七年级奥数-图形找规律
(完整版)初中数学规律题解题基本方法------图形找规律

初中数学规律题解题基本方法------图形找规律1.探索常见图形的规律,用火柴棒按下图的方式搭三角形⑴填写下表:⑵照这样的规律搭建下去,搭n 个这样的三角形需要多少根火柴棒? 2.若按图2方式摆放桌子和椅子⑴一张桌子可坐6人,2张桌子可坐人。
⑵按照上图方式继续排列桌子,完成下表:3.如果按图3的方式将桌子拼在一起⑴2张桌子拼在一起可坐多少人?3张呢?n 张呢?⑵教室有40张这样的桌子,按上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐 人。
⑶在⑵中,改成每8张桌子拼成1张大桌子,则共可坐 人。
4.如图,把一个面积为1的正方形分等分成两个面积为21的矩形,接着把面积为21的矩形等分成两个面积为41的正方形,再把面积为41的矩形等分成两个面积为81的矩形,如此进行下去,试利用图形提示的规律计算:=+++++++256112816413211618141215.把棱长为a 的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这种规律摆放,第五层的正方体的个数是 例8.观察下列图形并填表。
个数 1 2 3 4 5 6 7…n32121 41 811611126.用黑白两颜色的正六边形地面砖按如图所示规律,拼成若干个图案: (1)第4个图案中有白色地面砖 块; (2)第n 个图案中有白色地面砖 块。
……7.下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有)2(≥n n 个棋子,每个图案棋子总数为S ,按下图的排列规律推断,S 与n 之间的关系可以用式子 来表示。
……8.观察与分析下面各列数的排列规律,然后填空。
①5,9,13,17, , 。
②4,5,7,11,19, , 。
③10,20,21,42,43, , ,174,175。
④4,9,19,34,54, , ,144。
⑤45,1,43,3,41,5, , ,37,9。
⑥6,1,8,3,10,5,12,7, , 。
初一数学找规律题技巧

在初一数学中,找规律题是一种比较常见的题型。
这类题目通常会给出一些数字、图形或者算式,让学生通过观察和分析,找出其中的规律,从而得到下一个数字或图形。
以下是几个找规律题的技巧:
观察数字变化:找规律题中,数字的变化往往是有规律的,可以通过观察相邻两个数字之间的差值或倍数关系,找出规律。
观察图形排列:找规律题中,图形的排列也往往是有规律的,可以通过观察相邻两个图形之间的相同点和不同点,找出规律。
找出特殊点:找规律题中,特殊点往往可以成为解题的关键。
例如,在数列中,可以通过找出相邻两个数字之间的差值或倍数关系,得出下一个数字。
尝试猜想:在找不到明显的规律时,可以尝试对下一个数字或图形进行猜想,然后根据猜想进行验证。
转化题目:有些找规律题可能比较复杂,可以通过转化题目,将复杂的问题转化为简单的问题。
例如,可以将一个复杂数列中的数字按照一定规律分成不同的组,每组中的数字具有相同的规律。
总之,找规律题需要学生通过观察、分析、归纳和推理等方法,综合运用数学知识和其他学科知识来解决。
在解题过程中,要善于发现规律、善于运用规律、善于解决问题。
找规律(图形类)七年级数学

n=2, (3×2)×2 n=3, (4×3)×2
…
……
第n个, 2n (n+1)
【练11】(2010黑龙江哈尔滨)观察下列图形: 它们是按一定规律排列的,依照此规律, 第9个图形中共有 28 个★。
第1个图形 第2个图形
第3个图形
分析:
n=1, n=2, n=3, n=4,
……
n=9,
4 4+3 4+3+3 4+3+3+3
分析:
n=1
n=2
n=3
n=1, 1×4+1
n=2, 2×4+1+2
n=3, 3×4+1+2+2
…
……
第n个, n×4+1+(n −1)×2=6n −1
【练14】(2013重庆)下列图形都是由同样大小的棋子 按一定的规律组成,其中第①个图形有1颗棋子, 第②个图形一共有6颗棋子,第③个图形一共有16 颗棋子,…,则第⑥个图形中棋子的颗数为__76___
1×1+0×0 2×2+1×1 3×3+2×2 4×4+3×3
…… n=10, 10×10+9×9
第4个图案
【例4】(2010柳州)2010年广州亚运会吉祥物取名“乐羊羊”.下面各图 是按照一定规律排列的羊的组图,图①1有1只羊,图②有3只羊,……,
则图⑩有 55 只羊, 第n个图形有 2 n(n+1) 只羊.
n=3, 3×4+3×3
…
……
第n个, n× 4+n2=4n+n2
【例1】(2009年益阳市)下图是一组有规律的图案,第1
初一找规律的数学题及解题方法

初一找规律的数学题及解题方法初一找规律的数学题通常涉及数列、图形、数字变换等问题,需要观察、分析、归纳和推理。
下面是一些初一找规律的数学题及解题方法:一、数列规律题题目:观察数列1,3,7,15,31,...,求第n项的值。
解题方法:首先观察数列中相邻两项的差,发现差值分别为2,4,8,16...,即每次乘以2。
这是一个等比数列的差数列。
根据这个规律,我们可以推导出第n项的公式:第n项=2^(n-1)-1。
二、图形规律题题目:有一组图形,第一个图形有1个点,第二个图形有3个点,第三个图形有7个点,第四个图形有15个点,...,求第n个图形中点的个数。
解题方法:首先观察图形中点数的变化规律,发现相邻两项的差分别为2,4,8,...。
这是一个等比数列的差数列。
根据这个规律,我们可以推导出第n个图形中点的个数公式:第n个图形中点的个数=2^(n-1)-1。
三、数字变换规律题题目:观察数字序列1,11,21,1211,111221,...,求第n项的值。
解题方法:首先观察数字序列的变化规律,发现每个数字都是由前一个数字生成的。
具体地,第一个数字是“1”,第二个数字表示前一个数字有“1”个“1”,所以是“11”,第三个数字表示前一个数字有“2”个“1”,所以是“21”,以此类推。
这是一个描述性规律题,需要通过观察和描述来找出规律。
根据这个规律,我们可以逐步推导出第n项的值。
四、等差数列规律题题目:观察等差数列2,5,8,11,...,求第n项的值。
解题方法:首先观察等差数列的公差,发现相邻两项的差为3。
根据等差数列的通项公式an=a1+(n-1)d,其中a1为首项,d为公差,n为项数,我们可以推导出第n项的公式:第n项=2+3(n-1)。
以上是初一找规律的数学题及解题方法的一些例子。
对于找规律的数学题,重要的是通过观察和分析来发现其中的规律和模式,并根据这些规律和模式来推导出解决问题的方法。
七年级数学找规律经典题型

七年级数学找规律经典题型一、数字规律1. 数列规律例1:观察数列1,3,5,7,9,…,求第n个数。
解析:首先观察这个数列,发现相邻两个数的差值都是2。
第1个数是1 = 2×1 1;第2个数是3 = 2×2 1;第3个数是5 = 2×3 1;第4个数是7 = 2×4 1;第5个数是9 = 2×5 1。
所以可以得出第n个数为2n 1。
例2:观察数列2,4,8,16,32,…,求第n个数。
解析:这个数列中,后一个数都是前一个数的2倍。
第1个数是2 = 2^1;第2个数是4 = 2^2;第3个数是8 = 2^3;第4个数是16 = 2^4;第5个数是32 = 2^5。
所以第n个数为2^n。
2. 数字循环规律例:有一组数按照1, 1,1, 1,…的规律排列,求第n个数。
解析:观察这组数字,发现数字是1和 1交替出现。
当n为奇数时,第n个数为1;当n为偶数时,第n个数为 1。
可以用(-1)^(n + 1)来表示,当n = 1时,(-1)^(1+1)=1;当n = 2时,(-1)^(2 + 1)= 1。
二、图形规律1. 图形数量规律例1:用火柴棒搭三角形,搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒,搭3个三角形需要7根火柴棒,…,求搭n个三角形需要多少根火柴棒。
解析:搭1个三角形需要3根火柴棒,即2×1+1;搭2个三角形时,第二个三角形和第一个三角形共用一条边,所以需要3 + 2 = 5根火柴棒,即2×2+1;搭3个三角形时,第三个三角形和前面的三角形共用两条边,所以需要3+2×2 = 7根火柴棒,即2×3 + 1。
所以搭n个三角形需要2n+1根火柴棒。
例2:观察下列图形的点数规律:第1个图形有1个点;第2个图形有1 + 3 = 4个点;第3个图形有1+3 + 5 = 9个点;第4个图形有1+3+5 + 7 = 16个点;求第n个图形的点数。
七年级数学找规律题

奥数专题(三)找规律一、数字排列规律题1、观察下列各算式:1+3=4=,1+3+5=9=,1+3+5+7=16=…猜想:1+3+5+7+…+2015+2017=推广:1+3+5+7+9+…+(2n-1)+(2n+1)=2、下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 123 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第2016个()5、有一串数字 3 6 10 15 21 ___第6个是什么数?6、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2016个数是().7、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 _________个.二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2016个图形是(填图形名称).三、数、式计算规律题1、已知下列等式:① 13=12;② 13+23=32;③ 13+23+33=62;④ 13+23+33+43=102 ;由此规律知,第⑤个等式是.2、观察下面的几个算式:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1=____.3、1+2+3+ (100)经过研究,这个问题的一般性结论是1+2+3+…+,其中n是正整数.现在我们来研究一个类似的问题:1×2+2×3+…=?观察下面三个特殊的等式将这三个等式的两边相加,可以得到1×2+2×3+3×4=读完这段材料,请你思考后回答:⑴⑵⑶巩固练习:1.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则的值为2.有一列数:第一个数为x1=1,第二个数为x2=3,第三个数开始依次记为x3,x4,…,xn;从第二个数开始,每个数是它相邻两个数和的一半。
初中数学规律题解题基本方法---图形找规律

1.探索常见图形的规律,用火柴棒按下图的方式搭三角形⑵按照上图方式继续排列桌子,完成下表:桌子张数3456n可坐人数3.如果按图3的方式将桌子拼在一起(1)2张桌子拼在一起可坐多少人? 3张呢? n张呢?⑵教室有40张这样的桌子,按上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐人4. 如图,把一个面积为1的正方形分等分成两个面积为2的矩形,接着把面积为1的矩形等分成两个面积为1的正方形,再把面积为1的矩形等分成两个面积为8的矩形,如此进行下去,试利用图形提示的规律计5. 把棱长为a的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这种规律摆放,第五层的正方体的个数是 _______ 1初中数学规律题解题基本方法图形找规律⑴一张桌子可坐6人,2张桌子可坐算:111丄丄丄丄丄=2 4 8 16 32 64 128 25612141816132例8.观察下列图形并填表个数1234-Z567…n2.若按图2方式摆放桌子和椅子⑶在⑵中,改成每8张桌子拼成1张大桌子,则共可坐人。
O周长581114・・・6. 用黑白两颜色的正六边形地面砖按如图所示规律,拼成若干个图案:(1)第4个图案中有白色地面砖_______ 块;(2)第n个图案中有白色地面砖______ 块。
7. 下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n_2)个棋子,8观察与分析下面各列数的排列规律,然后填空。
①5, 9, 13, 17, ____ , _____ 。
②4, 5, 7, 11, 19, _____ , ____ 。
③10, 20, 21, 42, 43, ______ , ____ , 174, 175④4, 9, 19, 34, 54, _____ , ____ , 144。
⑤45, 1, 43, 3, 41, 5, _____ , ____ , 37, 9⑥6, 1, 8, 3, 10, 5, 12, 7, ______ , ____ 。
七年级奥数-图形找规律

七年级数学新题型能力训练题1、我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。
在电子数字计算机中用的是二进制,只要两个数码:0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数 。
2、从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…按此规律请你猜想从1开始,将前10个奇数(即当最后一个奇数是19时),它们的和是 。
3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入 (1)2345… 输出…21 52 103 174 265…那么,当输入数据是8时,输出的数据是( )A 、618 B 、638 C 、658 D 、6784、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要 枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n 个小房子用了 块石子.6、如下图是用棋子摆成的“上”字:(1)(2)(3)第4题第一个“上”字第二个“上”字第三个“上”字如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第四、第五个“上”字分别需用和枚棋子;(2)第n个“上”字需用枚棋子。
7、如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有_______颗.8、根据下列5个图形及相应点的个数的变化规律:猜想第6个图形有个点,第n个图形中有个点。
初中数学看图形找规律教案

初中数学看图形找规律教案【教学目标】1. 让学生通过观察和分析图形,培养学生的观察能力和逻辑思维能力。
2. 培养学生发现和总结图形规律的能力,提高学生的数学思维水平。
3. 引导学生运用数学知识解决实际问题,培养学生的数学应用能力。
【教学内容】1. 图形的基本概念和特征2. 常见图形的性质和规律3. 图形变换与图形规律的应用【教学过程】一、导入(5分钟)1. 教师通过展示一些日常生活中的图形,如建筑物、家具、标志等,引导学生观察和识别这些图形。
2. 学生分享自己观察到的图形,教师点评并总结。
二、新课导入(15分钟)1. 教师介绍图形的基本概念和特征,如点、线、面、角等。
2. 教师通过示例,讲解如何分析图形的基本性质和规律,如对称性、周期性等。
3. 学生跟随教师一起分析一些简单的图形规律,如正方形、矩形的性质。
三、实践操作(15分钟)1. 教师给出一些图形,要求学生观察和分析图形的性质和规律。
2. 学生独立观察和分析图形,教师巡回指导。
3. 学生分享自己发现的图形规律,教师点评并总结。
四、课堂小结(5分钟)1. 教师引导学生总结本节课所学的内容,如图形的基本概念、性质和规律等。
2. 学生分享自己的学习心得和收获。
五、课后作业(5分钟)1. 教师布置一些有关图形规律的练习题,要求学生在课后完成。
2. 学生认真完成作业,巩固所学知识。
【教学反思】本节课通过观察和分析图形,让学生掌握了图形的基本概念和特征,培养了学生的观察能力和逻辑思维能力。
同时,学生通过发现和总结图形规律,提高了数学思维水平。
在实践操作环节,学生独立观察和分析图形,培养了自主学习能力。
课堂小结和课后作业环节,帮助学生巩固所学知识,提高学生的数学应用能力。
然而,在教学过程中,教师要注意引导学生运用数学知识解决实际问题,提高学生的数学素养。
此外,教师还要关注学生的个体差异,因材施教,使每个学生都能在课堂上得到充分的锻炼和发展。
初中图形找规律教案

初中图形找规律教案教学目标:1. 让学生通过观察和分析,找出图形的变化规律。
2. 培养学生的观察能力、分析能力和推理能力。
3. 培养学生合作交流的意识,提高学生的解决问题的能力。
教学内容:1. 观察和分析各种图形的排列规律。
2. 运用规律解决问题。
教学重点:1. 帮助学生理解并掌握图形的变化规律。
2. 培养学生运用规律解决问题的能力。
教学难点:1. 引导学生发现和理解图形排列的规律。
2. 运用规律解决实际问题。
教学准备:1. 多媒体课件(或主题图)。
2. 各种图形的卡片或贴纸。
3. 练习题。
教学过程:一、导入(5分钟)1. 向学生介绍本节课的主题:图形找规律。
2. 引导学生观察和分析一些给定的图形,尝试找出它们的排列规律。
二、新课(20分钟)1. 教师通过多媒体课件或实物展示各种图形的排列规律。
2. 引导学生观察和分析这些图形的排列规律,并引导学生用语言描述这些规律。
3. 教师给出一些练习题,让学生独立完成,检验学生对图形排列规律的理解和掌握程度。
三、巩固练习(15分钟)1. 教师给出一些图形的排列规律,让学生根据规律画出相应的图形。
2. 学生分组合作,共同找出给定图形的排列规律,并完成练习题。
四、总结与反思(5分钟)1. 教师引导学生总结本节课所学的图形排列规律。
2. 学生分享自己在课堂上所学到的知识和经验,以及自己在解决问题时的思考过程。
教学评价:1. 通过学生在课堂上的表现,评价学生对图形排列规律的理解和掌握程度。
2. 通过学生在练习题上的表现,评价学生运用规律解决问题的能力。
教学反思:本节课通过观察和分析各种图形的排列规律,培养了学生的观察能力、分析能力和推理能力。
在教学过程中,教师应引导学生积极参与,鼓励学生提出自己的观点和想法,培养学生的合作交流意识。
同时,教师也应关注学生的个体差异,因材施教,使每个学生都能在课堂上得到锻炼和提高。
在今后的教学中,可以尝试引入更多的生活实例,让学生更好地理解图形排列规律的实际应用。
图形找规律(7年级)
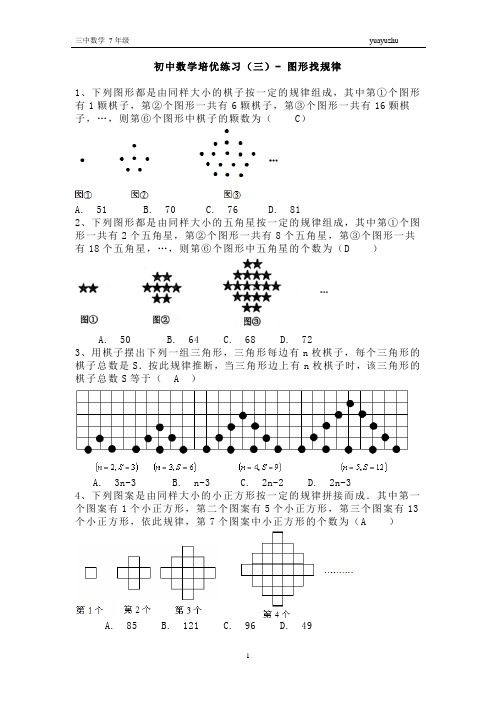
初中数学培优练习(三)- 图形找规律1、下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为(C)A. 51B. 70C. 76D. 812、下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为(D )A. 50B. 64C. 68D. 723、用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数是S.按此规律推断,当三角形边上有n枚棋子时,该三角形的棋子总数S等于( A )A. 3n-3B. n-3C. 2n-2D. 2n-34、下列图案是由同样大小的小正方形按一定的规律拼接而成.其中第一个图案有1个小正方形,第二个图案有5个小正方形,第三个图案有13个小正方形,依此规律,第7个图案中小正方形的个数为(A )A. 85B. 121C. 96D. 495、下列图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第8个图形中圆的个数为( A )A. 121B. 113C. 92D. 1916、下列图形都是由同样大小的矩形按一定的规律组成,其中第(1)个图形的面积为2cm2,第(2)个图形的面积为8cm2,第(3)个图形的面积为18c m2,…,则第(10)个图形的面积为(B )A. 196cm2B. 200cm2C. 216cm2D. 256cm27、观察下列图形及图形所对应的等式,探究其中的规律:1+8=32;1+8+16=52;1+8+16+24= ;(1)在横线上写出第3个图形所对应的算式的结果;(2)在横线上写出第4个图形所对应的等式;(3)根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为(用含n的代数式表示).8、将正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是( B )A. 502B. 503C. 504D. 5059、如图,是一组按照某种规律摆放成的图案,则图5中三角形的个数是( C )A. 8B. 9C. 16D. 17【解:由图可知:第一个图案有三角形1个.第二图案有三角形1+3=4个.第三个图案有三角形1+3+4=8个,第四个图案有三角形1+3+4+4=12第五个图案有三角形1+3+4+4+4=16】10、有边长为1的等边三角形卡片若干张,使用这些三角形卡片拼出边长分别是2,3,4…的等边三角形(如图所示).根据图形推断每个等边三角形卡片总数S与边长n的关系式s=n2(n≥2).11、如图由小正方形依次排出以下图形.那么第9个图形中共有(C )个小正方形。
初一找规律的数学题及解题方法

初一找规律的数学题及解题方法摘要:1.初一数学找规律题的特点2.解题方法及步骤3.实例分析4.提高找规律题解题能力的建议正文:初一数学找规律题是一种常见的题型,它不仅能培养学生的观察力和思维能力,还能帮助学生形成良好的数学素养。
这类题目要求学生通过观察数字、符号或图形的变化,找出其中的规律,并运用规律解决实际问题。
下面我们就来介绍一下初一找规律题的解题方法和步骤。
首先,我们要了解初一数学找规律题的特点。
这类题目通常有以下几个特点:1.数据量大,需要观察和分析;2.规律隐含在数据中,需要挖掘;3.题目形式多样,包括数字、符号和图形等;4.解题方法灵活,需要综合运用各种数学知识。
接下来,我们来介绍解题方法和步骤:1.仔细阅读题目,了解题意;2.观察数据的变化,找出规律;3.验证规律是否正确;4.根据规律解决问题。
为了更好地理解解题方法,我们通过一个实例进行分析。
例题:已知数列{an}如下:a1=1,a2=2,a3=3,a4=5,a5=8,……请问数列的通项公式是什么?解题步骤如下:1.观察数列{an},发现每个数字都是前两个数字之和;2.找出规律:a1+a2=a3,a2+a3=a4,a3+a4=a5,……;3.验证规律:a4+a5=a6,a5+a6=a7,……,符合上述规律;4.根据规律,得出数列的通项公式:an=a1+(n-1)×1。
最后,我们来谈谈如何提高找规律题的解题能力。
以下是一些建议:1.多做练习,熟能生巧;2.培养观察力和思维能力,善于发现数字、符号或图形之间的联系;3.学会总结规律,形成解题技巧;4.掌握相关数学知识,如代数、几何等,灵活运用。
通过以上方法,相信同学们在解决初一找规律题时会更加得心应手。
七年级找规律知识点总结

七年级找规律知识点总结在七年级数学学习中,找规律是一个重要的知识点。
它不仅是数学思维训练的关键,也是后续学习代数和函数的基础。
在此,我将从什么是找规律、找规律的方法、找规律的应用等方面进行总结。
一、什么是找规律找规律是指在一组数或图形中寻找规律性、相似性和变化规律的过程,通过对这些规律进行总结、归纳和推广,进一步加深对数学规律的理解,提高分析问题的能力。
二、找规律的方法找规律并不是看起来简单,实则需要有一定的技巧。
以下是几种常用的找规律方法:1. 数列数列是较为常见的一种找规律方法,它可以用表格列出其中的数字,以便快速发现规律。
常见的数列有等差数列和等比数列,可以应用对应的公式来计算每一项。
2. 分组讨论法通过分类讨论,把一组数据分解成不同的部分,从而来看出各部分的规律、特性和联系。
例如,把一组数字按奇偶分为两部分,可以发现每个奇数与其前一个偶数之和均为奇数等规律。
3. 拆分组合法将数列拆分成若干个小部分,分析小部分与大部分之间的联系,进而得出规律。
例如,把一组数据分为前后两个部分,看它们之间有什么联系,是否有递推、递归和循环等规律。
4. 数数法计算第n项与第n-1项之间的差值,看是否为固定数值或以某种规则变化,通过推算找出每一项的值。
三、找规律的应用找规律的能力是数学学科中的一个重要基础,不仅可以应用到中考、高考中,还可以在未来的数学学习中得到广泛的应用。
1. 应用到代数学习中代数学习是找规律的延伸,通过找出规律,我们可以总结、提炼更加高级的数学规律和知识。
2. 应用到函数学习中函数学习需要有对数量关系的理解和掌握,而找规律正是我们深入剖析数量关系的一个过程。
通过找规律,我们可以逐步掌握函数的性质和运算规则。
3. 应用到计算机编程中计算机编程中也需要具有找规律能力,因为它涉及到算法设计和程序逻辑。
只有通过找规律,才能快速地设计出便捷、高效的程序。
总之,在学习数学过程中,找规律是一个重要的知识点。
图形找规律

图形找规律标准化管理部编码-[99968T-6889628-J68568-1689N]
图形找规律
找规律是解决数学问题的一种重要的手段,而规律的寻找既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住以下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化。
对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.
板块一数量规律
例1:请找出下面哪个图形与其他图形不一样.例2:观察下面的图形,按规律在“”处填上适当的图形. 例3:观察下图中的点群,请回答:
(1)方框内的点群包含多少个点
(2)推测第10个点群中包含多少个点
(3)前10个点群中,所有点的总数是多少
例4:下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形(2)整个五层“宝塔”一共包含多少个小三角形
板块二旋转、轮换型规律
例5:观察下列各组图的变化规律,并在“”处画出相关的图形.
板块三其他
例9:请找出下面哪个图形与其他图形不一样。
例10:根据左边图形的关系,画出右边图形的另一半.
(1)
(2)
例11:仔细观察下图中图形的变化规律,并在“”处填入合适的图形.
例12:四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第五次交换位子后,小兔坐在第几号位子上。
图形找规律(7年级)

初中数学培优练习(三)- 图形找规律1、下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为(C)A. 51B. 70C. 76D. 812、下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为(D )A. 50B. 64C. 68D. 723、用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数是S.按此规律推断,当三角形边上有n枚棋子时,该三角形的棋子总数S等于( A )A. 3n-3B. n-3C. 2n-2D. 2n-34、下列图案是由同样大小的小正方形按一定的规律拼接而成.其中第一个图案有1个小正方形,第二个图案有5个小正方形,第三个图案有13个小正方形,依此规律,第7个图案中小正方形的个数为(A )A. 85B. 121C. 96D. 495、下列图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第8个图形中圆的个数为( A )A. 121B. 113C. 92D. 1916、下列图形都是由同样大小的矩形按一定的规律组成,其中第(1)个图形的面积为2cm2,第(2)个图形的面积为8cm2,第(3)个图形的面积为18c m2,…,则第(10)个图形的面积为(B )A. 196cm2B. 200cm2C. 216cm2D. 256cm27、观察下列图形及图形所对应的等式,探究其中的规律:1+8=32;1+8+16=52;1+8+16+24= ;(1)在横线上写出第3个图形所对应的算式的结果;(2)在横线上写出第4个图形所对应的等式;(3)根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为(用含n的代数式表示).8、将正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是( B )A. 502B. 503C. 504D. 5059、如图,是一组按照某种规律摆放成的图案,则图5中三角形的个数是( C )A. 8B. 9C. 16D. 17【解:由图可知:第一个图案有三角形1个.第二图案有三角形1+3=4个.第三个图案有三角形1+3+4=8个,第四个图案有三角形1+3+4+4=12第五个图案有三角形1+3+4+4+4=16】10、有边长为1的等边三角形卡片若干张,使用这些三角形卡片拼出边长分别是2,3,4…的等边三角形(如图所示).根据图形推断每个等边三角形卡片总数S与边长n的关系式s=n2(n≥2).11、如图由小正方形依次排出以下图形.那么第9个图形中共有(C )个小正方形。
初一数学,详解各种图形找规律方法,值得收藏

例题6、注意观察图形排列方式,左边都是1个,右边排列个数按照行和列相乘。
例题4如果把红色的正方形补齐右上角刚好是完整的图形并且小正方形的个数刚好是某个数的平方
初一数学,详解各种图形找规律方法,值得收藏
例题1、注意根据排列的规则,从上到下依次计算。
例题2、棋子的个数是每次增加的个数都是4个。
ቤተ መጻሕፍቲ ባይዱ例题3、看清题中的描述,不是计算所有正三角形的个数,计算的是小正三角形的个数。
例题4、如果把红色的正方形补齐右上角,刚好是完整的图形,并且小正方形的个数刚好是某个数的平方。
在图形中找规律经典实用

7.找一下规律,从a,b,c,d,e中选入一幅图填入空格内.
a
b
cd
e
选a.根据对角图形规律,可知右下角图形是a图.
•在图形中找规律
8.按照下列图形的变化规律,空白处应是什么样的图形.
?
分析:先看不变的部分.在整个变化过程中,图形中 大、小两个圆圈没有变化,因此可以肯定空白处的 图形一定也有大、小两个圆圈,位置一里一外. 变化的部分可为两部分:①图形中的直线部分,其变 化规律是每次顺时针旋转 ;②图形中的阴影部分, 其变化规律是每次逆时针旋转 ,黑色部分交替出现. 解:根据上面的分析,可画出空白处的图形如图所示.
(1)
(2)
(3)
?
(4)
(5)
•在图形中找规律
13、相传古时候一位老人留在人间很多宝盒,里面装着世界上最 宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒 的上面设置了密码,只有写出密码的人才会真正拥有这笔财富, 聪明的你你能找出密码吗?
○□☆△○□☆△ △○□☆△○□☆ ☆△○□☆△○□
•在图形中找规律
6.图的规律很容易发现,请你在最短的时间内得出答案.
ΟΟΟΟ
ΟΟΟ△
Ο Ο △△
Ο ? △△
横行观察,圆的个数逐次减少1个,所以到第4行, 圆的个数应为1,所以“?”处应是“△”.
或者从三角形考虑,三角形的个数为0、1、2, 是逐次增加1,所以第4行中三角形的个数应为3,所 以“?”处应为“△” 所以最后的图形为: “△” •在图形中找规律
其次我们看旗上星星的颗数.第1面是5颗,第2面是4颗,第4面是2颗, 可见颗数是依次减少1颗,所以第3面旗上应是3颗星星.所以“?”处 的图形应为:
•在图形中找规律
初中数学规律题解题基本方法------图形找规律.
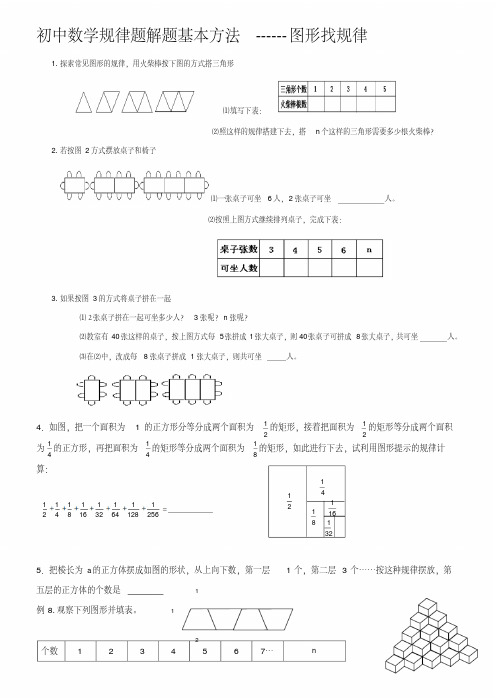
初中数学规律题解题基本方法------图形找规律1.探索常见图形的规律,用火柴棒按下图的方式搭三角形⑴填写下表:⑵照这样的规律搭建下去,搭n 个这样的三角形需要多少根火柴棒?2.若按图2方式摆放桌子和椅子⑴一张桌子可坐6人,2张桌子可坐人。
⑵按照上图方式继续排列桌子,完成下表:3.如果按图3的方式将桌子拼在一起⑴2张桌子拼在一起可坐多少人?3张呢?n 张呢?⑵教室有40张这样的桌子,按上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐人。
⑶在⑵中,改成每8张桌子拼成1张大桌子,则共可坐人。
4.如图,把一个面积为1的正方形分等分成两个面积为21的矩形,接着把面积为21的矩形等分成两个面积为41的正方形,再把面积为41的矩形等分成两个面积为81的矩形,如此进行下去,试利用图形提示的规律计算:256112816413211618141215.把棱长为a 的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这种规律摆放,第五层的正方体的个数是例8.观察下列图形并填表。
个数 1 2 3 4 5 6 7…n321214181161112周长 5 8 11 14 …6.用黑白两颜色的正六边形地面砖按如图所示规律,拼成若干个图案:(1)第4个图案中有白色地面砖块;(2)第n 个图案中有白色地面砖块。
……7.下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有)2(nn 个棋子,每个图案棋子总数为S ,按下图的排列规律推断,S 与n 之间的关系可以用式子来表示。
……8.观察与分析下面各列数的排列规律,然后填空。
①5,9,13,17,,。
②4,5,7,11,19,,。
③10,20,21,42,43,,,174,175。
④4,9,19,34,54,,,144。
⑤45,1,43,3,41,5,,,37,9。
⑥6,1,8,3,10,5,12,7,,。
⑦0,1,1,2,3,5,,。
七年级上图形规律题
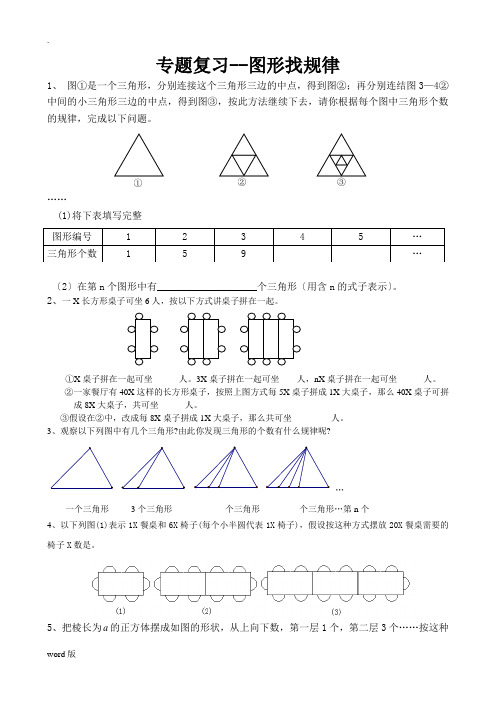
专题复习--图形找规律1、 图①是一个三角形,分别连接这个三角形三边的中点,得到图②;再分别连结图3—4②中间的小三角形三边的中点,得到图③,按此方法继续下去,请你根据每个图中三角形个数的规律,完成以下问题。
……(1)将下表填写完整〔2〕在第n 个图形中有____________________个三角形〔用含n 的式子表示〕。
2、一X 长方形桌子可坐6人,按以下方式讲桌子拼在一起。
①X 桌子拼在一起可坐______人。
3X 桌子拼在一起可坐____人,nX 桌子拼在一起可坐______人。
②一家餐厅有40X 这样的长方形桌子,按照上图方式每5X 桌子拼成1X 大桌子,那么40X 桌子可拼成8X 大桌子,共可坐______人。
③假设在②中,改成每8X 桌子拼成1X 大桌子,那么共可坐_________人。
3、观察以下列图中有几个三角形?由此你发现三角形的个数有什么规律呢?…一个三角形 3个三角形 ______个三角形 ______个三角形…第n 个4、以下列图(1)表示1X 餐桌和6X 椅子(每个小半圆代表1X 椅子),假设按这种方式摆放20X 餐桌需要的椅子X 数是。
5、把棱长为a 的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这种图形编号 1 2 3 4 5 … 三角形个数 159…①②③规律摆放,第五层的正方体的个数是6、观察以下列图形并填表。
7、用黑白两颜色的正六边形地面砖按如下列图规律,拼成假设干个图案: 〔1〕第4个图案中有白色地面砖块; 〔2〕第n 个图案中有白色地面砖块。
……8、以下每个图形都是假设干个棋子围成的正方形图案,图案的每条边〔包括两个顶点〕上都有)2(≥n n 个棋子,每个图案棋子总数为S ,按以下列图的排列规律推断,S 与n 之间的关系可以用式子来表示。
……9、把1到200的数像下表那样排列,用正方形框子围住横的3个数,竖的3个数,这9个12 第三个第一个第二个42==s n83==s n124==s n165==s n数的和是162。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学新题型能力训练题1、我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。
在电子数字计算机中用的是二进制,只要两个数码:0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数 。
2、从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…按此规律请你猜想从1开始,将前10个奇数(即当最后一个奇数是19时),它们的和是 。
3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入 (1)2345… 输出…2152 103 174 265…那么,当输入数据是8时,输出的数据是( )A 、618B 、638C 、658D 、6784、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要 枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n 个小房子用了 块石子.6、如下图是用棋子摆成的“上”字:第一个“上”字 第二个“上”字 第三个“上”字如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第四、第五个“上”字分别需用 和 枚棋子;(2)第n 个“上”字需用 枚棋子。
7、如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有_______颗.8、根据下列5个图形及相应点的个数的变化规律:猜想第6个图形有 个点,第n(1)(2)(3)第4题(1)(2)(3)(4)个图形中有个点。
9、下面是按照一定规律画出的一列“树型”图:经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”。
10、观察下面的点阵图和相应的等式,探究其中的规律: (1)在④和⑤后面的横线上分别写出相应的等式;(2)通过猜想写出与第n 个点阵相对应的等式_____________________。
11、用边长为1cm 的小正方形搭成如下的塔状图形,则第n 次所搭图形的周长是_______________cm (用含n 的代数式表示)。
12、如图,都是由边长为1的正方体叠成的图形。
例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位。
依此规律。
则第(5)个图形的表面积 个平方单位.13、图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( ) A 25 B 66 C 91 D 120…………①1=12; ②1+3=22; ③1+3+5=32;④ ;⑤ ;第1第2第3次···(1)(2)(3)⑴ ⑵ ⑶14题14、如图是由大小相同的小立方体木块叠入而成的几何体,图⑴中有1个立方体,图⑵中有4个立方体,图⑶中有9个立方体,……按这样的规律叠放下去,第8个图中小立方体个数是 .15、图1是棱长为a 的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续s .解答下列问题:(1)按照要求填表:(2)写出当n =10时,s= .16、如图用火柴摆去系列图案,按这种方式摆下去,当每边摆10根时(即10 n )时,需要的火柴棒总数为 根;17、用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个三角形需7支火柴棒,照这样的规律下去,搭n 个三角形需要S 支火柴棒,那么用n 的式子表示S 的式子是 _______ (n 为正整数).18、如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下图:则第n 个图形中需用黑色瓷砖 ____ 块.(用含n 的代数式表示)n 1 2 3 4 … s 136…图1 图2 图319、如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空: 当黑色瓷砖为20块时,白色瓷砖为 块;当白色瓷砖为n 2(n 为正整数)块时, 黑色瓷砖为 块.17题图20、观察下列由棱长为1的小立方体摆成的图形,寻找规律:如图1中:共有1 个小立方体,其中1个看得见,0个看不见;如图2中:共有8个小立方体,其中7个看得见,1个看不见;如图3中:共有27个小立方体,其中有19个看得见,8个看不见;……,则第6个图中,看不见的小立方体有 个。
21、下面的图形是由边长为l 的正方形按照某种规律排列而组成的.(1)观察图形,填写下表:图形① ② ③ 正方形的个数 8 图形的周长18(2)推测第n 个图形中,正方形的个数为________,周长为______________(都用含n 的代数式表示).22、观察下图,我们可以发现:图⑴中有1个正方形;图⑵中有5个正方形,图⑶中共有14个正方形,按照这种规律继续下去,图⑹中共有_______个正方形。
23、某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求....的是( )A DC B 第18题图A B C D24、如下图中的四个正方形的边长均相等,其中阴影部分面积最大的图形是( )25、如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是()A. <1>和<2>B. <2>和<3>C. <2>和<4>D. <1>和<4>26、某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;…依此方法,第n次铺完后,用字母n表示第n次镶嵌所使用的木块块数为. (n为正整数)27、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:⑴第4个图案中有白色地面砖块;⑵第n个图案中有白色地面砖块。
28、分析如下图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.29、将一圆形纸片对折后再对折,得到图2,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( )30.如图(1),小强拿一张正方形的纸,沿虚线对折一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线剪去一个角,再打开后的形状是()(A)(B)(C)(D)31、用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=度.32、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形).则∠OCD等于()A.108°B.144°C.126°D.129°33、如图,把一个正方形三次对折后沿虚线剪下则得到的图形是()_沿虚线剪开A B C D图3图2图1C DEBA图(2)AB C D34、某校教具制作车间有等腰三角形、正方形、平行四边形的塑料若干,数学兴趣小组的同学利用其中7块恰好拼成一个矩形(如图1),后来又用它们拼出了XYZ 等字母模型(如图2、图3、图4),每个塑料板保持图1的标号不变,请你参与:(1)将图2中每块塑料板对应的标号填上去;(2)图3中,点画出了标号7的塑料板位置,请你适当画线,找出其他6块塑料板, 并填上标号;(3)在图4中,找出7块塑料板,并填上标号。
图1 图2 图3 图435、将一张长方形的纸对折,如图5所示可得到一条折痕(图中虚线). 继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕 .如果对折n 次,可以得到 __________条折痕 。
36、观察图形:图中是边长为1,2,3 …的正方形:当边长n =1时,正方形被分成2个大小相等的小等腰直角三角形;当边长n =2时,正方形被分成8个大小相等的小等腰直角三角形;当边长n =3时,正方形被分成18个大小相等的小等腰直角三角形;以此类推:当边长为n 时,正方形被分成大小相等的小等腰直角三角形的个数是 。
37、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,1 2 3 45 6 7程 前你祝似锦是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、 “你”、 “前”分别表示正方体的___________________.38、如图是一块长方形ABCD 的场地,长AB =102m ,宽AD =51m ,从A 、B 两处入口的中路宽都为1m ,两小路汇合处路宽为2m ,其余部分种植草坪,则草坪面积为( ) (A )5050m 2 (B )4900m 2 (C)5000m 2(D)4998m 239、以给定的图形“○○、△△、=”(两个圆、两个三角形、两条平行线)为构件,构思出独特且有意义的图形。
举例:如图,右图中是符合要求的一个图形,你能构思出其它的图形吗请在右框中画出与之不同的一个图形,并写出一句贴切、诙谐的解说词。
A C SBS。
