第3章连续基础35~37
高中物理第3章原子核与放射性第2节原子核衰变及半衰期鲁科35鲁科高二35物理

第三十页,共五十页。
[解析] 21803Bi 经一次衰变变成210aX,由于质量数不变,所以只 发生了一次 β 衰变,核电荷数增加 1 即 a=83+1=84,①是 β 衰变.21803Bi 经一次衰变变成81bTi,由于核电荷数减少 2,所以只 发生了一次 α 衰变,质量数减少 4,即 b=210-4=206,②是 α 衰变,故 A、C 项均错误,B 项正确;20861Ti 变成20862Pb,质 量数不变,核电荷数增加 1,所以只能经过一次 β 衰变,故 D 项错误. [答案] B
第十六页,共五十页。
将 α、β、γ 三种射线分别射入匀强磁场和匀强电场, 如图表示射线偏转情况中正确的是( )
A.①③
B.①④
C.②③
D.②④
[思路点拨] 求解本题应把握以下两点:
(1)α 粒子、β 粒子在磁场中偏转,求半径再比较.
(2)α 粒子、β 粒子在电场中做平抛运动,求偏向位移再比较. 12/9/2021
12/9/2021
第十九页,共五十页。
对某一确定的 x 值,α、β 粒子沿电场线偏转距离之比为 yyαβ=qqαβ·mmβα·vv22βα
1 =21×1 8440×((00.9.19cc))22≈318. 由此可见③错误,④正确.
[答案] B
12/9/2021
第二十页,共五十页。
求解此类题目要熟知以下两点 (1)三种射线的带电性质. (2)正、负电荷在电场或磁场中的运动规律及解题方法.
速度
0.1c
0.9c
c
在电场或磁场
与 α 射线反向
偏转
不偏转
中
偏转
贯穿本领
最弱用纸能挡 较强穿透几毫 最强穿透几厘
第三章 沥青混合料

排水式沥青路面
排水式开级配沥青碎石ATPB基层 ——Asphalt-Treated Permeable Base
设计空隙率≥18%
9
10
(4) 间断级配沥青混合料
gap-graded bituminous paving mixtures(英) gap-graded asphalt mixtures(美)
47
48
8
2011/5/14
影响沥青混合料抗剪强度的外因
⑴ 温度的影响:温度↑C ↓
第二节 沥青混合料的技术性能
沥青路面的主要损坏类型 沥青混合料应具备的基本技术性能 评价方法与指标 影响因素与改善措施
受温度变化影响较少
⑵ 加载速率的影响:加载速率↑ τ ↑
形变速率的影响:变形速率↑粘度↓ C值↓
32
2. 沥青混合料的毛体积密度
f
沥青混合料质量与体积关系示意图
空隙
沥青 质量 m a 空隙体积 V 沥青体积 Va 空隙率 VV 沥青饱和度 VFA
矿料间隙率
ma mg Va Vse V
沥青
VMA
合成矿料有效体积 Vse
合成矿料表观体积
合成矿料毛体积
毛体积相对密度 水中重法 表干法
③ 温拌沥青混合料
19
20
沥青混合料组成与体积参数
空隙率VV 沥青体积率VA 矿料间隙率VMA
4~6. 沥青混合料试件的体积参数
空隙率
沥青混合料 最大理论密度
f VV 1 - t
100%
沥青混合料 毛体积密度
沥青
沥 青 玛 蹄 脂
集料
( 1 矿料间隙率VMA VMA
三菱FX3U系列PLC编程技术与应用 第三章

§3.2 串并联指令及其应用
第三章 基本指令系统及编程
3.2.2 PLC控制传送带贴商标
Date:
2020-1-15
Page: 10
检测随传送带运动物品的位置,自动贴商标装置。当产品从传送带上送过来时,
经过两个光电管,即可检测传送线上物品的位置。当信号被两个光电管同时被接收
到,贴商标执行机构自动完成贴商标操作。
梯形图 语句表
§3.2 串并联指令及其应用
定时器(T)
定时器通常分为以下两类: 1.非积算型定时器 T0~T199为100 ms定时器, 设定值为0.1~ 3276.7s; T200~T245为10 ms定时器,设 定值为0.01~327.67s。
第三章 基本指令系统及编程
Date:
2020-1-15
2020-1-15
Page: 15
§3.2 串并联指令及其应用
3.2.4 基础知识:并联指令
1.或指令OR 功能:常开触点并联连接。 操作元件:X、Y、M、T、
C、S、D□.b
第三章 基本指令系统及编程
Date:
2020-1-15
Page: 16
2.或非指令ORI 功能:常闭触点并联连接。
操作元件:X、Y、M、T、 C、S、D□.b
Page: 19
非积算型定时器的特点:当驱动定时器的条 件满足时,定时器开始定时,时间到达设定值后, 定时器动作;当驱动定时器的条件不满足时,定 时器复位。若定时器定时未到达设定值,驱动定 时器的条件由满足变为不满足时定时器也复位, 且当条件再次满足后定时器再次从0开始定时。
§3.2 串并联指令及其应用
§3.2 串并联指令及其应用
第三章 基本指令系统及编程
第三章、轨道力学分析

• 扣件和轨下基础等效刚度相当于两根串联 弹簧。不难得到钢轨支座刚度为:
DP Db D DP Db
一般轨道的扣件刚度远大于枕下基础等效刚 度,这时可近似的得到:
D Db
3. 钢轨基础弹性模量u • 采用连续基础梁模型时,钢轨基础弹性模量 表示钢轨基础的弹性特征,定义为使单位长度的 钢轨基础产生单位下沉所需施加在其上的分布力, 量纲为力/长度2。可由钢轨支座刚度除以轨枕间 距a得到:
• 计算假设: • (1)标准结构 • (2)对称结构 假设结构和受力均对称,即假设轨道 刚度均匀且对称于轨道中心,机车车辆不 偏载,从而两股钢轨上的静轮载相等,因 此模型都只取轨道的一半 • (3)不考虑轨道结构本身的自重
二、计算参数 1.道床系数C 道床系数是表征道床及路基的弹性特 征,定义为使道床顶面产生单位下沉时所 需施加于道床顶面的单位面积上的压力, 量纲为力/长度3。 2.钢轨支座刚度D • 钢轨支座刚度表示钢轨支座下扣件和 枕下基础的等效支承刚度,定义为使钢轨 支座顶面产生单位下沉时,所需施加于支 座顶面的力,其量纲为力/长度。
• 轨道结构的设计、养护和维修都需要了解 轨道结构各部件的应力和变形。 • 虽然轨道结构是在动荷载作用下工作,应 力和变形都是动态的,但目前的计算是在 静力分析的基础上再考虑动力因素的影响。 • 现有的轨道结构设计实质上还是静力强度 设计。 • 本章主要介绍静力分析理论。
第一节 轨道结构竖向静力分析模型 一、计算模型 我国规范轨道竖向静力分析两种: 点支承梁模型、连续支承梁模型 1.点支承梁模型 点支承梁模型中钢轨是按轨枕间距支 承于轨枕上,故称弹性点支承连续梁计算 模型
一、单个静轮载作用下的解 • 1.微分方程 • 在连续支承梁模型中,钢轨是连续弹性支 承上的梁,在静载作用下设位移曲线(以向下 为正)为y (x),轨下基础对钢轨的分布反力 (以向下为正)为q(x)。 根据文克尔假定,基 础反力与位移成正比,有 q( x) uy( x) • 即假设x坐标处的轨下基础反力与x处的钢 轨位移成正比。这相当于基础是由连续排列, 但相互独立的线性弹簧所组成,每个弹簧的变 形仅决定于作用在其上的力,而与相邻弹簧的 变形无关。
教案:第三章复习(1)

00≥≥ (a)2a =初 二 数 学(第三章 二次根式复习(1)教学目标:1.能够比较熟练地应用二次根式的性质进行化简; 2.能熟练进行二次根式的化简及运算;3.会运用二次根式的性质解决简单的实际问题.教学重点:二次根式性质的应用;二次根式的运算. 教学难点:二次根式性质的应用. 一、本章知识结构图: 二、本章基本概念:1.二次根式的定义:形如 a (a ≥ 0)的式子叫做二次根式. 2.二次根式的识别:(1)被开方数a ≥0; (2)根指数是2.例:下列各式中哪些是二次根式?哪些不是?为什么?①15 ②3a ③︱x-100︱ ④a 2+b 2 ⑤-a 2-1 ⑥-144 ⑦a 2-2a+1(1; (2); (3题型一:确定二次根式中被开方数所含字母的取值范围 1有意义的条件是 .2.当 时,3. 若11m +有意义,则m 的取值范围是 .4. 当x___________时,x311--是二次根式.说明:因为二次根式的被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组). 题型二:二次根式的非负数性的应用 1. 0, 试求 x -y 的值.2. 若2440y y +-+=,试求xy 的值.3. 已知,a b 为实数,且()10b -=,求20052006a b -的值.让学生抢答:判断下列二次根式是否是最简二次根式,并说明理由:① 50 ② a 2bc ③ x 2+y 2 ④ o.75 ⑤ (a+b)(a 2-b 2) ⑥ 12 错误!未定义书签。
6说明: 满足下列两个条件的二次根式,叫做最简二次根式(1)被开方数中的因数是整数,因式是整式;(2)被开方数中不含有能开得尽方的因数或因式. 例1.把下列各式化成最简二次根式:(1)54 (2) 4a 2+16a 2 (3) 412(4) x 2y x化简二次根式的方法: (1)如果被开方数是整数或整式,先因数分解或因式分解,然后利用积的算术平方根的性质,将式子化简. (2)如果被开方数是分数或分式时,先利用商的算术平方根的性质,将其变为二次根式相除的形式,然后利用分母有理化,将式子化简. 4. 二次根式性质及运算律:((a ≥0,b ≥0)(a ≥0,b ≥0)(a ≥0,b>0)a ≥0,b>0)5. 二次根式的应用:(1)二次根式的加减法:通常先把各个二次根式化成最简二次根式,再合并同类二次根式; (2)二次根式的乘法类似于多项式的乘法,运算公式为(a ≥0,b ≥0);对于二次根式的除法,通常是先化成分式的形式,然后通过分母有理化进行运算,有时可以约分,有时可以利用公式,但运算的结果都一定要化成最简二次根式. 题型一:化简下列各式-)2;-);+1)题型二:计算下列各题,并概括二次根式的运算的一般步骤 -)--)·÷1y)三、自主评价:1. 本节课你学到了哪些知识?2.本节课中你最大的收获是什么?四、教学反思:,0,0{a a a a a ≥-<==。
东南大学 基础工程 第三章 连续基础

§3.3 地基计算模型 在上部结构、基础与地基的共同作用分析中, 在上部结构、基础与地基的共同作用分析中, 或者在地基上的梁板分析中,都要用到土与基 或者在地基上的梁板分析中,都要用到土与基 础接触界面上的力与位移的关系, 础接触界面上的力与位移的关系,这种关系可 以用连续的或离散化形式的特征函数表示, 以用连续的或离散化形式的特征函数表示,这 就是所谓的地基计算模型 地基计算模型。 就是所谓的地基计算模型。 地基计算模型可以是线性或非线性的,且一般 地基计算模型可以是线性或非线性的, 是三维的,但常予以简化。 是三维的,但常予以简化。最简单的地基计算 模型是线性弹性模型 线性弹性模型, 模型是线性弹性模型,并且只考虑竖向力和位 几种线弹性地 移的关系,本节主要介绍常用的几种线弹性 移的关系,本节主要介绍常用的几种线弹性地 基模型。 基模型。
第三章
§3.1 §3.2 §3.3 §3.4
连续基础
概述 地基、基础与上部结构相互作用的概念 地基、 地基计算模型 Winkler地基梁的计算 Winkler地基梁的计算
§3.5 地基上梁的数值分析 §3.6 柱下条形基础 §3.7 柱下交叉条形基础 §3.8 筏形基础与箱形基础 刚性基础基底反力、 §3.9 刚性基础基底反力、沉降和倾斜计算的 数值分析方法
d 2ω EI 2 = M dx
dM =V dx
dV = bp q dx
d 4ω d 2M dV EI 4 = = = bp + q 2 dx dx dx
q = 0时
d 4ω EI 4 = bp dx p = ks = kω
d 4ω kb EI 4 + ω = 0 dx EI
d 4ω kb EI 4 + ω = 0 dx EI
基础工程 第三章 连续基础

s R
其中柔度系数按分层总和法计算:
ij
k 1
m
kijH ki
Eski
弹性半空间地基模型的优缺点: 能考虑应力扩散,能考虑相邻荷载的 影响。且能考虑地基土的分层变化。但仍 不能考虑土的应力应变非线性。 弹性半空间地基模型的适用条件: 分层的各种土组成的地基。
3.4文克勒地基上梁的计算
M 02 M 0 3 M M 剪力,归纳公式为: w Bx, C x,M 0 Dx,V 0 Ax kb kb 2 2
x x Ax e (cosx sin x),Bx e sin x 式中 x x C e (cos x sin x ) , D e cosx,均可按x查表获得。 x x 当 x 0 时,取其绝对值计算,所得结果 w、M取相反符号 、V 正负条形基础、十字交叉条形基础、筏板式基础和箱形基础等 的统称。也可简称为梁板式基础。 连续基础具有以下特点: (1)基底面积大、承载能力高,适用于荷载集中的高层建筑和荷载较大的工 业建筑; (2)能增大上部结构整体刚度,减小建筑物的不均匀沉降; (3)对于埋置深度较大的箱形基础,可以考虑挖除的土重对建筑物荷载的补 偿作用; (4)连续基础造价较高; (5)连续基础设计计算较为复杂。 连续基础是地基上的多跨连续受弯构件,其弯曲内力和挠曲变形都与地基 、基础以及上部结构的相对刚度有关,因此,综合考虑地基、基础与上部结构相 互作用,并选择适宜的地基计算模型,才能经济高效地完成连续基础的工程设计 。
2.弹性半空间地基模型
假定地基为弹性半空间力学介质,由Boussinesq解,
P(1 2 ) 地基沉降:s w( x, y,0) E0 r
si i1 p1 f1 i 2 p2 f 2 ... in pn f n ij R j 第i单元地基沉降:
北师大数学七年级第三章《整式及其加减》全章复习与巩固(基础)
《整式及其加减》全章复习与巩固(基础)知识讲解【学习目标】1、进一步理解用字母表示数的意义,能分析简单问题的数量关系,并用代数式表示.2、理解代数式的含义,能解释一些简单代数式的实际背景或几何意义,体会数学与世界的联系.3、会求代数式的值,能解释值的实际意义,能根据代数式的值推断代数式反映的规律.4.理解并掌握单项式与多项式的相关概念;5.理解整式加减的基础是去括号和合并同类项,并会用整式的加减运算法则,熟练进行整式的加减运算、求值;6.深刻体会本章体现的主要的数学思想----整体思想.【知识网络】【要点梳理】要点一、代数式诸如:16n ,2a+3b ,34 ,2n ,2)(b a 等式子,它们都是用运算符号(+、-、×、÷、乘方、开方)把数和表示数的字母连接而成的,像这样的式子叫做代数式,单独的一个数或一个字母也是代数式.要点诠释:代数式的书写规范:(1)字母与数字或字母与字母相乘时,通常把乘号写成“· ”或省略不写;(2)除法运算一般以分数的形式表示;(3)字母与数字相乘时,通常把数字写在字母的前面;(4)字母前面的数字是分数的,如果既能写成带分数又能写成假分数,一般写成假分数的形式;(5)如果字母前面的数字是1,通常省略不写.要点二、整式的相关概念1.单项式:由数字或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.要点诠释:(1)单项式的系数是指单项式中的数字因数.(2)单项式的次数是指单项式中所有字母的指数和.2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项. 要点诠释:(1)在多项式中,不含字母的项叫做常数项.(2)多项式中次数最高的项的次数,就是这个多项式的次数.(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.3. 多项式的降幂与升幂排列:把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.要点诠释:(1)利用加法交换律重新排列时,各项应带着它的符号一起移动位置;(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.4.整式:单项式和多项式统称为整式.要点三、整式的加减1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.要点诠释:辨别同类项要把准“两相同,两无关”:(1)“两相同”是指:①所含字母相同;②相同字母的指数相同;(2)“两无关”是指:①与系数无关;②与字母的排列顺序无关.2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.要点诠释:合并同类项时,只是系数相加减,所得结果作为系数,字母及字母的指数保持不变.3.去括号法则:括号前面是“+”,把括号和它前面的“+”去掉后,原括号里各项的符号都不改变;括号前面是“-”,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.4.添括号法则:添括号后,括号前面是“+”,括号内各项的符号都不改变;添括号后,括号前面是“-”,括号内各项的符号都要改变.5.整式的加减运算法则:几个整式相加减,通常用括号把每一个整式括起来,再用加、减号连接,然后去括号,合并同类项.要点四、探索与表达规律寻找规律并用字母表示这一规律体现了从特殊到一般和归纳、猜想的数学思想的运用.解题中应注意先从特殊的结果寻找规律,再用字母表示,最后加以验证.【典型例题】类型一、代数式1.(2016春•滨海县校级月考)做大小两个纸盒,尺规如下(单位:cm)长宽高小纸盒 a b c大纸盒3a 2b 2c(1)做这两个纸盒共用料多少平方厘米?(结果用含a、b、c的代数式表示)(2)做成的大纸盒比小纸盒的容积大多少立方厘米?(结果用含a、b、c的代数式表示)【思路点拨】(1)根据长方体表面积计算公式计算出两个长方体表面积,再相加化简可得;(2)根据长方体体积计算方法计算出两个长方体体积相减,化简可得.【答案与解析】解:(1)根据题意,做两个纸盒需用料2ab+2bc+2ac+12ab+8bc+12ac=14ab+10bc+14ac,答:做这两个纸盒共用料(14ab+10bc+14ac)平方厘米.(2)根据表格中数据可知,大纸盒比小纸盒的容积大3a×2b×2c﹣abc=11abc,答:做成的大纸盒比小纸盒的容积大11abc立方厘米.【总结升华】本题主要考查根据实际问题列代数式的能力,准确表示出各部分的面积或体积是关键.举一反三: 【变式】ba b a +-2的意义是( ) A.a 与b 差的2倍除以a 与b 的和B.a 的2倍与b 的差除以a 与b 和的商C.a 的2倍与b 的差除a 与b 的和D.a 与b 的2倍的差除以a 与b 和的商【答案】B类型二、整式的相关概念2.指出下列各式中的整式、单项式和多项式,是单项式的请指出系数和次数,是多项式的请说出是几次几项式.(1)3a - (2)5 (3)2b a - (4)2x y - (5)3xy (6)x π (7)5m n + (8)1+a% (9)1()2a b h +g 【答案与解析】解:整式:(1)、(2)、(4)、(5)、(6)、(7)、(8)、(9)单项式:(2)、(5)、(6),其中:5的系数是5,次数是0;3xy 的系数是3,次数是2;x π的系数是1π,次数是1. 多项式:(1)、(4)、(7)、(8)、(9),其中: 3a -是一次二项式;2x y -是一次二项式;5m n +是一次二项式;1+a%是一次二项式; 1()2a b h +g 是二次二项式. 【总结升华】①分母中出现字母的式子不是整式,故2b a -不是整式;②π是常数而不是字母,故x π是整式,也是单项式;③(7)、(9)表示的是加、减关系而不是乘积关系,而单项式中不能有加减.如5m n +其实质为55m n +,1()2a b h +其实质为1122ah bh +. 举一反三:【变式1】(1)3xy -的次数与系数的和是________;(2)已知单项式26x y 的系数是等于单项式52m x y -的次数,则m =________;(3)若nma b 是关于a 、b 的一个五次单项式,且系数为9,则-m+n =________.【答案】 (1)3 (2)1 (3)-5【变式2】多项式432231y y y y -+-+是________次________项式,常数项是________,三次项是________.【答案】四,五, 1 , 3y -【变式3】把多项式321325x x x --+按x 的降幂排列是________.【答案】322531x x x -+-+ 类型三、整式的加减运算3.(2015•遵义)如果单项式﹣xy b+1与xa ﹣2y 3是同类项,那么(a ﹣b )2015= . 【答案】1.【解析】解:由同类项的定义可知a ﹣2=1,解得a=3,b+1=3,解得b=2,所以(a ﹣b )2015=1.【总结升华】考查了同类项,要求代数式的值,首先要求出代数式中的字母的值,然后代入求解即可.举一反三:【变式】若47a x y 与579b x y -是同类项,则a =________,b =________. 【答案】 5 , 44. 计算 22232(12)[5(436)]x x x x x -----+【答案与解析】解法1: 22232(12)[5(436)]x x x x x -----+222324(5436)x x x x x =-+--+- 2234236x x x x =+---+224x x =++解法2:22232(12)[5(436)]x x x x x -----+2223245(436)x x x x x =-+-+-+ 22242436x x x x =-+-+-+224x x =++【总结升华】根据多重括号的去括号法则,可由里向外,也可由外向里逐层推进,在计算过程中要注意符号的变化.若括号前是“-”号,在去括号时,括号里各项都应变号,若括号前有数字因数,应把数字因数乘到括号里,再去括号.举一反三:【变式1】下列式子中去括号错误的是( ).A .5x -(x -2y +5z )=5x -x +2y -5zB .2a 2+(-3a -b )-(3c -2d )=2a 2-3a -b -3c +2dC .3x 2-3(x +6)=3x 2-3x -6D .-(x -2y )-(-x 2+y 2)=-x +2y +x 2-y 2【答案】C【变式2】化简:-2a+(2a-1)的结果是( ).A .-4a-1B .4a-1C .1D .-1【答案】D类型四、化简求值5. (1)直接化简代入已知12x =,1y =-,求225(23)2(43)x y x x x y ---的值. (2)条件求值 (烟台)若523m x y +与3n x y 的和是单项式,则n m =________.(3)整体代入已知x 2-2y =1,那么2x 2-4y+3=________.【答案与解析】解:(1)5(2x 2y-3x)-2(4x-3x 2y)=10x 2y-15x-8x+6x 2y=16x 2y-23x当12x =,y =-1时, 原式=211233116(1)2342222⎛⎫⨯⨯--⨯=--=- ⎪⎝⎭. (2) 由题意知:523m xy +和3n x y 是同类项,所以m+5=3,n =2,解得,m =-2,n =2,所以2(2)4n m =-=.(3)因为222432(2)3x y x y -+=-+, 而221x y -=所以22432135x y -+=⨯+=.【总结升华】整体代入的一般做法是对代数式先进行化简,然后找到化简结果与已知条件之间的联系.举一反三:【变式1】(2015•娄底)已知a 2+2a=1,则代数式2a 2+4a ﹣1的值为( )A .0B .1C .﹣1D .﹣2【答案】B【变式2】已知25m n -+=,求25(2)6360m n n m -+--的值.【答案】225(2)63605(2)3(2)60m n n m m n n m -+--=-+-- 225m n n m -+=-=Q所以,原式=255356080⨯+⨯-=.类型五、探索与表达规律6.将一张长方形的纸对折,如下图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到条折痕.如果对折n 次,可以得到 条折痕.【思路点拨】对前三次对折分析不难发现每对折1次把纸分成的部分是上一次的2倍,折痕比所分成的部分数少1,求出第4次的折痕即可;再根据对折规律求出对折n 次得到的部分数,然后减1即可得到折痕条数.【答案】15,2n -1【解析】解:由图可知,第1次对折,把纸分成2部分,1条折痕,第2次对折,把纸分成4部分,3条折痕,第3次对折,把纸分成8部分,7条折痕,所以,第4次对折,把纸分成16部分,15条折痕,…,依此类推,第n 次对折,把纸分成2n 部分,2n -1条折痕.故答案为:15;2n -1.【总结升华】本题是对图形变化规律的考查,观察得到对折得到的部分数与折痕的关系是解题的关键.类型六、综合应用7. 已知多项式2222(231)(543)mx x x x y x -++--+是否存在m ,使此多项式与x 无关?若不存在,说明理由;若存在,求出m 的值.【答案与解析】解: 要使原式与x 无关,则需该项的系数为0,即有260m -=,所以3m =答:存在m 使此多项式与x 无关,此时m 的值为3.【总结升华】一个多项式不含某项或说与某项无关,都是暗含此多项式中该项的系数为0.2222(215)(33)41(26)41m x x y m x y =--+-++=-++原式【巩固练习】 一、选择题 1.(2016•富顺县校级模拟)在-3,π2-1,-22x -,21x y π-,12a --,4x -六个代数式中,是单项式的个数( )A .2个B .3个C .4个D .5个2.(2015•厦门)已知一个单项式的系数是2,次数是3,则这个单项式可以是( )A .﹣2xy 2B . 3x 2C . 2xy 3D . 2x 3 3.有下列式子:12x yz +,2b ,2323x x --,abc ,0,y x ,x ,a b ab+,对于这些式子下列结论正确的是( ).A .有4个单项式,2个多项式B .有5个单项式,3个多项式C .有7个整式D .有3个单项式,2个多项式4.对于式子421.210x y -⨯,下列说法正确的是( ).A .不是单项式B .是单项式,系数为-1.2×10,次数是7C .是单项式,系数为-1.2×104,次数是3D .是单项式,系数为-1.2,次数是35.下面计算正确的是 ( )A .32x -2x =3B .32a +23a =55aC .3+x =3xD .-0.25ab +41ba =0 6.2a-(5b-c+3d-e)=2a □5b □c □3d □e ,方格内所填的符号依次是( ).A .+,-,+,-B .-,-,+,-C .-,+,-,+D .-,+,-,-7.某工厂现有工人a 人,若现有工人数比两年前减少了35%,则该工厂两年前工人数为( ).A .135%a +B .(1+35%)aC .135%a - D .(1-35%)a 8.若2237y y ++的值为8,则2469y y +-的值是( ).A .2B .-17C .-7D .7二、填空题9.比x 的15%大2的数是________.10.(2015•中江)单项式﹣x 2y 5的次数是 . 11.22372x y x -++是________次________项式,最高次项的系数是________. 12.化简:2a-(2a-1)=________.13.如果24a ab +=,21ab b +=-,那么22a b -=________.14.一个多项式减去3x 等于2535x x --,则这个多项式为________.15.(2016春•永春县校级月考)若与﹣3ab 3n -的和为单项式,则m+n= . 16.如图所示,外圆半径是R 厘米,内圆半径是r 厘米,四个小圆的半径都是2厘米,则图中阴影部分的面积是________平方厘米.三、解答题17.(2014秋•镇江校级期末)合并同类项①3a﹣2b ﹣5a+2b②(2m+3n ﹣5)﹣(2m ﹣n ﹣5)③2(x 2y+3xy 2)﹣3(2xy 2﹣4x 2y ) 18.已知:2263A x x =+-,213B x x =--,2451C x x =--,当32x =-时,求代数式32A B C -+的值.19. 计算下式的值:114x ,y ,==-其中甲同学把14x =错抄成14x =-,但他计算的结果也是正确的,你能说明其中的原因吗?20.某农场有耕地1000亩,种粮食、棉花和蔬菜. 其中蔬菜用地a 亩,粮食用地比蔬菜用地的6倍还多b 亩,求棉花用地多少亩?当a=120,b=4时,棉花用地多少亩?【答案与解析】一、选择题1. 【答案】A【解析】解:﹣3,﹣x 2y 是单项式.注意-22x -是分式, 4x -A . 2.【答案】D .【解析】此题规定了单项式的系数和次数,但没规定单项式中含几个字母.A 、﹣2xy 2系数是﹣2,错误;B 、3x 2系数是3,错误;C 、2xy 3次数是4,错误;D 、2x 3符合系数是2,次数是3,正确;故选D .3. 【答案】A【解析】单项式有2b ,abc ,0,x ;多项式有12x yz +,2323x x --,其中y x ,a b ab +不是整式.4.【答案】 C【解析】此单项式的系数是以科学记数法形式出现的数,所以系数为-1.2×104,次数应)4()2()242(33432242234y y x x y y x x y x y x x -+-++----为x 与y 的指数之和,不包括10的指数4,故次数为3.不要犯“见指数就相加”的错误.所以正确答案为C .5. 【答案】D6.【答案】 C【解析】因为括号前是“-”号,所以去括号时,括号里各项都变号,故选C .7. 【答案】C【解析】把减少前的工人数看作整体“1”,已知一个数的(1-35%)是a ,求这个数,则是135%a -,注意列式时不能用“÷”号,要写成分数形式. 8.【答案】C【解析】22378y y ++=,2231y y +=,22462(23)212y y y y +=+=⨯=,故24697y y +-=-.二、填空题9.【答案】15%x+2;10.【答案】7.11.【答案】三, 三 , 12-; 【解析】多项式的次数取决于次数最高项的次数,确定系数时不要忽视前面的“-”号.12.【答案】1;【解析】先根据去括号法则去括号,然后合并同类项即可,2a-(2a-1)=2a-2a+1=1.13.【答案】5;【解析】用前式减去后式可得225a b -=.14.【答案】255x -;【解析】要求的多项式实际上是2(535)3x x x --+,化简可得出结果.15.【答案】 4;【解析】解:∵与﹣3ab 3n -的和为单项式,∴2m ﹣5=1,n+1=3﹣n ,解得:m=3,n=1.故m+n=4.故答案为:4.16.【答案】22(16)R r πππ--;【解析】阴影部分的面积=大圆面积-最中间的圆的面积-4个小圆的面积.三、解答题17.【解析】解:(1)原式=(3a ﹣5a )+(﹣2b+2b )=﹣2a ;(2)原式=2m+3n ﹣5﹣2m+n+5=(2m ﹣2m )+(3n+n )+(﹣5+5)=4n ;(3)原式=2x 2y+6xy 2﹣6xy 2+12x 2y=(2x 2y+12x 2y )+(6xy 2﹣6xy 2)=14x 2y .18.【解析】解:∵222263,31,45 1.A x x B x x C x x ⎧=+-⎪=--+⎨⎪=--⎩ ∴ 222263,3393,2810 2.A x x B x x C x x ⎧=+-⎪⎪-=+-⎨⎪=--⎪⎩∴2321358A B C x x -+=+- 当32x =-时, 32A B C -+33915117303213()5()81388132242444=⨯-+⨯--=⨯--=--=. 19. 【解析】解: ∵化简结果与x 无关∴将x 抄错不影响最终结果.20.【解析】解:棉花用地:1000-a -(6a +b)=(1000-7a -b)亩.当a =120,b =4时,原式=1000-7×120-4=156(亩).答:棉花用地(1000-7a-b)亩.当a=120,b=4时,棉花用地为156亩.43224223433432242234333(242)(2)(4)242242yx x y x y x x y y x x y y x x y x y x x y y x x y y ----++-+-----+-- =+- = 。
信息学奥赛培训教程C++版--基础

6.9 构造算法与自上而下逐步完善:实例研究 3(嵌套控制结构) .......................................... 85 6.10 赋值运算符 ............................................................ 88 6.11 自增和自减运算符....................................................... 88 6.12 计数器控制循环的要点................................................... 91 6.13 for 重复结构............................................................ 92 6.14 for 结构使用举例........................................................ 94 6.15 switch 多项选择结构 ..................................................... 97 6.16 do/while 重复结构 ...................................................... 101 6.17 break 和 continue 语句 ................................................... 102 6.18 逻辑运算符 ........................................................... 104 6.19 混淆相等(==)与赋值(=)运算符............................................ 105 6.20 结构化编程小结 ....................................................... 106
第3章 连续基础

e 0 . 1W / A
2.筏板基础内力计算
2.筏板基础内力计算 (1)倒楼盖法 对上部荷载比较均匀或刚度比较大的结构体系,当基础 平面尺寸较小、筏板厚度较大及土层较软时,可以认为基础 板对地基而言是绝对刚性的,称之为刚性基础板。“刚性板 法”将基础板视为倒臵的楼盖,以柱子或剪力墙为支座、地 基净反力为荷载,按普通钢筋混凝土楼盖来计算。 (2)弹性地基上地基板的计算 当筏板基础的刚度较弱,属于柔性基础,应按弹性地 基上的梁板进行计算。若柱网及荷载分别比较均匀,按文 克尔地基梁模型计算。
(2)根据整体刚度大小,将地基变形对上部结构的影响
相对刚度为0,产生整体弯曲,排架结构, 不允许基础出现过量沉降量或沉降差 相对刚度为无穷大,产生局部弯曲,剪力墙、 筒体结构。
柔性结构: 刚性结构:
敏感性结构: 不均匀沉降会引起较大附加应力的结构 砌体结构、钢筋混凝土框架结构 若结构本身的强度储备不足,容易产生开裂 基础刚度愈大,挠曲愈小,则上部结构的次应力也愈小。因 此,对高压缩性地基上的框架结构,基础刚度宜刚,而对柔 性结构,在满足允许沉降值的前提下,基础刚度宜小不宜大, 而且不一定需要采用连续基础。
2.柱下条形基础的计算 (1)基础底面尺寸的确定 条形基础的长度由构造要求确定,即“条形基础的端 部宜向外伸出,其长度宜为第一跨距的0.25-0.30倍”, 然后将基础视为刚性矩形基础,按地基承载力特征值确定 基础底面宽度。在按构造要求确定基础长度时,应尽量使 其形心与基础所受外合力重心相重合,此时地基反力均匀 分布。否则按偏心受压计算。 (2)基础底板计算 柱下条形基础底板的计算方法与墙下钢筋混凝土条形基 础相同。在计算基底净反力设计值时,荷载沿纵向和横向 的偏向都要予以考虑。当各跨的净反力相差较大时,可依 次对各跨底板进行计算,净反力可取本跨内的最大值。
基础工程第3章3 连续基础3.4-3.6
w ex C3 cosx C4 sin x
对称性:在x=0处,dw/dx=0,代 入上式得C3-C4=0。令C3=C4=C, 则上式成为
w exCcosx sin x
静力平衡条件:再在O点处紧靠F0 的左、右侧把梁切开,则作用于O 点左右两侧截面上的剪力均等于F0 之半,且指向上方。根据符号规定, 在右侧截面有V=-F0 /2,由此得 C=F0λ/2kb 。 +V F0
解上述方程组得:
FA El Fl Dl Va El Fl Al M a Fl El Dl Vb Fl El Al M b Va M A El Fl Cl El Fl Dl M a 2 V Fl El Cl b Fl El Dl M b 2 FB Fl El Dl Va Fl El Al M a El Fl Dl Vb El Fl Al M b Va M B Fl El Cl Fl El Dl M a 2 Vb El Fl Cl El Fl Dl M b 2
3.4 文克勒地基上梁的计算
3.4.1 无限长梁的解答
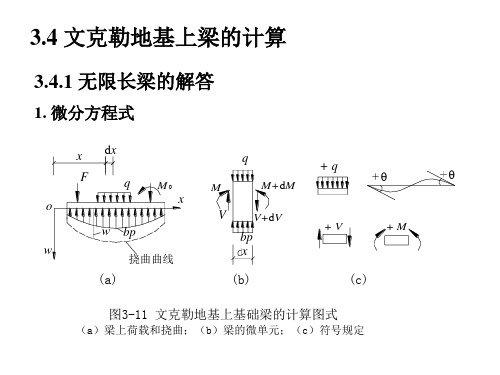
1. 微分方程式
x F o w w bp
挠曲曲线
dx q
M0 M
q
M+dM V+dV
+q
x
V bp x
+V
+M
(a)
(b)
(c)
图3-11 文克勒地基上基础梁的计算图式
(a)梁上荷载和挠曲;(b)梁的微单元;(c)符号规定
x F o
dx q
对短梁,可采用基底反力呈直线变化的简化方法计算;
2019-2020学年七年级数学上册 第三章练习(基础篇)教学案 苏科版.doc

2019-2020学年七年级数学上册 第三章练习(基础篇)教学案 苏科版一、选择题(2分×12=24分)1.下列式子中,符合代数式的书写格式的是( )A .(a-b )7 B.3a÷5b C.121ab D.a b2.计算a+(-a)的结果是( )A.2a B.0 C.-a 2D.-2a3.如果33-=-b a ,那么代数式b a 35+-的值是( )A .0B .2C .5D .84.一个两位数的个位数字是x ,十位数字是y ,这个两位数是( )A. xyB.yxC.10x+yD.10y+x 5.下列各组代数式中,不是同类项的是( ) 6.下列式子中正确的是 ( )A.527a b ab +=B.770ab ba -=C.45222x y xy x y -=-D.358235x x x +=7.火车站、机场、邮局等场所都有为旅客提供打包服务的 项目.现有一个长、宽、高分别为a 、b 、c 的箱子,按 如图所示的方式打包,则打包带的长(不计接头处的长) 至少应为 ( ) A.c b a 23++ B.c b a 642++ C.c b a 4104++ D.c b a 866++ 8.下列各组中,是同类项的是( )A.y x 23与23xyB. abc 2与ac 3-C. xy 2-与ab 2-D. 2与259.一个整式与x 2-y 2的和是x 2+y 2,则这个整式是( )A . 2x 2 B. 2y 2 C. -2x 2 D. -2y210.已知一个多项式与239x x +的和等于2341x x +-,则这个多项式是( )A .51x --B .51x +C .131x --D .131x +11.如图,用围棋子按下面的规律摆图形,则摆第n 个图形需要围棋子的枚数是( )A .5nB .5n -1C .6n -1D .2n 2+112.如图,从边长为(a +4)cm 的正方形纸片中剪去一个边长为()1a +cm 的正方形(0)a >,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( ). A .22(25)cm a a + B .2(315)cm a + C .2(69)cm a + D .2(615)cm a +二、填空题(2分×8=16分)13.单项式 y x -5352的系数是 ,次数是 .14. 若n m y x y x -和25是同类项,则n m 52-= . 15.若523m x y +与3n x y 的和是单项式,则m n = . 16.某服装原价为a 元,降价10%后的价格为 元. 17.已知a - b =1,则代数式2a -2b -3的值是18.如图是一个简单的数值运算程序,当输入n 的值为3时,则输出的结果为 .19.已知82=-ab a ,42-=-b ab ,则=-22b a ,=+-222b ab a20.若2320a a --=,则2526a a +-= .三、解答题 21.化简:(6分×2=12分)(1))32()54(722222ab b a ab b a b a --+-+.(2)()()22-25x 552215x x x -+--+22. (8分)先化简,再求值: )4(3)125(23m m m -+--,其中3-=m .23.在计算多项式M 加上,425,73,73222-++++-x x x x x x 得答案是误以为加上时 试求出正确案.(8分)24.(8分)(1)当a =5,b =3时,分别求代数式①222a ab b -+②2)(b a -的值. (2)当a =2,b= -1 时,分别求代数式①222a ab b -+②2)(b a -的值. (3)观察(1)(2)中代数式的值,222a ab b -+与2)(b a -有何关系? (4)利用你发现的规律,求227.357.357.13527.135+⨯⨯-的值.25.(8分)公安人员在破案时常常根据案发现场作案人员留下的脚印推断犯人的身高,如果用a 表示脚印长度,b 表示身高.关系类似满足于:b=7a —3.07 (1)某人脚印长度为24.5cm ,则他的身高约为多少?(精确到1cm )(2)在某次案件中,抓获了两可疑人员,一个身高为1.87m ,另一个身高1.82m ,现场测量的脚印长度为26.3cm ,请你帮助侦察一下,哪个可疑人员的可能性更大?26.(6分)用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案(1)第四个图案中有白色..地面砖多少块?(2)第n个图案中有白色..地面砖多少块?27.(10分)某公司在甲、乙两仓库分别存有某种机器12台和6台,现需调往A县10台,调往B县8台。
第3章:连续基础

基底压力的分布
1.柔性基础
抗弯刚度很小的基础可看 作柔性基础。柔性基础不具 备调整地基变形的能力,基 底反力分布与上部结构和基 础荷载的分布方式完全一致。a) 均布荷载下
b) 基础不发生挠曲时
2.刚性基础
刚性基础具有很大的调整地基变形的能力,在荷 载和地基都均匀的情况下发生均匀沉降,在偏心荷 载、相邻荷载下或地基不均匀时发生倾斜,但不会 发生基础的相对挠曲。
第3章:连续基础
❖ 概述 ❖ 地基、基础与上部结构共同工作
的概念 ❖ 地基计算模型 ❖ 文克勒地基上梁的计算 ❖ 柱下条形基础 ❖ 柱下交叉条形基础 ❖ 筏形基础与箱形基础
§3.1 概述
连续基础是指在柱下连续设置的单向或双向条形 基础,或底板连续成片的筏板基础和箱型基础。常 用在以下情况中: ➢ 1)需要较大的底面积去满足地基承载力要求,此 时可将扩展式基础的底板连接成条或片。 ➢ 2)需要利用连续基础的刚度去调整地基的不均匀 变形,或改善建筑物的抗震性能。 ➢ 3)建筑物的功能需要设置连续的底板时,例如地 下室、船坞、储液池等。
§3.2 地基、基础与上部结构 共同工作的概念
地基、基础和上部结构组成了一个完 整的受力体系,三者的变形相互制约、相 互协调,也就是共同工作的,其中任一部 分的内力和变形都是三者共同工作的结果。 但常规的简化设计方法未能充分考虑这一 点。
常规设计的步骤:
例如条形基础上多层平面框架的分析(如图):
(2)集中力偶作用
x , 0
M 02
kb
Bx
M 03
kb
Cx
M
M0 2
Dx
V
M 0
2
Ax
如计算截面在M0的左边(x<0) 时,且x取绝对值时,ω和M取 负,θ与V 不变。
奥数全集新篇

第一篇 基本方法 第一章 探索与发现“规律是数学的灵魂”------著名数学家高斯,“数学的伟大使命,在于从混沌中发现有序”------比利时科学家普利高津。
数学王国里到处充满了规律,运用规律能快速有效地解决一连串的数学实际问题。
我们要学会在日常生活中通过各种途径去探索、去发现、去猜测、去验证各种有规律的数学现象。
同学们要学会观察比较数字、图形、图表、数列的变化,并能从图形、数量间的关系中发现规律,这种能力对于同学们今后的学习将大有益处。
这一章将和同学们一起探索一些常见的数学规律。
一. 数字观察数字观察是最基本的找规律方法。
同学们观察下面几组算式,试着填一填,并说一说你发现了什么规律。
1. 1×9=9 2. 3×4=1212×9=108 33×34=1122 123×9=1107 333×334=1112221234×9=11106 3333×3334= 12345×9= 3. 6×7=42 123456×9= 66×67=44221234567×9= 666×667=44422212345678×9= 6666×6667=123456789×9= 66666×66667= 4.找规律约分:66666641666666=( )5. 142857×1=142857142857×2=285714142857×3=428571 142857×4=571428 142857×5= 142857×6= 142857×7=二. 数列观察按一定次序排列的一列数就叫数列。
列数按照某种规律排列起来,其中留有部分空缺的部分,只要从连续的数中找出规律,那么就可以知道所空缺的部分,从而把题目中给定的规律补充完整。
七年级数学上册第3章实数34实数的运算分层训练新版浙教版.docx

3.4实数的运算—课堂笔记1.实数的运算法则:____________ 的运算律和运算法则在实数范围内仍适用.2.实数的运算顺序:先算_____________ ,再算乘除,最后算 _____________ ;如果遇到括号,则先进行____________ 的运算.3.近似计算时按题目要求将用计算器算得的结果取I分层illl练A组基础训练1.下列说法中,正确的个数有()①两个无理数的和是无理数;②两个无理数的积是有理数;③无理数与有理数的和是无理数;④有理数除以无理数的商是无理数.A. 1个B. 2个C. 3个D. 4个2.下列运算中,正确的有()①②^冃戸二土旺A.1个B. 2个C. 3个D. 4个3.不小于4><飞gj的最小整数是()A.4B. 10C. 9D. 84.一个底而是正方形的水池,容积是11.52m3,池深2m,则水池底边长是( )A. 9.25mB. 13.52raC. 2.4m D・ 4.2m5.用计算器计算(结果精确到0.01)(1)p31400~ ;(2)±^0.618^ ______________ ;(3)_______________________ -勻0. 0005432= .6.计算下列各式:|1—寸引= _____________ : y/25—(―1)2= : yj (—3) 2 + (何= _______________ ;^27~\~2\=_______________ ;荷+储—訴= ________________ ;7-8X (2_&) = _______________(2)2X[9-2X(萌一 2)];7.⑴若 a<-l,化简 a+ |a+l| =(2) A(3)将希,平这三个数按从小到大的顺序用”〈”连接起来:⑷如图是一个简单的数值运算程序,若输入x 的值为萌,■输入x| —a罔―彳减i| —»|输出第7题图(5)已知一l 〈x<0,请把一x, —y[~x f x?按从大到小的顺序用X则输出的数值为” >”连接起来:8. 某数的立方的一半等于一丄,求这个数.9.计算:⑶(-1)?+ \ 2—y[2 \ —y[27+y[8;⑷2边宁迈一(一1严7+|萌一2|.10.已知一个立方体的棱长为6cm,再做一个立方体,使它的体积是原立方体的4倍, 求所做立方体的棱长(精确到0. 1cm)・11.跳伞运动员跳离飞机,在未打开降落伞前,下降的高度d(m)与下降的时间t(s)之间有关系式不计空气阻力,结果精确到0. 01s).(1)请完成下表:(2)如果共下降1000m,那么前一个500m与后一个500m所用的时间分别是多少?B组自主提高12.(1)写出两个无理数,使它们的和为5:____________ ・(2)对于实数a, b,给出以下三个判断:①若|a| = |b|,则后血②若|a|<|b|,则a<b;③若a=—b,贝9(—ajJbl其中正确的判断是_________________ .(3)如图,M, N, P, Q是数轴上的四个点,则这四个点屮最适合表示⑴的点是0 12 3 4第12题图13-观察:\/二1=\/1=\/字=2\/|,即弋;r~3" 127 [9X3 C 用V3-百=7 Io V ~w=3\ 帀即小寻彳诵请你猜想寸5—舊等于什么?并通过计算验证你的猜想.C组综合运用14.小明是一位善于思考,勇于创新的同学.在学习了有关平方根的知识后,小明知道负数没有平方根,比如:因为没有一个数的平方等于一1,所以一1没有平方根.有一天,小明想:如果存在一个数i,使i2=-l,那么(一i)J—1,因此一1就有两个平方根了.进一步,小明想:因为(±2i)2=-4,所以一4的平方根就是±2i;因为(±3i)2=-9,所以—9的平方根就是±3i・请你根据上而的信息解答下列问题:(1)求一16, —25的平方根;(2)求i3, i\ i5, i6, i7, i8,…的值,你发现了什么规律?将你发现的规律用式子表示出来.参考答案3. 4实数的运算【课堂笔记】1.有理数2•乘方和开方加减括号里3.近似值【分层训练】1. A2. A3. 2/4. C5. (1) 177. 20 (2)±0. 79 (3)-0. 086・£一1 4 6 1 11 一 9 + 8 仗8. 由 x'=—令X2,得 x =—-139. (1)—京 (2)26 —4念 (3)原式=1 + 2—住一3 + 2边=寸^. (4)原式= 2—( —1)+ 2—念=5—萌.10. 9. 5皿 11. (1)4. 47 6.3210. 00 14. 14 (2) 10. 00s 4.14s12. (1)答案不唯一:如和£ + 5 ⑵③(3)PF 門怎13-\5_26 = 5^26;验证:*14. (l)・・・(±4i)2= — 16,±V T716=±4i,即一16 的平方根是±4i.V (±5i)2=—25, /. ±yj — 2o= ±5i,即一25 的平方根是±5i. (2)i 3=i 2- i = -i, i 4=(i 2)2=(-l)2=l,规律:i 的n 次方(n 为正整数)的值每四个一循环,即i, -1, -i, 1.= -l,。
第三章 理想反应器

操作线方程
rAi
=
− CAi
τi
+
CAi−1
τi
动力学方程
rAi = k f (CAi )
(3.3-29)
(3.3-36)
(3.3-37)
(2)图解法步骤 若各级全混流反应器的温度相等,且各釜体积也相同,则作图法求解的步骤如下:
a.在rA~CA坐标系中标出动力学曲线,如图中曲线 OM;
b.由CA0为起点,以
本章讨论的主要内容: 1. 论述反应器内的流动模型,着重阐述混合与返混的异同
及理想流动模型的特征; 2. 以均相反应为背景,讨论理想反应器设计的基本方法; 3. 讨论理想流动反应器中复合反应的收率和选择率。
§3.1 概述
流动模型 是描述流体流经反应器时物料质点的流动与返混状况的模型,对各
种流动模型进行数学描述,便可得到流动的数学模型。
(3.3-33)
或
τ
=
1 k
⎡ ⎢
1
⎢⎣
(1
−
xAm
)
1 m
⎤ − 1⎥
⎥⎦
(3.3-34)
反应系统的总体积
VR
= mVRi
= mV0τ
=
mV0 k
⎡ ⎢
1
⎢⎣(1−
xAm
)
1 m
⎤ − 1⎥
⎥⎦
(3.3-35)
3. 多级串联全混流反应器的图解计算
(1) 图解法原理:
( ) VRi
= V0
CAi−1 −CAi rAi
−1 τ1
为斜率做出第一级反应的操作线与OM线交与A1,其横坐
则 Λ 可视为常数,将(3.3-22)积分得
T = T0 + Λx A
