16级大学物理A2复习题计算题解答

大学物理A2复习资料

大学物理A2复习资料电磁感应1．如图所示，一矩形金属线框，以速度v从无场空间进入一均匀磁场中，然后又从磁场中出来，到无场空间中．不计线圈的自感，下面哪一条图线正确地表示了线圈中的感应电流对时间的函数关系？(从线圈刚进入磁场时刻开始计时，I 以顺时针方向为正) 。

2．两根无限长平行直导线载有大小相等方向相反的电流I ，并各以d I /d t的变化率增长，一矩形线圈位于导线平面内(如图)，则：(A) 线圈中无感应电流．(B) 线圈中感应电流为顺时针方向．(C) 线圈中感应电流为逆时针方向．(D) 线圈中感应电流方向不确定．3．一块铜板垂直于磁场方向放在磁感强度正在增大的磁场中时，铜板中出现的涡流(感应电流)将 (A) 加速铜板中磁场的增加． (B) 减缓铜板中磁场的增加．(C) 对磁场不起作用． (D) 使铜板中磁场反向．4．一导体圆线圈在均匀磁场中运动，能使其中产生感应电流的一种情况是 (A) 线圈绕自身直径轴转动，轴与磁场方向平行． (B) 线圈绕自身直径轴转动，轴与磁场方向垂直． (C) 线圈平面垂直于磁场并沿垂直磁场方向平移．(D) 线圈平面平行于磁场并沿垂直磁场方向平移． 5．半径为a 的圆线圈置于磁感强度为B的均匀磁场中，线圈平面与磁场方向垂直，线圈电阻为R ；当把线圈转动使其法向与B的夹角 =60°时，线圈中通过的电荷与线圈面积及转动所用的时间的关系是(A) 与线圈面积成正比，与时间无关． (B) 与线圈面积成正比，与时间成正比． (C) 与线圈面积成反比，与时间成正比．(D) 与线圈面积成反比，与时间无关．BI O(D)I O(C)O (B)I6．将形状完全相同的铜环和木环静止放置，并使通过两环面的磁通量随时间的变化率相等，则不计自感时(A) 铜环中有感应电动势，木环中无感应电动势． (B) 铜环中感应电动势大，木环中感应电动势小． (C) 铜环中感应电动势小，木环中感应电动势大．(D) 两环中感应电动势相等．7．在无限长的载流直导线附近放置一矩形闭合线圈，开始时线圈与导线在同一平面内，且线圈中两条边与导线平行，当线圈以相同的速率作如图所示的三种不同方向的平动时，线圈中的感应电流(A) 以情况Ⅰ中为最大． (B) 以情况Ⅱ中为最大．(C) 以情况Ⅲ中为最大． (D) 在情况Ⅰ和Ⅱ中相同．8．在两个永久磁极中间放置一圆形线圈，线圈的大小和磁极大小约相等，线圈平面和磁场方向垂直．今欲使线圈中产生逆时针方向(俯视)的瞬时感应电流i (如图)，可选择下列哪一个方法？(A) 把线圈在自身平面内绕圆心旋转一个小角度．(B) 把线圈绕通过其直径的OO ′轴转一个小角度． (C) 把线圈向上平移．(D) 把线圈向右平移．9．一个圆形线环，它的一半放在一分布在方形区域的匀强磁场B 中，另一半位于磁场之外，如图所示．磁场B的方向垂直指向纸内．欲使圆线环中产生逆时针方向的感应电流，应使 (A) 线环向右平移． (B) 线环向上平移． (C) 线环向左平移． (D) 磁场强度减弱．10．如图所示，一载流螺线管的旁边有一圆形线圈，欲使线圈产生图示方向的感应电流i ，下列哪一种情况可以做到？(A) 载流螺线管向线圈靠近．(B) 载流螺线管离开线圈．(C) 载流螺线管中电流增大． (D) 载流螺线管中插入铁芯．11．一矩形线框长为a 宽为b ，置于均匀磁场中，线框绕OO ′轴，以匀角速度ω旋转(如图所示)．设t =0时，线框平面处于纸面内，则任一时刻感应电动势的大小为 (A) 2abB | cos ω t |． (B) ω abB (C) t abB ωωcos 21． (D) ω abB | cos ω t |． (E) ω abB | sin ω t |．12．如图所示，导体棒AB 在均匀磁场B 中绕通过C 点的垂直于棒长且沿磁场方向的轴OO ' 转动（角速度ω与B 同b c d b c d bc d v v I方向），BC 的长度为棒长的31，则(A) A 点比B 点电势高． (B) A 点与B 点电势相等．(B) A 点比B 点电势低． (D) 有稳恒电流从A 点流向B 点．13．如图，长度为l 的直导线ab 在均匀磁场B 中以速度v移动，直导线ab 中的电动势为(A) Bl v ． (B) Bl v sin α．(C) Bl v cos α． (D) 0．14．如图所示，直角三角形金属框架abc 放在均匀磁场中，磁场B平行于ab 边，bc 的长度为l ．当金属框架绕ab 边以匀角速度ω转动时，abc 回路中的感应电动势和a 、c 两点间的电势差U a – U c 为(A) =0，U a – U c =221l B ω． (B) =0，U a – U c =221l B ω-．(C) =2l B ω，U a – U c =221l B ω．(D) =2l B ω，U a – U c =221l B ω-．15．圆铜盘水平放置在均匀磁场中，B的方向垂直盘面向上．当铜盘绕通过中心垂直于盘面的轴沿图示方向转动时， (A) 铜盘上有感应电流产生，沿着铜盘转动的相反方向流动． (B) 铜盘上有感应电流产生，沿着铜盘转动的方向流动． (C) 铜盘上产生涡流． (D) 铜盘上有感应电动势产生，铜盘边缘处电势最高．(E) 铜盘上有感应电动势产生，铜盘中心处电势最高．16．一根长度为L 的铜棒，在均匀磁场 B中以匀角速度ω绕通过其一端O 的定轴旋转着，B的方向垂直铜棒转动的平面，如图所示．设t =0时，铜棒与Ob 成θ 角(b 为铜棒转动的平面上的一个固定点)，则在任一时刻t 这根铜棒两端之间的感应电动势是：(A) )cos(2θωω+t B L ． (B) t B L ωωcos 212．(C) )cos(22θωω+t B L ． (D)B L 2ω．(F) B L 221ω．17．两个通有电流的平面圆线圈相距不远，如果要使其互感系数近似为零，则应调整线圈的取向使(A) 两线圈平面都平行于两圆心连线． (B) 两线圈平面都垂直于两圆心连线．(C) 一个线圈平面平行于两圆心连线，另一个线圈平面垂直于两圆心连线．vBab clωB(C) 两线圈中电流方向相反．18．两个通有电流的平面圆线圈相距不远，如果要使其互感系数近似为零，则应调整线圈的取向使(A) 两线圈平面都平行于两圆心连线． (B) 两线圈平面都垂直于两圆心连线．(C) 一个线圈平面平行于两圆心连线，另一个线圈平面垂直于两圆心连线．(D) 两线圈中电流方向相反． 19．用线圈的自感系数L 来表示载流线圈磁场能量的公式221LI W m =(A) 只适用于无限长密绕螺线管． (B) 只适用于单匝圆线圈． (C) 只适用于一个匝数很多，且密绕的螺绕环．(E) 适用于自感系数Ｌ一定的任意线圈．20．两根很长的平行直导线，其间距离d 、与电源组成回路如图．已知导线上的电流为I ，两根导线的横截面的半径均为r 0．设用L 表示两导线回路单位长度的自感系数，则沿导线单位长度的空间内的总磁能W m 为(A)221LI ．(B) 221LI ⎰∞+π-+0d π2])(2π2[2002r r r r d I r I I μμ (C) ∞． (D) 221LI 020ln 2r dI π+μ21．真空中一根无限长直细导线上通电流I ，则距导线垂直距离为a 的空间某点处的磁能密度为 (A)200)2(21a I πμμ (B) 200)2(21aI πμμ (C) 20)2(21I a μπ (D) 200)2(21aI μμ1C 2B 3B 4B 5A 6D 7B 8C 9C 10B11D 12 A 13D 14 B 15 D 16 E 17C 18C 19D 20A21B振动与波1．一轻弹簧，上端固定，下端挂有质量为m 的重物，其自由振动的周期为T ．今已知振子离开平衡位置为x 时，其振动速度为v ，加速度为a ．则下列计算该振子劲度系数的公式中，错误的是：(A) 2max2max /x m k v =． (B) x mg k /=． (C) 22/4T m k π=． (D) x ma k /=．2．一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，（如图所示），作成一复摆．已知细棒绕通过其一端的轴的转动惯量231ml J =，此摆作微小振动的周期为 (A) g l π2. (B) gl 22π. (C) g l 322π. (D) gl 3π.3．把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π． (B) π/2． (C) 0 ． (D) θ．4．两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为x 1 = A cos(ωt + α)．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处．则第二个质点的振动方程为 (A) )π21cos(2++=αωt A x ． (B) )π21cos(2-+=αωt A x ． (C) )π23cos(2-+=αωt A x ． (D) )cos(2π++=αωt A x ．5．轻弹簧上端固定，下系一质量为m 1的物体，稳定后在m 1下边又系一质量为m 2的物体，于是弹簧又伸长了∆x ．若将m 2移去，并令其振动，则振动周期为(A) gm xm T 122∆π= ． (B) g m x m T 212∆π=．(C) g m x m T 2121∆π=． (D) gm m xm T )(2212+π=∆．6．一质点作简谐振动．其运动速度与时间的曲线如图所示．若质点的振动规律用余弦函数描述，则其初相应为(A) π/6． (B) 5π/6． (C) -5π/6． (D) -π/6． (E) -2π/3．v 217．一质点沿x 轴作简谐振动，振动方程为 )312cos(1042π+π⨯=-t x (SI)．从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A) s 81(B) s 61 (C) s 41(D) s 31(E)s 218．一物体作简谐振动，振动方程为)41cos(π+=t A x ω．在 t = T /4（T 为周期）时刻，物体的加速度为(A) 2221ωA -． (B) 2221ωA ． (C) 2321ωA -． (D) 2321ωA ．9．一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ． (C) φωcos A -． (D) φωcos A ．10．两个同周期简谐振动曲线如图所示．x 1的相位比x 2的相位(A) 落后π/2． (B) 超前π/2． (C) 落后π ． (D) 超前π．11．已知一质点沿ｙ轴作简谐振动．其振动方程为)4/3cos(π+=t A y ω．与之对应的振动曲线是12．一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为13．一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12． (B) T /8． (C) T /6． (D) T /4．14．一弹簧振子作简谐振动，总能量为E 1，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量E 2变为(A) E 1/4． (B) E 1/2．(C) 2E 1． (D) 4 E 1 ．15．当质点以频率ν 作简谐振动时，它的动能的变化频率为 (A) 4 ν． (B) 2 ν ． (C) ν． (D)ν21．16．一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的 (A) 1/4. (B) 1/2. (C) 2/1. (D) 3/4. (E) 2/3.17．一物体作简谐振动，振动方程为)21cos(π+=t A x ω．则该物体在t = 0时刻的动能与t = T /8（T 为振动周期）时刻的动能之比为：(A) 1:4． (B) 1:2． (C) 1:1． (D) 2:1． (E) 4:1．18．机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则(A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．19．一平面简谐波的表达式为 )3cos(1.0π+π-π=x t y (SI) ，t = 0时的波形曲线如图所示，则 (A) O 点的振幅为-0.1 m ．(B) 波长为3 m ． (C) a 、b 两点间相位差为π21．(D) 波速为9 m/s ．． -20．已知一平面简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则 (A) 波的频率为a ． (B) 波的传播速度为 b/a ． (C) 波长为 π / b ． (D) 波的周期为2π / a ．21．横波以波速u 沿x 轴负方向传播．t 时刻波形曲线如图．则该时刻(A) A 点振动速度大于零． (B) B 点静止不动．(C) C 点向下运动． (D)D 点振动速度小于零．22．若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则 (A) 波速为C ． (B) 周期为1/B ． (C) 波长为 2π /C ． (D) 角频率为2π /B ．23．在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反． (B) 大小和方向均相同．(C) 大小不同，方向相同． (D) 大小不同，而方向相反．24．一横波沿绳子传播时, 波的表达式为 )104cos(05.0t x y π-π= (SI)，则 (A) 其波长为0.5 m ． (B) 波速为5 m/s ． (C) 波速为25 m/s ． (D) 频率为2 Hz ．25．频率为 100 Hz ，传播速度为300 m/s 的平面简谐波，波线上距离小于波长的两点振动的相位差为π31，则此两点相距 (A) 2.86 m ． (B) 2.19 m ． (C) 0.5 m ． (D) 0.25 m ．26．如图所示，一平面简谐波沿x 轴正向传播，已知P 点的振动方程为)cos(0φω+=t A y ，则波的表达式为 (A) }]/)([cos{0φω+--=u l x t A y ． (B) })]/([cos{0φω+-=u x t A y ． (C) )/(cos u x t A y -=ω．(D) }]/)([cos{0φω+-+=u l x t A y ．27．图示一简谐波在t = 0时刻的波形图，波速 u = 200m/s ，则P 处质点的振动速度表达式为(A) )2cos(2.0π-ππ-=t v (SI)． (B) )cos(2.0π-ππ-=t v (SI)． (C) )2/2cos(2.0π-ππ=t v (SI)． (D) )2/3cos(2.0π-ππ=t v (SI)．28．一平面简谐波的表达式为 )/(2c o sλνx t A y -π=．在t = 1 /ν 时刻，x 1 = 3λ /4与x 2 = λ /4二点处质元速度之比是(A) -1． (B)31． (C) 1． (D) 329．一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它的能量是(A) 动能为零，势能最大． (B) 动能为零，势能为零． (C) 动能最大，势能最大． (D) 动能最大，势能为零．30．一平面简谐波在弹性媒质中传播时，某一时刻媒质中某质元在负的最大位移处，则它的能量是(A) 动能为零，势能最大． (B) 动能为零，势能为零． (C) 动能最大，势能最大． (D) 动能最大，势能为零． 31．一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中： (A) 它的动能转换成势能． (B) 它的势能转换成动能． (C) 它从相邻的一段质元获得能量其能量逐渐增大． (D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小．32．图示一平面简谐机械波在t 时刻的波形曲线．若此时A 点处媒质质元的振动动能在增大，则(A) A 点处质元的弹性势能在减小． (B) 波沿x 轴负方向传播．(C) B 点处质元的振动动能在减小．(D) 各点的波的能量密度都不随时间变化．33．如图所示，两列波长为λ 的相干波在P 点相遇．波在S 1点振动的初相是φ 1，S 1到P 点的距离是r 1；波在S 2点的初相是φ 2，S 2到P 点的距离是r 2，以k 代表零或正、负整数，则P 点是干涉极大的条件为：(A) λk r r =-12．(B) π=-k 212φφ．(C)π=-π+-k r r 2/)(21212λφφ．(D) π=-π+-k r r 2/)(22112λφφ．35．在波长为λ 的驻波中两个相邻波节之间的距离为 (A) λ ． (B) 3λ /4． (C) λ /2． (D) λ /4．1B 2C 3C 4B 5B 6C 7E 8B 9B 10B11B 12B 13C 14D 15B 16D 17D 18B 19C 20D21D 22C 23A 24A 25C 26A 27A 28A 29C 30B31D 32B 33D 34B 35CS波动光学1．在真空中波长为λ的单色光，在折射率为n 的透明介质中从A 沿某路径传播到B ，若A 、B 两点相位差为3π，则此路径AB 的光程为 (A) 1.5 λ． (B) 1.5 λ/ n ．(C) 1.5 n λ． (D) 3 λ．2．单色平行光垂直照射在薄膜上，经上下两表面反射的两束光发生干涉，如图所示，若薄膜的厚度为e ，且n 1＜n 2＞n 3，λ1为入射光在n 1中的波长，则两束反射光的光程差为 (A) 2n 2e ． (B) 2n 2 e - λ1 / (2n 1)．(C) 2n 2 e - n 1 λ1 / 2． (D) 2n 2 e - n 2 λ1 / 2．3．在相同的时间内，一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等，走过的光程相等． (B) 传播的路程相等，走过的光程不相等． (C) 传播的路程不相等，走过的光程相等．(D) 传播的路程不相等，走过的光程不相等．4．在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处(A) 仍为明条纹； (B) 变为暗条纹；(C) 既非明纹也非暗纹； (D) 无法确定是明纹，还是暗纹．5．在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是(A) 使屏靠近双缝．(B) 使两缝的间距变小． (C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源．6．在双缝干涉实验中，屏幕E 上的P 点处是明条纹．若将缝S 2盖住，并在S 1 S 2连线的垂直平分面处放一高折射率介质反射面M ，如图所示，则此时(A) P 点处仍为明条纹． (B) P 点处为暗条纹． (C) 不能确定P 点处是明条纹还是暗条纹． (D) 无干涉条纹．7．在双缝干涉实验中，光的波长为600 nm (1 nm ＝10－9 m )，双缝间距为2 mm ，双缝与屏的间距为300 cm ．在屏上形成的干涉图样的明条纹间距为 (A) 0.45 mm ． (B) 0.9 mm ．(C) 1.2 mm (D) 3.1 mm ．8．在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光3程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处(A) 仍为明条纹； (B) 变为暗条纹；(C) 既非明纹也非暗纹； (D) 无法确定是明纹，还是暗纹．9．在图示三种透明材料构成的牛顿环装置中，用单色光垂直照射，在反射光中看到干涉条纹，则在接触点P 处形成的圆斑为(A) 全明． (B) 全暗． (C) 右半部明，左半部暗． (D) 右半部暗，左半部明．10．一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为(A) λ / 4 ． (B) λ / (4n )．(C) λ / 2 ． (D) λ / (2n )．11．若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中，则干涉条纹(A) 中心暗斑变成亮斑． (B) 变疏．(C) 变密． (D) 间距不变．12．用劈尖干涉法可检测工件表面缺陷，当波长为λ的单色平行光垂直入射时，若观察到的干涉条纹如图所示，每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切，则工件表面与条纹弯曲处对应的部分(A) 凸起，且高度为λ / 4．(B) 凸起，且高度为λ / 2． (C) 凹陷，且深度为λ / 2． (D) 凹陷，且深度为λ / 4．13．如图，用单色光垂直照射在观察牛顿环的装置上．当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹(A) 向右平移． (B) 向中心收缩． (C) 向外扩张． (D) 静止不动． (E) 向左平移．14．在迈克耳孙干涉仪的一条光路中，放入一折射率为n ，厚度为d 的透明薄片，放入后，这条光路的光程改变了(A) 2 ( n -1 ) d ． (B) 2nd ．(C) 2 ( n -1 ) d +λ / 2． (D) nd ．(F) ( n -1 ) d ．15．在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a ＝4 λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为(A) 2 个． (B) 4 个．图中数字为各处的折射(C) 6 个． (D) 8 个．16．一束波长为λ的平行单色光垂直入射到一单缝AB 上，装置如图．在屏幕D 上形成衍射图样，如果P 是中央亮纹一侧第一个暗纹所在的位置，则BC 的长度为 (A) λ / 2．(B) λ．(C) 3λ / 2 ． (D) 2λ ．17．根据惠更斯－菲涅耳原理，若已知光在某时刻的波阵面为S ，则S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的(A) 振动振幅之和． (B) 光强之和．(C) 振动振幅之和的平方． (D) 振动的相干叠加．18．波长为λ的单色平行光垂直入射到一狭缝上，若第一级暗纹的位置对应的衍射角为θ=±π / 6，则缝宽的大小为(A) λ / 2． (B) λ．(C) 2λ． (D) 3 λ ．19．在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变小． (B) 对应的衍射角变大．(B) 对应的衍射角也不变． (D) 光强也不变．20．在单缝夫琅禾费衍射实验中，若减小缝宽，其他条件不变，则中央明条纹(A) 宽度变小；(B) 宽度变大；(C) 宽度不变，且中心强度也不变；（D ）宽度不变，但中心强度变小． 21．在如图所示的单缝夫琅禾费衍射实验装置中，S 为单缝，L 为透镜，C 为放在L 的焦面处的屏幕，当把单缝S 垂直于透镜光轴稍微向上平移时，屏幕上的衍射图样(A)向上平移． (B)向下平移．(C)不动． (D)消失．22．测量单色光的波长时，下列方法中哪一种方法最为准确？(A) 双缝干涉． (B) 牛顿环．(C) 单缝衍射． (D) 光栅衍射．23．一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是(A) 紫光． (B) 绿光． (C) 黄光． (D) 红光．24．对某一定波长的垂直入射光，衍射光栅的屏幕上只能出现零级和一级主极大，欲使屏幕上出现更高级次的主极大，应该(A) 换一个光栅常数较小的光栅．(B) 换一个光栅常数较大的光栅．(C) 将光栅向靠近屏幕的方向移动．(C)将光栅向远离屏幕的方向移动．25．一束光是自然光和线偏振光的混合光，让它垂直通过一偏振片．若以此入射光束为轴旋转偏振片，测得透射光强度最大值是最小值的5倍，那么入射光束中自然光与线偏振光的光强比值为(A) 1 / 2．(B) 1 / 3．(C) 1 / 4．(D) 1 / 5．26．一束光强为I0的自然光，相继通过三个偏振片P1、P2、P3后，出射光的光强为I＝I0 / 8．已知P1和P2的偏振化方向相互垂直，若以入射光线为轴，旋转P2，要使出射光的光强为零，P2最少要转过的角度是(A) 30°．(B) 45°．(C) 60°．(D) 90°．27．一束光强为I0的自然光垂直穿过两个偏振片，且此两偏振片的偏振化方向成45°角，则穿过两个偏振片后的光强I为(A) 4/0I2．(B) I0 / 4．(C) I0 / 2．(D) 2I0 / 2．28．三个偏振片P1，P2与P3堆叠在一起，P1与P3的偏振化方向相互垂直，P2与P1的偏振化方向间的夹角为30°．强度为I0的自然光垂直入射于偏振片P1，并依次透过偏振片P1、P2与P3，则通过三个偏振片后的光强为(A) I0 / 4．(B) 3 I0 / 8．(C) 3I0 / 32．(D) I0 / 16．29．两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过．当其中一偏振片慢慢转动180°时透射光强度发生的变化为：(A) 光强单调增加．(B) 光强先增加，后又减小至零．(C) 光强先增加，后减小，再增加．(D)光强先增加，然后减小，再增加，再减小至零．30．如果两个偏振片堆叠在一起，且偏振化方向之间夹角为60°，光强为I0的自然光垂直入射在偏振片上，则出射光强为(A) I0 / 8．(B) I0 / 4．(C) 3 I0 / 8．(D) 3 I0 / 4．斯特角i0，则在界面2的反射光(A) 是自然光．(B) 是线偏振光且光矢量的振动方向垂直于入射面．(C) 是线偏振光且光矢量的振动方向平行于入射面．(E)是部分偏振光．32．自然光以60°的入射角照射到某两介质交界面时，反射光为完全线偏振光，则知折射光为(A) 完全线偏振光且折射角是30°．(B) 部分偏振光且只是在该光由真空入射到折射率为3的介质时，折射角是30°．(C) 部分偏振光，但须知两种介质的折射率才能确定折射角．(D) 部分偏振光且折射角是30°．33．自然光以布儒斯特角由空气入射到一玻璃表面上，反射光是(A) 在入射面内振动的完全线偏振光．(B) 平行于入射面的振动占优势的部分偏振光．(C) 垂直于入射面振动的完全线偏振光．(D) 垂直于入射面的振动占优势的部分偏振光．1A 2 C 3 C 4B 5B 6B 7B 8B 9D 10B 11C 12C 13B 14A 15B 16B 17D 18C 19B 20B 21C 22D 23D 24B 25A 26B 27B 28C 29B 30A 31B 32D 33C。

大学物理A2复习题

R q q 1 1 1 1 V E d r dr ( ) 2 r r4 r 4 0 0r R
R
9. 两个同心的薄金属球壳，半径分别为 R 1 、 R 2 （R 1 >R 2 ）， q 2 ，将二球用导线联起来，（取无限远处作为带电量分别为 q 1、参考点）则它们的电势为。
q 3 q V 6 V 6 1 4 a 2 a 0 0
由于对称性，中心o点的场强大小为0。 6. 一个半径为R 的均匀带电的薄圆盘，电荷面密度为。在圆盘上挖去一个半径为r 的同心圆盘，则圆心处的电势将变小。（变大或变小） 7. 真空中一个半径为R 的球面均匀带电，面电荷密度为 0 ，在球心处有一个带电量为q的点电荷。取无限远处作为电势参考点，则球内距球心r 的P 点处的电势为。不放q时，均匀带电球面内是一个等势体，电势与球面的电势 2 相等： q 4 R R
4 0 R R 孤立球形导体的电容 C4 0R C R C r 4 0 r r
用一根细导线连接起来，使两个导体带电，则两导体球电势相等
2 Q S 4 R R R R R R V R 4 R4 R 4 R 0 0 0 0
q q A q V q ( ) 2 c 4 L4 L 0 0 2
2 q 2 A V ( 1 ) 2 q c 4 0L 2
最后把第4个点电荷q置于D点上，外力所做的功为
q q q Aq V q ( ) 3 D 4 L4 L4 L 0 0 0 2
负号表示磁力矩作正功时将使减小，现由 0 增大到 0 ，磁力矩作负功，因此，外力作正功。 180
外力矩的功为
2 A (2 ) 3 40L 2

大学物理A2的重要习题

1．如计算题7-1图所示，一根铜棒长为L=0.05m ，水平放置于一竖直向上的匀强磁场中，绕位于距a 端L/5处的竖直轴OO /在水平面内旋转，每秒钟转两圈。

已知该磁场的磁感应强度B=0.50×10-4T 。

求铜棒两端a 、b 的电位差。

计算题7-1图 1. 解:建立坐标系如图所示在ab 上任取线元dx,如图。

当铜棒旋转时产生的动生电动势xdx B i dx B v d ωε=⋅⨯=)(动整根铜棒产生的动生电动势⎰--⨯===545(1071.410382L L L B xdx B 伏）动ωωε 2．如计算题7-2图所示，无限长直导线，通以电流I ，有一与之共面的直角三角形线圈ABC ，已知AC 边长为b ，与长直导线平行，BC 边长为a 若线圈以垂直于导线方向的速度向右平移，当B 点与长直导线的距离为d 时，求线圈ABC 内的感应电动势的大小和感应电动势的方向。

计算题7-2图解：建立坐标系，长直导线为Y 轴，BC 边为X 轴，原点长直导线上，则斜边的方程为abr a bx y -= 式中r 是t 时刻B 点与长直导线的距离，三角形中的磁通量⎰⎰+++-=-==r a r r a rrr a a br b I dx ax br a b I dxxyI )ln (2)(22000πμπμπμφ td r d r a a r r a a b I dt d )(ln 20+-+=-=πμφε 当r = d 时，vr a a r r a a b I )(ln 20+-+=πμε 方向：ACBA （顺时针）3．两根平行无限长直导线相距为d ，载有大小相等方向相反的电流I ，电流变化率dI/dt=α>0。

一个边长为d 的正方形线圈位于导线平面内与一根导线相距d ，如计算题7-3图所示。

求线圈中的感应电动势ε，并说明线圈中的感应电动势是顺时针还是逆时针方向。

计算题7-3图解：（1）载流为I 的无限长直导线在与其相距为r 处产生的磁感应强度为： r I B πμ20=以顺时针绕向为线圈的正方向，与线圈相距较远的导线在线圈中产生的磁通量为： 23ln22034241πμπμφId r d rI d =⋅=⎰与线圈相距较近的导线在线圈中产生的磁通量为： 2ln 2202442πμπμφIdr d rI d -=⋅-=⎰ 总磁通量34ln2021πμφφφId -=+=感应电动势为：34ln234ln 200παμπμφεd t d I d d dt d ==-=由ε>0和回路正方向为顺时针，所以ε的绕向为顺时针方向，线圈中的感应电动势亦为顺时针方向。

大学物理A2-总复习

（1）相位差
∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0 ， 1， ) ± L
A = A1 + A2
（2）相位差
相互加强
∆ϕ = ϕ 2 − ϕ1 = (2k + 1) π (k = 0 ， 1， ) ± L
A = A1 − A2
相互削弱
大学物理A2-总复习大学物理A2A2
不同频率简谐振动的合成拍现象（了解）（2）同方向不同频率简谐振动的合成拍现象（了解））同方向不同频率
波腹波节
λ
1 (k + ) 2 2
相邻两波腹（节）之间的距离：xk +1 − xk = 之间的距离：相邻两波腹（
λ
2
长的许多段，所有波节点将媒质划分为 λ 长的许多段，每段中 2 各质点的振动振幅不同，相位皆相同；各质点的振动振幅不同，但相位皆相同；而相邻段间各质点的振动相位相反; 间各质点的振动相位相反; 即驻波中不存在相位的传播。传播。
x1(t) = A cos(ω t +ϕ1) 1 1
x2 (t) = A cos(ω2t +ϕ2 ) 2
频率相近的两个同方向不同频率的合振动：频率相近的两个同方向不同频率的合振动：
ν = (ν 1 + ν 2 ) 2
ν拍 =ν 2 −ν1
——拍频拍频
大学物理A2-总复习大学物理A2A2
第12章 12章
x
x
大学物理A2-总复习大学物理A2A2
5、简谐振动的能量、 6、简谐振动的合成、（1）同方向、同频率的简谐振动的合成）同方向、同频率的简谐振动的合成
x1 = A1 cos(ω t + ϕ 1 ) x2 = A2 cos(ω t + ϕ 2 )

大学物理A2期末总复习题及答案

大学物理A2期末总复习题及答案一、大学物理期末选择题复习1．一个质点在做圆周运动时,则有()(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变答案B2．如图所示,质量为m 的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为()(A) g sin θ(B) g cos θ(C) g tan θ(D) g cot θ答案D3．对质点组有以下几种说法：(1) 质点组总动量的改变与内力无关；(2) 质点组总动能的改变与内力无关；(3) 质点组机械能的改变与保守内力无关．下列对上述说法判断正确的是()(A) 只有(1)是正确的(B) (1) (2)是正确的(C) (1) (3)是正确的 (D) (2) (3)是正确的答案C4．一带电粒子垂直射入均匀磁场中，如果粒子的质量增加为原来的2倍，入射速度也增加为原来的2倍，而磁场的磁感应强度增大为原来的4倍，则通过粒子运动轨道所围面积的磁通量增大为原来的：（）(A) 2倍 (B) 4倍 (C) 0.5倍 (D) 1倍答案B5．一个电流元Idl 位于直角坐标系原点，电流沿z 轴方向，点P (x ，y ，z )的磁感强度沿x 轴的分量是：（）(A) 0(B) ()()2/32220/4/z y x Ixdl ++-πμ(C) ()()2/12220/4/z y x Ixdl ++-πμ(D)()()2220/4/z y x Ixdl ++-πμ答案B6．图为四个带电粒子在Ｏ点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹的照片. 磁场方向垂直纸面向外，轨迹所对应的四个粒子的质量相等，电量大小也相等，则其中动能最大的带负电的粒子的轨迹是（）(A) Oa (B) Ob(C) Oc (D) Od答案C7．下列说法正确的是（）（A ）闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过（B ）闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零（C ）磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D ）磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零答案B8．在图（ａ）和（ｂ）中各有一半径相同的圆形回路L 1 、L 2 ，圆周内有电流I 1 、I 2 ，其分布相同，且均在真空中，但在（ｂ）图中L 2 回路外有电流I 3 ，P 1 、P 2 为两圆形回路上的对应点，则（）（A ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B = （B ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B = （C ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B ≠ （D ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B ≠ 答案C9．用水平力N F 把一个物体压着靠在粗糙的竖直墙面上保持静止。

西南科技大学_大学物理A2练习题答案

Ox-a a y +σ+σ作业题一（静止电荷的电场）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 一均匀带电球面，电荷面密度为σ，球面内电场强度处处为零，球面上面元d S 带有σ d S 的电荷，该电荷在球面内各点产生的电场强度(A) 处处为零． (B) 不一定都为零． (C) 处处不为零． (D) 无法判定．[ ］ 2. 电荷面密度均为＋σ的两块“无限大”均匀带电的平行平板如图放置，其周围空间各点电场强度E随位置坐标x 变化的关系曲线为：(设场强方向向右为正、向左为负) ［］3. 将一个试验电荷q 0(正电荷)放在带有负电荷的大导体附近P 点处(如图)，测得它所受的力为F ．若考虑到电荷q 0不是足够小，则 (A) F / q 0比P 点处原先的场强数值大． (B) F / q 0比P 点处原先的场强数值小．(C) F / q 0等于P 点处原先场强的数值．(D) F / q 0与P 点处原先场强的数值哪个大无法确定．［］4. 如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于：(A)6εq ． (B)12εq ．(C)24εq ． (D)48εq．［］5. 高斯定理⎰⎰⋅=VSV S E 0/d d ερ(A) 适用于任何静电场． (B) 只适用于真空中的静电场．O E -a +a 02/εσx(A )0/εσOE-a +ax(B )-0/εσ0/εσOE-a +ax(D )/εσO E-a +ax(C )/εσ－P+q 0Abcd a q(C) 只适用于具有球对称性、轴对称性和平面对称性的静电场．(D) 只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场．［］6. 如图所示，两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电，沿轴线方向单位长度上所带电荷分别为λ1和λ2，则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小E 为： (A) r0212ελλπ+． (B)20210122R R ελελπ+π(C)1012R ελπ． (D) 0．［］7. 点电荷Q 被曲面S 所包围，从无穷远处引入另一点电荷q 至曲面外一点，如图所示，则引入前后： (A) 曲面S 的电场强度通量不变，曲面上各点场强不变． (B) 曲面S 的电场强度通量变化，曲面上各点场强不变． (C) 曲面S 的电场强度通量变化，曲面上各点场强变化． (D) 曲面S 的电场强度通量不变，曲面上各点场强变化．［］8. 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中，正确的是：(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零．(B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零． (C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零．(D) 闭合面上各点场强均为零时，闭合面内一定处处无电［］二、填空题9. A 、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小为E 0，两平面外侧电场强度大小都为E 0/3，方向如图．则A 、B 两平面上的电荷面密度分别为σA ＝_______________, σB ＝____________________．10. 三个平行的“无限大”均匀带电平面，其电荷面密度都是＋σ，如图所示，则A 、B 、C 、D 三个区域的电场强度分别为：E A ＝_________________，E B ＝_____________， E C ＝_________，E D =___________ (设方向向右为正)． Pr λ2λ1 R 1R 2Q SqA BEE 0/3E 0/3+σ+σ+σA B C D11. 一半径为R 的带有一缺口的细圆环，缺口长度为d (d<<R)环上均匀带有正电，电荷为q ，如图所示．则圆心O 处的场强大小E ＝__________________ __________，场强方向为______________________．12. 如图所示，真空中两个正点电荷Q ，相距2R ．若以其中一点电荷所在处O 点为中心，以R 为半径作高斯球面S ，则通过该球面的电场强度通量＝______________；若以 0r 表示高斯面外法线方向的单位矢量，则高斯面上a 、b 两点的电场强度分别为________________________．三、计算题13. 带电细线弯成半径为R 的半圆形，电荷线密度为λ=λ0sin φ，式中λ0为一常数，φ为半径R 与x 轴所成的夹角，如图所示．试求环心O 处的电场强度．14. “无限长”均匀带电的半圆柱面，半径为R ，设半圆柱面沿轴线OO'单位长度上的电荷为λ，试求轴线上一点的电场强度．15. 一半径为R 的带电球体，其电荷体密度分布为 ρ =Ar (r ≤R ) ， ρ =0 (r ＞R ) A 为一常量．试求球体内外的场强分布．R OdqO+Q RS +Q ba 2Ry RxφOO R’O'16. 图中虚线所示为一立方形的高斯面，已知空间的场强分布为：Ex ＝bx，Ey＝0，Ez＝0．高斯面边长a＝0.1 m，常量b＝1000 N/(C·m)．试求该闭合面中包含的净电荷．(真空介电常数 0＝8.85×10-12 C2·N-1·m-2 )a a a axzy O作业题二（电势）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 在点电荷+q 的电场中，若取图中P 点处为电势零点，则M 点的电势为(A) a q 04επ． (B) a q 08επ．(C)aq 04επ-． (D)aq 08επ-．［］2. 如图所示，两个同心球壳．内球壳半径为R 1，均匀带有电荷Q ；外球壳半径为R 2，壳的厚度忽略，原先不带电，但与地相连接．设地为电势零点，则在内球壳里面，距离球心为r 处的P 点的场强大小及电势分别为： (A) E ＝0，U ＝104R Q επ． (B) E ＝0，U ＝⎪⎪⎭⎫ ⎝⎛-π210114R R Qε． (C) E ＝204rQ επ，U ＝rQ 04επ (D) E ＝204rQ επ，U ＝104R Q επ．[ ]3. 关于静电场中某点电势值的正负，下列说法中正确的是： (A) 电势值的正负取决于置于该点的试验电荷的正负． (B) 电势值的正负取决于电场力对试验电荷作功的正负． (C) 电势值的正负取决于电势零点的选取．(D) 电势值的正负取决于产生电场的电荷的正负．［］4. 点电荷-q 位于圆心O 处，A 、B 、C 、D 为同一圆周上的四点，如图所示．现将一试验电荷从A 点分别移动到B 、C 、D 各点，则 (A) 从A 到B ，电场力作功最大．(B) 从A 到C ，电场力作功最大． (C) 从A 到D ，电场力作功最大．(D) 从A 到各点，电场力作功相等．［］5. 如图所示，直线MN 长为2l ，弧OCD 是以N点为中心，l 为半径的半圆弧，N 点有正电荷＋q ，M 点有负电荷-q ．今将一试验电荷＋q 0从O 点出发沿路径OCDP 移到无穷远处，设无穷远处电势为零，则电场力作功(A) A ＜0 , 且为有限常量． (B) A ＞0 ,且为有限常量．(C) A ＝≦． (D) A ＝0．［］ 6. 半径为r 的均匀带电球面1，带有电荷q ，其外有一同心的半径为R 的均匀aa+qPMOR 1R 2PrQ A B DC O-q7. N D P C +q M -q O带电球面2，带有电荷Q ，则此两球面之间的电势差U 1-U 2为： (A) ⎪⎭⎫⎝⎛-πR r q1140ε . (B) ⎪⎭⎫ ⎝⎛-πr R Q 1140ε .(C)⎪⎭⎫⎝⎛-πR Q r q 041ε . (D)rq 04επ . [ ] 7. 两块面积均为S 的金属平板A 和B 彼此平行放置，板间距离为d (d 远小于板的线度)，设A 板带有电荷q 1，B 板带有电荷q 2，则AB 两板间的电势差U AB 为 (A) d S q q 0212ε+． (B)d S q q 0214ε+． (C)d Sq q 0212ε-． (D)d Sq q 0214ε-．［］8. 面积为S 的空气平行板电容器，极板上分别带电量±q ，若不考虑边缘效应，则两极板间的相互作用力为 (A)Sq02ε． (B)S q022ε． (C)2022Sqε． (D)202Sqε．［］二、填空题9. 如图所示,两同心带电球面，内球面半径为r 1＝5 cm ，带电荷q 1＝3×10-8C ；外球面半径为r 2＝20 cm ，带电荷q 2＝－6×108C ，设无穷远处电势为零，则空间另一电势为零的球面半径r ＝ __________________．10. 真空中一半径为R 的均匀带电球面，总电荷为Q ．今在球面上挖去很小一块面积△S (连同其上电荷)，若电荷分布不改变，则挖去小块后球心处电势(设无穷远处电势为零)为________________．11. 把一个均匀带有电荷+Q 的球形肥皂泡由半径r 1吹胀到r 2，则半径为R (r 1＜R ＜r 2)的球面上任一点的场强大小E 由______________变为______________；电势U 由 __________________________变为________________(选无穷远处为电势零点)．12. 静电场的环路定理的数学表示式为：______________________．该式的物理意义是：____________________________________________________________．该定理表明，静电场是______ _________场．三、计算题dB ASSq 1q 2q 1q 2r 1r 213. 一“无限大”平面，中部有一半径为R的圆孔，设平面上均匀带电，电荷面密度为σ．如图所示，试求通过小孔中心O并与平面垂直的直线上各点的场强和电势(选O点的电势为零)．14. 图示为一个均匀带电的球层，其电荷体密度为ρ，球层内表面半径为R1，外表面半径为R2．设无穷远处为电势零点，求空腔内任一点的电势．σOROR1R215.两个带等量异号电荷的均匀带电同心球面，半径分别为R1＝0.03 m和R2＝0.10 m．已知两者的电势差为450 V，求内球面上所带的电荷．16. 有两根半径都是R的“无限长”直导线，彼此平行放置，两者轴线的距离是d (d≥2R)，沿轴线方向单位长度上分别带有＋λ和－λ的电荷，如图所示．设两带电导线之间的相互作用不影响它们的电荷分布，试求两导线间的电势差．R+λR-λd作业题三（导体和电介质）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. A 、B 为两导体大平板，面积均为S ，平行放置，如图所示．A 板带电荷+Q 1，B 板带电荷+Q 2，如果使B 板接地，则AB 间电场强度的大小E 为［］ (A) S Q 012ε ． (B)S Q Q 0212ε-．(C)SQ 01ε． (D)SQ Q 0212ε+．2. 一带正电荷的物体M ，靠近一原不带电的金属导体N ，N的左端感生出负电荷，右端感生出正电荷．若将N 的左端接地，如图所示，则(A) N 上有负电荷入地．(B) N 上有正电荷入地． (C ) N 上的电荷不动．(D) N 上所有电荷都入地．［］ 3. 一导体球外充满相对介电常量为εr 的均匀电介质，若测得导体表面附近场强为E ，则导体球面上的自由电荷面密度σ为［］ (A) ε 0 E ． (B) ε 0 ε r E ．(C) ε r E ． (D) (ε 0 ε r - ε 0)E ． 4. 一平行板电容器始终与端电压一定的电源相联．当电容器两极板间为真空时，电场强度为0E ，电位移为0D，而当两极板间充满相对介电常量为εr 的各向同性均匀电介质时，电场强度为E，电位移为D，则［］(A) r E E ε/0 =，0D D =． (B) 0E E =，0D D rε=．(C) r E E ε/0 =，r D D ε/0 =． (D) 0E E =，0D D=．5. 在静电场中，作闭合曲面S ，若有0d =⎰⋅SS D (式中D为电位移矢量)，则S面内必定［］(A) 既无自由电荷，也无束缚电荷． (B) 没有自由电荷． (C) 自由电荷和束缚电荷的代数和为零．(D) 自由电荷的代数和为零．+Q 1+Q2ABMN6. 一个大平行板电容器水平放置，两极板间的一半空间充有各向同性均匀电介质，另一半为空气，如图．当两极板带上恒定的等量异号电荷时，有一个质量为m 、带电荷为+q 的质点，在极板间的空气区域中处于平衡．此后，若把电介质抽去，则该质点［］ (A) 保持不动． (B) 向上运动． (C) 向下运动． (D) 是否运动不能确定． 7.一个平行板电容器，充电后与电源断开，当用绝缘手柄将电容器两极板间距离拉大，则两极板间的电势差U 12、电场强度的大小E 、电场能量W 将发生如下变化：［］(A) U 12减小，E 减小，W 减小．(B) U 12增大，E 增大，W 增大． (C) U 12增大，E 不变，W 增大．(D) U 12减小，E 不变，W 不变． 8. 如图所示, 一球形导体，带有电荷q ，置于一任意形状的空腔导体中．当用导线将两者连接后，则与未连接前相比系统静电场能量将 (A) 增大． (B) 减小． (C) 不变． (D) 如何变化无法确定．［］二、填空题9. 半径为R 1和R 2的两个同轴金属圆筒，其间充满着相对介电常量为εr 的均匀介质．设两筒上单位长度带有的电荷分别为+λ和-λ，则介质中离轴线的距离为r 处的电位移矢量的大小D =____________，电场强度的大小 E =____________．10. 一平行板电容器，充电后与电源保持联接，然后使两极板间充满相对介电常量为εr 的各向同性均匀电介质，这时两极板上的电荷是原来的______倍；电场强度是原来的 _________倍；电场能量是原来的_________倍．11. 一平行板电容器，充电后切断电源，然后使两极板间充满相对介电常量为εr 的各向同性均匀电介质．此时两极板间的电场强度是原来的____________倍；电场能量是原来的___________ 倍．12. 分子的正负电荷中心重合的电介质叫做_______________ 电介质．在外电场作用下，分子的正负电荷中心发生相对位移，形成________________________．三、计算题13. 如图所示，一内半径为a 、外半径为b 的金属球壳，带有电荷Q ，在球壳空腔内距离球心r 处有一点电荷q ．设无限远处为电势零点，试求：(1) 球壳内外表面上的电荷．(2) 球心O 点处，由球壳内表面上电荷产生的电势． (3) 球心O 点处的总电势．+q m+Q-Qqq Q a b O r14. 半径分别为R1和R2 (R2 > R1 )的两个同心导体薄球壳，分别带有电荷Q1和Q2，今将内球壳用细导线与远处半径为r的导体球相联，如图所示, 导体球原来不带电，试求相联后导体球所带电荷q．OR2R1r1115. 假想从无限远处陆续移来微量电荷使一半径为R的导体球带电．(1) 当球上已带有电荷q时，再将一个电荷元d q从无限远处移到球上的过程中，外力作多少功？(2) 使球上电荷从零开始增加到Q的过程中，外力共作多少功？16. 一电容器由两个很长的同轴薄圆筒组成，内、外圆筒半径分别为R1= 2 cm，R2 = 5 cm，其间充满相对介电常量为εr 的各向同性、均匀电介质．电容器接在电压U = 32 V的电源上，(如图所示)，试求距离轴线R = 3.5 cm处的A点的电场强度和A点与外筒间的电势差．作业题四（电流的磁场）A R1R2RεrU1213 班级:_____________ 姓名:_____________ 学号:_____________ 一、选择题1. 如图，边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷．此正方形以角速度ω 绕AC 轴旋转时，在中心O 点产生的磁感强度大小为B 1；此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时，在O 点产生的磁感强度的大小为B 2，则B 1与B 2间的关系为［］(A) B 1 = B 2． (B) B 1 = 2B 2． (C) B 1 =21B 2． (D) B 1 = B 2 /4．2. 电流I 由长直导线1沿平行bc 边方向经a 点流入由电阻均匀的导线构成的正三角形线框，再由b 点沿垂直ac 边方向流出，经长直导线2返回电源(如图)．若载流直导线1、2和三角形框中的电流在框中心O 点产生的磁感强度分别用1B 、2B和3B 表示，则O 点的磁感强度大小(A) B = 0，因为B 1 = B 2 = B 3 = 0．(B) B = 0，因为虽然B 1≠ 0、B 2≠ 0，但021=+B B，B 3 = 0． (C) B ≠ 0，因为虽然B 2 = 0、B 3= 0，但B 1≠ 0．(D) B ≠ 0，因为虽然021≠+B B，但B 3≠ 0．［］ 3. 通有电流I 的无限长直导线有如图三种形状，则P ，Q ，O 各点磁感强度的大小B P ，B Q ，B O 间的关系为：[ ](A) B P > B Q > B O . (B) B Q > B P > B O ． (C) B Q > B O > B P ． (D) B O > B Q > B P ．4. 边长为l 的正方形线圈，分别用图示两种方式通以电流I (其中ab 、cd 与正方形共面)，在这两种情况下，线圈在其中心产生的磁感强度的大小分别为： (A) 01=B ，02=B ． (B) 01=B ，lI B π=0222μ．(C) l I B π=0122μ，02=B ． (D) lI B π=0122μ,lI B π=0222μ．［］5. 如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知 (A)0d =⎰⋅Ll B，且环路上任意一点B = 0．ACqqqqO3.a bcIO12a I I I a a a a2a I PQ O Ia IB 1IB 1 2ab c d IL OI14 (B) 0d =⎰⋅Ll B，且环路上任意一点B ≠0． (C) 0d ≠⎰⋅Ll B，且环路上任意一点B ≠0．(D)0d ≠⎰⋅Ll B，且环路上任意一点B =常量．［］6. 如图，流出纸面的电流为2I ，流进纸面的电流为I ，则下述各式中哪一个是正确的？ (A)I l HL 2d 1=⎰⋅． (B)I l HL =⎰⋅2d(C)I l HL -=⎰⋅3d． (D)I l HL -=⎰⋅4d．［］7. 图中，六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大？(A) Ⅰ区域． (B) Ⅱ区域．(C) Ⅲ区域． (D) Ⅳ区域．(E) 最大不止一个．［］8. 如图两个半径为R 的相同的金属环在a 、b 两点接触(ab 连线为环直径)，并相互垂直放置．电流I 沿ab 连线方向由a 端流入，b 端流出，则环中心O 点的磁感强度的大小为(A) 0． (B) RI40μ． (C) R I 420μ． (D)RI0μ． (E)RI 820μ．［］二、填空题9. 如图，在无限长直载流导线的右侧有面积为S 1和S 2的两个矩形回路．两个回路与长直载流导线在同一平面，且矩形回路的一边与长直载流导线平行．则通过面积为S 1的矩形回路的磁通量与通过面积为S 2的矩形回路的磁通量之比为____________． 10. 如图，平行的无限长直载流导线A 和B ，电流强度均为I ，垂直纸面向外，两根载流导线之间相距为a ，则(1) AB 中点(P 点)的磁感强度=p B _____________．(2) 磁感强度B沿图中环路L 的线积分=⎰⋅Ll Bd __________________________________．L 2L 1L 3L 42IIⅠⅡⅢⅣIIbaS 1S 2a a 2a 10. BxAaL yP11. 图中所示的一无限长直圆筒，沿圆周方向上的面电流密度(单位垂直长度上流过的电流)为i，则圆筒内部的磁感强度的大小为B =________，方向_______________．12. 将半径为R的无限长导体薄壁管(厚度忽略)沿轴向割去一宽度为h ( h << R)的无限长狭缝后，再沿轴向流有在管壁上均匀分布的电流，其面电流密度(垂直于电流的单位长度截线上的电流)为i (如上图)，则管轴线磁感强度的大小是__________________．三、计算题13. 半径为R的无限长圆柱形导体和内半径为R0，外半径也为R的无限长圆筒形导体，都通有沿轴向的，在横截面上均匀分布的电流I，导体的磁导率都为 0．今取长为l、宽为2 R的矩形平面ABCD和A′B′C′D′，AD及A′D′正好在导体的轴线上，如图所示．(1) 通过ABCD的磁通量大小为多少？(2) 通过A′B′C′D′的磁通量为多少？(3) 若电流I不变，外半径R不变，圆筒壁变薄，直至壁厚趋于零，再求(2) ．14. 一根无限长导线弯成如图形状，设各线段都在同一平面内(纸面内)，其中第二段是半径为R的四分之一圆弧，其余为直线．导线中通有电流I，求图中O点处的磁感强度．15. 平面闭合回路由半径为R1及R2 (R1 > R2 )的两个同心半圆弧和两个直导线段组成(如图)．已知两个直导线段在两半圆弧中心O处的磁感强度为零，且闭合载流回路在O处产生的总的磁感强度B与半径为R2的半圆弧在O点产生的磁感强度B2的关系为B =2 B2/3，求R1与R2的关系．iOO′R ihA DBC lA′D′B′C′l12 34RROIR1R2OI151616. 如图所示，一半径为R 的均匀带电无限长直圆筒，面电荷密度为σ．该筒以角速度ω绕其轴线匀速旋转．试求圆筒内部的磁感强度．作业题五（电流在磁场中受力）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 按玻尔的氢原子理论，电子在以质子为中心、半径为r 的圆形轨道上运动．如果把这样一个原子放在均匀的外磁场中，使电子轨道平面与B垂直，如图所示，则在r 不变的情况下，电子轨道运动的角速度将：［］(A) 增加． (B) 减小． (C) 不变． (D) 改变方向．2. 如图，一个电荷为+q 、质量为m 的质点，以速度v沿x 轴射入磁感强度为B 的均匀磁场中，磁场方向垂直纸面向里，其范围从x = 0延伸到无限远，如果质点在x = 0和y = 0处进入磁场，则它将以速度v -从磁场中某一点出来，这点坐标是x = 0 和［］ (A) qBm y v +=． (B) qBm y v 2+=．Rωσepxy +q, mv BO17(C) qBm y v 2-=． (D) qBm y v -=．3. 一铜条置于均匀磁场中，铜条中电子流的方向如图所示．试问下述哪一种情况将会发生？(A) 在铜条上a 、b 两点产生一小电势差，且U a > U b ． (B) 在铜条上a 、b 两点产生一小电势差，且U a < U b ． (C) 在铜条上产生涡流．(D) 电子受到洛伦兹力而减速．［］ 4. 如图，无限长直载流导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将［］ (A) 向着长直导线平移． (B) 离开长直导线平移． (C) 转动． (D) 不动．5. 长直电流I 2与圆形电流I 1共面，并与其一直径相重合如图(但两者间绝缘)，设长直电流不动，则圆形电流将 (A) 绕I 2旋转． (B) 向左运动．(C) 向右运动． (D) 向上运动．(E) 不动．［］ 6. 如图，在一固定的载流大平板附近有一载流小线框能自由转动或平动．线框平面与大平板垂直．大平板的电流与线框中电流方向如图所示，则通电线框的运动情况对着从大平板看是：［］(A) 靠近大平板． (B) 顺时针转动．(C) 逆时针转动． (D) 离开大平板向外运动． 7. 两个同心圆线圈，大圆半径为R ，通有电流I 1；小圆半径为r ，通有电流I 2，方向如图．若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场)，当它们处在同一平面内时小线圈所受磁力矩的大小为［］ (A)RrI I 22210πμ． (B)Rr I I 22210μ．(C)rRI I 22210πμ． (D)0．8. 两根载流直导线相互正交放置，如图所示．I 1沿y 轴的正方向，I 2沿z 轴负方向．若载流I 1的导线不能动，载流I 2的导线可以自由运动，则载流I 2的导线开始运动的趋势是 [ ] (A) 沿x 方向平动． (B) 绕x 轴转动．I 1I 2 I 2I 1 6. I 1I 2O rR I 1I 2y zxI 1I 2a b B³ ³ ³ ³³ ³ ³ ³³ ³ ³ ³18 (C) 绕y 轴转动． (D) 无法判断．二、填空题9. 如图，均匀磁场中放一均匀带正电荷的圆环，其线电荷密度为λ，圆环可绕通过环心O 与环面垂直的转轴旋转．当圆环以角速度ω 转动时，圆环受到的磁力矩为_________________，其方向__________________________．10. 有一半径为a ，流过稳恒电流为I 的1/4圆弧形载流导线bc ，按图示方式置于均匀外磁场B中，则该载流导线所受的安培力大小为_______________________．11. 如图所示，在真空中有一半径为a 的3/4圆弧形的导线，其中通以稳恒电流I ，导线置于均匀外磁场B 中，且B与导线所在平面垂直．则该载流导线bc 所受的磁力大小为_________________．12. 如图所示，在真空中有一半圆形闭合线圈，半径为a ，流过稳恒电流I ，则圆心O 处的电流元l Id 所受的安培力Fd 的大小为_______________，方向_________________．OR ω λBOa c abBIaa IcbBOOIalI d19三、计算题13. 在一顶点为45°的扇形区域，有磁感强度为B方向垂直指向纸面内的均匀磁场，如图．今有一电子(质量为m ，电荷为-e )在底边距顶点O 为l 的地方，以垂直底边的速度 v射入该磁场区域，若要使电子不从上面边界跑出，电子的速度最大不应超过多少？14. 一圆线圈的半径为R ，载有电流I ，置于均匀外磁场B中(如图示)．在不考虑载流圆线圈本身所激发的磁场的情况下，求线圈导线上的张力．(载流线圈的法线方向规定与B的方向相同．)l45° vBOI RB2015. 一矩形线圈边长分别为a =10 cm 和b =5 cm ，导线中电流为I = 2 A ，此线圈可绕它的一边OO ＇转动，如图．当加上正y 方向的B =0.5 T 均匀外磁场B，且与线圈平面成30°角时，线圈的角加速度为β = 2 rad/s 2，求∶(1) 线圈对OO ＇轴的转动惯量J =？(2) 线圈平面由初始位置转到与B 垂直时磁力所做的功？16. 一根同轴线由半径为R 1的长导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成．中间充满磁导率为μ的各向同性均匀非铁磁绝缘材料，如图．传导电流I 沿导线向上流去，由圆筒向下流回，在它们的截面上电流都是均匀分布的．求同轴线内外的磁感强度大小B 的分布．O xyzI30° BO ′ a bIIR 1R 2R 3作业题六（电磁感应）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 将形状完全相同的铜环和木环静止放置，并使通过两环面的磁通量随时间的变化率相等，则不计自感时(A) 铜环中有感应电动势，木环中无感应电动势． (B) 铜环中感应电动势大，木环中感应电动势小． (C) 铜环中感应电动势小，木环中感应电动势大． (D) 两环中感应电动势相等．［］2. 如图所示，矩形区域为均匀稳恒磁场，半圆形闭合导线回路在纸面内绕轴O 作逆时针方向匀角速转动，O 点是圆心且恰好落在磁场的边缘上，半圆形闭合导线完全在磁场外时开始计时．图(A)—(D)的 --t 函数图象中哪一条属于半圆形导线回路中产生的感应电动势？［］3. 一块铜板垂直于磁场方向放在磁感强度正在增大的磁场中时，铜板中出现的涡流(感应电流)将 (A) 加速铜板中磁场的增加． (B) 减缓铜板中磁场的增加．(C) 对磁场不起作用． (D) 使铜板中磁场反向．［］4. 如图所示，导体棒AB 在均匀磁场B 中绕通过C 点的垂直于棒长且沿磁场方向的轴OO ' 转动（角速度ω与B同方向），BC 的长度为棒长的31，则(A) A 点比B 点电势高．(B) A 点与B 点电势相等．(B) A 点比B 点电势低．(D)有稳恒电流从A 点流向B 点． [ ]☜ t O (A ) ☜ t O (C ) ☜t O(B )☜ tO(D ) C D Oω BO O ′BBAC5. 如图所示，直角三角形金属框架abc 放在均匀磁场中，磁场B平行于ab 边，bc 的长度为l ．当金属框架绕ab 边以匀角速度ω转动时，abc 回路中的感应电动势和a 、c 两点间的电势差U a – U c为 [ ] (A) =0，U a – U c =221l B ω． (B) =0，U a – U c =221l B ω-．(C) =2l B ω，U a – U c =221l B ω．(D) =2l B ω，U a – U c =221l B ω-．6. 如图所示，两个线圈P 和Q 并联地接到一电动势恒定的电源上．线圈P 的自感和电阻分别是线圈Q 的两倍，线圈P 和Q 之间的互感可忽略不计．当达到稳定状态后，线圈P 的磁场能量与Q 的磁场能量的比值是［］(A) 4． (B) 2． (C) 1． (D)21．7. 在感应电场中电磁感应定律可写成tlE LKd d d Φ-=⎰⋅，式中K E为感应电场的电场强度．此式表明：(A) 闭合曲线L 上K E处处相等．(B) 感应电场是保守力场．(C) 感应电场的电场强度线不是闭合曲线． (D) 在感应电场中不能像对静电场那样引入电势的概念．［］ 8. 对位移电流，有下述四种说法，请指出哪一种说法正确． (A) 位移电流是指变化电场．(B) 位移电流是由线性变化磁场产生的． (C) 位移电流的热效应服从焦耳─楞次定律． (D) 位移电流的磁效应不服从安培环路定理．［］二、填空题9. 如图所示，aOc 为一折成∠形的金属导线(aO =Oc =L )，位于xy 平面中,磁感强度为 B的匀强磁场垂直于xy 平面．当aOc 以速度v沿x 轴正向运动时，导线上a 、c两点间电势差U ac =____________；当aOc 以速度v沿y 轴正向运动时，a 、c 两点的电势相比较, 是____________点电势高．Ba b clωPQv B yO xv ca θ³³³³³³³³³10. 一导线被弯成如图所示形状，acb 为半径为R 的四分之三圆弧，直线段Oa 长为R ．若此导线放在匀强磁场B 中，B的方向垂直图面向内．导线以角速度ω在图面内绕O 点匀速转动，则此导线中的动生电动势 i =___________ ，电势最高的点是________________________．11. 一长直导线旁有一长为b ，宽为a 的矩形线圈，线圈与导线共面，长度为b 的边与导线平行且与直导线相距为d ，如图．线圈与导线的互感系数为 ______________________．12. 一无铁芯的长直螺线管，在保持其半径和总匝数不变的情况下，把螺线管拉长一些，则它的自感系数将____________________．三、计算题13. 均匀磁场 B被限制在半径R =10 cm 的无限长圆柱空间内，方向垂直纸面向里．取一固定的等腰梯形回路abcd ，梯形所在平面的法向与圆柱空间的轴平行，位置如图所示．设磁感强度以d B /d t =1 T/s 的匀速率增加，已知 π=31θ，cm 6==Ob Oa ，求等腰梯形回路中感生电动势的大小和方向．14.如图所示，有一半径为r =10 cm 的多匝圆形线圈，匝数N =100，置于均匀磁场B中(B = 0.5 T )．圆形线圈可绕通过圆心的轴O 1O 2转动，转速 n =600rev/min ．求圆线圈自图示的初始位置转过π21时，(1) 线圈中的瞬时电流值(线圈的电阻R 为 100 Ω，不计自感)；(2) 圆心处的磁感强度．(μ0 =4π×10-7 H/m)ωa bc OBabdO 1O 2Brω×× × RB cb da O θ15. 两个半径分别为R和r的同轴圆形线圈相距x，且R>>r，x>>R．若大线圈通有电流I而小线圈沿x轴方向以速率v运动，试求x =NR时(N为正数)小线圈回路中产生的感应电动势的大小．16. 载有电流的I长直导线附近，放一导体半圆环MeN与长直导线共面，且端点MN的连线与长直导线垂直．半圆环的半径为b，环心O与导线相距a．设半圆环以速度v 平行导线平移，求半圆环内感应电动势的大小和方向以及MN两端的电压UMU N ．xrIRxvbM NeaIOv。

大学物理A2复习题(附答案)

大学物理A2复习题一、选择题：1. 一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ．(C) φωcos A -． (D) φωcos A ．［］2. 一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正方向运动时，开始计时．则其振动方程为： (A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x (C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x (E) t m /k A x cos = ［］3. 把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π． (B) π/2．(C) 0 ． (D) θ．［］4. 两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为x 1 =A cos(ωt + α)．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处．则第二个质点的振动方程为(A) )π21cos(2++=αωt A x ． (B) )π21cos(2-+=αωt A x ． (C) )π23cos(2-+=αωt A x ． (D) )cos(2π++=αωt A x ．［］5.一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2．将它们拿到月球上去，相应的周期分别为1T '和2T '．则有(A) 11T T >'且22T T >'． (B) 11T T <'且22T T <'．(C) 11T T ='且22T T ='． (D) 11T T ='且22T T >'．［］6.一质点沿x 轴作简谐振动，振动方程为 )312cos(1042π+π⨯=-t x (SI)．从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A)s 81 (B) s 61 (C) s 41 (D)s 31 (E) s 21 ［］7.一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1．若将此弹簧截去一半的长度，下端挂一质量为m 21的物体，则系统振动周期T 2等于 (A) 2 T 1 (B) T 1 (C) T 12/(D) T 1 /2 (E) T 1 /4 ［］8.轻弹簧上端固定，下系一质量为m 1的物体，稳定后在m 1下边又系一质量为m 2的物体，于是弹簧又伸长了∆x ．若将m 2移去，并令其振动，则振动周期为(A) g m x m T 122∆π= ． (B) gm x m T 212∆π=． (C) g m x m T 2121∆π=． (D) gm m x m T )(2212+π=∆．［］ 9.一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12． (B) T /8．(C) T /6． (D) T /4．10.两个同周期简谐振动曲线如图所示．x 1的相位比x 2的相位 (A) 落后π/2． (B) 超前π/2．(C) 落后π ． (D) 超前π．［］11.在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定 (A) 大小相同，而方向相反． (B) 大小和方向均相同．(C) 大小不同，方向相同． (D) 大小不同，而方向相反．［］12. 若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A) 波速为C ． (B) 周期为1/B ．(C) 波长为 2π /C ． (D) 角频率为2π /B ．［］13.一横波沿绳子传播时, 波的表达式为 )104cos(05.0t x y π-π= (SI)，则(A) 其波长为0.5 m ． (B) 波速为5 m/s ．(C) 波速为25 m/s ． (D) 频率为2 Hz ．［］14. 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则(A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．［］15.已知一平面简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则(A) 波的频率为a ． (B) 波的传播速度为 b/a ．(C) 波长为 π / b ． (D) 波的周期为2π / a ．［］16.一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它的能量是(A) 动能为零，势能最大．(B) 动能为零，势能为零．(C) 动能最大，势能最大．(D) 动能最大，势能为零．［］17.一平面简谐波在弹性媒质中传播时，某一时刻媒质中某质元在负的最大位移处，则它的能量是(A) 动能为零，势能最大．(B) 动能为零，势能为零．(C) 动能最大，势能最大．(D) 动能最大，势能为零．［］18.在波长为λ 的驻波中两个相邻波节之间的距离为(A) λ ．(B) 3λ /4．(C) λ /2．(D) λ /4．［］19.在波长为λ的驻波中，两个相邻波腹之间的距离为(A) λ /4．(B) λ /2．(C) 3λ /4．(D) λ ．［］20.在驻波中，两个相邻波节间各质点的振动(A) 振幅相同，相位相同．(B) 振幅不同，相位相同．(C) 振幅相同，相位不同．(D) 振幅不同，相位不同．［］21.在相同的时间内，一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等，走过的光程相等．(B) 传播的路程相等，走过的光程不相等．(C) 传播的路程不相等，走过的光程相等．(D) 传播的路程不相等，走过的光程不相等．［］22. 在真空中波长为λ的单色光，在折射率为n的透明介质中从A沿某路径传播到B，若A、B两点相位差为3π，则此路径AB的光程为(A) 1.5 λ．(B) 1.5 λ/ n．(C) 1.5 n λ．(D) 3 λ．［］23.用白光光源进行双缝实验，若用一个纯红色的滤光片遮盖一条缝，用一个纯蓝色的滤光片遮盖另一条缝，则(A) 干涉条纹的宽度将发生改变．(B) 产生红光和蓝光的两套彩色干涉条纹．(C) 干涉条纹的亮度将发生改变．(D) 不产生干涉条纹．［］24.在双缝干涉实验中，设缝是水平的．若双缝所在的平板稍微向上平移，其它条件不变，则屏上的干涉条纹(A) 向下平移，且间距不变．(B) 向上平移，且间距不变．(C) 不移动，但间距改变．(D) 向上平移，且间距改变．［］25.在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是(A) 使屏靠近双缝．(B) 使两缝的间距变小．(C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源．［］26. 在双缝干涉实验中，两条缝的宽度原来是相等的．若其中一缝的宽度略变窄(缝中心位置不变)，则(A)干涉条纹的间距变宽．(B)干涉条纹的间距变窄．(C)干涉条纹的间距不变，但原极小处的强度不再为零．(D)不再发生干涉现象．［］27.两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃慢慢地向上平移，则干涉条纹(A) 向棱边方向平移，条纹间隔变小．(B) 向棱边方向平移，条纹间隔变大．(C) 向棱边方向平移，条纹间隔不变．(D) 向远离棱边的方向平移，条纹间隔不变．(E) 向远离棱边的方向平移，条纹间隔变小．［］28.两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的(A) 间隔变小，并向棱边方向平移．(B) 间隔变大，并向远离棱边方向平移．(C) 间隔不变，向棱边方向平移．(D) 间隔变小，并向远离棱边方向平移．［］29.把一平凸透镜放在平玻璃上，构成牛顿环装置．当平凸透镜慢慢地向上平移时，由反射光形成的牛顿环(A)向中心收缩，条纹间隔变小．(B)向中心收缩，环心呈明暗交替变化．(C)向外扩张，环心呈明暗交替变化．(D)向外扩张，条纹间隔变大．［］30.若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中，则干涉条纹(A) 中心暗斑变成亮斑．(B) 变疏．(C) 变密．(D) 间距不变．［］31.在单缝夫琅禾费衍射实验中波长为的单色光垂直入射到单缝上．对应于衍射角为30°的方向上，若单缝处波面可分成3个半波带，则缝宽度a等于(A) λ．(B) 1.5 λ．(C) 2 λ．(D) 3 λ．［］32.在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a＝4 λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为(A) 2 个．(B) 4 个．(C) 6 个．(D) 8 个．［］33.波长为λ的单色平行光垂直入射到一狭缝上，若第一级暗纹的位置对应的衍射角为θ=±π / 6，则缝宽的大小为(A) λ / 2．(B) λ．(C) 2λ．(D) 3 λ．［］34.在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变小．(B) 对应的衍射角变大．(C) 对应的衍射角也不变．(D) 光强也不变．［］35.在单缝夫琅禾费衍射实验中，若增大缝宽，其他条件不变，则中央明条纹(A) 宽度变小．(B) 宽度变大．(C) 宽度不变，且中心强度也不变．(D) 宽度不变，但中心强度增大．［］36.在单缝夫琅禾费衍射实验中，若减小缝宽，其他条件不变，则中央明条纹(A) 宽度变小；(B) 宽度变大；(C) 宽度不变，且中心强度也不变；(D) 宽度不变，但中心强度变小．［］37.一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是(A) 紫光．(B) 绿光．(C) 黄光．(D) 红光．［］38.一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，距离中央明纹最近的是(A) 紫光．(B) 绿光．(C) 黄光．(D) 红光．［］39. 测量单色光的波长时，下列方法中哪一种方法最为准确？(A) 双缝干涉．(B) 牛顿环．(C) 单缝衍射．(D) 光栅衍射．［］40.设光栅平面、透镜均与屏幕平行．则当入射的平行单色光从垂直于光栅平面入射变为斜入射时，能观察到的光谱线的最高级次k(A) 变小．(B) 变大．(C) 不变．(D) 的改变无法确定．［］41. 一束光强为I 0的自然光垂直穿过两个偏振片，且此两偏振片的偏振化方向成45°角，则穿过两个偏振片后的光强I 为(A) 4/0I 2 ． (B) I 0 / 4．(C) I 0 / 2． (D)2I 0 / 2．［］ 42.如果两个偏振片堆叠在一起，且偏振化方向之间夹角为60°，光强为I 0的自然光垂直入射在偏振片上，则出射光强为(A) I 0 / 8． (B) I 0 / 4． (C) 3 I 0 / 8． (D) 3 I 0 / 4．［］43.在双缝干涉实验中，用单色自然光，在屏上形成干涉条纹．若在两缝后放一个偏振片，则(A) 干涉条纹的间距不变，但明纹的亮度加强．(B) 干涉条纹的间距不变，但明纹的亮度减弱．(C) 干涉条纹的间距变窄，且明纹的亮度减弱．(D) 无干涉条纹．［］44.两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过．当其中一偏振片慢慢转动180°时透射光强度发生的变化为：(A) 光强单调增加．(B) 光强先增加，后又减小至零．(C) 光强先增加，后减小，再增加．(D) 光强先增加，然后减小，再增加，再减小至零．［］45.一束光是自然光和线偏振光的混合光，让它垂直通过一偏振片．若以此入射光束为轴旋转偏振片，测得透射光强度最大值是最小值的5倍，那么入射光束中自然光与线偏振光的光强比值为(A) 1 / 2． (B) 1 / 3．(C) 1 / 4． (D) 1 / 5．［］二、填空题：1.在两个相同的弹簧下各悬一物体，两物体的质量比为4∶1，则二者作简谐振动的周期之比为_______________________．2.用40Ｎ的力拉一轻弹簧，可使其伸长20 cm ．此弹簧下应挂__________kg 的物体，才能使弹簧振子作简谐振动的周期T = 0.2π s ．3.一物体作余弦振动，振幅为15×10-2 m ，角频率为6π s -1，初相为0.5 π，则振动方程为 x = ________________________(SI)．4. 一简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A =_____________ ，初相φ =________________．5.两个弹簧振子的周期都是0.4 s ，设开始时第一个振子从平衡位置向负方向运动，经过0.5 s 后，第二个振子才从正方向的端点开始运动，则这两振动的相位差为____________．6.两质点沿水平x 轴线作相同频率和相同振幅的简谐振动，平衡位置都在坐标原点．它们总是沿相反方向经过同一个点，其位移x 的绝对值为振幅的一半，则它们之间的相位差为______________．7.一弹簧振子，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动周期为______________________．8.一竖直悬挂的弹簧振子，自然平衡时弹簧的伸长量为x 0，此振子自由振动的周期T = ____________________________．9. 一物体同时参与同一直线上的两个简谐振动：)314c o s (05.01π+π=t x (SI) ， )324cos(03.02π-π=t x (SI) 合成振动的振幅为__________________m ．10.两个同方向同频率的简谐振动，其振动表达式分别为：)215c o s (10621π+⨯=-t x (SI) ， )25c o s (10222π-⨯=-t x (SI) 它们的合振动的振辐为_____________,初相为____________．11. A ，B 是简谐波波线上距离小于波长的两点．已知，B 点振动的相位比A 点落后π31，波长为λ = 3 m ，则A ，B 两点相距L = ________________m ．12.一横波的表达式是 )30/01.0/(2sin 2x t y -π=其中x 和y 的单位是厘米、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ．13.频率为100 Hz 的波，其波速为250 m/s ．在同一条波线上，相距为0.5 m 的两点的相位差为________________．14.已知波源的振动周期为4.00×10-2 s ，波的传播速度为300 m/s ，波沿x 轴正方向传播，则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________．15.一列平面简谐波沿x 轴正向无衰减地传播，波的振幅为 2×10-3 m ，周期为0.01 s ，波速为400 m/s . 当t = 0时x 轴原点处的质元正通过平衡位置向y 轴正方向运动，则该简谐波的表达式为____________________．16.已知某平面简谐波的波源的振动方程为t y π=21sin 06.0 (SI)，波速为2 m/s ．则在波传播前方离波源5 m 处质点的振动方程为_______________________．17.两相干波源S 1和S 2的振动方程分别是)cos(1φω+=t A y 和)cos(2φω+=t A y .S 1距P 点3个波长，S 2距P 点 4.5个波长．设波传播过程中振幅不变，则两波同时传到P 点时的合振幅是________________．18.两个相干点波源S 1和S 2，它们的振动方程分别是 )21cos(1π+=t A y ω和 )21c o s (2π-=t A y ω．波从S 1传到P 点经过的路程等于2个波长，波从S 2传到P 点的路程等于7 / 2个波长．设两波波速相同，在传播过程中振幅不衰减，则两波传到P 点的振动的合振幅为__________________________．19.简谐驻波中，在同一个波节两侧距该波节的距离相同的两个媒质元的振动相位差是________________．20.在弦线上有一驻波，其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________．21.用波长为λ的单色光垂直照射置于空气中的厚度为e 折射率为1.5的透明薄膜，两束反射光的光程差δ ＝________________________．22.在双缝干涉实验中，两缝分别被折射率为n 1和n 2的透明薄膜遮盖，二者的厚度均为e ．波长为λ的平行单色光垂直照射到双缝上，在屏中央处，两束相干光的相位差∆φ＝_______________________．23.在双缝干涉实验中，若使两缝之间的距离增大，则屏幕上干涉条纹间距___________．24.在双缝干涉实验中，若使单色光波长减小，则干涉条纹间距_________________．25.用波长为λ的单色光垂直照射折射率为n 的劈形膜形成等厚干涉条纹，若测得相邻明条纹的间距为l ，则劈尖角θ＝_______________．26.波长为λ的平行单色光垂直照射到折射率为n 的劈形膜上，相邻的两明纹所对应的薄膜厚度之差是____________________．27.在双缝干涉实验中，若两缝的间距为所用光波波长的N 倍，观察屏到双缝的距离为D ，则屏上相邻明纹的间距为_______________ ．28.在双缝干涉实验中，双缝间距为d ，双缝到屏的距离为D (D >>d )，测得中央零级明纹与第五级明之间的距离为x ，则入射光的波长为_________________．29.用半波带法讨论单缝衍射暗条纹中心的条件时，与中央明条纹旁第二个暗条纹中心相对应的半波带的数目是__________．30.用半波带法讨论单缝衍射条纹中心的条件时，与中央明条纹旁第二个明条纹中心相对应的半波带的数目是__________．31.惠更斯－菲涅耳原理的基本内容是：波阵面上各面积元所发出的子波在观察点P 的_________________，决定了P 点的合振动及光强．32.惠更斯引入__________________的概念提出了惠更斯原理，菲涅耳再用______________的思想补充了惠更斯原理，发展成了惠更斯－菲涅耳原理．33.波长为λ的单色光垂直投射于缝宽为a ，总缝数为N ，光栅常数为d=a+b 的光栅上，光栅方程(表示出现主极大的衍射角ϕ应满足的条件)为__________________．34.若光栅的光栅常数d=a+b 、缝宽a 和入射光波长λ都保持不变，而使其缝数N 增加，则光栅光谱的同级光谱线将变得____________________________．35.一束单色光垂直入射在光栅上，衍射光谱中共出现5条明纹．若已知此光栅缝宽度与不透明部分宽度相等，那么在中央明纹一侧的两条明纹分别是第_____________级和第____________级谱线．36. 一束平行单色光垂直入射在一光栅上，若光栅的透明缝宽度a 与不透明部分宽度b 相等，则可能看到的衍射光谱的级次为___________________．37.当一衍射光栅的不透光部分的宽度b 与透光缝宽度a 满足b = 3a 关系时，衍射光谱中第_______________级谱线缺级．38.若在某单色光的光栅光谱中第三级谱线是缺级，则光栅常数与缝宽之比a b a /)(+ 的各种可能的数值为__________________．39. 一束自然光通过两个偏振片，若两偏振片的偏振化方向间夹角由α1转到α2，则转动前后透射光强度之比为________________．40.要使一束线偏振光通过偏振片之后振动方向转过90°，至少需要让这束光通过__________块理想偏振片．在此情况下，透射光强最大是原来光强的___________倍．41.布儒斯特定律的数学表达式为______________,式中________________为布儒斯特角，______________为折射媒质对入射媒质的相对折射率．42. 当一束自然光以布儒斯特角入射到两种媒质的分界面上时，就偏振状态来说反射光为____________________光，其振动方向__________于入射面．43.假设某一介质对于空气的临界角是45°，则光从空气射向此介质时的布儒斯特角是_______________________．44.光的干涉和衍射现象反映了光的________性质．光的偏振现像说明光波是_______波．45.一束光线入射到单轴晶体后，成为两束光线，沿着不同方向折射．这样的现象称为双折射现象．其中一束折射光称为寻常光，它________________________定律；另一束光线称为非常光，它____________________定律．三、简答题：1.什么是机械振动？2.什么是简谐振动？3.机械波产生的必备条件是什么？4.纵波与横波的区别是什么？5.机械波干涉的条件是什么？6.什么叫半波损失？7.哪些仪器是依据几何光学原理制成的？8.获得相干光的方法有哪些？9.薄膜干涉可分几类？ 10.牛顿环和劈尖属于哪一种干涉？ 11.何谓半波带法？ 12.简述惠更斯-菲涅耳原理。

大学物理A2总复习资料(修改版)(DOC)

元培学院大学物理学A2复习题一．选择题36．根据电介质中的高斯定律，下列说法正确的是（A ）若电位移矢量沿一闭合曲面的通量等于零，则这个曲面内一定没有自由电荷；（B ）若闭合曲面内没有自由电荷，则电位移矢量沿该闭合曲面的通量等于零；（C ）若闭合曲面内没有自由电荷，则曲面上的电位移矢量一定等于零；（D ）电位移矢量只与自由电荷的分布有关37．极化电荷与自由电荷的最大区别是（A ）自由电荷能激发电场，而极化电荷则不会；（B ）自由电荷能激发静电场，而极化电荷则只能产生涡旋电场；（C ）自由电荷有正负两种电荷，而极化电荷则没有正负之分；（D ）自由电荷能单独地自由运动，而极化电荷则不能脱离电介质中原子核而单独移动38．一个带电量为q ，半径为R 的薄金属壳外充满了相对电容率为r ε的均匀介质，球壳内为真空，则球壳的电势为（A ）R q 04πε （B ）R qr επε04 (C)０ (D))(40R r r qr >επε39．两个半径相同的金属球，一为空心，一为实心，把两者各自孤立时的电容值加以比较，则()A 空心球电容值大 ()B 实心球电容值大()C 两球电容值相等 ()D 大小关系无法确定40．如图所示，先接通开关K ，使电容器充电，然后断开K ；当电容器板间的距离增大时，假定电容器处于干燥的空气中，则()A 电容器上的电量减小 ()B 电容器两板间的场强减小 ()C 电容器两板间的电压变小 ()D 以上说法均不正确41．在感应电场中电磁感应定律可写成t l E LK d d d Φ-=⎰⋅ ，式中K E 为感应电场的电场强度．此式表明(A) 闭合曲线L 上K E 处处相等(B) 感应电场是保守力场(C) 感应电场的电场强度线不是闭合曲线(D) 在感应电场中不能像对静电场那样引入电势的概念42．关于产生感应电流的条件，下面说法正确的是（A ）任何导体在磁场中运动都产生感应电流（B ）只要导体在磁场中做切割磁感线运动时，导体中都能产生感应电流（C ）闭合电路的一部分导体，在磁场里做切割磁感线运动时，导体中就会产生感应电流（D ）闭合电路的一部分导体，在磁场里沿磁感线方向运动时，导体中就会产生感应电流43．由导体组成的一矩形线框，以匀速率v从无磁场的空间进入一个均匀磁场中，然后从磁场中出来，又在无磁场空间中运动。

大学物理A2稳恒磁场习题解答PPT课件

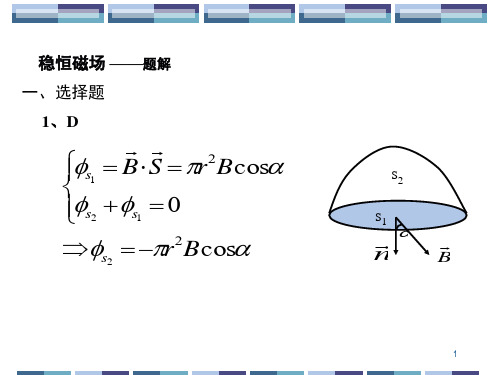
7、D
B
0 Ir , 2R 2 0I ,r 2r
rR R
8、B
3
2
1
45 6
6
9、C 10、C 11、B
12、D
Rm ,T2m ,m 4,Q 2
qB qB m H Q H
R m P
eB eB
Sin D eBD
RP
R BO•
-e
D
MP mB0
7
13、C
123 F3
F1
F2
1A 2A 3A
Ｌ３、Ｌ４在Ｏ点产生的磁感应强度的大小相等，方向相反，总值为０。即
B3B4 0
ቤተ መጻሕፍቲ ባይዱ19
Ｏ点的磁感应强度：
B0
B1B2 B3 B4
0I 4R
方向垂直图面向外。
20
3、带电粒子在均匀磁场中由静止开始下降，磁场方向与与重力方向（ X轴方向）垂直，求粒子下落距离为 X 时的速率 V，并叙述求解方法的理论依据。
16
2、用两根彼此平行的半无限长的直导线 L、1 L 2
把半径为 R的均匀导体圆环连到电源上，如图所
示，已知直导线上的电流为 I，求圆环中心 O
点的磁感应强度。
O
a
L1
R
b
L2
17
解：L1在O点产生的磁感应强度：由于L1与O点在一条直线，由毕奥—萨伐定律可求出
B1=0
L2在Ｏ点产生的磁感应强度：Ｌ２为半无限长直电流，它在Ｏ处产生的场是无限长直电流的一半，由安培环路定律和叠加原理有
0
I1
3
4、D I
a1 O1
I
O2
a2
B12a01I;B222a20I(见2题）

大学物理a2期末考试试题及答案

大学物理a2期末考试试题及答案一、选择题（每题3分，共30分）1. 光在真空中的传播速度是：A. 3×10^8 m/sB. 3×10^5 km/sC. 3×10^7 m/sD. 3×10^6 m/s答案：A2. 以下哪个选项不是牛顿三大定律之一？A. 惯性定律B. 作用与反作用定律C. 能量守恒定律D. 万有引力定律答案：C3. 一个物体在水平面上以恒定加速度运动，其速度与时间的关系是：A. v = u + atB. v = u - atC. v = u * tD. v = u / t答案：A4. 根据热力学第一定律，下列说法正确的是：A. 能量可以被创造或消灭B. 能量守恒C. 能量可以被转化为质量D. 能量可以被转化为信息5. 电磁波的频率与波长的关系是：A. 频率与波长成正比B. 频率与波长成反比C. 频率与波长无关D. 频率与波长成正比，但与波速无关答案：B6. 以下哪种物质的导电性能最好？A. 玻璃B. 橡胶C. 金属D. 陶瓷答案：C7. 根据麦克斯韦方程组，电磁波的传播速度与以下哪个因素无关？A. 真空的介电常数B. 真空的磁导率C. 光速D. 电磁波的频率答案：D8. 一个点电荷在电场中受到的力与以下哪个因素无关？A. 电荷的大小B. 电场的强度C. 电荷的正负D. 电荷的质量答案：D9. 根据量子力学，以下哪个概念是错误的？B. 测不准原理C. 光的波动性D. 粒子的波动性答案：C10. 以下哪个选项是正确的？A. 光子没有质量B. 光子具有能量C. 光子具有动量D. 光子具有静止质量答案：B二、填空题（每题2分，共20分）1. 根据牛顿第二定律，力等于________。

答案：质量乘以加速度2. 光的折射定律是斯涅尔定律，其表达式为n1 * sin(θ1) = n2 *sin(θ2)，其中n1和n2分别是光从介质1进入介质2时的________。

大学物理A2 作业答案

10 静电场（1）习题解10-1 （A ）由即得 ,0dq dF ,r4)q Q (q F 20=-=πε 10-2 （C ）10-3 （C ） 0x4Q214Q ,0i r 4Q 2i 14Q E 20202020=-=-=πεπεπεπε即可得. 10-4 （A ）2220(1)2Qq k k Q ⋅⋅=⇒=- 10-5 （A ） 10-6 0 ，214S a λπε∆⋅⋅；由圆心指向S ∆方向 10-7011()4a L aλπε-+ 10-8 解：2204()dxdq dx dE a x λλπε=⇒=+1222220cos 4()()x dxxdE dE a x a x λθπε=-=⋅++ 1222220sin 4()()y dxadE dE a x a x λθπε=-=⋅++积分后得到：04x E a λπε=-；04y E a λπε=；0()4E i j aλπε=-+ 10-9 解：取宽为dx 的细长条dx λσ=该细长条在P 处产生的电场强度为002()2()dxdE a b x a b x λσππεππε==+-+- ，则P 处的电场强度为：000ln 2()2b dx a bE dE a b x aσσπεπε+===+-⎰⎰ 指向+X 方向10-10 解：θθλλd sin R dl dq 0==， 200R4d sin R dE πεθθλ=，三11 静电场（2）习题解11-1 （A ）通过半球面的电通量与以R 为半径的圆平面的电通量等. 11-2 （C ）穿进高斯面的电通量与穿出高斯面的电通量相等。

11-3 （D ）把点电荷用空间立体面包围,则电通量为q/ε0,所给平面面积为空间立体面面积的1/6, ∴电通量也为过空间立体面的1/6.11-4 （D ）作一半径为r 的高斯面(球面),包围电荷为Q a , 即可得. 11-5 q/24ε0 ;若要把A 点全部包围,需要如图的8个立方体,封闭曲面表面积为24个abcd 面.11-6 Q ΔS/16π2ε0R 4; 由球心指向ΔS. 用补偿法: 球面看成完整带正电的, 球心场强为0;ΔS 带负电,所带电量q=σΔS=Q ΔS/(4πR 2), 场强由球心指向ΔS ，即可得叠加结果.11-7 4.43×10-13（C ·m -3）.⎰⎰⎰=-=-==ππθθπελθθθπελ02000200x x 0)2(d 2sin 41R 4Rd sin cos R 4RdE E R8 d sin R 4RdE E 0002200y y ελθθπελπ-=-==⎰⎰jR8j E i E E 00y xελ-=+=∴0dE E Ry Ry ==⎰θπεθθλθsin R 4d sin R sin dE dE 200y -=-=θπεθθλθcos R4d sin R cos dE dE 200x -=-=由高斯定理 012SSh S E S E S d E ε∆ρ∆∆=-=⋅⎰h)E E (120-=ερ11-8 解：分别在r a <，a r b <<，b r <建立高斯面r a <时，110Q E d S ε⋅=⎰ ；1100Q E =⇒=a rb <<时，22222004Q Q E d S E r πεε⋅=⇒⋅=⎰；3324()3Q r a ρπ=⋅-33332204()()343r a r a E r rρπρπεε⋅--== b r <时，23333004Q Q E d S E r πεε⋅=⇒⋅=⎰，3334()3Q b a ρπ=⋅-33333204()()343b a b a E r rρπρπεε⋅--== 11-9解：空腔内可看成电荷体密度大小相等的带异号电荷的球体叠加而成. 整个大球带正电, 作高斯面过P 点,场强32Sr 34r 4'E S d 'E επρπ==⋅⎰, 00233434'ερεππρrr r E ==,OP33r 'E 00ερερ==小球带负电, 同样作过P 点高斯面,场强32'34'4''''επρπr r E S d E S-==⋅⎰,P O r E '33'''00ερερ-=-=b P O OP E E E03)'(3'''ερερ=-=+=11-10 解：因为电荷分布以纵轴对称，电场线只能沿x 轴，作柱形高斯面，在平板内（小柱面）:0SS x 2Q ES 2S d E ερε===⋅⎰ ,2dx 2d -, x E 0<<=ερ ; 在平板外（大柱面）: , dS Q ES 2S d E0Sρε===⋅⎰ 2dx 2d , d 2E 0-≤≤=ερ 12 静电场（3）习题解12-1 （D ） a 8q )a 21a 1(4q r d e r 4qV l d E V 00a a 2r20p pM M πεπεπε-=--=⋅=+⋅=⎰⎰ 12-2 （E ）12-3 （C ）均匀电场场强处处相等；电势梯度常矢量=∂∂-=n e nV E(相等).12-4 （D ） 20202422R q r d e r q l d E V R rpMπεπε⎰⎰∞=⋅=⋅= 12-5 (1)U=0；（2）E 0=0 .电势和场强分别在点叠加 0r4q (2r4q 2V 2V 2V 00=-+=+=-+πεπε）设顶角分别为a 、b 、c 、d, 中点场强： d c b a E E E E E+++=因为对角线顶点为等量同号电荷，场强相等而反向，所以0E =12-6 45(V); -15(V) . 由电势定义 B Bp p V l d E V +⋅=⎰计算即得.12-7 E x =-2Ax/(x 2+y 2) ; E y =-2Ay/(x 2+y 2) .按场强与电势梯度关系 yV E x V E y x ∂∂-=∂∂-= , 12-8 (q A -q B )d/2ε0S .12-9 解：（1）由于D ，C 在1q ，2q 产生的电场中具有对称性，故D C U U =即0DC U ∆=。

大学物理A2复习题(附答案)

大学物理A2复习题一、选择题：1. 一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ．(C) φωcos A -． (D) φωcos A ．［］2. 一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正方向运动时，开始计时．则其振动方程为： (A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x (C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x (E) t m /k A x cos = ［］3. 把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π． (B) π/2．(C) 0 ． (D) θ．［］4. 两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为x 1 =A cos(ωt + α)．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处．则第二个质点的振动方程为(A) )π21cos(2++=αωt A x ． (B) )π21cos(2-+=αωt A x ． (C) )π23cos(2-+=αωt A x ． (D) )cos(2π++=αωt A x ．［］5.一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2．将它们拿到月球上去，相应的周期分别为1T '和2T '．则有(A) 11T T >'且22T T >'． (B) 11T T <'且22T T <'．(C) 11T T ='且22T T ='． (D) 11T T ='且22T T >'．［］6.一质点沿x 轴作简谐振动，振动方程为 )312cos(1042π+π⨯=-t x (SI)．从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A)s 81 (B) s 61 (C) s 41 (D)s 31 (E) s 21 ［］7.一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1．若将此弹簧截去一半的长度，下端挂一质量为m 21的物体，则系统振动周期T 2等于 (A) 2 T 1 (B) T 1 (C) T 12/(D) T 1 /2 (E) T 1 /4 ［］8.轻弹簧上端固定，下系一质量为m 1的物体，稳定后在m 1下边又系一质量为m 2的物体，于是弹簧又伸长了∆x ．若将m 2移去，并令其振动，则振动周期为(A) g m x m T 122∆π= ． (B) gm x m T 212∆π=． (C) g m x m T 2121∆π=． (D) gm m x m T )(2212+π=∆．［］ 9.一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12． (B) T /8．(C) T /6． (D) T /4．10.两个同周期简谐振动曲线如图所示．x 1的相位比x 2的相位 (A) 落后π/2． (B) 超前π/2．(C) 落后π ． (D) 超前π．［］11.在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定 (A) 大小相同，而方向相反． (B) 大小和方向均相同．(C) 大小不同，方向相同． (D) 大小不同，而方向相反．［］12. 若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A) 波速为C ． (B) 周期为1/B ．(C) 波长为 2π /C ． (D) 角频率为2π /B ．［］13.一横波沿绳子传播时, 波的表达式为 )104cos(05.0t x y π-π= (SI)，则(A) 其波长为0.5 m ． (B) 波速为5 m/s ．(C) 波速为25 m/s ． (D) 频率为2 Hz ．［］14. 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则(A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．［］15.已知一平面简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则(A) 波的频率为a ． (B) 波的传播速度为 b/a ．(C) 波长为 π / b ． (D) 波的周期为2π / a ．［］16.一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它的能量是(A) 动能为零，势能最大．(B) 动能为零，势能为零．(C) 动能最大，势能最大．(D) 动能最大，势能为零．［］17.一平面简谐波在弹性媒质中传播时，某一时刻媒质中某质元在负的最大位移处，则它的能量是(A) 动能为零，势能最大．(B) 动能为零，势能为零．(C) 动能最大，势能最大．(D) 动能最大，势能为零．［］18.在波长为λ 的驻波中两个相邻波节之间的距离为(A) λ ．(B) 3λ /4．(C) λ /2．(D) λ /4．［］19.在波长为λ的驻波中，两个相邻波腹之间的距离为(A) λ /4．(B) λ /2．(C) 3λ /4．(D) λ ．［］20.在驻波中，两个相邻波节间各质点的振动(A) 振幅相同，相位相同．(B) 振幅不同，相位相同．(C) 振幅相同，相位不同．(D) 振幅不同，相位不同．［］21.在相同的时间内，一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等，走过的光程相等．(B) 传播的路程相等，走过的光程不相等．(C) 传播的路程不相等，走过的光程相等．(D) 传播的路程不相等，走过的光程不相等．［］22. 在真空中波长为λ的单色光，在折射率为n的透明介质中从A沿某路径传播到B，若A、B两点相位差为3π，则此路径AB的光程为(A) 1.5 λ．(B) 1.5 λ/ n．(C) 1.5 n λ．(D) 3 λ．［］23.用白光光源进行双缝实验，若用一个纯红色的滤光片遮盖一条缝，用一个纯蓝色的滤光片遮盖另一条缝，则(A) 干涉条纹的宽度将发生改变．(B) 产生红光和蓝光的两套彩色干涉条纹．(C) 干涉条纹的亮度将发生改变．(D) 不产生干涉条纹．［］24.在双缝干涉实验中，设缝是水平的．若双缝所在的平板稍微向上平移，其它条件不变，则屏上的干涉条纹(A) 向下平移，且间距不变．(B) 向上平移，且间距不变．(C) 不移动，但间距改变．(D) 向上平移，且间距改变．［］25.在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是(A) 使屏靠近双缝．(B) 使两缝的间距变小．(C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源．［］26. 在双缝干涉实验中，两条缝的宽度原来是相等的．若其中一缝的宽度略变窄(缝中心位置不变)，则(A)干涉条纹的间距变宽．(B)干涉条纹的间距变窄．(C)干涉条纹的间距不变，但原极小处的强度不再为零．(D)不再发生干涉现象．［］27.两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃慢慢地向上平移，则干涉条纹(A) 向棱边方向平移，条纹间隔变小．(B) 向棱边方向平移，条纹间隔变大．(C) 向棱边方向平移，条纹间隔不变．(D) 向远离棱边的方向平移，条纹间隔不变．(E) 向远离棱边的方向平移，条纹间隔变小．［］28.两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的(A) 间隔变小，并向棱边方向平移．(B) 间隔变大，并向远离棱边方向平移．(C) 间隔不变，向棱边方向平移．(D) 间隔变小，并向远离棱边方向平移．［］29.把一平凸透镜放在平玻璃上，构成牛顿环装置．当平凸透镜慢慢地向上平移时，由反射光形成的牛顿环(A)向中心收缩，条纹间隔变小．(B)向中心收缩，环心呈明暗交替变化．(C)向外扩张，环心呈明暗交替变化．(D)向外扩张，条纹间隔变大．［］30.若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中，则干涉条纹(A) 中心暗斑变成亮斑．(B) 变疏．(C) 变密．(D) 间距不变．［］31.在单缝夫琅禾费衍射实验中波长为的单色光垂直入射到单缝上．对应于衍射角为30°的方向上，若单缝处波面可分成3个半波带，则缝宽度a等于(A) λ．(B) 1.5 λ．(C) 2 λ．(D) 3 λ．［］32.在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a＝4 λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为(A) 2 个．(B) 4 个．(C) 6 个．(D) 8 个．［］33.波长为λ的单色平行光垂直入射到一狭缝上，若第一级暗纹的位置对应的衍射角为θ=±π / 6，则缝宽的大小为(A) λ / 2．(B) λ．(C) 2λ．(D) 3 λ．［］34.在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变小．(B) 对应的衍射角变大．(C) 对应的衍射角也不变．(D) 光强也不变．［］35.在单缝夫琅禾费衍射实验中，若增大缝宽，其他条件不变，则中央明条纹(A) 宽度变小．(B) 宽度变大．(C) 宽度不变，且中心强度也不变．(D) 宽度不变，但中心强度增大．［］36.在单缝夫琅禾费衍射实验中，若减小缝宽，其他条件不变，则中央明条纹(A) 宽度变小；(B) 宽度变大；(C) 宽度不变，且中心强度也不变；(D) 宽度不变，但中心强度变小．［］37.一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是(A) 紫光．(B) 绿光．(C) 黄光．(D) 红光．［］38.一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，距离中央明纹最近的是(A) 紫光．(B) 绿光．(C) 黄光．(D) 红光．［］39. 测量单色光的波长时，下列方法中哪一种方法最为准确？(A) 双缝干涉．(B) 牛顿环．(C) 单缝衍射．(D) 光栅衍射．［］40.设光栅平面、透镜均与屏幕平行．则当入射的平行单色光从垂直于光栅平面入射变为斜入射时，能观察到的光谱线的最高级次k(A) 变小．(B) 变大．(C) 不变．(D) 的改变无法确定．［］41. 一束光强为I 0的自然光垂直穿过两个偏振片，且此两偏振片的偏振化方向成45°角，则穿过两个偏振片后的光强I 为(A) 4/0I 2 ． (B) I 0 / 4．(C) I 0 / 2． (D)2I 0 / 2．［］ 42.如果两个偏振片堆叠在一起，且偏振化方向之间夹角为60°，光强为I 0的自然光垂直入射在偏振片上，则出射光强为(A) I 0 / 8． (B) I 0 / 4． (C) 3 I 0 / 8． (D) 3 I 0 / 4．［］43.在双缝干涉实验中，用单色自然光，在屏上形成干涉条纹．若在两缝后放一个偏振片，则(A) 干涉条纹的间距不变，但明纹的亮度加强．(B) 干涉条纹的间距不变，但明纹的亮度减弱．(C) 干涉条纹的间距变窄，且明纹的亮度减弱．(D) 无干涉条纹．［］44.两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过．当其中一偏振片慢慢转动180°时透射光强度发生的变化为：(A) 光强单调增加．(B) 光强先增加，后又减小至零．(C) 光强先增加，后减小，再增加．(D) 光强先增加，然后减小，再增加，再减小至零．［］45.一束光是自然光和线偏振光的混合光，让它垂直通过一偏振片．若以此入射光束为轴旋转偏振片，测得透射光强度最大值是最小值的5倍，那么入射光束中自然光与线偏振光的光强比值为(A) 1 / 2． (B) 1 / 3．(C) 1 / 4． (D) 1 / 5．［］二、填空题：1.在两个相同的弹簧下各悬一物体，两物体的质量比为4∶1，则二者作简谐振动的周期之比为_______________________．2.用40Ｎ的力拉一轻弹簧，可使其伸长20 cm ．此弹簧下应挂__________kg 的物体，才能使弹簧振子作简谐振动的周期T = 0.2π s ．3.一物体作余弦振动，振幅为15×10-2 m ，角频率为6π s -1，初相为0.5 π，则振动方程为 x = ________________________(SI)．4. 一简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A =_____________ ，初相φ =________________．5.两个弹簧振子的周期都是0.4 s ，设开始时第一个振子从平衡位置向负方向运动，经过0.5 s 后，第二个振子才从正方向的端点开始运动，则这两振动的相位差为____________．6.两质点沿水平x 轴线作相同频率和相同振幅的简谐振动，平衡位置都在坐标原点．它们总是沿相反方向经过同一个点，其位移x 的绝对值为振幅的一半，则它们之间的相位差为______________．7.一弹簧振子，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动周期为______________________．8.一竖直悬挂的弹簧振子，自然平衡时弹簧的伸长量为x 0，此振子自由振动的周期T = ____________________________．9. 一物体同时参与同一直线上的两个简谐振动：)314c o s (05.01π+π=t x (SI) ， )324cos(03.02π-π=t x (SI) 合成振动的振幅为__________________m ．10.两个同方向同频率的简谐振动，其振动表达式分别为：)215c o s (10621π+⨯=-t x (SI) ， )25c o s (10222π-⨯=-t x (SI) 它们的合振动的振辐为_____________,初相为____________．11. A ，B 是简谐波波线上距离小于波长的两点．已知，B 点振动的相位比A 点落后π31，波长为λ = 3 m ，则A ，B 两点相距L = ________________m ．12.一横波的表达式是 )30/01.0/(2sin 2x t y -π=其中x 和y 的单位是厘米、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ．13.频率为100 Hz 的波，其波速为250 m/s ．在同一条波线上，相距为0.5 m 的两点的相位差为________________．14.已知波源的振动周期为4.00×10-2 s ，波的传播速度为300 m/s ，波沿x 轴正方向传播，则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________．15.一列平面简谐波沿x 轴正向无衰减地传播，波的振幅为 2×10-3 m ，周期为0.01 s ，波速为400 m/s . 当t = 0时x 轴原点处的质元正通过平衡位置向y 轴正方向运动，则该简谐波的表达式为____________________．16.已知某平面简谐波的波源的振动方程为t y π=21sin 06.0 (SI)，波速为2 m/s ．则在波传播前方离波源5 m 处质点的振动方程为_______________________．17.两相干波源S 1和S 2的振动方程分别是)cos(1φω+=t A y 和)cos(2φω+=t A y .S 1距P 点3个波长，S 2距P 点 4.5个波长．设波传播过程中振幅不变，则两波同时传到P 点时的合振幅是________________．18.两个相干点波源S 1和S 2，它们的振动方程分别是 )21cos(1π+=t A y ω和 )21c o s (2π-=t A y ω．波从S 1传到P 点经过的路程等于2个波长，波从S 2传到P 点的路程等于7 / 2个波长．设两波波速相同，在传播过程中振幅不衰减，则两波传到P 点的振动的合振幅为__________________________．19.简谐驻波中，在同一个波节两侧距该波节的距离相同的两个媒质元的振动相位差是________________．20.在弦线上有一驻波，其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________．21.用波长为λ的单色光垂直照射置于空气中的厚度为e 折射率为1.5的透明薄膜，两束反射光的光程差δ ＝________________________．22.在双缝干涉实验中，两缝分别被折射率为n 1和n 2的透明薄膜遮盖，二者的厚度均为e ．波长为λ的平行单色光垂直照射到双缝上，在屏中央处，两束相干光的相位差∆φ＝_______________________．23.在双缝干涉实验中，若使两缝之间的距离增大，则屏幕上干涉条纹间距___________．24.在双缝干涉实验中，若使单色光波长减小，则干涉条纹间距_________________．25.用波长为λ的单色光垂直照射折射率为n 的劈形膜形成等厚干涉条纹，若测得相邻明条纹的间距为l ，则劈尖角θ＝_______________．26.波长为λ的平行单色光垂直照射到折射率为n 的劈形膜上，相邻的两明纹所对应的薄膜厚度之差是____________________．27.在双缝干涉实验中，若两缝的间距为所用光波波长的N 倍，观察屏到双缝的距离为D ，则屏上相邻明纹的间距为_______________ ．28.在双缝干涉实验中，双缝间距为d ，双缝到屏的距离为D (D >>d )，测得中央零级明纹与第五级明之间的距离为x ，则入射光的波长为_________________．29.用半波带法讨论单缝衍射暗条纹中心的条件时，与中央明条纹旁第二个暗条纹中心相对应的半波带的数目是__________．30.用半波带法讨论单缝衍射条纹中心的条件时，与中央明条纹旁第二个明条纹中心相对应的半波带的数目是__________．31.惠更斯－菲涅耳原理的基本内容是：波阵面上各面积元所发出的子波在观察点P 的_________________，决定了P 点的合振动及光强．32.惠更斯引入__________________的概念提出了惠更斯原理，菲涅耳再用______________的思想补充了惠更斯原理，发展成了惠更斯－菲涅耳原理．33.波长为λ的单色光垂直投射于缝宽为a ，总缝数为N ，光栅常数为d=a+b 的光栅上，光栅方程(表示出现主极大的衍射角ϕ应满足的条件)为__________________．34.若光栅的光栅常数d=a+b 、缝宽a 和入射光波长λ都保持不变，而使其缝数N 增加，则光栅光谱的同级光谱线将变得____________________________．35.一束单色光垂直入射在光栅上，衍射光谱中共出现5条明纹．若已知此光栅缝宽度与不透明部分宽度相等，那么在中央明纹一侧的两条明纹分别是第_____________级和第____________级谱线．36. 一束平行单色光垂直入射在一光栅上，若光栅的透明缝宽度a 与不透明部分宽度b 相等，则可能看到的衍射光谱的级次为___________________．37.当一衍射光栅的不透光部分的宽度b 与透光缝宽度a 满足b = 3a 关系时，衍射光谱中第_______________级谱线缺级．38.若在某单色光的光栅光谱中第三级谱线是缺级，则光栅常数与缝宽之比a b a /)(+ 的各种可能的数值为__________________．39. 一束自然光通过两个偏振片，若两偏振片的偏振化方向间夹角由α1转到α2，则转动前后透射光强度之比为________________．40.要使一束线偏振光通过偏振片之后振动方向转过90°，至少需要让这束光通过__________块理想偏振片．在此情况下，透射光强最大是原来光强的___________倍．41.布儒斯特定律的数学表达式为______________,式中________________为布儒斯特角，______________为折射媒质对入射媒质的相对折射率．42. 当一束自然光以布儒斯特角入射到两种媒质的分界面上时，就偏振状态来说反射光为____________________光，其振动方向__________于入射面．43.假设某一介质对于空气的临界角是45°，则光从空气射向此介质时的布儒斯特角是_______________________．44.光的干涉和衍射现象反映了光的________性质．光的偏振现像说明光波是_______波．45.一束光线入射到单轴晶体后，成为两束光线，沿着不同方向折射．这样的现象称为双折射现象．其中一束折射光称为寻常光，它________________________定律；另一束光线称为非常光，它____________________定律．三、简答题：1.什么是机械振动？2.什么是简谐振动？3.机械波产生的必备条件是什么？4.纵波与横波的区别是什么？5.机械波干涉的条件是什么？6.什么叫半波损失？7.哪些仪器是依据几何光学原理制成的？8.获得相干光的方法有哪些？9.薄膜干涉可分几类？ 10.牛顿环和劈尖属于哪一种干涉？ 11.何谓半波带法？ 12.简述惠更斯-菲涅耳原理。

大学物理A2半期考试试题以与答案

大学物理A2半期考试试题以与答案2011-2012-2 《大学物理A1》半期考试试卷一、判断题 (回答正确或错误，每小题 2 分，共 8 分 )1、一对作用力与反作用力作功之和一定为零。

（）2、用r表示质点位置矢量，dr ds。

（）s 表示离开原点的路程，有dtdt3、两个同方向、不同频率的简谐振动的合振动仍是简谐振动。

（）4、由同时的相对性知道：在一个参照系中同时发生的两个事件，在另在一个参照系中一定不同时。

（）二、选择题(每小题 3 分，共39 分)1、一质点沿 x 轴运动的规律是x t 24t 5 （SI）。

前三秒内它的()A 、位移和路程都是 3 mB 、位移和路程都是 -3mC、位移是 -3m，路程是 3m D 、位移是 -3m，路程是 5m2、某物体的运动规律为 d v /d t k v t ，式中的k为大于零的常量．当t0 时，初速为v0，则速度 v 与时间t的函数关系是()v0 e kt v0 e kt 2v k v0 e t k v0 et 2(A)v, (B)v 2 ,(C),(D)v23、一绕定轴旋转的刚体，其转动惯量为I，转动角速度为0 。

现受一与转动角速度的成正比的阻力距M f k的作用，比例系数为 k(k0) 。

试求此刚体转动的角速度及刚体从0 到0 /2所需的时间是 ()。

(A)t I(B)tk(C)tI(D)k ln 2ln 2k ln 2tk I I ln 24、地球绕太阳作椭圆轨道运动，地球的动量和角动量是否守恒正确的说法是()A、动量不守恒，角动量不守恒 B 、动量守恒，角动量不守恒C、动量不守恒，角动量守恒 D 、动量守恒，角动量守恒5、花样滑冰运动员绕通过自身的竖直轴转动，开始时两臂伸开，转动惯量为I，角速度为0 ；然后将两手臂合拢，使其转动惯量为2I 3，则转动角速度变为()A、203B、203C、302D、3026．如图所示的弹簧振子，当振动到最大位移处恰好有一质量为m 的泥块从正上方落到质量为 m 的物体上，并与物体粘在一起运动，则下述结论正确的是()A 、振幅变小，周期变小B、振幅变小，周期不变m0C、振幅不变，周期变小kD、振幅不变，周期变大m7、质量为0.04kg 的质点在力F的作用下，由静止开始沿平面曲线x29 y 从点P（0，0）运动到点Q (3,1)，若力F 的两个分量为F x2xy, F y 3x 2，式中 F 以牛顿、 x 和y 以米计，那么质点运动到Q 点的速度的大小为 ()-1B -1-1-1A 、40m s、 30m s C、 20m s D 、 10m s8l、质量为 m 的均匀细杆置于光滑水平面上。

大学物理A2-A卷-3-选择题答案

（本科）试卷（A 卷）《大学物理A2》期末考试试卷开课单位：大学物理教研室，考试形式：闭卷，允许带计算器入场一、选择题（共20分，每题2分）（1）点电荷Q 被曲面S 所包围，从无穷远处引入另一点电荷q 至曲面外一点，如图所示，则引入前后：( D ) （A ）曲面S 上的电通量不变，曲面上各点场强不变．（B ）曲面S 上的电通量变化，曲面上各点场强不变．（C ）曲面S 上的电通量变化，曲面上各点场强变化．（D ）曲面S 上的电通量不变，曲面上各点场强变化．（2）真空中一“无限大”均匀带负电荷的平面如图所示，其电场的场强分布图线应是（设场强方向向右为正、向左为负）( D )（3）关于高斯定理，下列说法中哪一个是正确的？( C )（A ）高斯面内不包围自由电荷，则面上各点电位移矢量D为零．（B ）高斯面上处处D 为零，则面内必不存在自由电荷．（C ）高斯面的D 通量仅与面内自由电荷有关．（D ）以上说法都不正确．（4）把轻的导线圈用线挂在磁铁Ｎ极附近，磁铁的轴线穿过线圈中心，且与线圈在同一平面内，如图所示．当线圈内通以如图所示方向的电流时，线圈将( B ) （A ）不动．（B ）发生转动，同时靠近磁铁．（C ）发生转动，同时离开磁铁．（D ）不发生转动，只靠近磁铁．（E ）不发生转动，只离开磁铁．（5）一个圆形线环，它的一半放在一分布在方形区域的匀强磁场B中，另一半位于磁场之外，如图所示．磁场B的方向垂直指向纸内．欲使圆线环中产生逆时针方向的感应电流，应使 ( C )（A ）线环向右平移．（B ）线环向上平移．（C ）线环向左平移．（D ）磁场强度减弱．（6）在真空中波长为λ的单色光，在折射率为ｎ的透明介质中从A 沿某路径传播到B ，若A 、B 两点位相差为3π，则此路径AB 的光程为 ( A )（A ）1.5λ．（B ）1.5ｎλ．（C ）3λ．（D ）1.5λ／ｎ．（7）一衍射光栅对某一定波长的垂直入射光，在屏幕上只能出现零级和一级主极大，欲使屏幕上出现更高级次的主极大，应该 ( B ) （A ）换一个光栅常数较小的光栅．（B ）换一个光栅常数较大的光栅．（C ）将光栅向靠近屏幕的方向移动．（D ）将光栅向远离屏幕的方向移动．（8）如果两个偏振片堆叠在一起，且偏振化方向之间夹角为60°，假设二者对光无吸收，光强为I 0的自然光垂直入射在偏振片上，则出射光强为 ( A )（A ）I 0／8．（B ）3I 0／8．（C ）I 0／4．（D ）3I 0／4．（9）质量为m =0.02Kg ，速率为300m/s 子弹的德布罗意波长为 ( D ) m. (h =6.63⨯10-34) （A ）2.21⨯10-34．（B ）2.21⨯10-33．（C ）4.42⨯10-34．（D ）1.11⨯10-34．（10）已知一单色光照射在钠表面上，测得光电子的最大动能是 1.2 eV ，而钠的红限波长是5400Å，那么入射光的波长是 ( D )（A ）5350 Å．（B ）5000 Å．（C ）4350 Å．（D ）3550 Å．二、计算题（共80分，每题10分）1、如图2-1所示，直线上有A 、B 、C 三点，A-B 点、B-C 点的距离均+Q 的正电荷，B 点放置电量为+q 的检验电荷。

大学物理A2复习资料分解

波动光学1．在真空中波长为λ的单色光，在折射率为n 的透明介质中从A 沿某路径传播到B ，若A 、B 两点相位差为3π，则此路径AB 的光程为 (A) 1.5 λ． (B) 1.5 λ/ n ．(C) 1.5 n λ． (D) 3 λ．2．单色平行光垂直照射在薄膜上，经上下两表面反射的两束光发生干涉，如图所示，若薄膜的厚度为e ，且n 1＜n 2＞n 3，λ1为入射光在n 1中的波长，则两束反射光的光程差为 (A) 2n 2e ． (B) 2n 2 e - λ1 / (2n 1)．(C) 2n 2 e - n 1 λ1 / 2． (D) 2n 2 e - n 2 λ1 / 2．3．在相同的时间内，一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等，走过的光程相等． (B) 传播的路程相等，走过的光程不相等． (C) 传播的路程不相等，走过的光程相等．(D) 传播的路程不相等，走过的光程不相等．4．在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处(A) 仍为明条纹； (B) 变为暗条纹；(C) 既非明纹也非暗纹； (D) 无法确定是明纹，还是暗纹．5．在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是(A) 使屏靠近双缝．(B) 使两缝的间距变小． (C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源．6．在双缝干涉实验中，屏幕E 上的P 点处是明条纹．若将缝S 2盖住，并在S 1 S 2连线的垂直平分面处放一高折射率介质反射面M ，如图所示，则此时(A) P 点处仍为明条纹． (B) P 点处为暗条纹． (C) 不能确定P 点处是明条纹还是暗条纹．(D) 无干涉条纹．7．在双缝干涉实验中，光的波长为600 nm (1 nm ＝10－9 m )，双缝间距为2 mm ，双缝与屏的间距为300 cm ．在屏上形成的干涉图样的明条纹间距为 (A) 0.45 mm ． (B) 0.9 mm ．(C) 1.2 mm (D) 3.1 mm ．8．在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处n 1n 2n 3入射光反射光1反射光2eP EM S 1 S 2 S(A) 仍为明条纹； (B) 变为暗条纹；(C) 既非明纹也非暗纹； (D) 无法确定是明纹，还是暗纹． 9．在图示三种透明材料构成的牛顿环装置中，用单色光垂直照射，在反射光中看到干涉条纹，则在接触点P 处形成的圆斑为(A) 全明． (B) 全暗．(C) 右半部明，左半部暗．(D) 右半部暗，左半部明．10．一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为 (A) λ / 4 ． (B) λ / (4n )．(C) λ / 2 ． (D) λ / (2n )． 11．若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中，则干涉条纹(A) 中心暗斑变成亮斑． (B) 变疏．(C) 变密． (D) 间距不变．12．用劈尖干涉法可检测工件表面缺陷，当波长为λ的单色平行光垂直入射时，若观察到的干涉条纹如图所示，每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切，则工件表面与条纹弯曲处对应的部分(A) 凸起，且高度为λ / 4． (B) 凸起，且高度为λ / 2．(C) 凹陷，且深度为λ / 2． (D) 凹陷，且深度为λ / 4．13．如图，用单色光垂直照射在观察牛顿环的装置上．当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹(A) 向右平移． (B) 向中心收缩．(C) 向外扩张． (D) 静止不动．(E) 向左平移．14．在迈克耳孙干涉仪的一条光路中，放入一折射率为n ，厚度为d 的透明薄片，放入后，这条光路的光程改变了(A) 2 ( n -1 ) d ． (B) 2nd ． (C) 2 ( n -1 ) d +λ / 2． (D) nd ．(F) ( n -1 ) d ．15．在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a ＝4 λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为 (A) 2 个． (B) 4 个．(C) 6 个． (D) 8 个．P 1.521.75 1.52 图中数字为各处的折射λ 1.62 1.62平玻璃工件空气劈尖空气单色光16．一束波长为λ的平行单色光垂直入射到一单缝AB 上，装置如图．在屏幕D 上形成衍射图样，如果P 是中央亮纹一侧第一个暗纹所在的位置，则BC 的长度为 (A) λ / 2．(B) λ．(C) 3λ / 2 ． (D) 2λ ．17．根据惠更斯－菲涅耳原理，若已知光在某时刻的波阵面为S ，则S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的(A) 振动振幅之和． (B) 光强之和．(C) 振动振幅之和的平方． (D) 振动的相干叠加．18．波长为λ的单色平行光垂直入射到一狭缝上，若第一级暗纹的位置对应的衍射角为θ=±π / 6，则缝宽的大小为(A) λ / 2． (B) λ．(C) 2λ． (D) 3 λ ．19．在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变小． (B) 对应的衍射角变大．(A) 对应的衍射角也不变． (D) 光强也不变．20．在单缝夫琅禾费衍射实验中，若减小缝宽，其他条件不变，则中央明条纹(A) 宽度变小； (B) 宽度变大；(C) 宽度不变，且中心强度也不变；（D ）宽度不变，但中心强度变小．21．在如图所示的单缝夫琅禾费衍射实验装置中，S 为单缝，L 为透镜，C 为放在L 的焦面处的屏幕，当把单缝S 垂直于透镜光轴稍微向上平移时，屏幕上的衍射图样(A)向上平移． (B)向下平移． (C)不动． (D)消失．22．测量单色光的波长时，下列方法中哪一种方法最为准确？(A) 双缝干涉． (B) 牛顿环．(C) 单缝衍射． (D) 光栅衍射．23．一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是 (A) 紫光． (B) 绿光． (C) 黄光． (D) 红光．24．对某一定波长的垂直入射光，衍射光栅的屏幕上只能出现零级和一级主极大，欲使屏幕上出现更高级次的主极大，应该(A) 换一个光栅常数较小的光栅． (B) 换一个光栅常数较大的光栅．C屏f PD LABλSCL(C) 将光栅向靠近屏幕的方向移动．(B) 将光栅向远离屏幕的方向移动．25．一束光是自然光和线偏振光的混合光，让它垂直通过一偏振片．若以此入射光束为轴旋转偏振片，测得透射光强度最大值是最小值的5倍，那么入射光束中自然光与线偏振光的光强比值为(A) 1 / 2． (B) 1 / 3．(C) 1 / 4． (D) 1 / 5． 26．一束光强为I 0的自然光，相继通过三个偏振片P 1、P 2、P 3后，出射光的光强为I ＝I 0 / 8．已知P 1和P 2的偏振化方向相互垂直，若以入射光线为轴，旋转P 2，要使出射光的光强为零，P 2最少要转过的角度是(A) 30°． (B) 45°．(C) 60°． (D) 90°．27．一束光强为I 0的自然光垂直穿过两个偏振片，且此两偏振片的偏振化方向成45°角，则穿过两个偏振片后的光强I 为 (A) 4/0I 2 ． (B) I 0 / 4．(C) I 0 / 2． (D) 2I 0 / 2．28．三个偏振片P 1，P 2与P 3堆叠在一起，P 1与P 3的偏振化方向相互垂直，P 2与P 1的偏振化方向间的夹角为30°．强度为I 0的自然光垂直入射于偏振片P 1，并依次透过偏振片P 1、P 2与P 3，则通过三个偏振片后的光强为 (A) I 0 / 4． (B) 3 I 0 / 8．(C) 3I 0 / 32．(D) I 0 / 16．29．两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过．当其中一偏振片慢慢转动180°时透射光强度发生的变化为： (A) 光强单调增加．(B) 光强先增加，后又减小至零． (C) 光强先增加，后减小，再增加．(C) 光强先增加，然后减小，再增加，再减小至零．30．如果两个偏振片堆叠在一起，且偏振化方向之间夹角为60°，光强为I 0的自然光垂直入射在偏振片上，则出射光强为 (A) I 0 / 8． (B) I 0 / 4．(C) 3 I 0 / 8． (D) 3 I 0 / 4．31．一束自然光自空气射向一块平板玻璃(如图)，设入射角等于布儒斯特角i 0，则在界面2的反射光 (A) 是自然光．(B) 是线偏振光且光矢量的振动方向垂直于入射面．(C) 是线偏振光且光矢量的振动方向平行于入射面．(E) 是部分偏振光．32．自然光以60°的入射角照射到某两介质交界面时，反射光为完全线偏振光，则知折射光为(A) 完全线偏振光且折射角是30°．i 012(B) 部分偏振光且只是在该光由真空入射到折射率为3的介质时，折射角是30°．(C) 部分偏振光，但须知两种介质的折射率才能确定折射角．(D) 部分偏振光且折射角是30°．33．自然光以布儒斯特角由空气入射到一玻璃表面上，反射光是(A) 在入射面内振动的完全线偏振光．(B) 平行于入射面的振动占优势的部分偏振光．(C) 垂直于入射面振动的完全线偏振光．(D) 垂直于入射面的振动占优势的部分偏振光．1A 2 C 3 C 4B 5B 6B 7B 8B 9D 10B11C 12C 13B 14A 15B 16B 17D 18C 19B 20B21C 22D 23D 24B 25A 26B 27B 28C 29B 30A31B 32D 33C8、在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处(A) 仍为明条纹；(B) 变为暗条纹；(C) 既非明纹也非暗纹；(D) 无法确定是明纹，还是暗纹．9、在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变大．(B) 对应的衍射角变小．(C) 对应的衍射角也不变．(D) 光强也不变．10、三个偏振片P1，P2与P3堆叠在一起，P1与P3的偏振化方向相互垂直，P2与P1的偏振化方向间的夹角为30°．强度为I0的自然光垂直入射于偏振片P1，并依次透过偏振片P1、P2与P3，则通过三个偏振片后的光强为(A) I0 / 16．(B) 3I0 / 32．(C) 3 I0 / 8．(D) I0 / 4．5、一双缝干涉装置，在空气中观察时干涉条纹间距为1.0 mm．若整个装置放在水中，干涉条纹的间距将为____________________mm．(设水的折射率为4/3)6、在单缝夫琅禾费衍射实验中，设第一级暗纹的衍射角很小，若钠黄光(λ1≈589 nm) 中央明纹宽度为4.0 mm，则λ2=442 nm (1 nm = 10-9 m)的蓝紫色光的中央明纹宽度为____________________．7、一束平行的自然光，以60°角入射到平玻璃表面上．若反射光束是完全偏振的，则透射光束的折射角是____________________________。

大学物理A2半期考试试题和答案

西南科技大学2015-2016-1学期《大学物理A2》半期考试试卷一、选择题：（每题只有一个正确答案，每小题4分，共60分）1、一半径为R 的均匀带电球体，电荷q 均匀分布在整个球体内，则在球体内、距离球心为r 处的电场强度大小为： [ ] （A ） 0；（B ）304Qr R πε；（C ）204Qr R πε；（D ）04QrRπε2、如图所示，一边长为a 的正方形的四个顶点上各放置了一个正点电荷q ，取无穷远处的电势为零，则此正方形的中心点O 的电势为：[ ] （A ）a q 042πε；（B ）aq022πε；（C ）a q 02πε；（D ）a q 0πε。

3、一半径为R 的无限长均匀带电圆柱体，单位长度的电量为λ，则该圆柱体内半径)(R r r <处的电场强度大小为：[ ] （A ）202R r πελ；（B ）204R r πελ；（C ）r 02πελ；（D ）r04πελ。

4、A 、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小为320E ，两平面外侧电场强度大小都为0E ，方向如图所示，则A 、B 两平面上的电荷面密度分别为：[ ](A) 0035E B εσ=，0031E A εσ=； (B) 0037E B εσ=，0034E A εσ=；(C) 0034E B εσ=，0032E A εσ=； (D) 00310E B εσ=，0035E A εσ=。

5、如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量为 [ ](A) 04εq ； (B) 06εq ； (C) 012εq ； (D) 024εq。

6、两均匀带电球面，半径分别为R 1和R 2，带电量分别为q 1和q 2，取无穷远处的电势为零，则在两球面之间、半径为r 处P 点的电势为：[ ] （A ）r q q 0214πε+；（B ）2020144R q r q πεπε+；（C ）20210144R q R q πεπε+；（D ）rq R q 0210144πεπε+。

大学物理_下A2 期末练习题含解答汇编

xyoa∙∙∙a-(0,)P y qq-大学物理（下A2）练习题第八章真空中的静电场1．如图所示，在点((,0)a 处放置一个点电荷q +，在点(,0)a -处放置另一点电荷q -。

P 点在y 轴上，其坐标为(0,)y ，当y a 时，该点场强的大小为(A) 204q y πε； (B) 202q y πε；(C)302qa y πε； (D)304qa y πε.[ ]2．将一细玻璃棒弯成半径为R 的半圆形，其上半部均匀分布有电量Q +, 下半部均匀分布有电量Q -，如图所示。

求圆心o 处的电场强度。

3．带电圆环的半径为R ,电荷线密度0cos λλφ=,式中00λ>，且为常数。

求圆心O 处的电场强度。

4．一均匀带电圆环的半径为R ，带电量为Q ，其轴线上任一点P 到圆心的距离为a 。

求P 点的场强。

5．关于高斯定理有下面几种说法，正确的是(A) 如果高斯面上E 处处为零，那么则该面内必无电荷； (B) 如果高斯面内无电荷，那么高斯面上E 处处为零； (C) 如果高斯面上E 处处不为零，那么高斯面内必有电荷；(D) 如果高斯面内有净电荷，那么通过高斯面的电通量必不为零； (E) 高斯定理仅适用于具有高度对称性的电场。

[ ]6．点电荷Q 被闭合曲面S 所包围，从无穷远处引入另一点电荷q 至曲面S 外一点,如图所示，则引入前后(A) 通过曲面S 的电通量不变，曲面上各点场强不变；(B) 通过曲面S 的电通量变化，曲面上各点场强不变；(C) 通过曲面S 的电通量变化，曲面上各点场强变化；(D) 通过曲面S 的电通量不变，曲面上各点场强变化。

[ ]7．如果将带电量为q 的点电荷置于立方体的一个顶角上，则通过与它不相邻的每个侧面的电场强度通量为(A) 06q ε； (B) 012q ε； (C) 024q ε； (D) 048q ε. [ ]xq S Q8．如图所示，A 、B 为真空中两个平行的“无限大”均匀带电平面，A 面上的电荷面密度721.7718A C m σ--=-⨯⋅，B 面上的电荷面密度723.5418B C m σ--=⨯⋅。

大学物理A2课外题型

大学物理A2课外题型静电场一、选择题C 1、在坐标原点放一正电荷Q ，它在P 点(x =+1,y =0)产生的电场强度为E ．现在，另外有一个负电荷-2Q ，试问应将它放在什么位置才能使P 点的电场强度等于零？ (A) x 轴上x >1． (B) x 轴上0<x <1． (C) x 轴上x <0． (D) y 轴上y >0． (E) y 轴上y <0．A 2、电荷面密度分别为＋σ和－σ的两块“无限大”均匀带电的平行平板，如图放置，则其周围空间各点电场强度随位置坐标x 变化的关系曲线为：(设场强方向向右为正、向左为负) O E -a +a 02/εσx (D)0/εσ02/εσ- D 3、下面列出的真空中静电场的场强公式，其中哪个是正确的？ (A) 点电荷q 的电场：204r q E επ= ．(r 为点电荷到场点的距离) (B) “无限长”均匀带电直线(电荷线密度λ)的电场：r r E 302ελπ= (r 为带电直线到场点的垂直于直线的矢量)(C) “无限大”均匀带电平面(电荷面密度σ)的电场：02εσ=E (D) 半径为R 的均匀带电球面(电荷面密度σ)外的电场：r r R E 302εσ= (r 为球心到场点的矢量) D 4、一电场强度为E 的均匀电场，E 的方向与沿x 轴正向，如图所示．则通过图中一半径为R 的半球面的电场强度通量为(A) πR 2E ． (B) πR 2E / 2． (C) 2πR 2E ． (D) 0．D 5、点电荷Q 被曲面S 所包围，从无穷远处引入另一点电荷q 至曲面外一点，如图所示，则引入前后：(A) 曲面S 的电场强度通量不变，曲面上各点场强不变．O -a +a 0/εσ x (A) EO E -a +a 2/εσx (B) O x -a a y +σ-σO E -a +a 02/εσx (C)-02/εσ x O +Q P (1,0) x O E Q Sq(B) 曲面S 的电场强度通量变化，曲面上各点场强不变．(C) 曲面S 的电场强度通量变化，曲面上各点场强变化．(D) 曲面S 的电场强度通量不变，曲面上各点场强变化． C 6、如图所示，边长为l 的正方形，在其四个顶点上各放有等量的点电荷．若正方形中心O 处的场强值和电势值都等于零，则：(A) 顶点a 、b 、c 、d 处都是正电荷．(B) 顶点a 、b处是正电荷，c 、d 处是负电荷．(C) 顶点a 、c 处是正电荷，b 、d 处是负电荷． (D) 顶点a 、b 、c 、d 处都是负电荷．C 7、如图所示，边长为a 的等边三角形的三个顶点上，分别放置着三个正的点电荷q 、2q 、3q ．若将另一正点电荷Q 从无穷远处移到三角形的中心O 处，外力所作的功为： (A) a qQ 023επ ． (B) a qQ 03επ． (C) a qQ 0233επ． (D) a qQ 032επ． B 8、带有电荷－q 的一个质点垂直射入开有小孔的两带电平行板之间，如图所示．两平行板之间的电势差为U ，距离为d ，则此带电质点通过电场后它的动能增量等于(A) d qU -． (B) ＋qU ． (C) －qU ． (D) qU 21． D 9、图中实线为某电场中的电场线，虚线表示等势（位）面，由图可看出： (A) E A ＞E B ＞E C ，U A ＞U B ＞U C ． (B) E A ＜E B ＜E C ，U A ＜U B ＜U C ． (C) E A ＞E B ＞E C ，U A ＜U B ＜U C ． (D) E A ＜E B ＜E C ，U A ＞U B ＞U C ．10、设有一带电油滴，处在带电的水平放置的大平行金属板之间保持稳定，如图所示．若油滴获得了附加的负电荷，为了继续使油滴保持稳定，应采取下面哪个措施？(A) 使两金属板相互靠近些． (B) 改变两极板上电荷的正负极性． (C) 使油滴离正极板远一些． (D) 减小两板间的电势差．二、填空题0.4V/m 、向上 1、电荷为－5×10-9 C 的试验电荷放在电场中某点时，受到 20×10-9 N 的向下的力，则该点的电场强度大小为_________，方向_________．10q ε、120q q ε+ 2、电荷分别为q 1和q 2的两个点电荷单独在空间各点产生的静电场强分别为1E 和2E ，空间各点总场强为E ＝1E ＋2E ．现在作一封闭曲面S ，如图所示，则以下两式分别给出通过S 的电场强度通量⎰⋅S E d 1＝__________， ⎰⋅S E d ＝__________________．0、0/R r σε 3、一半径为R 的“无限长”均匀带电圆柱面，其电荷面密度为σ．该圆柱面内、外场强分布为(r 表示在垂直于圆柱面的平面上，从轴线处引出的矢径)：()r E ＝b3q 2 -- - +__ ___(r <R )， ()r E ＝_ _ ___(r >R )．0q ε、0、120q q ε+ 4、在点电荷＋q 和－q 的静电场中，作出如图所示的三个闭合面S 1、S 2、S 3，则通过这些闭合面的电场强度通量分别是：Φ1＝____，Φ2＝_____，Φ3＝____0、高斯面 5、如图，点电荷q 和－q 被包围在高斯面S 内，则通过该高斯面的电场强度通量⎰⋅S S E d ＝___________，式中E 为_____________处的场强．2130)1[]8q q q R πε+ 6、电荷分别为q 1，q 2，q 3的三个点电荷分别位于同一圆周的三个点上，如图所示．设无穷远处为电势零点，圆半径为R ，则b 点处的电势U ＝___ __ ．＜ 7、如图所示，在一个点电荷的电场中分别作三个电势不同的等势面A ，B ，C ．已知UU B ＞U C ，且U A －U B ＝U B －U C ，则相邻两等势面之间的距离的关系是：R B －R A ______ R C －R B ． (填＜，＝，＞)8、静电力作功的特点是_________________________________________________________，因而静电力属于__ ___力． ()22a r L -ρπ 9. 一“无限长”均匀带电的空心圆柱体，内半径为a ，外半径为b ，电荷体密度为ρ，若作一半径为r (a ＜r ＜b )、长度为L 的同轴圆柱形高斯柱面，则其中包含的电量q =_____________1：2 10、一质子和一α粒子进入到同一电场中，两者的加速度之比，a p ∶a α＝_______．静电场中的导体和电介质一、选择题(B) 1、如图所示，两同心导体球壳，内球壳带电荷+q ，外球壳带电荷-2q ．静电平衡时，外球壳的电荷分布为：内表面___________ ；外表面___________ ．(A) -q ，+q (B) -q ，-q (C) -2q ，0 (D) 0， -2q(D) 2、一空气平行板电容器，两极板间距为d ，充电后板间电压为U ．然后将电源断开，在两板间平行地插入一厚度为d /3的金属板，则板间电压变成U '=________________ ．(A) U 23 (B) U 31 (C) U 52 (D) U 32 二、填空题不变、减小 1、一平行板电容器充电后切断电源，若使二极板间距离增加，则二极板间场强__________，电容___________． (填增大或减小或不变)q/U 2.一个孤立导体，当它带有电荷q 而电势为U 时，则定义该导体的电容为C =___________，它是表征导体的____________的物理量．q 13恒定磁场一、选择题A 1、有一个圆形回路1及一个正方形回路2，圆直径和正方形的边长相等，二者中通有大小相等的电流，它们在各自中心产生的磁感强度的大小之比B 1 / B 2为(A) 0.90． (B) 1.00． (C) 1.11． (D) 1.22．D 2、通有电流I 的无限长直导线有如图三种形状，则P ，Q ，O 各点磁感强度的大小B P ，B Q ，B O 间的关系为： (A) B P > B Q > B O . (B) B Q > B P > B O ． (C) B Q > B O > B P ． (D) B O > B Q > B P ． B 3、一个电流元l I d 位于直角坐标系原点，电流沿z 轴方向，点P (x ，y ，z )的磁感强度沿x轴的分量是：(A) 0． (B) 2/32220)/(d )4/(z y x l Iy ++π-μ．(C) 2/32220)/(d )4/(z y x l Ix ++π-μ． (D) )/(d )4/(2220z y x l Iy ++π-μ．B 4.如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知 (A) 0d =⎰⋅L l B ，且环路上任意一点B = 0．(B) 0d =⎰⋅L l B ，且环路上任意一点B ≠0．(C) 0d ≠⎰⋅L l B ，且环路上任意一点B ≠0．(D) 0d ≠⎰⋅L l B ，且环路上任意一点B =常量． B 5、如图，两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I 从a 端流入而从d 端流出，则磁感强度B 沿图中闭合路径L 的积分⎰⋅L l B d 等于 (A) I 0μ． (B) I 031μ． (C) 4/0I μ． (D) 3/20I μ． D 6. A 、B 两个电子都垂直于磁场方向射入一均匀磁场而作圆周运动．A 电子的速率是B 电子速率的两倍．设R A ，R B 分别为A 电子与B 电子的轨道半径；T A ，T B 分别为它们各自的周期．则(A) R A ∶R B =2，T A ∶T B =2． (B) R A ∶R B 21=，T A ∶T B =1． (C) R A ∶R B =1，T A ∶T B 21=． (D) R A ∶R B =2，T A ∶T B =1． B 7、一电子以速度v 垂直地进入磁感强度为B 的均匀磁场中，此电子在磁场中运动轨道所围的面积内的磁通量将(A) 正比于B ，反比于v 2． (B) 反比于B ，正比于v 2．(C) 正比于B ，反比于v ． (D) 反比于B ，反比于v ．B 8. 有一矩形线圈AOCD ，通以如图示方向的电流I ，将它置于均匀a I I I a a a a 2aI P Q O I a L OI II a b c d L 120°v B y A D n磁场B 中，B 的方向与x 轴正方向一致，线圈平面与x 轴之间的夹角为α，α < 90°．若AO 边在y 轴上，且线圈可绕y 轴自由转动，则线圈将(A) 转动使α 角减小． (B) 转动使α角增大．(C) 不会发生转动． (D)如何转动尚不能判定．A 9、如图，无限长直载流导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将(A) 向着长直导线平移． (B) 离开长直导线平移．(C) 转动． (D) 不动．(B) 10. 电子在磁感应强度B=0.1T 的匀强磁场中沿圆周运动，电子运动形成的等效圆电流强度I=(A) A 191048.4-⨯ (B) A 101048.4-⨯ (C) A 81048.4-⨯ (D) A 121048.4-⨯ 二、填空题0、1：2 1.真空中有一载有稳恒电流I 的细线圈，则通过包围该线圈的封闭曲面S 的磁通量Φ=______．若通过S 面上某面元S d 的元磁通为d Φ，而线圈中的电流增加为2I 时,通过同一面元的元磁通为d Φ＇，则d Φ∶d Φ＇=_________________．/sin m f qv α 2.在非均匀磁场中，有一电荷为q 的运动电荷．当电荷运动至某点时，其速率为v ，运动方向与磁场方向间的夹角为α ，此时测出它所受的磁力为f m ．则该运动电荷所在处的磁感强度的大小为_________．磁力f m 的方向一定垂直___________． 04/R I πμ 3、在真空中，电流由长直导线1沿半径方向经a 点流入一由电阻均匀的导线构成的圆环，再由b 点沿切向从圆环流出，经长直导线2返回电源(如图)．已知直导线上的电流强度为I ，圆环半径为R ．a 、b 和圆心O 在同一直线上，则O 处的磁感强度B 的大小为__________________________． 4.在安培环路定理∑⎰⋅=i LI l B 0d μ 中，∑i I 是指___________ _______________________；B 是指_______________________________，它是由__________________________决定的．6.67×10-7 T7.20×10-7 A ·m 2 5.一质点带有电荷q =8.0×10-10 C ，以速度v =3.0×105 m ·s -1在半径为R =6.00×10-3 m 的圆周上，作匀速圆周运动．该带电质点在轨道中心所产生的磁感强度B =_____________，该带电质点轨道运动的磁矩p m =______________．(μ0 =4π×10-7 H ·m -1) 104 A ·m 2 6.电子以速率v =105 m/s 与磁力线成交角α =30°飞入匀强磁场中，磁场的磁感强度B = 0.2 T ，那么作用在电子上的洛伦兹力F =_______．(基本电荷e =1.6 ×10-19C)2Ia B 7、如图所示，一根通电流I 的导线，被折成长度分别为a 、b ，I夹角为 120°的两段，并置于均匀磁场B 中，若导线的长度为b 的一段与B 平行，则a ，b 两段载流导线所受的合磁力的大小为______________．0.036N 8. 一直导线放在B = 0.100 T 的均匀磁场中通以电流I = 2.00 A ，导线与磁场方向成120°角．导线上长 0.2 00m 的一段受的磁力f m =____________．30/B Ba μ9. 已知面积相等的载流圆线圈与载流正方形线圈的磁矩之比为2∶1，圆线圈在其中心处产生的磁感强度为B 0，那么正方形线圈(边长为a )在磁感强度为B 的均匀外磁场中所受最大磁力矩为____________．0.01m 90º 10. 在磁场中某点磁感强度的大小为 2.0 Wb/m 2，在该点一圆形试验线圈所受的最大磁力矩为6.28×10-6 N ·m ，如果通过的电流为10 mA ，则可知线圈的半径为____________m ，这时线圈平面法线方向与该处磁感强度的方向的夹角为__________________．电磁感应电磁场和电磁波一、选择题 A 1、一无限长直导体薄板宽为l ，板面与z 轴垂直，板的长度方向沿y 轴，板的两侧与一个伏特计相接，如图．整个系统放在磁感强度为B 的均匀磁场中，B 的方向沿z 轴正方向．如果伏特计与导体平板均以速度v 向y 轴正方向移动，则伏特计指示的电压值为(A) 0． (B) 21v Bl ． (C) v Bl ． (D) 2v Bl ． D 2、如图，长度为l 的直导线ab 在均匀磁场B 中以速度v 移动，直导线ab 中的电动势为 (A) Bl v ． (B) Bl v sin α． (C) Bl v cos α． (D) 0． C 3、有两个线圈，线圈1对线圈2的互感系数为M 21，而线圈2对线圈1的互感系数为M 12．若它们分别流过i 1和i 2的变化电流且t i t i d d d d 21>，并设由i 2变化在线圈1中产生的互感电动势为 12，由i 1变化在线圈2中产生的互感电动势为 21，判断下述哪个论断正确．(A) M 12 = M 21， 21 = 12． (B) M 12≠M 21， 21 ≠ 12．(C) M 12 = M 21， 21 > 12． (D) M 12 = M 21， 21 < 12．4、两根很长的平行直导线，其间距离d 、与电源组成回路如图．已知导线上的电流为I ，两根导线的横截面的半径均为r 0．设用L 表示两导线回路单位长度的自感系数，则沿导线单位长度的空间内的总磁能W m 为(A) 221LI ． (B) 221LI ⎰∞+π-+0d π2])(2π2[2002r r r r d I r I I μμB(C) ∞． (D) 221LI 020ln 2r d I π+μ （A ）5. 两根很长的平行直导线，其间距离为a ，与电源组成闭合回路，如图。