用一元二次方程解决几何图形问题含答案

合集下载

用一元二次方程解决几何图形问题含答案

用一元二次方程解决几何图形问题含答案用一元二次方程解决几何图形问题基础题知识点1：一般图形的问题1.绿苑小区在规划设计时，准备在两幢楼房之间设置一块面积为900平方米的矩形绿地，并且长比宽多10米。

设绿地的宽为x米，根据题意，可列方程为x(x+10)=900.2.从一块正方形的木板上锯掉2m宽的长方形木条，剩下的面积是48平方米，则原来这块木板的面积是64平方米。

3.一个直角三角形的两条直角边相差5cm，面积是7平方厘米，则它的两条直角边长分别为2cm和7cm。

4.一块矩形菜地的面积是120平方米，如果它的长减少2米，那么菜地就变成正方形，则原菜地的长是12米。

5.一个矩形周长为56厘米。

1) 当矩形面积为180平方厘米时，长、宽分别为18厘米和10厘米。

2) 不能围成面积为200平方厘米的矩形，因为方程y^2-28y+200=0无实数根。

知识点2：边框与甬道问题6.公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花，原空地一边减少了1米，另一边减少了2米，剩余空地的面积为18平方米。

求原正方形空地的边长，设原正方形空地的边长为x米，则可列方程为(x-1)(x-2)=18.7.在长为100米，宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644平方米，则道路的宽应为22米，因为可列方程为100×80-100x-80x=7644.10.某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2.设道路的宽为x m，则草坪的面积为(32-2x)(20-x)，因此正确的方程是A：(32-2x)(20-x)=570.11.在长为70 m，宽为40 m的长方形花园中，欲修宽度相等的观赏路(阴影部分所示)，要使观赏路面积占总面积的1/8，则路宽x应满足的方程是C：(40-2x)(70-3x)=2450.。

北师版九年级数学上册第二章一元二次方程应用一元二次方程第1课时利用一元二次方程解决几何问题

12．如图，已知一艘轮船以 20 海里/时的速度由西向东航行，途中接到台风警报，台风中心正以 40 海里/时的速度由南向北移动，距台风中心 20 10 海里的圆形区域(包括边界)都属台风区．当轮船航行到 A 处时，测得台风中心移到位于点 A 正南方向的 B 处，且 AB＝100 海里，若这艘轮船自 A 处按原速度继续航行，在途中会不会遇到台风？若会，试求经过多长时间轮船最初遇到台风；若不会，＝90°，AB＝5 cm，BC＝7 cm，点P 从点A开始沿AB边向点B以1 cm/s的速度移动，同时点Q从点B开始沿 BC边向点C以2 cm/s的速度移动，当其中一点到达终点时，另外一点也随之停止． (1)几秒后，△PBQ的面积等于4 cm2? (2)几秒后，PQ的长度等于5 cm? (3)△PBQ的面积能否等于7 cm2?
4．(2020·西藏)列方程(组)解应用题某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为600 m2的矩形试验茶园，便于成功后大面积推广．如图所示，茶园一面靠墙，墙长35 m，另外三面用69 m长的篱笆围成，其中一边开有一扇1 m宽的门(不包括篱笆).求这个茶园的长和宽．
知识点二：用一元二次方程解决动态几何图形问题 5．如图，AB⊥CB，AB＝10 cm，BC＝8 cm，一只螳螂从A点出发，以2 cm/s的速度向B爬行，与此同时，一只蝉从C点出发，以1 cm/s的速度向B爬行，当螳螂和蝉爬行x s后，它们分别到达了点M，N的位置，此时，△MNB的面积恰好为24 cm2，根据题意可得方程( D )
A.2x·x＝24 B．(10－2x)(8－x)＝24 C．(10－x)(8－2x)＝24 D．(10－2x)(8－x)＝48
6．(教材 P53 习题 2.9T2 变式)如图，在矩形 ABCD 中，AB＝6 厘米，BC＝12 厘米，点 P 从点 A 开始沿 AB 边向点 B 以 1 厘米/秒的速度移动(到点 B 终止)，点 Q 从点 B 开始沿 BC 边向点 C 以 2 厘米/秒的速度移动(到点 C 终止)，若两

2023年九年级数学中考复习一元二次方程的应用几何图形变换面积问题常考题型专题训练

2022-2023学年九年级数学中考复习一元二次方程的应用《几何图形变换+面积问题》常考题型专题训练（附答案）1．如图，一个长为acm，宽为bcm的矩形铁片．（1）如果a＝30，b＝20，在矩形的中央挖掉一个200cm2的矩形后，成为一个各条边一样宽的铁框，求这个铁框的宽度；（2）如果a＝2b，在四个角上分别裁掉四个边长为4cm的正方形，把它制作成一个体积为4576cm3的无盖长方体，求原矩形的面积．2．如图，用一面足够长的墙为一边，其余三边用总长36米的围栏建两个面积相同的生态园，由于场地限制，垂直于墙的一边长不超过6米．（围栏宽忽略不计）（1）每个生态园的面积为48平方米，求每个生态园的边长；（2）每个生态园的面积能否达到60平方米？请说明理由．3．为庆祝中国共产党成立100周年，某市举办了“学党史感党恩跟党走”建党100周年文艺汇演主题活动，活动前，主办方工作人员准备利用一面墙（墙的最大可利用长度为26米）作为一边，用48米隔栏绳作为另三边，设立一个面积为300平方米的矩形表演区，如图，为了方便进出，在两边空出两个各为1米的出入口（出入口不用隔栏绳），那么围成的这个矩形ABCD的长与宽分别是多少米呢？4．将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．（1）要使这两个正方形的面积之和等于17cm2，那么这段铁丝剪成两段后的长度分别是多少？（2）两个正方形的面积之和是否存在最小值？若存在，请求出最小值及此时两段铁丝的长度；若不存在，请说明理由．5．如图，一个边长为8m的正方形花坛由4块全等的小正方形组成．在小正方形ABCD中，点G，E，F分别在CD，AD，AB上，且DG＝1m，AE＝AF＝x，在△AEF，△DEG，五边形EFBCG三个区域上种植不同的花卉，每平方米的种植成本分别是20元、20元、10元．（1）当x＝2时，小正方形ABCD种植花卉所需的费用；（2）试用含有x的代数式表示五边形EFBCG的面积；（3）当x为何值时，大正方形花坛种植花卉所需的总费用是715元？6．学校准备利用操场开元旦晚会，师生坐在足球场区域，已知足球场宽度为72m（观众席不一定要占满球场宽度），其他三边利用总长为140m的移动围栏围成一个矩形的观众席，并在观众席内按行、列，摆放单人座椅，要求每个座位占地面积为1m2（如图所示），且观众席内的区域恰好都安排了座位．（1）若观众席内有x行座椅，用含x的代数式表示每行的座椅数，并求x的最小值；（2）若全校师生共2400人，那么座位够坐吗？请说明理由．7．某牧场准备利用现成的一堵“7”字形的墙面（粗线A﹣B﹣C表示墙面）建饲养场，已知AB⊥BC，AB＝3米，BC＝15米，现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF，并在每个区域开一个宽2米的门，如图（细线表示篱笆，饲养场中间用篱笆GH隔开），点F可能在线段BC上，也可能在线段BC的延长线上．（1）如图1，当点F在线段BC上时，①设EF的长为x米，则DE＝米；（用含x的代数式表示）②若围成的饲养场BDEF的面积为132平方米，求饲养场的宽EF的长；（2）如图2，当点F在线段BC延长线上，所围成的饲养场BDEF的面积能否为156平方米？如果能达到，求出EF的长；如果不能，请说明理由．8．如图①，某校进行校园改造，准备将一块正方形空地划出部分区域栽种鲜花，原空地一边减少了4m，另一边减少了5m，剩余部分面积为650m2．（1）求原正方形空地的边长；（2）在实际建造时，从校园美观和实用的角度考虑，按图②的方式进行改造，先在正方形空地一侧建成1m宽的画廊，再在余下地方建成宽度相等的两条小道后，其余地方栽种鲜花，如果栽种鲜花区域的面积为812m2，求小道的宽度．9．如图，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点D从点C开始沿CA边运动，速度为1cm/s，与此同时，点E从点B开始沿BC边运动，速度为2cm/s，当点E到达点C时，点D同时停止运动，连接AE，设运动时间为ts，△ADE的面积为S．（1）是否存在某一时刻t，使DE∥AB？若存在，请求出此时刻t的值，若不存在，请说明理由．（2）点D运动至何处时，S＝S△ABC？10．如图，在矩形ABCD中、AB＝15cm，AD＝5cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到点B为止，点Q以2cm/s的速度向点D移动（点P停止移动时，点Q也停止移动）．设移动时间为t（s）．连接PQ，QB．（1）当t为何值时，P、Q两点间的距离为13cm？（2）四边形APQD的形状可能为矩形吗？若可能，求出t的值；若不可能，请说明理由．11沿AC向点C方向运动，动点Q从点C出发，沿线段CB向点B方向运动．如果点P的速度是4cm/s，点Q的速度是2cm/s，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动的时间为ts，求：（1）用含t的代数式表示Rt△CPQ的面积S；（2）当t＝3秒时，这时，P、Q两点之间的距离是多少？（3）当t为多少秒时，S＝S△ABC？12．如图，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动．（1）如果P，Q同时出发，几秒钟后，可使PQ的长为4厘米？（2）点P，Q在移动过程中，是否存在某一时刻，使得△PCQ的面积等于△ABC的面积的一半．若存在，求出运动的时间；若不存在，说明理由．13．如图A，B，C，D为矩形的四个顶点，AB＝16cm，AD＝6cm，动点P，Q分别从点A，C同时出发，点P以3cm/s的速度向点B移动，一直到达B点为止，点Q以2m/s的速度向D点移动，当点P到达B点时点Q随之停止运动．（1）AP＝，BP＝，CQ＝，DQ＝（用含t的代数式表示）；（2）t为多少时，四边形PBCQ的面积为33cm2；（3）t为多少时，点P和点Q的距离为10cm．14．如图，在△ABC中，∠B＝90°，AB＝6厘米，BC＝8厘米．点P从A点开始沿AB边向点B以1厘米/秒的速度移动（到达点B即停止运动），点Q从B点开始沿BC边向点C以2厘米/秒的速度移动（到达点C即停止运动）．（1）如果P、Q分别从A、B两点同时出发，经过几秒钟，△PBQ的面积等于△ABC的三分之一？（2）如果P、Q两点分别从A、B两点同时出发，而且动点P从A点出发，沿AB移动（到达点B即停止运动），动点Q从B出发，沿BC移动（到达点C即停止运动），几秒钟后，P、Q相距6厘米？15．已知：如图，△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t（s），解答下列各问题：（1）经过秒时，求△PBQ的面积；（2）当t为何值时，△PBQ是直角三角形？（3）是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？如果存在，求出t的值；不存在请说明理由．16．如图，已知矩形ABCD的边长AB＝3cm，BC＝6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s 的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时间t，使△AMN的面积达到3.5cm2？若存在，求出时间t；若不存在，说明理由．17．在Rt△ABC中，AC＝6cm，BC＝8cm，点P从A点出发以每秒1个单位长的速度向C 点移动，点Q从C点出发以每秒2个单位长的速度向点B移动，点P、Q分别从起点同时出发，移动到某一位置所用的时间为t秒（1）当时间t＝3时，求线段PQ的长；（2）当移动时间t等于何值时，△PCQ的面积为8cm2？（3）点D为AB的中点，连接CD，移动P、Q能否使PQ、CD互相平分？若能，求出点P、Q移动时间t的值；若不能，请说明理由．18．如图，AO＝BO＝6厘米，OC是一条射线，OC⊥AB．一动点P从点A以1厘米/秒的速度向点B爬行，另一动点Q从点O以2厘米/秒的速度沿射线OC方向爬行，它们同时出发，当点P到达B点时点Q也停止运动．设运动时间为t秒．（1）直接写出OQ＝（用t的代数式）．（2）经过多少秒，△POQ的面积为8平方厘米．（3）当t＝时，△PBQ为等腰三角形（直接写出答案）19．如图，Rt△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，一动点P从点A出发沿边AC 向点C以1cm/s的速度运动，另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动．问：（1）运动几秒时，△CPQ的面积是8cm2？（2）运动几秒时，△CPQ与△ABC相似？20．在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发，沿AB边向点B以1cm/秒的速度移动，同时，点Q从点B出发沿BC边向点C以2cm/秒的速度移动．如果P、Q 两点在分别到达B、C两点后就停止移动，回答下列问题：（1）运动开始后第几秒时，△PBQ的面积等于8cm2？（2）设运动开始后第t秒时，五边形APQCD的面积为Scm2，写出S与t的函数关系式，并指出自变量t的取值范围；写出t为何值时，s的值最小．（3）当t＝时，试判断△DPQ的形状．（4）计算四边形DPBQ的面积，并探索一个与计算结果有关的结论．参考答案1．解：（1）设这个铁框的宽度为xcm，根据题意可得：（30﹣2x）（20﹣2x）＝200，解得：x1＝5，x2＝20（不合题意舍去），答：这个铁框的宽度为5cm；（2）由题意可得：4（a﹣8）（b﹣8）＝4576，则4（2b﹣8）（b﹣8）＝4576，解得：b1＝30，b2＝﹣18（不合题意舍去），则a＝30×2＝60（cm），故ab＝30×60＝1800（cm2），答：原矩形的面积为1800cm2．2．解：（1）设垂直于墙的一边长为x米，则平行于墙的一边长为米，根据题意得：x•＝48，整理得：x2﹣12x+32＝0，解得：x1＝4，x2＝8（不符合题意，舍去），∴＝＝12．答：每个生态园的长为12米，宽为4米．（2）每个生态园的面积不能达到60平方米，理由如下：设垂直于墙的一边长为y米，则平行于墙的一边长为米，根据题意得：y•＝60，整理得：y2﹣12y+40＝0，∵Δ＝（﹣12）2﹣4×1×40＝﹣16＜0，∴该方程没有实数根，即每个生态园的面积不能达到60平方米．3．解：设垂直于墙的一边长为x米，则平行于墙的一边长为（48+2﹣2x）米，根据题意得：x（48+2﹣2x）＝300，整理得：x2﹣25x+150＝0，解得：x1＝10，x2＝15，当x＝10时，48+2﹣2x＝48+2﹣2×10＝30＞26，不符合题意，舍去；当x＝15时，48+2﹣2x＝48+2﹣2×15＝20＜26，符合题意．答：围成的这个矩形ABCD的长为20米，宽为15米．4．解：（1）设其中一段铁丝长为xcm（0＜x≤10），则另一段铁丝长为（20﹣x）cm，根据题意得：（）2+（）2＝17，整理得：x2﹣20x+64＝0，解得：x1＝4，x2＝16（不符合题意，舍去），∴20﹣x＝20﹣4＝16．答：这段铁丝剪成两段后的长度分别是4cm，16cm．（2）设其中一段铁丝长为acm（0＜a≤10），则另一段铁丝长为（20﹣a）cm，两个正方形的面积之和为wcm2，根据题意得：w＝（）2+（）2，即w＝（a﹣10）2+，∵＞0，∴当a＝10时，w取得最小值，此时20﹣a＝20﹣10＝10，答：两个正方形的面积之和存在最小值，此时两段铁丝的长度均为10cm．5．解：（1）若x＝2，则DE＝2，∴S△AEF＝AE×AF＝2，S△DFG＝DG×DF＝×1×2＝1，∴S五边形EFBCG＝S正方形ABCD﹣S△AEF﹣S△DFG＝16﹣×4﹣2+×1＝13．∴所需费用为：20×2+20×1+10×13＝190（元）；（2）设AE＝AF＝x米，则DF＝（4﹣x）米．∴S△AEF＝AE×AF＝x2，S△DFG＝DG×DF＝×1×（4﹣x）＝2﹣x，∴S五边形EFBCG＝S正方形ABCD﹣S△AEF﹣S△DFG＝16﹣x2﹣2+x＝﹣x2+x+14，（3）根据题意得4×[20×x2+20×（2﹣x）+10×（﹣x2+x+14）]＝715，整理得4x2﹣4x+1＝0，解得x1＝x2＝．答：当AE＝AF＝米时，正方形花坛种植花卉所需的总费用是715元．6．解：（1）∵移动围栏的总长为140m，且观众席内有x行座椅，∴每行的座椅数为（140﹣2x）个．∵140﹣2x≤72，∴x≥34，∴x的最小值为34．（2）座位够坐，理由如下：依题意得：x（140﹣2x）＝2400，整理得：x2﹣70x+1200＝0，解得：x1＝30（不符合题意，舍去），x2＝40，∴若全校师生共2400人，那么座位够坐．7．解：（1）①设EF的长为x米，则DE＝38+2+2﹣（3x﹣3）＝（45﹣3x）（米）．故答案为：（45﹣3x）．②依题意得：x（45﹣3x）＝132，整理得：x2﹣15x+44＝0，解得：x1＝4，x2＝11．当x＝4时，45﹣3x＝45﹣3×4＝33＞15，不合题意，舍去；当x＝11时，45﹣3x＝45﹣3×11＝12＜15，符合题意．答：饲养场的宽EF的长为11米．（2）不能达到，理由如下：设EF的长为y米，则DE＝＝米，依题意得：y•＝156，整理得：y2﹣20y+104＝0，∵Δ＝（﹣20）2﹣4×1×104＝﹣16＜0，∴该方程没有实数根，即当点F在线段BC延长线上，所围成的饲养场BDEF的面积不能达到156平方米．8．解：（1）设原正方形空地的边长为xm，则剩余部分长（x﹣4）m，宽（x﹣5）m，依题意得：（x﹣4）（x﹣5）＝650，整理得：x2﹣9x﹣630＝0，解得：x1＝30，x2＝﹣21（不合题意，舍去）．答：原正方形空地的边长为30m．（2）设小道的宽度为ym，则栽种鲜花的区域可合成长（30﹣y）m，宽（30﹣1﹣y）m 的矩形，依题意得：（30﹣y）（30﹣1﹣y）＝812，整理得：y2﹣59y+58＝0，解得：y1＝1，y2＝58（不合题意，舍去）．答：小道的宽度为1m．9．解：（1）存在，理由如下：假设存在某一时刻t，使DE∥AB，∴＝，∵AC＝6，BC＝8，CD＝t，CE＝8﹣2t，∴＝，∴t＝，符合题意（t最大为8÷2＝4秒），∴存在某一时刻t＝秒，使DE∥AB；（2）设运动t秒时，S＝S△ABC，根据图示可知，S＝S△ACE﹣S△DCE＝S△ABC，∵S△ABC＝AC•CB＝×6×8＝24平方厘米，S△ACE＝AC•CE＝×6×（8﹣2t）＝（24﹣6t）平方厘米，S△DCE＝CD•CE＝t（8﹣2t）＝（4t﹣t2）平方厘米，∴S＝（24﹣6t）﹣（4t﹣t2）＝24﹣6t﹣4t+t2＝（t2﹣10t+24）平方厘米，∴S＝S△ABC，∴t2﹣10t+24＝×24，解一元二次方程得：t1＝7，t2＝3，∵点E到达点C时，点D同时停止运动，在整个运动过程中0≤t≤4，∴t＝3秒符合题意，∴此时CD＝3（cm），∴CD＝3cm时，S＝S△ABC．10．解：（1）设出发t秒后P、Q两点间的距离是13cm．则AP＝3t，CQ＝2t，作QM⊥AB于M，则PM＝|15﹣2t﹣3t|＝|15﹣5t|，（15﹣5t）2+52＝132，解得：t＝0.6或t＝5.4，答：P、Q出发0.6和5.4秒时，P，Q间的距离是13cm；（2）四边形APDQ的形状有可能为矩形；理由：当四边形APQD为矩形，则AP＝DQ，即3t＝15﹣2t，解得：t＝3．答：当P、Q出发3秒时四边形APQD为矩形．11．解：（1）若运动的时间为ts，则CP＝（20﹣4t）cm，CQ＝2tcm，∴S＝CP•CQ＝（20﹣4t）×2t＝20t﹣4t2．又∵，∴0≤t≤5．∴Rt△CPQ的面积S＝20t﹣4t2（0≤t≤5）．（2）当t＝3时，CP＝20﹣4t＝20﹣4×3＝8（cm），CQ＝2t＝2×3＝6（cm），∴PQ＝＝＝10（cm）．（3）依题意得：20t﹣4t2＝××15×20，整理得：t2﹣5t+6＝0，解得：t1＝2，t2＝3．∴t为2或3时，S＝S△ABC．12．解：（1）设x秒钟后，可使PQ的长为4cm，由题意得：（6﹣x）2+（2x）2＝（4）2，解得：x＝2或x＝，答：P、Q同时出发2或秒钟后，可使PQ的长为4厘米；（2）不存在．理由：设y秒时，△PCQ的面积等于△ABC的面积的一半，由题意得：（6﹣y）•2y＝×6×8，整理，得y2﹣6y+12＝0，∵Δ＝36﹣4×12＜0，∴方程无解，即：不存在．13．解：（1）当运动时间为ts时，AP＝3tcm，BP＝（16﹣3t）cm，CQ＝2tcm，DQ＝（16﹣2t）cm．故答案为：3tcm；（16﹣3t）cm；2tcm；（16﹣2t）cm．（2）依题意得：[（16﹣3t）+2t]×6＝33，整理得：16﹣t＝11，解得：t＝5.答：当t为5时，四边形PBCQ的面积为33cm2．（3）过点Q作QE⊥AB于点E，则PE＝|（16﹣3t）﹣2t|＝|16﹣5t|，如图所示．依题意得：|16﹣5t|2+62＝102，即（16﹣5t）2＝82，解得：t1＝，t2＝．答：当t为或时，点P和点Q的距离为10cm．14．解：（1）设t秒后，△PBQ的面积等于△ABC的三分之一，根据题意得：×2t（6﹣t）＝××6×8，解得：t＝2或4．答：2秒或4秒后，△PBQ的面积等于△ABC的三分之一．（2）设x秒时，P、Q相距6厘米，根据题意得：（6﹣x）2+（2x）2＝36，解得：x＝0（舍去）或x＝．答：秒时，P、Q相距6厘米．15．解：（1）经过秒时，AP＝cm，BQ＝cm，∵△ABC是边长为3cm的等边三角形，∴AB＝BC＝3cm，∠B＝60°，∴BP＝3﹣＝cm，∴△PBQ的面积＝BP•BQ•sin∠B＝×××＝；（2）设经过t秒△PBQ是直角三角形，则AP＝tcm，BQ＝tcm，△ABC中，AB＝BC＝3cm，∠B＝60°，∴BP＝（3﹣t）cm，△PBQ中，BP＝（3﹣t）cm，BQ＝tcm，若△PBQ是直角三角形，则∠BQP＝90°或∠BPQ＝90°，当∠BQP＝90°时，BQ＝BP，即t＝（3﹣t），t＝1（秒），当∠BPQ＝90°时，BP＝BQ，3﹣t＝t，t＝2（秒），答：当t＝1秒或t＝2秒时，△PBQ是直角三角形．（3）过P作PM⊥BC于M，△BPM中，sin∠B＝，∴PM＝PB•sin∠B＝（3﹣t），∴S△PBQ＝BQ•PM＝•t•（3﹣t），∴y＝S△ABC﹣S△PBQ＝×32×﹣×t×（3﹣t）＝t2﹣t+，∴y与t的关系式为y＝t2﹣t+，假设存在某一时刻t，使得四边形APQC的面积是△ABC面积的，则S四边形APQC＝S△ABC，∴t2﹣t+＝××32×，∴t2﹣3t+3＝0，∵（﹣3）2﹣4×1×3＜0，∴方程无解，∴无论t取何值，四边形APQC的面积都不可能是△ABC面积的．16．解：（1）设经过ts，△AMN的面积等于矩形ABCD面积的，则DN＝2tcm，AM＝tcm，AN＝AD﹣DN＝（6﹣2t）cm，∴AN•AM＝AD•AB，即（6﹣2t）t＝×6×3，整理得：t2﹣3t+2＝0，即（t﹣1）（t﹣2）＝0，解得：t1＝1，t2＝2，则经过1s或2s，△AMN的面积等于矩形ABCD面积的；（2）不存在，理由为：假设存在时间ts，使△AMN的面积达到3.5cm2，则AN•AM＝3.5，整理得：2t2﹣6t+7＝0，∵Δ＝36﹣56＝﹣20＜0，∴方程没有实数根，则△AMN的面积不能达到3.5cm2．17．解：（1）∵AP＝t，CQ＝2t，∴t＝3时，AP＝3，CQ＝6，∴PC＝6﹣3＝3在Rt△PCQ中，由勾股定理，得PQ＝＝3．答：PQ＝3；（2）∵AP＝t，CQ＝2t，∴PC＝6﹣t．∴（6﹣t）×2t＝8，解得：t1＝2，t2＝4．（3）PQ、CD不互相平分．当PQ、CD互相平分，∴四边形PCQD是平行四边形，∴PD∥CQ．PD＝CQ．∵点D为AB的中点，∴P是AC的中点，∴AP＝AC＝3，PD＝CQ＝BC＝4．∴t＝≠．∴PQ、CD不互相平分．18．解：（1）由函数图象，得OQ＝2t，故答案为：2t；（2）当P在AO上，，解得：t1＝2，t2＝4．∵t1＝2，t2＝4在0＜t＜6范围内，∴t1＝2，t2＝4．P在BO上，＝8，解得：t3＝3+，t4＝3﹣．∵t3＝3+在6＜t＜12范围内，∴t3＝3+；（3）在Rt△BOQ中，由勾股定理，得BQ2＝4t2+36，BP＝12﹣t，BP2＝144﹣24t+t2，∵△PBQ是等腰三角形，∴PB＝BQ，∴PB2＝BQ2，∴4t2+36＝144﹣24t+t2，解得：t1＝﹣4+2，t2＝﹣4﹣2（舍去）．当PB＝PQ时，BP2＝144﹣24t+t2，PQ2＝4t2+（6﹣t）2，t1＝，t2＝（舍去）．故答案为：﹣4+2或．19．解：（1）设x秒后，可使△CPQ的面积为8cm2．由题意得，AP＝xcm，PC＝（6﹣x）cm，CQ＝2xcm，则（6﹣x）•2x＝8，整理，得x2﹣6x+8＝0，解得x1＝2，x2＝4．则P、Q同时出发，2秒或4秒后可使△CPQ的面积为8cm2（2）设运动y秒时，△CPQ与△ABC相似．若△CPQ∽△CAB，则＝，即＝，解得y＝2.4秒；若△CPQ∽△CBA，则＝，即＝，解得y＝秒．综上所述，运动2.4秒或秒时，△CPQ与△ABC相似．20．解：（1）设经过t秒，△PBQ的面积等于8cm2则：BP＝6﹣t，BQ＝2t，所以S△PBQ＝×（6﹣t）×2t＝8，即t2﹣6t+8＝0，可得：t＝2或4，即经过2秒或4秒，△PBQ的面积等于8cm2．（2）根据（1）中所求出的S△PBQ＝PB•BQ＝×（6﹣t）×2t，整理得S△PBQ＝﹣t2+6t（0＜t＜6）．则S五边形APQCD＝S矩形ABCD﹣S△PBQ＝72﹣（﹣t2+6t）＝t2﹣6t+72＝（t﹣3）2+63（0＜t ＜6），当t＝﹣＝3时，S五边形APQCD＝63，故当t＝3秒，五边形APQCD的面积最小，最小值是63cm2，（3）当t＝1.5s时，AP＝1.5，BP＝4.5，CQ＝9，∴DP2＝146.25，PQ2＝29.25，DQ2＝117，∴PQ2+DQ2＝DP2，∴△DPQ为Rt△；（4）S DPBQ＝6×12﹣t×12﹣×6（12﹣2t），＝72﹣36，＝36，∴四边形DPBQ的面积是固定值36．。

一元二次方程解决几何图形问题

如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米，面积为S米2，（1）求S与x的函数关系式;（2）如果要围成面积为45米2的花圃，AB的长是多少米？
解：(1)设宽AB为x米，则BC为(24-3x)米，
S=x(24-3x)=-3x2+24x (2)由题意得 -3x2+24x=45
解：(1)设AB长为x米，则BC为(40-2x)米，得
x (40-2x) = 128
解：(1)设AB长为x米，则BC为(40-2x)米，得
x (40-2x) = 128 2x2-40x+128=0
x2-20x+64=0 解得x1=4，x2=16 当x1=4 时，40-2x=32>15，（舍去）当x2=16 时，40-2x=8<15。答：花圃的宽AB为16米
要设计一本书的封面,封面长27 ㎝,宽21㎝,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
解：设上、下边衬的宽均为9x cm，左、右边衬的宽均为7x cm.则中央矩形的长为（27-18x) cm，宽为（21-14x）cm，由题意得
(27-18x)(21-14x)=
3 4
27 21
整理，得
16x2-48x+9=0
解得 x 1

63 4
3
（舍去3
上、下边衬的宽均为_____cm,左、右边衬的宽均为_____cm.
方程的哪一个根更符合实际
意义？为什么？
如果换一种设未知数的方法，是否可以更简单的解决上面

一元二次方程解决几何问题

一元二次方程解决几何问题
一元二次方程是一种形式为ax^2 + bx + c = 0的方程，其中a、b和c是实数，而x是未知数。

它可以用于解决许多几何问题，如以下几个例子：
1. 高度和时间问题：假设一颗物体从一个高度h开始自由下落，利用物体的自由落体运动公式可以得到一个关于时间t的二次方程，通过解方程可以确定物体落地的时间点。

2. 路程和时间问题：假设一个物体以某个速度v在直线上运动，利用物体的匀速运动公式可以得到一个关于时间t的一次方程，通过解方程可以确定物体达到某个距离的时间点。

3. 面积问题：对于某些几何图形，如矩形、正方形和圆等，可以通过设定面积为某个值的条件，建立相应的二次方程来求解图形的尺寸。

这只是一些常见的例子，实际上，一元二次方程在几何问题中具有广泛的应用。

一元二次方程应用题(几何图形面积问题)

解题思路
假设长方形的长为l，宽为w，通过列方程建立方程组，然后求解得出面积。
解答与解析
通过解方程组，得出长方形的长、宽和面积的具体数值，详细解析计算过程和答案。
实例3 ：三角形面积问题
问题提出
已知直角三角形的斜边长度为c，某一直角边的长度为a，求三角形的面积。
解题思路
根据已知条件，利用勾股定理和三角形面积公式建立方程，然后求解得出面积。
一元二次方程应用题(几何图形面积问题)
本演示将介绍一元二次方程的应用，特别是在解决几何图形面积问题时的应用。通过精彩的实例和深入的讲解，帮助你全面理解和掌握这一知识点。
一元二次方程介绍
简要介绍一元二次方程的概念、形式和解法方法，以及元二次方程解决几何图形的面积问题，通过代入、求解方程，计算各种图形的面积。
解答与解析
通过解方程和应用三角形面积公式，得出三角形的面积的具体数值，详细解析计算过程和答案。
总结与实践建议
总结一元二次方程在解决几何图形面积问题中的应用要点，并提供一些建议和实践步骤，以帮助你更好地掌握这一知识。
实例1：正方形面积问题
1
问题提出
给定正方形的对角线长度为d，求正方形的面积。
2
解题思路
假设正方形的边长为x，利用勾股定理建立方程，然后求解得出面积。
3
解答与解析
通过解方程，得出正方形的边长和面积的具体数值，详细解析计算过程和答案。
实例2 ：长方形面积问题
问题提出
已知长方形的周长为P，求长方形的面积。

列一元二次方程解几何图形问题

列一元二次方程解几何图形问题代数、几何的综合题一直是中考的热点，用代数方法解几何问题，是初中数学的一种重要思想.在解几何题时，如果能根据几何问题中的数量关系，恰当地建立一元二次方程模型，并借助一元二次方程的相关知识来求解，定能收到事半功倍的效果.下面举例说明.一、利用勾股定理建立一元二次方程模型例1.（深圳中考题）在△ABC 中，AB 边上的中线CD=3，AB=6，BC+AC=8，则△ABC 的面积为______________________.分析：对于本题，先画出图形，判断出△ABC 为直角三角形后，再利用勾股定理建立一元二次方程模型求边长.解：如图，在△ABC 中，CD 是AB 边上的中线，∵ CD=3，AB=6，∴AD=BD=3，∴CD=AD=BD.∴∠A=∠ACD ，∠B=∠BCD.∵∠A ＋∠B ＋∠ACD ＋∠BCD=180°.∴∠A ＋∠B=90°.∴△ABC 为直角三角形，∴AC 2＋BC 2=AB 2=36.又∵BC+AC=8，∴设BC 的长为x ，则8AC x =-.∴22(8)36x x -+=，整理，得28140x x -+=.解得4x =.∴4BC =，4AC =或4BC =，4AC =. ∴12ABC S BC ∆=·1(472AC =+=. 说明：本题主要考查直角三角形中线的有关性质、一元二次方程的相关知识以及综合分析、解答问题的能力.二、利用面积公式建立一元二次方程模型例2. （辽宁十一市中考题）如图，在宽为20m ，长为32m 的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为2540m ，求道路的宽．（部分参考数据：2321024=，2522704=，2482304=）分析：本题是一道典型的列一元二次方程解决的实际应用问题.下面从两个角度给出如下的解法.解法（1）：由题意转化为右图，设道路宽为x 米.根据题意，可列出方程为()()2032540x x --=.整理得2521000x x -+=.解得150x =（舍去），22x =.答：道路宽为2米.解法（2）：由题意转化为右图，设道路宽为x 米，根据题意列方程得： ()220322032540x x ⨯-++=.整理得：2521000x x -+=.解得：12x =，250x =（舍去）.答：道路宽应是2米.说明：把不规则的图形转化为规则的图形是解决这类问题的关键所在，同时整体代换的思想方法在解题中起着化难为易的作用，同学们应该既能理解它，又会应用它.。

一元二次方程应用题(几何图形面积问题)

解:设道路宽为x米，则
(32 2x)(20 2x) 570 化简得，x2 36x 35 0
(x 35)(x 1) 0 x1 35, x2 1
其中的 x=35超出了原矩形的宽，应舍去.
答:道路的宽为1米.
例3. (2003年,舟山)如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米，面积为S米2，（1）求S与x的函数关系式;（2）如果要围成面积为 45米2的花圃，AB的长是多少米？
例1. 镜框有多宽?
一块四周镶有宽度相等的花边的镜框如下图，它的长为8m，宽为5m．如果镜框中央长方形图案的面积为 18m2 ，则花边多宽? 解：设镜框的宽为xm ，则镜框中央长方形图案的长为（8－2x）m, 宽为（5－2x） m,得
8
x
x
x
（8－2x）
5
１８m2
x
例1. 镜框有多宽?
一块四周镶有宽度相等的花边的镜框如下图，它的
例2：在一块长80米，宽60米的运动场外围修筑了一条宽度相等的跑道，这条跑道的面积是1500平方米，求这条跑道的宽度。
列一元二次方程解应题
补充练习： 1、（98年北京市崇文区中考题）如图，有一面积是150平方米的长方形鸡场，鸡场的一边靠墙（墙长18米），墙对面有一个2米宽的门，另三边（门除外）用竹篱笆围成，篱笆总长33米．求鸡场的长和宽各多少米？
例1 在矩形ABCD中,AB=6cm,BC=12cm, 点P从点A开始以1cm/s的速度沿AB边向点 B移动,点Q从点B开始以2cm/s的速度沿BC 边向点C移动,如果P、Q分别从A、B同时出发，几秒后⊿ PBQ的面积等于8cm2？

一元二次方程的应用(第3课时图形(行程)问题)

点,岛上有一个补给码头;小岛F位于BC的中点.一艘军舰从A出发,经B到C
匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批
物品送达军舰.
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与 A
北
补给船相遇于E处,那么相遇时补给船航行了多少海里？ (结果
D
精确到0.1 n mile )
根据题意，得
1 (8 x)(6 x) 1 1 8 6.
A
2
22
整理得 : x2 14x 24 0.
P
8m
解这个方程,得 :
x1 2; x2 12(不合题意,舍去).
答：2秒后，△ PCQ的面积是Rt △ABC面积的
C
Q
6m
B
一半.
随堂训练
1. 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从 A、B同时出发，几秒后⊿ PBQ的面积等于8cm2？
解：设x秒后⊿ PBQ的面积等于8cm2
根据题意，得
1 2x (6 x) 8 2
整理，得
x2 6x 8 0
解这个方程，得
x1 2, x2 4
0 x 6 ，∴2秒或4秒后⊿ PBQ的面积等于8cm2.
2.等腰直角⊿ ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点 P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?
解：设AP=x，则PR=x，PB=8-x
根据题意得：x8-x 16
整理得：x2 8x 16 0 解这个方程得：x1 x2 4 答：当AP 4cm时，四边形面积为16cm2

第3课时用一元二次方程解决几何图形问题

类型二:围成图形面积问题
例2 如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
(1)若墙长为18米,要围成鸡场的面积为150平方米,则鸡场的长和宽各为多少米? (2)围成鸡场的面积可能达到200平方米吗?
解:(1)设宽为 x 米,则 x(33-2x+2)=150,
第3课时用一元二次方程解决几何图形问题
1.规则几何图形面积问题:利用对应图形的面积计算公式建立一元二次方程的数学模型. 2.不规则几何图形面积问题:利用平移或割补的方法,将不规则几何图形面积问题转化为规则几何图形面积的和或差求解.
类型一:边框与甬道问题
例1 如图所示,在长为32 m、宽20 m的矩形耕地上,修筑同样宽的三条道路(两条纵向, 一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块作试验田,要使试验田面积为570 m2,问道路应多宽?
x cm,根据题意所列方程为
(60+2x)(40+2x)×54%=60×40
.
3.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
解:设AB=x,则BC=100-4x(BC≤25).根据题意,得x(100-4x)=400.解得x1=5,x2=20. 当x=5时,100-4x=80,不满足BC≤25,不符合题意舍去;当x=20时,100-4x=20.所以 AB为20米,BC为20米.
则根据题意可列出关于x的方程为( B )
(A)x(5+x)=6
(B)x(5-x)=6
(C)x(10-x)=6
(D)x(10-2x)=6

初中数学一元二次方程的应用题型分类——动态几何问题7(附答案)

初中数学一元二次方程的应用题型分类——动态几何问题7（附答案）1．如图，ABC 中，90C =∠，8AC cm =，4BC cm =，一动点P 从点C 出发沿着CB 方向以1/cm s 的速度运动，另一动点Q 从A 出发沿着AC 边以2/cm s 的速度运动，P ，Q 两点同时出发，运动时间为()t s ．()1若PCQ △的面积是ABC 面积的14，求t 的值？ ()2PCQ 的面积能否为ABC 面积的一半？若能，求出t 的值；若不能，说明理由．2．小张准备把一根长为32cm 的铁丝剪成两段，并把每一段各围成一个正方形．（1）要使这两个正方形的面积之和等于40cm 2，小张该怎么剪？（2）小李对小张说：“这两个正方形的面积之和不可能等于30cm 2．”他的说法对吗？请你用两种不同的方法说明理由．3．如图，在Rt △ABC 中，∠B=90°，AC=60cm ，∠A=60°，点D 从点C 出发沿CA 方向以4cm/秒的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以2cm/秒的速度向点B 匀速运动，当其中一个动点到达终点时，另一个动点也随之停止运动．设点D 、E 运动的时间是t 秒（0＜t≤15）．过点D 作DF ⊥BC 于点F ，连接DE ，EF.（1）当t 为何值时，DF=DA ？（2）当t 为何值时，△ADE 为直角三角形？请说明理由．（3）是否存在某一时刻t ，使点F 在线段AC 的中垂线上，若存在，请求出t 值，若不存在，请说明理由.（4）请用含有t 式子表示△DEF 的面积，并判断是否存在某一时刻t ，使△DEF 的面积是△ABC 面积的19，若存在，请求出t 值，若不存在，请说明理由.4．如图，在ABC 中，B 90∠=，AB 12cm =，BC 24cm =，动点P 从点A 开始沿着边AB 向点B 以2cm /s 的速度移动（不与点B 重合），动点Q 从点B 开始沿着边BC 向点C 以4cm /s 的速度移动（不与点C 重合）．若P 、Q 两点同时移动()t s ； 1（）当移动几秒时，BPQ 的面积为232cm ．2（）设四边形APQC 的面积为()2S cm ，当移动几秒时，四边形APQC 的面积为2108cm ？5．如图所示，在△ABC 中，∠B =90°，BC =8cm ，AB =6cm ．点P 从点A 开始沿AB 边向点B 以1cm ∕s 的速度移动，点Q 从点B 开始沿BC 边向点C 以4 cm ∕ s 的速度移动．如果点P 、Q 分别从点A 、B 同时出发，经过几秒钟，△PBQ 的面积等于10cm 2？6．已知：如图，在ABC 中，90B ∠=，5AB cm =，7BC cm =．点P 从点A 开始沿AB 边向点B 以1/cm s 的速度移动，同时点Q 从点B 开始沿BC 边向点C 以2/cm s 的速度移动．当一个点到达终点时另一点也随之停止运动，设运动时间为x 秒，()1求几秒后，PBQ 的面积等于26cm ？()2求几秒后，PQ 的长度等于5cm ？()3运动过程中，PQB 的面积能否等于28cm ？说明理由．7．由点P （14，1），A （a ，0），B （0，a ）确定的△PAB 的面积为18．（1）如图，若0＜a ＜14，求a 的值．（2）如果a ＞14，请画图并求a 的值．8．如图，在Rt ABC 中，90B ∠=，10AC cm =，6BC cm =，现有两点P 、Q 的分别从点A 和点C 同时出发，沿边AB ，CB 向终点B 移动．已知点P ，Q 的速度分别为2/cm s ，1/cm s ，且当其中一点到达终点时，另一点也随之停止移动，设P ，Q 两点移动时间为xs ．问是否存在这样的x ，使得四边形APQC 的面积等于216cm ？若存在，请求出此时x 的值；若不存在，请说明理由．9．如图，△ABC 中，∠ACB=90°，AB=5cm ，BC=4cm ，若点P 从点A 出发，以每秒2cm 的速度沿折线A ﹣B ﹣C ﹣A 运动，设运动时间为t 秒（t ＞0）．（1）若点P 在BC 上，且满足PA=PB ，求此时t 的值；（2）若点P 恰好在∠ABC 的角平分线上，求此时t 的值；10．A 、B 、C 、D 为矩形的四个顶点，16AB cm =，6AD cm =，动点P 、Q 分别从点A 、C 同时出发，点P 以3/cm s 的速度向点B 移动，一直到达B 为止，点Q 以2/cm s 的速度向D 移动．（1）P 、Q 两点从出发开始到几秒时四边形PBCQ 是矩形？（2）P 、Q 两点从出发开始到几秒时，点P 和点Q 的距离是10cm ？11．已知：如图所示，在ABC 中，90B ∠=，5AB cm =，7BC cm =，点P 从点A 开始沿AB 边向点B 以1/cm s 的速度移动，点Q 从点B 开始沿BC 边向点C 以2/cm s 的速度移动，当其中一点到达终点后，另外一点也随之停止运动．() 1如果P 、Q 分别从A 、B 同时出发，那么几秒后，PBQ 的面积等于24cm ？ ()2在()1中，PQB 的面积能否等于27cm ？请说明理由．12．如图，△ABC 中，∠C ＝90°，BC ＝6，AC ＝4．点P 、Q 分别从点A 、B 同时出发，点P 沿A →C 的方向以每秒1个单位长的速度向点C 运动，点Q 沿B →C 的方向以每秒2个单位长的速度向点C 运动．当其中一个点先到达点C 时，点P 、Q 停止运动．当四边形ABQP 的面积是△ABC 面积的一半时，求点P 运动的时间．13．如图，在ABC 中，B 90∠=，AB 12cm =，BC 24cm =，动点P 从点A 开始沿着边AB 向点B 以2cm /s 的速度移动（不与点B 重合），动点Q 从点B 开始沿着边BC 向点C 以4cm /s 的速度移动（不与点C 重合）．若P 、Q 两点同时移动()t s ；()1当移动几秒时，BPQ 的面积为232cm ．()2设四边形APQC 的面积为()2S cm ，当移动几秒时，四边形APQC 的面积为14．如图，在矩形ABCD 中，AB 6cm =，BC 12cm =，点P 从点A 沿边AB 向点B 以1cm/s 的速度移动；同时，点Q 从点B 沿边BC 向点C 以2cm /s 的速度移动，设运动的时间为t 秒，有一点到终点运动即停止．问：是否存在这样的时刻，使2DPQ S 28cm =？若存在，请求出t 的值；若不存在，请说明理由．15．已知：如图，在△ABC 中，∠B=90°，AB=5cm ，BC=7cm ．点P 从点A 开始沿AB边向点B 以1cm/s 的速度移动，点Q 从点B 开始沿BC 边向点C 以2cm/s 的速度移动．（1）如果P ，Q 分别从A ，B 同时出发，那么几秒后，△PBQ 的面积等于6cm 2？（2）如果P ，Q 分别从A ，B 同时出发，那么几秒后，PQ 的长度等于5cm ？（3）在（1）中，△PQB 的面积能否等于8cm 2？说明理由．16．如图，在ABC 中，90B ∠=，12AB cm =，24BC cm =，动点P 从点A 开始沿着边AB 向点B 以2/cm s 的速度移动，同时动点Q 从点B 开始沿着边BC 向点C 以4/cm s 的速度移动,P 、Q 分别到达B 、C 后运动停止．若P 、Q 两点同时移动()t s ；()1当t 为何值时，BPQ 的面积为232cm ．()2设四边形APQC 的面积为()2S cm ，当移动几秒时，四边形APQC 的面积为() 3 在P 、Q 运动过程中，BPQ 面积是否有最大值？若有，求出BPQ 面积最大时t 的值；若没有，请说明理由。

一元二次方程与几何图形的面积问题

解方程得: x1 9, x2 4
∵池底的边长不能为负数 ,∴取x=4答:池底的边长是4m.
练习、建造成一个长方体形的水池，原计划水池深3米，水池周围为1400米，经过研讨，修改原方案，要把长与宽两边都增加原方案中的宽的2 倍，于是新方案的水池容积为270万米3，求原来方案的水池的长与宽各是多少米？
40米
22米
4、如图，在宽为20m，长为32m的矩形耕地上，修筑同样宽的三条道路，（两条纵向，一条横向，横向与纵向相互垂直），把耕地分成大小相等的六块试验地，要使试验地面积为570m²，问道路的宽为多少？
SUCCESS
THANK YOU
2019/10/15
例3、求截去的正方形的边长
• 用一块长28cm、宽 20cm的长方形纸片，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体盒子，使它的底面积为180cm２，为了有效地利用材料，求截去的小正方形的边长是多少cm？
6、放铅笔的V形槽如图，每往上一层可以多放一支铅笔．现有190支铅笔，则要放几层 ? 解:要放x层,则每一层放(1+x) 支铅笔.得
再往下的计算、格式书写与解法1相同。
练习1：用一根长22厘米的铁丝，能否折成一个面积是30厘米的矩形？能否折成一个面积为32厘米的矩形？说明理由。
2：在一块长80米，宽60米的运动场外围修筑了一条宽度相等的跑道，这条跑道的面积是1500平方米，求这条跑道的宽度。
3. 如图，在长为40米，宽为22米的矩形地面上，修筑两条同样宽的互相垂直的道路，余下的铺上草坪，要使草坪的面积为760平方米，道路的宽应为多少？
xm
如图，设路宽为x米， 20m
xm
横向路面为 32x 米

一元二次方程的应用解决几何形状问题

一元二次方程的应用解决几何形状问题一元二次方程是数学中常见的一类方程，拥有广泛的应用领域。

在解决几何形状问题时，一元二次方程也扮演着重要的角色。

本文将讨论一元二次方程在几何形状问题中的应用，并探讨其解决问题的方法。

一、直线与抛物线交点的问题考虑一个几何形状问题，要求找到一条直线与一个抛物线的交点。

此类问题可以通过一元二次方程的解来轻松求解。

假设直线的方程为y = mx + c，抛物线的方程为y = ax^2 + bx + c。

将直线方程代入抛物线方程，可以得到一元二次方程ax^2 + (b - m)x + (c - c) = 0。

通过求解这个一元二次方程，可以得到交点的横坐标x。

将其带入直线方程，可以求解出交点的纵坐标y。

因此，一元二次方程为解决直线与抛物线交点问题提供了有效的方法。

二、求解几何形状的顶点坐标在几何形状中，有些形状可以用一元二次方程来表示。

其中，抛物线是一种常见的形状。

求解抛物线的顶点坐标，也可以通过一元二次方程来实现。

一元二次方程的标准形式为y = ax^2 + bx + c。

在标准形式中，a代表开口的方向和抛物线的形状，b代表抛物线在x轴上的平移，c代表抛物线与y轴的交点。

通过求解一元二次方程，可以得到抛物线的顶点坐标。

顶点坐标为(-b/(2a)，-Δ/(4a))，其中Δ为二次方程的判别式。

三、通过一元二次方程求解三角形面积三角形是几何学中的基本形状，而一元二次方程在求解三角形面积的问题中也大有作为。

以一个具体问题为例，假设已知三角形的三个顶点坐标为(x1, y1)，(x2, y2)，(x3, y3)。

根据三角形的面积公式S = 1/2 * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|，可以将三角形面积问题转化为一元二次方程的求解问题。

以求解三角形的面积为目标，可以通过一元二次方程求解出其中涉及的x和y的值。

将这些值代入面积公式，可以得到三角形的面积。

利用一元二次方程解图形问题

利用一元二次方程解图形问题作者：许广跃来源：《中学生数理化·中考版》2008年第07期一元二次方程的知识不仅可以用来解决实际问题，在解决许多几何图形问题时，若能运用所学知识，构造一元二次方程求解，也能起到避繁就简的作用.现举例说明.一、用于判断三角形的形状例1 已知a，b，c是△ABC的三条边，且满足a2+b2+c2=ab+bc+ca，试判断三角形的形状.解：将a2+b2+c2=ab+bc+ca整理为主元为a的一元二次方程，得a2-（b+c）a+b2-bc+c2=0.这个方程必有实数根，故Δ=（b+c）2-4（b2-bc+c2）=-3（b-c）2≥0.∴（b-c）2≤0，又（b-c）2≥0，故b-c=0，即b=c.把b=c代入原方程，得a2-2ac+c2=0.∴（a-c）2=0，得a=c.故a=b=c，即△ABC为等边三角形.二、方案设计问题例2 将一块长18 m、宽15 m的矩形荒地修建成一个花园，道路或四角活动地（阴影部分）所占的面积为原来荒地面积的三分之二.（精确到0.1 m）（1）设计方案1：如图1，花园中修两条互相垂直且宽度相等的小路.（2）设计方案2：如图2，花园中每个角的扇形都相同.以上两种方案是否都符合条件？若符合，请计算出图1中的小路的宽和图2中扇形的半径；若不符合条件，请说明理由.解：（1）符合条件.设小路宽为x m.可列方程18x+16x－x2＝ ×18×15.整理，得x2－34x+180＝0.解这个方程，得x＝，取x≈6.6.即路宽6.6 m.（2）符合条件.设扇形半径为r m，则3.14r2＝ ×18×15，即r2≈57.32.所以r≈7.6.即半径为7.6 m.三、动态几何问题例3 如图3所示，在△ABC中，∠C＝90°，AC＝6 cm，BC＝8 cm，点P从点A出发沿边AC向点C以1 cm/s的速度移动，点Q从C点出发沿CB边向点B以2 cm/s的速度移动.（1）如果P，Q同时出发，几秒钟后，可以使得△PCQ的面积为8 cm2？（2）点P，Q在移动过程中，是否存在某一时刻，使得△PCQ的面积等于△ABC的面积的一半？若存在，求出运动的时间；若不存在，说明理由.解：因为∠C＝90°，所以AB＝＝＝10 （cm）.（1）设x s后，可使△PCQ的面积为8 cm2.所以AP＝x cm，PC＝（6－x） cm，CQ＝2x cm.根据题意，得（6－x）•2x＝8.整理，得x2－6x+8＝0.解这个方程，得x1＝2，x2＝4.所以P，Q同时出发，移动2 s和4 s时△PCQ的面积为8 cm2.（2）设点P移动x s时，△PCQ的面积等于△ABC面积的一半.根据题意，得（6－x）•2x＝ × ×6×8.整理，得x2－6x+12＝0.由于此方程没有实数根，所以不存在使△PCQ的面积等于△ABC面积一半的时刻.四、平分几何图形的周长与面积问题例4 如图4，在等腰梯形ABCD中，AB＝DC＝5，AD＝4，BC＝10，点E在下底边BC 上，点F在腰AB上.（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积.（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE 的长；若不存在，请说明理由.（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分？若存在，求此时BE的长；若不存在，请说明理由.分析：为了能正确求得图形的面积，不妨过点F作FG⊥BC于G，过点A作AK⊥BC于K.这样，由三角形的面积公式即可列出含x的代数式.解：（1）由已知条件，可得梯形周长为24，高为4，面积为28.过点F作FG⊥BC于G，过点A作AK⊥BC于K.由 = ，可得FG＝ ×4.所以S△BEF ＝BE•FG＝－ x2+ x（7≤x≤10）.（2）存在.由（1）得－ x2+ x＝14.解这个方程，得x1＝7，x2＝5（舍去）.当BE=7时，FG= ×4=4，BF+BE=12.所以存在线段EF将等腰梯形ABCD的周长与面积同时平分，此时BE＝7.（3）不存在.假设存在，应该有S△BEF ∶S多边形AFECD＝1∶2和（BE+BF）∶（AF+AD+DC）＝1∶2同时成立.由面积比例式，得－ x2+ x＝ .整理，得3x2－36x+70＝0.由周长比例式，得BF+x= ×24=8.可知3≤x而方程3x2-36x+70=0的根不在这个范围内，所以不存在这样的实数x.即不存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分.注：“本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文。

专题六：一元二次方程实际应用中的篱笆和围栏问题(有答案)

专题六：一元二次方程实际应用中的篱笆和围栏问题（有答案）➢知识指引与几何图形面积有关的应用类问题是一元二次方程应用题型中较为重要的一类，在此类问题中要利用图形的面积公式，对图形进行分析，理清题意，引入未知数表示相应的量，并从中找到等量关系来列解方程，得到实际问题的答案.下面我们来看一下一元二次方程实际应用中的篱笆和围栏问题.➢知识回顾列一元二次方程解应用题的一般步骤1）解一元二次方程实际问题的原则，与一元一次方程的实际问题原则类似：①根据题意和实际问题涉及的类型，建立等量关系式；②以利于表示等量关系式为原则，设未知数x；③依据等量关系式和未知数x建立方程；④解方程并解答。

➢典型例题类型一：围栏不带门类型【例1】如图，利用一面墙（墙长度不超过45m），用80m长的篱笆围一个矩形场地．（1）怎样围才能使矩形场地的面积为750m2？（2）能否使所围矩形场地的面积为810m2，为什么？（80-x）米．【解答】（1）设所围矩形ABCD的长AB为x米，则宽AD为12依题意，得x•1（80-x）=750，2即x2-80x+1500=0，解得x1=30，x2=50．∵墙的长度不超过45m，∴x 2=50不合题意，应舍去．当x=30时，12（80-x ）=12（80-30）=25，所以，当所围矩形的长为30m 、宽为25m 时，能使矩形的面积为750m 2．（2）不能，理由如下：由x•12（80-x ）=810，得x 2-80x+1620=0．又∵b 2-4ac=（-80）2-4×1×1620=-80＜0，∴上述方程没有实数根．因此不能使所围矩形场地的面积为810m 2．【变式】如图，有长为30m 的篱笆，一面利用墙（墙的最大可用长度为10m ），围成中间隔有一道篱笆（平行于AB ）的长方形花圃．（1）设花圃的一边AB 为xm ，则BC 的长可用含x 的代数式表示为 m ；（2）当AB 的长是多少米时，围成的花圃面积为63平方米？【【解答】（1）BC 的长可用含x 的代数式表示为（30-3x ）m ．故答案为：（30-3x ）；（2）依题意有x （30-3x ）=63．解得x 1=7，x 2=3．当x=7时，30-3x=9＜10，符合题意；当x=3时，30-3x=21＞10，不符合题意，舍去．故当AB 的长是7米时，围成的花圃面积为63平方米．类型二：围栏带门类型【例2】如图，我区某中学计划用一块空地修建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米.计划建造车棚的面积为80平方米，已知现有的板材可使新建的板墙的总长为24米.为方便学生出行，学校决定在与墙平行的一面开一个2米宽的门.求这个车棚的长和宽分别是多少米？【解答】设垂直于墙的一边长为x米．根据题意，得x(24－2x+2)=80．解得x1=5，x2=8．当x1=5时，24－2x+2=16＞12，不符合题意，舍去；当x2=8时，24－2x+2=10＜12，符合题意；所以x=8．答：车棚的长和宽分别为10米和8米．【变式】如图，一农户要建一个矩形羊舍，羊舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形羊舍的长、宽分别为多少时，羊舍面积为80m2？【解答】设矩形羊舍垂直于住房墙一边长为xm，可以得出平行于墙的一边的长为(26-2x)m，由题意，得x（26-2x）=80．化简，得x2−13x+40=0．解得x1=5，x2=8．当x=5时，26－2x=16＞12（舍去），当x=8时，26－2x=10＜12．答：矩形羊舍的长为10m，宽为8m．➢跟踪训练1．如图，有长为24米的篱笆，一面利用墙(墙的最大可用长度为11米)，围成中间隔有一道篱笆的长方形花圃．(1)如果要围成面积为45平方米的花圃，那么AD的长为多少米？(2)能否围成面积为60平方米的花圃？若能，请求出AD的长；若不能，请说明理由．【解答】(1)设AD的长为x米，则AB为(24−3x)米，根据题意列方程得，(24−3x)⋅x=45，解得x1=3，x2=5；当x=3时，AB=24−3x=24−9=15>11，不符合题意，舍去；当x=5时，AB=24−3x=9<11，符合题意；答：AD的长为5米．(2)不能围成面积为60平方米的花圃．理由：假设存在符合条件的长方形，设AD的长为y米，于是有(24−3y)⋅y=60，整理得y2−8y+20=0，∵△=(−8)2−4×20=−16<0，∴这个方程无实数根，∴不能围成面积为60平方米的花圃．2.如图，某工程队在工地互相垂直的两面墙AE、AF处，用180米长的铁栅栏围成一个长方形场地ABCD，中间用同样材料分割成两个长方形．已知墙AE 长120米，墙AF长40米，要使长方形ABCD的面积为4000平方米，问BC 和CD各取多少米？【解答】设BC=x米，则CD=（180-2x）米．由题意，得：x（180-2x）=4000，整理，得：x2-90x+2000=0，解得：x=40或x=50＞40（不符合题意，舍去），∴180-2x=180-2×40=100＜120（符合题意）．答：BC=40米，CD=100米．3.如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度为11米），围成中间隔有一道篱笆的长方形花圃．（1）如果要围成面积为45平方米的花圃，那么AD的长为多少米？（2）能否围成面积为60平方米的花圃？若能，请求出AD的长；若不能，请说明理由．【解答】（1）设AD的长为x米，则AB为（24-3x）米，根据题意列方程得，（24-3x）•x=45，解得x1=3，x2=5；当x=3时，AB=24-3x=24-9=15＞11，不符合题意，舍去；当x=5时，AB=24-3x=9＜11，符合题意；答：AD的长为5米．（2）不能围成面积为60平方米的花圃．理由：假设存在符合条件的长方形，设AD的长为y米，于是有（24-3y）•y=60，整理得y2-8y+20=0，∵△=（-8）2-4×20=-16＜0，∴这个方程无实数根，∴不能围成面积为60平方米的花圃．4.如图，若要建一个长方形鸡场，鸡场的一边靠墙，墙对面有一个2米宽的门，另三边用竹篱笆围成，篱笆总长33米．（1）若墙长为18米，要围成鸡场的面积为150平方米，则鸡场的长和宽各为多少米？（2）围成鸡场的面积可能达到200平方米吗？【解答】（1）设宽为x米，则x（33-2x+2）=150，（不合题意舍去），解得：x1=10，x2=152答：长为15米，宽为10米；（2）设宽为x米，则x（33-2x+2）=200，即2x2−35x+200=0.∵∆=352−4×2×200=−375＜0，∴方程无解，故围成鸡场的面积不能达到200平方米．5．如图1，用篱笆靠墙围成矩形花圃ABCD，墙可利用的最大长度为15m，一面利用旧墙，其余三面用篱笆围，篱笆总长为24m，设平行于墙的BC边长为xm（1）若围成的花圃面积为40m2时，求BC的长；（2）如图2，若计划在花圃中间用一道篱笆隔成两个小矩形，且围成的花圃面积为50m2，请你判断能否成功围成花圃，如果能，求BC的长；如果不能，请说明理由(24−x)m，【解答】（1）根据题意得，AB=12(24−x）•x=40，则12∴x1=20，x2=4，∵20＞15，∴x=20舍去答：BC的长为4米；（2）不能围成花圃，(24−x)•x＝50，根据题意得，13方程可化为x2-24x+150=0∆=（-24）2-4×150＜0，∴方程无实数解，∴不能围成花圃；6.如图，利用一面足够长的墙，用铁栅栏围成一个矩形自行车场地ABCD，在AB和BC边各有一个2米宽的小门（不用铁栅栏），设矩形ABCD的宽AD为x米，矩形的长为AB（且AB＞AD）．（1）若所用铁栅栏的长为40米，用含x的代数式表示矩形的长AB；（2）在（1）的条件下，若使矩形场地面积为192平方米，则AD、AB的长应分别为多少米？【解答】（1）∵AD+BC-2+AB-2=40，AD=BC=x，∴AB=-2x+44；（2）由题意得-2x+44＞x，解得x＜44，3由题意，得（-2x+44）•x=192，即2x2-44x+192=0，解得x1=6，x2=16，（舍去），∵x2=16＞443∴AD=6，∴AB=-2×6+44=32．答：AD长为6米，AB长为32米．7.双流空港花田需要绿化的面积为52000米2，施工队在绿化了28000米2后，将每天的工作量增加为原来的1.5倍，结果提前4天完成了该项绿化工程．（1）该项绿化工程原计划每天完成多少米2？（2）该项绿化工程中，如图有长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃，为了方便出入，在建造篱笆花圃时，在BC 上用其他材料造了宽为1米的两个小门，此时花圃的面积刚好为45米2，求此时花圃的长和宽．【解答】（1）设该项绿化工程原计划每天完成x 米2，根据题意得：52000−28000x -52000−280001.5x =4，解得：x=2000，经检验，x=2000是原方程的解，答：该绿化项目原计划每天完成2000平方米；（2）设花圃的宽度为x 米，则BC=22+2-3x=24-3x ，根据题意，得（24-3x ）x=45，解得：x 1=3，x 2=5．∵当x=3时，24-3x=15＞14，∴不符合题意，舍去．∴宽为5米，长为9米．答：花圃的长为9米，宽为5米．8．某学校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米．计划建造车棚的面积为80平方米，已知现有的木板材料可使新建板墙的总长为26米．(1)为了方便学生出行，学校决定在与墙平行的一面开一个2米宽的门，那么这个车棚的长和宽分别应为多少米？(2)如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路，使得停放自行车的面积为54平方米，那么小路的宽为多少米？【解答】（1）设与墙垂直的一面为x 米，另一面为（26－2x+2）米，根据题意，得x(28－2x)=80.整理，得x 2－14x ＋40=0．解得x1=4，x2=10．当x=4时，28－2x=20＞12（舍去）．当x=10时，28－2x=8＜12，∴长为10米，宽为8米．（2）设宽为a米，根据题意，得（8－2a）(10－a)=54．整理，得a2－14a＋13=0．解得a1=13(舍去)，a2=1．答；小路的宽为1米．9.如图，利用一面墙（墙长25米），用总长度49米的栅栏（图中实线部分）围成一个矩形围栏ABCD，且中间共留两个1米的小门，设栅栏BC长为x米．（1）AB= 米（用含x的代数式表示）；（2）若矩形围栏ABCD面积为210平方米，求栅栏BC的长；（3）矩形围栏ABCD面积是否有可能达到240平方米？若有可能，求出相应x 的值；若不可能，则说明理由.【解答】（1）设栅栏BC长为x米，∵栅栏的全长为49米，且中间共留两个1米的小门，∴AB=49+2-3x=51-3x（米），故答案为：（51-3x）；（2）依题意，得：（51-3x）x=210，整理，得：x2-17x+70=0，解得：x1=7，x2=10．当x=7时，AB=51-3x=30＞25，不合题意，舍去，当x=10时，AB=51-3x=21，符合题意，答：栅栏BC的长为10米；（3）不可能，理由如下：依题意，得：（51-3x）x=240，整理得：x2-17x+80=0，∵△=（-17）2-4×1×80=-31＜0，∴方程没有实数根，∴矩形围栏ABCD面积不可能达到240平方米．。

初中数学一元二次方程的应用题型分类——图形相关问题6(附答案)

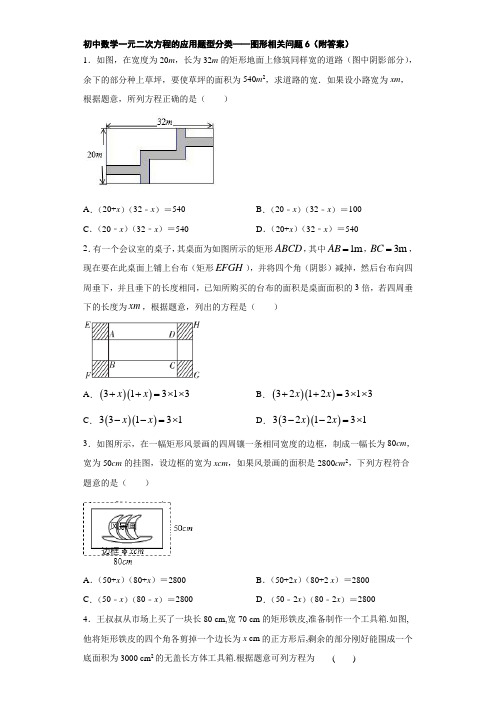
初中数学一元二次方程的应用题型分类——图形相关问题6（附答案）1．如图，在宽度为20m ，长为32m 的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为540m 2，求道路的宽．如果设小路宽为xm ，根据题意，所列方程正确的是（）A ．（20+x ）（32﹣x ）＝540B ．（20﹣x ）（32﹣x ）＝100C ．（20﹣x ）（32﹣x ）＝540D ．（20+x ）（32﹣x ）＝5402．有一个会议室的桌子，其桌面为如图所示的矩形ABCD ，其中1m =AB ，3m BC =，现在要在此桌面上铺上台布（矩形EFGH ），并将四个角（阴影）减掉，然后台布向四周垂下，并且垂下的长度相同，已知所购买的台布的面积是桌面面积的3倍，若四周垂下的长度为xm ，根据题意，列出的方程是（）A ．()()31313x x ++=⨯⨯B ．()()3212313x x ++=⨯⨯C ．()()33131x x --=⨯D ．()()3321231x x --=⨯3．如图所示，在一幅矩形风景画的四周镶一条相同宽度的边框，制成一幅长为80cm ，宽为50cm 的挂图，设边框的宽为xcm ，如果风景画的面积是2800cm 2，下列方程符合题意的是（）A ．（50+x ）（80+x ）＝2800B ．（50+2x ）（80+2 x ）＝2800C ．（50﹣x ）（80﹣x ）＝2800D ．（50﹣2x ）（80﹣2x ）＝28004．王叔叔从市场上买了一块长80 cm,宽70 cm 的矩形铁皮,准备制作一个工具箱.如图,他将矩形铁皮的四个角各剪掉一个边长为x cm 的正方形后,剩余的部分刚好能围成一个底面积为3000 cm 2的无盖长方体工具箱.根据题意可列方程为 ( )A ．(80-x )(70-x )=3000B ．80×70-4x 2=3000C ．(80-2x )(70-2x )=3000D ．80×70-4x 2-(70+80)x =30005．某校团委准备举办学生绘画展览，为美化画面，在长8 dm 、宽为5 dm 的矩形内画面四周镶上宽度相等的彩纸，并使彩纸的面积等于222dm （如图），若设彩纸的宽度为x dm ，则可得方程式为（）A ．4010x 16x 18--=B ．()()82x 52x 62++=C ．()()82x 52x 18--=D ．2405x 8x 422x --+=6．准备在一块长为30m ，宽为24m 的长方形花圃内修建四条宽度相等且与各边垂直的小路，如图所示，四条小路的中间部分恰好是一个正方形，且边长是小路宽度的4倍，若四条小路所占面积为80m 2，则小路的宽度为（）A ．1mB ．54m C ．2m D ．65m 7．如图是由三个边长分别是2，3和x 的正方形所组成的图形，若直线AB 将它分成面积相等的两部分，则x 的值是（）A ．1或4B ．2或3C ．3或4D ．1或28．公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m ，另一边减少了2m ，剩余空地的面积为18m 2，求原正方形空地的边长．设原正方形的空地的边长为xm ，则可列方程为（）A．（x+1）（x+2）=18 B．x2﹣3x+16=0 C．（x﹣1）（x﹣2）=18D．x2+3x+16=09．在一幅长为80cm，宽为50cm的矩形风景画的四周镶一条相同宽度的边框，制成一幅挂图，如图所示，设边框的宽为xcm，如果整个挂图的面积是5400cm2 ,那么下列方程符合题意的是（）A．(50-x)(80-x)=5400 B．(50-2x)(80-2x)=5400C．(50+x)(80+x)=5400 D．(50+2x)(80+2x)=540010．如图，一块长和宽分别为30cm和20cm的矩形铁皮，要在它的四角截去四个边长相等的小正方形，折成一个无盖的长方体盒子，使它的侧面积为272cm2，则截去的正方形的边长是（）cmA．4cm B．8.5cm C．4cm或8.5cm D．5cm或7.5cm 11．建一个面积为480平方米的长方形存车处，存车处的一面靠墙，另三面用铁栅栏围起来，已知铁栅栏的长是92米，存车处的长是________米,宽是________米.12．如图，用20 m长的铁丝网围成一个一面靠墙的矩形养殖场，其养殖场的最大面积________m2．13．给定一个边长为3的正方形，存在一个矩形，使它的周长和面积分别是这个正方形周长和面积的2倍，则这个矩形较长边的边长为______．14．为创建“国家生态园林城市”，某小区在规划设计时，在小区中央设置一块面积为1200平方米的矩形绿地，并且长比宽多40米．设绿地宽为x米，根据题意，可列方程为_____．84cm，则原15．从正方形的铁皮上，截去5cm宽的一个长方形铁皮，余下的面积为2正方形面积为______2cm.16．如图，有一块长30 m、宽20 m的矩形田地，准备修筑同样宽的三条直路，把田地分成六块，种植不同品种的蔬菜，并且种植蔬菜面积为矩形田地面积的78%，则道路的宽为___________17．如图，将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形（阴影部分即剪掉的部分），剩余的部分可以折成一个有盖的长方体盒子（纸板的厚度忽略不计）．若长方形纸板边长分别为40cm和30cm，且折成的长方体盒子表面积是950cm2，此时长方体盒子的体积为_____cm3．18．某养殖场为落实国家环保政策，建造一个池底为正方形、深度为2m的长方体无盖水池，池壁的造价为每平方米150元，池底的造价为每平方米300元，总造价为9600元，则该水池池底的边长为_____m．19．长方形的长比宽多4厘米，面积是60平方厘米，则它的长是______厘米.20．如图在一块长为22米,宽为17米的矩形地面上,要修建一条长方形道路LMPQ及一条平行四边形道路RSTK,剩余部分种上草坪,使草坪面积为300平方米,若LM=RS=x米,则根据题意可列出方程为______21．将一块面积为2120m的矩形菜地的长减少2m，它就变成了正方形，求原菜地的长.22．如图，从一块长80厘米，宽60厘米的铁片中间截去一个小长方形，使截去小长方形的面积是原来铁片面积的一半，并且剩下的长方框四周的宽度一样，求这个宽度．23．如图，要设计一幅宽为20cm，长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条宽度相等，如果要使余下的图案面积为504cm2，彩条的宽应是多少cm．24．如图，某小区规划在一个长30m，宽20m的矩形场地上，修建两横两竖四条同样宽的道路，且横、竖道路分别与矩形的长、宽平行，其余部分种草坪，若使每块草坪的56m.应如何设计道路的宽度？面积都为225．如图，一农户要建一个矩形猪舍，猪舍的一边利用长为15m的住房墙，另外三边用27m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长，宽分别为多少米时，猪舍面积为96m2？26．小李准备进行如下的操作，把一根长50cm的铁丝剪成两段，并把每段首尾相连各围成一个长宽不等的矩形，两矩形相似且相似比为2:3．78cm，较小矩形的长宽各是多少？（1）要使这两个矩形的面积之和为291cm，你同意吗？说明理由．（说明：相（2）小李认为这两个矩形的面积和不可能为2似多边形的周长比等于相似比，面积比等于相似比的平方）27．一张长为30cm，宽20cm的矩形纸片，如图1所示，将这张纸片的四个角各剪去一个边长相同的正方形后，把剩余部分折成一个无盖的长方体纸盒，如图1所示，如果折成的长方体纸盒的底面积为264cm2，求剪掉的正方形纸片的边长．28．小淇准备利用38m长的篱笆，在屋外的空地上围成三个相连且面积相等的矩形花园．围成的花园的形状是如图所示的矩形CDEF，矩形AEHG和矩形BFHG．若整个花园ABCD(AB＞BC)的面积是30m2，求HG的长．29．已知正方形ABCD的边长为10，现改变该正方形的边长，使其变为矩形．若AD 的长增加了x，AB的长减少了kx（其中k＞0，x＞0）．（1）若k＝2，请说明改变后得到的矩形面积是否可为125；（2）若改变后得到的矩形面积仍为100，求x与k的数量关系．30．如图，将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形，剩余部分折成一个无盖的盒子．（纸板的厚度忽略不计）．（1）若该无盖盒子的底面积为900cm2，求剪掉的正方形的边长；（2）求折成的无盖盒子的侧面积的最大值．参考答案1．C 【解析】【分析】设小路宽为x 米，利用平移把不规则的图形变为规则图形，如此一来，所有草坪面积之和就变为了（32﹣x ）（20﹣x ）米2，进而即可列出方程，求出答案．【详解】解：利用平移，原图可转化为右图，设小路宽为x 米，根据题意得：（20﹣x ）（32﹣x ）＝540．故选：C ．【点睛】本题考查由实际问题抽象出一元二次方程，这类题目体现了数形结合的思想，需利用平移把不规则的图形变为规则图形，进而即可列出方程，求出答案．另外还要注意解的合理性，从而确定取舍． 2．B 【解析】【分析】根据所购买的台布的面积是桌面面积的3倍，求出桌面面积即矩形ABCD ，的面积和台布面积即矩形EFGH 的面积，列出等式，即可得解. 【详解】根据题意，得桌面面积为：13ABCD S AB BC =⋅=⨯矩形台布面积为：()()3212EFGH S EF F x G x ⋅+==+矩形又由3EFGH ABCD S S =矩形矩形，可得()()3212313x x ++=⨯⨯ 故答案为B. 【点睛】此题主要考查一元二次方程的实际应用，解题关键是理解题意，列出等式. 3．D 【解析】【分析】根据图求出风景画的长、宽，再利用矩形的面积公式即可得出答案. 【详解】由题意得：风景画的长为：(802)x cm -，宽为：(502)x cm - 利用矩形的面积公式得：(802)(502)2800x x --= 故选：D. 【点睛】本题考查了一元二次方程的几何应用，依据题意求出风景画的长、宽是解题关键. 4．C 【解析】根据题意可知裁剪后的底面的长为（80-2x ）cm ，宽为（70-2x ）cm ，从而根据底面积可以列出相应的方程即可．解：由题意可得， (80−2x )(70−2x )=3000，故选C. 5．C 【解析】【分析】先求出中间空白矩形的面积，再根据大矩形的长、宽和彩纸的宽求出中间空白矩形的长、宽，最后利用面积公式即可得. 【详解】由题意得，中间空白矩形的面积为2852218()dm ⨯-=由图可知，中间空白矩形的长为：(82)x dm -，宽为：(52)x dm - 利用面积公式得：(82)(52)18x x --= 故选：C.本题考查了一元二次方程的几何应用，依题意得出中间空白矩形的长、宽是解题关键. 6．B【解析】【分析】设小路的宽度为x米，则小正方形的边长为4x米，根据小路的横向总长度（30＋4x）米和纵向总长度（24＋4x）米，结合矩形的面积公式得到：（30＋4x＋24＋4x）x＝80．通过解方程求得x的值即可．【详解】设小路的宽度为x米，则小正方形的边长为4x米，依题意得：（30＋4x＋24＋4x）x＝80整理得：4x2＋27x−40＝0解得x1＝−8（舍去），x2＝54．故选B.【点睛】考查了一元二次方程的应用，解题的关键是找到该小路的总的长度，利用矩形的面积公式列出方程并解答．7．D【解析】【分析】补全图形，然后根据面积相等列方程，解方程即可得到结论．【详解】解：如图，补全图形，∵直线AB将它分成面积相等的两部分，∴12（2+3+x）×3﹣x（3﹣x）＝12×（2+3+x）×3﹣2×1，解得x＝1或x＝2，【点睛】本题考查了一元二次方程的应用，补全图形，利用割补法表示出两部分的面积是解题的关键． 8．C 【解析】【详解】试题分析：可设原正方形的边长为xm ，则剩余的空地长为（x ﹣1）m ，宽为（x ﹣2）m ．根据长方形的面积公式列方程可得()()-1-2x x =18．故选C ．考点：由实际问题抽象出一元二次方程． 9．D 【解析】由题意可知当四周镶上一条宽为xcm 的边框后，整个挂图的长为（80+2x ）cm ，宽为（50+2x ）cm ，则这个挂图的面积可表达为(80+2x)(50+2x)，结合镶好边框后的挂图面积为5400cm 2，可得方程为：(80+2x)(50+2x)=5400. 故选D. 10．C 【解析】【分析】设截去的正方形的边长为xcm ，对于该长方形铁皮，四个角各截去一个边长为x 厘米的小正方形，长方体底面的长和宽分别是（30−2x ）cm 和（20−2x ）cm ，侧面积为2x[（30−2x ）＋（20−2x ）]cm 2，根据长方体的侧面积为272cm 2列方程求出x 的值即可．【详解】解：设截去正方形的边长为xcm ，依题意有：2x[（30−2x ）＋（20−2x ）]＝272，解得x 1＝4，x 2＝8.5，即截去的正方形的边长是4cm 或8.5cm ．故选：C ．【点睛】此题考查了一元二次方程的应用，解题的关键在于理解题意，找出等量关系列出方程进行求解．11．80 40 6 12【解析】【分析】根据题意设垂直于墙的边为x 米,另一边则为(92-2x )米,根据面积公式列出方程解出即可.【详解】设垂直于墙的一边是x 米,由题意可得：()922480x x -=,解得：140x =,26x =,则92212x -=或80,所以存车处的长和宽各是40米、12米或80米、6米.故答案为:80、40;6、12.【点睛】本题考查一元二次方程应用,关键在于正确设出各边长列出面积公式.12．50【解析】设与墙平行的一边长为xm ，则另一面为202x - ，其面积=2201·1022x x x x -=--， ∴最大面积为241005042ac b a -== ；即最大面积是50m 2．故答案是50．【点睛】求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a 的绝对值是较小的整数时，用配方法较好，如y=-x2-2x+5，y=3x2-6x+1等用配方法求解比较简单．13．【解析】【分析】设矩形较长边的边长为x （x ＞6），则较短边的边长为（3×4-x ），由矩形的面积公式结合矩形的面积，即可得出关于x 的一元二次方程，解之取其较大值即可得出结论．【详解】解：设矩形较长边的边长为x （x ＞6），则较短边的边长为（3×4-x ），由题意得：x （3×4-x ）=2×3×3，整理得：x 2-12x+18=0，解得：x 1x 2．故答案为：．【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键． 14．x （x+40）=1200．【解析】【分析】先表示出矩形场地的长，再根据矩形的面积公式即可列出方程．【详解】由题意可得，x （x+40）=1200，故答案是：x （x+40）=1200．【点睛】考查由实际问题抽象出一元二次方程，解题的关键是明确题意，列出相应的方程． 15．原正方形的面积1442cm【解析】【分析】可设正方形的边长是xcm ，根据“余下的面积是84cm 2”，余下的图形是一个矩形，矩形的长是正方形的边长，宽是x-5，根据矩形的面积公式即可列出方程求解．【详解】设原正方形的边长为cm x ，由题意可得：()584x x -=，解得：112x =，27x =-（舍去），原正方形的面积21212144cm =⨯=.本题考查了一元二次方程应用以及矩形及正方形面积公式，表示出矩形各边长是解题关键．16．2 m【解析】【详解】设道路为x米宽，由题意得：20×30−20x×2−30x+2x2=30×20×78%，整理得：x2−35x+66=0，解得：x=2，x=33，经检验是原方程的解，但是x=33>30，因此不合题意舍去．故答案是：2 m.【点睛】本题中,植蔬菜面积的面积=矩形耕地的面积-三条道路的面积+道路重叠部分的两个小正方形的面积.如果设道路宽x,可根据此关系列出方程求出x的值,然后将不合题意的舍去即可. 17．1500【解析】【分析】设剪掉的小正方形的边长为xcm，根据长方体盒子表面积是950cm2列出方程，求出方程的解得到x的值，再计算体积即可．【详解】解：设剪掉的小正方形的边长为xcm，根据题意，得：2x2+20x×2＝30×40﹣950，整理得：x2+20x﹣125＝0，解得：x1＝5，x2＝﹣25（不合题意，舍去），当x＝5时，长方体盒子的体积为：x（30﹣2x）（20﹣x）＝5×20×15＝1500（cm3），故答案为：1500．【点睛】此题考查了一元二次方程的应用，准确识别图形，弄清题中的等量关系是解本题的关键．18．4【解析】设正方形池底的边长为xm ，池壁的面积为4x×2m 2．根据池底的造价×池底的面积+池壁的造价×池壁的面积＝总造价，方程可列出，进而可求出正方形池底的边长．【详解】解：设池底的边长为xm ．300x 2+1200x ＝9600，解得x 1＝4，x 2＝﹣8（舍），答：池底的边长为4m ．故答案为：4．【点睛】本题考查了一元二次方程的应用．本题应熟记正方形的面积公式、长方体的表面积公式．注意本题池壁的造价，池底的造价不同．19．10【解析】【分析】首先设长为x cm ，根据长与宽的关系，得到宽为()4x cm -，然后根据长方形面积公式可列出方程并解方程即可.【详解】解：设长方形的长为x cm ，则它的宽为()4x cm -，根据题意得：()460x x -=解得：110x =，26x =-（舍去）答：这个长方形的长是为10cm .故答案为10.【点睛】本题考查的是一元二次方程的运用，要灵活运用长方形的面积公式对题意进行分析从而列出方程.20．(22−x)(17−x)=300.【解析】将每条道路平移到矩形的一边处，表示出新矩形的长和宽，利用矩形的面积的计算方法得到方程即可．【详解】根据题意得：(22−x)(17−x)=300；故答案为：(22−x)(17−x)=300.【点睛】此题考查由实际问题抽象出一元二次方程，解题关键在于理解题意列出方程.21．原菜地长为12m .【解析】【分析】设原菜地的长为xm ，根据正方形的性质可得原矩形菜地的宽，再根据矩形的面积公式列出方程求解即可.【详解】设原菜地的长为xm ，则原矩形菜地的宽(2)x m -由题意得：(2)120x x -=解得：112x =，210x =-(不合题意，舍去)答：原菜地的长为12m .【点睛】本题考查了一元二次方程的实际应用，依据题意正确建立方程是解题关键.22．长方框的宽度为10厘米【解析】【分析】设长方框的宽度为x 厘米，则减去小长方形的长为（80﹣2x ）厘米，宽为（60﹣2x ）厘米，根据长方形的面积公式结合截去小长方形的面积是原来铁片面积的一半，即可得出关于x 的一元二次方程，解之取其较小值即可得出结论．【详解】解：设长方框的宽度为x 厘米，则减去小长方形的长为（80﹣2x ）厘米，宽为（60﹣2x ）厘米，依题意，得：（80﹣2x ）（60﹣2x ）＝12×80×60，整理，得：x 2﹣70x+600＝0，解得：x 1＝10，x 2＝60（不合题意，舍去）．答：长方框的宽度为10厘米．【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键． 23．1cm ．【解析】【分析】设每个彩条的宽度为xcm ，根据剩余面积为504cm 2，建立方程求出其解即可．【详解】设每个彩条的宽度为xcm ，由题意，得（30﹣2x ）（20﹣2x ）＝504，解得：x 1＝24（舍去），x 2＝1．答：每个彩条的宽度为1cm ．【点睛】本题考查一元二次方程的应用，解题的关键是根据剩余面积=总面积-彩条面积列出方程. 24．道路的宽度应设计为1m.【解析】【分析】设道路的宽度为x m ，横、竖道路分别有2条，所以草坪的宽为：（20-2x ）m ，长为：（30-2x ）m ，草坪的总面积为56×9，根据长方形的面积公式即可得出结果．【详解】解：设道路的宽度为x m.由题意得：()()302202569x x --=⨯化简得：225240x x -+=()()1240x x --=解得：11x =，224x =（舍）答：道路的宽度应设计为1m．【点睛】本题考查的是一元二次方程的实际应用，根据题目条件进行设未知数，列出方程并且求解是解题的关键．25．所围矩形猪舍的长为12m、宽为8m【解析】【分析】设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(27﹣2x+1)m．根据矩形的面积公式建立方程求出其解就可以了．【详解】解：设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(27﹣2x+1)m，由题意得x(27﹣2x+1)＝96，解得：x1＝6，x2＝8，当x＝6时，27﹣2x+1＝16＞15(舍去)，当x＝8时，27﹣2x+1＝12．答：所围矩形猪舍的长为12m、宽为8m．【点睛】本题考查了列一元二次方程解实际问题的运用，矩形的面积公式的运用及一元二次方程的解法的运用，解答时寻找题目的等量关系是关键．26．（1）较小矩形宽4厘米，长6厘米；（2）同意，理由见解析．【解析】【分析】（1）根据相似多边形的性质，得较小的矩形周长为20厘米，再根据较小矩形的面积，列出方程，即可求解；（2）根据较小矩形的面积，列出一元二次方程，从而得判别式的值小于零，进而即可得到结论．【详解】（1）∵两矩形相似且相似比为2:3，∴23CC=小大，49SS=小大，∴C 小=20，设小矩形较短一边长x 厘米，则邻边长为（10-x ）厘米，则x （10-x ）=78×413，解得：x 1=4，x 2=6（舍去）， ∴较小矩形宽为4厘米，长为6厘米；（2）同意．理由如下：设小矩形较短一边长x 厘米，则邻边长为（10-x ）厘米，则x （10-x ）=91×413，即：x 2-10x +28=0， ∵Δ=2(10)412812--⨯⨯=-＜0，∴一元二次方程无解，∴两矩形的面积不可能为91cm 2．【点睛】本题主要考查相似多边形的性质，掌握相似多边形的周长比等于相似比，面积比等于相似比的平方是解题的关键．27．4cm【解析】试题分析：设剪掉的正方形纸片的边长为x cm ，则围成的长方体纸盒的底面长是（30-2x ）cm, 宽是（30-2x ）cm,根据底面积等于264 cm 2列方程求解.解：设剪掉的正方形纸片的边长为x cm ．由题意，得 (30-2x )(20-2x )=264．整理，得 x 2 -25x + 84=0．解方程，得14x =，221x =（不符合题意，舍去）．答：剪掉的正方形的边长为4cm ．28．HG 的长是2m【解析】【分析】设HG 的长为xm ，将BC ，AB 表示出来，再利用整个花园面积为30 m 2列出方程，解之即可.【详解】解：设HG 的长为xm ，则3384,23x BC xm AB m -==，由题意得，33843023x x ⋅=－解得，12152,2x x ==∵AB BC >， ∴2152x =不合题意，舍去．答：HG 的长是2m .【点睛】此题考查一元二次方程的实际运用，掌握长方形的面积计算公式是解决问题的关键． 29．（1）改变后得到的矩形面积不能为125；（2）x ＝1k k -．【解析】【分析】（1）根据矩形的面积公式结合改变后矩形的面积为125，即可得出关于x 的一元二次方程，由根的判别式△＝−100＜0，即可得出改变后得到的矩形面积不能为125；（2）根据矩形的面积公式结合改变后矩形的面积为100，即可得出关于x 的一元二次方程，由k ＞0，x ＞0，即可得出x 与k 的数量关系．【详解】（1）依题意，得：（10+x ）（10﹣2x ）＝125，整理，得：2x 2+10x+25＝0．∵△＝102﹣4×2×25＝﹣100＜0，∴改变后得到的矩形面积不能为125．（2）依题意，得：（10+x ）（10﹣kx ）＝100，整理，得：kx 2﹣（1﹣k ）x ＝0．∵k ＞0，x ＞0，∴x ＝1k k-．【点睛】本题考查了根的判别式以及一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．30．（1）5cm；（2）最大值是800cm2．【解析】【分析】（1）设剪掉的正方形的边长为x cm，则AB=（40-2x）cm，根据盒子的底面积为484cm2，列方程解出即可；（2）设剪掉的正方形的边长为x cm，盒子的侧面积为y cm2，侧面积=4个长方形面积；则y=-8x2+160x，配方求最值．【详解】（1）设剪掉的正方形的边长为x cm，则（40﹣2x）2＝900，即40﹣2x＝±30，解得x1＝35（不合题意，舍去），x2＝5；答：剪掉的正方形边长为5cm；（2）设剪掉的正方形的边长为x cm，盒子的侧面积为y cm2，则y与x的函数关系式为y＝4（40﹣2x）x，即y＝﹣8x2+160x，y＝﹣8（x﹣10）2+800，∵﹣8＜0，∴y有最大值，∴当x＝10时，y＝800；最大答：折成的长方体盒子的侧面积有最大值，这个最大值是800cm2．【点睛】本题考查了一元二次方程的应用和二次函数的最值问题，根据几何图形理解如何建立一元二次方程和函数关系式是解题的关键；明确正方形面积=边长×边长，长方形面积=长×宽；理解长方体盒子的底面是哪个长方形；解题时应该注意如何利用配方法求函数的最大值．。

用一元二次方程解决几何图形问题含答案