讲义2
讲义(2)《化学计量基础》课后练习答案(一)

第二章 化学计量基础【课后练习】一、物质的量1. 下列说法正确的是 ( )A. 水的摩尔质量是18g /molB. 1分子硫酸的质量是98/N A gC.4.4gCO 2的物质的量是0.1molD. 1mol 氢气的质量是2g2. 对于相同质量的SO 2和SO 3而言,下列关系正确的是 ( )A. 含氧原子的个数比为2∶3B. 含硫元素的质量比是5∶4C. 含氧元素的质量比为5∶6D. 含硫原子的个数比为1∶1解析:相同质量的SO 2和SO 3的物质的量之比为1/64 : 1/96 = 96 : 64 = 3 : 2,列出如下关系式:SO 2 ~ 1S ~ 2O SO 3 ~ 1S ~ 3OA 选项:氧原子个数比 = 3×2 : 2×3 = 1 : 1,错;B 选项:硫元素质量比 =3232:80:645:43216232163==+⨯+⨯ C 选项:氧元素质量比 =162163:3280:48645:63216232163⨯⨯=⨯⨯=+⨯+⨯ D 选项:硫原子个数比 = 3×1 : 2×1 = 3 : 2,错.3. 将a g 氯化钾溶于1.8L 水,恰使K +离子数与水分子数之比为1∶100,则a 值为 ( )A. 0.745B. 0.39C. 39D. 74.5解析:列出关系式:KCl ~ K + ~ 100H 2O1 mol 1 mol 100 mol1.8 L 水的质量为1800 g ,物质的量为100 mol ,则需要1 molKCl ,其质量为74.5 g 。
4. 在一定体积的容器中加入1.5mol 氙气和7.5mol 氟气,于400℃和2633kPa 下加热数小时,然后迅速冷却至25℃,容器内除得到一种无色晶体外,还余下4.5mol 氟气,则所得无色晶体产物中,氙与氟的原子个数之比是 ( )A. 1∶2B. 1∶3C. 1∶4D. 1∶6解析:实际消耗了所有的Xe 和3 mol F 2,则列出关系式:Xe ~ 2F 2 ~ XeF n根据原子守恒可得n = 4。
正交试验设计讲义(2)

素 C 1(1) 2(1.5) 3(2) 2 1 2 3 3 0.24 0.161 0.115 0.223 试验号 1 2 3 4 因 A 1(90) 1 1 2(88) B 1(40) 2(45) 3(50) 1 试验结果Yi 空列 粕中游离棉酚(%) 粕中残油率(%) 1.17 0.65 0.42 0.41
河南工业大学
因素 试验号 1 2 3 4 5 6 A 1 B 2 C 3
shiyanshujuchulishiyongfangfa
D 4 试验指标 I 17.8 12.2 6.2 8 4.5 4.1
II 29.8 41.3 59.9 24.3 综合评分 y 59.4 51.2 45.5 32.2
五、试验方案及结果分析(1)试验方案与试验结果表
河南工业大学
shiyanshujuchulishiyongfangfa
例3.2 白地雷核酸生产工艺的试验
一、试验目的: 原来生产中核酸的得率太低,成本太高,甚至 造成亏损。试验目的是提高含量,并寻找最好的工 艺条件。 二、因素与水平
因素 水平
1 2 3 白地雷核酸含量 腌制时间 加热时 加水量
A(%)
事实上,通过进一步的试验证明,上述最优条
件效果很好。投产后核酸质量得到显著提高,做到
了不经提纯一次可以入库。
河南工业大学
趋势图
指标
shiyanshujuchulishiyongfangfa
50 45 40 35 A1 A2 A3 B1 B2 B3 C1 C2 C3 D1 D2 D3
因素
指标(得分)-因素图
7.4 8.4 6.2
B(小时)
24 4 0
C(PH值)
新概念英语第3册课程讲义Lesson2

Lesson 2 Thirteen equals oneequal ['i:kwəl]v. 等于He equaled the world record.Nobody equals him in strength.Nobody matches him in strength.In English she has no equal in her class.be / stand head and shoulders above sb. be much better than others明显超过他人,鹤立鸡群5. In computer programming, Susan is head and shoulders above the rest of us. Answer: (A) Susan is much better than we are in this subject.Women demand equal pay for equal work.A is equal to Bequalityracial equalitysexual equalityWe wish to inform you that we specialize in garments for more than twenty years, and shall be pleased to establish business relations with you on the basis of equality and mutual benefits. raise [reɪz]v. 募集,筹措raiseone’s hand raise one’svoice raise one’s hatto sb. raise one’s glassto sb.raise the roofraise pigsHe has a big family to raise.We’re raising a fund for orphans.risearise arose arisenProblems arose.arousearouse one’s pity / anger …―You look happy today.―Yes. I got a raise.We pay two thousand Yuan monthly to start. It's our policy to hire on a trial basis. If you work out all right after three months you will be put on the permanent payroll and be given a raise.be always doing sth.He is always being late.People are always talking about the problems of youth.W: Mary is always complaining about her job.M: Maybe if you try typing letters every day, you'd see what it's like.Q: What does the man mean?Answer: A) The woman would understand if she did Mary's job.be forever doing sth.He is forever talking about the friendly people, the clean atmosphere, the closeness to nature and gentle pace of living.be constantly / continually doing sth.The boys are constantly / continually arguing.Your behavior reflects on me, and I can't do my job if you're constantly humiliating me. Constantly? Aside from today, give me one example.keep (on) doing sth.From the moment he arrived there, he kept on pestering his doctor to tell him when he would be able to go home.In the process, he enjoyed himself thoroughly and kept telling everybody how much he hated hospitals.do sth. all the timeW: I thought the doctor said you should stay off your foot until the swelling goes down.M: She did. It just makes me uncomfortable to ask my friends to wait on me all the time.What does the man mean?D) He doesn't like to bother people.Sam, mess up the kitchen (always)Sam is always messing up the kitchen.Bruce, leave his dirty dishes on the table (forever)Bruce is forever leaving his dirty dishes on the table.Peter, try to show me he’s smarter than me (constantly)Peter is constantly trying to show me he is smarter than me.Mary, borrow my clothes without asking me (continually)Mary is continually borrowing my clothes without asking me.Why, you, make the same mistakes (keep on doing)Why do you keep on making the same mistakes?Jane, forget to give me my phone messages (do sth. all the time)Jane forgets to give me my phone messages all the time.One would expect them to know their parts by heart and never have cause to falter.one … or anotherone cause or anotherHe is always asking me for money for one cause or another.Beginners will err at one time or another.Everyone can contribute to society in one way or another.one … after anotherone day after anotherencounter one difficulty after anotherachieve one success after anothermanage to do: 设法完成了某事As no pumas had been reported missing from any zoo in the country, this one must have been in the possession of a private collector and somehow managed to escape.fail to do: 没能完成某事When the journalist again failed to reply, the editor reluctantly published the article as it had originally been written.have sth. done 请某人做某事I'm going to have my hair cut this weekend.… people would rather pay large sums of money than have their life work destroyed by gangsters. King CharlesⅠhad his head cut off.The house had its window broken in the explosion.无灵主语/ 物称主语(inaminate subject)When reports came into London Zoo that a wild puma had been spotted forty-five miles south of London, they were not taken seriously.The sea bed was scoured with powerful nets and there was tremendous excitement on board when a chest was raised from the bottom.He lost his confidence.Confidence deserted him.I couldn't sleep that night.That night sleep eluded me.We only travelled half the distance at sunset.Sunset met us halfway.The past few years witnessed the great influx of foreigners to China, for travelling, studies or business.造句:我的小女儿总是抱怨(complain of) 各种各样的病,但她从未成功地得到允许(get permission) 呆在家里。
中级微观经济学讲义-2

第二讲 消费者理论
四、显示偏好简介
(一)显示偏好弱公理
与古典的从偏好关系到效用函数再到需 求函数的逻辑思路不同, 求函数的逻辑思路不同,萨缪尔森从行为结 果本身推导人的行为准则,抛却了效用理论 果本身推导人的行为准则, 中的许多主管假定,而仅需要一些隐含的、 中的许多主管假定,而仅需要一些隐含的、 弱的要求,比如一致性。 弱的要求,比如一致性。
第二讲 消费者理论
二、效用最大化与支出最小化
(二)效用最大化-续(2) 效用最大化-
罗伊恒等式】 【罗伊恒等式】 构造拉格朗日函数 L( x , λ ) = u( x ) + λ ( y − px ), ∂v ( p, y ) ∂L( x * , λ* ) 根据包络定理, 根据包络定理, = = λ*以及 ∂y ∂y ∂v ( p, y ) ∂L( x * , λ* ) = = − λ* x i*,可以得到 ∂ pi ∂p i ∂v ( p , y ) − ∂ pi x i* = x i ( p, y ) = ∂v ( p , y ) ∂y
x 2 f x1 , ∀t ∈ [0,1] ⇒ x t = tx 2 + (1 − t )x1 ~ x1 f ~ 公理 7 : 严格凸性 x 2 ≠ x1 , x 2 f x1 ⇒ x t f x1 ~ (排除了无差异集凹向原 点 < 多元化消费 > )
第二讲 消费者理论
一、偏好、效用与预算 偏好、
第二讲 消费者理论
一、偏好、效用与预算 偏好、
(一)偏好关系-续(1) 偏好关系-
偏好公理: 偏好公理: 公理 4 : 局部非饱和性 公理 5 : 严格单调性 公理 6 : 凸性 ∀x 0 ∈ R n , ∃ε > 0 , ∃x ∈ B ε ( x 0 ) I R n ⇒ x f x 0 + + (排除了无差异区域的存 在 ) ∀x 0, x1 ∈ R n , x1 ≥ x 0 ⇒ x1 f x 0 + ~ (排除了无差异集向上弯 曲)
西门子PLC讲义 2-2 功能和功能块 FCFBs

定义FC 20形式参数
定义
in out In_out
形式参数
使用方法
只能读 只能写 可读/可写
图形显示
在块的左侧 在块的右侧 在块的左侧
编辑可以分配参数的块
调用可以分配参数的块
练习: 编辑可以分配参数的FC块
练习: 调用可以分配参数的FC块
第一次调用FC20时 的参数分配
2. 创建一个新的背景数据块 在 SIMATIC Manager
练习: 编辑功能块
练习: 调用功能块并测试
之前
之后
之后插入/删除块的参数
Adding a parameter
Save
检查块的一致性
调用被修改过的块时应做的更正
单击鼠标右键
比较: 功能和功能块
特性 静态变量 变量的初始值 需要背景数据块 当被调用时必须使用所有的实际参数
FBD
FC1 CALL
FC1
EN
ENO
FC2
EN
Par3
Par1
Par2 ENO
DB2
FB1
EN
ENO
DB3
FB2
EN
Par3
Par1 Par2
ENO
FC 2
FC 3
?? . ? EN ENO
EN ENO
EN ENO
=
总结: 块的调用
语言
STL
LAD
无参数
• UC FC1 • CC FC1 • CALL FC1
FC1
( CALL )
FC1
EN
ENO
FC
有参数
• CALL FC2 Par1: ... Par2: ... Par3: ...
费恩曼物理学讲义第2卷

费恩曼物理学讲义第2卷
《费恩曼物理学讲义》是2013年4月由上海科学技术出版社出版的图书,作者是费恩曼。
该书主要根据费恩曼的讲稿组成完整地概括了电磁学方方面面的内容。
《费恩曼物理学讲义(第2卷)》主要介绍了电磁学,包括电场、磁场、波及其相互关系等,共42章。
费恩曼(R.P.Feynman)1918年生于布鲁克林区,1942年在普林斯顿获得博士学位。
第二次世界大战期间在洛斯阿拉莫斯,尽管当时他还很年轻,但已在曼哈顿计划中发挥了重要作用。
以后,他在康奈尔大学和加利福尼亚理工学院任教。
1965年,因他在量子电动力学方面的工作和朝永振一郎及施温格(J.Schwinger)同获诺贝尔物理学奖。
费恩曼博士获得诺贝尔奖是由于成功地解决了量子电动力学理论问题,他也创立了说是液氦中起流动性现象的数学理论。
此后,他和盖尔曼(M.Gell-Mann)在B衰变等弱相互作用领域内做出了奠基性的工作。
在以后的几年里,他在夸克理论的发展中起了关键性的作用,提出了他的高能质子碰撞过程的部分子模型。
除了这些成就之外,费恩曼博士将新的基本计算技术及记号法引时物理学,首先是无处不在的费恩曼图,在近代科学历史中,它比任何其他数学形式描述都更大地改变了对基本物理过程形成概念及进行计算的方法。
语文高考复习讲义第2部分 教材文言文复习 课时26 《〈论语〉十二章》《大学之道》《人皆有不忍人之心

课时26《〈论语〉十二章》《大学之道》《人皆有不忍人之心》活动一基础知识梳理1.通假字例句指出通假本字及意义①知.者不惑②非所以内.交于孺子之父母也③若火之始然.答案①同“智”,智慧②同“纳”,结交③同“燃”,燃烧2.古今异义词词语例句解析(古今义)①然后文质彬彬,然后..君子古义:_________________________今义:连词,表示一件事情之后接着又发生另一件事情②大学大学..之道古义:___________________________今义:实施高等教育的学校的一种答案①两个词,这样以后②指穷理、正心、修身、治人的学问3.多义实词词语例句意义(1)安①居无求安.②静而后能安.③思国之安.者,必积其德义(《谏太宗十思疏》)④卮酒安.足辞(《鸿门宴》)⑤然后得一夕安.寝(《六国论》)⑥衣食所安.,弗敢专也(《曹刿论战》)(2)克①克.己复礼为仁②能克.终者盖寡(《谏太宗十思疏》)③既克.,公问其故(《曹刿论战》)④三纳之而未克.(《中山狼传》)成功(3)恶①非恶.其声而然也②以小易大,彼恶.知之(《齐桓晋文之事》)③则思正身以黜恶.(《谏太宗十思疏》)(4)辞①辞.让之心,礼之端也②《归去来兮辞.》③辞.曰:“臣之壮也,犹不如人。
”(《烛之武退秦师》)④大礼不辞.小让(《鸿门宴》)⑤辞.楼下殿,辇来于秦(《阿房宫赋》)⑥其文约,其辞.微(《屈原列传》)(5)要①非所以要.誉于乡党朋友也②张良要.项伯(《鸿门宴》)③北收要.害之郡(《过秦论》)④虽与府吏要.,渠会永无缘(《孔雀东南飞》)⑤故治之要.在于知道(《荀子》)要领⑥要.之死日,然后是非乃定(《报任安书》)总括、总之(6)贼①有是四端而自谓不能者,自贼.者也②未及见贼.而士卒离散(《五代史伶官传序》)③是天下之大贼.也(《论积贮疏》)祸害④贼.二人得我,我幸皆杀之矣(《童区寄传》)强盗答案(1)①安逸、舒适②性情安和③安定④哪里⑤安稳⑥安身(2)①约束②能够③攻克(3)①厌恶②怎么、哪里③小人(4)①推让、谦让②古代的一种文体③推辞④讲究、计较⑤辞别、离开⑥文辞(5)①求取②同“邀”,邀请③重要的、关键的④相约(6)①伤害②敌人、仇敌4.词类活用例句活用类型及释义①就有道而正.焉②见贤.思齐焉③见不贤而内.自省也④譬如平.地⑤大学之道,在明.明德⑥先齐.其家⑦先正.其心⑧先诚.其意答案①形容词作动词,匡正②形容词作名词,贤能的人③名词作状语,在内心④形容词作动词,填平⑤形容词作动词,彰明⑥形容词的使动用法,使……整齐有序⑦形容词的使动用法,使……端正⑧形容词的使动用法,使……真诚5.特殊句式例句句式特点(指出标志词)①见不贤而内自省也②仁以为己任,不亦重乎③有一言而可以终身行之者乎④人而不仁,如乐何⑤克己复礼为仁答案①宾语前置句,“自”作“省”的宾语②宾语前置句,正常语序为“以仁为己任”;固定句式,“不亦……乎”,不也……吗③定语后置句,“而……者”为语言标志,正常语序为“有可以终身行(之)一言乎”④固定句式,“如……何”,把……怎么样呢、对……怎么办呢⑤判断句,标志词:为6.文化常识(1)小人:指地位低下的人,平民百姓,是统治者对劳动者的蔑称;又指__________________的人。
信号与系统讲义-2

f (t) u 3 10
p
u pf (t) 2p 10
u(t) (Ae5t B)U(t)
2 du(t) 10u(t) df (t)
dt
dt
u(t) 5Ae5t U(t) (A B)(t)
2(A B) 1 B0
u(t) 1 e5tU(t)V 2
H
(
p)
2p2 8p 3 ( p 1)( p 3)2
求系统的响应 y(t)。
解: D(p) (p 1)(p 3)2 0 p1 1 p2 p3 3
y0 (t) K1e t K 2e3t K 3te3t
y0 (0 ) K1 K2 =2 y0 (0 ) K1 3K 2 K3=1
3、共轭复根:(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
,
d
02 2 , 0
1 LC
4
三、 RLC串联电路全响应
d 2uc dt 2
R L
duc dt
1 LC
uc
1 LC Us
(二阶常系数线性非齐次微分方程)
t<0 , K在2,有 uc (0 ) U0
C
uc Aep1t Be p2t Us
2、重根:(临界阻尼) 即
R2
L C
(自然频率、固有频率)
uc (A Bt)ept Us
3、共轭复根:(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
d 02 2
平行线与相交线--学生讲义(2)
中正教育学生辅导讲义年级:初一课时数:3 班主任:学员姓名:李子扬辅导科目:数学学科教师:王梦珠授课类型T 立足课本,两条直线的位置关系C 两条直线垂直与平行中角的关系T熟练运用两直线平行的判定定理授课日期时段2015.530周六10:00-12:00教学内容一、立足课本【学习目标】1.熟练掌握对顶角,余角,补角,邻补角及垂线的概念及性质,了解点到直线的距离与两平行线间的距离的概念;2. 区别平行线的判定与性质,并能灵活运用;3. 了解尺规作图的概念,熟练掌握用尺规作角或线段的方法.【要点梳理】要点一、两条直线的位置关系1.同一平面内两条直线的位置关系:相交与平行要点诠释:(1)只有一个公共点的两条直线叫做相交直线,这个公共点叫做交点.(2)在同一平面内不相交的两条直线叫做平行线.平行用符号“∥”表示.2.对顶角、补角、余角(1)定义:①由两条直线相交构成的四个角中,有公共顶点且两边互为反向延长线的两个角叫做对顶角.②如果两个角的和是180°,那么这两个角互为补角,简称互补,其中一个角叫做另一个角的补角.类似地,如果两个角的和是90°,那么这两个角互为余角.简称互余,其中一个角叫做另一个角的余角.(2)性质:同角或等角的余角相等.同角或等角的补角相等.对顶角相等.3.垂线(1)垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足.垂直用符号“⊥”表示,如下图.(2)垂线的性质:①在同一平面内,过一点有且只有一条直线与已知直线垂直.②垂线段最短.(3)点到直线的距离:从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.要点二、平行线的判定与性质1.平行线的判定判定方法1:同位角相等,两直线平行.判定方法2:内错角相等,两直线平行.判定方法3:同旁内角互补,两直线平行.要点诠释:根据平行线的定义和平行公理的推论,平行线的判定方法还有:(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).(3)在同一平面内,垂直于同一直线的两条直线平行.(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.2.平行线的性质性质1:两直线平行,同位角相等;性质2:两直线平行,内错角相等;性质3:两直线平行,同旁内角互补.要点诠释:根据平行线的定义和平行公理的推论,平行线的性质还有:(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.3.两条平行线间的距离如图,直线AB∥CD,EF⊥AB于E,EF⊥CD于F,则称线段EF的长度为两平行线AB与CD间的距离.要点诠释:(1)两条平行线之间的距离处处相等.(2)初中阶级学习了三种距离,分别是两点间的距离、点到直线距离、平行线间的距离.这三种距离的共同点在于都是线段的长度,它们的区别是两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是一条直线上的一点到与之平行的另一直线的距离.(3)如何理解“垂线段”与“距离”的关系:垂线段是一个图形,距离是线段的长度,是一个量,它们之间不能等同.要点三、用尺规作线段和角1.用尺规作线段(1)用尺规作一条线段等于已知线段.(2)用尺规作一条线段等于已知线段的倍数.(3)用尺规作一条线段等于已知线段的和.(4)用尺规作一条线段等于已知线段的差.2.用尺规作角(1)用尺规作一个角等于已知角.(2)用尺规作一个角等于已知角的倍数.(3)用尺规作一个角等于已知角的和.(4)用尺规作一个角等于已知角的差.二、典例分析类型一、两条直线的位置关系1.如图,直线AB、CD、EF相交于点O,那么互为对顶角(平角除外)的角共有对,它们分别是,共有对邻补角.举一反三:【变式】如图所示,已知∠AOD=∠BOC,请在图中找出∠BOC的补角,邻补角及对顶角.2.已知:如图,直线a、b、c两两相交,且a⊥b,∠1=2∠3,,求∠4的度数.类型二、平行线的性质与判定3.如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整:因为EF∥AD,所以∠2= ()又因为∠1=∠2,所以∠1=∠3所以AB∥()所以∠BAC+ =180°()因为∠BAC=70°,所以∠AGD= .举一反三:【变式】如图,已知∠ADE=∠B,∠1=∠2,那么CD∥FG吗?并说明理由.4.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.1.(1)如图(1)已知直线AB,CD相交于点0.(2)如图(2)已知直线AE,BD相交于点C.分别指出两图中哪些角是邻补角? 哪些角是对顶角?2.直线AB、CD相交于点O,OE⊥AB于点O,∠COE=40°,求∠BOD的度数.举一反三:【变式】如图所示,O是直线AB上一点,射线OC、OD在AB的两侧,且∠AOC=∠BOD,试证明∠AOC与∠BOD是对顶角.类型二、平行线的性质与判定3.如图所示,AB∥CD,∠1=∠B,∠2=∠D,试说明BE⊥DE.举一反三:【变式1】已知直线AB∥CD,当点E在直线AB与CD之间时,有∠BED=∠ABE+∠CDE成立;而当点E在直线AB与CD之外时,下列关系式成立的是().A.∠BED=∠ABE+∠CDE或∠BED=∠ABE-∠CDEB.∠BED=∠ABE-∠CDEC.∠BED=∠CDE-∠ABE或∠BED=∠ABE-∠CDED.∠BED=∠CDE-∠ABE【变式2】如图,两直线AB、CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=.4.如图,已知CD∥EF,∠1+∠2=∠ABC,求证:AB∥GF.类型三、实际应用6.手工制作课上,老师先将一张长方形纸片折叠成如图所示的那样,若折痕与一条边BC的夹角∠EFB=30°,你能说出∠EGF的度数吗?举一反三:【变式】(山东滨州)如图,把—个长方形纸片对折两次,然后剪下—个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为().A.60° B.30° C.45° D.90°一、能力检测一、选择题1.下列图中,∠1和∠2是对顶角的有()个.A.1个B.2个C.3个D.4个2.如图所示是同位角关系的是().A.∠3和∠4 B.∠1和∠4 C.∠2和∠4 D.不存在3.下列说法正确的是().A.相等的角是对顶角.B.两条直线被第三条直线所截,内错角相等.C.如果两条直线都和第三条直线平行,那么这两条直线也互相平行.D.若两个角的和为180°,则这两个角互为余角.4.∠1和∠2是直线AB和CD被直线EF所截得到的同位角,那么∠1和∠2的大小关系是().A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定5.一个人从A点出发向北偏东60°方向走到B点,再从B点出发向南偏西15°方向走到C点,那么∠ABC等于().A.75°B.105°C.45°D.135°6.下列说法中,正确的是().A.过点P画线段AB的垂线.B.P是直线AB外一点,Q是直线AB上一点,连接PQ,使PQ⊥AB.C.过一点有且只有一条直线垂直于已知直线.D.过一点有且只有一条直线平行于已知直线.7.如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( ).A. 50°B. 60°C.70°D.80°二、填空题9. 如图所示,AB∥CD,EF分别交AB、CD于G、H两点,若∠1=50°,则∠EGB=________.10.如图所示,已知BC∥DE,则∠ACB+∠AOE=.11.每天小明上学时,需要先由家向东走150米到公共汽车站点,然后再乘车向西900米到学校,每天小明由家到学校移动的方向是________,移动的距离是________.12. (广东湛江)如图所示,请写出能判断CE∥AB的一个条件,这个条件是:①:________ ②:________ ③:________(第12题)(第13题)13.如图,已知AB∥CD,CE,AE分别平分∠ACD,∠CAB,则∠1+∠2=________.14.如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD= ,∠AOC=,∠BOC=.15. 如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西.16.如图所示,AC⊥BC于点C,CD⊥AB于点D,DE⊥BC于点E,能表示点到直线(或线段)的距离的线段有条.三、解答题17.如图所示,直线AB、CD、EF相交于点O,若∠1+∠2=90°,∠3=40°,求∠1的度数,并说明理由.18.如图所示,已知∠1=∠2,AC平分∠DAB,你能推断哪两条线段平行? 说明理由.19. 如图所示,已知∠1=50°,∠2=130°,∠4=50°,∠6=130°,试说明a∥b,b∥c,d∥e,a∥c.教师赠言:There is no elevator to success, only stairs. ----成功没有电梯,只有楼梯。
小学四年级奥数讲义(2)

小学四年级奥数讲义(2)姓名:课题第二讲:数列求和。
励志言小朋友们:你的快速反应能力、你的综合理解能力将体现在这些富有挑战的训练题中。
你的数学能力在这里将得到大大的提升!知识反思1、等差数列的定义及特点:像1,2,3,4,5,…,99,100这样的一列数一般叫做一个等差数列。
等差数列的特点是相邻两个数的差是相同的。
2、等差数列的各部分名称:公差:相邻两个数的差叫做公差。
项:数列中的每一个数叫做项。
首项:数列中的第一个数叫做首项。
末项:数列中的最后一个数叫做末项。
项数:数列中共有多少项(共有多少个数)叫做项。
3、等差数列求和公式:总和=(首项+末项)×项数÷2项数=(末项-首项)÷公差+1末项=首项+公差×(项数-1)首项=末项-公差×(项数-1)课前检测请大家用8分钟时间,背过上面的知识,过关的同学别忘记“※”,累计十个,可以得到老师的一份小礼物。
自主学习(一)例1.计算1+2+3+4+…+39+40合作探究例2.计算2+5+8+11+…+209+212(一)精讲释疑(一)例2,这是一个等差数列,首项是2,末项是212,公差是3,利用公式求和必须知道项数。
项数=(212-2)÷3+1=210÷3+1=71自主学习(二)例3.求首项是5,公差是3的等差数列的前199项的和。
(缺少什么?)合作探究(二)例4.一个有25项的等差数列,末项是204,公差是8,求这个等差数列的和是多少?精讲释疑(二)例4,要解答问题,看看知道什么,缺少什么。
想办法解决。
训练检测与能力挑战计算下面各题。
1、1+2+3+4+5+…+99+1002、1+2+3+…+49+50+49+…+3+2+13、1990+1991+…+2006+2007+20084、4+6+8+…+96+985、求首项是1,公差是2的等差数列的前50项的和。
6、一个有30项的等差数列,首项是1,公差是4,这个等差数列的和是多少?7、一个有50项的等差数列,末项是2007,公差是2,这个等差数列的和是多少?8、一个等差数列的首项是1,末项是1997,公差是2,这个等差数列的和是多少?课后巩(1)、5+10+15+…+215+220固(2)、求首项是7,末项是99,公差是4的等差数列的和。
2024年高考数学复习培优讲义专题2-指对同构(朗博同构)(含解析)
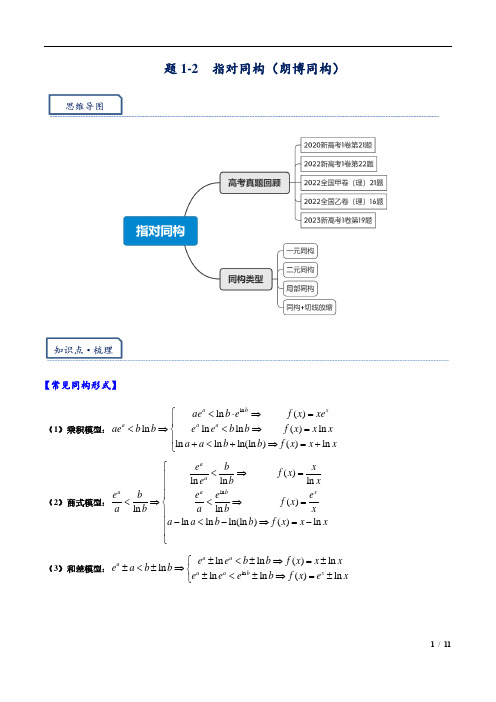
题1-2 指对同构(朗博同构)【常见同构形式】(1)乘积模型:ln ln ()ln ln ln ()ln ln ln ln(ln )()ln a b x aa a aeb e f x xe ae b b e e b b f x x x a a b b f x x x ⎧<⋅⇒=⎪<⇒<⇒=⎨⎪+<+⇒=+⎩(2)商式模型:ln ()ln ln ln ()ln ln ln ln ln(ln )()ln a aa ab x e b xf x e b x e b e e e f x a b a b x a a b b f x x x ⎧<⇒=⎪⎪⎪<⇒<⇒=⎨⎪−<−⇒=−⎪⎪⎩(3)和差模型:ln ln ln ()ln ln ln ln ()ln a a aaa b xe e b bf x x xe a b b e e e bf x e x ⎧±<±⇒=±±<±⇒⎨±<±⇒=±⎩【六大超越函数图像】(6)2020新高考1卷21(2)1.已知函数1()ln x f x ae x lna −=−+,若f (x )≥1,求a 的取值范围.2022新高考1卷第22题2.已知函数()x f x e x =−和()ln g x x x =−,证明:存在直线y b =,其与两条曲线()y f x =和()y g x =共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.2022全国甲卷(理)21题3.已知函数()ln xf x x a xx e −=+−.(1)若()0f x ≥,求a 的取值范围;(2)证明:若()f x 有两个零点12,x x ,则121x x <.2023新高考1卷T19(2) 同构+切线放缩或2次求导4.已知函数()()x f x a e a x =+−,证明:当a >0时,3()2ln 2f x a >+.2022全国乙卷(理)16题5.已知1x x =和2x x =分别是函数2()2e x f x a x =−(0a >且1a ≠)的极小值点和极大值点.若12x x <,则a的取值范围是 .题型一 一元同构2023深圳高二下期末·21(2)1.已知2()()x f x axe a R =∈,若关于x 的()2ln 0f x x x −−≥恒成立,求实数a 的取值范围.重点题型·归类精讲2.若关于x 的不等式ln ln 0e xx a a xx+−>对()0,1x ∀∈恒成立,则实数a 的取值范围为( ) A .1,e ⎛⎤−∞ ⎥⎝⎦B .1,e ∞⎡⎫+⎪⎢⎣⎭C .1,1e ⎡⎫⎪⎢⎣⎭D .10,e ⎛⎤ ⎥⎝⎦宁波九校高三上期末·22(2) 3.已知函数1()ln 2f x x x x x ⎛⎫=+− ⎪⎝⎭,e 是自然对数的底数.若不等式2()(1)4axf x a e x ≤+−对0x ∀>恒成立,求实数a 的取值范围.江苏盐城2023届高三5月三模·22 4.已知函数()(ln ).x a f x e e a x =−+ (1)当a =1时,求()f x 的单调递增区间; (2)()0f x ≥恒成立,求a 的取值范围.湖南九校联盟第二次联考·16 5.已知不等式))(1ln (0xa x e a a e −⎡⎤≥>⎢⎥⎣⎦恒成立,则实数a 的最大值为_______湖南省2023届高三下3月考试·16 6.已知e 是自然对数的底数.若()0x ∀∈+∞,,e ln mx m x ≥成立,则实数m 的最小值是 .7.若不等式0x ae lnx lna −+恒成立,则a 的取值范围是( )A .1[,)e +∞B .2[,)e +∞C .[,)2e+∞D .[e ,)+∞湖北鄂东南联考 ·88.已知函数()ln x f x x x xe k −=−−−恒有零点,则实数k 的取值范围是( )A .(],1−∞−B .1,1e⎛⎤−∞−− ⎥⎝⎦C .11,1e⎡⎤−−−⎢⎥⎣⎦D .11,0e⎡⎫−−⎪⎢⎣⎭福建龙岩九校联考·16 9.已知函数mx x m x f −+=)1ln()(,若不等式x e x x f −+>1)(在()+∞,0上恒成立,则实数m 的取值范围是____________ .湖南常德3月模拟10.已知不等式ln()x x a e a +≤−对[1,)x ∀∈+∞恒成立,则a 的取值范围为 .浙江省衢州、丽水、湖州三地市2023高三下学期4月教学质量检测·8 11.对任意的实数0x >,不等式22ln ln 0x ae x a −+≥恒成立,则实数a 的最小值为( )e2eC.2eD.12e2022湖北四地七校高二下期中·712.已知实数a >0,不等式()0x e aln ax ->恒成立,则a 的取值范围是( ) A .1<<a e eB .0<a <1C .0<a <eD .a >e湖南郴州高二下期末·16 13.函数.若对任意,都有,则实数m 的取值范围为_________.2023湖南邵阳二模·8 14.若不等式()1e 1ln 10txt x x ⎛⎫−−−≥ ⎪⎝⎭对任意[)2e 1,x ∞∈++恒成立,则正实数t 的取值范围是( )A. ln2,2e 1∞⎡⎫+⎪⎢+⎣⎭B. ln21,2e 1∞+⎡⎫+⎪⎢+⎣⎭C. ln210,2e 1+⎛⎫ ⎪+⎝⎭ D. ln2ln21,2e 12e 1+⎡⎤⎢⎥++⎣⎦15.已知函数ln 0x f xe a ax a a a ,若关于x 的不等式0f x恒成立,则实数a 的取值范围为( ) A .],0(eB .],0(2eC .],1[2eD .),1(2e()()()e1ln R mxf x m x x m =+−−∈0x >()0f x ≥16.关于x 的不等式ln 1axx e xe a x x−≤−−恒成立,则a 的取值范围为 .2022衡阳市八中高二期末·16 17.已知函数1()(0)a x f x x alnx x a e=++−<,若()0f x 在[2x ∈,)+∞上恒成立,则实数a 的取值范围为 . 2023届郴州三模·1618.设实数0m >,若对任意的21x e ∞⎛⎫∈+ ⎪⎝⎭,,不等式ln 1mx mx x e e m m mx−≥−恒成立,则实数m 的取值范围为 .湖北省部分学校高三下5月适应性考试·14 19.对于任意实数0x >,不等式22e ln ln 0x a x a −+≥恒成立,则a 取值范围是__________.2023·广东惠州·一模T22(2)20.已知函数()2ln f x x a x =−,若函数()(2)e x f x a x x ≥+−恒成立,求实数a 的取值范围.2023·广东深圳·南山区高三上期末联考·22 21.已知定义在()0,∞+上的函数()e ax f x x =. (1)若R a ∈,讨论()f x 的单调性;(2)若0a >,且当()0,x ∈+∞时,不等式2e ln aax xx ax ⎛⎫≥⎪⎝⎭恒成立,求实数a 的取值范围.2023·广东汕头·一模T2222.已知函数()e ln(2)ln 2x f x a x a =−++−.(1)若函数()f x 在2023x =处取得极值,求a 的值及函数的单调区间; (2)若函数()f x 有两个零点,求a 的取值范围.的题型二 二元同构2022届山东聊城一模·823.已知正数x ,y 满足ylnx +ylny =e x ,则xy ﹣2x 的最小值为( ) A .1122n B .222ln ﹣ C .1122n −D .222ln +24.实数x ,y 满足ln ln xe y x y y =+,则2ln xe y x−的最小值为________2022届T8第一次联考·825.设a ,b 都为正数,e 为自然对数的底数,若1a ae b blnb ++<,则( ) A .ab e >B .1a b e +>C .ab e <D .1a b e +<2023茂名市高三一模·1226.(多选)e 是自然对数的底数,,m n ∈R ,已知e ln ln m m n n n m +>+,则下列结论一定正确的是( ) A .若0m >,则0m n −> B .若0m >,则e 0m n −> C .若0m <,则ln 0m n +< D .若0m <,则e 2m n +>河北省衡水中学2023届高三下学期第三次综合素养评价·16 27.若正实数a ,b 满足()1ln ln e a a b a a b −−+≥,则1ab的最小值为 .28.设11110e ,11ln1.111a b ==,则( )A .1ab a <<B .1ab b <<C .1a ab <<D .1b ab <<题型三 局部同构华大新高考五月押题卷·1229.(多选)已知0λ>,若关于x 的方程()1ln 0x e x x xλλλ−−+=存在正零点,则实数λ的值可能为A .1eB .12C .eD .230.已知函数1ln )(−−=x ae x f x ,若0)(≥x f 恒成立,则实数a 的取值范围是 .2023·广东·海珠区高三2月联考·22 31.已知函数()()1e 02x f x ax a =−≠. (1)讨论函数()f x 的单调性; (2)已知函数()()ln xg x f x x=−有两个零点,求实数a 的取值范围.2023·广东3月·中学生标准学术能力诊断测试联考模拟预测T22(2) 部分同构+放缩 32.设()()e xxf x x =∈R ,若(e )()(ln 1)x f x k x ⋅≤⋅+在()1,x ∈+∞上恒成立,求k 的取值范围.2023·广东·深圳中学5月适应性测试T22(1) 部分同构33.已知函数()e ln xf x ax a x x =−−,若不等式()0f x <恒成立,求实数a 的取值范围.题型四 同构+切线放缩2023佛山一模T1134.(多选)若正实数x ,y 满足()1e 1ln x x y y −=+,则下列不等式中可能成立的是( )A .1x y <<B .1y x <<C .1x y <<D .1y x <<巴蜀中学2023届高考适应性月考卷(八)T8——局部构造+切线放缩35.已知函数22ln 1()e x x f x x a x+=−−,当()0,x ∈+∞时,()0f x ≥恒成立,则实数a 的取值范围是( ) A .(2,e 1⎤−∞−⎦B .(],e −∞C .(],2−∞D .(],1−∞2023届湖南四大名校5月“一起考”T736.若当π0,2x ⎛⎫∈ ⎪⎝⎭时,关于x 的不等式2e cos cos lncos 1x x x x x ax −++≥恒成立,则满足条件的a 的最小整数为( ) A. 1 B. 2 C. 3 D. 437.(2023·广东珠海·高三联考模拟考试)已知函数()()()()ln 2R ,e 1xf x x ax ag x x x a x =−−∈=−−+.(1)求函数()f x 的单调区间;(2)若不等式()()f x g x ≤恒成立,求实数a 的取值范围.38.(2023·广东·统考一模)已知函数()1e x f x x +=.(1)求()f x 的极值; (2)当0x >时,()()1ln 2f x a x x ≥+++,求实数a 的取值范围.补充练习杭州一模(高三上期末)T16——同构有一定难度,函数分析也比较麻烦1.已知不等式()ln ln 10,1()xa a a x a a >−>≠对)1,(x ∀∈+∞恒成立,a 的取值范围是________.2023湖北高三九师联盟1月·82.已知a >b >1,若1a a b e be ae a ++=+,则 A .ln(a +b )>1B .ln(a -b )<0C .333a b −+<D .133a b −<湖北名校联合体高三下学期开学考·163.已知关于x 的不等式()1ln 2x e a a ax a −+>−(0)a >恒成立,则实数a 的取值范围为________.4.对0x ∀>,恒有()112ln axa e x x x ⎛⎫+≥+⎪⎝⎭,则实数a 的最小值为________.专题1-2 指对同构(朗博同构)【常见同构形式】(1)乘积模型:ln ln ()ln ln ln ()ln ln ln ln(ln )()ln a b x aa a aeb e f x xe ae b b e e b b f x x x a a b b f x x x ⎧<⋅⇒=⎪<⇒<⇒=⎨⎪+<+⇒=+⎩(2)商式模型:ln ()ln ln ln ()ln ln ln ln ln(ln )()ln a aa ab x e b xf x e b x e b e e e f x a b a b x a a b b f x x x ⎧<⇒=⎪⎪⎪<⇒<⇒=⎨⎪−<−⇒=−⎪⎪⎩(3)和差模型:ln ln ln ()ln ln ln ln ()ln a a aaa b xe e b bf x x xe a b b e e e bf x e x⎧±<±⇒=±±<±⇒⎨±<±⇒=±⎩【六大超越函数图像】(6)2020新高考1卷21(2)1.已知函数1()ln x f x ae x lna −=−+,若f (x )≥1,求a 的取值范围.【答案】[)1+∞, [方法一]:【最优解】:同构由()1f x ≥得1e ln ln 1x a x a −−+≥,即ln 1ln 1ln a x e a x x x +−++−≥+,而ln ln ln x x x e x +=+,所以ln 1ln ln 1ln a x x e a x e x +−++−≥+.令()m h m e m =+,则()10m h m e +'=>,所以()h m 在R 上单调递增.由ln 1ln ln 1ln a x x e a x e x +−++−≥+,可知(ln 1)(ln )h a x h x +−≥,所以ln 1ln a x x +−≥,所以max ln (ln 1)a x x ≥−+. 令()ln 1F x x x =−+,则11()1xF x x x−'=−=. 所以当(0,1)x ∈时,()0,()F x F x '>单调递增; 当(1,)x ∈+∞时,()0,()F x F x '<单调递减. 所以max [()](1)0F x F ==,则ln 0a ≥,即1a ≥. 所以a 的取值范围为1a ≥. [方法二]:换元同构由题意知0,0a x >>,令1x ae t −=,所以ln 1ln a x t +−=,所以ln ln 1a t x =−+. 于是1()ln ln ln ln 1x f x ae x a t x t x −=−+=−+−+.由于()1,ln ln 11ln ln f x t x t x t t x x ≥−+−+≥⇔+≥+,而ln y x x =+在,()0x ∈+∞时为增函数,故t x ≥,即1x ae x −≥,分离参数后有1x xa e −≥.令1()x x g x e −=,所以1112222(1)()x x x x x e xe e x g x e e −−−−−−−=='. 当01x <<时,()0,()g x g x >'单调递增;当1x >时,()0,()g x g x <'单调递减. 所以当1x =时,1()x x g x e−=取得最大值为(1)1g =.所以1a ≥.[方法三]:通性通法1()ln ln x f x ae x a −=−+,11()x f x ae x−'∴=−,且0a >.设()()g x f x =',则121()0,x g x ae x −'=+> ∴g(x)在(0,)+∞上单调递增,即()f x '在(0,)+∞上单调递增, 当1a =时,()01f '=,∴()()11min f x f ==,∴()1f x ≥成立.当1a >时,11a < ,111a e −<∴,111()(1)(1)(1)0a f f a e a a−''∴=−−<,∴存在唯一00x >,使得01001()0x f x ae x −'=−=,且当0(0,)x x ∈时()0f x '<,当0(,)x x ∈+∞时()0f x '>,0101x ae x −∴=,00ln 1ln a x x ∴+−=−, 因此01min 00()()ln ln x f x f x ae x a −==−+000011ln 1ln 2ln 122ln 1a x a a x a x x =++−+≥−+⋅=+>1, ∴()1,f x >∴()1f x ≥恒成立;当01a <<时, (1)ln 1,f a a a =+<<∴(1)1,()1f f x <≥不是恒成立. 综上所述,实数a 的取值范围是[1,+∞). [方法四]:因为定义域为(0,)+∞,且()1f x ≥,所以(1)1f ≥,即ln 1a a +≥. 令()ln S a a a =+,则1()10S a a='+>,所以()S a 在区间(0,)+∞内单调递增. 因为(1)1S =,所以1a ≥时,有()(1)S a S ≥,即ln 1a a +≥. 下面证明当1a ≥时,()1f x ≥恒成立.令1()ln ln x T a ae x a −=−+,只需证当1a ≥时,()1T a ≥恒成立. 因为11()0x T a ea−=+>',所以()T a 在区间[1,)+∞内单调递增,则1min [()](1)ln x T a T e x −==−. 因此要证明1a ≥时,()1T a ≥恒成立,只需证明1min [()]ln 1x T a e x −=−≥即可.由1,ln 1x e x x x ≥+≤−,得1,ln 1x e x x x −≥−≥−.上面两个不等式两边相加可得1ln 1x e x −−≥,故1a ≥时,()1f x ≥恒成立. 当01a <<时,因为(1)ln 1f a a =+<,显然不满足()1f x ≥恒成立.所以a 的取值范围为1a ≥.【整体点评】(2)方法一:利用同构思想将原不等式化成ln 1ln ln 1ln a x x e a x e x +−++−≥+,再根据函数()m h m e m =+的单调性以及分离参数法即可求出,是本题的最优解;方法二:通过先换元,令1x ae t −=,再同构,可将原不等式化成ln ln t t x x +≥+,再根据函数ln y x x =+的单调性以及分离参数法求出;方法三:利用导数判断函数()f x 的单调性,求出其最小值,由min 0f ≥即可求出,解法虽稍麻烦,但是此类题,也是本题的通性通法;方法四:由特殊到一般,利用(1)1f ≥可得a 的取值范围,再进行充分性证明即可2022新高考1卷第22题2.已知函数()x f x e x =−和()ln g x x x =−,证明:存在直线y b =,其与两条曲线()y f x =和()y g x =共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列. 【解答】易得()f x 在()0,+∞↑,(),0−∞↓;()g x 在()0,1↓,()1,+∞↑只有y b =过()f x 与()g x 交点时,恰有3个不同交点 则有1223()()()()f x f x g x g x b ====,即12122233ln ln x xe x e x x x x x b −=−=−=−= ①∵111122ln ln xxxe x e e x x −==−− ,且1211,xe x <<,∴1212ln xe x x x =⇒= ② 又∵32ln 3332ln ln x x x x ex e x −=−=− ,且3200ln ,x x >>,∴2323ln x x x x e =⇒= ③由①②③可得:()()2132222ln 2xx x e x b x x b x +=+=++−=,证毕2022全国甲卷(理)21题3.已知函数()ln xf x x a x x e −=+−.(1)若()0f x ≥,求a 的取值范围;(2)证明:若()f x 有两个零点12,x x ,则121x x <. 【详解】(1)[方法一]:同构处理 由()0f x ≥得:ln ln 0x x e x x a −++−−≥令ln ,1t x x t −=≥,则()0tf t e t a =+−≥即t a e t ≤+ 令()[),1,tg t e t t =+∈+∞,则()'10tg t e =+>故()tg t e t =+在区间[)1,+∞上是增函数故()()min 11g t g e ==+,即1a e ≤+ 所以a 的取值范围为(,1]e −∞+ [方法二]:常规求导()f x 的定义域为(0,)+∞,则2111()1x f x e x x x ⎛⎫'=−−+ ⎪⎝⎭1111111x x x e e x x x x x ⎛⎫−⎛⎫⎛⎫=−+−=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭令()0f x '=,得1x =当(0,1),()0,()x f x f x '∈<单调递减当(1,),()0,()x f x f x >'∈+∞单调递增()(1)1f x f e a ≥=+−, 若()0f x ≥,则10e a +−≥,即1a e ≤+ 所以a 的取值范围为(,1]e −∞+ (2)法一:极值点偏移+同构简化计算由题知,()f x 一个零点小于1,一个零点大于1,不妨设121x x ,要证121x x <,即证121x x <因为121,(0,1)x x ∈,即证()121f x f x ⎛⎫> ⎪⎝⎭, 又因为()()12f x f x =,故只需证()221f x f x ⎛⎫> ⎪⎝⎭,即证11ln ln 0,(1,)x x e x x xe x x x x −+−−−>∈+∞同构,原不等式变形为:()1ln ln 1ln ln x x xxex x ex x+−++−>+ 令()xg x e x =+,则有1(ln )ln g x x g x x ⎛⎫−>+⎪⎝⎭即证:)1ln ln ,(1,x x x x x−>∈+∞+ 即证1()2ln 0(1,,)h x x x xx =+∈<+∞− ()()222121'()10,1x h x x x x x−−=−−=<>,即()h x 递减,故()(1)0h x h <=,证毕. [方法二]:对数平均不等式由题意得:()ln x xe ef x a x x=+−令1xe t x=>,则()ln f t t t a =+−,()1'10f t t =+>所以()ln g t t t a =+−在()1,+∞上单调递增,故()0g t =只有1个解又因为()ln x xe ef x a x x =+−有两个零点12,x x ,故1212x x e e t x x == 两边取对数得:1122ln ln x x x x −=−,即12121ln ln x x x x −=−()121212*ln ln x x x x x x −<−121x x <,即121x x <()121212*ln ln x x x x x x −<−121211212121222112ln ln ln ln ln x x xx xx x x x x x x x x x x −<⇔−⇔<−不妨设121x t x =>,则只需证12ln t t t <−构造()12ln ,1h t t t t t =−+>,则()22211'110h t t t t ⎛⎫=−−=−−< ⎪⎝⎭故()12ln h t t t t=−+在()1,+∞上单调递减故()()10h t h <=,即12ln t t t<−得证2023新高考1卷T19(2) 同构+切线放缩或2次求导4.已知函数()()x f x a e a x =+−,证明:当a >0时,3()2ln 2f x a >+. 解:即证:当a >0时,232ln 2xae a x a +−>+第一步,指数化,同构变形:()ln 2ln 2332ln ln ln 22a xa x ea x a e a x a a +++−>+⇒−+>−+ 第二步,换元:令ln t a x =+,t ∈R ,有23ln 2te t a a −>−+ 第三步,放缩:1t e t −≥(证明略),即证231ln 2a a >−+第四步,构造函数:令23()ln 2g a a a =−+,1'()2g a a a =−,故()g a 在202⎛⎫↑ ⎪ ⎪⎝⎭,,2,2⎫+∞↓⎪⎢⎪⎣⎭22132()ln ln 1122222g a g ⎛≤=−+=+< ⎝⎭2022全国乙卷(理)16题5.已知1x x =和2x x =分别是函数2()2e x f x a x =−(0a >且1a ≠)的极小值点和极大值点.若12x x <,则a的取值范围是 .【答案】1,1e ⎛⎫⎪⎝⎭【详解】[方法一]:转化法,零点的问题转为函数图象的交点因为()2ln 2e xf x a a x '=⋅−,所以方程2ln 2e 0x a a x ⋅−=的两个根为12,x x ,即方程ln e x a a x ⋅=的两个根为12,x x ,即函数ln x y a a =⋅与函数e y x =的图象有两个不同的交点,因为12,x x 分别是函数()22e x f x a x =−的极小值点和极大值点,所以函数()f x 在()1,x −∞和()2,x +∞上递减,在()12,x x 上递增, 所以当时()1,x −∞()2,x +∞,()0f x '<,即e y x =图象在ln x y a a =⋅上方 当()12,x x x ∈时,0fx,即e y x =图象在ln x y a a =⋅下方1a >,图象显然不符合题意,所以01a <<.令()ln x g x a a =⋅,则()2ln ,01xg x a a a '=⋅<<,设过原点且与函数()y g x =的图象相切的直线的切点为()00,ln x x a a⋅,则切线的斜率为()020ln x g x a a '=⋅,故切线方程为()0020ln ln x x y a a a a x x −⋅=⋅−,则有0020ln ln x x a a x a a −⋅=−⋅,解得01ln x a=,则切线的斜率为122ln ln eln a a a a ⋅=, 因为函数ln x y a a =⋅与函数e y x =的图象有两个不同的交点,所以2eln e a <,解得1e e a <<,又01a <<,所以11ea <<,综上所述,a 的取值范围为1,1e ⎛⎫⎪⎝⎭.[方法二]:【通性通法】构造新函数,二次求导 ()2ln 2e x f x a a x '=⋅−=0的两个根为12,x x因为12,x x 分别是函数()22e x f x a x =−的极小值点和极大值点,所以函数()f x 在()1,x −∞和()2,x +∞上递减,在()12,x x 上递增,设函数()()()g 2ln xx f x a a ex '==−,则()()2g 2ln 2x x a a e '=−,若1a >,则()g x '在R 上单调递增,此时若()0g 0x '=,则()f x '在()0-,x ∞上单调递减,在()0,x +∞上单调递增,此时若有1x x =和2x x =分别是函数()22(0x f x a ex a =−>且1)a ≠的极小值点和极大值点,则12x x >,不符合题意;若01a <<,则()g x '在R 上单调递减,此时若()0g 0x '=,则()f x '在()0,x −∞上单调递增,在()0,x +∞上单调递减,令()0g 0x '=,则02(ln )xea a =,此时若有1x x =和2x x =分别是函数()22(0x f x a ex a =−>且1)a ≠的极小值点和极大值点,且12x x <,则需满足()00f x '>,()()00002ln 20ln xe f x a a ex ex a ⎛⎫'=−=−> ⎪⎝⎭,即001ln 1ln x x a a <>,故()002ln ln ln 1ln x e a x a a ==>,所以11ea <<. [方法三]:同构+放缩(简证) ① 先得出01a << ② ()ln ln 2ln ln ln ln x a xx ae ea a ex ea ex x a a ⋅=⇒⋅=⇒=(ln 0x a >)③ 放缩:xxe e ex e x≥⇒≥()()221ln 11ln 01ln ee a a a ea >⇒<⇒−<<⇒<<题型一 一元同构2023深圳高二下期末·21(2)1.已知2()()x f x axe a R =∈,若关于x 的()2ln 0f x x x −−≥恒成立,求实数a 的取值范围.【答案】1a e≥【简证】()2ln 0f x x x −−≥恒成立等价于()22ln 0xaxe x x −−≥恒成立,即()()ln 2ln 22ln 2ln 0x xx x aee x x ae x x +−+=−+≥,则有ln 22ln x xx xa e++≥令2ln t x x =+,t ∈R ,则有max1t t a e e ⎛⎫≥=⎪⎝⎭(构造函数求导得出最值,过程略) 总结:同构+分参2.若关于x 的不等式ln ln 0e xx a a xx+−>对()0,1x ∀∈恒成立,则实数a 的取值范围为( ) A .1,e ⎛⎤−∞ ⎥⎝⎦B .1,e ∞⎡⎫+⎪⎢⎣⎭C .1,1e ⎡⎫⎪⎢⎣⎭D .10,e ⎛⎤ ⎥⎝⎦【答案】B【分析】由题意可知0a >,且ln e ln e xx a xa x >对()0,1x ∀∈恒成立,设()ln x g x x =,则问题转化为()()e xg a g x >在()0,1上恒成立,利用导数说明函数的单调性,再分e 1x a ≥和0e 1x a <<两种情况讨论,结合函数的取值情况及单调性,分别计算可得.重点题型·归类精讲【详解】由题意可知0a >,ln e ln ln e x x a a x x +>,即ln e ln e x x a xa x >对()0,1x ∀∈恒成立. 设()ln x g x x =,则问题转化为()()e xg a g x >在()0,1上恒成立,因为()21ln xg x x−'=,所以当0e x <<时,()0g x '>,当e x >时,()0g x '<, 所以()g x 在()0,e 上单调递增,在()e,+∞上单调递减,又()10g =,所以当()0,1x ∈时,()0g x <;当()1,x ∈+∞时,()0g x >. ①在()0,1x ∈上,若e 1x a ≥恒成立,即1a ≥,()()e0xg a g x ≥>;②在()0,1x ∈上,若0e 1x a <<,则e x a x >恒成立,即1e xxa <<恒成立, 令()e x x h x =,()0,1x ∈,则()10ex xh x −'=>,所以()h x 在()0,1上单调递增, 所以()()11e h x h <=,所以11e a <≤,综上所述,实数a 的取值范围为1,e ∞⎡⎫+⎪⎢⎣⎭.故选:B .宁波九校高三上期末·22(2) 3.已知函数1()ln 2f x x x x x ⎛⎫=+− ⎪⎝⎭,e 是自然对数的底数.若不等式2()(1)4axf x a e x ≤+−对0x ∀>恒成立,求实数a 的取值范围. 【答案】实数a 的取值范围为2,e ⎡⎫+∞⎪⎢⎣⎭.12()(1)42ln 4(1)4ax ax f x a e x x x x a e x x ⎛⎫≤+−⇒+−≤+− ⎪⎝⎭,整理,同乘x 得:()2212ln (1)1ln (1)ax axx x a e x x ax e x ⎛⎫+≤+⇒+≤+ ⎪⎝⎭, 比较一下2种构造方式,方式1:令()x g x xe x =+,()'()11xg x x e =++,易错:由洛必达可知(选填时用)——这里用不了错了!()111lim 1lim 0x x x x x x x e e e −−→−∞→−∞+−∞+=====−+∞−−∞,故()'()110()xg x x e g x =++>⇒↑()11'()111x xx xx x e g x x e e e−−−+++=++=+=,令()1xh x e x =−+,易知()h x ≥2恒成立, 故()11()0'()0()xx x e e x h x g x g x −−++=−−++=−>⇒>⇒↑由()2222ln 21ln (1)ln ln axx ax x x ax e x ex axe ax +≤+⇒+≤+,则有2(ln )()g x g ax ≤,由单调性可知22min ln 2ln x x ax a x e⎛⎫≤⇒≥= ⎪⎝⎭参考ln xy x=图像可以快速得出答案,解答题还是要写一下求导过程. 方式2:()ln g x x x x =+总结:(1)求导通分看极值点即可,注意2个增区间之间用“,”而不是“∪”(2)先同构再判断单调性. 江苏盐城2023届高三5月三模·22 4.已知函数()(ln ).x a f x e e a x =−+ (1)当a =1时,求()f x 的单调递增区间; (2)()0f x ≥恒成立,求a 的取值范围.【答案】(1)()1,+∞(2)(,1]−∞(1)解:当时,,,又,单调递增, ··············································· 2分 又,当时,当时,∴的单调递增区间为()1,+∞. ·························································· 4分 1a =()()1ln x f x e e x =−+()xe f x e x'=−()20xef x e x ''=+>()f x '∴()10f '=∴()0,1x ∈()0f x '<()1,x ∈+∞()0f x '>()f x(2)若恒成立,即恒成立.方法1:,,令, 则,在上单调递增,又,当时,故存在唯一正实数使得, ····················································· 6分 当时,,单调递减,当时,,单调递增,,由恒成立,得,由得,, ······ 8分 ∴,∴,∴,设,则恒成立,故在上递增,而,∴, 又且函数在上是增函数,故的取值范围为. ···································································· 12分 法2:同法一得,由得,∴ ,,故的取值范围为. ················· 12分方法3:令,则,,则,令,则, ················································ 8分 ∵,∴在上单调递增,当时,显然成立;当时,恒成立,即恒成立,可证(过程略),,,即,,综上,的取值范围为(,1]−∞. ······························································ 12分 ()0f x ≥()ln 0x ae e a x −+≥()ln x a af x e e x e a =−−()a x a x e xe e f x e x x−'=−=()x ag x xe e =−()0x x g x e xe '=+>()x ag x xe e ∴=−()0,+∞()00ag e =−<x →+∞()g x →+∞0x 00x a x e e =0x x <()0f x '<()f x 0x x >()0f x '>()f x ()()000min ln x a a f x f x e e x e a ∴==−−()0f x ≥()min 0f x ≥00x a x e e =00ln x x a +=()()00000min (2ln )0x xf x f x e x e x x ∴==−+≥0001(2ln )0x x x −+≥000(2ln )10x x x +−≤00012ln 0x x x +−≤1()2ln h x x x x=+−221()10h x x x '=++>()h x (0,)+∞(1)0h =001x <≤00ln x x a +=ln y x x =+(0,1]a (,1]−∞()()000min ln x a af x f x e e x e a ==−−00x a x e e =00ln x x a +=()000min00011ln ln aa a a a a a e f x e x e a e x e a e x a e a x x x ⎛⎫⎛⎫=−−=−−=+−− ⎪ ⎪⎝⎭⎝⎭()20a a e a e a ≥−−≥()220a e a ∴−≥a (,1]−∞a e t =ln a t =()()ln ln ln x e t t x t tx ≥+=()()()ln ln ln tx xxe tx tx tx e ≥=()(0)xg x xe x =>()()ln()g x g tx ≥()()10x g x x e '=+>()(0)xg x xe x =>()0,+∞()ln 0tx ≤()()ln()g x g tx ≥()ln 0tx >()ln ln ln x tx t x ≥=+ln ln t x x ≤−ln 1x x −≥∴ln 1t ≤∴t e ≤a e e ≤∴1a ≤a方法4:∵恒成立,∴,即,同法3考查函数可得, ··········································· 7分 反之,当时,, 又可证(过程略),∴,∴恒成立,故的取值范围为. ···································································· 12分 补充:同构和型+放缩ln (ln )0(ln )ln ln ln x a x a x a x a x e x x e a x e e a x e a x e x x a e −−−+≥⇒≥+⇒−≥+⇒+≥+=+令()x g x e x =+↑,则有()min ()(ln )ln ln 1g x a g x x a x a x x −≥⇒−≥⇒≤−=总结:(1)两次求导+取点(2)法一和法二是整体求导再用隐零点处理,法三和法四是同构处理相对简单 湖南九校联盟第二次联考·16 5.已知不等式))(1ln (0xa x e a a e −⎡⎤≥>⎢⎥⎣⎦恒成立,则实数a 的最大值为_______ 【答案】2e[]ln ln (1)lnln (1)1ln ln(1)1ln ln(1)1x x x a x a a x e a e a a x e a x x x e a x e−−−≥⇒≥−−−+⇒≥+−⇒−+−≥−令()x g x e x =+↑,则有()2(ln )ln(1)ln ln(1)ln(1)ln 2ln g x a g x x a x x x a a e a −≥−⇒−≥−⇒−−≥⇒≥⇒≥可放缩补充:构造函数求导令ln(1)()g x x x −−=,12()111x g x x x '−=−=−− 故g (x )在(1,2)上单调递减,在(2,+∞)上单调递增,因此min ()(2)2g x g ==. 因为不等式(1)ln(0)xa x e a a e−≥>恒成立,所以Ina ≤2,即2.a e ≤ 总结:指对分离,补全结构,最后的最值可以放缩得出. 补充:对右边的式子配凑也可以()0f x ≥(1)0f ≥a e e a ≥()(0)xg x xe x =>1a ≤1a ≤11x a a x −+≥+−ln 1,1x a x x e x a −≤−≥−+ln x a e a x −≥+()ln x ae e a x ≥+a (,1]−∞湖南省2023届高三下3月考试·166.已知e 是自然对数的底数.若()0x ∀∈+∞,,e ln mx m x ≥成立,则实数m 的最小值是 . 【答案】1e解析:由ln e ln e ln ln mx mx x m x mx x x e x ≥⇒≥=⋅.令()e x f x x =,则()f x 在()0+∞,上单调递增, 且()()ln f mx f x ≥,所以ln mx x ≥,即ln xm x≥对()0x ∀∈+∞,恒成立. 令()ln xg x x =,则()21ln x g x x−'=,所以当()0e x ∈,时,()0g x '>;当()e x ∈+∞,时,()0g x '<, 故()g x 在[)1+∞,上的最大值是1e ,所以1e m ≥,即实数m 的最小值是1e .故答案为:1e. 总结:同乘补全结构即可,入门型7.若不等式0x ae lnx lna −+恒成立,则a 的取值范围是( )A .1[,)e +∞B .2[,)e +∞C .[,)2e+∞D .[e ,)+∞【答案】A 【法一】:同构ln ln ln ln ln 0ln ln ln ln ln x a x a x x ae x a e e a x e a x x x e x +⇒+−+≥⇒≥+≥=+++构造函数()x g x e x =+,故ln ln ln ln (ln )(ln )a x x e a x e x g a x g x ++≥++≥+⇒ 而'()10x g x e =+>,则ln ln a x x +≥,即()max ln ln a x x ≥−令ln y x x =−,则1x y x '−=,故max 1y =−,则1ln 1a a e≥−⇒≥. 对于ln ln a x x +≥还可以直接分类参数:max1ln ln ln ln ln ln x xx xx a x x a x e a ee e ⎛⎫⎛⎫+≥⇒≥−=⇒≥= ⎪ ⎪⎝⎭⎝⎭ 总结:需要同加x 才能补全结构 【法二】:整体求导、取点设()x f x ae lnx lna =−+,则0x >,0a >,1()x f x ae x∴'=−, 易知()f x '在(0,)+∞上为增函数,存在0(0,)x ∈+∞,使得0001()0x f x ae x '=−=, 即01x ae x =, 两边取对数,可得00lna x lnx +=−,当00x x <<时,()0f x '<,函数()f x 单调递减, 当0x x >时,()0f x '>,函数()f x 单调递增,000001()()2x min f x f x ae lnx lna x lna x ∴==−+=++, 不等式0x ae lnx lna −+恒成立,∴00120x lna x ++恒成立, ∴12x lna x +−恒成立, 00001122x x x x +⋅=,当且仅当01x =时取等号, 22lna ∴−,即1ae ,故a 的取值范围是1[e,)+∞.湖北鄂东南联考 ·88.已知函数()ln x f x x x xe k −=−−−恒有零点,则实数k 的取值范围是( )A .(],1−∞−B .1,1e⎛⎤−∞−− ⎥⎝⎦C .11,1e⎡⎤−−−⎢⎥⎣⎦D .11,0e⎡⎫−−⎪⎢⎣⎭方法1:同构要使()ln x f x x x xe k −=−−−恒有零点,只需ln ln l =n x x x k x x xe x x e e −−=−−−− 设ln x x t −=,求导可知(],1t ∈−∞−而t k t e =−,求导可知函数t k t e =−在(],1−∞−上单调递增,故1,1k e ⎛⎤∈−∞−⎥⎝⎦方法2:分参求导ln xk x x xe −=−−,令()ln xg x x x xe −=−−,则()1'()1111x x x g x e x x x e x e −−⎪=⎛⎫+−=−−− ⎝⎭∵110xx e −> 故()ln x g x x x xe −=−−在(]0,1递增,()1,+∞递减,故max 1()(1)1g x g e==−−,故选B.注:由常见不等式1x e x ≥+得到,即1100xx e x x e−−>⇒>; 或者令11()x x xe e h x e x x x −=−=,221'()x x x e h x e−=,因为0x >,故'()0h x > 方法3:直接求导(可以消掉k )()()2111'()1xx x x x xxx x e x xe e x x f x x e e xe xe −−−−−=−+=++=,不难得出x x e −在()0,+∞上恒小于0,故()f x 在()0,1上单调递增,在[)1,+∞上递减,故max 1()(1)1f x f k e ==−−−,当0x →时,()f x →−∞,故()f x 的值域为1,1k e ⎛⎤−∞−−− ⎥⎝⎦,则11101k k e e−−−≥⇒≤−−. 福建龙岩九校联考·169.已知函数mx x m x f −+=)1ln()(,若不等式x e x x f −+>1)(在()+∞,0上恒成立,则实数m 的取值范围是____________ . 【答案】(],1−∞x e x x f −+>1)(在()+∞,0上恒成立等价于ln(1)1x m x mx x e +−>+−第一步,错位同构:()ln(1)1xm x x mx e +−+>−,第二步,构造对应函数:令()xg x mx e =−,则有[]ln(1)()g x g x +>第三步,分析单调性,定义域:易知0ln(1)x x <+<,故()g x 在()0,+∞上单调递减 第四步,由单调性求出参数范围:()min'()001xx g x m e x m e=−≤>⇒≤=总结:错位同构,很少见,最后要注意取等.湖南常德3月模拟10.已知不等式ln()x x a e a +≤−对[1,)x ∀∈+∞恒成立,则a 的取值范围为 . 【答案】11a e −<≤−解析:易得:()ln()ln()x xx a e a x a x a x e +≤−⇒+++≤+,1a >−即:ln()ln()x a x x a e x e +++≤+,构造函数()xg x x e =+,∴()()()ln g x a g x +≤.易知()g x 在[1,)x ∈+∞为增函数;∴()ln x x a ≥+, 令()()ln h x x x a =−+,()111x a h x x a x a+−'=−=++, 当0a ≥时,()0h x '≥,()h x 在[1,)x ∈+∞为增函数,()()10h x h ≥≥,∴01a e ≤≤−;当10a −<<时,11a −>;[1,1)x a ∈−,()0h x '<;()1x a ∈−+∞,时,()0h x '≥; ∴()()min 110h x h a a =−=−≥,∴11a −<≤,综上:11a e −<≤−. 总结:最后不等式要注意x 取值范围 补充:对于()ln x x a ≥+,也可以分参()()()minln ln ln 1x x x x x a e x a e x a a e x e ≥+⇒≥+⇒≥+⇒≤−=−浙江省衢州、丽水、湖州三地市高三下学期4月教学质量检测·811.对任意的实数0x >,不等式22ln ln 0x ae x a −+≥恒成立,则实数a 的最小值为( )e2eC.2eD.12e【答案】D总结:指对分离,补全结构2022湖北四地七校高二下期中·712.已知实数a >0,不等式()0x e aln ax ->恒成立,则a 的取值范围是( ) A .1<<a e eB .0<a <1C .0<a <eD .a >e【解答】解:令f (x )=e x ﹣aln (ax ),a >0,x ∈(0,+∞),f ′(x )=e x ﹣在x ∈(0,+∞)上单调递增,x →0时,f ′(x )→﹣∞;x →+∞时,f ′(x )→+∞. ∴存在唯一x 0>0,使得﹣=0,即=,x 0=lna ﹣lnx 0,∴x =x 0时,函数f (x )取得极小值即最小值,f (x 0)=+ax 0﹣2alna >0,∴2﹣2lna >0,解得0<a <e . 总结:补全结构即可。
讲义练习2 信息获取信息安全[答案]
![讲义练习2 信息获取信息安全[答案]](https://img.taocdn.com/s3/m/9db59a6ca98271fe910ef9c1.png)
第二章《信息获取》知识点2、1信息获取的一般过程信息获取的一般过程是:定位信息需求,选择信息来源,确定信息获取方法、获取信息,评价信息1、定位信息需求——信息需求表现在:(1)、时间范围(2)、地域范围(3)、内容范围2、选择信息来源3、确定信息获取方法,获取信息4、评价信息——评价信息的依据是(先前确定的信息需求)2.2 信息的安全与保护1. 威胁信息安全的常见因素人为的无意失误;人为的恶意攻击;软件的漏洞和“后门”;计算机病毒的侵害.2.病毒的概念:指编制或者在计算机程序中插入的破坏计算机功能或者毁坏数据,影响计算机使用,并能自我复制的一组计算机指令或者程序代码。
3.病毒的特征:潜伏性、隐蔽性、传染性、爆发性、破坏性。
4.计算机病毒的传染途径:移动存储设备(磁盘、移动硬盘、U盘、光盘),网络应用(电子邮件,在线聊天,文件下载)5.计算机感染病毒后的现象(1)打开程序的时间比平时长,运行异常(2)磁盘空间突然变小,或系统不能识别磁盘设备(3)有异常工作,如突然死机又自动重新启动(4)访问设备时有异常现象,如显示器显示乱码等(5)程序或数据无故丢失,找不到文件等(6)文件的长度发生变化(7)发现一些来历不明的隐藏文件(8)访问设备的时间比平时长,如长时间访问磁盘等现象(9)上网的计算机出现不能控制的自动操作现象等(10)机器发出怪声等6. 计算机病毒的预防措施(1)对重要的数据定期进行备份,如使用ghost等工具软件或刻录成光盘;(2)不适用来历不明的软盘、光盘;(3)不非法复制别人的软件;(4)对网络上下载的各种免费和共享软件,要先进行查杀病毒后再安装使用;(5)要谨慎处理收到的电子邮件附件;(6)在QQ聊天时接收到的一些网址和文件最好不要直接打开。
(7)安装杀毒软件和防火墙(扫描磁盘,查杀病毒、加强访问控制)。
7. 常用的信息安全防护方法(1)增强安全防范意识。
时常关注信息安全方面的信息,访问一些著名的网络安全站点;(2)禁用不必要的服务。
高中数学竞赛教案讲义(2)二次函数与命题

第二章 二次函数与命题一、基础知识1.二次函数:当≠a 0时,y =ax 2+bx +c 或f (x )=ax 2+bx +c 称为关于x 的二次函数,其对称轴为直线x =-ab2,另外配方可得f (x )=a (x -x 0)2+f (x 0),其中x 0=-ab 2,下同。
2 二次函数的性质:当a >0时,f (x )的图象开口向上,在区间(-∞,x 0]上随自变量x 增大函数值减小(简称递减),在[x 0, -∞)上随自变量增大函数值增大(简称递增)。
当a <0时,情况相反。
3.当a >0时,方程f (x )=0即ax 2+bx +c =0…①和不等式ax 2+bx +c >0…②及ax 2+bx +c <0…③与函数f (x )的关系如下(记△=b 2-4ac )。
1)当△>0时,方程①有两个不等实根,设x 1,x 2(x 1<x 2),不等式②和不等式③的解集分别是{x |x <x 1或x >x 2}和{x |x 1<x <x 2},二次函数f (x )图象与x 轴有两个不同的交点,f (x )还可写成f (x )=a (x -x 1)(x -x 2). 2)当△=0时,方程①有两个相等的实根x 1=x 2=x 0=a b 2-,不等式②和不等式③的解集分别是{x |x ab2-≠}和空集∅,f (x )的图象与x 轴有唯一公共点。
3)当△<0时,方程①无解,不等式②和不等式③的解集分别是R 和∅.f (x )图象与x 轴无公共点。
当a <0时,请读者自己分析。
4.二次函数的最值:若a >0,当x =x 0时,f (x )取最小值f (x 0)=a b ac 442-,若a <0,则当x =x 0=ab2-时,f (x )取最大值f (x 0)=ab ac 442-.对于给定区间[m,n ]上的二次函数f (x )=ax 2+bx +c (a >0),当x 0∈[m, n ]时,f (x )在[m, n ]上的最小值为f (x 0); 当x 0<m 时。
《2 的乘法口诀》 讲义

《2 的乘法口诀》讲义一、乘法的意义在我们学习 2 的乘法口诀之前,先来理解一下什么是乘法。
乘法其实就是求几个相同加数的和的简便运算。
比如说,2 + 2 + 2 = 6,我们用乘法可以写成 2×3 = 6,这里的 2 表示相同的加数,3 表示相同加数的个数。
二、2 的乘法算式我们从最简单的开始,一个 2 是多少呢?那就是 2×1 = 2 。
两个 2相加,2 + 2 = 4 ,用乘法算式表示就是 2×2 = 4 。
三个 2 相加,2 +2 + 2 = 6 ,乘法算式为 2×3 = 6 。
四个 2 相加,2 + 2 + 2 + 2 = 8 ,写成乘法就是 2×4 = 8 。
依此类推,我们可以得到 2×5 = 10 ,2×6 =12 ,2×7 = 14 ,2×8 = 16 ,2×9 = 18 。
三、2 的乘法口诀为了更方便地记住这些乘法算式的结果,我们有了乘法口诀。
2 的乘法口诀是:一二得二,意思是 1 个 2 是 2 ,乘法算式 2×1 = 2 。
二二得四,就是 2 个 2 是 4 ,算式为 2×2 = 4 。
二三得六,3 个 2 是 6 ,2×3 = 6 。
二四得八,4 个 2 是 8 ,2×4 = 8 。
二五一十,5 个 2 是 10 ,2×5 = 10 。
二六十二,6 个 2 是 12 ,2×6 = 12 。
二七十四,7 个 2 是 14 ,2×7 = 14 。
二八十六,8 个 2 是 16 ,2×8 = 16 。
二九十八,9 个 2 是 18 ,2×9 = 18 。
四、乘法口诀的作用乘法口诀可是个非常有用的工具。
当我们在计算乘法的时候,只要记住了乘法口诀,就能很快地得出答案,不用再一个一个地去相加。
比如,要算 2×7 是多少,我们马上就能想到“二七十四”,知道答案是14 。
二建市政工程重点 讲义(2)

2K311000城镇道路工程教材整体框架结构2K310000 市政公用工程施工技术2K311000 城镇道路工程2K311010 城镇道路工程结构与材料※重点导读:选择考点:城镇道路的分级(四级)、分类、高级路面适用范围、路面按力学特性分类、沥青路面的组成、面层性能要求(6个)、沥青混合料结构组成分类、改性SMA适用、水泥混凝土路面基层选用原则、水泥混凝土路面纵缝、横缝、胀缝、缩缝、施工缝区别与联系、挡土墙类型、三种土压力比较案例考点:水泥混凝土路面接缝问题配合施工方法2K311011 城镇道路分类一、城镇道路分级根据城市道路网中的地位、交通功能以及道路在城镇规划道路系统中所处的地位划分为快速路、主干路、次干路及支路;交通性减弱,服务性增强。
快速路应中央分隔、全部控制出入且控制出入口间距及形式,实现交通的连续通行;快速路两侧不应设置公共建筑物的出入口。
主干路应连接城市各主要分区,以交通功能为主。
主干路两侧不宜设置公共建筑物的出入口。
次干路应与主干路结合组成干路网,以集散交通的功能为主,兼有服务功能。
支路以解决局部地区交通,服务功能为主。
二、城市道路技术标准快速路必须设分隔带,支路不设。
三、城镇道路路面分类(一)按路面等级分类1.高级路面:路面强度高、刚度大、稳定性好是高级路面的特点。
它使用年限长,适应繁重交通量,且路面平整、车速高、运输成本低,建设投资高,养护费用少,适用于城市快速路、主干路、公交专用道路。
2.次高级路面:路面强度、刚度、稳定性、使用寿命、车辆行驶速度、适应交通量等均低于高级路面,但是维修、养护、运输费用较高,城市次干路、支路可采用。
(二)按力学特性分类1.柔性路面:荷载作用下产生的弯沉变形较大、抗弯强度小,在反复荷载作用下产生累积变形,它的破坏取决于极限垂直变形和弯拉应变。
柔性路面主要代表是各种沥青类路面,包括沥青混凝土(英国标准称压实后的混合料为混凝土)面层、沥青碎石面层、沥青贯入式碎(砾)石面层等。
《幼儿园课程》讲义-2

第二章幼儿园课程的基础目录结构:第一节幼儿园课程的心理学基础 (2)一、心理学流派与幼儿园课程 (2)(一)认知心理学与幼儿园课程21.皮亚杰理论与幼儿园课程2(1)皮亚杰建构理论概述2(2)皮亚杰理论的启示 3(3)皮亚杰理论的运用 3(4)皮亚杰理论的发展 32.历史 -文化学派维果茨基的理论与幼儿园课程 3(1)维果茨基理论概述 3(2)维果茨基理论的三个核心概念 3(3)维果茨基理论在课程中的运用:43.认知心理学研究的新进展与幼儿园课程 4(二)成熟理论与幼儿园课程 51.成熟理论概述52.成熟理论在幼儿园课程中的运用: 5(三)精神分析理论与幼儿园课程 51.弗洛伊德的理论 52.艾里克森的理论 53.精神分析理论在幼儿园课程中的运用 5(四)行为主义理论与幼儿园课程 61.行为主义理论概述 62.行为主义在课程中的运用6二、心理学对幼儿园课程的影响 (6)第二节幼儿园课程的哲学基础 (7)一、哲学流派与幼儿园课程 (7)(一)经验论和唯理论7(二)实用主义哲学71.实用主义的基本观点72.代表人物73.实用主义对课程的影响8二、哲学对幼儿园课程的影响 (8)第三节幼儿园课程的社会学基础 (9)第一节幼儿园课程的心理学基础一、心理学流派与幼儿园课程在当代,对幼儿园课程产生过重大影响作用的心理学流派主要是认知心理学、成熟理论、行为主义心理学和心理动力理论等。
(一)认知心理学与幼儿园课程1. 皮亚杰理论与幼儿园课程( 1)皮亚杰建构理论概述①认知的本质智慧的本质从生物学来说是一种适应,是同化和顺应之间的一种特殊的平衡。
同化感受外部刺激的主体,通过对刺激输入的过滤或改变,将它们纳入原有图式之内的过程称为同化。
顺应主体调节自身内部结构,建立新的图式,或者调节原有图式,以适应特定刺激环境的过程称为顺应。
皮亚杰②认知发展的阶段认知发展分成感知 - 运动阶段、前运算阶段、具体运算阶段和形式运算阶段等四个按不变顺序相继出现的、有着质的差异的阶段,揭示了儿童认知发展的规律。
古生物地史学讲义(2)

海底沉积物中底栖和浮游有孔虫的含量分布
二、“虫筳”类的生态
一般分布于温暖的浅海,常与珊瑚等化石共生;水深、盐度、水 动力条件等环境因素都对“虫筳”的分布产生影响。 “虫筳”的形态、结构与环境的关系表
三、 地史分布
有孔虫最早出现在寒武纪,一直发展到现代。 早古生代有孔虫是以胶结壳砂盘虫类为主,化石不多,地 层意义不大。 晚古生代的石炭二叠纪,是有孔虫发展的第一个繁盛期。 蜓类,演化快,分布广,成为这个时期有孔虫发展的标志。 晚白垩世是有孔虫的第二个繁盛时期。以螺旋壳的轮虫类 为主,开始出现底栖大有孔虫,并可成岩;浮游有孔虫开 始繁盛。 新生代是有孔虫的第三个繁盛时期。仍以轮虫类占优势。 自白垩纪以来,大有孔虫和浮游有孔虫演化迅速,更替频 繁,因此,成为白垩纪和新生代海相地层中的重要分带化 石。
变形虫
肉足虫纲:身体表面形 成有硬壳,发育有重 要化石
依据伪足等特征下分四目:
1. 根足虫目(表壳虫) 2. 有孔虫目:非“虫筳” 有孔虫亚目、虫筳 亚目 3. 放射虫目:等幅骨虫 4. 太阳虫目:太阳虫
第二节 有孔虫目(Foraminifera)
一、一般特征
分类位置:原生动 物门肉足虫纲有孔 虫目
假史塔夫 “虫筳”
小纺锤“虫 筳”
纺锤“虫筳”
壳小,由短轴型过渡到长轴型,隔壁相对平直,旋壁由致密层、内外疏 松层和透明层组成
晚石炭世的代表化石
个体变大, 形态多为 纺锤形或 球形,旋 脊弱或不 发育,出 现蜂巢层
拟纺锤“虫筳”
费伯克“虫筳”
早二叠世的 “虫筳”出 现拟旋脊、 列孔、副隔 壁等构造
新米斯“虫 筳”
新希瓦格“虫筳”
四、虫筳 的演化趋势及阶段性
高考英语一词多义学习讲义(2)

高考英语一词多义讲义(2)1.cut(1)vt.,vi.切,割,剪:Would you please cut the cake in half?请把蛋糕切成两半好吗?I read this story in the paper this morning and cut it out for you.今天上午我在报纸上读到这个故事便给你剪下来了。
(2)vt.割破,划破:He shaved hurriedly this morning and cut himself badly.他今天早上匆匆忙忙地刮脸,刮破了不少地方。
(3)vi.横穿,穿越(介词用across/through):The Wayle cut sacross a park.威尔河横穿过一个公园。
The road cuts across/through the forest.这条路穿过森林。
2.row(1)vt.,vi.划船:Have you ever learned to row (a boat)?你学过划船吗?John rowed across the lake quickly.约翰很快划到了湖那边。
(2)n. 排,行,列:The trees were planted in a row.树整齐地种了一排。
3. treat/triːt/vt. 对/看待;招/款待;治疗;处理拓展(1)treat sb. as...把某人看作……treat sb. of sth. 治疗某人的(病)treat sb. to sth..招待某人吃……;用……款待某人treat sb. with...以……方式对待某人(2)My treat.我请客。
(3)treatment n.治疗;处理;待遇under treatment 在治疗中例句①Police say they’re treating it as a case of attempted murder.警方说,他们把它当作谋杀未遂案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章海洋生物调查第一节概述一、名词1、叶绿素定义:是自养植物细胞中一类很重要的色素,是植物进行光合作用时吸收和传递光能的主要物质。
▪叶绿素a是其中的主要色素。
▪Chla表示海水中的叶绿素量。
2、初级生产力定义:自养生物通过光合作用生产有机物的能力。
通常以单位时间(年或天)内单位面积(或体积)中所产生的有机物(一般以有机碳表示)的重量来计算,相当于该时间内相同面积(或体积)中的初级生产量。
3、微生物定义:一群个体微小、结构简单、生理类型多样的单细胞或多细胞的低等生物,包括属于原核生物类的细菌、放线菌、支原体、立克次体、衣原体和蓝细菌,属于真核生物类的真菌(酵母菌和霉菌)、原生动物和显微藻类,以及属于非细胞类的病毒、类病毒和朊病毒。
4、浮游生物定义:缺乏发达的运动器官,没有或仅有微弱的运动能力,悬浮在水层中,常随水流移动的生物。
包括:浮游植物浮游动物按浮游生物的个体大小可分为⑴微微型(picoplankton):<2 µm 细菌⑵微型(nanoplankton):2~20 µm 金藻⑶小型(microplankton):20~200 µm 硅藻⑷中型(mesoplankton):0.2~2 mm 小型桡足类⑸大型(macroplankton):2~20 mm 大型桡足类⑹巨型(megaplankton):>20 mm 海蜇此外,鱼类浮游生物即为鱼卵和仔稚鱼。
5、底栖生物定义:栖息在水域基底表面或底内的生物。
在海洋中,这类生物自潮间带至水深大于万米以上的超深渊带(深海沟底部)都有分布,使海洋生物中种类最多的一个生态类型,包括大多数海洋动物门类、大型和微型定生海藻类和海洋种子植物。
6、潮间带生物定义:生活在潮间带底表的植物和底表与底内的动物。
7、污损生物定义:生长在船底、浮标、平台和海中一切其他设施表面或内部的生物。
这类生物一般是有害的。
8、游泳动物定义:具有发达的运动器官,在水层中能克服水流阻力自由游动的动物。
如:鱼类、大型虾、蟹类、头足类及海洋哺乳动物等。
二、调查内容、方式和采样深度1、海洋生物调查内容叶绿素、初级生产力和新生产力,微生物、微微型、微型和小型浮游生物,鱼类浮游生物,大型底栖生物,小型底栖生物,潮间带生物,污损生物和游泳生物。
必要时,渔业资源声学调查与评估。
辅助参数:海洋调查时,应视需要确定与其有关的辅助参数,并同步进行观测。
2、调查方式▪大面观测▪断面观测▪连续观测3、采水样(1)适用于叶绿素浓度、初级生产力和新生产力,微生物,微微型、微型和小型浮游生物等调查项目的水样采集。
(2)拖网采样适用于大、中型浮游生物、鱼类浮游生物、大型底栖生物、游泳动物调查和渔业资源声学调查与评估等项目的采样。
(3)底质采样适用于微生物、潮间带生物和大、小型底栖生物调查项目的采样。
(4)挂板和水面或水中设施上采样适用于污损生物调查的采样。
4、调查时间、调查次数和边缘海调查调查时间和调查次数应根据调查水域环境条件和调查目的确定。
(1)河口、港湾、沿岸海区和边缘海调查受气象、流系的季节性影响显著的边缘海应每季度调查一次;受气候、水文的季节性影响明显且物质来源复杂的河口、港湾和沿岸海区,通常应每月(至少每季度)调查一次(潮间带生物每年调查2次-4次);如有特殊需要可酌情调整调查次数。
若进行逐月和逐季调查,各季或各月调查的时间间隔应基本相等。
进行河口、港湾调查时,应充分考虑潮汐的影响。
一般以3-5月为春季,6-8月为夏季,9-11月为秋季,12月-2月为冬季,并分别以5月、8月、11月、2月代表春季、夏季、秋季和冬季。
但热带海域应根据具体的海洋环境条件和调查目的酌情调整调查时间和调查目的。
(2)大洋和极地海域调查应根据调查目的,选择调查时间,确定调查次数。
第二节叶绿素和初级生产力测定一、叶绿素a的测定(一)荧光分光光度法1、方法原理叶绿素a的丙酮萃取液受蓝光激发产生红色荧光,过滤一定体积海水所得的浮游植物用90%丙酮提取其色素,适用荧光计测定提取液酸化前后的荧光值,计算出海水叶绿素a的浓度。
2、试剂配制(1)丙酮溶液:9+l量取900mL丙酮于1OOOmL的量筒中,加水至标线。
保存在棕色试剂瓶中。
(2)碳酸镁悬浮液:1Og/L称取1g碳酸镁,加水至100mL,搅匀,盛试剂瓶中待用,用时需再摇匀。
(3)盐酸溶液:5+95在搅拌下,将5mL盐酸缓慢地加到95mL水中,混匀,保存于滴瓶中。
3、仪器设备•荧光计;•冰箱;•离心机:4000r/min•电动吸引器•过滤装置•玻璃纤维滤膜(WhatmanGF/C, 25mm)或0.45um的纤维素醋微孔滤膜•离心管:具塞,10mL,若干;•干燥器:1个•棕色试剂瓶:100,1000mL各1个•量筒:100,200,1000mL各1个•定量加液器:10mL,1个•滴瓶:l00mL,1个•镊子:2把•一般实验室常用设备4、分析步骤①样品制备②样品的提取③样品的离心④样品测定⑤仪器校正(1)样品制备量取一定体积海水(通常大洋水250-500mL,近岸或港湾水50-250mL),加2mL碳酸镁悬浮液,混匀,用滤膜过滤,过滤负压不得超过50kPa。
(2)样品的提取将带有样品的滤膜放人具塞离心管,加人丙酮溶液10mL,摇荡,放置冰箱贮存室中14-24h,提取叶绿素a。
若滤得的样品不能及时提取,应将该滤膜抽干、对折,再套上一张滤纸,置于含硅胶的干燥器内,贮存在低于1℃冰箱中。
(3)样品的离心•离心速度:3000-4000r/min。
•离心时间:10min。
(4)样品测定荧光计激发波长为436nm,发射波长670nm。
①零点调节:用丙酮溶液调节,使荧光计指针指零。
②将提取的上层提取液注入测定池。
③选择相应量程,测定样品的荧光值Rb。
④加2滴盐酸溶液至测定池,摇匀,经30s后再测其荧光值Ra。
(5)仪器校正用分光光度计校正取一定体积正处于指数生长期的单细胞藻类培养液,依上述方法提取其叶绿素a,用分光光度法测定、计算该提取液的叶绿素a浓度。
将它稀释至荧光计可测范围的浓度,用荧光计最低灵敏度量程测定此稀释液酸化前后的荧光值,依式(7),(8)计算该量程的换算因子和酸化因子。
5、记录与计算(二)分光光度法1、方法原理以丙酮溶液提取浮游植物色素,依次在664,647,630nm下测定吸光度,按Jeffrey-Humphrey的方程式计算,可分别得出叶绿素a,b,c的含量。
2、试剂配制(1)丙酮溶液:9+l量取900mL丙酮于1OOOmL的量筒中,加水至标线。
保存在棕色试剂瓶中。
(2)碳酸镁悬浮液:1Og/L称取1g碳酸镁,加水至100mL,搅匀,盛试剂瓶中待用,用时需再摇匀。
3、仪器设备•分光光度计:波带宽度应小于3nm,吸光值可读到0.001单位。
附3-10cm测定池。
•玻璃纤维滤膜(WhatmanGF/C, 47mm)或0.45um的纤维素酯微孔滤膜。
•离心管:具塞,10或15mL,若干。
•所需其他设备类同荧光光度法。
4、测定步骤(1)样品制备量取2-5L海水样品,加入3mL碳酸镁悬浮液,混匀,用滤膜过滤,过滤负压不得超过50kPa。
(2)样品的提取将带有样品的滤膜放人具塞离心管,加丙酮溶液10mL,摇荡,放置冰箱贮存室中14-24 h,提取叶绿素a。
若滤得样品不能及时提取,应将该滤膜抽干、对折,再套上一张滤张,置于含硅胶的干燥器内,贮存在低于1℃的冰箱中。
(3)样品的离心•离心速度:3000-4000r/min。
•离心时间:10min。
(4)样品测定小心将离心的上清液注入测定池。
用丙酮溶液作参比,分别在750,664,647,630nm波长处测定吸光值。
其中,750nm处的测定,用以校正提取液的浊度,当测定池1cm光程的吸光值超过0.005时,提取液应重新离心。
5、记录与计算(三)高效液相色谱(HPLC)法方法原理:浮游植物所含各种光合色素经提取后,在一定溶剂系统中,可经高效液相色谱柱进行分离,再由检测器进行检测并获得色谱图。
根据与标准色素比较保留时间及色谱图可鉴别色素种类,根据色谱峰的面积可计算含量。
二、初级生产力测定方法原理:取一定数量的H14CO3-加入到已知二氧化碳总浓度的海水样品中,在模拟现场海水温度和光照的情况下,经过一段时间的培养,测定浮游植物中固定有机14C的量,求出现场初级生产力的值。
1、采样层次按光学深度,在光强分别为表层的100%,50%,30%,10%,5%和1%的深度上采集水样,特殊情况时可减少采样层次。
2、采样与培养在预定深度采样后,尽快在弱光下将水样用孔径为180um左右的筛绢将水样过滤,并分装到相应层次的培养瓶中,每层样品设2个白瓶和1个黑瓶,第一层和第四层样品还应各分装一个零时间培养瓶(或根据现场调查情况选定)。
在每个培养瓶中加入相同体积的14C 工作液,在模拟设定的现场温度和光照条件下培养一定的时间(零培养瓶除外)。
3、过滤与储存培养结束后用滤膜将样品中的浮游植物过滤得滤膜上,在通风橱中将样品滤膜用浓硫酸蒸汽薰蒸15min,放入闪烁瓶中,密封保存。
4、测定用液体闪烁计数仪进行放射性活性的测定,并计算海水样品中的初级生产力。
第三节微生物调查一、粪大肠菌群检测(一)发酵法1、方法原理大肠菌群系一群在37℃或44℃生长时能使乳糖发酵、在24h内产酸产气的需氧及兼性厌氧的革兰氏阴性无芽抱杆菌。
大肠菌群数系指每升水样中所含有的“大肠菌群”的数目。
一般在37℃培养生长的称为“总大肠菌群”,在44℃培养生长的称为“粪大肠菌群”。
海水检验采用44℃培养法,以检出粪大肠菌群。
发酵法系通过初发酵及复发酵二个步骤,以证实海水水样中是否存在粪大肠菌群并测定其数目。
2、试剂及培养基配制(1)溴甲酚紫乙醇溶液:称取1.6g 的溴甲酚紫溶于2-3mL乙醇中,然后用蒸馏水定容到100mL。
(2)碳酸钠溶液:称取10.6g碳酸钠溶于蒸馏水,并定容到100mL。
(3)乳糖蛋白栋培养液成分:制法•将规定量的蛋白脉、牛肉膏、乳糖及氯化钠加热溶解于1000mL蒸馏水中,用碳酸钠溶液调节pH为7.2-7.4。
•加人1mL溴甲酚紫乙醇溶液,混匀,分装于置有倒管的试管内(10mL左右)。
置高压蒸气灭菌器中,于115 ℃(68.95kPa)灭菌20min。
•根据需要,可按上述配方将蒸馏水由l000mL减为333mL,制成浓缩三倍的乳糖蛋白陈培养液备用。
(4)EC培养基成分:制法将上述成分加热溶解,分装于内装倒管的试管中。
灭菌后pH值应为6.9。
此培养基用前不宜置冰箱,以防检测时出现假阳性。
3、仪器设备•恒温培养箱:37℃士1℃及44℃士0.5 ℃•干热灭菌箱•高压蒸气灭菌器•接种环•吸量管:1,10mL•试管:15mm×150mm,18mm×180mm;•发酵倒管:5mm×30mm;•纱布及棉花(塞试管用)•脱脂棉或白绒布:过滤培养基用•锥形瓶:500mL•采水样瓶:500mL广口瓶•接种箱:(折叠式)4、样品采集(1)采样瓶•用于细菌检查的采样瓶,宜用可耐灭菌处理的广口玻璃瓶或无毒的塑料瓶。
