中考数学复习一次函数图象的应用[人教版]
中考数学基础复习第10课一次函数的图象与性质课件

【知识清单】
一次函数的图象和性质 1.图象
正比例函数 y=kx(k≠0)
一次函数 y=kx+b(k≠0)
图象关系
是经过点(0,0)和点(1,___k___)的一条直线
是经过点(0,b__ )和点(____kb,0)的一条直线
一次函数y=kx+b的图象可由正比例函数y=kx的图象 平移得到,b>0,向___上____移动___b___个单位,b<0, 向___下____移动___-_b___个单位
∵m-n=4,∴m-(-2m+2)=4,解得m=2,n=-2,
∴点P的坐标为(2,-2).
反思:函数的性质可以结合图象来理解求解.
考点3 与方程(组)、不等式的关系 例3.(202X·乐山)直线y=kx+b在平面直角坐标系中的位置如图所示,求不等式 kx+b≤2的解.
【解析】根据图象得出直线y=kx+b经过(0,1),(2,0)两点,
2
.5
2
【联系课标】 【课标要求】 一次函数 (1)会利用待定系数法确定一次函数的表达式 (2)会画一次函数的图象 (3)能根据一次函数的图象和表达式探索并理解其性质 (4)体会一次函数与二元一次方程的关系
【考点剖析】 考点1 一次函数表达式的确定 例1.(202X·黔西南)如图,正比例函数的图象与一次函数y=-x+1的图象相交于 点P,点P到x轴的距离是2,求这个正比例函数的表达式.
变式1.(202X·广州)一次函数y=-3x+1的图象过点(x1,y1),(x1+1,y2),
(x1+2,y3),则 ( B )
A.y1<y2<y3
人教版八年级下册数学册第十九章 一次函数的图像和性质
2)、描点
y=2x+1
3)、连线
因为一次函数的图象是 一条直线,所以只要取 两个点就能画出函数的
图象
练习
选取适当的两点在坐标系中画出下面函数的图象 (同桌各画一组)
1)、y =2x 2)、y =-2x
y =2x+2 y =-2x+2
y =2x-2 y =-2x-2
练习
选取适当的两点在坐标系中画出下面函数的图象 (同桌各画一组)
1)、y =2x 2)、y =-2x
y =2x+2 y =-2x+2
y =2x-2 y =-2x-2
y=2x+2
y=-2x
y=2x-2
y=-2x+2
y=-2x-2
y=-2x
自学提示二
自学内容:
观察第一组函数的图象,根据你的观察完成导学 案中的3、4、5题。
自学方法:
阅读课本,利用数形结合、类比的数学思想 方法。
自学要求: 先独立思考后小组交流完成。
自学互帮
自学内容:
观察第一组函数的图象,根据你的观察完成导学 案中的问题。
自学方法:
阅读课本,利用数形结合、类比的数学思想 方法。
自学要求: 先独立思考后小组交流完成。
释疑
自学内容:1、 观察第一组函数的图象,根据你 的观察回答下列问题:
(1)这三个函数的图象形状都 是直线,并且倾斜程度 相同 ;
量x 可以是任意的实数,
解:1)、列表
列表表示几组对应值
x
. . . -2
-1 0 1
2
...
y=2x+1 . . .
-3 -1
1
3
5 ...
中考数学总复习 第三单元 函数及其图像 第11课时 一次函数的图像与性质课件

y=-x+2
.
图 11-1
2021/12/9
第十一页,共三十二页。
y= x
,图②
课前双基巩固
5. [八上 P164 探索改编] 已知一次函数 y=2x+4.
图 11-2
(1)在如图 11-2 所示的平面直角坐标系中,画出函数的图像;
(2)图像与 x 轴的交点 A 的坐标是 (-2,0) ,与 y 轴的交点 B 的坐标是 (0,4)
与 x 轴交点坐标
令 y=0,求出对应的 x 值
两直线的
与 y 轴交点坐标
令 x=0,求出对应的 y 值
交点坐标
与其他函数图
像的交点坐标
一条直线与坐标轴围
成的三角形的面积
2021/12/9
解由两个函数表达式组成的二元一次方程组,方程组的解即两函数
图像的交点坐标
1
2
直线 y=kx+b(k≠0)与 x 轴的交点为 - ,0 ,与 y 轴的交点为(0,b),三角形面积为 S△= - ×|b|(用
a2+a2=
直线 y=2x+1 向右、向上平移 3 个单位后的解析式是 y=2x-2.
2021/12/9
第二十二页,共三十二页。
2
3 2 ,解得 a=3.
高频考向探究
[方法模型] 直线 y=kx+b(k≠0)在平移过程中 k 值不变.平移的规律是:若上下平移,则直接在常数 b 后加上或减
去平移的单位长度数;若向左(或向右)平移 m 个单位长度,则直线 y=kx+b(k≠0)变为 y=k(x±m)+b,其口诀是上加
人教初中数学八下 19.2.2《一次函数》一次函数的图像和性质课件 【经典初中数学课件汇编】

(1)下列函数中,y的值随x值的增大而
增大的函数是__C______.
A.y=-2x B.y=-2x+1
直线y = kx+b (k≠0) 的平移规律
y
x o
y = kx+b(b>0)
y = kx y = kx+b(b<0)
特性:当k相同时,两直线平行 y
o
x y=kx+b
y=kx
活动二、怎样画一次函数y=kx+b的图像最简单?
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
度而得到;
推广: (1) 所有一次函数y=kx+b的图象都是_一__条__直__线_ ;
(2)直线 y=kx+b与直线y=kx_互__相__平__行___;
(3)直线 y=kx+b可以看作由直线y=kx_平__移_b__个__单__位_
而得到
当b>0,向上平移b个单位;
当b<0,向下平移 b 个单位。
16.1 二次根式
导入
1.如图所示的值表示正方形的
面积,则正方形的边长是 b 3 b-3
2.要修建一个面积为6.28m2的圆形喷水池,
它的半径为 2 m( 取3.14);
3、关系式中h 5t 2 ,用含有h的式子
表示t,则t为 h 。
5
新授:
你认为所得的各代数式有哪些共同特点?
中考数学复习一次函数图像及其性质[人教版]
![中考数学复习一次函数图像及其性质[人教版]](https://img.taocdn.com/s3/m/63c5e054852458fb770b562e.png)
(2006 浙江湖州课改)已知一次函数 y kx b( k,b 是常数, k 0 ),x与y的 部分对应值如下表所示:
那么不等式
kx b 0
的解集是(
)
x A. x 0 B.
0 C. x 1
D. x
1
(2006 绍兴课改)如图,一次函 数 y x 5 的图象经过点P(a,b)和 Q(c,d),则a(c-d)-b(c-d)的值 为 .
(2006 新疆课改)如图,把直线 l 向上平移2个单 位得到直线 l′ ,则 l′ 的表达式为( )
Байду номын сангаас
1 C. y x 1 2 1 D. y x 1 2
1 A. y x 1 2 1 B. y x 1 2
(2006 徐州非课改)(1)在如图-1所示的平面 直角坐标系中画出点A(2,3),再画出点A关于y轴 的对称点A’,则点A’的坐标为 ;
(4)请你根据自己在解 决以上问题的过程中所 获得的经验回答:直线
数,k 0 )关于y轴对 称的直线的函数关系式 为 .
y kx ( b k,b 是常
下讲介绍
2006中考赏析之
一次函数的应用
《食品包装设计》主要是对食品类包装设计进行了非常细致的分类介绍,比如:水、茶、果汁、酒类„„结合水与酒的不同特 性明确了包装设计不同的设计要求,体现了同是液态的商品,由于性质不同,其包装形式的差异也是非常明确的。糖果糕点类, 对于其不同的风格和形式也以对比的手法总结了其中的规律和特点。 书名 食品包装设计 目录1 简介2 无菌包装3 绿色包装4 功能包装5 智能包装6 方便化包装7 个性化包装 ; 食品包装设计 jzh96kbe 所有的产品都要被包装,随着经济的迅速发展和生活质量的不断提高,我国食品工业发展迅猛,人们的生活理念和消费模式正 在发生重大变化,包装在人们生活中也越来越重要,对食品包装也提出了新的要求,本世纪食品市场的竞争在很大程度上取决 于包装质量的竞争。科学技术突飞猛进,食品包装日新月异,而食品包装理念也显现出新特色,食品包装要以多样化满足现代 人不同层次的消费需求;无菌、方便、智能、个性化是食品包装发展的新时尚;拓展食品包装的功能、减轻包装废弃物对环境 污染的绿色包装已成为新世纪食品包装的发展趋势。 她的大头觉。老太太已经彻底对明蕙失望,所以倒不急了,得好好想想,明天怎么处置她,她毕竟不是丫头,不能一沓黄表纸 打发了。怎样才能既干净了眼前地界,又不至动静太大惹出流言来?还得好好想个法子。二老爷不在乎老太太怎么处置明蕙, 他在乎的是宝音还能不能进宫去?只有宝音再次得老太太首肯进宫,二房跟大房争竞还有希望。可宝音怎么就昏迷了呢!宝音 虽然昏迷,其实神智还在。她目不能视物,但知道自己倒下,也知道老婆子把她抱回房中,洛月坐在旁边哭,后来,医生来给 她把脉。这把脉的不是刘晨寂。尽管目不能视物,宝音还是可以分辨。刘晨寂的手指按上来,清凉、润和。即使没有药,单凭 他的手指触碰,仿佛都能让人安定似的。这一只把脉的手,却宽大、暖和,皮肤略有些粗糙。就是常给老太太诊视的那位老大 夫的手。他按着宝音的脉,没觉什么异样,只道体虚,开了些吃不死人的温补方子。宝音听在耳里,自己疑惑:哪有体虚成这 样的?神智无碍,也没觉得什么不舒服,就是张不开眼、动不得四肢?电光火石间她明白了:这一定是那撮药粉的功劳!所以 刘晨寂嘱咐,回家之前,药粉必须入腹。因她回家之后,立刻就要挨罚,只有药粉已在腹中,才能及时发挥作用,让她发场假 病,逃过漫漫长夜的罚跪,不至于受到实质伤害。可刘晨寂怎么知道宝音回府之后,就会挨罚?宝音只觉这人身上,疑团越来 越多,恨不能病好之后,即刻能寻到他,问个清楚。七王爷还不知出什么妖蛾子„„唉,走一步算一步罢!天有阴晴,月有圆 缺,谁能算定百年的基业?她方念及此,嘉颜气吁吁跑来,又把那老大夫请走了:老太太在二老爷那儿,休息了一会儿,胸闷 的毛病老是顺不过来,非得快些看看不可。老大夫过去,看了老太太气色、问了症候、把了脉。年纪大了,四肢百骸、五脏六 腑机能都下降,病灶丛生,药饵重不得、轻不得,大夫正斟酌,二老爷院子里又有诸人上气不接下气跑来报告:尤五姨娘捧着 肚子叫疼,要生了!这一晚上,苏府沸沸扬扬,没个清净的地方,连明蕙也被娘亲摇醒,听了几句话,脸色煞白,差点没晕死 过去。嘉颜一晚,头未沾枕,直至天快亮,老太太病势见缓和了,她才略眠了眠。那时候宝音也醒了。对于别人来说,宝音是 在昏迷中醒来。对于宝音来说,她在那奇怪的“昏迷”状态中,只能听、不能看,只能想、不能说,躺着无比憋闷,闷着闷着 睡了过去,似又见朱楼琼庭,持笔的仙人并不在案边,却有一兽,白首赤尾,马形虎纹,警惕而又温顺,过来拱她,一拱,她 就醒了,见到趴在自己床边睡觉的,是洛月,心中感念,手微抬了抬:“洛„„”“ 醒了!”洛月惊喜。宝音问:“外面什 么喧哗?”“尤五姨奶奶临盆了。”“五
一次函数图象的应用课件

目 录
• 一次函数图象的概述 • 一次函数图象在实际生活中的应用 • 一次函数图象与其他数学知识的结合应用 • 一次函数图象的应用实例分析 • 总结与展望
01
一次函数图象的概述
一次函数图象的定义
01
02
03
一次函数图象
一次函数y=kx+b(k≠0 )的图象是一条直线。
教学方法单一
部分教师在教授一次函数图象时 ,过于注重理论教学,缺乏实际 应用的结合,导致学生难以理解
其实际意义和应用价值。
技术应用不足
现代技术如几何画板、数学软件等 在课堂上的应用不足,限制了学生 对于函数图象动态变化的理解。
学生实践机会少
由于应试教育的影响,学生往往缺 乏实际操作和实践的机会,导致对 一次函数图象的理解停留在理论层 面。
对未来应用的展望与期待
加强技术与教学的结合
期待未来能更多地利用现代技术,使一次函数图象的教学更加生 动、形象,提高学生的学习兴趣和参与度。
注重实际应用与问题解决
希望教师在教学中能更多地引入实际问题,让学生在实际操作中理 解和掌握一次函数图象的应用。
培养学生的创新思维
期待未来的一次函数图象教学能够更加注重培养学生的创新思维和 解决问题的能力,而不仅仅是知识的灌输。
们的位置。
ቤተ መጻሕፍቲ ባይዱ
连线
用直线将这些点连接起 来,形成一次函数的图
象。
验证
根据题目要求或实际应 用需要,验证所绘制的 图象是否符合实际情况
。
02
一次函数图象在实际生活 中的应用
一次函数图象在物理中的应用
总结词
物理现象的数学描述
详细描述
中考数学考点10一次函数图像与性质总复习(解析版)

一次函数的图像与性质【命题趋势】在中考中.主要以选择题、填空题和解答题形式出现.主要考查一次函数的图像与性质.确定一次函数的解析式.一次函数与方程(组)、不等式的关系。
一次函数与二次函数、反比例函数综合也是中考重点之一。
【中考考查重点】一、结合具体情景体会一次函数的意义.能根据已知条件确定一次函数的表达式;二、利用待定系数法确定一次函数的表达式;三、根据一次函数画出图像.探索并理解k>0和k<0时.图像的变化情况;四、体会一次函数与二元一次方程的关系考点一:一次函数及其图像性质概念一般地.形如y=kx+b(k,b为常数.k≠0)的函数.叫做一次函数.当b=0十.即y=kx.这时称y是x的正比例函数(一次函数的特殊形式)增减性k>0k<0从左向右看图像呈上升趋势.y随x的增大而增大从左向右看图像呈下降趋势.y随x的增大而较少图像(草图)b>0b=0b<0b<0b=0 b<0经过象限一、二、三一、三一、三、四一、二、四二、四二、三、四与y轴的交点位置b>0.交点在y轴正半轴上;b=0,交点在原点;b<0.交点在y轴负半轴上【提分要点】:1.若两直线平行.则;2.若两直线垂直.则1.(2021春•大安市期末)一次函数y=2x﹣1图象经过象限()A.一、二、三B.一、二、四C.二、三、四D.一、三、四【答案】D【解答】解:∵一次函数y=2x﹣1.k=2>0.b=﹣1<0.∴该函数图象经过一、三、四象限.故选:D.2.(2021秋•肃州区期末)对于一次函数y=x+6.下列结论错误的是()A.函数值随自变量增大而增大B.函数图象与x轴正方向成45°角C.函数图象不经过第四象限D.函数图象与x轴交点坐标是(0.6)【答案】D【解答】解:A、∵一次函数y=x+6中k=1>0.∴函数值随自变量增大而增大.故A 选项正确;B、∵一次函数y=x+6与x、y轴的交点坐标分别为(﹣6.0).(0.6).∴此函数与x轴所成角度的正切值==1.∴函数图象与x轴正方向成45°角.故B选项正确;C、∵一次函数y=x+6中k=1>0.b=6>0.∴函数图象经过一、二、三象限.故C选项正确;D、∵令y=0.则x=﹣6.∴一次函数y=x+6与x轴的交点坐标分别为(﹣6.0).故D选项错误.故选:D.3.(2021秋•东港市期中)点A(﹣1.y1)和点B(﹣4.y2)都在直线y=﹣2x上.则y1与y2的大小关系为()A.y1>y2B.y1<y2C.y1=y2D.y1≥y2【答案】B【解答】解:∵k=﹣2<0.∴y随x的增大而减小.又∵点A(﹣1.y1)和点B(﹣4.y2)都在直线y=﹣2x上.且﹣1>﹣4.∴y1<y2.故选:B4.(2021秋•三水区期末)若一次函数y=kx+b的图象经过第一、二、四象限.则一次函数y=bx+k的图象大致是()A.B.C.D.【答案】D【解答】解:一次函数y=kx+b过一、二、四象限.则函数值y随x的增大而减小.因而k<0;图象与y轴的正半轴相交则b>0.因而一次函数y=bx﹣k的一次项系数b>0.y随x的增大而增大.经过一三象限.常数项k<0.则函数与y轴负半轴相交.因而一定经过一三四象限.故选:D.考点二:一次函数解析式的确定方法待定系数法步骤1.设:一般式y=kx+b(k≠0)(题干中未给解析式需设)2.代:找出一次函数图像上的两个点.并且将点坐标代入函数解析式.得到二元一次方程组;3.求:解方程(组)求出k、b的值;4.写:将k、b的值代入.直接写出一次函数解析式5.(2021秋•尤溪县期中)已知一次函数y=x+b过点(﹣1.﹣2).那么这个函数的表达式为()A.y=x﹣1B.y=x+1C.y=x﹣2D.y=x+2【答案】A【解答】解:把(﹣1.﹣2)代入y=x+b得:﹣2=﹣1+b.解得:b=﹣1.则一次函数解析式为y=x﹣1.故选:A.6.(2021春•海珠区期末)已知一次函数y=mx﹣4m.当1≤x≤3时.2≤y≤6.则m的值为()A.3B.2C.﹣2D.2或﹣2【答案】C【解答】解:当m>0时.一次函数y随x增大而增大.∴当x=1时.y=2且当x=3时.y=6.令x=1.y=2.解得m=.不符题意.令x=3.y=6.解得m=﹣6.不符题意.当m<0时.一次函数y随x增大而减小.∴当x=1时.y=6且当x=3时.y=2.令x=1.y=6.解得m=﹣2.令x=3.y=2.解得m=﹣2.符合题意.∴故选:C.7.(2021秋•萧山区月考)已知y与x﹣2成正比例.且当x=1时.y=1.则y与x之间的函数关系式为.【答案】y=﹣x+2【解答】解:设y=k(x﹣2)(k≠0).将x=1时y=1代入.得1=k(1﹣2).解得k=﹣1.所以y=﹣x+2;故答案为:y=﹣x+2.8.(2021春•古丈县期末)某个一次函数的图象与直线y=x+6平行.并且经过点(﹣2.﹣4).则这个一次函数的解析式为()A.y=﹣x﹣5B.y=x+3C.y=x﹣3D.y=﹣2x﹣8【答案】C【解答】解:由一次函数的图象与直线y=x+6平行.设直线解析式为y=x+b.把(﹣2.﹣4)代入得:﹣4=﹣1+b.即b=﹣3.则这个一次函数解析式为y=x﹣3.故选:C.考点三:一次函数图像的平移平移前平移方式(m>0)平移后简记y=kx+b 向左平移m个单位长度y=k(x+m)+bx左加右减向右平移m个单位长度y=k(x-m)+b向上平移m个单位长度y=kx+b+m等号右端整体上加下减向下平移m个单位长度y=kx+b-m9.(2021秋•金安区校级期中)将直线y=2x向右平移1个单位.再向上平移1个单位后.所得直线的表达式为()A.y=2x﹣1B.y=2x C.y=2x+4D.y=2x﹣2【答案】A【解答】解:将直线y=2x向右平移1个单位.再向上平移1个单位后.所得直线的解析式为y=2(x﹣1)+1.即y=2x﹣1.故选:A.10.(2021春•米易县期末)一次函数y=2x﹣4的图象由正比例函数y=2x的图象()A.向左平移4个单位长度得到B.向右平移4个单位长度得到C.向上平移4个单位长度得到D.向下平移4个单位长度得到【答案】D【解答】解:将正比例函数y=2x的图象向下平移4个单位即可得到y=2x﹣4的图象.故选:D.11.(2021秋•长丰县月考)已知点A(2.4)沿水平方向向左平移3个单位长度得到点A'.若点A'在直线y=x+b上.则b的值为()A.1B.3C.5D.﹣1【答案】C【解答】解:∵点A(2.4)沿水平方向向左平移3个单位长度得到点A'.∴点A'的坐标为(﹣1.4).又∵点A'在直线y=x+b上.∴4=﹣1+b.∴b=5.故选:C考点四:一次函数与方程(组)、不等式与一元一次方程的关系方程ax+b=0(a≠0)的解是一次函数y=ax+b(a≠0)的函数值为0时自变量的取值.还是直线y=ax+b(a≠0)与x轴交点的横坐标与二元一次方程组的关系方程组的解时直线的交点坐标与一元一次不等式的关系1.从“数”来看(1)kx+b>0的解集是y=kx+b中.y>0时x的取值范围(2)kx+b><0的解集是y=kx+b中.y<0时x的取值范围2.从“形”上看(1)kx+b>0的解集是y=kx+b函数图像位于x上方部分对应的点的横坐标(2)kx+b<0的解集是y=kx+b函数图像位于x下方部分对应的点的横坐标12.(2021秋•乐平市期中)一次函数y=kx+b的图象如图所示.则关于x的方程kx+b =0的解为()A.x=0B.x=3C.x=﹣2D.x=﹣3【答案】B【解答】解:∵直线与x轴交点坐标为(3.0).∴kx+b=0的解为x=3.故选:B.13.(2021秋•安徽期中)已知一次函数y=ax﹣1与y=mx+4的图象交于点A(3.1).则关于x的方程ax﹣1=mx+4的解是()A.x=﹣1B.x=1C.x=3D.x=4【答案】C【解答】解:∵一次函数y=ax﹣1与y=mx+4的图象交于点A(3.1).∴ax﹣1=mx+4的解是x=3.故选:C.14.(2021春•沧县期末)如图.直线y=x+5和直线y=ax+b相交于点P(20.25).根据图象可知.方程x+5=ax+b的解是()A.x=20B.x=5C.x=25D.x=15【答案】A【解答】解:∵直线y=x+5和直线y=ax+b相交于点P(20.25).∴方程x+5=ax+b的解为x=20.故选:A.15.(2020秋•建湖县期末)如图.一次函数y=kx+b(k≠0)的图象经过点A(﹣1.﹣2)和点B(﹣2.0).一次函数y=2x的图象过点A.则不等式2x<kx+b≤0的解集为()A.x≤﹣2B.﹣2≤x<﹣1C.﹣2<x≤﹣1D.﹣1<x≤0【答案】B【解答】解:∵由图象可知:正比例函数y=2x和一次函数y=kx+b的图象的交点是A(﹣1.﹣2).∴不等式2x<kx+b的解集是x<﹣1.∵一次函数y=kx+b的图象与x轴的交点坐标是B(﹣2.0).∴不等式kx+b≤0的解集是x≥﹣2.∴不等式2x<kx+b<0的解集是﹣2≤x<﹣1.故选:B.16.(2021秋•兴宁区校级月考)如图.直线y=kx+b交x轴于点A(﹣2.0).直线y=mx+n交x轴于点B(5.0).这两条直线相交于点C(2.c).则关于x的不等式组的解集为()A.x<5B.1<x<5C.﹣2<x<5D.x<﹣2【答案】D【解答】解:y=kx+b<0.则x<﹣2.y=mx+n>0.则x<5.关于x的不等式组的解集为:x<﹣2.故选:D.17.(2020秋•西林县期末)如图所示是函数y=kx+b与y=mx+n的图象.则方程组的解是()A.B.C.D.【答案】C【解答】解:∵函数y=kx+b与y=mx+n的图象交于点(3.4).∴方程组的解是.故选:C.1.(2021春•扎兰屯市期末)将直线y=﹣2x﹣2向右平移1个单位长度.可得直线的表达式为()A.y=2x B.y=﹣2x﹣4C.y=﹣2x D.y=﹣2x+4【答案】C【解答】解:由“左加右减”的原则可知.把直线y=﹣2x﹣2向右平移1个单位长度.可得直线的解析式为:y=﹣2(x﹣1)﹣2.即y=﹣2x.故选:C.2.(2021春•玉田县期末)下列有关一次函数y=﹣6x﹣5的说法中.正确的是()A.y的值随着x值的增大而增大B.函数图象与y轴的交点坐标为(0.5)C.当x>0时.y>﹣5D.函数图象经过第二、三、四象限【答案】D【解答】解:∵y=﹣6x﹣5.﹣6<0.﹣5<0.∴y随x的增大而减小.故选项A不符合题意;当x=0时.y=﹣6×0﹣5=﹣5.即函数图象与y轴的交点坐标为(0.﹣5).故选项B不符合题意;当x>0时.y<﹣5.故选项C不符合题意;函数图象经过第二、三、四象限.故选项D符合题意;故选:D.3.(2021春•红寺堡区期末)点P1(x1.y1).点P2(x2.y2)是一次函数y=﹣4x+3图象上的两个点.且x1<x2.则y1与y2的大小关系是()A.y1>y2B.y1>y2>0C.y1<y2D.y1=y2【答案】A【解答】解:∵k=﹣4<0.∴y随x的增大而减小.又∵x1<x2.∴y1>y2.故选:A.4.(2021秋•运城期中)在平面直角坐标系中.一次函数y=kx+3(k≠0)的图象经过点A(2.﹣1).则这个一次函数的表达式是()A.y=﹣2x+3B.y=x+3C.y=2x+3D.y=x+3【答案】A【解答】解:∵一次函数y=kx+3(k≠0)的图象经过点A(2.﹣1).∴2k+3=﹣1解得k=﹣2.∴一次函数的表达式是y=﹣2x+3.故选:A.5.(2021秋•南海区期中)如图.一次函数y=kx+b的图象经过点(2.0)、(0.1).则下列结论正确的是()A.k=1B.关于x的方程kx+b=0的解是x=2C.b=2D.关于x的方程kx+b=0的解是x=1【答案】B【解答】解:A.∵一次函数y=kx+b的图象经过点(2.0)、(0.1).∴.解得:.故选项A不符合题意;B.由图象得:关于x的方程kx+b=0的解为x=2正确.故选项B符合题意;C.由图象得:当x=0时.y=1.即b=1.故选项C不符合题意;D.由图象得:y=0.即kx+b=0时.x=2.∴关于x的方程kx+b=0的解是x=2.故选项D不符合题意;故选:B.6.(2021秋•滕州市期中)直线y=ax+b(a≠0)过点A(0.2).B(1.0).则关于x的方程ax+b=0的解为()A.x=0B.x=2C.x=1D.x=3【答案】C【解答】解:方程ax+b=0的解.即为函数y=ax+b图象与x轴交点的横坐标.∵直线y=ax+b过B(1.0).∴方程ax+b=0的解是x=1.故选:C.7.(2021秋•龙凤区期末)一次函数y=mx﹣n(m.n为常数)的图象如图所示.则不等式mx﹣n≥0的解集是()A.x≥2B.x≤2C.x≥3D.x≤3【答案】D【解答】解:由图象知:不等式mx﹣n≥0的解集是x≤3.故选:D.8.(2020秋•开化县期末)如图.直线y=2x+n与y=mx+3m(m≠0)的交点的横坐标为﹣1.则关于x的不等式2x+n<mx+3m<0的整数解为()A.﹣1B.﹣2C.﹣3D.﹣3.5【答案】B【解答】解:∵直线y=2x+n与y=mx+3m(m≠0)的交点的横坐标为﹣1.∴关于x的不等式2x+n<mx+3m的解集为x<﹣1.∵y=x+3=0时.x=﹣3.∴mx+3m<0的解集是x>﹣3.∴2x+n<mx+3m<0的解集是﹣3<x<﹣1.所以不等式2x+n<mx+3m<0的整数解为﹣2.故选:B.9.(2021春•单县期末)已知方程组的解为.则直线y=﹣x+2与直线y =2x﹣7的交点在平面直角坐标系中位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解答】解:∵方程组的解为.∴直线y=﹣x+2与直线y=2x﹣7的交点坐标为(3.﹣1).∵x=3>0.y=﹣1<0.∴交点在第四象限.故选:D.10.(2021春•武陵区期末)对于实数a.b.我们定义符号max{a.b}的意义为:当a≥b 时.max{a.b}=a;当a<b时.max{a.b}=b;如:max{4.﹣2}=4.max{3.3}=3.若关于x 的函数为y=max(2x﹣1.﹣x+2}.则该函数的最小值是()A.2B.1C.0D.﹣1【答案】B【解答】解:当2x﹣1≥﹣x+2时.解得:x≥1.此时y=2x﹣1.∵2>0.∴y随x的增大而增大.当x=1时.y最小为1;当2x﹣1<﹣x+2时.解得:x<1.此时y=﹣x+2.∵﹣1<0.∴y随x的增大而减小.综上.当x=1时.y最小为1.故选:B.11.(2020秋•成安县期末)如图.若直线y=kx+b与x轴交于点A(﹣4.0).与y轴正半轴交于B.且△OAB的面积为4.则该直线的解析式为()A.B.y=2x+2C.y=4x+4D.【答案】A【解答】解:∵A(﹣4.0).∴OA=4.∵×4×OB=4.解得OB=2.∴B(0.2).把A(﹣4.0).B(0.2)代入y=kx+b.∴.解得.∴直线解析式为y=x+2.故选:A.12.(2021春•饶平县校级期末)已知2y﹣3与3x+1成正比例.则y与x的函数解析式可能是()A.y=3x+1B.C.D.y=3x+2【答案】C【解答】解:∵2y﹣3与3x+1成正比例.则2y﹣3=k(3x+1).当k=1时.2y﹣3=3x+1.即y=x+2.故选:C.13.(2021秋•榆林期末)已知直线l1交x轴于点(﹣3.0).交y轴于点(0.6).直线l2与直线l1关于x轴对称.将直线l1向下平移8个单位得到直线l3.则直线l2与直线l3的交点坐标为()A.(﹣1.﹣4)B.(﹣2.﹣4)C.(﹣2.﹣1)D.(﹣1.﹣1)【答案】A【解答】解:设直线l1为y=kx+b.∵直线l1交x轴于点(﹣3.0).交y轴于点(0.6).∴.解得.∴b=﹣4.∴直线l1为y=2x+6.将直线l1向下平移8个单位得到直线l3:y=2x+6﹣8=2x﹣2.∵直线l2与直线l1关于x轴对称.∴直线l2交x轴于点(﹣3.0).交y轴于点(0.﹣6).∴直线l2为y=﹣2x﹣6.解得.∴直线l2与直线l3的交点坐标为(﹣1.﹣4).故选:A.1.(2021•长沙)下列函数图象中.表示直线y=2x+1的是()A.B.C.D.【答案】B【解答】解:∵k=2>0.b=1>0.∴直线经过一、二、三象限.故选:B.2.(2021•嘉峪关)将直线y=5x向下平移2个单位长度.所得直线的表达式为()A.y=5x﹣2B.y=5x+2C.y=5(x+2)D.y=5(x﹣2)【答案】A【解答】解:将直线y=5x向下平移2个单位长度.所得的函数解析式为y=5x﹣2.故选:A.3.(2021•陕西)在平面直角坐标系中.将直线y=﹣2x向上平移3个单位.平移后的直线经过点(﹣1.m).则m的值为()A.﹣1B.1C.﹣5D.5【答案】D【解答】解:将直线y=﹣2x向上平移3个单位.得到直线y=﹣2x+3.把点(﹣1.m)代入.得m=﹣2×(﹣1)+3=5.故选:D.4.(2021•抚顺)如图.直线y=2x与y=kx+b相交于点P(m.2).则关于x的方程kx+b =2的解是()A.x=B.x=1C.x=2D.x=4【答案】B【解答】解:∵直线y=2x与y=kx+b相交于点P(m.2).∴2=2m.∴m=1.∴P(1.2).∴当x=1时.y=kx+b=2.∴关于x的方程kx+b=2的解是x=1.故选:B.5.(2020•牡丹江)两个一次函数y=ax+b和y=bx+a.它们在同一个直角坐标系的图象可能是()A.B.C.D.【答案】B【解答】解:当a>0.b>0时.一次函数y=ax+b和y=bx+a的图象都经过第一、二、三象限.当a>0.b<0时.一次函数y=ax+b的图象经过第一、三、四象限.函数y=bx+a的图象经过第一、二、四象限.当a<0.b>0时.一次函数y=ax+b的图象经过第一、二、四象限.函数y=bx+a的图象经过第一、三、四象限.当a<0.b<0时.一次函数y=ax+b和y=bx+a的图象都经过第二、三、四象限.由上可得.两个一次函数y=ax+b和y=bx+a.它们在同一个直角坐标系的图象可能是B中的图象.故选:B.6.(2021•乐山)如图.已知直线l1:y=﹣2x+4与坐标轴分别交于A、B两点.那么过原点O且将△AOB的面积平分的直线l2的解析式为()A.y=x B.y=x C.y=x D.y=2x【答案】D【解答】解:如图.当y=0.﹣2x+4=0.解得x=2.则A(2.0);当x=0.y=4.则B(0.4).∴AB的中点坐标为(1.2).∵直线l2把△AOB面积平分∴直线l2过AB的中点.设直线l2的解析式为y=kx.把(1.2)代入得2=k.解得k=2.∴l2的解析式为y=2x.故选:D.7.(2021•娄底)如图.直线y=x+b和y=kx+4与x轴分别相交于点A(﹣4.0).点B(2.0).则解集为()A.﹣4<x<2B.x<﹣4C.x>2D.x<﹣4或x>2【答案】A【解答】解:∵当x>﹣4时.y=x+b>0.当x<2时.y=kx+4>0.∴解集为﹣4<x<2.故选:A.8.(2019•苏州)若一次函数y=kx+b(k.b为常数.且k≠0)的图象经过点A(0.﹣1).B (1.1).则不等式kx+b>1的解集为()A.x<0B.x>0C.x<1D.x>1【答案】D【解答】解:如图所示:不等式kx+b>1的解为:x>1.故选:D.9.(2021•德阳)关于x.y的方程组的解为.若点P(a.b)总在直线y=x上方.那么k的取值范围是()A.k>1B.k>﹣1C.k<1D.k<﹣1【答案】B【解答】解:解方程组可得..∵点P(a.b)总在直线y=x上方.∴b>a.∴>﹣k﹣1.解得k>﹣1.故选:B.10.(2021•呼和浩特)在平面直角坐标系中.点A(3.0).B(0.4).以AB为一边在第一象限作正方形ABCD.则对角线BD所在直线的解析式为()A.y=﹣x+4B.y=﹣x+4C.y=﹣x+4D.y=4【答案】A【解答】解:过D点作DH⊥x轴于H.如图.∵点A(3.0).B(0.4).∴OA=3.OB=4.∵四边形ABCD为正方形.∴AB=AD.∠BAD=90°.∵∠OBA+∠OAB=90°.∠OAB+∠DAH=90°.∴∠ABO=∠DAH.在△ABO和△DAH中..∴△ABO≌△DAH(AAS).∴AH=OB=4.DH=OA=3.∴D(7.3).设直线BD的解析式为y=kx+b.把D(7.3).B(0.4)代入得.解得.∴直线BD的解析式为y=﹣x+4.故选:A.11.(2019•江西)如图.在平面直角坐标系中.点A.B的坐标分别为(﹣.0).(.1).连接AB.以AB为边向上作等边三角形ABC.(1)求点C的坐标;(2)求线段BC所在直线的解析式.【答案】(1)(.2)(2)y=x+.【解答】解:(1)如图.过点B作BH⊥x轴.∵点A坐标为(﹣.0).点B坐标为(.1).∴|AB|==2.∵BH=1.∴sin∠BAH==.∴∠BAH=30°.∵△ABC为等边三角形.∴AB=AC=2.∴∠CAB+∠BAH=90°.∴点C的纵坐标为2.∴点C的坐标为(.2).(2)由(1)知点C的坐标为(.2).点B的坐标为(.1).设直线BC的解析式为:y=kx+b.则.解得.故直线BC的函数解析式为y=x+.1.(2021•庐阳区校级一模)一次函数y=﹣2x﹣3的图象和性质.叙述正确的是()A.y随x的增大而增大B.与y轴交于点(0.﹣2)C.函数图象不经过第一象限D.与x轴交于点(﹣3.0)【答案】C【解答】解:∵一次函数y=﹣2x﹣3.∴该函数y随x的增大而减小.故选项A错误;与y轴交于点(0.﹣3).故选项B错误;该函数图象经过第二、三、四象限.不经过第一象限.故选项C正确;与x轴交于点(﹣.0).故选项D错误;故选:C.2.(2021•陕西模拟)平面直角坐标系中.直线y=﹣2x+m沿x轴向右平移4个单位后恰好经过(1.2).则m=()A.﹣1B.2C.﹣4D.﹣3【答案】C【解答】解:直线y=﹣2x+m沿x轴向右平移4个单位后得到y=﹣2(x﹣4)+m.∵经过(1.2).∴2=﹣2(1﹣4)+m.解得m=﹣4.故选:C.3.(2021•商河县校级模拟)若一次函数y=kx+b的图象经过一、二、四象限.则一次函数y=﹣bx+k的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限【答案】A【解答】解:一次函数y=kx+b过一、二、四象限.则函数值y随x的增大而减小.因而k<0;图象与y轴的正半轴相交则b>0.因此一次函数y=﹣bx+k的一次项系数﹣b<0.y随x的增大而减小.经过二四象限.常数项k<0.则函数与y轴负半轴相交.因此一定经过二三四象限.因此函数不经过第一象限.故选:A.4.(2021•萧山区一模)已知y﹣3与x+5成正比例.且当x=﹣2时.y<0.则y关于x的函数图象经过()A.第一、二、三象限B.第一、二、四象限C.第一、三、四象限D.第二、三、四象限【答案】D【解答】解:∵y﹣3与x+5成正比例.∴设y﹣3=k(x+5).整理得:y=kx+5k+3.当x=﹣2时.y<0.即﹣2k+5k+3<0.整理得3k+3<0.解得:k<﹣1.∵k<﹣1.∴5k+3<﹣2.∴y=kx+5k+3的图象经过第二、三、四象限.故选:D.5.(2021•陕西模拟)一次函数y=kx+b的图象经过点A(2.3).每当x增加1个单位时.y 增加3个单位.则此函数表达式是()A.y=x+3B.y=2x﹣3C.y=3x﹣3D.y=4x﹣4【答案】C【解答】解;由题意可知一次函数y=kx+b的图象也经过点(3.6).∴.解得∴此函数表达式是y=3x﹣3.故选:C.6.(2021•蕉岭县模拟)在平面直角坐标系中.一次函数y=mx+b(m.b均为常数)与正比例函数y=nx(n为常数)的图象如图所示.则关于x的方程mx=nx﹣b的解为()A.x=3B.x=﹣3C.x=1D.x=﹣1【答案】A【解答】解:∵两条直线的交点坐标为(3.﹣1).∴关于x的方程mx=nx﹣b的解为x=3.故选:A.7.(2021•奉化区校级模拟)八个边长为1的正方形如图摆放在平面直角坐标系中.经过原点的一条直线l将这八个正方形分成面积相等的两部分.则该直线l的解析式为()A.y=﹣x B.y=﹣x C.y=﹣x D.y=﹣x【答案】D【解答】解:设直线l和八个正方形的最上面交点为A.过A作AB⊥OB于B.B过A 作AC⊥OC于C.∵正方形的边长为1.∴OB=3.∵经过原点的一条直线l将这八个正方形分成面积相等的两部分.∴S△AOB=4+1=5.∴OB•AB=5.∴AB=.∴OC=.由此可知直线l经过(﹣.3).设直线方程为y=kx.则3=﹣k.k=﹣.∴直线l解析式为y=﹣x.故选:D.8.(2021•遵义一模)如图.直线y=kx+b(k<0)与直线y=x都经过点A(3.2).当kx+b>x时.x的取值范围是()A.x<2B.x>2C.x<3D.x>3【答案】C【解答】解:由图象可知.当x<3时.直线y=kx+b在直线y=x上方.所以当kx+b>x时.x的取值范围是x<3.故选:C.9.(2021•饶平县校级模拟)如图.函数y=ax+b和y=﹣x的图象交于点P.则根据图象可得.关于x.y的二元一次方程组中的解是()A.B.C.D.【答案】C【解答】解:当y=1时.﹣x=1.解得x=﹣3.则点P的坐标为(﹣3.1).所以关于x.y的二元一次方程组中的解为.故选:C.10.(2021•杭州模拟)已知直线l:y=kx+b经过点A(﹣1.a)和点B(1.a﹣4).若将直线l向上平移2个单位后经过原点.则直线的表达式为()A.y=2x+2B.y=2x﹣2C.y=﹣2x+2D.y=﹣2x﹣2【答案】D【解答】解:将直线l向上平移2个单位后经过原点.则点A(﹣1.a)和点B(1.a﹣4)平移后对应的点的坐标为(﹣1.a+2)和(1.a﹣2).∵将直线l向上平移2个单位后经过原点.∴点(﹣1.a+2)和点(1.a﹣2)关于原点对称.∴a+2+a﹣2=0.∴a=0.∴A(﹣1.0).B(1.﹣4).把A、B的坐标代入y=kx+b得..解得.∴直线AB的解析式为y=﹣2x﹣2.故选:D.11.(2021•南山区校级二模)我国古代很早就对二元一次方程组进行了研究.古著《九章算术》记载用算筹表示二元一次方程组.发展到现代就是用矩阵式=来表示二元一次方程组.而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x.y)据此.则矩阵式=所对应两直线交点坐标是.【答案】(﹣1.2)【解答】解:依题意.得.解得.∴矩阵式=所对应两直线交点坐标是(﹣1.2).故答案为:(﹣1.2).12.(2021•杭州模拟)已知直线y=kx+b经过点A(5.0).B(1.4).(1)求直线AB的解析式;(2)若直线y=2x﹣4与直线AB相交于点C.求点C的坐标;(3)根据图象.写出关于x的不等式2x﹣4>kx+b的解集.【答案】(1)y=﹣x+5 (2)C(3.2)(3)x>3【解答】解:(1)∵直线y=kx+b经过点A(5.0).B(1.4).∴.解得.∴直线AB的解析式为:y=﹣x+5;(2)∵若直线y=2x﹣4与直线AB相交于点C.∴.解得.∴点C(3.2);(3)根据图象可得x>3.。
中考考点复习之一次函数专题
中考考点复习之一次函数专题考点精讲1.结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式。
2.会利用待定系数法确定一次函数的表达式。
3.能画出一次函数的图象,根据一次函数的图象和表达式()0≠+=k b kx y 探索并理解0>k 和0<k 时,图象的变化情况。
4.理解正比例函数。
5.体会一次函数和二元一次方程的关系。
考点解读考点1:一次函数图像与性质(1)概念:一般来说,形如y =kx +b (k ≠0)的函数叫做一次函数.特别地,当b =0时,称为正比例函数.(2)图象形状:一次函数y =kx +b 是一条经过点(0,b )和(-b /k ,0)的直线.特别地,正比例函数y =kx 的图象是一条恒经过点(0,0)的直线.(3)一次函数与坐标轴交点坐标1.求一次函数与x 轴的交点,只需令y =0,解出x 即可;2.求与y 轴的交点,只需令x =0,求出y 即可.故一次函数y =kx +b (k ≠0)的图象与x 轴的交点是)0,(kb -,与y 轴的交点是(0,b ); 3.正比例函数y =kx (k ≠0)的图象恒过点(0,0).考点2:一次函数解析式的确定(1)常用方法:待定系数法,其一般步骤为:①设:设函数表达式为y =kx +b (k ≠0);②代:将已知点的坐标代入函数表达式,解方程或方程组;③解:求出k 与b 的值,得到函数表达式.(2)常见类型:①已知两点确定表达式;②已知两对函数对应值确定表达式;③平移转化型:如已知函数是由y =2x 平移所得到的,且经过点(0,1),则可设要求函数的解析式为y =2x +b ,再把点(0,1)的坐标代入即可.考点3:一次函数图像的平移规律:“左加右减,上加下减”①一次函数图象平移前后k 不变,或两条直线可以通过平移得到,则可知它们的k 值相同. ②若向上平移h 单位,则b 值增大h ;若向下平移h 单位,则b 值减小h .考点4:一次函数与方程不等式的关系(1)一次函数与方程:一元一次方程kx +b =0的根就是一次函数y =kx +b (k 、b 是常数,k ≠0)的图象与x 轴交点的横坐标.(2)一次函数与方程组:二元一次方程组⎩⎨⎧+=+=bx k y b x k y 21的解⇔两个一次函数b x k y +=1和b x k y +=2图象的交点坐标.(3)一次函数与不等式(1)函数y =kx +b 的函数值y >0时,自变量x 的取值范围就是不等式kx +b >0的解集(2)函数y =kx +b 的函数值y <0时,自变量x 的取值范围就是不等式kx +b <0的解集 考点5:一次函数的应用.1.一般步骤:(1)设出实际问题中的变量;(2)建立一次函数关系式;(3)利用待定系数法求出一次函数关系式;(4)确定自变量的取值范围;(5)利用一次函数的性质求相应的值,对所求的值进行检验,是否符合实际意义;(6)做答.2.常见题型(1)求一次函数的解析式.(2)利用一次函数的性质解决方案问题.考点突破1.(2021秋•驻马店期末)若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为()A.±1B.﹣1C.1D.22.(2021秋•中原区校级期末)下列问题中,两个变量之间成正比例关系的是()A.圆的面积S(cm2)与它的半径r(cm)之间的关系B.某水池有水15m3,现打开进水管进水,进水速度为5m3/h,xh后这个水池有水ym3C.三角形面积一定时,它的底边a(cm)和底边上的高h(cm)之间的关系D.汽车以60km/h的速度匀速行驶,行驶路程y与行驶时间x之间的关系3.(2021秋•驿城区校级期末)在同一直角坐标系中,当ab>0时,y=ax2与y=ax+b的图象大致是()A.B.C.D.4.(2021春•新蔡县期末)正比例函数y=kx(k≠0)和一次函数y=k(1﹣x)在同一个直角坐标系内的图象大致是下图中的()A.B.C.D.5.(2021秋•白银期末)关于函数y=﹣2x+1,下列结论正确的是()A.图象必经过(﹣2,1)B.y随x的增大而增大C.图象经过第一、二、三象限D.当x>时,y<06.(2021春•巨野县期末)已知正比例函数y=kx(k≠0),函数值随x的增大而增大,则一次函数y=﹣kx+k的图象大致是()A.B.C.D.7.(2021秋•任城区校级期末)两个一次函数y1=mx+n,y2=nx+m,它们在同一坐标系中的图象可能是图中的()A.B.C.D.8.(2021秋•驿城区期末)一次函数y=﹣2x+6的图象与两坐标轴围成的三角形的面积是()A.6B.9C.12D.189.(2021秋•新郑市期末)若函数y=(m﹣3)x|m﹣2|+m﹣1是一次函数,则m的值为.10.(2021秋•驿城区校级期末)当k=时,函数y=(k﹣1)x+k2﹣1是一个正比例函数.11.(2021春•舞阳县期末)若式子+(k﹣1)0有意义,则一次函数y=(k﹣1)x+1﹣k的图象可能是.(填字母代号)A.B.C.D.12.(2019春•安阳期末)函数y=2x与y=6﹣kx的图象如图所示,则k=.13.(2021秋•东城区校级期末)请写出一个图象经过第一、第三象限的一次函数关系式.(写出一个即可).14.(2021•河南)请写出一个图象经过原点的函数的解析式.15.(2018春•确山县期末)点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OP A的面积为S.(1)用含x的解析式表示S为,其中x的范围是.(2)画出函数S的图象.(3)当点P的横坐标为5时,△OP A的面积为.(4)△OP A的面积能大于24吗?为什么?16.(2021春•会昌县期末)先完成下列填空,再在同一平面直角坐标系中画出以下函数的图象(不必再列表)(1)正比例函数y=2x的图象过(0,)和(1,);(2)一次函数y=﹣x+3的图象过(0,)和(,0).17.(2021秋•金水区校级期末)请根据学习“一次函数”时积累的经验和方法研究函数y =﹣|x|+2的图象和性质,并解决问题.(1)填空:①当x=0时,y=﹣|x|+2=;②当x>0时,y=﹣|x|+2=;③当x<0时,y=﹣|x|+2=;(2)在平面直角坐标系中作出函数y=﹣|x|+2的图象;(3)观察函数图象,写出关于这个函数的两条结论;(4)进一步探究函数图象发现:①函数图象与x轴有个交点,方程﹣|x|+2=0有个解;②方程﹣|x|+2=2有个解;③若关于x的方程﹣|x|+2=a无解,则a的取值范围是.18.(2021•禹州市模拟)如图1,在菱形ABCD中,AB=5,某数学兴趣小组从函数的角度对菱形ABCD的对角线长度进行如下探究:利用几何画板,测量出以下几组值:AC 1.00 2.00 3.00 4.00 5.00 6.007.008.009.009.549.809.95 BD9.959.809.549.168.668.007.14a 4.36 3.00 2.00 1.00(1)表格中a的值为.(2)设AC的长为自变量x,BD的长是关于自变量x的函数,记为y BD,现已在图2所示的平面直角坐标系中描出了表格中各组数据的对应点(x,y BD).①画出函数y BD的图象;②请在同一平面直角坐标系中画出直线y=x,结合所绘制的函数图象,写出函数y BD的一条性质.(3)在平面直角坐标系中,将三角板(含30°角的直角三角板)按如图3所示方式放置,顶点和坐标原点重合,斜边在x轴上,画出射线OA.若OA与绘制的函数图象交于点M,则此时菱形ABCD的面积为.。
人教版初中数学八年级下册19.2一次函数一次函数图像与性质应用课件

2、已知一次函数的图象经过点(3,5)与(-4, -9).求这个一次函数的解析式.
例3、已知一次函数y=kx+b(k≠0)在x=1时,y=5, 且它的图象与x轴交点的横坐标是6,求这个一 次函数的解析式。
4、 小明根据某个一次函数关系式填写了 下表:
已知:如图,平面直角坐标系xOy中,A(1,0), B(0,1),C(-1,0),过点C的直线绕点C旋 转,交y轴于点D,交线段AB于点E. (1)求∠OAB的度数及直线Az的解析式; (2)若△OCD与△BDE的面积相等, ①求直线CE的解析式; ②若y轴上的一点P满足∠APE=45°,请你直接写 出P点的坐标.
或3毫克以上时,治疗疾病最有效, 6
那么这个有效时间是_4__ 小时。.
点评(1)根据图像反映的信息解答有关问 3
题时,首先要弄清楚两坐标轴的实际意义,抓
住几个关键点来解决问题;
O2
5
(2)特别注意,第5问中由y=3对应的x值有两个;
x/时
(3)根据函数图像反映的信息来解答有关问题,比较形象、直观,从中能 进一步感受“数形结合思想”。
解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5
分别代入上式,得 b 40
解得 k 5
22.5 3.5k b
b
40
图象是包括
解析式为:Q=-5t+40 (0≤t≤8) Q (2)取点A(0,40),B(8,0),
40 然后连成 线段AB,即是所求的图形。
如图,直线y=kx+6与x、y轴分别交于E、F.点E 坐标为(-8,0),点A的坐标为(-6,0),P(x ,y)是直线y=kx+6上的一个动点. (1)求k的值; (2)若点P是第二象限内的直线上的一个动点,当 点P运动过程中,试写出三角形OPA的面积S与x的 函数关系式,并写出自变量x的取值范围; (3)探究:当P运动到什么位置时,三角形OPA的 面积为 27/8 ,并说明理由.
(名师整理)最新中考数学专题复习《一次函数的图象与性质》精品教案

中考数学人教版专题复习:一次函数的图象与性质考点考纲要求分值考向预测一次函数的图象与性质1. 理解函数、变量,正比例函数、一次函数定义;2. 掌握函数图象的性质,能够画出相应的函数图象;3. 掌握图象的运动变化规律,并能应用性质解决问题5~15分主要考查方向是自变量的取值范围,函数图象的性质,动点变化形成的图象,应用函数图象性质解决问题。
其中动点与图象问题难度较大一次函数1. 函数概念:一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,把y 称为因变量,y是x的函数。
用含有表示自变量的字母的代数式表示因变量的式子叫做函数的解析式。
提示:判断y是否为x的函数,只要看x取值确定的时候,y是否有唯一确定的值与之对应。
【方法指导】自变量的取值范围:(1)关系式为整式时,自变量的取值范围为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开方数大于等于零;1(4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,自变量的取值范围还要和实际情况相符合,使之有意义。
【随堂练习】x中的自变量x的取值范围是()(济宁)函数y=x1A. x≥0B. x≠﹣1C. x>0D. x≥0且x≠﹣1答案:解:根据题意得:x≥0且x+1≠0,解得x≥0,故选:A。
2. 一次函数的概念若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数(x为自变量),特别地,当b=0时,称y是x的正比例函数。
【重要提示】(1)一次函数的自变量的取值范围是一切实数,实际问题中要根据函数的实际意义来确定。
(2)一次函数y=kx+b(k,b为常数,k≠0)中的“一次”和一元一次方程、一元一次不等式中的“一次”意义相同,即自变量x的次数为1,一次项系数k必须是不为零的常数,b可为任意常数。
中考数学人教版 考点系统复习 第三章 函数 人教版 第二节 一次函数的图象与性质
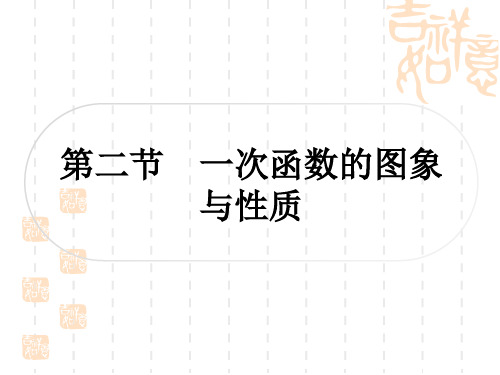
3.(2022·扬州)如图,函数y=kx+b(k<0) 的图象经过点P,则关于x 的不等式kx+b>3的解集为xx<<--11.
3 4.(2022·邵阳)在直角坐标系中,已知点A 2,m
,点B
7
2
,n
是直线y
=kx+b(k<0)上的两点,则m,n的大小关系是mm<<nn.
5.(2022·安徽)在同一平面直角坐标系中,一次函数y=ax+a2与y=
第二节 一次函数的图象 与性质
1.(2022·株洲)在平面直角坐标系中,一次函数y=5x+1的图象与y轴
的交点的坐标为
( D)
A.(0,-1)
B.-15,0 C.51,0 D.(0,1)
2.(2022·凉山州)一次函数y=3x+b(b≥0)的图象一定不经( D ) A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.★(2022·德阳)如图,已知点 A (-2,3),B (2,1),直线y= kx+k经过点P(-1,0).试探究直线与线段AB有交点时k的变化情况, 猜想k的取值范围是kk≤≤--33或或kk≥13 ≥.
9.★(2022·盐城)《庄子·天下篇》记载“一尺之棰,日取其半,万 1
世不竭”.如图,直线l1∶y= 2 x+1与y轴交于点A,过点A作x轴的平行 线交直线l2∶y=x于点O1,过点O1作y轴的平行线交直线l1于点A1,以此类 推,令OA=a1,O1A1=a2,…,On-1An-1=an,若a1+a2+…+an≤S对任意 大于1的整数n恒成立,则S的最小值为2 2 .
a2x+a的图象可能是
( D)
6.(2022·杭州)已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图 3x-y=1, xx==11,,
中考数学 考点系统复习 第三章 函数 第二节 一次函数 课时2 一次函数的实际应用
(RJ 八下 P99 习题 T11 改编)某市为了鼓励居民节约用水,采用分段 计费的方法按月计算每户家庭的水费,月用水量不超过 20 立方米时,按 2 元/立方米计费;月用水量超过 20 立方米时,超过部分按 2.6 元/立方 米计费.设某户家庭用水量为 x 立方米时,所交水费为 y 元.
解:(1)设去年 A 型车每辆售价 x 元,则今年售价每辆为(x-200)元,由 题意得 80 x000=80 00x0-(12-0010%), 解得 x=2 000. 经检验,x=2 000 是原方程的解. 答:去年 A 型车每辆售价为 2 000 元.
(2)设今年新进 A 型车 a 辆,则 B 型车(60-a)辆,获利 y 元,由题意得 y=(1 800-1 500)a+(2 400-1 800)(60-a). ∴y=-300a+36 000. ∵B 型车的进货数量不超过 A 型车数量的两倍, ∴60-a≤2a,∴a≥20. ∵y=-300a+36 000.∴k=-300<0, ∴y 随 a 的增大而减小.∴a=20 时,y 有最大值, ∴B 型车的数量为 60-20=40(辆). 答:当新进 A 型车 20 辆,B 型车 40 辆时,这批车获利最大.
(1)写出 y 与 x 之间的函数表达式;
解:由题意可得,当 0≤x≤20 时,y=2x, 当 x>20 时,y=20×2+(x-20)×2.6=2.6x-12,
2x(0≤x≤20), 综上可得,y=2.6x-第二季度交纳水费的情况如下: 月份 四月份 五月份
交费金额 30 元 34 元 小明家这个季度共用水多少立方米?
解:(1)设乙食材每千克进价为 a 元,则甲食材每千克进价为 2a 元,由 题意得820a-2a0=1,解得 a=20.经检验,a=20 是原方程的解,且符合题 意. ∴2a=40 元.答:甲、乙两种食材每千克进价分别为 40 元、20 元.
2019年人教版中考数学《一次函数的图象与性质》复习课件

一次函数与二元一次方程的关系
一次函数与二元一次方程组的关系
(1)一次函数y=mx+n(m≠0)与y=px+q(p≠0)的图象的交点坐标,即为二元
一次方程组 y px q 的解; y mx n,
y mx n, (2)以二元一次方程组 y px q 的解为坐标的点,是一次函数y=mx+
变式训练1 (2018衡水模拟)已知正比例函数y=kx(k≠0)的图象经过点(3,-6).
(1)求这个函数的解析式; (2)画出这个函数的图象; (3)判断点A(4,-2)、点B(-1.5,3)是否在这个函数的图象上; (4)图象上的两点C(x1,y1),D(x2,y2),如果x1>x2,比较y1,y2的大小.
3 ,0),∠ABC=30°, AE平分∠BAC交BC于点E. 0),C(
(1)求m的值,并在平面直角坐标系中画出△ABC及线段AE的大致位置; (2)求线段AE所在直线的函数表达式.
3 ,∠ACB=90°,故AB=2AC. 答案 (1)由△ABC的顶点坐标可知BC=
根据勾股定理,得(2AC)2=AC2+BC2,解得AC=1,∵Rt△ABC在第一象限内,∴m= 1,即A( 3 ,1). 画出的△ABC及线段AE如图所示. (2)根据题意,得∠AEC=60°,∠CAE=30°.
n(m≠0)与y=px+q(p≠0)的图象 的交点 一次函数与一元一次不等式的关系 (1)一次函数y=kx+b(k≠0)的图象位于x轴上方的部分所对应的自变量的 值,即为一元一次不等式kx +b>0的解集;反之亦然. (2)一次函数y=kx+b(k≠0)的图象位于x轴下方的部分所对应的自变量的 值,即为一元一次不等式kx+b <0的解集;反之亦然
中考数学复习一次函数的图像与性质

交点在 y 轴正半轴;当 b 小于 0 时,交点在 y 轴负半
轴.
(4)直线
y=kx+b
可以看作由直线
y=kx
平移 b
个单位长度得到(当 b>0 时,向上平移;当 b<0 时,
向下平移).
RED
(5)直线 y=k1x+b1,y=k2x+b2 的几种位置关 系:平行:k1=k2,b1≠b2;重合:k1=k2,b1=b2; 关于 y 轴对称:k1+k2=0,b1=b2;关于 x 轴对称: k1+k2=0,b1+b2=0;垂直:k1k2=-1.
图 1.10-7
RED
(1)求 k,b 的值; 解:当 x=1 时,y=3x=3,
RED
10 一次函数的图像与性质
RED
考点梳理
1.一次函数的图像与性质
RED
2.k,b 对一次函数图像的影响 (1)当 k>0 时,y 随 x 的增大而增大;当 k<0 时, y 随 x 的增大而减小. (2)k 决定着一次函数图像的倾斜程度,k越大, 其图像与 x 轴的夹角就越大.
RED
(3)b 决定着直线与 y 轴的交点,当 b 大于 0 时,
RED
3.一次函数与一次方程(组)、一次不等式(组) 的关系
(1)一次函数与一元一次方程的关系:一元一次 方程都可以转化成 ax+b=0(a,b 为常数,a≠0)的 形式,所以解一元一次方程可以转化为:当某个一 次函数的值为 0 时,求相应的自变量的值.从图像 上看,这相当于已知直线 y=ax+b,求它与 x 轴交 点的横坐标.
RED
(2)任何一个一元一次不等式都可以转化为 ax+ b>0 或 ax+b<0(a,b 为常数,a≠0)的形式,所以 解一元一次不等式可以看作:当一次函数值大(小) 于 0 时,求自变量的取值范围,也可以把一次函数 y =ax+b 在 x 轴上方的点所对应的 x 的取值范围看作 不等式 ax+b>0 的解集.
中考数学09 一次函数图象和性质及应用(含解析)新人教版

专题09 一次函数图象和性质及应用学校:___________姓名:___________班级:___________1.【2015届河北省保定市定州市中考三模】y与x成正比,当x=2时,y=8,那么当y=16时,x为()A.4 B.﹣4 C.3 D.﹣3【【答案】】A.【【分析】】[%#*~^]考点:待定系数法求正比例函数【分析】式.2.【湖北荆门2015年考数学试卷】在一次800米长跑比赛中,甲、乙两人所跑路程s(米)与各自所用时间t(秒)之间函数图象分别为线段OA和折线OBCD,则下列说法正确是()A.甲速度随时间增加而增大B.乙平均速度比甲平均速度大C.在起跑后第180秒时,两人相遇 [*#~%@]D.在起跑后第50秒时,乙在甲前面【【答案】】D. [@^*%#]【【分析】】考点:一次函数应用.3.【辽宁葫芦岛2015年考数学试卷】已知k 、b 是一元二次方程(21)(31)0x x +-=两个根,且k >b ,则函数y kx b =+图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限【【答案】】B .【【分析】】试题分析:∵k 、b 是一元二次方程(2x+1)(3x-1)=0两个根,且k >b ,∴k=31,b=-21,∴函数y=31x-21图象不经过第二象限,故选B . [#*&^@] 考点:1.一次函数图象与系数关系;2.解一元二次方程-因式分解法.4.【2014-2015学年山东省潍坊市诸城市实验中学中考三模】如图所示,函数y 1=|x|和y 2=13x+43图象相交于(﹣1,1),(2,2)两点.当y 1>y 2时,x 取值范围是( ).A .x <﹣1B .﹣1<x <2C .x >2D .x <﹣1或x >2 [^~@#&]【【答案】】D .【【分析】】试题分析:当x ≥0时,y 1=x ,又y 2=13x+43,所以两直线交点为(2,2),当当x<0时,y 1=﹣x ,又y 2=13x+43,所以两直线交点为(﹣1,1),由图象可知:当y 1>y 2时x 取值范围为:x <﹣1或x >2.故选D .考点:两条直线相交或平行问题. [^*&~#]5.【辽宁大连2015年中考数学试题】在平面直角坐标系中,点A 、B 坐标分别是(m ,3)、(3m-1,3).若线段AB 与直线y=2x+1相交,则m 取值范围为__________.【【答案】】32≤m ≤1. 【【分析】】考点:1.一次函数;2.分类讨论.6.【湖北武汉2015年中考数学试题】如图所示,购买一种苹果,所付款金额y (元)与购买量x (千克)之间函数图象由线段OA 和射线AB 组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元.【【答案】】2【【分析】】试题分析:根据函数图象可得:前面2千克,每千克10元,超过2千克每千克8元.则一次购买3千克需要钱数为:10×2+(3-2)×1=28元,分三次每次购买1千克需要钱数为:3×1×10=30元,30-28=2(元),即节省2元. 考点:一次函数应用.7.【2015届山东省济南市平阴县中考三模】新定义:[a ,b ,c]为函数y=ax 2+bx+c (a ,b ,c 为实数)“关联数”.若“关联数”为[m-2,m ,1]函数为一次函数,则m 值为 .【【答案】】2.【【分析】】试题分析:根据题意可得:m-2=0,且m ≠0,解得:m=2,考点:一次函数定义.8.【2015届山东省济南市平阴县中考三模】如图,已知函数y=x-2和y=-2x+1图象交于点P ,根据图象可得方程组221x y x y -=⎧⎨+=⎩解是 .【【答案】】⎩⎨⎧-==11y x . [@%^#&] 【【分析】】[~^@&*]考点:一次函数与二元一次方程(组). [%*^@#]9.【黑龙江绥化2015年中考数学试题】在平面直角坐标系xoy 中 ,直线y=-x+3 与x 轴、y 轴分别交于A 、B ,在△AOB 内部作正方形,使正方形四个顶点都落在该三角形边上,求正方形落在x 轴正半轴顶点坐标。
2020-2021学年人教版八年级数学下册第19章一次函数应用之图像专题 (三)

2020-2021学年人教版八年级数学下册第19章一次函数应用之图像专题(三)1.小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.(1)小张在路上停留小时,他从乙地返回时骑车的速度为千米/时;(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=12x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇次;(3)请你计算第一次相遇的时间.2.某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:(1)y与x之间的函数关系式;(2)每位旅客最多可免费携带行李的千克数.3.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.(1)填空:折线OABC表示赛跑过程中(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是米.(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)乌龟用了多少分钟追上了正在睡觉的兔子?(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.4.如图表示甲骑摩托车和乙驾驶汽车沿相同的路线行驶90千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的关系.请根据图象填空:(1)摩托车的速度为千米/小时;汽车的速度为千米/小时;(2)汽车比摩托车早小时到达B地.(3)在汽车出发后几小时,汽车和摩托车相遇?说明理由.5.小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:(1)小帅的骑车速度为千米/小时;点C的坐标为;(2)求线段AB对应的函数表达式;(3)当小帅到达乙地时,小泽距乙地还有多远?6.一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克西瓜出售的价格是多少?(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?(4)请问这个水果贩子一共赚了多少钱?7.秋高气爽,宜登高望远,张老师从小区大门出发,匀速步行前往南山,出发8分钟,他发现手机落在了小区大门,立即原速返回,张老师出发8分钟时,邻居老朱也匀速步行,从小区大门出发沿相同路线前往南山,张老师回到起点后用了4分钟才找到手机,之后一路小跑去追赶老朱,最终两人同时到达南山,开始了愉快的爬山之旅,两人之间的距离y(米)与张老师出发所用时间x(分)之间的关系如图所示,结合图象信息解答下列问题:(1)张老师最初出发的速度为米/分,a=,老朱步行的速度为米/分;(2)b=,c=,张老师回到起点,找到手机之后的速度为米/分;(3)小区大门与南山之间的距离为多少?8.从甲地到乙地,先是一段上坡路,然后是一段平路,小冲骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小冲骑车在上坡、平路、下坡时分别保持匀速前进,已知小冲骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小冲出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.(1)求小冲在平路上骑车的平均速度以及他在乙地的休息时间;(2)分别求线段AB、EF所对应的函数关系式;(3)从甲地到乙地经过丙地,如果小冲两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.9.某景区售票处规定:非节假日的票价打a折售票;节假日根据团队人数x(人)实行分段售票:若x≤10,则按原展价购买;若x>10,则其中10人按原票价购买,超过部分的按原那价打b折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y1元,在节假日的购票款为y2元,y1、y2与x之间的函数图象如图所示.(1)观察图象可知:a=,b=;(2)当x>10时,求y2与x之间的函数表达式;(3)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.10.李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,多宝鱼价格z(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示.(1)观察图象,直接写出日销售量的最大值;(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式;(3)试比较第10天与第12天的销售金额哪天多?11.甲乙两车从A市去往B市,甲比乙早出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,如图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:(1)A、B两市的距离是千米,甲到B市后小时乙到达B市;(2)求甲车返回时的路程S(千米)与时间t(小时)之间的函数关系式,并写出自变量t的取值范围;(3)请直接写出甲车从B市往回返后再经过几小时两车相遇.12.周末,甲、乙两人从学校出发去公园游玩,甲骑自行车出发0.5小时后到达苏果超市,在超市里休息了一段时间,再以相同的速度前往公园.乙因为一些事情耽搁了一些时间,在甲出发小时后,乙驾驶电瓶车沿相同的路线前往公园,如图,是他们离学校的路程y (km)与行走的时间x(h)的函数图象.已知乙驾驶电瓶车的速度是甲骑自行车的2倍.(1)求甲的速度和在苏果超市休息的时间;(2)乙出发后多长时间追上甲?13.如图是一辆摩托车从家里出发,离家的距离(千米)随行驶时间(分)的变化而变化的情况:(1)摩托车从出发到最后停止共经过了多少时间?离家最远的距离是多少?(2)摩托车在哪一段时间内速度最快?最快速度是多少?14.diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.15.甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:(1)货车在乙地卸货停留了多长时间?(2)货车往返速度,哪个快?返回速度是多少?16.A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.(1)求甲车行驶过程中y与x之间的函数关系式;(2)当它们行驶了7小时时,两车相遇,求乙车的速度.17.周末,小明和弟弟从家出发,步行去吉林省图书馆学习.出发2分钟后,小明发现弟弟的数学书忘记带了,弟弟继续按原速前往图书馆,小明按原路原速返回家取书,然后骑自行前往图书馆,恰好与弟弟同时到达图书馆.小明和弟弟各自距家的路程y(m)与小明步行的时间x(min)之间的函数图象如图所示.(1)求a的值.(2)求小明取回书后y与x的函数关系式.(3)直接写出小明取回书后与弟弟相距100m的时间.18.随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:(1)该市人均月生活用水不超过6吨时,求y与x的函数解析式;(2)该市人均月生活用水超过6吨时,求y与x的函数关系式;(3)若某个家庭有5人,六月份的生活用水费共75元,则该家庭这个月人均用了多少吨生活用水?19.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A的距离y(千米)与甲车行驶时间t(小时)之间的函数关系如图所示,根据图上信息回答.(1)A、B两城相距千米;乙车比甲车晚出发小时,却早到小时;(2)乙车出发后多少小时追上甲车?(3)多少小时甲、乙两车相距50千米时?20.甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A 地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:(1)图中点A表达的含义正确的是;(只填序号)①乙车出发时距离B地的路程.②甲车出发时距离A地的路程.③甲车出发时,乙车距离B地的距离.④乙车出发1小时后,距离B地的路程.(2)乙车的速度是千米/时,a=小时;甲车的速度是千米/时,t=小时.(3)在甲车到达C地之前,两车是否相遇?若相遇,求出在甲车出发后多久相遇?若没有相遇,说明理由.参考答案1.解:(1)由图象可知,小张在路上停留1小时,他从乙地返回时骑车的速度为:60÷(6﹣4)=30千米/时,故答案为:1,30;(2)如右图所示,图中虚线表示y=12x+10,由图象可知,小王与小张在途中相遇2次,故答案为:2;(3)设当2≤x≤4时,小张对应的函数解析式为y=kx+b,,得,∴当2≤x≤4时,小张对应的函数解析式为y=20x﹣20,∴,解得,,即小王与小张在途中第一次相遇的时间为小时.2.解:(1)设y与x之间的函数解析式为y=kx+b,,得,即y与x之间的函数关系式是y=x﹣6;(2)当y=0时,0=x﹣6,得x=30即每位旅客最多可免费携带行李30千克.3.解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻,∴折线OABC表示赛跑过程中兔子的路程与时间的关系;由图象可知:赛跑的全过程为1500米;故答案为:兔子,1500;(2)结合图象得出:兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).(3)700÷30=(分钟),所以乌龟用了分钟追上了正在睡觉的兔子.(4)∵兔子跑了700米停下睡觉,用了2分钟,∴剩余800米,所用的时间为:800÷400=2(分钟),∴兔子睡觉用了:50.5﹣2﹣2=46.5(分钟).所以兔子中间停下睡觉用了46.5分钟.4.解:(1)摩托车的速度为:90÷5=18千米/小时,汽车的速度为:90÷(4﹣2)=45千米/小时,故答案为:18、45;(2)5﹣4=1,即汽车比摩托车早1小时到达B地,故答案为:1;(3)解:在汽车出发后小时,汽车和摩托车相遇,理由:设在汽车出发后x小时,汽车和摩托车相遇,45x=18(x+2)解得x=∴在汽车出发后小时,汽车和摩托车相遇.5.解:(1)由图可得,小帅的骑车速度是:(24﹣8)÷(2﹣1)=16千米/小时,点C的横坐标为:1﹣8÷16=0.5,∴点C的坐标为(0.5,0),故答案为:16千米/小时,(0.5,0);(2)设线段AB对应的函数表达式为y=kx+b(k≠0),∵A(0.5,8),B(2.5,24),∴,解得:,∴线段AB对应的函数表达式为y=8x+4(0.5≤x≤2.5);(3)当x=2时,y=8×2+4=20,∴此时小泽距离乙地的距离为:24﹣20=4(千米),答:当小帅到达乙地时,小泽距乙地还有4千米.6.解:(1)由图可得农民自带的零钱为50元,答:农民自带的零钱为50元;(2)(330﹣50)÷80=280÷80=3.5元,答:降价前他每千克西瓜出售的价格是3.5元;(3)(450﹣330)÷(3.5﹣0.5)=120÷3=40(千克),80+40=120千克,答:他一共批发了120千克的西瓜;(4)450﹣120×1.8﹣50=184元,答:这个水果贩子一共赚了184元钱.7.解:(1)由函数图象可知,张老师出发8分钟行走了480米的路程,∴张老师最初出发的速度为:480÷8=60(m/min),由函数图象知,张老师出发a分钟后,与邻居老朱相距800米,此时为张老师回到起点的时候,∴a=8×2=16(min),老朱的速度为:800÷8=100(m/min),故答案为:60;16;100;(2)根据题意和图象可知,b分钟时张老师找到了手机,∴b=a+4=16+4=20(min),∵c为张老师找到手机时,两相距的路程,∴c=100×(20﹣8)=1200(m),由函数图象知,端点为(b,c)即(20,1200)和(22.5,800)的线段是张老师找到手机后两人相距的距离与张老师出发的时间的一段函数图象,∴张老师找到手机后的速度为:=260(m/min),故答案为:20;1200;260;(3)根据题意知,张老师找到手机后一路小跑去追上老朱时,所跑步的路程全是小区到南山的距离.=1950(m).答:小区大门与南山之间的距离为1950m.8.解:(1)小冲骑车上坡的速度为:(6.5﹣4.5)÷0.2=10(km/h),平路上的速度为:10+5=15(km/h);下坡的速度为:15+5=20(km/h),平路上所用的时间为:2(4.5÷15)=0.6h,下坡所用的时间为:(6.5﹣4.5)÷20=0.1h所以小冲在乙地休息了:1﹣0.1﹣0.6﹣0.2=0.1(h);(2)由题意可知:上坡的速度为10km/h,下坡的速度为20km/h,所以线段AB所对应的函数关系式为:y=6.5﹣10x,即y AB=﹣10x+6.5(0≤x≤0.2).线段EF所对应的函数关系式为y EF=4.5+20(x﹣0.9).即y EF=20x﹣13.5(0.9≤x≤1);(3)由题意可知:小冲第一次经过丙地在AB段,第二次经过丙地在EF段,设小冲出发a小时第一次经过丙地,则小冲出发后(a+0.85)小时第二次经过丙地,6.5﹣10a=20(a+0.85)﹣13.5,解得:a=.×10=1(千米).答:丙地与甲地之间的距离为1千米.9.解:(1)门票定价为80元/人,那么10人应花费800元,而从图可知实际只花费480元,是打6折得到的价格,所以a=6;从图可知10人之外的另10人花费640元,而原价是800元,可以知道是打8折得到的价格,所以b=8,故答案为:6,8;(2)当x>10时,设y=kx+b.2∵图象过点(10,800),(20,1440),∴,解得,=64x+160 (x>10),∴y2(3)设甲团有m人,乙团有n人.由图象,得y=48x,1当m>10时,依题意,得,解得,答:甲团有35人,乙团有15人.10.解:(1)观察图象,发现当x=12时,y=120为最大值,∴日销售量的最大值为120千克.(2)设李刚家多宝鱼的日销售量y与上市时间x的函数解析式为y=kx+b,当0≤x≤12时,有,解得:,∴此时日销售量y与上市时间x的函数解析式为y=10x;当12<x≤20时,有,解得:,∴此时日销售量y与上市时间x的函数解析式为y=﹣15x+300.综上可知:李刚家多宝鱼的日销售量y与上市时间x的函数解析式为y=.(3)设多宝鱼价格z与上市时间x的函数解析式为z=mx+n,当5≤x≤15时,有,解得:,∴此时多宝鱼价格z与上市时间x的函数解析式为y=﹣2x+42.当x=10时,y=10×10=100,z=﹣2×10+42=22,当天的销售金额为:100×22=2200(元);当x=12时,y=10×12=120,z=﹣2×12+42=18,当天的销售金额为:120×18=2160(元).∵2200>2160,∴第10天的销售金额多.11.解:(1)3×40=120,乙车所用时间:=6,2+6﹣3=5,答:A、B两市的距离是120千米,甲到B市后5小时乙到达B市;故答案为:120,5;(2)由题意得:A(10,120),B(13,0),设甲车返回时的路程S(千米)与时间t(小时)之间的函数关系式为:S=kt+b,把A(10,120),B(13,0)代入得:,解得:,∴甲车返回时的路程S(千米)与时间t(小时)之间的函数关系式为:S=﹣40t+520(10≤t≤13);(3)由题意得:C(8,10),120﹣(10﹣8)×20=80,∴D(10,80),设直线CD的解析式为:S=kt+b,把C(8,120)、D(10,80)代入得:,解得:,∴直线CD的解析式为:S=﹣20t+280,则:,﹣40t+520=﹣20t+280,t=12,12﹣10=2,答:甲车从B市往回返后再经过2小时两车相遇.12.解:(1)由图象得:甲骑车速度:10÷0.5=20(km/h);由函数图象得出,在苏果超市休息的时间是1﹣0.5=0.5h;(2)乙驾车速度:20×2=40(km/h)设直线OA的解析式为y=kx(k≠0),则10=0.5k,解得:k=20,故直线OA的解析式为:y=20x.∵甲走OA段与走BC段速度不变,∴OA∥BC.设直线BC解析式为y=20x+b,1=﹣10把点B(1,10)代入得b1∴y=20x﹣10,,把点D(,0),设直线DE解析式为y=40x+b2=﹣,代入得:b2∴y=40x﹣.∴,解得:x=.∴F点的横坐标为,﹣=,则乙出发小时追上甲.13.解:(1)摩托车从出发到最后停止共经过:100分钟;离家最远的距离是:40千米.(2)摩托车在20~50分钟内速度最快;最快速度是:30÷=60(千米/小时)14.解:由图象及题意,得故障前的速度为:80÷1=80海里/时,故障后的速度为:(180﹣80)÷1=100海里/时.设航行额全程有a海里,由题意,得=2+,解得:a=480,则原计划行驶的时间为:480÷80=6小时,解法二:设原计划行驶的时间为t小时,80t=80+100(t﹣2)解得:t=6,故计划准点到达的时刻为:7:00.15.解:(1)∵4.5﹣3.5=1(小时),∴货车在乙地卸货停留了1小时;(2)∵7.5﹣4.5=3<3.5,∴货车返回速度快,∵=70(千米/时),∴返回速度是70千米/时.16.解:(1)当0≤x≤6时,设甲车行驶过程中y与x之间的函数关系式为y=mx,把(6,600)代入y=mx,6m=600,解得m=100,∴y=100x;当6<x≤14时,设甲车行驶过程中y与x之间的函数关系式为y=kx+b,把(6,600)、(14,0)代入y=kx+b,得解得,∴y=﹣75x+1 050;即甲车行驶过程中y与x之间的函数关系式为:y=;(2)当x=7时,y=﹣75x+1 050解得,y=﹣75×7+1 050=525,525÷7=75(千米/时),即乙车的速度为75千米/时.17.解:(1)a=200÷2×8=800.(2)设小明取回书后y与x的函数关系式是y=kx+b.由题意,得解得(4分)∴小明取回书后y与x的函数关系式是y=200x﹣800.(3)由题意100x﹣(200x﹣800)=100,解得x=7∴7min后小明与弟弟相距100m.18.解:(1)该市人均月生活用水不超过6吨时,设y与x的函数解析式是y=kx,则9=6k,得k=1.5,即该市人均月生活用水不超过6吨时,y与x的函数解析式是y=1.5x;(2)该市人均月生活用水超过6吨时,设y与x的函数关系式是y=mx+n,则,解得,即该市人均月生活用水超过6吨时,y与x的函数关系式是y=3x﹣9;(3)由题意可得,人均月生活用水费为:75÷5=15,将y=15代入y=3x﹣9,得15=3x﹣9,解得,x=8,即该家庭这个月人均用了8吨生活用水.19.解:(1)由图可知,A、B两城相距300千米,乙车比甲车晚出发1小时,却早到1小时,故答案为:300,1,1;(2)设甲对应的函数解析式为:y=kx,300=5k解得,k=60,即甲对应的函数解析式为:y=60x,设乙对应的函数解析式为y=mx+n,解得,,即乙对应的函数解析式为y=100x﹣100,∴解得2.5﹣1=1.5,即乙车出发后1.5小时追上甲车;(3)由题意可得,当乙出发前甲、乙两车相距50千米,则50=60x,得x =,当乙出发后到乙到达终点的过程中,则60x﹣(100x﹣100)=±50,解得,x=1.25或x=3.75,当乙到达终点后甲、乙两车相距50千米,则300﹣50=60x,得x =,即小时、1.25小时、3.75小时、小时时,甲、乙两车相距50千米.20.解:(1)点A表达的含义正确的是甲车出发时,乙车距离B地的距离或乙车出发1小时后,距离B地的路程.故答案为③④.(2)乙车的速度是60千米/小时,a ==7小时,甲的速度==120千米/小时,t ==3小时.故答案为60,7,120,3.(3)相遇.设在甲车出发x小时后相遇.由题意(120+60)x=480﹣60解得x =,答:在甲车出发小时后相遇.21。
一次函数的图像与应用

一次函数的图像与应用一、引言一次函数是数学中常见且重要的一类函数类型。
它的图像呈现出一条直线的特点,具有简洁的数学表达形式和广泛的应用。
本文将分析一次函数的图像特征,并探讨其在实际问题中的应用。
二、一次函数的定义与表达形式一次函数又称为线性函数,其定义域和值域通常为实数集。
一次函数的一般表达形式为:f(x) = ax + b其中,a和b为常数,且a≠0。
函数图像为一条直线,斜率为a,截距为b。
三、一次函数的图像特征1. 斜率的意义一次函数的斜率代表了图像上每单位水平位移对应的垂直位移,即函数的变化率。
当斜率为正值时,图像呈现上升趋势;当斜率为负值时,图像呈现下降趋势;当斜率为零时,图像为水平线。
2. 截距的意义一次函数的截距代表了函数图像与y轴的交点,即当x=0时的函数值。
它反映了一次函数图像在垂直方向上的位置。
3. 变量对函数图像的影响一次函数的图像特征由斜率a和截距b决定。
增大a的绝对值会使图像更陡峭或更平缓,而改变b的值则会上下平移整个图像。
四、一次函数的应用1. 直线运动模型一次函数在直线运动模型中有着广泛的应用。
假设一个物体以固定速度运动,则其位移与时间的关系可以用一次函数表示。
斜率代表了物体的运动速度,截距则代表了物体在起点的位置。
2. 成本与收益分析在商业领域中,一次函数可以用来分析成本与收益之间的关系。
设某产品的生产成本与销售量之间呈现线性变化关系,则一次函数可以描述成本与销售量之间的关系。
商家可以通过分析这个函数来确定最大利润的销售量。
3. 折旧与资产价值在会计领域中,一次函数被用于计算资产的折旧和价值变化。
资产价值随着时间的推移而减少,这种变化可以用一次函数来描述。
斜率表示每年的折旧额,截距代表了初始价值。
4. 温度变化模型一次函数在气象学中也有重要的应用。
温度随着时间的变化通常呈现线性关系。
通过查找一次函数的斜率和截距,我们可以预测未来一段时间内的温度变化趋势。
五、总结一次函数作为一种常见的数学模型,具有简洁的形式和广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[单选,A2型题,A1/A2型题]关于造影剂的使用,哪项是错误的()A.胆影葡胺--胆道造影B.医用硫酸钡--消化道造影C.碘化油--心血管造影D.空气--脑室造影E.泛影葡胺--尿路造影 [单选]以下属于"编辑出版责任机制"中的"中期保障机制"的是()。A.坚持图书成批装订前的样书检查制度B.加强选题策划工作C.坚持图书书名页使用标准D.坚持重大选题备案制度 [多选]一般情况下,和易性包括以下含义()。A.流动性B.黏聚性C.保水性D.硬化性E.速凝性 [单选]可以在竖井、水中、有落差的地方敷设,且能承受外力的电力电缆型号为()。A.YJLV12B.YJLV22C.YJLV23D.YJLV32 [单选]不属于两栖纲无尾目蛙科的动物是()。A.黑魔蛙B.大树蛙C.金线蛙D.中国林蛙 [单选,A1型题]牛的性成熟期年龄是()A.8~14月龄B.15~23月龄C.18月龄D.15月龄E.10~12月龄 [单选]往浅绿色的Fe(NO3)2溶液中逐滴加入稀盐酸后,溶液的颜色应该是()。A.颜色变浅B.逐渐加深C.没有改变D.变棕黄色 [单选]发展心理学是研究()的科学。A.认知发展规律B.心理的种族发展C.心理的种系发展D.心理发展规律 [单选]甲烷化炉床温在低于()℃时,如有一氧化碳存在,将会生成剧毒物质羰基镍。A.200B.100C.180D.250 [单选]电潜泵变频器的输出频率范围是()HZ。A、30—50B、30—60C、30—80D、30—90 [单选,A2型题,A1/A2型题]胞体大,外形不规则,胞浆丰富,呈灰蓝色,核呈笔架形或S形,核染质纤细网状,急性白血病细胞形态学特征符合下列哪一项().A.急性粒细胞白血病(M1)B.急性早幼粒细胞白血病(M3)C.急性单核细胞白血病(M5)D.急性淋巴细胞白血病(L1)E.慢性淋巴细胞白 [判断题]储蓄存款的所有权发生争议,涉及办理过户的,储蓄机构依据上级行的指示办理过户手续。()A.正确B.错误 [单选,A2型题,A1/A2型题]终止心绞痛发作最有效的药物是()A.硝苯地平B.普萘洛尔C.阿司匹林D.硝酸甘油E.阿托品 [单选,A1型题]决定化学物质毒性大小最主要的因素是()。A.接触途径B.剂量C.接触时间D.接触速率和频率E.接触期限 [单选]受皮区的血液供应影响皮肤移植成活,以下哪项是错误的()A.颜面部血供好,植皮较易成活B.胫前部血供好,植皮较易成活C.陈旧性肉芽创面血供差,游离植皮成活率低D.老年人或糖尿病患者受皮区血供较一般差,皮肤移植成活率低E.放射性损伤创面除表面损伤外有深部组织损害, [单选]下列哪一项是腹水影响肝脏声像图的情况:()A.没有影响B.肝脏回声显示增强C.腹水使声波衰减导致肝回声减弱D.肝内管状结构不清 [单选]肌体疲劳主要是由于()活动加快,同时肌肉活动的耗氧量增加的缘故。A、大脑B、心脏C、神经系统 [单选]下列()船舶必须配备《程序和布置手册》。A、每艘散装运输有毒液体物质的船舶;B、每艘散装运输IBC规则第17章和第18章所列货品的船舶;C、每艘散装运输IBC规则和BCH规则第17章和第18章所列货品的船舶;D、每艘散装运输根据有毒液体物质分类指南确定为A类、B类、C类、D类有 [单选]RR表示()A.比值比B.相对危险度C.特异危险度D.人群特异危险度E.特异危险度百分比 [单选]物业服务成本或者物业服务支出构成一般由物业管理区域秩序维护费用、物业服务企业固定资产折旧和()组成。A.物业服务企业餐饮费用B.物业服务企业后勤管理费用C.物业服务企业交通费用D.物业共用部位、共用设施设备及公众责任保险费用 [单选]地形图的比例尺是1∶500,则地形图中的1mm表示地上实际的距离为()。A.0.05mB.0.5mC.5mD.50m [单选]关于预制梁模板设计要求,下述说法错误的是()A、能保证混凝土结构和构件各部分设计形状、尺寸和相互间位臵正确B、接缝不漏浆,制作简单,安装方便,便于拆卸和多次使用C、只需具有足够的强度即可,能承受新浇筑混凝土的重力、侧压力及施工中可能产生的各项荷载 [单选]A企业有关账户的期末余额如下:"现金"20000元,"银行存款"50000元,"应收票据"10000元,"其他货币资金"30000元。在资产负债表中,"货币资金"项目的金额为()。A.70000B.80000C.100000D.110000 [单选,B1型题]胎粪吸入性肺炎多见于()A.剖宫产儿B.早产儿C.过期产儿D.巨大儿E.小于胎龄儿 [单选]是否做到(),是人员招聘成败的关键。A.公开招聘B.择优录用C.公平公正D.效率优先 [单选]提高()是实现职业道德维护公德的手段A、专业B、知识C、理论D、专业技能 [单选]应当在海上打桩活动开始之日的()天前向所涉及海区的主管机关递交发布海上航行警告、航行通告的书面申请。A.3B.7C.15D.30 [单选,A2型题,A1/A2型题]有关肝动脉插管化疗的患者护理叙述不正确的是()A.严格无菌操作B.若出现发热,应使用抗菌药物C.注药后用肝素液冲洗导管D.定期局部换药E.剧烈腹痛时应警惕其他部位动脉栓塞及胆囊坏死等并发症 [填空题]测量工作的基准线是()。 [单选,A1型题]骨盆骨折最易损伤的尿道部位是()A.阴茎悬垂部B.球部尿道C.膜部尿道D.前列腺部尿道E.膀胱颈部 [名词解释]实生根系 [填空题]氨合成催化剂的毒物主要有()、()、()。 [问答题]家住楼房怎样避震? [单选]青年患者,反复发作左小腿红肿流脓,X线显示左胫骨增生硬化,并有死腔和死骨形成,应考虑A.急性骨髓炎B.慢性骨髓炎C.骨结核D.骨梅毒E.骨肉瘤 [单选]货运票据封套封口前,相关人员必须同时对票据封套记载的事项和实际运单、货票核对,保证运输票据()。A、整洁B、质量C、整齐D、齐全 [单选,A1型题]尿道损伤后最易造成的并发症是()A.尿瘘B.尿道狭窄C.慢性尿道周围脓肿D.尿失禁E.阳痿或阴茎萎缩 [单选]我国目前采用超率累进税率的是()。A.土地增值税B.个人所得税C.企业所得税D.消费税 [单选]人体细胞可分为肌细胞、()、上皮细胞和神经细胞。A.中性粒细胞B.淋巴细胞C.红细胞D.结缔组织细胞 [单选]为预防Rh阴性妇女发生致敏,下列哪些情况不适合预防性应用抗D球蛋白()A.第1次分娩Rh阳性婴儿后,于72小时内应用B.Rh(-)女婴出生时即应用C.流产(自然或人工流产)后D.在羊膜腔穿刺后E.产前出血、宫外孕、妊娠期高血压疾病 [填空题]通风机和鼓风机是化工厂常用的气体输送机机械,大体可分为()和()两类。
