2009-2010学年二学期高等数学期末考试试卷(最终卷)
2009—2010学年度第二学期期末试卷

2009—2010学年度第二学期期末试卷高 一 数 学数学试题卷共4页,满分150分,考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上;2.所有题目必须在答题卡上作答,在试题卷上答题无效。
第Ⅰ卷(选择题 共60分)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.cos 3π⎛⎫-=⎪⎝⎭A.12-B.12C. D2.若向量(2,1),(4,1),//,a b x a b ==+则x 的值为( ) A .1 B .7 C .-10 D .-93.sin cos cos sin 126126ππππ+的值为( )A.12D.14.若四边形ABCD 是正方形,E 是CD 的中点,且AB a = ,AD b = ,则BE =A.12b a +B.12a b +C.12b a -D.12a b -5.若0a b <<,则 A.11ab< B.01ab << C. 2ab b > D.b a a b> 6.若向量()1,3a m =+- ,()1,1b m =-,a b = ,则实数m 为A.21-B.2 C.2- D.不存在7.1sin cos 8αα=,且24παπ<<,则cos sin αα-的值为A.43B.34-C.23D.8.函数()sin y A x ωϕ=+ (其中0A >)的部分图象 如图所示,则此函数解析式为A.2sin 24x y π⎛⎫=+ ⎪⎝⎭ B.2sin 28y x π⎛⎫=+ ⎪⎝⎭C.2sin 4y x π⎛⎫=+ ⎪⎝⎭D.2sin 24y x π⎛⎫=+ ⎪⎝⎭9.把函数cos 2y x =的图象沿向量平移后得到函数sin(2)36y x π=-+的图象,则向量a是A.,33π⎛⎫ ⎪⎝⎭ B.,36π⎛⎫- ⎪⎝⎭C.,312π⎛⎫⎪⎝⎭D.,312π⎛⎫-- ⎪⎝⎭10.若1()2sin 23f x x π⎛⎫=- ⎪⎝⎭其中[]0,2x π∈,则()f x 的值域为A.[]2,2-B.2⎡⎤⎣⎦C.⎡⎣D.⎡-⎣11.已知tan α,tan β是方程240x ++=两根,且,,22ππαβ⎛⎫∈- ⎪⎝⎭,则αβ+等于 A.π-32B.π-32或3π C.3π-或π32 D.3π12.在ABC ∆所在的平面上有一点P ,满足PA PB PC BC ++=,则PBC ∆与ABC ∆的面积之比是( )A. 13B. 12C. 23D. 2第Ⅱ卷(非选择题 共100分)二.填空题(本大题共4小题,每题5分,满分20分,把答案填写在答题卡相应位置上)13.若实数0x >,则4x x+的最小值是___ ___.14.ABC ∆中,已知4a =,6b =,3sin 4B =,则A ∠=___ ___. 15.()1,C y 分AB 的比为35,()2,5A -、(),3B x -,则x y += .16.下面五个命题:(1)若α、β都是第一象限角,且αβ>,则sin sin αβ>;(2)2sin sin y x x=+在()0,x π∈的最小值是 (3)在ABC ∆中,若0AB BC ⋅<,则ABC ∆为钝角三角形;(4)若0a >,0b >,0m >,且1a b<,则a a mb b m +<+;(5)函数()sin cos sin cos f x x x x x =++-的值域是⎡⎤⎣⎦.其中,正确命题的序号是 (写出所有正确命题序号). 三.解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)已知(1,2)a = ,(1,0)b =-.(1)向量a b λ+ 与a b -共线时,求λ的值;(2)向量a b λ+ 与a b -垂直时,求λ的值.18.(本小题满分12分)已知cos α=,sin β=,且,0,2παβ⎛⎫∈ ⎪⎝⎭.(1)求sin α和cos β的值;(2)求αβ+.19.(本小题满分12分)已知正数x 、y 满足3xy x y =++. (1)求xy 的范围;(2)求x y +的范围.20. (本小题满分12分)一艘渔船在我海域遇险,且最多只能坚持45分钟,我海军舰艇在A 处获悉后,立即测出该渔船在方位角为45 距离为10海里的B 处,并测得渔船以9海里/时的速度正沿方位角为105 的方向漂移,我军舰艇立即以21海里/时的速度前往营救.求出我军舰艇赶上遇险渔船所需的最短时间,问能否营救成功?21.(本小题满分12分)已知(5sin ,cos )a x x =,(cos ,)b x x =- 其中x R ∈,()f x a b =⋅ .(1)求()f x 的最小正周期;(2)求()f x 图象的对称中心;(3)求()f x 在3,22x ππ⎡⎤∈⎢⎥⎣⎦上的单调递减区间.22.(本小题满分12分)是否存在实数a ,使253sin cos 82y x a x a =++-在闭区间0,2π⎡⎤⎢⎥⎣⎦上的最大值是1?若存在,求出对应的a 值;若不存在,说明理由. A。
湖北省孝感高中2009-2010学年高二数学下学期期末考试 理 旧人教版

;
(3)设 数列 的前n项和为 ,若存在整数m,使对任意 且 ,都有 成立,求m的最大值.
孝感高中2009—2010学年度下学期高二期末统一考试
数学(理)参考答案
一、选择题:BDBDA BCBDA
二、填空题:11.112. 13. 14.1815.
三、解答题:
16.解:(1)由 得:定义域 (2分)
C.1,2,3,4,5D.5,10,15,20,25
2.点E是正四面体ABCD的棱AD的中点,则异面直线BE与AC所成角的余弦值为()
A. B. C. D.
3.设随机变量 服从正态分布 ,则 可以被表示为()
A. B.
C. D.
4.一个到球心距离为1的平面截球所得截面的面积为 ,则球的体积为()
A. B. C. D.2分)
投2次骰子,棋子才到达顶点B有三种方式: .
故概率为 .(6分)
(2) 且 (9分)
(12分)
20.(1) (2分)
①若 则由 得 , 时, 时, ,故 无极值点.(4分)
② 时,由 得: , 时, ;
时, ; 时, .故 为极大值点,
且 , 为极小值点,且 = .(7分)
(2)因
.(8分)
令 ,因
故 在 上单增,故 ,即
取 ,故 .即 (11分)
而 .故 .
故 ,综合上述,可知 .(13分)
21.(1) 时, 时,
.故 (5分)
(2)由(1)知: ,原不等式即证
① 时, ,故 成立;
②假设 时, ,
则 时,
=
故 也成立;综合①、②知原不等式恒成立.(10分)
(3)由(1)知 ,令 ,
微积分试卷及答案【范本模板】

2009 — 2010 学年第 2 学期 课程名称 微积分B 试卷类型 期末A 考试形式 闭卷 考试时间 100 分钟 命 题 人 2010 年 6 月10日 使用班级教研室主任 年 月 日 教学院长 年 月 日姓 名 班 级 学 号一、填充题(共5小题,每题3分,共计15分)1。
2ln()d x x x =⎰ . 2。
cos d d x x =⎰ .3。
312d x x --=⎰ 。
4。
函数22xy z e+=的全微分d z = .5.微分方程ln d ln d 0y x x x y y +=的通解为 。
二、选择题(共5小题,每题3分,共计15分)1.设()1x f e x '=+,则()f x = ( ). (A) 1ln x C ++ (B ) ln x x C +(C ) 22x x C++ (D ) ln x x x C -+2。
设2d 11xk x +∞=+⎰,则k = ( ).(A ) 2π(B ) 22π(C) 2 (D ) 24π3.设()z f ax by =+,其中f 可导,则( ).(A) z z ab x y ∂∂=∂∂ (B)z z x y ∂∂=∂∂ (C ) z z ba xy ∂∂=∂∂ (D) z zx y ∂∂=-∂∂ 4。
设点00(,)x y 使00(,)0x f x y '=且00(,)0y f x y '=成立,则( ) (A ) 00(,)x y 是(,)f x y 的极值点 (B) 00(,)x y 是(,)f x y 的最小值点 (C ) 00(,)x y 是(,)f x y 的最大值点 (D ) 00(,)x y 可能是(,)f x y 的极值点 5.下列各级数绝对收敛的是( ).(A ) 211(1)nn n ∞=-∑(B) 1(1)n n ∞=-∑ (C) 13(1)2n nnn ∞=-∑ (D) 11(1)n n n ∞=-∑三、计算(共2小题,每题5分,共计10分)1。
2009-2010学年高二数学参考答案

2009-2010学年高二年级下学期期末考试数学参考答案及评分意见一、选择题(12×5 共计60分)理科:DBDAB DACCB CA 文科:DBDAD DACCB CC二、填空题 (理)13、210 ; 14、321 ; 15、y x 162-= ; 16、①②③ (文)13、210 ; 14、5 ; 15、y x 162-= ; 16、)123(∝+, 三、解答题 17、解:(Ⅰ)原不等式等价于⎩⎨⎧>+-<--06304322x x x x ②① ………… (3分) 不等式①即为0)1)(4(<+-x x ⇒ 41<<-x …(4分)不等式②的解为R …(5分)∴原不等式的解集为}{41|<<-x x …………(6分) 证明(Ⅱ)∵abb a b a b a b a a b 222))((-+=--+ …………(4分) 又00>>b a , ∴ b a b a a b +≥+22 …………(6分) 18、解:(Ⅰ)由题意知A )0(,k b -,B )0(b , ……(2分) 则AB =)(b kb , ……(4分) 又 j i AB 22+=∴2=kb ,2=b ∴ 1=k ,2=b ……(6分) (Ⅱ)⇒>)()(x g x f 622-->+x x x ⇒ 0822<--x x ∴ 42<<-x …(7分)25)(1)(2+--=+x x x x f x g =21)2(5)2(2+++-+x x x =521)2(-+++x x ……(10分) ∵ 02>+x ∴3)(1)(-≥+x f x g 当且仅当1-=x 时取等号 …………(11分) ∴ 3)(1)(-+的最小值是x f x g …………(12分) 19、解:(Ⅰ)建立如图所示的空间直角坐标系,则)3,4,0(),1,4,2(),0,4,0(),0,0,2(),0,4,2(),0,0,0(1C E C A B D设F AEC z F 1),,0,0(由为平行四边形知1EC = … (3即)2,0,2(),0,2(-=-z ∴2=z ,∴),2,4,2(--= …(4分)62= ……(6分) (Ⅱ)设)1,,(y x n =为平面F AEC 1的法向量, 由)1,41,1(02201400-=⎩⎨⎧=+-=+⎪⎩⎪⎨⎧=⋅=⋅x y 解得得 ……(8分)又33334cos ,),3,0,0(11===CC CC αα则与设 ……(10分) 所以到平面C F AEC 1的距离为11334==αd ……(12分) (理)20、解:(Ⅰ)解法一:设“甲投球一次命中”为事件A ,“乙投球一次命中”为事件B , 由题意得221(1())(1)16P B p -=-=, 解得34p =或54p =(舍去),所以乙投球的命中率为34. ……(4分) 解法二:设“甲投球一次命中”为事件A ,“乙投球一次命中”为事件B ,由题意得 1()()16P B P B =, 于是1()4P B =或1()4P B =-(舍去),故31()4p P B =-=.所以乙投球的命中率为34. (Ⅱ)解法一:由题设和(Ⅰ)知,1()2P A =,1()2P A =. 故甲投球2次至少命中1次的概率为31()4P A A -= . ……(8分) 解法二:由题设和(Ⅰ)知,1()2P A =,1()2P A =. 故甲投球2次至少命中1次的概率为123C ()()()()4P A P A P A P A +=. (Ⅲ)解:由题设和(Ⅰ)知,1()2P A =,1()2P A =,3()4P B =,1()4P B =. 甲、乙两人各投球2次,共命中2次有三种情况:甲、乙两人各中一次;甲中2次,乙2次均不中;甲2次均不中,乙中2次.概率分别为11223C ()()C ()()16P A P A P B P B =,1()()64P A A P B B = ,9()()64P A A P B B = . 所以甲、乙两人各投球2次,共命中2次的概率为3191116646432++= ……(12分) (文)20、1分,共6分)(Ⅱ)设“抽到6或10号”为事件A ,先后两次抛掷一枚均匀的骰子出现的点数为),(y x ……(7分) 则所有的基本事件有(1,1),(1,2),(1,3),……(6,6)共36个 …………(9分) 事件A 包含的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1),(4,6),(5,5),(6,4)共8个 …………(11分)∴P(A)=368=92 …………(12分) 21、(Ⅰ)证明:在PAD △中,由题设2PA =,2AD =,PD =可得222PA AD PD +=,于是AD PA ⊥.在矩形ABCD 中,AD AB ⊥,又PA AB A = ,所以AD ⊥平面PAB . ……(4分) (Ⅱ)解:由题设,BC AD ∥,所以PCB ∠(或其补角)是异面直线PC 与AD 所成的角.(5分)在PAB △中,由余弦定理得PB = ……(6分)由(Ⅰ)知AD ⊥平面PAB ,PB ⊂平面PAB ,所以AD PB ⊥,因而BC PB ⊥,于是PBC △是直角三角形,故tan 2PB PCB BC ==PC 与AD所成的角的大小为arctan 2.(8分) (Ⅲ)解:过点P 作PH AB ⊥于H ,过点H 作HE BD ⊥于E ,连结PE .因为AD ⊥平面PAB ,PH ⊂平面PAB ,所以AD PH ⊥.又AD AB A = ,因而PH ⊥平面ABCD ,故HE 为PE 在平面ABCD 内的射影.由三垂线定理可知,BD PE ⊥.从而PEH ∠是二面角P BD A --的平面角.……(10分)由题设可得,sin 60PH PA == cos601AH PA ==, 2BH AB AH =-=,BD =AD HE BH BD == .于是在Rt PHE △中,tan 4PH PEH HE == 所以二面角P BD A --的大小为 ……(12分) (理)22、解:(Ⅰ) ∵ F )0(,c ,)0(>c 且 222c b a =- ∴ 当直线的斜率为1时,方程为c x y -= 由题意有222=c得 1=c ……(2分)∴ 122=-b a ,又 31222==a c e ∴ 3=a 2=b ∴ 椭圆C 的方程为12322=+y x ……(4分) (Ⅱ) 当斜率k 存在时,直线l 的方程为)1(-=x k y ……(5分) A B C PH E设A ),(11y x ,B ),(22y x 若存在点P C y x ∈),(00,则由+=成立可得210x x x +=,210y y y += …(6分)⎪⎩⎪⎨⎧-==+)1(12322x k y y x ⇒ 0636)32(2222=-+-+k x k x k ……(7分) 显然对任意0>∆∈有R x 恒成立. ……(8分) 从而有210x x x +==22326k k + ……(9分) 210y y y +==)2(21-+x x k =2324k k +- ……(10分) 将0x ,0y 代入椭圆方程得:044324=--k k ⇒ 2±=k ……(11分)∴ 当直线不垂直于x 轴时,满足条件的点P 存在,其坐标为)22,23(± ……(12分) 直线l 的方程为)1(2-±=x y ……(13分) 当直线l 的斜率不存在时,即l 垂直于x 轴,不满足条件. ……(14分) (文)22、解:(Ⅰ)由已知602=+⇒=⇒=⋅=GM GN GN PG NQNP∴ 点G 的轨迹方程是14922=+y x . ……(4分) (Ⅱ)由为平行四边形四边形AOBS OB OA OS ⇒+= ……(5分) 若满足条件的直线l 存在,则四边形为矩形AOBS ∴0=⋅ ……(6分) ①如果直线斜率不存在,则由09163522149222≠=⋅⇒⎪⎩⎪⎨⎧±==⇒⎪⎩⎪⎨⎧=+=y x y x x ;…(8分) ②如果直线斜率存在,设为k ,,、),(),(),2(:2211y x B y x A x k y l -=0)1(3636)49(149)2(22222=-+-+⇒⎪⎩⎪⎨⎧=+-=k x k x k y x x k y 由 ……(10分) 4920]4)(2[49)1(36,493622212122122212221+-=++-=⇒+-=+=+∴k k x x x x k y y k k x x k k x x (12分) 由0=⋅得2302121±=⇒=+k y y x x ……(13分) ∴满足条件的直线l 存在其06230623=-+=--y x y x 或方程为 ……(14分)。
10级高等数学(A)2期末测试题答案

3.
设 L : 点 (1, 0)到 点 (2010, 2012) 再到点 (3, 0)的折 线段 .求 ( x 2 + y 3 ) dx + 3 xy 2 dy . ∫
L
2 3 2
∂P ∂Q 解:这里P ( x , y ) = x + y , Q(x , y )=3 xy ,由 =3 y = ,故此积分与路径无关.............2 分 ∂y ∂x 从而可选择 (1 , 0 )到(3, 0 )的直线段,方程为: y = 0,1 ≤ x ≤ 3................4 分 3 26 从而 ∫ ( x 2 + y 3 ) dx + 3 xy 2 dy = ∫ x 2 dx = ...........6分 1 3 L
D
】
解:积分区域D关于x轴对称,从而
∫∫ ( y + 3)d σ = ∫∫ yd σ +∫∫ 3d σ...........................2分
D D D
1 = ∫∫ 3d σ =3 ⋅ ⋅1⋅ 2=3........................................6分 2 D
第 2 页共 3 页
解:(1) 联立方程可求得交线为: x 2 + y 2 = 1, z = 1, 从而D xy = {( x, y ) x 2 + y 2 ≤ 1}..........................2分
∫∫ zdxdy = − ∫∫ ( x
∑2 Dxy
2
+ y 2 )dxdy........................4分
).
32π
1. 设 zLeabharlann = 4 x3 y + y 2 e3 x + ln( x + tan x) + sec 2, 求
2009-2010(2)期末考试试卷(A)(高等数学)

9. 计算 zdS ,其中∑是上半球面 z 4 x 2 y 2 介于 z 1, z 2 之间的部分
10. 计算 xzdydz yzdzdx 2zdxdy ,其中∑是 x y z 1与三个坐标面围成区域的整个边界面 的外侧。
11. 已知连续函数 fΒιβλιοθήκη (x) 满足 f (x) e x
ds
=____________.
4.设 D: x2+y2≤1, 则 (4 1 x 2 y 2 )dxdy __________.
D
5. 若 y 1, y x, y x 2 为某个二阶线性非齐次微分方程的三个解,则该方程的通解为 。
二、解答下列各题(1-6 小题每个 6 分,7-13 每题 7 分,总计 85 分)
武汉工业学院 2009 –2010 学年第 2 学期 期末考试试卷(A 卷)
课程名称 高等数学 2
学号:
注:1、考生必须在答题纸的指定位置答题,主观题要有必要的步骤。
2、考生必须在答题纸的密封线内填写姓名、班级、学号。
姓名:
班级:
3、考试结束后只交答题纸。
------------------------------------------------------------------------------------------------------------------------------------一、填空题(每小题 2 分, 共 10 分)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
2009-2010学年第二学期高等数学(2)期末试卷及其答案

2009-2010学年第二学期高等数学(2)期末试卷及其答案2009 至 2010 学年度第 2 期 高等数学(下)课程考试试题册A试题使用对象 : 2009 级 理科各 专业(本科)命题人: 考试用时 120 分钟 答题方式采用:闭卷说明:1.答题请使用黑色或蓝色的钢笔、圆珠笔在答题纸上书写工整.2.考生应在答题纸上答题,在此卷上答题作废.一.填空题(本题共15 分,共5 小题,每题 3 分) 1.已知(2,1,),(1,2,4)a mb ==r r,则当m = 时,向量a b⊥r r .2.(,)(2,0)sin()limx y xy y →= .3.设区域D 为22y x +≤x 2,则二重积分Dd σ=⎰⎰ .4.函数(,),(,)P x y Q x y 在包含L 的单连通区域G 内具有一阶连续偏导数,如果曲线积分(,)(,)LP x y dx Q x y dy+⎰与路径无关,则(,),(,)P x y Q x y 应满足条件 .5. 当p 时,级数211pn n +∞=∑收敛.二.选择题(本题共15分,共5小题,每题3 分)1.直线221:314x y z L -+-==-与平面:6287x y z π-+=的位置关系是 .A .直线L 与平面π平行;B .直线L 与平面π垂直;C .直线L 在平面π上;D .直线L 与平面π只有一个交点,但不垂直.2. 函数(,)f x y 在点(,)x y 可微分是(,)f x y 在该点连续的( ).A .充分条件; B. 必要条件; C. 充分必要条件; D. 既非充分也不必要条件 3.改变积分次序,则100(,)y dy f x y dx⎰⎰.A .1(,)xdx f x y dy ⎰⎰; B .11(,)dx f x y dy ⎰⎰;C .11(,)x dx f x y dy ⎰⎰;D .11(,)xdx f x y dy ⎰⎰4.下列级数中收敛的是 . A .∑∞=+1884n n nn B .∑∞=-1884n n nn C .∑∞=+1824n n nnD .1248n nn n ∞=⨯∑.5.级数1...-++A. 发散B. 绝对收敛C. 条件收敛D. 既绝对收敛又条件收敛 三. 求解下列各题(本题共70分,共9小题,1~2每题7 分,3~9每题8 分). 1.设sin uz e v=,而u xy =,v x y =- 求xz .2.设22(,tan())u f x y xy =-,其中f 具有一阶连续偏导数,求yz . 3.求旋转抛物面221z x y =+-在点(2,1,4)处的切平面方程及法线方程. 4.计算 22Dx d y σ⎰⎰,其中D 是由直线y x =.2x =和曲线1xy =所围成的闭区域. 5.计算L⎰,其中L 是圆周222x y a +=(0a >).6.计算22()(sin )Lxy dx x y dy--+⎰,其中L 是上半圆周y =x 轴所围区域的边界,沿逆时针方向.7.将函数1()3f x x =+展开成(3)x -的幂级数. 8.计算曲面积分xydydz yzdzdx xzdxdy ∑++⎰⎰,其中∑为1x y z ++=,0,x =y =,0z =所围立体的外侧.9.求抛物面22z xy =+到平面10x y z +++=的最短距离.2009 至 2010 学年度第 2 期高等数学(下)课程试题A 参考答案试题使用对象: 2009 级 理科各专业(本科) 向瑞银一.填空题(本题共15 分,共5 小题,每题 3 分) 1. 1-; 2. 2; 3. π; 4.y P ∂∂=xQ ∂∂; 5.12p >二.选择题(本题共15分,共5小题,每题3 分) 1.B ; 2.A ; 3.D ; 4.C ; 5.C 三. 求解下列各题(本题共70分,共9小题,1~2每题7 分,3~9每题8 分).1.z z u z vx u x v x∂∂∂∂∂=+∂∂∂∂∂……4分sin cos u u ye v e v=+(sin()cos())xy e y x y x y =-+-……7分 2.2212()(tan())y y uf x y f xy y∂''''=⋅-+∂ ……4分2122sec ()()yyf f xy xy '''=-+2122sec ()yf xf xy ''=-+……7分 3. 令22(,,)1F x y z xy z=+--,则法向量(2,2,1)n x y =-r,(2,1,4)(4,2,1)n=-r ……3分在点(2,1,4)处的切平面方程为 4(2)2(1)(4)0x y z -+---=.即4260x y z +--=. (6)分法线方程为214421x y z ---==-. ……8分 4.22Dx d yσ⎰⎰22121xxx dx dy y=⎰⎰……4分221/11()x xx dxy=-⎰……6分231()x x dx =-⎰322111()42x x =-94=……8分5.令cos ,sin x a y a θθ==,则sin ,cos x a y a θθ''=-=,ds θ=ad θ= ……3分20a Le ad πθ=⎰⎰ ……6分=2aae π ……8分6.2P xy=-,1P y ∂=-∂ ,2(sin )Q x y =-+,1Q x∂=-∂ , ……4分()0DDQ PI dxdy dxdy x y∂∂=-=∂∂⎰⎰⎰⎰ ……6分=……8分 7.1136(3)x x =++-113616x =-+ ……4分 当316x -<,即 39x -<<时,13x +013()66nn x +∞=-=-∑ ……8分8. ⎰⎰∑++zxdxdy yzdzdx xydydz=()x y z dxdydz Ω++⎰⎰⎰……4分 =1110()xx ydx dy x y z dz---++⎰⎰⎰……6分81=……8分9.设抛物面一点(,,)x y z ,它到平面的距离为1d x y z =+++满足条件220x y z +-= ……3分 拉格朗日函数为222(1)()3x y z L x y z λ+++=++- ……5分2(1)203x x y z L x λ+++=+=,2(1)203yx y z Ly λ+++=+=2(1)3z x y z L λ+++=-=,220Lx y z λ=+-=解方程组得,12x y ==-,12z =. 由问题本身知最短距离存在,所以最短距离为0.5,0.5,0.5)d --=6=……8分。
北京五中2009-2010年第二学期高二数学期末考试试卷及答案

北京五中2009-2010年第二学期高二数学期末考试试卷一. 选择题(每题5分,共50分.请把答案填在第4页表中)1.设集合⎭⎬⎫⎩⎨⎧∈+==Z k k x x M ,412,⎭⎬⎫⎩⎨⎧∈+==Z k k x x N ,214,则( ). N M A =)( N M B ⊆)( N M C ⊇)( ∅=N M D )(2.已知b a >,R x ∈,则下列各式正确的是( ))(A x b x a lg lg >(0>x ) )(B 22bx ax > )(C 22b a > )(D x x b a 22⋅>⋅3.已知4≠+y x p :,1≠x q :或3≠y ,则p 是q 的( ))(A 充分而不必要条件 )(B 必要而不充分条件)(C 充要条件 )(D 既不充分也不必要条件4.若函数)(x f y =的值域为⎥⎦⎤⎢⎣⎡3,21,则函数)(1)()(x f x f x F +=的值域为( ) )(A ⎥⎦⎤⎢⎣⎡3,21 )(B ⎥⎦⎤⎢⎣⎡310,2 )(C ⎥⎦⎤⎢⎣⎡310,25 )(D ⎥⎦⎤⎢⎣⎡25,2 5.极坐标方程sin 2cos ρθθ=+表示的曲线为( )、)(A 直线 )(B 圆 )(C 椭圆 )(D 双曲线6.已知双曲线2=xy 上任意一点处的切线与坐标轴构成的三角形面积为定值,则这个定值为( ))(A 2 )(B 4 )(C 8 )(D 167.直线112()3332x t t y t ⎧=+⎪⎪⎨⎪=-+⎪⎩为参数和圆2216x y +=交于,A B 两点,则AB 的中点坐 标为( ))(A (3,3)- )(B (3,3)- )(C (3,3)- )(D (3,3)-8.设随机变量ξ服从正态分布2(1,)(0)N σσ>,若(01)0.4P ξ<<=,则(2)P ξ>等于( ))(A 0.8 )(B 0.5 )(C 0.2 )(D 0.19.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以1A ,2A 和3A 表示由甲罐取出的球是红球,白球和黑球的事件.再从乙罐中随机取出一球,以B 表示由乙罐取出的球是红球的事件.给出下列结论:①P (B )=25; ②P (B|1A )=511; ③事件B 与事件1A 相互独立;④1A ,2A ,3A 是两两互斥的事件;⑤P (B )的值不能确定,因为它与1A ,2A ,3A 中究竟哪一个发生有关;其中正确的有( ))(A ②④ )(B ①③ )(C ②④⑤ )(D ②③④⑤10.3位男生和3位女生共6位同学排成一排,若男生甲不站两端,且3位女生中有且仅有两位女生相邻,则不同的排法共有( )种)(A 360 )(B 288 )(C 216 )(D 144二.填空题(每题5分,共60分)11.“若022=+y x ,则y x ,都是0”的否命题为12.计算536lg 27lg 321240lg 9lg 211+--+的值为 13.不等式()()02sin 113>---x x 的解集为14.设0≠t ,点)0,(t P 是函数at x x f +=3)(与c bx x g +=2)(图象的一个公共点,两函数的图象在点P 处有相同的切线,则用t 表示c 为15.随机变量ξ的分布列如下: 其中a bc ,,成等差数列, ξ1- 0 1 P a b c若13E ξ=,则D ξ的值为 . 16.今有2个红球、3个黄球和4个白球,同色球不加区分,将这9个球排成一排共有 种不同的方法17.方程0233=+-ax x 有3个不等实根,则a 的取值范围为18.某次竞赛规则如下:在主办方预设的5个问题中,选手若能连续..回答出两个问题,即 停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于19.用长90cm ,宽48cm 的长方形铁皮做一个无盖的长方体容器,先在四角分别截去一个小正方形,然后把四边翻转90º角,再焊接而成,则截去的小正方形边长为 时,长方体体积最大20.6本不同的书分给4个人,每人至少一本的概率为21.若a 、b 、0>c ,且324)(-=+++bc c b a a ,则c b a ++2的最小值为班级 姓名 学号 成绩22.一个圆环直径为22m ,通过金属链条BC 、1CA 、 2CA 、3CA (1A 、2A 、3A 是圆上三等分点)悬挂在B 处,圆环呈水平状态,并距天花板2m (如图所示),为使金属链条总长最小,BC 的长应为三.解答题(共40分)23.解关于x 的不等式:12>-x ax24.某射手每次射击击中目标的概率是23,且各次射击的结果互不影响. (Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率(Ⅱ)假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记ξ为射手射击3次后的总得分数,求ξ的分布列25.设函数)1ln()(2++=x b x x f ,其中0≠b(1) 求)(x f 的单调增区间(2) 对任意的正整数n ,证明:2222ln e e e e e e n n -≤+答案一. 选择题题号1 2 3 4 5 6 7 8 9 10答案B D A B B B D D AB二.填空题11.若022≠+y x ,则y x ,不都是012.-1 13.)32,0( 14.323t c -= 15.95 16.1260 17. 1>a 18.0.128 19.10cm 20.512195 21.)13(2- 22.1.5m三. 解答题24.(1)24340 (2)818 (3) ξ0 1 2 3 6 P 271 92 274 278 278 25. 解:(1)当0<b 时,增区间为⎪⎪⎭⎫ ⎝⎛∞+-+-,2211b 当210<<b 时,增区间为⎪⎪⎭⎫ ⎝⎛∞+-+-,2211b 和⎪⎪⎭⎫ ⎝⎛----2211,1b 当21≥b 时,增区间为()+∞-,1(2)由(1)得1-=b 时,)(x f 在⎪⎪⎭⎫ ⎝⎛∞++-,231增 欲证2222ln ee e e e e n n -≤+,只需证1)21ln(221-≤+--n n e e 只需证12ln )1ln()1(21-≤-+--n n e e令)1ln()(2x x x g +-=()1≥x因为)(x f 在⎪⎪⎭⎫ ⎝⎛∞++-,231增,又1231<+-, 所以2ln 1)1()(-=≥g x g所以当1≥x 时,2ln 1)1ln(2-≥+-x x故12ln )1ln()1(21-≤-+--n n e e 成立。
高数期末考试试卷

2009-2010年度第二学期 高等数学(二)期末考试试卷B一、填空题(每小题3分,共5小题,15分)1. 定积分x x x d )(sin 114⎰-= 0 .2.微分方程0)0(,2=='-y e y yx 的特解为21212+=x y e e . 3.函数22y x z +=在点)2,1(P 的梯度为 6 . 4. 求极限xy xy y x 24lim-+→→=41.5. 级数=+∑∞=1)1(1n n n 1 .二、选择题(每小题3分,共5小题,15分)1.函数),(y x f 在点),(00y x 处连续,两个偏导数),(),,(0000y x f y x f y x 存在是),(y x f 在该点可微的( B ) A.充分但不必要条件 B.必要但不充分条件 C.充分必要条件D.既不充分也不必要条件2. 设2232y xy x z -+=,则=∂∂∂yx z2( B ) A. 6 B. 3 C. 2- D. 2 3.设L 为圆周222R y x =+,则积分⎰=+Lds y x )(22 ( D ).A. 52R π B. 72R π C. 92R π D. 32R π 4.设常数项级数20=∑∞=n nu,则级数=-∑∞=0)212(n n n u (D ).D. 2 A. 0 B. 1 C. 25. 设函数xy y x f =),(则)0,0(是该函数的( A ) A. 不是极值点 B. 极小值点C. 极大值点D. 驻点但不是极值点 三、解答题:(共6题,每题6分,共36分)1.设函数xy y x z 222++=,求)2,1(d z.解:x y yzy x x z 22,22+=∂∂+=∂∂……………………………2分 在点)2,1(处,有6,6)2,1()2,1(=∂∂=∂∂yz xz……………………4分则dy dx z 66d )2,1(+=. ………………………………………6分2.计算定积分⎰+411d xx .解:令dt dx t x t x 22=⇒=⇒=,当4,0==x x 时,2,0==t t ,…………………………….2分 则原积分为⎰⎰+-+=+2020111212dt t t dt t t22020)1ln(4112t dt tt +-=+-=⎰………………………….4分 3ln 4-=……………………………………………………….6分3. 计算σd )(I 22⎰⎰+=Dy x ,其中区域}1),{(22≤+=y x y x D . 解:用极坐标积分,θθsin ,cos r y r x ==,则积分区域D 化为:10,20:≤≤≤≤r D πθ………………………………………….2分则ππθπ214121410220=⋅=⋅=⎰⎰r rdr r d I ……………….6分4. 判断级数∑∞=⋅131n nn 的敛散性. 解:正项级数,用比值审敛法:因为131133)1(1lim lim 11<=⋅+=+∞→+∞→n n n nn n n n u u …………………5分所以,原级数收敛………………………………………………..6分5.计算曲线积分L dy y x dx y x L,)()(⎰+--为点)0,1(-到点)0,1(的直线段.解:]1,1[,0:-∈=x y L ,则原积分为…………………………2分21211021==⎰x xdx ……………………………………………6分 6. 求曲线t z t y t x L 2,sin ,cos :===,在点)2,0,1(π-处的切线方程和法平面方程.解:2,cos .sin ='='-='z t y t x ,………………………………1分 在点)2,0,1(π-处,π=t ,……………………………………….2分 则在该点的切线方程的方向向量为:)2,1,0(-…………………..4分 所以切线方程为:22101π-=-=+z y x …………………………5分 法平面方程为:042=+-πz y …………………………………6分 四、解答下列各题:1.求函数22)(4),(y x y x y x f ---=的极值.(10分) 解:y yzx x z 24,24--=∂∂-=∂∂……………………………2分 令024,024=--=∂∂=-=∂∂y yz x x z ………………………3分解得驻点:)2,2(-……………………………………………4分又0,2,222222=∂∂∂-=∂∂-=∂∂y x z yz x z ;…………………………6分在驻点)2,2(-处0,04,0,22<>=-⇒=-==A B AC B C A ,所)2,2(-是极大值点.极大值为8)2,2(=-f …………………………10分2.求级数 ++++nx x x n22的收敛区间与和函数.(8分) 解:收敛半径:111lim=+⋅=∞→nn n R n ,则收敛区间为)1,1(-…….3分 令=)(x s ++++nx x x n 22, 则xx xx x s n n n -==++++='∑∞=-111)(01………………..6分 则)1ln(11)(0x dx x x s x--=-=⎰………………………………..8分3..求解常微分方程0365=-'+''y y y 的通解.(6分) 解:特征方程为:03652=-+r r ,特征根为:9,421-==r r ……………………………………..4分 则原方程的通解为:x xe C e C y 9241-+=…………………….2分4. 计算dv z y x I )(222++=⎰⎰⎰Ω,其中Ω是由 1222=++z y x 所围成的闭区域.(6分)解:用球面坐标积分:10,0,20:≤≤≤≤≤≤Ωr πφπθ………3分 则⎰⎰⎰⋅=122020sin drr r d d I ππϕϕθ[]πφππ5451cos 21050=⎥⎦⎤⎢⎣⎡⋅-⋅=r ……………………………………6分 5.求曲线4,1,===x x x y 及x 轴绕x 轴旋转一周所得旋转体的体积.(4分)解:所求体积为:πππ2152141241===⎰x dx x V ……………………4分(注:本资料素材和资料部分来自网络,仅供参考。
09-10高等数学期末试题参考答案(A)
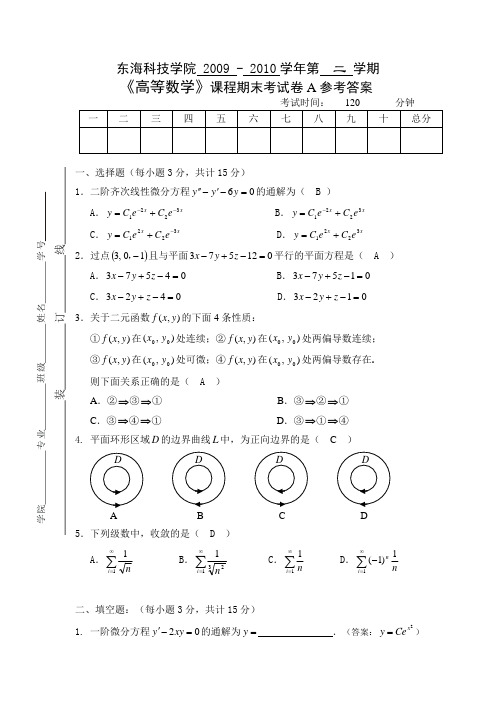
东海科技学院 2009 - 2010学年第 二 学期 《高等数学》课程期末考试卷A 参考答案一、选择题(每小题3分,共计15分)1.二阶齐次线性微分方程06=-'-''y y y 的通解为( B ) A .x x e C e C y 3221--+= B .x x e C e C y 3221+=- C .x x e C e C y 3221-+= D .x x e C e C y 3221+=2.过点()10,3-,且与平面012573=-+-z y x 平行的平面方程是( A ) A .04573=-+-z y x B .01573=-+-z y x C .0423=-+-z y x D .0123=-+-z y x 3.关于二元函数),(y x f 的下面4条性质:①),(y x f 在),(00y x 处连续;②),(y x f 在),(00y x 处两偏导数连续; ③),(y x f 在),(00y x 处可微;④),(y x f 在),(00y x 处两偏导数存在. 则下面关系正确的是( A )A .②⇒③⇒①B .③⇒②⇒①C .③⇒④⇒①D .③⇒①⇒④ 4. 平面环形区域D 的边界曲线L 中,为正向边界的是( C )A B C D5.下列级数中,收敛的是( D ) A .∑∞=11i nB .∑∞=1321i n C .∑∞=11i n D .∑∞=-11)1(i n n二、填空题:(每小题3分,共计15分)1. 一阶微分方程02=-'xy y 的通解为=y .(答案:2x Ce y =)学院专业班级姓名学2.=+→xy yx y x 2lim)2,1(),( .(答案:2)3. 222y x z +=表示空间曲面 .(答案:抛物面)4.⎰⎰=1010xydy dx .(答案:41)5. 若L 表示抛物线2x y =上点)0,0(与点)1,1(的一段弧,则第一类曲线积分⎰Lds y = .(答案:)155(121-)三、计算题:(每小题6分,共计48分) 1.设2221y x z +=,求全微分dz . 解:x xz=∂∂ ……………………………………………………………….2分 y yz2=∂∂……………………………………………………………….2分 y d y x d x dz 2+=………………………………………………………2分 2.设}2,0,1{-=a ,}1,1,3{-=b ,求b a ⋅和b a ⨯.解:51)2(10)3(1-=⨯-+⨯+-⨯=⋅b a …………………………….3分}1,5,2{52113201=++=--=⨯k j i k j ib a ………………………..3分3.求过点()132,,-且平行于直线⎩⎨⎧=-+=+-025032z y x z y x 的直线方程.解:直线⎩⎨⎧=-+=+-025032z y x z y x 的方向向量为k j i kj i 135251132++=-- …………………………………….4分 所求直线方程为1315312-=-=+z y x ……………………………….2分 4.设z xy x z y x f +-=23),,(,求),,(z y x f 在)0,1,1(0P 的梯度f ∇及f ∇.解:k j i k f j f i f f z y x +-=++=∇22 ………………………………….4分31)2(222=+-+=∇f …………………………………………….2分5.计算二重积分σd xy ⎰⎰D,其中D 是由直线1=y 、2=x 和x y =所围闭区域.解:把D 看成X 型区域{}x y x y x ≤≤≤≤1,21),(………..……………2分89)(21213211D=-==⎰⎰⎰⎰⎰dx x x xydy dx d xy xσ………………………….4分 6.计算三重积分dV x e y )2sin (2⎰⎰⎰Ω+,其中Ω:10,10,11≤≤≤≤≤≤-z y x .解:注意到积分区域Ω关于YOZ 面对称,x e y sin 2为x 的奇函数…….2分4112212sin )2sin (22=⨯⨯⨯=+=+⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩdV dV x e dV x ey y …...4分7.L 为封闭正向圆周曲线122=+y x ,求⎰-Lydx x dy xy 22.解:y x P 2-=,2xy Q =………………………………………………….2分由格林公式⎰-Lydx x dy xy 22σσd y x d y Px Q DD⎰⎰⎰⎰+=∂∂-∂∂=)()(22 ⎰⎰=⋅=ππρρρθ20122d d …..………………4分8.判断级数πn n n ncos 2)12(12∑∞=+的敛散性. 解:注意到πn n n n cos 2)12(12∑∞=+≤∑∞=+122)12(n nn …………………………….2分 而级数∑∞=+122)12(n nn 利用比值审敛法,得 121lim1<=+∞→nn n u u ………………………....2分则由比较审敛法,级数πn n n ncos 2)12(12∑∞=+收敛.…………………....2分四、解答题(每小题8分,共计16分)1. 求二阶非齐次线性微分方程x e y y y 244-=+'+''的通解.解:注意到右端项为x m e x P x f λ)()(=型(其中2,1)(-==λx P m )…….2分 且原方程对应的齐次方程的特征方程为0442=++r r ,特征根2-=λ为二重根.......................................................................................2分 设原方程的一个特解为x e ax y 22*-=代入原方程解出21=a ………………....2分 则原方程通解为()xx e x e x C C y 2222121--++=....................................................2分 2.设)(x f 的周期为π2,且在],[ππ-上2)(x x f =,试将)(x f 展开成傅里叶级数. 解:依题)(x f 在],[∞-∞上连续,且满足狄利克雷收敛定理条件,则0=n b ),2,1( =n ,…………………………………………....2分3222020πππ==⎰dx x a ,…………………………………….……2分⎰⎰⎰===ππππππ02020sin 2cos 2cos )(2nx d x n dx nx x dx nx x f a n⎰⎰=⎥⎦⎤⎢⎣⎡-=πππππ02002c o s 4s i n 2s i n 2nx xd n dx nx x nx x n 2002)1(4cos cos 4n nxdx nx x n n -=⎥⎦⎤⎢⎣⎡-=⎰πππ ),2,1( =n ……2分由收敛性定理可知,∑∞=-+=1222c o s )1(43n n n nx x π …………….……………….……2分 五、应用题(本题6分)某养殖场饲养两种鱼。
2009-2010学年第二学期高等数学(2)期末试卷及其答案

2009-2010学年第二学期高等数学(2)期末试卷及其答案2009 至2010 学年度第2 期高等数学(下)课程考试试题册A试题使用对象:2009 级理科各专业(本科)命题人:考试用时120 分钟答题方式采用:闭卷说明:1.答题请使用黑色或蓝色的钢笔、圆珠笔在答题纸上书写工整.2.考生应在答题纸上答题,在此卷上答题作废.一.填空题(本题共15 分,共5 小题,每题 3 分)1.已知(2,1,),(1,2,4)a m b==,则当m=时,向量a b⊥.2.(,)(2,0)sin()lim x yxy y→=.3.设区域D为22yx+≤x2,则二重积分D dσ=⎰⎰.4.函数(,),(,)P x y Q x y在包含L的单连通区域G内具有一阶连续偏导数,如果曲线积分(,)(,)LP x y dx Q x y dy+⎰与路径无关,则(,),(,)P x y Q x y 应满足条件 .5. 当p 时,级数211pn n +∞=∑收敛.二.选择题(本题共15分,共5小题,每题3 分)1.直线221:314x y z L -+-==-与平面:6287x y z π-+=的位置关系是 .A .直线L 与平面π平行;B .直线L 与平面π垂直;C .直线L 在平面π上;D .直线L 与平面π只有一个交点,但不垂直.2. 函数(,)f x y 在点(,)x y 可微分是(,)f x y 在该点连续的( ).A .充分条件; B. 必要条件; C. 充分必要条件; D. 既非充分也不必要条件 3.改变积分次序,则100(,)y dy f x y dx⎰⎰.A .1(,)xdx f x y dy ⎰⎰; B .11(,)dx f x y dy ⎰⎰;C .11(,)x dx f x y dy ⎰⎰;D .11(,)xdx f x y dy ⎰⎰6.计算22()(sin )Lxy dx x y dy--+⎰,其中L 是上半圆周y =x 轴所围区域的边界,沿逆时针方向.7.将函数1()3f x x =+展开成(3)x -的幂级数. 8.计算曲面积分xydydz yzdzdx xzdxdy ∑++⎰⎰,其中∑为1x y z ++=,0,x =y =,0z =所围立体的外侧.9.求抛物面22z xy =+到平面10x y z +++=的最短距离.2009 至 2010 学年度第 2 期高等数学(下)课程试题A 参考答案试题使用对象: 2009 级 理科各专业(本科) 向瑞银一.填空题(本题共15 分,共5 小题,每题 3 分) 1. 1-; 2. 2; 3. π; 4.y P ∂∂=xQ ∂∂; 5.12p >二.选择题(本题共15分,共5小题,每题3 分) 1.B ; 2.A ; 3.D ; 4.C ; 5.C 三. 求解下列各题(本题共70分,共9小题,1~2每题7 分,3~9每题8 分).1.z z u z vx u x v x∂∂∂∂∂=+∂∂∂∂∂……4分sin cos u u ye v e v=+(sin()cos())xy e y x y x y =-+-……7分 2.2212()(tan())y y uf x y f xy y∂''''=⋅-+∂ ……4分2122sec ()()yyf f xy xy '''=-+2122sec ()yf xf xy ''=-+……7分 3. 令22(,,)1F x y z xy z=+--,则法向量(2,2,1)n x y =-,(2,1,4)(4,2,1)n=- ……3分在点(2,1,4)处的切平面方程为 4(2)2(1)(4)0x y z -+---=.即4260x y z +--=. (6)分法线方程为214421x y z ---==-. ……8分 4.22Dx d yσ⎰⎰22121xxx dx dy y=⎰⎰……4分221/11()x xx dxy=-⎰……6分231()x x dx =-⎰322111()42x x =-94=……8分5.令cos ,sin x a y a θθ==,则sin ,cos x a y a θθ''=-=,ds θ=ad θ= ……3分20a Le ad πθ=⎰⎰ ……6分=2aae π ……8分6.2P xy=-,1P y ∂=-∂ ,2(sin )Q x y =-+,1Q x∂=-∂ , ……4分()0DDQ PI dxdy dxdy x y∂∂=-=∂∂⎰⎰⎰⎰ ……6分=……8分 7.1136(3)x x =++-113616x =-+ ……4分 当316x -<,即 39x -<<时,13x +013()66nn x +∞=-=-∑ ……8分8. ⎰⎰∑++zxdxdy yzdzdx xydydz=()x y z dxdydz Ω++⎰⎰⎰……4分 =1110()xx ydx dy x y z dz---++⎰⎰⎰……6分81=……8分9.设抛物面一点(,,)x y z ,它到平面的距离为1d x y z =+++满足条件220x y z +-= ……3分 拉格朗日函数为222(1)()3x y z L x y z λ+++=++- ……5分2(1)203x x y z L x λ+++=+=,2(1)203yx y z Ly λ+++=+=2(1)3z x y z L λ+++=-=,220Lx y z λ=+-=解方程组得,12x y ==-,12z =. 由问题本身知最短距离存在,所以最短距离为0.5,0.5,0.5)d --=6=……8分。
2009-2010-2高数期末试题及解答

2π
2
而
∫∫ xdydz + ( z
Σ0
2
− y )dzdx + ( x 2 − z )dxdy = ∫∫ x 2dxdy =
Dxy
2 1 1 2π ( x 2 + y 2 )dxdy = ∫ dθ ∫ r 3dr = 2π , ∫∫ 0 2 Dxy 2 0
故
∫∫ xdydz + ( z
Σ
2
− y )dzdx + ( x 2 − z )dxdy = −4π 。
2dxdy ;
2 2
积分曲面Σ 2 : z = 1 ,( x, y ) ∈ Dxy = ( x, y ) 0 ≤ x + y ≤ 1 ,
{
}
′ 面积微元素为:dS = 1 + z′ x + z y dxdy = dxdy ;
2 2
Ò ∫∫ ( x
Σ
2
+ y 2 )ds = ( 2 + 1) ∫∫ ( x 2 + y 2 )dxdy = ( 2 + 1) ∫ dθ ∫ r 3dr =
−1 −1
1
1
1 nπ x 2 dx = 2 ∫ (2 + x ) cos nπ xdx = [( −1) n − 1] 0 2 ( nπ ) 2
,
(n = 1, 2,L ) 1 1 bn = ∫ f ( x )sin nπ xdx = 0 ,( n = 1, 2,L ) 2 −1 5 ∞ 2 f ( x) = + ∑ [( −1) n − 1]cos nπ x , x ∈ [ −1,1) 2 2 n =1 ( nπ ) 令 x = −1 可得 ∞ ∞ ∞ ∞ 1 1 1 1 π2 = ,又∑ 2 = ∑ +∑ , ∑ 2 2 2 8 n =1 (2n − 1) n =1 n n =1 (2n − 1) n =1 (2n )
09-10第2学期高数A试卷A

)
班级
高等数学(A)
A.
2009 —2010 学年度第二学期期末考试(A)卷
注意事项:1. 考前请将密封线内填写清楚 2. 所有答案请直接答在试卷上 3.考试形式:闭卷 4. 本试卷共四大题,满分 100 分,考试时间 100 分钟
∫0
1
dy ∫
y− y2 0
1
f(x,y)dx ;
B.
∫0
1
1
dy ∫
学号
∫
2 1
dy ∫
2 y
sin x dx = x −1
2 时,级数 ∑ n sin n =1 ∞
5.设常数 p > 0 ,则当 p 满足条件
π n
p
收敛
6.设 L 为从点(1,1)沿曲线 x = y 2 到点(1,-1)的曲线段,则曲线积分
3 . 函数 z = x 3 + y 3 − 3x 2 − 3 y 2 的极小值点是( A. (0,0) ; B.(2,2) ;
D
y = 0, x =
π
2
所围的区域.
第2页 共3页
得分 评卷人 复查人
四、综合与证明题(本题共 3 小题,每小题 7 分, 共 21 分) 1.验证: (2 x cos y + y 2 cos x)dx + (2 y sin x − x 2 sin y )dy 为某
3.
2 2 2 设球体 x + y + z ≤ 2 Rz 内,各点处的密度等于该点到原点距离的平方,试求
一、单项选择题(本题共 5 小题,每小题 4 分,共 20 分)在 每小题列出的四个选项中只有一个是符合题目要求的, 请将其代 码填在题后的括号内。错选或未选均无分。
2009—2010学年度下学期高二数学期末测试选编 理 新人教A版

2009—2010学年度下学期高二数学理期末测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分共150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一.选择题(本大题共12个小题,每小题5分,共60分.在每个小题的四个选项中,只有一项是符合题目要求的.) 1.复数13)31(2-+i i 的值是 ( )A .2B .21C .21-D .2- 2.)('0x f =0是可导函数)(x f 在点0x x =处取极值的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3a 的取值范围是 ( )A .)22,22(-BC .D 4.已知(p x x-22)的展开式中,不含x 的项是2720,那么正数p 的值是 ( )A . 1B .2C .3D .45.如果654321,,,,,a a a a a a 的方差为3,那么2)3(1-a .2)3(2-a . 2)3(3-a .2)3(4-a .2)3(5-a .2)3(6-a 的方差是( )A .0B .3C .6D .12 6.今天为星期四,则今天后的第20062天是( )A .星期一B .星期二C .星期四D .星期日7.函数22()()x a y x a b+=++的图象如右图所示,则 ( D ) A .(0,1),(0,1)a b ∈∈B .(0,1),(1,)a b ∈∈+∞C .(1,0),(1,)a b ∈-∈+∞D .(1,0),(0,1)a b ∈-∈8.有一排7只发光二级管,每只二级管点亮时可发出红光或绿光,若每次恰有3只二级管点亮,但相邻的两只二级管不能同时点亮,根据这三只点亮的二级管的不同位置或不同颜色来表示不同的信息,则这排二级管能表示的信息种数共有 ( ) A .10 B .48 C .60 D .80 9.设随机变量~(0,1)N ξ,记)()(x P x <=Φξ,则(11)P ξ-<<等于 ( )A .2(1)1Φ-B .2(1)1Φ--C .(1)(1)2Φ+Φ-D .(1)(1)Φ+Φ-10.把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里,如果数学必须比历史先上,则不同的排法有 ( ) A .48 B .24 C .60 D .120 11. 口袋里放有大小相同的2个红球和1个白球,有 放回的每次模取一个球,定义数列{}n a :⎩⎨⎧-=次摸取白球第次摸取红球第n n a n 11 如果n S 为数列{}n a 的前n 项之和,那么37=S 的概率为( )A .729224 B .72928C .238735D .7528 12.有A .B .C .D .E .F6个集装箱,准备用甲.乙.丙三辆卡车运送,每台卡车一次运两个.若卡车甲不能运A 箱,卡车乙不能运B 箱,此外无其它任何限制;要把这6个集装箱分配给这3台卡车运送,则不同的分配方案的种数为 ( ) A .168 B .84 C .56 D .42第Ⅱ卷(非选择题满分90)二、填空题:(本题共4小题,每小题4分,共16分)13. (2x+x )4的展开式中x 3的系数是14.曲线1,0,2===y x x y ,所围成的图形的面积可用定积分表示为__________.15.从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,推广到第n 个等式为_________. 16.已知函数)0(1)1(3)(223>+-+-=k k x k kx x f ,若)(x f 的单调减区间是 (0,4),则在曲线)(x f y =的切线中,斜率最小的切线方程是_________________. 三、解答题17.(12分)求证:(1)223)a b ab a b ++≥++; (2)6+7>22+5.18.(12分)已知(41x +3x 2)n展开式中的倒数第三项的系数为45,求:(1)含x 3的项; (2)系数最大的项.19.(本小题满分12分)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.(Ⅰ)记“函数x x x f ξ+=2)(为R 上的偶函数”为事件A ,求事件A 的概率; (Ⅱ)求ξ的分布列和数学期望.20.(12分)已知函数3()3f x x x =-(1)求函数()f x 在3[3,]2-上的最大值和最小值(2)过点(2,6)P -作曲线()y f x =的切线,求此切线的方程21.(12分)函数数列{})(x f n 满足:)0(1)(21>+=x xx x f ,)]([)(11x f f x f n n =+(1)求)(),(32x f x f ;(2)猜想)(x f n 的表达式,并证明你的结论.22.(14分)已知a 为实数,函数23()()()2f x x x a =++.(I )若函数()f x 的图象上有与x 轴平行的切线,求a 的取值范围; (II )若(1)0f '-=,(ⅰ) 求函数()f x 的单调区间;(ⅱ) 证明对任意的12,(1,0)x x ∈-,不等式125()()16f x f x -<恒成立参考答案一、选择题 ABDCD A D DAC BD 二、填空题13.24 14.3215.)321()1()1(16941121n n n n ++++-=⋅-++-+-++ 16.1280x y +-=三、解答题17.证明:(1) ∵222a b ab +≥,23a +≥,23b +≥ ;将此三式相加得:222(3)2a b ab ++≥++,∴223)a b ab a b ++≥++.(2)要证原不等式成立,只需证(6+7)2>(22+5)2,即证402422>.∵上式显然成立, ∴原不等式成立. 18.解:(1)由题设知2245,45,10.n nn C C n -==∴=即21113010363341211010710433101130()(),3,6,12210.r rrrr r r T C x x C xr x T C xC x x ---+-=⋅======令得含的项为 (2)系数最大的项为中间项,即55302551212610252.T C xx -==19.解:设该学生选修甲、乙、丙的概率分别为x 、y 、z依题意得⎪⎩⎪⎨⎧===⎪⎩⎪⎨⎧=----=-=--5.06.04.0,88.0)1)(1)(1(1,12.0)1(,08.0)1)(1(z y x z y x z xy z y x 解得 (I )若函数x x x f ξ+=2)(为R 上的偶函数,则ξ=0当ξ=0时,表示该学生选修三门功课或三门功课都没选.)1)(1)(1()0()(z y x xyz P A P ---+===∴ξ=0.4×0.5×0.6+(1-0.4)(1-0.5)(1-0.6)=0.24∴事件A 的概率为0.24(II )依题意知ξ=0.2则ξ的分布列为∴ξ的数学期望为E ξ=0×0.24+2×0.76=1.5220.解:(1)'()3(1)(1)f x x x =+-当[3,1)x ∈--或3(1,]2x ∈时,'()0f x >,3[3,1],[1,]2∴--为函数()f x 的单调增区间当(1,1)x ∈-时,'()0f x <,[1,1]∴-为函数()f x 的单调减区间 又39(3)18,(1)2,(1)2,()28f f f f -=--==-=-,∴当3x =-时,min ()18f x =- 当1x =-时,max ()2f x =(2)设切点为3(,3)Q x x x -,则所求切线方程为32(3)3(1)()y x x x x x --=--由于切线过点(2,6)P -,326(3)3(1)(2)x x x x ∴---=--,解得0x =或3x =所以切线方程为30x y +=或24540x y --= 21.解:(1)221111221)(1)())(()(x x x f x f x f f x f +=+==222221331)(1)())(()(xx x f x f x f f x f +=+==(2)猜想:)(1)(2*∈+=N n nx x x f n下面用数学归纳法证明: ①当n=1时,211)(xx x f +=,已知,显然成立②假设当)(*∈=N K K n 时 ,猜想成立,即21)(kxx x f k +=则当1+=K n 时,2222211)1(1)1(11)(1)())(()(xk x kx x kx xx f x f x f f x f k k k k ++=+++=+==+即对1+=K n 时,猜想也成立. 由①②可得)(1)(2*∈+=N n nx x x f n 成立22.解: 解:(Ⅰ) ∵3233()22f x x ax x a =+++,∴23()322f x x ax '=++.∵函数()f x 的图象上有与x 轴平行的切线,∴()0f x '=有实数解. ∴2344302a D =-⨯⨯≥,…………………4分 ∴292a ≥. 因此,所求实数a的取值范围是32(,(,)-∞-+∞. (Ⅱ) (ⅰ)∵(1)0f '-=,∴33202a -+=,即94a =.∴231()323()(1)22f x x ax x x '=++=++. 由()0f x '>,得1x <-或12x >-; 由()0f x '<,得112x -<<-.因此,函数()f x 的单调增区间为(,1]-∞-,1[,)2-+∞;单调减区间为1[1,]2--.(ⅱ)由(ⅰ)的结论可知,()f x 在1[1,]2--上的最大值为25(1)8f -=,最小值为149()216f -=; ()f x 在1[,0]2-上的的最大值为27(0)8f =,最小值为149()216f -=. ∴()f x 在[1,0]-上的的最大值为27(0)8f =,最小值为149()216f -=.因此,任意的12,(1,0)x x ∈-,恒有1227495()()81616f x f x -<-=.。
湖北省2009-2010学年高二下学期期末测试(数学)

图112009—2010学年度下学期高二数学期末测试[原人教版]说明:本试卷分第一卷和第二卷两部分,第一卷60分,第二卷90分,共150分;答题时间150分钟.第Ⅰ卷(选择题,共60分)一、选择题:每小题5分,共60分,在每小题给出的四个选项中,只有一个选项是正确的,请把正确地选项填在题后的括号内.1.图1是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,则豆 子落入圆内的概率是 A .8π B .4πC .2πD .π2.甲打靶一次,中靶的概率为0.8,乙打靶一次,中靶的概率为0.7,现甲乙两人同时打靶一次,则恰有一人中靶的概率为 ( ) A .0.56 B .0.46 C . 0.38 D .0.643.将一个各个面上均涂有颜色的正方体,锯成64个同样大小的小正方体,从这些小正方体中任取一个,其中恰好有2面涂有颜色的概率是 ( ) A .916B .2764 C .38 D .11324.在一圆的圆周上有10个等分点,以这些点为顶点,每三个点可以构成一个三角形,如果随机选择三个点,刚好可以构成直角三角形的概率是 ( )A .41 B .31 C .21D .51 5.有5条长度分别为1,3,5,7,9的线段,从中任意取出3条,则所取3条线段可构成 三角形的概率为 ( )A .53 B .103 C .52 D .107 6.坛子里放有3个白球,2个黑球,从中进行不放回摸球. A 1表示第一次摸得白球,A 2表示第二次摸得白球,则A 1与A 2是 ( ) A .互斥事件 B .独立事件 C .对立事件 D .不独立事件7.以正方体的顶点为顶点作正四面体,则正方体的表面积与正四面体的表面积之比为( )A .3:1B .1:3C .2:3D .3:28.已知水平平面α内的两条相交直线a, b 所成的角为θ,如果将角θ的平分线l '绕着其顶点,在竖直平面内作上下转动, 转动到离开水平位值的l '处,且与两条直线a,b 都成角α,则α与2θ的大小关系是( )A .2θα≤或2θα≥B .α>2θ或 α<2θC .α>2θD .α<2θ9.地球半径为R ,A 、B 两地均在北纬45°圈上,两地的球面距离为3R π,则A 、B 两地的经度之差的绝对值为( )A .3πB .2πC .32πD .4π10.在(312xx -)8的展开式中常数项是 ( )A .-28B .-7C .7D .2811.从6种小麦品种中选出4种,分别种植在不同土质的4块土地上进行试验,已知1号、2号小麦品种不能在试验田甲这块地上种植,则不同的种植方法有 ( )A .144种B .180种C .240种D .300种12.两位同学去某大学参加自主招生考试,根据右图学校负责人与他们两人的对话,可推断出参加考 试的人数为 ( ) A .19 B . 20 C .21 D .22第Ⅱ卷(非选择题,共90分)二、填空题:每小题5分,共20分,把正确答案填写在题中的横线上,或按题目要求作答. 13.在的系数为的展开式中226,)1()1(x x x x ++- .14.甲说:“我有4个朋友,有男的,有女的且女的数不少于男的数,他们的年龄都不相同”;乙说:“我猜其中年龄最大的是女的,年龄最小的是男的。
河北省邯郸市09-10学年度高二第二学期期末考试--数学

邯郸市2009-2010学年度第二学期期末教学质量检测高二数学试题注意:本试卷分第I 卷(选择题)和第H 卷(非选择题)两部分,满分 150分,时间120分钟.题号前注明示范性高中做 的,普通中学不做;注明 普通中学做 的,示范性高中不做,注明 文科做的理科不做;注 明理科做的文科不做,没有注明的,所有学生都做 .题号前注明示范性高中做 的,普通中学不做;注明普通中学做 的,示范性高中不做,注明 文科做的理科不 做;注明理科做的文科不做,没有注明的,所有学生都做 .参考公式:如果事件A 、B 互斥,那么球的体积公式43P (A +B )= P (A ) +P ( B )7 - R 3其中R 表示球的半径3如果事件A B 相互独立,那么P (A- B )= P (A ) • P (B )如果事件A 在一次试验中发生的概率是 P, 那么n 次独立重复试验中恰好发生 k 次的 概率 P n (k)二 C :P k (1 _P)n “第I 卷(选择题,共60 分)、选择题(每题只有一个正确结论,把正确结论前的代号填在 涂卡.每小题5分,共60分) 2. 某地区的年降水量(单位: mr )在[100 , 150)、[150 , 200)、[200 , 250)范围内的概率分别为0.25、0.16,则年降水量在[100 , 200)范围内的概率为 A.0.53B.0.25C.0.37D.0.283. 一道竞赛题,甲同学解出它的概率为丄,乙同学解出它的概率为1,丙同学解出它的概率为 丄,则独234立解答此题时,三人中只有一人解出的概率为 A .丄B. HC.I 7 D. 12424244. 符合下面哪种条件的多面体一定是长方体A.直平行六面体B.侧面是矩形的四棱柱C.对角面是全等的四棱柱D.底面是矩形的直棱柱第I 卷答题栏 内,用答题卡的学校,直接1. 2C :00A . 9900B.9800C. 2000D. 2200 0.12、5. 三棱锥P - ABC中,若有两组相对的棱互相垂直,则点P在平面ABC上的射影一定是ABC的A.夕卜心B.内心C. 垂心D. 重心2 1 66. 二项式(x ・)的展开式中,常数项为xA . 9B . 12 C. 15 D. 277. 将红,黄,蓝,绿四种颜色共4个小球,放入红,黄,蓝,绿四种颜色的盒子里,每个盒子放一个小球,则小球的颜色和盒子的颜色均不相同的放法有A . 6 种B . 9 种C. 11 种D. 23 种8. 北纬45;圈上有A,B 两地分别是东经 40:和西经50,若设地球半径为 R,则A, B 的球面距离为JT-R 212. 已知三棱柱ABC-AB 1C 1的侧棱与底面边长都相等,A 在底面ABC 内的射影为ABC 的中心,则 AB 1与底面ABC 所成角的正弦值等于1 A.-3B .乏C .二3 32 D .-3第H 卷(非选择题共90分)注意事项:1•用钢笔或蓝圆珠笔直接答在答题卡上.2 .答卷前将密封线内的项目填写清楚.611 用 0、 1、 2、有A. 288 个B. 600个 C. 360个 D. 3123 4 23、4、5六个数字能组成没有重复数字的六位数,这样的六位数中奇数、填空题:本大题共4个小题,每小题4分,共16分.2 1 713. (x 一―)的二项展开式中的第5项的二项式系数二;x14. (文科做)某地区有300家宾馆和旅店,其中高档宾馆有30家,中档宾馆有75家,大众型旅店有195家.为了解宾馆和旅店的入住率,要从中抽取一个容量为20的样本.若采用分层抽样的方法,抽取的中档宾馆的数是;(理科做)随机变量E的分布列如下表:E—101P a B c其中a,b,c成等差数列,若E E =—,则D E = ;3 ---------------------15. 把正方形ABCD&对角线AC折起,当A、B C、D四点为顶点的三棱锥体积最大时,直线BD与平面ABC所成的角的大小为_; ____16. 从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是三、解答题:本大题共6个小题•共70分•解答要写出文字说明、证明过程或解题步骤.17. (本小题满分10分)已知—)n的展开式中第五项的系数与第三项的系数之比是10 :1,求展开式中x的系数.x18. (本小题满分1—分)(普通中学做)如图,四棱锥P—ABCD中,底形,AB=8, AD=4\3,侧面PAD为等边三角形,并且面角为60° .求PA与底面ABCD所成角的大小面ABCD为矩与底面所成二D(示范性高中做)如图,四面体ABCD 中,ABD和「'BCD均为等边三角形,AB =2,AC — 6.(I)求证:AO _平面BCD ;(n)求二面角A _ BC -D的余弦值.19. (本小题满分12分)书桌上一共有六本不同的书•问:(I) 6本书排成一排,要求其中的2本数学书排在一起,共有多少种不同的排法?(n) 6本书分给甲、乙、丙三个同学,每人2本,共有多少种不同方法?(川)(示范性高中做)6本书分给甲、乙、丙三个同学,如果一个人得1本,一个人得2本,一个人得3本,共有多少种不同的分法?20. (本小题满分12分)设进入某商场的每一位顾客购买甲种商品的概率是0.5,购买乙种商品的概率是0.6 ,且购买甲种商品和购买乙种商品是相互独立的,各顾客之间购买商品也是互相独立的(I)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;(n)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率21. (本小题满分12分)(文科做)某商场进行促销活动,促销方案是:顾客每消费100元,便可以获得奖券一张,每张奖券中奖的概率1为丄,若中奖,则商场返还顾客现金100元某顾客购买价格为340元的商品,得到3张奖券5(I )求商场恰好返还该顾客现金100元的概率;(II )求商场至少返还该顾客现金100元的概率.(理科做)甲、乙两队进行一场排球比赛•根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束•设各局比赛相互间没有影响•令的概率分为本场比赛的局数•求布和数学期望.(精确到0.0001)22. (本小题共12分)(普通高中做)如图,在直三棱柱AB& ABG中,AC= 3, BC= 4, AA= 4,点D是AB的中点,(I )求证:ACL BG;(II )求证:AC// 平面CDB;(III )求异面直线AC与BC所成角的余弦值.(示范性高中做)已知正方体ABCD -A三CD,的棱长为1,点M是棱AA的中点,点N是棱CC的中点,上底面A B C D啲中心.(I)求证:MO/平面NBD(H)求二面角M -BN -B,的大小;(川)求三棱锥M -OBN的体积•2009-2010学年第二学期高二数学参考答案及评分标准 6.26、选择题1---5 ACBDC 6---10 CBACA 11---12 AB、填空题5 o1113. 35 ; 14. 5 , ; 15. 45 ° ;16.9 21三、解答题17•解:依题意有(C: 24):(C: 22)=10:1,二n=8. ------- 4 分28 3—=1,有r =2•「1 二c;(..x)8丄(2)r=2r c;x 丁x••• T2厂4C;x =112x,即展开式中x的系数为112.-------10分18.(普通中学做)解:如图,取AD的中点E,连结PE,则PE± AD. 作PO L平面ABCD垂足为O,连结OE.根据三垂线定理的逆定理得OEL AD,所以/ PEO为侧面PAD与底面所成的二面角的平面角由已知条件可知/ PEO=60 , PE=6所以PO=3. 3,连结AO,则.PAO就是PO 3 '3 3PA与底面ABCD所成角•在直角三角形POA中, sin. PAOPA 4J 3 43-PAO =arcsin --------- 12 分418.(示范性高中做)解: (I)连结OC ,: ABD和CBD为等边三角形,O为BD的中点,O为BD的中点, AO _ BD ,CO _ BD ,又AB =2,AC ,AO 二CO 〜3 .在AOC中,;AO2CO2= AC2,AOC =90,即AO — OCV BD PlOC -O ,••• AO _ 平面BCD ...............(n)过O作OE — BC于E,连结AE ,:AO —平面BCD ,AE在平面BCD上的射影为OEAE — BC..AEO 为二面角A - BC - D 的平面角.在 Rt.AEO 中,AO =、3,OE 3,ta n . AEO 二竺=2,cos. AEO 52 OE 5面角A - BC - D 的余弦值为19 .解:(n)分二步完成,第一步甲先选有C |种不同的方法,然后乙选有 C 4种不同的方法,第三丙选有 C :种不同的方法,所以一共有2 2 2N = C 6 C 4C 2 = 90种不同的分法...................... 12 (8)分(川)因为没有明确甲乙丙三个人哪一个得1本,哪一个得2本,哪一个得3本,所以共有N =C 6C |C 33A 3 = 360种不同的分法...................... (12)分20.解:记A 表示事件:进入商场的 1位顾客购买甲种商品; 记B 表示事件:进入商场的 1位顾客购买乙种商品; 记C 表示事件:进入商场的 1位顾客购买甲、乙两种商品中的一种 ; 记D 表示事件:进入商场的 1位顾客至少购买甲、乙两种商品中的一种• ............ 2分(I) C = A B A B, P(C)=P (A B A B) = P(A B) P(A B)= P(A) P(B) P(A) P(B) = 0.5 0.40.5 0.6 =0.5 .............. 7 分(n) D = A B,P(D) =P(A B) =P(A)卩(B) =0.5 0.4-0.2P(D) =1 _P(D) =0.8 ........... 12分21.(文科做)解:(I )商场恰好返还给该顾客现金100元,即该顾客的三张奖券有且只有一张中奖 .................... 2分1 1 4 248P =C 3( ) ( )..................................... 4分(结果不对扣1分) 5 5125(II )法一:设商场至少返还给该顾客现金 100元为事件A,这位顾客的三张奖券有且只有一张中奖为事 件A,有且只有两张中奖为事件 如 有且只有三张中奖为事件 如 则A=A+A+A , A 1A 2A 3是互斥事件••… 6分 P (A ) =P (A 1) + ( PA ) +P (A 3) ................. 8 分= c 3(2)£)2 c 2(1)2 (4) c f (1)3 ................................................ 10分5 5 5 5 512分(I)共有N 二A f A ; =240种排列的方法6 (4)分=:48 .竺•丄__61 ................................................................ 12 分125 125 125 "125法二:商场至少返还给该顾客现金100元即这位顾客的三张奖券中至少有一张中奖,设为事件B,对立事件为B :三张奖券全没有中奖............. 6分P(B)=1-P(B) .................................................................. 8 分则它的o/1、0 /4、3 64P(B) =C3()( ) ..................................... 10分5 5 125••• P(B) =1 _ P(B)』............................. 12 分12521.(理科做)解:E的所有取值为3,4,5 ........................................ 2分P( e=3)= C3 (0.6)3 (0.4)0 C0 (0.6)0 (0.4)3=0.28 ;..................... 4 分P( =4)= C32 (0.6)2 (0.4)1 0.6 C3 (0.6)1 (0.4)2 0.4 = 0.3744 ;............. 6 分P(=5)=C: (0.6)2 (0.4)2 0.6 C2 (0.6)2 (0.4)2 0.4 = 0.3456 ........................ 8 分• E的分布列为:E 3 4 5P 0.28 0.3744 0.3456• E^3X 0.28+4 X 0.3744+5 X 0.3456=0.84+1.4976+1.728=4.0656••…12 分22.(普通高中做)解:(I)直三棱柱ABC— A1B1C1,底面三边长AC=3, BC=4AB=5AC丄BC,且BC1在平面ABC内的射影为BC,「. AC丄BC1 ............... 4分(II)设CBi与GB的交点为E,连结DE,T D是AB的中点,E是BG的中点,二DE//A& DEU 平面CDB, AC1U平面CDB,「・AG// 平面CDB ;..... 8 分(III) DE//AC , • / CED为AC 与B1C所成的角, 亠亠1 5 1 5在厶CED 中,ED^— AC 1= , CD=—AB=—,2 2 2 2CE=1CB1=2 ■. 2 ,2cos—CED = 2.2 5异面直线AG与B1C所成角的余弦值1 X3 1222.(示范性高中做)解:(I)连接AC 则0点必为AC 的中点,连结AC 交DB 于P 点,连结AC ,连结 PN ,则有 M0 // AC ' // PN.所以 M 0// 平面 NBD. .......... 4 分(H)过 M 作MQ 丄BB 于Q,过Q 作QRL BN,连结MR,则.MRQ 就是所求二面角 M _BN -B •的平面角•易知 Rt. QBR s Rt. :BNCBQ=AM =NC=1 , BN = p'BC 2 +NC 2 =、:1 + (*)1 z MQ 厂QR=— ,tan MRO 5 ,Q5 QR 所以二面角 M 「BN -B ■的大小为arctan 52yf25 .12分 1S OMN = MN AM - 4所以V M qBN =V B-OMN 1(立方单位)12分 (川)V M _OBN - V B _OMN 易知B 点到底面OMN 的距离=BP=」 2 8分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⎰=+L dx y x )(2_________ 。
0D
ydxdy 奇偶性】
则I =________________。
【
332dv =⋅ 】 64分)
-8 y 所确定,求1
02
2==y x x
z
∂∂。
)z z x +-=30 ;
∂∂z
x
x y ===01
2
∂∂22
01
4z
x
x y ===
14⎫
⎭⎪ D z z z z x x xx xy yx yy ==--=-6112121
214033,xx z ⎛⎫=> ⎪⎝⎭
13⎫⎭⎪处取极小值。
学院 _____________班级名称_______________学号_____________姓名_____________ 教师________________
………密……………封……………线……………以……………内……………答……………题……………无……………效……………
_
12.设闭区域),(.0,:22y x f x y y x D ≥≤+为D 上的连续函数,且
,),(8
1),(22dudv v u f y x y x f D
⎰⎰
-
--=π 求),(y x f
解 设A dudv v u f D
=⎰⎰
),(,在已知等式两边求区域D 上的二重积分,有
,81),(22dxdy A
dxdy y x dxdy y x f D
D
D
⎰⎰
⎰⎰
⎰⎰
-
--=π
从而.122A dxdy y x A D
---=
⎰⎰
所以 ⎰⎰⎰-=⋅-=203202
sin 0)cos 1(3112π
π
θ
θθθd rdr r d A .32231⎪⎭
⎫
⎝⎛-=π 故 .32261⎪⎭⎫ ⎝⎛-=πA 于是 .322341),(2
2⎪⎭
⎫ ⎝⎛----=ππy x y x f
【注意关键点:
(,)(,)D
D
f u v dudv f u v dudv A =⎰⎰
⎰⎰是一个常数,从而可设】
13.计算二重积分D
xdxdy ⎰⎰,其中D 是由抛物线21
2y x =及直线y =x +4所围成的区域。
解:原式2
4
44
2
31
2
22
1
(4)182
+--=
=+-=⎰
⎰⎰x x xdx dy x x x dx
【注意:先求2
12
y x =与y =x +4的交点,从而2:24,/2 4.X D x x y x -≤≤≤≤+】
14.计算I =Ω⎰⎰⎰
2yz d v ,其中Ω是由x 2+z 2=1,y =0,y =1所围的位于z ≥0部分的立体。
解一.1
1
2d d I x =⎰⎰111
220
22d (1)(1)3
x y x x dx =-=-=
⎰⎰⎰ 解一.22221
21
:10:1002
2
sin 3
xz xz D x z D x z I zdzdx ydy zdzdx d r rdr π
θθ+≤+≤===⋅=⎰⎰⎰⎰⎰
⎰⎰ 【注意: 22:1:02,01,cos ,sin .xz r D x z D r x r z r θθπθθ+≤⇒≤≤≤≤==】
15.已知L 是由221,0x y y x +≤≤≤所确定的平面域的边界线,求⎰+L ds y x 22cos 。
解:D 由 L OA AB BO =++.
其中(0,0),(1,0),O A B
:0,01;OA y x ds dx
=≤≤==
:cos ,sin ,0/4,.AB x t y t t ds dt π==≤≤==
:.0BO y x x ds =≤≤==
cos
d L
s ⎰
1
1cos d cos d )d x x t x π4=
+
+
⋅⎰
⎰
2
2
)2sin(1cos 41sin x +π
+
=1cos 4
1sin 2π
+
= 16.计算曲线积分⎰+++L dy y x y dx y x x )cos()sin(2222,式中L 是正向圆周 222
x y π
+=
11.解:法一。
(L
参数化后直接计算),2x t y t π=
=
≤≤,
2220
1
sin
cos
)cos 02
2
22
L
I x dx y dy td t t
π
ππ
π
π=⋅+⋅==
⋅=⎰⎰
法二. (直接用格林公式+对称区间上积分考虑被积函数的奇偶性)
2222()(2sin()2cos())20x y D
D
D
I Q P dxdy xy x y xy x y dxdy xydxdy =-=-+-+==⎰⎰⎰⎰⎰⎰
法三(先化简,再计算)22
:/2L x y π+=注意,从而先将积分化简再按法一法二处理即可。
sin
cos
(00)02
2
L
L
D
I x dx y dy x dxGreen dxdy π
π
=⋅+⋅=⋅-=⎰⎰⎰⎰ 公式,或
20
sin
cos )0
2
L
L
I x dx y dy x dx td t π
π
π
=⋅+⋅=⋅=⎰⎰⎰
参数化L .
四、证明 (1小题,共8分)
17.试证曲面xyz a =3的切平面与三个坐标面所围四面体的体积为常数。
证明:曲面上点()x y z 000,,处的切平面法向量
{}
y z z x x y =000000,, 切平面方程为 y z x x z x y y x y z z 0000000000()()()-+-+-= 即
x x y y z z 3331000
++= 切平面与三个坐标平面所围四面体的体积
V x y z a =
⋅⋅=163339
2
0003为常数。
