信号与线性系统分析第二章1
信号与系统课后题解第二章

⑺
对⑺式求一阶导,有:
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中,有:
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ,则有:
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为:
由联立方程可得 故系统的零输入响应为:
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
(2)由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )
信号与系统 2.1

所以,特解为
1 2 2 10 y p (t ) = t + t − 3 9 27
8
d 2 y (t ) dt2
+2
d y (t ) d f (t ) + 3 y (t ) = + f (t ) dt dt
7
P1 cos(β t ) + P2 sin (β t )(特征根不等于 ± j β )
Signals & Systems
例:给定微分方程式
d 2 y (t ) dt2
d y (t ) d f (t ) +2 + 3 y (t ) = + f (t ) dt dt
如果已知: (1) f (t ) = t 2 ; (2 ) f (t ) = e t , 方程的特解。 解: (1)由于f(t)=t2,故特解函数式为 代入方程,整理得
10
Signals & Systems
全解举例2.1-1
例 描述某LTI系统的微分方程为 y”(t) + 5y’(t) + 6y(t) = f(t) 求当f(t) = 2e-t,t≥0;y(0)=2,y’(0)= -1时的全解 解: (1) 特征方程为λ2 + 5λ+ 6 = 0 其特征根λ1= – 2, λ2= – 3。齐次解为 yh(t) = C1e – 2t + C2e – 3t (2)当f(t) = 2e – t时,其特解可设为 yp(t) = Pe – t 将其代入微分方程得 Pe – t + 5(– Pe – t) + 6Pe – t = 2e – t 解得 P=1,于是特解为 yp(t) = e – t (3)全解为: y(t) = yh(t) + yp(t) = C1e – 2t + C2e – 3t + e – t 其中 待定常数C1,C2由初始条件确定。 y(0) = C1+C2+ 1 = 2,y’(0) = – 2C1 – 3C2 – 1= – 1 解得 C1 = 3 ,C2 = – 2 最后得全解 y(t) = 3e – 2t – 2e – 3t + e – t , t≥0
信号与系统第二章第一讲

则相应于1的k阶重根,有k项:
( A1t k 1 A2t k 2 Ak 1t Ak )e1t ( Ai t k i )e1t
i 1
k
例2-3
信 号 与 系 统
求如下所示的微分方程的齐次解。
Hale Waihona Puke d3 d2 d r (t ) 7 2 r (t ) 16 r (t ) 12r (t ) e(t ) 3 dt dt dt
等式两端各对应幂次的系数应相等,于是有:
信 号 与 系 统
特解为: 联立解得:
3B1 1 4 B1 3B2 2 2 B 2 B 3 B 0 2 3 1
统
线性时不变系统
线性的常系数微分方程
按照元件的约束特性及 系统结构的约束特性
也即:
具体系统物理模型
常系数微分方程建立
(1)元件端口的电压与电流约束关系
iR (t ) R
信 号 与 系 统
vR (t )
C
vR (t ) iR (t ) R
dvC (t ) iC (t ) C dt
vR (t ) Ri R (t )
与
时域经典法就是直接求解系统微分方程的方法。这种方 系 法的优点是直观,物理概念清楚,缺点是求解过程冗繁,应 用上也有局限性。所以在20世纪50年代以前,人们普遍喜欢 统 采用变换域分析方法(例如拉普拉斯变换法),而较少采用时 域经典法。20世纪50年代以后,由于δ(t)函数及计算机的普 遍应用,时域卷积法得到了迅速发展,且不断成熟和完善, 已成为系统分析的重要方法之一。时域分析法是各种变换域 分析法的基础。
信 号 与 系 统
is (t )
信号与系统分析第二章 连续时间系统的时域分析

第二章 连续时间系统的时域分析
2.1.1
对系统进行分析时, 首先要建立系统的数学模型。 对于电的系统, 只要利用理想的电路元件, 根据基尔霍 夫定律, 就可以列出一个或一组描述电路特征的线性 微分方程。 现举例来说明微分方程的建立方法。
第二章 连续时间系统的时域分析
例2.1 图2.1所示为RLC串联电路, 求电路中电流i(t) 与激励e(t)之间的关系。
第二章 连续时间系统的时域分析
(3)
y(t) C 1 e t C 2 e 6 t5 2c 0 1o 2 t)s 5 3 (s0i2 n t) (
D(p)y(t)=N(p)f(t)
y(t) N(p) f (t) D(P)
式(2.15)中的 N ( p ) 定义为转移算子, 用H(p)表示,
D (P)
(2.14) (2.15)
H (p ) N D ( (P p ) ) b a m n p p m n a b n m 1 1 p p n m 1 1 a b 1 1 p p a b 0 0 (2.16)
t0
解 (1) 齐次解。 由例2.4 yh (t)=C1e-t+C2e-6t
第二章 连续时间系统的时域分析
(2) 特解。 查表2.2, yp(t)=B1cos (2t)+B2sin(2t)
-14B1+2B2-6=0 2B1+14B2=0
于是,
B15201,
B2530
yp(t)5 20 c 1o2ts) (530 si2 nt)(
第二章 连续时间系统的时域分析
3. 用算子符号表示微分方程, 不仅书写简便, 而且在建 立系统的数学模型时也很方便。 把电路中的基本元件R、 L、 C的伏安关系用微分算子形式来表示, 可以得到相应 的算子模型, 如表2.1所示。
信号与线性系统分析第2章

e t
cos t sin t
Pe t (不等于特征根) t (P t P )e (等于特征单根) 1 0
(Pr t r Pr 1t r 1 P0 )e t (等于r重特征根)
例:f1(t), f2(t)如图,求f1(t)* f2(t) 解: f1(t) = 2ε (t) –2ε (t –1) f2(t) = ε (t+1) –ε (t –1) f1(t)* f2(t) = 2 ε (t)* ε (t+1) –2 ε (t)* ε (t –1) –2ε (t –1)* ε (t+1) +2ε (t –1)* ε (t –1) 由于ε (t)* ε (t) = tε (t) 据时移特性,有 f1(t)* f2(t) = 2 (t+1) ε (t+1) - 2 (t –1) ε (t –1) –2 tε (t) +2 (t –2) ε (t –2)
f (t ) f1 ( ) f 2 (t )d
为f1(t)与f2(t)的卷积积分,简称卷积;记为 f(t)= f1(t)*f2(t) 注意:积分是在虚设的变量τ下进行的,τ为积分变量, t为参变量。结果仍为t 的函数。
y zs (t )
f ( )h(t ) d f (t ) * ) d
▲ ■ 第 13 页
2 .任意信号作用下的零状态响应
f ( t) 根据h(t)的定义: δ(t)
LTI系统 零状态
yzs(t) h(t) h(t -τ) f (τ) h(t -τ)
由时不变性:
信号系统第二章(第2-4讲)

第二章 连续时间系统的时域分析§2-1 引 言线性连续时间系统的时域分析,就是一个建立和求解线性微分方程的过程。
一、建立数学模型主要应用《电路分析》课程中建立在KCL 和KVL 基础上的各种方法。
线性时不变系统的微分方程的一般形式可以为:)()(...)()()()(...)()(0111101111t e b t e dtd b te dt d b t e dt d b t r a t r dtd a t r dt d a t r dt d m m m m m m n n n n n ++++=++++------二、求解(时域解)1、时域法将响应分为通解和特解两部分:1) 通解:通过方程左边部分对应的特征方程所得到的特征频率,解得的系统的自然响应(或自由响应);2) 特解:由激励项得到系统的受迫响应;3)代入初始条件,确定通解和特解中的待定系数。
经典解法在激励信号形式简单时求解比较简单,但是激励信号形式比较复杂时求解就不容易,这时候很难确定特解的形式。
2、卷积法(或近代时域法,算子法)这种方法将响应分为两个部分,分别求解:1)零输入响应:系统在没有输入激励的情况下,仅仅由系统的初始状态引起的响应r)(t;zi2)零状态响应: 状态为零(没有初始储能)的条件下,仅仅由输入信号引起的响应r)(t。
zs●系统的零输入响应可以用经典法求解,在其中只有自然响应部分;●系统的零状态响应也可以用经典法求解,但是用卷积积分法更加方便。
借助于计算机数值计算,可以求出任意信号激励下的响应(数值解)。
●卷积法要求激励信号是一个有始信号,否则无法确定初始状态。
● 零输入响应与自然响应、零状态响应与受迫响应之间并不相等,具体对比见§2-9经典法在高等数学中已有详细介绍。
本课程中重点介绍近代时域法。
§2-2 系统微分方程的算子表示一、算子通过微分算子可以简化微分方程的表示。
微分算子:令dt d p =,n n n dtd p =, 积分算子:⎰∞-=t d p τ)()(1● 利用算子可以将电路中的电感和电容的伏安特性记为:L L L i p L dt di L u ⋅⋅== C t C C i pC d i C u ⋅⋅==⎰∞-11τ 即可以将电感和电容记成阻值为p L ⋅和p C ⋅1的电阻,即感抗和容抗。
信号与系统王明泉版本~第二章习题解答
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
《信号与系统分析基础》第二章部分习题参考答案

第二章部分习题参考答案2-6 试求下列各函数1()f t 与2()f t 之卷积。
121212(-)01(1) ()() ()() (0) ()()()(-) ()(-)11(1) 0(2) ()t tt t tt t f t u t f t e u t f t f t f f t d u eu t d e e d e e e t f t ααταατααταατττττττααδ-+∞-∞+∞---∞--==>*===⋅=⋅=-≥=⎰⎰⎰,解:,2121212() ()cos(45)()()()cos[()45] cos(45)(3) ()(1)[()(1)] ()(1)(2) ()()t f t t f t f t t d t f t t u t u t f t u t u t f t f t ωδτωττω+∞-∞=+*=-+=+=+--=---*⎰,解:,解:ττ222221211211()(-1)(-1)-2(-2)(-2)(-1)(-1)-(-2)(-2)2211-(-2)(-2)(-3)(-3)-(-2)(-2)(-3)(-3)22()*()()1,()0123, (1-)(1)21(1)--(12ttf t t u t t u t t u t t u t t u t t u t t u t t u t f t f t f t t f t t t dt t ft t t t τττ=+++=<=<<+=+-=++⎰222-112222212111)-222123, (1-)(1)-221()2(1)-2(1-)(-1)211121---152223, ()*()0.t t t t t t d t f t t t t t t t t t t t f t f t ττττ-+=<<+=+=+++=+++=++>=⎰121221--(4) cos , (1)-(-1)()*()()(-) [(1)-(-1)][cos(-)] cos[(1)]-cos[(-1)]f t t f t t t f t f t f f t d t t t d t t ωδδτττδδωττωω+∞∞+∞∞==+==+⋅=+⎰⎰ -212-212--2-220(5) ()(), ()sin ()()()*()()sin(-)(-) sin(-)sin t t ttt tf t e u t f t t u t f t f t f t e u t u t d e t d ee d τττττττττ+∞∞==⋅==⋅⋅⋅=⋅=⋅⎰⎰⎰-12-(-)--0022-(-)-33-2-3(6) ()2[()-(-3)], ()4()-(-2)0, ()0.02,()2488-825, 88()8(-)5, ()0.t tt t t tt t t t t f t e u t u t f t u t u t t f t t f t e d e e e t ft ed ef t e e e t f t ττττττ-==<=<<==⋅=<<===>=⎰⎰2-8 求阶跃响应为32()(21)()t t s t e e u t --=-+的LTI (线性时不变)系统对输入()()t x t e u t =的响应。
信号与系统第二章_连续时间系统时域分析(青岛大学)

n
rzi (t) Azikekt k 1
(b)
r(k zi
)
(0
)
r(k) (0 )
k 0,1,L ,(n 1)
系数Azik可直接由 r(k) (0 ) 来确定。
例:已知描述某二阶LTI连续时间系统的动态方程
d2 dt 2
r(t)
5
d dt
r(t)
6r(t)
e(t)
起始状态 r(0 ) 1,r(0 ) ,2激励信号
(t)
2
p3
5
2p p2
5
p
3
e(t)
2
d3 dt3
vo
(t)
5
d2 dt 2
vo
(t)
5
d dt
vo
(t)
3vo
(t)
2
d dt
e(t)
总结: (1)引入算子符号后,RLC 电路可借助纯电阻电路的分析方法;
(2)是否可消去公共因子的原则:微分方程的阶数应等于电路 阶数(独立储能元件的个数)。
§2.3 微分方程的经典解法 r(t) rh (t) rp (t)
r(0 ) r(0 ) 1
(4)由 0状态确定待定系数
r(t) A1et A2e2t 0.5e3t
rr((00))
A1 A1
A2 0.5 1 2A2 1.5
3
A1 A2
5.5 5
全响应 r(t) 5.5et 5e2t 0.5e3t ,t 0
(一)经典法求解微分方程步骤:
r(t) 0 u(t) r(0 ) r(0 )
代入
d2 dt 2
r(t)
3
d dt
r(t)
信号与线性系统分析总结

•两个周期信号x(t),y(t)的周期分别为T1和T2,若其周期之比T1/T2为有理数,则其 和信号x(t)+y(t)仍然是周期信号,其周期为T1和T2的最小公倍数。
总结
➢ 能量信号与功率信号
将信号f (t)施加于1Ω电阻上,它所消耗的瞬时功率为| f (t) |2, 在区间(–∞ , ∞)的能量和平均功率定义为
-2 -1 0 1 2 3 ki
总结
例2 f1(k) ={0, 2 , 1 , 5,0} ↑k=1
f2(k) ={0, 3 , 4,0,6,0} ↑k=0
解:
3 , 4, 0, 6
×—————2 ,——1 ,—5 15 ,20, 0, 30
3 , 4, 0, 6 6 ,8, 0, 12 + ———————————— 6 ,11,19,32,6,30
总结
第二章 连续系统的时域分析
➢系统的时域求解,冲激响应,阶跃响应。
➢时域卷积: f1 (t) * f2 (t) f1 ( ) f2 (t )d
图解法一般比较繁琐,但若只求某一时刻卷积 值时还是比较方便的。确定积分的上下限是关
f1(-τ)
键。
f 1( τt )
2
f1(2-τ)
f1(t)、 f2(t)如图所示,已知f(t) = f2(t)* f1(t),求f(2) =?
*
d
n f 2 (t dtn
)
t
t
t
[
f1
(
)
*
f 2 ( )]d
[
f1 ( ) d ] *
f 2 (t)
f1 (t) *[
第二章 信号与线性系统 吴大正 教材课件

对于t>0时
yf (t ) 3 yf (t ) 2 y f (t ) 6 (t )
第2章 离散信号与系统的Z域分析 连续系统的时域分析
y f (t ) C f 1e t C f 2e 2t 3;
y f (t ) 4e t e 2t 3, t 0
y (t ) an 1 y
(n)
( n 1)
(t ) a0 y (t ) bm f
m j 0
( m)
(t ) b0 f (t )
(2.1-1)
可表示为:
ai y ( i ) (t ) b j f ( j ) (t )
i 0
n
式中an-1,…,a1,a0和bm,…,b1,b0均为常数。该方程的全解由齐 次解和特解组成。齐次方程的解即为齐次解,用yh(t)表示。非齐 次方程的特解用yp(t)表示。即有 y(t)=yh(t)+yp(t) (2.1-2)
例2―3 求微分方程y″(t)+3y′(t)+2y(t)=f(t)的齐次解。 解:由特征方程
2 3 2 0 解得特征根λ1=-1,λ2=-2。
因此该方程的齐次解
yh(t)=c1e-t+c2e-2t
第2章 离散信号与系统的Z域分析 连续系统的时域分析 例2-1 求微分方程y″(t)+2y′(t)+y(t)=f(t)的齐次解。 解 由特征方程 2 2 1 0 解得二重根λ1=λ2=-1,
y x (t ) 4e t 2e 2t , t 0
第2章 离散信号与系统的Z域分析 连续系统的时域分析 2、零状态响应yf(t)
信号与系统-线性系统分析__第二章

一.微分方程的经典解法
• n阶常系数线性微分方程
n
m
aiy(i) (t) bjf (j) (t)
i0
j0
(an 1)
y(n) (t) an-1y(n-1)(t) a0y(t)
bmf (m) (t) bm-1f (m-1)(t) b0f(t)
微分方程的全解由齐次解yh(t)和特解yp(t)组成
上例中,可令f(t)=10ejt,得解为 yp(t)=(1−j)ejt=cost+sint+j(sint−cost)
▪ 求微分方程也就是确定解的形式与全部待定系数。 ▪ 解的形式根据表2−1和表2−2确定,待定系数由初始
条件求出。
11
• 用算子方法求微分方程
微分算子:p d dt
积分算子:1 t ( )d
Pet (i) 或 et[Prtr+Pr−1tr−1+…+P0]
Pcos(t)+Qsin(t) 或 Aetcos(t+)
5
f(t)为常数1时,则特解为b0/a0。 考察函数f(t)在t0时作用,则全解的定义域[0,)。
全解由齐次解和特解组成,待定常数由初始条件y(0)、
y(1)(0)、…、y(n−1)(0)确定。
j1
j1
自由响应:由系统 本身的特性确定的 响应形式
强迫响应:由激 励信号确定的响 应形式
当输入信号含有阶跃函数或有始的周期函数时,系 统的全响应可分解为瞬态响应和稳态响应。
18
例:微分方程为 y''(t)+3y'(t)+2y(t)=2f '(t)+6f(t);
初始状态y(0−)=2,y'(0−)=1;输入函数f(t)=(t)。 求零输入响应和零状态响应。
第二章线性系统的状态空间描述1

第二章 线性系统的状态空间描述§2-1 状态空间的基本概念1、状态:系统的状态,是指系统的过去、现在和将来的状况。
(如:一个质点作直线运动,它的状态就是它每个时刻的位置和速度)2、状态变量:能完全表征系统运行状态的最小数目的一组变量。
(如果用最少的n 个变量x 1(t), x 2(t),……, x n (t)就能完全描述系统的状态,那么这n 个变量就是一组状态变量。
)3、状态向量:设一个系统有n 个状态变量,即x 1(t),x 2(t),……,x n (t),用这n 个状态变量作为分量构成的向量x(t)称为该系统的状态向量。
记为Tn t x t x t x t x )](,),(),([)(21 =4、状态空间:由n 个状态变量作为坐标轴所构成的n 维空间,称为状态空间。
引入了状态和状态空间的概念之后,就可以建立动力学系统的状态空间描述了。
从结构的角度讲,一个动力学系统可用图2-1所示的方块图来表示。
其中x(t)表征系统的状态变量,u(t)为系统控制量(即输入量),y(t)为系统的输出变量。
与输入—输出描述不同,状态空间描述把系统动态过程的描述考虑为一个更为细致的过程:输入引起系统状态的变化,而状态和输入则决定了输出的变化。
5、状态方程:状态变量的一阶导数与状态变量、输入量的关系,称为系统的状态方程。
例:设单输入线性定常系统(LTI-Linear Time Invariant )的状态变量为x 1(t),x 2(t),……,x n (t),输入为u(t),则一般形式的状态方程为:)()()()()()()()()()()()()()()()()()()()()(2211222221212112121111t u b t x t a t x t a t x a t x t u b t x t a t x t a t x a t x t u b t x t a t x t a t x a t x n n nn n n nn n n n ++++='++++='++++='图2-1 动力学系统结构示意图上式可写成向量—矩阵形式:其中:6、输出方程:在指定系统输出的情况下,该输出与状态变量、输入量之间的函数关系式,称为系统的输出方程。
《信号与系统》第二版第二章:LTI连续时间系统的时域分析
零状态(zero state)响应 yzs (t ) :不考虑起始时刻系统储能的作用,即Y(0-) ≡0,由系统的外加激励信号 v (t ) = v (t )u (t ) ≠ 0 所产生的响应。
零输入响应 yzi (t ) :
5
《信号与系统》
第二章:LTI 连续时间系统的时域分析
∏(p −αi )
i =1
(αi 为互异特征根)
= N (p) ⎡⎣eαnt ∗ ∗ eα1t ∗ v (t )⎤⎦
(2-19)
n
∑ yzs (t ) = 齐次解 Aieαit +特解 B (t ) i =1
(2-20)
特解 B (t ) 反映系统输入对输出的强迫。
非零状态线性系统: 定义(非零状态线性系统):系统 T 的初始状态为X(0-)≠0
令: D (p) pn + an−1pn−1 + ... + a1p + a0
N (p) bmpm + ... + b1p + b0
4
《信号与系统》
有:
第二章:LTI 连续时间系统的时域分析
y
(t)
=
N (p) D(p)
v(t
)
H (p)v(t)
(2-13)
其中,
H
(p)
=
N (p) D(p)
称为系统算子。
≤ ∫ ∫ f (τ ) g (t −τ ) dτ dt ΩΩ
= ∫ f (τ ) ∫ g (t −τ ) dtdτ
Ω
Ω
=∫
f (τ )
g (t ) dτ = 1
f (t) 1
g (t ) 1
信号与系统第2章ppt课件

(B) u(t)Limetu(t) 0
假设u(t)的傅立叶变换为:
F ()A ()jB ()
e t u (t ) 的傅立叶变换为 :
依据傅立叶变换具有唯一性:
F e()A e()jB e()
F()li m0Fe()
所以
A()li m0Ae()精选pBpt()li m0Be()
第二章 傅立叶变换
F ()A ()jB () A()li m0Ae() B()li m0Be()
,这种频谱搬移技术在通信系统中
得到广泛的应用。调幅,调频都是
在该基础上进行的。
精选ppt
由此可见,将时间信号f(t)乘以Cs(ω0t) 或Sin(ω0t)
,等效于将f(t)的频谱一分
为二,即幅度减小一半,沿
频率轴向左和向右各平移ω0.
第二章 傅立叶变换
例2 求如下矩形调幅信号的频谱函数
f(t) G (t)c o s 0 t
例7 如图a所示系统,已知乘法器的输入为
f (t) sin(2t) s(t)co3st)(
t
系统的频率响应为:
求输出y(t).
精选ppt
第二章 傅立叶变换
f (t) sin(2t) s(t)co3st)(
t
乘法器的输出信号为: x(t)f(t)s(t)
依频域卷积定理可知:X(j)21F(j)*S(j) 这里 f(t)F(j) s(t)S(j)
精选ppt
第二章 傅立叶变换
11周期信号的傅里叶变换
周期信号的频谱------用傅里叶级数表示。 非周期信号的频谱——用傅里叶变换表示。 周期信号的频谱可以用傅里叶变换表示吗? (1)正弦、余弦信号的傅里叶变换 直流信号的博立叶变换为
信号与线性系统 管致中 第2章 线性时不变系统

0
2T
t T
0
t
y(t ) x(t ) h(t ) x( )h(t )d
x(t )h( )d
① 当 t 0 时, y(t ) 0 ② ③ ④ ⑤
1 2 y 当 0 t T 时, (t ) 0 d t 2 t 1 2 y 当 T t 2T 时, (t ) t T d Tt 2 T 2T 1 2 y (t ) d 2T (t T ) 2 当 2T t 3T 时, t T 2 当 t 3T 时, y(t ) 0
个 t 的值,将 x( ) 和 h(t ) 对应相乘,再计算相
乘后曲线所包围的面积。
通过图形帮助确定积分区间和积分上下限是很有
用的。
x(t )* h(t )
x( )h(t )d
要完成卷积运算的步骤: 1. 变量臵换:将x(t) ,h(t)变为x(), h() , 以 为积分变量 ; 2. 反褶:将h()变为h(- );
n h( n) 0
x(k )
1
0n4 otherwise
1, 0 n 6
otherwise
h(n k ) nk
k
0
k
n6
0
4
n
① n 0 时,
y ( n) 0
n n k 0 k 0
y ( n) n k n k ② 0 n 4 时, 1 ( n 1) 1 n 1 n 1 1 1
通过图形帮助确定反转移位信号的区间表示,对 于确定卷积和计算的区段及各区段求和的上下限是 很有用的。 例3. 列表法 分析卷积和的过程,可以发现有如下特点:
信号与线性系统分析-(吴大正-第四版)习题答案第二章

第二章2-1已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)y''(t) 5y'(t) 6y(t) f (t), y(0) 1, y'(0 ) 1(4)y''(t) y(t) f(t), y(0) 2, y'(0 ) 0解(l)已知方程的特征方程为A2+ 5A + 6 = 0 其特征根为初=-2"? =-36澈分方程的齐次解为央⑴=CL十C代7 由于y(0_) = Kj/70_) =- 1,且激励为零•故有比(0 十〉=y^(0-) = y(O-)= 1 必(0+)=y x(o_)= y(o_)=—i 即并d= G十G = 1 y\(O~) ——2Ci —3G =—1 由上式解得C\ =2,C =-l则系统的零输入响应为y z(n= 2厂孫—色一常d $ 0(4)已知方程的特征方程为A2 -H 1 = 0 其特征根为和=人兀=—人微分方程的齐次解为片(D = Cicos/ + Cg sin/ 由于激励为零,故有>7 (0-r )=力(。
一)=y(0-)= 2 心(0 十)== y(O-)= 0 即划(0_)= Ci = 23/上(0一)= C?2 = 0则系统的零输人响应为几(f)= 2cosz^ 02-2已知描述系统的微分方程和初始状态如下,试求其0值y(0 )和y'(0 )(2)y''(t) 6y'(t) 8y(t) f''(t),y(0 ) 1, y'(0 ) 1, f(t) (t)(4)y''(t) 4y'(t) 5y(t) f'(t),y(0 ) 1,y'(0 ) 2, f (t) e2t (t)解:⑵ y (7)+ 6『⑺一 8了⑺=©"(/) 设/(/> =力一处‘仃)+必(“ +儿(门 则有 丿⑺=必‘(r 〉+处(了)一兀(r )•f/! (r ) = a : (r ) + /0(r )d^同理 y(/) = u (5(z)—人(r) y 2 (r) = /as(r) + 兀(r)dz■ —X 整理得 力"(C + (6u + 6)y (r) + (8a + 6〃 + Cd(r) +L8/2(r)+671(r) + 70(r)]=『⑴<a = 1 = 1・ J 6a 十 Z> = 0=> J )=— 6 丨 8Q + 6〃 + c = 0c = 28r o ・••有 J(O-) - J(O-)= 飞'(r)dr — 6 - Jo. J 0_ =—6 ・:y(0-) = y(0_) — 6 =— 5 (J(r)dr + /i (r)dr J O- ro y Z (0+ ) — y(0_ ) = 8 ( t)dt — 6 8 (/) dz + o_ 0. =28 ■・・y'(0J = 295(/)d/ + Jo. YQ (t)dt(4) /(/) +□></) =-2c_?£(f) + 肮。
信号与系统 第二章 线性时不变系统的时域分析
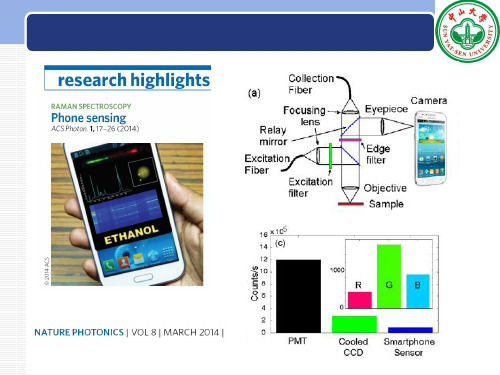
外加信号 常数A
特解 常数B
r 1i k t i r 1 i 1
tr
sin t或cos t
eλt
k1 cost k2 sin t keλt, λ不是方程的特征根 kteλt, λ是方程的特征根
k t
i 1 i
r 1
r 1i t
e , λ是方程的r阶特征重根
一、微差分方程的建立以及经典解法
'' 1
di1 (t ) 1 t L i2 ( )d R2i2 (t ) f (t ) dt C
一、微差分方程的建立以及经典解法
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
(1)
t
i ( )d
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
例题,已知线性时不变系统方程如下: y˝(t)+6y΄(t)+8y(t)= f(t), t>0. 初始条件y(0)=1, y΄(0)=2,输入信号f(t)=e-tu(t) , Q求系统的完全响应y(t)。
解:1)求方程的齐次解 特征方程为:m2+6m+8=0 显然特征根为:m1=-2,m2=-4
故原方程的齐次解为:yn(t)= Ae-2t+Be-4t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
jt
y p (t )
自由响应
强迫响应
零输入响应
零状态响应
21
2.2 冲激响应和阶跃响应
• 一、冲激响应 • 由单位冲激函数δ (t)所引起的零状态响应称为 单位冲激响应,简称冲激响应,记为h(t)。 h(t)=T[{0},δ (t)]
• 例1 描述某系统的微分方程为 y”(t)+5y’(t)+6y(t)=f(t),求其冲激响应h(t)。 • 解:根据h(t)的定义有 • h”(t) + 5h’(t) + 6h(t) = δ (t) • h’(0-) = h(0-) = 0 • 先求h’(0+)和h(0+)。
λ2 + 5λ+ 6 = 0 λ1= – 2,λ2= – 3
yh(t) = C1e – 2t + C2e – 3t yp(t) = Pe – t
特解带入方程:Pe – t + 5(– Pe – t) + 6Pe – t = 2e – t 解得 : P=1 特解: yp(t) = e – t
12
全解: y(t) = yh(t) + yp(t) = C1e – 2t + C2e – 3t + e – t 其中 待定常数C1,C2由初始条件确定。
(cr 1t
齐次解
n
yh (t )
i1
cie
r2
it
r 1
cr 2t
c1 t c 0 )e
at 或 Ae at cos(
t
at
C cos( t )
D sin( t ) e
t ), Ae
C jD
5
齐次解举例
求微分方程 的齐次解。 d
def
用g(t)表示阶跃响应
g ( t ) T [{ 0 }, ( t )]
30
三、 冲激响应与阶跃响应的关系
g (t )
t
h( )d
h(t )
d dt
g (t )
系统的阶跃响应g(t)可通过对冲激响应 h(t)的积 分得出,冲激响应h(t)可通过对阶跃响应h(t)的微分
1
特征方程:
a n 1
n
n1
a1 a 0 0
i i 1 , 2 , n 特征根: 齐次解的形式由特征根定: 待定系数Ci在求得全解 后由初始条件定
特征根λ n个单实特征根 r重实根 1对共轭复根 1, a j 2 r重共轭复根
11
例 描述某系统的微分方程为 y”(t) + 5y’(t) + 6y(t) = f(t) 求(1)当f(t) = 2e-t,t≥0;y(0)=2,y’(0)= -1时的全解; (2)当f(t) = e-2t,t≥0;y(0)= 1,y’(0)=0时的全解。
解: (1) 特征方程: 其特征根: 齐次解: 特解:
得出。
31
2.3 卷积积分
一、信号的时域分解与卷积积分 1 .信号的时域分解 (1) 预备知识
问f1(t) = ? p(t)
32
(2) 任意信号分解
• “0”号脉冲高度f(0) ,宽度为△, • 用p(t)表示为:f(0) △ p(t) • “1”号脉冲高度f(△) ,宽度为 △,用p(t - △)表示为: • f(△) △ p(t - △) • “-1”号脉冲高度f(-△) 、宽度为△,用p(t +△)表示 为: f ( - △) △ p(t + △)
20
y zs ( t ) C zsj e
j1
n
jt
y p (t )
其中:Czsj------待定系数
yp(t)----特解
(3). y(t) 全响应
y(t ) C i e
i 1 n
it
y p ( t ) C zij e
j1
n
jt
C zsj e
若把f(t)作用于LTIS,则响应为:
根据h(t)的定义: δ(t) h(t) 由时不变性: δ(t -τ) h(t -τ) 由抽样性:f (τ)δ(t -τ) f(τ) h(t -τ)
-
f t d
f h t d f t h t
对应的齐次解为
y h t C 1 t C 2 e
2t
C 3e
3t
6
2. 特解
• 特解的函数形式由激励确定,称为强迫响应。
问:若f(t)=c(常数),特解形式??
7
特解举例:
例:给定微分方程式
d
2
y t
2
2
d y t dt
3 y t
d f t dt
第二章 连续系统的时域分析
概述: 对于给定的激励,根据微 1.LTI连续系统的时域分析: 分方程求出响应与激励关系 时域分析法:函数的变量----t 2.特点:比较直观、物理概念清楚,是学习各种变换 域分析法的基础
1
本章主要内容
2.1 LTI连续系统的响应 2.2 冲激响应和阶跃响应
2.3 卷积积分
34
2 .卷积积分的定义
已知定义在区间( – ∞,∞)上的两个函数f1(t)和f2(t),
则定义积分
为f1(t)与f2(t)的卷积积分,简称卷积,记为f(t)= f1(t)*f2(t)
注意:积分是在虚设的变量τ 下进行的,τ 为积分
由于(t)及其导数在 t≥0+ 时都为零,因而方程式 右端的自由项恒等于零,这样原系统的冲激响应形式 与齐次解的形式相同。
29
二、阶跃响应 *阶跃响应是激励为单位阶跃函数(t)时,系统的零
状态响应,如下图所示。
(t)
g(t) 1
(t)
0 t
{x(0)}={0}
线性非时 变系统
g(t)
0
t
阶跃响应示意图
2.4 卷积积分的性质
2
2.1 LTI连续系统的响应
一、微分方程的经典解
二、关于0-和0+值 三、零输入响应
四、零状态响应
五、全响应
3
一、微分方程的经典解
y(n)(t) + an-1y (n-1)(t) + …+ a1y(1)(t) + a0y (t) = bmf(m)(t) + bm-1f (m-1)(t) + …+ b1f(1)(t) + b0f (t)
25
§2.2 冲激响应和阶跃响应
概述: 1. 学习了2种求LTI系统响应的方法 自由响应+强迫响应 零输入相应+零状态响应 下面一节的内容,针对零状态响应的求取, 找寻一种好方法。
26
一、冲激响应
1.定义
由单位冲激函数δ(t)所引起的零状态响应称为 单位冲激响应,简称冲激响应,记为h(t)。
h(t)=T[{0},δ(t)]
8
等式两端各对应幂次的系数应相等,于是有
3 P2 1 4 P2 3 P1 2 2 P 2 P 3P 0 1 0 2
联解得到
P2 1 3 , P1 2 9 , P0 10 27
特解为
y p t 1 3 t
2
2 9
t
10 27
9
t
ht
T {0}
27
冲激响应示意图
28
h
n
( t ) a n 1 h
m
n 1
(t ) a1 h
m 1
1
(t ) a 0 h (t )
1
bm
( t ) b m 1
( t ) b1
(t ) b0 (t )
f t
dt
如果已知: 1 f t t 2 ; 2 f t e t , 分别求两种情况下此 方程的特解。 解: (1)由于f(t)=t2,故特解函数式为
y p t P2 t
2
2
P1 t P0
2
3 P2 t 4 P2 3 P1 t 2 P2 2 P1 3 P0 t 2 t
(2)当f(t)= et 时
特解为yp(t)=P et ,代入方程后有:
Pe 2 Pe 3Pe e e
t t t t t
P
1 3
于是,特解为
1 3
e。
t
10
3. 全解
自由响应
强迫响应
完全解 = 齐次解 + 特解
注意:特解中待定系数:特解带入非齐次方程,对比求;
齐次解中待定系数:在全解求得后由初始条件定。 • 齐次解的函数形式:仅与系统本身的特性有关 与激励f(t)的函数形式无关 又叫固有响应或自由响应 •特解的函数形式: 由激励确定 又叫强迫响应
yzit): 没有外加输入信号,只由起始状态所产生的响应; yzst): 不考虑起始储能的作用(起始状态=0),只由系
统外加输入信号所产生的响应。ห้องสมุดไป่ตู้全响应 y(t) = yzi(t) + yzs(t)的求取方法: 借助经典方法
卷积积分法(后面学)
19
2.经典分析及求解
y(t) = y zi(t) + yzs(t) (1). yzi(t) 零输入响应 微分方程:齐次
LTI连续系统:常系数的n阶线性常微分方程 高等数学中经典解法:完全解 = 齐次解 + 特解 齐次解: 满足齐次方程的通解,又叫齐次解 特解: 满足非齐次方程的解,叫特解
