勾股定理综合测试题1

合集下载

北师大版2020八年级数学上册第一章勾股定理自主学习单元综合能力达标测试题1(附答案详解)

北师大版2020八年级数学上册第一章勾股定理自主学习单元综合能力达标测试题1（附答案详解）1．在△ABC中，∠C=90°，AC=6cm，BC=8cm，则AB等于（）A．2cm B．8cm C．10cm D．100cm2．等腰三角形底长为24，底边上的高为5，则这个三角形的周长为( )A．37 B．60 C．34 D．533．古埃及人曾经用如图所示的方法画直角：把一根长绳打上等距离的13个结，然后以3个结间距、4个结间距、5个结间距的长度为边长，用木桩钉成一个三角形，其中一个角便是直角，这样做的道理是（）A．直角三角形两个锐角互补B．三角形内角和等于180°C．如果三角形两条边长的平方和等于第三边长的平方D．如果三角形两条边长的平方和等于第三边长的平方，那么这个三角形是直角三角形4．如图，等腰三角形ABC底边上的高AD为4 cm，周长为16 cm，则△ABC的面积是（）A．14 cm2B．13 cm2C．12 cm2D．8 cm25．如图，在波平如镜的湖面上，有一朵盛开的美丽的红莲，它高出水面3尺．突然一阵大风吹过，红莲被吹至一边，花朵刚好齐及水面，如果知道红莲移动的水平距离为6尺，则水是（）尺．A．3.5 B．4 C．4.5 D．56．如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为（）A．35B．45C．23D．327．如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度(滑轮上方的部分忽略不计)为( )A．12 m B．13 m C．16 m D．17 m8．如图，数轴上点A，B表示的数分别是1，2，过点B作PQ⊥AB，以点B为圆心，AB 长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M表示的数是( )A．3B．5C．6D．79．以下各组数为边长，不能组成直角三角形的是（）．A．1.5，2，2.5 B．40，50，60 C．7，25，24 D．54，1，3410．有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了右图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2018次后形成的图形中所有的正方形的面积和是（）A．2017 B．2018 C．2019 D．111．在ABC ∆中，90,ACB CD ∠=︒是高，若,,BC a AC b ==,,AB c CD h ==,AD k BD p ==，且3,4a b ==，则____,____,____,____c p k h ====．12．如图，一架云梯长10米，斜靠在一面墙上，梯子顶端离地面6米，要使梯子顶端离地面8米，则梯子的底部在水平面方向要向左滑动______米．13．已知，如图，△OBC 中是直角三角形，OB 与x 轴正半轴重合，∠OBC=90°，且OB=1，BC=3，将△OBC 绕原点O 逆时针旋转60°再将其各边扩大为原来的2倍，使OB 1=OC ，得到△OB 1C 1，将△OB 1C 1绕原点O 逆时针旋转60°再将其各边扩大为原来的2倍，使OB 2=OC 1，得到△OB 2C 2，…，如此继续下去，得到△OB 2015C 2015，则点C 2015的坐标是_____．14．如图ABC 与ADE 都是以A 为直角顶点的等腰直角三角形，DE 交AC 于点F ，若5AB =，32=AD ，当CEF △是直角三角形时，则BD 的长为__________．15．如图，在四边形ABCD 中，AD BC ∥，DE BC ⊥，垂足为点E ，连接AC 交DE 于点F ，点G 为AF 的中点，2ACD ACB ∠=∠．若4DG =，1EC =，则DE 的长为__________．16．如图，在ABC 中，AB 32=，BC 1=，ABC 45∠=，以AB 为边作等腰直角ABD ，使ABD 90∠=，连接CD ，则线段CD 的长为________．17．如图，△OPQ 是边长为2的等边三角形，若正比例函数的图象过点P ，则它的表达式是y ＝_____18．如图，正方形网格中，每个小正方形的边长为1，则网格上的ABC △是__________三角形．19．三角形中两条较短的边为a ＋b ，a-b(a>b),则当第三条边为_______时，此三角形为直角三角形．20．如图，在直角三角形纸片ABC 中，∠ACB ＝90°，AC ＝2，BC ＝4，点D 在边AB 上，以CD 为折痕将△CBD 折叠得到△CPD ，CP 与边AB 交于点E ，若△DEP 为直角三角形，则BD 的长是_____21．如图，在等边△ABC 中，D 为BC 上一点，∠BAD =3∠CAD, BC=2．（1）求△ABC 的面积；（2）求CD 的值．22．（1）在右面的方格纸中，以线段AB为一边，画一个正方形；（2）如果图中小方格的面积为1平方厘米，你知道（1）中画出的正方形的面积是多大吗？解释你的计算方法.23．如图，直角坐标系中的网格由单位正方形构成.△ABC中，A点坐标为（2，3）、B （-2，0）、C（0，-1）.（1）AB的长为_____，∠ACB的度数为______；（2）若以A、B、C及点D为顶点的四边形为平行四边形，请写出D点的坐标___________，并在图中画出平行四边形.24．如图是一个三级台阶,它的每一级的长、宽和高分别等于5 cm,3 cm和1 cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?25．小明剪了两张直角三角形纸片，进行了如下的操作：操作一：如图1，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE．（1）如果AC＝6cm，BC＝8cm，则△ACD的周长为cm；（2）如果∠B0，则∠CAD= 度；35操作二：如图2，小明拿出另一张Rt△ABC纸片，将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，若AC＝9cm，BC＝12cm，请求出CD的长．26．如图1所示，等边△ABC 中，AD 是BC 边上的中线，根据等腰三角形的“三线合一”特性，AD 平分∠BAC ，且AD ⊥BC ，则有∠BAD=30°，BD=CD=12AB ．于是可得出结论“直角三角形中， 30°角所对的直角边等于斜边的一半”．请根据从上面材料中所得到的信息解答下列问题：（1）如图2所示，在△ABC 中，∠ACB=90°，BC 的垂直平分线交AB 于点D ，垂足为E ，当BD=5cm ，∠B=30°时，△ACD 的周长= ．（2）如图3所示，在△ABC 中，AB=AC ，∠A=120°，D 是BC 的中点，DE ⊥AB ，垂足为E ，那么BE ：EA= ．（3）如图4所示，在等边△ABC 中，D 、E 分别是BC 、AC 上的点，且AE=DC ，AD 、BE 交于点P ，作BQ ⊥AD 于Q ，若BP=2，求BQ 的长．27．已知四边形ABCD 中，10AB =，8BC =，26CD =，45DAC ∠=︒，15DCA =︒∠．（1）求ADC 的面积．（2）若E 为AB 中点，求线段CE 的长．28．在Rt△ABC 中，∠C=90°，BC=3，AC=4．现在要将交ABC 扩充成等腰三角形，且扩充的部分是以AC为直角边的直角三角形，求扩充后等腰三角形的周长．赵佳同学是这样操作的：如图 1 所示，延长BC 到点 D，使CD=BC，连接AD．所以，△ADB 为符合条件的三角形．则此时△ADB的周长为____________．请你在图2、图3中再设计两种扩充方案，并直接写出扩充后等腰三角形的周长．图2的周长：______________；图3的周长：______________.29．如图（1），Rt△AOB中，∠A=90°，∠AOB=60°，OB=23，∠AOB的平分线OC交AB于C，过O点做与OB垂直的直线ON．动点P从点B出发沿折线BC﹣CO 以每秒1个单位长度的速度向终点O运动，运动时间为t秒，同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动，当点P到达点O时P、Q同时停止运动．（1）求OC、BC的长；（2）设△CPQ的面积为S，求S与t的函数关系式；（3）当P在OC上Q在ON上运动时，如图（2），设PQ与OA交于点M，当t为何值时，△OPM为等腰三角形？求出所有满足条件的t值．30．如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?参考答案1．C【解析】【分析】已知直角三角形两直角边，可以直接利用勾股定理来求斜边.【详解】解：∵在△ABC中，∠C=90°，AC=6cm，BC=8cm，∴斜边22AB=+=.6810故选C.【点睛】运用勾股定理：a，b，c是直角三角形的三条边，c为斜边，则满足c2=a2+b2是解题的关键. 2．B【解析】【分析】根据等腰三角形的性质和勾股定理可求得等腰三角形的腰，据此即可得解．【详解】解：如图：BC=24cm，AD=5cm，△ABC中，AB=AC，AD⊥BC；则BD=DC=BC=6cm；Rt△ABD中，AD=5cm，BD=12cm；由勾股定理，得：AB===13cm,∴△ABC的周长是13+13+24=60cm，故选：B．【点睛】本题主要考查了等腰三角形的性质以及勾股定理的应用．3．D【解析】分析：根据勾股定理的逆定理即可判断．详解：设相邻两个结点的距离为m，则此三角形三边的长分别为3m、4m、5m，∵（3m）2+（4m）2=（5m）2，∴以3m、4m、5m为边长的三角形是直角三角形．（如果三角形的两条边的平方和等于第三边的平方，那么这个三角形是直角三角形）故选D．点睛：此题考查了勾股定理的证明，属于基础题，注意仔细阅读题目所给内容，得到解题需要的信息，比较简单．4．C【解析】【分析】设BD=xcm，由题意表示出AB的长度，根据勾股定理列方程求出x，进而求出△ABC的面积．【详解】设BD=xcm，∵等腰△ABC，∴AB=AC，∵AD⊥BC，∴BD=CD=xcm，∴AB=12（16﹣2x），由勾股定理可得：[12（16﹣2x）]2=x2+42，解得x=3，∴BC=2BD=6cm，∴S△ABC=12×6×4=12cm2．故选C．【点睛】本题关键在于设未知数，根据勾股定理列方程求解．5．C【解析】试题分析：如图，设水深h尺，在Rt△ABC中，AB＝h，AC＝h＋3，BC＝6，由勾股定理得，AC 2＝AB 2＋BC 2，即（h+3）2＝h 2＋62，∴h 2＋6h ＋9=h 2＋36，6h ＝27，解得h=4．5．故答案选C ．考点：勾股定理．6．B 【解析】【分析】首先根据折叠可得CD=AC=3，BC=4，∠ACE=∠DCE ，∠BCF=∠B /CF ，CE ⊥AB ，然后求得△BCF 是等腰直角三角形，进而求得∠B /GD=90°，CE-EF=125，ED=AE=95，从而求得B /D=1，DF=35，在Rt △B /DF 中，由勾股定理即可求得B /F 的长．【详解】解：根据首先根据折叠可得CD=AC=3，B /C=B4，∠ACE=∠DCE ，∠BCF=∠B /CF ，CE ⊥AB ，∴BD=4-3=1，∠DCE+∠B /CF=∠ACE+∠BCF ，∴∠ACB=90°，∴∠ECF=45°，∴△ECF 是等腰直角三角形，∴EF=CE ，∠EFC=45°，∴∠BFC=∠B /FC=135°，∴∠B /FD=90°，∵S △ABC =12AC×BC=12AB×CE ， ∴AC×BC=AB×CE ，∵根据勾股定理求得AB=5，∴CE=125，∴EF=125，22AC CE -=95∴DE=EF-ED=35， ∴B /22B D DF '-=45 故选：B ．【点睛】此题主要考查了翻折变换，等腰三角形的判定和性质，勾股定理的应用等，根据折叠的性质求得相等的角是解本题的关键．7．D【解析】【分析】根据题意画出示意图，设旗杆高度为x，可得AC=AD=x，AB=（x﹣2）m，BC=8m，在Rt△ABC中利用勾股定理可求出x．【详解】设旗杆高度为x，则AC=AD=x，AB=（x﹣2）m，BC=8m，在Rt△ABC中，AB2+BC2=AC2，即（x﹣2）2+82=x2，解得：x=17，即旗杆的高度为17米．故选D．【点睛】考查了勾股定理的应用，解答本题的关键是构造直角三角形，构造直角三角形的一般方法就是作垂线．8．B【解析】【分析】先依据勾股定理可求得OC的长，从而得到OM的长，于是可得到点M对应的数．【详解】解：由题意得可知：OB=2，BC=1，依据勾股定理可知：∴故选：B．【点睛】本题考查勾股定理、实数与数轴，熟练掌握相关知识是解题的关键．9．B【解析】分析：判断是否可以作为直角三角形的三边长，则判断两小边的平方和是否等于最长边的平方即可．详解：A. ()()2221.52 2.5+=，是直角三角形，故此选项错误；B. 222405060，+≠不是直角三角形，故此选项正确；C. 22272425，+=是直角三角形，故此选项错误；D. 22235144⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，是直角三角形，故此选项错误. 故选B.点睛：考查勾股定理的逆定理：如果三角形两条边的平方和等于第三条边的平方，那么这个三角形是直角三角形.10．C【解析】【分析】根据勾股定理和正方形的面积公式，知“生长”1次后，以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积，即所有正方形的面积和是2×1=2；“生长”2次后，所有的正方形的面积和是3×1=3，推而广之即可求解．【详解】设直角三角形的是三条边分别是a ，b ，c ．根据勾股定理，得a 2+b 2=c 2，即正方形A 的面积+正方形B 的面积=正方形C 的面积=1．推而广之，“生长”了2019次后形成的图形中所有的正方形的面积和是2019×1=2019．故选：C ．【点睛】此题主要是能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系．11．5，91612,,555【解析】【分析】运用勾股定理可求解c，由三角形面积公式可求解h，再利用勾股定理可分别求解出k和p. 【详解】由勾股定理得：c2=a2+b2=9+16=25，则c=5；由三角形面积公式可得：ab=ch，则3×4=5×h，则h=125；由勾股定理得：b2=k2+h2，则16= k2+(125)2，则k=165，a2=p2+h2，则9= p2+(125)2，则p=95.【点睛】本题考查了勾股定理和三角形面积公式的应用.12．2【解析】【分析】如图，先利用勾股定理求出BC的长，再利用勾股定理求出CE的长，根据BE=BC-CE即可得答案.【详解】如图，AB=DE=10，AC=6，DC=8，∠C =90°，∴BC=2222106AB AC-=-=8，CE=2222108DE DC-=-=6，∴BE=BC-CE=2（米），故答案为2.【点睛】本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键.13．（22016，0）【解析】∵∠OBC=90°，OB=1，BC=，∵将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍，使OB1=OC，∴OC1=2OC=2×2=4=22，OC2=2OC1=2×4=8=23，OC3=2OC2=2×8=16=24，…，OC n=2n+1，∴OC2015=22016，∵2015÷6=335…5，∴点C2015与点C5在同一射线上，在x轴正半轴，坐标为（22016，0）．点睛：根据直角三角形得出∠BOC=60°，然后求出OC1、OC2、OC3、…、OC n的长度，再根据周角等于360°，每6个为一个循环组，求出点C2015是第几个循环组的第几个点，再根据变化规律写出点的坐标即可．14．113【解析】∵△ABC、△ADE都是以A为直角顶点的等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°，∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，∴在△ABD和△ACE中：AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△ACE，∴BD=CE.①如图1，当∠CFE=90°时，AF⊥DE，∴AF=EF=22AE=23232=，∴CF=AC-AF=5-3=2，∴在Rt△CEF中，223213+=∴13②如图2：当∠CEF=90°时，∠AEC=90°+45°=135°，∵△ABD ≌△ACE ，∴∠ADB=∠AEC=135°，∴∠ADB+∠ADE=135°+45°=180°，∴点B 、D 、F 三点共线，过点A 作AG ⊥DE 于点G ，则AG=DG=22AD=2323⨯=， ∴在Rt △ABG 中，BG=22534-=，∴BD=BG-DG=4-3=1.综上所述，131.1515【解析】∵AD BC ∥，DE BC ⊥．∴DAC ACB ∠=∠，90ADE DEC ∠=∠=︒．∵G 为AF 的中点．∴AG GD GF ==．∴ADG DAG ACB ∠=∠=∠．∴2DGC ADG DAG ACB ∠=∠+∠=∠．∵DG DC =．∵4DG =，1EC =．∴4DC =，∵90DEC ∠=︒． ∴222241DE DC EC =-=-15=．点睛：本题考查了勾股定理，直角三角形斜边上中线性质的应用，解此题的关键是求出DG=DC 后利用勾股定理求DE 的长．16．13【解析】【分析】延长BC 交AD 于点E ，根据等腰直角三角形的性质求出AD ，再求出BE=DE=12AD 并得到BE ⊥AD ，然后求出CE ，在Rt △CDE 中，利用勾股定理列式计算即可得CD 的长．【详解】延长BC 交AD 于点E ，∵∠ABD=90°,∠ABC=45°，∴∠DBC=45°，∵AB=BD ，∴BE=DE=12AD ，BE ⊥AD ， ∵2，∴AD=6，∴DE=BE=3，∵BC=1，∴CE=2，∴CD2=DE2+CE2∴【点睛】本题考查的是等腰三角形和勾股定理，熟练掌握这两点是解题的关键.17．【解析】分析：过点P作PD⊥x轴于点D，由等边三角形的性质可知OD=12OQ=1，再根据勾股定理求出PD的长，故可得出P点坐标，再利用待定系数法求出直线OP的解析式即可．详解：解：过点P作PD⊥x轴于点D，∵△OPQ是边长为2的等边三角形，∴OD=12OQ=12×2=1，在Rt△OPD中，∵OP=2，OD=1，∴PD=∴P（1，设直线OP的解析式为y=kx（k≠0），k，∴直线OP的解析式为y．．点睛：本题考查的是用待定系数法求正比例函数的解析式，先根据题意得出点P 的坐标是解答此题的关键．18．直角三角形【解析】∵2223213AB =+=，2224652BC =+=，2221865AC =+=，∴222AB BC AC +=,∴ABC △为直角三角形．点睛：本题考查了勾股定理逆定理的应用，如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.192222a b +【解析】 22a b a b ++-（）（）2222a b +. 2222a b +204552．【解析】【分析】分两种情形：①如图1中，当∠EDF =90°时，作CH ⊥AB 于H ．只要证明CH =DH ，即可解决问题；②如图2中，当∠DEF =90°时，设DE =x ，则EF =2x ，DF =BD 5，构建方程即可解决问题．【详解】解：如图1中，当∠EDF =90°时，作CH ⊥AB 于H ．在Rt△ACB中，∵AC=2，BC=4，∴AB=2224+=25，∴CH=AC BCAB⋅=455．∵∠ACB=∠AHC=90°，∴∠ACH+∠BCH=90°，∠BCH+∠B=90°，∴∠ACH=∠B=∠F．∵CH∥DF，∴∠F=∠HCE，∴∠ACH=∠HCE，∠DCE=∠DCB，∴∠HCD=45°，∴HC=HD=45．∵AH=22AC CH-=255，∴BD=AB﹣AH﹣DH=25﹣655=455．如图2中，当∠DEF=90°时，设DE=x，则EF=2x，DF=BD=5x．∵AE+DE+BD=25，∴255+x+5x=25，∴x=2﹣255，∴BD=5x=25﹣2．综上所述：BD的长为455或25﹣2．故答案为455或52．【点睛】本题考查了翻折变换、勾股定理、等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会用分类讨论的首先思考问题，属于中考填空题中的压轴题．21．（1）S△ABC32）3【解析】【分析】（1）过点A作AM⊥BC于M，根据已知可得BM=CM=12BC=1，然后根据勾股定理求得AM的长，再利用三角形的面积公式进行求解即可；（2）过点D作DN⊥AC于N，根据已知则可得到△ADM≌△AND，从而得DM=DN，AN=AM=3，继而得CN=AC-AB=2-3，设DM=DN=x，则CD=CM-DM=1-x，在Rt△CDN中，利用勾股定理求得x即可得.【详解】(1) 过点A作AM⊥BC于M，∵△ABC是等边三角形，∴BM=CM=12BC=1，∠BAM=∠CAM=30°，在Rt△CAM中，AM2+CM2=AC2，∴AM 2+12=22 ，∴AM=3，∴S△ABC=12BC·AM =12×2×3=3；（2）∵∠BAD=3∠CAD，∠BAD+∠CAD=∠BAC=60°，∴∠CAD=14∠BAC=15°，∠MAD=∠MAC-∠DAC=15°，∴AD平分∠MAC ，过点D作DN⊥AC于N，则△ADM≌△AND，∴DM=DN，3∴3，设DM=DN=x，则CD=CM-DM=1-x，在Rt△CDN中，DN2+CN2=CD2，x232=(1-x)2 ，解得：3-3，∴3【点睛】本题考查了等边三角形的性质，勾股定理、全等三角形的判定与性质等，添加辅助构造直角三角形进行解题是关键.22．（1）作图见解析；（2）正方形的面积是53，解释见解析.【解析】试题分析：（1）在网格中分别过点A作AD⊥AB于点A，过点B作BC⊥AB于点B，并使AD=AB=BC，再连接CD即可得到所求正方形；（2）如图，由勾股定理易得AB=22+=，再由正方形的面积公式即可计算出正2753方形ABCD的面积了.试题解析：（1）如图，过A、B分别作AD⊥AB，BC⊥AB，并且使得AD=BC=AB，连接CD，则图中所得四边形ABCD为所求正方形；（2）如图，∵图中小方格为的面积为1cm2，∴小方格的边长为1cm，∴AB=222753+=,=AB2=53.∴S正方形ABCD23．（1）5 90°（2）（0，4）或（4，2）或（-4，-4），平行四边形如图.【解析】分析：（1）由勾股定理即可求得AB，BC，AC的值，然后由勾股定理逆定理，可判定△ABC是直角三角形；（2）首先根据题意画出图形，然后根据图可求得平行四边形中D 点的坐标．详解：（1）根据点A 和点B 的坐标可知：AB =()22223++=5；同理可得BC =()22111++=5，AC =2224+=5，所以有(5)2+(25)2=52，即222BC AC AB +=，故△ABC 是直角三角形，且∠ACB =90°. （2）点D 的坐标为（0，4）或（4，2）或（-4，-4），所作平行四边形如图所示.点睛：考查平行四边形的性质, 坐标与图形性质，注意数形结合思想在解题中的应用. 24．蚂蚁爬行的最短线路为13 cm .【解析】试题分析：根据题意，先将图形平面展开（如图所示），根据“两点之间，线段最短”可得蚂蚁爬行的最短距离为线段AB 的长，再用勾股定理求得AB 的长即可.试题解析：如图所示,将台阶展开.∵AC=3×3+1×3=12,BC=5,∴AB 2=AC 2+BC 2=132,∴AB=13(cm).∴蚂蚁爬行的最短线路为13 cm .点睛：本题考查了平面展开-最短路径问题，解决这类问题的基本思路是化曲面问题为平面问题，再用所学的知识解决．25．操作一：（1）14 cm ；（2）∠CAD =20度；操作二：CD=4.5cm【解析】【分析】操作一：（1）依据DE 垂直平分AB ，可得AD=BD ，依据△ACD 的周长=AD+CD+AC=BD+CD+AC=BC+AC 进行计算即可；（2）依据DE 垂直平分AB ，可得AD=BD ，即可得出∠B=∠BAD=35°，再根据Rt △ABC中，∠BAC=90°-35°=55°，即可得到∠CAD=55°-35°=20°；操作二：设CD=DE=x ，则BD=12-x ，Rt △ABC 中，15AB ==,BE=15-9=6，依据Rt △BDE 中，DE 2+BE 2=BD 2，可得方程x 2+62=（12-x ）2，即可得CD=4.5cm ．【详解】操作一：(1)由折叠可得，DE 垂直平分AB ，∴AD =BD ，∴△ACD 的周长为AD +CD +AC =BD +CD +AC =BC +AC =8+6=14(cm )故答案为14；(2)由折叠可得，DE 垂直平分AB ，∴AD =BD ，∴35B BAD ∠=∠=，又∵Rt △ABC 中,903555BAC ∠=-=，∴553520CAD ∠=-=，故答案为20；操作二：∵AC=9cm ，BC=12cm ，∴15AB ==（cm ），根据折叠性质可得AC=AE=9cm ，∴BE=AB ﹣AE=6cm ，设CD=x ，则BD=12﹣x ，DE=x ，在Rt △BDE 中，由题意可得方程x 2+62=（12﹣x ）2，解之得x=4.5，∴CD=4.5cm ．【点睛】考查线段的垂直平分线的性质，三角形的内角和以及勾股定理，掌握勾股定理是解题的关键.26．（1）15cm ；（2）3：1；（3）【解析】整体分析：(1)由“直角三角形中，30°角所对的直角边等于斜边的一半”求AC 的长；(2)连接AD ，由“三线合一”得∠BAD=60°，利用直角三角形中的30°角所对的直角边的性质，分别把BE ，EA 用BD 表示；(3)证明△BAE≌△ACD，得∠BPQ=60°，结合勾股定理求解.解：(1)∵DE 是线段BC 的垂直平分线，∠ACB=90°，∴CD=BD，AD=BD ．又∵在△ABC 中，∠ACB=90°，∠B=30°， ∴AC=12AB ， ∴△ACD 的周长=AC+AB=3BD=15cm ．故答案为15cm ；(2)连接AD ，如图所示．∵在△ABC 中，AB=AC ，∠A=120°，D 是BC 的中点，∴∠BAD=60°．又∵DE⊥AB，，EA=12AD ，AD ，∴EA=1212AD ， ∴BE:AE=3:1．故答案为3:1．(3)∵△ABC 为等边三角形．∴AB=AC，∠BAC=∠ACB=60°，在△BAE 和△ACD 中，AE=CD ，∠BAC=∠ACB，AB=AC ，∴△BAE≌△ACD(SAS)，∴∠ABE=∠CAD．∵∠BPQ 为△ABP 外角，∴∠BPQ=∠ABE+∠BAD．∴∠BPQ=∠CAD+∠BAD=∠BAC=60°，∵BQ⊥AD，∴∠PBQ=30°，∴BP=2PQ=2，∴PQ=1，2BP PQ -2221-3．27．（1）933-（2）5【解析】试题分析：（1）如图，过点C 作CF ⊥AD 于点F ，由此可得∠CFA=90°，由已知条件可得∠CDF=60°，从而可得∠DCF=30°，即可由CD 的长度求得DF 、CF 及AF 的长度，从而可得AD 的长度，就可计算出△ADC 的面积了；（2）在Rt △ACF 中由CF 32CAF=45°可求得AC 的长，结合已知的AB=10、BC=8可的AC 2+BC 2=AB 2，从而可证得∠ACB=90°，结合点E 是AB 的中点，即可得到CE=12AB=5. 试题解析：（1）过点C 作CF AD ⊥，交AD 延长线于点F ，∵45DAC ∠=︒，15DCA ∠=︒，∴CDF DAC DCA ∠=∠+∠ 451560=︒+︒=︒，在Rt CFD 中，26CD =，∴ 162DF CD ==， ()()222226632CF CD DF =-=-=，∴ 326AD AF DF =-=-，∴ 12ADC S AD CF =⨯ ()1236322=⨯-⨯ 933=-．（2）在Rt AFC 中，∵ 45DAC ∠=︒，32CF =∴ 22326AC CF ===，在ABC 中，∵ 2222268AC BC AB +=+=∴ △ABC 是直角三角形，又∵ E 为AB 中点，∴ 1110522CE AB ==⨯=． 28．16 5 403 【解析】试题分析：利用勾股定理可求出AB 的长进而得出△ADB 的周长；再根据题目要求扩充成AC 为直角边的直角三角形，利用AB=BD ，AD=BD ，分别得出答案．试题解析：∵在Rt △ABC 中，∠C=90°，BC=3，AC=4，CD=BC ，∴5=，则AD=AB=5，故此时△ADB 的周长为：5+5+6=16；如图2所示：AD=BD 时，设DC=x ，则AD=x+3，在Rt △ADC 中，（x+3）2=x 2+42，解得：x=76，故AD=3+76=256 ，则此时△ADB 的周长为：256+256+5=403 ；如图3所示：AB=BD 时，在Rt △ADC 中，=则此时△ADB的周长为：故答案为（1）16；（2）403．【点睛】本题主要考查对勾股定理，等腰三角形的性质等知识点的理解和掌握，能通过分类求出等腰三角形的所有情况是解此题的关键．29．（1）OC=2，BC=2；（2）S 与t 的函数关系式是：S=22(02)4)t t ⎧<≤⎪⎪-+<≤；（3）当t 为83时，△OPM 是等腰三角形．【解析】整体分析：（1）先求出OA ，判断OC=CB ，再在Rt △AOC 中用勾股定理列方程求解；（2）分点P 在BC 上，与点C 重合，在CO 上，与点O 重合四种情况分类讨论，注意画出相应的图形，利用三角形的面积公式和三角形面积的和差关系求解；（3）因为等腰三角形的腰不确定，所以需要分三种情况讨论，利用等腰三角形的性质列方程求解.（1）解：∵∠A=90°，∠AOB=60°，∴∠B=30°，∴OA=12由勾股定理得：AB=3，∵OC平分∠AOB，∴∠AOC=∠BOC=30°=∠B，∴OC=BC，在△AOC中，AO2+AC2=CO2，∴(3)²+（3﹣OC）2=OC2，∴OC=2=BC，答：OC=2，BC=2．（2）解：①当P在BC上，Q在OC上时，0＜t＜2，则CP=2﹣t，CQ=t，过P作PH⊥OC于H，∴∠HCP=60°，∠HPC=30°，∴CH=12CP=12（2﹣t），HP=32（2﹣t），∴S△CPQ=12CQ×PH=12×t×3（2﹣t），即S=﹣3t2+3t；②当t=2时，P在C点，Q在O点，此时，△CPQ不存在，∴S=0，③当P在OC上，Q在ON上时2＜t＜4，过P作PG⊥ON于G，过C作CZ⊥ON于Z，∵CO=2，∠NOC=60°，∴3CP=t﹣2，OQ=t﹣2，∠NOC=60°，∴∠GPO=30°，∴OG=12OP=12（4﹣t），34﹣t），∴S△CPQ=S△COQ﹣S△OPQ=12×（t﹣2）×3﹣12×（t﹣2）×34﹣t），即3233．④当t=4时，P 在O 点，Q 在ON 上，如图（3）过C 作CM ⊥OB 于M ，CK ⊥ON 于K ，∵∠B=30°，由（1）知BC=2，∴CM=12BC=1，有勾股定理得：3∵3，∴333，∴S=12PQ×CK=12×2×33 综合上述：S 与t 的函数关系式是：S=2233(02)333(24)t t t ⎧+<≤⎪⎪⎨⎪+<≤⎪；（3）解：如图（2），∵ON ⊥OB ，∴∠NOB=90°，∵∠B=30°，∠A=90°，∴∠AOB=60°， ∵OC 平分∠AOB ，∴∠AOC=∠BOC=30°，∴∠NOC=90°﹣30°=60°， ①OM=PM 时，∠MOP=∠MPO=30°， ∴∠PQO=180°﹣∠QOP ﹣∠MPO=90°， ∴OP=2OQ ，∴2（t ﹣2）=4﹣t ，解得：t=83， ②PM=OP 时，∠PMO=∠MOP=30°， ∴∠MPO=120°，∵∠QOP=60°，∴此时不存在； ③OM=OP 时，过P 作PG ⊥ON 于G ，OP=4﹣t ，∠QOP=60°， ∴∠OPG=30°，∴GO=12（4﹣t ），34﹣t ）， ∵∠AOC=30°，OM=OP ，∴∠OPM=∠OMP=75°， ∴∠PQO=180°﹣∠QOP ﹣∠QPO=45°，∴34﹣t ），∵OG+QG=OQ，∴12（4﹣t）+3（4﹣t）=t﹣2，解得：t=623+综合上述：当t为83或6233+时，△OPM是等腰三角形．30．25cm【解析】分析: 将立体图形展开成平面图形,然后根据两点之间线段距离最短,利用根据勾股定理进行求解,根据立体展开成平面图形情况分类讨论进行进行比较.详解:将长方体沿CH,HE,BE剪开翻折,使面ABCD和面BEHC在同一个平面内,连接AM,如图1,由题意可得:MD=MC+CD=5+10=15cm,AD=20cm,在Rt△ADM中,根据勾股定理得:AM=25cm,将长方体沿CH、GD、GH剪开翻折,使面ABCD和面D CH G在同一个平面内,连接AM，如图2,由题意得:BM=BC+MC=20+5=25（cm）,AB=10cm,在Rt△ABM中,根据勾股定理得:AM29cm,将长方体沿CD、CH、GH剪开翻折,连接AM,如图3,由题意得:AC=AB+BC=10+20=30（cm）,MC=5cm,在Rt△ACM中,根据勾股定理得:AM37cm,∵25＜29＜37则需要爬行的最短距离是25cm.点睛:本题考查了勾股定理的拓展应用,“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.。

第1章勾股定理单元综合测试题 2022—2023学年北师大版数学八年级上册(含答案)

2022-2023学年北师大版八年级数学上册《第1章勾股定理》单元综合测试题（附答案）一．选择题（共10小题，满分40分）1．我国汉代的赵爽在注释《周髀算经》时给出了勾股定理的无字证明，人们称它为“赵爽弦图”，“赵爽弦图”指的是（）A．B．C．D．2．下列各组数中，属于勾股数的是（）A．1，1.7，2B．1.5，2，2.5C．6，8，10D．5，6，73．如图，以Rt△ABC的三边为直径分别向外作半圆，若斜边AB＝3，则图中阴影部分的面积为（）A．9πB．C．D．3π4．如图，在△ABC中，AB＝AC＝10，BC＝12，AD平分∠BAC，则AD等于（）A．6B．7C．8D．95．在△ABC中，AB＝AC＝5，BC＝6，若点P在边AC上移动，则BP的最小值是（）A．5B．6C．4D．4.86．如图，某自动感应门的正上方A处装着一个感应器，离地AB＝2.5米，当人体进入感应器的感应范围内时，感应门就会自动打开．一个身高1.6米的学生CD正对门，缓慢走到离门1.2米的地方时（BC＝1.2米），感应门自动打开，则人头顶离感应器的距离AD等于（）A．1.2米B．1.5米C．2.0米D．2.5米7．如图，一根长25m的梯子，斜立在一竖直的墙上，这时梯足距离底端7m．如果梯子的顶端下滑4m，那么梯足将滑动（）A．7m B．8m C．9m D．10m8．如图，一圆柱高8cm，底面半径为cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是（）A．6cm B．8cm C．10cm D．12cm9．以下列各组数为边长，能构成直角三角形的是（）A．3，4，5B．4，5，6C．1，2，3D．32，42，52 10．现有四块正方形纸片，面积分别是4，6，8，10，从中选取三块按如图的方式组成图案，若要使所围成的三角形是直角三角形，则要选取的三块纸片的面积分别是（）A．4，6，8B．4，6，10C．4，8，10D．6，8，10二．填空题（共7小题，满分28分）11．直角三角形的两直角边长分别为6和8，则斜边中线的长是．12．直角三角形中，两边长为3，4，则第三边长的平方为．13．一个三角形的三边长分别为15cm、20cm、25cm，则这个三角形最长边上的高是cm．14．如图，每个小正方形的边长都相等，A，B，C是小正方形的顶点，则∠ABC的度数为．15．观察右面几组勾股数，①3，4，5；②5，12，13；③7，24，25；④9，40，41；并寻找规律，请你写出有以上规律的第⑤组勾股数：，第n组勾股数是．16．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b，若ab＝8，大正方形的面积为25，则小正方形的边长为．17．在Rt△ABC中，∠C＝90°，若AB﹣AC＝2，BC＝8，则AB的长是．三．解答题（共6小题，满分52分）18．如图是单位长度为1的正方形网格．（1）在图1中画出一条长度的平方为10的线段AB；（2）在图2中画出一个以格点为顶点，面积为5的正方形．。

《第17章勾股定理》期末复习综合提升训练1(附答案)-2020-2021学年人教版八年级数学下册

2021学年人教版八年级数学下册《第17章勾股定理》期末复习综合提升训练1（附答案）1．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AB＝5，角平分线CD交AB于点D，则点D到AC的距离是（）A．B．2C．D．32．已知三角形的三边长分别为a，b，c，且a+b＝10，ab＝18，c＝8，则该三角形的形状是（）A．等腰三角形B．直角三角形C．钝角三角形D．等腰直角三角形3．《九章算术》是我国古代数学的经典著作，书中有一个“折竹抵地”问题：“今有竹高丈，末折抵地，问折者高几何？“意思是：一根竹子，原来高一丈（一丈为十尺），虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子根部三尺远，问：原处还有多高的竹子？（）A．4尺B．4.55尺C．5尺D．5.55尺4．已知a，b，c是△ABC的三条边，满足下列条件的△ABC中，不是直角三角形的是（）A．b2＝c2﹣a2B．∠A：∠B：∠C＝3：4：5C．∠C＝∠A﹣∠B D．a：b：c＝5：12：135．一架长10m的梯子斜靠在墙上，梯子底端到墙的距离为6m．若梯子顶端下滑1m，那么梯子底端在水平方向上滑动了（）A．1m B．小于1m C．大于1m D．无法确定6．已知△ABC中，AB＝10，AC＝17，BC边上的高AD＝8，则△ABC的面积为（）A．168B．84C．84或36D．168或727．如图，正方形ABCD是由四个全等的直角三角形围成的，若CF＝5，AB＝13，则EF的长为．8．在Rt△ABC中，∠C＝90°，若a＝6，b＝8，则斜边c上的高h＝．9．如图，△ABC中，∠C＝90°，BC＝，AB＝10，D在边AC上，且CD＝2AD．（1）D点到AB的距离为；（2）若M、N两点都在边AB上，△DMN是等腰三角形，且∠DMN＝∠BDC，则MN 长为．10．△ABC中，AB＝AC＝6，∠BAC＝120°，P是BC上的动点，Q是AC上的动点（Q不与A，C重合）．（1）线段P A的最小值为；（2）当△ABP为直角三角形时，△PCQ也为直角三角形时，则CQ的长度为．11．如图，在△ABC中，BC＝5，AC＝6，AB＝7，则△ABC的面积S△ABC＝．12．如图，点D在△ABC的边AB上，∠ACB＝90°，∠A＝2∠BCD，BC＝20，BD＝8，则△ABC的周长为．13．如图，在四边形ABCD中，∠B＝90°，AB＝3，BC＝6，点E在BC上，AE⊥DE．且AE＝DE，若EC＝1．则CD＝．14．如图，在Rt△ABC中，∠ACB＝90°，点D在AB的延长线上，BD＝BC，AE平分∠BAC交CD于点E，若AE＝5，则点A到直线CD的距离AH为．15．如图，在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1.0，1.21，1.44，正放置的四个正方形的面积为S1、S2、S3、S4，则S1+S4＝．16．如图，四个全等的直角三角形围成一个大正方形ABCD，中间阴影的部分是一个小正方形EFGH，这样就组成了一个“赵爽弦图”．若AB＝13，AE＝12，则正方形EFGH的面积为．17．如图，Rt△ABC中，∠ACB＝90°，CD是AB边上的高，AC＝8，BC＝6，则AD＝．18．如图，在四边形ABCD中，AD∥BC，∠B＝∠DEC＝90°，AB＝8cm，AD＝24 cm，BC＝26cm，点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．若过点P作PF⊥BC于F，从运动开始算，运动到第秒时，△DEC≌△PFQ．19．将一根24cm的筷子，置于底面直径为5cm、高为12cm的圆柱体中，如图，设筷子露出在杯子外面长为hcm，则h的最小值，h的最大值．20．如图，四边形ABCD中，∠C＝90°，AD＝13，AB＝2，BC＝9，DC＝12，则四边形ABCD的面积为．21．如图，△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF．（1）求证：BF＝2AE；（2）若CD＝2，求AD的长．22．四边形ABCD中，AB＝12，BC＝3，CD＝4，AD＝13，∠C＝90°．（1）求证：∠ABD＝90°；（2）求四边形ABCD的面积．23．为了绿化环境，我县某中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量，∠ADC＝90°，CD＝3米，AD＝4米，AB＝13米，BC＝12米．（1）求出空地ABCD的面积．（2）若每种植1平方米草皮需要300元，问总共需投入多少元？24．如图，学校有一块三角形空地ABC，计划将这块三角形空地分割成四边形ABDE和△EDC，分别摆放“秋海棠”和“天竺葵”两种不同的花卉．经测量，∠EDC＝90°，DC ＝6m，CE＝10m，BD＝14m，AB＝16m，AE＝2m．（1）求DE的长；（2）求四边形ABDE的面积．25．如图，已知△ABC中，∠ACB＝90°，过点B作BD∥AC，交∠ACB的平分线CD于点D，CD交AB于点E．（1）求证：BC＝BD；（2）若AC＝3，AB＝6，求CD的长．26．如图，△ABC中，∠ACB＝90°，AB＝5cm，BC＝3cm，若点P从点A出发，以每秒2cm的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．（1）若点P在AC上，且满足P A＝PB时，求出此时t的值；（2）若点P恰好在∠BAC的角平分线上，求t的值；（3）在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．27．如图，已知在△ABC中，CD⊥AB于D，BD＝9，BC＝15，AC＝20．（1）求CD的长；（2）求AB的长；（3）判断△ABC的形状．参考答案1．解：作DE⊥AC于E，作DF⊥BC于F，在Rt△ACB中，AC＝＝＝4，∵CD是角平分线，∴DE＝DF，∴AC•DE+BC•DF＝AC•BC，即×4DE+×3DE＝×4×3，解得DE＝．故点D到AC的距离是．故选：A．2．解：∵c＝8，∴c2＝64，∵（a+b）2﹣2ab＝100﹣36＝64，∴a2+b2＝c2，∴此三角形是直角三角形．故选：B．3．解：设竹子折断处离地面x尺，则斜边为（10﹣x）尺，根据勾股定理得：x2+32＝（10﹣x）2解得：x＝4.55．答：原处还有4.55尺高的竹子．故选：B．4．解：A、∵b2＝c2﹣a2，∴此三角形是直角三角形，故本选项不符合题意；B、∵∠A+∠B+∠C＝180°，∠A：∠B：∠C＝3：4：5，∴最大角∠C＝×180°＝75°，此三角形不是直角三角形，故本选项符合题意；C、∵∠A﹣∠B＝∠C，∴∠B+∠C＝∠A，∵∠A+∠B+∠C＝180°，∴∠A＝90°，此三角形是直角三角形，故本选项不符合题意；D、∵a：b：c＝5：12：13，∴设a＝5k，b＝12k，c＝13k，∵a2+b2＝（5k）2+（12k）2＝（13k）2＝c2，此三角形是直角三角形，故本选项不符合题意；故选：B．5．解：在△ABC中，∠ACB＝90°，AB＝10米，BC＝6米，由勾股定理得AC＝8米，△A1BC1中，∠C＝90°，A1B1＝10米，A1C＝7米，由勾股定理得B1C＝米，∴BB1＝B1C﹣BC＝（﹣6）米．∵，∴﹣6＞1，∴梯子底端在水平方向上滑动了小于1m，故选：C．6．解：在直角三角形ABD中，根据勾股定理，得BD＝15，在直角三角形ACD中，根据勾股定理，得CD＝6当AD在三角形的内部时，BC＝15+6＝21，所以△ABC的面积为×21×8＝84；当AD在三角形的外部时，BC＝15﹣6＝9，所以△ABC的面积为×9×8＝36．故选：C．7．解：如图，∵正方形ABCD是由四个全等的直角三角形围成的，∴AH＝BE＝CG＝DF，AE＝BG＝CF＝DH，∴EG＝GF＝GH＝HE，∴四边形EGFH为菱形，∵△ABE为直角三角形，∴∠AEB＝∠GEH＝90°，∴四边形EGFH为正方形，∵四边形ABCD为正方形，∴CD＝AB＝13，在Rt△CDF中，∠DFC＝90°，CF＝5，根据勾股定理得，DF＝12，∴GF＝DF﹣DH＝GC﹣FC＝7，在△GEF中，GE＝GF＝7，∠EGF＝90°，根据勾股定理得，EF＝＝7．故答案为：7．8．解：∵∠C＝90°，若a＝6，b＝8，∴c＝＝10，而S△ABC＝a•b＝×6×8＝24，∵斜边c上的高h，∴S△ABC＝c•h，∴24＝×10•h，∴h＝．故答案为：．9．解：（1）过D作DF⊥AB于F，∴D到AB的距离为DF，∵∠C＝90°，BC＝，AB＝10，∴，sin∠A＝，∵CD＝2AD，∴CD＝2，AD＝，故答案为：1；（2）①若以DM，DN为腰，∵∠DMN＝∠BDC，∵△DMN是等腰三角形，DF⊥MN，∴DF平分MN，∴MN＝2MF＝4，②若以DM，MN为腰，∴BD＝，∵DF⊥MN，∴MN＝DM＝，③当ND＝NM时，MN＝DM＝1.25，综上所述，MN长为1.25或4或．故答案为：（1）1；（2）1.25或4或．10．解：（1）作AP⊥BC于P，∵△ABC中，AB＝AC＝6，∠BAC＝120°，∴∠B＝∠C＝30°，由垂线段最短可知，线段P A的最小值为AB＝3．故答案为：3；（2）如①，∠APB＝90°，∠PQC＝90°时，AQ＝AP＝1.5，CQ＝6﹣1.5＝4.5；如②，∠BAP＝90°，∠QPC＝90°时，BP2﹣AP2＝AB2，即BP2﹣（BP）2＝62，解得BP＝±4（负值舍去），由勾股定理得BP＝3，∴BC＝6，∴CP＝2，由勾股定理得CQ＝±4（负值舍去）；∠BAP＝90°，∠PQC＝90°时，CP＝2，由勾股定理得CQ＝±3（负值舍去）．综上所述，CQ的长度为4.5或4或3．故答案为：4.5或4或3．11．解：过点C作CD⊥AB于点D，设BD＝x，则AD＝7﹣x，在Rt△ACD中，CD＝＝，在Rt△BCD中，CD＝＝，∴＝，解得：x＝，∴CD＝CD＝＝＝，∴S△ABC＝AB•CD＝×7×＝6．故答案为：6．12．解：设∠DCB＝α，则∠CAB＝2α，则∠ACD＝∠ACB﹣∠DCB＝90°﹣α，∵∠CBA＝180°﹣∠ACB﹣∠CAB＝90°﹣2α，又∵∠CDA＝∠DCB+∠DBC＝90°﹣2α+α＝90°﹣α，∴∠ACD＝∠CDA＝90°﹣α，∴AC＝AD，设AC＝x，则AD＝AC＝x，∵AC2+BC2＝AB2，∴x2+202＝（8+x）2，∴x2+400＝64+16x+x2，∴x＝21，∴△ABC的周长＝AC+CB+AD+DB＝21+20+8+21＝70．故答案为：70．13．解：过点D作DF⊥BC，交BC延长线于点F，由题意得，BE＝BC﹣EC＝5，∵∠B＝90°，∴∠BAE+∠AEB＝90°，∵AE⊥DE，∴∠AEB+∠DEC＝90°，∴∠BAE＝∠DEC，∵AE＝DE，∠B＝∠DFE＝90°，∴△ABE≌△EFD（AAS），∴EF＝AB＝3，DF＝BE＝5，∴CF＝EF﹣CE＝2，∵∠DFC＝90°，∴DC＝．故答案为：．14．解：∵BC＝BD，∴∠D＝∠BCD，∵AH⊥DH，∴∠H＝∠ACB＝90°，∴∠ACH+∠HAC＝90°，∠ACH+∠BCD＝90°，∴∠HAC＝∠BCD＝∠D，∵AE平分∠CAB，∴∠EAC＝∠EAD，∵∠HAE＝∠HAC+∠EAC，∠AEH＝∠D+∠EAD，∴∠HAE＝∠AEH，∴HA＝HE，∵AE＝5，∴AH＝HE＝AE＝5，故答案为：5．15．解：由勾股定理的几何意义可知：S1+S2＝1，S2+S3＝1.21，S3+S4＝1.44，∴S1+S4＝1.23．故填：1.23．16．解：直角三角形直角边的较短边为，正方形EFGH的面积＝13×13﹣4×＝169﹣120＝49．故答案为：49．17．解：∵AC＝8，BC＝6，∴AB＝＝＝10，∵S△ABC＝×6×8＝×10×CD，∴CD＝．在Rt△ACD中，AD＝＝，故答案为：．18．解：∵AD∥BC，∠B＝∠DEC＝90°，∴∠A＝180°﹣∠B＝90°，∠ADE＝∠DEC ＝90°，∴∠A＝∠B＝∠ADE＝90°，∴四边形ABED是矩形，∴BE＝AD＝24cm，∵BC＝26cm，∴EC＝BC﹣BE＝2cm．∵∠DEC＝90°，PF⊥BC于F，AD∥BC，∴DE＝PF，∠DEC＝∠PFQ＝90°，∴当EC＝FQ＝2cm时△DEC≌△PFQ．设运动时间为t秒，∵点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动，∴BF＝AP＝t，CQ＝3t，0＜t≤．分两种情况：①Q在F的右边时，∵BF+FQ+CQ＝BC，∴t+2+3t＝26，∴t＝6，符合题意；②Q在F的左边时，∵BF﹣FQ+CQ＝BC，∴t﹣2+3t＝26，∴t＝7，符合题意；综上，从运动开始算，运动到第6或7秒时，△DEC≌△PFQ．故答案为：6或7．19．解：当筷子与杯底垂直时h最大，h最大＝24﹣12＝12（cm）．当筷子与杯底及杯高构成直角三角形时h最小，此时，在杯子内部分＝＝13（cm），故h＝24﹣13＝11（cm）．故h的取值范围是11≤h≤12．故答案为：11cm；12cm．20．解：连接BD，∵∠C＝90°，BC＝9，DC＝12，∴BD＝＝＝＝15，∵AB2+AD2＝（2）2+132＝56+169＝225＝DB2，∴△ABD是直角三角形，且∠A＝90°，∴四边形ABCD的面积为：AB•AD+CB•CD＝2×13+×9×12＝13+54，故答案为：13+54．21．（1）证明：∵AD⊥BC，∠BAD＝45°，∴△ABD是等腰直角三角形，∴AD＝BD，∵BE⊥AC，AD⊥BC，∴∠CAD+∠ACD＝90°，∠CBE+∠ACD＝90°，∴∠CAD＝∠CBE，在△ADC和△BDF中，，∴△ADC≌△BDF（ASA），∴BF＝AC，∵AB＝BC，BE⊥AC，∴AC＝2AE，∴BF＝2AE；（2）解：∵△ADC≌△BDF，∴DF＝CD＝2，在Rt△CDF中，CF＝＝＝2，∵BE⊥AC，AE＝EC，∴AF＝CF＝2，∴AD＝AF+DF＝2+2．22．解：（1）∵∠C＝90°，BC＝3，CD＝4，∴BD＝＝＝5，在△ABD中，∵AB2+BD2＝122+52＝144+25＝169＝AD2，∴△ABD是直角三角形，∠ABD＝90°；（2）由图形可知：S四边形ABCD＝S△ABD+S△BCD＝AB•BD+BC•CD＝×12×5+×3×4＝30+6＝36．23．解：（1）连接AC，在Rt△ACD中，AC2＝CD2+AD2＝32+42＝52，在△ABC中，AB2＝132，BC2＝122，而52+122＝132，即AC2+BC2＝AB2，∴∠ACB＝90°，S四边形ABCD＝S△ACB﹣S△ACD＝C•BC﹣AD•CD＝×5×12﹣×4×3＝24（m2）．（2）需费用24×300＝7200（元），答：总共需投入7200元．24．解：（1）在Rt△EDC中，∠EDC＝90°，DC＝6m，CE＝10m，∴m；（2）如图，连接BE，在Rt△EBD中，BD＝14m，ED＝8m，∴BE2＝BD2+ED2＝142+82＝260，∵AB＝16m，AE＝2m，∴AB2+AE2＝162+22＝260，∴AB2+AE2＝BE2，∴△ABE是直角三角形，∠A＝90°，∴S△ABE＝×16×2＝16（m2）．又∵S△BDE＝×14×8＝56（m2）．∴四边形ABDE的面积＝S△ABE+S△BDE＝72（m2）．25．（1）证明：∵∠ACB＝90°，CD平分∠ACB，∴∠BCD＝∠ACD＝∠ACB＝×90°＝45°，∵BD∥AC，∴∠D＝∠ACD＝45°，∴∠D＝∠BCD，∴BC＝BD；（2）解：在Rt△ACB中，BC＝＝＝3，∴BD＝3，∵∠BCD＝∠D＝45°，∴∠CBD＝90°，∴CD＝＝＝3．26．解：（1）设存在点P，使得P A＝PB，此时P A＝PB＝2t，PC＝4﹣2t，在Rt△PCB中，PC2+CB2＝PB2，即：（4﹣2t）2+32＝（2t）2，解得：t＝，∴当t＝时，P A＝PB；（2）当点P在∠BAC的平分线上时，如图1，过点P作PE⊥AB于点E，此时BP＝7﹣2t，PE＝PC＝2t﹣4，BE＝5﹣4＝1，在Rt△BEP中，PE2+BE2＝BP2，即：（2t﹣4）2+12＝（7﹣2t）2，解得：t＝，当t＝6时，点P与A重合，也符合条件，∴当或6时，P在△ABC的角平分线上；（3）在Rt△ABC中，∵AB＝5cm，BC＝3cm，∴AC＝4cm，根据题意得：AP＝2t，当P在AC上时，△BCP为等腰三角形，∴PC＝BC，即4﹣2t＝3，∴t＝，当P在AB上时，△BCP为等腰三角形，①CP＝PB，点P在BC的垂直平分线上，如图2，过P作PE⊥BC于E，∴BE＝BC＝，∴PB＝AB，即2t﹣3﹣4＝，解得：t＝，②PB＝BC，即2t﹣3﹣4＝3，解得：t＝5，③PC＝BC，如图3，过C作CF⊥AB于F，∴BF＝BP，∵∠ACB＝90°，由射影定理得；BC2＝BF•AB，即32＝×5，解得：t＝，∴当时，△BCP为等腰三角形．27．解：（1）在△BCD中，因为CD⊥AB，所以BD2+CD2＝BC2．所以CD2＝BC2﹣BD2＝152﹣92＝144．所以CD＝12．（2）在△ACD中，因为CD⊥AB，所以CD2+AD2＝AC2．所以AD2＝AC2﹣CD2＝202﹣122＝256．所以AD＝16．所以AB＝AD+BD＝16+9＝25．（3）因为BC2+AC2＝152+202＝625，AB2＝252＝625，所以AB2＝BC2+AC2．所以△ABC是直角三角形。

中考数学勾股定理综合练习(含答案)

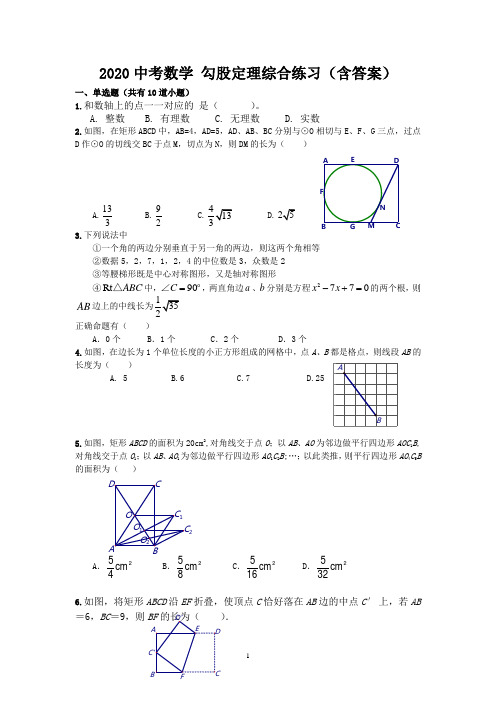
2020中考数学勾股定理综合练习（含答案）一、单选题（共有10道小题）1.和数轴上的点一一对应的是（）。

A. 整数B. 有理数C. 无理数D. 实数2.如图，在矩形ABCD 中，AB=4，AD=5，AD 、AB 、BC 分别与⊙O 相切与E 、F 、G 三点，过点D 作⊙O 的切线交BC 于点M ，切点为N ，则DM 的长为（）A.133B.92D.3.下列说法中①一个角的两边分别垂直于另一角的两边，则这两个角相等 ②数据5，2，7，1，2，4的中位数是3，众数是2 ③等腰梯形既是中心对称图形，又是轴对称图形④Rt ABC △中，90C =o ∠，两直角边a 、b 分别是方程2770x x -+=的两个根，则AB正确命题有（）A ．0个B ．1个C ．2个D ．3个4.如图，在边长为1个单位长度的小正方形组成的网格中，点A 、B 都是格点，则线段AB 的长度为（） A. 5 B.6 C.7 D.255.如图，矩形ABCD 的面积为20cm 2,对角线交于点O ；以AB 、AO 为邻边做平行四边形AOC 1B ,对角线交于点O 1；以AB 、AO 1为邻边做平行四边形AO 1C 2B ;…；以此类推，则平行四边形AO 4C 5B 的面积为（）A ．54cm 2B ．58cm 2C ．516cm 2 D ．532cm 26.如图，将矩形ABCD 沿EF 折叠，使顶点C 恰好落在AB 边的中点C ′上，若AB＝6，BC ＝9，则）．FA CD E MN2A ．4B．C ．4.5D ．57.如图，两个连接在一起的菱形的边长都是1 cm ，一只电子甲虫从点A 开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行，当电子甲虫爬行2014cm 时停下，则它停的位置是( )A ．点FB ．点EC ．点AD ．点C8.如图，正方形网格中，每个小正方形的边长为1，则网格上的三角形ABC 中，边长为无理数的边数是（）A ．0B ．1C ．2D ．39.下列图形都是由边长为1厘米的小正方形连接组成的．按照图形的变化规律，第2009个图形的周长是（）厘米． A 、4018 B 、4020 C 、8036 D 、602710.如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE 。

第一章勾股定理章末综合测试-

第一章勾股定理章末综合测试一. 填空题1. 求图1-1中直角三角形中未知的长度:b=__________,c=____________.b1591024c图1-12. 传说,古埃及人曾用＂拉绳”的方法画直角,现有一根长24厘米的绳子,请你利用它拉出一个周长为24厘米的直角三角形,那么你拉出的直角三角形三边的长度分别为_______厘米,______厘米,________厘米,其中的道理是______________________.3. 直角三角形的两直角边是3,4,则以斜边长为直径的圆的面积是_______________.4. 已知正方形的面积为16cm 2,以这个正方形的边长为边作等边三角形,则其一边上的高的平方等于_____________.5. 等腰三角形的腰长为10,底边上的高为6,则底边的长为__________.6. 斜边长8cm 2的等腰直角三角形的面积等于__________cm 2.7. 如图1-3,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD 的长等于______________.DCA16925BDCAB图1-3 图1-4 图1-58. 已知三角形的三边长分别是2n+1,2n 2+2n, 2n 2+2n+1,则最大角等于_________度. 9. 在∆ABC 中,AB=20,AC=15,高AD=12,则S ABC ∆=__________________. 二. 选择题10. 如图1-4,字母B 所代表的正方形的面积是 ( ) A. 12 B. 13 C. 144 D. 19411. 下列几组数中,不能作为直角三角形三边长度的是 ( ) A. a=7, b=24, c=25; B. a=1.5, b=2, c=2.5C. a=32, b=2, c=45; D. a=15, b=8, c=17 12. 如图1-5,小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( )A. 25B. 12.5;C. 9D. 8.513. 如果梯子的底端离建筑物5米,13米长的梯子可以达到该建筑物的高度是 ( ) A. 12米 B. 13米 C. 14米 D. 15米14. 小强量得家里新购置的彩电荧光屏的长为58厘米,宽为46厘米,则这台电视机的尺寸是(实际测量的误差可不计) ( )A. 9英寸(23厘米);B. 21英寸(54厘米);C. 29英寸(74厘米);D. 34英寸(87厘米) 15. 观察下列几组数据:(1) 8, 15, 17; (2) 7, 12, 15; (3)12, 15, 20; (4) 7, 24, 25. 其中能作为直角三角形的三边长的有( )组A. 1B. 2C. 3D. 4 16. 等边三角形的三条高把这个三角形分成( )个直角三角形A. 8B. 10C. 11D. 12 17. 下列说法中, 不正确的是 ( )A. 三个角的度数之比为1:3:4的三角形是直角三角形B. 三个角的度数之比为3:4:5的三角形是直角三角形C. 三边长度之比为3:4:5的三角形是直角三角形D. 三边长度之比为5:12:13的三角形是直角三角形18. 若三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( ) A. 12 cm B. 10 cm C. 8 cm D. 6 cm19. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( ) A. ab=h B. a 2+b 2=2h 2; C.a 1+b 1=h1 D.21a +21b =21h 三. 解答题20. 如图1-6,一个高1.5米,宽3.6米的大门,需要在相对的顶点间用一条木板加固,求这条木板的长.图1-621. 某零件截面形状如图,由一个直角三角形和一个半圆组成.(1)求出这个零件的截面积;(2)求出这个截面图形的周长(单位:厘米,∏取3.14,结果精确到个位)22. 学习了勾股定理以后,有同学提出”在直角三角形中,三边满足a2+b2=c2,或许其他的三角形三边也有这样的关系’’.让我们来做一个实验!(1)画出任意一个锐角三角形,量出各边的长度(精确到1毫米),较短的两条边长分别是a=______mm;b=_______mm;较长的一条边长c=_______mm. 比较a2+b2=______c2(填写’’>’’ , ”<’’, 或’’=’’);(2)画出任意的一个钝角三角形,量出各边的长度(精确到1毫米),较短的两条边长分别是a=______mm;b=_______mm;较长的一条边长c=_______mm. 比较a2+b2=______c2(填写’’>’’ , ”<’’, 或’’=’’);(3)根据以上的操作和结果,对这位同学提出的问题,你猜想的结论是:_________________.23. 一辆汽车以16千米/时的速度离开甲城市,向东南方向行驶,另一辆汽车在同时同地以12千米/时的速度离开甲城市,向西南方向行驶,它们离开城市3个小时后相距多远?24. 如图,有一个长方体的长,宽,高分别是 6, 4, 4,在底面A 处有一只蚂蚁,它想吃到长方体上面B 处的食物,需要爬行的最短路程是多少?464AB四. 综合题25. 如图,已知:∆ABC 中,CD ⊥AB 于D, AC=4, BC=3, BD=59. (1) 求CD 的长; (2) 求AD 的长; (3) 求AB 的长;(4) ∆ABC 是直角三角形吗?26. 如图,折叠矩形纸片ABCD,先折出对角线BD,再折叠使AD 边与BD 重合,得到折痕DG,若AB=8. BC=6,求AG 的长.DCAG B27. 如图,∠C=90°,D为AC的中点,DE⊥AB于E,请说明BC2=BE2-AE2的理由.CDA E B28. 如图1-12所示, ∆ABC中,∠ACB=90°,AC=BC,P是∆ABC内一点,满足PA=3,PB=1,PC=2,求∠BPC的度数.CPA五. 知识擂台街道的两旁共有45盏街灯,每两盏灯之间间隔30米.每一盏灯的位置正好在对面街道相对的两盏灯的中间,请问这条街道有多长?。

《勾股定理》练习题及答案

《勾股定理》练习题测试1 勾股定理(一)课堂学习检测一、填空题1．若一个直角三角形的两边长分别为12和5，则此三角形的第三边长为______．2．甲、乙两人同时从同一地点出发，已知甲往东走了4km ，乙往南走了3km ，此时甲、乙两人相距______km ．3．如图，有一块长方形花圃，有少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了______m 路，却踩伤了花草．4．如图，有两棵树，一棵高8m ，另一棵高2m ，两树相距8m ，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少要飞______m ．二、选择题5．如图，一棵大树被台风刮断，若树在离地面3m 处折断，树顶端落在离树底部4m 处，则树折断之前高( )．(A)5m (B)7m (C)8m (D)10m6．如图，从台阶的下端点B 到上端点A 的直线距离为( )． (A)212 (B)310 (C)56 (D)58三、解答题7．在一棵树的10米高B 处有两只猴子，一只猴子爬下树走到离树20米处的池塘的A 处；另一只爬到树顶D 后直接跃到A 处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树高多少米?8．在平静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲移到一边，花朵齐及水面，已知红莲移动的水平距离为2米，求这里的水深是多少米?综合、运用、诊断一、填空题9．如图，一电线杆AB 的高为10米，当太阳光线与地面的夹角为60°时，其影长AC 为______米．10．如图，有一个圆柱体，它的高为20，底面半径为5．如果一只蚂蚁要从圆柱体下底面的A 点，沿圆柱表面爬到与A相对的上底面B点，则蚂蚁爬的最短路线长约为______(取3)二、解答题：11．长为4 m的梯子搭在墙上与地面成45°角，作业时调整为60°角(如图所示)，则梯子的顶端沿墙面升高了______m．12．如图，在高为3米，斜坡长为5米的楼梯表面铺地毯，则地毯的长度至少需要多少米?若楼梯宽2米，地毯每平方米30元，那么这块地毯需花多少元?9 10 11 12拓展、探究、思考13．如图，两个村庄A、B在河CD的同侧，A、B两村到河的距离分别为AC＝1千米，BD ＝3千米，CD＝3千米．现要在河边CD上建造一水厂，向A、B两村送自来水．铺设水管的工程费用为每千米20000元，请你在CD上选择水厂位置O，使铺设水管的费用最省，并求出铺设水管的总费用W．测试2 勾股定理(三)学习要求熟练应用勾股定理解决直角三角形中的问题，进一步运用方程思想解决问题．课堂学习检测一、填空题1．在△ABC中，若∠A＋∠B＝90°，AC＝5，BC＝3，则AB＝______，AB边上的高CE＝______．2．在△ABC中，若AB＝AC＝20，BC＝24，则BC边上的高AD＝______，AC边上的高BE＝______．3．在△ABC中，若AC＝BC，∠ACB＝90°，AB＝10，则AC＝______，AB边上的高CD＝______．4．在△ABC中，若AB＝BC＝CA＝a，则△ABC的面积为______．5．在△ABC中，若∠ACB＝120°，AC＝BC，AB边上的高CD＝3，则AC＝______，AB＝______，BC边上的高AE＝______．二、选择题6．已知直角三角形的周长为62+，斜边为2，则该三角形的面积是( )． (A)41 (B)43 (C)21 (D)17．若等腰三角形两边长分别为4和6，则底边上的高等于( )．(A)7(B)7或41 (C)24 (D)24或7三、解答题8．如图，在Rt △ABC 中，∠C ＝90°，D 、E 分别为BC 和AC 的中点，AD ＝5，BE ＝102求AB 的长．9．在数轴上画出表示10-及13的点．综合、运用、诊断10．如图，△ABC 中，∠A ＝90°，AC ＝20，AB ＝10，延长AB 到D ，使CD ＋DB ＝AC ＋AB ，求BD 的长．11．如图，将矩形ABCD 沿EF 折叠，使点D 与点B 重合，已知AB ＝3，AD ＝9，求BE 的长．12．如图，折叠矩形的一边AD ，使点D 落在BC 边的点F 处，已知AB ＝8cm ，BC ＝10cm ，求EC 的长．13．已知：如图，△ABC 中，∠C ＝90°，D 为AB 的中点，E 、F 分别在AC 、BC上，且DE ⊥DF ．求证：AE 2＋BF 2＝EF 2．拓展、探究、思考14．如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2，l2，l3之间的距离为3，求AC的长是多少?15．如图，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去，……已知正方形ABCD的面积S1为1，按上述方法所作的正方形的面积依次为S2，S3，…，S n(n为正整数)，那么第8个正方形的面积S8＝______，第n个正方形的面积S n＝______．测试3 勾股定理的逆定理学习要求掌握勾股定理的逆定理及其应用．理解原命题与其逆命题，原定理与其逆定理的概念及它们之间的关系．课堂学习检测一、填空题1．如果三角形的三边长a、b、c满足a2＋b2＝c2，那么这个三角形是______三角形，我们把这个定理叫做勾股定理的______．2．在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题叫做____________；如果把其中一个命题叫做原命题，那么另一个命题叫做它的____________．3．分别以下列四组数为一个三角形的边长：(1)6、8、10，(2)5、12、13，(3)8、15、17，(4)4、5、6，其中能构成直角三角形的有____________．(填序号)4．在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，①若a2＋b2＞c2，则∠c为____________；②若a2＋b2＝c2，则∠c为____________；③若a2＋b2＜c2，则∠c为____________．5．若△ABC 中，(b －a )(b ＋a )＝c 2，则∠B ＝____________；6．如图，正方形网格中，每个小正方形的边长为1，则网格上的△ABC 是______三角形．7．若一个三角形的三边长分别为1、a 、8(其中a 为正整数)，则以a －2、a 、a ＋2为边的三角形的面积为______．8．△ABC 的两边a ，b 分别为5，12，另一边c 为奇数，且a ＋b ＋c 是3的倍数，则c 应为______，此三角形为______．二、选择题9．下列线段不能组成直角三角形的是( )．(A)a ＝6，b ＝8，c ＝10 (B)3,2,1===c b a (C)43,1,45===c b a (D)6,3,2===c b a 10．下面各选项给出的是三角形中各边的长度的平方比，其中不是直角三角形的是( )． (A)1∶1∶2 (B)1∶3∶4 (C)9∶25∶26(D)25∶144∶169 11．已知三角形的三边长为n 、n ＋1、m (其中m 2＝2n ＋1)，则此三角形( )．(A)一定是等边三角形 (B)一定是等腰三角形 (C)一定是直角三角形(D)形状无法确定综合、运用、诊断一、解答题12．如图，在△ABC 中，D 为BC 边上的一点，已知AB ＝13，AD ＝12，AC ＝15，BD ＝5，求CD 的长．13．已知：如图，四边形ABCD 中，AB ⊥BC ，AB ＝1，BC ＝2，CD ＝2，AD ＝3，求四边形ABCD 的面积．14．已知：如图，在正方形ABCD 中，F 为DC 的中点，E 为CB 的四等分点且CE ＝CB 41，求证：AF ⊥FE ．15．在B 港有甲、乙两艘渔船，若甲船沿北偏东60°方向以每小时8海里的速度前进，乙船沿南偏东某个角度以每小时15海里的速度前进，2小时后，甲船到M岛，乙船到P岛，两岛相距34海里，你知道乙船是沿哪个方向航行的吗?拓展、探究、思考16．已知△ABC中，a2＋b2＋c2＝10a＋24b＋26c－338，试判定△ABC的形状，并说明你的理由．17．已知a、b、c是△ABC的三边，且a2c2－b2c2＝a4－b4，试判断三角形的形状．18．观察下列各式：32＋42＝52，82＋62＝102，152＋82＝172，242＋102＝262，…，你有没有发现其中的规律?请用含n的代数式表示此规律并证明，再根据规律写出接下来的式子．参考答案3测试1 勾股定理(二)1．13或.119 2．5． 3．2． 4．10．5．C ． 6．A ． 7．15米． 8．23米． 9．⋅3310 10．25． 11．.2232- 12．7米，420元． 13．10万元．提示：作A 点关于CD 的对称点A ′，连结A ′B ，与CD 交点为O ．测试2 勾股定理(三)1．;343415,34 2．16，19.2． 3．52，5． 4．.432a 5．6，36，33． 6．C ． 7．D8．.132 提示：设BD ＝DC ＝m ，CE ＝EA ＝k ，则k 2＋4m 2＝40，4k 2＋m 2＝25．AB ＝.1324422=+k m9．,3213,31102222+=+=图略．10．BD ＝5．提示：设BD ＝x ，则CD ＝30－x ．在Rt △ACD 中根据勾股定理列出(30－x )2＝(x ＋10)2＋202，解得x ＝5．11．BE ＝5．提示：设BE ＝x ，则DE ＝BE ＝x ，AE ＝AD －DE ＝9－x ．在Rt △ABE 中，AB 2＋AE 2＝BE 2，∴32＋(9－x )2＝x 2．解得x ＝5．12．EC ＝3cm ．提示：设EC ＝x ，则DE ＝EF ＝8－x ，AF ＝AD ＝10，BF ＝622=-AB AF ，CF ＝4．在Rt △CEF 中(8－x )2＝x 2＋42，解得x ＝3． 13．提示：延长FD 到M 使DM ＝DF ，连结AM ，EM ．14．提示：过A ，C 分别作l 3的垂线，垂足分别为M ，N ，则易得△AMB ≌△BNC ，则.172,34=∴=AC AB 15．128，2n －1．测试3 勾股定理的逆定理1．直角，逆定理． 2．互逆命题，逆命题． 3．(1)(2)(3)．4．①锐角；②直角；③钝角． 5．90°． 6．直角．7．24．提示：7＜a ＜9，∴a ＝8． 8．13，直角三角形．提示：7＜c ＜17．9．D ． 10．C ． 11．C ．12．CD ＝9． 13．.51+14．提示：连结AE，设正方形的边长为4a，计算得出AF，EF，AE的长，由AF2＋EF2＝AE2得结论．15．南偏东30°．16．直角三角形．提示：原式变为(a－5)2＋(b－12)2＋(c－13)2＝0．17．等腰三角形或直角三角形．提示：原式可变形为(a2－b2)(a2＋b2－c2)＝0．18．352＋122＝372，[(n＋1)2－1]2＋[2(n＋1)]2＝[(n＋1)2＋1]2．(n≥1且n为整数)。

勾股定理练习题及答案(共6套)

勾股定理课时练（1）1.在直角三角形ABC 中，斜边AB=1，则AB 222AC BC ++的值是（）A.2B.4C.6D.82.如图18－2－4所示,有一个形状为直角梯形的零件ABCD ，AD ∥BC ，斜腰DC 的长为10cm ，∠D=120°，则该零件另一腰AB 的长是______cm （结果不取近似值）.3.直角三角形两直角边长分别为5和12，则它斜边上的高为_______．4.一根旗杆于离地面12m 处断裂，犹如装有铰链那样倒向地6.飞机在空中水平飞行上方4000米处,过了209.如图，在四边形CD=3，求AB 的长10.如图，一个牧童在小河的南的小屋B 的西8km 2m 的楼道上铺地毯,已知地毯平方米18元，请你帮助计算一下，铺完这个楼道至少需要多少元钱?12.甲、乙两位探险者到沙漠进行探险，没有了水，需要寻找水源．为了不致于走散，他们用两部对话机联系，已知对话机的有效距离为15千米．早晨8：00甲先出发，他以6千米/时的速度向东行走，1小时后乙出发，他以5千米/时的速度向北行进，上午10：00，甲、乙二人相距多远？还能保持联系吗？第一课时答案：1.A ，提示：根据勾股定理得122=+AC BC ，所以AB222AC BC ++=1+1=2；2.4，提示：由勾股定理可得斜边的长为5m ，而3+4-5=2m ，所以他们少走了4步.3.1360，提示：设斜边的高为x ，根据勾股定理求斜边为1316951222==+，再利用面积法得，136011米,由勾所以飞机飞行的速度为CE=60.2⨯，由勾股定理，得CF=)(3416302222cm EF CE =+=+8.解：在直角三角形ABC 中，根据勾股定理，得在直角三角形CBD 中，根据勾股定理，得CD 2=BC 2+BD 2=25+122=169，所以CD=13. 9.解：延长BC 、AD 交于点E.（如图所示）第5题图第8题∵∠B=90°，∠A=60°，∴∠E=30°又∵CD=3，∴CE=6，∴BE=8，设AB=x ，则AE=2x ，由勾股定理。

勾股定理练习题(含答案)

勾股定理练习题一、基础达标:1. 下列说法正确的是（）A.若 a 、b 、c 是△ABC 的三边，则a 2＋b 2＝c 2；B.若 a 、b 、c 是Rt△ABC 的三边，则a 2＋b 2＝c 2；C.若 a 、b 、c 是Rt△ABC 的三边，ο90=∠A ，则a 2＋b 2＝c 2；D.若 a 、b 、c 是Rt△ABC 的三边，ο90=∠C ，则a 2＋b 2＝c 2．2. Rt △ABC 的三条边长分别是a 、b 、c ，则下列各式成立的是（）A ．c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+3．如果Rt △的两直角边长分别为k 2－1，2k （k >1），那么它的斜边长是（）A 、2kB 、k+1C 、k 2－1D 、k 2+1 4. 已知a ，b ，c 为△ABC 三边，且满足(a 2－b 2)(a 2+b 2－c 2)＝0，则它的形状为（）A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形 5．直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（）A ．121B ．120C ．90D ．不能确定 6． △ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（） A ．42 B ．32 C ．42 或 32 D ．37 或 33 7.※直角三角形的面积为S ，斜边上的中线长为d ，则这个三角形周长为（）（A 2d （B d（C ）2d （D ）d8、在平面直角坐标系中，已知点P 的坐标是(3,4)，则OP 的长为（）A ：3B ：4C ：5D ：79．若△ABC 中，AB=25cm ，AC=26cm 高AD=24,则BC 的长为（）A ．17 B.3 C.17或3 D.以上都不对10．已知a 、b 、c 是三角形的三边长，如果满足2(6)100a c --=则三角形的形状是（）A ：底与边不相等的等腰三角形B ：等边三角形C ：钝角三角形D ：直角三角形 11．斜边的边长为cm 17，一条直角边长为cm 8的直角三角形的面积是．12. 等腰三角形的腰长为13，底边长为10，则顶角的平分线为＿＿. 13. 一个直角三角形的三边长的平方和为200，则斜边长为 14．一个三角形三边之比是6:8:10，则按角分类它是三角形． 15. 一个三角形的三边之比为5∶12∶13，它的周长为60，则它的面积是＿＿＿.16. 在Rt △ABC 中，斜边AB=4，则AB 2＋BC 2＋AC 2=_____．17．若三角形的三个内角的比是3:2:1，最短边长为cm 1，最长边长为cm 2，则这个三角形三个角度数分别是，另外一边的平方是．18．如图，已知ABC ∆中，︒=∠90C ，15=BA ，12=AC ，以直角边BC 为直径作半圆，则这个半圆的面积是．19．一长方形的一边长为cm 3，面积为212cm ，那么它的一条对角线长是．ACB二、综合发展:1．如图，一个高4m 、宽3m 的大门，需要在对角线的顶点间加固一个木条，求木条的长．2、有一个直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠，使它落在斜边AB 上，且与AE 重合，你能求出CD 的长吗？3.一个三角形三条边的长分别为cm 15，cm 20，cm 25，这个三角形最长边上的高是多少？4．如图，要修建一个育苗棚，棚高h=3m ，棚宽a=4m ，棚的长为12m ，现要在棚顶上覆盖塑料薄膜，试求需要多少平方米塑料薄膜？AECDB5．如图，有一只小鸟在一棵高13m 的大树树梢上捉虫子，它的伙伴在离该树12m ，高8m 的一棵小树树梢上发出友好的叫声，它立刻以2m/s 的速度飞向小树树梢，它最短要飞多远？这只小鸟至少几秒才可能到达小树和伙伴在一起？15．“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70km/h.如图，，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪正前方30m 处，过了2s 后，测得小汽车与车速检测仪间距离为50m ，这辆小汽车超速了吗？A小汽车小汽车BC观测点答案:一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角．答案: D.2. 解析：本题考察三角形的三边关系和勾股定理.答案：B.3．解析：设另一条直角边为x ，则斜边为（x+1）利用勾股定理可得方程，可以求出x ．然后再求它的周长. 答案：C ．4．解析：解决本题关键是要画出图形来，作图时应注意高AD 是在三角形的内部还是在三角形的外部，有两种情况，分别求解. 答案：C.5．解析: 勾股定理得到：22215817=-，另一条直角边是15，所求直角三角形面积为21158602cm ⨯⨯=．答案: 260cm ．6．解析：本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立．答案:222c b a =+，c ，直角，斜，直角．7．解析:本题由边长之比是6:8:10 可知满足勾股定理，即是直角三角形．答案：直角． 8．解析：由三角形的内角和定理知三个角的度数,断定是直角三角形．答案：︒30、︒60、︒90，3． 9．解析：由勾股定理知道：22222291215=-=-=AC AB BC ，所以以直角边9=BC 为直径的半圆面积为10.125π．答案：10.125π．10．解析:长方形面积长×宽，即12长×3，长4=，所以一条对角线长为5．答案：cm 5．二、综合发展11．解析：木条长的平方=门高长的平方+门宽长的平方．答案：5m ．12解析：因为222252015=+，所以这三角形是直角三角形，设最长边（斜边）上的高为xcm ，由直角三角形面积关系，可得1115202522x ⨯⨯=⨯⋅，∴12=x ．答案：12cm13．解析：透阳光最大面积是塑料薄膜的面积，需要求出它的另一边的长是多少，可以借助勾股定理求出.答案：在直角三角形中，由勾股定理可得：直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是：5×20=100(m 2) ．14．解析：本题的关键是构造直角三角形，利用勾股定理求斜边的值是13m ，也就是两树树梢之间的距离是13m ，两再利用时间关系式求解. 答案：6.5s ． 15．解析：本题和14题相似，可以求出BC 的值，再利用速度等于路程除以时间后比较.BC=40米，时间是2s ，可得速度是20m/s=72km/h ＞70km/h ．答案：这辆小汽车超速了．。

人教版八年级数学下册第十七章勾股定理综合测试题(一)

C5米3米2013-2014学年度第二学期八年级数学试卷（二）（第十七章：勾股定理）一、选一选，看完四个选项后再做决定呀！（每小题3分，共30分）1.满足下列条件的三角形中，不是直角三角形的是（）A.、三内角之比为1∶2∶3B.、三边长的平方之比为1∶2∶3C.、三边长之比为3∶4∶5 D 、.三内角之比为3∶4∶52. 直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长 A 、4 cm B 、8 cmC 、10 cmD 、12 cm3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（） A 、25B 、14C 、7D 、7或254. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) A 、13 B 、8 C 、25 D 、645. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）72425207152024257252024257202415(A)(B)(C)(D)6. 在Rt △ABC 中，∠B ＝90°，BC ＝15，AC ＝17，以AB 为直径作半圆，则此半圆的面积为（）． A ．16π B ．12π C ．10π D ．8π7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) A 、 25 B 、 12.5 C 、 9 D 、 8.58. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A 、等边三角形B 、钝角三角形C 、直角三角形D 、锐角三角形.9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°，AC=30米，AB=50米，如果要在这块空地上种植草皮，按每平方米草皮a 元计算，那么共需要资金（）. A 、0a 元 B 、600a 元 C 、1200a 元 D 、1500a 元10.如图，A B ⊥CD 于B ，△ABD 和△BCE 都是等腰直角三角形，如果CD=17，BE=5，那么AC 的长为（）.A 、12B 、7C 、5D 、13二、填一填，要相信自己的能力！（每小题3分，共18分）11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要_____米.12. 在直角三角形ABC 中，斜边AB =2，则222AB AC BC ++=______. 13. 直角三角形的三边长为连续偶数，则其周长为 .14.如图，在△ABC 中，∠C=90°，BC=3，AC=4.以斜边AB 为直径作半圆，则这个半圆的面积是________.（第14题）（第15题）（第16题）15. 如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___________米.16. 如图，△ABC 中，∠C =90°，AB 垂直平分线交BC 于D 若BC =8，AD =5，则AC 等于______________.三、做一做，要注意认真审题呀！（5大题，17—20题每题10分，21题12分，共52分）17. 如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.密封线内不得答题C18、如图，一架2.5米长的梯子AB ，斜靠在一竖直的墙AC 上，这时梯足B 到墙底端C 的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯足将向外移多少米？19.如图，在平面直角坐标系中，点A 、B 的坐标分别为A （3，1），B （2，4），△OAB 是直角三角形吗？借助于网格，证明你的结论.20. 如图，A 、B 两个小集镇在河流CD 的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A 、B 两镇供水，铺设水管的费用为每千米3万，请你在河流CD 上选择水厂的位置M ，使铺设水管的费用最节省，并求出总费用是多少？21、去年某省将地处A 、B 两地的两所大学合并成了一所综合性大学，为了方便A 、B 两地师生的交往，学校准备在相距2km 的A 、B 两地之间修筑一条笔直公路（即图中的线段AB ），经测量，在A 地的北偏东60°方向、B 地的西偏北45°方向C 处有一个半径为0.7km 的公园，问计划修筑的这条公路会不会穿过公园？为什么？（3≈1.732）ABC DL。

人教版勾股定理综合检测题检测试题及答案(共2套)

数学：第18章勾股定理综合检测题检测试题（1）（总分：120分，时间：90分钟）一、认真选一选，你一定很棒！（每题3分，共30分）1，分别以下列五组数为一个三角形的边长：①6，8，10；②13，5，12 ③1，2，3；④9，40，41；⑤321，421，521.其中能构成直角三角形的有（）组 A.2B.3C.4D.52，已知△ABC 中，∠A ＝12∠B ＝13∠C ，则它的三条边之比为（）A.1∶1∶2 B.1∶3∶2 C.1∶2∶3 D.1∶4∶13，已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（） A.52B.3C.3+2D.332+ 4，如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（） A.12米 B.13米 C.14米 D.15米5，放学以后，萍萍和晓晓从学校分手，分别沿东南方向和西南方向回家，若萍萍和晓晓行走的速度都是40米/分，萍萍用15分钟到家，晓晓用20分钟到家，萍萍家和晓晓家的距离为（）A.600米B.800米C.1000米D.不能确定6，如图1所示，要在离地面5•米处引拉线固定电线杆，使拉线和地面成60°角，若要考虑既要符合设计要求，又要节省材料，则在库存的L 1＝5.2米，L 2＝6.2米，L 3＝7.8米，L 4＝10米四种备用拉线材料中，拉线AC 最好选用（）A.L 1 C.L 3 D.L 47，（2006年山西吕梁课改）如图2，分别以直角△ABC 的三边AB ，BC ，CA 为直径向外作半圆.设直线AB 左边阴影部分的面积为S 1，右边阴影部分的面积和为S 2，则（）A.S 1＝S 2B.S 1＜S 2C.S 1＞S 2D.无法确定8，在△ABC 中，∠C ＝90°，周长为60，斜边与一直角边比是13∶5，则这个三角形三边长分别是A.5，4，3B.13，12，5C.10，8，6D.26，24，109，如图3所示，AB ＝BC ＝CD ＝DE ＝1，AB ⊥BC ，AC ⊥CD ，AD ⊥DE ，则AE ＝（）A.1B.2C.3D.210，直角三角形有一条直角边长为13，另外两条边长都是自然数，则周长为（） A.182 B.183 C.184 D.185 二、仔细填一填，你一定很准！（每题3分，共24分）11，根据下图中的数据，确定A ＝_______，B ＝_______，x ＝_______.12，直角三角形两直角边长分别为5和12，则它斜边上的高为_______. 13，直角三角形的三边长为连续偶数，则这三个数分别为__________.14，如图5，一根树在离地面9米处断裂，树的顶部落在离底部12米处.树折断之前有______米. 15，如果一个三角形的三个内角之比是1∶2∶3，且最小边的长度是8，最长边的长度是________. 16，在△ABC 中，AB ＝8cm ，BC ＝15cm ，要使∠B ＝90°，则AC 的长必为______cm.17，[2008年河北省]如图是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若6AC =，5BC =，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是．18，甲、乙两只轮船同时从港口出发，甲以16海里/时的速度向北偏东75°的方向航行，乙以12海里/时的速度向南偏东15°的方向航行，若他们出发1.5小时后，•两船相距＿＿＿海里. 三、细心做一做，你一定会成功！（共66分）19，古埃及人用下面方法画直角：把一根长绳打上等距离的13个结，然后用桩钉成如图所示的一AB CABC图25mBCAD图1BCAED 图3图5图420，从旗杆的顶端系一条绳子，垂到地面还多2米，小敏拉起绳子下端绷紧，刚好接触地面，发现绳子下端距离旗杆底部8米，小敏马上计算出旗杆的高度，你知道她是如何解的吗？21，如图7，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km 处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？22，（1）四年一度的国际数学家大会于2002年8月20日在北京召开，大会会标如图8，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13，每个直角三角形两直角边的和是5，求中间小正方形的面积.（2）现有一张长为6.5cm，宽为2cm的纸片，如图9，请你将它分割成6块，再拼合成一个正方形.（要求：先在图9中画出分割线，再画出拼成的正方形并标明相应数据）23，清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日，西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为3、4、5的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数（面积），以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”.用现在的数学语言表述是：“若直角三角形的三边长分别为3、4、5的整数倍，设其面积为S ，则第一步：6S＝m；第二步：m＝k；第三步：分别用3、4、5乘以k，得三边长”.（1）当面积S等于150时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；（2）你能证明“积求勾股法”的正确性吗？请写出证明过程.24，学校科技小组研制了一套信号发射、接收系统.在对系统进行测试中，如图10，小明从路口A处出发，沿东南方向笔直公路行进，并发射信号，小华同时从A处出发，沿西南方向笔直公路行进，并接收信号.若小明步行速度为39米／分，小华步行速度为52米／分，恰好在出发后30分时信号开始不清晰.（1）你能求出他们研制的信号收发系统的信号传送半径吗？（以信号清晰为界限）（2）通过计算，你能找到题中数据与勾股数3、4、5的联系吗？试从中寻找求解决问题的简便算法.图6AB小河东北牧童小屋图7图8 图9北A图10数学：第18章勾股定理综合检测题检测试题（1）参考答案：一、1，B ；2，B ；3，D ；4，A ；5，C .点拨：画出图形，东南方向与西南方向成直角；6，B .点拨：在Rt △ACD 中，AC ＝2AD ，设AD ＝x ，由AD 2+CD 2＝AC 2，即x 2+52＝(2x )2，x ＝253≈2.8868，所以2x ＝5.7736；7，A ；8，D .点拨：设斜边为13x ，则一直角边长为5x ，另一直角边为22(13)(5)x x -＝12x ，所以 13x +5x +12x ＝60，x ＝2，即三角形分别为10、24、26；9，D .点拨：AE ＝22DE AD +＝221CD AC++＝2211BC AB+++＝211++＝2；10，A .二、11，15、144、40；12，1360；13，6、8、10；14，24；15，16；16，17；17，：76 ；18，30.三、19，设相邻两个结点的距离为m ，则此三角形三边的长分别为3m 、4m 、5m ，有(3m )2+(4m )2＝(5m )2，所以以3m 、4m 、5m 为边长的三角形是直角三角形.20，15m.21，如图，作出A 点关于MN 的对称点A ′，连接A ′B 交MN 于点P ，则A ′B 就是最短路线.在Rt △A ′DB 中，由勾股定理求得A ′B ＝17km.22，（1）设直角三角形的两条边分别为a 、b （a ＞b ），则依题意有22513a b a b +=⎧⎨+=⎩由此得ab＝6，(a －b )2＝(a+b)2－4ab ＝1，所以a －b ＝1，故小正方形的面积为1.（2）如图：23，（1）当S ＝150时，k ＝m＝1502566S ==＝5，所以三边长分别为：3×5＝15，4×5＝20，5×5＝25；（2）证明：三边为3、4、5的整数倍，设为k 倍，则三边为3k ，4k ，5k ，•而三角形为直角三角形且3k 、4k 为直角边.其面积S ＝12(3k )·(4k )＝6k 2，所以k 2＝6S，k ＝6S （取正值），即将面积除以6，然后开方，即可得到倍数.24，（1）利用勾股定理求出半径为1950米；（2）小明所走的路程为39×30＝3×13×30，小华所走的路程为52×30＝4×13×30，根据前面的探索，可知勾股数3、4、5的倍数仍能构成一组勾股数，故所求半径为5×13×30=1950（米）.ABDPNM数学：第18章勾股定理综合检测题检测试题（2）一﹑选择题(每小题3分, 共30分)1. 一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（）A . 4B . 8C . 10D . 122.小丰的妈妈买了一部29英寸(74cm)的电视机,下列对29英寸的说法中正确的是( ) A. 小丰认为指的是屏幕的长度 B. 小丰的妈妈认为指的是屏幕的宽度 C. 小丰的爸爸认为指的是屏幕的周长 D. 售货员认为指的是屏幕对角线的长度3.如图1，中字母A 所代表的正方形的面积为( ) A. 4 B. 8 C. 16 D. 644. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( ) A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等腰三角形5. 一直角三角形的一条直角边长是7cm , 另一条直角边与斜边长的和是49cm , 则斜边的长( ) A. 18cm B. 20 cm C. 24 cm D. 25cm6. 适合下列条件的△ABC 中, 直角三角形的个数为( ) ①;51,41,31===c b a ②,6=a ∠A=450;③∠A=320, ∠B=580;④;25,24,7===c b a⑤.4,2,2===c b aA. 2个B. 3个C. 4个D. 5个 7. 在⊿ABC 中，若1,2,122+==-=n c n b n a ，则⊿ABC 是（）A . 锐角三角形B . 钝角三角形C . 等腰三角形D . 直角三角形8. 直角三角形斜边的平方等于两条直角边乘积的2倍, 这个三角形有一个锐角是( ) A. 15° B. 30° C. 45° D. 60° 9.已知，如图2，长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为（） 2222北方向航行，另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行，离开港口2小时后，则两船相距（） A ．25海里B ．30海里C ．35海里D ．40海里二﹑填空题 (每小题3分, 共24分)11. (2008年湖州市)利用图（1）或图（2）两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理，这个定理称为，该定理的结论其数学表达式是．12.如图5，等腰△ABC 的底边BC 为16, 底边上的高AD 为6, 则腰长AB 的长为____________. 13.如图6，某人欲横渡一条河，由于水流的影响，实际上岸地点C 偏离欲到达点B200m ，结果他在水中实际游了520m ，求该河流的宽度为_________ m.14. 小华和小红都从同一点O 出发，小华向北走了9米到A 点，小红向东走了12米到了B 点，则________=AB 米．15. 一个三角形三边满足(a+b)2-c 2＝2ab, 则这个三角形是三角形.16. 木工做一个长方形桌面, 量得桌面的长为60cm, 宽为32cm, 对角线为68cm, 这个桌面(填”合格”或”不合格”).17. 直角三角形一直角边为cm 12，斜边长为cm 13，则它的面积为．18. 如图7，一个三级台阶，它的每一级的长宽和高分别为20、3、2，A 和B 是这个台阶两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物，则蚂蚁沿着A289225（图1）（图4）（图5） AB C200m520mDCBA（图6）D CB AOA BEFD北南 A东（图3）D ˊABCD A ˊB ˊC ˊ三、解答题 (共66分)19. (8分) 如图，有一只小鸟从小树顶飞到大树顶上，请问它飞行的最短路程是多少米？（先画出示意图，然后再求解）20. (8分)如图, 在△ABC 中, AD ⊥BC 于D, AB=3, BD=2, DC=1, 求AC 2的值. AB D C21. (10分) “中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪正前方30米处，过了2秒后，测得小汽车与车速检测仪间距离为50米，这辆小汽车超速了吗？22. (10分)小明的叔叔家承包了一个矩形鱼池，已知其面积为48m 2，其对角线长为10m ，为建栅栏，要计算这个矩形鱼池的周长，你能帮助小明算一算吗？23．(10分)印度数学家什迦逻（1141年-1225年）曾提出过“荷花问题”： “平平湖水清可鉴，面上半尺生红莲；出泥不染亭亭立，忽被强风吹一边，渔人观看忙向前，花离原位二尺远；能算诸君请解题，湖水如何知深浅？”24．(10分)如图，A 城气象台测得台风中心在A 城正西方向320km 的B 处，以每小时40km 的速度向北偏东60°的BF 方向移动，距离台风中心200km 的范围内是受台风影响的区域.（1） A 城是否受到这次台风的影响？为什么？（2）若A 城受到这次台风影响，那么A 城遭受这次台风影响有多长时间？四、创新探索题（10分）一只蚂蚁如果沿长方体的表面从A 点爬到B ’点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm 、宽为1cm 、高为4cm.八年级勾股定理单元检测题参考答案（2）一1.C 2.D 3.D 4.C 5.D 6.A 7.D 8.C 9.A 10.D 二11、勾股定理，222ab c +=；12、10；13、480； 14、15；15、直角；16、合格；17、观测点BCA东北 FE AB30；18、25. 三19、13米 20、AC 2＝6 21、20 v米/秒＝72千米/时＞70千米/时，超速。

(完整版)勾股定理综合测考试试题

1 / 3勾股定理全章综合测试题（120分）一。

选择题(每小题3分，共30分)1. △ABC 中, AD ⊥BC 于D ，AB=3，BD=2，DC=1，则AC 等于（） A. 6. B.6 C.5 D.42.（如图）在Rt △ABC 中，∠C=90°,D 为BC 上一点，∠DAC=30°， BD=2，AB=32，则AC 的长是（） A.3 B. 23 C. 3 D.323 3．△ABC 中，∠B=30°,∠C=45°,AB=8, 则AC 等于( ) A .4 B.24 C.34 D.64 4.等腰三角形一腰上的高是a, 且这条高与底边的夹角为60°，则这个三角形的面积为（）A.22a B.23a C.2321a D.2331a 5. △ABC 在下列条件中不是直角三角形的是（）A.a ﹕b ﹕c=1﹕3﹕2B.222c a b -= C.∠C=2∠A-∠B D. ∠A ﹕∠B ﹕∠C=1﹕2﹕36.一个直角三角形斜边的平方等于两条直角边乘积的2倍，则这个三角形中有一个角是（）A.15°B.30°C. 45°D. 75°7.直角三角形两条直角边上的中线长分别是4和7，则这个直角三角形的面积是（）A ．133 B. 64 C.136 D.以上都不对8.在直角三角形中，两直角边分别为a ﹑b ，斜边为c ，斜边上的高为h ，则（）A.c b a 111=+ B. 2222h b a =+ C.22111b a h +=D.bah =1 9．已知三角形三内角之比为1﹕2﹕3，它的最长边为10，则此三角形的面积为（） A.20 B.103 C.35 D.2325 10. (如图)在△ABC 中，AC=8，BC=6，在△ABE 中，DE 为AB 边上的高， DE=12，60=∆ABE S ，则△ABC 的面积为（）A.24B.48C.64D.72二．填空题（(每小题3分，共30分)11．在RT △ABC 中，∠C=90°,三内角A 、B 、C 的对边分别为a 、b 、c ，当∠A=30°时， a ﹕b ﹕c= ；当∠A=45°时, a ﹕b ﹕c= ；12.直角三角形的两直角边长为8和10，则斜边上的高为。

第一章勾股定理综合素质评价

第一章勾股定理综合素质评价一、选择题(每题3分，共30分)1．如图，在Rt△ABC中，∠A＝90°，BC＝2.5 cm，AC＝1.5 cm，则AB的长为() A．3.5 cm B．2 cm C．3 cm D．4 cm(第1题)(第3题)(第4题)2．【教材P16复习题T2改编】下列长度的线段能构成直角三角形的一组是() A．30，40，50 B．7，12，13C．5，9，12 D．3，4，63．【教材P7习题T2改编】历史上对勾股定理的一种验证方法采用了如图所示的图形，其中两个全等直角三角形的边AE，EB在一条直线上，其中用到的面积相等的关系式是()A．S△EDA＝S△CEB B．S△EDA＋S△CEB＝S△CDEC．S四边形CDAE＝S四边形CDEB D．S△EDA＋S△CDE＋S△CEB＝S四边形ABCD 4．如图，在Rt△ABC中，∠ACB＝90°，若AB＝15 cm，则正方形ADEC和正方形BCFG的面积之和为()A．150 cm2B．200 cm2C．225 cm2D．无法计算5．【教材P14习题T1改编】如图，阴影部分是一个长方形，则长方形的面积是() A．3 cm2B．4 cm2C．5 cm2D．6 cm2(第5题)(第7题)6．满足下列条件的△ABC，不是．．直角三角形的为()A．∠A＝∠B－∠C B．∠A∶∠B∶∠C＝1∶1∶2C．b2＝a2－c2D．a∶b∶c＝2∶3∶47．如图，在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，DE⊥AB，垂足为点E，则DE等于()A.1013 B.1513 C.6013 D.75138．【教材P15习题T5改编】【2021·襄阳】我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭(j iā)生其中央，出水一尺，引葭赴岸，适与岸齐，问水深几何”．(丈、尺是长度单位，1丈＝10尺)其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面(如图，单位：尺)，水的深度是多少？则水深为()A．10尺B．11尺C．12尺D．13尺(第8题)(第9题)(第10题)9．【2020·恩施州】如图，正方形ABCD的边长为4，点E在AB上且BE＝1，F 为对角线AC上一动点，则△BFE周长的最小值为()A．5 B．6 C．7 D．810．如图，圆柱的底面直径为16π，BC＝12，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离为()A．10 B．12 C．20 D．14二、填空题(每题3分，共24分)11．请任意写出一组勾股数：__________．12．如图，某人从A点出发欲横渡一条河，由于水流的影响，实际上岸地点C 偏离欲到达地点B 300 m，结果他在水中实际游了500 m，则该河的宽度为__________．(第12题)(第13题)(第15题)(第16题)13．如图，在Rt△ABC中，∠B＝90°，AB＝3 cm，AC＝5 cm，将△ABC折叠，使点C与点A重合，得到折痕DE，则△ABE的周长等于__________．c－b＝0，14．已知a，b，c是△ABC的三边长，且满足关系式(a2－c2－b2)2＋||则△ABC的形状为____________________．15．【中考·邵阳】公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾a＝6，弦c＝10，则小正方形ABCD的面积是________．16．【2021·玉林】如图，某港口P位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A，B处，且相距20海里，如果知道甲船沿北偏西40°方向航行，则乙船沿________方向航行．17．【中考·南京】无盖圆柱形杯子的展开图如图所示．将一根长为20 cm的细木筷斜放在该杯子内，木筷露在杯子外面的部分至少有________cm.(第17题)(第18题)18．【2020·雅安】对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O.若AD＝2，BC＝4，则AB2＋CD2＝________．三、解答题(每题11分，共66分)19．如图，在锐角三角形ABC中，高AD＝12，边AC＝13，BC＝14，求AB的长．20．如图，在4×4的正方形网格中，每个小正方形的边长都是1.线段AB，AE分别是图中两个1×3的长方形的对角线，请你说明：AB⊥AE.21．【教材P14习题T3变式】某消防部队进行消防演练．在模拟演练现场，有一建筑物发生了火灾，消防车到达后，发现离建筑物的水平距离最近为12 m，如图，即AD＝BC＝12 m，此时建筑物中距地面12.8 m高的P处有一被困人员需要救援．已知消防车的车身高AB是3.8 m，问此消防车的云梯至少应伸长多少米？22．如图，在四边形ABCD中，AB＝AD＝2，BC＝3，CD＝1，∠A＝90°，求∠ADC的度数．23．【教材P15习题T4变式】如图，长方体的底面(正方形)边长为3 cm，高为5 cm.若一只蚂蚁从点A开始经过四个侧面爬行一圈到达点B，求蚂蚁爬行的最短路径有多长．24．如图，在长方形ABCD中，DC＝5 cm，在DC上存在一点E，沿直线AE把△AED折叠，使点D恰好落在BC边上，设落点为F. 若△ABF的面积为30cm2，求△ADE的面积．第一章勾股定理综合素质评价答案一、1.B 2.A 3.D 4.C 5.C 6.D7.C8．C9 .B点技巧：根据B，D两点关于AC对称，利用对称的性质将线段和的最小值转化为一条线段的长(可求解)．点拨：如图，连接ED交AC于点F，连接BF.因为四边形ABCD是正方形，所以点B与点D关于AC对称．所以BF＝DF.所以△BFE的周长＝BF＋EF＋BE＝DE＋BE，此时△BFE的周长最小．根据勾股定理易求DE＝5，所以△BFE的周长最小为DE＋BE＝5＋1＝6.10．A点拨：将圆柱的侧面沿DA展开，如图，连接BC，AS，则AB＝12×16π×π＝8，BS＝12BC＝6.在Rt△ABS中，由勾股定理得AS＝10，即动点P从点A沿着圆柱的侧面移动到点S的最短距离为10.二、11.3，4，5(答案不唯一)12.400 m13.7 cm14．等腰直角三角形15.416.北偏东50°17.518.20点思路：由勾股定理得AB2＋CD2＝AO2＋BO2＋CO2＋DO2，AD2＋BC2＝AO2＋DO2＋BO2＋CO2，所以AB2＋CD2＝AD2＋BC2＝22＋42＝20.三、19.解：在Rt△ADC中，AC＝13，AD＝12，由勾股定理得CD2＝AC2－AD2＝25，所以CD＝5.因为BC＝14，所以BD＝BC－CD＝9.在Rt△ABD中，由勾股定理得AB2＝AD2＋BD2＝225，所以AB＝15. 20．解：如图，连接BE.因为AE2＝12＋32＝10，AB2＝12＋32＝10，BE2＝22＋42＝20，所以AE2＋AB2＝BE2.所以△ABE是直角三角形，且∠BAE＝90°，即AB⊥AE.21．解：由题意知CD＝AB＝3.8 m，所以PD＝PC－CD＝12.8－3.8＝9(m)．在Rt△ADP中，AP2＝AD2＋PD2，所以AP2＝122＋92.所以AP＝15 m.答：此消防车的云梯至少应伸长15 m.22．解：连接BD.在Rt△BAD中，因为AB＝AD＝2，所以∠ADB＝45°，BD2＝AD2＋AB2＝22＋22＝8.在△BCD中，因为BD2＋CD2＝8＋1＝9＝BC2，所以△BCD是直角三角形，且∠BDC＝90°.所以∠ADC＝∠ADB＋∠BDC＝45°＋90°＝135°.23．解：将长方体的侧面展开如图所示，连接AB′.因为在Rt△AA′B′中，AA′＝12 cm，A′B′＝5 cm，所以AB′2＝AA′2＋A′B′2＝169.所以AB′＝13 cm.所以蚂蚁爬行的最短路径长为13 cm. 24．解：由折叠可知AD＝AF，DE＝EF.由S△ABF ＝12BF·AB＝30 cm2，AB＝DC＝5 cm，得BF＝12 cm.在Rt△ABF中，由勾股定理得AF2＝AB2＋BF2＝52＋122＝169，所以AF＝13 cm.所以BC＝AD＝AF＝13 cm.设DE＝x cm，则EC＝(5－x)cm，EF＝x cm.在Rt△ECF中，FC＝13－12＝1(cm)，由勾股定理得EC2＋FC2＝EF2，即(5－x)2＋12＝x2，解得x＝13 5.所以DE＝135cm.所以△ADE的面积为12AD·DE＝12×13×135＝16.9 (cm2)．。

勾股定理应用综合练习1

勾股定理的应用
• 1．如图,某人到岛上去探宝，从A处登陆后先往东走4km，又往北走1.5km，遇到障碍后又往西走2km，再折回向北走到4.5km处往东一拐，仅走0.5km就找到宝藏。问登陆点A与宝藏埋藏点B之间的距离是多少？
• 2．如图，将一根25㎝长的细木棒放入长、宽、高分别为8
㎝、6㎝和10
• 14、如图所示,有一条小路穿过长方形的草地ABCD,若 AB=60m,BC=84m,AE=100m,• 则这条小路的面积是多少?
• 15、如图，已知在△ABC中，CD⊥AB于D，AC＝20，BC ＝15，DB＝9。 • (1)求DC的长。 • (2)求AB的长。
• 17、“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70 km/h.如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪正前方30 m处，过了2s后，测得小汽车与车速检测仪间距离为50 m，这辆小汽车超速了吗？
• 18、如图一个圆柱，底圆周长6cm，高4cm，一只蚂蚁沿外壁爬行，要从A点爬到B点，则最少要爬行多少cm？
• 19.已知：如图，∠B=∠D=90°，∠A=60°，AB=4， CD=2。求：四边形ABCD的面积。
A
D E C
B
• 20．有一个长方体盒子，它的长是70cm，宽和高都是 50cm．在A点处有一只蚂蚁，它想吃到B点处的食物．那么它爬行的最短路程是多少
• 8.已知如图，在ΔABC中，∠ACB=90°，AB=5cm, BC=3cm, CD⊥AB于D，求CD的长。
• 9．如图,一梯子AB长25m顶端A斜靠在墙AC上,梯子底端离墙7m,则梯子的顶端离地面多远？如果梯子的底端在水平面上向墙外滑动8m,则梯子的顶端下滑多远？

人教版八年级下册数学第17章《勾股定理》章末综合测试题(含答案)

人教版八年级下册数学第17章《勾股定理》章末综合测试题一．选择题（共10小题，满分30分）1．判断下列各组数能作为直角三角形三边的是（）A．3，4，6B．4，5，7C．2，3，D．7，6，2．已知三角形的三边分别为6，8，10，则最长边上的高等于（）A．10B．14C．4.8D．2.43．如图，在△ABC中，AB＝AC＝10，BC＝12，AD平分∠BAC，则AD等于（）A．6B．7C．8D．94．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别是9、16、1、9，则最大正方形E的边长是（）A．35B．C．70D．无法确定5．下面的三角形中：①△ABC中，∠C＝∠A﹣∠B；②△ABC中，∠A：∠B：∠C＝1：2：3；③△ABC中，a：b：c＝5：12：13；④△ABC中，三边长分别为，其中，直角三角形的个数有（）A．1个B．2个C．3个D．4个6．如图，分别以数轴的单位长度1和2为直角边长作Rt△OBC，然后以点B为圆心，线段BC的长为半径画弧，交数轴于点A，那么点A所表示的数为（）A．B．1+C．+2D．3.27．如图，在Rt△ABC中，∠ACB＝90°，AE为△ABC的角平分线，且ED⊥AB，若AC＝6，BC＝8，则BD的长（）A．2B．3C．4D．58．小明准备测量一段河水的深度，他把一根竹竿直插到离岸边6米远的水底，竹竿高出水面2米，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（）A．7m B．8m C．9m D．10m9．已知直角三角形纸片的两条直角边长分别为m和3（m＜3），过锐角顶点把该纸片剪成两个三角形，若这两个三角形都为等腰三角形，则（）A．m2+6m+9＝0B．m2﹣6m+9＝0C．m2+6m﹣9＝0D．m2﹣6m﹣9＝0 10．如图，Rt△ACB中，∠ACB＝90°，AB＝13cm，AC＝5cm，动点P从点B出发沿射线BC以2cm/s的速度运动，设运动时间为ts，当△APB为等腰三角形时，t的值为（）A．或B．或12或4C．或或12D．或12或4二．填空题（共6小题，满分18分）11．若一个直角三角形的两直角边长分别是1、2，则第三边长为．12．如图，已知在Rt△ABC中，∠A＝90°，AB＝3，BC＝5，分别以Rt△ABC三条边为直径作半圆，则图中阴影部分的面积为．13．如图，在平面直角坐标系中，A（8，0），B（0，6），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C的坐标为．14．如图，在△ABC中，AB＝5，AC＝4，BC＝3，分别以点A、点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN交AB于点O，连接CO，则CO的长为．15．如图，斜靠在一面墙上的一根竹竿，它的顶端A距离地面的距离AO为4m，底端B远离墙的距离BO为3m，当它的顶端A下滑2m时，底端B在地面上水平滑行的距离是m．16．如图①，是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成．若直角三角形一个锐角为30°，将各三角形较短的直角边分别向外延长一倍，得到图②所示的“数学风车”设AB＝a，则图中阴影部分面积为（用含a的代数式表示）三．解答题（共8小题，满分52分）17．在Rt△ABC中，∠C＝90°，a、b、c分别表示∠A、∠B、∠C的对边．（1）如图1，已知：a＝7，c＝25，求b；（2）如图2，已知：c＝25，a：b＝4：3，求a、b．18．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，AC＝12，BC＝5，求BD的长．19．如图，在4×4的正方形网格中，每个小正方形的边长都为1．（1）△ABC的周长为；（2）∠ABC＝度；（3）△ABC的面积为．20．某港口P位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行20nmile，“海天”号每小时航行15nmile，它们离开港口两个小时后，“远航”号到达A处，“海天”号到达B处，A，B相距50nmile，且知道“远航”号沿东北方向航行，那么“海天”号沿什么方向航行？21．如图，小明将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端9米处，发现此时绳子底端距离打结处约3米，请算出旗杆的高度．22．为了绿化环境，我县某中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量，∠ADC＝90°，CD＝6m，AD＝8m，AB＝26m，BC＝24m，（1）求出空地ABCD的面积．（2）若每种植1平方米草皮需要200元，问总共需投入多少元？23．在Rt△ABC中，∠B＝90°，AB＝3cm，BC＝4cm．（1）如图1，点P从点A出发，沿AB匀速运动；点Q从点C出发，沿CB匀速运动．两点同时出发，在B点处首次相遇．设点P的速度为xcm/s．则点Q的速度可以表示为cm/s（用含x的代数式表示）；（2）在（1）的条件下，两点在B点处首次相遇后，点P的运动速度每秒提高了2cm，并沿B→C→A的路径匀速运动；点Q保持原速度不变，沿B→A→C的路径匀速运动，如图2．两点在AC边上点D处再次相遇后停止运动．又知AD＝1cm．求点P原来的速度x的值．24．如图，△ABC中，∠ACB＝90°，AB＝5cm，BC＝4cm，若点P从点A出发，以每秒2cm的速度沿折线A﹣B﹣C﹣A运动，设运动时间为t（t＞0）秒．（1）AC＝cm；（2）若点P恰好在∠ABC的角平分线上，求此时t的值；（3）在运动过程中，当t为何值时，△ACP为等腰三角形（直接写出结果）？参考答案一．选择题（共10小题）1．【解答】解：A、∵32+42≠62，∴不能作为直角三角形三边；B、∵42+52≠72，∴不能作为直角三角形三边；C、∵22+（）2≠32，∴不能作为直角三角形三边；D、∵62+（）2＝72，∴能作为直角三角形三边．故选：D．2．【解答】解：∵三角形的三边长分别为6，8，10，符合勾股定理的逆定理62+82＝102，∴此三角形为直角三角形，则10为直角三角形的斜边，设三角形最长边上的高是h，根据三角形的面积公式得：×6×8＝×10h，解得h＝4.8．故选：C．3．【解答】解：∵AB＝AC，AD平分∠BAC，∴AD⊥BC，BD＝DC＝BC＝6，在Rt△ABD中，AD＝＝＝8，故选：C．4．【解答】解：正方形A、B、C、D的面积分别是9、16、1、9，由勾股定理得，正方形G的面积为：9+16＝25，正方形H的面积为：1+9＝10，则正方形E的面积为：25+10＝35，最大正方形E的边长＝，故选：B．5．【解答】解：①△ABC中，∠C＝∠A﹣∠B，即∠C+∠B＝∠A，∵∠A+∠B+∠C＝180°，∴∠A＝90°，∴△ABC是直角三角形，故①正确；②△ABC中，∠A：∠B：∠C＝1：2：3，∵∠A+∠B+∠C＝180°，∴∠C＝90°，∴△ABC是直角三角形，故②正确；③∵△ABC中，a：b：c＝5：12：13，∴a2+b2＝c2，即△ABC是直角三角形，故③正确；④∵△ABC中，三边长分别为，∴（）2+（）2≠（）2，即△ABC不是直角三角形，故④错误；即正确的个数是3个，故选：C．6．【解答】解：∵Rt△OBC中，OC＝2，OB＝1，∴BC＝＝，∵以点B为圆心，线段BC的长为半径画弧，交数轴于点A，∴BA＝BC＝，∴OA＝1+，∴点A所表示的数为1+，故选：B．7．【解答】解：∵在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，∴AB＝，∵AE为△ABC的角平分线，ED⊥AB，∴AD＝AC＝6，∴BD＝10﹣6＝4，故选：C．8．【解答】解：在直角△ABC中，AC＝6m．AB﹣BC＝2m．设河深BC＝xm，则AB＝2+x（m）．根据勾股定理得出：∵AC2+BC2＝AB2∴62+x2＝（x+2）2解得：x＝8．即河水的深度为8m，故选：B．9．【解答】解：如图，m2+m2＝（3﹣m）2，2m2＝32﹣6m+m2，m2+6m﹣9＝0．故选：C．10．【解答】解：∵∠C＝90°，AB＝13cm，AC＝5cm，∴BC＝12cm．①当BP＝BA＝13时，∴t＝s．②当AB＝AP时，BP＝2BC＝24cm，∴t＝12s．③当PB＝P A时，PB＝P A＝t cm，CP＝（12﹣t）cm，AC＝5 cm，在Rt△ACP中，AP2＝AC2+CP2，∴（t）2＝52+（12﹣t）2，解得t＝s．综上，当△ABP为等腰三角形时，t＝s或12s或s，故选：C．二．填空题（共6小题）11．【解答】解：∵直角三角形的两直角边长分别是1和2，∴斜边＝＝，故答案为．12．【解答】解：在Rt△BAC中，∠BAC＝90°，AB＝3，BC＝5，由勾股定理得：AC＝＝4，所以阴影部分的面积S＝×π×（）2+×π×（）2+×3×4﹣×π×（）2＝6．故答案为：6．13．【解答】解：由题意得，OB＝6，OA＝8，∴AB＝＝10，则AC＝10，∴OC＝AC﹣OA＝2，∴点C坐标为（﹣2，0），故答案为：（﹣2，0）．14．【解答】解：∵AB＝5，AC＝4，BC＝3，∴AB2＝AC2+BC2，∴∠ACB＝90°，由作图可知：MN是AB的垂直平分线，∴O是AB的中点，∴CO＝AB＝，故答案为：．15．【解答】解：∵∠C＝90°，AO＝4m，BO＝5m，∴AB＝＝5m；∵梯子的顶端A下滑2m，∴OA′＝4﹣2＝2m，∴OB′＝＝＝（m），∴BB′＝B′C﹣BC＝﹣3（m）．∴底端B在地面上水平滑行的距离是（﹣3）m．16．【解答】解：如图，设AC＝x，则BC＝AD＝a+x，∵∠ADC＝30°，∴AD＝AC，∴a+x＝x，∴x＝，∴AC＝，∴图中阴影部分面积＝4×AC2＝4××（）2＝（2+）a2．故答案为：（2+）a2．三．解答题（共8小题）17．【解答】解：（1）b＝，（2）设a＝4x，b＝3x，可得：c＝＝5x＝25，解得：x＝5，所以a＝20，b＝15．18．【解答】解：∵在Rt△ABC中，∠ACB＝90°，AC＝12，BC＝5，∴AB＝＝13，∵AB•CD＝AC•BC∴CD＝＝，∴BD＝＝．19．【解答】解：（1）AB＝＝2，BC＝＝，AC＝＝5，△ABC的周长＝2++5＝3+5；（2）∵AC2＝25，AB2＝20，BC2＝5，∴AC2＝AB2+BC2，∴∠ABC＝90°．（3）△ABC的面积为2×÷2＝5．故答案为：3+5；90；5．20．【解答】解：如图所示：由题意得：P A＝2×20＝40（nmile），PB＝2×15＝30（nmile），AB＝50nmile，∵402+302＝502，∴P A2+PB2＝AB2，∴△P AB是直角三角形，∴∠APB＝90°，∵“远航”号沿东北方向航行，∴“海天”号沿西北方向或东南方向航行．21．【解答】解：设旗杆的高度为x米，根据勾股定理，得x2+92＝（x+3）2，解得：x＝12；答：旗杆的高度为12米22．【解答】解：（1）连接AC，在Rt△ACD中，AC2＝CD2+AD2＝62+82＝102，在△ABC中，AB2＝262，BC2＝242，而102+242＝262，即AC2+BC2＝AB2，∴∠ACB＝90°，S四边形ABCD＝S△ACB﹣S△ACD＝•AC•BC﹣AD•CD，＝×10×24﹣×8×6＝96（m2）．（2）需费用96×200＝19200（元）．23．【解答】解解：（1）设点Q的速度为ycm/s，由题意得3÷x＝4÷y，∴y＝x，故答案为：x；（2）AC＝＝5，CD＝5﹣1＝4，在B点处首次相遇后，点P的运动速度为（x+2）cm/s，由题意得＝，解得：x＝（cm/s），经检验x＝是原方程的根，答：点P原来的速度为cm/s．24．【解答】解：（1）∵△ABC中，∠ACB＝90°，AB＝5cm，BC＝4cm，∴AC＝cm，故答案为：3；（2）如图，过P作PD⊥AB于D，∵BP平分∠ABC，∠C＝90°，∴PD＝PC，BC＝BD＝4，∴AD＝5﹣4＝1，设PD＝PC＝y，则AP＝3﹣y，在Rt△ADP中，AD2+PD2＝AP2，∴12+y2＝（3﹣y）2，解得y＝，∴CP＝，∴t＝；当点P与点B重合时，点P也在∠ABC的角平分线上，此时，t＝；综上所述，点P恰好在∠ABC的角平分线上，t的值为或；（3）分四种情况：①如图，当P在AB上且AP＝CP时，∠A＝∠ACP，而∠A+∠B＝90°，∠ACP+∠BCP＝90°，∴∠B＝∠BCP，∴CP＝BP，∴P是AB的中点，即AP＝AB＝，∴t＝；②如图，当P在AB上且AP＝CA＝3时，t＝；③如图，当P在AB上且AC＝PC时，过C作CD⊥AB于D，则CD＝，∴Rt△ACD中，AD＝，∴AP＝2AD＝，∴t＝；④如图，当P在BC上且AC＝PC＝3时，BP＝4﹣3＝1，∴t＝＝3．综上所述，当t＝或或或3s时，△ACP为等腰三角形．。

人教版八年级下册第17章《勾股定理》综合考试测试卷(附答案)

2020年春季八年级下册第17章《勾股定理》综合测试卷时间100分钟，满分120分班级____________姓名____________学号____________成绩____________一．选择题（共12小题，满分36分）1．下列各组数是勾股数的是（）A．1，2，3B．0.3，0.4，0.5C．6，8，10D．5，11，122．由下列条件不能判定△ABC为直角三角形的是（）A．∠A：∠B：∠C＝3：4：5B．∠A﹣∠B＝∠CC．a＝1，b＝2，c＝D．（b+c）（b﹣c）＝a23．如图，一个梯形分成一个正方形（阴影部分）和一个三角形（空白部分），已知三角形的两条边分别是12cm和13cm，那么阴影部分的面积是（）cm2．A．16B．25C．36D．494．如图，数轴上的点A表示的数是﹣2，点B表示的数是1，CB⊥AB于点B，且BC＝2，以点A为圆心，AC为半径画弧交数轴于点D，则点D表示的数为（）A．B．+2C．﹣2D．25．如图，在Rt△ABC中，∠C＝90°，D为AC上一点．若DA＝DB＝15，△ABD的面积为90，则CD的长是（）A．6B．9C．12D．6．如图，已知由16个边长为1的小正方形拼成的图案中，有五条线段P A、PB、PC、PD、PE，其中长度是有理数的有（）A．1条B．2条C．3条D．4条7．如图，等腰△ABC中，AB＝AC＝10cm，BC＝12cm，D为BC上一点，连接AD，E为AD上一点，连接BE，若∠ABE＝∠BAE═∠BAC，则DE的长为（）A．cm B．cm C．cm D．1cm8．如图，高速公路上有A、B两点相距10km，C、D为两村庄，已知DA＝4km，CB＝6km．DA ⊥AB于A，CB⊥AB于B，现要在AB上建一个服务站E，使得C、D两村庄到E站的距离相等，则EB的长是（）km．A．4B．5C．6D．9．如图，用4个相同的直角三角形与一个小正方形拼成的大正方形，若图中直角三角形较短的直角边长是5，小正方形的边长是7，则大正方形的面积是（）A．121B．144C．169D．19610．如图，在Rt△ABC中，∠ABC＝90°，BC＝12，AB＝5．分别以A，C为圆心，以大于线段AC长度的一半为半径作弧，两弧相交于点E，F，过点E，F作直线EF，交AC于点D，连结BD，则△ABD的周长为（）A．13B．17C．18D．2511．某工厂的厂门形状如图（厂门上方为半圆形拱门），现有四辆装满货物的卡车，外形宽都是2.0米，高分别为2.8米，3.1米，3.4米，3.7米，则能通过该工厂厂门的车辆数是（）（参考数据：≈1.41，≈1.73，≈2.24）A．1B．2C．3D．412．正方形ABCD的边长为1，其面积记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积为S2，…按此规律继续下去，则S5的值为（）A．B．C．D．二．填空题（共8小题，满分24分）13．直角三角形的直角边长分别为8，15，斜边长为x，则x2＝．14．如果点A的坐标为（﹣4，0），点B的坐标为（0，3），则AB＝．15．已知一个等腰三角形的一边长为4，一边长为6，则这个三角形底边上的高的长为．16．《九章算术》勾股卷有一题目：今有垣高一丈．依木于垣，上于垣齐．引木却行四尺，其木至地，问木长几何？意即：一道墙髙一丈，一根木棒靠于墙上，木棒上端与墙头齐平，若木棒下端向后退，则木棒上端会随着往下滑，当木棒下端向后退了四尺时，木棒上端恰好落到地上，则木棒长尺（1丈＝10尺）．17．如图，分别以直角△ABC的三边为直径作半圆，若两直角边分别为6，8，则阴影部分的面积是．18．已知三角形三边长分别为、、（a＞0，b＞0），请借助构造图形并利用勾股定理进行探究，得出此三角形面积为（用含a、b的代数式表示）．19．如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AB＝4cm，动点P从点B出发沿射线BC方向以2cm/s的速度运动．设运动的时间为t秒，则当t＝秒时，△ABP 为直角三角形．20．如图，在平面直角坐标系中，OA1＝2，∠A1Ox＝30°，以OA1为直角边作Rt△OA1A2，并使∠A1OA2＝60°，再以A1A2为直角边作Rt△A1A2A3，并使∠A2A1A3＝60°，再以A2A3为直角边作Rt△A2A3A4，并使∠A3A2A4＝60°，…，按此规律进行下去，则A2020的坐标是．三．解答题（共8小题，满分60分）21．某中学八（1）班小明在综合实践课上剪了一个四边形ABCD，如图，连接AC，经测量AB＝12，BC＝9，CD＝8，AD＝17，∠B＝90°．求证：△ACD是直角三角形．22．如图所示，在△ABC中，AB＝AC＝5，BC＝8，CD是AB边上的高．求线段AD的长．23．如图，学校有一块空地ABCD，准备种草皮绿化已知∠ADC＝90°，AD＝4米，CD＝3米，AB＝13米，BC＝12米，求这块地的面积．24．某条道路限速70km/h，如图，一辆小汽车在这条道路上沿直线行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处，过了2s，小汽车到达B处，此时测得小汽车与车速测检测仪间的題离为50m，这辆小汽车超速了吗？25．利用如图4×4方格，每个小正方形的边长都为1．（1）请求出图1中阴影正方形的面积与边长；（2）请在图2中画出一个与图1中阴影部分面积不相等的正方形，要求它的边长为无理数，并求出它的边长；（3）把分别表示图1与图2中的正方形的边长的实数在数轴上表示出来．26．如图，已知一架竹梯AB斜靠在墙角MON处，竹梯AB＝13m，梯子底端离墙角的距离BO＝5m．（1）求这个梯子顶端A距地面有多高；（2）如果梯子的顶端A下滑4m到点C，那么梯子的底部B在水平方向上滑动的距离BD ＝4m吗？为什么？27．如图，△ABC中，∠ABC＝90°，AC＝25cm，BC＝15cm．（1）设点P在AB上，若∠P AC＝∠PCA．求AP的长；（2）设点M在AC上．若△MBC为等腰三角形，求AM的长．28．（1）我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成了一个大的正方形（如图1），这个矩形称为赵爽弦图，验证了一个非常要的结论：在直角三角形中两直角边a、b与斜边c满足关系式a2+b2＝c2．称为勾股定理．证明：∵大正方形面积表示为S＝c2，又可表示为S＝∴＝c2∴．即直角三角形两直角边的平方和等于斜边的平方．（2）爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形（如图2），也能验证这个结论，请你帮助小明完成验证的过程，（3）如图3所示，∠ABC＝∠ACE＝90°，请你添加适当的辅助线证明结论a2+b2＝c2．参考答案一．选择题（共12小题）1．【解答】解：A、∵12+22≠32，∴这组数不是勾股数；B、∵0.32+0.42＝0.52，但不是整数，∴这组数不是勾股数；C、∵62+82＝102，∴这组数是勾股数；D、∵52+112≠122，∴这组数不是勾股数．故选：C．2．【解答】解：A、由题意：∠C＝×180°＝75°，△ABC是锐角三角形，本选项符合题意．B、∵∠A﹣∠B＝∠C，∠A+∠B+∠C＝180°，∴∠A＝90°，∴△ABC是直角三角形，本选项不符合题意．C、∵a＝1，b＝2，c＝，∴a2+b2＝c2，∴∠C＝90°，∴△ABC是直角三角形，本选项不符合题意．D、∵（b+c）（b﹣c）＝a2，∴b2﹣c2＝a2，∴b2＝a2+c2，∴△ABC是直角三角形，本选项不符合题意．故选：A．3．【解答】解：如图所示：Rt△CDE中，DE＝12，CE＝13，∴CD＝＝5，∴阴影部分的面积＝5×5＝25cm2；故选：B．4．【解答】解：由题意可得，AB＝3，BC＝2，AB⊥BC，∴AC＝＝＝，∴AD＝．∴点D表示数为﹣2．故选：C．5．【解答】解：∵∠C＝90，DA＝15，∴S△DAB＝DA•BC＝90，∴BC＝12在Rt△BCD中，CD2+BC2＝BD2，即CD2+122＝152，解得：CD＝9（负值舍去）．故选：B．6．【解答】解：观察图形可知P A＝4，由勾股定理得：PB＝＝，PC＝＝5，PD＝＝2，PE＝＝，故其中长度是有理数的有2条．故选：B．7．【解答】解：∵AB＝AC，∠BAE═∠BAC，∴AD⊥BC，∴∠BDE＝90°，BD＝BC＝6，∵AB＝10，∴AD＝＝8，∵∠ABE＝∠BAE，∴AE＝BE，设DE＝x，则AE＝BE＝8﹣x，在Rt△BDE中，BE2＝DE2+BD2，∴（8﹣x）2＝x2+62，解得：x＝，即DE＝cm，故选：C．8．【解答】解：设BE＝x，则AE＝（10﹣x）km，由勾股定理得：在Rt△ADE中，DE2＝AD2+AE2＝42+（10﹣x）2，在Rt△BCE中，CE2＝BC2+BE2＝62+x2，由题意可知：DE＝CE，所以：62+x2＝42+（10﹣x）2，解得：x＝4km．所以，EB的长是4km．故选：A．9．【解答】解：∵直角三角形较短的直角边长是5，小正方形的边长是7，∴直角三角形的较长直角边＝5+7＝12，∴直角三角形斜边长＝13，∴大正方形的边长是13，∴大正方形的面积是13×13＝169．故选：C．10．【解答】解：∵∠ABC＝90°，BC＝12，AB＝5，∴AC＝＝13，根据题意可得EF是AC的垂直平分线，∴D是AC的中点，∴AD＝AC＝6.5，BD＝AC＝6.5，∴△ABD的周长为6.5+6.5+5＝18．故选：C．11．【解答】解：∵车宽2米，∴卡车能否通过，只要比较距厂门中线1米处的高度与车高．在Rt△OCD中，由勾股定理可得：CD＝＝＝≈1.73（米），CH＝CD+DH＝1.73+1.6＝3.33，∴两辆卡车都能通过此门，故选：B．12．【解答】解：在图中标上字母E，如图所示．∵正方形ABCD的边长为1，△CDE为等腰直角三角形，∴DE2+CE2＝CD2，DE＝CE，∴S2+S2＝S1．观察，发现规律：S1＝12＝1，S2＝S1＝，S3＝S2＝，S4＝S3＝，…，∴S n＝（）n﹣1．当n＝5时，S5＝（）5﹣1＝（）4，故选：A．二．填空题（共8小题）13．【解答】解：∵直角三角形的直角边长分别为8，15，∴由勾股定理得，x2＝82+152＝64+225＝289，故答案为：289．14．【解答】解：由两点间的距离公式可得AB＝＝5．故答案为：5．15．【解答】解：①若等腰三角形的腰长为4，底边为6，如图1，在△ABC中，AB＝AC＝4，AD⊥BC，则AD为BC边上的中线，即D为BC中点，∴BD＝DC＝3，在直角△ABD中AD＝＝．②若等腰三角形的腰长为6，底边为4，如图2，AB＝AC＝6，AD⊥BC，BC＝4，同理可得AD＝＝4．∴AD的长为或4．故答案为：或4．16．【解答】解：如图，设木杆AB长为x尺，则木杆底端B离墙的距离即BC的长有（x﹣1）尺，在Rt△ABC中，∵AC2+BC2＝AB2，∴102+（x﹣4）2＝x2，解得，x＝14.5故答案为：14.5．17．【解答】解：S阴＝S半圆AC+S半圆BC+S△ABC﹣S半圆AB＝+＝＝24故答案为：24．18．【解答】解：如图所示，AB＝＝，AC＝＝，BC＝＝，∴S△ABC＝S矩形DEFC﹣S△ABE﹣S△ADC﹣S△BFC＝20ab﹣﹣＝．故答案为：．19．【解答】解：∵∠C＝90°，AB＝4cm，∠B＝30°，∴AC＝2cm，BC＝6cm．①当∠APB为直角时，点P与点C重合，BP＝BC＝6 cm，∴t＝6÷2＝3s．②当∠BAP为直角时，BP＝2tcm，CP＝（2t﹣6）cm，AC＝2cm，在Rt△ACP中，AP2＝（2）2+（2t﹣6）2，在Rt△BAP中，AB2+AP2＝BP2，∴（4）2+[（2）2+（2t﹣6）2]＝（2t）2，解得t＝4s．综上，当t＝3s或4s时，△ABP为直角三角形．故答案为：3或4．20．【解答】解：∵∠A1Ox＝30°，∠A1OA2＝60°，∴∠A2Ox＝90°，∴A2在y轴上，Rt△A1A2O中，OA1＝2，∴OA2＝2OA1＝4，A1A2＝2，∴A2的纵坐标为：4＝+1，∴A2（0，4），Rt△A1A2A3中，∠A2A1A3＝60°，∴∠A1A3A2＝30°，∴A1A3＝2A1A2＝4，∵∠BA1O＝∠A1Ox＝30°，∴A1B∥x轴，∴A1B⊥A2O，∵∠A1A2B＝30°，∴A1B＝A1A2＝，A1B＝3，∴A3B＝4﹣＝3，OB＝4﹣3＝1，∴A3的横坐标为：﹣3＝﹣，∴A3（﹣3，1），Rt△A2BA3中，A2A3＝2A2B＝6，Rt△A2A3A4中，A2A4＝2A2A3＝12，∴OA4＝12﹣4＝8，∴A4的纵坐标为：﹣[﹣1]，A4（0，﹣8），由此发现：点A1，A2，A3，A4，…，A n，每四次一循环，2020÷4＝505，∴点A2020在y轴的负半轴上，纵坐标是：﹣[﹣1]＝1﹣31010．则A2020的坐标是（0，1﹣31010）；故答案为：（0，1﹣31010）．三．解答题（共8小题）21．【解答】证明：∵∠B＝90°，AB＝12，BC＝9，∴AC2＝AB2+BC2＝144+81＝225，∴AC＝15，又∵AC2+CD2＝225+64＝289，AD2＝289，∴AC2+CD2＝AD2，∴△ACD是直角三角形．22．【解答】解：设AD＝x∵CD⊥AB，∴∠D＝90°，∴CD2＝BC2﹣BD2＝AC2﹣AD2，∴82﹣（5+x）2＝52﹣x2，∴x＝，∴AD＝．23．【解答】解：连接AC．由勾股定理可知：AC＝＝＝5，又∵AC2+BC2＝52+122＝132＝AB2，∴△ABC是直角三角形，∴这块地的面积＝△ABC的面积﹣△ACD的面积＝×5×12﹣×3×4＝24（米2）．24．【解答】解：在Rt△ABC中，AC＝30m，AB＝50m；据勾股定理可得：BC＝＝＝40（m）∴小汽车的速度为v＝＝20（m/s）＝20×3.6（km/h）＝72（km/h）；∵72（km/h）＞70（km/h）；∴这辆小汽车超速行驶．答：这辆小汽车超速了．25．【解答】解（1）面积为4×4﹣4××1×3＝10，边长为；（2）如图所示，正方形的边长为均可．（答案不唯一，合理即可．）（3）表示或或的点如图所示．（答案不唯一，画出表示的点亦可）26．【解答】解：（1）∵AO⊥DO，∴AO＝，＝，＝12m，∴梯子顶端距地面12m高；（2）滑动不等于4m，∵AC＝4m，∴OC＝AO﹣AC＝8m，∴OD＝，＝，∴BD＝OD﹣OB＝，∴滑动不等于4m．27．【解答】解：（1）∵∠ABC＝90°，AC＝25cm，BC＝15cm，∴AB＝＝20cm，∵∠P AC＝∠PCA，∴AP＝PC，设AP＝BP＝x，∴PB＝20﹣x，∴（20﹣x）2+152＝x2，解得：x＝，∴AP＝；（2）当CM＝BC＝15时，△MBC为等腰三角形，∴AM＝AC﹣CM＝10；当BM＝BC＝15，时，△MBC为等腰三角形，过B作BH⊥AC于H，∴BH＝＝＝12，∴CH＝＝9，∴AM＝AC﹣2CH＝7；当BM＝CM时，△MBC为等腰三角形，连接BM，设AM＝x，则BM＝CM＝25﹣x，∴（25﹣x）2＝122+（25﹣x﹣9）2，解得：x＝，∴AM＝，综上所述，若△MBC为等腰三角形，AM的长为10，7，．28．【解答】（1）证明：∵大正方形面积表示为S＝c2，又可表示为S＝4×ab+（b﹣a）2，∴4×ab+（b﹣a）2＝c2．∴2ab+b2﹣2ab+a2＝c2，∴a2+b2＝c2，即直角三角形两直角边的平方和等于斜边的平方．故答案为：4×ab+（b﹣a）2，4×ab+（b﹣a）2，a2+b2＝c2；（2）证明：由图得，大正方形面积＝×ab×4+c2＝（a+b）×（a+b），整理得，2ab+c2＝a2+b2+2ab，即a2+b2＝c2；（3）解：如图3，过A作AF⊥AB，过E作EF⊥AF于F，交BC的延长线于D，则四边形ABDF是矩形，∵△ACE是等腰直角三角形，∴AC＝CE＝c，∠ACE＝90°＝∠ACB+∠ECD，∵∠ACB+∠BAC＝90°，∴∠BAC＝∠ECD，∵∠B＝∠D＝90°，∴△ABC≌△CDE（AAS），∴CD＝AB＝b，DE＝BC＝a，S矩形ABDF＝b（a+b）＝2×ab+c2+（b﹣a）（a+b），∴a2+b2＝c2．。

人教版八年级下册第17章《勾股定理》章末综合测试(带答案)

人教版八年级下册第17章《勾股定理》章末综合测试满分100分班级__________姓名__________成绩__________一．选择题（共10小题，30分）1．下列各组数中，能作为直角三角形三边长的是（）A．4，5，6B．5，7，12C．3，5，D．1，，2．已知点A的坐标为（2，﹣1），则点A到原点的距离为（）A．3B．C．D．13．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（）A．13B．26C．34D．474．如图，以数轴的单位长度线段为边作一个正方形，以1为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（）A．1B．﹣1C．1﹣D．5．若等腰三角形的腰长为13，底边长为10，则底边上的高为（）A．6B．7C．9D．126．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab＝8，大正方形的面积为25，则小正方形的边长为（）A．9B．6C．4D．37．满足下列条件的△ABC是直角三角形的是（）A．∠A：∠B：∠C＝3：4：5B．a：b：c＝1：2：3C．∠A＝∠B＝2∠C D．a＝1，b＝2，c＝8．下列说法正确的是（）A．一个三角形的三边长分别为：a，b，c，且a2﹣b2＝c2，则这个三角形是直角三角形B．三边长度分别为1，1，的三角形是直角三角形，且1，1，是组勾股数C．三边长度分别是12，35，36的三角形是直角三角形D．在一个直角三角形中，有两边的长度分别是3和5，则另一边的长度一定是49．如图，一架云梯AB长为25米，顶端A靠在墙AC上，此时云梯底端B与墙角C距离为7米，云梯滑动后停在DE的位置上，测得AE长为4米，则云梯底端B在水平方向滑动了（）米A．4B．6C．8D．1010．如图，在高为3米，斜坡长为5米的楼梯台阶上铺地毯，则地毯的长度至少要（）A．4米B．5米C．6米D．7米二．填空题（共8小题，24分）11．如图是由三个直角三角形组成的梯形，根据图形，写出一个正确的等式．12．已知直角坐标平面上点P（3，2）和Q（﹣1，5），那么PQ＝．13．在Rt△ABC中，∠C＝90°，AB＝15，BC：AC＝3：4，则BC＝．14．已知三角形三边长分别为5，12，13，则此三角形的最大边上的高等于．15．如图所示的网格是正方形网格，∠APB＝°．16．如图，△ABC中，AC＝5，BC＝12，AB＝13，以AB为直径的半圆过点C，再分别以BC、AC为直径向上作三个半圆，则阴影部分面积为．17．观察下列式子：当n＝2时，a＝2×2＝4，b＝22﹣1＝3，c＝22+1＝5n＝3时，a＝2×3＝6，b＝32﹣1＝8，c＝32+1＝10n＝4时，a＝2×4＝8，b＝42﹣1＝15，c＝42+1＝17…根据上述发现的规律，用含n（n≥2的整数）的代数式表示上述特点的勾股数a＝，b＝，c＝．18．现有两根长6分米和3分米的木条，小华想再找一根木条为老师制作一个直角三角形教具，则第三根木条的长度应该为分米．三．解答题（共8小题，46分）19．（5分）如图，等腰△ABC中，AB＝AC＝13cm，BC＝10cm，求△ABC的面积．20．（5分）如图所示，在△ABC中，AD⊥BC，AB＝13，BD＝12，CD＝．（1）求AD的长；（2）求△ABC的周长．21．（5分）勾股定理是初中数学学习的重要定理之一，这个定理的验证方法有很多，你能验证它吗？请你根据所给图形选择一种方法画出验证勾股定理的方法并写出验证过程．22．（5分）如图，△ABC中，AB＝4，∠ABC＝45°，D是BC边上一点，且AD＝AC，若BD﹣DC＝1．求DC的长．23．（6分）平面直角坐标系中如果任意两点A、B的坐标分别为（x1，y1）、（x2，y2），则A、B两点之间的距离可表示为|AB|＝；在平面直角坐标系中．（1）若点C的坐标为（3，4），O为坐标原点，则C、O两点之间的距离为．（2）若点E（﹣2，3）、F（4，﹣5），求E、F两点之间的距离．24．（6分）如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点D的位置，问船向岸边移动了多少米？（假设绳子是直的）25．（6分）如图，有一块等腰三角形草地，测得腰CA＝CB，AB＝6米，腰比底边上的高多1米，现在园艺师想更换一下草坪，已知每平方米草坪售价200元，请你帮园艺师计算一下全部更换草坪需要少资金？26．（8分）如图，已知∠MAN＝30°，点B在射线AM上，且AB＝6，点C在射线AN上．（1）若△ABC是直角三角形，求AC的长；（2）若△ABC是等腰三角形，则满足条件的C点有个；（3）设BC＝x，当△ABC唯一确定时，直接写出x的取值范围．参考答案一．选择题（共10小题）1．下列各组数中，能作为直角三角形三边长的是（）A．4，5，6B．5，7，12C．3，5，D．1，，【解答】解：A、∵52+42≠62，∴三条线段不能组成直角三角形，故A选项错误；B、∵52+72≠122，∴三条线段不能组成直角三角形，故B选项错误；C、∵32+（）2≠52，∴三条线段不能组成直角三角形，故C选项错误；D、∵12+（）2＝（）2，∴三条线段能组成直角三角形，故D选项正确；故选：D．2．已知点A的坐标为（2，﹣1），则点A到原点的距离为（）A．3B．C．D．1【解答】解：点A的坐标为（2，﹣1）到原点O的距离：OA＝＝．故选：C．3．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（）A．13B．26C．34D．47【解答】解：由勾股定理得，正方形F的面积＝正方形A的面积+正方形B的面积＝32+52＝34，同理，正方形G的面积＝正方形C的面积+正方形D的面积＝22+32＝13，∴正方形E的面积＝正方形F的面积+正方形G的面积＝47，故选：D．4．如图，以数轴的单位长度线段为边作一个正方形，以1为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（）A．1B．﹣1C．1﹣D．【解答】解：∵正方形的边长为1，∴BC＝＝，∴AC＝，即|A﹣1|＝，故点A表示1﹣．故选：C．5．若等腰三角形的腰长为13，底边长为10，则底边上的高为（）A．6B．7C．9D．12【解答】解：如图：AB＝AC＝13，BC＝10．△ABC中，AB＝AC，AD⊥BC；∴BD＝DC＝BC＝5；Rt△ABD中，AB＝13，BD＝5；由勾股定理，得：AD＝＝＝12．故选：D．6．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab＝8，大正方形的面积为25，则小正方形的边长为（）A．9B．6C．4D．3【解答】解：由题意可知：中间小正方形的边长为：a﹣b，∵每一个直角三角形的面积为：ab＝×8＝4，∴4×ab+（a﹣b）2＝25，∴（a﹣b）2＝25﹣16＝9，∴a﹣b＝3，故选：D．7．满足下列条件的△ABC是直角三角形的是（）A．∠A：∠B：∠C＝3：4：5B．a：b：c＝1：2：3C．∠A＝∠B＝2∠C D．a＝1，b＝2，c＝【解答】解：A、∵∠A：∠B：∠C＝3：4：5，∠A+∠B+∠C＝180°，∴∠A＝45°，∠B＝60°，∠C＝75°，∴△ABC不是直角三角形；B、∵12+22≠32，∴△ABC不是直角三角形；C、∵∠A＝∠B＝2∠C，∠A+∠B+∠C＝180°，∴∠A＝∠B＝75°，∠C＝37.5°，∴△ABC不是直角三角形；D、∵12+（）2＝22，∴△ABC是直角三角形．故选：D．8．下列说法正确的是（）A．一个三角形的三边长分别为：a，b，c，且a2﹣b2＝c2，则这个三角形是直角三角形B．三边长度分别为1，1，的三角形是直角三角形，且1，1，是组勾股数C．三边长度分别是12，35，36的三角形是直角三角形D．在一个直角三角形中，有两边的长度分别是3和5，则另一边的长度一定是4【解答】解：A、一个三角形的三边长分别为：a，b，c，且a2﹣b2＝c2，则这个三角形是直角三角形，正确，符合题意；B、因勾股数必须都是整数，故原命题错误，不符合题意；C、∵122+352≠362，∴三边长度分别是12，35，36的三角形是直角三角形错误，不符合题意；D、在一个直角三角形中，有两边的长度分别是3和5，则另一边的长度是4或，故错误，不符合题意，故选：A．9．如图，一架云梯AB长为25米，顶端A靠在墙AC上，此时云梯底端B与墙角C距离为7米，云梯滑动后停在DE的位置上，测得AE长为4米，则云梯底端B在水平方向滑动了（）米A．4B．6C．8D．10【解答】解：在直角△ABC中，已知AB＝25米，BC＝7米，∴AC＝＝＝24米，在直角△CDE中，已知CE＝CE+EA＝24米，DE＝AB＝25米，AE＝4米，∴CE＝AC﹣AE＝20米，∴CD＝＝＝15米，∴BD＝15﹣7＝8米故云梯底端B在水平方向滑动了8米，故选：C．10．如图，在高为3米，斜坡长为5米的楼梯台阶上铺地毯，则地毯的长度至少要（）A．4米B．5米C．6米D．7米【解答】解：在Rt△ABC中，AC＝＝4米，故可得地毯长度＝AC+BC＝7米，故选：D．二．填空题（共8小题）11．如图是由三个直角三角形组成的梯形，根据图形，写出一个正确的等式c2＝a2+b2．【解答】解：依题意得：ab+c2+ab＝（a+b）（a+b），整理，得c2＝a2+b2．故答案是：c2＝a2+b2．12．已知直角坐标平面上点P（3，2）和Q（﹣1，5），那么PQ＝5．【解答】解：∵P（3，2）和Q（﹣1，5），∴PQ＝，故答案为：513．在Rt△ABC中，∠C＝90°，AB＝15，BC：AC＝3：4，则BC＝9．【解答】解：设BC＝3x，AC＝4x，又其斜边AB＝15，∴9x2+16x2＝152，解得：x＝3或﹣3（舍去），∴BC＝3x＝9．故答案为：9．14．已知三角形三边长分别为5，12，13，则此三角形的最大边上的高等于．【解答】解：∵52+122＝132，∴根据勾股定理的逆定理，△ABC是直角三角形，最长边是13，设斜边上的高为h，则S△ABC＝×5×12＝×13h，解得：h＝，故答案为．15．如图所示的网格是正方形网格，∠APB＝135°．【解答】解：延长AP交格点于D，连接BD，则PD2＝BD2＝12+22＝5，PB2＝12+32＝10，∴PD2+DB2＝PB2，∴∠PDB＝90°，∴∠DPB＝45°，∴∠APB＝135°．故答案为：135．16．如图，△ABC中，AC＝5，BC＝12，AB＝13，以AB为直径的半圆过点C，再分别以BC、AC为直径向上作三个半圆，则阴影部分面积为30．【解答】解：∵52+122＝169＝132，∴△ABC是直角三角形，S阴影＝π（）2+π（）2﹣[π（）2﹣×5×12]＝30．故答案为：30．17．观察下列式子：当n＝2时，a＝2×2＝4，b＝22﹣1＝3，c＝22+1＝5n＝3时，a＝2×3＝6，b＝32﹣1＝8，c＝32+1＝10n＝4时，a＝2×4＝8，b＝42﹣1＝15，c＝42+1＝17…根据上述发现的规律，用含n（n≥2的整数）的代数式表示上述特点的勾股数a＝2n，b＝n2﹣1，c＝n2+1．【解答】解：∵当n＝2时，a＝2×2＝4，b＝22﹣1＝3，c＝22+1＝5n＝3时，a＝2×3＝6，b＝32﹣1＝8，c＝32+1＝10n＝4时，a＝2×4＝8，b＝42﹣1＝15，c＝42+1＝17…∴勾股数a＝2n，b＝n2﹣1，c＝n2+1．故答案为：2n，n2﹣1，n2+1．18．现有两根长6分米和3分米的木条，小华想再找一根木条为老师制作一个直角三角形教具，则第三根木条的长度应该为3或3分米．【解答】解：第三根木条的长度应该为或分米；故答案为：3或3．三．解答题（共8小题）19．如图，等腰△ABC中，AB＝AC＝13cm，BC＝10cm，求△ABC的面积．【解答】解：过点A作AD⊥BC交BC于点D，∵AB＝AC＝13cm，BC＝10cm，∴BD＝CD＝5cm，AD⊥BC，由勾股定理得：AD＝＝12（cm），∴△ABC的面积＝×BC×AD＝×10×12＝60（cm2）．20．如图所示，在△ABC中，AD⊥BC，AB＝13，BD＝12，CD＝．（1）求AD的长；（2）求△ABC的周长．【解答】解：（1）在Rt△ABD中，AD＝＝5；（2）在Rt△ADC中，AC＝＝2，则△ABC的周长＝AB+BC+AC＝13+12++2＝25++2．21．勾股定理是初中数学学习的重要定理之一，这个定理的验证方法有很多，你能验证它吗？请你根据所给图形选择一种方法画出验证勾股定理的方法并写出验证过程．【解答】解：则由图形可知：（a+b）2﹣4×ab＝a2+b2+2ab﹣4×ab＝c2，整理得：a2+b2＝c2．答案不唯一．22．如图，△ABC中，AB＝4，∠ABC＝45°，D是BC边上一点，且AD＝AC，若BD ﹣DC＝1．求DC的长．【解答】解：过点A作AE⊥BC于点E，如图所示．∵AD＝AC，AE⊥BC，∴∠AEB＝90°，DE＝CE．∵∠ABC＝45°，∴∠BAE＝45°，∴AE＝BE．在Rt△ABE中，AB＝4，∴AE2+BE2＝AB2，即BE2+BE2＝（4）2，∴BE＝4，∴BD+DC＝4．又∵BD﹣DC＝1，∴DC+1+DC＝4，∴DC＝2．23．平面直角坐标系中如果任意两点A、B的坐标分别为（x1，y1）、（x2，y2），则A、B两点之间的距离可表示为|AB|＝；在平面直角坐标系中．（1）若点C的坐标为（3，4），O为坐标原点，则C、O两点之间的距离为5．（2）若点E（﹣2，3）、F（4，﹣5），求E、F两点之间的距离．【解答】解：（1）∵O为原点，∴O坐标为（0，0），∵点C的坐标为（3，4），∴CO＝＝5，故答案为：5；（2）∵点E（﹣2，3）、F（4，﹣5），E、F两点之间的距离可表示为|EF|＝，∴EF＝＝＝10．24．如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点D的位置，问船向岸边移动了多少米？（假设绳子是直的）【解答】解：在Rt△ABC中：∵∠CAB＝90°，BC＝17米，AC＝8米，∴AB＝＝15（米），∵此人以1米每秒的速度收绳，7秒后船移动到点D的位置，∴CD＝17﹣1×7＝10（米），∴AD＝＝＝6（米），∴BD＝AB﹣AD＝15﹣6＝9（米），答：船向岸边移动了9米．25．如图，有一块等腰三角形草地，测得腰CA＝CB，AB＝6米，腰比底边上的高多1米，现在园艺师想更换一下草坪，已知每平方米草坪售价200元，请你帮园艺师计算一下全部更换草坪需要少资金？【解答】解：过C作CD⊥AB于D，∵AC＝BC，∴AD＝AB＝3，∵腰比底边上的高多1米，∴AC＝CD+1，∵AC2＝AD2+CD2，∴（CD+1）2＝32+CD2，解得：CD＝4，∴S△ABC＝AB•CD＝×6×4＝12（m2），∴全部更换草坪需要12×200＝2400（元），答：全部更换草坪需要2400元资金．26．如图，已知∠MAN＝30°，点B在射线AM上，且AB＝6，点C在射线AN上．（1）若△ABC是直角三角形，求AC的长；（2）若△ABC是等腰三角形，则满足条件的C点有3个；（3）设BC＝x，当△ABC唯一确定时，直接写出x的取值范围．【解答】解：（1）当∠ABC＝90°时，∵∠A＝30°，∴BC＝，∴设BC＝x，则AC＝2x，在Rt△ABC中，由勾股定理得36+x2＝4x2，解得x＝2，x＝﹣2（舍去）．∴AC＝4，当∠ACB＝90°时，∵∠A＝30°∴BC＝，∴AC＝3．（2）如图3，当AC＝BC时，满足题意．如图4，当AC＝AB时，满足题意．如图3，当AB＝BC时，满足题意．故答案为：3．（3）当BC≥6或BC＝3时，△ABC唯一确定．即x＝3或x≥6．。

勾股定理综合应用题(含答案)

勾股定理应用综合题汇编一・解答題（共29小題）1. 如图所示，缜峑警方在基地B处获知有贩浚分子分别在P2）和行羞品交易后，缉飆立即出矣已知甲題沿北偏东60方向以毋小时40海里的速度前逬，乙艇沿南偏东30。

方向以野小时30海里的速度前逬，半小时后甲51 MS.乙到PS.则M S^PS之间的距篦是多少？2. 小明家有一块三角形菜地，重得两边长分别为80耒，100米，第三边上的高为印米，诸你帮小明计算这块菜地册面积.3. 如图.一探险者在某海出探宝，登陆后，先往东走了8千米，又往北走了2千米，又向西走了3千来，再又向北走了6千米，往东一拐，仅走了1千米就找到了宝藏，试冋他走的是遅近的路吗？如果是，谙求出这个路雄长, 如果不是:，诫在图上画出最近旳路线.并求出眾近的路线长.丄B6384如图，在笔直的菜公路上有A、B两点相距50km. C^D为两村庄,DAJAB亍点A，CB-1AB于点B，已知DA・30km，CB=20km.现在蔓在公路的AB段上建一个土特产品收购站E・使得C、D两村到收购站E的距离相等.则收购站E应建在囱A点多远处？5. 如图.一艘渔政船从小£ A处出发.向正北方向以每小时20海里的逮废行驶了1.5小时到达B谢丸行任务.再向正东方向以相同的速度行驶了2小时到达C处继续执行任务，然后以相同的速度直播从Cid：i0a A处.：1）分别求AB、BC的长》：2）问返回时比出去时节省了多少时间？6. 如图.一块草坪的形状为四边形ABCD・亘中Q=90°・ AB=8m. BC=6m，CD=24m，AD=26m・求这块草坪的面积.7. 如图.斜坡AC总米./AD=30°・坡顶有一旗杆BC （旗杆与地而AD垂丙）•旗杆顶端B点与A点有一彩带A3相连.AB=10米.试求旗杆BC的高慶？（结果保留根号）&如图所示，在3米高的柱子顶端A处有一只老圏它看到一条蛇从距柱脚9米B处向注脚的蛇涓C游来，老鹰主眄卜下.如果它们的违度相等.间老鹰在距蛇洞多远处捉住蛇？（设老動直线飞行）9・如图.为修铁路需凿通随道AC・测得厶=50°・zBXO°，AB=5km. BC=4km.若每天凿隧道0 3km・间几天才能把随道凿通？10・如图，在树上距地面10m的D处有两只猴子，它们同时发现地面上C处有一筐水果，一只猴子从D处向上飓到树顶A处.択后利用拉在A处的滑绸AC滑到C处，另一只猴子从D处先滑封地而B，再由B跑到C・已知两號子所经过的路程裁是15m，求树高AB・12.（2008＞义马市）如图.小胡用一块有一个锐角为30°册直角三角板测童树高，已知小朋离树的距离为3米DE 为1.68米，那么这探树大约有多高？（楕确到0.1米，“3汛732）13.（2005•双柏且）如图.有两櫟树.一櫟高10米.另一棵高4米.两树相距8米.一只小鸟从一鮒的树梢飞鱼另一棵树的树梢，间小乌至少飞行多少米？1＜已知某开发区有一块四边形的空地ABCD.如图所示二现计划在空地上冲植草皮，经测重如90°. AB«3m.BA12m ，CD-13m ，DA-4m ，若每平方米草庆需S 200元，间要多少投入°15.英校把一块形状为直角三角形的陵迪开辟为生物园.如图所示.4CB=90°・ AC 割米，BC=60米.若线段CD 是F 小渠.且D 点在边AB 上，已知水渠的造价为10元/米，间D 点在距A 点多远处时.水渠的造价聂低？盪底18.如图，是一个三级台阶，它的每一级的长、宽和高分别等于5cm. 3cm 和lcm. A 和B 是这个台阶的两个相对的端点，A 点上有一只蚂蚁，想到B 点去吃可□的良物.请你想一想，这只蚂蚊从A 点出矣沿着台阶面爬到B 点.最短线路是多少？19・甲、乙两人在沙漠逬行探险某日早舄& 00甲先出发，他以6千米时逋度向东南方向行走，1小时后乙出发, 他以5千米耐速度向西南方向行走.上午2 CD 时.甲、乙两人相距多远？严S 一 ------------ 东16.印度数学家什泗逻（1141年-1225年）旨提出过商花T 可题”: 平平湖水洁可鉴，面上半尺生红莲'出泥不染亭亭立，忽被强风吹一边，旌人观看忙向前，花篦康位二尺远：能算诸君请解•题，湖水如何知深浅” 适用学过的敌学知识回答这个问题.P.如图，小强在江南岸选定逹這物A.并在江北岸的B 处观弱此时，極绕与江岸BE 所成的夫角是30°，小强沼江岸BE 向东走了 500m ，到C 处，再观麋A ，此时视线AC 与江岸所戚的夹角4CE ・60°・根据小强提供的信息, 你能测出江宽吗？若能.写出求解过程（结果可保留根号几若不能.诵说朗理由.20.如图一个长方体盒子，棱长AB-3cm« BF・3cm，BC-4cm・ <1）连授BD，求BD的长；（2）一根长为6cm的木棒能放进这个盒子里去吗？说明你的理由.2：.如图，某会展中心在会展期间准备将高5m>长13m，宽2m的楼梯上铺地毯，已知地毯每平方米18元谙你帮助计算一下，铺完这个楼道至少需要多少元钱？22. 在甲村至乙村的公路有一块山地正在开发•现有一C处需要爆破.已知点C与公路上旳停靠站A的距离为300X.与公路上的另一停軒站B的距离为400米，且CAJCB.如图所示.対了安全起见，爆破点C周围半径250米•范围内不得进入，间在进行爆舉时，公路AB段是否有危险，是否需要暂时封锁？23. 如图，小翩秋千，秋千架高2.4米秋千座位商地04米，小红荡起战高时，坐位葛地0 8*・此肘小红荡出的水平距离是多少？（荡到秋千架两边的爱高点之间的距藹）24. 如图，将穿好彩旗的旗杆垂直插在樓场上，旗杆从旗顶到地而的高度为320皿在无风的天气里.彩旗自然下垂，如图.求彩旗下垂时最低处离地而的最小高度h.彩旗完全展平时的尺于如左图的长方形（单位：an）.25. 如图，一根竹竿在离地面5米处断裂，竹竽顶部珞在离竹竿底部12米处，间竹竿折断之前有多长?26・如图，要测一也塘两端A、B的距務请你利用三角形知识设计一个测重方案・要求，血述测量方法；Q®出示意图（原图画），觀你测童的数据（用宇母表示〉叢示AB.芥说明理由，说明：池塘周围在司一高度，芥且比较平坦.力.有一块询长为加米的&方牺绿的，如图审示.左绿地旁询R外有傅身器林由干民住在A外的住戻跋曙了绿地，小明想在A处树立f 标牌少走踏之何忍”，情你计算石帮小明在标牌的■［上适当的数字.28.如图，是一个长8n宽6m，高5m的仓库，在其内壁的A （长的四等分点）处有一只壁％B （宽的三等分点）处有一只蚊子，则壁虎爬到蚊子处的最短距冏犬多少米.答案1、25 海里2、2400 平方米或者3987.5 平方米3、10 千米4、20km5、（1）AB=30 海里BC=40 海里（2）省1 小时6、96 平方米7、 2 V 3 - 48、 4 米9、10 天10、A B=12m11、7米12、3.4 米13、10 米14、7200 元15、480 元16、（x+0.5）A2=x A2+2A2 x=3.7517、250V3 米18、13cm19、13km20、（1）BD=5cm （2）V34cm小于6cm 不够21、648 元22、240m<250m 没有危险，不需要封锁23、1.2 米24、170cm25、18 米26、略27、6米28、V89 米。

勾股定理综合训练

长为（）
A． 6 B． 2√5
C．√7
D．5
6．（2014•德阳）如图，在 Rt△ABC 中，∠ACB=90°，点 D 是 AB 的中点，且 CD=，
如果 Rt△ABC 的面积为 1，则它的周长为（）
7．（2014•牡丹江一模）在△ABC 中，若 AB=AC=15，BC=24，若 P 是△ABC 所在的
三．解答题（共 9 小题） 21．（2007•牡丹江）小强家有一块三角形菜地，量得两边长分别为 40m，50m，第三边上的高为 30m．请你帮小强计算这块菜地的面积．（结果保留根号）
22.如图，Rt△ABC 中，∠ACB=90°．在 AB 的同侧分别以 AB、BC、AC 为直径作三个半圆．图中阴影部分的面积分别记作为 S1 和 S2．（1）求证：S1+S2=S△ ABC；（2）若 Rt△ABC 的周长是 2+√6，斜边长为 2，求图中阴影部分面积的和．
图 9：
图 10：
19．（2012•青海）如图 10，在 Rt△ABC 中，∠C=90°，AC=4，BC=2，分别以 AC、 BC 为直径画半圆，则图中阴影部分的面积为 _________ （结果保留π）． 20．如图，以 AB 为直径画一个大半圆，BC=2AC，分别以 AC，CB 为直径在大半圆内部画两个小半圆，那么阴影部分的面积与大半圆面积的比等于 _________
勾股定理综合训练一．选择题（共 10 小题） 1．（2014•淮安）如图 1，在边长为 1 个单位长度的小正方形组成的网格中，点 A、 B 都是格点，则线段 AB 的长度为（）
图 1：
图2
A．5
B．6
C．7
D．25
2．（2014•乐山）如图 2，△ABC 的顶点 A、B、C 在边长为 1 的正方形网格的格点

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

勾股定理综合测试题
班级_________ 学号__________ 姓名____________ 成绩
一．选择题（每题3分，共30分）
1、在下列以线段a ，b ，c 的长为三边的三角形中，不能构成直角三角形的是（） A 、 a ＝5，b ＝12，c ＝13 B 、 a ＝b ＝5，c ＝25 C 、 a ：b ：c ＝3：4：5 D 、 a ＝11，b ＝12，c ＝15
2、下面是直角三角形具备的几条性质：
①两个较小的内角之和等于较大的内角；②三个内角的和等于180°；③面积等于较短的两边的乘积的一半；④有斜边和一条直角边相等的两个直角三角形全等。

其中一般三角形不具备的有（）
A.4条
B.3条
C.2条
D.1条
3、如图所示，在△ABC 中，三边a ,b ,c 的大小关系是（） A.a ＜b ＜c B. c ＜a ＜b C. c ＜b ＜a D. b ＜a ＜c
4、如图，一个圆桶儿，底面直径为16cm ，高为18cm ，则一只小虫底部点A 爬到上底B 处，则小虫所爬的最短路径长是（π取3）（）
A.20cm
B.30cm
C.40cm
D.50cm
5、如图，有一块直角三角形纸片，两直角边AC ＝6cm ，BC ＝8cm ，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（）
A.2cm
B.3 cm
C.4 cm
D.5 cm
6、如图，在△ABC 中，∠ACB=90°，AC=12，BC=5，AM=AC ，BN=BC ，则MN 的长为（）
A 、2
B 、2.6
C 、3
D 、4
7、若等腰△ABC 的腰长AB ＝2，顶角∠BAC ＝120°，以 BC 为边的正方形面积为（）
A.3
B.12
C.427
D.3
16
8、直角三角形三条边的比是3∶4∶5.则这个三角形三条边上的高的比是（） A 、15∶12∶8 B 、15∶20∶12 C 、12∶15∶20 D 、20∶15∶12
9、若三角形ABC 中，∠A ∶∠B ∶∠C=2∶1∶1,a 、b 、c 分别是∠A 、∠B 、∠C 的对边，则下列各等式成立的是（）
A 、2
2
2
c b a =+ B 、2
2
2c a = C 、2
2
2a c = D 、2
2
2b c =
10、△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（） A.42 B.32 C.42 或32 D.37 或 33
二．填空题（每题3分，共30分）
11、在△ABC 中，∠C ＝90°，BC ＝60cm ，CA ＝80cm ，一只蜗牛从C 点出发，以每分20cm 的速度沿CA →AB →BC 的路径再回到C 点，需要＿＿＿分的时间．
12、已知一个直角三角形的两条直角边分别为6cm 、8cm ，那么这个直角三角形斜边上的高为。

13、若正方形的面积为18cm 2，则正方形对角线长为__________cm 。

14、在△ABC 中，∠C=90°，若AB
＝2
AB +2AC +2
BC =__________。

15、一座桥横跨一江，桥长12m ，一般小船自桥北头出发，向正南方驶去，因水流原因到达南岸以后，发现已偏离桥南头5m ，则小船实际行驶＿＿＿m 。

16、一个长方体同一顶点的三条棱长分别是3、4、12，则这个长方体内能容下的最长的木棒为。

17、如图，学校有一块长方形花铺，长BC=12m ，CD=8m ，有极少数人为了避开拐角走“捷径”，从BC 边走到AC 边，在花铺内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却
踩伤了花草。

18、如图，AC ⊥CE ，AD=BE=13，BC=5，DE=7，那么AC= 。

19、如图，已知矩形ABCD 沿着直线BD 折叠，使点C 落在C /处，BC /交AD 于E ，AD ＝8，AB ＝
4，则DE 的长为。

20、在△ABC 中，∠B ＝90°，两直角边AB ＝7，BC ＝24，三角形内有一点P 到各边的距离相等，则这个距离是＿＿＿。

B
D
19题图
A
B
C
D
E
18题图
8
17题图
B
第6题
B
A
D
E
第5题图
18cm
第4题图
B 第3题图
三．解答题（每题10分，共40分）
21
1
线段.请在图中画出△ABC，其中AB BC CA
===
22、有一个小朋友拿着一根竹竿要通过一个长方形的门，如果把竹竿竖放就比门高出1尺，斜放就
恰好等于门的对角线，已知门宽4尺，求竹竿高与门高。

23、如图，折叠长方形一边AD，点D落在BC边的点F处，BC＝10cm，AB＝8cm，求EF的长。

24、将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为320cm，在无风的天气里，
彩旗自然下垂，如右图. 求彩旗下垂时最低处离地面的最小高度h.彩旗完全展平时的尺寸如左图的长方形（单位：cm）.
四、附加题（10分）
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，设AC＝a，BC＝b，AB＝c，CD＝h．
求证：（1）
2
2
2
1
1
1
h
b
a
=
+；(2) h
c
b
a+
<
+；
(3) 以b
a+、h、h
c+为边的三角形，是直角三角形．
B
C
D
A
23题图。