D3_6图形
图形与坐标 教学设计

图形与坐标教学设计教学设计思想第一课时主要学习了根据图形特点和问题的需要而能够灵活建立直角坐标系。
可先让学生尝试建立适当的直角坐标系,写出顶点坐标,然后与教科书给出的方法对比,最后在小组或全班交流选择坐标系的理由。
第二、三课时主要学习图形上点坐标变化与图形变化的关系,要学生多动手描点、连线、测量,小组讨论,体会点的位置变化与点的坐标的变化规律。
教学目标知识与技能根据图形特点和问题的需要而能够灵活建立直角坐标系。
在同一直角坐标系中,感受坐标变化导致图形位置与形状的变化,并能找出变化规律。
通过探索图形上点的坐标变化与图形变换之间的关系,发展形象思维能力。
过程与方法经历有选择性地建立直角坐标系并表示图形上点的坐标的过程;经历图形上点坐标的变化导致图形位置与形状变化的探索过程,通过实际操作,小组讨论得出在同一直角坐标系中图形变换与点的坐标变化之间的关系。
(多动手描点、连线、测量、体会点的位置变化与点的坐标的变化规律。
)情感态度价值观进一步体会数形结合的思想;通过归纳、总结变化规律,体会从特殊到一般的数学思想方法。
重点难点重点:有选择性地建立直角坐标系并表示图形上点的坐标;图形上点坐标变化与图形变化的关系。
难点:图形的伸缩变换与坐标变化之间的关系。
教学方法合作探究、小组讨论教具准备多媒体或投影仪课时安排3课时教学设计过程复习:点的坐标。
新授第一课时把图形放在直角坐标系中,图形上的点就有了相应的坐标。
有一个边长为4的正方形。
建立适当的坐标系,写出这个正方形各顶点的坐标。
(一)一起探究1.小明、小亮分别建立了图18—10(1)和图18—10(2)的直角坐标系。
他们写出的正方形各顶点坐标相同吗?2.他们建立的坐标系各有什么优点?3.你还能用其他方法建立坐标系吗?注:可先让学生尝试建立适当的直角坐标系,写出顶点坐标,然后与教科书给出的两种方法对比;最后在小组或全班交流选择坐标系的理由,增进对图形对称性质及其他性质的理解。
找规律画图形方法教案小班

找规律画图形方法教案小班教案标题:找规律画图形方法教案(小班)教学目标:1. 学习观察并发现图形中的规律。
2. 培养小班学生的形状识别能力和图形创造能力。
3. 培养小班学生的思维逻辑和创新思考能力。
教学资源:1. 图形卡片(包括不同形状的图形:圆、方形、三角形等)。
2. 彩色纸张、彩笔、剪刀等绘画工具。
教学准备:1. 准备好图形卡片,确保每个学生都能看清楚图形。
2. 准备足够的彩色纸张和绘画工具。
教学步骤:引入活动:1. 与学生进行简短的谈话,询问学生是否喜欢画图,并讨论一些他们已经学习过的图形。
2. 出示图形卡片,引导学生观察和描述不同的形状,培养他们对图形的兴趣。
探索活动:1. 指导学生使用彩色纸张和绘画工具来重现教师展示的一个简单的图形(例如圆形)。
2. 引导学生思考并尝试使用不同的方法和工具来画同一个图形。
例如:画一个圆形可以用剪纸,也可以用铅笔和专用工具。
3. 引导学生细心观察每种方法的特点和区别,并讨论为什么会有这样的区别。
规律总结:1. 引导学生回顾之前探索的不同画图方法,并让他们讨论以找出画图形方法的规律。
2. 引导学生将这些规律总结为简单的句子或口诀,并鼓励他们将这些规律应用到其他形状的图形中。
创作活动:1. 提供不同形状的图形卡片,让学生选择一个图形并运用之前学习到的规律和方法来画出自己创造的图形。
2. 鼓励学生展示自己的作品,并与同学分享他们的创意和方法。
总结活动:1. 回顾学生们的作品,让他们用自己的话来描述他们的图形并解释他们选择的画图方法。
2. 引导学生总结整堂课的学习内容,并强调找到规律的重要性。
拓展活动(根据学生水平调整):1. 引导学生尝试画出更复杂的图形,例如星形、椭圆、正方形等。
2. 鼓励学生用创意的方式来创建新的图形,并共享和展示他们的创作成果。
教学评估:1. 观察学生在探索和创作活动中的参与程度。
2. 评估学生是否能准确地运用之前学习到的规律和方法来画出图形。
元器件PCB封装图形大全

SIL-100-02
SIL-100-02R
SIL-100-20
SIL-100-20R
类似的还有: SIL-100-03 , SIL-100-03R , SIL-100-04 , SIL-100-04R ,SIL-100-05 ,SIL-100-05R
SIL-100-06 , SIL-100-06R , SIL-100-07 , SIL-100-07R ,SIL-100-08 ,SIL-100-08R
CR3216
CR3225
FMD
IMD MELF2012 MELF3216
MELF3516
MELF5923
SC70-5 SC70-6 SOT143 SOT223-4 SOT23-5 SOT23-6 SOT23-8
UM6
UB
六、电容
CAP-RAD10 CAP-RAD20
CAP-RAD30
CAP10
CAP110
TO92-2
TO92-50
二、晶振
TO92-70
TO92-75
TO92-80
TO92/5
TO98
XTAL18
三、电感
RESONATOR XTAL
XTAL30
IND1210 IND1812
IND603 IND805 IND2012
IND2825
IND3216
IND3225
IND3225_MOL IND3230
SIL-100-10 , SIL-100-10R , SIL-100-15 , SIL-100-15R ,SIL-100-20 ,SIL-100-20R
SIL-156-02
SIL-156-02R
2024年西师大一年级数学上册几何图形分类专项综合练习题

2024年西师大一年级数学上册几何图形分类专项综合练习题班级:__________ 姓名:__________1. 数一数,填一填。
有______个三角形。
2. 用不同的颜色把下面的图形分成大小和形状完全相同的两部分。
3. 下面的图案分别是由哪些图形组成的?填一填。
______________ ______________ ______________4. 数一数,填一填。
圆形______个长方形______个正方形______个三角形______个圆柱形______个形平行四边形______个5. 能用七巧板拼出来的图形画“√”,不能的画“×”。
6. 图中共有()个正方体。
A .4B .5C .6D .77. 照样子用同样长的小棒搭正方形,想一想,最少要用几根?搭1个用4根搭2个用7根搭3个用______根搭4个用______根8. 想一想,填一填。
(1)三角形比长方形少______条边,六边形比三角形多______条边。
(2)要拼一个大正方形最少需要______个小正方形,或______个小三角形。
(3)七巧板是由______种图形组成,其中有______个□,有______个△(4)黑板的面是______形,地板砖的面是______形,红领巾的面是______形,硬币的面是______形。
(5)正方形有______条边,长方形有______条边,三角形有______条边。
9. 下面图形是长方体的是()。
A .B .C .10. 找规律,画一画。
11. 想一想,填一填。
(1)魔方的每个面都是______形,正方形的四条边都______。
(2)三角形有______条边,长方形和正方形各有______条边。
12. 圈出合适的图形。
13. 判断下图中哪些是长方体,哪些不是,是的打“√”,不是的打“×”。
(________)(________)(________)14. 从右图中找出1个和左上角形状相同的图形,涂上漂亮的颜色。
六年级美术《图形的魔术组合》说课稿

六年级美术《图形的魔术组合》说课稿一. 教材分析《图形的魔术组合》是人教版六年级美术教材中的一课,本课主要让学生通过观察、分析、实践,探索图形的组合方式,培养学生的创新意识和动手能力。
教材以生活中的实例为导入,激发学生的学习兴趣,接着引导学生进行图形组合的实践,最后通过评价、展示,使学生感受到美术的魅力。
二. 学情分析六年级的学生已经具备了一定的美术基础,对图形、色彩、构图等方面有一定的认识。
但部分学生对图形的组合创意还不够清晰,需要在实践中进一步培养。
此外,学生对新鲜事物充满好奇,善于模仿,合作意识强,有利于开展小组合作学习。
三. 说教学目标1.知识与技能:让学生掌握图形组合的基本方法,能够独立创作出有创意的图形组合作品。
2.过程与方法:通过观察、实践、评价等环节,培养学生的创新意识和动手能力。
3.情感、态度和价值观:培养学生对美术的热爱,提高审美情趣,增强团队协作精神。
四. 说教学重难点1.教学重点:图形组合的基本方法。
2.教学难点:创作出有创意的图形组合作品。
五. 说教学方法与手段1.教学方法:采用启发式教学法、案例分析法、小组合作法等。
2.教学手段:多媒体课件、实物模型、绘画工具等。
六. 说教学过程1.导入:以生活中的实例引入,激发学生的学习兴趣。
2.讲解:讲解图形组合的基本方法,引导学生观察、分析实例。
3.实践:学生分组进行图形组合创作,教师巡回指导。
4.展示:学生展示作品,进行自评、互评、教师评。
5.总结:总结本节课的学习内容,强调图形组合的重要性。
七. 说板书设计板书设计要简洁明了,突出教学重点。
可以采用流程图、图示、关键词等形式,帮助学生理解和记忆。
八. 说教学评价教学评价分为过程性评价和终结性评价。
过程性评价主要关注学生在实践过程中的创新意识、合作精神、动手能力等;终结性评价主要评价学生的作品创意、构图、色彩等方面。
通过评价,激发学生的学习兴趣,提高教学质量。
九. 说教学反思在课后,教师应认真反思本节课的教学效果,从教材处理、教学方法、学生反馈等方面进行总结,为改进今后的教学提供依据。
高等数学(解析几何)图形

P M
Sz
N (0, y1 , z1 ) .
z1 C
o
y1
y
.
S:f ( x 2 y2 , z) 0.
x
11. 双叶旋转双曲面
双
曲
线
x a
y b
z
绕 x 轴一周
x
0
y
11. 双叶旋转双曲面
双
曲
线
x a
y b
z
绕 x 轴一周
.
x
z
0
y
11. 双叶旋转双曲面
双
曲
线
x a
y b
z
图形
28 作出曲面x2 y 2 a, 2 x2 z 2 a2 , x 0, y 0, z 0所围立体 图形
29 作出曲面 z 1 x2 y2 和 x2 y2 z 1 所围立体图形 30 平面 x a, y a, z a, x y z a 在第一卦限所围立体图形
的截口椭圆任意接近,即: x
双曲面和锥面任意接近。
z
o
y
20. 单叶双曲面是直纹面
x2 y2 z2 1
a2 b2 c2
含两个直母线系
.
直纹面在建筑学上有意义
例如,储水塔、 电视塔等建筑都 有用这种结构的。
21. 双曲抛物面是直纹面
x2 y2 z
a2 b2
含两个直母线系
22. 一般锥面
方程 F(x,y,z)= 0是 n次齐次的若:F (tx, ty, tz) t n F ( x, y, z). t是任意数
曲面S外的每一点都不满足方程
6. 一般柱面 F(y,
z)=0
(不含x)
z 准线
常用的电气图形符号补
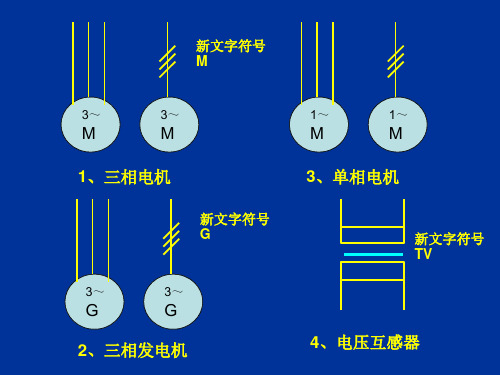
KMLeabharlann KM接触器 常开接点
接触器 常闭接点
KA
KA
KM
KM
中间继电器 常开接点
中间继电器 常闭接点
接触器 常开接点
接触器 常闭接点
说明:开关或触点在垂直画时,推荐向左为常开向右为常 闭;水平画时推荐向下为常开向上为常闭。
新文字 符号FH
P
新文字
符号KP
15、热继电器
16、压力继电器动合接点
G
新文字
高压负荷开关具有简单的灭弧装置。主要用 在高压侧接通和断开正常工作的负荷电流,但因 灭弧能力不高,故不能切断断路电流,它必须和 高压熔断器串联使用,靠熔断器切断短路电流。
(4)高压熔断器(FU)
高压熔断器当所在电路的电流超过规定值并 经过一定时间后,能使其熔体熔化而切断电路, 如果发生短路故障,其熔体会快速熔断而切断电 路。因此,熔断器主要功能是对电路进行短路保 护,也具有过负荷保护的功能。
(5)高压开关柜
高压开关柜是按照一定的接线方案将有关的 一、二次设备(如开关设备、监察测量仪表、保 护电器及操作辅助设备等)组装而成的一种高压 成套配电装置。高压开关柜有固定式和手车式两 大类型。
2、低压配电装置 (1)低压断路器;(2)低压隔离开关;(3)低 压负荷开关;(4)低压熔断器;(5)低压配电柜; (6)其他设备
断电延时断 开常开接点
KT
~ —
新文字 符号U
23、整流器
新文字 符号D
25、二极管
新文字 符号G
24、电池
新文字 符号C
26、电容器
新文字 符号XP
27、插座
新文字 符号XS
28、插头
29、插头插座组合
颗粒的粒度描述

圆盘
H=d/2 H=d/4
H=d/10
1:1:1 长方体 1:1:2
1:1:4
球形度 1.0 0.87 0.83 0.73 0.83 0.69 0.58 0.81 0.77 0.68
颗粒形状
正四面体
正八面体
长方体
1:2:2 1:2:4
1:4:4
1:1:2
椭球体
1:1:4 1:2:2
1:2:4
1:4:4
Dst
18ust m g p f
粒度/粒度的定义
☻粒度或当量直径/三轴径
粒度/粒度的定义
☻粒度或当量直径/投影径
☆定方向径(Feret径) ☆定方向等分径(Martin径) ☆定向最大径 ☆Heywood径
Feret 径 > 投 影 圆 当 量 径 (Heywood径)>Martin径
体积、表面积、比表面积形 状系数、球形度
数据种类
三轴径
三轴径、投影面积、体 积
体积、表面积、投影面 积、周长、各种相当径
曲率半径
投影轮廓曲线各参数及各种 代表径
立体几何各量
颗粒的形状
1、形状系数 (shape factor)
体积形状系数
V
V
d
3 p
对于球ΦV=π/6,对于立方体ΦV=1
表面积形状系数
非球形颗 粒
数学 - 组合图形面积的计算

数学 - 组合图形面积的计算引言在数学中,组合图形是指由多个基本图形组合而成的复合图形。
而要计算组合图形的面积,需要先计算组合图形中各个基本图形的面积,然后将这些面积相加。
本文将介绍如何计算常见的组合图形的面积。
一、矩形和正方形的面积计算矩形和正方形是最简单的组合图形,其面积的计算公式分别为:•矩形的面积:$S = l \\times w$,其中l为矩形的长,w为矩形的宽。
•正方形的面积:$S = a \\times a$,其中a为正方形的边长。
示例:假设有一个矩形,长为 5,宽为 3,那么它的面积可以通过以下计算得到:S = 5 * 3 = 15因此,该矩形的面积为 15。
二、三角形的面积计算三角形是另一个常见的组合图形,其面积的计算公式为:$S = \\frac{1}{2} \\times b \\times h$,其中b为三角形的底边长,ℎ为三角形的高。
示例:假设有一个底边长为 4,高为 6 的三角形,那么它的面积可以通过以下计算得到:S = 0.5 * 4 * 6 = 12因此,该三角形的面积为 12。
三、圆的面积计算圆是另一种常见的组合图形,其面积的计算公式为:$S = \\pi \\times r^2$,其中r为圆的半径。
需要注意的是,计算圆的面积时,需要使用 $\\pi$(圆周率)的近似值,通常取 3.14 或更精确的值。
示例:假设有一个半径为 5 的圆,那么它的面积可以通过以下计算得到:S = 3.14 * (5^2) = 78.5因此,该圆的面积为 78.5。
四、组合图形的面积计算当组合图形由多个基本图形组合而成时,其面积的计算可以通过计算各个基本图形的面积,然后将这些面积相加得到。
示例:假设有一个由一个矩形和一个三角形组成的图形,如下图所示:---------------| ▲ || ╱╲ || ╱╲ || ╱╲ || ╱______╲ || ▔ |--------------矩形的长和宽分别为 6 和 4,三角形的底边长为 4,高为 3。
电路符号及对应图形大全

电路符号及对应的图大全序号名称旧代号新代号一导线敷设方式的标注1 用瓷瓶或瓷柱敷设 CP K2 用塑料线槽敷设 XC PR3 用钢线槽敷设 GC SR4 穿焊接钢管敷设 G SC5 穿电线管敷设 DG TC6 穿硬聚氯乙烯管敷设 VG PC7 穿阻燃半硬聚氯乙烯管敷设 ZVG FPC8 用电缆桥架敷设 CT9 用瓷夹敷设 CJ PL10 用塑料夹敷设 VJ PCL11 穿蛇皮管敷设 CP在管道工程中:TC—表示电线管SC—表示焊接钢管RC—表示水煤气钢管FPC—表示聚氯乙烯半硬质塑料电线管KPC—表示聚氯乙烯塑料波纹管FC—表示普通灰口铸件,如FC20,FC25分别表示才质为FC20,FC25的灰口铸铁。
二导线敷设部位的标注1 沿钢索敷设 S SR2 沿屋架或跨屋架敷设 LM BE3 沿柱或跨柱敷设 ZM CLE4 沿墙面敷设 QM WE5 沿天棚面或顶板面敷设 PM CE6 在能进入的吊顶内敷设 PNM ACE7 暗敷设在梁内 LA BC8 暗敷设在柱内 ZA CLC9 暗敷设在墙内 QA WC10 暗敷设在地面或地板内 DA FC11 暗敷设在屋面或顶板内 PA CC12 暗敷设在不能进入的吊顶内 PNA ACC从电源引入端开始向配出端顺序看:1、SCB10-2000 10/0.4 D/Yn11干式变压器,10KV/0.4KV,容量2000KVA,高压侧三角形接法,低压侧为星形接法,连接组别为D/Yn11(星三角11点接法);2、TMY-3[2*(125*10)]+1*(125*10)低压进线柜主母线或低压水平母线规格,125*10硬铜排,3条相线为双排,PEN为单排;3、MT40H1/3P MIC5.0 I=3200A低压总进线自动(万能)断路器施耐德品牌,电流规格4000A,整定电流(长延时)3200A,性能要求查厂家样本;4、4000/5A进线侧电流互感器变比,4000/55、NS100H/3P I=100A GPU3-60II浪涌保护辅助回路,配施耐德NS100H/3P开关、GPU3-60II浪涌吸收保护器;6、D1:MNS 1000*1000*2200低压柜编号、型号,MNS系列,进线柜尺寸为1000宽、1000深、2200高;7、D2、D3:无功功率补偿电容补偿柜8、GLR-1250/3P,ZWK ARC-12/J带熔断器隔离开关1250A/3P,无功功率自动补偿控制器(安科瑞品牌)12路;9、FYS-0.22浪涌吸收保护(避雷器);10、NT100-100A熔断器,100A;11、LC1-DPK12M7C施耐德产接触器,需要查产品样本(略),用于自动切换电容器组;12、FK-Dr30/440/7电容器组回路串接电抗器,防止瞬间切换过电流;13、10*MKPg0.44-30-3 10组电容器,MKPg0.44型号,30KVar、三相;14、D7,含4套NS系列断路器低压出线柜NS400N/3P 200A表示施耐德NS400N断路器,400A框架,整定电流为200A;15、112KW WDZA-YJY-4*185+E95该出线回路为112KW负荷,出线电缆为无卤低烟A级阻燃(交联聚乙烯绝缘、交联聚乙烯护套),规格为4*185+E95,E95表示PE线规格95;16、ACR220E、300/5安科瑞品牌仪表(出线回路电流表),配300/5电流互感器;17、D9含MT25H1/3P MIC5.0 I=1600A及2000/5A低压母联柜,断路器为MT25H1/3P MIC5.0,整定电流1600A,配2000/5A电流互感器。
d3的功能主治

D3的功能主治1. 数据可视化•D3(Data-Driven Documents)是一个用于创建动态、交互式、可视化数据的JavaScript库。
•使用D3,可以通过将数据绑定到HTML、SVG和CSS等标准的Web 技术上,快速创建丰富的数据可视化图表和图形。
•D3提供了强大的数据操作和处理功能,能够帮助用户灵活地创建各种类型的数据可视化。
2. 矢量图形渲染•D3是基于SVG(Scalable Vector Graphics)的Web图形库,可以创建高质量的矢量图形。
•用户可以使用D3来绘制各种形状、路径、线条、文本等图形元素,进行自定义的图形渲染。
•D3的矢量图形渲染功能可以帮助用户实现各种漂亮、精细的图形效果。
3. 数据驱动的交互•D3的强项之一是数据驱动的交互,可以根据数据的变化实时更新页面中的图表和图形。
•用户可以轻松地实现通过鼠标、键盘等交互事件来控制和操作可视化图形。
•D3还提供了丰富的交互功能,例如拖拽、缩放、动画等,可以增强用户的交互体验。
4. 多维数据处理•D3提供了强大的多维数据处理功能,用户可以对数据进行聚合、过滤、排序、统计等操作。
•用户可以利用D3的数据处理功能,对大规模、复杂的数据进行加工和转换,以便于可视化呈现。
•D3中的数据处理功能能够帮助用户更好地理解和分析数据,从而获取有价值的信息。
5. 地图可视化•D3在地图可视化方面有出色的表现,可以帮助用户创建各种类型的地图可视化。
•用户可以使用D3来绘制各种地图元素,例如地图边界、区域填充、标签等,实现高度自定义的地图可视化效果。
•D3的地图可视化功能可以帮助用户更直观地呈现地理数据,展示地理空间的分布和关系。
6. 数据绑定与更新•D3的核心理念之一是数据绑定,用户可以将数据与HTML文档中的元素进行绑定。
•用户可以使用D3的数据绑定功能,根据数据的变化自动更新页面中的元素,实现动态数据的展示。
•D3还提供了丰富的数据更新方式,例如插入、删除、过渡等,可以实现平滑的数据更新效果。
几何图形初步知识点

几何图形初步知识点归纳1.几何图形1、几何图形:从形形色色的物体外形中得到的图形叫做几何图形。
2、立体图形:这些几何图形的各部分不都在同一个平面内。
3、平面图形:这些几何图形的各部分都在同一个平面内。
4、虽然立体图形与平面图形是两类不同的几何图形,但它们是互相联系的。
立体图形中某些部分是平面图形。
5、三视图:从左面看,从正面看,从上面看6、展开图:有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形。
这样的平面图形称为相应立体图形的展开图。
7、⑴几何体简称体;包围着体的是面;面面相交形成线;线线相交形成点; ⑵点无大小,线、面有曲直;⑶几何图形都是由点、线、面、体组成的; ⑷点动成线,线动成面,面动成体; ⑸点:是组成几何图形的基本元素。
练习:1、下列叙述正确的有 ( ) (1)棱柱的底面不一定是四边形;(2)棱锥的侧面都是三角形;(3)柱体都是多面体;(4)锥体一定不是多面体A.1个B.2个C.3个D.4个2、若一个多面体的顶点数20,面数为12,则棱数为 ( )A.28B.32C.30D.26 3、在世界地图上,一个城市可以看作 ( )A.一个点B.一条直线C.一个面D.一个几何体4、直线AB 上有一点C ,直线AB 外有一点D ,则A 、B 、C 、D 四点能确定的直线有( )A.3条B.4条C.1条或4条D.4条或6条 5、C 为线段AB 延长线上的一点,且AC=23AB ,则BC 为AB 的 ( ) A.32 B.31 C.21 D.23 6、如图中是正方体的展开图的有( )个A 、2个B 、3个C 、4个D 、5个二、填空题 1 2、手电筒发出的光给我们的形象是。
3、下列说法中:①直线是射线长度的2倍;②线段AB 是直线AB 的一部分;③延长射线OA 到B 。
a4、已知:线段AC和BC在同一直线上,如果AC=10㎝,BC=6㎝,D为AC的中点,E为BC 的中点,则DE=。
23.6.2 图形的变换与坐标 说课稿 2022—2023学年华东师大版数学九年级上册

23.6.2 图形的变换与坐标说课稿 2022—2023学年华东师大版数学九年级上册一、教材分析《2022—2023学年华东师大版数学九年级上册》是针对九年级学生编写的数学教材。
该教材包括了多个章节,其中第23章是关于图形的变换与坐标的内容。
该章节主要包括平移、旋转和对称三种图形的变换方法,并且通过坐标系的引入,使学生能够更好地理解和描述图形的变换过程。
本节课的内容是23.6.2小节,重点学习了图形的变换与坐标的关系。
通过本节课的学习,学生可以掌握图形在坐标平面上的平移、旋转和对称变换的方法,并能够运用所学知识解决实际问题。
二、教学目标1.知识目标:了解平移、旋转和对称变换的定义和基本原理,学会在坐标平面上描述图形的变换过程。
2.能力目标:掌握图形在坐标平面上进行平移、旋转和对称变换的方法,能够准确描述变换后的图形。
3.情感目标:培养学生的思维观察力和动手能力,增强学生对数学的兴趣和自信心。
三、教学重、难点1.教学重点:通过示例和实例,引导学生理解图形的平移、旋转和对称变换,并能够在坐标平面上进行描述。
2.教学难点:学生能够自主运用所学知识,准确进行图形的变换和描述。
1. 导入新知识教师可以通过提问的方式,回顾和巩固学生对平移、旋转和对称变换的基本概念和定义。
同时,引入坐标系的概念,并说明图形的变换与坐标之间的关系。
2. 示范与练习教师先给出一个图形的坐标,然后引导学生根据给定的坐标,在坐标平面上进行平移、旋转和对称变换,并让学生描述变换前后的图形特点。
接着,教师让学生分组进行练习,每组给出一个图形的坐标和一个变换方式,要求学生在坐标平面上进行对应变换,并准确描述变换后的图形。
3. 拓展与应用教师让学生通过实际生活中的例子,运用所学知识解决实际问题。
例如,给出一个房间平面图,让学生根据给定的条件进行平移、旋转和对称变换,找出满足条件的位置。
同时,教师可以引导学生思考图形变换的数学性质,例如平移、旋转和对称变换对图形的某些性质是否有影响,让学生能够运用数学推理的方法解决问题。
第六章-多元函数微分学基础

z
V
O
y
V
V
V
x
图6-3 八卦限示意图
下面将平面上两点间的距离公式推广到空间(证明从略)
设M
1
(
x1
,
y1
,
z1
)和M
2
(
x2
,
y2
,
z2
)为空间两点,
则点M
1与M
间的
2
距离为
M1M 2 (x2 x1)2 ( y2 y1)2 (z2 z1)2 (6-1)
例1 在x轴上求一点P,使它到点A(3,2, 2)的距离为3.
0和G(x, y, z) 0是两个曲面方程,它们交线上的每一点的坐标
都同时满足上述两个曲面方程;反过来,曲时满足上述两个曲面
方程的点都在这条交线上.因此,联立方程组
z
F(x, y, z) 0
L
F(x, y, z) 0 G(x, y, z) 0
G(x, y, z) 0
叫做空间曲线L的一般方程
由两点距离公式知
M1M (x a1)2 ( y b1)2 (z c1)2 M 2M (x a2 )2 ( y b2 )2 (z c2 )2 又因为 M1M M 2M ,故知
(x a1)2 ( y b1)2 (z c1)2 (x a2 )2 ( y b2 )2 (z c2 )2
称上式为平面的一般方程,式中,A, B,C, D分别为变量x, y, z的系数; D为常数 Nhomakorabea.z
p3 c
例2 求过点P1(a, 0, 0), P2 (0,b, 0),
P3 (0, 0, c)的平面方程(其中a,b, c 0)
(见图6 5)
p1 a
犀牛在三维图形捕捉点

犀牛在三维图形捕捉点
3D图形捕捉点以犀牛Python作为其中的一种有很多一般应用。
一般来说,犀牛Python
用于捕捉三维场景中的多个图形,包括三角形、立方体、多边形、圆柱形,并可以处理复杂图像,确保复杂部分得到有效表达。
三维图形捕捉有两个主要过程:计算和渲染。
在计算过程中,犀牛Python将应用,根据
指定的参数计算三维图形,通过数学运算预计算出需要的样式,以保证最终的渲染图像的
精度和准确度。
然后,在渲染过程中,犀牛Python将计算出的图形渲染成真实感的图像,并可以捕捉复杂图形的手柄点,以便提高图形的处理效率和可操作性。
同时,犀牛Python还可以处理多种不同的图形,比如三角形和其他基本形状,而且可以
根据不同的纹理和复杂度编写自定义图形,以获得更高质量的图形。
此外,犀牛Python
还可以让用户在渲染过程中添加灯光进行实时渲染,以获得更真实的渲染效果。
总之,犀牛Python在三维图形捕捉中的应用不可忽视,它能够计算和渲染多种三维图形,而且能够捕捉复杂图形的手柄点,保证精度和准确度。
此外,它还可以根据不同需求编写
自定义图形,是三维图形捕捉一个十分重要的工具。
幼儿园《图形》教案推荐8篇

幼儿园《图形》教案推荐8篇幼儿园《图形》教案篇1活动目标:1、通过操作,感知立方体与平面图形之间的关系,了解正方体的特征。
2、能开动脑筋设计制作教具。
3、初步学习用对唱的方式演唱歌曲。
4、在学习歌表演的基础上,结合游戏情节,注意随着音乐的变化而变换动作。
活动准备:1、正方体积木若干、同样大小的白色及彩色的正方形纸若干。
2、制作礼盒的平面图形若干、正方体的插片若干。
3、胶水及彩色水笔。
活动过程:1、分组操作,感知正方体的特征第一组:做礼品盒。
用画有6个一样大的正方形的图形纸,动手动脑做成礼品盒。
第二组:做数学角教具。
"数一数,这块积木有几个一样大的正方形的面,就拿这样的正方形的纸,在每张正方形的纸上写1个数字或符号(+、一、_),写好贴在积木的每一个面上,供数学教学游戏用"。
第三组:让积木变漂亮。
"这些积木旧了,你们数一数它们有几个什么形状、大小是怎样的面?""请你选用大小、形状一样的彩色纸,把积木贴起来。
"第四组:插积木。
用插片插出一个正方体。
2、教师引导幼儿介绍自己的小制作(1)"礼品盒是什么形状的?数数看,它有几个面,大小是怎么样的?是什么形状的面?"(2)"你们给数学角做的教具是什么形状的?它有几个什么形状的、大小是怎样的面?每个面有几个数字?""用你们做的玩具,合在一起给小朋友出一道算术题好吗?"(3)"这些五颜六色的积木真漂亮!数数看,一块积木用了几张什么形状的、大小是怎样的纸贴好的?你们把积木摞在一起吧。
"(4)"插了这么多积木,它们是什么形状的?插好一块积木需要用几块插片?插片的大小一样吗?一共有多少块积木?能用这些积木搭成一个大正方体吗?试试看。
"教学反思:在执教的过程中缺少激情,数学本身就是枯燥的,那在教孩子新知识的时候,就需要老师以自己的激情带动孩子的学习,在今后的教学中这方面也要注意。
机械制图6-轴测图

机械制图6-轴测图介绍在机械制图中,轴测图是一种用于三维物体表示的图形方法。
其中的6-轴测图是最常用和基本的一种形式。
通过6-轴测图,可以将三维物体的外形、结构和尺寸以简明清晰的方式展示出来。
本文将介绍6-轴测图的基本原理、绘制方法和应用场景。
1. 基本原理6-轴测图是通过对物体的外形进行透视投影得到的,它包括三个主要方位:前顶展开、左侧展开和右侧展开。
其中,前顶展开主要展示物体的前、顶面,左右两侧面隐藏;左侧展开主要展示物体的左、顶面,前后两侧面隐藏;右侧展开主要展示物体的右、顶面,前后两侧面隐藏。
通过这三个方位的展开,可以全面地了解物体的形状和结构。
2. 绘制方法绘制6-轴测图的方法如下:步骤一:确定主方位根据物体的特点和要求,确定主方位,即选择展示物体的前、顶面的方位。
主方位确定后,左右两侧面的相对位置也随之确定。
步骤二:绘制前顶展开在纸上绘制两根垂直线段,分别代表物体的前方和顶方,线段的长度可以根据需要确定。
然后,按照实际尺寸比例,在前顶线上绘制物体的外形,细节可以使用线段、弧线等几何图形表示。
需要注意的是,前顶展开是在不考虑透视效果的情况下绘制的,因此不同部位的线段要保持平行关系。
同时,为了方便展示物体的外形,可以适度放大一些细节。
步骤三:绘制左右展开在前顶展开的基础上,根据主方位确定左右两侧面的相对位置。
然后,依照前顶展开的尺寸和平行关系,通过线段和弧线来绘制左右展开。
需要注意的是,左侧展开显示的是物体的左、顶面,右侧展开显示的是物体的右、顶面。
因此,在绘制线段时,要根据左右关系的不同,适当调整线段的位置和长度。
步骤四:标注尺寸在绘制好6-轴测图后,需要给图形标注尺寸。
通过测量前顶展开图上的线段长度,可以获得物体的实际尺寸。
将这些尺寸标注到适当的位置上,以便读者了解物体的尺寸和比例关系。
3. 应用场景6-轴测图在工程领域有广泛的应用,特别是在机械制图中。
它可以用于展示各种机械零件、设备和装置的外形、结构和尺寸。
第五讲数数方块

举一反三练习: 1、数一数,有多少个正方形木块?
3、下图积木块如果按上层、下层把它 分开,上层、下层各是哪幅图?
( )个 ( )个 ( )个
2、哪两个图形可以拼成 一连。
?用线连
• 周四 • 经典例题
• 把图(1)和图(2)方木块按箭头组合起来,与哪幅图相同? •
• 名师导航: • 看图示,把图(1)和图(2)组合时,图(2)放在图(1)的右边,即
数、还可以按看得见和看不见的来数。 • •
举一反三练习 1、右图由正方体堆成, 请数一数再填空。按 层数:第一层有( ) 个正方体,第二层有 ( )个正方 9 体, 第三层有( )个正方体,第四层(最 下层)有( )个正方体,按排数, 前排有( )个正方体,中排有( ) 个正方体,后排有( )个正方体, 或先数看的见的有( )个正方体, 看不见的有( )个正方体,一共有 ( )个正方体。
•
• 温馨提示:(★)
•
动手搭一搭、画一画,搭(画)的时候要注意正方体的6个面都相等哦!
•
•
举一反三练习: 1、连一连,哪两个图形可以拼成一个
2、动手试一试,用 6 个小正方体木块 可以搭出几种不同的长方体?
3、要搭成一个大正方体,你知道下面 每组图形至少还少几个小正方体木块 吗?
• 周三 • 经典例题
2、数一数,下面图形中的小方块各有 多少个?
( )个
( )个
3、下面的图形都是由小正方体拼成的, 数数各是多少个?
( )个 ( )个 ( )个
• 周二 • 经典例题
• 用 搭成 一个大的正方体,至少需要几个这样的小正方体木块? •
• 名师导航: • 小朋友可以试着搭一搭,先用2个小正方体木块搭,搭出的形状有下面这几种,它们都不是正方体。如图:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y x2
3
1
所以有铅直渐近线 x 3 及 x 1
f ( x) x2 又因 k lim lim 2 x x x x 2x 3
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2x 3
第三章
第六节 函数图形的描绘
一、 曲线的渐近线 二、 函数图形的描绘
一、 曲线的渐近线 (P76 题14)
定义 . 若曲线 C上的点M 沿着曲线无限地远离原点 时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为 曲线C 的渐近线 . y C 或为“纵坐标差” 例如, 双曲线
L
y f (x)
思考与练习
1. 曲线 y
1 e
x2
2
1 e x
(D )
(B) 仅有水平渐近线;
(A) 没有渐近线;
(C) 仅有铅直渐近线;
(D) 既有水平渐近线又有铅直渐近线. 提示: lim
1 e
x2
2
x 1 e x
1;
x 0 1 e x
lim
1 e
x2
2
2 1
y 2 为水平渐近线; 1 lim ( 2) , x 1 为垂直渐近线. x1 x 1
2. 斜渐近线 若
(或 x )
( k x b)
斜渐近线 y k x b .
( k x b)
f ( x) b k lim [ ] x x x f ( x) k lim x x
(或 x )
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
b lim [ f ( x) k x]
x (或 x )
例2. 求曲线
的渐近线 .
x3 解: y , lim y , ( x 3)(x 1) x3
笛卡儿叶形线 3at x 3 1 t t 1 2 3at y 1 t3 点击图中任意点 动画开始或暂停 参数的几何意义: t tan t (,1) ( , )
图形在第四象限
2 4
t (1, 0] ( 34 , ]
图形在第二象限 图形在第一象限
t [0 , ) [0 , ) 2
1
(极小)
(3 , )
4) 求渐近线
lim y , x 1 为铅直渐近线
x1
2 ( x 3)( x 1) ( x 3) , y y , y 4( x 1) ( x 1)3 4( x 1) 2
2
y 1 1 又因 lim , 即k x x 4 4 ( x 3) 2 1 1 x] b lim ( y x) lim [ x 4( x 1) 4 x 4 5x 9 5 lim ( x 3) 2 x 4( x 1) 4 y 4( x 1) 1 5 y x 为斜渐近线 ( x 3)( x 1) 4 4 y 4( x 1) 2 2 0 5) 求特殊点 x 2 1 y y 9 ( x 1)3 4 4
的图形. 图形对称于 y 轴.
1 y e 2
x2 2
(1 x 2 )
令 y 0 得 x 0 ; 令 y 0得 x 1
3) 判别曲线形态
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
x y y y
M
PN
y kxb
o
x y 0 a b
无渐近线 .
y
x
有渐近线
但抛物线
o
x
1. 水平与铅直渐近线 若 则曲线
(或 x )
有水平渐近线 y b . 有垂直渐近线 x x0 .
若
(或 x x0 )
则曲线
例1. 求曲线
解: lim (
x
的渐近线 .
1 2) 2 x 1
1 2
(
1 ,1 e 2 2
1
)
o
x
作业
P76 14 (2);
P169 2 ;
5
思考题 求笛卡儿叶形线 x 3 y 3 3a x y 的渐近线 . 解: 令 y = t x , 代入原方程得曲线的参数方程 :
3a t 2 3a t , y t 1 x 3 3 1 t 1 t 当 x 时 t 1, 因 y 3a t 2 3a t 1 lim lim t 1 1 t 3 x x 3 1 t 3a t 2 3a t 3 at (1t ) lim y ( x) lim lim (1t )(1t t 2 ) 3 3 x t 1 1 t t 1 1 t a 所以笛卡儿叶形线有斜渐近线 y x a
6)绘图
x ( , 1) 1 (1,1)
y
铅直渐近线 斜渐近线 特殊点
(极大)
1
无 定 义
(1, 3)
3
0
(极小)
(3 , )
2
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
1
0 12 3
例5. 描绘函数
解: 1) 定义域为 2) 求关键点 2 x2 1 xe , y 2
y x 2 为曲线的斜渐近线 .
二、函数图形的描绘
步骤 : 1. 确定函数 期性 ; 2. 求 的点 ; 3. 列表判别增减及凹凸区间 , 求出极值和拐点 ; 4. 求渐近线 ; 并求出 及 为 0 和不存在 的定义域 , 并考察其对称性及周
5. 确定某些特殊点 , 描绘函数图形 .
例3. 描绘
解: 1) 定义域为
的图形. 无对称性及周期性.
2) y x 2 2 x , y 2 x 2 , 令 y 0 , 令 y 0 ,
1
1
2
3
3)
x ( , 0) y y y x 1 3 y 2 2 3
0 0
2
(极大)
(0 ,1) 1 0
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
4) 求渐近线 lim y 0
x
y
1 2
y
1 2
e
x2 2
y 0 为水平渐近线
5) 作图
A
B
o
x
内容小结
1. 曲线渐近线的求法 水平渐近线 ; 垂直渐近线; 斜渐近线 2. 函数图形的描绘 按作图步骤进行
2. 曲线 y 1 e
x2
( 1 , 的凹区间是 2
1 , ) 2
1 ) 2
,
( , 1 ) 及 ( 凸区间是 2
拐点为 提示:
,
(
1 1 ,1 e 2 ) 2
, 渐近线
y 1
.
y
x2
y 2 e
(1 2 x 2 )
1
( 1 ,1 e ) 2
2 4 y 8 y 4 x y 0 1 4 y y 2( x 1)
令 y 0, 得 x 1, 3 ;
3) 判别曲线形态
x ( , 1) 1 (1,1) y 0 y y 2
(极大)
(1, 3) 3 0 无 定 义 0
4 3
(1, 2)
2 ( 2 , ) 0
2 3
(拐点)
(极小)
4)
例4. 描绘方程
的图形.
( x 3) 2 , 定义域为 解: 1) y 4( x 1) 2) 求关键点 2( x 3) 4 y 4 y 4 x y 0
x 3 2y y 2( x 1)
