弦振动偏微分方程的求解
偏微分方程的求解方法

偏微分方程的求解方法偏微分方程(Partial Differential Equation,简称PDE)是一类重要的数学问题,其应用范围遍及自然科学、工程技术以及金融等领域。
如何求解偏微分方程是一个具有挑战性的问题,通常需要采用多种方法结合起来进行求解。
本文将简要介绍几种常见的偏微分方程求解方法。
1. 分离变量法分离变量法是一种简单而重要的偏微分方程求解方法。
该方法基于以下假设:偏微分方程的一个解可以写成一系列单一变量的函数乘积的形式。
具体地说,对于一个偏微分方程u(x, y) = 0(其中x, y为自变量),假设其解可以表示为u(x, y) = X(x)Y(y),其中X(x)和Y(y)分别是关于x和y的单一变量函数。
将u(x, y)代入原方程,得到X(x)Y(y) = 0。
由于0的任何一侧都是0,因此可得到两个单一变量方程:X(x) = 0和Y(y) = 0。
这两个方程的部分解(即使其中一个变量为常数时的解)可以结合在一起,形成原偏微分方程的一般解。
2. 特征线法特征线法是另一种重要的偏微分方程求解方法。
该方法的基本思想是将原方程转化为常微分方程,进而求解。
具体地说,对于一个二阶线性偏微分方程:a(x, y)u_xx + 2b(x, y)u_xy + c(x, y)u_yy + d(x, y)u_x + e(x, y)u_y + f(x, y)u = g(x, y),通过变量的代换,可以将该方程化为一个与一次微分方程组相关的形式。
进一步地,可以选择沿着特定的方向(例如x或y方向)进行参数化,从而得到关于变量的一阶微分方程。
该微分方程的解通常可以通过传统的常微分方程求解技巧来获得。
3. 数值方法数值方法是目前应用最广泛的偏微分方程求解方法之一。
由于大多数偏微分方程的解析解很难获得,因此数值方法成为了一种有效的、可行的替代方法。
常见的数值方法包括有限差分法、有限元法和边界元法等。
这些方法通过将偏微分方程离散化为一个有限维的计算问题,然后使用数值方法求解这个问题的解。
弦振动方程的导出与定解条件

弦的一端的运动规律已知, 以
为例,若以
表示其运动规律,则边界条件可以表达为
特别的,若
非齐次边界 条件
端被固定,则相应的边界条件为
u |x0 0.
齐次边界条件
20
2、第二类边界条件(诺伊曼Neumann)
若弦的一端(例如
)在垂直于 x 轴的直线
上自由滑动,且不受到垂直方向的外力,这种边界
成为自由边界. 根据边界微元右端的张力沿垂直方
1、购买练习册(以小班为单位购买) 时间:本周三到周六早上8:00-12:00 下午2:00-5:30 地点:科技楼602(应用数学系办公室)
2、答疑:从第六周开始
3、综合成绩: 平时成绩:30%(考勤+作业) 卷面成绩:70%
典型的数学物理方程的导出
1.1 弦振动方程与定解条件 1.2 热传导方程与定解条件 1.3 拉普拉斯方程与定解条件
4
3.弦在某一平面内作微小横振动 即弦的位置始终在一直线段附近(平衡位 置),而弦上各点均在同一平面内垂直于该 直线的方向上作微小振动。(“微小”是指 弦振动的幅度及弦上任意点切线的倾角都很 小) 我们将在上述假定下来导出弦振动方程。 先讨论振动过程中不受外力作用时弦 振动的情形
5
为此,选择坐标系如下
2
lx
这个方程称为弦的自由横振动方程。
15
u
1
M1 M2
T0
2
T0
O x1 x2
lx
若还有外力作用到弦上,其方向垂直于
轴,
设其力密度为
由于弦段
其上各点处的外力近似相等,
很小,
因此作用在该段上的外力近似地等于
16
u
1
M1 M2
弦振动偏微分方程的求解

弦振动偏微分方程的求解(郑州航空工业管理学院数理系 田硕 450015)摘要:本文列出了不同情况下的弦振动问题的定解方程及其成立条件,给出了不同情况下偏微分方程的求解方法,对于我们的生活和学习有一定的指导意义。
关键词:数学物理方程;偏微分方程;弦振动;拉普拉斯变换Method for solving partial differential equations of string vibration (Tianshuo Department of mathematics and physics, Zhengzhou Institute ofAeronautics Industry Management, henna zhengzhou 450015)Abstract : This article lists the definite solution of the equation of string vibration problems in different situations and the establishment of conditions, given the method for solving partial differential equations under different circumstances, for our lives and learning have a certain significance. Keywords : mathematical physics equations; partial differential equations; vibrating string; Laplace transform在数学物理方程中,根据常见物理模型,可以建立求解的偏微分方程。
如在很多物理实际问题中要遇到的拉普拉斯方程,泊松方程,波动方程,热传导方程等等。
弦振动方程的导出与定解条件

2、答疑:从第六周开始
3、综合成绩: 平时成绩:30%(考勤+作业) 卷面成绩:70%
典型的数学物理方程的导出
1.1 弦振动方程与定解条件 1.2 热传导方程与定解条件 1.3 拉普拉斯方程与定解条件
在考察弦振动问题时的基本假设为:
1.弦是均匀的,弦的截面直径与弦的长度
相比可以忽略,弦的线密度 是常数。
2.弦是柔软的,它在形变时不抵抗弯曲, 弦上各点所受的张力方向与弦的切线方向一 致,而弦的伸长形变与张力的关系服从胡克
(Hooke)定律。(即指在弹性限度内, 物体的形变跟引起形变的外力成正比)
分量的代数和为
T0 sin 2 T0 sin 1 T0 (sin 2 sin 1).
由于小振动:
u u T0[ x |x2 x |x1 ]
sin 2
tan2
u x
|x2 ,
sin 1
tan1
u x
| x1 ,
12
u
1
M1 M2
T0
2
T0
O x1 x2
lx
应用微分中值定理:
T0
[
u x
|x2
接下来, 我们只须说明张力与位置 x 无关
9
u
M2
T2
1
M1
T1
O x1 x2
2
lx
我们分别把在点 M1, M2 处的张力记作 T1, T2, 由前所述知他们的方向分别是沿着弦在点
M1, M2 处的切线方向。
由假定,弦只作横向振动,因此张力在
弦振动频率计算公式推导

弦振动频率计算公式推导全文共四篇示例,供读者参考第一篇示例:弦振动频率是指弦在振动时产生的频率,它是弦的长度、材质、张力等因素共同作用的结果。
在物理学中,弦振动频率的计算是一个重要的问题,它可以帮助我们了解弦的振动特性以及音乐乐器的原理。
为了计算弦的振动频率,我们需要首先推导出弦振动频率的计算公式。
在这里,我们将通过弦的基本原理和波动方程来推导这个公式。
我们假设一根长度为L、质量为m的弦被拉紧,并在两端固定。
弦上的振动可以被描述为横波传播,其波速v可以用张力T和线密度μ来表示:v = √(T/μ)弦的振动频率f可以用波速v和波长λ来表示:f = v/λ我们知道波长λ与弦的长度L有关系:其中n为弦的振动模态数。
当n=1时,弦的整数倍分之一波长的振动称为基频振动,也称为第一次共振;当n=2时,弦的整数倍分之二波长的振动称为第二次共振,如此类推。
将λ带入频率计算公式中,得到:将波速v的公式代入,得到:f = (1/2L)√(T/μ) * n这就是弦振动频率的计算公式。
从这个公式可以看出,弦振动频率与弦的长度L、张力T、线密度μ以及振动模态数n有关。
当我们改变这些参数时,弦的振动频率也会相应改变。
通过这个公式,我们可以更好地理解弦的振动特性,并且可以应用于乐器的设计和制作中。
通过调节张力和长度,可以改变乐器的音调,使得音乐更加美妙动听。
弦振动频率的计算公式是一个重要的物理公式,它可以帮助我们理解弦的振动原理和音乐乐器的工作原理。
希望通过本文的介绍,读者能够更加深入地了解弦振动频率的计算方法,并且能够应用于实际问题中。
【这是我对于弦振动频率计算公式的一些理解,希望能够对您有所帮助。
】第二篇示例:弦振动是物理学中常见的一种现象,例如吉他、小提琴等乐器中的琴弦就是一种典型的弦振动系统。
在弦振动中,弦线上的每一个微小的部分都在进行横向振动,形成一系列波动。
而弦振动的频率则是指每秒钟弦线振动的次数,是描述弦振动特性的重要参数之一。
弦振动方程中D'Alembert公式的算子算法

其 中 , 是 ( ( 的任意连续可微 函数. 由上式可得
(, e
G +J (
啦
个主要方 法. 本文主要 从 另一角 度 即算子 的方法 进一 步
令 F 一J ( ( , 啦, 则
( , 一G( + F( e
讨论了 DA e et lmbr 公式的推导过程 , 面将作 简单介绍. 下
其中 c,z c 为任 意常数. 作变量变换
 ̄
我们首先引入另两个定解 问题
+口 £
e x- a , = - t叩
f 一 口 M 一 O ~ ∞ < < + ∞ ,> O t (*1 u x, ) ) ( 0 一 ( 或(D 钾 , u 一0
加原理知道
u x,) “ ( ,) U ( f ( f 一 1 f + 2 ,) () 6
詈+ 一( n n +£ )
再联立 ( z 中的初始条件 U ,) , *) z 0 一0 则问题( *z的求解 等价于下列问题 ( 。 的求解 : *)
公式.
关键 词 : 弦振动 方程 DAl et e r 公式 ; mb 算子方法
中图 分 类 号 : 7 . 7 O15 2 文献标识码 : A
特 征线 的方法是求解 一维 双 曲型方程 C u h ac y问题 的
最基本方法 , 也是 推导弦振 动方程 中的 EA e et r lmb r 公式 的
弦振动方程中 DAlmb r 公 式的算子算法 ' e et
陈 名 中
(成 宁学 院 数 学 系 ,湖北
摘
成宁
47 O ) 3 1O
要: 主要讨论 了运用算子的方法推导 出弦振动 方程 中的 EAl et 式. r e r公 mb 弦振 动方程 中的 DA e et lmb r 公式
基本波动方程的求解方法

基本波动方程的求解方法 This model paper was revised by the Standardization Office on December 10, 2020关于弦振动的求解方法李航一、无界弦振动1、一维齐次波动方程达朗贝尔方程解无界的定解问题⎰+-+-++=at x atx d a at x at x t x u ξξϕφϕ)(21)]()([21),( <达朗贝尔公式> 在常微分方程的定解问题中,通常是先求方程的通解,然后利用定解条件确定通解所含的任意常数,从而得到定解问题的解。
考虑无界的定解问题一般方程为 由达郎贝尔公式,解在点),(t x 的值由初始条件在区间],[at x at x +-内的值决定,称区间],[at x at x +-为点),(t x 的依赖区域,在t x -平面上,它可看作是过点),(t x ,斜率分别a 1± 为的两条直线在x 轴上截得的区间。
2、一维非齐次波动方程的柯西问题达朗贝尔方程解非齐次定解问题令),(),(),(t x V t x U t x u +=,可将此定解分解成下面两个定解问题: (I) ⎪⎪⎩⎪⎪⎨⎧=∂∂=>+∞<<∞-∂∂=∂∂== , )(|),(|0,0022222x t u x u t x x u a t u t x φϕ(II) ⎪⎪⎩⎪⎪⎨⎧=∂∂=>+∞<<∞-+∂∂=∂∂== , 0|,0|0,),(0022222t x t u u t x t x f x u a t u 其中问题(I)的解可由达朗贝尔公式给出:⎰+-+-++=at x atx d a at x at x t x U ξξϕϕϕ)(21)]()([21),(。
对于问题(II),有下面重要的定理。
定理(齐次化原理)设),,(τωt x 是柯西问题的解)0(≥τ,则⎰=t d t x t x V 0),,(),(ττω是问题(II)的解。
偏微分方程的解法

偏微分方程的解法偏微分方程(Partial Differential Equation,简称PDE)是数学中一种重要的方程形式,广泛应用于物理、工程、金融等领域。
本文将介绍几种常见的偏微分方程的解法,并对其原理和应用进行详细的讨论。
一、分离变量法分离变量法是求解偏微分方程中最常用的方法之一。
该方法的基本思想是将偏微分方程中的未知函数表示为多个单变量函数的乘积,然后通过分别求解这些单变量函数的常微分方程来得到原方程的解。
以下以一个简单的例子来说明该方法的具体步骤。
考虑一个常见的一维热传导方程:\[\frac{{\partial u}}{{\partial t}} = \alpha \frac{{\partial^2 u}}{{\partial x^2}}\]假设 u(x,t) 可以表示为两个单变量函数的乘积形式:u(x,t) =X(x)T(t),将其代入原方程,可以得到如下的形式:\[\frac{1}{\alpha}\cdot\frac{1}{X(x)}\cdot\frac{{d^2X}}{{dx^2}} =\frac{1}{T(t)}\cdot\frac{{dT}}{{dt}} = -\lambda\]通过解这两个单变量函数所满足的常微分方程,可以得到 X(x) 和T(t) 的解,再将其组合即可得到原方程的通解。
二、变换方法变换方法是另一种重要的求解偏微分方程的技巧。
通过对原方程进行适当的变换,可以将其转化为常微分方程或者其他更容易求解的形式。
以下介绍两种常见的变换方法。
1. 傅立叶变换法傅立叶变换法被广泛应用于分析和求解各种偏微分方程。
通过将原方程进行傅立叶变换,可以将其转化为代数方程,并通过解代数方程来得到原方程的解。
具体来说,假设原方程为:\[L[u(x,t)] = f(x,t)\]将其进行傅立叶变换,可以得到:\[L[\hat{u}(k,\omega)] = \hat{f}(k,\omega)\]然后通过解代数方程来求得 \(\hat{u}(k,\omega)\),再进行逆傅立叶变换即可得到 u(x,t) 的解。
第八章 弦振动方程初值问题的达朗贝尔解

at x
0
c ( )d 2
固得:
u( x , t ) f 2 ( ( x at )) f 2 ( x at ) 1 1 [ (at x ) ( x at )] x ( )d 2 2a at
at x
综上得:
( x at ) ( x at ) 1 x at at ( )d , x at 2 2a x u( x , t ) x at (at x ) ( x at ) 1 x ( )d , x at 2 2a at
解:
0 ( x) 0 ( x ) 0
x at x at
x1 x x2 x1 x , x2 x
x at
1 1 1 u( x, t ) at ( )d 2a ( )d 2a ( )d 2a x
1 ( x) ( )d 2a
( x) 0
(x)
u0
x
x1
x1 x2 2
x2
u( x , t )
1 ( x) 2
x1
u0
x2
x x x
1 u( x , t ) [ ( x at ) ( x at )] 2
例:初位移为0,在 x1 x x2 范围有恒定速度。 相当于用一定宽度的物件敲击弦。
2 代入方程 utt a uxx
得: u 0
u c( )
u( , ) c( )d f1 ( ) f 2 ( )
代回原变量得: u( x, t ) f1 ( x at ) f 2 ( x at )
容易验证,只要这两个任意函数具有二阶连续偏导数,则 上式就是所求弦振动方程的的解,且是通解(一般解).
弦振动方程

演奏弦乐器(如提琴、二胡)的人用弓在 弦上来回拉动. 弓所接触的只是弦的很小一段, 似乎应该只引起这个小段的振动. 实际上,振 动总是传播到整根弦,弦的各处都振动起来. 人们力求用数学方法研究这种弦振动传播现 象.
弦振动方程
考虑一根绷紧的弦,它在不振动时是一根 直线,就取此直线作为x 轴. 在时刻t=0 将此弦 拨动一下使其振动. 令u(x,t)表示弦上对应与横 坐标x 的点在时刻t 的横向位移. 则用讨论张力 的方法可推得u(x,t)满足偏微分方程
2u 2u ξ 2u η 2u ξ 2u η = 2 + + + 2 2 x ξ x ξη x ξη x η x 2u 2u 2u = 2 +2 + 2 ξ ξη η
弦振动方程
u u ξ u η u u = + = a( ) t ξ t η t ξ η
2u 2u ξ 2u η 2u ξ 2u η = a[ 2 + 2 ] 2 t ξ t ξη t ξη t η t 2u 2u 2u = a2 ( 2 2 + 2) ξ ξη η
代入原方程得 先对 η 积分,得
2u =0 ξη u = f (ξ ) ξ
弦ቤተ መጻሕፍቲ ባይዱ动方程
再对 ξ 积分,就得到通解
u = ∫ f (ξ )dξ + f 2 (η ) f1 (ξ ) + f 2 (η )
= f1 ( x + at ) + f 2 ( x at )
其中f1,f2为任意函数. 通解有很鲜明的物理意义. 事实上,凡f(x-at) 形状的函数描述的是沿x 的正方向传播的波, 其速度为a. 而f(x+at)形状的函数描述的是沿x 的负方向传播的波,其速度也为a.
偏微分方程数值解流程

偏微分方程数值解流程1.网格划分:将求解域划分为网格,这是将偏微分方程离散化的基础。
可以使用等距网格或非等距网格,具体取决于问题的特点。
2.离散化:根据偏微分方程的类型和边界条件,将偏微分方程的导数转换为离散的差分或有限差分格式。
常用的数值离散化方法有前向差分,后向差分和中心差分等。
3.初值条件:根据问题的初始状态,确定在初始时间步骤上网格点的值。
常用的方法是根据问题的初始条件进行数值插值。
4.边界条件:确定在边界网格点上的值。
根据问题的边界条件,可以采用数值插值法或手动设置边界值。
5. 迭代求解:根据离散化的差分方程,通过迭代方法求解离散化的方程组。
常用的迭代方法有Jacobi方法,Gauss-Seidel方法,SOR方法等。
6.收敛性判断:根据设定的收敛准则,判断数值解是否达到了预期的精度。
通常可以通过比较相邻两次迭代的差异来判断收敛性。
7.后处理:根据求解得到的数值解,计算并绘制出感兴趣的物理量。
还可以评估数值方法的误差和稳定性,并进行必要的修正。
8.参数选择:在数值解的迭代过程中,可能需要选择合适的参数,如网格大小和时间步长等。
这需要根据问题的特性和数值方法的准则进行选择。
9.优化和改进:根据数值解的结果和收敛性,可以对数值方法进行改进和优化。
可能需要调整离散化方法,调整网格布局或改进迭代算法。
总之,偏微分方程的数值解流程是一个迭代过程,通过将偏微分方程离散化为差分方程,并进行迭代求解和收敛性判断,获得问题的数值解。
这个过程需要认真的数值计算和对问题的物理背景知识的深刻理解。
偏微分方程及其求解实例ppt课件
(hn1-2.*h(k,n)+h(k,n-1))./dr.^2);
end plot(r(3:n)./ra,p(k,3:n).*theta.*2./rb)
h hi1 hi1 r i 2r
2h hi1 2hi hi1
r 2
r 2
i
P
1 rb 4
1
r
h r
2h r 2
偏微分方程的求解实例2:
2u A x2
2u B
xy
C
2u y 2
D u x
E u y
Fu
f
x,
y,u,
u x
,
u y
(1) 导热方程:
u 2u
t x2 (2) 拉普拉斯方程: 如稳态静电场和稳态温度分布模型
2u 2u 0
x2 y2
(3) 波动方程: 一维弦振动模型
2u 2 2u
t 2
x2
偏微分方程的边界条件
function PDE1Dd_CrankNicolson % 使用Crank-Nicolson有限差分方法求解一维动态传
热模型
c1 = 100; c2 = 0; a = 10; b = 8; alpha = 2; n = 6; m = 8; U = CrankNicolson(@ic,c1,c2,a,b,alpha,n,m)
h t 3 9c
9c
h3 h33
4h r 4
3
h5 4h4
6h3 4h2 r 4
h1
h t
n
V
r i 2r
2h hi1 2hi hi1
r 2
r 2
i
3h r 3
hi2
2hi1 2hi1 2r 3
偏微分方程模型

偏微分方程模型一、弦的微小横振动给定一根两端固定且拉紧的均匀,柔软的细弦,其长度为L .在垂直于弦线的外力作用下,弦在其平衡位置附近作微小的横振动,求弦的运动规律.术语及假设:柔软:抗拉伸,不抗弯曲,从而拉力与弦线相切.均匀:弦的线密度为常数,可设为kg/m. 细:弦的截面直径比长度远远小于1,可视为理想的曲线.外力:已知,外力密度可表示为).,(t x f 弦:有弹性,且在其弹性限度内.弦的振动是一种机械运动.其基本定律是质点力学的牛顿运动学第二定律:.ma F 然而弦不是质点,该定律对整根弦并不适用.但整根弦可以细分为许多极小的小段,每小段可以抽象为质点,即每个小段(质点)可以运用上述定律.差分方程及其模型)()1(1t f t f y y y t t t -+=-=∆+1. 差分的定义定义1设函数称为函数的一阶差分;t y 一、差分方程的基本概念,2,1,0),(==t t f y t称2()t t y y ∆=∆∆1t ty y +=∆-∆211()()t t t t y y y y +++=---212t t ty y y ++=-+为函数t y 的二阶差分. 为三阶差分. 同样,称32()t t y y ∆=∆∆依此类推,函数的n 阶差分等.定义2含有自变量、未知函数及其差分的方程, 称为差分方程.差分方程的一般形式为F(t,y t ,∆y t ,⋅⋅⋅, ∆n y t )= 0. (1)差分方程中可以不含自变量t和未知函数y,但必须t含有差分.式(1)中, 当n = 1时, 称为一阶差分方程;当n = 2时, 称为二阶差分方程.例如,差分方程∆2y t+ 2∆y t= 0可将其表示成不含差分的形式:∆y t= y t+1-y t, ∆2y t= y t+2-y t+1+ y t,代入得y t+2-y t= 0.由此可以看出, 差分方程能化为含有某些不同下标的整标函数的方程.定义3含有未知函数几个时期值的符号的方程, 称为差分方程.其一般形式为G(t,y t,y t+1, ⋅⋅⋅, y t+n) = 0. (2)定义3中要求y,y t+1, ⋅⋅⋅, y t+n不少于两个.t例如,y+y t+1= 0 为差分方程,t+2y t= t 不是差分方程.差分方程式(2)中, 未知函数下标的最大差数为n, 则称差分方程为n 阶差分方程.t S t t S r ,)1(1t t t t S r rS S S +=+=+,,2,1,0 =t t S ,)1(0S r S tt +=,,2,1,0 =t 0S 例1(存款模型)为期存款总额,利率,按年复利计息,则与有如下关系式:这是关于的一个一阶常系数齐次线性差分方程,其中为初始存款总额.为存款其通解为设r 差分方程在经济问题中的简单应用例3(筹措教育经费模型)某家庭从现在着手从每月工资中拿出一部分资金存入银行,用于投资子女的教育. 并计划20年后开始从投资帐户中每月支取1000元,共计支取10年,直到子女完成学业并用完全部资金.要实现这个投资目标,20年内共要筹措多少资金?每月要向银行存入多少钱?假设投资的月利率为0.5%,10年后子女大学毕业用完全部资金.该问题可分为两个阶段,第一阶段是在前面20年分析解设从现在到20年内共要筹措x 元资金,第n 个月每月存入资金a 元. 同时.投资账户资金为I n 元,也设20 年后第n 个月投资帐户资金为S n 元,于是,20 年后,关于S n 的差分方程模型为每月向银行存入一定数量的资金,第二阶段是在20 年后将所有资金用于子女教育,每月支取1000元,10内用完所有资金..95.194=a 以及从而有即要达到投资目标,20 年内要筹措资金90073.45 元,平均每月要存入银行194.95 元.,45.90073200005.11240240=-=a C I .020010=-=a C I。
偏微分方程解法

偏微分方程解法一、概述偏微分方程是数学中的一个重要分支,广泛应用于物理、工程、经济等领域。
解决偏微分方程的方法有很多种,其中最常用的方法是数值解法和解析解法。
本文将重点介绍偏微分方程的解析解法。
二、基本概念1. 偏微分方程:含有多个自变量和它们的偏导数的方程。
2. 解析解:能够用一定的代数式或函数表示出来的解。
3. 常微分方程:只含一个自变量和它的导数的方程。
4. 偏微分方程分类:(1)线性偏微分方程:各项次数之和为1或2。
(2)非线性偏微分方程:各项次数之和大于2。
5. 解析解法分类:(1)可分离变量法(2)相似变量法(3)积分因子法(4)特征线法(5)变换法三、可分离变量法可分离变量法是求解一类特殊形式线性偏微分方程最常用的方法,其基本思想是将未知函数表示成各自变量之积,然后将其带入原偏微分方程中得到一组常微分方程,再求解这些常微分方程,最后将得到的解代回原方程中即可。
以一阶线性偏微分方程为例:$$\frac{\partial u}{\partial t}+a(t)u=b(t)$$其中$a(t)$和$b(t)$为已知函数,$u=u(x,t)$为未知函数。
将未知函数表示成各自变量之积:$$u=X(x)T(t)$$将其带入原方程中得到:$$XT'+aXT=bXt$$将$X$和$T$分离变量并整理得到:$$\frac{1}{X}\frac{dX}{dx}=\frac{1}{at+b}-\frac{c}{X}$$其中$c$为常数。
对上式两边同时积分得到:$$ln|X|=ln|at+b|-ct+D_1,D_1为常数。
$$即可得到$X(x)$的解析解。
同理,对于$T(t)$也可以通过可分离变量法求出其解析解。
最后将$X(x)$和$T(t)$的解代入原方程中即可得到未知函数$u=u(x,t)$的解析解。
四、相似变量法相似变量法是一种适用于非线性偏微分方程的方法,其基本思想是通过引入新的自变量和因变量,将原偏微分方程转化成一个形式相似但更简单的方程,从而求出原方程的解析解。
弦振动 偏微分方程

弦振动偏微分方程弦振动是一种自然现象,指的是弦线在受到外力驱动后产生的振动。
这种振动可以通过偏微分方程进行描述和分析,以便更好地理解和预测弦线振动的特性。
偏微分方程是一种数学表达式,用于描述多个变量之间的关系。
在弦振动的分析中,最常使用的偏微分方程为一维波动方程。
该方程可表示为:∂^2y/∂t^2=c^2∂^2y/∂x^2其中,y表示弦线上任意一点的位移(以某个平衡位置为基准),t表示时间,x表示该点在弦线上的位置,c表示波速。
该方程表达的是弦线上任意一点的位移随时间和位置的变化情况。
解一维波动方程需要使用波动方程的通解形式。
通解形式有多种,其中最常用的是分离变量法。
首先,将y分解为关于时间t和位置x的两个未知函数F和G的积:y=F(t)G(x)由于y随时间的变化是二阶导数,所以F需要满足二阶常微分方程:∂^2F/∂t^2+c^2kF=0其中,k为常数,由于F只是时间t的函数,所以k只是一个常数。
同样,由于y随空间位置的变化是二阶导数,所以G需要满足二阶常微分方程:∂^2G/∂x^2+kG=0利用该方程的通解形式,可以得到F和G的解析形式:F=Acos(ct)+Bsin(ct)G=Ccos(kx)+Dsin(kx)其中,A、B、C和D均为常数。
将F和G合并为y,即可得到y关于时间t和位置x的通解形式。
波动方程的解析解无法描述所有情况,但可以帮助我们了解弦振动的特性。
通过偏微分方程的求解,我们可以得到弦振动的幅度、波长、波速等参数,从而更好地进行振动相关的工程设计和控制。
在日常生活中,弦振动广泛应用于乐器演奏、声波传递、振动摄影等领域。
了解弦振动的特性和使用偏微分方程进行分析,可以更好地理解这些现象,同时也有助于我们将弦振动应用于更多的领域。
偏微分方程数值求解方法

偏微分方程数值求解方法偏微分方程(Partial Differential Equations, PDEs)是数学中的一个重要研究领域,也是应用领域中关键的数学工具之一。
在科学与工程领域中,偏微分方程广泛地应用于描述许多自然现象和物理过程,例如流体力学、电磁学、量子力学等。
在实际问题中,往往很难找到偏微分方程的解析解,这时就需要使用数值求解方法来近似求解。
数值求解方法可以分为两大类:直接法和间接法。
直接法基于有限差分(Finite Difference)思想,将偏微分方程中的导数转化为差商,通过离散化空间和时间的方法,将连续的问题转化为离散的问题。
常见的有限差分方法有:显式格式、隐式格式和Crank-Nicolson格式。
显式格式是最直观的方法,通过将一阶导数展开到下一个时间点的差商来逼近导数,但它的稳定性条件限制了时间步长的选取,以保证数值解的稳定性。
隐式格式则是通过将未知数展开到下一个时间点的差商来逼近导数,从而避免了时步限制,但会导致一个隐式的线性系统,需要通过迭代方法求解。
Crank-Nicolson格式则是将显式格式和隐式格式的结果进行加权平均,可以通过选择合适的权重来平衡时间精度和稳定性。
间接法则是基于变分原理,将偏微分方程转化为变分问题,通过寻找变分问题的极值得到偏微分方程的近似解。
常见的间接法有有限元方法(Finite Element Method, FEM)和边界元方法(BoundaryElement Method, BEM)。
有限元方法将求解区域分割为许多小的单元,通过构建基函数展开的近似解,并将原方程带入到变分问题中,得到一个离散的代数方程组。
边界元方法则是将求解区域的边界分割为许多小的面元,通过将边界上的值表示为边界上的基函数的线性组合,从而将偏微分方程转化为一个边界积分方程。
无论是有限元方法还是边界元方法,都可以通过求解离散的方程组得到原偏微分方程的数值解。
需要注意的是,数值求解方法的选取应该根据具体问题的性质和要求来进行选择。
求解偏微分方程三种数值方法

求解偏微分方程三种数值方法偏微分方程是数学中研究包含多个变量及其偏导数的方程。
解决偏微分方程的数值方法有很多,但本文将重点介绍三种常用的数值方法,分别是有限差分法、有限元法和谱方法。
一、有限差分法:有限差分法是一种常用的数值方法,用于求解偏微分方程的数值解。
其基本思想是通过建立网格来离散化偏微分方程中的空间变量,并近似替代导数,将偏微分方程转化为代数方程组,进而求解。
常见的有限差分格式有向前差分、向后差分和中心差分。
有限差分法主要包括以下步骤:1.空间离散化:将区域划分为网格点,在每个网格点上计算方程中的函数值。
2.近似代替导数:使用差分公式,将导数近似替代为函数在相邻网格点上的差分。
3.建立代数方程组:根据近似的导数和偏微分方程的形式,可以建立相应的代数方程组。
4.求解方程组:使用求解线性方程组的方法,如高斯消元法或迭代法,求解代数方程组。
5.恢复连续解:通过插值或者其他方法,将离散解恢复为连续解。
二、有限元法:有限元法是一种广泛应用的数值方法,用于求解偏微分方程的数值解。
其基本思想是将区域划分为有限个小区域,称为单元,通过求解单元上的局部方程,最终得到整个区域上的数值解。
有限元法主要包括以下步骤:1.离散化:将区域划分为单元,并选择适当的有限元空间。
2.建立局部方程:在每个单元上,根据选择的有限元空间和边界条件,建立局部方程。
3.组装全局方程:将所有单元上的局部方程组装成整个区域上的全局方程。
4.施加边界条件:根据问题的边界条件,施加适当的边界条件。
5.求解方程组:使用求解线性方程组的方法,求解全局方程组,得到数值解。
6.后处理:通过插值等方法,将离散解恢复为连续解,并进行后续的分析。
三、谱方法:谱方法是一种高精度的数值方法,适用于求解偏微分方程的数值解。
其基本思想是将区域上的函数展开为一组基函数的线性组合,通过选取适当的基函数和系数,来逼近求解方程。
谱方法主要包括以下步骤:1. 选择基函数:根据问题的性质,选择合适的基函数,如Legendre多项式、Chebyshev多项式等。
具有非齐次定解条件的弦振动方程的解

具有非齐次定解条件的弦振动方程的解解决实际物理问题的关键在于对有关方程的可解性,而有关非齐次定解条件的方程解,是很多物理问题研究中不可缺少的重要内容。
本文就以弦振动方程为例,从定义开始,考察非齐次定解条件的解方式,总结出一系列可行的解决办法,以期能够对同学们对理论计算与实际解决物理问题中相关内容的了解产生一定的裨益。
2.振动方程的定义弦振动方程,即线性微分方程,是由描述弦振动现象的一种数学模型。
一般的弦振动方程的形式为:$$frac{d^2y}{dx^2}+P(x) frac{dy}{dx}+Q(x)y=f(x)$$ 式中P(x),Q(x)和f(x)为弦振动方程的非齐次定解条件,可以通过求解这个弦振动方程来实现对弦振动的研究.3.齐次定解条件的求解非齐次定解条件的解法可以采用几种不同的方式进行求解,其中包括积分法、特解法、递推法以及解析法等。
3.1分法积分法是基于对弦振动方程进行积分求解的方法,即从未知函数的参数到函数的构建的过程,其具体实现需要解决相应的积分等价问题,但求解的复杂度很高。
3.2解法特解法是基于特解求解弦振动方程的方法,即针对特定的非齐次定解条件而求解的特解,它可以通过积分系数的方式发现特解的解析解,而无需计算就可以求出特定的解。
3.3推法递推法是基于递推法求解弦振动方程的方法,即针对特定的非齐次定解条件而求解的解析解,它可以通过将相关系数纳入递推式而求出解析解。
3.4析法解析法是基于解析法求解弦振动方程的方法,即针对特定的非齐次定解条件而求解的解析解,它可以通过分解解析解的参数和系数而求出解析解。
4.语本文以弦振动方程的解为例,探讨了关于非齐次定解条件的不同解法及其实现方式。
从定义、几种不同解法到实现方式,本文对弦振动方程的解有了比较详细的介绍,以期能够对同学们在解决物理问题中的用到的非齐次定解条件有更深入的了解,为实际的应用提供前期的理论基础。
2.3.2弦振动方程的一般解

2.3.2弦振动⽅程的⼀般解( 2-3-14 )这⾥,是仅包含位置变量的函数;是仅包含时间变量的函数。
将( 2-3-15 )上式等号的左边仅与有关,右边仅与有关,⽽和都是独⽴变量,因⽽如果 (2-1-15) 式对任何的 x 与 t 都成⽴,则其等号两边应恒等于⼀个与,都⽆关的常数。
如果令这⼀常数为,并且,那么 (2-1-15) 式可写成( 2-3-16 )于是可以分别得到两个独⽴的⽅程( 2-3-17 )( 2-3-18 )经过上⾯分离变量后,就把⼀个偏微分⽅程分解成两个具有单⼀独⽴变量的常微分⽅程。
⽽这种形式的微分⽅程我们在第 1章中⼰遇到过,因此我们可以仿照⽅程 (1-2-4) 的求解结果,直接写出 (2-1-17) 与 (2-l-18) ⽅程的解为( 2-3-19 )( 2-3-20 )式中都是待定常数。
将上⾯⼆式代⼈( 2-3-14 )可得( 2-3-21 )其中仍是待定常数。
如果弦的两端固定,可以利⽤对任意时间都满⾜的边界条件( 2-3-8 )式。
将代⼈ (2-1-21) 式可以定得常数,再将代⼈ (2 - 1-21) 式可得如下关系( 2-3-22 )这时不能为零,否则和都为零,则整个弦不振动,这显然是没有意义的。
因此要得到⾮零解就必须令( 2-3-23 )要正弦函数等于零。
显然应该使其宗量满⾜如下关系( 2-3-24 )⽤⼀新的符号来代替,于是( 2-3-24 )式可写成( 2-3-25 )或( 2-3-26 )从 (2-1-21) 式可知弦的位移对时间是⼀简谐函数,因⽽应该代表振动的圆频率,⽽代表弦的振动频率。
从 (2-1-26) 式知,对于两端固定的弦,振动频率具有⼀系列持定的数值,即,并且仅同弦本⾝的固有⼒学参量有关,因⽽称为弦的固有频率。
但是它与第 1 章讨论的质点振动之间有⼀明显区别,⼀个单振⼦系统仅有⼀个固有频率,旧弦的固有频率不⽌⼀个,⽽有个,亦即⽆限多个。
并且固有频率的数值不是任意的,其变化也不是连续的,⽽是以等次序离散变化的。
03-1 弦的振动
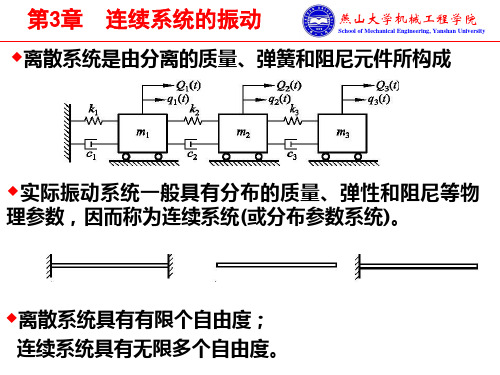
◆离散系统和连续系统具有相同的动力特性。连续系统的振动理 论在概念方面严格地与离散系统相似;分析计算的过程也相似: (1)建立系统运动微分方程 离散系统:常微分方程组; 连续系统:偏微分方程组。 (2)求固有频率、振型、正则振型 离散系统:根据特征方程求固有频率、确定振型向量;根据正交性 确定正则振型向量。 连续系统:根据边界条件求固有频率、确定振型函数;根据正交性 确定正则振型函数。 (3)求正则坐标下的响应 离散系统:正则坐标数为系统自由度数。 连续系统:正则坐标数为无限个。 (4)求原广义坐标下的响应
F(t)表示弦的振动规律,只 取决于时间t。
●
2 y 2 2 y a 2 ★将上式代入自由振动的波动方程 2 t x 2 1 d 2 F t 1 d Y x 2 a 2 F t dt Y x dx 2
燕山大学机械工程学院
School of Mechanical Engineering, Yanshan University
式中,不计 dx 的二次项, 两边同时除 以 dx ,整理 得
2 y 2 y T y 2 f x ,t T 2 t x x x
式中
2 y T y y T 2 T x x x x x
燕山大学机械工程学院
School of Mechanical Engineering, Yanshan University
连续系统具有无限多个自由度。
燕山大学机械工程学院
School of Mechanical Engineering, Yanshan University
◆在数学上,离散系统的运动方程为方程数目与自由度
数目相等的二阶常微分方程组;
◆连续系统需要用时间和坐标的函数来描述它的运动状
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弦振动偏微分方程的求解(郑州航空工业管理学院数理系 田硕 450015)摘要:本文列出了不同情况下的弦振动问题的定解方程及其成立条件,给出了不同情况下偏微分方程的求解方法,对于我们的生活和学习有一定的指导意义。
关键词:数学物理方程;偏微分方程;弦振动;拉普拉斯变换Method for solving partial differential equations of string vibration (Tianshuo Department of mathematics and physics, Zhengzhou Institute ofAeronautics Industry Management, henna zhengzhou 450015)Abstract : This article lists the definite solution of the equation of string vibration problems in different situations and the establishment of conditions, given the method for solving partial differential equations under different circumstances, for our lives and learning have a certain significance. Keywords : mathematical physics equations; partial differential equations; vibrating string; Laplace transform在数学物理方程中,根据常见物理模型,可以建立求解的偏微分方程。
如在很多物理实际问题中要遇到的拉普拉斯方程,泊松方程,波动方程,热传导方程等等。
对偏微分方程求解的讨论,有很重要的意义和运用。
对不同的偏微分方程,往往有不同的求解方法,这要根据方程本身的特点而定。
选取合适的方法不仅可以使问题简化,有时候也能体现出方程背后更深层次的物理意义。
理想弦的振动方程就是一个一维波动方程的特例,本文将给出不同情况下的弦振动偏微分方程,并对它们的求解给予一定的讨论。
一、无界弦的自由振动问题无界弦的自由振动问题既是满足下面条件的偏微分方程[1]:⎩⎨⎧+∞<<-∞==>+∞<<-∞=)(),(),0(),(),0(),0,(2x x x u x x u t x u a u t xx tt φϕ 对于该偏微分方程,我们可以类似常微分方程初始问题的解法,先求出通解,然后把初始条件代入通解,以确定任意常数,从而求得初始问题的解。
做变量代换at x -=ξ,at x +=η,代入偏微分方程,整理可得:02=∂∂∂ηξu,得方程的通解为:)()()()(at x g at x f g f u ++-=+=ηξ 再代入初始条件,有:⎩⎨⎧='+'-==+=)2()()()(),0()1()()()(),0(x x g a x f a x u x x g x f x u t φϕ 对(2)式积分:)3()(1)()(0c d ax g x f x+=+-⎰λλφ将(1)式和(3)式联立,解之则得:2)(212)()(0cd a x x f x --=⎰λλφϕ2)(212)()(0cd a x x g x ++=⎰λλφϕ 于是我们便得到了:⎰+-+++-=++-=atx atx d a at x at x at x g at x f x t u λλφϕϕ)(212)()()()(),( 这便是一维无界弦的自由振动解的表达式, 称作达朗贝尔公式。
由于对u 没有任何限制,只要一维波动方程有解,解必由达朗贝尔公式给出,且解是唯一的。
二、有界弦的自由振动问题。
描述两端固定的有界弦的自由振动的混合问题:⎪⎩⎪⎨⎧====>+∞<<-∞=(初始条件)边界条件),),(),0(),(),0((0),()0,()0,(2x x u x x u l t u t u t x u a u t xx tt φϕ 对于该问题,适合用分离变量方法进行求解。
第一步,分离变量,分析求一族满足泛定方程和边界条件的分离变量形式的非零特解,可以先不估计初始条件。
令:)()(),(t T x X x t u =,把它代入方程,得)()()()(2t T x X a t T x X ''=''两边除以)()(2t T x X a ,得)()()()(2x X x X t T a t T ''='' 此式左端仅是t 的函数,右端仅是x 的函数,而x 与t 是两个相互独立的变量,所以只有两边都是常数时,等式才能成立,令这个常数为λ-,就得到一个常微分方程:02=+''T a T λ及其边值问题(因,0)()0()0,(==t T X t u 所以0)0(=X ;同理,0)()(),(==t T l X l t u 所以0)(=l X ) 故第二个常微分方程是:⎩⎨⎧==<<=+''0)(0)0(0))(l X X l x x X x X )((λ第二步,解固有值问题怎么找到满足条件的固有值λ,使常微分方程的边值问题有非零解。
分三种情况讨论。
(1)0=λ,这时方程为:, 0=''X ,通解为:B Ax X +=,由边界条件0)()0(==l X X ,得A=0;B=0,0)(≡x X ,不满足要求。
(2)0<λ,不妨设2k -=λ,这时方程0))(2=-''x X k x X (的通解为:kx kx Be Ae X -+=由边界条件0)()0(==l X X ,得⎩⎨⎧=+=+-0klkl Be Ae B A 不难求出A=B=0,同样不满足要求。
(3)0>λ,不妨设2k =λ(0>k ),这时方程0))(2=+''x X k x X (的通解为:kx B kx A X sin cos +=由条件X(0)=0,知,A=0,再由条件0)(=l X ,得0sin =kl B ,由于B 不能再为零,则必有),2,1( ==n ln k π或者:),2,1(2=⎪⎭⎫ ⎝⎛=n l n πλ我们把),2,1(2=⎪⎭⎫⎝⎛=n l n n πλ叫做固有值,与固有值对应的非零解为:lx n B x X n n πsin)(=,n B 是任意常数。
求固有值和固有函数的边值问题称为固有值问题。
把固有值2⎪⎭⎫⎝⎛=l n n πλ代入确定T 的常微分方程:latn D l at n C t T n n n ππsincos)(+=,n C ,n D 为任意常数。
这样得到: ),2,1(sinsin cos )()(),( =⎪⎭⎫ ⎝⎛+==n l x n l at n D l at n C t T x X x t u n n n n n πππ 把n B 归入常数n C ,n D第三步,写出级数形式解由于方程和边界条件都是线性齐次的,故由叠加原理,级数:∑∑+∞=+∞=⎪⎭⎫ ⎝⎛+==11sinsin cos ),(),(n n n n n l x n l at n D l at n C x t u x t u πππ 仍满足方程和边界条件。
第四步,确定级数解中的系数n C 和nD由初始条件:∑+∞===1sin),0()(n nlxn Cx u x πϕ及 ∑+∞===1sin ),0()(n n t l xn D l a n x u x ππφ,由正弦展开的系数公式,得: ⎰=l n dx l xn x l C 0sin )(2πϕ⎰=l n dx lx n x a n D 0sin )(2πφπ 这样我们得到该问题的定解为:∑⎰⎰+∞=⎪⎭⎫ ⎝⎛⋅+⋅=100sin sin sin )(2cos sin )(2),(n l ll x n l at n d l n a n l at n d l n lx t u ππξπξξφππξπξξϕ三、无界弦的受迫振动问题 该问题的偏微分方程为:⎩⎨⎧==>+∞<<-∞+=(初始条件)),(),0(),(),0()0,(),(2x x u x x u t x t x f u a u t xx tt φϕ 对该问题,用拉普拉斯变换计算比较方便[2]。
对泛定方程施行拉普拉斯变换dt e t x u x p u pt ⎰+∞-=0),(),(得:0),(2002=----==p x f u a u u p u p xx t tt代入初始条件得:0),(22=----p x f u a p u p xx φϕ该非齐次常微分方程的通解是d p p f pe e a d p pf pe e a BeAep x u x apx a px x a px a px apx apx )](),()([21)](),()([21),()()(ξϕξξφξξϕξξφ+++++-+=⎰⎰---考虑到+∞→x 和-∞→x 时u 不应为无穷大,所以A=0,B=0,另为保证积分收敛,第一个积分下限取∞+,第二个积分下限取∞-。
所以⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+=+++++=+++++-=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∞---∞+--∞---∞+--∞---∞+--∞---∞+--∞---∞--ξξϕξξϕξξξξξξφξξφξξϕξξφξξϕξξφξξϕξξφξξϕξξφξξξξξξξξξξd p p e a d p p e a d p f p e a d p f p e a d p e a d p e a d p p f p e a d p p f p e a d p p f p e a d p p f pe a p x u x x p x a x p x ax p x a x p x a x p x a x p x x p x a x p x x p x ax p )(21)(21),(21),(21)(21)(21)](),()([21)](),()([21)](),()([21)](),()([21),()()()()()()()()()()(对于第一个中括号,运用延迟定理,),(1t H P⇔则⎩⎨⎧+>+<=--⇔--)(0)(1)()(at x at x a x t H p e a x p ξξξξ所以ξξφξξφξd a d p e a atx x x a x p )(21)(21)(⎰⎰+∞+--⇔ 同理ξξφξφξd ad pe a x at x x a x p )(21)(21)(⎰⎰-∞---⇔ 对第三个中括号,)(ξϕ代替了)(ξφ且多了一个因子p ,则对第一个中括号中原函数中)(ξφ替换行为)(ξϕ并对t 求导即得第三个中括号里的原函数分别为: ξξϕξd p pe a x x p )(21)(⎰∞+--)(21at x a +⇔ϕ ξξϕξd p p e a x x p )(21)(⎰∞---)(21at x a-⇔ϕ对第二个中括号,运用卷积定理⎰-⇔td t f f p f p f 02121)()()()(ττττξτξτξξττξξξτξd d f a d d axt H f a d p f p e a t t a x xt x x a x p ⎰⎰⎰⎰⎰-+∞+∞+--=---=0)(0)(),(21)(),(21),(21同理:τξτξξξτξd d f ad p f pe a t x t a x x a x p ⎰⎰⎰--∞---=0))()(),(21),(21 于是得到该问题解的表达式为:⎰⎰⎰+--+--++-++=at x at x t t a x t a x d d f ad a at x at x t x u τξτξξξφϕϕττ0)()(),(21)(21)]()([21),( 四、半无界弦的自由振动问题该问题即求下面问题的解[3]:⎪⎩⎪⎨⎧===>+∞<≤=∞→(初始条件)边界条件)有限,,),0(,0),0((,0)0,()0,0(2b x u x u u t u t x u a u t x xx tt 对t 做拉普拉斯变换。
