欧阳志强
岳麓区第十四届“迪克——朝善”杯

岳麓区第十五届中小学生田径运动会秩序册主办单位:岳麓区教育局岳麓区文体局比赛地点:麓山国际实验学校田径场二0一一年五月岳麓区第十五届中小学生田径运动会竞赛规程一、主办单位岳麓区教育局二、承办单位岳麓区业余体校三、竞赛日期与地点时间:2011年5月21日地点:麓山国际实验学校田径场四、竞赛项目及分组中学组:以区属各中学为单位组队。
竞赛项目:100米、200米、400米、800米、1500米、3000米(女)、5000米(男)、跳高、跳远、三级跳、铅球、4╳100米接力小学组:以区直属小学、子弟学校、教学片为单位组队。
竞赛项目:100米、200米、400米、800米(女)、1500米(男)、跳高、跳远、立定三级跳、垒球、铅球、4╳100米接力五、参加办法每参赛单位可报队1支,每队可报领队1人,教练2人,每个项目限报3人,每人限报两项(接力除外)六、竞赛办法1、采用国家体育总局最新审定的田径竞赛规程2、运动员比赛号码由大会统一编号,号码布由大会统一制作,各单位在赛前领取,比赛后统一归还,如有遗失照价赔偿。
七、运动员资格与审查1、运动员必须是思想品德好,经医院体检证明身心健康、文化成绩合格的在籍、在校、在读学生2、参赛运动员必须持有在岳麓区业余体校注册的“岳麓区中小学生体育竞赛注册证”3、初中组必须是1996年1月1日以后出生的在籍在读初中生,小学组必须是1999年1月1日以后出生的在籍在读小学生。
4、比赛前、比赛中、比赛后,均对运动员资格进行审查。
对违反规定弄虚作假,冒名顶替者一经查实,取消该队员参赛资格和学校团体总分的录取,并对该校和有关责任人予以通报批评。
停止该校参赛资格一年以上。
八、报名时间凡参赛队报名单须填写完整交学校审查同意,加盖公章于5月6日前送区体校,同时带运动员寸照两张、户口(或第二代身份证)、学籍册、30元注册费办理报名注册手续,以前办理的注册证可以继续使用,报名的时候带来验证即可。
XY-4L型岩心钻机的研制与应用

钻机净质量 ( g k)
3 1 ×1 5 ×14 0 2 5 90 0 0
50 00
2 钻 机 的结构 及原 理
X Y~ L型岩心钻机是一种机 械传 动、 4 液压给 进、 履带行走 的立轴式岩心钻机 。钻机由动力机 、 回
转器 、 动箱 、 分 卷扬 机 、 机架及 履 带 、 液压 系统 、 钻塔 、 液压 绞 车等 主要部 件组 成 , 构 如 图 1所示 。 结
轴等 优质通 用 部件 , 效 地 提 高 了钻 机 的可靠 性 和 有 使用寿命 , 极大地方便 了钻机的维修保养 。
关键词 : 岩心钻机
目前我 国广泛使用 的岩心钻机 主要是机械传 动 、 压 给进 的立 轴式 钻机 , 液 该类 钻机 经过 长期 的不
断改进和完善, 结构性能已趋合理 , 但也存在钻机搬 迁困难 、 不易实现斜孔钻进 、 须单独配置钻塔、 不能 完 全满 足多种 钻 探工 艺 的要 求 等诸 多 缺 点 , 全 液 而 压动力头岩心钻机虽具有优势 , 但其整机及配件价
21 年 2 00 月
地 质 装备
XY一4 L型岩 心 钻 机 的研 制 与应 用
卢春阳 欧阳志强
( 阳中地装备探矿工程机械有限公 司 湖南衡 阳 4 10 ) 衡 20 2 摘 要 : 文首先分析 了钻机研 发的必要性, 本 介绍 了 X 4 Y一 L型钻机 的参数 、 结构形 式、 应用效果及特 点。 机械传 动 履 带行走 塔机 一体
素质要求高等缺点 , 严重制约 了该钻机在 国内的普 遍 推广 。 因此 开发 一 种 能满 足 多种 钻 探 工艺 需 要 、 容易搬迁 , 主要适用 于山区、 平原 、 沙漠的钻探设备 是很 有必要 的 , 阳 中地 装 备探 矿 工 程 机 械有 限公 衡
欧阳院士讲座的心得体会

近日,我有幸参加了欧阳院士的讲座,聆听了他关于科技创新与国家发展的精彩论述。
此次讲座不仅让我对科技创新有了更深入的理解,也激发了我对科研事业的热爱。
以下是我对此次讲座的心得体会。
一、科技创新的重要性欧阳院士在讲座中强调,科技创新是推动国家发展的重要动力。
当今世界,科技日新月异,各国之间的竞争愈发激烈。
只有紧跟科技发展趋势,加大科技创新力度,才能在国际竞争中立于不败之地。
以下是我对科技创新重要性的几点认识:1. 科技创新是提升国家综合实力的关键。
一个国家的综合实力不仅体现在经济、政治、文化等方面,更体现在科技创新能力上。
科技创新能够带动产业升级,提高生产效率,增强国家竞争力。
2. 科技创新是解决民生问题的关键。
随着社会的发展,人们对生活质量的要求越来越高。
科技创新能够为人们提供更多便利,解决生活中的实际问题,提高人民群众的生活水平。
3. 科技创新是推动社会进步的关键。
科技创新能够促进社会制度的改革,推动社会进步。
例如,互联网、大数据、人工智能等新兴技术的出现,已经深刻改变了人们的生活方式。
二、科技创新的发展趋势欧阳院士在讲座中介绍了当前科技创新的发展趋势,主要包括以下几个方面:1. 新一代信息技术:以5G、人工智能、物联网、大数据等为代表的新一代信息技术正在快速发展,为各行业带来前所未有的机遇。
2. 生物科技:生物科技在医疗、农业、环保等领域具有广泛应用前景,如基因编辑、生物制药、生物能源等。
3. 新材料科技:新材料科技在航空航天、新能源、电子信息等领域具有广泛应用前景,如石墨烯、碳纳米管、超导材料等。
4. 空间科技:随着我国航天事业的快速发展,空间科技在通信、导航、遥感等领域具有广泛应用前景。
三、我国科技创新的现状与挑战欧阳院士在讲座中分析了我国科技创新的现状和挑战。
他指出,我国在科技创新方面取得了一定的成绩,但仍存在以下问题:1. 基础研究薄弱。
与发达国家相比,我国在基础研究方面的投入和成果仍有较大差距。
宁波市滨海学校2010学年第二学期高中部教科

宁波市滨海学校2010学年第二学期高中部教科研成果汇总一、教师获奖情况(一)、论文发表、获奖、交流情况1、徐大土关于2010年浙江省高考自选模块的解法发表于《数学教学》(2010.12)2徐大土《中学数学解题纠错实用宝典》第一章第十五节陕西师范大学出版社(11.4)、石友才农村中学作文教学优胜策略获中国教育学会中语会论文一等奖(2011.4)、陈晓涛万有引力真的就提供向心力吗象山县2010年教育教学论文二等奖、马国顺曲径通幽,别有洞天象山县2010年教育教学论文三奖、修勇恰当的运用组织教法,提高体育课堂的实效性发表于《体育博览》(2011.2)张昌培高考英语浙江卷完形填空的效度分析获宁波市论文一等奖(2011.4)、朱宝林运用“破窗理论”提高管理效能市三等奖、石友才谈民办学校德育系统工程的构建市二等奖0朱宝林调控教学氛围给力课堂效率发表于《新教师教学》(2011.2)1刘成达尤胜利关于象山高中篮球队训练的调查分析与解决对策发表于《教育科研》(2011.6)(二)、课题立项、获奖情况1、.省级课题《“131”学生自主学习的教学模式》获浙江省第四届教研课题成果评比三等奖主要成员:方德懿俞宏达朱宝林陈秉忠胡庆彪石友才2、浙江省教科规划2011年度重点研究课题《中学自主学习背景下问题教学法的实践研究》主持人:王恕成3、市级课题《中学教师教学实绩发展性增量评价的实践与研究》主持人:王恕成4、市级课题《民办学校教师教学实绩发展性增量评价的实践与研究》负责人,主持人:王恕成5、2011年浙江省教研课题《自主学习背景下高中生物实施问题教学法的研究与实践》主持人:朱宝林6、“6+1”校园文化建设研究与实践象山县教育课题研究科研优秀成果三等奖方德懿石友才等(三)教师业务竞赛获奖1、陈玲娣2010年度高中体育与健康优质课评比二等奖2、戚满兰第二届全国青少年英语读写大赛辅导金奖3、戚满兰象山县高中英语课堂教学评比二等奖4、高玲莉象山县第十一届高中教坛新秀语文三等奖5、王寒阳象山县第十一届高中教坛新秀数学二等奖6、徐小伟象山县第十一届高中教坛新秀数学三等奖7、何芸芸象山县第十一届高中教坛新秀英语二等奖8、桂莹象山县第十一届高中教坛新秀英语三等奖9、陈晓涛象山县第十一届高中教坛新秀物理三等奖10、赵淑明象山县第十一届高中教坛新秀生物二等奖11、刘广二象山县第十一届高中教坛新秀政治三等奖12、李春明象山县第十一届高中教坛新秀历史二等奖13、刘成达象山县第十一届高中教坛新秀体育三等奖14、邱丹象山县第十一届高中教坛新秀信息技术三等奖15、欧阳志强象山县第十一届高中教坛新秀通用技术三等奖16、朱宝林象山县名优教师考核优秀奖17、郑康祥象山县名优教师考核优秀奖18、石友才象山县名优教师考核优秀奖(四)、教师荣誉1朱豫国2010年度县优秀教育工会干部(五)集体荣誉1、《滨海教科》获宁波市2010年度优秀教育科研校刊一等奖2、高一(6)班被评为第二届全国青少年英语读写示范班二、学生获奖情况1、舞蹈《且吟春雨》宁波市教育系统第十届艺术节中小学生舞蹈比赛中获高中组三等奖指导老师陈雅菲2、史建威2011年浙江省高中生物学竞赛省二等奖指导老师朱宝林赵淑明3、韩贤威2011年浙江省高中生物学竞赛市三等奖指导老师朱宝林赵淑明4、董鹏飞2011年浙江省高中生物学竞赛县一等奖指导老师朱宝林赵淑明5、张涛2011年浙江省高中生物学竞赛县一等奖指导老师朱宝林赵淑明6、周易2011年浙江省高中生物学竞赛县二等奖指导老师朱宝林赵淑明7、孔华2011年浙江省高中生物学竞赛县三等奖指导老师朱宝林赵淑明8、杨泽东2011年浙江省高中生物学竞赛县三等奖指导老师朱宝林赵淑明9、陈镔2011年浙江省高中生物学竞赛县三等奖指导老师朱宝林赵淑明10、史建威2011年浙江省高中化学竞赛省二等奖指导老师刘元思李志刚11、邵杰2011年浙江省高中化学竞赛市二等奖指导老师刘元思李志刚12、石承乾2011年浙江省高中化学竞赛市二等奖指导老师刘元思李志刚13、茅琪2011年浙江省高中化学竞赛县一等奖指导老师刘元思李志刚14、朱元杰2011年浙江省高中化学竞赛县二等奖指导老师刘元思李志刚15、陈辽开2011年浙江省高中化学竞赛县三等奖指导老师刘元思李志刚16、陈相助2011年浙江省高中化学竞赛县三等奖指导老师刘元思李志刚17、夏智超宁波市高一化学竞赛县三等奖指导老师梁斌18、郑宏宁波市高一化学竞赛县三等奖指导老师梁斌19石雨宁波市高一化学竞赛县三等奖指导老师王松良20、胡越浙江省高中数学竞赛市三等奖指导老师邱亚珍21、张泽南浙江省高中数学竞赛市三等奖指导老师邱亚珍22、陈家雷浙江省高中数学竞赛县三等奖指导老师邱亚珍23、李再芝第二届全国青少年英语读写大赛银奖指导老师戚满兰24、何佳儿第二届全国青少年英语读写大赛铜奖指导老师戚满兰25、卢瑞瑞第二届全国青少年英语读写大赛金奖指导老师戚满兰26、徐秀民第二届全国青少年英语读写大赛金奖指导老师戚满兰27、汪佳男第二届全国青少年英语读写大赛金奖指导老师戚满兰28、叶腾冠第二届全国青少年英语读写大赛金奖指导老师戚满兰29、王继乐第二届全国青少年英语读写大赛金奖指导老师戚满兰30、蒋珊珊第二届全国青少年英语读写大赛银奖指导老师戚满兰31、蒋吉星第二届全国青少年英语读写大赛银奖指导老师戚满兰32、林婉璐第二届全国青少年英语读写大赛银奖指导老师戚满兰33、章佳乐第二届全国青少年英语读写大赛银奖指导老师戚满兰34、郑涵萧第二届全国青少年英语读写大赛铜奖指导老师戚满兰35、石丽文第二届全国青少年英语读写大赛铜奖指导老师戚满兰36、杨家欢第二届全国青少年英语读写大赛铜奖指导老师戚满兰37、张佳蓉象山县高中生英语口语比赛一等奖指导老师蒋海38、钱曙来象山县高中生英语口语比赛三等奖指导老师梁黎丽39、高波象山县第七届中小学生棋类比赛中国象棋第一名指导老师尤胜利。
(桂林市级奖)

张帮国
颜丽青
李锦凤 莫慧文
一等奖: 张峻源
二等奖: 杨仁贵
三等奖: 陈前梨 毛意娟
秦开茂
陈美勤
石春燕 覃久军
一等奖: 张弛
二等奖: 陈李卉 莫心妍
三等奖: 李匡媛 费煜淇
俸云
黄嘉慧 秦白云飞
李哲 彭岱仪
一等奖: 刘宏斌
二等奖: 马正华
三等奖: 姚鉴纯
黄斯文 谢林钢
一等奖: 欧阳宇
一等奖: 朱继超
陈鹏远
二等奖:
邓凌媛 赵莉洁
莫小龙 秦欢
文惠 陈善超
姚元武 李婷婷
徐嘉智 秦丽珍
李方韬 阳桂花
刘成德 黎海林
刘鑫
秦建强
以济兴
十九中
徐晓 莫富冰 唐玲珺 何海宁
陈俊宏 黄中南 刘艳萍 刘凤玲
庄翔中
莫明辉
刘霜
师大附外
卿宇翔 杨诗綦 刘小瑗
马曙徽 陈沐源
梁晨 刘钰 余瑞玲
阳洁 刘廷钧 吴肇倩
曾邵辉
一等奖: 申婷
二等奖: 秦觅 陈伟
邓晶晶 三等奖:
姚继燕 秦静
俸云龙
蒋琴
黄新云 韩泽渠
阳舒 庾子华 罗海娟
一等奖: 蒋耀程
二等奖: 唐海美 俞园园
三等奖: 汤翠云 秦锋
蒋春香
莫义忠 黄琦
苏晶 俸安友
王坊庭
李路
吴乔鹏 陈玛莎 刘洋
任远学校
十二县
灵川县 灵川中学
秦家园
李娜
李伟特 熊远香
文芬燕 马玉秋
一等奖: 吴一乐
二等奖: 李琳
三等奖: 韦佳瑛
一等奖: 谢仁杰 董尚博
泥浆泵泵阀的特点及应用

表"VWKC!!"!泥浆泵不同泵阀性能测试对比 M.;/7"@7+43+<.2-7-3<9.+&:32340&447+72*9,<98./87:43+<,09,<9:
工作 挡位
泵速* 469-#
球阀 流量* 排出压力* !H-469-## `'5
噪声* CL
容积效率* >
泵速* 469-#
片阀 流量* 排出压力* !H-469-## `'5
图?为 L[3&""*#$型泥浆泵的片阀结构图"该 泵阀的阀体与阀片为一体制造"限位套和阀体均为 精铸件"加工制造成本较高%在较大流量泵上使用 时"阀座与泵头接触的锥面加工精度要求较高"否则 容易松开脱落"造成泵阀损坏"脱落的泵阀被柱塞顶 坏"见图$%
图1 为 L[3%?"*#" 和 L[3#"""*#! 泥浆泵的
Copyright©博看网. All Rights Reserved.
#%
卢春阳等泥浆泵泵阀的特点及应用
图#为 L[3#?"泥浆泵的排水阀"阀球为钢球" 阀球和阀座直接金属接触密封"冲击较大"容易产生 较大的噪声"为降低噪声"在阀盖上安装消声垫"起 到降噪缓冲的作用%球阀的阀隙流道圆滑"流液阻 力小"也常用于砂浆泵的泵阀上"图!为 L[b3#?"* #)?水泥砂浆泵的吸排阀"砂浆泵要求阀座通径大" 通过性好"与之相配的阀球较重"泵的吸入排出要克 服阀球的重量"为解决这一矛盾"通常采用空心阀球 减轻重量以满足砂浆泵的性能要求%
2012地质找矿成果奖公示
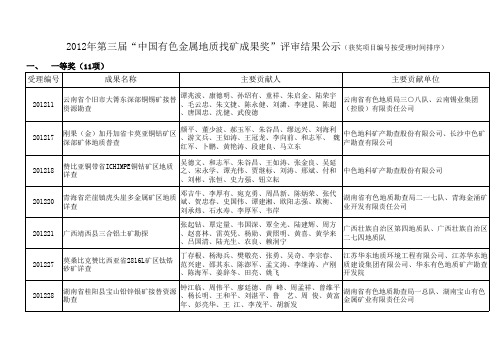
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排一、 一等奖(11项)
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排二、二等奖(35项)
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排三、三等奖(21项)
2012年第三届“中国有色金属地质找矿成果奖”评审结果公示(获奖项目编号按受理时间排
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)
示(获奖项目编号按受理时间排序)。
南昌大学2014-2015-1学期个性课课表

纪昌品 林刚,阮禄章,欧阳珊,夏斌,王尚洪 辛天蓉 姜水生,姜水生 陈钢 许小明 许小明 胡东平 陈友华 陈友华 习青华 谢建宏 吴禄慎 廖小建,廖小建 彭杰 欧阳志强 欧阳志强 赵刚 赵刚 赵刚 韩艺 张明锋 陆明 陈奇伟 陆明 吴晓红 郭朝晖
讲师 副教授,教授,教授,教授,副教授 讲师 教授,教授 副教授 副教授 副教授 讲师 副教授 副教授 讲师 副教授 教授 教授,教授 副教授 讲师 讲师 讲师 讲师 讲师 副教授 副教授 讲(Ⅱ) 机械制造技术应用 机械制造装备设计 建筑材料(Ⅱ) 建筑法规 交通工程学 节目主持人通论 金融学 金融学 金融学 金融学 金融学 金融学 金融学 金融学 经济学 经济学原理 经济学原理 客户关系管理 空调用制冷技术 控制工程专题 跨文化管理 领导科学 流体输配管网 伦理学 媒介经营管理
经济管理学院 信息工程学院 法学院 法学院 机电工程学院 经济管理学院 经济管理学院 经济管理学院 经济管理学院 经济管理学院 经济管理学院 经济管理学院 资源环境与化工学院 法学院 资源环境与化工学院 资源环境与化工学院 经济管理学院 经济管理学院 经济管理学院 经济管理学院 经济管理学院 建筑工程学院 信息工程学院 法学院 体育与教育学院 外国语学院 生命科学与食品工程学院
2 2 2 2 2 2 2 2 3 3 2 2 1.5 3 2 3 3 2 2 2 3 3 32 32 32 3 3 2014-12-28
40 32 32 36 32 32 32 32 48 48 40 32 24 48 32 48 48 32 32 32 48 48 32 32 32 48 48
24 32 32 32 32 32 32 32 48 48 24 32 24 48 32 48 48 32 32 32 48 48 32 32 32 48 48
图书馆南昌大学图书馆CASHL文献传递工作总结

结
2020/11/10
图书馆南昌大学图书馆CASHL文献 传递工作总结
目录
宣传推广 培训情况 文献传递服务 工作体会 存在问题 工作设想
图书馆南昌大学图书馆CASHL文献 传递工作总结
第一部分 宣传推广
一、宣传推广
o 主页显著位置发出通知 o 致全校人文社会科学教师与学者的一封信 o 制作成PPT挂在主页上 o 会议宣传
南昌大学图书馆 2007.3.1
图书馆南昌大学图书馆CASHL文献 传递工作总结
1.主页显著位置发出通知
2007年3月三周年庆典优惠活动
免费获得人文社科类外文期刊文献原文! 为满足我校教师和研究生在人文社科外文文献方面的更广泛 的深层次需求,2007年3 月 12 日— 3 月 19 日期间,图书馆为教 师和研究生提供中国高校人文社会科学文献中心(CASHL)文献传递 服务。图书馆对于文献传递申请费用在CASHL补贴50%的基础上,再 补贴50%,即读者申请CASHL文献传递全部免费,欢迎读者到南昌大 学图书馆信息研究室(前湖校区二楼 A204 )提交申请。 联系人: 胡小飞 联系电话: 3969265
图书馆南昌大学图书馆CASHL文献 传递工作总结
五、存在问题
✓ 宣传力度不够 ✓ 用户使用情况与满意度调研有待加强
图书馆南昌大学图书馆CASHL文献 传递工作总结
六、工作设想
o 加大宣传力度,深入学校院系举办讲座。 o 进一步提升CASHL的共享度,做好相关服务。 o 建立信息代理机制,实施网络信息推送。
图书馆南昌大学图书馆CASHL文献 传递工作总结
4.会议宣传
2008年1月江西省高校图书馆馆长会议
面对面帮扶企业手把手解决问题-株洲公共资源交易中心

面对面帮扶企业手把手解决问题
市公共资源交易中心真心实意为民营企业解难
本网讯尹清连报道9月22日,市政府企业帮扶联络员、市公共资源交易中心副调研员罗春武带领业务二科人员来到市高科集团当起民营企业推销员,帮助湖南旭日陶瓷有限公司促销产品。
湖南旭日陶瓷有限公司是市公共资源交易中心帮扶的企业之一,为贯彻落实市“企业帮扶”工作要求,切实为企业协调解决问题,交易中心把帮扶工作摆上日常工作议程,专门成立帮扶领导小组,中心主要领导多次深入湖南旭日陶瓷有限公司了解情况,掌握企业准确的信息和需要解决的难题,并通过市场调查分析,明确制订帮助企业解决困难的计划,进行面对面指导,针对性帮扶,做到有的放矢。
日前,交易中心了解到市高科集团是墙砖、地板砖等产品的销售大户,罗副调研员亲自带队到高科集团搞营销,向高科集团领导介绍旭日陶瓷有限公司的主打产品“白兔”牌墙砖、地板砖。
集团领导被罗副调研员的真诚打动,如是说旭日陶瓷是本地区生产墙砖、地板砖的唯一一家民营企业,生产技术过硬,产品质量有保证,当场表示给旭日陶瓷提供一个展示平台,尽快安排开发经营部与企业对接。
湖南旭日陶瓷有限公司负责人表示,能够在高科集团这么大平台展示自己的产品,想都没想过,有交易中心做后盾,企业发展前途明亮,我们很有信心。
附图一张:。
自然资源部关于实施海砂采矿权和海域使用权“两权合一”招拍挂出让的通知

低温元素;第三类以具有挥发性、低温热液元素Hg为代表;说明矿区可能存在多期次的热液流体活动。
(3)全区共圈出7处综合异常,依地球化学—地质成因,划分为乙1类1个(Ap2);乙2类2个(Ap1、Ap7);乙3类2个(Ap3、Ap4、Ap6);丙类1个(Ap5)。
Ap2综合异常不论规模、伴生元素、含量等化探特征来看都是1∶1万土壤地球化学测量叠加最好的一带,异常大部分分布在断裂附近。
从元素组合(Pb、Zn、Ag、Ba、Au、Cu、Co、Sb、As、Hg)及规模、含量强度、出露地层看,区内异常发育主要与区内断裂破碎带有关;异常带北部见民采行为,显示曾有采矿活动。
在已采矿污染的高异常值影响下,该区域有异常显示已说明该异常具一定的找矿意义。
而且Pb、Zn、Cu、Ag、Au等元素异常重叠性好,具有矿致异常的特征,对寻找Pb、Zn多金属矿有重要的指导意义。
在地球化学地质成因和找矿远景的基础上,结合异常,Ap2可作为找矿靶区,建议开展对该异常的相关查证工作。
参 考 文 献[1] 付建明,陈希清,马丽艳,等.南岭成矿带锡多金属找矿成果及找矿方向[J].矿床地质,2010(S1):204 205.[2] 罗华彪,欧阳志强,史国伟,等.湖南省祁东县大路边铅锌矿普查项目总体设计和2013年工作方案[R].衡阳:湖南有色地质勘查局二一七队,2013.[3] 王崇云.地球化学找矿基础[M].北京:地质出版社,1986.[4] 黎彤.化学元素的地球化学丰度[J].地球化学,1976,5(3):167 174.[5] 谢学锦.区域化探[M].北京:地质出版社,1979.[6] 余金生,李裕伟.地质因子分析[M].北京,地质出版社,1985.[7] 关显东,钱建平,王硕,等.因子分析在冀东峪耳崖金矿地球化学找矿中的应用[J].现代矿业,2020(1):19 25.[8] 章贤能,寇尚文,刘艾华.安徽宁国东山坞地区土壤地球化学特征与评价[J].物探与化探,2017,41(1):71 78.[9] 袁和,徐云鹏,邵华,等.藏南邦卓玛地区金多金属矿土壤地球化学特征及找矿前景[J].金属矿山,2019(3):147 155[10] 李保平,陈玉华,周晓中.青海叶陇沟金矿地质地球化学特征及找矿方向[J].黄金科学技术,2011,1(2):31 34[11] 孙雨,神元,鲁正清,等.河南卢氏三官庙钼多金属矿区土壤地球化学特征及成矿预测[J].金属矿山,2018(1):128 136[12] 唐志祥,朱贤,宁勇云,等.大义山羊角脑地区土壤地球化学特征及找矿预测研究[J].现代矿业,2020(3):14 19[13] 中华人民共和国地质矿产行业标准.DZ/T0167 95.区域地球化学勘查规范[S].北京:中国标准出版社,1995.(收稿日期2020 10 26櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄櫄)·记者在线·自然资源部关于实施海砂采矿权和海域使用权“两权合一”招拍挂出让的通知 为切实解决海砂采矿权和海域使用权“两权”出让中不衔接、不便民的问题,适应机构改革后职能重构的要求,落实党中央、国务院关于推进政府职能转变、加快放管服务改革部署,充分发挥市场在自然资源配置中的决定性作用,现就精简、优化海砂采矿权和海域使用权出让环节和办事流程,通知如下。
关于2006年全市中学高级教师高评会

5.方茴说:“那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢,就算喜欢也是偷偷摸摸的。
”6.方茴说:“我觉得之所以说相见不如怀念,是因为相见只能让人在现实面前无奈地哀悼伤痛,而怀念却可以把已经注定的谎言变成童话。
”7.在村头有一截巨大的雷击木,直径十几米,此时主干上唯一的柳条已经在朝霞中掩去了莹光,变得普普通通了。
8.这些孩子都很活泼与好动,即便吃饭时也都不太老实,不少人抱着陶碗从自家出来,凑到了一起。
9.石村周围草木丰茂,猛兽众多,可守着大山,村人的食物相对来说却算不上丰盛,只是一些粗麦饼、野果以及孩子们碗中少量的肉食。
关于2006年全市中学高级教师高评会评审结果的报告九江市人事局:九江市中学高级教师评审委员会下设语文、数学、英语、物理、生化、综合等6个专业评委会,6个专业评委会评委人数共60人,于2006年11月5日至11月10日对申报中学高级教师(含小学特高)的对象进行了为期4天的评审,现将评审结果报告如下:中学高评委会共收到申报中学高级教师材料927份,其中正常申报903人,破格申报24人。
经评审通过具备中学高级教师任职资格的有755人,未获通过的有172人,通过率为81.5%。
一、评审通过的人员名单如下(共计755人)1、共青城(共计15人):语文(6人):段汉文、熊远征、徐根生、余凯民、曹佑星、彭益秀;数学(3人);游健钧、周镮、王志宇;英语(1人):胡雪珍;物理(1人):王全托;化学(1人):李炳金;政治(1人):陶玉平;历史(2人):柯有清、胡济光;2、德安县(共计40人):语文(10人):张四龙、殷小红、李海桂、余英、王英、李书菊、程峰、余伟清、刘秀英、郭庆生;数学(8人):吴逢友、祝学红、黄荣火、程萍娥、周金球、吴敦旭、黄源、袁华;英语(7人):胡振、刘军华、邹时富、毕兆亨、王晓玲、彭翃岚、王桂金;物理(5人):吴家发、罗华锌、殷绍贵、蔡锦宝、祝小利;化学(3人):戴明胜、万峰、梅雪艳;生物(2人):洪和平、涂其玉;政治(1人):詹德红;历史(2人):陈旸、胡银春;体育(2人):徐小良、黄振生;。
XY一4L型岩心钻机的研制与应用

地质蓑备
11
XY一4L型岩心钻机的研制与应用
卢春阳欧阳志强
(衡阳中地装备探矿工程机械有限公司湖南衡阳421002)
摘要:本文首先分析了钻机研发的格要性,介绍了XY一4L型钻机的参数、结构形式、应用效果及特点。 关键词:岩心钻机机械传动履带行走塔机一体
目前我国广泛使用的岩心钻机主要是机械传 动、液压给进的立轴式钻机,该类钻机经过长期的不 断改进和完善,结构性能已趋合理,但也存在钻机搬 迁困难、不易实现斜孔钻进、须单独配置钻塔、不能 完全满足多种钻探工艺的要求等诸多缺点,而全液 压动力头岩心钻机虽具有优势,但其整机及配件价 格高,动力消耗大,保养维修技术要求高、对操作者 素质要求高等缺点,严重制约了该钻机在国内的普 遍推广。因此开发一种能满足多种钻探工艺需要、 容易搬迁,主要适用于山区、平原、沙漠的钻探设备 是很有必要的,衡阳中地装备探矿工程机械有限公 司研发设计的XY一4L型钻机正是为解决这些不足 而研制的。
The Development and Application of XY一4L Coring Drill
Abstract:This paper firstly analyses the necessity for the development of this kind core drilling machine. Then the authors introduce in detail the parameters,structure,features as well as its application in Jiangxi
3钻机的应用效果 XY一4L型钻机已小批量生产,样机由中国地
质科学院探矿工艺研究所在青海进行生产试验,随 后,江西和南美洲的秘鲁等工地应用于地质勘探、岩 心钻探和地质勘察等,使用情况均达到预期的目的, 多处工地在山区或高原地区,地质结构十分复杂,交 通条件非常不便。图2为秘鲁施工现场。经实践证 明,XY~4L型钻机技术性能良好,钻进效率高,各 项技术指标合理,主要技术参数和使用性能完全满 足多种钻探工艺要求,具有较强的处理孔内事故的 能力和完成特种钻进工作的能力。除保持了原机械 岩心钻机制造成本低、可靠性能高、维修方便等优点 外,还通过合理的、巧妙的结构设计,提高了钻机的 性价比。钻机真正实现了钻机塔机一体化,方便了
企业须穿信息安全“防护衣”

设计 、
建设 、
运维、
管理 的专业化 服务 , 在数据运 维 、 信息
安全服务方面经验丰富。 宝景公司以
IT IL 最佳服务实践的技术管理 流程管 、
理 以及服务管理 三 条主 线为基 础 , 构建
了宝景信息的特色IT 服务架构模型 , 旨
在 向客户提供 完整贯 穿 I T 系统应用 全
生命周 期— —
案 , 提升信息 系统应用安全 水平 。
在国际化程度越来越高的今天 , “ 顺德 制造 ” 是 广东 的一 张重 要 名 片 。
为进 一 步推动广东省佛 山市顺德 区 的
企 业 信息化建设 , 协助企 业建 立 完善
的信息 安全 体系 , 1 1 月 2 8 日, 由顺德
区科学技术局 、 顺德区信息产业局指
中国信息化杂志社执行社 长助理 肖菁在会 议 上 强调 , 企 业 要 构建 信 息 安 全 防护体系来降低企 业运 营风 险, 建 立 完善的安全制度 , 要让 每个 网络安全的 参 与者提 高 自身 的安 全 意 识 。
广 东北 电研 发 中心 的苏 宪恒 指 出 , 建立 企业安全控制和治理 体系应该注意 对企 业 信息安全 的风险评估是根据信息 对业 务 的重 要 程度 以及 丢 失/泄漏 后对 企 业 的影 响; 信 息 安 全 的控 制和 治理 是 服 务于 企 业 的 业 务 目标和 策略 , 两者 需 协调一 致 ; 管理 层 从 上 而 下 的 支持 , 全 体员工 强制执行 和惩罚性是成功的关
键。 作为著名安全 产 品 厂 商 S y m a n t e c
华南核心 代理 商 , 宝 景 公 司是 中国华南 地 区最早一 家通 过基于 IT IL 标 准及流
DKZ系列钻机的研制

9在液压系统中采用双泵供油高压大流量 油路与低压小流量油路分别独立行走时只需开启 大液压泵正常钻进时大液压泵停止只需开启小 液压泵采用变频电机控制因此液压系统能耗小 油温温升极小可以确保液压元件的可靠性延长使 用寿命
-2
欧阳志强等6<@系列钻机的研制
第!-卷第!期
6<@ 系列钻机的研制
欧阳志强贺建波谭颖卢春阳
衡阳中地装备探矿工程机械有限公司湖南衡阳#!-""!
摘要本文简要介绍了地下反循环桩孔的施工方法和施工设备的现状以及目前存在的问题并从地铁站施工的 环境条件和施工质量技术要求等角度分析提出了对未来施工的要求重点介绍了为满足地下空间灌注桩 工程施工而研发 @ZY系列钻机应用的关键创新技术和性能保证措施以及系列产品的主要技术参数和工 地使用情况
目前该设备品种多基本上都是从原来的泵吸 反循环工程施工和水井钻机照搬变型过来的钻机 是电机驱动液压系统整套设备含泵吸系统钻进 回转给进提升电控液压钻塔等系统功能放在 履带底盘上移动方便在地面的塔架高给进行程 长而在地铁导洞施工受到空间尺寸限制给进行程 短目前整体设备按离心砂石泵的排渣口直径有 !"066!1#660"#O966 等规格
根据使用方评价钻机的整体性能达到了设计 的要求#采用的电传动比液压传动可靠性高$运 行和维护成 本 较 低% 施 工 效 率 高& 利 用 变 频 控 制数字显示方便操作提高了智能化减轻了劳动 强度期间陆续也出现了一些问题#使用初期出 现了泥浆泵小机械密封的动环易碎改变密封件材
上诉人万日升诉被上诉人丰城市公安局不履行保护公民财产安全职责一案二审行政判决书

上诉人万日升诉被上诉人丰城市公安局不履行保护公民财产安全职责一案二审行政判决书【案由】行政行政行为种类其他行政行为【审理法院】江西省宜春市中级人民法院【审理法院】江西省宜春市中级人民法院【审结日期】2021.03.03【案件字号】(2021)赣09行终27号【审理程序】二审【审理法官】吴建平黄礼潘丽平【审理法官】吴建平黄礼潘丽平【文书类型】判决书【当事人】万日升;丰城市公安局【当事人】万日升丰城市公安局【当事人-个人】万日升【当事人-公司】丰城市公安局【法院级别】中级人民法院【原告】万日升【被告】丰城市公安局【本院观点】本案的争议焦点是被上诉人丰城市公安局是否履行了法定职责。
【权责关键词】行政强制合法违法警告拒绝履行(不履行)管辖新证据证据不足维持原判改判发回重审【指导案例标记】0【指导案例排序】0【本院查明】二审查明的事实与一审法院查明的事实一致。
【本院认为】本院认为,本案的争议焦点是被上诉人丰城市公安局是否履行了法定职责。
公民在遇到问题时,有权利向公安机关报警或求助,公安机关接到公民的报警或求助后,也应及时进行处理,但并不是公民所有的报警或求助事项都属于公安机关职责范围之内。
本案中,上诉人因土地被平整向被上诉人丰城市公安局报警求助,该局接警后指派民警到现场处理,根据调查了解,案涉土地被平整属征收土地的后续行为,因上诉人对案涉土地征收问题存在异议引发的纠纷,现场并未发生打架等违反治安管理的行为,民警告知在场人员该报警事项不属于公安机关的管辖事项并向在场社区干部释明有关规定后离开,已经履行了法定职责。
需要指出的是,被上诉人指派的民警因处置其他在先的报警事件而迟延到达本案报警现场,民警到达时,上诉人已经离开现场,民警未能告知上诉人处理结果,存在瑕疵,但因该报警事项并不属于被上诉人的职责范围,且上诉人对平整土地的行为正在进行行政诉讼,被上诉人的上述工作瑕疵并不会对上诉人的权益产生实际影响,故本院对该瑕疵仅予以指正。
浅谈二项式定理及其应用

浅谈二项式定理及其应用欧阳志强(伊犁师范学院数学与统计学院09-2A班新疆伊宁 835000)摘要:二项式定理是初等数学中的一个重要的定理, 在高等数学中更是许多重要公式的共同基础.本文主要讨论了二项式定理在解决组合理论、开高次方,以及不等式问题等方面的应用.关键词:二项式定理;不等式;展开式中图分类号:O122.4 文献标识码:A一引言二项式定理的应用非常广泛, 也很重要, 主要表现在两个方面: 一是它所揭示的方法富有启发性; 二是它与高等数学联系紧密.学习与掌握它, 既有利于培养学生联想和抽象思维的能力, 也有利于其今后进一步的学习.二项式定理在中国被称为“贾宪三角”或“杨辉三角”,一般认为是北宋数学家贾宪所首创.它记载于杨辉的《详解九章算法》(1261)之中.在阿拉伯数学家卡西的著作《算数之钥》(1427)中也给出了一个二项式定理系数表,他所用的计算方法与贾宪的完全相同.在欧洲,德国数学家阿皮安努斯在他1527年出版的算数书的封面上刻有此图,但一般称之为“帕斯卡三角形”.因为帕斯卡在1654年也发现了这个结果.杨辉-贾宪三角而在1664年和1665年间,也就是由于瘟疫流行而迫使牛顿从剑桥躲开的前夕,牛顿就开始了二项式定理的研究,值得注意的是,牛顿只处理了二项式的自乘幂是分数或负数的情况.牛顿第一次提到二项式定理是在1676年6月13日他写给奥尔登堡转给莱布尼兹的一封信中,此后牛顿对于该定理进行不断的推理、猜想和证明,最终建立了二项式定理.牛顿在建立了二项式定理以后,马上就抛弃了他以前用于求积的插值法,而把这个定理当做确定曲线下方面积的一个最简单最直接的方法来使用.随着时间的推移,二项式定理被越来越多的人运用,直到今天,二项式定理已经是中学数学内容的重要部分,也是当今高考的难点之一.二项式定理是在处理有关两个元素和的方幂的问题时常常考虑到的一个重要公式,是组合数学中一个基础而重要的定理,在微积分、概率论、初等数论等许多数学分支中都可见其踪影. 二 预备知识二项式定理:(a +(n .理解二项式定理应注意:(1)二项式中,a 是第一项,b 是第二项,顺序不能变; (2)展开式中有1n +项(比指数多1); (3)01,,,n n n n C C C 是二项式系数;(4)a 的指数降幂,b 的指数是升幂,两者的指数的和等于n ; (5)二项式展开时要注意各项的符号规律; (6)注意二项式定理的可逆性.二项式定理除了要注意以上几点外还具有一些性质:性质一 ()na b +的二项展开式中,与首末两端“等距离”的两项的二项式系数相等,即m n mn n C C -=.性质二 二项式系数表中,除两端以外其余位置的数都等于它肩上两个数之和,11m m m n n n C C C -++=.性质三 ()na b +的二项展开式中,所有二项式系数的和等于2n ,即012.nn n n n C C C +++=(令1a b ==即得,或用集合的子集个数的两种计算方法结果相等来解释).性质四 ()na b +的二项展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和,即022132112.r r n n n n n n n C C C C C C +-++++=++++=(令1,1a b ==-即得).性质五 ()na b +的二项展开式中,当n 为偶数时,中间一项的二项式系数2n n C 取得最大值;当n 为奇数时,中间两项的二项式系数12n n C -,12n n C +相等,且同时取得最大值.(即中间项的二项式系数最大)了解了二项式定理的特点与性质的同时,也要学会如何合理的应用二项式定理,下面则介绍一些二项式定理在高中数学题中的应用. 三 二项式定理的应用3.1 二项式定理可计算展开式问题 3.1.1二项式定理可计算展开式中的系数例162⎛⎫⎝的展开式中2x 的系数为 .(2011年高考天津卷理科5) A.154-B.154C.38-D.38解:因为6111226328T C x -⎛⎛=⋅⋅=- ⎝⎝⎭, 所以2x 的系数为38-.例2 在(1-的展开式中,含x 的项的系数是( ).(2005年浙江卷)A.74B.121C.-74D.121 解:由等比数列求和公式得:原式.要求展开式中的项的系数.即求中的的系数与中的系数的差.而中含的项为()4445515T C x x =⋅⋅-=,中含的项为()4454591126T C x x =⋅⋅-=,所以在的展开式中,含的项的系数是5-126=-121.例3 设()21221012211x a a x a x a x -=++++,则1011a a += .(2011年高考安徽卷理科12)解:因为()21211202192021212111x x C x C x C x -=-+-+-,则0021a C =-,20121a C =,19221a C =-,,12021a C =-,212121a C =,故111010112121a a C C +=-+, 又因为11102121C C =,所以10110a a +=.例4 (1)若1nx x ⎛⎫+ ⎪⎝⎭的展开式中第3项与第7项的二项式系数相等,则该展开式中21x 的系数为 ;(2012高考真题全国卷理15)(2)求412x x ⎛⎫+ ⎪⎝⎭的展开式中各项的二项式系数和及各项系数和.解:(1)因为展开式中的第3项和第7项的二项式系数相同,即26n n C C =,所以628n =+=,所以展开式的通项为8821881kk k k k k T C x C x x --+⎛⎫=⋅⋅= ⎪⎝⎭,令822k -=-,解得5k =,所以25681T C x ⎛⎫=⋅ ⎪⎝⎭, 所以21x的系数为5856C =. (2)该展开式的各项二项式系数和为:01234444444216C C C C C ++++==.令二项式中变量1x =,得各项系数之和为4381=.小结:二项式的考查注重基本概念,尤其是二项式系数和系数的相关问题.而解决此类问题的关键是正确认识它们的本质区别.两者本质差别在:展开式中第1r +项的二项式系数是()0,1,2,,r n C r n =,而第1r +项的系数是指经过化简整理后该项未知数前的最简系数(含正负).特别提醒:(1)求二项式系数最大的项,根据二项式系数的性质,n 为奇数时中间两项的二项式系数最大,n 为偶数时,中间一项的二项式系数最大.求展开式中系数最大的项需先判断各项系数的正、负情况,再列不等式组求解.(2)各项二项式系数和总是012nn n n n C C C +++=;而各项系数和是令展开式中各变量都为1时所得的值.3.1.2二项式定理可求展开式中的特定项例 5 若将函数()5f x x =表示为()()()()250125111f x a a x a x a x =+++++++,其中0125,,,,a a a a 为实数,则3a = .解:方法一:根据等式两边对应的系数相等.即545543315544310100a C a a a C a C a a =⎧⎪+=⇒=⎨⎪++=⎩. 方法二:对等式()()()()2550125111f x x a a x a x a x ==+++++++两边连续对x 求导三次,得到()()22345606241601x a a x a x =++++,再运用赋值法,令1x =-,得到3606a =, 即360610a =÷=.例6 ()522121x x ⎛⎫+- ⎪⎝⎭的展开式中常数项为( ).(2012高考真题安徽理7)A.-3B.-2C.2D.3 解:由题意可知,当第一个因式取2x 时,第二个因式就取21x,得到()415115C ⨯-=, 当第一个因式取2时,第二个因式取()51-,得到()5212⨯-=-, 所以展开式的常数项是()523+-=. 例712的展开式中,含x 的正整数幂的项数共有( ).(2005年浙西卷)解:设展开式中1r +项的幂为正整数,则121262361121212r rr rrr r rr T CC xC x--+-+===.依题意,r 是6的倍数,且012r ≤≤,所以r 共有3个值.即12的展开式中,含x 的正整数幂的项数共有3个.小结:在求展开式中某个特定项时,主要是考察二项式定理,写出二项展开式的通项公式是解决这类问题的常规办法,首先要知道特定项都有哪些特点,在根据题意将这些特点带入式子中.例如常数项就是x 的指数为0,而有理数就是x 的指数为整数.3.2二项式定理可解决整除或余数问题 3.2.1二项式定理可解决整除问题 例8 证明:()11nn +-能被2n 整除.证明:因()11221nn n n nnn n n n C n C n C --+=++++则()11nn +-=11222n n n n n n C n C n n --++++.由二项式定理的性质知,n 的指数是自左向右逐项递减1的,易见上式n 的最低指数是2,故()11nn +-=()222241n n n n n n n C n ---++++,又因为22421n n n C n --+++是整数.则()11nn +-能被2n 整除.例9 当*n N ∈时,求证:22389n n +--能被64整除. 证明:22389n n +--=1989n n +-- =()11889n n ++--=012233111111118888889n n n n n n n n n n C C C C C C n +++++++++⋅+⋅+⋅++⋅+⋅-- =()2233111111118888889n n n n n n n n n C C C C n ++++++++⋅+⋅+⋅++⋅+⋅-- =()22321111118888n n n n n n n n C C C C --++++++++⋅+⋅, 因为232111111888n n n n n n n n C C C C --++++++++⋅+⋅ 是整数.所以22389n n +--能被64整除. 3.2.2二项式定理可解决余数问题 例10 求9291除以100所得的余数.解:因为()92929219129029191929292929110091001009100910099C C C =-=-⨯+⨯--⨯+所以要求9291被100除所得的余数,只要求929被100除所得余数.因为()()929292921912909029192929292910110101010101C C C C =-=-⨯+⨯-+⨯-⨯+-,又因为9219129090292929210101010C C C -⨯+⨯-+⨯能被100整除.所以只要求()9291921019201919100081C -⨯+-=-+=-=-+被100除所得的余数,显然所得余数为81. 例11 求3023-除以7的余数.解:3023-=()()10103102383713-=-=+-=01019910101010107773C C C C ++++-=091891010107(77)2C C C ⨯+++-.又因为余数不能为负数,需转化为正数, 所以3023-除以7的余数为5.小结:证明整除性问题,或求余数问题.关键是找准指数式中的底数和除数的联系,将指数式分拆成与除数有关联的两个数的和或差,再用二项式定理展开,要注意余数为非负数且不大于除数.3.3二项式定理可计算近似值例12 求61.05的近似值,使结果精确到0.001. 解:()661.0510.05=+23160.05150.05200.05=+⨯+⨯+⨯+10.30.03750.0025=++++其中40.00250.01T =<,舍去.所以61.0510.30.0375 1.34≈++=.例13 求()551.99720.003=-精确到0.001的近似值.解:()555432231.99720.0032520.0031020.0031020.003=-=-⨯⨯+⨯⨯-⨯⨯+若用k T 表示展开式中第k 项的值,显然654||||||0.00000108T T T <<=,654||0.000004T T T ++=故51.997320.240.0007231.761≈-+≈.3.4二项式定理可证明恒等式或不等式 3.4.1二项式定理可证明恒等式例14 证明:0224411333242n nn n n n n n C C C C --++++=⋅+(n 为偶数,*n N ∈).证明:因为n 为偶数,所以()012213333nn n nn n n C C C C +=++++,()012213333nn nnn n n C C C C -=-+-+两式相加得 ()02244422333n n n nn n n n C C C C +=+++,所以0224411333242n nn n n n nn C C C C --+++=⋅+.例15 求证12122nn n n n C C nC n -+++=.证明:由二项式定理有:()1111nn n n nnn n x x C x C x C --+=++++.对上式以x 为自变量求导得:()()()1112231111n n n n n n n n n x nx C n x C n x C x -----+=+-+-++.取1x =有()()1121212n n n nn n n n C n C C --=+-+-+.又因组合数性质:m n mn n C C -=得()()1121212n n n nn n n n C n C C --=+-+-+.小结:关于组合恒等式的证明,关键在于十分熟悉二项式定理的展开形式及结构特点,要善于把所论问题用数学方法合理的化为二项式定理数学表达式形式.3.4.2二项式定理可证明不等式 例16 求证2n n > ()n N ∈.证明:()0121211nn n nn n n n C C C C C n =+=++++>=(舍去多余的项).证得2n n >.例17 求证(0,0)22nn n a b a b a b ++⎛⎫≥>> ⎪⎝⎭.证明:2nna b +122222n na b a b a b a b ⎧⎫+-+-⎪⎪⎛⎫⎛⎫=++-⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭22222n n nn a b a b a b C -+++⎛⎫⎛⎫⎛⎫=++≥ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. (应用二项式定理展开后,留下有用的项,舍去多余项)小结:不等式的变形是以左边开始的,而右边是较为标准的二项式定理形式,所以,我们要盯着这个要证的目标,通过各种手段将左边变形后,使其部分具有右边的形式,这就是我们的目标.四 总结二项式定理有着广泛的应用,如果不能够准确把握其本质,则可能导致无法预测的结果.二项式定理多出现在高考题中,其中比较突出的就是利用二项式的通项公式解决特定项问题,除此之外,二项式定理在整除问题,余数问题,近似值问题等都有出现,但又不是所有问题都可以用二项式定理去做,因此要合理运用二项式定理,掌握其中的技巧,以便于快速解决问题,提高利用二项式定理解决实际问题的能力.参考文献:[1]单意明.二项式定理的几点应用[J].青海师专学报,1999,(1):81-82.[2]孙幸荣,曹学峰.二项式定理的推广及应用[J].广西教育学院学报,2004,(5):53-54.[3]方厚良,罗灿.二项式定理的应用[J].数学通讯,2004,(7):19-20.[4]孟桂芬.二项式定理的应用[J].承德名族职业技术学院学报,2003,(3):56-57.[5]王荣峰.二项式定理的应用[J].高中数学教与学,2006,(10):24-25.[6]黄陂,张友力,吴红梅.二项式定理的应用[J].高中生学习(第二版),2012,(12):30-32.[7]赵建勋. 二项式定理的应用[J].数理化学习(高中版),2010,(6):12-14.[8]唐先成.二项式地管理及其应用[J].数学教学通讯,2002,(5):82-89.[9]邓勇.基于二项式定理应用的探究[J].大庆师范学院学报,2008,(5):71-73.[10]马富强.浅谈二项式定理的基本应用[J].中学生数学,2010,(9):10-12.[11]宋丽萍.浅谈二项式定理的应用[J].呼伦贝尔学院学报 ,2001,(4):65-67.Introduction to Binomial Theorem And Its ApplicationsOuYang Zhi-qiang(Mathematics and Applied Mathematics 09-2A of School of Mathematics and Statistics,Yili NormalUniversity,Yining835000,Xinjiang,China)Abstract:The binomial theorem is an important theorem in elementary mathematics,and it’s also the common basis of many important formula in higher mathematics.This paper mainly discusses the application of binomial theorem in solving combinatorial theory,a high order and inequality problems.Keywords:binomial Theorem;inequality;expand form。
太原市劳动人事争议仲裁委员会关于石磊诉山西恒光微电子集成科技有限公司劳动争议案件的仲裁公告

太原市劳动人事争议仲裁委员会关于石磊诉山西恒光微电子集成科技有限公司劳动争议案件的仲裁公告
文章属性
•【制定机关】太原市人力资源和社会保障局
•【公布日期】2022.11.01
•【字号】
•【施行日期】2022.11.01
•【效力等级】地方规范性文件
•【时效性】现行有效
•【主题分类】仲裁
正文
太原市劳动人事争议仲裁委员会关于石磊诉山西恒光微电子集成科技有限公司劳动争议案件的仲裁公告
山西恒光微电子集成科技有限公司:
本委已受理石磊诉你单位劳动争议案件(并劳人仲案字〔2022〕第238号),因受送达人无法通过直接送达等其他方式送达,现依法向你单位公告送达申请书副本及证据材料、应诉通知书、开庭通知书等,自本公告发布之日起经过30日即视为送达。
提交答辩书的期限为公告送达期满后10日内。
本委定于2022年12月21日上午9时在本委仲裁庭(地址:太原市桃园三巷11号)开庭审理此案,请准时参加庭审,未依法到庭本委将依法缺席裁决。
特此公告
太原市劳动人事争议仲裁委员会
2022年11月1日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mondays to Fridays 9:30 am - 1:00 pm 3:30 pm - 6:30 pm (Wednesdays PM Closed) Saturdays 9:30 am - 2:00 pm Sundays and Public Holidays Closed.
132 Record(s) Foun
Consultation Hours :
Mondays to Fridays 10:00 am - 1:00 pm 3:00 pm - 6:00 pm Saturdays 10:00 am - 1:00 pm Sundays and Public Holidays Closed. By Appointment Only.
Medical Enquiry System
第 2 頁,共 22 頁
Fortune Plaza Tai Po, N.T.
Telephone No.: 2665 2272
Remarks :
Dr. CHAN Kwok Pui, Brian
20/F Oterprise Square 26 Nathan Road Tsim Sha Tsui Kowloon
Monday - Friday 8:30am - 12:30pm 4:00pm - 8:00pm Sat, Sun
Consultation Hours :
Mondays to Fridays
https:///application/IMES/queryMed.do
6/5/2009
Consultation Hours :
Mondays to Saturdays 8:30 am - 1:00 pm 4:00 pm - 8:30 pm Sundays and Public Holidays 8:30 am - 1:00 pm
Dr. CHEUNG Y.W., Arnold
Rm. 705, Belgian Bank Bldg. 721 Nathan Rd. Mong Kok, Kln.
歐陽恆 新界元朗教育路 元朗商業中心401-2號
Dr. AU YEUNG, Henry
Shop M11, Shek Ping Mansion Long Ping Est. Yuen Long, N.T.
Telephone No.: 2475 8823
Remarks :
歐陽恆 新界元朗 朗屏村石屏樓M11號
張炎桓 九龍旺角 彌敦道721號 華比銀行大廈705室
Telephone No.: 2395 0313 , 2395 5555
Remarks :
Dr. CHIU Hong Sing, Ronald
Rm. 1012 Hang Shing Bldg. 363-373 Nathan Rd. Yau Ma Tei, Kln.
Telephone No.: 2893 7650
Remarks :
張麗瑪 澳門 司打口25號 海運大廈2樓D座
Dr. CHEONG Lai Ma
Rua Do Commandante Mata E Oliverrira Macau
Telephone No.: 2871 3892
Fax No.:
2871 3893
Telephone No.: 2391 2822
Remarks :
新界大埔 昌運中心 1樓56號
陳國培 香港尖沙咀彌敦道26號 東企業廣場20樓
Dr. CHAN, Michael
G/F, Jade Court 35A Belcher's St. Kennedy Town, H.K.
Telephone No.: 2819 8688
Mondays to Saturdays 10:00 am - 1:00 pm 4:00 pm - 8:00 pm Sundays Closed Public Holidays Open As Uaual
Consultation Hours :
Mondays to Fridays 4:00pm - 8:00pm Saturday and Sundays closed
Mondays to Saturdays 8:30 am - 12:30 pm 3:30 pm - 7:30 pm
Consultation Hours :
Mondays to Fridays 9:00 am - 1:00 pm 3:00 pm - 7:00 pm Saturdays 9:00 am - 1:00 pm 3:00 pm - 5:00 pm Sundays and Public Holidays 10:00am - 1:00pm
Telephone No.: 27799689
Remarks :
陳洪昭醫生 九龍深水步巴域街 27號地下
Dr. CHAN Kin Hing
Shop 56, 1/F
陳建慶
AIACC
Back to Index - About MES
Type Any
submit Close
Male Doctors
Female Doctors
Remarks :
Dr. CHANG Hoi Man
40C, R/C, RUA Pedro Coutinho Macau
Telephone No.: 2855 0568
Remarks :
曾靄文 澳門 高地烏街40號 恆利大廈C座地下
Dr. CHENG Chee Tung
Rm. 1602, Island Centre 1 Great George St. Causeway Bay, H.K.
Mondays to Fridays 9:30 am - 1:30 pm 3:30 pm - 8:30 pm Saturdays 9:30 am - 1:30 pm Sundays and Public Holidays 9:30 am - 1:30 pm 3:00 pm - 6:30 pm
Consultation Hours :
Consultation Hours :
Mon, Wed, Thurs, Fri 11:30am - 2:00pm 7pm -8pm Tuesday 11:30am -2pm Evening closed Sat, Sun & Public Holiday 11:30am - 1pm Evening closed (By appointment)
Consultation Hours :
Mondays to Fridays 9:00 am - 1:00 pm 4:00 pm - 7:30 pm Saturdays, Sundays and Public Holidays 9:00 am - 12:00 pm
Consultation Hours :
歐陽志強 九龍尖沙咀 加拿芬道18號 恆生銀行大廈607室
Dr. AU YEUNG, Henry
Rm. 401-2, Yuen Long Commercial Centre 24 Kau Yuk Rd. Yuen Long, N.T.
Telephone No.: 2477 5522
Remarks :
Consultation Hours :
Mondays to Fridays 10:00 am - 1:00 pm 3:00 pm - 6:00 pm (Wednesdays PM Closed) Saturdays 10:00 am - 3:00 pm Public Holidays 10:00 am - 1:00 pm Sundays Closed.
Medical Enquiry System
第 1 頁,共 22 頁
Medical Laboratories : Hong Kong - Kowloon - New Territories - Macau
Doctor Name
Sex Any
District Any
Friday June 5,2009
Consultation Hours :
Mon, Wed, Thurs, Fri 10:30am - 11:30am 3pm - 6:30pm Tuesdays 10:30am - 11:30am Afternoon Closed Saturday 10:30am -1130am 5:30pm - 7:30pm Sun and Public Holiday 8:30am -11am Afternoon Closed (By appointment)
Remarks :
Dr. CHEUNG Mun Wah
Shop 212, Commercial Centre Hing Tin Est. Lam Tin, Kln.
Telephone No.: 2727 3901
Remarks :
張敏華 九龍藍田 興田村商場2樓212號
Consultation Hours :
Telephone No.: 2780 7878
Remarks :
Remarks :
張麗瑪 澳門馬統領街 8號地下
Dr. CHEUNG Kwok Kwong
Rm. 1001, Argyle Centre Phase 1 688 Nathan Rd. Mong Kok, Kln.
張國光 九龍旺角 彌敦道688號 旺角中心第一期1001室
Telephone No.: 2380 3833 , 2381 6600
Telephone No.: 2577 5906
Remarks :
鄭至東 香港銅鑼灣 紀利佐治街1號 金堡中心1602室
Dr. CHENG Suk Tung
Shop 12, CB 4 Kwong Yuen Est. Shatin, N.T.
