123等腰三角形水平测试题
等腰三角形测试题

等腰三角形测试题等腰三角形测试题:探索几何世界的奇妙之旅在我们的数学学习中,等腰三角形就像是一个神秘而有趣的小伙伴,总是带着各种谜题等待我们去解开。
今天,咱们就一起来面对一场关于等腰三角形的测试挑战,看看你能在这个几何世界中闯出怎样的精彩!先来几道基础题热热身。
比如说:“一个等腰三角形的顶角是80 度,那它的一个底角是多少度?”这就像是在问,三角形的两个底角小伙伴,你们要怎么分配角度,才能和顶角一起组成完美的 180 度大家庭呀。
再看看这道:“已知等腰三角形的两条边长分别是 5 厘米和 11 厘米,那它的周长是多少?”这可有点小陷阱哦,得好好想想等腰三角形两条腰的长度关系,可别一不小心掉进去啦。
还有稍微难一点的,“在等腰三角形 ABC 中,AB = AC,BD 是角ABC 的平分线,交 AC 于点 D,如果角 A = 36 度,求角 BDC 的度数。
”这就像是在一个错综复杂的几何迷宫里找出口,得把各种角度关系理得清清楚楚。
说到等腰三角形,我想起有一次在课堂上,老师让我们用折纸的方式来理解等腰三角形的性质。
我拿起一张正方形的纸,按照老师说的步骤,先对折,再对折,然后展开,一个等腰三角形就出现在眼前啦。
我仔细地观察着这个亲手折出来的三角形,突然发现,原来等腰三角形的两条腰就像是一对双胞胎,长得一模一样,而且它们和底边形成的角度也有着特别的关系。
那一刻,我感觉自己仿佛和等腰三角形成为了好朋友,它不再是书本上冷冰冰的图形,而是充满了生命力和趣味。
接下来,咱们继续挑战难题。
“在等腰三角形中,作一条中线将其分成两个三角形,这两个三角形全等吗?为什么?”这可需要我们对全等三角形的判定条件了如指掌,还要结合等腰三角形的特殊性质来思考。
还有“等腰三角形一腰上的高与另一腰的夹角为 40 度,求这个等腰三角形的顶角。
”这道题可真是让人有点头疼,得考虑是锐角等腰三角形还是钝角等腰三角形两种情况呢。
做完这些测试题,你是不是对等腰三角形有了更深的了解呢?其实,数学就像一场探险,每一个几何图形都是一个神秘的宝藏,等待着我们用智慧去发现。
八年级数学12.3等腰三角形水平测试题及答案

12.3等腰三角形水平测试题一.选择题(每小题3分;共24分)1. 小明将两个全等且有一个角为60的直角三角形拼成如图1所示的图形;其中两条较长直角边在同一直线上;则图中等腰三角形的个数是( )A.4 B.3 C.2 D.12、已知等腰三角形的一个角等于42°;则它的底角为 ( ). A 、42 ° B 、69° C 、69°或84° D 、42°或69°3、如图;ABC △中;AB AC =;30A ∠=;DE 垂直平分AC ;则BCD ∠的度数为( )A.80 B.75 C.65 D.454、等腰三角形的顶角是80°;则一腰上的高与底边的夹角是( ) A .40° B .50° C .60° D .30°5、如图;已知等边三角形ABC 中;BD CE =;AD 与BE 交于点P ;则APE ∠的度数是( ) A .45B .55C .60D .756、如图是一个等边三角形木框;甲虫P 在边框AC 上爬行(A ;C 端点除外);设甲虫P 到另外两边的距离之和为d ;等边三角形ABC 的高为h ;则d 与h 的大小关系是( ) A.d h > B.d h < C.d h = D.无法确定7. 如图;15A =∠;AB BC CD DE EF ====;则DEF ∠等于( )A F C H BME G AD EE DC AB F A .90 B .75C .70D .608、如图;△MNP 中; ∠P=60°;MN=NP ;MQ ⊥PN ;垂足为Q ;延长MN 至G ;取NG=NQ ;若△MNP 的周长为12;MQ=a ;则△MGQ 周长是( )PQMNGA .8+2aB .8+aC .6+aD .6+2a二.选择题(每小题3分;共24分)1. 在△ABC 中;AB=AC ;若∠B=56º;则∠C=__________.2.等腰三角形底边中点与一腰的距离为6;则腰上的高为______.3.如图;在△ABC 中;AB=AC ;CD 平分∠ACB 交AB 于点D ;AE ∥DC 交BC 的延长线于点E ;已知∠E=36°;则∠B= .4.如图;在ABC △中;点D 是BC 上一点;80BAD ∠=°;AB AD DC ==;则C ∠= .5. 等腰三角形至少有a 条对称轴;至多有b 条对称轴;则b a -= .6. 有一个等腰三角形;三边分别是3x -2;4x -3;6-2x ;则等腰三角形的周长___.7. 如图;△ABC 中AB=AC ;EB=BD=DC=CF ;∠A=40°;则∠EDF•的度数是_____.8.在△ABC 中;B C ⊥AC ;D E ⊥AC ;D 是AB 的中点;若∠A=300;AB=8;则BC= ;DE= 。
湘教版八年级数学上册《2.3.2等腰三角形的判定》同步测试题及答案

湘教版八年级数学上册《2.3.2等腰三角形的判定》同步测试题及答案班级:___________姓名:___________得分:__________(满分:100分,考试时间:40分钟)一.选择题(共5小题,每题8分)1.下列推理中,错误的是( )A.∵∠A=∠B=∠C,∴△ABC是等边三角形B.∵AB=AC,且∠B=∠C,∴△ABC是等边三角形C.∵∠A=60°,∠B=60°,∴△ABC是等边三角形D.∵AB=AC,∠B=60°,∴△ABC是等边三角形2.如果一个三角形是轴对称图形,且有一个内角是60°,那么这个三角形是( )A.等边三角形B.等腰直角三角形C.等腰三角形D.含30°角的直角三角形3.如图,△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线BE、CD交于点F,则图中共有等腰三角形( )A.8个B.7个C.6个D.5个第3题图第5题图4.下列能判定三角形是等腰三角形的是( )A.有两个角为30°、60°B.有两个角为40°、80°C.有两个角为50°、80°D.有两个角为100°、120°5.如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )A.7 B.8 C.9 D.10二.填空题(共4小题,每题5分)6.如图,在ΔABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是__________第6题图第7题图第8题图7.如图,已知OC平分∠AOB,CD∥OB,若OD=6㎝,则CD的长等于____________ .8.小明从A处出发,要到北偏东60°方向的C处,他先沿正东方向走了200米到达B处,再沿北偏东30°方向走恰能到达目的地C处. 则B、C两地的距离为________9.在△ABC中,∠A=80°,当∠B=__________时,△ABC是等腰三角形.三.解答题(共3小题,第10题10分,第11、12题各15分)10.△ABC是等边三角形,点D在边BC上,DE∥AC,△BDE是等边三角形吗?试说明理由.11.如图,在△ABC中,∠BAD=∠B,∠EAC=∠C,若△ADE的周长是12,则BC的长是多少?12.如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.(1)求∠B的度数,并判断△ABC的形状;(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.参考答案与解析1.B【解析】A∵∠A=∠B=∠C,∴△ABC是等边三角形,故正确;B条件重复且条件不足,故不正确;C∵∠A=60°,∠B=60°,∴∠C=60°,∴△ABC是等边三角形60°,故正确;D根据有一个角是60°的等腰三角形是等边三角形可以得到,故正确.故选B.2.A【解析】∵这个三角形是轴对称图形∴一定有两个角相等∴这是一个等腰三角形.∵有一个内角是60°∴这个三角形是等边三角形.故选A.3.A【解析】△ABC, △BCE,△CDB, △BFC,△BFD,△CEF,△AEB,△ADC,故选A.4.C【解析】A、因为有两个角为30°、60°,则第三个角为90°,所以此选项不正确;B、因为有两个角为40°、80°,则第三个角为60°,所以此选项不正确;C、因为有两个角为50°、80°,则第三个角为50°,有两个角相等,所以此选项正确;D、因为100°+120°>180°,所以此选项不正确;故选:C.5.D【解析】利用角平分线及平行线性质,结合等腰三角形的判定得到MB=MO,NC=NO,将三角形AMN 周长转化为AB+AC,求出即可.解:∵BO为∠ABC的平分线,CO为∠ACB的平分线,∴∠ABO=∠CBO,∠ACO=∠BCO.∵MN∥BC,∴∠MOB=∠OBC,∠NOC=∠BCO,∴∠ABO=∠MOB,∠NOC=∠ACO,∴MB=MO,NC=NO,∴MN=MO+NO=MB+N C.∵AB=4,AC=6,∴△AMN周长为AM+MN+AN=AM+MB+AN+NC=AB+AC=10.故答案为:10.6.3【解析】由已知条件,利用三角形的内角和定理及角平分线的性质得到各角的度数,根据等腰三角形的定义及等角对等边得出答案.解:∵AB=AC,∴△ABC是等腰三角形.∵∠A=36°,∴∠C=∠ABC=72°.∵BD平分∠ABC交AC于D∴∠ABD=∠DBC=36°∵∠A=∠ABD=36°∴△ABD是等腰三角形.∠BDC=∠A+∠ABD=36°+36°=72°=∠C∴△BDC是等腰三角形.∴共有3个等腰三角形.故答案为:3.7.6cm【解析】∵OC平分∠AOB∴∠AOC=∠BOC;又∵CD∥OB∴∠C=BOC∴∠C=∠AOC;∴CD=OD=6cm.故答案为:6cm.8.200米【解析】根据题中的角的关系证明∠BAC=∠C.解:根据题意得,∠BAC=90°-60°=30°,∠ABC=90°+30°=120°所以∠C=30°,所以∠BAC=∠C,所以BC=AB=200.故答案为200米.9.80°或50°或20°【解析】分三种情况分析解:∵∠A=80°∴①当∠B=80°时,△ABC是等腰三角形;②当∠B=(180°﹣80°)÷2=50°时,△ABC是等腰三角形;③当∠B=180°﹣80°×2=20°时,△ABC是等腰三角形;故答案为:80°或50°或20°10.证明见解析.【解析】根据△ABC是等边三角形得出∠A=∠B=∠C=60°,利用DE∥AC,求得∠B=∠BED=∠BDE 即可得出结论.解:△BDE是等边三角形理由:∵△ABC是等边三角形∴∠A=∠B=∠C=60°∵DE∥AC∴∠BED=∠A=60°,∠BDE=∠C=60°∴∠B=∠BED=∠BDE∴△BDE是等边三角形.11.12.【解析】结合图形,利用等腰三角形的判定,可所求出BC的长度.解:∵∠BAD=∠B∴BD=AD∵∠EAC=∠C∴AE=CE.∵AD+DE+DE=12∴BC=BD+DE+EC=12.12.(1)△ABC是等腰三角形,∠B=40°;(2)见解析.【解析】分析:(1)、根据Rt△ADE的内角和得出∠DAC=70°,根据平行线的性质得出∠C=70°,从而根据有两个角相等的三角形是等腰三角形得出答案;(2)、根据等腰三角形底边上的三线合一定理得出DB为顶角的角平分线.。
最新初中数学八年级上册《123等腰三角形》

初中数学八年级上册《123等腰三角形》新课标人教版初中数学八年级上册《12.3等腰三角形》精品试题一、填空题1、等腰三角形的一内角是40°,则其他两角的度数分别是2、等腰三角形顶角的外教是138°,它的一个底教是3、已知一等腰三角形两边为2,4,则它的周长为4、等腰三角形中,和顶角相邻的外角的平分线和底边的位置关系是5、等腰三角形一腰上的高与另一腰的夹角为30°,腰长为a,则其底边上的高为二、选择题6、下列判断正确的是()A、有两边和其中一边的对角对应相等的两个三角形全等。
B、有两边对应相等,且有一角为30°的两个等腰三角形全等。
C、有一角和一边对应相等的两个直角三角形全等。
D、有两角和一边对应相等的两个三角形全等。
7、下列命题中的假命题是()A、等腰三角形的底角一定是锐角。
B、等腰三角形至少有两个角全等。
C、等腰三角形的顶角一定是锐角。
D、等腰三角形顶角的外角是底角的2倍。
8、下列命题中假命题是()A、等腰三角形一定是锐角三角形。
B、等腰直角三角形一定是直角三角形。
C、等边三角形一定是等腰三角形。
D、等边三角形一定锐角三角形。
9、两个等腰三角形全等的条件是()A、有两条边对应相等。
B、有两个角对应相等。
C、有一腰和一底角对应相等。
D、有一腰和一角对应相等。
10、下列作图语句中,正确的是()A、作等腰三角形底边上的高,使它平分底边。
B、作等腰三角形底边上的高,使它平分顶角。
C、作等腰三角形底边上的高,使它平分底边且平分顶角。
D、作等腰三角形底边上的高,则高平分底边且平分顶角。
三、证明题11、已知,如图,△ABC中,AB = AC,AD ⊥ BC于D,BE ⊥ AC于E,AD和BE交于H,且BE = AE,求证:AH = 2BD。
AH EB D C12、已知,如图,△ABC的∠ABC的平分线BD与∠ACB的外角平分线交于D点,DE∥BC交AB于E,交AC于F,求证:EF = BE – DF。
12.3.1 等腰三角形(二)及答案
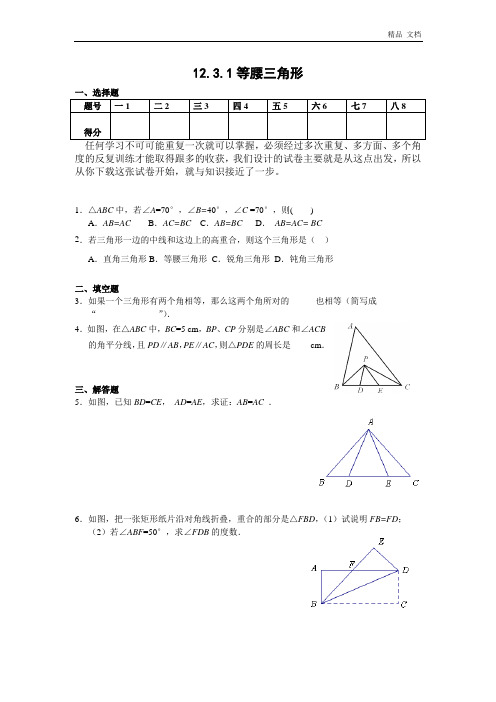
12.3.1等腰三角形题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
1.△ABC中,若∠A=70°,∠B=40°,∠C =70°,则( )A.AB=AC B.AC=BC C.AB=BC D.AB=AC=BC2.若三角形一边的中线和这边上的高重合,则这个三角形是()A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形二、填空题3.如果一个三角形有两个角相等,那么这两个角所对的______也相等(简写成“______________”).4.如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是____ cm.三、解答题5.如图,已知BD=CE,AD=AE,求证:AB=AC.6.如图,把一张矩形纸片沿对角线折叠,重合的部分是△FBD,(1)试说明FB=FD;(2)若∠ABF=50°,求∠FDB的度数.7.已知四边形ABCD、EFGC为全等的矩形,B、C、E在一条直线上,试判断三角形△ACF 的形状,并说明理由.参考答案一、选择题1.C2.B二、填空题3.边,等边对等角4.5三、解答题5.过A做AF⊥BC,垂足为F,∵AD=AE∴DF=EF,又∵BD=CE∴BF=CF ∴AB=AC.6.(1)证明略(2)20°7.△ACF是等腰直角三角形,提示:证明△ABC≌△CE F,再零用三角形全等的性质This document is collected from the Internet, which is convenient for readers to use. Ifthere is any infringement, please contact the author and delete it immediately.可以编辑的试卷(可以删除)。
2022-2023学年人教版八年级数学上册《13-3等腰三角形》同步达标测试题(附答案)

2022-2023学年人教版八年级数学上册《13.3等腰三角形》同步达标测试题(附答案)一.选择题(共10小题,满分40分)1.已知等腰三角形三边的长分别为4,x,10,则x的值是()A.4B.10C.4 或10D.6 或102.已知等腰三角形ABC的周长为20cm,BC=8cm,则AB的长度是()A.8cm B.6cmC.8cm或6cm D.8cm或6cm或4cm3.已知等腰三角形的一个底角为70°,则其顶角为()A.50°B.60°C.30°D.40°4.等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为()A.65°B.105°C.55°或105°D.65°或115°5.如图,在△ABC中,D、E是两边AB、AC上的点,DE∥BC,DE=BE,若∠DBC=20°,∠C=65°,则∠A的度数是()A.60°B.65°C.70°D.75°6.如图,已知点B,C,D,E在同一直线上,△ABC是等边三角形,且CG=CD,DF=DE,则∠E=()A.35°B.30°C.25°D.15°7.三个等边三角形的摆放位置如图,若∠3=60°,则∠1+∠2的度数为()°A.150B.120C.90D.808.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD于点D.∠ABD=∠A,若BD=1,BC=3,则AC的长为()A.2B.3C.4D.59.如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是()A.10B.8C.6D.410.如图,在△ABC中,∠B=60°,∠EDC=∠BAC,且D为BC中点,DE=CE,则AE:AB的值为()A.B.C.D.无法确定二.填空题(共6小题,满分30分)11.等腰三角形一边长等于4,一边长等于9,它的周长是.12.已知△ABC中有一个内角是30°,AB=AC,AB边上的中垂线交直线BC于点D,连结AD,则∠DAC=.13.如图,AD是△ABC的高,且AB+BD=DC,∠BAD=40°,则∠C的度数为.14.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E =60°,若BE=4cm,DE=3cm,则BC=cm.15.如图,∠ABC的平分线BF与△ABC的相邻外角∠ACG的平分线CF相交于F,过F 作DF∥BC,交AB于D,交AC于E,若BD=8cm,CE=5cm,则DE的长为.16.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB 于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn.其中正确的结论是.(填序号)三.解答题(共5小题,满分50分)17.已知:如图,E为△ABC的外角平分线上的一点,AE∥BC,BF=AE,求证:(1)△ABC是等腰三角形;(2)AF=CE.18.如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)求证:∠B=∠DEF;(3)当∠A=40°时,求∠DEF的度数.19.如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.(1)求证:AE=BD;(2)求证:MN∥AB.20.已知:在△AOB和△COD中,OA=OB,OC=OD.(1)如图①,若∠AOB=∠COD=60°,求证:①AC=BD②∠APB=60°.(2)如图②,若∠AOB=∠COD=α,则AC与BD间的等量关系式为,∠APB 的大小为(直接写出结果,不证明)21.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.参考答案一.选择题(共10小题,满分40分)1.解:当x=4时,4+4<10,不符合三角形三边关系,舍去;当x=10时,4+10>10,符合三角形三边关系.故选:B.2.解:(1)当BC=8cm为底边时,AB为腰,由等腰三角形的性质,得AB=(20﹣BC)=6cm;(2)当BC=8cm为腰时,①若AB为腰,则BC=AB=8cm;②若AB为底,则AB=20﹣2BC=4cm,故选:D.3.解:∵等腰三角形的一个底角为70°,∴顶角=180°﹣70°×2=40°.故选:D.4.解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部.根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+25°=115°;②如图2,当等腰三角形的顶角是锐角时,腰上的高在其内部,故顶角是90°﹣25°=65°.故选:D.5.解:∵DE=BE,∴∠EBD=∠EDB,∵DE∥BC,∴∠EDB=∠DBC=20°,∴∠DBE=∠BDE=20°,∴∠ABC=40°,∵∠C=65°,∴∠A=180°﹣∠ABC﹣∠C=180°﹣40°﹣65°=75°,故选:D.6.解:如图所示,∵△ABC是等边三角形,∴∠B=∠1=60°,∵CD=CG,∴∠CGD=∠2,∴∠1=2∠2,同理有∠2=2∠E,∴4∠E=60°,∴∠E=15°.故选:D.7.解:∵图中是三个等边三角形,∠3=60°,∴∠ABC=180°﹣60°﹣60°=60°,∠ACB=180°﹣60°﹣∠2=120°﹣∠2,∠BAC=180°﹣60°﹣∠1=120°﹣∠1,∵∠ABC+∠ACB+∠BAC=180°,∴60°+(120°﹣∠2)+(120°﹣∠1)=180°,∴∠1+∠2=120°.故选:B.8.解:延长BD交AC于E,如图,∵CD平分∠ACB,BD⊥CD,∴△BCE为等腰三角形,∴DE=BD=1,CE=CB=3,∵∠A=∠ABD,∴EA=EB=2,∴AC=AE+CE=2+3=5.故选:D.9.解:如图,延长BD交AC于点E,∵AD平分∠BAE,AD⊥BD,∴∠BAD=∠EAD,∠ADB=∠ADE,在△ABD和△AED中,,∴△ABD≌△AED(ASA),∴BD=DE,∴S△ABD=S△ADE,S△BDC=S△CDE,∴S△ABD+S△BDC=S△ADE+S△CDE=S△ADC,∴S△ADC=S△ABC=×12=6,故选:C.10.解:∵DE=CE∴∠EDC=∠C,∵∠EDC=∠BAC,∴∠EDC=∠BAC=∠C,∵∠B=60°,∴△ABC及△DCE是等边三角形,∵D为BC中点,∴DE是△ABC的中位线,∴AE:AB=1:2.故选:A.二.填空题(共6小题,满分30分)11.解:∵4+4=8<9,0<4<9+9=18∴腰的不应为4,而应为9∴等腰三角形的周长=4+9+9=22故填:22.12.解:∠B=30°是底角,如图1:∵AB=AC,∠B=30°,∴∠C=30°,∵AB边上的中垂线交直线BC于点D,∴∠BAD=∠B=30°,∴∠ADC=30°+30°=60°,∴∠DAC=180°﹣30°﹣60°=90°;∠BAC=30°的角是顶角,如图2:∵AB=AC,∠BAC=30°,∴∠B=∠ACB=(180°﹣30°)÷2=75°,∵AB边上的中垂线交直线BC于点D,∴∠BED=∠AED=90°﹣75°=15°,∴∠ADC=15°+15°=30°,∴∠DAC=75°﹣30°=45°.故∠DAC=90°或45°.故答案为:90°或45°.13.解:在线段DC上取一点E,使DE=DB,连接AE,∵AD是△ABC的高,∴AD⊥BC,∴AD垂直平分BE,∴AB=AE,∴∠EAD=∠BAD=40°,∠AEB=∠B=90°﹣∠BAD=50°,∵AB+BD=DC,DE+CE=DC,∴AB=CE,∴AE=CE,∴∠EAC=∠C,∵∠AEB=∠EAC+∠C=2∠C,∴∠C=∠AEB=25°,故答案为:25°.14.解:延长ED交BC于M,延长AD交BC于N,作DF∥BC,∵AB=AC,AD平分∠BAC,∴AN⊥BC,BN=CN,∵∠EBC=∠E=60°,∴△BEM为等边三角形,∴△EFD为等边三角形,∵BE=4cm,DE=3cm,∴DM=1cm,∵△BEM为等边三角形,∴∠EMB=60°,∵AN⊥BC,∴∠DNM=90°,∴∠NDM=30°,∴NM=cm,∴BN=cm,∴BC=2BN=7cm,故答案为7.15.解:∵BF、CF分别平分∠ABC、∠ACB的外角,∴∠DBF=∠CBF,∠FCE=∠FCG,∵DE∥BC,∴∠DFB=∠CBF,∠EFC=∠FCG,∴∠DBF=∠DFB,∠FCE=∠EFC,∴BD=FD=8cm,EF=CE=5cm,∴BD﹣CE=FD﹣EF=DE=8﹣5=3(cm),故答案为:3cm.16.解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故②正确;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF,∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=AE•OM+AF•OD=OD•(AE+AF)=mn;故④错误;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故③正确.故答案是:①②③三.解答题(共5小题,满分50分)17.证明:(1)∵AE∥BC,∴∠DAE=∠B,∠EAC=∠ACB,∵E为△ABC的外角平分线上的一点,∴∠DAE=∠EAC,∴∠B=∠ACB,∴AB=AC,∴△ABC是等腰三角形;(2)在△ABF和△CAE中,,∴△ABF≌△CAE(SAS),∴AF=CE.18.(1)证明:∵AB=AC,∴∠B=∠C,在△DBE和△ECF中,,∴△DBE≌△ECF,∴DE=FE,∴△DEF是等腰三角形;(2)∵△BDE≌△CEF,∴∠FEC=∠BDE,∴∠DEF=180°﹣∠BED﹣∠FEC=180°﹣∠DEB﹣∠EDB=∠B (3)∵由(2)知△BDE≌△CEF,∴∠BDE=∠CEF,∴∠CEF+∠DEF=∠BDE+∠B,∴∠DEF=∠B,∴AB=AC,∠A=40°,∴∠DEF=∠B==70°.19.证明:(1)∵△ACD和△BCE是等边三角形,∴AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,∵∠DCA=∠ECB=60°,∴∠DCA+∠DCE=∠ECB+∠DCE,∠ACE=∠DCB,在△ACE与△DCB中,∵,∴△ACE≌△DCB,∴AE=BD;(2)∵由(1)得,△ACE≌△DCB,∴∠CAM=∠CDN,∵∠ACD=∠ECB=60°,而A、C、B三点共线,∴∠DCN=60°,在△ACM与△DCN中,∵,∴△ACM≌△DCN(ASA),∴MC=NC,∵∠MCN=60°,∴△MCN为等边三角形,∴∠NMC=∠DCN=60°,∴∠NMC=∠DCA,∴MN∥AB.20.解:(1)①证明:∵∠AOB=∠COD=60°,∴∠AOB+∠BOC=∠COD+∠BOC,∴∠AOC=∠BOD.在△AOC和△BOD中,,∴△AOC≌△BOD(SAS),∴AC=BD;②证明:∵△AOC≌△BOD,∴∠OAC=∠OBD,∴∠OAC+∠AOB=∠OBD+∠APB,∴∠OAC+60°=∠OBD+∠APB,∴∠APB=60°;(2)AC=BD,∠APB=α.21.解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,∠BDA逐渐变小;故答案为:25°,115°,小;(2)当DC=2时,△ABD≌△DCE,理由:∵∠C=40°,∴∠DEC+∠EDC=140°,又∵∠ADE=40°,∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,又∵AB=DC=2,∴△ABD≌△DCE(AAS),(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,理由:∵∠BDA=110°时,∴∠ADC=70°,∵∠C=40°,∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,∴∠DAC=∠AED,∴△ADE的形状是等腰三角形;∵当∠BDA的度数为80°时,∴∠ADC=100°,∵∠C=40°,∴∠DAC=40°,∴∠DAC=∠ADE,∴△ADE的形状是等腰三角形.。
等腰三角形的练习题

等腰三角形的练习题一、选择题1. 等腰三角形的两边相等,这个性质称为()A. 对称性B. 等边性C. 等腰性D. 等角性2. 在等腰三角形中,底角相等的原因是()A. 三角形内角和定理B. 等腰三角形的性质C. 相似三角形的判定D. 直角三角形的性质3. 等腰三角形的底边高等于腰上的高,这是因为()A. 直角三角形的斜边中线性质B. 等腰三角形的三线合一性质C. 勾股定理D. 相似三角形的性质4. 已知等腰三角形的顶角为60°,那么这个三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定5. 如果等腰三角形的底边长为10厘米,腰长为13厘米,那么其面积是()A. 30平方厘米B. 65平方厘米C. 100平方厘米D. 无法计算二、填空题6. 等腰三角形的两个底角相等,其大小为______。
7. 如果等腰三角形的顶角为120°,那么底角的大小为______。
8. 在等腰三角形ABC中,AB=AC,如果AB边上的高为h,那么AC边上的高也是______。
9. 等腰三角形的三线合一性质指的是______、______和______在同一直线上。
10. 如果等腰三角形的腰长为x,底边长为y,且x>y,那么面积公式为S=______。
三、解答题11. 已知等腰三角形的顶角为40°,求其底角的大小。
12. 一个等腰三角形的底边长为8厘米,腰长为10厘米,求其面积。
13. 证明:等腰三角形的底边上的中线、高线和角平分线重合。
14. 如果一个三角形的两边相等,且这两边所夹的角为70°,求这个三角形的另外两个内角的大小。
15. 已知等腰三角形的周长为32厘米,底边长为10厘米,求其腰长。
四、应用题16. 一个等腰三角形的花园,其底边长为20米,腰长为13米。
如果需要在花园的周围铺设一圈围栏,问需要多少米的围栏?17. 在一个等腰三角形ABC中,AB=AC,AB边上的高为h,求证:AC边上的高也是h。
初中数学:等腰三角形测试题(含答案)

初中数学:等腰三角形测试题(含答案)时间40分钟总分100分一、选择题(每题5分)1、若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为()A、75°或15°B、30°或60°C、75°D、30°【答案】A【解析】试题分析:分等腰三角形的顶角是锐角和钝角两种情况求解.解:当等腰三角形的顶角是锐角时,如图所示,∵BD=12 AB,∴∠A=30°,∴∠ABC=∠C=75°;当等腰三角形的顶角是钝角时,如图所示,∵BD=12 AB,∴∠BAD=30°,∴∠BAC=150°,∴∠ABC=∠C=15°.故应选A.考点:等腰三角形的性质.2、等腰三角形的底边为7cm,一边上的中线把其周长分为两部分的差为3cm,则腰长为()A.20cm B.10cm C.10cm或4cm D.4cm 【答案】C【解析】试题分析:解:等腰三角形底边上的中线把等腰三角形分成的两部分的长度相等,∴把等腰三角形的周长分成差为3cm的两部分的中线是腰上的中线,设等腰三角形的腰长是2xcm,则被分成的两部分的长度分别是3xcm和(7+x)cm,当3x-(7+x)=3时,解得:x=5,则2x=10,∴等腰三角形的腰长为5cm;当(7+x)-3x=3时,解得:x=2,则2x=4,∴等腰三角形的腰长是4cm或10cm.故应选C考点:等腰三角形的性质.3、如图,坐标平面内一点A(2,﹣1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为()A. 2 B. 3 C. 4 D. 5【答案】C【解析】试题分析:根据等腰三角形的定义分情况讨论.解:如下图所示,当OA为等腰三角形的底边时,点P是线段OA的垂直平分线与x轴的交点;当AP为等腰三角形的底边时,符合条件的点P有2个;当OP为等腰三角形的底边时,符合条件的点P有1个.符合条件的点共有4个.故应选C考点:等腰三角形的定义.4、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有()A.2种B.3种C.4种D.6种【答案】C【解析】试题分析:利用等腰三角形的定义和判定定理进行判断.解:可以证明△ABC是等腰三角形的方法有:①②①③②④③④,所以共有4种,故应选C.考点:等腰三角形的判定5、下列说法中:(1)顶角相等,并且有一腰相等的两个等腰三角形全等;(2)底边相等,且周长相等的两个等腰三角形全等;(3)腰长相等,且有一角是50°的两个等腰三角形全等;(4)两条直角边对应相等的两个直角三角形全等;错误的有()A.1个B. 2个C.3个D.4个【答案】A【解析】试题分析:根据等腰三角形的性质和全等三角形的判定定理进行判断.解:(1)顶角相等,并且有一腰相等的两个等腰三角形,根据SAS可证全等,故(1)正确;(2) 底边相等,且周长相等的两个等腰三角形,根据SSS可证全等,故(2)正确;(3)腰长相等,且有一角是50°的两个等腰三角形,50°角可能是等腰三角形的顶角也可能是等腰三角形的底角,所以这两个等腰三角形不一定全等,故(3)错误;(4) 两条直角边对应相等的两个直角三角形,根据SAS可证全等,故(4)正确.所以错误的有1个.故应选A.考点:1.等腰三角形的性质;2.全等三角形的判定6、已知:如图,下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是()A.①③④B.①②③④C.①②④D.①③【答案】A【解析】试题分析:根据三角形各内角的度数进行划分.解:如下图所示,所以①③④都可以.故应选A.考点:等腰三角形的判定二、填空题(每题6分)7、若一个等腰三角形的周长是20cm,一边长是5cm,则另两边的长是__________。
部编版人教初中数学八年级上册《13.3 等腰三角形 同步练习题及答案》最新精品优秀测试题

前言:该同步练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点,精心编辑而成。
以高质量的同步练习题助力考生查漏补缺,在原有基础上更进一步。
(最新精品同步练习题)13.3等腰三角形基础巩固1.(知识点2)下列能判定△ABC为等腰三角形的是()A.∠A=30°,∠B=60°B.∠A=50°,∠B=80°C.AB=AC=2,BC=4D.AB=3,BC=7,周长为102.(题型一)如图13-3-1,O是△ABC的两条垂直平分线的交点,∠BAC=70°,则∠BOC=()图13-3-1A.120°B.125°C.130°D.140°3.(知识点1)如图13-3-2,D是Rt△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.若α=10°,则β的度数是()图13-3-2A.40°B.50°C.60°D.不能确定4.(知识点3)已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P与P关于OA对称,则P1,O,P2三点所组成的三角形是()2A.直角三角形B.钝角三角形C.等腰三角形D.等边三角形5.(知识点3)如图13-3-3,M,N是△ABC的边BC上的两点,且BM=MN=NC=AM=AN,则∠BAN= .图13-3-3 图13-3-46.(知识点1)如图13-3-4,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=12∠B,∠C=50°,则∠BAC的度数为 .7.(题型一)如图13-3-5,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC= °.图13-3-5 图13-3-68.(知识点2)如图13-3-6,在△ABC中,BC=5 cm,BP,CP分别是∠ABC 和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是 cm.9.(知识点1)如图13-3-7,在△ABC中,AB=AC,BE=EC.求证:∠ABE=∠ACE.图13-3-710.(知识点1)如图13-3-8,在△ABC中,AB=AC,AD是△ABC的中线,E 是AC的中点,连接DE,DF⊥AB于点F.求证:∠BDF=∠ADE.(注:直角三角形斜边上的中线等于斜边的一半)图13-3-8能力提升。
《等腰三角形》测试题

《等腰三角形》测试题一、选择题(每题 5 分,共 25 分)1、等腰三角形的一个角是 80°,则它顶角的度数是()A 80°B 80°或 20°C 80°或 50°D 20°2、已知等腰三角形的两边长分别为 3 和 6,则它的周长为()A 9B 12C 15D 12 或 153、等腰三角形一腰上的高与另一腰的夹角为 40°,则顶角的度数为()A 50°B 130°C 50°或 130°D 40°或 140°4、如图,在△ABC 中,AB = AC,∠A = 36°,BD 平分∠ABC 交 AC 于点 D,则图中的等腰三角形有()A 1 个B 2 个C 3 个D 4 个5、若等腰三角形的底边长为 6,底边上的中线长为 4,则它的腰长为()A 7B 6C 5D 4二、填空题(每题 5 分,共 25 分)6、等腰三角形的两边长分别为 4 和 9,则它的周长为______7、等腰三角形的一个外角为 110°,则它的底角为______8、若等腰三角形一腰上的中线把其周长分为 12 和 9 两部分,则这个等腰三角形的腰长是______9、如图,在△ABC 中,AB = AC,AD 是 BC 边上的中线,BE⊥AC 于点 E 若 AD = 5,BE = 4,则△ABC 的面积是______10、等腰三角形一腰上的高与另一腰的夹角为 36°,则该等腰三角形的底角的度数为______三、解答题(共 50 分)11、(10 分)如图,在△ABC 中,AB = AC,点 D、E 在 BC 上,且 AD = AE 求证:BD = CE12、(10 分)已知等腰三角形的周长为 12,其一边长为 5,求另外两边的长13、(15 分)如图,在△ABC 中,AB = AC,∠A = 120°,AB的垂直平分线交 BC 于点 M,交 AB 于点 E,AC 的垂直平分线交 BC于点 N,交 AC 于点 F 求证:BM = MN = NC14、(15 分)如图,在△ABC 中,AB = AC,D 是 BC 边上一点,E 是 AD 上一点,且∠BED = 2∠CED =∠BAC 求证:BD = 2CD答案解析一、选择题1、解:当80°的角是顶角时,顶角就是80°;当80°的角是底角时,顶角是 180° 80°×2 = 20°,所以顶角的度数是 80°或 20°,故选 B2、解:当腰长为 3 时,3 + 3 = 6,不能构成三角形;当腰长为 6 时,周长为 6 + 6 + 3 = 15,故选 C3、解:分两种情况:当等腰三角形为锐角三角形时,顶角为50°;当等腰三角形为钝角三角形时,顶角为 130°,故选 C4、解:∵AB = AC,∠A = 36°,∴∠ABC =∠C = 72°∵BD平分∠ABC,∴∠ABD =∠CBD = 36°,∴△ABD,△BDC 都是等腰三角形又∵AB = AC,∴△ABC 也是等腰三角形,共 3 个,故选 C5、解:因为等腰三角形底边上的中线也是底边上的高,根据勾股定理可得腰长为√(4²+ 3²) = 5,故选 C二、填空题6、解:当腰长为 4 时,4 + 4 < 9,不能构成三角形;当腰长为 9 时,周长为 9 + 9 + 4 = 22、7、解:当外角为顶角的外角时,顶角为 180° 110°= 70°,底角为55°;当外角为底角的外角时,底角为 70°8、解:设腰长为 2x,底边长为 y 则有 2x + x = 12,x + y = 9或 2x + x = 9,x + y = 12、解得 x = 4,y = 5 或 x = 3,y = 9、所以腰长为 8 或 6、9、解:因为 AB = AC,AD 是中线,所以 BC = 2BD 根据三角形面积公式,S = 1/2 × BC × BE = 1/2 × 2BD × 4 = 4BD 又因为 AD = 5,在直角三角形 ABD 中,BD =√(AB² AD²) =√(AB² 25) 根据勾股定理,AB²= AD²+ BD²,即 AB²= 25 +(AB² 25),解得 AB =√25 = 5、所以 BD = 3,S = 4 × 3 = 12、10、解:当等腰三角形为锐角三角形时,底角为(180° 90° 36°)÷ 2 = 27°;当等腰三角形为钝角三角形时,底角为 90° 36°= 54°三、解答题11、证明:过点 A 作 AF⊥BC 于点 F∵AB = AC,AD = AE,∴BF = CF,DF = EF,∴BF DF = CF EF,即 BD = CE12、解:当边长为 5 的边为腰时,则底边长为 12 5 5 = 2,此时另外两边长分别为 5 和 2;当边长为 5 的边为底时,则腰长为(12 5)÷ 2 = 35,此时另外两边长分别为 35 和 35、综上,另外两边的长为 5 和 2 或 35 和 35、13、证明:连接 AM,AN∵AB = AC,∠A = 120°,∴∠B =∠C = 30°∵ME 是 AB 的垂直平分线,∴AM = BM,∴∠BAM =∠B = 30°,∴∠CAM = 120° 30°= 90°,∴AM = 1/2 CM同理,AN = CN,∴∠CAN = 90°,∴AN = 1/2 BN∴BM = AM = 1/2 CM,CN = AN = 1/2 BN,∴BM = MN = NC14、证明:作∠BED 的平分线交 BC 于点 F∵∠BED = 2∠CED =∠BAC,∴∠BEF =∠CEF =∠BAC/2、∵AB = AC,∴∠ABC =∠ACB∵∠BFE =∠BAC +∠ABE,∠FEC =∠ABC +∠EBC,∴∠ABE =∠EBC∵∠EBF =∠EBC,∴∠EBF =∠ABE,∴BE 是∠ABC 的平分线过点 E 作 EG⊥AB 于点 G,EH⊥BC 于点 H∵BE 是∠ABC 的平分线,∴EG = EH∵∠BED =∠BAC,∠BDE =∠ADC,∴△BDE∽△ADC,∴BD/AD = BE/AC∵S△ABE/S△BCE = 1/2 AB × EG/1/2 BC × EH = AB/BC,S△ABE/S△BCE = BD/DC,∴AB/BC = BD/DC∵AB = AC,∴BD = DC综上所述,BD = 2CD。
2022-2023学年人教版八年级数学上册《13-3等腰三角形》同步达标测试题(附答案) (2)

2022-2023学年人教版八年级数学上册《13.3等腰三角形》同步达标测试题(附答案)一.选择题(共10小题,满分30分)1.如果等腰三角形两边长是6 cm和12 cm,那么它的周长是()A.18 cm B.24 cm C.30 cm D.24或30 cm 2.若等腰三角形的一个内角比另一个内角大30°,则这个等腰三角形的底角度数是()A.50°B.80°C.50°或70°D.80°或40°3.如图,在△ABC中,AB=AC>BC,点D、E分别在AB、AC上,连接BE、CD,相交于点F,BE=BC,∠ABE=∠BCD,若CE=5,则CF的长为()A.6B.5C.4D.34.若(a﹣2)2+|b﹣5|=0,则以a、b为边长的等腰三角形的周长为()A.7B.12C.9D.9或125.如图,已知AE交CD于点O,AB∥CD,OC=OE,∠A=50°,则∠C的大小为()A.10°B.15°C.25°D.30°6.如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为()A.3B.4C.5D.67.如图,在△ABC中,AB=AC,D是BC的中点,下列结论不一定正确的是()A.∠B=∠C B.AB=2BD C.∠1=∠2D.AD⊥BC8.如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12cm2,则图中阴影部分的面积为()A.2cm2B.4cm2C.6cm2D.8cm29.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD 于点G,交BE于点H,下面说法正确的是()①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠F AG=2∠ACF;④BH=CH.A.①②③B.②③④C.①③④D.①②③④10.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A =18°,则∠GEF的度数是()A.108°B.100°C.90°D.80°二.填空题(共10小题,满分30分)11.等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为.12.等腰三角形的一个内角是80°,则它顶角的度数是.13.如果等腰三角形的一个外角是100°,那么它的底角为.14.等腰三角形的一边长为3,另一边长为6,则该三角形的周长是.15.如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,则∠CDE的度数为.16.等腰三角形的一个角是70°,则它的一腰上的高与底边的夹角是.17.在等腰△ABC中,∠A:∠B:∠C=1:m:4,则m的值是.18.如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有个.19.如图,在△ABC中,边AB的垂直平分线分别交AB、AC于点D,E,若AD为4cm,△ABC的周长为26cm,则△BCE的周长为cm.20.如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A 运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是秒.三.解答题(共7小题,满分60分)21.等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,求这个等腰三角形的底边长.22.如图,在△ABC中,∠ABC=90°,点E在BC上,点F在AB的延长线上,连接AE,CF,且AE=CF,BF=BE.求证:△ABC是等腰三角形.23.如图,△ABC中,AB=AC,D点在BC上,∠BAD=30°,且∠ADC=60°,BD=3,求CD.24.已知:如图,在等腰三角形ADC中,AD=CD,且AB∥DC,CB⊥AB于B,CE⊥AD 交AD的延长线于E.(1)求证:CE=CB;(2)如果连接BE,请写出BE与AC的关系并证明.25.如图所示,在△ABC中,AB=AC,分别在边AB、AC上取点D、E,使DE∥BC,△ADE是等腰三角形吗?说明理由.26.如图,在△ABC中,AB=BC,BE平分∠ABC,AD为BC边上的高,且AD=BD.(1)∠1=∠2=°.(2)∠1与∠3相等吗?为什么?(3)试判断线段AB与BD,DH之间有何数量关系,并说明理由.27.已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.参考答案一.选择题(共10小题,满分30分)1.解:当12为腰,6为底时,12﹣6<12<12+6,能构成等腰三角形,周长为12+12+6=30;当6为腰,12为底时,6+6=12,不能构成三角形.故选:C.2.解:在△ABC中,设∠A=x,∠B=x+30°,分情况讨论:当∠A=∠C为底角时,2x+(x+30°)=180°,解得x=50°,底角∠A=50°;当∠B=∠C为底角时,2(x+30°)+x=180°,解得x=40°,底角∠B=70°.故这个等腰三角形的底角的度数为50°或70°.故选:C.3.解:∵AB=AC,BE=BC,∴∠ABC=∠ACB.∠BEC=∠BCE,∴∠ABC=∠ACB=∠BEC,∵∠ABE=∠BCD,∴∠EBC=∠ECD,∵∠CFE为△CBF的外角,∴∠CFE=∠CBF+∠FCB,∵∠ABE=∠BCD,∴∠CFE=∠CBF+∠FCB=∠ABC,∴∠CFE=∠CEF,∴CF=CE=5,故选:B.4.解:∵(a﹣2)2+|b﹣5|=0,∴a﹣2=0,b﹣5=0,解得a=2,b=5,∴等腰三角形的三边长分别为2,2,5或2,5,5,∵2+2<5,2+5>5,∴边长分别为2,2,5的等腰三角形不存在,∴以a、b为边长的等腰三角形的周长为2+5+5=12,5.解:∵AB∥CD,∠A=50°,∴∠DOE=∠A=50°,∵OC=OE,∴∠C=∠E,∴∠C=∠DOE=25°,故选:C.6.解:∵△ABC中,AB=AC,AD⊥BC,∴AD是△ABC的中线,∴S△ABC=2S△ABD=2×AB•DE=AB•DE=2AB,∵S△ABC=AC•BF,∴AC•BF=2AB,∵AC=AB,∴BF=2,∴BF=4,故选:B.7.解:∵△ABC中,AB=AC,D是BC中点,∴∠B=∠C(故A正确)∠1=∠2(故C正确)AD⊥BC(故D正确)无法得到AB=2BD,(故B不正确).故选:B.8.解:∵S△ABC=12cm2,∴阴影部分面积=12÷2=6cm2.9.解:∵BE是△ABC的中线,∴AE=CE,∴△ABE的面积等于△BCE的面积,故①正确;∵AD是△ABC的高线,∴∠ADC=90°,∴∠ABC+∠BAD=90°,∵∠BAC=90°,∴∠BAD+∠CAD=90°,∴∠ABC=∠CAD,∵CF为△ABC的角平分线,∴∠ACF=∠BCF=∠ACB,∵∠AFC=∠ABD+∠BCF,∠AGF=∠ACF+∠CAD,∴∠AFC=∠AGF,故②正确;∵∠BAD+∠CAD=∠ACB+∠CAD=90°,∴∠BAD=∠ACD,∴∠F AG=2∠ACF,故③正确;根据已知条件无法证明BH=CH,故④错误,故选:A.10.解:∵∠A=18°,AB=BC=CD=DE=EF,∴∠ACB=18°,根据三角形外角和外角性质得出∠BCD=108°,∴∠CBD=∠CDB=×(180°﹣108°)=36°,∵∠ECD=180°﹣∠BCD﹣∠ACB=180°﹣108°﹣18°=54°,∴∠ECD=∠CED=54°∴∠CDE=180°﹣54°×2=72°,∵∠EDF=∠EFD=180°﹣(∠CDB+∠CDE)=72°,∴∠DEF=180°﹣(∠EDF+∠EFD)=36°,∴∠GEF=180°﹣(∠CED+∠DEF)=90°,即∠GEF=90°.二.填空题(共10小题,满分30分)11.解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部.根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+25°=115°;②如图2,当等腰三角形的顶角是锐角时,腰上的高在其内部,故顶角是90°﹣25°=65°.故答案为:115°或65°.12.解:当80°是等腰三角形的顶角时,则顶角就是80°;当80°是等腰三角形的底角时,则顶角是180°﹣80°×2=20°.故答案为:80°或20°.13.解:∵等腰三角形的一个外角是100°,∴与这个外角相邻的内角是180°﹣100°=80°,①80°角是顶角时,它的底角为:(180°﹣80°)=50°,②80°角是底角时,它的底角80°,所以,它的底角是50°或80°.故答案为:50°或80°.14.解:∵等腰三角形的一边长为3,另一边长为6,∴有两种情况:①6为底,3为腰,而3+3=6,那么应舍去;②3为底,6为腰,那么6+6+3=15;∴该三角形的周长是6+6+3=15.故填15.15.解:∵AB=AC,AD⊥BC,∴∠CAD=∠BAD=40°,∠ADC=90°,又∵AD=AE,∴∠ADE=(180°﹣∠CAD)=70°,∴∠CDE=90°﹣70°=20°,故答案为:20°.16.解:如图:△ABC,AB=AC,BD⊥AC当底角为70°时,即∠ABC=∠C=70°,∵BD⊥AC,∴∠BDC=90°,∴∠CBD=90°﹣∠C=90°﹣70°=20°;当顶角为70°时,即∠A=70°,∵AB=AC,∴∠ABC=∠C=55°,∵BD⊥AC,∴∠DBC=90°﹣∠C=90°﹣55°=35°,综上,它的一腰上的高与底边的夹角是20°或35°.故答案为20°或35°.17.解:当∠A为顶角时,此时∠B和∠C为底角,∴此时∠A:∠B:∠C=1:4:4,即:m=4;当∠A为底角时,此时∠C为顶角,所以,∠A:∠B:∠C=1:1:4,即:m=1,故答案为1或4.18.解:∵∠C=72°,∠DBC=36°,∠A=36°,∴∠ABD=180°﹣72°﹣36°﹣36°=36°=∠A,∴AD=BD,△ADB是等腰三角形,∵根据三角形内角和定理知∠BDC=180°﹣72°﹣36°=72°=∠C,∴BD=BC,△BDC是等腰三角形,∵∠C=∠ABC=72°,∴AB=AC,△ABC是等腰三角形.故图中共3个等腰三角形.故答案为:3.19.解:∵ED垂直平分AB,∴AE=BE,∴BD=AD=4cm,AB=8cm,∵△ABC的周长为26cm,∴AC+BC=18cm,△BCE的周长=BC+CE+AE=BC+CE+AE=18cm.故填18.20.解:设运动的时间为x,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,当△APQ是等腰三角形时,AP=AQ,AP=20﹣3x,AQ=2x即20﹣3x=2x,解得x=4.故答案为:4.三.解答题(共7小题,满分60分)21.解:如图,AB=AC,BD为腰AC上的中线,设AD=DC=x,BC=y,根据题意得或,解得或,当x=4,y=17时,等腰三角形的三边为8,8,17,显然不符合三角形的三边关系,舍去;当x=7,y=5时,等腰三角形的三边为14,14,5,答:这个等腰三角形的底边长是5.22.证明:∵∠ABC=90°,∴∠CBF=180°﹣∠ABC=90°,在Rt△ABE和Rt△CBF中,∴Rt△ABE≌Rt△CBF(HL),∴AB=CB,∴△ABC是等腰三角形.23.证明:∵∠ADC=60°,∠BAD=30°,∴∠B=∠ADC﹣∠BAD=60°﹣30°=30°=∠BAD,∴BD=AD=3,∵AB=AC,∴∠B=∠C=30°,∴∠BAC=120°,∴∠DAC=120°﹣30°=90°,∴CD=2AD=6.24.(1)证明:∵AD=CD,∴∠DAC=∠DCA,∵AB∥CD,∴∠DAC=∠CAB,∴AC是∠EAB的角平分线,∵CE⊥AE,CB⊥AB,∴CE=CB;(2)AC垂直平分BE,证明:由(1)知,CE=CB,∵CE⊥AE,CB⊥AB,∴∠CEA=∠CBA=90°,在Rt△CEA和Rt△CBA中,,∴Rt△CEA≌Rt△CBA(HL),∴AE=AB,CE=CB,∴点A、点C在线段BE的垂直平分线上,∴AC垂直平分BE.25.解:△ADE是等腰三角形,理由:在△ABC中,AB=AC,∴∠B=∠C,∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∴∠ADE=∠AED,∴AD=AE,∴△ADE是等腰三角形.26.解:(1)∵AD为BC边上的高,∵AD=BD,∴∠ABD=∠BAD=(180°﹣∠ADB)=45°,∵BE平分∠ABC,∴∠1=∠2=ABD=22.5°,故答案为:22.5;(2)∠1=∠3,理由是:∵AB=BC,BE平分∠ABC,∴BE⊥AC,∴∠BEA=90°=∠ADB,∵∠3+∠BEA+∠AHE=180°,∠2+∠ADB+∠BHD=180°,∠AHE=∠BHD,∴∠2=∠3,∵∠1=∠2,∴∠1=∠3;(3)AB=BD+DH,理由是:∵在△BDH和△ADC中,∴△BDH≌△ADC(ASA),∴DH=DC,∴BC=BD+DC=BD+DH,∵AB=BC,∴AB=BD+DH.27.解:∵AB=AC,∴∠B=∠C(等边对等角),∵DE⊥BC于E,∴∠FEB=∠FEC=90°,∴∠B+∠EDB=∠C+∠EFC=90°,∴∠EFC=∠EDB(等角的余角相等),∵∠EDB=∠ADF(对顶角相等),∴∠EFC=∠ADF,∴AD=AF,∴△ADF是等腰三角形.。
等腰三角形测试题及答案

等腰三角形测试题及答案1. 等腰三角形的两个底角相等。
(判断题)答案:正确。
2. 已知等腰三角形的顶角为60°,求底角的度数。
答案:底角的度数为60°。
3. 若等腰三角形的周长为18cm,且底边长为6cm,求腰长。
答案:腰长为6cm。
4. 等腰三角形的顶角平分线与底边垂直。
(判断题)答案:正确。
5. 一个等腰三角形的顶角为50°,求另外两个内角的度数。
答案:另外两个内角的度数均为65°。
6. 已知等腰三角形的腰长为10cm,底边长为8cm,求三角形的面积。
答案:面积为24cm²。
7. 等腰三角形的底边长为12cm,腰长为15cm,求顶角的度数。
答案:顶角的度数为30°。
8. 一个等腰三角形的底角为45°,求顶角的度数。
答案:顶角的度数为90°。
9. 等腰三角形的底边长为20cm,腰长为25cm,求三角形的高。
答案:高为15cm。
10. 等腰三角形的底边长为8cm,腰长为10cm,求三角形的内切圆半径。
答案:内切圆半径为2cm。
11. 等腰三角形的顶角为80°,求底角的度数。
答案:底角的度数为50°。
12. 已知等腰三角形的周长为30cm,底边长为12cm,求腰长。
答案:腰长为9cm。
13. 等腰三角形的底边长为10cm,腰长为13cm,求顶角的度数。
答案:顶角的度数为30°。
14. 一个等腰三角形的顶角为40°,求另外两个内角的度数。
答案:另外两个内角的度数均为70°。
15. 等腰三角形的底边长为14cm,腰长为10cm,求三角形的面积。
答案:面积为48cm²。
16. 已知等腰三角形的腰长为8cm,底边长为6cm,求三角形的高。
答案:高为5cm。
17. 等腰三角形的底边长为16cm,腰长为20cm,求三角形的内切圆半径。
答案:内切圆半径为4cm。
18. 等腰三角形的顶角为120°,求底角的度数。
(新)初中数学《等腰三角形》专项测试题附答案解析(全汇编)

(新)初中数学《等腰三角形》专项测试题(全汇编)一、选择题1.等腰三角形的一个角是80°,则它顶角的度数是()A.80° B.80°或20° C.80°或50° D.20°2.已知等腰三角形的两边长分别是3和5,则该三角形的周长是()A.8 B.9 C.10或12 D.11或133.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为()A.7 B.11 C.7或11 D.7或104.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为()A.60° B.120° C.60°或150° D.60°或120°5.在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=()A.36° B.54° C.18 ° D.64°6. 在△ABC中,D是BC上的点,AB=AD=DC,∠B=70°,则∠C的度数为()A.35° B.40° C.45° D.50°7. 在△ABC中,∠B=∠C,AB=5,则AC的长为()A.2 B.3 C.4 D.58. 在矩形ABCD中,AB<BC,AC,BD相交于点O,则等腰三角形的个数是()A.8 B.6 C.4 D.29. 在等腰△ABC中,AB=AC,其周长为20 cm,则AB边的取值范围是()A.1 cm<AB<4 cm B.5 cm<AB<10 cm C.4 cm<AB<8 cm D.4 cm<AB<10cm10. 在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于()A. 4 cm B.2 cm C. 3 cm D.1 cm11.在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )A.2 B.3 C.4 D.512. 在△ABC中,AB=20 cm,AC=12 cm,点P从点B出发以每秒3 cm的速度向点A运动,点Q从点A同时出发以每秒2 cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是以PQ为底的等腰三角形时,运动的时间是()A.2.5秒B.3秒C.3.5秒D.4秒13. 等腰但不等边的三角形的角平分线、高线、中线的总条数是()A.3 B.5 C.7 D.914. 已知△ABC中,三边a,b,c满足|b-c|+(a-b)2=0,则∠A等于()A. 60° B.45° C.90° D.不能确定15.等腰三角形周长为36cm,两边长之比为4:1,则底边长为()A.16cm B.4cm C.20cm D.16cm或4cm二、填空题16. 等腰三角形的一个外角为110°,则底角的度数可能是_______.17. 等腰三角形的对称轴是____________.18.△ABC中,AB=AC,∠A=36°,BD平分∠ABC,则∠BD C=_______度,此图有___个等腰三角形.19. 在△ABC中,与∠A相邻的外角是100°,要使△ABC是等腰三角形,则∠B的度是_________.20. 在△ABC中,若∠A=80°,∠B=50°,AC=5,则AB=_______.三、解答题.21.在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长.22.在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC23.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,求证:(1)△BCE≌△ACD(2)CF=CH(3)△FCH是等边三角形;24. 如图,已知AB=AC=AD,且AD∥BC,求证:∠C = 2∠D25.在△ABC中,∠A BC与∠A CB的平分线交于点O,过O点作DE∥BC,分别交AB、AC于D、E,若AB=5,AC=4,求△ADE的周长.参考答案与解析一、选择题1. B 2D 3C 4D 5B 6A 7D 8C 9B 10C 11B 12D 13C 14A 15B二 填空:(16) 70°或55°(17) 底边上的高(顶角平分线或底边的中线)所在的直线(18)72°,3个 (19) 50°或80°或20° (20)5三、解答题.(21) 27°/2 (25) 93解析:解答:设AB =AC =x BC =y则有12,2152x x x y +=+=⎧⎨⎩或者12,2152x x x y +=+=⎧⎨⎩ 所以x =8, y =11或者x =10,y =7.即三角形AB =AC =8,BC =11.或AB =AC =10,BC =7.故选C.分析:等腰三角形两腰相等,会解二元一次方程.4.解析:解答:分两种情况:一种是这个高在三角形内,即此三角形是锐角三角形顶角=180°-90°-30°=60°,另一种是这个高落在一腰延长线上,即此三角形为钝角三角形顶角的补角=180°-90°-30°=60°,顶角=180°-60°=120°.分析:此题要注意分两种情况,要考虑锐角三角形和钝角三角形.6解析:解答:∵AB =AD , ∴∠ADB =∠B =70°.∵AD =DC , ∴12C DAC ADB ∠=∠=∠=35°. 分析:等腰三角形两底角相等,再根据三角形的外角等于和它不相邻的两个内角和.8解析:解答:∵四边形ABCD 是矩形,∴AO =BO =CO =DO ,∴△ABO ,△BCO ,△DCO ,△ADO 都是等腰三角形.分析:根据矩形的对角线相等且互相平分可得AO =BO =CO =DO ,进而得到等腰三角形.9解析:解答:∵在等腰△ABC 中,AB =AC ,其周长为20cm ,∴设AB=AC=x cm,则BC=(20-2x)cm,∴2x>20−2x,即20−2x>0.解得5 cm<x<10 cm.分析:设AB=AC=x,则BC=20-2x,根据三角形的三边关系即可得出结论.10解析:解答:∵ED⊥AB,∠A=30°,∴AE=2ED,∵AE=6cm,∴ED=3cm.∵∠ACB=90°,BE平分∠ABC,∴ED=CE,∴CE=3cm.分析:根据在直角三角形中,30度所对的直角边等于斜边的一半得出AE=2ED,求出ED,再根据角平分线到两边的距离相等得出ED=CE,即可得出CE的值11.解析:解答:AB的垂直平分线与直线y=x相交于点C1,∵A(0,2),B(0,6),∴AB=6-2=4,点A为圆心,以AB的长为半径画弧,与直线y=x的交点为C2,C3∵OB=6,∴点B到直线y=x的距离为=∵4,∴以点B为圆心,以AB的长为半径画弧,与直线y=x没有交点,所以,点C的个数是1+2=3.分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AB的垂直平分线与直线y=x的交点为点C再求出AB的长,以点A为圆心,以AB的长为半径画弧,与直线y=x的交点为点C,求出点B到直线y=x的距离可知以点B为圆心,以AB的长为半径画弧,与直线没有交点12.解析:解答:设运动的时间为x cm/s,在△ABC中,AB=20cm,AC=12cm点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动当△APQ是等腰三角形时,AP=AQ,AP=20-3x,AQ=2x即20-3x=2x,解得x=4.分析:设运动的时间为x,则AP=20-3x,当APQ是等腰三角形时,AP=AQ,则20-3x=2x,解得x即可.13解析:解答:等腰但不等边的三角形底边上的角平分线、中线、高线三线重合成一条;腰上的三条线不重合,因而共有7条线.分析:画出图形,根据等腰三角形的性质进行分析即可得到答案14.解析:解答:△ABC中,三边a,b,c满足|b-c|+(a-b)2=0∴b-c=0,a-b=0,∴a=b=c,∴a=b=c,∴三角形是等边三角形,∴∠A=60°.分析:根据非负数的性质列式求解得到a=b=c,然后选择答案即可.15解析:解答:因为两边长之比为4:1,所以设较短一边为x,则另一边为4x;(1)假设x为底边,4x为腰;则8x+x=36,x=4,即底边为4;(2)假设x为腰,4x为底边,则2x+4x=36,x=6,4x=24;∵6+6<24,∴该假设不成立.所以等腰三角形的底边为4cm.分析:题中只给出了两边之比,没有明确说明哪个是底哪个是腰,所以应该分两种情况进行分析,再结合三角形三边的关系将不合题意的解舍去.16解析:解答:当110°是等腰三角形底角的外角时,底角为70°;当110°是等腰三角形顶角的外角时,因为等腰三角形两底角相等,所以一个底角的度数等于外角110°的一半,即55°分析:外角与它相邻的内角互补,外角等于和它不相邻的两个内角和.17答案:底边上的高(顶角平分线或底边的中线)所在的直线18.解析:解答:∵AB=AC,∠A=36°,∴△ABC是等腰三角形,∠C=∠ABC=(180°−36°)12⨯=72°.∵BD为∠ABC的平分线,∴∠ABD=∠A=∠DBC=36°,∴AD=BD,△ADB是等腰三角形,∴∠1=180°-36°-72°=72°=∠C,∴BC=BD,△CDB是等腰三角形.图中共有3个等腰三角形.分析:由已知条件,根据三角形内角和等于180、角的平分线的性质求得各个角的度数,然后利用等腰三角形的判定进行找寻,注意做到由易到难,不重不漏.19解析:解答:∵∠A的相邻外角是100°,∴∠A=80°.分两种情况:(1)当∠A为底角时,另一底角∠B=∠A=80°;(2)当∠A为顶角时,则底角∠B=∠C= (180°−80°)12⨯=50°(3)当∠B是顶角时,∠B=180°-2∠A=20°.综上所述,∠B的度数是80°或50°或20°.分析:已知给出了∠A的相邻外角是100°,没有明确是顶角还是底角,所以要进行分类讨论,分类后还有用内角和定理去验证每种情况是不是都成立.20解析:解答:∵∠A=80°,∠B=50°,∴∠C=180°-80°-50°=50°.∴AB=AC=5.分析:由已知条件先求出∠C的度数是50°,根据等角对等边的性质求解即可.三、解答题.21.解答:∵AB=AC,∠C=63°,∴∠B=∠C=63°,∴∠BAC=180°-63°-63°=54°.又∵AD是BC边上的高,∴AD是∠BAC的平分线,AD是BC边上的中线,∴∠BAD=12∠BAC=27°,DC=12BC=2.解析:分析:根据等腰三角形的两个底角相等求出顶角∠BAC的度数,再由等腰三角形的三线合一性质即可求出∠BAD=12∠BAC=27°,DC=12BC=2.22.证明:∵AB=AC,∴∠ABC=∠ACB.又∵BD⊥AC,CE⊥AB,∴∠BEC=∠CDB=90°.在△BCE和△CBD中,∠ABC=∠ACB,∠BEC=∠CDB,BC=BC.∴△BCE≌△CBD(AAS).∴BE=CD.∵AB=AC,BE=CD,∴AB-BE=AC-CD,∴AE=AD.∴在△AEF和△ADF中,AE=AD, AF=AF.△AEF≌△ADF(HL).∴∠EAF=∠DAF,AF平分∠BAC.解析:分析:要通过两次三角形全等,再结合等腰三角形的性质得出结论. 23(1)证明:∵△ABC和△CDE都是等边三角形,∴∠BCA=∠DCE=60°,BC=AC=AB,EC=CD=ED,∴∠BCE=∠ACD.在△BCE和△ACD中,,,,BC AC BCE ACD CE CD =⎧∠=∠=⎪⎨⎪⎩∴△BCE ≌△ACD (S A S );(2)CF =CH ; ∵△BCE ≌△ACD ,∴∠CBF =∠CAH .∵∠ACB =∠DCE =60°,在△BCF 和△ACH 中,∴∠ACH =60°,∴∠BCF =∠ACH ,,,,CBF CAH BC AC BCF ACH ∠=∠=∠=∠⎧⎪⎨⎪⎩∴△BCF ≌△ACH (A S A ),∴CF =CH ;(3)△FCH 是等边三角形;∵CF =CH ,∠ACH =60°,∴△CFH 是等边三角形. 24.证明:∵AB =AC =AD ,∴∠C =∠ABC ,∠D =∠ABD.∴∠ABC =∠CBD +∠D .∵AD ∥BC ,∴∠CBD =∠D ,∴∠ABC =∠D +∠D =2∠D ,又∵∠C =∠ABC ,∴∠C =2∠D .解析:分析:首先根据AB =AC =AD ,∵AD ∥BC ,∴∠D =∠DBC 可得∠C =∠ABC ,∠D =∠ABD ,∠ABC =∠CBD +∠D ;然后根据AD ∥BC ,可得∠CBD =∠D ,据此判断出∠ABC =2∠D ,再根据∠C =∠ABC ,即可判断出∠C =2∠D25.如图,在△ABC 中,∠B 与∠C 的平分线交于点O , 过O 点作DE ∥BC ,分别交AB 、AC 于D 、E ,若AB =5,AC=4,求△ADE的周长.答案:解答:∵在△ABC中,∠B与∠C的平分线交于点O,∴∠DBO=∠CBO,∠ECO=∠BCO,∵DE∥BC,∴∠DOB=∠CBO,∠EOC=∠BCO,∴∠DBO=∠DOB,∠ECO=∠EOC,∴OD=BD,OE=CE,∵AB=5,AC=4,∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9.解析:分析:由在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,易证得△DOB与△EOC是等腰三角形,即DO=DB,EO=EC,继而可得△ADE的周长等于AB+AC,即可求得答案.。
等腰三角形水平测试题及答案

八年级上册第等腰三角形水平测试题 一.选择题(每小题3分,共24分) 1.小明将两个全等且有一个角为 直线上,则图中等腰三角形的个数是 60°的直角三角形拼成如图 ( ) 1所示的图形,其中两条较长直角边在同一 A. .4 B . 3 C . 2 D . 1 2、 : 42 °,则它的底角为 ( ) 已知等腰三用形的 个用等于 A 42 ° B 69° C 、69° 或 84° D 42° 或 69° 3、 如图, △ ABC 中, ABAC , A 30°, DE 垂直平分 AC , 贝 U BCD 数为( ) A. .80° B . 75°C . .65°D . 45°4、 等腰三角形的顶角是 80° ,则一腰上的高与底边的夹角是( ) O 的度 A . 40° B . 50°5、如图,已知等边三角形 /APE 的度数是( )C . 60 ABC 中, BD D . 30°CE , AD 与BE 交于点P ,则 A . 45° B . 55° D . 75°6、如图是一个等边三角形木框,甲虫 C 端点除外),设甲虫P 到另外两边的距离之和为 形ABC 的高为h ,贝U d 与h 的大小关系是(P 在边框AC 上爬行d ,等 ) C A . d h B . d h C . d h D . 无法确定 7. 如图, ZA 15°, AB BC CD DE EF , 则 /DEF 等于() A . ° 90 B . 75°C . 70°D . 60° 8、 如图, △ MNP 中, Z P=60 ° , MN=NP ,MQ 丄 PN , 垂足为 Q 延长MN 至G , 取 NG=NQ ,若△ MNP 的周长为12, MQ=a ,则△ A . 8+2a B . 8+a C . 6+a D . 6+2a.选择题(每小题3分,共24分)1.在厶 ABC 中, AB=AC 若/ B=56°,则/ C= _____________ B MGQ 周长是( (A , 边三角2. 等腰三角形底边中点与一腰的距离为 6,则腰上的高为 __________ .3. 如图,在△ ABC 中,AB=AC ,CD 平分/ ACB 交AB 于点D ,AE II DC 交BC 的延长线于点 E ,已知 / E=36°,则/ B= _______ .4. 如图,在△ABC 中,点D 是BC 上一点, AB AD DC ,则 C ____________ 5. 等腰 角形至 有a 条 称轴, 多有b3、解:因为在△ ABC 中,Z ACB 900 ,对称轴,则a b = ___________ .6.有一个等腰三角形,三边分别是 3x — 2, 4x — 3, 6 — 2x ,则等腰三角形的周长 ____7. 如图,△ ABC 中 AB=AC , EB=BD=DC=CF , Z A=40 °,则Z EDF?的度数是 __8. _______ 在△ ABC 中,BC 丄 AC , DE 丄 AC , D 是 AB 的中点,若Z A=30 0, AB=8,贝U BC= DE= 。
八年级数学上册13.3等腰三角形同步测试题

八年级数学上册13.3等腰三角形同步测试题A. 6B.8c.10D.无法确定已知a、b、C是AABc的三条边,且满足a□+bc=b□+ac,则Z∖ABc是()A.锐角三角形B.钝角三角形c.等腰三角形D.等边三角形如图,下列条件不能推出AABc是等腰三角形的是()A.ZB=ZCB.AD丄Be,ZBAD=ZCADc.AD丄Be,ZBAD=ZACDD.AD丄Be,BD=CD如图,四边形AB题,共16.0分)如图1,在Z∖ABc中,AE丄BC于E,AE=BE,D是AE上的一点,且DE=cE,连接BD,cD.(1)试判断BD与AC的位置关系和数量关系,并说明理由;(2)如图2,若将ADcE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.①试猜想BD与AC的数量关系,请直接写出结论;②你能求出BD与AC的夹角14.32或3415.816.417.1718.2019.3620.60/1321.(1)证明:VZDEC=ZB+ZBDE=ZcEF+ZDEF,ZDEF=ZB,∙∙∙ZCEF=ZBDE・VAB=Ac,Zc=ZB.又VcE=BD,.∖∆BDE^ΔcEF・(2)解:V∆BDE^ΔcEFΛDE=FE.所以ADEF是等腰三角形•∙∙∙ZEDF=ZEFD@ZBDF=ZAD C@BD=AD)H,.∖∆BDF^∆ADc(AAS),ΛBF=Ac;(2)连接cF,V∆BDF^∆ADc,•:DF=Dc,.∙.∆DFcÆ等腰直角三角形. VCD=3,cF=√2cD=3√2,VAB=Bc,BE丄Ac,.∙.AE=Ec,BE是AC的垂直平分线•ΛAF=c F,.∙.AF=3√2・【解析】1.【分析】此题考查了平行四边形的性质以及等腰三角形的判定与性质.能证得ABcE是等腰三角形是解此题的关键.由平行四边形ABCD中,CE 平分ZBcD,可证得ABcE是等腰三角形,继而利用AE=BE-AB,求得答案.【解答】解:•・•四边形ABCD是平行四边形,ΛAD∕∕Bc,AD=BC=5,・;ZE=ZECD,TcE平分ZBcD,ΛZBCE=ZEcD,ΛZE=ZBCE,.°.BE=BC=5,ΛAE=BE-AB=5-3=2;故选c.2.【分析】此题考查了菱形5+5+8=18c;(2)当腰是8c时,三角形的三边是:5c,8c,8c,能构成三角形,则等腰三角形的周长=5+8+8=21c.因此这个等腰三角形的周长为18或21c.故选:c.题目给出等腰三角形有两条边长为5c和8c,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构+b)(a-b)-C(a-b)=O,即(a~b)(a+b~c)=0,*.*a+b-c≠0,a-b=O,即a=b,则AABc为等腰三角形.故选:c.已知等式左边分解因式后,利用两数相乘积为O两因式中至少有一个为O得到a=b,即可确定出三角形形状.此题考查了因式分解的应用,熟练掌握因式分解的方法是解本题的关键.9.解:由ZB=ZC可得AB=Ac,则Z∖ABc为等腰三角形,故A可以;由AD丄BC且ZBAD=ZcAD,可得△BAD竺AcAD,则可得AB=Ac,即AABc为等腰三角形,故B可以;由AD丄Be,ZBAD=ZAcD,无法求得AB=AC或AC=BC,故C不可以;由AD丄Be,BD=cD,可得AD为线段BC的垂直平分线,可得AB=Ac,故D可以;故选c.根据等腰三角形的判定逐项判断即可.本题主要考查等腰三角形的判定,掌握等角对等边是解题的关键.10.解:解法一:如图1,过作k丄CD于k,过N作NP丄CD于P,过作H丄PN于H,则k//EF辅助线,构建全等三角形,证明△EF竺ZkcD,则E=c,利用勾股定理得:BD=√(6□+6□)=6√2,EC=√(4□+6□)=2√13,可得AEBG 是等腰直角三角形,分别求E=C的长,利用勾股定理的逆定理可得AEc是等腰直角三角形,根据直角三角形斜边中线的性质得N的长.本题考查了正方形的性质、三角形全等的性质和判定、等腰直角三角形的性质和判定、直角三角形斜边中线的性质、勾股定理的逆定理,属于基础题,本题的关键是证明AEc是直角三角形.11•解:延长CE交AB4.解:•••四边形ABCD是平行四边形,.∖AD=Bc,AB=cD,AD//Bc,•IZAEB=ZcBE,TBE平分ZABc,∙∙∙ZABE=ZcBE,∙∙∙ZABE=ZAEB,.∖AB=AE,(1)当AE=5时,AB=5,平行四边形ABCD的周长是2X(5+5+6)=32;(2)当AE=6时,AB=6,平行四边形ABCD的周长是2X(5+6+6)=34;故答案为:32或34.由平行四边形ABCD推出ZAEB=ZcBE,由已知得到ZABE=ZcBE,推出AB=AE,分两种情况(1)当AE=5时,求出AB的长;(2)当AE=6时,求出AB的长,进一步求出平行四边形的周长.本题主要考查了平行四边形的性质,等腰三角形的判定,三角形的角平分线等知识点,解此题的关键是求出AE=AB.用的数学思想是分类讨论思想.15.解:连接AD交EF与点',连结A.V∆ABc⅛等腰三角形,点D是BC边的中点,∙°∙AD丄Bc,∙∙∙S_(∆ABc)=1/2BC・AD=1∕2X4XAD二12,解得AD二6,VEF是线段AB的垂直平分线,ΛA=B.∙'∙B+D=D+A.・•・当点位于点'处时,B+D有最小值,最小值6.•••△BD的周长的最小值为DB+AD二2+6二8・连接AD交EF与点',连结A,由线段垂直平分线的性质可知A=B,则B+D=A+D,故此当A-D在一条直线上时,B+D有最小值,然后依据要三角形三线合一的性质可证明AD为∆ABc底边上的高线,依据三角形的面积为12可求得AD的长.本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键・16.【分析】本题考查了等腰三角形的性质和勾股定理.关键要熟知等腰三角形的三线合一可得.先根据等腰三角形的性质求出BD的长,再根据勾股定理解答即可.【解答】解:根据等腰三角形的三线合一可得:BD=l/2Bc=l/2X6=3c,在直角AABD中,由勾股定理得:AB□=BD□+AD□,所以,AD=√(AB□-BD□)=√(5□-3□)=4c.故答案为4.17.解:(1)若3为腰长,7为底边长,由于3+3 (2)若7为腰长,则符合三角形的两边之和大于第三边.所以这个三角形的周长为7+7+3=17.故答案为:17.求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为3和7,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论c=l/2Bc=5.在Rt∆ABF中,由勾股定理,得AF=√(K133□-5□)=12,.∙.S_(∆ABc)=1/2BC∙AF=60,VAD=BD,.∙.S_(∆ADc)=S_(∆BcD)=l∕2S.(∆ABc)=30,TS_(∆ADc)=1/2AC∙DE=30,ΛDE=(2×30)∕Ac=60∕13.故答案为:60/13.过A作BC的垂线,由勾股定理易求得此垂线的长,即可求出AABc 的面积;连接cD,由于AD=BD,则本题考查了等腰三角形的性质和判定、三角形的外角与内角的关系及全等三角形的判定及性质;证得三角形全等是正确解答本题的关键.22.EF与BC垂直,理由为:由三角形ABC为等腰三角形且AD为底边上的高,利用三线合一得到AD为角平分线,再由AE=AF,利用等边对等角得到一对角相等,利用外角性质得到一对内错角相等,利用内错角相等两直线平行得到EF与AD平行,进而确定出EF与BC 垂直.此题考查了等腰三角形的性质,外角性质,以及平行线的判定与性质,熟练掌握等腰三角形的性质是解形的性质得到DF=Dc,得到ADFc 是等腰直角三角形.推出AE=Ec,BE是AC的垂直平分线.于是得到结论.本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了等腰三角形底边三线合一的性质,本题中求证△BDF竺AAcD是解题的关键.11。
12.3 等腰三角形水平测试(含答案)

12.3 等腰三角形一、选择题题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
1.等腰三角形的周长为26㎝,一边长为6㎝,那么腰长为()A.6㎝B.10㎝C.6㎝或10㎝D.14㎝2.已知△ABC,AB =AC,∠B=65°,∠C度数是( )A.50°B.65°C.70°D.75°3.等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边的垂线C.顶角的平分线所在的直线D.腰上的高所在的直线二、填空题4.等腰三角形的两个_______相等(简写成“____________”).5.已知△ABC,AB =AC,∠A=80°,∠B度数是_________.6.等腰三角形的两个内角的比是1:2,则这个等腰三角形的顶角的度数是_______________.7.等腰三角形的腰长是6,则底边长5,周长为__________.三、解答题8.如图AB=AD,AD∥BC,求证:BD平分∠ABC.(写出每步证明的重要依据)9.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB。
求∠A的度数参考答案一、选择题1.B2.B3.C二、填空题4.底角,等边对等角5.50°6.36°或90°7.16或17三、解答题8.如图AB=AD,AD∥BC,求证:BD平分∠ABC.证明:∵AB=AD(已知)∴∠ABD=∠ADB(等边对等角)∵AD∥BC(已知)∴∠ADB=∠CBD(两直线平行,内错角相等)∴∠ABD=∠CBD(等量代换)∴BD平分∠ABC.(角平分线定义)9.4512.3.2等边三角形一、选择题1.△ABC是等边三角形,D、E、F为各边中点,则图中共.有正三角形( ) A.2个B.3个C.4个D.5个2.△ABC中,∠A:∠B:∠C=1:2:3,则BC:AB等于( )A.2:1 B.1:2 C.1:3 D.2 :3二、填空题3.等边三角形的周长为6㎝,则它的边长为________.4.等边三角形的两条高线相交所成钝角的度数是__________.5.在△ABC中,∠A=∠B=∠C,则△ABC是_____三角形.6.△ABC中,∠AC B=90°∠B=60°,BC=3㎝,则AB=_______.三、解答题7.△ABC是等边三角形,点D在边BC上,DE∥AC,△BDE是等边三角形吗?试说明理由.8.已知:如图,P,Q是△ABC边上BC上的两点,且BP=PQ=QC=AP=AQ。
最新初中人教版数学人教八年级上册《13.3等腰三角形》测试与评价

《13.3等腰三角形》测试与评价本测评考查的主要内容有:等腰三角形的判定和性质、等边三角形的判定和性质.以下题目分为三个水平等级:水平1(用★☆☆表示):运用基本知识、基本技能就能解决的题目;水平2(用★★☆表示):灵活运用基本知识、基本技能,并要具备一定的运算能力和推理能力才能解决的题目;水平3(用★★★表示):综合运用基本知识、基本技能、方法技巧,并要具备一定的运算能力和推理能力才能解决的题目.一、选择题1.在△ABC中,∠B=∠C,AB=5,则AC的长为().A.2 B.3 C.4 D.5考查目的:本题主要考查等腰三角形“等角对等边”的性质.水平等级:★☆☆.解析:根据“等边对等角”可知,AC=AB=5.故选D.答案:D.2.若一个等腰三角形的两边长分别为2和5,则它的周长为().A.12B.9 C.12或9D.9或7考查目的:本题考查等腰三角形的性质和分类讨论思想.水平等级:★☆☆.解析:由已知可知该等腰三角形的三边长分别为2,5,5(不可能是2,2,5,因为三角形两边之和大于第三边),所以周长为12.答案:A.3.下面几个三角形中,不可能是等腰三角形的是().A.有两个内角分别为85°,85°的三角形B.有两个内角分别为110°和40°的三角形C.有一个外角为100°,一个内角为50°的三角形D.有一个外角为80°,一个内角为100°的三角形考查目的:本题主要考查等腰三角形的判定和三角形内角和定理.水平等级:★★☆.解析:利用“等角对等边”可知,有两个角相等的三角形是等腰三角形.根据等腰三角形内角和定理和外角的性质可得出选项A、C、D正确,选项B错误.答案:B.4.下面给出的几种三角形:①有两个角为60°的三角形;②三个外角都相等的三角形;③一边上的高也是这边上的中线的等腰三角形;④有一个角为60°的等腰三角形.其中一定是等边三角形的有().A.4个B.3个C.2个D.1个考查目的:本题主要考查等边三角形的判定.水平等级:★★☆.解析:一个三角形是等腰三角形,必须满足三个内角都是60°.在③中,一边上的高也是这边上的中线的等腰三角形,也有可能是非等边三角形的等腰三角形.而①②④都能判定三角形是等边三角形,所以选B.答案:B.二、填空题5.一个三角形三个内角度数的比为1︰1︰2,则这个三角形是三角形.考查目的:本题主要考查等腰三角形的判定和三角形内角和定理.水平等级:★☆☆.解析:由三个内角度数的比可求出三个内角的度数:1180454⨯=,2180904⨯=,则这个三角形三个内角的度数分别为45°,45°,90°,故这个三角形是等腰直角三角形.答案:等腰直角.6.如图,欲测塔高AB,选取一点C,使仰角∠ACB=45°,测出BC的长度为20米,则塔高AB为米.(第6题)考查目的:本题主要考查三角形内角和定理和“等角对等边”.水平等级:★☆☆.解析:根据三角形内角和定理可求出∠BAC=45°,从而AB=BC=20米.答案:20.7.在△ABC中,∠B=∠C=15°,AB=2,CD⊥AB交BA的延长线与点D,则CD的长为___________.考查目的:本题考查等腰三角形的性质以及含30°角的直角三角形的性质.水平等级:★★☆.解析:因为∠B=∠C=15°,所以AC=AB=2,∠CAD=∠B+∠ACB=30°.在Rt△ACD中,CD=1.答案:1.8.在△ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B的度数为___________.考查目的:本题主要考查等腰三角形的判定和性质以及分类讨论思想.水平等级:★★☆.解析:分两种情况:一种是AB边的中垂线与线段AC相交,此时∠B=70°;另一种是AB边的中垂线与线段AC的反向延长线相交,此时∠B=20°.答案:20°或70°.三、解答题9.已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC.求证:△ABC 是等腰三角形.ADO ECB(第9题)考查目的:本题主要考查等腰三角形的判定.水平等级:★★☆.解析:利用△BDC≌△CEB,证明∠DBC=∠ECB.证明:∵OB=OC,∴∠OBC=∠OCB.∵BE,CD是△ABC的两条高,∴∠BDC=∠CEB=90°.又∵BC=CB,∴△BDC≌△CEB(AAS).∴∠DBC=∠ECB,∴AB=AC,∴△ABC是等腰三角形.10.已知,如图,△ABC中,D是BC上一点,P是AD上一点,若∠1=∠2,PB=PC.求证:AD ⊥BC .(第10题)考查目的:本题考查全等三角形的判定以及等腰三角形的性质等.水平等级:★★☆.解析:先利用“等角对等边”证明△ABC 是等腰三角形,再利用等腰三角形三线合一的性质证明AD ⊥BC .证明:作PM ⊥AB 于M ,PN ⊥AC 于N .(第10题答案)∵∠1=∠2,∴PM =PN .在Rt △BPM 和Rt △CPN 中,,,PM PN PB PC ==⎧⎨⎩ ∴Rt △BPM ≌Rt △CPN (HL ).∴∠ABP =∠ACP .∵PB =PC ,∴∠PBC =∠PCB .∴∠ABP +∠PBC =∠ACP +∠PCB ,即∠ABC =∠ACB .∴AB =AC .∵∠1=∠2,∴AD⊥BC.。
人教新课标数学八年级上册123等腰三角形练习题

人教新课标数学八年级上册12.3等腰三角形练习题(2)一、选择题(每小题3分,共18分)1.已知一个等腰三角形内角的度数之比为1∶4,则这个等腰三角形顶角的度数为()A.20°B.120°C.20°或120° D.36°2.在等腰三角形中,腰上的高在三角形的外部,则这个三角形是()A.等边三角形B.直角三角形C.钝角三角形D.不存在3.在△ABC中,如果只给出条件∠A=60°,还不能判定△ABC是等边三角形,给出下面三种说法:(1)如果再加上条件“AB=AC”,那么△ABC是等边三角形;(2)如果再加上条件“D是BC的中点,且AD⊥BC”,则△ABC是等边三角形;(3)如果再加上条件“AB、AC边上的高相等”,那么△ABC是等边三角形.其中正确的说法有()A.0 B.1个C.2个D.3个4.已知△ABC是等边三角形,D是BC边上任一点,连接AD并作等边△ADE,若DE⊥AB,则BDCD的值是()A.12B.23C.1 D.325.如图16所示,两个全等的直角三角形中都有一个锐角为30°,且较长的直角边在同一直线上,则图中的等腰三角形有()A.4个B.3个C.2个D.1个图16 图176.如图17所示,AB=AC,∠BAD=α,且AE=AD,则∠EDC等于()A.12α B.13α C.14α D.23α二、填空题(每小题6分,共24分)7.等腰三角形的两边长分别为4 cm和9 cm,则它的周长为________cm.8. 请你仔细观察图18中等边三角形图形的变换规律,写出你所发现关于等边三角形内一点到三边距离的数学事实:____________.图189.如图19,在四个正方形拼接成的图形内,以A1、A2、A3…A10这十个点中任意三点为顶点,共能组成________个等腰直角三角形,你愿意把得到上述结论的方法与他人交流吗?若愿意,请在下方简要写出你的探究过程:__________________.图19 图2010.如图20,△ABC和△CDE是等边三角形,则AD________BE.三、解答题(共58分)11.(10分)如图21所示,△ABC中,AD⊥BC于D,E为BD上一点,EG∥AD,分别交AB,CA的延长线于点F,G,∠AFG=∠G.图21(1)求证:△ABD≌△ACD;(2)若∠B=40°,求∠G和∠FAG的大小.12.(10分)如图22,C为线段AB上一点,分别以AC、CB为边在AB同侧作等边△ACD和等边△BCE,AE交DC于G点,DB交CE于H点,你能说明GH∥AB吗?图2213.(10分)如图23,△ABC中,AB=AC,D、E、F分别为AB、BC、CA上的点且BD=CE,∠DEF=∠B,你能说明△DEF是等腰三角形吗?图2314.(14分)已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高为h,AM是BC边上的高.若点P在一边BC上,如图24①,此时h3=0,可得结论h1+h2+h3=h.请直接应用上述信息解决下列问题:(1)当点P在△ABC内如图24②,(2)当点P在△ABC外如图24③,这两种情况时,上述结论是否还成立?若成立,请给予说明;若不成立,h1、h2、h3与h之间又有怎样的关系?请写出你的猜想,不需说明.图2415.(14分)如图25所示,点C为线段AB上一点,△ACM,△CBN是等边三角形,可证AN =BM.图25(1)将△ACM绕C点按逆时针方向旋转180°,使A点落在CB上,请画出符合要求的图形(不写作法,保留作图痕迹);(2)在(1)所得到的图形中,结论“AN=BM”是否还成立?若成立,请证明;若不成立,请说明理由;(3)在(1)得到的图形中,设AM的延长线与BN相交于D点,请你判断△ABD与四边形MDNC的形状.参考答案一、选择题1.C 解析根据等腰三角形的性质两底角相等知,两内角度数为1∶4是顶角与一个底角度数之比为1∶4或一个底角与顶角度数之比为1∶4,然后用三角形内角和定理可得顶角度数.2.C 3.D 4.C 5.B6.A 解析设∠EDC=x,∠C=y,∵AB=AC,∴∠B=∠C=y,得∠AED=∠EDC+∠C,∵AD =AE,∴∠ADE=∠AED=x+y,∴∠ADC=∠ADE+∠EDC=2x+y=∠B+∠BAD=y+a,∴2x=a,∴x=a 2 .二、填空题7.228.等边三角形内任意一点到三边的距离之和等于该等边三角形的高(叙述清楚即可得分)9.24 以A1、A2、A3、A10、A9为直角顶点有1+1+4+5+1=12个等腰直角三角形,再根据轴对称性质知,在整个图形内共可组成12×2=24个等腰直角三角形.10.=三、解答题11.解(1)∵AD⊥BC,EG∥AD,∴EG⊥BC,∴∠C+∠G=90°,又∠G=∠AFG=∠BFE,∠G +∠C=∠B+∠BFE=∠B+∠G=90°,∴∠B=∠C,又AD=AD,∠ADB=∠ADC,∴△ABD≌△ACD (AAS)或得AB=AC,又AD=AD,∴Rt△ABD≌Rt△ACD(HL);(2)若∠B=40°,则∠G=90°-∠C=90°-∠B=90°-40°=50°,∠FAG=∠B+∠C=2×40°=80°.12.解在等边△ACD和等边△BCE中,AC=CD,BC=CE,∠ACD=∠BCE=60°.∵∠ACD+∠DCE+∠BCE=180°,∴∠DCE=60°,∠ACE=∠DCB=120°.在△ACE和△DCB中,AC=DC,,∠ACE=∠DCB,,CE=CB,∴△ACE≌△DCB(SAS).∴∠AEC=∠DBC,又∵CE=CB,∠ECB=∠GCE=60°,∴在△CHB与△CGE中,∠AEC=∠DBC,,CE=CB,,∠ECB=∠GCE,∴△CHB≌△CGE(ASA).∴CH=CG.∴∠CGH=∠CHG.∵∠GCH+∠GHC+∠CGH=180°,∴∠GHC=∠CGH=60°,∴∠ACG=∠CGH=60°,∴GH∥AB.13.解在△ABC中,∵AB=AC,∴∠B=∠C,又∵∠B+∠BDE=∠DEF+∠FEC,∠DEF=∠B,∴∠BDE=∠FEC,则在△DBE与△ECF中,∠B=∠C,,BD=CE,,∠BDE=∠FEC,∴△DBE≌△ECF,故DE=EF,∴△DEF是等腰三角形.14.解(1)当点P在△ABC内时,结论成立,如解图.过点P作GN∥BC分别交AB、AC于G、N,与AM交于点H.作PF∥AM交BC于点F,由于GN∥BC,△ABC是等边三角形,∴△AGN也是等边三角形.由题知,可得PD+PE=AH. 第14题解图又∵PF∥AM,GN∥BC,∴PF=HM,∴h1+h2+h3=h;(2)当点P在△ABC外时,h1+h2+h3=h这一结论此时不成立,此时有如下关系:h1+h2-h3=h.15.解(1)如解图所示:第14题解图(2)AN=BM依然成立,证明过程如下:旋转后,△ACM仍为等边三角形,在△NCA和△BCM 中,CN=CB,∠NCA=∠BCM=60°,AC=MC,∴△NCA≌△BCM,AN=BM;〓(3)△ABC是等边三角形,四边形MDNC是平行四边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上册第12.3等腰三角形水平测试题
一.选择题(每小题3分,共24分)
1. 小明将两个全等且有一个角为60的直角三角形拼成如图1所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是( )
A.4 B.3 C.2 D.1
2、已知等腰三角形的一个角等于42°,则它的底角为 ( ). A 、42 ° B 、69° C 、69°或84° D 、42°或69°
3、如图,ABC △中,AB AC =,30A ∠=,DE 垂直平分AC ,则BCD ∠的度数为( )
A.80 B.75 C.65 D.45
4、等腰三角形的顶角是80°,则一腰上的高与底边的夹角是( ) A .40° B .50° C .60° D .30°
5、如图,已知等边三角形ABC 中,BD CE =,AD 与BE 交于点P ,则APE ∠的度数是( ) A .45
B .55
C .60
D .75
6、如图是一个等边三角形木框,甲虫P 在边框AC 上爬行(A ,C 端点除外),设甲虫P 到另外两边的距离之和为d ,等边三角形ABC 的高为h ,则d 与h 的大小关系是( ) A.d h > B.d h < C.d h = D.无法确定
7. 如图,15A =∠,AB BC CD DE EF ====,则DEF ∠等于( )
A F C H B
M
E G A
D E
E D
C A
B F A .90 B .75
C .70
D .60
8、如图,△MNP 中, ∠P=60°,MN=NP ,MQ ⊥PN ,垂足为Q ,延长MN 至G ,取NG=NQ ,若△MNP 的周长为12,MQ=a ,则△MGQ 周长是( )
P
Q
M
N
G
A .8+2a
B .8+a
C .6+a
D .6+2a
二.选择题(每小题3分,共24分)
1. 在△ABC 中,AB=AC ,若∠B=56º,则∠C=__________.
2.等腰三角形底边中点与一腰的距离为6,则腰上的高为______.
3.如图,在△ABC 中,AB=AC ,CD 平分∠ACB 交AB 于点D ,AE ∥DC 交BC 的延长线于点E ,已知∠E=36°,则∠B= .
4.如图,在ABC △中,点D 是BC 上一点,80BAD ∠=°,AB AD DC ==,则C ∠= .
5. 等腰三角形至少有a 条对称轴,至多有b 条对称轴,则b a -= .
6. 有一个等腰三角形,三边分别是3x -2,4x -3,6-2x ,则等腰三角形的周长___.
7. 如图,△ABC 中AB=AC ,EB=BD=DC=CF ,∠A=40°,则∠EDF•的度数是_____.
8.在△ABC 中,B C ⊥AC ,D E ⊥AC ,D 是AB 的中点,若∠A=300,AB=8,则BC= ,DE= 。
三.解答题(共38分)
1. (8分)下午2时,一轮船从A 处出发,以每小时40海里的速度向正南方向行驶,下午4时,到达B 处,在A 处测得灯塔C 在东南方向,在B 处测得灯塔C 在正东方向,在图中画出示意图 ,并求出B 、C 之间的距离.
A C B
D
80
2. (9分) 如图,在四边形ABCD 中,AB=AD ,CB=CD ,求证:∠ABC=∠ADC.
D
C
A
B
3. (10分)在△ABC 中,∠ACB=900,点
D 、
E 都在AB 上,且AD=AC ,BC=BE ,求∠
DCE 的度数。
4. (11分)已知在△ABC 中,AB=AC ,∠BAC=1200,AC 的垂直平分线EF 交AC 于点E ,交BC 于点F ,试说明BF=2CF 。
四.拓广与探究(14分)
如图, ΔABC 是等边三角形,D 是AC 上一点,BD=CE,∠1=∠2,试判断ΔADE
形状,并证明你的结论.
备选题
1. 如图,在ABC △中,D 、E 分别是AC 、AB 上的点,BD 与CE
交于点O ,给出下列四个条件:①EBO ∠=DOC ∠;②BEO ∠=CDO ;③BE =CD ;④OB =OC .
(1)上述四个条件中,哪两个条件可判定ABC △是等腰三角形(用序号写出所有情况);
(2)选(1)小题中的一种情形,说明ABC △是等腰三角形 O
E D C
B A
A B C E D 1
2
2.如图,已知等边△ABC 和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距
离分别为h 1、h 2、h 3,△ABC 的高为h .
在图(1)中, 点P 是边BC 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(4)中,点P 分别在线段MC 上、MC 的延长线上、△ABC 内. (1)请探究:图(2)--(4)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论) (2)请说明根据图(2)所得的结论。
参考答案:
一.1、B 2、D 3、D 4、A 5、C 6、C 7、D 8、D 二.1.560 2.12 3. 72° 4. 25 °5.-2 6.9 或8.5 7.700 8.4,2 三.
1.解:B 、C 之间的距离为80海里。
图略。
2.解:连结BD 。
因为AB=AD ,
所以ABD ADB =∠∠。
因为CB=CD ,
所以CBD CDB =∠∠。
所以ABC ABD CBD ADB CDB ADC =+=+=∠∠∠∠∠∠。
3、解:因为在△ABC 中,0
90ACB =∠, 所以0
90A B +=∠∠。
因为AC=AD ,
所以01802
A
ACD -=∠∠。
因为BC=BE ,
所以01802
B
BCE -=∠∠。
所以01352
A B ACD BCE ++=
=0360-(∠∠)
∠∠。
所以0
1359045DCE ACD BCE ACB =+-=-=∠∠∠∠。
4. 解:连结AF ,
因为EF 是AC 的垂直平分线, 所以FA=FC ,
所以C FAC =∠∠。
又因为0
120BAC =∠, 所以060B C +=∠∠。
又因为AB=AC ,所以0
30B C ==∠∠。
所以0
1203090BAF BAC FAC =-=-=∠∠∠。
在Rt △ABF 中,0
90BAF =∠,0
30B =∠, 所以12AF FB =
,所以1
2
CF FB =,即BF=2CF 。
四. 解:ΔADE 为等边三角形.
因为ΔABC 为等边三角形, 所以AB=AC 。
又因为∠1=∠2,BD=CE , 所以⊿ABD ≌⊿ACE (SAS )。
所以AD=AE, ∠CAE=∠BAD=60°。
所以⊿ADE 为等边三角形。
备选题 1. 解:(1)有①③,①④,②③,②④四种情况可判定ABC △是等腰三角形; (2)下面以①③两个条件证明ABC △是等腰三角形。
因为EBO ∠=DCO ∠,BE =CD ,EOB ∠=DOC ∠, 所以△EOB DOC ∆≅∆(AAS )。
所以OB =OC 。
所以OBC ∠=OCB ∠。
又因为EBO ∠=DCO ∠, 所以EBC ∠=DCB ∠。
所以ABC △是等腰三角形。
2、解:(1)图(2)---(4)中的关系依次是:
h 1+h 2+h 3=h ; h 1-h 2+h 3=h ; h 1+h 2+h 3=h . (2)图②中,h 1+h 2+h 3=h .
连结AP , 则S ΔAPB +S ΔAPC =S ΔABC .
所以
12111
222
AB h AC h BC h ⨯+⨯=⨯. 又因为h 3=0,AB=AC=BC ,
所以h 1+h 2+h 3==h .。
