平面与 组合回转体相交
考试大纲(模板)

《机械制图》课程考试大纲一、课程的性质与要求(一)课程的性质本课程是机械类专业的一门专业基础课,为学习专业技术课和培养专业岗位能力服务。
(二)课程的基本要求学完本课程后,应达到下列要求:(1)掌握正投影法的基本理论及其应用;了解轴测投影的基本知识,掌握其基本画法;掌握用换面法求线段实长、平面图形真形的方法。
(2)能正确使用一般的绘图工具和仪器,掌握绘图的基本技能,做到作图准确、图线分明、字体工整、图面整洁。
初步掌握徒手画草图的技巧。
(3)能正确绘制和阅读一般的零件图和中等复杂的装配图。
在绘图和读图过程中,具有相应的分析能力和空间想象能力。
(4)能严格遵守《技术制图》和《机械制图》国家标准的有关规定,会查阅本课程所涉及的标准结构、标准零件以及《极限与配合》等的国家标准。
(5) 了解计算机绘图的发展概况及其在经济建设中的作用,和计算机绘图系统的组成及图形输入偷出设备的主要功能,并会初步运用绘图软件绘制简单的机械图。
此外,在本课程的学习和作业训练的过程中,考生还应注意树立认真负责的工作态度和严谨细致的工作作风。
(三)本课程与相关课程的联系和分工学习本课程之前,需有金工实践的知识,同时本课程与中学的平面几何、立体几何也有一定的衔接关系。
本课程涉及到的有关结构、工艺等专业知识,应在有关的后续课程中获得解决。
本课程只能为考生的绘图、读图能力奠定必要的基础,该能力还需要通过后续课程进一步培养和提高。
本课程计算机绘图部分的教学要求,也仅限于二维的范围,为能掌握计算机辅助设计技术,还须在有关后续课程中补充三维的计算机绘图内容。
二、课程内容与考核目标本课程的内容除绪论外,包括:I.投影基础部分Ⅱ.制图基础部分Ⅲ.机械图部分Ⅳ .计算机绘图基础部分绪论(一)学习目的与要求通过绪论的学习,要求了解本课程的研究对象,明确学习本课程的目的、任务和要求。
并在具体了解本课程的研究对象中,还要求理解有关投影法的基本知识和工业生产中广泛使用的正投影图的主要特点及优点,为以后学习点、线、面的投影作必要的知识准备。
平面与回转体相交

2、通槽侧面投影的作图:两侧平面 距球心等远,两圆弧的半径相等,两 段圆弧的侧面投影重合。
精品课件
平面与回转体的相对位置,初步判断截交线的形状及其投影。 ➢ 求出截交线上的点,首先找特殊点再补充中间点。 ➢ 补全轮廓线,光滑地连接各点,得截交线的投影。
精品课件
一、平面与圆柱体相交 截平面与圆柱面截交线的形状取决于截平面与圆
柱轴线的相对位置。
P
PH
截平面与圆柱轴线 平行截交线为矩形
精品课件
P
P
c ' a' •2'
6'(7 •
')
4 8''(d'•)(•b (•9 ')
(5')
')
75
••
• d9
b
•
•
3
•1
6 • 4•
•2
•
8
c
•
a
1"
·
3" • b" • d" 9" •
5(" • )7"
• 2" • a"
c" • 8"
• (4" 6)"
分析:圆柱的轴线是侧垂线, 截断体分别由侧平面、正垂面、 水平面截切圆柱体而成的。
e
h •
•
•
C
• f•
•a
g ••
db
a"
e
•
"c"•
•
h "
11 第五章第三讲 相贯线

3'
4' 6' • • •• 7' 5' R3
•
R4 R5 R4 R1
•Ⅰ •Ⅱ
•Ⅲ •Ⅳ
完
R5
•1 • 7) ( •2 (6) R2 •3 • • (4)5) • ( R3
求相贯线作图步骤:
1、求特殊点; 2、求一般点; 3、找出分界点; 4、顺次连接各点(连接原则是:如果两曲面的 两个共有点分别位于一曲面的相邻两素线 上, 同时也分别在另一曲面的相邻两素线 上,则 这两点才能相连)。 5、判别可见性(其判别原则是:两曲面的可见 部分的交线才是可见的;否则是不可见的)。
三、相贯线的类型
三、相贯线的类型
四、作图方法
(1)重影性法。 (2)辅助平面法。 (3)辅助球面法。
二、相贯线的作图
1、方法: (1)求特殊点。(一定要标注) (2)求一般点。
(3)光滑连接。
(4)判别可见性。
(5)体的完整。(画完剩余转向线)
2、连线的原则:
两立体表面上都处于相邻两素线之间的点才能相连。
已知直三棱柱与圆柱贯穿后的两面投影,求作其W面投影
3’ (10)’ 2’ (11)’ 11’’ (10)’’ 3’’ 2’’
1’
1’’ (8)’ 6’ (9)’ 5’ 9’’ 5’’
7’
8’’
7’’
6’’
(8) 11 10 (9)
1 (7)
3 (5) 2 (6)
例:93题:求三棱柱与圆球的相贯线
●
●
★ 外形交线
◆ 两外表面相贯 ◆ 一内表面和一外表面相贯
● ● ● ●
பைடு நூலகம்★ 内形交线
◆ 两内表面相贯
《机械制图》模拟考试题(附答案)

《机械制图》模拟考试题(附答案)一、判断题(共100题,每题1分,共100分)1、推拔销之锥度为 1 : 50 。
A、正确B、错误正确答案:A2、退刀槽和砂轮越程槽可按“槽宽×直径”的形式标注。
A、正确B、错误正确答案:A3、装配图必须有明细栏A、正确B、错误正确答案:A4、水平面的水平投影积聚为直线。
A、正确B、错误正确答案:B5、尺寸公差有可能是负值A、正确B、错误正确答案:B6、螺钉旋转一周,就沿轴向位移三个螺距者为三线螺纹。
A、正确B、错误正确答案:A7、同一标称直径之细螺纹,可有不同之节距。
A、正确B、错误正确答案:A8、用剖视图来表示物体内部特征,比用虚线表示之视图要清楚。
A、正确B、错误正确答案:A9、装配图上已注明的尺寸,零件图上可以省略。
A、正确B、错误正确答案:B10、420×594为4张A4的大小。
A、正确B、错误正确答案:A11、汉字的书写应求端正划一,大小间隔适当,清晰易认即可。
A、正确B、错误正确答案:A12、在相同工件条件下,钻头直径愈小,转速要愈快。
A、正确B、错误正确答案:A13、与他件组合有关之尺寸称为功能尺寸。
A、正确B、错误正确答案:A14、一个实心小圆点,有时可以代替相邻的两箭头。
A、正确B、错误正确答案:A15、沿垂直轴线方向所量得之螺峰与螺谷间的距离称为螺距。
A、正确B、错误正确答案:B16、平面与回转体相交,截交线在特殊情况时可能由直线和曲线或完全由直线组成A、正确B、错误正确答案:A17、薄片弯曲物体,仅用一视图表示即可。
B、错误正确答案:B18、槽孔之表面符号可用指引线引至适当位置标注。
A、正确B、错误正确答案:A19、多个同方向之位置尺寸,应用基准面标注法标注之。
A、正确B、错误正确答案:A20、一物体之各视图,剖面线需保持相同的间隔与方向。
A、正确B、错误正确答案:A21、机件表面局部特殊处理之范围须加细链线表明。
A、正确B、错误正确答案:B22、长仿宋体汉字,字宽为字高的 4 / 3 倍。
工程制图平面与立体相交

返回
•工程制图平面与立体相交
返回
整理棱线投影
•工程制图平面与立体相交
浏览三维动画
二、平面与回转体相交
平面截切回转体,在回转体表面留有的交线, 称为回转体的截交线。
㈠ 回转体截交线性质
1、截交线是截平面与回转 体表面的公有线。截交线上 的点为截平面与回转体表面 的公有点。
2、截交线的形状通常为平 面曲线,特殊情况下可含有 直线段组成。截交线的形状 取决于回转体表面性质和截 平面与回转体的相对位置。
一、截交线概述
平面截切立体,在立体表面留有的交线成为截交线。 依据立体表面性质不同,立体的截交线可分为:
平面体截交线和曲面体截交线
•工程制图平面与立体相交
二、平面与平面立体相交
平面截切平面立体,在平面立体表面留有的交 线,称为平面立体的截交线。
㈠ 平面体截交线的性质:
⒈平面体截交线是截平面与平面 立体表面的公有线。
2、投影作图
运用锥面取点方法作 出抛物线顶点和底端点、 转向轮廓线上点和一般 点,用曲线光滑连接各 点。
3、整理轮廓线
•工程制图平面与立体相交
【例题3】完成圆锥截切后的水平投影和侧面投影。
1、空间与投影分析
截交线为圆弧和两根 直线段,两截平面间有 一条交线。截交线的正 面投影落在截平面的正 面积聚性投影上,求作 截交线的水平投影和侧 面投影。
3、整理轮廓线
浏览三维动画•工程制图平面与立体相交
3、圆球的截交线 平面截切圆球,其截交线的形状为圆。
当截平面平行于投影面时,则截交线圆的投影反映实形; 当截平面垂直于投影面时,则截交线圆的投影为直线段; 当截平面倾斜于投影面时,则截交线圆的投影为椭圆。
•工程制图平面与立体相交
平面与回转体表面相交(1)

平面与回转体表面相交引入:物体表面上经常出现平面与回转面的交线,画图时通常把平面看成截平面,把交线看成截交线,再应用截交线的作图方法作出该交线的投影。
1.截交线的特点平面与回转体相交产生的截交线通常是一条封闭的平面曲线,或曲线和直线围成的平面图形或多边形。
截交线是截平面与回转体表面的共有线。
截交线的形状取决于回转体表面的形状。
截交线的形状取决于截平面与回转体轴线的相对位置。
2.求回转体表面截交线投影的分析方法1)分析截平面与回转体轴线之间的相互位置——搞清楚截交线的空间形状。
2)分析截平面与投影面的位置关系——初步掌握截交线的投影特点。
3.求平面与回转体表面截交线的步骤:1)求截交线的特殊点这些点通常是转向轮廓线上的点、极限位置点(最高、最低点,最前、最后点,最左、最右点)。
2)求一般点是指在各特殊点之间插入一些点,目的是使截交线连接得更加平顺、光滑。
通常是在具有积聚性投影的截平面投影上插入这些点,完成这些点的各面投影。
3)判别可见性并光滑连线。
4.回转体被截切的情况、投影分析和作图1)平面与圆柱相交截交情况:依据截平面与圆柱体轴线的相对位置不同,其截交线的形状有圆、椭圆、和两条直线三种。
表4.1平面与圆柱面的交线作图举例:例题完成圆柱被切割后的俯视图和左视图。
分析:从立体图及已知条件可知,这是圆柱被正垂面截切,截平面与圆柱轴线斜交,截交线是椭圆。
截交线正面投影重影为一直线,水平投影与圆柱面的投影重影积聚为圆;其侧面投影可根据投影规律和圆柱表面取点的方法求出。
作图:①作截交线上的特殊点:椭圆长短轴的四个端点,转向轮廓线上点,最高、最低、最前和最后的点。
②作一般点:在主视图中插入Ⅰ、Ⅱ、Ⅲ、Ⅳ点的投影1’(2’)和3’(4’)。
按圆柱表面取点方法作出相应点的水平和侧面投影。
③依顺序连接各点,作图结果如图c所示。
(a)(b)(c)例题如图a所示为接头的立体图及已知条件,完成接头的投影图。
分析:接头由左端的凹榫和右端的凸榫组成。
3[1] 4 平面与回转体相交
![3[1] 4 平面与回转体相交](https://img.taocdn.com/s3/m/7232c830b42acfc789eb172ded630b1c58ee9b77.png)
3[1] 4 平面与回转体相交平面和回转体是几何学中的两个基本概念。
一个平面是一个无限大的二维区域,它由无数个点组成。
一个回转体是一个三维空间中的体积,它围绕一个轴旋转而形成。
在几何学中,平面和回转体是常常被使用来描述和分析物体在空间中的形状和位置。
而当平面和回转体相交时,我们可以得到一些有趣的几何图形和问题。
平面和回转体相交的形状可以分为三种:圆形、椭圆形和长方形。
因此,在讨论平面和回转体相交时,我们将分别讨论这三种形状的情况。
圆形的情况当一个平面与一个回转体相交时,如果相交部分的形状是圆形,那么我们可以得到一个非常有用的结论:相交部分的圆心在回转体的轴上。
这个结论可以用于计算一个回转体的体积。
我们可以采用以下的步骤来计算一个回转体的体积。
步骤1:通过相交部分的圆心和轴的交点确定回转体的高度(高度等于交点到圆心的距离)。
步骤2:计算相交部分圆形面积(面积等于半径的平方乘以π)。
步骤1:通过相交部分的两个焦点和轴的交点构成一个锥形体。
步骤2:计算锥形体的体积(体积等于锥形体的高度乘以底面积的1/3)。
平行截面定理是指,若一个回转体被一组平面所截,这些平面与轴平行且相邻平面之间的距离为Δx,那么回转体的体积为:V=∫a^bA(x)dx其中,a和b是相邻平面的横坐标,A(x)是第x个平面所截的面积。
步骤1:将椭圆形或圆形的相交部分分成若干个长方形。
步骤2:通过平行截面定理计算回转体的体积。
总结通过以上的分析,我们可以得到平面与回转体相交的计算方法。
不仅可以计算回转体的体积,还可以用于解决其他一些几何问题。
因此,了解平面与回转体相交的特点和计算方法对于学习和应用几何知识非常重要。
《机械制图习题集》习题答案——第2章
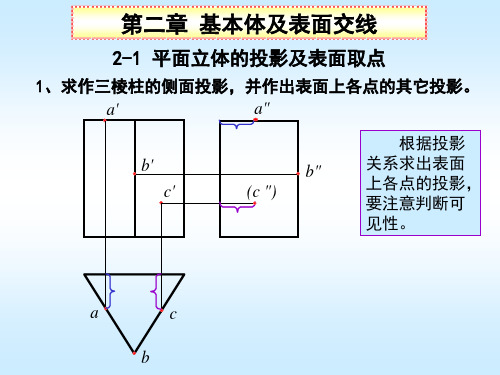
由于棱
锥体的棱面 无积聚性, 表面取点要 利用辅助线 法。
2-2 回转体的投影及表面取点
完成回转体的投影,并作出表面上各点的三面投影。
(1
)
a'
a"
b'
(b")
(b) a
回转体表面取点, 根据已知点的可见性 判断点所处的位置, 按投影关系,找出各 点的投影。
(2 )
(c') 1'
a'
b'
1" c" a"
4、完成相贯体的三视图。
1'
5'(6') 3'(4') 2' 7'(8')
1"
5" 6"
4"
3"
8"
7" 2"
4 86 21
75 3
圆锥体与圆
柱形孔正交。因 圆锥面的投影无 积聚性,利用辅 助平面求一般位 置的点。
5、完成相贯体的三视图。
1'
5'(6') 3'(4') 7'(8') 2'
1"
6"
b"
c
a
b
圆锥面的投
影无积聚性,表 面取点利用辅助 素线或辅助纬圆 法求解。底面上 的点可利用投影 关系直接求出。
(3 )
a'
b'
a" (b")
1a
圆锥台的表面
2 b
投影无积聚性,表 面上取点利用辅助
纬圆法。
(4 )
平面与回转体表面相交

完整版pt
求截交线的方法:棱线法 棱面法
二、平面截切回转体,截交线的形状取决于截
平面与被截立体轴线的相对位置。
截交线是截平面与回转体表面的共有线。
完整版pt
23
三、解题方法与步骤
⒈ 空间及投影分析
⑴ 分析截平面与被截立体的相对位置,以
确定截交线的形状。
⑵ 分析截平面与被截立体对投影面的相对
位置,以确定截交线的投影特性。
2.3.4 复合回转体的截切
例:求 作顶尖 的俯视 图
●
●
●●
●
●●
●
●
●
● ● ●
● ● ●
首先分析复合回转体由哪些基本回转体组成以及它们的连接关 系,然后分别求出这些基本回转完体整版的pt 截交线,并依次将其连接。22
小结
一、平面体的截交线一般情况下是由直线组成 的封闭的平面多边形,多边形的边是截平 面与棱面的交线。
完整版pt
10
作图步骤如下:
(1)先作出完整基本形体的三面投影图。 (2)然后作出槽口三面投影图。
( 3) 作出穿孔的三面投影图。
Q
平面与圆柱相完交整版pt
P11ຫໍສະໝຸດ 例4:求左视图● ● ● ●
同一立体被多个平面 截切,要逐个截平面进行 截交线的分析和作图。
解题步骤:
★空间及投影分析
截平面与体的相对位置
8
6
ⅥⅤ
1
5
Ⅶ
Ⅳ
Ⅲ
2
4
3
Ⅷ ⅠⅡ
平面与圆柱相交
完整版pt
5
比较不同角度的正垂面截交圆柱所得的截交 线的投影。
﹥45°
﹤45°
平面与圆柱相交
机械制图讲义之第二章_立体的投影
第2章立体的投影2.1 立体及其表面上的点与线立体由其表面所围成,可分为两类:表面都是平面的平面立体和表面是曲面或曲面与平面的曲面立体。
一、平面立体平面立体由若干多边形所围成,因此,绘制平面立体的投影,可归结为绘制它的所有多边形表面的投影,也就是绘制这些多边形的边和顶点的投影。
多边形的边是平面立体的轮廓线,分别是平面立体的每两个多边形表面的交线。
当轮廓线的投影为可见时,画粗实线;不可见时,画虚线;当粗实线与虚线相重合时,应画粗实线。
常见的平面立体有棱柱和棱锥。
1、棱柱2、棱锥平面立体的投影的外围轮廓总是可见的,应画粗实线;而在投影的外围轮廓内部的图线,则应根据线、面的投影分析,按前遮后、上遮下、左遮右直接判断投影的可见性,决定画粗实线或虚线,必要时还可利用交叉两直线的重影点的可见性进行判断。
二、曲面立体曲面立体由曲面或曲面与平面所围成。
有的曲面立体有轮廓线,即表面之间的交线,如圆柱;有的曲面立体有尖点,如圆锥;有的曲面立体全部由光滑的曲面所围成,如圆球。
在画曲面立体的投影时,除了画出轮廓线和尖点外,还要画出曲面投影的转向轮廓线。
曲面立体的转向轮廓线是切于曲面的诸投射线与投影面的交点的集合,也就是这些投射线所组成的平面或柱面与曲面的切线的投影,常常是曲面的可见投影和不可见投影的分界线。
曲面立体的投影就是它的所有曲面表面或曲面表面与平面表面的投影,也就是曲面立体的轮廓线、尖点的投影和曲面投影的转向轮廓线。
常见的曲面立体有圆柱、圆锥、圆球,圆环。
1、圆柱圆柱由圆柱面、顶面和底面所围成。
圆柱面由直线绕与它平行的轴线旋转而成。
因此,画圆柱的投影就是画顶面和底面及轮廓线、圆柱面投影的转向轮廓线、轴线。
当圆柱的轴线与投影面垂直时,圆柱面在轴线垂直的投影面上的投影具有积聚性。
因此,作圆柱表面2、 圆锥圆锥由圆锥面和底面所围成。
圆锥面由直线绕与它相交的轴线旋转而成。
因此,画圆锥的投影就是画尖点(即锥顶)、底面及轮廓线、圆锥面投影的转向轮廓线、轴线。
立体表面的交线

(1) 2
§3-2
平面与回转体表面相交
综合举例
3” 6” 5”
3’ 6’
5’
7’
4’
7” 4”
6 5
(7) 3 (4)
§3-2
平面与回转体表面相交
综合举例
§3-3 两回转体表面相交
• 相贯线及其性质 • 回转体表面相交的情况 • 求相贯线的方法
• 应用举例
• 相贯线的特殊情况
§3-3 两回转体表面相交
§3-3 两回转体表面相交
Q2V Q1V (6’) 5’
(8’) 7’
Q2W
Q1W
(8”)
(7”)
6”
5”
6
8
m1
5
7 l1
求相贯线上的一般点
§3-3 两回转体表面相交
(k’2) (k’1)
k’1(k’2)
k’2
k’1
§3-3 两回转体表面相交
辅助球面法
辅助球面法的原理
设置一辅助球面 (球心位于两回转体 轴线的交点),求辅 助球面与两回转体表 面的交线圆,两圆的 交点为两体表面和辅 助球面三面的共点, 即相贯线上的点。
1’’(2’’)
3’
(7’)
7’’
(8’’)
3’’(4’’)
5(7) 6(8)
1(3)
2(4)
§3-2
平面与回转体表面相交
轴套
§3-2
a’ (m’2) m’1 (d’) c’ (k’2) k’1 b’ m”2 d’’ a’’
平面与回转体表面相交
m”1 c”
PV
b’’
d k2 b m2
a
k1 c
m1
相贯线的性质
两立体表面的交线相贯线

第六讲两立体表面的交线——相贯线教学目标:掌握相贯线的画法教学重点:特殊位置平面与回转体的交线一、相贯线的概念两立体相交,在其表面产生的交线,称为相贯线。
二、相贯线的性质1.表面性相贯线位于两立体表面。
2.封闭性相贯线通常是封闭的空间曲线,特殊情况下为平面曲线或直线。
3.共有性相贯线是两立体表面的共有线。
求相贯线的作图实质是找出相贯的两立体表面的若干共有点的投影。
三、平面立体与回转体相交相贯线是由若干段平面曲线或直线组成的空间折线,每一段是平面体的棱面与回转体表面的交线。
求交线的实质是求各棱面与回转面的截交线。
求相贯线的步骤:分析各棱面与回转体表面的相对位置,从而确定交线的形状。
求出各棱面与回转体表面的截交线。
连接各段交线,并判断可见性。
举例:四、两圆柱相交本节是此讲的重点,让学生学会从空间到投影分析,掌握相贯线的作图方法。
两圆柱相交,相贯线通常为封闭的空间曲线,它是两圆柱表面的共有线。
常用的作图方法为表面取点法。
(其中一形体表面必须有积聚性的特点)举例:作图步骤:1.空间及投影分析:交线为封闭的空间曲线,利用圆柱表面的积聚性,先找到已知的投影。
2.作图方法:表面取点法。
3.作图步骤:通过投影规律找到特殊点,以确定交线范围;再补充一些中间点以确定交线的弯曲趋势;最后光滑连接。
讨论:1.相贯线产生:两外圆柱面相交、内外圆柱面相交、两内圆柱面相交。
1.两圆柱直径变化对相贯线的影响。
3.两圆柱正交的简化画法介绍:四个要点①轮廓线的交点②大圆柱半径③小圆柱轴线④弯向大圆柱轴线举一些实例分析相贯线的产生和画法。
目的使学生掌握相贯线的画法。
五、圆柱与圆锥相交介绍辅助平面法,让学生理解三面共点的原理,会应用其作交线。
空间及投影分析:相贯线为一光滑的封闭的空间曲线。
它的侧面投影有积聚性,正面投影、水平投影没有积聚性,应分别求出。
作图方法:辅助平面法,利用三面共点的原理,用一辅助平面截切相贯体,分别与两个立体产生两组交线,两组交线的交点即为三面共点,就是所求的相贯线。
