平行四边形的面积公式推导(正式)
平行四边形面积的计算公式是什么
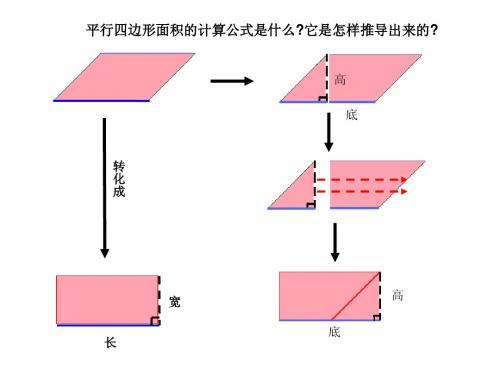
高
底
转 化 成
宽 长 底
高
高 底
S=ah 5×2.5 =12.5(平方米)
答:它的面积是12.5平方米。
1、画出底和高。
h
h
a a
2、量出底和高的长度。 3、把数据代入平行四边形面积的计算公式中。
(1)算术解题的方法:
(2)列方程解题的方法:
28÷7=4(m)
设:平行四边形的高为x 米。 根据:ah=S 7x=28 解:7x÷7=28÷7 x=4
答:这个平行四边形的高少公顷?
(2)平均每公顷收小麦多少吨?
根据:小麦总吨数÷麦田面积=每公顷收小麦的吨数
S=ah
250×84 =21000(平方米)
14.7÷2.1= 7(吨)
15cm
18cm
21000平方米=2.1公顷
答:这块麦田有2.1 公顷, 平均每公顷收小麦7吨。
两个等底等高的平行四边形的面积是相等的。 S=ah 2.5×1.4 =3.5(平方厘米)
答:它们的面积各是3.5平方厘米。
两个等底等高的正方形和平行四边形的面积是相等的。
(1)求出正方形的边长是多少? (2)正方形的边长就是平行四边形的底和高。 (3)求出平行四边形的面积。
平行四边形、三角形面积推导

1、平行四边形面积推导过程:
方法一:
平行四边形面积计算公式的推导过程:
平行四边形从顶点做高,并沿高剪开,分成一个三角形和一个梯形,把三角形向右平移,拼成一个长方形,拼成长方形的长等于原平行四边形的底,拼成长方形的宽等于原平行四边形的高,因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
方法二:
将一个平行四边形沿任意一条高剪开,平移到另一边,则拼成一个长方形。
a
平行四边形的面积等于长方形的面积。
原平行四边形的底等于拼成长方形的长,原平行四边形的高等于拼成的长方形的宽。
因为长方形的面积= 长×宽
平行四边形的面积=底×高
所以,平行四边形的面积等于底乘高。
2、三角形面积推导过程
平行四边形的底等于原三角形的底,平行四边形的高等于原三角形的高,平行四边形的面积等于原三角形面积的2倍,(原三角形的面积等于拼成的平行四边形面积的一半)。
即三角形的面积=等于平行四边形面积的一半。
(三角形的面积=底×高÷2)
沿一个三角形两边终点剪开,然后拼补成平行四边形。
⑴原三角形的面积等于拼成的平行四边形的面积。
⑵拼成的平行四边形的底等于原三角形的底,高等于原三角形的一半。
⑶平行四边形的面积= 底×高
(原三角形的底)(原三角形的高÷2)
三角形的面积= 底×高÷2
(三角形的面积=底×高÷2)。
人教版五年级平行四边形和三角形的面积

1.平行四边形的面积:1)平行四边形的面积推导:总结:平行四边形可以通过割补法拼成一个长方形,长方形的长就是平行四边形的的底,长方形的宽就是平行四边形的高。
所以平行四边形的面积=底(长)×高(宽)。
(用字母表示:S=ah)注意:通过平行四边形的面积公式可以得到:平行四边形的高=面积÷底,平行四边形的底=面积÷高。
把一个长方形拉伸成一个平行四边形,它的周长不变,面积将变小。
2)知平行四边形的面积求高或者底的公式:因为平行四边形的底×高=面积,所以平行四边形的底=面积÷高,三角形的高=面积÷底2.三角形的面积:1)三角形的面积公式推导:总结:两个完全一样的三角形可以拼成一个平行四边形,那么三角形的面积就等于平行四边形面积的一半.所以三角形的面积=底×高÷2。
(用字母表示:S=ah÷2)注意:要两个完全一样的三角形的才能拼成一个平行四边形。
(等地等高的三角形不能拼成平行四边形)面积相等的两个三角形不一定能拼成平行四边形。
2)知道三角形的面积求高或者底的公式:因为三角形的底×高÷2=面积,这样:底×高=面积×2。
所以三角形的底=面积×2÷高,三角形的高=面积×2÷底3.典型例题:1)2)求长是24cm的高所对求长是4cm的底所对应的高应的底3)一块平行四边形菜地,底是5.5米,高是16米。
如果每平方米产白菜15千克,这块菜地能产白菜多少千克?4)一块三角形菜地,底长是150m,高是50m,共收油菜籽1726.5kg,平均每公顷产油菜籽多少千克?5)下面三角形的面积相等吗?为什么?6)思考:下图中两个平行四边形的面积相等吗?为什么?每个平行四边形的面积是多少?4.随堂练习:1)计算下面各平行四边形图形的面积(单位:cm)2)已知平行四边形的面积是84平方厘米,它的高是21厘米,这个平行四边形的底是多少厘米?3)一个三角形的面积是24平方分米,高是6分米,底是多少分米?4)一个三角形的面积是25平方米,底是10米,高是多少米?5)一块平行四边形的菜地长20m,高15m,如果每平方米收获20kg稻谷。
平行四边形的面积怎么求公式

平行四边形的面积怎么求公式面积=底×高其中,底指的是平行四边形的任意一条边的长度,高指的是与底垂直的线段的长度。
同时,平行四边形也可以看作是由两个相邻边及其夹角所组成的三角形。
在这种情况下,我们可以利用三角形的面积公式求解平行四边形的面积。
要使用三角形的面积公式求解平行四边形的面积,可以有以下两种方法:方法一:使用高和底边长首先,选择一个边作为底边,并将其长度标记为b。
然后,选择从底边上一点引出的线段作为高,并将其长度标记为h。
这个高线段必须与底边垂直。
接下来,我们可以使用以下公式求解平行四边形的面积:面积=底×高=b×h此方法适用于已知平行四边形的两个相邻边和夹角,而不是直接给出高和底的长度。
方法二:使用三角形的面积公式面积=1/2×底×高在平行四边形中,高等于垂直于底边的线段长度,底等于平行四边形的一条边的长度。
因此,平行四边形的面积可以通过将两个相等三角形的面积相加得到,即:面积=2×(1/2×底×高)=底×高以上就是求解平行四边形面积的两种方法。
除了这两种方法之外,还可以根据平行四边形的特性结合其他几何概念来求解面积,比如利用正方形和长方形的性质,或者将平行四边形拆分为直角三角形等等。
但这些方法都是基于基本的几何原理进行推理和计算。
最后,值得注意的是,无论采用哪种方法,求解平行四边形面积的关键是准确测量和确立底边和高的长度。
如果底边或高的长度有误,将导致计算的面积结果不准确。
因此,在进行计算之前,务必要确保所用的测量值准确无误。
平行四边形的面积公式推导

平行四边形的面积公式推导
1.基本原理
任意一个矩形的面积都是由两条对角线的积确定的,令矩形的长为a,宽为b,那么它的面积S等于两条对角线的乘积:
S=ab
如果要求平行四边形的面积,则需要注意到矩形的两个对角线可以表
示为有两条对角线的平行四边形,所以可以推导出平行四边形的面积公式:S=a*b
其中a,b分别为两条对角线的长度。
2.关于各种边长的情况
(1)若知道两条对角线的长度a,b,则可直接应用上述面积公式求
出面积:
S=a*b
(2)若对角线长度已知,而对角线的边长未知,则可以利用勾股定
理求出边长:
若已知a,b为对角线的长度,则一条对角线上的两条边的长度分别为:c1=sqrt(a*a-b*b/4),c2=sqrt(a*a+b*b/4)
(3)若已知四条边的长度,则可以利用下图将平行四边形分解为两
个三角形,由勾股定理求出两条对角线的长度。
长方形面积推导平行四边形面积的公式

长方形面积推导平行四边形面积的公式
我们要通过长方形的面积来推导平行四边形的面积公式。
首先,我们需要理解两者的面积是如何计算的。
假设长方形的长为 l,宽为 w。
长方形的面积A_rectangle = l × w。
对于平行四边形,假设它的底为 b,高为 h。
平行四边形的面积A_parallelogram = b × h。
为了从长方形推导出平行四边形的面积,我们可以考虑一个特殊的情况:当平行四边形是一个矩形时,它的长就是宽,也就是说 l = b 和 w = h。
所以,在这种情况下,平行四边形的面积A_parallelogram = l × w。
这意味着,对于矩形,平行四边形的面积与长方形的面积是相等的。
因此,对于矩形,平行四边形的面积公式是:A_parallelogram = lw
这意味着,对于矩形,平行四边形的面积与长方形的面积是相等的。
平行四边形面积的推导过程怎么写

平行四边形面积的推导过程怎么写平行四边形是初中数学中的一个重要几何形状,它的面积的推导过程也是数学学习的基本内容之一。
本文将详细介绍平行四边形面积的推导过程,并探讨一些相关的性质和定理。
一、平行四边形的定义和性质平行四边形是指有四条边,且对边平行的四边形。
平行四边形具有以下性质:1.相邻两边相等:平行四边形的相邻两边相等,即AB=CD,BC=AD。
2.对角线互相平分:平行四边形的对角线互相平分,即AC和BD互相平分。
3.对角线长度相等:平行四边形的对角线长度相等,即AC=BD。
4.对角线互相垂直:平行四边形的对角线互相垂直。
二、平行四边形面积的推导过程要推导平行四边形的面积,我们可以借助三角形的面积和平行四边形的性质来进行推导。
设平行四边形的边长分别为a和b,高为h,我们可以将平行四边形分割为两个等腰直角三角形。
1.首先,连接平行四边形的对角线AC和BD,如图所示:A___________C////B/_________D/2.根据平行四边形的性质,对角线互相平分,所以AC=BD,设其长度为d。
3.根据等腰直角三角形的性质,直角边等于斜边的一半,所以AC=2h。
4.根据勾股定理,我们可以得到平行四边形的高h与对角线d的关系:d^2=a^2+b^2。
5.将等腰直角三角形ACD分割为两个等腰直角三角形ADC和BCD。
根据等腰直角三角形的性质,我们可以得到这两个三角形的面积:S1=1/2*AD*hS2=1/2*BC*h6.将两个三角形的面积相加,即可得到整个平行四边形的面积S:S=S1+S2=1/2*AD*h+1/2*BC*h=1/2*(AD+BC)*h=1/2*(a+b)*h三、平行四边形面积的计算公式通过上述推导过程,我们可以得到平行四边形的面积计算公式:S=1/2*(a+b)*h其中,a和b分别表示平行四边形的两个邻边的长度,h表示平行四边形的高。
这个公式可以方便地计算平行四边形的面积,只需要知道两个邻边的长度和高的值即可。
平行四边形面积怎么求
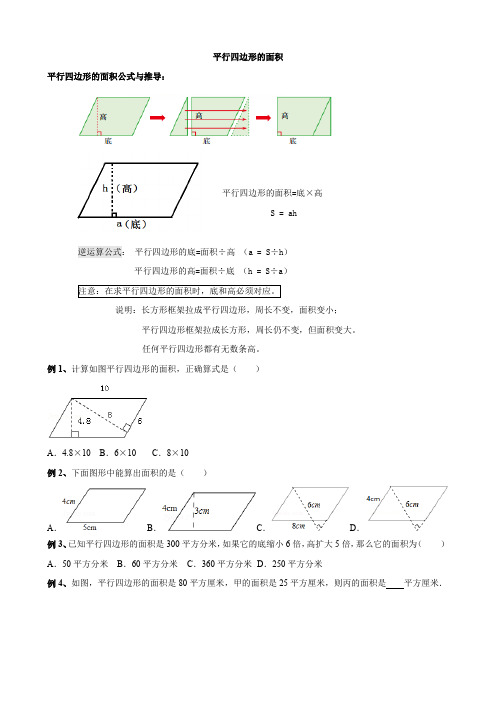
平行四边形的面积平行四边形的面积公式与推导:平行四边形的面积=底×高S = ah逆运算公式:平行四边形的底=面积÷高(a = S÷h)平行四边形的高=面积÷底(h = S÷a)注意:在求平行四边形的面积时,底和高必须对应。
说明:长方形框架拉成平行四边形,周长不变,面积变小;平行四边形框架拉成长方形,周长仍不变,但面积变大。
任何平行四边形都有无数条高。
例1、计算如图平行四边形的面积,正确算式是()A.4.8×10B.6×10C.8×10例2、下面图形中能算出面积的是()A.B.C.D.例3、已知平行四边形的面积是300平方分米,如果它的底缩小6倍,高扩大5倍,那么它的面积为()A.50平方分米B.60平方分米C.360平方分米D.250平方分米例4、如图,平行四边形的面积是80平方厘米,甲的面积是25平方厘米,则丙的面积是平方厘米.例4图例5图例5、如图,图A和图B的面积相比较,()A.图A的面积大B.图B的面积大C.两者一样大D.无法确定例6、用两根长4厘米和两根长5厘米的小棒围成一个平行四边形,面积最大不会超过()平方厘米.A.25B.18C.20D.81例7、北京奥运会期间北京市某单位做了一个如图所示的宣传标语牌,已知标语牌的周长是16米,两边上的高如图所示,求这个标语牌的面积是多少平方米?课堂练习1、平行四边形的高是6cm,底是5cm,面积是,如果把高和底各扩大2倍,那么面积就扩大为原来的倍.2、已知一个平行四边形的面积是60平方分米,底是12分米,高是分米.3、底为4分米,高为0.2米的平行四边形的面积是平方分米.4、一个平行四边形的面积是188平方分米,一个长方形的长和宽分别与平行四边形的底和高相等,这个长方形的面积是平方分米.5、两个平行四边形的面积相等,一个平行四边形的底是9厘米,高是8厘米,另一个平行四边形的高是6厘米,底是厘米.6、一个平行四边形的面积是12.5平方米.它的底是2.5米,对应高是米.7、如图,平行四边形的底为8厘米,高为4.5厘米,面积为36平方厘米,阴影部分面积为平方厘米.第7题图第13题图第14题图8、一个平行四边形的底是8分米,面积是48平方分米,它的高是厘米.9、一个平行四边形的面积是5.4平方米,高是3.6米,底是米.10、一个平行四边形的高4分米,比它的底短1分米,它的面积是.11、平行四边形的底是12米,它的两条高分别是9米、15米,这个平行四边形的面积是平方米.12、一个平行四边形的面积是24平方分米,它的底是6分米,高是分米.13、如图平行四边形的面积是48平方厘米.线段CD长5厘米,线段AF长4.8厘米,那么平行四边形的周长是厘米.14、如图,平行四边形的面积是20平方厘米,图中阴影部分的面积是平方厘米.如果阴影部分的面积是15平方厘米,平行四边形的底是6厘米,则它的高是厘米.15、如果把一个平行四边形的底和高都扩大原来的2倍,那么它的面积将()A.扩大原来2倍B.缩小原来4倍C.扩大原来4倍16、平行四边形相邻的两条边长度分别为12厘米和8厘米,已知其中的一条高是10厘米,那么这个平行四边形的面积是()平方厘米.A.120B.96C.80D.6017、计算如图平行四边形面积的正确算式是()A.8×12B.10×12C.8×10第17题图第18题图18、如图,平行四边形的面积是()平方厘米A.32B.24 C.48D.以上答案都不可能课后习题1、一个平行四边形的底是9分米,高是底的2倍,它的面积是.2、一个平行四边形的面积是80平方米,高是5米,底是.3、有一块平行四边形土地,底边长28m,高是底的,这块地的面积是平方米.4、如图是一个平行四边形,阴影部分的面积是8平方厘米,那么这个平行四边形的面积是平方厘米.第4题图第7题图第9题图5、王师傅从一个上底是5.5厘米、下底是7.5厘米、高是4厘米的梯形铁片上截取一个最大的平行四边形.这个平行四边形的面积是()平方厘米.A.22B.30C.无法选择6、平行四边形的两邻边长分别是6厘米和8厘米,夹角是30°,这个平行四边形的面积是()A.12厘米2B.24厘米2C.40厘米2D.都不对7、求下面平行四边形的面积,正确的列式是()A.6×4.8B.10×4.8C.8×10D.8×4.88、一个平行四边形的高减少了5cm,底增加了5cm,它的面积比原来()A.增加B.减小C.不变D.无法确定9、如图计算平行四边形的面积列式为()A.7.5×8 B.8×6 C.10×8 D.10×7.510、计算下面平行四边形面积的正确算式是()A.12×10B.7.5×12C.9×12D.7.5×1011、平行四边形的底扩大2倍,高也扩大2倍,面积()A.扩大2倍B.扩大4倍C.不变D.无法判断12、把一个平行四边形沿着高切开,拼成一个长方形.()A.面积变小,周长变小B.面积不变,周长不变C.面积变小,周长不变D.面积不变,周长变小13、平行四边形两边长分别是8厘米和6厘米,其中一条边上的高是4厘米,这个平行四边形的面积是()平方厘米.A.32B.24C.80或5614、把一个长6厘米,宽4厘米的长方形拉成一个平行四边形后面积减少6平方厘米,平行四边形的高是()A.3B.4C.515、将﹣个边长为4分米的正方形框架拉成一个高是3分米的平行四边形,则平行四边形的面积是()平方分米.A.12B.16C.无法确定。
平行四边形的面积公式推导

努 力 吧 !
有一块地近似平行四边形,底43米, 高20.1米,面积是多少平方米?
填表
底(米) 高(米)
38 70 22 20 6.2 11
面积(平方米) 760 434 242
判断: (1) 平行四边形的底是 7米,高是4米,面积是28米。 ( ) (2) a=5分米,h=2米, S=100平方分米。 ( )
×
下面对平行四边形面积的计算对吗?
6米
6×3=18(平方米)(
x)
下面对平行四边形面积的计算对吗?
8×7=56(平方分米)(
x)
思考题:你有几种方法求下面图形的面积?
宽高 底 长
平行四边形的面积 长方形的面积
= = 长
× ×
=
宽
①画 ②剪 ③移、拼
画
剪、旋转
拼
通过割补的方法,我们可清楚地看 到,任何一个 平行四边形 都可以转化 为 长方形 ,而且长方形的 长 和 宽 恰 好等于平行四边形的 底 和 高 。 所以, 平行四边形的面积= 底×高 S=a × h 还可以写成:S=a· h 或 S=ah
平行四边形花坛的底是
6m,高是 4m,它的面积是多
少?
4m 6m
S =ah =6 × 4
= 24(m2) 答:它的面积是 24 m2。
S =ah =5×2.5 = 12.5(m2) 答:它的面积是 12.5 m2。
算出下列平行四边形面积?
10 厘米
8 厘米 12 厘米
15 厘米
方法一
方法二
S=ah S=ah =15×8 =10×12 =120(平方厘米) =120(平方厘米)
(2)
面积 ( A )
平行四边形的三种面积公式

平行四边形的三种面积公式
1.基于底和高的公式
2.基于两边和夹角的公式
这个公式的推导基于平行四边形的高也就是两个非邻边之间的距离。
从一个顶点向另外一条边引垂线,可以得到一个直角三角形。
根据正弦定理可以得到sin(θ) = h / b,即h = b * sin(θ)。
结合平行四边形的面积公式S = b * h,可以得到S = a * b * sin(θ)。
3.基于三个顶点坐标的公式
平行四边形的面积还可以通过已知三个顶点的坐标来计算。
假设平行四边形的三个顶点分别为A(x1,y1),B(x2,y2)和C(x3,y3),则其面积公式为S=,(x1y2+x2y3+x3y1)-(y1x2+y2x3+y3x1),/2、其中,x,表示取x 的绝对值。
这个公式的推导基于行列式的性质。
将三个顶点的坐标分别代入到行列式中,然后按照特定的顺序进行计算,可以得到平行四边形的面积。
综上所述,平行四边形的面积可以通过这三种公式进行计算。
根据实际问题的不同,我们可以选择合适的公式来求解。
五年级数学上册教案-6.1平行四边形的面积公式的推导过程128-人教版

五年级数学上册教案6.1 平行四边形的面积公式的推导过程128人教版教案:五年级数学上册教案6.1 平行四边形的面积公式的推导过程我作为一名经验丰富的教师,对于五年级数学上册的平行四边形的面积公式的推导过程有着深入的理解和丰富的教学经验。
一、教学内容本节课的教学内容是平行四边形的面积公式的推导过程。
我们将通过实际的例题和练习,让学生理解和掌握平行四边形的面积公式,并能够运用到实际问题中。
二、教学目标通过本节课的学习,我希望学生能够理解平行四边形的面积公式的推导过程,并能够运用该公式计算平行四边形的面积。
同时,我也希望学生能够通过解决实际问题,提高他们的数学应用能力。
三、教学难点与重点本节课的重点是让学生理解和掌握平行四边形的面积公式,并能够运用到实际问题中。
而教学难点则是如何让学生理解并推导出平行四边形的面积公式。
四、教具与学具准备五、教学过程1. 实践情景引入:我会向学生展示一个实际的平行四边形,并让他们观察和描述这个平行四边形的特征。
2. 例题讲解:我会通过一个具体的例题,引导学生理解和推导出平行四边形的面积公式。
我会让学生观察和分析例题中的平行四边形,并引导他们通过实际的操作,推导出平行四边形的面积公式。
3. 随堂练习:在讲解完例题后,我会给学生一些随堂练习题,让他们通过实际的操作和计算,巩固他们对平行四边形的面积公式的理解和掌握。
4. 作业设计:我会布置一些有关平行四边形的面积公式的作业题,让学生在课后进一步巩固和应用所学的内容。
六、板书设计在教学过程中,我会通过板书来展示和强调平行四边形的面积公式的推导过程,以便学生更好地理解和记忆。
七、作业设计1. 请用彩笔和剪刀,剪出一个平行四边形,并计算出它的面积。
答案:学生可以通过实际的操作,剪出一个平行四边形,并计算出它的面积。
2. 如果一个平行四边形的底是6厘米,高是4厘米,那么它的面积是多少?答案:36平方厘米。
八、课后反思及拓展延伸在课后,我会反思本节课的教学效果,并根据学生的实际情况,进行拓展延伸,以帮助学生更好地理解和掌握平行四边形的面积公式的推导过程。
平行四边形、三角形、梯形面积公式的推导

.
一、平行四边形面积公式的推导过程:
1、把平行四边形沿着它的一条高剪开,就拼成了一个长方形。
2、平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。
3、因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
二、三角形面积公式的推导过程:
1、两个完全一样的三角形可以拼成一个平行四边形。
2、三角形的底等于平行四边形的底,三角形的高等于平行四边形的高。
3、三角形的面积等于平行四边形的一半,因为平行四边形的面积=底×高,所以三角形的面
积=底×高÷2.
三、梯形面积公式的推导过程:
1、两个完全一样的梯形可以拼成一个平行四边形。
2、平行四边形的底等于梯形的上底加下底,平行四边形的高等于梯形的高。
3、梯形的面积等于平行四边形面积的一半,因为平行四边形的面积=底×高,所以梯形的面
积=(上底+下底)×高÷2.
'.。
平行四边形面积推导过程6种

平行四边形面积推导过程6种平行四边形的面积推导,听上去是不是有点枯燥?别急,咱们轻松聊聊这个话题,保证让你乐在其中,学得也快。
想象一下,平行四边形就像是一个被撑开的巧克力盒,四个角巴巴地站着,里面的面积藏得好好的。
咱们今天就来撬撬这巧克力盒,看看里面的秘密。
平行四边形的特点就挺有意思的。
对吧?两组对边平行且相等,真是聪明得让人忍不住想赞叹。
要说面积嘛,想象一下,你在海边挖沙子,平行四边形就是你挖的沙子堆。
为了计算面积,咱们得找个好方法。
这里就有个简单的办法,就是找出底边的长度和高度,像咱们量米一样,简单直接。
说到这里,有个小秘密要告诉你,面积的公式其实就是底边乘以高度,听起来是不是很简单?就像买水果,称几斤苹果,结果一算,嘿,账单上显示的就是你买的苹果的总重量。
平行四边形的底边和高度,就像那称苹果的秤,给你一目了然的结果,面积自然就出来了。
咱们再换个角度看。
这时候想象一下,如果把这个平行四边形撕成两半,是不是就变成了两个三角形?哈哈,这可真是个妙招!这时候,咱们可以用三角形的面积公式,反过来推算,平行四边形的面积也就呼之欲出了。
就像把一块蛋糕切成两半,吃的时候心里想着,其实这蛋糕还是一整块。
咱们也可以用平行四边形的对角线来玩。
把这对角线想象成一根绳子,把平行四边形一拉一扯,它就会变得更美妙。
对角线把平行四边形分成了两个三角形,面积又能轻松算出来。
没错,就是这个道理,面积不就是在这些小细节中找到的吗?还有一种方式,咱们可以用三角形的分割法,真的是个绝招。
想象一下,把平行四边形从一角斜着切过去,嘿,那又是两个三角形。
用三角形的面积公式再计算一次,平行四边形的面积就又出来了。
就像逛超市,没事买点小零食,最后发现原来是一次大采购,哈哈,感觉赚到了。
再说说重叠法。
你可以把两个相同的平行四边形叠在一起,像双胞胎一样,互相依偎。
然后把其中一个的底边放到另一个的上面,刚好就形成了一个矩形。
矩形的面积计算起来简直是小菜一碟,宽乘以高,结果就到了手。
图形的面积公式推导

二、三角形面积公式推导 倍拼法(1)
高
底 平行四边形面积 = 底×高 三角形面积 = 底×高 ÷ 2
二、三角形面积公式推导 倍拼法(2)
高
宽
底
长
长方形面积 = 长×宽 三角形面积 = 底×高 ÷2
二、三角形面积公式推导 割补法(1)
高÷2 底 平行四边形面积 = 底×高 三角形面积 = 底×高÷2
一、平行四边形面积公式推导 割补法(3)
高
宽
底
长
长方形面积 = 长×宽 平行四边形面积 = 底× 高
一、平行四边形面积公式推导 折叠法
高
宽
(高÷2)
底
长
长方形面积 = 长×宽
平行四边形面积 = 底×高÷2×2 = 底×高
目
录
Contents
A 平行四边形面积推导 B 三角形面积推导 C 梯形面积推导
梯形的面积=(下底-上底)×高÷2 + 上底×高 =(上底+下底)×高÷2
三、梯形面积公式推导 分割法(2)
上底
高
=高
+
下底
梯形的面积 = 下底 × 高 ÷ 2 + 上底 × 高 ÷ 2 = (上底+下底)×高÷2
三、梯形面积公式推导 折叠法
上底
高
宽
(高÷2)
下底 长=(上底+下底)÷2
长方形面积=
二、三角形面积公式推导 割补法(2)
高
宽
(高÷2)
底长 长方形面积 = 长×宽 三角形面积 = 底×高÷2
二、三角形面积公式推导 割补法(3)
高
长
底 宽(底÷ 2)
长方形面积 = 长×宽 三角形面积 = 高×底÷2
平行四边形面积计算公式推导

平行四边形面积计算公式推导咱都知道,在数学的世界里,图形那可是相当重要的角色。
今天咱就来好好唠唠平行四边形面积计算公式的推导,这可是个相当有趣的事儿!还记得有一次,我去朋友家,看到他正在为孩子辅导数学作业,刚好就碰到了平行四边形面积计算的问题。
那孩子一脸的迷茫,朋友也是急得抓耳挠腮。
我在旁边看着,心里就想,这其实没那么难嘛。
咱们先来说说平行四边形。
平行四边形就是对边平行且相等的四边形。
那怎么计算它的面积呢?这就得从我们熟悉的长方形说起啦。
咱们假设手里有一张平行四边形的纸,把它沿着高剪一刀,然后通过平移,是不是就可以把它拼成一个长方形啦?这个过程可有意思了。
就好像是给这个平行四边形变了个魔术,一下子就变成了长方形。
那为什么要这样做呢?因为咱们熟悉长方形的面积计算呀,长方形的面积等于长乘宽。
而通过刚才的操作,我们发现,平行四边形的底就相当于长方形的长,平行四边形的高就相当于长方形的宽。
所以,平行四边形的面积也就等于底乘高。
比如说,有一个平行四边形,底是 5 厘米,高是 3 厘米,那它的面积就是 5×3 = 15 平方厘米。
是不是挺简单的?再举个例子,在咱们的生活中,经常能看到平行四边形的影子。
像小区的伸缩门,不就是一个个平行四边形组成的嘛。
要是咱们想知道这伸缩门的面积,用底乘高的方法就能轻松算出来。
回到学习中,同学们在做相关题目时,可一定要找准底和高。
有的时候题目会故意设置一些小陷阱,比如给你好几条线段,让你判断哪条是底对应的高。
这时候可别马虎,要仔细分辨。
总之,平行四边形面积计算公式的推导,其实就是一个巧妙的转化过程。
把不熟悉的平行四边形转化成熟悉的长方形,问题就迎刃而解啦。
就像我们在生活中遇到困难,有时候换个角度,换个方法,也许就能轻松解决。
希望同学们都能牢牢掌握这个知识,在数学的海洋里畅游,轻松应对各种挑战!。
平行四边形和三角形的面积公式推导过程

平行四边形和三角形的面积公式推导过程大家好,今天我们来聊聊平行四边形和三角形的面积公式推导过程。
我们要明白什么是平行四边形和三角形。
平行四边形就是两组对边分别平行的四边形,而三角形呢,就是有三条边的图形。
那么,它们有什么关系呢?别急,我们先来看看它们的面积是怎么计算的吧!1. 平行四边形的面积公式推导过程我们先来看平行四边形的面积公式。
假设我们有一个平行四边形ABCD,其中AB和CD是两条平行的边,BC和DA也是两条平行的边。
我们可以把这个平行四边形分成两个三角形:三角形ABC和三角形ADC。
这两个三角形的高都是垂直于底边的线段,而且它们的底边分别是AB和CD。
那么,这两个三角形的面积分别是什么呢?我们知道,三角形的面积等于底边乘以高的一半。
所以,三角形ABC的面积就是(AB * 高)/2,而三角形ADC的面积就是(CD * 高)/2。
那么,平行四边形ABCD的面积就是这两个三角形面积之和,即(AB * 高)/2 + (CD * 高)/2。
但是,我们发现这里有一个问题,既然AB和CD是平行的,那么它们的高也应该是相等的。
所以,我们可以把上面的公式简化为:平行四边形ABCD的面积 = AB * 高。
这就是平行四边形的面积公式。
2. 三角形的面积公式推导过程接下来,我们再来聊聊三角形的面积公式。
我们还是用上面的例子来说吧。
假设我们有一个三角形ABC,其中AB、AC和BC分别是三条边。
我们可以从顶点A作一条垂线到底边BC上,这样就把这个三角形分成了两个直角三角形:直角三角形ABD和直角三角形ACD。
这两个直角三角形的高都是从顶点A到底边的垂线段。
那么,这两个直角三角形的面积分别是什么呢?我们知道,直角三角形的面积等于底边乘以高的一半。
所以,直角三角形ABD的面积就是(BD * 高)/2,而直角三角形ACD的面积就是(CD * 高)/2。
那么,整个三角形ABC的面积就是这两个直角三角形面积之和,即(BD * 高)/2 + (CD * 高)/2。
平行四边形和三角形的面积公式推导过程

平行四边形和三角形的面积公式推导过程大家好,我今天要给大家讲解一下平行四边形和三角形的面积公式推导过程。
我们要知道什么是平行四边形和三角形。
平行四边形就是一个有四个角的四边形,它的对边是平行的。
而三角形就是一个有三个角的多边形,它的三个角之和是180度。
接下来,我们要分别推导出它们的面积公式。
我们来看平行四边形的面积公式。
我们知道,平行四边形可以分成两个相等的三角形,这两个三角形的底分别是平行四边形的两条相邻边,高分别是平行四边形的高。
那么,这两个三角形的面积之和就是平行四边形的面积。
所以,平行四边形的面积公式就是:平行四边形的面积= 2 × (底× 高) / 2这个公式告诉我们,只要知道一个平行四边形的底和高,就可以算出它的面积。
现在我们来看三角形的面积公式。
我们知道,三角形可以分成两个相等的梯形,这两个梯形的高分别是三角形的高,上底和下底分别是从顶点到对应底边的中点的线段。
那么,这两个梯形的面积之和就是三角形的面积。
所以,三角形的面积公式就是:三角形的面积 = (上底 + 下底) × 高 / 2这个公式告诉我们,只要知道一个三角形的底和高,就可以算出它的面积。
下面,我来给大家演示一下如何使用这两个公式来求解实际问题。
假设我们有一个平行四边形,它的底是10厘米,高是5厘米。
那么,我们可以用平行四边形的面积公式来求解它的面积:平行四边形的面积= 2 × (10 × 5) / 2 = 50平方厘米同样地,假设我们有一个三角形,它的底是8厘米,高是6厘米。
那么,我们可以用三角形的面积公式来求解它的面积:三角形的面积= (8 + 6) × 6 / 2 = 42平方厘米通过这两个例子,我们可以看出,无论是平行四边形还是三角形,只要知道它们的底和高,就可以轻松地求出它们的面积。
这就是平行四边形和三角形的面积公式推导过程。
希望大家能够理解并掌握这些知识。
平行四边形的三种面积公式

平行四边形的三种面积公式
(2)平行四边形的面积等于两组邻边的积乘以夹角的正弦值。
(3)平行四边形周长:四边之和。
周长c=2(a+b)。
平行四边形就是在同一个二维平面内,由两组平行线段共同组成的滑动图形,通常用
图形名称提四个顶点依次命名。
平行四边形的相对或相对的侧面具有相同的长度,并且其相反的角度是相等的,只有
一对平行边的四边形是梯形,其三维对应是平行六面体。
该图形的特点是对边平行且相等、容易变形。
【有关排序】
1、(1)平行四边形的面积公式:底×高(可运用割补法,推导方法如图);如用“h”表示高,“a”表示底,“s”表示平行四边形面积,则s平行四边形=a*h。
(2)平行四边形的面积等同于两组邻边的积除以夹角的正弦值;例如用“a”“b”
则表示两组邻边长,α则表示两边的夹角,“s”则表示平行四边形的面积,则s平行四
边形=ab*sinα。
2、平行四边形周长:四边之和。
可以二乘(底1+底2);如用“a”表示底1,“b”表示底2,“c平”表示平行四边形周长,则平行四边的周长c=2(a+b)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 探究平行四边形面积的计算公式,能运用公式解 决实际问题。 • 学会用猜想-验证-结论的方法来探究数学问题。
学过的几何图形有哪些?
长方形面积=长×宽
正方形面积=边长×边长
说一说:有关平行四边形的知识。
高
平行四边形特点: ①对边平行且相等 ②对角相等 ③相邻的角互补(即180°)
a=5分米
S=15平方分米
由S=ah得: h=S÷a =15÷5 =3(分米)
要在公路中间的一块平行四边形空地 上(见下图)种草坪。1平方米草坪的 价格是12元。种这片草坪需要多少元?
s = ah =8×12.5 =100(m 2 )
8m
12.5m
12×100=1200(元)
答:种这片草坪需要1200元。
底
? =
长=6m 宽=4m 底=6m 高=4m
用数方格的方法试一试!
怎样比较这两个花坛的大小呢?
(用数方格的方法算出这两个图形的面积。一个 方格表示1m2 ,不满一格都按半格计算。)
平行四边形 长方形
底 长
高 宽
面积
6m 4m 6m 4m
24m2
面积
观察表格的数据, 你发现了什么?
24m2
你猜想平行四边形的面积该 怎样计算呢?
拓展1.比较下列平行四边形的面积
高
底 结论: 等底等高的平行四边形面积 相等。
想一想:把一个长方形拉成一个平行四边形(如
图),它的面积( ),周长( )。
A、不变 B、变大 C、变小
7厘米
12厘 米
小结: 1.平行四边形的面积=底×高 2.猜想——验证——结论 3.转化思想.
2.平行四边形的高 和长方形的宽 相等.
因 为: 长 方 形 的 面 积 = 长
所以:平行四边形的面积就= 底
× ×
宽 高
做 一做 一个平行四边形停车位的底是5米,高是2.5米,
这个停车位的面积是多少平方米?
S=ah=5×2.5=12.5(平方米)
高 底
答:这个停车位的面积是 12.5平方米
计算出下面平行四边形的高?
( 长 方 形 的 宽 )
原来平行四边形的底 原 来 平 行 四 边 形 的 高
(长方形的长) ( 长 方 形 的 宽 )
长方形的面积 = 长
×
宽
平行四边形的面积 =
底
×
高
讨论:平行四边形有多少条高? 沿任意一条高剪开,然后将右 半部分向左或将左半部分 向右平移都能得到一 个长方形吗?
高 底
• 验证:割补法
1、通过剪拼的方法,你把平行四边形转化成了什么图 形?(只剪一刀) 2、转化后的图形与原来的平行四边形相比,你发现它 们之间有什么联系?(面积、底、高) 3、说说你最后得出了什么结论?
抓住数学灵魂 转化思想贯穿全课
原来平行四边形的底
(长方形的长)
原 来 平 行 四 边 形 的 高
宽
长
高
底 长
宽
想一想:
宽
高
底
长
转化后的长方形和原平行四边形比, ( 形状 )变了,( 面积 )不变。
长方形的长和宽与平行四边形的底和高 有什么关系?
求平行四边形的面积,
必须知道什么?
底
和
高
底边上的 高
平行四边形的面积计算
高
平行四边形 宽
变成了
长方形
底
长
1.平行四边形的 底 和长方形的 长相等.
