六年级奥数应用题浓度问题

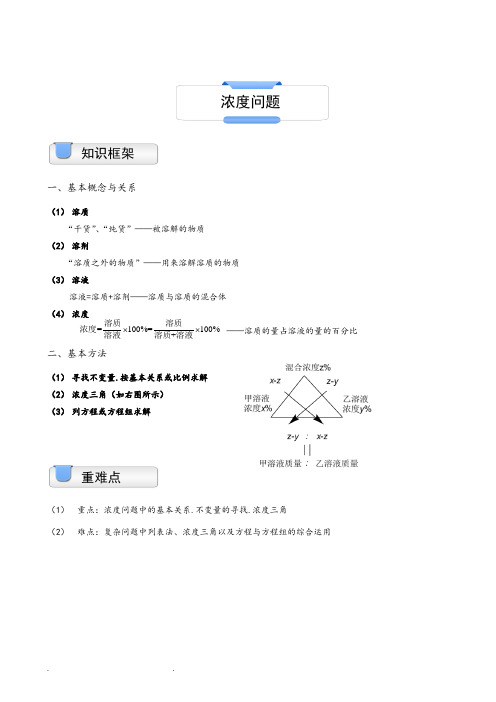
一、基本概念与关系

（1） 溶质

“干货”、“纯货”——被溶解的物质

（2） 溶剂 “溶质之外的物质”——用来溶解溶质的物质

（3） 溶液 溶液=溶质+溶剂——溶质与溶质的混合体

（4） 浓度

——溶质的量占溶液的量的百分比

二、基本方法

（1） 寻找不变量，按基本关系或比例求解

（2） 浓度三角（如右图所示）

知识框架 浓度问题 =100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液

::乙溶液质量甲溶液质量z-y x-z z-y

x-z 乙溶液浓度y %

浓度x %混合浓度z%

（3）列方程或方程组求解

重难点

（1）重点：浓度问题中的基本关系，不变量的寻找，浓度三角

（2）难点：复杂问题中列表法、浓度三角以及方程与方程组的综合运用

例题精讲

一、抓住不变量和浓度基本关系解决问题

【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到，那么这种溶液的食盐浓度为多少？

【巩固】一容器内有浓度为25％的糖水，若再加入20千克水，则糖水的浓度变为15％，问这个容器内原来含有糖多少千克？

【例 2】浓度为20％的糖水40克，要把它变成浓度为40％的糖水，需加多少克糖？【巩固】浓度为10％，重量为80克的糖水中，加入多少克水就能得到浓度为8％的糖水？

【例 3】买来蘑菇10千克，含水量为99％，晾晒一会儿后，含水量为98％，问蒸发掉多少水份？

【巩固】1000千克葡萄含水率为96.5%，一周后含水率降为96%，这些葡萄的质量减少了千克.

【例 4】将含农药30%的药液，加入一定量的水以后，药液含药24%，如果再加入同样多的水，药液含药的百分比是________．

【巩固】一杯盐水，第一次加入一定量的水后，盐水的含盐百分比变为15%；第二次又加入同样多的水，盐水的含盐百分比变为12%，第三次再加入同样多的水，盐水的含盐百分比将变为_______%.

二、通过浓度三角解决浓度和实际生活中的配比问题

【例 5】有浓度为20％的盐水300克，要配制成40％的盐水，需加入浓度为70％的盐水多少克？

【巩固】将75％的酒精溶液32克稀释成浓度为40％的稀酒精，需加入水多少克？【例 6】瓶中装有浓度为15%的酒精溶液1000克，现在又分别倒入100克和400克的A、B两种酒精溶液，瓶中的浓度变成了14%．已知A种酒精溶液浓度是B种酒精溶

液浓度的2倍，那么A种酒精溶液的浓度是百分之几？

【巩固】有两种溶液，甲溶液的酒精浓度为15%，盐浓度为10%，乙溶液中的酒精浓度为45%，盐浓度为5%．现在有甲溶液1千克，那么需要多少千克乙溶液，将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍？

【例 7】甲瓶中酒精的浓度为70%，乙瓶中酒精的浓度为60%，两瓶酒精混合后的浓度是66%．如果两瓶酒精各用去5升后再混合，则混合后的浓度是66.25%．问原来甲、

乙两瓶酒精分别有多少升？

【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%．如果每种酒精都多取20克，混合后纯酒精的含量变为45%．求甲、乙两种酒精原有多少克？

【例 8】甲种酒精纯酒精含量为72%，乙种酒精纯酒精含量为58%，混合后纯酒精含量为62%．如果每种酒精取的数量比原来都多取15升，混合后纯酒精含量为

63.25%．第一次混合时，甲、乙两种酒精均取了多少升？

【巩固】甲、乙两只装满硫酸溶液的容器，甲容器中装有浓度为8%的硫酸溶液600千克，乙容器中装有浓度为40%的硫酸溶液400千克．均取多少千克分别放入对方容器中，才能使这两个容器中的硫酸溶液的浓度一样？

【例 9】某班有学生48人，女生占全班的37.5％，后来又转来女生若干人，这时人数恰好是占全班人数的40％，问转来几名女生？

【巩固】小明到商店买红、黑两种笔共66支．红笔每支定价5元，黑笔每支定价9元．由于买的数量较多，商店就给予优惠，红笔按定价85%付钱，黑笔按定价80%付钱，

如果他付的钱比按定价少付了18%，那么他买了红笔多少支？

【例 10】有两包糖，第一包糖由奶糖和水果糖组成，其中1

4

为奶糖；第二包糖由酥糖和

水果糖组成，其中1

5

为酥糖．将两包糖混合后，水果糖占78%，那么奶糖与酥糖的

比例是________.

【巩固】某商品76件，出售给33位顾客，每位顾客最多买三件．如果买一件按原定价，买两件降价10%，买三件降价20%，最后结算，平均每件恰好按原定价的85%出售．那么买三件的顾客有多少人？

三、综合运用各种方法解决多溶液、多次配比问题

【例 11】甲容器中有纯酒精11升，乙容器中有水15升，第一次将甲容器中的一部分纯酒精倒入乙容器，使酒精与水混合。第二次将乙容器中的混合液倒入甲容器。这

样甲容器中纯酒精含量为62.5％，乙容器中纯酒精的含量为40％。那么第二次从乙容器中倒入甲容器的混合液是多少升？

【巩固】 甲容器中有纯酒精11立方分米，乙容器中有水15立方分米．第一次将甲容器

中的一部分纯酒精倒入乙容器，使酒精与水混合；第二次将乙容器中的一部分混合液倒入甲容器．这样甲容器中的纯酒精含量为62.5%，乙容器中的纯酒精含量为25%．那么，第二次从乙容器倒入甲容器的混合液是多少立方分米？

【例 12】 甲种酒精纯酒精含量为72%，乙种酒精纯酒精含量为58%，混合后纯酒精含量

为62%．如果每种酒精取的数量比原来都多取15升，混合后纯酒精含量为63.25%．第一次混合时，甲、乙两种酒精各取了多少升？

【巩固】 若干升含盐70%的溶液与若干升含盐58%的溶液混合后得到含盐62%的溶液。如

果每种溶液各多取15升，混合后就得到含盐63.25%的溶液，那么第一次混合时含盐70%的溶液取了

升.

【例 13】 林林倒满一杯纯牛奶，第一次喝了

31，然后加入豆浆，将杯子斟满并搅拌均匀，第二次，林林又喝了3

1，继续用豆浆将杯子斟满并搅拌均匀，重复上述过程，那么第四次后，林林共喝了一杯纯牛奶总量的 .（用分数表示）

【巩固】 有甲、乙、丙三个容器，容量为毫升．甲容器有浓度为40%的盐水400毫升；

乙容器中有清水400 毫升；丙容器中有浓度为20%的盐水400毫升．先把甲、丙两容器中的盐水各一半倒入乙容器搅匀后，再把乙容器中的盐水200毫升倒入甲容器，200毫升倒入丙容器．这时甲、乙、丙容器中盐水的浓度各是多少？