人教版五年级数学下册表面积
人教版数学五年级下册-三2《长方体和正方体的表面积》教案设计
上课解决方案教案设计教学目标知识与技能1.理解表面积的意义，初步掌握长方体和正方体表面积的计算方法。
2.能运用长方体、正方体表面积的计算方法解决生活中的实际问题。
过程与方法经历长方体、正方体表面积计算方法的探究过程，培养学生的分析能力和空间想象能力。
情感、态度与价值观在探究过程中，获得积极的情感体验，感受数学与生活的密切联系，培养学生应用数学的意识。
重点难点重点：理解长方体、正方体表面积的意义，掌握长方体、正方体表面积的计算方法。
难点：运用长方体、正方体表面积的计算方法解决实际问题。
课前准备教师准备PPT课件学生准备长方体、正方体纸盒剪刀教学过程板块一趣味成语，引入新课e师：同学们，老师这里有一则有趣的成语故事画面，你能找到这则成语，并解释吗？预设生1：金玉其外，败絮其中。
生2：外表像金、像玉，里面却是破棉絮。
比喻外表很华丽，而里面一团糟。
师：我们要做一个有内涵、有真才实学的人，不要外表看着一表人才，实则不学无术。
任何事物都有自己的外表，像我们学过的长方体或正方体也有外表，就是表面，长方体或正方体外表的面积的大小，我们就叫作长方体或正方体的表面积。
（板书课题：长方体和正方体的表面积）学生拿出自己的长方体或正方体纸盒，触摸外表，体会表面积。
师：看一看，长方体或正方体的表面是由几个面组成的？生：长方体和正方体的表面都是由6个面组成的。
师：什么叫作长方体或正方体的表面积？生：长方体或正方体6个面的总面积，叫作它的表面积。
操作指导先通过猜成语，在游戏中让学生初步体会什么是外表，引起学生的兴趣，再通过触摸长方体或正方体纸盒，建立长方体或正方体表面积的概念，引起学生研究长方体或正方体表面积的想法，同时引发学生的讨论，使学生主动思考，寻求解决问题的方法。
板块二演示操作，形成表象活动1小组合作，引发思考手工操作，尝试总结求表面积的方法。
出示合作提纲：（1）在长方体纸盒棱的边缘标上长、宽、高。
（2）把准备好的长方体纸盒沿一些棱剪开并展开，分别用“上、下、前、后、左、右”标明6个面，观察并思考以下问题：长方体哪些面的面积相等？长方体每个面的长和宽与长方体的长、宽、高有什么关系？（3）长方体每个面的面积怎么求？小组合作标长、宽、高，剪开长方体纸盒并展开，找到每个面的长和宽。
人教版五年级下册数学第三单元第5课 长方体和正方体的表面积(3)
第五课长方体和正方体的表面积（3）投我以桃，报之以李。
《诗经·大雅·抑》原创不容易，【关注】店铺，不迷路！原创不容易，为有更多动力，请【关注、关注、关注】，谢谢！新竹高于旧竹枝，全凭老干为扶持。
出自郑燮的《新竹》开心回顾1．正方体的6个面的面积之和叫做正方体的表面积．正方体每个面的面积= ×棱长正方体的表面积=棱长×棱长×，用字母表示为：S=6a2．【答案】棱长、6【解析】试题分析：正方体的表面积是6个面的总面积，正方体的6个面都相等，正方体的每个面都是正方形，每个面的面积=棱长×棱长，正方体的表面积=棱长×棱长×6，解答即可．解：正方体的6个面的面积之和叫做正方体的表面积．正方体每个面的面积=棱长×棱长，正方体的表面积=棱长×棱长×6，用字母表示为：S=6a2．故答案为：棱长、6．2．长方体6个面的面积之和叫做长方体的表面积．长方体上面或下面的面积= ×宽长方体的表面积=长×宽×2+长×高×2+宽×高×2．【答案】长【解析】试题分析：根据长方体的特征：6个面都是长方形（特殊情况有两个相对的面是正方形），相对的面的面积相等．长方体的表面积是指它的6个面的总面积．解答即可．解：长方体6个面的面积之和叫做长方体的表面积．长方体上面或下面的面积=长×宽，长方体的表面积=长×宽×2+长×高×2+宽×高×2，公式：s=2（ab+a] 课前导学学习目标：1.使学生熟练地掌握长方体和正方体表面积的计算方法,能灵活地解决一些实际问题。
2.培养学生分析、解决问题的能力,以及良好的思维品质。
知识讲解：[来源:学_科_网Z_X_X_K]【例题】用12个拼长方体，画出草图。
人教版数学五年级下册 长方体、正方体表面积的计算
没有底面，这个布罩就只有5个面，要求的就是 前、后、左、右面和上面这5个面的面积和。
0.75×1.6×2＋0.5×1.6×2＋0.75×0.5 0.75 m
＝2.4＋1.6＋0.375
＝4.375（m²） 答：至少需要用4.375 m²的布料。
1 求下列图形的表面积。
5cm 8cm
4cm 7cm
6×5×2＋ 6×4 ×2 ＋ 5×4 ×2
＝30×2＋24×2＋20×2 ＝148（dm²）
我这样算！
上、下每个面， 长 6 dm ，宽 5 dm，面积是 (6×5)dm2；
前、后每个面， 长 6 dm ，宽 4 dm，面积是 (6×4)dm2； 左、右每个面， 长 5 dm ，宽 4 dm，面积是(5×4)dm2。
这节课有什么收获呢？
长方体、正方体表面积计算： 长方体表面积＝(长×宽十长×高十宽×高)×2 正方体表面积＝棱长×棱长×6
用三个长5dm、宽4dm、高2dm的长方体拼成一个大 长方体，大长方体的表面积最大是多少？最小呢？
2×3 = 6 （ dm ） （5×4 + 5×6 + 4×6）×2
= （20 + 30 + 24）×2
6 dm 5 dm 4 dm
= 74×2
= 148（dm ²） 答：大长方体的表面积最小是 148dm²。
5dm 5dm
5dm
3 一个无盖的长方体金鱼缸，长是9分米，宽是6 分米，高是7分米。做这样的一个鱼缸需要多大 面积的玻璃？ 长方体的上9面×不6＋用(算9×，7＋6×7)×2 即长×宽＝算5一4＋次1即0可5×。2
＝54＋210
＝264（平方分米）
答：做这样的一个鱼缸需要264平方分米的玻璃。
五年级下册数学课堂课件--长方体与正方体表面积人教版(38张)
宽、高
已知，利用长方体的表面积公式即可求解
【解答】解：5×5×2+5×20×4 =50+400 =450（平方厘米） 答：做一只这样的纸盒至少需要硬纸450平方厘米．
17
走进生活，解决问题
一个长方体的长是宽的3倍，高是宽的2倍．已知这个长方体的长是 12厘米，求长方体的表面积．
18
走进生活，解决问题
（2）要使割后的表面积之和最小，沿平行6×8面切割，这 样表面积 就会增加两个原来长方体的最小的面，由此把原来 长方体的表面积 加上增加的面积就是切割后的长方体表面积之 25
切把一拼个问长16题厘米，宽6厘米，高8厘米的大长方体切成两个小长方
体，这两个小长方体的表面积的和最大是多少平方厘米，最小是 多少？
22
走进生活，解决问题
有个长方体铁盒，它的高与宽相等．如果长缩短15厘米，就成为表面积 是54平方厘米的正方体，这个长方体盒的宽是长的几分之几？
【解答】解：54÷6=9（平方厘米），
因为3×3=9平方厘米，
所以正方体的棱长为3厘米，
则长方体的长为3+15=18厘米，宽为3厘米，
3÷18=16．
答：这个长方体盒的宽是长的1．
走进生活，解决问题
纸盒厂加工一批装工具的纸盒，盒长20厘米，宽和高都是5厘米， 做一只这样的纸盒至少需要硬纸多少平方厘米？
16
走进生活，解决问题
纸盒厂加工一批装工具的纸盒，盒长20厘米，宽和高都是5厘米，做一只这样 的纸盒至少需要硬纸多少平方厘米？
【分析】求制作这样一个纸盒积，实际上是求纸盒的表面积，长方体的长、
2.一个正方体的木料，它的底面积是10cm ，把它横截成4段，表面积增加 （ ）。
五年级下册数学课件-第三单元2.长方体和正方体的表面积第2课时长方体和正方体表面积的计算人教版
三、梯度练习
简单练习
将下面3本词典包成一包，你能想出几种包装方案？每种包装方案至
少用多大的包装纸？哪种包装方案最省包装纸？
第四页，编辑于星期日：二十三点 三十九分。
①3本词典摞在一起：
此时需要包装成一个长为10cm、宽为4×3＝
12（cm）、高为15cm的长方体，需要包装纸为：（10×12＋10×15＋
二、探究新知
一个正方体墨水盒，棱长6.5cm。制作这个墨水盒至少需 要多少平方厘米的硬纸板？
求至少用多少平方厘米 的硬纸板，就是要求什 么?自己试一试！
6.5×6.5×6 ＝42.25×6 ＝253.5（cm2）
答：制作这个墨水盒至少需要253.5cm2的硬纸板。
第三页，编辑于星期日：二十三点 三十九分。
是 平方厘米。 292
3. 一个正方体的棱长之和为48分米，这个正方体的表面积是
平方分米。
96
4. 一个正方体的棱长扩大为原来的3倍，表面积扩大为原来的 倍。
9
第六页，编辑于星期日：二十三点 三十九分。
拓展练习
一个长方体的木料，长是3分米，宽是2分米，厚是1分米
，现在从这块木料上截去一个尽可能大的正方体木块，剩下的 因为：900cm2＜1260cm2＜1340cm2，故3本词典摞在一起包装最省包装纸。
第十页，编辑于星期日：二十三点 三十九分。
谢谢!
第十一页，编辑于星期日：二十三点 三十九分。
10×45＋4×45）×2＝1340（cm2）
因为：900cm2＜1260cm2＜1340cm2，故3本词典摞在一起包装最省包装纸。
第五页，编辑于星期日：二十三点 三十九分。
中等练习
想一想，填一填。
人教版数学五年级下册《长方体和正方体的表面积》教案
人教版数学五年级下册《长方体和正方体的表面积》教案一、教学目标•知识与能力：掌握长方体和正方体的表面积计算方法，能够灵活运用公式解决相关问题。
•过程与方法：培养学生观察问题、分析问题、解决问题的能力，培养学生数学思维。
•情感态度与价值观：培养学生正确的学习态度，激发学生学习数学的兴趣，提高学生的自信心。
二、教学重点与难点1. 教学重点•掌握长方体和正方体的表面积的概念。
•掌握长方体和正方体的表面积计算方法。
2. 教学难点•理解长方体和正方体的表面积计算方法，学会灵活运用。
三、教学准备•教材：人教版数学五年级下册《长方体和正方体的表面积》教材。
•工具：教学板书、长方体和正方体的模型。
四、教学过程第一步：导入教师可通过问题启动学生思维，引出长方体和正方体的表面积概念。
例如：“如果我们想知道一个长方体或正方体的表面有多大，应该怎么计算呢？”第二步：提出问题教师出示一个长方体和一个正方体的模型，提出如下问题：1.长方体的表面积如何计算？2.正方体的表面积如何计算？第三步：学习长方体表面积计算方法1.介绍长方体的概念。
2.利用模型演示如何计算长方体的表面积。
3.讲解长方体表面积的计算公式，并通过例题进行讲解。
第四步：学习正方体表面积计算方法1.介绍正方体的概念。
2.利用模型演示如何计算正方体的表面积。
3.讲解正方体表面积的计算公式，并通过例题进行讲解。
第五步：练习与巩固1.学生自主练习长方体和正方体的表面积计算方法。
2.教师抽查部分学生回答，并给予指导和帮助。
第六步：课堂总结教师对本节课内容进行总结，概括长方体和正方体的表面积计算方法，强调重点难点。
五、课堂小结通过本节课的学习，学生掌握了长方体和正方体的表面积计算方法，提高了数学思维能力和解决问题的能力。
六、课后作业1.完成课本上相关练习题。
2.拓展思维：除了长方体和正方体，还有哪些几何体的表面积你能计算出来？七、教学反思在教学过程中，要注意引导学生主动思考问题、积极参与讨论，激发学生的学习兴趣，提高学生的学习效果。
数学人教版五年级下册长、正方体公式集合
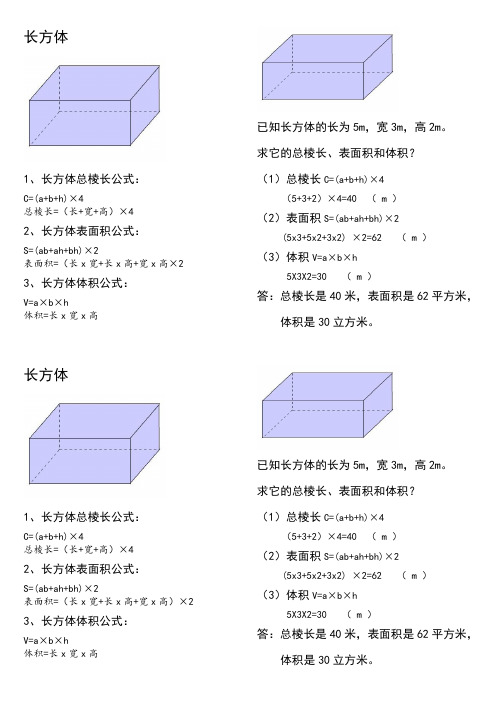
1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高×2 3、长方体体积公式：V=a×b×h体积=长x宽x高长方体1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高）×2 3、长方体体积公式：V=a×b×h体积=长x宽x高已知长方体的长为5m，宽3m，高2m。
求它的总棱长、表面积和体积？（1）总棱长C=(a+b+h)×4（5+3+2）×4=40 （ m ）（2）表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 （ m ）（3）体积V=a×b×h5X3X2=30 （ m ）答：总棱长是40米，表面积是62平方米，体积是30立方米。
已知长方体的长为5m，宽3m，高2m。
求它的总棱长、表面积和体积？（1）总棱长C=(a+b+h)×4（5+3+2）×4=40 （ m ）（2）表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 （ m ）（3）体积V=a×b×h5X3X2=30 （ m ）答：总棱长是40米，表面积是62平方米，体积是30立方米。
1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长正方体1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长已知正方体的棱长为5m。
数学人教版新版五年级下册 《长方体和正方体的表面积》教学设计
数学人教版新版五年级下册《长方体和正方体的表面积》教学设计删除明显有问题的段落。
教学目标：1.通过动手操作，建立表面积的概念，经历探索长方体和正方体表面积计算方法的过程。
2.掌握长方体和正方体表面积计算方法，能正确地计算长方体和正方体的表面积。
过程与方法：1.在探索研究中建立初步的空间观念，发展初步的推理能力。
2.培养学生的动手操作能力和合作探究问题的惯。
情感态度与价值观：1.体验数学问题的探索性，感受数学思考过程的合理性，并从中体验数学活动充满着探索与创造。
2.渗透具体问题具体分析的唯物主义观点，培养学生主动探索的欲望和创新精神。
教学重、难点：教学重点：长方体表面积计算的基本思路和方法。
教学难点：根据长方体的长、宽、高，确定长方体每个面的长、宽是多少。
教学方法：通过小组自主合作探究等方法。
教学准备：教具：多媒体课件。
课时安排：1课时教学流程：一、复旧知、引入新课1.温故知新（课件出示练）1）长方体有（）个面，每个面都是（）形，特殊情况有两个相对的面是（），相对的面完全（），相对的棱长度（）。
2）正方体有(。
)个面，每个面都（）。
3）长方体有（）组相对的面。
2.谈话导入：通过前面知识的研究，我们已经能够求出长方体或正方体中任何一个面的面积，下面请同学们看这个礼品盒，（出示课件）我们怎样才能求出这个礼品盒包装纸的面积是多少呢？这就是这节课我们要来探究的新知识。
板书课题：《长方体和正方体的表面积》【设计意图】：通过回顾旧知、使学生知道本节知识与前面知识点的联系，从而激发学生的好奇心，为学新知识奠定了浓厚的研究兴趣。
二、相互合作、研究新知一）明确表面积概念。
1.课件出示长方体。
1）理解“表面”？（露在外面的面。
）2）提问：正方体和长方体都有几个面？2.明确表面积：长方体或正方体6个面的总面积，叫做它的表面积。
二）、探索长方体、正方体的表面积计算方法教师导语：同学们，我们通过探究，合作交流的方式，学会了这么多关于长方体或正方体的知识，又知道了表面积。
五年级下册数学_2长方体与正方体的表面积与体积人教版(39张)精品课件
（2）30×20×3÷6=1800÷6=300（分钟） 答：200分钟后水深能到达2m，300分钟后能将池塘注满水． 这个游泳池可装多少立方米的水？ 5平方分米= （）平方厘米 先求出假山和水一共的体积：46×25×28=32200（立方厘米） 拼成的这个长方体的表面积比原来16个小正方体的表面积之和少了多少平方分米？
（2）同理，用池塘的容积，除以每分钟注水量6立方米，即可求 出注水的时 间．
29
真题训练营
2.小明家门前有一个长30m，宽20m，深3m的池塘，现在要养鱼，需 要往池塘注水，如果每分钟能注水6m3，那么多少分钟后水深能到达 2m，多少分钟后能将池塘注满水？ 解：（1）30×20×2÷6=1200÷6=200（分钟）
没第？三关---实物5实0验×班25×2=2500（立方米）
6
旧识回顾
在一个长60cm,宽30cm的水箱中放入两个大小一样的西瓜（西瓜完 全浸没），水面上升了8cm,平均每个西瓜的体积是多少？
7
旧识回顾
在一个长60cm,宽30cm的水箱中放入两个大小一样的西瓜（西瓜完 全浸没），水面上升了8cm,平均每个西瓜的体积是多少？ 解：根据长方体体积公式：长×宽×高
14
3.长方体与正方体的体积之会旧友
什么是体积：物体所占空间的大小叫做物体的体积 计量体积要用体积单位：常用的体积单位有立方厘米(cm^3)、立 方分米(dm^3)、立方米(m^3)
15
3.制胜宝典
长方体体积=长×宽×高 (V=abh)或底面积×高(V=sh) 正方体体积=棱长×棱长×棱长(V=a*a*a) • 长方体或正方体底面的面积叫做底面积
人教版五年级数学下册《长方体和正方体的表面积(2)》课件
合作交流 探索新知
例1.制作尺寸如下图所示的长方体和正方体保温箱， 各需要多少平方分米的泡沫板？（单位：dm）
组内讨论：怎样计 算长方体的表面积？
想：长方体有6个面。 上、下每个面，长__6_d_m__，宽__5_d_m__，面积是_3_0__d_m_2_； 前、后每个面，长__6_d_m__，宽__4_d_m__，面积是_2_4__d_m_2_； 左、右每个面，长__5_d_m__，宽__4_d_m__，面积是_2_0__d_m_2_。
5 cm
（2） 哪些面的面积相等？
9
（高） cm（长）
4
cm（宽）
（3）
什么是长方体的表面积？
长方体6个面的总面积， 叫作它的表面积。
例1.制作尺寸如下图所示的长方体和正方体保温箱， 各需要多少平方分米的泡沫板？（单位：dm）
求需要多少平方 分米的泡沫板就 是要求什么？
求保温箱的表面积，就是计算保温箱6个面的面积之和。
一个面的面积： 5×5 ×6
棱长×棱长
=25×6
=150（平方分米）
答：制作正方体保温箱需要150平方分米的泡沫板。
小结
正方体表面积计算公式：
文字
棱长：表面积，a:棱长）
应用迁移 巩固提高
1.选一选。
（1）如图，一个长方体木箱，箱底和左侧面被虫蛀， 修理工需重新配置的两块木板的面积分别是（ B ）。
3 把一个棱长46 cm的正方体纸箱各面都贴上红纸，作为 捐款箱。（教材P25第6题）
（2）如果只在棱上粘贴一圈胶带纸，一卷4.5 m长的胶带纸 够用吗？ 正方体的棱长总和=棱长×12 46×12=552（cm） 552 cm=5.52 m 5.52 m＞4.5 m 答：一卷4.5 m长的胶带纸不够用。
人教版五年级下册数学第三单元《长方体和正方体》表面积
2、一个长方体的长是 15 厘米，宽是 12 厘米，高是 8 厘米，这 个长方体的表面积是平方厘米。
3、一个正方体的棱长是８分米，它的棱长总和是，表面积是。
4、用 60 厘米长的铁丝焊接成一个正方体的框架，这个正方体的 表面积是平方厘米。
5、用铁丝焊接成一个长 12 厘米，宽 10 厘米，高 5 厘米的长方 体的框架，至少需要铁丝厘米 6、一个长方体的长是 25 厘米，宽是 20 厘米，高是 18 厘米，的 面的长是厘米，宽是厘米，一个这样的面的面积是平方厘米；最小的 面长是厘米，宽是厘米，一个这样的面的面积是平方厘米。
7、一个长方体的长是 1 米 4 分米，宽是 5 分米，高是 5 分米， 这个长方体有个面是正方形，每个面的面积是平方分米；其余四个面 是长方形的面积大小，每个面的面积是平方分米；这个长方体的表面 积是平方分米。
8、一个长方体的金鱼缸，长是 8 分米，宽是 5 分米，高是 6 分 米，不小心前面的玻璃被打坏了，修理时配上的玻璃的面积是。
9、一个正方体的棱长总和是 72 厘米，它的一个面是边长厘米的 正方形，它的表面积是平方厘米。
二、应用题。
1、一个通风管的横截面是边长是 05 米的正方形，长 25 米。
如果用铁皮做这样的通风管 50 只，需要多少平方米的铁皮？ _____________________________________2、一个长方体的游泳池，长 20 米，宽 18 米，水深 25 米，如在 四壁和底面抹水泥，求抹水泥的面积是多少平方米？_____________________________________ 3、做一个长方体的浴缸无盖，长 8 分米，宽 4 分米，高 6 分米， 至少需要多少平方分米的玻璃？如果每平方分米玻璃 4 元钱，至少需 要多少钱买玻璃？ _____________________________________ 4、一个房间的长 6 米，宽 35 米，高 3 米，门窗面积是 8 平方米。
【新】五年级下册数学 人教版 长方体和正方体的表面积(知识点+试题)
长方体和正方体二、内容讲解：知识点一：长方体和正方体的特征(1)长方体：由6个长方形围成的立体图形。
(2)正方体：由6个完全相同的正方形围成的立体图形叫做正方体（也叫做立方体）。
它是一种特殊的长方体。
(3)两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
特征：①有几个面？面的位置和大小有什么关系？②有多少条棱？棱的位置、长短有什么关系？③有多少个顶点？例一：1、（a）图是（）体，它的6个面是（）形。
（b）图是（）体，它的6个面是（）形。
2、长方体有（）个面，（）条棱，（）个顶点。
相对的棱的长度（），相对的面完全（）。
3、正方体所有的面都（），（）条棱都（）。
4、长、宽、高相等的长方体叫做（）。
知识点二：长方体、正方体棱长的计算（1）各棱长之间的关系及棱长的计算方法长方体的棱长总和=（长+宽+高）×4 L=（a＋b＋h）×4 长=棱长总和÷4－宽－高a=L÷4－b－h宽=棱长总和÷4－长－高b=L÷4－a－h高=棱长总和÷4－长－宽h=L÷4－a－b正方体的棱长总和=棱长×12 L=a×12正方体的棱长=棱长总和÷12 a=L÷12例二：1、一个长方体的长8厘米，宽7厘米，高6厘米，棱长和是多少厘米？2、如果用一根长72厘米的铁丝做一个宽4厘米，高6厘米的长方体框架，长是多少厘米？知识点三：长方体、正方体的表面积表面积：长方体或正方体6个面的总面积，叫做它的表面积已知长、宽、高，求面积S=(ɑb+bc+ɑc)×2长方体的表面积= ( 长×宽+ 长×高+ 宽×高) × 2正方体的表面积=（长×宽）×6例三：1、一个长方体油箱，从里面量长是70厘米，宽是30厘米，高是85厘米，如果每升汽油重约0. 73千克，这个油箱最多能装多重的汽油？（一）已知棱长和求面积长方体棱长和=（长+宽+高）×4正方体棱长和=棱长×12例四：1、一个正方体框架是用一根长48分米的铁丝焊接成的，如果给这个正方体粘上一层塑料，至少需要多少平方分米的塑料？（二）已知长、宽、高的关系求面积例五：1、已知一个长方体的长是20分米，这个长方体的宽是长的4/5，高是宽的一半，求这个长方体的面积？2、一个长方体房间，长8米，宽比长短1/4，高比宽短1/3，这个房间的表面积是多少？（三）已知棱长和，求转换后图形面积例六：1、一根铁丝可以围成一个长6分米、宽4.5分米、高2.5分米长方体框架，现在想将其围成一个正方体，这个正方体的表面积是多少？（四）求面不全的长方体（正方体）表面积柱子：求四个面的面积，不算上下两面（长×宽）鱼缸：正面是玻璃，1、求其他五个面的面积，不算正面（长×高）2、前面的玻璃坏了，若求配上的玻璃面积，则只求正面的面积。
人教版五年级下册数学专题学习之第三模块 有关长方体、正方体的棱长和表面积问题
第三模块有关长方体、正方体的棱长和表面积问题【教法剖析】我们认识了长方体和正方体，知道它们都有6个面、12条棱，12条棱长的和是它们的棱长总和，长方体或正方体6个面面积的总和叫做长方体或正方体的表面积。
公式法：长方体的棱长总和=（长+宽+高）×4正方体的棱长总和=棱长×12长方体的表面积=（长×宽+长×高+宽×高）×2正方体的表面积=棱长×棱长×6经验判断法：在实际生活中，长方体或正方体的表面积的计算要根据具体的情况而定。
（1）计算6个面的总面积，如纸箱、油箱、茶叶盒、牛奶盒等。
（2）计算5个面的总面积，如洗衣机罩、水池、鱼缸、教室粉刷墙面、蚊帐等。
（3）计算4个面的总面积，通风管、大楼雨管、烟囱、食品盒商标纸等。
（4）表面积的变化要会分析：长方体或正方体被锯开后，一次会增加两个面；反之，两个相同的正方体或长方体拼在一起，一次会减少两个面。
【题例教案】例1 制作一个长5dm，宽3dm，高4dm的长方体灯笼框架，至少需要多少米长的竹条？【助教解读】这道题是已知长方体的长、宽、高，求长方体的棱长总和，直接运用公式：长方体的棱长=（长+宽+高）×4来进行解答。
长方体的棱长=（长+宽+高）×4=（5+3+4）×4=48（dm）=4.8(m)答：至少需要4.8米长的竹条。
【经验总结】解答这道题的关键是要知道长方体的长、宽、高或知道长、宽、高的和。
若求正方体的棱长总和只需要用棱长乘12即可。
例2 一个房间长6米，宽3.5米，高3米，门窗面积是8m2。
现在要把这个房子的四壁和顶面粉刷水泥，粉刷水泥的面积是多少平方米？【助教解读】求粉刷水泥的面积，实际是求房间的表面积，但是粉刷房子时，地面不用粉刷，也就是求5个面的面积，在运用公式计算时，长×宽不需要乘2，还要减去门窗的面积。
6×3.5+(6×3＋3.5×3)×2－8 ＝21＋57－8 ＝70（m2)答：粉刷水泥的面积是70平方米。
五年级下册数学课件3.2.1长方体和正方体的表面积 人教版 (共13张PPT)【完美版课件】
人教版 五年级下相对 ）的面面积相等；有（12 ）条棱， 相对的棱长度（相等 ）。
2、相交于一个顶点的三条棱的长度分别叫做长方体的（ 长 ）、 （
）、宽（ ）。高 如图：这个长方体的长是（8cm），宽是（5cm）， 高是（ 6cm）。 3、正方体有（ 6 ）个面，每个面都是（ 正方 ）形，
6cm 5cm
8cm
每个的面积都（ 相等 ），有（ 12 ）棱，它们的长度都（ 相等 ）。
4、思考长方体和正方体的展开图是怎样的？。
新知讲解
要沿着棱剪 开！
我展开了一个 长方体纸盒。
正方体展开 后是这样的。
把一个长方体或正方体的纸盒展开是什么形状呢？
新知讲解
把这个长方体的纸盒展开（如下图）
上 前右
左、右每个面的长=长方体的宽，宽=长方体的高； 正方体的展开图中
：每个面的边长=正方体的棱长
作业布置
1、完成书上第25页，第1、2题的作业。 2、探究生活中的长方体和正方体。
每个人都有潜在的能量，只是很容易被习惯所掩盖，被时间所迷离，被惰性所消磨。把命运寄托在自己身上，这是这个世界上最美妙的心思。为此努力，拼搏，不舍昼夜。每个人的内心都充 满了魔鬼，学会控制他。如果你还认为自己还年轻，还可以蹉跎岁月的话，你终将一事无成，老来叹息。在实现理想的路途中，必须排除一切干扰，特别是要看清那些美丽的诱惑。忍一时之 气，免百日之忧信心、毅力、勇气三者具备，则天下没有做不成的事改变自己是自救，影响别人是救人。当你感到无助的时候，还有一种坚实的力量可以依靠，那就是你自己。想过去是杂念， 想未来是妄想，最好把握当下时刻。幸福不在得到多，而在计较少。改变别人，不如先改变自己。一个人能走多远，要看他有谁同行；一个人有多优秀，要看他有谁指点；一个人有多成功， 要看他有谁相伴。同样的一瓶饮料，便利店里2块钱，五星饭店里60块，很多的时候，一个人的价值取决于所在的位置。忙碌是一种幸福，让我们没时间体会痛苦；奔波是一种快乐，让我们真 实地感受生活；疲惫是一种享受，让我们无暇空虚。10、我是世界上独一无二的，我一定会成功！成功者往往有个计划，而失败者往往有个托辞。成功者会说：“我帮你做点什么吧！而失败 者说：那不是我的事。成功三个条件：机会；自己渴望改变并非常努力；贵人相助亿万财富买不到一个好的观念；好的观念却能让你赚到亿万财富。一个讯息从地球这一端到另一端只需要 0.05秒，而一个观念从脑外传到脑里却需要一年，三年甚至十年。要改变命运，先改变观念。人生的成败往往就在于一念之差。鸟无翅膀不能飞，人无志气不成功。成功99%是心志，1%是能力。 一个人不成功是因为两个字——恐惧。一个会向别人学习的人就是一个要成功的人。人要是惧怕痛苦，惧怕种种疾病，惧怕不测的事情，惧怕生命的危险和死亡，他就什么也不能忍受了，人 格的完善是本，财富的确立是末。傲不可长，欲不可纵，乐不可极，志不可满。在人之上，要把人当人；在人之下，要把自己当人。锲而舍之，朽木不折；锲而不舍，金石可镂。真者，精诚 之至也，不精不诚，不能动人。我觉得坦途在前，人又何必因为一点小障碍而不走路呢？对时间的慷慨，成功不是将来才有的，而是从决定去做的那一刻起，持续累积而成。天下之事常成于 困约，而败于奢靡。企业家收获着梦想，又在播种着希望；原来一切辉煌只代表过去，未来永远空白。一个最困苦、最卑贱、最为命运所屈辱的人，只要还抱有希望，便无所怨惧。你生而有 翼，为何一生匍匐前进，形如蝼蚁世界上只有想不通的人，没有走不通的路。世上那有什么成功，那只是努力的另一个代名词罢了。所谓英雄，其实是指那些无论在什么环境下都能够生存下 去的人。微笑不用本钱，但能创造财富。赞美不用花钱，但能产生气力。分享不用过度，但能倍增快乐。微笑向阳，无畏悲伤。我们不知道的事情并不等于没发生，我们不了解的事情并不代 表不存在。我们渴望成功，首先要志在成功。我要让未来的自己为现在的自己感动。想哭就哭，想笑就笑，不要因为世界虚伪，你也变得虚伪了。小鸟眷恋春天，因为它懂得飞翔才是生命的 价值。笑对人生，能穿透迷雾；笑对人生，能坚持到底；笑对人生，能化解危机；笑对人生，能照亮黑暗。学在苦中求，艺在勤中练。不怕学问浅，就怕志气短。一个细节足以改变一生。一 切成就都缘于一个梦想和毫无根据的自信。永远不要嘲笑你的教师无知或者单调，因为有一天当你发现你用瞌睡来嘲弄教师实际上很愚蠢时，你在社会上已经碰了很多钉子了。幽默胜过直白， 话少胜过多言；坦率胜过伪装，自然胜过狡辩；心静何来多梦，苦索不如随缘。有一种落差是，你配不上自己的野心，也辜负了所受的苦难。最可怕的不是有人比你优秀，而是比你优秀的人 还比你更努力。最有希望的成功者，并不是才干出众的人而是那些最善利用每一时机去发掘开拓的人。昨天如影——记住你昨天的挫折和失败的教训；今天如画快乐和幸福的人生要靠你自己 去描绘；明天如梦——珍惜今天,选择好自己的目标，努力地为自己的明天去寻求和拼搏。不曾扬帆，何以至远方。不论你在什么时候开始，重要的是开始之后就不要轻言放弃。不去耕耘，不 去播种，再肥的沃土也长不出庄稼，不去奋斗，不去创造，再美的青春也结不出硕果。不要盘算太多，要顺其自然。该是你的终会得到。成大事不在于力量多少，而在能坚持多久。成为一个 成功者最重要的条件，就是每天精力充沛的努力工作，不虚掷光阴。从未跌倒算不得光彩，每次跌倒后能再战起来才是最大的荣耀。脆弱的心灵创伤太多，追求才是愈合你伤口最好的良药。 挫折经历的太少，所以总是把一些琐碎的小事看得很重。当你知道你不在是你的时候，你才是真正的你！漫无目的的生活就像出海航行而没有指南针。人生多一份感恩，就多一份美化。所有 的豪言都收起来，所有的呐喊都咽下去。成功六机握机当你握着两手沙子时，一定就拿不到地上那颗珍珠了。快乐在满足中求，烦恼多从欲中来。人若有志，万事可为。为明天做准备的最好 方法，就是要集中你所有的智慧，所有的热诚，把今天的事情做得尽善尽美。在茫茫沙漠，唯有前进时的脚步才是希望的象征。在我们了解什么是生命之前，我们已将它消磨了一半。这个世 界既不是有钱人的世界，也不是有权人的世界，它是有心人的世界。这个世界上任何奇迹的产生都是经过千辛万苦的努力而得的，首先承认自己的平凡，然后用千百倍的努力来弥补平凡。真 正的导者，其厉害之处不在于能指
人教版五年级下册数学长方体的表面积及表面积的变化课件
2、一个正方体木块的表面积是36cm2，把它沿着各面中的线切割成相 等的8个小正方体，这时表面积增加了多少平方厘米？
3、一个长方体，如果高增加了4cm，那么就变成一个正方体，这时表 面积比原来增加128cm2，原来长方体的表面积多少平方厘米？
4、一个正方体，如果高增加了2cm，那么就变成一个长方体，这时长 方体的表面积比原来正方体的表面积增加96cm2，原来正方体的表面积 多少平方厘米？
P26
8、一个玻璃鱼缸的形状是正方体，棱长3dm。制作这个鱼缸时至少 需要玻璃多少平方分米? (鱼缸的上面没有盖。)
P26
11、学校要粉刷新教室。已知教室的长是8m，宽是6m，高是3m，门
窗的面积是11.4m2。如果每平方米需要花4元涂料费，粉刷这个教室需
要花费多少钱？
一个长方体，它的长、宽、高分别是10dm、8dm、5dm，在它的上面 焊接另一个正方体，棱长是2dm，现在要在前后、左右面涂上黄色，其 它露出的面涂上蓝色，涂黄色、蓝色的面积各是多少？
长方体或正方体6个面的总面积，叫做它的表面积。
后h
h
aa
b
几何体外表面的面积之和就是它的表面积。
P25
4、光华街口装了一个新的长方体铁皮邮箱。长50cm，宽40cm， 高78cm，做这个邮箱至少需要多少平方厘米的铁皮？
一个长方体的饼干盒，长10 cm、宽6 cm、高12 cm。如果围着它 贴一圈商标纸(上下面不贴)，这张商标纸的面积至少多少平方厘米？
2、一个长方体木块被截成两个完全相同的正方体（如下图）。如果两 个正方体的棱长总和比原来长方体的棱长总和增加了24cm，那么原来 长方体的长是多少厘米？
3、一个三阶魔方被挖掉了一个小正方体后，剩下的图形与原图 形的表面积相比较有何变化？
(人教版)五年级数学下册 长方体和正方体的表面积和体积
（人教版）五年级数学下册长方体和正方体的表面积和体积（人教版）五年级数学下册长方体和正方体的表面积和体积班级姓名分数一、填空题。
1.一个长方体框架长8厘米，宽6厘米，高4厘米，做这个框架共要（）厘米铁丝，是求长方体（），在表面贴上塑料板，是求长方体（），在里面能盛（）升水是求（），这个盒子有（）立方米是求（）。
长方体的短就是6厘米，阔就是4厘米，低就是4厘米，它的棱长总和就是（）厘米，六个面中最小的面积就是（）平方厘米，表面积就是（）平方厘米，体积就是（）立方厘米，（）条棱成正比。
2.一瓶可乐的容积大约是230（）；一个雪糕的体积是20（）；一台冰箱的容积大约是180（）；一瓶眼药水约有12（）。
3.1立方分米的1个正方体可以分为（）个1立方厘米的小正方体，如果把这些大正方体排在一排，一共短（）分后米。
4.用长2厘米、宽1厘米、高1厘米的长方体木块拼成一个正方体，至少用（）个这样的长方体。
拼成的正方体的表面积是（）平方厘米。
5.搞一个长6分米，阔4分米，低1.5分米的抽屉，至少须要木板（）。
6．一根铁丝长36厘米，如果搞一个正方体框架，棱长就是（）厘米；如果搞一个低和阔都就是2厘米的长方体框架，短就是（）厘米。
7．一个长方体水池占地6平方米，他深1.5米，池内最多能容水（）升。
8．把一个棱长2分米的正方体，切成两个相等的长方体，表面积增加了（）。
9．至少（）个棱长2厘米的小正方体可以拼成一个大正方体。
10．一个长方体的长、阔、低各不断扩大了3倍，它的体积不断扩大了（）倍。
11．把5个棱长1厘米的小正方体拆成长方体，这个长方体的表面积就是（）。
12．一个长方体的玻璃缸，长4分米、宽3分米、高5分米，倒入水后量得水深3.5分米，倒入的水有（）升。
13.用两个长6厘米，阔3厘米，低1厘米的长方体拆成一个表面积尽可能大的正方体，这个拆成的长方体的表面积就是（）平方厘米。
14.一个长方体的体积是30立方厘米，长是5厘米，高是3厘米，宽是（）。
五年级数学下册长方体的表面积人教版ppt课件
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
左 左。
上
上
后 前
下下
右 右
前
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
1.6
2、这题求长方体几个面的面积。
5个面的面积
自己独立解答：
0.75 0.5
方法一：
（0.75×0.5＋0.75×1.6＋0.5×1.6）×2－0.75×0.5
方法二： 0.75×1.6×2＋0.5×1.6×2＋0.75×0.5
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
课前准备： 1. 任意一个长方体纸盒。 2. 一把剪刀。 3. 一支水彩笔。 4. 笔和练习本。
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
左
上
后后
右
下
前、后每个面 长＝长方体的长 宽＝长方体的高
前
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
左
上
后后
右
下
左、右每个面 长＝长方体的宽 宽＝长方体的高
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
长方体和正方体表面积的认识
教学目标：
1 ．通过观察操作，使学生建立长方体和正方体表面积的概念。
2 ．使学生初步学会长方体表面积的计算方法。
3 ．建立空间观念，培养学生学习几何知识的兴趣。
重点难点：建立表面积的概念，初步学会计算长方体的表面积。
教具准备：长方体、正方体纸盒，剪刀。
教学方法：演示法观察法练习法
教学过程：
（一）导入
投影出示练习。
1 ．说一说下列长方体的长、宽、高各是多少，再分别指出各长方体前面的长和宽，并口算前面的面积。
（单位：厘米）
学生算完后，指名回答，集体订正，还可以请同学说一说各长方体后面的面积是多少？
2 ．算一算。
同桌互相说出每个长方体各面的长和宽各是多少，算出各长方体左面的面积是多少。
（二）教学实施
1 ．学习长方体、正方体表面积的概念。
（1）请同学们拿出准备好的长方体纸盒，在上面分别标出“上”“下”前”“后”“左”“右”六个面，边观察边回答下面问题：长方体有几个面？(六个面）
每个面都是什么形状？长方体有哪些面的形状是完全相同的？（上面和下面、前面和后面、左面和右面）它们的面积怎么样？（相对的面的面积相等）有几组面积相等的长方形？（有三组）
请同学们沿长方体纸盒的前面和上面相交的棱剪开，得到下面左边这幅展开图。
（2）请同学们拿出准备好的正方体纸盒，分别标出“上”“下”“前”，“后”, “右”六个面，并回答下列问题。
正方体有几个面？每个面是什么形状？正方体有几组面积相等的正方形？
让学生分别沿着正方体的棱剪开，得到上面右边的正方体展开图。
（3）观察长方体展开图，看一看哪些面的面积相等，每个面的长和宽与长方体的长、宽、高有什么关系。
观察后，小组议一议。
引导学生总结长方体、正方体表面积的概念。
老师板书：长方体或正方体6 个面的总面积，叫做它的表面积。
2 ．学习长方体表面积的计算方法。
同学们知道了长方体、正方体表面积的含义，那么在日常生活和生产中，我们经常需要计算一些长方体或正方体的表面积。
现在我们就来学习长方体表面积的计算方法。
（1）老师板书教材第34 页的例1 。
做一个微波炉的包装箱（如下图），至少要用多少平方米的硬纸板？
（2）学生读题，理解题意。
（3）提问：
求至少要用多少平方米的硬纸板就是求什么？（就是要计算这个长方体的表面积）
先确定每个面的长和宽，再分别口算出每个面的面积。
最后把每个面的面积合起来就是这个长方体的表面积。
（4 ）尝试独立解答。
老师巡视，辅导学生。
（5 ）集体交流反馈。
老师根据学生解题思路，进行板书。
方法一：
长方体表面积＝6 个面的面积和
0.7×0.4+0.7×0.4+0.5×0.4+0.5×0.4+0.7×0.5+0.7×0.5
=0.28+0.28+0.2+0.35+0.35
=1.66 (m2)
方法二：
长方体表面积=上、下两面面积＋前、后两面面积＋左、右两面面积
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
=0.7+0.5+0.4
=1.66 (m2)
方法三：
长方体表面积=（上面面积十前面面积＋左面面积）× 2
(0.7×0.5+0.7×0.4+0.5×0.4）× 2
＝( o .35 + 0 .28 + 0.2 ) × 2
＝0.83 × 2
＝1 .66 (m2)
答：至少要用1 . 66 平方米的硬纸板。
（6 ）比较三种方法。
提问：上面三种计算方法有什么不同？
引导学生回顾三种计算方法的不同。
讨论：你认为哪种方法简便？
引导学生理解：第三种方法简便些。
（7 ）小结。
通过上面的计算，你认为求长方体表面积最关键的是找出什么？（是根据长方体的长、宽、高找出每个面的长和宽）
老师提示：在实际生活和生产中要结合实际情况灵活运用计算表面积的方法。
（三）思维训练
一个长方体，若长增加3 厘米，宽和高不变，则体积增加96 平方厘米；若宽减少5 厘米，长和高不变，则体积减少55 平方厘米；若高增加4厘米，长和宽不变，则体积增加68 平方厘米。
求原长方体的表面积
（四）课堂小结
这节课我们学习了什么知识？（长方体和正方体表面积的概念）
什么是长方体的表面积？( 6 个面的总面积叫长方体的表面积)计算长方体表面积的关键是根据长方体的长、宽、高确定每个面的长和宽。
作业布置：
板书设计：
课后反思：。