第3章 习题
物理初三第3章练习题

物理初三第3章练习题在物理学习的过程中,练习题是巩固和深化知识的重要方式。
第3章的练习题是进一步检验你对力的理解以及应用能力的机会。
本文将对第3章的练习题进行详细的解答,帮助你更好地掌握力的概念和相关计算方法。
1. 一个物体质量为10kg,受到一个20N的重力,地面对该物体的支持力大小是多少?解答:根据牛顿第三定律,该物体受到的地面支持力大小应该等于物体受到的重力大小,即20N。
2. 一个物体受到两个力的作用,一个力的大小为8N,方向向右,另一个力的大小为6N,方向向左,这两个力的合力大小是多少?合力的方向是什么?解答:根据力的合成原理,合力的大小等于两个力的代数和,即8N - 6N = 2N。
合力的方向取决于两个力的相对方向,即向右减去向左,所以合力的方向是向右。
3. 如果一个物体所受合力为零,这个物体是处于静止还是匀速直线运动?为什么?解答:如果一个物体所受合力为零,则根据牛顿第一定律,该物体将保持静止或匀速直线运动。
这是因为合力为零意味着物体所受的各个力相互平衡,在没有外力作用下,物体将不会改变其静止状态或匀速直线运动状态。
4. 一个力为5N的物体,受到一个摩擦力的作用,摩擦力的大小为3N,方向与物体运动的方向相反,该物体的加速度是多少?解答:根据牛顿第二定律,物体所受的合力等于物体的质量乘以加速度。
所以,5N - 3N = 2N的合力将导致物体产生加速度。
因此,该物体的加速度为2N/物体的质量。
5. 一个物体做斜抛运动,抛出的初速度大小为20m/s,抛射角度为30°,求物体的水平速度和垂直速度分量。
解答:物体的水平速度分量等于初速度乘以余弦值30°,即20m/s * cos30° = 17.3m/s。
物体的垂直速度分量等于初速度乘以正弦值30°,即20m/s * sin30° = 10m/s。
通过解答上述练习题,我们不仅巩固了力的概念和计算方法,还进一步加深了对牛顿运动定律的理解。
操作系统第3章习题带答案

第三章一、问答题1、用户级线程与内核级线程的区别是什么?2、PCB中包含哪些信息?进程状态属于哪类信息?3、什么是操作系统的内核?4、简述时间片轮转调度算法的基本思想。
5、某系统采用时间片轮转调度算法的处理机调度算法,某个时刻根据用户要求创建了一个进程P,进程P在其存在过程中依次经历了:进程调度选中了进程P 占用处理机运行,进程P运行中提出资源申请,要求增加内存使用量,没有得到;进程等待一段时间后得到内存;进程调度再次选中了进程P占用处理机运行;进程P的时间片到;一段时间后,进程P再次占用处理机;有紧急进程Q进入,系统停止进程P的运行,将处理机分配进程Q;进程Q运行完,进程调度再次选中了进程P占用处理机运行;进程P运行完。
请分析进程P在其整个生命过程中的状态变化。
进程调度选中了进程P占用处理机运行(就绪→运行),进程P运行中提出资源申请,要求增加内存使用量,没有得到(运行→阻塞);进程等待一段时间后得到内存(阻塞→就绪);进程调度再次选中了进程P占用处理机运行(就绪→运行);进程P的时间片到(运行→就绪);一段时间后,进程P再次占用处理机(就绪→运行);有紧急进程Q进入,系统停止进程P的运行,将处理机分配进程Q(运行→就绪);进程Q运行完,进程调度再次选中了进程P占用处理机运行(就绪→运行);进程P运行完。
请分析进程P在其整个生命过程中的状态变化。
6、试比较进程与程序的异同。
7、引起创建进程的事件通常有哪些?简述进程的创建过程。
8、简述进程的阻塞过程。
911、简述操作系统的三级调度。
12、为什么要了解进程间的家族关系?因为父进程和子进程之间是隶属关系,子进程可以继承使用父进程的资源;如果父进程被撤销,还应撤销其所有的子孙进程。
13、什么是进程?。
14、试比较进程和线程的区别。
15、简述进程的基本状态,画出其状态转换图。
二、计算题1、若程序Pa,Pb和Pc单独执行时间分别Ta,Tb和Tc,Ta=1小时,Tb=1.5小时,Tc=2小时,其中处理机工作时间分别为Ta=10分钟,Tb=15分钟,Tc=35分钟。
第三章习题

第三章习题(2)班级:______ 姓名:_________一、选择题(每小题有1~2个正确答案)1、下列各物质投入水中,因促进水的电离而使溶液呈酸性的是( ) A 、NaHSO 4B 、Na 3PO 4C 、CH 3COOHD 、Al 2(SO 4)32、物质的量浓度相同的三种盐NaX 、NaY 和NaZ 的溶液,其pH 值依次为8、9、10,则HX 、HY 、HZ 的酸性由强到弱的顺序是( )A 、HX 、HY 、HZB 、HZ 、HY 、HXC 、HX 、HZ 、HYD 、HY 、HZ 、HX3、将滴有甲基橙的醋酸钠饱和溶液加热,溶液的颜色是( ) A 、黄色不变B 、黄色变橙色C 、黄色变红色D 、橙色不变4、下列关于盐类水解的叙述中,错误的是( )A 、盐类水解是中和反应的逆反应B 、盐类水解过程是吸热过程C 、含有弱酸根盐的水溶液一定显碱性D 、盐溶液的酸碱性主要决定于形成盐的酸和碱的相对强弱5、下列各组离子中能在溶液中大量共存,且溶液呈碱性透明的是( ) A 、Na +、OH -、H 2PO 4-、NO 3- B 、AlO 2-、K +、CO 32-、Na + C 、Al 3+、Cl -、AlO 2-、Na +D 、Fe 2+、K +、H +、NO 3-6、用物质的量都是0.1mol 的CH 3COOH 和CH 3COONa 配制成1L 混合溶液,已知其中c(CH 3COO -)大于c(Na +)。
对该混合溶液的下列判断正确的是( )A 、c(H +)>c(OH -)B 、c(CH 3COOH)+c(CH 3COO -)=0.2mol/LC 、c(CH 3COOH)>c(CH 3COO -)D 、c(CH 3COO -)+c(OH -)=0.2mol/L7、100mLpH=11的氨水与100mLpH=3的盐酸相混合,所得的混合液( ) A 、显碱性B 、显酸性C 、显中性D 、不能确定其酸碱性8、物质的量浓度相同的下列溶液:①Na 2CO 3 ②NaHCO 3 ③H 2CO 3 ④(NH 4)2CO 3 ⑤NH 4HCO 3,按c(CO 32-)由小到大排列顺序正确的是( )A 、⑤<④<③<②<①B 、③<⑤<②<④<①C 、③<②<⑤<④<①D 、③<⑤<④<②<①9、为了使Na 2S 溶液中c(Na +)/c(S 2-)的比值变小,可加入的物质是( )A 、适量盐酸B 、适量NaOHC 、适量KOHD 、适量KHS10、将0.1mol 下列物质置于1L 水中充分搅拌后,溶液中阴离子数最多的是( ) A 、KCl B 、Mg(OH)2 C 、Na 2CO 3 D 、MgSO 4二、填空题:11、写出下列盐溶液水解的离子方程式。
七年级数学第三章练习题

12、一辆汽车以每小时60千米的速度由甲地驶 往乙地,当车行驶了4小时30分后,遇雨路滑,车不 能开快,这样将速度每小时减少20千米,结果比预 计时间晚45分钟到达乙地,求甲,乙两地的距离. 解:设甲乙两地相距x千米,则计划用时 x/60 小时,实际用时 【4.5+x-(4.5*60)/(60-20)】小时。 依题有: (4.5*60)/(60-20)-x/60=3/4 解得:x=360 答:甲乙两地相距360千米.
甲的年龄/岁 现在 如甲所说 如乙所说 x 2x-61 61 乙的年龄/岁 X-(61-x)=2x-61 4 x 年龄差 61-x 2x-65 61-x
• •
• 因为,年龄差恒定不变,所以· ,2x-65=61-x • 解得:x=42 2x-61=23 • 答:甲现年42岁,乙现年23岁。
4.甲对乙说:"当我是你现在的年龄,你才4岁."乙对甲 说:"当我是你现在的年龄时,你将61岁."问甲,乙现在 的年龄各是多少?
3.在下列方程中,解是x=2的方程是( x 1 2 0 A. 3x+6=0 B. 4 2 C. 3 x 2 D. 5-3x=1 4.当x=2时,代数式ax-2x的值为4, 当x=-2时,这个代数式的值为( A.-8 B.-4 C.-2 )
)
D.8
• 5.如果x=2 是方程 2x+m-4=0的解,那么 的 值是( ) • A.-8 B.0 C.2 D.8 • 6.若x=a是方程4x+3a=-7的解,则a的值 为( ) • A.7 B.-7 C.1 D.-1
2、
赵刚 期末考试语文、数学、外语
的成绩分别为三个连续偶数, 其和为270 ,则数学成绩为多少? 解:设数学成绩为x分,则语文、 外语分别为(x-2)分、(x+2)分。 (x+2)+x+(x-2)=270 解得:x=90. 答:赵刚的数学成绩为90分。
第3章作业参考答案

λ2l
l!
e− λ2 ,
l = 0,1,2,"
P( X + Y = n) = ∑ P{ X = k}P{Y = n − k}
k =0
=∑
k =0
n
λ1
k
k!
e −λ1
λ2
n−k
(n − k )!
e −λ2 =
e −( λ1+λ2 ) n λ1 λ2 e −( λ1+λ2 ) n k k n−k e −( λ1+λ2 ) n ! = ∑ ∑ Cn λ1 λ2 = n! (λ1 + λ2 )n n! k =0 k! (n − k )! n! k =0
18. 设随机变量 X 和 Y 的联合概率密度为
λ1k
e
−λ1
λ2n−k
e−λ2
⎛ λ2 ⎞ ⎜ ⎜λ +λ ⎟ ⎟ ⎝ 1 2⎠
n−k
f ( x, y ) =
1 − 2 (x2 + y2 ) e , ( x, y ) ∈ R 2 2π
1
计算概率 P{− 2 < X + Y < 2 2} 。 解:
19. 随机变量 X 与 Y 相互独立,X 服从参数为 λ 的指数分布,Y~U(0, h), 求 X+Y 的概率密 度。 解:
20. 一射手向某个靶子射击,设靶心为坐标原点,弹着点坐标(X,Y)服从二维正态分布 N(0,1;0,1;0). 求弹着点与靶心的距离 Z 的概率密度函数。 解: (X,Y)的联合概率密度为
f ( x, y ) =
1 − 2(x2 + y2 ) e , ( x, y ) ∈ R 2 2π
1
弹着点与靶心的距离 Z 的分布函数为
03第三章结缔组织习题

03第三章结缔组织习题第3章结缔组织一、选择题(一)A型题A1型题1.疏松结缔组织中的纤维和基质是由下列哪个细胞分泌的?A.成纤维细胞B.巨噬细胞C.浆细胞D.肥大细胞E.脂肪细胞2.与过敏反应有关的细胞是:A.成纤维细胞B.巨噬细胞C.浆细胞D.肥大细胞E.未分化的间充质细胞3.蛋白多糖亚单位的主干是:A.硫酸肝素B.硫酸角质素C.硫酸软骨素D.透明质酸E.纤维黏连蛋白4.免疫球蛋白是以下哪种细胞分泌的?A.成纤维细胞B.巨噬细胞C.浆细胞D.肥大细胞E.未分化的间充质细胞5.形成分子筛结构的是:A.蛋白多糖B.纤维黏连蛋白C.组织液D.弹性蛋白E.网状纤维6.具有抗原提呈作用的细胞是:A.成纤维细胞B.巨噬细胞C.浆细胞D.肥大细胞E.未分化的间充质细胞7.不规则致密结缔组织的纤维成分是:A.成纤维细胞B.巨噬细胞C.浆细胞D.肥大细胞E.未分化的间充质细胞9.胞质内含有嗜碱性颗粒,颗粒内含组胺和肝素的细胞是:A.成纤维细胞B.巨噬细胞C.浆细胞D.肥大细胞E.未分化的间充质细胞10.能产生胶原纤维中的胶原蛋白的细胞是:A.成纤维细胞B.浆细胞C.肥大细胞D.单核细胞E.巨噬细胞11.浆细胞胞质呈嗜碱性是因为含有丰富的:A.滑面内质网B.粗面内质网C.高尔基复合体D.线粒体E.溶酶体12.结缔组织中能分泌肝素的细胞是:A..成纤维细胞B.浆细胞C.肥大细胞D.未分化的间充质细胞E.巨噬细胞13.电镜下可见周期性横纹的结构是:A.神经原纤维B.胶原原纤维C.平滑肌纤维D.神经纤维E.弹性纤维14.疏松结缔组织基质的生物大分子是:A.蛋白多糖和纤维黏连蛋白B.透明质酸C.蛋白质D.硫酸肝素E.糖蛋白15.疏松结缔组织中具有防御屏障作用的结构是:A.组织液B.基质C.弹性纤维D.网状纤维E.胶原纤维16.组织细胞是指:A.成纤维细胞B.浆细胞C.巨噬细胞D.肥大细胞E.未分化的间充质细胞17.具有嗜银性的纤维是:A.胶原纤维B.胶原原纤维C.弹性纤维D.网状纤维E.微原纤维18.血清中不存在的成分是:A.白蛋白B.球蛋白C.纤维蛋白原D.脂蛋白E.激素19.呈双凹圆盘状的成分是:A.红细胞B.血小板C.单核细胞D.淋巴细胞E.中性粒细胞17.无核也无细胞器的细胞是:A.血小板B.红细胞C.网织红细胞D.中性粒细胞E.嗜酸性粒细胞20.网织红细胞的中的细网状结构是:A.粗面内质网B.滑面内质网C.核糖体D.线粒体E.高尔基复合体21.核呈分叶状且分叶数目与细胞年龄相关的细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞22.数量最多的白细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞23.主要以吞噬细菌为主的白细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞24.参与过敏反应的白细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞25.胞质内的颗粒中内含组胺和肝素的细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞26.颗粒内含有组胺酶和芳基硫酸酯酶等的细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞27.体积最大的白细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞26.与肥大细胞功能相似的白细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞28.人的血型是由下面哪个细胞决定的?A.红细胞B.血小板C.网织红细胞D.淋巴细胞E.单核细胞29.颗粒内含溶菌酶、吞噬素的白细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞30.关于中性粒细胞的特点,以下哪项是正确的?A.是数量最少的白细胞B.胞质内的颗粒含有组胺和肝素C.胞质内含有大量的特殊颗粒和少量的嗜天青颗粒D.在过敏性疾病和寄生虫感染时增多E.细胞核呈圆形31.关于嗜酸性粒细胞的特点,以下哪项是正确的?A.数量最多B.胞质中含特殊颗粒和嗜天青颗粒C.急性感染性炎症时候增多D.核多分2叶E.颗粒内含组胺、肝素等32参与凝血和止血的成分是:A.红细胞B.血小板C.白蛋白D.中性粒细胞E.单核细胞33.血小板是:A.有核无细胞器的成分B.有核有细胞器的成分C.无核无细胞器的成分D.无核有细胞器的成分E.富含血红蛋白的成分34.红骨髓的主要成分是:A.脂肪组织B.造血干细胞C.造血组织和血窦D.基质细胞E.造血祖细胞35.血小板透明区主要有:A.微丝和微管B.血小板颗粒C.开放小管系统D.溶酶体E.致密小管系统36.单核细胞内的嗜天青颗粒是:A.线粒体B.溶酶体C.高尔基复合体D.核糖体E.微体37.颗粒内可见长方形或方形结晶体的是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞238.红细胞的形态是:A.双凸圆盘状B.双凹圆盘状C.圆球状D.圆盘状E.不规则形39.具有抗寄生虫和抗过敏作用的细胞是:A.中性粒细胞B.嗜酸性粒细胞C.嗜碱性粒细胞D.单核细胞E.淋巴细胞40.中性粒细胞的核分叶状,以()居多:A.1~2叶B.2~3叶C.3~4叶D.4~5叶E.5~6叶41.人的血细胞最早发生在:A.卵黄囊的血岛B.肝C.骨髓D.脾脏E.心脏42.中性粒细胞的中性颗粒内含:A.肝素和组胺B.吞噬素和溶菌酶C.白三烯和组胺D.组胺酶和芳基硫酸酯酶E.过氧化物酶和酸性磷酸酶43.嗜碱性粒细胞的嗜碱性颗粒内含有的物质:A.嗜酸性粒细胞趋化因子B.组胺酶C.白三烯D.溶菌酶E.吞噬素44.嗜酸性粒细胞的嗜酸性颗粒中含有的物质:A.溶菌酶B.吞噬素C.芳基硫酸酯酶D.嗜酸性粒细胞趋化因子E.白三烯42.软骨中部的软骨细胞的形态是:A.扁圆形B.圆形或椭圆型C.扁椭圆型D.矮柱状E.梭形43.软骨周边的软骨细胞的形态是:A.扁圆形B.圆形或椭圆型C.扁椭圆型D.矮柱状E.梭形44.软骨的主要区别是:A.分布部位不同B.基质成分不同C.软骨膜结构不同D.纤维种类不同E.软骨细胞结构不同45.软骨囊是指:A.软骨表面覆盖的致密结缔组织B.软骨细胞周围的纤维C.软骨陷窝周围的纤维D.软骨陷窝周围的基质E.软骨细胞周围的腔隙46.透明软骨内的纤维特点是:A.大量平行或交织排列的胶原纤维束B.大量交织排列的弹性纤维C.大量交织排列的胶原纤维D.大量交织排列的胶原原纤维E.大量平行排列的弹性纤维47.软骨细胞在基质中所在的腔隙称:A.骨陷窝B.软骨陷窝C.软骨囊D.软骨膜E.软骨基质48.弹性软骨内的纤维特点是:A.大量平行或交织排列的胶原纤维束B.大量交织排列的弹性纤维C.大量交织排列的胶原纤维D.大量交织排列的胶原原纤维E.大量平行排列的弹性纤维49.纤维软骨内纤维特点是:A.大量平行或交织排列的胶原纤维束B.大量交织排列的弹性纤维C.大量交织排列的胶原纤维D.大量交织排列的胶原原纤维E.大量平行排列的弹性纤维50.对软骨细胞起到保护和营养作用的是:A.软骨囊B.软骨膜C.软骨陷窝D.纤维E.基质51.HE染色切片中不能分辨纤维是由于:A.基质内不含纤维B.纤维为嗜银性C.纤维量太少D.纤维为细小的胶原原纤维,折光性与基质接近E.基质量太多52.骨基质是指:A.蛋白多糖B.胶原纤维、基质和骨盐C.羟基磷灰石结晶D.有机成分E.无机成分53.骨基质中最多的是:A.蛋白多糖B.骨盐C.胶原纤维D.基质E.水354.骨祖细胞的形态是:A.梭形B.椭圆形C.圆形D.不规则形E.矮柱状55.分布在骨质内的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞56.成骨细胞的形态是:A.梭形B.椭圆形C.圆形D.不规则形E.矮柱状57.成骨细胞胞质呈嗜碱性是因为:A.有大量的滑面内质网B.有大量的粗面内质网C.有大量溶酶体D.有大量线粒体E.有大量基质小泡58.合成和分泌类骨质的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞59.骨干内与骨干长轴垂直走行的是:A.中央管B.穿通管C.骨小管D.骨陷窝E.间骨板60.具有溶解骨盐和分解骨质有机成分的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞59.骨干密质骨的主要结构是:A.外环骨板B.内环骨板C.骨单位D.间骨板E.骨小梁60.光镜下有皱褶缘的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞61.不规则的平行骨板是指:A.外环骨板B.内环骨板C.骨单位D.间骨板E.骨小梁62.电镜下胞质内以溶酶体和线粒体为主的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞63.具有干细胞性质的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞64.成骨细胞的形态是:A.梭形B.椭圆形C.圆形D.不规则形E.矮柱状65.相邻骨小管内的骨细胞之间的细胞连接是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞67.穿通纤维属于:A.胶原原纤维B.胶原纤维C.嗜银纤维D.网状纤维E.弹性纤维68..骨单位中可见:A.中央管B.穿通管C.骨小管D.骨陷窝E.间骨板69.骨细胞的形态是:A立方形B.矮柱状C.梭形D.不规则形E.扁圆形70.相邻成骨细胞以以下哪种方式连接?:A.紧密连接B.中间连接C.桥粒D.半桥粒E.缝隙连接71.具有吞噬功能的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞72.穿通管在骨表面的开口称:A.骨小管B.滋养孔C.骨陷窝D.骨小梁E.横小管73.长骨骨髓腔面的结构是:4A.外环骨板B.内环骨板C.松质骨D.哈弗斯形态E.间骨板74.可释放基质小泡的细胞是:A.骨祖细胞B.破骨细胞C.骨细胞D.成骨细胞E.软骨细胞76.纤维软骨中的纤维是:A.胶原原纤维B.胶原纤维.C.弹性纤维D.网状纤维E.微原纤维77.骨板的组成是:A..平行排列的胶原纤维和骨盐由基质黏合在一起B.平行排列的细胞和骨盐由基质黏合在一起C.交叉排列的胶原纤维和骨盐由基质黏合在一起D.平行排列的胶原纤维和细胞由骨盐黏合在一起E.平行排列的细胞和基质由胶原纤维黏合在一起79.软骨囊的位置在:A.软骨细胞周围B.软骨陷窝周围C.软骨膜周围D.软骨周边E.软骨中部80.骨基质的纤维成分是;A.胶原原纤维B.胶原纤维.C.弹性纤维D.网状纤维E.微原纤维81.透明软骨中的纤维是:A.胶原原纤维B.胶原纤维.C.弹性纤维D.网状纤维E.微原纤维82.纤维软骨中的纤维是:A.胶原原纤维B.胶原纤维.C.弹性纤维D.网状纤维E.肌原纤维83.软骨囊形成的原因是含有较多的:A.透明质酸B.硫酸软骨素C.硫酸角质素D.胶原纤维E.纤维黏连蛋白A2型题1.以下哪种细胞胞质内不包含有大量的粗面内质网和高尔基复合体?A.浆细胞B.成纤维细胞C.软骨细胞D.骨祖细胞E.成骨细胞2.结缔组织的功能不包括:A.支持B.营养C.保护D.吸收E.连接3.固有结缔组织不包括:A.疏松结缔组织B.致密结缔组织C.脂肪组织D.网状组织E.淋巴组织4.成纤维细胞的结构特点不包括:A.有突起B.形态不规则C.胞质嗜碱性D.胞质内大量溶酶体和线粒体5.浆细胞的结构特点不包括:A.圆形或椭圆形B.核圆形偏于一侧C.核染色质呈车轮状D.胞质嗜碱性E.胞质内大量圆形的膜包颗粒6.巨噬细胞的特点不包括:A.可为不规则形B.胞质嗜碱性C.胞质内大量溶酶体D.表面由皱褶或突起E.具有分泌功能7.不参与构成分子筛结构的是:A.透明质酸B.硫酸肝素C.蛋白质D.纤维黏连蛋白E.硫酸角质素8.成纤维细胞不分泌:A.胶原蛋白B.原纤维蛋白C.弹性蛋白D.纤维黏连蛋白E.免疫球蛋白9.巨噬细胞功能不包括:A.趋化性B.吞噬作用C.抗原提呈作用D.分泌功能E.参与过敏反应10.基质中的蛋白多糖成分不包括:A.硫酸软骨素B.硫酸角质素C.透明质酸D.硫酸肝素E.纤维黏连蛋白11.血清内不含有:5。
第3章 习题解答 哈工大习题册
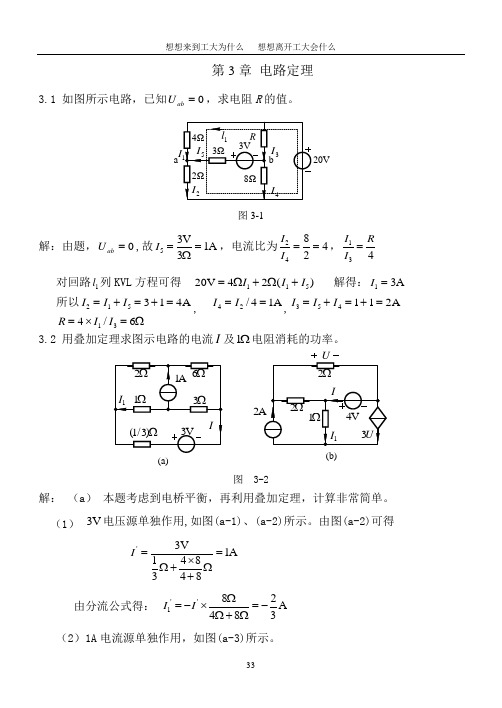
第3章 电路定理3.1 如图所示电路,已知0=ab U ,求电阻R 的值。
a图3-1解:由题,0=ab U ,故53V1A 3I ==Ω,电流比为24842I I ==,134I R I =对回路1l 列KVL 方程可得 11520V 42()I I I =Ω+Ω+ 解得:13AI =所以215314A I I I =+=+=, 42/41A I I ==,354112A I I I =+=+=134/6R I I =⨯=Ω3.2 用叠加定理求图示电路的电流I 及1Ω电阻消耗的功率。
(a)(b)2图 3-2解: (a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1) 3V 电压源单独作用,如图(a-1)、(a-2)所示。
由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得: ''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
考虑到电桥平衡,0I ''=,133(1A)A 134I ''=-⨯=-+ (3)叠加:1A I I I '''=+=,11117/12A I I I '''=+=-2111 2.007WP I Ω=⨯=(a-1)(a-2)(a-3)(b )(1)4V 电压源单独作用,如图(b-1)所示。
24V 2V 22U Ω'=⨯=Ω+Ω,136A I U ''=-=-,125A I I I '''=+=- (2)2A 电流源单独作用,如图(b-2)所示。
'2I '(b-1)(b-2)222A 2V 22U Ω⨯Ω''=⨯=Ω+Ω,22/21A I U ''''== 对节点②列KCL 方程得1234A I U ''''=-=-对节点③列KCL 方程得235A I I U ''''''=-=- (3) 叠加 '"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=注释:不能用各独立源单独作用时电阻消耗的功率之和来计算电阻在电路中消耗的功率。
第三章例题习题

作业1 试推导方程 (
∂U ∂p )T = T ( )V − p ∂V ∂T
式中,T,V为独立变量
2。设氯在27 ℃ 、0.1MPa下的焓、熵为零,求227 ℃ 、10MPa下氯的 焓、熵值,已知氯在理想气体状态下的定压摩尔热容为 Cp*=31.696+10.144×10-3T-4.038×10-6T2 J/mol .K 3. 试用普遍化方法计算丙烷气体从378K、0.507MPa变到463K、 2.535MPa时过程的焓变、熵变。 已知Cp*=22.99+0.1775T 4. 有一贮缸,盛有处于平衡态的液氨、气氨共5Kg,若气氨的体积占 总体积的五分之三,缸内压力为10atm,该压力下有关参数如下表, 求缸内物质总焓,若节流到3atm,节流后气氨为多少千克?
T/ ℃ Cp/J.g-1.K-1 0 2.151 50 2.351 100 2.548 150 2.732 200 2.900
例3 有人用A,B两股蒸汽通过绝热混和得到0.5MPa的饱和蒸汽。其中A股 为XA=0.98,压力0.5MPa,流量1.0Kg/s 的湿蒸汽,B股为473.15K, 0.5MPa的过热蒸汽,求B股流量
有机化学例题与习题会计基础第三章习题财务管理第三章习题浮力典型例题双代号网络图例题财经法规第三章习题排列组合例题决策树例题数学建模例题错位相减法例题
第三章 例题 例1 估算93℃,2.026MPa下,1mol 乙烷的体积、内能、焓和熵。设 0.1013MPa,-18 ℃时乙烷;239.304×10-3T-73.358×10-6T2 例2 利用R-K方程计算p1=0.1013MPa,T1=0 ℃,压缩到p2= 2.026MPa,T2=200 ℃时,1mol甲烷的焓变。已知甲烷在0.1013MPa时 Cp数据如下表:
第三章习题参考答案

第三章习题参考答案一、填空题1、指令格式是由操作码和操作数所组成,也可能仅由操作码组成。
2、若用传送指令访问MCS-51的程序存储器,它的操作码助记符应为MOVC 。
3、若用传送指令访问MCS-51的片内数据存储器,它的操作码助记符应为MOV 。
4、若访问MCS-51的片外数据存储器,它的操作码助记符应为MOVX 。
5、累加器(A)=80H,执行完指令ADD A,#83H后,进位位C= 1 。
6、执行ANL A,#0FH指令后,累加器A的高4位= 0000 。
7、JZ rel的操作码地址为1000H,rel=20H,它的转移目的地址为1022H 。
8、JBC 00H,rel 操作码的地址为2000H,rel=70H,它的转移目的地址为2073H 。
9、累加器(A)=7EH,(20H)= #04H,MCS-51执行完ADD A,20H指令后PSW.0= 0 。
10、MOV PSW,#10H是将MCS-51的工作寄存器置为第 2 组。
11、指令LCALL 37B0H,首地址在2000H,所完成的操作是2003H 入栈,37B0H →PC。
12、MOVX A,@DPTR源操作数寻址方式为寄存器间接寻址。
13、ORL A,#0F0H是将A的高4位置1,而低4位保持不变。
14、SJMP rel的指令操作码地址为0050H,rel=65H,那么它的转移目标地址为 00B7H 。
15、设DPTR=2000H,(A)=80H,则MOVC A,@A+DPTR的操作数的实际地址为2080H 。
16、MOV C,20H源寻址方式为位寻址。
17、在直接寻址方式中,只能使用8 位二进制数作为直接地址,因此其寻址对象只限于片内RAM 。
18、在寄存器间接寻址方式中,其“间接”体现在指令中寄存器的内容不是操作数,而是操作数的地址。
19、在变址寻址方式中,以 A 作变址寄存器,以PC 或DPTR 作基址寄存器。
20、假定累加器A中的内容为30H,执行指令1000H:MOVC A,@A+PC后,把程序存储器1031H 单元的内容送入累加器A中。
第三章习题与思考题参考答案

习题与思考题3-8 按要求写出相应的指令。
(1)把寄存器R6的内容送到累加器A中。
(2)把外部RAM 1000H单元的内容传送到内部RAM 30H单元中。
(3)清除内部RAM 3FH 单元的高4位。
(4)使累加器A的最低位置1。
(5)清除进位位。
(6)使ACC.4和ACC.5置1。
(7)把外部ROM 2000H单元中的内容送到内部RAM的20H单元中。
(8)把外部ROM 2000H单元中的内容送到外部RAM的3000H单元中。
答案:(1)MOV A,R6(2)MOV DPTR,#1000HMOVX A,@DPTRMOV R0,#30HMOV @R0,A(3)ANL 3FH,#0FH(4)ORL A,#01H(5)CLR C(6)ORL A,#30H(7)CLR AMOV DPTR,#2000HMOVC A,@A+DPTRMOV 20H,A(8)CLR AMOV DPTR,#2000HMOVC A,@A+DPTRMOV DPTR,#3000HMOVX @DPTR,A3-10 编写程序段完成如下要求。
(1)将寄存器R0中的内容乘以10(积小于256)。
(2)将片内RAM 30H单元开始的15个字节的数据传送到片外RAM 3000H开始的单元中。
(3)将片外RAM 2000H开始的5个字节的数据传送到片内RAM 20H开始的单元中。
(4)有10个字节的二进制数存放在片内RAM以40H开始的单元内,编程找出其中的最大值并存于内部50H单元中。
(5)将片外RAM空间2000H~200AH中的数据的高4位变零,低4位不变,原址存放。
(6)将外部RAM 2040H单元的内容与3040H单元的内容互换。
答案:(1) MOV B,#0AHMOV A,R0MUL ABMOV R0,A(2) ORG 0000HMOV R0,#30HMOV DPTR,#3000HMOV R7,#0FHLOOP: MOV A,@R0MOVX @DPRT,AINC R0INC DPTRDJNZ R7,LOOPSJMP $END(3) MOV DPTR,#2000HMOV R0,#20HMOV R7,#05HLOOP: MOVX A,@DPTRMOV @R0,AINC R0INC DPTRDJNZ R7,LOOPEND(4) ORG 0000HMOV A,40H;A寄存器放最大值,且初始化最大值(默认第一个数)MOV R3,#09H;比较次数MOV R0,#41HSTART: CJNE A,@R0,LOOPLOOP: JNC LOOP1;如果比A小,则跳转到LOOP1MOV A,@R0;如果比A大,则更新A的值LOOP1: INC R0DJNZ R3 STARTMOV 50H,ASJMP $END(5) MOV DPTR,#20000HMOV R1,#0BHLOOP: MOVX A,@DPTRANL A,#0FHMOVX @DPTR,AINC DPTRDJNZ R1,LOOPSJMP $(6) MOV DPTR,#2040HMOVX A,@DPTRMOV R0,#20HMOV @R0,AMOV DPTR,#3040HMOVX A,@DPTRXCH @R0,AMOVX @DPTR AMOV A,@R0MOV DPTR,#2040HMOVX @DPTR,A3-15 设有一带符号的十六位数以补码形式存放在R2、R3寄存器中,试编制求其原码的程序。
第三章习题答案

习(A )1. 将两封信随机地往编号为Ⅰ,Ⅱ, Ⅲ, Ⅳ 的4个邮筒内投,Y X ,分别表示第Ⅰ个和第Ⅱ个邮筒内信的数目,写出),(Y X 的概率分布.解 ),(Y X 可能的取值为)0,2(),1,1(),0,1(),2,0(),1,0(),0,0(.25.016422}0,0{42=====Y X P ,25.016422}1,0{412==⋅===C Y X P ,0625.016121}2,0{4=====Y X P , 25.016422}0,1{412==⋅===C Y X P ,125.01622}1,1{412=====C Y X P ,0625.016121}0,2{4=====Y X P . 2. 袋中装有标号为3,2,2,1的4个球,从中任取一个而且不再放回,然后再从袋中任取一球,以Y X ,分别记为第一次,第二次取到球的号码,求),(Y X 的概率分布. 解 ),(Y X 可能的取值是)2,3(),1,3(),3,2(),2,2(),1,2(),3,1(),2,1(.61}2,1{2412====A A Y X P ,1211}3,1{24====A Y X P , 61}1,2{2412====A A Y X P61}2,2{2412====A A Y X P ,61}3,2{2412====A A Y X P ,1211}1,3{24====A Y X P , 61}2,3{2412====A A Y X P .3. 袋内有四张卡片,分别写有数字4,3,2,1,每次从中任取一张,不放回地抽取两次,记Y X ,分别表示两次取到的卡片上数字的最小值和最大值,求),(Y X 的概率分布及X 与Y 的边缘概率分布. 解 ),(Y X 可以取为)4,3(,),3,1(),2,1( .事件}2,1{==Y X 是两个互不相容事件"第一次取到数字1且第二次取到数字2"与"第一次取到数字2且第二次取到数字1"的和,其概率为6/1,类似地可以计算出其他的ij p 的值(见下表).4⋅i p26161 63 061 61 j p ⋅61 62 634. 一个袋中有个球,其中有红球个,白球个,黑球个,不放回地抽取两次,每次一个,记X 表示两次中取到的红球数目,Y 表示取到的白球数目,求),(Y X 的概率分布及X 与Y 的边缘概率分布. 解 显然),(Y X 的全部取值为)0,2(,),2,0(),1,0( .455}1,0{21015====C C Y X P , 类似地可以计算出其他的ij p 的值(见下表).2⋅i p0 04510 4515 454456456 j p ⋅4510 4525 4510⎪⎩⎪⎨⎧=.,2,,1,,0次取到黑球第次取到白球第次取到红球第i i i X i 2,1=i ,求二维随机变量),(21X X 的概率分布,计算两次取到的球颜色相同的概率.解 易见),(21X X 的全部可能取值为)1,2(,),1,0(),0,0( .应用乘法公式 }|{}{},{i X j Y P j X P j Y i X P ====== 不难计算出ij p 的全部值(见下表):2904 905 2904 905 045}1,1{}0,0{}{212121===+====X X P X X P X X P . 6. 第4题中袋内球的组成及抽取次数不变,但是改为有放回抽取,求第5题中定义的二维随机变量),(21X X 的概率分布.解 ),(21X X 的取值为)2,2(,),1,0(),0,0( .且}{}{},{2121j X P i X P j X i X P =====,因此,),(21X X 的联合概率分布为下表所示:2 04.0 05.0 204.005.001.07. 将3个球随机地放入四个盒子,记i X 表示第i 个盒子内球的个数,2,1=i ,求随机变量1X 与2X 的联合概率分布及关于2X 的边缘概率分布. 解 ),(21X X 的取值为)0,3(,),1,0(),0,0( .64842}0,0{3321====X X P ,641242}0,1{}1,0{32132121=⋅======C X X P X X P , 6464}0,2{}2,0{312232121=======C C X X P X X P , 64124}1,1{312121321====C C C X X P , 6434}1,2{}2,1{3132121=======C X X P X X P ,64141}0,3{}3,0{32121=======X X P X X P , 列成联合分布表如下,表中最下一行为2X 的边缘分布j p j X P ⋅==}{2,3,2,1,0=j .23646 641 643 02 646 643 03641 0j p ⋅6427 6427 649 641 8. 将个球随机地放入四个盒子,设表示第一个盒子内球的个数,表示有球的盒子个数,求二维随机变量),(Y X 的概率分布.解 ),(1Y X 的取值为)2,2(),3,1(),2,1(),3,0(),2,0(),1,0(.6434}1,0{313====C Y X P ,类似地可以依次计算出ij p 的值(见下表):3643646 03641 00 9. 求第题中在条件下关于的条件概率分布.解 166}1,1{}1,0{}1{===+====Y X P Y X P Y P .3216/616/4}1{}1,0{}1|0{========Y P Y X P Y X P ,3116/616/2}1{}1,1{}1|1{========Y P Y X P Y X P .10. 某射手在射击中,每次击中目标的概率为)10(<<p p ,射击进行到第二次击中目标为止.i X 表示第i 次击中目标时所进行的射击次数)2,1(=i .求1X 和2X 的联合概率分布以及它们的条件概率分布.解 ),(21X X 可以取),(j i ,1-≤j i , ,3,2=j .2221},{-====j ij q p j X i X P p , ,3,2=j )1(p q -=.11)1(}|{222221-=-====--⋅j q p j q p p p j X i X P j j j ij)1,,2,1(-=j i . 112212}|{----⋅=====i j i j i ijpq pqq p p p i X j X P ),2,1( ++=i i j . 11. 已知随机变量X 与Y 的联合概率分布为1.01.02.0 完成下表,使之成为在条件下随机变量的条件概率分布表.Y1 23 — p — 4.0— 解 5.01.02.02.0}0{=++==X P ,4.05.02.0}0{}1,0{}0|1{========X P Y X P X Y P ,2.05.01.0}0{}2,0{}0|2{========X P Y X P X Y P ,所以有Y 1232 p4.04.02.012. 设二维随机变量),(Y X 的概率分布由下表给出,求X 在0=Y 的条件下的条件概率分布: 1.005.01.0 22.0 1.02.0解 2.01.005.005.0}0{=++==Y P ,25.02.005.0}0{}0,0{}0|0{========Y P Y X P Y X P ,25.02.005.0}0{}0,1{}0|1{========Y P Y X P Y X P ,5.02.01.0}0{}0,2{}0|2{========Y P Y X P Y X P .13. 设随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤=.,0,10,10,4),(其他y x xy y x f求条件概率密度)|(|y x f Y X 及)|(|x y f X Y . 解 X 与Y 的边际概率密度)(x f X 与)(y f Y 分别为⎪⎩⎪⎨⎧≤≤=⎰.,0,104)(10其他x xydy x f X⎩⎨⎧≤≤=.,0,102其他x x ⎪⎩⎪⎨⎧≤≤=⎰.,0,104)(10其他y xydx y f Y⎩⎨⎧≤≤=.,0,102其他y y ⎩⎨⎧≤≤==.0102)(),()|(|其他x x y f y x f y x f Y Y X ⎩⎨⎧≤≤==.0102)(),()|(|其他y y x f y x f x y f X X Y 14. 设二维连续随机变量),(Y X 的概率密度为⎩⎨⎧<<<<=.,0,0,10,3),(其他x y x x y x f试求条件概率密度)|(|x y f X Y . 解 X 的边际概率密度)(x f X 为⎪⎩⎪⎨⎧<<=⎰,0,103)(0其他x xdy x f x X⎩⎨⎧<<=.,1032其他x x⎪⎩⎪⎨⎧<<==.,01)(),()|(|其他x y x x f y x f x y f X X Y15. 设二维连续随机变量),(Y X 概率密度为⎩⎨⎧<<<=.,0,10,||,1),(其他x x y y x f 求条件概率密度)|(|y x f Y X . 解 Y 的边际概率密度)(y f Y 为⎪⎩⎪⎨⎧<=⎰.0,1||1)(1||其他y dx y f y Y⎩⎨⎧<-=.0,1||||1其他y y⎪⎩⎪⎨⎧<<-==.0,1||||11)(),()|(|其他x y y y f y x f y x f Y Y X16. 已知二维随机变量),(Y X 只取)0,0(,)1,1(-,)2,1(-及)0,2(四对值,相应概率依次为31,61,121和125,列出),(Y X 的概率分布表,求Y 的边缘概率分布及Y X +的概率分布.),(Y X 的联合概率分布如上表所示,表中最下一行为Y 的边缘分布,Y X +的分布如下表:Y X + 0 1 2 P41 31 125 17. 袋中有10张卡片,其中有m 张卡片上写有数字m ,,4,3,2,1=m 从中不重复地抽取2张,每次一张,记i X 表示第i 次取到的卡片上数字,2,1=i .求),(21X X 的概率分布以及21X X +,21X X 的概率分布.解 ),(21X X 可以取)4,4(,),3,1(),2,1( 其相应概率见下表:134903 904 906 908 3903 906 906 9012 4904 908 9012 9012 21X X +可以取8,,4,3 各值,21X X 可以取16,12,9,8,6,4,3,2各值,其相应概率见以下二表: 34678P452 454 4510 4512 456 23689P.18设),(Y X 的概率分布为2202 202202204204 证明:Y X ,相互独立. 证明2202 202 202204204 表中最左一列和最下一行分别为与边缘概率分布.由上表可知 101202}1,21{==-==Y X P , 而101208205}1{}21{=⋅=-==Y P X P ,故}1{}21{}1,21{-===-==Y P X P Y X P .类似还可以证明 }{}{},{j Y P i X P j Y i X P =====,2,1,21=i ;2,0,1-=j . 故Y X ,相互独立.19. 分别判断第4、8、16各题中的随机变量X 与Y 是否独立? 解 第4题中 0}0,0{===Y X P ,而 045104515}0{}0{≠⋅==⋅=Y P X P . 第8题中 643}1,0{===Y X P ,而 643641646}1{}0{≠⋅==⋅=Y P X P . 第16题中 0}0,1{==-=Y X P , 而 02131}0{}1{≠⋅==⋅-=Y P X P .故三个题中的随机变量X 与Y 均不独立. 20. 二维随机变量),(Y X ~),(y x f ,)1)(1(),(22y x Ay x f ++=0,>y x .确定系数A 的值,求联合分布函数),(y x F .解dxdy y x Adxdy y x f ⎰⎰⎰⎰+∞∞-+∞∞-+∞+∞++=022)1)(1(),( 142==A π,24π=A .⎪⎩⎪⎨⎧>=.,0,0,,arctan arctan 4),(2其他y x y x y x F π21. 随机变量),(Y X 服从区域D 上的均匀分布,求概率密度),(y x f ,其中D 为下面给定的区域:)1(}21,11),,{(≤≤≤≤-=y x y x D )2(}144),,{(22≤+=y x y x D )3(}2),,{(22y y x y x D ≤+=解 )1(2=D S ,⎩⎨⎧≤≤≤≤-=.,0,21,11,5.0),(其他y x y x f)2(π6=D S ,⎪⎩⎪⎨⎧≤+=.,0,194,61),(22其他y x y x f π)3(π=D S ,⎪⎩⎪⎨⎧≤+=.,0,2,1),(22其他y y x y x f π22. 求上题中关于X 及关于Y 的边缘概率密度.解 )1(⎩⎨⎧>≤=.1||,0,1||,5.0)(x x x f X⎩⎨⎧≤≤=.,0,21,1)(其他y y f Y )2(24/14/1421613)(22x dy x f x x X -==⎰---ππ,2||≤x ,当2||>x 时,0)(=x f X ,类似地⎪⎩⎪⎨⎧>≤-= .3||,0,3||,992)(2y y y y f Y π)3(当1||≤x 时,21111121)(22x dy x f x xX -==⎰++--ππ,当1||>x 时,0)(=x f X ,类似地,⎪⎩⎪⎨⎧≤≤-=.,0,20,22)(2其他y y y y f Y π23. 判断第20、21各题中的随机变量X 与Y 是否独立?解 在第20题中,⎪⎩⎪⎨⎧≤>=≤=.00,0arctan 2}{)(x x xx X P x F X π⎪⎩⎪⎨⎧≤>=.00,0arctan 2)(y y yy F Y π由于对任何y x ,均有)()(),(y F x F y x F Y X =,因此随机变量X 与Y 独立.在第21题)1(中的)()(),(y f x f y x f Y X =,因此X 与Y 是独立的,而在第21题的)2(与)3(中,不能对所有的y x ,均满足等式)()(),(y f x f y x f Y X ⋅=,因此)2(与)3(中的X 与Y 是不独立的.24. 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<= .,0,10,10,),(2其他y x cxy y x f )1(求参数c ;)2(证明X 与Y 相互独立. 解 )1(6110121012c dy y xdx c dxdy cxy ===⎰⎰⎰⎰, 6=c .)2(⎪⎩⎪⎨⎧<<=⎰ .,0,10,6)(102其他x dy xy x f X⎩⎨⎧<<=.0,102其他x x⎪⎩⎪⎨⎧<<=⎰ .,0,10,6)(102其他y dx xy y f Y⎩⎨⎧<<=.,1032其他y y由于)()(),(y f x f y x f Y X ⋅=,所以X 与Y 是独立的. 25. 随机变量),(Y X 的概率密度⎪⎩⎪⎨⎧≥+<++-= .,0,),(),(22222222R y x R y x y x R c y x f求)1(参数c .)2(随机变量落在圆)(222R r r y x <≤+内的概率.解 )1(3)()(132022222R c rdrd r R c dxdy y x R c RR y x πθπ=-=+-=⎰⎰⎰<+,33R c π=. )2(⎰⎰⎰-=+-=<+πθππ201113223)(3)(3222rr y x d dr r r R R dxdy y x R R p32)(2)(3Rr R r -=. 26. 设),(Y X 的概率密度是)1)(1(),(22y x cy x f ++=.求)1(参数c ;)2(),(Y X 落在以)1,1(),0,1(),1,0(),0,0(为顶点的正方形内的概率;)3(X 与Y 是否独立.解 )1()|)(arctan |(arctan ),(1∞+∞-+∞∞-+∞∞-∞+∞-⎰⎰==y x c dxdy y x f2πc =, 21π=c .)2(161)|)(arctan |(arctan 1),(10101102===⎰⎰y x dxdy y x f p π. )3( )1(1|arctan )1(1).()(222x y x dy y x f x f X +=+==∞+∞-+∞∞-⎰ππ, 同理可得 )1(1)(2y y f Y +=π.由于 )()(),(y f x f y x f Y X ⋅=,所以X 与Y 是独立的. 27. 设随机变量1X 与2X 独立,其概率分布如下表所示,令21X X X +=,21X X Y ⋅=,求随机变量),(21X X 的概率分布及X 、Y 的概率分布.2X1 2 3P 5.03.02.01X0 1 P 6.04.0解 由于1X 与2X 独立,因此有}{}{},{j Y P i X P j Y i X P =⋅====, 具体计算结果列于下表 13 12.0 08.0X 的取值为4,3,2,1.30.0}1,0{}1{}1{2121=====+==X X P X X P X P , 类似地,可以计算出.4,3,2},{==i i X P 列于下表X 1 2 3 4 P 30.0 38.0 24.0 08.0随机变量Y 可以取3,2,1,0各值.60.0}0{}0{}0{121======X P X X P Y P , 20.0}1,1{}1{}1{2121=======X X P X X P Y P , 12.0}2,1{}2{}2{2121=======X X P X X P Y P , 08.0}3,1{}3{}3{2121=======X X P X X P Y P .28. 有一种两版面的报纸,每版印刷错误数服从参数为1的泊松分布,假定各版印刷错误相互独立,求一份这种报纸上印刷错误总数X 的概率分布.解 设21,X X 分别表示第1、第2版面上的印刷错误,21X X X +=,X 可以取一切非负整数.∑=-====+==nk k n X k X P n X X P n X P 02121},{}{}{}{}{201k n X P k XP nk -===∑=∑∑=---=-=-=nk nk k n k n n e e k n ek 02110)!(!!!)!(1!122!2!-=-==∑e n C n e n nk k n),2,1,0( =n 29. 设随机变量1X 与2X 独立,且i X ~)8.0,2(B ,2,1=i .令21X X X +=,21X X Y ⋅=,求X ,Y 的概率分布.解 X 可以取4,3,2,1,0各值,∑=-====+==km m k X m XP k X X P k X P 02121},{}{}{}{}{201m k X P m X P km -===∑=m k m k mk m m km m C C+----=⨯⨯⨯=∑222022.08.02.08.0k k m k km m C C--=⨯⨯=∑42022.08.0kk kC -⨯=442.08.0 )4,3,2,1,0(=kY 可以取4,2,1,0各值)}0()0{(}0{21=⋃===X X P Y P0784.0}0{}0{}0{}0{2121===-=+==X P X P X P X P ,1024.0}1{}1{}1{21=====X P X P Y P , 4096.0}2{}2{}4{21=====X P X P Y P ,4096.0}4{}1{}0{1}2{==-=-=-==Y P Y P Y P Y P .30. 随机变量X 与Y 独立,且X 服从]2,0[上的均匀分布,Y 服从2=λ的指数分布,写出随机变量),(Y X 的概率密度,计算概率}{Y X P ≤.解 ⎪⎩⎪⎨⎧<≤=;,2021)(其他x x f X ⎩⎨⎧≤>=-.00,02)(2y y e y f yY由于X 与Y 独立,因此有⎩⎨⎧>≤≤=⋅=-.,0,20)()(),(2其他y x e y f x f y x f yY Xdy e dx dxdy y x f Y X P yx xy ⎰⎰⎰⎰≤+∞-==≤22),(}{)1(4121422---==⎰e dx e x . 31. 一个靶面由五个同心圆组成,半径分别为25,20,15,10,5(单位:厘米),假定射击时弹着点的位置为),(Y X ,且),(Y X 服从二维正态分布,其概率密度为200222001),(y x e y x f +-=π,现规定弹着点落入最小的圆域得5分,落入其他各圆域(从小到大)的得分依次为4分、3分、2分及1分,W 为1次射击的得分数,写出W 的概率分布.解 设随机变量W 为一次射击的得分,则W 可以取5,4,3,2,1,0.⎰⎰>+==62522),(}0{y x dxdy y x f W P令θcos r x =,θsin r y =,0439.020020025202==-∞+⎰⎰dr e r d r πθπ. 同样方法可以计算出0914.0}1{==W P , 1893.0}2{==W P ,2819.0}3{==W P , 2760.0}4{==W P , 1175.0}5{==W P .32. 上题中设Z 为弹着点到靶心的距离,求Z 的概率密度)(z f Z . 解 依题意随机变量Z 是X 与Y 的函数,且 22Y X Z +=,当0>Z 时,dxdy e z Z P z F y x z y x Z 200222222001}{)(+-≤+⎰⎰=≤=π,令θcos r x =,θsin r y =,20020020221200)(z r zZ edr e r d z F ---==⎰⎰πθ,⎪⎩⎪⎨⎧≤>=-.00,0100)(2002z z e z z f z Z 33. 设X 与Y 是两个相互独立的随机变量,其概率密度分别为⎩⎨⎧≤≤= .,0,10,1)(其他x x f X ⎩⎨⎧≤≥=- .0,0,0,)(y y e y f y Y 求Y X T +=的概率密度.解 ⎩⎨⎧>≤≤=-.,0,10),(其他y x e y x f y当0≤t 时,0)(=t f T , 当10≤<t 时,t tT e dy e t f y---==⎰1)(0,当1>t 时,)1()(1-==---⎰e e dy e tf t tt T y.⎪⎩⎪⎨⎧>-≤<-≤=--.1)1(,101,00)(t e e t et t f t tT 34.设X 与Y 是相互独立的随机变量,且均服从)1,0(N ,求123++=Y X T 的概率密度. 解 T ~)13,1(N ,T 的概率密度为26)1(2261)(--=t e t f π∞<<∞-t .35. 设二维随机变量),(Y X 的概率密度为),(y x f ,求Y X T -=的概率密度. 解 ⎰⎰≤-=≤-=≤=ty x T dxdy y x f t Y X P t T P t F ),(}{}{)(⎰⎰⎰⎰+∞∞-∞-+∞∞-+∞-++==tty du y u y f dy u y x dx y x f dy ),(),(令⎰⎰∞-+∞∞-+=tdu dy y u y f ]),([,故Y X T -=的概率密度函数为 ⎰+∞∞-+=dy y t y f t f T ),()(.⎰⎰≤-=≤-=≤=ty x T dxdy y x f t Y X P t T P t F ),(}{}{)(⎰⎰⎰⎰+∞∞--∞+∞∞-+∞----==ttx du u x x f dx u x y dy y x f dx ))(,(),(令⎰⎰∞-+∞∞--=tdu dx u x x f ]),([故Y X T -=的概率密度函数为 ⎰+∞∞--=dx t x x f t f T ),()(.36. 设X 与Y 相互独立, 概率密度为⎩⎨⎧>>≤==-.0,0,,0,0)()(a x ae x y f x f axY X 试求YXZ =的概率密度)(z f Z . 解 当0>z 时,dy y f yz yf z f Y X Z )()()(0⎰+∞= dy ye a dy ae yae y z a ay ayz ⎰⎰+∞+--+∞-==)1(20)|(10)1(0)1(dy e ye za y z a y z a ⎰+∞+-∞++--+-=20)1()1(1)|)1(1(1z e z a z a y z a +=+-+=∞++-, 当0≤z 时, 0)(=z f Z .所以有 ⎪⎩⎪⎨⎧≤>+=.0,0,0,)1(1)(2z z z z f Z(B ).1已知随机变量1X 与2X 的概率分布1X1- 0 1P41 21 412X1P21 21 而且1}0{21==X X P .)1(求1X 与2X 的联合概率分布. )2(问1X 与2X 是否独立?为什么?解 )1(由联合概率分布与边缘概率分布的关系可知,求1X 与2X 的联合概率分布有如下形式: 41 21 131p41 j p ⋅21 21 其中03212==p p 是由于1}0{21==X X P ,所以,0}0{21=≠X X P ,再根据边缘概率分布与联合概率分布的关系可写出联合概率分布如下: 41 21 141 041)2(由联合概率分布表可以看出41}0,1{21==-=X X P , 而 2141}0{}1{21⨯==-=X P X P ,所以,1X 与2X 不独立.2.设随机变量U 在区间]2,2[-上服从均匀分布,随机变量⎩⎨⎧->-≤-=.1,1,1,1U U X 若若⎩⎨⎧>≤-= .1,11,,1Y U U 若若 求X 和Y 的联合概率分布.解 因为U 在区间]2,2[-上服从均匀分布,所以⎪⎩⎪⎨⎧<<-=.,2241)(~其他u u f U从而可求得41}1{}1,1{}1,1{=-≤=≤-≤=-=-=U P U U P Y X P , 41}1{}1,1{}1,1{=>=>->===U P U U P Y X P , 0}{}1,1{}1,1{=Φ=>-≤==-=P U U P Y X P , 21}11{}1,1{}1,1{=≤<-=≤->=-==U P U U P Y X P , 或2141411}1,1{=--=-==Y X P . 41 433. 设),(Y X 在矩形}10,20|),{(≤≤≤≤=y x y x G 上服从均匀分布.记⎩⎨⎧>≤= .,1,,0Y X Y X U 若若⎩⎨⎧>≤= .2,12Y,,0V Y X X 若若 求U 和V 的联合概率分布及边缘概率分布.解 画出区域G 的图形(图3.1),由图3.1可知41}{=≤Y X P , 21}2{=>Y X P , 41}2{=≤<Y X Y P .图3.1),(V U 的取值为)1,1(),0,1(),1,0(),0,0(,且41}{}2,{}0,0{=≤=≤≤===Y X P Y X Y X P V U P ,0}{}2,{}1,0{=Φ=>≤===P Y X Y X P V U P ,41}2{}2,{}0,1{=≤<=≤>===Y X Y P Y X Y X P V U P , 21}2{}2,{}1,1{=>=>>===Y X P Y X Y X P V U P , 于是可得到),(V U 的联合分布及边缘分布 00 41 141 21 43 j p ⋅21 214. 设B A ,为两个随机事件,且41)(=A P ,31)|(=AB P ,21)|(=B A P ,令 ⎩⎨⎧=.,0,,1不发生发生A A X ⎩⎨⎧= .0,,1,Y 不发生发生B B )1(二维随机变量),(Y X 的概率分布及边缘概率分布; )2(22Y X Z +=的概率分布.解 )1(),(Y X 的取值为)0,0(,)1,0(,)0,1(,)1,1(,相应的概率为121)|()()(}1,1{=====A B P A P AB P Y X P , 61)()()()(}0,1{=-=-====AB P A P AB A P B A P Y X P , )()()()(}1,0{AB P B P AB B P B A P Y X P -=-==== 12112161)()|()(=-=-=AB P B A P AB P ,)(1)(}0,0{B A P B A P Y X P ⋃-=⋅===32)()()(1=+--=AB P B P A P . )2(随机变量222Y X Z +=只取三个值:2,1,0,相应概率为32}0,0{}0{=====Y X P Z P , 121}1,1{}2{=====Y X P Z P ,41}0,1{}1,0{}1{===+====Y X P Y X P Z P . 5. 已知X 的概率分布及给定1,0==X X 下Y 的条件概率分布:求)1(Y X ,的联合概率分布; )2(在给定1≠Y 时X 的条件概率分布. 解 )1(由题设条件414.0}1,0{}0{}1,0{}0|1{==========Y X P X P Y X P X Y P ,得 1.0414.0}1,0{=⨯===Y X P . 同理可以计算其他概率值.)2(由概率分布表可得216.03.0}1{}1,0{}1|0{==≠≠==≠=Y P Y X P Y X P ,216.03.0}1{}1,0{}1|1{==≠≠==≠=Y P Y X P Y X P .6. 设),(Y X 服从区域}0,2|),{(22≥≤+=y x y x y x D 上的均匀分布,令⎩⎨⎧<≥=.,1,,0X Y X Y U ⎪⎪⎩⎪⎪⎨⎧<≥= ,.33,133,0X X Y Y V求),(V U 的概率分布.解 画出区域D 的图形,由于),(Y X 服从区域D 上的均匀分布,所以概率密度⎪⎩⎪⎨⎧∉∈=.),(,0;),(,2),(D y x D y x y x f π图3.2由此可得ππθπθππ222}{}0,0{cos 2024-==≥===⎰⎰rdr d X Y P V U P , πθπθπ23312}33{}1,1{cos 2060+==<===⎰⎰rdr d X Y P V U P ,rdr d X Y X P V U P ⎰⎰=<<===θππθπcos 20462}33{}0,1{ π23261-+=, 0}1,0{===V U P7. 设随机变量X 在区间)1,0(上服从均匀分布,在)10(<<=x x X 的条件下,随机变量Y 在区间),0(x 上服从均匀分布,求:)1(随机变量X 和Y 的联合概率密度; )2(Y 的概率密度; )3(概率)1(>+Y X P . 解 )1(X 与Y 的联合概率密度为⎪⎩⎪⎨⎧<<<==.,0,10,1)|()(),(|其他x y x x y f x f y x f X Y X)2(画出区域}10|),{(<<<=x y y x D 的图形⎰+∞∞-=dx y x f y f Y ),()(当0≤y 或1≥y 时,0)(=y f Y ;当10<<y y dx xdx y x f y f y Y ln 1),()(1-===⎰⎰+∞∞-图3.3)3(在区域D 的图形中画出直线1=+y x ,则2ln 11),()1(11211-===>+⎰⎰⎰⎰>+-dy xdx dxdy y x f y x P y x xx .图3.48. 设随机变量的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<-=.,0,20,41,01,21)(其他x x x f X令2X Y =,),(y x F 为二维随机变量),(Y X 的分布函数.求)1(Y 的概率密度)(y f Y ;)2()4,21(-F .解 )1(}{}{)(2y X P y Y P y F Y ≤=≤=.当0<y 时,0)(=y F Y ;当10<≤y 时,y dx dx y X y P y F y y Y 434121}{)(00=+=≤≤-=⎰⎰-; 当41<≤y 时,y dx dx y X y P y F y Y 41214121}{)(001+=+=≤≤-=⎰⎰-; 当4≥y 1)(=y F Y .⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤+<≤<= .4,1,41,4121,10,43,0,0)(y y y y y y y F Y于是⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<=.4,0,41,81,10,83,0,0)(y y y y yy y f Y)2(}4,21{}4,21{2≤-≤=≤-≤X X P Y X P4121}212{211==-≤≤-=⎰--dx X P .9. 设随机变量X 和Y 独立,其中,X 的概率分布为X1 2 3.0 7.0而Y 的概率密度为)(y f ,求随机变量Y X U +=的概率密度)(u g .解 设Y 的分布函数为)(y F ,Y X U +=的分布函数为)(u G .因为事件}1{=X 与}2{=X 构成完备事件组,所以,由全概率公式可得)]}2()1[(){(}{}{)(=⋃=⋂≤+=≤+=≤=X X u Y X P u Y X P u U P u G}2,{}1,{=≤++=≤+=X u Y X P X u Y X P}1|{}1{=≤+==XuYXPXP}2|{}2{=≤+=+XuYXPXP}2|2{7.0}1|1{3.0=≤++=≤+=XuYPXuYP}2|2{7.0}1|1{3.0=-≤+=-≤=XuYPXuYP由于X与Y相互独立,所以}1{}1|1{-≤==-≤uYPXuYP ,}2{}2|2{-≤==-≤uYPXuYP ,}2{7.0}1{3.0)(-≤+-≤=uYPuYPuG)2(7.0)1(3.0-+-=uFuF,由此得U的概率密度为)2(7.0)1(3.0)()('''-+-==uFuFuGug)2(7.0)1(3.0-+-=ufuf.10. 设随机变量X服从参数为λ的指数分布,随机变量⎩⎨⎧>-≤=.1||,,1||,XXXXY,求)1(}0{=+YXP;)2(Y的分布函数)(yF.解)1(因为随机变量X服从参数为λ的指数分布,所以概率密度为⎩⎨⎧≤>=-.0,0,0,)(xxexfxλλ分布函数⎩⎨⎧≤>-=-.0,0,0,1)(xxexFxλ于是}1{}1{}1|{|}{}0{-<+>=>=-===+XPXPXPXYPYXP)1()1(1}1{}1{1---=-<-≤-=F F X P X P1)1()1(1-+=----=--λλλλe e e e.)2(}1||,{}1||,{}{)(>≤+≤≤=≤=X y Y P X y Y P y Y P y F}1,{}1,{}1||,{-<≤-+>≤-+≤≤=X y X P X y X P X y X P}.1,{}10,{>-≥+≤<≤=X y X P X y X P(因为X 服从参数为λ的指数分布,所以上式中的 0}01,{=≤≤-≤X y X P ,0}1,{=-<≤-X y X P .) 1-<y y yx e dx e y X P y F λλλ==-≥=⎰+∞--}{)(,01<≤-y 时,λ-=>=e X P y F }1{)(,10<≤y 时, λλ--+-=>+≤=e e X P y X P y F y 1}1{}{)(, 1≥y 1}1{}10{)(=>+≤<=X P X P y F .⎪⎪⎩⎪⎪⎨⎧≥<≤+-<≤--<=---.1,1,10,1,01,,1,)(y y e e y e y e y F y y λλλλ11. 设随机变量X 服从参数为1=λ的指数分布,Y 服从区间]2,2[-上的均匀分布,X 与Y 独立,且⎩⎨⎧>≤=.1||,2,1||,Y a Y a Z 其中0>a 为常数.求随机变量Z XU =的概率密度. 解 设X 的分布函数为)(x F X ,ZXU =的分布函数为)(u G .因为事件}{a Z =与}2{a Z =构成完备事件组,所以由全概率公式可得)]}2()[(){(}{}{)(a Z a Z u Z XP u Z X P u U P u G =⋃=⋂≤=≤=≤=}2,{},{a Z u ZXP a Z u Z X P =≤+=≤=}|{}{a Z u Z XP a Z P =≤==}2|{}2{a Z u ZXP a Z P =≤=+}2|2{21}|{21aZuaXPaZuaXP=≤+=≤=}2|2{21}|{21aZauXPaZauXP=≤+=≤=.由于X与Y相互独立,所以X与Z相互独立,故}{}|{auXPaZauXP≤==≤,}2{}2|2{auXPaZauXP≤==≤,)2(21)(21}2{21}{21)(auFauFauXPauXPuGXX+=≤+≤=.X~⎩⎨⎧≤>=-.0,0,0,)(xxexfx于是,ZXU=的概率密度''')]2([21)]([21)()(auFauFuGugXX+==)]2(2)([21auafauafXX+=.当0>u)2(21)(2auau aeaeug--+=,当0≤u0)(=ug.⎪⎩⎪⎨⎧≤>+=--.0,0,0),2(21)(2uueeaugauau12. 设二维随机变量),(YX在矩形}10,20|),{(≤≤≤≤=yxyxG上服从均匀分布,试求长为X和Y的矩形面积S的概率密度)(sf.解由题意知X和Y的联合概率密度为⎪⎩⎪⎨⎧∈=.,0,),(,21),(其他Gyxyxf画出区域}10,20|),{(≤≤≤≤=yxyxG的图形,用分布函数法求随机变量XYS=的概率密度)(sf.图3.5)()(s S P s F ≤=表示S 的分布函数.0≤s 时,0)(=s F .当2≥s 时,1)(=s F .20<<s 时,在区域G 中画出曲线s xy =如图3.5所示,则有⎰⎰>-=>-=≤=sxy dxdy y x f s XY P s XY P s F ),(1}{1}{)( ⎰⎰-+=-=21)ln 2ln 1(2211x x s s s dy dx .⎪⎩⎪⎨⎧≥<<-+≤=.2,1,20),ln 2ln 1(2,0,0)(s s s s s s F于是,随机变量XY S =的概率密度⎪⎩⎪⎨⎧<<-=.,0,20),ln 2(ln 21)(其他s s s f13. 设随机变量X 和Y 相互独立,且概率密度分别为⎪⎩⎪⎨⎧+∞<<=-.,0,0,2)(2其他x e x f x X π⎪⎩⎪⎨⎧+∞<<=-.,0,0,2)(2其他y e y f y Y π求随机变量22Y X Z +=的概率密度)(z f Z . 解 由题意,X 与Y 相互独立,于是联合概率密度为⎪⎩⎪⎨⎧>>=+- .,0,0,0,2),()(22其他y x e y x f y x π 当0≤z 时,0)(=z F Z 0)(=z f Z . 当0>z 时,画出222z y x =+的图形.如图3.6,则}{}{}{)(22222z Y X P z Y X P z Z P z F Z ≤+=≤+=≤= ⎰⎰⎰⎰--≤+-===2002222214),(πθπz z r z y x e rdr e d dxdy y x f , 所以,随机变量22Y X Z +=的概率密度⎩⎨⎧>≤=- .0,2,0,0)(2z ze z z f z Z图3.6。
第三章习题-ddg.概要

习题1.给出以下概念的解释说明。
机器语言程序机器指令汇编语言汇编指令汇编语言程序汇编助记符汇编程序反汇编程序机器级程序通用寄存器定点通用寄存器栈指针寄存器指令指针寄存器标志寄存器条件标志(条件码)控制标志寻址方式立即寻址寄存器寻址存储器操作数实地址模式保护模式比例变址非比例变址比例系数(比例因子)MMX指令SSE指令集SIMD 多媒体扩展通用寄存器栈(Stack)调用者保存寄存器被调用者保存寄存器帧指针寄存器当前栈帧按值传递参数按地址传递参数嵌套调用递归调用缓冲区溢出缓冲区溢出攻击栈随机化2.简单回答下列问题。
(1)一条机器指令通常由哪些字段组成?各字段的含义分别是什么?(2)将一个高级语言源程序转换成计算机能直接执行的机器代码通常需要哪几个步骤?(3)IA-32中的逻辑运算指令如何生成条件标志?移位指令可能会改变哪些条件标志?(4)执行条件转移指令时所用到的条件标志信息从何而来?请举例说明。
(5)无条件转移指令和调用指令的相同点和不同点是什么?(6)按值传递参数和按地址传递参数两种方式有哪些不同点?(7)为什么在递归深度较深时递归调用的时间开销和空间开销都会较大?(8)为什么数据在存储器中最好按地址对齐方式存放?(9)造成缓冲区溢出的根本原因是什么?3.对于以下AT&T格式汇编指令,根据操作数的长度确定对应指令助记符中的长度后缀,并说明每个操作数的寻址方式。
(1)mov 8(%ebp, %ebx, 4), %ax(2)mov %al, 12(%ebp)(3)add ( , %ebx,4), %ebx(4)or (%ebx), %dh(5)push $0xF8(6)mov $0xFFF0, %eax(7)test %cx, %cx(8)lea 8(%ebx, %esi), %eax4.使用汇编器处理以下各行AT&T格式代码时都会产生错误,请说明每一行存在什么错误。
(1)movl 0xFF, (%eax)(2)movb %ax, 12(%ebp)(3)addl %ecx, $0xF0(4)orw $0xFFFF0, (%ebx)(5)addb $0xF8, (%dl)(6)movl %bx, %eax(7)andl %esi, %esx(8)movw 8(%ebp, , 4), %ax5.假设变量x和ptr的类型声明如下:src_type x;dst_type *ptr;这里,src_type和dst_type是用typedef声明的数据类型。
第三章习题解答及参考答案

(
)
①
2 式中 m 为整数。令 u = αr ,显然上式是 u 的周期函数,周期为 2π ,故可展开成傅里 ∞ 1 1 + sgn (cos u ) = ∑ Cn e inu 2 2 n = −∞
叶级数:
其中,
Cn =
1 2π
∫
π 2
−π 2
e −inu du =
sin (nπ 2) nπ
②
遂有:
∞ 1 1 sin (nπ 2 ) inαr 2 e + sgn cos αr 2 = ∑ 2 2 nπ n= −∞
②
σ ( f x ,0 ) 2λd i =1− f x = 1− f x f0 σ0 l
l l ≤ λd i f x ≤ (见附图3 - 4(b)) 4 2
2 1 l l σ ( f x ,0 ) = (l − λd i f x ) l − = − λd i l f x 2 2 2
λd ;两个一级分量与中央亮斑 L
附图 3-2
习题[3-2]图示
附图 3-3
归一化强度分布
[3-3]
将面积为 10 mm × 10 mm 的透射物体置于一傅里叶变换透镜的前焦面上作频谱分析。
用波长 λ = 0.5 µ m 的单色平面波垂直照明,要求在频谱面上测得的强度在频率 140 线/mm 以下能准确代表物体的功率谱。并要求频率为 140 线/mm 与 20 线/mm 在频谱面上的间隔为 30mm,问该透镜的焦距和口径各为多少? 解:取面积为10mm ×10mm 的透射物体的对角线方向为 x 轴。因要求在 140 线/mm 以下的 空间频率成分不受到有限孔径的渐晕效应的影响,故透镜的口径 D 应满足条件:
第三章习题参考答案
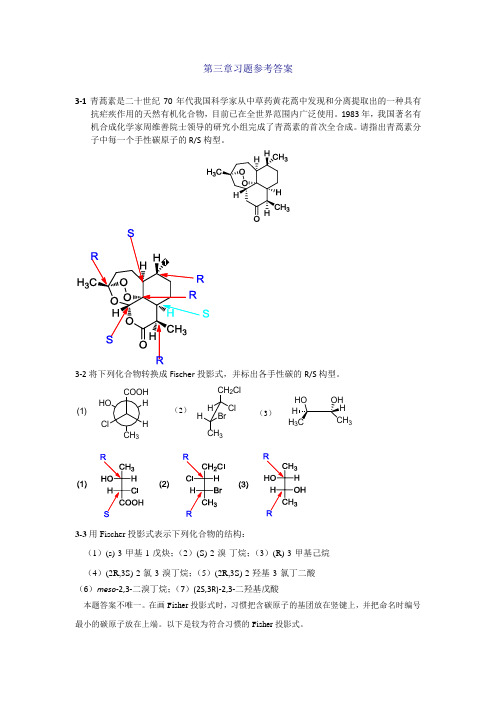
第三章习题参考答案3-1青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrH3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔;(2)(S)-2-溴-丁烷;(3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷;(7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher 投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher 投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(.Chem.2013,78,6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
(R)-A(S)-A3-6山梗烷定是从印度烟叶中分离到的一种化合物,它没有旋光性,也不可被拆分。
第三章课后习题

3-1变截面连续梁桥和等截面连续梁桥分别在何种情况下采用?为什么?答:连续梁桥采用等截面布置,构造简单、预制定型、施工方便,随着预应力锚具施工方法的发展愈来愈受到重视。
中等跨径,若采用预制装配施工和就地浇筑施工的连续梁桥,为便于预制安装和模板周转使用,宜选用等截面布置。
采用顶推法施工,为便于布置顶推和滑移设备,一般均采用等截面梁。
对于长大桥梁,选用中等跨径(40-60m),采用逐跨施工和移动模架法施工,按等截面布置最为有利,它可以使用少量施工设备完成全桥的施工。
等截面连续梁主要适用情况为:(1)桥梁一般为中等跨径,以40-60m为多数。
采用等截面布置使桥梁构造简单,施工迅速。
由于跨径不大,梁的各截面内力差异不大,可采用构造措施予以调节。
(2)等截面布置以等跨布置为宜。
对于长桥,由于各种原因需要对个别跨径改交跨长时,也以等截面为宜。
(3)采用有支架施工,逐跨架设施工、移动模架法和顶推法施工的连续梁桥较多采用等截面布置。
(4)双层桥梁在无需做大跨径的情况下,选用等截面布置可使结构构造筒化。
变截面连续梁主要使用于大跨径的连续梁,截面高度的变化根据弯矩影响线而变化,结构受力更合理,减轻结构自重,节约建造成本。
从已建桥梁实例的统计资料分析,跨径大于100m的预应力混凝土连续梁桥有90%以上是选用变截面梁。
因为大跨桥梁在外载和自重作用下,支点截面将出现较大的负弯矩。
从预应力锚具的绝对值来看,支点截面的负弯矩大于跨中截面的正弯矩,因此,采用变截面梁能符合梁的内力分布规律。
同时,大跨连续梁桥宜选用悬臂法施工,而变截面梁又与施工的内力状态相吻合。
在跨径布置上,为减小边跨跨中正弯矩,宜选用不等跨布置,这样安排也便于悬臂对称施工。
此外,有些采用有支架施工和预制装配施工的大跨径连续梁桥,也以梁的受力需要选用变截面梁。
变截面连续梁主要适用情况为:(1)连续梁的主跨访径接近100m或100m以上时,从经济的角度考虑,要求截面的变化规律基本符合梁的锚具内力变化规律而采用变截面布置。
第3章 习题(3)-带答案

第5章交流-直流变换器习题(3)第1部分:填空题1.实际工作中,整流电路输出的电压是周期性的非正弦函数,当 α 从0°~90°变化时,整流输出的电压u d的谐波幅值随 α 的增大而增大,当 α 从90°~180°变化时,整流输出的电压 ud 的谐波幅值随 α 的增大而减小。
2.三相桥式全控整流电路带阻感负载时,设交流侧电抗为零,直流电感L为足够大。
当 α =30°时,三相电流有效值与直流电流的关系为I=Id ,交流侧电流中所含次谐波次数为6k+1 ,其整流输出电压中所含的谐波次数为6k 。
3.对于三相半波可控整流电路,换相重迭角的影响,将使输出电压平均值降低。
4.带平衡电抗器的双反星形可控整流电路适用于低电压大电流的场合,当它带电感负载时,移相范围是0°~90°,带电阻负载时,移相范围是0°~120°;如果不接平衡电抗器,则每管最大的导通角为 60°,每管的平均电流为 1/6 I d。
5.多重化整流电路可以提高功率因数,其中移相多重联结有并联多重联接和串联多重联接两大类。
6.PWM整流电路可分为电压型和电流型两大类,目前研究和应用较多的是PWM整流电路。
7.PWM整流电路的控制方法有间接电流控制和直接电流控制,基于系统的静态模型设计、动态性能较差的是间接电流控制,电流响应速度快、系统鲁棒性好的是间接电流控制。
第2部分:简答题1.无功功率和谐波对公用电网分别有那些危害?答:无功功率,对公用电网带来不利影响有:1)无功功率会导致电流增大和视在功率增加,导致设备容量增加。
2)无功功率增加,会使总电流增加,从而使设备和线路的损耗增加。
3)使线路压降增大,冲击性无功负载还会使电压剧烈波动。
谐波,对公用电网危害包括:1)谐波使电网中的元件产生附加的谐波损耗,降低发电、输电及用电设备的效率,大量的3次谐波流过中性线会使线路过热甚至发生火灾。
第3章 习题、答案

(一)1.目的练习材料按定额费用的比例分配。
2.资料某企业生产甲、乙两种产品,耗用原材料费用共计62 400元。
本月投产甲产品220件,乙产品256件。
单件原材料费用定额:甲产品120元,乙产品100元。
3.要求采用原材料定额费用比例分配甲、乙产品实际耗用原材料费用。
解:(1)计算每种产品的材料定额消耗额甲产品材料定额消耗量=220×120=26 400(元)乙产品材料定额消耗量=256×100=25 600(元)(2)材料费用分配率=62400 2640025600+=1.2(3)每种产品应分配的材料费用甲产品应分配的材料费用=26400×1.2=31 680(元)乙产品应分配的材料费用=25600×1.2=30 720(元)(二)1.目的练习材料按定额消耗量的比例分配法。
2.资料某企业生产A、B两种产品,本月两种产品共同领用主要材料12 375千克,单价20元,共计247500元。
本月投产A产品为425件,B产品为525件,A产品的材料消耗定额为20千克,B产品的材料消耗定额为10千克。
3.要求按材料定额消耗量比例分配材料费用。
解:(1)计算每种产品的材料定额消耗量A产品材料定额消耗量=425×20=8500(千克)B产品材料定额消耗量=525×10=5250(千克)(2)材料消耗量分配率=12375 85005250+=0.9(3)每种产品应分配的材料数量A产品应分配的材料数量=8500×0.9=7 650(千克)B产品应分配的材料数量=5250×0.9=4 725(千克)(4)每种产品应分配的材料费用A产品应分配的材料费用=7 650×20=153 000(元)B产品应分配的材料费用=4 725×20=94 500(元)(三)1.目的练习直接材料费用分配的系数分配法。
2.资料某厂生产A1、A2、A3、A4,和A5五种产品,五种产品单位产品甲材料消耗定额分别为30、27.5、25、20、17.5元,本月实际产量分别为400、500、1 000、200、160件,本月实际消耗甲材料59 850元,见表。
中职信息技术(基础模块)第三章课后习题一

三、练习题第3章图文编辑(一)选择题1. Word 是_AA,文字编辑软件B.播放软件C、硬件D.操作系统2、退出Word 的快捷操作是按【_B_】组合键。
A. Alt+F4B.Ctrl+F4c.Shift+F4D.Ctrl+Esc3.在Word 中快速访问工具栏上的按钮的功能是_D-A.撤销上次操作B.加粗C.设置下画线D. 保存4.在Word 中进行编辑时,要将选定区域的内容放到剪贴板上,可单击“开始”功能区中的C_按钮。
A.剪切或替换B.剪切或清除C.剪切或复制D.剪切或粘贴5.在Word 使用过程中,可以利用【_C_】键获得系统帮助。
A.EscB.Ctrl+F1C. FID. Enter6. Word 文档的默认扩展名是_A__·A..docxB..pptxC..xlsxD. .txt7.Word 的工作窗口中不包括_D_·A,快速访问工具栏 B. 标题栏C,编辑区 D.主题8. 在Word 中完成一个文档的编辑后,要想知道它打印后的效果,可使用_A_-_功能。
A.打印预览B.模拟打印C,提前打印D,屏幕打印9.如果用户想保存一个正在编辑的文档,但希望以不同文件名存储,可用_-B_命令A,保存B,另存为C,比较D,限制编辑10.在Word 中,执行命令有多种方法,其中弹出快捷菜单的方法是B_-A.单击鼠标左键B,单击鼠标右键C.双击鼠标左键D.双击鼠标右键(二)填空题1.主流的图文编辑软件有WPS_和__Word软件2. Word 是一个_图文编辑__软件。
3.Word 的编辑功能主要包括选择、_-替换_、查找、_剪切_、复制、_粘贴_、格式等。
4.退出Word 还可以采用单击标题栏右侧_X_按钮的方法。
5、单击-保存_按钮可以对已命名的文档进行保存。
6、在输入文本时,一些键盘上没有的特殊的符号(如俄、日、希腊文字符,数学符号,图形符号等),除了用键盘输入外,还可以使用_插入符号_功能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U 1 2 1 2
1 2
2
2U 2 sin t
2
dt
2U 2 2U 2
2
2
sin 2 tdt
2
4
1 U2 2
1 0 .5 2
7/21
cos
例6、电感性负载采用单相桥式半控接线,有续流二极管,见图,负载的电 阻值为5Ω ,输入的交流电压 U 2 220 V ,负载的额定励磁电压为100V. 求晶闸管和续流二极管电流平均值和有效值?
U d 0.45U 2 1 cos 1 0 0.45 100 22.5V 2 2
Id
I VT
U d 12.5 4.5 A R 5
2
2U 2 sin t 1 dt 2 2 R
2
2U 2 1 2 R 2U 2 R
10/21
2、VT2两端波形
11/21
12/21
解:1、ω L=2π fL=2×3.14×50×0.1=31.4>>0.946 。 故负载可看为纯电感性。
Id Ud R 2.34 U 2 cos 0.946
3 136 U 110V 2
选择晶闸管应折成 0 0 时的情况: Ud0=2.34U2×cos00=2.34×110=257(V)
2
sin 2 tdt
2U 2 1 U 2 1 100 1 10A 2 4 2 2 R 2 R 2 5
6/21
2、Ud、Id的波形图
3、功率因素
2 I VT R U I VT p cos s U 2 I VT U 2 I VT
其中U为负载的电压有效值:
第3章
习题
例1、求工频正弦半波的电流波形的通态平均电流ITAV 、电流有效值及波 形系数? 通态平均电流ITAV :
I TAV
电流有效值:
1 2
0
Im I m sin tdt 0.318I m
1 1 2 I m sin t dt I m 0.5I m IT 0 2 2
Im 2
1 cos 0.27I m 4
1 2 2 1 1 1 3 1 I1 I m 0.48 I m I m sin d I m 2 4 4 4 2 4 4 2
解:由于是半可控桥式整流,故
U d 0.9U 2
1 cos 1 cos 1 100 0.9 220 900 2 2 2 U d 100 I d 20A R 5
8/21
晶闸管平均电流:
I dVT
I VT
1800 900 Id 20 5 A 0 2 360
Id0 I VT Ud0 257 272 A R 0.946 1 1 Id0 272 157 A 3 3
IVT折成标准波形时的额定电流: I VT AV
I VT 157 100 A 1.57 1.57
取安全系数为2,则晶闸管电流为200(A)
WL=2π fL=2×3.14×50×0.2=62.8>>5Ω 故电流波形近似当一条水平线
4/21
SCR平均值:
I dVT
1800 900 Id 10 2.5 A 0 2 2 180
Id 2
Id 2
2 1 2
触发脉冲丢失。 求:1、画出输出电压的波形,计算输出电压的大小? 2、画出VT2两端电压波形?
1、输出波形及大小:
1 Ud 2
6 3
2U 2 2U 2 sin tdt 2
2
sin tdt
2U 2 2U 2 cost 49.5V 2 2 2
0.48I m K1 1.78 0.27I m
2/21
例3、上题中如果不考虑安全裕量,问100A的晶闸管能送出的平均电流 Id1为多少?这时相应的电流最大值Im1为多少?
I d1
157 157 88.2 A K1 1.78
88.2=0.27Im1 Im1= 326.7 A
3/21
例4、具有续流二极管的单相半波晶闸管整流电路,对发电机励 磁绕组供电。绕组的电阻为5Ω,电感为0.2亨,励磁直流平均电流 为10A,交流电源电压为220V,计算晶闸管和续流二极管的电流 有效值?
解:整流电路输出的直流电压,其平均值为: Ud=IdR=10×5=50伏
U d 0.45U 2
1 cos 50 cos 0 90 0 2
波形系数(电流有效值与平均值之比):
I VT 1 1 Kf I m / I m 1.57 I TAV 2
1/21
例2、下图中阴影部分为晶闸管处于通态区间的电流波形,各波形的流最大 值均为Im ,试计算各波形的电流平均值Id1与电流有效值I1?
I d1
1 2
4
I m sin d
U m 6U 2 6 110 270V
取安全系数为2,则晶闸管电压为700(V) 故选择KP200—7晶闸管
13/21
0 2、 60 时,输出电压波形:
14/21
SCR有效值:
I VT
2
1 2
10 5 A
二极管平均值:
I dVDR
10 7.5 A
二极管的有效值:
I VDR
Id 2
2
1 2
10 8.66A
5/21
例5、单相半波可控整流的电路,纯电阻性负载。已知:U2=100V,R=5Ω ,α =900 求:1、输出电流平均值Id 及有效值IVT ? 2、画出Ud、Id的波形图 ? 3、 co s ? 解1 :
晶闸管有效值:
900 Id 20 10A 0 2 360
2 900 Id 20 10A 0 2 180
续流二极管平均:
I dVDR
续流二极管有效值:
I VDR
900 Id 20 14.1A 0 180
9/21
0 例7、如图电路,已知变压器副边相电压U2=220V,当 60 时,VT2、VT3的
