仿真系统时间类型定义
系统仿真的类型

0.3 系统仿真的类型1.根据模型的物理属性分类物理仿真:按照真实系统的物理性质构造系统的物理模型,并在物理模型上进行实验的过程称为物理仿真。
∙物理仿真的优点是:直观、形象,也称为“模拟”。
∙物理仿真的缺点是:模型改变困难,实验限制多,投资较大。
数学仿真:对实际系统进行抽象,并将其特性用数学关系加以描述而得到系统的数学模型,对数学模型进行实验的过程称为数学仿真。
计算机技术的发展为数学仿真创造了环境,亦称为计算机仿真∙数学仿真优点是:方便、灵活、经济∙数学仿真缺点是:受限于系统建模技术,即系统数学模型不易建立。
半实物仿真:即将数学模型与物理模型甚至实物联合起来进行实验。
∙对系统中比较简单的部分或对其规律比较清楚的部分建立数学模型,并在计算机上加以实现∙对比较复杂的部分或对规律尚不十分清楚的系统,其数学模型的建立比较困难,则采用物理模型或实物∙仿真时将两者连接起来完成整个系统的实验2.根据仿真计算机类型分类模拟计算机仿真:模拟计算机本质上是一种通用的电气装置,这是50-60年代普遍采用仿真设备。
将系统数学模型在模拟机上加以实现并进行实验称为模拟机仿真。
模拟机仿真是一种并行仿真,仿真时,代表模型的各部件是并发执行的。
例如: d ydtad ydtbdydtcy f td ydtad ydtbdydtcy f td ydtd ydtdtdydtd ydtdt ydydtdt 33223322223322+++==---+===⎰⎰⎰()()数字计算机仿真:将系统数学模型用计算机程序加以实现,通过运行程序来得到数学模型的解,从而达到系统仿真的目的。
早期的数字计算机仿真则是一种串行仿真,因为计算机只有一个中央处理器(CPU),计算机指令只能逐条执行。
数字模拟混合仿真:为了发挥模拟计算机并行计算和数字计算机强大的存贮记忆及控制功能,以实现大型复杂系统的高速仿真,将系统模型分为两部分,其中一部分放在模拟计算机上运行,另一部分放在数字计算机上运行,两个计算机之间利用模/数和数/模转换装置交换信息。
simulink 步长概念

simulink 步长概念
Simulink 是MATLAB 的一个功能强大的可视化仿真工具,它主要用于对动态系统进行建模、仿真和分析。
在Simulink 中,步长(step size) 是指仿真时间步的长度。
步长决定了仿真时间推进的速度,并影响仿真结果的精度。
步长的概念
在仿真过程中,步长表示从一个仿真时间点到下一个仿真时间点的间隔。
这个间隔可以是固定的,也可以是变化的。
步长可以是自动计算的,也可以是用户定义的。
步长的选择对仿真的精度和速度有着直接的影响。
选择合适的步长
选择合适的步长需要考虑仿真系统的动态特性和精度需求。
较小的步长会提供更高的精度,但需要更多的计算资源,可能会减慢仿真速度。
较大的步长会加快仿真速度,但可能会降低精度。
因此,需要根据仿真的需求在精度和速度之间做出权衡。
自动步长和固定步长
在Simulink 中,可以选择自动步长或固定步长。
自动步长让Simulink 自动选择适当的步长以获得满意的精度。
固定步长则让用户定义一个固定的步长值。
在大多数情况下,自动步长是一个好的选择,因为它可以根据需要动态调整步长,以在精度和速度之间找到最佳的平衡。
步长是Simulink 中一个重要的概念,它决定了仿真时间推进的速度和精度。
了解步长的概念和如何选择合适的步长对于获得准确的仿真结果是至关重要的。
通过选择适当的步长,可以在满足精度需求的同时提高仿真的效率。
simulink 步长概念 -回复

simulink 步长概念-回复Simulink是一种用于建模、仿真和分析动态系统的工具。
在Simulink中,步长是模拟或仿真模型时使用的一个重要概念。
步长定义了模型在每个模拟时间步长上进行计算的精度,影响着仿真的准确性和效率。
本文将逐步回答关于Simulink步长的一些常见问题,并探讨步长对模型仿真的影响。
第一步:什么是Simulink步长?步长是Simulink模型在仿真期间使用的时间间隔,用于获取系统的当前状态并计算下一个时刻的状态。
在仿真中,模型将时间分成一系列小的离散步长,每个步长模型计算一遍模型的状态,并将结果用作下一个时间点的初始条件。
步长的选择是一个重要的决策,因为它直接影响着模型分析的准确性和计算效率。
第二步:如何选择适当的步长?选择适当的步长是确保模型仿真准确性的关键一步。
步长的选择需要考虑到系统动态的特性以及仿真的可接受误差。
一般而言,步长应足够小,以捕捉到系统动态的细节,但又不应过小,以至于使仿真时间过长或导致不稳定的计算。
以下是一些考虑步长选择的重要原则:1. 系统的动态特性:不同类型的系统具有不同的动态响应特征,如快速响应、慢速响应、高频振荡等。
快速响应系统的仿真步长应该相对较小,以捕捉高频率的变化。
而慢速响应系统可以使用较大的步长,以提高仿真效率。
2. 模型的非线性特性:如果模型具有非线性特性,例如非线性函数或激活函数,那么较小的步长可能更合适,以捕捉non-linearity的行为特征。
3. 仿真误差:在某些应用中,需要控制仿真结果与实际结果之间的误差。
较小的步长可以减小仿真误差,但也会增加仿真时间和计算负载。
因此,需要在精度和效率之间进行权衡。
第三步:在Simulink中如何设置步长?在Simulink中,可以通过多种方式来指定仿真步长。
以下是一些常见的设置选项:1. 固定步长:使用固定步长时,仿真将在每个模拟时间步长上进行计算。
可以通过在模型参数对话框中设置固定步长的值来指定步长。
Systemview仿真环境使用教程

Systemview仿真环境一、实验目的1、熟悉Systemview软件的界面;2、熟悉常用菜单和工具栏;3、掌握系统定时、信号源、函数模块、数据接收器、接收计算器等概念及使用方法。
4、能利用软件进行简单系统的仿真设计。
二、实验设备Systemview软件、计算机三、实验内容1、选择Help/Demo..菜单项,单击Start Demo 按键,观察实例演示。
调节Demo Speed ,可改变演示速度。
2、在观察演示过程中,特别注意如何设置系统时间,如何选择模块和设置模块参数,如何选择滤波器和设置滤波器的参数。
3、建立如下系统:该系统实现对输入信号进行平方运算。
4、操作步骤如下:1)每次构建一个新的仿真系统时,都首先需要对系统时间进行定义。
单击系统工具栏上的定时按扭,“No.of Samples”(采样点数)设置为128,单击“OK”。
2)双击信号源库“Source”图符。
双击该图符显示出信号源库窗口,单击“Sinusoid”,单击参数“Parameters”按扭,在频率框“Frequency”内输入“4”,单击“OK”。
这样就定义了一个幅度为1,频率为4HZ 的正弦波信号。
3)现在弹出函数图符。
与信号源图符的处理相同,双击该图符显示出函数库窗口,选择“Algebraic”,选择“X^a”,单击参数“Parameters”按扭,在“Exponent”框内输入“2”。
这个图符被用于对输入的正弦波进行平方运算。
4)弹出数据接收器“Sink”图符。
双击该图符并选择“Graphic Display”,选择“SystemView”做为信号接收器的类型。
5)点击(连接按扭),再点击信号源图符“Source”,出现“Select Output”对话框,选择“0:sine”点击“OK”,再点击“Sink”图符,这样“Source”图符就连接到了“Sink”图符。
6)弹出另一个“Sink”图符并同样选择“SystemView”类型。
仿真概念归纳总结

仿真概念归纳总结近年来,仿真技术在各个领域中得到了广泛应用,成为解决实际问题、预测结果和培训等方面的重要工具。
本文将对仿真概念进行归纳总结,从定义、分类到应用领域等方面进行探讨。
一、仿真概念定义仿真是指利用计算机模拟真实世界过程、系统或行为的过程。
它通过建立模型并对模型进行计算,以求得关于真实世界的有用信息。
仿真技术以模拟实验的方式,通过模型的演化和结果的观察,在模型中模拟和分析实际系统的运行,并据以进行决策。
二、仿真分类1. 离散事件仿真(DES)离散事件仿真是一种基于事件驱动的仿真方法,它以离散事件为时间推进单位,模拟系统中的离散事件及其之间的发生、处理和发展关系。
这种仿真方法适用于涉及到系统内离散事件交互和非持续性系统行为的问题,如排队、交通流、生产流程等。
2. 连续仿真连续仿真是一种通过对仿真对象的状态进行连续变化而推进仿真时间的方法。
这种仿真方法适用于涉及到系统内连续状态变化和持续性系统行为的问题,如物理模型、流体力学等。
3. 混合仿真混合仿真是离散事件仿真和连续仿真的结合体,将两种仿真方法结合起来,以更好地模拟复杂系统。
这种仿真方法适用于既涉及到离散事件交互,又涉及到连续状态变化的问题,如交通系统、航空系统等。
三、仿真应用领域1. 工业制造仿真在工业制造中的应用非常广泛,可以对生产线、物料流动、装配过程等进行建模和仿真,以优化生产效率、降低成本、提高产品质量。
2. 交通运输仿真技术在交通运输领域的应用可以模拟交通流量、道路网络、交通信号等,以实现交通拥堵预测、交通规划优化和交通管理等目标。
3. 医疗领域仿真可以用于医疗培训和手术模拟,使医生和护士能够在虚拟环境中进行实践,提高医疗技术和减少医疗事故。
4. 军事训练仿真技术在军事训练中的应用可以模拟战场环境、交战双方、武器系统等,提供真实的虚拟训练环境,以提高军事人员的战斗能力和决策水平。
5. 城市规划仿真可以对城市的建筑、交通、人口等进行精确建模和仿真,以帮助城市规划者分析城市发展策略、优化城市布局和改善城市运行。
系统时间响应及其仿真概述

系统时间响应及其仿真概述系统时间响应是指系统对于输入信号的变化做出的相应。
它描述了系统在时间上的动态特性,包括系统的稳定性、阻尼比、过渡过程等。
在控制系统中,系统时间响应的分析及仿真是非常重要的,它能够帮助工程师评估系统性能,并进行系统设计和调整。
系统时间响应可以通过分析系统的传递函数得到,传递函数是系统输入和输出之间的关系描述。
通过对传递函数的分析,可以获得系统的零点、极点和阻尼比等参数,进而推导出系统的时间响应。
时间响应通常用单位阶跃响应和单位冲激响应来表示。
仿真是对系统时间响应的模拟,在计算机上通过数学模型和仿真工具来模拟系统的动态特性。
仿真可以方便地对系统进行分析、优化和测试,为系统设计和调整提供参考。
在进行系统时间响应的仿真时,一般需要以下步骤:1. 确定系统的传递函数:通过系统的物理特性和传感器的性质,可以得到系统的传递函数。
传递函数的形式可以是标准形式,如一阶、二阶系统,也可以是非线性的。
2. 选择仿真工具:根据实际情况选择适合的仿真工具。
常用的仿真工具有MATLAB/Simulink、LabVIEW等。
3. 建立仿真模型:根据系统的传递函数建立仿真模型。
在仿真模型中,需要包括输入信号、传递函数和输出信号的关系。
4. 设定仿真参数:确定仿真方式、仿真步长和仿真时间等参数,并进行相应的设定。
5. 运行仿真模型:根据设定的参数,运行仿真模型,并获得系统的时间响应结果。
6. 分析仿真结果:根据仿真结果,对系统的时间响应进行分析,评估系统的性能,并进行可能的调整和优化。
通过对系统时间响应的仿真,可以直观地了解系统的动态特性,从而对系统进行设计和调整。
因此,系统时间响应的分析与仿真在控制系统设计和优化中起着重要的作用。
系统时间响应是控制系统中的重要性能指标之一,它描述了系统对输入信号变化的反应情况。
系统的时间响应能够体现系统的稳定性、动态特性以及对不同输入信号的响应速度。
通过对系统时间响应的分析和仿真,可以帮助工程师评估系统性能,并进行系统设计和调整。
系统仿真PDPSPDPS入门到精通详细教程

优化系统设计
仿真技术可以帮助工程师在设计阶段发现潜在的问 题并进行优化,提高设计的可靠性和效率。
加速产品开发周期
通过仿真技术,可以缩短产品开发周期,加 快产品上市时间,提高企业竞争力。
PDPS/PDPS概述
PDPS/PDPS简介
PDPS/PDPS是一款功能强大的系统仿真软件,广泛应用于各个领 域。它具有丰富的功能和工具,支持多种仿真方法和算法。
并行计算与分布式仿真技术
并行计算原理与实现
01
介绍并行计算的基本原理和实现方法,包括任务并行
和数据并行两种方式。
分布式仿真技术
02 详细讲解分布式仿真的原理和实现方法,包括基于消
息传递的分布式仿真和基于共享内存的分布式仿真。
PDPS中的并行计算与分布式仿真支持
03
探讨PDPS如何支持并行计算和分布式仿真,包括提
数值积分方法
03
离散事件仿真方法
利用数值积分算法对连续系统进 行仿真,如欧拉法、龙格-库塔 法等。
通过模拟离散事件的发生和处理 过程来仿真系统,适用于排队系 统、生产流程等。
系统仿真软件介绍
MATLAB/Simulink
功能强大的数学计算和仿真软件,提供丰富的工具箱和模型库,适用 于多种领域的系统仿真。
供的并行计算库、分布式仿真框架等工具和技术。
07
总结与展望
回顾本次课程重点内容
系统仿真基本概念和原理
介绍了系统仿真的定义、分类、应用 领域以及基本原理,包括建模、仿真 实验设计和结果分析等。
系统建模与仿真实验设计
深入阐述了系统建模的方法和步骤, 包括模型构建、参数设置、仿真实验 设计等,以及如何通过仿真实验验证 模型的正确性和有效性。
stateflow中duration用法

stateflow中duration用法Stateflow中duration用法Stateflow是一种用于模型和仿真离散事件系统的Matlab/Simulink工具。
它提供了一种图形化的界面来描述状态转换和事件处理。
在Stateflow中,duration(持续时间)是用来表示时间间隔的一种类型,它可以在状态之间进行条件判断和控制流程的转换。
下面是一些常见的Stateflow中duration的用法及详细讲解:1. duration的基本用法duration 是一个数值类型,用来表示一段时间间隔。
它可以以秒(s)、毫秒 (ms)、微秒 (us) 等单位进行表示。
在Stateflow中,可以使用内置的函数来操作和比较这些时间间隔。
duration dt = ; // 定义一个持续时间为5秒的变量dt duration t = ; // 定义一个持续时间为10秒的变量tif(dt > t){// 如果dt大于t,则执行该语句块}else{// 如果dt小于等于t,则执行该语句块}2. duration与状态转换在Stateflow中,duration可以与条件判断语句一起使用,来控制状态之间的转换。
比如,当某个任务持续时间达到一定阈值时,自动切换到下一个状态。
duration taskTime = ; // 定义任务持续时间为秒if(taskTime > ){// 如果任务持续时间大于2秒,则切换到下一个状态next_state();}else{// 如果任务持续时间小于等于2秒,则保持当前状态}3. duration与事件处理在Stateflow中,duration还可以与事件处理一起使用,来控制状态之间的触发和处理。
duration timeout = ; // 定义超时时间为1秒// 定义一个事件处理函数,当超时发生时,触发事件,并执行相应的操作on timeout_event() do{// 超时事件处理逻辑}// 定义一个定时器,当持续时间达到超时时间时,触发超时事件timer(t, timeout_event());在上述代码中,当定时器的持续时间达到超时时间时,会自动触发timeout_event()事件,从而执行相应的事件处理逻辑。
离散时间和连续时间模型的仿真

计算机仿真
用于模拟计算机系统的性能和行为,如操作系 统、网络通信等。
数字电路仿真
用于模拟数字电路的行为和性能,如逻辑门电路、微处理器等。于模拟控制系统的动态行为,如飞机、汽 车、机器人等。
电路仿真
用于模拟电路的动态行为和性能,如模拟电 路、数字电路等。
流体动力学仿真
05
离散时间和连续时间模型仿
真的发展趋势
离散时间模型仿真的发展趋势
01
离散时间模型仿真在计算机技 术的推动下,正朝着高精度、 高效率、高逼真度的方向发展 。
02
随着数值计算方法的改进,离 散时间模型仿真在处理复杂系 统时能够更准确地反映其动态 特性。
03
离散时间模型仿真在工程设计 、产品开发、生产制造等领域 的应用越来越广泛,成为解决 实际问题的有力工具。
骤或过程来模拟仿真过程。
02
连续时间模型仿真
连续事件的定义
连续事件
在连续时间模型中,事件的发生是在一个连续的时间段内,而不是离散的时刻。这些事 件通常与物理过程或自然现象相关,如温度变化、速度变化等。
时间变量
在连续时间模型中,时间是一个连续变化的变量,可以表示为实数轴上的一个点或一段 长度。
状态变化
用于模拟流体动力学系统的行为和性能,如 流体流动、热传导等。
离散时间和连续时间模型的适用性分析
离散时间模型适用于模拟离散事件系统,而连续时间模型适用于模拟连续 动态系统。
在选择使用离散时间模型还是连续时间模型时,需要考虑系统的特性和需 求,以及仿真的精度和计算成本等因素。
在某些情况下,可能需要结合离散时间模型和连续时间模型进行仿真,以 获得更准确的结果。
感谢观看
THANKS
仿真系统时间类型定义
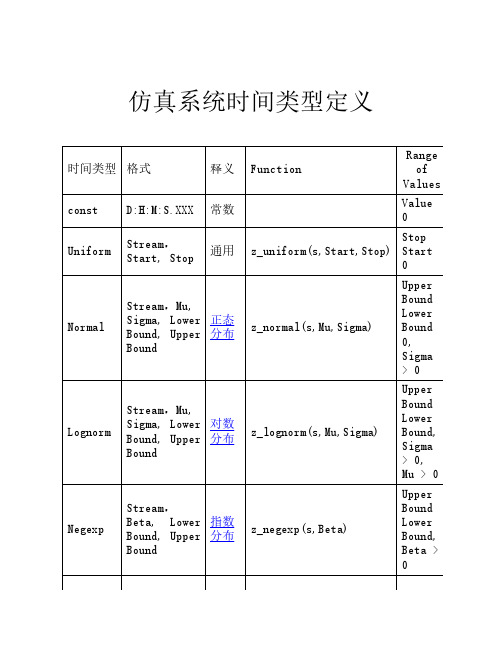
仿真系统时间类型定义Distribution FunctionsYou can create random numbers with objects of type Generator and Variables of data type time as well as with the functions described below, which return random numbers according to the desired distribution.你可以根据需要的数据分布形态,使用下面所述的针对时间变量的类型生成器,生成任意数值。
The argument s stands for the random number stream and is of data type integer. All other arguments are the arguments of the corresponding distribution function as described under Statistical Distributions. They all either are of data type real orTypeUsage:<attribute_path>.Type := <string>; The attribute Type defines the type of a statistical distribution for the attribute named. Attribute_path designates anattribute of data type time or a customExample:singleProc.proctime.Type :="uniform";The different distributions have different attributes. You can set these:With the method setParam.With the method setTypeAndAttr.By direct assignments to theattribute.Example:singleProc.proctime.Mu := 0.50;singleProc.proctime.Sigma :=0.1;数学基础NORMDIST正态分布返回指定平均值和标准偏差的正态分布。
系统建模与仿真-第3章 系统仿真方法与技术

3.4 系统仿真技术的应用
3.4.5 仿真技术在CIMS中的应用
(1)CIMS的需求分析仿真 (2)CIMS的设计仿真 (3)CIMS的仿真测试 (4)CIMS运行与维护的仿真支持
3. 5 系统仿真技术的特点
(1)安全性 (2)经济性 (3)可重复性
Add Your Company Slogan
3.2 系统仿真技术的分类
2.根据仿真计算机类型分类
根据所使用的仿真计算机类型也可将仿真分为三类: (1)模拟计算机仿真; (2)数字计算机仿真; (3)数字模拟混合仿真。
3.2 系统仿真技术的分类
3.根据仿真时钟与实际时钟的比例关系分类
实际动态系统的时间基称为实际时钟。而系统仿真时模 型所采用的时钟称为仿真时钟。根据仿真时钟与实时时 钟的比例关系,系统仿真分类如下: (1)实时仿真。 (2)亚实时仿真。 (3)超实时仿真。
3.4 系统仿真技术的应用
3.4.4 仿真在产品开发及制造过程中的应用
设计人员或用户甚至可“进入”虚拟的制造环境检验其 设计、加工、装配和操作,而不依赖于传统的原型样机的反 复修改。这样使得产品开发走出主要依赖于经验的狭小天地 ,发展到了全方位预报的新阶段。下图简要表示了虚拟制造 与实际制造的联系与区别。
(5) 试验时间太长、费用太大或者有危险等。
3.4 系统仿真技术的应用
3.4.3 仿真在教育与训练中的应用
训练仿真系统是利用计算机并通过运动设备、操纵设备、显 示设备、仪器仪表等复现所模拟的对象行为,并产生与之适 应的环境,从而成为训练操纵、控制或管理这类对象的人员 的系统。 根据模拟对象、训练目的,可将训练仿真系统分为三大类: (1)载体操纵型:这是与运载工具有关的仿真系统,包括航空 、航天、航海、地面运载工具,以训练驾驶员的操纵技术为 主要目的。 (2)过程控制型用于训练各种工厂(如电厂、化工厂、核电站 、电力网等)的运行操作人员。 (3)博弈决策型用于企业管理人员(厂长、经理)、交通管制人 员(火车调度、航空管制、港口管制、城市交通指挥等)和军 事指挥人员(空战、海战、电子战等)的训练。
仿真的基本形式

仿真的基本形式
仿真是利用计算机技术来模拟现实世界或虚拟世界中的事件或过程的过程。
它的基本形式有以下几种:
1. 离散事件仿真:离散事件仿真是一种基于离散时间步的仿真技术,适用于模拟离散事件系统,如调度系统、生产线、运输系统等。
该技术将时间分成离散的时间步,每个时间步中模拟系统状态的改变和事件的发生。
2. 连续仿真:连续仿真是一种基于连续时间的仿真技术,适用于模拟连续系统,如物理系统、气候系统、经济系统等。
该技术将时间看作一个连续的变量,根据系统的物理特性和方程式模拟系统状态的变化。
3. 混合仿真:混合仿真是将离散事件仿真和连续仿真相结合的一种仿真技术,适用于模拟同时包含离散事件和连续过程的系统,如交通系统、军事系统等。
该技术将时间分为离散事件和连续时间两部分,同时考虑系统中的离散事件和连续过程,模拟系统状态的变化。
4. 随机仿真:随机仿真是一种基于随机过程的仿真技术,适用于模拟存在随机因素的系统,如金融系统、风险评估等。
该技术采用随机变量模拟系统中的随机因素对系统状态的影响。
总之,仿真技术的不同形式都是为了更好地模拟不同类型的系统和过程,以便更好地预测、分析和优化系统性能。
比例控制的直流调速系统的仿真参数

比例控制的直流调速系统的仿真参数一、电机特性参数:1.电机额定电流(I_N):直流电机的额定电流,可以根据电机的额定功率和电压通过功率公式计算得到。
2.电机内阻(R):电机内部电阻,决定了电机的电流分布和阻尼特性。
可以通过实际测量或者从电机的技术手册中获取。
3.电机电感(L):电机的电感,反映了电机的自感特性,也会对电机的动态响应产生影响。
可以通过实际测量或者从电机的技术手册中获取。
4.电机转动惯量(J):电机的转动惯量,决定了电机的惯性和动态响应。
可以通过实际测量或者从电机的技术手册中获取。
5.电机反电动势常数(Ke):电机反电动势常数,反映了电机的输出电压与转速之间的关系。
可以通过实际测量或者从电机的技术手册中获取。
二、控制回路参数:1.比例增益(Kp):比例速度调节器的增益,决定了控制输出与误差之间的线性关系。
可以根据系统的要求进行选择。
2.采样周期(T):控制系统的采样周期,决定了控制器的调节速度和控制精度。
通常根据系统的性能指标进行选择,如超调量、调节时间等。
3.控制器类型:可以选择不同类型的控制器,如比例控制器、积分控制器、微分控制器或者PID控制器等。
4.控制器输出限制:对控制器的输出做限制,可以避免电机超调或者过负荷运行。
5.反馈方式:可以选择转速反馈或者位置反馈,一般采用转速反馈。
三、仿真环境参数:1.仿真时间:仿真的总时间长度,可以根据系统的稳态要求进行选择。
2.仿真步长:仿真器的时间步长,决定了仿真器的计算精度。
可以根据系统的要求进行选择。
3.仿真误差容限:控制系统的输出与设定值之间的允许误差范围。
可以根据系统的控制精度要求进行选择。
4.扰动信号:可以在仿真中添加加性或者乘性噪声,模拟实际工作环境中的扰动。
综上所述,比例控制的直流调速系统的仿真参数包括电机的特性参数、控制回路参数和仿真环境参数等。
根据具体的系统要求和性能指标,可以选择适当的参数值来进行仿真建模和分析,以评估系统的控制性能和稳定性。
各种仿真分析的定义与理解

各种仿真分析的定义与理解仿真分析是指使用计算机模型和模拟技术来模拟和分析实际系统的行为和性能的一种方法。
它可以在系统设计、性能评估、决策支持等领域中发挥重要作用。
仿真分析可以帮助我们深入理解系统的复杂性和相互关联性,预测系统的行为变化,并优化系统设计和运营策略。
仿真分析可以分为离散事件仿真和连续仿真两种类型。
离散事件仿真是一种基于事件驱动的仿真方法,模拟系统中的离散事件的发生和处理过程,如顾客到达一些进程、任务完成、装备故障等。
离散事件仿真适用于需要模拟离散事件的系统,如生产线、交通系统等。
连续仿真是一种基于不断变化的连续时间的仿真方法,模拟系统在连续时间下的行为变化,如流体流动、结构力学等。
连续仿真适用于需要模拟连续变化的系统,如天气模拟、飞行模拟等。
在仿真分析中,需要建立系统的数学模型和计算机模型。
数学模型是对实际系统的抽象描述,包括系统的结构和行为规则等。
计算机模型是将数学模型转化为计算机程序,利用计算机来模拟系统的行为和性能。
计算机模型可以是基于模型的仿真或是基于仿真的优化。
基于模型的仿真通过模拟系统的行为来分析系统的性能,可以提供系统的详细行为和性能指标,但是计算复杂度较高。
基于仿真的优化通过多次运行仿真模拟来最佳设计参数,以达到系统的最优性能。
在仿真分析中,需要选择适当的建模方法和仿真工具。
建模方法包括系统动力学、离散事件、代理模型等。
系统动力学是一种基于系统结构和变量间的相互关系建立数学模型的方法,适用于非线性且高度相互依赖的系统。
离散事件建模主要关注事件的发生和处理顺序,适用于需要考虑事件的影响和交互的系统。
代理模型是一种通过建立不同角色的代理来模拟系统行为的方法,适用于多层次、多个参与者的系统。
仿真工具包括专业的仿真软件和编程语言等,如Simulink、Arena、AnyLogic等。
在仿真分析中,需要进行实验设计和参数优化。
实验设计包括确定仿真的目标、选择输入参数和输出指标、设计实验方案等。
仿真概念归纳总结

仿真概念归纳总结简介仿真是一种通过模拟真实系统的运行,通过模型来预测系统的行为和性能的方法。
它广泛应用于各个领域,例如物理、工程、计算机科学等。
本文将对仿真的概念进行归纳总结,包括仿真的定义、分类、应用和优势等方面。
1. 仿真的定义仿真是通过创建一个模型来模拟现实系统的行为和性能。
这个模型可以是一个数学模型、物理模型或计算机模型。
仿真通过表达模型中的各个元素之间的关系和规则来模拟系统的运行。
与现实系统相比,仿真可以为我们提供更多的机会来观察、分析和预测系统的行为。
2. 仿真的分类根据仿真系统的类型和目标,仿真可以分为以下几类:2.1 连续仿真连续仿真是指模拟连续系统的行为和性能,其中系统的状态随时间的变化而连续变化。
连续仿真通常使用微分方程来描述系统的动态变化。
2.2 离散仿真离散仿真是指模拟离散系统的行为和性能,其中系统的状态在一系列离散的时间点上发生变化。
离散仿真通常使用差分方程或状态转移图来描述系统的行为。
2.3 混合仿真混合仿真是指同时模拟连续和离散系统的行为和性能。
混合仿真通常使用混合系统理论来描述系统的动态变化。
3. 仿真的应用仿真在各个领域都有广泛的应用,以下是一些常见的仿真应用示例:3.1 物理仿真物理仿真用于模拟物理系统的行为和性能。
例如,通过模拟重力、摩擦等物理规律,可以预测物体的运动轨迹和碰撞结果。
3.2 工程仿真工程仿真用于模拟工程系统的行为和性能。
例如,在设计一座桥梁时,可以使用仿真来测试桥梁的耐久性、承重能力等。
3.3 计算机仿真计算机仿真用于模拟计算机系统的行为和性能。
例如,在开发软件时,可以使用仿真来测试软件的性能、稳定性等。
3.4 生物仿真生物仿真用于模拟生物系统的行为和性能。
例如,通过模拟人体器官的功能和相互作用,可以预测药物的副作用和疾病的发展趋势。
4. 仿真的优势仿真作为一种研究和预测系统行为的方法,具有以下几个优势:4.1 降低成本和风险通过仿真,可以在现实系统投入大量时间和资源之前,预测系统的性能、问题和风险。
并行与分布式仿真系统中的时间管理技术研究

近年来,分布式仿真运行支撑平台的发展迅速,广泛应用于军事、工业、科研 等领域。然而,随着系统规模的扩大和复杂性的增加,时间管理服务也面临着 越来越多的挑战。例如,如何确保仿真时间的同步精度、如何处理节点之间的 通信延迟、如何提高时间管理服务的可扩展性等。
本次演示采用文献调研、技术分析和系统设计等方法,对分布式仿真运行支撑 平台中时间管理服务进行深入研究。首先,我们对时间管理服务的相关理论进 行研究,建立相应的数学模型,以提高时间同步精度和分配的效率。其次,我 们分析现有时间管理服务的优缺点,针对不足之处提出改进措施。最后,我们 设计并实现了一个高效的时间管理服务系统,并在实际应用中进行了验证。
2、存储策略:对于海量空间数据,需要制定合适的存储策略,以满足其对存 储容量、查询速度和数据安全等方面的需求。例如,可以采用分布式哈希表 (DHT)或基于冗余的分布,管理机制至关重要。需要实现包括数据复制、 数据迁移、数据备份和恢复等在内的多种管理任务,以保证数据的可靠性和一 致性。
2、任务完成率:任务完成率是指仿真系统中完成任务的数量占任务总数的比 例。这个指标可以用来衡量时间管理技术的有效性。
3、任务执行顺序:任务执行顺序是指任务在仿真系统中的执行顺序。这个指 标可以用来衡量时间管理技术的合理性和准确性。
在评估时间管理技术时,可以通过真实数据采集和模拟实验的方式进行。真实 数据采集可以直接在真实系统中采集实际运行数据,但需要考虑实验环境和实 验条件的影响。模拟实验可以在模拟环境中模拟各种实际情况,但需要设计合 理的模拟实验方案。
二、并行处理技术
并行处理技术是一种可以提高数据处理速度和效率的技术。在并行处理中,通 过将任务分解为多个子任务,并分配给多个处理器同时处理,可以大大提高处 理速度和处理效率。
仿真系统时间类型定义
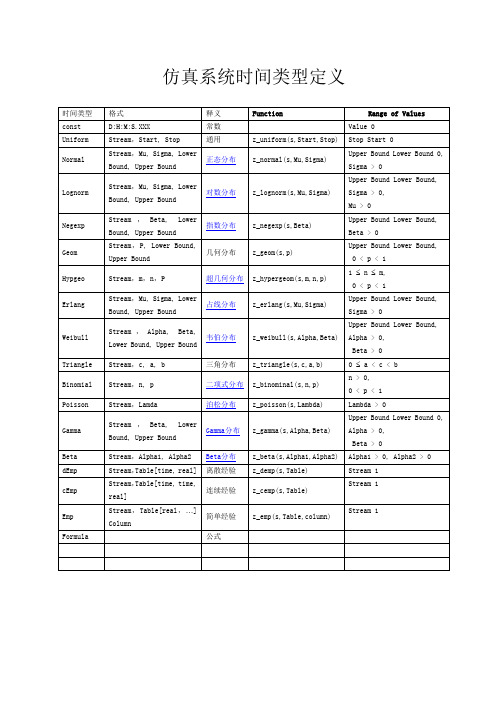
仿真系统时间类型定义Distribution FunctionsYou can create random numbers with objects of type Generator and Variables of data type time as well as with the functions described below, which return random numbers according to the desired distribution.你可以根据需要的数据分布形态,使用下面所述的针对时间变量的类型生成器,生成任意数值。
The argument s stands for the random number stream and is of data type integer. All other arguments are the arguments of the corresponding distribution function as described under Statistical Distributions. They all either are of data type real or integer.TypeUsage:<attribute_path>.Type := <string>;The attribute Type defines the type of a statistical distribution for the attribute named. Attribute_path designates an attribute of data type time or a custom attribute of data type randtime.Example:singleProc.proctime.Type := "uniform";The different distributions have different attributes. You can set these: •With the method setParam.•With the method setTypeAndAttr.•By direct assignments to the attribute.Example:singleProc.proctime.Mu := 0.50;singleProc.proctime.Sigma := 0.1;Assign arguments according to this list:数学基础NORMDIST正态分布返回指定平均值和标准偏差的正态分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仿真系统时间类型定义Distribution FunctionsYou can create random numbers with objects of type Generator and Variables of data type time as well as with the functions described below, which return random numbers according to the desired distribution.你可以根据需要的数据分布形态,使用下面所述的针对时间变量的类型生成器,生成任意数值。
The argument s stands for the random number stream and is of data type integer. All other arguments are the arguments of the corresponding distribution function as described under Statistical Distributions. They all either are of data type real orTypeUsage:<attribute_path>.Type := <string>; The attribute Type defines the type of a statistical distribution for the attribute named. Attribute_path designates anattribute of data type time or a customExample:singleProc.proctime.Type :="uniform";The different distributions have different attributes. You can set these:With the method setParam.With the method setTypeAndAttr.By direct assignments to theattribute.Example:singleProc.proctime.Mu := 0.50;singleProc.proctime.Sigma :=0.1;数学基础NORMDIST正态分布返回指定平均值和标准偏差的正态分布。
此函数在统计方面应用范围广泛(包括假设检验)。
语法NORMDIST(x,mean,standard_dev,cumulative)X 是需要计算其分布的数值。
Mean 分布的算术平均值。
Standard_dev 分布的标准偏差。
Cumulative 为一逻辑值,指明函数的形式。
如果 cumulative 为TRUE,则 NORMDIST 返回累积分布函数;如果为 FALSE,则返回概率密度函数。
说明如果 mean 或 standard_dev 为非数字型,则 NORMDIST 返回错误值 #VALUE!。
如果 standard_dev ≤ 0,则 NORMDIST 返回错误值 #NUM!。
如果 mean = 0,standard_dev = 1,且 cumulative = TRUE,则NORMDIST 返回标准正态分布,即 NORMSDIST。
正态分布密度函数 (cumulative = FALSE) 的计算公式如下:如果 cumulative = TRUE,则公式为从负无穷大到公式中给定的 X 的积分。
示例X Mean StdDev公式说明(结果)4240 1.5=NORMDIST([X],[Mean],[StdDev],TRUE)在指定的参数条件下的累积分布函数值 (0.908789)4240 1.5=NORMDIST([X],[Mean],[StdDev],FALSE)在指定的参数条件下的概率密度函数值 (0.10934005)LOGNORMDIST对数累积分布返回 x 的对数累积分布,其中 ln(x) 是服从参数 mean 和standard_dev 的正态分布。
使用此函数可以分析经过对数变换的数据。
语法LOGNORMDIST(x,mean,standard_dev)X 是用于计算函数的数值。
Mean ln(x) 的平均值。
Standard_dev ln(x) 的标准偏差。
说明如果任一参数是非数字型,则 LOGNORMDIST 返回错误值#VALUE!。
如果 x ≤ 0 或 standard_dev ≤ 0,则 LOGNORMDIST 返回错误值#NUM!。
对数累积分布函数的计算公式如下:示例X Mean StdDev公式说明(结果)4 3.5 1.2=LOGNORMDIST([X],[Mean],[StdDev])在指定的参数条件下 4 的对数累积分布函数值(0.039084)EXPONDIST 指数分布返回指数分布。
使用 EXPONDIST 可以建立事件之间的时间间隔模型,如银行自动提款机支付一次现金所花费的时间。
例如,可以使用函数EXPONDIST 来确定这一过程最长持续一分钟的发生概率。
语法EXPONDIST(x,lambda,cumulative)X 函数的数值。
Lambda 参数值。
Cumulative 是一逻辑值,指出提供的指数函数的形式。
如果cumulative 为 TRUE,则 EXPONDIST 返回累积分布函数;如果为FALSE,则它返回概率密度函数。
说明如果 x 或 lambda 为非数字型,则 EXPONDIST 返回错误值#VALUE!。
如果 x < 0,则 EXPONDIST 返回错误值 #NUM!。
如果 lambda ≤ 0,则 EXPONDIST 返回错误值 #NUM!。
概率密度函数的计算公式如下:累积分布函数的计算公式如下:示例 1公式说明(结果)=EXPONDIST(0.2,10,FALSE)概率指数分布函数 (1.353353)示例 2X Lambda公式说明(结果)0.210=EXPONDIST([X,][Lambda],TRUE)累积指数分布函数(0.864665)HYPGEOMDIST超几何分布返回超几何分布。
在给定样本容量、样本总体成功次数和样本总体容量时,HYPGEOMDIST 返回样本取得给定成功次数的概率。
使用HYPGEOMDIST 可解决有限总体的问题,其中每个观察值或为成功或为失败,且其中给定样本容量的每一个子集有相等的发生概率。
语法HYPGEOMDIST(sample_s,number_sample,population_s,number_population) Sample_s 样本中成功的次数。
Number_sample 样本容量。
Population_s 样本总体中成功的次数。
Number_population 样本总体容量。
说明所有参数都将被截尾取整。
如果任一参数为非数字型,则 HYPGEOMDIST 返回错误值#VALUE!。
如果 sample_s < 0 或 sample_s 大于 number_sample 或 population_s中的较小值,则 HYPGEOMDIST 返回错误值 #NUM!。
如果 sample_s 小于 0 或 (number_sample - number_population +population_s) 中的较大值,则 HYPGEOMDIST 返回错误值#NUM!。
如果 number_sample < 0 或 number_sample > number_population,则 HYPGEOMDIST 返回错误值 #NUM!。
如果 population_s < 0 或 population_s > number_population,则HYPGEOMDIST 返回错误值 #NUM!。
如果 number_population < 0,则 HYPGEOMDIST 返回错误值#NUM!。
超几何分布的计算公式如下:式中:x = sample_sn = number_sampleM = population_sN = number_populationHYPGEOMDIST 用于在有限样本总体中进行不退回抽样的概率计算。
示例抽样器里有 20 块巧克力。
其中 8 块是焦糖的,其余 12 块是果仁的。
如果随机选出 4 块,下面函数返回正好有一块是焦糖的概率。
Sample_s Number_sample Population_s Number_Population公式14820=HYPGEOMDIST([Number_sample],[Population_s],[Number_PopulationWEIBULL分布返回韦伯分布。
使用此分布可以进行可靠性分析,例如计算设备失效的平均时间。
语法WEIBULL(x,alpha,beta,cumulative)X 用于计算函数的数值。
Alpha 分布参数。
Beta 分布参数。
Cumulative 决定函数的形式。
说明如果 x、alpha 或 beta 为非数字型,则 WEIBULL 返回错误值#VALUE!。
如果 x < 0,则 WEIBULL 返回错误值 #NUM!。
如果 alpha ≤ 0 或 beta ≤ 0,则 WEIBULL 返回错误值 #NUM!。
韦伯累积分布函数的计算公式如下:韦伯概率密度函数的计算公式如下:当 alpha = 1 时,WEIBULL 返回指数分布:示例X Alpha Beta公式说明(结果)10520100=WEIBULL([X],[Alpha],[Beta],TRUE)在指定的参数条件下韦伯累积分布函数 (0.929581)10520100=WEIBULL([X],[Alpha],[Beta],FALSE)在指定的参数条件下韦伯概率密度函数 (0.035589)BINOMDIST一元二项式分布返回一元二项式分布的概率值。
函数 BINOMDIST 适用于固定次数的测试或试验,当任何试验的结果仅包含成功或失败两种情况,当试验是独立试验,且当在整个试验过程中成功的概率固定不变。
例如,函数BINOMDIST 可以计算三个婴儿中两个是男孩的概率。
语法BINOMDIST(number_s,trials,probability_s,cumulative)Number_s 是试验中成功的次数。
Trials 是独立试验的次数。
Probability_s 是每次试验中成功的概率。
