高中数学必修三算法案例知识点
高考数学必修三算法初步知识点

高考数学必修三算法初步知识点
1、算法的概念:
①由基本运算及规定的运算顺序所构成的完整的解题步骤,或者是按照要求设计好的有限的计算序列,并且这样的步骤或序列能解决一类问题。
②算法的五个重要特征:
ⅰ有穷性:一个算法必须保证执行有限步后结束;
ⅱ确切性:算法的每一步必须有确切的定义;
ⅲ可行性:算法原则上能够精确地运行,而且人们用笔和纸做有限次即可完成;
ⅳ输入:一个算法有0个或多个输入,以刻划运算对象的初始条件。
所谓0个输入是指算法本身定出了初始条件。
ⅴ输出:一个算法有1个或多个输出,以反映对输入数据加工后的结果。
没有输出的算法是毫无意义的。
2、程序框图也叫流程图,是人们将思考的过程和工作的顺序进行分析、整理,用规定的文字、符号、图形的组合加以直观描述的方法
(1)程序框图的基本符号:
(2)画流程图的基本规则:
①使用标准的框图符号
②从上倒下、从左到右
③开始符号只有一个退出点,结束符号只有一个进入点,判
断符号允许有多个退出点
④判断可以是两分支结构,也可以是多分支结构
⑤语言简练
⑥循环框可以被替代
3、三种基本的逻辑结构:顺序结构、条件结构和循环结构(1)顺序结构:
顺序结构描述的是是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的。
(2)条件结构:分支结构的一般形式。
高中数学必修三知识点大全

知識點串講必修三第一章:演算法1. 1.1 演算法得概念1、演算法(algorithm)一詞源於算術(algorism),即算術方法,是指一個由已知推求未知得運算過程。
後來,人們把它推廣到一般,把進行某一工作得方法和步驟稱為演算法。
廣義地說,演算法就是做某一件事得步驟或程式。
2、任意給定一個大於1得整數n,試設計一個程式或步驟對n是否為質數做出判定。
解析:根據質數得定義判斷解:演算法如下:第一步:判斷n是否等於2,若n=2,則n是質數;若n>2,則執行第二步。
第二步:依次從2至(n-1)檢驗是不是n得因數,即整除n得數,若有這樣得數,則n不是質數;若沒有這樣得數,則n是質數。
3、一個人帶三隻狼和三隻羚羊過河,只有一條船,同船可以容納一個人和兩隻動物.沒有人在得時候,如果狼得數量不少於羚羊得數量,狼就會吃掉羚羊.請設計過河得演算法。
解:演算法或步驟如下:S1 人帶兩隻狼過河;S2 人自己返回;S3 人帶一隻羚羊過河;S4 人帶兩隻狼返回;S5 人帶兩隻羚羊過河;S6 人自己返回;S7 人帶兩隻狼過河;S8 人自己返回;S9 人帶一隻狼過河.1.1.2程式框圖(1得流程圖得首末兩端必須是起止框。
(2表示資料得輸入或結果得輸出,它可用在演算法中得任何需要輸入、輸出得位置。
(3(4判斷框一般有一個入口和兩個出口,有時也有多個出口,它是惟一得具有兩個或兩個以上出口得符號,在只有兩個出口得情形中,通常都分成“是”與“否”(也可用“Y ”與“N ”)兩個分支。
2、順序結構:順序結構描述得是是最簡單得演算法結構,語句與語句之間,框與框之間是按從上到下得順序進行得。
3、已知一個三角形得三邊分別為2、3、4,利用海倫公式設計一個演算法,求出它得面積,並畫出演算法得程式框圖。
演算法分析:這是一個簡單得問題,只需先算出p 得值,再將它代入公式,最後輸出結果,只用順序結構就能夠表達出演算法。
解:程式框圖:24、條件結構:根據條件選擇執行不同指令得控制結構。
高中数学必修三知识点

高中数学必修三知识点引言高中数学必修三通常包括概率统计、数列、算法、复数等重要数学领域,这些知识点对于培养学生的逻辑思维和解决问题的能力至关重要。
一、概率与统计1.1 随机事件与概率概念:随机事件的定义、概率的计算方法。
1.2 概率的性质总结:概率的基本性质,如非负性、规范性、加法法则。
1.3 条件概率与独立事件定义:条件概率的概念、独立事件的判断。
1.4 统计初步指标:均值、中位数、众数、方差、标准差的计算与意义。
1.5 统计图类型:条形图、直方图、饼图的绘制与解读。
二、数列2.1 等差数列公式:等差数列的通项公式、求和公式。
2.2 等比数列公式:等比数列的通项公式、求和公式。
2.3 数列的极限概念:数列极限的定义、无穷等比数列的极限。
2.4 数列的应用案例:数列在实际问题中的应用,如分期付款、人口增长模型。
三、算法3.1 算法的概念定义:算法的定义、特征。
3.2 程序框图绘制:程序框图的绘制方法,如顺序结构、条件结构、循环结构。
3.3 算法案例分析:常见算法问题的解决步骤,如排序、查找。
四、复数4.1 复数的概念定义:复数的定义、实部与虚部。
4.2 复数的运算规则:复数的四则运算、共轭复数、复数的模。
4.3 复数的几何意义解释:复数与复平面的关系、复数的代数表示与几何意义。
4.4 复数的应用案例:复数在电气工程、流体力学等领域的应用。
五、解析几何5.1 坐标系介绍:直角坐标系、极坐标系的基本概念。
5.2 直线的方程形式:直线的点斜式、斜截式、一般式。
5.3 圆的方程形式:圆的标准方程、一般方程。
5.4 圆锥曲线类型:椭圆、双曲线、抛物线的方程和性质。
六、逻辑推理6.1 逻辑与推理概念:逻辑推理的定义、演绎推理与归纳推理。
6.2 逻辑语句分析:逻辑语句的真假判断、逻辑运算。
6.3 推理方法总结:直接证明、间接证明、反证法的应用。
七、推理与证明7.1 推理的概念定义:推理的定义、日常生活中的推理应用。
高中数学之算法案例

算法案例(讲义)➢ 知识点睛典型算法举例: 1. 辗转相除法①方法概述:两数相除,较大数除以较小数,得商和余数,继而较小数除以余数,重复操作,直至除尽,此时除数即为最大公约数.②原理:在a =bq +r 中,除数b 和余数r 能被同一个数整除,那么被除数a 也能被这个数整除.或者说,除数与余数的最大公约数,就是被除数与除数的最大公约数. 2. 秦九韶算法把一个n 次多项式改写成如下形式:1110121102312101210()()(())((()))n n n n n n n n n n n n n n n f x a x a x a x a a x a x a x a a x a x a x a x a a x a x a x a x a ----------=++++=++++=+++++==+++++……………… 记0n v a =,11n n v a x a -=+,…,10n n v v x a -=+.求多项式的值时,首先计算最内层括号内一次多项式的值,即v 1,然后由内向外逐层计算. 3. 进位制①k 进制:若k 是一个大于1的整数,那么以k 为基数的k 进制数可以表示为一串数字连写在一起的形式.110()n n k a a a a -…11011000n n n n a a a a N a k a a a k --∈<<<≤(,,…,,,,,…,,)②进位制数相互转化:k 进制转十进制,计算k 进制数a 的右数第i 位数字i a 与1i k -的乘积1i i a k -⋅,再将其累加,重复操作求和.十进制数转k 进制数(除k 取余法): 如右图,十进制数化为二进制数, 89=1011001(2).➢ 精讲精练1. 用“辗转相除法”求下列数的最大公约数:(1)459和357的最大公约数是____________;余数2222222012511224489(2)三个数324243135,,的最大公约数是____________.2. 用秦九韶算法求多项式的值:(1)计算多项式x x x x x x x f 876543)(23456+++++=在1.0=x 时的值时,需要做乘法和加法的次数分别是_______,_______;(2)求多项式23456()1235879653f x x x x x x x =+-++++在x =-4的值时,4v 的值为_______;(3)计算多项式5432()853261f x x x x x x =+++++,当2x =时的值为________. 3. 完成下列进制的转化:(3)(10)10202____=; (10)__________(8)101=;1231(5)=_____________(7).4. 三位七进制的数表示的最大的十进制的数是( )A .322B .402C .342D .3655. 在下列各数中,最小的数是( )A .)9(85B .)6(210C .)4(1000D .(2)1111116. 已知三个数12(16),25(7),33(4),按照从小到大的顺序排列为________________.7. 已知()175r =(10)125,则r =________.8. 如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 的值分别为14,18,则输出的a 的值为( ) A .0B .2C .4D .149. 如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n ,x 的值分别为3,2,则输出v 的值为( ) A .35B .20C .18D .910.下面是把二进制数(2)11111化为十进制数的一个程序框图,判断框内应填入的条件是()A.5i>?B.4i≤?C.4i>?D.5i≤?11.执行如图所示的程序框图后,输出的值为4,则P的取值范围是()A.715816P<≤B.1516P>C.3748P<≤D.715816P<≤12.设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=________.13. 已知函数232 1 01 012 1x x y x x x x x -<⎧⎪=+<⎨⎪+⎩≤≥()()(),写出求该函数的函数值的算法,并画出程序框图.14. 设计一算法,求使20063212222>++++n Λ成立的最小正整数n 的值.15.设计算法计算:1112131415167S=++++++,画出程序框图.【参考答案】1. (1)51;(2)272. (1)6;5;(2)220;(3)3813. 101 145 3624. C5. D6. (4)(16)(7)331225<<7. 88. B9. C 10. C 11. C 12. 495 13. 略 14. 略 15. 略算法案例(随堂测试)1. 372和684的最大公约数是( )A .36B .186C .12D .5892. 用秦九韶算法计算多项式65432()3567983512f x x x x x x x =+++-++在x =-4时的值时,v 2的值为( )A .-57B .-22C .34D .743. 1234(8)=________(10);300=________(5);300=_______(6).4. 设计一个算法,输入正整数n ,输出111123n++++….【参考答案】1. C2. C3. 668;2 200;1 2204. 略算法案例(习题)➢ 巩固练习5. 求下列数的最大公约数:(1)1 443与999的最大公约数是_____________;(2)319,377,116的最大公约数是___________.6. 用秦九韶算法求n 次多项式1110()n n n n f x a x a x a x a --=++++…,当x =x 0时,0()f x 需要算乘法、加法的次数分别为( ) A .n 2,nB .2n ,nC .n ,2nD .n ,n7.已知532=++++,运用秦九韶算法计算x=3时的值时,v3的值为()()231f x x x x xA.27 B.11 C.109 D.368.用秦九韶算法求多项式765432=++++++在x=3时的值为________.()765432f x x x x x x x x9.把21化为二进制数,则此数为()A.10011(2)B.10110(2)C.10101(2)D.11001(2)10.一个k进制的三位数与某六进制的二位数等值,则k不可能是()A.3 B.4 C.5 D.711.下列各数中,最小的数是()A.75B.210(6)C.111111(2)D.85(9)12.若a=33(10),b=52(6),c=11111(2),则三个数的大小关系是()A.c>b>a B.b>c>a C.c>a>b D.a>b>c13.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()A.7B.12C.17D.34第9题图第10题图14.如图是一个算法的程序框图,该算法所输出的结果是()A.11112310++++…B.11113519++++…C.111124620++++…D.231011112222++++…15.某程序框图如图所示,若输出的S=57,则判断框内为()A.k>4?B.k>5?C.k>6?D.k>7?11第11题图 第12题图16. 执行如图所示的程序框图,若输入k 的值为8,则判断框图可填入的条件是( )A .S ≤34?B .S ≤56?C .S ≤1112? D .S ≤1524?17. 设计一个算法,输入两个数,输出两个数中较大的一个.18.已知函数21111131x x y x x x x ⎧-<-⎪=+-⎨⎪+>≤≤()()(),试画出求函数值的程序框图.19. 对任意给定的正整数n ,写出一个求13+23+33+…+n 3的算法程序框图.20.设计算法求111112233499100++++⨯⨯⨯⨯…的值,要求画出程序框图.【参考答案】1.(1)111 (2)292.D3.D4.213245.C6.D7.C8.D9.C10.C11.A12.C13.略14.略15.略16.略12。
高中数学必修3-算法初步精讲

高中数学必修3-算法初步精讲高中数学必修3-算法初步精讲§13.1 流程图一、知识导学1.流程图:是由一些图框和带箭头的流线组成的,其中图框表示各种操作的类型,图框中的文字和符号表示操作的内容,带箭头的流线表示操作的先后次序.2.算法的三种基本的逻辑结构:顺序结构、条件结构、循环结构.3.根据对条件的不同处理,循环结构又分为两种:直到型(until型)循环:在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体.满足则停止.如图13-1-3,先执行A框,再判断给定的条件p是否为“假”,若p为“假”,则再执行A,如此反复,直到p为“真”为止.当型(while型)循环:在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,不满足则停止.如图13-1-4,当给定的条件p成立(“真”)时,反复执行A框操作,直到条件p为“假”时才停止循环.图13-1-1 图13-1-2二、疑难知识1.“算法“没有一个精确化的定义,教科书只对它作了描述性说明,算法具有如下特点:(1)有限性:一个算法的步骤是有限的,必须在有限操作之后停止,不能是无限的.(2)确定性:算法的每一步骤和次序应当是确定的.(3)有效性:算法的每一步骤都必须是有效的.2. 画流程图时必须注意以下几方面:(1)使用标准的图形符号.(2)流程图一般按从上到下、从左到右的方向画.(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框具有超过一个退出点的唯一符号.(4)判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.(5)在图形符号内描述的语言要非常简练清楚.3. 算法三种逻辑结构的几点说明:(1)顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.在流程图中的体现就是用流程线自上而下地连接起来,按顺序执行算法步骤.(2)一个条件结构可以有多个判断框.(3)循环结构要在某个条件下终止循环,这就需要条件结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用语输出结果,计数变量和累加变量一般是同步执行的,累加一次,计数一次. 三、经典例题[例1] 已知三个单元存放了变量x,y,z的值,试给出一个算法,顺次交换x,y,z的值(即y取x的值,z取y的值,x取z的值),并画出流程图.错解:第一步xy←第二步yz←第三步zx←流程图为图13-1-3错因:未理解赋值的含义,由上面的算法使得y,z均取x的值.举一形象的例子:有蓝和黑两个墨水瓶,但现在却把蓝墨水装在了黑墨水瓶中,黑墨水错装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题.对于这种非数值性问题的算法设计问题,应当首先建立过程模型,根据过程设计步骤完成算法. 我们不可将两个墨水瓶中的墨水直接交换,因为两个墨水瓶都装有墨水,不可能进行直接交换.正确的解法应为:S1 取一只空的墨水瓶,设其为白色;S2 将黑墨水瓶中的蓝墨水装入白瓶中;S3 将蓝墨水瓶中的黑墨水装入黑瓶中;S4 将白瓶中的蓝墨水装入蓝瓶中;S5 交换结束.p←{先将z的值赋给变量p,这时存放z的单元可作它正解:第一步z用}第二步yz←{再将y的值赋给z,这时存放y的单元可作它用}第三步xy←{同样将x的值赋给y,这时存放x的单元可作它用}第四步px←{最后将p的值赋给y,三个变量x,y,z的值就完成了交换}流程图为图13-1-4点评:在计算机中,每个变量都分配了一个存储单元,为了达到交换的目的,需要一个单元存放中间变量p.[例2]已知三个数a,b,c.试给出寻找这三个数中最大的一个算法,画出该算法的流程图.解:流程图为图13-1-5点评:条件结构可含有多个判断框,判断框内的内容要简明、准确、清晰.此题也可将第一个判断框中的两个条件分别用两个判断框表示,两两比较也很清晰.若改为求100个数中的最大数或最小数的问题则选择此法较繁琐,可采用假设第一数最大(最小)将第一个数与后面的数依依比较,若后面的数较大(较小),则进行交换,最终第一个数即为最大(最小)值.点评:求和时根据过程的类同性可用循环结构来实现,而不用顺序结构. [例3]画出求222210022+--Λ的值的算法流程图.++991-423解:这是一个求和问题,可采用循环结构实现设计算法,但要注意奇数项为正号,偶数项为负号.思路一:采用-1的奇偶次方(利用循环变量)来解决正负符号问题;图13-1-6 图13-1-7 思路二:采用选择结构分奇偶项求和;图13-1-8思路三:可先将222100222-++-Λ化简成+299431---Λ,转化为一个等差数列求和问题,易利用循环结构求出结果.199--1173-[例4] 设计一算法,求使200621232>22Λ成立的最小正整数n的+n+++值.解:流程图为图13-1-9点评:这道题仍然是考察求和的循环结构的运用问题,需要强调的是求和语句的表示方法.若将题改为求使200621232<22Λ成立的最大正整数++n++n的值时,则需注意的是输出的值.[例5]任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判断.解:算法为:S1 判断n是否等于2,若n=2,则n是质数;若n>2,则执行S2 S2 依次从2~n-1检验是不是的因数,即整除n的数,若有这样的数,则n不是质数;若没有这样的数,则n是质数.点评:要验证是否为质数首先必须对质数的本质含义作深入分析:(1)质数是只能被1和自身整除的大于1的整数.(2)要判断一个大于1的整数n是否为质数,只要根据定义,用比这个整数小的数去除n.如果它只能被1和本身整除,而不能被其它整数整除,则这个数便是质数.图13-1-10[例6]设计一个求无理数2的近似值的算法.分析:无理数2的近似值可看作是方程022=-x 的正的近似根,因此该算法的实质是设计一个求方程022=-x 的近似根的算法.其基本方法即运用二分法求解方程的近似解.解:设所求近似根与精确解的差的绝对值不超过0.005,算法:S1 令2)(2-=x x f .因为0)2(,0)1(><f f ,所以设2,121==x xS2 令2)(21x x m +=,判断)(m f 是否为0,若是,则m 为所求;若否,则继续判断)()(1m f x f 大于0还是小于0.S3 若)()(1m f x f >0,则m x =1;否则,令m x =2.S4 判断005.021<-x x 是否成立,若是,则21,x x 之间的任意值均为满足条件的近似根;若否,则返回第二步.点评:二分法求方程近似解的算法是一个重要的算法案例,将在第三节中详细阐述.四、典型习题1.已知两个单元分别存放了变量A 和B 的值,则可以实现变量B A ,交换的算法是( ). A .S1 A B ← B .S1 A C ←C .S1 A C ←D .S1 A C ← S2 B A ← S2 C B ←S2 B A ← S2 B D ← S3 BC ← S3 C B ← 1. 下面流程图中的错误是( )图13-1-11A .i 没有赋值B .循环结构有错C .S 的计算不对D .判断条件不成立3.将“打电话”的过程描述成一个算法,这个算法可表示为,由此说明算法具有下列特性 .4. 在表示求直线0byax(a,b为常数,且a,b不同时为0)的斜率的+c=+算法的流程图中,判断框中应填入的内容是5. 3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画出这个算法的流程图.6.一队士兵来到一条有鳄鱼的深河的左岸.只有一条小船和两个小孩,这条船只能承载两个小孩或一个士兵.试设计一个算法,将这队士兵渡到对岸,并将这个算法用流程图表示.§13.2基本算法语句一、知识导学1.赋值语句用符号“←”表示,“yx←”表示将y的值赋给x,其中x是一个变量,y是一个与x同类型的变量或表达式.2.条件语句主要有两种形式:“行If 语句”和“块If语句”.“行If 语句”的一般形式为:If A Then B [Else C] .一个行If 语句必须在一行中写完,其中方括号中的Else部分可以缺省.“块If 语句”的一般格式为:If A ThenBElseCEnd ifThen 部分和Else 部分是可选的,但块If语句的出口“End if”不能省. 3.循环语句主要有两种类型:For语句和While语句.当循环的次数已经确定,可用“For”语句表示.“For”语句的一般形式为:For I from“初值”to step“步长”…End for上面“For”和“End for”之间缩进的步骤称为循环体.当循环次数不能确定是,可用“While”语句来实现循环.“While”语句的一般形式为:While A…End while其中A表示判断执行循环的条件.上面“While”和“End While”之间缩进的步骤称为循环体.二、疑难知识1.有的条件语句可以不带“Else”分支,即满足条件时执行B,否则不执行任何操作.条件语句也可以进行嵌套,在进行条件语句的嵌套时,书写要有层次.例如:If A ThenBElse if C ThenDElseEEnd if2.“For”语句是在执行过程中先操作,后判断.而“While”语句的特点是“前测试”,即先判断,后执行.若初始条件不成立,则一次也不执行循环体中的内容.任何一种需要重复处理的问题都可以用这种前测试循环来实现.三、经典例题[例1] 下列程序的运行结果是 .X←9Y8←If X>5 Then 7+Y←YIf X>4 Then 6+←YYIf X>3 Then 6+Y←YPrint Y错解:8+7=15错因:误认为在一个程序中只执行一个条件语句,与在一个条件语句中只选择其中一个分支相混淆.If A Then B [Else C] 若满足条件A 则执行B,否则是执行C,B和C是这个条件语句的分支,而这个程序省略了Else部分.正解:这里是有三个条件语句,各个条件语句是独立的,三个条件均成立,所以按顺序依次执行,结果为8+7+6+6=27.[例2] 下面的伪代码的效果是0←iWhile i <102⨯←i iEnd WhileEnd错解:执行10次循环错因:将For 语句和While 语句混淆. For 语句中有步长使循环变量不断变化,而While 语句则无.正解:无限循环下去,这是因为这里i 始终为0,总能满足条件“10<i ”,故是一个“死循环”.点评:“死循环”是设计循环结构的大忌,此题可改变i 的初始值或每一次循环i 都增加一个值.[例3]下面的程序运行时输出的结果是( )1←IWhile 5<I0←S1+←I II I S S *+←End whilePrint SEnd错解:第一次循环时,I 被赋予2,S 被赋予4;第二次循环时,I 被赋予3,S 被赋予4+23=13;第三次循环时,I 被赋予4,S 被赋予13+24=29;第四次循环时,I 被赋予5,S 被赋予545292=+.由于此时5=I ,故循环终止,输出S 为54.正解:由于0←S 在循环内,每经过一次循环后S 都被赋值0,因此,只要求满足条件的最后一次循环S 的值,即当4=I 时,16440=⨯+=S .[例4]用语句描述求使10007531<⨯⨯⨯⨯⨯n Λ成立的最大正整数n 的算法过程.解: 1←n1←TWhile 1000<T2+←n n n T T ⨯←End whilePrint 2-n点评:此题易错的是输出值,根据While 循环语句的特征当1000≥T 时跳出循环体,此时n 的值是1000≥T 时的最小的整数,则使1000<T 的最大整数应为n 的前一个奇数即2-n .[例5]已知当100100<<-x 时,1+=x y ,当100-≤x 时,4=y ,当100≥x 时,4-=x y ,设计一算法求y 的值.解: Read xIf 100100<<-x then1+←x yElse if 100≥x Then4-←x yElse4←yEnd ifEnd点评:嵌套If 语句可用如上的紧凑形式书写,要注意的是如不是采取紧凑形式,则需注意一个块If 语句对应一个End If ,不可省略或缺少.[例6]设计一个算法,使得输入一个正整数n ,输出1!+2!+3!+…+n !的值.写出伪代码.解:思路一:利用单循环,循环体中必须包括一个求各项阶乘的语句以及一个求和语句.Read n1←←S T For I from 1 to nTS S I T T +←⨯← End ForPrint S思路二:运用内外双重循环,但尤其注意的是每一次外循环T 的值都要从1开始.Read n0←SFor I from 1 to n1←TFor J from 1 to IJ T T ⨯←End ForT S S +←End ForPrint S四、典型习题1.下列的循环语句循环的次数为()For I from 1 to 7For J from 1 to 9Pint I+JEnd forEnd forEndA.7次B.9次C.63次D.16次2.运行下面的程序后输出的结果是,若将程序中的A语句与B语句的位置互换,再次执行程序后输出的结果为 .x←1y←While 3<x←′A语句y+yxx′B语句←x+1End WhilePrint x,yEnd3.伪代码描述的求T的代数式是,求S的代数式是 .Read n1←T0←SFor I from 1 to nI T T ⨯←I S S +←End forPrint T,S4.运行下面程序后输出的结果为For I from 10 to 1 step -2Print IEnd forEnd5. 将100名学生的一门功课的成绩依次输入并计算输出平均成绩.§ 13.3 算法案例一、知识导学1.算法设计思想:(1)“韩信点兵—孙子问题”对正整数m 从2开始逐一检验条件,若三个条件中有任何一个不满足,则m 递增1,一直到m 同时满足三个条件为止(循环过程用Goto 语句实现)(2)用辗转相除法找出b a .的最大公约数的步骤是:计算出b a ÷的余数r ,若0=r ,则b 为b a ,的最大公约数;若0≠r ,则把前面的除数b 作为新的被除数,继续运算,直到余数为0,此时的除数即为正整数b a ,的最大公约数.2.更相减损术的步骤:(1)任意给出两个正数,判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.(2)以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.(3)二分法求方程0)(=x f 在区间[]b a ,内的一个近似解*x 的解题步骤可表示为 S1 取[b a ,]的中点()b a x +=210,将区间 一分为二; S2 若()00=x f ,则0x 就是方程的根;否则判别根*x 在0x 的左侧还是右侧:若()()00>⋅x f a f ,()b x x ,*0∈,以0x 代替a ;若()()00<⋅x f a f ,则()0,*x a x ∈,以0x 代替b ;S3 若c b a <-,计算终止,此时0x x ≈*,否则转S1.二、疑难知识1.)int(x 表示不超过x 的整数部分,如0)32.0int(,5)86.5int(==,但当x 是负数时极易出错,如1)14.1int(-=-就是错误的,应为-2.2.),mod(b a 表示a 除以b 所得的余数,也可用a mod b 表示.3.辗转相除法与更相减损术求最大公约数的联系与区别:(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显.(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.4.用二分法求方程近似解,必须先判断方程在给定区间[b a ,]上是否有解,即()x f 连续且满足()()0<b f a f .并在二分搜索过程中需对中点处函数值的符号进行多次循环判定,故需要选择结构、循环结构,即可用Goto 语句和条件语句实现算法.三、经典例题[例1]=)5int(π , =-)05.0int( ,=)9,67mod( , 45 mod 7= .A .16,-1,4,3 B.15,0,4,3 C.15,-1,3,4 D.15,-1,4,3 错解:根据)int(x 表示不超过x 的整数部分, ),mod(b a 表示a 除以b 所得的余数,选择B.错因:对)int(x 表示的含义理解不透彻,将不超过-0.05的整数错认为是0,将负数的大小比较与正数的大小比较相混淆.正解:不超过-0.05的整数是-1,所以答案为D.[例2] 所谓同构数是指此数的平方数的最后几位与该数相等.请设计一算法判断一个大于0且小于1000的整数是否为同构数.错解: 算法思想:求出输入数的平方,考虑其个位或最后两位或最后三位与输入数是否相等,若相等,则为同构数.Read xx x y *=If )10(y x = or )100(y x = or )1000(y x = ThenPrint xEnd ifEnd错因:在表示个位或最后两位或最后三位出现错误,“/”仅表示除,y/10,y/100,y/1000都仅仅表示商.正解:可用)1000,mod(),100,mod(),10,mod(y y y 来表示个位,最后两位以及最后三位.Read x=y*xxIf ))1000x=or )),mod((yx=(ymod(10,(ymod(,100x=or ))ThenPrint xEnd ifEnd[例3]《孙子算经》中的“物不知数”问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”可以用下面的算法解决:先在纸上写上2,每次加3,加成5除余3的时候停下来,再在这个数上每次加15,到得出7除2的时候,就是答数.试用流程图和伪代码表示这一算法.解:流程图为:伪代码为:10 2m←20 3+m←m30 If ()35,m od ≠m Then Goto 2040 If 2)7,mod(=m ThenPrint mGoto 8050 End if60 15+←m m70 Goto 4080 End点评:这是孙子思想的体现,主要是依次满足三个整除条件.[例4]分别用辗转相除法、更相减损法求192与81的最大公约数.解:辗转相除法:S1 30281192ΛΛΛΛ=÷S2 2123081ΛΛΛΛ=÷S3 912130ΛΛΛΛ=÷S4 32921ΛΛΛΛ=÷S5 0339ΛΛΛΛ=÷故3是192 与81 的最大公约数.更相减损法:S1 11181192=-S2 3081111=-S3 513081=-S4 213051=-S5 92130=-S6 12921=-S7 3912=-S8 639=-S9 336=-故3 是192与81的最大公约数.点评:辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少.辗转相除法是当大数被小数整除时停止除法运算,此时的小数就是两者的最大公约数,更相减损术是当大数减去小数的差等于小数时减法停止,较小的数就是最大公约数.[例5]为了设计用区间二分法求方程0123=-+x x 在[0,1]上的一个近似解(误差不超过0.001)的算法,流程图的各个框图如下所示,请重新排列各框图,并用带箭头的流线和判断符号“Y”、“N ”组成正确的算法流程图,并写出其伪代码.(其中b a ,分别表示区间的左右端点)图13-3-2流程图为图13-3-3伪代码为10 Read b a ,20 2)(0b a x +←30 1)(23-+←a a a f40 1)(20300-+←x x x f 50 If 0)(0=x f Then Goto 12060 If 0)()(0<x f a f Then70 0x b ←100 End if80 Else90 0x a ←100 End if110 If 001.0≥-b a Then Goto 20120 Print 0x130 End点评:二分法的基本思想在必修一中已渗透,这里运用算法将二分法求方程近似解的步骤更清晰的表述出来.[例6] 用秦九韶算法计算多项式654323567983512)(x x x x x x x f ++++-+=在4-=x 时的值时,3v 的值为 .解: 根据秦九韶算法,此多项式可变形为()()()()()()1235879653++-+++=x x x x x x x f按照从内到外的顺序,依次计算一次多项式当4-=x 时的值:40-=v75)4(31-=+-⨯=v346)7()4(2=+-⨯-=v577934)4(3-=+⨯-=v故当4-=x 时多项式的值为57-.点评:秦九韶算法的关键是n 次多项式的变形.把一个n 次多项式0111)(a x a x a x a x f n n n n ++++=--Λ改写成0121)))(()(a x a x a x a x a x f n n n +++++=--ΛΛ,求多项式的值,首先计算最内层括号内一次多项式的值,然后由内向外逐层计算一次多项式的值,这样把求n 次多项式的值问题转化为求n 个一次多项式的值的问题,这种方法成为秦九韶算法.这种算法中有反复执行的步骤,因此,可考虑用循环结构实现.四、典型习题1.以下短文摘自古代《孙子算经》一书,其引申出的“大衍求一术”称为“中国剩余原理”:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”答曰( ).A .二十一 B.二十二 C.二十三 D.二十四2.用辗转相除法求52与39的最大公约数的循环次数为( ).A .1次 B.2次 C.3次 D.5次3.下面程序功能是统计随机产生的十个两位正整数中偶数和奇数的个数,并求出偶数与奇数各自的总和.For I from 1 to 1010)90int(+*←Rnd xPrint x;If Thenxs s n n +←+←22122 Elsex s s +←11End IfEnd forPrintPrint “奇数个数=”;1n,“偶数个数=”;2n4.若一个数的各因子之和正好等于该数本身,则该数成为完数.请补充完整下列找出1~100之间的所有完数的伪代码.For a from 2 to 100c1For b from 2 toIf mod(a,b)=0 ThenEnd ifEnd ForIf ThenPrint aEnd ifEnd ForEnd5.设计求被9除余4,被11除余3的最小正整数的算法,画出流程图,写出伪代码.6.利用辗转相除法或更相减损术求324,243,135的最大公约数.。
高中数学必修三算法初步知识点讲解

高中数学必修三算法初步知识点讲解前言在现代社会中,算法是极其重要的。
无论是互联网公司的搜索引擎、电子商务平台,还是金融市场的投资分析、量化交易,都离不开算法的支持。
因此,在高中阶段学习并掌握一些基础的算法,不仅能提高数学素养和思维能力,还有利于今后的学习和工作。
本文就是要介绍高中数学必修三中一些初步的算法知识点。
下面将分别从排序算法、查找算法和递推算法三个方面展开讲解,以帮助读者加深对算法的理解和掌握。
排序算法冒泡排序冒泡排序是一种基础的排序算法,其思路是通过不断地交换相邻元素的位置,将大的元素逐渐往后移动。
具体实现过程如下:1.从第一个元素开始,一直到倒数第二个元素,依次比较相邻元素的大小。
2.如果前一个元素大于后一个元素,则交换它们的位置。
3.重复以上步骤,直到没有需要交换的元素为止。
冒泡排序的时间复杂度为O(n2),因此对于较大的数据集来说,效率较低。
选择排序选择排序是另一种基础的排序算法,其思路是每次选出剩下元素中最小的一个,放在已排好序的部分的末尾。
具体实现过程如下:1.从第一个元素开始,一直到倒数第二个元素,依次找出剩下元素中的最小值。
2.将找出的最小值与当前位置的元素进行交换。
3.重复以上步骤,直到所有元素都排好序。
选择排序的时间复杂度为O(n2),与冒泡排序相同,但是其空间复杂度较低。
插入排序插入排序是一种简单而有效的排序算法,它类似于整理扑克牌的过程,将未排序的部分依次插入已经排序的部分。
具体实现过程如下:1.从第二个元素开始,将其与已经排好序的部分进行比较。
如果它小于前面的元素,则将它插入到前面的合适位置。
2.重复以上步骤,直到所有元素都排好序。
插入排序的时间复杂度为O(n2),但是对于小规模数据集,效率较高。
查找算法顺序查找顺序查找是一种基础的查找算法,其思路是从头到尾依次查找目标元素。
具体实现过程如下:1.从第一个元素开始,逐个与目标元素进行比较。
2.如果找到目标元素,则返回对应位置的索引值。
人教版高中数学必修三 第一章 算法初步算法案例——辗转相除法

算法案例——辗转相除法一、教材分析1、地位作用:与传统教学内容相比,《算法初步》为新增内容,算法是计算机科学的重要基础,从日常生活的电子邮件发送到繁忙的交通管理,从与人们生产、生活息息相关的天气预报到没有硝烟的战争模拟等等都离不开计算机算法。
算法思想已经渗透到社会的方方面面,算法思想也逐渐成为每个现代人应具有的数学素养。
在以前的学习中,虽然没有出现算法这个名词,但实际上在数学教学中已经渗透了大量的算法思想,如四则运算的过程,求解方程的步骤,以及将要学习的数列求和等等,完成这些工作都需要一系列程序化的步骤,这就是算法思想。
本节内容是探究古代算法案例――辗转相除法,巩固算法三种描述性语言(自然语言、流程图和伪代码),提高学生分析和解决问题的能力。
2、教学目标:(1)知识目标:①理解辗转相除法原理;②能用自然语言、流程图和伪代码表达辗转相除法;③能应用迭代算法思想。
(2)能力目标:①培养学生把具体问题抽象转化为算法语言的能力;②培养学生自主探索和合作学习的能力。
(3)情感目标:①使学生进一步了解从具体到抽象,抽象到具体的辨证思想方法,对学生进行辨证唯物主义教育;②创设和谐融洽的教学氛围和阶梯形问题,使学生在活动中获得成功感,从而培养学生热爱数学、积极学习数学、应用数学的热情。
3、教学重点与难点:(1)教学重点:①理解辗转相除法原理;②能用自然语言、流程图和伪代码表达辗转相除法。
(2)教学难点:①理解和区分两种循环结构表达辗转相除法;②能应用迭代算法思想。
二、教法学法1、教法:以问题为载体,有引导的对话,让学生经历知识的形成过程和发展过程,从而突出教学重点,并采用多媒体教学,增加课堂容量,有利于学生活动的充分展开。
2、学法:以观察、讨论、思考、分析、动手操作、自主探索、合作学习多种形式相结合,引导学生多角度、多层面认识事物,突破教学难点。
三、教学过程设计:1、情景设置――感知辗转相除法(发给每位学生一张长为22cm ,宽为6cm 的纸条)【问1】这张长方形的纸,先拿短边往长边上折,得到一个正方形,从长方形上裁掉这个正方形后继续将短边往长边上折,一直到最后剩下来的是正方形为止,最后得到的边长是几的正方形?【师生互动解答】22=6×3+4;6 = 4×1+2;4 = 2×2+0 => 最后正方形的边长为2cm 。
高中数学_算法案例

算法案例知识图谱算法案例知识精讲一.更相减损术应用:求两个整数的最大公约数的算法更相减损术的步骤:1.任意给定两个正整数;判断它们是否都是偶数.若是,则用2约简;若不是则执行第二步.2.以两个数中较大的数减去较小的数,以差数和较小的数构成一对新的数,对这一对数再用大数减小数,以同样的操作一直做下去,直到产生一对相等的数为止,则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数.等值算法:用“更相减损术”设计出来的算法求最大公约数的算法称为“等值算法”,用等值算法可以求任意两个正整数的最大公约数.说明:《九章算法》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数.以具体的例子来说明更相减损术求最大公约数的原理:以求117和182的最大公约数为例:,,,,,,,,(117182)(11765)(6552)(5213)(1339)(1326)(1313)→→→→→→每次操作后得到的两个数与前两个数的最大公约数相同,而且逐渐减少,故总能得到相等的两个数,即为所求的最大公约数.二.辗转相除法又称欧几里得算法,是由欧几里得在公元前300年左右首先提出来的求两个数的最大公约数的算法.辗转相除法的步骤:对于给定的两个数,以其中较大的数除以较小的数得到一个余数,将较小的数与余数看成一对新的数,重复上面的步骤,直到余数为零为止,此时上一步中较小的数即为所求的最大公约数.以求117和182的最大公约数为例:,,,,,,故13即为所求.→→→→(117182)(11765)(6552)(5213)(130)三.秦九韶算法—求多项式的值的算法应用:快速的求解对于任意一个n次的多项式在某点所取到的值.秦九韶算法:已知一个多项式函数,计算多项式在某点处的函数值的一种算法,是我国古代数学家秦九韶提出的,具体如下.对任意一个n 元多项式1110()n n n n f x a x a x a x a --=++++ ,改写成如下形式:12110()()n n n n f x a x a x a x a ---=++++ 231210(())n n n n a x a x a x a x a ---=+++++ = 1210((()))n n n a x a x a x a x a --=+++++ ,求多项式的值时,先计算最内层括号内的一次多项式的值,即11n n v a x a -=+,然后由内向外逐层计算一次多项式的值,即212n v v x a -=+,323n v v x a -=+, ,10n n v v x a -=+.这样,求一个n 次多项式的值,就转化为求n 个一次多项式的值.令1(1)(())k n n n k n k v a x a x a x a ----=++++ ,则递推公式为01n kk n k v a v v x a --=⎧⎨=+⎩,其中12k n = ,,,.到目前为止,此算法仍然是世界上多项式求值的最先进的算法.秦九韶算法与其它算法在计算量上面的比较:1110()n n n n f x a x a x a x a --=++++ ,1.直接求和法:先计算各个单项式的值,再把它们相加,乘法次数为(1)(1)212n n n n ++-+++= ,加法次数n ;2.逐项求和法:先计算x 的各项幂的值,再分别相乘,计算幂值需要乘法1n -次,将幂值与多项式系数k a 相乘需要乘法n 次,故共需要乘法21n -次,加法n 次.此方法对直接求和法有所改进,但仍然比秦九韶算法计算量大很多.3.秦九韶算法:计算量仅为乘法n 次,加法n 次.<备注>秦九韶算法是多项式求值的优秀算法,秦九韶算法的特点:(1)化高次多项式求值为一次多项式求值;(2)减少了运算次数,提高了效率;(3)步骤重复执行,容易用计算机实现.利用秦九韶算法计算多项式的值关键是能正确地将所给多项式改写,然后由内向外逐次计算,由于后项计算用到前项的结果,故应认真、细心,确保中间结果的准确性.若在多项式中有几项不存在时,可将这些项的系数看成0,即把这些项看做0·x n .三点剖析一.注意事项1.辗转相除法与更相减损术联系(1)都是求最大公约数的方法,计算上,辗转相除法以除法为主,更相减损术以减法为主,计算次数上,辗转相除法计算次数相对较少,特别当两个数大小差距较大时,计算次数的区别比较明显;(2)从结果的体现形式来看,辗转相除法体现结果是以相除余数为零而得到,而更相减损术则是以减数与差相等而得到;(3)辗转相除法与更相减损术是统一的,因为做一次除法与做若干次减法的效果相同.二.方法点拨1.两个整数的最大公约数是两个整数的公约数中最大的数,与此类似,两个整数的最小公倍数是两个整数的公倍数中最小的数.2.穷举法是将集合中的元素进行一一列举,逐个条件进行验证,知道找出满足条件的元素为止,穷举法可以解决所有问题看,但是一般来说常常可以用来解决一些无规律可循的问题,例如求不定方程的解或者不定方程组的解,运用穷举法思想设计算法时,常常采用循环结构,将验证条件为循环结构的判断条件,将每一个元素作为循环体.求两个正整数的最大公约数例题1、8251与6105的最大公约数是____.例题2、用更相减损来求80和36的最大公约数?例题3、用更相减损术求294与84的最大公约数.随练1、两个数153和119的最大公约数是______________.随练2、用更相减损术求294与84的最大公约数.随练3、有甲、乙、丙三种溶液分别重147g、343g、133g,现要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同,问每瓶最多装多少?秦九韶算法例题1、用秦九韶算法求多项式f(x)=x4+2x3+x2-3x-1,当x=2时的值,则v3=______例题2、使用秦九韶算法计算x=2时f(x)=6x6+4x5-2x4+5x3-7x2-2x+5的值,所要进行的乘法和加法的次数分别为________随练1、用秦九韶算法求多项式f(x)=1+2x+x2-3x3+2x4在x=-1时的值,v2的结果是______随练2、用秦九韶算法计算多项式f(x)=5x5+4x4+3x3-2x2-x-1在x=-4时的值时,需要进行的乘法、加法的次数分别是_______拓展1、用更相减损术求78和36的最大公约数_________.2、三个数208,351,429的最大公约数是()A.65B.91C.26D.133、用“辗转相除法”求得459和357的最大公约数是()A.3B.9C.17D.514、用秦九韶算法求多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4的值时,其中V1的值=_______5、用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.4时的值时,需要做乘法和加法的次数分别是。
高中数学人教A版必修3课件:1.3 算法案例

1.3 算法案例
题型1 辗转相除法与更相减损术
4.分别用辗转相除法和更相减损术求36和80的最大公约数.
解
辗转相除法:
80=36×2+8,36=8×4+4,8=4×2.
故36和80的最大公约数是4.
更相减损术:
80-36=44,44-36=8,36-8=28,28-8=20,
20-8=12,12-8=4,8-4=4.
解析
111÷2=55……1,55÷2=27……1,27÷2=13……1,13÷2=6……1, 6÷2=3……0,3÷2=1……1,1÷2=0……1, 故111(10)=1101111(2).故选C.
1.3 算法案例
题型3 进位制
11.把十进制数189化为四进制数,则末位数字是( B )
A.0
B.1
1.3 算法案例
刷基础
题型3 进位制
13.十六进制数与十进制数的对应如下表:
十 六 进 1 2 3 4 5 6 7 8 9 10 A B C D E F 制 数 十 进 制 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 数
例如:A+B=11+12=16+7=F+7=17(16),所以A+B的值用十六进制表示就等于17(16).
f(x)=anxn+an-1xn-1+…+a1x+a0的具体函数值,运用常规方法计算出结果最多需要n次加法和
n(n 2
1)
次乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计
算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算的
A.2
B.3
C.4
D.5
高中数学必修三知识讲解,巩固练习(复习补习,期末复习资料):06【提高】算法案例

算法案例【学习目标】1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析;2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序;3.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质;4.了解各种进位制与十进制之间转换的规律,会利用各种进位制与十进制之间的联系进行各种进位制之间的转换.【要点梳理】要点一:辗转相除法也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的.利用辗转相除法求最大公约数的步骤如下:第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;第三步:若r1=0,则r0为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;……依次计算直至r n=0,此时所得到的r n-1即为所求的最大公约数.用辗转相除法求最大公约数的程序框图为:INPUT “m=”;m INPUT “n=”;n IF m<n THEN x=m m=n n=x END IF r=m MOD n WHILE r<>0 r=m MOD n m=n n=r WEND PRINT n END要点诠释:辗转相除法的基本步骤是用较大的数除以较小的数,考虑到算法中的赋值语句可以对同一变量多次赋值,我们可以把较大的数用变量m 表示,把较小的数用变量n 表示,这样式子)0(n r r q n m <≤+⋅=就是一个反复执行的步骤,因此可以用循环结构实现算法. 要点二:更相减损术我国早期也有解决求最大公约数问题的算法,就是更相减损术.更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.翻译出来为:第一步:任意给出两个正整数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步. 第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.理论依据:由r b a r b a +=→=-,得b a ,与r b ,有相同的公约数 更相减损术一般算法:第一步,输入两个正整数)(,b a b a >;第二步,如果b a ≠,则执行3S ,否则转到5S ; 第三步,将b a -的值赋予r ;第四步,若r b >,则把b 赋予a ,把r 赋予b ,否则把r 赋予a ,重新执行2S ; 第五步,输出最大公约数b . 程序:INPUT “a=”,a INPUT “b=”,b WHILE a<>b IF a>=bELSE b=b-a WEND ENDPRINT b 或者INPUT “请输入两个不相等的正整数”;a ,b i=0WHILE a MOD 2=0 AND b MOD 2=0 a=a/2 b=b/2 i=i+1 WEND DOIF b<a THEN t=a a=b b=t END IF c=a -b a=b b=cLOOP UNTIL a=b PRINT a^i END要点诠释:用辗转相除法步骤较少,而更相减损术虽然有些步骤较长,但运算简单. 要点三:秦九韶计算多项式的方法12121012312102312101210()()(())((()))n n n n n n n n n n n n n n n n n n n f x a x a x a x a x a a x a x a x a x a a x a x a x a x a a x a x a x a x a --------------=+++++=+++++=+++++==+++++令12(1)((()))k n n n n k n k v a x a x a x a x a -----=+++++,则有01nk k nkv a v v x a--=⎧⎨=+⎩,其中n k ,2,1=.这样,我们便可由0v 依次求出n v v v ,,21;1323212101,,,a x v v a x v v a x v v a x v v n n n n n +=+=+=+=----要点诠释:显然,用秦九韶算法求n 次多项式的值时只需要做n 次乘法和n 次加法运算 要点四:进位制进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值.可使用数字符号的个数称为基数,基数为n ,即可称n 进位制,简称n 进制.现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数.对于任何一个数,我们可以用不同的进位制来表示.比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的.表示各种进位制数一般在数字右下角加注来表示,如111001(2)表示二进制数,34(5)表示5进制数. 1.k 进制转换为十进制的方法:012211)(0121a k a k a k a k a a a a a a a n n n n k n n +⨯+⨯++⨯+⨯=--- ,把k 进制数a 转化为十进制数b 的算法程序为:INPUT “ a,k,n=”;a,k,n i=1 b=0WHILE i<=n t=GET a[i] b=b+t*k^(i-1) i=i+1 WEND PRINT b END2.十进制转化为k 进制数b 的步骤为:第一步,将给定的十进制整数除以基数k ,余数便是等值的k 进制的最低位; 第二步,将上一步的商再除以基数k ,余数便是等值的k 进制数的次低位;第三步,重复第二步,直到最后所得的商等于0为止,各次所得的余数,便是k 进制各位的数,最后一次余数是最高位,即除k 取余法.要点诠释:1、在k 进制中,具有k 个数字符号.如二进制有0,1两个数字.2、在k 进制中,由低位向高位是按“逢k 进一”的规则进行计数.3、非k 进制数之间的转化一般应先转化成十进制,再将这个十进制数转化为另一种进制的数,有的也可以相互转化.【典型例题】类型一:辗转相除法与更相减损术例1.分别用辗转相除法和更相减损术求378与90的最大公约数. 【答案】18【解析】 用辗转相除法:378=90×4+18,90=18×5.∴378与90的最大公约数是18.用更相减损术:∵378与90都是偶数,∴用2约分后得189和45.189-45=144,144-45=99,99-45=54,54-45=9,45-9=36,36-9=27,27-9=18,18-9=9.∴378与90的最大公约数为2×9=18.【总结升华】比较辗转相除法与更相减损术的区别(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显;(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.由该题可以看出,辗转相除法得最大公约数的步骤较少.对比两种方法控制好算法的结束,辗转相除法是到达余数为0,更相减损术是到达减数和差相等.举一反三:【变式1】(1)用更相减损术求两个正数84与72的最大公约数.(2)利用辗转相除法求3869与6497的最大公约数与最小公倍数.【解析】(1)因为84=21×4,72=18×4,所以21-18=3,18-3=15,15-3=12,12-3=9,9-3=6,6-3=3.所以21和18的最大公约数等于3.所以84和72的最大公约数等于12.【总结升华】先约简,再求21与18的最大公约数,然后乘以约简的4得84与72的最大公约数.(2)6497=3869×1+2628,3869=2628×1+1241,2628=1241×2+146,1241=146×8+73,146=73×2+0.所以3 869与6 497的最大公约数为73,最小公倍数为3 869×6497÷73=344341.例2.求三个数:168,54,264的最大公约数.【思路点拨】运用更相减损术或辗转相除法,先求168和54的最大公约数a,再求a与264的最大公约数.【答案】6【解析】采用更相减损术先求168和54的最大公约数.(168,54)→(114,54)→(60,54)→(6,54)→(6,48)→(6,42)→(6,36)→(6,30)→(6,24)→(6,18)→(6,12)→(6,6).故168和54的最大公约数为6.采用辗转相除法求6和264的最大公约数.∵264=44×6+0,∴6为264与6的最大公约数,也是这三个数的最大公约数.【总结升华】求最大公约数通常有两种方法:一是辗转相除法;二是更相减损术,对于3个数的最大公约数的求法,则是先求其中两个数的最大公约数m,再求m与第三个数的最大公约数.同样可推广到求3个以上数的最大公约数.举一反三:【变式1】求三个数324,243,135的最大公约数.【答案】27【解析】∵324=243×1+81,243=81×3+0,∴324与243的最大公约数为81.又135=81×1+54,81=54×1+27,54=27×2+0,∴81与135的最大公约数为27.∴三个数324,243,135的最大公约数为27.更相减损术:∵324-243=81,243-81=162,162-81=81,∴81是324和243的最大公约数.又135-81=54,81-54=27,54-27=27,∴27是81与135的最大公约数.∴三个数324,243,135的最大公约数为27.例3.甲、乙、丙三种溶液分别重147g、343g、133g,现要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同,问每瓶最多装多少?【思路点拨】由题意,每个小瓶最多能装的溶液的质量应是三种溶液质量的最大公约数.【答案】7g【解析】先求147与343的最大公约数.343-147=196,196-147=49,147-49=98,98-49=49,∴147与343的最大公约数是49.再求49与133的最大公约数.133-49=84,84-49=35,49-35=14,35-14=21,21-14=7, 14-7=7.∴147,343,133的最大公约数是7. 故每瓶最多装7g .【总结升华】本题关键是分析清楚题意,找出三个数的最大公约数.求三个以上(含三个数)的数的最大公约数时,可依次通过求两个数的最大公约数与第三个数的最大公约数来求得.类型二:秦九韶算法例4.(2018春 河北邯郸月考)用秦九韶算法求多项式5432()254367f x x x x x x =--+-+当x =5时的值.【思路点拨】利用秦九韶算法计算多项式的值,先将多项式转化为((((25)4)3)6)7x x x x x --+-+的形式,然后逐步计算0v 到5v 的值,即可得到答案.【答案】2677【解析】5432()254367((((25)4)3)6)7f x x x x x x x x x x x =--+-+=--+-+12555v =⨯-=, 255421v =⨯-=, 32153108v =⨯+=, 410856534v =⨯-=, 5534572677v =⨯+=.所以f (5)=2677.【总结升华】秦九韶算法的原理是01(1,2,3,,)nk k nk v a v v x ak n --=⎧⎨=+=⎩.在运用秦九韶算法进行计算时,应注意每一步的运算结果,像这种一环扣一环的运算,如果错一步,则下一步,一直到最后一步就会全部算错.同学们在计算这种题时应格外小心. 举一反三:【变式1】用秦九韶算法求多项式764()85321f x x x x x =++++当x=2时的值. 【答案】1397 【解析】765432()85030021((((((85)0)3)0)0)2)1f x x x x x x x x x x x x x x x =++⋅++⋅+⋅++=+++++++.v 0=8,v 1=8×2+5=21,v 2=21×2 -0=42, v 3=42×2 -3=87, v 4=87×2+0=174, v 5=174×2+0=348, v 6=348×2+2=698, v 7=698×2+1=1397,所以,当x=2时,多项式的值为1397.【变式2】用秦九韶算法计算多项式65432()654327f x x x x x x x =++++++在x=0.4时的值时,需做加法和乘法的次数和是( )A .10B .9C .12D .8 【答案】 C【解析】 ()(((((65)4)3)2)1f x x x x x x x =++++++.∴加法6次,乘法6次, ∴6+6=12(次),故选C .类型三:进位制 例5.(1)试把十进制数136转化为二进制数; (2)试把十进制数1 234转化为七进制数. 【答案】(1)10001000(2)(2)3412(7) 【解析】 (1)由于136=2×68+0, 68=2×34+0. 34=2×17+0. 17=2×8+1. 8=2×4+0. 4=2×2+0. 2=2×1+0. 1=2×0+1.所以136=10001000(2). (2)1234=7×176+2, 176=7×25+1. 25=7×3+4. 3=7×0+3.所以1234=3412(7). 【总结升华】(1)应注意搞清每一次除法中的被除数、除数,当商为零时停止除法,把每步所得的余数倒着排成一个数,就是相应的二进制数.(2)十进制数转化为七进制数与转化为二进制数的方法类似,要认真体会其原理. 举一反三: 【变式1】(1)把十进制数89转化为二进制数; (2)将十进制数2l 转化为五进制数. 【解析】(1)用除2取余法:∴89=2×(2×(2×(2×(2×(2×(2×0+1)+0)+1)+1)+0)+0)+1=2×(2×(2×(2×2×(22×0+2+0)+1)+1)+0)+0)+1 =……=1×26+0×25+1×24+1×23+0×22×0×21+1×20=1011001(2)(2)用除5取余法,可得∴21=41(5). 例6.(2017春 湖南娄底月考)若二进制数100y 011和八进制数x 03相等,求x +y 的值. 【思路点拨】直接利用进位制运算法则化简求解即可. 【答案】1【解析】63100011122121678y y y =⨯+⨯+⨯+=+,20383643x x x =⨯+=+,∴67+8y =64x +3,∵y =0或1,x 可以取1、2、3、4、5、6、7, y =0时,x =1;y =1时,64x =72,无解; ∴x +y =1. 举一反三:【变式1】在十进制中,01232004410010010210=⨯+⨯+⨯+⨯,那么在五进制中数码2 004折合成十进制为( )A .29B .254C .602D .2 004 【答案】B解析:0123200445050525254=⨯+⨯+⨯+⨯=,故选B . 【变式2】把四进制数2132化为七进制数________. 【答案】314(7)【解析】先将“四进制”数2132(5)化为十进制数为32124143424158(1)⨯+⨯+⨯+⨯= 然后将十进制的158化为七进制: 158÷7=22余4, 22÷7=3余1, 3÷7=0余3,所以,结果是314(7) 故答案为:314(7)【巩固练习】1.1337与382的最大公约数是( ). A .3 B .382 C .191 D .2012.用辗转相除法求得459和357的最大公约数是( ). A .3 B .9 C .17 D .51 3.下列各数中最小的是( )A .)2(111111B .)6(210C .)4(1000D .(9)814.(2017春 河南灵宝市月考)若用秦九韶算法求多项求52()42f x x x =-+当x =3时的值,则需要做乘法运算和加减法运算的次数分别为( ) A .4,2 B .5,3 C .5,2 D .6,2 5.把67转化为二进制数为( ).A .1100001(2)B .1000011(2)C .110000(2)D .100011l (2)6.(2018 湖北天门模拟)已知多项式5432()42 3.5 2.6 1.70.8f x x x x x x =++-+-,用秦九韶算法算f (5)时的1v 值为( )A .22B .564.9C .20D .14130.27.已知一个k 进制数132与十进制数30相等,那么k 等于( ). A .-7或4 B .-7 C .4 D .都不对 8. 计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A ~F 共16个计数符号,A .6EB .72C .5FD .B09.三个数72,120,168的最大公约数是 .10.(2018春 河南期中)若a =111111(2),b =210(6),c =1000(4),d =110(8),则a ,b ,c ,d 的大小顺序为________.11.已知a=333,b=24,则使得a=bq+r (q ,r 均为自然数,且0≤r <b )成立的q 和r 的值分别为________.12. 秦九韶的算法中有n 个一次式,若令0n v a =,我们可以得到01___(12).n k k v a v v x k n -=⎧⎨=+=⎩,,,,我们可以利用 结构来实现.13.(2018春 河北卢龙县期中)用“更相减损术”求(1)中两数的最大公约数,用“辗转相除法”求(2)中两数的最大公约数.用秦九韶算法求函数532()1f x x x x x =++++,当x =3时的函数值.(1)72,168; (2)98,280.14.古时候,当边境有敌人来犯时,守边的官兵通过在烽火台上举火向国内报告,如下图,若烽火台上点火,则用数字1表示,若不点火用数字0表示,约定二进制数对应的十进制数的单位是1000,请你计算一下,这组烽火台表示边境有多少敌人入侵?15.设有甲、乙、丙三种溶液,质量分别为146kg 、334kg 、229kg .要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同.每瓶最多装多少?16.(2017春 甘肃临夏州月考)比较85(9)、210(6)、1000(4)、111111(2)这四个数的大小.【答案与解析】1.【答案】C【解析】 1337=382×3+191,382=191×2+0,1337与382的最大公约数为191.2.【答案】D【解析】 ∵459=357×1+102,357=102×3+51,102=51×2+0,即51为459和357的最大公约数.3.【答案】A【解析】把这四个数都化为十进制数63111111)2(=,78210)6(=,641000)4(=,(9)8173=,故选A .4.【答案】C【解析】∵f (x )=((((4x )x )x -1)x )x +2,∴乘法要运算5次,加减法要运算2次.故选C .5.【答案】B【解析】利用除2取余法易得67=1000011(2).6.【答案】A【解析】∵f (x )=((((4x +2)x +3.5)x ―2.6)x +1.7)x ―0.8,∴04v =,145222v =⨯+=.故选:A .7. 【答案】C【解析】∵132(k )=1×k2+3k+2=30,∴k=-7或k=4.又∵k >0,∴k=4.故选C .8. 【答案】A【解析】A×B 用十进制可以表示为10×11=110,而110=6×16+14,所以用十六进制表示为6E ,故选A .9. 【答案】24【解析】12072148,7248124,48242,168247=⨯+=⨯+=⨯=⨯10.【答案】b >d >a >c .【解析】∵2345111111(2)112121212121248163263a ==+⨯+⨯+⨯+⨯+⨯=+++++=; 12210(6)162667278b ==⨯+⨯=+=;31000(4)1448c ==⨯=;2110(8)181886472d ==⨯+⨯=+=.∴b >d >a >c .故答案为:b >d >a >c .11.【答案】13,21【解析】 用333除以24,商即为q ,余数就是r .333=24×13+21.12.【答案】n k a -;循环13.【答案】(1)24;(2)14;(3)283【解析】(1)∵168―72=96,96―72=24,72―24=4848―24=24,故72和168的最大公约数是24;(2)∵280=2×98+84,98=1×84+14,84=6×14,故98和280的最大公约数是14;(3)532()1((((0)1)1)1)1f x x x x x x x x x x =++++=+++++,当x =3时 01v =,10303v v =⨯+=;213110v v =⨯+=;323131v v =⨯+=;433194v v =⨯+=;5431283v v =⨯+=,即x =3时的函数值为283.14.【答案】27000【解析】由题图可知,从左到右的五个烽火台,表示二进制数的自左到右的五个数位.这组烽火台表示的二进制数是11011(2),转化为十进制数为11011(2)=1×24+1×23+0×22+1×21+1×20=16+8+2+1=27.又27×1000=27000,所以,这组烽火台表示边境共有27000个敌人入侵.15.【答案】536【解析】12515046636==,31513534436==,2208029936==.15013515363636-=,13515120363636-=,12015105363636-=, 1051590363636-=,901575363636-=,751560363636-=, 601545363636-=,451530363636-=,301515363636-=, 即146与334的最大公约数为1536. 801565363636-=,651550363636-=,501535363636-=, 351520363636-=,20155363636-=,155********-=,1055363636-=. 综上所述,146、334、229的最大公约数是536. 16.【答案】210(6)>85(9)>1000(4)>111111(2).【解析】85(9)=8×9+5=77,2(6)210261678=⨯+⨯=,3(4)10001464=⨯=,6(2)11111112163=⨯-=,故210(6)>85(9)>1000(4)>111111(2).。
高中数学必修三1.3算法案例-辗转相除法
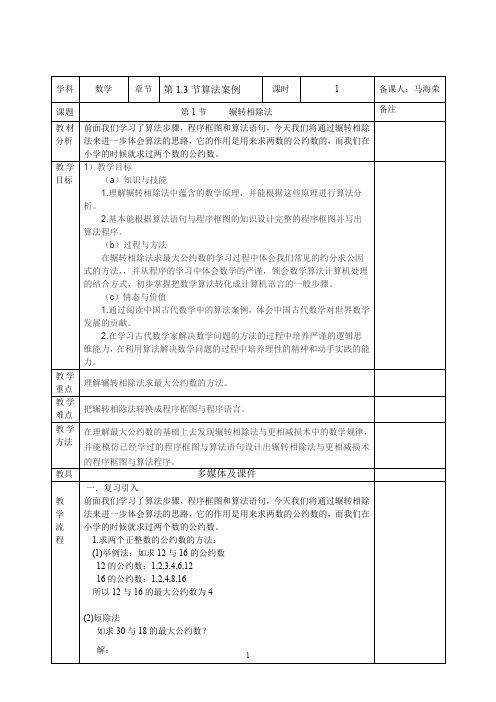
1734=816×2+102
816=102×8
2)再求102与1343的最大公约数
1343=102×13+17
102=17×6
所以17为102与1343的最大公约数
所以17为1734、816、1343这三个数的最大公约数
板
书
设
计
第1.3节算法案例-----辗转相除法
............................... ................................... ...............
课后作业
P45练习:1.
P48习题1.3A组:1.
课
后
反
思
1.辗转相除法的思想2.辗转相除法算法框图3.例题讲解
................................ ................................... ...............
............................... ................................... ...............
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序。
(b)过程与方法
在辗转相除法求最大公约数的学习过程中体会我们常见的约分求公因式的方法,,并从程序的学习中体会数学的严谨,领会数学算法计算机处理的结合方式,初步掌握把数学算法转化成计算机语言的一般步骤。
(c)情态与价值
1.通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献。
PRINT m
END
课堂练习:1.求两数4081与20723的最大公约数.
高一数学必修3算法知识点

高一数学必修3算法知识点在高中数学的学习过程中,必修3是一门非常重要的课程,其中包含了许多与算法相关的知识点。
算法作为计算机科学的核心之一,也是数学学科中的一个重要分支。
掌握数学算法知识,对于培养学生的逻辑思维和解决问题的能力具有重要的意义。
下面,我们将介绍一些高一数学必修3中与算法相关的知识点。
一、排序算法排序算法是计算机科学中的基础问题之一,也是高中数学必修3中的重点内容。
常见的排序算法有冒泡排序、插入排序、选择排序、快速排序等。
这些排序算法能够将一组无序的数列按照某种规则重新排列,使得数列有序。
通过学习排序算法,学生能够提高对问题的分析和解决能力,锻炼自己的思维逻辑。
二、递归算法递归算法是一种常用的问题解决方法,也是高中数学必修3中的重要内容之一。
递归算法通过将一个问题分解为一个或多个更小的同类问题来解决。
递归算法能够提高学生的抽象思维和问题拆解能力。
在实际应用中,递归算法被广泛应用于许多领域,如数据结构、图形图像处理等。
三、图论算法图论是高中数学中一个重要的分支,也是计算机科学中的常用工具。
图论算法主要研究图的各种性质和算法的设计与分析。
在高一数学必修3中,学生会学习到图的表示方法、最短路径算法、最小生成树算法等。
图论算法能够帮助学生理解和解决实际问题,提高他们的计算思维和创新能力。
四、搜索算法搜索算法是解决问题的一种常用方法,也是高中数学必修3中的重点知识。
搜索算法通过遍历问题的解空间,寻找问题的解。
其中,深度优先搜索和广度优先搜索是最常用的搜索算法。
深度优先搜索通过栈实现,从起始节点出发,沿着一条路径一直深入,直到找到解或无路可走,然后回溯到上一个节点继续搜索。
广度优先搜索通过队列实现,从起始节点出发,依次访问与当前节点相邻的节点,并将它们加入到队列中,直到找到解或队列为空。
通过学习搜索算法,学生能够提高问题分析和解决能力,培养自己的逻辑思维和创新意识。
总结起来,高一数学必修3中的算法知识点涉及了排序算法、递归算法、图论算法和搜索算法等。
高中数学必修三知识点大全

知识点串讲必修三第一章:算法1. 1.1 算法的概念1、算法(algorithm)一词源于算术(algorism),即算术方法,是指一个由已知推求未知的运算过程。
后来,人们把它推广到一般,把进行某一工作的方法和步骤称为算法。
广义地说,算法就是做某一件事的步骤或程序。
2、任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定。
解析:根据质数的定义判断解:算法如下:第一步:判断n是否等于2,若n=2,则n是质数;若n>2,则执行第二步。
第二步:依次从2至(n-1)检验是不是n的因数,即整除n的数,若有这样的数,则n不是质数;若没有这样的数,则n是质数。
3、一个人带三只狼和三只羚羊过河,只有一条船,同船可以容纳一个人和两只动物.没有人在的时候,如果狼的数量不少于羚羊的数量,狼就会吃掉羚羊.请设计过河的算法。
解:算法或步骤如下:S1 人带两只狼过河;S2 人自己返回;S3 人带一只羚羊过河;S4 人带两只狼返回;S5 人带两只羚羊过河;S6 人自己返回;S7 人带两只狼过河;S8 人自己返回;S9 人带一只狼过河.1.1.2程序框图1、基本概念:(1的流程图的首末两端必须是起止框。
(2表示数据的输入或结果的输出,它可用在算法中的任何需要输入、输出的位置。
(3(4判断框一般有一个入口和两个出口,有时也有多个出口,它是惟一的具有两个或两个以上出口的符号,在只有两个出口的情形中,通常都分成“是”与“否”(也可用“Y”与“N”)两个分支。
2、顺序结构:顺序结构描述的是是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的。
3、已知一个三角形的三边分别为2、3、4,利用海伦公式设计一个算法,求出它的面积,并画出算法的程序框图。
算法分析:这是一个简单的问题,只需先算出p 的值,再将它代入公式,最后输出结果,只用顺序结构就能够表达出算法。
解:程序框图:24、条件结构:根据条件选择执行不同指令的控制结构。
人教课标版高中数学必修3知识归纳:基本算法语句和算法案例

1.2基本算法语句1.2.1输入、输出语句和赋值语句1.输入语句在该程序中的第1行中的INPUT语句就是输入语句.这个语句的一般格式是:其中,“提示内容”一般是提示用户输入什么样的信息.如每次运行上述程序时,依次输入-5,-4,-3,-2,-1,0,1,2,3,4,5,计算机每次都把新输入的值赋给变量“x”,并按“x”新获得的值执行下面的语句.2.输出语句在该程序中,第3行和第4行中的PRINT语句是输出语句.它的一般格式是:3.赋值语句用来表明赋给某一个变量一个具体的确定值的语句.除了输入语句,在该程序中第2行的赋值语句也可以给变量提供初值.它的一般格式是:4.INPUT语句不但可以给单个变量赋值,还可以给多个变量赋值,其格式为:5.(1)赋值语句中的“=”叫做赋值号.(2)赋值语句的作用:先计算出赋值号右边表达式的值,然后把这个值赋给赋值号左边的变量,使该变量的值等于表达式的值.(3)赋值号左边只能是变量名字,而不能是表达式.如:2=X是错误的.(4)赋值号左右不能对换.如“A=B”“B=A”的含义运行结果是不同的.(5)不能利用赋值语句进行代数式的演算.(如化简、因式分解、解方程等)(6)赋值号“=”与数学中的等号意义不同.1.3算法案例1.利用辗转相除法求最大公约数的步骤如下:(1)用较大的数m 除以较小的数n 得到一个商0S 和一个余数0R ;(2):若0R =0,则n 为m ,n 的最大公约数;若0R ≠0,则用除数n 除以余数0R 得到一个商1S 和一个余数1R ;(3):若1R =0,则1R 为m ,n 的最大公约数;若1R ≠0,则用除数0R 除以余数1R 得到一个商2S 和一个余数2R ;……依次计算直至n R =0,此时所得到的1n R 即为所求的最大公约数.2.直接插入排序的基本思想:插入排序的思想就是读一个,排一个.将第1个数放入数组的第1个元素中,以后读入的数与已存入数组的数进行比较,确定它在从大到小的排列中应处的位置.将该位置以及以后的元素向后推移一个位置,将读入的新数填入空出的位置中.(由于算法简单,可以举例说明)3.冒泡排序的基本思想:依次比较相邻的两个数,把大的放前面,小的放后面.即首先比较第1个数和第2个数,大数放前,小数放后.然后比较第2个数和第3个数......直到比较最后两个数.第一趟结束,最小的一定沉到最后.重复上过程,仍从第1个数开始,到最后第2个数...... 由于在排序过程中总是大数往前,小数往后,相当气泡上升,所以叫冒泡排序.4.进位制是一种记数方式用有限的数字在不同的位置表示不同的数值.可使用数字符号的个数称为基数,基数为n ,即可称n 进位制,简称n 进制.现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数.对于任何一个数,我们可以用不同的进位制来表示.比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的.5.辗转相除法与更相减损术的区别:(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显.(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到6. 一般地,若k 是一个大于一的整数,那么以k 为基数的k 进制可以表示为: 110()110...(0,0,...,,)n n k n n a a a a a k a a a k --<<≤<,而表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表示5进制数.。
高中数学人教A版必修三第一章1.3.3进位制-算法案例课件

把89化为五进制的数.
5 89 5 17 53
0
余数
4 2 3
∴ 89=324(5)
练习:把3282化为16进制的数.
10
11
12
13
14
15
A
B
C
D
E
F
思考 你会把三进制数10221(3)化为二进制数吗?
解:第一步:先把三进制数化为十进制数: 10221(3)=1×34+0×33+2×32+2×31+1×30
51
把89化为二进制的数.
2 89
2 44 2 22 2 11 25
22 21
0
余数
1 0 0 1 1 0 1
把算式中各步所得的余 数从下到上排列,得到
89=1011001(2) 可以用2连续去除89或所得 商(一直到商为0为止),然后 取余数---除2取余法.
这种方法也可以推广为把 十进制数化为k进制数的 算法,称为除k取余法.
=81+18+6+1=106. 第二步:再把十进制数化为二进制数:
106=1101010(2). ∴10221(3)=106=110就是几,基数都是大于1的数.
按照十进制数的运算规则计算出结果, 结果就是十进制下该数的大小了.
1.3算法案例
进位制
十进制数3721中的3表示3个千,7表示7个百,2表示2个 十,1表示1个一,从而它可以写成下面的形式:
3721=3×103+7×102+2×101+1×100.
同理: 3421(5)= 3×53+4×52+2×51+1×50.
每一位上的数都是整数.
高三数学必修三算法知识点

高三数学必修三算法知识点一、算法概述算法是指解决问题的一系列明确指令的有限序列。
在高三数学必修三中,算法是解决数学问题的基本工具,它可以用来求解数值计算问题、优化问题以及数学模拟等。
二、二分法1. 概述:二分法是一种通过将问题分解为更小的子问题进行求解的算法。
它适用于有序列表的搜索和函数求根等计算问题。
2. 原理:二分法的基本思想是不断将搜索范围缩小一半,通过将目标值与中间值进行比较,逐步逼近目标值。
3. 实例:求解有序列表中某个元素的位置。
三、迭代法1. 概述:迭代法是一种通过不断逼近目标值的方法来求解问题的算法。
它适用于函数求解、线性方程组求解、递归关系求解等问题。
2. 原理:迭代法的基本思想是通过不断迭代计算的方式,逐步逼近目标值。
通常通过设置初始值和递推公式来实现迭代。
3. 实例:使用牛顿迭代法求解方程的根。
四、贪心法1. 概述:贪心法是一种通过每一步选择当前最优解来求解问题的算法。
它适用于某些优化问题,如最小生成树、背包问题等。
2. 原理:贪心法的基本思想是每一步都选择当前最优解,以期望整体解能够达到最优。
贪心法通常需要证明某种贪心策略的正确性。
3. 实例:使用贪心法求解背包问题。
五、动态规划1. 概述:动态规划是一种通过将问题分解为相互重叠的子问题,并保存子问题的解来求解问题的算法。
它适用于具有重叠子问题和最优子结构性质的问题。
2. 原理:动态规划的基本思想是通过解决子问题的方式,逐步构建最优解。
动态规划一般需要设计递推关系和确定初始条件。
3. 实例:使用动态规划求解最长公共子序列问题。
六、快速排序1. 概述:快速排序是一种通过将数组分为两个子数组并对每个子数组进行排序来实现整体排序的算法。
它是一种高效的排序算法。
2. 原理:快速排序的基本思想是选择基准元素,将数组分为小于基准元素和大于基准元素的两部分,然后递归地对这两部分进行排序。
3. 实例:使用快速排序对数组进行排序。
七、图论算法1. 概述:图论算法是解决图相关问题的一类算法。
高三数学必修三算法初步要点归纳

高三数学必修三算法初步要点归纳以下是作者为大家整理的关于《高三数学必修三算法初步要点归纳》的文章,供大家学习参考!(1)算法的含义、程序框图①通过对解决具体问题进程与步骤的分析(如二元一次方程组求解等问题),体会算法的思想,了解算法的含义。
②通过仿照、操作、探索,经历通过设计程序框图表达解决问题的进程。
在具体问题的解决进程中(如三元一次方程组求解等问题),知道程序框图的三种基本逻辑结构:顺序、条件分支、循环。
(2)基本算法语句:经历将具体问题的程序框图转化为程序语句的进程,知道几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句,进一步体会算法的基本思想。
(3)通过浏览中国古代数学中的算法案例,体会中国古代数学对世界数学发展的奉献。
2. 统计(约16课时)(1)随机抽样①能从现实生活或其他学科中提出具有一定价值的统计问题。
②结合具体的实际问题情境,知道随机抽样的必要性和重要性。
③在参与解决统计问题的进程中,学会用简单随机抽样方法从整体中抽取样本;通过对实例的分析,了解分层抽样和系统抽样方法。
④能通过实验、查阅资料、设计调查问卷等方法收集数据。
(2)用样本估计整体①通过实例体会散布的意义和作用,在表示样本数据的进程中,学会列频率散布表、画频率散布直方图、频率折线图、茎叶图(参见例1),体会它们各自的特点。
②通过实例知道样本数据标准差的意义和作用,学会运算数据标准差。
③能根据实际问题的需求公道地选取样本,从样本数据中提取基本的数字特点(如平均数、标准差),并作出公道的说明。
④在解决统计问题的进程中,进一步体会用样本估计整体的思想,会用样本的频率散布估计整体散布,会用样本的基本数字特点估计整体的基本数字特点;初步体会样本频率散布和数字特点的随机性。
⑤会用随机抽样的基本方法和样本估计整体的思想,解决一些简单的实际问题;能通过对数据的分析为公道的决策提供一些根据,认识统计的作用,体会统计思维与肯定性思维的差异。
高中数学必修3算法初步知识点

高中数学必修3算法初步知识点高中数学必修3算法初步知识点:概念(1)算法概念:在数学上,现代意义上的〝算法〞通常是指可以用计算机来处置的某一类效果是顺序或步骤,这些顺序或步骤必需是明白和有效的,而且可以在有限步之内完成.(2)算法的特点:①有限性:一个算法的步骤序列是有限的,必需在有限操作之后中止,不能是有限的.②确定性:算法中的每一步应该是确定的并且能有效地执行且失掉确定的结果,而不应当是模棱两可.③顺序性与正确性:算法从初始步骤末尾,分为假定干明白的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只要执行完前一步才干停止下一步,并且每一步都准确无误,才干完成效果.④不独一性:求解某一个效果的解法不一定是独一的,关于一个效果可以有不同的算法.⑤普遍性:很多详细的效果,都可以设计合理的算法去处置,如心算、计算器计算都要经过有限、事前设计好的步骤加以处置。
高中数学必修3算法初步知识点:三种基本逻辑结构(1)顺序结构:顺序结构是最复杂的算法结构,语句与语句之间,框与框之间是按从上到下的顺序停止的,它是由假定干个依次执行的处置步骤组成的,它是任何一个算法都离不开的一种基本算法结构。
顺序结构在顺序框图中的表达就是用流程线将顺序框自上而下地衔接起来,按顺序执行算法步骤。
如在表示图中,A框和B框是依次执行的,只要在执行完A框指定的操作后,才干接着执行B框所指定的操作。
(2)条件结构:条件结构是指在算法中经过对条件的判别依据条件能否成立而选择不同流向的算法结构。
条件P能否成立而选择执行A框或B框。
无论P条件能否成立,只能执行A框或B框之一,不能够同时执行A框和B框,也不能够A框、B框都不执行。
一个判别结构可以有多个判别框。
(3)循环结构:在一些算法中,经常会出现从某处末尾,依照一定条件,重复执行某一处置步骤的状况,这就是循环结构,重复执行的处置步骤为循环体,显然,循环结构中一定包括条件结构。
循环结构又称重复结构,循环结构可细分为两类:①一类是当型循环结构,如下左图所示,它的功用是当给定的条件P成立时,执行A框,A框执行终了后,再判别条件P能否成立,假设依然成立,再执行A框,如此重复执行A框,直到某一次条件P不成立为止,此时不再执行A框,分开循环结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修三算法案例知识点
算法案例:
主要有辗转相除法、更相减损术、秦九韶算法、k进制化十进制的算法。
辗转相除的定义:
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。
若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较
小的数就是原来两个数的最大公约数。
更相减损术的定义:
就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一
对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等
的两数便为原来两个数的最大公约数。
比较辗转相除法与更相减损术的区别:
1都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区
别较明显。
2从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损
术则以减数与差相等而得到。
辗转相除法的一个程序算法的步骤:
第一步:输入两个正整数m,nm>n.
第二步:计算m除以n所得的余数r.
第三步:m=n,n=r.
第四步:若r=0,则m,n的最大公约数等于m;否则转到第二步.第五步:输出最大公约
数m.
更相减勋术的一个程序算法步骤:
第一步:输入两个正整数a,ba>b;
第二步:若a不等于b,则执行第三步;否则转到第五步;
第三步:把a-b的差赋予r;
第四步:如果b>r,那么把b赋给a,把r赋给b;否则把r赋给a,执行第二步;
第五步:输出最大公约数b.
1、算法概念:
在数学中,算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.现在,算法通常可以编成计算机程序,让计算机执行并解决问题.
2、算法的特征
①有限性:算法中的步骤序列是有限的,必须在有限操作之后停止,不能是无限的。
②确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可。
③顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后续步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题。
④不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法。
⑤普通性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算其计算都要经过有限、事先设计好的步骤加以解决。
<>的人还:
感谢您的阅读,祝您生活愉快。
