实验三自顶向下语法分析--递归下降法

合集下载

递归下降语法分析

实验项目名称：递归下降语法分析实验学时： 6 同组学生姓名：实验地点：实验日期：实验成绩：批改教师：批改时间：一、实验目的和要求通过本实验，了解递归下降预测分析的原理和过程以及可能存在的回溯问题，探讨解决方法，为预测分析表方法的学习奠定基础。

分析递归下降子程序的优缺点。

二、实验仪器和设备硬件系统：586以上计算机、服务器要求内存256以上、Cpu 2.0GHz以上、Clinet内存128以上、CPU奔腾III以上，硬盘，光驱等软件系统：Visual Studio 2005中文版软件三、实验过程1、设计框架图1-1 递归下降程序框架图2、设计步骤1)给定文法：E→E+T｜TT→T*F｜FF→(E)｜i2)构造FIRST()集和FOLLOW()集表2-1 FIRST()集和FOLLOW()集3、程序源代码using System;using System.Collections.Generic;using System.Text;namespace递归下降语法分析{public class Program{public static char []a=new char[50];public static char []b=new char[50];public static char []d=new char[200];public static char []e=new char[10];public static char ch;public static int n1,i1=0,flag=1,n=5;public static int total=0;/*步骤计数器*/public static int E1(){int f,t;Console.Write(total);Console.Write("\tE-->TG\t");total++;flag=1;input();input1();f=T();if (f==0) return(0);t=G();if (t==0) return(0);else return(1);}public static int E(){int f,t;Console.Write(total);Console.Write("\tE-->TG\t");total++;e[0]='E';e[1]='=';e[2]='>';e[3]='T';e[4]='G';e[5]='#'; output();flag=1;input();f=T();if (f==0) return(0);t=G();if (t==0) return(0);else return(1);}public static int T(){int f,t;Console.Write(total);Console.Write("\tT-->FS\t");total++;e[0]='T';e[1]='=';e[2]='>';e[3]='F';e[4]='S';e[5]='#';output();flag=1;input();input1();f=F();if (f==0) return(0);t=S();if (t==0) return(0);else return(1);}public static int G(){int f;if(ch=='+') {b[i1]=ch;Console.Write(total);Console.Write("\tG-->+TG\t");total++;e[0]='G';e[1]='=';e[2]='>';e[3]='+';e[4]='T';e[5]='G';e[6]='#'; output();flag=0;input();input1();ch=a[++i1];f=T();if (f==0) return(0);G();return(1);}Console.Write(total);Console.Write("\tG-->^\t");total++;e[0]='G';e[1]='=';e[2]='>';e[3]='^';e[4]='#';output();input();input1();return(1);}public static int S(){int f,t;if(ch=='*') {b[i1]=ch;Console.Write(total);Console.Write("\tS-->*FS\t");total++;e[0]='S';e[1]='=';e[2]='>';e[3]='*';e[4]='F';e[5]='S';e[6]='#'; output();flag=0;input();input1();ch=a[++i1];f=F();if (f==0) return(0);t=S();if (t==0) return(0);else return(1);}Console.Write(total);Console.Write("\tS-->^\t");total++;e[0]='S';e[1]='=';e[2]='>';e[3]='^';e[4]='#';output();flag=1;a[i1]=ch;input();input1();return(1);}public static int F(){int f;if(ch=='(') {b[i1]=ch;Console.Write(total);Console.Write("\tF-->(E)\t");total++;e[0]='F';e[1]='=';e[2]='>';e[3]='(';e[4]='E';e[5]=')';e[6]='#'; output();flag=0;input();input1();ch=a[++i1];f=E();if (f==0) return(0);if(ch==')') {b[i1]=ch;Console.Write(total);Console.Write("\tF-->(E)\t");total++;flag=0;input();input1();ch=a[++i1];}else {Console.Write("error\n");return(0);}}else if(ch=='i') {b[i1]=ch;Console.Write(total);Console.Write("\tF-->i\t");total++;e[0]='F';e[1]='=';e[2]='>';e[3]='i';e[4]='#';output();flag=0;input();input1();ch=a[++i1];}else {Console.Write("error\n");return(0);}return(1);}public static void input(){int j=0;for (;j<=i1-flag;j++)Console.Write(b[j]); /*输出分析串*/Console.Write("\t\t");Console.Write("\t\t",ch); /*输出分析字符*/ }public static void input1(){int j;for (j=i1+1-flag;j<n1;j++)Console.Write(a[j]); /*输出剩余字符*/ Console.Write("\n");}public static void output(){ /*推导式计算*/int m,k,j,q;int i=0;m=0;k=0;q=0;i=n;d[n]='=';d[n+1]='>';d[n+2]='#';n=n+2;i=n;i=i-2;while(d[i]!='>'&&i!=0) i=i-1;i=i+1;while(d[i]!=e[0]) i=i+1;q=i;m=q;k=q;while(d[m]!='>') m=m-1;m=m+1;while(m!=q) {d[n]=d[m];m=m+1;n=n+1;}d[n]='#';for(j=3;e[j]!='#';j++){d[n]=e[j];n=n+1;}k=k+1;while(d[k]!='=') {d[n]=d[k];n=n+1;k=k+1;}d[n]='#';//system("pause");}static void Main(string[] args){ /*递归分析*/int f,p,j=0;char x;d[0]='E';d[1]='=';d[2]='>';d[3]='T';d[4]='G';d[5]='#';Console.Write("请输入字符串(长度<50,以#号结束）\n");do{ch=(char)Console.Read();a[j]=ch;j++;}while(ch!='#');n1=j;ch=b[0]=a[0];Console.Write("步骤\t文法\t分析串\t\t分析字符\t剩余串\n");f=E1();if (f==0) return;if (ch=='#'){Console.Write("accept\n");p=0;x=d[p];while(x!='#') {Console.Write(x);p=p+1;x=d[p]; /*输出推导式*/ }}else {Console.Write("error\n");Console.Write("回车返回\n");Console.ReadLine();Console.ReadLine();return;}Console.Write("\n");Console.Write("回车返回\n");Console.ReadLine();Console.ReadLine();}}}程序输入输出举例:1、输入“(i+i)*i”，分析如下图所示：2、输入“i#”，分析如下图所示：3、输入“i+i#”，分析如下图所示：四、实验结果与分析通过本次实验基本掌握了语法分析的原理和递归下降子程序分析方法，并且能将学到的知识学以致用，提高了对代码的分析能力，掌握了递归下降语法的构造，对自上再而下的语法分析模式有了更好的认识和理解。

第3章语法分析-编译原理及实践教程(第3版)-黄贤英-清华大学出版社

• 文法是被用来精确而无歧义地描述语言的句子的构成方式. • 文法描述语言的时候不考虑语言的含义。
3.2.1 文法的定义
例1：有如下规则
<句子><主语><谓语> <主语><代词>|<名词> <代词>我 <名词>大学生 <谓语><动词><直接宾语> <动词>是 <直接宾语><代词>|<名词>
(表示由…组成)
• 归约:推导的逆过程。
• 直接归约：直接推导的逆过程
几个概念的形式定义
• 直接推导: 如果αβ是文法 G=（Vn,Vt,P,S）
的产生式，γ和δ是Ｖ*中的任意符号，若有符号串v,w满足： v=γαδ,w=γβδ,则说v直接产生w，(w是v的直接推导)记作：v=>w 例：S01, 0S0=>0010(直接推导γ＝０,δ＝０) • 如果存在v=>w0=>w1=>w2...=>Wn=w(n>0)，则称v推导出w（长度为n），记作v+=>w(至少一步) • 若有ｖ=>w或v=w，则记作v*=>w(0步或若干步)
一个非终结符号，β∈V*)
–上例中： G=（Vn,Vt,P,<句子>）
Vn=（<句子>，<主语>，<谓语>，<代词>，<动词>，
<名词>，<直接宾语>）
Vt= (我，是，大学生)
P=
<句子><主语><谓语>
<主语> <代词>|<名词>

编译原理用递归下降法进行表达式分析实验报告

《编译原理》课程实验报告题目用递归下降法进行表达式分析专业班级学号姓名一.实验题目用递归下降法进行语法分析的方法二.实验日期三.实验环境（操作系统，开发语言）操作系统是Windows开发语言是C语言四.实验内容（实验要求）词法分析程序和语法分析程序已经提供。

此语法分析程序能够实现：正确的输入可以给出结果。

例：输入表达式串为：（13+4）*3则应给出结果为51。

要求：（1）读懂源代码，理解内容写入实验报告（语法分析及语法分析程序和词法分析程序的接口）（2）把语法分析中使用的yyval，用yytext实现。

（3）在语法分析程序用加入出错处理（尽量完整，包括出错的位置，出错的原因，错误的重定位）五.实验步骤1.生成lex.yy.c文件：将已给的mylexer.l文件打开，先理解，然后再在DOS环境下用flex运行此文件，这时会生成一个lex.yy.c文件。

2.创建工程：打开C-Free 5.0(注：用C-Free 4.0会出错)，在菜单栏中的“工程（project）”菜单下选择“新建”；在新建工程中选择“控制台程序”，添加工程名字为“myleb”和保存位置后点“确定”；第1步选择“空的程序”点“下一步”；第2步再点“下一步”；最后点击“完成”。

3.在创建的工程中添加文件：在Source files文件夹中添加之前生成的lex.yy.c文件和syn.c文件，然后找到parser.h文件，将其添加到新建工程中的Header files文件夹中，这时就能将三个文件组成一个类似于.exe文件类型的文件，最后运行。

如图：4.理解并修改syn.c文件：首先，将num = yyval.intval修改成num = atoi(yytext)；将num = yyval.fval修改成num = atof(yytext)。

可以这样修改的原因：在.l文件中所写的规则中，有{DIGIT}+ { yyval.intval = atoi(yytext);return INTEGER; }和{DIGIT}+"."{DIGIT}* {yyval.fval = atof(yytext); return DOUBLE; } 这两句代码，其中yyval.intval = atoi(yytext)和yyval.fval = atof(yytext)就说明两者可以相互替代。

递归下降语法分析设计原理与实现技术实验报告

}
else
error();
}
void E1()
{
if(current=='+' || current=='-')
{
A();
T();
E1();
}
else
if(!(current==')' || current=='#'))
error();
}
void T()
{
if(current=='i' || current=='(')
}
void F()
{
if(current=='(')
{
advance();
E();
if(current==')')
advance();
}
else
if(current=='i')
advance();
error()
{
cout<<"ERROR!"<<endl;
exit(0);
cout<<"SUCCESS!"<<endl;
return 1;
}
九、
/****************************************************
课题名称:递归下降语法分析设计原理与实现技术
作者:房皓进修生13410801
最后修改时间:2014、4、16 13:52
***************************************************/

编译原理6-4.2-4.3- 自顶向下翻译-递归下降翻译

对于自顶向下分析，对于自顶向下分析，我们假定动作是在处于相同位置上的符号被展开匹配成功）时执行的。被展开（置上的符号被展开（匹配成功）时执行的。
E T.val=9 num.val=9 R.i=9 － T.val=5 num.val=5 + R.i=4 T.val=2 R.i= 6 ε
num.val=2
图6.15
计算表达式 9 – 5 + 2
下面我们把转换左递归翻译模式的方法推广到一以便进行自顶向下分析。般，以便进行自顶向下分析。假设我们有下面的翻译模式，假设我们有下面的翻译模式，它的每个文法符号都有一个综合属性，用小写字母表示，和是任都有一个综合属性，用小写字母表示，g和f是任意函数。意函数。
procedure R; begin if sym = addop then begin advance; T; R end else begin /* 什么也不做 */ * end end; 产生式R 图6.19 产生式 → addop TR | ε 的分析过程
function R (in :↑ AST-node) :↑ AST-node; var nptr , i1, s1, s : ↑ AST-node; addoplexeme : char; begin if sym = addop then begin /* 产生式 R → addop T R */ nptr: T.nptr addoplexeme := lexval; i1: R1.i advance; s1: R1.s nptr := T; s: R.s i1 := mknode(addoplexme, in , nptr) ; s1 := R (i1); addoplexeme: s : = s1 addop (+|-) end else s := in; /* 产生式 R → ε */ return s end; 图6.20 递归下降构造抽象语法树

实验二：语法分析(递归下降法)

实验二：语法分析（递归下降法）一、实验目的1、掌握语法分析的基本原理；2、掌握递归下降的分析法；3、熟悉C语言程序设计。

二、实验准备微机CPU主频1.3G以上，128M内存，安装好C语言，PASCAL语言，或C++。

三、实验时间2学时四、实验内容已给语言文法，写出该文法的递归下降法语法分析器。

输入：源符号串。

输出：语法是否合法。

：文法：(1) <程序> ::= begin<语句串>end(2) <语句串> ::= <语句>{;<语句>}(3) <语句> ::= <赋值语句>(4) <赋值语句> ::= ID:=<表达式>(5) <表达式> ::= <项>{+<项>|-<项>}(6) <项> ::= <因子>{*<因子>|/<因子>}(7) <因子> ::= ID|NUM|(<表达式>)五:源程序：lrparser()对应 <程序>yucu() 对应 <语句串>statement() 对应 <语句>expression()对应 <表达式>term() 对应 <项>factor() 对应 <因子>关键字，数字，字母，符号对应码如下"begin", "if", "then", "while", "do", "end" 1——6字母 10 数字11+,-,*,/,:,:=,<,<>,<=,>,>=,=,;,(,),# 13——28,0factor()#include "stdio.h"#include "string.h"char prog[80], token[8];char ch;int syn, p, m, n, sum, kk=0;char *rwtab[6]={"begin", "if", "then", "while", "do", "end"};void scaner();void lrparser();void yucu();void statement();void expression();void term();void factor();void main(){p=0;printf("Please input string:\n");do{scanf("%c", &ch);prog[p++]=ch;}while(ch!='#'); //当遇到‘#’，结束输入p=0;scaner();lrparser();}void scaner(){for(n=0; n<8; n++) token[n]=NULL;ch=prog[p++];while(ch==' '||ch=='\n') ch=prog[p++];m=0;if((ch>='A'&&ch<='Z') || (ch>='a'&&ch<='z')){while((ch>='A'&&ch<='Z') || (ch>='a'&&ch<='z')||(ch>='0'&&ch<='9')){token[m++]=ch;ch=prog[p++];//将prog数组的字母复制到ch数组中}token[m++]='\0';//把token的末尾设置结束符\0p--;//标记到当前token数组中不是字母的当前位置syn=10; //标记字母的对应码for(n=0; n<6; n++){if(strcmp(token, rwtab[n])==0)//判断token对应rwtab中的哪一个,并进行对应赋对应码{syn=n+1;break;}}}else if(ch>='0'&&ch<='9'){sum=0;while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';//number用来记录所对应的数字ch=prog[p++];}p--;syn=11;//标记数字的对应码}else{switch(ch){case '<':m=0;token[m++]=ch;ch=prog[p++];if(ch=='>'){syn=21; //标记”<>”的对应码token[m++]=ch;}else if(ch=='='){syn=22; //标记”<=”的对应码token[m++]=ch;}else{syn=20; //标记”<”的对应码p--;}break;case '>':token[m++]=ch;ch=prog[p++];if(ch=='='){syn=24; //标记”>=”的对应码token[m++]=ch;}else{syn=23; //标记”>”的对应码p--;}break;case ':':token[m++]=ch;ch=prog[p++];if(ch=='='){syn=18; //标记”:=”的对应码token[m++]=ch;}else{syn=17; //标记”:”的对应码p--;}break;case '+':syn=13; //标记”+”的对应码token[m++]=ch;break;case '-':syn=14; //标记”-”的对应码token[m++]=ch;break;case '*':syn=15; //标记”*”的对应码token[m++]=ch;break;case '/':syn=16; //标记”/”的对应码token[m++]=ch;break;case '=':syn=25; //标记”=”的对应码token[m++]=ch;break;case ';':syn=26; //标记”；”的对应码token[m++]=ch;break;case '(':syn=27; //标记”（”的对应码token[m++]=ch;break;case ')':syn=28; //标记”）”的对应码token[m++]=ch;break;case '#':syn=0; //标记”#”的对应码token[m++]=ch;break;default:syn=-1; //当不是上述字母，数字，符号时，设置syn=-1 }token[m++]='\0';}}void factor()//因子{if(syn==10 || syn==11) //当扫描的是数字或字母时，继续扫描{scaner();}else if(syn==27) //当扫描的‘（’时，继续扫描{scaner();expression();if(syn==28) //当扫描的是‘）’时，继续扫描scaner();else{kk=1;printf("ERROR: )错误\n");//表达式缺乏‘）‘，出错}}else{kk=1;printf("ERROR: 表达式错误\n");//扫描表达式，表达式开头不是‘（‘，出错}}void term()//项{factor();while(syn==15 || syn==16) //当开头扫描的是’*’或’/’时，继续扫描{scaner();factor();}}void expression()//表达式{term();while(syn==13 || syn==14) //当开头扫描的是’+’或’-’时，继续扫描{scaner();term();}}void statement()//语句{if(syn==10) //当开头扫描的是字母时，继续扫描{scaner();if(syn==18) //扫描的是’:=’时，继续扫描{scaner();expression();}else{kk=1;printf("ERROR: 赋值号错误\n");//当扫描的是’:=’，出错}}else{kk=1;printf("ERROR: 语句错误\n");}}void yucu()//语句串{statement();while(syn==26) //当开始扫描到的是’；’，继续扫描{scaner();statement();}}void lrparser()//程序{if(syn==1) //当开头扫描的是‘begin‘时，继续扫描{scaner();yucu();if(syn==6){scaner();if(syn==0 && kk==0) //当数字串的最后扫描的是‘#‘，而且并无出错，分析成功printf("success!\n");else if(syn!=0 && kk==0){kk=1;printf("ERROR: END后未正常结束\n");//数字串的最后并没有扫描到符号‘#‘，出// 错}}else{if(kk!=1){kk=1;printf("ERROR: 缺少end\n");//程序分析结束并没有扫描到’end’，出错}}}else{kk=1;printf("ERROR: begin错误\n");//开始时并没有扫描到’begin’，出错}}。

第四章3-递归下降法

冲突
Predict(A→β 定义 Predict(A→β) First(β λ∉First( First(β = First(β) ，当λ∉First(β) (First( First(β })∪ λ∈First( First(β = (First(β)-{λ})∪Follow(A) ，当λ∈First(β)
满足产生式预测集合不相交条件的文法为递归下降文法
递归子程序方法要求的条件
predict(A→βk)∩ predict(A→βj )= ∅， β ∩ β 当k ≠ j
结论
如果文法中每个非终极符只有一个产生式，则没有上述限制。因为其递归下降子程序中没有多分支的选择问题。递归下降条件是针对具有多产生式的非终极符而言的。
必须消除选择的二义性
产生式A→β被选择的条件是：产生式A→β被选择的条件是： A→ 当前要匹配的输入符属于predict(A→β 当前要匹配的输入符属于predict(A→β)。 predict(A→ 至多一个产生式被选择的条件是：至多一个产生式被选择的条件是： predict(A→βk) ∩ predict(A→βj )=∅，当k ≠ j predict(A→β )=∅ predict(A→β
//调用Exp子程序 //调用Exp子程序调用Exp
Match($do)； Match($do)； Stm end
//调用调用Exp子程序调用子程序
Match（#while）（）表示检查当前输入的Token是输入的是不是#while，若不是，是，则输入指针移一位，针移一位，读下一个Token，下一个，否则表示有错
具有多个产生式的非终极符
当产生式中形如: 当产生式中形如: A → β1| β2| …| βn 也可以写成 | 则按下面的方法编写子程序A 则按下面的方法编写子程序A： Case结构结构 procedure A( ) token∈Predict(A→β begin if token∈Predict(A→β1) then θ(β1) else if token∈Predict(A→β2) then θ(β2) else token∈Predict(A→β …… token∈Predict(A→β →βn) if token∈Predict(A→βn) then θ(βn) else err( ) end 其中对β 其中对βi=X1X2…Xn，θ(βi) = θ’(X1);θ’(X2);…;θ’(Xn); β θ θ 如果X 如果 i∈VN，θ’(Xi)= Xi 如果X 如果 i∈VT，θ’(Xi)= Match(Xi) 如果X 空语句) 如果 i= ε , θ(ε) = skip(空语句 ε 空语句

递归下降分析算法

数学与计算机学院编译原理实验报告年级09软工学号姓名成绩专业软件工程实验地点主楼指导教师湛燕实验项目递归下降分析算法实验日期2012.6.10一、实验目的和要求使用递归子程序法设计一个语法分析程序，理解自顶向下分析方法的原理，掌握手工编写语法分析程序的方法。

重点和难点：本实验的重点是理解自顶向下分析方法的原理；难点是如何把文法改写成EBNF形式。

2、该词法分析器以子程序形式出现，当需要进行词法分析时进行调用；3、能够识别正确和错误的表达式；4、在进行语法分析的过程中，计算输入表达式的值。

三、程序设计主要变量有：boolIsDigit(char ch);//判断字符是否是数字static string s;//staticinti=0;//staticint flag=0;//staticint result;//主要函数有：staticintexp();//staticint exp1(int temp);//staticint term();//staticint term1(int temp);//staticint factor();//static intReadNum();//提取数字递归下降的主要原理是：对每个非终结符按其产生结构构造相应语法分析子程序，其中终结符产生匹配命令，而非终结符则产生过程调用命令。

因为文法递归相应子程序也递归，所以称这种方法为递归子程序下降法或递归下降法。

五、代码和截图自己写程序如下：#include<stdio.h>#include<conio.h>#include<cstdlib>#include<string>#include <iostream>#include <fstream>#include <stdlib.h>using namespace std;staticintexp();staticint exp1(int temp);staticint term();staticint term1(int temp);staticint factor();staticintReadNum();boolIsDigit(char ch);static string s;staticinti=0;staticint flag=0;staticint result;int main(){cout<<"请输入一个语句，以“#”结束，输入“#”退出"<<endl;while(1){cin>>s;s+='#';if(s[0]=='#')return 0;result = exp();if (flag == 0){cout<<"结果是"<<endl<<result<<endl;}}return 1;}staticboolIsDigit(char ch){if (ch>= 48 &&ch<= 57)return true;elsereturn false;}staticintReadNum(){int add = 0;stringstr = "";while (s[i]!= '#'){if (s[i] == '+'||s[i] =='-'||s[i]=='*'||s[i]=='/'||s[i]==')'){break;}else if (s[i]>= 48&&s[i]<=57){str +=s[i];}else{flag= 1;cout<<"输入了错误的字符!"<<endl;return -1;}i++;}str += "!";int n = 0;while (str[n] != '!'){cout<<str<<"（数字）"<<endl;n++;}int m = 0;while (str[m] != '!'){add += (int)(str[m] - 48);add *= 10;m++;}add = add / 10; cout<<add<<endl;return add;}staticintexp(){int temp;temp = term();temp = exp1(temp);return temp;}staticint exp1(int temp) {if(s[i]=='+'){++i;temp += term(); temp = exp1(temp);}else if(s[i]=='-'){++i;temp -= term(); temp = exp1(temp);}return temp;}staticint term(){int temp;temp = factor();temp = term1(temp); return temp;}staticint term1(int temp) {if(s[i]=='*'){++i;temp *= factor();temp = term1(temp);}else if(s[i]=='/'){++i;temp /= factor();temp = term1(temp);}return temp;}staticint factor(){int temp = 0;if (IsDigit(s[i])){temp = ReadNum();}else if(s[i]=='('){++i;temp=exp();if(s[i]==')')++i;else{flag = 1;cout<<"缺少右括号！"<<endl;}}else{flag = 1;cout<<"请输入正确的格式！"<<endl;}return temp;}输入的句子不正确时，提示，如下图：输入了正确的句子后，分析如下图：。

语法分析-递归下降分析法

char *rwtab[6]={"begin","if","then","while","do","end"};//关键字
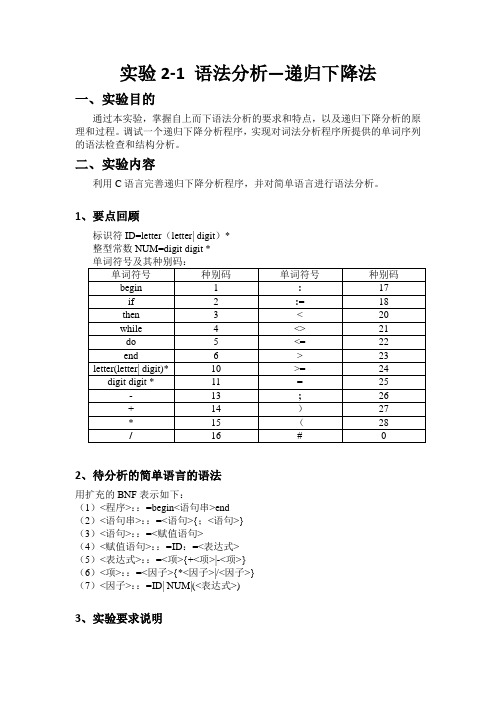
void scaner();//扫描函数
void factor();//因子
void term();//项
void expression();//表达式
void statement();//语句
else
{
cout<<"错误,表达式缺乏')'"<<endl;
kk=1;
}
}
else
{
cout<<"表达式错误,表达式开头不是'('"<<endl;
kk=1;
}
return;
}
//项
void term()
{
factor();
//问题---补充判断条件
while(syn==15 || syn==16)//当开头扫描的是'*'或'/'时，继续扫描
{
scaner();
factor();
}
return;
}
//表达式
void expression()
{
//问题---补充程序代码
term();
while(syn==14 || syn==13)//当开头扫描的是'+'或'-'时，继续扫描
{
scaner();
term();
}
return;
}

语法分析—递归下降分析法

实验2 语法分析——递归下降分析法一、实验目的1、通过该课程设计要学会用消除左递归的方法来使文法满足进行确定自顶向下分析的条件。

2、学会用C/C++高级程序设计语言来设计一个递归下降分析法的语法分析器；3、通过该课程设计，加深对语法分析理论的理解，培养动手实践的能力。

二、设计内容参考算数运算的递归子程序构造方法及代码，完成以下任务：构造布尔表达式的文法，并编写其递归子程序。

程序设计语言中的布尔表达式有两个作用，一是计算逻辑值，更多的情况是二，用作改变控制流语句中条件表达式，如在if-then，if-then-else或是while-do 语句中使用。

布尔表达式是由布尔算符(and,or,not)施予布尔变量或关系运算表达式而成。

可适当减少工作量，暂时忽略id的定义，输入时直接用数字或字母表示。

三、语法分析器的功能该语法分析器能够分析词法分析器的结果，即单词二元式。

在输入单词二元式后，能输出分析的结果。

四、算法分析1、语法分析的相关知识；2、递归子程序法的相关理论知识；3、根据递归子程序法相关理论，具体针对文法的每一条规则编写相应得递归子程序以及分析过程等。

//在递归子程序的编写过程中，当要识别一个非终结符时，需时刻留意该非终结符的FIRST集与FOLLOW集。

程序示例一：G：P→begin d；X end G’：P→begin d；X endX→d；X|Y X→d；X|YY→Y；s|s Y→sZ Z→；sZ|ε相应的递归子程序设计如下：P（）{ if（token==“begin“）{ Read(token);If(token==’d’)Read(token);ElseERROR;If (token==’;’)Read(token);ElseERROR;If (token==’d’ || ‘s’)X();Else ERROR;If(token==’end’) OK;}Else ERROR;}X() //X→d；X|Y{if(token==’d’){read(token);if(token==’;’)read(token);elseERROR;If(token==’d’)X();Else if (token==’s’) //注意：对Y的识别也可以是在X的过程中一开始就进行，所以在最外层分支中，加上一个token==s的分支Y();Else ERROR;}Else ERROR;}Y() //Y→sZ{if(token==’s’){read(token);If(token==’;’ || ‘end’)Z();Else ERROR;Else ERROR;}Z() //Z→；s Z|ε{if(token==’;’){read(token);If(token==’s’)Read(token);Else ERROR;If(token==’;’)Z()；Else if (token==’end’) // 类似的，这里对于读到end，也要最外层添加一个分支Return;Else ERROR;}Else ERROR;}程序示例二（参考代码）：构造文法G[E]：E→E + T | T T→T * F | F F→（E）| d的递归子程序（即语法分析器）。

c语言_递归下降分析程序实验_共13页

实验二递归下降语法分析程序的设计与实现、实验目的：加深对语法分析器工作过程的理解；加强对递归下降法实现语法分析程序的掌握；能够采用一种编程语言实现简单的语法分析程序；能够使用自己编写的分析程序对简单的程序段进行语法翻译。

、实验内容：在实验1的基础上，用递归下降分析法编制语法分析程序，语法分析程序的实现可以采用任何一种编程工具。

三、实验要求：1.对语法规则有明确的定义；2.编写的分析程序能够进行正确的语法分析；3.*对于遇到的语法错误，能够做出简单的错误处理，给出简单的错误提示，保证顺利完成语法分析过程；4.实验报告要求用文法的形式对语法定义做出详细说明，说明语法分析程序的工作过程，说明错误处理的实现*。

四、实验学时：4学时五、实验步骤：1.定义目标语言的语法规则；2.根据语法规则输入语句段，用递归下降分析的方法进行语法分析，直到结束；3.*对遇到的语法错误做出错误处理。

六、实验内容：1.编程实现给定文法的递归下降分析程序。

E—T|E+TT—F|T*FF—(E)|i2.（参考课本P74）对文法先进行消除左递归。

3.分析程序由一组递归过程组成，文法中每个非终结符对应一个过程几个全局过程和变量：ADVANCE，把输入串指示器IP指向下一个输入符号，即读入一个单字符号SYM，IP当前所指的输入符号ERROR，出错处理子程序每个非终结符有对应的子程序的定义，首先在分析过程中，当需要从某个非终结符出发进行展开（推导）时，就调用这个非终结符对应的子程序。

4.具体实现时:当遇到终结符，编写：if （当前读到的输入符号=i）读入下一个输入符号当遇到非终结符E时，编写语句：调用E（）当遇到E--＞编写语句if （当前读到的输入符号不属于Follow （E））Error（）；（4）当某个非终结符的规则有多个候选式时，按LL（1）文法的条件能唯一的选择一个候选式进行推导。

#in elude <iostream> using n ames pace std;char〃字符串的存入a[80];char sym; 〃单个的判断字符int//字符串下标i=0;void//功能识别函数E();void//功能识别函数E2();void//功能识别函数T();void//功能识别函数T2();void input(); // 输入函数void advance(); // 字符串小标进一函数5. 代码实现：#include <stdio.h> #include<dos.h>#include<stdlib.h> #include<string.h>char a[50] ,b[50],d[200],e[10];char ch;int n1,i1=0,flag=1,n=5;int total=0;/* 步骤计数器 */ int E();int E1();int T();int F();void input();void input1();void F(); //功能识别函数 int G();/*E*/ int S();/*T ' */voidoutput();void main() /*递归分析*/int f,p,j=0;char x;d[0]='E';d[1]='=';d[2]='>';d[3]='T';d[4]='G';d[5]='#';printf（"请输入字符串（长度＜50,以#号结束）\n"）;do{scanf("%c",&ch);a[j]=ch;j++;}while(ch!='#');n1=j;ch=b[0]=a[0];printf（"步骤吐文法\t分析串\t\t分析字符\t剩余串\n"）;f=E1();if (f==0) return;if (ch=='#'){printf("accept\n");int E1(){p=0; x=d[p];while(x!='#') {printf("%c",x);p=p+1;x=d[p];printf("error\n");printf(" 回车返回 \n");getchar();getchar();return;printf("\n");printf("回车返回 \n");getchar();getchar();式*/}else{ /*输出推导int f,t;printf("%d\tE-->TG\t",total);total++;flag=1;input();input1();f=T();if (f==0) return(0);t=G();if (t==0) return(0);else return(1);int E()int f,t;printf("%d\tE-->TG\t",total);total++;e[0]='E';e[1]='=';e[2]='>';e[3]= 'T';e[4]='G';e[5]='#';output();flag=1;input();input1();f=T();if (f==0) return(0);{t=G();printf("accept\n");int E1(){int f;if (t==0) return(0); else return(1);int f,t; printf("%d\tT-->FS\t",total);total++; e[0]='T';e[1]='=';e[2]='>';e[3]='F';e[4]='S';e[5]='#'; output(); flag=1; input(); input1(); f=F(); if (f==0) return(0); t=S(); if (t==0) return(0); else return(1);intT()in t G()if(ch=='+') {b[i1]=ch;printf("%d\tG-->+TG\t",total);total++;e[0]='G';e[1]='=';e[2]='>';e[3]='+';e[4]='T';e[5]='G' ;e[6]='#';output();flag=0;input();input1();ch=a[++i1];f=T();if (f==0)return(0);G();return(1);prin tf("%d\tG-->A\t",total);total++;e[0]='G';e[1]='=';e[2]='>';e[3]='A';e[4]=#;output();flag=1;input();input1();return(1);intS()int f,t;if(ch=='*') {b[i1]=ch;printf("%d\tS-->*FS\t",total);total++;e[0]='S';e[1]='=';e[2]='>';e[3]='*';e[4]='F';e[5]='S ';e[6]='#';output();flag=0;input();input1();ch=a[++i1];f=F();if (f==0) return(0);t=S();if (t==0) return(0);else return(1);}prin tf("%d\tS-->A\t",total);total++;e[0]='S';e[1]='=';e[2]='>';e[3]='A';e[4]=#;output();flag=1;a[i1]=ch;input();input1();}return(1); }intF()intf;if(ch=='(') {b[i1]=ch;printf("%d\tF-->(E)\t",total);total++;e[0]='F';e[1]='=';e[2]='>';e[3]='(';e[4]='E';e[5]=' )';e[6]='#';output();flag=0;input();input1();ch=a[++i1];f=E();if (f==0)return(0);if(ch==')') {b[i1]=ch;printf("%d\tF-->(E)\t",total);total++;flag=0;input();input1();ch=a[++i1];else{printf("error\n");return(0);}elseif(ch=='i') {b[i1]=ch;printf("%d\tF-->i\t",total);total++;e[0]='F';e[1]='=';e[2]='>';e[3]='i';e[4]='#';output();flag=0;input();input1();ch=a[++i1];else{printf("error\n");return(0);return(1)};voidinput()intj=0;for (;j<=i1-flag;j++)printf("%c",b[j/*输出分析串*/ ]);printf("\t\t");/*输出分析字符*/ printf("%c\t\t",ch);voidinput1()intj;for (j=i1+1-flag;j<n1;j++)/*输出剩余字符*/ printf("%c",a[j]);}int m,k,j,q;int i=0;m=0;k=0;q=0;i=n;d[n]='=';d[n+1]='>';d[n+2]='#';n=n+2;i=n;i=i-2;while(d[i]!='>'&&i!=0) i=i-1; i=i+1;while(d[i]!=e[0]) i=i+1;q=i;m=q;k=q;while(d[m]!='>') m=m-1;m=m+1;while(m!=q) {d[n]=d[m];m=m+1;n=n+1;printf("\n ");void output(){ /*推导式计算 */d[n]='#';for(j=3;e[j]!='#';j++){d[n]=e[j];n=n+1;k=k+1;while(d[k]!='=') {d[n]=d[k];n=n+1;k=k+1;d[n]='#';system("pause");}。

编译原理(3)语法_3(自顶向下语法分析：递归下降)33页PPT

G[S]: S → Q c | c
Q → R b | b
R → S a | a
(3.3)
中的S、Q、R都具有间接左递归
S Qc Rbc Sabc
3.3 自顶向下的语法分析
3、消除间接左递归如何消除一个文法的一切左递归呢？如果一个文法不含回路(
形如A=+>A的推导)，且产生式的右部也不含ε的候选式，那么
（3.1）
G[E]:E → TE' E' → +TE' | ε T → FT' T' → *FT' | ε F → (E) | i
（3.2）
可以通过文法(3.2)构造递归下降分析器：
(1)文法(3.2)无左递归 (2) E ' 、 T ' 、F的候选式首字符无交集
3.3 自顶向下的语法分析
4、递归下降分析器
3.3 自顶向下的语法分析 4、递归下降分析器
– 子程序的调用关系：
主程序
子程序
1.简单子程序
主程序
子程序1
2.嵌套子程序
子程序2
主程序
子程序
3.直接递归子程序
主程序
子程序1
子程序2
4.间接递归子程序
递归下降分析器的设计示例
G[E]:E → E+T | T T → T*F | F
F → (E) | i
A … Aα Aαα Aααα βααα
3.3 自顶向下的语法分析
再看下面不含A的直接左递归的产生式： A → βA' A' → α A' | ε
这两个产生式所能推导的句子如下：
A βA' β A βA' βαA' βα A βA' βαA' βααA' βαα A βA' βαA' βααA' βαααA' βααα

语法分析器的设计与实现

语法分析器的设计与实现一、设计概述1.定义语法规则：根据所设计的编程语言，确定其语法规则。

可以使用文法或者EBNF（扩展巴科斯-诺尔范式）来定义语法规则。

2. 设计语法分析算法：选择适合的语法分析算法，常见的有自顶向下（Top-Down）和自底向上（Bottom-Up）两种。

自顶向下算法从语法规则的起始符号开始，逐步向下匹配源代码，构建语法树。

自底向上算法则通过逐步将输入的源代码规约为语法规则的右侧，最终得到语法树。

3.实现语法分析器：根据所选择的语法分析算法，实现相应的算法，根据文法定义和源代码进行语法分析。

二、自顶向下语法分析自顶向下语法分析是一种递归的、自上而下构造语法树的方法。

它以文法的起始符号为目标，通过不断向下匹配文法规则，构造出整个语法树。

自顶向下语法分析的步骤如下：1.设计非终结符的产生规则：根据文法的非终结符定义产生规则。

非终结符表示语法规则的左侧。

2.设计终结符的匹配规则：根据文法的终结符定义匹配规则。

终结符表示具体的代码元素，如标识符、关键字等。

3.设计递归下降分析算法：根据文法的产生规则，设计递归下降分析算法。

算法的入口是文法的起始符号，通过递归调用不同的产生规则，不断向下匹配源代码，构造语法树。

三、自底向上语法分析自底向上语法分析是一种逆推的、以产生规则的右侧为目标的方法。

它通过逐步将源代码的串规约为文法规则的右侧，最终得到语法树。

自底向上语法分析的步骤如下：1.设计终结符的匹配规则：根据文法的终结符定义匹配规则。

2.设计产生规则的规约动作：根据文法的产生规则，为每个规则设计规约动作。

规约动作通常是将产生规则的右侧转化为左侧的非终结符。

3.设计移进-规约分析算法：根据终结符的匹配规则和产生规则的规约动作，实现移进-规约分析算法。

算法通过逐步将输入的源代码进行移进和规约操作，直到得到语法树。

四、错误处理在语法分析的过程中，可能会出现各种错误，如语法错误、缺失分号、括号不匹配等。

编译原理之自顶向下语法分析方法(25页)

自顶向下的语法分析(实验报告一)

武汉轻工大学编译原理实验报告姓名朱春桃院（系）数学与计算机学院班级软件工程1203学号 1205110605指导教师李禹生2014 年11 月10 日一、实验目的完成自顶向下语法分析算法的程序设计。

二、实验内容设计、调试并测试自顶向下语法分析算法程序。

三、设计思路根据课堂讲授的自顶向下语法分析方法，可以根据递归下降子程序方法设计语法分析程序，也可以根据LL（1）算法设计语法分析程序，针对文法：G[E]E→E+T | TT→T*F | FF→( E ) | i（1）由于文法G[E]不满足LL（1）文法条件，需要进行必要的等价文法变换。

变换后的等价文法为：H[E]E→TAA→+TA | εT→FBB→*FB | εF→( E ) | i（2）等价文法H[E]不含左递归，可以证明文法H[E]满足LL（1）文法条件（3）根据递归下降子程序方法设计语法分析程序①递归程序清单②调试过程说明③测试语句设计④测试结果列表⑤测试结论分析（4）根据LL（1）算法设计语法分析程序①预测分析表②预测分析程序清单③调试过程说明④测试语句设计⑤测试结果列表⑥测试结论分析四、程序清单/*E->TA,A->+TA|ε,T->FB,B->*FB|ε,F->i|(E).*/#include<stdio.h>void E(char str[80],int &i,int &err or);void A(char str[80],int &i,int &error);void T(char str[80],int &i,int &error);void B(char str[80],int &i,int &error);void F(char str[80],int &i,int &error);void main(){int i=0,j=0,error=0;char str[80];printf("请输入字符串（'#'为结束字符）:");while ((str[j]=getchar())!='#')j++;str[j]='#';E(str,i,error);if(error)printf("error\n");elseprintf("right\n");}void E(char str[80],int &i,int &error){printf("E->TA\n");T(str,i,error);A(str,i,error);}void A(char str[80],int &i,int &error){if(str[i]=='+'){printf("A->+TA|ε\n");i++;T(str,i,error);A(str,i,error);else if (str[i]=='#'||str[i]==')'){}elseerror++;}void T(char str[80],int &i,int &error) {printf("T->FB\n");F(str,i,error);B(str,i,error);}void B(char str[80],int &i,int &error) {if (str[i]=='*'){printf("B->*FB|ε\n");i++;F(str,i,error);B(str,i,error);}}void F(char str[80],int &i,int &error) {if (str[i]=='('){printf("F->i|(E)\n");i++;E(str,i,error);if(str[i]==')'){i++;}elseerror++;}else{if(str[i]=='i'){printf("F->i|(E)\n");i++;}elseerror++;}五、测试结果六、实验总结实验在老师提前给出的算法指导下，完成自顶向下语法分析的程序实际上是不困难的。

自顶向下语法分析方法

7
PL/0语言文法的EBNF表示
PL/0语言文法的EBNF表示 <程序>∷=<分程序>. <分程序>∷=[<常量说明部分>][<变量说明部分>][<过程说明部分>]<语句> <常量说明部分>∷=CONST<常量定义部分>{，<常量定义>}； <无符号整数>∷=<数字>{<数字>} <变量说明部分>∷=VAR<标识符>{，<标识符>}； <标识符>∷=<字母>{<字母>|<数字>} <过程说明部分>∷=<过程首部><分程序>{；<过程说明部分>}； <过程首部>∷=PROCEDURE <标识符>； <语句>∷=<赋值语句>|<条件语句>|<当型循环语句>|<过程调用语句>| <读语句>|<写语句>|<复合语句>|<空> <赋值语句>∷=<标识符>:=<表达式> <复合语句>∷=BEGIN <语句>{；<语句>} END <条件>∷=<表达式><关系运算符><表达式>|ODD<表达式>
例如对文法G3[S]： S→aAS|b A→bA| SELECT(S→aAS)={a} SELECT(S→b)={b} SELECT(A→bA)={b} SELECT(A→)={a,b}

递归下降分析实验报告

实习二递归下降分析一、实验目的：根据某一文法编制调试递归下降分析程序，以便对任意输入的符号串进行分析。

本次实验的目的主要是加深对递归下降分析法的理解。

二、实验预习提示1、递归下降分析法的功能词法分析器的功能是利用函数之间的递归调用模拟语法树自上而下的构造过程。

2、递归下降分析法的前提改造文法：消除二义性、消除左递归、提取左因子，判断是否为LL（1）文法，3、递归下降分析法实验设计思想及算法为G的每个非终结符号U构造一个递归过程,不妨命名为U。

U的产生式的右边指出这个过程的代码结构：(1)若是终结符号，则和向前看符号对照，若匹配则向前进一个符号；否则出错。

(2)若是非终结符号，则调用与此非终结符对应的过程。

当A的右部有多个产生式时,可用选择结构实现。

具体为：（1）对于每个非终结符号U->u1|u2|…|un处理的方法如下：U( ){ch=当前符号;if(ch可能是u1字的开头) 处理u1的程序部分;else if(ch可能是u2字的开头)处理u2的程序部分;…else error()}（2）对于每个右部u1->x1x2…x n的处理架构如下：处理x1的程序；处理x2的程序；…处理x n的程序；（3）如果右部为空，则不处理。

（4）对于右部中的每个符号x i①如果xi为终结符号：if(xi= = 当前的符号){NextChar()；/% NextChar为前进一个字符函数。

%/return;}else 出错处理②如果xi为非终结符号，直接调用相应的过程xi()三、实验要求程序输入/输出示例：对下列文法，用递归下降分析法对任意输入的符号串进行分析：（1）E->TG（2）G->+TG|－TG|ε（3）T->FS（4）S->*FS|/FS|ε（5）F->(E)|i输出的格式如下：(1)输入一以#结束的符号串(包括+—*/（）i#)(2)备注：输入一符号串如i+i*#,要求输出为“非法的符号串”。