八年级数学第一章轴对称图形(B卷)

合集下载

八年级数学复习考点1 轴对称及轴对称图形的意义

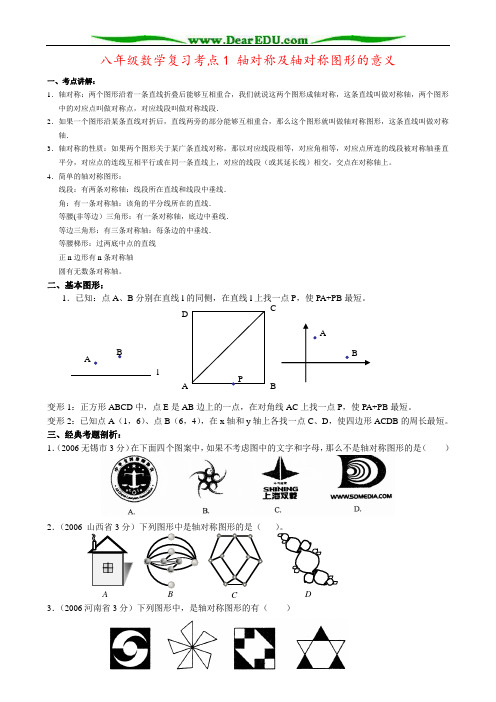
ABCDP八年级数学复习考点1 轴对称及轴对称图形的意义一、考点讲解：1．轴对称：两个图形沿着一条直线折叠后能够互相重合，我们就说这两个图形成轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点，对应线段叫做对称线段．2．如果一个图形沿某条直线对折后，直线两旁的部分能够互相重合，那么这个图形就叫做轴对称图形，这条直线叫做对称轴．3．轴对称的性质：如果两个图形关于某广条直线对称，那以对应线段相等，对应角相等，对应点所连的线段被对称轴垂直平分，对应点的连线互相平行或在同一条直线上，对应的线段（或其延长线）相交，交点在对称轴上。

4．简单的轴对称图形：线段：有两条对称轴：线段所在直线和线段中垂线．角：有一条对称轴：该角的平分线所在的直线．等腰(非等边）三角形：有一条对称轴，底边中垂线．等边三角形：有三条对称轴：每条边的中垂线．等腰梯形：过两底中点的直线正n 边形有n 条对称轴圆有无数条对称轴。

二、基本图形：1．已知：点A 、B 分别在直线l 的同侧，在直线l 上找一点P ，使PA+PB 最短。

变形1：正方形ABCD 中，点E 是AB 边上的一点，在对角线AC 上找一点P ，使PA+PB 最短。

变形2：已知点A （1，6）、点B （6，4），在x 轴和y 轴上各找一点C 、D ，使四边形ACDB 的周长最短。

三、经典考题剖析：1．（2006无锡市3分）在下面四个图案中，如果不考虑图中的文字和字母，那么不是轴对称图形的是（）2．（2006 山西省3分）下列图形中是轴对称图形的是（）。

3．（2006河南省3分）下列图形中，是轴对称图形的有（）ABABlB A CDＡ．4个Ｂ．3个Ｃ．2个Ｄ．1个4．（2006鸡西市3分）在下列四个图案中，既是轴对称图形，又是中心对称图形的是( )(A) (B) (C) (D)5．（2006苏州市3分）如图，如果直线m 是多边形ABCDE 的对称轴，其中∠A=1300， ∠B=1100．那么∠BCD 的度数等于（） A. 400B.500C ．60D.7006．（2006梅州市3分）小明在镜中看到身后墙上的时钟，实际时间最接近8时的是下图中的（）7．（2006 湛江市6分）如图5，请你画出方格纸中的图形关于点O 的中心对称图形，并写出整个图形的对称轴的条数．四、针对性训练：1．（2006宜昌市3分）从汽车的后视镜中看见某车车牌的后5位号码是，该车的后5位号码实际是。

初中数学八上第一章单元测试卷

BCADE第5题八上第一章单元测试卷一、精心选一选1. 以下图形中，是轴对称图形的是（）(A)①② （B ）③④ （C ）②③ （D ）①④2. 如图1 所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（ ) A .△ABC 的三条中线的交点 B .△ABC 三边的中垂线的交点 C .△ABC 三条角平分线的交点 D .△ABC 三条高所在直线的交点3. 如下图的正方形网格中，网格线的交点称为格点．已知A 、B 是两格点，假如C 也是图中的格点，且使得ABC 为等腰三角形．．．．．，则点C 的个数是（） A ．6B ．7C ．8D ．94. .如图，AD 是△ABC 的角平分线，DF ⊥AB ，垂足为F ，DE=DG ，△ADG 和△AED 的面积分别为50和39，则△EDF 的面积为：（）A 、11B 、5.5C 、7D 、3.5 5.如图，△ABC 的周长为30cm ，把△ABC 的边AC 对折，使顶点C 和点A 重合，折痕交BC 边于点D ，交AC 边于点E ，连接AD ，若AE =4cm ，则△ABD 的周长是（） A ．22cm B ．20 cm C ．18cm D ．15cm6. 如图，在Rt △ABC 中，CD 是中线，且CD ＝4cm ，则AB 的长为（） A 、 4cm B 、 6cm C 、 8cm D 、10cm7. 如图，在△ABC 中，AB=AC ，D 、E 分别在AC 、AB 边上，且ＢＣ＝ＢＤ，ＡＤ＝ＤＥ＝ＥＢ，则∠A 的度数等于（） A.36° B.40° C.45° D.50°① ② ③ ④ BC图1B ADCBA第6题8.在等腰梯形ABCD中，AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E,F,AD=4,BC=8,则AE+EF=（）A．9 B．10 C．11 D．20第九题二、用心填一填9.如图,在△ABC中,∠C=90 ，点D在AC上，,将△BCD沿着直线BD翻折，使点C落在斜边AB上的点E处，DC=5cm，则点D到斜边AB的距离是cm.．10. 已知等腰三角形的两边长分别是4和6，则第三边的长是11.等腰梯形的上底是4cm，下底是10 cm，一个底角是60︒，则等腰梯形的腰长是cm．12.如图，上面各图都是用全等的等边三角形拼成的一组图形，则在第10个这样的图形中，共有个等腰梯形．13.已知等边△ABC中，点D,E分别在边AB,BC上，把△BDE沿直线DE翻折，使点B落在点Bˊ处，DBˊ,EBˊ分别交边AC于点F，G，若∠ADF=80º，则∠EGC的度数为14.如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG＝CD，DF＝DE，则∠E＝度．14题图13题图15.B、D、F在AN上，C、E在AM上，且AB=BC=CD，EC=ED=EF，∠A=20°，则∠FEM度数是16.已知∆ABC中∠BAC=140°，AB、AC的垂直平分线分别交BC于E、F.则∠EAF的度数为；若BC=12，则△AEF周长为ABDFNMC E15题图三、耐心解一解17. 如图：某通信公司要修建一座信号发射塔，要求发射塔到两城镇P 、Q 的距离相等，同时到两条高速公路l 1、l 2的距离也相等．在图上作出发射塔的位置．（不写作法，保留作图痕迹）18.已知：如图，锐角△ABC 的两条高BD 、CE 相交于点O ，且OB=OC ，（1）求证：△ABC 是等腰三角形；（2）判断点O 是否在∠B AC 的角平分线上，并说明理由。

2024年重庆市中考数学试题B卷(含答案)

重庆市2024年初中学业水平暨高中招生考试数学试题（B卷）（全卷共三个大题，满分150分，考试时间120分钟）注意事项：1．试题的答案书写在答题卡上，不得在试题卷上直接作答；2．作答前认真阅读答题卡上的注意事项；3．作图（包括作辅助线）请一律用黑色2B铅笔完成；4．考试结束，由监考人员将试题卷和答题卡一并收回．参考公式：抛物线()20y ax bx c a=++≠的顶点坐标为24,24b ac ba a⎛⎫-- ⎪⎝⎭，对称轴为2bxa=-．一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．1.下列各数中最小的数是（）A.1-B.0C.1D.2【答案】A【解析】【分析】根据正数大于0，0大于负数，即可作出判断．【详解】1-是负数，其他三个数均是非负数，故1-是最小的数；故选：A．【点睛】本题考查了有理数大小的比较：负数小于一切非负数，明确此性质是关键．2.下列标点符号中，是轴对称图形的是（）A.B.C.D.【答案】A【解析】【分析】本题考查轴对称图形的识别．解题的关键是理解轴对称的概念（如果一个平面图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴），寻找对称轴，图形两部分沿对称轴折叠后可重合．据此对各选项逐一进行判断即可．【详解】解：A．该标点符号是轴对称图形，故此选项符合题意；B．该标点符号不是轴对称图形，故此选项不符合题意；C．该标点符号不是轴对称图形，故此选项不符合题意；D ．该标点符号不是轴对称图形，故此选项不符合题意．故选：A ．3.反比例函数10y x =-的图象一定经过的点是（）A.()1,10 B.()2,5- C.()2,5 D.()2,8【答案】B【解析】【分析】本题考查了求反比例函数值．熟练掌握求反比例函数值是解题的关键．分别将各选项的点坐标的横坐标代入，求纵坐标，然后判断作答即可．【详解】解：解：当1x =时，10101y =-=-，图象不经过()1,10，故A 不符合要求；当2x =-时，1052y =-=-，图象一定经过()2,5-，故B 符合要求；当2x =时，1052y =-=-，图象不经过()2,5，故C 不符合要求；当2x =时，1052y =-=-，图象不经过()2,8，故D 不符合要求；故选：B ．4.如图，AB CD ∥，若1125∠=︒，则2∠的度数为（）A .35︒ B.45︒ C.55︒ D.125︒【答案】C【解析】【分析】本题考查了平行线的性质，邻补角的定义，根据邻补角的定义求出3∠，然后根据平行线的性质求解即可．【详解】解：如图，∵1125∠=︒，∴3180155∠=︒-∠=︒，∵AB CD ∥，∴2355∠=∠=︒，故选：C ．5.若两个相似三角形的相似比为1:4，则这两个三角形面积的比是（）A.1:2B.1:4C.1:8D.1:16【答案】D【解析】【分析】本题主要考查了相似三角形的性质，根据相似三角形的面积之比等于相似比的平方进行求解即可．【详解】解：∵两个相似三角形的相似比为1:4，∴这两个三角形面积的比是221:41:16=，故选：D ．6.估计的值应在（）A.8和9之间B.9和10之间C.10和11之间D.11和12之间【答案】C【解析】【分析】本题考查的是二次根式的乘法运算，无理数的估算，先计算二次根式的乘法运算，再估算即可．6=，而45<=，∴10611<<，故答案为：C7.用菱形按如图所示的规律拼图案，其中第①个图案中有2个菱形，第②个图案中有5个菱形，第③个图案中有8个菱形，第④个图案中有11个菱形，…，按此规律，则第⑧个图案中，菱形的个数是（）A.20B.21C.23D.26【答案】C【解析】【分析】本题考查了图形类的规律探索，解题的关键是找出规律．利用规律求解．通过观察图形找到相应的规律，进行求解即可．【详解】解：第①个图案中有()131112+⨯-+=个菱形，第②个图案中有()132115+⨯-+=个菱形，第③个图案中有()133118+⨯-+=个菱形，第④个图案中有()1341111+⨯-+=个菱形，∴第n 个图案中有()131131n n +-+=-个菱形，∴第⑧个图案中菱形的个数为38123⨯-=，故选：C ．8.如图，AB 是O 的弦，OC AB ⊥交O 于点C ，点D 是O 上一点，连接BD ，CD ．若28D ∠=︒，则OAB ∠的度数为（）A.28︒B.34︒C.56︒D.62︒【答案】B【解析】【分析】本题考查了圆周角定理，等腰三角形的性质等知识，利用圆周角定理求出COB ∠，根据等腰三角形的三线合一性质求出AOB ∠，等边对等角然后结合三角形内角和定理求解即可．【详解】解：∵28D ∠=︒，∴256BOC D ∠=∠=︒，∵OC AB ⊥，OA OB =，∴2112AOB BOC ∠=∠=︒，OAB OBA ∠=∠，∴()1180342OAB AOB ∠=︒-∠=︒，故选：B ．9.如图，在边长为4的正方形ABCD 中，点E 是BC 上一点，点F 是CD 延长线上一点，连接AE ，AF ，AM 平分EAF ∠．交CD 于点M ．若1BE DF ==，则DM 的长度为（）A.2B.C.D.125【答案】D【解析】【分析】本题主要考查了正方形的性质，全等三角形的性质与判定，勾股定理，先由正方形的性质得到904ABE ADC ADF C AB AD CD BC ====︒====∠∠∠∠，，再证明()SAS ABE ADF △≌△得到AE AF =，进一步证明()SAS AEM AFM △≌△得到EM FM =，设DM x =，则14EM FM DF DM x CM CD DM x ==+=+=-=-，，在Rt CEM △中，由勾股定理得()()222134x x +=+-，解方程即可得到答案．【详解】解：∵四边形ABCD 是正方形，∴904ABE ADC ADF C AB AD CD BC ====︒====∠∠∠∠，，又∵1BE DF ==，∴()SAS ABE ADF △≌△，∴AE AF =，∵AM 平分EAF ∠，∴EAM FAM ∠=∠，又∵AM AM =，∴()SAS AEM AFM △≌△，∴EM FM =，设DM x =，则14EM FM DF DM x CM CD DM x ==+=+=-=-，，在Rt CEM △中，由勾股定理得222EM CE CM =+，∴()()222134x x +=+-，解得125x =，∴125DM =，故选：D ．10.已知整式1110:n n n n M a x a x a x a --++++ ，其中10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ．下列说法：①满足条件的整式M 中有5个单项式；②不存在任何一个n ，使得满足条件的整式M 有且只有3个；③满足条件的整式M 共有16个．其中正确的个数是（）A.0B.1C.2D.3【答案】D【解析】【分析】本题考查的是整式的规律探究，分类讨论思想的应用，由条件可得04n ≤≤，再分类讨论得到答案即可．【详解】解：∵10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ，∴04n ≤≤，当4n =时，则2104345a a a a a +++++=，∴41a =，23100a a a a ====，满足条件的整式有4x ，当3n =时，则210335a a a a ++++=，∴()()3210,,,2,0,0,0a a a a =，()1,1,0,0，()1,0,1,0，()1,0,0,1，满足条件的整式有：32x ，32x x +，3x x +，31x +，当2n =时，则21025a a a +++=，∴()()210,,3,0,0a a a =，()2,1,0，()2,0,1，()1,2,0，()1,0,2，()1,1,1，满足条件的整式有：23x ，22x x +，221x +，22x x +，22x +，21x x ++；当1n =时，则1015a a ++=，∴()()10,4,0a a =，()3,1，()1,3，()2,2，满足条件的整式有：4x ，31x +，3x +，22x +；当0n =时，005a +=，满足条件的整式有：5；∴满足条件的单项式有：4x ，32x ，23x ，4x ，5，故①符合题意；不存在任何一个n ，使得满足条件的整式M 有且只有3个；故②符合题意；满足条件的整式M 共有1464116++++=个．故③符合题意；故选D二、填空题：（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上．11.计算：023-+=______．【答案】3【解析】【分析】原式第一项利用绝对值的代数意义化简，第二项利用零指数幂法则计算即可得到结果．【详解】解：原式=2+1=3，故答案为：3．【点睛】此题考查了有理数的运算，熟练掌握运算法则是解本题的关键．12.甲、乙两人分别从A 、B 、C 三个景区中随机选取一个景区前往游览，则他们恰好选择同一景区的概率为________．【答案】13【解析】【分析】本题考查了列表法与树状图法：画树状图展示所有9种等可能的结果数，找出甲、乙恰好游玩同一景点的结果数，然后根据概率公式求解．【详解】解：画树状图如下：由图可知，共有9种等可能的情况，他们选择同一个景点有3种，故他们选择同一个景点的概率是：3193=，故答案为：13．13.若正多边形的一个外角是45°，则该正多边形的边数是_________.【答案】8【解析】【分析】根据多边形外角和是360度，正多边形的各个内角相等，各个外角也相等，直接用36045︒÷︒可求得边数．【详解】解：多边形外角和是360度，正多边形的一个外角是45︒，360458∴︒÷︒=即该正多边形的边数是8，故答案为：8．【点睛】本题主要考查了多边形外角和以及多边形的边数，解题的关键是掌握正多边形的各个内角相等，各个外角也相等．14.重庆在低空经济领域实现了新的突破．今年第一季度低空飞行航线安全运行了200架次，预计第三季度低空飞行航线安全运行将达到401架次．设第二、第三两个季度安全运行架次的平均增长率为x ，根据题意，可列方程为________．【答案】()22001401x +=【解析】【分析】本题主要考查了一元二次方程的实际应用，设第二、第三两个季度安全运行架次的平均增长率为x ，则第二季度低空飞行航线安全运行了()2001x +架次，第三季度低空飞行航线安全运行了()22001x +架次，据此列出方程即可．【详解】解：设第二、第三两个季度安全运行架次的平均增长率为x ，由题意得，()22001401x +=，故答案为：()22001401x +=．15.如图，在ABC 中，AB AC =，36A ∠=︒，BD 平分ABC ∠交AC 于点D ．若2BC =，则AD 的长度为________．【答案】2【解析】【分析】本题主要考查了等腰三角形的性质与判定，三角形内角和定理，三角形外角的性质，先根据等边对等角和三角形内角和定理求出72C ABC ∠=∠=︒，再由角平分线的定义得到36ABD CBD ∠=∠=︒，进而可证明A ABD BDC C ==∠∠，∠∠，即可推出2AD BC ==．【详解】解：∵在ABC 中，AB AC =，36A ∠=︒，∴180722A C ABC ︒︒-∠∠=∠==，∵BD 平分ABC ∠，∴1362ABD CBD ABC ∠=∠=∠=︒，∴72A ABD BDC A ABD C ==+=︒=∠∠，∠∠∠∠，∴AD BD BD BC ==，，∴2AD BC ==,故答案为：2．16.若关于x 的一元一次不等式组2133423x x x a +⎧≤⎪⎨⎪-<+⎩的解集为4x ≤，且关于y 的分式方程8122a y y y --=++的解均为负整数，则所有满足条件的整数a 的值之和是________．【答案】12【解析】【分析】本题主要考查了根据分式方程解的情况求参数，根据不等式组的解集求参数，先解不等式组中的两个不等式，再根据不等式组的解集求出2a >；解分式方程得到102a y -=，再由关于y 的分式方程8122a y y y --=++的解均为负整数，推出10a <且6a ≠且a 是偶数，则210a <<且6a ≠且a 是偶数，据此确定符合题意的a 的值，最后求和即可．【详解】解：2133423x x x a +⎧≤⎪⎨⎪-<+⎩①②解不等式①得：4x ≤，解不等式②得：2x a <+，∵不等式组的解集为4x ≤，∴24a +>，∴2a >；解分式方程8122a y y y --=++得102a y -=，∵关于y 的分式方程8122a y y y --=++的解均为负整数，∴1002a -<且102a -是整数且102202a y -+=+≠，∴10a <且6a ≠且a 是偶数，∴210a <<且6a ≠且a 是偶数，∴满足题意的a 的值可以为4或8，∴所有满足条件的整数a 的值之和是4812+=．故答案为：12．17.如图，AB 是O 的直径，BC 是O 的切线，点B 为切点．连接AC 交O 于点D ，点E 是O 上一点，连接BE ，DE ，过点A 作AF BE ∥交BD 的延长线于点F ．若5BC =，3CD =，F ADE ∠=∠，则AB 的长度是________；DF 的长度是________．【答案】①.203##263②.83##223【解析】【分析】由直径所对的圆周角是直角得到90ADB BDC ∠=∠=︒，根据勾股定理求出4BD =，则3cos 5CD C BC ==，由切线的性质得到90ABC ∠=︒，则可证明C ABD ∠=∠，解直角三角形即可求出20cos 3BD AB ABD ==∠；连接AE ，由平行线的性质得到BAF ABE ∠=∠，再由F ADE ∠=∠，ADE ABE ∠=∠，推出F BAF ∠=∠，得到203BF AB ==，则208433DF BF BD =-=-=．【详解】解：∵AB 是O 的直径，∴90ADB BDC ∠=∠=︒，在Rt BDC中，由勾股定理得4BD ==，∴3cos 5CD C BC ==，∵BC 是O 的切线，∴90ABC ∠=︒，∴90C CBD CBD ABD +=+=︒∠∠∠∠，∴C ABD ∠=∠，在Rt △ABD 中，4203cos 35BD AB ABD ===∠；如图所示，连接AE，∵AF BE ∥，∴BAF ABE ∠=∠，∵F ADE ∠=∠，ADE ABE ∠=∠，∴F BAF ∠=∠，∴203BF AB ==，∴208433DF BF BD =-=-=；故答案为：203；83．【点睛】本题主要考查了切线的性质，同弧所对的圆周角相等，直径所对的圆周角是直角，勾股定理，解直角三角形，等腰三角形的判定等等，证明F BAF ∠=∠是解题的关键．18.一个各数位均不为0的四位自然数M abcd =，若满足9a d b c +=+=，则称这个四位数为“友谊数”．例如：四位数1278，∵18279+=+=，∴1278是“友谊数”．若abcd 是一个“友谊数”，且1b a c b -=-=，则这个数为________；若M abcd =是一个“友谊数”，设()9M F M =，且()13F M ab cd++是整数，则满足条件的M 的最大值是________．【答案】①.3456②.6273【解析】【分析】本题主要考查了新定义，根据新定义得到9a d b c +=+=，再由1b a c b -=-=可求出a 、b 、c 、d 的值，进而可得答案；先求出9999099M a b =++，进而得到()36981313F M ab cda b a ++++=++，根据()13F M ab cd++是整数，得到369813a b a ++++是整数，即3613a b ++是整数，则36a b ++是13的倍数，求出8a ≤，再按照a 从大到小的范围讨论求解即可．【详解】解：∵abcd 是一个“友谊数”，∴9a d b c +=+=，又∵1b a c b -=-=，∴45b c ==，，∴36a d ==，，∴这个数为3456；∵M abcd =是一个“友谊数”，∴100010010M a b c d=+++()10001001099a b b a=++-+-9999099a b =++，∴()11110119M F M a b ==++，∴()13F M ab cd++1111011101013a b a b c d++++++=()111101*********a b a b b a +++++-+-=12011013a b ++=1173104613a a b ++++=369813a b a ++=++，∵()13F M ab cd++是整数，∴369813a b a ++++是整数，即3613a b ++是整数，∴36a b ++是13的倍数，∵a b c d 、、、都是不为0的正整数，且9a d b c +=+=，∴8a ≤，∴当8a =时，313638a b ≤++≤，此时不满足36a b ++是13的倍数，不符合题意；当7a =时，283635a b ≤++≤，此时不满足36a b ++是13的倍数，不符合题意；当6a =时，253632a b ≤++≤，此时可以满足36a b ++是13的倍数，即此时2b =，则此时37d c ==，，∵要使M 最大，则一定要满足a 最大，∴满足题意的M 的最大值即为6273；故答案为：3456；6273．三、解答题：（本大题8个小题，第19题8分，其余每题各10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．19.计算：（1）()()()312a a a a -+-+；（2）22241244x x x x -⎛⎫+÷ ⎪--+⎝⎭．【答案】（1）42a -（2）2x x +【解析】【分析】本题主要考查了整式的混合计算，分式的混合计算∶（1）先根据单项式乘以多项式的计算法则和多项式乘以多项式的计算法则去括号，然后合并同类项即可得到答案；（2）先把小括号内的式子通分，再把除法变成乘法后约分化简即可得到答案．【小问1详解】解：()()()312a a a a -+-+22322a a a a a =-+-+-42a =-；【小问2详解】解：22241244x x x x -⎛⎫+÷ ⎪--+⎝⎭()()()2222222x x x x x +--+=÷--()()()22222x x x x x -=⋅-+-2x x =+．20.数学文化有利于激发学生数学兴趣．某校为了解学生数学文化知识掌握的情况，从该校七、八年级学生中各随机抽取10名学生参加了数学文化知识竞赛，并对数据（百分制）进行整理、描述和分析（成绩均不低于70分，用x 表示，共分三组：A ．90100x ≤≤，B ．8090x ≤<，C ．7080x ≤<），下面给出了部分信息：七年级10名学生的竞赛成绩是：76，78，80，82，87，87，87，93，93，97．八年级10名学生的竞赛成绩在B 组中的数据是：80，83，88，88．七、八年级抽取的学生竞赛成绩统计表年级平均数中位数众数七年级8687b 八年级86a 90根据以上信息，解答下列问题：（1）填空：=a ________，b =________，m =________；（2）根据以上数据，你认为该校七、八年级中哪个年级学生数学文化知识较好？请说明理由（写出一条理由即可）；（3）该校七年级学生有500人，八年级学生有400人．估计该校七、八年级学生中数学文化知识为“优秀”()90x ≥的总共有多少人？【答案】（1）88；87；40（2）八年级学生数学文化知识较好，理由见解析（3）310人【解析】【分析】本题主要考查了中位数，众数，用样本估计总体，扇形统计图等等：（1）根据中位数和众数的定义可求出a 、b 的值，先求出把年级A 组的人数，进而可求出m 的值；（2）根据八年级学生成绩的中位数和众数都比七年级学生成绩的高即可得到结论；（3）用七年级的人数乘以七年级样本中优秀的人数占比求出七年级优秀人数，用八年级的人数乘以八年级样本中优秀的人数占比求出八年级优秀人数，再二者求和即可得到答案．【小问1详解】解：八年级C 组的人数为1020%2⨯=人，而八年级B 组有4人，则把八年级10名学生的成绩按照从低到高排列，处在第5名和第6名的成绩分别为88分，88分，∴八年级学生成绩的中位数8888882a +==；∵七年级10名学生成绩中，得分为87分的人数最多，∴七年级的众数87b =；由题意得，1041020%%100%40%10m --⨯=⨯=，∴40m =；故答案为：88；87；40；【小问2详解】解：八年级学生数学文化知识较好，理由如下：∵两个年级10名学生的平均成绩相同，但是八年级学生成绩的中位数和众数都比七年级学生成绩的高，∴八年级学生数学文化知识较好；【小问3详解】解：350040040%31010⨯+⨯=人，∴估计该校七、八年级学生中数学文化知识为“优秀”的总共有310人．21.在学习了矩形与菱形的相关知识后，小明同学进行了更深入的研究，他发现，过矩形的一条对角线的中点作这条对角线的垂线，与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形，可利用证明三角形全等得到此结论．根据他的想法与思路，完成以下作图与填空：（1）如图，在矩形ABCD 中，点O 是对角线AC 的中点．用尺规过点O 作AC 的垂线，分别交AB ，CD 于点E ，F ，连接AF ，CE ．（不写作法，保留作图痕迹）（2）已知：矩形ABCD ，点E ，F 分别在AB ，CD 上，EF 经过对角线AC 的中点O ，且EFAC ⊥．求证：四边形AECF 是菱形．证明：∵四边形ABCD 是矩形，∴AB CD ．∴①，OCF OAE ∠=∠．∵点O 是AC 的中点，∴②．∴CFO AEO ≅△△（AAS ）．∴③．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．进一步思考，如果四边形ABCD 是平行四边形呢？请你模仿题中表述，写出你猜想的结论：④．【答案】（1）见解析（2）①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形【解析】【分析】本题主要考查了矩形的性质，平行四边形的性质与判定，菱形的判定，垂线的尺规作图：（1）根据垂线的尺规作图方法作图即可；（2）根据矩形或平行四边形的对边平行得到OFC OEA ∠=∠，OCF OAE ∠=∠，进而证明()AAS CFO AEO ≌，得到OF OE =，即可证明四边形AECF 是平行四边形．再由EF AC ⊥，即可证明四边形AECF 是菱形．【小问1详解】解：如图所示，即为所求；【小问2详解】证明：∵四边形ABCD 是矩形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．猜想：过平行四边形的一条对角线的中点作这条对角线的垂线，与平行四边形两边相交的两点和这条对角线的两个端点构成的四边形是菱形；证明：∵四边形ABCD 是平行四边形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．故答案为：①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形．22.某工程队承接了老旧小区改造工程中1000平方米的外墙粉刷任务，选派甲、乙两人分别用A 、B 两种外墙漆各完成总粉刷任务的一半．据测算需要A 、B 两种外墙漆各300千克，购买外墙漆总费用为15000元，已知A 种外墙漆每千克的价格比B 种外墙漆每千克的价格多2元．（1）求A 、B 两种外墙漆每千克的价格各是多少元？（2）已知乙每小时粉刷外墙面积是甲每小时粉刷外墙面积的45，乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时．问甲每小时粉刷外墙的面积是多少平方米？【答案】（1）A 种外墙漆每千克的价格为26元，则B 种外墙漆每千克的价格为24元．（2）甲每小时粉刷外墙的面积是25平方米．【解析】【分析】本题考查的是分式方程的应用，一元一次方程的应用，理解题意建立方程是解本题的关键；（1）设A 种外墙漆每千克的价格为x 元，则B 种外墙漆每千克的价格为()2x -元，再根据总费用为15000元列方程求解即可；（2）设甲每小时粉刷外墙面积为y 平方米，则乙每小时粉刷外墙面积是45y 平方米；利用乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时．从而建立分式方程求解即可．【小问1详解】解：设A 种外墙漆每千克的价格为x 元，则B 种外墙漆每千克的价格为()2x -元，∴()300300215000x x +-=，解得：26x =，∴224x -=，答：A 种外墙漆每千克的价格为26元，B 种外墙漆每千克的价格为24元．【小问2详解】设甲每小时粉刷外墙面积为y 平方米，则乙每小时粉刷外墙面积是45y 平方米；∴500500545y y -=，解得：25y =，经检验：25y =是原方程的根且符合题意，答：甲每小时粉刷外墙的面积是25平方米．23.如图，在ABC 中，6AB =，8BC =，点P 为AB 上一点，过点P 作PQ BC ∥交AC 于点Q ．设AP 的长度为x ，点P ，Q 的距离为1y ，ABC 的周长与APQ △的周长之比为2y．（1）请直接写出1y ，2y 分别关于x 的函数表达式，并注明自变量x 的取值范围；（2）在给定的平面直角坐标系中画出函数1y ，2y 的图象；请分别写出函数1y ，2y 的一条性质；（3）结合函数图象，直接写出12y y >时x 的取值范围．（近似值保留一位小数，误差不超过0.2）【答案】（1）()()124606063y x x y x x=<≤=<≤，（2）函数图象见解析，1y 随x 增大而增大，2y 随x 增大而减小（3）2.26x <≤【解析】【分析】本题主要考查了一次函数与反比例函数综合，相似三角形的性质与判定：（1）证明APQ ABC ∽，根据相似三角形的性质得到APQABC C PQ AP C BC AB==△△，据此可得答案；（2）根据（1）所求利用描点法画出对应的函数图象并根据函数图象写出对应的函数图象的性质即可；（3）找到一次函数图象在反比例函数图象上方时自变量的取值范围即可．【小问1详解】解：∵PQ BC ∥，∴APQ ABC ∽，∴APQABC C PQ AP C BC AB==△△，∴12686y x AB y AP x ===，∴()()124606063y x x y x x =<≤=<≤，；【小问2详解】解：如图所示，即为所求；由函数图象可知，1y 随x 增大而增大，2y 随x 增大而减小；【小问3详解】解：由函数图象可知，当12y y >时x 的取值范围2.26x <≤．24.如图，A ，B ，C ，D 分别是某公园四个景点，B 在A 的正东方向，D 在A 的正北方向，且在C 的北偏西60︒方向，C 在A 的北偏东30︒方向，且在B 的北偏西15︒方向，2AB =千米．1.41≈，1.73≈2.45≈）（1）求BC 的长度（结果精确到0.1千米）；（2）甲、乙两人从景点D 出发去景点B ，甲选择的路线为：D C B --，乙选择的路线为：D A B --．请计算说明谁选择的路线较近？【答案】（1）2.5千米（2）甲选择的路线较近【解析】【分析】本题主要考查了解直角三角形的实际应用：（1）过点B 作BE AC ⊥于E ，先求出45ACB ∠=︒，再解Rt ABE △得到BE =千米，进一步解Rt BCE即可得到 2.5sin BE BC BCE ==≈∠千米；（2）过点C 作CF AD ⊥于D ，先解Rt ABE △得到1AE =千米，则(1AC AE CE =+=+千米，再Rt AFC △得到12CF +=千米，32AF +=千米，最后解Rt DCF 得到36DF +=千米，333CD +=千米，即可得到33 4.033CD BC ++=+千米， 5.15AD AB +≈千米，据此可得答案．【小问1详解】解：如图所示，过点B 作BE AC ⊥于E ，由题意得，903060901575CAB ABC =︒-︒=︒=︒-︒=︒∠，∠，∴18045ACB CAB ABC ∠=︒-∠-∠=︒，在Rt ABE △中，902AEB AB =︒=∠，千米，∴cos 2cos60BE AB BAE =⋅=⋅︒=∠千米，在Rt BCE 中， 2.5sin sin 45BE BC BCE ===︒∠千米，∴BC 的长度约为2.5千米；【小问2详解】解：如图所示，过点C 作CF AD ⊥于D ，在Rt ABE △中，cos 2cos601AE AB BAE =⋅=⋅︒=∠千米，∴(13AC AE CE =+=+千米，在Rt AFC △中，(13sin 13sin 302CF AC CAF +=⋅∠=+⋅︒=千米，(33cos 13cos302AF AC CAF =⋅∠=⋅︒=千米，在Rt DCF 中，3090DCF DFC =︒=︒∠，∠，∴1333tan tan 3026DF CF DCF +=⋅=⋅︒=∠千米，13332cos cos303CF CD DCF ++===︒∠千米，∴336 4.033CD BC ++=+≈千米，33332 5.1562AD AB DF AF AB +++=++=++≈千米，∵4.03 5.15<，∴甲选择的路线较近．25.如图，在平面直角坐标系中，抛物线23y ax bx =+-与x 轴交于()1,0A -，B 两点，交y 轴于点C ，抛物线的对称轴是直线52x =．（1）求抛物线的表达式；（2）点P 是直线BC 下方对称轴右侧抛物线上一动点，过点P 作PD x ∥轴交抛物线于点D ，作PE BC ⊥于点E ，求52PD PE +的最大值及此时点P 的坐标；（3）将抛物线沿射线BC 552PD PE +取得最大值的条件下，点F 为点P 平移后的对应点，连接AF 交y 轴于点M ，点N 为平移后的抛物线上一点，若45NMF ABC ∠-∠=︒，请直接写出所有符合条件的点N 的坐标．【答案】（1）215322y x x =--（2）52PD PE +最大值为152；()5,3P -；（3）573,4732N ⎛- ⎝⎭或131113,2⎛⎫- ⎪ ⎪⎝⎭【解析】【分析】（1）直接利用待定系数法求解抛物线的解析式即可；（2）如图，延长PE 交x 轴于G ，过P 作PH y ∥轴于H ，求解223635BC =+=，可得625sin 535OB BCO BC ∠===，证明255PE PH =，设215,322P x x x ⎛⎫-- ⎪⎝⎭，2132PH x x =-+，25PD x =-，再建立二次函数求解即可；（3）由抛物线沿射线BC 方向平移5个单位，即把抛物线向左平移2个单位，再向下平移1个单位，可得新的抛物线为：211722y x x =--，()3,4F -，如图，当N 在y 轴的左侧时，过N 作NK y ⊥轴于K ，证明()0,1M -，可得45AMO OAM FMK ∠=∠=︒=∠，证明NMK ABC ∠=∠，如图，当N 在y 轴的右侧时，过M 作y 轴的垂线，过N '作N T '⊥过M 的垂线于T ，同理可得：N MT ABC '∠=∠，再进一步结合三角函数建立方程求解即可．【小问1详解】解：∵抛物线23y ax bx =+-与x 轴交于()1,0A -，B 两点，交y 轴于点C ，抛物线的对称轴是直线52x =，∴30522a b b a --=⎧⎪⎨-=⎪⎩，解得1252a b ⎧=⎪⎪⎨⎪=-⎪⎩，∴215322y x x =--；【小问2详解】解：如图，延长PE 交x 轴于G ，过P 作PH y ∥轴于H，∵当2153022y x x =--=时，解得：11x =-，26x =，∴()6,0B ，当0x =时，=3y -，∴()0,3C -，∴BC ==，∴25sin 5OB BCO BC ∠===，∵PD x 轴，∴PHE BCO ∠=∠，∴25sin 5PE PHE PH ∠==，∴255PE PH =，∵()6,0B ，()0,3C -，设BC 为3y mx =-，∴630m -=，解得：12m =，∴直线BC 为：132y x =-，设215,322P x x x ⎛⎫-- ⎪⎝⎭，∴1,32H x x ⎛⎫- ⎪⎝⎭，∴2132PH x x =-+，∵抛物线215322y x x =--的对称轴为直线52x =，∴25PD x =-，∴2552512532252PD PE x x x ⎛⎫+=-+-+ ⎪⎝⎭21552x x =-+-，当55122x =-=⎛⎫⨯- ⎪⎝⎭时，52PD PE +取得最大值，最大值为152；此时()5,3P -；【小问3详解】解：∵抛物线沿射线BC方向平移个单位，即把抛物线向左平移2个单位，再向下平移1个单位，∴新的抛物线为：211722y x x =--，()3,4F -，如图，当N 在y 轴的左侧时，过N 作NK y ⊥轴于K ，∵()1,0A -，同理可得：直线AF 为=1y x --，当0x =时，1y =-，∴()0,1M -，∴45AMO OAM FMK ∠=∠=︒=∠，∵45NMF ABC ∠-∠=︒，∴4545NMK ABC ∠+︒-∠=︒，∴NMK ABC ∠=∠，∴1tan tan 2NMK ABC ∠=∠=，设211,722N n n n ⎛⎫-- ⎪⎝⎭，∴211121722NKn MK n n -==--++，解得：5732n =或5732+（舍去）∴573,42N ⎛- ⎝；如图，当N 在y 轴的右侧时，过M 作y 轴的垂线，过N '作N T '⊥过M 的垂线于T，同理可得：N MT ABC '∠=∠，设211,722N x x x ⎛-'⎫- ⎪⎝⎭，则(),1T x -，同理可得：211711222x x x --+=，∴1x =+或1，∴13112N ⎛⎫+ ⎝'⎪⎪⎭．【点睛】本题属于二次函数的综合题，难度很大，考查了待定系数法，二次函数的性质，锐角三角函数的应用，关键是做出合适的辅助线进行转化，清晰的分类讨论是解本题的关键．26.在Rt ABC △中，90ACB ∠=︒，AC BC =，过点B 作BD AC ∥．（1）如图1，若点D 在点B 的左侧，连接CD ，过点A 作AE CD ⊥交BC 于点E ．若点E 是BC 的中点，求证：2AC BD =；（2）如图2，若点D 在点B 的右侧，连接AD ，点F 是AD 的中点，连接BF 并延长交AC 于点G ，连接CF ．过点F 作FM BG ⊥交AB 于点M ，CN 平分ACB ∠交BG 于点N ，求证：2AM CN BD =+；（3）若点D 在点B 的右侧，连接AD ，点F 是AD 的中点，且AF AC =．点P 是直线AC 上一动点，连接FP ，将FP 绕点F 逆时针旋转60︒得到FQ ，连接BQ ，点R 是直线AD 上一动点，连接BR ，QR ．在点P 的运动过程中，当BQ 取得最小值时，在平面内将BQR 沿直线QR 翻折得到TQR △，连接FT ．在点R 的运动过程中，直接写出FT CP 的最大值．【答案】（1）证明见解析（2）证明见解析（3）2++【解析】【分析】（1）证明()ASA ACE CBD ≌得到BD CE =，再由点E 是BC 的中点，得到22BC CE BD ==，即可证明2AC BD =；（2）如图所示，过点G 作GH AB ⊥于H ，连接HF ，先证明()AAS AGF DBF ≌，得到AG BD =，BF GF =，再证明AHG 是等腰直角三角形，得到2222AH AG ==；由直角三角形斜边上的中线的性质可得12FH FC BF BG ===，则FBH FHB FBC FCB ==∠∠，∠∠，进而可证明290HFC ABC ==︒∠∠，则HFM CFN =∠∠；设CBG x ∠=，则4590ABG x CGB x =︒-=︒-∠，∠，可得135HMF BFM FBM x =+=︒-∠∠∠由角平分线的定义可得1452GCN ACB ==︒∠∠，则可证明HMF CNF =∠∠，进而证明()AAS HFM CFN ≌，得到HM CN =，即可证明22AM BD CN =+；（3）如图所示，过点D 作DH AC ⊥交AC 延长线与H ，连接FH ，则四边形BCHD 是矩形，可得BC DH AC ==，证明FDH △是等边三角形，得到60DFH FDH ==︒∠∠，进而得到30BDA DAH ==︒∠∠，30FHA FAH ==︒∠∠；由旋转的性质可得60FQ FP PFQ DFH ==︒=，∠∠，证明()SAS DFQ HFP ≌，得到30FDQ FHP ==︒∠∠，则点Q 在直线DQ 上运动，设直线DQ 交FH 于K ，则113022DK FH FK FH FDK FDH ===︒⊥，，∠，可得60BDQ ∠=︒，由垂线段最短可知，当BQ DQ ⊥时，BQ 有最小值，则30DBQ ∠=︒，设6AC DH a ==，则AH ==6BD CH a ==-，则3DQ a =-，9BQ a =-；再求出3FK a =，则DK =，3QK DK DQ a =-=，由勾股定理得FQ =；由全等三角形的性质可得3PH DQ a ==-，则3CP a =-；由折叠的性质可得9TQ BQ a ==-，由FT FQ TQ ≤+，得到当点Q 在线段FT 上时，FT CP 此时有最大值，最大值为FQ TQ CP+，据此代值计算即可．【小问1详解】证明：∵90ACB ∠=︒，BD AC ∥，∴18090CBD ACB ∠∠︒︒=-=，∵AE CD ⊥，∴90ACD CAE ∠+∠=︒，∵90ACD BCD ∠+∠=︒，∴CAE BCD ∠=∠，又∵90AC CB CBD ACE ===︒，∠∠，∴()ASA ACE CBD ≌，∴BD CE =，∵点E 是BC 的中点，∴22BC CE BD ==，∴2AC BD =；【小问2详解】证明：如图所示，过点G 作GH AB ⊥于H ，连接HF ，∵BD AC ∥，∴FBD FGA D FAG ==∠∠，∠∠，∵点F 是AD 的中点，∴AF DF =，∴()AAS AGF DBF ≌，∴AG BD =，BF GF =，∵90AC BC ACB =∠=︒，，∴45CAB ACB ∠=∠=︒，∵GH AH ⊥，∴AHG 是等腰直角三角形，∴2222AH AG BD ==；∵90BHG BCG BF GF ==︒=∠∠，，∴12FH FC BF BG ===，∴FBH FHB FBC FCB ==∠∠，∠∠，∴22GFH FBH FHB FBH GFC FBC FCB FBC =+==+=∠∠∠∠，∠∠∠∠，∴22290HFC GFH GFC FBH FBC ABC =+=+==︒∠∠∠∠∠∠，∵FM BG ⊥，∴90BFM ∠=︒，∴HFM CFN =∠∠；设CBG x ∠=，则4590ABG x CGB x =︒-=︒-∠，∠，∴135HMF BFM FBM x =+=︒-∠∠∠，∵CN 平分ACB ∠，∴1452GCN ACB ==︒∠，∴135CNF CGN GCN x =+=︒-∠∠∠，∴HMF CNF =∠∠，∴()AAS HFM CFN ≌，∴HM CN =，∵AM AH HM =+，∴22AM BD CN =+；【小问3详解】解：如图所示，过点D 作DH AC ⊥交AC 延长线与H ，连接FH ，∵90BD AC ACB =︒∥，∠，∴90BCH CBD ==︒∠∠，∵DH AC ⊥，∴四边形BCHD 是矩形，∴BC DH AC ==，∵点F 是AD 的中点，且AF AC =，∴2222AD AF DH FH DF ====，∴FDH △是等边三角形，∴60DFH FDH ==︒∠∠，∴30BDA DAH ==︒∠∠，∴30FHA FAH ==︒∠∠，由旋转的性质可得60FQ FP PFQ DFH ==︒=，∠∠，∴DFQ HFP =∠∠，。

人教版八年级上册数学《轴对称》单元测试卷(含答案)

人教版数学八年级上学期《轴对称》单元测试考试时间：100分钟；总分：120分一、单选题（每小题3分，共30分)1．（2019·江苏南京一中初二期中）下列图案中,不是轴对称图形的是()A．B．C．D．2．（2018·河北初二期中）如果点P（﹣2，b）和点Q（a，﹣3）关于x轴对称，则a+b的值是（）A．﹣1 B．1 C．﹣5 D．53．（2018·河北初二期中）如图，AB的垂直平分线分别交AB、AC于点D、E，AC=9，AE：EC=2：1，则点E到点B的距离为（）A．5 B．6 C．7 D．8关于直线MN的轴对称图形，其中正确的是( ) 4．（2019·江苏初二期中）下面是四位同学作ABCA．B．C．D．5．（2019·江苏初二期中）如图，正方形网格中的每个小正方形边长都是1．已知A、B是两格点，若△ABC 为等腰三角形，且S△ABC＝1.5，则满足条件的格点C有（）A．1个B．2个C．3个D．4个6．（2019·江苏省盐城市初级中学初二期中）如图，点E是等腰三角形△ABD底边上的中点，点C是AE延长线上任一点，连接BC、DC，则下列结论中：①BC=AD；②AC平分∠BCD；③AC=AB；④∠ABC=∠ADC。

一定成立的是（）A．②④B．②③C．①③D．①②7．（2019·山东初二期中）等腰三角形的两条边长分别为3cm和6cm，则它的周长为( ).A．12cm B．15cm C．12cm或15cm D．18cm或36cm8．（2019·山东初二期中）如图，在△ABC中，DE是边AB的垂直平分线，BC=8cm，AC=5cm，则△ADC 的周长为（）A．14cm B．13cm C．11cm D．9cm9．（2017·广东初二月考）下列各点中，到三角形各顶点的距离相等的是（）A．三个内角平分线的交点B．三条边的垂直平分线的交点C．三条中线的交点D．三条高线的交点10．（2019·湖北初二期中）上午8时，一条船从海岛A出发，以15n mile/h（海里/时，1n mile＝1852m）的速度向正北航行，10时到达海岛B处，从A、B望灯塔C，测得NAC＝42°，NBC＝84°．则从海岛B到灯塔C的距离为（）A ．45n mileB ．30n mileC ．20n mileD ．15n mile二、填空题（每小题4分，共24分)11．（2019·南京市浦口外国语学校初二期中）如图，四边形ABCD 是轴对称图形，BD 所在的直线是它的对称轴，AB ＝5 cm ，CD ＝3.5 cm ，则四边形ABCD 的周长为_____cm ．12．（2019·如东县新店镇初级中学初二期中）如图，在△ABC 中，AB ＝AC ，D 是BC 的中点，∠BAD ＝34°，则∠C ＝_________°．13．（2019·安徽初二期中）如图，ABC △与A B C '''关于直线l 对称，且105A ∠=︒，30C '∠=︒，则B ∠=______．14．（2019·广西初二期中）如图，在ABC ∆中，DE 垂直平分AC ，若BCD ∆的周长是12，4BC =，则AB 的长______.15．（2019·北京市三帆中学初二期中）如图，在Rt △ABC 中，90B =∠ ，ED 是AC 的垂直平分线，交AC 于点D ，交BC 于点E ．已知40C ∠=，则BAE ∠的度数为_________。

数学八年级上册《轴对称》单元测试题(带答案)

∴∠A=40°．
∵A B=A C，
∴
故选A．
[点睛]此题考查等腰三角形的性质及三角形的内角与外角等知识点的掌握情况．根据已知求得∠A=40°是正确解答本题的关键．
二、填空题
11.请写出两个具有轴对称性的汉字.
[答案]甲、由、中、田、日等(答案不唯一).
[解析]
[分析]
根据轴对称图形的概念，即可写出:甲，日，田等字．
6.已知M(0，2)关于x轴对称的点为N，线段MN的中点坐标是()
A.(0，﹣2)B.(0，0)C.(﹣2，0)D.(0，4)
[答案]B
[解析]
根据轴对称的性质，知线段MN的中点就是原点，即线段MN的中点坐标是(0，0)．
故选B
7.在△A B C中,A B=A C,D为B C的中点,则下列结论:①∠B=∠C;②A D⊥B C;③∠B A C=2∠B A D;④A B,A C边上的中线的长相等.其中正确的结论有( )
故答案选:A．
[点睛]本题考查了用坐标表示轴对称的知识点，熟练掌握点关于x轴、y轴对称的点的坐标特点是解题的关键．
3.已知线段A B和点C,D,且C A=C B,D A=D B,那么直线C D是线段A B的( )
A. 垂线B. 平行线
C. 垂直平分线D. 过中点的直线
[答案]C
[解析]
[分析]
由已知C A=C B根据线段垂直平分线的性质的逆定理可得点C在A B的垂直平分线上，同理得点D的位置
[答案]D
[解析]
[分析]
此题中没有明确指出等边三角形的边长是等腰三角形的底边还是腰长，所以我们应该分两种情况进行分析．先求出等边三角形的边长，再分两种情况进行分析求解．
[详解]解:∵等边三角形周长为45Cm，

人教版初中数学八年级上单元试卷第章轴对称【B卷】(解析版)

第13章轴对称B卷一、单选题1. ( 3分) 下列图标中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.【答案】A【考点】轴对称图形，中心对称及中心对称图形【解析】【解答】A.即是轴对称图形，又是中心对称图形.故该选项正确；B.是轴对称图形，但不是中心对称图形.故该选项错误；C.是中心对称图形，但不是轴对称图形.故该选项错误；D.是中心对称图形，但不是轴对称图形.故该选项错误.故答案为：A【分析】根据轴对称图形和中心对称图形的概念即可判断.2. ( 3分) 如图，在△ABC中，BC=8，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长为18，则AC的长等于（）A. 6B. 8C. 10D. 12【答案】C【考点】线段垂直平分线的性质【解析】【解答】由已知条件，利用线段垂直平分线的性质得AE+CE=BE+CE，再利用给出的周长即可求出AC的长．∵△BCE的周长等于18cm，BC=8cm∴BE+EC=10cm∵DE垂直平分AB∴AE＝BE∴AE+EC=10cm，即AC=10cm【分析】由△BCE的周长及BC的长可求出BE与EC的和，根据相段的垂直平分线的性质可求出AE=BE,进而求出AC的长。

3. ( 3分) 点P（2，﹣3）关于x轴的对称点是（）A. （﹣2，3）B. （2，3）C. （﹣2，-3）D. （2，﹣3）【答案】B【考点】关于坐标轴对称的点的坐标特征【解析】【解答】解：点P（2，﹣3）关于x轴的对称点坐标为：（2，3）．故选：B．【分析】根据平面直角坐标系中对称点的规律解答．4. ( 3分) 下列图形中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.【答案】B【考点】轴对称图形【解析】【解答】解：A、不是轴对称图形，是中心对称图形，故此选项错误；B、是轴对称图形，是中心对称图形，故此选项正确；C、是轴对称图形，不是中心对称图形，故此选项错误；D、是轴对称图形，不是中心对称图形，故此选项错误；故选：B．【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴；把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．进行分析即可．5. ( 3分) 用两个完全相同的直角三角形拼下列图形：(1)平行四边形，(2)矩形，(3)菱形，(4)正方形，(5)等腰三角形，(6)等边三角形，一定可以拼成的图形是（）A. (1)(4)(5);B. (2)(5)(6);C. (1)(2)(3);D. (1)(2)(5).【答案】D【考点】三角形全等及其性质，等腰三角形的判定，平行四边形的判定，矩形的判定【解析】【解答】解：根据题意，用形状和大小完全相同的直角三角形一定能拼出平行四边形、矩形和等腰三角形，共3种图形.画出图形如下所示：故答案为：D.【分析】根据全等三角形的性质、平行四边形的判定方法、矩形的判定方法、菱形的判定方法、正方形的判定方法、等腰三角形的判定方法、等边三角形的判定方法，动手操作或画图即可判断.6. ( 3分) 等腰三角形的一个内角是70°,则它顶角的度数是( )A. 70°B. 70°或40°C. 70°或50°D. 40°【答案】B【考点】三角形内角和定理，等腰三角形的性质【解析】【解答】解：本题可分两种情况：①当70°角为底角时，顶角为180°−2×70°=40°；②70°角为等腰三角形的顶角；因此这个等腰三角形的顶角为40°或70°．故答案为：B．【分析】首先要进行分析题意，“等腰三角形的一个内角”没明确是顶角还是底角，所以要分两种情况进行讨论．7. ( 3分) 下列与防疫有关的图案中不是轴对称图形的有（）A. 1个B. 2个C. 3个D. 4个【答案】B【考点】轴对称图形【解析】【解答】解：AB、为轴对称图形，对称轴为等边三角形的高，符合题意；CD、没有对称轴，不是轴对称图形，不符合题意；故答案为：B.【分析】根据轴对称图形特点分析判断，轴对称图形沿一条轴折叠180°，被折叠两部分能完全重合.8. ( 3分) 若a、b、c为△ABC的三条边，且满足条件：点（a+c，a）与点（2b，﹣b）关于x轴对称，则△ABC的形状是（）A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形【答案】B【考点】等边三角形的判定，关于坐标轴对称的点的坐标特征【解析】【解答】∵点（a+c，a）与点（2b，﹣b）关于x轴对称，∴a+c=2b，a=b，∴a=b=c，∴△ABC的形状是等边三角形．故答案为：B【分析】根据关于x轴对称的点横坐标相同、纵坐标互为相反数的特征，可得a+c=2b，a=b，可得a=b=c，判定△ABC的形状是等边三角形。

模拟卷：2018-2019学年八年级数学上学期期末原创卷B卷(河北)

数学试题第1页（共6页）数学试题第2页（共6页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________绝密★启用前2018-2019学年上学期期末原创卷B 卷（河北）八年级数学（考试时间：120分钟试卷满分：120分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

5．考试范围：冀教版八上全册。

第Ⅰ卷一、选择题（本大题共16小题，共42分，1~10小题各3分，11~16小题各2分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．下列图形中，是轴对称图形，但不是中心对称图形的是（）A ．B ．C ．D ．2．16的算术平方根是（） A ．4B ．±4C ．±2D ．23．在实数|-3|，-2，0，π中，最小的数是（） A ．|-3|B ．-2C ．0D ．π4．要使得代数式12x x --在实数范围内有意义，则x 的取值范围是（） A ．2x ≥ B ．1x ≥ C ．2x ≠D ．1x ≥且2x ≠5．如果132x y x +=，那么yx的值为（） A ．12 B ．23 C ．13D ．256．下列运算错误的是（） A ．532-=B ．632÷=C ．6332⨯=D ．2333-=7．已知a 、b 、c 是三角形的三边长，如果满足2(6)8|10|0a b c -+-+-=，则三角形的形状是（） A ．底与边不相等的等腰三角形B ．等边三角形C ．钝角三角形D ．直角三角形8．下列命题中，真命题的是（）A ．相等的两个角是对顶角B ．若a >b ，则|a |>|b |C ．两条直线被第三条直线所截，内错角相等D ．等腰三角形的两个底角相等9．如图，在△ABC 中，AB =AC ，∠A =40°，AB 的垂直平分线交AB 于点D ，交AC 于点E ，连接BE ，则 ∠CBE 的度数为（）A ．80°B ．70°C ．40°D ．30°10．如图，一架云梯长25米，斜靠在一面墙上，梯子底端离墙7米，如果梯子的顶端下滑4米，那么梯子的底部在水平方向上滑动了（）A ．4米B ．6米C ．8米D ．10米11．数学课上，小丽用尺规这样作图：（1）以点O 为圆心，任意长为半径作弧，交OA ，OB 于D ，E 两点；（2）分别以点D ，E 为圆心，大于12DE 的长为半径作弧，两弧交于点C ；（3）作射线OC 并连数学试题第3页（共6页）数学试题第4页（共6页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………此卷只装订不密封………………○………………外………………○………………装………………○………………订………………○………………线………………○………………接CD，CE，下列结论不正确的是（）A．∠1=∠2 B．S△OCE=S△OCD C．OD=CD D．OC垂直平分DE12．如图，△ABC中，AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则下列结论不正确的是（）A．BF=DF B．∠1=∠EFD C．BF>EF D．FD∥BC13．已知：如果二次根式28n是整数，那么正整数n的最小值是（）A．1 B．4 C．7 D．2814．如图，∠AOB=30º，∠AOB内有一定点P，且OP=12，在OA上有一动点Q，OB上有一动点R．若△PQR 周长最小，则最小周长是（）A．6 B．12 C．16 D．2015．若关于x的方程2222x mx x++=--的解为正数，则m的取值范围是（）A．m<6 B．m>6 C．m<6且m≠0D．m>6且m≠816．在△ABC中，AB=BC，将△ABC绕点B顺时针旋转α度，得到△A1BC1，A1B交AC于E，A1C1分别交AC、BC于点D、F，下列结论：①∠CDF=α，②A1E=CF，③DF=FC，④AD=CE，⑤A1F=CE．其中一定正确的有（）A．①②④B．②③④C．①②⑤D．③④⑤第Ⅱ卷二、填空题（本大题共3小题，共12分．17~18小题各3分；19小题有两个空，每空3分）17．同学们都知道，蜜蜂建造的蜂房既坚固又省料．那你知道蜂房蜂巢的厚度吗？事实上，蜂房的蜂巢厚度仅仅约为0.000073m．此数据用科学记数法表示为__________．18．已知：如图，在△AOB中，∠AOB=90°，AO=3 cm，BO=4 cm．将△AOB绕顶点O，按顺时针方向旋转到△A1OB1处，此时线段OB1与AB的交点D恰好为AB的中点，则线段B1D=__________cm．19．在方格纸中，选择标有序号的一个小正方形涂黑，与图中阴影构成中心对称图形，涂黑的小正方形序号为__________；若与图中阴影构成轴对称图形，涂黑的小正方形序号为__________．三、解答题（本大题共7小题，共66分．解答应写出文字说明、证明过程或演算步骤）20．（本小题满分8分）计算下列各题：（1）03816(21)-++-；（2）211(3)||292----+-．21．（本小题满分9分）如图，某公路上A，B两点的正南方有D，C两村庄，现要在公路AB上建一个车站E，使C，D两村到E站的距离相等，已知AB=50 km，DA=20 km，CB=10 km，请你设计出E站的位置，并计算车站E距A点多远？数学试题第5页（共6页）数学试题第6页（共6页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________22．（本小题满分9分）如图，△ABC 中，AB 的垂直平分线分别交AB ，BC 于D ，E ，AC 的垂直平分线分别交AC ，BC 于F ，G ．（1）若△AEG 的周长为10，求线段BC 的长．（2）若∠BAC =128°，求∠EAG 的度数．23．（本小题满分9分）如图，在△ABC 中，∠BAC =90°，AC =AB ，点D 为BC 边上的一个动点（点D 不与B ，C 重合），以AD 为边作等腰直角△ADE ，∠DAE =90°，连接CE ．（1）求证：△ABD ≌△ACE ．（2）试猜想线段BD ，CD ，DE 之间的等量关系，并证明你的猜想．24．（本小题满分10分）某地下管道，若由甲队单独铺设，恰好在规定时间内完成；若由乙队单独铺设，需要超过规定时间15天才能完成，如果先由甲、乙两队合做10天，再由乙队单独铺设正好按时完成．（1）这项工程的规定时间是多少天？（2）已知甲队每天的施工费用为5000元，乙队每天的施工费用为3000元，为了缩短工期以减少对居民交通的影响，工程指挥部最终决定该工程由甲、乙两队合做来完成，那么该工程施工费用是多少？ 25．（本小题满分10分）如图，在△ABC 中，AB =AC ，D ，E ，F 分别在三边上，且BE =CD ，BD =CF ，G为EF 的中点．（1）若∠A =40°，求∠B 的度数；（2）试说明：DG 垂直平分EF ．26．（本小题满分11分）如图1，△ABC 中，CD ⊥AB 于D ，且BD ∶AD ∶CD =2∶3∶4，（1）试说明△ABC 是等腰三角形；（2）已知S △ABC =40 cm 2，如图2，动点M 从点B 出发以每秒1 cm 的速度沿线段BA 向点A 运动，同时动点N 从点A 出发以相同速度沿线段AC 向点C 运动，当其中一点到达终点时整个运动都停止．设点M 运动的时间为t （秒），①若△DMN 的边与BC 平行，求t 的值；②若点E 是边AC 的中点，问在点M 运动的过程中，△MDE 能否成为等腰三角形？若能，求出t 的值；若不能，请说明理由．。

苏教版数学八年级上册第一章第二章单元试卷及答案

苏教版八上数学第一章轴对称图形测试题一、选择题1．下列命题中：①两个全等三角形合在一起是一个轴对称图形；②等腰三角形的对称轴是底边上的中线；③等边三角形一边上的高就是这边的垂直平分线；④一条线段可以看着是以它的垂直平分线为对称轴的轴对称图形. 正确的说法有（）个 A ．1个 B ．2个 C ．3个 D ．4个2．下列图形中：①平行四边形；②有一个角是30°的直角三角形；③长方形；④等腰三角形. 其中是轴对称图形有（）个A ．1个B ．2个C ．3个D ．4个 3．已知∠AO B ＝30°，点P 在∠AOB 的内部，P 1与P 关于OA 对称，P 2与P 关于OB 对称，则△P 1OP 2是（） A ．含30°角的直角三角形； B ．顶角是30的等腰三角形；C ．等边三角形D ．等腰直角三角形. 4．如图：等边三角形ABC 中，BD ＝CE ，AD 与BE 相交于点P ，则 ∠APE 的度数是（） A ．45° B ．55° C ．60° D ．75° 5. 等腰梯形两底长为4cm 和10cm ，面积为21cm 2，则这个梯形较小的底角是（）度.A ．45°B ．30°C ．60°D ．90°6．已知点P 在线段AB 的中垂线上，点Q 在线段AB 的中垂线外，则（） A ．PA+PB ＞QA+QB B ．PA+PB ＜QA+QB D ．PA+PB ＝QA+QB D ．不能确定 7．已知△ABC 与△A 1B 1C 1关于直线MN 对称，且BC 与B 1C 1交与直线MN 上一点O ，则（） A ．点O 是BC 的中点 B ．点O 是B 1C 1的中点 C ．线段OA 与OA 1关于直线MN 对称 D ．以上都不对 8．如图：已知∠AOP=∠BOP=15°，PC∥OA， PD⊥OA，若PC=4，则PD= （） A ．4 B ．3 C ．2 D ．1 9．∠AOB 的平分线上一点P 到OA 的距离为5，Q 是OB 上任一点，则（） A ．PQ ＞5 B ．PQ≥5C ．PQ ＜5D ．PQ≤510．等腰三角形的周长为15cm ，其中一边长为3cm ．则该等腰三角形的底长为（）A ．3cm 或5cmB ．3cm 或7cmC ．3cmD ．5cm 二．填空题11．线段轴是对称图形，它有_______条对称轴． 12．等腰△ABC 中，若∠A=30°，则∠B=________．A O P AEC B D13．在Rt△ABC 中，∠C=90°，AD 平分∠BAC 交BC 于D ，若CD=4，则点D 到AB 的距离是__________． 14．等腰△ABC 中，AB=AC=10，∠A=30°，则腰AB 上的高等于___________．15．如图：等腰梯形ABCD 中，AD∥BC，AB=6，AD=5，BC=8，且AB∥DE，则△DEC 的周长是____________．16．等腰梯形的腰长为2，上、下底之和为10且有一底角为60°，则它的两底长分别为____________．17．若D 为△ABC 的边BC 上一点，且AD=BD ，AB=AC=CD ，则∠BAC=____________． 18．△ABC 中，AB 、AC 的垂直平分线分别交BC 于点E 、F ，若∠BAC=115°，则∠EAF=___________．三．解答题19．如图：已知∠AOB 和C 、D 两点，求作一点P ，使PC=PD ，且P 到∠AOB 两边的距离相等．20．如图：AD 为△ABC 的高，∠B=2∠C，用轴对称图形说明：CD=AB+BD ．21．有一本书折了其中一页的一角，如图：测得AD=30cm,BE=20cm ，∠BEG=60°，求折痕EF的长．OB22．如图：△ABC 中，AB=AC=5，AB 的垂直平分线DE 交AB 、AC 于E 、D ，① 若△BCD 的周长为8，求BC 的长； ② 若BC=4，求△BCD 的周长．23．等边△ABC 中，点P 在△ABC 内，点Q 在△ABC 外，且∠ABP=∠ACQ，BP=CQ ，问 △APQ是什么形状的三角形？试说明你的结论．B CD EAA CBPQ苏教版八上数学第一章轴对称图形测试题参考答案一、选择题（每小题3分，共30分）1．A 2．B 3．C 4．C 5．A 6．D 7．C 8．C 9．B 10．C 二、填空题（每小题3分，共24分）11．2 12．30°、75°、120°13．4 14．5 15．15 16．4、6 17．72°18．50°三解答题：（共46分）19．提示：作CD的中垂线和∠AOB的平分线，两线的交点即为所作的点P；20．提示：在CD上取一点E使DE＝BD，连结AE；21．EF＝20㎝；22．①BC＝3，②9；23．提示：△APQ为等边三角形，先证△ABP≌△ACQ得AP＝AQ，再证∠PAQ＝60°即可.苏教版第二章勾股定理与平方根测试题一、选择题1．下列几组数中不能作为直角三角形三边长度的是（）A ．7,24,25a b c ===B ． 1.5,2, 2.5a b c ===C ．25,2,34a b c ===D ．15,8,17a b c ===2．小强量得家里彩电荧屏的长为cm 58，宽为cm 46，则这台电视机尺寸是（） A ．9英寸（23cm ） B ．21英寸（54cm ） C ．29英寸（74cm ） D ．34英寸（87cm ） 3．等腰三角形腰长10cm ，底边16cm ，则面积（）A ．296cmB ．248cmC ．224cmD ．232cm4．三角形三边c b a ,,满足ab c b a 2)(22+=+，则这个三角形是（）A ．锐角三角形B ．钝角三角形C ．直角三角形D ．等腰三角形 5．2(6)-的平方根是（）A ．6-B ．36C ．±6D ．6±6．下列命题正确的个数有：a a a a ==233)2(,)1(（3）无限小数都是无理数（4）有限小数都是有理数（5）实数分为正实数和负实数两类（）A ．1个B ．2个C ．3个D ．4个 7．x 是2)9(-的平方根，y 是64的立方根，则=+y x（）A ．3B ．7C ．3，7D ．1，7 8．直角三角形两直角边长度为5，12，则斜边上的高（）A ．6B ．8C ．1813D ．60139．直角三角形边长为b a ,，斜边上高为h ，则下列各式总能成立的是（）A 、2h ab =B ．2222h b a =+C ．hb a 111=+ D ．222111hb a =+ 10．如图一直角三角形纸片，两直角边cm BC cm AC 8,6==，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（）A ．cm 2B ．cm 3C ．cm 4D ．cm 5AE B D C 第10题图二、填空题11．下列实数(1)3.1415926 .(2)0.3 22(3)7(5)-(6)2π(7)0.3030030003...其中无理数有________，有理数有________．（填序号） 12．49的平方根________，0.216的立方根________．13的平方根________的立方根________．14．算术平方根等于它本身的数有________，立方根等于本身的数有________．15．若2256x =，则=x ________，若3216x =-，则=x ________．16．已知Rt ABC ∆两边为3，4，则第三边长________．17．若三角形三边之比为3：4：5，周长为24，则三角形面积________．18．已知三角形三边长n n n n n n ,122,22,1222++++为正整数，则此三角形是________三角形．19．如果0)6(42=++-y x ，则=+y x ________．20．如果21a -和5a -是一个数m 的平方根，则.__________,==m a 21．三角形三边分别为8，15，17，那么最长边上的高为________．22．直角三角形三角形两直角边长为3和4，三角形内一点到各边距离相等，那么这个距离为________．三、计算题23．求下列各式中x 的值2(1)16490x -=；2(2)(1)25x -=；3(3)(2)8x =-；3(4)(3)27x --=．四、作图题24．在数轴上画出8-的点．25．下图的正方形网格，每个正方形顶点叫格点，请在图中画一个面积为10的正方形．五、解答题26．已知如图所示，四边形ABCD 中，3,4,13,12,AB cm AD cm BC cm CD cm ====090A ∠=求四边形ABCD 的面积．27．如图所示，在边长为c 的正方形中，有四个斜边为c 、直角边为b a ,的全等直角三角形，你能利用这个图说明勾股定理吗？写出理由．第24题图第25题图第27题图A第26题图28．如图所示，15只空油桶（每只油桶底面直径均为60cm ）堆在一起，要给它盖一个遮雨棚，遮雨棚起码要多高？29．如图所示，在Rt ABC ∆中，090ACB ∠=，CD 是AB 边上高，若AD=8，BD=2，求CD ．30．如图，有一只小鸟从小树顶飞到大树顶上，请问它飞行的最短路程是多少米？（先画出示意图，然后再求解）．第29题图CADB第28题图苏教版八上数学第二章勾股定理与平方根参考答案一、选择题（每小题3分，共30分）1．C 2．C 3．C 4．C 5．C 6．B 7．D 8．D 9．D 10．B 二、填空题：（每空2分，共34分） 11． (4)(6)(7)；(1)(2)(3)(5)12．23±,0.613．2±,214．0,1；0，1± 15．16±,-6 16．5717．24 18．直角 19．-220．2或－4；9或8121．1201722．1三、解答题：（共56分）23.(1) x=74± (2) x=6或x=－4 （3）x=-1 (4) x=024．略 25．如图 26．3627．2222222214(),22,2ab b a c ab a b ab c a b c ⨯+-=∴++-=∴+=28．h=360 29．4 30．13苏教版八上数学第三章中心对称图形（一）一．选择题1．下列图形中，是中心对称图形而不是轴对称图形的是（） A ．平行四边形 B ．矩形 C ．菱形 D ．正方形2．正方形具有而菱形不一定具有的性质是（） A ．对角线互相垂直 B ．对角线互相平分 C ．对角线相等 D ．对角线平分一组对角3．平行四边形的对角线长为x 、y ，一边长为12，则x 、y 的值可能是（） A ．8和14 B ．10和14 C ．18和20 D ．10和344．下面说法正确的是（） A ．一个三角形中，至多只能有一个锐角 B ．一个四边形中，至少有一个锐角 C ．一个四边形中，四个内角可能全是锐角 D ．一个四边形中，不能全是钝角5．一个凸n 边形的边数与对角线条数的和小于20，且能被5整除，则n 为（） A ．4 B ．5 C ．6D ．5或66．如图：在□ABCD 中，AE⊥BC 于E ，AF⊥CD 于F 。

人教版八年级数学轴对称章检测卷

第1页共8页 ◎ 第2页共8页人教版八年级数学轴对称章检测卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知点A (a ，2)与点B (3，b )关于x 轴对称，则a +2b ＝（） A ．-4B ．-1C ．-2D ．42．下列图标中，是轴对称图形的是（）A ．B ．C ．D ．3．在平面直角坐标系中，点A （3，﹣1）关于x 轴对称的点的坐标为（） A ．（﹣3，1）B ．（1，﹣3）C ．（﹣3，﹣1）D ．（3，1）4．如图，在ABC 中，DE 是AC 的垂直平分线，且分别交BC 、AC 于点D 和E ，70B ∠=︒，25C ∠=︒，则BAD ∠为（）A ．55︒B ．60︒C ．65︒D ．70︒5．剪纸是我国传统的民间艺术．将一张正方形纸片按图1，图2中的方式沿虚线依次对折后，再沿图3中的虚线裁剪，最后将图4中的纸片打开铺平，所得图案应该是（）A ．B ．C ．D ．6．如图，在△ABC 中，BD 平分△ABC ，BC 的垂直平分线交BD 于点E ，连接CE ，若△A =60°，△ACE =24°，则△ABE 的度数为（）A ．24°B ．30°C ．32°D ．48°7．下列图案中，是轴对称图形的是（）A ．B ．C ．D ．第3页共8页 ◎ 第4页共8页8．如图，△ABC 与A B C '''关于直线MN 对称，BB '交MN 于点O ，则下列结论不一定正确的是（）A ．AC AC =''B ．BO B O ='C ．AA MN '⊥D ．AB B C ''∥9．下列图形中，轴对称图形的个数是（）A ．1个；B ．2个；C ．3个；D ．4个；10．如图，△ABC 中△A ＝40°，E 是AC 边上的点，先将△ABE 沿着BE 翻折，翻折后△ABE 的AB 边交AC 于点D ，又将△BCD 沿着BD 翻折，点C 恰好落在BE 上的点G 处，此时△BDC ＝82°，则原三角形的△B 的度数为（）A ．57°B ．60°C ．63°D ．70°二、填空题11．把一张长方形纸条ABCD 沿EF 折叠成图△，再沿HF 折叠成图△，若△DEF ＝β（0°＜β＜90°），用β表示△C ''FE ，则△C ''FE ＝_______．12．如图，将ABC 沿AB 边对折，使点C 落在点D 处，延长CA 到E ，使AE AD =，连接CD 交AB 于F ，连接ED ，则下列结论中：△若ABC 的周长为12，5DE =，则四边形ABDE 的周长为17；△AB DE ∥；△90CDE ∠=︒；△2ADE ADF S S =△△，正确的有_____________．13．如图，在△ABC 中，△B 、△C 的平分线交于点F ，过点F 作DE △BC 交AB 于点D ，交AC 于点E ，下列结论：△△BDF ，△ADE 都是等腰三角形；△DE ＝BD ＋CE ；△△ADE 的周长等于AB ＋AC ；△BF＝CF ；△若△A ＝80°，则△BFC ＝130°，其中正确的有_________14．如图，在平行四边形ABCD 中，60C ∠=︒，以点A 为圆心，AB 长为半径画弧交AD 于点F ，再分别以点B ，F 为圆心，大于12BF 的长为半径画弧，两弧交于一点P ，连接AP 并延长交BC 于点E ，连接EF ．设AE 与BF 相交于点O ，若四边形ABEF 的周长为16，则四边形ABEF 的面积是_________．第5页共8页 ◎ 第6页共8页15．如图，四边形ABCD 的对角线AC 、BD 相交于点O ，△ABO △△ADO ，下列结论：△AC △BD ；△CB =CD ；△△ABC △△ADC ；△DA =DC ．其中不正确结论的序号是____．16．如图，在ABC 中，90ACB ∠=︒，15B ∠=︒，DE 的垂直平分线AB 分别交AB 、BC 于点D 、E ，连接AE ，若6cm BE =，则AC 等于___________cm ．17．等腰三角形的顶角是100︒，那么它的一个底角的度数是________．18．如图，在△ABC 中，AB ＝8，BC ＝9，AC ＝5，直线m 是△ABC 中BC 边的垂直平分线，P 是直线上的一动点，则△APC 的周长的最小值为________．三、解答题19．如图，在△ABC 中，AB ＝BC ，△ABC ＝120°，AB 的垂直平分线DE 交AC 于点D ，连接BD ，若AC ＝12(1)求证：BD △BC ． (2)求DB 的长．20．如图，E 为ABC 的外角CAD ∠平分线上的一点，AE //BC ，BF AE =．(1)求证：ABC 是等腰三角形；(2)若4AF =，求CE 的长．21．如图，△ABC 是边长为6的等边三角形，三边上分别有点E 、D 、F ，使得AE ＝BD ＝CF ，过点E 作EP △DF ，垂足为点P（1）求证：△BDE △△CFD ；（2）求△DEP 的度数；第7页共8页 ◎ 第8页共8页（3）当点E 、D 、F 分别在三边BA 、CB 及AC 的延长线上时，过点E 作EP △DF ，垂足为点P ，若AE ＝BD ＝CF ＝2，若△BDE 的周长为19，求DP 的长． 22．如图，AB 是线段，AD 和BC 是射线，AD//BC ．（1）尺规作图：作AB 的垂直平分线EF ，垂足为O ，且分别与射线BC 、AD 相交于点E 、F （不写作法，保留作图痕迹）；（2）在（1）条件下，连接AE ，求证：AE=AF ．23．已知：如图，△ABC 是等边三角形，边长为6，点D 为动点，AD 绕点A 逆时针旋转60°得到AE ．(1)如图1，连接BD ，CE ，求证BD CE =；(2)如图2，BAD DBC ∠=∠，连接DE ，求证：点B ，D ，E 三点在同一条直线上； (3)如图3，点D 在△ABC 的高BF 上，连接EF ，求EF 的最小值． 24．已知：Rt ABC ，90B ．求作：点P ，使点P 在ABC 内部，且,45PB PC PBC =∠=︒．25．在正方形网格中，建立如图所示的平面直角坐标系，△ABC 的三个顶点都在格点上，△ABC 关于y 轴对称图形为△A 1B 1C 1（要求：A 与A 1，B 与B 1，C 与C 1相对应）（1）写出A 1，B 1，C 1的坐标，并画出△A 1B 1C 1的图形；（2）求△A 1B 1C 1的面积；（3）点P 是y 轴上一动点，画出P A ＋PC 最短时，点P 的位置．（保留作图痕迹，不写画法）26．如图，在平面直角坐标系中，A （3，4），B （1，2），C （5，1）.(1)作出△ABC 关于y 轴的对称图形△1A 1B 1C ； (2)写出△1A 1B 1C 的三个顶点的坐标；(3)连接1AA ，1BB ，并求出四边形11ABB A 的面积.参考答案：1．B【分析】先根据关于x轴对称的点的坐标特点求出a、b，再代入计算即可．【详解】解：△点A(a，2)与点B(3，b)关于x轴对称，所以a=3，b=−2，△a+2b=3+2×(−2)=-1．故选B．【点睛】此题主要考查关于x轴对称的点的坐标特点．关于x轴对称的点的坐标特点：横坐标不变，纵坐标互为相反数．2．D【分析】根据轴对称图形的定义“如果一个平面图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形”逐项判断即可．【详解】A、不是轴对称图形，此项不符题意；B、不是轴对称图形，此项不符题意；C、不是轴对称图形，此项不符题意；；D、是轴对称图形，此项符合题意；故选：D．【点睛】本题考查了轴对称图形的定义，熟记定义是解题关键．3．D【分析】关于x轴对称的点，横坐标相同，纵坐标互为相反数，可得答案．【详解】解：点P（3，−1）关于x轴对称的点的坐标是（3，1）故选：D．【点睛】本题考查了关于x轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．4．B【分析】根据线段垂直平分线的性质得到DA=DC，根据等腰三角形的性质得到△DAC=△C，根据三角形内角和定理求出△BAC的度数，计算出结果．【详解】解：△DE是AC的垂直平分线，△DA=DC，△△DAC=△C=25°，△△B=70°，△C=25°，△△BAC=85°，△△BAD=△BAC-△DAC=60°，故选：B．【点睛】本题考查的是线段垂直平分线的性质的知识，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．5．A【分析】依据翻折变换，将图4中的纸片按顺序打开铺平，即可得到一个图案．【详解】解：将图4中的纸片打开铺平，所得图案应该是：故选：A．【点睛】本题主要考查了剪纸问题，解决这类问题要熟知轴对称图形的特点，关键是准确地找到对称轴．一般方法是动手操作，拿张纸按照题目的要求剪出图案，展开即可得到正确的图案．6．C【分析】先根据BC的垂直平分线交BD于点E证明△BFE△△CFE（SAS），根据全等三角形∠=∠=∠，再根据三角形内角和定理即可得到的性质和角平分线的性质得到ABE EBF ECF答案．【详解】解：如图：△BC的垂直平分线交BD于点E，△BF=CF，△BFE=△CFE=90°，在△BFE和△CFE中，EF EF EFB EFC BF CF =⎧⎪∠=∠⎨⎪=⎩， △△BFE △△CFE （SAS ），△EBF ECF ∠=∠（全等三角形对应角相等），又△BD 平分△ABC ， △ABE EBF ECF ∠=∠=∠，又△180ABE EBF ECF ACE A ∠+∠+∠+∠+∠=︒（三角形内角和定理）， △180602496ABE EBF ECF ∠+∠+∠=︒-︒-︒=︒， △196323ABE ∠=⨯︒=︒，故选：C ．【点睛】本题主要考查了三角形全等的判定与性质、角平分线的性质、三角形内角和定理，解题的关键是证明ABE EBF ECF ∠=∠=∠． 7．C【分析】根据轴对称图形的定义：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，对各选项判断即可．【详解】根据轴对称图形的定义可知A 、B 、D 均不是轴对称图形，只有C 是轴对称图形．故选：C ．【点睛】本题考查了轴对称图形的知识，属于基础题，解答本题的关键是找出对称轴从而判段是否是轴对称图形． 8．D【分析】根据轴对称的性质逐项判断即可得．【详解】解：A ．AC AC=''，则此项正确，不符合题意； B ．BO B O ='，则此项正确，不符合题意； C ．AA MN '⊥，则此项正确，不符合题意； D ．AB B C ''∥不一定正确，则此项符合题意；故选：D ．【点睛】本题考查了轴对称的性质，解题的关键是熟练掌握轴对称的性质：成轴对称的两个图形的对应边相等，对应角相等，对称轴垂直平分对应点连接的线段．9．C【分析】根据轴对称图形的概念对各图形分析判断即可得解．【详解】解：第1个不是轴对称图形；第2个是轴对称图形；第3个是轴对称图形；第4个是轴对称图形；故选：C ．【点睛】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合． 10．C【分析】根据折叠的性质可知：△BDG ＝△BDC ＝82°，△ABE ＝△A 'BE ＝△A 'BG=△A 'BC ，根据三角形外角性质可得：△DBA ＝△BDC ﹣△A ＝82°﹣40°＝42°，进一步可求出△ABE ＝△A 'BE ＝21°，△ABC ＝3×21°＝63°，即原三角形的△B =63°．【详解】解：由折叠性质可得，△BDG ＝△BDC ＝82°，△ABE ＝△A 'BE ＝△A 'BG=△A 'BC ， △△BDC 是△BDA 的外角，△△DBA ＝△BDC ﹣△A ＝82°﹣40°＝42°， △△ABE ＝△A 'BE ＝21°，△△ABC ＝3×21°＝63°，即原三角形的△B =63°，故选：C ．【点睛】此题主要考查的是图形的折叠及三角形外角性质，能够根据折叠的性质发现△BDG ＝△BDC ＝82°，△ABE ＝△A 'BE ＝△A 'BG=△A 'BC 是解答此题的关键． 11．1803β︒-【分析】先利用平行线的性质得到EFH DEF β∠=∠=，180EFC β∠=︒-，再根据折叠的性质得到180EFC β∠'=︒-，所以1802HFC β∠'=︒-，接着再利用折叠的性质得到1802C FH C FH β∠''=∠'=︒-，然后计算C FH EFH ''∠-∠即可．【详解】四边形ABCD 为长方形，//AD BC ∴，EFH DEF β∴∠=∠=，180EFC β∠=︒-，方形纸条ABCD 沿EF 折叠成图△， 180EFC EFC β∴∠'=∠=︒-，1801802HFC EFC EFH βββ∴∠'=∠'-∠=︒--=︒-，长方形ABCD 沿HF 折叠成图△， 1802C FH C FH β∴∠''=∠'=︒-，18021803C FE C FH EFH βββ∴∠=∠-∠=︒--=''︒-''．故答案为：1803β︒-．【点睛】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等． 12．△△△△【分析】△由题知AE ＝AC ，BD ＝BC ，可得结论正确；△由三角形外角知△CAB +△DAB ＝△ADE +△AED ，又知△CAB ＝△DAB ，△ADE ＝△AED ，即可得△CAB ＝△DAB ＝△ADE ＝△AED ，即可得证结论； △由对称知CD △AB ，由AB △DE 可得结论；△由△知S △ADE ＝12DF •DE ，S △ADF ＝12DF •AF ，证AF 是中位线可得AF ＝12DE ，即可得证结论．【详解】解：△由图形翻折可知，AD ＝AC ，BD ＝BC ， △AE ＝AD ， △AE ＝AC ，△C 四边形ABDE ＝C △ABC +DE ， △C △ABC ＝12，DE ＝5， △C 四边形ABDE ＝17， △△正确；△由图形翻折知，△CAB ＝△DAB ， △AE ＝AD ， △△ADE ＝△AED ，又△△CAB +△DAB ＝△ADE +△AED ， △△CAB ＝△DAB ＝△ADE ＝△AED ， △AB //DE ， △△正确；△由△知，AB //DE ，由图形翻折知，CD△AB，△△CF A＝△CDE＝90°，△△正确；△由△知，△CF A＝△CDE＝90°，△S△ADE＝12DF•DE，S△ADF＝12DF•AF，△A是EC的中点，AB//DE，△AF是△CDE的中位线，△AF＝12DE，△S△ADE＝2S△ADF，△△正确，故答案为：△△△△．【点睛】本题主要考查图形的翻折，三角形的面积，平行线的判定和性质等知识点，证明AB DE是解题的关键．13．△△△【分析】由平行线得到角相等，由角平分线得角相等，根据平行线的性质及等腰三角形的判定和性质．【详解】解：△△B、△C的角平分线交于点F，△△DBF＝△CBF，△ECF＝△BCF，设△DBF＝△CBF＝α，△ECF＝△BCF＝β，△DE BC∥，△△DFB＝△CBF＝α，△EFC＝△BCF＝β，△△DBF＝△DFB，△EFC＝△ECF，△DB＝DF，EF＝EC，△△BDF与△CEF为等腰三角形，△DE＝DF＋EF＝BD＋CE，故△正确；△△ADE的周长为AD＋AE＋DE＝AD＋AE＋BD＋CE＝AB＋AC，故△正确；只有当△ABC是等腰三角形时，即△ABC=△ACB，则△FBC=△FCB，△ADE=△AED，则BF ＝CF，AD=AE，根据现有条件无法证明BF=CF，并且无法证明△ADE=△A或△AED=△A，即无法证明△ADE为等腰三角形，故△、△错误；△△A ＝80°，△△FBC ＋△FCB ＝218080︒-︒＝50°， △△BFC ＝180°－50°＝130°，故△正确．故答案为△△△．【点睛】本题考查了等腰三角形的性质与判定及角平分线的定义及平行线的性质，三角形内角和定理；题目利用了两直线平行，内错角相等，及等角对等边来判定等腰三角形的；等量代换的利用是解答本题的关键．14．【分析】根据题意可知AE 是BF 的垂直平分线，可得AB=AF ，BE=EF ，再根据“AAS ”证明△AOF △△EOB ，可得AF=BE ，进而根据“四边相等的四边形是菱形”得出四边形ABEF 是菱形，可知AF=AB=4，再说明△ABF 是等边三角形，可求出BF=4，然后根据勾股定理求出AO ，最后根据菱形的面积等于对角线乘积的一半得出答案即可．【详解】根据题意可知AE 是BF 的垂直平分线，△AB=AF ，BE=EF ．△△F AO=△BEO ，△AOF=△BOE ，BO=FO ，△△AOF △△EOB ，△AF=BE ，△AB=BE=EF=AF ，△四边形ABEF 是菱形，△AF=AB=4．△四边形ABCD 是平行四边形，且△C =60°，△△BAF =60°，△△ABF 是等边三角形，△BF=4，△OF=2．在Rt △AOF 中，AO ===，△AE =△11==422ABEF S AE BF ⨯⋅⨯⨯四边形故答案为：【点睛】本题主要考查了尺规作垂直平分线，菱形的判定和性质，平行四边形的性质，等边三角形的判定和性质，勾股定理等，掌握菱形面积的计算方法是解题的关键．15．△【分析】根据全等三角形的性质可得AOB AOD ∠=∠，根据平角的定义可得1180902AOB AOD ∠=∠=⨯︒=︒，即可判断△，根据全等三角形的性质得出AB AD =，BO DO =，结合△可得AC 是BD 的垂直平分线，即可判断△，根据SSS 即可证明△，不能得出结论△．【详解】解：△△ABO △△ADO ，△AOB AOD ∠=∠，AB AD =，BO DO =△四边形ABCD 的对角线AC 、BD 相交于点O ， △1180902AOB AOD ∠=∠=⨯︒=︒， △△AC △BD 正确；△AB AD =，BO DO =△AC 是BD 的垂直平分线，△△CB =CD 正确；△,,AB AD BC DC AC AC ===，△△△ABC △△ADC 正确；由已知条件不能判断△DA =DC ．故答案为：△．【点睛】本题考查了全等三角形的性质与判定，垂直平分线的性质与判定，掌握以上知识是解题的关键．16．3【分析】根据垂直平分线的性质，可知6AE BE ，再由三角形外角的性质得出30AEC ABE BAE ∠=∠+∠=︒，最后由含30°的直角三角形的性质得出AC 的值即可．【详解】解：△DE 垂直平分AB ，6BE =△6AE BE ，又15B ∠=︒△15ABE BAE ∠=∠=︒，△30AEC ABE BAE ∠=∠+∠=︒，又△90ACB ∠=︒△在Rt AEC 中，132AC AE == 故答案为：3．【点睛】本题考查了垂直平分线的性质、三角形的外角的性质、含30°的直角三角形的性质，解题的关键在于对知识的灵活运用．17．40︒##40度【分析】根据等腰三角形的性质即可得．【详解】解：根据题意得，底角的度数为：1(180100)402⨯︒-︒=︒，故答案为：40︒．【点睛】本题考查了等腰三角形的性质，解题的关键是熟记等腰三角形的性质． 18．13【分析】首先连接PC ，由中垂线的性质可得PB =PC ，由于△APC 的周长为AC +P A +PC ，AC 长度固定，则只要P A +PB 最小即可，此时可推出P 、A 、B 三点共线，即P A +PB =AB ，由此计算即可．【详解】解：如图，连接PC ，则由中垂线的性质可得PB =PC ，△△APC 的周长=AC +P A +PC ，△△APC 的周长=AC +P A +PB ，△AC =5，△要使得△APC 的周长最小，使得P A +PB 最小即可，显然，根据两点之间线段最短，可知当P 、A 、B 三点共线时，P A +PB 最小此时，P 点即在AB 边上，P A +PB =AB ，△P A +PB 最小值为8，△△APC 的周长最小为：8+5=13，故答案为：13．【点睛】本题考查最短路径问题，以及中垂线的性质，理解并掌握中垂线的性质，以及最短路径问题的基本处理方式是解题关键．19．(1)见解析(2)4【分析】(1)根据等腰三角形的性质和三角形内角和定理求出△A=△C=30°，再根据线段垂直平分线的性质得出AD=BD，求出△DBA=30°，据此即可证得；(2)根据含30°角的直角三角形的性质求出BD=12CD，求出AD=12CD，据此求出答案即可．【详解】（1）证明：△AB＝BC，△ABC＝120°，△1180302A C ABC∠=∠=︒-∠︒（）＝，△AB的垂直平分线是DE，△AD＝BD，△△DBA＝△A＝30°，△△DBC＝△ABC﹣△DBA＝120°﹣30°＝90°，△BD△BC；（2）解：△△DBC＝90°，△C＝30°，△12BD CD=，△AD＝BD，△1123AD CD AC==，△AC=12，△AD＝4，△BD＝AD＝4．【点睛】本题考查了线段垂直平分线的性质，含30°角的直角三角形的性质，三角形内角和定理，等腰三角形的性质等知识点，能灵活运用知识点进行推理和计算是解此题的关键．20．(1)证明见解析(2)4【分析】（1）先根据平行线的性质可得DAE B ∠=∠，EAC ACB ∠=∠，再根据角平分线的定义可得DAE EAC ∠=∠，从而可得B ACB ∠=∠，然后根据等腰三角形的判定即可得证；（2）先根据三角形全等的判定证出ABF CAE ≅，再根据全等三角形的性质即可得．【详解】（1）证明：△AE //BC ，DAE B ∴∠=∠，EAC ACB ∠=∠， E 为ABC 的外角CAD ∠平分线上的一点，DAE EAC ∴∠=∠，B ACB ∴∠=∠，AB AC ∴=，ABC ∴是等腰三角形．（2）解：由（1）已得：,DAE B DAE EAC ∠=∠∠=∠，B EAC ∴∠=∠，在ABF △和CAE 中，AB CA B EAC BF AE =⎧⎪∠=∠⎨⎪=⎩，(SAS)ABF CAE ∴≅，AF CE ∴=，4AF =，4CE ∴=．【点睛】本题考查了等腰三角形的判定、三角形全等的判定与性质等知识点，熟练掌握等腰三角形的判定是解题关键．21．（1）见解析；（2）30°；（3）4.5【分析】（1）直接根据SAS 证明△BDE △△CFD 即可；（2）由（1）得△BDE △△CFD ，则△BED =△CDF ，即可推出△ EDP =△B =60°，再由EP △DF ，即可得到△ DEP =30° ；（2）根据△ABC 边长为6, AE =BD =2，得到BE =AB +AE =8，由△BDE 的周长为19，求出DE =19-BD -BE =9，然后证明△BDE △△CFD 得到△DEB =△FDC ，推出△EDP =60°，即可利用含30度角的直角三角形的性质求解．【详解】解：（1）△△ABC是等边三角形，△△B=△C=60°，AB=BC，△AE=BD=CF，△AB-AE=BC-BD，即BE=CD，△△BDE△△CFD（SAS）；（2）由（1）得△BDE△△CFD，△△BED=△CDF，又△△EDC=△B+△BED，△△ EDP+△CDF=△B+△BED，△△ EDP=△B=60°，△EP△DF，△△EPD=90°，△△ DEP=30° ；（2）△△ABC边长为6,AE=BD =2，△BE=AB+AE=8，又△△BDE的周长为19，△ DE=19-BD-BE=9，△△ABC是等边三角形，△△ABC=△ACB=60°，BA=CB，△△EBD=180°-△ABC=180°-△ACB=△DCF=120°，又△BD=AE，△BA+AE=CB+BD，即BE=CD，△△BDE△△CFD（SAS），△△DEB=△FDC，△△EBC=△EDB+△DEB=60°，△△EDB+△FDC=60°，即△EDP=60°，又△EP△DF，△△EPD=90°，△△ DEP=30°，△DE=2DP，△DP= 4.5．【点睛】本题主要考查了等边三角形的性质，全等三角形的性质与判定，三角形外角的性质，含30度角的直角三角形的性质，解题的关键在于能够熟练掌握全等三角形的性质与判定条件．22．（1）见详解；（2）见详解【分析】（1）按照垂直平分线的作法画出AB的垂直平分线即可；（2）通过平行线的性质及垂直平分线的性质得出BAF EAB∠=∠，然后通过ASA证明≅，再由全等三角形的性质即可得出结论．AOE AOF【详解】（1）如图（2）如图，连接AE//AD BCEBA BAF∴∠=∠△EF是AB的垂直平分线,90 EB EA AOE AOF∴=∠=∠=︒EBA EAB∴∠=∠BAF EAB∴∠=∠在AOE△和AOF中，EAO FAO AO AOAOE AOF ∠=∠⎧⎪=⎨⎪∠=⎩()AOE AOF ASA∴≅AE AF∴=【点睛】本题主要考查尺规作图及全等三角形的判定及性质，掌握垂直平分线的作法和全等三角形的判定方法及性质是解题的关键．23．(1)见解析(2)见解析(3)3 2【分析】（1）证明△BAD△△CAE，从而得出结论；（2）△BAD=△CAE=△CBE，所以△ABC=△ABD+△CBE=△ABD+△BAD=60°，从而得出△ADB=120°，进一步得出结论；（3）可证得△ACE=△ABF=30°，从而得出点E的运动轨迹，进而求得EF的最小值．【详解】（1）△△ABC是等边三角形，△AB=AC，△BAC=60°，△AD 绕点A 逆时针旋转60°得到AE ，△△DAE =60°，AD =AE ，△△BAC =△DAE ，△△BAC -△DAC =△DAE -△DAC ，即：△BAD =CAE ，在△BAD 和△CAE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝， △△BAD △△CAE （SAS ），△BD =CE ；（2）由（1）知：△CAE =△BAD ，△△CAE =△CBE ，△△BAD =△CBE ，△△ABC 是等边三角形，△△ABC =60°，△△ABD +△CBE =60°，△△ABD +△BAD =60°，△△ADB =180°-（△ABD +△BAD ）=120°，△AD =AE ，△DAE =60°，△△ADE 是等边三角形，△△ADE =60°，△△ADB +△ADE =180°，△B 、D 、E 在同一条直线上；（3）如图，连接CE ，由（1）得：△BAD △△CAE ，△△ACE=△ABD，△△ABC是等边三角形，△AB=BC，△ACB=△ABC=60°，△BF△AC，△△ABF=12△ABC＝30°，CF=AF=12AC=3，△△ACE=30°，△△BCE=△ACB+△ACE=90°，△点E在过点C且与BC垂直的直线上运动，△当FE垂直于该直线时，CE最小（图中点CE′），△△CE′F=90°，△ACE=30°，△FE′=12CF＝32，△EF的最小值为：32．【点睛】本题考查了等边三角形性质，直角三角形性质，全等三角形的判定和性质等知识，解决问题的关键是熟练掌握“手拉手”模型．24．见解析【分析】分别以点B、C为圆心，大于BC长的一半为半径画弧，交于两点，连接这两点，然后再以点B为圆心，适当长为半径画弧，交AB、BC于点M、N，以点M、N为圆心，大于MN长一半为半径画弧，交于一点Q，连接BQ，进而问题可求解．【详解】解：如图，点P即为所求：【点睛】本题主要考查角平分线与垂直平分线的尺规作图，熟练掌握角平分线与垂直平分线的尺规作图是解题的关键．25．（1）A1(4，1) ；B1(2，-1)；C1(1，3)；见解析；（2）5；（3）见解析【分析】（1）根据关于y轴对称的点的坐标特征，纵坐标相同，横坐标互为相反数，先找到A 、B 、C 关于y 轴对称的点，然后顺次连接即可；（2）根据111A B C △的面积等于其所在的长方形面积减去周围三个三角形面积求解即可；（3）连接1A C 与y 轴交于点P 即为所求．【详解】解：（1）如图所示，111A B C △即为所求；由图可知，1A 的坐标为（4，1），1B 的坐标为（2，-1），1C 的坐标为（1，3）；（2）由图可知111111341422325222A B C S =⨯-⨯⨯-⨯⨯-⨯⨯=△；（3）如图所示，连接1A C 与y 轴交于点P 即为所求；【点睛】本题主要考查了画轴对称图形，坐标与图形变化，轴对称最短路径等等，解题的关键在于能够熟练掌握关于y 轴对称的点的坐标特征．26．(1)作图见详解(2)1(3,4)A -，1(1,2)B -，1(5,1)C -(3)作图见详解，四边形11ABB A 的面积为8【分析】（1）先依次作A ，B ，C 关于y 轴的对称点，再顺次连接即可．（2）由图写出1A ，1B ，1C 坐标即可．（3）由图可知四边形11ABB A 为梯形，用梯形面积公式即可求得面积．【详解】（1）（2）解：由（1）中图可知1(3,4)A -，1(1,2)B -，1(5,1)C -（3）解：如图四边形11ABB A 的面积=1(26)282+⨯= 【点睛】本题考查了轴对称的作图，以及平面直角坐标系相关知识点．掌握轴对称的作图步骤是解题关键．。

八年级数学上册试卷轴对称

一、选择题（每题3分，共15分）1. 下列图形中，不是轴对称图形的是（）A. 正方形B. 等边三角形C. 长方形D. 梯形2. 若一个图形关于某条直线对称，那么这条直线称为（）A. 对称轴B. 中线C. 高D. 角平分线3. 下列关于轴对称的说法中，正确的是（）A. 轴对称图形的两部分完全重合B. 轴对称图形的两部分一定相等C. 轴对称图形的两部分一定平行D. 轴对称图形的两部分一定垂直4. 已知点A（2，3）关于x轴的对称点为B，则点B的坐标是（）A. （2，-3）B. （-2，3）C. （-2，-3）D. （2，9）5. 若一个图形关于y轴对称，那么它的对称轴是（）A. x轴C. 两条互相垂直的直线D. 两条互相平行的直线二、填空题（每题5分，共25分）6. 图形关于x轴对称，那么它的对称轴是__________。

7. 若点A（-4，5）关于y轴的对称点为B，则点B的坐标是__________。

8. 一个等腰三角形的底边长为6cm，腰长为8cm，那么这个三角形的周长是__________cm。

9. 在平面直角坐标系中，点P（3，-2）关于x轴的对称点是__________。

10. 一个长方形的长是8cm，宽是5cm，那么这个长方形的面积是__________cm²。

三、解答题（每题10分，共30分）11. （10分）画出下列图形的轴对称图形，并标出对称轴。

（1）一个等腰直角三角形；（2）一个正方形；（3）一个圆。

12. （10分）已知点A（2，-3）关于y轴的对称点为B，求线段AB的长度。

13. （10分）已知长方形ABCD，AB=6cm，BC=4cm，求长方形ABCD的面积。

四、探究题（10分）14. （10分）观察下列图形，探究它们之间的关系，并说明理由。

（1）图形①是一个正方形，图形②是一个等边三角形；（2）图形③是一个长方形，图形④是一个平行四边形。

请写出你的探究结果。

答案：一、选择题2. A3. B4. A5. B二、填空题6. x轴7. （4，5）8. 289. （-3，-2）10. 40三、解答题11.（1）图形①的轴对称图形为图形①本身，对称轴为直线y=x；（2）图形②的轴对称图形为图形②本身，对称轴为直线y=x；（3）图形③的轴对称图形为图形③本身，对称轴为直线y=x；12. 线段AB的长度为4cm。

新苏教版八年级数学上册第一章测试试卷(附答案)

新苏教版八年级数学上册第一章测试试卷（满分：150分时间：120分钟）一、选择题（将正确答案的序号填入题后的括号，共30分）1.下面有4个汽车标志图案，其中是轴对称图形的是（）①②③④A、②③④B、①③④C、①②④D、①②③2．下列图形中只有一条对称轴的是（）。

A B C D3．小亮在镜中看到身后墙上的时钟如下, 你认为实际时间最接近8:00的是( )A. B. C. D.4．如图，在△ABC中，AB=AC，∠A=44°，CD⊥AB于D，则∠DCB等于（）A、44°B、68°C、46°D、22°5．已知等腰三角形的一个内角是75º，则它的顶角是（）A．30ºB．75ºC．30º或75ºD．105º6．如图，把矩形ABCD沿EF对折，若150∠=，则AEF∠等于（）A．115B．130C．120D．65AB CD EF17．等腰梯形一底角为60°，它的两底长分别为8cm和20cm，则它的周长是（）A．36cm B．44cm C．48cm D．52cm8．△ABC中，①若AB＝BC＝CA，则△ABC是等边三角形；②一个底角为60°的等腰三角形是等边三角形；③顶角为60°的等腰三角形是等边三角形;④有两个角都是60°的三角形是等边三角形．上述结论中正确的有（）A．1个B．2个C．3个D．4个9．下列说法中, 不正确的是( )A. 三个角的度数之比为1:3:4的三角形是直角三角形；B. 三个角的度数之比为3:4:5的三角形是直角三角形；C. 三边长度之比为3:4:5的三角形是直角三角形；D. 三边长度之比为5:12:13的三角形是直角三角形10. 如图，在钝角△ABC中，点D、E分别是边AC、BC的中点，且DA＝DE。

有下列结论：①∠1=∠2②∠1=∠3 ③∠B=∠C ④∠B=∠3；其中一定正确的结论有（）个。

2020年人教版八年级数学上册13.2《画轴对称图形》课时作业(含答案)

2020年人教版八年级数学上册13.2《画轴对称图形》课时作业一、选择题1．下列说法正确的是（）A．任何一个图形都有对称轴; B．两个全等三角形一定关于某直线对称;C．若△ABC与△A′B′C′成轴对称，则△ABC≌△A′B′C′;D．点A，点B在直线1两旁，且AB与直线1交于点O，若AO=BO，则点A与点B 关于直线l对称.2．已知两条互不平行的线段AB和A′B′关于直线1对称，AB和A′B′所在的直线交于点P，下面四个结论：①AB=A′B′；②点P在直线1上；③若A、A′是对应点，则直线1垂直平分线段AA′；④若B、B′是对应点，则PB=PB′，其中正确的是（）A．①③④ B．③④ C．①② D．①②③④二、填空题线对称的图形，这个图形与原图形的_________、___________完全一样．4．数的运算中会有一些有趣的对称形式，仿照等式①的形式填空，并检验等式是否成立．①12×231=132×21;②12×462=___________;③18×891=__________;④24×231=___________.5．如图，点P在∠AOB的内部，点M、N分别是点P关于直线OA、OB 的对称点，线段MN交OA、OB于点E、F，若△PEF的周长是20cm，则线段MN的长是___________．三、解答题6．如图，C 、D 、E 、F 是一个长方形台球桌的4个顶点，A 、B 是桌面上的两个球，怎样击打A 球，才能使A 球撞击桌面边缘CF 后反弹能够撞击B 球？请画出A 球经过的路线，并写出作法．7．如图，A 、B 是两个蓄水池，都在河流a 的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A 、B 两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点（保留作图痕迹）8．如图，仿照例子利用“两个圆、两个三角形和两条平行线段”设计一个轴对称图案，并说明你所要表达的含义．例:一辆小车9．如图，已知牧马营地在P 处，每天牧马人要赶着马群先到河边饮水，再带到草地吃草，然后回到营地，请你替牧马人设计出最短的放牧路线．草地河流营地P答案:1．C；2．D3．形状；大小4．264×21；198×81；132×42 5．20cm6．作点A关于直线CF对称的点G，连接BG交CF于点P，则点P即为A 球撞击桌面边缘CF的位置7．作点A关于直线a对称的点C，连接BC交a于点P，则点P就是抽水站的位置8．略9．分别作P点关于河边和草地边对称的点C、D，连接CD分别交河边和草地于A、B两点，则沿PA→AB→BP的线路，所走路程最短．。

苏教版八年级数学全册知识点总结

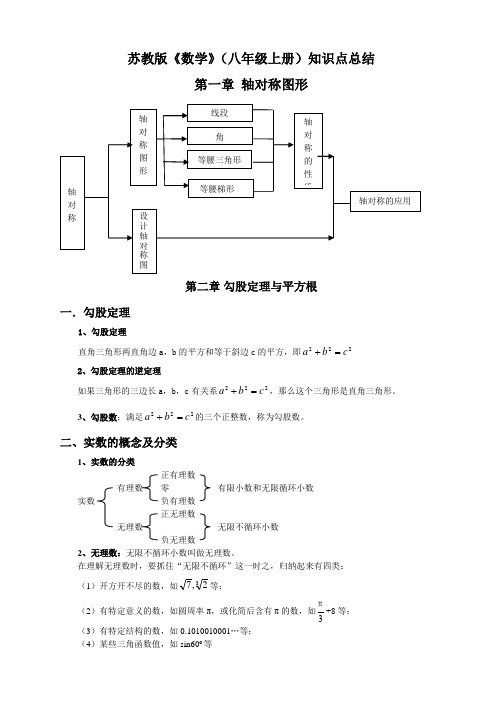
苏教版《数学》（八年级上册）知识点总结第一章轴对称图形第二章勾股定理与平方根一．勾股定理1、勾股定理直角三角形两直角边a ，b 的平方和等于斜边c 的平方，即222c b a =+ 2、勾股定理的逆定理如果三角形的三边长a ，b ，c 有关系222c b a =+，那么这个三角形是直角三角形。

3、勾股数：满足222c b a =+的三个正整数，称为勾股数。

二、实数的概念及分类1、实数的分类正有理数有理数零有限小数和无限循环小数实数负有理数正无理数无理数无限不循环小数负无理数2、无理数：无限不循环小数叫做无理数。

在理解无理数时，要抓住“无限不循环”这一时之，归纳起来有四类：（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等；（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数值，如sin60o 等轴对称轴对称的性质轴对称图形线段角等腰三角形轴对称的应用等腰梯形设计轴对称图案三、平方根、算数平方根和立方根1、算术平方根：一般地，如果一个正数x 的平方等于a ，即x 2=a ，那么这个正数x 就叫做a 的算术平方根。

特别地，0的算术平方根是0。

表示方法：记作“a ”，读作根号a 。

性质：正数和零的算术平方根都只有一个，零的算术平方根是零。

2、平方根：一般地，如果一个数x 的平方等于a ，即x 2=a ，那么这个数x 就叫做a 的平方根（或二次方根）。

表示方法：正数a 的平方根记做“a ±”，读作“正、负根号a ”。

性质：一个正数有两个平方根，它们互为相反数；零的平方根是零；负数没有平方根。

开平方：求一个数a 的平方根的运算，叫做开平方。

0≥a注意a 的双重非负性：a ≥03、立方根一般地，如果一个数x 的立方等于a ，即x 3=a 那么这个数x 就叫做a 的立方根（或三次方根）。

表示方法：记作3a性质：一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

人教版初中数学八年级上单元试卷第章轴对称【培优卷】(解析版)

第13章轴对称培优一、单选题1. ( 3分) 平面直角坐标系中，点P(﹣2，3)关于x轴对称的点的坐标为（）A. (2，﹣3)B. (﹣2，3)C. (﹣2，﹣3)D. (2，3) 【答案】C【考点】关于坐标轴对称的点的坐标特征【解析】【解答】解：∵关于x轴对称点的坐标特点：横坐标相同，纵坐标互为相反数，∴点P（﹣2，3）关于x轴的对称点坐标是（﹣2，﹣3），故答选：C．【分析】关于x轴对称点的坐标特点：横坐标相同，纵坐标互为相反数；可得.2. ( 3分) 下列图案中，既是中心对称图形也是轴对称图形的个数为（）A. 1个B. 2个C. 3个D. 4个【答案】B【考点】轴对称图形【解析】【解答】解：第一个图形是轴对称图形，不是中心对称图形；第二个图形是轴对称图形，是中心对称图形；第三个图形不是轴对称图形，是中心对称图形；第四个图形是轴对称图形，也是中心对称图形．故选：B．【分析】根据轴对称图形与中心对称图形的概念进行判断即可．3. ( 3分) 在下列命题中，正确的是（）A. 一组对边平行的四边形是平行四边形B. 有一个角是直角的四边形是矩形C. 有一组邻边相等的四边形是菱形D. 对角线互相垂直平分的四边形是菱形【答案】D【考点】平行四边形的判定，菱形的判定，矩形的判定【解析】【解答】解：A、有一组对边平行且相等的四边形是平行四边形，错误；B、有一个角是直角的平行四边形是矩形，错误；C、有一组邻边相等的平行四边形是菱形，错误；D、对角线互相垂直平分的四边形是菱形，正确；故答案为：D.【分析】分别利用矩形的判定方法、以及菱形的判定与性质和平行四边形的判定方法分析得出答案.4. ( 3分) 如图，已知AB=AC=BD，那么∠1与∠2之间的关系是（）A. ∠1=2∠2B. 2∠1+∠2=180°C. ∠1+3∠2=180°D. 3∠1-∠2=180°【答案】D【考点】三角形内角和定理，三角形的外角性质，等腰三角形的性质【解析】【解答】解：∵AB=AC=BD，∴∠BAD=∠1，∠B=∠C，∴∠B=180°－2∠1=∠C，∵∠C=∠1－∠2，∴180°－2∠1=∠1－∠2，∴3∠1－∠2=180°.故答案为：D.【分析】根据等边对等角可得∠BAD=∠1，∠B=∠C，利用三角形的内角和可得∠B=180°－2∠1=∠C，由三角形外角的性质可得∠C=∠1－∠2，从而可得180°－2∠1=∠1－∠2，据此即得结论.5. ( 3分) 下列图形既是轴对称图形又是中心对称图形的图形是( )A. 等腰三角形B. 等边三角形C. 长方形D. 梯形【答案】C【考点】轴对称图形，中心对称及中心对称图形【解析】【解答】解：A、等腰三角形是轴对称图形，不是中心对称图形；B、等边三角形是轴对称图形，不是中心对称图形；C、长方形是轴对称图形，是中心对称图形；D、梯形既不是轴对称图形，又不是中心对称图形.故答案为：C.【分析】把一个图形沿着某一条直线折叠，如果直线两旁的部分能够完全重合，那么这个图形就是轴对称图形,把一个图形绕着某个点旋转180°，如果它能与原图形完全重合，那么这个图形就是中心对称图形，据此作出判断即可.6. ( 3分) 在平面直角坐标系中，点P（3，-4）关于x轴对称的点的坐标是( )A. （3，4）B. （3，－4）C. （－3，－4）D. （4，3）【答案】A【考点】关于坐标轴对称的点的坐标特征【解析】【分析】平面直角坐标系中任意一点P（x，y)，关于x轴的对称点的坐标是（x，-y)，据此即可求得点（3，-4)关于x轴对称的点的坐标．【解答】∵点（3，-4)关于x轴对称；∴对称的点的坐标是（3，4)．故选A．【点评】这一类题目是需要识记的基础题7. ( 3分) 如图，已知∠AOB=60°，点P在边OA上，OP=12，点M，N在边OB上，PM=PN，若MN=2，则OM=（）A. 8B. 6C. 5D. 3【答案】C【考点】等腰三角形的性质，含30°角的直角三角形【解析】【解答】解：过P作PQ⊥MN，∵PM=PN，∴MQ=NQ=1，在Rt△OPQ中，OP=12，∠AOB=60°，∴∠OPQ=30°，OP=6，∴OQ= 12则OM=OQ-QM=6-1=5.故答案为：C.【分析】过P作PQ⊥MN，根据等腰三角形的性质可得MQ=NQ=1，然后在Rt△OPQ中根据含30°角的直角三角形的边之间的关系可求出OQ的值，进而得到OM的值.8. ( 3分) 如图，正方形网格中的每个小正方形边长都是1．已知A、B是两格点，若△ABC为等腰三角形，且S△ABC=1.5，则满足条件的格点C有（）A. 1个B. 2个C. 3个D. 4个【答案】B【考点】等腰三角形的判定【解析】【解答】解：如上图：分情况讨论．①AB为等腰△ABC底边时，符合△ABC为等腰三角形的C点有4个；②AB为等腰△ABC其中的一条腰时，符合△ABC为等腰三角形的C点有4个．因为S△ABC=1.5，所以满足条件的格点C只有两个，如图中蓝色的点．故选B．【分析】根据题意，结合图形，分两种情况讨论：①AB为等腰△ABC底边；②AB为等腰△ABC其中的一条腰；然后根据S△ABC=1.5，再确定点C的位置．9. ( 3分) 如图，在△ABC中，∠ABC=50°，∠ACB=100°，点M是射线AB上的一个动点，过点M作MN∥BC 交射线AC于点N，连结BN。

八年级数学：轴对称图形与轴对称练习（含答案）

八年级数学：轴对称图形与轴对称练习（含答案）八年级数学：轴对称图形与轴对称练习（含答案）一、选择题（共8小题）1．下列各图,不是轴对称图形的是（）A．B．] C．D．2．下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是（）A．上海自来水来自海上B．有志者事竞成C．清水池里池水清D．蜜蜂酿蜂蜜3．下列说法错误的是（）A．等边三角形有3条对称轴B．正方形有4条对称轴C．角的对称轴有2条D．圆有无数条对称轴4．如图是经过轴对称变换后所得的图形,与原图形相比（）A．形状没有改变,大小没有改变B．形状没有改变,大小有改变C．形状有改变,大小没有改变D．形状有改变,大小有改变5．观察图形…并判断照此规律从左到右第四个图形是( )A ．B ．C．D．6．把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换．在自然界和日常生活中,大量地存在这种图形变换（如图1）．结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形（如图2）的对应点所具有的性质是（）A．对应点连线与对称轴垂直B．对应点连线被对称轴平分C．对应点连线被对称轴垂直平分 D．对应点连线互相平行第5题图第6题图第7题图7．如图,两个三角形关于某条直线成轴对称,其中已知某些边的长度和某些角的度数,则x的度数是（）A．55°B．60°C．65°D．70°8．小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是（）A．B．C．D．二、填空题（共10小题）9．2011年11月2日,即20111102,正好前后对称,因而被称为“完美对称日”,请你写出本世纪的一个“完美对称日”：_________ ．10．写出一个至少具有2条对称轴的图形名称_________ ．11．如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中的一个小正方形涂黑,所得图案是一个轴对称图形,则涂黑的小正方形可以是_________ （填出所有符合要求的小正方形的标号）12．在轴对称图形中,对应点的连线段被_________ 垂直平分．13．下列图形中,一定是轴对称图形的有_________ ；（填序号）（1）线段（2）三角形（3）圆（4）正方形（5）梯形．14．如图是汽车牌照在水中的倒影,则该车牌照上的数字是_________ ．15．请同学们写出两个具有轴对称性的汉字_________ ．16．如图,国际奥委会会旗上的图案由5个圆环组成．每两个圆环相交的部分叫做曲边四边形,如图所示,从左至右共有8个曲边四边形,分别给它们标上序号．观察图形,我们发现标号为2的曲边四边形（下简称“2”）经过平移能与“6”重合,2又与_________ 成轴对称．（请把能成轴对称的曲边四边形标号都填上）第11题图第14题图第16题图17．如图,长方形ABCD中,长BC=a,宽AB=b,（b＜a＜2b）,四边形ABEH和四边形ECGF都是正方形．当a、b满足的等量关系是_________ 时,图形是一个轴对称图形．18．请利用轴对称性,在下面这组图形符号中找出它们所蕴含的内在规律,然后在横线上的空白处填上恰当的图形：三、解答题（共5小题）19．判断下列图形是否为轴对称图形？如果是,说出它有几条对称轴．20．如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角．21．如图,l是该轴对称图形的对称轴．（1）试写出图中二组对应相等的线段：；（2）试写出二组对应相等的角：；（3）线段AB、CD都被直线l ．22．如图是由两个等边三角形（不全等）组成的图形．请你移动其中的一个三角形,使它与另一个三角形组成轴对称图形,并且所构成的图形有尽可能多的对称轴．画出你所构成的图形,它有几条对称轴？23．有一些整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如：22,131,1991,123321,…,像这样的数,我们叫它“回文数”．回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数（两位以上）,经过一定的计算,可以变成“回文数”,办法很简单：只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文数,比如：①132+231=363②7299+9927=17226,17226+62271=79497,成功了！（1）你能用上述方法,将下列各数“变”成回文数吗？①237 ②362（2）请写出一个四位数,并用上述方法将它变成回文数．参考答案一、选择题（共8小题）1．A 2．B 3．C 4．A 5．D 6．B 7．B 8．D二．填空题（共10小题）9．20011002,20100102（答案不唯一）；10．矩形；11．2,3,4,5,712．对称轴；13．（1）（3）（4）；14．21678 ．；15．甲、由、中、田、日等．；16．1,3,7 ；17．；18.三．解答题（共5小题）19．解：根据轴对称图形的概念：如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形．则（1）（3）（5）（6）（9）不是轴对称图形；（2）（4）有1条对称轴；（7）有4条对称轴；（8）有1条对称轴；（10）有2条对称轴．20．解：相等的线段：AB=AE,CB=DE,CF=DF；相等的角：∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC．21．（1）AC=BD,AE=BE,CF=DF,AO=BO ；（2）∠BAC=∠ABD,∠ACD=∠BDC；（3）垂直平分．22．解：如图,小正三角形再大正三角形的内部,该图形有3条对称轴．23．解：（1）①237+732=969,②362+263=625,（2）1151+1511=2662；。

八年级数学(上)整章测试(B卷7套合)参考答案

八年级数学（上）第一单元自主学习达标检B 卷一、填空题1．一定，一定不 2．50度 3．40度 4．AD=BC 5．HL 6．∠A=∠C 7．4 8．∠A=∠D ，∠B=∠C 9．9.5或4 10．5 11．8 12．15 13．正确 14．5，30度 15．16．35度二、解答题17．略 18．略 19．略 20．在同一直线上 21．略22．情况一：已知：AD BC AC BD ==，求证：CE DE =（或D C ∠=∠或DAB CBA ∠=∠）情况二：已知：D C DAB CBA ∠=∠∠=∠，求证：AD BC =（或AC BD =或CE DE =）23略 24．BF= 1 25．上面证明过程不正确; 错在第一步。

正确过程如下：在△BEC 中，∵BE =CE ， ∴∠EBC =∠ECB ，又∵∠ABE =∠ACE ，∴∠ABC =∠ACB ， ∴AB =AC 。

在△AEB 和△AEC 中，AE =AE 。

BE =CE ，AB =AC ，∴△AEB ≌△AEC ，∠BAE =∠CAE 。

26．略27．（1）△ADE ≌△A ′DE ，∠ADE =∠A ′DE ，∠AED =∠A ′ED ，∠A =∠A ′；（2）11802,21802x y ∠=︒-∠=︒-；（3）2∠A =∠1+∠228．（1）ABC △与AEG △面积相等（证等底等高）；（2）由（1）知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和，所以这条小路的面积为(2)a b +平方米．八年级数学（上）第二单元自主学习达标检B 卷一、填空题1．2，3 2．④，不是轴对称图形3．75度或30度4．3 5．4 6．（1）（3）（6）是轴对称图形，（2）（4）（5）不是轴对称图形 7．5 8．12 9．点O 到BC 两端的距离相等 10．1511．正反写的4和6 12．4，6 13．353cm 或5cm 14．2、4，2 15．30度 16．130度二、解答题17．9 18．垂直 19．BC=6cm 20．略 21．略 22．22度，66度 23．20cm 24．（1）90度；（2）90度；（3）90度；（4）三角形中，一边上的中线等于这边的一半，那么这边所对的角等于90度 25．略 26．略 27．是等边三角形 28．略八年级数学（上）第三单元自主学习达标检B 卷一、填空题1．12- 2．2± 3．3- 4．22-,±，0.08159 7．2-+8．34.2810⨯ 9．1 10． 11．10 12．0 13．1- 14．7 15．3，4 16．40，11二、解答题17．（1）4个全对；（2= 18．略 19．（1）110；（2）16-；（3）58；（4）4.21 20．14 21．12- 22．略 23． 24． 25．cm ，cm 26．．约42次 28．表格中依次填，积为200.8。

八年级上册数学《轴对称》单元综合检测(附答案)

11.如图,将长方形A B C D对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是B C的中点且MN与折痕PQ交于F,连接A C′,B C′,则图中共有等腰三角形的个数是( )
A.1B.2C.3D.4
12. 如图,过边长为1的等边△A B C的边A B上一点P,作PE⊥A C于E,Q为B C延长线上一点,当PA＝CQ时,连PQ交A C边于D,则DE的长为()
故选C．
4.如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是()
A.1号袋B.2号袋C.3号袋D.4号袋
[答案]B
[解析]
[分析]
根据轴对称的性质画出图形即可得出正确选项．
[详解]解：根据轴对称的性质可知,台球走过的路径为：
(1)请用尺规作图法作出B C的垂直平分线DE,垂足为D,交A C于点E,(保留作图痕迹,不写作法)；
(2)请用尺规作图法作出∠C 角平分线CF,交A B于点F,(保留作图痕迹,不写作法)；
(3)请用尺规作图法在B C上找出一点P,使△PEF的周长最小.(保留作图痕迹,不写作法).
四、解答题:
20.已知点A(2A-B,5＋A),B(2B－1,-A＋B).
∴∠NMC=15°+15°=30°,
∴BM所在的直线是△C DM的角平分线,
又∵CM=DM,
∴BM所在的直线垂直平分C D；
(4)根据(2)同理可求∠D A B=105°,∠B C D=75°,
∴∠D A B+∠A B C=180°,
∴A D∥B C,
24.如图点O是等边内一点, ,∠A C D=∠B CO,OC=C D,