2012北京高三期末试卷

合集下载

北京市西城区2012届高三上学期期末考试试

北京市西城区2012届高三上学期期末考试试语文北京市西城区2012届高三上学期期末考试语文试题第一部分（选择题，共27分）一、本大题共5小题，每小题3分，共15分。

1．下列词语中，字形和加点的字的读音全都正确的一项是A.照相馆两全齐美胡诌(zhōu)悬崖勒（lēi）马B.伤元气倾刻之间匕(bì)首戎马倥(kǒng)偬C.陪小心首屈一指市侩(huì)惊魂甫(fǔ)定D.座谈会金榜题名逮(dài)捕徇(xùn)私舞弊2．依次填入下列语段横线处的词语，最恰当的一项是宋词仿佛一朵芬芳绚丽的奇葩，它以的风格，散发着迷人的馨香。

千百年来，代代中国文人对宋词的品鉴、仿作，已成为他们的，凝聚着独特的美学追求。

在现当代，有的诗人创作的旧体堪称，甚至足以与古人的佳作比肩，只是宋词的时代已不可能复现。

A. ①独树一帜②情趣③精致B. ①独具匠心②情趣③精品C. ①独具匠心②雅趣③精致D. ①独树一帜②雅趣③精品3．下列句子中，加点的成语使用正确的一项是A.18名路人看到遭受了碾轧的小悦悦后，居然义无反顾地离去，这一事件引发了全社会对于“道德”话题的热烈讨论。

B.中国高铁自从开通以来，不断出现安全方面的负面新闻，老百姓对此噤若寒蝉，纷纷对高铁建设的质量问题提出质疑。

C.近年来，“红色”旅游、农业旅游、科技旅游、探险旅游等特色旅游方兴未艾，甚至成为一些地区经济发展的新名片。

D.在纪念辛亥革命100周年之际，各地以各种形式缅怀革命先驱，颂扬他们敢为天下先的英雄气概，溢美之词不绝于耳。

4．下列句子中，没有语病的一句是A.美国苹果公司前任总裁乔布斯是一位传奇人物，他引领了一个时代的风尚，所以缔造了自己的企业，不断开发出最先进的电子产品。

B.2012年伦敦夏季奥运会的吉祥物是精灵文洛克，它以英格兰的萨罗普羊为原型，造型活泼而且富有动感，其设计充满了想象力。

C. 美国民众在纽约发起了“占领华尔街”示威活动，抗议政府的权钱交易和贫富差距日增等问题，如今已成为席卷全美的社会运动。

2012届北京市海淀区高三期末语文试题答案

2012 届北京海淀区高三年级第一学期期末语文练习答案第一部分（共27 分）一、本大题共 5 小题，每小题 3 分，共15 分。

1.B2.C3.B4.D5.D二、本大题共4小题，每小题3分，共12 分。

6.A7.D8.D9.C第二部分（共123 分）三、本大题共 4 小题，共30分。

10. （10 分）第一问：（2 分）“以天下为务”具体所指，国君（政府、官员）恤民、知怨、修政（照抄原文不得分，答对12 个得1 分，答对 3 个得 2 分；信息转换正确即可）。

第二问：（8 分）观点明确 2 分；联系实际或阅读积累2分（恰当1分，具体1 分）；分析有理有据2分；语言2分（顺畅 1 分，表达清晰 1 分）。

11. （5 分）“/ ”处为必断句处，“ // ”处为可断可不断处。

必断处每答对 2 处得 1 分。

在可断可不断处断句，不得分。

答错 2 处扣 1 分，扣完 5 分为止。

赵简子曰：“厥也// 爱我/ 铎也// 不爱我/ 厥之谏我也/ 必于无人之所/ 铎之谏我也/ 喜质我于人中/ 必使我丑/ 尹铎对曰：“厥也爱君之丑也，而不爱君之过也；铎也爱君之过也，而不爱君之丑也。

臣尝闻相人于师/ 敦颜而土色者忍丑/ 不质君于人中/ 恐君之不变也。

”翻译：赵简子说：“赵厥敬重我，尹铎不敬重我。

赵厥劝谏我的时候，一定在没有人的地方；尹铎劝谏我的时候，喜欢当着别人的面质问我，一定要让我出丑。

” 尹铎回答说：“赵厥顾及您出丑，却不顾及您的过错；我顾及您的过错，却不顾及您出丑。

我曾经从老师那里听说过如何观察人，（那些）相貌敦厚、脸色土黄的人能够承受住出丑。

（我如果）不在别人面前质问您，恐怕您不能改正啊。

”12. （8 分）答案略。

（每句1 分，句中有错该句不得分）13. （7 分）①（3分）C②（4分）诗中所描写的金山月如玉镜般透亮，如白银般明亮，如冰雪般洁净（特点 1 分，结合诗句 1 分），万里皓月营造了澄澈、清明、旷远的意境（1 分），诗人借此映衬自己高洁的追求、旷达的胸襟（1 分）。

北京市9区2012届高三上学期期末考试试题--数学AnllAM

昌平区2011－2012学年第一学期高三年级期末质量抽测数学试卷（文科）2012 .1考生注意事项：1.本试卷共6页，分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分，满分150分，考试时间120分钟．2.答题前，考生务必将学校、班级、考试编号填写清楚．答题卡上第一部分(选择题)必须用2B铅笔作答，第二部分(非选择题)必须用黑色字迹的签字笔作答，作图时可以使用2B铅笔．3.修改时，选择题用塑料橡皮擦干净，不得使用涂改液．请保持卡面整洁，不要折叠、折皱、破损．不得在答题卡上作任何标记．4.请按照题号顺序在各题目的答题区域内作答，未在对应的答题区域作答或超出答题区域的作答均不得分．第Ⅰ卷（选择题共40分）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．)1．设全集}7,5,3,1{=U，集合}7,3,1{},5,3{==BA，则()UA BIð等于A．{5} B．{3，5} C．{1，5，7} D．Φ2．21i-等于A．22i-B．1i-C．i D．1i+3．“x y>”是“22x y>”的A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件4.从3名男同学，2名女同学中任选2人参加体能测试，则选到的2名同学中至少有一名男同学的概率是A．910B．45C．25D．125.若某空间几何体的三视图如图所示，则该几何体的体积是A．2 B．4C．6. D．86. 某程序框图如图所示，则输出的S= A．120 B．57C．56 D．26 主视俯视7.某类产品按工艺共分10个档次，最低档次产品每件利润为8元.每提高一个档次，每件利润增加2元. 用同样工时，可以生产最低档产品60件，每提高一个档次将少生产3件产品.则获得利润最大时生产产品的档次是A.第7档次B.第8档次C.第9档次D.第10档次8. 一圆形纸片的圆心为点O ,点Q 是圆内异于O 点的一定点，点A 是圆周上一点.把纸片折叠使点A 与Q 重合，然后展平纸片，折痕与OA 交于P 点.当点A 运动时点P 的轨迹是 A ．圆 B ．椭圆 C ．双曲线 D ．抛物线第Ⅱ卷（非选择题共110分）填空题（本大题共6小题，每小题5分，共30分）． 9.已知函数x x y cos sin = ，则函数的最小正周期是 .10.已知向量(2,1)=a ，10⋅=a b ，7+=a b ，则=b .11.某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100)，[100，102)，[102，104)，[104，106] .已知样本中产品净重小于100克的个数是48，则a =___________ ；样本中净重在[98，104）的产品的个数是__________ .12. 已知双曲线122=-y m x 的右焦点恰好是抛物线x y 82=的焦点，则m = .13. 已知D是由不等式组0,0,x y x -≥⎧⎪⎨+≥⎪⎩所确定的平面区域，则圆224x y +=在区域D 内的弧长为_____________；该弧上的点到直线320x y ++=的距离的最大值等于__________ .14.设函数)(x f 的定义域为R ，若存在与x 无关的正常数M ，使|||)(|x M x f ≤对一切实数x 均成立，a则称)(x f 为有界泛函.在函数①x x f 5)(-=，②x x f 2sin )(=，③xx f )21()(=，④x x x f cos )(=中，属于有界泛函的有__________(填上所有正确的序号) .三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．) 15.（本小题满分13分）在ABC ∆中，AA A cos cos 2cos 212-=．（I ）求角A 的大小；（II ）若3a =，sin 2sin B C =，求ABCS ∆．16．（本小题满分13分）已知数列}{n a 是等差数列,22, 1063==a a ，数列}{n b 的前n 项和是nS ，且131=+n n b S .（I ）求数列}{n a 的通项公式；（II ）求证：数列}{n b 是等比数列；17.（本小题满分14分）如图在四棱锥P ABCD -中，底面ABCD 是正方形，ABCD PA 底面⊥，垂足为点A ，2==AB PA ,点M ，N 分别是PD ，PB 的中点．（I ）求证:ACM PB 平面// ；（II ）求证:⊥MN 平面PAC ；（III ）求四面体A MBC -的体积.18.(本小题满分13分)已知函数ax x x x f ++=1ln )(（a 为实数）.（I ）当0=a 时，求)(x f 的最小值；（II ）若)(x f 在),2[+∞上是单调函数，求a 的取值范围.19.(本小题满分14分)已知椭圆C 的中心在原点，左焦点为(，离心率为23．设直线l 与椭圆C 有且只有一个公共点P ，记点P 在第一象限时直线l 与x 轴、y 轴的交点分别为B A 、，且向量OM +=.求：（I ）椭圆C 的方程；（II ）||OM 的最小值及此时直线l 的方程.20. (本小题满分13分)M 是具有以下性质的函数()f x 的全体：对于任意s ，0t >，都有()0f s >，()0f t >，且()()()f s f t f s t +<+.（I ）试判断函数12()log (1)f x x =+，2()21x f x =-是否属于M ？（II ）证明：对于任意的0x >，0(x m m +>∈R 且0)m ≠都有[()()]0m f x m f x +->；（III ）证明：对于任意给定的正数1s >，存在正数t ，当0x t <≤时，()f x s <.昌平区2011－2012学年第一学期高三年级期末质量抽测数学(文科)试卷参考答案及评分标准 2012.1二、填空题(本大题共6小题，每小题5分，共30分．) 9．π 10. 26 11. 0.125；120 12. 313． 65π;5102+14. ① ② ④三、解答题(本大题共6小题，共80分)15.（本小题满分13分）解：（I ）由已知得：AA A cos cos )1cos 2(2122-=-，……2分.21cos =∴A ……4分 π<<A 0Θ， .3π=∴A …………6分（II ）由C c B b sin sin = 可得：2sin sin ==c b C B ………7分∴ c b 2= …………8分214942cos 222222=-+=-+=c c c bc a c b A ………10分解得：32b , 3==c ………11分2332333221sin 21=⨯⨯⨯==A bc S . ……13分16（本小题满分13分）解：（1）由已知⎩⎨⎧=+=+.225,10211d a d a 解得 .4,21==d a .244)1(2-=⨯-+=∴n n a n ………………6分（2）由于nn b S 311-=， ① 令n =1，得.31111b b -= 解得431=b ，当2≥n 时，11311---=n n b S ② －②得n n n b b b 31311-=- ， 141-=∴n n b b 又0431≠=b , .411=∴-n n b b∴数列}{n b 是以43为首项，41为公比的等比数列.……………………13分17.（本小题满分14分）证明：（I ）连接O BD AC MN MO MC AM BD AC =I 且,,,,,,的中点分别是点BD PD M O ,,Θ ACM PB PB MO 平面⊄∴,//∴ACM PB 平面//. …… 4分(II) ABCD PA 平面⊥Θ，ABCD BD 平面⊂BD PA ⊥∴是正方形底面ABCD Θ BD AC ⊥∴又A AC PA =⋂Θ PAC BD 平面⊥∴ (7)分在中PBD ∆，点M ，N 分别是PD ，PB 的中点．∴BD MN //PAC MN 平面⊥∴. …… 9分（III ）由h S V V ABC ABC M MBC A ⋅⋅==∆--31 ……11分PAh 21= ……12分 32212131=⋅⋅⋅⋅⋅=∴-PA AD AB V MBC A . ……14分18.(本小题满分13分)解：(Ⅰ) 由题意可知：0>x ……1分当0=a 时21)(x x x f -=' …….2分当10<<x 时，0)(<'x f 当1>x 时，0)(>'x f ……..4分故1)1()(min ==f x f . …….5分(Ⅱ) 由222111)(x x ax a x x x f -+=+-='① 由题意可知0=a 时，21)(x x x f -=',在),2[+∞时，0)(>'x f 符合要求 …….7分② 当0<a 时，令1)(2-+=x ax x g 故此时)(x f 在),2[+∞上只能是单调递减0)2(≤'f 即04124≤-+a 解得41-≤a …….9分当0>a 时，)(x f 在),2[+∞上只能是单调递增 0)2(≥'f 即,04124≥-+a 得41-≥a 故0>a …….11分综上),0[]41,(+∞⋃--∞∈a …….13分19. （本小题满分14分）解：(Ⅰ)由题意可知3=c ，23==a c e ，所以2=a ，于是12=b ，由于焦点在x 轴上，故C 椭圆的方程为2214x y += ………………………………5分（Ⅱ）设直线l 的方程为：m kx y +=)0(<k ，),0(),0,(m B k mA -⎪⎩⎪⎨⎧=++=,14,22y x m kx y 消去y 得：012)41(222=-+++m kmx x k …………………7分Q 直线l 与曲线C 有且只有一个公共点，0)1)(41(42222=-+-=∆m k m k即1422+=k m ① …………………… 9分 ∵+=222||mk m +=∴② ……………………11分将①式代入②得：||3OM =≥=u u u u r当且仅当22-=k 时，等号成立，故min ||3OM =u u u u r，此时直线方程为：03222=-+y x . …………………14分20（本小题满分13分）(Ⅰ)由题意可知，0)(,0)(,0)(,0)(2211>>>>t f s f t f s f 若)1(log )1(log )1(log 222++<+++t s t s 成立则1)1)(1(++<++t s t s 即0<st与已知任意s ，0t >即0>st 相矛盾，故M x f ∉)(1； ……2分若12222-<-++ts ts成立则01222<--++ts t s即0)21)(12(<--t s Θs ，0t > 021,12<->∴t s 即0)21)(12(<--ts 成立 …..4分故M x f ∈)(2.综上，M x f ∉)(1，M x f ∈)(2. ……5分 (II) 当0>m 时，)()()()(x f m f x f m x f >+>+ 0)()(>-+∴x f m x f 当0<m 时，)()()()()(m x f m f m x f m m x f x f +>-++>-+=0)()(<-+∴x f m x f故0)]()([ >-+x f m x f m . ……9分(III) 据（II ））上为增函数在（∞+.0)(x f ，且必有)(2)2(x f x f >（*） ①若s f <)1(，令1=t ，则t x ≤<0时 s x f <)(；②若,)1(s f >则存在*N ∈k ，使t f k 12)1(=<由（*）式可得s f f f kk k <<<<<-1)1(21)21(21)21(1Λ即当s x f t x <≤<)(0时，综①、②命题得证。

北京市海淀区2012届高三上学期期末考试(有答案 )

北京市海淀区2012届高三年级期末考试语文试题 2012·1第一部分(共27分)一、本大题共5小题，每小题3分，共15分。

1. 下列词语中，字形和加点的字读音全都正确的一项是 BA. 果腹珠联璧和合木讷．（nà）nè嘉言懿．（yì）行B. 奇葩独辟蹊径裹挟．（xié）曲．（qū）突徙薪C. 法码砝语焉不详信笺．（qiān）jiān舐．（shì）犊情深D. 雾霾认人唯贤任丰腴．（yú）握发吐哺．（fǔ）fǔ2. 下列句子中，加点的成语使用不正确的一项是 CA. 据报道，近日科学家们发现了迄今已知的两个最大的黑洞，它们的质量是太阳的100亿倍，整个太阳系在它们面前都显得相形见绌．．．．。

形：对照；绌：不够，不足。

和同类的事物相比较，显得远远不足。

B. 尽管如今搞收藏的人越来越多，但社会上不少拍卖会却与平民无关，普通的收藏者只能望洋兴叹．．．．，因为一般的藏品进不了拍卖会的门槛。

原指在伟大事物面前感叹自己的渺小。

现多比喻做事时因力不胜任或没有条件而感到无可奈何。

C.姜文在电影《关云长》中饰演曹操，他的表演栩栩如生．．．．，极具个性，有人评论他诠释了一个前所未有的带有“姜文”印记的曹操。

活泼生动的样子。

指艺术形象非常逼真，如同活的一样。

D.孙家栋院士如数家珍．．．．地向前来参观的人们介绍了我国绕月探测工程五大系统的特点，并特别强调这五大系统处处是“中国制造”。

好像数自己家藏的珍宝那样清楚。

比喻对所讲的事情十分熟悉。

3.下列句子中，没有语病的一句是 BA.为迅速平息“冰箱门事件”，西门子公司就此向消费者诚恳道歉，以避免对公司终端产品的销售和品牌形象造成更大的损毁。

（不合逻辑）B.德班气候大会举行期间，场外的示威抗议活动持续不断，环保人士高喊口号，要求各国政要在应对气候变化上做出更多努力。

C.在日本那些再现曲水宴的表演中，有着不少“中国元素”，但是由于现代年轻人对古代中国文化了解甚少，并不知道哪些元素来自中国。

北京市各区2012届高三第一学期语文期末试卷汇编

北京市101中学2012届上学期高三统考试卷二（语文）北京市朝阳区2012届高三上学期期末考试试题（语文）北京市东城区2012届高三上学期期末教学统一检测（语文）北京市丰台区2012届高三上学期期末考试试题（语文）北京市海淀区2012届高三上学期期末考试试题（语文）北京市石景山区2012届高三上学期期末考试试题（语文）北京市西城区2012届高三上学期期末考试试题（语文）2012年2月北京市101中学2012届上学期高三统考试卷二（语文）第I卷（选择题共38分）一、本大题共13小题，每小题2分，共26分。

1. 下列词语中加点字的读音，全都正确的一组是A. 吮．吸（shǔn）拂．晓（fó）嫉．妒（jí）摈．弃（bìn）B. 泥．古（nì）内疚．（jiù）辟．谣（pì）稽．首（qǐ）C. 下载．（zǎi）包扎．（zā）重创．（chuàng）滂．沱（pāng）D. 肖．像（xiào）粗犷．（guǎng）关卡．（kǎ）胡诌．（zōu）2. 下列词语中加点字的读音，全都正确的一组是A. 咄．咄逼人（duō）叱咤．风云（zhà）纵横捭．阖（bǎi）锲．而不舍（qì）B. 不容置喙．（huì）蓦．然回首（mò）乘．人之危（chèng）度德量．力（liàng）C. 栉．风沐雨（zhì）无稽．之谈（jī）间．不容发（jiān）舐．犊情深（shì）D. 装模．作样（mú）荷．枪实弹（hé）方枘．圆凿（ruì）自出机杼．（zhù）3. 下列各组词语中，没有错别字的一组是A. 录像范畴斑马线绿草如茵B. 装潢沧桑霓红灯水乳交溶C. 仓皇暇疵必需品安分守已D. 缅怀影牒捅娄子山清水秀4. 下列各组词语中，没有错别字的一组是A. 没精打采轻歌曼舞积腋成裘弥天大谎B. 人情世故旁证博引振聋发聩老生长谈C. 墨守成规掉以轻心平心而论曲意逢迎D. 名门望族突如奇来变本加厉英雄辈出5. 依次填入下列各句横线处的词语，最恰当的一项是①面对记者的拍照和采访，这位在华尔街工作的女士并不___________自己的投票决定：“我投奥巴马的票，我的家人和朋友基本都一样。

北京市西城区2012高三期末语文答案

北京市西城区2011 — 2012学年度第一学期期末试卷高三语文参考答案及评分标准 2012、1[试题解析]1．D [A项应为“两全其．美”“悬崖勒．（lè）马”；B项应为“顷．刻之间”“匕(bǐ)首”；C项应为“赔小心”“市侩(kuài)”。

]2．D [①“独树一帜”，单独树立起一面旗帜，比喻自成一家。

“独具匠心”，指具有与众不同的巧妙的构思。

与“风格”搭配，应用“独树一帜”。

②“情趣”，性情志趣或情调趣味。

“雅趣”，高雅的意趣。

在“对宋词的品鉴、仿作”“独特的美学追求”等语境中，用“雅趣”更佳。

③“精致”，精巧细致，为形容词。

“精品”，精心制作的上乘物品或作品，为名词。

前面的中心词是“旧体词”，后文又有“古人佳作”，应用名词“精品”。

]3．C [A项中“义无反顾”的意思是在道义上只有勇往直前，绝对不能退缩回头。

含褒义，用于此处褒贬失当。

B项中“噤若寒蝉”的意思是像深秋的蝉那样一声不吭，比喻因害怕或有所顾虑而不敢说话。

与下文“纷纷提出质疑”相矛盾。

D项中“溢美之词”的意思是过分夸赞的言论。

褒贬失当。

用在此处不合语境。

C项中“方兴未艾”的意思是事物正在发展，一时不会终止。

符合本句语境。

]4．B [A不合逻辑，用“所以”联系上下句，强加因果。

C结构混乱，开始的主语为“美国民众”，最后分句的主语暗换成了“占领华尔街活动”；搭配不当，“抗议……问题”动宾搭配不当。

D表意不明。

前面提出答案具有两面性的两个问题，后句中代词“此”，指向不明确。

]5．B [《阿房宫赋》的作者杜牧并非“唐宋八大家”之一。

]6．D [备，防备，防人之心。

]7．A [A项：于是，就。

B项：①于是，因此；②凭借。

C项：①给，替；②表被动。

D项：①指示代词，那里的；②语气副词，加强反问语气。

]8．C [官军或者朝廷讨伐叛军不力，而非裴度。

]9．A [裴寰并没有痛骂小使的丑恶行径，是小使诬陷裴寰狂言侮辱朝廷。

]第二部分（共123分）三、（30分）10．上闻景州录事参军张玄素名，召见，问以政道。

北京市9区2012届高三上学期期末考试试题数

北京市西城区2011—2012学年度第一学期期末试卷高三数学（文科） 2012.1第Ⅰ卷（选择题共40分）一、选择题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项. 1．复数i (1i)⋅+=（）（A ）1i + （B ）1i -（C ）1i -+（D ）1i --2．若向量=a ，(0,2)=-b ，则与2+a b 共线的向量可以是（）（A）1)- （B）(1,-（C）(1)-（D）(1-3.下列函数中，既是偶函数又在(0,)+∞单调递增的函数是（）（A ）1y x=-（B ）||e x y = （C ）23y x =-+ （D ）cos y x =4．“直线l 的方程为0x y -=”是“直线l 平分圆221x y +=的周长”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分又不必要条件5．一个几何体的主视图和左视图如图所示，则这个几何体的俯视图不可能．．．是（）（A ）（B ）（C ）（D ）6．执行如图所示的程序框图，输出的S 值为（）（A ）3 （B ）6- （C ）10 （D ）15-7．已知0a b >>，给出下列四个不等式：① 22a b >； ② 122ab ->； ③> ④ 3322a b a b +>．其中一定成立的不等式为（）（A ）①、②、③ （B ）①、②、④ （C ）①、③、④ （D ）②、③、④8．有限集合P 中元素的个数记作card()P .已知card()10M =，A M ⊆，B M ⊆，A B =∅ ，且card()2A =，card()3B =.若集合X 满足X M ⊆，且A X ⊄，B X ⊄，则集合X 的个数是（）（A ）672 （B ）640（C ）384（D ）352第Ⅱ卷（非选择题共110分）二、填空题共6小题，每小题5分，共30分.9．函数()f x =______.10．双曲线221169x y -=的一个焦点到其渐近线的距离是______．11．若曲线3y x ax =+在原点处的切线方程是20x y -=，则实数a =______．12．在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ．若b =4B π∠=， tan 2C =，则c =______．13．已知{}n a 是公比为2的等比数列，若316a a -=，则1a = ；22212111na a a +++= ______． 14．设0λ>，不等式组 2,0,20x x y x y λλ≤⎧⎪-≥⎨⎪+≥⎩所表示的平面区域是W ．给出下列三个结论：① 当1λ=时，W 的面积为3； ② 0λ∃>，使W 是直角三角形区域； ③ 设点(,)P x y ,对于P W ∀∈有4yx λ+≤．其中，所有正确结论的序号是______．三、解答题共6小题，共80分. 解答应写出文字说明，演算步骤或证明过程. 15.（本小题满分13分）已知函数2()sin cos f x x x x =+，π[,π]2x ∈. （Ⅰ）求2π()3f 的值；（Ⅱ）求()f x 的最大值和最小值.16.（本小题满分13分）某种零件按质量标准分为5,4,3,2,1五个等级.现从一批该零件中随机抽取20个，对其等级进行统计分析，得到频率分布表如下：（Ⅰ）在抽取的20个零件中，等级为5的恰有2个，求n m ,；（Ⅱ）在（Ⅰ）的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级恰好相同的概率.17．（本小题满分14分）如图，正三棱柱111C B A ABC -的侧棱长和底面边长均为2，D 是BC 的中点．（Ⅰ）求证：AD ⊥平面11B BCC ；（Ⅱ）求证：1A B ∥平面1ADC ；（Ⅲ）求三棱锥11ADB C -的体积．18.（本小题满分13分）已知函数21()ln 2f x ax x =+，其中a ∈R . （Ⅰ）求)(x f 的单调区间；（Ⅱ）若)(x f 在(0,1]上的最大值是1-，求a 的值.19.（本小题满分14分）已知椭圆:C 22221(0)x y a b a b+=>>的一个焦点是(1,0)F ，且离心率为12.（Ⅰ）求椭圆C 的方程；（Ⅱ）设经过点F 的直线交椭圆C 于,M N 两点，线段MN 的垂直平分线交y 轴于点0(0,)P y ，求0y 的取值范围.20.（本小题满分13分）已知数列12:,,,n n A a a a .如果数列12:,,,n n B b b b 满足1n b a =，11k k k k b a a b --=+-，其中2,3,,k n = ，则称n B 为n A 的“衍生数列”. （Ⅰ）写出数列4:2,1,4,5A 的“衍生数列”4B ；（Ⅱ）若n 为偶数，且n A 的“衍生数列”是n B ，证明：1n b a =；（Ⅲ）若n 为奇数，且n A 的“衍生数列”是n B ，n B 的“衍生数列”是n C ，….依次将数列n A ，n B ，n C ，…的首项取出，构成数列111:,,,a b c Ω .证明：Ω是等差数列.北京市西城区2011 — 2012学年度第一学期期末高三数学（文科）参考答案及评分标准2012.1一、选择题：本大题共8小题，每小题5分，共40分.1. C ；2. D ；3. B ；4. A ；5. D ；6. C ；7. A ；8. A .二、填空题：本大题共6小题，每小题5分，共30分.9. {|1}x x ≥； 10.3； 11.2；12. 13.2，1(14)3n--； 14. ①、③.注：13题第一问2分，第二问3分；14题多选、少选、错选均不给分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分. 15.（本小题满分13分）（Ⅰ）解：22π2π2π2π()sin cos 3333f =+==. ………………4分（Ⅱ）解：1π()1cos2sin 2sin(2)23f x x x x =-+=-） ………………8分因为π[,π]2x ∈，所以π2π5π2[]333x -∈,. ………………9分当π2π233x -=，即π2x =时，)(x f ………………11分当π3π232x -=，即11π12x =时，)(x f 的最小值为1- ………………13分16.（本小题满分13分）（Ⅰ）解：由频率分布表得 0.050.150.35m n ++++=，即 0.45m n +=. ………………2分由抽取的20个零件中，等级为5的恰有2个，得 1.0202==n . ………………4分所以0.450.10.35m =-=. ………………5分（Ⅱ）解：由（Ⅰ）得，等级为3的零件有3个，记作123,,x x x ；等级为5的零件有2个，记作12,y y .从12312,,,,x x x y y 中任意抽取2个零件，所有可能的结果为：12131112232122313212(,),(,),(,),(,),(,),(,),(,),(,),(,),(,)x x x x x y x y x x x y x y x y x y y y共计10种. ………………9分记事件A 为“从零件12312,,,,x x x y y 中任取2件，其等级相等”.则A 包含的基本事件为12132312(,),(,),(,),(,)x x x x x x y y 共4个. ………………11分故所求概率为 4()0.410P A ==.………………13分17.（本小题满分14分）（Ⅰ）证明：因为111C B A ABC -是正三棱柱，所以 1CC ⊥平面ABC . 又 AD ⊂平面ABC ，所以 AD CC ⊥1. ………………3分因为 △ABC 是正三角形，D 是BC 的中点，所以 AD BC ⊥， ………………4分所以 AD ⊥平面11B BCC . ………………5分（Ⅱ）证明：连结1AC ，交1AC 于点O ，连结OD .由 111C B A ABC -是正三棱柱，得四边形11ACC A 为矩形，O 为1AC 的中点.又D 为BC 中点，所以OD 为1A BC △中位线，所以 1A B ∥OD ， ………………8分因为 OD ⊂平面1ADC ，1A B ⊄平面1ADC ，所以 1A B ∥平面1ADC . ………………10分（Ⅲ）解：因为 1111D C B A AD B C V V --=， ………………12分所以 1111Δ13C ADB B DC V S AD -=⋅=. ………………14分 18.（本小题满分13分）（Ⅰ）解：21(),(0,)ax f x x x+'=∈+∞. ………………3分当0≥a 时，()0f x '>，从而函数)(x f 在),0(+∞上单调递增. ………………4分当0<a 时，令()0f x '=，解得x =x =………………5分此时，()f x 与()f x '的情况如下：所以，()f x 的单调增区间是；单调减区间是),1(∞+-a.…………7分（Ⅱ）① 当0≥a 时，由（Ⅰ）得函数)(x f 在]1,0(上的最大值为(1)2a f =. 令12a=-，得2a =-，这与0≥a 矛盾，舍去2a =-. ………………9分 ② 当10a -≤<时，11≥-a，由（Ⅰ）得函数)(x f 在]1,0(上的最大值为(1)2a f =.令12a=-，得2a =-，这与10a -≤<矛盾，舍去2a =-. ………………10分③ 当1-<a 时，01<，由（Ⅰ）得函数)(x f 在]1,0(上的最大值为f .令1f =-，解得e a =-，适合1-<a . ………………12分综上，当)(x f 在(0,1]上的最大值是1-时，e a =-. ………………13分19.（本小题满分14分）（Ⅰ）解：设椭圆C 的半焦距是c .依题意，得 1c =. ………………1分因为椭圆C 的离心率为12，所以22a c ==，2223b a c =-=. ………………3分故椭圆C 的方程为 22143x y +=. ………………4分（Ⅱ）解：当MN x ⊥轴时，显然00y =. ………………5分当MN 与x 轴不垂直时，可设直线MN 的方程为(1)(0)y k x k =-≠.由 22(1),3412,y k x x y =-⎧⎨+=⎩消去y 整理得 0)3(48)43(2222=-+-+k x k x k .………………7分设1122(,),(,)M x y N x y ，线段MN 的中点为33(,)Q x y .则 2122834k x x k +=+. ………………8分所以 212324234x x k x k +==+，3323(1)34k y k x k -=-=+.线段MN 的垂直平分线方程为)434(1433222k k x k k k y +--=++. 在上述方程中令0=x ，得k kk k y 4314320+=+=. ………………10分当0k <时，34k k +≤-0k >时，34k k+≥所以0012y -≤<，或0012y <≤. ………………12分综上，0y 的取值范围是[]1212. ………………13分20.（本小题满分13分）（Ⅰ）解：4:5,2,7,2B -. ………………3分（Ⅱ）证明：因为 1n b a =，1212b b a a +=+， 2323b b a a +=+，……11n n n n b b a a --+=+，由于n 为偶数，将上述n 个等式中的第2,4,6,,n 这2n个式子都乘以1-，相加得 11223112231()()()()()()n n n n n b b b b b b b a a a a a a a ---+++--+=-+++--+ 即1n b a -=-，1n b a =. ………………8分（Ⅲ）证明：对于数列n A 及其“衍生数列”n B ，因为 1n b a =，1212b b a a +=+， 2323b b a a +=+，……11n n n n b b a a --+=+，由于n 为奇数，将上述n 个等式中的第2,4,6,,1n - 这12n -个式子都乘以1-，相加得11223112231()()()()()()n n n n n b b b b b b b a a a a a a a ---+++-++=-+++-++即112n n n n b a a a a a =-+=-.设数列n B 的“衍生数列”为n C ，因为 1n b a =，112n n c b a a ==-，所以 1112b a c =+，即111,,a b c 成等差数列. ………………12分同理可证，111111,,;,,,b c d c d e 也成等差数列. 从而Ω是等差数列. ………………13分。

北京市9区2012届高三上学期期末考试试题--数学AnllPl

北京市房山区2012届高三上学期期末统测数学（理）试题第I 卷选择题（共40分）一、选择题（本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.）1. 已知集合{}{}0,1,2,3,4,1,3,5,,M N P M N ===I 则P 的子集共有( ) A.7个 B. 6个 C. 5个 D. 4个2．已知向量==),2,1()4,(-x ，若a ∥，则=⋅（） A.-10 B.-6 C.0 D.6 3．已知命题22:bm am p <，命题b a q <:，则p 是 q 的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分又不必要条件4．极坐标方程θρsin 2=和参数方程⎩⎨⎧--=+=t y tx 132（t 为参数）所表示的图形分别为（）A. 圆，圆B. 圆，直线C. 直线，直线D.直线，圆5．已知奇函数)(x f 在区间（－∞，0）内单调递增，且0)2(=-f ，则不等式()0f x ≤的解集为（） A []2,2- B (](]2,02,Y -∞- C (][)+∞-∞-,22,Y D [][)+∞-,20,2Y6．在数列{}n a 中，若12a =，且对任意的正整数,p q 都有q p q p a a a =+，则8a 的值为（） A ．256 B ．128 C ．64 D ．327．已知点),(y x P 的坐标满足条件⎪⎩⎪⎨⎧≥+-≥≥0321y x x y x ，那么点P 到直线0943=--y x 的距离的最小值为( )A.514 B.56C.2D.1 8.已知函数22()1,(,)f x x ax b b a b R =-++-+∈对任意实数x 都有(1)(1)f x f x -=+成立，若当[11]x ∈-，时，()0f x >恒成立，则b 的取值范围是（）A ．10b -<<B ．2b >C ．21b b ><-或D ．1b <- 第II 卷非选择题(共110分）二、填空题（本大题共6小题,每小题5分,共30分.把答案填在答题纸上指定位置.） 9. 若复数ii--121的实部为a ，虚部为b ，则b a += . 10. 如图，有一圆盘,其中的阴影部分圆心角为45o，若向圆内投镖，则投中阴影部分的概率为 .11．某程序框图如图所示，该程序运行后输出的值是 .12．已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是 3cm .13.圆O 的直径AB ＝6，C 为圆周上一点，BC ＝3，过C 作圆的切线l ，则点A 到直线l 的距离AD 为 .ABCDEOl是否结束1i =50S >21S S =+21i i =+输出i开始0S = ？14．规定记号“⊗”表示一种运算，即),(为正实数b a b a ab b a ++=⊗.若31=⊗k ，则k 的值为，此时函数()f x=的最小值为 .三、解答题（本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.） 15．（本小题共13分）设函数2cos 22sin 3)(2++=x x x f ．（I ）求)(x f 的最小正周期和值域；（II ）在△ABC 中，a 、b 、c 分别是角A 、B 、C 的对边，若3π=A ，△ABC 的面积为23，求)(A f 及a 的值．16.（本小题共13分）已知直线:l 0834=-+y x （R a ∈）过圆C: 022=-+ax y x 的圆心交圆C 于A 、B 两点,O 为坐标原点.（I ）求圆C 的方程;(II) 求圆C在点P（1,3）处的切线方程;∆的面积.(III)求OAB17.（本小题共14分）如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD=，E，F分别是AB，PB的中点．为正方形，PD=DC2EF平面PAD；（Ⅰ）求证：//（Ⅱ）求直线EF 与CD 所成的角；（Ⅲ）求二面角B EC F --的余弦值．18.（本小题共13分）已知数列{}n a 的前n 项和为n S ，11=a ,且3231=++n n S a (n •∈N ).(I ) 求32,a a 的值,并求数列{}n a 的通项公式;(II )若对任意正整数nn S k ≤,恒成立,求实数k 的最大值.19.（本小题共14分）已知函数()2ln pf x px x x=--，R p ∈．（I ）若2p =，求曲线()f x 在点(1,(1))f 处的切线方程；（II ）若函数()f x 在其定义域内为增函数，求正实数p 的取值范围；（III ）设函数22()()p g x f x x+=+，求函数()g x 的单调区间．20．（本小题共13分）已知函数23()3x f x x+=，数列}{n a 对N n n ∈≥,2总有111(),1n n a f a a -==. （I ）求{n a }的通项公式；(II) 求和：1122334451(1)n n n n S a a a a a a a a a a -+=-+-++-L ；（III ）若数列}{n b 满足：①}{n b 为1{}n a 的子数列（即}{n b 中的每一项都是1{}n a 的项，且按在1{}na 中的顺序排列）②}{nb 为无穷等比数列，它的各项和为21。

北京市各区2012届高三第一学期化学期末试卷汇编

北京市昌平区高三年级第一学期期末化学考试北京市朝阳区高三年级第一学期期末统一考试北京市东城区2012届高三上学期期末教学统一检测丰台区2011-2012学年度第一学期高三化学期末试题石景山区2011—2012学年第一学期期末考试试卷石景山区2011—2012学年第一学期期末考试试卷2012年2月北京市昌平区高三年级第一学期期末化学考试(2012.01)相对原子质量：H 1 C 12 O 16 F 19 Na 23 Si 28 Cu 64一、单选题(每小题3分，共48分)6．下列做法用到物质氧化性的是( ) A．明矾净化水B．纯碱除去油污C．臭氧消毒餐具D．食醋清洗水垢7．下列说法中正确的是( ) A．热稳定性H2O＞HF＞H2SB．原子半径Na＞Mg＞OC．酸性H3PO4＞H2SO4＞HClOD．金属性Na＞K＞Ca8．下列说法中正确的是( ) A．2.4g金属Mg变为镁离子失去0.1×6.02×1023个电子B．1.6gCH4所含的质子数是6.02×1023C．1L0.1mol/LNH4Cl溶液中所含有的NH4+数是0.1×6.02×1023D．标准状况下，5.6LCCl4中所含的分子数是0.25×6.02×10239．“茶倍健”牙膏中含有茶多酚，期中没食子儿茶素(EGC)的结构如下图所示。

关于EGC 的下列叙述中正确的是( )A．分子式为C15H12O7B．EGC可在强碱的醇溶液中发生消去反应C．1molEGC最多消耗6molNaOHD．1molEGC可与4molBr2发生取代反应10．下列说法中正确的是A．可用Na2CO3溶液处理水垢中含有的CaSO4B．SO2通入BaCl2溶液中有白色沉淀产生C．过量CO2通入Na2SiO3溶液，最终无沉淀产生D．在海轮外壳上装若干铜块以减缓腐蚀11．下列离子方程式书写不正确的是( )A．向H2SO4酸化的KI溶液中滴加H2O2：2I－+H2O2+2H+I2+2H2OB．小苏打治疗胃酸过多：H++HCO3H2O+CO2↑C．氯气溶于水：Cl2+H2O H++ Cl－+HClOD．检验溴乙烷中含有的溴元素：Br－+Ag+AgBr↓12．常温下，浓度均为0.1mol/L的三种溶液：①CH3COOH溶液②NaOH溶液③CH3COONa 溶液。

2012年北京市朝阳区高三文科数学第一学期期末试题和答案

北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷（文史类） 2012.1（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）注意事项：考生务必将答案答在答题卡上，在试卷上答无效。

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1.已知集合2{|3},{|log 1}M x x N x x =<=>，则M N 等于（）A ．φB ．}321|{<<x x C ．}30|{<<x xD ．{|23}x x <<2.已知平面向量(3,1)=a ，(,3)x =b ，且a ⊥b ，则实数x 的值为（）A ．9-B ．1-C ．1D ．93. 函数⎪⎩⎪⎨⎧≥-<=)0(12)0(2x x x y x的图象大致是（）4. 设数列{}n a 是公差不为0的等差数列，11a =且136,,a a a 成等比数列，则{}n a 的前n 项和n S 等于（）A ． 2788n n +B ．2744n n+ C ．2324n n +D ．2n n +5.执行如图所示的程序框图，输出的S 值为（）A ．1B ．1-C ． 2-D ．06. 函数2()2xf x a x=--的一个零点在区间(1,2)内，则实数a 的取值范围是（） A ．(1,3) B ．(1,2) C ．(0,3) D ． (0,2)7.已知函数()sin f x x x =+，设()7a f π=，()6b f π=，()3c f π=，则,,a b c 的大小关系是（） A. a b c << B.c a b << C.b a c << D.b c a << 8. 已知集合{(,)|,,}A x y x n y na b n ===+∈Z ,{(,)|,B x y x m ==2312,y m =+m ∈Z }.若存在实数,a b 使得A B ≠∅成立,称点(,)a b 为“￡”点，则“￡”点在平面区域22{(,)|108}C x y x y =+≤内的个数是 ( ) A. 0 B. 1 C. 2 D. 无数个第二部分（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.9. 若变量x ，y 满足约束条件1,,236,x y x x y ≥⎧⎪≥⎨⎪+≤⎩则2z x y =+的最大值为 .10. 已知有若干辆汽车通过某一段公路，从中抽取200辆汽车进行测速分析，其时速的频率分布直方图如图所示，则时速在区间[60,70)上的汽车大约有辆.11. 某几何体的三视图如图所示，则这个几何体时速（km/h ）01002 003 00440 50 60 70 80的体积是 .12. 设直线10x my --=与圆22(1)(2)4x y -+-=相交于A ，B 两点，且弦AB的长为m 的值是 .13. 某公司购买一批机器投入生产，据市场分析每台机器生产的产品可获得的总利润y （万元）与机器运转时间x （年数，x *∈N ）的关系为21825y x x =-+-.则当每台机器运转年时，年平均利润最大，最大值是万元.14. 已知两个正数,a b ,可按规则c ab a b =++扩充为一个新数c ,在,,a b c 三个数中取两个较大的数,按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作.（1）若1,3a b ==,按上述规则操作三次,扩充所得的数是__________；（2）若0p q >>，经过6次操作后扩充所得的数为(1)(1)1mnq p ++-（,m n 为正整数），则,m n 的值分别为______________.三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本题满分13分）在锐角三角形ABC 中，a ，b ，c 分别为内角A ，B ，C所对的边，且满足2sin 0b A -=．（Ⅰ）求角B 的大小；（Ⅱ）若b =2c =，求AB AC 的值．16. （本题满分14分）如图，在四棱锥S ABCD -中，平面SAD ⊥平面ABCD ．四边形ABCD 为正方形，且P 为AD 的中点，Q 为SB 的中点．（Ⅰ）求证：CD ⊥平面SAD ；（Ⅱ）求证：//PQ 平面SCD ；（Ⅲ）若SA SD =，M 为BC 中点，在棱SC 上是否存在点N，使得平面DMN ⊥平面ABCD ，并证明你的结论.17. （本题满分13分）如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘，转盘停止转动时，箭头A 所指区域的数字就是每次游戏所得的分数（箭头指向两个区域MSD CAP Q·的边界时重新转动），且箭头A 指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后各转动一次游戏转盘，得分记为(,)a b （假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动）．（Ⅰ）请列出一个家庭得分(,)a b 的所有情况；（Ⅱ）若游戏规定：一个家庭的总得分为参与游戏的两人所得分数之和，且总得分为偶数的家庭可以获得一份奖品．请问一个家庭获奖的概率为多少？18. （本题满分13分）设函数2()ln 2,R 2ax f x a x x a =+-∈. （Ⅰ）当1a =时,试求函数()f x 在区间[1,e]上的最大值; （Ⅱ）当0a ≥时,试求函数()f x 的单调区间. 19. （本题满分13分）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12，且过点3(1,)2P ，F 为其右焦点.（Ⅰ）求椭圆C 的方程；（Ⅱ）设过点(4,0)A 的直线l 与椭圆相交于M 、N 两点（点M 在,A N 两点之间），若AMF △与MFN △的面积相等，试求直线l 的方程.20. （本题满分14分）数列{}n a ，{}n b （1,2,3,n =）由下列条件确定：①110,0a b <>；②当2k ≥时，k a 与k b 满足：当011≥+--k k b a 时，1-=k k a a ,211--+=k k k b a b ；当011<+--k k b a 时，211--+=k k k b a a ，1-=k k b b . （Ⅰ）若11a =-，11b =，求2a ，3a ，4a ，并猜想数列}{n a 的通项公式（不需要证明）；（Ⅱ）在数列}{n b 中，若s b b b >>> 21(3s ≥,且*s ∈N )，试用11,b a 表示k b ，},,2,1{s k ∈；（Ⅲ）在（Ⅰ）的条件下，设数列}{n c (*)n ∈N 满足211=c ，0n c ≠，2212m n n n mc c c ma -+=-+(其中m 为给定的不小于2的整数)，求证：当m n ≤时，恒有1<n c .北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷（文史类）答案 2012.1二、填空题：注：若有两空，则第一个空第二个空三、解答题：（15）（本小题满分13分）解：2sin 0b A -=，根据正弦定理得：2sin sin 0A B A -=.………………………………………………………3分因为sin 0A ≠，所以23sin =B . ………………………………………………5分又B 为锐角，则3B π=. …………………………………………………6分（Ⅱ）由（Ⅰ）可知，3B π=．因为b =2c =，根据余弦定理，得 2744cos3a a π=+-， ……………………………………8分整理，得2230a a --=．由于0a >，得3a =． ……………………………10分于是222cos214b c a A bc +-===， ………………………………11分所以 cos cos 2114AB AC AB AC A cb A ====． ……………13分（16）（本小题满分14分）证明：（Ⅰ）因为四边形ABCD 为正方形，则CD AD ⊥. …………………1分又平面SAD ⊥平面ABCD ，且面SAD 面ABCD AD =，所以CD ⊥平面SAD . ………………………………………………………3分（Ⅱ）取SC 的中点R ，连QR, DR ．由题意知：PD ∥BC 且PD =12BC ．…………………4分在SBC ∆中，Q 为SB 的中点，R 为SC 的中点，所以QR ∥BC 且QR =12BC ．所以QR ∥PD 且QR=PD ，则四边形PDRQ 为平行四边形. …………………………………………………7分所以PQ ∥DR .又PQ ⊄平面SCD ，DR ⊂平面SCD ，所以PQ ∥平面SCD ． ……………………………………………………………10分（Ⅲ）存在点N 为SC 中点，使得平面DMN ⊥平面ABCD ． ………………11分连接PC DM 、交于点O ，连接PM 、SP ，因为//PD CM ，并且PD CM =，所以四边形PMCD 为平行四边形，所以PO CO =. 又因为N 为SC 中点，所以//NO SP ．………………………………………………………………………12分因为平面SAD ⊥平面ABCD ，平面SAD 平面ABCD =AD ，并且SP AD ⊥，所以SP ⊥平面ABCD ，所以NO ⊥平面ABCD ， ……………………………………………………13分又因为NO ⊂平面DMN ，所以平面DMN ⊥平面ABCD ．……………………………………………………14分（17）（本小题满分13分）解：（Ⅰ）由题意可知，一个家庭的得分情况共有9种，分别为(2,2),(2,3),(2,5),(3,2)，(3,3),(3,5),(5,3),(5,2),(5,5)． …………………………………………………………7分（Ⅱ）记事件A ：一个家庭在游戏中获奖，则符合获奖条件的得分情况包括 (2,2)，(3,3),(3,5),(5,3),(5,5)共5种， ……………………………………………11分所以5()9P A =．所以一个家庭获奖的概率为59． …………………………………………………13分（18）（本小题满分13分）解: （Ⅰ）函数()f x 的定义域为(0,)+∞. ………………………………………………1分当1a =时,2()ln 22x f x x x =+-，因为21(1)()20x f x x x x -'=+-=≥， …3分 M SDBCAPQ·R (N )O所以函数()f x 在区间[1,e]上单调递增，则当=e x 时,函数()f x 取得最大值2e (e )12e 2f =+-. …………………………………………………………………5分（Ⅱ）22()ax x af x x-+'=. ………………………………………………………6分当0a =时,因为()20f x '=-<，所以函数()f x 在区间(0,)+∞上单调递减；…7分当0a >时，⑴当2440a ∆=-≤时，即1a ≥时，()0f x '≥，所以函数()f x 在区间(0,)+∞ 上单调递增； …………………………………………………………9分⑵当2440a ∆=->时，即01a <<时，由()0f x '>解得，10x a <<1x a +>. …………………………………………10分由()0f x '<解得11x a a +<<； ………………………………11分所以当01a <<时，函数()f x 在区间1(0,a上单调递增；在上单调递减，)+∞单调递增. ………13分（19）（本小题满分13分）解：（Ⅰ）因为12c a =，所以2a c =，b =. …………………………………1分设椭圆方程为2222143x y c c +=，又点3(1,)2P 在椭圆上,所以2213144c c+=，解得21c =， …………………………………………………………………………3分所以椭圆方程为22143x y +=. …………………………………………………………4分（Ⅱ）易知直线l 的斜率存在,设l 的方程为(4)y k x =-， ……………………………………………………………5分由22(4),1,43y k x x y =-⎧⎪⎨+=⎪⎩消去y 整理，得 2222(34)3264120k x k x k +-+-=， ………………………………………………6分由题意知2222(32)4(34)(6412)0k k k ∆=-+->，解得1122k -<<. ……………………………………………………………………7分设11(,)M x y ，22(,)N x y ，则21223234k x x k +=+，⋅⋅⋅⋅⋅⋅ ①， 2122641234k x x k-=+.… ②. 因为AMF △与MFN △的面积相等，所以AM MN =，所以1224x x =+.⋅⋅⋅⋅⋅⋅ ③ ……………………………………10分由①③消去2x 得21241634k x k +=+.⋅⋅⋅⋅⋅⋅ ④将2124x x =-代入②得21126412(24)34k x x k --=+.⋅⋅⋅⋅⋅⋅ ⑤ 将④代入⑤2222224164166412(24)343434k k k k k k ++-⨯-=+++，整理化简得2365k =，解得k =，经检验成立. …………………………12分所以直线l的方程为4)6y x =±-. …………………………………………13分（20）（本小题满分14分）（Ⅰ）解：因为011=+b a ，所以112-==a a ,02112=+=b a b . ……1分因为0122<-=+b a ,则212223-=+=b a a ,320b b ==. ………………2分 333421222a b a a +===-. ……………………………………………………3分猜想当2n ≥时，22221111222n n n n a a ---⎛⎫⎛⎫=⨯=-⋅=-⎪⎪⎝⎭⎝⎭.则21,1,1, 2.2n n n a n -⎧-=⎪=⎨-≥⎪⎩ …………………………………………………………4分（Ⅱ）解：当s k ≤≤2时，假设110k k a b --+<，根据已知条件则有1-=k k b b ，与s b b b >>> 21矛盾，因此110k k a b --+<不成立， ……………………5分所以有110k k a b --+≥，从而有1k k a a -=，所以1a a k =. ……………………6分当011≥+--k k b a 时，1-=k k a a ，211--+=k k k b a b , 所以111111()22k k k k k k k a b b a a b a -----+-=-=-; …………………………8分当s k ≤≤2时，总有111()2k k k k b a b a ---=-成立. 又110b a -≠，所以}{k k a b -(s k ,,2,1 =)是首项为11b a -，公比为12的等比数列， ……9分 11121)(-⎪⎭⎫⎝⎛-=-k k k a b a b ，1,2,,k s =,又因为1a a k =，所以111121)(a a b b k k +⎪⎭⎫⎝⎛-=-. …………………………10分（Ⅲ）证明：由题意得2212m n n n mc c c ma -+=-+n n c c m+=21. 因为211n n n c c c m +=+，所以2110n n n c c c m+-=>.所以数列{}n c 是单调递增数列. ………………………………………………11分因此要证)(1m n c n ≤<，只须证1<m c . 由2≥m ，则n n n c c m c +=+211<n n n c c c m++11，即1111n n c c m +->-. …12分因此1122111)11()11()11(1c c c c c c c c m m m m m +-++-+-=--- m m m m 121+=+-->. 所以11m mc m <<+.故当m n ≤,恒有1<n c . ………………………………………………………14分。

北京市朝阳区2012届高三上学期期末考试试题

北京市朝阳区2012届高三上学期期末考试试题语文本试卷答题纸共4页。

考生务必将答案答在机读卡和答题纸上，在试卷上作答无效。

考试结束后，请收回机读卡和答题纸。

第一部分（27分）一、本大题共5小题，每小题3分，共15分。

1．下列词语中，字形和加点的字的读音全都正确的一项是A．步后尘美仑美奂绯．（féi）闻拾．（shè）级而上B．报不平戒骄戒躁模．（mó）样称．（chèn）心如意C．破天荒披沙捡金戏谑．（xuě）海外同胞．（pāo）D．耐用品流离失所包扎．（zā）独当．（dāng）一面2．下列句子中，加点的成语使用恰当的一项是A．在刚刚结束的第72届男子举重世界锦标赛中，中国选手吕小军不孚众望．．．．，获得了抓举和总成绩两枚金牌。

B．随着美国金融危机的进一步扩大蔓延，多家跨国企业面临银行一次性收回全部贷款的釜底抽薪．．．．的严峻局面。

C．“斗茶”是一种评比茶技高下的比赛活动，富有生活情趣和文化内涵，曾经在宋代的文人雅士间风靡一时．．．．。

D．一顿美餐之后，有的人甘之如饴．．．．，有的人却会暖气、泛酸、胃痛，这些症状很可能是患有胃肠疾病的信号。

3．下列句子中，没有语病的一句是A．为加强校车安全管理，防止校车安全事故不再发生，国务院法制办起草公布了《校车安全条例（草案征求意见稿）》。

B．中科院紫金山天文台研究员王思潮介绍，本次月全食是继今年1月10日之后我国境内观测条件最好的一次月全食。

C．地沟油不仅脏而且危害极大，其中含有多种有毒有害物质，会使人导致肠癌、胃癌等恶性疾病，严重威胁身体健康。

D．比赛中有很多实力弱的球队战胜强队，是因为他们做到了坚持到底、士气高昂，不到最后一秒钟不罢休的顽强信念。

4．下列有关文学常识的表述，有错误的一项是A．“楚辞”是战国时代伟大诗人屈原创造的一种诗体，他的诗集《楚辞》是我国第一部浪漫主义诗歌总集。

B．清代文学家蒲松龄以毕生精力创作的《聊斋志异》，艺术成就很高，是中国古代优秀的文言短篇小说集。

2012北京海淀期末语文高三上学期含答案

北京市海淀区高三年级第一学期期末练习语文2012.1第一部分(共27分)一、本大题共5小题，每小题3分，共15分。

1. 下列词语中，字形和加点的字读音全都正确的一项是A. 果腹珠联璧和木讷．（n à）嘉言懿．（y ì）行 B. 奇葩独辟蹊径裹挟．（xi é）曲．（q ū）突徙薪 C. 法码语焉不详信笺．（qi ān ）舐．（sh ì）犊情深 D. 雾霾认人唯贤丰腴．（y ú）握发吐哺．（f ǔ） 2. 下列句子中，加点的成语使用不正确．．．的一项是 A. 据报道，近日科学家们发现了迄今已知的两个最大的黑洞，它们的质量是太阳的100亿倍，整个太阳系在它们面前都显得相形见绌．．．．。

B. 尽管如今搞收藏的人越来越多，但社会上不少拍卖会却与平民无关，普通的收藏者只能望洋兴叹．．．．，因为一般的藏品进不了拍卖会的门槛。

C.姜文在电影《关云长》中饰演曹操，他的表演栩栩如生．．．．，极具个性，有人评论他诠释了一个前所未有的带有“姜文”印记的曹操。

D.孙家栋院士如数家珍．．．．地向前来参观的人们介绍了我国绕月探测工程五大系统的特点，并特别强调这五大系统处处是“中国制造”。

3.下列句子中，没有语病的一句是A.为迅速平息“冰箱门事件”，西门子公司就此向消费者诚恳道歉，以避免对公司终端产品的销售和品牌形象造成更大的损毁。

B.德班气候大会举行期间，场外的示威抗议活动持续不断，环保人士高喊口号，要求各国政要在应对气候变化上做出更多努力。

C.在日本那些再现曲水宴的表演中，有着不少“中国元素”，但是由于现代年轻人对古代中国文化了解甚少，并不知道哪些元素来自中国。

D.历史和现实表明，一个民族是否具有高度的文化自觉与文化自信，不仅决定着一个民族的前途命运，而且关系到文化自身的繁荣。

4.下列有关文学常识的表述，有错误的一项是A.赋、比、兴是《诗经》中常用的表现手法，《关雎》开头的“关关雎鸠，在河之洲。

北京市东城区2012届高三上学期期末考试语文试题

东城区 2011—2012 学年度第一学期期末教课一致检测高三语文本试卷共 6 页， 150 分。

考试时长 150 分钟。

考生务势必答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（27 分）一、本大题共 5 小题，每题 3 分，共 15 分。

1.以下词语中，字形和加点的字读音全都正确的一项为哪一项A. 勘误表察言观色付梓(zǐ)．B. 度难关山清水秀下载(zài)．C.综合征蛛丝蚂迹胡扯(zōu)．D.孤零零独辟溪径谄谀(chǎn)．焚膏继晷 ( ɡuǐ)．爱憎分明 (j ìnɡ)．酩酊烂醉 (mǐnɡ)．心宽体胖 (p ànɡ)．2.以下句子中，加点的成语使用正确的一项为哪一项A. 教育专家就“怎样打造美好讲堂” 的问题坐而论道，一线教师听后特别激动，感觉受益匪浅。

．．．．B. 在新加坡你能够品味到星洲辣蟹、肉骨茶和娘惹菜等美食，品类之丰，实在是擢发难数。

．．．．C.时隔二十多年，我们再次欢聚一堂，与以前沥尽心血培养我们的韩教练共享天伦之乐。

．．．．D.秦始皇的焚书之举及其对诸子百家的监禁，造成了当时中国社会万籁俱寂的烦闷场面。

．．．．3.以下句子中，没有语病的一句是A. 受投资者对欧洲出台债务危机解决方案的乐观预期等要素的影响，纽约油价再次重返每桶 90 美元。

B.当苏格拉底、柏拉图与学生对话的时候，中国也出现了孔墨孟荀等人弟子众多、充满天下的盛况。

C. 领土资源部禁止工商公司借口“租借”“流转”之名下乡圈地、私自改变土地用途、损害农民利益的行为。

D.占有关部门介绍，全国律师代理的各种诉讼案件有效保护了当事人的合法权益，促使了司法公正。

4.以下有关文学知识的表述，有错误的一项为哪一项A.《诗经》是我国最早的一部诗歌总集，它创始了现实主义诗歌创作的先河，与《书》《礼》《易》《春秋》合为儒家“五经” 。

B.“未入麒麟阁，不时望帝乡。

北京市9区2012届高三上学期期末考试试题--数学AnllPK

石景山区2011—2012学年第一学期期末考试试卷高三数学（文科）第Ⅰ卷选择题一、选择题：本大题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合{}4,3,2,1=U ，{}2,1=A ,{}4,2=B ,则=⋃)(B A C U （） A ． }3{ B ． }2{C ．}4,2,1{D ．}4,1{2．已知复数i1i1z -+=，则复数z 的模为（） A ． 2B ． 2C ．1D ．03．设)(x f 是定义在R 上的奇函数，当0≤x 时，x x x f -=22)(，则=)1(f （）4．如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为2，那么这个几何体的体积为（）A ．38 B ．34 C ．4 D ．25．执行右面的框图，若输入实数2=x ，则输出结果为（）A ．-3B ．-1C ．1D ．3正视图侧视图俯视图A ．22 B ．41 C ．12- D ．216.设抛物线x y 82=上一点P 到y 轴的距离是4，则点P 到该抛物线准线的距离为（）A ．4B ．6C ．8D ．127.以下四个命题中，真命题的个数是（） ①命题“若0232=+-x x ，则1=x ”的逆否命题为“若1≠x ，则0232≠+-x x ”； ②若q p ∨为假命题，则p 、q 均为假命题；③命题p ：存在R x ∈,使得012<++x x ，则p ⌝：任意R x ∈,都有012≥++x x ；④在ABC ∆中,B A <是B A sin sin <的充分不必要条件. A ．1 B ．2 C ．3 D ．48.对于使M x x ≤+-22成立的所有常数M 中，我们把M 的最小值1叫做22x x -+的上确界,若+∈R b a 、，且1=+b a ，则122a b--的上确界为（） A ．92B ．92-C ．41 D ．-4第Ⅱ卷非选择题二、填空题：本大题共6个小题，每小题5分，共30分． 9．在ABC ∆中，若32,120,2=︒=∠=a A c ，则=∠B ．10．统计某校1000名学生的数学会考成绩，得到样本频率分布直方图如下图，规定不低于60分为及格，不低于80分为优秀．则及格人数是；优秀率为．11．已知向量)1,3(=a ，)1,0(=b ，)3,(k c =，若b a 2+与c 垂直，则=k ．12．已知等差数列{}n a 的前n 项和为n S ，若4518a a =-，则8S = ．13．若实数,x y 满足条件⎪⎩⎪⎨⎧≤≥+≥+-.1,2,01x y x y x 则2x y +的最大值为．14.已知函数)1,0(log )(≠>+-=a a b x x x f a 且，当2131<<a 且43<<b 时，函数)(x f 的零点*0),1,(N n n n x ∈+∈，则=n ．三、解答题：本大题共6个小题，共80分．应写出文字说明，证明过程或演算步骤． 15．（本小题满分13分）已知函数x x x f 2sin 21cos 3)(2+=．（Ⅰ）求)(x f 的最小正周期；（Ⅱ）求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ，上的最大值和最小值．16．（本小题满分13分）甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下：甲乙FCA1 8 6 0 02 4 4 23（Ⅰ）求乙球员得分的平均数和方差；（Ⅱ）分别从两人得分中随机选取一场的得分，求得分和超过55分的概率．（注：方差[]222212)()()(1x x x x x x ns n -++-+-=其中x 为1x ，2x ，⋯n x 的平均数）17．（本小题满分13分）如图，矩形ADEF 与梯形ABCD 所在的平面互相垂直，AD CD ⊥，AB ∥CD ，2AB AD ==，4CD =，M 为CE 的中点．（Ⅰ）求证：BM ∥平面ADEF ；（Ⅱ）求证：BC ⊥平面BDE ．18．（本小题满分14分）已知椭圆12222=+by a x （0>>b a ）过点M （0，2），离心率36=e .（Ⅰ）求椭圆的方程；（Ⅱ）设直线1+=x y 与椭圆相交于B A 、两点，求AMB S ∆.19．（本小题满分14分）已知.,ln )(R a x ax x f ∈-=（Ⅰ）当2=a 时，求曲线)(x f 在点))1(,1(f 处的切线方程；（Ⅱ）若)(x f 在1=x 处有极值，求)(x f 的单调递增区间；（Ⅲ）是否存在实数a ，使()f x 在区间(]e ,0的最小值是3，若存在，求出a 的值；若不存在，说明理由.20．（本小题满分13分）对于给定数列{}n c ，如果存在实常数,p q 使得1n n c pc q +=+对于任意*n N ∈都成立，我们称数列{}n c 是 “κ类数列”．（Ⅰ）若n a n 2=，32n n b =⋅，*n N ∈，数列{}n a 、{}n b 是否为“κ类数列”？若是，指出它对应的实常数,p q ，若不是，请说明理由；（Ⅱ）证明：若数列{}n a 是“κ类数列”，则数列}{1++n n a a 也是“κ类数列”；（Ⅲ）若数列{}n a 满足12a =，)(23*1N n t a a n n n ∈⋅=++，t 为常数．求数列{}n a 前2012项的和．并判断{}n a 是否为“κ类数列”，说明理由．石景山区2011—2012学年第一学期期末考试试卷高三数学（文科）参考答案一、选择题：本大题共8个小题，每小题5分，共40分．二、填空题：本大题共6个小题，每小题5分，共30分．注：两空的题第1个空3分，第2个空2分.三、解答题：本大题共6个小题，共80分．应写出文字说明，证明过程或演算步骤． 15．（本小题满分13分）解：（Ⅰ）x x x f 2sin 2122cos 13)(++∙= 232sin 212cos 23++=x x 23)32sin(++=πx ……………5分π=T ……………7分（Ⅱ）因为46ππ≤≤-x ，所以ππ65320≤+≤x …………9分当232ππ=+x 时，即12π=x 时，)(x f 的最大值为231+；………11分当032=+πx 时，即6π-=x 时，)(x f 的最小值为23. ………13分16．（本小题满分13分）解：（Ⅰ）由茎叶图可知，乙球员四场比赛得分为18,24,24,30，所以平均数24430242418=+++=x ； ……………………2分[]18)2430()2424()2424()2418(4122222=-+-+-+-=s . ……5分（Ⅱ）甲球员四场比赛得分为20,20,26,32，分别从两人得分中随机选取一场的得分，共有16种情况：（18，20）（18，20）（18，26）（18，32）（24，20）（24，20）（24，26）（24，32）（24，20）（24，20）（24，26）（24，32）（30，20）（30，20）（30，26）（30，32） …………9分得分和超过55分的结果有：（24，32）（24，32）(30，26)（30，32） …………11分求得分和超过55分的概率为41. ………13分17．（本小题满分13分）解：（Ⅰ）证明：取DE 中点N ，连结,MN AN ．在△EDC 中，,M N 分别为,EC ED 的中点， ………2分所以MN ∥CD ，且12MN CD =．由已知AB ∥CD ，12AB CD =，所以MN ∥AB ，且MN AB =．所以四边形ABMN 为平行四边形． ………4分所以BM ∥AN ．又因为AN ⊂平面ADEF ，且BM ⊄平面ADEF ，所以BM ∥平面ADEF ． ………………………………6分（Ⅱ）证明：在矩形ADEF 中，ED AD ⊥．又因为平面ADEF ⊥平面ABCD ，且平面ADEF平面ABCD AD =，所以ED ⊥平面ABCD ．所以ED BC ⊥． ………………………………9分在直角梯形ABCD 中，2AB AD ==，4CD =，可得BC =在△BCD中，4BD BC CD ===，因为222BD BC CD +=，所以BC BD ⊥．因为BD DE D ⋂=,所以BC ⊥平面BDE ．………………………13分18．（本小题满分14分）解：（Ⅰ）由题意得36,2==a c b 结合222c b a +=，解得122=a所以，椭圆的方程为141222=+y x . ………………5分（Ⅱ）由⎪⎪⎩⎪⎪⎨⎧+==+1141222x y y x 得12)1(322=++x x ………………6分即09642=-+x x ，经验证0>∆. 设),(),,(2211y x B y x A . 所以49,232121-=⋅-=+x x x x ， ………………8分 221221221)2)()AB x x y y x x -=-+-=（（，2103]4)[2AB 21221=-+=x x x x （ ………………11分因为点M 到直线AB 的距离222120=+-=d ， ………………13分所以4532221032121=⨯⨯=⨯⨯=∆d AB S AMB . ………………14分19．（本小题满分14分）解：（Ⅰ）由已知得)(x f 的定义域为(0)+∞，，因为()ln f x ax x =-，所以'1()f x a x =-当2a =时，()2ln f x x x =-，所以(1)2f =，因为'1 ()2f x x =-，所以'1 (1)211f =-=……………………2分所以曲线)(x f 在点))1(,1(f 处的切线方程为2(1)(1)y f x '-=-，即10x y -+=. …………………………4分（Ⅱ）因为)(x f 在1=x 处有极值，所以(1)0f '=，由（Ⅰ）知(1)1f a '=-，所以1a =经检验，1a =时)(x f 在1=x 处有极值． …………………………5分所以()ln f x x x =-，令'1()10f x x=->解得10x x ><或；因为)(x f 的定义域为(0)+∞，，所以'()0f x >的解集为(1)+∞，，即)(x f 的单调递增区间为(1)+∞，. …………………………………………8分（Ⅲ）假设存在实数a ，使x ax x f ln )(-=（],0(e x ∈）有最小值3， ① 当0≤a 时，因为(]e x ,0∈，所以0)('<x f ，所以)(x f 在],0(e 上单调递减，31)()(min =-==ae e f x f ，解得ea 4=，舍去. ……………………10分 ②当e a<<10时，)(x f 在)1,0(a 上单调递减，在],1(e a 上单调递增，3ln 1)1()(min =+==a a f x f ，解得2e a =，满足条件. …………………12分③ 当e a≥1时，因为(]e x ,0∈，所以0)('<x f ，所以)(x f 在],0(e 上单调递减，31)()(min =-==ae e f x f ，解得ea 4=，舍去. 综上，存在实数2e a =，使得当],0(e x ∈时()f x 有最小值3. ……………14分20．（本小题满分13分）解：（Ⅰ）因为2,n a n =则有12,n n a a +=+*n N ∈故数列{}n a 是“κ类数列”，对应的实常数分别为1,2； …………… 1分因为32n n b =⋅，则有12n n b b +=，*n N ∈.故数列{}n b 是“κ类数列”，对应的实常数分别为2,0. ……………3分（Ⅱ）证明：若数列{}n a 是“κ类数列”，则存在实常数q p 、，使得1n n a pa q +=+对于任意*n N ∈都成立，且有21n n a pa q ++=+对于任意*n N ∈都成立，因此()()1212n n n n a a p a a q ++++=++对于任意*n N ∈都成立，故数列{}1n n a a ++也是“κ类数列”．对应的实常数分别为,2p q ． ……………6分（Ⅲ）因为 *132()n n n a a t n N ++=⋅∈ 则有1232a a t +=⋅，33432a a t +=⋅，20092009201032a a t +=⋅20112011201232a a t +=⋅故数列{}n a 前2012项的和2012S =()12a a ++()34a a +++()20092010a a ++()20112012a a +()320092011201232323232221t t t t t =⋅+⋅++⋅+⋅=-……………9分若数列{}n a 是“κ类数列”，则存在实常数q p 、使得1n n a pa q +=+对于任意*n N ∈都成立，且有21n n a pa q ++=+对于任意*n N ∈都成立，因此()()1212n n n n a a p a a q ++++=++对于任意*n N ∈都成立，而*132()n n n a a t n N ++=⋅∈，且)(23*121N n t a a n n n ∈⋅=++++，则有132322n n t t p q +⋅=⋅+对于任意*n N ∈都成立，可以得到(2)0,0t p q -==，当2,0p q ==时，12n n a a +=，2n n a =，1t =，经检验满足条件. 当0,0t q == 时，1n n a a +=-，12(1)n n a -=-，1p =-经检验满足条件. 因此当且仅当1t =或0t =时，数列{}n a 是“κ类数列”.对应的实常数分别为2,0或1,0-． ………………… 13分注：若有其它解法，请酌情给分．。

北京市9区2012届高三上学期期末考试试题--数学_-_方法AnllAA

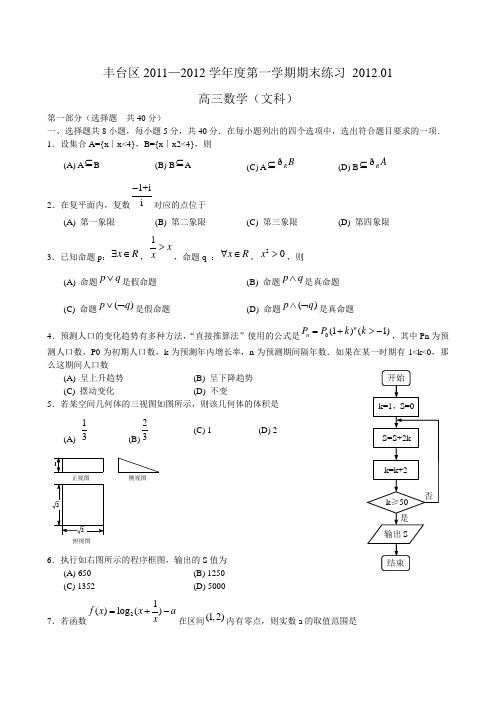
丰台区2011—2012学年度第一学期期末练习 2012.01高三数学（文科）第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．设集合A={x ∣x<4}，B={x ∣x2<4}，则(A) A ⊆B(B) B ⊆A(C) A ⊆R Bð(D) B ⊆R Að2．在复平面内，复数1+ii -对应的点位于(A) 第一象限(B) 第二象限(C) 第三象限(D) 第四象限3．已知命题p ：x R ∃∈，1x x >，命题q ：x R ∀∈，20x >，则(A) 命题p q ∨是假命题 (B) 命题p q ∧是真命题 (C) 命题()p q ∨⌝是假命题(D) 命题()p q ∧⌝是真命题4．预测人口的变化趋势有多种方法，“直接推算法”使用的公式是0(1)(1)n n P P k k =+>-，其中Pn 为预测人口数，P0为初期人口数，k 为预测年内增长率，n 为预测期间隔年数．如果在某一时期有-1<k<0，那么这期间人口数(A) 呈上升趋势 (B) 呈下降趋势 (C) 摆动变化 (D) 不变5．若某空间几何体的三视图如图所示，则该几何体的体积是 (A) 13(B)23(C) 1(D) 2俯视图侧视图正视图6．执行如右图所示的程序框图，输出的S 值为(A) 650 (B) 1250 (C) 1352 (D) 50007．若函数21()log ()f x x ax =+-在区间(1,2)内有零点，则实数a 的取值范围是(A) 25(log ,1)2--(B) (1,)+∞(C) 25(0,log )2 (D)25(1,log )28．如图，P 是正方体ABCD —A1B1C1D1对角线AC1上一动点，设AP 的长度为x ，若△PBD 的面积为f(x)，则f(x)的图象大致是y xO(A)yxO(B)yxO(C) yxO(D)第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．过点(-1,3)且与直线x-2y+3=0平行的直线方程为．10．已知函数2log ,(0),()2,(0).xx x f x x >⎧=⎨≤⎩ 若1()2f a =，则a= ． 11．某个容量为100的样本的频率分布直方图如图所示，则数据在区间[8,10) 上的频数是．12．若向量a r ，b r 满足2a =r ，2b =r ，()a b a -⊥r r r ，则向量a r 与b r 的夹角等于___．13．设Sn 是等比数列{an}的前n 项和，若S1，2S2，3S3成等差数列，则公比q 等于．14．函数()f x 的导函数为'()f x ，若对于定义域内任意1x ，2x 12()x x ≠，有121212()()'()2f x f x x xf x x -+=-恒成立，则称()f x 为恒均变函数．给出下列函数：①()=23f x x +；②2()23f x x x =-+；③1()=f x x ；D 1C 1B 1A 1PDCBA④()=xf x e ；⑤()=ln f x x ．其中为恒均变函数的序号是．（写出所有满足条件的函数序号）三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数2()2cos 2xf x x =．（Ⅰ）求函数()f x 的最小正周期和值域；（Ⅱ）若α为第二象限角，且1()33f πα-=，求cos 21tan αα-的值．16.（本小题共14分）如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC ，AC=BC ，M ，N 分别是CC1，AB 的中点．（Ⅰ）求证：CN ⊥AB1；（Ⅱ）求证：CN //平面AB1M ．17.（本小题共13分）为了解某地区中学生的身体发育状况，拟采用分层抽样的方法从甲、乙、丙三所中学抽取6个教学班进行调查.已知甲、乙、丙三所中学分别有12，6，18个教学班.NMC 1B 1A 1CB A（Ⅰ）求从甲、乙、丙三所中学中分别抽取的教学班的个数；（Ⅱ）若从抽取的6个教学班中随机抽取2个进行调查结果的对比，求这2个教学班中至少有1个来自甲学校的概率.18.（本小题共13分）在平面直角坐标系xOy 中，O 为坐标原点，以O 为圆心的圆与直线40x --=相切．（Ⅰ）求圆O 的方程；（Ⅱ）直线l ：3y kx =+与圆O 交于A ，B 两点，在圆O 上是否存在一点M ，使得四边形OAMB 为菱形，若存在，求出此时直线l 的斜率；若不存在，说明理由．19.（本小题共14分）已知函数x x bax x f ln 2)(++=．（Ⅰ）若函数)(x f 在1=x ，21=x 处取得极值，求a ，b 的值；（Ⅱ）若(1)2f '=，函数)(x f 在),0(+∞上是单调函数，求a 的取值范围．20.（本小题共13分）函数()f x 的定义域为R ，数列{}n a 满足1=()n n a f a -（*n N ∈且2n ≥）．（Ⅰ）若数列{}n a 是等差数列，12a a ≠，且11()()()n n n n f a f a k a a ---=-(k 为非零常数， *n N ∈且2n ≥)，求k 的值；（Ⅱ）若()(1)f x kx k =>，12a =，*ln ()n n b a n N =∈，数列{}n b 的前n 项和为n S ，对于给定的正整数m ，如果(1)m nmn S S +的值与n 无关，求k 的值．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2011—2012学年度第一学期期末练习2012．01 高三数学（文科）答案及评分参考一、选择题共8小题，每小题5分，共40分。

北京市海淀区2012届高三上学期期末考试试题

北京市海淀区2012届高三上学期期末考试试题数学（文）2012.01一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. （1）复数i(12i)-=（A ）2i -+ （B ）2i + （C ）2i - （D ）2i -- （2）如图，正方形ABCD 中，点E ，F 分别是DC ，BC 的中点，那么=EF（A ）1122AB AD +（B ）1122AB AD -- （C ）1122AB AD -+（D ）1122AB AD -（3）已知数列{}n a 满足：22111, 0, 1(*)n n n a a a a n +=>-=∈N ，那么使5n a <成立的n 的最大值为（）（A ）4 （B ）5 （C ）24 （D ）25 （4）某程序的框图如图所示，若执行该程序，则输出的i 值为（A ）5 （B ）6 （C ）7 （D ）8（5）已知直线1l ：110k x y ++=与直线2l ：210k x y +-=，那么“12k k =”是“1l ∥2l ”的（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件（6）函数()sin(2)(,)f x A x A ϕϕ=+?R 的部分图象如图所示，那么(0)f =（A ）12- （B ）1- （C）- （D）-F（7）已知函数()2f x x x x =-，则下列结论正确的是（A ）()f x 是偶函数，递增区间是()0,+?（B ）()f x 是偶函数，递减区间是(,1)-?（C ）()f x 是奇函数，递减区间是()1,1- （D ）()f x 是奇函数，递增区间是(),0-?（8）点A 到图形C 上每一个点的距离的最小值称为点A 到图形C 的距离. 已知点(1,0)A ，圆C ：2220x x y ++=，那么平面内到圆C 的距离与到点A 的距离之差为1的点的轨迹是（A ）双曲线的一支（B ）椭圆（C ）抛物线（D ）射线二、填空题：本大题共6小题，每小题6分，共30分，把答案填在题中横线上.（9）双曲线22145x y -=的离心率为 .（10）已知抛物线2y ax =过点1(,1)4A ，那么点A 到此抛物线的焦点的距离为 .（11）若实数,x y 满足40,250,10,x y x y y ì+-?ïïï+-?íïï-?ïïî 则2z x y =+的最大值为 .（12）甲和乙两个城市去年上半年每月的平均气温（单位：C °）用茎叶图记录如下，根据茎叶图可知，两城市中平均温度较高的城市是_____________，气温波动较大的城市是____________.（13）已知圆C ：22(1)8x y -+=，过点(1,0)A -的直线l 将圆C 分成弧长之比为1:2的两段圆弧，则直线l 的方程为 .（14）已知正三棱柱'''ABC A B C -的正（主）视图和侧（左）视图如图所示. 设,'''ABC A B C ∆∆的中心分别是,'O O ，现将此三棱柱绕直线'OO 旋转，射线OA 旋转所成的角为x 弧度（x 可以取到任意一个实数），对应的俯视图的面积为()S x ，则函数()S x 的最大值为；最小正周期为 .甲城市乙城市9 087 7 3 1 2 4 72 2 0 4 7侧（左）视图正（主）视图说明：“三棱柱绕直线'OO 旋转”包括逆时针方向和顺时针方向，逆时针方向旋转时，OA 旋转所成的角为正角，顺时针方向旋转时，OA 旋转所成的角为负角.三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤. （15）（本小题满分13分）在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ， 2A B =，sin B =. （Ⅰ）求cos A 的值；（Ⅱ）若2b =，求边,a c 的长.(16)（本小题满分13分）为加强大学生实践、创新能力和团队精神的培养，促进高等教育教学改革，教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序.通过预赛，选拔出甲、乙和丙三支队伍参加决赛.（Ⅰ）求决赛中甲、乙两支队伍恰好排在前两位的概率；（Ⅱ）求决赛中甲、乙两支队伍出场顺序相邻的概率.（17）（本小题满分13分）在四棱锥P ABCD -中，底面ABCD 是菱形，PAC BD O =.（Ⅰ）若AC PD ⊥，求证：AC ⊥平面PBD ；（Ⅱ）若平面PAC ^平面ABCD ，求证：PB PD =；（Ⅲ）在棱PC 上是否存在点M （异于点C ）使得BM ∥平面PAD ，若存在，求PMPC的值；若不存在，说明理由.(18)（本小题满分13分）已知函数2()e ()xf x x ax a =+-，其中a 是常数. （Ⅰ）当1a =时，求()f x 在点(1,(1))f 处的切线方程；（Ⅱ）求()f x 在区间[0,)+∞上的最小值.（19）（本小题满分13分）已知椭圆C :22221(0)x y a b a b+=>>的右焦点为1F (1,0)，离心率为12. （Ⅰ）求椭圆C 的方程及左顶点P 的坐标；（Ⅱ）设过点1F 的直线交椭圆C 于,A B 两点，若PAB ∆的面积为3613，求直线AB 的方程.（20）（本小题满分14分）若集合A 具有以下性质： ①A ∈0，A ∈1；②若A y x ∈,，则A y x ∈-，且0≠x 时，A x∈1. 则称集合A 是“好集”.（Ⅰ）分别判断集合{1,0,1}B =-，有理数集Q 是否是“好集”，并说明理由；（Ⅱ）设集合A 是“好集”，求证：若A y x ∈,，则A y x ∈+；（Ⅲ）对任意的一个“好集”A ，分别判断下面命题的真假，并说明理由. 命题p ：若A y x ∈,，则必有A xy ∈；命题q ：若A y x ∈,，且0≠x ，则必有A xy∈；参考答案及评分标准 2012．01一.选择题：本大题共8小题，每小题5分，共40分.题号 1 2 3 4 5 6 7 8 答案BDCACBCD二.填空题：本大题共6小题，每小题5分，共30分.（9）32 （10）54（11）7 （12）乙，乙（13）1y x =+或1y x =-- （14）8；3π注：（13）题正确答出一种情况给3分，全对给5分；（12）、（14）题第一空3分；第二空2分. 三.解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤. （15）（本小题满分13分）解：（Ⅰ）因为2A B =，所以2cos cos 212sin A B B ==-. ………………………………………2分因为sin 3B =，所以11cos 1233A =-?. ………………………………………3分（Ⅱ）由题意可知，(0,)2B πÎ.所以cos B ==………………………………………5分所以sin sin 22sin cos 3A B B B ===. ………………………………………7分因为sin sin b aB A=，2b =，=.所以a =. ………………………………………10分由1cos 3A =可知，(0,)2A πÎ.过点C 作CD AB ^于D .所以110cos cos 233c a B b A=???. ………………………………………13分(16)（本小题满分13分）解：基本事件空间包含的基本事件有“甲乙丙，甲丙乙，乙甲丙，乙丙甲，丙甲乙，丙乙甲”. ………………………………………2分（Ⅰ）设“甲、乙两支队伍恰好排在前两位”为事件A ，事件A 包含的基本事件有“甲乙丙，乙甲丙”，则 ………………………………………4分()2163P A ==. 所以甲、乙两支队伍恰好排在前两位的概率为13. ………………………………………7分（Ⅱ）设“甲、乙两支队伍出场顺序相邻”为事件B ，事件B 包含的基本事件有“甲乙丙，乙甲丙，丙甲乙，丙乙甲”，则………………………………………10分()4263P B ==. 所以甲、乙两支队伍出场顺序相邻的概率为23. ………………………………………13分(17)（本小题满分14分）（Ⅰ）证明：因为底面ABCD 是菱形所以 AC BD ⊥. ………………………………………1分因为 AC PD ⊥，PDBD D =，所以 AC ⊥平面PBD . ………………………………………3分（Ⅱ）证明：由（Ⅰ）可知AC BD ⊥. 因为平面PAC ^平面ABCD ，平面PAC平面ABCD AC =，BD Ì平面ABCD ，所以 BD ⊥平面PAC . ………………………………………5分因为 PO Ì平面PAC ，所以 BD PO ⊥. ………………………………………7分因为底面ABCD 是菱形，所以 BO DO =.所以 PB PD =. ………………………………………8分（Ⅲ）解：不存在. 下面用反证法说明. ………………………………………9分假设存在点M （异于点C ）使得BM ∥平面PAD . 在菱形ABCD 中，BC ∥AD ，因为 AD Ì平面PAD ，BC Ë平面PAD ，所以 BC ∥平面PAD .………………………………………11分因为 BM Ì平面PBC ，BC Ì平面PBC ，BC BM B =，所以平面PBC ∥平面PAD .………………………………………13分而平面PBC 与平面PAD 相交，矛盾. ………………………………………14分(18)（本小题满分13分）解：（Ⅰ）由2()e ()xf x x ax a =+-可得2'()e [(2)]xf x x a x =++. ………………………………………2分当1a =时,(1)e f = ,'(1)4e f =. ………………………………………4分所以曲线()y f x =在点(1,(1))f 处的切线方程为()e 4e 1y x -=-，即4e 3e y x =-. ………………………………………6分（Ⅱ）令2'()e [(2)]0xf x x a x =++=，解得(2)x a =-+或0x =. ………………………………………8分当(2)0a -+≤，即2a ≥-时，在区间[0,)+∞上，'()0f x ≥，所以()f x 是[0,)+∞上的增函数.MBCDO AP所以()f x 的最小值为(0)f ＝a -; ………………………………………10分当(2)0a -+>，即2a <-时, ()'(),f x f x 随x 的变化情况如下表由上表可知函数()f x 的最小值为2((2))e a f a +-+=. ……………………………………13分（19）（本小题满分13分）解：（Ⅰ）由题意可知：1c =，12c a =，所以2a =. 所以 2223b a c =-=.所以椭圆C 的标准方程为22143x y +=，左顶点P 的坐标是(2,0)-. ……………………………………4分（Ⅱ）根据题意可设直线AB 的方程为1x my =+，1122(,),(,)A x y B x y .由221,431x y x my ìïï+=ïíïï=+ïî可得：22(34)690my my ++-=. 所以 223636(34)0m m ∆=++>，122634m y y m +=-+，122934y y m =-+. ……………………………………7分所以 PAB ∆的面积12111322S PF y y =-=创……………………………………9分= ………………………………………10分因为PAB ∆的面积为3613，213=.令t =22(1)3113t t t =?+.解得116t =（舍），22t =.所以m =?所以直线AB 的方程为10x -=或10x --=.……………………………………13分（20）（本小题满分14分）解：（Ⅰ）集合B 不是“好集”. 理由是：假设集合B 是“好集”. 因为1B -?，B ∈1，所以112B --=-?. 这与2B -?矛盾.………………………………………2分有理数集Q 是“好集”. 因为0ÎQ ，1ÎQ , 对任意的,x y ÎQ ，有x y -?Q ，且0≠x 时，1xÎQ . 所以有理数集Q 是“好集”. ………………………………………4分（Ⅱ）因为集合A 是“好集”，所以 A ∈0.若,x y A Î，则A y ∈-0，即A y ∈-.所以A y x ∈--)(，即A y x ∈+. ………………………………………7分（Ⅲ）命题q p ,均为真命题. 理由如下： ………………………………………9分对任意一个“好集”A ，任取,x y A Î，若y x ,中有0或1时，显然A xy ∈. 下设y x ,均不为0，1. 由定义可知：A xx x ∈--1,11,1. 所以111A x x -?-，即1(1)A x x Î-. 所以 (1)x x A -?.由（Ⅱ）可得：(1)x x x A -+?，即2x A Î. 同理可得2y A Î.---WORD 格式--可编辑-----WORD 格式--可编辑-- 若0x y +=或1x y +=，则显然2()x y A +?. 若0x y +?且1x y +?，则2()x y A +?. 所以 A y x y x xy ∈--+=222)(2.所以 A xy∈21. 由（Ⅱ）可得：A xy xy xy ∈+=21211. 所以 A xy ∈.综上可知，A xy ∈，即命题p 为真命题. 若,x y A Î，且0x ¹，则1A x Î. 所以1y y A x x =孜，即命题q 为真命题. ……………………………………14分。