人教版数学七年级下册第五章达标检测卷(含解析)
(完整)人教版七年级下册数学第五章测试题及答案,推荐文档
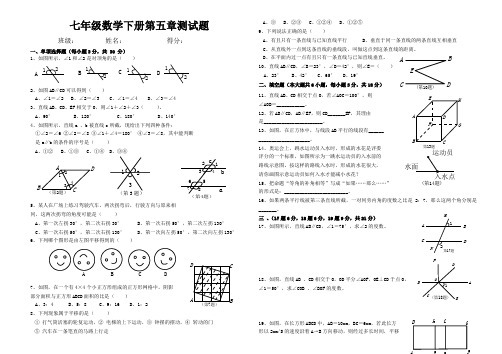
A BC D E(第10题)(第14题)ABCDEF G H第13题ABCD 1234(第2题)12345678(第4题)ab cABCD(第7题)1A BOFDEC (第18题)第17题A B CDMN12七年级数学下册第五章测试题班级:______ 姓名:_________ 得分:__________一、单项选择题(每小题3分,共 30 分) 1、如图所示,∠1和∠2是对顶角的是( )ABC D121212122、如图AB∥CD 可以得到( )A 、∠1=∠2 B、∠2=∠3 C 、∠1=∠4 D、∠3=∠4 3、直线AB 、CD 、EF 相交于O ,则∠1+∠2+∠3( )。
A 、90° B 、120°C 、180°D 、140° 4、如图所示,直线a 、b 被直线c 所截,现给出下列四种条件: ①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断 是a∥b 的条件的序号是( ) A 、①② B、①③ C、①④ D 、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相 同,这两次拐弯的角度可能是( )A 、第一次左拐30°,第二次右拐30°B 、第一次右拐50°,第二次左拐130°C 、第一次右拐50°,第二次右拐130°D 、第一次向左拐50°,第二次向左拐130° 6、下列哪个图形是由左图平移得到的( )BD7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影 部分面积与正方形ABCD 面积的比是( ) A 、3:4 B 、5:8 C 、9:16 D 、1:2 8、下列现象属于平移的是( )① 打气筒活塞的轮复运动,② 电梯的上下运动,③ 钟摆的摆动,④ 转动的门 ⑤ 汽车在一条笔直的马路上行走A 、③ B、②③ C、①②④ D、①②⑤ 9、下列说法正确的是( )A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
人教版七年级下册数学第五章测试题及答案

人教版七年级下册数学第五章测试题及答案 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-123(第三题)12345678(第4题)ab c七年级数学下册第五章测试题姓名 ________ 成绩 _______一、单项选择题(每小题3分,共 30 分) 1、如图所示,∠1和∠2是对顶角的是( ) 2、如图AB ∥CD 可以得到( )A 、∠1=∠2 B、∠2=∠3 C 、∠1=∠4 D、∠3=∠4 3、直线AB 、CD 、EF 相交于O ,则∠1+∠2+∠3( )。
A 、90° B 、120°C 、180°D 、140°4、如图所示,直线a 、b 被直线c 所截,现给出下列四种条件:①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a ∥b 的条件的序号是( ) A 、①② B、①③ C、①④ D、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( ) A 、第一次左拐30°,第二次右拐30° B 、第一次右拐50°,第二次左拐130° C 、第一次右拐50°,第二次右拐130°A B C DE(第10题)ADEF G HABCD(第7题)D 、第一次向左拐50°,第二次向左拐130° 6、下列哪个图形是由左图平移得到的( )7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD 面积的比是( ) A 、3:4 B 、5:8 C 、9:16 D 、1:2 8、下列现象属于平移的是( )① 打气筒活塞的轮复运动,② 电梯的上下运动,③ 钟摆的摆动,④ 转动的门,⑤ 汽车在一条笔直的马路上行走 A 、③ B、②③ C、①②④ D、①②⑤ 9、下列说法正确的是( ) A 、有且只有一条直线与已知直线平行 B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段,叫做这点到这 条直线的距离。
(完整word版)人教版七年级数学下册第五章测试题(含答案),推荐文档

第五章订交线与平行线检测题一、选择题〔每题 3 分,共 30 分〕1.以下命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有〔〕A.1 个B.2个C.3 个D.4 个2.点 P 是直线 l 外一点, A 为垂足,,且 PA=4 cm,那么点P 到直线 l 的距离〔〕A.小于 4 cm B.等于 4 cm C.大于 4 cm D.不确定3.〔2021 ?安徽〕如图,AB∥CD,∠A+∠E=75°,那么∠C为〔〕A. 60 °B. 65 °C. 75°D. 80°8.如图, DH∥ EG∥ BC, DC∥ EF,那么与∠DCB 相等的角的个数为〔A.2 个B.3 个C.4 个D.5 个9. 以下条件中能获取平行线的是〔〕①邻补角的角均分线;②平行线内错角的角均分线;③平行线同旁内角的角均分线.A.①②B.②③C.②D.③10. 两平行直线被第三条直线所截,同位角的均分线〔〕A.互相重合B.互相平行线号题答第3题图4.〔 2021 ?襄阳〕如图,BD 平分∠ ABC,CD∥ AB ,假设∠ BCD=70 °,那么∠ ABD 的度数为〔〕5.〔2021 ?孝感〕如图,∠1=∠ 2,∠3=40°,那么∠4 等于〔〕B 封不A. 120 °B. 130 °C. 140 °D. 40°名6.如图, AB∥ CD, AC⊥ BC,图中与∠ CAB 互余的角有〔〕姓内A.1 个B.2 个C.3 个D.4 个线封密级第 5题图第 6图班密A 中,先作AB⊥ CD,足为 B,尔校A.∠ 1=∠ 2B.∠ 3=∠ 4学C.∠ 5=∠D.∠ +∠ BDC=180°第7题图第8题图第1页,共8页第2页,共8页第15题图 第 16题图 16.如图, AB ∥ CD ,直线 EF 分别交 AB 、CD 于 E 、F ,EG 均分∠ BEF ,假设∠ 1=72°,那么∠ 2=.17.如图,直线 a ∥ b ,那么∠ ACB= .线号学题答第17题图第18题图18.〔2021 ?郴州〕如图,∥ ,∠1=60°, 那么∠2=度 .ABCD得 三、解答题〔共 6 小题,总分值 46 分〕19.〔 7 分〕读句画图:如图,直线CD 与直线 AB 订交于 C ,名 封 不依照以下语句画图:〔 1〕过点 P 作 PQ ∥ CD ,交 AB 于点 Q ;姓内〔 2〕过点 P 作 PR ⊥ CD ,垂足为 R ;线 〔 3〕假设∠ DCB=120°, 猜想∠ PQC 是多少度?并说明原由.封密级第 19 题图20.〔 7 分〕如图,方格中有一条美丽可爱的小金鱼.班密〔 1〕假设方格的边长为 1,那么小鱼的面积为;校〔 2〕画出小鱼向左平移3 格后的图形. 〔不要求写作图步骤和过程〕学第20题图21.〔8 分〕:如图,∠BAP +∠ APD =180 °,∠ 1 = ∠ 2. 求证:∠ E = ∠ F .22.〔8 分〕:如图,∠1 = ∠2,∠ 3 = ∠ 4,∠ 5 = ∠ 6. 求证: ED ∥ FB .23.〔 8 分〕如图, CD 均分∠ ACB , DE ∥ BC ,∠ AED=80°,求∠ EDC 的度数.第23题图24.〔 8 分〕如图,AB ∥ CD ,∠ B=65°, CM 均分∠ BCE ,∠ MCN=90°,求∠ DCN 的度数.第五章订交线与平行线检测题参照答案 1.B 剖析:①是正确的,对顶角相等;②正确,在同一平面内,垂直于同一条直线的两直线平行;③错误,角均分线分成的两个角相等但不是对顶角;④错误,同位角只有在两直线平行的情况下才相等.故①②正确,③④错误,因此错误的有两个,应选 B.2.B 剖析:依照点到直线的距离为点到直线的垂线段的长度〔垂线段最短〕,因此点 P 到直线 l 的距离等于 4 cm,应选 B.3.C 剖析:∵∠ A+∠E=75°,线∴∠ EOB=∠ A+∠E=75°.号∵AB∥CD,∴∠ C=∠EOB=75°,应选 C.4. A 剖析:∵ CD∥AB,∴∠ ABC+∠ DCB=180°.学∵∠ BCD=70°,∴∠ ABC=180°-70°=110°.题∵BD 均分∠ ABC,∴∠ ABD=55° .答5. C 剖析:如题图所示,∵∠ 1=∠2,∴a∥b,∴∠ 3=∠5.∵∠ 3=40°,∴∠ 5=40°,∴∠ 4=180°-∠ 5=180°-40°=140°,得应选 C.封不6. C 剖析:∵ AB∥CD,∴∠ABC=∠BCD.名设∠ ABC的对顶角为∠ 1,那么∠ ABC=∠ 1.又∵ AC⊥BC,∴∠ACB=90°,姓内∴ ∠CAB+∠ABC=∠CAB+∠ BCD=∠ CAB+∠1=90°,线因此与∠ CAB互余的角为∠ ABC,∠ BCD,∠ 1.应选 C.封7. A 剖析:选项 B 中,∵∠ 3=∠4,∴ AB∥CD 〔内错角相等,两直线平行〕,故正确;密〔内错角相等,两直线平行〕,故正确;选项 C 中,∵∠ 5=∠B,∴ AB∥CD级选项 D 中,∵∠B+∠ BDC=180°,∴ AB∥CD〔同旁内角互补,两直线平行〕,故正确;班密而选项 A 中,∠ 1 与∠ 2 是直线 AC、BD 被直线 AD 所截形成的内错角,∵ ∠ 1=∠2,校∴ AC∥ BD,故 A 错误.选 A.学8.D 剖析:如题图所示,∵ DC∥EF,∴∠DCB=∠ EFB.∵ DH∥ EG∥ BC,∴ ∠GEF=∠EFB,∠ DCB=∠HDC,∠ DCB=∠CMG=∠DME,故与∠ DCB相等的角共有 5 个.应选 D.9.C 剖析:结合条件,利用平行线的判判定理依次推理判断.10.B 剖析:∵ 两条平行直线被第三条直线所截,同位角相等,∴ 它们角的均分线形成的同位角相等,∴同位角相等的均分线平行.应选 B.11.144°剖析:由题图得,∠ 1 与∠ 2 互为邻补角,即∠ 1+∠2=180°.又∵∠ 1=36°,∴ ∠2=180°36° =144°.12.50 剖析:∵∠ BAC=80°,∴∠ EAC=100° .∵AD 均分△ ABC的外角∠ EAC,∴∠ EAD=∠DAC=50° .∵AD∥BC,∴∠ B=∠EAD=50°.故答案为 50.13.垂线段定理:直线外一点与直线上所有点的连线中,垂线段最短剖析:依照垂线段定理,直线外一点与直线上所有点的连线中,垂线段最短,∴沿 AB开渠,能使所开的渠道最短.14.∠ 1+∠2=90°剖析:∵ 直线 AB、EF订交于 O 点,∴∠1=∠ DOF.又∵ AB⊥CD,∴∠2+∠ DOF=90°,∴ ∠1+∠ 2=90°.15.65°剖析:∵∠ 1=155°,∴∠ EDC=180°-155°=25°.∵DE∥BC,∴∠ C=∠EDC=25° .∵在△ ABC中,∠ A=90°,∠ C=25°,∴∠ B=180°-90°-25°=65°.故答案为 65°.16.54°剖析:∵ AB∥ CD,∴ ∠BEF=180°∠ 1=180°72° =108°,∠ 2=∠BEG.又∵ EG均分∠ BEF,∴∠BEG=∠ BEF=× 108°=54°,故∠ 2=∠BEG=54°.17.78°剖析:延长 BC与直线 a 订交于点 D,∵a∥b,∴∠ADC=∠DBE=50°. ∴ ∠ACB=∠ADC +28°=50°+28° =78°.故应填 78°.18. 120 剖析:∵ AB∥CD,∴∠ 1=∠3,而∠ 1=60°,∴∠ 3=60°.又∵∠ 2+∠ 3=180°,∴∠ 2=180° -60°=120°.故答案为 120.19.解:〔1〕〔 2〕以以下图 .第 19 题答图〔3〕∠ PQC=60°.原由:∵ PQ∥ CD,∴ ∠ DCB+∠PQC=180°.∵∠DCB=120°,∴ ∠PQC=180°120° =60°.20.解:〔 1〕小鱼的面积为 7×6 ×5×6 ×2×5 ×4×2 ××1 × ×11=16.〔2〕将每个要点点向左平移 3 个单位,连接即可.线号学题答得封不名姓内线封密第 20 题答图21.证明:∵∠ BAP+∠APD = 180°,∴AB∥ CD.∴ ∠ BAP =∠APC.又∵∠1 =∠2,∴ ∠BAP-∠1 =∠APC-∠2.即∠ EAP =∠APF∴. AE∥FP.∴ ∠E =∠F.22.证明:∵∠ 3 =∠ 4,∴ AC∥BD.∴ ∠6+∠2+∠ 3 = 180°.∵ ∠6 =∠5,∠ 2 =∠1,∴ ∠5+∠1+∠3 = 180°.∴ED∥FB.23.解:∵ DE∥BC,∠ AED=80°,∴ ∠ EDC=∠ BCD,∠ ACB=∠ AED=80°. ∵ CD均分∠ ACB,∴ ∠BCD= ∠ ACB=40°,∴ ∠ EDC=∠ BCD=40°.24.解:∵ AB∥ CD,∴∠ B+∠BCE=180°〔两直线平行,同旁内角互补〕 . ∵ ∠B=65°,∴ ∠ BCE=115° .∵ CM 均分∠ BCE,∴∠ ECM= ∠°.∵ ∠ECM +∠MCN +∠ NCD =180°,∠ MCN=90°,∴ ∠NCD=180°-∠ECM-∠MCN=180°°-90°°.级班校学密。
人教版七年级数学下册第五章测试题(含答案)

农村管理创新探讨随着城市化的推进和农村经济的快速发展,农村管理面临着新的挑战和需求。
如何利用现代科技和管理理念,提升农村管理水平,助力农村发展,成为亟待解决的问题。
本文将从不同角度出发,探讨农村管理的创新。
一、数字农村建设随着信息技术的迅猛发展,数字化已经成为农村管理的关键词之一。
数字农村建设将现代化技术引入到农村,实现农村基础设施的信息化和智能化。
通过建设农村信息化平台,实现数据的互通共享,可以提高资源的配置效率,并为农村发展提供积极支持。
二、贫困农村的创新案例在农村管理创新的过程中,贫困地区的农村发展是重点和难点。
为了解决贫困问题,一些地方政府和社会组织提出了一些创新案例。
例如,通过发展特色农业和乡村旅游,传统贫困地区的农民可以增加收入。
此外,推动农民参与农产品加工和电商平台的建设,也为贫困地区农民创造了更多就业机会。
三、农村土地管理农村土地管理一直是一个复杂而重要的问题。
传统的土地占有权和承包权制度已经无法满足现代农村管理的需求。
一些地方已经开始尝试土地流转和农地集体经营的改革,以适应现代产业发展的需求。
改革可以通过确保农民权益和保护农村环境等方面,推动农村土地资源的更加合理利用。
四、农村金融服务创新传统金融服务往往难以满足农村的需求,例如小额贷款和农民保险等。
现代金融服务的创新可以提供更多种类的金融产品和服务,满足农村发展的多样化需求。
例如,一些地方政府和金融机构合作,成立农村金融合作社,为农民提供方便快捷的金融服务。
五、农村社会组织建设农村社会组织是促进农村管理创新的重要力量。
传统的村民自治组织在一些地方存在效率低下和权力滥用等问题。
为了解决这些问题,一些地方政府开始鼓励和支持农村社会组织的建设。
通过培育和引导有效的农村社会组织,可以提高村民的自治能力,推动农村管理的创新。
六、农村教育创新农村教育是农村人才培养和农村社会发展的重要基础。
农村教育普及和教师素质提升一直是农村管理创新的重要方向。
人教版七年级下册数学第五章测试题及答案.doc
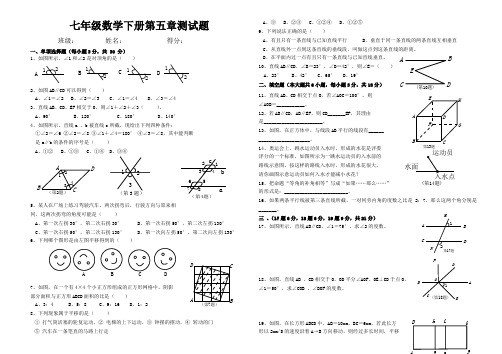
A BC D E(第10题)(第14题)ABCDEF G H第13题ABCD 1234(第2题)12345678(第4题)ab cABCD(第7题)1A BOFDEC (第18题)第17题A B CDMN12七年级数学下册第五章测试题班级:______ 姓名:_________ 得分:__________一、单项选择题(每小题3分,共 30 分) 1、如图所示,∠1和∠2是对顶角的是( )ABC D121212122、如图AB∥CD 可以得到( )A 、∠1=∠2 B、∠2=∠3 C 、∠1=∠4 D、∠3=∠4 3、直线AB 、CD 、EF 相交于O ,则∠1+∠2+∠3( )。
A 、90° B 、120°C 、180°D 、140° 4、如图所示,直线a 、b 被直线c 所截,现给出下列四种条件: ①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断 是a∥b 的条件的序号是( ) A 、①② B、①③ C、①④ D 、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相 同,这两次拐弯的角度可能是( )A 、第一次左拐30°,第二次右拐30°B 、第一次右拐50°,第二次左拐130°C 、第一次右拐50°,第二次右拐130°D 、第一次向左拐50°,第二次向左拐130° 6、下列哪个图形是由左图平移得到的( )BD7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影 部分面积与正方形ABCD 面积的比是( ) A 、3:4 B 、5:8 C 、9:16 D 、1:2 8、下列现象属于平移的是( )① 打气筒活塞的轮复运动,② 电梯的上下运动,③ 钟摆的摆动,④ 转动的门 ⑤ 汽车在一条笔直的马路上行走A 、③ B、②③ C、①②④ D、①②⑤ 9、下列说法正确的是( )A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
人教版数学七年级(下册)第五章测试卷(附参考答案)

人教版数学七年级(下册)第五章测试卷1.下面四个图形中,∠1=∠2一定成立的是( )A.B.C.D.2.如图1所示,∠ADE和∠CED是()图1A.同位角B.内错角C.同旁内角D.互为补角3.如图2所示,AB、CD相交于点O,OE⊥AB,那么下列结论错误的是( )图2A.∠AOC与∠COE互为余角B.∠BOD与∠COE互为余角C.∠COE与∠BOE互为补角D.∠AOC与∠BOD是对顶角4.下列说法错误的是( )A.在同一平面内,两条不平行的直线是相交线B.与同一条直线平行的两条直线必平行C.与同一条直线相交的两条直线必相交D.过直线外一点有且只有一条直线与已知直线平行5.如图3所示,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为( )图3A.40°B.60°C.80°D.100°6.如图4所示,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )图4A.70°B.60°C.50°D.40°7.如图5所示,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )图5A.28°B.30°C.34°D.56°8.如图6所示,△DEF经过怎样的平移得到△ABC( )图6A.把△DEF向左平移4个单位,再向下平移2个单位B.把△DEF向右平移4个单位,再向下平移2个单位C.把△DEF向右平移4个单位,再向上平移2个单位D.把△DEF向左平移4个单位,再向上平移2个单位9.如图7所示,直线a和直线b相交于点O,∠1=50°,则∠2=.图710.如图8所示,AD、BC相交于点O,若∠A=∠AOB,∠D=∠COD,则∠A与∠D的数量关系是.图811.如图9所示,直线a∥b,则∠ACB=.图912.如图10所示,直线a∥b,小明把三角板的直角顶点放在直线b上,量得∠1=55°,则∠2=.图1013.如图11所示,AB∥CD,AD⊥AC,∠ADC=32°,则∠CAB度数是.图1114.某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价50元,主楼梯道宽2米,其侧面如图12所示,则购买地毯至少需要元.图1215.动手操作:(1)画出图中△ABC的高AD,并请标注出点D的位置;(2)画出把△ABC沿射线AD方向平移1 cm后得到的△A1B1C1;(3)在(2)中,根据“图形平移”的性质,得BB1=cm,AC与A1C1的关系是.图1316.如图14所示,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2. 求证:EF∥CD.补全下面证明过程.图14证明:∵ DG⊥BC,AC⊥BC( ),∴∠DGB=∠ACB=90°(垂直的定义).∴ DG∥AC( ).∴∠2 =( ).∵∠1=∠2( ).∴∠1=∠DCA(等量代换).∴ EF∥CD ( ).17.如图15所示,AB、CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD、∠AOE的度数.图1518.已知,如图16所示,AB⊥BC,BC⊥CD且∠1=∠2,求证BE∥CF.图1619.如图17所示,已知AB∥CD,分别写出下列四个图形中∠P与∠A、∠C的关系,请你从所得的四个关系中任选一个加以证明.(1) (2) (3) (4)图1720.阅读:如图18所示,∵CE∥AB,∴∠1=∠A,∠2=∠B.∴∠ACD=∠1+∠2=∠A+∠B.这是一个有用的事实,请用这个事实,在图19中四边形ABCD内引一条和边平行的直线,求出∠A+∠B+∠C+∠D的度数.图18图19参考答案1.B2.B3.C4.C5.D6.C7.A8.A9.50°10.∠A=∠D11.78°12.35°13.122°14.84015.解:画图略.(3)1AC=A1C116.已知同位角相等,两直线平行∠ACD两直线平行,内错角相等已知同位角相等,两直线平行17.解:∵∠AOC=120°(已知),∴∠BOD=120°(对顶角相等).∵∠AOC+∠AOD=180°(平角定义),∴∠AOD=180°-120 °=60°.∵OE平分∠AOD(已知),∴∠AOE=∠AOD=30°(角平分线定义).18.证明:∵AB⊥BC,BC⊥CD,∴∠ABC=∠DCB=90°.∵∠1=∠2,∴∠ABC-∠1=∠DCB-∠2.∴∠CBE=∠BCF.∴BE∥CF.19.解:(1)∠P+∠A+∠C=360°;(2)∠P=∠A+∠C;(3)∠C=∠P+∠A;(4)∠A=∠P+∠C.证明略.20.解:过D作直线DE∥AB,交BC于点E,∴∠ABC=∠DEC,∠A+∠ADE=180°.∵∠CDE+∠DEC+∠C=180°,∴∠A+∠B+∠C+∠D=∠A+∠ADE+∠CDE+∠DEC+∠C=180°+180°=360°.。
人教版七年级数学下册第五章检测卷(含答案解析)
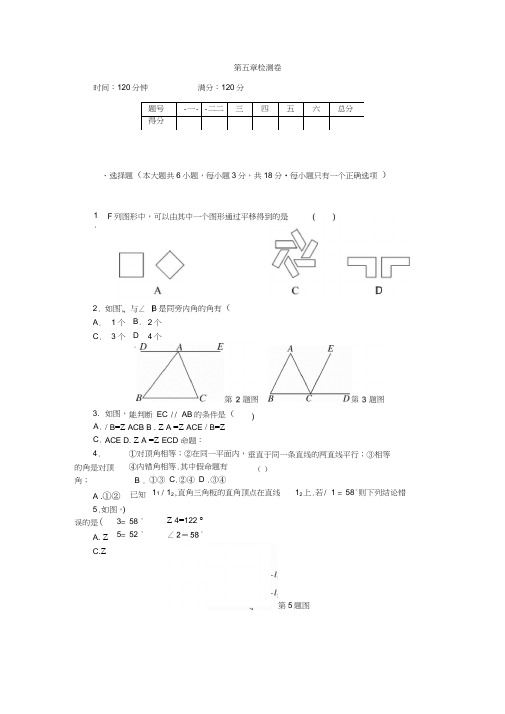
第5题图
6•如图,直线li〃I2,/A=125°ZB=85°则/1+Z2的度数为()
A•30°B•35°C.36°D.40°
二、填空题(本大题共6小题,每小题3分,共18分)
7•如图是一把剪刀,若Z1与Z2互为余角,则Z1=
9•如图,如果Z=Z,那么根据可
10.如图,一张三角形纸片ABC,ZB=45°现将纸片的一角向内折叠, 折痕ED//BC,
在小方格的顶点上•要求:①将三角形ABC平移,使点P落在平移后的三角形内部;②平
移后的三角形的顶点在方格的顶点上.
请你在图甲和图乙中分别画出符合要求的一个示意图,并写出平移的方法.
14. 如图,直线allb,BC平分/ABD,
15.如图,/AOB内有一点P.根据下列语句画图:
(1)过点P作0B的垂线段,垂足为Q;
⑵过点P作线段PC//0B交0A于点C,作线段PD//0A交0B于点D;
(3)写出图中与/0相等的角.
16.如图,在方格纸中,每个小方格的边长均为1,三角形ABC的三个顶点和点P都
第五章检测卷
时间:120分钟
1.
题号
-一-
-二二
三
四
五
六
总分
得分
满分:120分
、选择题(本大题共6小题,每小题3分,共18分•每小题只有一个正确选项)
F列图形中,可以由其中一个图形通过平移得到的是
2.
A.
C.
如图,
1个
3个
能判断EC//AB的条件是(
)
B.
D.
B是同旁内角的角有(
2个
4个
3.
A.
C.
则ZAEB的度数为
人教版七年级数学下册第五章测试题(附答案)

人教版七年级数学下册第五章测试题(附答案)一、单选题(共15题;共30分)1.数轴上一动点A 向左移动2个单位长度到达点B ,再向右移动6个单位长度到达点C ,若点C 表示的数是1,则点A 表示的数为()A. 7B. 3C. -3D. -22.在数轴上,点A,B在原点O的同侧,分别表示数a,3,将点A向左平移5个单位长度得到点C,若点C与点B所表示的数互为相反数,则a的值为()A. 2B. 3C. −1D. 03.点A表示数轴上的一个点,将点A向右移动7个单位,再向左移动4个单位,终点恰好是原点,则点A 表示的数是()A. ﹣3B. 0C. 3D. ﹣24.数轴上一点A表示的数是-2,将点A先向左移动3个单位长度到达点B,再向右移动7个单位长度到达点C,则点C表示的数是()A. 1B. 2C. -1D. -25.数轴上点A表示的数是−3,将点A在数轴上平移7个单位长度得到点B.则点B表示的数是()A. 4B. −4或10C. −10D. 4或−106.在数轴上,A、B两点所表示的数分别为﹣2、3,若移动A点到B点,应把A点()个单位长度.A. 向左移动5B. 向右移动5C. 向右移动4D. 向左移动1或向右移动57.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为()A. 0B. 1C. 2D. 38.如图,已知直线l1∥l2,将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于()A. 39°B. 45°C. 50°D. 51°9.如图.直线a∥b,直线L与a、b分别交于点A,B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为10.如图,能判定EB//AC的条件是()A. ∠1=∠2B. ∠3=∠4C. ∠5=∠6D. ∠2=∠311.在平面直角坐标系中,点P(2,1)向左平移3个单位长度得到的点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限12.如图A、B、C三点共线,C、D、E三点共线,且∠1=∠2,∠1=∠C,下列结论错误的是()A. CE//BFB. ∠F=∠2C. ∠1+∠CBF=180°D. ∠C=∠CBF13.如图,平行线AB,CD被直线AE所截,∠1=75°,则∠2的度数是()A. 75°B. 95°C. 105°D. 115°14.如图,AB//CD,则下列等式正确的是()A. ∠1=∠2+∠3B. ∠1−∠2=180°−∠3C. ∠1−∠3=180°−∠2D. ∠1+∠2+∠3=180°15.如图,将周长为18的△ABC沿BC方向平移2个单位得△DEF,则四边形ABFD的周长为()二、填空题(共4题;共4分)16.如图,数轴上的点A向左移动2个单位长度得到点B,则点B表示的数是________.17.已知点A在数轴上,若一个点从点A处向右移动4个单位长度,再向左移动1个单位长度,此时该点所对应的数是1,那么点A表示的数是________.18.如果点A表示+3,将A向左移动7个单位长度,再向右移动3个单位长度,则终点表示的数是________.19.如图,将两个含角30°的直角三角板的最长边靠在一起滑动,可知直角AB//CD边,依据是________.三、解答题(共1题;共5分)20.如图,已知,∠1=∠3,∠2=∠E,求证:BE//CD.四、综合题(共1题;共10分)21.如图,在平面直角坐标系中,点A、B的坐标分别为(−1,0)、(3,0),现同时先将点A、B分别向上平移2个单位长度,再向右平移1个单位长度,得到A、B的对应点C、D,连接AC、BD、CD.(1)直接写出点C、D的坐标;(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍?若存在,请求出点F的坐标;若不存在,请说明理由.答案一、单选题1. C2. A3. A4. B5. D6. B7. D8. D9. C 10. D 11. B 12. D 13. C 14. B 15. A二、填空题16. -1 17. -2 18. -119. 内错角相等,两直线平行三、解答题20. 证明:∵∠1=∠3,∴AE//DB,∴∠E=∠4∵∠2=∠E,∴∠4=∠2∴BE//CD四、综合题21. (1)解:因为A(−1,0),B(3,0),所以由点坐标的平移变换规律得:C(−1+1,0+2),D(3+1,0+2),即C(0,2),D(4,2)(2)解:存在,求解过程如下:设点F的坐标为F(a,0),∵C(0,2),D(4,2),∴CD//x轴,即CD//AB,∴△DFC边CD上的高与△DFB边BF上的高相等,则当CD=2BF时,△DFC的面积是△DFB面积的2倍,又∵C(0,2),D(4,2),B(3,0),F(a,0),×4=2,∴CD=4−0=4,BF=|3−a|,∴|3−a|=12解得a=1或a=5,故F(1,0)或F(5,0).。
人教版七年级数学下册 第五章 达标检测卷(含答案)
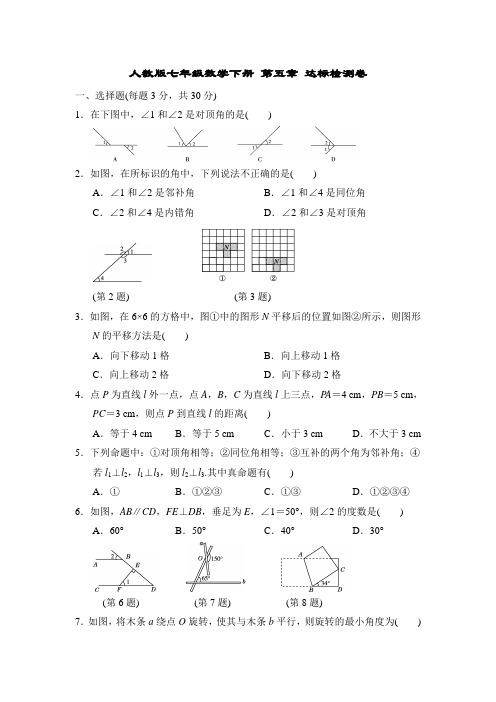
人教版七年级数学下册第五章达标检测卷一、选择题(每题3分,共30分)1.在下图中,∠1和∠2是对顶角的是()2.如图,在所标识的角中,下列说法不正确的是()A.∠1和∠2是邻补角B.∠1和∠4是同位角C.∠2和∠4是内错角D.∠2和∠3是对顶角(第2题)(第3题)3.如图,在6×6的方格中,图①中的图形N平移后的位置如图②所示,则图形N的平移方法是()A.向下移动1格B.向上移动1格C.向上移动2格D.向下移动2格4.点P为直线l外一点,点A,B,C为直线l上三点,P A=4 cm,PB=5 cm,PC=3 cm,则点P到直线l的距离()A.等于4 cm B.等于5 cm C.小于3 cm D.不大于3 cm 5.下列命题中:①对顶角相等;②同位角相等;③互补的两个角为邻补角;④若l1⊥l2,l1⊥l3,则l2⊥l3.其中真命题有()A.①B.①②③C.①③D.①②③④6.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是() A.60°B.50°C.40°D.30°(第6题)(第7题)(第8题)7.如图,将木条a绕点O旋转,使其与木条b平行,则旋转的最小角度为()A.65°B.85°C.95°D.115°8.将一张长方形纸片折叠成如图所示的形状,则∠ABC等于() A.73°B.56°C.68°D.146°9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于()A.81°B.99°C.108°D.120°(第9题)(第10题)10.图①是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中∠CFE的度数是()A.160°B.150°C.120°D.110°二、填空题(每题3分,共30分)11.下列语句:①同旁内角相等;②如果a=b,那么a+c=b+c;③对顶角相等吗?④画线段AB;⑤两点确定一条直线.其中是命题的有__________;是真命题的有__________.(只填序号)12.如图,∠3的同旁内角是________,∠4的内错角是________,∠7的同位角是________.(第12题)(第13题)(第14题)13.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠COM=________.14.如图,跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离________4.6米(填“大于”“小于”或“等于”).15.如图,小明从A处出发,沿北偏东60°的方向行走至B处,又沿北偏西20°的方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是________.(第15题)(第16题)(第17题)16.将一张长方形纸条折成如图所示的形状,若∠1=110°,则∠2=________.17.如图,将三角形ABC沿着点B到点C的方向平移3 cm得到三角形DEF,且DE交AC于点H,AB=6 cm,BC=9 cm,DH=2 cm,那么图中阴影部分的面积为________cm2.18.如图,a∥b,∠1=65°,∠2=140°,则∠3的度数是________.(第18题)(第19题)(第20题)19.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.20.以下三种沿AB折叠的方法:(1)如图①,展开后测得∠1=∠2;(2)如图②,展开后测得∠1=∠2且∠3=∠4;(3)如图③,测得∠1=∠2.其中能判定纸带两条边线a,b互相平行的是________(填序号).三、解答题(24题10分,25题12分,26题14分,其余每题8分,共60分) 21.如图是一条河,C是河岸AB外一点.(1)过点C要修一条与河平行的绿化带(用直线表示),请作出正确的示意图;(2)现欲用水管从河岸AB将水引到C处,问:从河岸AB上的何处开口,才能使所用的水管最短?画图表示,并说明设计的理由.(第21题)22.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.(1)试在图中标出点D,并画出该四边形的另两条边;(2)将四边形ABCD向下平移5个单位长度,画出平移后得到的四边形A′B′C′D′.(第22题)23.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.(第23题)24.如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.(第24题)25.如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.(第25题)26.如图,MN∥EF,C为两直线之间一点.(1)如图①,∠CAM与∠CBE的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.(2)如图②,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.(3)如图③,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请写出∠ACB与∠ADB的数量关系,并证明你的结论.(第26题)答案一、1.C 2.C 3.D 4.D 5.A 6.C 7.B 8.A(第9题)9.B 点拨:如图,过点B 作MN ∥AD ,∴∠ABN =∠A =72°.∵CH ∥AD ,AD∥MN ,∴CH ∥MN ,∴∠NBC +∠BCH =180°,∴∠NBC =180°-∠BCH=180°-153°=27°.∴∠ABC =∠ABN +∠NBC =72°+27°=99°.10.B 点拨:在题图①中,因为四边形ABCD 为长方形,所以AD ∥BC ,所以∠BFE =∠DEF =10°,则∠EFC =180°-∠BFE =170°.在题图②中,∠BFC=∠EFC -∠BFE =170°-10°=160°.在题图③中,∠CFE =∠BFC -∠BFE =160°-10°=150°.故选B .二、11.①②⑤;②⑤12.∠4,∠5;∠2,∠6;∠1,∠4 13. 38° 14. 大于15.向右转80°16.55° 点拨:∵∠1=110°,纸条的两条对边互相平行,∴∠3=180°-∠1=180°-110°=70°.根据折叠的性质可知∠2=12(180°-∠3)=12(180°-70°)=55°.17.15 点拨:由平移的性质知,DE =AB =6 cm ,HE =DE -DH =4 cm ,CF =BE =3 cm ,所以EC =6 cm ,所以S 阴影部分=S 三角形EFD -S 三角形ECH =12DE ·EF -12EH ·EC =12×6×9-12×4×6=15(cm 2). 18.105° 点拨:反向延长射线b ,如图,∵∠2+∠5=180°,∴∠5=180°-∠2=180°-140°=40°.∴∠4=180°-∠1-∠5=180°-65°-40°=75°.又∵a∥b ,∴∠3=180°-∠4=180°-75°=105°.(第18题)19.140°20.(1)(2)三、21.解:(1)如图,过点C画一条平行于AB的直线MN,则MN为绿化带.(2)如图,过点C作CD⊥AB于点D,从河岸AB上的点D处开口,才能使所用的水管最短.设计的理由是垂线段最短.(第21题)22.解:(1)点D及四边形ABCD的另两条边如图所示.(第22题)(2)得到的四边形A′B′C′D′如图所示.23.解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°.∵BC平分∠ABD,∴∠ABD=2∠ABC=130°.∴∠BDC=180°-∠ABD=50°.∴∠2=∠BDC=50°.24.解:如图,过点C作∠ACF=∠A,则AB∥CF.∵∠A+∠ACD+∠D=360°,∴∠ACF+∠ACD+∠D=360°.又∵∠ACF+∠ACD+∠FCD=360°,∴∠FCD=∠D,∴CF∥DE,∴AB∥DE.点拨:本题运用了构造法,通过添加辅助线构造平行线,从而利用平行公理的推论进行判定.(第24题)25.解:∵AD∥BC,∴∠FED=∠EFG=55°,∠2+∠1=180°.由折叠的性质得∠FED=∠FEG,∴∠1=180°-∠FED-∠FEG=180°-2∠FED=70°,∴∠2=180°-∠1=110°.26.解:(1)如图①,过点C作CG∥MN,过点D作DH∥MN,(第26题)因为MN∥EF,所以MN∥CG∥DH∥EF,所以∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG.因为∠MAC与∠EBC的平分线相交于点D,所以∠1=12∠MAC=12∠ACG,∠2=12∠EBC=12∠BCG,所以∠ADB=12(∠ACG+∠BCG)=12∠ACB.因为∠ACB=100°,所以∠ADB=50°.(2)∠ADB=180°-12∠ACB.证明:如图②,过点C作CG∥MN,过点D作DH∥MN,因为MN∥EF,所以MN∥CG∥DH∥EF,所以∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG. 因为∠MAC与∠EBC的平分线相交于点D,所以∠1=12∠MAC,∠2=12∠EBC,所以∠ADB=∠1+∠2=12(∠MAC+∠EBC)=12(180°-∠ACG+180°-∠BCG)=12(360°-∠ACB),所以∠ADB=180°-12∠ACB.(3)∠ADB=90°-12∠ACB.证明:如图③,过点C作CG∥MN,过点D作DH∥MN,因为MN∥EF,所以MN∥CG∥DH∥EF,所以∠DBE=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG.因为∠MAC的平分线与∠FBC的平分线所在的直线相交于点D,所以∠CAD=12∠MAC,∠DBE=12∠CBF,所以∠ADB=180°-∠CAD-∠CAN-∠BDH=180°-12∠MAC-∠ACG-12∠CBF=180°-12∠MAC-∠ACG-12∠BCG=180°-12(180°-∠ACG)-∠ACG-12∠BCG=180°-90°+12∠ACG-∠ACG-12∠BCG=90°-12∠ACG-12∠BCG=90°-12(∠ACG+∠BCG)=90°-12∠ACB.点拨:解答本题的关键是过“拐点”(折线中两条线段的公共端点)作直线的平行线,利用平行线的判定和性质求角的度数或探究角的数量关系;由于条件类似,因此其解题过程也可以类比完成,所不同的是结论虽类似但也有些变化.。
人教版七年级下册数学第五章测试题(附答案)

人教版七年级下册数学第五章测试题(附答案)一、单选题(共12题;共24分)1.下列命题不正确的是()A. 如果AB∥CD,那么∠1=∠4B. 如果AB∥CD,那么∠1=∠3C. 如果AD∥BC,那么∠3=∠4D. 如果AD∥BC,那么∠3+∠2=180°2.如图,直线a、b被直线c所截,下列条件:(1)∠1=∠3;(2)∠3=∠4;(3)∠1=∠4;(4)∠2+∠4=180°,其中能判定a∥b的有( )A. 1个B. 2个C. 3个D. 4个3.如图,能判定EC∥AB的条件是()A. ∠B=∠ACEB. ∠B=∠ECDC. ∠A=∠ACBD. ∠A=∠ECD4.下列命题正确的是()A. 对角线相等的四边形是矩形B. 对角线垂直的四边形是菱形C. 对角线互相垂直平分的四边形是矩形D. 对角线相等的菱形是正方形5.下列四个命题:①等边三角形是中心对称图形;②在同圆或等圆中,相等的弦所对的圆周角相等;③三角形有且只有一个外接圆;④垂直于弦的直径平分弦所对的两条弧.其中真命题的个数有()A. 1个B. 2个C. 3个D. 4个6.下列四种说法:①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;②将2020减去它的,再减去余下的,再减去余下的,再减去余下的,……,依此类推,直到最后减去余下的,最后的结果是1;③实验的次数越多,频率越靠近理论概率;④对于任何实数x、y,多项式的值不小于2.其中正确的个数是()A. 1B. 2C. 3D. 47.如图,已知:AB∥CD,∠2=40°,则∠1 =()A. 40°B. 50°C. 60°D. 80°8.如图将△ABC水平向右平移到△DEF,若A、D间的距离为1,CE=2,则BF=()A. 3B. 4C. 5D. 不能确定9.下列说法不正确的个数有( )①. 两条直线被第三条直线所截,同位角相等②. 对顶角一定相等,邻补角的和一定为180°;③.平面直角坐标系把平面上的点分为四部分;④. 体育老师测定同学的跳远成绩的依据是垂线段最短。
(完整版)人教版七下第五章数学测试题(含)

(完整版)人教版七下第五章数学测试题(含) ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★学校------------班级------------姓名------------★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★七年级 2021年春季学期数学跟踪检测七年级数学测试题〔一〕内容:第五章相交线与平行线一、选择题:〔每题 3分,共 36分〕题号 1 2 3 4 5 6 7 8 9 10 11 12答案1. 邻补角是〔〕A. 和为 180°的两个角B. 有公共顶点且互补的两个角C.有一条公共边且相等的两个角D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角2.下面四个图形中,∠ 1 与∠ 2 是对顶角的图形的个数是〔〕A .0B . 1C .2D . 32 2 21 2 1 1 13.同一平面内的四条直线假设满足a⊥ b, b⊥c, c⊥ d,那么以下式子成立的是〔〕A . a∥ dB . b⊥ dC . a⊥ dD .b∥ c4.如图,假设 m∥n,∠ 1=105 o,那么∠ 2=〔〕A.55o oB.60C.65 o D.75 o5.以下说法正确的选项是( )〔第 4 题〕A. 互补的角是邻补角B. 同旁内角互补.C. 同角的补角相等.D. 相等的角是对顶角.6.如图,点 E 在 BC的延长线上,以下条件中不能判定AB∥ CD的是 ( )A.∠ 3=∠ 4 B .∠ 1=∠ 2C.∠ B=∠ DCE D .∠ D+∠ DAB=180°7.以下说法正确的选项是〔〕〔第 6 题〕A.有且只有一条直线垂直于直线。
人教版数学七年级下册第五章测试卷(含答案)

初中数学人教版七年级下学期第五章测试卷一、单选题(共6题;共12分)1. ( 2分) 如图所示,下列条件中不能判定DE∥BC的是()A. ∠1=∠CB. ∠2=∠3C. ∠1=∠2D. ∠2+∠4=180°2. ( 2分) 下面四个图形中,∠1与∠2是对顶角的是()A. B. C.D.3. ( 2分) 如图,,若,则的度数是( )A. B. C.D.4. ( 2分) 下列命题中,为真命题的是( )A. 对角线互相垂直的四边形是菱形B. 四边相等的四边形是正方形C. 对角线相等的四边形是矩形D. 两组对角分别相等的四边形是平行四边形5. ( 2分) 如图,已知CD∥BE,如果∠1=60°,那么∠B的度数为()A. 70°B. 100°C. 110°D. 120°6. ( 2分)已知直线m∥n,将一块含30°角的直角三角板ABC,按如图所示方式放置,其中A,B两点分别落在直线m、n上,若∠1=25°,则∠2的度数是( )A. 25°B. 30°C. 35°D. 55°二、填空题(共6题;共10分)7. ( 1分) 如图,直线AB,CD相交于点O,射线OE⊥CD,给出下列结论:①∠2和∠4互为对顶角;②∠3+∠2=180°;③∠5与∠4互补;④∠5=∠3-∠1;其中正确的是________。
(填序号)8. ( 1分) 如图,直线a、b 被直线c所截,若满足________,则a∥b.9. ( 1分) 命题“等角的余角相等”的逆命题是________命题.10. ( 5分) 已知:如图,射线OA 与OB 被直线CD 和EF 所截,∠1+ ∠2 = 180°,求证:∠3 = ∠4 .11. ( 1分) 直角三角形从点出发沿着方向匀速平移得到三角形(如图1),当点平移至点时停止运动(如图2).若,当点恰好将分为两部分时,四边形的面积为,那么平移的距离是________.12. ( 1分) 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积为________.三、解答题(共3题;共15分)13. ( 5分) 如图,已知∠B=∠C,∠B+∠D=180°,指出图中的平行线,并说明理由.14. ( 5分) 如图18,∠1=∠2,∠C=∠D,问∠A与∠F相等吗?为什么?15. ( 5分) 如图,,,,试求的大小.四、综合题(共2题;共21分)16. ( 10分) 如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于F.(1)求证:AD∥BC;(2)若∠1=36°,求∠2的度数.17. ( 11分) 问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.(1)数学活动小组经过讨论形成下列推理,请你补全推理依据.如图2,过点P作PE∥AB,∵PE∥AB(作图知)又∵AB∥CD,∴PE∥CD.________∴∠A+∠APE=180°.∠C+∠CPE=180°.________∵∠PAB=130°,∠PCD=120°,∴∠APE=50°,∠CPE=60°∴∠APC=∠APE+∠CPE=110°.(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=α,∠BCP=β,求∠CPD与α、β之间有何数量关系?请说明理由.(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与α、β之间的数量关系.答案解析部分一、单选题1.【答案】C【考点】同位角、内错角、同旁内角【解析】【解答】A、∵∠1=∠C,∴DE∥BC(同位角相等两直线平行),正确,不符合题意;B、∵∠2=∠3,∴DE∥BC(内错角相等两直线平行),正确,不符合题意;C、∠1=∠2,∴DF∥AC(内错角相等两直线平行),而不能得到DE∥BC,错误,符合题意;D、∠2+∠4=180°,∴DE∥BC(同旁内角互补两直线平行),正确,不符合题意;故答案为:C.【分析】根据平行线的判定定理分别分析判断即可,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行.2.【答案】B【考点】对顶角、邻补角【解析】【解答】解:根据对顶角的定义,A,D,C,不符合其中一个角是另一个角的边的反向延长线,是对顶角的只有第二个图形,故答案为:B【分析】根据对顶角的概念,即可.3.【答案】B【考点】同位角、内错角、同旁内角【解析】【解答】∵,∴.∵,∴,故答案为:B.【分析】根据互相平行的两条直线同位角相等、平角为180°的性质,可得出结果。
(完整word版)人教版七下数学第五章测试题及答案

人教版七下数学第五章测试题一、选择题(共12小题;共36分)1。
如图,与是A。
对顶角B。
同位角C。
内错角D。
同旁内角2。
如图,能判定的条件是A。
B. C。
D.3. 下列结论中不正确的是()A. 互为邻补角的两个角的平分线互相垂直B。
互不相等的两个角,一定不是对顶角C. 两条直线相交,若有一个角为,则这四个角中任取两个角都互为补角D。
不是对顶角的两个角互不相等4. 下列命题是真命题的有① 对顶角相等;② 两直线平行,内错角相等;③ 两个锐角对应相等的两个直角三角形全等;④ 有三个角是直角的四边形是矩形;⑤ 平分弦的直径垂直于弦,并且平分弦所对的弧.A. 个B。
个C。
个 D. 个5。
下列语句是命题的有个.①两点之间线段最短;②不平行的两条直线有一个交点;③ 与的和等于吗?④对顶角不相等;⑤互补的两个角不相等;⑥作线段.A。
B. C. D。
6. 下列图形中,和不是内错角的是( )A. B。
C. D。
7。
某校九年级四个班的代表队准备举行篮球友谊赛.甲、乙、丙三位同学预测比赛的结果如下:甲说:“902 班得冠军,904 班得第三”;乙说:“901 班得第四,903 班得亚军”;丙说:“903 班得第三,904 班得冠军”.赛后得知,三人都只猜对了一半,则得冠军的是( )A. 901 班B。
902 班 C. 903 班 D. 904 班8. 希望一中初一21班班主任邓老师打电话通知班上名同学,每名被通知到的同学再打电话通知其他的同学,如果打电话每分钟可以通知个人,要将全班名同学全部通知到,至少要用分钟.A。
B。
C. D。
9. 如图,直线,,相交于点,,平分,,则为A. B。
C。
D.10. 如图,,与,分别相交于点,,,与的平分线相交于点,且,则度.A。
B。
C. D.11. 如图所示,,分别是和的平分线,且,那么与的关系是A. 可能平行也可能相交B。
一定平行C. 一定相交D. 以上答案都不对12。
人教版七年级下册数学第五章检测试卷(附答案)

人教版七年级下册数学第五章检测试卷(附答案)一、单选题(共20题;共39分)1.在平面直角坐标系内点A、点B的坐标分别为(0,3)、(4,3),在坐标轴上找一点C,使△ABC是等腰三角形,则符合条件的点C的个数是()A. 5个B. 6个C. 7个D. 8个2.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(﹣1,0),AC=2.将Rt△ABC先绕点C 顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是()2题图3题图A. (2,2)B. (1,2)C. (﹣1,2)D. (2,﹣1)3.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠1与∠4是内错角;④∠1与∠3是同位角. 其中正确的个数是A. 4个B. 3个C. 2个D. 1个4.如图,4根火柴棒形成象形“口”字,只通过平移火柴棒,原图形能变成的汉字是( )A. B. C. D.5.同一平面内的三条直线满足a⊥b,b⊥c,则下列式子成立的是()A. a∥cB. b⊥aC. a⊥cD. b∥c6.如图,一辆超市购物车放置在水平地面上,其侧面四边形ABCD与地面某条水平线l在同一平面内,且AB∥l,若∠A=93°,∠D=111°,则直线CD与l所夹锐角的度数为()A.15°B. 18°C. 21°D. 24°A. 对角线互相平分且相等的四边形是矩形B. 对角线垂直的四边形是菱形C. 对角线相等的四边形是矩形D. 对角线互相垂直平分的四边形是正方形8.如图,BC∥DE,∠1=105°, ∠AED=65°, 则∠A的大小是( )A. 25°B. 35°B. C. 40° D. 60°9.将点A(2,1)向上平移2个单位长度得到点A′,则点A′的坐标是()A. (2,3)B. (0,1)C. (4,1)D. (2,-1)10.如图,DE∥BC,CD平分∠ACB,∠AED=50°,则∠EDC的度数是()10题图11题图A. 50°B. 40°C. 30°D. 25°11.如图,与∠1是内错角的是()A. ∠2B. ∠3C. ∠4D. ∠512.如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则()A. 点B到AO的距离为sin54°B. 点B到AO的距离为tan36°C. 点A到OC的距离为sin36°sin54°D. 点A到OC的距离为cos36°sin54°13.已知∠AOB,作图.步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;步骤2:过点M作PQ的垂线交于点C;步骤3:画射线OC.则下列判断:① = ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为()13题图14题图15题图A. 1B. 2C. 3D. 414.如图,,,,则的度数是()A. B. C. D.15.如图,与∠1是内错角的是( )A. ∠2B. ∠3C. ∠4D. ∠5A. 一个锐角与一个钝角一定互补B. 锐角的补角一定是钝角C. 互补的两个角一定不相等D. 互余的两个角一定不相等17.如图所示,图中内错角有()17题图18题图A. 2对B. 3对C. 4对D. 5对18.如图,△ABC中,BD平分∠ABC,交AC于D,CF平分∠ACB的邻补角∠ACE,CF交BA延长线于点F,交BD延长线于点M.在下列结论中:①∠BMC=∠MBC+∠F;②∠ABD+∠BAD=∠DCM+∠DMC;③2∠BMC=∠BAC;④3(∠BDC+∠F)=4∠BAC;其中正确的有()个.A. 1个B. 2个C. 3个D. 4个19.如图,,、、分别平分、和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版数学七年级下册第五章达标检测卷一、选择题(每题3分,共30分)1.在下图中,∠1和∠2是对顶角的是()2.如图,在所标识的角中,下列说法不正确的是()A.∠1和∠2是邻补角B.∠1和∠4是同位角C.∠2和∠4是内错角D.∠2和∠3是对顶角(第2题)(第3题)3.如图,在6×6的方格中,图①中的图形N平移后的位置如图②所示,则图形N的平移方法是()A.向下移动1格B.向上移动1格C.向上移动2格D.向下移动2格4.点P为直线l外一点,点A,B,C为直线l上三点,P A=4 cm,PB=5 cm,PC=3 cm,则点P到直线l的距离()A.等于4 cm B.等于5 cm C.小于3 cm D.不大于3 cm 5.下列命题中:①对顶角相等;②同位角相等;③互补的两个角为邻补角;④若l1⊥l2,l1⊥l3,则l2⊥l3.其中真命题有()A.①B.①②③C.①③D.①②③④学校:班级:姓名:考号:6.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是() A.60°B.50°C.40°D.30°(第6题)(第7题)(第8题)7.如图,将木条a绕点O旋转,使其与木条b平行,则旋转的最小角度为() A.65°B.85°C.95°D.115°8.将一张长方形纸片折叠成如图所示的形状,则∠ABC等于() A.73°B.56°C.68°D.146°9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于()A.81°B.99°C.108°D.120°(第9题)(第10题)10.图①是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中∠CFE的度数是()A.160°B.150°C.120°D.110°二、填空题(每题3分,共30分)11.下列语句:①同旁内角相等;②如果a=b,那么a+c=b+c;③对顶角相等吗?④画线段AB;⑤两点确定一条直线.其中是命题的有__________;是真命题的有__________.(只填序号)12.如图,∠3的同旁内角是________,∠4的内错角是________,∠7的同位角是________.(第12题)(第13题)(第14题)13.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠COM=________.14.如图,跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离________4.6米(填“大于”“小于”或“等于”).15.如图,小明从A处出发,沿北偏东60°的方向行走至B处,又沿北偏西20°的方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是________.(第15题)(第16题)(第17题)16.将一张长方形纸条折成如图所示的形状,若∠1=110°,则∠2=________.17.如图,将三角形ABC沿着点B到点C的方向平移3 cm得到三角形DEF,且DE交AC于点H,AB=6 cm,BC=9 cm,DH=2 cm,那么图中阴影部分的面积为________cm2.18.如图,a∥b,∠1=65°,∠2=140°,则∠3的度数是________.(第18题)(第19题)(第20题)19.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.20.以下三种沿AB折叠的方法:(1)如图①,展开后测得∠1=∠2;(2)如图②,展开后测得∠1=∠2且∠3=∠4;(3)如图③,测得∠1=∠2.其中能判定纸带两条边线a,b互相平行的是________(填序号).三、解答题(24题10分,25题12分,26题14分,其余每题8分,共60分) 21.如图是一条河,C是河岸AB外一点.(1)过点C要修一条与河平行的绿化带(用直线表示),请作出正确的示意图;(2)现欲用水管从河岸AB将水引到C处,问:从河岸AB上的何处开口,才能使所用的水管最短?画图表示,并说明设计的理由.(第21题) 22.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.(1)试在图中标出点D,并画出该四边形的另两条边;(2)将四边形ABCD向下平移5个单位长度,画出平移后得到的四边形A′B′C′D′.(第22题)23.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.(第23题) 24.如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.(第24题)25.如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.(第25题)26.如图,MN∥EF,C为两直线之间一点.(1)如图①,∠CAM与∠CBE的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.(2)如图②,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.(3)如图③,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请写出∠ACB与∠ADB的数量关系,并证明你的结论.(第26题)答案一、1.C 2.C 3.D 4.D 5.A 6.C 7.B 8.A(第9题)9.B 解析:如图,过点B 作MN ∥AD ,∴∠ABN =∠A =72°.∵CH ∥AD ,AD∥MN ,∴CH ∥MN ,∴∠NBC +∠BCH =180°,∴∠NBC =180°-∠BCH =180°-153°=27°.∴∠ABC =∠ABN +∠NBC =72°+27°=99°.10.B 解析:在题图①中,因为四边形ABCD 为长方形,所以AD ∥BC ,所以∠BFE =∠DEF =10°,则∠EFC =180°-∠BFE =170°.在题图②中,∠BFC =∠EFC -∠BFE =170°-10°=160°.在题图③中,∠CFE =∠BFC -∠BFE =160°-10°=150°.故选B . 二、11.①②⑤;②⑤12.∠4,∠5;∠2,∠6;∠1,∠4 13. 38° 14. 大于 15.向右转80°16.55° 解析:∵∠1=110°,纸条的两条对边互相平行,∴∠3=180°-∠1=180°-110°=70°.根据折叠的性质可知∠2=12(180°-∠3)=12(180°-70°)=55°.17.15 解析:由平移的性质知,DE =AB =6 cm ,HE =DE -DH =4 cm ,CF =BE =3 cm ,所以EC =6 cm ,所以S 阴影部分=S 三角形EFD -S 三角形ECH =12DE ·EF -12EH ·EC =12×6×9-12×4×6=15(cm 2). 18.105° 解析:反向延长射线b ,如图,∵∠2+∠5=180°,∴∠5=180°-∠2=180°-140°=40°.∴∠4=180°-∠1-∠5=180°-65°-40°=75°.又∵a ∥b,∴∠3=180°-∠4=180°-75°=105°.(第18题)19.140°20.(1)(2)三、21.解:(1)如图,过点C画一条平行于AB的直线MN,则MN为绿化带.(2)如图,过点C作CD⊥AB于点D,从河岸AB上的点D处开口,才能使所用的水管最短.设计的理由是垂线段最短.(第21题)22.解:(1)点D及四边形ABCD的另两条边如图所示.(第22题)(2)得到的四边形A′B′C′D′如图所示.23.解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°.∵BC平分∠ABD,∴∠ABD=2∠ABC=130°.∴∠BDC=180°-∠ABD=50°.∴∠2=∠BDC=50°.24.解:如图,过点C作∠ACF=∠A,则AB∥CF.∵∠A+∠ACD+∠D=360°,∴∠ACF+∠ACD+∠D=360°.又∵∠ACF+∠ACD+∠FCD=360°,∴∠FCD=∠D,∴CF∥DE,∴AB∥DE.解析:本题运用了构造法,通过添加辅助线构造平行线,从而利用平行公理的推论进行判定.(第24题)25.解:∵AD∥BC,∴∠FED=∠EFG=55°,∠2+∠1=180°.由折叠的性质得∠FED=∠FEG,∴∠1=180°-∠FED-∠FEG=180°-2∠FED=70°,∴∠2=180°-∠1=110°.26.解:(1)如图①,过点C作CG∥MN,过点D作DH∥MN,(第26题)因为MN∥EF,所以MN∥CG∥DH∥EF,所以∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG.因为∠MAC与∠EBC的平分线相交于点D,所以∠1=12∠MAC=12∠ACG,∠2=12∠EBC=12∠BCG,所以∠ADB=12(∠ACG+∠BCG)=12∠ACB.因为∠ACB=100°,所以∠ADB=50°.(2)∠ADB=180°-12∠ACB.证明:如图②,过点C作CG∥MN,过点D作DH∥MN,因为MN∥EF,所以MN∥CG∥DH∥EF,所以∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG. 因为∠MAC与∠EBC的平分线相交于点D,所以∠1=12∠MAC,∠2=12∠EBC,所以∠ADB=∠1+∠2=12(∠MAC+∠EBC)=12(180°-∠ACG+180°-∠BCG)=12(360°-∠ACB),所以∠ADB=180°-12∠ACB.(3)∠ADB=90°-12∠ACB.证明:如图③,过点C作CG∥MN,过点D作DH∥MN,因为MN∥EF,所以MN∥CG∥DH∥EF,所以∠DBE=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG.因为∠MAC的平分线与∠FBC的平分线所在的直线相交于点D,所以∠CAD=12∠MAC,∠DBE=12∠CBF,所以∠ADB=180°-∠CAD-∠CAN-∠BDH=180°-12∠MAC-∠ACG-12∠CBF=180°-12∠MAC-∠ACG-12∠BCG=180°-12(180°-∠ACG)-∠ACG-12∠BCG=180°-90°+12∠ACG-∠ACG-12∠BCG=90°-12∠ACG-12∠BCG=90°-12(∠ACG+∠BCG)=90°-12∠ACB.解析:解答本题的关键是过“拐点”(折线中两条线段的公共端点)作直线的平行线,利用平行线的判定和性质求角的度数或探究角的数量关系;由于条件类似,因此其解题过程也可以类比完成,所不同的是结论虽类似但也有些变化.。
