§3.2周期信号的频谱分析——傅里叶级数
合集下载
傅里叶级数及频谱
三角形式的傅里叶级数 周期信号可表示为
x(t ) = x(t + mT )(m = 0,±1,±2,L)
任何周期函数在满足狄义赫利的条件下，可以展成正交函 任何周期函数在满足狄义赫利的条件下， 数线性组合的无穷级数。 数线性组合的无穷级数。如果正交函数集是三角函数集或指数 函数集，此时周期函数所展成的级数就是“傅里叶级数” 函数集，此时周期函数所展成的级数就是“傅里叶级数”。
∫
T0 2 T − 0 2
x (t )d t
2 an = T0
bn 2 = T0
∫
∫
T0 2 T − 0 2
x ( t ) c o s n ω 0 td t
x (t ) s in nω 0td t
T0 2 T − 0 2
T0 T0 ~ 以上各式中的积分限一般取： 以上各式中的积分限一般取： 0 ~ T0 或 − 2 2 三角形式的傅里叶级数也可表示成： 三角形式的傅里叶级数也可表示成：
( n = 2 , 4 ,6 L ) ( n = 1,3,5 L )
可见，在奇谐函数的傅里叶级数中，只会含有基波和奇次 谐波的正弦、余弦分量，而不会包含直流和偶次谐波分量。
（4）偶谐函数 ）
T1 f (t ± ) = f (t ) 2 f (t )
L
T1 T1 − − 2 4 T1 4 T1 2
L
0t
这就是傅立叶级数的指数形式
0
1 ∞ x (t ) = ∑ An e jϕ n e jn ω 0 t = 2 n = −∞
n = −∞
∑ X (nω
∞
)e
jn ω 0 t
1 X (nω 0 ) = An e jϕn 2
2 an = T0 ∫ 可求得如下
(完整版)周期信号傅里叶级数
C e dt T0 n0
j(nk )0t
n =
由{en (t)}的正交性得：
T0
0
e
dt j(nk )0t
T0
[n k]
T0 n=k 0 n不等于k
Ck
1 T
T
2 T
fT (t)e jk 0t dt
2
2. 指数形式傅立叶级数
连续时间周期信号可以用指数形式傅立叶级数表示为
f (t)
bn
2 T
T
2 T
2
f (t)sin n0tdt
(n = 1,2 )
纯余弦形式傅立叶级数
其中
f（t）
a0 2
n1
An
co（ s n0t
）
n
An an2 bn2
n
arctg
bn an
a0 2
称为信号的直流分量，
An cos(n0+ n)称为信号的n次谐波分量。
例题1 试计算图示周期矩形脉冲信号的傅立叶级数展 开式。
Cn e jn0t
jn 2 t
Cn e T
n =
n =
物理含义：周期信号f(t)可以分解为不同频率虚指数信号之和。
其中
Cn
1 T
T
2 T
fT (t)e jn0t dt
（傅立叶系数）
2
n 1 两项的基波频率为f0，两项合起来称为信号的基波分量
n 2 的基波频率为2f0，两项合起来称为信号的2次谐波分量
若 f (t)为实函数，则有 Cn Cn
利用这个性质可以将指数Fourier级数表示写为
1
f (t) C0
Cne jn0t
周期信号的傅里叶级数表
傅里叶级数与复变函数的关系
傅里叶级数可以看作是复数域中的三角函数，即复数域中的正弦和余弦。在复数域中，正弦和余弦函数表现为复指数函数的 形式。
复数的使用使得傅里叶级数的系数可以表示为实数，从而简化了计算。此外，复数的共轭也提供了相位信息，这在信号处理 中非常重要。
傅里叶级数与小波分析的关系
小波分析是傅里叶分析的进一步发展，它提供了更灵活的时频分析工具。小波变 换可以看作是傅里叶变换的一种扩展，它允许我们在不同的频率段使用不同的基 本函数。
三角函数形式
傅里叶级数的另一种表示形式，利用三角函数来表示周期信号。
傅里叶级数的三角函数形式
01
02
03
正弦形式
余弦形式
系数
傅里叶级数的正弦函数形式，用 于表示只包含正弦波的周期信号。
傅里叶级数的余弦函数形式，用 于表示只包含余弦波的周期信号。
在傅里叶级数中，每个正弦或余 弦函数都对应一个系数，表示该 函数在周期信号中的贡献程度。
03
傅里叶级数的性质
傅里叶级数的收敛性
傅里叶级数在数学上具有收敛性，意味着它可以将一个 周期函数表示为无穷级数，每个项都是正弦或余弦函数。
收敛的速度取决于函数的特性，例如，对于具有快速衰 减的周期函数，傅里叶级数收敛得更快。
傅里叶级数的对称性
傅里叶级数的对称性质是指，对于一个周期函数，其傅里叶级数的正弦和余弦项具有对称性。 这意味着，对于一个给定的周期函数，其傅里叶级数的正弦和余弦项的系数是相同的。
周期信号的傅里叶级 数表
目录
• 傅里叶级数简介 • 周期信号的傅里叶级数表示 • 傅里叶级数的性质 • 傅里叶级数的应用实例 • 傅里叶级数与其他数学工具的关系
01
第三章周期信号的傅里叶级数表示
1、复指数傅里叶级数
sk =jk0，即:
eskt e jk0t , k 0, 1, 2,L
一个周期为T的周期信号x(t) 的复指数傅里叶级数：
x(t) ake jk0 t k
0 2 / T
其中系数 ak一般来说是 k0 的复函数。
e jk0t , k 0, 1, 2, 成谐波关系的复指数信号集
0
xˆ4
a4e j 40t
a4e j 40t
0
x(t) ake jk0 t
k
k
即：x(t) a0 xˆ1(t) xˆ3(t) xˆ5(t)
xˆ1 xˆ3 xˆ5 xˆ9 xˆ19
a0 xˆ1 xˆ3 a0 xˆ1 xˆ3 xˆ5 a0 xˆ1 xˆ7 a0 xˆ1 xˆ19 a0 xˆ1 xˆ99 x(t)
est 是连续LTI系统的特征函数
zn 是离散LTI系统的特征函数
对一个特定 sk 或 zk , H (sk )或 H (z就k ) 是对应的特征值。
7
4、将一个信号分解为特征函数(复指数信号) 的线性加权和
如果一个LTI系统的输入信号（连续/离散）可以分解 为复指数信号的线性加权和：
x(t) ak e skt
因此xn可以分解为n个不同的特征函数的线性加权和其傅里叶级数只需对连续n个独立k值求和记为352傅里叶级数系数的确定两边同乘以并在n内求和范围同的取值其中周期内求和为一个周期正弦信号在以下推导供学有余力同学参考36离散时间周期信号周期为n的傅里叶级数是一个有限项级数n个不同的复指数信号求和但a本身是一个周期为n的周期信号
T x(t)e jn0tdt T
0
0
ak e e jk0t jn0t dt
信号与系统 第三章 周期信号的傅里叶级数展开
1 T
2 n 2
T1
f (t ) dt
F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1
三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E
T1
t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集
2 n 2
T1
f (t ) dt
F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1
三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E
T1
t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集
信号与系统分析基础----周期信号的频谱周期信号的频谱分析——傅里叶级数
n1t
sin
m1t
0
2
T 2 T 2
cos n1t
cos m1t
T , 2 0,
mn mn
T 2 T 2
sin n1t
sin m1t
T , 2 0,
mn mn
3
2．级数形式
周期信号
f t ,周期为T1
, 基波角频率为1
2
T1
在满足狄氏条件时，可展成:
f (t) a0 an cos n1t bn sin n1t
§3.2 周期信号的频谱分析——傅里叶级数
1
主要内容
•三角函数形式的傅氏级数 • 指数函数形式的傅氏级数 •两种傅氏级数的关系 • 频谱图
2
一．三角函数形式的傅里叶级数
1.三角函数集
cosn1t , sin n1 t是一个完备的正交函数集
由积分可知
t在一个周期内，n=0,1,....
T
2 T
cos
周期信号可分解为直流，基波（1）和各次谐波 （n1 : 基波角频率的整数倍）的线性组合．
cn ~ 关系曲线称为幅度频谱图 n ~ 关系曲线称为相位频谱图
可画出频谱图
周期信号频谱具有离散性，谐波性，收敛性
9
二．指数函数形式的傅里叶级数
1．复指数正交函数集 e jn1t n 0,1,2
2．级数形式 f (t ) F (n1 ) e jn1t
f
2
(
t
)dt
t2 t1
f 2 (t )
f
1
(t
)dt
0
若在区间(t1,t2)内，复变函数集 {gr (t)}(r 1,2,...,n)
满足关系
周期信号的分解-傅里叶级数
傅里叶级数
傅里叶级数是一种将周期信号分 解为不同频率的正弦和余弦函数 的数学方法。
三角函数系
傅里叶级数使用正弦和余弦函数 作为基底，将周期信号表示为这 些函数的线性组合。
频谱分析
通过傅里叶级数，可以分析周期 信号的频谱，了解信号中各个频 率分量的强度和分布。
周期信号的频谱分析
频谱图
频谱图是用来表示周期信 号中各个频率分量强度的 图形，横轴表示频率，纵 轴表示幅度。
傅里叶级数的发展经历了多个阶段， 包括早期的数学证明和后来的完善， 最终成为数学和工程领域中分析周期 信号的重要工具。
傅里叶级数的应用领域
1 2 3
通信领域
傅里叶级数用于信号处理和调制解调，例如在频 分复用（FDM）和调频（FM）中分析信号的频 谱特性。
振动分析
傅里叶级数用于分析机械振动，通过将振动信号 分解为不同频率的分量，可以研究振动的模式和 频率成分。
图像处理
傅里叶变换在图像处理中广泛应用，通过将图像 信号表示为傅里叶级数，可以实现图像的滤波、 去噪、压缩等处理。
02 傅里叶级数的数学基础
三角函数和正弦函数三角Fra bibliotek数包括正弦函数、余弦函数、正切函数 等，它们在周期信号的分解中起着关 键作用。
正弦函数
正弦函数是周期函数，其基本周期为 $2pi$，在信号处理中常用于描述周 期信号。
周期信号的频谱分析
频谱分析
通过将周期信号分解为不同频率的正弦波分量，可以分析信号中各频率分量的 幅度和相位。
频谱密度函数
描述了信号中各频率分量的分布情况，其图形称为频谱图或频谱密度图。
傅里叶级数的收敛性
傅里叶级数
是一个无穷级数，可以用来表示任何周期信号。
信号与系统第3章 傅里叶变换
P
f
2 (t) 1 T1
t0 T1 t0
f
2 (t)d t
a0 2
1 2
n1
(an
2
bn 2 )
2
Fn _____ 帕塞瓦尔定理
n
结论：周期信号的平均功率等于傅里叶级数展开 式中基波分量及各谐波分量有效值的平方 和，即时域和频域的能量守恒。
五. 周期信f号(t)的频c0 谱 （c三n c角os函(n数1t形 式n )） n1
(1) 偶函数 f (t) f (t)
4
an T1
T1
2 0
f (t) cos(n1t)dt
Fn
Fn
an 2
bn 0
傅里叶级数中不会含有正弦项， 只可能含有直流项和余弦项。
(2) 奇函数 f (t) f (t)
a0 0 , an 0
bn
4 T1
T1
2 0
f (t) sin(n1t)d t
e j n1t
T1 n 2
画频谱图：
c0
a0
E
T1
an
2E
T1
Sa
n1
2
, n
1,2,
cn an
1）令 m
2
得
2
m
即在
2
m，m为整数处有零点。
2）
2
2
T1
T1
零点间谱线个数
3) c n值为正，相位为0，值为负，相位为π
4)谱线间隔为 1 带宽
2
T1
，第一个过零点带宽定义为信号的
1 3
s in31t
1 4
sin41t
E
1 n1
信号与系统分析宗伟 3
2
1
fT t
n jn1t F n e 1
由傅里叶级数的指数形式出发： 其傅氏变换(用定义)
FT F fT t
F F n 1 e j n1t F n 1 F e j n1t
3.2 非周期信号的频谱分析 ─ 傅里叶变换
1.从傅立叶级数到傅立叶变换
当周期信号的周期T1无限大时,就演变成了 非周期信号的单脉冲信号 频率也变成连续变量
频谱演变的定性观察
-T/2
T/2
-T/2
T/2
傅立叶 变换
傅立叶的逆变换
傅立叶 逆变换
物理意义：非周期信号可以分解为无数个频率为， 复振幅为[F()/2]d 的复指数信号ej t的线性组合。
傅立叶变换一般为复数
FT一般为复函数
若f(t)为实数，则幅频为偶函数,相频为奇函数
傅立叶变换存在的充分条件
用广义函数的概念，允许奇异函数也 能满足上述条件，因而象阶跃、冲激 一类函数也存在傅立叶变换
傅立叶正变换：
傅立叶反变换： 符号表示：
试求图示非周期矩形脉冲信号的频谱函数
[解] 非周期矩形脉冲信号f(t)的时域表示式为
A
/ 2
/2
t
6. 卷积定理
(1)时域卷积定理
若 f1 (t ) F1 ( j ) , f 2 (t ) F2 ( j )
则 f1 (t ) f 2 (t ) F1 ( j ) F2 ( j )
证明：F[ f1 (t ) f 2 (t )] [
n 1
3．确定信号的基频和周期
当不考虑信号的直流分量时, 的3个分量的角频率分别时 1/2,2/3,和7/6,相邻两个频率之比为3/4,4/7,和3/7,显然 三者之间呈现谐波关系,他们之中的最大公约数时1/6,因 此1/6是基频 ,也就时说该信号具有3次,4次和7次谐波, 进一步可求得周期
周期信号的傅里叶级数表示
弦波叠加起来，合成复杂的周期信号。
信号分析
02
对于给定的周期信号，可以利用傅里叶级数进行频谱分析，得
到信号中各个频率分量的幅度和相位信息。
频谱特性
03
通过傅里叶级数展开，可以清晰地展示信号在频域上的特性，
如主频、谐波分量等。
信号调制与解调
01 02
调制
在通信系统中，常常需要将低频信号调制到高频载波上进行传输。利用 傅里叶级数，可以将低频信号表示为一系列正弦波的叠加，进而实现调 制过程。
WENKU DESIGN
WENKU DESIGN
2023-2026
END
THANKS
感谢观看
KEEP VIEW
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
https://
PART 01
傅里叶级数基本概念
周期信号与非周期信号
周期信号
具有固定时间周期的信号，即信 号在某个时间周期内重复出现。
非周期信号
不具有固定时间周期的信号，即 信号不会重复出现。
傅里叶级数定义及公式
傅里叶级数定义
将周期信号表示为一系列正弦波和余弦波的叠加，这些正弦波和余弦波具有不 同的频率和幅度。
数值计算与仿真实验
数值计算方法简介
01
离散傅里叶变换 （DFT）
将连续时间信号在时域上进行离 散化，并通过傅里叶变换得到频 域上的离散表示。
02
快速傅里叶变换 （FFT）
利用DFT中冗余计算的特点，采 用分治策略减少计算量，提高计 算效率。
03
迭代法
通过逐步逼近的方式求解傅里叶 系数，如雅可比迭代和高斯-赛 德尔迭代等。
3.1-2 周期信号的傅里叶级数分析
2 t0 T1 an t0 f (t ) cos n1tdt T1
2 t0 T1 bn t0 f (t ) sin n1tdt T1
an jbn jn1t an jbn jn1t f (t ) a0 e e n1 n1 2 2 F0 Fn e
还得出了关于非周期信号的表示不是成谐波关系的正弦信 号的加权和，而是不全成谐波关系的正弦信号的加权和。和傅 立叶级数一样，傅立叶积分(或变换)仍然是分析LTI系统的最 强有力的工具之一。 当时指定了四位著名的科学家和数学家来评审1807年傅立 叶的论文，其中三位即S.F.拉克劳克斯、G.孟济和P.S.拉普拉 斯赞成发表傅立叶的论文，而第四位J.L.拉格朗日仍然顽固地 坚持他于50年前就已经提出过的关于拒绝接受三角级数的论点。 由于拉格朗日的强烈反对，傅立叶的论文从未公开露过面，为 了使他的研究成果能让法兰西研究院接受并发表，在经过了几 次其它的尝试后，傅立叶才把他的成果以另一种方式出现在 “热的分析理论”这本书中。这本书出版于1822年，也即比他 首次在法兰西研究院宣读他的成果时晚15年。
n1
jn1t
Fn e jn1t
n1 jn1t
F0 Fn e
n1
jn1t
Fn e
n1
又有
F0 Fn e jn1t
n 0
于是，可将上式写成紧凑的形式：
f (t ) Fn e
n
jn1t
（注意n的取值范围与 三角形傅氏级数不同）
到1807年，傅立叶已完成了关于热传理论实质部分的研究， 并于1807年12月21日向法兰西研究院提交了他的研究成果。在 他的研究过程中，傅立叶发现在表示一个物体的温度分布时， 成谐波关系的正弦函数是非常有用的，另外，他还断言“任何” 周期信号都可以用这样的级数来表示！虽然在这一问题上，他 的论述是很有意义的，但是隐藏在这一问题后面的其它很多基 本概念已经被其他科学家们所发现；同时傅立叶的数学证明也 不是很完善的。后来1829年P.L.狄里克雷给出了若干精确的条 件，在这些条件下一个周期信号才可以用一个傅立叶级数来表 示，因此，傅立叶并没有对傅立叶级数的数学理论作出贡献， 然而，他确实洞察出这个级数表示法的潜在威力，并且在很大 程度上正是由于他的工作和断言，才大大激励和推动着傅立叶 级数问题的深入研究。另外，傅立叶在这一问题上的研究成果 比他的任何前驱者都大大前进了一步，这指的是他
周期信号的频谱分析——傅里叶级数
（ n 的整 线数 性倍 组） 合。 1:基 波 角 频 率 的 cn ~ 关系曲线称为幅度频谱图；幅度谱
周期信号可分 ，解 基为 波 ） 直 （ 和 流 各次谐波 1
n ~ 关系曲线称为相位频谱图。相位谱
可画出频谱图。 周期信号频谱具有离散性、谐波性、收敛性 。 cn φn c1 c2 π c3 c0 0 ω1 3ω1 nω1 ω 0 ω1 3ω1 nω1 ω
1 1
1
1
1 1 T T F ( n ) f ( t ) cos n t d t j f ( t ) sin n t d t 1 1 1 0 0 T T 1 1
1 1
1 an jbn 2
n
j F n F ( n ) e F ( n ), F ( n ) 是 复 数 1 1 1 1
§3.2
周期信号傅里叶 级数分析
主要内容
•三角函数形式的傅氏级数 • 指数函数形式的傅氏级数
•两种傅氏级数的关系
• 频谱图
•函数的对称性与傅里叶级数的关系
•周期信号的功率 •傅里叶有限级数与最小方均误差
一．三角函数形式的傅里叶级数
1.三角函数集
由积分可知 是一个完备的正交函数集 cos n t , sin n t 1 1 t在一个周期内，n=0,1,...
0 1 0
1
2t T f( t ) cos n t d t 余弦分量的幅度 a n 1 t T 1
0 1 0
1 t T a f( t)d t 0 t T 1
2t T 正弦分量的幅度 b f( t ) sin n t d t n 1 t T 1
周期信号可分 ，解 基为 波 ） 直 （ 和 流 各次谐波 1
n ~ 关系曲线称为相位频谱图。相位谱
可画出频谱图。 周期信号频谱具有离散性、谐波性、收敛性 。 cn φn c1 c2 π c3 c0 0 ω1 3ω1 nω1 ω 0 ω1 3ω1 nω1 ω
1 1
1
1
1 1 T T F ( n ) f ( t ) cos n t d t j f ( t ) sin n t d t 1 1 1 0 0 T T 1 1
1 1
1 an jbn 2
n
j F n F ( n ) e F ( n ), F ( n ) 是 复 数 1 1 1 1
§3.2
周期信号傅里叶 级数分析
主要内容
•三角函数形式的傅氏级数 • 指数函数形式的傅氏级数
•两种傅氏级数的关系
• 频谱图
•函数的对称性与傅里叶级数的关系
•周期信号的功率 •傅里叶有限级数与最小方均误差
一．三角函数形式的傅里叶级数
1.三角函数集
由积分可知 是一个完备的正交函数集 cos n t , sin n t 1 1 t在一个周期内，n=0,1,...
0 1 0
1
2t T f( t ) cos n t d t 余弦分量的幅度 a n 1 t T 1
0 1 0
1 t T a f( t)d t 0 t T 1
2t T 正弦分量的幅度 b f( t ) sin n t d t n 1 t T 1
傅里叶级数
傅里叶变换：（频域分析）连续系统频谱分析：就是将时域的信号（可以是周期信号与非周期信号）变成频域形式并加以分析的方法。
其目的是把复杂的时域波形，经过某种变换分解为若干单一的谐波分量来研究，以获得信号的频率结构以及各谐波和相位信息。
这某种变换可以是傅里叶级数，也可以是傅里叶变换。
它们的作用都是把时域信号变成频域信号以便于信号分析。
傅里叶级数有三角级数形式和指数级数形式两种表示形式。
例如，假设有个周期信号,周期为，角频率，频率为。
要作频谱分析时，按傅里叶级数展开：三角形式的傅里叶级数******(a)直流分量：****** (a1)余弦分量幅度：****** (a2)正弦分量幅度：****** (a3)由上可见，公式a左边是一个周期信号，而右边是一个三角函数的线性组合，或也可以称为三角级数表示方式，这种三角级数的表示方式就称为傅里叶级数。
但公式(a)有个问题，就是说在每个频率点上可能会有两个三角函数，这不利于信号能量的计算或图形表示，为了便于画图我们做了一些变换，用三角公式中的合角公式对公式(a)进行了转换，把同频率的项加以合并，于是得到了余弦形式的傅里叶级数或正弦形式的傅里叶级数，如式(b),(c)。
余弦形式：****** (b)正弦形式：****** (c)由上总结：1、一个周期信号可以分解成直流分量、基波（）和各次谐波（基波角频率整数倍）的线性组合。
2、周期信号频谱具有离散型，谐波性，收敛性。
为幅度频谱关系由此可画出频谱图为相位频谱关系欧拉公式：****** (d1)****** (d2)将公式（d1）、（d2）带入公式（a）可得：****** (d3)**** (d4)**** (d5)将公式(d4)、(d5)带入(d3)可得：****** (d6)令:****** (d7)从而得到f(t)得到指数形式的傅里叶级数:****** (e)将(a2)、(a3)带入(d4)，其中可以简写成。
由此可得可得到指数形式傅里叶级数的系数：。
傅里叶级数及频谱
对于离散的数据点，可以使用数值方法（如快速傅里叶变换）来高效计算傅里叶系 数。
收敛性与吉布斯现象
傅里叶级数的收敛性是指当基本分量 的数量增加时，傅里叶级数的和逐渐 逼近原周期函数。
吉布斯现象是由于傅里叶级数在逼近不连续 点时产生的截断误差所导致的，增加基本分 量的数量可以减小但无法完全消除吉布斯现 象。
谢谢
THANKS
旋转因子
在FFT算法中，旋转因子e^{-j*2π*k/N}起着重要作用。它可以将输入信号的每个样本点映射 到频域上的相应位置，从而实现信号的频谱分析。
FFT在信号处理中应用举例
• 频谱分析：FFT可以用于信号的频谱分析，将时域信号转换为频域信号，以便 观察和分析信号的频率成分。这在音频处理、图像处理等领域具有广泛应用。
域实现滤波。
时频分析
结合时间和频率信息，对信号进行 时频分析，实现非平稳信号的滤波 和去噪。
小波变换
利用小波基函数对信号进行多尺度 分解，实现信号在不同频率和时间 尺度上的滤波和去噪。
信号调制与解调
调制
01
将低频信号通过傅里叶变换转换到频域，与高频载波信号相乘，
实现信号调制。
解调
02
对已调信号进行傅里叶变换，提取出低频信号的频谱信息，实
对于某些不连续或具有跳跃点的周期函 数，傅里叶级数在跳跃点附近会出现过 冲和振荡现象，这被称为吉布斯现象。
02 频谱分析原理及方法
CHAPTER
频谱定义及性质
频谱定义
频谱是频率域中信号幅度和相位 的分布，表示信号在不同频率分 量上的贡献。
频谱性质
频谱具有幅度谱和相位谱两部分 ，幅度谱表示信号各频率分量的 幅度大小，相位谱表示各频率分 量的相位信息。
收敛性与吉布斯现象
傅里叶级数的收敛性是指当基本分量 的数量增加时，傅里叶级数的和逐渐 逼近原周期函数。
吉布斯现象是由于傅里叶级数在逼近不连续 点时产生的截断误差所导致的，增加基本分 量的数量可以减小但无法完全消除吉布斯现 象。
谢谢
THANKS
旋转因子
在FFT算法中，旋转因子e^{-j*2π*k/N}起着重要作用。它可以将输入信号的每个样本点映射 到频域上的相应位置，从而实现信号的频谱分析。
FFT在信号处理中应用举例
• 频谱分析：FFT可以用于信号的频谱分析，将时域信号转换为频域信号，以便 观察和分析信号的频率成分。这在音频处理、图像处理等领域具有广泛应用。
域实现滤波。
时频分析
结合时间和频率信息，对信号进行 时频分析，实现非平稳信号的滤波 和去噪。
小波变换
利用小波基函数对信号进行多尺度 分解，实现信号在不同频率和时间 尺度上的滤波和去噪。
信号调制与解调
调制
01
将低频信号通过傅里叶变换转换到频域，与高频载波信号相乘，
实现信号调制。
解调
02
对已调信号进行傅里叶变换，提取出低频信号的频谱信息，实
对于某些不连续或具有跳跃点的周期函 数，傅里叶级数在跳跃点附近会出现过 冲和振荡现象，这被称为吉布斯现象。
02 频谱分析原理及方法
CHAPTER
频谱定义及性质
频谱定义
频谱是频率域中信号幅度和相位 的分布，表示信号在不同频率分 量上的贡献。
频谱性质
频谱具有幅度谱和相位谱两部分 ，幅度谱表示信号各频率分量的 幅度大小，相位谱表示各频率分 量的相位信息。
3.2 周期信号的傅里叶级数分析
n=1
1
∞
f (t) = a0 + ∑(an cos nω1t + bn sin nω1t), n为正整数
n=1
∞
1 直流分量： a 0 = T1
∫
t 0 + T1
t0
f ( t ) dt
2 t0 +T1 余弦分量的幅度：n = ∫ a f (t ) cos(nω1t )dt T1 t0
2 正弦分量的幅度： bn = T1
sin(ω1t )
4 T1 a1 = ∫ 2 f (t) cos(ω1t)dt T 0 1
4 T1 b = ∫ 2 f (t) sin( ω1t)dt 1 T 0 1
cos(2ω1t )
sin(2ω1t )
∞
令：Fn = Fn e
∞
jϕn
1 − jϕn 1 = (an − jbn ) F−n = F−n e = (an + jbn ) 2 2
jnwt 1
f (t) = F0 + ∑Fne
n=1
+ ∑F−ne
n=1
∞
− jnwt 1
= ∑Fne
n=0
∞
jnwt 1
+ ∑Fne jnw1t
n=−∞
−1
周期函数: f (t) =
7
周期信号的复数频谱 F0
complex frequency spectrum
F = Fn n − F = c0 0
1 = cn 2
8
周期信号的功率特性
1 t0 +T1 2 周期信号f (t )的平均功率 : P = f (t ) = ∫ f (t )dt T1 t0
2
1
∞
f (t) = a0 + ∑(an cos nω1t + bn sin nω1t), n为正整数
n=1
∞
1 直流分量： a 0 = T1
∫
t 0 + T1
t0
f ( t ) dt
2 t0 +T1 余弦分量的幅度：n = ∫ a f (t ) cos(nω1t )dt T1 t0
2 正弦分量的幅度： bn = T1
sin(ω1t )
4 T1 a1 = ∫ 2 f (t) cos(ω1t)dt T 0 1
4 T1 b = ∫ 2 f (t) sin( ω1t)dt 1 T 0 1
cos(2ω1t )
sin(2ω1t )
∞
令：Fn = Fn e
∞
jϕn
1 − jϕn 1 = (an − jbn ) F−n = F−n e = (an + jbn ) 2 2
jnwt 1
f (t) = F0 + ∑Fne
n=1
+ ∑F−ne
n=1
∞
− jnwt 1
= ∑Fne
n=0
∞
jnwt 1
+ ∑Fne jnw1t
n=−∞
−1
周期函数: f (t) =
7
周期信号的复数频谱 F0
complex frequency spectrum
F = Fn n − F = c0 0
1 = cn 2
8
周期信号的功率特性
1 t0 +T1 2 周期信号f (t )的平均功率 : P = f (t ) = ∫ f (t )dt T1 t0
2
周期信号的连续时间傅里叶级数
傅里叶级数是无穷级数，但只有在满足一定条件下才能收敛。对于周期信号，其傅里叶级数在频域上 是收敛的，即其频谱在无穷大频率处的值趋近于零。在时域上，傅里叶级数在每个周期内的积分值是 有限的，因此也是收敛的。
傅里叶级数的收敛性取决于信号的形状和频率范围。对于具有快速衰减特性的信号，其傅里叶级数可 能具有良好的收敛性；而对于具有缓慢衰减特性的信号，其傅里叶级数可能具有较差的收敛性。在实 际应用中，通常需要对信号进行截断或加窗处理，以提高傅里叶级数的收敛性。
傅里叶级数的重要性和应用价值
信号分析
傅里叶级数提供了将周期信号 分解为正弦和余弦波的方法，
是信号分析中的重要工具。
通信系统
在通信系统中，傅里叶级数用 于信号调制和解调，实现信号 的传输和接收。
控制系统
在控制系统中，傅里叶级数用 于频域分析和系统稳定性分析 。
物理和工程领域
在物理、化学、生物和工程领 域，傅里叶级数用于分析各种
DTFS的主要应用包括信号分析和数字信号处理中的频谱分析。
快速傅里叶变换（FFT）
1
快速傅里叶变换（FFT）是一种高效的计算离散 傅里叶变换（DFT）和其逆变换的算法。
2
FFT的主要思想是将长度为$N$的DFT分解为多 个较短的DFT，然后利用旋转因子的周期性和对 称性来减少计算的复杂度。
3
FFT的出现极大地促进了数字信号处理领域的发 展，使得实时信号处理成为可能。
滤波器设计
滤波器是信号处理中的重要元件，用于提取或抑制特定频率范围的信号。通过傅 里叶级数，可以设计出各种类型的滤波器，如低通、高通、带通和带阻滤波器等 。
滤波器设计在音频处理、图像处理、雷达和通信等领域有广泛应用，例如在音频 处理中可以通过滤波器来消除噪音或增强特定音色。
傅里叶级数的收敛性取决于信号的形状和频率范围。对于具有快速衰减特性的信号，其傅里叶级数可 能具有良好的收敛性；而对于具有缓慢衰减特性的信号，其傅里叶级数可能具有较差的收敛性。在实 际应用中，通常需要对信号进行截断或加窗处理，以提高傅里叶级数的收敛性。
傅里叶级数的重要性和应用价值
信号分析
傅里叶级数提供了将周期信号 分解为正弦和余弦波的方法，
是信号分析中的重要工具。
通信系统
在通信系统中，傅里叶级数用 于信号调制和解调，实现信号 的传输和接收。
控制系统
在控制系统中，傅里叶级数用 于频域分析和系统稳定性分析 。
物理和工程领域
在物理、化学、生物和工程领 域，傅里叶级数用于分析各种
DTFS的主要应用包括信号分析和数字信号处理中的频谱分析。
快速傅里叶变换（FFT）
1
快速傅里叶变换（FFT）是一种高效的计算离散 傅里叶变换（DFT）和其逆变换的算法。
2
FFT的主要思想是将长度为$N$的DFT分解为多 个较短的DFT，然后利用旋转因子的周期性和对 称性来减少计算的复杂度。
3
FFT的出现极大地促进了数字信号处理领域的发 展，使得实时信号处理成为可能。
滤波器设计
滤波器是信号处理中的重要元件，用于提取或抑制特定频率范围的信号。通过傅 里叶级数，可以设计出各种类型的滤波器，如低通、高通、带通和带阻滤波器等 。
滤波器设计在音频处理、图像处理、雷达和通信等领域有广泛应用，例如在音频 处理中可以通过滤波器来消除噪音或增强特定音色。
周期信号频谱分析
周期信号频谱分析作者：王慧申志平程晨来源：《科技与创新》2014年第14期摘要：周期信号频谱分析在信号与系统这一学科中占有极其重要的地位。
满足狄里赫利条件的非正弦周期函数可以展开为傅里叶级数，基于此事实，以傅里叶变化作为信号分析的理论基础，可以将非正弦周期信号视为一个直流分量与若干个不同频率的正弦分量之和。
通过对频谱宽带的理解，研究了矩形脉冲波形的变化对其频谱的影响。
关键词：周期信号；频谱；矩形脉冲；波形中图分类号：TN911.6 文献标识码：A 文章编号：2095-6835（2014）14-0139-011 实验原理与说明为了直观、方便地表达信号分解后所包含的频率分量和各分量所占的“比重”，将长度与各频率分量的振幅大小相对应的线段按频率高低依次排列，就得到了周期信号的振幅频谱图。
与此类似，将长度与各频率分量的初相相对应的线段按频率高低依次排列起来，就得到了周期信号的相位频谱图。
对周期信号进行傅里叶展开，基波的频率即为原周期信号的频率。
而频谱图中的谱线间隔为基波频率，所以，随着周期信号周期的增大，频谱的谱线将渐趋密集。
进一步分析可知，随着周期信号周期的增大，频谱的幅度将渐趋减小。
从理论上讲，周期信号的谐波分量是无限多的，所取的谐波分量越多，叠加后的波形越接近原信号的波形。
谐波振幅具有收敛性，这类信号能量的主要部分集中在低频分量中，所以可以忽略谐波次数过高的频率分量。
对于一个信号，自零频率开始到需要考虑的最高频率之间的频率范围是信号所占有的频带宽度。
对于一般的频谱，也常把自零频率开始到频谱振幅降为包络线最大值的101倍时的频率之间的频率范围定义为信号的频带宽度。
可以证明，对于矩形脉冲信号而言，频谱频带宽度与脉冲时间宽度成反比。
2 实验内容与方法2.1 单频正弦量的频谱观察单频正弦量的频谱观察的步骤主要有：①设置信号发生器为正弦波，频率为500 Hz，幅值为2 V。
②启动仿真开关，通过示波器观测波形。
第三章§3.2 周期信号的频谱分析——傅里叶级数
T
2 T 2
T , cos n 1 t cos m 1 t dt 2 0, T , sin n 1 t sin m 1 t dt 2 0,
m n m n m n m n
X
T
2 T 2
请画出其幅度谱和相位谱。
化为余弦形式
f (t ) 1 π 5 cos( 1 t 0 . 15 π ) cos 2 1 t 4
c0 1
三角函数形式的傅里叶级数的谱系数
三角函数形式的频谱图
cn
c1
0 0
5 2 . 236
n
2 . 24 c2
a n
j bn
T
T 0
f ( t ) co s n 1t d t j
T
1 T
T 0
f ( t ) sin n 1t d t
1 T
f ( t )e
0
j n 1t
dt
t 0 T1 t0
因 此 F n 1
1 T
f (t ) e
j n 1t
n
j n 1t
n 0 , 1, 2
jn 1t
f (t )
F (n 1 ) e
4
a
n 1
n
co s n 1t b n sin n 1t
利用欧拉公式
sin n 1 t
co s n 1 t
周期信号
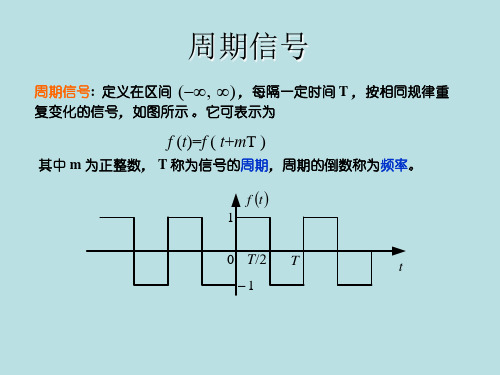
周期信号: 定义在区间 ( , ) ，每隔一定时间 T ，按相同规律重 复变化的信号，如图所示 。它可表示为
周期函数的傅里叶级数
2
f (t) a0
A e e n jn 1t n
j n1 t n
2 n1 2
§ 周期信号的傅立叶级数
又A-n
A（A 是n的偶函数）
n
n
n
（n n是n的奇函数）
b0 0，A0
a2 0
b02
a， 0
故
f (t)
1 2
Ane
n
j n1
t
n
1 2
Ane
n
j
n
e jn1 t
f t
Fne jn1t 用FS分析是对周期信号进行谐波分解，即
用谐n波 加权和来合成信号，因此，FS分析又称为谐波分析。
周期信号的对称性与付立叶系数的关系。
f (t)的对称条件
展开式中系数特点
f (t)
f (t)，纵轴对称（偶函数 ）
bn
0，an
4 T
t0
T 2
t0
f (t) cos n1tdt
nT
2
n
n
0
Sa( n1 ) 0
2
即 Fn>0
Sa( n1 ) 0 即 Fn<0
2
F e n
1 2
An
j n
§ 周期信号的傅立叶级数
此例中F n
A
T
Sa( n
2
)为一实数。幅度频谱与相位频谱可以合
画在一张图上。
c n
1 2
A n
-4
2
2
4 A
T
1 213141 51
101
第四步：讨论频谱结构与 、T 的关系
§ 周期信号的傅立叶级数
An