2017——2018年八年级上学期第二章测试卷 (1) (1)
2018学年八年级(上)物理试卷(1-2章)

八年级(上)物理试卷(1-2章)一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)下列现象中不属于机械运动的是()A.一江春水向东流 B.海水奔腾C.心潮澎湃D.流星似箭2.(3分)王迪同学在测量记录中忘记写单位,下列哪个数据的单位是cm()A.普通课本一张纸的厚度是7 B.茶杯的高度是10C.物理书的长度是252 D.他自己的身高是16.73.(3分)小明利用最小分度值为1mm的刻度尺测量一个物体的长度,三次测量的数据分别为2.35cm、2.36cm、2.36cm,则测量结果应记为()A.2.36cm B.2.357cm C.2.35cm D.2.4cm4.(3分)某车站并排停着两列待发的列车甲和乙。
一段时间后,甲车内一个人看见车外树木向西移动,乙车内的人通过车窗看到甲车没动,如果以地面为参照物,则甲、乙两车的运动情况是()A.甲列车向东运动,乙列车静止不动B.甲列车向东运动,乙列车向西运动C.乙列车向东运动,甲列车不动D.甲、乙两列车同时同速向东运动5.(3分)如图所示,刻度尺的使用方法正确的是()A. B. C. D.6.(3分)如图所示为不同物体运动时的频闪照片,其中做匀速直线运动的是()A.B.C.D.7.(3分)如图所示是一个小球在相同时间间隔里运动情景的大致物理模型图,下列对这个小球的运动情景描述正确的可能是()A.小球从高处自由落下B.小球沿斜面上下运动C.小球做匀速圆周运动D.小球做匀速直线运动8.(3分)运动会上,100m决赛,中间过程张明落后于王亮,冲刺阶段张明加速追赶,结果他们同时到达终点。
关于全过程中的平均速度,下列说法中正确的是()A.张明的平均速度比王亮的平均速度大B.张明的平均速度比王亮的平均速度小C.二者的平均速度相等D.不是匀速直线运动,无法比较9.(3分)神舟十号运载火箭长58m.分别从视频中截取火箭发射前和发射后第10s的位置图象,如图所示,则火箭发射后10s内的平均速度最接近于()A.5m/s B.9m/s C.12m/s D.15m/s10.(3分)如图是相向而行的甲、乙两物体的s﹣t图象,下列说法正确的是()A.相遇时两物体通过的路程均为100mB.0﹣30s内甲、乙均做匀速直线运动C.甲的运动速度为10m/sD.甲、乙是同时出发的二、填空题(本大题共8小题,每空1分,共18分)11.(1分)小明用刻度尺和三角板按图测一枚纽扣的直径,纽扣的直径是cm。
2017——2018学年度上学期八年级物理期末模拟试题(二)

2017——2018学年度上学期期末质量检测八年级物理模拟试题(二)一、选择题(下列各小题中1—10题为单项选择题,11—12题为多项选择题,每小题共36分。
多项选择题选对但不全得2分,选错得零分。
请将正确答案填入上表栏中)1.2017年4月20日,中国首个货运飞船“天舟一号”在海南文昌发射升空,升空后,“天舟一号”与空间站“天宫二号”成功实现了交会对接,如图2为对接模拟图,对接后“天舟一号”相对以下哪个参照物是静止的:A.地球 B.“天舟一号” C.“天宫二号” D.太阳2.某物体从地面上某一点出发沿直线运动,其s-t图象如图2所示.对物体的运动情况进行分析,得出结论不正确的是:A.物体在6s内运动的路程为15m B.以地球为参照物,物体在中间2s内静止C.物体在前2s内和后2s内的速度相等 D.物体在6s内的平均速度为2.5m/s3.在旅游景区,导游常利用扩音器进行讲解,如图所示。
关于扩音器的作用以下说法正确的是:A.提高声音的音调 B.增大声音的响度C.改变声音的音色 D.改变声音的传播速度4.下列四种现象中,由光的直线传播形成的是:A.镜中的花朵 B.小孔成像 C.水中“断”笔 D.仙鹤的倒影5.关于平面镜成像特点及其实验探究,下列说法正确的是:A.使用光屏是为了验证平面镜所成像的虚实 B.将蜡烛靠近玻璃板的同时像将远离玻璃板C.做多次试验获得多组数据是为了减小误差D.平面镜成像的大小与物体到平面镜的距离有关6.下列关于光的知识应用的说法,不正确的是:A.照相机的原理是利用凸透镜能成正立、缩小的实像B.电视机遥控器是利用红外线实现遥控的C.近视眼镜是利用凹透镜对光的发散作用 D.投影仪的原理是利用凸透镜能成倒立、放大的实像7.如图所示,早期照相馆里摄影师取景时看到的像是倒立的.有几位同学对此现象展开了讨论正确的是:甲.将照相机靠近两位照相的人,可以看到两位照相人的全身像乙.调整相机和两位照相人之间的距离,人像变小时,应减小相机镜头和胶片之间的距离丙.要使人像更亮,必须在两位照相的人身后进行“补光”丁.现在的相机利用光学或电子技术,把倒立的像转变成正立的,便于观察.A.甲与乙 B.甲与丙 C.乙与丁 D.丙与丁8.对于水银体温计的认识,下列说法正确的是:A.其分度值为0.01℃ B.它利用了气体热胀冷缩的原理C.读数时可以离开人体 D.可以不采取任何措施进行连续测量9.沂蒙革命老区四季分明,非常适合人类居住,下列热现象中,需要吸热的是:10.下列关于声现象说法正确的是:A.剧院四壁做成凹凸不平或用蜂窝状的材料,是为了增强声音的响度B.医生用“B超”给病人做检查,说明声音可以传递能量C.百米赛跑时,终点计时员以看到发令枪冒烟开始计时,而不是以听到枪声开始计时,是因为声速远小于光速D.学校路段“禁鸣喇叭”,是在传播过程中阻断噪声11.甲、乙两种物质的m-V图象如图所示,分析图象得出结论不正确的是:A.若甲、乙的质量相等,则甲的体积较大;B.若甲、乙的体积相等,则甲的质量较小;C.两物质的密度之比为4:1;D.两物质的密度之比为1:4。
2017-2018学年度上学期八年级语文第一次摸底考试试题(1-2单元)

2017-2018学年度上学期八年级语文第一次摸底考试试题(1-2单元)(时间:120分钟,满分:120分)一、积累运用(30分)1.下列加点字的读音全部正确的一项是()(2分)A.蹊.跷qī膝.盖xī呜咽.yè祈.祷qíB.嫣.红yān 愠.怒wèn 字帖.tiè挟.持xiéC.逶迤.yí蔫.巴niān 惩.罚chěng 猝.然cùD.焦灼.zhuó逮.捕dài 霎.时chà眷.念juàn2、下列对课文内容表述不正确的一项是(2分)()A、虽然同样是以长征为题材,但《<长征>节选》和《老山界》两篇课文的体裁并不相同。
B、王愿坚的《草》,以红军爬雪山为创作背景,塑造了以周副主席为代表的无产阶级革命家的高大形象。
C、《枣核》选自《美国点滴》,作者萧乾,现在代作家、翻译家、记者。
D、《始终眷恋着祖国》一文讲述了钱学森虽然在美国获得了巨大的成就,但仍心系祖国,最终历经艰辛回到祖国的故事。
3.对病句的修改不正确的一项是 (2分) ( )A.在语文学习之旅中,我们将领会到名人的光辉形象。
将“领会”改为“领悟”B.“中国梦”不仅在国际社会产生强烈反响,而且在国内引发强烈共鸣将“在国际社会产生强烈反响”和“在国内引发强烈共鸣”互换位置。
C.通过调查,使我们了解了真实情况删掉“通过”或“使”。
D.为了防止今后不再发生类似的事件,有关部门进一步完善了安全措施。
去掉“防止”或“不”4.下列加点成语使用正确的一项是()(2分)A.他处理这类事情可谓轻车熟路....,一点也不费力。
B.实现小康的宏伟蓝图是需付出艰苦努力的,不可能一挥而就。
.....C.经过大家的努力,我们终于登峰造极....,在山顶欣赏了美好的景色。
D.这件事我明明不愿做,他却偏要我去做,这是差强人意....吗?依次填入下面一段文字横线处的语句,衔接最恰当的一项是(行。
2017-2018学年浙教版八年级数学上第2章单元检测题有答案AKKHAl
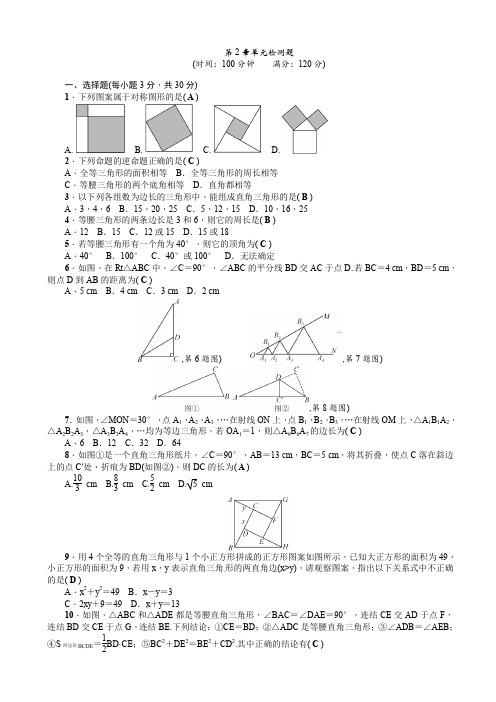
第2章单元检测题(时间:100分钟 满分:120分)一、选择题(每小题3分,共30分) 1.下列图案属于对称图形的是( A )A. B. C. D. 2.下列命题的逆命题正确的是( C )A .全等三角形的面积相等B .全等三角形的周长相等C .等腰三角形的两个底角相等D .直角都相等3.以下列各组数为边长的三角形中,能组成直角三角形的是( B ) A .3,4,6 B .15,20,25 C .5,12,15 D .10,16,25 4.等腰三角形的两条边长是3和6,则它的周长是( B ) A .12 B .15 C .12或15 D .15或185.若等腰三角形有一个角为40°,则它的顶角为( C ) A .40° B .100° C .40°或100° D .无法确定6.如图,在Rt △ABC 中,∠C =90°,∠ABC 的平分线BD 交AC 于点D.若BC =4 cm ,BD =5 cm ,则点D 到AB 的距离为( C )A .5 cmB .4 cmC .3 cmD .2 cm,第6题图) ,第7题图),第8题图)7.如图,∠MON =30°,点A 1,A 2,A 3,…在射线ON 上,点B 1,B 2,B 3,…在射线OM 上,△A 1B 1A 2,△A 2B 2A 3,△A 3B 3A 4,…均为等边三角形,若OA 1=1,则△A 6B 6A 7的边长为( C )A .6B .12C .32D .648.如图①是一个直角三角形纸片,∠C =90°,AB =13 cm ,BC =5 cm ,将其折叠,使点C 落在斜边上的点C′处,折痕为BD(如图②),则DC 的长为( A )A.103 cmB.83 cmC.52cm D. 5 cm9.用4个全等的直角三角形与1个小正方形拼成的正方形图案如图所示,已知大正方形的面积为49,小正方形的面积为9,若用x ,y 表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( D )A .x 2+y 2=49B .x -y =3C .2xy +9=49D .x +y =1310.如图,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,连结CE 交AD 于点F ,连结BD 交CE 于点G ,连结BE.下列结论:①CE =BD ;②△ADC 是等腰直角三角形;③∠ADB =∠AEB ;④S 四边形BCDE =12BD·CE ;⑤BC 2+DE 2=BE 2+CD 2.其中正确的结论有( C )A .1个B .2个C .3个D .4个,第10题图) ,第14题图) ,第15题图),第16题图)二、填空题(每小题4分,共24分)11.命题“等腰三角形两腰上的高相等”的逆命题是__两边上的高相等的三角形是等腰三角形__,这个逆命题是__真__命题.12.在△ABC 中,AB =AC ,AD 是中线,若∠B =60°,则∠BAD =__30°__. 13.在Rt △ABC 中,AB =5,BC =3,则斜边上的中线长为__2.5或2. 14.如图,在△ABC 中,CD ⊥AB 于点D ,E 是AC 的中点.若AD =6,DE =5,则CD 的长等于__8__. 15.如图,BD ,CE 分别是△ABC 两个外角的角平分线,DE 过点A 且DE ∥BC.若DE =14,BC =7,则△ABC 的周长为__21__.16.如图,已知D 为等边三角形ABC 内的一点,DB =DA ,BF =AB ,∠1=∠2,则∠BFD =__30°__.点拨:证△BCD ≌△ACD 得∠BCD =30°,再证△BFD ≌△BCD 得∠BFD =∠BCD =30° 三、解答题(共66分)17.(7分)如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 为半径画弧,两弧相交于点M ,N ,连结MN ,与AC ,BC 分别交于点D ,E ,连结AE.(1)求∠ADE 的度数;(直接写出结果)(2)当AB =3,AC =5时,求△ABE 的周长.解:(1)由题意可知MN 是线段AC 的垂直平分线,∴∠ADE =90°(2)由勾股定理可求BC =4,∵MN 是线段AC 的垂直平分线,∴AE =CE ,∴△ABE 的周长=AB +(AE +BE )=AB +BC =718.(8分)如图,AD =BC ,AC =BD.求证:△EAB 是等腰三角形.证明:易证△ABD ≌△BAC (SSS ),∴∠ABD =∠BAC ,∴AE =BE ,即△EAB 是等腰三角形19.(8分)在等腰三角形ABC 中,AB =AC ,∠C =30°,AB ⊥AD ,AD =2,求BC 的长.解:BC =620.(8分)如图,在△ABC 中,点D 是BC 边上一点,且BA =BD ,∠DAC =12∠B ,∠C =50°,求∠BAC的度数.解:设∠DAC =x °,则∠B =2x °,∠BDA =∠C +∠DAC =50°+x °.∵BD =BA ,∴∠BAD =∠BDA =50°+x °.∵∠B +∠BAD +∠BDA =180°,∴2x +50+x +50+x =180,解得x =20,∴∠BAD =∠BDA =70°,∠BAC =∠BAD +∠DAC =90°21.(8分)如图,AD ⊥BC 于点D ,∠B =∠DAC ,点E 在BC 上,△EAC 是以EC 为底的等腰三角形,AB =4,AE =3.(1)判断△ABC 的形状,并说明理由; (2)求△ABC 的面积.解:(1)△ABC 是直角三角形.理由:∵AD ⊥BC ,∴∠DAC +∠C =90°,∵∠B =∠DAC ,∴∠B +∠C =90°,∴△ABC 是直角三角形 (2)S △ABC =622.(8分)一牧童在A 处牧马,牧童的家在B 处,A ,B 处距河岸的距离分别是AC =500 m ,BD =700 m ,且C ,D 两地间的距离也为500 m ,天黑前牧童从点A 将马牵到河边去饮水,再赶回家,为了使所走的路程最短.(1)牧童应将马赶到河边的什么地点?请你在图中画出来; (2)问:他至少要走多少路?解:(1)如图①,作点A 关于河岸的对称点A′,连结BA′交河岸于点P ,则PB +PA =PB +PA ′=BA′最短,故牧童应将马赶到河边的点P 处(2)如图②,过点A′作A′B′⊥BD 交BD 的延长线于点B′,∴B ′A ′=CD =500 m ,B ′D =A′C =AC =500 m .在Rt △BB ′A ′中,BB ′=BD +DB′=1200 m ,A ′B ′=500 m ,∴BA ′=12002+5002=1300(m ),即他至少要走1300 m 路23.(9分)如图,△ABC 和△CDE 均为等边三角形,且点B ,C ,D 在同一直线上,连结AD ,BE ,分别交CE 和AC 于点G ,H ,连结GH.(1)请说出AD =BE 的理由;(2)试说出△BCH ≌△ACG 的理由;(3)试猜想△CGH 是什么特殊的三角形,并加以证明.解:(1)∵△ABC 和△CDE 均为等边三角形,∴AC =BC ,EC =DC ,∠ACB =∠ECD =60°,∴∠AC D =∠BCE ,∴△ACD ≌△BCE (SAS ),∴AD =BE(2)∵△ACD ≌△BCE ,∴∠CBH =∠CAG .∵∠ACB =∠ECD =60°,点B ,C ,D 在同一条直线上,∴∠ACB =∠ECD =∠ACG =60°.又∵AC =BC ,∴△BCH ≌△ACG (ASA ) (3)△CGH 是等边三角形,理由:∵△ACG ≌△BCH ,∴CG =CH ,又∵∠ACG =60°,∴△CGH 是等边三角形24.(10分)(1)如图①,在正方形ABCD 中,△AEF 的顶点E ,F 分别在BC ,CD 边上,高线AG 与正方形的边长相等,求∠EAF 的度数;(2)如图②,在Rt △BAD 中,∠BAD =90°,AB =AD ,点M ,N 是BD 边上的任意两点,且∠MAN =45°.将△AB M 绕点A 逆时针旋转90°至△ADH 位置,连结NH ,试判断MN ,ND ,DH 之间的数量关系,并说明理由.解:(1)易证Rt △ABE ≌Rt △AGE (HL ),Rt △AGF ≌Rt △ADF (HL ),∴∠BAE =∠GAE ,∠DAF =∠GAF ,∵∠BAD =90°,∠EAF =12∠BAD =45° (2)MN 2=ND 2+DH 2.理由:可证△AMN ≌△AHN (SAS ),∴MN=HN.∵∠BAD =90°,AB =AD ,∴∠AB D =∠ADB =45°,∴∠HDN =∠HDA +∠ADB =∠ABD +∠ADB =90°,∴HN 2=ND 2+DH 2.∴MN 2=ND 2+DH 2。
人教版八年级上册数学第二章测试题

人教版八年级上册数学第二章测试题一、选择题(每题3分,共30分)A. 2cm,3cm,5cmB. 5cm,6cm,10cmC. 1cm,1cm,3cmD. 3cm,4cm,9cm解析:根据三角形三边关系“任意两边之和大于第三边,任意两边之差小于第三边”。
A选项中,2 + 3 = 5,不满足两边之和大于第三边,不能组成三角形;B选项中,5+6 = 11>10,6 + 10 = 16>5,5+10 = 15>6,满足三边关系,可以组成三角形;C选项中,1+1 = 2<3,不满足三边关系,不能组成三角形;D选项中,3+4 = 7<9,不满足三边关系,不能组成三角形。
所以答案是B。
2. 一个三角形的两边长分别为3和8,第三边长是一个偶数,则第三边的长不能为()A. 6B. 8C. 10D. 12解析:设第三边为x,根据三边关系8 3<x<8+3,即5<x<11。
因为第三边是偶数,所以x可以为6、8、10,不能为12。
所以答案是D。
3. 在△ABC中,∠A = 55°,∠B比∠C大25°,则∠B的度数为()A. 50°B. 75°C. 100°D. 125°解析:设∠C = x°,则∠B=(x + 25)°,因为三角形内角和为180°,所以55+x+(x + 25)=180,化简得2x+80 = 180,2x=100,x = 50,则∠B=x + 25=75°。
所以答案是B。
4. 等腰三角形的一边长为3cm,另一边长为7cm,则这个等腰三角形的周长为()A. 13cmB. 17cmC. 13cm或17cmD. 无法确定解析:当3cm为腰时,3+3 = 6<7,不满足三角形三边关系,不能构成三角形;当7cm为腰时,周长为7 + 7+3=17cm。
所以答案是B。
5. 如图,在△ABC中,∠ACB = 90°,CD⊥AB于点D,则图中互余的角有()对。
2017-2018学年八年级数学上册(浙教版)课件:第2章达标测试题 (共29张)

19.(8分)如图,AB=AC,CD⊥AB于点D, BE⊥AC于点E,BE与CD相交于点O. (1)求证:AD=AE; (2)连结OA,BC,试判断直线OA,BC的位置关系 并说明理由.
解:(1)在△ACD与△ABE中,∵∠A=∠A, ∠ADC=∠AEB=90°,AB=AC, ∴△ACD≌△ABE.∴AD=AE;(2)OA与BC互相垂 直.在Rt△ADO与Rt△AEO中,∵OA=OA,AD =AE,∴Rt△ADO≌Rt△AEO.∴∠DAO=∠EAO, 即OA是∠BAC的平分线.又∵AB=AC, ∴OA⊥BC.
22.(8分)如图,△ABC是等腰直角三角形,BC是 斜边,P为△ABC内一点,将△ABP绕点A逆时针 旋转后与△ACP′重合.如果AP=3,求线段PP′的 长.
证明:∵△ACB和△ECD都是等腰直角三角 形.∴AC=BC,EC=DC.∵∠ACB=∠ECD= 90°,∴∠ACE=∠BCD,在△ACE和△BCD中,
∴△ACE≌△BCD(SAS);
(2)由(1)得∠EAC=∠B=45,AE=BD=12,又 ∵∠BAC=45°,∴∠EAD=∠EAC+∠BAC= 90°,∴△EAD是直角三角形, ∴DE= ∴DE=13. =13,
∴△AMF≌△DCF(AAS),∴MF=CF,∴∠FMC =∠FCM;(2)AD⊥MC.∵△ADE与△MFC均为等 腰Rt△,∴∠FED=∠ACM,∴DE∥MC,又 ∵AD⊥DE,∴AD⊥MC.
21.(8分)如图,△ACB和△ECD都是等腰直角三 角形,∠ACB=∠ECD=90°,D为AB边上一 点. (1)求证:△ACE≌△BCD; (2)若AD=5,BD=12,求DE的长.
一、选择题(每小题3分,共30分) 1.下列图形中,不是轴对称图形的是( D ) A.线段 B.角 C.等腰三角形 D.直角三角形 2.等腰三角形的一边长是8,周长是18,那么它的 腰长是( D ) A.8 B.5 C.2 D.8或5 3.等腰三角形是轴对称图形,它的对称轴是(C) A.过顶点的直线 B.底角的角平分线所在的直线 C.顶角的角平分线所在的直线 D.腰上的高所在的直线
八年级上册数学第二章测试题

八年级上册数学第二章测试题一、选择题(每题3分,共30分)1. 4的平方根是()A. 2B. -2C. ±2D. 16解析:一个正数有两个平方根,它们互为相反数。
因为(±2)^2 = 4,所以4的平方根是±2,答案为C。
2. 下列实数中,属于无理数的是()A. 0B. (1)/(3)C. √(3)D. 3.14解析:无理数是无限不循环小数。
0是整数,属于有理数;(1)/(3)是分数,属于有理数;3.14是有限小数,属于有理数;√(3)是无限不循环小数,是无理数,答案为C。
3. √(16)的算术平方根是()A. 4B. 2C. -2D. ±2解析:先计算√(16)=4,4的算术平方根是2(算术平方根是非负的),答案为B。
4. 下列说法正确的是()A. -81的平方根是±9B. 任何数的平方是非负数,因而任何数的平方根也是非负数C. 任何一个非负数的平方根都不大于这个数D. 2是4的平方根解析:A选项,负数没有平方根, 81是负数,所以A错误。
B选项,任何数的平方是非负数,但正数的平方根有两个,一正一负,0的平方根是0,所以B错误。
C选项,(1)/(4)的平方根是±(1)/(2),(1)/(2)>(1)/(4),所以C错误。
D选项,因为2^2 = 4,所以2是4的平方根,D正确。
答案为D。
5. 在实数-√(2),0,(1)/(3),π,√(16)中,无理数有()个A. 1B. 2C. 3D. 4解析:-√(2)是无理数,0是有理数,(1)/(3)是有理数,π是无理数,√(16) = 4是有理数,所以无理数有2个,答案为B。
6. 若x^2=16,则x的值为()A. 4B. -4C. ±4D. ±2解析:因为x^2=16,所以x=±√(16)=±4,答案为C。
7. 一个数的算术平方根是它本身,则这个数是()A. 1B. 0C. -1D. 0或1解析:0的算术平方根是0,1的算术平方根是1, 1没有算术平方根,所以这个数是0或1,答案为D。
2018年浙教版八年级数学上《第2章特殊三角形》同步测试含答案

本文为Word版,可任意修改编辑《特殊三角形》测试一、选择题(本大题共8小题,共32.0分)()1.等腰三角形两边长为3和6,则周长为 A. 12B. 15C. 12或15D. 无法确定△ABC AB=AC=5BC=62.如图,在中,,,AD是BC边上的中线,点()E、F、M、N是AD上的四点,则图中阴影部分的总面积是 A. 6B. 8C. 4D. 1236∘()3.有一个角是的等腰三角形,其它两个角的度数是 36∘108∘36∘72∘A. ,B. ,72∘72∘36∘108∘72∘72∘C. ,D. ,或,Rt△ABC∠C=90∘∠ABC D.BC=4cm4.如图,在中,,的平分线BD交AC于点若,BD=5cm(),则点D到AB的距离是 A. 5cmB. 4cmC. 3cmD. 2cm.5.如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”下列各组数据中,能()作为一个智慧三角形三边长的一组是 233A. 1,2,3B. 1,1,C. 1,1,D. 1,2,△ABC△ABC6.如图,的顶点都在正方形网格的格点上,若小方格的边长为1,则的形()状是 A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰直角三角形7.如图,已知:,点、、在射线ON 上,点、、在射线OM 上,、∠MON =30∘A 1A 2A 3…B 1B 2B 3…△A 1B 1A 2、均为等边三角形,若,则的边长为 △A 2B 2A 3△A 3B 3A 4…OA 1=1△A 6B 6A 7()A. 6B. 12C. 32D. 648.如图,和都是等腰直角三角形,,连结CE 交AD△ABC △ADE ∠BAC =∠DAE =90∘于点F ,连结BD 交CE 于点G ,连结下列结论中,正确的结论有 BE.();①CE =BD 是等腰直角三角形;②△ADC ;③∠ADB =∠AEB ;④S 四边形BCDE =12BD ⋅CE .⑤BC 2+DE 2=BE 2+CD 2A. 1个 B. 2个 C. 3个 D. 4个二、填空题(本大题共7小题,共28.0分)9.如图,在中,,,于D ,则 ______ .△ABC AB =AC BC =6AD ⊥BC BD =10.如图,在中,CD 是斜边AB 上的中线,若,则 ______Rt △ABC ∠A =20∘∠BDC =.11.如图,在等边中,,D 是BC 的中点,将绕点A 旋转后△ABC AB =6△ABD得到,那么线段DE 的长度为______.△ACE12.如图,中,于D ,E 是AC 的中点若,,则CD 的长等于△ABC CD ⊥AB .AD =6DE =5______.本文为Word 版,可任意修改编辑13.如图,折叠长方形的一边AD ,使点D 落在BC 边上的F 点处,若,AB =8cm ,则EC 长为______ .BC =10cm14.如图,在中,,,AE 是经过A 点的一条直线,△ABC ∠BAC =90∘AB =AC 且B 、C 在AE 的两侧,于D ,于E ,,,则BD ⊥AE CE ⊥AE CE =2BD =6DE 的长为______ .15.如图,在中,,,将其绕点A 逆时针旋转得到Rt △ABC ∠C =90∘AC =BC 15∘,交AB 于E ,若图中阴影部分面积为,则的长为Rt △AB'C'B'C'23B'E ______.三、解答题(本大题共5小题,共40.0分)16.如图,在中,,分别以点A 、C 为圆心,大于长为半径画弧,两弧相交于点M 、N ,Rt △ABC ∠B =90∘12AC 连接MN ,与AC 、BC 分别交于点D 、E ,连接AE .求;直接写出结果(1)∠ADE ()当,时,求的周长.(2)AB =3AC =5△ABE17.如图,在等边三角形ABC 中,点D ,E 分别在边BC ,AC 上,且,过点E 作,交BC 的延DE//AB EF ⊥DE 长线于点F .求的度数;(1)∠F 若,求DF 的长.(2)CD =218.现在给出两个三角形,请你把图分割成两个等腰三角形,把图分割成三个等腰三角形要求:在图、(1)(2).(1)上分割:标出分割后的三角形的各内角的度数.(2)19.如图,在中,D 是BC 边上一点,且,,求△ABC BA =BD ∠DAC =12∠B ∠C =50∘.的度数.∠BAC本文为Word版,可任意修改编辑△ABC△ABC∠DCE=∠ACD20.已知:如图,在中,AD是的高,作,交AD的延长线于点E,点F是点C关于直线AE的对称点,连接AF.(1)CE=AF求证:;(2)CD=1AD=3∠B=20∘∠BAF若,,且,求的度数.答案1. B2. A3. D4. C5. D6. B7. C8. C9. 310. 40∘11. 3312. 813. 3cm14. 415. 23‒2(1)∵16. 解:由题意可知MN是线段AC的垂直平分线,∴∠ADE=90∘;(2)∵Rt△ABC∠B=90∘AB=3AC=5在中,,,,∴BC=52‒32=4,∵MN是线段AC的垂直平分线,∴AE=CE,∴△ABE=AB+(AE+BE)=AB+BC=3+4=7的周长.(1)∵△ABC17. 解:是等边三角形,∴∠B=60∘,∵DE//AB,∴∠EDC=∠B=60∘,∵EF⊥DE,∴∠DEF=90∘,∴∠F=90∘‒∠EDC=30∘;(2)∵∠ACB=60∘∠EDC=60∘,,∴△EDC是等边三角形.∴ED=DC=2,∵∠DEF=90∘∠F=30∘,,∴DF=2DE=4.18. 解:如图所示:∠DAC=x∘∠B=2x∘∠BDA=∠C+∠DAC=50∘+x∘19. 解:设,则,.∵BD=BA,∴∠BAD=∠BDA=50∘+x∘,∵∠B+∠BAD+∠BDA=180∘,2x+50+x+50+x=180即,x=20解得.∴∠BAD=∠BDA=50∘+20∘=70∘,∴∠BAC=∠BAD+∠DAC=70∘+20∘=90∘.(1)∵AD△ABC20. 证明:是的高,∴∠ADC=∠EDC=90∘∠DCE=∠ACD,,本文为Word 版,可任意修改编辑为等腰三角形,∴△ACE ,∴AC =CE 又点F 是点C 关于AE 的对称点,∵,∴AF =AC ;∴CE =AF 解:在中,,,根据勾股定理得到:,(2)Rt △ACD CD =1AD =3AC =AD 2+CD 2=2,∴CD =12AC .∴∠DAC =30∘同理可得,∠DAF =30∘在中,,Rt △ABD ∠B =20∘. ∴∠BAF =90∘‒∠B ‒∠DAF =40∘。
2017-2018学年度八年级上学期第二次教学质量检测

石门实验中学2017-2018学年度第一学期第二次教学质量检测试卷初二年级物理学科第Ⅰ卷选择题部分一、单项选择题(7小题,每小题3分,共21分。
下列各题所列答案中,只有一项是符合题目要求的,选对的得3分,选错或不答的得0分。
请将答案写在答题卷上)1.如图2所示的光路图中,能正确表示光从空气射人水中时发生的反射和折射现象是()2.关于声音,下列说法中正确的是()A.我们能区分出小提琴和二胡的声音,是因为它们发出声音的音调不同B.我们无法听到蝴蝶飞过的声音,是因为它发出声音的响度太小C.敲锣时用力越大,它发出声音的响度越大D.歌唱演员引吭高歌,其中的“高”是指音调高3.下列物态变化过程需要吸热的是()A.初夏,清晨林中弥漫白雾 B.俗话说“水缸穿裙子,老天要下雨”C.衣柜中樟脑丸放置一段时间后变小 D.深秋,柿子树上的柿子挂满了白霜4.某火车站并列停靠着甲、乙两列火车,甲车上的乘客突然发现自己所在的列车向东运动了,关于两列火车运动情况的说法可能的是()A.甲车不动,乙车向东B.甲车不动,乙车向西C.甲车向西,乙车不动D.甲车向西,乙车向东5.已知酒精、煤油、水银的熔点分别为-117℃、-30℃、-38.8℃,南极的最低气温可达-89.2℃,要测量南极的气温,应该选用()A.酒精温度计 B.煤油温度计 C.水银温度计 D.煤油温度计和水银温度计6.一盏探照灯装在东面看台上,灯光朝西斜向下射到没有水的游泳池底的中央,在将游泳池逐渐灌满水的过程中,池底的光斑将()A.先东移动后静止B.向西移动后静止C.先向东移动后向西移动D.仍在原来位置7.如图,沿同一条直线向东运动的物体A、B,其运动相对同一参考点O的距离S随时间t变化的图象,以下说法正确的是()①两物体由同一位置O点开始运动,但物体A比B迟3s才开始运动;②t=0时刻,A在O点,B在距离O点5m处;③在第4秒时,A的速度更快,在第5s末A、B相遇;④5s内,A、B的平均速度相等.A.只有①④正确B.只有③④正确C.只有①③正确D.只有②③正确第Ⅱ卷非选择题部分二、填空题(7小题,每空1分,共21分。
2018年秋北师大版八年级上《第二章实数》检测卷含答案

16 x -1 , 的第二章检测卷时间:120 分钟满分:120 分一、选择题(本大题共 6 小题,每小题 3 分,共 18 分,每小题只有一个正确的选项)1.下列各数中,最小的是( )A .0B .1C .-1D .- 22.在-1.414, 2,π,2+ 3,3.212212221…,3.14这些数中,无理数的个数为() A .5 个 B .2 个C .3 个D .4 个3.下列计算正确的是( ) A. 18- 2=2 2 B. 2+ 3= 5C. 12÷ 3=4D. 5× 6= 114.若 m = 30-3,则 m 的取值范围是( )A .1<m <2B .2<m <3C .3<m <4D .4<m <55.如图,在 Rt △PQR 中,∠PRQ =90°,RP =RQ ,边 QR 在数轴上.点 Q 表示的数为 1,点 R 表示的数为 3,以 Q 为圆心,QP 的长为半径画弧交数轴负半轴于点 P 1,则 P 1 表示的数是( )A .-2B .-2 2C .1-2 2D .2 2-16.若 6- 13的整数部分为 x ,小数部分为 y ,则(2x + 13)y 的值是() A .5-3 13 B .3C .3 13-5D .-3二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)1 7. 的算术平方根为________.x 8.若代数式 有意义,则实数 x 的取值范围是______________.9.若最简二次根式 5m -4与 2m +5可以合并,则 m 的值可以为________.10.如图,直径为 1 个单位长度的圆从原点沿数轴向右滚动一周,圆上在原点 O 处的点到达点 O ′ 点 P 表 示的数是 2.6,那么 PO ′ 长度是________.42.现已知△ABC223(2)(6-215)×3-6111.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式.即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S=的三边长分别为2,3,4,则△ABC的面积为________.1ab-a2+b2-c2212.已知|a|=5,b2=7,且|a+b|=a+b,则b-a的值为________.三、(本大题共5小题,每小题6分,共30分)13.求下列各式中x的值:(1)(x-2)+1=17;(2)(x+2)+27=0.14.计算:3(1)(-3)2+-8+|1-2|;2.15.一个正数x的平方根分别是3a+2与4-a,求a和x的值.16.实数a,b在数轴上的位置如图所示,请化简:(a-b)2-a2-b2..17.如图,在四边形ABCD中,AB=AD,∠BAD=90°若AB=22,CD=43,BC=8,求四边形ABCD 的面积.四、(本大题共3小题,每小题8分,共24分)18.已知a-17+217-a=b+8.(1)求a的值;(2)求a2-b2的平方根.19.已知x=5+2,y=5-2,求下列各式的值.(1)xy;(2)x2-y2.m)近似满足公式t=h12120.如图,每个小正方形的边长为1.(1)求四边形ABCD的面积和周长;(2)∠BCD是直角吗?请说明理由.五、(本大题共2小题,每小题9分,共18分)21.高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:5(不考虑风速的影响).(1)从50m高空抛物到落地所需时间t是________s,从100m高空抛物到落地所需时间t是________s;(2)t是t的多少倍?(3)经过1.5s,高空抛物下落的高度是多少?22.已知实数a,b满足|2017-a|+a-2018=a.(1)a的取值范围是________,化简:|2017-a|=________;(2)张敏同学求得a-20172的值为2019,你认为她的答案正确吗?为什么?2 22 4 43 2.六、(本大题共 12 分)23.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 3+2 2= (1+ 2) .善于思考的小明进行了以下探索:设 a + 2b =(m + 2n) (其中 a ,b ,m ,n 均为整数),则有 a + 2b = m 2+2n 2+2 2mn .∴a =m 2+2n 2,b =2mn .这样小明就找到了一种把类似 a + 2b 的式子化为平方式的方法,请你 仿照小明的方法探索并解决下列问题:(1)当 a ,b ,m ,n 均为正整数时,若 a + 3b =(m + 3n) ,用含 m ,n 的式子分别表示 a 、b ,得 a =________,b =________; (2)利用所探索的结论,找一组正整数 a ,b ,m ,n 填空:________+ 3________=(________+ 3________) ; (3)若 a +4 3=(m + 3n) ,且 a ,m ,n 均为正整数,求 a 的值.参考答案与解析1.D 2.D 3.A 4.B 5.C6.B 解析:∵3< 13<4,∴6- 13的整数部分 x =2,则小数部分 y =6- 13-2=4- 13,则(2x + 13)y =(4+ 13)(4- 13)=16-13=3.1 3 15 7. 8.x≥0 且 x≠19.3 10.π-2.6 11. 12.2 或 12 解析:∵|a |=5,∴a =±5.∵ b 2=7,∴b =±7.∵|a +b|=a +b ,∴a +b >0.∴当 a =5 时,b =7,此时 b -a =7-5=2;当 a =-5 时,b =7,此时 b -a =7-(-5)=12,故 b -a 的值为 2 或 12.13.解:(1)(x -2) =16,x -2=±4,∴x =6 或-2.(3分)(2)(x +2) =-27,x +2=-3,∴x =-5.(6分) 14.解:(1)原式=3-2-1+ 2= 2.(3分)(2)原式= 18-2 45-3 2=3 2-6 5-3 2=-6 5.(6分)15.解:由题意得 3a +2+4-a =0,解得 a =-3,(2 分)则 3a +2=-7,(4 分)故这个正数 x =(-7) =49.(62 5 2+3 5+5,面积为 7×5- ×1×7- ×4×2- ×1×2- ×(1+5)×3=17.5.(5分)=1.5,即 =2.25,∴h =11.25m.(8分) BC 2=64,∴BD 2+CD 2=BC △2,∴ BCD 为直角三角形,且∠BDC =90° 分)∴S 四边形 ABCD △=S ABD △+S BCD = ×2 22 t 1 10 (3)由题意得h 2 2 1分) 16.解:由数轴可知 a<0,b>0,∴a -b<0,(2 分)则 (a -b )2- a 2- b 2=|a -b|-|a |-|b |=-(a -b)+a -b =0.(6分)17.解:∵AB =AD ,∠BAD =90°,AB =2 2,∴BD = AB 2+AD 2=4.(2分)∵BD 2+CD 2=42+(43) =64, 1 .(41 ×2 2+ ×4 3×4=4+8 3.(6分)18.解:(1)由题意知 a -17 与 17-a 均有算术平方根,∴a -17 与 17-a 均为非负数,(2 分)而 a -17 与 17 -a 又互为相反数,∴a -17=0,∴a =17.(4分)(2)由(1)可知 a =17,∴b +8=0,∴b =-8.(6分)∴a 2-b 2=172-(-8) =225,∴a 2-b 2 的平方根为± a 2-b 2=±15.(8分)19.解:(1)原式=( 5+2)( 5-2)=5-4=1.(4分)(2)原式=( 5+2) -( 5-2) =5+4+4 5-5-4+4 5=8 5.(8分)20.解:(1)由勾股定理可得 AB 2=12+72=50,则 AB = 50=5 2.∵BC 2=42+22=20,∴BC =2 5.∵CD 2 =22+12=5,∴CD = 5.∵AD 2=32+42=25,∴AD =5,(2 分)故四边形 ABCD 的周长为 5 2+2 5+ 5+5= 1 1 1 1 2 2 2 2 (2)∠BCD 是直角.(6 分)理由如下:连接 BD ,由(1)得 BC 2=20,CD 2=5,而 BD 2=32+42=25,∴DC 2+BC 2 =BD △2,∴ BCD 是直角三角形,且∠BCD =90°.(8分)21.解:(1) 10 2 5(2 分)t 2 5 (2)∵ 2= = 2,∴t 是 t 的 2倍.(5 分)h 5 5答:经过 1.5s ,高空抛物下落的高度是 11.25m.(9分)22.解:(1)a≥2018 a -2017(4 分)(2)她的答案不正确.(5 分)理由如下:∵|2017-a|+ a -2018=a ,∴a -2017+ a -2018=a ,∴ a -2018 =2017,(7 分)∴a -2018=20172,∴a -20172=2018.∴她的答案不正确.(9 分)23.解:(1)m 2+3n 2 2mn (2 分)(2)4 2 1 1(答案不唯一)(6分)(3)由题意得 a =m 2+3n 2,b =2mn ,∴4=2mn ,且 m ,n 为正整数,(8 分)∴m =2,n =1 或 m =1,n =2,∴a =22+3×12=7 或 a =12+3×22=13.(12分)。
浙教版八年级上第二章特殊三角形20172018学年章末复习含答案

章末复习(二)特别三角形1基础题知识点 1轴对称图形与轴对称1、以下四个手机APP 图标中,是轴对称图形的是(C)2、(萧山区期中)以下图案中,是轴对称图形的有(B)A、1 个B、2 个C、3 个D、4 个知识点2等腰三角形的性质与判断3、(丽水岭头中学月考)已知a、b、c 是△ ABC的三边长,且满足c2- a2- b2+ |a- b|= 0,则△ABC 的形状为(C)A 、等腰三角形B 、直角三角形C、等腰直角三角形 D 、等边三角形4、(杭州青春中学期中)已知等腰三角形的一个外角等于100 °,则它的顶角是(C)A 、80°B 、20°C、 80°或20° D 、不可以确立5、如图,已知△ABC 中,∠ ACB= 120 °, CE 均分∠ ACB, AD ∥EC,交BC的延长线于点 D.(1)求∠ BCE 的度数;(2)试找出图中的等边三角形,并说明原由、解:( 1)∵∠ ACB= 120°, CE 均分∠ ACB,∴∠ BCE=12∠ ABC= 60°.(2)△ ACD 是等边三角形,原由:∵∠ BCE= 60°, AD ∥ EC,∴∠ BCE=∠ D= 60°.∵∠ ACB= 120°,∴∠ ACD = 60°.∴△ ACD 是等边三角形、6、(杭州下城区校级期中)如图,△ABC 中,AB =AC,AE =BC,AC 的垂直均分线交AB 于 E,D 为垂足,连结 EC.(1)若 CE= 12,求 BC 长;(2)求∠ ECD 的度数、解:( 1)∵ ED 垂直均分 AC,∴AE= EC.∵AE= BC,∴BC= CE= 12.(2)∵ AE=CE= BC,∴∠ A=∠ ACE,∠ B=∠ CEB.∵AB= AC,∴∠ B=∠ ACB.∵∠ BEC=∠ A+∠ ECA=2∠ A,∴设∠ A= x,则∠ BEC=∠ B=∠ ACB= 2x.∴5x=180°, x= 36°.∴∠ ECD =∠ A= 36°.知识点 3抗命题与逆定理7、命题:“平行四边形是中心对称图形”的抗命题为拥有中心对称的图形是平行四边形、知识点 4直角三角形的性质与判断8、如图,将三角尺与直尺贴在一起,使三角尺的直角极点C(∠ ACB= 90°)在直尺的一边上,若∠ 2= 60°,则∠ 1 的度数等于( D )A 、75°B 、60°C 、 45°D 、30°9、如图,在△ABC第 8题图中,∠ ACB = 90°,∠ ABC = 60°,BD第均分∠9 题图ABC ,P点是BD的中点,若AD = 8,则CP的长为( C )A 、3B 、3.5C 、 4D 、4.510、(萧山区期中)命题 “直角三角形斜边上的中线等于斜边的一半 ”的抗命题是什么?是真命题还是假命题?假如真命题请你证明,假如假命题请你举反例说明、解:抗命题:有一边的中线等于该边一半的三角形是直角三角形;为真命题;1已知:在△ ABC 中, AD 是 BC 边的中线, AD =2BC.求证:△ ABC 是直角三角形、证明:∵ AD 是 BC 边的中线,∴ BD = CD =1BC.21∵AD =2BC ,∴ AD = BD =CD .∴∠ 1=∠ B ,∠ 2=∠ C.∴∠ 1+∠ 2=∠ B +∠ C ,即∠ BAC =∠ B +∠ C.∵ 2∠BAC =∠ BAC +∠ B +∠ C = 180°, ∴∠ BAC = 90°.∴△ ABC 是直角三角形、知识点 5 勾股定理11、直角三角形的斜边比向来角边长 A 、4 cm B 、8 cm2 cm ,另向来角边长为C 、 10 cm 6 cm ,则它的斜边长为(D 、 12 cmC )12、(平阳县校级月考)如图,校园内有两棵树,相距8 米,一棵树高AB= 13米,另一棵树高CD= 7 米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟最少要飞10 米、a b c13、(金华月考)已知,在△ABC 中, AB= c,BC= a, AC= b,==, 2c- b= 12,求△ ABC 的面积、a b c解:∵==,∴设 a= 3k,则 b= 4k, c= 5k.∵2c-b=12,∴ 10k-4k= 12.∴k= 2.∴a= 6, b= 8,c= 10.∵62+ 82= 102,222∴ a + b = c .∴△ ABC 为直角三角形、∴△ ABC 的面积为:12×6×8= 24.知识点 6直角三角形全等的判断14、如图,∠ACB=∠CFE=90°,AB=DE,BC=EF,求证:AD=CF.证明:∵∠ ACB=∠ CFE = 90°,∴∠ ACB=∠ DFE = 90°.在 Rt△ ACB 和 Rt△ DFE 中,AB= DE , BC= EF,∴Rt△ ACB≌ Rt△ DFE ( HL )、∴AC= DF .∴AC- AF= DF -AF,即 AD= CF.2中档题15、如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.若α=10°,则β的度数是( B)A 、40°B 、50°C、60°D、不可以确立第 15题图第16题图16、如图1是我国古代有名的“赵爽弦图”的表示图,它是由四个全等的直角三角形围成的、若AC= 6,BC = 5,将四个直角三角形中边长为 6 的直角边分别向外延长一倍,获得图2所示的“数学风车”,则这个风车的外头周长是(D)A 、72B 、52C、80D、 7617、如图,底面周长为12,高为 8 的圆柱体上有一只小蚂蚁要从点 A 爬到点 B,则蚂蚁爬行的最短距离是( A)A 、10B、8C、5D、4第17题图第18题图18、(下城区校级期中)如图,Rt△ABC 中, AC= BC= 4,点 D ,E 分别是 AB,AC 的中点,在CD 上找一点 P,使 PA+PE 最小,则这个最小值是(C)A、2B、2 2C、2 5D、419、(萧山区期中)如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角均分线AE交CD于H,EF⊥ AB 于 F,以下结论:①∠ ACD =∠ B;② CH = CE= EF ;③ AC= AF;④ CH = HD .此中正确的结论为( B)A 、①②④B 、①②③C、②③ D 、①③第19题图第20题图20、(台州月考)如图,在△ABC 中, AB= AC, D、 E 是△ ABC 内的两点, AD 均分∠ BAC,∠ EBC=∠ E =60°.若 BE= 6 cm, DE = 2 cm,则 BC 的长为( B)A 、4 cmB 、6 cm C、 8 cm D 、12 cm21、如图,在△ABC 中, AB= 15, BC= 14, AC= 13.求BC 边上的高AD .解:设 BD= x,则 CD = 14- x.∵ AD 是△ ABC 中 BC 边上的高,∴在 Rt△ ABD 和 Rt△ADC 中,由勾股定理,得AD2= AB2-BD2=AC 2-CD 2,即 152- x2= 132-( 14- x)2,解得 x= 9.∴AD = 152- 92= 12.22、已知:如图,△ABC 为等边三角形, D 是 BC 延长线上一点,连结AD ,以 AD 为边作等边△ ADE ,连结 CE,用你学过的知识探究AC, CD ,CE 三条线段的长度有何关系?试写出证明过程、解: CE =AC+CD .证明:∵△ ABC 为等边三角形,∴AB= AC,∠ BAC = 60°.又∵△ ADE 为等边三角形,∴AD = AE,∠ DAE = 60°.∴∠ BAC+∠ CAD=∠ DAE +∠ CAD ,即∠ BAD=∠ CAE.在△ ABD 和△ ACE 中,AB =AC ,∠BAD =∠ CAE ,AD =AE ,∴△ ABD ≌△ ACE( SAS)、∴BD = CE.∵AC= BC,∴BD = BC+CD = AC+ CD,即 CE= AC+ CD .23、如图,在△ABC 中,∠ C= 90°, AD 是∠ BAC 的均分线, DE⊥ AB 于 E, F 在 AC 上, BD=DF .求证:(1)CF =EB ;(2)AB= AF+2EB .证明:( 1)∵ AD 是∠ BAC 的均分线, DE ⊥ AB, DC ⊥ AC,∴DE = DC.在 Rt△ CDF 和 Rt△EDB 中,DF =DB ,DC =DE ,∴Rt△ CDF ≌ Rt△ EDB( HL )、∴CF = EB.(2)在 Rt△ ADC 和 Rt△ ADE 中,DC =DE ,AD =AD ,∴Rt△ ADC ≌ Rt△ ADE( HL )、∴AC= AE.∴AB= AE+ BE= AC+ EB= AF+ CF + EB= AF+ 2EB.24、已知:在△ABC 中, AC= BC,∠ ACB= 90°,点 D 是 AB 的中点,点 E 是 AB 边上一点、( 1)直线 BF 垂直于 CE 于点 F ,交 CD 于点 G(如图 1),求证: AE= CG;BE 相等的线段,并( 2)直线 AH 垂直于 CE,垂足为H ,交 CD 的延长线于点M(如图 2),找出图中与说明原由、解:( 1)证明:∵点 D 是 AB 的中点, AC= BC,∠ ACB= 90°,∴CD ⊥AB,∠ ACD =∠ BCD = 45°,∠ CAD =∠ CBD =45°.∴∠ CAE=∠ BCG.∵BF⊥ CE,∴∠ CBG+∠ BCF = 90°.又∵∠ ACE +∠ BCF= 90°,∴∠ ACE=∠ CBG.又∵ AC =CB,∴△ AEC≌△ CGB.∴AE= CG.(2)BE= CM.原由:∵ CH ⊥ HM, CD⊥ ED ,∴∠CMA +∠ MCH = 90°,∠ BEC+∠ MCH = 90°.∴∠ CMA =∠ BEC.又∵ AC =BC,∠ ACM =∠ CBE = 45°,∴△ CAM ≌△ BCE.∴BE= CM .3综合题25、如图1,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、 DE 的中点、(1)求证: MN ⊥DE ;(2)连结 DM , ME,猜想∠ A 与∠ DME 之间的关系,并写出推理过程;(3)若将锐角△ ABC 变成钝角△ ABC,如图 2,上述( 1)(2)中的结论能否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明原由、解:( 1)证明:连结DM,ME ,∵ CD 、BE 分别是 AB、 AC 边上的高, M 是 BC 的中点,∴DM=1BC,ME=1B C. 22∴DM=ME.又∵N 为 DE 中点,∴MN⊥DE.(2)在△ ABC 中,∠ ABC+∠ ACB = 180°-∠ A,∵DM =ME =BM= MC,∴∠ BMD +∠ CME =( 180°- 2∠ ABC)+( 180°- 2∠ACB)= 360°- 2(∠ ABC+∠ ACB)= 360°- 2( 180°-∠ A)= 2∠A.∴∠ DME = 180°- 2∠ A.(3)结论( 1)成立,结论( 2)不成立、原由以下:在△ ABC 中,∠ ABC+∠ ACB= 180°-∠ A,∵DM =ME =BM= MC,∴∠ BME +∠ CMD = 2∠ ACB +2∠ ABC=2( 180°-∠ A)=360°- 2∠ A.∴∠ DME = 180°-( 360°- 2∠ A)= 2∠ A- 180°.。
2018-2017学年度八年级物理第一学期第二学段考试科试卷

2018-2018学年度八年级物理第一学期第二学段考试科试卷说明:1.本卷共四大题,29小题,共5页,满分120分,考试时间为80分钟。
2.答卷前,考生请将自己的班级、姓名、位号填写在密封线左边的相应位置。
一、选择题<每小题3分,共45分)1、我国正在进行登月计划的研究,按照计划,我国在2007年将“嫦娥一号”送上月球,宇航员登上月球后,若有一块陨石落在他附近,则下列判断正确的是 < )6dfiwhH0RuA.宇航员能够听到陨石撞击月球的声音B.陨石撞击月球时不会使月球的地面产生振动C.宇航员虽然不能听到陨石撞击月球的声音,但他可以感受到这个声音的存在D.陨石撞击月球的声音可以在月球的表面向四周传播2、为了保护学习的环境,减少噪声污染,下列措施不可行的是( >A.不要在教学区域内大声喧哗B.在校园内及其附近栽花种草C.将教室的所有门窗全部封死D.教学楼的内外墙面尽量做得粗糙些3、弦乐器在使用一段时间后需请调音师进行调音,调音师通过调节弦的长度将琴音调准,在此过程中调音师改变了琴弦的< )6dfiwhH0RuA.响度B.音调C.音色D.振幅4、利用“B超”可以对病人的内脏进行检测,在提高诊断的准确性的同时又避免了对病人的伤害,但我们即使站在“B超”的旁边也无法听到它产生的声音,这是因为< )6dfiwhH0RuA.“B超”发出的声音的频率大于人能够听到的声音的频率B.“B超”发出的声音的频率小于人能够听到的声音的频率C.“B超”发出的声音响度太大D.“B超”发出的声音响度太小5、晚上,在桌面上铺一张白纸,把一块小平面镜平方在白纸上,让手电筒的光正对手电筒和白纸照射,从侧面看去< )6dfiwhH0RuA.镜子比较亮,因为它发生了镜面反射B.镜子比较亮,因为它发生了漫反射C.白纸比较亮,因为它发生了镜面反射D.白纸比较亮,因为它发生了漫反射6、一个人站在平面前,在他远离平面镜的过程中,他在镜中所成的像< )A.逐渐变大B.逐渐变小C.大小不变D.大小由平面镜大小决定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017——2018年八年级上学期第二章测试卷
姓名:___________班级:___________成绩:___________
一、单选题(本大题共15小题,共30.0分)
1.下列叙述和对应的地形区相对的是()
A.青藏高原--雪山连绵,冰川广布
B.内蒙古高原--地面崎岖,支离破碎
C.东北平原--地势低平,河网密布
D.塔里木盆地--有“天府之国”美誉
2.如图为我国部分地区示意图,对图中序号表示的区域描述正确的是
A.①降水稀少,河流均为内流河
B.②光照充足,植被类型为荒漠
C.③雨热同期,主要为湿润和半湿润地区
D.④水热充足,主要为热带和暖温带地区
读我国甲、乙、丙、丁四条河流示意图,完成以下问题。
3.关于图中甲、乙、丙、丁四条河流说法正确的是()
A.甲河流在四河流中结冰期最长
B.乙河流中游为“地上河”
C.丙河流因水能丰富被称为“黄金水道”
D.丁河流流出国境叫“湄公河”
4.关于上面四条河流流域农业发展说法错误的是()
A.甲河流域为我国重要的商品粮基地之一
B.乙河流域中下游为我国重要的产棉区
C.丙河流域是我国最大的油菜产区
D.丁河谷地因为海拔低,不利于当地农业发展
5.下列对我国东部地区河流的叙述,错误的是()
A.河水的主要补给形式是大气降水
B.汛期最长的河流是珠江
C.自北向南河流汛期逐渐缩短
D.开发长江的主要任务是开发水能资源
6. 读某河流水系图判断下列说法错误的是()
A.图中字母A山脉走向为西北-东南走向,此山脉为阿尔
泰山
B.该河③-④处河段流经黄土高原,水土流失严重
C.山脉B为我国重要的地理分界线,北侧主要种植粮食作
物为小麦
D.该河为我国第二长河,最终注入渤海
如图是气温年变化曲线和将水月份柱
状分布图,读图完成7-8题.
7.和台湾南部气候类型相同的是
A.甲
B.乙
C.丙
D.丁
8.符合“夏季炎热干燥,冬季温和多
雨”气候特征的是()
9. 今年第22号台风“海马”,10月21日12时40分在广东汕尾海丰鲘门镇沿海登陆,登陆时中心最大风力14级(42米/秒),之后强度迅速减弱,21日22时进入江西境内并减弱为热带低压。
下列关于台风的叙述正确的是( )
A.多发生于秋末、春初季节
B.除西藏、云贵高原外,我国其余地区都受台风影响
C.台风是灾害性天气,带来大风降温和霜冻
D.台风带来的大量降水,可缓解伏旱
读南北朝时期流传的民歌:“敕勒川,阴山下。
天似穹庐,笼盖四野。
天苍苍,野茫茫,风吹草低见牛羊”。
完成10-12题
10.民歌中所描述的自然景观位于
A.北方地区
B.西北地区
C.南方地区
D.青藏地区
11.民歌中阴山山脉走向是
A.东西走向
B.南北走向
C.东北西南走向
D.西北东南走向
12.民歌中所描述地区,农业生产以
A.种植小麦为主
B.种植水稻为主
C.种植经济作物
D.畜牧业为主
13.读图“长江流域示意图”下列说法正确的是()
A.①为面积最大的淡水湖-鄱阳湖
B.②为湘江
C.a为三峡水利枢纽
D.城市A为重庆
14.一人初冬穿棉衣、带皮帽乘火车外出旅游,途中衣服越穿越少,最后只穿单衣你认为此人的旅行路线应是()
A.上海一北京
B.杭州一昆明
C.哈尔滨一广州
D.济南一西安
15.下列河流中,具有“水量丰富,含沙量小、结冰期长”的特征的河流是()
A.珠江
B.长江
C.黄河
D.黑龙江
二、综合题(本大题共5小题,共50.0分)
1. 读三江平原、三江源和三江并流地区分布图,完成下列问题。
(11分)
(1)河流A是___________,图二是某水文站测得的该河多年平均径流量图,由图可知该河M、N两次汛期出现的季节分别是________和_______,请解释汛期M形成的原因(2分)
______________________________________。
(2)三江源地区位于__________高原上,是黄河、长江和__________(河流)的发源地,其源头水源补给形式主要是_____________________________。
(3)三江并流位于我国______________(地形区),是世界上罕见的高山峡谷地貌代表地区,试分析此地水能资源丰富的原因(2分)
________________________________________________________
2.自2010年以来,“应对气候变化·记录中国”专家组先后在7省8地进行了考察活动。
2015年陕西行启动。
读图,回答问题。
(11分)
(1)⑨省主要位于(地形区)。
甲山脉的冰雪融水是⑧甘肃省河西走廊的重要灌溉水源。
近年来,由于全球气候变暖,冰川消融,出现湿地萎缩等现象,位于
①省的“三江源”发出告急。
(2)内蒙古主要位于我国西部的区(季风、非季风区),其自然景观自东向西是“草原一荒漠草原一荒漠”的变化,产生这种变化主要原因是。
(3)⑥省简称是,和③省都是我国的粮食生产基地,主要的粮食作物是,位于带(填所属温度带)影响其农业生产有利的气候条件是。
(2分)
3. 下图为我国长江水系图,读图回答问题。
(7分)
(1)长江源远流长,支流众多,其中最大的支流②是江。
(2)划分长江上、中游的分界点A是湖北省的。
(3)a是我国最大的水利枢纽工程。
(4)D是我国最大的淡水湖_________,D湖所在省的简称是______。
(5)长江干流横贯东西,宜宾以下四季通航,航运价值高,人们把长江称为“______________”。
(6)长江上游河段的最大生态问题是_______________。
4. 读“黄河水系示意图”回答下列问题.(11分)
(1)图中A、B、C三点中,表示黄河中、下游分
界点的是.
(2)图中黄河两条最大支流的名称
①,②.
(3)黄河上最大水利枢纽工程③是
水利枢纽;著名的水电站④为水电
站.
(4)黄河流经的主要地形区:⑤平
原,⑥高原.
(5)黄河中游存在的忧患是;下游存在的忧患是和.
(6)治理黄河的关键是.。
