2019年“超级全能生”全国卷26省联考高考数学(理)试题(甲卷)及答案
2019届河北省“超级全能生”高考全国卷26省9月联考甲卷-语文试题(word版)

“超级全能生”2019高考全国卷26省9月联考甲卷语文注意事项:1.本试题共8页,满分150分,考试时间150分钟。
2.答题前,考生务必将自己的姓名、准考证号等填写在答题卡的相应位置。
3.全部答案在答题卡上完成,答在本试题上无效。
4.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
5.考试结束后,将本试题和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
近年来,关于汉语在各国持续升温的报道不断见诸国内外媒体。
语言是民族的重要特征之一,语言的影响力和传播力也日益成为民族国家综合实力的体现。
海外“汉语热”实际上反映的是中国合作共赢、大国担当和文化自信的国际魅力。
互利共赢是重要动力汉语难学,但挡不住学习的热情,海外汉语热出现的根本原因是中国综合国力和国际影响力的大幅度提升,经济上的互利共赢是推动海外汉语热的根本动力。
首先,海外中资企业对熟悉汉语的当地员工的需求越来越大,尤其是对从事国际贸易的企业来说,懂汉语的员工在录用和薪酬方面往往都具有较大优势。
择业方面的语言优势以引领和示范作用影响着海外青年的外语学习选择。
其次,中国游客海外旅游数量屡破新高,而且展现出强大的消费能力,“学说中国话”成为外国商铺每天必须面对的市场现实。
经济搭台,文化唱戏,一些从业人员开始有意识地了解中国文化,了解中国人的生活习惯、行为方式甚至文化传统。
同时,一些有远见的海外家庭看好中国的发展前景,着手培养下一代的汉语语言能力,认为掌握汉语能让孩子站在更好的起点。
由于学习汉语的主要难点是汉字识别和四声发音,需要耳濡目染,因此懂汉语的家政服务人员格外受欢迎,成为高级私教,收入明显高于普通家政服务人员。
为了保持不间断的汉语语言学习环境,这些家庭还在生活中大量使用智能语音服务或其他支持中外互译的手机软件。
“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案

“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案注意事项:1.本试题满分150分,考试时间150分钟;2.答题考生务必将自己准考证号填写在答题卡的相应位置;3.全部答案在答题卡,答在本试题卷上无效.一、现代文阅(3分)(一)论述类文本(本题共3小题,共9分)阅读下面的,宽1~3题。
展览通过实物、摹本、AR技术、仿制洞窟等方式将不便移动的壁画呈现在公众面前。
其中,大量数字化技术的运用对传统壁画临摹带来了新挑战。
人们不禁发问:当数字复制技术愈发成熟,古代壁画还需要临摹吗?过去,古代壁画临摹常常出于研究保护之目的,为历史而摹。
如山西永乐宫在进行整体搬迁保护工程前,组织中央美术学院师生进行了全部壁画临摹工作,以为后续搬迁工作服务。
这样的临摹,不仅对壁画保护具有重要意义,在这一过程中,通过对壁画形式语言结构的深入分析,也培养出了一批年轻的壁画研究人才。
另外,临摹流失海外的古代壁画也为还原文化遗产面貌提供了有益借鉴。
还有一批画家、学者是为艺术而摹。
出于对古代壁画艺术的崇敬向往,他们在临摹中更强调梳理壁画创作媒介、图像及方法。
如敦煌研究院,在临摹壁画艺术宝库作品时,探索出了一套从起稿、线稿、上色、画面整体调整到完稿的临摹技法体系。
又如段文杰先生临摹的《都督夫人礼佛图》,通过长达两年时间对唐人的研究,最终使本已残破的原壁画重绽光辉。
类似这样的“整理临摹”“复原临摹”等研究性临摹实践,在“客观临摹”的基础上,进一步凸显了当代研究者对壁画的理解感悟。
然而,这些实践成果的应用却面临着传播困境。
传统临摹作品虽具备较高的学术性,但因数量少、临摹耗时长等因素,大多用于研究、保护、教学工作,很少以展览、研究成果的形式走出洞窟,走向大众。
此时,数字技术的合理介入是满足公众诉求的必由之路,也是让静默千年的文化遗产“活”起来的必然要求。
数字复制、VR技术、3D动画复原演示、线上展览、配套互动游戏等高科技,为盘活传统壁画这个超级IP提供了无限可能,也为壁画保护提供了新思路。
超级全能生2019高考全国卷26省12月联考乙卷(理科)数学试题及答案
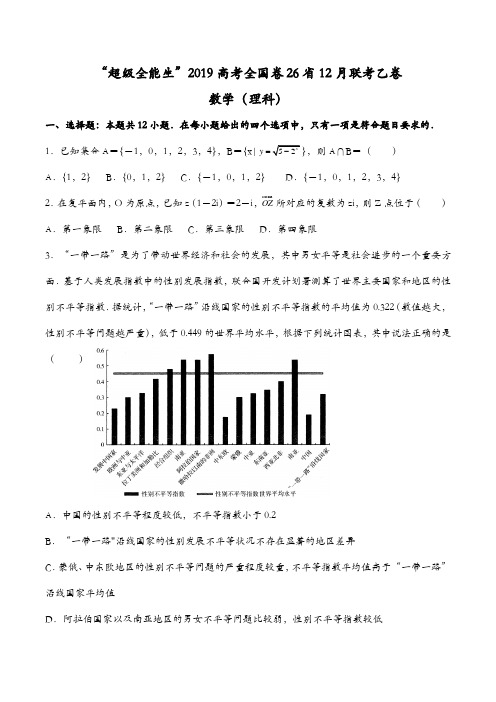
“超级全能生”2019高考全国卷26省12月联考乙卷数学(理科)一、选择题:本题共12小题.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={-1,0,1,2,3,4},B={x|y=,则A∩B=()A.{1,2} B.{0,1,2} C.{-1,0,1,2} D.{-1,0,1,2,3,4}2.在复平面内,O为原点,已知z(1-2i)=2-i,OZ 所对应的复数为zi,则Z点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.“一带一路”是为了带动世界经济和社会的发展,其中男女平等是社会进步的一个重要方面.基于人类发展指数中的性别发展指数,联合国开发计划署测算了世界主要国家和地区的性别不平等指数.据统计,“一带一路”沿线国家的性别不平等指数的平均值为0.322(数值越大,性别不平等问题越严重),低于0.449的世界平均水平,根据下列统计图表,其中说法正确的是()A.中国的性别不平等程度较低,不平等指数小于0.2B.“一带一路"沿线国家的性别发展不平等状况不存在显著的地区差异C.蒙俄、中东欧地区的性别不平等问题的严重程度较重,不平等指数平均值高于“一带一路”沿线国家平均值D.阿拉伯国家以及南亚地区的男女不平等问题比较弱,性别不平等指数较低4.已知2sin()63απ+=,则cos(2)3α2π-=( )A .19-B .19C .23 D5.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,E 为△ABC 的中线BD 的中点,0AB BC ⋅= 且1AE =,则ac 的最大值为( ) A .23 B .43 C .163 D .836.已知某几何体的三视图如图所示,则该几何体的内切球半径为( )ABC.12 D.127.已知(x +1)n 的展开式中,奇数项的二项式系数和为32,则22()nx x -的展开式的常数项为( )A .32B .64C .120D .608.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若角A ,32B,C成等差数列,2a c +==,则△ABC 的面积为( ) A.12 B.12C1 D1 9.已知实数x ,y 满足230,240,210,x y a x y x y --⎧⎪+-⎨⎪++⎩≤≥≥且z =x -2y +2的最大值为4,则实数a 的值为( )A .2B .92C .52D .3210.过抛物线x 2=8y 焦点的直线交抛物线于M ,N 两点,则OM NO ⋅=( )A .-20B .12C .-12D .2011.函数f (x )=sin (ωx+φ)(ω>0,02ϕπ<<)的部分图象如图所示,则下列选项中是函数1()3f x +的单调递增区间的是( )A .[19,29]和[49,79]B .[59-,29-]∪[19,49]C .[59-,29-]和[19,49]D .[-1,59-]∪[19,29]12.已知f (x ),g (x )都是定义在R 上的函数,对任意x 均满足f (-x )=-f (x ),g (-x )=g (x )≠0,当x >0时,总有f′(x )·g (x )>f (x )·g′(x ),f (2)=0,则()()303f x g x --≥的解集为( )A .[1,3]∪[5,+≦)B .[-2,0]∪[2,+≦)C .(-3,-2)∪(-1,+≦)D .[-5,-2]∪[3,+≦) 二、填空题:本题共4小题.13.命题“x ∃∈R ,sinx +cosx <1”的否定是________.14.已知非零向量a ,b ,满足|a |=|b |.若|a +b |=|2b -a |,则向量a ,b 的夹角为________.15.双曲线x 2-y 2=4的渐近线与圆C :(x -3)2+(y -2)2=4交于A ,B 两点,则|AB|=________.16.如图,点P 在长方体ABCD —A 1B 1C 1D 1的体对角线A 1C 上(不包含线段端点),若AB =2AD =2AA 1=2,则下列结论正确的有________.①存在P 点,使直线A 1C 与平面D 1AP 所成角为直角; ②无论P 点在何位置,都有∠APD 1<90°; ③当112A P PC =时,D 1P ∥平面BDC 1. 三、解答题:解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答. (一)必考题:17.设S n 为数列{a n }的前n 项和,且a 1=3,S n =An 2+Bn (A ,B 为常数).(Ⅰ)证明:数列n S n ⎧⎫⎨⎬⎩⎭为等差数列;(Ⅱ)若a 8=17,求数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和T n .18.某羽毛球俱乐部规定,每天一人打球1小时收费30元(不足1小时部分按1小时收费,以此类推),注册成为会员,对会员一天连续打球2小时、3小时的优惠标准如下表:该俱乐部从注册的会员中,随机抽取了40人进行统计,得到统计数据如下表:假设该俱乐部一人一小时活动的成本为5元,根据所给数据,解答下列问题:(Ⅰ)估计该俱乐部一位会员至少打球2小时的概率;(Ⅱ)假设每个会员每天最多打球3小时,以事件发生的频率作为相应事件发生的概率,从该俱乐部的会员中随机抽取2人,记俱乐部从这2位会员的消费中每小时获得的平均利润之和为X,求X的分布列和数学期望E(X).19.如图,在四棱锥P —ABCD 中,底面ABCD 的对角线互相垂直,且BC =CD ,PA ⊥平面ABCD .(Ⅰ)证明:平面PAC ⊥平面PBD ;(Ⅱ)若1cos 2BAD ∠=-,12AB PA AC ==,M 在PC 上,且2PM MC = ,试求直线BM 与平面PBD 所成角的正弦值.20.已知F 1,F 2分别为椭圆C :2221x y a+=(a >1)的左、右焦点,过F 1且斜率不为零的直线l 与C 交于A ,B 两点.若△AF 1F 2的周长为2+ (Ⅰ)求C 的方程;(Ⅱ)设l 的倾斜角为θ,若2cos 3θ=,直线F 2A ,AB ,F 2B 与直线21x a=-分别交于P ,Q ,R 三个不同的点,记P ,Q ,R 三点的纵坐标分别为y P ,y Q ,y R ,求证:|y P |·|y R |=|y Q |2.21.已知函数f (x )=(e x -1)mx -e x +x +1,m ∈R . (Ⅰ)若m =0时,求函数f (x )的极值;(Ⅱ)若关于x 的不等式(m -1)e x +x +1>m 在x ∈[12,3)上恒成立,求m 的取值范围.(二)选考题:请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题记分,作答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.[选修4—4:坐标系与参数方程]已知曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩(θ为参数).(Ⅰ)求曲线C 1的普通方程;(Ⅱ)设P 是曲线C 1上的动点,M (-2,5),N (6,1),求|PM|2+|PN|2的最大值.23.[选修4—5:不等式选讲]已知函数f (x )=|2x -1|-|2x -a|(a >2且a ∈R ). (Ⅰ)当a =4时,求不等式f (x )≥x 的解集; (Ⅱ)若f (x )的最大值为M ,且正实数m ,n 满足12m a m n ++=,求2112m n +--的最小值.“超级全能生”2019高考全国卷26省12月联考乙卷数学(理科) 答案详解1 2 3 4 5 6 7 8 9 10 11 12 CBAADBDBBBCA13.x ∀∈R ,sinx +cosx≥1 14.3π 15.16.①③17.解:(Ⅰ)证明:依题意,S n =An 2+Bn ,所以nS An B n =+, 所以11n n S SA n n+-=+,所以数列n S n ⎧⎫⎨⎬⎩⎭为等差数列.(Ⅱ)依题意可得{a n }为等差数列,183,17,a a =⎧⎨=⎩所以183,30,S S =⎧⎨=⎩所以1,2,A B =⎧⎨=⎩所以S n =n 2+2n ,所以11(2)n S n n =+, 所以数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和11111111[(1)()()(2324112n n T n n n n n n+=-+-++-+--++++ . 18.解:(Ⅰ)在40名会员中,至少打球2小时的会员有12+8=20(人), 故估计至少打球2小时的概率为201402P ==.(Ⅱ)某会员打球1小时,该俱乐部每小时的平均利润为30-5=25(元),概率为1201 402P==;某会员打球2小时,该俱乐部每小时的平均利润为1(2300.910)222⨯⨯-=(元),概率为2123 4010P==;某会员打球3小时,该俱乐部每小时的平均利润为1(3300.815)193⨯⨯-=(元),概率为381 405P==;由题意可知,X的所有可能取值为50,47,44,41,38.111(50)224P X==⨯=,133(47)221010P X==⨯⨯=,331129(44)2101025100P X==⨯+⨯⨯=,313(41)210525P X==⨯⨯=,111(38)5525P X==⨯=.所以X的分布列为所以数学期望()504744413845.84101002525100E X=⨯+⨯+⨯+⨯+⨯==.19.解:(Ⅰ)证明:因为底面ABCD的对角线瓦相垂直,所以BD⊥AC,又因为PA⊥平面ABCD,所以BD⊥PA,因为PA∩AC=A,所以BD⊥平面PAC,又因为BD⊂平面PBD,所以平面PAC⊥平面PBD.(Ⅱ)因为1cos 2BAD ∠=-,所以∠BAC =∠DAC =60°, 又因为12AB AC =,所以∠ABC =90°, 如图,以BC ,BA ,Bz (Bz ∥AP )所在直线分别为x ,y ,z 轴建立空间直角坐标系.设PA =AB =1,所以B (0,0,0),C0,0),A (0,1,0),P (0,1,1),D,32,0), 又因为2PM MC =,所以M(3,23,23),所以22(,)333BM = ,设平面PBD 的法向量为m =(x ,y ,z ),3(,0)22BD = ,(0,1,1)BP = ,所以0,0,BD BP ⎧⋅=⎪⎨⋅=⎪⎩m m 令y =1,有1,1,x y z ⎧=⎪=⎨⎪=-⎩所以(,1)=-m ,所以cos ,55||||BM BM BM ⋅==- m m m 故直线BM 与平面PBD. 20.解:(Ⅰ)由椭圆的定义得|AF 1|+|AF 2|=2a ,所以△AF 1F 2的周长为1212||||||2AF AF FF ++=,所以22a +=+a =所以C 的方程为2212x y +=. (Ⅱ)证明:由题意得直线l的方程为(1)2y x =+,联立方程221),1,2y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩ 可得7x 2+10x +1=0,设A (x 1,y 1),B (x 2,y 2),显然x 1≠1,x 2≠1, 所以12107x x +=-,1217x x =. 因为l 与直线12x =-交点Q的纵坐标为Q y = 所以25||16Q y =. 因为直线F 2A 的方程为11(1)1y y x x =--, 故直线F 2A 与直线12x =-交点P 的纵坐标为1132(1)P y y x -=-, 同理,点R 的纵坐标为2232(1)R y y x -=-,所以121233||||2(1)2(1)P R y y y y x x --⋅=⋅-- 121294(1)(1)y y x x =-- 1212121259(1)44[()1]x x x x x x x x ⋅+++=-++ 516=, 所以|y P |·|y R |=|y Q |2.21.解:(Ⅰ)若m =0时,f (x )=-e x +x +1,所以f′(x )=-e x +1,令f′(x )=0,得x =0.故x ∈(-≦,0)时,f′(x )>0,f (x )单调递增;x ∈(0,+≦)时,f′(x )<0,f (x )单调递减,所以函数f (x )的极大值为f (0)=0,无极小值.(Ⅱ)由(m -1)e x +x +1>m ,得m (e x -1)>e x -x -1,由x ∈[12,3)知,e x -1>0, 所以e 11e 1e 1x x x x x m -->=---, 令()1e 1x x h x =--,x ∈[12,3), 所以2e (1)1()(e 1)x x x h x -+'=-, 令g (x )=e x (x -1)+1,g′(x )=e x (x -1)+e x =xe x ,因为x ∈[12,3),所以g′(x )>0, 即g (x )=e x (x -1)+1在[12,3)上单调递增,又1102g ⎛⎫=> ⎪⎝⎭,所以g (x )>0恒成立, 即2e (1)1()0(e 1)x x x h x -+'=>-, 所以h′(x )>0在[12,3)上恒成立, 所以()1e 1x x h x =--在[12,3)上单调递增, 所以33()(3)1e 1h x h <=--, 所以331e 1m --≥. 22.解:(Ⅰ)因为曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩(θ为参数),则曲线C 1的普通方程为x 2+y 2=16.(Ⅱ)设P (4cosθ,4sinθ)(θ为参数),又因为M (-2,5),N (6,1),所以|PM|2+|PN|2=(4cosθ+2)2+(4sinθ-5)2+(4cosθ-6)2+(4sinθ-1)2=98-16(3sinθ+2cosθ)98)θϕ=-+(其中cosϕ=). 因为-1≤sin(θ+φ)≤1,所以|PM|2+|PN|2的最大值为98+. 23.解:(Ⅰ)将函数f (x )=|2x -1|-|2x -4|去绝对值, 当12x ≤时,f (x )=-3≥x ⇒x≤-3; 当122x <<时,5()4523f x x x x =-⇒<≥≤; 当x≥2时,f (x )=3≥x ⇒2≤x≤3,综上所述,不等式的解集为(-≦,-3]∪[53,3]. (Ⅱ)由绝对值三角不等式可得||2x -1|-|2x -a||≤|(2x -1)-(2x -a )|=|a -1|=a -1,所以f (x )的最大值为a -1,因为正实数m ,n 满足12M a m n +==, 所以121m n +=,所以2nm n =-,所以2121122122212n n m n n n n +=+=-+=------≥(当且仅当1232n n n -=⇒=-时,取等号), 所以2112m n +--的最小值为2。
“超级全能生”2019高考全国卷26省12月联考甲卷-数学理科答案

2019年全国统一高考数学试卷(理科)真题解析(解析版)

状元考前提醒拿到试卷:熟悉试卷刚拿到试卷一般心情比较紧张,建议拿到卷子以后看看考卷一共几页,有多少道题,了解试卷结构,通览全卷是克服“前面难题做不出,后面易题没时间做”的有效措施,也从根本上防止了“漏做题”。
答题策略答题策略一共有三点:1. 先易后难、先熟后生。
先做简单的、熟悉的题,再做综合题、难题。
2. 先小后大。
先做容易拿分的小题,再做耗时又复杂的大题。
3. 先局部后整体。
把疑难问题划分成一系列的步骤,一步一步的解决,每解决一步就能得到一步的分数。
立足中下题目,力争高水平考试时,因为时间和个别题目的难度,多数学生很难做完、做对全部题目,所以在答卷中要立足中下题目。
中下题目通常占全卷的80%以上,是试题的主要构成,学生能拿下这些题目,实际上就是有了胜利在握的心理,对攻克高档题会更放得开。
确保运算正确,立足一次性成功在答卷时,要在以快为上的前提下,稳扎稳打,步步准确,尽量一次性成功。
不能为追求速度而丢掉准确度,甚至丢掉重要的得分步骤。
试题做完后要认真做好解后检查,看是否有空题,答卷是否准确,格式是否规范。
要学会“挤”分考试试题大多分步给分,所以理科要把主要方程式和计算结果写在显要位置,文科尽量把要点写清晰,作文尤其要注意开头和结尾。
考试时,每一道题都认真思考,能做几步就做几步,对于考生来说就是能做几分是几分,这是考试中最好的策略。
检查后的涂改方式要讲究发现错误后要划掉重新写,忌原地用涂黑的方式改,这会使阅卷老师看不清。
如果对现有的题解不满意想重新写,要先写出正确的,再划去错误的。
有的同学先把原来写的题解涂抹了,写新题解的时间又不够,本来可能得的分数被自己涂掉了。
考试期间遇到这些事,莫慌乱!绝密★启用前2019年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案

“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案注意事项:1.本试题满分150分,考试时间150分钟;2.答题考生务必将自己准考证号填写在答题卡的相应位置;3.全部答案在答题卡,答在本试题卷上无效.一、现代文阅(3分)(一)论述类文本(本题共3小题,共9分)阅读下面的,宽1~3题。
展览通过实物、摹本、AR技术、仿制洞窟等方式将不便移动的壁画呈现在公众面前。
其中,大量数字化技术的运用对传统壁画临摹带来了新挑战。
人们不禁发问:当数字复制技术愈发成熟,古代壁画还需要临摹吗?过去,古代壁画临摹常常出于研究保护之目的,为历史而摹。
如山西永乐宫在进行整体搬迁保护工程前,组织中央美术学院师生进行了全部壁画临摹工作,以为后续搬迁工作服务。
这样的临摹,不仅对壁画保护具有重要意义,在这一过程中,通过对壁画形式语言结构的深入分析,也培养出了一批年轻的壁画研究人才。
另外,临摹流失海外的古代壁画也为还原文化遗产面貌提供了有益借鉴。
还有一批画家、学者是为艺术而摹。
出于对古代壁画艺术的崇敬向往,他们在临摹中更强调梳理壁画创作媒介、图像及方法。
如敦煌研究院,在临摹壁画艺术宝库作品时,探索出了一套从起稿、线稿、上色、画面整体调整到完稿的临摹技法体系。
又如段文杰先生临摹的《都督夫人礼佛图》,通过长达两年时间对唐人的研究,最终使本已残破的原壁画重绽光辉。
类似这样的“整理临摹”“复原临摹”等研究性临摹实践,在“客观临摹”的基础上,进一步凸显了当代研究者对壁画的理解感悟。
然而,这些实践成果的应用却面临着传播困境。
传统临摹作品虽具备较高的学术性,但因数量少、临摹耗时长等因素,大多用于研究、保护、教学工作,很少以展览、研究成果的形式走出洞窟,走向大众。
此时,数字技术的合理介入是满足公众诉求的必由之路,也是让静默千年的文化遗产“活”起来的必然要求。
数字复制、VR技术、3D动画复原演示、线上展览、配套互动游戏等高科技,为盘活传统壁画这个超级IP提供了无限可能,也为壁画保护提供了新思路。
【精品】2019年全国卷Ⅱ理数高考试题文档版附答案

( 2)由( 1)知, an bn
1 2n 1 , an bn
2n 1.
1
1
1
所以 an
2[( an bn ) (an bn)]
2n
n, 2
1
1
1
bn
[( an bn) (an 2
bn )]
2n
n. 2
20.解:( 1) f ( x)的定义域为( 0, 1),( 1, +∞)单调递增.
因为 f (e) =1 e 1 0 , f (e2 ) e1
点 G. ( i )证明: △ PQG 是直角三角形; ( ii )求 △ PQG 面积的最大值 .
(二)选考题:共 10 分.请考生在第 22、 23 题中任选一题作答。如果多做,则按所做的第一题计分. 22. [ 选修 4-4 :坐标系与参数方程 ] ( 10 分)
在极坐标系中, O为极点, 点 M ( 0, 0 )( 0 0) 在曲线 C :
D. α,β 垂直于同一平面
8.若抛物线 y2=2px( p>0) 的焦点是椭圆 x2
y2 1 的一个焦点,则 p=
3p p
A. 2 C. 4
B. 3 D. 8
9.下列函数中,以 为周期且在区间 ( , ) 单调递增的是
2
42
A. f ( x)= │cos 2 x│
B. f ( x)= │ sin 2 x│
x2 y2 a2交于 P, Q两点 . 若 PQ OF ,则 C的离心率为
A. 2
B. 3
C. 2
D. 5
12.设函数 f ( x) 的定义域为 R,满足 f (x 1) 2 f (x) ,且当 x (0,1] 时, f (x) x(x 1) . 若对任意
“超级全能生”2019高考全国卷26省12月联考乙卷-数学理科答案

[
)
( 分) 5 由绝对值三角不等式可得 | ( 2 x-1 | -| 2 x- Ⅱ) ( ) ( ) , a |≤ | 2 x - 1 - 2 x -a | =| a - 1 | =a - 1 所以 f ( ) 的最大值为 a , x - 1 1 2 因为正实数 m , 满足 + +M =a , n m n n 1 2 , ( 分) , 所以 m= 所以 + = 7 1 m n - 2 n 1 2 1 2 1 所以 + + = =n -2 + ≥ 1 n - 2 n - 2 - 2 n m- n - 1 - 2 n 1 1 ) 2 ( = 2 当且仅当 n -2 = n = n - 2 ˑ n - 2 - 2 n
(
)
(
)
(
)
( {
)
{
3 5 5 故直线 B M 与平面 P B D所成角的正弦值为 槡 . 5 5 分) ( 1 2
— 数学( 理科) ·答 1—
解: ( 由椭圆的定义得 | , 2 0 . A F +| A F = 2 a Ⅰ) 1| 2| 的周长为 所以△ A | A F F | +| A F | +| F = F 1 2 1 2 1F 2| , 2 2 + 2 槡
[
) [
)
{
(
)
2 2 所以 | 的最大值为 9 P M| +| P N| 8 + 1 6 3 . 槡1 ( 分) 1 0 解: ( ) 将函数 ( ) 去绝对值, 2 3 . Ⅰ fx =| 2 x - 1 | -| 2 x - 4 | 1 x ( ) ; 当x f x =- 3 3 ≥x ≤- ≤ 2时, 1 5≤ x ; 当 <x 时, ( ) < 2 < 2 f x = 4 x - 5 ≥x 2 3
2019年普通高等学校招生全国统一考试数学试题及答案(理)

2019年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至8页.共150分.考试时间120分钟.第Ⅰ卷(选择题共60分)注意事项:1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2. 每小题选出答案后,用铅笔把答题卡上对应答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3. 考试结束,监考人将本试卷和答题卡一并收回.参考公式:一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的(1) 若siniθcosθ>0,则θ在( )(A) 第一、二象限(B) 第一、三象限(C) 第一、四象限(D) 第二、四象限(2) 过点A (1,-1)、B (-1,1)且圆心在直线x+y-2 = 0上的圆的方程是( )(A) (x-3) 2+(y+1) 2 = 4 (B) (x+3) 2+(y-1) 2 = 4(C) (x-1) 2+(y-1) 2 = 4 (D) (x+1) 2+(y+1) 2 = 4(3) 设{a n }是递增等差数列,前三项的和为12,前三项的积为48,则它的首项是( )(A) 1(B) 2(C) 4(D) 6(4) 若定义在区间(-1,0)的函数f (x ) = log 2a (x +1)满足f (x )>0,则a 的取值范围是( )(A)(210,)(B)⎥⎦⎤ ⎝⎛210,(C) (21,+∞) (D) (0,+∞)(5) 极坐标方程)4sin(2πθρ+=的图形是( )(6) 函数y = cos x +1(-π≤x ≤0)的反函数是 ( )(A) y =-arc cos (x -1)(0≤x ≤2) (B) y = π-arc cos (x -1)(0≤x ≤2) (C) y = arc cos (x -1)(0≤x ≤2)(D) y = π+arc cos (x -1)(0≤x ≤2)(7) 若椭圆经过原点,且焦点为F 1 (1,0) F 2 (3,0),则其离心率为 ( )(A)43 (B)32 (C)21 (D)41 (8) 若0<α<β<4π,sin α+cos α = α,sin β+cos β= b ,则 ( )(A) a <b(B) a >b(C) ab <1(D) ab >2(9) 在正三棱柱ABC -A 1B 1C 1中,若12BB AB =,则AB 1 与C 1B 所成的角的大小为( )(A) 60°(B) 90°(C) 105°(D) 75°(10) 设f (x )、g (x )都是单调函数,有如下四个命题:① 若f (x )单调递增,g (x )单调递增,则f (x )-g (x )单调递增; ② 若f (x )单调递增,g (x )单调递减,则f (x )-g (x )单调递增; ③ 若f (x )单调递减,g (x )单调递增,则f (x )-g (x )单调递减; ④ 若f (x )单调递减,g (x )单调递减,则f (x )-g (x )单调递减. 其中,正确的命题是( )(A) ①③ (B) ①④ (C) ②③ (D) ②④(11) 一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P 1、P 2、P 3.若屋顶斜面与水平面所成的角都是α,则 ( ) (A) P 3>P 2>P 1(B) P 3>P 2 = P 1(C) P 3 = P 2>P 1(D) P 3 = P 2 = P 1(12) 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )(A) 26 (B) 24(C) 20(D) 19第Ⅱ卷(非选择题共90分)注意事项:1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中.2.答卷前将密封线内的项目填写清楚.二.填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.(13)若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积是 (14)双曲线116922=-y x 的两个焦点为F 1、F 2,点P 在双曲线上.若PF 1⊥PF 2,则点P 到x 轴的距离为(15)设{a n }是公比为q 的等比数列,S n 是它的前n 项和.若{S n }是等差数列,则 q =(16)圆周上有2n 个等分点(n >1),以其中三个点为顶点的直角三角形的个数为三.解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.(17) (本小题满分12分)如图,在底面是直角梯形的四棱锥S —ABCD 中,∠ABC = 90°,SA ⊥面ABCD ,SA = AB = BC = 1,21=AD . (Ⅰ)求四棱锥S —ABCD 的体积;(Ⅱ)求面SCD 与面SBA 所成的二面角的正切值. (18) (本小题满分12分) 已知复数z 1 = i (1-i ) 3. (Ⅰ)求arg z 1及1z ;(Ⅱ)当复数z 满足1z =1,求1z z -的最大值. (19) (本小题满分12分)设抛物线y 2 =2px (p >0)的焦点为F ,经过点F 的直线交抛物线于A 、B 两点,点C 在抛物线的准线上,且BC ∥x 轴.证明直线AC 经过原点O .(20) (本小题满分12分)已知i ,m ,n 是正整数,且1<i ≤m <n .(Ⅰ)证明in i i m i P m P n <;(Ⅱ)证明(1+m ) n > (1+n ) m . (21) (本小题满分12分)从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入800万元,以后每年投入将比上年减少51.本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加41. (Ⅰ)设n 年内(本年度为第一年)总投入为a n 万元,旅游业总收入为b n 万元.写出a n ,b n 的表达式;(Ⅱ)至少经过几年旅游业的总收入才能超过总投入? (22) (本小题满分14分)设f (x ) 是定义在R 上的偶函数,其图像关于直线x = 1对称.对任意x 1,x 2∈[0,21]都有f (x 1+x 2) = f (x 1) · f (x 2).且f (1) = a >0. (Ⅰ)求f (21) 及f (41); (Ⅱ)证明f (x ) 是周期函数; (Ⅲ)记a n = f (2n +n21),求()n n a ln lim ∞→.2001年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答及评分标准说明:一. 本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生物解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二. 对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定部分的给分,但不得超过该部分正确解答得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三. 解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四. 只给整数分数.选择题和填空题不给中间分.一.选择题:本题考查基本知识和基本运算.每小题5分,满分60分.(1)B (2)C (3)B (4)A (5)C (6)A (7)C (8)A (9)B (10)C (11)D (12)D二.填空题:本题考查基本知识和基本运算.每小题4分,满分16分.(13)2π (14)516(15)1 (16)2n (n -1)三.解答题:(17)本小题考查线面关系和棱锥体积计算,以及空间想象能力和逻辑推理能力.满分12分.解:(Ⅰ)直角梯形ABCD 的面积是 M 底面()43125.0121=⨯+=⋅+=AB AD BC , ……2分 ∴ 四棱锥S —ABCD 的体积是⨯⨯=SA V 31M 底面43131⨯⨯=41=.……4分 (Ⅱ)延长BA 、CD 相交于点E ,连结SE 则SE 是所求二面角的棱. ……6分∵ AD ∥BC ,BC = 2AD ,∴ EA = AB = SA ,∴ SE ⊥SB ,∵ SA ⊥面ABCD ,得SEB ⊥面EBC ,EB 是交线, 又BC ⊥EB ,∴ BC ⊥面SEB , 故SB 是CS 在面SEB 上的射影, ∴ CS ⊥SE ,所以∠BSC 是所求二面角的平面角. ……10分 ∵ 22AB SA SB +=2=,BC =1,BC ⊥SB ,∴ tan ∠BSC =22=SB BC . 即所求二面角的正切值为22. ……12分 (18)本小题考查复数基本性质和基本运算,以及分析问题和解决问题的能力.满分12分.解:(Ⅰ)z 1 = i (1-i ) 3 = 2-2i , 将z 1化为三角形式,得⎪⎭⎫⎝⎛+=47sin47cos 221ππi z ,∴ 47arg 1π=z ,221=z . ……6分 (Ⅱ)设z = cos α+i sin α,则z -z 1 = ( cos α-2)+(sin α+2) i , ()()22212sin 2cos ++-=-ααz zsin 249+=(4πα-), ……9分当sin(4πα-) = 1时,21z z -取得最大值249+.从而得到1z z -的最大值为122+. ……12分 (19)本小题考查抛物线的概念和性质,直线的方程和性质,运算能力和逻辑推理能力.满分12分.证明一:因为抛物线y 2 =2px (p >0)的焦点为F (2p,0),所以经过点F 的直线的方程可设为2pmy x +=; ……4分 代入抛物线方程得y 2 -2pmy -p 2 = 0,若记A (x 1,y 1),B (x 2,y 2),则y 1,y 2是该方程的两个根,所以y 1y 2 = -p 2. ……8分因为BC ∥x 轴,且点c 在准线x = -2p 上,所以点c 的坐标为(-2p,y 2),故直线CO 的斜率为111222x y y p p y k ==-=. 即k 也是直线OA 的斜率,所以直线AC 经过原点O . ……12分证明二:如图,记x 轴与抛物线准线l 的交点为E ,过A 作AD ⊥l ,D 是垂足.则 AD ∥FE ∥BC . ……2分连结AC ,与EF 相交于点N ,则ABBF AC CN AD EN ==,,ABAF BCNF = ……6分 根据抛物线的几何性质,AD AF =,BC BF =, ……8分∴ NF ABBC AF ABBF AD EN =⋅=⋅=,即点N 是EF 的中点,与抛物线的顶点O 重合,所以直线AC 经过原点O . ……12分 (20)本小题考查排列、组合、二项式定理、不等式的基本知识和逻辑推理能力.满分12分.(Ⅰ)证明: 对于1<i ≤m 有im p = m ·…·(m -i +1),⋅-⋅=m m m m m p i i m 1…mi m 1+-⋅, 同理 ⋅-⋅=n n n n n p i in 1…ni n 1+-⋅, ……4分由于 m <n ,对整数k = 1,2…,i -1,有mkm n k n ->-, 所以 i im i i n mp n p >,即im i i n i p n p m >. ……6分(Ⅱ)证明由二项式定理有()in ni i nC m m ∑==+01, ()i mmi i mCn n ∑==+01, ……8分由 (Ⅰ)知i n i p m >im i p n (1<i ≤m <n =,而 !i p C i m im=,!i p C i n in =, ……10分所以, im i i n i C n C m >(1<i ≤m <n =.因此,∑∑==>mi im i mi i niC n Cm 22. 又 10000==m n C n C m ,mn nC mC m n ==11,()n i m C m in i ≤<>0.∴∑∑==>mi im i ni i niC n Cm 0. 即 (1+m )n >(1+n )m . ……12分 (21)本小题主要考查建立函数关系式、数列求和、不等式等基础知识;考查综合运用数学知识解决实际问题的能力.满分12分.解:(Ⅰ)第1年投入为800万元,第2年投入为800×(1-51)万元,……,第n 年投入为800×(1-51)n -1万元. 所以,n 年内的总投入为a n = 800+800×(1-51)+…+800×(1-51)n -1∑=--⨯=nk k 11)511(800= 4000×[1-(54)n]; ……3分 第1年旅游业收入为400万元,第2年旅游业收入为400×(1+41)万元,……,第n 年旅游业收入为400×(1+41)n -1万元.所以,n 年内的旅游业总收入为b n = 400+400×(1+41)+…+400×(1+41)n -1∑=-⨯=nk k 11)45(400= 1600×[ (54)n-1]. ……6分 (Ⅱ)设至少经过n 年旅游业的总收入才能超过总投入,由此b n -a n >0,即 1600×[(45)n -1]-4000×[1-(54)n ]>0.化简得 5×(54)n +2×(54)n -7>0, ……9分 设=x (54)n,代入上式得 5x 2-7x +2>0,解此不等式,得52<x ,x >1(舍去). 即 (54)n <52,由此得 n ≥5.答:至少经过5年旅游业的总收入才能超过总投入. ……12分。
“超级全能生”陕西省2019届高三第二次教学质量检测数学(理)试题(解析版)

“超级全能生”陕西省2019届高三第二次教学质量检测数学(理)试题一、选择题(本大题共12小题,共60.0分)1.已知集合M={x|−2<x<2},N={x|log2x>0},则M∩N为()A. (−2,2)B. (1,+∞)C. (1,2)D. (−2,+∞)【答案】C【解析】解:∵集合M={x|−2<x<2},N={x|log2x>0}={x|x>1},∴M∩N={x|1<x<2}=(1,2).故选:C.分别求出集合M,N,由此能求出M∩N.本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.2.已知复数z满足z=−1+5i2,则|z|=()A. 3B. √26C. 4D. √262【答案】D【解析】解:由复数模的运算法则可得:|z|=|−1+5i2|=|−1+5i||2|=√262.故选:D.由题意结合复数模的运算法则计算z的模即可.本题主要考查复数的模的求解等知识,属于基础题.3.若实数x,y满足约束条件{x+y≤4y−x≥0x−1≥0,则目标函数z=√x2+y2的最大值为()A. √6B. √10C. 2√2D. √7【答案】B【解析】解:作出实数x,y满足约束条件{x+y≤4 y−x≥0 x−1≥0,所对应的可行域,而目标函数z=√x2+y2表示可行域内的点A到原点距离的平方,由:{x +y =4x=1,解得A(1,3)数形结合可得最大值为:√1+9=√10, 故选:B .作出可行域,z =√x 2+y 2表示可行域内的点到原点距离,数形结合可得. 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.4. 已知命题p :对∀x >0,总有x <sinx ;命题q :直线l 1:ax +2y +1=0,l 2:x +(a −1)y −1=0若l 1//l 2,则a =2或a =−1;则下列命题中是真命题的是( )A. p ∧qB. (¬p)∧(¬q)C. (¬p)∨qD. p ∨q【答案】D【解析】解:设f(x)=sinx −x ,则f′(x)=cosx −1≤0,则函数f(x)在x ≥0上为减函数, 则当x >0时,f(x)<f(0)=0,即此时sinx <x 恒成立,即命题p 是真命题, 若a =0,则两直线方程为l 1:2y +1=0,l 2:x −y −1=0,此时两直线不平行,不满足条件.若a ≠0,若两直线平行,则满足1a =a−12≠−11,由1a =a−12得a(a −1)=2,即a 2−a −2=0得a =2或a =−1,由1a ≠−1得a ≠−1,则a =2,即命题q 是假命题, 则p ∨q 是真命题,其余为假命题, 故选:D .根据条件判断命题p ,q 的真假,结合复合命题真假关系进行判断即可.本题主要考查复合命题真假的判断,根据条件判断命题p ,q 的真假是解决本题的关键.5. 陕西省西安市周至县的旅游景点楼观台,号称“天下第一福地”,是我国著名的道教圣地,古代圣哲老子曾在此著《道德经》五千言.景区内有一处景点建筑,是按古典著作《连山易》中记载的金、木、谁、火、土之间相生相克的关系,如图所示,现从五种不同属性的物质中任取两种,则取出的两种物质恰好是相克关系的概率为( )A. 23 B. 12 C. 15 D. 25【答案】B【解析】解:现从五种不同属性的物质中任取两种,基本事件总数n=C52=10,取出的两种物质恰好是相克关系包含的基本事件个数m=C51=5,则取出的两种物质恰好是相克关系的概率为p=mn =510=12.故选:B.基本事件总数n=C52=10,取出的两种物质恰好是相克关系包含的基本事件个数m= C51=5,由此能求出取出的两种物质恰好是相克关系的概率.本题考查概率的求法,考查古典概型等基础知识,考查运算求解能力,是基础题.6.如图是计算12+14+16+18+110值的一个程序框图,其中判断框内应填入的条件是()A. k≥5B. k<5C. k>5D. k≤6【答案】C【解析】解:∵算法的功能是计算12+14+16+18+110值,共循环5次,∴跳出循环体的n值为12,k值为6,∴判断框内应填的条件是k>5或k≥6.故选:C.根据算法的功能确定循环的次数是5,确定跳出循环体的n值为12,k值为6,由此可得判断框内应填的条件.本题考查了循环结构的程序框图,根据算法的功能确定循环的次数,从而求得跳出循环体的k值是关键.7. 已知点(2,8)在幂函数f(x)=x n 图象上,设a =f((45)0.3),b =f((54)0.2),c =f(log 1254),则a ,b ,c 的大小关系是( )A. b >a >cB. a >b >cC. c >b >aD. b >c >a【答案】A【解析】解:点(2,8)在幂函数f(x)=x n 图象上, ∴f(2)=2n =8,解得n =3,∴f(x)=x 3,设a =f((45)0.3),b =f((54)0.2),c =f(log 1254),∴45<a =[(45)0.3]3=(45)0.9<(45)0=1,54>b =[(54)0.2]3=(54)0.6>(54)0=1, c =(log 1254)3<(log 121)3=0,∴a ,b ,c 的大小关系是b >a >c . 故选:A .推导出f(x)=x 3,从而45<a =[(45)0.3]3=(45)0.9<(45)0=1,54>b =[(54)0.2]3=(54)0.6>(54)0=1,c =(log 1254)3<(log 121)3=0,由此能判断a ,b ,c 的大小关系.本题考查三个数的大小的判断,考查幂函数性质等基础知识,考查运算求解能力,是基础题.8. 要得到函数y =sin(2x +π12)的图象,只需将函数y =sinx 的图象经过下列两次变换而得到的( )A. 先将y =sinx 的图象上各点的横坐标缩短为原来的一半,再将所得图象向左平移π6个单位B. 先将y =sinx 的图象上各点的横坐标伸长为原来的2倍,再将所得图象向左平移π24个单位C. 先将y =sinx 的图象向左平移π12个单位,再将所得图上各点的横坐标缩短为原来的一半D. 先将y =sinx 的图象向左平移π12个单位,再将所得图上各点的横坐标伸长为原来的2倍 【答案】C【解析】解:要得到函数y =sin(2x +π12)的图象,只需将函数y =sinx 的图象向左平移π12个单位,得到y=sin(x+π12),再将所得图上各点的横坐标缩短为原来的一半,得到y=sin(2x+π12),故选:C.根据三角函数的图象变换关系进行判断即可.本题主要考查三角函数的图象和性质,根据三角函数的图象变换关系是解决本题的关键.9.某三棱锥的三视图如图所示,其俯视图是一个等腰直角三角形,在此三棱锥的六条棱中,最长棱的长度为()A. 2B. 2√2C. √6D. √2【答案】B【解析】解:由题意可知几何体的直观图如图:可知PA⊥底面ABC,三角形ABC是等腰三角形,AB⊥BC,可知PC是最长的棱长:√4+4=2√2.故选:B.画出几何体的直观图,利用三视图的数据求解几何体的最长棱长.本题考查三视图求解几何体的棱长,考查计算能力.10.已知抛物线y2=4x的准线过双曲线x2a2−y2b2=1(a>0,b>0)的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为32,则双曲线的离心率为()A. 32B. 4C. 3D. 2【答案】D【解析】解:∵抛物线y2=4x的准线方程为x=−1,∴双曲线x2a2−y2b2=1(a>0,b>0)的左焦点为(−1,0)x=−1时,代入双曲线方程,由b2=1−a2,可得y=±1−a2a,∵△AOB 的面积为32, ∴12⋅1⋅2(1−a 2)a=32,∴a =12,∴e =ca =2. 故选:D .求出抛物线y 2=4x 的准线方程,可得双曲线x 2a 2−y 2b 2=1(a >0,b >0)的左焦点,求出x =−1时,y 的值,利用△AOB 的面积为32,求出a ,即可求双曲线的离心率.本题考查抛物线、双曲线的几何性质,考查三角形面积的计算,正确运用抛物线、双曲线的几何性质是关键.11. 一布袋中装有n 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由甲先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )A. 若n =9,则甲有必赢的策略B. 若n =11,则乙有必赢的策略C. 若n =6,则乙有必赢的策略D. 若n =4,则甲有必赢的策略【答案】A【解析】解:若n =9,则甲有必赢的策略, 必赢策略如下: 第一步:甲先抓1球,第二步:①当乙抓1球时,甲再抓3球时; ②当乙抓2球时,甲再抓2球时; ③当乙抓3球时,甲再抓1球时;第三步:这时还有4个球,轮到乙抓,按规定乙最少抓一个球,最多抓三个球, 则布袋中都会剩余1--3个球,第四步:甲再抓走剩下所有的球,从而甲胜. 故选:A .甲若想必胜,则必须最后取球时还剩1--3个球,通过简单的合情推理可以得解. 本题考查了实际操作的能力及进行简单的合情推理,属简单题.12. 已知函数f(x)={xe x ,x ≥0−x,x <0,又函数g(x)=f 2(x)+tf(x)+1(t ∈R)有4个不同的零点,则实数t 的取值范围是( )A. (−∞,−e 2+1e )B. (e 2+1e ,+∞)C. (−e 2+1e ,−2)D. (2,e 2+1e )【答案】A【解析】解:由已知有f(x)=xe x (x ≥0), f′(x)=1−x e x,易得0≤x <1时,f′(x)>0,x >1时,f′(x)<0, 即f(x)在[0,1)为增函数,在(1,+∞)为减函数, 设m =f(x),则h(m)=m 2+tm +1, 设h(m)=m 2+tm +1的零点为m 1,m 2 则g(x)=f 2(x)+tf(x)+1(t ∈R)有4个不同的零点等价于t =f(x)的图象与直线m =m 1,m =m 2的交点有4个, 函数t =f(x)的图象与直线m =m 1,m =m 2的位置关系如图所示, 由图知:0<m 2<1e <m 1, 即h(1e )<0,解得:t <−e 2+1e,故选:A .由函数的零点与函数图象的交点问题得:g(x)=f 2(x)+tf(x)+1(t ∈R)有4个不同的零点等价于t =f(x)的图象与直线m =m 1,m =m 2的交点有4个,结合利用导数研究函数的图象可作出函数t =f(x)的图象与直线m =m 1,m =m 2的位置, 由二次方程区间根问题得:h(1e )<0,解得:t <−e 2+1e,得解本题考查了函数的零点与函数图象的交点问题、利用导数研究函数的图象及二次方程区间根问题,属中档题二、解答题(本大题共11小题,共102.0分)13. 若S 1=∫x 221dx,S 2=∫1x 21dx,S 3=∫e x 21dx ,则S 1,S 2,S 3的大小关系为______. 【答案】S 2<S 1<S 3【解析】解:S 1=13×(23−13)=73, S 2=ln2−ln1=ln2, S 3=e 2−e ,其中0<S 2<1,2<S 1<3,S 3>3, 故答案为S 2<S 1<S 3运用微积分基本定理可解决此问题. 本题考查定积分的简单应用.14. 公比为√2的等比数列{a n }的各项都是正数,且a 2a 12=16,则log 2a 15=______. 【答案】6【解析】解:∵a 2a 12=a 72=16,∴a 7=4, ∴log 2a 15=log 2a 7q 8=log 24×(√2)8=6. 故答案为:6.等比中项结合对数的运算性质可得结果.本题考查了等比数列的性质及对数的运算性质,属基础题.15. 圆x 2+y 2=1的任意一条切线与圆x 2+y 2=4相交于A(x 1,y 1),B(x 2,y 2)两点,O为坐标原点,则x 1x 2+y 1y 2=______. 【答案】−2【解析】解:根据题意,设AB 与圆x 2+y 2=1相切于点P ,分析可得|OP|=1,|OA|=|OB|=2, 又由OP ⊥AB ,则∠BOP =60∘, 则∠AOB =120∘, 又由A(x 1,y 1),B(x 2,y 2),则OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=|OA||OB|cos120∘=−2, 则x 1x 2+y 1y 2=−2; 故答案为:−2.根据题意,设AB 与圆x 2+y 2=1相切于点P ,由两个圆的方程分析可得|OP|=1,|OA|=|OB|=2,又由OP ⊥AB ,分析可得∠AOB =120∘;结合数量积的计算公式可得OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=|OA||OB|cos120∘=−2,即可得答案.本题考查直线与圆相交的性质,涉及圆与圆的位置关系以及数量积的计算公式,属于基础题.16. 在实数集R 中定义一种运算“∗”,具有性质:(1)对任意a ,b ∈R ,a ∗b =b ∗a ; (2)对任意a ,a ∗0=0;(3)对任意a ,b ∈R ,(a ∗b)∗c =c(ab)+(a ∗c)+(b ∗c)−5c . 则函数f(x)=x ∗1x (x >0)的最小值为______. 【答案】−3【解析】解:根据定义的运算性质得:f(x)=x ∗1x =(x ∗1x )∗1 =1×(x ⋅1x )+(x ∗1)+(1x ∗1)−5×1=1+1∗x +1∗1x =x +1x −5,因为x >0,由均值不等式得f(x)=x +1x−5≥2√x ⋅1x−5=2−5=−3(当且仅当x =1时取“=”), 即f(x)的最小值为−3. 故答案为−3.根据题目给出的新定义,写出函数的解析式f(x)=x +1x −5,然后运用基本不等式求最值.本题考查了函数值域的求法,考查了利用基本不等式求函数最值的方法,解答此题的关键是能够根据题目所给的新定义,正确写出熟悉的函数表达式.17. 某市规划一个平面示意图为如下图五边形ABCDE 的一条自行车赛道,ED ,DC ,CB ,BA ,AE 为赛道(不考虑宽度),BE 为赛道内的一条服务通道,∠BCD =∠CDE =∠BAE =2π3,DE =4km ,BC =CD =√3km .(1)求服务通道BE 的长度;(3)应如何设计,才能使折线段赛道BAE 最长?【答案】解:(1)∵连接BD ,∠BCD =∠CDE =∠BAE =2π3,DE =4km ,BC =CD =√3km∴在△BCD 中,由余弦定理可得:BD 2=BC 2+CD 2−2BC ⋅CD ⋅cos∠BCD =3+3+2×√3×√3×12=9, ∴BD =3, ∵BC =CD ,∴∠CBD =∠CDB =π6, 又∵∠CDE =2π3,∴∠BDE =π2,在Rt △BDE 中,BE =√BD 2+DE 2=5. (2)在△BAE 中,∠BAE =2π3,BE =5,由余弦定理可得:BE 2=AB 2+AE 2−2AB ⋅AE ⋅cos∠BAE ,即:25=AB 2+AE 2+AB ⋅AE ,可得:(AB +AE)2−25=AB ⋅AE ≤(AB+AE 2)2, 从而34(AB +AE)2≤25,即:AB +AE ≤10√33,当且仅当AB =AE 时,等号成立,即设计为AB =AE 时,折线段赛道BAE 最长.【解析】(1)连接BD ,在△BCD 中,由余弦定理可得BD 的值,由BC =CD ,可求∠CBD =∠CDB =π6,可求∠BDE =π2,利用勾股定理可求BE 的值. (2)在△BAE 中,∠BAE =2π3,BE =5,由余弦定理,基本不等式可求AB +AE ≤10√3,当且仅当AB =AE 时,等号成立,即可得解AB =AE 时,折线段赛道BAE 最长. 本题主要考查了余弦定理,勾股定理,基本不等式在解三角形中的综合应用,考查了转化思想和数形结合思想的应用,属于中档题.18. 某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续6个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示 (1)由折线图可以看出,可用线性回归模型拟合月利润y(单位:百万元)与月代码x 之间的关系,求y 关于x 的线性回归方程,并预测该公司2019年3月份的利润; (2)甲公司新研制了一款产品,需要采购一批新型材料,现有A ,B 两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对A ,B 两种新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的聘书统计如下表: 寿命类型 1个月 2个月 3个月 4个月 总计 A 20 35 35 10 100 B10304020100经甲公司测算平均每包新型材料每月可以带来5万元收入,不考虑除采购成本之外的其它成本,假设每包新型材料的使用寿命都是整数月,且以频率作为每包新型材料使用寿命的概率,如果你是甲公司的负责人,以每包新型材料产生利润的期望值为决策依据,你会选择采购哪款新型材料?参考数据:∑y i 6i=1=96,∑x i 6i=1y i =371.参考公式:回归直线方程为y ̂=b ̂x +a ̂,其中b ̂=∑(n i=1x i −x −)(y i −y −)=96∑(n i=1x i −x −)2.【答案】解:(1)由折现图可知统计数据(x −,y −)共6组, 即(1,11),(2,13),(3,16),(4,15),(5,20),(6,21), 计算可得x −=16(1+2+3+4+5+6)=3.5,y −=16∑y i 6i=1=16⋅96=16,故b ̂=371−6⋅3.5⋅1617.5=2,故a ̂=y −−b ̂x −=16−2⋅3.5=9, ∴x 关于y 的线性回归方程为y ̂=2x +9, 故x =11时,则y ̂=2×11+9=31,即预测公司2018年1月份(即x =7时)的利润为31百万元;(2)由频率估计概率,A 型材料可使用1个月,2个月,3个月、4个月的概率分别为0.2,0.35,0.35,0.1,∴A 型材料利润的数学期望为(5−10)×0.2+(10−10)×0.35+(15−10)×0.35+(20−10)×0.1=1.75万元;B 型材料可使用1个月,2个月,3个月、4个月的概率分别为0.1,0.3,0.4,0.2, ∴B 型材料利润的数学期望为(5−12)×0.1+(10−12)×0.3+(15−12)×0.4+(20−12)×0.2=1.50万元; ∵1.75>1.50, ∴应该采购A 型材料.【解析】(1)求出回归系数,可得回归方程,即可得出结论; (2)分别计算相应的数学期望,即可得出结论.本题考查数学知识在实际生活中的应用,考查学生的阅读能力,对数据的处理能力,属于中档题.19. 如图所示,等腰梯形ABCD 的底角∠BAD =∠ADC =60∘,直角梯形ADEF 所在的平面垂直于平面ABCD ,且∠EDA =90∘,ED =AD =2AF =2AB =2. (1)证明:平面ABE ⊥平面EBD ;(2)点M 在线段EF 上,试确定点M 的位置,使平面MAB 与平面ECD 所成角的锐二面角的余弦值为√34.【答案】证明:(1)∵平面ABCD ⊥平面ADEF ,平面ABCD ∩平面ADEF =AD ,ED ⊥AD ,∴EAD ⊥平面ABCD ,AB ⊂平面ABCD ,∴ED ⊥AD , ∵AB =1,AD =2,∠BAD =60∘, ∴BD =√1+4−2×1×2cos60∘=√3, ∴AB 2+BD 2=AD 2,∴AB ⊥AD ,又BD ⊂平面BDE ,ED ⊂平面BDE ,BD ∩ED =D , ∴AB ⊥平面BDE ,又AB ⊂平面ABE ,∴平面ABE ⊥平面EBD .解:(2)以B 为坐标原点,以BA ,BD 为x 轴,y 轴,建立如图所示的空间直角坐标系,则A(1,0,0),B(0,0,0),C(−12,√32,0),D(0,√3,0),E(0,√3,2),F(1,0,1),则CD⃗⃗⃗⃗⃗ =(12,√32,0),DE ⃗⃗⃗⃗⃗ =(0,0,2),BA ⃗⃗⃗⃗⃗ =(1,0,0),EF ⃗⃗⃗⃗ =(1,−√3,−1), 设EM ⃗⃗⃗⃗⃗⃗ =λEF ⃗⃗⃗⃗ =(λ,−√3λ,−λ),(0≤λ≤1), 则BM⃗⃗⃗⃗⃗⃗ =BE ⃗⃗⃗⃗⃗ +EM ⃗⃗⃗⃗⃗⃗ =(λ,√3−√3λ,2−λ), 设平面CDE 的法向量为m⃗⃗⃗ =(x,y ,z),平面ABM 的法向量为n ⃗ =(x,y ,z), 则{m ⃗⃗⃗ ⋅CD ⃗⃗⃗⃗⃗ =0m ⃗⃗⃗ ⋅DE ⃗⃗⃗⃗⃗ =0,即{12x +√32y =02z =0,取y =1,得m ⃗⃗⃗ =(−√3,1,0), {n ⃗ ⋅BA ⃗⃗⃗⃗⃗ =0n ⃗ ⋅BM⃗⃗⃗⃗⃗⃗ =0,即{x =0λx +(√3−√3λ)y +(2−λ)z =0, 取y =2−λ,得n ⃗ =(0,2−λ,√3λ−√3),∵平面MAB 与平面ECD 所成角的锐二面角的余弦值为√34.∴|cos <m ⃗⃗⃗ ,n ⃗ >|=|m ⃗⃗⃗ ⋅n ⃗ ||m ⃗⃗⃗ |⋅|n ⃗ |=|2−λ|2√4λ2−10λ+7=√34, 解得λ=12,∴点M 中线段EF 中点时,使平面MAB 与平面ECD 所成角的锐二面角的余弦值为√34.【解析】(1)推导出EAD ⊥平面ABCD ,ED ⊥AD ,AB ⊥AD ,由此能证明AB ⊥平面BDE ,从而平面ABE ⊥平面EBD .(2)以B 为坐标原点,以BA ,BD 为x 轴,y 轴,建立空间直角坐标系,利用向量法能求出点M 中线段EF 中点时,使平面MAB 与平面ECD 所成角的锐二面角的余弦值为√34.本题考查面面垂直的证明,考查满足二面角的余弦值的点的位置的确定与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.20. 已知F 1,F 2为椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左右焦点,点P(2,3)为其上一点,且|PF 1|+|PF 2|=8. (1)求椭圆C 的标准方程;(2)若直线l :y =kx −4交椭圆C 于A ,B 两点,且原点O 在以线段AB 为直径的圆的外部,试求k 的取值范围.【答案】解:(1)由题意可得{4a 2+9b 2=12a =8,解得a 2=16,b 2=12,∴椭圆的方程为x 216+y 212=1, (2)设A(x 1,y 1)、B(x 2,y 2),由{x 216+y 212=1y =kx −4得(4k 2+3)x 2−32kx +16=0, ∴x 1+x 2=32k4k 2+3,x 1x 2=164k +3,由△>0,即(−32k 2)−4×16(4k 2+3)>0,解得k >12或k <−12.① ∵原点O 在以线段AB 为直径的圆的外部,则OA ⃗⃗⃗⃗⃗ ⋅OB⃗⃗⃗⃗⃗ >0, ∴OA ⃗⃗⃗⃗⃗ ⋅OB⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=x 1x 2+(kx 1−4)(kx 2−4)=(k 2+1)x 1x 2−4k(x 1+x 2)+16=(k 2+1)⋅164k 2+3−4k ⋅32k 4k 2+3+16=16(4−3k 2)4k 2+3>0解得−2√33<k <2√33.② 由①②解得实数k 的范围是(−2√33,−12)∪(12,2√33). 【解析】(1)由题意可得{4a 2+9b 2=12a =8,解得a 2=16,b 2=12求椭圆C 的方程. (2)设A(x 1,y 1)、B(x 2,y 2),联立直线与椭圆方程,利用韦达定理以及判别式大于0,通过原点O 在以线段AB 为直径的圆的外部,推出OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ >0,然后求解k 的范围即可. 本题考查直线与椭圆的位置关系的综合应用,圆锥曲线的综合应用,考查分析问题解决问题的能力.21. 函数f(x)=ln(x +t)+ax ,其中t 、a 为实常数.(1)若t =0时,讨论函数f(x)的单调性;(2)t =0时,不等式f(x)≥1在x ∈(0,1]上恒成立,求实数a 的取值范围; (3)若g(x)=e x +ax ,当t ≤2时,证明:g(x)>f(x). 【答案】解:(1)当t =0时,f(x)=lnx +ax ,x >0, ∴f′(x)=1x −ax 2=x−a x 2,当a ≤0时,f′(x)>0恒成立,则f(x)在(0,+∞)上单调递增,当a >0时,若0<x <a ,则f′(x)<0,函数单调递减,若x >a ,则f′(x)>0,函数单调递增,∴f(x)在(0,a)上单调递减,在(a,+∞)单调递增, (2)∵不等式f(x)≥1在x ∈(0,1]上恒成立,∴a≥x−xlnx,设h(x)=x−xlnx,x∈(0,1]∴h′(x)=1−1−lnx=−lnx≥0恒成立,∴h(x)在(0,1]上单调递增,∴h(x)max=h(1)=1,∴a≥1(3)g(x)−f(x)=e x+ax −ln(x+t)−ax=e x−ln(x+t),t≤2,∴x+t>0,∴x>−t≥−2,设m(x)=e x−x−1,∴m′(x)=e x−1,当x>0时,m′(x)>0,函数m(x)单调递增,当x<0时,m′(x)<0,函数m(x)单调递减,∴m(x)>m(0)=1−1>0,∴e x>x+1,要证g(x)>f(x),只要证x+1−ln(x+t)>0,设φ(x)=x+1−ln(x+t),∴φ′(x)=1−1x+t =x+t−1x+t,令φ′(x)=0,解得x=1−t>−1,当x>1−t时,φ′(x)>0,函数φ(x)单调递增,当−t<x<1−t时,φ′(x)<0,函数φ(x)单调递减,∴φ(x)min=φ(1−t)=2−t≥0,∴g(x)>f(x).【解析】(1)当t=0时,f(x)=lnx+ax ,x>0,f′(x)=1x−ax2=x−ax2,对a分类讨论即可得出函数的单调性.(2)不等式f(x)≥1在x∈(0,1]上恒成立,可得a≥x−xlnx,设h(x)=x−xlnx,x∈(0,1],利用导数研究其单调性极值与最值即可得出.(3)g(x)−f(x)=e x+ax −ln(x+t)−ax=e x−ln(x+t),t≤2,由x+t>0,可得x>−t≥−2,设m(x)=e x−x−1,利用导数研究函数的单调性可得e x>x+1.因此要证g(x)>f(x),只要证x+1−ln(x+t)>0,设φ(x)=x+1−ln(x+t),利用导数研究其单调性即可证明结论.本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、分类讨论方法、等价转化方法,考查了推理能力与计算能力,属于难题.22.在平面直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1:x2+y2−x=0,C2:x2+y2−2y=0.(1)以过原点的直线的倾斜角θ为参数,写出曲线C2的参数方程;(2)直线l过原点,且与曲线C1,C2分别交于A,B两点(A,B不是原点),求|AB|的最大值.【答案】解:(1)如图,C 1:x 2+y 2−x =0,即(x −12)2+y 2=14, 是以C 1(12,0)为圆心,12为半径,且过原点的圆,设∠PC 1x =α(0≤α<π). 则{x =12+12cosαy =12sinα, 由已知,以过原点的直线倾斜角为参数,则0≤θ<π,而α=2θ, 所以圆的参数方程为:{x =12+12cos2θy =12sin2θ(θ为参数,且0≤θ<π). (2)根据已知C 1,C 2的极坐标方程分别为ρ=cosα,ρ=2sinα(ρ>0), 故|AB|=|ρ1±ρ2|=|2sinα±cosα|=√5|sin(α±φ)|≤√5,其中tanφ12. 故当|sin(α±φ)|=1时,等号成立. 综上,|AB|的最大值为√5.【解析】(1)先设出圆C 2的参数方程的标准形式,再根据两个参数之间的关系可得; (2)利用极坐标方程的极径的几何意义可求得. 本题考查了简单曲线的极坐标方程,属中档题.23. 已知对任意实数x ,都有|x +2|+|x −4|−m ≥0恒成立.(1)求实数m 的取值范围;(2)若m 的最大值为n ,当正实数a ,b 满足4a+5b +13a+2b =n6时,求4a +7b 的最小值. 【答案】解:(1)对任意实数x ,都有|x +2|+|x −4|−m ≥0恒成立; 因为|x +2|+|x −4|≥|(x +2)−(x −4)|=6, 所以6≥m ,即m ≤6, 实数m 的取值范围是m ≤6;(2)由(1)知n =6,所以4a+5b +13a+2b =n6=1, 所以4a +7b =(4a +7b)(4a+5b +13a+2b )=[(a +5b)+(3a +2b)](4a +5b +13a +2b)=4+1+4(3a+2b)a+5b+a+5b 3a+2b ≥5+2√4(3a+2b)a+5b ⋅a+5b3a+2b =9,当且仅当b =5a ,即a =313,b =1513时取“=”; 所以4a +7b 的最小值为9.【解析】(1)不等式化为|x+2|+|x−4|≥m恒成立,利用绝对值不等式求出|x+2|+ |x−4|的最小值,即可得出m的取值范围;(2)由(1)知n=6,得4a+5b +13a+2b=n6=1,则4a+7b=(4a+7b)(4a+5b+13a+2b),再利用基本不等式求出它的最小值.本题考查了绝对值不等式以及基本不等式的应用问题,是中档题.。
“超级全能生”全国卷26省联考2019届高考英语试题(甲卷)及答案

“超级全能生”2018高考全国卷26省联考(甲卷)英语第I卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1. 5分,满分7. 5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A,B,C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一题。
每段对话仅读一遍。
1. What is the weather like today?A. Cold.B. Warm.C. Rainy.2. Where does this conversation probably take place?A. At a hotel.B. At a bank.C. At a post office.3. How much will the man pay for the tickets?A.$18.B.$28.C.$32.4. What is the man's attitude towards his job?A. He is satisfied with his job.B. He wants to quit his job.C. He was too busy to have a rest.5. How does the man feel about the play?A. He doesn't want to stay at home.B. He is pleased with the play.C. He felt disappointed about the play.第二节(共15小题;每小题1. 5分,满分22. 5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各个小题将给出5秒钟的作答时间。
2019年全国统一高考数学试卷(理科)(新课标ⅰ)(含解析版)

即 ,可得 .
由于 ,所以 ,故
.
18.解:(1)连结B1C,ME.
因为M,E分别为BB1,BC的中点,
所以ME∥B1C,且ME= B1C.
又因为N为A1D的中点,所以ND= A1D.
由题设知A1B1 DC,可得B1C A1D,故ME ND,
因此四边形MNDE为平行四边形,MN∥ED.
1.已知集合 ,则 =
A. B. C. D.
【答案】C
【解析】
【分析】
本题考查集合的交集和一元二次不等式的解法,渗透了数学运算素养.采取数轴法,利用数形结合的思想解题.
【详解】由题意得, ,则
.故选C.
【点睛】不能领会交集的含义易致误,区分交集与并集的不同,交集取公共部分,并集包括二者部分.
2.设复数z满足 ,z在复平面内对应的点为(x,y),则
A. B. C. D.
11.关于函数 有下述四个结论:
①f(x)是偶函数②f(x)在区间( , )单调递增
③f(x)在 有4个零点④f(x)的最大值为2
其中所有正确结论的编号是
A.①②④B.②④C.①④D.①③
12.已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,PB的中点,∠CEF=90°,则球O的体积为
22.[选修4—4:坐标系与参数方程](10分)
在直角坐标系xOy中,曲线C的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
(1)求C和l的直角坐标方程;
(2)求C上的点到l距离的最小值.
23.[选修4—5:不等式选讲](10分)
超级全能生2019高考全国卷26省2月联考乙卷理科数学
参考答案
“超级全能生”2019高考全国卷26省2月联考乙卷
数学(理科)
1.D
2.C
3.A
4.B
5.C
6.A
7.B
8.D
9.C
10.D
11.C
12.B
13.
14.60
15.18
16.6
17.解法一(I )如图,过点D作DE⊥AB,
15.若ln(2a + 8b) =lna+lnb,则a+b的最小值为________.
16.我国南北朝时期的数学家祖暅提出体积的计算原理(祖暅原理)“幂势既同则积不容异”,“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同等高处的截面积相等,那么这两个几何体的体积相等.已知双曲线 ,直线y = 0与y=6在第一象限内与双曲线及其渐近线围成如图中阴影部分所示的图形,则该图形绕y轴旋转一周所得几何体的体积为________.
手机依赖症
非手机依赖症
合计
男生
100
女生
100
合计
200
试运用独立性检验的思想方法分析:是否有90%的把握认为“手机依赖症”与“性别”有关?附:参考公式与临界值表: ,其中
0.100
0.050
0.025
0.010
0.001
k
2.706
3.841
5.024
6.635
10.828
19.(12分)
如图,已知AB丄平面ACD,AB//DE,△ACD为等边三角形,AD = DE = 2AB, F为CE的中点.
A. 36
B. 48
2019年数学普通高等学校招生全国统一考试数学(理)全国甲卷

2019年数学普通高等学校招生全国统一考试数学(理)全国甲卷2019年数学高考全国2卷全国(Ⅱ)理一、选择题(共11小题;共55分)1. 已知z=(m+3)+(m?1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )A. (?3,1)B. (?1,3)C. (1,+∞)D. (?∞,?3)2. 已知集合A={1,2,3},B={x∣ (x+1)(x?2)<0,x∈Z},则A∪B=( )A. {1}B. {1,2}C. {0,1,2,3}D. {?1,0,1,2,3}3. 已知向量a?=(1,m),b??=(3,?2),且(a?+b??)⊥b??,则m=( )A. ?8B. ?6C. 6D. 84. 如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A. 24B. 18C. 12D. 95. 圆x2+y2?2x?8y+13=0的圆心到直线ax+y?1=0的距离为1,则a=( )A. ?43B. ?34C. √3D. 26. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A. 20πB. 24πC. 28πD. 32π7. 若将函数y=2sin2x的图象向左平移π12个单位长度,则平移后图象的对称轴为( )A. x=kπ2?π6(k∈Z) B. x=kπ2+π6(k∈Z)C. x=kπ2?π12(k∈Z) D. x=kπ2+π12(k∈Z)8. 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )A. 7B. 12C. 17D. 349. 若cos (π4?α)=35,则sin2α= ( )A. 725B. 15C. ?15D. ?72510. 从区间 [0,1] 随机抽取 2n 个数 x 1,x 2,?,x n ,y 1,y 2,?,y n ,构成 n 个数对 (x 1,y 1),(x 2,y 2),?,(x n ,y n ),其中两数的平方和小于 1 的数对共有 m 个,则用随机模拟的方法得到的圆周率的近似值为 ( )A. 4nmB. 2nmC. 4mnD. 2mn11. 已知 F 1,F 2 是双曲线 E :x 2a 2?y 2b 2=1 的左,右焦点,点 M 在 E 上,MF 1 与 x 轴垂直,sin∠MF 2F 1=13,则 E 的离心率为 ( )A. √2B. 32C. √3D. 2二、填空题(共1小题;共5分)12. 三角形 ABC 的内角 A ,B ,C 的对边分别为 a ,b ,c ,若cosA =45,cosC =513,a =1,则b = .三、选择题(共1小题;共5分)13. 已知函数f (x )(x ∈R ) 满足 f (?x )=2?f (x ),若函数 y =x+1x与 y =f (x ) 图象的交点为(x 1,y 1),(x 2,y 2),?,(x m ,y m ),则∑(x i +y i )m i=1= ( ) A.0 B. m C. 2mD. 4m四、填空题(共3小题;共15分)14. 有三张卡片,分别写有 1 和 2,1 和 3,2 和 3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是.15. α,β 是两个平面,m ,n 是两条线,有下列四个命题:① 如果m⊥n,m⊥α,n∥β,那么α⊥β.② 如果m⊥α,n∥α,那么m⊥n.③ 如果α∥β,m?α,那么m∥β.④ 如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.则上述四个命题真命题的是16. 若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,b=.五、解答题(共8小题;共104分)17. S n为等差数列{a n}的前n项和,且a1=1,S7=28.记b n=[lga n],其中[x]表示不超过x的最大整数,如[0.9]=1,[lg99]=1.Ⅰ求b1,b11,b101;Ⅱ求数列{b n}的前1000项和.18. 某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:ⅠⅡ若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;Ⅲ求续保人本年度的平均保费与基本保费的比值.19. 如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=54,EF交BD于点H.将三角形DEF沿EF折到三角形D?EF的位置OD?=√10.Ⅰ证明:D?H⊥平面ABCD;Ⅱ求二面角B?D?A?C的正弦值.20. 已知椭圆E:x2t +y23=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E 于A,M两点,点N在E上,MA⊥NA.Ⅰ当t=4,∣AM∣=∣AN∣时,求三角形AMN的面积;Ⅱ当2∣AM∣=∣AN∣时,求k的取值范围.21. (1)讨论函数 f (x )=x?2x+2?e x 的单调性,并证明当 x >0 时,(x ?2)?e x +x +2>0Ⅱ 证明:当a ∈[0,1) 时,函数 g (x )=e x ?ax?ax 2(x >0) 有最小值.设 g (x ) 的最小值为 ?(a ),求函数 ?(a ) 的值域.22. 如图,在正方形 ABCD ,E ,G 分别在边 DA ,DC 上(不与端点重合),且 DE =DG ,过 D 点作DF ⊥CE ,垂足为 F .Ⅰ 证明:B ,C ,G ,F 四点共圆;Ⅱ 若 AB =1,E 为 DA 的中点,求四边形 BCGF 的面积.23. 在直角坐标系 xOy 中,圆 C 的方程为 (x +6)2+y 2=25.Ⅰ 以坐标原点为极点,轴正半轴为极轴建立极坐标系,求 C 的极坐标方程;Ⅱ 直线 l 的参数方程是{x =tcosα,y =tsinα,(t 为参数),l 与 C 交于 A ,B 两点,∣AB∣=√10,求l 的斜率.24. 已知函数f (x )=∣∣x ?12∣∣+∣∣x +12∣∣,M 为不等式 f (x )<2 的解集.Ⅰ 求 M ;Ⅱ 证明:当 a ,b ∈M 时,∣a +b∣<∣1+ab∣.答案第一部分1. A2. C3. D4. B5. A6. C7. B8. C9. D 10. C11. A第二部分12. 2113第三部分13. B第四部分14. 1和315. ②③④16. 1?ln2第五部分17. (1)设{a n}的公差为d,S7=7a4=28,所以a4=4,所以d=a4?a13=1,所以a n=a1+(n?1)d=n.所以b1=[lga1]=[lg1]=0,b11=[lga11]=[lg11]=1,b101=[lga101]=[lg101]=2.(2)记{b n}的前n项和为T n,则T1000=b1+b2+?+b1000=[lga1]+[lga2]+?+[lga1000].当0≤lga n<1时,n=1,2,?,9;当1≤lga n<2时,n=10,11,?,99;当2≤lga n<3时,n=100,101,?,999;当lga n=3时,n=1000.所以T1000=0×9+1×90+2×900+3×1=1893.18. (1)设续保人本年度的保费高于基本保费为事件A,P(A)=1?P(A)=1?(0.30+0.15)=0.55.(2)设续保人保费比基本保费高出60%为事件B,P(B∣ A)=P(AB)P(A)=0.10+0.050.55=311.(3)设本年度所交保费为随机变量X.平均保费EX =0.85a ×0.30+0.15a +1.25a ×0.20+1.5a ×0.20+1.75a ×0.10+2a ×0.05=0.255a +0.15a +0.25a +0.3a +0.175a +0.1a=1.23a.所以平均保费与基本保费比值为1.23. 19. (1)因为AE =CF =54,所以 AEAD =CFCD ,所以EF ∥AC .因为四边形 ABCD 为菱形,所以AC ⊥BD ,所以EF ⊥BD ,所以EF ⊥DH ,所以EF ⊥D?H .因为 AC =6,所以 AO =3;又 AB =5,AO ⊥OB ,所以 OB =4,所以 OH = AE AOOD =1,所以DH =D?H =3,所以∣OD?∣2=∣OH∣2+∣D?H∣2,所以D?H ⊥OH .又OH ∩EF =H ,所以D?H ⊥面ABCD .(2)建立如图坐标系 H ?xyz .B (5,0,0),C (1,3,0),D?(0,0,3),A (1,?3,0),AB =(4,3,0),AD=(?1,3,3),AC =(0,6,0),设面 ABD? 法向量 n 1=(x,y,z ),由 {n 1AB =0,n 1AD???=0, 得 {4x +3y =0,?x +3y +3z =0, 取 {x =3,y =?4,z =5,所以n 1=(3,?4,5).同理可得面AD?C 的法向量n 2=(3,0,1),所以∣cosθ∣=∣n 1n 2??????∣∣∣n 1??????∣∣∣∣n2∣∣=5√2?√10=7√525,所以sinθ=2√9525.20. (1)当 t =4 时,椭圆 E 的方程为 x 24+y 23=1,A 点坐标为 (?2,0),因为∣AM ∣=∣AN ∣,MA ⊥NA ,由椭圆的对称性,k =1,则直线 AM 的方程为 y =x +2.联立 {x 24+y 23=1,y =x +2,并整理得 7x 2+16x +4=0,所以 M (?27,127 ),所以S △AMN =12×(2?27)×127×2=14449.(2)直线 AM 的方程为y =k(x +√t),联立 {x 2 t +y 23=1,y =k(x +√t),并整理得(3+tk 2)x 2+2t √tk 2x +t 2k 2?3t =0.解得x =?√t 或 x =?t √tk 2?3√t 3+tk 2,所以∣AM∣=√1+k 2∣∣∣?t √tk 2?3√t3+tk 2+√t ∣∣∣=√1+k 2?6√t3+tk 2.所以∣AN∣=√1+k 2?6√t 3k+t k.因为2∣AM∣=∣AN∣,所以2?√1+k 26√t3+tk 2=√1+k 2?6√t 3k+t k,整理得 t =6k 2?3k k 3?2.因为椭圆 E 的焦点在 x 轴,所以 t >3,即6k 2?3k k ?2>3,整理得(k 2+1)(k?2)k ?2<0,解得√23<2.<="" p="">21. (1)因为 f (x )=x?2x+2e x ,所以 f?(x )=e x (x?2x+2+4x+2)=x 2e xx+2.因为当x ∈(?∞,?2)∪(?2,+∞) 时,f?(x )>0,所以 f (x ) 在(?∞,?2) 和(?2,+∞) 上单调递增.所以 x >0 时,x?2x+2?e x >f (0)=?1,所以 (x ?2)e x +x +2>0 得证.(2)因为g?(x )=(e x ?a )x 2?2x (e x ?ax ?a )x 4=x (xe x ?2e x +ax +2a )x 4=(x +2)?(x ?2x +2?e x+a)x 3,a ∈[0,1), 令 ?(x )=x?2x+2e x +a ,则 ?(0)=a ?1<0,?(2)=a ≥0,由(1)的结论,?(x ) 在 (0,2] 上有唯一零点 x =t .可得函数 g (x ) 在 (0,t ) 上单调递减,在(t,+∞) 上单调递增,因此 x =t 也是函数 g (x ) 的极小值点,亦为最小值点.因此当 a ∈[0,1) 时,函数 g (x ) 有最小值 g (t ).由于t ?2t +2e t+a =0, 即 a =?t?2t+2e t ,当a ∈[0,1) 时,有t ∈(0,2].所以函数 g (x ) 的最小值g (t )=e t +(t +1)t ?2t +2?e tt 2=e t t +2.令 r (t )=e tt+2(m ∈(0,2]),则其导函数r?(t )=t +1()2e t>0,因此函数 r (t ) 在 (0,2] 上单调递增,从而函数 ?(a ) 的值域,即函数 g (x ) 的最小值的取值范围是(r (0),r (2)],即 (12,14e 2].22. (1)因为DF ⊥CE ,所以Rt △DEF ∽Rt △CED .所以∠GDF =∠DEF =∠BCF ,DFDG =CFBC .因为 DE =DG ,CD =BC ,所以DE DG=CF BC.所以△GDF ∽△BCF ,所以∠CFB =∠DFG .所以∠GFB =∠GFC +∠CFB =∠GFC +∠DFG =∠DFC =90°.所以∠GFB +∠GCB =180°.所以 B ,C ,G ,F 四点共面.(2)因为 E 为 AD 中点,AB =1,所以 DG =CG =DE =12,所以在Rt △GFC 中,GF =GC ,连接GB ,Rt △BCG ≌Rt △BFG ,所以 S 四边形BCGF =2S △BCG =2×12×1×12=12.23. (1)由{x =ρcosθ,y =ρsinθ, 可得,(ρcosθ+6)2+ρ2sin 2θ=25,整理得ρ2+12ρcosθ+11=0 即为所求.(2)令直线l 的斜率为k ,可得直线的直角坐标方程为kx ?y =0.圆的半径为 r =5,圆心到直线的距离d =√k 2+1,又因为∣AB∣=√10,所以可得∣AB∣24+d 2=r 2,即 52+36k 2k 2+1=25,解得k =±√153. 24. (1)当x ≤?12 时,原不等式可以化为 12?x ?x ?12<2,解得 x >?1,所以此时不等式的解集为 (?1,?12];当x ≥12 时,原不等式可以化为 x ?12+x +12<2,解得 x <1,所以此时不等式的解集为 [12,1);当 ?12<1<="" p="">2 时,原不等式可以化为 x +12+12?x <2,解得x ∈R ,所以此时不等式的解集为 (?12,12);综上可得原不等式的解集为 M =(?1,1).(2)要证明∣a +b∣<∣1+ab∣,则只需要证明(a +b )2<(1+ab )2.因为(1+ab)2?(a+b)2=a2b2+1?a2?b2=(a2?1)(b2?1),而由1可得a2<1,b2<1,所以(a2?1)(b2?1)>0.所以原不等式得证.。
“超级全能生”2019高考全国卷26省5月联考-丙A-数理DA

故选 "!
知识拓展二 项 式 的 展 开 式 有 关 问 题 的 解 题 策 略%
求展开式中的第/ 项)可 依 据 二 项 式 的 通 项 公 式 直
接求出第/ 项*求展开式中的特定项)可依据 条 件 写
* 出第-(* 项)再 由 特 定 项 的 特 点 求 出- 值 即 可* 已
1
O
π
π
超级全能生 高考全国卷 省 月联考丙卷 数学理科!答案详解
! " # $ % & ' ( ) !* !! !"
!""#!!"!!#!"
!!!!解析本 题 考 查 集 合 的 运 算 知 识!考 查 运 算 求 解 * 线*的方程为%$(#&'$+!圆 $$&+%%( $#(%%% $)
视图一样宽)正"主#视图和侧"左#视图一样 高!若 相 邻 两物体的表面相交)表面的交线是它们的分界 线)在 三
* * *
视 图 中 )要 注 意 实 '虚 线 的 画 法 !
*
$!#!解析本 题 考 查 余 弦 函 数 的 图 象(几 何 概 型 等 知 *
识!考 查 识 图(用 图 能 力!考 查 直 观 想 象 核 心 素 养!如 *
能力!考 查 数 学 运 算 核 心 素 养!因 为 "$ "#"#$$% & *
'$()!$#+#$ "#"#$ $$&%%% (*!$#+#$ "#"#$ *#!%$"$"+%$&'#!所以 "'%$&*!''!故选 !!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学精品复习资料
2019.5
“超级全能生”20xx 高考全国卷26省联考(甲卷)
理科数学试卷
一.选择题(本题共12小题,,每小题5分,共60分)
1. 已知集合B ={1},C ={3},A B ={1,2},则()
A 、A
B =∅ B 、A
C =∅ C 、A C ={1,2,3}
D 、A C ={2,3}
2. 若复数31z i =,22z i =+,则12z z =()
A 、-1-2i
B 、-1+2i
C 、1+2i
D 、1-2i 3. 掷一枚均匀的硬币4次,则出现正面的次数多于反面的次数的概率为() A 、
12 B 、25 C 、516 D 、14
4. “0xy ≠”是“0x ≠”的()
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
5. 一个蜂巢里有1只蜜蜂,第一天它飞出去找回3个伙伴;第2天有4只蜜蜂飞出去各自找回了3个伙伴,...,如果这个找伙伴的过程继续下去,第6天所有的蜜蜂归巢后,蜂巢中一共有 只蜜蜂。
()
A. 972
B. 1456
C. 4096
D. 5460
6. 如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体表面积是()
A. 80-2π
B. 80
C. 80+4π
D. 80+6π 7. 对任意非零实数a,b,若
的运算原理如图所示,则
的值为()
C.
2 D. 12
8. 下列函数中在3(
,)44
ππ
上为减函数的是()
A. tan y x =-
B.cos(2)2
y x π
=--
C. sin 2cos 2y x x =+
D. 22cos 1y x =- 9. 下列函数中满足121212()()
(
)()22
x x f x f x f x x ++<≠的是() A. ()f x ax b =+ B. ()f x x α= C. ()log (0,1)a f x x a a =>≠ D. 2()f x x ax b =++
10. 双曲线22
221(0,0)x y a b a b
-=>>的一条渐近线的斜率为2,过右焦点F 作x 轴的垂线交双曲线与
A,B 两点,△OAB (O 为坐标原点)的面积为F 到一条渐近线的距离为()
11. 半径为R 的球O 中有两个半径分别为它们所在的平面互相垂直,且两圆的公共弦长为R ,则R= ()
12. 以下关于(0)x x ≥的不等式2
ln(1)0x kx x ++-≥的结论中错误的是()
14k ∃≤
,使不等式恒成立 B. 1
4k ∀≥,使不等式恒成立 C. 12k ∃≤,使不等式恒成立 D. 1
2k ∀≥,使不等式恒成立
二、填空题(本题共4小题,每小题5分,共20分)
13、等腰直角三角形的直角顶点位于原点,另外两个点在抛物线2
4y x =上,则这个等腰直角三角形的面积为
14、若关于x 的不等式2
x x mx -+>的解集为{}|10x x -<<,则二项式2016
(1)mx +的展开式中的
x 系数为
15、等比数列{}n a 中,130,256,448,n n a a S T >==为数列{}n a 的前n 项乘积,则n T 当取得最大值时,n =
16、已知向量(,),(1,1)a m n b ==,满足a b ≥2,且(2)0a a b -≤,则a b 的取值范围是 三、解答题(本题共6小题,共70分)
17、(12分)△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若2sin sin 2sin()B C A C -=- (1)求cosA ;
(2)若5a b c =+=,求△ABC 的面积。
18、(12分)某超市某种面包进货价为每个4元,实际售价为每个4.5元,若当天不能卖完,就在闭店前以每个3元的价格全部处理,据以往统计日需求量(单位:个)的情况如下:
若某日超市面包进货量为600。
(1)若以日需求量x 所在区间的中间值为估计值,根据上表列出当日利润y 的分布列; (2)估计超市当日利润y 的均值。
19.(12分)已知三棱柱ABC —A 1B 1C 1,侧棱AA 1垂直于底面ABC ,∠2
ABC π
=,AB=BC=AA 1=4,D 为
BC 的中点.
(1)若E 为棱CC 1的中点,求证:DE ⊥A 1C
(2)若E 为棱CC 1上异于端点的任意一点,设C E 与平面ADE 所称角为α,
求满足sin 61
α=
时CE 的长
20.(12分)已知直线l :y=x+1,圆O :2
2
3
2
x y +=
直线l 被圆截得的弦长与椭圆C :
22221(0)x y a b a b +=>>的短轴长相等,椭圆的离心率e (1)求椭圆C 的方程; (2)过点M(0,-
1
3
)的直线l 0交椭圆于A,B 两点,试问,在坐标平面上是否存在一个定点T,使得无论l 0如何旋转,以AB 为直径的圆恒过定点T?若存在,求出T 的坐标;若不存在,请说明理由
21.(12分)已知函数1
()ln 1f x x x
=+
-。
(1)求函数的单调性;
(2)证明:ln(x+1)!>2n -*)n N ∈
22.(10分) 选修4-1: 几何证明题选讲
如图所示,AB 为圆O 的直径,BC ,CD 为圆O 的切线,B 、D 为切点。
(1)求证:AD //OC
(2)若圆的半径为1,求AD ·OC 的值
23.(10分)选修4-4: 坐标系与参数方程
已知A ,B(不与原点O 重合)分别在圆221:(2)4C x y -+=与圆222:(1)1C x y -+=上, 且OA ⊥OB.
(1) 若以原点为极点,x 轴的正半轴为极轴建立极坐标系,当A 的极角为3
π
时,求A, B 的极坐标; (2) 求||||OA OB 的最大值
24. (10分) 选修4-4: 不等式选讲
如果关于x 的不等式|3||4|||x x a -+-≤的解集为空集 (1) 求实数a 的取值范围;
(2) 若实数b 与实数a 取值范围完全相同,求证:|1|||ab a b ->-
理科数学参考答案 1-5:BACAC 6-10:CCBDB 11-12:DB 13、16
14、4032
15、8或9
16、[2,4]
17、
18、
19、
20、
21、
22、
23、
24、。
