2019_年普通高等学校招生全国统一考试(天津卷)_数学(文史类)
2019年天津高考语文、数学(文史类)、文综、英语真题及答案解析汇总word版-40页文档资料

2019年天津高考语文、数学(文史类)、文综、英语真题及答案解析汇总2019年普通高等学校招生全国统一考试(天津卷)语文本试卷分第I卷和第II卷两部分,共150分,考试用时150分钟,第I卷1至6页,第II卷7至12页。
答卷前,考生务必奖自己的姓名、准考证号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净以后,再选涂其他答案标号。
2.本卷共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的。
一、(15分)1.下列词语中加点字的读音,全都正确的一组是A.裨.(bì)益窠.(kē)臼偌.(nuò)大潜.(.qián)移默化B.发轫.(rěn) 烘焙.(péi) 禀.(bǐng)赋既往不咎.(jiù)C.臧否.(pǐ) 契.(qiè)合澄.(chéng)澈乳臭.(xiù)未干D.造诣.(.yì) 编纂.(zuǎn) 泊.(bó)位游目骋.(chěng)怀2.下列词语中没有..错别字的一组是A.膏梁青涩雍容华贵豆寇年华B.缴纳戍边平心而论得鱼忘筌C.桀骜羁旅摩肩接踵励精图治D.袅娜覆盖开城布公呕心沥血3.下面语段横线处应填入的词语,是恰当的一组是长期以来,人们把图书馆当成“知识宝库”,当成“知识殿堂”,似乎对图书馆_________有㖙,然而,“宝库”和“殿堂”虽好,但它们离普通百姓很远,甚至很遥远,普通百姓往往_______。
一些人从不进图书馆,恐怕同这种心态不无关系,图书馆_________“宝库”“殿堂”,______“知识公园”。
A.崇敬望而生畏不仅是而且是B.尊崇望而生畏不应是而应是C.崇敬敬而远之不应是而应是D.尊崇敬而远之不仅是而且是4.下列各句中没有..语病的一句是A.在学校开设的各种选修课中,同学们尤其更喜欢“生活中的法律”“电脑音乐制作”等体验性强、新鲜有趣的课程。
2019年普通高等学校招生全国统一考试(天津卷)文科数学及答案解析

绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)文科数学答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={﹣1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=()A.{2}B.{2,3}C.{﹣1,2,3}D.{1,2,3,4} 2.(5分)设变量x,y满足约束条件则目标函数z=﹣4x+y的最大值为()A.2B.3C.5D.63.(5分)设x∈R,则“0<x<5”是“|x﹣1|<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.(5分)阅读如图的程序框图,运行相应的程序,输出S的值为()A.5B.8C.24D.295.(5分)已知a=log27,b=log38,c=0.30.2,则a,b,c的大小关系为()A.c<b<a B.a<b<c C.b<c<a D.c<a<b6.(5分)已知抛物线y2=4x的焦点为F,准线为l.若l与双曲线﹣=1(a>0,b >0)的两条渐近线分别交于点A和点B,且|AB|=4|OF|(O为原点),则双曲线的离心率为()A.B.C.2D.7.(5分)已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<π)是奇函数,且f(x)的最小正周期为π,将y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g(x).若g()=,则f()=()A.﹣2B.﹣C.D.28.(5分)已知函数f(x)=若关于x的方程f(x)=﹣x+a(a∈R)恰有两个互异的实数解,则a的取值范围为()A.[,]B.(,]C.(,]∪{1}D.[,]∪{1}二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)i 是虚数单位,则||的值为 .10.(5分)设x ∈R ,使不等式3x 2+x ﹣2<0成立的x 的取值范围为 . 11.(5分)曲线y =cos x ﹣在点(0,1)处的切线方程为 . 12.(5分)已知四棱锥的底面是边长为的正方形,侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为 .13.(5分)设x >0,y >0,x +2y =4,则的最小值为 .14.(5分)在四边形ABCD 中,AD ∥BC ,AB =2,AD =5,∠A =30°,点E 在线段CB 的延长线上,且AE =BE ,则•= .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(13分)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.(Ⅰ)应从老、中、青员工中分别抽取多少人?(Ⅱ)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A ,B ,C ,D ,E ,F .享受情况如表,其中“〇”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.A BCDEF子女教育 〇 〇 × 〇 × 〇 继续教育 × × 〇 × 〇 〇 大病医疗 × × × 〇 × × 住房贷款利息 〇 〇 × × 〇 〇 住房租金 × × 〇 × × × 赡养老人〇〇×××〇(i )试用所给字母列举出所有可能的抽取结果;(ii)设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.16.(13分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2a,3c sin B =4a sin C.(Ⅰ)求cos B的值;(Ⅱ)求sin(2B+)的值.17.(13分)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面P AC⊥平面PCD,P A⊥CD,CD=2,AD=3.(Ⅰ)设G,H分别为PB,AC的中点,求证:GH∥平面P AD;(Ⅱ)求证:P A⊥平面PCD;(Ⅲ)求直线AD与平面P AC所成角的正弦值.18.(13分)设{a n}是等差数列,{b n}是等比数列,公比大于0.已知a1=b1=3,b2=a3,b3=4a2+3.(Ⅰ)求{a n}和{b n}的通项公式;(Ⅱ)设数列{c n}满足c n=求a1c1+a2c2+…+a2n c2n(n∈N*).19.(14分)设椭圆+=1(a>b>0)的左焦点为F,左顶点为A,上顶点为B.已知|OA|=2|OB|(O为原点).(Ⅰ)求椭圆的离心率;(Ⅱ)设经过点F且斜率为的直线l与椭圆在x轴上方的交点为P,圆C同时与x轴和直线l相切,圆心C在直线x=4上,且OC∥AP.求椭圆的方程.20.(14分)设函数f(x)=lnx﹣a(x﹣1)e x,其中a∈R.(Ⅰ)若a≤0,讨论f(x)的单调性;。
【2019年高考真题—普通高等学校统一考试—文科数学(天津卷)—解析版】

《【2019年高考真题—普通高等学校统一考试—文科数学(天津卷)—解析版】》摘要:2019年普通高等学校招生全国统一考试(天津卷)文科数学本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟,因此当时,,从而,所以在内单调递增. (II)证明:(i)由(I)知,,令,由,可知在内单调递减,又,且,故在内有唯一解,从而在内有唯一解,不妨设为,则,当时,,所以在内单调递增,因此是的唯一极值点. 令,则当时,,故在内单调递减,从而当时,,所以,从而,又因为,所以在内有唯一零点,又在内有唯一零点1,从而,在内恰有两个零点. (ii)由题意,,即,从而,即,以内当时,,又,故,两边取对数,得,于是,整理得,【点睛2019年普通高等学校招生全国统一考试(天津卷)文科数学本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利第Ⅰ卷注意事项: 1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分共40分。
参考公式:·如果事件A,B互斥,那么. ·圆柱的体积公式,其中表示圆柱的底面面积,表示圆柱的高·棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,,,则 A. {2} B. {2,3} C. {-1,2,3} D. {1,2,3,4} 【答案】D 【解析】【分析】先求,再求。
【详解】因为,所以. 故选D。
【点睛】集合的运算问题,一般要先研究集合中元素的构成,能化简的要先化简,同时注意数形结合,即借助数轴、坐标系、韦恩图等进行运算. 2.设变量满足约束条件,则目标函数的最大值为 A. 2 B. 3 C. 5 D. 6 【答案】D 【解析】【分析】画出可行域,用截距模型求最值。
【2019年高考真题—普通高等学校统一考试—文科数学(天津卷)—解析版】

【2019年高考真题—普通高等学校统一考试—文科数学(天津卷)—解析版】2019年普通高等学校招生全国统一考试(天津卷)文科数学本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分共40分。
参考公式:·如果事件A,B互斥,那么. ·圆柱的体积公式,其中表示圆柱的底面面积,表示圆柱的高·棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,,,则A. {2} B. {2,3} C. {-1,2,3} D. {1,2,3,4} 【答案】D 【解析】【分析】先求,再求。
【详解】因为,所以. 故选D。
【点睛】集合的运算问题,一般要先研究集合中元素的构成,能化简的要先化简,同时注意数形结合,即借助数轴、坐标系、韦恩图等进行运算. 2.设变量满足约束条件,则目标函数的最大值为A. 2 B. 3 C. 5 D. 6 【答案】D 【解析】【分析】画出可行域,用截距模型求最值。
【详解】已知不等式组表示的平面区域如图中的阴影部分。
目标函数的几何意义是直线在轴上的截距,故目标函数在点处取得最大值。
由,得,所以。
故选C。
【点睛】线性规划问题,首先明确可行域对应的是封闭区域还是开放区域,分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值或范围.即:一画,二移,三求. 3.设,则“”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B 【解析】【分析】求出的解集,根据两解集的包含关系确定. 【详解】等价于,故推不出;由能推出。
2019年天津卷文数高考真题及答案解析(word精编)

2019年天津卷文数高考真题及答案解析(word精编)绝密★启用前 xx年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名.准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分共40分。
参考公式:·如果事件A,B互斥,那么. ·圆柱的体积公式,其中表示圆柱的底面面积,表示圆柱的高·棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合,,,则(A){2}(B){2,3}(C){-1,2,3}(D){1,2,3,4} (2)设变量满足约束条件则目标函数的最大值为(A)2(B)3(C)5(D)6 (3)设,则“”是“”的(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分也不必要条件(4)阅读右边的程序框图,运行相应的程序,输出的值为(A)5(B)8(C)24(D)29 (5)已知,,,则的大小关系为(A)(B)(c)(D)(6)已知抛物线的焦点为,准线为.若与双曲线的两条渐近线分别交于点A和点B,且(为原点),则双曲线的离心率为(A)(B)(C)2(D)(7)已知函数是奇函数,且的最小正周期为,将的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为.若,则(A)-2(B)(C)(D)2 (8)已知函数若关于的方程恰有两个互异的实数解,则的取值范围为(A)(B)(C)(D)绝密★启用前 xx年普通高等学校招生全国统一考试(天津卷)数学(文史类)第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年高考天津卷文科数学试卷(更多试卷看个人主页)
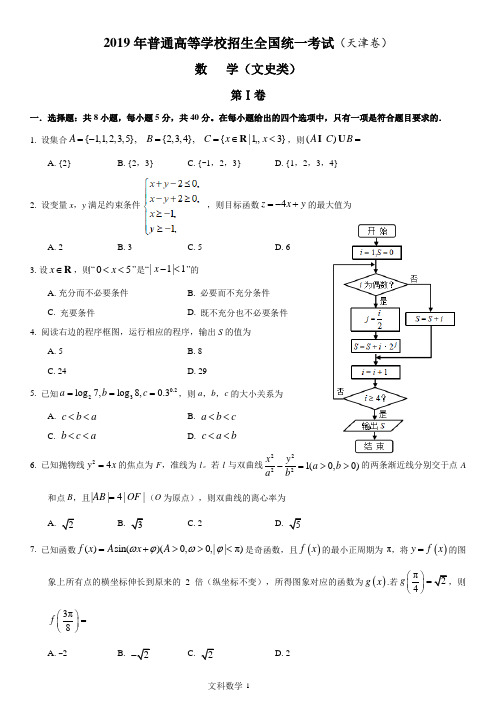
2019年普通高等学校招生全国统一考试(天津卷)数 学(文史类)第Ⅰ卷一.选择题:共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R …,则()A CB =A. {2}B. {2,3}C. {-1,2,3}D. {1,2,3,4}2. 设变量x ,y 满足约束条件,则目标函数4z x y =-+的最大值为A. 2B. 3C. 5D. 63. 设x ∈R ,则“05x <<”是“|1|1x -<”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件4. 阅读右边的程序框图,运行相应的程序,输出S 的值为A. 5B. 8C. 24D. 295. 已知0.223log 7,log 8,0.3a b c ===,则a ,b ,c 的大小关系为A. c b a <<B. a b c <<C. b c a <<D. c a b <<6. 已知抛物线24y x =的焦点为F ,准线为l 。
若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为A.B.C. 2D.7. 已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若π4g ⎛⎫=⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭A. -2B.C.D. 28.已知函数01,()1,1.x f x x x ⎧≤≤⎪=⎨>⎪⎩若关于x 的方程1()()4f x x a a =-+∈R 恰有两个互异的实数解,则a 的取值范围为 A. 59,44⎡⎤⎢⎥⎣⎦B. 59,44⎛⎤⎥⎝⎦C. 59,{1}44⎛⎤⎥⎝⎦D. 59,{1}44⎡⎤⎢⎥⎣⎦第Ⅱ卷二.填空题:本大题共6小题,每小题5分,共30分. 9. i 是虚数单位,则5i1i-+的值为__________. 10. 设x ∈R ,使不等式2320x x +-<成立的x 的取值范围为__________. 11. 曲线cos 2xy x =-在点(0,1)处的切线方程为__________. 12..若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________. 13. 设0,0,24x y x y >>+=,则(1)(21)x y xy ++的最小值为__________.14. 在四边形ABCD中,,5,30AD BC AB AD A ==∠=︒∥,点E 在线段CB 的延长线上,且AE BE =,则BD AE ⋅=__________.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15. (本小题满分13分)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除。
2019年高考天津卷文科数学试题(含解析)

天津2019年普通高等学校招生全国统一考试数学(文史类)一、选择题1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x R x =-==∈≤<,则()A C B =( )A.{2}B.{2,3}C.{1,2,3}-D.{1,2,3,4} 【答案】D 【解析】{1,2}AC =,(){1,2,3,4}A C B =,故选D.2.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为( )A.2B.3C.5D.6 【答案】C【解析】画出可行域,如图,当4E x y =-+经过(1,1)D -时,取最大值max 415z =+=.3.设x R ∈,则“05x <<”是“|1|1x -<”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 【答案】B【解析】由|1|1x -<,得02x <<,“05x <<”不可以推出“02x <<”, 而“02x <<”可推出“05x <<”,故为的必要不充分条件,故选B.4.阅读的程序框图,运行相应的程序,输出S 的值为( )A.5B.8C.24D.29 【答案】B【解析】1,1i S ==;2,1,1225i j S ===+⨯=;3,538i S ==+=;4i =,满足4i ≥,输出8S =.5.已知0.223log 7,log 8,0.3a b c ===,则,,a b c 的大小关系为( )A.c b a <<B.a b c <<C.b c a <<D.c a b << 【答案】A 【解析】0.2332230.3log 8log 19log 2log 4lo 3g 7c b a ==<=<=<==<.6.己知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为( )2【答案】D【解析】由题意知(1,0)F ,:1l x =-,||4AB =,所以24ba=,e ==.7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x:若()4g π=3()8f π=( ) A.2-B.2 【答案】C【解析】由题意知(0)00f ϕ=⇒=,所以()sin()f x A x ω=,()()sin()22x xg x f A ω==,()g x 的最小正周期为2π,且()4g π=()2sin 2f x x =,3()8f π=.8.已知函数1,()1, 1.x f x x x⎧≤≤⎪=⎨>⎪⎩若关于x 的方程1()()4f x x a a R =-+∈恰有两个互异的实数解,则a 的取值范围为( )A.59[,]44B.59(,]44C.59(,]{1}44D.59 [,]{1}44【答案】D【解析】方法一:当1a =时,令104x+=即2840([0,1])t t t +-==,解得4(0,1)t =∈,令110(1)4x x x+-=>,解得2x =,排除A,B ; 当54a =时,令5044x +=即2850([0,1])t t t +-==,解得4(0,1)t =∈,令150(1)44x x x +-=>,解得4x =,排除C. 方法二:如图,当直线14y x a =-+过(1,2)点时,有2191044a a -=-⇒=-, 过(1,1)点时,有1151044a a -=-⇒=-, 当直线14y x a =-+与曲线1(1)y x x =>相切时,可求得切点1(2,)2, 此时1121204a a -=-⇒=-,综上,实数a 的取值范围为59 [,]{1}44.二.填空题 9.i 是虚数单位,则5||1ii-+的值为 .【解析】5(5)(1)231(1)(1)i i i i i i i ---==-=++-.10.设x R ∈,使不等式2320x x +-<成立的x 的取值范围为 . 【答案】(21,)3-【解析】2320x x +-<,即(1)(32)0x x +-<,即213x -<<,故x 的取值范围是2(1,)3-.11.曲线cos 2xy x =-在点(0,1)处的切线方程为 . 【答案】220x y +-=【解析】1'sin 2y x =--,当0x =时其值为12-,故所求的切线方程为112y x-=-,即220x y +-=.12.的正方核侧枝长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一底面的圆心为四棱锥底面的中心,则该圆柱的体积为 . 【答案】4π【解析】显然圆柱的直径等于1,圆柱的高等于1,所以圆柱的体积等于4π.13.设0,0,24x y x y >>+=,则(1)(21)x y xy++的最小值为 .【答案】92【解析】∵0,0,24x y x y >>+=,∴42x y =+≥≤2xy ≤,当且仅当22x y ==时等号成立.,∵(1)(21)221255592222x y xy x y xy xy xy xy xy ++++++===+≥+=.14.在四边形ABCD 中,//,5,30AD BC AB AD A ==∠=︒,点E 在线段CB 的延长线上,且AE BE =,则BD AE ⋅= . 【答案】1-【解析】如图所示,//,5,30AD BC AB AD BAC ==∠=︒,又AE BE =,所以120AEB ∠=︒,根据余弦定理222cos1202AE BE AB AE BE +-︒=⋅⋅,解得2AE BE ==,所以25BE AD =-,又BD AD AB =-,25AE AB BE AB AD =+=-,所以72()()(12525)15525AB A BD AE AD A D B ⋅=-⋅=--⨯⨯⨯=--.三、解答题15.2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除,某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.(1)应从老、中、青员工中分别抽取多少人?(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为,,,,,A B C D E F .享受情况如右表,其中“”表示享受.“⨯”表示不享受.现从这6人中随机抽取2人接受采访. (i )使用所给字母列举出所有可能的抽取结果;(ii )设M 为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M 发生的概率. 【解析】(1)由已知老、中、青员工人数之比为6:9:10,由于采用分层抽样的方法从中抽取25为员工,因此应从老、中、青员工中分别抽取6人,9人,10人. (2)(i )从已知6人中随机抽取2人的所有可能结果为{,},{,},{,},{,},{,},{,},{,},{,},{,},{,},{,},{,},{,},{,},{,}A B A C A D A E A F B C B D B E B F C D C E C F D E D F E F 共15种.(ii )由表格知,符合题意的所有可能结果为{,},{,},{,},{,},{,},{,},{,},{,},{,},{,},{,}A B A D A E A F B D B E B F C E C F D F E F 共11种.所以,事件M 发生的概率11()15P M =.16.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c .已知2b c a +=,3sin 4sin c B a C =.(1)求cos B 的值; (2)求in 6(s 2)B π-的值.【答案】(1)14-;(2)【解析】(1)在ABC ∆中,由正弦定理sin sin b cB C=,得sin sin b C c B =,又由3sin 4sin c B a C =,得3sin 4sin b C a C =,即34b a =.又因为2b c a +=,得到43b a =,23c a =,由余弦定理可得222222416199cos 22423a a a a cb B ac a a +-+-===-⋅⋅. (2)由(1)可得sin B ==,从而sin 22sin cos B B B ==,227cos 2cos sin 8B B B =-=-,故717sin 2sin 2coscos 2sin666828(2)16B B B πππ+=+=--⨯=-17.如图,在四棱锥P ABCD -中底面ABCD 为平行四边形,PCD ∆为等边三角形,平面PAC ⊥平面PCD ,PA CD ⊥,2CD =,3AD =.(1)设G ,H 分别为PB ,AC 的中点,求证://GH 平面PAD ; (2)求证:PA ⊥平面PCD ;(3)求直线AD 与平面PAC 所成角的正弦值.【答案】(1)见解析;(2)见解析;(3. 【解析】(1)证明:连接BD ,易知AC BD H =,BH DH =.又由BG PG =,故//GH PD ,又因为GH ⊄平面PAD ,PD ⊂平面PAD ,所以//GH 平面PAD . (2)证明:取棱PC 的中点N ,连接DN .依题意,得D N P C ⊥,又因为平面PAC ⊥平面PCD ,平面PAC平面PCD PC =,所以DN ⊥平面PAC ,又PA ⊂平面PAC ,故DN PA ⊥,又已知PA CD ⊥,CD DN D =,所以PA ⊥平面PCD .(3)解:连接AN ,由(2)中DN ⊥平面PAC ,可知DAN ∠为直线AD 与平面PAC 所成的角.因为PCD ∆是等边三角形,2CD =且N 为PC 的中点,所以DN =DN AN ⊥,在Rt AND ∆中,sin 3DN DAN AD ∠==.所以,直线AD 与平面PAC 所成角的正弦值为3. 18.设{}n a 是等差数列,{}n b 是等比数列,公比大于0,已知113a b ==,23b a =,3243b a =+. (1)求{}n a 和{}n b 的通项公式;(2)设数列{}n c 满足.求*112222()n n a c a c a c n N +++∈.【答案】(1)3n a n =;3n nb =;(2)22*(21)3692()n n n n N +-++∈.【解析】(1)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,依题意,得23323154q d q d =+⎧⎨=+⎩,解得33d q =⎧⎨=⎩,故33(1)3n a n n =+-=,1333n nn b -=⨯=.所以,{}n a 的通项公式为3n a n =,{}n b 的通项公式为3n nb =.(2)112222n n a c a c a c +++135212142632(())n b n a a a a a b a b a b a b -=+++++++++123(1)366[3123183632]()n n n n n -=⨯+⨯+⨯+⨯+⨯++⨯2123613233()n n n =+⨯+⨯++⨯.记1213233nn T n =⨯+⨯++⨯,① 则231313233n n T n +=⨯+⨯++⨯,②②-①得,231233333n n n T n +=-----+⨯11313(21)333132()n n n n n ++--+=-+⨯=-. 所以122112222(21)3336332n n n n n a c a c A a c n T n +-++++=++⨯22*(21)3692()n n n n N +-++=∈.19.设椭圆22221(0)x y a b a b+=>>的左焦点为F ,左顶点为B .|2||OA OB =(O 为原点).(1)求椭圆的离心率; (2)设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ,圆C 同时与x 轴和直线l 相切,圆心C 在直线4x =上.且//OC AP ,求椭圆的方程.【答案】(1)12;(2)2211612x y +=.【解析】(1)设椭圆的半焦距为c2b =,又由222a b c =+,消去b得222(2)a a c =+,解得12c a =. 所以,椭圆的离心率为12. (2)由(1)知,2a c =,b =,故椭圆方程为2222143x y c c+=.由题意,(,0)F c -,则直线l 的方程为3()4y x c =+.点P 的坐标满足22221433()4x y c c y x c ⎧+=⎪⎪⎨⎪=+⎪⎩,消去y 并化简,得到2276130x cx c +-=,解得1x c =,2137c x =-.代入到l 的方程,解得132y c =,2914y c =-.因为点P 在x 轴上方,所以2()3,P c c .(2)由圆C 在直线4x =上,可设(4,)c t .因为//OC AP ,且由(1)知(2,0)A c -,故3242ct c c=+,解得2t =.因为圆C 与x 轴相切,所以圆的半径长为2,又由圆C 与l||3(4)22c +-=,可得2c =. 所以,椭圆的方程为2211612x y +=.20.设函数()ln (1)x f x x a x e =--,其中a R ∈. (1)若0a ≤,讨论()f x 的单调性; (2)若10ea <<. (i )证明()f x 恰有两个零点;(ii )设0x 为()f x 的极值点,1x 为()f x 的零点,且10x x >,证明0132x x ->. 【解析】(1)由已知()f x 的定义域为(0,)+∞,且2[11()(]1)x x xax e f x ae a x e x x-'=-+-=.因此当0a ≤时,210x ax e ->,从而()0f x '>,所以()f x 在(0,)+∞内单调递增.(2)证明:(i )由(1)知,21()x ax e f x x -'=.令2()1xg x ax e =-,由10a e <<,可知()g x 在(0,)+∞内单调递减,又(1)10g ae =->,且22()()1111ln 1ln 1ln 0()g a a a a a=-=-<,故()0g x =在(0,)+∞内有唯一解,从而()0f x '=在(0,)+∞内有唯一解,不妨设0x ,则011ln x a<<.当0()0,x x ∈时,0(())()0g x g x f x x x '=>=,所以()f x 在0(0,)x 内单调递增;当0(,)x x ∈+∞时,0()()()0g x g x x x f x<'==,所以()f x 在0(,)x +∞内单调递减,因此0x 是()f x 的唯一极值点.令()ln 1h x x x =-+,则当1x >时,1()10h x x'=-<,故()h x 在(1,)+∞内单调递减,从而当1x >时,()(1)0h x h <=,所以ln 1x x <-,从而1ln 111111ln ln ln ln ()1ln ln ln ln 0())1(a f a e h a a a a a a=--=-+=<,又因为0()(1)0f x f >=,所以()f x 在0(),x +∞内有唯一零点.又()f x 在0(0,)x 内有唯一零点1,从而,()f x 在(0,)+∞内恰好有两个零点. (ii )由题意01()()00f x f x '=⎧⎨=⎩,即0120111ln )1(x x ax x a e x e⎧=⎨=-⎩,从而1011201ln x x x x e x --=,即102011ln 1x x x x e x -=-. 因为当1x >时,ln 1x x ≤-,又101x x >>,故10220101()11x x x x e x x --<=-,两边取对数,得020ln ln x x e x -<,于是100021(ln )2x x x x -<<-,整理得0132x x ->.。
2019年天津市高考数学试卷(文科)(解析版)

绝密★启用前2019 年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150 分,考试用时 120 分钟。
第Ⅰ卷 1 至 2 页,第Ⅱ卷 3 至 5 页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共 8 小题,每小题 5 分共 40 分。
参考公式:·如果事件A,B 互斥,那么P (A B)=P (A)+P (B).·圆柱的体积公式V =Sh ,其中S 表示圆柱的底面面积,h 表示圆柱的高V =1 Sh·棱锥的体积公式 3 ,其中S 表示棱锥的底面面积,h 表示棱锥的高一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合A ={-1,1, 2, 3, 5},B ={2, 3, 4},C = {x ∈R |1x < 3},则( A C) B =A. {2}B. {2,3}C. {-1,2,3}D. {1,2,3,4}【答案】D【解析】【分析】先求A ⋂B ,再求( A C) B 。
【详解】因为A C = {1, 2} ,⎪ ⎪ 由⎩ 所以( A C ) B = {1, 2, 3, 4}.故选 D 。
【点睛】集合的运算问题,一般要先研究集合中元素的构成,能化简的要先化简,同时注意数形结合,即借助数轴、坐标系、韦恩图等进行运算.⎧x + y - 2 ≤ 0, ⎪x - y + 2 ≥ 0, ⎨x -1, 2.设变量 x , y 满足约束条件⎪⎩ y -1,,则目标函数 z = -4x + y 的最大值为A. 2B. 3C. 5D. 6【答案】D【解析】【分析】画出可行域,用截距模型求最值。
【高考】2019年天津卷文数高考试题文档版有答案

绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数 学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P A B P A P B =+U .·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R „,则()A C B =I U(A ){2}(B ){2,3}(C ){-1,2,3}(D ){1,2,3,4}(2)设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为(A )2(B )3(C )5(D )6(3)设x ∈R ,则“05x <<”是“|1|1x -<”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读下边的程序框图,运行相应的程序,输出S 的值为(A )5 (B )8(C )24 (D )29(5)已知0.223log 7,log 8,0.3a b c ===,则a ,b ,c 的大小关系为(A )c b a << (B )a b c << (c )b c a <<(D )c a b <<(6)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 (A 2(B 3(C )2(D 5(7)已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若2π4g ⎛⎫=⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭(A )-2(B )2-(C 2(D )2(8)已知函数2,01,()1,1.x x f x x x⎧≤≤⎪=⎨>⎪⎩若关于x 的方程1()()4f x x a a =-+∈R 恰有两个互异的实数解,则a 的取值范围为 (A )59,44⎡⎤⎢⎥⎣⎦(B )59,44⎛⎤⎥⎝⎦(C )59,{1}44⎛⎤⎥⎝⎦U(D )59,{1}44⎡⎤⎢⎥⎣⎦U第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷文数高考试题文档版有答案【2020新】

2019年普通高等学校招生全国统一考试(天津卷)数 学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P A B P A P B =+U .·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R „,则()A C B =I U(A ){2}(B ){2,3}(C ){-1,2,3}(D ){1,2,3,4}(2)设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为(A )2(B )3(C )5(D )6(3)设x ∈R ,则“05x <<”是“|1|1x -<”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读下边的程序框图,运行相应的程序,输出S 的值为(A )5 (B )8(C )24 (D )29(5)已知0.223log 7,log 8,0.3a b c ===,则a ,b ,c 的大小关系为(A )c b a << (B )a b c << (c )b c a <<(D )c a b <<(6)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 (A 2(B 3(C )2(D 5(7)已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若2π4g ⎛⎫=⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭(A )-2(B )2-(C 2(D )2(8)已知函数2,01,()1,1.x x f x x x⎧≤≤⎪=⎨>⎪⎩若关于x 的方程1()()4f x x a a =-+∈R 恰有两个互异的实数解,则a 的取值范围为 (A )59,44⎡⎤⎢⎥⎣⎦(B )59,44⎛⎤⎥⎝⎦(C )59,{1}44⎛⎤⎥⎝⎦U(D )59,{1}44⎡⎤⎢⎥⎣⎦U第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
【高考】2019年天津卷文数高考试题文档

绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数 学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P A B P A P B =+U .·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R „,则()A C B =I U(A ){2}(B ){2,3}(C ){-1,2,3}(D ){1,2,3,4}(2)设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为(A )2(B )3(C )5(D )6(3)设x ∈R ,则“05x <<”是“|1|1x -<”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读下边的程序框图,运行相应的程序,输出S 的值为(A )5 (B )8(C )24 (D )29(5)已知0.223log 7,log 8,0.3a b c ===,则a ,b ,c 的大小关系为(A )c b a << (B )a b c << (c )b c a <<(D )c a b <<(6)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 (A 2(B 3(C )2(D 5(7)已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若2π4g ⎛⎫=⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭(A )-2(B )2-(C 2(D )2(8)已知函数2,01,()1,1.x x f x x x⎧≤≤⎪=⎨>⎪⎩若关于x 的方程1()()4f x x a a =-+∈R 恰有两个互异的实数解,则a 的取值范围为 (A )59,44⎡⎤⎢⎥⎣⎦(B )59,44⎛⎤⎥⎝⎦(C )59,{1}44⎛⎤⎥⎝⎦U(D )59,{1}44⎡⎤⎢⎥⎣⎦U第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷(理科、文科)数学高考真题

2019年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P AB P A P B =+.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R ,则()A CB =(A ){2}(B ){2,3}(C ){-1,2,3}(D ){1,2,3,4}(2)设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩则目标函数4z x y =-+的最大值为(A )2(B )3(C )5(D )6(3)设x ∈R ,则“05x <<”是“|1|1x -<”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读下边的程序框图,运行相应的程序,输出S 的值为(A )5 (B )8(C )24 (D )29(5)已知0.223log 7,log 8,0.3a b c ===,则a ,b ,c 的大小关系为(A )c b a << (B )a b c << (c )b c a <<(D )c a b <<(6)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为(A(B(C )2(D(7)已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若π4g ⎛⎫= ⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭(A )-2(B)(C(D )2(8)已知函数01,()1,1.x f x x x⎧≤≤⎪=⎨>⎪⎩若关于x 的方程1()()4f x x a a =-+∈R 恰有两个互异的实数解,则a 的取值范围为 (A )59,44⎡⎤⎢⎥⎣⎦(B )59,44⎛⎤⎥⎝⎦(C )59,{1}44⎛⎤⎥⎝⎦(D )59,{1}44⎡⎤⎢⎥⎣⎦2019年普通高等学校招生全国统一考试(天津卷)数学(文史类)第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
09【精校版2019】天津卷 文数高考试题WORD版2019(含答案)

1绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数 学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P A B P A P B =+U .·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R …,则()A C B =I U(A ){2}(B ){2,3}(C ){-1,2,3}(D ){1,2,3,4}2(2)设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为(A )2(B )3(C )5(D )6(3)设x ∈R ,则“05x <<”是“|1|1x -<”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(4)阅读下边的程序框图,运行相应的程序,输出S 的值为(A )5 (B )8(C )24 (D )29(5)已知0.223log 7,log 8,0.3a b c ===,则a ,b ,c 的大小关系为3(A )c b a << (B )a b c << (c )b c a <<(D )c a b <<(6)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 (A )2(B )3(C )2(D )5(7)已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若2π4g ⎛⎫=⎪⎝⎭,则3π8f ⎛⎫= ⎪⎝⎭(A )-2(B )2-(C )2(D )2(8)已知函数2,01,()1,1.x x f x x x⎧≤≤⎪=⎨>⎪⎩若关于x 的方程1()()4f x x a a =-+∈R 恰有两个互异的实数解,则a 的取值范围为 (A )59,44⎡⎤⎢⎥⎣⎦(B )59,44⎛⎤⎥⎝⎦(C )59,{1}44⎛⎤⎥⎝⎦U(D )59,{1}44⎡⎤⎢⎥⎣⎦U绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数 学(文史类)第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年普通高等学校招生全国统一考试(天津卷)数学(文)试卷及解析

2019年普通高等学校招生全国统一考试数学(文)试卷(解析版)(天津卷)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P A B P A P B =+.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高 ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{}1,1,2,3,5A =-,{}2,3,4B = ,{|13}C x R x =∈<… ,则()A C B =A. {2}B. {2,3}C. {-1,2,3}D. {1,2,3,4}【答案】D【解析】【分析】先求A B ⋂,再求()A CB 。
【详解】因为{1,2}A C =,所以(){1,2,3,4}A C B =.故选D 。
2.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……,则目标函数4z x y =-+的最大值为A. 2B. 3C. 5D. 6 【答案】D【解析】【分析】画出可行域,用截距模型求最值。
【详解】已知不等式组表示的平面区域如图中的阴影部分。
目标函数的几何意义是直线4y x z =+在y 轴上的截距, 故目标函数在点A 处取得最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019 年普通高等学校招生全国统一考试(天津卷)数学(文史类)一、选择题1. 设集合A={−1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=( )A.{2}B.{2,3}C.{−1,2,3}D.{1,2,3,4}2. 设变量x,y满足约束条件{x+y−2≤0,x−y+2≥0,x≥−1,y≥−1,则目标函数z=−4x+y的最大值为()A.2B.3C.5D.63. 设x∈R,则“0<x<5”是“|x−1|<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4. 阅读下边的程序框图,运行相应的程序,输出S的值为()A.5B.8C.24D.295. 已知a=log27,b=log38,c=0.30.2,则a,b,c的大小关系为( )A.c<b<aB.a<b<cC.b<c<aD.c<a<b6. 已知抛物线y2=4x的焦点为F,准线为l,若l与双曲线x2a −y2b=1 (a>0,b>0)的两条渐近线分别交于点A和点B,且|AB|=4|OF|(O为原点),则双曲线的离心率为()A.√2B.√3C.2D.√57. 已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<π)是奇函数,将y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g(x).若g(x)的最小正周期为2π,且g(π4)=√2,则f(3π8)=( )A.−2B.−√2C.√2D.28. 已知函数f(x)={2√x,0≤x≤11x,x>1若关于x的方程f(x)=−14x+a(a∈R)恰有两个互异的实数解,则a的取值范围为( )A.[54,94] B.(54,94] C.(54,94]∪{1} D.[54,94]∪{1}二、填空题9. i是虚数单位,则|5−i1+i|的值为________.10. 设x∈R,使不等式3x2+x−2<0成立的x的取值范围为________11. 曲线y=cos x−x2在点(0,1)处的切线方程为________.12. 已知四棱锥的底面是边长为√2的正方形,侧棱长均为√5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为________.13. 设x>0,y>0,x+2y=4,则(x+1)(2y+1)xy的最小值为________.14. 在四边形ABCD中,AD//BC,AB=2√3,AD=5,∠A=30∘,点E在线段CB的延长线上,且AE=BE,则BD→⋅AE→=________.三、解答题15. 2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.(1)应从老、中、青员工中分别抽取多少人?(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如表,其中“O”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.①试用所给字母列举出所有可能的抽取结果;②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.16. 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2a,3c sin B=4a sin C.(1)求cos B的值;(2)求sin(2B+π6)的值.17. 如图,在四棱锥P−ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD, CD=2, AD=3.(1)设G,H分别为PB,AC的中点,求证:GH//平面PAD;(2)求证:PA⊥平面PCD;(3)求直线AD与平面PAC所成角的正弦值18. 设{a n}是等差数列,{b n}是等比数列,公比大于0,已知a1=b1=3,b2=a3,b3=4a2+3.(1)求{a n}和{b n}的通项公式;(2)设数列{c n}满足c n={1,n为奇数,b n2,n为偶数,求a1c1+a2c2+⋯+a2n c2n (n∈N∗).19. 设椭圆x2a2+y2b2=1(a>b>0)的左焦点为F,左顶点为A,上顶点为B,已知√3|OA|=2|OB|(O为原点).(1)求椭圆的离心率;(2)设经过点F且斜率为34的直线l与椭圆在x轴上方的交点为P,圆C同时与x轴和直线l相切,圆心C在直线x=4上,且OC//AP,求椭圆的方程.20. 设函数f(x)=ln x−a(x−1)e x,其中a∈R.(1)若a≤0,讨论f(x)的单调性;(2)若0<a<1e,证明f(x)恰有两个零点.参考答案与试题解析2019 年普通高等学校招生全国统一考试(天津卷)数学(文史类)一、选择题1.【答案】D【考点】交、并、补集的混合运算【解析】此题暂无解析【解答】解:由题意解得,A∩C={1,2},(A∩C)∪B={1,2,3,4}.故选D.2.【答案】C【考点】求线性目标函数的最值简单线性规划【解析】此题暂无解析【解答】解:不等式组表示的可行域如图所示:目标函数z=−4x+y,即y=4x+z,平移直线y=4x+z,当直线平移到点(−1,1)时截距最大,即z最大,为5.故选C.3.【答案】B【考点】必要条件、充分条件与充要条件的判断【解析】此题暂无解析【解答】解:∵|x−1|<1⇒0<x<2,故“0<x<5”是“|x−1|<1”的必要而不充分条件.故选B.4.【答案】B【考点】程序框图【解析】此题暂无解析【解答】解:根据程序框图可得:第一次循环,i=1,不满足i为偶数,S=0+1=1,i=1+1=2,不满足i≥4,继续循环;第二次循环,i=2,满足满足i为偶数,j=22=1,S=1+2×21=5,i=2+1=3,不满足i≥4,继续循环;第三次循环,i=3,不满足i为偶数,S=5+3=8,i=3+1=4,满足i≥4,跳出循环,输出S=8. 故选B.5.【答案】A【考点】指数式、对数式的综合比较【解析】此题暂无解析【解答】解:c=0.30.2<0.30=1,log27>log24=2,1<log38<log39=2,故c<b<a.故选A.6.【答案】D【考点】双曲线的渐近线抛物线的性质双曲线的离心率双曲线的标准方程【解析】此题暂无解析【解答】解:∵抛物线y2=4x的焦点为(1,0),准线l为x=−1,双曲线的两条渐近线分别为y=ba x和y=−bax,∵l与双曲线的两条渐近线分别交于点A和点B,∴A(−1,−ba ),B(−1,ba),|AB|=2ba,∵|OF|=1,∴|AB|=4|OF|,即2ba=4,∴b=2a,在双曲线中a2+b2=c2,即a2+4a2=c2,解得e=ca=√5.故选D.7.【答案】C【考点】三角函数的恒等变换及化简求值函数y=Asin(ωx+φ)的图象变换三角函数的周期性及其求法函数奇偶性的性质【解析】此题暂无解析【解答】解:根据题意,将y=f(x)的图象上所有点的横坐标伸长到原来的2倍之后的图象为g(x)=A sin(ωx2+φ).因为f(x)是奇函数,所以g(x)也为奇函数,又因为g(x)的最小正周期为2π,由三角函数周期公式可得:2π=2πω2解得ω=2所以g(x)=A sin(x+φ),f(x)=A sin(2x+φ),所以f(3π8)=A sin(3π4+φ).由三角恒等变换公式可得,A sin(3π4+φ)=A sin[π−(3π4+φ)]即A sin(3π4+φ)=A sin(π4−φ)所以f(3π8)=A sin(π4−φ).又g(π4)=√2,因为g(x)为奇函数,所以−g(−π4)=g(π4)即−A sin(−π4+φ)=√2即A sin(π4−φ)=√2即所求f(3π8)=√2,故选C.8.【答案】D【考点】分段函数的应用函数的零点与方程根的关系【解析】此题暂无解析【解答】解:根据函数f(x)的解析式可画出函数图象,如图所示.当x >1时,f(x)=1x ,f ′(x)=−1x 2, 令−1x 2=−14,解得x =2,所以当x >1时,直线y =−14x +a 与函数f(x)相切时的切点坐标为(2,12), 所以此时直线y =−14x +a 与函数f(x)在x ∈[0,+∞)上有两个交点,此时−14×2+a =12,a =1.由图象可知,当直线y =−14x +a 在直线l 1和直线l 2之间移动时(包括直线l 1和l 2), 函数f(x)和直线y =−14x +a 有两个不同的交点, l 1过(1,1),此时1=−14+a, a =54, l 2过(1,2),此时2=−14+a, a =94, 所以a ∈[54,94],综上,a 的取值范围为[54,94]∪{1}. 故选D .二、填空题 9.【答案】√13【考点】 复数的模复数代数形式的乘除运算 【解析】 此题暂无解析 【解答】解:∵ 5−i1+i =(5−i)(1−i)(1+i)(1−i)=4−6i 2=2−3i ,∴ |5−i 1+i|=√22+(−3)2=√13.故答案为:√13. 10.【答案】(−1,23)【考点】一元二次不等式的解法 【解析】 此题暂无解析 【解答】解:3x 2+x −2<0, 即(3x −2)(x +1)<0, 即−1<x <23. 故答案为:(−1,23) 11.【答案】x +2y −2=0 【考点】利用导数研究曲线上某点切线方程 【解析】 此题暂无解析 【解答】解:y ′=−sin x −12,曲线y 在点(0,1)处的切线的斜率为y ′=−12,则曲线y =cos x −x2在点(0,1)处的切线方程为: y −1=−12(x −0), 即x +2y −2=0. 故答案为:x +2y −2=0. 12. 【答案】π4【考点】柱体、锥体、台体的体积计算 【解析】 此题暂无解析 【解答】解:根据题意画出空间几何体以及它的截面图,因为四棱锥的底面是边长为√2的正方形, 所以BC 2=(√2)2+(√2)2=4,可得BO =1, 由此可求出四棱锥的高为√(√5)2−1=2.因为圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,所以根据截面图可得圆柱的底面半径为12BO =12,由此可以解出圆柱的高ℎ为√(√52)2−(12)2=1,根据圆柱的体积公式可得圆柱的体积为π×(12)2×1=14π.故答案为:π4.13. 【答案】92【考点】基本不等式在最值问题中的应用 基本不等式 【解析】 此题暂无解析【解答】解:∵ x +2y =4,x >0,y >0, ∴ x +2y =4≥2√x ⋅2y ,即√2xy ≤2,0<xy ≤2,当且仅当x =2y ,即x =2,y =1时取等号. 又∵ (x+1)(2y+1)xy=2xy +x +2y +1xy=2+5xy≥2+5×12=92,∴(x+1)(2y+1)xy的最小值为92.故答案为:92. 14.【答案】 −1【考点】向量加减法的应用数量积表示两个向量的夹角 平面向量数量积向量加减混合运算及其几何意义【解析】 此题暂无解析 【解答】解:由题意,可以画出示例图形如下图所示:∵ AD//BC ,∠A =30∘, ∴ ∠ABE =30∘,∵ AE =BE ,∴ ∠BAE =∠ABE =30∘, ∵ AB =2√3,易求AE =BE =2, BD →⋅AE →=(BA →+AD →)⋅AE →=BA →⋅AE →+AD →⋅AE →=|BA →|×|AE →|×cos (π−30∘)+|AD →|×|AE →|×cos (30∘+30∘) =2√3×2×cos 150∘+5×2×cos 60∘=−6+5 =−1. 故答案为:−1. 三、解答题15.【答案】解:(1)由已知,老、中、青员工人数之比为6:9:10,由于采用分层抽样的方法从中抽取25位员工, 因此应从老、中、青员工中分别抽取6人,9人,10人. (2)①从已知的6人中随机抽取2人的所有可能结果为 {A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}, 共15种.②由表格知,符合题意的所有可能结果为 {A,B},{A,D},{A,E},{A,F},{B,D},{B,E} {B,F},{C,E},{C,F},{D,F},{E,F},共11种. 所以,事件M 发生的概率P(M)=1115.【考点】列举法计算基本事件数及事件发生的概率 分层抽样方法【解析】 此题暂无解析 【解答】解:(1)由已知,老、中、青员工人数之比为6:9:10,由于采用分层抽样的方法从中抽取25位员工, 因此应从老、中、青员工中分别抽取6人,9人,10人. (2)①从已知的6人中随机抽取2人的所有可能结果为 {A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}, 共15种.②由表格知,符合题意的所有可能结果为 {A,B},{A,D},{A,E},{A,F},{B,D},{B,E} {B,F},{C,E},{C,F},{D,F},{E,F},共11种. 所以,事件M 发生的概率P(M)=1115. 16.【答案】解:(1)在△ABC 中,由正弦定理b sin B =csin C 得b sin C =c sin B , 又由3c sin B =4a sin C 得3b sin C =4a sin C ,即3b =4a , 又因为b +c =2a ,得到b =43a, c =23a , 由余弦定理可得cos B =a 2+c 2−b 22ac=a 2+49a 2−169a 22⋅a⋅23a=−14.(2)由(1)得sin B =√1−cos 2B =√154, 从而sin 2B =2sin B cos B =−√158, cos 2B =cos 2B −sin 2B =−78, 故sin (2B +π6)=sin 2B cos π6+cos 2B sin π6 =−√158×√32−78×12=−3√5+716. 【考点】二倍角的正弦公式 二倍角的余弦公式 两角和与差的正弦公式 余弦定理 正弦定理 【解析】 此题暂无解析 【解答】解:(1)在△ABC 中,由正弦定理b sin B=c sin C得b sin C =c sin B ,又由3c sin B =4a sin C 得3b sin C =4a sin C ,即3b =4a , 又因为b +c =2a ,得到b =43a, c =23a ,由余弦定理可得cos B =a 2+c 2−b 22ac=a 2+49a 2−169a 22⋅a⋅23a=−14.(2)由(1)得sin B =√1−cos 2B =√154, 从而sin 2B =2sin B cos B =−√158,cos2B=cos2B−sin2B=−78,故sin(2B+π6)=sin2B cosπ6+cos2B sinπ6=−√158×√32−78×12=−3√5+716.17.【答案】证明:(1)连接BD,易知AC∩BD=H, BH=DH,又由BG=PG,故GH//PD,又因为GH⊄平面PAD,PD⊂平面PAD,所以GH//平面PAD.(2)证明:取棱PC的中点N,连接DN,依题意,得DN⊥PC,又因为平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,所以DN⊥平面PAC,又PA⊂平面PAC,故DN⊥PA,又已知PA⊥CD,CD∩DN=D,所以PA⊥平面PCD.(3)解:连接AN,由(2)中DN⊥平面PAC,可知∠DAN为直线AD与平面PAC所成的角,因为△PCD为等边三角形,CD=2且N为PC的中点,所以DN=√3,又DN⊥AN,在Rt△AND中,sin∠DAN=DNAD =√33.所以,直线AD与平面角PAC所成角的正弦值为√33. 【考点】直线与平面所成的角直线与平面垂直的判定直线与平面平行的判定【解析】此题暂无解析【解答】证明:(1)连接BD,易知AC∩BD=H, BH=DH,又由BG=PG,故GH//PD,又因为GH⊄平面PAD,PD⊂平面PAD,所以GH//平面PAD.(2)证明:取棱PC的中点N,连接DN,依题意,得DN⊥PC,又因为平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,所以DN⊥平面PAC,又PA⊂平面PAC,故DN⊥PA,又已知PA⊥CD,CD∩DN=D,所以PA⊥平面PCD.(3)解:连接AN,由(2)中DN⊥平面PAC,可知∠DAN为直线AD与平面PAC所成的角,因为△PCD为等边三角形,CD=2且N为PC的中点,所以DN=√3,又DN⊥AN,在Rt△AND中,sin∠DAN=DNAD=√33.所以,直线AD与平面角PAC所成角的正弦值为√33.18.【答案】解:(1)设等差数列{a n}的公差为d,等比数列{b n}的公比为q,依题意得{3q=3+2d,3q2=15+4d,解得{d=3,q=3,故a n=3+3(n−1)=3n,b n=3×3n−1=3n所以,{a n}的通项公式为a n=3n,{b n}的通项公式为b n=3n.(2)解:a1c1+a2c2+⋯+a2n c2n=(a1+a3+a5+⋯+a2n−1)+(a2b1+a4b2+a6b3+⋯+a2n b n)=[n×3+n(n−1)2×6]+(6×31+12×32+18×33+⋯+6n×3n)=3n2+6(1×31+2×32+⋯+n×3n)T n =1×31+2×32+⋯+n ×3n .① 3T n =1×32+2×33+⋯+n ×33+1.② ②−①得,2T n =−3−32−33−⋯−3n +n ×3n+1 =−3(1−3n )1−3+n ×3n+1=(2n−1)3n+1+32.T n =(2n −1)3n+1+34所以,a 1c 1+a 2c 2+⋯+a 2n c 2n =3n 2+6T n=3n 2+6×(2n −1)3n+1+34=(2n−1)3n+2+6n 2+92(n ∈N ∗).【考点】等差数列与等比数列的综合 数列的求和 等比数列的通项公式 等差数列的通项公式【解析】 此题暂无解析 【解答】解:(1)设等差数列{a n }的公差为d , 等比数列{b n }的公比为q ,依题意得{3q =3+2d,3q 2=15+4d,解得{d =3,q =3,故a n =3+3(n −1)=3n, b n =3×3n−1=3n所以,{a n }的通项公式为a n =3n , {b n }的通项公式为b n =3n .(2)解:a 1c 1+a 2c 2+⋯+a 2n c 2n =(a 1+a 3+a 5+⋯+a 2n−1)+(a 2b 1+a 4b 2+a 6b 3+⋯+a 2n b n )=[n ×3+n(n −1)2×6]+(6×31+12×32+18×33+⋯+6n ×3n ) =3n 2+6(1×31+2×32+⋯+n ×3n ) T n =1×31+2×32+⋯+n ×3n .① 3T n =1×32+2×33+⋯+n ×33+1.② ②−①得,2T n =−3−32−33−⋯−3n +n ×3n+1 =−3(1−3n )1−3+n ×3n+1=(2n−1)3n+1+32.T n =(2n −1)3n+1+34所以,a 1c 1+a 2c 2+⋯+a 2n c 2n =3n 2+6T n=3n 2+6×(2n −1)3n+1+34=(2n−1)3n+2+6n 2+92(n ∈N ∗).19. 【答案】解:(1)设椭圆的半焦距为c ,由已知有√3a =2b , 又由a 2=b 2+c 2, 消去b 得a 2=(√32a)2+c 2,解得ca=12.所以,椭圆的离心率为12.(2)由(1)知,a =2c, b =√3c , 故椭圆方程为x 24c 2+y 23c 2=1,由题意,F(−c,0),则直线l 的方程为y =34(x +c),点P 的坐标满足{x 24c2+y 23c 2=1,y =34(x +c),消去y 并化简,得到7x 2+6cx −13c 2=0, 解得x 1=c,x 2=−13c 7,代入到l 的方程,解得y 1=32c,y 2=−914c , 因为点P 在x 轴上方,所以P (c,32c), 由圆心C 在直线x =4上,可设C(4,t), 因为OC//AP ,且由(1)知A(−2c,0), 故t4=32c c+2c ,解得t =2,因为圆C 与x 轴相切,所以圆的半径为2,又由圆C 与l 相切,得|34(4+c)−2|√1+(4)2=2,可得c =2. 所以,椭圆的方程为x 216+y 212=1.【考点】圆锥曲线的综合问题 椭圆的离心率 椭圆的标准方程 椭圆的定义 直线与圆的位置关系 【解析】 此题暂无解析 【解答】解:(1)设椭圆的半焦距为c ,由已知有√3a =2b , 又由a 2=b 2+c 2, 消去b 得a 2=(√32a)2+c 2,解得ca=12.所以,椭圆的离心率为12. (2)由(1)知,a =2c, b =√3c , 故椭圆方程为x 24c 2+y 23c 2=1,由题意,F(−c,0),则直线l 的方程为y =34(x +c),点P 的坐标满足{x 24c 2+y 23c 2=1,y =34(x +c),消去y 并化简,得到7x 2+6cx −13c 2=0, 解得x 1=c,x 2=−13c 7,代入到l 的方程,解得y 1=32c,y 2=−914c , 因为点P 在x 轴上方,所以P (c,32c), 由圆心C 在直线x =4上,可设C(4,t), 因为OC//AP ,且由(1)知A(−2c,0), 故t4=32c c+2c ,解得t =2,因为圆C 与x 轴相切,所以圆的半径为2,又由圆C 与l 相切,得|34(4+c)−2|√1+(4)2=2,可得c =2.所以,椭圆的方程为x 216+y 212=1.20. 【答案】(1)解:由已知,f(x)的定义域为(0,+∞), 且f ′(x)=1x −[ae x+a(x −1)ex ]=1−ax 2e xx,因此当a ≤0时,1−ax 2e x >0,从而f ′(x)>0, 所以f(x)在(0,+∞)内单调递增. (2)证明:由(1)知,f ′(x)=1−ax 2e xx ,令g(x)=1−ax 2e x ,由0<a <1e, 可知g(x)在(0,+∞)内单调递减, 又g(1)=1−ae >0, 且g (ln 1a )=1−a (ln 1a )21a=1−(ln 1a )2<0, 故g(x)=0在(0,+∞)内有唯一解,从而f ′(x)=0在(0,+∞)内有唯一解, 不妨设为x 0,则1<x 0<ln 1a , 当x ∈(0,x 0)时,f ′(x)=g(x)x >g (x 0)x=0,所以f(x)在(0,x 0)内单调递增; 当x ∈(x 0,+∞)时,f ′(x)=g(x)x<g (x 0)x=0,所以f(x)在(x 0,+∞)内单调递减,因此x 0是f(x)唯一极值点. 令ℎ(x)=ln x −x +1,则当x >1时,ℎ′(x)=1x −1<0,故ℎ(x)在(1,+∞)内单调递减, 从而当x >1时,ℎ(x)<ℎ(1)=0,所以ln x <x −1. 从而f (ln 1a )=ln (ln 1a )−a (ln 1a −1)e ln1a=ln (ln 1a )−ln 1a +1=ℎ(ln 1a )<0, 又因为f (x 0)>f(1)=0,所以f(x)在(1,+∞)内有唯一零点. 又f(x)在(0,x 0)内有唯一零点1,从而,f(x)在(0,+∞)内恰有两个零点.【考点】利用导数研究函数的单调性函数的零点【解析】此题暂无解析【解答】(1)解:由已知,f(x)的定义域为(0,+∞),且f′(x)=1x −[ae x+a(x−1)e x]=1−ax2e xx,因此当a≤0时,1−ax2e x>0,从而f′(x)>0,所以f(x)在(0,+∞)内单调递增.(2)证明:由(1)知,f′(x)=1−ax2e xx,令g(x)=1−ax2e x,由0<a<1e,可知g(x)在(0,+∞)内单调递减,又g(1)=1−ae>0,且g(ln1a )=1−a(ln1a)21a=1−(ln1a)2<0,故g(x)=0在(0,+∞)内有唯一解,从而f′(x)=0在(0,+∞)内有唯一解,不妨设为x0,则1<x0<ln1a,当x∈(0,x0)时,f′(x)=g(x)x >g(x0)x=0,所以f(x)在(0,x0)内单调递增;当x∈(x0,+∞)时,f′(x)=g(x)x <g(x0)x=0,所以f(x)在(x0,+∞)内单调递减,因此x0是f(x)唯一极值点. 令ℎ(x)=ln x−x+1,则当x>1时,ℎ′(x)=1x−1<0,故ℎ(x)在(1,+∞)内单调递减,从而当x>1时,ℎ(x)<ℎ(1)=0,所以ln x<x−1.从而f(ln1a )=ln(ln1a)−a(ln1a−1)e ln1a=ln(ln1a )−ln1a+1=ℎ(ln1a)<0,又因为f(x0)>f(1)=0,所以f(x)在(1,+∞)内有唯一零点.又f(x)在(0,x0)内有唯一零点1,从而,f(x)在(0,+∞)内恰有两个零点.第21页共22页◎第22页共22页。
