《圆柱的认识和表面积》习题
圆柱的认识测试题及答案

圆柱的认识测试题及答案一、选择题1. 圆柱的侧面展开图通常是什么形状?A. 正方形B. 长方形C. 三角形D. 圆形答案:B2. 圆柱的底面是什么形状?A. 正方形B. 长方形C. 圆形D. 椭圆形答案:C3. 圆柱的体积计算公式是什么?A. V = πr²hB. V = πr² + hC. V = 2πrhD. V = πr² - h答案:A二、填空题4. 圆柱的侧面展开后是一个 ________,其长等于圆柱的 ________,宽等于圆柱的 ________。
答案:长方形;底面周长;高5. 圆柱的表面积计算公式为:S = 侧面积+ 2 × 底面积,其中侧面积计算公式为 S_侧 = ________。
答案:底面周长× 高三、判断题6. 所有圆柱的侧面展开图都是长方形。
()答案:正确7. 圆柱的高可以是任意长度。
()答案:正确四、计算题8. 一个圆柱的底面半径为3厘米,高为5厘米,请计算其体积。
答案:V = πr²h = π × 3² × 5 = 45π 立方厘米9. 一个圆柱的底面周长为12.56厘米,高为4厘米,请计算其侧面积和表面积。
答案:侧面积 S_侧 = 底面周长× 高= 12.56 × 4 = 50.24 平方厘米底面半径 r = 底面周长÷ (2 × π) = 12.56 ÷ (2 × 3.14) ≈ 2 厘米底面积 S_底= πr² = 3.14 × 2² = 12.56 平方厘米表面积 S = 侧面积+ 2 × 底面积= 50.24 + 2 × 12.56 = 75.36 平方厘米五、解答题10. 如何用一张长方形纸片制作一个圆柱?答案:首先,将长方形纸片的一条边作为圆柱的高,将纸片卷绕成一个圆筒,使得纸片的另一边成为圆筒的底面周长。
圆柱认识、表面积、体积操作综合思维训练练习题(立体图形的表面积和体积复习)

圆柱表面积、体积操作练习题姓名:提示:请同学们先用卡纸制作下列立体图形的模型(制作时请注意预留接口粘贴处),再解决问题。
本次练习共需制作5个模型,你全做对了吗?一、制作一个长、宽、高分别为8厘米、6厘米、4厘米的长方体。
再分别计算出它的表面积和体积。
1、模型是否已经制作?()。
画出它的草图,标出有关数据:2、长方体的表面积计算公式是:()这个长方体的表面积:3、长方体的体积计算公式是:()这个长方体的体积:4、如果把这个长方体看作是一块长方体木料,要将加工成一个最大的圆柱。
这个圆柱的高应该是()厘米,底面半径是()厘米。
(可以模型或草图上画一画)这个圆柱的表面积是多少?这个圆柱的体积是多少?二、制作一个棱长为6厘米的正方体。
再分别计算出它的表面积和体积。
1、模型是否已经制作?()。
画出它的草图,标出有关数据:2、正方体的表面积计算公式是:()这个正方体的表面积:3、正方体的体积计算公式是:()这个正方体的体积:4、如果把这个正方体看作是一块正方体木料,要将加工成一个最大的圆柱。
这个圆柱的高应该是()厘米,底面半径是()厘米。
(可以模型或草图上画一画)这个圆柱的表面积是多少?这个圆柱的体积是多少?这个圆柱的体积是原来正方体体积的几分之几?三、制作一个底面直径是4厘米,高也是4厘米的圆柱。
1、模型是否已经制作?()2、画出侧面展开图的草图,并标上有关数据:3、画出该圆柱沿直径劈成相等的两半,所得到的截面的草图,并标出相关数据:4、求出这个圆柱的表面积(写出每一步的计算公式)。
5、求出圆柱的体积(写出每一步的计算公式)。
6、如果把这圆柱看作是一块圆柱形木料,沿横截面切成两段,表面积多出多少?7、如果把这圆柱看作是一块圆柱形木料,沿直径劈成相等的两半,表面积多出多少?四、用一张长25.12厘米,宽18.84厘米的长方形卡纸围成一个圆柱有几种围法?()1、请以长方形的长作为圆柱的高,制作出1号圆柱,1号圆柱的底面半径是多少厘米?2、求出1号圆柱的表面积(写出每一步的计算公式)。
圆柱的认识、表面积

圆柱的认识一、下面图形中,哪些是圆柱体,请将序号填写在括号里。
上面图形是圆柱体的有()。
二、想一想,填一填。
1、圆柱的两个圆面叫做(),它们是()的圆形;周围的面叫做();圆柱两个底面之间的距离叫做()。
一个圆柱有()条高。
2、把一张长方形的纸的一条边固定贴在一根木棒上,然后快速转动,得到一个()。
3、一个圆柱,底面周长是 21 厘米,高 14 厘米,则它的侧面展开图形是一个长()厘米,宽()厘米的()形。
4、把一张正方形纸卷成一个圆柱体,这个圆柱体的()与()相等。
5、一个圆柱的侧面展开后得到一个正方形,它的边长是9.42厘米。
这个圆柱的底面周长是()厘米,高是()厘米。
三、小法官,请判断。
(对的打,“√”,错的打“x”)1、圆柱的底面是两个大小相同的圆。
()2圆柱的上下两个底面面积相等。
()3、圆柱的侧面沿着高展开后会得到一个长方形或者正方形。
()4、圆柱的底面直径就是它侧面展开图长方形的长。
()5、圆柱的底面半径是 r ,高是2兀 r , 那么它的侧面沿着高展开后一定是正方形。
()四、标出下面圆柱的底面、侧面、高。
圆柱的表面积一、想一想,填一填。
1、把圆柱的侧面沿高剪开,展开得到一个( )形,这个图形的长等于这个圆柱的( ),宽等于这个圆柱的( )。
2、圆柱的( )面积加上( )的面积,就是圆柱的表面积。
3、计算做一个圆柱形的茶叶筒要用多少铁皮,要计算圆柱的( )。
计算做一个圆柱形的烟囱要用多少铁皮,要计算圆柱的( )。
4、一个圆柱底面的半径是 5 厘米,高是 3 厘米,它的侧面积是( )。
5、一个圆柱,它的高是 8 厘米,侧面积是 200.96 平方厘米,它的底面积是 ( )。
6、把一个底面积是 15.7 平方厘米的圆柱,切成两个同样大小的圆柱,表面积增加了( )平方厘米。
7、用一张长20厘米,宽15厘米的长方形纸围成一个圆柱,这个圆柱的侧面积是( )平方厘米。
8、一个圆柱的底面周长是6.28分米,高10分米,这个圆柱的表面积是( )平方米。
人教版六年级下册《31_圆柱的认识》小学数学-有答案-同步练习卷

人教版六年级下册《3.1 圆柱的认识》小学数学-有答案-同步练习卷1. 如图的图形哪些是圆柱?在它下面的()里画“√”.二、填一填圆柱的上、下两个底面都是________形,它们的面积________.把一个圆柱的侧面展开,得到一个长方形,这个长方形的长等于圆柱底面的________,宽等于圆柱的________.把一个圆柱的侧面展开得到一个正方形,则此圆柱的________和________相等。
指出如图圆柱的底面、侧面和髙。
一、判断题.正确的在横线上画“√”,错误的画“×”.圆柱的高只有一条。
________.(判断对错)同一个圆柱的两个底面的直径相等。
________(判断对错)一个圆柱的底面周长和高相等,沿着它的高剪下后展开的侧面图一定是正方形。
________.(判断对错)一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体。
________.(判断对错)一、选一选.将正确答案的序号填在()里.下面的物体中,形状是圆柱的是()A. B. C.下面图形中是圆柱的展开图的是(单位:cm)()A. B.C. D.将圆柱体的侧面展开,将得不到()A.长方形B.正方形C.平行四边形D.梯形三、解决问题.一个圆柱的侧面展开图是一个长是18.84dm、宽是9.42dm的长方形,这个圆柱的底面半径是多少分米?一个圆柱的底面半径是4.5cm,它的侧面展开图是正方形,这个圆柱的高是多少厘米?把一个边长是56.52dm的正方形钢板卷成一个最大的圆柱,给这个圆柱配上一个底面,这个底面的面积是多少平方分米?一、填一填.圆柱的侧面积=________×________;圆柱的表面积=________+底面积×2.计算做一个圆柱形的烟囱要用多少铁皮,要计算圆柱的________.计算做一个易拉罐要用多少铁皮,要计算圆柱的________.填表。
做一个无盖的圆柱形水桶,需要铁皮的面积是()A.侧面积+底面积B.侧面积+底面积×2C.侧面积×2+底面积一个圆柱的底面半径为r,高是ℎ求这个圆柱表面积的式子是()A.2πrℎB.2πr2+rℎC.πr2+2πrℎD.2πr2+2πrℎ一个圆柱的底面直径是10cm,高是4cm,它的侧面积是()A.12.56cm2B.125.6cm2C.1256cm2若一个圆柱的高不变,底面半径扩大到原来的3倍,则底面直径扩大到原来的________倍,底面积扩大到原来的________倍,侧面积扩大到原来的________倍。
六年级数学下册《圆柱的认识》练习题(附答案解析)

六年级数学下册《圆柱的认识》练习题(附答案解析)学校:___________姓名:___________班级:___________一、选择题1.一个圆柱的底面半径是2cm,高是12.56cm,它的侧面沿高剪开是()。
A.长方形B.正方形C.平行四边形2.用一个高9厘米的圆锥形容器盛满水,再将水倒入和它等底等高的圆柱形容器中,水的高度是()厘米。
A.3B.6C.9D.273.压路机滚筒滚动一周能压多少路面是求滚筒的()。
A.表面积B.侧面积C.体积4.用一块长18.84厘米,宽12.56厘米的长方形铁皮,以长方形的宽为高,配上下面()圆形铁片可以做成一个无盖的圆柱形容器。
(单位:厘米)A.B.C.D.5.下面物体中,()的形状是圆柱。
A.B.C.D.6.王大伯挖一个底面直径是3m,深是1.2m的圆柱体水池。
求这个水池占地多少平方米?实际是求这个水池的()。
A.底面积B.容积C.表面积D.体积7.圆柱的高和底面上任意一条半径所组成的角是()。
A.锐角B.直角C.钝角8.()可以立起来,放倒后很容易滚动。
A.长方体B.圆柱体C.球9.圆柱的底面半径扩大2倍,高不变。
它的底面积扩大()倍。
A.2B.4C.8D.1610.一个长方形的长是8cm,宽是4cm。
分别以长和宽为轴旋转一周,得到两个圆柱体,它们的体积相比,()。
A.以长为轴旋转一周得到的圆柱体积大B.以宽为轴旋转一周得到的圆柱体积大C.一样大二、填空题11.小明用一张边长为20cm的正方形彩纸和两张圆形彩纸刚好可以围成一个圆柱,这个圆柱的侧面积是( )2cm。
12.把一块体积是60cm3的正方体木块削成一个最大的圆柱体,圆柱体的体积是( )。
13.圆柱的表面有个________面,圆锥的表面有________个面。
14.下面各图中h表示的是圆柱的高吗?是的在括号里画“√”,不是的画“×”。
( )( )( )( )( )15.把一张长6.28分米、宽3.14分米的长方形纸卷成一个圆柱并把它直立在桌面上,它的容积可能是( )立方分米或( )立方分米。
圆柱的认识和表面积复习
你
基础梳理
圆柱的认识
借助实物模型,掌握圆柱的特征
下面这些都是圆柱吗?
以长方形的一条长或宽所在的直线为轴,旋转一周所得到的几何体叫圆柱体你知道圆柱各部分的名称吗?圆柱有哪些特征呢?
侧面高
底面
底面
《圆柱的认识和表面积》
圆柱上、下两个面叫做底面
圆柱上、下两个底面是大小相等的两个圆
圆柱的上下是一样粗的。
下面的图形是圆柱吗?
圆柱表面积
观察一个圆柱模型,说说圆柱的表面积由哪几部分组成?
圆柱侧面积=长×宽=底圆周长×高
C 表示圆柱底面的周长,h 表示圆柱的高,S 表示圆柱的侧面积 则S 侧=Ch=2πr ×h
圆柱表面积=长方形面积+2×底面圆面积 S 表=S 侧+2S 底
=2πrh+2πr 2
=2πr ×(h+r )=C ×(h+r )
侧面
底面
底面
侧面底面
圆柱有一个曲面
围成圆柱的后面,叫做圆柱的侧面
圆柱两个底面之间的距离叫做圆柱的高。
圆柱的高有无数条,而且都相等。
例1、一个圆柱的底面直径是10cm,高是15cm,它的表面积是多少cm2?
例2、制作一个底面直径是20cm,高是25cm的圆柱形灯笼,在它的下底面和侧面糊上红纸,至少需要多少cm2的红纸?
例3、如图,一台压路机的前轮是圆柱体的,轮宽1.5米,直径1米,前轮转动10周,压过的路面面积是多少平方米?
例4、把三个完全一样的圆柱拼成一个大圆柱,这个大圆柱的表面积比原来每个小圆柱的表面积多188.4平方厘米,每个小圆柱的高是5厘米,原来每个小圆柱的表面积是多少平方厘米?。
北师大版小学数学六年级下册第一单元《圆柱的表面积》教学建议及课后习题解析

圆柱的表面积学习目标1.经历圆柱展开与卷成圆柱等活动,理解圆柱的表面积的意义,知道圆柱的侧面展开后可以是一个长方形,探索圆柱侧面积的计算方法,并掌握圆柱的表面积的计算方法,能正确计算圆柱的表面积。
2.能根据具体情境的不同情况,灵活运用圆柱表面积的计算方法解决生活中一些简单的问题,体会数学与生活的联系,丰富对现实空间的认识。
编写说明在学习长方体和正方体的表面积时,学生已经初步理解了表面积的含义,这是圆柱的表面积的学习基础。
圆柱的表面是由两个相同的底面和一个侧面构成的,计算圆柱底面面积就是计算圆面积,对学生来说并不是新知识,所以教学的重点是探索圆柱侧面积的计算方法。
教科书突出了圆柱侧面展开图的探索过程,以及侧面展开图的长、宽与圆柱有关量之间的关系。
·如果接口不计,至少需要用多大面积的纸板?先说说你是怎么想的。
教科书创设了“做一个圆柱形纸盒,至少需要用多大面积的纸板”的简单情境,引导学生结合具体物体理解圆柱表面积的意义。
结合实际问题,让学生理解所面临的问题实际上就是求圆柱的表面积的问题,而圆柱的表面是由圆柱的两个底面与一个侧面组成的,因此可知,圆柱的表面积就是两个底面的面积与侧面面积的和。
其中,怎样求圆柱的侧面积,对学生而言,是个新问题。
·圆柱的侧面展开后是一个怎样的图形呢?你能想办法说明吗?在初步理解圆柱表面积的意义后,教科书安排了探索圆柱侧面是一个怎样的图形的内容。
这是解决求圆柱侧面积的关键问题,而且要由学生自己想办法把圆柱的侧面展开成平面,再判断是什么图形。
事实上,学生已经具有把圆周变成线段,即“化曲为直”的活动经验,所以也就有了把圆柱的曲面化为平面的可能性。
教科书呈现了两种说明的方法:一种是把圆柱形纸盒沿圆柱的高剪开,侧面展开后是一个长方形;另一种是用一张长方形纸卷成圆柱。
除了这两种办法外,还有其他的一些方法,如“把圆柱沿着直尺边缘滚动一周,圆柱的侧面印下的区域是一个长方形”等。
人教版六年级数学下册第2讲圆柱的表面积专题精讲练习试题及答案

【专题讲义】人教版六年级数学下册第2讲圆柱的表面积专题精讲(学生版)知识要点梳理页12.会归纳出侧面展开图是正方形的圆柱的侧面积及表面积的计算方法。
(讲解,比较,练习。
)(一)圆柱的基本特征(1)圆柱的底面圆柱的上、下两个面叫做圆柱的底面。
圆柱的底面是两个完全相同的圆形。
(2)圆柱的侧面围成圆柱的曲面叫做圆柱的侧面。
(3)圆柱的高圆柱两个底面之间的距离叫做圆柱的高。
圆柱有无数条高,每条高都相等。
(4)圆柱的透视图如果把圆柱形实物画在平面上,它的透视图如上图。
(二)圆柱侧面展开图示页2页 3注意:把圆柱的侧面打开,得到一个长方形,这个长方形的长就是圆柱的底周长。
(三)圆柱的侧面积与底面积公式(1)圆柱的侧面积=底面的周长×高 S C 2h r h π==圆侧(2)圆柱的底面积2221S 24d r d πππ⎛⎫=== ⎪⎝⎭圆(3)圆柱的表面积=侧面积+两个底面积 22=22S S S r h r ππ=++圆侧表归纳:1.上、下两个面都是面积相等的圆圆柱从上到下粗细相同2.侧面展开一般是一个长方形。
这个长方形的长等于圆柱体底面的周长,宽等于圆柱体的高。
长方形注意:沿高剪斜着剪:平行四边形正方形3.圆柱的侧面积。
圆柱的侧面积=底面周长×高页44.圆柱表面积的含义。
圆柱的表面积=圆柱侧面积+两个底面的面积指出:使用的材料要比计算得到的结果多一些。
因此,这里不能用四舍五入法取近似值。
如果一道题结果要保留整百平方厘米,省略的十位上即使是4或比4小,都要向前一位进1。
这种取近似值的方法叫做进一法。
在实际应用中计算圆柱形物体的表面积,要根据实际情况计算各部分的面积。
如计算烟筒用铁皮只求一个侧面积,水桶用铁皮是侧面积加上一个底面积,油桶用铁皮是侧面积加上两个底面积,求用料多少,一般采用进一法取值,以保证原材料够用。
1、圆柱的侧面积和表面积的计算,必需先理解圆柱的侧面展开是长方形,其中长为底面周长,宽为圆柱的高;2、探索出圆柱表面积的计算方法,能根据实际情况正确计算,解决简单的实际问题。
圆柱的表面积练习题答案

圆柱的表面积练习题答案【篇一:圆柱的表面积测试题】O (将正确答案的序号填在括号里,每小题2分)1、下面物体中,()的形状是圆柱。
a> b 、c 、 d 、 3. 下面()图形是圆柱的展开图。
(单位:Cm )4、 下面()杯中的饮料最多。
5、 一个圆柱有()条高。
a 、一b 、二c 、三d 、无数条 6、 一个圆柱的侧面展开以后正好是一个正方形,那么圆柱的高等于 它的底面()。
a ・半径b.直径c ∙周长d ∙面积7•压路机滚筒滚动一周能压多少路面是求滚筒的O a>表面积b 、侧面积c 、体积8、一个棱长4分米的正方体木块削成一个最大的圆柱体, 体积是()立方分米。
a 、50.24b 、100.48 c. 649,圆柱体的底面半径扩大3倍,高不变高不变,,体积扩大()a> 3倍b 、9倍c 、6倍2, 求长方体求长方体,,正方体正方体,,圆柱体的体积共同的公式是Oa> V= abhb. V= a3Cy V= Sh 二、頃空(每空3分) K 将一张长12.56厘米,宽9.42厘米的长方形纸卷成一个圆柱体厘米的长方形纸卷成一个圆柱体, , , 圆柱体的圆柱体的体积是()立方厘米。
2、 一个圆柱体的侧面展开后,正好得到一个边长25.12厘米的正方 形,圆柱体的高是()厘米。
3、 有一个圆柱形罐头盒,高是1分米,底面周长6.28分米,盒的 侧面商标纸的面积最大是()平方分米,这个盒至少要用() 平方分米的铁皮©4、用一张长4.5分米,宽1・2分米的长方形铁皮制成一个圆柱,这 个圆柱的侧面积最多是()平方分米。
(接口处不计) 三、判断(每小题2分)K 圆柱的体积一般比它的表面积大。
()Iil 1:12、 底面积相等的两个圆柱,体积也相等。
()3、 两个圆柱的体积相等那么它们的表面积也相等。
() 柱体的侧面积等于底面积乘O5、圆柱两底面之间的距离处处相等。
O四、计算题O 计算下列圆柱的表面积和体积。
西师大版六年级数学下册 圆柱1(认识圆柱及表面积的计算)

茶 叶
圆柱体的几何图形 上面的图形都是圆柱。
O O
底面
高
O
底面
侧面
圆柱上、下两个圆面叫底面。
周围的面叫侧面。 两个面之间的距离叫高。
圆柱有多少条高?它们之间有什么关系?
两个面之间 的距离叫高。
圆柱的侧面是展开后是一个什么图形呢?
大 小 相 等
沿高剪开后展开得到一个长方形; 也可能得到一个正方形;斜着剪得到 一个平行四边形。
答:这个圆柱的表面积是254.34平方厘米。
3.14 10 40 2 =628(cm2)
3.14 ( 10 2) =78.5(cm2)
2
40 10 =400(cm2) 628 78.5 400 =1106.5(cm2)
答:它的表面积是1106.5平方厘米。
2
S侧 2 3.14 3 5
=94.2(cm2)
2
5cm
3cm
答:这个圆柱的侧面积 是94.2cm 。
S侧 2rh
S侧 2 3.14 (8 2) 6
2 =150.72(cm )
6cm
8cm
2
答:这个圆柱的侧面积 是150.72 cm 。
S侧 2rh
油桶的侧面积:
3.14 4 6 =75.36(dm2)
油桶的底面积:
4 2 3.14 ( ) 2 =12.56(dm2) 2
油桶的表面积:
75.36 12.56 =87.92(dm2)
答:至少需要 87.92dm 的铁皮。
2底Βιβλιοθήκη 侧面底面不是是
不是
是
不是
是
不是
不是
六年级下册数学试题-圆柱的认识及圆柱的侧面积和表面积(无答案)人教版

圆柱的认识及圆柱的侧面积和表面积____________________________________________________________________________________________________________________________________________________________________1、在初步认识圆柱的基础上理解圆柱的侧面积和表面积的含义,掌握圆柱侧面积和表面积的计算方法,会正确计算圆柱的侧面积和表面积,能解决一些有关实际生活的问题。
2、培养良好的空间观念和解决简单的实际问题的能力。
3、通过实践操作,在理解圆柱侧面积和表面的含义的同时,培养学生的理解能力和探索意识。
考点1:圆柱的形成圆柱是以长方形的一边为轴旋转而得到的。
考点2:圆柱的相关概念圆柱上、下两个面叫做圆柱的底面,它们是完全相同的两个圆。
形成圆柱的面还有一个曲面,叫做圆柱的侧面。
圆柱两个底面之间的距离叫做圆柱的高。
考点3:圆柱的侧面展开图a 沿着高展开,展开图形是长方形,长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高,当底面周长和高相等时(h=2πR),侧面沿高展开后是一个正方形,展开图形为正方形。
b. 不沿着高展开,展开图形是平行四边形或不规则图形。
C.无论如何展开都得不到梯形侧面积=底面周长×高 S侧=Ch=πd×h =2πr×h考点4:圆柱的表面积圆柱体表面的面积,叫做这个圆柱的表面积.圆柱的表面积=2×底面积+侧面积即S表=S侧+S底×2=2πr×h + 2×πr2侧面积=底面周长×高 S侧=Ch=πd×h =2πr×hA.梯形B.正方形C.长方形【规范解答】【分析】根据圆柱的特征,圆柱的侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,特殊情况当圆柱的底面周长和高相等时,侧面沿高展开是一个正方形,如果沿斜线展开,得到的是一个平行四边形.侧面无论怎样展开绝对不是梯形.由此做出选择.解:圆柱的侧面沿高展开是长方形或正方形,如果沿斜线展开得到的图形是一个平行四边形,侧面无论怎样展开绝对不是梯形;故选:A.例2圆柱的侧面可以展开成平行四边形,也可以展开成长方形,平行四边形与长方形相【规范解答】【分析】因为侧面积一定,所以无论展开成什么形状,面积都是一样的;可由长方形展成平行四边形后,上下边长没变,左右两边由垂直底边变成倾斜的,所以周长变长了;从而问题得解.解:因为侧面积一定,所以无论展开成什么形状,面积都是一样的;可由长方形展成平行四边形后,上下边长没变,左右两边由垂直底边变成倾斜的,所以周长变长了;故选:D.)【规范解答】【分析】由圆柱体的侧面展开图是一个正方形可知,圆柱体的高和底面周长相等,由此写出圆柱底面直径与高的比并化简即可.解:底面周长即圆柱的高=πd;圆柱底面直径与高的比是:d:πd=1:π;故选:A.例4 把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体,表面积比原来增加了100cm2,已知圆柱的高是10cm,圆柱的侧面积是()cm2.【规范解答】【分析】根据题意可知:把一个圆柱体的底面平均分成若干个扇形,然后切开拼成一个近似的长方体,表面积比原来增加了100cm2,表面积比原来增加了两个长方形的面积.这个长方形长是圆柱的高,宽是圆的底面半径.因此,圆柱的底面半径是100÷2÷10=5厘米,圆柱体的侧面积=底面周长×高;由此列式解答.解:圆柱的底面半径是:100÷2÷10=50÷10=5(厘米);圆柱的侧面积是:2×3.14×5×10=31.4×10=314(平方厘米);答:圆柱的侧面积是314平方厘米.故选:A.)平方米.【规范解答】【分析】要求圆柱的侧面积,根据“圆柱的侧面积=底面周长×高”,代入数字,进行解答,即可解决问题.解:3.14×0.5×1.8,=1.57×1.8,=2.826,≈2.83(平方米);故选:C.例6 把一个棱长是2分米的正方体木块削成一个最大的圆柱体,圆柱体的表面积是A.12.56 B.6.28 C.18.84 D.25.12利用圆柱的表面积公式即可解答.解:3.14×(2÷2)2×2+3.14×2×2=6.28+12.56=18.84(平方分米)答:这个圆柱体的表面积是18.84平方分米.故选:C.例7 计算一个圆柱形无盖水桶要用多少铁皮,应该是求()A.侧面积 B.侧面积十1个底面积C.侧面积十2个底面积 D.体积【规范解答】【分析】根据圆柱的特征,圆柱的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高.根据题意可知,因为铁皮水桶无盖,因此计算做一个无盖的圆柱形铁皮水桶需要多少铁皮,其实就是计算水桶的侧面积和一个底面积的和.解:因为铁皮水桶无盖,因此计算做一个无盖的圆柱形铁皮水桶需要多少铁皮,其实就是计算水桶的侧面积和一个底面积的和.故选:B.例8 要包装100个圆柱形状易拉罐的侧面,至少需要()平方分米的广告纸.(用进一法取近似值,得数保留整平方分米)A.340 B.339 C.227 D.226【规范解答】【分析】根据题干分析可得,这个广告纸的面积,就是这个圆柱形易拉罐的侧面积,据此利用圆柱的侧面积=底面周长×高,计算即可解答.解:3.14×6×12×100=22608(平方厘米)≈227平方分米,答:至少需要227平方分米的广告纸.故选:C.基础演练一、填空1、把圆柱体的侧面展开,得到一个(),它的()等于圆柱底面周长,()等于圆柱的高.2、一个圆柱体,底面周长是94.2厘米,高是25厘米,它的侧面积是()平方厘米.3、一个圆柱体,底面半径是2厘米,高是6厘米,它的侧面积是()平方厘米.4、一个圆柱体的侧面积是12.56平方厘米,底面半径是2分米,它的高是()厘米.5、把一张长8分米,宽5分米的白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米.6、把一张边长为5.5厘米的正方形白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米.二、判断1、圆柱的侧面展开后一定是长方形.()2、6立方厘米比5平方厘米显然要大.()3、一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体.()4、把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,并装上两个底面,那么制的圆柱的高、侧面积、表面积一定相等.()5、圆柱体的表面积=底面积×2+底面积×高.()6、圆柱体的表面积一定比它的侧面积大.()7、圆柱体的高越长,它的侧面积就越大.()三、解决问题(1)有一个圆柱,底面直径是5厘米,高是12厘米。
六年级数学下第3周小卷及答案(圆柱的认识及表面积)
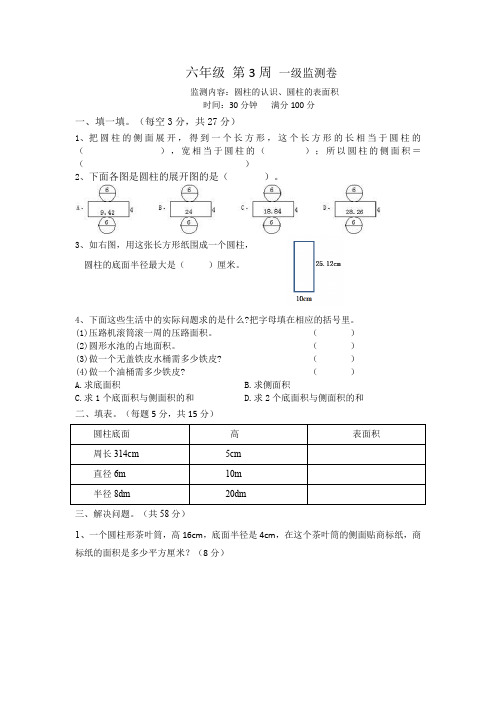
六年级第3周一级监测卷监测内容:圆柱的认识、圆柱的表面积时间:30分钟满分100分一、填一填。
(每空3分,共27分)1、把圆柱的侧面展开,得到一个长方形,这个长方形的长相当于圆柱的(),宽相当于圆柱的();所以圆柱的侧面积=()2、下面各图是圆柱的展开图的是()。
3、如右图,用这张长方形纸围成一个圆柱,圆柱的底面半径最大是()厘米。
4、下面这些生活中的实际问题求的是什么?把字母填在相应的括号里。
(1)压路机滚筒滚一周的压路面积。
()(2)圆形水池的占地面积。
()(3)做一个无盖铁皮水桶需多少铁皮? ()(4)做一个油桶需多少铁皮? ()A.求底面积B.求侧面积C.求1个底面积与侧面积的和D.求2个底面积与侧面积的和二、填表。
(每题5分,共15分)圆柱底面高表面积周长314cm5cm直径6m10m半径8dm20dm三、解决问题。
(共58分)1、一个圆柱形茶叶筒,高16cm,底面半径是4cm,在这个茶叶筒的侧面贴商标纸,商标纸的面积是多少平方厘米?(8分)2、一个底面半径是3cm的水杯,高1dm。
现往杯中加入6cm高的水。
水与水杯接触部分的面积是多少?(10分)3、一个圆柱形铁皮礼品盒,高12cm,底面直径8cm。
用塑料绳扎成如下图的形状,打花结处用去绳子18cm。
请问:(1)共用去塑料绳多少厘米?(10分)(2)做这个礼品盒至少需要铁皮多少平方厘米?(10分)4、一台压路机的前轮是圆柱形的,轮宽2.5米,直径是1.2米,每分钟滚动8周。
这台压路机前进1分钟压过的路面是多少平方米?(10分)5、如图是一个机器零件,上面小圆柱的底面半径是4dm,高是6dm,下面大圆柱的底面半径是6dm,高是10dm。
如果要在这个零件的表面涂上一层漆,涂漆的面积是多少平方分米?(10分)六年级第3周二级监测卷监测内容:圆柱的认识、圆柱的表面积时间:30分钟满分100分一、下面是圆柱体的展开图。
(单位:cm)(每空5分,共20分)AB=();6cm表示圆柱的();这个圆柱的侧面积是()cm2, 表面积是()cm2。
小学数学六下“第二单元圆柱(认识表面积部分)”专项训练

小学数学六下“第二单元圆柱(认识、表面积部分)”专项训练一、填空1.把圆柱的侧面沿高展开,得到一个长方形,它的长等于圆柱的(),宽等于圆柱的()。
2. 当圆柱的底面周长和高相等时,沿着高剪开,把圆柱的侧面展开得到的是()。
3.一个圆柱形铁盒底面半径和高都是4cm,它的侧面积是()cm²,表面积是()平方厘米。
4.用一张长方形纸卷成一个底面直径是10cm,高20cm的圆柱体(接头不计),这张长方形纸的长是()cm,宽是()cm。
5.一个圆柱侧面展开后是一个边长6.28cm的正方形,这个圆柱的高是()cm,底面半径是()cm。
6.一根圆木的底面周长是12.56dm,高是10dm,把它横截成三个大小不等的小圆柱,其表面积增加了()dm²。
7.做一节底面直径10cm,高0.5m的圆柱形铁皮烟囱,需铁皮()平方分米。
(得数保留整数)8. 3.25m²=()m²()dm² 0.75m²=()dm²=()cm²9.一个圆柱的侧面积是188.4dm²,底面半径是2dm,它的高是()dm。
10.圆柱的底面直径是2cm,高是5cm,沿高把侧面展开,它的侧面展开图的周长是()cm,侧面积是()dm²。
二、选择1.求圆柱形通风管所用铁皮材料就是求它的()A 底面积 B侧面积 C容积2.用一块长28.26cm,宽15.7cm的长方形铁皮做一个圆柱形容器,配()当底更能节省铁皮材料。
A 底面半径4.5cm B底面直径6cm C 底面直径5cm3.一个圆柱的侧面展开得不到()A 长方形 B正方形 C平行四边形 D梯形4.一个圆柱侧面展开是正方形,它的高是底面直径的()倍A πB 2πC 2三、判断题1.如果两个圆柱的侧面相等,那么底面周长也相等。
()2.一个圆柱的底面直径扩大3倍,高不变,侧面积扩大9倍。
()3.将3个完全一样的圆柱拼在一起组成一个大圆柱,减少了6个底面积。
2020年圆柱的认识和圆柱的表面积必考题型

必考题:圆柱认识和圆柱的表面积考点一:与长度有关的问题1、奶奶过生日,妈妈买了一个大蛋糕.蛋糕盒是圆柱形的,妈妈准备配上十字形的丝带再打上蝴蝶结,你知道买多长的丝带合适吗?(蝴蝶结需要25cm)2、某种饮料罐的形状为圆柱形,底面直径是7cm,高是12cm。
将24罐这种饮料按如图所示的方式放入箱内,这个纸箱的长、宽、高至少各是多少厘米?考点二:圆柱的侧面积3、一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。
前轮转动一周,压路的面积是多少平方米?4、一个圆柱的侧面积是62.82cm,高是5cm,这个圆柱的底面积是多少平方厘米?考点三:圆柱的表面积(5个面或6个面)5、修建一个圆柱形的沼气池,底面直径是4米,深2米。
这个蓄水池的占地面积是多少?在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?6、一个封闭式圆柱油桶的外表要刷上防锈油漆,每平方米需要防锈3,刷这个油桶大约需要多油漆0.2千克,油桶高1米,直径是高的5少千克防锈油漆?(得数保留两位小数)考点四:圆柱的表面积(组合图形)7、下图是用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个直径2米的半圆。
这个大棚的种植面积是多少?覆盖在大棚上的塑料薄膜约有多少平方米?(得数保留整数)8、一顶帽子,上面是圆柱形,用黄色布料做;帽檐部份是圆环,用紫色布料做(如下图)。
制作这顶帽子需要多少布料?(单位:cm)考点五:圆柱面积增加9、把一个半径为4厘米的圆柱从直径处沿高剖成两个半圆柱,这两个半圆柱的表面积比原来增加80平方厘米,求原来圆柱的表面积?10、把一根是2米、底面周长是12.56分米的圆柱形木头,锯成同样的2段圆柱形,表面积增加了多少平方米?。
圆柱的认识练习题

圆柱的认识练习题一、选择题1. 下列哪个几何体不属于圆柱?A. 圆锥体B. 球体C. 圆台体D. 正方体2. 圆柱的底面是一个圆,且与母线垂直相交。
母线又称为圆柱的A. 高度B. 直径C. 半径D. 对称轴3. 如果圆柱的高度为10cm,半径为5cm,其体积为A. 100π cm³B. 150π cm³C. 200π cm³D. 250π cm³4. 圆柱的表面积公式是A. S = πr²B. S = 2πrC. S = 2πrhD. S = 2π(r + h)5. 已知圆柱的半径为3cm,表面积为75π cm²,求其高度h的值。
A. 3B. 4C. 5D. 6二、填空题1. 圆柱的体积计算公式是________。
2. 圆柱的侧面积计算公式是________。
3. 如果圆柱的底面半径r = 6cm,高度h = 10cm,则其体积为________。
4. 若圆柱的底面周长C = 18π cm,高度h = 5cm,其侧面积S =________。
5. 圆柱的两底面半径相等,高度为h,若侧面积等于底面积的2倍,则圆柱的高度h为________。
三、解答题1. 一个圆柱的底面直径为6cm,高度为8cm,求其侧面积和体积。
解:首先根据底面直径可以得到底面半径r = 6cm / 2 = 3cm。
侧面积公式为S = 2πrh,代入已知值得S = 2π × 3cm × 8cm = 48πcm²。
体积公式为V = πr²h,代入已知值得V = π × (3cm)² × 8cm = 72π cm³。
2. 若一个圆柱的高度为10cm,体积为100π cm³,求其半径和侧面积。
解:根据体积公式V = πr²h,可以解得半径r = √(V / (πh)) = √(100π cm³ / (π × 10cm)) = √10cm = 3.16cm(保留两位小数)。
六年级下册数学试题-第二单元圆柱圆锥的认识 圆柱表面积 苏教版(无答案)

【第1课时:圆柱、圆锥的认识】一、填空1.下面的物体是圆柱的画“⚪”,是圆锥的画“√”2. 圆柱.上、下两个面叫作( ) ,它们是 ( )的两个圆,围成圆柱的曲面叫作( ),圆柱的两个底面之间的距离叫作圆柱的(),圆柱有()条高。
3.圆锥的底面是一个( ), 圆锥的侧面是一个( ) 面。
从圆锥的顶点到底面圆心的距离是圆锥的( )。
圆锥有( )条高。
4.把圆柱的侧面沿它的一条高剪展开,可能得到一个( )形或( )形,若展开后是长方形,长等于圆柱的( ),宽等于圆柱的( ),圆锥的侧面展开是一个()形。
5.如果把一个圆柱的侧面展开得到一个正方形,那么这个圆柱的高等于()。
6.将一个圆柱沿着它的高平均切成两半,会增加()个截面,所得截面是一个( )形或()。
将一个圆锥沿着它的高平均切成两半,截面是一个( )形。
7.如图以竖线为轴旋转一周,会得到一个(),它的底面半径是()厘米,高是()厘米。
二、我是小法官,对错我会判。
(1) 圆柱和圆锥都只有一条高。
( )(2)圆柱的侧面展开可以得到一个长方形、正方形或平行四边形( )(3)圆柱是立体图形。
( )(4) 圆柱有3个面。
( ) 三、连一连四、小芳给爷爷买了一盒生日蛋糕(如图),捆扎这个蛋糕盒所用的彩带至少有多长?(打结处大约用20厘米)【第2课时:圆柱的侧面积】一、填空1. 圆柱的侧面积等于( )乘高。
2.把圆柱的侧面沿高展开,得到一个长方形,它的()等于圆柱的底面周长,( )等于圆柱的高。
3.一个圆柱体,底面周长是94.2厘米,高是25厘米,它的侧面积是( )平方厘米。
3.一个圆柱的底面半径是5cm,高是10cm,它的侧面积是( )cm²6.把一张长8分米,宽5分米的白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是( ) 平方分米。
圆的相关计算公式:给直径求圆的周长: c=πd给半径求圆的周长: c=2πr给周长求圆的直径: d=c÷π 给周长求圆的半径: r=c÷π÷2圆的面积: s=πr²【如果已知条件是直径或圆的周长先求出半径】7.一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是( )。
小学数学西师大版第十二册第二单元 圆柱和圆锥圆柱的认识-章节测试习题(1)

章节测试题1.【答题】是一个圆柱.()【答案】×【分析】此题考查的是认识立体图形.【解答】圆柱是直直的,上下一样粗,两端都是圆平面,的上下不是一样粗,所以不是一个圆柱.故此题错误.2.【答题】一个圆柱体的底面直径是,高是,它的侧面展开图形是正方形.()【答案】✓【分析】此题考查的是认识圆柱的侧面展开图.【解答】圆的周长=.已知圆柱底面的直径是,则圆柱底面周长为,圆柱高是,所以圆柱侧面展开图是正方形.故此题正确.3.【答题】下图是圆柱.()【答案】✓【分析】此题考查的是认识圆柱.【解答】圆柱的上下底是两个完全相同的圆形,圆柱的侧面是一个曲面.故此题正确.4.【答题】这是一个圆柱.()【答案】×【分析】此题考查的是认识圆柱.【解答】圆柱特征:直直的,上下一样粗,上下两个圆面一样大.上下不一样粗,上下两个圆面不一样大,所以这不是一个圆柱.故此题错误.5.【答题】一张长方形纸沿长和宽可以围成不同的圆柱.圆柱A的侧面积()圆柱B的侧面积.A.等于B.大于C.小于D.无法比较【答案】A【分析】此题考查的知识点是圆柱的侧面展开图.【解答】圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的一边长等于圆柱的底面周长,另一边长等于圆柱的高.同一张长方形纸,沿长或宽围成的圆柱的侧面积相等,都等于这个长方形的面积.选A.6.【答题】已知圆柱的底面半径为,高为,求这个圆柱表面积的式子是().A.B.C.D.【答案】D【分析】此题考查的知识点是圆柱的表面积.【解答】底面积=,底面周长=,圆柱的表面积=2×底面积+底面周长×高.已知圆柱的底面半径为,高为,求这个圆柱表面积的式子是.选D.7.【答题】圆柱的底面面积是,侧面面积是,则该圆柱的表面积是().A.B.【答案】A【分析】此题考查的知识点是圆柱的表面积.【解答】已知圆柱的底面面积是,侧面面积是,则该圆柱的表面积是()cm².选A.8.【答题】把一根圆柱形的木头横截成两段,两个圆柱的表面积之和与原来的圆柱的表面积比,().A.减少了B.增加了C.不变【答案】B【分析】此题考查的知识点是切割圆柱体表面积的变化.【解答】把一根圆柱形的木头横截成两段,截断处多出两个底面,所以两个圆柱的表面积之和与原来的圆柱的表面积比增加了.选B.9.【答题】李师傅准备用下左图卷成一个圆柱的侧面,再从右面的四个图形中选一个做底面,可直接选用的底面有().(接缝处忽略不计,无盖,π的取值为3.14)A.1个B.2个C.3个D.4个【答案】B【分析】此题考查的知识点是圆柱侧面积的计算.【解答】圆柱的侧面积=底面周长×高,底面周长=2πr.如果把12.56cm当作底面周长,那么底面半径为:12.56÷2π=2cm,底面直径为4cm;如果把25.12cm当作底面周长,那么底面半径为:25.12÷2π=4cm.所以可以选用的底面有半径为4cm的圆和直径为4cm的圆两个.选B.10.【答题】将一个底面直径为4厘米,高为5厘米的圆柱切成两个完全相等的部分,()切法表面积增加得大.A.(1)B.(2)C.一样大D.无法确定【答案】B【分析】此题考查的知识点是圆柱的表面积.【解答】由题可知,将一个底面直径为4厘米,高为5厘米的圆柱切成两个完全相等的部分(1)圆柱的切法,表面积增加了两个底面圆的面积,增加的面积为:(2)圆柱的切法,表面积增加了两个长方形的面积,增加的面积为:4×5×2=40(平方厘米)25.12<40,所以(2)圆柱增加的面积多.选B.11.【答题】有一顶少数民族的帽子(如下图),帽顶部分(包括上面的侧面)是圆柱形,用黑布做;帽檐部分是一个圆环,用白布做.帽顶的半径、高和帽檐的宽都是厘米,黑布和白布相比,().A.黑布用的多B.白布用的多C.两种布用的一样多【答案】C【分析】此题考查的知识点是圆柱的侧面积.【解答】为半径,为高,圆的面积=,所以圆柱的侧面积=.帽子的帽顶部分(包括上面的侧面)是圆柱形,用黑布做;帽檐部分是一个圆环,用白布做.帽顶的半径、高和帽檐的宽都是厘米,则黑布用了:(平方厘米),白布用了:(平方厘米),所以黑布和白布用的一样多.选C.12.【答题】圆柱的侧面积=()×高.A.底面积B.底面周长【答案】B【分析】此题考查的知识点是圆柱的侧面积.【解答】圆柱的侧面积=底面周长×高.选B.13.【答题】圆柱侧面积的大小是由()决定的.A.圆柱的底面周长B.底面直径和高C.圆柱的高【答案】B【分析】此题考查的知识点是圆柱的侧面积.【解答】圆柱的侧面积=底面周长×高,因为底面周长是由底面直径决定的,故圆柱侧面积的大小是由底面直径和高决定的.选B.14.【答题】圆柱侧面积的计算方法用字母表示是().A.B.C.【答案】B【分析】此题考查的知识点是圆柱侧面积的计算公式.【解答】圆柱侧面积=底面周长×高,底面周长用字母表示是或,高用字母表示是,所以圆柱侧面积用字母表示是或.选B.15.【答题】圆柱侧面积的大小是由圆柱的()决定的.A.高B.底面周长C.底面半径和高【答案】C【分析】此题考查的知识点是圆柱侧面积的计算.【解答】圆柱侧面积=底面周长×高,底面周长是由底面半径决定的.圆柱侧面积的大小是由圆柱的底面半径和高决定的.选C.16.【答题】下面()图形是圆柱的展开图.(单位:cm)A. B.C. D.【答案】B【分析】此题考查的知识点是圆柱的展开图.【解答】圆柱的侧面是长方形,底面是圆形,长方形的长与圆形的周长相等.由题可知:底面圆形的直径为3cm,故底面周长为:3.14×3=9.42(cm),即侧面长方形的长为9.42cm.选B.17.【答题】把一个圆柱平均截成两个小圆柱,每个小圆柱的表面积相当于原来圆柱的表面积的.()【答案】×【分析】此题考查的知识点是切割圆柱体后表面积的变化.【解答】把一个圆柱平均截成两个小圆柱,小圆柱的侧面积为原来圆柱侧面积的,但是小圆柱的底面积与原圆柱的底面积相等.所以每个小圆柱的表面积不等于原来圆柱的表面积的.故此题错误.18.【答题】圆柱的侧面积等于底面积乘高.()【答案】×【分析】此题考查的知识点是圆柱侧面积的计算.【解答】圆柱侧面积=底面周长×高.故此题错误.19.【答题】侧面积相等的两个圆柱,表面积也相等.()【答案】×【分析】此题考查的知识点是圆柱表面积的计算.【解答】圆柱的表面积=侧面积+底面积,当两个圆柱的侧面积相等时,底面积不一定相等,所以表面积不一定相等.故此题错误.20.【答题】两个圆柱的侧面积相等,它们的底面周长也一定相等.()【答案】×【分析】此题考查的知识点是圆柱表面积的计算.【解答】此题错误.圆柱的侧面积=圆柱的底面周长×高,圆柱的侧面积与底面周长和高有关,所以两个圆柱的侧面积相等,它们的底面周长不一定相等.。
圆柱、圆锥的认识,圆柱的表面积

圆柱、圆锥的认识,圆柱的表面积圆柱的表面积1、把一张长9.42分米,宽3.14分米的长方形铁皮圈成一个圆柱形无盖容器,要配上底面半径多少分米的圆形铁皮。
2、一个圆柱体底面周长和高相等,如果高缩短了2厘米,表面积就减少12.56平方厘米。
求这个圆柱体的表面积。
3、取出直角三角尺(30度、60度、90度),进行操作观察:将三角尺的一条直角边平放在桌面上,以另一条直角边为轴作快速的旋转,看到了什么?试画出示意图。
怎样旋转后图形的底面积才会最大?4、下面的圆柱沿着箭头方向竖着切开,表面积增加了40平方厘米,求圆柱的表面积。
5、一个圆柱的表面积是50.24平方分米,底面半径是2分米,则这个圆柱的高是多少分米?6、一个高是20厘米的圆柱,把高增加4厘米后,圆柱表面积比原来增加了25.12平方厘米,那么新的圆柱表面积是多少平方厘米?圆柱的体积1、把一块长31.4厘米,宽20厘米,高4厘米的长方体钢坯熔化后浇铸成底面半径是4厘米的圆柱体,圆柱体的高是多少厘米?2、一根空心的钢管长2米,量得内直径6厘米,管壁厚1厘米。
如果每立方厘米钢重7.8克,这根钢管大约重多少千克?(得数保一位小数)3、一个圆柱形底面周长是25.12厘米,高10厘米,把它装满盐水后,再倒入一个长10厘米,宽8厘米的长方体容器中,水面高多少厘米?4、把一个长7厘米,宽6厘米,高4.5厘米的长方体铁块和一个棱长5厘米的正方体的铁块,熔铸成一个大圆柱体,这个圆柱体的底面积是78.5平方厘米,那圆柱的高应是多少厘米?5、把一个直径是2分米的圆柱的底面分成许多相等的扇形,然后沿直径把圆切开,拼成一个和它体积相等的长方体,这个长方体表面积比原来圆柱的表面积增加8平方分米,这个长方体的体积是多少?6、如右图,是一个棱长为4分米的正方体零件,它的上、下、左、右面上各有一个半径为2厘米的圆孔,孔深为1分米,这个零件的表面积是多少?体积是多少?7、一个酒瓶里面深30厘米,底面直径是8厘米,瓶里有酒深12厘米,把酒瓶塞紧后倒置(瓶口向下),这时酒深20厘米,你能算出酒瓶的容积是多少毫升吗?8、下面的是装可乐的盒子,已知沿着长可以放6听,沿着宽可以放4听,可乐罐的底面直径是8厘米,高是13厘米,那么这个盒子的容积至少是多少立方厘米。
小学一年级综合专项练习题认识圆柱体

小学一年级综合专项练习题认识圆柱体圆柱体是一种常见的几何体,它在我们的日常生活中随处可见。
了解圆柱体的属性和特点对于我们认识世界具有重要意义。
下面是一些小学一年级综合专项练习题,帮助大家进一步认识圆柱体。
第一题:街边的垃圾桶是什么形状?解析:垃圾桶通常是圆柱体,它的底部和顶部是圆形的,侧面是直的,形状像一个竖立的圆筒。
第二题:你家冰淇淋蛋筒是什么形状?解析:冰淇淋蛋筒也是圆柱体。
它的底部是一个圆形的筒状空间,并且顶部是一个半球形的封口,形状上类似于一个立体的圆筒。
第三题:如果你用一张纸卷起来,会是什么形状?解析:如果你将一张纸卷起来,形状就像一个圆柱体。
纸的两端是圆形,而中间则是不断变化的直线。
第四题:下面这些物体中,哪个是圆柱体?A. 铅笔B. 鸟巢C. 鸭蛋D. 棒棒糖解析:选项C和D是圆柱体。
铅笔是长方形,鸟巢是球体,所以不符合圆柱体的形状。
第五题:如何计算圆柱体的体积?解析:计算圆柱体的体积可以使用以下公式:V = π * r² * h。
其中,V代表体积,π是一个近似值,约等于3.14,r是圆柱体底部的半径,h是圆柱体的高度。
第六题:如何计算圆柱体的表面积?解析:计算圆柱体的表面积可以使用以下公式:A = 2π * r * (r + h)。
其中,A代表表面积,π是近似值3.14,r是底部圆的半径,h是圆柱体的高度。
第七题:如果一个圆柱体的底面直径为10厘米,高度为20厘米,那么它的体积是多少?解析:这个圆柱体的底面半径是5厘米(直径除以2),高度是20厘米。
将这些值代入体积公式V = π * r² * h,得出V = 3.14 * 5² * 20,计算得到V = 1570立方厘米。
通过以上练习题,我们可以更好地认识圆柱体的形状、特点和计算方法。
希望大家能够通过实际操作和观察,进一步加深对圆柱体的理解,为以后的学习打下基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《圆柱的认识和表面积》习题
一、填空。
1、圆柱的两个圆面叫做(),它们是()的圆形;周围的面叫做();圆柱两个底面之间的距离叫做()。
一个圆柱有()条高。
2、把一张长方形的纸的一条边固定贴在一根木棒上,然后快速转动,得到一个()。
以直角三角形的一条直角边为轴,旋转一周,可以得到一个()。
3、一个圆柱的侧面展开后得到一个长方形,长是12.56厘米,宽是3厘米。
这个圆柱的底面周长是()厘米,高是()厘米。
4、一个圆柱的侧面展开后得到一个正方形,边长是9.42厘米。
这个圆柱的底面周长是()厘米,高是()厘米。
5、圆柱的侧面是一个()面,把它展开得到一个长方形,长方形的长等于圆柱的(),宽等于圆柱的()当圆柱的底面周长和高相等时,把它的侧面展开得到一个()形。
6、一个圆柱的侧面展开正好是一个正方形,它的高是直径的()倍。
2、火眼金睛判对错。
(1)一张长訟厘米、宽10厘米的长方形纸,围成一个圆柱形纸筒(接头除外),纸筒的侧面积是30平方厘米。
()
(1)圆柱的底面半径扩大到原来的5倍,圆柱的侧面积就扩大到原来的5倍。
()(2)圆柱的底面周长和高相等,侧面展开可以得到一个正方形。
()
(3)圆柱的底面积越大,它的表面积就越大。
()
(4)圆柱的底面半径和高都扩大到原来的2倍,它的侧面积就扩大到原来的2倍。
()(5)两个圆柱的底面直径相等,它们的表面积一定相等。
()
(6)给一个圆柱形茶叶筒周围贴标签,要求标签纸的大小就是求这个圆柱的表面积。
()
3、一个高10厘米、直径为8厘米的圆柱形罐头盒,至少需要多少平方厘米铁皮?
4、—种没有盖的圆柱形铁皮水桶,底面半径是2分米,高是5分米,做两个这样的水桶,最少要用铁皮多少平方分米?
5、箱底面半径是S分米,髙是a分米要把这个油箱的表面涂上油漆,涂油漆部分的面积是多少?
6、有一段长1米、横截面半径是12厘米的圆木,若沿着它的底面直径锯成两份,则它的表面积增加了多少平方厘米?。
