课堂新坐标2013届高三数学(文)一轮复习6-5
课堂新坐标2013届高三数学(文)一轮复习阶段知能检测5

阶段知能检测(五)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2012·汕尾模拟)已知等差数列{a n }中,a 5+a 9-a 7=10,记S n =a 1+a 2+…+a n ,则S 13的值是( )A .130B .260C .156D .1682.设等差数列{a n }的公差为非零常数d ,且a 1=1,若a 1,a 3,a 13成等比数列,则公差d =( )A .1B .2C .3D .53.已知各项均为正数的等比数列{a n }中,lg(a 3a 8a 13)=6,则a 1a 15的值为( ) A .100 B .1 000 C .10 000 D .104.(2012·湛江调研)已知S n 为等比数列{a n }的前n 项和,a 1=2,若数列{1+a n }也是等比数列,则S n 等于( )A .2nB .3nC .2n +1-2 D .3n -15.已知等差数列{a n }的前n 项和为S n ,且S 2=10,S 5=55,则过点P (n ,a n )和Q (n +2,a n +2)(n ∈N *)的直线的斜率是( )A .4B .3C .2D .16.数列{x n }满足x 1=1,x 2=23,且1x n -1+1x n +1=2x n (n ∈N *,n ≥2),则x n 等于( )A.2n +1 B .(23)n -1 C .(23)n D.2n +27.已知数列-1,a 1,a 2,-4成等差数列,-1,b 1,b 2,b 3,-4成等比数列,则a 2-a 1b 2的值为( )A.12 B .-12 C.12或-12 D.148.在等差数列{a n }中,首项a 1=0,公差d ≠0,若a k =S 6,则k 的值为( )A .15B .16C .17D .189.设数列{2n -1}按第n 组有n 个数(n 是正整数)的规则分组如下:(1),(2,4),(8,16,32),…,则第101组中的第一个数为( )A .24 951B .24 950C .25 051D .25 05010.某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产.已知该生产线连续生产n 年的产量为f (n )=12n (n +1)(2n +1)吨,但如果年产量超过150吨,将会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是( )A .5年B .6年C .7年D .8年第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)11.已知{a n }是各项都为正数的等比数列,S n 是{a n }的前n 项和,若a 1=1,5S 2=S 4,则a 5=________.12.(2012·惠州模拟)设S n 是等差数列{a n }的前n 项和,S 5=3(a 2+a 8),则a 5a 3的值为________.13.已知函数f (x )对应关系如表所示,数列{a n }满足a 1=3,a n +1=f (a n ),则a 2013=________.14.已知数列{a n }的前n 1≥2时,a n 是S n 与S n -1的等差中项,则S 5=________.三、解答题(本大题共6小题,共80分.解答时应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分12分)(2012·潮州模拟)已知{a n }是公比大于1的等比数列,a 1,a 3是函数f (x )=x +9x-10的两个零点.(1)求数列{a n }的通项公式;(2)若数列{b n }满足b n =log 3a n +n +2,且b 1+b 2+b 3+…+b n ≥80,求n 的最小值.16.(本小题满分13分)已知数列{a n}是等差数列,数列{b n}是正项等比数列,且满足a1=1,b1=4,a2+b2=10,a26-b3=10.(1)求数列{a n},{b n}的通项公式;(2)记c n=a n b n,求数列{c n+2c n c n+1}的前n项和S n.17.(本小题满分13分)(2012·云浮调研)已知正项数列{a n}中,a1=1,点(a n,a n+1)(n∈N*)在函数y=x2+1的图象上,数列{b n}的前n项和S n=2-b n.(1)求数列{a n}和{b n}的通项公式;(2)设c n=-1a n+1log2b n+1,求{c n}的前n项和T n.18.(本小题满分14分)已知数列{a n}的前n项和为S n,对任意的n∈N*,点(a n,S n)都在直线2x-y-2=0的图象上.(1)求{a n}的通项公式;(2)是否存在等差数列{b n},使得a1b1+a2b2+…+a n b n=(n-1)·2n+1+2对一切n∈N*都成立?若存在,求出{b n}的通项公式;若不存在,说明理由.19.(本小题满分14分)已知数列{a n}满足a1=3,a n+1-3a n=3n(n∈N*).数列{b n}满足b n=3-n a n.(1)求证:数列{b n}是等差数列;(2)设S n=a13+a24+a35+…+a nn+2,求满足不等式1128<S nS2n<14的所有正整数n的值.20.(本小题满分14分) (2011·山东高考)等比数列{a n}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.(1)求数列{a n}的通项公式;(2)若数列{b n}满足:b n=a n+(-1)n ln a n,求数列{b n}的前2n项和S2n.答案及解析1.【解析】 由a 5+a 9=2a 7得a 5+a 9-a 7=a 7=10, ∴S 13=13(a 1+a 13)2=13a 7=130.【答案】 A2.【解析】 由已知得,a 23=a 1·a 13,即(1+2d )2=1+12d . 又d ≠0,∴d =2. 【答案】 B3.【解析】 ∵lg(a 3a 8a 13)=6,∴a 3a 8a 13=a 38=106,∴a 8=100,∴a 1a 15=a 28=10 000. 【答案】 C4.【解析】 ∵数列{1+a n }是等比数列, ∴(1+2q )2=3(1+2q 2)⇒q =1,∴S n =2n . 【答案】 A5.【解析】 设等差数列{a n }的公差为d , 则⎩⎨⎧ 2a 1+d =10,5a 1+10d =55解得⎩⎨⎧a 1=3,d =4 ∴直线PQ 的斜率k =a n +2-a n2=d =4. 【答案】 A6.【解析】 数列{1x n }是首项为1,公差为12∴1x n =1+12(n -1)=n +12,∴x n =2n +1. 【答案】 A7.【解析】 由题意知3(a 2-a 1)=-4-(-1)=-3, ∴a 2-a 1=-1,又b 22=(-1)×(-4)=4,且b 2<0,∴b 2=-2,∴a 2-a 1b 2=12.【答案】 A8.【解析】 由a k =S 6得(k -1)d =15d , ∴k -1=15,∴k =16. 【答案】 B9.【解析】 前100组共有1+2+3+…+100=5 050个数,则第101组中的第1个数为数列{2n -1}的第5 051项,该数为25 050.【答案】 D10.【解析】 由题意a 1=f (1)=12×1×2×3=3(吨);以后第n (n =2,3,…)年的产量分别为 a n =f (n )-f (n -1)=12n (n +1)(2n +1)-12(n -1)·n ·(2n -1)=3n 2(吨). 令3n 2≤150,得1≤n ≤5 2.又n ∈N *,所以1≤n ≤7,即生产期限最长为7年. 【答案】 C11.【解析】 设等比数列{a n }的公比为q ,则由5S 2=S 4 得5(1+q )=1-q 41-q ,∴q 2=4,∴q =2,∴a 5=a 1q 4=24=16. 【答案】 1612.【解析】 ∵S 5=5(a 1+a 5)2=5a 3,a 2+a 8=2a 5,∴由S 5=3(a 2+a 8),得5a 3=6a 5,∴a 5a 3=56.【答案】5613.【解析】 由题意知a 2=f (a 1)=f (3)=1, a 3=f (a 2)=f (1)=3,∴数列{a n }是周期为2的数列,∴a 2013=a 1=3. 【答案】 314.【解析】 由题意知2a n =S n +S n -1(n ≥2), ∴2a n +1=S n +1+S n ,∴2a n +1-2a n =a n +1+a n ,即a n +1=3a n (n ≥2), 又2a 2=S 2+S 1,且S 1=a 1=1,∴a 2=2. 则数列{a n }从第2项起,以后各项成等比数列, ∴S 5=a 1+a 2+a 3+a 4+a 5=1+2(1-34)1-3=81.【答案】 8115.【解】 (1)∵a 1,a 3是函数f (x )=x +9x -10的两个零点,∴a 1,a 3是方程x 2-10x +9=0的两根, 又公比大于1,故a 1=1,a 3=9,则q =3, ∴等比数列{a n }的通项公式为a n =3n -1. (2)由(1)知b n =log 3a n +n +2=2n +1,∴数列{b n }是首项为3,公差为2的等差数列, ∴b 1+b 2+…+b n =n 2+2n ≥80, 解得n ≥8或n ≤-10(舍), 故n 的最小值是8.16.【解】 (1)设数列{a n }的公差为d ,数列{b n }的公比为q (q >0),由已知条件得⎩⎨⎧1+d +4q =10,1+25d -4q 2=10.解得d =1,q =2. 故数列{a n }的通项公式是a n =n ,数列{b n }的通项公式是b n =4·2n -1=2n +1.(2)由(1)得c n =n ·2n +1,记d n =c n +2c n c n +1=(n +2)·2n +3n (n +1)·22n +3=n +2n (n +1)·2n =2(n +1)-n n (n +1)·2n =1n ·2n -1-1(n +1)·2n ,所以S n =d 1+d 2+…+d n =(11×20-12×21)+(12×21-13×22)+…+[1n ·2n -1-1(n +1)·2n ]=1-1(n +1)·2n.17.【解】 (1)∵点(a n ,a n +1)(n ∈N *)在函数y =x 2+1图象上, ∴a n +1=a n +1,∴数列{a n }是公差为1的等差数列. ∵a 1=1,∴a n =1+(n -1)=n , ∵S n =2-b n , ∴S n +1=2-b n +1,两式相减得:b n +1=-b n +1+b n ,即b n +1b n =12,由S 1=2-b 1即b 1=2-b 1,得b 1=1.∴数列{b n }是首项为1,公比为12的等比数列,∴b n =(12)n -1.(2)log 2b n +1=log 2(12)n =-n ,∴C n =1n (n +1)=1n -1n +1,∴T n =C 1+C 2+…+C n +1=(1-12)+(12-13)+(13-14)+…+(1n -1n +1)=1-1n +1=nn +1. 18.【解】 (1)由题意得2a n -S n -2=0, 当n =1时,2a 1-S 1-2=0得a 1=2, 当n ≥2时,由2a n -S n -2=0,① 得2a n -1-S n -1-2=0②①-②得2a n -2a n -1-a n =0,即a n =2a n -1,因为a 1=2所以a n a n -1=2,所以{a n }是以2为首项,2为公比的等比数列,所以a n =2·2n -1=2n .(2)假设存在等差数列{b n },使得a 1b 1+a 2b 2+…+a n b n =(n -1)·2n +1+2对一切n ∈N *都成立,则当n =1时,a 1b 1=(1-1)·21+2得b 1=1,当n ≥2时,由a 1b 1+a 2b 2+…+a n b n =(n -1)·2n +1+2③ 得a 1b 1+a 2b 2+…a n -1b n -1=(n -1-1)·2n +2④ ③-④得a n b n =n ·2n ,即b n =n , 当n =1时也满足条件,所以b n =n ,因为{b n }为等差数列,故存在b n =n (n ∈N *)满足条件.19.【证明】 (1)由b n =3-n a n 得a n =3n b n ,则a n +1=3n +1b n +1代入a n +1-3a n =3n 中,得3n +1b n +1-3n +1b n =3n ,即得b n +1-b n =13,所以数列{b n }是等差数列.(2)因为数列{b n }是首项为b 1=3-1a 1=1,公差为13的等差数列,则b n =1+13(n -1)=n +23,则a n =3n b n =(n +2)×3n -1.从而有a n n +2=3n -1, 故S n =a 13+a 24+a 35+…+a n n +2=1+3+32+…+3n -1=1-3n1-3=3n -12. 则S n S 2n =3n -132n -1=13n +1, 由1128<S n S 2n <14,得1128<13n +114∴3<3n <127,得1<n ≤4.故满足不等式1128<S n S 2n <14的所有正整数n 的值为2,3,4.20.【解】 (1)由题意知a 1=2,a 2=6,a 3=18, 因为{a n }是等比数列,所以公比为3, 所以数列{a n }的通项公式a n =2·3n -1.(2)b n =a n +(-1)n ln a n =2·3n -1+(-1)n [ln 2+(n -1)ln 3]=2·3n -1+(-1)n ln 2+(-1)n (n -1)ln 3,所以S 2n =(2·30+2·31+2·32+…+2·32n -1)+[(-1)1+(-1)2+…+(-1)2n ]ln 2+[(-1)1·0+(-1)2·1+(-1)3·2+…+(-1)2n ·(2n -1)]ln 3=2(1-32n)1-3+(-1+1-1+1-…-1+1)ln 2+[0+1-2+3-4+…-(2n-2)+2n-1]ln 3=9n-1+0·ln 2+n ln 3=9n-1+n ln 3.。
课堂新坐标2013届高考数学一轮复习课件:第三章第六节 简单的三角恒等变换(广东专用)

例 探 究
=sin(x-π4)+sin(x-π4)=2sin(x-π4).
· 提
∴T=2π,f(x)的最小值为-2.
知 能
自 主
(2)∵cos(β-α)=45,cos(β+α)=-45.
落 实 ·
∴cos βcos α+sin βsin α=45,
高 考 体 验
固 基 础
cos βcos α-sin βsin α=-45, 两式相加得 2cos βcos α=0.
菜单
第十八页,编辑于星期日:二十点 十四分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
已知向量 m=(sin A,cos A),n=( 3,-1),m·n=1, 例
且 A 为锐角.
探 究
(1)求角 A 的大小;
·
(2)求函数 f(x)=cos 2x+4cos Asin x(x∈R)的最大值.
提 知
固 基 础
∴cos 2α=sin(2α+π2)
高 考 体 验
· 明 考 情
=2sin(α+π4)cos(α+π4)=-2245.
sin 2α=-cos(2α+π2)=1-2cos2(α+π4)=275,
课 时 知
∴cos(2α+π4)=-3510 2.
能 训 练
菜单
第十五页,编辑于星期日:二十点 十四分。
验 · 明
础
∴原式=2sinx+π4cosx+π4=sin x+cos x
考 情
2cosπ4+x·sin x
sin x
课 时
=1+ta1n x=1+(-34)=14.
知 能 训
练
菜单
第十三页,编辑于星期日:二十点 十四分。
课堂新坐标2013届高三数学(文)一轮复习阶段知能检测6

阶段知能检测(六)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若a 2<b 2,则下列不等式成立的是( ) A .a <b B.1a 2>1b 2C .|a |<|b |D .a 3<b 32.如果a >b >c ,且有a +b +c =0,则( ) A .a ·b >a ·c B .a ·c >b ·c C .a ·|b |>c ·|b | D .a 2>b 2>c 23.(2011·浙江高考)若实数x ,y 满足不等式组⎩⎨⎧x +2y -5≥0,2x +y -7≥0,x ≥0,y ≥0,则3x +4y的最小值是( )A .13B .15C .20D .284.设n 为正整数,f (n )=1+1213+…+1n ,经计算得f (2)=32,f (4)>2,f (8)>52,f (16)>3,f (32)>72,观察上述结果,可推测出一般结论( ) A .f (2n )>2n +12 B .f (n 2)≥n +22C .f (2n )≥n +22D .以上都不对5.已知不等式x 2+ax +4<0的解集不是空集,则实数a 的取值范围是( ) A .-4≤a ≤4 B .-4<a <4 C .a ≥4,或a ≤-4 D .a <-4,或a >46.已知2x +8y=1(x >0,y >0),则x +y 的最小值为( )A .12B .14C .16D .187.若不等式f (x )=ax 2-x -c >0的解集为{x |-2<x <1},则函数y =f (-x )的图象为()8.设函数f (x )=⎩⎨⎧x 2-4x +6,x ≥0,x +6,x <0,则不等式f (x )>f (1)的解集是( )A .(-3,1)∪(3,+∞)B .(-3,1)∪(2,+∞)C .(-1,1)∪(3,+∞)D .(-∞,-3)∪(1,3)9.(2011·广东高考)已知平面直角坐标系xOy 上的区域D 由不等式组⎩⎨⎧0≤x ≤2,y ≤2,x ≤2y给定,若M (x ,y )为D 上的动点,点A 的坐标为(2,1),则z=OM →·OA→的最大值为( ) A .4 2 B .3 2 C .4 D .310.已知正项等比数列{a n }满足:a 7=a 6+2a 5,若存在两项a m ,a n 使得a m a n =4a 1,则1m +4n的最小值为( )A.32B.53C.256D .不存在 第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)11.若点P (x ,y )在直线x +3y -2=0上,则3x +27y 的最小值是________.12.若实数x ,y 满足⎩⎨⎧x ≤2y ≤2,x +y ≥2,则目标函数z =yx +1的最大值是________.13.给出下列命题:命题1:点(1,1)是直线y =x 与双曲线y =1x 的一个交点;命题2:点(2,4)是直线y =2x 与双曲线y =8x 的一个交点;命题3:点(3,9)是直线y =3x 与双曲线y =27x的一个交点; ……请观察上面命题,猜想出命题n (n 是正整数)为________. 14.若log a (a 2+1)<log a (2a )<0,则a 的取值范围是________.三、解答题(本大题共6小题,共80分.解答时应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分12分)已知a >0,b >0,求证:b 2a +a 2b≥a +b .16.(本小题满分13分)已知二次函数f (x )=ax 2+bx +c (a >0)的图象与x 轴有两个不同的交点,若f (c )=0,且0<x <c 时,f (x )>0.(1)证明:1a 是f (x )=0的一个根;(2)证明:1a>c .17.(本小题满分13分)某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A 、B ,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:最大收益是多少?18.(本小题满分14分)祖国大陆开放台湾农民到大陆创业以来,在11个省区设立了海峡两岸农业合作试验区和台湾农民创业园,台湾农民在那里申办了个体工商户可以享受“绿色通道”的申请、受理、审批一站式服务.某台商到大陆一创业园投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元.设f(n)表示前n年的纯利润(f(n)=前n年的总收入-前n年的总支出-投资额).(1)从第几年开始获取纯利润?(2)若干年后,该台商为开发新项目,有两种处理方案;①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万美元出售该厂.问哪种方案更合算?19.(本小题满分14分)某少数民族的刺绣有着悠久的历史,如图1(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n 个图形包含f(n)个小正方形.图1(1)求出f(5)的值;(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;(3)求1f(1)1f(2)-11f(3)-1+…+1f(n)-1的值.20.(本小题满分14分)(2012·佛山模拟)设函数f(x)=tx2+2t2x+t-1(x∈[-1,1]).(1)若t>0,求f(x)的最小值h(t);(2)对于(1)中的h(t),若t∈(0,2]时,h(t)<-2t+m2+4m恒成立,求实数m的取值范围.答案及解析1.【解析】 ∵a 2<b 2,∴a 2<b 2,即|a |<|b |. 【答案】 C2.【解析】 ∵a >b >c ,a +b +c =0, ∴a >0,c <0,∴a ·b >a ·c . 【答案】 A3.【解析】 作出可行域,如图所示,两条直线的交点为A (3,1),作直线3x +4y =0,并将它向右上平移,当过点A (3,1)时,3x +4y 取得最小值,且最小值为3×3+4×1=13.【答案】 A4.【解析】 ∵f (2)=32,f (4)>2=42,f (8)>52,f (16)>3=62,f (32)>72,∴猜想:f (2n )≥n +22.【答案】 C5.【解析】 由题意知Δ=a 2-16>0,解得a >4或a <-4. 【答案】 D6.【解析】 x +y =(x +y )(2x +8y )=10+2y x 8x y ≥10+22y x ×8xy=18,当且仅当2y x =8xy时取等号.【答案】 D7.【解析】 方程ax 2-x -c =0的两根为x 1=-2,x 2=1, 则有⎩⎪⎨⎪⎧1a =-2+1,-ca =-2×1,∴⎩⎨⎧a =-1c =-2. ∴f (x )=-x 2-x +2, ∴f (-x )=-x 2+x +2,令f (-x )=0得x =2或x =-1,选B. 【答案】 B8.【解析】 易知f (1)=3,则不等式f (x )>f (1)等价于⎩⎨⎧x ≥0,x 2-4x +6>3或⎩⎨⎧x <0,x +6>3,解得-3<x <1或x >3. 【答案】 A9.【解析】由线性约束条件⎩⎨⎧0≤x ≤2,y ≤2,x ≤2y ,画出可行域如图所示,目标函数z =OM →·OA →=2x +y ,将其化为y =-2x +z ,结合图形可知,目标函数的图象过点(2,2)时,z 最大,将点(2,2)的坐标代入z =2x +y ,得z 的最大值为4.【答案】 C10.【解析】 设正项等比数列{a n }的公比为q ,且q >0. 由a 7=a 6+2a 5,得q 2-q -2=0, 解得q =2.由a m a n =4a 1,得2m +n -2=24, 即m +n =6.故1m +4n =16(m +n )(1m +4n )=56+16(4m n +n m )≥56+46=32,当且仅当n =2m 时等号成立.【答案】 A11.【解析】 由题意知,x +3y =2, ∴3x +27y ≥23x ·27y =23x +3y=6,当且仅当3x =27y , 即x =1,y =13时等号成立.【答案】 612.【解析】 线性约束条件对应的可行域为△ABC (如图).而z =y x +1为点(x ,y )与(-1,0)连线的斜率.由图形知,z max =20+1=2.【答案】 213.【解析】 观察所给命题知,命题n 中交点坐标为(n ,n 2), 直线方程为y =nx ,双曲线方程为y =n 3x,故命题n 是“点(n ,n 2)是直线y =nx 与双曲线y =n 3x的一个交点”.【答案】 点(n ,n 2)是直线y =nx 与双曲线y =n3x的一个交点14.【解析】 ∵a 2+1≥1且log a (a 2+1)<0,∴0<a <1, 由log a (a 2+1)<log a (2a ),得a 2+1>2a ,恒成立, 由log a (2a )<0得2a >1,∴a >12.综上知12<a <1.【答案】 (12,1)15.【证明】 b 2a +a 2b -(a +b )=(b 2a -a )+(a 2b b )=(b +a )(b -a )a +(a +b )(a -b )b=(a -b )(a +b )(1b -1a )=1ab (a -b )2(a +b ),∵a >0,b >0, ∴1ab>0,a +b >0,(a -b )2≥0, ∴1ab(a -b )2(a +b )≥0, 即b 2a +a 2b (a +b )≥0, ∴b 2a +a 2ba +b . 16.【证明】 (1)∵f (x )图象与x 轴有两个不同的交点, ∴f (x )=0有两个不相等的实根x 1,x 2. ∵f (c )=0,∴x 1=c 是f (x )=0的一个根. 又x 1·x 2=c a ,∴x 2=1a (1a 0).∴1a 是f (x )=0的一个根. (2)假设1a <c ,又1a>0,由0<x <c 时,f (x )>0,知f (1a )>0,这与f (1a )=0矛盾,∴1a ≥c .又∵1a ≠c .∴1a >c .17.【解】 设搭载产品A x 件,产品B y 件, 预计总收益z =80x +60y .则⎩⎨⎧20x +30y ≤300,10x +5y ≤110,x ∈N ,y ∈N ,作出可行域,如图.作出直线l 0:4x +3y =0并平移,由图象得,当直线经过M 点时z 能取得最大值,由⎩⎨⎧ 2x +3y =30,2x +y =22,解得⎩⎨⎧x =9,y =4,即M (9,4). 所以z max =80×9+60×4=960(万元).即搭载产品A 9件,产品B 4件,可使得总预计收益最大,为960万元. 18.【解】 由题意知,每年的经费是以12为首项,4为公差的等差数列,设纯利润与年数的关系为f (n ),则f (n )=50n -[12n +n (n -1)2×4]-72 =-2n 2+40n -72.(1)获取纯利润就是要求f (n )>0,即-2n 2+40n -72>0, 解得2<n <18.又n ∈N ,故从第三年开始获利. (2)①年平均利润=f (n )n =40-2(n +36n )≤16. 当且仅当n =6时取等号.故此方案共获利6×16+48=144(万美元),此时n =6. ②f (n )=-2(n -10)2+128, 当n =10时,f (n )max =128故第②种方案共获利128+16=144(万美元). 故比较两种方案,获利都是144万美元.但第①种方案只需6年,而第②种方案需10年,故选择第①种方案更合算. 19.【解】 (1)∵f (1)=1,f (2)=5,f (3)=13,f (4)=25, ∴f (5)=25+4×4=41.(2)∵f (2)-f (1)=4=4×1, f (3)-f (2)=8=4×2, f (4)-f (3)=12=4×3, f (5)-f (4)=16=4×4,由上式规律得出f (n +1)-f (n )=4n . ∴f (n )-f (n -1)=4(n -1), f (n -1)-f (n -2)=4·(n -2), f (n -2)-f (n -3)=4·(n -3), …f (2)-f (1)=4×1,∴f (n )-f (1)=4[(n -1)+(n -2)+…+2+1] =2(n -1)·n , ∴f (n )=2n 2-2n +1.(3)当n ≥2时,1f (n )-1=12n 2-2n +1-1=12(1n -1-1n ), ∴1f (1)+1f (2)-1+1f (3)-1+…+1f (n )-1=1+12(1-12+12-13+…+1n -1-1n )=1+12(1-1n )=32-12n.20.【解】 (1)∵f (x )=t (x +t )2-t 3+t -1,①当-t <-1,即t >1时,f (x )在[-1,1]上单调递增,f (x )的最小值为 f (-1)=-2t 2+2t -1;②当-1≤-t <0,即0<t ≤1时, f (x )在[-1,1]上的最小值为 f (-t )=-t 3+t -1;∴h (t )=⎩⎨⎧-t 3+t -1 t ∈(0,1]-2t 2+2t -1 t ∈(1,+∞)(2)令g (t )=h (t )+2t=⎩⎨⎧-t 3+3t -1 t ∈(0,1]-2t 2+4t -1 t ∈(1,2]. ①0<t ≤1时,由g ′(t )=-3t 2+3≥0,∴g (t )在(0,1]上单调递增,②1<t ≤2时,g (t )=-2t 2+4t -1=-2(t -1)2+1,g (t )在(1,2]上单调递减,由①、②可知,g (t )在区间(0,2]上的最大值为g (1)=1.所以h (t )<-2t +m 2+4m 在(0,2]内恒成立,等价于g (t )<m 2+4m 在(0,2]内恒成立,即只要1<m 2+4m 即可,解m 2+4m -1>0得m <-2-5或m >-2+ 5.所以m 的取值范围为(-∞,-2-5)∪(-2+5,+∞).。
课堂新坐标2013届高三数学(文)一轮复习阶段知能检测4

阶段知能检测(四)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2011·辽宁高考)i 为虚数单位,1i +1i 3+1i 5+1i 7=( ) A .0 B .2i C .-2i D .4i2.设i ,j 是不共线的单位向量,a =5i +3j ,b =3i -5j ,则a ⊥b 是i ⊥j 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既非充分又非必要条件3.(2011·浙江高考)若复数z =1+i ,i 为虚数单位,则(1+z )·z =( )A .1+3iB .3+3iC .3-iD .34.(2012·江门模拟)若四边形ABCD 满足AB →+CD →=0,(AB →-AD →)·AC →=0,则该四边形一定是( )A .直角梯形B .菱形C .矩形D .正方形5.平面向量a 与b 的夹角为60°,a =(2,0),|b |=1,则|a +2b |=( ) A. 3 B .2 3 C .4 D .126.(2011·课标全国卷)复数2+i 1-2i的共轭复数是( ) A .-35i B.35i C .-i D .i 7.已知向量a 、b 不共线,c =k a +b (k ∈R ),d =a -b .如果c ∥d ,那么( )A .k =1且c 与d 同向B .k =1且c 与d 反向C .k =-1且c 与d 同向D .k =-1且c 与d 反向8.(2011·课标全国卷)a ,b 为平面向量,已知a =(4,3),2a +b =(3,18),则a ,b 夹角的余弦值等于( )A.865 B .-865 C.1665 D .-16659.已知两点M (-2,0),N (2,0),点P 为坐标平面内的动点,满足|MN →|·|MP→|+MN →·NP→=0,则动点P (x ,y )的轨迹方程为( ) A .y 2=8x B .y 2=-8xC .y 2=4xD .y 2=-4x10.设a =(a 1,a 2),b =(b 1,b 2),定义一种向量积:a ⊗b =(a 1b 1,a 2b 2).已知点P (θ,sin θ),m =(2,12),n =(π3,0),点Q 在y =f (x )的图象上运动,满足OQ →=m ⊗OP→+n (其中O 为坐标原点),则y =f (x )的最大值A 及最小正周期T 分别为( )A .2,πB .2,4πC.12,4πD.12,π 第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)11.若向量a =(1,1),b =(2,5),c =(3,x )满足条件(8a -b )·c =30,则x =________.12.(2011·广东高考改编)设复数z 满足(1+i)z =2,其中i 是虚数单位,则z =________.13.|a |=1,|b |=2,且a ⊥(a -b ),则向量a 与向量b 的夹角是________.14.在四边形ABCD 中,AB →=DC →=(1,1),1|BA →|BA →+1|BC →|BC →=3|BD→|BD →,则四边形ABCD 的面积为________.三、解答题(本大题共6小题,共80分.解答时应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分12分)设存在复数z 同时满足下列条件:(1)复数z 在复平面内对应点位于第二象限;(2)z ·z +2i z =8+a i(a ∈R ).试求a 的取值范围.16.(本小题满分13分)已知A (3,0),B (0,3),C (cos α,sin α).(1)若AC →·BC →=-1,求sin(α+π4)的值; (2)若|OA →+OC →|=13,且α∈(0,π),求OB →与OC →的夹角.17.(本小题满分13分)已知向量OP →=(2cos x +1,cos 2x -sin x +1),OQ →=(cos x ,-1),定义f (x )=OP →·OQ →.(1)求函数f (x )的最小正周期;(2)若x ∈(0,2π),当OP →·OQ →<-1时,求x 的取值范围.18.(本小题满分14分)设O 为坐标原点,已知向量OZ 1→,OZ 2→分别对应复数z 1,z 2,且z 1=3a +5+(10-a 2)i ,z 2=21-a+(2a -5)i(其中a ∈R ),若z 1+z 2可以与任意实数比较大小,求OZ 1→·OZ 2→的值.19.(本小题满分14分)已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ,设向量m =(a ,b ),n =(sin B ,sin A ),p =(b -2,a -2).(1)若m ∥n ,求证:△ABC 为等腰三角形;(2)若m ⊥p ,边长c =2,角C =π3,求△ABC 的面积. 20.(本小题满分14分)已知两点M (-1,0),N (1,0),且点P 使NM →·NP →,PM →·PN→,MP →·MN→成公差为非负的等差数列. (1)求点P 的轨迹方程;(2)若θ为PM →与PN →的夹角,求θ的最大值及此时点P 的坐标.答案及解析1.【解析】 原式=-i +i +(-i)+i =0.【答案】 A2.【解析】 a ·b =(5i +3j )·(3i -5j )=15|i |2-16i ·j -15|j |2=-16i ·j .∴a ⊥b 是i ⊥j 的充要条件.【答案】 C3.【解析】 ∵z =1+i ,∴(1+z )·z =(2+i)(1+i)=1+3i.【答案】 A4.【解析】 由AB→+CD →=0知,AB →=DC →, ∴四边形ABCD 是平行四边形.又(AB →-AD →)·AC→=0, ∴DB →·AC→=0,即AC ⊥BD , 因此四边形ABCD 是菱形.【答案】 B5.【解析】 ∵|a |=2,且|b |=1,∴|a +2b |2=(a +2b )2=a 2+4a ·b +4b 2=4+4×2×1×cos 60°+4×12=12.∴|a +2b |=2 3.【答案】 B6.【解析】 ∵2+i 1-2i =(2+i )(1+2i )(1-2i )(1+2i )=2+i +4i -25=i , ∴2+i 1-2i的共轭复数为-i. 【答案】 C7.【解析】 ∵c ∥d 且a ,b 不共线,∴存在唯一实数λ,使c =λd . ∴k a +b =λa -λb ,∴⎩⎨⎧ k =λ,1=-λ,∴⎩⎨⎧k =-1,λ=-1.【答案】 D8.【解析】 ∵a =(4,3),2a +b =(3,18),∴b =(3,18)-2(4,3)=(-5,12),∴cos 〈a ,b 〉=a ·b |a |·|b |=(4,3)·(-5,12)5×13=1665【答案】 C9.【解析】 ∵MN→=(4,0),MP →=(x +2,y ),NP →=(x -2,y ), ∴|MN →|·|MP →|+MN →·NP→ =4·(x +2)2+y 2+4(x -2)=0. 整理,得(x +2)2+y 2=2-x ,化简得y 2=-8x .【答案】 B10.【解析】 设点Q (x ,y ),由OQ →=m ⊗OP →+n ,得OQ →=(2θ,12sin θ)+(π3,0)=(2θ+π312sin θ), ∴x =2θ+π3,且y =12sin θ, 消去θ,得y =12sin(x 2-π6), 依题意f (x )=12sin(x 2-π6), 因此A =12,最小正周期T =4π. 【答案】 C11.【解析】 由(8a -b )·c =30,得18+3x =30,x =4.【答案】 412.【解析】 z =21+i =2(1-i )(1+i )(1-i )1-i. 【答案】 1-i13.【解析】 设向量a 与b 的夹角为θ,由a ⊥(a -b ),得 a ·(a -b )=0,即|a |2-a ·b =0,∴|a ||b |cos θ=|a |2,∴cos θ=|a ||b |=22,故θ=π4.【答案】 π414.【解析】 如图所示,由AB →=DC →=(1,1)知AB 綊DC .又1|BA →|→+1|BC →|→=3|BD →|BD →, 知四边形ABCD 为菱形,且AB =AD =2,又∵(1|BA →|·BA →+1|BC →|·BC →)2=3, ∴∠ABC =60°.∴S 四边形ABCD =2×2×32= 3. 【答案】 3 15.【解】 设z =x +y i(x ,y ∈R ),由(1)得x <0,y >0.由(2)得x 2+y 2+2i(x +y i)=8+a i ,即x 2+y 2-2y +2x i =8+a i.由复数相等,得⎩⎨⎧x 2+y 2-2y =8,2x =a .解得-6≤a <0. 因此实数a 的取值范围是-6≤a <0.16.【解】 (1)∵AC→=(cos α-3,sin α),BC →=(cos α,sin α-3), ∴AC →·BC→=(cos α-3)cos α+sin α(sin α-3)=-1, 得cos 2α+sin 2α-3(cos α+sin α)=-1,∴cos α+sin α=23∴sin(α+π4)=23. (2)∵|OA →+OC →|=13,∴(3+cos α)2+sin 2α=13,∴cos α=12,∵α∈(0,π),∴α=π3,sin α=32,∴C (12,32), ∴OB →·OC →=332, 设OB→与OC →的夹角为θ,且θ∈[0,π], 则cos θ=OB →·OC →|OB →|·|OC→|3323=32.故θ=π6为所求. 17.【解】 (1)f (x )=OP →·OQ→ =2cos 2x +cos x -cos 2x +sin x -1=sin x +cos x =2sin(x +π4), 则f (x )的最小正周期为T =2π.(2)由OP →·OQ →<-1,得sin(x +π4)<-22. 又x ∈(0,2π),则5π4<x +π4<7π4,即π<x <3π2. 故x 的取值范围是(π,3π2). 18.【解】 依题意z 1+z 2为实数,由z 1=3a +5-(10-a 2)i , ∴z 1+z 2=3a +5+21-a+[(a 2-10)+(2a -5)]i 的虚部为0, ∴a 2+2a -15=0,解得a =-5,或a =3.又分母不为零,∴a =3,此时z 1=38+i ,z 2=-1+i , 即OZ 1→=(38,1),OZ 2→=(-1,1), ∴OZ 1→·OZ 2→=38×(-1)+1×1=58. 19.【解】 (1)证明 ∵m ∥n ,∴a sin A =b sin B ,由正弦定理,得a 2=b 2,∴a =b .∴△ABC 为等腰三角形.(2)由题意可知m ·p =0,即a (b -2)+b (a -2)=0.∴a +b =ab .由余弦定理可知,4=a 2+b 2-ab =(a +b )2-3ab ,即(ab )2-3ab -4=0,∴ab =4(舍去ab =-1),∴S =12ab sin C =124×sin π3= 3. 20.【解】 (1)设点P 的坐标为(x ,y ),又M (-1,0),N (1,0), 则PM →=-MP →=(-1-x ,-y ),PN →=-NP →=(1-x ,-y ),MN →=-NM →=(2,0). ∴NM →·NP→=2(1-x ), PM →·PN →=x 2+y 2-1,MP →·MN→=2(1+x ), 依题意得⎩⎨⎧ 2(x 2+y 2-1)=2(1+x )+2(1-x ),2(1+x )-2(1-x )≥0⇔⎩⎨⎧x 2+y 2=3,x ≥0.∴点P 的轨迹方程为x 2+y 2=3(x ≥0).(2)∵PM →·PN →=(-1-x ,-y )·(1-x ,-y )=x 2+y 2-1=2,|PM →|·|PN→|=(-1-x )2+(-y )2·(1-x )2+(-y )2 =24-x 2.∴cos θ=PM →·PN →|PM →|·|PN →|=14-x 2. ∵0≤x ≤3,∴12≤cos θ≤1,∴0≤θ≤π3. ∴θ的最大值为π3,此时x =0,∴点P的坐标为(0,±3).。
课堂新坐标2013届高三数学(文)一轮复习阶段知能检测10

阶段知能检测(十)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.有3张奖券,其中2张可中奖,现3个人按顺序依次从中抽一张,小明最后抽,则他抽到中奖券的概率是( )A.23B.38C.59D.782.盒子内装有红球、白球、黑球三种,其数量分别为3,2,1,从中任取两球,则互斥而不对立的两个事件为( )A .至少有一个白球;都是白球B .至少有一个白球;至少有一个红球C .恰有一个白球;一个白球一个黑球D .至少有一个白球;红黑球各一个图13.如图1所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为23,则阴影区域的面积为( )A.43B.83C D .无法计算4.古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木,木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率是( )A.310 B.25 C.12 D.355.已知直线y =x +b ,b ∈[-2,3],则直线在y 轴上的截距大于1的概率是( )A.15B.25C.35D.456.某班准备到郊外野营,为此向商店定了帐篷,如果下雨与不下雨是等可能的,能否准时收到帐篷也是等可能的,只有帐篷如期运到,他们就不会淋雨,则下列说法正确的是( )A .一定不会淋雨B .淋雨的可能性为34C .淋雨的可能性为12D .淋雨的可能性为14图27.如图2所示,墙上挂有边长为a 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为a2的扇形,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )A .1-π4 B.π4C .1-π8D .与a 的取值有关8.在一个袋子中装有分别标注1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同,现从中随机取出2个小球,则取出小球标注的数字之差的绝对值为2或4的概率是( )A.110 B.310 C.25 D.14图39.如图3所示,ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点.取到的点到O的距离大于1的概率为()A.π4B.1-π4C.π8D.1-π810.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为X、Y,则log2X Y=1的概率为()A.16B.536C.112D.12第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)11.在区间[-1,2]上随机取一个数x,则|x|≤1的概率为________.12.某家庭电话,打进的电话响第一声时被接的概率为110,响第二声时被接的概率为310,响第三声时被接的概率为25,响第四声时被接的概率为110,则电话在响前四声内被接的概率为________.13.已知函数f(x)=6x-4(x=1,2,3,4,5,6)的值域为集合A,函数g(x)=2x-1(x =1,2,3,4,5,6)的值域为集合B,任意x∈A∪B,则x∈A∩B的概率是________.14.(2012·佛山模拟)已知平面区域U={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≤4,y≥0,x-2y≥0},若向区域U内随机投一点P,则点P落在区域A内的概率为________.三、解答题(本大题共6小题,共80分.解答时应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分12分)袋中有大小、形状相同的红、黑球各一个,现依次有放回地随机摸取3次,每次摸取一个球.(1)试问:一共有多少种不同的结果?请列出所有可能的结果;(2)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.16.(本小题满分13分)汽车厂生产A ,B ,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A 类轿车10辆.(1)求z 的值;(2)用分层抽样的方法在C 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.17.(本小题满分13分)(2012·深圳质检)已知集合A ={x |x 2+2x -3<0},B ={x |x +2x -3<0}. (1)在区间(-4,4)上任取一个实数x ,求“x ∈A ∩B ”的概率;(2)设(a ,b )为有序实数对,其中a ∈A ,b ∈B ,且a ,b 为整数,求“b -a ∈A ∪B ”的概率.18.(本小题满分14分)设关于x 的一元二次方程x 2+2ax +b 2=0.(1)若a 是从-4,-3,-2,-1四个数中任取的一个数,b 是从1,2,3三个数中任取的一个数,求上述方程有实根的概率;(2)若a 是从区间[-4,-1]任取的一个数,b 是从区间[1,3]任取的一个数,求上述方程有实根的概率.19.(本小题满分14分)(2011·福建高考)某日用品按行业质量标准分成五个等级,等级系数X 依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:(1)若所抽取的203件,等级系数为5的恰有2件,求a ,b ,c 的值;(2)在(1)的条件下,将等级系数为4的3件日用品记为x 1,x 2,x 3,等级系数为5的2件日用品记为y 1,y 2.现从x 1,x 2,x 3,y 1,y 2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.20.(本小题满分14分)某中学的高二(1)班男同学有45名,女同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;(3)试验结束后,第一次做试验的同学得到的试验数据为68,70,71,72,74,第二次做试验的同学得到的试验数据为69,70,70,72,74,请问哪位同学的实验更稳定?并说明理由.答案及解析1.【解析】 因为每张奖券都可能被小明抽到,且等可能,共有3种结果,其中中奖的结果有2种,故小明抽到中奖券的概率为23.【答案】 A2.【解析】 红黑球各取一个,则一定取不到白球,故“至少有一个白球,红黑球各一个”为互斥事件,又任取两球还包含“两个红球”等事件,故不是对立事件.【答案】 D3.【解析】 由几何概型知:S 阴S 正方形23.故S 阴=23×22=83.【答案】 B4.【解析】 基本事件为:金木、金水、金火、金土、木水、木火、木土、水火、水土、火土,共10个.不相克的事件数为10-5=5,∴抽取的两种物质不相克的概率是51012.【答案】 C5.【解析】 试验的全部结果构成的区域是[-2,3],所求事件构成的区域为(1,3],故所求概率为P =3-13-(-2)=25【答案】 B6.【解析】 基本事件有“下雨帐篷到”“不下雨帐篷到”“下雨帐篷未到”“不下雨帐篷未到”4种情况,又只有“下雨帐篷未到”时会淋雨,故淋雨的可能性为14.【答案】 D7.【解析】 阴影部分的面积S 阴影=a 2-π(a 2)2=(1-π4)a 2,∴所求事件的概率P =(1-π4)a 2/a 2=1-π4.【答案】 A8.【解析】 从袋中随机取出2个小球,其基本事件是(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种,其中符合条件的有(1,3),(1,5),(2,4),(3,5)四种情况.故所求概率为P =410=25. 【答案】 C9.【解析】 设事件A 表示“在长方形ABCD 内取点,到点O 的距离大于1”,则试验的全部结果构成的区域为长方形ABCD ,事件A 发生的区域是图中的阴影部分,所以S 阴影=2-π2,因此P (A )=2-π22=1-π4.【答案】 B10.【解析】 由log 2X Y =1得Y =2X ,满足条件的X 、Y 有3对,而骰子朝上的点数X 、Y 共有6×6=36对,∴概率为336=112. 【答案】 C11.【解析】 [-1,2]的长度为3,|x |≤1的解集为[-1,1]的长度为2,所以概率是23.【答案】2312.【解析】 设响n 声时被接的概率为P n ,则P 1=110,P 2=310,P 3=25,P 4=110.故前四声内被接的概率为P 1+P 2+P 3+P 4=910.【答案】91013.【解析】 根据已知条件可得A ={2,8,14,20,26,32}, B ={1,2,4,8,16,32}.∴A ∪B ={1,2,4,8,14,16,20,26,32},A ∩B ={2,8,32}. 所以任取x ∈A ∪B ,则x ∈A ∩B 的概率是39=13.【答案】 1314.【解析】 作出可行域知,平面区域U 为△OAB 及其内部,平面区域A 为△ODC 及其内部,又S △OAB =12×6×6=18,S △ODC =12×4×2=4,故所求事件的概率P =S △ODC S △OAB =418=29. 【答案】2915.【解】 (1)一共有8种不同的结果,列举如下:(红、红、红)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑).(2)记“3次摸球所得总分为5”为事件A .事件A 包含的基本事件为(红、红、黑)、(红、黑、红)、(黑、红、红),事件A 包含的基本事件数为3.由(1)可知,基本事件总数为8,所以事件A 的概率为P (A )=38.16.【解】 (1)设该厂本月生产轿车为n 辆, 由题意得50n =10100+300.所以n =2 000.z =2 000-(100+300)-(150+450)-600=400.(2)设所抽样本中有m 辆舒适型轿车,因为用分层抽样的方法在C 类轿车中抽取一个容量为5的样本,所以4001 000=m5,解得m =2. 也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作A 1,A 2,B 1,B 2,B 3,则从中任取2辆的所有基本事件为(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 2,B 1),(A 2,B 2),(A 2,B 3),(B 1,B 2),(B 1,B 3),(B 2,B 3)共10个.其中至少有1辆舒适型轿车的基本事件有7个:(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 2,B 1),(A 2,B 2),(A 2,B 3).∴从中任取2辆,至少有1辆舒适型轿车的概率为710.17.【解】 (1)A ={x |-3<x <1},B ={x |-2<x <3}, 设事件“x ∈A ∩B ”的概率为P 1,又A ∩B ={x |-2<x <1}, 这是一个几何概型,则P 1=38.(2)因为a ,b ∈Z ,且a ∈A ,b ∈B ,所以,基本事件共12个:(-2,-1),(-2,0),(-2,1),(-2,2),(-1,-1),(-1,0),(-1,1),(-1,2),(0,-1),(0,0),(0,1),(0,2).设事件E 为“b -a ∈A ∪B ”,则E 包含9个基本事件. 所以事件E 的概率P (E )=912=34. 18.【解】 设事件A 为“方程x 2+2ax +b 2=0有实根”.当a <0,b >0时,方程x 2+2ax +b 2=0有实根的充要条件为a +b ≤0. (1)基本事件共12个:(-4,1),(-4,2),(-4,3),(-3,1),(-3,2),(-3,3),(-2,1),(-2,2),(-2,3),(-1,1),(-1,2),(-1,3).其中第一个数表示a 的取值,第二个数表示b 的取值.事件A 中包含9个基本事件.事件A 发生的概率为P (A )=912=34. (2)试验的全部结果所构成的区域为{(a ,b )|-4≤a ≤-1,1≤b ≤3},构成事件A 的区域为{(a ,b )|-4≤a ≤-1,1≤b ≤3,a +b ≤0},所求概率为这两区域面积的比. 所以所求的概率P =3×2-12×223×2=23.19.【解】 (1)由频率分布表得a +0.2+0.45+b +c =1, ∴a +b +c =0.35,因为抽取的20件日用品中,等级系数为4的恰有3件. 所以b =320=0.15. 等级系数为5的恰有2件,所以c =220=0.1, 从而a =0.35-b -c =0.1, 所以a =0.1,b =0.15,c =0.1.(2)从日用品x 1,x 2,x 3,y 1,y 2中任取两件,所有可能的结果为{x 1,x 2},{x 1,x 3},{x 1,y 1},{x 1,y 2},{x 2,x 3},{x 2,y 1},{x 2,y 2},{x 3,y 1},{x 3,y 2},{y 1,y 2}.共10个基本事件.设事件A 表示“从日用品x 1,x 2,x 3,y 1,y 2中任取两件,其等级系数相等”, ∴事件A 包含的基本事件为{x 1,x 2},{x 1,x 3},{x 2,x 3},{y 1,y 2},共4个.故所求的概率P (A )=410=0.4.20.【解】 (1)用古典概型的定义,P =m n =460=115.∴某同学被抽到的概率为115.设有x 名男同学,则4560=x4,∴x =3,∴男、女同学的人数分别为3与1.(2)把3名男同学和1名女同学记为a 1,a 2,a 3,b ,则选取两名同学的基本事件有(a 1,a 2),(a 1,a 3),(a 1,b ),(a 2,a 1),(a 2,a 3),(a 2,b ),(a 3,a 1),(a 3,a 2),(a 3,b ),(b ,a 1),(b ,a 2),(b ,a 3)共12种,其中有一名女同学的有6种.选出的两名同学中恰有一名女同学的概率为P =612=12(3)x 1=68+70+71+72+745=71,x 2=69+70+70+72+745=71,s 21=(68-71)2+…+(74-71)25=4,s 22=(69-71)2+…+(74-71)25=3.2,则x 1=x 2,s 21>s 22,∴第二次做试验的同学得到的数据更稳定.。
《课堂新坐标》高考数学(文)一轮总复习(人教新课标·广东专用)课件:第五章 第三节 等比数列

菜单
新课标 ·文科数学(广东专用)
高 考 体 验 · 明 考 情
课 后 作 业
新课标 ·文科数学(广东专用)
(2013·清远调研)已知{an}是各项均为正数的等
自 主
比数列,且 a1+a2=2(a11+a12),a3+a4+a5=64(a13+a14+a15).
高 考
1.本题求解常见的错误:(1)计算失误,不注意对方
明 考
础 程的根(公差 d)的符号进行判断;(2)不能灵活运用数列的 情
性质简化运算.
2.证明数列{an}是等比数列一般有两种方法:
典 例 探 究
· 提
(1)定义法:aan+n 1=q(q 是不为零的常数,n∈N*); (2)等比中项法:an2+1=an·an+2≠0(n∈N*).
自14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月18日星期六2021/9/182021/9/182021/9/18
高
主15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/182021/9/182021/9/189/18/2021
能
菜单
新课标 ·文科数学(广东专用)
(2)证明 ∵an+Sn=n,∴a1+S1=1,得 a1=12,
自
高
主 落 实
∴c1=a1-1=-12.
考 体 验
· 固
又 an+1+Sn+1=n+1,an+Sn=n,
· 明
基 础
∴2an+1-an=1,即 2(an+1-1)=an-1.
究
· 提 知 能
化简得aa2121qq= 6=26,4.又 a1>0,故 q=2,a1=1.
课堂新坐标2013届高考数学一轮复习课件:第六章第七节 数学归纳法及其应用(广东专用)

考
落
体
实
基础,也叫归纳奠基,第二步是递推的依据,也叫归纳递推.两
验
·
·
固
者缺一不可.另外,在第二步中证明n=k+1时命题成立,必须利用
明
基
考
础
归纳假设,否则就不是数学归纳法.
情
课 时 知 能 训 练
菜单
第四页,编辑于星期日:二十点 十七分。
一轮复习 ·新课标 ·数学(理)(广东专用
)
典
例
探
1.(教材改编题)在应用数学归纳法证明凸 n 边形的对角线为21n(n
D.非以上答案
高
主
考
落
体
实 · 固
【解析】 f(1)=1+21+31+41+15.
验 · 明
基
考
础
情
【答案】 C
课 时 知 能 训 练
菜单
第七页,编辑于星期日:二十点 十七分。
一轮复习 ·新课标 ·数学(理)(广东专用
)
典
例
探
4.(2012·揭阳模拟)设 f(n)=1+21+31+41+…+3n1-1(n∈N*),则
【解析】 k为偶数,则k+2为偶数,选B.
考 情
【答案】 B
课 时 知 能 训 练
菜单
第六页,编辑于星期日:二十点 十七分。
一轮复习 ·新课标 ·数学(理)(广东专用
)
典
例
3.若 f(n)=1+21+13+…+6n1-1(n∈N*),则 f(1)为(
)
探 究 ·
A.1
1 B.5
提 知 能
自
C.1+12+13+14+15
课 时 知 能 训 练
菜单
课堂新坐标2013届高三数学(文)一轮复习6-1

课时知能训练一、选择题1.(2012·梅州模拟)已知a ,b ,c 满足c <b <a 且ac <0,则下列选项中不一定能成立的是( )A.c a <b aB.b -a c>0 C.b 2c <a 2c D.a -c ac<0 2.若0<a <1,则下列不等式中正确的是( )A .(1-a )13>(1-a )12B .log (1-a )(1+a )>0C .(1-a )3>(1+a )2D .(1-a )1+a >13.设α∈(0,π2),β∈[0,π2],那么2α-β3的取值范围是( ) A .(0,5π6) B .(-π6,5π6) C .(0,π) D .(-π6,π) 4.若a ,b ,x ,y ∈R ,则⎩⎨⎧ x >a y >b 是⎩⎨⎧x +y >a +b (x -a )(y -b )>0成立的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件5.若a >b >0,则下列不等式中一定成立的是( )A .a +1b >b +1a B.b a >b +1a +1C .a -1b >b -1a D.2a +b a +2b >a b二、填空题6.x 2+y 2+1与2(x +y -1)的大小关系是________.7.(2012·潮州模拟)设x ,y 为实数,满足3≤xy 2≤8,4≤x 2y ≤9,则x 3y 4的最大值是________.8.如果一辆汽车每天行驶的路程比原来多19 km ,那么8天的行程就超过2 200 km ;如果它每天行驶的路程比原来少12 km ,那么它行驶同样的路程就得花9天多的时间,则这辆汽车原来每天行驶的路程(单位:km)的范围是______.三、解答题9.已知b >a >0,x >y >0,求证:x x +a >y y +b. 10.若实数a 、b 、c 满足b +c =5a 2-8a +11,b -c =a 2-6a +9,试比较a 、b 、c 的大小.11.下表为广州全运会官方票务网站分布的几种球类比赛的门票价格,某球迷赛前准备1 200元,预订15张下表中球类比赛的门票.该球迷想预订上表中三种球类比赛门票,其中篮球比赛门票数与乒乓球比赛门票数相同,且篮球比赛门票的费用不超过足球比赛门票的费用,求可以预订的足球比赛门票数.答案及解析1.【解析】 ∵c <b <a ,且ac <0,∴c <0,a >0,∴c a <b a ,b -a c >0,a -c ac<0, 但b 2与a 2的关系不确定,故b 2c <a 2c不一定成立. 【答案】 C2.【解析】 ∵0<a <1,∴0<1-a <1,∴(1-a )13>(1-a )12. 【答案】 A2.【解析】 由已知得0<2α<π,0≤β3≤π6∴-π6≤-β3≤0,∴-π6<2α-β3<π. 【答案】 D4.【解析】 ⎩⎨⎧ x >a ,y >b ,⇒⎩⎨⎧ x +y >a +b ,(x -a )(y -b )>0, 且⎩⎨⎧ x +y >a +b ,(x -a )(y -b )>0,⇒⎩⎨⎧x >a ,y >b .【答案】 C5.【解析】 ∵a >b >0,∴1b >1a >0,∴a +1b >b +1a. 【答案】 A6.【解析】 ∵(x 2+y 2+1)-2(x +y -1)=(x -1)2+(y -1)2+1>0,∴x 2+y 2+1>2(x +y -1).【答案】 x 2+y 2+1>2(x +y -1)7.【解析】 ∵3≤xy 2≤8,∴18≤1xy 213, ∵4≤x 2y ≤9,∴16≤x 4y 2≤81, ∴2≤x 3y 4≤27,故x 3y 4的最大值是27. 【答案】 278.【解析】 设原来每天行驶的路程为x km ,则⎩⎨⎧ 8(x +19)>2 200,8(x +19)>9(x -12),解得256<x <260. 【答案】 (256,260)9.【证明】x x +a -y y +b =x (y +b )-y (x +a )(x +a )(y +b ) =bx -ay (x +a )(y +b ). ∵b >a >0,x >y >0,∴bx >ay ,x +a >0,y +b >0,∴bx -ay (x +a )(y +b )>0, ∴x x +a >y y +b. 10.【解】 ∵b -c =a 2-6a +9=(a -3)2≥0,∴b ≥c .①又⎩⎨⎧b +c =5a 2-8a +11,b -c =a 2-6a +9.∴c =2a 2-a +1, 则c -a =2a 2-2a +1=2(a -12)2+12>0, ∴c >a .②由①②得b ≥c >a .11.【解】 设预订篮球比赛门票数与乒乓球比赛门票数都是n 张,则足球比赛门票预订(15-2n )张,由题意得 ⎩⎨⎧ 80n +60n +100(15-2n )≤1 200,80n ≤100(15-2n ),n ∈N *.解得5≤n ≤5514, 由n ∈N *知,n =5,∴15-2n =5,故可预订足球比赛门票5张.。
课堂新坐标2013届高三数学(文)一轮复习课时知能训练5-4

课时知能训练一、选择题1.数列{a n }中,a n +1=a 2n 2a n -5,已知该数列既是等差数列又是等比数列,则该数列的前20项的和等于( )A .100B .0或100C .100或-100D .0或-1002.数列{a n }的通项公式a n =1n +n +2(n ∈N *),若前n 项和为S n ,则S n为( )A.n +2-1B.n +2+n +1-2-1C.12(n +2-1)D.12(n +2+n +1-2-1) 3.(2012·惠州模拟)已知S n 为等差数列{a n }的前n 项和,若a 1=-2010,S 2 0102 010-S 2 0042004=6,则S 2011=( ) A .2011 B .2010 C .0 D .24.已知数列{a n }:12,13+23,14+24+34,…,110210+310+…+910,…,那么数列{b n }={1a n a n +1}的前n 项和S n 为( ) A.n n +1 B.4n n +1 C.3n n +1 D.5n n +1 5.设数列{x n }满足log a x n +1=1+log a x n (n ∈N *,a >0且a ≠1),且x 1+x 2+x 3+…+x 100=100,则x 101+x 102+x 103+…+x 200的值为( )A .100a 2B .101a 2C .100a 100D .101a 100二、填空题6.数列3,33,333,…的前n 项和S n =________.7.数列{a n }的前n 项和为S n ,a 1=1,a 2=2,a n +2-a n =1+(-1)n (n ∈N *),则S 100=________.8.已知{a n }是公差为-2的等差数列,a 1=12,则|a 1|+|a 2|+|a 3|+…+|a 20|=________.三、解答题9.(2012·韶关模拟)已知数列{a n }是各项均不为0的等差数列,S n 为其前n项和,且满足a 2n =S 2n -1,n ∈N *.(1)求数列{a n }的通项公式;(2)数列{b n }满足b n =1a n ·a n +1,求数列{b n }的前n 项和T n . 10.设函数y =f (x )的定义域为R ,其图象关于点(12,12)成中心对称,令a k =f (k n)(n 是常数且n ≥2,n ∈N *),k =1,2,…,n -1,求数列{a k }的前n -1项的和.11.(2012·汕头模拟)已知等差数列{a n }的前3项和为6,前8项和为-4.(1)求数列{a n }的通项公式;(2)设b n =(4-a n )q n -1(q ≠0,n ∈N *),求数列{b n }的前n 项和S n .答案及解析1.【解析】 由题意知a n +1=a n ≠0,由a n +1=a 2n 2a n -5得a 2n -5a n =0,∴a n =5, ∴S 20=100.【答案】 A2.【解析】 ∵a n =1n +n +2=12(n +2-n ), ∴S n =12(3-1+4-2+5-3+6-4+…+n -n -2+n +1-n -1+n +2-n )=12(-1-2+n +1+n +2) =12(n +2+n +1-2-1). 【答案】 D3.【解析】 设等差数列的公差为d ,则S n =na 1+n (n -1)2, ∴S n n =d 2n -2010-d 2, ∴数列{S n n }是以-2010为首项, 以d 2为公差的等差数列, 由S 20102010-S 20042004=6得6×d 2=6,∴d =2. ∴S 2011=2011×(-2010)+2011×20102×2=0. 【答案】 C4.【解析】 a n =1+2+3+…+n n +1=n 2, ∴b n =1a n a n +1=4n (n +1)=4(1n -1n +1), ∴S n =4[(1-12)+(12-13)+…+(1n -1n +1)] =4(1-1n +1)=4n n +1. 【答案】 B5.【解析】 log a x n +1=1+log a x n ,得x n +1=ax n 且a >0,a ≠1,x n >0,∴数列{x n }是公比为a 的等比数列,∴x 101+x 102+x 103+…+x 200=x 1a 100+x 2a 100+x 3a 100+…+x 100a 100=100a 100.【答案】 C6.【解析】 数列3,33,333,…的通项公式a n =13(10n -1), ∴S n =13(10-1)+13(102-1)+…+13n -1) =13[(10+102+103+…+10n )-n ] =13×10(1-10n )1-10-n 3=127×10n +1-10+9n 27. 【答案】 127×10n +1-10+9n 277.【解析】 由a n +2-a n =1+(-1)n 知a 2k +2-a 2k =2,a 2k +1-a 2k -1=0,∴a 1=a 3=a 5=…=a 2n -1=1,数列{a 2k }是等差数列,a 2k =2k .∴S 100=(a 1+a 3+a 5+…+a 99)+(a 2+a 4+a 6+…+a 100) =50+(2+4+6+…+100)=50+(100+2)×502=2 600. 【答案】 2 6008.【解析】 由题意知,a n =12+(n -1)×(-2)=-2n +14, 令-2n +14≥0,得n ≤7,∴当n ≤7时,a n ≥0;当n >7时,a n <0.∴|a 1|+|a 2|+|a 3|+…+|a 20|=(a 1+a 2+…+a 7)-(a 8+a 9+…+a 20)=2S 7-S 20=2[7×12+7×62×(-2)]-[20×12+20×192×(-2)] =224.【答案】 2249.【解】 (1)法一 设等差数列{a n }的公差为d ,首项为a 1, 在a 2n =S 2n -1中,令n =1,n =2,得⎩⎨⎧ a 21=S 1,a 22=S 3,即⎩⎨⎧a 21=a 1,(a 1+d )2=3a 1+3d , 解得a 1=1,d =2,∴a n =2n -1.法二 ∵{a n }是等差数列,则a 1+a 2n -1=2a n .∴S 2n -1=a 1+a 2n -12(2n -1)=(2n -1)a n . 由a 2n =S 2n -1,得a 2n =(2n -1)a n ,又∵a n ≠0,∴a n =2n -1,则a 1=1,d =2.∴a n =2n -1.(2)∵b n =1a n a n +1=1(2n -1)(2n +1)=12(12n -1-12n +1), ∴T n =12(1-13+13-15+…+12n -1-12n +1)=n 2n +1. 10.【解】 ∵y =f (x )的图象关于点(12,12)成中心对称, 所以f (x )+f (1-x )=1.令S n -1=a 1+a 2+…+a n -1则S n -1=f (1n )+f (2n )+…+f (n -1n), 又S n -1=f (n -1n )+f (n -2n )+…+f (1n), 两式相加,得2S n -1=[f (1n )+f (n -1n )]+[f (2n )+f (n -2n )]+…+[f (n -1n )+f (1n)]=n -1,∴S n -1=n -12. 11.【解】 (1)设{a n }的公差为d .由已知得⎩⎨⎧3a 1+3d =6,8a 1+28d =-4.解得a 1=3,d =-1.故a n =3-(n -1)=4-n .(2)由(1)可得,b n =n ·q n -1,于是S n =1·q 0+2·q 1+3·q 2+…+n ·q n -1. 若q ≠1,将上式两边同乘以q , qS n =1·q 1+2·q 2+…+(n -1)·q n -1+n ·q n . 两式相减得到(q -1)S n =nq n -1-q 1-q 2-…-q n -1=nq n -q n -1q -1=nq n +1-(n +1)q n +1q -1于是,S n =nq n +1-(n +1)q n +1(q -1)2若q =1,则S n =1+2+3+…+n =n (n +1)2, 所以,S n =⎩⎪⎨⎪⎧ n (n +1)2,(q =1),nq n +1-(n +1)q n +1(q -1)2,(q ≠1).。
课堂新坐标2013届高三数学(文)一轮复习4-1-2
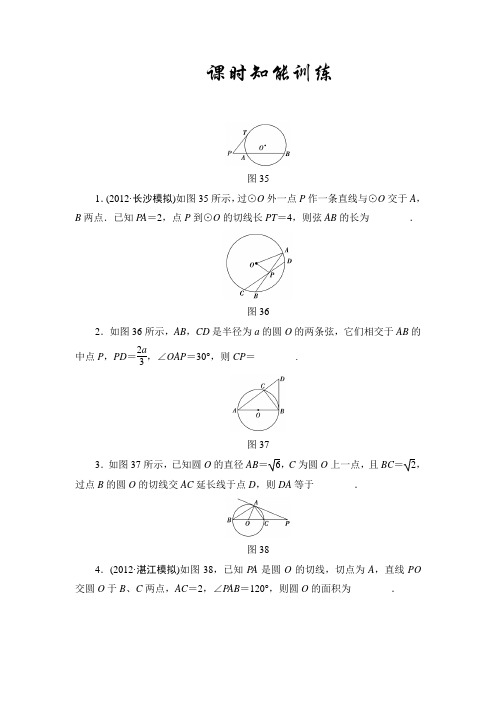
课时知能训练图351.(2012·长沙模拟)如图35所示,过⊙O 外一点P 作一条直线与⊙O 交于A ,B 两点.已知PA =2,点P 到⊙O 的切线长PT =4,则弦AB 的长为________.图362.如图36所示,AB ,CD 是半径为a 的圆O 的两条弦,它们相交于AB 的中点P ,PD =2a3,∠OAP =30°,则CP =________.图373.如图37所示,已知圆O 的直径AB =6,C 为圆O 上一点,且BC =2,过点B 的圆O 的切线交AC 延长线于点D ,则DA 等于________.图384.(2012·湛江模拟)如图38,已知PA 是圆O 的切线,切点为A ,直线PO 交圆O 于B 、C 两点,AC =2,∠PAB =120°,则圆O 的面积为________.图395.如图39,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,则AB=________,AC=________,BC=________.图406.(2012·韶关调研)如图40所示,⊙O和⊙O′相交于A、B两点,过A作两圆的切线分别交两圆于C、D,若BC=4,BD=9,则AB=________.图417.如图41所示,在△ABC中,AD是高,△ABC的外接圆直径AE交BC 边于点G,有下列四个结论:①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确的结论有________.图428.(2012·佛山模拟)如图42,AB是⊙O的直径,D为⊙O上一点,过D作⊙O的切线交AB的延长线于点C,若DA=DC,且BC=5,则AB=________.9.如图43,AB为⊙O的直径,C为⊙O上一点,AP和过C的切线互相垂直,垂足为P,过B的切线交过C的切线于T,PB交⊙O于Q,若∠BTC=120°,AB =4,则PQ ·PB =________.图43图4410.如图44所示,在梯形ABCD 中,AD ∥BC ,点E 、F 分别在边AB ,CD 上,设ED 与AF 相交于点G ,若B ,C ,F ,E 四点共圆.且AG =1,GF =2,DG =2,则GE =________.答案及解析1.【解析】 由切割线定理得PT 2=PA ·PB , ∴42=2(2+AB ), ∴AB =6. 【答案】 62.【解析】 由题意知OP ⊥AB ,且AP =32a , 根据相交弦定理AP 2=CP ·PD ,CP =98a .【答案】98a 3.【解析】 ∵AB 为直径,∴∠ACB =90°. 又AB =6,BC =2,得AC =2. BD 是圆O 的切线,则AB ⊥BD , 由射影定理得BC 2=AC ·CD . 故CD =1,所以AD =2+1=3. 【答案】 34.【解析】由题意知∠BAC=90°,则∠PAC=120°-90°=30°,由弦切角定理知,∠B=30°,∴BC=2AC=4,∴圆O的面积S=4π.【答案】4π5.【解析】∵∠CAE=∠EAB,∠EAB=∠ACB,∴∠ACB=∠CAE=∠EAB.又∵CB⊥AD,∴∠ACB=∠CAE=∠EAB=30°.又∵AE=2,∴AB=3,AC=23,BC=3.【答案】323 36.【解析】因为AC、AD分别是两圆的切线,所以∠C=∠2,∠1=∠D,所以△ACB∽△DAB.所以BCAB=ABBD,所以AB2=BC·BD,又BC=4,BD=9因此AB=6.【答案】 67.【解】①中仅当∠BAC为直角时才成立;在②中仅当BG⊥AE时才成立;由△AEB∽△ACD,故ABAD=AEAC,即AE·AD=AB·AC,故③正确;由相交弦定理知④正确.【答案】③④8.【解析】如图所示,连OD,∵CD是⊙O的切线,∴∠ODC=90°.设∠C=θ,则∠A=θ,∠ADO=θ.∵θ+θ+θ+90°=180°,∴θ=30°,∴OC=2OD.设圆O半径为r,则OC=2r,∴BC=r.∴AB=2BC=10.【答案】109.【解析】连结OC、AC,则OC⊥PC,则O、C、T、B四点共圆,∠COB =60°,故∠AOC=120°.由AO=OC=2,知AC=23,在Rt△APC中,∠ACP=60°,因此PC= 3.根据切割线定理得PQ·PB=PC2=3.【答案】 310.【解】如图所示,连结EF.∵B,C,F,E四点共圆,∴∠ABC=∠EFD.∵AD∥BC,∴∠BAD+∠ABC=180°.∴∠BAD+∠EFD=180°.∴A,D,F,E四点共圆.由相交弦定理,可得AG ·GF =DG ·GE . 因此GE =AG ·GF DG =1×22= 2.【答案】2。
课堂新坐标2013届高三数学(文)一轮复习阶段知能检测1

阶段知能检测(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2011·安徽高考)集合U ={1,2,3,4,5,6},S ={1,4,5},T ={2,3,4},则S ∩(∁U T )等于( )A .{1,4,5,6}B .{1,5}C .{4}D .{1,2,3,4,5}2.命题“若f (x )是奇函数,则f (-x )是奇函数”的否命题是( )A .若f (x )是偶函数,则f (-x )是偶函数B .若f (x )不是奇函数,则f (-x )不是奇函数C .若f (-x )是奇函数,则f (x )是奇函数D .若f (-x )不是奇函数,则f (x )不是奇函数3.若向量a =(x,3)(x ∈R),则“x =4”是“|a |=5”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件4.已知直线l ⊥平面α,直线m ⊂平面β,有下面四个命题: ①α∥β⇒l ⊥m ;②α⊥β⇒l ∥m ;③l ∥m ⇒α⊥β;④l ⊥m ⇒α∥β. 其中正确的命题是( )A .①与②B .①与③C .②与④D .③与④5. (2011·广东高考)已知集合A ={(x ,y )|x ,y 为实数,且x 2+y 2=1},B ={(x ,y )|x ,y 为实数,且y =x },则A ∩B 的元素个数为( )A .0B .1C .2D .36.(2011·陕西高考)设集合M ={y |y =|cos 2x -sin 2x |,x ∈R},N ={x ||x -1i|<2,i 为虚数单位,x ∈R},则M ∩N 为( )A .(0,1)B .(0,1]C .[0,1)D .[0,1]7.(2011·湖南高考) “x >1”是“|x |>1”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件8.有下列四个命题:①“若xy =1,则x ,y 互为倒数”的逆命题.②“面积相等的三角形全等”的否命题;③“若m ≤1,则x 2-2x +m =0有实数解”的逆否命题;④“若A ∩B =B ,则A B ”的逆否命题.其中真命题为( )A .①②B .②③C .④D .①②③9.(2012·汕尾质检)设0<x <π2,则“x sin 2x <1”是“x sin x <1”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件10.(2012·梅州模拟)已知命题p :∃a ,b ∈(0,+∞),当a +b =1时,1a +1b=3,命题q :∀x ∈R ,x 2-x +1≥0恒成立,则下列命题是假命题的是( )A .綈p ∨綈qB .綈p ∧綈qC .綈p ∨qD .綈p ∧q第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)11.命题“∃x ∈R ,x =sin x ”的否定是______.12.非零向量a 、b ,“a +b =0”是“a ∥b ”的________条件.13.设P 和Q 是两个集合,定义集合P -Q ={x |x ∈P ,且x ∉Q },若P ={1,2,3,4},Q ={x | x +12<2,x ∈R},则P -Q =________. 14.(2012·揭阳模拟)已知函数y =lg(4-x )的定义域为A ,集合B ={x |x <a },若P :“x ∈A ”是Q :“x ∈B ”的充分不必要条件,则实数a 的取值范围________.三、解答题(本大题共6小题,共80分.解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分12分)写出下列命题的否定,并判断真假.(1)p :正数的对数都是正数;(2)p :∀x ∈Z ,x 2的个位数字不等于3.16.(本小题满分13分)已知集合A ={y |y 2-(a 2+a +1)y +a (a 2+1)>0},B={y |y =12x 2-x +52,0≤x ≤3}. (1)若A ∩B =∅,求a 的取值范围;(2)当a 取使不等式x 2+1≥ax 恒成立的最小值时,求(∁R A )∩B .17.(本小题满分13分)(2012·广州模拟)已知函数f (x )=4sin 2(π4+x )-23cos 2x -1,x ∈[π4,π2]. (1)求f (x )的最大值及最小值;(2)若条件p :f (x )的值域,条件q :“|f (x )-m |<2”,且p 是q 的充分条件,求实数m 的取值范围.18.(本小题满分14分)已知命题p :方程a 2x 2+ax -2=0在[-1,1]上有解;命题q :只有一个实数x 满足不等式x 2+2ax +2a ≤0,若命题“p 或q ”是假命题,求a 的取值范围.19.(本小题满分14分)命题p :实数x 满足x 2-4ax +3a 2<0,其中a <0;命题q :实数x 满足x 2-x -6≤0或x 2+2x -8>0.若綈p 是綈q 的必要不充分条件,求a 的取值范围.20.(本小题满分14分)设命题甲:直线x =y 与圆(x -a )2+y 2=1有公共点,命题乙:函数f (x )=2-|x +1|-a 的图象与x 轴有交点,试判断命题甲与命题乙的条件关系,并说明理由.答案及解析1.【解析】 ∁U T ={1,5,6},S ∩(∁U T )={1,5}.【答案】 B2.【解析】 “奇函数”的否定,是“不是奇函数”,因此否命题应为“若函数f (x )不是奇函数,则f (-x )不是奇函数”.【答案】 B3.【解析】 a =(4,3),|a |=42+32=5;当|a |=5时,x =±4.【答案】 A4.【解析】 对于②,l 与m 可相交、平行、异面,不正确,对于④,α与β可相交,不正确.【答案】 B5.【解析】 ∵直线y =x 与单位圆x 2+y 2=1有两个交点,∴A ∩B 的元素有2个.【答案】 C6.【解析】 由y =|cos 2x -sin 2x |=|cos 2x |,得M =[0,1];因为|x -1i|<2,所以|x +i|<2,即x 2+1<2, 所以-1<x <1,即N =(-1,1),∴M ∩N =[0,1).【答案】 C7.【解析】 |x |>1⇔x >1或x <-1,故x >1⇒|x |>1,但|x |>1D /⇒x >1(如x =-2),∴x >1是|x |>1的充分不必要条件.【答案】 A8.【解析】 ①的逆命题为:“若x ,y 互为倒数,则xy =1”是真命题;②的否命题为:“面积不相等的三角形不是全等三角形”是真命题;命题③是真命题,所以它的逆否命题也是真命题.命题④是假命题,所以它的逆否命题也是假命题.【答案】 D9.【解析】 ∵0<x <π2, ∴0<sin x <1,由x ·sin x <1知x sin 2x <sin x <1,因此必要性成立.由x sin 2x <1得x sin x <1sin x ,而1sin x>1, 因此充分性不成立.【答案】 B10.【解析】 当a ,b ∈(0,+∞),且a +b =1时,1a +1b =(a +b )(1a +1b )=2+b a +a b≥4≠3, ∴p 为假命题.对∀x ∈R ,x 2-x +1=(x -12)2+34≥34≥0恒成立. ∴命题q 是真命题,∴綈p ∧綈q 是假命题.【答案】 B11.【解析】 ∵所给命题是特称命题,∴它的否定应为全称命题.【答案】 ∀x ∈R ,x ≠sin x12.【解析】 对于非零向量a ,b ,若a +b =0,则a =-b ,∴a ∥b .但a ∥b ,有a =λb (λ∈R),不一定有a +b =0,∴“a +b =0”是“a ∥b ”的充分不必要条件.【答案】 充分不必要13.【解析】 因为x ∉Q ,所以x ∈∁R Q ,∵Q ={x |-12≤x <72},∴∁R Q ={x |x <-12或x ≥72},则P -Q ={4}. 【答案】 {4}14.【解析】 由4-x >0,知A =(-∞,4).又B ={x |x <a },且“x ∈A ”是“x ∈B ”的充分不必要条件.∴A B ,∴a >4.【答案】 (4,+∞)15.【解】 (1)綈p :存在一个正数,它的对数不是正数.真命题.(2)綈p :∃x ∈Z ,x 2的个位数字等于3,假命题.16.【解】 A ={y |y <a 或y >a 2+1},B ={y |2≤y ≤4}.(1)当A ∩B =∅时,⎩⎨⎧ a 2+1≥4a ≤2, 所以a ≤-3或3≤a ≤2.(2)由x 2+1≥ax ,得x 2-ax +1≥0,依题意知,Δ=a 2-4≤0,则-2≤a ≤2,即a 的最小值为-2.当a =-2时,A ={y |y <-2或y >5},所以∁R A ={y |-2≤y ≤5},故(∁R A )∩B ={y |2≤y ≤4}.17.【解】 (1)∵f (x )=2[1-cos(π2+2x )]-23cos 2x -1 =2sin 2x -23cos 2x +1=4sin(2x -π3)+1. 又∵π4≤x ≤π2, ∴π6≤2x -π3≤2π3, 即3≤4sin(2x -π3)+1≤5, ∴f (x )max =5,f (x )min =3.(2)∵|f (x )-m |<2,∴m -2<f (x )<m +2.又∵p 是q 的充分条件,∴⎩⎨⎧m -2<3m +2>5,解之得3<m <5. 因此实数m 的取值范围是(3,5).18.【解】 由题意知a ≠0,若命题p 正确,由于a 2x 2+ax -2=(ax +2)(ax -1)=0.∴x =1a 或x =-2a. 若方程在[-1,1]上有解,满足-1≤1a ≤1或-1≤-2a≤1, 解之得a ≥1或a ≤-1.若q 正确,即只有一个实数x 满足x 2+2ax +2a ≤0.则有Δ=0,即a =0或2.若p 或q 是假命题.则p 和q 都是假命题,有⎩⎨⎧ -1<a <1,a ≠0且a ≠2.所以a 的取值范围是(-1,0)∪(0,1).19.【解】 由x 2-4ax +3a 2<0,且a <0.得3a <x <a .∴记p :对应集合A ={x |3a <x <a ,a <0}.又记B ={x |x 2-x -6≤0或x 2+2x -8>0}={x |x <-4或x ≥-2}.∵綈p 是綈q 的必要不充分条件,∴q 是p 的必要不充分条件.因此A B .∴a ≤-4或3a ≥-2(a <0),解之得-23≤a <0或a ≤-4. 20.【解】 命题甲:若直线x =y 与圆(x -a )2+y 2=1有公共点. 则|a -0|12+12≤1,-2≤a ≤ 2.命题乙:函数f (x )=2-|x +1|-a 的图象与x 轴有交点,等价于a =2-|x +1|有解. ∵|x +1|≥0,-|x +1|≤0,∴0<2-|x +1|≤1,因此0<a ≤1.∴命题乙⇒命题甲,但命题甲D ⇒/命题乙.故命题乙是命题甲的充分不必要条件.。
《课堂新坐标》高考数学一轮总复习课件:第二章 第六节 对数与对数函数(共39张PPT)

=(llgg 23+2llgg23)·(2llgg32+3llgg32)
=32llgg 23·56llgg 32=54.
高考体验·明
探究·提知能
课后作
菜单
新课标 ·文科数学(广东专用)
1.对数运算法则是在化为同底的情况下进行的,因 落实·固基础此经常用到换底公式及其推论;在对含字母的对数式化 高考体验·明
在(0,+∞)上为 ___增__函__数____
当0<x<1时,y>0; 当x>1时,___y_<__0__.
课后作
在(0,+∞)上为 ____减_函__数____
菜单
新课标 ·文科数学(广东专用)
4.反函数 指数函数y=ax(a>0且a≠1)与对数函数 __y_=__lo_g_a_x____(a 落实·固基>础 0且a≠1)互为反函数,它们的图象关于直线______y_=对x称.高考体验·明
|lg x| 落实·固基础-21x+6
0<x≤10,
x>10,
若 a、b、c 互不相等,且 f(a)=f(b高) 考体验·明
=f(c),则 abc 的取值范围是( )
A.(1,10)
B.(5,6)
C.(10,12)
D.(20,24)
【思路点拨】 (1)根据函数 y=ax2+bx 与 x
探究·提知能 轴的交点确定|ba|的范围.
【答案】 2
探究·提知能
课后作
菜单
新课标 ·文科数学(广东专用)
落实·固基础
(1)计算(1-log63)lo2g+64log62·log618; (2)计算(log32+log92)·(log43+log83).
高考体验·明
【思路点拨】 (1)根据乘法公式和对数运算性质进行计
课堂新坐标2013届高三数学(文)一轮复习6-4

课时知能训练一、选择题1.(2011·重庆高考)若函数f (x )=x +1x -2(x >2)在x =a 处取最小值,则a =( )A .1+2B .1+3C .3D .42.若M =a 2+4a(a ∈R ,a ≠0),则M 的取值范围为( ) A .(-∞,-4]∪[4,+∞) B .(-∞,-4]C .[4,+∞)D .[-4,4]3.(2011·上海高考)若a ,b ∈R ,且ab >0,则下列不等式中恒成立的是( )A .a 2+b 2>2abB .a +b ≥2abC.1a +1b >2abD.b a +a b ≥2 4.已知a >0,b >0,且ab =1,α=a +4a ,β=b +4b,则α+β的最小值为( ) A .8 B .9 C .10 D .125.已知x >0,y >0,x +2y +2xy =8,则x +2y 的最小值是( )A .3B .4 C.92 D.112二、填空题6.(2011·湖南高考)设x ,y ∈R ,且xy ≠0,则(x 2+1y 2)(1x24y 2)的最小值为________.7.若正数a ,b 满足1a +4b=2,则ab 的最小值为________. 8.若a >0,b >0,a +b =2,则下列不等式对一切满足条件的a ,b 恒成立的是________(写出所有正确命题的编号).①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④a 3+b 3≥3.三、解答题9.已知a ,b ,c 是正实数,求证:bc a +ac b +ab c≥a +b +c .10.求函数y =x 2+x +3x +1(x >-1)的值域. 11.某国际化妆品生产企业为了占有更多的市场份额,拟在2012年英国伦敦奥运会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量x 万件与年促销费t 万元之间满足3-x 与t +1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2012年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完.(1)将2012年的利润y (万元)表示为促销费t (万元)的函数.(2)该企业2012年的促销费投入多少万元时,企业的年利润最大?(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)答案及解析1.【解析】 ∵x >2,∴x -2>0,∴f (x )=x +1x -2=(x -2)+1x -2+2≥2 (x -2)·1x -2+2=4, 当且仅当x -2=1x -2(x >2),即x =3时等号成立, ∴a =3.【答案】 C2.【解析】 M =a 2+4a =a +4a, 当a >0时,M ≥4,当且仅当a =2时等号成立,当a <0时,M ≤-4,当且仅当a =-2时等号成立,故M 的取值范围是(-∞,-4]∪[4,+∞).【答案】 A3.【解析】 当a =b 时,a 2+b 2=2ab ,排除A ;当a <b ,b <0时,a +b<0<2ab ,1a +1b <0<2ab,排除B 、C ,选D.【答案】 D4.【解析】 α+β=(a +b )+4a +4b =(a +b )+4(a +b )ab=5(a +b )≥10ab =10,当且仅当a =b =1时等号成立.【答案】 C5.【解析】 ∵x +2y +2xy =8,∴y =8-x 2x +2>0, ∴-1<x <8,∴x +2y =x +2·8-x 2x +2=(x +1)+9x +12≥2 (x +1)·9x +1-2=4, 当且仅当x +1=9x +1时“=”成立,此时x =2,y =1. 【答案】 B6.【解析】 (x 2+1y 2)(1x 2+4y 2)=5+4x 2y 2+1x 2y2 ≥5+24x 2y 2·1x 2y 2=9, 当且仅当4x 2y 2=1x 2y 2,即|xy |=22时等号成立. 【答案】 97.【解析】 ∵a >0,b >0,∴1a +4b ≥2 1a ·4b =4 1ab , ∴4 1ab≤2,∴ab ≥4, 当且仅当1a =4b 且1a +4b=2时等号成立. 【答案】 48.【解析】 ab ≤(a +b )24=1,当且仅当a =b 时取等号,①对; (a +b )2=a +b +2ab =2+2 ab ≤4,当且仅当a =b 时取等号,得a +b ≤2,故②错误.由于a 2+b 22≥(a +b )24=1,故a 2+b 2≥2成立,故③正确. a 3+b 3=(a +b )(a 2+b 2-ab )=2(a 2+b 2-ab ),∵ab ≤1,又a 2+b 2≥2,∴a 2+b 2-ab ≥1,∴a 3+b 3≥2,故④错误.【答案】 ①③9.【证明】 ∵a ,b ,c 是正实数∴bc a +ac b≥2 bc a ·ac b =2c (当且仅当a =b 时取等号) ac b +ab c≥2 ac b ·ab c =2a (当且仅当b =c 时取等号) ab c +bc a ≥2 ab c ·bc a=2b (当且仅当a =c 时取等号) ∴2·(bc a +ac b +ab c)≥2a +2b +2c , 故bc a +ac b +ab c≥a +b +c . 10.【解】 y =x 2+x +3x +1=(x +1)2-(x +1)+3x +1=x +1+3x +1-1, 由x >-1,知x +1>0.∴(x +1)+3x +12(x +1)×3x +1=23, 当且仅当x +1=3x +1,即x =3-1时等号成立, ∴y ≥23-1,故函数的值域为[23-1,+∞).11.【解】 (1)由题意可设3-x =k t +1, 将t =0,x =1代入,得k =2.∴x =3-2t +1. 当年生产x 万件时,∵年生产成本=年生产费用+固定费用,∴年生产成本为32x +3=32(3-2t +1)+3. 当销售x (万件)时,年销售收入为150%[32(3-2t +1)+3]+12t . 由题意,生产x 万件化妆品正好销完,得年利润y =-t 2+98t +352(t +1)(t ≥0). (2)y =-t 2+98t +352(t +1)=50-(t +12+32t +1) ≤50-2t +12×32t +1=50-216=42(万元), 当且仅当t +12=32t +1,即t =7时,y max =42, ∴当促销费定在7万元时,年利润最大.。
课堂新坐标2013届高考数学一轮复习课件:第二章第六节 对数与对数函数(广东专用)

考
情
之间进行转化.
课 时 知 能 训 练
菜单
第十五页,编辑于星期日:二十点 十五分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
(1)化简 lg37+lg 70-lg 3- lg23-lg 9+1;
究 · 提
知
4
能
自 主
(2)计算:log3 327·log5[412log210-(3 3)23-7log72].
高 考 体
· 固 基
而抛物线对称轴|-2ba|<12,∴|ba|<1.
②
验 · 明
础
因此①、②矛盾.A、B 不正确.
考
对于 C 项,对称轴 x=-2ba<-12,|ba|>1.
体 验
固 基
∴a>c>b.
· 明
础
【答案】 B
考 情
课 时 知 能 训 练
菜单
第十一页,编辑于星期日:二十点 十五分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
究
·
提
4.计算(lg 14-lg 25)÷100-12=________.
知 能
自
主
高
落
考
实 ·
【解析】 原式=lg(14×215)÷(102)-12
体 验
固 基
=-2÷10-1=-20.
· 明
础
考
情
【答案】 -20
课
时
知
能
训
练
菜单
第十二页,编辑于星期日:二十点 十五分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
课堂新坐标2013届高考数学一轮复习课件:第五章第五节 数列的综合应用(广东专用)

典
第五节 数列的综合应用
例 探
究
·
提
知
能
自
高
主
考
落
体
实
验
·
·
固
明
基
考
础
情
课 时 知 能 训 练
菜单
第一页,编辑于星期日:二十点 十六分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
1.解答数列应用题的步骤
究
·
(1)审题——仔细阅读材料,认真理解题意.
典
例
探
银行储蓄单利公式及复利公式是什么模型?
究 ·
【提示】 单利公式——设本金为a元,每期利率为r,存期为n,则
提 知
能
本利和an=a(1+rn),属于等差模型.
自 主
复利公式——设本金为a元,每期利率为r,存期为n,则本利和an=a(1+
高 考
落 实
r)n,属于等比模型.
体 验
·
·
固
明
基
考
础
情
课 时 知 能 训 练
考 体
实 · 固
第 2 年投入为 800×(1-15)万元,…,
基 础
第 n 年投入为 800×(1-15)n-1万元,
验
· 明 考 情
所以,n 年内的总投入为
an=800+800×(1-15)+…+800×(1-15)n- 1
课 时
=4 000×[1-(45)n].
知 能 训
练
菜单
第十六页,编辑于星期日:二十点 十六分。
典
例
探
课堂新坐标2013届高考数学一轮复习课件:第五章第二节 等差数列(广东专用)

自 主 落 实
(2)通项公式:an=__a_1+__(_n_-__1_)d___.an=am+_(_n_-__m_)_d___. (3)前 n 项和公式:Sn=na1+nn-2 1d=na12+an.
· 固
a+b
高 考 体 验
· 明
基
(4)a、b 的等差中项 A=____2______.
础
考 情
课 时 知 能 训 练
∴a1n=-1+(n-1)×(-1)=-n,
· 明 考
础
∴an=-n1.
情
课 时 知 能 训 练
菜单
第十页,编辑于星期日:二十点 十六分。
一轮复习 ·新课标 ·数学(理)(广东专用)
(2)①∵an=
2-an1-
(n≥2,n∈N*),且
1
bn=an-1 1,
典 例 探
∴bn+
1-bn=an+
1 1-
练
菜单
第十八页,编辑于星期日:二十点 十六分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
究
·
提
知
能
(2)法一 由(1)知 Sn=32n-n2=-(n-16)2+256,
自 主 落
∴当 n=16 时,Sn有最大值,Sn的最大值是 256. 法二 由 Sn=32n-n2=n(32-n),
高 考 体
课 时 知 能 训 练
菜单
第十二页,编辑于星期日:二十点 十六分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
已知数列{an}的前 n 项和为 Sn,且满足 Sn=2SSn-n-1+1 1(n≥2),a1
探 究 ·
课堂新坐标2013届高考数学一轮复习课件:第二章第五节 指数与指数函数(广东专用)

究 ·
提
知
自
已知函数 y=(13)|x+1|.
能
主 落
(1)作出图象;
高 考
实 ·
(2)由图象指出其单调区间;
固
(3)由图象指出当 x 取什么值时函数有最值.
体 验 ·
基
明
础
考
情
课 时 知 能 训 练
菜单
第十四页,编辑于星期日:二十点 十五分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
【尝试解答】 (1)由已知可得
· 固 基
(2)原式=(-287)-23+(5100)-12- 51-0 2+1
验 · 明
础
=(-287)23+50012-10( 5+2)+1
考 情
=49+10 5-10 5-20+1=-1967.
课
时
知
能
训
练
菜单
第十一页,编辑于星期日:二十点 十五分。
一轮复习 ·新课标 ·数学(理)(广东专用)
知 能
自 主
式子n a叫___根__式_____
高
落
实 ·
(2)根式的性质:①(n a)n=__a__;
考 体 验
固
基 础
②n
a an=|a|=a-aa≥a0< 0
n为奇数, n为偶数;
· 明 考 情
课 时 知 能 训 练
菜单
第二页,编辑于星期日:二十点 十五分。
一轮复习 ·新课标 ·数学(理)(广东专用)
基
称变换得到其图象.
明
础
2.本题利用指数型函数的图象研究其性质化抽象为直观.
考 情
3.如果指数函数的底数含有参数,一般需分类讨论.
课堂新坐标2013届高考数学一轮复习课件:第五章第一节 数列的概念与简单表示法(广东专用)

一轮复习 ·新课标 ·数学(理)(广东专用)
网
典
络
例
构
探
建
1.(教材改编题)下列说法正确的是( )
· 览
A.数列 1,3,5,7 可表示为{1,3,5,7}
究 · 提
全 局
B.数列 0,2,4,6,…可记为{2n}
知 能
策 略 指 导
C.数列12,31,41,…n1,…的通项公式为 an=1n D.数列{n+n 1}的第 k 项为 1+1k
一轮复习 ·新课标 ·数学(理)(广东专用)
网
典
络 构
2.(2012·揭阳模拟)把1,3,6,10,15,21,…这些数叫做三角形数,这是
例 探
建
因为以这些数目的点可以排成一个正三角形(如图5-1-1).
·
究 ·
览
提
全
知
局
能
策 略 指 导
高 考 体 验
·
备
则第7个三角形数是( )
高
考
A.27
B.28
项数_有__限_____
考 情
项数__无__限____
an+1___>_____an
课 时
an+1___<_____an
其中n∈N*
知 能
训
an+1=an
练
第六页,编辑于星期日:二十点 十六分。
一轮复习 ·新课标 ·数学(理)(广东专用)
网
典
络 3.数列的通项公式
构
例 探
建 ·
如果数列{an}的第n项与________序__号_之n间的关系可以用一个式子来表示,
究 ·
览
那么这个公式叫做这个数列的通项公式.
课堂新坐标2013届高考数学一轮复习课件:第四章第五节 数系的扩充与复数的引入(广东专用)

典
例
探
若将复数 z 改为“z=1+i i”,且复数 z 与12+32i 分别在
究 · 提
知
复平面内对应点 Z 与 A,试求O→Z+O→A对应点的坐标(O 为原点).
能
自
主 落 实
【解】 ∵z=1+i i=i1-2 i=21+2i,
·
高 考 体 验
固 基 础
又 z 与12+32i 对应点 Z 和 A. 由复数及其加法的几何意义,
例 探 究
为 m+ni(m,n∈R)的形式,用纯虚数定义求 a 的值.
· 提
知
能
【尝试解答】 (1)因为(x-i)i=y+2i,所以 xi+1=y+2i.
自 主
又 x,y∈R,由复数相等的定义,
高
落 实
∴x=2,y=1;因此 x+yi=2+i.
考 体
· 固 基
(2)12+-aii=12+-aii·22++ii=2-a+52a+1i,
C.1-2i
D.1+2i
· 明
(2)(2011·安徽高考)设 i 是虚数单位,复数12+-aii为纯虚数,则
考 情
实数 a 为( )
A.2
B.-2
课 时
C.-21
1 D.2
知 能 训
练
菜单
第十页,编辑于星期日:二十点 十九分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
【思路点拨】 (1)由复数相等定义,求 x+yi;(2)将12+-aii化
高
落 实 ·
∴复数 z 对应的点的坐标为(35,-45),在第四象限.
考 体 验
固
·
基
明
础
【答案】 D
课堂新坐标2013届高考数学一轮复习课件:第五章第三节 等比数列(广东专用)

究 ·
y=0 上,则数列{an}的前 n 项和 Sn=________. (2)数列{an}的前 n 项和为 Sn,若 an+Sn=n,cn=an-1,求证:
提 知 能
数列{cn}是等比数列.
自
高
主
落
【解】 (1)由题意知 an- 2 an-1=0,
考 体
实 ·
∴an=2an- 1(n≥2),
验 ·
典
例
4.(2011·广东高考)已知{an}是递增的等比数列,a2=2,a4-a3=4,
探 究
则此数列的公比q=________.
· 提
知
【解析】 由a4-a3=4,得a2q2-a2q=4,即2q2-2q=4.
能
自 解得q=2或q=-1(舍).
高
主
考
落
体
实
验
· 固
【答案】 2
· 明
基
考
础
情
课 时 知 能 训 练
体 验 ·
固 基 础
=4n-1+4n1-1+2.因此 Tn=(1+4+…+4n-1)+(1+14+…+4n1-1)
明 考 情
+2n
=44n--11+11--4411n+2n=13(4n-41- n)+2n+ 1.,
课 时 知 能 训
练
菜单
第十六页,编辑于星期日:二十点 十六分。
一轮复习 ·新课标 ·数学(理)(广东专用)
明 考
础
论.此外在运算过程中,还应善于运用整体代换思想与化归思想
情
(如第(2)问).
课 时 知 能 训 练
菜单
第十七页,编辑于星期日:二十点 十六分。
一轮复习 ·新课标 ·数学(理)(广东专用)
