2017九下数学27.3圆中的计算问题(华师大共2份)全面版
九年级数学下册第27章圆27.3圆中的计算问题27.3.1弧长和扇形的面积练习华东师大版(2021

2018-2019学年九年级数学下册第27章圆27.3 圆中的计算问题27.3.1 弧长和扇形的面积同步练习(新版)华东师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年九年级数学下册第27章圆27.3 圆中的计算问题27.3.1 弧长和扇形的面积同步练习(新版)华东师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年九年级数学下册第27章圆27.3 圆中的计算问题27.3.1 弧长和扇形的面积同步练习(新版)华东师大版的全部内容。
27。
3 圆中的计算问题第1课时弧长和扇形的面积知|识|目|标1.通过计算特殊角度的圆心角所对的弧长,能推导并理解弧长公式.2.通过计算特殊角度的圆心角所对的扇形面积,能由特殊到一般地推导理解扇形面积公式.目标一能推导并理解弧长的计算公式例1 教材练习第1题针对训练(1)如图27-3-1,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则错误!的长为()图27-3-1A。
错误! B。
错误!C.错误! D。
错误!(2)教材补充例题若一个扇形的圆心角为60°,它的弧长为2π cm,则这个扇形的半径为( )A.6 cm B.12 cmC.2错误! cm D。
错误! cm【归纳总结】利用弧长公式进行计算的一般步骤:第一步:从问题中找出公式所涉及的三个量(弧长l、弧所对的圆心角n°、半径r)中的两个;第二步:把已知的两个量代入弧长公式;第三步:求出公式中的未知量.目标二能归纳并掌握扇形面积公式例2 (1)教材例1针对训练在圆心角为120°的扇形AOB中,半径OA=6 cm,则扇形AOB的面积是( )A.6π cm2 B.8π cm2C.12π cm2 D.24π cm2(2)教材补充例题已知扇形的半径为6 cm,面积为10π cm2,求该扇形的弧长.【归纳总结】扇形面积公式的选择:(1)当已知半径r和圆心角的度数求扇形的面积时,选用公式S=错误!;(2)当已知半径r和弧长l求扇形的面积时,选用公式S=错误!lr。
华东师大初中数学九下《27.3圆中的计算问题》word教案 (1)

27.3 实践与探索教材:华东师大版九年级下1.教学目标1)知识目标:①掌握如何将实际问题抽象出二次函数模型;②能运用函数关系中的对应法则并解释自变量取值范围的实际意义;③学会根据题意,合理建系,并准确标识题意;④能运用并合理解释二次函数模型。
2)能力目标:①数学思考能力:联系实际,感知数学与现实世界的密切联系,让学生经历数学建模过程,渗透数学建模思想,体会二次函数是刻画现实世界的有效数学模型。
②解决问题的能力:结合具体情境,发现并提出问题,并寻找解决问题的方法。
能与他人合作交流,并通过反思来体验解决问题策略的多样性,以此来获得解决问题的经验。
3)情感目标:了解数学理论的实用价值,提高学生对数学的好奇心和求知欲;增强学数学的自信心,同时借助题目中丰富的背景知识来充实自己的精神世界,形成良好的个性品质。
2.教学重点——建立并合理解释数学模型3.教学难点——实际问题数学化过程4.教学过程1)教学思路实际问题的提出,说明引入二次函数模型的必要性。
——体现构建二次函数数学模型解决实际问题的思想——通过丰富的问题情景,形成用二次函数解决实际问题的一般性策略和方法。
——合理解释相应的数学模型2)教学环节分析环节一:抛砖引玉,点明主旨环节二:自主探索,实践新知环节三:拓展转化,加深理解环节四:合作探索,学以致用环节五:反思小结,形成新知环节六:布置作业,巩固新知用活几1)喷出的水流距水平面的最大高度是多少?2) 如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?(x-2最大高度为-教榜样启发、同伴启发在三份获奖作品中任选一份,模仿问题计题。
反思和发表对本堂课时,测得涵洞顶点与水面的距离为2.4m离开3)一只宽为1m,高为1.5m的小船能否通过?为什么?让学生充分探究各种AE D学§27.3 二次函数的实践与探索 课堂卷例1:某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A 处安装一个喷头向外喷水。
【最新】华师大版九年级数学下册第二十七章《圆中的计算问题》公开课课件 (2).ppt

D B
度AB=40m,拱形的半
径R=29m,求拱形的高.
O
1
倍 速 课
解:如图:由垂径定理得:BD= AB=20m 2
在直角三角形BOD中: OD2 =OB2 - BD2
时
学 OD2 =292 - 202 OD=21 m
练
所以拱形的高CD=29-
一、弧长的计算公式
l n 2r nr
360
180
速 课
长是_________;____
时 学 练
答案: 23
2s
240°,
36
r
例题讲解
例1 如图23.3.5,圆心角为60°的扇形的半径为 10厘米,求这个扇形的面积和周长.(π≈3.14)
解:因为n=60°,r=10厘米,所以扇形面积为
Snr2 603.14102 ≈52.33(平方厘米);
360 360
• 10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 4:50:53 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/162020/12/162020/12/16Dec-2016-Dec-20 • 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/162020/12/162020/12/16Wednesday, December 16, 2020 • 13、志不立,天下无可成之事。2020/12/162020/12/162020/12/162020/12/1612/16/2020
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
华东师大版初中九年级下册数学精品授课课件 第27章 圆 27.3 圆中的计算问题 习题27.3

解:由题意,得2πr圆柱=a,2πr圆锥底= 90 2πr a ,
a
360
所以 r圆柱 = 2π 2 , r圆锥底 1 a π 4
∴该圆柱与圆锥两者的底面半径之比为 2 .
π
4.如果两个扇形的圆心角相等,大扇形的半径是小扇形半 径的2倍,那么大扇形的面积是小扇形面积的多少倍?
解:设小扇形半径为r,则大扇形的半径为2r.由题意,得
即分针在钟面扫过的面积为26.18cm2.
2.火车机车上主动轮的直径为1.2m,如果主动轮每分钟转 400圈,那么火车每小时行多少千米?(精确到0.1km)
解:由题意,得 60×400×1.2π= 28800π(m)=28.8π(km)≈90.5km 即火车每小时行90.5km.
3.将一个边长为a的正方形纸片卷起来,恰好可以围住一个 圆柱的侧面;又在这个正方形纸片上剪下最大的一个扇形, 卷起来,恰好可以围住一个圆锥的侧面.那么该圆柱与圆锥 两者的底面半径之比为多少?(结果保留π)
nπ2r2 nπr2
=4. 360 360
∴大扇形的面积是小扇形的面积的4倍.
华东师大版·九年级下册
习题27.3
1.钟面上分针的长为5cm,经过20min,分针在钟面上扫过 的面积是多少平方厘米?(精确到0.01cm2)
解:如图,20分钟即分针从OA转到OB的位置,圆心角 ∠AOB=4×30° = 120°,
∴S扇形= nπr2 = 120 π 52 = 25π 26.18 cm2 . 360 360 3
27.3 圆中的计算问题 华东师大版九年级数学下册同步练习(含答案)
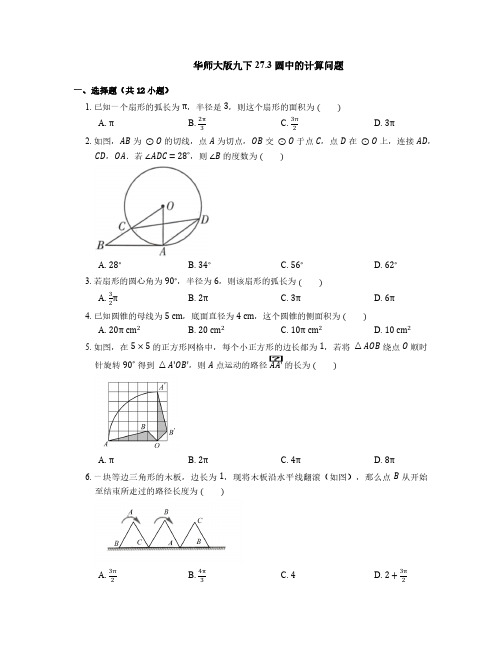
华师大版九下 27.3 圆中的计算问题一、选择题(共12小题)1. 已知一个扇形的弧长为 π,半径是 3,则这个扇形的面积为 ( )A. πB. 2π3C. 3π2D. 3π2. 如图,AB 为 ⊙O 的切线,点 A 为切点,OB 交 ⊙O 于点 C ,点 D 在 ⊙O 上,连接 AD ,CD ,OA .若 ∠ADC =28∘,则 ∠B 的度数为 ( )A. 28∘B. 34∘C. 56∘D. 62∘ 3. 若扇形的圆心角为 90∘,半径为 6,则该扇形的弧长为 ( )A. 32πB. 2πC. 3πD. 6π4. 已知圆锥的母线为 5 cm ,底面直径为 4 cm ,这个圆锥的侧面积为 ( )A. 20π cm 2 B. 20 cm 2 C. 10π cm 2 D. 10 cm 25. 如图,在 5×5 的正方形网格中,每个小正方形的边长都为 1,若将 △AOB 绕点 O 顺时针旋转 90∘ 得到 △AʹOBʹ,则 A 点运动的路径 AAʹ 的长为 ( )A. πB. 2πC. 4πD. 8π6. 一块等边三角形的木板,边长为 1,现将木板沿水平线翻滚(如图),那么点 B 从开始至结束所走过的路径长度为 ( )A. 3π2B. 4π3C. 4D. 2+3π27. 如图,AB 为 ⊙O 的直径,AB =30,点 C 在 ⊙O 上,∠A =24∘,则 AC 的长为 ( )A. 9πB. 10πC. 11πD. 12π8. 如图所示,草地上一根长 5 米的绳子,一端拴在墙角的木桩上,另一端栓着一只小羊 R .那么,小羊在草地上的最大活动区域的面积是 ( )A. 132π m 2B. 274π m 2C. 132π m 2D. 274π m 29. 如图,半径为 10 的扇形 AOB 中,∠AOB =90∘,C 为 AB 上一点,CD ⊥OA ,CE ⊥OB ,垂足分别为 D ,E .若 ∠CDE 为 36∘,则图中阴影部分的面积为 ( )A. 10πB. 9πC. 8πD. 6π10. 如图,线段 AB 经过 ⊙O 的圆心,AC ,BD 分别与 ⊙O 相切于点 C ,D ,若AC =BD =4,∠A =45∘,则 CD 的长度为 ( )A. πB. 2πC. 22πD. 4π11. 如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积是( )A. 4π―4B. 4π―8C. 8π―4D. 8π―812. 如图,在Rt△ABC中,∠C=90∘,∠B=30∘,AC=1,以A为圆心,AC为半径画圆,交AB于点D,则阴影部分面积是( )A. 32―π3B. 32―π6C. 3―π6D. 23―π二、填空题(共6小题)13. 如图,图中阴影部分的面积等于.14. 如图,将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为.15. 已知圆锥的底面半径为2 cm,侧面积为10π cm2,则该圆锥的母线长为cm. cm2,则这个扇形的弧长为cm(结果保16. 若一个扇形的圆心角为60∘,面积为π6留π).17. 如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE,若∠A=65∘,则∠DOE=.18. 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心、AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为.三、解答题(共7小题)19. 若120∘的圆心角所对的弧长是12π cm,则此弧所在圆的半径为多少cm?20. 如果圆的直径d=8 cm,那么圆心角为90∘的扇形面积是多少?21. 如图,大正方形ABCD与小正方形BEFH并排放在一起,已知大正方形的边长是6,以点B为圆心,边AB长为半径画圆弧,连接AF,CF.(1)计算:(1)当小正方形边长是2,求阴影部分的面积;(2)当小正方形边长是3,求阴影部分的面积.(2)探究:由上述计算,你感到阴影部分的面积与小正方形边长有关吗?请说明理由.22. 如图,正方形的边长为2,以各边为直径在正方形内画半圆,求所围成的图形(阴影部分)的面积.23. 一支手枪的有效射程是300米,如果在90∘范围内射击,则它的控制面积是多少平方米?24. 如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(AB)对应的圆心角(∠AOB)为120∘,OC的长为2 cm,求三角板和量角器重叠部分的面积.25. 如图,在△ABC中,∠C=90∘,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,求⊙O的半径.答案一选择题1. C【解析】扇形面积为S=nπr2360,弧长公式为l=nπr180,∴S=12lr,∵l=π,r=3,∴S=3π2.2. B3. C【解析】该扇形的弧长=90×π×6180=3π.4. C5. B6. B7. C【解析】如图,连接OC,∵OA=OC,∴∠OCA=∠A=24∘,∴∠AOC=180∘―24∘×2=132∘,∴AC的长=132π×5180=11π.故选C.8. B【解析】S=90π×52360+2×90π×12360=274π m2.9. A【解析】连接OC交DE为F点,如下图所示:由已知得:四边形 DCEO 为矩形,∵∠CDE =36∘,且 FD =FO ,∴∠FOD =∠FDO =54∘,△DCE 面积等于 △DCO 面积, S 阴影=S 扇形AOB ―S 扇形AOC =90⋅π⋅102360―54⋅π⋅102360=10π.10. B【解析】如图,连接 OC ,OD ,∵AC ,BD 分别与 ⊙O 相切于 C ,D ,∴OC ⊥AC ,OD ⊥BD ,∵∠A =45∘,∴∠AOC =45∘,∴AC =OC =4,∵AC =BD =4,OC =OD =4,∴OD =BD ,∴∠BOD =45∘,∴∠COD =180∘―45∘―45∘=90∘,∴CD 的长度为90π×4180=2π.11. A【解析】利用对称性可知,S 阴影=S 扇形EAF ―S △ABD =90×π×42360―12×4×2=4π―4.12. B【解析】在 Rt △ACB 中,∠ACB =90∘,∠B =30∘,AC =1, ∴BC =3AC =3,∠A =60∘,∴S △ABC =12AC ⋅BC =12×1×3=32, S 扇形ACD =60∘π×12360=16π,∴S 阴影部分=S △ABC ―S 扇形ACD =32―π6.二 填空题13. 1.1414. 36【解析】∵ 正方形的边长为 6,∴ 弧 BD 的弧长 =6+6=12,∴S 扇形ABD =12lr =12×12×6=36.15. 516. π3【解析】设扇形的半径为 r cm ,则60πr 2360=π6.解得 r =1(cm) 或 r =―1(cm)(不符题意,舍去).则这个扇形的弧长为60π×1180=π3(cm).17. 50∘18. 9三 解答题19. 由题意得 120πr180=12π,解得 r =18.20. 12.56 cm 221. (1) (1)28.26.(2)28.26.(2) 无关(理由略).22. 2.28.23. 70650 平方米.24. 因为 ∠AOB =120∘,所以 ∠BOC =60∘.在 Rt △OBC 中,OC =2 cm ,∠BOC =60∘,所以 ∠OBC =30∘.所以 OB =4 cm ,BC =23 cm .则 S 扇形OAB =120π×42360=16π3(cm 2), S △OBC =12OC ×BC =23(cm 2).故 S 重叠=S 扇形OAB +S △OBC =+2) .25. ∵BP =2⋅BC =62,设半径为 r ,OP =2r .∴BO=BP―OP,而BO2=OE2+BE2,而AE=FA=PA+FP=2+r,∴(BP―OP)2=OE2+(BA―EA)2,即:(62―r2)2=r2+[10―(2+r)]2,∴r=1.提示:过点O分别作OE⊥AB,OF⊥AC,⊙O的半径为1.。
九年级下册数学课件(华师版)圆中的计算问题

知识要点
弧长公式
l n 2 R n R
360
180
注意 用弧长公式 l n R ,进行计算时,要注意公式中n的
180
意义.n表示1°圆心角的倍数,它是不带单位的.
算一算 已知弧所对的圆心角为60°,半径是4,则弧 长为__43__.
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下 料,试计算图所示管道的展直长度l.(单位:mm,精确到1mm)
则整个旋转过程中线段OH所扫过的面积为 (C )
A1
A.
7 3
7 8
C.
3
B.
4 3
7 8
3
D. 4 3 3
H
A
O
C
O1 H1
B
C1
3.如图,☉A、☉B、 ☉C、 ☉D两两不相交,且半径都是2cm,
则图中阴影部分的面积是12cm2 .
C B
A
D
4.(例题变式题)如图、水平放置的圆柱形排水管道的截面 半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
.
3
3.已知扇形的圆心角为120°,半径为2,则这个扇形的
面积S扇=
4 3
.
例2 如图,圆心角为60°的扇形的半径为10cm.求这个扇形的 面积和周长.(精确到0.01cm2和0.01cm)
解:∵n=60,r=10cm,
∴扇形的面积为
S = n r2 = 60 102 = 50 52.36(cm2 ).
扇形.
B B
弧 圆心角 O
A
扇形 O
A
判一判
下列图形是扇形吗?
想一想
问题1 半径为R的圆,面积是多少?
华师大版九年级数学下册第二十七章《圆中的计算问题》优课件 (2)

2、扇形的面积是它所在圆的面积的 ,这个扇
形的圆心角的度数是_________°. 3
3、扇形的面积是S,它的半径是r,这个扇形的弧 长是_________;____
答案: 23 36
2s 240°, r
例题讲解
例1 如图23.3.5,圆心角为60°的扇形的半径为 10厘米,求这个扇形的面积和周长.(π≈3.14)
(精确到 m20).1.c
解:∵n=1200,r=12厘米 ∴弧AB为 l nr
180
120 3.1412
25.12 25.1cm
180
∴扇形AOB面积为
s
1
lr
1 25.1212
22
=150.72 15.07cm2
下面是圆弧形桥拱,其每拱的跨度为40m,拱形 的半径为29m,求拱形的高.
C
90 2r
360
45 2r
360
n 2r
360
结论:
如果弧长为l,圆心角度数为n,圆的半径为r,那
么,弧长的计算公式为:
l n 2r nr
练一练:
360
180
已知圆弧的半径为50厘米,圆心角为60°,求此
圆弧的长度。
解:l n 2r nr
360
18答0 :此圆弧的长度为50 cm
=
50 3
cm
3
扇形: 如图,由组成圆心角的两条半径
和圆心角所对的弧所围成的图形 叫扇形.
Q
l
扇形面积S
n° Or
怎样计算圆心角是n0 的扇形面积?
圆心角占整个周角的 所对扇形面积是
1800
180
360
180 r 2
360
【数学课件】2017九下数学27.3圆中的计算问题(华师大共2份)(2)

好好学习,天天向上。
圆柱的侧面积=圆柱的高×底面圆周长 圆柱的全面积=侧面积+两个底面积
圆锥及侧面展开图的相关概念
圆锥的侧面积和全面积
圆锥的侧面积就是弧长为圆锥底面的周 长、半径为圆锥的一条母线的长的扇形面 积. 圆锥的全面积=圆锥的侧面积+底面积.
P a r
h A O
B
圆锥的侧面积和全面积 如图:设圆锥的母线长为a,底面 半径为r.则圆锥的侧面积 P 公式为:
S侧 1 2r a. 2
l 2r
= ra
h A O r
a B
全面积公式为:
S全 S侧 S底
= πra +2πr
例1、根据圆锥的下列条件, 求它的侧面积和全面积 ( 1)
( 2)
r=12cm, a=20cm
h=12cm, r=5cm
图 23.3.6
例2.一个圆锥形零件的高4cm,底面 半径3cm,求这个圆锥形零件的侧面积 和全面积。
2
填空、根据下列条件求值(其中r、h、a 分别是圆锥的底面半径、高线、母线长) (1)a = 2, r=1 则 h=_______
(2) h = 3,
r=4 则 a=_______
则 r=_______
(3) a = 10, h=8
驶向胜 利的彼 岸
圆柱侧面展开图
圆柱的侧面展开图是一个矩 形,它的一边长是圆柱的高; 它的另一边长是圆柱的底面 圆周长
PhLeabharlann aAOr
B
童心玩具厂欲生产一种圣诞老人的帽子,其 圆锥形帽身的母线长为15cm,底面半径为5cm, 生产这种帽身10000个,你能帮玩具厂算一算 至少需多少平方米的材料吗(不计接缝用料和 余料,π取3.14 )? 解:∵ a=15cm,r =5cm, ∴S 侧 =πra 3.14×15×5 = 235.5(cm 2 )
九年级数学下册 27.3 圆中的计算问题同步练习题 华东师大版(2021学年)

2017年九年级数学下册27.3 圆中的计算问题同步练习题(新版)华东师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年九年级数学下册27.3 圆中的计算问题同步练习题(新版)华东师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年九年级数学下册27.3圆中的计算问题同步练习题(新版)华东师大版的全部内容。
27.3圆中的计算问题练习题一.选择题(共8小题)1.一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )A.cm B.cmﻩC.3cmﻩD.cm2.圆心角为120°,弧长为12π的扇形半径为()A.6 B.9C.18ﻩD.363.已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是( )A.10cm2B.5π cm2ﻩC.10πcm2D.20πcm24.一个扇形的半径为8cm,弧长为cm,则扇形的圆心角为( )A.60°B.120°ﻩC.150°ﻩD.180°5.已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是()A.30°B.60°ﻩC.90°ﻩD.180°6.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为()A.10cm2 B.10πcm2ﻩC.20cm2ﻩD.20πcm27.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为( )A.9cmB.12cm C.15cm D.18cm8.如图是一个几何体的三视图,则这个几何体的侧面积是( )A.πcm2B.2πcm2ﻩC.6πcm2D.3πcm2二.填空题(共6小题)9.若扇形的圆心角为60°,弧长为2π,则扇形的半径为_______.10.一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为_________ .11.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是_________ cm2.(结果保留π)12.圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数为________ 度.13.半径为4cm,圆心角为60°的扇形的面积为_________ cm2.14.如图,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是__ _______ .三.解答题(共8小题)15.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,求图中阴影部分的面积.16.如图所示,在⊙O中,=,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. (1)求证:AC2=AB•AF;(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.17.在△ABC中,∠C=90°,∠A=30°,BC=3.(1)将△ABC绕AB所在的直线旋转一周,求所得几何体的侧面积;(2)折叠△ABC,使BC边与CA边重合,求折痕长和重叠部分的面积.18..如图,圆锥底面的半径为10cm,高为10cm.(1)求圆锥的全面积;(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.19.如图,一个圆锥的高为cm,侧面展开图是半圆.求:(1)圆锥的母线长与底面半径之比;(2)求∠BAC的度数;(3)圆锥的侧面积(结果保留π).答案:1.A 2.C 3.C4.D5。
九年级数学 圆中的计算问题华东师大版知识精讲

九年级数学 圆中的计算问题华东师大版【本讲教育信息】一. 教学内容:§28.3 圆中的计算问题二. 重点、难点: 1. 重点:⑴弧长和扇形的面积; ⑵圆锥的侧面积和全面积 2. 难点:弧长和扇形面积公式的推导三. 知识梳理:(一)弧长和扇形的面积 1. 弧长的计算公式如果弧长为l ,圆心角度数为n ,圆的半径为r ,那么,弧长的计算公式为:2360180n n rl r ππ=⋅=. 2. 扇形的面积公式如果设圆心角是n °的扇形面积为S ,圆的半径为r ,那么扇形面积为213602n r S S lr π==或 说明:⑴对于弧长公式和扇形面积公式,无须死记硬背,应在明确其“来历”的基础上理解掌握.⑵在应用弧长公式180n rl π=或扇形面积公式2360n r S π=进行计算时,要注意公式中的n的意义,n 表示1°的圆心角的倍数,因此不带单位.⑶扇形的另一个面积公式12S lr =与三角形的面积公式有些类似.形式基本一样,可以联系起来记忆.(二)圆锥的侧面积和全面积如图,我们把圆锥底面圆周上任意一点与圆锥顶点的连线叫做圆锥的母线.连结顶点与底面圆心的线段叫做圆锥的高.如图,沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长.圆锥的侧面积就是弧长为圆锥底面的周长、半径为圆锥的一条母线的长的扇形面积,而圆锥的全面积就是它的侧面积与它的底面积的和.说明:⑴研究圆锥的侧面积和全面积,必须先将其展开.圆锥的侧面展开图是扇形,这个扇形的半径是圆锥的母线长,弧长是圆锥底面圆的周长.⑵若设圆锥的母线长为l ,底面半径为r ,则圆锥的侧面积就是其展开图——扇形的面积,122r l rl ππ⋅⋅=S=;圆锥的全面积是侧面积与底面积的和,是2rl r ππ+.另外,知道扇形的半径和弧长,还可以求得扇形的圆心角.【典型例题】例1. 如图,一块长为8的正方形木板ABCD ,在水平桌面上绕点A 按逆时针方向旋转到ADEF 的位置,则顶点C 从开始到结束所经过的路径长为( )A. 16 ;B. 162 ;C. 8π ;D. 42π分析:在旋转过程中,AC 的长度保持不变,所以顶点C 从开始到结束所经过的路径长是以A 为圆心,AC 长为半径的90°的弧长,因为AC =82,所以,ππ241802890=⋅⋅=l ,故选D .例2. 如图,⊙A 、⊙B 、⊙C 、⊙D 互相外离,它们的半径都是1,顺次连结四个圆心得到四边形ABCD ,则图中四边形内的四个扇形面积之和为( )A. 2π;B.π;C.32π ; D. 21π分析:根据题中的条件无法求出四个扇形的圆心角的度数,因而从整体考虑,可以发现四个扇形的圆心角分别是四边形的四个内角,所以四个扇形的圆心角的度数之和为360°,故选B .例3. 如图,如果圆锥的底面圆的半径是8,母线长是15,那么这个圆锥侧面展开图的扇形的圆心角的度数是 .分析:由圆锥的底面圆的半径是8,可以求出底面圆的周长,也就是扇形CAB 的弧长,再利用弧长公式2360180n n rl r ππ=⋅=即可求扇形的圆心角的度数. 解:∵圆锥底面圆的半径是8,∴BC l r C ==⋅=ππ162 ∵母线长为15∵180Rn l BC ⌒π=∴1801516⋅=ππn 192=n∴圆心角的度数为192°.例4. 如图,一把纸扇完全打开后,外侧两竹条AB 和AC 的夹角为120°,AB 长为25cm ,贴纸部分的宽BD 为17cm ,则贴纸部分的面积为_______.(结果保留π)分析:扇形面积公式有两个,一是2360n r S π=,另一个是12S lr =,贴纸部分的面积实际是由两个扇形的面积相减所得.由解意很容易列出关于所求贴纸部分的面积:2212025120(2517)360360ππ⋅⋅⋅⋅--=187π(cm 2).例5. 如图1,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图2所示的一个圆锥模型.设圆的半径为r ,扇形半径为R ,则圆的半径与扇形半径之间的关系为A. R =2rB. R =94r C. R =3r D. R =4r分析:注意题中的“底面圆的半径”与“扇形的半径”是两个不同的概念.要找到圆的半径与扇形半径之间的关系,需要得到一个等量关系,由圆锥的有关概念,根据圆锥底面圆的周长等于扇形的弧长,可得2πr =90180πR∴R =4r ∴答案选D例6. 如图所示,半径是10cm 的圆纸片,剪去一个圆心角是120°的扇形(图中阴影部分),用剩下部分围成一圆锥,求圆锥的高和底面圆的半径.分析:首先,根据题意画出圆锥体的示意图,从图中可知,要求圆锥的底面圆的半径需求出其所在圆的周长,而底面圆的周长为左图中剩下扇形的弧长,这样转化到求弧长的问题;关于圆锥的高,只要由底面半径与圆锥的母线长构造直角三角形即可.解:如答图中的甲、乙图,∵n =360°-120°=240°,R =10cm ,如图(甲)所示,24010401801803OAmB n r l πππ⨯===扇形(cm ) 如图乙中连结O ′P ,则O ′P ⊥CD ,设⊙O ′半径为r , ∵'',2OAmB O O C l C r π==扇形,∴4023r ππ=,∴r =203(cm ) ∴ O ′P =22'22201010533PD O D ⎛⎫-=-=⎪⎝⎭(cm )例7. 已知矩形ABCD 中,AB =1cm ,BC =2cm ,以B 为圆心,BC 长为半径作41圆弧交AD 于F ,交BA 的延长线于E ,求阴影部分面积.分析:要求阴影部分面积,只须将它转化为求规则图形的面积的和差,故需连结BF ,ABF BFE S S S △扇形阴-=解:连结BF∵BC =2,F 点在以B 为圆心,BC 为半径的圆上 ∴BF =2∵矩形ABCD ,AB =1,BF =2 ∴∠ABF =60° ∴ππ323602602=⋅⋅=BFES 扇形3BA BF AF ,BAF Rt 22=-=∆中231321=⨯⨯=ABF S △∴ABF BFE S S S △扇形阴-= =2cm )2332(-π 答:阴影部分面积为2cm )2332(-π.例8. 如图已知圆锥的底面半径r =10cm ,母线长为40cm .⑴求它的侧面展开图的圆心角和表面积;⑵若一只甲虫从A 点出发沿着圆锥侧面绕行到母线SA 的中点B ,它所走的最短路程是多少?SAB分析:⑴把圆锥的侧面沿母线SA 展开,如图 则⋂'AA 的长为2πr =20π,SA =40 所以20π=40180n π⋅所以n =90°所以圆锥的侧面展开图的圆心角是90°S 表面=S 侧+S 底=29040360π⋅+π·102=500π(cm 2)⑵由圆锥的侧面展开图可见,甲虫从A 点出发沿着圆锥侧面绕行到母线SA 的中点B 所走的最短路程是线段AB 的长在Rt △ASB 中,∠ASB =90°,SA =40,SB =20所以AB =22SA +SB =205cm答:圆锥的侧面展开图的圆心角是90°,圆锥的表面积是500π2cm ,甲虫所走的最短路程长205cm .例9. 如图,扇形OAB 的圆心角为90°,分别以OA 、OB 为直径在扇形内作半圆,P 和Q 分别表示两个封闭图形的面积,那么P 和Q 的大小关系是( )A. P =Q ;B. P >Q ;C. P <Q ;D. 无法确定.分析:本题中两个封闭图形的面积不易直接求,可用代数方法来求,根据图形的对称性,另两个封闭图形的面积相等,不妨设为M ,再设OA =2r ,由图形可得M +Q =221r ⋅π,2M +P +Q =2r ⋅π,解得P =Q ,故选A .[方法探究]在一个问题不能直接解决的情况下,就要善于从另一个角度来寻找其它的途径.本题是通过设未知数,把几何问题转化为代数问题,即通过方程思想,使问题迎刃而解.例10. 如图,秋千拉绳长AB 为3米,静止时踩板离地面0.5米,某小朋友荡该秋千时,秋千在最高处时踩板离地面2米(左右对称),请计算该秋千所荡过的圆弧长(精确到0.1米)?解析:由题意要求圆弧BF 的长,只要求得圆心角∠BAF 的度数即可,根据左右对称,所以将∠BAC 置于一个直角三角形中来计算其度数.过点B 作BE ⊥地面于点E ,作BG ⊥AD 于点G ,则有GD =BE =2,又AD =AC +CD =3.5,所以AG =1.5,则在Rt ΔABG 中,AB =3,AG =1.5,所以∠BAC =60°,所以∠BAF =120°.则弧BF 的长=1203180π⋅⋅=2π≈6.3(米).例11. 如图是某学校田径体育场一部分的示意图,第一条跑道每圈为400米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与同心的半圆型,弯道与直道相连接.已知直道BC 的长为86.96米,跑道的宽为1米(π=3.14,结果精确到0.01米) ⑴求第一条跑道的弯道部分⋂AB 的半径;⑵求一圈中第二条跑道比第一条跑道长多少米?⑶若进行200米比赛,求第六道的起点F 与圆心O 的连线FO 与OA 的夹角∠FOA 的度数.解析:⑴弯道的半圆周长为400286.962-⨯=113.04(米),由圆周长L =2πr ,所以半圆弧线长'l r π=,则第一道弯道部分的半径r ='113.043.14l π==36.00(米)⑵第二道与第一道的直跑道长相等,第二道与第一道的弯跑道的半径之差为1米,第二道与第一道的弯跑道长的差即为两圆周长之差,即2π(r +1)-2πr =2π=6.28(米).⑶从第一道200米,是以A 点为始点,第六道上的运动员需要跑86.96米的直道和113.04米的弯道,即弧长为113.04米,又第六道弯道半圆的半径为41米, 由弧长与半圆、圆心角的关系得n =,所以∠FOA =180°°°.【模拟试题】(答题时间:30分钟)1. 一个扇形的弧长是20πcm ,面积是240π2cm ,则扇形的半径是( )A. 6cmB. 21cmC. 24 cmD. 62 cm2. 一个圆锥的侧面积是底面积的3倍,这个圆锥的侧面展开图的圆心角是( ) A. 60° B. 90° C. 120° D. 180°3. 底面圆半径为3cm ,高为4cm 的圆锥侧面积是( )A. 7. 5π2cmB. 12π2cmC. 15π2cmD. 24π2cm4. 扇形的半径OA =20cm ,∠AOB =135 ,用它做成一个圆锥的侧面,此圆锥底面的半径是( )A. B. C. 15cm D. 30cm5. 如图,⊙A ,⊙B ,⊙C 两两不相交,且半径都是,则圆中的三个扇形即(三个阴影部分)的面积之和为( )A.12π2cm B.8π2cm C. 6π2cm D.4π2cm6. 一个圆锥的底面积是25π2cm ,母线长13cm ,则这个圆锥的侧面积是 .7. 一个圆锥的侧面展开图是一个面积为8π的半圆,则这个圆锥的全面积是________. 8. 如图所示,已知⊙1O 内切于扇形AOB ,切点为C 、D 、E ,⊙1O 的面积为16π,∠AOB =60°,求扇形AOB 的周长和面积.9. 如图所示是一管道的横截面示意图,某工厂想测量管道横截面的面积,工人师傅使钢尺与管道内圆相切并交外圆于A 、B 两点,测量结果为AB =30cm , 求管道阴影部分的面积为多少?【试题答案】1. C2. C3. C4. B5. B6. 65π2cm7.12π8. 24π提示:连结O 1C ,OO 1并延长OO 1,则必过切点E ,设⊙O 1的半径为r ∴1O S 圆21,16r S O ππ==圆,∴216r ππ=,r =4, ∴O 1C =4, ∵OA ,OB 切圆1O 于C ,D ,∠AOB =60°, ∴∠AOE =30° ∵∠COO 1=30°,O 1C =4,∴O 1O =8, ∴R =OE =OO 1+O 1E =8+4=12 ∴24412242,41801260+=⨯+=+==⨯=⋂⋂ππππr l l lAOB OAB AOB扇形∴224360OABn R S ππ==扇形. 9. 解:设钢尺AB 与管道内圆相切于C 点,连结OC 、OA ,则OC ⊥AB ,设OC =r ,OA =R ,∵AB =30cm ,OC ⊥AB ,∴AC =152AB=, ∴222222()15225S OA OC R r AC ππππππ=⋅-⋅=-=⨯=⨯=阴影(cm 2)。
九年级数学下册27.3圆中的计算问题(一)教案(新版)华东师大版

27.3圆中的计算问题(一)教学内容:课本P58~61教学目标:1、掌握扇形的弧长和面积计算公式;会用公式求阴影部分的面积;2、对图形进行正确的切分,综合运用所学知识进行计算;教学重难点重点:掌握扇形的弧长和面积计算公式;会用公式求阴影部分的面积;难点:对图形进行正确的切分,综合运用所学知识进行计算;教学准备:课件教学方法:讲授法教学过程:一、引入100m,圆心角为90°, 1、提出问题:如图是圆弧形状的铁轨示意图,其中铁轨的半径为你能求出这段铁轨的长度吗?(精确到0.1m)2、学生回答后,老师总结:我们容易石岀这段铁轨址圆周的j,所以,挟轨的氏度2二$ * "舱二50TT“ 15X08(卷}.43、提出新的问题:如果圆心角是任意的角度,如何计算它所对的弧长呢?二、思考与探索1、思考:如图,各圆心解所对的弧长分别是圆周长的几分之几?2、探索180(1 )圆心角是180°,占整个周角的180,因此它所对的弧长是圆周长的36090(2)圆心角是90°,占整个周角的上0,因此它所对的弧长是圆周长的360(3)圆心角是45°,占整个周角的 _____________ ,因此它所对的弧长是圆周长的 _____________ ;(4 )圆心角是1°,占整个周角的________________ ,因此它所对的弧长是圆周长的 _____________ ;(5)圆心角是n°,占整个周角的________________ ,因此它所对的弧长是圆周长的 _____________ ;3、教师总结如果弧长为I,圆心角的度数为n,圆的半径为r,那么,弧长为因此弧长的计算公式为I =4、提出问题扇形的面积与组成扇形的弧所对的圆心角的大小有关。
圆心角越大,扇形的面积也越大。
怎样计算圆心角为n的扇形的面积呢?三、思考与探索扇形的面积1、思考:如下图所示的各扇形面积分别是圆面积的几分之几?2、探索180(1 )圆心角是180°,占整个周角的180,因此圆心角是180°的扇形面积是圆面积360的______________ ;90(2)圆心角是90°,占整个周角的上0,因此圆心角是90°的扇形面积是圆面积360的______________ ;(3)________________________________________ 圆心角是45°,占整个周角的,因此圆心角是45。
华师大版九年级数学下册第二十七章《圆中的计算问题》公开课课件 (2)

扇形: 如图,由组成圆心角的两条半径
和圆心角所对的弧所围成的图形 叫扇形.
Q
l
扇形面积S
n° Or
怎样计算圆心角是n0 的扇形面积?
圆心角占整个周角的 所对扇形面积是
1800
180
360
180 r 2
360
900
90
360
90 r 2
360
450
45
360
n0
n
360
45 r 2
2
2、扇形的面积是它所在圆的面积的 ,这个扇
形的圆心角的度数是_________°. 3
3、扇形的面积是S,它的半径是r,这个扇形的弧 长是_________;____
答案: 23 36
2s 240°, r
例题讲解
例1 如图23.3.5,圆心角为60°的扇形的半径为 10厘米,求这个扇形的面积和周长.(π≈3.14)
解:因为n=60°,r=10厘米,所以扇形面积为
Snr2 603.14102
360 360
≈52.33(平方厘米);
扇形的周长为
lnr2r6 03.1 41 020
180 180
≈ 30.47(厘米)。
图 2 3 .3 .
例.2扇形 AO的 B 半径为12AcO m=B, 1
求AB的 长 ( 精 确 到 0.1cAm O的 ) B
转化为数学模型为: A
D
B
有一圆弧形桥拱Βιβλιοθήκη 拱的跨度AB=40m,拱形的半
径R=29m,求拱形的高.
O
1 解:如图:由垂径定理得:BD= AB=20m
2
在直角三角形BOD中: OD2 =OB2 - BD2
新华东师大版九年级数学下册《27章 圆 27.3 圆中的计算问题 圆锥的侧面积和全面积》课件_19

a=R
R 2.圆锥的底面周长= 扇形的弧长
n
C=l 3.圆锥的侧面积= 扇形的面积
S侧=S扇形
圆锥的侧面积公式
圆锥的侧面积=扇形的面积
S侧=S扇形
n
1 la 1 2ra ra
22
公式: S侧 ra
例1、一个圆锥形零件的母线长为a,
底面的半径为r,求这个圆锥形零件的
2、圆锥的母线与高的夹角为30°,母线 长为6cm ,它的全面积为 2_7_π,
3、如图,若圆锥的侧面展 开图是半圆,那么这个展开 图的圆心角是_1_8_0度; 圆锥底半径 r与母线a的比
r :a = _1_:_2 .
S
hl A Or
B
如图,圆锥的底面半径为2,母线长 为6,一只蚂蚁要从底面圆周上一点B 出发,沿圆锥侧面爬行一圈再回到点 B,问它爬行的最短路线是多少?
圆锥的侧面积l
2.5
s圆锥侧S侧 s=扇π形ra
圆锥的全面积
360
·l 2
r ·36 l
s全 s侧 s底 ra r 2
P
a h
A
O r
B
ha
r
即时训练 及时评价
(1)已知圆锥的底面半径为4,母线长为6,则它的侧面
积为___2__4____.
(2)已知圆锥的底面直径为20cm,母线长为12cm,则它
圆锥的侧面展开图
1.圆锥的侧面展开图是一个扇形
2. 圆 锥 的 底 面 圆 周 长 就 是 其
侧面展开图扇形的弧长
ha
3.圆锥的母线就是其侧面展开图
r
扇形的半径。
4.圆锥的侧面积就是弧长为圆锥底面的周长、 半径为圆锥的一条母线的长的扇形面积.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
90 r 2
360
45 r 2
360
n r 2
360
结论:
如果扇形面积为s,圆心角度数为n,圆
半径是r,那么 扇形面积计算公式为
Q
l
扇形面积S
n° Or
s n r 2
360
nr r 1 lr
180 2 2
s n r 2
360
或s 1 lr 2
180 180
≈ 30.47(厘米)。
例2. 扇形AOB的半径为12cmA, OB=120,
求AB的长(精确到0.1cm)A和 OB的 扇面 形积 (精确到0m.21)c .
解:∵n=1200,r=12厘米 ∴弧AB为 l nr
120 3.1412 25.12 25.1cm 180
180
50
=3
cm
答:此圆弧的长度为 50 cm
3
扇形: 如图,由组成圆心角的两条半径
和圆心角所对的弧所围成的图形 叫扇形.
Q
l
扇形面积S
n° Or
怎样计算圆心角是n0 的扇形面积?
圆心角占整个周角的
1800
180
360
900
90
360
450
45
360
n0
n
360
所对扇形面积是
180 r 2
2
在直角三角形BOD中: OD2 =OB2 - BD2
OD2 =292 - 202 OD=21 m 所以拱形的高CD=29-21=8m
小结
一、弧长的计算公式
l n 2r nr
360
180
二、扇形面积计算公式
s n r 2 或s 1 lr
360
2
只要我们坚持了,就没有克服不了的困难。或许,为了将来,为了自己的发展,我们会把一件事情想得非常透彻,对自己越来越严,要求越来越高,对任何机会都不曾错过,其 目的也只不过是不让自己随时陷入逆境与失去那种面对困难不曾屈服的精神。但有时,“千里之行,始于足下。”我们更需要用时间持久的用心去做一件事情,让自己其中那小 小的浅浅的进步,来击破打破突破自己那本以为可以高枕无忧十分舒适的区域,强迫逼迫自己一刻不停的马不停蹄的一直向前走,向前看,向前进。所有的未来,都是靠脚步去 丈量。没有走,怎么知道,不可能;没有去努力,又怎么知道不能实现?幸福都是奋斗出来的。那不如,生活中、工作中,就让这“幸福都是奋斗出来的”完完全全彻彻底底的 渗入我们的心灵,着心、心平气和的去体验、去察觉这一种灵魂深处的安详,侧耳聆听这仅属于我们自己生命最原始最动人的节奏。但,这种聆听,它绝不是仅限于、执着于 “我”,而是观察一种生命状态能够扩展和超脱到什么程度,也就是那“幸福都是奋斗出来的”深处又会是如何?生命不止,奋斗不息!又或者,对于很多优秀的人来说,我们 奋斗了一辈子,拼搏了一辈子,也只是人家的起点。可是,这微不足道的进步,对于我们来说,却是幸福的,也是知足的,因为我们清清楚楚的知道自己需要的是什么,隐隐约 约的感觉到自己的人生正把握在自己手中,并且这一切还是通过我们自己勤勤恳恳努力,去积极争取的!“宝剑锋从磨砺出,梅花香自苦寒来。”当我们坦然接受这人生的终局, 或许,这无所皈依的心灵就有了归宿,这生命中觅寻处那真正的幸福、真正的清香也就从此真正的灿烂了我们的人生。一生有多少属于我们的时光?陌上的花,落了又开了,开 了又落了。无数个岁月就这样在悄无声息的时光里静静的流逝。童年的玩伴,曾经的天真,只能在梦里回味,每回梦醒时分,总是多了很多伤感。不知不觉中,走过了青春年少, 走过了人世间风风雨雨。爱过了,恨过了,哭过了,笑过了,才渐渐明白,酸甜苦辣咸才是人生的真味!生老病死是自然规律。所以,面对生活中经历的一切顺境和逆境都学会 了坦然承受,面对突然而至的灾难多了一份从容和冷静。这世上没有什么不能承受的,只要你有足够的坚强!这世上没有什么不能放下的,只要你有足够的胸襟! 一生有多少 属于我们的时光?当你为今天的落日而感伤流泪的时候,你也将错过了明日的旭日东升;当你为过去的遗憾郁郁寡欢,患得患失的时候,你也将忽略了沿途美丽的风景,淡漠了 对未来美好生活的憧憬。没有十全十美的生活,没有一帆风顺的旅途。波平浪静的人生太乏味,抑郁忧伤的人生少欢乐,风雨过后的彩虹最绚丽,历经磨砺的生命才丰盈而深刻。 见过了各样的人生:有的轻浮,有的踏实;有的喧哗,有的落寞;有的激扬,有的低回。肉体凡胎的我们之所以苦恼或喜悦,大都是缘于生活里的际遇沉浮,走不出个人心里的 藩篱。也许我们能挺得过物质生活的匮乏,却不能抵挡住内心的种种纠结。其实幸福和欢乐大多时候是对人对事对生活的一种态度,一花一世界,一树一菩提,就是一粒小小的 沙子,也有自己精彩的乾坤。如果想到我们终有一天会灰飞烟灭,一切象风一样无影亦无踪,还去争个什么?还去抱怨什么?还要烦恼什么?未曾生我谁是我?生我之时我是谁? 长大成人方是我,合眼朦胧又是谁?一生真的没有多少时光,何必要和生活过不去,和自己过不去呢。你在与不在,太阳每天都会照常升起;你愁与不愁,生活都将要继续。时
4
问题探究
上面求的是的圆心角900所对的弧长,若圆 心角为n0,如何计算它所对的弧长呢?
思考:
请同学们计算半径为 r,圆心角分别为1800、 900、450、n0所对的弧长。
图23.3.2
圆心角占整个周角的
180
180
0
360
90
90
0
36045450来自360nn
0
360
所对弧长是
180 2r
360
90 2r
360
45 2r
360
n 2r
360
结论:
如果弧长为l,圆心角度数为n,圆的半径为r,
那么,弧长的计算公式为:
l n 2r nr
练一练:
360
180
已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
解:l n 2r nr
360
180
∴扇形AOB面积为
s
1
lr
1 25.1212
22
=150.72 15.07cm2
下面是圆弧形桥拱,其每拱的跨度为40m,拱形的 半径为29m,求拱形的高.
C
转化为数学模型为:
有一圆弧形桥拱,拱的
D
跨度AB=40m,拱形的半 A
B
径R=29m,求拱形的高.
O
1 解:如图:由垂径定理得:BD= AB=20m
240°, 2 s r
例题讲解
例1 如图23.3.5,圆心角为60°的扇形的半径为 10厘米,求这个扇形的面积和周长.(π≈3.14)
解:因为n=60°,r=10厘米,所以扇形面积为
Snr2 603.14102 ≈52.33(平方厘米);
360 360
扇形的周长为
lnr2r6 03.1 41 020
小试牛刀:
1、如果扇形的圆心角是230°,那么这个扇形的 面积等于这个扇形所在圆的面积的____________;
2
2、扇形的面积是它所在圆的面积的 ,这个扇
形的圆心角的度数是_________°; 3
3、扇形的面积是S,它的半径是r,这个扇形的弧 长是_____________.
23 答案: 36
弧长和扇形的面积
知识回顾
o rp
圆的周长公式
C=2πr
圆的面积公式
S=πr2
问题情景:
如图23.3.1是圆弧形状的铁轨示意图,其中铁 轨的半径为100米,圆心角为90°.你能求出 这段铁轨的长度吗?
解:∵圆心角900
∴铁轨长度是圆周长的 1
图 2 3 .3 .1
4
则铁轨长是 1210050米
