数据库系统原理教程课后习题及答案(第三章)
《数据库系统原理》04735课后习题答案(2018版)

《数据库系统原理》04735课后习题答案(2018版)答案仅供参考第一章数据库系统概述选择题B、B、A简答题1.请简述数据,数据库,数据库管理系统,数据库系统的概念。
P27数据是描述事物的记录符号,是指用物理符号记录下来的,可以鉴别的信息。
数据库即存储数据的仓库,严格意义上是指长期存储在计算机中的有组织的、可共享的数据集合。
数据库管理系统是专门用于建立和管理数据库的一套软件,介于应用程序和操作系统之间。
数据库系统是指在计算机中引入数据库技术之后的系统,包括数据库、数据库管理系统及相关实用工具、应用程序、数据库管理员和用户。
2.请简述早数据库管理技术中,与人工管理、文件系统相比,数据库系统的优点。
数据共享性高数据冗余小易于保证数据一致性数据独立性高可以实施统一管理与控制减少了应用程序开发与维护的工作量3.请简述数据库系统的三级模式和两层映像的含义。
P31答:数据库的三级模式是指数据库系统是由模式、外模式和内模式三级工程的,对应了数据的三级抽象。
两层映像是指三级模式之间的映像关系,即外模式/模式映像和模式/内模式映像。
4.请简述关系模型与网状模型、层次模型的区别。
P35使用二维表结构表示实体及实体间的联系建立在严格的数学概念的基础上概念单一,统一用关系表示实体和实体之间的联系,数据结构简单清晰,用户易懂易用存取路径对用户透明,具有更高的数据独立性、更好的安全保密性。
第二章关系数据库选择题C、C、D简答题1.请简述关系数据库的基本特征。
P48答:关系数据库的基本特征是使用关系数据模型组织数据。
2.请简述什么是参照完整性约束。
P55答:参照完整性约束是指:若属性或属性组F是基本关系R的外码,与基本关系S的主码K相对应,则对于R中每个元组在F上的取值只允许有两种可能,要么是空值,要么与S 中某个元组的主码值对应。
3.请简述关系规范化过程。
答:对于存在数据冗余、插入异常、删除异常问题的关系模式,应采取将一个关系模式分解为多个关系模式的方法进行处理。
《数据库系统原理》04735课后习题答案(2018版)

答案仅供参考第一章数据库系统概述选择题B、B、A简答题1.请简述数据,数据库,数据库管理系统,数据库系统的概念。
P27数据是描述事物的记录符号,是指用物理符号记录下来的,可以鉴别的信息。
数据库即存储数据的仓库,严格意义上是指长期存储在计算机中的有组织的、可共享的数据集合。
数据库管理系统是专门用于建立和管理数据库的一套软件,介于应用程序和操作系统之间。
数据库系统是指在计算机中引入数据库技术之后的系统,包括数据库、数据库管理系统及相关实用工具、应用程序、数据库管理员和用户。
2.请简述早数据库管理技术中,与人工管理、文件系统相比,数据库系统的优点。
数据共享性高数据冗余小易于保证数据一致性数据独立性高可以实施统一管理与控制减少了应用程序开发与维护的工作量3.请简述数据库系统的三级模式和两层映像的含义。
P31答:数据库的三级模式是指数据库系统是由模式、外模式和内模式三级工程的,对应了数据的三级抽象。
两层映像是指三级模式之间的映像关系,即外模式/模式映像和模式/内模式映像。
4.请简述关系模型与网状模型、层次模型的区别。
P35使用二维表结构表示实体及实体间的联系建立在严格的数学概念的基础上概念单一,统一用关系表示实体和实体之间的联系,数据结构简单清晰,用户易懂易用存取路径对用户透明,具有更高的数据独立性、更好的安全保密性。
第二章关系数据库选择题C、C、D简答题1.请简述关系数据库的基本特征。
P48答:关系数据库的基本特征是使用关系数据模型组织数据。
2.请简述什么是参照完整性约束。
P55答:参照完整性约束是指:若属性或属性组F是基本关系R的外码,与基本关系S的主码K 相对应,则对于R中每个元组在F上的取值只允许有两种可能,要么是空值,要么与S中某个元组的主码值对应。
3.请简述关系规范化过程。
答:对于存在数据冗余、插入异常、删除异常问题的关系模式,应采取将一个关系模式分解为多个关系模式的方法进行处理。
一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式,这就是所谓的规范化过程。
分享:数据库系统原理第三章基本概念及课后习题有答案

分享:数据库系统原理第三章基本概念及课后习题有答案一、关系模式的设计准则1.数据冗余:同一个数据在系统中多次重复出现。
2.关系模式设计不当引起的异常问题:数据冗余、操作异常(包括修改异常、插入异常和删除异常)3.关系模式的非形式化设计准则1)关系模式的设计应尽可能只包含有直接联系的属性,不要包含有间接联系的属性。
也就是,每个关系模式应只对应于一个实体类型或一个联系类型。
2)关系模式的设计应尽可能使得相应关系中不出现插入异常、删除和修改等操作异常现象。
3)关系模式的设计应尽可能使得相应关系中避免放置经常为空值的属性。
4)关系模式的设计应尽可能使得关系的等值连接在主键和外键的属性上进行,并且保证以后不会生成额外的元组。
4.习惯使用的一些符号:1)英文字母表首部的大写字母“A,B,C,…”表示单个的属性。
2)英文字母表尾部的大写字母“…,U,V,W,X,Y,Z”表示属性集。
3)大写字母R表示关系模式,小写字母r表示其关系。
4)关系模式的简化表示方法:R(A,B,C,…)或R(ABC…)5)属性集X和Y的并集简写为XY。
二、函数依赖1.函数依赖(FD)的定义:设有关系模式R(U),X和Y是属性集U的子集,函数依赖是形成X→Y的一个命题,只要r是R的当前关系,对r中任意两个元组t和s,都有t[X]=s[X]蕴涵t[Y]=s[Y],那么称FD X→Y在关系模式R(U)中成立。
说明: 1)t[X]表示元组t在属性集X上的值,其余类同。
2)X→Y读作“X函数决定Y”或“Y函数依赖于X”。
3)FD是对关系模式R的一切可能的关系r定义的。
对于当前关系r的任意两个元组,如果X值相同,则要求Y值也相同,即有一个X 值就有一个Y值与之对应,或者说Y值由X值决定。
例:设关系模式R(ABCD),在R的关系中,属性值间有这样的联系:A值与B值有一对多联系;C值与D值之间有一对一联系。
试根据这些规则写出相应的函数依赖。
B→A C→D D→C2.如果X→Y和Y→X同时成立,则可记为:X↔Y3.FD的逻辑蕴涵:设F是在关系模式R上成立的函数依赖的集合,X→Y是一个函数依赖。
《数据库系统原理》04735课后习题答案(2018版)

答案仅供参考第一章数据库系统概述选择题B、B、A简答题1.请简述数据,数据库,数据库管理系统,数据库系统的概念。
P27数据是描述事物的记录符号,是指用物理符号记录下来的,可以鉴别的信息。
数据库即存储数据的仓库,严格意义上是指长期存储在计算机中的有组织的、可共享的数据集合。
数据库管理系统是专门用于建立和管理数据库的一套软件,介于应用程序和操作系统之间。
数据库系统是指在计算机中引入数据库技术之后的系统,包括数据库、数据库管理系统及相关实用工具、应用程序、数据库管理员和用户。
2.请简述早数据库管理技术中,与人工管理、文件系统相比,数据库系统的优点。
数据共享性高数据冗余小易于保证数据一致性数据独立性高可以实施统一管理与控制减少了应用程序开发与维护的工作量3.请简述数据库系统的三级模式和两层映像的含义。
P31答:数据库的三级模式是指数据库系统是由模式、外模式和内模式三级工程的,对应了数据的三级抽象。
两层映像是指三级模式之间的映像关系,即外模式/模式映像和模式/内模式映像。
4.请简述关系模型与网状模型、层次模型的区别。
P35使用二维表结构表示实体及实体间的联系建立在严格的数学概念的基础上概念单一,统一用关系表示实体和实体之间的联系,数据结构简单清晰,用户易懂易用存取路径对用户透明,具有更高的数据独立性、更好的安全保密性。
第二章关系数据库选择题C、C、D简答题1.请简述关系数据库的基本特征。
P48答:关系数据库的基本特征是使用关系数据模型组织数据。
2.请简述什么是参照完整性约束。
P55答:参照完整性约束是指:若属性或属性组F是基本关系R的外码,与基本关系S的主码K 相对应,则对于R中每个元组在F上的取值只允许有两种可能,要么是空值,要么与S中某个元组的主码值对应。
3.请简述关系规范化过程。
答:对于存在数据冗余、插入异常、删除异常问题的关系模式,应采取将一个关系模式分解为多个关系模式的方法进行处理。
一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式,这就是所谓的规范化过程。
数据库第三章习题及答案

第3章关系数据库标准语言SQL一、选择题1、SQL语言是的语言,易学习。
A.过程化 B.非过程化 C.格式化 D.导航式答案:B2、SQL语言是语言。
A.层次数据库 B.网络数据库 C.关系数据库 D.非数据库答案:C3、SQL语言具有的功能。
A.关系规范化、数据操纵、数据控制 B.数据定义、数据操纵、数据控制C.数据定义、关系规范化、数据控制 D.数据定义、关系规范化、数据操纵答案:B4、SQL语言具有两种使用方式,分别称为交互式SQL和。
A.提示式SQL B.多用户SQL C.嵌入式SQL D.解释式SQL 答案:C5、假定学生关系是S(S#,SNAME,SEX,AGE),课程关系是C(C#,CNAME,TEACHER),学生选课关系是SC(S#,C#,GRADE)。
要查找选修“COMPUTER”课程的“女”学生姓名,将涉及到关系。
A.S B.SC,C C.S,SC D.S,C,SC 答案:D6、若用如下的SQL语句创建一个student表:CREATE TABLE student(NO C(4) NOT NULL,NAME C(8) NOT NULL,SEX C(2),AGE N(2))可以插入到student表中的是。
A.(‘1031’,‘曾华’,男,23) B.(‘1031’,‘曾华’,NULL,NULL)C.(NULL,‘曾华’,‘男’,‘23’) D.(‘1031’,NULL,‘男’,23) 答案:B7、当两个子查询的结果时,可以执行并,交,差操作.A.结构完全不一致 B.结构完全一致C.结构部分一致D.主键一致答案:B第8到第10题基于这样的三个表即学生表S、课程表C和学生选课表SC,它们的结构如下:S(S#,SN,SEX,AGE,DEPT)C(C#,CN)SC(S#,C#,GRADE)其中:S#为学号,SN为姓名,SEX为性别,AGE为年龄,DEPT为系别,C#为课程号,CN为课程名,GRADE为成绩。
数据库系统原理教程课后习题答案

第1章绪论1 .试述数据、数据库、数据库系统、数据库管理系统的概念。
答:( l )数据( Data ) :描述事物的符号记录称为数据。
数据的种类有数字、文字、图形、图像、声音、正文等。
数据与其语义是不可分的。
解析在现代计算机系统中数据的概念是广义的。
早期的计算机系统主要用于科学计算,处理的数据是整数、实数、浮点数等传统数学中的数据。
现代计算机能存储和处理的对象十分广泛,表示这些对象的数据也越来越复杂。
数据与其语义是不可分的。
500 这个数字可以表示一件物品的价格是 500 元,也可以表示一个学术会议参加的人数有 500 人,还可以表示一袋奶粉重 500 克。
( 2 )数据库( DataBase ,简称 DB ) :数据库是长期储存在计算机内的、有组织的、可共享的数据集合。
数据库中的数据按一定的数据模型组织、描述和储存,具有较小的冗余度、较高的数据独立性和易扩展性,并可为各种用户共享。
( 3 )数据库系统( DataBas 。
Sytem ,简称 DBS ) :数据库系统是指在计算机系统中引入数据库后的系统构成,一般由数据库、数据库管理系统(及其开发工具)、应用系统、数据库管理员构成。
解析数据库系统和数据库是两个概念。
数据库系统是一个人一机系统,数据库是数据库系统的一个组成部分。
但是在日常工作中人们常常把数据库系统简称为数据库。
希望读者能够从人们讲话或文章的上下文中区分“数据库系统”和“数据库”,不要引起混淆。
( 4 )数据库管理系统( DataBase Management sytem ,简称 DBMs ) :数据库管理系统是位于用户与操作系统之间的一层数据管理软件,用于科学地组织和存储数据、高效地获取和维护数据。
DBMS 的主要功能包括数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能。
解析 DBMS 是一个大型的复杂的软件系统,是计算机中的基础软件。
目前,专门研制 DBMS的厂商及其研制的 DBMS 产品很多。
数据库系统原理(2018年版)课后习题参考答案解析

第三代数据库系统必须保持或集成第二代数据库系统技术
第三代数据库系统必须对其他系统开放
2.描述数据仓库粒度的概念P182
粒度是指数据仓库数据单位中保存数据的细化或综合程度
3.描述数据挖掘技术的能P183
概念描述
关联分析
分类与预测
聚类
孤立点检测
趋势和演变分析
视图的内容是由存储在数据库中进行查询操作的SQL语句定义的,它的列数据与行数据均来自于定义视图的查询所引用的基本表。
视图不适宜数据集的形式存储在数据库中的,它所对应的数据实际上是存储在视图所引用的基本表中的。
视图是用来查看存储在别处的数据的一种虚拟表,本身不存储数据。
第五章 数据库编程
简答题
1.请简述存储过程的概念P125
答:参照完整性约束是指:若属性或属性组F是基本关系R的外码,与基本关系S的主码K相对应,则对于R中每个元组在F上的取值只允许有两种可能,要么是空值,要么与S中某个元组的主码值对应。
3.请简述关系规范化过程。
答:对于存在数据冗余、插入异常、删除异常问题的关系模式,应采取将一个关系模式分解为多个关系模式的方法进行处理。一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式,这就是所谓的规范化过程。
数据库系统是指在计算机中引入数据库技术之后的系统,包括数据库、数据库管理系统及相关实用工具、应用程序、数据库管理员和用户。
2.请简述早数据库管理技术中,与人工管理、文件系统相比,数据库系统的优点。
数据共享性高
数据冗余小
易于保证数据一致性
数据独立性高
可以实施统一管理与控制
减少了应用程序开发与维护的工作量
数据库系统原理(2018版)课后习题参考答案

选择题
A、D、D
填空题
数据库系统就是指在计算机中引入数据库技术之后得系统,包括数据库、数据库管理系统及相关实用工具、应用程序、数据库管理员与用户。
2、请简述早数据库管理技术中,与人工管理、文件系统相比,数据库系统得优点。
数据共享性高
数据冗余小
易于保证数据一致性
数据独立性高
可以实施统一管理与控制
减少了应用程序开发与维护得工作量
一对多联系:对于实体集A中得每个实体,实体集B中有N个实体与之联系,反之,对于实体集B中得每个实体,实体集A中最多只有一个实体与之联系。举例:班级与班级成员,每个班级对应多个班级成员,每个班级成员只对应一个班级。
多对多联系:对于实体集A中得每个实体,实体集B中有N个实体与之联系,反之,对于实体集B中得每个实体,实体集A中有M个实体与之联系。举例:授课班级与任课教师,每个班级对应多名任课教师,每个任课教师也对应多个授课班级。
答案仅供参考
第一章 数据库系统概述
选择题
B、B、A
简答题
1、请简述数据,数据库,数据库管理系统,数据库系统得概念。 P27
数据就是描述事物得记录符号,就是指用物理符号记录下来得,可以鉴别得信息。
数据库即存储数据得仓库,严格意义上就是指长期存储在计算机中得有组织得、可共享得数据集合。
数据库管理系统就是专用于建立与管理数据库得一套软件,介于应用程序与操作系统之间。
建立在严格得数学概念得基础上
概念单一,统一用关系表示实体与实体之间得联系,数据结构简单清晰,用户易懂易用
存取路径对用户透明,具有更高得数据独立性、更好得安全保密性。
第二章 关系数据库
选择题
C、C、D
简答题
数据库系统原理教程课后习题及答案(第三章)

第3章关系数据库标准语言1 .试述语言的特点。
答:(l)综合统一。
语言集数据定义语言、数据操纵语言、数据控制语言的功能于一体。
(2)高度非过程化。
用语言进行数据操作,只要提出“做什么”,而无需指明“怎么做”,因此无需了解存取路径,存取路径的选择以与语句的操作过程由系统自动完成。
(3)面向集合的操作方式。
语言采用集合操作方式,不仅操作对象、查找结果可以是元组的集合,而且一次插入、删除、更新操作的对象也可以是元组的集合。
(4)以同一种语法结构提供两种使用方式。
语言既是自含式语言,又是嵌入式语言。
作为自含式语言,它能够独立地用于联机交互的使用方式;作为嵌入式语言,它能够嵌入到高级语言程序中,供程序员设计程序时使用。
(5)语言简捷,易学易用。
2 .试述的定义功能。
的数据定义功能包括定义表、定义视图和定义索引。
语言使用语句建立基本表,语句修改基本表定义,语句删除基本表;使用语句建立索引,语句删除索引;使用语句建立视图,语句删除视图。
3 .用语句建立第二章习题5 中的4 个表。
答:对于S 表:S ( , , , ) ;建S 表:S ( C(2) ,C(6) ,C(2),C(4));对于P 表:P ( , , , );建P 表:P( C(2) ,C(6),C(2),);对于J 表:J ( , , );建J 表:J( C(2) ,C(8),C(4))对于表:( , , , );建表:()( C(2),C(2),C(2),))4.针对上题中建立的4 个表试用语言完成第二章习题5 中的查询。
( l )求供应工程零件的供应商号码;’J1’( 2 )求供应工程零件的供应商号码;'J1' 'P1'( 3 )求供应工程零件为红色的供应商号码;'J1' '红'( 4 )求没有使用天津供应商生产的红色零件的工程号;( '天津' '红' )。
数据库原理课后习题及解答(常用版)

数据库原理课后习题及解答(常用版)(可以直接使用,可编辑完整版资料,欢迎下载)《数据库原理》课后习题及解答课后习题:第一章第二章第三章第四章第五章第六章第七章第八章第九章习题答案:第一章第二章第三章第四章第五章第六章第七章第八章第九章第一章概论1.试解释下列术语:数据库;数据库管理系统;数据库系统2.试述数据库管理系统的组成内容。
3.试比较文件系统与数据库系统的异同。
4.什么叫数据的物理独立性与逻辑独立性?并说明它的重要性。
5.试述数据库系统的优点。
6.什么叫数据的冗余与数据的不一致性?7.什么叫数据库管理员?他的主要工作是什么?8.试述数据库系统发展的几个阶段。
返回第一章答案第二章数据模型1.什么叫数据库模型,它分哪几种类型?2.试区别数据模型与数据模式。
3.什么叫数据模式,它分哪三级?4.试述数据模型四个世界的基本内容。
5.试介绍E-R模型,EE-R模型及面向对象模型、谓词模型,并各举一例说明之。
6.层次网状模型有什么特点?并各举一例说明之。
7.试比较层次、网状、关系模型之优缺点。
8.试说明关系模型的基本结构与操作。
9.目前流行的关系型数据库管理系统,有哪些你比较熟悉,试介绍其特点。
10.你认为“数据模型”在整个数据库领域中是否有重要作用和地位,试详细说明之。
11.一图书馆借阅书刊,请你画出书刊、读者及借阅三者间的E-R模型。
12.一人事档案中,有干部、职工,干部又有高级干部与一般干部,请用EE-R模型画出他们之间关系。
13.试述物理模型的主要内容。
14.试叙述四个世界的转化关系。
15.请你比较四种数据模型的异同。
返回第二章答案第三章关系数据库系统1.试述关系数据库系统的优点。
2.试述关系型的12条标准,并说明FOXBASE为何是半关系型的。
3.关系代数与关系演算的表示能力是否相同?试证明之。
4.从关系模型的数学表示中,你是否认为网状与层次模型也可以用数学方法表示?试说明理由。
5.设有如图3-1所示的医院组织。
04735数据库系统原理(2018版)课后习题参考答案.pdf

2.请简述什么是参照完整性约束。 P55
答:参照完整性约束是指:若属性或属性组 F 是基本关系 R 的外码,与基本关系 S 的主码 K
相对应,则对于 R 中每个元组在 F 上的取值只允许有两种可能,要么是空值,要么与
S中
某个元组的主码值对应。
3.请简述关系规范化过程。
答:对于存在数据冗余、 插入异常、 删除异常问题的关系模式,应采取将一个关系模式分解
实体集 B 中的每个实体,实体集 A 中最多只有一个实体与之联系。举例:班级与班级成员,
每个班级对应多个班级成员,每个班级成员只对应一个班级。
多对多联系:对于实体集 A 中的每个实体,实体集 B 中有 N 个实体与之联系,反之,对于
实体集 B 中的每个实体,实体集 A 中有 M 个实体与之联系。举例:授课班级与任课教师,
3.请简述数据库系统的三级模式和两层映像的含义。
P31
答:
数据库的三级模式是指数据库系统是由模式、 外模式和内模式三级工程的, 对应了数据的三
级抽象。
两层映像是指三级模式之间的映像关系,即外模式
/ 模式映像和模式 / 内模式映像。
4.请简述关系模型与网状模型、层次模型的区别。
P35
使用二维表结构表示实体及实体间的联系
来自于定义视图的查询所引用的基本表。 视图不适宜数据集的形式存储在数据库中的,
它所对应的数据实际上是存储在视图所引用的
基本表中的。
视图是用来查看存储在别处的数据的一种虚拟表,本身不存储数据。
文档鉴赏
第五章 数据库编程
简答题
1. 请简述存储过程的概念 P125
存储过程是一组为了完成某项特定功能的
SQL 语句集,经过编译后存储在数据库中,可以
数据库系统原理教程课后习题答案

第1章绪论1 .试述数据、数据库、数据库系统、数据库管理系统的概念。
答:( l )数据(Data ) :描述事物的符号记录称为数据。
数据的种类有数字、文字、图形、图像、声音、正文等。
数据与其语义是不可分的。
解析在现代计算机系统中数据的概念是广义的。
早期的计算机系统主要用于科学计算,处理的数据是整数、实数、浮点数等传统数学中的数据。
现代计算机能存储和处理的对象十分广泛,表示这些对象的数据也越来越复杂。
数据与其语义是不可分的。
500 这个数字可以表示一件物品的价格是500 元,也可以表示一个学术会议参加的人数有500 人,还可以表示一袋奶粉重500 克。
( 2 )数据库(DataBase ,简称DB ) :数据库是长期储存在计算机内的、有组织的、可共享的数据集合。
数据库中的数据按一定的数据模型组织、描述和储存,具有较小的冗余度、较高的数据独立性和易扩展性,并可为各种用户共享。
( 3 )数据库系统(DataBas 。
Sytem ,简称DBS ) :数据库系统是指在计算机系统中引入数据库后的系统构成,一般由数据库、数据库管理系统(及其开发工具)、应用系统、数据库管理员构成。
解析数据库系统和数据库是两个概念。
数据库系统是一个人一机系统,数据库是数据库系统的一个组成部分。
但是在日常工作中人们常常把数据库系统简称为数据库。
希望读者能够从人们讲话或文章的上下文中区分“数据库系统”和“数据库”,不要引起混淆。
( 4 )数据库管理系统(DataBase Management sytem ,简称DBMs ) :数据库管理系统是位于用户与操作系统之间的一层数据管理软件,用于科学地组织和存储数据、高效地获取和维护数据。
DBMS 的主要功能包括数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能。
解析DBMS 是一个大型的复杂的软件系统,是计算机中的基础软件。
目前,专门研制DBMS 的厂商及其研制的DBMS 产品很多。
04735数据库系统原理(2018年版)课后习题参考答案与解析

答案仅供参考第一章数据库系统概述选择题B、B、A简答题1.请简述数据,数据库,数据库管理系统,数据库系统的概念。
P27数据是描述事物的记录符号,是指用物理符号记录下来的,可以鉴别的信息。
数据库即存储数据的仓库,严格意义上是指长期存储在计算机中的有组织的、可共享的数据集合。
数据库管理系统是专门用于建立和管理数据库的一套软件,介于应用程序和操作系统之间。
数据库系统是指在计算机中引入数据库技术之后的系统,包括数据库、数据库管理系统及相关实用工具、应用程序、数据库管理员和用户。
2.请简述早数据库管理技术中,与人工管理、文件系统相比,数据库系统的优点。
数据共享性高数据冗余小易于保证数据一致性数据独立性高可以实施统一管理与控制减少了应用程序开发与维护的工作量3.请简述数据库系统的三级模式和两层映像的含义。
P31答:数据库的三级模式是指数据库系统是由模式、外模式和内模式三级工程的,对应了数据的三级抽象。
两层映像是指三级模式之间的映像关系,即外模式/模式映像和模式/内模式映像。
4.请简述关系模型与网状模型、层次模型的区别。
P35使用二维表结构表示实体及实体间的联系建立在严格的数学概念的基础上概念单一,统一用关系表示实体和实体之间的联系,数据结构简单清晰,用户易懂易用存取路径对用户透明,具有更高的数据独立性、更好的安全保密性。
第二章关系数据库选择题C、C、D简答题1.请简述关系数据库的基本特征。
P48答:关系数据库的基本特征是使用关系数据模型组织数据。
2.请简述什么是参照完整性约束。
P55答:参照完整性约束是指:若属性或属性组F是基本关系R的外码,与基本关系S的主码K 相对应,则对于R中每个元组在F上的取值只允许有两种可能,要么是空值,要么与S中某个元组的主码值对应。
3.请简述关系规范化过程。
答:对于存在数据冗余、插入异常、删除异常问题的关系模式,应采取将一个关系模式分解为多个关系模式的方法进行处理。
一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式,这就是所谓的规范化过程。
数据库管理系统原理 第三章测验 测验答案 慕课答案 UOOC优课 课后练习 深圳大学
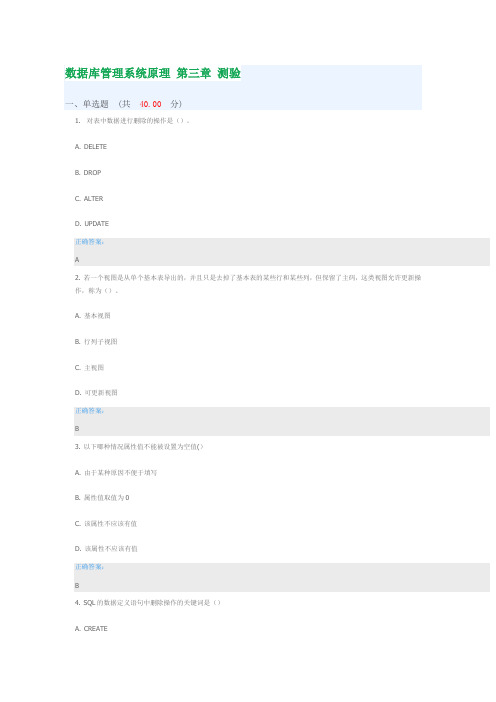
数据库管理系统原理第三章测验一、单选题(共40.00分)1. 对表中数据进行删除的操作是()。
A. DELETEB. DROPC. ALTERD. UPDATE正确答案:A2. 若一个视图是从单个基本表导出的,并且只是去掉了基本表的某些行和某些列,但保留了主码,这类视图允许更新操作,称为()。
A. 基本视图B. 行列子视图C. 主视图D. 可更新视图正确答案:B3. 以下哪种情况属性值不能被设置为空值()A. 由于某种原因不便于填写B. 属性值取值为0C. 该属性不应该有值D. 该属性不应该有值正确答案:B4. SQL的数据定义语句中删除操作的关键词是()A. CREATEC. ALTERD. DELETE正确答案:B二、多选题(共33.00分)1. 请下列选项选出SQL语言具有哪些?()A. 数据定义B. 数据查询C. 数据操纵D. 数据控制正确答案:A B C D答案解析:SQL语言功能2. 请下列选项选出SQL语言的数据定义功能()。
A. 模式定义B. 表定义C. 视图定义D. 索引定义正确答案:A B C D答案解析:SQL语言的数据定义功能3. SQL语句支持“修改”(ALTER)功能的数据对象是()A. 模式B. 表D. 索引正确答案:B D三、判断题(共27.00分)1. 视图不仅可以从单个基本表导出,还可以从多个基本表导出。
A. 正确B. 错误正确答案:A2. 不是所有的视图都可以进行更新,但视图都可以进行插入。
A. 正确B. 错误正确答案:B3. SELECT子句中的目标列可以是表中的属性列也可以是表达式。
A. 正确B. 错误正确答案:A。
数据库系统基础教程课后答案第三章

The superkeys are any subset that contains {A1,A2 } or {A3,A4}. There are 2(n-2) such subsets when considering {A1,A2} and the n-2 attributes A3 through An. There are 2(n-2) – 2(n-4) such subsets when considering {A3,A4} and attributes A5 through An along with the individual attributes A1 and A2. We get the 2(n-4) term because we have to discard the subsets that contain the key {A1,A2} to avoid double counting. The total number of subsets is 2(n-2) + 2(n-2) – 2(n-4). Exercise 3.1.3d The superkeys are any subset that contains {A1,A2 } or {A1,A3}. There are 2(n-2) such subsets when considering {A1,A2} and the n-2 attributes A3 through An. There are 2(n-3) such subsets when considering {A1,A3} and the n-3 attributes A4 through An We do not count A2 in these subsets because they are already counted in the first group of subsets. The total number of subsets is 2(n-2) + 2(n-3). Exercise 3.2.1a We could try inference rules to deduce new dependencies until we are satisfied we have them all. A more systematic way is to consider the closures of all 15 nonempty sets of attributes. For the single attributes we have {A}+ = A, {B}+ = B, {C}+ = ACD, and {D}+ = AD. Thus, the only new dependency we get with a single attribute on the left is CA. Now consider pairs of attributes: {AB}+ = ABCD, so we get new dependency ABD. {AC}+ = ACD, and ACD is nontrivial. {AD}+ = AD, so nothing new. {BC}+ = ABCD, so we get BCA, and BCD. {BD}+ = ABCD, giving us BDA and BDC. {CD}+ = ACD, giving CDA. For the triples of attributes, {ACD}+ = ACD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABCD, ABDC, and BCDA. Since {ABCD}+ = ABCD, we get no new dependencies. The collection of 11 new dependencies mentioned above are: CA, ABD, ACD, BCA, BCD, BDA, BDC, CDA, ABCD, ABDC, and BCDA. Exercise 3.2.1b From the analysis of closures above, we find that AB, BC, and BD are keys. All other sets either do not have ABCD as the closure or contain one of these three sets. Exercise 3.2.1c The superkeys are all those that contain one of those three keys. That is, a superkey that is not a key must contain B and more than one of A, C, and D. Thus, the (proper) superkeys are ABC, ABD, BCD, and ABCD.
(完整word版)数据库系统基础教程第三章答案

Exercise 3.1.1Answers for this exercise may vary because of different interpretations.Some possible FDs:Social Security number → nameArea code → stateStreet address, city, state → zipcodePossible keys:{Social Security number, street address, city, state, area code, phone number}Need street address, city, state to uniquely determine location. A person couldhave multiple addresses. The same is true for phones. These days, a person couldhave a landline and a cellular phoneExercise 3.1.2Answers for this exercise may vary because of different interpretationsSome possible FDs:ID → x-position, y-position, z-positionID → x-velocity, y-velocity, z-velocityx-position, y-position, z-position → IDPossible keys:{ID}{x-position, y-position, z-position}The reason why the positions would be a key is no two molecules can occupy the same point.Exercise 3.1.3aThe superkeys are any subset that contains A1. Thus, there are 2(n-1) such subsets, since each of the n-1 attributes A2 through A n may independently be chosen in or out.Exercise 3.1.3bThe superkeys are any subset that contains A1 or A2. There are 2(n-1) such subsets when considering A1 and the n-1 attributes A2 through A n. There are 2(n-2) such subsets when considering A2 and the n-2 attributes A3 through A n. We do not count A1 in these subsets because they are already counted in the first group of subsets. The total number of subsets is 2(n-1) + 2(n-2).Exercise 3.1.3cThe superkeys are any subset that contains {A1,A2} or {A3,A4}. There are 2(n-2) such subsets when considering {A1,A2} and the n-2 attributes A3 through A n. There are 2(n-2) – 2(n-4) such subsets when considering {A3,A4} and attributes A5 through A n along with the individual attributes A1 and A2. We get the 2(n-4) term because we have to discard the subsets that contain the key {A1,A2} to avoid double counting. The total number of subsets is 2(n-2) +2(n-2) – 2(n-4).Exercise 3.1.3dThe superkeys are any subset that contains {A1,A2} or {A1,A3}. There are 2(n-2) such subsets when considering {A1,A2} and the n-2 attributes A3 through A n. There are 2(n-3) such subsets when considering {A1,A3} and the n-3 attributes A4 through A n We do not count A2 in these subsets because they are already counted in the first group of subsets. The total number of subsets is 2(n-2) + 2(n-3).Exercise 3.2.1aWe could try inference rules to deduce new dependencies until we are satisfied we have them all. A more systematic way is to consider the closures of all 15 nonempty sets of attributes.For the single attributes we have {A}+ = A, {B}+ = B, {C}+ = ACD, and {D}+ = AD. Thus, the only new dependency we get with a single attribute on the left is C→A.Now consider pairs of attributes:{AB}+ = ABCD, so we get new dependency AB→D. {AC}+ = ACD, and AC→D is nontrivial. {AD}+= AD, so nothing new. {BC}+ = ABCD, so we get BC→A, and BC→D. {BD}+ = ABCD, giving us BD→A and BD→C. {CD}+ = ACD, giving CD→A.For the triples of attributes, {ACD}+ = ACD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABC→D, ABD→C, and BCD→A.Since {ABCD}+ = ABCD, we get no new dependencies.The collection of 11 new dependencies mentioned above are:C→A, AB→D, AC→D, BC→A, BC→D, BD→A, BD→C, CD→A, ABC→D, ABD→C, and BCD→A.Exercise 3.2.1bFrom the analysis of closures above, we find that AB, BC, and BD are keys. All other sets either do not have ABCD as the closure or contain one of these three sets.Exercise 3.2.1cThe superkeys are all those that contain one of those three keys. That is, a superkeythat is not a key must contain B and more than one of A, C, and D. Thus, the (proper) superkeys are ABC, ABD, BCD, and ABCD.Exercise 3.2.2ai) For the single attributes we have {A}+ = ABCD, {B}+ = BCD, {C}+ = C, and {D}+ = D. Thus, the new dependencies are A→C and A→D.Now consider pairs of attributes:{AB}+ = ABCD, {AC}+ = ABCD, {AD}+ = ABCD, {BC}+ = BCD, {BD}+ = BCD, {CD}+ = CD. Thus the new dependencies are AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BC→D and BD→C.For the triples of attributes, {BCD}+ = BCD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABC→D, ABD→C, and ACD→B.Since {ABCD}+ = ABCD, we get no new dependencies.The collection of 13 new dependencies mentioned above are:A→C, A→D, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BC→D, BD→C, ABC→D, ABD→C and ACD→B.ii) For the single attributes we have {A}+ = A, {B}+ = B, {C}+ = C, and {D}+ = D. Thus, there are no new dependencies.Now consider pairs of attributes:{AB}+ = ABCD, {AC}+ = AC, {AD}+ = ABCD, {BC}+ = ABCD, {BD}+ = BD, {CD}+ = ABCD. Thus the new dependencies are AB→D, AD→C, BC→A and CD→B.For the triples of attributes, all the closures of the sets are each ABCD. Thus, we get new dependencies ABC→D, ABD→C, ACD→B and BCD→A.Since {ABCD}+ = ABCD, we get no new dependencies.The collection of 8 new dependencies mentioned above are:AB→D, AD→C, BC→A, CD→B, ABC→D, ABD→C, ACD→B and BCD→A.iii) For the single attributes we have {A}+ = ABCD, {B}+ = ABCD, {C}+ = ABCD, and {D}+ = ABCD. Thus, the new dependencies are A→C, A→D, B→D, B→A, C→A, C→B, D→B and D→C.Since all the single attributes’ closures are ABCD, any superset of the singleattributes will also lead to a closure of ABCD. Knowing this, we can enumerate the restof the new dependencies.The collection of 24 new dependencies mentioned above are:A→C, A→D, B→D, B→A, C→A, C→B, D→B, D→C, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BC→A, BC→D, BD→A, BD→C, CD→A, CD→B, ABC→D, ABD→C, ACD→B and BCD→A.Exercise 3.2.2bi) From the analysis of closures in 3.2.2a(i), we find that the only key is A. All other sets either do not have ABCD as the closure or contain A.ii) From the analysis of closures 3.2.2a(ii), we find that AB, AD, BC, and CD are keys.All other sets either do not have ABCD as the closure or contain one of these four sets.iii) From the analysis of closures 3.2.2a(iii), we find that A, B, C and D are keys. All other sets either do not have ABCD as the closure or contain one of these four sets.Exercise 3.2.2ci) The superkeys are all those sets that contain one of the keys in 3.2.2b(i). The superkeys are AB, AC, AD, ABC, ABD, ACD, BCD and ABCD.ii) The superkeys are all those sets that contain one of the keys in 3.2.2b(ii). The superkeys are ABC, ABD, ACD, BCD and ABCD.iii) The superkeys are all those sets that contain one of the keys in 3.2.2b(iii). The superkeys are AB, AC, AD, BC, BD, CD, ABC, ABD, ACD, BCD and ABCD.Exercise 3.2.3aSince A1A2…A n C contains A1A2…A n, then the closure of A1A2…A n C contains B. Thus it follows that A1A2…A n C→B.Exercise 3.2.3bFrom 3.2.3a, we know that A1A2…A n C→B. Using the concept of trivial dependencies, we can show that A1A2…A n C→C. Thus A1A2…A n C→BC.Exercise 3.2.3cFrom A1A2…A n E1E2…E j, we know that the closure contains B1B2…B m because of the FD A1A2…A n→B1B2…B m. The B1B2…B m and the E1E2…E j combine to form the C1C2…C k. Thus the closure ofA1A2…A n E1E2…E j contains D as well. Thus, A1A2…A n E1E2…E j→D.Exercise 3.2.3dFrom A1A2…A n C1C2…C k, we know that the closure contains B1B2…B m because of the FD A1A2…A n→B1B2…B m. The C1C2…C k also tell us that the closure of A1A2…A n C1C2…C k contains D1D2…D j. Thus, A1A2…A n C1C2…C k→B1B2…B k D1D2…D j.Exercise 3.2.4aIf attribute A represented Social Security Number and B represented a person’s name,then we would assume A→B but B→A would not be valid because there may be many peoplewith the same name and different Social Security Numbers.Exercise 3.2.4bLet attribute A represent Social Security Number, B represent gender and C represent name. Surely Social Security Number and gender can uniquely identify a person’s name (i.e.AB→C). A Social Security Number can also uniquely identify a person’s name (i.e. A→C). However, gender does not uniquely determine a name (i.e. B→C is not valid).Exercise 3.2.4cLet attribute A represent latitude and B represent longitude. Together, both attributes can uniquely determine C, a point on the world map (i.e. AB→C). However, neither A nor B can uniquely identify a point (i.e. A→C and B→C are not valid).Exercise 3.2.5Given a relation with attributes A1A2…A n, we are told that there are no functional dependencies of the form B1B2…B n-1→C where B1B2…B n-1 is n-1 of the attributes from A1A2…A n and C is the remaining attribute from A1A2…A n. In this case, the set B1B2…B n-1 and any subset do not functionally determine C. Thus the only functional dependencies that we can make are ones where C is on both the left and right hand sides. All of these functional dependencies would be trivial and thus the relation has no nontrivial FD’s.Exercise 3.2.6Let’s prove this by using the contrapositive. We wish to show that if X+ is not a subset of Y+, then it must be that X is not a subset of Y.If X+ is not a subset of Y+, there must be attributes A1A2…A n in X+ that are not in Y+. If any of these attributes were originally in X, then we are done because Y does not contain any of the A1A2…A n. However, if the A1A2…A n were added by the closure, then we must examine the case further. Assume that there was some FD C1C2…C m→A1A2…A j where A1A2…A j is some subset of A1A2…A n. It must be then that C1C2…C m or some subset of C1C2…C m is in X. However, the attributes C1C2…C m cannot be in Y because we assumed that attributes A1A2…A n are only in X+ and are not in Y+. Thus, X is not a subset of Y.By proving the contrapositive, we have also proved if X ⊆ Y, then X+⊆ Y+.Exercise 3.2.7The algorithm to find X+ is outlined on pg. 76. Using that algorithm, we can prove that (X+)+ = X+. We will do this by using a proof by contradiction.Suppose that (X+)+≠ X+. Then for (X+)+, it must be that some FD allowed additional attributes to be added to the original set X+. For example, X+→ A where A is some attribute not in X+. However, if this were the case, then X+ would not be the closure of X. The closure of X would have to include A as well. This contradicts the fact that we weregiven the closure of X, X+. Therefore, it must be that (X+)+ = X+ or else X+ is not the closure of X.Exercise 3.2.8aIf all sets of attributes are closed, then there cannot be any nontrivial functional dependencies. Suppose A1A2...A n→B is a nontrivial dependency. Then {A1A2...A n}+ contains B and thus A1A2...A n is not closed.Exercise 3.2.8bIf the only closed sets are ø and {A,B,C,D}, then the following FDs hold:A→B A→C A→DB→A B→C B→DC→A C→B C→DD→A D→B D→CAB→C AB→DAC→B AC→DAD→B AD→CBC→A BC→DBD→A BD→CCD→A CD→BABC→DABD→CACD→BBCD→AExercise 3.2.8cIf the only closed sets are ø, {A,B} and {A,B,C,D}, then the following FDs hold:A→BB→AC→A C→B C→DD→A D→B D→CAC→B AC→DAD→B AD→CBC→A BC→DBD→A BD→CCD→A CD→BABC→DABD→CACD→BBCD→AExercise 3.2.9We can think of this problem as a situation where the attributes A,B,C represent cities and the functional dependencies represent one way paths between the cities. The minimal bases are the minimal number of pathways that are needed to connect the cities. We do not want to create another roadway if the two cities are already connected.The systematic way to do this would be to check all possible sets of the pathways. However, we can simplify the situation by noting that it takes more than two pathways to visit the two other cities and come back. Also, if we find a set of pathways that is minimal, adding additional pathways will not create another minimal set.The two sets of minimal bases that were given in example 3.11 are:{A→B, B→C, C→A}{A→B, B→A, B→C, C→B}The additional sets of minimal bases are:{C→B, B→A, A→C}{A→B, A→C, B→A, C→A}{A→C, B→C, C→A, C→B}Exercise 3.2.10aWe need to compute the closures of all subsets of {ABC}, although there is no need to think about the empty set or the set of all three attributes. Here are the calculations for the remaining six sets:{A}+=A{B}+=B{C}+=ACE{AB}+=ABCDE{AC}+=ACE{BC}+=ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC is: C→A and AB→C. Note that BC->A is true, but follows logically from C->A, and therefore may be omitted from our list.Exercise 3.2.10bWe need to compute the closures of all subsets of {ABC}, although there is no need to think about the empty set or the set of all three attributes. Here are the calculations for the remaining six sets:{A}+=AD{B}+=B{C}+=C{AB}+=ABDE{AC}+=ABCDE{BC}+=BCWe ignore D and E, so a basis for the resulting functional dependencies for ABC is: AC→B.Exercise 3.2.10cWe need to compute the closures of all subsets of {ABC}, although there is no need tothink about the empty set or the set of all three attributes. Here are the calculationsfor the remaining six sets:{A}+=A{B}+=B{C}+=C{AB}+=ABD{AC}+=ABCDE{BC}+=ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC is: AC→B and BC→A.Exercise 3.2.10dWe need to compute the closures of all subsets of {ABC}, although there is no need tothink about the empty set or the set of all three attributes. Here are the calculationsfor the remaining six sets:{A}+=ABCDE{B}+=ABCDE{C}+=ABCDE{AB}+=ABCDE{AC}+=ABCDE{BC}+=ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC is: A→B, B→C and C→A.Exercise 3.2.11For step one of Algorithm 3.7, suppose we have the FD ABC→DE. We want to use Armstrong’s Axioms to show that ABC→D and ABC→E follow. Surely the functional dependencies DE→D and DE→E hold because they are trivial and follow the reflexivity property. Using the transitivity rule, we can derive the FD ABC→D from the FDs ABC→DE and DE→D. Likewise, we can do the same for ABC→DE and DE→E and derive the FD ABC→E.For steps two through four of Algorithm 3.7, suppose we have the initial set ofattributes of the closure as ABC. Suppose also that we have FDs C→D and D→E. Accordingto Algorithm 3.7, the closure should become ABCDE. Taking the FD C→D and augmenting both sides with attributes AB we get the FD ABC→ABD. We can use the splitting method in stepone to get the FD ABC→D. Since D is not in the closure, we can add attribute D. Taking the FD D→E and augmenting both sides with attributes ABC we get the FD ABCD→ABCDE.Using again the splitting method in step one we get the FD ABCD→E. Since E is not in the closure, we can add attribute E.Given a set of FDs, we can prove that a FD F follows by taking the closure of the left side of FD F. The steps to compute the closure in Algorithm 3.7 can be mimicked by Armstrong’s axioms and thus we can prove F from the given set of FDs using Armstrong’s axioms.Exercise 3.3.1aIn the solution to Exercise 3.2.1 we found that there are 14 nontrivial dependencies, including the three given ones and eleven derived dependencies. They are: C→A, C→D,D→A, AB→D, AB→ C, AC→D, BC→A, BC→D, BD→A, BD→C, CD→A, ABC→D, ABD→C, and BCD→A.We also learned that the three keys were AB, BC, and BD. Thus, any dependency above that does not have one of these pairs on the left is a BCNF violation. These are: C→A, C→D,D→A, AC→D, and CD→A.One choice is to decompose using the violation C→D. Using the above FDs, we get ACD and BC as decomposed relations. BC is surely in BCNF, since any two-attribute relation is. Using Algorithm 3.12 to discover the projection of FDs on relation ACD, we discover that ACD is not in BCNF since C is its only key. However, D→A is a dependency that holds in ABCD and therefore holds in ACD. We must further decompose ACD into AD and CD. Thus, the three relations of the decomposition are BC, AD, and CD.Exercise 3.3.1bBy computing the closures of all 15 nonempty subsets of ABCD, we can find all thenontrivial FDs. They are B→C, B→D, AB→C, AB→D, BC→D, BD→C, ABC→D and ABD→C. From the closures we can also deduce that the only key is AB. Thus, any dependency above that does not contain AB on the left is a BCNF violation. These are: B→C, B→D, BC→D andBD→C.One choice is to decompose using the violation B→C. Using the above FDs, we get BCD and AB as decomposed relations. AB is surely in BCNF, since any two-attribute relation is. Using Algorithm 3.12 to discover the projection of FDs on relation BCD, we discover that BCD is in BCNF since B is its only key and the projected FDs all have B on the left side. Thus the two relations of the decomposition are AB and BCD.Exercise 3.3.1cIn the solution to Exercise 3.2.2(ii), we found that there are 12 nontrivial dependencies, including the four given ones and the eight derived ones. They are AB→C, BC→D, CD→A, AD→B, AB→D, AD→C, BC→A, CD→B, ABC→D, ABD→C, ACD→B and BCD→A.We also found out that the keys are AB, AD, BC, and CD. Thus, any dependency above that does not have one of these pairs on the left is a BCNF violation. However, all of the FDs contain a key on the left so there are no BCNF violations.No decomposition is necessary since all the FDs do not violate BCNF.Exercise 3.3.1dIn the solution to Exercise 3.2.2(iii), we found that there are 28 nontrivial dependencies, including the four given ones and the 24 derived ones. They are A→B, B→C, C→D, D→A, A→C, A→D, B→D, B→A, C→A, C→B, D→B, D→C, AB→C, AB→D, AC→B, AC→D,AD→B, AD→C, BC→A, BC→D, BD→A, BD→C, CD→A, CD→B, ABC→D, ABD→C, ACD→B and BCD→A.We also found out that the keys are A,B,C,D. Thus, any dependency above that does nothave one of these attributes on the left is a BCNF violation. However, all of the FDs contain a key on the left so there are no BCNF violations.No decomposition is necessary since all the FDs do not violate BCNF.Exercise 3.3.1eBy computing the closures of all 31 nonempty subsets of ABCDE, we can find all the nontrivial FDs. They are AB→C, DE→C, B→D, AB→D, BC→D, BE→C, BE→D, ABC→D, ABD→C, ABE→C, ABE→D, ADE→C, BCE→D, BDE→C, ABCE→D, and ABDE→C. From the closures we canalso deduce that the only key is ABE. Thus, any dependency above that does not contain ABE on the left is a BCNF violation. These are: AB→C, DE→C, B→D, AB→D, BC→D, BE→C, BE→D, ABC→D, ABD→C, ADE→C, BCE→D and BDE→C.One choice is to decompose using the violation AB→C. Using the above FDs, we get ABCDand ABE as decomposed relations. Using Algorithm 3.12 to discover the projection of FDs on relation ABCD, we discover that ABCD is not in BCNF since AB is its only key and the FD B→D follows for ABCD. Using violation B→D to further decompose, we get BD and ABC as decomposed relations. BD is in BCNF because it is a two-attribute relation. Using Algorithm 3.12 again, we discover that ABC is in BCNF since AB is the only key and AB→Cis the only nontrivial FD. Going back to relation ABE, following Algorithm 3.12 tells us that ABE is in BCNF because there are no keys and no nontrivial FDs. Thus the three relations of the decomposition are ABC, BD and ABE.Exercise 3.3.1fBy computing the closures of all 31 nonempty subsets of ABCDE, we can find all the nontrivial FDs. They are: C→B, C→D, C→E, D→B, D→E, AB→C, AB→D, AB→E, AC→B, AC→D, AC→E, AD→B, AD→C, AD→E, BC→D, BC→E, BD→E, CD→B, CD→E, CE→B, CE→D, DE→B,ABC→D, ABC→E, ABD→C, ABD→E, ABE→C, ABE→D, ACD→B, ACD→E, ACE→B, ACE→D, ADE→B, ADE→C, BCD→E, BCE→D, CDE→B, ABCD→E, ABCE→D, ABDE→C and ACDE→B. From the closures we can also deduce that the keys are AB, AC and AD. Thus, any dependency above that does not contain one of the above pairs on the left is a BCNF violation. These are: C→B, C→D,C →E,D →B, D →E, BC →D, BC →E, BD →E, CD →B, CD →E, CE →B, CE →D, DE →B, BCD →E, BCE →D and CDE →B.One choice is to decompose using the violation D →B. Using the above FDs, we get BDE and ABC as decomposed relations. Using Algorithm 3.12 to discover the projection of FDs on relation BDE, we discover that BDE is in BCNF since D, BD, DE are the only keys and all the projected FDs contain D, BD, or DE in the left side. Going back to relation ABC,following Algorithm 3.12 tells us that ABC is not in BCNF because since AB and AC are its only keys and the FD C →B follows for ABC. Using violation C →B to further decompose, we get BC and AC as decomposed relations. Both BC and AC are in BCNF because they are two-attribute relations. Thus the three relations of the decomposition are BDE, BC and AC.Exercise 3.3.2Yes, we will get the same result. Both A →B and A →BC have A on the left side and part ofthe process of decomposition involves finding {A}+to form one decomposed relation and Aplus the rest of the attributes not in {A}+as the second relation. Both cases yield the same decomposed relations.Exercise 3.3.3Yes, we will still get the same result. Both A →B and A →BC have A on the left side andpart of the process of decomposition involves finding {A}+to form one decomposedrelation and A plus the rest of the attributes not in {A}+as the second relation. Both cases yield the same decomposed relations.Exercise 3.3.4This is taken from Example 3.21 pg. 95.Suppose that an instance of relation R only contains two tuples.The projections of R onto the relations with schemas {A,B} and {B,C} are:If we do a natural join on the two projections, we will get:The result of the natural join is not equal to the original relation R.Exercise 3.4.1aThis is the initial tableau:→A.Since there is not an unsubscripted row, the decomposition for R is not lossless for this set of FDs.We can use the final tableau as an instance of R as an example for why the join is not lossless. The projected relations are:The joined relation is:The joined relation has three more tuples than the original tableau.Exercise 3.4.1bThis is the initial tableau:This is the final tableau after applying FDs AC→E and BC→DSince there is an unsubscripted row, the decomposition for R is lossless for this set of FDs.Exercise 3.4.1cThis is the initial tableau:This is the final tableau after applying FDs A→D, D→E and B→D.Since there is an unsubscripted row, the decomposition for R is lossless for this set of FDs.Exercise 3.4.1dThis is the initial tableau:This is the final tableau after applying FDs A→D, CD→E and E→DSince there is an unsubscripted row, the decomposition for R is lossless for this set of FDs.Exercise 3.4.2When we decompose a relation into BCNF, we will project the FDs onto the decomposed relations to get new sets of FDs. These dependencies are preserved if the union of these new sets is equivalent to the original set of FDs.For the FDs of 3.4.1a, the dependencies are not preserved. The union of the new sets of FDs is CE→A. However, the FD B→E is not in the union and cannot be derived. Thus the two sets of FDs are not equivalent.For the FDs of 3.4.1b, the dependencies are preserved. The union of the new sets of FDs is AC→E and BC→D. This is precisely the same as the original set of FDs and thus the two sets of FDs are equivalent.For the FDs of 3.4.1c, the dependencies are not preserved. The union of the new sets of FDs is B→D and A→E. The FDs A→D and D→E are not in the union and cannot be derived. Thus the two sets of FDs are not equivalent.For the FDs of 3.4.1d, the dependencies are not preserved. The union of the new sets of FDs is AC→E. However, the FDs A→D, CD→E and E→D are not in the union and cannot be derived. Thus the two sets of FDs are not equivalent.Exercise 3.5.1aIn the solution to Exercise 3.3.1a we found that there are 14 nontrivial dependencies. They are: C→A, C→D, D→A, AB→D, AB→ C, AC→D, BC→A, BC→D, BD→A, BD→C, CD→A,ABC→D, ABD→C, and BCD→A.We also learned that the three keys were AB, BC, and BD. Since all the attributes on the right sides of the FDs are prime, there are no 3NF violations.Since there are no 3NF violations, it is not necessary to decompose the relation.Exercise 3.5.1bIn the solution to Exercise 3.3.1b we found that there are 8 nontrivial dependencies. They are B→C, B→D, AB→C, AB→D, BC→D, BD→C, ABC→D and ABD→C.We also found out that the only key is AB. FDs where the left side is not a superkey or the attributes on the right are not part of some key are 3NF violations. The 3NF violations are B→C, B→D, BC→D and BD→C.Using algorithm 3.26, we can decompose into relations using the minimal basis B→C andB→D. The resulting decomposed relations would be BC and BD. However, none of these two sets of attributes is a superkey. Thus we add relation AB to the result. The final set of decomposed relations is BC, BD and AB.Exercise 3.5.1cIn the solution to Exercise 3.3.1c we found that there are 12 nontrivial dependencies. They are AB→C, BC→D, CD→A, AD→B, AB→D, AD→C, BC→A, CD→B, ABC→D, ABD→C, ACD→B and BCD→A.We also found out that the keys are AB, AD, BC, and CD. Since all the attributes on the right sides of the FDs are prime, there are no 3NF violations.Since there are no 3NF violations, it is not necessary to decompose the relation.Exercise 3.5.1dIn the solution to Exercise 3.3.1d we found that there are 28 nontrivial dependencies. They are A→B, B→C, C→D, D→A, A→C, A→D, B→D, B→A, C→A, C→B, D→B, D→C, AB→C,AB→D, AC→B, AC→D, AD→B, AD→C, BC→A, BC→D, BD→A, BD→C, CD→A, CD→B, ABC→D,ABD→C, ACD→B and BCD→A.We also found out that the keys are A,B,C,D. Since all the attributes on the right sidesof the FDs are prime, there are no 3NF violations.Since there are no 3NF violations, it is not necessary to decompose the relation.Exercise 3.5.1eIn the solution to Exercise 3.3.1e we found that there are 16 nontrivial dependencies. They are AB→C, DE→C, B→D, AB→D, BC→D, BE→C, BE→D, ABC→D, ABD→C, ABE→C, ABE→D, ADE→C, BCE→D, BDE→C, ABCE→D, and ABDE→C.We also found out that the only key is ABE. FDs where the left side is not a superkey or the attributes on the right are not part of some key are 3NF violations. The 3NFviolations are AB→C, DE→C, B→D, AB→D, BC→D, BE→C, BE→D, ABC→D, ABD→C, ADE→C, BCE→D and BDE→C.Using algorithm 3.26, we can decompose into relations using the minimal basis AB→C,DE→C and B→D. The resulting decomposed relations would be ABC, CDE and BD. However,none of these three sets of attributes is a superkey. Thus we add relation ABE to the result. The final set of decomposed relations is ABC, CDE, BD and ABE.Exercise 3.5.1fIn the solution to Exercise 3.3.1f we found that there are 41 nontrivial dependencies. They are: C→B, C→D, C→E, D→B, D→E, AB→C, AB→D, AB→E, AC→B, AC→D, AC→E, AD→B, AD→C, AD→E, BC→D, BC→E, BD→E, CD→B, CD→E, CE→B, CE→D, DE→B, ABC→D, ABC→E,ABD→C, ABD→E, ABE→C, ABE→D, ACD→B, ACD→E, ACE→B, ACE→D, ADE→B, ADE→C, BCD→E, BCE→D, CDE→B, ABCD→E, ABCE→D, ABDE→C and ACDE→B.We also found out that the keys are AB, AC and AD. FDs where the left side is not a superkey or the attributes on the right are not part of some key are 3NF violations. The3NF violations are C→E, D→E, BC→E, BD→E, CD→E and BCD→E.Using algorithm 3.26, we can decompose into relations using the minimal basis AB→C, C→D, D→B and D→E. The resulting decomposed relations would be ABC, CD, BD and DE. Since relation ABC contains a key, we can stop with the decomposition. The final set of decomposed relations is ABC, CD, BD and DE.Exercise 3.5.2aThe usual procedure to find the keys would be to take the closure of all 63 nonempty subsets. However, if we notice that none of the right sides of the FDs contains。
数据库系统原理04735课后习题答案

数据库系统原理04735课后习题答第一章.数据库系统基本概念1.1.名词解释(省略)1.2.人工管理阶段的数据管理有哪些特点?1)数据不保存在计算机里2)没有专门的软件进行对数据库管理3)只有程序概念,没有文件概念4)数据面向程序1.3.文件系统阶段的数据管理有哪些特点?1)数据以文件形式长期存储在外部存储器的磁盘上2)数据的逻辑结构和物理结构有了区别,但比较简单3)文件组织多样化,有了索引文件、链接文件和直接存取文件等4)数据不再属于某个特定程序,可重复使用,即数据面向应用5)对数据的操作以记录为单位1.4.文件系统阶段的数据管理有哪些缺陷?请举例说明?1)数据冗余、数据不一致、数据联系弱2)比如建立了职工档案、职工工资和职工保健三个文件,职工的电话在三个文件中重复出现,即数据冗余。
1.5.数据管理的数据库阶段产生的标志是哪三件事情?1)1968年IBM公司推出层次模型IMS系统2)1969年美国CODASYL组织发布了DBTG报告3)1970年IBM公司的E .F.Codd连续发表论文,提出关系模型1.6.数据库阶段的数据管理有哪些特色?1)采用了数据模型表示复杂的数据结构2)有较高的数据独立性3)数据库系统提供了方便的用户接口4)数据库系统提供了四个方面的数据控制功能:数据库的恢复、数据的并发控制、数据的完整性、数据完全性。
5)增加了系统的灵活性:对数据的操作不一定以记录为单位,可以以数据项为单位。
1.7.高级数据库阶段有哪些技术?面向对象的概念建模、开放数据库互联技术1.8.逻辑记录与物理记录,逻辑文件与物理文件有哪些联系和区别?数据描述有两种形式:物理数据描述和逻辑物理描述。
物理数据描述是指数据在存储设备上的描述,物理数据是存储在物理设备上的数据,物理记录和物理文件都是用来描述存储数据的细节。
逻辑数据描述是用户或程序员以操作的数据形式的描述,逻辑记录和逻辑文件都是用户观点的数据描述。
1.9.数据抽象过程有哪些步骤?1)根据用户的需求,设计数据的概念模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章关系数据库标准语言
1 .试述语言的特点。
答:
(l)综合统一。
语言集数据定义语言、数据操纵语言、数据控制语言的功能于一体。
(2)高度非过程化。
用语言进行数据操作,只要提出“做什么”,而无需指明“怎么做”,因此无需了解存取路径,存取路径的选择以与语句的操作过程由系统自动完成。
(3)面向集合的操作方式。
语言采用集合操作方式,不仅操作对象、查找结果可以是元组的集合,而且一次插入、删除、更新操作的对象也可以是元组的集合。
(4)以同一种语法结构提供两种使用方式。
语言既是自含式语言,又是嵌入式语言。
作为自含式语言,它能够独立地用于联机交互的使用方式;作为嵌入式语言,它能够嵌入到高级语言程序中,供程序员设计程序时使用。
(5)语言简捷,易学易用。
2 .试述的定义功能。
的数据定义功能包括定义表、定义视图和定义索引。
语言使用语句建立基本表,语句修改基本表定义,语句删除基本表;使用语句建立索引,语句删除索引;使用语句建立视图,语句删除视图。
3 .用语句建立第二章习题5 中的
4 个表。
答:
对于S 表:S ( , , , ) ;
建S 表:
S ( C(2) ,C(6) ,C(2),C(4));
对于P 表:P ( , , , );
建P 表:
P( C(2) ,C(6),C(2),);
对于J 表:J ( , , );
建J 表:
J( C(2) ,C(8),C(4))
对于表:( , , , );
建表:()
( C(2),C(2),C(2),))
4.针对上题中建立的4 个表试用语言完成第二章习题5 中的查询。
( l )求供应工程零件的供应商号码;
’J1’
( 2 )求供应工程零件的供应商号码;
'J1' 'P1'
( 3 )求供应工程零件为红色的供应商号码;
'J1' '红'
( 4 )求没有使用天津供应商生产的红色零件的工程号;
( '天津' '红' )。
( 5 )求至少用了供应商所供应的全部零件的工程号;
由于不允许子查询嵌套太深,将查询分为两步
A、查询S1供应商供应的零件号
'S1'结果是(P1,P2)
B、查询哪一个工程既使用P1零件又使用P2零件。
'P1'
( 'P2')
5.针对习题3中的四个表试用语言完成以下各项操作:(1)找出所有供应商的姓名和所在城市。
S
(2)找出所有零件的名称、颜色、重量。
P
(3)找出使用供应商S1所供应零件的工程号码。
'S1'
(4)找出工程项目J2使用的各种零件的名称与其数量。
'J2'
(5)找出上海厂商供应的所有零件号码。
'上海'
(6)出使用上海产的零件的工程名称。
'上海'
(7)找出没有使用天津产的零件的工程号码。
注意: ( '天津') 适用于是唯一或不唯一的情况.
注意: <>'天津'适用于是唯一的情况
(8)把全部红色零件的颜色改成蓝色。
P '蓝' '红'
(9)由S5供给J4的零件P6改为由S3供应。
'S3' 'S5' 'J4' 'P6'
(10)从供应商关系中删除供应商号是S2的记录,并从供应情况关系中删除相应的记录。
A、S ’S2’
B、‘S2’
(11)请将(S2,J6,P4,200)插入供应情况关系。
(‘S2’,‘J6’,‘P4’,200)
6 .什么是基本表?什么是视图?
答
两者的区别和联系是什么?基本表是本身独立存在的表,在中一个关系就对应一个表。
视图是从一个或几个基本表导出的表。
视图本身不独立存储在数据库中,是一个虚表。
即数据库中只存放视图的定义而不存放视图对应的数据,这些数据仍存放在导出视图的基本表中。
视图在概念上与基本表等同,用户可以如同基本
表那样使用视图,可以在视图上再定义视图。
7 .试述视图的优点。
答
( l )视图能够简化用户的操作;( 2 )视图使用户能以多种角度看待同一数据;( 3 )视图对重构数据库提供了一定程度的逻辑独立性;( 4 )视图能够对机密数据提供安全保护。
8 .所有的视图是否都可以更新?为什么?
答:
不是。
视图是不实际存储数据的虚表,因此对视图的更新,最终要转换为对基本表的更新。
因为有些视图的更新不能惟一有意义地转换成对相应基本表的更新,所以,并不是所有的视图都是可更新的.
9 .哪类视图是可以更新的?哪类视图是不可更新的?各举一例说明。
答:基本表的行列子集视图一般是可更新的。
若视图的属性来自集函数、表达式,则该视图肯定是不可以更新的。
10 .试述某个你熟悉的实际系统中对视图更新的规定。
答
11.请为三建工程项目建立一个供应情况的视图,包括供应商代码()、零件代码()、供应数量()。
'三建'
针对该视图完成下列查询:
(1)找出三建工程项目使用的各种零件代码与其数量。
(2)找出供应商S1的供应情况。
* 'S1'。
