计时双基练7
人教版新课标A版高中数学必修5双基限时练及答案7.doc

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】双基限时练(七)1.下列叙述正确的是( )A .数列1,3,5,7与7,5,3,1是同一数列B .数列0,1,2,3,…的通项公式为a n =n C. 0,1,0,1,…是常数列D .数列⎩⎨⎧⎭⎬⎫n n +1是递增数列答案 D2.数列23,45,67,89,…的第10项是( ) A.1617 B.1819 C.2021 D.2223答案 C3.数列1,3,6,10,x,21,…中,x 的值是( ) A .12 B .13 C .15 D .16 答案 C4.下列说法不正确的是( ) A .数列可以用图形表示 B .数列的通项公式不唯一 C .数列的项不能相等 D .数列可能没有通项公式 答案 C5.已知a n +1-a n -3=0,则数列{a n }是( )A .递增数列B .递减数列C .常数列D .摆动数列解析 由a n +1-a n -3=0,得a n +1=a n +3, ∴数列{a n }是递增数列. 答案 A6.数列1,3,6,10,15,…的递推公式是( ) A .a n +1=a n +n (n ∈N *) B .a n =a n -1+n (n ∈N *,n ≥2) C .a n +1=a n +(n +1)(n ∈N *,n ≥2) D .a n =a n -1+(n -1)(n ∈N *,n ≥2)解析 把数的前5项代入验证,知a n =a n -1+n 适合. 答案 B7.观察数列的特点,用适当的一个数填空:1,3,5,7,________,11,….答案 38.在数列-1,0,19,18,…,n -2n 2,…中,0.08是它的第________项.解析 令n -2n 2=0.08,得2n 2-25n +50=0,解得n =10,或n =52(舍去), ∴a 10=0.08. 答案 109.若数列的通项公式是a n =3-2n,则a 2n =________;a 2a 3=________.解析 ∵a n =3-2n ,∴a 2n =3-22n =3-4n ,a 2a 3=3-223-23=15.答案 3-4n 1510.已知数列{a n }的通项公式是a n =n 2-8n +12,那么该数列中为负数的项一共有________项.解析 由a n =n 2-8n +12<0, 得(n -2)(n -6)<0, ∴2<n <6,又n ∈N +, ∴n =3,4,5共3项. 答案 311.根据数列的通项公式,写出下列数列的前5项,并用图象表示出来.(1)a n =(-1)n +2; (2)a n =2nn +1.解 (1)∵a n =(-1)n +2,∴a 1=1,a 2=3,a 3=1,a 4=3,a 5=1. ∴数列的前5项是1,3,1,3,1. 图象如图①.① ②(2)数列{a n }的前5项依次是:1,43,32,85,53.图象如图②. 12.已知数列{a n }的通项公式为a n =3n -23n +1.(1)求a 10;(2)710是否为该数列中的项?若是,它为第几项? (3)求证:0<a n <1.解 (1)a 10=3×10-23×10+1=2831.(2)令a n =710,即3n -23n +1=710,解得n =3,∴710为数列{a n }中的项,为第3项. (3)证明:a n =3n -23n +1=1-33n +1.∵n ∈N *,∴3n +1>3.∴0<33n +1<1,∴0<1-33n +1<1,即0<a n <1.。
计时双基练

计时双基练(一)走近细胞(计时:45分钟满分:100分)一、选择题(每小题4分,共56分)1.据英国《皇家学会学报B》上发表的一项研究显示,台湾乳白蚁粪便具有一种特殊功效,其所含有的起保护作用的细菌能阻止杀死乳白蚁的真菌的入侵。
下列相关叙述中不正确的是()A.台湾乳白蚁、细菌和真菌三种生物都含有以核膜为界限的细胞核B.对台湾乳白蚁具有保护作用的细菌所含有的DNA是裸露的C.台湾乳白蚁在咀嚼木材时消耗的能量主要由线粒体提供D.台湾乳白蚁、细菌和真菌都含有生产蛋白质的机器——核糖体2.下列有关颤藻、水绵和黑藻所具有的共同结构和生理功能的叙述,正确的是() A.都含有叶绿素和类胡萝卜素,进行光合作用B.都含中心体,决定细胞分裂方向C.都含核糖体,作为蛋白质合成的装配机器D.都不含染色体,只在分子水平产生可遗传变异3.下列有关细胞及细胞学说的叙述,正确的是()A.小麦细胞和发菜细胞的结构有差异,不具有统一性B.原核细胞构成的原核生物都是营腐生或寄生生活的异养生物C.原核细胞没有核膜,结构也比较简单,所以不具有多样性D.细胞学说主要揭示了细胞的统一性和生物体结构的统一性4.细胞行使的功能不同,其形态一般也不同,无论动物细胞还是植物细胞,形态总是与功能相适应,这是生物在长期进化过程中逐渐形成的,下列叙述不正确的是() A.神经细胞有长的突起,有利于接收细胞外的刺激和传导兴奋B.鸵鸟的卵细胞较大,有利于从外界环境中吸收营养物质供给胚胎的发育C.叶表皮保卫细胞呈半月形,2个细胞围成一个气孔,有利于呼吸又有利于蒸腾作用D.人体内的白细胞形状不规则,与其免疫功能相适应5.波浪热是由布鲁氏杆菌引起急性或慢性人畜共患传染病。
下列相关说法正确是() A.布鲁氏杆菌细胞中有线粒体、核糖体B.布鲁氏杆菌在分裂过程中不出现基因重组C.布鲁氏杆菌所含元素中O是最基本的元素D.布鲁氏杆菌的遗传物质分布于细胞核内6.下列是关于几类生物的特点的叙述,正确的是()A.细菌和蓝藻在结构上有统一性,具体体现在它们都有细胞壁、细胞膜、核糖体及相同类型的遗传物质等B.硝化细菌与变形虫结构上的根本区别是前者有细胞壁,营养方式为自养型,后者无细胞壁,营养方式为异养型C.颤藻与发菜共同点都能进行光合作用,但颤藻含光合色素,而发菜细胞中含叶绿体D.一个动物体不同细胞形态和功能有其多样性。
高二数学 双基限时练7

双基限时练(七)1.函数f(x)的定义域为开区间(a,b),导数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内极小值有()A.1个B.2个C.3个D.4个解析设x0为f(x)的一个极小值点,则在x0左侧f′(x)<0,右侧f′(x)>0,由y=f′(x)的图象知,只有一个适合.答案A2.已知实数a,b,c,d成等比数列,且曲线y=3x-x3的极大值点坐标为(b,c),则ad等于()A.2 B.1C.-1 D.-2解析y′=3-3x2,令y′=0,得x=±1.可判断函数y=3x-x3在x=1处取得极大值,因此极大值点的坐标为(1,2),即b=1,c=2,又ad=bc,∴ad=2.答案A3.三次函数当x=1时,有极大值,当x=3时,有极小值,且函数的图象过原点,则该三次函数为()A.y=x3+6x2+9x B.y=x3-6x2+9xC .y =x 3-6x 2-9xD .y =x 3+6x 2-9x解析 本题若直接求解,相当于解一个大题,本题按照小题小做的原则,可采用试验找答案,显然四个函数的图象都过原点,下面分别求导函数,验证x =1和x =3都是导函数的根,对于B ,y ′=3x 2-12x +9=3(x -1)(x -3).当x =1和x =3时,有y ′=0.而其他不适合题意.答案 B4.已知函数y =2x 3+ax 2+36x -24在x =2处有极值,则该函数的一个递增区间是( )A .(2,3)B .(3,+∞)C .(2,+∞)D .(-∞,3)解析 y ′=6x 2+2ax +36.依题意知6×22+4a +36=0,∴a =-15,∴y ′=6x 2-30x +36=6(x -2)(x -3),易知当x >3时,y ′>0,∴函数的一个增区间为(3,+∞).答案 B5.函数f (x )=13x 3-2ax 2+3a 2x 在(0,1)内有极小值,则实数a 的取值范围是( )A .(0,+∞)B .(-∞,3)C.⎝⎛⎭⎪⎫0,13 D.⎝ ⎛⎭⎪⎫0,32 解析 f ′(x )=x 2-4ax +3a 2=(x -a )(x -3a ),易知a ≠0,∴f ′(0)=3a 2>0,Δ=(-4a )2-12a 2=4a 2>0,依题意可得⎩⎪⎨⎪⎧0<3a <1,f ′(1)=1-4a +3a 2>0.解得0<a <13. 答案 C6.已知函数f (x )=x 3+3ax 2+3(a +2)x +1既有极大值,又有极小值,则实数a 的取值范围是________.解析 f ′(x )=3x 2+6ax +3(a +2),由题意知f ′(x )=0有两个不同的实数根,∴Δ=36a 2-36(a +2)>0,解得a <-1,或a >2.答案 a >2或a <-17.已知函数f (x )=-x 3+3x 2+9x +m ,在R 上的极大值为20,则实数m =________.解析 f ′(x )=-3x 2+6x +9=-3(x +1)(x -3),当-1<x <3时,f ′(x )>0,当x >3时,f ′(x )<0,∴当x =3时,f (x )有极大值,则f (3)=-33+3×32+9×3+m =20,∴m =-7.答案 -78.曲线y =12x 2+4ln x 上切线斜率的极小值为________.解析 y ′=x +4x (x >0),令g (x )=x +4x ,则g ′(x )=1-4x 2.令g ′(x )=0,得x =2.当x ∈(0,2)时,g ′(x )<0;当x ∈(2,+∞)时g ′(x )>0,∴当x =2时,g (x )有极小值g (2)=2+42=4.答案 49.函数y =f (x )的导函数f ′(x )的图象如图所示,给出下列命题:①-3是函数y=f(x)的极值点;②-1是函数y=f(x)的最小值点;③y=f(x)在区间(-3,1)上单调递增;④y=f(x)在x=0处切线的斜率小于零.以上正确命题的序号是________.解析由f′(x)的图象知,在-3的左右两侧f′(x)符号左负右正,是极值点,故①正确;②错;在(-3,1)上f′(x)≥0,故③正确;k=f′(0)>0,故④错.答案①③10.设x=-2,x=4是函数f(x)=x3+ax2+bx的两个极值点.(1)求常数a,b;(2)判断x=-2,x=4是函数f(x)的极大值点还是极小值点,并说明理由.解(1)f′(x)=3x2+2ax+b,由极值点的必要条件可知,x=-2,x=4是方程f′(x)=0的两根.∴a=-3,b=-24.(2)f′(x)=3x2-6x-24=3(x+2)(x-4)当x<-2时,f′(x)>0,当-2<x<4时,f′(x)<0,当x>4时,f′(x)>0,∴x=-2是f(x)的极大值点,x=4是f(x)的极小值点.11.设函数f(x)=2x3-3(a-1)x2+1,其中a≥1.(1)求f(x)的单调区间;(2)讨论f(x)的极值.解由已知得,f′(x)=6x[x-(a-1)],令f′(x)=0,解得x1=0,x2=a-1,(1)当a=1时,f′(x)=6x2,f(x)在(-∞,+∞)上单调递增.当a>1时,f′(x)=6x[x-(a-1)].f′(x),f(x)随x的变化情况如下表:调递减;在(a-1,+∞)上单调递增.(2)由(1)知,当a=1时,函数f(x)没有极值.当a>1时,函数在x=0处取得极大值1,在x=a-1处取得极小值1-(a-1)3.12.设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=2a,f′(2)=-b,其中常数a,b∈R.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)设g(x)=f′(x)e-x,求函数g(x)的极值.解 ∵f (x )=x 3+ax 2+bx +1,∴f ′(x )=3x 2+2ax +b .令x =1,得f ′(1)=3+2a +b ,又f ′(1)=2a ,∴3+2a +b =2a ,∴b =-3.令x =2,得f ′(2)=12+4a +b ,又f ′(2)=-b ,∴12+4a +b =-b ,解得a =-32.∴f (x )=x 3-32x 2-3x +1.从而f (1)=-52.又∵f ′(1)=2×(-32)=-3.故曲线y =f (x )在点(1,f (1))处的切线方程为y -(-52)=-3(x -1),即6x +2y -1=0.(2)由(1)知,g (x )=(3x 2-3x -3)e -x ,∴g ′(x )=(-3x 2+9x )e -x =-3x (x -3)e -x .令g ′(x )=0,得x 1=0,x 2=3.当x ∈(-∞,0)时,g ′(x )<0,故g (x )在(-∞,0)上为减函数; 当x ∈(0,3)时,g ′(x )>0,故g (x )在(0,3)上为增函数;当x ∈(3,+∞)时,g ′(x )<0,故g (x )在(3,+∞)上为减函数. 从而可知,函数g (x )在x =0处取得极小值g (0)=-3, 在x =3处取得极大值g (3)=15e -3.新课标第一网系列资料 。
人教B版高中数学必修三双基限时练7.docx

双基限时练(七)循环语句基础强化1.关于for循环和w hile循环的说法错误的是()A.在for循环中,循环变量也称为循环体B.在for循环中,步长为1,可以省略不写;若为其他值,则不可省略C.w hile循环中,只有当表达式为真时,才执行循环体D.在for循环和w hile循环中,必须都有“end”结尾解析for循环中,循环表达式也称为循环体,故A错.答案A2.关于下面一段程序,其中正确的说法是()k=10;w hile k==0k=k+1;endA.语句中的循环体共执行了10次B.循环体是无限循环的C.语句中的循环体一次也不执行D.语句中的循环体只进行了一次解析由于k=10,则k=0不成立,则不执行循环体.答案C3.程序S=1;for i=1:1:10S=(3^ i)*S;endprint (%io(2),S);上面程序的功能为()A.用来计算3×103的值B.用来计算355的值C.用来计算310的值D.用来计算1×2×3×…×10的值解析当i=10时,S=31·32·33·…·310=355.故选B.答案 B4.下面两个程序最后输出的S的值为()程序1:i=1;while i<8i=i+2;S=2]程序2:i=1;w hile i<8S=2]i=i+2;enddisp(S);A.都是17B.都是21C.21,17 D.14,21解析程序1中:当i=7时进入循环体后,i=9,S=21,退出循环.程序2中:当i=7时进入循环体,S=2×7+3=17,i=9,退出循环.答案 C5.下面程序的运算结果为()i=0;S=0;While S<=20S=S+i;i=i+1;endprint(%io(2),i);A.6B.7C.8 D.9解析S=0+1+2+3+4+5+6=21>20,由于循环体为“S=S +i;i=i+1”,∴程序终止时i=7.答案 B6.执行程序:S=0;for i=1:2:100S=S+i;Print(%io(2),S);end该程序输出的第10个数为()A.181 B.100C.210 D.221解析该程序输出第10个数为S=1+3+…+19=100.答案 B7.当下列程序中运行后,输出的结果为________.i=1;s=1;while s<5s=s*(i+1)/i;i=i+1;endprint(%io(2),i);解析第一步:s=2,i=2;第二步:s=3,i=3;第三步:s=4,i=4;第四步:s=5,i=5.程序终止时,i=5.答案 58.s=1;for i=1:2:7s=3]上面程序输出的结果为________.解析∵i的终值为7,∴输出最终结果为S=3×7=21.答案219.若下面程序的运行结果为240,则“表达式”应为i>________.S=1;w hile i>S=S*i;i=i-1;endprint(%io(2),S);解析w hile循环语句中,当表达式为真时执行循环体,否则退出循环.由于输出的结果为240=15×16,所以执行了两次循环,因此表达式应为i>14.答案14能力提升10.编写计算11×2+12×3+13×4+…+199×100的算法程序.解程序为:S=0;for i=1:1:99S=S+1/(i*(i+1));endprint(%io(2),S);11.试编写程序确定S=1+4+7+10+…中至少加到第几项时S≥300.解程序如下:n=1;i=0;w hile S<300S=S+n;n=n+3;i=i+1;endprint(%io(2),i);12.设计一个程序将全班60名学生考试及格者的平均分计算并打印出来.解程序为:S=0;n=1;i=0;w hile n≤60G=input(“输入学生成绩”);if G>=60i=i+1;S=S+G;endn=n+1;enda v er=S/i;print(%io(2),a v er);品味高考13.下列问题可以用循环语句设计程序的有()①求1+3+32+…+39的和;②比较a,b两个数的大小;③对于分段函数,要求输入自变量,输出函数值;④求平方值小于100的最大自然数.A.0个B.1个C.2个D.3个解析①④可以用循环语句设计程序,②③要用条件语句设计程序.答案C。
人教A版选修2-3双基限时练7.docx

高中数学学习材料唐玲出品双基限时练(七)1.在(x -3)10的展开式中,x 6的系数是( )A .-27C 510B .27C 410C .-9C 510D .9C 410解析 通项T r +1=C r 10x 10-r (-3)r =(-3)r C r 10x10-r. 令10-r =6,得r =4.∴x 6的系数为9C 410. 答案 D2.在(32x -12)20的展开式中,系数是有理数的项共有( )A .4项B .5项C .6项D .7项解析T r +1=C r 20(32x )20-r(-12)r=(-1)r C r 20220-r 3-r2·x 20-r .要使系数为有理数,只要20-r 3-r 2为整数,即40-5r6为整数. ∵0≤r ≤20,∴r =2,8,14,20,∴共有4项. 答案 A3.(2x -1x )9的展开式中,常数项为( )A .-672B .672C .-288D .288解析T r +1=C r 9(2x )9-r(-1x)r =(-1)r 29-r C r9·x 9-r -r 2,令9-r -r 2=0,得r =6.∴常数项为23C 69=8C 39=672.答案 B4.设P =1+5(x +1)+10(x +1)2+10(x +1)3+5(x +1)4+(x +1)5,则P 等于( )A .x 5B .(x +2)5C .(x -1)5D .(x +1)5解析 P =C 05+C 15(x +1)+C 25(x +2)2+…+C 55(x +1)5=(x +1+1)5=(x +2)5.答案 B5.在(x +2x )n的展开式中,常数项为60,则n 等于( ) A .3 B .6 C .9 D .12解析T r +1=C r n (x )n -r(2x )r =2r C rn xn -r2-r .令n -3r2=0,则n =3r .∴2r C r3r =60,试验知r =2,∴n =6.答案 B6.(x 2+2x )8的展开式中x 4的系数是( )A .16B .70C .560D .1120解析 (x 2+2x )8的展开式的通项是T r +1=C r 8·(x 2)8-r ·(2x )r =2r ·C r 8·x 16-3r,令16-3r =4,得r =4.因此x 4的系数为24·C 48=1120. 答案 D7.对于二项式(1x +x 3)n(n ∈N +),四位同学作出四种判断: 甲:存在n ∈N +,展开式中有常数项; 乙:对任意n ∈N +,展开式中没有常数项; 丙:对任意n ∈N +,展开式中没有x 的一次项; 丁:存在n ∈N +,展开式中有x 的一次项. 其中判断正确的是________. 解析 由通项公式 T r +1=C r n (1x)n -r ·(x 3)r =C r n x 4r -n若r =1,则n =4,T 2就是常数项,令r =1,n =3时,就存在x的一次项.因此应填甲、丁. 答案 甲丁8.在(1+x )3+(1+x )3+(1+3x )3的展开式中,x 的系数为________(用数字作答).解析 x 的系数为C 13C 22+C 23C 11+C 33=3+3+1=7.答案 79.若⎝ ⎛⎭⎪⎫a x-x 29的展开式中x 3的系数为94,则常数a 的值为________.解析答案 410.在(4x -2-x )6的展开式中,常数项为________.解析 (4x -2-x )6展开式的通项为T r +1=C r 6(4x )6-r·(-2-x )r =(-1)r C r 6(2x )2(6-r )-r ,由2(6-r )-r =0,得r =4,∴(-1)4C 46=15.即常数项为15.答案 1511.设f (x )=(1+x )m +(1+x )n 展开式中x 的系数是19(m ,n ∈N *). (1)求f (x )展开式中x 2的系数的最小值;(2)当f (x )展开式中x 2的系数取最小值时,求f (x )展开式中x 7的系数.解 (1)由题设条件,得m +n =19. ∴m =19-n ,x 2的系数为C 2m +C 2n =C 219-n +C 2n =(19-n )(18-n )2+n (n -1)2=n 2-19n +171=(n -192)2+3234,∵n ∈N *,∴当n =9,或n =10时, x 2的系数取最小值(12)2+3234=81.(2)当n =9,m =10或n =10,m =9时,x 2的系数取最小值,此时x 7的系数为C 710+C 79=C 310+C 29=156.12.已知数列{a n }是公比为q 的等比数列.(1)求和:a1C02-a2C12+a3C22,a1C03-a2C13+a3C23-a4C33;(2)由(1)的结果归纳概括出关于正整数n的一个结论,并证明.解(1)a1C02-a2C12+a3C22=a1-2a1q+a1q2=a1(1-q)2,a1C03-a2C13+a3C23-a4C33=a1-3a1q+3a1q2-a1q3=a1(1-q)3.(2)归纳概括的结论为:若数列{a n}是首项为a1,公比为q的等比数列,则a1C0n-a2C1n+a3C2n-a4C3n+…+(-1)n a n+1C n n=a1(1-q)n,n 为正整数.证明:a1C0n-a2C1n+a3C2n-a4C3n+…+(-1)n a n+1C n n=a1C0n-a1q C1n+a1q2C2n-a1q3C3n+…+(-1)n a1q n C n n=a1[C0n-q C1n+q2C2n-q3C3n+…+(-1)n q n C n n]=a1(1-q)n.。
双基能力训练习题及答案

双基能力训练习题及答案双基能力训练Ⅰ.单词辨音:判断下列各题画线部分分别有几种读音:A.一种B.两种 C.三种D.四种,Put them away, please! 双基能力训练。
1.[ ]class same want bag2.[ ]goodness broken empty get3.[ ]wrong worry only not4.[ ]put mum ruler student5.[ ]say play Sunday today6.[ ]flower window know how7.[ ]China school catch chair8.[ ]nine know think orangeⅡ.从A、B、C、D中找出其重音与其它几个重音不同的选项。
1.[ ]A.yellow B.pencilC.fourteen D.sweater2.[ ]A.bedroom B.middleC.very D.Chinese3.[ ]A.basket B.excuseC.begin D.today4.[ ]A.apple B.dutyC.orange D.thirteen5.[ ]A.worry B.aboutC.other D.brokenⅢ.单词拼写:根据下列句子及所给单词的首字母,完成以下单词的`拼写。
1.“I can see some books there. ”“What o________ things can you see? ” 2.Here are your clothes. Please put them a________.3.Don't w________. I can help you.4.“Is seventy and twenty ninety? ”“Yes. That's r________.”5.What's w________ with your kite?Ⅳ.找出下列各组单词中范畴与其它几个均不相同的选项。
人教版八年级物理上册(国庆)横道中学双基训练七

年班姓名成绩:1、有一山峡宽1200m,两旁都是竖直的陡壁,有一人在山峡内开了一枪,听到第一、第二两次回声间隔5s,则人到两壁的距离分别是(声速v=340m/s )()A.700m,500m B.860m,340m C.1000m,200m D.1025m,175m2、人耳能听到回声的条件是回声到达人耳比原声晚0.1s,你面向一高墙喊话,如果想听到回声,那么你和高墙之间的距离至少应()A.大于34m B.大于17m C.等于17m D.等于34m3、关于声的利用,下列哪种做法是不可行的()A.可以利用回声探测海底沉船的位置B.可以利用向宇宙飞船发射超声波的方法来测量飞船距地面的高度C.可以利用超声波除去人体内的结石D.可以利用声波来清洗精细的机械4、下列控制噪声的措施中,属于防止噪声产生的是()A.晚上休息时关闭房间的门窗B.公共场所不要高声喧哗C.街道上安装噪声监测仪D.纺织车间的工作人员使用防噪声耳罩5、下列做法属于在传播过程中减弱噪声的是()A.摩托车装有消声器B.城市路旁设有隔声板C.工人带防噪声耳罩D.考场附近禁止鸣笛6、关于声现象,下列说法错误的是()A.“隔墙有耳”说明固体能传声B.用超声波清洗眼镜,说明声波具有能量C.听诊器能增大振幅,使响度增大D.“闻其声而知其人”是根据声音的音色来判断的7、吼猴是世界上叫声最响的动物之一,它以雷鸣般吼声警告其它动物不要侵犯它的领地,吼猴的叫声是由舌骨产生的,并通过传入其它动物耳中:这里的“雷鸣般”描述的是声音的.8、爱动脑筋的刘畅在学习声现象后,将喝酸奶的吸管剪成不同的长度,并用胶带将吸管底部密封,然后排在一起,如图所示.对着管口吹气,由于空气柱就会产生声音.管的长短不同,发出声音的(填“音调、响度、音色”)就不同,这样就做成了一个小吸管乐器.能听出来该乐器与商店出售的乐器的声音明显不同,原因是它们的不同.9、汽车在行驶时,发动机因而产生较大的噪声,噪声通过传入我们的耳朵,减少噪声的主要途径有:①在声源处控制噪声;②在传播途中控制噪声;③在人耳处减弱噪声.人们在发动机周围安装带有很多小孔的吸音槽,当声音传进小孔,就会由于摩擦而被减弱,这是通过上述途径减少噪声的.(填序号)命题:横道中学物理组敬请批评指正初中物理试卷灿若寒星制作。
人教A版数学必修一双基限时练7.docx

高中数学学习材料马鸣风萧萧*整理制作双基限时练(七)1.y 与x 成反比例,且当x =2时,y =1,则y 关于x 的解析式为( )A .y =2x B .y =1x C .y =-2x D .y =-1x答案 A2.已知正方形的周长为x ,它的外接圆的半径为y ,则y 关于x 的解析式为( )A .y =12x (x >0) B .y =24x (x >0) C .y =28x (x >0)D .y =216x (x >0) 解析 正方形外接圆的直径是它的对角线,又正方形的边长为x4,由勾股定理得(2y )2=⎝ ⎛⎭⎪⎫x 42+⎝ ⎛⎭⎪⎫x 42,∴y 2=x 232,∴y =28x (x >0).答案 C3.“龟兔赛跑”讲述了这样一个故事:领先的兔子看着缓缓爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到了终点….用S 1和S 2分别表示乌龟和兔子所行的路程,t 为时间,S 为路程,则下列图象中与故事情节相吻合的是( )答案 D4.若y =f (x )的定义域是[0,2],则函数g (x )=f (2x )x -1的定义域是( )A .[0,1]B .[0,1)C .[0,1)∪(1,4]D .(0,1)解析 由⎩⎪⎨⎪⎧ 0≤2x ≤2,x -1≠0,得⎩⎪⎨⎪⎧0≤x ≤1,x ≠1.∴g (x )的定义域为[0,1). 答案 B5.已知x ≠0,函数f (x )满足f ⎝⎛⎭⎪⎫x -1x =x 2+1x 2,则f (x )的表达式为( )A .f (x )=x +1x B .f (x )=x 2+2 C .f (x )=x 2D .f (x )=⎝ ⎛⎭⎪⎫x -1x 2 解析 ∵f ⎝ ⎛⎭⎪⎫x -1x =x 2+1x 2=⎝ ⎛⎭⎪⎫x -1x 2+2, ∴f (x )=x 2+2. 答案 B6.一旅社有100间相同的客房,经过一段时间的经营实践,发现每间客房每天的定价与住房率有如下关系:每间房定价 100元 90元 80元 60元 住房率65%75%85%95%要使每天的收入最高,每间房的定价应为( ) A .100元 B .90元 C .80元D .60元解析 100×65=6500(元),90×75=6750(元), 80×85=6800(元),60×95=5700(元). 比较结果知,每间房定价为80元收入最高. 答案 C7.已知函数的关系由下表给出:x -3 -2 -1 0 1 2 3 f (x )-4-3-2-112则函数f (x )的解析式可表示为____________. 解析 观察表可知f (x )的值比x 的值小1, 因此f (x )=x -1. 答案 f (x )=x -18.若f (x )-12f (-x )=2x (x ∈R ),则f (2)=________.解析由⎩⎪⎨⎪⎧f (2)-12f (-2)=4,f (-2)-12f (2)=-4,得⎩⎨⎧2f (2)-f (-2)=8,f (-2)-12f (2)=-4.相加得32f (2)=4,f (2)=83. 答案 839.已知函数f (x ),g (x )分别由下表给出.x 1 2 3 f (x )211x 1 2 3 g (x )321 则f [g (1)]的值为________;当g [f (x )]=2时,x =________. 解析 由表知,g (1)=3,g (2)=2. ∴f [g (1)]=f (3)=1.由g [f (x )]=2,得f (x )=2,∴x =1. 答案 1 110.已知f (x )为二次函数,其图象顶点为(1,3),且过原点,求f (x ). 解 解法一:由于图象的顶点是(1,3), 故设f (x )=a (x -1)2+3(a ≠0).∵图象过原点(0,0), ∴a +3=0,∴a =-3. 故f (x )=-3(x -1)2+3.解法二:设f (x )=ax 2+bx +c (a ≠0),依题意得⎩⎪⎨⎪⎧-b2a =1,4ac -b24a =3,c =0,即⎩⎪⎨⎪⎧b =-2a ,b 2=-12a ,c =0.解得⎩⎪⎨⎪⎧a =-3,b =6,c =0.∴f (x )=-3x 2+6x .11.画出函数f (x )=-x 2+2x +3的图象,并根据图象回答下列问题:(1)比较f (0)、f (1)、f (3)的大小; (2)若x 1<x 2<1,比较f (x 1)与f (x 2)的大小; (3)求函数f (x )的值域.解 因为函数f (x )=-x 2+2x +3的定义域为R ,列表:x … -2 -1 0 1 2 34…y … -53430 -5 …连线,描点,得函数图象如图:(1)根据图象,容易发现f (0)=3,f (1)=4,f (3)=0, 所以f (3)<f (0)<f (1).(2)根据图象,容易发现当x 1<x 2<1时,有f (x 1)<f (x 2).(3)根据图象,可以看出函数的图象是以(1,4)为顶点,开口向下的抛物线,因此,函数的值域为(-∞,4].12.已知函数f (x )(x ∈R )满足f (x )=2bx ax -1,a ≠0,f (1)=1且使f (x )=2x 成立的实数x 只有一个,求函数f (x )的表达式.解 由f (x )=2bxax -1,f (1)=1,得a =2b +1.由f (x )=2x 只有一个解,即2bxax -1=2x ,也就是2ax 2-2(1+b )x =0(a ≠0)只有一解, ∴b =-1,∴a =-1. 故f (x )=2xx +1.。
双基练习题答案

双基练习题答案一、选择题1. 以下哪个选项是双基教育的核心内容?A. 体育B. 音乐C. 语文D. 数学答案:D2. 双基教育强调的“双基”指的是什么?A. 基础体能和基础技能B. 基础知识和基本技能C. 基础理论和基础实践D. 基础文化和基本素养答案:B3. 双基教育的实施目的是什么?A. 培养学生的应试能力B. 培养学生的创新能力C. 培养学生的基础知识和基本技能D. 培养学生的道德品质答案:C4. 双基教育在教学中通常采用哪种教学方法?A. 启发式教学B. 讲授式教学C. 互动式教学D. 以上都是答案:D5. 以下哪项不是双基教育的实施原则?A. 面向全体学生B. 注重学生个性发展C. 只注重知识传授D. 因材施教答案:C二、填空题6. 双基教育强调学生应该掌握的________和________。
答案:基础知识,基本技能7. 双基教育认为,教育应该________学生的全面发展。
答案:促进8. 在双基教育中,教师应该根据学生的________进行教学。
答案:实际情况9. 双基教育倡导的是一种________的教学模式。
答案:全面发展10. 双基教育要求学生在学习过程中,不仅要掌握知识,还要培养________。
答案:基本技能三、简答题11. 简述双基教育的重要性。
答案:双基教育的重要性在于它为学生提供了扎实的基础知识和基本技能,使学生能够在未来的学习和工作中具备必要的能力。
同时,它也有助于培养学生的创新思维和解决问题的能力。
12. 描述一下双基教育在课堂教学中的实施策略。
答案:在课堂教学中实施双基教育,教师应该采用多样化的教学方法,激发学生的学习兴趣,注重学生基础知识的掌握和基本技能的培养。
同时,教师还应该关注学生的个体差异,实施因材施教,确保每个学生都能在学习过程中得到发展。
四、论述题13. 论述双基教育与学生终身发展的关系。
答案:双基教育与学生终身发展密切相关。
首先,双基教育为学生提供了坚实的知识基础和技能基础,这为他们未来的学习和工作奠定了基础。
物理双基练习题

物理双基练习题1. 引言物理是一门自然科学,其涉及研究物质、能量和其相互作用的规律。
掌握物理基础概念和解题技巧对于培养学生的科学思维和解决实际问题的能力至关重要。
本文将介绍一些物理双基练习题,以便提高读者对物理知识的理解和应用。
2. 力学题2.1 问题描述:一辆质量为1000千克的小汽车以10米/秒的速度行驶,经过5秒后速度降至5米/秒。
请问,此时小汽车所受到的平均减速度是多少?解析:减速度定义为速度变化量除以时间,即a = (v2 - v1) / t。
代入已知数值,可得a = (5 - 10) / 5 = -1 单位:米/秒²2.2 问题描述:一个质量为2千克的物体以10米/秒的速度水平投射,抛射角度为30°,求此物体的飞行时间和飞行距离。
解析:水平速度v_x = v * cosθ = 10 * cos30° ≈ 8.66 米/秒垂直速度v_y = v * sinθ = 10 * sin30° ≈ 5 米/秒飞行时间t = 2v_y / g ≈ 2 * 5 / 9.8 ≈ 1.02 秒飞行距离d = v_x * t ≈ 8.66 * 1.02 ≈ 8.84 米3. 热学题3.1 问题描述:一块物体的质量为2千克,它的温度从20℃升高到60℃时,吸收了400焦耳的热量,求该物体的比热容。
解析:热量Q = mcΔθ,其中m为物体质量,c为比热容,Δθ为温度变化量。
代入已知数值,400 = 2c(60 - 20),解得c = 10 J/(kg·℃)。
3.2 问题描述:一杯水质量为0.2千克,初始温度为25℃,最后与环境达到热平衡时的温度为30℃。
求水的吸热量。
解析:吸热量Q = mcΔθ,其中m为物体质量,c为比热容,Δθ为温度变化量。
代入已知数值,Q = 0.2 * 4186 * (30 - 25) ≈ 418.6 焦耳4. 光学题4.1 问题描述:一面镜子与平面成30°的角,入射光线方向与法线成60°的角。
八年级物理上册课时双基目标训练

横道中学八年物理阶段性双基目标测试题二年班姓名时间50分钟满分70分成绩:一、选择题(每题2分共12分)1、用天平称出一个塑料瓶的质量,然后将其剪碎再放到天平上称,比较这个物体在形状变化前后的质量()A.变大B.变小C.不变D.无法确定2、用托盘天平测出一枚邮票的质量,下列做法中最合理的是()A.把一枚邮票放在托盘天平上称量B.先测出一枚邮票和一螺母的总质量,再减去螺母的质量C.先测出200枚邮票总质量,再除以200D.先测出200枚邮票的总质量,再加一枚邮票测出201枚邮票的总质量,求其差就是一枚邮票的质量3、在测量铁块的密度时,用了下面几个步骤,则测量步骤合理顺序是()①计算铁块的体积;②记录铁块放入量筒后水面上升到的刻度;③观察量筒中水的体积;④用天平测出铁块的质量;⑤调节好天平;⑥计算铁块的密度.A.⑤④②③①⑥B.④⑤③②①⑥C.③②①⑤④⑥D.⑤④③②①⑥4、托盘天平横梁上都有标尺和游码,向右移动游码的作用是()A.相当于向左调节平衡螺母B.代替指针用来指示平衡C.相当于在左盘中加小砝码D.相当于在右盘中加小砝码5、老花镜掉在地上,镜片裂成两块,但仍留在镜框内,则用这个眼镜看书上的字时()A.一个字会变成两个字B.看不到字C.仍能看到一个完整的字,只是字上有一条缝D.仍能看到一个完整的字6、关于照相机的使用,下列说法正确的是()A.拍摄远景时,应将镜头向前伸B.拍摄近景时,应将镜头向前伸C.晴天拍摄景物时,应开大光圈D.阴天拍摄景物时,应缩短曝光时间二、填空题(每空1分共18分)放大后正立的像.三、计算题(每题5分共10分)15、如图所示,一容积为3×10-4m3的瓶内盛有0.2kg的水,一只口渴的乌鸦每次将一块质量为0.01kg的小石子投入到瓶中,当乌鸦投入了25块相同的小石子后,水面升到瓶口,求:(1)瓶内石块的总体积;(2)石块的密度.16、一个实心铅球的质量是4kg,经测量它的体积是0.57×10-3m3,这个铅球是用纯铅制成的吗?(已知ρ3kg/m3)铅=11.3×10四、简答题(每题2分共6分)17、飞机为什么用铝合金制造而不用钢铁制造?18、实验室有一架托盘天平和砝码,横梁调节螺母已丢失,其他部件都完好准确,将它放在水平桌面上,游码移到零刻度线上时,指针总偏向中央标尺左端,现要利用这架天平准确测出一小金属块的质量,请你简述出一种测量方法.(可选用生活中常见的材料)19、望远镜物镜的直径比我们眼睛的瞳孔大得多,这是为什么?五、作图与实验题(20题2分21题10分22题4分23题5分24题3分共24分)20、如图所示,OO′是凸透镜的主光轴,A′B′是蜡烛AB通过凸透镜成的像,试在图中画出光线AC经凸透镜后的折射光线,并用作图的方法找出右侧焦点的位置.21、小华在观察凸透镜成像的条件的实验中:(1)把蜡烛、凸透镜、光屏从左向右依次放在同一上,点燃蜡烛并调整烛焰、凸透镜、光屏的高度,使它们的中心大致在同一.(2)确定像的位置时,沿凸透镜主光轴移动光屏,直到光屏上出现明亮、的烛焰像;(3)从蜡烛到凸透镜距离等于2倍焦距处开始,向焦点方向移动蜡烛,在这过程中,像到透镜的距离(增大/减小/不变),像(变大/变小/不变);(4)实验得到的结论是:凸透镜成放大实像的条件是:;凸透镜成缩小实像的条件是:;凸透镜放大虚像的条件是:.(以上三空均填字母符号)(5)小华看到装满清水的透明玻璃酒杯很像一个凸透镜(如图),就想探究它是否具有凸透镜的性质.请你帮他想出一个验证的方法.。
高中数学 双基限时练7 新人教B版必修4

双基限时练(七)基 础 强 化1.sin ⎝ ⎛⎭⎪⎫-14π3+cos ⎝⎛⎭⎪⎫-20π3的值为( ) A.-3+12 B.3-12 C.3+12D.-3-12解析 原式=-sin 14π3+cos 20π3=-sin ⎝ ⎛⎭⎪⎫4π+2π3+cos ⎝ ⎛⎭⎪⎫6π+2π3=-sin 2π3+cos 2π3 =-sin ⎝ ⎛⎭⎪⎫π-π3+cos ⎝ ⎛⎭⎪⎫π-π3 =-sin π3-cos π3=-3+12.答案 D2.sin1680°+tan2010°的值为( ) A.16 B.36 C .-16D .-36解析 sin1680°+tan2010°=sin(4×360°+240°)+tan(5×360°+210°) =sin(180°+60°)+tan(180°+30°) =-sin60°+tan30°=-32+33=-36. 答案 D3.下列各式不正确的是( ) A .sin(α+180°)=-sin α B .cos(-α+β)=-cos(α-β) C .sin(-α-360°)=-sin α D .cos(-α-β)=cos(α+β)解析 cos(-α+β)=cos(α-β).故B 选项错. 答案 B4.已知cos(3π-α)=-45,α是第四象限角,则sin(-α-π)的值为( )A.45 B .-35C .±35D .±45解析 ∵cos(3π-α)=-45,∴cos α=45.∵α是第四象限角,∴sin α=-35.∴sin(-α-π)=sin α=-35.答案 B5.已知tan(α-π)=-3,则sin 3π+α-cos -α+πsin α-2π-cos α-3π的值为( )A .2B .-2 C.12D .-12解析 tan(α-π)=-3,则tan α=-3. sin 3π+α-cos -α+πsin α-2π-cos α-3π=-sin α+cos αsin α+cos α=-tan α+1tan α+1=3+1-3+1=-2.答案 B 6.已知A =sink π+αsin α+cos k π+αcos α(k ∈Z ),则由A 的值构成的集合为( )A .{-1,1,-2,2}B .{-1,1}C .{2,-2}D .{1,-1,0,2,-2}解析 当k 为偶数时,A =sin αsin α+cos αcos α=2;当k 为奇数时,A =-sin αsin α+-cos αcos α=-2.答案 C7.已知cos ⎝ ⎛⎭⎪⎫α-π6=23,则cos ⎝ ⎛⎭⎪⎫5π6+α=________.解析 cos ⎝⎛⎭⎪⎫5π6+α=cos ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6-α =-cos ⎝ ⎛⎭⎪⎫π6-α=-cos ⎝⎛⎭⎪⎫α-π6=-23.答案 -238.化简:cos θ+4πcos 2θ+πsin 2θ+3πsin θ-4πsin 5π+θcos 2-π-θ=______. 解析 原式=cos θ·cos 2θ·sin 2θsin θ·-sin θ·cos 2θ=-cos θ. 答案 -cos θ能 力 提 升9.若函数f (x )=a sin(πx +α)+b cos(πx +β),其中a ,b ,α,β都是非零实数,且满足f (2 014)=2,则f (2 015)=________.解析 ∵f (2 014)=a sin(2 014π+α)+b cos(2 014π+β)=2, ∴f (2 015)=a sin(2 015π+α)+b cos(2 015π+β) =a sin[π+(2 014π+α)]+b cos[π+(2 014π+β)] =-[a sin(2 014π+α)+b cos(2 014π+β)] =-2. 答案 -210.求下列函数的值:(1)sin ⎝ ⎛⎭⎪⎫-113π; (2)cos(-1 035°);(3)sin315°sin(-1 260°)+cos390°sin(-1 020°). 解析 (1)sin ⎝ ⎛⎭⎪⎫-113π=sin ⎝ ⎛⎭⎪⎫-123π+π3=sin π3=32.(2)cos(-1 035°)=cos1 035°=cos(1 080°-45°)=cos45°=22. (3)sin315°sin(-1 260°)+cos390°sin(-1 020°)=sin(360°-45°)sin(-1 080°-180°)+cos30°·sin(-1 080°+60°) =-sin45°·0+cos30°·sin60°=34.11.已知sin(α-π)=2cos(2π-α), 求sin π-α+5cos 2π-α3cos π-α-sin -α的值.解析 ∵sin(α-π)=2cos(2π-α), ∴-sin α=2cos α. ∴tan α=-2.sin π-α+5cos 2π-α3cos π-α-sin -α=sin α+5cos α-3cos α+sin α=tan α+5-3+tan α=-2+5-3-2=-35.12.求证:tan2π-αsin -2π-αcos 6π-αcos α-πsin 5π-α=-tan α.证明 左边=sin 2π-αcos 2π-α·sin -α·cos -αcos π-αsin π-α=-sin α·-sin α·cos αcos α·-cos α·sin α=-sin αcos α=-tan α=右边. ∴等式成立.品 味 高 考13.cos300°=( ) A .-32B .-12C.12D.32解析 cos300°=cos(-60°)=cos60°=12.答案 C。
人教A版高中数学必修四双基限时练7.docx
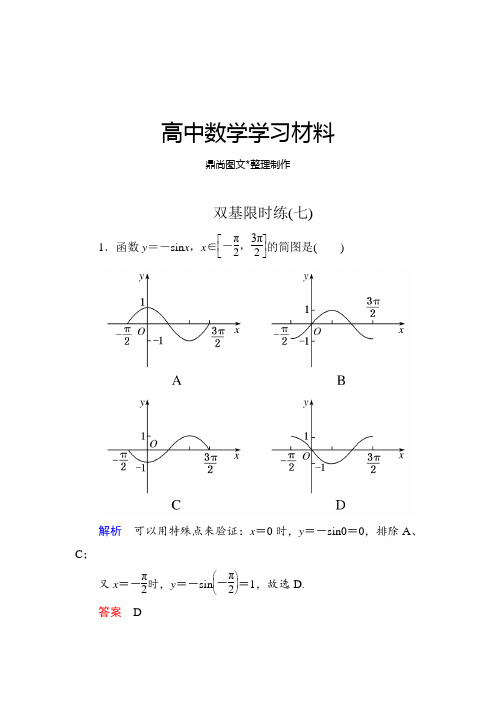
高中数学学习材料鼎尚图文*整理制作双基限时练(七)1.函数y =-sin x ,x ∈⎣⎢⎡⎦⎥⎤-π2,3π2的简图是( )解析 可以用特殊点来验证:x =0时,y =-sin0=0,排除A 、C ;又x =-π2时,y =-sin ⎝ ⎛⎭⎪⎫-π2=1,故选D.答案 D2.用五点法作y =2sin2x 的图象时,首先应描出的五点的横坐标可以是( )A .0,π2,π,3π2,2π B .0,π4,π2,3π4,π C .0,π,2π,3π,4πD .0,π6,π3,π2,2π3解析 令2x 分别等于0,π2,π,3π2,2π时,得x =0,π4,π2,3π4,π.答案 B3.若cos x =0,则角x 等于( ) A .k π(k ∈Z ) B.π2+k π(k ∈Z ) C.π2+2k π(k ∈Z ) D .-π2+2k π(k ∈Z )答案 B4.已知f (x )=sin ⎝⎛⎭⎪⎫x +π2,g (x )=cos ⎝⎛⎭⎪⎫x -π2,则f (x )的图象( )A .与g (x )的图象相同B .与g (x )的图象关于y 轴对称C .向左平移π2个单位,得g (x )的图象 D .向右平移π2个单位,得g (x )的图象 答案 D5.函数y =cos x +|cos x |,x ∈[0,2π]的大致图象为( )答案 D6.函数y =sin x ,x ∈[0,2π]的图象与直线y =-12的交点有( ) A .1个 B .2个 C .3个 D .4个答案 B7.下列函数图象相同的序号是________. ①y =cos x 与y =cos(x +π); ②y =sin ⎝ ⎛⎭⎪⎫x -π2与y =sin ⎝ ⎛⎭⎪⎫π2-x ;③y =sin x 与y =sin(2π-x ); ④y =sin(2π+x )与y =sin x . 答案 ④8.函数y =sin x 的图象和y =cos x 的图象在[0,2π]内的交点坐标为________.解析 在同一坐标系内画出图象即可.答案 ⎝ ⎛⎭⎪⎫π4,22和⎝ ⎛⎭⎪⎫5π4,-229.利用正弦曲线,写出函数y =2sin x ⎝⎛⎭⎪⎫π6≤x ≤2π3的值域是________.解析 y =sin x 的图象如图.由图知,当x =π2时,sin x 取到最大值1, 当x =π6时,sin π6=12.∴当π6≤x ≤2π3时,1≤y ≤2. 答案 [1,2]10.函数y =2cos x -2的定义域是________.答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪⎪2k π-π4≤x ≤2k π+π4,k ∈Z11.用“五点法”画函数y =-2+sin x (x ∈[0,2π])的简图. 解 按五个关键点列表:x 0 π2 π 3π2 2π sin x 01-1-2+sin x-2 -1 -2 -3 -2利用正弦函数的性质描点作图(如下图所示).12.作出函数y =-sin x ,x ∈[-π,π]的图象,并回答下列问题: (1)观察函数的图象,写出满足下列条件的区间: ①sin x >0;②sin x <0;(2)直线y =12与y =-sin x 的图象有几个交点? 解 用五点法作图如下:x -π -π2 0 π2 π y =-sin x 01-1(1)根据图象可知,图象在x 轴上方的部分-sin x >0,在x 轴下方的部分-sin x <0,所以当x ∈(-π,0)时,-sin x >0;当x ∈(0,π)时,-sin x <0.即当x ∈(0,π)时,sin x >0;当x ∈(-π,0)时,sin x <0.(2)画出直线y =12,知有两个交点.13.若函数y =2cos x (0≤x ≤2π)的图象和直线y =2围成一个封闭的平面图形,求这个封闭图形的面积.解观察图可知:图形S 1与S 2,S 3与S 4是两个对称图形;有S 1=S 2,S 3=S 4,因此函数y =2cos x 的图象与直线y =2所围成的图形面积,可以转化为求矩形OABC 的面积.因为|OA |=2,|OC |=2π, 所以S 矩形OABC =2×2π=4π. 所以所求封闭图形的面积为4π.。
高中数学 双基限时练7 新人教A版必修3

双基限时练(七)1.求函数f (x )=⎩⎪⎨⎪⎧x 2x >2,x -1 -2<x ≤2,6x -6 x ≤-2.在x =x 0时的值的算法中,下列语句用不到的是( )A .输入语句B .输出语句C .条件语句D .循环语句解析 因为是求分段函数f (x )在x =x 0时的值,所以须用条件语句,当然输入、输出语句必不可少,因此应选D.答案 D2.关于WHILE 语句的一般格式的说法正确的是( ) A .总是执行循环体 B .执行一次循环体C .循环控制条件为真时执行循环体D .遇到WEND 就结束解析 由当型循环结构的特征知,在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环体,因此应选C.答案 C 3.下列算法:①求和1+12+13+…+1100;②已知两个数求它们的商;③已知函数的定义域在区间上,将该区间十等分求端点及各分点处的函数值;④已知三角形的一边长及此边上的高,求其面积.其中可能要用到循环语句的是( ) A .①② B .①③ C .②④ D .③④答案 B4.编写程序求1+2+3+…+n 的和(n 由键盘输入).程序如下:在上述程序的横线上应填( )A.i<n B.i<=nC.i>n D.i>=n解析该程序应用的是当型循环结构,i为控制变量,每次循环增加1,因此应填i<=n,故选B.答案 B5.下面的程序执行后输出的结果是( )n=5S=0WHILE S<15S=S+nn=n-1WENDPRINT nENDA.-1 B.0 C.1 D.2解析阅读该程序知,该程序运行了5次,此时S=5+4+3+2+1=15,终止运行,因此n=5-5=0,应选B.答案 B6.下图给出的是计算12+14+16+…+120的值的一个程序,其中横线处应填入的条件是________.(填关于i的表达式)解析结合算式及程序知,该程序循环10次,应用的是当型循环结构,因此应填i<=10.答案i<=107.下面程序运行后,输出的值为________.解析∵44×44=1936,45×45=2025>2000.∴i=45,i-1=44.答案448.下列程序运行的结果为________.i=1S=0WHILE S<=20S=S+ii=i+1WENDPRINT iEND解析第一次循环,S=0+1=1,i=1+1=2;第二次循环,S=1+2=3,i=2+1=3;第三次循环,S=3+3=6,i=3+1=4;第四次循环,S=6+4=10,i=4+1=5;第五次循环,S=10+5=15,i=5+1=6;第六次循环,S=15+6=21>20.i=6+1=7,故输出的值为7.答案79.根据下列程序画出相应的程序框图.S=1n=1WHILE S<1000S=S*nn=n+1WENDPRINT nEND解程序框图如图.10.计算1+2+3+…+100的值有如下算法:第一步,令i=1,S=0.第二步,计算S+i,仍用S表示.第三步,计算i+1,仍用i表示.第四步,判断i>100是否成立.若是,则输出S,结束算法;否则,返回第二步.请用UNTIL语句写出这个算法对应的程序.解程序如下:11.计算1+2+3+…+100的值又有如下算法:第一步,令i=1,S=0.第二步,若i≤100,则执行第三步;否则,输出S,结束算法.第三步,S=S+i.第四步,i=i+1,返回第二步.请用WHILE语句写出这个算法对应的程序.解程序如下:i=1S=0WHILE i≤100S=S+ii=i+1WENDPRINT SEND12.阅读下面的程序,回答下面的问题.i=1sum=0WHILE i<=100sum=sum+ii=i+1WENDPRINT sumEND(1)此程序的算法逻辑结构是________型循环结构;(2)画出此程序的程序框图;(3)试用UNTIL语句编写此程序.解(1)由程序知,运行时先对条件进行判断,根据判断的结果决定是否进入循环体,故是当型循环结构.(2)程序框图如图所示.(3)用UNTIL语句编写此程序如下.i=1sum=0DOsum=sum+ii=i+1LOOP UNTIL i>100PRINT sumEND。
人教A版选修一双基限时练7.docx

双基限时练(七)1.应用反证法推出矛盾的推导过程中要把下列哪些作为条件使用( )①结论相反的判断,即假设 ②原命题的条件 ③公理、定理、定义等 ④原结论A .①②B .①②④C .①②③D .②③答案 C2.如果两个实数之和为正数,则这两个数( ) A .一个是正数,一个是负数 B .两个都是正数 C .两个都是非负数 D .至少有一个是正数 答案 D3.已知a +b +c >0,ab +bc +ca >0,abc >0,用反证法求证a >0,b >0,c >0时的假设为( )A .a <0,b <0,c >0B .a ≤0,b >0,c >0C .a ,b ,c 不全是正数D .abc <0答案 C4.否定“至多有两个解”的说法中,正确的是( ) A .有一个解 B .有两个解 C .至少有两个解 D .至少有三个解 答案 D5.设a ,b ,c 都是正数,则三个数a +1b ,b +1c ,c +1a( )A.都大于2B.至少有一个大于2 C.至少有一个不小于2 D.至少有一个不大于2 解析∵a>0,b>0,c>0,∴a+1b+b+1c+c+1a=(a+1a )+(b+1b)+(c+1c)≥2+2+2=6.由此可断定三个数a+1b,b+1c,c+1a至少有一个不小于2.答案 C6.命题“a,b∈R,若|a-1|+|b-1|=0,则a=b=1”用反证法证明时应假设为________.答案a≠1,或b≠17.用反证法证明“一个三角形不能有两个直角”有三个步骤:①∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°矛盾,故假设错误;②所以一个三角形不能有两个直角;③假设△ABC中有两个直角,不妨设∠A=90°,∠B=90°.以上步骤正确的顺序是________.答案③①②8.有下列四个命题:①同一平面内,与两条相交直线分别垂直的两条直线必相交;②两个不相等的角不是直角;③平行四边形的对角线互相平分;④已知x ,y ∈R ,且x +y >2,求证:x 、y 中至少有一个大于1. 其中适合用反证法证明的是________. 答案 ①②④9.如果函数f (x )在区间[a ,b ]上是增函数,那么方程f (x )=0在区间[a ,b ]上至多有一个实根.证明 假设方程f (x )=0在[a ,b ]上至少有两个实根α,β,即f (α)=f (β)=0,∵α≠β,不妨设α>β, 又∵f (x )在[a ,b ]上单调递增,∴f (α)>f (β),这与f (α)=f (β)=0矛盾. ∴f (x )=0在[a ,b ]上至多有一个实根.10.若下列方程:x 2+4ax -4a +3=0,x 2+(a -1)x +a 2=0,x 2+2ax -2a =0至少有一个方程有实根,求实数a 的取值范围.解 设三个方程均无实根,则有⎩⎪⎨⎪⎧Δ1=16a 2-4(-4a +3)<0,Δ2=(a -1)2-4a 2<0,Δ3=4a 2-4(-2a )<0,解得⎩⎪⎨⎪⎧-32<a <12,a <-1,或a >13,-2<a <0,所以-32<a <-1.所以当a ≥-1,或a ≤-32时,三个方程至少有一个方程有实根.11.如果非零实数a ,b ,c 两两不相等,且2b =a +c . 证明:2b =1a +1c不成立.证明 假设2b =1a +1c 成立,则2b =a +c ac =2bac,∴b 2=ac . 又∵b =a +c2,∴(a +c2)2=ac ,即a 2+c 2=2ac ,即(a -c )2=0,∴a =c ,这与a ,b ,c 两两不相等矛盾,∴2b =1a +1c不成立.12.如右图所示,已知两个正方形ABCD 和DCEF 不在同一平面内,M ,N 分别为AB ,DF 的中点.(1)若CD =2,平面ABCD ⊥平面DCEF ,求MN 的长; (2)用反证法证明:直线ME 与BN 是两条异面直线.解(1)如右图,取CD的中点G,连接MG,NG,∵ABCD,DCEF为正方形,且边长为2,∴MG⊥CD,MG=2,NG= 2.∵平面ABCD⊥平面DCEF,∴MG⊥平面DCEF.∴MG⊥GN.∴MN=MG2+GN2= 6.(2)证明假设直线ME与BN共面,则AB⊂平面MBEN,且平面MBEN∩平面DCEF=EN.由已知,两正方形ABCD和DCEF不共面,故AB⊄平面DCEF.又AB∥CD,∴AB∥平面DCEF,∴EN∥AB,又AB∥CD∥EF.∴EF∥NE,这与EF∩EN=E矛盾,故假设不成立.∴ME与BN不共面,它们是异面直线.。
人教A版选修2-3双基限时练7.docx

双基限时练(七)1.在(x -3)10的展开式中,x 6的系数是( )A .-27C 510B .27C 410C .-9C 510D .9C 410解析 通项T r +1=C r 10x 10-r (-3)r =(-3)r C r 10x10-r. 令10-r =6,得r =4.∴x 6的系数为9C 410. 答案 D2.在(32x -12)20的展开式中,系数是有理数的项共有( )A .4项B .5项C .6项D .7项解析T r +1=C r 20(32x )20-r(-12)r=(-1)r C r 20220-r 3-r2·x 20-r .要使系数为有理数,只要20-r 3-r 2为整数,即40-5r6为整数. ∵0≤r ≤20,∴r =2,8,14,20,∴共有4项. 答案 A3.(2x -1x)9的展开式中,常数项为( )A .-672B .672C .-288D .288解析 T r +1=C r 9(2x )9-r(-1x)r =(-1)r 29-r C r 9·x 9-r -r 2,令9-r -r2=0,得r =6.∴常数项为23C 69=8C 39=672.答案 B4.设P =1+5(x +1)+10(x +1)2+10(x +1)3+5(x +1)4+(x +1)5,则P 等于( )A .x 5B .(x +2)5C .(x -1)5D .(x +1)5解析 P =C 05+C 15(x +1)+C 25(x +2)2+…+C 55(x +1)5=(x +1+1)5=(x +2)5.答案 B5.在(x +2x )n的展开式中,常数项为60,则n 等于( ) A .3 B .6 C .9D .12解析 T r +1=C r n(x )n -r (2x )r =2r C rn x n -r2-r .令n -3r2=0,则n =3r .∴2r C r3r =60,试验知r =2,∴n =6.答案 B6.(x 2+2x )8的展开式中x 4的系数是( ) A .16B .70C .560D .1120解析 (x 2+2x )8的展开式的通项是T r +1=C r 8·(x 2)8-r ·(2x )r=2r ·C r 8·x 16-3r,令16-3r =4,得r =4.因此x 4的系数为24·C 48=1120. 答案 D7.对于二项式(1x +x 3)n (n ∈N +),四位同学作出四种判断: 甲:存在n ∈N +,展开式中有常数项; 乙:对任意n ∈N +,展开式中没有常数项; 丙:对任意n ∈N +,展开式中没有x 的一次项; 丁:存在n ∈N +,展开式中有x 的一次项. 其中判断正确的是________. 解析 由通项公式 T r +1=C r n (1x)n -r ·(x 3)r =C r n x 4r -n若r =1,则n =4,T 2就是常数项,令r =1,n =3时,就存在x的一次项.因此应填甲、丁. 答案 甲丁8.在(1+x )3+(1+x )3+(1+3x )3的展开式中,x 的系数为________(用数字作答).解析 x 的系数为C 13C 22+C 23C 11+C 33=3+3+1=7.答案 79.若⎝ ⎛⎭⎪⎫a x-x 29的展开式中x 3的系数为94,则常数a 的值为________.解析答案 410.在(4x -2-x )6的展开式中,常数项为________.解析 (4x -2-x )6展开式的通项为T r +1=C r 6(4x )6-r·(-2-x )r =(-1)r C r 6(2x )2(6-r )-r ,由2(6-r )-r =0,得r =4,∴(-1)4C 46=15.即常数项为15.答案 1511.设f (x )=(1+x )m +(1+x )n 展开式中x 的系数是19(m ,n ∈N *). (1)求f (x )展开式中x 2的系数的最小值;(2)当f (x )展开式中x 2的系数取最小值时,求f (x )展开式中x 7的系数.解 (1)由题设条件,得m +n =19. ∴m =19-n ,x 2的系数为C 2m +C 2n =C 219-n +C 2n =(19-n )(18-n )2+n (n -1)2=n 2-19n +171=(n -192)2+3234,∵n ∈N *,∴当n =9,或n =10时, x 2的系数取最小值(12)2+3234=81.(2)当n =9,m =10或n =10,m =9时,x 2的系数取最小值,此时x 7的系数为C 710+C 79=C 310+C 29=156.12.已知数列{a n }是公比为q 的等比数列.(1)求和:a1C02-a2C12+a3C22,a1C03-a2C13+a3C23-a4C33;(2)由(1)的结果归纳概括出关于正整数n的一个结论,并证明.解(1)a1C02-a2C12+a3C22=a1-2a1q+a1q2=a1(1-q)2,a1C03-a2C13+a3C23-a4C33=a1-3a1q+3a1q2-a1q3=a1(1-q)3.(2)归纳概括的结论为:若数列{a n}是首项为a1,公比为q的等比数列,则a1C0n-a2C1n+a3C2n-a4C3n+…+(-1)n a n+1C n n=a1(1-q)n,n 为正整数.证明:a1C0n-a2C1n+a3C2n-a4C3n+…+(-1)n a n+1C n n=a1C0n-a1q C1n+a1q2C2n-a1q3C3n+…+(-1)n a1q n C n n=a1[C0n-q C1n+q2C2n-q3C3n+…+(-1)n q n C n n]=a1(1-q)n.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计时双基练七 二次函数与幂函数A 组 基础必做1.(2015·湖北孝感调研)函数f (x )=(m 2-m -1)x m 是幂函数,且在x ∈(0,+∞)上为增函数,则实数m 的值是( )A .-1B .2C .3D .-1或2解析 f (x )=(m 2-m -1)x m 是幂函数⇒m 2-m -1=1⇒m =-1或m =2。
又x ∈(0,+∞)上是增函数,所以m =2。
答案 B2.二次函数y =-x 2+4x +t 图像的顶点在x 轴上,则t 的值是( )A .-4B .4C .-2D .2解析 二次函数图像的顶点在x 轴上,所以Δ=42-4×(-1)×t =0,解得t =-4。
答案 A3.(2015·东北三校联考)设函数f (x )=x 2+(a -2)x -1在区间[2,+∞)上是增函数,则实数a 的最小值为( )A .-2B .-1C .1D .2解析 由题意得a -2-2≤2,解得a ≥-2,所以实数a 的最小值为-2。
答案 A4.(2016·淮南模拟)函数f (x )=ax 2+bx +5满足条件f (-1)=f (3),则f (2)的值为( )A .5B .6C .8D .与a ,b 的值有关解析 ①当a =0时,由f (-1)=f (3)可知b =0,此时f (x )=5,所以f (2)=5。
②当a ≠0时,因为函数f (x )=ax 2+bx +5满足条件f (-1)=f (3),所以f (x )=ax 2+bx +5的图像关于x =-1+32=1对称,则f (2)=f (0)=5。
答案 A5.已知函数f (x )=x 2+bx +c 且f (1+x )=f (-x ),则下列不等式中成立的是( )A .f (-2)<f (0)<f (2)B .f (0)<f (-2)<f (2)C .f (0)<f (2)<f (-2)D .f (2)<f (0)<f (-2)解析 ∵f (1+x )=f (-x ),∴(x +1)2+b (x +1)+c =x 2-bx +c 。
∴x 2+(2+b )x +1+b +c =x 2-bx +c 。
∴2+b =-b ,即b =-1。
∴f (x )=x 2-x +c ,其图像的对称轴为x =12。
∴f (2)=f (-1),又∵x <12时,f (x )为减函数, ∴f (0)<f (-1)<f (-2), ∴f (0)<f (2)<f (-2)。
答案 C6.已知y =f (x )是偶函数,当x >0时,f (x )=(x -1)2,若当x ∈⎣⎢⎡⎦⎥⎤-2,-12时,n ≤f (x )≤m 恒成立,则m -n 的最小值为( )A.13B.12 C.34D .1解析 当x <0时,-x >0, f (x )=f (-x )=(x +1)2, ∵x ∈⎣⎢⎡⎦⎥⎤-2,-12, ∴f (x )min =f (-1)=0,f (x )max =f (-2)=1,∴m ≥1,n ≤0,m -n ≥1。
∴m -n 的最小值是1。
答案 D7.已知函数f (x )=x 2-2ax +5(a >1),若f (x )的定义域和值域均是[1,a ],则实数a 的值为________。
解析 由于f (x )=(x -a )2+5-a 2,又a >1,所以f (x )在区间[1,a ]上单调递减,所以⎩⎪⎨⎪⎧f (1)=a ,f (a )=1,即⎩⎪⎨⎪⎧1-2a +5=a ,a 2-2a 2+5=1,解得a =2。
答案 28.已知二次函数y =f (x )的顶点坐标为⎝⎛⎭⎪⎫-32,49,且方程f (x )=0的两个实根之差等于7,则此二次函数的解析式是________。
解析 设二次函数的解析式为f (x )=a ⎝⎛⎭⎪⎫x +322+49(a ≠0),方程a ⎝ ⎛⎭⎪⎫x +322+49=0的两个根分别为x 1,x 2,则|x 1-x 2|=2 -49a =7,∴a =-4,故f (x )=-4x 2-12x +40。
答案 f (x )=-4x 2-12x +409.(2016·淮南模拟)已知函数f (x )=x 2+mx +4,若对于任意x ∈[1,2]时,都有f (x )<0成立,则实数m 的取值范围是________。
解析 由x ∈[1,2]时f (x )<0得x 2+mx +4<0, 即m <-⎝ ⎛⎭⎪⎫x +4x ,x ∈[1,2],令g (x )=-⎝ ⎛⎭⎪⎫x +4x ,则g ′(x )=4-x 2x 2≥0,x ∈[1,2],所以g (x )在[1,2]上是增加的,所以g (x )min =g (1)=-5,所以m <-5。
答案 (-∞,-5)10.已知幂函数f (x )=x (m 2+m )-1(m ∈N +),经过点(2,2),试确定m 的值,并求满足条件f (2-a )>f (a -1)的实数a 的取值范围。
解 ∵幂函数f (x )经过点(2,2), ∴2=2(m 2+m )-1,即212=2(m 2+m )-1。
∴m 2+m =2。
解得m =1或m =-2。
又∵m ∈N +,∴m =1。
∴f (x )=x 12,则函数的定义域为[0,+∞),并且在定义域上为增函数。
由f (2-a )>f (a -1)得⎩⎪⎨⎪⎧2-a ≥0,a -1≥0,2-a >a -1,解得1≤a <32。
∴a 的取值范围为⎣⎢⎡⎭⎪⎫1,32。
11.已知函数f (x )=ax 2-2ax +2+b (a ≠0),若f (x )在区间[2,3]上有最大值5,最小值2。
(1)求a ,b 的值;(2)若b <1,g (x )=f (x )-mx 在[2,4]上单调,求m 的取值范围。
解 (1)f (x )=a (x -1)2+2+b -a 。
当a >0时,f (x )在[2,3]上为增函数,故⎩⎪⎨⎪⎧ f (3)=5,f (2)=2,即⎩⎪⎨⎪⎧ 9a -6a +2+b =5,4a -4a +2+b =2,解得⎩⎪⎨⎪⎧a =1,b =0。
当a <0时,f (x )在[2,3]上为减函数,故⎩⎪⎨⎪⎧f (3)=2,f (2)=5,即⎩⎪⎨⎪⎧9a -6a +2+b =2,4a -4a +2+b =5, 解得⎩⎪⎨⎪⎧a =-1,b =3。
(2)∵b <1,∴a =1,b =0,即f (x )=x 2-2x +2, g (x )=x 2-2x +2-mx =x 2-(2+m )x +2, ∵g (x )在[2,4]上单调,∴2+m 2≤2或m +22≥4, ∴m ≤2或m ≥6。
故m 的取值范围为(-∞,2]∪[6,+∞)。
B 组 培优演练1.已知函数f (x )=x 2-2x ,g (x )=ax +2(a >0),若∀x 1∈[-1,2],∃x 2∈[-1,2],f (x 1)=g (x 2),则实数a 的取值范围是( )A.⎝ ⎛⎦⎥⎤0,12 B.⎣⎢⎡⎦⎥⎤12,3 C .(0,3]D .[3,+∞)解析 由题意得g (x )min ≤f (x )min 且g (x )max ≥f (x )max ,f (x )在区间[-1,2]上的最大值f (x )max =f (-1)=3,f (x )在区间[-1,2]上的最小值f (x )min =f (1)=-1。
由于g (x )=ax +2(a >0)在区间[-1,2]上单调递增,则g (x )min =g (-1)=-a +2,g (x )max =g (2)=2a +2,故⎩⎪⎨⎪⎧-a +2≤-1,2a +2≥3,解得a ≥3。
答案 D2.(2016·广东省广州市五校联考高三年级试题)已知函数f (x )=⎩⎪⎨⎪⎧-x -2x ,x ≥0x 2-2x ,x <0,若f (3-a 2)<f (2a ),则实数a 的取值范围是________。
解析 如图,画出f (x )的图像,由图像易得f (x )在R 上单调递减,∵f (3-a 2)<f (2a ),∴3-a 2>2a ,解得-3<a <1。
答案 (-3,1)3.(2015·陕西质检二)若方程x 2+ax +2b =0的一个根在(0,1)内,另一个根在(1,2)内,则b -2a -1的取值范围是________。
解析 令f (x )=x 2+ax +2b ,∵方程x 2+ax +2b =0的一个根在(0,1)内,另一个根在(1,2)内,∴⎩⎪⎨⎪⎧f (0)>0,f (1)<0,f (2)>0。
∴⎩⎪⎨⎪⎧b >0,a +2b <-1,a +b >-2。
根据约束条件作出可行域,可知14<b -2a -1<1。
答案 ⎝ ⎛⎭⎪⎫14,1 4.(2016·雅安模拟)已知函数f (x )=3ax 2+2bx +c ,a +b +c =0,且f (0)·f (1)>0。
(1)求证:-2<ba <-1;(2)若x 1,x 2是方程f (x )=0的两个实根,求|x 1-x 2|的取值范围。
解 (1)证明:当a =0时,f (0)=c ,f (1)=2b +c ,又b +c =0, 则f (0)·f (1)=c (2b +c )=-c 2<0与已知矛盾,因而a ≠0, 则f (0)·f (1)=c (3a +2b +c )=-(a +b )(2a +b )>0即⎝ ⎛⎭⎪⎫b a +1⎝ ⎛⎭⎪⎫b a +2<0,从而-2<b a <-1。
(2)x 1,x 2是方程f (x )=0的两个实根, 则x 1+x 2=-2b3a ,x 1x 2=-a +b 3a ,那么(x 1-x 2)2=(x 1+x 2)2-4x 1x 2=⎝⎛⎭⎪⎫-2b 3a 2+4×a +b 3a =49·⎝ ⎛⎭⎪⎫b a 2+4b 3a+43=49⎝ ⎛⎭⎪⎫b a +322+13。
∵-2<b a <-1,∴13≤(x 1-x 2)2<49,∴33≤|x 1-x 2|<23,即|x 1-x 2|的取值范围是⎣⎢⎡⎭⎪⎫33,23。
