Independent set on trees
ACM术语

ACM术语.txt我退化了,到现在我还不会游泳,要知道在我出生之前,我绝对是游的最快的那个ACM/ICPC 术语:ICPC (International Collegiate Programming Contest) 国际大学生程序设计竞赛AC (Accepted) 程序通过WA (Wrong Answer) 错误的答案 (读做“哇”)PE (Presentation Error) 输出格式错误RE (Runtime Error) 程序执行错误 (常见于数组溢出、递归层数太多 ...)CE (Compile Error) 编译错误MLE (Memory Limit Exceeded) 内存超界 (正式比赛没有内存限制,但如果用太多可能 RE) TLE (Time Limit Exceed) 程序超时错误 (死循环或算法有问题)OLE (Output Limit Exceed) 输出超界 (一般不太常见,除非你输出了超过 1024K ...)dp (Dynamic Programming) 动态编程,动态规划dfs (Depth First Search) 深度优先搜索bfs (Breadth First Search) 宽度/广度优先搜索LCS (longest common subsequence) 最长公共子串算法常用术语英中对照Approximate String Matching 模糊匹配Arbitrary Precision Arithmetic 高精度计算Bandwidth Reduction 带宽压缩Bin Packing 装箱问题Calendrical Calculations 日期Clique 最大团Combinatorial Problems 组合问题Computational Geometry 计算几何Connected Components 连通分支Constrained and Unconstrained Optimization 最值问题Convex Hull 凸包Cryptography 密码Data Structures 基本数据结构Determinants and Permanents 行列式Dictionaries 字典Discrete Fourier Transform 离散Fourier变换Drawing Graphs Nicely 图的描绘Drawing Trees 树的描绘Edge and Vertex Connectivity 割边/割点Edge Coloring 边染色Eulerian Cycle / Chinese Postman Euler回路/中国邮路Factoring and Primality Testing 因子分解/质数判定Feedback Edge/Vertex Set 最大无环子图Finite State Machine Minimization 有穷自动机简化Generating Graphs 图的生成Generating Partitions 划分生成Generating Permutations 排列生成Generating Subsets 子集生成Graph Data Structures 图Graph Isomorphism 同构Graph Partition 图的划分Graph Problems — hard 图论-NP问题Graph Problems — polynomial 图论-多项式算法Hamiltonian Cycle Hamilton回路Independent Set 独立集Intersection Detection 碰撞测试Job Scheduling 工程安排Kd-Trees 线段树Knapsack Problem 背包问题Linear Programming 线性规划Longest Common Substring 最长公共子串Maintaining Line Arrangements 平面分割Matching 匹配Matrix Multiplication 矩阵乘法Medial-Axis Transformation 中轴变换Median and Selection 中位数Minimum Spanning Tree 最小生成树Minkowski Sum Minkowski和Motion Planning 运动规划Nearest Neighbor Search 最近点对查询Network Flow 网络流Numerical Problems 数值问题Planarity Detection and Embedding 平面性检测和嵌入Point Location 位置查询Polygon Partitioning 多边形分割Priority Queues 优先队列Random Number Generation 随机数生成Range Search 范围查询rate of convergence 收敛速度robustness 鲁棒性Satisfiability 可满足性Searching 查找Set and String Problems 集合与串的问题Set Cover 集合覆盖Set Data Structures 集合Set Packing 集合配置Shape Similarity 相似多边形Shortest Common Superstring 最短公共父串Shortest Path 最短路径Simplifying Polygons 多边形化简Solving Linear Equations 线性方程组Sorting 排序Steiner Tree Steiner树String Matching 模式匹配Text Compression 压缩Topological Sorting 拓扑排序Transitive Closure and Reduction 传递闭包Traveling Salesman Problem 旅行商问题Triangulation 三角剖分Vertex Coloring 点染色Vertex Cover 点覆盖Voronoi Diagrams Voronoi图。
2024年6月上海市秋季高考英语全真模拟试卷03(含答案)

2024年上海市秋季高考英语全真模拟试卷03(考试时间:120分钟试卷满分:140分)I.Listening Comprehension (第1-10题, 每题1分;第11-20题,每题1.5分;共25分)Section ADirections: In Section A, you will hear ten short conversations between two speakers. At the end of each conversation, a question will be asked about what was said. The conversations and the questions will be spoken only once. After you hear a conversation and the question about it, read the four possible answers on your paper, and decide which one is the best answer to the question you have heard.1.A.They are not used to living in hot places.B.They will get away from the hot days.C.They will not be back until it gets cold.D.They are reluctant to go on holiday.2.A.Advertise for a job. B.Find another job through ads.C.Keep the news a secret from his wife. D.Serve at the coffee shop.3.A.He was a firefighter. B.He was excited to get the medal.C.He was responsible for the fire. D.He was very brave.4.A.Doctor and patient. B.Teacher and student.C.Magician and audience. D.Driver and passenger.5.A.Manager and clerk. B.Teacher and student.C.Saleswoman and customer. D.Official and citizen.6.A.She did it out of passion.B.She did it out of necessity.C.She wanted to become a fashion designer.D.She was a successful businesswoman.7.A.She has fixed the computer. B.She has replaced the monitor.C.She has removed the mouse. D.She has given a computer lesson.8.A.She’s excited about her new job.B.She finds the office is too big for her.C.She thinks the work load unbearable.D.She’s not so excited about her new position.9.A.He will be too nervous to make his point.B.He will get up the courage to ask Rite out.C.If he fails to ask Rita out, he will live in fear.D.If he asks Rita out, he will definitely be rejected.10.A.A restaurant. B.A pet shop. C.A parking garage. D.A park.Section BDirections: In Section B, you will hear two short passages and one longer conversation, and you will be asked several questions on each of the short passages and the longer conversation. The short passages and the longer conversation will be read twice, but the questions will be spoken only once. When you hear a question, read the four possible answers on your paper and decide which one is the best answer to the question you have heard.Questions 11 through 13 are based on the following passage.11.A.By offering thanks orally to the loved ones.B.By showing gratefulness on a regular basis.C.By developing good sleeping and eating habits.D.By taking exercise with close friends regularly.12.A.Noticing the positive helps cure eating disorders.B.Practicing gratitude can lengthen your sleep cycle.C.Showing thankfulness contributes to your career promotion.D.Admiring others’ value can improve relationship in workplaces.13.A.It is a blessing that we are valued.B.Extending gratitude has multiple benefits.C.We should stop counting sheep or calories.D.People can learn to be appreciative by heart.Questions 14 through 16 are based on the following passage.14.Why do airports have to look good?A.They represent international significance.B.They need keep up with air travel growth.C.They are symbols of a city’s development.D.They are designed by well-known architects.15.What do airports provide to meet the competition and customer demand?A.Notice of fli ghts’ delay.B.Luxurious departure halls.C.Road and rail connections. D.Nearby shopping areas. 16.Why are airports often located far away from cities?A.Aircraft are noisier than before.B.Aircraft are getting larger in size.C.Aircraft need much space to land and take off.D.Aircraft need regular examination with engines.Questions 17 through 20 are based on the following passage. 17.A.Because she knew a lot of retired teachers.B.Because she wanted to teach classes online.C.Because she knew the program would be influential.D.Because she wanted to help disadvantaged kids learn.18.A.Many Indian children organize their own learning.B.One of the problems facing the school is communication by text. C.Students must stay in the same group when working on a question. D.Children are encouraged to think of their own questions in the project.19.A.That many retired teachers want to join the program.B.That teachers should be good at using modern technology.C.That students play a central role in their learning activities.D.That there are many opportunities in the School in the Cloud.20.A.A TV program. B.An educational project.C.The role of retired teachers. D.New technologies in education.II.Grammar and Vocabulary (每题1分;共20分)Section ADirections: After reading the passage below, fill in the blanks to make the passage coherent and grammatically correct. For the blanks with a given word, fill in each blank with the proper form of the given word; for the other blanks, use one word that best fits each blank.Living a Life Full of Wild AdventuresHelen Skelton was brought up on a remote farm, and her family wasn't full of "runners and rock climbers". However, she has since travelled the world on 21 series of record breaking adventures. The former Blue Peter presenter has kayaked(划皮划艇)down the Amazon River, cycled to the South Pole and done a tightrope walk between the chimneys of Batter-sea Power Station in London. Now, Skelton 22 (share) the secrets of her success in a new book called Wild Girl: How to Have Incredible Outdoor Adventures.23 she's got plenty of stamps in her passport, Skelton says you don't need to go to the Amazon or Antarctica in order to have an adventure - there's plenty to do here in the UK. She grew up in Cumbria, and would go bike-riding and skateboarding with her mum, as well as building rafts. She hopes to pass on these adventures to her own children.Despite the title, Skelton says that the book isn't just for girls. She believes adventure is a leveller - an activity 24 men and women are equal. Adventures 25 also be educational. Skelton says when you're at the mercy of the elements you have to adapt and be flexible, which is a great lesson for life.Of all the places she 26 (be) to, Skelton says the South Pole was particularly hard. "It's like living in a freezer. It's the windiest, driest, coldest place on Earth." Skelton explains, "You can't even put up your tent, which is your only shelter, 27 putting on huge gloves, otherwise you'll get a frostbite. 28 (put) up a tent in oven gloves isn't easy."Her advice to any aspiring adventurers would be to "not worry about 29 comments other peoplemight make. When I said I'm going to kayak the Amazon, people told me that's madness. And, if I had listened to them, I never would have done 30 of it. So just try."Section BDirections: Fill in each blank with a proper word chosen from the box. Each word can be used only once. Note that there is one word more than you need.Young Chinese opera director broadens traditional art form“Chinese opera art is like a huge sponge, constantly absorbing, transforming, merging and flourishing,” says traditional Chinese opera director Li Zhuoqun, who is 31 with creating a market for traditional opera shows in small theaters across China.Performed in 2013, Li Zhuoqun’s first 32 work “Death Do Us Part” is a story 33 from the 14th-century Chinese classic novel “Water Margin”. Li, a graduate of the National Academy of Chinese Theater Arts, says that performing this classic piece for today’s audience is an experiment and a challenge.“We de cided to shorten the divorce scene that lasted four or five days in order to 34 the effect of our vocals and dramatic performances. We also invited modern dancers to work with us. We 35 the performance methods of traditional opera with the r hythm of modern dance.”Li defines her team as “small, deep, refined and broad”. She explained, “‘Small’ in its size, volume and36 . ‘Deep’ refers to our performance and the depth of the script. ‘Refined’ refers to the production of the37 makeup, props, sound and light. ‘Broad’ refers to its 38 and operation.”“We target all ages and a wider audience.” To Li, traditional opera is “the art of regret” due to the unique charm of 39 performances. She aims to allow the audience to enjoy every minute of the show and draw more people to the theater. Li said, “We hope to find a possibility for small theater opera to make a breakthrough in terms of the market and target audience. With the development of aesthetics (审美) and society, our generation needs to 40 a wider and more varied artistic vocabulary into traditional opera. Yet it should still develop on the basis of maintaining the characteristics of traditional opera.”III.Reading Comprehension (共45分。
大学英语综合第一册第二单元答案

9) We had a family [reunion] where I saw relatives I hadn't seen for 20 years.
BOOK 1 - Unit 2 - Language Focus - Vocabulary
10) I guess Henry has been busy writing an article [or ssoommeetthhiningg]] recently. That's why he couldn't accept the invitation.
11) Scientists [estimate] that smoking reduces life expectancy by around 12 years on average.
12) Although it is unlikely that everyone will be able to come, they are still [going ahead] with the plan to hold a class reunion.
3) What was their conversation centered on [Their conversation was centered on the lifelong friendship between the driver and Old Ed.]
Module6Unit2-2024-2025学年初中英语八年级上册(外研版)上课课件

Language points
1. There are only about 1, 600 pandas living in the wild today. There be+sb./ sth+doing sth. 有某人/物在做某事 doing sth.作前面名词的后置定语,动词和前面的名 词之间是逻辑上的主谓关系,且该动作正在发生。
4 Complete the passage with the words in the box.
baby government nature produce save Scientists situation symbol
Zoos and research centres protect animals. (1) __S_c_ie_n_t_is_t_s_ do a lot of research to help pandas (2) __p_r_o_d_u_c_e___ more babies.
2. How is the nature park? The nature park will be big and there will be more bamboo to feed the pandas.
Learning to learn Sometimes you can learn new words through translation. For example, when you learn “government”, you can take a card and write the English word on one side and the Chinese on the other. Practise saying “government” and check that you remember the meaning.
dynamic programming 动态规划

A B C D with total cost 20 300 10 + 40 20 10 + 40 10 100 = 108; 000. Among
the ve possible orders the ve possible binary trees with four leaves this latter method is
2. Travelling Salesman Problem:
The traveling salesman problem. Suppose that you are given n cities and the distances dij between any two cities; you wish to nd the shortest tour that takes you from your home city to all cities and back.
for all j 2 S; j 6= 1 do
opt:=
mfCinjS6=;1jC :=f1m; 2i;n:i6=: :j;;in2Sg;
英汉互译之文学名篇翻译赏析

文学翻译赏析一、雄健阳刚类艰难的国运与雄健的国民李大钊历史的道路,不会是坦平的,有时走到艰难险阻的境界。
这是全靠雄健的精神才能够冲过去的。
一条浩浩荡荡的长江大河,有时流到很宽阔的境界,平原无际,一泻万里。
有是流到很逼狭的境界,两岸丛山迭岭,绝壁断崖,江河流于其间,回环曲折,极其险峻。
民族生命的进展,其经历亦复如是。
人类在历史上的生活正如旅行一样。
旅途上的征人所经过的地方,有时是坦荡平原,有时是崎岖险路。
老于旅途的人,走到平坦的地方,固是高高兴兴地向前走,走到崎岖的境界,愈是奇趣横生,觉得在此奇绝壮绝的境界,愈能感到一种冒险的美趣。
中华民族现在所逢的史路,是一段崎岖险阻的道路。
在这一段道路上,实在亦有一种奇绝壮绝的景致,使我们经过此段道路的人,感得一种壮美的趣味。
但这种壮美的趣味,是非有雄健的精神的人不能够感觉到的。
我们的扬子江,黄河,可以代表我们的民族精神。
扬子江及黄河遇见沙漠,遇见山峡都是浩浩荡荡的往前流过去,以成其浊流滚滚,一泻万里的魄势。
目前的艰难境界,那能阻抑我们民族生命的曲调,在这悲壮歌声中,走过这崎岖险阻的道路。
要知在艰难的国运中建造国家,亦是人生最有趣味的事。
The Bad Luck of China and the Strong Will of the ChineseLi DazhaoThe progress of history sometimes comes into a territory full of hardships and hindrances, and only by means of strong will can it run through the territory.Sometimes in an extensive and open terrain with boundless plains, a huge and mighty river flows vigorously down thousands of miles. Sometimes it runs in an imposing and narrow terrain with ranges of high mountains, crags and cliffs. It zigzags its way down through them, which is drastically hazardous and precipitous. The progress of a nation undergoes the same experience.The life of human race in history is just like a journey. The places the travelers have traversed are open and flat here, but craggy and risky there. Walking on a flat and level road, an experienced traveler certainly feels delighted. However, walking in a rugged and rough terrain, one can enjoy more wits and humor. Walking in such an area of wonderful and magnificent scenes, one can savor more tastes of adventure.The road of history taken today by the Chinese nation is one full of twists and turns. But in this section of the road, there is an extremely fabulous and magnificent view which makes those of us who are going and have gone through it feel glorious and hallowed. It is a feel only those strongly-determined people are capable of enjoying.The Yangtze River and Yellow River stand well for our national spirit. They run into deserts and mountains, and mightily they run. They develop into huge muddy streams and vigorously theydash and roar down thousands of miles. The current crisis can never stop our nation from advancing forward. Strongly determined, we should sing a march and, accompanied by this touching and tragic song.白杨礼赞矛盾……那就是白杨树,西北极普通的一种树,然而实在不是平凡的一种树。
Paths, Trees, and Flowers

Paths,Trees,and Flowers“Jack Edmonds has been one of the creators of the field of combinatorial optimization and polyhedral combinatorics.His1965paper‘P aths,Trees,and Flowers’[1]was one of the first papers to suggest the possibility of establishing a mathematical theory of efficient combinatorial algorithms...”[from the award citation of the1985John von Neumann Theory Prize,awarded annually since1975by the Institute for Operations Research and the Management Sciences].In1962,the Chinese mathematician Mei-Ko Kwan proposed a method that could be used to minimize the lengths of routes walked by mail carriers.Much earlier, in1736,the eminent Swiss mathematician Leonhard Euler,who had elevated calculus to unprecedented heights,had investigated whether there existed a walk across all seven bridges that connected two islands in the river Pregel with the rest of the city of Ko¨nigsberg on the adjacent shores,a walk that would cross each bridge exactly once.Different as they may sound,these two inquiries have much in common.They both admit schematic represen-tations based on the concept of graphs.Thus they are problems in graph theory,a twentieth century discipline which combines aspects of combinatorics and topology. Given a set of items called nodes and a second set of items called arcs,a graph is defined as a relationship between such sets:For each arc,two of the nodes are specified to be joined by this arc.The actual,say physical,meaning of such nodes and arcs is not what distinguishes graphs.Only formal relationships count. In particular,the bridges of Ko¨nigsberg may be consid-ered as arcs,each joining a pair of the four nodes whichcorrespond to the two islands and the two shores. The commonality between the two graph-theoretical problem formulations reaches deeper.Given any graph, for one of its nodes,say i0,find an arc a1that joins node i0and another node,say i1.One may try to repeat this process and find a second arc a2which joins node i1to a node i2and so on.This process would yield a sequence of nodes—some may be revisited—successive pairs of which are joined by arcs(Fig.3).The first andthe last node in that sequence are then connected by this“path.”Fig.2.The graph of the bridges of Ko¨nigsberg.Fig.1.The bridges of Ko¨ningsberg.Fig.3.Open and closed paths in the graph.(Think of a route along street segments joining inter-sections.)If each pair of nodes in a graph can be con-nected by a path,then the whole graph is considered connected.A path in a graph is called closed if it returns to its starting point(Fig.3).Mei-Ko Kwan’s“Chinese Postman Problem,”as it is now generally called(since first suggested by Alan Goldman,then of NBS),is to determine,in a given connected graph,a shortest closed path which traverses every arc at least once—delivers mail on every assigned street block.Euler also considers closed paths meeting all arcs,but aims at characterizing all graphs which accommodate an Euler tour,a closed path that crosses each arc exactly once.As Euler found,they are precisely those connected graphs in which each node attaches to an even number of arcs,or in other words,every node is of even degree.By this result,there can be no Euler tour over the bridges of Ko¨nigsberg.Euler’s examination typifies the classical combinatorial query:Do certain constructs exist and if so,how many?The following question also illustrates the flavor of classical combinatorics:how many isomers are there of the hydrocarbon C n H2n+2?Each such isomer(Fig.4)is characterized by the joining patterns of the carbon atoms as nodes and bonds as arcs.The corresponding arrangements,therefore,represent graphs.These graphs have a very special property:For any two of their nodes there exists a unique connecting path without repeat arcs.Such a graph is called a“tree.”Every isomer defines a tree of carbon atoms whose nodes are of degree four or less.Conversely,every such tree uniquely characterizes an isomer.In graph-theoret-ical terms,the question is:How many trees with n nodes are there with node degrees not exceeding four?(For n=40,the number is62,481,801,147,341,as deter-mined by ingenious use of“generating functions.”) Here is one more topic in the same vein.A match-maker has a list of k single men and l single women.Her experience of many years enables her to discern which pairs are compatible.She considers a number of com-patible matches that might be arranged simultaneously. How can she be sure that she arrived at the largest possible number of such matches?A theorem by one of the founders of graph theory, the Hungarian mathematician De´nes Ko¨nig in1931, suggests an answer to that question.He considered theFig.4.The carbon graphs of the isomers of C6H14.Fig.5.A matching in a graph;two of the augmenting paths arehighlighted by........graph whose nodes are the matchmaker’s clients and whose arcs join the compatible pairs,leading to the graph-theoretical concept of matching.A matching in a graph is any subset of its arcs such that no two arcs in the matching meet at a common node(Fig.5). Similar concepts are that of a packing or independent set,namely,a subset of the nodes no two of which are connected by an arc,and of a cover,namely,a subset of the nodes that meets every arc.The matchmaker’s graph has the special property that each of its nodes is of one of two kinds,male or female, and every arc connects nodes of different gender.For such a bipartite graph,Ko¨nig’s theorem states that the number of arcs in a maximum matching equals the number of nodes in a minimum cover.However,this deep result ignores the problem of actually finding a minimum cover in order to prove the optimality of a matching.Given a particular matching in any graph,an exposed node is one that is not met by any arc of the matching.An alternating path,that is,a path whose every other arc is part of the matching,is called augmenting if it connects two exposed nodes.Indeed,switching arcs in and out of the matching along an augmenting path results in a new matching with one more arc in it.It is a1957theorem by the French mathematician Claude Berge that a larger matching exists not merely if,but also only if,the current matching admits an augmenting path.The classical graph theorist would look at this elegant characterization of maximum matchings and ask:what more needs to be said?That outlook had been changing during and after W orld W ar II.The extensive planning needs,military and civilian,encountered during the war and post-war years now required finding actual solutions to many graph-theoretical and combinatorial problems,but with a new slant:Instead of asking questions about existence or numbers of solutions,there was now a call for “optimal”solutions,crucial in such areas as logistics, traffic and transportation planning,scheduling of jobs, machines,or airline crews,facility location,microchip design,just to name a few.George B.Dantzig’s celebrated“Simplex Algorithm”for linear program-ming was a key achievement of this era.The Chinese Postman is a case in point.He does not care about how many tours of his street blocks there are to choose from nor whether there are indeed Euler tours. He cares about delivering his mail while walking the shortest possible distance.(Admittedly,mail carriers, Chinese and otherwise,don’t really think in terms of the Chinese Postman Problem.But how about garbage collection in a big city?)And then there were computers,and the expectation that those electronic wizards would handle applied combinatorial optimizations even if faced with the large numbers of variables which typically rendered manual computations impractical.Enter Jack Edmonds.Edmonds did his undergradu-ate work at the George W ashington University.He recounts—as one of the pioneers featured in the volume History of Mathematical Programming:A Collection of P ersonal Reminiscences[20]Ϫhis varied interests and activities of that period.Thus he designed toys and games with expectations of monetary rewards, which unfortunately did not materialize.A stint as a copy boy at the W ashington Post found him at the night desk during President Eisenhower’s heart attack in1955.Mathematics,however,survived as his over-riding interest.Fascinated by the study of polytopes by the Canadian Mathematician H.S.M.Coxeter, Edmonds’master thesis at the University of Maryland (1959)addressed the problem of embedding graphs into surfaces[6].Fig.6.Jack Edmonds.In1959he joined NBS,became a founding member of Alan Goldman’s newly created Operations Research Section in1961,and was steered towards precisely the endeavor of developing optimization algorithms for problems in graph theory and combinatorics.In particular,he was drawn to two fundamental problems: the“Maximum Packing Problem”and the“Minimum Cover Problem”of determining largest packings and smallest covers,respectively,in a given graph[2]. Edmonds quickly recognized the major challenge of that task,a challenge that he called“the curse of exponentiality.”While plainly“finite,”many of the known graph-theoretical algorithms required exponen-tial effort,or their authors had not detailed their proce-dures in a way that avoided such exponentiality. Consider the“Maximum Matching Problem”of finding the largest matching in a given graph.Recall that a matching can be enlarged whenever there is an augmenting path,that is,an alternating path connecting two exposed nodes.As a consequence,there exists an “algorithm”which in a finite number of steps—every-thing is finite here—determines whether a matching is maximum or shows how to improve it.“All”that’s needed is to examine,at each step,the alternating paths originating at exposed nodes.It’s just that there are so darn many of them!In a general framework,computational problems have a natural size,for instance,the number of nodes or arcs in a graph.For algorithms,computational effort can then be defined as the number of basic computational steps,such as individual additions or multiplications, and depends on problem size.If computational effort increases as fast or faster than exponentially with problem size,then it is said to require exponential effort. P olynomial time,by contrast,—Edmonds used the term good—prevails if computational effort is bounded by a power d of problem size n.The notation O(n d)is used to indicate that level of complexity.Regardless of technological progress,computers are helpless when faced with exponential effort.T o wit, the“Traveling Salesman Problem.”Here a connected graph is given along with a particular length for each arc.What is wanted is a closed path of least total length that visits every node.The sequence of visits essentially defines such a round trip.Consider,for instance,the 48state capitals of the contiguous United States and W ashington,DC,as nodes of a graph with an arc between any two of them.From a base in W ashington, all those capitals are to be visited while minimizing the total distance traveled.Thus there are48!(factorial) round trips in the running.A future supercomputer, spending1nanosecond per trip,would require more than3ϫ1044years to examine all possible trips.Stressing the integral role of complexity,Edmonds became the leading proponent of a new direction:to develop good algorithms for problems in graph theory and combinatorics(or to identify problems for which such algorithms can be proven not to exist).This has spawned a new area of research that has grown and flourished for four decades and is still going strong.It is not by accident that a graph-theoretical optimization problem,namely,the Traveling Salesman Problem,is now frequently used as a complexity standard,calling a problem NP-complete if it requires computational effort equivalent to that of the Traveling Salesman Problem. In1961,while attending a summer workshop at the RAND corporation in Santa Monica,California, Jack Edmonds discovered a good algorithm for the Maximum Matching Problem,whose complexity he conservatively pegged at O(n4).That algorithm is described in the paper P aths,Trees, and Flowers[1].In its title,the words“paths”and “trees”refer to the standard graph-theoretical concepts. The algorithms augmenting paths are found by a“tree search”combined with a sophisticated process of shrinking certain subgraphs called blossoms into single nodes of a reduced graph.Hence the term“flowers”in the title.Why was it a breakthrough?The answer is that all good graph-theoretical algorithms known at the time addressed“unimodular”problems such as the“Shortest Path”and“Network Flow”problems,the rigorous proof for the latter having been given by Edmonds with collab-oration by Richard M.Karp[13].These are problems that could be formulated as integrality-preserving linear programs,which by themselves did not create good algorithms but indicated the potential for such. Edmonds’matching algorithm was the very first instance of a good algorithm for a problem outside that mold.In addition,P aths,Trees,and Flowers contributed a major theoretical result:a generalization of Ko¨nig’s theorem that holds for matchings in all kinds of graphs, not just bipartite ones.Edmonds also conjectured in this paper that both the Maximum Packing Problem and the Minimum Cover Problem were intrinsically harder than the Maximum Matching Problem.Indeed,both of the former problems were subsequently shown to be NP-complete.In one of his seminal papers[3-10]published in the Journal of Research of the National Bureau of Standards,Edmonds[7]extended his algorithm to find matchings that optimize the sum of given arc weights, and,perhaps more importantly,he laid the foundationfor a polyhedral interpretation of matching theory which was pursued,for instance,in the doctoral thesis by William R.Pulleyblank[15]advised by Edmonds. Subsequently,Edmonds found other good algorithms, for instance,in his path-breaking research on combina-torial abstractions of matrices,called matroids[4,12, 14-17,19].And,last but not least,he and Ellis L. Johnson used the matching paradigm to arrive at a first good algorithm for the Chinese Postman Problem[18]. In1969,Edmonds accepted a professorship of mathematics at the University of W aterloo,where a list of distinguished doctoral students is testament to his special gift of guiding and motivating young mathemati-cians.He remains to this day an active and highly influential researcher in the field of graph theory and combinatorics.Why is it important to identify even a few graph-theoretical and combinatorial problems with good solution algorithms,when there is such a great variety of real-life optimization tasks,most of them defined in a less clear-cut fashion?The utility of good algorithms for idealized problems and their theory is that they sug-gest generalizations,variations,promising avenues of attack,treatable approximations,iterative applications, and also flag problem formulations best to avoid.In all these roles,Edmonds’matching algorithm has been an indispensable and inspirational part of the toolkit for combinatorial optimization and its multiple applications to modern technology.Prepared by Christoph Witzgall with help by Ronald Boisvert,Geraldine Cheok,Saul Gass,Alan Goldman, and James Lawrence.Bibliography[1]Jack Edmonds,Paths,Trees,and Flowers,Canad.J.Math.17,449-467(1965).[2]Jack Edmonds,Covers and Packings in a Family of Sets,Bull.Amer.Math.Soc.68,494-499(1962).[3]Jack Edmonds,Existence of k-Edge Connected Ordinary Graphswith Prescribed Degrees,J.Res.Natl.Bur.Stand.68B,73-74 (1964).[4]Jack Edmonds,Minimum Partition of a Matroid into Indepen-dent Subsets,J.Res.Natl.Bur.Stand.69B,67-72(1965).[5]Jack Edmonds,Lehman’s Switching Game and a Theorem ofTutte and Nash-Williams,J.Res.Natl.Bur.Stand.69B,73-77 (1965).[6]Jack Edmonds,On the Surface Duality of Linear Graphs,J.Res.Natl.Bur.Stand.69B,121-123(1965).[7]Jack Edmonds,Maximum Matching and a Polyhedron with0,1-V ertices,J.Res.Natl.Bur.Stand.69B,125-130(1965). [8]Jack Edmonds and D.R.Fulkerson,Transversals and MatroidPartition,J.Res.Natl.Bur.Stand.69B,147-153(1965). [9]Jack Edmonds,Optimum Branchings,J.Res.Natl.Bur.Stand.71B,233-240(1967).[10]Jack Edmonds,Systems of Distinct Representatives and LinearAlgebra,J.Res.Natl.Bur.Stand.71B,241-245(1967). [11]Jack Edmonds,Matroid Partition,in Mathematics of the Deci-sion Sciences,P art I,(Proceedings of the Fifth Summer Seminar on the Mathematics of the Decision Sciences,Stanford Univer-sity,Stanford,CA,1967),American Mathematical Society, Providence,RI(1968)pp.335-345.[12]Jack Edmonds,Submodular Functions,Matroids,and CertainPolyhedra,in Combinatorial Structures and their Applications (Proceedings of the Calgary International Conference on Combi-natorial Structures and their Applications,University of Calgary, Calgary,Alberta,Canada,1969),Gordon and Breach,New Y ork (1970)pp.69-81.[13]Jack Edmonds and Richard M.Karp,Theoretical Improvementsin Algorithmic Efficiency for Network Flow Problems,in Combinatorial Structures and their Applications(Proceedings of the Calgary International Conference on Combinatorial Structures and their Applications,University of Calgary, Calgary,Alberta,Canada,1969),Gordon and Breach,New Y ork (1970)pp.93-96.[14]Jack Edmonds,Matroids and the Greedy Algorithm,Math.Programming1,127-136(1971).[15]W.Pulleyblank and Jack Edmonds,Facets of1-MatchingPolyhedra,in Hypergraph Seminar(Proceedings of the First W orking Seminar on Hypergraphs,Ohio State Univ.,Columbus, Ohio,1972)Lecture Notes in Mathematics V ol.411,Springer-V erlag,Berlin(1974)pp.214-242.[16]Jack Edmonds,Edge-Disjoint Branchings,in CombinatorialAlgorithms(Courant Computer Science Symposium9,Naval Postgraduate School,Monterey,CA,1972),Algorithmics Press, New Y ork(1973)pp.91-96.[17]Peyton Y oung and Jack Edmonds,Matroid Designs,J.Res.Natl.Bur.Stand.77B,15-44(1973).[18]Jack Edmonds and Ellis L.Johnson,Matching,Euler T ours,andthe Chinese Postman,Math.Programming5,88-124(1973).[19]Jack Edmonds,Matroid Intersection,in Discrete Optimization I(Proceedings of the Advanced Research Institute on Discrete Optimization and Systems Applications,Alberta,Canada,1977);Ann.Discrete Math.4,39-49(1979).[20]Jan Karel Lenstra,Alexander H.G.Rinnooy Kan,AlexanderSchrijver,History of Mathematical Programming,A Collection of P ersonal Reminiscences,North-Holland,Amsterdam(1991).。
Unit 4 Lesson 3 My Favourite Comedian(含视频)课件

Deliver a speech to introduce Rowan Atkinson to the class.
British
6 January, 1955
actor, comedian, screenwriter
...a scholarship
...the highest marks ...master’s degree in electrical engineering
showed a talent for acting decided to become an actor discovered his face
Bean’s actions.
Scene 2
Find out all the verbs or verb phrases used to describe Mr Bean’s actions. Scene 2
takes all the money...
puts it in...
shocked to cannot hide finds... discover… his feelings
3. Why does Mr Bean pretend to like the food when the waiters ask him?
Because he wants to be elegant. /gentleman/ behave properly / conduct himself 4. Why does the author say that he wouldn’t want to meet someone like Mr Bean in real life? Mr Bean’s manners are not socially acceptable so it would be embarrassing to sit with him at a dinner table.
Set-problems课件.ppt

union is X.
– From DS to Set Covering: For each vertex v, take a set Sv in the collection, with Sv = {v} N(v).
Proof continues
Sx S cx Si=1…k (ui-1 – ui)/ ui-1 Si=1…k (H(ui-1) – H(ui)) = H(u0) – H(uk) = H(|S|) – 0.
• Use H(b) – H(a) (b – a)/b • Now we showed: Sx S cx H(|S|)
• Independent set: Set of vertices W with for all v, w W: {v,w} E.
• Clique problem: find largest clique. • Independent set problem: find largest
independent set
– Trees, bounded treewidth – Bipartite graphs – Interval graphs, circular arc graphs
5
Interval graphs and generalizations
Interval graphs
• Each vertex represents an interval • Edge between two vertices when their intervals
Independent-tree ad hoc multicast routing
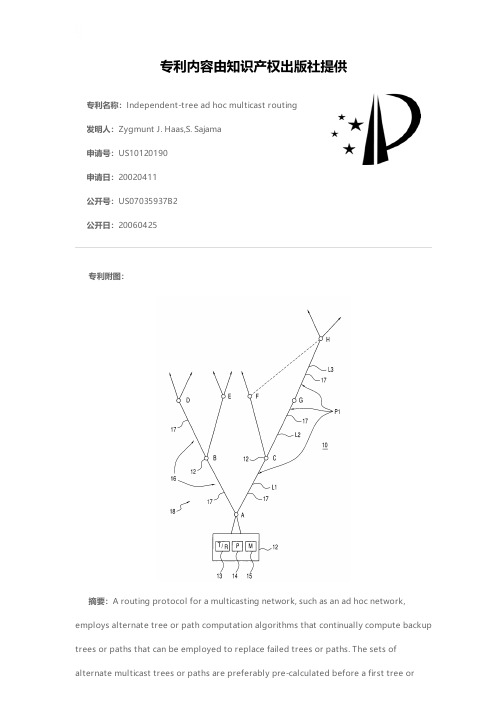
专利名称:Independent-tree ad hoc multicast routing发明人:Zygmunt J. Haas,S. Sajama申请号:US10120190申请日:20020411公开号:US07035937B2公开日:20060425专利内容由知识产权出版社提供专利附图:摘要:A routing protocol for a multicasting network, such as an ad hoc network,employs alternate tree or path computation algorithms that continually compute backup trees or paths that can be employed to replace failed trees or paths. The sets ofalternate multicast trees or paths are preferably pre-calculated before a first tree orpath fails to minimize delay in replacing a failed tree or path. Preferably, the algorithms are designed to compute the alternate multicast trees or paths in such a manner that they are maximally independent of the original set of trees and paths to minimize correlation between the original trees or paths and the replacement trees or paths and to possibly increase the useful time of the calculated trees. This helps insure that the replacement trees or paths will not be likely themselves to fail soon after failure of the original trees or paths.申请人:Zygmunt J. Haas,S. Sajama地址:Summit NJ US,La Jolla CA US国籍:US,US代理机构:Jones, Tullar & Cooper, P.C.更多信息请下载全文后查看。
用independent造句简单

用independent造句简单1. I want to be independent, just like a bird flying freely in the sky! For example, I can choose my own clothes without asking for others' opinions.2. She is so independent that she can handle everything by herself. Look, she's decorating her room all alone!3. Are you an independent person? Can you go to a movie by yourself like I do?4. He became independent after going through many difficulties. Just like a warrior who has overcome countless battles.5. We should encourage children to be independent. Don't you think it's important? For instance, let them do their own homework.6. Being independent is not easy, but it's so rewarding! Isn't it like climbing a mountain and enjoying the beautiful view at the top?7. She strives to be independent, like a flower blooming brightly in the wild. Example? She started her own business!8. You need to be independent to face life's challenges. Can't you see those independent people living a fulfilling life?9. How can you become independent? By taking small stepsevery day, just like building a house brick by brick.10. I really admire those independent souls. They are like stars shining in the darkness. Example? They travel around the world alone!In my opinion, being independent is crucial for a person's growth and happiness. It allows us to be ourselves and explore the world with confidence.。
保护树木的英语作文

Trees are an essential part of our ecosystem,providing oxygen,absorbing carbon dioxide,and offering habitats for various species of wildlife.They also play a crucial role in maintaining the balance of our environment and preventing soil erosion.Here are some points to consider when writing an essay on protecting trees:1.Importance of Trees:Begin your essay by highlighting the significance of trees in our daily lives.Explain how they contribute to the air we breathe,the food chain,and the overall health of our planet.2.Threats to Trees:Discuss the various threats that trees face today,such as deforestation, pollution,climate change,and disease.Provide examples of how these threats are impacting forests and the species that depend on them.3.Consequences of Deforestation:Elaborate on the negative consequences of deforestation,including loss of biodiversity,increased greenhouse gas emissions,and the disruption of water cycles.4.Individual Actions:Suggest ways in which individuals can contribute to tree conservation.This could include planting trees,participating in tree planting initiatives, and supporting organizations that work towards forest preservation.ernment and Corporate Responsibility:Discuss the role of governments and corporations in protecting trees.Mention policies and regulations that promote sustainable forestry practices and the importance of corporate social responsibility in this context.cation and Awareness:Stress the importance of educating the public about the value of trees and the need for their protection.Suggest ways to raise awareness,such as campaigns,school programs,and community events.7.Technological Solutions:Mention how technology can aid in tree conservation efforts, such as using satellite imagery to monitor deforestation and employing drones for planting seeds in hardtoreach areas.8.International Cooperation:Highlight the need for international cooperation in protecting trees,as forests are a global resource.Discuss agreements and treaties that aim to preserve forests,such as the Paris Agreement.9.Sustainable Practices:Advocate for sustainable practices in agriculture,construction, and other industries that may impact forests.Explain how sustainable practices canreduce the need for deforestation.10.Conclusion:Conclude your essay by reiterating the importance of trees and the urgent need for their protection.Encourage readers to take action and contribute to the conservation of trees in their own ways.Remember to use clear and persuasive language to convey the importance of the topic and to engage your readers in the discussion about tree conservation.。
不乱砍伐树木建造设施的英语作文

不乱砍伐树木建造设施的英语作文全文共5篇示例,供读者参考篇1Don't Cut Down the Trees!Hi! My name is Emily and I'm 10 years old. Today I want to tell you about why we shouldn't cut down trees to build new buildings, houses, roads and stuff like that. Trees are really important and we need to protect them!Trees are like the lungs of the Earth. They take in carbon dioxide and bad air that we breathe out, and they make fresh oxygen for us to breathe in. Without trees, the air would be super dirty and polluted and it would be hard for people and animals to breathe. Trees also help keep the temperature from getting too hot by providing shade and cooling the air around them. If there weren't any trees, everywhere would be really hot in the summer!The forest is home to so many cool animals like birds, squirrels, deer, bears, tigers and elephants. Trees give them a safe place to live, build their nests and find food. If we cut down the forests, those poor animals would have nowhere to go andmight go extinct! That means they would be gone forever. I don't want beautiful animals like tigers and elephants to disappear.Trees are really pretty and they make the world look nicer. Forests are peaceful places where people can hike, camp, and explore nature. Isn't it nice to look at big tall trees waving their branches in the breeze? I feel calm when I'm in the woods. Parks and green areas in cities with lots of trees make me happy too. Ugly concrete jungles of buildings and roads without any trees or plants are kind of depressing.The roots of trees help hold the soil together so when it rains a lot, the soil doesn't get washed away as easily. Trees prevent landslides from happening and their leaves collect rain water and release it into rivers and lakes. Trees are like nature's clean water filters!People cut down trees to use the wood for building houses, furniture, paper products and fires. But there are other ways we can get wood without destroying whole forests. We can use wood from tree farms where they carefully replant after cutting down trees. And we can use other materials besides wood like metal, plastic and brick to make houses, tables, etc. Recycling paper, plastics and other stuff means we don't need to chop down as many trees too.Indigenous people who have lived in rainforests for thousands of years understand that they need to protect the forests because their lives depend on it. We should learn from them about how to live in harmony with nature. Mass deforestation by big companies is threatening rainforests that have been around for millions of years. It makes me really sad to think of those amazing and ancient rainforests disappearing forever.In conclusion, trees are like the lungs of the planet and we need them to breathe clean air. They provide homes for animals and their root systems prevent soil erosion and flooding. Trees make our world beautiful and green spaces are good for our mental health. We shouldn't destroy forests to make room for buildings, roads and other human developments. There are smarter ways for us to grow and expand that don't involve tearing down trees. We need to protect trees because they are life!篇2Here's an English essay of around 2,000 words, written in the tone of an elementary school student, about not cutting down trees carelessly to build facilities:The Importance of Protecting TreesHi there! Today, I want to talk to you about something really important – trees! Trees are amazing, aren't they? They provide us with oxygen, shade, and even fruits to eat. But did you know that many trees are being cut down to make way for buildings, roads, and other things? This is really sad because trees are our friends, and we need to protect them.Let me tell you a story about a place called Treeville. Treeville was a beautiful town surrounded by lush green forests and tall, majestic trees. The people who lived there loved their trees and took good care of them. They would often go for walks in the forest, have picnics under the shade of the trees, and climb them for fun.One day, a group of people came to Treeville with plans to build a huge shopping mall. They wanted to cut down a large part of the forest to make space for the mall. The people of Treeville were very upset. They tried to explain to the builders how important the trees were to them and how cutting them down would be harmful to the environment.The builders didn't listen. They started cutting down the trees one by one. The people of Treeville were heartbroken. Theywatched helplessly as their beloved friends, the trees, were chopped down and taken away.But then, something strange started happening. The air in Treeville became harder to breathe. The sun felt hotter than ever before, and there was no shade to protect them from its scorching rays. The animals that lived in the forest had nowhere to go, and many of them disappeared.The people of Treeville realized that they had made a big mistake by letting the builders cut down the trees. They tried to stop them, but it was too late. The damage had been done.After the shopping mall was built, the people of Treeville noticed that it was always very hot inside, and they had to use a lot of air conditioning to keep cool. They also had to pay a lot of money for electricity bills because there were no trees to provide natural shade and cooling.The animals that used to live in the forest were gone, and the children of Treeville couldn't play in the forest anymore. They missed climbing trees, building tree houses, and listening to the birds sing.The people of Treeville learned a valuable lesson that day. They realized that trees are not just plants; they are living beingsthat are essential to our survival. They provide us with oxygen, shade, food, and homes for animals. Without trees, the world would be a very different and much less beautiful place.From that day on, the people of Treeville made sure to protect the remaining trees and plant new ones wherever they could. They also taught their children about the importance of trees and how to take care of them.Whenever someone wanted to build something new in Treeville, they made sure to do it in a way that didn't harm the trees. They would carefully plan around the trees and find ways to incorporate them into their buildings and designs.The people of Treeville also started a tree-planting program, where they would plant new trees every year to replace the ones that were lost. They involved the children in this program, teaching them how to plant and care for trees.Today, Treeville is once again a beautiful and green town, with trees lining the streets and parks filled with lush foliage. The people of Treeville are proud of their efforts to protect the trees and the environment, and they hope that others will learn from their mistakes and do the same.So, remember, trees are our friends, and we need to take care of them. They provide us with so many things that we often take for granted. Let's all do our part to protect trees and make sure that future generations can enjoy their beauty and benefits.That's all from me for today, folks! I hope you enjoyed my story and learned something new about the importance of trees. Until next time, keep hugging those trees and planting new ones wherever you can!篇3Don't Cut Down Trees to Build Things!Hi friends! Today I want to talk about something super important. Trees are amazing and we should protect them instead of cutting them down to make buildings and stuff. Let me tell you why.Trees are like the lungs of the Earth. They breathe in carbon dioxide (that's a gas that can be bad for us in large amounts) and breathe out oxygen, which is the air that we all need to live! Without trees, we wouldn't have fresh air to breathe. Isn't that crazy? Trees are like our air filters.Not only that, but trees give us shade and shelter. Have you ever built a fort or clubhouse using trees and branches? Orclimbed up into a tree to get away from annoying little brothers and sisters? Trees are so fun to play in and around! And they provide homes for lots of animals like birds, squirrels, raccoons, and bugs.Trees are also really pretty and make our parks and neighborhoods look nice. Can you imagine if there were no trees anywhere, just buildings and roads? It would be so bland and ugly. Trees add beautiful colors when their leaves change in the fall too. Some of my favorite childhood memories are playing in piles of crunchy leaves!Another awesome thing about trees is that they help prevent soil erosion. That's when wind and rain wash away the soil, which we need to grow plants and crops. Tree roots hold the soil in place so it doesn't get carried away. Trees also help absorb excess rain water so it doesn't cause flooding.So you can see, trees do SO MUCH for us and for the whole planet. That's why I get really sad when I see trees getting cut down, especially for buildings we don't really need. It makes me want to chain myself to the trees to try to stop the bulldozers and chainsaws!I know we need houses, schools, stores and other buildings to live in. But we should be smarter about how we constructthem. Like, builders could put up new buildings in areas where there aren't many trees already instead of clearing out a whole forest. Or they could build taller rather than taking up a huge footprint of land.We could also re-use old buildings instead of knocking them down to make new ones all the time. My school is over 100 years old and the building is still in great shape! With some renovations, old buildings can be just as good as new.And when new construction happens, builders should replace every tree they cut down by planting new seedlings somewhere else. That way there's no net loss of trees. It would be even better if they planted two or three new trees for every one they take down to make up for all the benefits we'd be missing while those new trees are still tiny.I really wish adults would think more about the environment and how their actions impact the future of the planet. We kids have to live here for like 80 more years, so we want things to be okay! Trees are one of the most important things for keeping the Earth healthy.Instead of cutting down trees for buildings we don't absolutely need, people should focus on taking care of the trees we already have. Trees get stressed out too when there'spollution, lack of water, disease or insect problems. We should make sure they have everything they need to thrive.If we all work together to protect trees, the world will be a much better place. Healthy trees mean healthy people and a healthy planet for plants, animals and humans alike. We need to be the tree heroes and stand up for our tall, leafy friends!What do you think? Will you join me in promising to love trees and be respectful when we need to construct new buildings? We can make a difference if we're committed to taking care of our amazing planet.Thank you trees for all that you do! Let's make sure future generations can enjoy your shade, climb among your branches, and breathe your fresh oxygen-filled air. The Earth wouldn't be the same without you!篇4Trees Are Our Green FriendsHi everyone! Today I want to talk about something really important - trees! Trees are like big green friends that live all around us. They make our neighborhoods look pretty with their colorful leaves and flowers. They give us shade to play under onhot sunny days. And most importantly, trees make the air we breathe nice and clean.But you know what? Some people have been cutting down way too many trees lately. They chop them down to build new houses, stores, roads and other stuff. While I understand we need places to live and go, I don't think cutting down a bunch of trees is a very good idea. Let me tell you why.First of all, trees are living things just like you and me. Wouldn't it be really mean to chop someone's head off just because you wanted to put up a new building where they were standing? Trees can't run away or move, so it's not fair that we hurt them by cutting them down without a good reason. They were here on Earth first, way before humans came along!Trees also do so many important jobs for our planet. Their leaves breathe out oxygen that we all need to live. They take in carbon dioxide and other stinky gases that can make people and animals sick. Trees keep soil from washing away into rivers and streams when it rains a lot. Birds and squirrels make their nests in trees to stay safe and warm. Chopping down too many trees means losing homes for all the cute forest creatures.When a lot of trees get cut down in one area, it can actually change the weather too! Trees help keep the air cooler byproviding shade and releasing water vapor. If they're all gone, the temperature gets hotter which can lead to things like droughts where rain doesn't come as often. Plus, fewer trees means less rain gets soaked up by the soil, so everywhere gets way more flooding after storms. Not awesome!Not only that, but having less trees around is just sad. Hiking in the woods and seeing tons of pretty green trees all over is amazing. Building parking lots, stores and houses everywhere until there's no nature left would be so boring and ugly. I wouldn't want to live in a big city with no trees or plants. Would you?Now, I know sometimes new buildings do need to be made. More houses have to be built if the population grows, and we need schools, hospitals and grocery stores too. But I think there are better ways to do it than just clearing out a whole forest. Why don't we try to build up in the city areas that are already developed instead of tearing down more trees? Or build in places that don't have many trees to begin with? Architects could also try to plan building layouts that keep some of the trees on the property.We can't just take away trees' homes without giving them a new place to live too! So whenever trees have to go to makeroom for something new, we should always plant even more new trees somewhere else. Kids could have tree planting field trips at school to make it an interesting learning activity. Wouldn't it be fun to put a new tree seed or sapling in the ground and watch it sprout up over time? Tree planting could turn into a cool competition between classrooms to see who can grow the most!Grownups always talk about going "green" and beingeco-friendly, but you can't be very green if you knock down all the actual green things! Trees don't just grow back overnight, so we need to take care of the ones we have. Let's keep our big tree friends around to keep our planet happy, healthy and beautiful! Who's with me?篇5Don't Cut Down Trees for Buildings! An Essay by a KidHi friends! Today I want to talk about something really important. Trees are being cut down to make room for buildings and that's just not okay. Trees are living things too and we need to protect them.Trees are like the lungs of the planet. They breathe in air like we do, but instead of breathing out carbon dioxide, they breathe out oxygen for us to breathe. Isn't that cool? Without treesmaking oxygen for us, we couldn't live. We need those tree lungs working hard every day!But trees don't just make oxygen, they also make shade to keep us cool on sunny days. Have you ever sat under a big tree when it's really hot out? It feels so nice and breezy in that shady spot. Trees are like natural umbrellas protecting us from too much sun. If we cut them all down, we'll be really hot and sweaty all the time. No thanks!One of my favorite things about trees is that they're homes for lots of different animals. Squirrels and birds make nests in the branches to live and have babies. Bugs and worms live in the bark and underground by the roots. If we destroy the trees, those poor animals won't have anywhere to go. Their homes and food will be gone. We can't let that happen!Trees are also just plain beautiful to look at. Can you imagine if all the forests and parks nearby were cut down and replaced by boring buildings? How ugly and sad that would be. Trees have gorgeous colored leaves, pretty flowers, and cool twisted branches. Buildings are just gray concrete boxes. No thanks, I'll take the trees!Another amazing thing about trees is that they help prevent soil erosion. What's that? It's when soil gets washed or blownaway, leaving the dirt lumpy and gross. Tree roots grip the soil and hold it in place so it doesn't erode away. If too many trees get cut down, we could have soil erosion problems. Yuck!As you can see, trees do so much awesome stuff for our planet and for us humans. We seriously need to stop tearing them down just to put up more buildings, houses, malls, and parking lots. There's already plenty of those things. Let's focus on protecting the trees we have left.If we really need to build something new, we should put it somewhere that doesn't have any trees growing. There's plenty of empty land in fields and deserts that doesn't need to be cleared of trees first. We can build there instead of destroying forests.Or better yet, let's make buildings out of other stuff like recycled plastic or metal instead of wood from trees. That way we don't need to cut down any trees at all! How cool would it be to have a school made out of recycled bottles or something? Pretty awesome if you ask me.So in conclusion, trees are super important for giving us oxygen, shade, homes for animals, beauty, and protecting the soil. We need to take really good care of them and stop cutting them down for buildings and stuff. Trees were here first and theydeserve to stay. Let's find better ways to make the buildings we need that don't hurt trees. Who's with me? Let's save the trees!。
八年级英语独立主格结构单选题40题

八年级英语独立主格结构单选题40题1.The meeting over, we went home. “会议结束了,我们回家了。
”这里独立主格结构“The meeting over”表示时间,会议结束后我们回家。
答案:无选项,本题是语法结构分析题。
解析:“The meeting over”是独立主格结构,其中“over”是形容词,表示“结束的”,“meeting”和“over”之间是逻辑上的主谓关系,这种结构在句中作时间状语。
2.School being over, the students went home. “放学了,学生们回家了。
”这里“School being over”表示时间,放学的时候学生们回家。
答案:无选项,本题是语法结构分析题。
解析:“School being over”是独立主格结构,“being over”表示“正在结束”,“school”和“being over”之间是逻辑上的主谓关系,这种结构在句中作时间状语。
3.The sun having set, it grew dark. “太阳落山了,天变黑了。
”这里“The sun having set”表示时间,太阳落山后天变黑。
答案:无选项,本题是语法结构分析题。
解析:“The sun having set”是独立主格结构,“having set”表示“已经落山”,“sun”和“having set”之间是逻辑上的主谓关系,这种结构在句中作时间状语。
4.The rain having stopped, we went on our journey. “雨停了,我们继续我们的旅程。
”这里“The rain having stopped”表示时间,雨停后我们继续旅程。
答案:无选项,本题是语法结构分析题。
解析:“The rain having stopped”是独立主格结构,“having stopped”表示“已经停止”,“rain”和“having stopped”之间是逻辑上的主谓关系,这种结构在句中作时间状语。
中考英语独立主格结构高级综合用法练习题30题

中考英语独立主格结构高级综合用法练习题30题1<背景文章>In the early morning, the sun slowly rises, casting a warm glow over the landscape. The fields are covered in dew, and the grass glistens as if adorned with tiny diamonds. The gentle breeze blowing, the leaves on the trees rustle softly. With the sky a beautiful shade of blue and clouds floating lazily, it is a scene of pure tranquility.The sight of a small brook meandering through the meadow is particularly enchanting. The water flows smoothly, making a soothing sound. Along the banks, wildflowers are in full bloom, adding splashes of color to the scenery. The birds chirping in the trees and the bees buzzing around the flowers complete the idyllic picture.In this beautiful natural setting, the independent nominative structure is often used to describe the various elements. For example, “The sun having risen, the day begins to unfold.” Here, “The sun having risen” is an independent nominative structure, adding more vividness and detail to the description.Another example is “The wind blowing gently, the leaves dance in the air.” In this sentence, “The wind blowing gently” is the independent nominative structure that helps to create a more immersive description ofthe natural scene.1. In the sentence “The sun having risen, the day begins to unfold.”, “The sun having risen” is an example of ___.A. a simple sentenceB. a compound sentenceC. an independent nominative structureD. a complex sentence答案:C。
Zero-skew clock routing trees with minimum wirelength

ltTahhyeSeMoimanMvieltaMrharegirmeessaprumerldotesuv,ecbmateinonedncnht1ism2nw%awerrkviersee,rolsebauntssagittsnhhheeodwwrafenossrui1lEnt6sl%mToafovbrTeelressdau2eys-..
TttihohenDeopMorofesEmitthiao1elnsZiosoepprforrtoohSdvekuedecswoeisunCrtchl4eoe]c.ikos pRtxiomeudat.ilnZTgShPTisroienbxltteehmnesiwvoahnreitraoeawssteornietutyUehrScincne,dodp-enwseulirnanhteykittcchotehdeipqneuoilglsilaanoylStgeht.ayioenr, DomamnMiZoen-dESihmeTalw,.ulfimWDltlhMiefneeEnafdoasiiawcabtlmslpeocerortomnaevsrdietniroutiufmhsctatifhtzoaeergsZsiavitSnnheTknye aciwtdd2Snaoiiius\nnsitDkFshdhssdioiiedwossgliwtikesfuininkts"narehenegiaticseshcare5odotana)fliipbtd(Irdnponsaile(toseidds.oki;tinihtrnIu;ltton)ieessosk-joeMcdhrw)btoeaahiejannltefnsshodar0tihitiir;tn.ewaTaussmtTojcaRttdtrhaho2iRpdaennearsmSde,wdpMsZgaeil(ciaaS.taterMemhn.TniLgrbeha.e.aee,,antfmdoestcthurrtromraacrraotShnepa--f
学术英语(理工)详解答案_Unit 3

1 Preparing for listening
to a lecture
Unit 3 Listening to Lectures
1 Preparing for listening to a lecture
Tips before listening to a lecture:
1) Find out the topic of the lecture to be delivered.
Unit 3 Listening to Lectures
2 Paying attention to the introduction
Read the following introductions of two lectures and guess the topic and content of each of them.
2 What is the relationship between carbon dioxide, greenhouse gases and the thinning ozone layer with global warming? Carbon dioxide is a greenhouse gas. Burning oil, coal and fossil fuels leads to a sharp increase in the greenhouse gas which build up and condense, forming a thick gas layer of carbon dioxide. This gas traps heat from the sun and destroys the ozone layer, the layer which protects the Earth from harmful radiation, causing global warming.
保护野生动物__英语作文

②滥用农药 ◎use too much pesticide v. ◎ the abuse of pesticide n. 害死一◑ kill some animals 些动物◑ cause some animals to die ♡♡ ◑ endanger the lives of some animals Sentences: ☎ Farmers use too much pesticide and this causes some animals to die. / and this endangers the lives of some animals. Farmers use too much pesticide, ◆which endangers the lives of some animals. causing some animals to die. ☎ The farmers’ abuse of pesticide causes some animals to die. endangers the lives of some animals.
罗列观点常用词: @ To begin with, then, furthermore, finally @ To start with, next, in addition / additionally, finally @ Most important of all, moreover, last but not least @ For one thing, for another @ On the one hand, on 现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Weighted independent set on trees
Weighted independent set on trees. Given a tree and node weights wv > 0, find an independent set S that maximizes Σv ∈ S wv. Dynamic programming solution. Root tree at some node, say r. OPTin (u) = max weight independent set of subtree rooted at u, containing u. OPTout (u) = max weight independent set of subtree rooted at u, not containing u. OPT = max { OPTin (r), OPTout (r) }.
OPTin (u)
delete u and v and all incident edges
= wu +
v ∈ children( u )
∑ OPTout ( v )
u v w x
OPTout (u) =
v ∈ children( u )
∑ max {OPTin ( v ), OPTout ( v )}
r
S ← ∅. WHILE (F has at least 1 edge) e ← (u, v) such that v is a leaf. S ← S ∪ { v }. F ← F – { u, v }. RETURN S.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
if u ∉ S and v ∉ S, then S ∪ { v } is independent ⇒ S not maximum if u ∈ S and v ∉ S, then S ∪ { v } − { u } is independent ▪
4
Independent set on trees: greedy algorithm
Key observation. If node v is a leaf, there exists a max cardinality independent set containing v. Pf. [exchange argument]
SECTION 10.2
u v
Consider a max cardinality independent set S. If v ∈ S, we're done. Let (u, v) be some edge.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Remark. Can implement in O(n) time by considering nodes in postorder.
5
€
children(u) = { v, w, x }
6
Weighted independent set on trees: dynamic programming algorithm
Theorem. The dynamic programming algorithm finds a max weighted independent set in a tree in O(n) time.
can also find independent set itself (not just value)
2
Independent set on trees
I NTRACTABILITY III
‣ special cases: trees ‣ approximation algorithms ‣ exact exponential algorithms
Independent set on trees. Given a tree, find a maximum cardinality subset of nodes such that no two are adjacent. Fact. A tree has at least one node that is a leaf (degree = 1).
