2015年北京西城初三一模大排名
2015年_海淀_东城、西城、丰台、朝阳、石景山、两区中考一模试题及答案_Word版本

18. (本小题满分 5 分) 解:
x , 2① 3x 4 5 1 4 x≥ x . ② 3 3
由不等式①得
x 3.
……………………………………………………2 分 ……………………………………………………4 分
由不等式②得 x≥ 2 .
∴不等式组的解集为 2≤x 3 . ……………………………………………………5 分 19. (本小题满分 5 分) 解: ( x 2 y)2 ( x y)( x y) 2 y 2
海淀区九年级第二学期期中练习
数学试卷答案及评分参考
2015.5
一、 选择题(本题共 30 分,每小题 3 分) 题号 答案 1 B 2 A 3 C 4 D 5 B 6 A 7 C 8 B 9 D 10 B
二、填空题(本题共 18 分,每小题 3 分) 题号 11 12 13 14 15 小明(1 分) ; 一组对边平行且 相等的四边形是 平行四边形 (2 分) 16 30° 或 150° (只答对 一个 2 分, 全对 3 分)
D D
A
E
C
A
E
C
B
B
备用图 (2)求证: EG BC ; (3)用等式表示线段 AE , EG , BG 之间的数量关系:_____________________________.
29.在平面直角坐标系 xOy 中,对于点 P(a, b) 和点 Q (a, b) ,给出如下定义:
b, a≥1 若 b ,则称点 Q 为点 P 的限变点.例如:点 2,3 的限变点的坐标是 2,3 ,点 2,5 的限变 b , a 1
四、解答题(本题共 20 分,每小题 5 分) 23.如图,在□ ABCD 中,∠BAD 的平分线交 CD 于点 E,交 线于点 F,连接 BE,∠F=45°. (1)求证:四边形 ABCD 是矩形; (2)若 AB=14,DE=8,求 sin∠AEB 的值.
西城区初三数学一模试卷含答案

合用优选文件资料分享2015 年西城区初三数学一模试卷( 含答案 )北京市西城区 2015 年初三一模试卷数学2015. 4考生须知 1 .本试卷共 6 页,共五道大题, 29 道小题,满分 120 分。
考试时间 120 分钟。
2 .在试卷和答题卡上正确填写学校名称、姓名和准考据号。
3 .试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4 .在答题卡上,选择题、作图题用 2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5 .考试结束,将本试卷、答题卡和底稿纸一并交回。
一、选择题 ( 此题共 30 分,每题 3 分) 下面各题均有四个选项,其中只有一个是符合题意的. 1 .的相反数是 A. B. C. D. 2 .据市烟花办有关负责人介绍, 2015 年大年夜零时至正月十五 24 时,全市共销售烟花鞭炮约 196 000 箱,同比下降了 32%.将 196 000 用科学记数法表示应为 A. B. C. D. 3.以下运算正确的选项是 A. B. C.D. 4 .如图是一个几何体的直观图,则其主视图是 5 .甲、乙、丙、丁四名选手参加 100 米决赛,赛场共设 1,2,3,4 四条跑道,选手以随机抽签的方式决定各自的跑道.若甲第一抽签,则甲抽到 1 号跑道的概率是 A. 1 B. C. D. 6 .以下列图形中,既是轴对称图形又是中心对称图形的是 7 .如图,线段 AB是⊙O的直径,弦 CD? AAB,如果∠ BOC=70°,那么∠ BAD等于 A. 20 ° B. 30 ° C. 35 ° D.70 °8.在平面直角坐标系 xOy 中,第一象限内的点 P 在反比率函数的图象上,若是点 P的纵坐标是 3,OP=5,那么该函数的表达式为 A. B. C. D. 9 .为认识某小区“全民健身”活动的睁开情况,某志愿者对居住在该小区的 50 名成年人一周的体育锻炼时间进行了统计,并绘制成以以下列图的条形统计图.这组数据的众数和中位数分别是 A. 6,4 B. 6 ,6 C. 4 ,4 D. 4 ,6 10 .如图,过半径为 6 的⊙O上一点 A 作⊙O的切线,P 为⊙O上的一个动点,作 PH⊥于点 H,连结 PA.如果 PA= ,AH= ,那么以下列图象中,能大概表示与的函数关系的是二、填空题 ( 此题共 18 分,每题 3 分) 11 .若是分式存心义,那么的取值范围是. 12 .半径为 4cm,圆心角为 60°的扇形的面积为cm2. 13 .分解因式: = . 14 .如图,△ABC中,AB=AC,点 D,E 在 BC边上,当时,△ABD≌△ ACE.(增加一个适合的条件即可)15.如是板的表示,立柱 OC与地面垂直,以 O 横板 AB 的中点,AB点 O上下,横板 AB 的 B 端最大高度 h 可否会随横板度的化而化呢?一位同学做了以下研究:他先 AB=2 m, OC=0.5 m,通算获取此的 h1,再将横板 AB 成横板 A′B′,O横板 A′B′的中点,且 A′B′=3m,此 B′点的最大高度 h2,由此得到 h1 与 h2 的大小关系是: h1 h2 (填“>”、“=”或“<”).可一步得出, h 随横板的度的化而(填“不”或“改”).16.如,数上,点 A 的初始地址表示的数 1,点 A 做以下移:第 1 次点A 向左移 3 个位度至点,第 2 次从点向右移6 个位度至点,第 3 次从点向左移 9 个位度至点,⋯,依照种移方式行下去,点表示的数是,若是点与原点的距离不小于 20,那么的最小是.三、解答(本共30分,每小 5 分) 17 .算:.18.如,∠ C=∠E,∠ EAC=∠DAB, AB=AD.求: BC=DE.19.解不等式20.先化,再求:,其中.21.从北京到某市可乘坐一般列或高.已知高的行行程是400 千米,一般列的行行程是520千米.若是高的平均速度是一般列平均速度的 2.5 倍,且乘坐高比乘坐一般列少用3小.求高的平均速度是多少千米/ .22.已知对于 x 的一元二次方程.(1)求:此方程有两个不相等的数根;(2)若是此方程的一个根,求数m的.四、解答 ( 本共 20 分,每小 5 分) 23.如,四形 ABCD中,BD垂直均分AC,垂足点 F,E四形 ABCD外一点,且∠ ADE=∠BAD,AE⊥AC.(1)求:四形 ABDE是平行四形;(2)若是 DA均分∠ BDE,AB=5,AD=6,求AC的.24.在北京,乘坐地是市民出行常采用的一种交通方式.据,新票价改革政策的施北京市道交通客流来很大化.根据 2015 年 1 月宣布的调价后市民当时乘坐地铁的有关检查数据,制作了以下统计表以及统计图.依照以上信息解答以下问题:(1)补全扇形图;(2)题目所给出的线路中,调价后客流量下降百分比最高的线路是,调价后里程 x(千米)在范围内的客流量下降最明显.对于表中客流量不降反增而且增加率最高的线路,若是连续按此变化率增加,预计 2016 年 1月这条线路的日均客流量将达到万人次;(精准到 0.1 )(3)小王同学上学时,需要乘坐地铁 15.9 公里抵达学校,每天上下学共乘坐两次.问调价后小王每周(按 5 天计算)乘坐地铁的花销比调价前多支出元.(不考虑使用市政一卡通刷卡优惠,调价前每次乘坐地铁票价为 2 元)25.如图,AB为⊙O的直径, M为⊙O外一点,连结 MA与⊙ O 交于点C,连结 MB并延伸交⊙O 于点 D,经过点 M的直线 l 与 MA所在直线对于直线 MD对称.作 BE⊥l于点 E,连结 AD,DE.(1)依题意补全图形;(2)在不增加新的线段的条件下,写出图中与∠ BED相等的角,并加以证明.26.阅读下面的资料:小敏在数学课外小组活动中碰到这样一个问题:若是α,β都为锐角,且,,求的度数.小敏是这样解决问题的:如图 1,把,放在正方形网格中,使得,,且 BA,BC在直线 BD的两侧,连结 AC,可证得△ ABC是等腰直角三角形,因此可求得=∠ABC= °. 请参照小敏思虑问题的方法解决问题:若是,都为锐角,当,时,在图 2 的正方形网格中,利用已作出的锐角α,画出∠ MON=,由此可得 =______°.五、解答题 ( 此题共 22 分,第 27 题 7 分,第 28 题 7 分,第 29 题 8分) 27.已知二次函数的图象经过,两点.(1)求对应的函数表达式;(2)将先向左平移1 个单位,再向上平移4 个单位,获取抛物线,将对应的函数表达式记为,求对应的函数表达式;(3)设,在(2)的条件下,若是在≤x≤a内存在某一个 x 的值,使得≤建立,利用函数图象直接写出 a 的取值范围.28.△ABC中,AB=AC.取BC边的中点D,作DE⊥AC于点E,取DE 的中点F,连结BE,AF交于点H.(1)如图1,若是,那么,;(2)如 2,若是,猜想的度数和的,并明你的;(3)若是,那么.(用含的表达式表示)29.出以下定:两个形G1和 G2,点 P G1上任一点,点 QG2上任一点,若是段 PQ的度存在最小,就称最小两个形 G1和G2之的距离.在平面直角坐系 xOy中, O坐原点.(1)点 A的坐,点和射 OA之的距离 ________,点和射 OA之的距离 ________;(2)若是直 y=x 和双曲之的距离,那么 k= ;(可在 1 中行研究)(3)点 E 的坐 (1, ),将射OE原点O逆旋,获取射OF,在坐平面内所有和射 OE,OF之的距离相等的点所成的形形 M.①在 2 中画出形 M,并描绘形 M的成部分;(若波及平面中某个地区能够用阴影表示)②将射 OE,OF成的形形 W,抛物与形 M的公共部分形 N,直接写出形 W和形 N之的距离.北京市西城区 2015 年初三一模卷数学卷参照答案及分准 2015. 4 一、(本共30分,每小 3分)号答案 BACCD A C A B C 二、填空(本共 18 分,每小 3 分) 11 12 13 14 1516BD=CE,∠ BAD=∠CAE,∠ ADB=∠AEC, BE=CD,∠ BAE=∠CAD,∠ADE=∠AED,AE=AD(只填一个即可) = ,不 7 ,13 三、解答(本共30 分,每小 5 分) 17 .解:= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分 ==3.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 18 .明:如 1.∵ ∠EAC=∠DAB,∴ .即∠BAC=∠DAE.⋯⋯⋯⋯⋯⋯⋯⋯ 1 分在△ ABC和△ ADE中,⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分∴△ABC≌△ ADE.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分∴BC=DE.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分 19 .解:由①,得.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分由②,得.移,归并,得.系数化 1,得.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分因此原不等式的解集.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分 20 .解: = ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分=⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分当,原式=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分 21 .解:一般列的平均速度 x 千米 /.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分高的平均速度是 2.5x 千米 / .依意,得.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分解得.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分,是原方程的解,且符合意.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分因此.答:高的平均速度是 300 千米 /. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 22.(1)明:.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵≥0,∴>0.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分∴方程有两个不相等的数根.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分(2)解:∵ 是此方程的一个根,∴ .整理得.解得,.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分四、解答(本共20 分,每小 5 分) 23 .(1)明:∵,∴∥ .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∵ BD 垂直均分 AC,垂足 F,∴,AF=FC.又∵ ,∴ .∴ AE∥BD.∴四形 ABDE是平行四形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分(2)解:如 2,接 BE交 AD于点 O.∵ DA 均分∠ BDE,∴∠ADE=∠1.又∵ ,∴ ∠1=∠BAD.∴ AB=BD.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分∴ ABDE是菱形.∵ AB=5,AD=6,∴ BD=AB=5,,.在 Rt△中,.∵,∴ .解得.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分∵ BD 垂直均分 AC,∴ .⋯⋯⋯⋯⋯⋯⋯⋯5分注:其他解法相分.24 .解:(1)全扇形如 3 所示.⋯⋯⋯⋯⋯⋯⋯1 分(2)2 号,52<x≤72 , 22.2 .(各 1 分)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分(3)30.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 25 .解:(1)依意,全形如 4.⋯⋯⋯⋯⋯⋯ 1 分(2).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分明:如 5,接BC,CD.∵直 l 与直 MA对于直 MD称,∴ .⋯⋯⋯⋯⋯⋯⋯⋯⋯3分∵ AB⊙O的直径,∴,即.又∵,∵,,∴MC=ME.又∵ C, E 两点分在直 MA与直 l 上,可得 C,E 两点对于直MD称.∴ .⋯⋯⋯⋯⋯⋯⋯ 4 分又∵ ,∴ .⋯⋯⋯⋯⋯⋯ 5 分 26.解:45.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分画6.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分45.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分五、解答(本共 22 分,第 23 7 分,第 24 7 分,第 25 8 分) 27 .解:(1)∵ 二次函数的象,两点,∴⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分解得⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分∴抛物的函数表达式.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分(2)∵ ,∴抛物的点.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∴平移后抛物的点,它的函数表达式.⋯ 5 分(3)a≥(7).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分28.解:(1)90,.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分(2):,.明:如 8,接 AD.∵ AB=AC,∠BAC=60°,∴ △ABC是等三角形.∵ D BC的中点,∴ AD⊥BC.∴∠1+∠2=90°.又∵ DE⊥AC,∴ ∠DEC=90°.∴∠2+∠C=90°.∴ ∠1=∠C=60°.AB=BC=k(),,.∵F DE的中点,∴ ,.∴ ,.∴ .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分又∵∠1=∠C,∴△ADF∽△ BCE .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∴,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分∠3=∠4.又∵ ∠4+∠5=90°,∠ 5=∠6,∴∠3+∠6=90°.∴ .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分(3).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分注:写或其他答案相分. 29 .解:(1)3,.(每空各 1分)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分(2).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分(3)①如 9,点 O分作射 OE、OF的垂 OG、OH,形 M:y 正半,∠ GOH的及其内部的所有点(中的阴影部分).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分明:(画 2 分,描绘 1 分)(形 M也可描绘:y 正半,直下方与直下方重叠的部分(含界))③ .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分。
2015年北京市西城区中考数学一模试卷-含详细解析

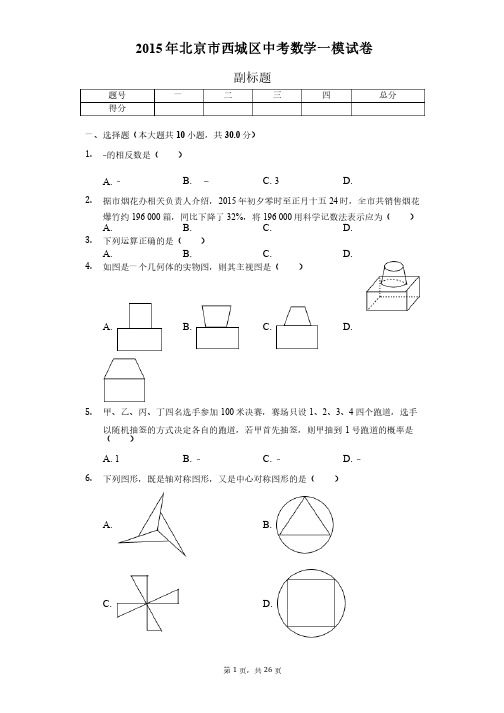
2015年北京市西城区中考数学一模试卷副标题一、选择题(本大题共10小题,共30.0分)1.的相反数是()A. B. C. 3 D.2.据市烟花办相关负责人介绍,2015年初夕零时至正月十五24时,全市共销售烟花爆竹约196 000箱,同比下降了32%,将196 000用科学记数法表示应为()A. B. C. D.3.下列运算正确的是()A. B. C. D.4.如图是一个几何体的实物图,则其主视图是()A. B. C. D.5.甲、乙、丙、丁四名选手参加100米决赛,赛场只设1、2、3、4四个跑道,选手以随机抽签的方式决定各自的跑道,若甲首先抽签,则甲抽到1号跑道的概率是()A. 1B.C.D.6.下列图形,既是轴对称图形,又是中心对称图形的是()A. B.C. D.7.如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于()A.B.C.D.8.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为()A. B. C. D.9.为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是()A. 6,4B. 6,6C. 4,4D. 4,610.如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是()A.B.C.D.二、填空题(本大题共6小题,共18.0分)11.如果分式有意义,那么的取值范围是______.12.半径为4cm,圆心角为60°的扇形的面积为______cm2.13.分解因式:12m2-3=______.14.如图,△ABC中,AB=AC,点D,E在BC边上,当______时,△ABD≌△ACE.(添加一个适当的条件即可)15.如图是跷跷板的示意图,立柱OC与地面垂直.以O为横板AB的中点,AB绕点O上下转动,横板AB的B端最大高度h是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设AB=2m,OC=0.5m,通过计算得到此时的h1,再将横板AB换成横板A′B′,O为横板A′B′的中点,且A′B′=3m,此时B′点的最大高度为h2,由此得到h1与h2的大小关系是:h1______h2(填“>”、“=”或“<”).可进一步得出h随横板的长度的变化为______(填“不变”或“改变”)16.如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第一次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A4表示的数是______,如果点A n与原点的距离不小于20,那么n的最小值是______.三、计算题(本大题共3小题,共15.0分)17.计算:.18.化简求值:,其中a=2.19.阅读下面的材料小敏在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且tanα=,tan,求α+β的度数.小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,因此可求得α+β=∠ABC=______°请参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ=时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α-β,由此可得α-β=______°.四、解答题(本大题共10小题,共57.0分)20.如图,∠C=∠E,∠EAC=∠DAB,AB=AD.求证:BC=DE.21.解不等式组:.22.从北京到某市可乘坐普通列车或高铁.已知高铁的行驶路程是400千米,普通列车的行驶路程是520千米.如果高铁的平均速度是普通列车平均速度的2.5倍,且乘坐高铁比乘坐普通列车少用3小时,求高铁的平均速度是多少千米/时?23.已知关于x的一元二次方程x2-2(m-1)x-m(m+2)=0.(1)求证:方程总有两个不相等的实数根;(2)若x=-2是此方程的一个根,求实数m的值.24.如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC(1)求证:四边形ABDE是平行四边形;(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.25.在北京,乘坐地铁是市民出行时经常采用的一种交通方式,据调查,新票改革政策的实施给北京市轨道交通客流带来很大变化.根据2015年1月公布的调价后市民当时乘坐地铁的相关调查数据,制作了一下统计表以及统计图.根据以上信息解答下列问题:(1)补全扇形图;(2)题目所给出的线路中,调价后客流量下降百分比最高的线路是______,调价后里程x(千米)在______范围内的客流量下降最明显.对于表中客流量不降反增而且增长率最高的线路,如果继续按此变化率增长,预计2016年1月这条线路的日均客流量将达到______万人次(精确到0.1)(3)小王同学上学时,需要乘坐地铁15.9公里到达学校,每天上下学共乘坐两次.问调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出______元.(不考虑使用一卡通刷卡优惠,调价前每次乘坐地铁票价为2元)26.如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称,作BE⊥l 于点E,连接AD,DE(1)依题意补全图形;(2)在不添加新的线段的条件下,写出图中与∠BED相等的角,并加以证明.27.已知二次函数y1=x2+bx+c的图象C1经过(-1,0),(0,-3)两点.(1)求C1对应的函数表达式;(2)将C1先向左平移1个单位,在向上平移4个单位,得到抛物线C2,将C2对应的函数表达式记为y2=x2+mx+n,求C2对应的函数表达式;(3)设y3=2x+3在(2)的条件下,如果在-2≤x≤a内存在某一个x的值,使得y2≤y3成立,结合函数图象直接写出a的取值范围.28.△ABC中,AB=AC,取BC的中点D,做DE⊥AC与点E,取DE的中点F,连接BE,AF交于点H.(1)如图1,如果∠BAC=90°,那么∠AHB=______°,=______;(2)如图2,如果∠BAC=60°,猜想∠AHB的度数和的值,并证明你的结论;(3)如果∠BAC=α,那么=______.(用含α表达式表示)29.给出如下规定:两个图形G1和G2,点P为G1上任一点,点Q为G2上任一点,如果线段PQ的长度存在最小值,就称该最小值为两个图形G1和G2之间的距离.在平面直角坐标系xOy中,O为坐标原点.(1)点A的坐标为A(1,0),则点(2,3)和射线OA之间的距离为______,点(-2,3)和射线OA之间的距离为______;(2)如果直线y=x和双曲线y=之间的距离为,那么k=______;(可在图1中进行研究)(3)点E的坐标为(1,),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.①请在图2中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)②将射线OE,OF组成的图形记为图形W,抛物线y=x2-2与图形M的公共部分记为图形N,请直接写出图形W与图形N之间的距离.答案和解析1.【答案】B【解析】解:的相反数是-,添加一个负号即可.故选:B.根据相反数的概念解答即可.本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.【答案】A【解析】解:将196 000用科学记数法表示为:1.96×105.故选:A.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.【答案】C【解析】解:A、3a与3b不是同类项,不能合并,错误;B、a3与a不是同类项,不能合并,错误;C、(a2)3=a6,正确;D、a6÷a3=a3,错误;故选:C.分别根据同底数幂的除法、幂的乘方与积的乘方、合并同类项的法则进行逐一计算即可.本题考查合并同类项、同底数幂的除法、幂的乘方,熟练掌握性质和法则是解题的关键.4.【答案】C【解析】解:从正面看可得到一个矩形和一个下底和矩形相邻的梯形的组合图,故选C.找到从正面看所得到的图形即可.本题考查了三视图的知识,主视图是从物体的正面看得到的视图.5.【答案】D【解析】解:∵设1、2、3、4四个跑道,甲抽到1号跑道的只有1种情况,∴甲抽到1号跑道的概率是:.故选D.由设1、2、3、4四个跑道,甲抽到1号跑道的只有1种情况,直接利用概率公式求解即可求得答案.此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.6.【答案】D【解析】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误;B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;C、此图形旋转180°后能与原图形重合,此图形是中心对称图形,不是轴对称图形,故此选项错误;D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.故选:D.根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.此题主要考查了中心对称图形与轴对称的定义,根据定义得出图形形状是解决问题的关键.7.【答案】C【解析】解:∵弦CD⊥直径AB,∴=,∴∠BAD=∠BOC=×70°=35°.故选C.先根据垂径定理得到=,然后根据圆周角定理得∠BAD=∠BOC=35°.本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.8.【答案】A【解析】解:在RT△OPD中,过P作PD⊥x轴于D,则PD=3,∴OD==4,∴P(4,3),∴代入反比例函数y=得,3=,解得k=12,∴反比例函数的解析式为y=,故选A.过P作PD⊥x轴于D,则PD=3,根据勾股定理求得OD,得出D的坐标,然后根据待定系数法即可求得反比例函数的解析式.本题考查了待定系数法求反比例函数的解析式,熟练掌握待定系数法是解题的关键.9.【答案】B【解析】解:出现最多的是6小时,则众数为6;按大小顺序排列在中间的两个人的锻炼时间都为6小时,则中位数为6.故选:B.在这50人中,参加6个小时体育锻炼的人数最多,则众数为6;50人中锻炼时间处在第25和26位的都是6小时,则中位数为6.本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.10.【答案】C【解析】解:如图,当PH与圆O相切时,∵四边形OAHP是正方形,∴AH=6,PA=6,当点P在圆O上运动时,y与x之间的关系既不是一次函数也不是二次函数,并且在x=6时,函数取得最大值6,因为6<6<12,故选:C.当PH与圆O相切时,y取得最大值6,x=6,据此分析即可得出结论.本题主要考查了动点问题的图象,通过计算发现在函数取得最大值时,x的值大于6是解决问题的关键.11.【答案】x≠5【解析】解:分式有意义,得x-5≠0.解得x≠5,故答案为:x≠5.根据分母为零,分式无意义;分母不为零,分式有意义.本题考查了分式有意义的条件,从以下三个方面透彻理解分式的概念:分式无意义⇔分母为零;分式有意义⇔分母不为零;分式值为零⇔分子为零且分母不为零.12.【答案】π【解析】解:半径为4cm,圆心角为60°的扇形的面积为:=π(cm2).故答案为:π.直接利用扇形面积公式求出即可.此题主要考查了扇形的面积公式应用,熟练记忆扇形面积公式是解题关键.13.【答案】3(2m+1)(2m-1)【解析】解:12m2-3=3(4m2-1)=3(2m+1)(2m-1).故答案为:3(2m+1)(2m-1).首先提取公因式3,进而利用平方差公式分解因式得出即可.此题主要考查了提取公因式法以及公式法分解因式,正确应用平方差公式是解题关键.14.【答案】BD=CE【解析】解:BD=CE,理由是:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中∴△ABD≌△ACE(SAS),故答案为:BD=CE.根据等边对等角得出∠B=∠C,根据全等三角形的判定推出即可.本题考查了等腰三角形的性质,全等三角形的判定的应用,此题是一道开放型的题目,答案不唯一,只要填上一个符合的即可.15.【答案】=;不变【解析】解:过点B作BD⊥AD,B′D′⊥A′B′,∵OC是△ABD与△A′B′D′的中位线,∴BD=B′D′=OC,即h1=h2,故答案为:=,不变.过点B作BD⊥AD,B′D′⊥A′B′,根据三角形中位线定理即可得出结论.本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.16.【答案】7 13【解析】解:第一次点A向左移动3个单位长度至点A1,则A1表示的数,1-3=-2-2;第2次从点A1向右移动6个单位长度至点A2,则A2表示的数为-2+6=4;第3次从点A2向左移动9个单位长度至点A3,则A3表示的数为4-9=-5;第4次从点A3向右移动12个单位长度至点A4,则A4表示的数为-5+12=7;第5次从点A4向左移动15个单位长度至点A5,则A5表示的数为7-15=-8;…;则A7表示的数为-8-3=-11,A9表示的数为-11-3=-14,A11表示的数为-14-3=-17,A13表示的数为-17-3=-20,A6表示的数为7+3=10,A8表示的数为10+3=13,A10表示的数为13+3=16,A12表示的数为16+3=19,所以点A n与原点的距离不小于20,那么n的最小值是13.故答案为7,13.序号为奇数的点在点A的左边,各点所表示的数依次减少3,序号为偶数的点在点A的右侧,各点所表示的数依次增加3,于是可得到A13表示的数为-17-3=-20,A12表示的数为16+3=19,则可判断点A n与原点的距离不小于20时,n的最小值是13.本题考查了规律型:认真观察、仔细思考,找出点表示的数的变化规律.17.【答案】解:原式=.【解析】本题涉及零指数幂、负指数幂、二次根式化简、特殊角的三角函数值等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.18.【答案】原式=×-,=,=,当a=2时,原式==.【解析】将原式的分子、分母因式分解,除法化为乘法,约分,再代值计算.本题考查了分式的化简求值.解答此题的关键是把分式化到最简,然后代值计算.19.【答案】45;45【解析】解:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,因此可求得α+β=∠ABC=45°;参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ=时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α-β,由此可得α-β=45°.故答案为:45;45如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,可求得α+β=∠ABC=45°如图2,把α,β放在正方形网格中,使得∠MOG=α,∠NOH=β,且ON在∠MOG 内,连接MN,可证得△MON是等腰三角形,可求得α-β=45°.本题考查了作图-应用与设计图,等腰三角形的性质,解直角三角形等,根据函数值作出直角三角形是解题的关键.20.【答案】证明:∵∠DAB=∠EAC,∴∠DAB+∠BAE=∠EAC+∠BAE,即∠DAE=∠BAC,在△DAE和△BAC中,∴△DAE≌△BAC,∴BC=DE.【解析】因为∠DAB=∠EAC,从图上可以看出∠DAB+∠BAE=∠EAC+∠BAE,即∠DAE=∠BAC,又因为,∠C=∠E,AB=AD,所以很容易证明△DAE≌△BAC,从而得出结论.本题考查全等三角形的判定定理,根据ASA可证明三角形全等,从而可得出结论.21.【答案】解:∵解不等式①得:x≥2,解不等式②得:x>-1,∴不等式组的解集为x≥2.【解析】先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是能根据找不等式组解集的规律找出不等式组的解集,难度适中.22.【答案】解:设普通列车平均速度是x千米/时,则高铁平均速度是2.5x千米/时,根据题意得:-=3,解得:x=120,经检验x=120是原方程的解,则高铁的平均速度是120×2.5=300(千米/时),答:高铁的平均速度是300千米/时.【解析】设普通列车平均速度是x千米/时,则高铁的平均速度是2.5x千米/时,根据乘坐高铁比乘坐普通列车少用3小时,列出分式方程,然后求解即可.此题考查了分式方程的应用,关键是分析题意,找到合适的数量关系列出方程,解分式方程时要注意检验.23.【答案】(1)证明:∵关于x的一元二次方程x2-2(m-1)x-m(m+2)=0.∴△=4×(m-1)2+4m(m+2)=8m2+4>0,∴方程总有两个不相等的实数根;(2)解:∵x=-2是此方程的一个根,∴把x=-2代入方程中得到4-2(m-1)×(-2)-m(m+2)=0,∴4+4(m-1)-m(m+2)=0,∴m2-2m=0,∴m1=0,m2=2.【解析】(1)根据根的判别式求出△的值,再进行判断即可;(2)先把x=-2代入方程,然后解关于m的一元二次方程,即可求出m的值.此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.24.【答案】(1)证明:∵∠ADE=∠BAD,∴AB∥DE,∵AE⊥AC,BD⊥AC,AE∥BD,∴四边形ABDE是平行四边形;(2)解:∵DA平分∠BDE,∴∠AED=∠BDA,∴∠BAD=∠BDA,∴BD=AB=5,设BF=x,则DF=5-x,∴AD2-DF2=AB2-BF2,∴62-(5-x)2=52-x2,∴x=,∴AF==,∴AC=2AF=.【解析】(1)由平行四边形的判定定理:两组对边分别平行得到结论;(2)由角平分线、等量代换得到角相等,由等角对等边得到BD=AB=5,根据勾股定理列方程求解.本题考查了平行四边形的判定和性质,角平分线的性质,勾股定理的应用,解题的关键是利用勾股定理列方程.25.【答案】2号线;52<x≤72;22.2;30【解析】解:(1)每周乘地铁1-2次的所占的百分比是:1-29.7%-12.1%-9.0%-12.2%=37%;;(2)调价后客流量下降百分比最高的线路是2号线,调价后里程x(千米)在52<x≤72范围内的客流量下降最明显.增长率最高的线路是15号线,预计2016年1月这条线路的日均客流量将达到:17.3×(1+28.15%)≈22.2(万人);故答案是:2号线,52<x≤72,22.2;(3)调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出:5×2×(5-2)=30(元).故答案是:30.(1)利用1减去其它组的百分比,即可求得每周乘地铁1-2次的所占的百分比;(2)根据调整后部分路线的客流量及变化率即可直接求得;(3)根据15.9公里确定调整后的票价,即可求解.本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.26.【答案】解:(1)如图,(2)∠BAD=∠BED.理由如下:连结BC、CD,如图,∴AB为⊙O的直径,∴∠ACB=90°,∴BC⊥AC,∵直线l与MA所在直线关于直线MD对称,∴MD平分∠EMC,∴BC=BE,∴点C与点E关于直线MD对称,∴△BCD≌△BED,∴∠BCD=∠BED,∵∠BCD=∠BAD,∴∠BAD=∠BED.【解析】(1)连结两条线段即可;(2)连结BC、CD,如图,根据圆周角定理得到∠ACB=90°,则BC⊥AC,再根据轴对称的性质得到MD平分∠EMC,于是根据角平分线的性质得BC=BE,所以可判断点C与点E关于直线MD对称,得到△BCD≌△BED,则∠BCD=∠BED,再由圆周角定理得∠BCD=∠BAD,于是得到∠BAD=∠BED.本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了轴对称的性质.27.【答案】解:(1)∵二次函数y1=x2+bx+c的图象C1经过(-1,0),(0,-3)两点,∴ .解得,∴抛物线C1的函数解析式为y=x2-2x-3;(2)∵y1=x2-2x-3=(x-1)2-4,∴抛物线的顶点坐标为(1,-4),∵C1先向左平移1个单位,在向上平移4个单位,得到抛物线C2,∴平移后C2的顶点坐标为(0,0),C2对应的函数表达式记为y2=x2;(3)如图:由图象,得只要-1≤a就肯定存在-2≤x≤a中的某一个x的值使得y2≤y3成立【解析】(1)根据待定系数法,可得函数解析式;(2)根据抛物线平移的规律:向左平移加,向上平移加,可得答案;(3)根据函数与不等式的关系,可得答案.本题考查了二次函数与不等式组,函数图象平移的规律是:左加右减,上加下减;利用函数图象在上方的部分函数值大是解不等式组的关键.28.【答案】90;;tan(90°-α)【解析】解:连接AD,∵AB=AC,点D是BC的中点,∴∠ABC=∠C,∠BAD=∠DAC=∠BAC,AD⊥BC,∵AD⊥BC,DE⊥AC,∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,∴∠ADE=∠C.又∵∠ADB=∠DEC=90°,∴△ADB∽△DEC,∴=即AD•CE=BD•DE.∵点D是BC的中点,点F是DE的中点,∴BD=BC,DE=2DF,∴AD•CE═BC•2DF=BC•DF,∴=,又∵∠ADE=∠C,∴△AFD∽△BEC,∴=.在Rt△ADB中,∵∠ABD=90°-∠BAD=90°-∠BAC,BD=BC,∴tan∠ABD=tan(90°-∠BAC)==,∴==tan(90°-∠BAC).∵△AFD∽△BEC,∴∠DAF=∠CBE.∵∠CBE+∠BOD=90°,∠AOH=∠BOD,∴∠DAF+∠AOH=∠CBE+∠BOD=90°,∴∠AHO=180°-90°=90°,即∠AHB=90°.(1)如图1,根据以上结论可得:∠AHB=90°,=tan(90°-×90°)=.故答案分别为:90°、;(2)如图2,猜想:∠AHB=90°,=.证明:根据以上结论可得:∠AHB=90°,=tan(90°-×60°)=.(3)如图3,根据以上结论可得:=tan(90°-α).故答案为:tan(90°-α).连接AD,根据等腰三角形的性质可得∠ABC=∠C,∠BAD=∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得AD•CE=BD•DE.由此可得AD•CE=BC•2DF=BC•DF,即=,由此可证到△AFD∽△BEC,则有=.在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-∠BAC)==,从而可得=tan(90°-∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的三个问题.本题主要考查的是相似三角形的判定与性质、三角函数的定义、等腰三角形的性质、同角的余角相等等知识,证到△AFD∽△BEC是解决本题的关键.29.【答案】3;;-1【解析】解:(1)点(2,3)和射线OA之间的距离为3,点(-2,3)和射线OA之间的距离为=,故答案分别为:3、;(2)∵直线y=x和双曲线y=之间的距离为,∴k<0(否则直线y=x和双曲线y=相交,它们之间的距离为0).过点O作直线y=x的垂线,与双曲线y=交于点A、B,过点B作BH⊥x轴,如图1,在Rt△OHB中,∠HOB=∠HBO=45°,OB=,则有OH=BH=OB=1,∴点B的坐标为(1,-1),∴k=1×(-1)=-1,故答案为:-1;(3)①过点O分别作射线OE、OF的垂线OG、OH,如图2,则图形M为:y轴的正半轴、∠GOH的边及其内部所有的点(图2中的阴影部分);②图形W与图形N之间的距离为.提示:设抛物线y=x2-2与射线OG的交点为N,如图3,图形N上点的坐标可设为(x,x2-2),则图形W与图形N之间的距离为的最小值.易求出点N的坐标为(,-),从而有0≤x2≤,由此可得x2+(x2-2)2=(x2-)2+的最小值为(-)2+=,则图形W与图形N之间的距离为=.(1)只需根据新定义即可解决问题;(2)过点O作直线y=x的垂线,与双曲线y=交于点A、B,过点B作BH⊥x轴,如图1,根据新定义可得直线y=x和双曲线y=之间的距离就是线段OB 的长,如何只需求出点B的坐标,运用待定系数法就可求出k的值;(3)①过点O分别作射线OE、OF的垂线OG、OH,如图2,根据新定义可得图形M为y轴的正半轴、∠GOH的边及其内部所有的点;②设抛物线y=x2-2与射线OG的交点为N,如图3,图形N上点的坐标可设为(x,x2-2),根据新定义可得图形W与图形N之间的距离为的最小值.可通过求出点N的坐标得到x2的范围,然后利用二次函数的增减性求出x2+(x2-2)2=(x2-)2+的最小值,就可解决问题.本题属于新定义型,考查了用待定系数法求反比例函数的解析式、抛物线的增减性、勾股定理、求直线与抛物线的交点等知识,解决本题的关键是对新定义的理解.。
2015年北京市西城区中考数学一模试卷-含详细解析
第1页,共26页2015年北京市西城区中考数学一模试卷副标题题号题号 一 二 三 四 总分总分 得分得分一、选择题(本大题共10小题,共30.0分)分) 1.的相反数是(的相反数是( ) A.B.C. 3D.2. 据市烟花办相关负责人介绍,2015年初夕零时至正月十五24时,全市共销售烟花爆竹约196 000箱,同比下降了32%,将196 000用科学记数法表示应为(用科学记数法表示应为( )A.B.C. D. 3. 下列运算正确的是(下列运算正确的是( )A. B.C. D. 4. 如图是一个几何体的实物图,则其主视图是(如图是一个几何体的实物图,则其主视图是()A.B.C.D.5. 甲、乙、丙、丁四名选手参加100米决赛,赛场只设1、2、3、4四个跑道,选手以随机抽签的方式决定各自的跑道,若甲首先抽签,则甲抽到1号跑道的概率是( )A. 1B.C.D.6. 下列图形,既是轴对称图形,又是中心对称图形的是(下列图形,既是轴对称图形,又是中心对称图形的是( )A.B.C.D.7. 如图,线段AB 是圆O 的直径,弦CD ⊥AB ,如果∠BOC =70°,那么∠BAD 等于(等于( )A. B.C. D.8. 在平面直角坐标系xOy 中,第一象限内的点P 在反比例函数的图象上,如果点P的纵坐标是3,OP =5,那么该函数的表达式为(,那么该函数的表达式为( )A.B.C.D.9. 为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,并绘制成如图所示的条形统计图,并绘制成如图所示的条形统计图,这组数据的这组数据的众数和中位数分别是(众数和中位数分别是( )A. 6,4B. 6,6C. 4,4D. 4,610. 如图,过半径为6的圆O 上一点A 作圆O 的切线l ,P 为圆O 的一个动点,作PH ⊥l 于点H ,连接P A .如果P A =x ,AH =y ,那么下列图象中,那么下列图象中,能大致表示能大致表示y 与x 的函数关系的是(数关系的是( )A.B.C.D.二、填空题(本大题共6小题,共18.0分)分)11. 如果分式有意义,那么的取值范围是______.12. 半径为4cm ,圆心角为60°的扇形的面积为______cm 2. 13. 分解因式:12m 2-3=______.14. 如图,△ABC 中,AB =AC ,点D ,E 在BC 边上,当______时,△ABD ≌△ACE .(添加一个适当的条件即可).(添加一个适当的条件即可)15. 如图是跷跷板的示意图,如图是跷跷板的示意图,立柱立柱OC 与地面垂直.与地面垂直.以以O 为横板AB 的中点,AB 绕点O上下转动,横板AB 的B 端最大高度h 是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设AB =2m ,OC =0.5m ,通过计算得到此时的h 1,再将横板AB 换成横板A ′B ′,O 为横板A ′B ′的中点,且A ′B ′=3m ,此时B ′点的最大高度为h 2,由此得到h 1与h 2的大小关系是:h 1______h 2(填“>”、“=”或“<”).可进一步得出h 随横板的长度的变化为______(填“不变”或“改变”) 16. 如图,数轴上,点A 的初始位置表示的数为1,现点A 做如下移动:第一次点A 向左移动3个单位长度至点A 1,第2次从点A 1向右移动6个单位长度至点A 2,第3次从点A 2向左移动9个单位长度至点A 3,…,按照这种移动方式进行下去,点A 4表示的数是______,如果点A n 与原点的距离不小于20,那么n 的最小值是______.三、计算题(本大题共3小题,共15.0分)分) 17. 计算:计算:.18. 化简求值:,其中a =2.19. 阅读下面的材料小敏在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且tanα= ,tan,求α+β的度数.小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD =α,∠CBE =β,且BA ,BC 在直线BD 的两侧,连接AC ,可证得△ABC 是等腰三角形,因此可求得α+β=∠ABC =______°请参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ=时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON =α=α--β,由此可得α-β=______°.四、解答题(本大题共10小题,共57.0分)分) 20. 如图,∠C =∠E ,∠EAC =∠DAB ,AB =AD .求证:BC =DE .21. 解不等式组:解不等式组:.22. 从北京到某市可乘坐普通列车或高铁.已知高铁的行驶路程是400千米,普通列车从北京到某市可乘坐普通列车或高铁.已知高铁的行驶路程是的行驶路程是520千米.如果高铁的平均速度是普通列车平均速度的2.5倍,且乘坐高铁比乘坐普通列车少用3小时,求高铁的平均速度是多少千米/时?时?23. 已知关于x的一元二次方程x2-2(m-1)x-m(m+2)=0.(1)求证:方程总有两个不相等的实数根;)求证:方程总有两个不相等的实数根;(2)若x=-2是此方程的一个根,求实数m的值.的值.24. 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC(1)求证:四边形ABDE是平行四边形;的长.(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.25. 在北京,乘坐地铁是市民出行时经常采用的一种交通方式,据调查,新票改革政策的实施给北京市轨道交通客流带来很大变化.根据2015年1月公布的调价后市民当时乘坐地铁的相关调查数据,制作了一下统计表以及统计图.根据以上信息解答下列问题:(1)补全扇形图;(2)题目所给出的线路中,调价后客流量下降百分比最高的线路是______,调价后里程x(千米)在______范围内的客流量下降最明显.对于表中客流量不降反增而且增长率最高的线路,如果继续按此变化率增长,预计2016年1月这条线路的日均客流量将达到______万人次(精确到0.1)(3)小王同学上学时,需要乘坐地铁15.9公里到达学校,每天上下学共乘坐两次.问调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出______元.(不考元)虑使用一卡通刷卡优惠,调价前每次乘坐地铁票价为2元)26. 如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称,作BE⊥l 于点E,连接AD,DE(1)依题意补全图形;相等的角,并加以证明. (2)在不添加新的线段的条件下,写出图中与∠BED相等的角,并加以证明.27. 已知二次函数y1=x2+bx+c的图象C1经过(-1,0),(0,-3)两点.(1)求C1对应的函数表达式;(2)将C1先向左平移1个单位,在向上平移4个单位,得到抛物线C2,将C2对应的函数表达式记为y2=x2+mx+n,求C2对应的函数表达式;(3)设y3=2x+3在(2)的条件下,如果在-2≤x≤a内存在某一个x的值,使得y2≤y3成立,结合函数图象直接写出a的取值范围.的取值范围.28. △ABC中,AB=AC,取BC的中点D,做DE⊥AC与点E,取DE的中点F,连接BE,AF交于点H.(1)如图1,如果∠BAC=90°,那么∠AHB=______°,=______;(2)如图2,如果∠BAC=60°,猜想∠AHB的度数和的值,并证明你的结论;的值,并证明你的结论;(3)如果∠BAC=α,那么=______.(用含α表达式表示)29. 给出如下规定:两个图形G1和G2,点P为G1上任一点,点Q为G2上任一点,如果线段PQ的长度存在最小值,就称该最小值为两个图形G1和G2之间的距离.在平面直角坐标系xOy中,O为坐标原点.(1)点A的坐标为A(1,0),则点(2,3)和射线OA之间的距离为______,点(-2,3)和射线OA之间的距离为______;(2)如果直线y=x和双曲线y=之间的距离为 ,那么k=______;(可在图1中进行研究)(3)点E的坐标为(1, ),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.①请在图2中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)②将射线OE,OF组成的图形记为图形W,抛物线y=x2-2与图形M的公共部分记之间的距离.为图形N,请直接写出图形W与图形N之间的距离.答案和解析1.【答案】B【解析】解:的相反数是-,添加一个负号即可. 故选:B .根据相反数的概念解答即可.本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0. 2.【答案】A【解析】解:将196 000用科学记数法表示为:1.96×1.96×10105. 故选:A .科学记数法的表示形式为a×a×1010n的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数. 此题考查科学记数法的表示方法.科学记数法的表示形式为a×a×1010n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值. 3.【答案】C【解析】解:A 、3a 与3b 不是同类项,不能合并,错误; B 、a 3与a 不是同类项,不能合并,错误; C 、(a 2)3=a 6,正确; D 、a 6÷a 3=a 3,错误; 故选:C .分别根据同底数幂的除法、幂的乘方与积的乘方、合并同类项的法则进行逐一计算即可.本题考查合并同类项、同底数幂的除法、幂的乘方,熟练掌握性质和法则是解题的关键.4.【答案】C【解析】解:从正面看可得到一个矩形和一个下底和矩形相邻的梯形的组合图,故选C. 找到从正面看所得到的图形即可.本题考查了三视图的知识,主视图是从物体的正面看得到的视图.5.【答案】D【解析】解:∵设1、2、3、4四个跑道,甲抽到1号跑道的只有1种情况,∴甲抽到1号跑道的概率是:.故选D.由设1、2、3、4四个跑道,甲抽到1号跑道的只有1种情况,直接利用概率公式求解即可求得答案.此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.6.【答案】D【解析】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误;B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;C、此图形旋转180°后能与原图形重合,此图形是中心对称图形,不是轴对称图形,故此选项错误;D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.故选:D.根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.此题主要考查了中心对称图形与轴对称的定义,根据定义得出图形形状是解决问题的关键.7.【答案】C【解析】解:∵弦CD⊥直径AB,∴=,∴∠BAD=∠BOC=×70°70°=35°=35°.故选C.先根据垂径定理得到=,然后根据圆周角定理得∠BAD=∠BOC=35°. 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.8.【答案】A【解析】解:在RT△OPD中,过P作PD⊥x轴于D,则PD=3,∴OD==4,∴P(4,3),∴代入反比例函数y=得,3=,解得k=12,∴反比例函数的解析式为y=,故选A.过P作PD⊥x轴于D,则PD=3,根据勾股定理求得OD,得出D的坐标,然后根据待定系数法即可求得反比例函数的解析式.本题考查了待定系数法求反比例函数的解析式,熟练掌握待定系数法是解题的关键.9.【答案】B【解析】解:出现最多的是6小时,则众数为6;按大小顺序排列在中间的两个人的锻炼时间都为6小时,则中位数为6.故选:B.在这50人中,参加6个小时体育锻炼的人数最多,则众数为6;50人中锻炼时间处在第25和26位的都是6小时,则中位数为6.本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.10.【答案】C【解析】解:如图,当PH与圆O相切时,∵四边形OAHP是正方形,∴AH=6,PA=6,当点P在圆O上运动时,y与x之间的关系既不是一次函数也不是二次函数,并且在x=6时,函数取得最大值6,因为6<6<12,故选:C.当PH与圆O相切时,y取得最大值6,x=6,据此分析即可得出结论. 本题主要考查了动点问题的图象,通过计算发现在函数取得最大值时,x的值大于6是解决问题的关键.11.【答案】x≠5【解析】解:分式有意义,得x-x-5≠05≠0.解得x≠5,故答案为:x≠5.根据分母为零,分式无意义;分母不为零,分式有意义.本题考查了分式有意义的条件,从以下三个方面透彻理解分式的概念:分式无意义⇔分母为零;分式有意义⇔分母不为零;分式值为零⇔分子为零且分母不为零.12.【答案】π【解析】解:半径为4cm,圆心角为60°的扇形的面积为:=π(cm2).故答案为:π.直接利用扇形面积公式求出即可.此题主要考查了扇形的面积公式应用,熟练记忆扇形面积公式是解题关键. 13.【答案】3(2m+1)(2m-1)【解析】解:12m2-3=3(4m2-1)=3(2m+1)(2m-1).故答案为:3(2m+1)(2m-1).首先提取公因式3,进而利用平方差公式分解因式得出即可.此题主要考查了提取公因式法以及公式法分解因式,正确应用平方差公式是解题关键.14.【答案】BD=CE【解析】解:BD=CE,理由是:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中∴△ABD≌△ACE(SAS),故答案为:BD=CE.根据等边对等角得出∠B=∠C,根据全等三角形的判定推出即可.本题考查了等腰三角形的性质,全等三角形的判定的应用,此题是一道开放型的题目,答案不唯一,只要填上一个符合的即可.15.【答案】=;不变;不变【解析】解:过点B作BD⊥AD,B′D′⊥A′B′,∵OC是△ABD与△A′B′D′的中位线,∴BD=B′D′=OC,即h1=h2,故答案为:=,不变.过点B作BD⊥AD,B′D′⊥A′B′,根据三角形中位线定理即可得出结论.本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.16.【答案】7 13【解析】解:第一次点A向左移动3个单位长度至点A1,则A1表示的数,1-3=-2-2; 第2次从点A1向右移动6个单位长度至点A2,则A2表示的数为-2+6=4;第3次从点A2向左移动9个单位长度至点A3,则A3表示的数为4-9=-5;第4次从点A3向右移动12个单位长度至点A4,则A4表示的数为-5+12=7;第5次从点A4向左移动15个单位长度至点A5,则A5表示的数为7-15=-8; …;则A7表示的数为-8-3=-11,A9表示的数为-11-3=-14,A11表示的数为-14-3=-17,A13表示的数为-17-3=-20,A6表示的数为7+3=10,A8表示的数为10+3=13,A10表示的数为13+3=16,A12表示的数为16+3=19,所以点A n与原点的距离不小于20,那么n的最小值是13.故答案为7,13.序号为奇数的点在点A的左边,各点所表示的数依次减少3,序号为偶数的点在点A的右侧,各点所表示的数依次增加3,于是可得到A13表示的数为-17-3=-20,A12表示的数为16+3=19,则可判断点A n与原点的距离不小于20时,n的最小值是13.本题考查了规律型:认真观察、仔细思考,找出点表示的数的变化规律. 17.【答案】解:原式=.【解析】本题涉及零指数幂、负指数幂、二次根式化简、特殊角的三角函数值等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.18.【答案】原式=×- ,= ,=,当a=2时,原式==.【解析】将原式的分子、分母因式分解,除法化为乘法,约分,再代值计算.本题考查了分式的化简求值.解答此题的关键是把分式化到最简,然后代值计算.19.【答案】45;45【解析】解:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,因此可求得α+β=∠ABC=45°;参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ=时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=αMON=α--β,由此可得α-β=45°. 故答案为:45;45如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA ,BC 在直线BD 的两侧,连接AC ,可证得△ABC 是等腰三角形,可求得α+β=∠ABC=45° 如图2,把α,β放在正方形网格中,使得∠MOG=α,∠NOH=β,且ON 在∠MOG 内,连接MN ,可证得△MON 是等腰三角形,可求得α-β=45°.本题考查了作图-应用与设计图,等腰三角形的性质,解直角三角形等,根据函数值作出直角三角形是解题的关键. 20.【答案】证明:∵∠DAB =∠EAC ,∴∠DAB +∠BAE =∠EAC +∠BAE ,即∠DAE =∠BAC ,在△DAE 和△BAC 中,∴△DAE ≌△BAC , ∴BC =DE . 【解析】因为∠DAB=∠EAC ,从图上可以看出∠DAB+∠BAE=∠EAC+∠BAE ,即∠DAE=∠BAC ,又因为,∠C=∠E ,AB=AD ,所以很容易证明△DAE ≌△BAC ,从而得出结论.本题考查全等三角形的判定定理,根据ASA 可证明三角形全等,从而可得出结论. 21.【答案】解:∵解不等式①得:x ≥2, 解不等式②得:x >-1, ∴不等式组的解集为x ≥2. 【解析】先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是能根据找不等式组解集的规律找出不等式组的解集,难度适中. 22.【答案】解:设普通列车平均速度是x 千米/时,则高铁平均速度是2.5x 千米/时,根据题意得:-=3, 解得:x =120,经检验x =120是原方程的解,是原方程的解,则高铁的平均速度是120×120×2.5=3002.5=300(千米/时), 答:高铁的平均速度是300千米/时. 【解析】设普通列车平均速度是x 千米/时,则高铁的平均速度是2.5x 千米/时,根据乘坐高铁比乘坐普通列车少用3小时,列出分式方程,然后求解即可. 此题考查了分式方程的应用,关键是分析题意,找到合适的数量关系列出方程,解分式方程时要注意检验.23.【答案】(1)证明:∵关于x 的一元二次方程x 2-2(m -1)x -m (m +2)=0.∴△=4×(m -1)2+4m (m +2)=8m 2+4>0, ∴方程总有两个不相等的实数根;(2)解:∵x =-2是此方程的一个根,∴把x =-2代入方程中得到4-2(m -1)×(-2)-m (m +2)=0, ∴4+4(m -1)-m (m +2)=0, ∴m 2-2m =0, ∴m 1=0,m 2=2. 【解析】(1)根据根的判别式求出△的值,再进行判断即可;(2)先把x=-2代入方程,然后解关于m 的一元二次方程,即可求出m 的值.此题考查了一元二次方程ax 2+bx+c=0(a≠0)的根的判别式△=b 2-4ac :当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.24.【答案】(1)证明:∵∠ADE=∠BAD,∴AB∥DE,∵AE⊥AC,BD⊥AC,AE∥BD,∴四边形ABDE是平行四边形;(2)解:∵DA平分∠BDE,∴∠AED=∠BDA,∴∠BAD=∠BDA,∴BD=AB=5,设BF=x,则DF=5-x,∴AD2-DF2=AB2-BF2,∴62-(5-x)2=52-x2,∴x=,∴AF= =,∴AC=2AF=.【解析】(1)由平行四边形的判定定理:两组对边分别平行得到结论;(2)由角平分线、等量代换得到角相等,由等角对等边得到BD=AB=5,根据勾股定理列方程求解.本题考查了平行四边形的判定和性质,角平分线的性质,勾股定理的应用,解题的关键是利用勾股定理列方程.25.【答案】2号线;52<x≤72;22.2;30【解析】解:(1)每周乘地铁1-2次的所占的百分比是:1-29.7%-12.1%-9.0%-12.2%=37%;;(2)调价后客流量下降百分比最高的线路是2号线,调价后里程x (千米)在52<x≤72范围内的客流量下降最明显.增长率最高的线路是15号线,预计2016年1月这条线路的日均客流量将达到:17.3×(1+28.15%)≈22.2(万人); 故答案是:2号线,52<x≤72,22.2;(3)调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出:5×5×2×2×(5-2)=30(元). 故答案是:30.(1)利用1减去其它组的百分比,即可求得每周乘地铁1-2次的所占的百分比; (2)根据调整后部分路线的客流量及变化率即可直接求得; (3)根据15.9公里确定调整后的票价,即可求解.本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小. 26.【答案】解:(1)如图,(2)∠BAD =∠BED .理由如下:连结BC 、CD ,如图,∴AB 为⊙O 的直径,的直径, ∴∠ACB =90°, ∴BC ⊥AC ,∵直线l 与MA 所在直线关于直线MD 对称, ∴MD 平分∠EMC ,∴BC =BE ,∴点C 与点E 关于直线MD 对称, ∴△BCD ≌△BED , ∴∠BCD =∠BED , ∵∠BCD =∠BAD , ∴∠BAD =∠BED . 【解析】(1)连结两条线段即可;(2)连结BC 、CD ,如图,根据圆周角定理得到∠ACB=90°,则BC ⊥AC ,再根据轴对称的性质得到MD 平分∠EMC ,于是根据角平分线的性质得BC=BE ,所以可判断点C 与点E 关于直线MD 对称,得到△BCD ≌△BED ,则∠BCD=∠BED ,再由圆周角定理得∠BCD=∠BAD ,于是得到∠BAD=∠BED . 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了轴对称的性质.27.【答案】解:(1)∵二次函数y 1=x 2+bx +c 的图象C 1经过(-1,0),(0,-3)两点,∴.解得解得 , ∴抛物线C 1的函数解析式为y =x 2-2x -3;(2)∵y 1=x 2-2x -3=(x -1)2-4, ∴抛物线的顶点坐标为(1,-4),∵C 1先向左平移1个单位,在向上平移4个单位,得到抛物线C 2, ∴平移后C 2的顶点坐标为(0,0),C 2对应的函数表达式记为y 2=x 2; (3)如图:由图象,得只要-1≤a 就肯定存在-2≤x ≤a 中的某一个x 的值使得y 2≤y 3成立 【解析】(1)根据待定系数法,可得函数解析式;(2)根据抛物线平移的规律:向左平移加,向上平移加,可得答案; (3)根据函数与不等式的关系,可得答案.本题考查了二次函数与不等式组,函数图象平移的规律是:左加右减,上加下减;利用函数图象在上方的部分函数值大是解不等式组的关键.28.【答案】90; ;tan (90°90°--α) 【解析】解:连接AD ,∵AB=AC ,点D 是BC 的中点,∴∠ABC=∠C ,∠BAD=∠DAC=∠BAC ,AD ⊥BC , ∵AD ⊥BC ,DE ⊥AC , ∴∠ADE+∠CDE=90°,∠C+∠CDE=90°, ∴∠ADE=∠C .又∵∠ADB=∠DEC=90°,∴△ADB ∽△DEC , ∴=即AD•CE=BD•DE .∵点D 是BC 的中点,点F 是DE 的中点,∴BD=BC ,DE=2DF , ∴AD•CE═BC•2DF=BC•DF , ∴=,又∵∠ADE=∠C ,∴△AFD ∽△BEC , ∴=.在Rt △ADB 中,∵∠ABD=90°ABD=90°--∠BAD=90°BAD=90°--∠BAC ,BD=BC ,∴tan ∠ABD=tan (90°90°--∠BAC )==,∴==tan (90°90°--∠BAC ).∵△AFD ∽△BEC ,∴∠DAF=∠CBE . ∵∠CBE+∠BOD=90°,∠AOH=∠BOD , ∴∠DAF+∠AOH=∠CBE+∠BOD=90°, ∴∠AHO=180°AHO=180°-90°-90°-90°=90°=90°,即∠AHB=90°. (1)如图1,根据以上结论可得: ∠AHB=90°,=tan (90°90°--×90°)=.故答案分别为:90°、;(2)如图2, 猜想:∠AHB=90°,=.证明:根据以上结论可得: ∠AHB=90°,=tan (90°90°--×60°)=.(3)如图3,根据以上结论可得:=tan (90°90°--α). 故答案为:tan (90°90°--α). 连接AD ,根据等腰三角形的性质可得∠ABC=∠C ,∠BAD=∠BAC ,AD ⊥BC ,然后根据同角的余角相等可得∠ADE=∠C .易证△ADB ∽△DEC ,可得AD•CE=BD•DE .由此可得AD•CE=BC•2DF=BC•DF ,即=,由此可证到△AFD ∽△BEC ,则有=.在Rt △ADB 中根据三角函数的定义可得90°--90°--∠BAC)==,从而可得=tan(90°tan∠ABD=tan(90°∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的三个问题.本题主要考查的是相似三角形的判定与性质、三角函数的定义、等腰三角形的性质、同角的余角相等等知识,证到△AFD∽△BEC是解决本题的关键. 29.【答案】3; ;-1【解析】解:(1)点(2,3)和射线OA之间的距离为3,点(-2,3)和射线OA之间的距离为=,故答案分别为:3、;(2)∵直线y=x和双曲线y=之间的距离为,∴k<0(否则直线y=x和双曲线y=相交,它们之间的距离为0).过点O作直线y=x的垂线,与双曲线y=交于点A、B,过点B作BH⊥x轴,如图1,在Rt△OHB中,∠HOB=∠HBO=45°,OB=,则有OH=BH=OB=1,∴点B的坐标为(1,-1),∴k=1×(-1)=-1,故答案为:-1;(3)①过点O分别作射线OE、OF的垂线OG、OH,如图2,则图形M为:y轴的正半轴、∠GOH的边及其内部所有的点(图2中的阴影部分);②图形W与图形N之间的距离为.提示:设抛物线y=x2-2与射线OG的交点为N,如图3,图形N上点的坐标可设为(x,x2-2),则图形W与图形N之间的距离为的最小值.易求出点N的坐标为(,-),从而有0≤x2≤,由此可得x2+(x2-2)2=(x2-)2+的最小值为(-)2+=,则图形W与图形N之间的距离为=.(1)只需根据新定义即可解决问题;(2)过点O作直线y=x的垂线,与双曲线y=交于点A、B,过点B作BH⊥x 轴,如图1,根据新定义可得直线y=x和双曲线y=之间的距离就是线段OB 的长,如何只需求出点B的坐标,运用待定系数法就可求出k的值; (3)①过点O分别作射线OE、OF的垂线OG、OH,如图2,根据新定义可得图形M为y轴的正半轴、∠GOH的边及其内部所有的点;②设抛物线y=x2-2与射线OG的交点为N,如图3,图形N上点的坐标可设为(x,x 2-2),根据新定义可得图形W与图形N之间的距离为的最小值.可通过求出点N的坐标得到x2的范围,然后利用二次函数的增减性求出x2+(x2-2)2=(x2-)2+的最小值,就可解决问题.本题属于新定义型,考查了用待定系数法求反比例函数的解析式、抛物线的增减性、勾股定理、求直线与抛物线的交点等知识,解决本题的关键是对新定义的理解.。
北京市西城区2015届中考语文一模试题(word版,含答案)

北京市西城区2015届中考语文一模试题一、基础·运用(共22分)(一)选择。
下面各题均有四个选项,其中只有一个..符合题意,选出答案后在答题卡上用铅笔把对应题目的选项字母涂黑涂满。
(共12分)1.阅读下面的文字,完成第(1)~(5)题。
(共10分)中国历代的家训是中国传统文化中根源最为深厚的一部分,最早可追溯到周公告诫子侄周成王的诰辞(诰,音gào,“诰辞”是古代的一种告诫性的话或文章),从此绵(yán)接续数千年。
好的家训(甲)承载.着一个家庭或家族的生活方式、文化氛围、价值追求,(乙)体现了中华民族优秀传统,(丙)逐渐成为国人“修身”“齐家”“治国”的标准,乃至_①_。
例如,“一粥一饭,当思________;________,恒念物力维艰”的节俭持家思想,今天看来于家于国都有着积极意义。
当然,家训并非_②_,它也随着文明的进步,不断发展与深化。
在思想多变、文化多元的今天,我们更应该在________的基础上,________,________,________,让这面家国同在的千年旗帜凝聚民族精神,除旧貌,换新颜,引领千千万万个家庭成为国家发展、民族进步、社会和谐的重要基石。
(1)从文意及字义解释来看,上文画波浪线词语中“yán”字的字形和加点字“载”的注音判断都正确的一项是(2分)A. 延(意义为“延长”)载(zǎi,意义为“记载”)B. 延(意义为“延长”)载(zài,意义为“装载”)C. 沿(意义为“顺着”)载(zài,意义为“装载”)D. 沿(意义为“顺着”)载(zǎi,意义为“记载”)(2)在文中①②处依次填入词语,最恰当的一项是(2分)A. 规范千篇一律B. 规范一成不变C. 典范一成不变D. 典范千篇一律(3)在第一段横线处依次填入词语,将这则对偶句式的家训补充完整,正确的一项是(2分)一粥一饭,当思________;________,恒念物力维艰。
2015年西城区中学排名

西城区中学2015年排名2015年德胜学区学区内小学裕中小学;实验二小(德胜校区);育翔小学;五路通小学;西师附小属地内初中校与排名三帆中学,第2名师大二附中初中部,第14名三帆中学裕中学校,第21名北京七中,第27名调配初中校与排名十三中分校,第1名北京八中,第4名北京四中,第5名北京十三中,第12名2015年什刹海学区学区内小学雷锋小学、西什库小学、黄城根小学、厂桥小学、鸦儿小学、什刹海小学、新街口东街小学、十三中附小属地内初中校与排名北京四中,第5名;北京156中学,第7名;北京十三中,第12名;北京三中,第22名;北京39中,第29名调配初中校与排名十三中分校,第1名三帆中学,第2名北京161中学,第6名2015年金融街学区学区内小学宏庙小学、西单小学、实验二小本部、奋斗小学本部、实验二小受水河分校、华嘉小学属地内初中校与排名北师大实验中学,第3名北京八中,第4名鲁迅中学,第25名北京159中学,第28名北师大实验二龙路中学,第39名调配初中校与排名北京四中,第5名161中学,第6名北师大附中,第9名2015年西长安街学区学区内小学一六一中附小、实验二小长安校区、自忠小学、顺城街一小、力学小学属地内初中校与排名161中学,第6名31中学,第19名调配初中校与排名北师大实验中学,第3名北京四中,第5名北师大附中,第9名北京14中学,第10名北京35中,第13名西城外国语学校,第15名2015年新街口学区学区内小学黄城根小学、实验二小玉桃园分校、四根柏小学、中华路小学、西四北四条小学属地内初中校与排名北京35中,第13名北京三中,第22名市教院附中,第35名北京41中,第38名调配初中校与排名十三中分校,第1名三帆中学,第2名北京四中,第5名一六一中学,第6名2015年展览路学区学区内小学西外附小、展一小、奋斗小学银河校区、阜外一小、进步小学、建筑大学附小属地内初中校与排名北京35中学,第13名西城外国语学校,第15名北京八中(并154中学),第32名北京56中学,第36名调配初中校与排名三帆中学,第2名北京四中,第5名北京14中学,第10名铁二中,第11名2015年月坛学区学区内小学育民小学、中古友谊小学、三里河三小、复兴门外一下、实验二小白云路分校属地内初中校与排名北京八中(并八中分校),第4名铁二中,第11名北京44中学,第23名214中学(拟更名北大元培中学),第31名外交学院月坛中学,第40名调配初中校与排名北师大实验中学,第3名北京35中学,第13名西城外国语学校,第15名2015年大栅栏、椿树、天桥学区学区内小学实验一小前门分校、北京实验一小、香厂路小学、新世纪实验小学、炭儿胡同小学属地内初中校与排名北师大附中本部,第9名中央美院徐悲鸿中学,第41名北京43中学,第42名调配初中校与排名北京八中,第4名北京161中学,第6名北京14中,第10名铁二中,第11名北京15中,第13名2015年广安门内、牛街学区学区内小学北京小学、康乐里小学、北京小学走读部、回民小学、登莱小学属地内初中校与排名北京十四中,第11名北京66中学,第20名北京回民学校,第33名调配初中校与排名北师大实验中学,第3名北京八中,第4名北师大附中本部,第9名北京15中,第13名北京四中南址,第44名2015年广外学区学区内小学椿树馆小学、实验一小广外分校、实验二小广外分校、北京小学广外分校、北京小学天宁寺分校、北京小学红山分校、青年湖小学、三义里小学、红莲小学属地内初中校与排名北京14中,第10名宣武外国语学校,第17名北京四中南址,第44名调配初中校与排名北师大实验中学,第3名北京八中,第4名铁二中,第11名北京15中,第13名西城外国语学校,第15名2015年陶然亭、白纸坊学区学区内小学八中附小、陶然亭小学、宣师一附小、半步桥小学、西城实验小学、白纸坊小学属地内初中校与排名育才学校(并宣武分院附中),第8 15中(并140中),第13名六十六中(并广安中学),第20师大附中南校区(并62中),第34四中南校区(并63中),第44调配初中校与排名北京八中,第4名北京一六一中学,第6名北京14中学,第10名。
2014-2015学年北京市西城区初三一模数学试题.docx

北京市西城区 2015 年初三一模试卷数学2015. 4一、选择题 ( 本题共30 分,每小题 3 分 )下面各题均有四个选项,其中只有一个是符合题意的.1.1的相反数是311C. 3D.3 A. B.332.据市烟花办相关负责人介绍,2015 年除夕零时至正月十五24 时,全市共销售烟花爆竹约196 000 箱,同比下降了32%.将 196 000 用科学记数法表示应为A. 1.96105B. 1.96104C. 19.6104D. 0.196 1063.下列运算正确的是A. 3a3b 6abB. a3a a2C. a23a6D. a6a3a24.如图是一个几何体的直观图,则其主视图是5.甲、乙、丙、丁四名选手参加100 米决赛,赛场共设1, 2, 3, 4 四条跑道,选手以随机抽签的方式决定各自的跑道.若甲首先抽签,则甲抽到 1 号跑道的概率是A. 11C.11 B.3D.246.下列图形中,既是轴对称图形又是中心对称图形的是7.如图,线段AB 是⊙ O 的直径,弦CD 丄 AB,如果∠ BOC=70 °,那么∠ BAD 等于A. 20°B.30 °C. 35°D.70°8.在平面直角坐标系 xOy 中,第一象限内的点 P 在反比例函数的图象上,如果点 P 的纵坐标是 3,OP= 5,那么该函数的表达式为1212A.yB.yx x1515C. yD. yx x9.为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50 名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图.这组数据的众数和中位数分别是A. 6 ,4B. 6 , 6C. 4,4D. 4, 610.如图,过半径为 6 的⊙ O 上一点 A 作⊙ O 的切线l, P 为⊙ O 上的一个动点,作PH ⊥l于点 H,连接 PA.如果 PA= x, AH= y,那么下列图象中,能大致表示y 与x的函数关系的是二、填空题 (本题共 18 分,每小题 3 分 )11.如果分式1有意义,那么x 的取值范围是.x 512.半径为 4cm,圆心角为60°的扇形的面积为cm2.13.分解因式:12m2 3 =.14.如图,△ ABC 中, AB=AC ,点 D,E 在 BC 边上,当时,△ ABD ≌ △ACE.(添加一个适当的条件即可)15.如图是跷跷板的示意图,立柱OC 与地面垂直,以 O为横板 AB 的中点, AB 绕点 O 上下转动,横板 AB..的 B 端最大高度 h 是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设AB= 2 m,OC= 0.5 m,通过计算得到此时的h1,再将横板 AB换成横板 A′B′, O 为横板 A′B′的中点,且 A′B′=3m,此时 B′点的最大高度为h2,由此得到h1与 h2的大小关系是: h1 h2(填“>”、“=”或“<” ).可进一步得出, h 随横板的长度的变化而(填“不变”或“改变” ).16.如图,数轴上,点 A 的初始位置表示的数为1,现点 A 做如下移动:第 1 次点 A 向左移动 3 个单位长度至点 A1,第2次从点 A1向右移动6个单位长度至点 A2,第3次从点 A2向左移动9个单位长度至点A3,,,按照这种移动方式进行下去,点A4表示的数是,如果点A n与原点的距离不小于20,那么n的最小值是.三、解答题 (本题共 30分,每小题 5分 )17.计算:12π0 1 )1 6 tan30 .2008(218.如图,∠ C=∠ E,∠ EAC=∠ DAB, AB=AD .求证: BC=DE .2 x0,19.解不等式组3 5x 1 4x8.a23a a 3120.先化简,再求值:,其中a 2.a22a 1 a 1 a 121.从北京到某市可乘坐普通列车或高铁.已知高铁的行驶路程是400 千米,普通列车的行驶路程是520千米.如果高铁的平均速度是普通列车平均速度的 2.5 倍,且乘坐高铁比乘坐普通列车少用 3 小时.求高铁的平均速度是多少千米/时.22.已知关于 x 的一元二次方程x22( m1) x m(m 2) 0 .( 1)求证:此方程总有两个不相等的实数根;( 2)若x 2 是此方程的一个根,求实数m 的值.四、解答题 ( 本题共 20 分,每小题 5 分 )23.如图,四边形 ABCD 中,BD 垂直平分 AC,垂足为点 F ,E 为四边形 ABCD 外一点,且∠ ADE =∠ BAD ,AE⊥ AC.(1)求证:四边形 ABDE 是平行四边形;(2)如果 DA 平分∠ BDE , AB= 5,AD= 6,求 AC 的长.\24.在北京,乘坐地铁是市民出行时经常采用的一种交通方式.据调查,新票价改革政策的实施给北京市轨道交通客流带来很大变化.根据 2015 年 1 月公布的调价后市民当时乘坐地铁的相关调查数据,制作了以下统计表以及统计图.根据以上信息解答下列问题:( 1)补全扇形图;( 2)题目所给出的线路中,调价后客流量下降百分比最高的线路是,调价后里程x(千米)在范围内的客流量下降最明显.对于表中客流量不降反增而且增长率最高的线路,如果继续按此变化率增长,预计2016 年 1 月这条线路的日均客流量将达到万人次;(精确到 0.1)(3)小王同学上学时,需要乘坐地铁15.9 公里到达学校,每天上下学共乘坐两次.问:调价后小王每周(按 5 天计算)乘坐地铁的费用比调价前多支出元.(不考虑使用市政一卡通刷卡优惠,调价前每次乘坐地铁票价为 2 元)25.如图,AB为⊙ O 的直径,M为⊙ O 外一点,连接 MA 与⊙ O 交于点 C,连接 MB 并延长交⊙ O 于点D,经过点 M 的直线 l 与 MA 所在直线关于直线 MD 对称.作 BE⊥ l 于点 E,连接 AD, DE.( 1)依题意补全图形;( 2)在不添加新的线段的条件下,写出图中与∠BED 相等的角,并加以证明.26.阅读下面的材料:小敏在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且tan 11的度数., tan,求23小敏是这样解决问题的:如图 1,把,放在正方形网格中,使得 ABD, CBE,且 BA,BC 在直线 BD 的两侧,连接AC,可证得△ ABC 是等腰直角三角形,因此可求得=∠ ABC=°.请参考小敏思考问题的方法解决问题:如果,都为锐角,当 tan 4 , tan 32 的正方形网格中,利用已作出的锐角α,画出时,在图5∠ MON=,由此可得=______°.五、解答题 (本题共 22 分,第 27 题 7 分,第 28 题 7 分,第 29 题 8 分 )27、已知二次函数 y 1 x 2 bx c 的图象 C 1 经过 ( 1,0) , (0, 3) 两点.( 1)求 C 1 对应的函数表达式;( 2)将 C 1 先向左平移 1 个单位,再向上平移 4 个单位,得到抛物线 C 2 ,将 C 2对应的函数表达式记为y 2 x 2 mx n ,求 C 2 对应的函数表达式;3y 3 2x 3 ,2 x ≤ a..x( )设在( )的条件下,如果在 2 ≤ 内存在 某一个的值,使得 y 2 ≤ y 3 成立,利用函数图象直接写出a 的取值范围.28、 △ ABC 中, AB=AC .取 BC 边的中点 D ,作 DE ⊥ AC 于点 E ,取 DE 的中点 F ,连接 BE , AF 交于点H .( 1)如图 1,如果BAC 90 ,那么 AHB ,AF;BE( 2)如图 2,如果 BAC60 ,猜想AHB 的度数和AF的值,并证明你的结论;BE( 3)如果BAC ,那么AF.(用含的表达式表示)BE29、给出如下规定:两个图形G1和 G2,点P为 G 1上任一点,点Q 为G2上任一点,如果线段PQ 的长度存在最小值,就称该最小值为两个图形 G1和 G2之间的距离.在平面直角坐标系 xOy 中, O 为坐标原点.(1)点 A 的坐标为A(1,0),则点B(2,3)和射线 OA 之间的距离为 ________,点C ( 2,3)和射线 OA 之间的距离为 ________;( 2)如果直线 y=x 和双曲线y k2 ,那么 k=;(可在图 1 中进行研究)之间的距离为x( 3)点 E 的坐标为 (1, 3 ),将射线 OE 绕原点 O 逆时针旋转60 ,得到射线 OF ,在坐标平面内所有和射线 OE, OF 之间的距离相等的点所组成的图形记为图形M .①请在图 2 中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)②将射线 OE ,OF 组成的图形记为图形W,抛物线y x2 2 与图形M的公共部分记为图形N ,请直接写出图形 W 和图形 N 之间的距离.北京市西城区2015 年初三一模试卷数学试卷参考答案及评分标准2015. 4一、选择题(本题共30 分,每小题 3 分)题号12345678910答案B A C C D A C A B C 二、填空题(本题共18 分,每小题 3 分)1112131415168BD=CE,∠ BAD=∠ CAE,∠ ADB =∠AEC,=,x 3 2m1 2m 1 BE=CD,∠BAE=∠CAD,∠ADE =∠AED,57, 13不变3AE=AD(只填一个即可)三、解答题(本题共30 分,每小题5 分)17.解:0( 1)16tan3012 π 200823= 2 3 1 2 6,,,,,,,,,,,,,,,,,,,,,, 4 分3=2 3 3 2 3=3. ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, 5 分18.证明:如图1.∵∠ EAC=∠DAB ,∴ EAC1DAB1.即∠ BAC=∠DAE .,,,,,,,, 1 分在△ ABC 和△ ADE 中,C E,BAC DAE , ,,,,,,,,, 3 分图 1AB AD ,∴△ ABC≌△ ADE .,,,,,,,,,,,,,,,,,,,,,,, 4 分∴ BC = DE .,,,,,,,,,,,,,,,,,,,,,,,,,, 5 分2x,①19.解:14x8. ②3 5x由①,得 x 2 .,,,,,,,,,,,,,,,,,,,,,,,,, 2 分由②,得 15x 3 4x 8 .系数化 1,得 x 1 .,,,,,,,,,,,,,,,,,,,,,,4 分所以原不等式组的解集为 x2 .,,,,,,,,,,,,,,,,,,,5 分20.解:a 2 3aa 3 1a22a 1 a 1a 1=a a3a 31 ,,,,,,,,,,,,,,,,,,,,,,,2 分a2a1a 11a a3 a 11a2a 3 a 11= a1 ,,,,,,,,,,,,,,,,,,,,,,,,,,,,3 分a 1 a1= a1.,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,4 分a 1当 a2 时, 原式 =211.,,,,,,,,,,,,,,,,,,,,, 5 分2 1 321.解:设普通列车的平均速度为 x 千米 / 时. ,,,,,,,,,,,,,,,,, 1 分则高铁的平均速度是2.5x 千米 /时.依题意,得400 3520 . ,,,,,,,,,,,,,,,,,,,,2 分2.5xx解得 x120 .,,,,,,,,,,,,,,,,,,,,,,,,,, 3 分 经检验, x 120 是原方程的解,且符合题意. ,,,,,,,,,,,, 4 分所以 2. 5x 300 .答:高铁的平均速度是300 千米 /时 . ,,,,,,,,,,,,,,,,,,,5 分22.( 1)证明:2(m 1) 24m( m 2)4m 2 8m 4 4m 28m8m 2 4 . ,,,,,,,,,,,,,,,,,,,,,,,,,,1 分∵ 8m 2 ≥ 0,∴ 8m 2 4 > 0. ,,,,,,,,,,,,,,,,,,,,,,,,2 分∴方程总有两个不相等的实数根. ,,,,,,,,,,,,,,,3 分( 2)解:∵ x2 是此方程的一个根,∴ ( 2)22 ( 2)(m 1)m(m 2) 0 .22m 0 .整理得 m解得 m 1 0 , m 2 2 . ,,,,,,,,,,,,,,,,,,,,,5 分四、解答题(本题共20 分,每小题 5 分)23.( 1)证明:∵ ADE BAD ,∴ AB ∥ ED .,,,,,,,,,,,,,,,,,,,,,,,1 分∵ BD 垂直平分 AC ,垂足为 F ,∴ BDAC , AF=FC .又∵ AE AC ,∴EAC DFC90 .∴四边形ABDE 是平行四边形. ,,,,,,,,,,,,,,,,(2)解:如图 2,连接 BE 交 AD 于点 O.∵DA 平分∠ BDE,∴∠ ADE= ∠ 1.又∵ ADE BAD ,∴∠ 1= ∠ BAD .∴ AB= BD .,,,,,,,,,,,, 3 分∴ ABDE 是菱形.∵ AB= 5, AD= 6,∴ BD=AB= 5,AD BE ,OA 1AD 3 .2在 Rt△OAB中,OB AB2OA2 4 .∵ S V ABD 11AD OB BD AF ,22∴ 6 4 5 AF .解得 AF 4.8 .,,,,,,,,,, 4 分∵ BD 垂直平分 AC,∴ AC 2 AF9.6 .,,,,,,,, 5 分注:其他解法相应给分.24.解:( 1)补全扇形图如图 3 所示. ,,,,,,, 1 分(2) 2 号线, 52< x≤ 72 , 22.2.(各 1 分),,,,,,,,,,,,,,,, 4 分( 3) 30.,,,,,,,,,,,,,,, 5 分25.解:( 1)依题意,补全图形如图4. ,,,,,, 1 分( 2)BAD .,,,,,,,,,,,,,, 2 分证明:如图5,连接 BC, CD.∵直线 l 与直线 MA 关于直线MD 对称,∴12.,,,,,,,,, 3 分∵ AB 为⊙O的直径,∴ACB 90 ,即BC MA .又∵ BE l ,∵ MC MB cos 1 , ME MB cos 2 ,∴MC=ME .又∵ C, E 两点分别在直线 MA 与直线 l 上,可得 C, E 两点关于直线 MD 对称.∴3BED .,,,,,,, 4 分又∵3BAD ,∴BAD BED .,,,,,, 5 分26.解: 45. ,,,,,,,,,,,,,,,,,,, 1 分2 分图2图 3图 4图 511画图见图 6.,,,,,,,,,,,,,,, 3 分45. ,,,,,,,,,,,,,,,,,,, 5 分五、解答题(本题共 22 分,第 23 题 7 分,第 24 题 7 分,第 25 题 8 分)27.解:( 1)∵二次函数y1x2bx c 的图象C1经过 ( 1,0) , (0,3)两点,1 b c 0,1 分∴,,,,,,,,,,,,c 3.b2,2 分解得,,,,,,,,,,,,,c 3.∴抛物线 C 的函数表达式为y1x 22x 3 .1,,,,,,,,,,,,,, 3 分( 2)∵y1x2 2 x 3=(x1)2 4 ,图 7∴抛物线 C1的顶点为(1,4) .,,,,,,,,,,,,,,,,,, 4 分∴平移后抛物线 C 2的顶点为(0,0),它对应的函数表达式为y2x2.,5分(3)a≥1(见图 7).,,,,,,,,,,,,,,,,,,,,,,,,28.解:( 1) 90,1.,,,,,,,,,,,,,,,,,,,,,,,,,,, 2( 2)结论: AHB 90, AF3.BE2证明:如图8,连接 AD.∵AB=AC,∠ BAC=60°,∴△ ABC 是等边三角形.∵D 为 BC 的中点,∴ AD⊥ BC.∴∠ 1+∠ 2=90°.又∵ DE ⊥ AC,∴∠ DEC =90°.∴∠ 2+∠ C=90°.∴∠ 1=∠ C=60°.设 AB=BC=k (k0 ),7 分2 分图8则 CE 1CDk, DE3k .244∵ F 为 DE 的中点,∴ DF 1DE3k , AD3328AB k .22∴ AD 3 , DF 3 .BC2CE212∴ ADDF .,,,,,,,,,,,,,,,,,,,,,, 3 分BCCE又∵∠ 1=∠ C ,∴△ ADF ∽△ BCE .,,,,,,,,,,,,,,,,,,, 4 分 ∴ AFAD 3 , ,,,,,,,,,,,,,,,,,,, 5 分BEBC 2∠ 3=∠ 4.又∵∠ 4+∠ 5=90°,∠ 5=∠6,∴∠ 3+∠ 6=90°.∴ AHB 90 .,,,,,,,,,,,,,,,,,,,,,6 分( 3) 1tan (90). ,,,,,,,,,,,,,,,,,,,,,,,, 7 分22注:写 1 cos或其他答案相 分.2sin29.解:( 1) 3,13 .(每空各 1 分) ,,,,,,,,,,,,,,,,,,,,2 分 (2) 1.,,,,,,,,,,,,,,,,,,,,,,,,,,,,,4 分(3)①如 9, 点 O 分 作射 OE 、OF 的垂 OG 、OH , 形 M :y 正半 ,∠ GOH的 及其内部的所有点( 中的阴影部分).,,,,,,,,7 分9明:(画 2 分,描述 1 分)( 形 M 也可描述 : y 正半 ,直 y3x 下方与直 y3x33下方重叠的部分(含 界) )② 4. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分313。
2015年北京市西城区初三一模数学试题及答案

北京市西城区2015年初三一模试一、选择题(本题共30分,每小题3分) 1.13的相反数是A.13 B.13- C.3 D.3-2.据市烟花办相关负责人介绍,2015年除夕零时至正月十五24时,全市共销售烟花爆竹 约196 000箱,同比下降了32%.将196 000用科学记数法表示应为A.51.9610⨯B.41.9610⨯C.419.610⨯D. 60.19610⨯ 3.下列运算正确的是A. 336a b ab+=B.32a a a -=C.()326a a = D.632a a a ÷=4.如图是一个几何体的直观图,则其主视图是5.甲、乙、丙、丁四名选手参加100米决赛,赛场共设1,2,3,4四条跑道,选手以随机 抽签的方式决定各自的跑道.若甲首先抽签,则甲抽到1号跑道的概率是A. 1B.12 C. 13 D.146.下列图形中,既是轴对称图形又是中心对称图形的是7.如图,线段AB 是⊙O 的直径,弦CD 丄AB ,如果∠BOC =70°, 那么∠BAD 等于A. 20°B. 30°C. 35°D.70° 8.在平面直角坐标系xOy 中,第一象限内的点P 在反比例函数的图象如果点P 的纵坐标是3,OP=5,那么该函数的表达式为A. 12y x =B. 12y x =-C. 15y x =D. 15y =-9.为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图.这组数据的众数和中位数分别是 A. 6,4 B. 6,6 C. 4,4 D. 4,610.如图,过半径为6的⊙O 上一点A 作⊙O 的切线l ,P 为⊙O 上的一个动点,作PH ⊥l 于点H ,连接P A .如果P A =x ,AH=y , 那么下列图象中,能大致表示y 与x 的函数关系的是二、填空题(本题共18分,每小题3分) 11.如果分式15x -有意义,那么x的取值范围是 .12.半径为4cm ,圆心角为60°的扇形的面积为 cm 2. 13.分解因式:2123m -= .14.如图,△ABC 中,AB =AC ,点D ,E 在BC 边上,当 时, △ABD ≌△ACE .(添加一个适当的条件即可) 15.如图是跷跷板的示意图,立柱OC 与地面垂直,以O为横板AB 的中点..,AB 绕点O 上下转动,横板AB 的B 端最大高度h 是否会随横板长度的变化而变化 呢?一位同学做了如下研究:他先设AB=2 m , OC=0.5 m ,通过计算得到此时的h 1,再将横板AB换成横板A ′B ′,O 为横板A ′B ′的中点,且A ′B ′=3m ,此时B ′点的最大高度为h 2,由此得 到h 1与h 2的大小关系是:h 1 h 2(填“>”、“=”或“<”).可进一步得出,h 随横板的长度的变化而 (填“不变”或“改变”).16.如图,数轴上,点A 的初始位置表示的数为1,现点A 做如下移动:第1次点A 向左移动3个单位长度至点1A ,第2次从点1A 向右移动6个单位长度至点2A ,第3次从点2A 向左移动9个单位长度至点3A ,…,按照这种移动方式进行下去,点4A 表示的数是 ,如果点n A 与原点的距离不小于20,那么n 的最小值是 .三、解答题(本题共30分,每小题5分)17()011π2008()6tan302--+-︒.18.如图,∠C =∠E ,∠EAC =∠DAB ,AB=AD .求证:BC=DE .19.解不等式组 ()2035148.x x x -≤⎧⎪⎨+>-⎪⎩,20.先化简,再求值:223312111a a a a a a a ++÷-++++,其中2a =.21.从北京到某市可乘坐普通列车或高铁.已知高铁的行驶路程是400千米,普通列车的行驶路程是520千米.如果高铁的平均速度是普通列车平均速度的2.5倍,且乘坐高铁比 乘坐普通列车少用3小时.求高铁的平均速度是多少千米/时.22.已知关于x 的一元二次方程0)2()1(22=+---m m x m x . (1)求证:此方程总有两个不相等的实数根; (2)若2x =-是此方程的一个根,求实数m 的值.四、解答题(本题共20分,每小题5分)23.如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.(1)求证:四边形ABDE是平行四边形;(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.24.在北京,乘坐地铁是市民出行时经常采用的一种交通方式.据调查,新票价改革政策的实施给北京市轨道交通客流带来很大变化.根据2015年1月公布的调价后市民当时乘坐地铁的相关调查数据,制作了以下统计表以及统计图.根据以上信息解答下列问题:(1)补全扇形图;(2)题目所给出的线路中,调价后客流量下降百分比最高的线路是,调价后里程x(千米)在范围内的客流量下降最明显.对于表中客流量不降反增而且增长率最高的线路,如果继续按此变化率增长,预计2016年1月这条线路的日均客流量将达到 万人次;(精确到0.1)(3)小王同学上学时,需要乘坐地铁15.9公里到达学校,每天上下学共乘坐两次.问 调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出 元.(不 考虑使用市政一卡通刷卡优惠,调价前每次乘坐地铁票价为2元)25.如图,AB 为⊙O 的直径,M 为⊙O 外一点,连接MA 与⊙O交于点C ,连接MB 并延长交⊙O 于点D ,经过点M 的直线l 与MA 所在直线关于直线MD 对称.作BE ⊥l 于点E ,连接 AD ,DE .(1)依题意补全图形;(2)在不添加新的线段的条件下,写出图中与∠BED 相等 的角,并加以证明.26.阅读下面的材料:小敏在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且1tan 2α=,1tan 3β=,求αβ+的度数. 小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得ABD α∠=, CBE β∠=,且BA ,BC 在直线BD 的两侧,连接AC ,可证得△ABC 是等腰直角三角形,因此可求得αβ+=∠ABC = °.请参考小敏思考问题的方法解决问题: 如果α,β都为锐角,当tan 4α=,3tan 5β=时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=αβ-,由此可得αβ-=______°.五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.已知二次函数21y x bx c =++的图象1C 经过(1,0)-,(0,3)-两点.(1)求1C 对应的函数表达式;(2)将1C 先向左平移1个单位,再向上平移4个单位,得到抛物线2C ,将2C 对应的函数表达式记为22y x mx n =++,求2C 对应的函数表达式;(3)设323y x =+,在(2)的条件下,如果在2-≤x ≤a 内存在..某一个x 的值,使得2y ≤3y 成立,利用函数图象直接写出a 的取值范围.28.△ABC 中,AB=AC .取BC 边的中点D ,作DE ⊥AC 于点E ,取DE 的中点F ,连接BE ,AF 交于点H . (1)如图1,如果90BAC ∠=︒,那么AHB ∠= ︒,AFBE= ; (2)如图2,如果60BAC ∠=︒,猜想AHB ∠的度数和AFBE的值,并证明你的结论; (3)如果BAC α∠=,那么AFBE= .(用含α的表达式表示)29.给出如下规定:两个图形G 1和G 2,点P 为G 1上任一点,点Q 为G 2上任一点,如果线段PQ 的长度存在最小值,就称该最小值为两个图形G 1和G 2之间的距离. 在平面直角坐标系xOy 中,O 为坐标原点.(1)点A 的坐标为(1,0)A ,则点(2,3)B 和射线OA 之间的距离为________,点(2,3)C - 和射线OA 之间的距离为________;(2)如果直线y =x 和双曲线ky x=k = ;(可在图1中进 行研究)(3)点E 的坐标为(1,3),将射线OE 绕原点O 逆时针旋转60︒,得到射线OF ,在坐标平面内所有和射线OE ,OF 之间的距离相等的点所组成的图形记为图形M . ① 请在图2中画出图形M ,并描述图形M 的组成部分;(若涉及平面中某个区域时可以用阴影表示) ② 将射线OE ,OF 组成的图形记为图形W ,抛物线22-=x y 与图形M 的 公共部分记为图形N ,请直接写出图形W 和图形N 之间的距离.北京市西城区2015年初三一模试卷数学试卷参考答案及评分标准 2015. 4一、选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)三、解答题(本题共30分,每小题5分) 17()011π2008()6tan302--+-︒ =3362132⨯-++………………………………………………………… 4分 =32332-+=3.…………………………………………………………………………………… 5分 18.证明:如图1.∵ ∠EAC =∠DAB ,∴ 11EAC DAB ∠+∠=∠+∠.即 ∠BAC =∠DAE . …………………… 1分 在△ABC 和△ADE 中,,,,C E BAC DAE AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩………………………3分∴ △ABC ≌△ADE .…………………………………………………………… 4分 ∴ BC = DE .…………………………………………………………………… 5分19.解:()2035148.x x x -≤⎧⎪⎨+>-⎪⎩, 由①,得2x ≥. ………………………………………………………………… 2分由②,得 15348x x +>-.移项,合并,得 1111x >-.系数化1,得 1x >-. ………………………………………………………… 4分 所以原不等式组的解集为2x ≥.…………………………………………………5分20.解: 223312111a a a a a a a ++÷-++++ =()()2331111a a a a a a ++÷-+++……………………………………………………………2分()()2311311a a a a a a ++=⋅-+++ =111+-+a a a …………………………………………………………………………3分 =11a a -+.………………………………………………………………………………4分 当2=a 时,原式=311212=+-.………………………………………………………5分 21.解:设普通列车的平均速度为x 千米/时.…………………………………………… 1分 则高铁的平均速度是2.5x 千米/时.依题意,得40052032.5x x+=.…………………………………………………… 2分 解得 120=x .……………………………………………………………………3分 经检验,120=x 是原方程的解,且符合题意.……………………………… 4分 所以 30052=x .. 答:高铁的平均速度是300千米/时.………………………………………………… 5分22.(1)证明: []22(1)4(2)m m m ∆=--++ 2248448m m m m =-+++284m =+.……………………………………………………………………1分∵ 28m ≥0,∴ 284m +>0.………………………………………………………………2分∴ 方程总有两个不相等的实数根. ……………………………………… 3分(2)解:∵ 2x =-是此方程的一个根,∴ 2(2)2(2)(1)(2)0m m m --⨯---+=.整理得 220m m -=.解得 10m =,22m =.……………………………………………………… 5分四、解答题(本题共20分,每小题5分)23.(1)证明:∵ ADE BAD ∠=∠,∴ AB ∥ED .…………………………………………………………… 1分 ∵ BD 垂直平分AC ,垂足为F ,∴ BD AC ⊥,AF=FC .又∵ AE AC ⊥,∴ 90EAC DFC ∠=∠=︒.∴AE ∥BD .∴ 四边形ABDE 是平行四边形.…………………………………………2分(2)解:如图2,连接BE 交AD 于点O .∵ DA 平分∠BDE ,∴ ∠ADE=∠1.又∵ ADE BAD ∠=∠,∴ ∠1=∠BAD .∴ AB= BD .………………………………3分∴ABDE 是菱形.∵ AB=5,AD=6,∴ BD=AB=5,AD BE ⊥,132OA AD ==.在Rt △OAB 中,4OB .∵ 1122ABD S AD OB BD AF =⋅=⋅V , ∴ 645AF ⨯=.解得 4.8AF =. …………………………4分∵ BD 垂直平分AC ,∴ 29.6AC AF ==.……………………5分注:其他解法相应给分.24.解:(1)补全扇形图如图3所示.…………………1分(2)2号线,52<x≤72 ,22.2.(各1分)………………………………………… 4分(3)30.……………………………………… 5分25.解:(1)依题意,补全图形如图4.……………… 1分(2)BAD ∠.…………………………………… 2分证明:如图5,连接BC ,CD .∵ 直线l 与直线MA 关于直线MD 对称,∴ 12∠=∠.………………………3分∵ AB 为⊙O 的直径,∴ 90ACB ∠=︒,即BC MA ⊥.又∵ BE l ⊥,∵ cos 1MC MB =⋅∠,cos 2ME MB =⋅∠,∴ MC=ME .又∵ C ,E 两点分别在直线MA 与直线l 上,可得C ,E 两点关于直线MD 对称.∴ 3BED ∠=∠. ………………… 4分又∵ 3BAD ∠=∠,∴ BAD BED ∠=∠. ……………… 5分26.解:45. …………………………………………………1分画图见图6. ………………………………………3分45.………………………………………………… 5分 五、解答题(本题共22分,第23题7分,第24题7分,第2527.解:(1)∵ 二次函数21y x bx c =++的图象1C 经过(1,0)-,∴10,3.b c c -+=⎧⎨=-⎩………………………………1分 解得2,3.b c =-⎧⎨=-⎩ (2)分 ∴ 抛物线1C 的函数表达式为3221--=x x y . …………………………………… 3分(2)∵ 22123=(1)4y x x x =----,∴ 抛物线1C 的顶点为(1,4)- ∴ 平移后抛物线2C 的顶点为(0,0),它对应的函数表达式为22y x =.… 5分(3)a ≥1-(见图7).………………………………………………………………7分28.解:(1)90,12.……………………………………………………………………… 2分 (2)结论:90AHB ∠=︒,AF BE =. 证明:如图8,连接AD .∵ AB =AC ,∠BAC =60°,∴ △ABC 是等边三角形.∵ D 为BC 的中点,∴ AD ⊥BC .∴ ∠1+∠2=90°.又∵ DE ⊥AC ,∴ ∠DEC =90°.∴ ∠2+∠C =90°.∴ ∠1=∠C =60°.设AB =BC=k (0k >), 则124k CE CD ==,DE =. ∵ F 为DE 的中点,∴ 12DF DE ==,AD AB ==. ∴AD BC ,DF CE =. ∴ =BC AD CEDF .…………………………………………………………3分 又∵ ∠1=∠C ,∴ △ADF ∽△BCE .………………………………………………… 4分∴AF AD BE BC ==,………………………………………………… 5分 ∠3=∠4.又∵ ∠4+∠5=90°,∠5=∠6,∴ ∠3+∠6=90°.∴ 90AHB ∠=︒.………………………………………………………6分 (3)1tan 9022α︒-().………………………………………………………………7分 注:写1cos 2sin αα+或其他答案相应给分.29.解:(1)3.(每空各1分)…………………………………………………… 2分(2)-1.…………………………………………………………………………… 4分(3)①如图9,过点O 分别作射线OE 、OF 的垂线OG 、OH ,则图形M 为:y 轴正半轴,∠GOH 的边及其内部的所有点(图中的阴影部分).……………………………………………………………………………… 7分说明:(画图2分,描述1分)(图形M 也可描述为:y 轴正半轴,直线x y 33=下方与直线x y 33-=下方重叠的部分(含边界)) ③34.…………………………………………………………………………8分。
北京市西城区2015年初三一模数学试卷参考答案及评分标准

北京市西城区2015年初三一模试卷数学试卷参考答案及评分标准 2015. 4一、选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)三、解答题(本题共30分,每小题5分) 17()01112π2008()6tan302--+-︒=3362132⨯-++………………………………………………………… 4分 =32332-+=3.…………………………………………………………………………………… 5分 18.证明:如图1.∵ ∠EAC =∠DAB ,∴ 11EAC DAB ∠+∠=∠+∠.即 ∠BAC =∠DAE . …………………… 1分 在△ABC 和△ADE 中,,,,C E BAC DAE AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩………………………3分∴ △ABC ≌△ADE .…………………………………………………………… 4分 ∴ BC = DE.…………………………………………………………………… 5分 19.解:()2035148.x x x -≤⎧⎪⎨+>-⎪⎩,由①,得2x ≥. ………………………………………………………………… 2分由②,得 15348x x +>-.移项,合并,得 1111x >-.系数化1,得 1x >-. ………………………………………………………… 4分所以原不等式组的解集为2x ≥.…………………………………………………5分20.解: 223312111a a a a a a a ++÷-++++=()()2331111a a a a a a ++÷-+++……………………………………………………………2分 ()()2311311a a a a a a ++=⋅-+++ =111+-+a a a …………………………………………………………………………3分 =11a a -+.………………………………………………………………………………4分 当2=a 时,原式=311212=+-.………………………………………………………5分 21.解:设普通列车的平均速度为x 千米/时.…………………………………………… 1分 则高铁的平均速度是2.5x 千米/时.依题意,得40052032.5x x+=.…………………………………………………… 2分 解得 120=x .……………………………………………………………………3分 经检验,120=x 是原方程的解,且符合题意.……………………………… 4分 所以 30052=x ..答:高铁的平均速度是300千米/时.………………………………………………… 5分 22.(1)证明: []22(1)4(2)m m m ∆=--++ 2248448m m m m =-+++284m =+.……………………………………………………………………1分∵ 28m ≥0,∴ 284m +>0.………………………………………………………………2分∴ 方程总有两个不相等的实数根. ……………………………………… 3分(2)解:∵ 2x =-是此方程的一个根,∴ 2(2)2(2)(1)(2)0m m m --⨯---+=.整理得 220m m -=.解得 10m =,22m =.……………………………………………………… 5分四、解答题(本题共20分,每小题5分) 23.(1)证明:∵ ADE BAD ∠=∠,∴ AB ∥ED .…………………………………………………………… 1分 ∵ BD 垂直平分AC ,垂足为F , ∴ BD AC ⊥,AF=FC .又∵ AE AC ⊥,∴ 90EAC DFC ∠=∠=︒. ∴AE ∥BD .∴ 四边形ABDE 是平行四边形.…………………………………………2分(2)解:如图2,连接BE 交AD 于点O . ∵ DA 平分∠BDE ,∴ ∠ADE=∠1.又∵ ADE BAD ∠=∠, ∴ ∠1=∠BAD .∴ AB= BD .………………………………3分 ∴ ABDE 是菱形. ∵ AB=5,AD=6,∴ BD=AB=5,AD BE ⊥,132OA AD ==. 在Rt △OAB 中,224OB AB OA -=.∵ 1122ABD S AD OB BD AF =⋅=⋅V , ∴ 645AF ⨯=.解得 4.8AF =. …………………………4分∵ BD 垂直平分AC ,∴ 29.6AC AF ==.……………………5分 注:其他解法相应给分. 24.解:(1)补全扇形图如图3所示.…………………1分 (2)2号线,52<x ≤72 ,22.2.(各1分)………………………………………… 4分 (3)30.……………………………………… 5分 25.解:(1)依题意,补全图形如图4.……………… 1分 (2)BAD ∠.…………………………………… 2分 证明:如图5,连接BC ,CD .∵ 直线l 与直线MA 关于直线MD 对称, ∴ 12∠=∠.………………………3分 ∵ AB 为⊙O 的直径,∴ 90ACB ∠=︒,即BC MA ⊥. 又∵ BE l ⊥,∵ cos 1MC MB =⋅∠,cos 2ME MB =⋅∠, ∴ MC=ME . 又∵ C ,E 两点分别在直线MA 与直线l 上, 可得C ,E 两点关于直线MD 对称.图3∴ 3BED ∠=∠. ………………… 4分 又∵ 3BAD ∠=∠,∴ BAD BED ∠=∠. ……………… 5分26.解:45. …………………………………………………1分画图见图6. ………………………………………3分 45.………………………………………………… 5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 27.解:(1)∵ 二次函数21y x bx c =++的图象1C 经过(1,0)-,∴10,3.b c c -+=⎧⎨=-⎩ ………………………………1分解得2,3.b c =-⎧⎨=-⎩…………………………………2分∴ 抛物线1C 的函数表达式为3221--=x x y . …………………………………… 3分 (2)∵ 22123=(1)4y x x x =----,∴ 抛物线1C 的顶点为(1,4)- ∴ 平移后抛物线2C 的顶点为(0,0),它对应的函数表达式为22y x =.… 5分 (3)a ≥1-(见图7).………………………………………………………………7分28.解:(1)90,12.……………………………………………………………………… 2分 (2)结论:90AHB ∠=︒,AF BE . 证明:如图8,连接AD .∵ AB =AC ,∠BAC =60°, ∴ △ABC 是等边三角形. ∵ D 为BC 的中点, ∴ AD ⊥BC . ∴ ∠1+∠2=90°.又∵ DE ⊥AC ,∴ ∠DEC =90°. ∴ ∠2+∠C =90°. ∴ ∠1=∠C =60°. 设AB =BC=k (0k >),则124kCE CD ==,DE =. ∵ F 为DE 的中点,∴ 12DF DE ==,AD AB ==.∴AD BC =,DF CE =. ∴ =BC AD CE DF .…………………………………………………………3分 又∵ ∠1=∠C ,∴ △ADF ∽△BCE .………………………………………………… 4分∴AF AD BE BC ==,………………………………………………… 5分 ∠3=∠4. 又∵ ∠4+∠5=90°,∠5=∠6, ∴ ∠3+∠6=90°.∴ 90AHB ∠=︒.………………………………………………………6分(3)1tan 9022α︒-().………………………………………………………………7分注:写1cos 2sin αα+或其他答案相应给分.29.解:(1)313.(每空各1分)…………………………………………………… 2分(2)-1.…………………………………………………………………………… 4分(3)①如图9,过点O 分别作射线OE 、OF 的垂线OG 、OH ,则图形M 为:y 轴正半轴,∠GOH 的边及其内部的所有点(图中的阴影部分).……………………………………………………………………………… 7分 说明:(画图2分,描述1分)(图形M 也可描述为:y 轴正半轴,直线x y 33=下方与直线x y 33-=下方重叠的部分(含边界)) ②34.…………………………………………………………………………8分。
