2020年辽宁省沈阳市高中三年级教学质量监测(三)理数试题含答案
2020 年沈阳市高中三年级教学质量监测(三)

2019年沈阳市高中三年级教学质量监测(三)理科综合能力测试命题:高晓楠刘占武李铁军周际虹芦峰耿迎俊王宏利彭杨曹传英主审:金秀梅黄南万佩华注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.答选考题时,用2B铅笔在答题卡上将所选题目对应题号下方的方框涂黑。
4.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H 1 B 11 C 12 N 14 O 16 Ca 40一、选择题:本题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列关于细胞膜上蛋白质的叙述,错误的是A.可以催化反应,也可以被催化B.可以作为抗原,也可以识别抗原C.可以维持细胞内外某些物质的浓度差D.不参与细胞和外界环境之间的能量转换2.下列关于细胞结构的叙述正确的是A.癌变细胞中的线粒体和核糖体明显少于正常细胞B.液泡主要存在于植物细胞中,含有色素和大量核酸C.因溶酶体中缺乏分解硅尘的酶而使人患上某种遗传病D.细胞骨架与细胞的运动、分裂、分化等生命活动密切相关3.将酵母中编码某种蛋白质的基因进行改造,使其转录的mRNA上对应精氨酸的密码子由AGA变为CGG(仍然决定精氨酸),下列相关叙述,错误的是A.该蛋白质氨基酸序列不变B.配对的反密码子变为GCCC.编码该蛋白质的基因热稳定性降低D.编码该蛋白质mRNA的碱基序列改变4.以基因型为AaBb的植物为材料,培育出基因型为aabb个体的过程如下:上图所示的可遗传变异类型有①基因突变②基因重组③染色体变异④不遗传变异A.①③B.②③C.①④D.②④5.最新研究表明,晒太阳能改善学习和记忆,与其能促进脑内神经元合成和释放谷氨酸有关。
下列有关叙述错误的是A.每个神经元轴突末梢都形成一个突触小体B.神经元轴突末梢释放谷氨酸的方式是胞吐C.记忆是对学习获得的经验进行贮存和再现D.长期记忆的形成可能与新突触的建立有关6.下列有关物种、种群和群落的叙述正确的是A.凡是能够交配产生后代的生物就是一个物种B.不同群落中同种生物种群的环境容纳量相同C.在裸岩上进行初生演替时首先定居的是地衣D.物种丰富度是指一个群落中生物个体的多少7.化学与材料、生活和环境密切相关。
2020年辽宁省沈阳市高考数学三模试卷(理科)

2020年辽宁省沈阳市高考数学三模试卷(理科)一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合{|(1)(2)0}M x x x =--…,{|0}N x x =>,则( ) A .N M ⊆B .M N ⊆C .M N =∅ID .M N R =U2.(5分)复数12z i =+,若复数1z ,2z 在复平面内的对应点关于虚轴对称,则12(z z =) A .5-B .5C .34i -+D .34i -3.(5分)已知抛物线22x py =上一点(,1)A m 到其焦点的距离为3,则(p = ) A .2B .2-C .4D .4±4.(5分)《九章算术》中介绍了一种“更相减损术”,用于求两个正整数的最大公约数,将该方法用算法流程图表示如图,若输入15a =,12b =,0i =,则输出的结果为( )A .4a =,4i =B .4a =,5i =C .3a =,4i =D .3a =,5i =5.(5分)被誉为“中国现代数学之父”的著名数学家华罗庚先生倡导的“0.618优选法”在生产和科研实践中得到了非常广泛的应用,0.618就是黄金分割比51m -=的近似值,黄金分割比还可以表示成2sin18︒24(m m -= ) A .4B 51C .2D 516.(5分)已知某不规则几何体三视图如图,其中俯视图中的圆弧为14圆周,则该几何体的侧面积为( )A .344π+B .722π+C .752π+D .752π+7.(5分)设函数2()cos sin f x x b x =+,则“0b =”是“()f x 的最小正周期为π”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.(5分)2020年初,新型冠状肺炎在欧洲爆发后,我国第一时间内向相关国家捐助医疗物资,并派出由医疗专家组成的医疗小组奔赴相关国家.现有四个医疗小组甲、乙、丙、丁,和有4个需要援助的国家可供选择,每个医疗小组只去一个国家,设事件A = “4个医疗小组去的国家各不相同”,事件B = “小组甲独自去一个国家”,则(|)(P A B = ) A .29B .13C .49 D .599.(5分)已知O 为ABC ∆的外接圆的圆心,且345OA OB OC +=-u u u r u u u r u u u r,则C ∠的值为( )A .4πB .2π C .6π D .12π10.(5分)我们打印用的4A 纸的长与宽的比约为2,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为2,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD 为一张4A 纸,若点E 为上底面圆上弧AB 的中点,则异面直线DE 与AB 所成的角约为( )A .6πB .4π C .3π D .23π11.(5分)已知x 与y 之间的几组数据如表:如表数据中y 的平均值为2.5,若某同学对m 赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为11y b x a =+,22y b x a =+,33y b x a =+,对应的相关系数分别为1r ,2r,3r ,下列结论中错误的是( )参考公式:线性回归方程ˆˆy bxa =+中,其中121()()ˆ()niii nii x x yy b x x ==--=-∑∑,ˆˆay bx =-.相关系数()()nii xx y y r --∑.A .三条回归直线有共同交点B .相关系数中,2r 最大C .12b b >D .12a a >12.(5分)已知函数3()4f x x x =-,过点(2,0)A -的直线l 与()f x 的图象有三个不同的交点,则直线l 斜率的取值范围为( ) A .(1,8)-B .(1-,8)(8⋃,)+∞C .(2-,8)(8⋃,)+∞D .(1,)-+∞二、填空题:本题共4小题,每小题5分,共20分.13.(5分)已知m 是常数,55432543210(1)mx a x a x a x a x a x a -=+++++,且1234533a a a a a ++++=,则m = .14.(5分)已知1()f x x x =+,若25(log )2f b =,则1(log )2b f = . 15.(5分)在平面直角坐标系xOy 中,F 是双曲线22221(0,0)x y a b a b-=>>的右焦点,直线2y b =与双曲线交于B ,C 两点,且90BFC ∠=︒,则该双曲线的离心率为 .16.(5分)在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,设ABC ∆的面积为S ,若2224sin 3sin 2sin A B C =+,则SAB ACu u u r u u u r g 的最大值为 . 三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22-23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)已知数列{}n a 的前n 项和2n S n pn =+,且4a ,7a ,12a 成等比数列. (1)求数列{}n a 的通项公式; (2)若14nnn n S b a a +=g ,求数列{}n b 的前n 项和n T .18.(12分)随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台.已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取100名点外卖的用户进行统计,按送餐距离分类统计结果如表: 送餐距离(千米)(0,1](1,2](2,3](3,4](4,5]频数15 25 25 20 15以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.(1)若某送餐员一天送餐的总距离为100千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数,且同一组中的数据用该组区间的中点值为代表).(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份7元,超过4千米为远距离,每份12元.记X 为送餐员送一份外卖的收入(单位:元),求X 的分布列和数学期望.19.(12分)如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60DAB ∠=︒,AD PD ⊥,点F 为棱PD 的中点.(1)在棱BC 上是否存在一点E ,使得//CF 平面PAE ,并说明理由; (2)若AC PB ⊥,二面角D FC B --的余弦值为6时,求直线AF 与平面BCF 所成的角的正弦值.20.(12分)已知椭圆2222:1(0)x y C a b a b+=>>,四点13)P ,22)P ,36(P -,。
辽宁省沈阳市2020届高三数学教学质量监测试题(三)理(含解析)

辽宁省沈阳市2020 届高三数学教学质量监测试题(三)理(含解析)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知i 为虚数单位,则i i2i3L i2019等于( ).A. iB. 1C. iD. 1 【答案】D【解析】【分析】利用i(n n N ) 的周期求解.【详解】由于i i2 i3 i4 i 1 i 1 0 ,且i(n n N ) 的周期为4,2019=4 504+3 ,所以原式=i i2 i3 i 1 i 1.故选:D【点睛】本题主要考查复数的计算和i(n n N ) 的周期性,意在考查学生对这些知识的理解掌握水平和分析推理能力.2.已知集合A {(x, y)|x y 2,x, y N},则A中元素的个数为( ).A. 1B. 5C. 6D. 无数个【答案】C【解析】【分析】直接列举求出A和A中元素个数得解.【详解】由题得A {(0,0),(0,1),(0,2),(1 ,0),(1,1),(2,0)} ,所以A中元素的个数为 6.故选: C 【点睛】本题主要考查集合的表示和化简,意在考查学生对这些知识的理解掌握水平和分析推理能力.3•“ k — ”是“直线3 l: y k(x 2)与圆 x 2 y 21 相切”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】【分析】先化简直线1: yk(x 2)与圆x 22y 1相切,再利用充分必要条件的定义判断得解【详解】因为直线 l:yk(x 2)与圆x 2 y 21相切,所以 _|2k L 1,kJk 21,3所以“ k 3”是“直线l : y k(x 2)与圆x 2 y 21相切”的充分不必要条件3 故选:A【点睛】本题主要考查直线和圆的位置关系和充分不必要条件的判定,意在考查学生对这些 知识的理解掌握水平和分析推理能力•r r r4.若非零向量a,b 满足|a| |b |,(2a b) b 0,则a,b 的夹角为().5 A.B.C.6 36【答案】D 【解析】 【分析】直接利用数量积的运算法则化简已知即得解【点睛】本题主要考查数量积的运算和向量的夹角的求法,意在考查学生对这些知识的理解 掌握水平和分析推理能力【详解】由题得 r r 门2a b+b =0,r 22b cos所以cos a,b 丄r r a,b2 23故选:Do2r br b5.己知数列 a n 是等差数列,且a i a 4 a 7 2 ,则tan a 3 a §的值为(A. 3B. ,3C . 3D. J33【答案】 A【解析】试题 分析 :a 1 a 4 a 7 2,所 以3a 42 2,a 4小,a 3 3a 5 2a 43 ,tan(a 3 a 5) tan^. 3考点:1、、等差数列;2、 三角函数求值6.我国古代有着辉煌的数学研究成果. 《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》、……《缉古算经》等 10部专著,有着十分丰富多彩的内容,是了解我国古代数学的重 要文献•这10部专著中有7部产生于魏晋南北朝时期•某中学拟从这 10部专著中选择2部作为“数学文化”校本课程学习内容,则所选 2部专著中至少有一部是魏晋南北朝时期专著的概率为( ).14 1 27A.B.C.—D.151599【答案】A【解析】【分析】部疋魏晋设所选 2 部专著中至少有南北朝时期专者为事件A ,可以求P (A ),运用公式P(A) 1 P(A),求出 P(A).【详解】设所选2部专著中至少有一部是魏晋南北朝时期专著为事件 A ,丄,因此P(A) 1 P(A)=1 丄 14 ,故本题选A.1515 15【点睛】本题考查了求对立事件的概率问题,考查了运算能力7.设 a log 2018 2019 ,b log 2019 2018,c 2018总,则 a ,b ,c 的大小关系是( ).A. a b c).所以P(A)=C i 20 B. a c bC. c a bD. c b a【答案】C【解析】【分析】根据所给的对数式和指数式的特征可以采用中间值比较法,进行比较大小1【详解】因为1 log20182018 a log2018. 2019 log2018. 2018 —,21 1b log2019 .2018 log2019 ,2019 ^,c 2018麺2018°1,故本题选。
辽宁省沈阳市2020届高三年级教学质量监测(三)数学(理科)试题 含答案

参考公式:线性回归方程 y = b x + a 中,其中 b = i=1 n
,a = y− b x .相
−
(xi − x)2
i =1
关系数 r =
ቤተ መጻሕፍቲ ባይዱ
n
−
−
(xi − x)( yi − y)
i =1
.
n
−n
−
(xi − x)2 ( yi − y)2
i =1
i =1
12.已知函数 f (x) = x3 − 4x ,过点 A(−2, 0) 的直线l 与 f (x) 的图象有三个不同的交点,
A. 4
B. 2
C. 5 +1
D. 5 −1
6.已知某不规则几何体三视图如图,其中俯视图中的圆弧
为 1 圆周,则该几何体的侧面积为 4
A. 4 + 3 4
B. 7 + 22
C. 7 + 5 24
D. 7 + 5 28
7.设函数 f (x) = cos2 x + bsin x ,则“ b = 0 ”是“ f (x) 的最小正周期为 ”的
A. 2
B. −2
C. 4
D. 4
4.《九章算术》中介绍了一种“更相减损术”,用于求两个正整数的最大公约数,将该方法用
算法流程图表示如下,若输入 a = 15 , b = 12 , i = 0 ,则输出的结果为 A. a = 4 , i = 4
开始 输入a, b, i
B. a = 4 , i = 5 C. a = 3 , i = 4 D. a = 3 , i = 5
C. 4 9
D. 5 9
9.已知 O 为 ABC 的外接圆的圆心,且 3OA + 4OB = −5OC ,则 C 的值为
2020年高中高三教学质量检测 含答案

2020年高中高三教学质量检测数 学 (理科)本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生要务必填写答题卷上的有关项目.2.选择题每小题选出答案后,用黑色字迹的钢笔或签字笔把答案代号填在答题卷对应的空格内.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回. 参考公式: 锥体的体积公式:13V Sh =.其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设U =R ,集合{}|1A y y x =≥,}{240B x Z x =∈-≤,则下列结论正确的是A .}{2,1A B =--I B . ()(,0)U A B =-∞U ðC .[0,)A B =+∞UD . }{()2,1U A B =--I ð 2.已知向量a =r ,(1,0)b =-r ,则|2|a b +=r rA .1B.C. 2D. 43.如图:正方体ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 、K 、L 分别为AB 、BB 1、B 1C 1、C 1D 1、D 1D 、DA的中点,则六边形EFGHKL 在正方体面上的射影可能是4.已知i 是虚数单位,使(1)ni +为实数的最小正整数n 为A .2B .4C .6D .85.已知sin()sin ,0,352ππααα++=--<<则2cos()3πα+等于A .45-B .35-C .35D .456.下列说法中,不正确...的是ABC DABC D A 1B 1C 1D 1H G FK LEA .“x y =”是“x y =”的必要不充分条件;B .命题:p x ∀∈R ,sin 1x ≤,则:p x ⌝∃∈R ,sin 1x >;C .命题“若,x y 都是偶数,则x y +是偶数”的否命题是“若,x y 不是偶数,则x y +不是偶数”;D .命题:p 所有有理数都是实数,:q 正数的对数都是负数,则()()p q ⌝∨⌝为真命题.7.已知实数,m n 满足01n m <<<,给出下列关系式 ①23mn= ②23log log m n = ③23m n = 其中可能成立的有A .0个B .1个C .2个D .3个8.设12,,,(4)n a a a n ≥L 是各项均不为零的等差数列,且公差0d ≠.设()n α是将此数列删去某一项得到的数列(按原来的顺序)为等比数列的最大的n 值,则()n α=A .4B .5C .6D .7二、填空题:本大共7小题,考生作答6小题,每小题5分,满分30分) (一)必做题(9~13题)9. 某体育赛事志愿者组织有1000名志愿者,其中参加过2008北京奥运会志愿服务的有250名,新招募的2010年广州亚运会愿者750名.现用分层抽样的方法从中选出100名志愿者调查他们的服务能力,则选出新招募的广州亚运会志愿者的人数是 .10. 已知函数2()(sin cos )1f x x x =+-,x ∈R , 则()f x 的最小正周期是 . 11. 右图给出的是计算201614121++++Λ的 值的一个框图,其中菱形判断框内应填入的条件是_________.12. 若实数x 、y 满足20,,,x y y x y x b -≥⎧⎪≥⎨⎪≥-+⎩且2z x y =+的最小值为3,则实数b 的值为_____.13.若等差数列{}n a 的首项为1,a 公差为d ,前n 项的和为n S ,则数列{}nS n为等差数列,且通项为1(1)2n S da n n =+-⋅.类似地,若各项均为正数的等比数列{}nb 的首项为1b ,公比为q ,前n 项的积为n T ,第11题图则数列{}n n T 为等比数列,通项为____________________. (二)选做题(14~15题,考生只能从中选做一题)14.(坐标系与参数方程)极坐标系中,直线l 的极坐标方程为sin()26πρθ+=,则极点在直线l 上的射影的极坐标是____________.15.(几何证明选讲)如图,以4AB =为直径的圆与△ABC 的两边 分别交于,E F 两点,60ACB ∠=o,则EF = .三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16.(本题满分12分)已知海岸边,A B 两海事监测站相距60 mile n ,为了测量海平面上两艘油轮,C D 间距离,在,A B 两处分别测得75CBD ∠=o,30ABC ∠=o , 45DAB ∠=o ,60CAD ∠=o (,,,A B C D 在同一个水平面内).请计算出,C D 两艘轮船间距离.17.(本题满分12分)某市为鼓励企业发展“低碳经济”,真正实现“低消耗、高产出”,施行奖惩制度.通过制定评分标准,每年对本市50%的企业抽查评估,评出优秀、良好、合格和不合格四个等次,并根据等级给予相应的奖惩(如下表).某企业投入100万元改造,由于自身技术原因,能达到以上四个等次的概率分别为111123824,,,,且由此增加的产值分别为60万元、40万元、20万元、5-万元.设该企业当年因改造而增加利润为ξ.(Ⅰ)在抽查评估中,该企业能被抽到且被评为合格以上等次的概率是多少? (Ⅱ)求ξ的数学期望.评估得分 (0,60)[)7060, [)8070, []10080,评定等级 不合格合格良好优秀奖惩(万元)80- 30 60 10018.(本题满分14分)如图,在棱长为1的正方体1111ABCD A B C D -中,P 为线段1AD 上的点,且满足1(0)D P PA λλ=>u u u u r u u u r.(Ⅰ)当1λ=时,求证:平面11ABC D ⊥平面PDB ; (Ⅱ)试证无论λ为何值,三棱锥1D PBC -的体积 恒为定值;(Ⅲ)求异面直线1C P 与1CB 所成的角的余弦值.第18题图第16题图CAEF第15题图19.(本题满分14分)已知函数2()ln f x x ax b x =++(0x >,实数a ,b 为常数). (Ⅰ)若1,1a b ==-,求函数()f x 的极值; (Ⅱ)若2a b +=-,讨论函数()f x 的单调性.20.(本题满分14分)如图,抛物线21:8C y x =与双曲线22222:1(x y C a a b-=12,C C 在第一象限的交点,且25AF =. (Ⅰ)求双曲线2C 的方程;(Ⅱ)以1F 为圆心的圆M 与双曲线的一条渐近线相切,圆N :22(2)1x y -+=.平面上有点P 满足:存在过点P 的无穷多对互相垂直的直线12,l l ,它们分别与圆,M N 相交,且直线1l 被圆M 截得的弦长与直线2l 被圆N 截得的弦长的比,试求所有满足条件的点P 的坐标.21.(本题满分14分)设0a >,函数21()f x x a=+. (Ⅰ)证明:存在唯一实数01(0,)x a∈,使00()f x x =;(Ⅱ)定义数列{}n x :10x =,1()n n x f x +=,*n N ∈.(i )求证:对任意正整数n 都有2102n n x x x -<<; (ii) 当2a =时, 若10(2,3,4,)2k x k <≤=L , 证明:对任意*m N ∈都有:1134m k k k x x +--<⋅.2020年高三教学质量检测数学试题(理科)参考答案和评分标准一、选择题:(每题5分,共40分)题号 12345678选项D C B B D C C A二、填空题(每题5分,共30分) 9.75 10. π 11.10?i > 12.94 1311n b -= 14. (2,)3π 15.2 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16.(本题满分12分)解:方法一:在ABD ∆中,由正弦定理得:sinAD ABABD =∠,∴6060sin(3075)60sin 7541sin[180(453075)]sin 302AD +====-++o o oo o o o o…………………4分 同理,在在ABC ∆中,由正弦定理得:sin sin AC ABABC ACB =∠∠ 16060sin 302sin[180(453060)]sin 45AC ⨯====-++oo o o o o ……………………………………………8分∴计算出,AD AC 后,再在ACD ∆中,应用余弦定理计算出CD 两点间的距离:CD ==………………………………………………………10分===∴,C D 两艘轮船相距 mile n .………………………………………………………………12分方法二:在ABC ∆中,由正弦定理得:sin sin BC ABBAC=∠,∴6060sin(6045)60sin 751)sin[180(456030)]sin 452BC +====-++o o oo o o o o…………………4分 同理,在在ABD∆中,由正弦定理得:BD ABADB=606060sin 45221sin[180(453075)]sin 302BD ====-++oo o o o o……………………………………8分 ∴计算出,BC BD 后,再在BCD ∆中,应用余弦定理计算出CD 两点间的距离:CD == ………………………………………………………10分== =∴,C D 两艘轮船相距 mile n . ………………………………………………………12分 17.(本题满分12分)解:(Ⅰ)设该企业能被抽中的概率且评为合格以上等次的概率为P ,则111123238248P ⎛⎫=++⨯= ⎪⎝⎭………………………………………………………4分 (Ⅱ)依题意,ξ的可能取值为185,105,80,60,50,40,0,60,------则1612181)50(,612131)0(,412121)60(=⨯=-==⨯===⨯==ξξξP P P412121)40(,48121241)185(=⨯=-==⨯=-=ξξP P ,111111111(60),(80),(105)326821624248P P P ξξξ=-=⨯==-=⨯==-=⨯=则其分布列为10分第18题图 ∴1111115(60406050801851054616486E ξ=-⨯+-⨯+--⨯+--⨯=-)()()()(万元) ………………………………………………………12分18.(本题满分12分)方法一、证明:(Ⅰ)∵正方体1111ABCD A B C D -中,AB ⊥面11AA D D ,又11AB ABC D ⊂∴平面11ABC D ⊥平面11AA D D , ………………………2分 ∵1λ=时,P 为1AD 的中点,∴1DP AD ⊥, 又∵平面11ABC D I 平面11AA D D 1AD =, ∴DP ⊥平面11ABC D ,又DP ⊂平面PDB ,∴平面11ABC D ⊥平面PDB .……………………………………………………4分 (Ⅱ)∵11//AD BC , P 为线段1AD 上的点, ∴三角形1PBC 的面积为定值,即1122122PBC S ∆==,……………………………………………6分 又∵//CD 平面11ABC D ,∴点D 到平面1PBC 的距离为定值,即22h =, ……………………………………………………8分 ∴三棱锥1D BPC -的体积为定值,即111122133226D PBC PBC V S h -∆=⋅⋅=⨯=. 也即无论λ为何值,三棱锥1D PBC -的体积恒为定值16;……………………………………………10分(Ⅲ)∵由(Ⅰ)易知1B C ⊥平面11ABC D ,又1C P ⊂平面11ABC D ,∴11B C C P ⊥, ……………………………………………12分 即异面直线1C P 与1CB 所成的角为定值90o,从而其余弦值为0.………………………………………14分 方法二、如图,以点D 为坐标原点,建立如图所示的坐标系.(Ⅰ)当1λ=时,即点P 为线段1AD 的中点,则11(,0,)22P ,又(0,0,0)D 、(1,1,0)B∴11(,0,)22PD =--u u u r ,11(,1,)22PB =-u u u r ,设平面PDB 的法向量为(,,)n x y z =r ,……………………1分则00PD n PB n ⎧⋅=⎪⎨⋅=⎪⎩u u u r r r u u u r r r ,即11002211022x z x y z ⎧-+-=⎪⎪⎨⎪+-=⎪⎩,令1y =,解得(1,1,1)n =-r , ……………………2分 又∵点P 为线段1AD 的中点,∴1DP AD ⊥,∴DP ⊥平面11ABC D ,∴平面11ABC D 的法向量为11(,0,)22PD =--u u u r , ……………………3分∵110022PD n ⋅=+-=u u u r r ,∴平面11ABC D ⊥平面PDB , ………………………………………4分(Ⅱ)略;(Ⅲ)∵1(0)D P PA λλ=>u u u u r u u u r ,∴1(,0,)11P λλλ++, ………………………………………11分又1(0,1,1)C 、(0,1,0)C 、1(1,1,1)B ,∴1(,1,)11C P λλλλ-=-++u u u r ,1(1,0,1)CB =u u u r , ………………………………………12分∵110011C P CB λλλλ-⋅=++=++u u u r u u u r ………………………………………13分∴不管λ取值多少,都有11C P CB ⊥,即异面直线1C P 与1CB 所成的角的余弦值为0.……………14分19.(本题满分12分)解:(Ⅰ)函数2()ln f x x x x =+-,则1()21f x x x'=+-,………………………………………1分 令()0f x '=,得1x =-(舍去),12x =. ……………………………………………2分 当102x <<时,()0f x '<,函数单调递减; ……………………………………………3分 当12x >时,()0f x '>,函数单调递增; ……………………………………………4分 ∴()f x 在12x =处取得极小值3ln 24+. ……………………………………………5分(Ⅱ)由于2a b +=-,则2a b =--,从而2()(2)ln f x x b x b x =-++,则(2)(1)()2(2)b x b x f x x b x x --'=-++=……………………………………………5分 令()0f x '=,得12bx =,21x =. ……………………………………………7分① 当02b≤,即0b <时,函数()f x 的单调递减区间为(0,1),单调递增区间为(1,)+∞;…8分② 当01b<<,即02b <<时,列表如下:所以,函数()f x 的单调递增区间为(0,)2,(1,)+∞,单调递减区间为(,1)2b ;…………………10分③ 当12b=,即2b =时,函数()f x 的单调递增区间为(0,)+∞;………………………………11分 ④当1b>,即2b >时,列表如下:所以函数()f x 的单调递增区间为(0,1),(,)2b +∞,单调递减区间为(1,)2b ; …………………13分综上:当02b≤,即0b <时,函数()f x 的单调递减区间为(0,1),单调递增区间为(1,)+∞; 当012b <<,即02b <<时,函数()f x 的单调递增区间为(0,)2b ,(1,)+∞,单调递减区间为(,1)2b;当12b=,即2b =时,函数()f x 的单调递增区间为(0,)+∞; 当12b >,即2b >时,函数()f x 的单调递增区间为(0,1),(,)2b +∞,单调递减区间为(1,)2b . ………………………………14分20.(本题满分12分)解:(Ⅰ)∵抛物线21:8C y x =的焦点为2(2,0)F ,∴双曲线2C 的焦点为1(2,0)F -、2(2,0)F , ……………………………………………… 1分设00(,)A x y 在抛物线21:8C y x =上,且25AF =,由抛物线的定义得,025x +=,∴03x =, ………………………………………………2分∴2083y =⨯,∴0y =± ……………………………………………… 3分∴1||7AF ==, ……………………………………………… 4分 又∵点A 在双曲线上,由双曲线定义得,2|75|2a =-=,∴1a =, ……………………………………………… 5分∴双曲线的方程为:2213y x -=. ……………………………………………… 6分 (Ⅱ)设圆M 的方程为:222(2)x y r ++=,双曲线的渐近线方程为:y =,∵圆M 与渐近线y =相切,∴圆M 的半径为d ==,………………………………… 7分 故圆M :22(2)3x y ++=, ………………………………… 8分 设点00(,)P x y ,则1l 的方程为00()y y k x x -=-,即000kx y kx y --+=,2l 的方程为001()y y x x k-=--,即000x ky x ky +--=,∴点M 到直线1l 的距离为1d =,点N 到直线2l 的距离为2d =,∴直线1l 被圆M 截得的弦长s = 直线2l 被圆N 截得的弦长t = ………………………………… 11分 由题意可得,s t ==2200003(2)(2)x ky k kx y +-=+-,00002k kx y -=+- ①00002k kx y -=--+②……… 12分由①得:0000(2)0x k y +-+-=, ∵该方程有无穷多组解,∴0000200x y ⎧+=⎪+-=,解得001x y =⎧⎪⎨=⎪⎩,点P 的坐标为.………………………………… 13分由②得:0000(2)0x k y ++--=,∵该方程有无穷多组解,∴0000200x y ⎧++=⎪--=,解得001x y =⎧⎪⎨=⎪⎩P 的坐标为(1,.∴满足条件的点P 的坐标为或(1,. ………………………………… 14分21.(本题满分12分)(Ⅰ)证明: ①3()10f x x x ax =⇔+-=. ………………………………… 1分 令3()1h x x ax =+-,则(0)10h =-<,311()0h a a =>, ∴1(0)()0h h a⋅<. ………………………………… 2分 又/2()30h x x a =+>,∴3()1h x x ax =+-是R 上的增函数. ………………………………… 3分 故3()1h x x ax =+-在区间10,a ⎛⎫⎪⎝⎭上有唯一零点, 即存在唯一实数010,x a ⎛⎫∈ ⎪⎝⎭使00()f x x =. ………………………………… 4分 ②当1n =时, 10x =,211()(0)x f x f a ===,由①知010,x a ⎛⎫∈ ⎪⎝⎭,即102x x x <<成立;………… 5分 设当(2)n k k =≥时, 2102k k x x x -<<,注意到21()f x x a=+在()0,+∞上是减函数,且0k x >, 故有:2102()()()k k f x f x f x ->>,即2021k k x x x +>>∴2021()()()k k f x f x f x +<<, ………………………………… 7分 即21022k k x x x ++<<.这就是说,1n k =+时,结论也成立.故对任意正整数n 都有:2102n n x x x -<<. ………………………………… 8分 (2)当2a =时,由10x =得:211()(0)2x f x f ===,2112x x -= ………………………………… 9分222132222221211122(2)(2)x x x x x x x x --=-=++++22121211114244x x x x x x -+⎛⎫<=⋅-= ⎪⎝⎭……………………………… 10分 当2k ≥时,102k x <≤Q , ∴22112222111122(2)(2)k k k k k k k k x x x x x x x x -+----=-=++++114k k k k x x x x ---+<14k k x x --< 2212321144k k k x x x x ---⎛⎫⎛⎫<⋅-<<⋅- ⎪ ⎪⎝⎭⎝⎭L 14k ⎛⎫< ⎪⎝⎭ ………………………………… 12分 对*m N ∀∈,1121()()()m k k m k m k m k m k k k x x x x x x x x +++-+-+-+-=-+-++-L 1121m k m k m k m k k k x x x x x x ++-+-+-+≤-+-++-L ………………………………… 13分1122111114444k k m m x x +--⎛⎫≤+++++- ⎪⎝⎭L 111114141141134343414m k k k k m k k x x x x ++--⎛⎫=-=⋅-⋅-<⋅= ⎪⋅⎝⎭- ………………………………… 14分。
2020年辽宁省第三次高考模拟考试理科数学试题与答案

2020年辽宁省第三次高考模拟考试理科数学试题与答案(满分150分,考试时间120分钟)注意事项:1.答题前,考生务必将自己的姓名、准考证号码填写在答题卡和试卷指定位置上,并将条形码准确粘贴在条形码区域内。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合{}{}22|22,|log A x Z x B x y x =∈-<<==,则AB =( )A .{}1,1-B .{}1,0,1-C .{}1D .{}0,12. 复数z 满足(1)|1|z +=+,则z 等于( )A .1B .1C .12D 12i -3. 已知实数,满足约束条件,则的最大值为( )A.B.C. D. 24. 在由直线,和轴围成的三角形内任取一点,记事件为,为,则( )A.B. C. D.5. 《孙子算经》是我国古代的数学名著,书中有如下问题:“今有五等诸侯,共分橘子六十颗,人别加三颗.问: 五人各得几何?”其意思为: 有5个人分60个橘子,他们分得的橘子数成公差为3的等差数列,问5人各得多少个橘子.这个问题中,得到橘子最多的人所得的橘子个数是( ) A. 15B. 16C. 18D. 216. 某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4为朋友,每位朋友1本,则不同的赠送方法共有( )A. 4种B. 10种C. 18种D. 20种7. 若1x 是方程4xxe =的解,2x 是方程ln 4x x =的解,则12x x +等于( ) A .4B .2C .eD .18. 已知函数()2()12sin 06f x x πωω⎛⎫=-+> ⎪⎝⎭在区间,62ππ⎡⎤⎢⎥⎣⎦为单调递减函数,则ω的最大值是( ) A .12 B .35 C .23 D .349. 已知三棱锥的底面是以为斜边的等腰直角三角形,且,则该三棱锥的外接球的表面积为 A.B.C.D.10. 函数的图象大致是( )A. B. C. D.11.已知函数a x ax e ex f +--+=)(,若c b a ==3log 3,则( )A.)(a f <)(b f <)(c fB.)(b f <)(c f <)(a fC.)(a f <)(c f <)(b fD.)(c f <)(b f <)(a f12.已知函数1,)21(1,2542{)(≤>-+-=x x x x x x f ,若函数()()g x f x mx m =--的图象与x 轴的交点个数不少于2个,则实数m 的取值范围为( )A.1,64⎡⎢⎣ B.1,64⎡⎢⎣C .][1,2ln2,64⎛-∞-⋃ ⎝ D .][1,2ln2,64e ⎛-∞-⋃ ⎝ 二、填空题:本题共4小题,每小题5分,共20分。
2020年沈阳市高三质量监测(三)理科综合能力测试 化学答案

沈阳市高三教学质量监测(三)理科综合能力测试化学试题答案及评分细则一、选择题二、非选择题26、(13分)(1)c (2分)(2)6Li 0.5CoO 2 == 3LiCoO 2 + Co 3O 4 + O 2(分数配平也可以)(2分)(3)0.4 (2分)(4)低pH 范围时, C 2O 42-水解为H 2C 2O 4和HC 2O 4-;随着pH 增高,C 2O 42-水解程度降低。
(或H +与Co 2+竞争C 2O 42-)(2分)(5)3CoC 2O 4 +2O 2 == Co 3O 4 + 6CO 2(分数配平也给分,)(2分)(6)温度的提高有利于增加Co 2+与C 2O 42-的有效碰撞(或沉淀速率)(1分 ),同时由于草酸钴的沉淀反应是吸热反应,温度升高有利于沉淀反应正移(1分);由于草酸钴的溶解度在较高温度下可能会增大,因此过高温度反而在一定程度上降低Co 2+的沉淀率(1分)。
27、(15分)(1)+124.2(2分) ①升高温度(2分)② 丙烷直接裂解是吸热反应,通入足量O 2可提供裂解所需的能量,并保持热平衡(2分) (2)① BCD (3分)② >(考查按计量数之比投料,平衡时生成物的百分含量最大)(2分)(3)①0.09(2分) ②0.21(2分)28、(15分)(1)b (1分)(2)催化剂 吸水剂(2分)(答脱水性,不扣分)(3)受热均匀,便于控制温度 (2分)防止空气中水蒸气进入锥形瓶,使硼酸三甲酯水解(2分)(4)2403343B(OCH )+4NaH =NaBH +3CH ONa ℃(2分) (5)圆底烧瓶 (2分)(6)蒸馏(2分)(7)0.21 (2分)。
2020 年辽宁省高三教学质量监测考试理科数学试卷-含答案

作圆 C 的一条切线,切点为 B,则|AB|=
A.4
B.4 2
C.6
D.6 2
12.定义在 R 上的奇函数 f (x)又是周期为 4 的周期函数,已知在区间[-2,0)∪(0,2]上,
f (x)=aaxx-+1b,,-0<2≤x≤x<2.0 ,则 f (2019)+f (2020)=
A.12
B.-12
A.若 m∥α,n∥α,则 m∥n
B.若 m∥α,m⊥n,则 n⊥α
C.若 m⊥α,n⊂α,则 m⊥n
D.若 m⊥α,m⊥n,则 n∥α
9.已知 tan(α-π4)=17,则 cos2α=
A.-275
B.275
C.-2254
D.2245
10.将函数 y=cos(2x+φ)(-π2<φ<2π)的图象向右平移38π个单位长度单位后得函数 f (x)图
D.c<b<a
5.如图所示,是一个空间几何体的三视图,且这个空间几何 体的所有顶点都在同一个球面上,则这个球的表面积是 A.4π B.7π C.16π D.28π学试题 第 1 页(共 4 页)
6.中国古代《易经》一书中记载,远古时期,人们通过在绳子上打 结来记录数量,即“结绳计数”.如图,一位古人在从右到左依次
排列的绳子上打结,满五进一,用来记录捕鱼条数,由图可知,
这位古人共捕鱼
A.89 条
B.113 条
C.324 条
D.445 条
7.同时抛掷 2 枚质地均匀的硬币 4 次,设 2 枚硬币均正面向上的次数为 X,则 X 的数学
方差是
A.12
B.34
C.1
D.32
8.已知 m,n 表示两条不同直线,α 表示平面,下列说法正确的是
2020届辽宁省沈阳市高三年级教学质量监测(三)数学(理科)试题答案
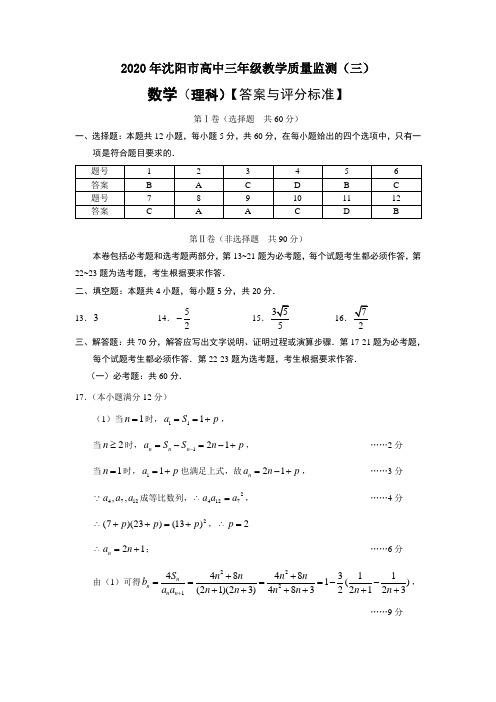
2020年沈阳市高中三年级教学质量监测(三)数学(理科)【答案与评分标准】第Ⅰ卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分,第13~21题为必考题,每个试题考生都必须作答,第22~23题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分,共20分. 13.314.52-15.516三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22-23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(本小题满分12分)(1)当1n =时,111a S p ==+, 当2n ≥时,121n n n a S S n p -=-=-+,……2分 当1n =时,11a p =+也满足上式,故21n a n p =-+,……3分 ∵4712,,a a a 成等比数列,∴24127a a a =,……4分∴2(7)(23)(13)p p p ++=+,∴2p = ∴21n a n =+;……6分由(1)可得2221448483111()(21)(23)48322123n n n n S n n n n b a a n n n n n n +++====--++++++,……9分∴231111111322()23557212324623n n nT n n n n n n +=--+-+⋅⋅⋅+-=-+=++++.……12分18.(本小题满分12分)(1)估计每名外卖用户的平均送餐距离为:0.50.15 1.50.25 2.50.25 3.50.2 4.50.15 2.45⨯+⨯+⨯+⨯+⨯=千米. ……3分所以送餐距离为100千米时,送餐份数为:100412.45≈份; ……5分 (2)由题意知X 的可能取值为:3,7,12.……6分 ()40310025P X ===, ……7分 ()710904502P X ===, ……8分 ()1512100230P X ===. ……9分所以X 的分布列为:……10分∴()3712 6.1522930205E X =⨯+⨯+⨯=. ……12分19.(本小题满分12分)(1)在棱BC 上存在点E ,使得CF P 平面PAE ,点E 为棱BC 的中点. 证明:取PA 的中点Q ,连结EQ 、FQ , 由题意,FQ AD P 且12FQ AD =, CE AD P 且12CE AD =,故CE FQ P 且CEFQ =.∴四边形CEQF 为平行四边形. ……2分 ∴CF EQ P ,又CF ⊄平面PAE , ∴CF P 平面PAE .……4分(2)菱形ABCD 中,AC BD ⊥,又AC PB ⊥,PB BD B =I . ∴AC ⊥平面PBD ,又PD ⊂面PBD ,∴AC PD ⊥, ∵AD PD ⊥,AC AD A =I ,∴PD ⊥平面ABCD . ……6分取AB 中点为M ,则DM AB ⊥.以D 为原点,DM ,DC ,DP 为x ,y ,z 轴建立如图空间直角坐标系,设FD a =, 则由题意知()0,0,0D ,()0,0,F a ,()0,2,0C,)B,)1,0A-.()0,2,FC a =-u u u v,)1,0CB =-u u u v ,……7分设平面FBC 的法向量为(),,m x y z =v,则由00m FC m CB ⎧⋅=⎨⋅=⎩u u u v v u u u vv得200y az y -=⎧⎪-=, 令1x =,则y =z =m ⎛= ⎝⎭v , ……9分显然可取平面DFC 的法向量()1,0,0n =v,由题意:cos ,6m n ==v v,所以a =……10分1,FA =-u u u v ,设直线AF 与平面BCF 所成的角为θ,则sin cos ,5m FA θ===u r u u u r . ……12分20.(本小题满分12分)解:(1)易知3(-P,4P 关于y 轴对称,一定都在椭圆上.所以1P一定不在椭圆上.根据题意2P 也在椭圆上.……2分将2P,4P 带入椭圆方程,解得椭圆方程为22162x y +=.……4分 (2)设直线l 方程为(2)y k x =+(0k ≠),()11,P x y ,()22,Q x y ,联立22162(2)x y y k x ⎧+=⎪⎨⎪=+⎩,可得()222231121260k x k x k ++-=+. ……5分则224(1)0k ∆=+>,且21221231+=-+k x x k ,212212631-=+k x x k , ……6分设PQ 的中点00(,)N x y ,则212262310x x k x k +==-+,22262(2)31310k k y k k k =-+=++, ∴N 坐标为22262,3131⎛⎫- ⎪++⎝⎭k k k k ,||=PQ221)31+=+k k . ……8分因此直线ON 的方程为13y x k =-,从而点M 为1(3,)k-,又1(2,0)F -,1||MF = ……9分2222221(||241)||(31)PQ k k MF k +=+,令2311u =k +≥, 则222(1)(2)1611116119()8()[()]33223416u u h u u u u u -+==---=---,因此当4u =,即1k =±时h(u)最大值为3.所以1||||PQ MF……12分21.(本小题满分12分)(1)由已知定义域为{|0}x R x ∈≠,2()()()bxabx a e f x ax -'=,由22(2)(2)0(2)b ab a e f a -'==,又0a ≠,得12b =, 2(2)222b e e ef a a ===,所以1a =,……2分从而22(1)2()xxe f x x-'=又0x ≠。
2024辽宁省沈阳市高三下学期教学质量监测(三)数学试题及答案

2024年沈阳市高中三年级教学质量监测(三)数学 参考答案及评分标准一、选择题:本题共8小题,每小题5分,共40分.1.B2.D3.D4.B5.A6.C7.C8.A二、选择题:本题共3小题,每小题6分,共18分.9. ACD 10.BCD 11.AC三、填空题:本题共3小题,每小题5分,共15分.12.13.3 14. 109 【部分题目解析】8.因为(21)f x -是偶函数,则()f x 的图象关于直线1x =-轴对称,又因为(2)f x -是奇函数,则()f x 的图象关于点(2,0)中心对称,故函数()f x 具有周期性,且周期为4,则(7)(1)(1)1f f f =-=-=-.11.21()cos cos sin(2)62f x nx nx nx nx π=+=++, 对于A ,当[0,]2x π∈时,72[,]666nx πππ+∈,1sin(2[,1]62nx π+∈-,min ()0f x =; 对于B ,函数()f x 图象的对称中心的纵坐标应为12; 对于C ,22[,]62636n n nx πππππ+∈++, 解2226,232362n k k Z n k ππππππππ⎧+≤+⎪⎪∈⎨⎪+≤+⎪⎩得到214[,2][,5]33n ∈ ,所以1,2,5n =; 对于D ,方程等价于1sin(2)64nx π+=,函数()sin(2)6g x nx π=+的图象和直线14y =的交点如图函数()g x 的最小正周期13||T A A =,设12||A A dT =,23||A A DT =,(其中1D d =-) 因为10sin 46π<<,所以由下图可知112323d D <<<<,26364d D <<<<因为在区间00(,6x x π+内的解的个数[5,9]m ∈,所以区间长度6π应满足:(2)(4)6D T d T π+<+ ,由T n π=,则(2)(4)6D d n n πππ+<+ ,化简得126246D n d +<+ ,所以[16,26]n ∈.正整数的n 值有11个.12.由2(4)44+⋅=⋅+=a b b a b b ,得2222|2|4442420+=+⋅+=⨯+=a b a a b b ,所以|2|+=a b 13.由题意11||||sin120||||sin 6022ABC ABD ACD S S S BD AD CD AD =+=⋅⋅︒+⋅⋅︒△△△,又||2||CD BD =,||1AD =,ABC S =△43BD =,在ABD △中,由余弦定理解,得22237||||||2||||cos1209AB BD AD BD AD =+-⋅⋅︒=,则3c =. 14.由题意得,2log ,2y p y q ==,2log 22024y y +=,设2()log 2xf x x =+,显然()f x 是增函数,从而y 是方程()2024f x =的唯一解, 由101121024,22048==,且当[10,11]x ∈时,2log (3,4)x ∈可得102(10)log 102(1027,1028)f =+∈,112(11)log 112(2051,2052)f =+∈, 从而y 应略小于11,需要判断y 与10.9的大小关系,先估算10.92的近似值。
2020年高考理科数学新课标Ⅲ三真题及答案

K
累计确诊病例数I(t)(t的单位:天)的Logistic模型: ( )= 0.23( 53) ,其中K为最大确诊病例数.当I(
It
t
*
1 e t
)=0.95K时,标志着已初步遏制疫情,则t* 约为( )(ln19≈3)
A. 60 【答案】C 【解析】 【分析】
B. 63
C. 66
D. 69
K
将 t t 代入函数
(2)若 AB 2 , AD 1 , AA1 3 ,求二面角
的正弦值.
A EF A
1
x y
2
2
20.已知椭圆C
m
:
1(0
25 m
2
的离心率为 5)
15 , A , B 分别为C 的左、右顶点.
4
(1)求C 的方程;
(2)若点 P 在 C 上,点Q 在直线 x 6 上,且| BP || BQ | , BP BQ ,求AAPQ 的面积.
2020年普通高等学校招生全国统一考试
理科数学
注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上. 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改 动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本 试卷上无效. 3.考试结束后,将本试卷和答题卡一并交回. 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是 符合题目要求的. 1.已知集合 A {(x, y) | x, y N* , y x}, B {(x, y) | x y 8},则 A B 中元素的个数为( )
(1)证明:ab+bc+ca<0;
2024 年沈阳市高中三年级教学质量监测数学试卷

2024 年沈阳市高中三年级教学质量监测数学试卷全文共四篇示例,供读者参考第一篇示例:一、选择题(每题2分,共40分)1. 一组数据的方差是5,标准差是多少?A. 5B. 2C. 10D. 254. 一个球从100米高度自由落下,第n次弹起的高度为多少?A. 100/(2^(n-1))B. 100*(2^n)C. 100*(1/2)^nD. 100*n^25. 函数y = 2x + 1和y = 3x - 2的交点为(x,y)=?A. (1, 3)B. (-1, -1)C. (2, 5)D. (0, 2)10. 在直角三角形中,已知两条直角边分别为3和4,求斜边的长。
A. 5B. 7C. 8D. 1011. P(A) = 0.4,P(B) = 0.5,P(A∩B) = 0.2,则P(A并B的补集) = ?12. 已知log10 2 ≈ 0.3010,求log10 20的值。
13. 集合{1, 2, 3, 4, 5} 的排列数是多少?14. 一个圆的周长是20π,它的直径是多少?15. 在一组数据中,若中位数是10,众数是8,平均数是12,则范围是多少?16. 已知直角三角形的一条直角边为6,斜边比另一条直角边长2,求另一条直角边的长。
17. 在长方形的一条对角线上,已知长为10,宽为6,求长方形的面积。
18. 在一个等差数列中,已知第二项是5,公差是3,求这个数列的通项公式。
19. 在平面直角坐标系中,已知一次函数y = 3x - 4和y = -2x + 5的交点为(x, y),求(x, y)的值。
四、综合题(20分)20. 一条铁轨长500米,两列火车同时从两端开往中间,速度分别为30m/s和40m/s,求两列火车相遇的时间。
以上就是2024年沈阳市高中三年级教学质量监测数学试卷的所有内容,希望同学们能够认真答题,取得优异的成绩!祝大家学业有成,前程似锦!第二篇示例:第一部分选择题(共80分)1. 下列各组数中,互质数是()A. 6和9B. 15和25C. 10和15D. 21和352. 已知△ABC中,sinA = 0.6,sinB = 0.8,那么角C的大小为()A. 30°B. 45°C. 60°D. 90°3. 若函数f(x) = (x^2 +3x +1)(x^2 -3x +1),则f(x)的零点个数为()A. 2B. 3C. 4D. 54. 已知向量a = 2i + 3j,向量b = i - 2j,求向量a与向量b的数量积ab的大小。
辽宁省2020年高考数学三模试卷(理科)D卷(新版)

辽宁省2020年高考数学三模试卷(理科)D卷姓名:________ 班级:________ 成绩:________一、选择题: (共12题;共24分)1. (2分)已知集合M=,则M∩P等于()A . {x|0<x≤3,x∈Z}B . {x|0≤x≤3,x∈Z}C . {x|﹣1≤x≤0,x∈Z}D . {x|﹣1≤x<0,x∈Z}2. (2分) (2018高二下·巨鹿期末) 已知( 为虚数单位),则复数()A .B .C .D .3. (2分)若的定义域为,恒成立,,则解集为()A .B .C .D .4. (2分)从1,2,3,4,5中任取三个数,则这三个数成递增的等差数列的概率为()A .B .C .D .5. (2分)如果执行框图,输入N=5,则输出的数等于()A .B .C .D .6. (2分) (2017高二下·孝感期末) 已知双曲线﹣ =1(a>0,b>0)的离心率为,则此双曲线的渐近线方程为()A . y=±2xB .C .D .7. (2分)已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是()A .B .C . 1D . 28. (2分)已知A(2,1),O(0,0),点M(x,y)满足,则z=的最大值为()A . -5B . -1C . 0D . 19. (2分)如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:①f(x)=sinxcosx;②;③;④.其中“同簇函数”的是()A . ①②B . ①④C . ②③D . ③④10. (2分)在二项式( + )n的展开式中,只有第五项的二项式系数最大,把展开式中所有的项重新排成一列,则有理项不相邻的概率为()A .B .C .D .11. (2分) (2016高一上·珠海期末) 关于x的函数y=ax , y=xa , y=loga(x﹣1),其中a>0,a≠1,在第一象限内的图象只可能是()A .B .C .D .12. (2分) (2016高二上·自贡期中) 以下对于几何体的描述,错误的是()A . 以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球B . 一个等腰三角形绕着底边上的高所在直线旋转180°形成的封闭曲面所围成的图形叫做圆锥C . 用平面去截圆锥,底面与截面之间的部分叫做圆台D . 以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱二、填空题: (共4题;共5分)13. (2分)(2019·北京模拟) 已知平面向量的夹角为 ,且满足则________;________.14. (1分) (2019高一下·鹤岗期中) 在数列中,,,则数列的通项 ________.15. (1分)若点P(x,y)是曲线上任意一点,则的最小值为________.16. (1分) (2020高二上·汪清期中) 的内角、、的对边分别为、、,已知,,,则 ________三、解答题 (共8题;共70分)17. (10分) (2017高一下·怀仁期末) 已知等差数列的公差,它的前项和为,若,且成等比数列.(1)求数列的通项公式及前项和;(2)令,求数列的前项和.18. (15分)(2020·新课标Ⅱ·理) 某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi , yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,, .(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(xi , yi)(i=1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数r= , =1.414.19. (10分)如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为矩形,且PD=AD= AB,E为PC的中点.(1)过点A作一条射线AG,使得AG∥BD,求证:平面PAG∥平面BDE;(2)求二面角D﹣BE﹣C得余弦值的绝对值.20. (10分) (2015高二上·滨州期末) 已知椭圆C:(a>b>0)的左、右焦点为F1(﹣2,0),F2(2,0),点M(﹣2,)在椭圆C上.(1)求椭圆C的标准方程;(2)已知斜率为k的直线l过椭圆C的右焦点F2 ,与椭圆C相交于A,B两点.①若|AB|= ,求直线l的方程;②设点P(,0),证明:• 为定值,并求出该定值.21. (5分)(2017·临沂模拟) 已知函数f(x)= .(I)求函数f(x)的单调区间;(II)若不等式f(x)>恒成立,求整数k的最大值;(III)求证:(1+1×2)•(1+2×3)…(1+n(n×1))>e2n﹣3(n∈N*).22. (5分) (2017高三下·黑龙江开学考) 如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.(Ⅰ)求证:AD∥EC;(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.23. (5分)(2017·湖北模拟) 已知在直角坐标系xOy中,直线l的参数方程为,若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos2θ+4cosθ=ρ(ρ≥0,0≤θ≤2π).(Ⅰ)当时,求直线l的普通方程;(Ⅱ)若直线l与曲线C相交A,B两点.求证:是定值.24. (10分) (2018·河南模拟) 已知函数, . (1)解不等式;(2)对于,使得成立,求的取值范围.参考答案一、选择题: (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题: (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共8题;共70分) 17-1、17-2、18-1、18-2、18-3、19-1、19-2、20-1、20-2、22-1、23-1、24-1、24-2、。
辽宁省2020版高考数学三模试卷(理科)A卷

辽宁省2020版高考数学三模试卷(理科)A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2018高一上·营口期中) 已知集合,集合,则=()A .B .C . 或D .2. (2分)(2016·山东模拟) i为虚数单位,负数i2016的共轭复数为()A . 1B . iC . ﹣1D . ﹣i3. (2分)等于()A .B .C .D .4. (2分) (2019高二上·沧县月考) 一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,从中任意取出一个,则取出的小正方体两面涂有油漆的概率是()A .B .C .D .5. (2分)若直线y=kx与圆的两个交点关于直线对称,则()A . k=-1,b=2B . k=1,b=2C . k=1,b=-2D . k=-1,b=-26. (2分) (2019高一上·月考) 已知 , ,则下列等式一定成立的是()A .B .C .D .7. (2分) (2019高一下·包头期中) 在中分别为角所对的边,若 ,则此三角形一定是()A . 等腰直角三角形B . 直角三角形C . 等腰三角形D . 等腰三角形或直角三角形8. (2分)已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为()A .B .C .D .9. (2分) (2018高一下·云阳期末) 执行如图所示的程序框图,若输出的值在集合中,则输入的实数的取值集合是()A .B .C .D .10. (2分)若|,且,则与的夹角是()A .B .C .D .11. (2分) (2020高二上·永安月考) 作三棱锥中,平面,,,则该三棱锥外接球的表面积为()A .B .C .D .12. (2分)已知函数的导函数为,那么“”是“是函数的一个极值点”的()A . 充分而不必要条件B . 必要而不充分条件C . 充要条件D . 既不充分也不必要条件二、填空题 (共4题;共4分)13. (1分) (2016高二上·吉林期中) 定积分 dx的值为________14. (1分)(2017·福建模拟) 设不等式,表示的平面区域为M,若直线y=k(x+2)上存在M内的点,则实数k的最大值是________.15. (1分) (2015高一下·普宁期中) 抛物线y2=12x上一点M到抛物线焦点的距离为9,则点M到x轴的距离为________16. (1分)有下列4个命题:①若函数f(x)定义域为R,则g(x)=f(x)﹣f(﹣x)是奇函数;②若函数f(x)是定义在R上的奇函数,∀x∈R,f(x)+f(2﹣x)=0,则f(x图象关于x=1对称;③已知x1和x2是函数定义域内的两个值(x1<x2),若f(x1)>f(x2),则f(x)在定义域内单调递减;④若f(x)是定义在R上的奇函数,f(x+2)也是奇函数,则f(x)是以4为周期的周期函数.其中,正确命题是________ (把所有正确结论的序号都填上).三、解答题 (共7题;共65分)17. (5分)数列{an}满足a1=2,an+1=an2+6an+6(n∈N×)(Ⅰ)设Cn=log5(an+3),求证{Cn}是等比数列;(Ⅱ)求数列{an}的通项公式;18. (10分) (2017高二下·赤峰期末) 如图,在四棱锥中,底面,底面为直角梯形,,,,为的中点,平面交于点.、(1)求证:;(2)求二面角的余弦值.19. (15分)(2018·全国Ⅲ卷理) 某工厂为提高生产效率,开展技术创新活动,提出了完成项目生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随即分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:超过m不超过m第一种生产方式第二种生产方式(3)根据2中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:,20. (10分)(2019·随州模拟) 已知长轴长为4的椭圆过点,点是椭圆的右焦点.(1)求椭圆方程;(2)轴上是否存在定点D (在椭圆外),使得过的直线交椭圆于两点.设点为点关于轴的对称点,且三点共线?若存在,求点坐标;若不存在,说明理由.21. (10分)(2017·山东模拟) 已知函数f(x)=ax2ex+blnx,且在P(1,f(1))处的切线方程为(3e﹣1)x﹣y+1﹣2e=0,g(x)=(﹣1)ln(x﹣2)+ +1.(1)求a,b的值;(2)证明:f(x)的最小值与g(x)的最大值相等.22. (5分)(2017·湖北模拟) 已知在直角坐标系xOy中,直线l的参数方程为,若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos2θ+4cosθ=ρ(ρ≥0,0≤θ≤2π).(Ⅰ)当时,求直线l的普通方程;(Ⅱ)若直线l与曲线C相交A,B两点.求证:是定值.23. (10分)(2019·汉中模拟) 已知函数 .(1)解不等式;(2)若关于的不等式的解集不是空集,求的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共65分) 17-1、18-1、18-2、19-1、19-2、19-3、20-1、20-2、21-1、第11 页共13 页第12 页共13 页21-2、22-1、23-1、23-2、第13 页共13 页。
辽宁省2020年高考数学三模试卷(理科)(II)卷

辽宁省2020年高考数学三模试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题: (共12题;共24分)1. (2分)全集,则=().A .B .C .D . 或2. (2分)已知复数 a=3+2i,b=4+mi,若复数()2<0,则实数m 的值为()A . 3B . ﹣3C . 6D . ﹣63. (2分)已知非负实数满足,则关于的一元二次方程有实根的概率是()A .B .C .D .4. (2分) (2015高一下·普宁期中) 已知a、b为实数,则2a>2b是log2a>log2b的()A . 必要非充分条件B . 充分非必要条件C . 充要条件D . 既不充分也不必要条件5. (2分) (2017高二上·四川期中) 设为双曲线:的右焦点,过坐标原点的直线依次与双曲线的左、右支交于点,若,,则该双曲线的离心率为()A .B .C .D .6. (2分) (2017高三上·赣州期中) 若变量x,y满足|x|﹣ln =0,则y关于x的函数图象大致是()A .B .C .D .7. (2分) (2019高三上·抚州月考) 执行如图所示的程序框图,若输出的结果是7,则判断框内的取值范围是()A .B .C .D .8. (2分)如图为一个几何体的三视图,则该几何体外接球的表面积为()A . 4πB . 12πC . 12πD . 24π9. (2分)(2017·辽宁模拟) 定义为n个正数P1 ,P2…Pn的“均倒数”,若已知正整数数列{an}的前n项的“均倒数”为,又bn= ,则 + +…+ =()A .B .C .D .10. (2分)二项式(x﹣1)n的奇数项二项式系数和64,若(x﹣1)n=a0+a1(x+1)+a2(x+1)2+…+an(x+1)n ,则a1等于()A . ﹣14B . 448C . ﹣1024D . ﹣1611. (2分)椭圆=1的焦点为F1 ,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M 的纵坐标是()A .B .C .D .12. (2分) (2019高三上·富平月考) 对于一个声强为为(单位:)的声波,其声强级(单位:)可由如下公式计算:(其中是能引起听觉的最弱声强),设声强为时的声强级为70 ,声强为时的声强级为60 ,则是的()倍A . 10B .C .D .二、填空题 (共4题;共4分)13. (1分) (2019高二下·上海期末) 课本中,在形如… … 的展开式中,我们把)叫做二项式系数,类似地在…的展开式中,我们把叫做三项式系数,则… … 的值为________.14. (1分) (2019高二下·镇海期末) 若对于任意x∈[1,4],不等式0≤ax2+bx+4a≤4x恒成立,|a|+|a+b+25|的范围为________.15. (1分) (2016高二上·南通开学考) 若将函数y=sin2x的图象向左平移θ,个单位后所得图象关于y轴对称,则θ=________.16. (1分) (2019高一下·马鞍山期中) 已知数列中,,,则 ________.三、解答题 (共7题;共65分)17. (10分) (2018高一下·汕头期末) 已知△ 内角,,的对边分别为,,,.(1)求;(2)若,,求△ 的面积.18. (10分)(2017·南京模拟) 如图,在直三棱柱ABC﹣A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.(1)求证:B1C1∥平面A1DE;(2)求证:平面A1DE⊥平面ACC1A1 .19. (10分)(2017·河南模拟) 某地区拟建立一个艺术搏物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标总是中随机抽取3个总题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正面回答每道题目的概率均为,甲、乙两家公司对每题的回答都是相独立,互不影响的.(1)求甲、乙两家公司共答对2道题目的概率;(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?20. (5分) (2019高三上·雷州期末) 设、分别是椭圆:的左、右焦点,若是该椭圆上的一个动点,的最大值为.(I)求椭圆的方程;(II)设直线与椭圆交于、两点,点关于轴的对称点为(与不重合),试判定:直线与轴是否交于定点?若是,请写出定点坐标,并证明你的结论;否则,请说明理由.21. (10分) (2019高三上·凤城月考) 已知函数, .(1)讨论函数的单调性;(2)当,时,若对于任意,都存在,使得,证明: .22. (10分) (2017高二下·新乡期末) 已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标是ρ=2asinθ,直线l的参数方程是(t为参数).(1)若a=2,M为直线l与x轴的交点,N是圆C上一动点,求|MN|的最大值;(2)若直线l被圆C截得的弦长为,求a的值.23. (10分)(2017·运城模拟) 设函数f(x)=|2x﹣1|,x∈R.(1)若不等式f(x)≤a的解集为{x|0≤x≤1},求a的值;(2)若g(x)= 的定义域为R,求实数m的取值范围.参考答案一、选择题: (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共65分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、21-1、21-2、22-1、22-2、23-1、23-2、。
2020年秋期高中三年级期终质量评估数学(理)试题及答案【完整版】

Ã
v
H槡)#=
%
£
U
0#
º
h
9#& {q/ÅÃv*
#;$!& $ E + #! + " , h£q[ \ ¤ 4#B C 5#!,##""#£ U:,$* ,(#W 0 H h " / # W#` W 0 õ£U: /$U#$FHW 3#^!!0+5*#,0+3*".!!0+5*#.0+3*"*"#W 0 /%&HÌU&$ !#"=ÌU & /!!"> 5!!##""#` 5! ^º$ X x ' : / £ U7 º Ì U& ( ¿ f x ) / W ##%*A '5##% /"*¦/hn8+,,u'v/ M,,#= . - 1 u ' v . ´ ¹ £ U7 / M x , , #/ ç è % 0 $
!"!"!"#$%&!'#()*+,
! " # $%
!"#$
#$!"#$%!#&'() % " #* & ' (+ , $$- . / ( 0 1 2 3 2 4 2 ( 5 6 7 8 9 : ; 4 ! " # ; 2 ( < = $
!$2 ( > - . ? @ A 1 B C 6 D E F - G H I J 4 2 ( 5 ; $ %$&'(23KL!& MNIO*&'(23KL"$'PQ6RSTUV WN X Y Z N [ J W \ ] ^ N _ ` a $ ($b c d ( H 4 e ( 6 2 ( f g R S h i j k 2 l m 2 ( f g [ J 6 2 3 < = $ '$n o # p ` q r s t r u v $
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年辽宁省沈阳市高中三年级教学质量监测(三)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必将自己的姓名、考号填写在答题卡上,并将条码粘贴在答题卡指定区域。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动用橡皮擦干净后,再选涂其他答案标号。
第Ⅱ卷用黑色墨水签字笔在答题卡指定位置书写作答,在本试题卷上作答无效。
3.考试结束后,考生将答题卡交回。
第Ⅰ卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|(1)(2)0},{|0}=--≤=>M x x x N x x ,则A .N M ⊆B .M N ⊆C .M N =∅ID .M N =R U2.复数12z i =+,若复数1z ,2z 在复平面内的对应点关于虚轴对称,则12z z =A .5-B .5C .34i -+D .34i -3.已知抛物线22x py =上一点(,1)A m 到其焦点的距离为3,则p =A .2B .2-C .4D .4±4.《九章算术》中介绍了一种“更相减损术”,用于求两个正整数的最大公约数,将该方法用算法流程图表示如下,若输入15a =,12b =,0i =,则输出的结果为A .4a =,4i =B .4a =,5i =C .3a =,4i =D .3a =,5i =5.被誉为“中国现代数学之父”的著名数学家华罗庚先生倡导的“0.618优选法”在生产和科研实践中得到了非常广泛的应用,0.618就是黄金分割比512m -=的近似值,黄金分割比还可以表示为2sin18︒,则24m m -= A .4 B .2C .51+D .51-6.已知某不规则几何体三视图如图,其中俯视图中的圆弧为14圆周,则该几何体的侧面积为 A .344π+B .722π+ C .7524π+D .7528π+ 7.设函数2()cos sin f x x b x =+,则“0b =”是“()f x 的最小正周期为π”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.2020年初,新型冠状肺炎在欧洲爆发后,我国第一时间内向相关国家捐助医疗物资,并派出由医疗专家组成的医疗小组奔赴相关国家.现有四个医疗小组甲、乙、丙、丁,和有4个需要援助的国家可供选择,每个医疗小组只去一个国家,设事件A =“4个医疗小组去的国家各不相同”,事件B =“小组甲独自去一个国家”,则()P A B = A .29B .13C .49D .599.已知O 为ABC ∆的外接圆的圆心,且345OA OB OC +=-u u u r u u u r u u u r,则C ∠的值为A .4πB .2πC .6πD .12π10.我们打印用的4A 纸的长与宽的比约为2,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为2,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD 为一张4A 纸,若点E 为上底面圆上弧AB 的中点,则异面直线DE 与AB 所成的角约为 A .6πB .4π C .3π D .32π CE11.已知x 与y 之间的几组数据如下表:上表数据中y 的平均值为2.5,若某同学对m 赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为11y b x a =+,22y b x a =+,33y b x a =+,对应的相关系数分别为1r ,2r ,3r ,下列结论中错误的是 A .三条回归直线有共同交点 B .相关系数中,2r 最大 C .12b b >D .12a a >参考公式:线性回归方程yb x a ∧∧=+中,其中121()()()niii nii x x y y b x x --∧=-=--=-∑∑,a y b x ∧-∧-=-.相关系数()()niix x y y r----=∑.12.已知函数3()4f x x x =-,过点(2,0)A -的直线l 与()f x 的图象有三个不同的交点,则直线l 斜率的取值范围为 A .(1,8)-B .(1,8)(8,)-+∞UC .(2,8)(8,)-+∞UD .(1,)-+∞第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分,第13~21题为必考题,每个试题考生都必须作答,第22~23题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分,共20分.13.已知m 是常数,()543252054311 a x a x a x a x a x a mx +++++-=,且1234533a a a a a ++++=,则m =________.14.已知1()f x x x =+,若25(log )2f b =,则1(log )2b f =________.15.在平面直角坐标系xOy 中,F 是双曲线22221(0,0)x y a b a b-=>>的右焦点,直线2y b=与双曲线交于,B C 两点,且90BFC ∠=︒,则该双曲线的离心率为________. 16.在△ABC 中,角,,A B C 的对边分别为,,a b c ,设△ABC 的面积为S ,若2224sin sin s 3n +2i A B C =,则SAB AC⋅u u u r u u u r 的最大值为________. 三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22-23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(本小题满分12分)已知数列{}n a 的前n 项和2n S n pn =+,且4712,,a a a 成等比数列. (1)求数列{}n a 的通项公式; (2)若14nn n n S b a a +=⋅,求数列{}n b 的前n 项和n T .18.(本小题满分12分)随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台.已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取100名点外卖的用户进行统计,按送餐距离分类统计结果如下表:以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率. (1)若某送餐员一天送餐的总距离为100千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数,且同一组中的数据用该组区间的中点值为代表)(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份7元,超过4千米为远距离,每份12元.记X 为送餐员送一份外卖收入(单位:元),求X 的分布列和数学期望.19.(本小题满分12分)如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60DAB ∠=︒,AD PD ⊥,点F 为棱PD 的中点.(1)在棱BC 上是否存在一点E ,使得CF P 平面PAE ,并说明理由; (2)若AC PB ⊥,二面角D FC B --的余弦值为6AF 与平面BCF 所成的角的正弦值.20.(本小题满分12分)已知椭圆2222:1(0)+=>>x y C a b a b ,四点1P,2P,3(2,3-P,4P 中恰有三个点在椭圆C 上,左、右焦点分别为1F 、2F . (1)求椭圆C 的方程;(2)过左焦点1F 且不平行坐标轴的直线l 交椭圆于P 、Q 两点,若PQ 的中点为N ,O 为原点,直线ON 交直线3x =-于点M ,求1||||PQ MF 的最大值.21.(本小题满分12分)已知函数()bx e f x ax =在2x =处取到极值为2e.(1)求函数()f x 的单调区间;(2)若不等式2()ln 1x f x kx x ≥++在(0,)x ∈+∞上恒成立,求实数k 的取值范围.ABCDPF(二)选考题:共10分,请考生在22、23题中任选一题作答,如果多做则按所做的第一题计分. 22.【选修4-4坐标系与参数方程】(本小题满分10分)在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为sin 2ρθ=.(1)M 为曲线1C 上的动点,点P 在线段OM 上,且满足4PO OM ⋅=-u u u r u u u u r,求点P 的轨迹2C 的直角坐标方程; (2)曲线2C 上两点1(,)3A ρπ与点2(,)B ρα,求OAB ∆面积的最大值.23.【选修4-5:不等式选讲】(本小题满分10分)已知,,a b c 均为正数,设函数()f x x b x c a =--++,x ∈R . (1)若222a b c ===,求不等式()3f x <的解集; (2)若函数()f x 的最大值为1,证明:14936a b c++≥.2020年沈阳市高中三年级教学质量监测(三)数学(理科)【答案与评分标准】第Ⅰ卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分,第13~21题为必考题,每个试题考生都必须作答,第22~23题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分,共20分. 13.314.52-15.516三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22-23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(本小题满分12分)(1)当1n =时,111a S p ==+, 当2n ≥时,121n n n a S S n p -=-=-+,……2分 当1n =时,11a p =+也满足上式,故21n a n p =-+,……3分 ∵4712,,a a a 成等比数列,∴24127a a a =,……4分∴2(7)(23)(13)p p p ++=+,∴2p = ∴21n a n =+;……6分由(1)可得2221448483111()(21)(23)48322123n n n n S n n n n b a a n n n n n n +++====--++++++,……9分∴231111111322()23557212324623n n nT n n n n n n +=--+-+⋅⋅⋅+-=-+=++++.……12分18.(本小题满分12分)(1)估计每名外卖用户的平均送餐距离为:0.50.15 1.50.25 2.50.25 3.50.2 4.50.15 2.45⨯+⨯+⨯+⨯+⨯=千米. ……3分所以送餐距离为100千米时,送餐份数为:100412.45≈份; ……5分 (2)由题意知X 的可能取值为:3,7,12.……6分 ()40310025P X ===, ……7分 ()710904502P X ===, ……8分 ()1512100230P X ===. ……9分所以X 的分布列为:……10分∴()3712 6.1522930205E X =⨯+⨯+⨯=. ……12分19.(本小题满分12分)(1)在棱BC 上存在点E ,使得CF P 平面PAE ,点E 为棱BC 的中点. 证明:取PA 的中点Q ,连结EQ 、FQ , 由题意,FQ AD P 且12FQ AD =, CE AD P 且12CE AD =,故CE FQ P 且CEFQ =.∴四边形CEQF 为平行四边形. ……2分 ∴CF EQ P ,又CF ⊄平面PAE , ∴CF P 平面PAE .……4分(2)菱形ABCD 中,AC BD ⊥,又AC PB ⊥,PB BD B =I . ∴AC ⊥平面PBD ,又PD ⊂面PBD ,∴AC PD ⊥, ∵AD PD ⊥,AC AD A =I ,∴PD ⊥平面ABCD . ……6分取AB 中点为M ,则DM AB ⊥.以D 为原点,DM ,DC ,DP 为x ,y ,z 轴建立如图空间直角坐标系,设FD a =, 则由题意知()0,0,0D ,()0,0,F a ,()0,2,0C,)B,)1,0A-.()0,2,FC a =-u u u v,)1,0CB =-u u u v ,……7分设平面FBC 的法向量为(),,m x y z =v,则由00m FC m CB ⎧⋅=⎨⋅=⎩u u u v v u u u vv得200y az y -=⎧⎪-=, 令1x =,则y =z =m ⎛= ⎝⎭v , ……9分显然可取平面DFC 的法向量()1,0,0n =v,由题意:cos ,6m n ==v v,所以a =……10分1,FA =-u u u v ,设直线AF 与平面BCF 所成的角为θ,则sin cos ,5m FA θ===u r u u u r . ……12分20.(本小题满分12分)解:(1)易知3(-P,4P 关于y 轴对称,一定都在椭圆上.所以1P一定不在椭圆上.根据题意2P 也在椭圆上.……2分将2P,4P 带入椭圆方程,解得椭圆方程为22162x y +=.……4分 (2)设直线l 方程为(2)y k x =+(0k ≠),()11,P x y ,()22,Q x y ,联立22162(2)x y y k x ⎧+=⎪⎨⎪=+⎩,可得()222231121260k x k x k ++-=+. ……5分则224(1)0k ∆=+>,且21221231+=-+k x x k ,212212631-=+k x x k , ……6分设PQ 的中点00(,)N x y ,则212262310x x k x k +==-+,22262(2)31310k k y k k k =-+=++, ∴N 坐标为22262,3131⎛⎫- ⎪++⎝⎭k k k k ,||=PQ221)31+=+k k . ……8分因此直线ON 的方程为13y x k =-,从而点M 为1(3,)k-,又1(2,0)F -,1||MF = ……9分2222221(||241)||(31)PQ k k MF k +=+,令2311u =k +≥, 则222(1)(2)1611116119()8()[()]33223416u u h u u u u u -+==---=---,因此当4u =,即1k =±时h(u)最大值为3.所以1||||PQ MF……12分21.(本小题满分12分)(1)由已知定义域为{|0}x R x ∈≠,2()()()bxabx a e f x ax -'=,由22(2)(2)0(2)bab a e f a -'==,又0a ≠,得12b =, 2(2)222b e e ef a a ===,所以1a =,……2分从而22(1)2()xxe f x x-'=又0x ≠。
