【潍坊_文数】2015年4月潍坊一中2015届高三过程性检测数学试题(文)word含答案数
2015潍坊一模_山东省潍坊市2015届高三下学期三月一模考试数学(文)试题_含答案

2015潍坊⼀模_⼭东省潍坊市2015届⾼三下学期三⽉⼀模考试数学(⽂)试题_含答案⾼三数学(⽂史类)第Ⅰ卷(选择题共50分)⼀、选择题(本⼤题共10个⼩题,每⼩题5分,共50分,在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的)1、集合1{|()1},{|lg(2)}2x M x N x y x =≥==+,则M N 等于()A .[)0,+∞B .(]2,0-C .()2,-+∞D .()[),20,-∞-+∞2、设复数12,z z 在复平⾯内的对应点关于虚轴对称,若112z i =-,则21z z 的虚部为() A .35 B .35- C .45 D .45- 3、如果双曲线22221(0,0)x y a b a b-=>>的⼀条渐近线与直线0y -平⾏,则双曲线的离⼼率为()A.2 D .34、已知函数()y f x =的定义域为{|0}x x R x ∈≠且,且满⾜()()0f x f x +-=,当0x >时,()ln 1f x x x =-+,则函数()y f x =的⼤致图象为()5、某同学寒假期间对其30位亲属的饮⾷习惯进⾏了⼀次调查,列出了如下22?列联表:则可以说其亲属的饮⾷习惯与年龄有关的把握为()A .90%B .95%C .99%D .99.9%附:参考公式和临界值表:22112212211212()n n n n n n n n n χ++++-=6、下列结论中正确的是()①命题:3(0,2),3x x x ?∈>的否定是3(0,2),3x x x ?∈≤;②若直线l 上有⽆数个点不在平⾯α内,则//l α;③若随机变量ξ服从正态分布2(1,)N σ,且(2)0.8P ξ<=,则(01)0.2P ξ<<=;④等差数列{}n a 的前n 项和为n S ,若43a =,则721S =A .①②B .②③C .③④ D.①④7、如图,在ABC ?中,点D 在AC上,,5,sin 3AB BDBC BD ABC ⊥==∠=,则CD 的长为()A .4 C ..58、某⼏何体的三视图是如图所⽰,其中左视图为半圆,则该⼏何体的体积是()A.3B .2π C .3 D .π 9、圆22:(1)25C x y -+=,过点(2,1)P -作圆的所有弦中,以最长弦和最短弦为对⾓线的四边形的⾯积是()A .. C ..10、对于实数,m n 定义运算“⊕”:2221m mn m n m n n mn m n ?-+-≤?⊕=?->??,设()(21)(1)f x x x =-⊕-,且关于x 的⽅程()f x a =恰有三个互不相等的实数根123,,x x x ,则123x x x 的取值范围是()A .1(,0)32-B .1(,0)16-C .1(0,)32D .1(0,)16第Ⅱ卷⼆、填空题:本⼤题共5⼩题,每⼩题5分,共25分,把答案填在答题卷的横线上。
潍坊市2015届高三4月第二次模拟考试各科(数学理)

潍坊高三数学(理工农医学)2015.04本试卷共5页,分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
第Ⅰ卷 选择题(共50分)一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集R U =,已知集合}1|||{≤=x x A ,}1log |{2≤=x x B ,则UA B ⋂=A .]1,0(B .]1,1[-C .]2,1(D .]2,1[)1,( --∞ 2. 设i 是虚数单位,若复数)(310R a ia ∈--是纯虚数,则a 的值为 A .-3 B .-1 C .1 D .3 3. 已知命题44,0:≥+>∀x x x p ;命题212),,0(:00=+∞∈∃x x q ,则下列判断正确的是 A .p 是假命题B .q 是真命题C .)(q p ⌝∧是真命题D .q p ∧⌝)(是真命题4. 设n m ,是不同的直线,βα,是不同的平面,下列命题中正确的是A .若n m n m ⊥⊥,,//βα,则βα⊥;B .若n m n m //,,//βα⊥,则βα⊥;C .若n m n m ⊥⊥,,//βα,则βα//;D .若n m n m //,,//βα⊥,则βα//;5.若)2,0(πα∈,且103)22cos(cos 2=++απα,则=αtan A .21 B .31 C .41 D .516. 已知定义在R 上的函数)(x f y =满足)(2)2(x f x f =+,当]2,0[∈x 时,⎩⎨⎧∈+-∈=]2,1[,2)1.0[,)(2x x x x x x f ,则函数)(x f y =在]4,2[上的大致图像是7. 已知三棱锥S —ABC 的所有顶点都在球O 的球面上,底面△ABC 是边长为1的正三角形,棱SC 是球O 的直径且SC=2,则此三棱锥的体积为A .62B .63C .32D .22 8.某公司新招聘5名员工,分给下属的甲,乙两个部门,其中两名英语翻译人员不能分给同一个部门;另三名电脑编程人员不能都分给同一个部门,则不同的分配方案和数是 A.6 B.12 C.24 D.369. 已知圆()()22:341C x y -+-=和两点()()(),0,,00A m B m m ->.若圆C 上存在P 点,使得90APB ∠=,则m 的最大值为 A.7 B.6 C.5 D.410. 已知函数()23420142015123420142015x x x x x f x x =+-+-+⋅⋅⋅-+,若函数()f x 的零点均在区间[](),,,a b a b a b Z <∈内,则b a -的最小值是A.1B.2C.3D.4第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.某校对高三年级1600名男女学生的视力状况进行调查,现用分 层抽样的方法抽取一个容量是200的样本,已知样本中女生比男生 少10人,则该校高三年级的女生人数是 ;12. 当输入的实数]30,2[∈x 时,执行如图所示的程序框图,则输 出的x 不小于103的概率是 ;13. 已知G 为△ABC 的重心,令AB=a uu u r ,AC b =uuu r,过点G 的直线分别交AB 、AC 于P 、Q 两点,且AP ma =uu u r ,AQ nb =uuu r ,则nm 11+=__________.14. 抛物线)0(2:2>=p px y C 的焦点为F ,点O 是坐标原点,过点O 、F 的圆与抛物线C 的准线相切,且该圆的面积为36π,则抛物线的方程为 ;15. 定义在()0,+∞上的函数()f x 满足:对()0,x ∀∈+∞,都有()()22f x f x =;当(]()1,22x f x x ∈=-时,,给出如下结论: ①对(),20xm Z f ∀∈=有;②函数()f x 的值域为[)0,+∞;③存在n Z ∈,使()219xf +=;④函数()f x 在区间(),a b 上单调递减的充分条件是“存在k Z ∈,使得()()1,2,2mkk a b -⊆.其中所有正确结论的序号是 。
高三英语月考试题及答案-潍坊第一中学2015届高三4月过程性检测

山东省潍坊第一中学2015届高三4月过程性检测英语试题第I卷第一部分:听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上.第一节(共5小题;每小题1.5分,满分7.5分)听下面五段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.15.C.£9.18.答案是B。
1.How long will the concert last?A.One hour.B.Two hours.C.One and a half hours.2.What is Mary like according to the man?A.Easygoing.B.Rude.C.Kind.3.What problem is the man facing?A.He is too busy to call Carl.B.He hasn’t been able to reach Carl.C.He will be late for the football game.4.When will the man see his parents?A.At 10:00 am.B.At 8:00 am.C.At 6:00 am.5.What does the woman suggest they do?A.Walk to the theater.B.Have dinner first.C.Go to another theater.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
山东省潍坊市2015届高三第一次模拟考试 数学理

第一次 选择题 和第 II 卷
理
试题
非选择题 两部分.共 150 分.考试时 间 120 分钟. 选择题 共 50 分
第 I 卷
注意事项: 1.答第 I 卷前,考生务必将自己的姓 准考证号 考试科目用铅笔涂写在答题卡 . 2. 题选出答案 ,用 2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮 擦 净 , 再改涂其它答案标号 一 选择题:本大题共 10 小题, 小题 5 分,共 50 分 1.集合 等于
2.设复数 z1·z2 在复 面内的对应点关于虚轴对称,若
的虚部为
3.如果双曲线
的一条渐近线与直线
行,则双曲线的离心率为
·1 ·
·2 ·
·3 ·
·4 ·
·5 ·
·6 ·
·7 ·
·8 ·
山东省潍坊一中2015届高三4月过程性检测

山东省潍坊一中2015届高三4月过程性检测山东省潍坊一中2015届高三4月过程性检测高三过程性检测语文试题【试卷综析】山东省潍坊一中高三4月过程性检测考试语文试题。
作为检测性考试试题,该卷有以下特色。
第一,特别注重基础知识的考查。
如第1、2题的字音和字形,引领考生平时要注重基础知识积累。
第二,题型稳定。
词语、病句和连贯题等常规题型依然存在,文言文阅读、现代文阅读等常规题型与高考接轨。
第三,题目不难,有一定的梯度,对高考知识点涵盖较广,如阅读题的设置往往不止一个考点。
第四,关注时下热点,如压缩题和作文材料,都紧扣热点,又有一定深度。
说明:本试卷分I卷(选择题)和II卷(非选择题)两部分,满分150分,考试时间150分钟。
请将I卷选择题答案填写在答题卡上,请将II卷答在答题纸上。
第I卷(共36分)一、(每小题3分,共15分)91【题文】A01.下列各组词语中,加点字的注音全都正确的一组是A.颤动(chn)悲恸(tng)口头禅(chn)翘首以待(qio)B.晕车(yn))处方(ch)爆冷门(bo)龇牙咧嘴(z)C.瓜蔓(mn)伯仲(zhng)一溜烟(1i)天遂人愿(su)D.茎叶(jng)连累(1i)露马脚(1u)按捺不住(ni)【知识点】本题考查考生识记现代汉语普通话常用字的字音的能力,能力层次为A(识记)。
【答案解析】A解析:B项,“处方(ch)”应为“ch”;C项,“瓜蔓(mn)”应为“wn”,“伯仲(zhng)”应为“zhng”;D项,“露马脚(1u)”应为“lu”,“按捺不住(ni)”应为“n”。
【思路点拨】字音题需要针对字音不同情况采用不同的方法:多音字需要切记据义定音,形声字需要谨防声旁误导,形近字需要注意细微差别,方言字需要矫正地区缺陷。
【题文】B02.下列各组词语中,没有错别字的一组是A.亵赎膏梁变速挡奇貌不扬树倒猢狲散B.诧异埂塞拌脚石心无旁骛有志者事竟成C.低炭临摹亲和力要言不烦废力不讨好D.畅销枯燥候车室举步维艰快刀斩乱麻【知识点】本题考查考生识记并正确书写现代常用规范汉字的能力,能力层次为A(识记)。
潍坊一中2015届高三4月考数学试题(文)word含答案数

高三过程性检测 数学(文科)试题本试卷分第I 卷(选择题)和第II 卷进(非选择题)两部分,满分150分。
考试用时120分钟。
注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号、班级和科类填写在答题卡和试卷规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3.第II 卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
第I 卷(共50分)一.选择题:(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.设全集(){}{}(),ln 1,11,U U R A x y x B x x C A B ===-=-<⋂=则 A.()2,1-B. (]2,1-C. [)1,2D. ()1,22.已知i 为虚数单位,复数121iz i +=-,则z 的共轭复数虚部是 A.32i B.32C. 12i - D. 32-3.平面向量a b 与的夹角为()602,012a b a b ==+,,,则等于A. B. C.12D.4.如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平均数分别为x x 甲乙、,中位数分别为m m甲乙,,则A. ,m m x <<甲甲乙乙B. ,m m x ><甲甲乙乙C.,m m x x >>甲甲乙乙D.,m m x x <>甲甲乙乙5. 已知双曲线的中心在原点,一个焦点为()1F ,点p 在双曲线上,且线段1PF 的中点坐标为(0,2),则此双曲线的方程是A. 2214x y -= B. 2214y x -= C. 22123x y -=D. 22132x y -=6.下列命题正确的是:(1)已知命题:,2 1.,21x x p x R p x R ∃∈=⌝∃∈≠则是:(2)设,l m 表示不同的直线,α表示平面,若//,////m l m l αα且,则; (3)利用计算机产生0~1之间的均匀随机数a ,则事件“310a ->”发生的概率为23(4)“0,0a b >>”是“2a bb a+≥”的充分不必要条件. A.(1)(4) B.(2)(3) C.(1)(3)D.(3)(4)7.如图,长方体1111ABCD A BC D -中,12,2A B A D A==设长方体的截面四边形11ABC D 的内切圆为O ,圆O 的正视图是椭圆O ',则椭圆O '的离心率等于A.3 B.2C.3D.2 8.执行如图的程序,则输出的结果等于 A.14950B.200101C.9950D.150509.函数()22sin 1,0,24,0x x x f x x x x ⎧-+>⎪=⎨--≤⎪⎩的零点个数为A.0B.1C.2D.310.如果函数()y f x =在区间I 上是增函数,而函数()f x y x=在区间I 上是减函数,那么称函数()y f x =是区间I 上“缓增函数”,区间I 叫做“缓增区间”.若函数()21322f x x x =-+是区间I 上“缓增函数”,则“缓增区间”I 为A. [)1,+∞B. ⎡⎣C. []0,1D. ⎡⎣二、填空题:本大题共5小题,每小题5分,共25分。
山东省潍坊一中2015届高三上学期期末模拟(四)文科综合试题 Word版含答案

潍坊一中高66级考试题(四)文科综合本试卷分第I卷和第Ⅱ卷两部分,共12页。
满分300分。
考试用时150分钟。
答题前,考生务必将自己的姓名、准考证号写在试卷和答题卡规定的位置。
考生注意:第一卷按题号涂在答题卡上;第二卷按题号答在答题纸上。
第Ⅰ卷(选择题共140分)一、单项选择题(共35题,每题4分)在拼搏中放飞青春梦想,让奥林匹克精神薪火相传。
第二届夏季青年奥林匹克运动会于北京时间2014年8月16日20时在中国南京正式开幕。
据此回答1~2题。
1.在南京青奥会开幕时,西五区的区时是()A. 2014年8月16日7 时B. 2014年8月16日17时C. 2014年8月17日9时D. 2014年8月15日17时2.开幕式次日,运动员们观察到南京日落的方位最可能是()A. 西北B. 西南C. 正西D.东南下图为非洲大陆局部区域某月份平均气温(单位:℃)分布图,读图完成3~5题。
3.影响图中①②③三条等温线基本走向及数值递变的主导因素是()A. 地形B. 洋流C. 海陆位置D.纬度4.图中R地的气温数值,最可能是()A. 16B. 20C. 23D.135.图中甲乙丙丁四地,年降水量最多的是()A. 甲B.乙C. 丙D.丁北疆阿尔泰山和准噶尔盆地以西山地的河流,常在4~6月发生洪水灾害,其特征为“一日一峰”,白天流量很大,夜晚消退。
结合材料,回答下面6~7题。
6.此类洪水的直接补给水为()A.大气降水B.季节性积雪融水C.冰川融水D.湖泊决堤7.“一日一峰”反映的当地环境特征是()A.气候大陆性强B.降水变率大C.冰雪融化快D.自然灾害多下图为我国部分省区2005—2010年人口净迁移率(迁入率与迁出率之差,正数表示人口净迁入.反之为净迁出)与人口自然增长率分布图。
读图完成8~9题。
8.下列有关我国部分省区2005—2010年人口变化状况的叙述,正确的是()①江西省净迁入人口数增加②天津人口增长率大于四川③广东自然增长人口数大于净迁入人口数④贵州人口净减少A.①②B.③④C.②③D.①④9.图中人口数量的变化()A.加剧了北京、上海、天津城市交通拥堵B.引起江西、贵州的人口合理容量增大C.增强了广东、浙江第一产业的活力D.使北京、上海人口老龄化问题更加严重10.读右图(图中曲线数值分别为等高线的高程和等深线的深度,单位是米),该城市在发展规划中,a、b、c、d四处为预留土地,准备选择其中一个建港口,从港口的建设条件考虑,最优的是()A.a B.b C.C D.d沪宁(上海至南京)高铁多段地基采用水泥粉煤灰碎石(CFG)桩施工技术。
山东省潍坊市某重点中学2015届高三上学期12月阶段性教

高三阶段性教学质量检测 高三文科数学试题本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟. 第Ⅰ卷一、选择题:本题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,恰有..一项..是符合题目要求的,把正确答案涂在答题卡上. 1.设集合{1}A x x =<,2{log 0}B x x =≤,则A B ⋂=( )A .{}11<<-x x B. {}10<<x x C. {}11≤<-x x D. {}1x x 0<≤ 2.下列说法正确的是( )A .命题“若2x =,则24x =”的否命题为“若24x ≠,则2x ≠”B .命题“2,10x R x x ∀∈+-<”的否定是“2,10x R x x ∃∈+->” C .“x y =”是“sin sin x y =”的充分不必要条件A.B.3-34.已知132a -=,21log 3b =,2log 3c =,则( ) A .c a b >> B .a c b >> C .c b a >> D .a b c >> 5. 函数()x x f 2log 1+=与12)(+-=x x g 在同一直角坐标系下的图象大致是( )A.B. C. D.6.设,m n 是两条不同的直线,,αβ是两个不同的平面,则下列命题不正确的是( ) A .若,,m n m n αα⊥⊥⊄,则n ∥α B .若m ∥α,αβ⊥,则m β⊥ C .若m β⊥,αβ⊥,则m ∥α或m α⊂ D .若,,m n m n αβ⊥⊥⊥,则αβ⊥7. 已知a =(1,2),b =(0,1),c =(-2,k ),若(a +2b )⊥c ,则k =( ) A .12 B .2 C .12- D .2- 8.若直线:10 l ax by ++=始终平分圆M :224210x y x y ++++=的周长,则21a b+的最小值为( ) AB .3C .5D .99.已知抛物线22(0)y px p =>的焦点F 与双曲线22145x y -=的右焦点重合,抛物线的准线与x 轴的交点为K ,点A在抛物线上且AK =,则A 点的横坐标为( )A..3 C..4 10.已知定义在R 上的偶函数()f x ,设其导函数为()x f ',当(]0,∞-∈x 时,恒有()()0≤+'x f x f x ,令()()x xf x F =,则满足()(3)21F F x >-的实数x 的取值范围是( )A. (),2-∞B.()1,-+∞C. ()2,+∞D. ()1,2-第II 卷二、填空题:(本大题共5小题,每小题5分,共25分,把答案直接填在横线上) 11.等比数列{}n a 的各项均为正数,且154a a =,则2log 1a +2log 2a +2log 3a +2log 4a +2log 5a =________.12.设点P 是双曲线)0,0(12222>>=-b a by ax 上一点,21,F F 分别是双曲线的左、右焦点,12PF PF ⊥,且213PF PF =,则双曲线的离心率是__________________13.已知),(y x P 满足约束条件⎪⎩⎪⎨⎧≥-≤--≤-+010103x y x y x ,则y x 2-的最大值是__________14.定义,(),()a ab a b b a b ≤⎧*=⎨>⎩,则函数()13xf x =*的值域是__________________ 15.定义12142334a a a a a a a a =-,若函数 () cos x x f x x x=,给出下列四个命题:①()f x 在区间⎥⎦⎤⎢⎣⎡85,8ππ上是减函数;②()f x 关于308π(,)中心对称;③)(x f y =的表达式可改写成 )14y x --π;④由0)()(21==x f x f 可得21x x -必是π的整数倍; 其中正确命题的序号是三、解答题:(本大题6小题,共75分,解答写出文字说明,证明过程或演算步骤) 16.(本小题满分12)已知ABC ∆1,且sin sin A B C +=(I )求边AB 的长; (Ⅱ)若ABC ∆的面积为1sin 6C ,求角C 的度数. 17. (本小题满分12分)设命题p :函数21()lg()16f x ax x a =-+的定义域为R ;命题q :不等式a xx<-93对一切正实数x 均成立.(I )如果p 是真命题,求实数a 的取值范围;(Ⅱ)如果命题“p 或q ”为真命题,且“p 且q ”为假命题,求实数a 的取值范围. 18.(本小题满分12分)已知四棱锥P ABCD -的三视图如下,E 是侧棱PC 上的动点. (I )求四棱锥P ABCD -的体积;(Ⅱ)不论点E 在何位置,是否都有BD AE ⊥? 证明你的结论; (Ⅲ)是否存在E 点使得PA //平面BDE ? 证明你的结论.19.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且22n n S a =-,数列{}n b 满足11b =,且12n n b b +=+. (I )求数列{}n a ,{}n b 的通项公式;已知倾斜角为60︒的直线l 过点(0,-和椭圆2222:1(0)x y C a b a b+=>>的右焦点,且椭(I )求椭圆C 的方程;(II )过(3,0)-点的直线l 与椭圆相交于,A B 两点,若以线段,A B 为直径的圆过椭圆的左焦点,求直线l 的方程. 21.(本小题满分14分)已知函数1()ln xf x x ax-=+(0)a >(I )若函数()f x 在[1,)+∞上为增函数,求a 的取值范围;(II )当1a =时,函数()()g x f x m =-在1[,2]2上有两个零点,求实数m 的取值范围: (Ⅲ)当1a =时,求证:对大于1的任意正整数1111,ln 234n n n>++++…恒成立. 高三文科数学参考答案2014.12一、选择题1.B2.C3.D4.A5.C6.B7.A8.D9.B 10.D 二、填空题11. 5 12.2(]0,1 15. ①③ 三、解答题:(本大题6小题,共75分,解答写出文字说明,证明过程或演算步骤) 16.解:(I )由题意及正弦定理,得1,AB BC AC BC AC ++=+=两式相减,得1AB =……………………………………………………………………6分(Ⅱ)由ABC ∆的面积111sin sin ,263BC AC C C BC AC ⋅⋅=⋅=得,……………9分 由余弦定理,有22222()21cos 222AC BC AB AC BC AC BC AB C AC BC AC BC +-+-⋅-===⋅⋅, 所以60C ︒= …………………………………………………………………………12分17. 解:(I )若命题为p 真,即21016ax x a -+>恒成立 ①当0a =时,0x ->不合题意 …………………………………………………2分②当0a ≠时,可得00a >⎧⎨∆<⎩,即201104a a >⎧⎪⎨-<⎪⎩ 2a ∴> ………………………6分(II )令21139(3)24xxxy =-=--+由0x >得31x> 若命题q 为真,则0a ≥………………………………………………………………8分 由命题“p 或q ”为真且“p 且q ”为假,得命题p 、q 一真一假……………10分 ①当p 真q 假时,a 不存在②当p 假q 真时,02a ≤≤…………………………………………………………12分 18. 解: (I )由该四棱锥的三视图可知,该四棱锥P ABCD -的底面是边长为1的正方形,侧棱PC ⊥ 底面ABCD ,且2PC = .1233P ABCD ABCD V S PC -∴==……………………3分(II )不论点E 在何位置,都有BD ⊥AE . ………………………………………4分 证明:连接AC ,ABCD 是正方形,∴BD ⊥AC .PC ⊥ 底面ABCD ,且BD ⊂平面ABCD ,∴BD ⊥PC . ……………5分 又AC ⋂PC C =, ∴BD ⊥平面PAC . 不论点E 在何位置,都有AE ⊂平面PAC .∴不论点E 在何位置,都有BD ⊥AE . ………………………………………8分 (Ⅲ)当E 点为PC 中点时,PA //平面BDE ………………………………9分 证明:连结AC 交BD 于O 点,连结OE四边形ABCD 为正方形∴O 点为AC 中点,又E 点为PC 中点∴OE //PA ,又PA ⊄平面BDE ,OE ⊂平面BDE∴ PA //平面BDE ………………………………………………………………12分19.解:(I )当1=n ,21=a ;…………………………………………………………1分当2≥n 时,1122n n n n n a S S a a --=-=- ,∴ 12n n a a -=.…………………2分 ∴{}n a 是等比数列,公比为2,首项12a =, ∴2n n a =.…………………3分 由12n n b b +=+,得{}n b 是等差数列,公差为2. ……………………………4分又首项11=b ,∴ 21n b n =-. ……………………………………………6分(II )2(21)n n c n ⎧=⎨--⎩ 为偶数为奇数n n ……………………………………8分3212222[37(41)]n n T n -=+++-+++- ………………………10分2122223n n n +-=--.…………………………………………………… 12分20.解: (I )∵直线l 的倾斜角为60︒∴直线l的斜率为k =l过点(0,-∴直线l的方程为y += …………………………………………………3分 ∵a b >,∴椭圆的焦点为直线l 与x 轴的交点 ∴椭圆的焦点为(2,0)∴2c =,又∵3c e a ==∴a =,∴2222b a c =-= ∴椭圆方程为22162x y += ………………………………………………………… 5分 (Ⅱ)设直线l 的方程为3x my =-,1122(,),(,)A x y B x y …………………………6分联立直线与椭圆的方程221623x y x my ⎧+=⎪⎨⎪=-⎩,得22(3)630m y my +-+= 12122263,33m y y y y m m +==++ …………………………………………………7分由题意可知11AF BF ⊥,即111AF BF k k ⋅=- ………………………………………8分 ∴121212212121212122(1)(1)()1y y y y y y x x my my m y y m y y ⋅===-++---++ 整理得:21212(1)()10m y y m y y +-++= ……………………………………10分∴22223(+1)61033m m m m -+=++,解得m =…………………………………11分代入22=3612(3)24336360m m ∆-+=⨯-=>………………………………12分所以直线l 的方程为3030x x +=+=或 ………………………13分22.解:(I )因为 1()ln x f x x ax -=+,所以21'()(0)ax f x a ax -=>………1分 依题意可得,对21[1,).'()0ax x f x ax-∀∈+∞=≥恒成立, 所以 对[1,),10x ax ∀∈+∞-≥恒成立,所以 对1[1,),x a x ∀∈+∞≥恒成立,max 1()a x≥,即1a ≥……………………4分(Ⅱ)函数()()g x f x m =-在1[,2]2上有两个零点,即()f x m =在1[,2]2上有两个不同的实数根,即函数()y f x =的图像与直线y m =在1[,2]2上有两个零点。
山东省潍坊市某重点中学2015届高三上学期12月阶段性教

高三文科数学参考答案2014.12一、选择题1.B2.C3.D4.A5.C6.B7.A8.D9.B 10.D二、填空题11. 5 12. 2(]0,1 15. ①③ 三、解答题:(本大题6小题,共75分,解答写出文字说明,证明过程或演算步骤)16.解:(I )由题意及正弦定理,得1,AB BC AC BC AC ++=+=两式相减,得1AB =……………………………………………………………………6分(Ⅱ)由ABC ∆的面积111sin sin ,263BC AC C C BC AC ⋅⋅=⋅=得,……………9分 由余弦定理,有22222()21cos 222AC BC AB AC BC AC BC AB C AC BC AC BC +-+-⋅-===⋅⋅, 所以60C ︒= …………………………………………………………………………12分17. 解:(I )若命题为p 真,即21016ax x a -+>恒成立 ①当0a =时,0x ->不合题意 …………………………………………………2分 ②当0a ≠时,可得00a >⎧⎨∆<⎩,即201104a a >⎧⎪⎨-<⎪⎩ 2a ∴> ………………………6分 (II )令21139(3)24x x x y =-=--+ 由0x >得31x > 若命题q 为真,则0a ≥………………………………………………………………8分 由命题“p 或q ”为真且“p 且q ”为假,得命题p 、q 一真一假……………10分 ①当p 真q 假时,a 不存在②当p 假q 真时,02a ≤≤…………………………………………………………12分18. 解: (I )由该四棱锥的三视图可知,该四棱锥P ABCD -的底面是边长为1的正方形,侧棱PC ⊥ 底面ABCD ,且2PC = .1233P ABCD ABCD V S PC -∴==........................3分 (II )不论点E 在何位置,都有BD ⊥AE . (4)分 证明:连接AC ,ABCD 是正方形,∴BD ⊥AC .PC ⊥ 底面ABCD ,且BD ⊂平面ABCD ,∴BD ⊥PC . ……………5分 又AC ⋂PC C =, ∴BD ⊥平面PAC .不论点E 在何位置,都有AE ⊂平面PAC .∴不论点E 在何位置,都有BD ⊥AE . ………………………………………8分(Ⅲ)当E 点为PC 中点时,PA //平面BDE ………………………………9分证明:连结AC 交BD 于O 点,连结OE四边形ABCD 为正方形∴O 点为AC 中点,又E 点为PC 中点∴OE //PA ,又PA ⊄平面BDE ,OE ⊂平面BDE∴ PA //平面BDE ………………………………………………………………12分19.解:(I )当1=n ,21=a ;…………………………………………………………1分当2≥n 时,1122n n n n n a S S a a --=-=- ,∴ 12n n a a -=.…………………2分∴{}n a 是等比数列,公比为2,首项12a =, ∴2n n a =.…………………3分 由12n n b b +=+,得{}n b 是等差数列,公差为2. ……………………………4分又首项11=b ,∴ 21n b n =-. ……………………………………………6分(II )2(21)n n c n ⎧=⎨--⎩ 为偶数为奇数n n ……………………………………8分3212222[37(41)]n n T n -=+++-+++- ………………………10分2122223n n n +-=--.…………………………………………………… 12分 20.解: (I )∵直线l 的倾斜角为60︒∴直线l的斜率为k =l过点(0,- ∴直线l的方程为y += …………………………………………………3分 ∵a b >,∴椭圆的焦点为直线l 与x 轴的交点∴椭圆的焦点为(2,0)∴2c =,又∵3c e a ==∴a =,∴2222b a c =-= ∴椭圆方程为22162x y += ………………………………………………………… 5分 (Ⅱ)设直线l 的方程为3x my =-,1122(,),(,)A x y B x y …………………………6分 联立直线与椭圆的方程221623x y x my ⎧+=⎪⎨⎪=-⎩,得22(3)630m y my +-+= 12122263,33m y y y y m m +==++ …………………………………………………7分 由题意可知11AF BF ⊥,即111AF BF k k ⋅=- ………………………………………8分 ∴121212212121212122(1)(1)()1y y y y y y x x my my m y y m y y ⋅===-++---++整理得:21212(1)()10m y y m y y +-++= ……………………………………10分 ∴22223(+1)61033m m m m -+=++,解得m =…………………………………11分 代入22=3612(3)24336360m m ∆-+=⨯-=>………………………………12分 所以直线l的方程为3030x x +=+=或 ………………………13分22.解:(I )因为 1()ln x f x x ax -=+,所以21'()(0)ax f x a ax-=>………1分 依题意可得,对21[1,).'()0ax x f x ax -∀∈+∞=≥恒成立, 所以 对[1,),10x ax ∀∈+∞-≥恒成立,所以 对1[1,),x a x∀∈+∞≥恒成立,max 1()a x ≥,即1a ≥……………………4分 (Ⅱ)函数()()g x f x m =-在1[,2]2上有两个零点, 即()f x m =在1[,2]2上有两个不同的实数根, 即函数()y f x =的图像与直线y m =在1[,2]2上有两个零点。
【潍坊一模_文数】山东省潍坊市2015届高三3月一模数学(文)试题及答案(Word版)
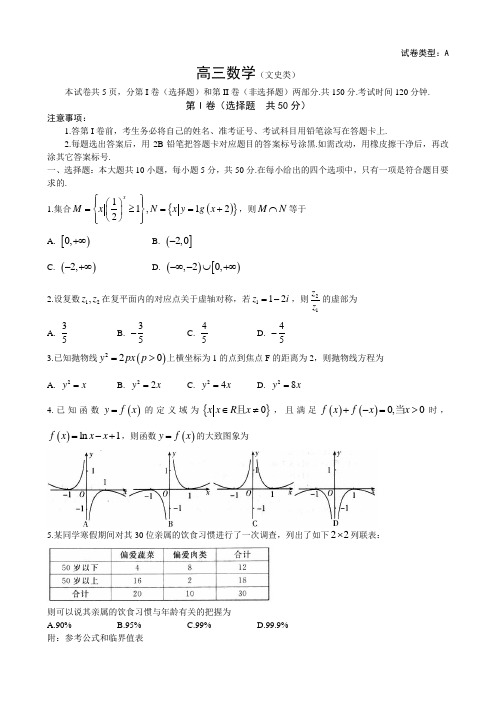
试卷类型:A高三数学(文史类)本试卷共5页,分第I 卷(选择题)和第II 卷(非选择题)两部分.共150分.考试时间120分钟.第I 卷(选择题 共50分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再改涂其它答案标号.一、选择题:本大题共10小题,每小题5分,共50分.在每小给出的四个选项中,只有一项是符合题目要求的.1.集合(){}11,122xM x N x y g x ⎧⎫⎪⎪⎛⎫=≥==+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,则M N ⋂等于A. [)0,+∞B. (]2,0-C. ()2,-+∞D. ()[),20,-∞-⋃+∞2.设复数12,z z 在复平面内的对应点关于虚轴对称,若112z i =-,则21z z 的虚部为 A.35B. 35-C.45D. 45-3.已知抛物线()220y px p =>上横坐标为1的点到焦点F 的距离为2,则抛物线方程为 A. 2y x =B. 22y x =C. 24y x =D. 28y x =4.已知函数()y f x =的定义域为{}0x x Rx ∈≠且,且满足()()0,0f x f x x +-=>当时,()l n 1f x x x =-+,则函数()y f x =的大致图象为5.某同学寒假期间对其30位亲属的饮食习惯进行了一次调查,列出了如下22⨯列联表:则可以说其亲属的饮食习惯与年龄有关的把握为 A.90% B.95% C.99% D.99.9%附:参考公式和临界值表6.下列结论中正确的是①命题:()30,2,3x x x ∀∈>的否定是()30,2,3x x x ∃∈≤; ②若直线l 上有无数个点不在平面α内,则//l α;③射击比赛中,比赛成绩的方差越小的运动员成绩越不稳定; ④等差数列{}n a 的前n 项和为473=21.n S a S =,若,则 A.①②B.②③C.③④D.①④7.如图,在ABC ∆中,点D 在AC上,,5,sin AB BD BC BD ABC ⊥==∠=,则CD 的长为A.B.4C.D.58.某几何体的三视图如图所示,其中左视图为半圆,则该几何体的体积是A.3B.2πC.3D.π9.圆()22:125C x y -+=,过点()2,1P -作圆的所有弦中,以最长弦和最短弦为对角线的四边形的面积是A.B.C.D. 10.对于实数,m n 定义运算“⊕”: ()()2221,21m mn m nm n f x x n mnm n ⎧-+-≤⎪⊕==-⊕⎨->⎪⎩设 ()1x -,且关于x 的方程()f x a =恰有三个互不相等的实数根123,,,x x x 则123,,x x x 的取值范围是A. 1,032⎛⎫-⎪⎝⎭B. 1,016⎛⎫-⎪⎝⎭C. 10,32⎛⎫ ⎪⎝⎭D. 10,16⎛⎫⎪⎝⎭第II 卷(非选择题 共100分)注意事项:1.将第II 卷答案用0.5mm 的黑色签字笔答在答题纸的相应位置上.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共5小题,每小题5分,共25分.11.已知0,0,x y >>且满足1221x y x y+=+,则的最小值是_________. 12.运行右面的程序框图,如果输入的x 的值在区间[]2,3-内,那么输出的()fx的取值范围是_________.13.若变量,x y 满足约束条件20,3260,3x y x y z x y y k +-≥⎧⎪--≤=+⎨⎪≥⎩且的最小值为4,则k=_________.14.对于实数[],x x 表示不超过x的最大整数,观察下列等式:按照此规律第n 个等式的等号右边的结果为______________________.15.设双曲线()222210,0x y a b a b-=>>的左焦点为F ,过点F 作与x 轴垂直的直线l 交两条渐近线于M 、N两点,且与双曲线在第二象限的交点为P.设O 为坐标原点,若()1,,8OP mOM nON m n R mn =+∈=且,则双曲线的离心率为________.三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤. 16. (本小题满分12分) 已知函数()()2sin 24sin 206f x x x πωωω⎛⎫=--+> ⎪⎝⎭,其图象与x 轴相邻两个交点的距离为2π. (I )求函数()f x 的解析式;(II )若将()f x 的图象向左平移()0m m >个长度单位得到函数()g x 的图象恰好经过点,03π⎛⎫-⎪⎝⎭,求当m 取得最小值时,()7612g x ππ⎡⎤-⎢⎥⎣⎦在,上的单调递增区间. 17. (本小题满分12分)如图,已知平行四边形ABCD 与直角梯形ABEF 所在的平面互相垂直,11,//,2AB BE AF BE AF AB AF ===⊥,4CBA BC π∠==,P 为DF的中点.(I )求证:PE//平面ABCD ; (II )求三棱锥A BCE -的体积.18. (本小题满分12分)某校从参加某次数学能力测试学生中抽出36名学生,并统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率分布直方图如图所示,其中成绩分组区间是:[)[)[)[]809090.100100110110120,,,,,,.(I )求实数a 的值并求这36名学生成绩的样本平均数x (同一组中的数据用该组区间的中点值作代表); (II )已知数学成绩为120分有4位同学,从这4位同学中任选两位同学,再从数学成绩在[)8090,中任选一位同学组成“二帮一”小组.已知甲同学的成绩为81分,乙同学的成绩为120分,求甲、乙两同学恰好被安排在同一个“二帮一”小组的概率.19. (本小题满分12分)已知各项都为正数的等比数列{}n a 的前n 项和为n S ,数列{}n b 的通项公式{}n b 的通项公式().1n n n b n N n n *⎧=∈⎨+⎩为偶数为奇数若2352441,S b a a b =+⋅=. (I )求数列{}n a 的通项公式; (II )求数列{}n n a b ⋅的前n 项和n T . 20. (本小题满分13分)椭圆2222:1x y C a b+=的左、右焦点分别为12,F F ,直线1:l x my +=C 的右焦点2F 且与椭圆交于P ,Q 两点,已知1F PQ ∆的周长为8,点O 为坐标原点. (I )求椭圆C 的方程;(II )设直线:l y kx t =+与椭圆C 相交于M,N 两点,以线段OM ,ON 为邻边作平行四边形OMGN ,其中点G 在椭圆C 上,当112t ≤≤时,求OG 的取值范围.21. (本小题满分14分)已知函数()()2ln f x x ax x a R =--∈.(I )当1a =时,求函数()f x 在()1,2-处的切线方程; (II )当0a ≤时,讨论函数()f x 的单调性;(III )问当0a >时,函数()y f x =的图象上是否存在点()()00,P x f x ,使得以P 点为切点的切线()l y f x =将的图象分割成12,C C 两部分,且12,C C 分别位于l 的两侧(仅点P 除外)?若存在,求出0x 的值;若不存在,说明理由.。
山东省潍坊市2015届高三下学期四县联考模拟训练数学(文)试题

2015年高三模拟训练数学试题(文科)本试卷分第I 卷和第Ⅱ卷两部分,共5页。
满分150分。
考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中。
只有一项是符合题目要求的.1.已知集合{}24,,2x M x x x N y y x M M N ⎧⎫⎪⎪=>==∈⋂=⎨⎬⎪⎪⎩⎭,则 A.102x x ⎧⎫<<⎨⎬⎩⎭ B. 112x x ⎧⎫<<⎨⎬⎩⎭ C. {}01x x << D. {}2x x 1<<2.已知i 为虚数单位,2,i a R a i -∈+若为纯虚数,则复数()21z a =+的模等于A. B. C. D. 3.经过圆2220x x y -+=的圆心且与直线20x y +=平行的直线方程是A. 210x y +-=B. 220x y --=C. 210x y -+=D. 220x y ++= 4.已知()01110b a a a a b >≠>->且,则是的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5. 已知函数()sin 2f x x =向左平移6π个单位后,得到函数()y g x =,下列关于()y g x =的说法正确的是A.图象关于点,03π⎛⎫- ⎪⎝⎭中心对称B.图象关于6x π=-轴对称C.在区间5,126ππ⎡⎤--⎢⎥⎣⎦单调递增D.在,63ππ⎡⎤-⎢⎥⎣⎦单调递减 6. 设m n 、是两条不同的直线,αβ、是两个不同的平面,下列四个命题正确的是A.若//,//,//m n m n αββαβ⊂、,则B. 若//,m ααββ⊂,则m//C.若,//,m n ααββ⊥⊥⊥,则m nD. 若,,αγβγαβ⊥⊥⊥则7. 一算法的程序框图如图所示,若输出的12y =,则输入的x 的值可能为A. 1-B.0C.1D.5 8.能够把圆O :229x y +=的周长和面积同时分为相等的两部分的函数()f x 称为圆O 的“亲和函数”,下列函数:①()324f x x x =+,②()5ln 5x f x x -=+,③()2x x e e f x -+=,④()tan5x f x =是圆O 的“亲和函数”的是 A.①③ B.②③ C.②④ D.①④9.已知双曲线()22122:10,0x y C a b a b-=>>的离心率为2,若抛物线()22:20C x py p =>的焦点到双曲线1C 的渐近线的距离为2,则抛物线2C 的方程为A. 2x y =B. 2x y =C. 28x y =D. 216x y = 10. 若直线:1l ax by -=与不等式组1320320y x y x y <⎧⎪--<⎨⎪++>⎩表示的平面区域无公共点,则32a b-的最小值为 A. 72 B. 112- C.2 D. 2-第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.若不等式23208kx kx +-≥的解集为空集,则实数k 的取值范围是________. 12.若一个底面是正三角形的直三棱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为_________.13. ()G x 表示函数2cos 3y x =+的导数,在区间,3ππ⎡⎤-⎢⎥⎣⎦上,随机取值a ,则()1G a <的概率为__________.14.已知cos 0,sin 2423πππθθθ⎛⎫⎛⎫⎛⎫+=∈-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则__________. 15.已知()f x 是定义在()0,+∞上的单调函数,()()f x f x '是的导函数,若对()0,x ∀∈+∞,都有()23x f f x ⎡⎤-=⎣⎦,则方程()40f x x'-=的解所在的区间是________. 三、解答题:本大题共6小题,共75分.16. 已知函数()2sin 22cos 1,6f x x x x R π⎛⎫=-+-∈ ⎪⎝⎭, (I )求()f x 的最小正周期和单调递增区间;(II )在ABC ∆中,三内角A,B,C 的对边分别为a,b,c ,已知()1,,,2f A b a c =成等差数列,且9AB AC ⋅=uu u r uuu r ,求ABC S ∆及a 的值.17.如右图所示,正方形ABCD 与直角梯形ADEF 所在平面互相垂直,90,//,22ADE AF DE DE DA AF ∠====o . (I )求证:AC//平面BEF ;(II )求四面体BDEF 的体积.18. 下图是某市今年1月份前30天空气质量指数(AQI )的趋势图.(I )根据该图数据在答题卷中完成频率分布表,并在下图中作出这些数据的频率分布直方图;(II )当空气质量指数(AQI )小于100时,表示空气质量优良.某人随机选择当月(按30天计)某一天到达该市,根据以上信息,能否认为此人到达当天空气质量优良的可能性超过60%?19. (本小题满分12分)已知数列{}n a 的前n 项和为()21n n n S n N a S n *∈+=+,且满足.(I )求证:数列{}2n a -是等比数列,并求数列{}n a 的通项公式;(II )求证:21223111112223n n n a a a a a a +++⋅⋅⋅+<.20. (本小题满分13分)已知函数()22ln f x a x ax x =+-. (I )当0a >时,求函数()f x 的单调区间;(II )设()()22g x a x f x =-,且函数()g x 在点1x =处的切线为l ,直线//l l l y '',且在轴上的截距为1,求证:无论a 取任何实数,函数()g x 的图象恒在直线l '的下方.21. (本小题满分14分)已知抛物线2y =的焦点为椭圆()222210x y a b a b +=>>的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B ,经过椭圆左焦点的直线l 与椭圆交于C 、D (异于A,B )两点. (I )求椭圆标准方程;(II )求四边形ADBC 的面积的最大值;(III )若()()1122,,M x y N x y 、是椭圆上的两动点,且满足121220x x y y +=,动点P 满足2OP OM ON =+uu u r uuu r uuu r (其中O 为坐标原点),是否存在两定点12,F F 使得12PF PF + 为定值,若存在求出该定值,若不存在说明理由.。
【2015潍坊三模】山东省潍坊市2015届高三5月高考模拟 数学(文)试题 Word版含答案

2015潍坊三模 高三数学(文)2015.5本试卷共5页,分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.第I 卷(选择题 共50分)注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、考试科目填写在规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.i 是虚数单位,复数221ii-=+ A.2B. 2-C.2iD. 2i -2.已知集合(){}{}22ln ,90A x y x x B x xA B ==-=-≤⋂=,则A. [][]3013-⋃,,B. [](]3013-⋃,,C. ()01,D. []33-,3.在ABC ∆中,内角A,B,C 的对边分别为,,,3,2,cos a b c a b B A A ==∠=∠若则的值为A.B.C.D.4.设01a a >≠且.则“函数()()log 0a f x x =+∞是,上的增函数”是“函数()()1xg x a a =-⋅”是R 上的减函数的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.一个几何体的三视图如图所示,其中左视图为直角三角形,则该几何体的体积为A.B.C.D.6.运行如图所示的程序框图,若输出的S 是254,则①处应为 A. 5n ≤ B. 6n ≤ C. 7n ≤D. 8n ≤7.已知函数()2321cos ,,,432f x x x f f f ⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭则的大小关系是A. 132243f f f ⎛⎫⎛⎫⎛⎫-<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B. 123234f f f ⎛⎫⎛⎫⎛⎫-<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C. 321432f f f ⎛⎫⎛⎫⎛⎫<<- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D. 213324f f f ⎛⎫⎛⎫⎛⎫<-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭8.当0a >时,函数()()22xf x x ax e =+的图象大致是9.已知抛物线21:2C y x =的焦点F 是双曲线()22222:10,0x y C a b a b-=>>的一个顶点,两条曲线的一个交点为M ,若32MF =,则双曲线2C 的离心率是A.B.C.D.10.已知函数()f x 和()g x 是两个定义在区间M 上的函数,若对任意的x M ∈,存在常数0x M ∈,使得()()()()()()0000,f x f x g x g x f x g x ≥≥≤,且,则称函数()f x 和()g x 在区间M 上是“相似函数”.若()()()322log 138f x x b g x x x =-+=-+与在5,34⎡⎤⎢⎥⎣⎦上是“相似函数”,则函数()f x 在区间5,34⎡⎤⎢⎥⎣⎦上的最大值为A.4B.5C.6D.92第II 卷(非选择题 共100分)注意事项:将第II 卷答案用0.5mm 的黑色签字笔答在答题卡的相应位置上. 二、填空题:本大题共5小题,每小题5分,共25分. 11.在区间[]3,3-上随机取一个数x ,使得301xx -≥+成立的概率为_________.12.已知圆C 的圆心是直线10x y x -+=与轴的交点,且圆C 与圆()()22238x y -+-=相外切,则圆C 的方程为__________.13.已知,x y 满足约束条件002040x y x y x y <⎧⎪>⎪⎨+-≤⎪⎪-+≥⎩,若目标函数()0z x my m =+≠取得最大值时最优解有无数个,则m 的值为___________.14.已知数列{}n a 是等差数列,n S .是它的前n 项和,则数列n S n ⎧⎫⎨⎬⎩⎭是等差数列.由此类比:数列{}n b 是各项为正数的等比数列,n T 是它的前n 项积,则数列{}_______为等比数列(写出一个正确的结论).15.已知函数()f x 对任意x R ∈满足()()()11f x f x f x +=-,且是偶函数,当[]1,0x ∈-时,()21f x x =-+,若方程()f x a x =至少有4个相异实根,则实数a 的取值范围是___________.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)如右图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A 实践的次数和乙班4名同学在同一学年中去社会实践基地B 实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x 表示.(I )如果7x =,求乙班4名同学实践基地B 实践次数的中位数和方差;(II )如果9x =,从实践次数大于8的同学中任选两名同学,求选出的两名同学分别在甲、乙两个班级且实践次数的和大于20的概率.17. (本小题满分12分) 已知函数())()2sin sin f x xx x x R ωωω=+∈的图象的一条对称轴为x π=,其中ω为常数,且1,13ω⎛⎫∈ ⎪⎝⎭. (I )求函数()f x 的最小正周期;(II )在ABC ∆中,角A,B,C 的对边分别为,,a b c ,若63,35f A b c ⎛⎫=+= ⎪⎝⎭,求a 的最小值.18. (本小题满分12分)如右图,斜三棱柱1111111ABC A B C A B A C -=中,,点E,F 分别是1111,B C A B 的中点,111,60AA AB BE A AB ===∠=.(I )求证:1//AC 平面1A BE ; (II )求证:BF ⊥平面111A B C .19. (本小题满分12分)已知数列{}n a 与{}n b 满足:(){}1232log .n n n a a a a b n N a *+++⋅⋅⋅+=∈若为等差数列,且1322,64a b b ==. (I )求n n a b 与;(II )设(){}212n a n n n c a n c -=++⋅,求数列的前n 项和n T .20. (本小题满分13分)已知椭圆()2222:10x y C a b a b +=>>O 为坐标原点,椭圆C 与曲线y x =的交点分别为A,B (A 在第四象限),且32OB AB ⋅=uu u r uu u r .(I )求椭圆C 的标准方程;(II )定义:以原点O 22221x y a b+=的“伴随圆”.若直线l 交椭圆C 于M,N 两点,交其“伴随圆”于P ,Q 两点,且以MN 为直径的圆过原点O ,证明:PQ 为定值.21. (本小题满分14分)已知函数()()()21ln ,f x x x g x a x =-=,其中a R ∈.(I )若曲线()y f x =与曲线()2y g x x ==在处的切线互相垂直,求实数a 的值; (II )记()()()1F x f x g x =+-,讨论函数()F x 的单调性;(III )设函数()()()G x f x g x =+两个极值点分别为1212,x x x x <,且, 求证:()211ln 242G x >-.。
山东省潍坊第一中学2015届高三第一次(10月)月考数学(文)试题

潍坊一中2015届高三年级第一次月考数 学 试 卷(文)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合}111|{≥-+=x x x M ,集合}032|{>+=x x N ,则=⋂N M C R )(( ) A .(-1,23) B .(-1,23] C .[-1,23) D .[-1,23] 2.已知α是第二象限角,且sin(53)-=+απ,则tan2α的值为( ) A .54 B .723- C .724- D .924- 3.下列函数中,在其定义域是减函数的是( ) A. 12)(2++-=x x x f B. x x f 1)(=C. ||)41()(x x f = D. )2ln()(x x f -= 4. 下列函数中,最小正周期为π,且图象关于直线x=3π对称的函数是( )A .y=2sin(2x+3π) B .y=2sin(2x-6π)C .y=2sin(32π+x ) D .y=2sin(2x-3π) 5.已知二次函数4)(2+-=ax x x f ,若)1(+x f 是偶函数,则实数的值为( )A. -1B. 1C. -2D. 2xy-1127π 3π 6. 2||,0)(sin(πϕωϕω<>+=x y )的图象的一部分图形如图所示,则函数的解析式为( )A .y=sin(x+3π) B .y=sin(x-3π)C .y=sin(2x+3π)D .y=sin(2x-3π)7. 设a 为实数,函数f (x )=x 3+ax 2+(a -2)x 的导数是)('x f ,且)('x f 是偶函数,则曲线y =f (x )在原点处的切线方程为( )A .y =-2xB .y =3xC .y =-3xD .y =4x8.已知函数⎩⎨⎧≤<+-<≤---=)10(1)01(1)(x x x x x f ,则1)()(->--x f x f 的解集为( )A .(-∞,-1)∪(1,+∞) B. [-1,-21)∪(0,1] C .(-∞,0)∪(1,+∞) D. [-1,-21]∪(0,1) 9.对于任意的实数a 、b ,记max{a,b}=⎩⎨⎧<≥)()(b a b b a a .若F(x)=max{f(x),g(x)}(x ∈R),其中函数y=f(x)(x ∈R)是奇函数,且在x=1处取得极小值-2,函数y=g(x) (x ∈R)是正比例函数,其图象与x ≥0时的函数y=f(x)的图象如图所示,则下列关于函数y=F(x)的说法中,正确的是( ) A .y=F(x)为奇函数 B .y=F(x)有极大值F(-1)C .y=F(x)的最小值为-2,最大值为2D .y=F(x)在(-3,0)上为增函数10.已知函数f (x )是定义在R 上的偶函数,且对任意的x ∈R ,都有f (x +2)=f (x ).当0≤x ≤1时,f (x )=x 2.若直线y =x +a 与函数y =f (x )的图像在[0,2]内恰有两个不同的公共点,则实数a 的值是( )A .0B .0或-12C .-14或-12D .0或-14二.填空题:(本大题共4小题,每小题5分。
山东省潍坊市2015年高三一模试题

山东省潍坊市2015届高三第一次模拟考试文综试题本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分300分,考试用时150分钟。
考试结束后,将答题卡和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在答题卡规定的地方。
第I卷(必做,共140分)注意事项:1.第I卷共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不涂在答题卡上,只答在试卷上无效。
每年六月到七月初,我国东部地区常会出现右图所示的天气系统,读图回答1~2题。
1.该天气系统在此地区停留期间,甲地 A.正午日影逐渐变短B.6时以后日出 C.正午太阳高度比乙地小D.昼长比乙地短2.如果该天气系统在此地区停留时间过短,我国东部地区可能会 A.南旱北涝 B.南涝北旱 C.南北皆旱 D.南北皆涝进入2015年以来,国内奶源价格持续走低。
而从新西兰等地大包装进口的奶源数量不减反增。
读图回答3~5题。
3.近年来,国内制奶企业大量从新西兰进口奶源的主要原因是①国内生产供不应求,需大量进口②新西兰劳动力、土地价格低③新西兰环境优美、奶源质量好④大包装进口,成本较低 A.①② B.②③ C.①③ D.③④4.关于新西兰自然特征描述正确的是 A.植被以常绿阔叶林为主 B.B岛地势东南坡缓,西北坡陡 C.位于板块生长边界,多火山分布 D.河流夏汛明显,结冰期长5.B岛西南部海岸多U型峡湾,其形成的地质作用主要是 A.地壳断裂下沉 B.海浪侵蚀 C.古冰川侵蚀 D.河流冲积“人口红利期”是指随着生育率的下降和总人口中劳动适龄人口比重的上升,形成了一个劳动力资源相对丰富、人口抚养负担相对较轻的时期。
读我国不同年龄段人口比例随时间变化图,田答6~7题。
6.在人口红利期A.65岁以上老龄人口总量减少 B.15—64岁劳动力人口比重持续上升 C.0—14岁青少年人口数量减少 D.2010年前后人口抚养负担最轻7.我国要想适度延长人口红利期,下列措施可行的是①实施“单独”二胎政策②完善养老保障体制③渐进式延迟退休年龄④促进国内人口迁移 A.①② B.①③ C.②③ D.①④读某城市用地功能区规划示意图(从环境因素考虑,图中各功能区用地规划合理),回答8~9题。
2015年山东省潍坊市高考一模数学试卷(文科)【解析版】

2015年山东省潍坊市高考数学一模试卷(文科)一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)集合M={x|()x≥1},N={x|y=lg(x+2)},则M∩N等于()A.[0,+∞)B.(﹣2,0]C.(﹣2,+∞)D.(﹣∞,﹣2)∪[0,+∞)2.(5分)设复数z1,z2在复平面内对应的点关于虚轴对称,若z1=1﹣2i,则的虚部为()A.B.﹣C.D.﹣3.(5分)如果双曲线﹣=1(a>0,b>0)的一条渐近线与直线x﹣y+=0平行,则双曲线的离心率为()A.B.C.2D.34.(5分)已知函数y=f(x)的定义域为{x|x≠0},满足f(x)+f(﹣x)=0,当x>0时,f(x)=1gx﹣x+1,则函数)y=f(x)的大致图象是()A.B.C.D.5.(5分)某同学寒假期间对其30位亲属的饮食习惯进行了一次调查,列出了如下2×2列联表:则可以说其亲属的饮食习惯与年龄有关的把握为()附:参考公式和临界值表:Χ2=A.90%B.95%C.99%D.99.9%6.(5分)下列结论中正确的是()①命题:∀x∈(0,2),3x>x3的否定是∃x∈(0,2),3x≤x3;②若直线l上有无数个点不在平面α内,则l∥α;③若随机变量ξ服从正态分布N(1,σ2),且P(ξ<2)=0.8,则P(0<ξ<1)=0.2;④等差数列{a n}的前n项和为S n,若a4=3,则S7=21.A.①②B.②③C.③④D.①④7.(5分)如图,在△ABC中,点D在AC上,AB⊥BD,BC=3,BD=5,sin∠ABC=,则CD的长为()A.B.4C.2D.58.(5分)某几何体的三视图是如图所示,其中左视图为半圆,则该几何体的体积是()A.πB.C.πD.π9.(5分)圆C:(x﹣1)2+y2=25,过点P(2,﹣1)作圆的所有弦中,以最长弦和最短弦为对角线的四边形的面积是()A.10B.9C.10D.910.(5分)对于实数m,n定义运算“⊕”:m⊕n=,设f(x)=(2x﹣1)⊕(x﹣1),且关于x的方程f(x)=a恰有三个互不相等的实数根x1,x2,x3,则x1x2x3的取值范围是()A.(﹣,0)B.(﹣,0)C.(0,)D.(0,)二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卷的横线上..11.(5分)已知x>0,y>0,且2x+y=1,则+的最小值是.12.(5分)运行右面的程序框图,如果输入的x的值在区间[﹣2,3]内,那么输出的f(x)的取值范围是13.(5分)若变量x,y满足约束条件,且z=x+3y的最小值为4,则k=.14.(5分)对于实数x,[x]表示不超过x的最大整数,观察下列等式:[]+[]+[]=3[]+[]+[]+[]+[]=10[]+[]+[]+[]+[]+[]+[]=21…按照此规律第n个等式的等号右边的结果为.15.(5分)设双曲线=1(a>0,b>0)的左焦点为F,过点F作与x 轴垂直的直线l交两条渐近线于M,N两点,且与双曲线在第二象限的交点为P,设O为坐标原点,若(m,n∈R),且mn=,则双曲线的离心率为.三、解答题:本大题共6小题,满分75分,解答应写出文字说明、证明过程或演算步骤16.(12分)已知函数f(x)=sin(2wx﹣)﹣4sin2wx+2(w>0),其图象与x轴相邻两个交点的距离为.(1)求函数f(x)的解析式;(2)若将f(x)的图象向左平移m(m>0)个长度单位得到函数g(x)的图象恰好经过点(﹣,0),求当m取得最小值时,g(x)在[﹣,]上的单调增区间.17.(12分)如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=AF=1,BE∥AF,AB⊥AF,∠CBA=,BC=,P为DF的中点.(1)求证:PE∥平面ABCD;(2)求三棱锥A﹣BCE的体积.18.(12分)某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,其中成绩分组间是:[80,90),[90,100),[100,110),[110,120](1)求实数a的值并求这36名学生成绩的样本平均数(同一组中的数据用该组的中点值作代表);(2)已知数学成绩为120分有4位同学,从这4位同学中任选两位同学,再从数学成绩在[80,90)中任选以为同学组成“二帮一”小组,已知甲同学的成绩为81分,乙同学的成绩为120分,求甲、乙两同学恰好被安排在同一个“二帮一”小组的概率.19.(12分)已知各项为正数的等比数列数列{a n}的前n项和为S n,数列{b n}的通项公式b n=(n∈N*),若S3=b5+1,b4是a2和a4的等比中项.(1)求数列{a n}的通项公式;(2)求数列{a n•b n}的前n项和为T n.20.(13分)椭圆=1的左右焦点分别为F1,F2,直线l:x+my=恒过椭圆的右焦点F2,且与椭圆交于P,Q两点,已知△F1PQ的周长为8,点O 为坐标原点.(1)求椭圆C的方程;(2)若直线l:y=kx+t与椭圆C交于M,N两点,以线段OM,ON为邻边作平行四边形OMGN其中G在椭圆C上,当≤|t|≤1时,求|OG|的取值范围.21.(14分)已知函数f(x)=lnx﹣ax2﹣x(a∈R)(1)当a=1时,求函数f(x)在(1,﹣2)处的切线方程;(2)当a≤0时,讨论函数f(x)的单调性;(3)问当a>0时,函数y=f(x)的图象上是否存在点P(x0,f(x0)),使得以P点为切点的切线l将y=f(x)的图象分割成C1,C2两部分,且C1,C2分别位于l的两侧(仅点P除外)?若存在,求出x0的值;若不存在,说明理由.2015年山东省潍坊市高考数学一模试卷(文科)参考答案与试题解析一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)集合M={x|()x≥1},N={x|y=lg(x+2)},则M∩N等于()A.[0,+∞)B.(﹣2,0]C.(﹣2,+∞)D.(﹣∞,﹣2)∪[0,+∞)【解答】解:因为集合M={x|≥1}={x|≥},所以M={x|x≤0},N={x|y=lg(x+2)}={x|x>﹣2},所以A∩B={x|x≤0}∩{x|x>﹣2}={x|﹣2<x≤0},故选:B.2.(5分)设复数z1,z2在复平面内对应的点关于虚轴对称,若z1=1﹣2i,则的虚部为()A.B.﹣C.D.﹣【解答】解:复数z1,z2在复平面内对应的点关于虚轴对称,若z1=1﹣2i,z2=﹣1﹣2i,则====.复数的虚部为:.故选:D.3.(5分)如果双曲线﹣=1(a>0,b>0)的一条渐近线与直线x﹣y+=0平行,则双曲线的离心率为()A.B.C.2D.3【解答】解:∵双曲线﹣=1(a>0,b>0)的一条渐近线与直线x﹣y+=0平行∴双曲线的渐近线方程为y=±x∴=,得b2=3a2,c2﹣a2=3a2,此时,离心率e==2.故选:C.4.(5分)已知函数y=f(x)的定义域为{x|x≠0},满足f(x)+f(﹣x)=0,当x>0时,f(x)=1gx﹣x+1,则函数)y=f(x)的大致图象是()A.B.C.D.【解答】解:因为函数y=f(x)的定义域为{x|x≠0},满足f(x)+f(﹣x)=0,所以函数是奇函数,排除C、D.又函数当x>0时,f(x)=lgx﹣x+1,当x=10时,y=1﹣10+1=﹣8,就是的图象在第四象限,A正确,故选:A.5.(5分)某同学寒假期间对其30位亲属的饮食习惯进行了一次调查,列出了如下2×2列联表:则可以说其亲属的饮食习惯与年龄有关的把握为()附:参考公式和临界值表:Χ2=A.90%B.95%C.99%D.99.9%【解答】解:设H0:饮食习惯与年龄无关.因为Χ2==10>6.635,所以有99%的把握认为其亲属的饮食习惯与年龄有关.故选:C.6.(5分)下列结论中正确的是()①命题:∀x∈(0,2),3x>x3的否定是∃x∈(0,2),3x≤x3;②若直线l上有无数个点不在平面α内,则l∥α;③若随机变量ξ服从正态分布N(1,σ2),且P(ξ<2)=0.8,则P(0<ξ<1)=0.2;④等差数列{a n}的前n项和为S n,若a4=3,则S7=21.A.①②B.②③C.③④D.①④【解答】解:①命题:∀x∈(0,2),3x>x3的否定是∃x∈(0,2),3x≤x3,正确;②若直线l上有无数个点不在平面α内,则l∥α或l与α相交,故不正确;③若随机变量ξ服从正态分布N(1,σ2),且P(ξ<2)=0.8,则P(ξ>2)=0.2,P(0<ξ<1)=0.5﹣0.2=0.3,不正确;④等差数列{a n}的前n项和为S n,若a4=3,则S7==7a4=21,正确.故选:D.7.(5分)如图,在△ABC中,点D在AC上,AB⊥BD,BC=3,BD=5,sin∠ABC=,则CD的长为()A.B.4C.2D.5【解答】解:由题意可得sin∠ABC==sin(+∠CBD)=cos∠CBD,再根据余弦定理可得CD2=BC2+BD2﹣2BC•BD•cos∠CBD=27+25﹣2×3×5×=16,可得CD=4,故选:B.8.(5分)某几何体的三视图是如图所示,其中左视图为半圆,则该几何体的体积是()A.πB.C.πD.π【解答】解:根据几何体的三视图,得;该几何体是平放的半圆锥,且圆锥的底面半径为1,母线长为3,∴圆锥的高为=2;∴该几何体的体积为V半圆锥=×π×12×2=π.故选:A.9.(5分)圆C:(x﹣1)2+y2=25,过点P(2,﹣1)作圆的所有弦中,以最长弦和最短弦为对角线的四边形的面积是()A.10B.9C.10D.9【解答】解:∵圆的方程为:(x﹣1)2+y2=25,∴圆心坐标为M(1,0),半径r=5.∵P(2,﹣1)是该圆内一点,∴经过P点的直径是圆的最长弦,且最短的弦是与该直径垂直的弦.结合题意,得AC是经过P点的直径,BD是与AC垂直的弦.∵|PM|=,∴由垂径定理,得|BD|=2=2.因此,四边形ABCD的面积是S=|AC|•|BD|=×10×2=10.故选:C.10.(5分)对于实数m,n定义运算“⊕”:m⊕n=,设f(x)=(2x﹣1)⊕(x﹣1),且关于x的方程f(x)=a恰有三个互不相等的实数根x1,x2,x3,则x1x2x3的取值范围是()A.(﹣,0)B.(﹣,0)C.(0,)D.(0,)【解答】解:由2x﹣1≤x﹣1,得x≤0,此时f(x)=(2x﹣1)*(x﹣1)=﹣(2x﹣1)2+2(2x﹣1)(x﹣1)﹣1=﹣2x,由2x﹣1>x﹣1,得x>0,此时f(x)=(2x﹣1)*(x﹣1)=(x﹣1)2﹣(2x ﹣1)(x﹣1)=﹣x2+x,∴f(x)=(2x﹣1)⊕(x﹣1)=,作出函数的图象可得,要使方程f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,不妨设x1<x2<x3,则0<x2<<x3<1,且x2和x3,关于x=对称,∴x 2+x3=2×=1.则x2+x3≥2,0<x2x3<,等号取不到.当﹣2x=时,解得x=﹣,∴﹣<x1<0,∵0<x2x3<,∴﹣<x1•x2•x3<0,即x1•x2•x3的取值范围是(﹣,0),故选:A.二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卷的横线上..11.(5分)已知x>0,y>0,且2x+y=1,则+的最小值是8.【解答】解:∵2x+y=1,∴+=(+)×(2x+y)=2+2+≥4+2=8当且仅当=,即x=,y=时等号成立,∴+的最小值是8故答案为:812.(5分)运行右面的程序框图,如果输入的x的值在区间[﹣2,3]内,那么输出的f(x)的取值范围是[,9].【解答】解:模拟执行程序,可得其功能是求分段函数f(x)=的值,所以,当x∈[﹣2,2]时,f(x)=2x∈[,4],当x∈(2,3]时,f(x)=x2∈(4,9].故如果输入的x的值在区间[﹣2,3]内,那么输出的f(x)的取值范围是[,9].故答案为:[,9].13.(5分)若变量x,y满足约束条件,且z=x+3y的最小值为4,则k=1.【解答】解:由z=x+3y,得,作出不等式对应的可行域,平移直线,由平移可知当直线,经过点B时,直线,的截距最小,此时z取得最小值为4,即x+3y=4,由,解得,即B(1,1),B同时也在直线y=k上,则k=1,故答案为:114.(5分)对于实数x,[x]表示不超过x的最大整数,观察下列等式:[]+[]+[]=3[]+[]+[]+[]+[]=10[]+[]+[]+[]+[]+[]+[]=21…按照此规律第n个等式的等号右边的结果为2n2+n.【解答】解:因为[x]表示不超过x的最大整数,所以=1,=2,…,因为等式:,,,…,所以第1个式子的左边有3项、右边1+1+1=1×3=3,第2个式子的左边有5项、右边2+2+2+2+2=2×5=10,第3个式子的左边有7项、右边3×7=21,则第n个式子的左边有(2n+1)项、右边=n(2n+1)=2n2+n,故答案为:2n2+n.15.(5分)设双曲线=1(a>0,b>0)的左焦点为F,过点F作与x 轴垂直的直线l交两条渐近线于M,N两点,且与双曲线在第二象限的交点为P,设O为坐标原点,若(m,n∈R),且mn=,则双曲线的离心率为.【解答】解:双曲线=1(a>0,b>0)的渐近线为:y=±x,设左焦点F(﹣c,0),则M(﹣c,),N(﹣c,﹣),P(﹣c,),因为(m,n∈R),所以(﹣c,)=(﹣(m+n)c,(m﹣n)),所以m+n=1,m﹣n=,解得:m=,n=,又由mn=,得:=,解得:=,所以,e==.故答案为:.三、解答题:本大题共6小题,满分75分,解答应写出文字说明、证明过程或演算步骤16.(12分)已知函数f(x)=sin(2wx﹣)﹣4sin2wx+2(w>0),其图象与x轴相邻两个交点的距离为.(1)求函数f(x)的解析式;(2)若将f(x)的图象向左平移m(m>0)个长度单位得到函数g(x)的图象恰好经过点(﹣,0),求当m取得最小值时,g(x)在[﹣,]上的单调增区间.【解答】解:(1)函数f(x)=sin(2wx﹣)﹣4sin2wx+2(w>0)=sin2wx﹣cos2wx﹣4•+2=sin2wx+cos2wx=sin(2wx+),根据图象与x轴相邻两个交点的距离为,可得函数的最小正周期为2×=,求得w=1,故函数f(x)=sin(2x+).(2)将f(x)的图象向左平移m(m>0)个长度单位得到函数g(x)=sin[2(x+m)+]=sin(2x+2m+)的图象,再根据g(x)的图象恰好经过点(﹣,0),可得sin(2m﹣)=0,故m =,g(x)=sin(2x+).令2kπ﹣≤2x+≤2kπ+,k∈z,求得kπ﹣≤x≤kπ﹣,故函数g(x)的增区间为[kπ﹣,kπ﹣],k∈z.再结合x∈[﹣,],可得增区间为[﹣,﹣]、[,].17.(12分)如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=AF=1,BE∥AF,AB⊥AF,∠CBA=,BC=,P为DF的中点.(1)求证:PE∥平面ABCD;(2)求三棱锥A﹣BCE的体积.【解答】(1)证明:取AD的中点M,连接MP,MB,∵P为DF的中点,∴,又∵,∴,∴四边形BEPM是平行四边形,∴PE∥BM,又PE⊄平面ABCD,BM⊂平面ABCD.∴PE∥平面ABCD.(2)解:在△ABC中,由余弦定理可得:AC2=AB2+BC2﹣2AB•BC cos∠ABC==1,∴AC=1,∴AC2+AB2=BC2,∴AC⊥AB.∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,∴AC⊥平面ABEF,∵==.∴V A﹣BCE =V C﹣ABE===.18.(12分)某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,其中成绩分组间是:[80,90),[90,100),[100,110),[110,120](1)求实数a的值并求这36名学生成绩的样本平均数(同一组中的数据用该组的中点值作代表);(2)已知数学成绩为120分有4位同学,从这4位同学中任选两位同学,再从数学成绩在[80,90)中任选以为同学组成“二帮一”小组,已知甲同学的成绩为81分,乙同学的成绩为120分,求甲、乙两同学恰好被安排在同一个“二帮一”小组的概率.【解答】解:(Ⅰ)由频率分布直方图知,10a=1﹣()×10=,故a==×10×85+×10×95+×10×115=,(Ⅱ)成绩在[80,90)分的学生有=3人,分别记为甲,A,B,数学成绩为120分有4位同学记为乙,1,2,3,则“二帮一”小组共有18种,分别去下:甲乙1,甲乙2,甲乙3,甲12,甲13,甲23,A乙1,A乙2,A乙3,A12,A13,A23,B乙1,B乙2,B乙3,B12,B13,B23,其中甲、乙两同学恰好被安排在同一个“二帮一”小组有3种情况,甲乙1,甲乙2,甲乙3故甲、乙两同学恰好被安排在同一个“二帮一”小组的概率为=19.(12分)已知各项为正数的等比数列数列{a n}的前n项和为S n,数列{b n}的通项公式b n=(n∈N*),若S3=b5+1,b4是a2和a4的等比中项.(1)求数列{a n}的通项公式;(2)求数列{a n•b n}的前n项和为T n.【解答】解:(1)∵数列{b n}的通项公式b n=(n∈N*),∴b5=6,b4=4,设各项为正数的等比数列数列{a n}的公比为q,q>0,∵S3=b5+1=7,∴,①∵b4是a2和a4的等比中项,∴,解得,②由①②得3q2﹣4q﹣4=0,解得q=2,或q=﹣(舍),∴a1=1,.(2)当n为偶数时,T n=(1+1)•20+2•2+(3+1)•22+4•23+(5+1)•24+…+[(n﹣1)+1]•2n﹣2+n•2n﹣1=(20+2•2+3•22+4•23+…+n•2n﹣1)+(20+22+…+2n﹣2),设H n=20+2•2+3•22+4•23+…+n•2n﹣1,①2H n=2+2•22+3•23+4•24+…+n•2n,②①﹣②,得﹣H n=20+2+22+23+…+2n﹣1﹣n•2n=﹣n•2n=(1﹣n)•2n﹣1,∴H n=(n﹣1)•2n+1,∴+=(n﹣)•2n+.当n为奇数,且n≥3时,T n=T n﹣1+(n+1)•2n﹣1==+,经检验,T1=2符合上式,∴T n=.20.(13分)椭圆=1的左右焦点分别为F1,F2,直线l:x+my=恒过椭圆的右焦点F2,且与椭圆交于P,Q两点,已知△F1PQ的周长为8,点O 为坐标原点.(1)求椭圆C的方程;(2)若直线l:y=kx+t与椭圆C交于M,N两点,以线段OM,ON为邻边作平行四边形OMGN其中G在椭圆C上,当≤|t|≤1时,求|OG|的取值范围.【解答】解:(1)∵直线l:x+my=恒过定点,∴椭圆的右焦点F2.∴.∴△F1PQ的周长为8,∴4a=8,解得a=2,∴b2=a2﹣c2=1,∴椭圆C的方程为=1;(2)联立,化为(1+4k2)x2+8ktx+4t2﹣4=0,由△=64k2t2﹣4(1+4k2)(4t2﹣4)>0,可得4k2+1>t2.设M(x1,y1),N(x2,y2),G(x0,y0),则,∵四边形OMGN是平行四边形,∴,y0=y1+y2=k(x1+x2)+2t=kx0+2t=,可得G,∵G在椭圆C上,∴+=1,化为4t2(4k2+1)=(4k2+1)2,∴4t2=4k2+1,∴|OG|2=====4﹣,∵≤|t|≤1,∴,∴,∴|OG|的取值范围是.21.(14分)已知函数f(x)=lnx﹣ax2﹣x(a∈R)(1)当a=1时,求函数f(x)在(1,﹣2)处的切线方程;(2)当a≤0时,讨论函数f(x)的单调性;(3)问当a>0时,函数y=f(x)的图象上是否存在点P(x0,f(x0)),使得以P点为切点的切线l将y=f(x)的图象分割成C1,C2两部分,且C1,C2分别位于l的两侧(仅点P除外)?若存在,求出x0的值;若不存在,说明理由.【解答】解:(1)当a=1时,f(x)=lnx﹣x2﹣x,f′(x)=﹣2x﹣1,函数f(x)在(1,﹣2)处的切线斜率为k=1﹣2﹣1=﹣2,则函数f(x)在(1,﹣2)处的切线方程为y+2=﹣2(x﹣1),即为y=﹣2x;(2)f′(x)=﹣2ax﹣1=(x>0),①当a=0时,f′(x )=,当0<x<1时,f′(x)>0,f(x)递增,当x>1时,f′(x)<0,f(x)递减.②当a<0时,f′(x)=0,即﹣2ax2﹣x+1=0,当△=1+8a≤0时,即a ≤﹣,﹣2ax2﹣x+1≥0在(0,+∞)恒成立,即f′(x)≥0在(0,+∞)恒成立,f(x)在(0,+∞)递增;当△=1+8a>0,即﹣<a<0时,﹣2ax2﹣x+1=0的两根为x1=x2=,f′(x )=(x>0)且x1>0,x2>0,x1<x2,则0<x<x1,f′(x)>0,f(x)递增,x1<x<x2,f′(x)<0,f(x)递减.综上可得,a=0,f(x)的增区间为(0,1),减区间为(1,+∞);a ≤﹣时,f(x)的增区间为(0,+∞);﹣<a<0时,f(x)的增区间为(0,),(,+∞),f(x )的减区间为(,).(3)f′(x )=﹣2ax﹣1,P(x0,f(x0)),在P点的切线方程为y=f′(x0)(x﹣x0)+f(x0),令g(x)=f(x)﹣f′(x0)(x﹣x0)+f(x0),且g(x0)=0,g′(x)=f′(x)﹣f′(x0)=﹣2ax﹣1﹣+2ax0+1=﹣(x﹣x0)•(x>0),由a>0,当0<x<x0,g′(x)>0,g(x)递增,当x>x0,g′(x)<0,g(x)递减,故g(x)≤g(x0)=0,即f(x)≤f′(x0)(x﹣x0)+f(x0),也就是y=f(x)的图象永远在切线的下方.故不存在这样的点P.第21页(共21页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
潍坊一中2015届高三过程性检测
数学(文科)试题
2015.04
本试卷分第I 卷(选择题)和第II 卷进(非选择题)两部分,满分150分。
考试用时120分钟。
注意事项:
1.答题前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号、班级和科类填写在答题卡和试卷规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3.第II 卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
第I 卷(共50分)
一.选择题:(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)
1.设全集(){}{}
(),ln 1,11,U U R A x y x B x x C A B ===-=-<⋂=则 A.()2,1-
B. (]2,1-
C. [)1,2
D. ()1,2
2.已知i 为虚数单位,复数121i
z i +=-,则z 的共轭复数虚部是 A.
32
i B.
32
C. 12
i - D. 32-
3.平面向量a b 与的夹角为()602,012a b a b ==+,,,则等于
A. B. C.12
D.
4.如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平
均数分别为x x 甲乙
、,中位数分别为m m
甲乙
,,则
A. ,m m x <<甲甲乙乙
B. ,m m x ><甲甲乙乙
C.
,m m x x >>甲甲乙乙
D.
,m m x x <>甲甲乙乙
5. 已知双曲线的中心在原点,一个焦点为()
1F ,
点p 在双曲线上,且线段1PF 的中点坐标为(0,2),则此双曲线的方程是
A. 2
214x y -= B. 2
214
y x -= C. 22123x y -=
D. 22132
x y -=
6.下列命题正确的是:
(1)已知命题:,2 1.,21x x p x R p x R ∃∈=⌝∃∈≠则是:
(2)设,l m 表示不同的直线,α表示平面,若//,////m l m l αα且,则; (3)利用计算机产生0~1之间的均匀随机数a ,则事件“310a ->”发生的概率为
23
(4)“0
,0a b >>”是“
2a b
b a
+≥”的充分不必要条件. A.(1)(4) B.(2)(3) C.(1)(3)
D.(3)(4)
7.
如
图
,
长
方
体
1111
ABCD A BC D -中
,
12,
2A B A D A
==设长方体的截面四边形11ABC D 的内切圆为O ,圆O 的正视图是椭圆O ',则椭圆O '的离心率等于
A.
3 B.
2
C.
3
D.
2 8.执行如图的程序,则输出的结果等于 A.
1
4950
B.
200
101
C.
9950
D.
15050
9.函数()22sin 1,0,
24,0
x x x f x x x x ⎧-+>⎪=⎨--≤⎪⎩的零点个数为
A.0
B.1
C.2
D.3
10.如果函数()y f x =在区间I 上是增函数,而函数()
f x y x
=
在区间I 上是减函数,那么称函数()y f x =是区间I 上“缓增函数”,区间I 叫做“缓增区间”.若函数()213
22
f x x x =-+是区间I 上“缓增函数”,则“缓增区间”I 为
A. [)1,+∞
B. ⎡⎣
C. []0,1
D. ⎡⎣
二、填空题:本大题共5小题,每小题5分,共25分。
请将答案填写在试题的横线上。
11.已知某几何体的三视图如右图所示,则该几何体的外接球体积为___________.
12.2by +=(其中a 、b 为非零实数)与圆221x y +=相交于A 、B 两点,O 为坐标原点,且AOB ∆为直角三角形,则
2212a b
+的最小值为________. 13.设O 为坐标原点,点()1,1,,4A M x y ⎛⎫
⎪⎝⎭若满足不等式组2
1
,2
x y x OM OA y +≥⎧⎪≤⎨⎪≤⎩
则uuu r uu r g 的最小值是___________.
14.如图为了测量A,C 两点间的距离,选取同一平面上B ,D 两点,测出四边形ABCD 的各边的长度(单
位:km ):5,8,3,5A B B C C D D A ====
,如图所
示,且A 、B 、C 、D 四点共圆,则AC 的长为
___________km.
15.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请120名同学,每人随机写下一个都小于1的正实数对(x ,y );再统计两数能与1构成钝角三角形三边的数对(x,y )的个数m ;最后再根据统计数m 来估计π的值.假如统计结果是m=94,那么可以估计π≈__________.(用分数表示)
三、解答题:本大题共6小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤.
16. (本小题满分12分)
已知函数()()sin 0,02f x x πωϕωφ⎛⎫
=+><< ⎪⎝
⎭
的图象经过点10,2⎛⎫ ⎪⎝⎭
,且相邻两条对
称轴的距离为
2
π. (1)求函数()f x 的解析式及其在[]0,π上的单调递增区间; (2)在,,ABC a b c ∆中,分别是A,B,C 的对边,若1cos ,122A f A bc ⎛⎫
-==
⎪
⎝⎭
且,3b c +=,求a 的值.
17. (本小题满分12分)
已知三棱柱111ABC A B C -中,11=90BCA AA AC BC A ∠===,在底面ABC 上
的射影恰为AC 的中点D. (1)求证:11AC BA ⊥; (2)求四棱锥111A BCC B -的体积.
18. (本小题满分12分)
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[)2025,,第2组[)25,30,第3组[)305,3,第4组[)35,40,第5组[)405,4,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
19. (本小题满分12分) 已知数列{}n a 满足{}11222,1
,2,n n n n a n n a a a a n n ++-⎧=
=⎨--⎩为奇数,数列为偶数
的前n 项和为2,n n n S b a =,其中n N *∈.
(I )试求23,a a 的值并证明数列{}n b 为等比数列; (II )设21n n n c b a +=+求数列11n n c c +⎧⎫
⎨⎬⎩⎭
的前n 项和.
20. (本小题满分13分)
已知圆1C 的圆心在坐标原点O ,
且恰好与直线1:20l x y -+=相切,点A 为圆上一
动点,AM x ⊥轴于点M ,且动点N
满足2233
3ON OA OM ⎛⎫=+- ⎪ ⎪⎝⎭uuu r uu r uuu r
,设动点N 的轨迹为曲线C.
(I )求椭圆C 的方程;
(II )若直线()1l 与中E 相交于不同两点A,B ,且满足OA OB ⊥u u r u u u r
(O 为坐标原点),求
线段AB 长度的取值范围.
21. (本小题满分14分)
已知函数()1x
f x e ax =--(0,a e >为自然对数的底数)
(I )若函数()f x 的最小值;
(II )若()0f x ≥在其定义域上恒成立,求实数a 的值; (III )在(2)的条件下,证明:()()111
11123n n n N n
*+
++⋅⋅⋅+>+∈。
