3.4 数据的离散程度 (1)
数据的离散程度教案

数据的离散程度教案教案标题:数据的离散程度教案教案目标:1. 理解数据的离散程度是指数据分布的分散程度,能够区分离散数据和连续数据。
2. 掌握计算数据的离散程度的方法,包括极差、方差和标准差。
3. 能够分析和比较不同数据集的离散程度,从而对数据的特征有更深入的了解。
教案步骤:步骤一:导入与概念讲解1. 引入数据的离散程度的概念,并解释离散程度与数据分布的关系。
2. 介绍离散数据和连续数据的区别,并给出实际例子进行说明。
步骤二:计算离散程度的方法1. 介绍极差的概念和计算方法,即最大值减去最小值。
2. 介绍方差的概念和计算方法,即每个数据与平均值的差的平方的平均值。
3. 介绍标准差的概念和计算方法,即方差的平方根。
步骤三:实例分析1. 给出一个实际数据集,要求学生计算其极差、方差和标准差。
2. 引导学生分析计算结果,比较不同数据集的离散程度。
3. 讨论离散程度与数据分布的关系,以及离散程度对数据分析的意义。
步骤四:拓展应用1. 提供更多实际数据集,要求学生计算其离散程度,并进行比较和分析。
2. 引导学生思考离散程度在不同领域的应用,如金融、医学等。
3. 鼓励学生提出自己的问题和观点,展开讨论和思考。
步骤五:总结与评价1. 总结本节课的内容,强调数据的离散程度对数据分析的重要性。
2. 对学生的参与和表现进行评价,鼓励积极思考和提问。
教学资源:1. PowerPoint演示文稿或白板,用于展示概念和计算方法。
2. 实际数据集,用于学生计算和分析。
评估方式:1. 学生计算离散程度的准确性和理解程度。
2. 学生对数据分析和离散程度的思考和应用能力。
3. 学生的课堂参与和表现。
教学延伸:1. 引导学生进一步学习其他数据分析方法,如偏度和峰度等。
2. 给予学生更多实际数据集,让他们自主进行数据分析和离散程度计算。
3. 鼓励学生进行小组或个人项目,以探索数据分析在实际问题中的应用。
数据的离散程度(课件)

离散程度反映的是数据值的分散 程度,如果数据值比较集中,则 离散程度较小;如果数据值比较 分散,则离散程度较大。
离散程度的度量方法
方差
方差是离散程度最常用的度量方法,它计算的是数据值与 平均值的差的平方的平均值。方差越大,说明数据值的离 散程度越大。
极差
极差是指数据中的最大值与最小值之差,它表示数据值的 最大离散程度。极差越大,说明数据值的离散程度越大。
优化数据收 集
算法改进
将多个来源的数据进行融合,综合利用不同数据源的 优势,提高数据的可靠性和一致性,降低数据的离散
程度。
数据融合
通过改进算法,提高数据处理的准确性和稳定性,从 而降低数据的离散程度。例如,采用更先进的统计分 析方法、优化决策树算法等。
未来发展前景
人工智能和机器学习在离散程度分析中的应用: 随着人工智能和机器学习技术的发展,未来可以 将这些技术应用于离散程度分析中,提高数据处 理的自动化和智能化水平。
详细描述
消费者行为数据分析是另一个应用数据离散程度的领域。通过对消费者的购买行为、偏 好、满意度等数据进行离散程度分析,企业可以更好地理解客户需求和市场趋势,从而
制定更有效的营销策略。
案例三:人口普查数据离散程度分析
总结词
人口普查数据离散程度分析
VS
详细描述
人口普查数据离散程度分析是评估国家或 地区人口统计数据可靠性和一致性的重要 手段。通过对人口普查数据的离散程度进 行测量,可以发现数据中的异常值和误差 ,提高数据质量。这对于政策制定、资源 分配和规划具有重要意义。
影响因素
影响数据离散程度的因素有很多,如测量误差、样本大小、数据来源等。在分 析数据的离散程度时,需要综合考虑这些因素,以确保结果的准确性和可靠性。
数据的离散程度(优质课)获奖课件

你还累?这么大的 个,才比我多驮 了2个.
哼,我从你背上拿来 1个,我的包裹数就 是你的2倍!
真的?!
我从你背上拿来 1个,我的包裹数 就是你的 2 倍!
你还累?这么大 的个,才比我 多驮了2个.
它们各驮了多少包裹呢?
【解析】设老牛驮了 x 个包裹 , 小马驮了 y个包裹.
老牛的包裹数比小马的多2个,
82 80 78 76 74 72 70 0 5 10 乙厂 15 20 25
结论
平均质量只能反映总体的集中趋势,并不能反映个体
的变化情况.从图中看,甲厂的产品更符合要求.
甲厂鸡腿规格比较稳定,最大值和最小值只相差6 g;
乙厂鸡腿规格比较不稳定,最大值和最小值相差9 g.
现实生活中,除了关心数据的“平均水平”外,人
结论
极差大,偏离平均数越大,产品的质量(性能)越不稳定.
想一想
如果丙厂也参与了竞争,从该厂也抽查20只鸡腿,
80 79 78 77 76 75 74 73 72 71 0 5 10 丙厂 15 20 25
平均数:
x 丙 75( g )
极差: 79 72 7( g )
问题6:丙厂这20只鸡腿质量的平均数和极差分别是多少?
C.
6x+4y=9
y=1
D.
y=3x+4
4.(嘉兴·中考)根据以下对话,可以求得小红所买的 笔和笔记本的价格分别是( D )
小红,你上周买的笔和笔 记本的价格是多少啊? 哦……我忘了!只记得 先后买了两次,第一次 买了5支笔和10本笔记 本花了42元钱,第二次 买了10支笔和5本笔记 本花了30元钱.
x=4, y=4呢? 你还能找到其他x , y的值适合方程x+y=8吗 ? (2) x=5 , y=3适合方程5x+3y=34吗?
第3章 数据的分析 单元备课 2022—2023学年鲁教版(五四制)八年级数学上册
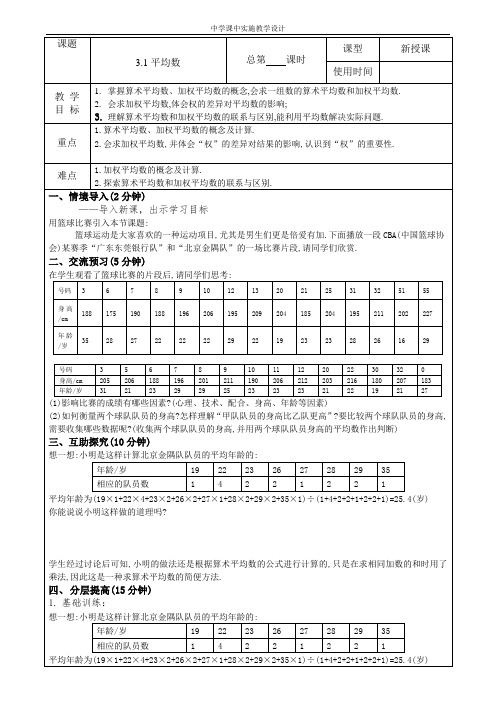
课题3.1平均数总第课时课型新授课使用时间教学目标1.掌握算术平均数、加权平均数的概念,会求一组数的算术平均数和加权平均数.2.会求加权平均数,体会权的差异对平均数的影响;3.理解算术平均数和加权平均数的联系与区别,能利用平均数解决实际问题.重点1.算术平均数、加权平均数的概念及计算.2.会求加权平均数,并体会“权”的差异对结果的影响,认识到“权”的重要性.难点1.加权平均数的概念及计算.2.探索算术平均数和加权平均数的联系与区别.一、情境导入(2分钟)——导入新课,出示学习目标用篮球比赛引入本节课题:篮球运动是大家喜欢的一种运动项目,尤其是男生们更是倍爱有加.下面播放一段CBA(中国篮球协会)某赛季“广东东莞银行队”和“北京金隅队”的一场比赛片段,请同学们欣赏.二、交流预习(5分钟)在学生观看了篮球比赛的片段后,请同学们思考:号码3678910121320212531325155身高/cm188175190188196206195209204185204195211202227年龄/岁352827222222292219232328261629号码356789101112202230320身高/cm205206188196201211190206212203216180207183年龄/岁3121232929252323232122192127(1)影响比赛的成绩有哪些因素?(心理、技术、配合、身高、年龄等因素)(2)如何衡量两个球队队员的身高?怎样理解“甲队队员的身高比乙队更高”?要比较两个球队队员的身高,需要收集哪些数据呢?(收集两个球队队员的身高,并用两个球队队员身高的平均数作出判断)三、互助探究(10分钟)想一想:小明是这样计算北京金隅队队员的平均年龄的:年龄/岁1922232627282935相应的队员数14221221平均年龄为(19×1+22×4+23×2+26×2+27×1+28×2+29×2+35×1)÷(1+4+2+2+1+2+2+1)=25.4(岁)你能说说小明这样做的道理吗?学生经过讨论后可知,小明的做法还是根据算术平均数的公式进行计算的,只是在求相同加数的和时用了乘法,因此这是一种求算术平均数的简便方法.四、分层提高(15分钟)1.基础训练:想一想:小明是这样计算北京金隅队队员的平均年龄的:年龄/岁1922232627282935相应的队员数14221221平均年龄为(19×1+22×4+23×2+26×2+27×1+28×2+29×2+35×1)÷(1+4+2+2+1+2+2+1)=25.4(岁)你能说说小明这样做的道理吗?学生经过讨论后可知,小明的做法还是根据算术平均数的公式进行计算的,只是在求相同加数的和时用了乘法,因此这是一种求算术平均数的简便方法.2.提升训练:某市是一个严重缺水的城市,为鼓励市民珍惜每一滴水,某居委会表扬了100个节约用水模范户,5月份这100户节约用水的情况如下表:每户节约用水量(单位:t)1 1.2 1.5节水户数523018那么5月份这100户平均每户节约用水的吨数为 t.教师引导师友订正答案,对师友出现的错题和重点题目进行有选择性讲解、点拨,组织师友有针对性地进行互助交流。
数据的离散程度1

Байду номын сангаас流与发现
甲乙两名运动员在8次百米跑训练中,成绩如下表: 序数 1 2 3 4 5
甲的成绩/秒 乙的成绩/秒
6 12.5
7 12.4
8 12.2
12.0
12.2
13.0
12.6
13.1
12.2
12.4
12.7
12.5
12.9
成绩 /秒
12.2
12.8
12.3
你能用折线统计图表示上述数据吗? 成绩/秒
1.平均数
1 x ( x1 x2 xn ) n
x x1 f1 x2 f 2 xk fk
2.众数 在一组数据中,出现次数最多的数据叫做这组数据的众数. 3.中位数 把一组数据从小到大排列,最中间的一个数(或
最中间两个数的平均数)
平均数、众数、中位数描述数据集中趋势
(2)小亮说:“甲、乙两名运动员的百米跑成绩的平均数、众数中 不合适. 位数对应相同,因此他们的成绩一样”,你认为这种说法合适吗? (3)观察图象,你发现哪名运动员的成绩波动较大?谁的成绩 比较稳定?由此你认为分析一组数据,仅关心这组数据的平均数、 众数、中位数,就能得到前面的结论吗?
通常用数据的离散程度来描述一组数据的波动范围和偏 离平均数的差异程度.
成绩/秒
13.4 13.2 13.0 12.8 12.6 12.4 12.2 12.0 3 4 5 6 7 8 序数
成绩 /秒
1
2
1
2
乙的成绩统计图
3
4
5
6
7
8 序数
(1)在这8次训练中,甲、乙两名运动员的百米跑成绩的平均数、 众数、中位数分别是多少?成绩平均数都是12.5秒,众数都是12.2 秒
离散程度的概念

离散程度的概念离散程度(dispersion)是指一组数据中各个数据值之间的分散程度或波动程度,用于了解数据分布的形状以及其中的变异程度。
离散程度是统计学中一个重要的概念,它能够提供有关数据集中程度的信息,从而帮助我们更好地理解数据。
在现实生活中,离散程度在很多领域和实际问题中都具有重要的应用,例如金融领域的风险评估、市场波动性的分析,以及工程领域中对测量数据的分析等。
离散程度有很多不同的度量方法,下面将详细介绍几种常见的离散程度度量方法。
1.极差(range):极差是指数据集中最大值与最小值之间的差值。
极差可以很容易地计算出来,并且能够提供数据集中的最大范围。
然而,它只考虑了最大和最小值,忽略了其他值的分布情况。
因此,在考虑整体分布情况时,极差的分析能力较弱。
2.平均绝对差(mean absolute deviation):平均绝对差是指数据集中各个数据值与平均值之间的差值的绝对值的平均。
平均绝对差能够考虑数据集中所有值的偏离程度,因此对数据的分散程度有更好的反映。
然而,平均绝对差受到极端值(outliers)的影响较大,容易受到异常值的扰动。
3.方差(variance):方差是指数据集中各个数据值与平均值之间的差值的平方的平均。
方差是离散程度度量中最常用的方法之一。
方差能够较好地反映数据集的分散程度,且在统计推断中有很重要的应用。
但是方差的单位是平方,无法与原始数据具有直接可比性。
4.标准差(standard deviation):标准差是方差的平方根。
标准差是离散程度度量中最常用的方法之一,它能够提供与原始数据具有直接可比性的度量。
标准差在正态分布和抽样理论中有很重要的应用。
5.百分位数(percentile):百分位数是指将数据按大小排序后,处于某个位置的数据值。
例如,第25百分位数是指将数据按大小排序后,在从小到大的顺序下,位于中间位置的数据值。
百分位数能够提供数据集的分布位置信息,例如中位数(50%百分位数)能够提供数据集的中间位置信息。
《数据的离散程度》数据的分析

《数据的离散程度》数据的分析数据的离散程度是指数据变量之间的差异程度。
离散程度越大,数据之间的差异越大,反之亦然。
在数据分析中,了解和评估数据的离散程度对于了解和解释数据的分布特点和趋势非常重要。
数据的离散程度可以通过多种统计指标和图表来描述和分析。
下面将介绍几种常用的方法。
1. 平均差距(Mean deviation)平均差距是数据离散程度的简单度量方法之一、它计算每个数据点与均值之间的差距,并求取这些差距的平均值。
平均差距越大,数据离散程度越大。
2. 方差(Variance)方差是数据离散程度的常用度量方法之一、它计算每个数据点与均值之间的差距的平方,并求取这些差距平方的平均值。
方差越大,数据离散程度越大。
3. 标准差(Standard deviation)标准差是方差的平方根。
它可以快速度量数据的离散程度,并且易于解释。
标准差越大,数据离散程度越大。
4. 四分位间距(Interquartile range)四分位间距是数据的分布特征的度量方法之一、它测量了数据中25%和75%之间数据点的差距。
四分位间距越大,数据离散程度越大。
5. 离群值检测(Outlier detection)离群值是与其他数据点显著不同的异常值。
通过检测和处理离群值,可以更准确地评估数据的离散程度。
6.统计图表直方图和箱线图是用于可视化数据离散程度的常用图表。
直方图将数据分布在一系列柱状图中,可以清晰地显示数据的离散性。
箱线图显示了数据的分布范围、中位数和四分位间距,可以直观地了解数据的离散程度。
了解数据的离散程度可以帮助我们更好地分析和解释数据,从而做出有意义的决策。
不同的离散程度描述方法可以结合使用,以便全面地评估数据的离散程度。
在实际应用中,我们需要根据具体问题和数据类型选择合适的离散程度度量方法,并结合其他统计分析方法进行综合分析。
《数据的离散程度》

数据的离散程度在统计学中,我们经常会关注数据的分布情况和离散程度。
数据的离散程度是指数据值在分布中的散布程度,也就是数据点相对于平均值的偏离程度。
偏离程度的度量方法常见的度量偏离程度的方法有四个:方差、标准差、极差和平均绝对偏差。
方差方差是偏离程度的最常用指标之一。
它计算对于均值的平均偏离的平方。
我们可以用以下公式来计算方差:$$ s^2 = \\frac{1}{n-1} \\sum_{i=1}^{n} (X_i - \\bar{X})^2 $$其中,n是样本大小,X i是第i个数据点,$\\bar{X}$是样本的平均值。
标准差标准差是方差的平方根。
它测量了数据点对于均值的平均偏离,并提供了一种标准化的度量。
我们可以用以下公式来计算标准差:$$ s = \\sqrt{\\frac{1}{n-1} \\sum_{i=1}^{n} (X_i - \\bar{X})^2} $$极差极差是样本数据中最大值与最小值的差。
它提供了数据集中数据较为分散的程度。
我们可以用以下公式来计算极差:r=X max−X min其中,X max是最大值,X min是最小值。
平均绝对偏差平均绝对偏差是测量样本与均值之间平均差异的度量方法,计算了数据点与平均值的绝对偏差的平均值。
我们可以用以下公式来计算平均绝对偏差:$$ MAD = \\frac{1}{n} \\sum_{i=1}^{n} |X_i - \\bar{X}| $$应用离散程度是数据分析和数据处理中非常重要的概念。
例如,在金融领域中,我们可以使用离散程度来衡量投资组合的风险,进而作出更好的投资决策。
在生物医学研究中,研究者们可以使用离散程度来分析药物试验数据及对疾病的影响。
在市场营销中,离散程度可以用来研究客户对于一款产品的反馈,进而制定更有针对性的市场营销策略。
总结数据的离散程度是衡量数据分布状态的重要指标。
使用方差、标准差、极差以及平均绝对偏差这些量化离散程度的方法,可以帮助我们分析数据分布的特征,做出更加准确的结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.在一次射击测试中,甲、乙、丙、丁的平均环数均相同,而方差分别为8.7,6.5,9.1,7.7,则这四人中,射击成绩最稳定的是()
A.甲B.乙C.丙D.丁
3.在方差的计算公式 中,数字10和20分别表示的意义是和.
4.如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的()
泰山博文中学学生课堂学习设计
学科:数学年级:初三学制:四制设计人:董备课组长:刘
课题:3.4数据的离散程度(1)课型:新授课
一、学习目标:
1.经历表示数据离散程度的几个量度的探索过程;
2.了解刻画数据离散程度的三个量度——极差、方差和标准差,,理解方差、标准差刻画数据波动情况的作用,并在具体问题情境中加以应用.
A.平均数和方差都不变B.平均数不变,方差改变
C.平均数改变,方差不变D.平均数和方差都改变
5、已知一组数据1,3,2,5,x,它们的平均数为3,则这组数据的方差是.
6、(2014•徐州)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数
众数
二、学习重点:
重点:方差和标准差的求法;
难点:为什么用方差能较好地描述数据的离散程度.
三、自学指导:
(一)、认真阅读课本62页,完成课本中4个题目.
总结:1、方差能够描述数据的离散程度,公式为 =,
其中, 是 的平均数, 是方差.
四、典型例题例1、计算数据13,14,15,16,17的方差.
练习一
1、甲乙丙丁四人进行射击测试,每人10次射击成绩的平均数均是9.2环,方差分别是 =0.56, =0.60, =0.50, =0.45,则成绩最稳定的是。
2、要从甲乙两射击运动员中选拔一名参加比赛,在预选赛中,他们每人各打了10发子弹,命中的环数如下:
甲:10,10,9,10,9,9,9,9,9,9;
乙:10,9,8,10,8,9,10,9,9,9.
根据这次成绩应该选择谁去参加比赛?
五、当堂检测
1.在统计中,样本的极差、方差、标准差可以近似地反应总体的()
中位数
方差
甲
8
8练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差.(填“变大”、“变小”或“不变”).
