数学四年级上2019秋浙江省台州市三门县-期末试卷
浙江省台州市三门县2019-2020学年第一学期浙教版九年级数学期末调考试卷(PDF版)

三门县2019学年九年级(上)期末统考数学参考答案一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选,多选、错选,均不给分)1~5:BCCAD;6~10:ADDBC二、填空题(本题有6小题,每小题5分,共30分)11.如-1,(是负数即可);12.-5 13.0.8814.3 cm 15.722516.116三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分)17.解方程:(1)x2-2x=0;解;x1=0 , x2=2 ……………4分(2)2x(x+1)=3.解;x1, x2……………8分18.(1)13;……………2分(2)49(过程略). ……………8分19.(1)y=-2x;……………4分(2)-2<x<0或x>1. ……………8分20.(1)40-x,20+2x;……………2分(2)(40-x)(20+2x)=1200,……………5分x=10或20,……………7分因为了扩大销售,增加盈利,尽快减少库存,故取x=20,答:每件衬衫应降价20元. …………8分21.(1)∵FG是⊙O的切线∴∠1+∠2=90°. ……………1分∵AB⊥CD∴∠DEH+∠3=90°. ……………2分∵OF=OD∴∠2=∠3.∴∠DEH=∠1 ……………3分∵FG∥BD,∴∠1=∠BDF. ……………4分∴∠DEH=∠BDF∴BE=BD……………6分(2)∵CD是⊙O的直径,弦AB⊥CD,垂足为H∴AH=BH=12AB=4……………7分∵DH=3∴BD=5……………8分∵BE=BD∴BE=5……………9分∴EH=BE-BH=1……………10分22.(1)135°; ……………2分(2)解法1:根据两个图形的面积相等关系列得方程GH (GH +a +b )=12(GH +a )(GH +b ),5分 化简得GH 2+(a +b )GH -ab =0,所以GH 的长是关于x 的方程x 2+(a +b )x -ab =0的一个根. …7分解法2:在图2直角三角形中,由勾股定理列得方程(GH +a )2+(GH +b )2=(a +b )2,解法3:根据图2直角三角形中的面积关系列得方程12GH (a +b )+12GH (GH +a )+12GH (GH +b )=12(GH +a )(GH +b ). (3)因为GH =2,GJ =k ,所以a +b =k -2 ,22+2(k -2)-ab =0,即 ab =2k ,……………9分所以22a b k ab k +-=……………10分 化简得11112a b k +=-,所以11112a b k ++=. ……………12分23.(1)①设解析式为2()y a x h k =-+,将(2,1),(5,7),h =3代入,得221(23)7(53)a k a k ⎧=-+⎪⎨=-+⎪⎩,……………2分 解得a =2,k =-1. ……………3分所以,解析式为22(3)1y x =--,即221217y x x =-+. ……………4分②t=1或t=4. ……………7分(2)设解析式为2()y a x h k =-+,由2(0)y ax bx c a =++≠知图象过(0,c ), 所以2c ah k =+. ……………8分因为点P 在函数2-3y x x c =+的图象上,所以2-3k h h c =+. ……………9分 所以2230h h ah -+=,……………10分因为h ≠0,所以31h a =+. ……………11分因为12≤a ≤2,h 随a 的增大而减小,所以,当12a =时,h 的值最大,h 的最大值为2. ……………12分24.(1)∵AB 是⊙O 的直径, ∴∠AMB =90°. ……………1分 ∵AN BN = ∴∠AMN =∠BMN =45°. ……………2分 ∵OM =OB∴∠OMB =∠OBM =30°. ……………3分 ∴∠CMO =45°-30°=15° ……………4分(2)连接OA ,OB ,ON . ∵AN BN =∴∠AON =∠BON 又∵OA =OB∴ON ⊥AB ,……………5分∵OD ∥AB∴∠DON =90°……………6分 ∵OM =ON∴∠OMN =∠ONM ……………7分∵∠OMN +∠ONM +∠MOD +∠DON =180° ∴∠MOD +2∠DMO =90°. ……………8分(3)延长MB 至点M ',使BM '=AM ,连接NM ',作NE ⊥MM '于点E.. 设AM =a ,BM =b .∵四边形AMBN 是圆内接四边形 ∴∠A +∠MBN =180°……………9分 ∵∠NBM '+∠MBN =180°∴∠A =∠NBM '……………10分∵AN BN = ∴AN =BN∴△AMN ≌△BM 'N (SAS)∴MN = N M ',BM '= AM =a ,……………11分 ∵NE ⊥MM '于点E.. ∴ME = EM '=12 MM '=1()2a b +,BE =b -1()2a b +=1()2b a - ……………12分∵ME 2+(BN 2-BE 2) =MN 2∴22211[()][()]1622a b BN b a ++--=,……………13分化简得216ab NB +=,∴16AM MB AN NB ⋅+⋅=. ……………14分。
2019年小学四年级数学上册期末考试试卷及答案
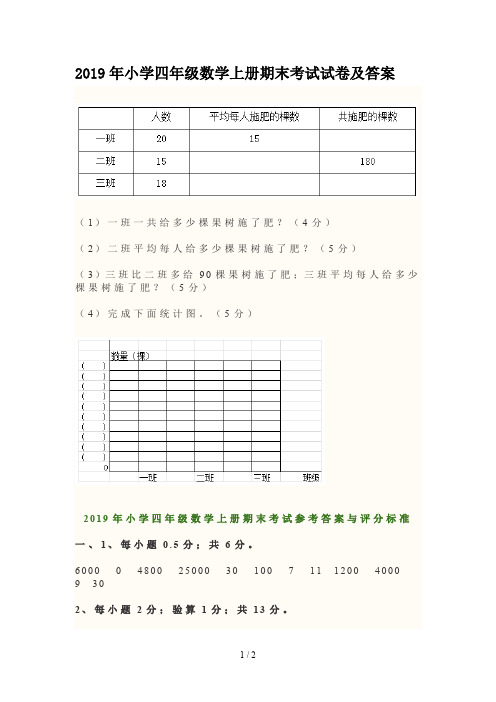
2019年小学四年级数学上册期末考试试卷及答案(1)一班一共给多少棵果树施了肥?(4分)(2)二班平均每人给多少棵果树施了肥?(5分)(3)三班比二班多给90棵果树施了肥;三班平均每人给多少棵果树施了肥?(5分)(4)完成下面统计图。
(5分)2019年小学四年级数学上册期末考试参考答案与评分标准一、1、每小题0.5分;共6分。
600004800250003010071112004000 9302、每小题2分;验算1分;共13分。
18081146202168…7224288竖式略3、每小题3分;共12分。
41545831二、每空1分;共17分。
1、千万5个千万十万7个十万两亿五千二百七十九万两千3亿2、垂直线段点到直线的距离3、平行相交4、8888005、一十6、五四12三、每小题1分;共5分。
√× × × ×四、每小题2分;共10分。
A B D A B A五、共4分;答案略。
六、共33分。
1、362×26=9412(本)答语略(4分)2、(264-180)÷6=14(元)答语略(5分)3、36÷6+1=7(棵)答语略(5分)4、(1)20×15=300(棵)答语略(4分)(2)180÷15=12(棵)答语略(5分)(3)(180+90)÷18=15(棵)答语略(5分)(4)略(5分)评分标准:4分值题列式、计算、单位名称、答语各2、1、0.5、0.5分。
5分值题列式、计算、单位名称、答语各3、1、0.5、0.5分。
2019年最新人教版四年级数学第一学期期末测试卷(含答案)

2018-2019学年小学四年级上册数学期末试卷第一部分基本知识(共30分)一、填空。
(每题2分,共20分)1. 据报道,受8号台风“莫拉克”的严重影响,给温州地区造成直接经济损失达993700000元,改写成以“万”做单位的数是( )万元,省略亿后面的尾数约是( )亿元。
2. 一个十位数,最高位是7,百万位和百位都是5,其他各数位上都是0,这个数写作( ),这个数最高位是( )位。
3. 1个周角= ( )个平角= ( )个直角。
4. 右边( )里最大能填几?( )×24 < 10053×() < 3025. 4时整,时针与分钟夹角是( )º;6时整,时针与分钟夹角是( )º。
6. 要使4□6÷46的商是两位数,□里最小可填( ),要使商是一位数,□最大可填( )。
7. 在下面〇里填上“>”、“<”或“=”。
3654879〇3654897 26900100000〇27万480÷12〇480÷3018×500〇50×1808. 两个数的积是240,如果一个因数不变,另一个因数缩小10倍,则积是( )。
9. 在A÷15=14……B中,余数B最大可取( ),这时被除数A是( )。
10.一本词典需39元,王老师带376元钱,最多能买( )本这样的词典。
二、判断:对的在括号里打“√”,错的打“×”。
(每题1分,共5分)1. 角的大小跟边的长短无关,跟两边叉开的大小有关。
………………………( )2. 整数数位顺序表中,任何两个计数单位之间的进率都是10。
……………()3. 钝角一定比直角大,比直角大的角一定是钝角。
…………………………()4. 长方形是特殊的平行四边形。
………………………………………………()5. 两个数相除,把被除数乘以10,除数除以10,商不变。
………………()三、选择:把正确答案的序号填在括号里。
2019-2020学年浙江省台州市三门县九年级数学期末统考卷二(含答案解析)

浙江省台州市三门县期末统考卷二姓名:得分:日期:一、选择题(本大题共 10 小题,共 40 分)1、(4分) 方程:x2﹣9=0的解是A.x=3B.x=±3C.4.5D.±4.52、(4分) 我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是A.①③B.①④C.②③D.②④3、(4分) 商场举行摸奖促销活动,对于“抽到一等奖的概率为0.01”.下列说法正确的是B.抽100次奖必有一次抽到一等奖A.抽101次也可能没有抽到一等奖C.抽一次不可能抽到一等奖D.抽了99次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖4、(4分) 如图,AB是⊙O的直径,弦CD丄AB,∠CAB=25°,则∠BOD等于A.70°B.65°C.50°D.45°5、(4分) 如图,在正方形网格中,线段A′B′是线段AB绕某点顺时针旋转一定角度所得,点A′与点A是对应点,则这个旋转的角度大小可能是A.45°B.60°C.90°D.135°6、(4分) 对于二次函数y=2(x+1)(x-3),下列说法正确的是A.图象过点(0,-3)B.图象与x轴的交点为(1,0),(-3,0)C.此函数有最小值为-6D.当x<1时,y随x的增大而减小7、(4分) 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,若此蓄电池为某用电器的电源,限制电流不能超过12A,那么用电器的可变电阻R应控制在什么范围?A.R≥3ΩB.R≤3ΩC.R≥12ΩD.R≥24Ω8、(4分) 如图,AB是⊙O的直径,AC,BC分别为⊙O交于点D,E,则下列说法一定正确的是()A.连接BD,可知BD时△ABC的中线B.连接AE,可知AE是△ABC的高线C.连接DE,可知DEAB =CEBCD.连接DE,可知SΔCDE:SΔABC=DE:AB9、(4分) 如图,这是一个由四个半径都为1米的圆设计而成的花坛,圆心在同一直线上,每个圆都会经过相邻的圆心,则这个花坛的周长(实线部分)为A.4π米B.113π米C.3π米D.2π米10、(4分) 如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8米,水流在喷出口的水平距离1.25米处达到最高,密集的水滴在水面上形成了一个半径为3m 的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m ,则应把出水口的高度调节为高出水面A.0.55米B.1130米C.1330米D.0.4米二、填空题(本大题共 6 小题,共 30 分)11、(5分) 抛物线y=2(x-1)2-5的顶点坐标是 12、(5分) 如图.若点P 在反比例函数y =−3x (x <0)的图象上,过点P 作PM⊥x 轴于点M ,PN⊥y 轴于点N ,则矩形PMON 的面积为 13、(5分) 某学习小组做摸球实验,在一个不透明的口袋里装有颜色不同的黄,白两种颜色的乒乓球若干只,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:n现从这个口袋中摸出一球,恰好是黄球的概率为14、(5分) 如图,一人口的弧形台阶,从上往下看是一组同心圆被一条直线所截得的一组圆弧.已知每个台阶宽度为32cm(即相邻两弧半径相差32cm),测得AB=200cm,AC=BD=40cm,则弧AB所在的圆的半径为 cm15、(5分) 函数y=kx,y=ax ,y=bx的图象如图所示,下列判断正确的有(填序号)①k,a,b都是正数;②函数y=ax ,y=bx的图象会出现四个交点;③A,D两点关于原点对称;④若B是OA的中点,则a=4b.16、(5分) 如图,矩形ABCD绕点A旋转90°,得矩形AB′C′D′,若B,D,C′三点在同一直线上,则ABAD的值为三、解答题(本大题共 8 小题,共 80 分)17、(8分) 如图,点A的坐标为(0,2),点B的坐标为(-3,2)。
台州市2019年实验小学四年级数学上学期期末考试试卷 附答案

台州市2019年实验小学四年级数学上学期期末考试试卷附答案班级:_________ 姓名:_________ 学号:_________题号填空题选择题判断题计算题综合题应用题总分得分考试须知:1、考试时间:90分钟,满分为100分(含卷面分2分)。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
3、不要在试卷上乱写乱画,卷面不整洁扣2分。
一、用心思考,正确填空(共10小题,每题2分,共20分)。
1、如图,其中有()个三角形,有()个直角三角形,有()个钝角三角形。
2、动电信的铁塔有许多三角形的结构,这是因为三角形具有()。
3、王老板进货,买了16套服装,每套服装145元。
根据条件完成填空。
4、一个数有6个百,7个千万,3个十亿组成,这个数写作(),省略“亿”后面的尾数约是()亿。
5、小明期末考试语文、数学的平均分是96分,其中语文92分,数学()分。
6、4×12+24÷6添上括号,使其运算顺序是:加—除—乘.则加了括号的算式是( )。
7、钟面上()时整的时候,时针和分针成平角。
8、写出下面各数。
四万零五百五十五四十万零四写作:__________ 写作:__________二百万零二百零九六千零三十万零三百写作:__________ 写作:__________9、将下面各数改写成用“万”或“亿”作单位的数。
570000=( )万 73200000=( )万8900000000=( )亿 506000000000=( )亿10、在下面的括号里填上合适的分数。
1.2时=()时()分 2千克50克=()千克40平方厘米=()平方分米 25厘米=()分米二、反复比较,慎重选择(共8小题,每题2分,共16分)。
1、与345÷15结果相等的算式是()。
A.345÷10÷5 B.345÷5÷3 C.345÷5×32、一个等腰三角形中,其中一底角是75度,顶角是( )。
2024届浙江省台州市三门县数学八上期末调研模拟试题含解析

2024届浙江省台州市三门县数学八上期末调研模拟试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题(每题4分,共48分)1.一个缺角的三角形ABC 残片如图所示,量得∠A =60°,∠B =75°,则这个三角形残缺前的∠C 的度数为()A .75°B .60°C .45°D .40°2.已知2310x x -+=,则223x x -++值为( )A .10B .9C .12D .33.如图,将一张三角形纸片ABC 的一角折叠,使点A 落在ABC ∆处的'A 处,折痕为DE .如果A α∠=,'CEA β∠=,'BDA γ∠=,那么下列式子中正确的是( )A .2γαβ=+B .2γαβ=+C .γαβ=+D .180γαβ=--4.下列图形中,中心对称图形是( )A .B .C .D .5.如图,CE 是ABC 的角平分线,//EF BC ,交AC 于点F .已知68AFE ∠=︒,则FEC ∠的度数为( )A .68︒B .34︒C .32︒D .22︒6.人体中红细胞的直径约为0.0000077 m ,用科学记数法表示数的结果是( )A .0.77×10-5 mB .0.77×10-6 mC .7.7×10-5 mD .7.7×10-6 m7.若等腰三角形的两边长分别为6和8,则周长为( )A .20或22B .20C .22D .无法确定8.如图,已知30MON ∠=︒,点1A ,2A ,3A ,在射线ON 上,点1B ,2B ,3B ,在射线OM 上,112A B B ∆,223A B B ∆,334A B B ∆,均为等边三角形.若11OB =,则889A B B ∆的边长为( )A .64B .128C .132D .2569.已知A 、B 两地相距12km,甲、乙两人沿同一条公路分别从A 、B 两地出发相向而行,甲, 乙两人离B 地的路程s(km)与时间t(h)的函数关系图象如图所示, 则两人在甲出发后相遇所需的时间是()A .1.2hB .1.5hC .1.6hD .1.8h10.如图所示,将正方形纸片三次对折后,沿图中AB 线剪掉一个等腰直角三角形,展开铺平得到的图形是( )A .B .C .D .11.根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误..的是( )A .扇形统计图能反映各部分在总体中所占的百分比B .每天阅读30分钟以上的居民家庭孩子超过50%C .每天阅读1小时以上的居民家庭孩子占20%D .每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°12.要使分式242x x -+有意义,则x 的取值范围是( ) A .2x ≠- B .2x = C .2x =- D .2x ≠±二、填空题(每题4分,共24分)13.如图,AB AC =,AB 的垂直平分线交AB 于点E ,交AC 于点D ,若40A ∠=︒,则DBC ∠=______°.14.直线y kx b =+与直线21y x =-+平行,且经过点(﹣2,3),则kb = .15.如果关于x 的方程111ax x x+=--2无解,则a 的值为______. 16.在Rt △ABC 中,∠ACB=90°,D 为AB 上的中点,若CD=5cm ,则AB=_____________cm.17.不等式13x -≥ 的解集为________. 18.如图所示,为估计池塘两岸边A ,B 两点间的距离,在池塘的一侧选取点C ,分别取CA 、CB 的中点E ,F ,测的18EF m =,则A ,B 两点间的距离是______m .三、解答题(共78分)19.(8分)如图,已知△ABC 的其中两个顶点分别为:A (-4,1)、B (-2,4).(1)请根据题意,在图中建立平面直角坐标系,并写出点C 的坐标;(2)若△ABC 每个点的横坐标保持不变,纵坐标分别乘-1,顺次连接这些点,得到△A 1B 1C 1,画出△A 1B 1C 1,判断△A 1B 1C 1与△ABC 有怎样的位置关系?并写出点B 的对应点B 1的坐标.20.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?21.(8分)在ABC ∆中,AB AC =,在ABC ∆的外部作等边三角形ACD ,E 为AC 的中点,连接DE 并延长交BC 于点F ,连接BD .(1)如图1,若96BAC ∠=︒,求BDF ∠的度数;(2)如图2,ACB ∠的平分线交AB 于点M ,交EF 于点N ,连接BN .①补全图2;②若BN DN =,求证:MB MN =.22.(10分)如图1,在Rt △ABC 中,∠C =90°,AC =BC ,点D ,E 分别在边AC ,BC 上,CD =CE ,连接AE ,点F ,H ,G 分别为DE ,AE ,AB 的中点连接FH ,HG(1)观察猜想图1中,线段FH 与GH 的数量关系是 ,位置关系是(2)探究证明:把△CDE 绕点C 顺时针方向旋转到图2的位置,连接AD ,AE ,BE 判断△FHG 的形状,并说明理由 (3)拓展延伸:把△CDE 绕点C 在平面内自由旋转,若CD =4,AC =8,请直接写出△FHG 面积的最大值23.(10分)小明在证明“有两个角相等的三角形是等腰三角形”这一命题时,先画出图形,再写出“已知”,“求证”(如图),证明时他对所作的辅助线描述如下:“过点A 作BC 的中垂线AD ,垂足为D ”.(1)请你判断小明辅助线的叙述是否正确;如果不正确,请改正.(2)根据正确的辅助线的做法,写出证明过程.24.(10分)如图,在等腰直角三角形ABC 中,4AC BC ==,90ACB ∠=︒,CD AB ⊥.将等腰直角形ABC 沿高CD 剪开后,拼成图2所示的正方形EFGH .(1)如图1,等腰直角三角形ABC的面积是______________.(2)如图2,求正方形EFGH的边长是多少?(3)把正方形EFGH放到数轴上(如图3),使得边EF落到数轴上,其中一个端点所对应的数为-1,直接..写出另一个端点所对应的数.25.(12分)把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子.(1)图1是由几个面积不等的小正方形与小长方形拼成的一个边长为a+b+c的正方形,试用不同的方法计算这个正方形的面积,你发现了什么结论?请写出来;(2)图2是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连结BD、BF,若两正方形的边长满足a+b=10,ab=20,试求阴影部分的面积.26.两个工程队共同参与一项筑路工程,若先由甲、乙两队合作30天,剩下的工程再由乙队单独做15天可以完成,共需施工费810万元;若由甲、乙合作完成此项工程共需36天,共需施工费828万元.(1)求乙队单独完成这项工程需多少天?(2)甲、乙两队每天的施工费各为多少万元?(3)若工程预算的总费用不超过840万元,则乙队最少施工多少天?参考答案一、选择题(每题4分,共48分)1、C【分析】利用三角形内角和定理求解即可.【题目详解】因为三角形内角和为180°,且∠A = 60°,∠B = 75°,所以∠C=180°–60°–75°=45°. 【题目点拨】三角形内角和定理是常考的知识点.2、A【分析】由题意根据等式和分式的基本性质以及完全平方公式对式子进行变形,进而整体代入求解. 【题目详解】解:由222221133()1x x x x x x-++=++=++,可知0x ≠, 已知2310x x -+=,等式两边同时除以x 可得:13x x+=, 将13x x +=,代入221()13110x x ++=+=, 所以22310x x -++=.故选:A.【题目点拨】本题考查完全平方公式,结合等式和分式的基本性质运用整体替换的思想进行分析是解题的关键.3、A【题目详解】分析:根据三角形的外角得:∠BDA'=∠A+∠AFD ,∠AFD=∠A'+∠CEA',代入已知可得结论. 详解:由折叠得:∠A=∠A',∵∠BDA'=∠A+∠AFD ,∠AFD=∠A'+∠CEA',∵∠A=α,∠CEA′=β,∠BDA'=γ,∴∠BDA'=γ=α+α+β=2α+β,点睛:本题考查了三角形外角的性质,熟练掌握三角形的外角等于与它不相邻的两个内角的和是关键.4、C【分析】根据中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形进行解答.【题目详解】解:A 、不是中心对称图形,故本选项错误;B 、不是中心对称图形,故本选项错误;C 、是中心对称图形,故本选项正确;D 、不是中心对称图形,故本选项错误.故选:C .【题目点拨】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合.5、B【分析】根据平行线的性质和角平分线的性质即可求解.【题目详解】解:∵//EF BC∴∠ACB=68AFE ∠=︒∵CE 是ABC 的角平分线∴FEC ∠=∠BCE=12ACB ∠=34︒ 故选:B【题目点拨】此题主要考查平行线的性质和角平分线的性质,灵活运用性质解决问题是解题关键.6、D【解题分析】解:0.0000077 m = 7.7×10-6 m .故选D . 7、A【解题分析】若6是腰长,则三角形的三边分别为6、6、8,能组成三角形,周长=6+6+8=20,若6是底边长,则三角形的三边分别为6、8、8,能组成三角形,周长=6+8+8=1,综上所述,三角形的周长为20或1.8、B【分析】根据等腰三角形的性质以及平行线的性质得出112233////.B A A B A B 以及221222A B A B ==,得出231334422, .... 2n n n A B A B A B -===,进而得出答案.【题目详解】解:∵112A B B ∆ 是等边三角形,∴111211122,60A B A B A B B A B O =∠=∠=︒,∵∠O=30°,∴2121290A A B A B O O ∠=∠+∠=︒,∵11211A B B OA B O ∠=∠+∠,∴1130O OA B ∠=∠=︒,∴111211,OB A B A B ===在212Rt A A B 中,∵22130A A B ∠=︒∴221222A B A B ==,同法可得231334422, .... 2n n n A B A B A B -===,∴889A B B ∆的边长为:72128= ,故选:B.【题目点拨】本题考查的是等边三角形的性质以及等腰三角形的性质,根据已知得出221222A B A B ==,得出231334422, .... 2n n n A B A B A B -===,进而发现规律是解题关键.9、C【解题分析】先根据图象求出甲、乙两人的s 与t 的函数关系式,再联立求出交点坐标即可得出答案.【题目详解】设甲的s 与t 的函数关系式为s mt a =+由图象可知,点(2,0)、(0,12)在s mt a =+的图象上则2012m a a +=⎧⎨=⎩,解得612m a =-⎧⎨=⎩故甲的s 与t 的函数关系式为612s t =-+设乙的s 与t 的函数关系式为s nt b =+由图象可知,点(1,0)、(4,12)在s nt b =+的图象上则0412n b n b +=⎧⎨+=⎩,解得44n b =⎧⎨=-⎩故乙的s 与t 的函数关系式为44s t =-联立61244s t s t =-+⎧⎨=-⎩,解得 1.62.4t s =⎧⎨=⎩即两人在甲出发后相遇所需的时间为1.6h故选:C .【题目点拨】本题考查了一次函数的实际应用,依据图象求出甲、乙两人的s 与t 的函数关系式是解题关键.10、A【解题分析】试题分析:找一张正方形的纸片,按上述顺序折叠、裁剪,然后展开后得到的图形如图所示: 故选A .考点:剪纸问题.11、C【解题分析】根据扇形统计图中的百分比的意义逐一判断即可得.【题目详解】解:A .扇形统计图能反映各部分在总体中所占的百分比,此选项正确;B .每天阅读30分钟以上的居民家庭孩子的百分比为,超过,此选项正确;C .每天阅读1小时以上的居民家庭孩子占,此选项错误;D .每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是,此选项正确; 故选:C .【题目点拨】本题主要考查扇形统计图,扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数. 12、A【分析】分式有意义的条件是分母不能为0即可. 【题目详解】要使分式22-4x x +有意义,分母不为0,即x+1≠0,∴x≠-1,则x 的取值范围是x≠-1.故选择:A .【题目点拨】本题考查分式有意义的条件问题,掌握分式有意义就是满足分母不为0,会解不等式是关键.二、填空题(每题4分,共24分)13、1【分析】根据等边对等角和三角形的内角和定理即可求出∠ABC,然后根据垂直平分线的性质可得DA=DB,从而得出∠A=∠DBA=40°,即可求出DBC ∠.【题目详解】解:∵AB AC =,40A ∠=︒∴∠ABC=∠ACB=()1180702A ︒-∠=︒ ∵DE 垂直平分AB∴DA=DB∴∠A=∠DBA=40°∴∠DBC=∠ABC -∠DBA=1°故答案为:1.【题目点拨】此题考查的是等腰三角形的性质和垂直平分线的性质,掌握等边对等角和线段垂直平分线上的点到这条线段两个端点的距离相等是解决此题的关键.14、1.【分析】根据两直线平行可得k 值相等,进一步求得b 的值即可得解.【题目详解】∵直线y kx b =+与直线21y x =-+平行,∴k=﹣1,∴直线2y x b =-+,把点(﹣1,3)代入得:4+b=3,∴b=﹣1,∴kb=1.故答案为1.考点:两条直线相交或平行问题.15、1或1.【分析】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于2.【题目详解】去分母得:ax﹣1=1(x﹣1)ax﹣1x=﹣1,(a﹣1)x=﹣1,当a﹣1=2时,∴a=1,此时方程无解,满足题意,当a﹣1≠2时,∴x12a=--,将x12a=--代入x﹣1=2,解得:a=1,综上所述:a=1或a=1.故答案为:1或1.【题目点拨】本题考查分式方程的解法,解题的关键是熟练运用分式方程的解法,本题属于基础题型.16、1【解题分析】根据直角三角形斜边上的中线等于斜边的一半解答.【题目详解】∵在Rt△ABC中,∠ACB=90°,D是AB的中点,∴线段CD是斜边AB上的中线;又∵CD=5cm,∴AB=2CD=1cm.故答案是:1.【题目点拨】本题考查了直角三角形斜边上的中线.直角三角形斜边上的中线等于斜边的一半.17、3x≤-【解题分析】首先去分母,再系数化成1即可;【题目详解】解:去分母得:-x≥3系数化成1得:x≤-3故答案为:x≤-3【题目点拨】本题考查了解一元一次不等式,主要考查学生的计算能力.18、36【分析】根据E、F是CA、CB的中点,即EF是△CAB的中位线,根据三角形的中位线定理:三角形的中位线平行于第三边且等于第三边的一半,即可求解.【题目详解】解:据E、F是CA、CB的中点,即EF是△CAB的中位线,∴EF=12 AB,∴AB=2EF=2×18=36.故答案为36.【题目点拨】本题考查了三角形的中位线定理应用,灵活应用三角形中位线定理是解题的关键.三、解答题(共78分)19、(1)图见解析,点C的坐标为(3,3);(2)图见解析,B1的坐标为(-2,-4)【分析】(1)直接利用已知点建立平面直角坐标系进而得出答案;(2)利用坐标之间的关系得出△A1B1C1各顶点位置,进而得出答案.【题目详解】解:(1)平面直角坐标系如图所示.点C的坐标为(3,3).(2)△A 1B 1C 1如图所示.△A 1B 1C 1与△ABC 关于x 轴对称.点B 的对应点B 1的坐标为(-2,-4).【题目点拨】此题主要考查了轴对称变换,正确得出各对应点位置是解题关键.20、(1)大本作业本每本0.1元,小本作业本每本0.5元.(2)大本作业本最多能购买1本.【解题分析】(1)设小本作业本每本x 元,则大本作业本每本(x+0.3)元,根据数量=总价÷单价结合用1元购买大本作业本的数量与用5元购买小本作业本的数量相同,即可得出关于x 的分式方程,解之经检验后即可得出结论;(2)设大本作业本购买m 本,则小本作业本购买2m 本,根据总价=单价×数量结合总费用不超过15元,即可得出关于m 的一元一次不等式,解之取其中的最大整数值即可得出结论.【题目详解】解:(1)设小本作业本每本x 元,则大本作业本每本(x +0.3)(0.3)x +元, 依题意,得:850.3x x=+, 解得:0.5x =,经检验,0.5x =是原方程的解,且符合题意,∴0.30.8x +=.答:大本作业本每本0.1元,小本作业本每本0.5元.(2)设大本作业本购买m 本,则小本作业本购买2m 本,依题意,得:0.80.5215m m +⨯, 解得:506m ≤. ∵m 为正整数,∴m 的最大值为1.答:大本作业本最多能购买1本.【题目点拨】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.21、(1)18BDF ∠=︒;(2)①补全图形,如图所示.见解析;②见解析.【解题分析】(1)分别求出∠ADF ,∠ADB ,根据∠BDF=∠ADF-∠ADB 计算即可;(2)①根据要求画出图形即可;②设∠ACM=∠BCM=α,由AB=AC ,推出∠ABC=∠ACB=2α,可得∠NAC=∠NCA=α,∠DAN=60°+α,由△ABN ≌△ADN (SSS ),推出∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+α,∠BAC=60°+2α,在△ABC 中,根据∠BAC+∠ACB+∠ABC=180°,构建方程求出α,再证明∠MNB=∠MBN 即可解决问题;【题目详解】(1)解:如图1中,在等边三角形ACD ∆中,60CAD ADC ∠=∠=︒,AD AC =.∵E 为AC 的中点, ∴1302ADE ADC ∠=∠=︒, ∵AB AC =,∴AD AB =,∵BAD BAC CAD ∠=∠+∠,96BAC ∠=︒,60CAD ∠=︒,∴156BAD BAC CAD ∠=∠+∠=︒,∴12ADB ABD ∠=∠=︒,∴18BDF ADF ADB ∠=∠-∠=︒.(2)①补全图形,如图所示.②证明:连接AN .∵CM 平分ACB ∠,∴设AOM BCM a ∠=∠=,∵AB AC =,∴2ABC ACB a ∠=∠=.在等边三角形ACD ∆中,∵E 为AC 的中点,∴DN AC ⊥,∴NA NC =,∴NAC NCA a ∠=∠=,∴60DAN a ∠=︒+,在ABN ∆和ADN ∆中,AB AD BN DN AN AN =⎧⎪=⎨⎪=⎩∴()ABN ADN SSS ∆∆≌,∴30ABN ADN ∠=∠=︒,60BAN DAN a ∠=∠=︒+,∴602BAC a ∠=︒+,在ABC ∆中,180BAC ACB ABC ∠+∠+∠=︒∴60222180a a a ︒+++=︒,∴20a =︒,∴10NBC ABC ABN ∠=∠-∠=︒,∴30MNB NBC NCB ∠=∠+∠=︒,∴MNB MBN ∠=∠,∴MB MN =.【题目点拨】本题考查全等三角形的判定和性质,等边三角形的性质,等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.22、(1)FH =GH ,FH ⊥HG ;(2)△FGP 是等腰直角三角形,理由见解析;(3)2【分析】(1)直接利用三角形的中位线定理得出FH =GH ,再借助三角形的外角的性质即可得出∠FHG =90°,即可得出结论;(2)由题意可证△CAD ≌△CBE ,可得∠CAD =∠CBE ,AD =BE ,根据三角形中位线定理,可证HG =HF ,HF ∥AD ,HG ∥BE ,根据角的数量关系可求∠GHF =90°,即可证△FGH 是等腰直角三角形;(3)由题意可得S △HGF 最大=12HG 2,HG 最大时,△FGH 面积最大,点D 在AC 的延长线上,即可求出△FGH 面积的最大值.【题目详解】解:(1)∵AC =BC ,CD =CE ,∴AD =BE ,∵点F 是DE 的中点,点H 是AE 的中点,∴FH=12 AD,∵点G是AB的中点,点H是AE的中点,∴GH=12 BE,∴FH=GH,∵点F是DE的中点,点H是AE的中点,∴FH∥AD,∴∠FHE=∠CAE∵点G是AB的中点,点H是AE的中点,∴GH∥BE,∴∠AGH=∠B,∵∠C=90°,AC=BC,∴∠BAC=∠B=45°,∵∠EGH=∠B+∠BAE,∴∠FHG=∠FHE+∠EHG=∠CAE+∠B+∠BAE=∠B+∠BAC=90°,∴FH⊥HG,故答案为:FH=GH,FH⊥HG;(2)△FGP是等腰直角三角形理由:由旋转知,∠ACD=∠BCE,∵AC=BC,CD=CE,∴△CAD≌△CBE(SAS),∴∠CAD=∠CBE,AD=BE,由三角形的中位线得,HG=12BE,HF=12AD,∴HG=HF,∴△FGH是等腰三角形,由三角形的中位线得,HG∥BE,∴∠AGH=∠ABE,由三角形的中位线得,HF∥AD,∴∠FHE=∠DAE,∵∠EHG=∠BAE+∠AGH=∠BAE+∠ABE,∴∠GHF=∠FHE+∠EHG=∠DAE+∠BAE+∠ABE=∠BAD+∠ABE=∠BAC+∠CAD+∠ABC ﹣∠CBE=∠CBA+∠CAB ,∵∠ACB =90°,AC =BC ,∴∠CBA =∠CAB =45°,∴∠GHF =90°,∴△FGH 是等腰直角三角形;(3)由(2)知,△FGH 是等腰直角三角形,HG =HF =12AD , ∵S △HGF =12HG 2, ∴HG 最大时,△FGH 面积最大,∴点D 在AC 的延长线上,∵CD =4,AC =8∴AD =AC+CD =12,∴HG =12×12=1. ∴S △PGF 最大=12HG 2=2. 【题目点拨】此题是几何变换综合题,主要考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,旋转的性质,三角形的中位线定理,判断出HG ⊥FH 是解本题的关键.23、(1)不正确,应该是:过点A 作AD BC ⊥;(2)见解析【分析】(1)不正确.过一点可以作已知直线的垂线,不能作线段的中垂线.(2)利用ASA 证明ADB ADC ∆≅∆即可.【题目详解】解:(1)不正确.应该是:过点A 作AD BC ⊥.(2)∵AD BC ⊥,∴90ADB ADC ∠=∠=︒,∵AD AD =,B C ∠=∠,∴()ADB ADC ASA ∆∆≌,∴AB AC =.【题目点拨】本题考查等腰三角形的判定,线段的垂直平分线的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.24、(1)8;(2)3)-1+-1-【分析】(1)根据面积公式进行计算;(2)根据所拼图形,可知正方形的边长为△ABC 的高,从而计算可得;(3)根据(2)中所求边长,当点E 在-1,和点F 在-1处分别得出另一个点对应的数.【题目详解】解:(1)1=2ABC S AC BC ⨯△=1442⨯⨯=8; (2)由题意可知,拼成正方形EFGH 后,△ABC 的高CD 变成了正方形的边长,∵CD=12AB =12∴正方形EFGH 的边长为(3)当点E 在-1处时,F 所对应的数为:-1+当点F 在-1处时,F 所对应的数为:-1-∴另一个端点所对应的的数为-1+或-1-【题目点拨】本题考查了等腰直角三角形的性质,数轴上的点表示数,实数的加减运算,关键是数形结合,了解拼图的过程,并且注意在数轴上分类讨论.25、(1)a 2+b 2+c 2+2ab+2bc+2ac ;(2)20【解题分析】试题分析:(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,另一种是大正方形的面积,可得等式2222()222a b c a b c ab ac bc ++=+++++;(2)利用S 阴影=正方形ABCD 的面积+正方形ECGF 的面积-三角形BGF 的面积-三角形ABD 的面积求解.试题解析:(1)2222()222a b c a b c ab ac bc ++=+++++;(2)1020a b ab +==,, 22222221111113131020503020222222222S a b a b b a a b ab a b ab ∴=+-+⨯-=+-=+-=⨯-⨯=-=阴影()().考点:因式分解的应用 26、(1)乙队单独完成这项工程需90天;(2)甲队每天的施工费为15万元,乙队每天的施工费为8万元;(3)乙队最少施工30天【分析】(1)设乙队单独完成这项工程需x天,根据“甲、乙合作30天的工作量+乙队15天的工作量=1”列分式方程即可;(2)设甲队每天的施工费为a万元,乙队每天的施工费为b万元,根据题意列二元一次方程组即可求出a、b的值;(3)先求出甲的效率,设乙队施工y天,则甲队还需施工119060y⎛⎫-÷⎪⎝⎭天完成任务,然后根据“总费用不超过840万元”列出不等式即可得出结论.【题目详解】解:(1)设乙队单独完成这项工程需x天由题意可得:11×30+151 36x⨯=解得:x=90经检验:x=90是原方程的解答:乙队单独完成这项工程需90天.(2)设甲队每天的施工费为a万元,乙队每天的施工费为b万元由题意可知:()() 3015810 36828a b ba b⎧++=⎪⎨+=⎪⎩解得:158 ab=⎧⎨=⎩答:甲队每天的施工费为15万元,乙队每天的施工费为8万元.(3)甲的效率为111 369060 -=设乙队施工y天,则甲队还需施工119060y⎛⎫-÷⎪⎝⎭天完成任务根据题意可得15×119060y⎡⎤⎛⎫-÷⎪⎢⎥⎝⎭⎣⎦+8y≤840解得:y≥30答:乙队最少施工30天.【题目点拨】此题考查的是分式方程的应用、二元一次方程组的应用和不等式的应用,掌握实际问题中的等量关系和不等关系是解决此题的关键.。
数学四年级下2020春浙江省台州市三门县期末测试卷
浙江省台州市三门县四年级数学(下) 期末检测卷班级: 姓名: 学号:一、用心思考,正确填写。
(每空1分,共22分)1.看图写数。
阴影部分用小数表示是( ),它的计数单位是( ),不改变数的大小,把它改成三位小数是( )。
2.2018年天猫“双十一”再创辉煌,最终整日成交额定格于213549300000元,物流订单超过十亿。
横线上的数改成以“亿”作单位的数是( )亿元,精确到十分位约是( )亿元。
3.钓鱼岛自古以来就是中国的领土,钓鱼岛列岛总面积约6.3平方千米,合( )公顷;一 间教室的占地面积是70平方米,钓鱼岛列岛总面积大约有( )间教室那么大。
4.一个数缩小到它的1100是0.063,原数扩大到它的10倍是( )。
5.小马虎在计算10+☆×5时,先算加法,后算乘法,得到的结果是240,正确的结果是( )。
6.学校运动会上,四个同学100米决赛的成绩如下表,如果丁是第4名,那么第三名是( ); 如果乙是第一名,那么他可能跑了( )秒。
7.如右图,一张三角形纸片被撕去了一角,撕去的这个角是( )°, 原来这张纸片的形状是( )三角形,也是( )三角形。
8.一个三条边长均是整厘米数的三角形的两条边长分别是4厘米和9厘米,第三条边的长度最小 是( )厘米,最大是( )厘米。
9.小学阶段学习了很多的数学知识,知识之间有着密切的联系。
右图中,若A 表示长方形,那么B 可以表示正方形;若A 表示等腰三角形,那么 B 可以表示( )。
10.在里填上“>”“<”或“=”。
25.8025.8 4公顷80平方米4.08公顷7.83-0.45+0.557.83-(0.45+0.55)姓名甲乙丙丁成绩/秒13.1513.□714.011□.1070°55°A B11.一辆小汽车的牌照是浙J·B○□△8,已知○+○=□,○+□+□=10,△+△=○,那么它的牌照号码是浙J·B( )。
浙江省台州市三门县2019-2020学年九年级数学期末统考卷二(含解析)

浙江省台州市三门县期末统考卷二姓名:得分:日期:一、选择题(本大题共 10 小题,共 40 分)1、(4分) 方程:x2﹣9=0的解是A.x=3B.x=±3C.4.5D.±4.52、(4分) 我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是A.①③B.①④C.②③D.②④3、(4分) 商场举行摸奖促销活动,对于“抽到一等奖的概率为0.01”.下列说法正确的是B.抽100次奖必有一次抽到一等奖A.抽101次也可能没有抽到一等奖C.抽一次不可能抽到一等奖D.抽了99次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖4、(4分) 如图,AB是⊙O的直径,弦CD丄AB,∠CAB=25°,则∠BOD等于A.70°B.65°C.50°D.45°5、(4分) 如图,在正方形网格中,线段A′B′是线段AB绕某点顺时针旋转一定角度所得,点A′与点A是对应点,则这个旋转的角度大小可能是A.45°B.60°C.90°D.135°6、(4分) 对于二次函数y=2(x+1)(x-3),下列说法正确的是A.图象过点(0,-3)B.图象与x轴的交点为(1,0),(-3,0)C.此函数有最小值为-6D.当x<1时,y随x的增大而减小7、(4分) 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,若此蓄电池为某用电器的电源,限制电流不能超过12A,那么用电器的可变电阻R应控制在什么范围?A.R≥3ΩB.R≤3ΩC.R≥12ΩD.R≥24Ω8、(4分) 如图,AB是⊙O的直径,AC,BC分别为⊙O交于点D,E,则下列说法一定正确的是()A.连接BD,可知BD时△ABC的中线B.连接AE,可知AE是△ABC的高线C.连接DE,可知DEAB =CEBCD.连接DE,可知SΔCDE:SΔABC=DE:AB9、(4分) 如图,这是一个由四个半径都为1米的圆设计而成的花坛,圆心在同一直线上,每个圆都会经过相邻的圆心,则这个花坛的周长(实线部分)为A.4π米B.113π米C.3π米D.2π米10、(4分) 如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8米,水流在喷出口的水平距离1.25米处达到最高,密集的水滴在水面上形成了一个半径为3m 的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m ,则应把出水口的高度调节为高出水面A.0.55米B.1130米C.1330米D.0.4米二、填空题(本大题共 6 小题,共 30 分)11、(5分) 抛物线y=2(x-1)2-5的顶点坐标是 12、(5分) 如图.若点P 在反比例函数y =−3x (x <0)的图象上,过点P 作PM⊥x 轴于点M ,PN⊥y 轴于点N ,则矩形PMON 的面积为 13、(5分) 某学习小组做摸球实验,在一个不透明的口袋里装有颜色不同的黄,白两种颜色的乒乓球若干只,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:n现从这个口袋中摸出一球,恰好是黄球的概率为14、(5分) 如图,一人口的弧形台阶,从上往下看是一组同心圆被一条直线所截得的一组圆弧.已知每个台阶宽度为32cm(即相邻两弧半径相差32cm),测得AB=200cm,AC=BD=40cm,则弧AB所在的圆的半径为 cm15、(5分) 函数y=kx,y=ax ,y=bx的图象如图所示,下列判断正确的有(填序号)①k,a,b都是正数;②函数y=ax ,y=bx的图象会出现四个交点;③A,D两点关于原点对称;④若B是OA的中点,则a=4b.16、(5分) 如图,矩形ABCD绕点A旋转90°,得矩形AB′C′D′,若B,D,C′三点在同一直线上,则ABAD的值为三、解答题(本大题共 8 小题,共 80 分)17、(8分) 如图,点A的坐标为(0,2),点B的坐标为(-3,2)。
