《圆》测试题A

合集下载

《圆》基础测试(含答案)

《圆》基础测试一、选择题（每题2分，共20分）1．有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有………………（）（A）4个（B）3个（C）2个（D）1个2．下列判断中正确的是…………………………………………………………（）（A）平分弦的直线垂直于弦;（B）平分弦的直线也必平分弦所对的两条弧（C）弦的垂直平分线必平分弦所对的两条弧（D）平分一条弧的直线必平分这条弧所对的弦3．如图，在两半径不同的同心圆中，∠AOB＝∠A′OB′＝60°，则…………（）（A ）＝（B ）＞（C ）的度数＝的度数（D ）的长度＝的长度4．如图，已知⊙O的弦AB、CD相交于点E ，的度数为60°，的度数为100°，则∠AEC等于……………………………………………………………（）（A）60°（B）100°（C）80°（D）130°5．圆内接四边形ABCD中，∠A、∠B、∠C的度数比是2︰3︰6，则∠D的度数是（）（A）67.5°（B）135°（C）112.5°（D）110°6．OA平分∠BOC，P是OA上任一点，C不与点O重合，且以P为圆心的圆与OC 相离，那么圆P与OB的位置关系是………………………………………（）（A）相离（B）相切（C）相交（D）不确定7．△ABC的三边长分别为a、b、c，它的内切圆的半径为r，则△ABC的面积为（）（A ）21（a ＋b ＋c ）r （B ）2（a ＋b ＋c ）（C ）31（a ＋b ＋c ）r （D ）（a ＋b ＋c ）r 8．如图，已知四边形ABCD 为圆内接四边形，AD 为圆的直径，直线MN 切圆于点B ，DC 的延长线交MN 于G ，且cos ∠ABM ＝23，则tan ∠BCG 的值为……（）（A ）33 （B ）23 （C ）1 （D ）39．在⊙O 中，弦AB 和CD 相交于点P ，若P A ＝3，PB ＝4，CD ＝9，则以PC 、PD 的长为根的一元二次方程为…………………………………………………（）（A ）x 2＋9 x ＋12＝0 （B ）x 2－9 x ＋12＝0（C ）x 2＋7 x ＋9＝0 （D ）x 2－7 x ＋9＝010．已知半径分别为r 和2 r 的两圆相交，则这两圆的圆心距d 的取值范围是…（）（A ）0＜d ＜3 r （B ）r ＜d ＜3 r （C ）r ≤d ＜3 r （D ）r ≤d ≤3 r三、填空题（每题2分，共20分）11．某公园的一石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为_____．12．如图，已知AB 为⊙O 的直径，∠E ＝20°，∠DBC ＝50°，则∠CBE ＝______．13．圆内接梯形是_____梯形，圆内接平行四边形是_______．．14．如图，AB、AC是⊙O的切线，将OB延长一倍至D，若∠DAC＝60°，则∠D＝_____．15．如图，BA与⊙O相切于B，OA与⊙O相交于E，若AB＝5，EA＝1，则⊙O 的半径为______．16．已知两圆的圆心距为3，半径分别为2和1，则这两圆有______条公切线．17．正八边形有_____条对称轴，它不仅是______对称图形，还是_____对称图形．18．边长为2 a的正六边形的面积为______．19．扇形的半径为6 cm，面积为9 cm2，那么扇形的弧长为______，扇形的圆心角度数为_____．20．用一张面积为900 cm2的正方形硬纸片围成一个圆柱的侧面，则这个圆柱的底面直径为_____．三、判断题（每题2分，共10分）21．相交两圆的公共弦垂直平分连结这两圆圆心的线段………………………（）22．各角都相等的圆内接多边形是正多边形……………………………………（）23．正五边形既是轴对称图形，又是中心对称图形……………………………（）24．三角形一定有内切圆…………………………………………………………（）25．平分弦的直径垂直于弦………………………………………………………（）四、解答题：（共50分）26．（8分）如图，⊙O的直径AB和弦CD相交于点E，且AE＝1 cm，EB＝5 cm，∠DEB＝60°，求CD的长．27．（8分）如图，AB 为⊙O 的直径，P 为BA 的延长线上一点，PC 切⊙O 于点C ，CD ⊥AB ，垂足为D ，且P A ＝4，PC ＝8，求tan ∠ACD 和sin ∠P 的值．28．（8分）如图，已知ABCD 是圆内接四边形，EB 是⊙O 的直径，且EB ⊥AD ，AD与BC 的延长线交于F ，求证FD AB ＝DCBC ．29．（12分）已知：如图，⊙O 1与⊙O 2内切于点P ，过点P 的直线交⊙O 1于点D ，交⊙O 2于点E ；DA 与⊙O 2相切，切点为C ．*（1）求证PC 平分∠APD ；（2）若PE ＝3，P A ＝6，求PC 的长．30．（14分）如图，⊙O 是以AB 为直径的△ABC 的外接圆，点D 是劣弧的中点，连结AD 并延长，与过C 点的切线交于P ，OD 与BC 相交于点E ．（1）求证OE ＝21AC ；（2）求证：AP DP ＝22AC BD ；（3）当AC ＝6，AB ＝10时，求切线PC 的长．参考答案1.【提示】若三点在一条直线上，则不能作出过这三点的圆，故②不对．【答案】B ．【点评】本题考查直径、过不在同一条直线上的三点的圆、外心、等圆与等弧等概念，其中第②个命题不对的原因在于忽视了过三点作图的条件．2.【提示】弦的垂直平分线平分弦、垂直于弦，因此平分弦所对的两条弧．【答案】C ．3.【提示】因为在圆中，圆心角的度数与它所对的弧的度数相等，而∠AOB ＝∠A ′OB ′，所以的度数＝的度数．【答案】C ．4.【提示】连结BC ，则∠AEC ＝∠B ＋∠C ＝21×60°＋21×100°＝80°．【答案】C ．5.【提示】因为圆内接四边形的对角之和为180°，则∠A ＋∠C ＝∠B ＋∠D ＝180°．又因为∠A ︰∠B ︰∠C ＝2︰3︰6，所以∠B ︰∠D ＝3︰5，所以∠D 的度数为85×180°＝112.5°．【答案】C ．6.【提示】因为以点P 为圆心的圆与OC 相离，则P 到OC 的距离大于圆的半径．又因为角平分线上的一点到角的两边的距离相等，则点P 到OB 的距离也大于圆的半径，故圆P 与OB 也相离．【答案】A ．7.【提示】连结内心与三个顶点，则△ABC 的面积等于三个三角形的面积之和，所以△ABC 的面积为21a ·r ＋21b ·r ＋21c ·r ＝21（a ＋b ＋c ）r ．【答案】A 8.【提示】连结BD ，则∠ABM ＝∠ADB ．因为AD 为直径，所以∠A ＋∠ADB ＝90°，所以cos ∠ABM ＝23＝cos ∠ADB ＝sin A ，所以∠A ＝60°．又因四边形ABCD 内接于⊙O ，所以∠BCG ＝∠A ＝60°．则tan ∠BCG ＝3．【答案】D ．9.【提示】设PC 的长为a ，则PD 的长为（9－a ），由相交弦定理得3×4＝a ·（9－a ）．所以a 2－9 a ＋12＝0，故PC 、PD 的长是方程x 2－9 x ＋12＝0的两根．【答案】B ．10.【提示】当两圆相交时，圆心距d 与两圆半径的关系为2 r －r ＜d ＜2 r ＋r ，即r ＜d ＜3 r ．【答案】B ．11.【提示】如图，AB 为弦，CD 为拱高，则CD ⊥AB ，AD ＝BD ，且O 在CD 的延长线上．连结OD 、OA ，则OD ＝22AD OA -＝221213-＝5（米）．所以CD ＝13－5＝8（米）．【答案】8米．12.【提示】连结AC ．设∠DCA ＝x °，则∠DBA ＝x °，所以∠CAB ＝x °＋20°．因为AB 为直径，所以∠BCA ＝90°，则∠CBA ＋∠CAB ＝90°．又 ∠DBC ＝50°，∴ 50＋x ＋（x ＋20）＝90．∴ x ＝10．∴ ∠CBE ＝60°．【答案】60°．13.【提示】因平行弦所夹的弧相等，等弧所对的弦相等，所以圆内接梯形是等腰梯形．同理可证圆内接平行四边形是矩形．【答案】等腰，矩形．14.【提示】连结OA ．∵ AB 、AC 是⊙O 的切线，∴ AO 平分∠BAC ，且OB ⊥AB ．又 OB ＝BD ，∴ OA ＝DA ．∴ ∠OAB ＝∠DAB ．∴ 3∠DAB ＝60°．∴ ∠DAB ＝20°．∴ ∠D ＝70°15.【提示】延长AO ，交⊙O 于点F ．设⊙O 的半径为r ．由切割线定理，得AB 2＝AE ·AF ．∴ （5）2＝1·（1＋2 r ）．∴ r ＝2．【答案】2．16.【提示】因为圆心距等于两圆半径之和，所以这两圆外切，故有两条外公切线，一条内公切线．【答案】3．17.【提示】正n 边形有n 条对称轴．正2n 边形既是轴对称图形，又是中心对称图形．【答案】8，轴，中心．18.【提示】把正六边形的中心与六个顶点连结起来，所得六个等边三角形全等．每个等边三角形的面积为43·（2 a ）2＝3a 2，所以正六边形的面积为63a 2 19.【提示】已知扇形面积为9 cm 2，半径为6 cm ，则弧长l ＝692⨯＝3；设圆心角的度数为n ，则1806π⋅n ＝3 cm ，所以n ＝π90．【答案】3；π90︒． 20.【提示】面积为900 cm 2的正方形的边长为30 cm ，则底面圆的周长30 cm ．设直径为d ，则πd ＝30，故d ＝π30（cm ）．【答案】π30 cm ． 21.【答案】×．【点评】相交两圆的连心线垂直平分公共弦，反过来公共弦不一定平分连结两圆圆心的线段．22.【答案】×．【点评】矩形内接于以对角线为直径的圆，但它不是正多边形．23.【答案】×．【点评】正五边形是轴对称图形，但不是中心对称图形．24.【答案】√．【点评】作三角形的两条角平分线，设交点为I ，过I 作一边的垂线段，则以点I 为圆心，垂线段长为半径的圆即三角形的内切圆．25.【答案】×．【点评】当被平分的弦为直径时，两直径不一定垂直． 26.【分析】因为AE ＝1 cm ，EB ＝5 cm ，所以OE ＝21（1＋5）－1＝2（cm ）．在Rt △OEF 中可求EF 的长，则EC 、ED 都可用DF 表示，再用相交弦定理建立关于DF 的方程，解方程求DF 的长．【略解】∵ AE ＝1 cm ，BE ＝5 cm ，∴ ⊙O 的半径为 3 cm ．∴ OE ＝3－1＝2（cm ）．在Rt △OEF 中，∠OEF ＝60°，∴ EF ＝cos 60°·OE ＝21·2＝1（cm ）． ∵ OF ⊥CD ，∴ FC ＝FD ．∴ EC ＝FC －FE ＝FD －FE ，ED ＝EF ＋FD ．即 EC ＝FD －1，ED ＝FD ＋1．由相交弦定理，得 AE ·EB ＝EC ·ED ．∴ 1×5＝（FD －1）（FD ＋1）．解此方程，得 FD ＝6（负值舍去）．∴ CD ＝2FD ＝26（cm ）．27.【提示】连结CB ，易证△PCA ∽△PBC ，所以BC AC ＝PB PC ．由切割线定理可求PB 的长，所以tan ∠ACD ＝tan ∠CBA ＝BC AC ＝PBPC ．连结OC ，则在Rt △OCP 中可求sin ∠P 的值．【略解】连结OC 、BC ．∵ PC 为⊙O 的公切线，∴ PC 2＝P A ·PB ．∴ 82＝4·PB ．∴ PB ＝16．∴ AB ＝16－4＝12．易证△PCA ∽△PBC ．∴ BC AC ＝PBPC ． ∵ AB 为⊙O 的直径，∴ ∠ACB ＝90°．又 CD ⊥AB ，∴ ∠ACD ＝∠B ．∴ tan ∠ACD ＝tan B ＝BC AC ＝PB PC ＝168＝21． ∵ PC 为⊙O 的切线，∴ ∠PCO ＝90°．∴ sin P ＝PO OC ＝106＝5328.【提示】连结AC ，证△ABC ∽△FDC ．显然∠FDC ＝∠ABC ．因为AD ⊥直径EB ，由垂径定理得＝，故∠DAB ＝∠ACB ．又因为∠FCD ＝∠DAB ，所以∠FCD ＝∠ACB ，故△ABC ∽△FDC ，则可得出待证的比例式．【略证】连结AC ．∵ AD ⊥EB ，且EB 为直径，∴＝． ∴ ∠ACB ＝∠DAB ．∵ ABCD 为圆内接四边形，∴ ∠FCD ＝∠DAB ，∠FDC ＝∠ABC ．∴ ∠ACB ＝∠FCD ．∴ △ABC ∽△FDC ．∴ FD AB ＝DCBC 29.【提示】（1）过点P 作两圆的公切线PT ，利用弦切角进行角的转换；在（2）题中，可通过证△PCA ∽△PEC ，得到比例式PE PC ＝PCPA ，则可求PC ． *（1）【略证】过点P 作两圆的公切线PT ，连结CE ．∵ ∠TPC ＝∠4，∠3＝∠D ．∴ ∠4＝∠D ＋∠5，∴ ∠2＋∠3＝∠D ＋∠5．∴ ∠2＝∠5．∵ DA 与⊙O 相切于点C ，∴ ∠5＝∠1．∴ ∠1＝∠2．即PC 平分∠APD ．（2）【解】∵ DA 与⊙O 2相切于点C ，∴ ∠PCA ＝∠4．由（1），可知∠2＝∠1．∴ △PCA ∽△PEC ．∴ PE PC ＝PCPA ．即 PC 2＝P A ·PE ． ∵ PE ＝3，P A ＝6，∴ PC 2＝18．∴ PC ＝32．30.【提示】（1）因为AO ＝BO ，可证OE 为△ABC 的中位线，可通过证OE ∥AC 得到OE 为中位线；（2）连结CD ，则CD ＝BD ，可转化为证明AP DP ＝22AC CD ．先证△PCD ∽△P AC ，得比例式AC CD ＝PCPD ，两边平方得22AC CD ＝22PC PD ，再结合切割线定理可证得22AC CD ＝PA PD PD ⋅2＝PA PD ；（3）利用（2）可求DP 、AP ，再利用勾股定理、切割线定理可求出PC 的长．（1）【略证】∵ AB 为直径，∴ ∠ACB ＝90°，即 AC ⊥BC ．∵ D 为的中点，由垂径定理，得OD ⊥BC ．∴ OD ∥AC ．又∵ 点O 为AB 的中点，∴ 点E 为BC 的中点． ∴ OE ＝21AC ． *（2）【略证】连结CD ．∵ ∠PCD ＝∠CAP ，∠P 是公共角，∴ △PCD ∽△P AC ．∴ PC PD ＝ACCD ． ∴ 22PCPD ＝22AC CD ．又 PC 是⊙O 的切线，∴ PC 2＝PD ·DA ． ∴ PA PD PD ⋅2＝22ACCD ， ∴ PA PD ＝22AC CD ．∵ BD ＝CD ，∴ PA PD ＝22AC BD ．（3）【略解】在Rt △ABC 中，AC ＝6，AB ＝10，∴ BC ＝22610-＝8．∴ BE ＝4．∵ OE ＝AC 21＝3，∴ ED ＝2．则在Rt △BED 中，BD ＝22BE ED +＝25，在Rt △ADB 中，AD ＝22BD AB -＝45．∵ AC PD ＝22ACBD ， ∴ 54+PD PD ＝3620．解此方程，得 PD ＝55，AP ＝95．又 PC 2＝DP ·AP ， ∴ PC ＝5955 ＝15．。

北师大版数学六年级上册第一单元《圆》单元测试卷(A卷含答案)

28．圆的周长一定，是62.8米，它的半径是多少米？
29．一辆自行车轮胎的外直径约70厘米．小方骑这辆自行车从家到学校用了10分．如果车轮每分转100圈，小方家到学校的路程大约是多少米？
五、图形计算
30．用尺子量出如图图形的边长，并计算它们的周长．
参考答案
1．B
2．B
3．B
4．C
5．B
6．C
7．C
8．A
A．4×2×3.14B．4×4×3.14C．3.14×2D．2×4
3．一根绳子可围成一个半径是6米的圆，若用它围成一个正三角形，那么它的边长是( )米
A． B．4 C．6 D．12
4．如图中的五个半圆，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿，，，路线爬行，乙虫沿ACB路线爬行，则下列结论正确的是（）
北师大版数学六年级上册第一单元《圆》单元测试卷
学校:___姓名：___班级：___考号：___
一、选择题（20分）
1．一个圆环，外圆半径是2分米，内圆直径是2分米，圆环的面积是（）
A．3.14平方分米B．9.42平方分米C．12.56平方分米
2．用4米长的绳子把一只羊拴在一根木桩上，这只羊吃草面积最大是（）平方米．
20．一个圆的直径是20厘米，这个圆的周长是（）厘米，面积是（）平方厘米．
21．一个环形垫圈，内圆半径是3厘米，外圆直径是10厘米，这个环形垫圈的面积是（）平方厘米．
22．计算下圆的周长，请记住这些常用数据.
d=3厘米，c=（）厘米
23．半径2厘米的圆，周长是（）厘米，面积是（）平方厘米．
24．在一个面积为16平方厘米的正方形内，画一个最大的圆，这个圆的面积是（）平方厘米．
10．一个半圆，它的半径是r，这个半圆的周长是多少？（）

(必考题)小学数学六年级上册第五单元《圆》测试题(含答案解析)(3)

12．D
解析： D 【解析】【解答】解：大圆面积是小圆面积的 32=9 倍。故答案为：D。【分析】已知大圆半径是小圆半径的几倍，那么大圆面积是小圆面积的（几 2）倍。
二、填空题
13．8【解析】【解答】314×20=628（平方分米）所以圆的面积是 628 平方分米故答案为：628【分析】正方形的面积=边长×边长圆的面积=π×半径的平方根据已知条件一个正方形的边长和一个圆的半径相等可
6．D
解析： D 【解析】【解答】解：根据圆环的面积公式列式为：3.14×242÷2-3.14×202÷2。故答案为：D。【分析】外圆半径是 24 米。内圆半径是 20 米，用外半圆的面积减去内半圆的面积即可求出小路的面积。
7．C
解析： C 【解析】【解答】解：根据圆面积公式可知，一个圆的周长扩大 3 倍，它的面积就扩大 9 倍。故答案为：C。【分析】圆的周长、半径、直径扩大的倍数是相同的，圆面积扩大的倍数是半径扩大倍数的平方倍。
C. 6 倍
二、填空题
D. 9 倍
13．一个正方形的边长和一个圆的半径相等，已知正方形的面积是 20 平方分米，圆的面积是________平方分米。 14．用圆规画一个周长是 12.56dm 的圆，圆规两脚之间的距离是________dm，这个圆的面积是________dm2。 15 ．下图中，正方形的面积是 9cm2 ，这个圆的周长是 ________cm ，面积是 ________cm2。
A. 2
B. 6.28
C. 12.56
11．下面两个图形阴影部分的周长和面积的大小关系是（）。
D. 18.84
A. 周长相等，面积不相等
B. 周长和面积都相等

(压轴题)小学数学六年级上册第五单元《圆》测试(包含答案解析)

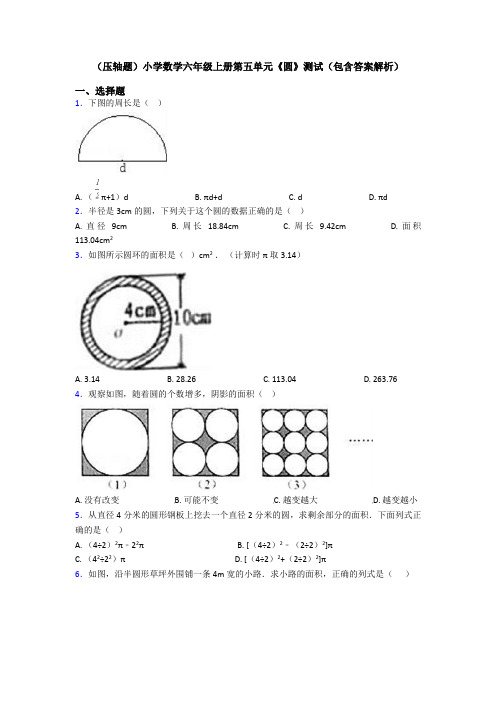
（压轴题）小学数学六年级上册第五单元《圆》测试（包含答案解析）一、选择题1．下图的周长是（）A. （π+1）dB. πd+dC. dD. πd2．半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm23．如图所示圆环的面积是（）cm2．（计算时π取3.14）A. 3.14B. 28.26C. 113.04D. 263.76 4．观察如图，随着圆的个数增多，阴影的面积（）A. 没有改变B. 可能不变C. 越变越大D. 越变越小5．从直径4分米的圆形钢板上挖去一个直径2分米的圆，求剩余部分的面积．下面列式正确的是（）A. （4÷2）2π﹣22πB. [（4÷2）2﹣（2÷2）2]πC. （42÷22）πD. [（4÷2）2+（2÷2）2]π6．如图，沿半圆形草坪外围铺一条4m宽的小路．求小路的面积，正确的列式是（）A. 3.14×42÷2B. 3.14×202÷2C. 3.14×（202﹣42）÷2D. 3.14×242÷2﹣3.14×202÷2 7．大圆的半径是小圆的直径，则大圆面积是小圆面积的（）。

A. 2倍B. 4倍C. 12D. 14 8．周长相等的长方形、正方形、圆中，（）的面积最大。

A. 长方形B. 正方形C. 圆9．如果一个圆的半径由1分米增加到2分米，它的周长增加了（）分米。

A. 2B. 6.28C. 12.56D. 18.84 10．半圆的周长是直径的（）。

A. π倍B. π倍C. （π+1）倍11．一个圆和一个正方形的周长相等，他们的面积比较（）A. 圆的面积大B. 正方形的面积大C. 一样大12．将圆的半径按3：1放大后，面积将扩大到原来的（）。

六年级数学上册第五单元《圆》测试卷-人教版(含答案)

六年级数学上册第五单元《圆》测试卷-人教版（含答案）一、单选题(总分：40分本大题共8小题，共40分)1.(本题5分)圆的周长扩大2倍，面积就（）A.扩大2倍B.扩大4倍C.不变2.(本题5分)大圆的周长除以它的直径（）小圆的周长除以它的直径．A.大于B.小于C.等于3.(本题5分)如果圆的半径等于正方形的边长，那么圆的周长（）正方形的周长．A.大于B.等于C.小于4.(本题5分)两个圆的周长不相等，是因为它们的（）A.圆心位置不同B.圆周率不相等C.直径不相等5.(本题5分)圆的大小与（）有关．A.圆心B.半径C.圆周率6.(本题5分)一张长13厘米，宽9厘米的长方形纸板，最多可以剪（）个半径2厘米的圆．A.7B.8C.67.(本题5分)半径不同的两个圆，它们的（）相同．A.圆周率B.周长C.面积8.(本题5分)画圆时，圆规两脚间的距离是（）A.半径长度B.直径长度C.圆的大小二、填空题(总分：25分本大题共5小题，共25分)9.(本题5分)一根铁丝可以围成一个半径是3厘米的圆，如果用它围成一个等边三角形，这个三角形的边长是____厘米．10.(本题5分)圆周率表示一个圆的____和____的倍数关系．π约等于____．11.(本题5分)时针长5厘米，分针长6厘米，从上午10时到下午4时，时针尖经过的路线长____分米，分针扫过的面积是____．12.(本题5分)在同一个圆里，直径的长度是半径的____．13.(本题5分)通过圆心，两端都在圆上的线段叫做半径．____．（判断对错）三、解答题(总分：35分本大题共5小题，共35分)14.(本题7分)如图，正方形的周长是24dm，其中一个半圆的周长是多少？15.(本题7分)在下边的正方形中画一个最大的圆．16.(本题7分)列式计算．（1）d=5厘米，求周长．（2）C=12.56dm，求面积．17.(本题7分)笑笑想在室外画一个直径约6米的圆，他可以如何去完成？18.(本题7分)用圆规画一个直径6厘米的半圆，这个半圆的周长是____厘米．在这个半圆里画一个最大的三角形，画出的这个三角形的面积是____平方厘米．参考答案1.【答案】：B;【解析】：解：圆的周长=2πr，其中2π是一个定值，所以圆的周长与r成正比例，周长扩大2倍，则半径也是扩大了2倍；圆的面积公式：S=πr2，其中r2看成一个因数，π是恒值，那么S和r2成正比例；半径扩大2倍，面积就扩大22=4倍；答：圆的面积是扩大4倍．故选：B．2.【答案】：C;【解析】：解：根据圆周率的含义可知：大圆的周长除以它的直径等于小圆的周长除以它的直径；故选：C．3.【答案】：A;【解析】：解：设圆的半径为r，则正方形的边长也是r，圆的周长：3.14×r×2=6.28r，正方形的周长：4r，因为6.28r＞4r，所以圆的周长大于正方形的周长．故选：A．4.【答案】：C;【解析】：解：由“圆的周长=2πr=πd”可知：圆的周长和半径或直径、圆周率有关系，因为圆周率不变，所以只与半径或直径有关，则两个圆的周长不相等，是因为半径或直径不同．故选：C．5.【答案】：B;【解析】：解：因为圆心决定圆的位置，半径决定圆的大小；所以得出：圆的大小与半径的长短有关；故选：B．6.【答案】：C;【解析】：解：13÷（2×2）=13÷4=3（个）…1（厘米）9÷（2×2）=9÷4=2（个）…1（厘米）3×2=6（个）．答：最多可画6个．故选：C．7.【答案】：A;【解析】：解：半径不同的两个圆，它们的圆周率相同．故选：A．8.【答案】：A;【解析】：解：根据画圆的方法可知，圆规两脚之间的距离就是圆的半径．故选：A．9.【答案】：6.28;【解析】：解：（2×3.14×3）÷3，=18.84÷3，=6.28（厘米）；答：这个三角形的一条边长6.28厘米．故答案为：6.28．10.【答案】：周长;直径;3.14;【解析】：解：圆周率表示一个圆的周长和直径的倍数关系．π约等于3.14；故答案为：周长，直径，3.14．11.【答案】：1.57;56.52平方厘米;【解析】：解：（1）时针“走过”了：2×3.14×5×÷2，=3.14×5，=15.7（厘米），=1.57（分米）；（2）时针“扫过”的面积：πr2，=×3.14×62，=56.52（平方厘米）；答：时针尖经过的路线长1.57分米，分针扫过的面积是56.52平方厘米．故答案为：1.57，56.52平方厘米．12.【答案】：2倍;【解析】：解：通过半径和直径的定义可知，直径的长度是半径的2倍．故答案为：2倍．13.【答案】：x;【解析】：解：由分析可知：半径是连接圆心和圆上任意一点的线段；故答案为：×．14.【答案】：解：24÷4=6（dm）3.14×6÷2+6=9.42+6=15.42（dm），答：一个半圆的周长是15.42分米．;【解析】：根据题意，正方形的周长是24dm，据此可求出正方形的边长，也就是半圆的直径，半圆的周长等于半圆所在圆周长的一半再加上一条直径的长即可，根据圆的周长公式C=πd 进行计算即可得到答案．15.【答案】：解：由分析作图如下：;【解析】：根据在正方形中画一个最大的圆，要使正方形内的圆最大，圆的直径必须等于正方形的边长，量出正方形的边长，即圆的直径，然后画圆即可．16.【答案】：解：（1）3.14×5=15.7（厘米）答：圆的周长是15.7厘米．（2）12.56÷3.14÷2=2（分米）3.14×22=12.56（平方分米）答：圆的面积是12.56平方分米．;【解析】：（1）根据圆的周长公式C=πd进行计算即可得到答案；（2）根据圆的周长公式C=2πr先求出圆的半径，再根据圆的面积公式是：S=πr2，把数据代入公式解答即可．17.【答案】：解：笑笑可以找一根6÷2=3米的绳子，先将绳子的一端固定在地面上，再用手牵着绳子的另一端，绕固定的一端旋转一周，即可画出直径约6米的圆．;【解析】：圆心确定圆的位置，半径确定圆的大小．以任意一点为圆心，以（6÷2）米为半径，即可画出符合要求的圆．18.【答案】：15.429;【解析】：解：（1）以任意一点O为圆心，以6÷2=3厘米为半径的半圆如图所示：半圆的周长为：3.14×6÷2+6=9.42+6=15.42（厘米）（2）6×（6÷2）÷2=6×3÷2=18÷2=9（平方厘米）答：这个三角形的面积是9平方厘米．故答案为：15.42，9．。

六年级上册小学数学第五单元《圆》测试(包含答案解析)(1)

六年级上册小学数学第五单元《圆》测试（包含答案解析）(1)一、选择题1．下面图案中，对称轴条数最多的是（）。

A. B. C. D.2．同圆中扇形甲的弧长是扇形乙的弧长的，那么扇形乙的面积是扇形甲面积的（）A. 36倍 B. 12倍 C. 6倍 D. 3倍3．将半径分别为2厘米和3厘米的两个半圆如图那样放置，则阴影部分的周长是（）A. 18.7厘米B. 19厘米C. 10厘米D. 19.7厘米4．半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm25．已知大圆半径是小圆半径的3倍，则大圆面积是小圆面积的（）A. 3倍B. 6倍C. 9倍D. 12倍6．如图所示圆环的面积是（）cm2．（计算时π取3.14）A. 3.14B. 28.26C. 113.04D. 263.76 7．如图，两只蚂蚁分别选择甲、乙两条线路从A地爬向B地．下面说法正确的是（）A. 甲线路路程多B. 乙线路路程多C. 两条线路的路程一样多D. 不能确定8．在圆内剪去一个圆心角为45的扇形，余下部分的面积是剪去部分面积的（）倍．A. 9 B. 8 C. 79．东方公园有一个圆形的喷水池，经测量得出这个喷水池的周长是37 .68m。

这个喷水池占地（）m2。

A. 37.68B. 113.04C. 452.1610．周长相等的长方形、正方形、圆中，（）的面积最大。

A. 长方形B. 正方形C. 圆11．如果一个圆的半径由1分米增加到2分米，它的周长增加了（）分米。

A. 2B. 6.28C. 12.56D. 18.84 12．修一个如图的羊圈，需要（）米栅栏。

A. 25.12B. 12.56C. 20.56D. 50.24二、填空题13．两个圆的半径比是4：9，则它们的周长比是________，面积比是________．14．一个正方形的边长和一个圆的半径相等，已知正方形的面积是20平方分米，圆的面积是________平方分米。

2020版人教版数学六年级上册第五单元《圆》单元测试卷A卷

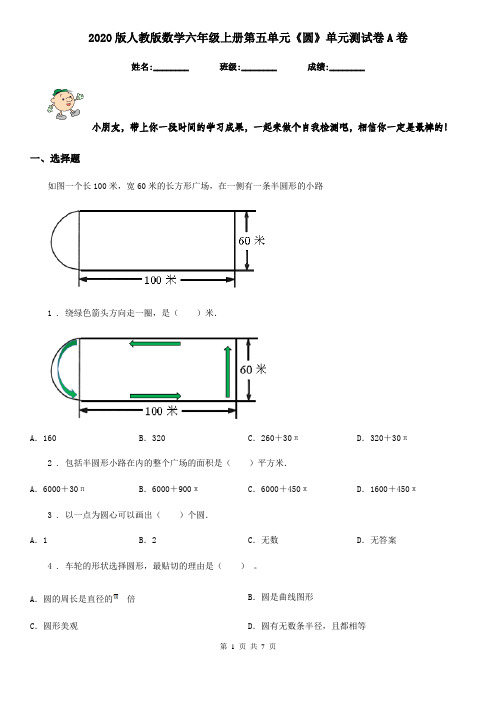
2020版人教版数学六年级上册第五单元《圆》单元测试卷A卷姓名:________ 班级:________ 成绩:________小朋友，带上你一段时间的学习成果，一起来做个自我检测吧，相信你一定是最棒的！一、选择题如图一个长100米，宽60米的长方形广场，在一侧有一条半圆形的小路1 . 绕绿色箭头方向走一圈，是（）米．A．160B．320C．260＋30πD．320＋30π2 . 包括半圆形小路在内的整个广场的面积是（）平方米．A．6000＋30πB．6000＋900πC．6000＋450πD．1600＋450π3 . 以一点为圆心可以画出（）个圆．A．1B．2C．无数D．无答案4 . 车轮的形状选择圆形，最贴切的理由是（）。

A．圆的周长是直径的倍B．圆是曲线图形C．圆形美观D．圆有无数条半径，且都相等5 . 一个环形，外圆直径是40厘米，环的宽度是10厘米，它的内圆半径是（）A．10厘米B．20厘米C．30厘米D．50厘米6 . 一个圆的半径由3厘米变成5厘米，圆的面积增加了（）平方厘米．A．2πB．4C．16D．16π7 . 所有的车轮都做成圆形是利用了圆的（）特性．A．曲线B．美观C．圆心到圆上任意一点的距离相等8 . 下图的周长是（）。

B．πd+dA．(π+1)dC．d D．πd9 . 圆中两端都在圆上的线段可能是（）。

A．圆的直径B．圆的半径C．圆的周长D．圆的面积二、填空题10 . 画圆时，圆规两脚之间的距离是4厘米，画出的圆的周长是（______）厘米，面积是（______）平方厘米。

11 . 地球赤道是一个近似的圆，如果它的直径增加1米，它的周长增加________米．12 . 将圆均分成360份，其中的1份所对的角的大小叫做_____．13 . 在一个圆中，圆的周长是直径的倍，是半径的倍．14 . 圆的直径越小，它的半径就越小．．15 . 填写下表。

16 . 圆的周长总是直径的多一些．17 . 一个直径是10厘米的圆，它的任意一条直径将它分成2个半圆，半圆的周长为（）cm。

《常考题》小学数学六年级上册第五单元《圆》测试卷(含答案解析)

2.5 米，在花坛一周铺了一条宽 0.5 米的碎石小路，小路的面积11．两个圆的周长之比是 2：5，则它的面积之比是（A. 18.84 二、填空题13．如图，正方形 ABCD 的边 AB=1，弧 BD 和弧 AC 都是以 1 为半径的圆弧，则无阴影的两部分的面积之差为。

常考题》小学数学六年级上册第五单元《圆》测试卷（含答案解析）一、选择题 1．圆是轴对称图形，它有（）条对称轴。

A. 一 B. 两 C. 无数 D. 四 2．把一个直径 10 厘米圆分成两个相等的半圆，两个半圆的周长的和是（） A. 31.4 B . 62.8 C . 41.4 D . 51.4 3．已知圆的周长是 18.84 厘米，它的直径是（） B. 12.56 厘米 A. 6 厘米 C. 12 厘米 4．在圆内剪去一个圆心角为 45 的扇形，余下部分的面积是剪去部分面积的（）倍． A. 9 5．两个圆的周长不相等，是因为它们的（ A. 圆心位置不同 B. 半径不相等）。

C. 圆周率不相等 6．大圆的半径是小圆的直径，则大圆面积是小圆面积的 A. 2 倍 B. 倍4 ）。

C. 12 D. 14 5cm，周长是（ A. 6.28cm 2 个半圆后，每个半圆的周长是） cm 。

C. 10π D. 10 π +10 ）。

B . 3.14cm C . 4.14cm D . 5.14cm A. 27.475 B . 9.42 C . 8.635 D .28.26 10．如果一个圆的半径由 A. 2 1 分米增加到 2 分米，它的周长增加了（ B . 6.28 C . 12.56 ）分米。

D . 18.84 A. 2： 5 B. ：5 2 C.： 425 D. 2：5 4 12．一个圆的半径是 6 厘米，它的周长是）厘米。

9．一个圆形花坛的半径是是（）平方米。

）。

B. 37.68C. 113.0414．如图所示的图形由 1 个大半圆弧和 6 个小半圆弧组成，已知最大半圆弧的直径是这个图形的周长为 _____ 。

《圆》精选测试题及参考答案

圆精选测试题（一）一、填空题̂=CD̂=BD̂，M是AB上一动点，则CM+DM的最1.在⊙O中，AB是⊙O的直径，AB=8cm，AC小值为____________.2.如图，正三角形ABC的边长为2，D、E、F分别为BC、CA、AB的中点，以A、B、C三点为圆心，半径为1作圆，则圆中阴影部分的面积是____________.3.如图，在△ABC中，∠C=90°，∠A=25°，以点C为圆心，BC为半径的圆交AB于点D，̂的度数为．交AC于点E，则BD4.如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC=110°．连接AC，则∠A的度数是．5.如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为4，则阴影部分的面积等于___ ．6.如图，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，点D是⊙上一点，连接PD．已知PC=PD=BC．下列结论：（1）PD与⊙O相切;（2）四边形PCBD是菱形;（3）PO=AB;（4）∠PDB=120°.其中正确的是_____________.7.如图，半径为2，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为____________.二、解决问题1.如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，求图中阴影部分的面积．2.如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=BFD．（1）求证：FD是⊙O的切线；（2）若AB=10，AC=8，求DF的长．3.如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．（1）求AC、AD的长；（2）试判断直线PC与⊙O的位置关系，并说明理由．4.如图，AB是⊙O的直径，点C在0O上，连接BC，AC，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．（1)求证：DE是⊙O的切线；(2)若CEDE =23，求tan∠E和cos∠ABC的值.5.如图，AB，AC分别是半⊙O的直径和弦，OD⊥AC于点D，过点A作半⊙O的切线AP，AP 与OD的延长线交于点P,连接PC并延长与AB的延长线交于点F．（1）求证：PC是半⊙O的切线；（2）若∠CAB=30°，AB=10，求线段BF的长．6.如图，AB 是⊙O 的直径，延长AB 至P ，使BP=OB ，BD 垂直于弦BC ，垂足为点B ，点D 在PC 上．设∠PCB=α，∠POC=β．(1)下列结论：①BD ∥AC;②tan β2=BC AC ;③△PBD ∽△PAC.其中正确的有________________.(2)求证：tan α• tanβ=137.如图1，在⊙O 中，E 是弧AB 的中点，C 为⊙O 上的一动点（C 与E 在AB 异侧），连接EC 交AB 于点F ，r 是⊙O 的半径，EB=2r3，D 为AB 延长线上一点. (1)下列结论：①若DC=DF ，直线DC 是⊙O 的切线;②△EBF ∽△ECB;③EF•EC = 49r 2.其中正确的有____________________.(2)如图2，若F 是AB 的四等分点，求EF 和EC 的值.圆精选测试题（二）一、填空题1.如图，AB 是半圆的直径，点O 为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E ，交⊙O 于D ，连接BE ．设∠BEC=α，则sinα的值为____________.2.如图，水平放置的圆柱形排水管道的截面直径是1m ，其中水面的宽AB 为0.8m ，则排水管内水的深度为____________.3.如图，等腰直角△ABC 中， AB = AC = 8，以AB 为直径的半圆O 交斜边BC 于D ，阴影部分面积为____________. (结果保留π).4.如图，要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为____________．5.图，圆内接正六边形的边长为4，以其各边为直径作半圆，则图中阴影部分的面积为____________.6.直线AB 与⊙O 相切于点A ，弦CD∥AB，E ，F 为圆上的两点，且∠CDE=∠ADF．若⊙O 的半径为52，CD=4，则弦EF 的长为____________. BA7.菱形ABCD 的边长为2，∠A=60°，以点B 为圆心的圆与AD ，DC 相切，与AB ，CB 的延长线分别相交于点E 、F ，则图中阴影部分的面积为____________.8.AB 是⊙O 的直径，且经过弦CD 的中点H ，过CD 延长线上一点E 作⊙O 的切线，切点为F.若∠ACF=65°，则∠E=____________.二、解决问题1.如图，⊙O 的半径为1，A ，P ，B ，C 是⊙O 上的四个点，∠APC=∠CPB=60°.（1）判断△ABC 的形状：______________；（2）试探究线段PA ，PB ，PC 之间的数量关系，并证明你的结论；（3）当点P 位于AB̂的什么位置时，四边形APBC 的面积最大？求出最大面积． B C P OA ACB O ABCHO D2.已知在△ABC 中，∠B=90o，以AB 上的一点O 为圆心，以OA 为半径的圆交AC 于点D ，交AB 于点E ．（1）求证：AC ·AD=AB ·AE ；（2）如果BD 是⊙O 的切线，D 是切点，E 是OB 的中点，当BC=2时，求AC 的长．3.如图,在△ABC 中,BA=BC,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，BC 的延长线与⊙O 的切线AF 交于点F.(1)求证：∠ABC=2∠CAF ；(2)若AC=2√10，CE:EB=1:4,求CE 的长. 4.如图，在△ABC 中，AB=AC ，以AC 为直径的⊙O 交AB 于点D ，交BC 于点E ．（1）求证：BE=CE ；（2）若BD=2，BE=3，求AC 的长．5.如图，点C 在以AB 为直径的⊙O 上，点D 是半圆AB 的中点，连接AC ，BC ，AD ，BD ，过点D 作DH ∥AB 交CB 的延长线于点H.（1）求证：直线DH 是⊙O 的切线；E DA O（2）若AB=10，BC=6，求AD ，BH 的长.6.如图，A 为⊙O 外一点，AB 切⊙O 于点B ，AO 交⊙O 于C ，CD ⊥OB 于E ，交⊙O 于点D ，连接OD ．若AB=12，AC=8．（1）求OD 的长；（2）求CD 的长．参考答案测试题（一）一、填空题1. 82. √3−π23. 50°4. 35°5. 16π36. ①②③④7. π2−1 二、解决问题1（1）提示：计算∠OCD=90°（2）2√3−2π32（1）提示：证明FD ∥AC（2）提示：相似，DF=203 3(1)AC=5√3,AD=5√2(2) 提示：计算∠OCP=90°4(1) 提示：证明△OCD ≌△OAD(2) tan ∠E=√24，cos ∠ABC =√335(1) 提示：证明△OCP ≌△OAP(2) BF=56(1) ①②③(2) tan α• tanβ=BD BC ∙BC AC =BD AC =13 7(1) ①②③(2) EF=2√3r 9,EC=2√3r 3测试题（二）一、填空题1. 3√313 提示：连接BC ，sin α=BC BE2. 0.8m3. 4π+244. 288°5. 24√3−4π6. 2√57. 3π+2√348. 50°二、解决问题1(1) 等边三角形.(2)PC=PA+PB 提示：在PC 上截取PD ，使PD ＝PA ，证明△PAB ≌△DAC.(3)中点，最大面积是√3.2(1) 提示：接连DE,证明△ADE ∽△ABC.(2) 30°3(1) 提示：接连BD,证明∠CBD=∠ABD ，∠ABD=∠CAF.(2) CE=2.提示：设CE=x,则BE=4x,AB=5x,勾股定理列方程可解. 4(1) 提示：三线合一.(2) AC=9.提示：连接DE ，△BDE ∽△BCA ．5(1)提示：平行法.（2）析：∠CAD=∠DBH ，∠ACD=∠BDH, △ACD ∽△BDH,AD BH =AC BD ,BH=254. 6(1) AC=5.提示：设半径是x,勾股定理.（2）析： CE∥AB ,△OEC∽△OBA，∠CAD=∠DBH ，∠ACD=∠BDH, △ACD ∽△BDH,CD=2013.。

人教版小学数学六年级上册数学第五单元圆的水平测试题

最新人教版小学数学六年级上册第五单元《圆》的水平测试题A一、判断是否：1、圆的半径有无数条。

…………………………………………………………( )2、圆的直径是半径的2倍。

……………………………………………………（)3、圆有无数条对称轴。

………………………………………………………( ）4、圆的半径都相等。

…………………………………………………………（）5、直径4厘米的圆与半径2厘米的圆一样大。

………………………………（）6、半径2分米的圆的周长和面积一样大。

…………………………………（）二、细心填写：1、用圆规画一个周长50.24厘米的圆,圆规两脚之间的距离是（）厘米，所画的圆的面积是（)平方厘米。

2、圆的半径扩大3倍，直径扩大（)倍，周长扩大（）倍;面积扩大（）倍。

3、一根铁丝正好围成一个直径2米的圆，这根铁丝长（）米；如果改围成一个正方形，正方形的边长是（）米，面积是（)平方米。

4、小圆半径6厘米,大圆半径8厘米.大圆和小圆半径的比是（);直径的比是（);周长的比是（)；面积的比是（）.三、解决问题：1、一辆自行车轮胎外直径50厘米，如果自行车每分钟转120周，这辆自行车每小时能行多少千米？（得数保留整千米）2、在长8分米宽6分米的长方形中画一个最大的圆，圆的周长和面积各是多少?3、在长8分米宽6分米的长方形中画一个最大的半圆,半圆的周长和面积各是多少？4、一个圆形喷水池的周长62.8米,在水池外边有一条0.5米宽的水泥路。

路的面积是多少平方米？圆的复习B一、谨慎选择:1、圆周率π的值（）。

A 等于3.14B 大于3.14C 小于3。

142、一个圆的半径2米,那么它的周长和面积相比，( ）。

A 面积大B 周长大C 同样大D 无法比较3、直径是通过圆心并且两端都在圆上的（）。

A 线段B 直线C 射线4、把一张圆形纸片沿半径平均分成若干份，拼成一个近似长方形，其周长（）.A 等于圆周长B 大于圆周长C 小于圆周长D 无法比较5、圆的直径扩大2倍，它的面积扩大（）。

(必考题)小学数学六年级上册第五单元《圆》测试题(答案解析)

（必考题）小学数学六年级上册第五单元《圆》测试题（答案解析）一、选择题1．下图的周长是（）A. （π+1）dB. πd+dC. dD. πd2．将半径分别为2厘米和3厘米的两个半圆如图那样放置，则阴影部分的周长是（）A. 18.7厘米B. 19厘米C. 10厘米D. 19.7厘米3．一个圆的半径扩大到原来的2倍，面积就扩大到原来的（）A. 2倍B. 3倍C. 4倍4．长方形纸长20厘米，宽16厘米，它最多能够剪下（）个半径是3厘米的圆形纸片。

A. 6B. 8C. 115．已知一个圆的半径是R，且R满足3：R=R：4，则这个圆的面积为（）A. 7πB. 7C. 12πD. 无法求出6．半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm27．已知大圆半径是小圆半径的3倍，则大圆面积是小圆面积的（）A. 3倍B. 6倍C. 9倍D. 12倍8．已知圆的周长是18.84厘米，它的直径是（）A. 6厘米B. 12.56厘米C. 12厘米9．一个圆的周长扩大3倍，它的面积就扩大（）倍．A. 3B. 6C. 910．在长4厘米，宽3厘米的长方形内画最大半圆，这个半圆的周长是（）A. 6.28厘米B. 7.71厘米C. 10.28厘米D. 12.56厘米11．周长相等的长方形、正方形、圆中，（）的面积最大。

A. 长方形B. 正方形C. 圆12．一个圆和一个正方形的周长相等，他们的面积比较（）A. 圆的面积大B. 正方形的面积大C. 一样大二、填空题13．一个半圆的周长是25.7 cm，这个半圆的面积是________cm2.14．用三根同样长的铁丝分别围成一个圆、一个长方形和一个正方形，其中________的面积最大。

15．圆心角为90°，半径为6米的扇形，它的面积是________平方米．16．在一个周长为40cm的正方形纸片内，要剪一个最大的圆，那么这个圆的半径是________cm，面积是________cm2。

人教版六年级数学上册第5单元《圆》测试题(含答案)

人教版六年级数学上册第5单元《圆》测试题（含答案）（满分：100分，完成时间：60分钟）一．选择题（满分16分，每小题2分）1．推导圆的周长公式时，我们是用( )的方法得出计算公式C d π=或2C r π=。

A ．画圆为方B ．化曲为直C ．化直为曲D ．没有方法2．如图，大圆直径2cm ，小圆贴着大圆的内侧从P 点开始按箭头所指方向滚动，小圆至少需要滚动( )周才能回到P 点。

A ．2B ．3C ．43．如图是一个半圆，求它的周长的正确算式是( )A ．3.141522⨯⨯ B ．3.14(152)152⨯⨯+C ．3.1415152⨯+⨯D ．3.141521522⨯⨯+÷ 4．如图，把一个圆沿半径分成若干等份后，拼成一个近似的长方形，近似长方形的周长比圆的周长增加了20厘米，这个圆的面积是( )平方厘米。

A ．400πB ．100πC ．25πD ．20π5．周长相等的平面图形中，( )的面积最大。

A ．圆B ．长方形C ．正方形D ．平行四边形6．一个圆滚动一周的示意图，那么这个圆的直径大约是( )厘米。

A．4B．3C．2D．1 7．如果大圆的半径等于小圆的直径，那么小圆的面积是大圆面积的()A．2倍B．4倍C．12D．148．为了美化校园环境，学校准备在半径是4米的花坛外围铺一条1米宽的环形小路。

这条环形小路的面积是()平方米。

A．6.28B．12.56C．28.26D．50.24二．填空题（满分16分，每小题2分）9．如果要画一个周长是28.26厘米的圆，圆规两脚分开的距离是毫米。

10．一个圆环，内圆周长是9.42厘米，环宽是2厘米，内圆半径是，外圆半径厘米，环形面积是平方厘米。

11．如果把一个圆平均分成32份，拼成如图所示的长方形，长方形的长是31.4厘米，那么圆的半径是厘米，圆的面积是平方厘米。

12．如图，学校操场两端是半圆形，中间是正方形，程老师绕操场跑了2圈，一共跑了米。

(压轴题)小学数学六年级上册第五单元《圆》测试题(含答案解析)(4)

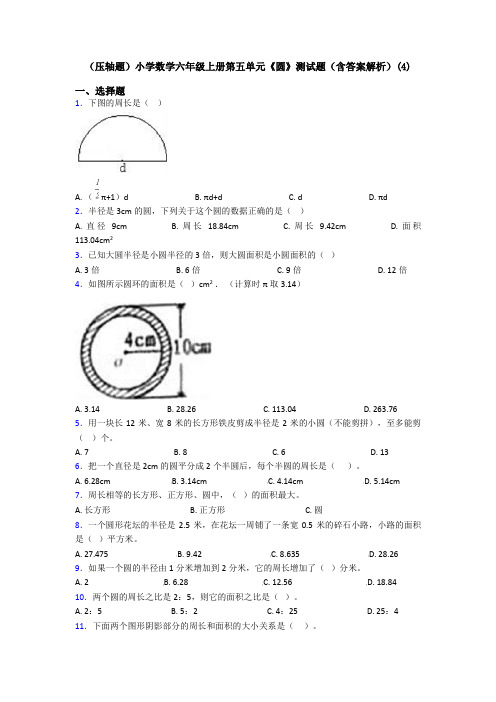
（压轴题）小学数学六年级上册第五单元《圆》测试题（含答案解析）(4)一、选择题1．下图的周长是（）A. （π+1）dB. πd+dC. dD. πd2．半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm23．已知大圆半径是小圆半径的3倍，则大圆面积是小圆面积的（）A. 3倍B. 6倍C. 9倍D. 12倍4．如图所示圆环的面积是（）cm2．（计算时π取3.14）A. 3.14B. 28.26C. 113.04D. 263.76 5．用一块长12米、宽8米的长方形铁皮剪成半径是2米的小圆（不能剪拼），至多能剪（）个。

A. 7B. 8C. 6D. 136．把一个直径是2cm的圆平分成2个半圆后，每个半圆的周长是（）。

A. 6.28cmB. 3.14cmC. 4.14cmD. 5.14cm 7．周长相等的长方形、正方形、圆中，（）的面积最大。

A. 长方形B. 正方形C. 圆8．一个圆形花坛的半径是2.5米，在花坛一周铺了一条宽0.5米的碎石小路，小路的面积是（）平方米。

A. 27.475B. 9.42C. 8.635D. 28.26 9．如果一个圆的半径由1分米增加到2分米，它的周长增加了（）分米。

A. 2B. 6.28C. 12.56D. 18.84 10．两个圆的周长之比是2：5，则它的面积之比是（）。

A. 2：5B. 5：2C. 4：25D. 25：4 11．下面两个图形阴影部分的周长和面积的大小关系是（）。

A. 周长相等，面积不相等B. 周长和面积都相等C. 周长和面积都不相等D. 周长不相等，面积相等12．修一个如图的羊圈，需要（）米栅栏。

A. 25.12B. 12.56C. 20.56D. 50.24二、填空题13．一个半圆的周长是25.7 cm，这个半圆的面积是________cm2.14．在一个圆内，以它的半径为边长作一个正方形，已知正方形的面积是36平方厘米，圆的面积是________平方厘米。

(易错题)小学数学六年级上册第五单元《圆》测试题(答案解析)

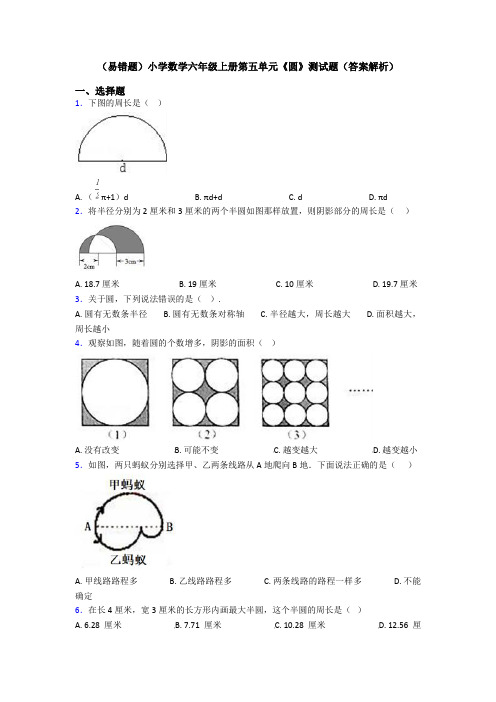
（易错题）小学数学六年级上册第五单元《圆》测试题（答案解析）一、选择题1．下图的周长是（）A. （π+1）dB. πd+dC. dD. πd2．将半径分别为2厘米和3厘米的两个半圆如图那样放置，则阴影部分的周长是（）A. 18.7厘米B. 19厘米C. 10厘米D. 19.7厘米3．关于圆，下列说法错误的是（）.A. 圆有无数条半径B. 圆有无数条对称轴C. 半径越大，周长越大D. 面积越大，周长越小4．观察如图，随着圆的个数增多，阴影的面积（）A. 没有改变B. 可能不变C. 越变越大D. 越变越小5．如图，两只蚂蚁分别选择甲、乙两条线路从A地爬向B地．下面说法正确的是（）A. 甲线路路程多B. 乙线路路程多C. 两条线路的路程一样多D. 不能确定6．在长4厘米，宽3厘米的长方形内画最大半圆，这个半圆的周长是（）A. 6.28厘米B. 7.71厘米C. 10.28厘米D. 12.56厘米7．大圆的半径是小圆的直径，则大圆面积是小圆面积的（）。

A. 2倍B. 4倍C. 12D. 14 8．把一个直径是2cm的圆平分成2个半圆后，每个半圆的周长是（）。

A. 6.28cmB. 3.14cmC. 4.14cmD. 5.14cm 9．半圆的周长是直径的（）。

A. π倍B. π倍C. （π+1）倍10．两个圆的周长之比是2：5，则它的面积之比是（）。

A. 2：5B. 5：2C. 4：25D. 25：4 11．一个圆和一个正方形的周长相等，他们的面积比较（）A. 圆的面积大B. 正方形的面积大C. 一样大12．将圆的半径按3：1放大后，面积将扩大到原来的（）。

A. 9倍B. 6倍C. 3倍二、填空题13．一个正方形的边长和一个圆的半径相等，已知正方形的面积是20平方分米，圆的面积是________平方分米。

14．从一个长10cm，宽8cm的长方形纸上剪下一个最大的圆，这个圆的面积是________cm2，剩下部分的面积是________cm2。

《易错题》小学数学六年级上册第五单元《圆》测试卷(答案解析)(1)

《易错题》小学数学六年级上册第五单元《圆》测试卷（答案解析）(1)一、选择题1．下图的周长是（）A. （π+1）dB. πd+dC. dD. πd2．一个圆的半径扩大到原来的2倍，面积就扩大到原来的（）A. 2倍B. 3倍C. 4倍3．已知大圆半径是小圆半径的3倍，则大圆面积是小圆面积的（）A. 3倍B. 6倍C. 9倍D. 12倍4．如图，两只蚂蚁分别选择甲、乙两条线路从A地爬向B地．下面说法正确的是（）A. 甲线路路程多B. 乙线路路程多C. 两条线路的路程一样多D. 不能确定5．一个圆的周长扩大3倍，它的面积就扩大（）倍．A. 3B. 6C. 96．用一块长12米、宽8米的长方形铁皮剪成半径是2米的小圆（不能剪拼），至多能剪（）个。

A. 7B. 8C. 6D. 137．两个圆的周长不相等，是因为它们的（）。

A. 圆心位置不同B. 半径不相等C. 圆周率不相等8．大圆的半径是小圆的直径，则大圆面积是小圆面积的（）。

A. 2倍B. 4倍C. 12D. 14 9．把一个直径是2cm的圆平分成2个半圆后，每个半圆的周长是（）。

A. 6.28cmB. 3.14cmC. 4.14cmD. 5.14cm 10．周长相等的长方形、正方形、圆中，（）的面积最大。

A. 长方形B. 正方形C. 圆11．如果一个圆的半径由1分米增加到2分米，它的周长增加了（）分米。

A. 2B. 6.28C. 12.56D. 18.84 12．修一个如图的羊圈，需要（）米栅栏。

A. 25.12B. 12.56C. 20.56D. 50.24二、填空题13．如图，正方形ABCD的边AB=1，弧BD和弧AC都是以1为半径的圆弧，则无阴影的两部分的面积之差为________。

14．用三根同样长的铁丝分别围成一个圆、一个长方形和一个正方形，其中________的面积最大。

15．从一个长10cm，宽8cm的长方形纸上剪下一个最大的圆，这个圆的面积是________cm2，剩下部分的面积是________cm2。

人教版九年级数学上册圆单元测试题及答案

九年级数学第二十四章圆测试题（A)时间：45分钟分数:100分一、选择题(每小题3分，共33分）1．若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为10,最小距离为4则此圆的半径为（ )A ．14B ．6C ．14 或6D ．7 或32．如图24—A-1，⊙O 的直径为10，圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长是（）A ．4B ．6C ．7D ．83．已知点O 为△ABC 的外心，若∠A=80°,则∠BOC 的度数为（）A ．40°B ．80°C ．160°D ．120°4．如图24—A-2，△ABC 内接于⊙O ，若∠A=40°，则∠OBC 的度数为( ）A ．20°B ．40°C ．50°D ．70°5．如图24—A-3，小明同学设计了一个测量圆直径的工具，标有刻度的尺子OA 、OB 在O 点钉在一起，并使它们保持垂直,在测直径时，把O 点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的直径为（ )A ．12个单位B ．10个单位C ．1个单位D ．15个单位6．如图24—A-4，AB 为⊙O 的直径，点C 在⊙O 上，若∠B=60°，则∠A 等于( ）A ．80°B ．50°C ．40°D ．30°7．如图24—A-5,P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B ，CD 切⊙O 于点E,分别交PA 、PB 于点C 、D ，若PA=5,则△PCD 的周长为（）A ．5B ．7C ．8D ．108．若粮仓顶部是圆锥形，且这个圆锥的底面直径为4m ，母线长为3m ，为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是（）A ．B ．C ．D ．9．如图24—A —6,两个同心圆,大圆的弦AB 与小圆相切于点P ，大圆的弦CD 经过点P ，且CD=13,PC=4,则两圆组成的圆环的面积是（ )A ．16πB ．36πC ．52πD ．81π10．已知在△ABC 中，AB=AC=13，BC=10，那么△ABC 的内切圆的半径为（） A ． B ． C ．2 D ．311．如图24-A —7，两个半径都是4cm 的圆外切于点C ，一只蚂蚁由点A 开始依A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断爬行,直到行走2006πcm 后才停下来,则蚂蚁停的那一个点为（）A ．D 点B ．E 点C ．F 点D ．G 点二、填空题（每小题3分，共30分）12．如图24—A-8，在⊙O 中，弦AB 等于⊙O 的半径,OC ⊥AB 交⊙O 于点C ，则∠AOC= 。

(常考题)人教版小学数学六年级上册第五单元《圆》测试卷(有答案解析)

（常考题）人教版小学数学六年级上册第五单元《圆》测试卷（有答案解析）一、选择题1．下图的周长是（）A. （π+1）dB. πd+dC. dD. πd2．已知一个圆的半径是R，且R满足3：R=R：4，则这个圆的面积为（）A. 7πB. 7C. 12πD. 无法求出3．半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm24．下图中，正方形的面积是16平方厘米，圆的面积是（）cm2。

A. 50.24B. 47.1C. 43.98D. 37.68 5．如图所示圆环的面积是（）cm2．（计算时π取3.14）A. 3.14B. 28.26C. 113.04D. 263.76 6．从直径4分米的圆形钢板上挖去一个直径2分米的圆，求剩余部分的面积．下面列式正确的是（）A. （4÷2）2π﹣22πB. [（4÷2）2﹣（2÷2）2]πC. （42÷22）πD. [（4÷2）2+（2÷2）2]π7．用一块长12米、宽8米的长方形铁皮剪成半径是2米的小圆（不能剪拼），至多能剪（）个。

A. 7B. 8C. 6D. 138．在圆内剪去一个圆心角为45的扇形，余下部分的面积是剪去部分面积的（）倍．A. 9 B. 8 C. 79．大圆的半径是小圆的直径，则大圆面积是小圆面积的（）。

A. 2倍B. 4倍C. 12D. 14 10．东方公园有一个圆形的喷水池，经测量得出这个喷水池的周长是37 .68m。