小学奥数专题——计算综合
沪教版小学三年级数学上册奥数.计算综合.数字谜(A级)(含答案)

【解析】赛×赛的个位是9,赛=3或7,赛=3,小学希望杯赛=333333,不合题意,舍去;故赛=7,小学希望杯赛=999999÷7=142857
【答案】
【例 10】在□内填入适当的数字,使下列除法竖式成立:
【考点】与数论结合的数字谜之特殊数字 【难度】2星 【题型】填空
【解析】被除数与除数的和为 ,被除数比除数的21倍多3,所以除数为 。
【答案】
(1)12×23□=□32×21;(2)12×46□=□64×21;
(3)□8×891=198×8□;(4)24×2□1=1□2×42;
(5)□3×6528=8256×3□。
【考点】横式数字谜【难度】2星【题型】解答
【答案】
【例 2】将0~9这10个数码填入下列3个算式的□中,使得3个等式同时成立:
(2)逆推法:常是从算式的最后一个数字开始,逐步向前推想,从而得到等式。
最值问题
(1)横式转化为竖式数字谜,乘法转化为除法;
(2)找突破口:末位和首位、进位和借位、个位数字、位数的差别等.
(3)采用特殊分析方法:个位数字分析法、高位数字分析法、数字大小估算分析法、进位错位分析法、分解质因数法、奇偶分析法等.
【答案】
【例 6】在□内填入适当的数字,使下列乘法竖式成立:
【考点】竖式数字谜【难度】2星【题型】解答
【解析】与7相乘末尾为7的只有4,17×4=68.与17相乘结果为三位数的一位数有6、7、8、9.经试验只有6符合题意。
【答案】
【巩固】在□内填入适当的数字,使下列乘法竖式成立:
【考点】竖式数字谜【难度】2星【题型】解答
【考点】与数论结合的数字谜之特殊数字【难度】2星【题型】填空
高思奥数导引小学五年级含详解答案第17讲:计算综合一

第17讲计算综合一内容概述了解等比数列的基本概念,学会利用错位相减的方法进行求和;灵活使用各种方法简化比较复杂的分数算式;具有一定综合性的“定义新运算”问题;较复杂的数列与数表问题。
典型问题兴趣篇1.计算:(1)1248163264128256++++++++;(2)111111111248163264128256 ++++++++。
2.计算:23456333333+++++。
3.计算:199519951995199519951995 200920092009200920092009 ++++。
4.计算:131435 415263 342556⨯+⨯+⨯。
5.计算:1111111111 123456789100 2342342342+-++-++-++。
6.规定新运算“*”为:*32a b a b=⨯-⨯。
(1)计算:456**345⎛⎫⎪⎝⎭;(2)已知456**345x⎛⎫=⎪⎝⎭,求x。
7.图17-1中除了每行两端的数之外,其余每个数都是与它相连的上一行的两个数的平均数,例如:2.75是2.5和3的平均数。
请问:第100行中的各数之和是多少?8.有这样一列数,前两个数分别是0和1,从第三个数开始,每一个数都是前两个数的和:0,1,1,2,3,5,8,13,21,34,…。
请问:这个数列的第1000个数除以8所得的余数是多少?9.观察下面的数阵:根据前五行数所表达的规律,求(1)3367这个数在由上至下的第几行?在这一行中,它是由左向右第几个?(2)第28行第19个数是什么?10.观察数列11,12,22,12,13,23,33,13,14,24,34,44,34,24,14,…,求:(1)数列中第150项;(2)数列中前300项的和。
拓展篇1.如图17-2,有一个边长为81厘米的等边三角形,将它每条边三等分,以中间那一份为边向外作等边三角形,得到图17-3。
由图17-3通过同样方法又得到图17-4。
小学奥数六年级上第17讲《整数型计算综合》教学课件

例题讲解
mathematics
练习2:把从1开始的所有奇数进行分组,其中每一组的第一个数都等于这一段中所有数的个 数,例如:(1),(3,5,7),(9,11,13,15,17,19,21,23,25),(27,29…,79),(81, 83,…),那么第8组中所有数的和是多少? 答案:9563751
知识精讲 一、多位数计算 1.凑整、凑9的思想;
2.数字和问题:999 99与一个不大于它的数相乘,积的数字和是9×n
二、等差数列 n个9 1.等差数列的“配对”思想; 2.求和公式: • Culture (1)(首项+末项)×项数÷2; (2)中间项×项数; 3.项数公式:(末项-首项)÷公差+1; 4.第n项:首项+(n-1)×公差. 三、等比数列 等比数列“错位相减”法求和,基本步骤是: (1)设等比数列的和为S;(2)等式两边同时乘以公比(或者公比的倒数);(3)两式对应的项相减,消去同 样的项,求出结果.
六年级上第17讲
整数型计算综合
• Culture
知识树
mathematics
• Culture
知识树
mathematics
• Culture
知识树
mathematics
数学知识点
mathematics
• Culture
1.知识精讲 3.极限挑战
2.例题讲解 4.巩固提升
数学知识点
mathematics
巩固提升
mathematics
作业2:甲、乙二人每天背单词,甲背单词的数量每天增加5个,乙背单词的数量每天增加1 倍,已知第一天二人共背了33单词,第二天二人共背了40个单词,那么从第几天起乙每天背 的单词要比甲多,从第几天起乙背过的单词数量要比甲多? 答案:6;8
三年级混合运算奥数题

三年级混合运算奥数题在三年级的数学学习中,混合运算是一个重要的内容,通过解答混合运算题目,可以提高学生的综合运算能力和思维能力。
本文将提供一些三年级混合运算奥数题,帮助学生巩固所学知识。
题目一:加减运算1.小明有5本书,他借给小红3本书,借给小刚2本书,还剩下多少书?2.班级里有25个学生,其中18个学生去了游乐园,剩下多少个学生在班级?3.母鸡筑了10个蛋,它卖掉7个,还剩下多少个蛋?题目二:乘法运算1.有3个篮球,每个篮球上有5个红色小点,一共有多少个红色小点?2.一个班级里有7个学生,每个学生手中有10本书,一共有多少本书?3.爸爸买了8包牛奶,每包牛奶里有6瓶,一共有多少瓶牛奶?题目三:除法运算1.一个篮子里有30颗橙子,每个篮子里装6颗橙子,一共需要多少个篮子?2.有24本书,每个书架上放4本书,一共需要多少个书架?3.购物车里有20个苹果,每个购物袋里放2个苹果,一共需要多少个购物袋?题目四:混合运算1.粉笔盒里有10支粉笔,小红拿走了3支粉笔,小强又拿走了4支粉笔,粉笔盒里还剩下多少支粉笔?2.小明有12颗苹果,他平均分给了3个朋友,每个朋友得到几颗苹果?3.小明一共有28元,他花掉了9元,还剩下多少元?解答题目一:加减运算1.小明有5本书,借出去3本书,再借出去2本书,还剩下5-3-2=0本书。
2.班级里有25个学生,去了游乐园的有18个学生,还剩下25-18=7个学生。
3.母鸡筑了10个蛋,卖掉了7个蛋,还剩下10-7=3个蛋。
题目二:乘法运算1.3个篮球上每个篮球有5个红色小点,一共有3*5=15个红色小点。
2.班级里有7个学生,每个学生手中有10本书,一共有7*10=70本书。
3.爸爸买了8包牛奶,每包牛奶里有6瓶,一共有8*6=48瓶牛奶。
题目三:除法运算1.一个篮子里有30颗橙子,每个篮子里装6颗橙子,一共需要30/6=5个篮子。
2.有24本书,每个书架上放4本书,一共需要24/4=6个书架。
高思奥数导引小学六年级含详解答案第9讲计算综合二
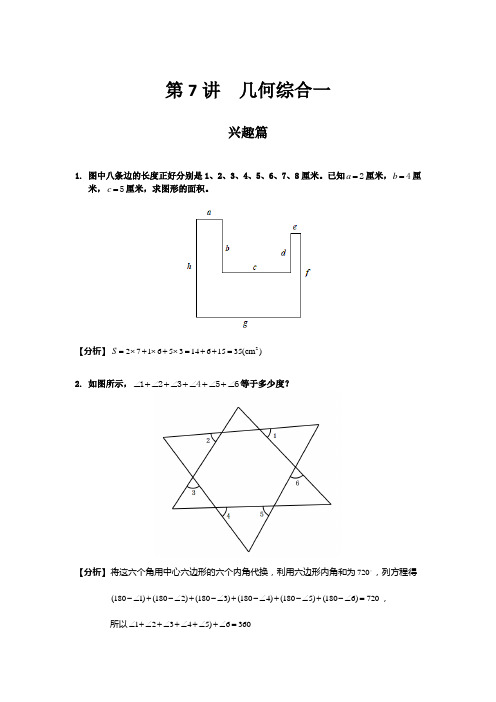
第7讲几何综合一兴趣篇1. 图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米。
已知a=2厘米,b=4厘米,c=5厘米,求图形的面积。
【分析】2S=⨯+⨯+⨯=++=2716531461535(cm)2. 如图所示,∠+∠+∠+∠+∠+∠123456等于多少度?【分析】将这六个角用中心六边形的六个内角代换,利用六边形内角和为720,列方程得(1801)(1802)(1803)(1804)(1805)(1806)720-∠+-∠+-∠+-∠+-∠+-∠=,所以12345)6360∠+∠+∠+∠+∠+∠=3. 如图,平行四边形ABCD 的周长为75厘米。
以BC 为底时高是14厘米,以CD 为底时高是16厘米。
求平行四边形ABCD 的面积。
【分析】 75237.5BC CD +=÷=,根据面积相等,底的比与高的比成反比例,所以:16:148:7BC CD ==,因此37.5(87)820BC =÷+⨯=,平行四边形ABCD 的面积是2014280⨯=平方厘米4. 如图所示,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是310平方米、25平方米、15平方米和110平方米。
已知图中的阴影部分是正方形,那么它的面积是多少平方米?【分析】 1251110CH HD ==,因此23CH =,13HD =,3310245AE EB ==,所以37AE =,47EB =,因此2353721FG =-=,那么它的面积是252521441⎛⎫= ⎪⎝⎭平方米5. 如图,红、黄、绿三块大小一样的正方形纸片,放在一个正方体盒内,它们之间相互重叠。
已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是10。
那么,正方体盒子的底面积是多少?绿黄红【分析】 将黄色纸片推到左边,则每块纸片露出的形状如右上图.黄、绿两色的面积之和保持14+10=24不变,则在右图中这两块面积相等,均为24212÷=.根据公式可知,空白处面积=黄⨯绿÷红=1212207.2⨯÷=,则正方形盒底面积是7.212122051.2+++=.6. 如图,在三角形ABC 中,IF 和BC 平行,GD 和AB 平行,HE 和AC 平行。
小学奥数:计算专题《加减法的巧算》练习题

小学奥数:计算专题《加减法的巧算》练习题一.填空题(共15小题)1.计算:(1+3+5+…+2019)-(2+4+6+…+2018)=10102.计算:3-5+7-9+11-13+…+1995-1997+1999=-10003.计算200-(16+17+18+…+23+24)=844.a=4,b=25,则a+b=29,a×b=100,a÷b=4/255.计算:1+2+3+4+5+6+7+8+9=456.1+3+5+7+…+97+99-10-12-14…-96-98=507.计算:13+75-37+427+85-23=5608.计算:(2017-1)+(2016-2)+…+(2011-7)=9.计算:-+-+-+-+-=7010.计算1000-257-84-43-16=60011.计算:2+3+5-6+7+1-10=212.193-191+189-187+……+93-91=5113.算式(1+3+5+…+89)-(1+2+3+…+63)的计算结果是72714.计算:1+2+4+5+7+8+10+11+13+14+16+17+19+20=12015.算式1+3+4+6+7+9+10+12的计算结果是52二.计算题(共15小题)16.计算:30-29-28+27+26-25-24+23+22-21-20+19=-217.计算:xxxxxxxx+XXX999+99+9=xxxxxxxx18.计算:1-2+3-4+5-6+7-8+9-10+11-12+…+991-992+993-994+995-996+997-998+999=-49919.直接写出得数。
5.43+1.47=6.94.5×0.4=1.820.计算:(2004-1)+(2003-2)+(2002-3)+…+(1003-1002)=100121.计算:1+2+3+……+50+49+……+2+1=255022.计算:1+2+3+…+1999=xxxxxxx5-3.28=1.72,0.46÷4.6=0.1,4×0.25=19.58×101-9.58=957,85÷(1-0.9)=850,3÷0.3=10,0.63÷0.7=0.9,1.8×0.4=0.7223.计算2+4+6+8+…+1990的和=24.用简便方法计算:略。
三年级上册数学试题-奥数.计算综合.等量代换(B级)(含答案)沪教版(2015秋)

(1) 生活中有很多相等的量,如平衡的天平、平衡的跷跷板两边的重量相等.我们可以根据这些相等的关系进行推理,进而可以等量代换,找到答案(2) “等量代换”是指一个量用与它相等的量去代替,它是数学中一种基本的思想方法,也是代数思想方法的基础.(1) 寻找等量关系【例 1】 有一天,小狗老师要在动物学校挑选队员参加数学竞赛,小松鼠很高兴也跑来了.小狗老师说:“那我就来考考你!你把下面的题做对了就可以参加了.”小松鼠看了半天说:“老师,你写的这是什么?”小狗老师说:“哈哈!看来你要好好学一学图文算式了,欢迎你下次再来.”小朋友们,上面的题你会吗?【考点】等量代换 【难度】2星 【题型】解答【解析】 通过这个故事引入新课,在这里不要求学生能马上做出来,可放在最后来解决.如果学生的能力较强,也可把这两个题作为引入新课的切入点进行讲解.(1)因为,所以=5,又因为,把=5替换,就变成例题精讲重难点知识框架等量代换,这样我们就可以得出=10.(2)我们把上下两个算式进行比较,我们发现下面比上面多了一个,得数多了18-14=4,所以我们可以推断出=4,,根据第一个算式我们可以得出;那么=5.【答案】=5 =10 =4 =5【巩固】求下面图形所表示的数.【考点】等量代换【难度】1星【题型】解答【解析】(1)△=( 9 ),○=( 6 ),☆=( 7 );(2)△=( 3 ),□=( 4 ).【答案】(1)△=( 9 ),○=( 6 ),☆=( 7 );(2)△=( 3 ),□=( 4 )【例 2】下面的天平是不平衡的,但除了天平上的砝码,周围已找不到别的砝码了.你能通过移动天平上的砝码,使天平平衡吗?【考点】等量代换【难度】2星【题型】解答【解析】我们可先看看天平两边各有多少克:天平左边:551020++++=++=(克).天平右边:10421118 (克).显然,天平左边如果减少1克,放到天平右边,20119-=(克),18+1=19(克),天平两边就都平衡了,但天平左边没有l克的砝码,怎么办?可以用天平左边5克的砝码和天平右边4克的砝码交换一下,就可以达到要求了.这样天平左边是541019++=(克).右边是10521119++++= (克).【答案】左边5克的砝码和天平右边4克的砝码交换一下【巩固】你能通过移动天平上的砝码,使下面的天平平衡吗?【考点】等量代换【难度】2星【题型】解答【解析】把左边的3克和右边的6克对换.或把左边的4克和右边的7克对换.【答案】左边的4克和右边的7克对换【例 3】1只猴子的体重等于3只猫的体重,3只狗的体重等于9只猫的体重.如果1只猴子重3千克,请问1只狗重多少千克?【考点】等量代换【难度】1星【题型】解答【解析】由3只狗的体重=9只猫的体重,得1只狗的体重=3只猫的体重.又1只猴子的体重=3只猫的体重,1只狗的体重=1只猴子的体重.1只猴子重3千克,1只狗重3千克.【答案】1只狗重3千克【巩固】1串葡萄的重量等于3个梨的重量,2个梨的重量等于80克,1串葡萄重多少克?【考点】等量代换【难度】1星【题型】解答【解析】2个梨的重量是80克,那么1个梨的重量就是40克,1串葡萄的重量等于3个梨的重量,1串葡萄就是403120⨯=克.【答案】120克【例 4】1个西瓜的重量等于2个哈密瓜的重量,1个哈密瓜的重量等于8个苹果的重量,2个苹果的重量等于3个柿子的重量,那么1个西瓜的重量等于几个柿子的重量?【考点】等量代换【难度】2星【题型】解答【解析】因为2个苹果的重量等于3个柿子的重量,所以8个苹果的重量等于12个柿子的重量.又因为1个哈密瓜的重量等于8个苹果的重量,所以1个哈密瓜的重量等于12个柿子的重量.而1个西瓜的重量等于2个哈密瓜的重量,因此1个西瓜的重量=12224⨯=个柿子的重量.【答案】24个柿子【巩固】 一只小猴重4千克,一只小猴的重量等于两只小兔的重量,两只小兔的重量等于4只小猫的重量.一只小兔和一只小猫的重量共多少千克?【考点】等量代换 【难度】2星 【题型】解答【解析】 一只小猴的重量等于两只兔子的重量,这样可以求出一只兔子的重量.而两只兔子的重量等于4只小猫的重量,可以求出一只小猫的重量.最后一只小兔和一只小猫的总重量就求出来了.一只兔子的重量:422÷=(千克,)一只小猫的重量:441÷=(千克),一只小兔和一只小猫的总重量:213+=(千克)【答案】3千克【例 5】 学校第一次买了3个水瓶和20个茶杯,共用去134元;第二次又买了同样的3个水瓶和16个茶杯,共用去118元.问水瓶和茶杯的单价各是多少元?【考点】等量代换 【难度】2星 【题型】解答【解析】 引导学生学会审题,找出两次购买的相同点及差异,让学生思考解决.我们用数量关系式来比较对应的未知数量的情况:320134316118416+=+==个水瓶的价钱个茶杯的价钱元-个水瓶的价钱个茶杯的价钱元个茶杯的价钱元比较上面两个等式,我们可以看出,134元和118元的差正好是4个茶杯的价钱.利用这一条件,把3个水瓶的价钱消去,先求出每个茶杯的价钱,再求出每个水瓶的价钱.每个茶杯的价钱:(134118)(2016)-÷-164=÷4=(元)每个水瓶的价钱:(134420)318-⨯÷=(元)或(118416)318-⨯÷=(元)【答案】每个茶杯的价钱: 4元;每个水瓶的价钱:18元【巩固】 奶奶去买水果,如果她买4千克梨和5千克荔枝,需要花掉58元;如果她买6千克梨和5千克荔枝,需要花掉62元.问1千克梨和1千克荔枝各多少元?【考点】等量代换 【难度】2星 【题型】解答【解析】 我们可以把两次的情况进行比较:4千克梨的价钱5+千克荔枝的价钱58=(元) ⑴6千克梨的价钱5+千克荔枝的价钱62=(元) ⑵比较⑴和⑵式,发现两式中荔枝的千克数相等.⑵式比⑴式多了642-=千克梨,也就是62584-=元,说明1千克梨的价钱为422÷=元.那么1千克荔枝的价钱也就好求了.(6258)(64)2-÷-=(元),(5824)510-⨯÷=(元)或(6226)510-⨯÷=(元)【答案】1千克梨的价钱为2元;1千克荔枝的价钱10元【例 6】 李老师第一次买回5个篮球和3个排球,用去318元.第二次又买回7个篮球和6个排球,用去510元.问:一个篮球和一个排球的价格各是多少元?【考点】等量代换 【难度】2星 【题型】解答【解析】 可引导学生读题、审题,找出此题与例7的不同之处,并转化成例7的模型.此题有篮球单价与排球单价两个未知数量,而从题里所给条件分析,两次购买篮球与排球的数量各不相同,不能直接用消去法消去哪一个未知数,所以解题关键是使篮球或排球中的某一对未知数变换得相同,则可消去其中一个.通过比较,第一次购买的排球为3个;第二次购买的排球为6个,恰为第一次的2倍.若将第一次购买的排球、篮球各扩大2倍,付的钱也扩大2倍,则能使购买的排球个数与第二次购买的排球个数相同,从而设法消去排球这个未知数量,先求出每个篮球的价格,再求每一个排球的价格.533182106636⨯个篮球个排球元个篮球个排球元 106636765103126-个篮球个排球元个篮球个排球元个篮球元列式:(3182510)(527)⨯-÷⨯-126342=÷=(元)……篮球的单价.(318425)-⨯÷108336=÷=(元)……排球的单价.【答案】篮球的单价42元;排球的单价36元【巩固】 3头牛和8只羊每天共吃青草93千克,5头牛和15只羊每天共吃青草165千克.问一头牛和一只羊每天各吃青草多少千克?【考点】等量代换 【难度】2星 【题型】解答【解析】 3头牛吃草的重量8+只羊吃草的重量93=千克 ⑴5头牛吃草的重量15+只羊吃草的重量165=千克 ⑵如果把⑴式扩大5倍,⑵式扩大3倍,那么两个式子中牛的数量就一样多了.这样就得到:⑴5⨯:15头牛吃草的重量40+只羊吃草的重量465=千克⑶ ⑵3⨯:15头牛吃草的重量45+只羊吃草的重量495=千克⑷⑷-⑶:5只羊吃草的重量30=千克1只羊吃草的重量6=千克1头牛每天吃草的重量:(9368)3-⨯÷453=÷15=(千克)【答案】1只羊吃草6千克;1头牛每天吃草15千克【例 7】李宁的妈妈去菜市场买菜,买了6斤土豆和5斤柿子椒,共花了13元5角.己知3斤土豆的价钱与2斤柿子椒的价钱相等.那么1斤土豆和1斤柿子椒各多少钱?【考点】等量代换【难度】2星【题型】解答【解析】可引导学生读题、审题,让学生自己思考解答.老师可以画图进行分析,已知条件为:6斤土豆+5斤柿子椒=13元5角.3斤土豆=2斤柿子椒.从第一个式子不能算出1斤土豆、1斤柿子椒的价钱.若把土豆转化成柿子椒或把柿子椒转化成土豆的价钱就可求该种菜的价钱了.由第二个式子知3斤土豆=2斤柿子椒,则6斤土豆应等于4斤柿子椒的价钱.即:6斤土豆+5斤柿子椒=13元5角,6斤土豆=4斤柿子椒.4斤柿子椒+5斤柿子椒=13元5角,9斤柿子椒=13元5角.13元5角等于135角,135角买了9斤柿子椒,所以1斤柿子椒的价钱为:135915÷=(角)= 1元5角.4斤柿子椒的价钱为:15460÷=(元).所以1斤土豆的价钱⨯=(角)=6(元).1斤土豆的价钱为:661为1元,1斤柿子椒的价钱为1元5角.【答案】1斤土豆的价钱为1元,1斤柿子椒的价钱为1元5角【巩固】3米绵绸的价格与6米花布的价格相等.王云买了6米绵绸和18米花布,共花费了120元.棉绸和花布的单价各是多少?【考点】等量代换【难度】2星【题型】解答【解析】由题意可知3米棉绸与6米花布的价格相等,由此可推知1米棉绸与2米花布的价格相等.因此可用花布的价格去替换棉绸的价格,而使棉绸价格转变为花布的价格.消去棉绸价格这个未知数量可以先求出花布的单价,进而求出棉绸的单价.120(2618)÷⨯+120304=÷=(元)……每米花布的单价428⨯=(元)……每米棉绸的单价.【答案】每米花布的单价4元每米棉绸的单价8元【例 8】学校买2张桌子和3把椅子共用90元钱,每张桌子的价钱是每把椅子价钱的3倍.每张桌子多少钱?【考点】等量代换【难度】2星【题型】解答【解析】引导学生读题、审题,让学生自己思考解答,教师集体订正.2张桌子的价钱3=(元) ⑴+把椅子的价钱901张桌子的价钱3=把椅子的价钱⑵将⑵代入⑴式,消去桌子这个未知量,问题就可以解决.(32=(元)⨯)把椅子的价钱3+把椅子的价钱909把椅子的价钱90=(元)1把椅子的价钱10=(元)1张桌子的价钱10330=⨯=(元)【答案】1张桌子的价钱30元【巩固】红、黄、蓝三个纸盒里共有彩票56张,其中红色纸盒里的彩票是黄色纸盒里彩票张数的2倍,蓝色纸盒里的彩票是红色纸盒里彩票张数的2倍.红、黄、蓝三个纸盒里各有多少张彩票?【考点】等量代换【难度】2星【题型】解答【解析】以黄色纸盒里的彩票张数为1倍数.红纸盒里的彩票张数是这样的2倍.蓝纸盒是红纸盒里彩票张数的2倍,也就是黄纸盒里彩票张数的4倍.一共是(124)++倍.这样就可以消去两个未知量而先求出黄纸盒里彩票的张数,再分别求出红色和蓝色盒子里彩票的张数.÷++56756(124)=(张)……黄盒里的彩票张数,=÷8⨯=(张)……蓝盒里的彩票张数.⨯=(张)……红盒里的彩票张数,84328216【答案】黄盒里的彩票张数8张红盒里的彩票张数16张蓝盒里的彩票张数32张【例 9】第一只茶壶能装10大杯水,第二只茶壶可以装15小杯水.已知5大杯水与9小杯水同样多,哪个茶壶大?【考点】等量代换【难度】2星【题型】解答【解析】读题,抓住大杯数目,引导学生进行扩倍来解决题目.因为5大杯水与9小杯水同样多,那么10大杯水就等于18小杯的水,而现在只有15小杯的水,10大杯水和15小杯水比较,10大杯水要多一些,所以第一个茶壶大.【答案】第一个茶壶大【巩固】如图,第一只壶里的茶只有一半,小华倒出了5大杯,第二只壶里的茶是一满壶,小明倒出了15小杯.已知3小杯的茶与2大杯的茶同样多,现在问你哪个壶大?【考点】等量代换【难度】2星【题型】解答【解析】我们可以按以下三个步骤来思考:⑴第二只壶满壶茶倒出15小杯,而每3小杯可以倒满2杯,所以第二只壶可以装茶10大杯.⑵一只壶的一半倒出了5大杯,那么满壶茶可以倒出10大杯.由⑴⑵可知,两个茶壶一样大.【答案】两个茶壶一样大【例 10】如果鱼尾重4公斤,鱼头重量等于鱼尾加上鱼身一半的重量,而鱼身重量等于鱼头加鱼尾的重量,问这条鱼有多少公斤重?【考点】等量代换【难度】3星【题型】解答【解析】依题意列出下列等式:尾=4 (1)头=尾+身÷2 (2)身=头+尾(3)由于等式左右两边同乘以一个数,结果仍相等所以把(2)式两边同乘以2得:2头=2尾+身(4)把(3)式代入(4)式得:2头=2尾+头+尾即:头=3尾=3×4=12公斤身=头+尾=12+4=16公斤所以,全鱼=头+身+尾=12+16+4=32公斤【答案】32公斤【巩固】已知13个李子的重量等于2个苹果和1个桃子的重量,而4个李子和1个苹果的重量等于1个桃子的重量.问多少个李子的重量等于1个桃子的重量?【考点】等量代换【难度】3星【题型】解答【解析】:由题意列等式:13李=2苹+1桃(1)4李+1苹=1桃(2)把(2)式代入(1)式得:13李=2苹+4李+1苹即 9李=3苹;即 3李=1苹 (3)把(3)式代入(2)式得4李+3李=1桃即 7李=1桃即 7个李子重量等于1个桃子的重量.【答案】7个【随练1】 甲、乙两人共储蓄32元,乙、丙两人共储蓄30元,甲、丙两人共储蓄22元.三人各储蓄多少元?【考点】等量代换 【难度】2星 【题型】解答【解析】 可先让学生自己去思考,教师巡视指正.此题要求三个未知数,甲储蓄多少元?乙储蓄多少元?丙储蓄多少元?关系较为复杂,为了化繁为简,采用消去法来解.首先用加减消去法消去乙和丙,只剩下甲,然后求出甲储蓄多少元,再求乙、丙各储蓄多少元.解法1:()甲乙→32元+甲丙→22元2甲乙丙→54元-乙丙→30元2甲→24元由2倍甲储蓄为24元,可求出甲储蓄多少元.列表:(322230)2+-÷24212=÷=(元)……甲储蓄款.321220-=(元)……乙储蓄款, 302010-=(元)……丙储蓄款.此题也可用另一种方法求解.解法2:甲乙+乙丙+甲丙32223084=++=(元),即2倍的(甲+乙+丙)等于84元.甲+乙+丙84242=÷=(元).423210-=(元)……丙储蓄款,423012-=(元)……甲储蓄款,422220-=(元)……乙储蓄款.【答案】甲储蓄12元,乙储蓄20元,丙储蓄10元,课堂检测【随练2】 图书室里的故事书与科技书共有720本,又知故事书比科技书多160本,这两种图书各有多少本?【考点】等量代换 【难度】2星 【题型】解答【解析】 题目中给出了两个未知量“故事书”和“科技书”的数量关系,即已知故事书与科技书共有720本和故事书与科技书本数之差,属于典型应用题中的“和差问题”,一般用消去法来解.7201602880++-故事书本数科技书本数本故事书本数科技书本数本倍故事书本数本消去科技书本数后,可先求出故事书的本数.列式:(720160)2440+÷=(本)……故事书,44016028-=(本)……科技书.也可以先求出科技书的本数.【答案】故事书440本,科技书280本【随练3】 学校要买足球和排球.买3个足球和4个排球共需190元,如果买6个足球和2个排球需要230元.一个足球和一个排球各需要多少元?【考点】等量代换 【难度】2星 【题型】解答【解析】 我们可以把两次情况进行比较;3个足球的价钱4+个排球的价钱190=(元)⑴ 6个足球的价钱2+个排球的价钱230=(元) ⑵我们发现两组条件不管相加还是相减,都不可能求出足球和排球的单价,因为这里没有一个相同的条件可减去.再观察,我们发现,如果把⑴式扩大2倍,可以得到6个足球和8个排球共380元,即⑴2⨯:6个足球的价钱8+个排球的价钱380=元 ⑶⑶-⑵,可知6个排球的价钱150=元.容易得出排球和足球的价钱各是多少.排球:150625÷=(元),足球:(190254)330-⨯÷=(元)【答案】排球为25元,足球为30元【作业1】 你能通过移动天平上的砝码,使下面的天平平衡吗?家庭作业【考点】等量代换【难度】2星【题型】解答【解析】可引用线段图帮助学生理解多的部分给少的部分多少,可达到一样多,然后再讲解此题.左边= ++=克,右边=1016430++=克,左边比右边多8克.只有从左边拿4克到右边,两边1020838的重量才一样多.这样可以把左边8克的砝码和右边4克的砝码互换一下,左右两边重量都是34克,天平平衡.【答案】左边8克的砝码和右边4克的砝码互换一下【作业2】已知:(见下图)求:最大的球的重量是多少克?【考点】等量代换【难度】2星【题型】解答【解析】:由图(1)得:3●=2●+48,所以●=48(克).由图(2)得:3○=2●,即:3○=2×48,所以○=2×48÷3=32(克).由图(3)得:○=4○=4×32=128(克).【答案】128克【作业3】2只兔子的重量等于6只小鸡的重量,3只袋鼠的重量相当于4只兔子的重量,那么1只袋鼠的重量相当于多少只小鸡的重量?【考点】等量代换【难度】2星【题型】解答【解析】2只兔相当于6只小鸡的重量,那么4只兔相当于12只小鸡的重量.3只袋鼠的重量相当于4只兔子的重量,所以3只袋鼠相当于12只小鸡的重量.1234÷=,即1只袋鼠相当于4只小鸡的重量.【答案】4只【作业4】 百货商店运来300双球鞋,分别装在2个木箱、6个纸箱里。
四年级奥数综合计算练习题

四年级奥数综合计算练习题
题目一
某班有35名学生,其中有15名男生。
请问这个班级男生占总人数的百分之几?
题目二
小明参加了一场长跑比赛,他以每分钟7米的速度跑了15分钟。
请问他跑了多少米?
题目三
某个果园里有25棵苹果树,每棵树上有30个苹果。
请问这个果园总共有多少个苹果?
题目四
一家商店原价出售一只玩具熊是25元。
现在这只玩具熊打折,降价15%。
请问现在这只玩具熊的价格是多少元?
题目五
小红的妈妈去超市买了3千克苹果和1.5千克橙子,苹果的价
格是每千克8元,橙子的价格是每千克6元。
请问小红的妈妈一共
花了多少钱?
题目六
小明今年7岁,小弟弟比他小3岁。
请问小弟弟今年几岁了?
题目七
一个长方形的长是10米,宽是5米。
请问这个长方形的周长
是多少米?
题目八
小明今年身高1.2米,每年平均长高5厘米。
请问10年后他的身高将是多少米?
题目九
某地有175个学生,这些学生乘以3之后的数目是多少?
题目十
某家公司有35个员工,其中25个是男性,剩下的是女性。
请问这家公司女性员工的比例是多少?
以上是四年级奥数综合计算练习题,希望对同学们的数学能力有所帮助。
加油!。
(完整版)小学的奥数面积计算(综合题型)

第十八周面积计算(一)专题简析:计算平面图形的面积时,有些问题乍一看,在已知条件与所求问题之间找不到任何联系,会使你感到无从下手。
这时,如果我们能认真观察图形,分析、研究已知条件,并加以深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题的小“桥”,就会使你顺利达到目的。
有些平面图形的面积计算必须借助于图形本身的特征,添加一些辅助线,运用平移旋转、剪拼组合等方法,对图形进行恰当合理的变形,再经过分析推导,方能寻求出解题的途径。
图形面积)简单的面积计算是小学数学的一项重要内容.要会计算面积,首先要能识别一些特别的图形:正方形、三角形、平行四边形、梯形等等,然后会计算这些图形的面积.如果我们把这些图形画在方格纸上,不但容易识别,而且容易计算.上面左图是边长为4的正方形,它的面积是4×4=16(格);右图是3×5的长方形,它的面积是3×5=15(格).上面左图是一个锐角三角形,它的底是5,高是4,面积是5×4÷2=10(格);右图是一个钝角三角形,底是4,高也是4,它的面积是4×4÷2=8(格).这里特别说明,这两个三角形的高线一样长,钝角三角形的高线有可能在三角形的外面.上面左图是一个平行四边形,底是5,高是3,它的面积是5×3=15(格);右图是一个梯形,上底是4,下底是7,高是4,它的面积是(4+7)×4÷2=22(格).上面面积计算的单位用“格”,一格就是一个小正方形.如果小正方形边长是1厘米,1格就是1平方厘米;如果小正方形边长是1米,1格就是1平方米.也就是说我们设定一个方格的边长是1个长度单位,1格就是一个面积单位.在这一讲中,我们直接用数表示长度或面积,省略了相应的长度单位和面积单位.一、三角形的面积用直线组成的图形,都可以划分成若干个三角形来计算面积.三角形面积的计算公式是:三角形面积= 底×高÷2.这个公式是许多面积计算的基础.因此我们不仅要掌握这一公式,而且要会灵活运用.例1 右图中BD长是4,DC长是2,那么三角形ABD的面积是三角形ADC面积的多少倍呢?解:三角形ABD与三角形ADC的高相同.三角形ABD面积=4×高÷2.三角形ADC面积=2×高÷2.因此三角形ABD的面积是三角形ADC面积的2倍.注意:三角形的任意一边都可以看作是底,这条边上的高就是三角形的高,所以每个三角形都可看成有三个底,和相应的三条高.例2右图中,BD,DE,EC的长分别是2,4,2.F是线段AE的中点,三角形ABC的高为4.求三角形DFE的面积.解:BC=2+4+2=8.三角形ABC面积= 8×4÷2=16.我们把A和D连成线段,组成三角形ADE,它与三角形ABC的高相同,而DE长是4,也是BC的一半,因此三角形ADE面积是三角形ABC面积的一半.同样道理,EF是AE的一半,三角形DFE面积是三角形ADE面积的一半.三角形DFE面积= 16÷4=4.例3右图中长方形的长是20,宽是12,求它的内部阴影部分面积.解:ABEF也是一个长方形,它内部的三个三角形阴影部分高都与BE一样长.而三个三角形底边的长加起来,就是FE的长.因此这三个三角形的面积之和是FE×BE÷2,它恰好是长方形ABEF面积的一半.同样道理,FECD也是长方形,它内部三个三角形(阴影部分)面积之和是它的面积的一半.因此所有阴影的面积是长方形ABCD面积的一半,也就是20×12÷2=120.通过方格纸,我们还可以从另一个途径来求解.当我们画出中间两个三角形的高线,把每个三角形分成两个直角三角形后,图中每个直角三角形都是某个长方形的一半,而长方形ABCD是由这若干个长方形拼成.因此所有这些直角三角形(阴影部分)的面积之和是长方形ABCD面积的的一半.例4 右图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?解:把A和C连成线段,四边形ABCD就分成了两个,三角形ABC和三角形ADC.对三角形ABC来说,AB是底边,高是10,因此面积=4×10÷2=20.对三角形ADC来说,DC是底边,高是8,因此面积=7×8÷2=28.四边形ABCD面积= 20+28=48.这一例题再一次告诉我们,钝角三角形的高线有可能是在三角形的外面.例5在边长为6的正方形内有一个三角形BEF,线段AE=3,DF=2,求三角形BEF 的面积.解:要直接求出三角形BEF的面积是困难的,但容易求出下面列的三个直角三角形的面积三角形ABE面积=3×6×2=9.三角形BCF面积= 6×(6-2)÷2=12.三角形DEF面积=2×(6-3)÷2=3.我们只要用正方形面积减去这三个直角三角形的面积就能算出:三角形BEF面积=6×6-9-12-3=12.例6 在右图中,ABCD是长方形,三条线段的长度如图所示,M是线段DE的中点,求四边形ABMD(阴影部分)的面积.解:四边形ABMD中,已知的太少,直接求它面积是不可能的,我们设法求出三角形DCE与三角形MBE的面积,然后用长方形ABCD的面积减去它们,由此就可以求得四边形ABMD的面积.把M与C用线段连起来,将三角形DCE分成两个三角形.三角形DCE的面积是7×2÷2=7.因为M是线段DE的中点,三角形DMC与三角形MCE面积相等,所以三角形MCE 面积是7÷2=3.5.因为BE=8是CE=2的4倍,三角形MBE与三角形MCE高一样,因此三角形MBE面积是3.5×4=14.长方形ABCD面积=7×(8+2)=70.四边形ABMD面积=70-7- 14=49.二、有关正方形的问题先从等腰直角三角形讲起.一个直角三角形,它的两条直角边一样长,这样的直角三角形,就叫做等腰直角三角形.它有一个直角(90度),还有两个角都是45度,通常在一副三角尺中.有一个就是等腰直角三角形.两个一样的等腰直角三角形,可以拼成一个正方形,如图(a).四个一样的等腰直角三角形,也可以拼成一个正方形,如图(b).一个等腰直角三角形,当知道它的直角边长,从图(a)知,它的面积是直角边长的平方÷2.当知道它的斜边长,从图(b)知,它的面积是斜边的平方÷4例7 右图由六个等腰直角三角形组成.第一个三角形两条直角边长是8.后一个三角形的直角边长,恰好是前一个斜边长的一半,求这个图形的面积.解:从前面的图形上可以知道,前一个等腰直角三角形的两个拼成的正方形,等于后一个等腰直角三角形四个拼成的正方形.因此后一个三角形面积是前一个三角形面积的一半,第一个等腰直角三角形的面积是8×8÷2=32.这一个图形的面积是32+16+8+ 4 +2+1=63.例8 如右图,两个长方形叠放在一起,小长形的宽是2,A点是大长方形一边的中点,并且三角形ABC是等腰直角三角形,那么图中阴影部分的总面积是多少?解:为了说明的方便,在图上标上英文字母D,E,F,G.三角形ABC的面积=2×2÷2=2.三角形ABC,ADE,EFG都是等腰直角三角形.三角形ABC的斜边,与三角形ADE的直角边一样长,因此三角形ADE面积=ABC面积×2=4.三角形EFG的斜边与三角形ABC的直角边一样长.因此三角形EFG面积=ABC面积÷2=1.阴影部分的总面积是4+1=5.例9如右图,已知一个四边形ABCD的两条边的长度AD=7,BC=3,三个角的度数:角B和D是直角,角A是45°.求这个四边形的面积.解:这个图形可以看作是一个等腰直角三角形ADE,切掉一个等腰直角三角形BCE.因为A是45°,角D是90°,角E是180°-45°-90°=45°,所以ADE是等腰直角三角形,BCE也是等腰直角三角形.四边形ABCD的面积,是这两个等腰直角三角形面积之差,即7×7÷2-3×3÷2=20.这是1994小学数学奥林匹克决赛试题.原来试题图上并没有画出虚线三角形.参赛同学是不大容易想到把图形补全成为等腰直角三角形.因此做对这道题的人数不多.但是有一些同学,用直线AC把图形分成两个直角三角形,并认为这两个直角三角形是一样的,这就大错特错了.这样做,角A是45°,这一条件还用得上吗?图形上线段相等,两个三角形相等,是不能靠眼睛来测定的,必须从几何学上找出根据,小学同学尚未学过几何,千万不要随便对图形下结论.我们应该从题目中已有的条件作为思考的线索.有45°和直角,你应首先考虑等腰直角三角形.现在我们转向正方形的问题.例10 在右图11×15的长方形内,有四对正方形(标号相同的两个正方形为一对),每一对是相同的正方形,那么中间这个小正方形(阴影部分)面积是多少?解:长方形的宽,是“一”与“二”两个正方形的边长之和,长方形的长,是“一”、“三”与“二”三个正方形的边长之和.长-宽=15-11=4是“三”正方形的边长.宽又是两个“三”正方形与中间小正方形的边长之和,因此中间小正方形边长=11-4×2=3.中间小正方形面积=3×3=9.如果把这一图形,画在方格纸上,就一目了然了.例11从一块正方形土地中,划出一块宽为1米的长方形土地(见图),剩下的长方形土地面积是15.75平方米.求划出的长方形土地的面积.解:剩下的长方形土地,我们已知道长-宽=1(米).还知道它的面积是15.75平方米,那么能否从这一面积求出长与宽之和呢?如果能求出,那么与上面“差”的算式就形成和差问题了.我们把长和宽拼在一起,如右图.从这个图形还不能算出长与宽之和,但是再拼上同样的两个正方形,如下图就拼成一个大正方形,这个正方形的边长,恰好是长方形的长与宽之和.可是这个大正方形的中间还有一个空洞.它也是一个正方形,仔细观察一下,就会发现,它的边长,恰好是长方形的长与宽之差,等于1米.现在,我们就可以算出大正方形面积:15.75×4+1×1=64(平方米).64是8×8,大正方形边长是8米,也就是说长方形的长+宽=8(米).因此长=(8+1)÷2=4.5(米).宽=8-4.5=3.5(米).那么划出的长方形面积是4.5×1=4. 5(平方米).例12 如右图.正方形ABCD与正方形EFGC并放在一起.已知小正方形EFGC的边长是6,求三角形AEG(阴影部分)的面积.解:四边形AECD是一个梯形.它的下底是AD,上底是EC,高是CD,因此四边形AECD面积=(小正方形边长+大正方形边长)×大正方形边长÷2三角形ADG是直角三角形,它的一条直角边长DG=(小正方形边长+大正方形边长),因此三角形ADG面积=(小正方形边长+大正方形边长)×大正方形边长÷2.四边形AECD与三角形ADG面积一样大.四边形AHCD是它们两者共有,因此,三角形AEH与三角形HCG面积相等,都加上三角形EHG面积后,就有阴影部分面积=三角形ECG面积=小正方形面积的一半= 6×6÷2=18.十分有趣的是,影阴部分面积,只与小正方形边长有关,而与大正方形边长却没有关系.三、其他的面积这一节将着重介绍求面积的常用思路和技巧.有些例题看起来不难,但可以给你启发的内容不少,请读者仔细体会.例13 画在方格纸上的一个用粗线围成的图形(如右图),求它的面积.解:直接计算粗线围成的面积是困难的,我们通过扣除周围正方形和直角三角形来计算.周围小正方形有3个,面积为1的三角形有5个,面积为1.5的三角形有1个,因此围成面积是4×4-3-5-1.5=6.5.例6与本题在解题思路上是完全类同的.例14 下图中ABCD是6×8的长方形,AF长是4,求阴影部分三角形AEF的面积.解:三角形AEF中,我们知道一边AF,但是不知道它的高多长,直接求它的面积是困难的.如果把它扩大到三角形AEB,底边AB,就是长方形的长,高是长方形的宽,即BC 的长,面积就可以求出.三角形AEB的面积是长方形面积的一半,而扩大的三角形AFB是直角三角形,它的两条直角边的长是知道的,很容易算出它的面积.因此三角形AEF面积=(三角形AEB面积)-(三角形AFB面积)=8×6÷2-4×8÷2=8.这一例题告诉我们,有时我们把难求的图形扩大成易求的图形,当然扩大的部分也要容易求出,从而间接地解决了问题.前面例9的解法,也是这种思路.例15 下左图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积(阴影部分)有多大?解:我们首先要弄清楚,平行四边形面积有多大.平行四边形的面积是底×高.从图上可以看出,底是2,高恰好是长方形的宽度.因此这个平行四边形的面积与10×2的长方形面积相等.可以设想,把这个平行四边形换成10×2的长方形,再把横竖两条都移至边上(如前页右图),草地部分面积(阴影部分)还是与原来一样大小,因此草地面积=(16-2)×(10-2)=112.例16 右图是两个相同的直角三角形叠在一起,求阴影部分的面积.解:实际上,阴影部分是一个梯形,可是它的上底、下底和高都不知道,不能直接来求它的面积.阴影部分与三角形BCE合在一起,就是原直角三角形.你是否看出,ABCD也是梯形,它和三角形BCE合在一起,也是原直角三角形.因此,梯形ABCD的面积与阴影部分面积一样大.梯形ABCD的上底BC,是直角边AD的长减去3,高就是DC的长.因此阴影部分面积等于梯形ABCD面积=(8+8-3)×5÷2=32.5.上面两个例子都启发我们,如何把不容易算的面积,换成容易算的面积,数学上这叫等积变形.要想有这种“换”的本领,首先要提高对图形的观察能力.例17 下图是两个直角三角形叠放在一起形成的图形.已知AF,FE,EC都等于3,CB,BD都等于4.求这个图形的面积.解:两个直角三角形的面积是很容易求出的.三角形ABC面积=(3+3+3)×4÷2=18.三角形CDE面积=(4+4)×3÷2=12.这两个直角三角形有一个重叠部分--四边形BCEG,只要减去这个重叠部分,所求图形的面积立即可以得出.因为AF=FE=EC=3,所以AGF,FGE,EGC是三个面积相等的三角形.因为CB=BD=4,所以CGB,BGD是两个面积相等的三角形.2×三角形DEC面积= 2×2×(三角形GBC面积)+2×(三角形GCE面积).三角形ABC面积= (三角形GBC面积)+3×(三角形GCE面积).四边形BCEG面积=(三角形GBC面积)+(三角形GCE面积)=(2×12+18)÷5=8.4.所求图形面积=12+18- 8.4=21.6.例18 如下页左图,ABCG是4×7长方形,DEFG是2×10长方形.求三角形BCM与三角形DEM面积之差.解:三角形BCM与非阴影部分合起来是梯形ABEF.三角形DEM与非阴影部分合起来是两个长方形的和.(三角形BCM面积)-(三角形DEM面积)=(梯形ABEF面积)-(两个长方形面积之和=(7+10)×(4+2)÷2-(4×7 +2×10)=3.例19 上右图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?解:所求的影阴部分,恰好是三角形ABC 与三角形CDE 的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC 与三角形CDE 盖住的部分,因此(三角形 ABC 面积)+(三角形CDE 面积)+(13+49+35)=(长方形面积)+(阴影部分面积).三角形ABC ,底是长方形的长,高是长方形的宽;三角形CDE ,底是长方形的宽,高是长方形的长.因此,三角形ABC 面积,与三角形CDE 面积,都是长方形面积的一半,就有阴影部分面积=13 + 49+ 35= 97.例题1。
高斯小学奥数五年级下册含答案第04讲_计算综合一

第四讲计算综合一看完前面的故事,同学们可能有些疑问,真的需要那么多麦子吗?同学们可以试着算一算:从第一个棋盘开始,需要的麦子数分别为:1粒、2粒、4粒、8粒、16粒、32粒、64粒、128粒、256粒、512粒、1024粒、2048粒、……写到这里,同学们可以看出,开始的时候麦粒数量并不大,但越到后面数量越多,最终会达到全世界都无法承受的程度.我们的直觉往往是正确的,但有的时候我们也会被直觉所欺骗.麦粒数量形成的这串数列,就叫做等比数列.等比数列就是按照相同的倍数增加(或减少)的数列,例如“麦粒数列”就是按照2倍的速度增加的,这个相同的倍数就是公比,“麦粒数列”的公比就是2.同等差数列一样,等比数列同样有首项,末项及项数,同学们可以想一想如何通过首项和公比将等比数列的每一项都表示出来.等差数列求和是利用“倒序相加”或“配对求和”的方法,那么等比数列如何求和呢?我们来看一个例题.例题1.计算:(1)1248163264128256++++++++;(2)2618541624861458++++++.分析:这是一个等比数列求和的问题.如果一个一个的计算会有点复杂,那么该如何简便地算出数列的和呢?练习1.(1)3456789++++++;2222222(2)2373333++++.(836561=)有关等比数列的知识,同学们到中学以后还会继续学习,在这里只需掌握简单的等比数列求和即可.下面我们看一些技巧性比较强的分数计算的题目,首先我们先来看一个整体约分的题目.例题2.计算:123246481271421 13526104122072135⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯.分析:注意到246⨯⨯是123⨯⨯的32倍,4812⨯⨯是123⨯⨯的34倍,71421⨯⨯是123⨯⨯的37倍,那么可以把123⨯⨯都提出来.分母也可以同样处理.练习2.计算:234468691281216 345681091215121620⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯.除了整体约分,有时候我们也可以对计算中的某些数进行适当的拆分,从而避免很多冗繁的计算.使得计算过程呈现出“四两拨千斤”的效果.例题3.计算:113114115 151617 131414151516⨯+⨯+⨯.分析:把算式里的某些数适当拆分,可以简化计算的过程.练习3.计算:115116117 333537 151616171718⨯+⨯+⨯.例题4.计算:201111 20112011227201262013÷+÷+.分析:利用前面两道题目用过的技巧,就可以解决这道题目了.练习4.计算:19811 19819864919917200÷+÷+.例题5.定义新运算a bΩ为a与b之间(包含a,b)所有与a奇偶性相同的自然数的平均数,例如:()714791113410Ω=+++÷=,()18101816141210514Ω=++++÷=.(1)计算:1019Ω;(2)在算式()199980ΩΩ=的方框中填入恰当的自然数后可使等式成立,请问:所填的数是什么?分析:根据题意,可知a bΩ是公差为2的等差数列的平均数.想一下,等差数列的平均数有什么简便算法吗?最后我们来看一下数列数表的问题,数列数表的问题一般难度比较大,需要我们仔细观察,寻找规律.例题6.观察数列11212312341223334444,,,,,,,,,,的规律,求:(1)150是数列中第几项?(2)数列中第100个分数是多少?分析:观察数列,你找到什么规律了吗?又如何来利用这些规律呢?心算能力超强的数学家“欧拉进行计算看起来毫不费劲儿,就像人进行呼吸,像鹰在风中盘旋一样.”(数学家阿拉戈语)欧拉是历史上最多产的数学家,写下了浩如烟海的书籍和论文.他心算能力极强,如果你问他前一百个质数中任何一个数的六次方,他都可以瞬间告诉你结果.有一次欧拉的两个学生算无穷级数求和,算到第17项时两人在小数点后第50位数字上发生争执,欧拉这时进行心算,迅速给出了正确答案.莱昂哈德·欧拉(Leonhard Euler)约翰·冯·诺依曼(John Von Neumann)(1707年4月15日~1783年9月18日)(1903年12月28日~1957年2月8日)约翰·冯·诺依曼,被誉为“现代电子计算机之父”,也是公认的数学天才.据说:六岁时他能心算八位数乘除法,八岁时掌握微积分,十二岁就读懂领会了波莱尔的大作《函数论》要义.有一次,美国物理学家塞格雷(诺贝尔奖获得者)和同事(也是个诺贝尔奖牛人)为一个积分问题奋斗了一个下午,却毫无进展.这时他们从开着的门缝中看到冯·诺依曼正沿着走廊朝他们的办公室走来,于是他们问冯·诺依曼:“您能帮我们解决这个积分问题吗?”困扰他们的积分问题就写在移动黑板上,冯·诺依曼走到门口,看了一眼黑板,立即给出了答案(大概花了3秒钟).1. 计算:212222++2. 计算:361224384+++++.3. 计算:111112252711121213⨯+⨯. 4. 计算:12324651015125241051025⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯. 5. 数列23、25、45、27、47、67、29、…中,第100项是多少?100105是数列的第几项?第四讲 计算综合一例题1. 答案:(1)511;(2)2186详解:(1)设1248163264128256S =++++++++,2248163264128256512S =++++++++,二式相减得5121511S =-=.(2)设261458S =+++,36184374S =+++,两式相减得2437424372S =-=,2186S =.例题2. 答案:25 详解:整体约分,原式333333123123212341237135135212341237⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯ 33333312312471351247⨯⨯⨯+++=⨯⨯⨯+++()()25=.例题3. 答案:45 详解:11311411514+115+116+1131414151516=⨯+⨯+⨯原式()()()131413141514151615=14++15++16+141314151415161516⨯⨯⨯⨯⨯⨯=13+1+14+1+15+1=45例题4. 答案:146详解:171=11+(21+)7+201262013÷÷原式201217=++217+7201320136÷÷1=46.例题5. 答案:(1)14;(2)101或100详解:(1)10191018214Ω=+÷=();(2)199********Ω=+÷=();方框里有两种填法,80259101⨯-=或者80260=100⨯-.例题6. 答案:(1)1226;(2)914详解:(1)150是()1494921=1226+⨯÷+项.(2)因为()11313291+⨯÷=,114是第92个数.那么第100个数就是从114开始数的第9个,是914.练习1. 答案:(1)1016;(2)3279简答:(1)原式932221016=⨯-=;(2)原式83332792-==.练习2. 答案:25简答:原式23423455⨯⨯==⨯⨯.练习3. 答案:99 简答:原式115116117321341361151616171718⎛⎫⎛⎫⎛⎫=+⨯++⨯++⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 30132134199=+++++=.练习4. 答案:2817简答:原式11119921211631978199172002001720017⎛⎫=÷++÷+=+++= ⎪⎝⎭.作业1. 答案:8190 简答:原式.作业2. 答案:765简答:原式38423765=⨯-=.作业3. 答案:48 简答:原式1111122412612212414811121213⎛⎫⎛⎫=+⨯++⨯=+++= ⎪ ⎪⎝⎭⎝⎭. 作业4. 答案:35 简答:原式12331255⨯⨯==⨯⨯. 作业5. 答案:1829,第1376项 简答:把数列改写成一个三角形的数表,然后再做就可以了.122228190=⨯-=。
小学六年级奥数 分数计算题型综合

分数计算题型综合整体约分——观察的威力连锁约分——多米诺骨牌循环小数——分小的联系【例1】(★★)(走进美妙的数学花园·六年级初赛)211 3计算:541 1_____7997【例2】(★★★)(数学解题能力展示·读者评选活动小学六年级组初赛试题) 计算:89109101110111211121378910_____111 178910【例3】(★★★)计算:2009个20082008200820082008200820082009200920092009200920092009个2009____【例4】(★★★)计算:【例6】(★★★★)计算:124248100200400 1392618100300900 _____111 1111 113243520072009____【例5】(★★★)(清华附中分班考试)计算:11_____11111 120082007100110001【例7】(★★★★★)已知循环小数化分数A135979924698100,纯循环小数化分数:B2469698=,13579799,C=试求A、B、C三者大小关系。
10混循环小数化分数:abc0.abc=999abc9900.abc=a理解:分母:9=;0=的个数循环节位数的个数不循环小数位数分子:,从小数点后开始到第一个循环节结束-不循环部分【例8】(★★)0291019203750526....计算:⑴03300186..⑵【例9】(★★★)计算:0.160.1428570.1250.1一、本讲重点知识回顾1.整体约分:分母对应相等,带假互化2.连锁约分:多分数连乘吐血推荐:大分数运算想约分小分数连加要裂项二、本讲经典例题例2,例4,例5,例7,例82。
小学奥数思维训练整数计算综合_通用版

2019年四年级数学思维训练:整数计算综合1.计算:(1)121×32÷8;(2)4×(250÷8);(3)25×83×32×125.2.计算:(1)56×22+56×33+56×44;(2)222×33+889×66.3.计算:(1)37×47+36×53;(2)123×76﹣124×75.4.计算:100﹣99+98﹣97+96﹣95+…+12﹣11+10.5.计算:50+49﹣48﹣47+46+45﹣44﹣43+…﹣4﹣3+2+1.6.计算:(1+3+5+7+…+199+201)﹣(2+4+6+8+…+198+200).7.计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.8.下面是一个叫做“七上八下”的数字游戏.游戏规则是:对一个给定的数,按照由若干个7和8组成的口令进行一连串的变换.口令“7”是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8”是指将这个数中的一个数字去掉,也要使新生成的数尽量大.例如:给出的数是2019,口令是“8→7,”在第一个口令“8”发出后变成995,在第二个口令“7”发出后变成9995.如果给出数“6595”以及口令“8→7→8→7→8→8”,问:变换后依次得到的6个数的和是多少?9.规定运算“▽”为:a▽b=(a+1)×(b﹣1),请计算:(1)8▽10;(2)10▽8.10.规定运算“☺”为:a☺b=a×b﹣(a+b),请计算:(1)5☺8;(2)8☺5;(3)(6☺5)4;(4)6☺(5☺4)11.计算:(1)72×27×88÷(9×11×12);(2)31×121﹣88×125÷(1000÷121).12.计算:(1)555×445﹣556×444;(2)42×137﹣80÷15+58×138﹣70÷15.13.计算:20092009×2009﹣20092019×2019﹣20092019.14.计算:1+2﹣3+4+5﹣6+7+8﹣9+…+97+98﹣99.15.计算:100×99﹣99×98+98×97﹣97×96+96×95﹣95×94+…+4×3﹣3×2+2×1.16.在不大于1000的自然数中,A为所有个位数字为8的数之和,B为所有个位数字为3的数之和.A与B的差是多少?17.求图中所有数的和.18.已知平方差公式:a2﹣b2=(a+b)×(a﹣b),计算:202﹣192+182﹣172+162﹣152+…+22﹣12.19.计算:951×949﹣52×48.第1页/共13页20.规定运算“Θ”为:aΘb=a+2b﹣2,计算:(1)(8Θ7)Θ6;(2)8Θ(7Θ6)21.规定运算“○”为:a○b=(a+1)×(b﹣2).如果6○(□○5)=91,那么方格内应该填入什么数?22.规定:符号“△”为选择两数中较大的数的运算,“▽”为选择两数中较小的数的运算,例如:3△5=5,3▽5=3,请计算:1△2△3▽4△5△6▽7△…▽100.(运算的顺序是从左至右)23.观察下面算式的规律:2019+1991﹣1988﹣1982+1976+1970﹣1964﹣1958+1952+1946﹣1940﹣1934+…一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?24.从1,2,…,9,10 中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积,把所有这样的乘积全部加起来,总和是多少?25.计算:1﹣3+6﹣10+15﹣21+28﹣ (4950)26.已知平方差公式:a2﹣b2=(a+b)×(a﹣b),计算:1002+992﹣982﹣972+962+952﹣942﹣932+…+42+32﹣22﹣12.27.aΘb表示从a开始依次增加的b个连续自然数的和,例如:4Θ3=4+5+6=15,5Θ4=5+6+7+8=26,请计算:(1)4Θ15;(2)在算式(□Θ7)Θ11=1056中,方框里的数应该是多少?28.定义两种运算:aΩb=a﹣b+1,a∀b=a×b+1,用“Ω”、“∀”和括号填入下面的式子,使得等式成立(不能用别的计算符号):7 3 4 5=3.29.现定义四种操作的规则如下:①“一分为二”:如果一个自然数是偶数,就把它除以2;如果是奇数,就先加上1,然后除以2.例如从16可以得到8,从27可以得到14.②“丢三落四”:如果一个自然数中包含数字“3”或“4”,就将其划掉,例如从5304可以得到50,从408可以得到8.(不含数字3和4的自然数不能进行“丢三落四”操作)③“七上八下”:如果一个自然数中包含数字“7”,就将所有“7”移到最左边;如果一个自然数中包含数字“8”,就将所有“8”移到最右边.例如从98707可以得到77908,从802可以得到28.(不含数字7和8的自然数不能进行“七上八下”操作)④“十全十美”:将一个自然数的个位数字换成0.例如从111可以得到110,从905可以得到900.(个位是0的自然数不能进行“十全十美”操作)(1)请写出对4176依次进行③①③②④操作后的结果;(2)从655687开始,最少经过几次操作以后可以得到0?(3)一个三位数除了“丢三落四”外,其他三个操作各进行一次之后得到的结果是;求有多少个这样的三位数?30.如图是同学们都很熟悉的九九乘法口诀表,表中所有乘积的总和是多少?参考答案1.484;125;8300000;【解析】试题分析:(1)按照从左到右的顺序计算;(2)先算除法,再算乘法;(3)把32=4×8,利用乘法交换律与结合律简算.解:(1)121×32÷8=3872÷8=484;(2)4×(250÷8)=4×31.25=125;(3)25×83×32×125=25×4×(8×125)×83=100×1000×83=8300000.点评:整数混合运算的关键是抓住运算顺序,正确按运算顺序计算,适当利用运算定律简算..2.5544;66000.【解析】试题分析:(1)根据乘法分配律,把这几个乘式的公因数56提出来放在括号外,括号内的数相加是99,再把99看作(100﹣1),再应用乘法分配律解答.(2)把66看作2×33,即可用乘法分配律解答.解:(1)56×22+56×33+56×44=56×(22+33+44)=56×99=56×(100﹣1)=56×100﹣56)=5600﹣56=5544;(2)222×33+889×66=33×(222+889×2)=33×(222+1778)=33×2019=66000.点评:此题是整数的四则混合运算的简便算法,主要是考查乘法分配律的灵活运用.3.3647;48.【解析】试题分析:(1)把37×7看作(36+1)×47,根据乘法分配律,(36+1)×47=36×47+47,原式=36×47+47+36×53,再用乘法分配律,36×47+47+36×53=36×(47+53)+47,即可解答.(2)把123×76看作123×75+123,124×75看作123×75+75,原式═(123×75+123)﹣(123×75+75),去括号解答即可.解:(1)37×7+36×53=(36+1)×47+36×53=36×47+47+36×53第1页/共13页=36×(47+53)+47=36×100+47=3600+47=3647;(2)123×76﹣124×75=(123×75+123)﹣(123×75+75)=123×75+123﹣123×75﹣75=123﹣75=48.点评:此题是考查整数的四则混合运算,两个小题看似没有简便算法,只要将原式适当变形,即可用乘法分配律,使计算简便.4.55【解析】试题分析:通过观察,相邻两个数字相差1,因此原式变为(100﹣99)+(98﹣97)+(96﹣95)+…+(12﹣11)+10,共有(100﹣12)÷2+1=45个1,然后加上10即可.解:100﹣99+98﹣97+96﹣95+…+12﹣11+10=(100﹣99)+(98﹣97)+(96﹣95)+…+(12﹣11)+10=1+1+1+…+1+10=45+10=55点评:此题解答的关键仔细分析数据,根据数字特点进行合理分组,达到简算的目的.5.51【解析】试题分析:此题中的隔项相差2,因此把原式变成(50﹣48)+(49﹣47)+…+(6﹣4)+(5﹣3)+2+1,计算即可.解:50+49﹣48﹣47+46+45﹣44﹣43+…﹣4﹣3+2+1=(50﹣48)+(49﹣47)+…+(6﹣4)+(5﹣3)+2+1=2+2+2+…+2+1=2×25+1=51点评:认真观察,根据数字特点进行组合,从而达到巧算的目的.6.101【解析】试题分析:通过观察,括号内的算式都是公差为2的等差数列,运用等差数列公式解答即可.解:(1+201)×101÷2﹣(2+200)×100÷2=202×101÷2﹣202×50=10201﹣10100=101点评:仔细观察数据,运用等差数列公式进行解答.7.2500【解析】试题分析:把1+2+3+…+49+50+49+48+…+3+2+1分成两段来计算,即原式=(1+2+3+…+49+50)+(49+48+…+3+2+1),把第二段加上50再减去50,每部分运用高斯求和公式计算即可.解:1+2+3+…+49+50+49+48+…+3+2+1=(1+2+3+…+49+50)+(50+49+48+…+3+2+1﹣50)=(1+50)×50÷2+(1+50)×50÷2﹣50=1275+(1275﹣50)=1275+1225=2500点评:此题主要运用了高斯求和公式进行计算.8.22478【解析】试题分析:先根据口令,6595在8发出后变为695,7发出后变为9695,8发出后为995,7发出后为9995,6发出后为999,最后一次8发出后为99,把这六个数加起来即可.解:根据游戏规则得:6595”以及口令“8→7→8→7→8→8分别变为:695→9695→995→9995→999→99695+9695+995+9995+999+99=(695+995)+(9695+9995)+1000﹣1+100﹣1=1690+19690+1100﹣2=22478点评:解答本题的根据是根据题意先把这6个数照出来,然后加起来即可.9.81;77.【解析】试题分析:规定运算“▽”为:a▽b=(a+1)×(b﹣1),也就是等于第一个因数与1的和乘第二个因数与1的差的乘积,据此解答即可.解:1)8▽10=(8+1)×(10﹣1)=9×9=81(2)10▽8=(10+1)×(8﹣1)=11×7=77点评:根据新运算的规则,等于第一个因数与1的和乘第二个因数与1的差的乘积.10.27;27;53;49.【解析】试题分析:a☺b=a×b﹣(a+b)表示两数的乘积减去这两个数的和,据此解答即可.解:因为a☺b=a×b﹣(a+b),所以:(1)5☺8=5×8﹣(5+8)=40﹣13=27(2)8☺5=8×5﹣(8+5)第3页/共13页=40﹣13=27(3)(6☺5)☺4=(6×5﹣6﹣5)☺4=19☺4=19×4﹣(19+4)=76﹣23=53(4)6☺(5☺4)=6☺(5×4﹣5﹣4)=6☺11=6×11﹣(6+11)=66﹣17=49点评:根据新运算的法则:这种新运算等于两数的乘积减去这两个数的和.11.144;2420.【解析】试题分析:(1)利用a÷(b×c)=a÷b÷c即可;(2)88×125=8×125×11=11×1000,再利用a÷(b÷c)=a÷b×c即可.解:(1)72×27×88÷(9×11×12)=72×27×88÷(9×11×12)=(72÷12)×(27÷9)×(88÷11)=6×3×8=18×8=144(2)31×121﹣88×125÷(1000÷121)=31×121﹣8×125×11÷1000×121=31×121﹣11×121=121×(31﹣11)=121×20=2420点评:巧妙的利用合适的简便方法使计算简便.12.111;13748.【解析】试题分析:(1)利用555=5×111,444=4×111,然后利用乘法分配律即可;(2)58×138=58×137+58,80÷15+70÷15=(80+70)÷15,再利用乘法分配律即可.解:(1)555×445﹣556×444=111×5×445﹣4×111×556=111×2225﹣111×2224=111×(2225﹣2224)=111(2)42×137﹣80÷15+58×138﹣70÷15=42×137﹣(80+70)÷15+58×137+58=137×(42+58)﹣150÷15+58=137×100﹣10+58=13700+48=13748点评:解决本题的关键是注意对原题的恒等变形.13.2009.【解析】试题分析:每项都有20092019,那么利用20092009×2009=(20092019+1)×2009后,再利用乘法分配律即可.解:20092009×2009﹣20092019×2019﹣20092019=(20092019+1)×2009﹣20092019×2019﹣20092019=20092019×(2009﹣2019﹣1)+2009=2009点评:解答本题的关键是把20092009×2009转化为:(20092019+1)×2009.14.1584.【解析】试题分析:先进行分组,从前往后分别把三个数分为一组,即(1+2﹣3)+(4+5﹣6)+(7+8﹣9)…+(97+98﹣99)=0+3+6+…+96,变成首项为0,公差是3的前33项和,用等差公式计算即可.解:1+2﹣3+4+5﹣6+7+8﹣9+…+97+98﹣99=(1+2﹣3)+(4+5﹣6)+(7+8﹣9)…+(97+98﹣99)=0+3+6+…+96=(0+96)×33÷2=96×33÷2=1584.点评:合理分组,运用运算技巧或公式,进行简便计算.15.4182.【解析】试题分析:通过仔细观察,此题可通过数字变形,即原式变为100×(100﹣1)﹣98×(98﹣1)+96×(96﹣1)﹣94×(94﹣1)+...+4×(4﹣1)﹣2×(2﹣1)=(1002﹣100)﹣(982﹣98)+(962﹣96)+...+(42﹣4)﹣(22﹣2),运用平方差公式和加法结合律,进一步变为(1002﹣982+962﹣942+...+42﹣22)﹣(100+98+96+ (2),运用高斯求和公式,解决问题.解:100×99﹣98×97+96×95﹣94×93+…+4×3﹣2×1=100×(100﹣1)﹣98×(98﹣1)+96×(96﹣1)﹣94×(94﹣1)+…+4×(4﹣1)﹣2×(2﹣1)=(1002﹣100)﹣(982﹣98)+(962﹣96)+…+(42﹣4)﹣(22﹣2)=(1002﹣982+962﹣942+...+42﹣22)﹣(100+98+96+ (2)=(1002﹣982)+(962﹣942)﹣…+(42﹣22)﹣(100+2)×50÷2=198×2+190×2+…+6×2﹣2550=(198+190+182+…+6)×2﹣2550=(198+6)×33÷2×2﹣2550=6732﹣2550=4182点评:通过转化的数学思想,巧妙灵活地运用运算定律,使复杂的问题简单化.第5页/共13页【解析】试题分析:分析:从1到10有2,8;,从11到20,即这样每10个数中有一个个位数是3的数,一个个位数是8的数.如1到10里,有3和8;11到20里有13和18,这两个数的差都是5,如8﹣3=5,18﹣13=5.又1000÷10=100,所以A与B的差是5×100=500.解:8﹣3=51000÷10=100,100×5=500.答:A与B的差是500.点评:完成此类题目要注意分析数据,从中找出规律后解答.17.510.【解析】试题分析:每一行把第一个与第九个相加,第二个与第把个相加,第三个与第七个相加,第四个与第六个相加,再加第五个,第一行是4个18与9;第二行4个20与10;第三行4个22与11;第四行4个24与12;第五行4个26与13相加即可.解:18×4+9+20×4+10+22×4+11+24×4+12+26×4+13=72+9+80+10+88+11+96+12+104+13=510.点评:本题考查了数字和问题,关键是得出第一行是4个18与9;第二行4个20与10;第三行4个22与11;第四行4个24与12;第五行4个26与13.18.210.【解析】试题分析:把算式进行必要的变形,进而利用平方差公式计算得解.解:202﹣192+182﹣172+162﹣152+…+22﹣12=(20+19)(20﹣19)+(18+17)(18﹣17)+(16+15)(16﹣15)+…+(2+1)(2﹣1)=39+35+31+…+3=(39+3)+(35+7)+(31+11)+(27+15)+(23+19)=42+42+42+42+42=210.点评:本题考查了平方差公式的应用.关键是把原式化为(20+19)(20﹣19)+(18+17)(18﹣17)+(16+15)(16﹣15)+…+(2+1)(2﹣1).19.900003.【解析】试题分析:先算乘法,再算减法,由此顺序计算即可.解:951×949﹣52×48=902499﹣2496=900003.点评:整数混合运算的关键是抓住运算顺序,正确按运算顺序计算即可.20.30;40.【解析】试题分析:规定运算“Θ”为:aΘb=a+2b﹣2,第一个数加上第二个数的2倍再减去2,按照这个规律即可;有括号先算括号里面的.解:因为aΘb=a+2b﹣2,(1)(8Θ7)Θ6=(8+2×7﹣2)Θ6=20Θ6=20+2×6﹣2=32﹣2=30(2)8Θ(7Θ6)=8Θ(7+2×6﹣2)=8Θ17=8+2×17﹣2=8+34﹣2=40点评:本题考查根据新运算规则计算:正确找准计算规则是关键.21.4.【解析】试题分析:根据题意a○b=(a+1)×(b﹣2),即为第一个加1与第二个数减去2的差的乘积;设□○5=x,6○(□○5)=91就变为6○x=91,据此解出x,然后代入即可求得□.解:设□○5=x因为:a○b=(a+1)×(b﹣2)所以:6○(□○5)=91即为:6○x=91(6+1)×(x﹣2)=917x﹣14=917x﹣14+14=91+147x=1057x÷7=105÷7x=15所以:□○5=15(□+1)×(5﹣2)=153□+3=153□+3﹣3=15﹣33□=123□÷3=12÷3□=4答:方格内应该填4.点评:本题考查根据新运算规则计算:正确找准计算规则是关键.22.99.【解析】试题分析:因为符号“△”为选择两数中较大的数的运算,“▽”为选择两数中较小的数的运算,第7页/共13页而△2△3▽4△5△6▽7△…▽100,两个向上的,一个向下的,3个是一周期,△取大,▽取小,所以正好是取3的倍数,到最后还剩99,据此解答即可.解:因为3△5=5,3▽5=31△2△3▽4△5△6▽7△…▽100两个向上的,一个向下的,3个是一周期,△取大,▽取小,所以正好是取3的倍数,到最后还剩99,所以:1△2△3▽4△5△6▽7△…▽100=2△3▽4△5△6▽7△…▽100=3▽4△5△6▽7△…▽100=3△5△6▽7△…▽100=6▽7△…▽100=6△8…▽100=99▽100=99点评:本题考查根据新运算规则计算:正确找准计算规则是关键.23.这四个数为24,18,12,6;24+18﹣12﹣6;24.【解析】试题分析:通过分析可知,每四个数为一循环,每一循环的第一个数相差24,后边的数相差6,所以最后4个自然数分别24,18,12,6,为24+18﹣12﹣6,据解答即可.解:根据规律可知,这四个数为24,18,12,6,算式为24+18﹣12﹣6结果为:24+18﹣12﹣6=24答:这四个数为24,18,12,6;24+18﹣12﹣6;24.点评:先找到各数量之间的关系,再根据这个关系求解.24.750.【解析】试题分析:在1、2、3、4、5、6、7、8、9、10这10个数中,奇数为1,3,5,7,9;偶数为2,4,6,8,10.奇数与偶数各5个,则每个奇数都可与其它5个偶数相乘得到5个不同的积,它们的和为:1×2+1×4+1×6+1×8+1×10=(2+4+6+8+10)×1,同理3与这五个偶数相乘积的和为(2+4+6+8+10)×3,由此可我们根据乘法分配律即求出在1、2、3、4、5、6、7、8、9、10这10个数中,每次取一个奇数和一个偶数相乘,它们所有积和的大小.解:(1×2+1×4+1×6+1×8+1×10)+(3×2+3×4+…+3×10)+…+(9×2+9×4+…+9×10)=(2+4+6+8+10)×1+(2+4+6+8+10)×3+…+(2+4+6+8+10)×9,=(1+3+5+7+9)×(2+4+6+8+10),=25×30,=750.点评:在列出算式的基础上通过分析找出算式中数据之间的特点及内在联系,然后连续运用乘法分配律是完成本题的关键.25.2500.【解析】试题分析:我们观察这个算式中的每一项,3=1+2,6=1+2+3,10=1+2+3+4,….4990=1+2+3…+99,那么原式变为:1﹣(1+2)+(1+2+3)﹣(1+2+3+4)+…+(1+2+3+…+99),计算即可.解:1﹣3+6﹣10+15﹣21+28﹣…+4950=1﹣(1+2)+(1+2+3)﹣(1+2+3+4)+...+(1+2+3+ (99)=1+3+5+…+99=(1+99)×50÷2=2500点评:仔细观察算式,根据数据特点,把数据进行拆分,变成从第二项开始相邻两式部分相同的式子,通过加减相互抵消,变成1+3+5+…+99,运用高斯求和公式计算求得结果.26.10100.【解析】试题分析:解答此题先运用平方差公式把相邻两个偶数或两个奇数平方的差转化成因数相乘的形式进行计算即可求解.解:1002+992﹣982﹣972+962+952﹣942﹣932+…+42+32﹣22﹣12=(1002﹣982)+(992﹣972)+(962﹣942)+(952﹣932)+…+(42﹣22)+(32﹣12)=(100﹣98)×(100+98)+(99﹣97)×(99+97)+…+(4﹣2)×(4+2)+(3﹣1)×(3+1)=2×(100+98)+2×(99+97)+…+2×(4+2)+2×(3+1)=2×(100+98+99+97+4+2+3+1)=2×=101×100=10100.点评:解答此题主要运用平方差公式、乘法分配律、加法结合律,高斯求和公式进行计算.27.165;10.【解析】试题分析:由题意可知:这种新运算是从第一个数开始,连续自然数相加,加数的个数就是后一个数;(2)设□Θ7=x,根据条件求出x,然后根据新运算规则再求得方框即可.解:因为4Θ3=4+5+6=15,5Θ4=5+6+7+8=26,所以:(1)4Θ15=4+5+6+7+ (18)=(4+17)×7+18=21×7+18=147+18=165(2)因为:(□Θ7)Θ11=1056设□Θ7=x,原算式变为:x+(x+1)+…(x+10)=105611x+(1+10)×5=105611x+55=105611x+55﹣55=1056﹣5511x=100111x÷11=1001÷11x=91所以□Θ7=91第9页/共13页□+(□+1)+…(□+6)=917□+21=917□+21﹣21=91﹣217□=707□÷7=70÷7□=10答;方框里的数应该是10.点评:本题考查根据新运算规则计算:正确找准计算规则是关键.28.﹣7Ω{﹣[(3∀4 )Ω 5]}=3.【解析】试题分析:根据aΩb=a﹣b+1,a∀b=a×b+1,要多次实验到底用几个Ω,几个∀,或者是单独用其中一个符号,让右边等于3即可.解:因为aΩb=a﹣b+1,a∀b=a×b+13∀4=3×4+1=1313Ω5=13﹣5+1=9﹣7Ω(﹣9)=﹣7+9+1=3所以:﹣7Ω{﹣[(3∀4 )Ω 5]}=3.点评:本题考查根据新运算规则计算:正确找准计算规则是关键.29.(1)4176﹣7416﹣3708﹣7308﹣708﹣700(2)即经过7次可以得到0.(3)234经过①得117,再经过③得711,再经过④得710.【解析】试题分析:(1)(2)根据操作规则进行分析操作即可得出相应结果.(3)第一问可选择一个数根据操作规则进行操作得出结果即可,第二问可按不同的操作顺序分析完成.解:(1)4176依次进行③①③②④操作后的结果:4176﹣7416﹣3708﹣7308﹣708﹣700(2)从655687开始,655687经过“一分为二”的操作,得到327844;再经过“丢三落四”的操作,得到278;再经过“七上八下”的操作,得到728;再经过经过“一分为二”的操作,得到364;再经过“丢三落四”的操作,得到6;最后经过“十全十美”的操作,得到0.共6步完成操作,得到0.655687经过①得327844﹣经过②得278﹣经过①得139﹣经过②得19﹣经过①得10﹣经过①得5﹣经过④得0.即经过7次可以得到0.(3)一个三位数除了“丢三落四”外,其他三个操作各进行一次之后得到的结果是如:234经过①得117,再经过③得711,再经过④得710.步骤①③④,经过步骤①之后个位含有7,百位含有1的,有10个;分别是214,234,254,274,294,314,334,354,374,394;经过步骤①之后十位含有7,百位为1,有10个;分别是340,342,344,346,348,350,352,354,356,358.重复354;总共有10+10﹣1=19个.步骤①④③,经过步骤①之后十位含有7,百位含有1,有10个;分别是340,342,344,346,348,350,352,354,356,358步骤③①④,③④①,都没有步骤④①③,个位数有10种可能,分别是340,341,342,343,344,345,346,347,348,349步骤④③①,没有.根据上面的分类,除去重复的数据,那么总共有:19+5=24个.故答案为:710.点评:完成本题要注意条件中所给的操作规则,然后按操作规则分析即可.30.1155.【解析】试题分析:根9的乘法口诀表,把表中的各个乘积相加即可得出结论.解:(1+2+3+4+5+6+7+8+9)+(4+6+8+10+12+14+16+18)+(9+12+15+18+21+24+27)+(16+20+24+28+32+36)+(25+30+35+40+45)+(36+42+48+54)+(49+56+63)+(64+72)+81=[(1+9)×4+5]+[(4+18)×4]+[(9+27)×3+18]+[(16+36)×3]+[(25+45)×2+35]+[(36+54)×2]+168+136+81=45+88+126+156+175+180+168+136+81=1155点评:此题也可以按行累计九九乘法表里共有:1个1,1+2个2,1+2+3个3…以此类推,得1个1,3个2,6个3,10个4,15个5,21个6,28个7,36个8,45个9,由此解答即可.第11页/共13页。
四年级奥数整数计算综合

整数计算是数学学科的基础内容之一,是学生数学能力的重要组成部分。
在四年级的奥数中,整数计算题目往往是综合性的,包括加法、减法、乘法和除法等运算,并且常常涉及到多步运算和应用问题。
下面我将列举一些常见的整数计算综合题目,并给出详细解答。
例题一:计算题小明骑着自行车从家里出发,先向东骑200米,然后向西骑300米,再向南骑400米,最后向北骑500米,小明最后停在哪里?解答:我们可以用坐标系来解答这个题目。
在北方是向上,南方是向下,东方是向右,西方是向左,这样我们可以假设小明的初始位置是原点(0,0),向东骑行200米即向右移动200个单位,所以位置变为(200,0),然后向西骑行300米即向左移动300个单位,所以位置变为(200-300,0)=(-100,0),再向南骑行400米,所以位置变为(-100,0-400)=(-100,-400),最后向北骑行500米,所以位置变为(-100,-400+500)=(-100,100)。
所以小明最后停在坐标为(-100,100)的位置。
例题二:综合应用题超市在一天内进行了货物的进销存计算,结果如下:上午9:00时存货50件,销售了80件,下午14:00时存货60件,进货了100件,晚上19:00时存货70件,售出了60件。
请问该超市最后一共进了多少件货物?最后还剩下多少件货物?解答:首先,我们需要把问题中的信息整理清楚。
上午9:00时存货50件,销售了80件,所以上午9:00时存货数量50-80=-30件。
下午14:00时存货60件,进货了100件,所以下午14:00时存货数量60+100=160件。
晚上19:00时存货70件,售出了60件,所以晚上19:00时存货数量70-60=10件。
最后,我们只需要把所有进货的数量加起来,再减去所有售出的数量,就可以得到该超市最后一共进了多少件货物。
进货数量为:100件最后,我们将最后一共进的货物数量与最后剩下的货物数量相加,即可得到该超市最后一共进了多少件货物。
小学奥数小升初计算高频考点汇总与方法总结

本讲重点模块一、不识“计算”真面目,只因学习不系统——计算专题系统梳理模块二、计算专题综合性题目选讲模块一:计算专题系统梳理一、计算基础知识:1.两个重要数列2.四个重要公式:3.三条常用结论小升初计算高频考点汇总与方法总结二、升初计算三宝三、计算题目类型:1.定义新运算:照猫画虎,or看透本质。
2.比较与估算:化小数,通分法,比倒数,设标准,糖水法,放缩法等等。
模块二、计算专题综合性题目选讲计算:13524.33 3.66.7 1.231350.0935183⎛⎫⎛⎫⨯⨯-+÷-÷--⎪ ⎪⎝⎭⎝⎭【巩固】要使等式()2142315.62 1.625133101535⎡⎤÷⨯+--÷=⎢⎥⎣⎦□成立,方格内应填入多少?若下面的等式成立,x应该等于多少?1811111214x=+++【巩固】将下面这个繁分数化为最简真分数:11514112+++(迎春杯竞赛试题)计算: 212391239112923912341023410223103410⎛⎫⎛⎫⎛⎫⎛⎫+++++++++⨯-++++⨯+++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭我们规定:△n =n ×(n +1),比如:△1=1×2,△2=2×3,△3=3×4。
请问: ⑴要使等式1111299100+++=∆∆∆∆□成立,那么方框内应填入多少? ⑵计算:△1+△2+△3+…+△100。
已知111112345619992000A =++++⨯⨯⨯⨯,11111000100110021999B =++++,比较A 和B 的大小,并计算出它们的差。
计算专题考点分析与技巧总结——谷老师感悟:1.计算是数学基本功,基本功一定要扎实,各重点中学都 很看重,为必考考点。
2.计算常考题型有两种:区重点:分数小数四则混合运算——乘法分配律逆用。
市重点:抵消思想——裂项,整体约分与连锁约分等。
小学奥数思维训练整数计算综合_通用版

2022年四年级数学思维训练:整数计算综合1.计算:〔1〕121×32÷8;〔2〕4×〔250÷8〕;〔3〕25×83×32×125.2.计算:〔1〕56×22+56×33+56×44;〔2〕222×33+889×66.3.计算:〔1〕37×47+36×53;〔2〕123×76﹣124×75.4.计算:100﹣99+98﹣97+96﹣95+…+12﹣11+10.5.计算:50+49﹣48﹣47+46+45﹣44﹣43+…﹣4﹣3+2+1.6.计算:〔1+3+5+7+…+199+201〕﹣〔2+4+6+8+…+198+200〕.7.计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.8.下面是一个叫做“七上八下〞的数字游戏.游戏规那么是:对一个给定的数,按照由假设干个7和8组成的口令进展一连串的变换.口令“7〞是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8〞是指将这个数中的一个数字去掉,也要使新生成的数尽量大.例如:给出的数是2022,口令是“8→7,〞在第一个口令“8〞发出后变成995,在第二个口令“7〞发出后变成9995.假如给出数“6595〞以及口令“8→7→8→7→8→8〞,问:变换后依次得到的6个数的和是多少?9.规定运算“▽〞为:a▽b=〔a+1〕×〔b﹣1〕,请计算:〔1〕8▽10;〔2〕10▽8.10.规定运算“☺〞为:a☺b=a×b﹣〔a+b〕,请计算:〔1〕5☺8;〔2〕8☺5;〔3〕〔6☺5〕4;〔4〕6☺〔5☺4〕11.计算:〔1〕72×27×88÷〔9×11×12〕;〔2〕31×121﹣88×125÷〔1000÷121〕.12.计算:〔1〕555×445﹣556×444;〔2〕42×137﹣80÷15+58×138﹣70÷15.13.计算:20212021×2021﹣20212022×2022﹣20212022.14.计算:1+2﹣3+4+5﹣6+7+8﹣9+…+97+98﹣99.15.计算:100×99﹣99×98+98×97﹣97×96+96×95﹣95×94+…+4×3﹣3×2+2×1.16.在不大于1000的自然数中,A为所有个位数字为8的数之和,B为所有个位数字为3的数之和.A与B的差是多少?17.求图中所有数的和.18.平方差公式:a2﹣b2=〔a+b〕×〔a﹣b〕,计算:202﹣192+182﹣172+162﹣152+…+22﹣12.19.计算:951×949﹣52×48.20.规定运算“Θ〞为:aΘb=a+2b﹣2,计算:〔1〕〔8Θ7〕Θ6;第 1 页〔2〕8Θ〔7Θ6〕21.规定运算“○〞为:a○b=〔a+1〕×〔b﹣2〕.假如6○〔□○5〕=91,那么方格内应该填入什么数?22.规定:符号“△〞为选择两数中较大的数的运算,“▽〞为选择两数中较小的数的运算,例如:3△5=5,3▽5=3,请计算:1△2△3▽4△5△6▽7△…▽100.〔运算的顺序是从左至右〕23.观察下面算式的规律:2022+1991﹣1988﹣1982+1976+1970﹣1964﹣1958+1952+1946﹣1940﹣1934+…一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?24.从1,2,…,9,10 中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积,把所有这样的乘积全部加起来,总和是多少?25.计算:1﹣3+6﹣10+15﹣21+28﹣ (4950)26.平方差公式:a2﹣b2=〔a+b〕×〔a﹣b〕,计算:1002+992﹣982﹣972+962+952﹣942﹣932+…+42+32﹣22﹣12.27.aΘb表示从a开场依次增加的b个连续自然数的和,例如:4Θ3=4+5+6=15,5Θ4=5+6+7+8=26,请计算:〔1〕4Θ15;〔2〕在算式〔□Θ7〕Θ11=1056中,方框里的数应该是多少?28.定义两种运算:aΩb=a﹣b+1,a∀b=a×b+1,用“Ω〞、“∀〞和括号填入下面的式子,使得等式成立〔不能用别的计算符号〕:7 3 4 5=3.29.现定义四种操作的规那么如下:①“一分为二〞:假如一个自然数是偶数,就把它除以2;假如是奇数,就先加上1,然后除以2.例如从16可以得到8,从27可以得到14.②“丢三落四〞:假如一个自然数中包含数字“3〞或“4〞,就将其划掉,例如从5304可以得到50,从408可以得到8.〔不含数字3和4的自然数不能进展“丢三落四〞操作〕③“七上八下〞:假如一个自然数中包含数字“7〞,就将所有“7〞移到最左边;假如一个自然数中包含数字“8〞,就将所有“8〞移到最右边.例如从98707可以得到77908,从802可以得到28.〔不含数字7和8的自然数不能进展“七上八下〞操作〕④“十全十美〞:将一个自然数的个位数字换成0.例如从111可以得到110,从905可以得到900.〔个位是0的自然数不能进展“十全十美〞操作〕〔1〕请写出对4176依次进展③①③②④操作后的结果;〔2〕从655687开场,最少经过几次操作以后可以得到0?〔3〕一个三位数除了“丢三落四〞外,其他三个操作各进展一次之后得到的结果是;求有多少个这样的三位数?30.如图是同学们都很熟悉的九九乘法口诀表,表中所有乘积的总和是多少?参考答案1.484;125;8300000;【解析】试题分析:〔1〕按照从左到右的顺序计算;〔2〕先算除法,再算乘法;〔3〕把32=4×8,利用乘法交换律与结合律简算.解:〔1〕121×32÷8=3872÷8=484;〔2〕4×〔250÷8〕=4×31.25=125;〔3〕25×83×32×125=25×4×〔8×125〕×83=100×1000×83=8300000.点评:整数混合运算的关键是抓住运算顺序,正确按运算顺序计算,适当利用运算定律简算..2.5544;66000.【解析】试题分析:〔1〕根据乘法分配律,把这几个乘式的公因数56提出来放在括号外,括号内的数相加是99,再把99看作〔100﹣1〕,再应用乘法分配律解答.〔2〕把66看作2×33,即可用乘法分配律解答.解:〔1〕56×22+56×33+56×44=56×〔22+33+44〕=56×99=56×〔100﹣1〕=56×100﹣56〕=5600﹣56=5544;〔2〕222×33+889×66=33×〔222+889×2〕=33×〔222+1778〕=33×2022=66000.点评:此题是整数的四那么混合运算的简便算法,主要是考察乘法分配律的灵敏运用.3.3647;48.【解析】试题分析:〔1〕把37×7看作〔36+1〕×47,根据乘法分配律,〔36+1〕×47=36×47+47,原式=36×47+47+36×53,再用乘法分配律,36×47+47+36×53=36×〔47+53〕+47,即可解答.〔2〕把123×76看作123×75+123,124×75看作123×75+75,原式═〔123×75+123〕﹣〔123×75+75〕,去括号解答即可.解:〔1〕37×7+36×53=〔36+1〕×47+36×53第 1 页=36×47+47+36×53=36×〔47+53〕+47=36×100+47=3600+47=3647;〔2〕123×76﹣124×75=〔123×75+123〕﹣〔123×75+75〕=123×75+123﹣123×75﹣75=123﹣75=48.点评:此题是考察整数的四那么混合运算,两个小题看似没有简便算法,只要将原式适当变形,即可用乘法分配律,使计算简便.4.55【解析】试题分析:通过观察,相邻两个数字相差1,因此原式变为〔100﹣99〕+〔98﹣97〕+〔96﹣95〕+…+〔12﹣11〕+10,共有〔100﹣12〕÷2+1=45个1,然后加上10即可.解:100﹣99+98﹣97+96﹣95+…+12﹣11+10=〔100﹣99〕+〔98﹣97〕+〔96﹣95〕+…+〔12﹣11〕+10=1+1+1+…+1+10=45+10=55点评:此题解答的关键仔细分析数据,根据数字特点进展合理分组,到达简算的目的.5.51【解析】试题分析:此题中的隔项相差2,因此把原式变成〔50﹣48〕+〔49﹣47〕+…+〔6﹣4〕+〔5﹣3〕+2+1,计算即可.解:50+49﹣48﹣47+46+45﹣44﹣43+…﹣4﹣3+2+1=〔50﹣48〕+〔49﹣47〕+…+〔6﹣4〕+〔5﹣3〕+2+1=2+2+2+…+2+1=2×25+1=51点评:认真观察,根据数字特点进展组合,从而到达巧算的目的.6.101【解析】试题分析:通过观察,括号内的算式都是公差为2的等差数列,运用等差数列公式解答即可.解:〔1+201〕×101÷2﹣〔2+200〕×100÷2=202×101÷2﹣202×50=10201﹣10100=101点评:仔细观察数据,运用等差数列公式进展解答.7.2500【解析】试题分析:把1+2+3+…+49+50+49+48+…+3+2+1分成两段来计算,即原式=〔1+2+3+…+49+50〕+〔49+48+…+3+2+1〕,把第二段加上50再减去50,每局部运用高斯求和公式计算即可.解:1+2+3+…+49+50+49+48+…+3+2+1=〔1+2+3+…+49+50〕+〔50+49+48+…+3+2+1﹣50〕=〔1+50〕×50÷2+〔1+50〕×50÷2﹣50=1275+〔1275﹣50〕=1275+1225=2500点评:此题主要运用了高斯求和公式进展计算.8.22478【解析】试题分析:先根据口令,6595在8发出后变为695,7发出后变为9695,8发出后为995,7发出后为9995,6发出后为999,最后一次8发出后为99,把这六个数加起来即可.解:根据游戏规那么得:6595〞以及口令“8→7→8→7→8→8分别变为:695→9695→995→9995→999→99695+9695+995+9995+999+99=〔695+995〕+〔9695+9995〕+1000﹣1+100﹣1=1690+19690+1100﹣2=22478点评:解答此题的根据是根据题意先把这6个数照出来,然后加起来即可.9.81;77.【解析】试题分析:规定运算“▽〞为:a▽b=〔a+1〕×〔b﹣1〕,也就是等于第一个因数与1的和乘第二个因数与1的差的乘积,据此解答即可.解:1〕8▽10=〔8+1〕×〔10﹣1〕=9×9=81〔2〕10▽8=〔10+1〕×〔8﹣1〕=11×7=77点评:根据新运算的规那么,等于第一个因数与1的和乘第二个因数与1的差的乘积.10.27;27;53;49.【解析】试题分析:a☺b=a×b﹣〔a+b〕表示两数的乘积减去这两个数的和,据此解答即可.解:因为a☺b=a×b﹣〔a+b〕,所以:〔1〕5☺8=5×8﹣〔5+8〕=40﹣13=27〔2〕8☺5=8×5﹣〔8+5〕第 3 页=40﹣13=27〔3〕〔6☺5〕☺4=〔6×5﹣6﹣5〕☺4=19☺4=19×4﹣〔19+4〕=76﹣23=53〔4〕6☺〔5☺4〕=6☺〔5×4﹣5﹣4〕=6☺11=6×11﹣〔6+11〕=66﹣17=49点评:根据新运算的法那么:这种新运算等于两数的乘积减去这两个数的和.11.144;2420.【解析】试题分析:〔1〕利用a÷〔b×c〕=a÷b÷c即可;〔2〕88×125=8×125×11=11×1000,再利用a÷〔b÷c〕=a÷b×c即可.解:〔1〕72×27×88÷〔9×11×12〕=72×27×88÷〔9×11×12〕=〔72÷12〕×〔27÷9〕×〔88÷11〕=6×3×8=18×8=144〔2〕31×121﹣88×125÷〔1000÷121〕=31×121﹣8×125×11÷1000×121=31×121﹣11×121=121×〔31﹣11〕=121×20=2420点评:巧妙的利用适宜的简便方法使计算简便.12.111;13748.【解析】试题分析:〔1〕利用555=5×111,444=4×111,然后利用乘法分配律即可;〔2〕58×138=58×137+58,80÷15+70÷15=〔80+70〕÷15,再利用乘法分配律即可.解:〔1〕555×445﹣556×444=111×5×445﹣4×111×556=111×2225﹣111×2224=111×〔2225﹣2224〕=111〔2〕42×137﹣80÷15+58×138﹣70÷15=42×137﹣〔80+70〕÷15+58×137+58=137×〔42+58〕﹣150÷15+58=137×100﹣10+58=13700+48=13748点评:解决此题的关键是注意对原题的恒等变形.13.2021.【解析】试题分析:每项都有20212022,那么利用20212021×2021=〔20212022+1〕×2021后,再利用乘法分配律即可.解:20212021×2021﹣20212022×2022﹣20212022=〔20212022+1〕×2021﹣20212022×2022﹣20212022=20212022×〔2021﹣2022﹣1〕+2021=2021点评:解答此题的关键是把20212021×2021转化为:〔20212022+1〕×2021.14.1584.【解析】试题分析:先进展分组,从前往后分别把三个数分为一组,即〔1+2﹣3〕+〔4+5﹣6〕+〔7+8﹣9〕…+〔97+98﹣99〕=0+3+6+…+96,变成首项为0,公差是3的前33项和,用等差公式计算即可.解:1+2﹣3+4+5﹣6+7+8﹣9+…+97+98﹣99=〔1+2﹣3〕+〔4+5﹣6〕+〔7+8﹣9〕…+〔97+98﹣99〕=0+3+6+…+96=〔0+96〕×33÷2=96×33÷2=1584.点评:合理分组,运用运算技巧或公式,进展简便计算.15.4182.【解析】试题分析:通过仔细观察,此题可通过数字变形,即原式变为100×〔100﹣1〕﹣98×〔98﹣1〕+96×〔96﹣1〕﹣94×〔94﹣1〕+...+4×〔4﹣1〕﹣2×〔2﹣1〕=〔1002﹣100〕﹣〔982﹣98〕+〔962﹣96〕+...+〔42﹣4〕﹣〔22﹣2〕,运用平方差公式和加法结合律,进一步变为〔1002﹣982+962﹣942+...+42﹣22〕﹣〔100+98+96+ (2),运用高斯求和公式,解决问题.解:100×99﹣98×97+96×95﹣94×93+…+4×3﹣2×1=100×〔100﹣1〕﹣98×〔98﹣1〕+96×〔96﹣1〕﹣94×〔94﹣1〕+…+4×〔4﹣1〕﹣2×〔2﹣1〕=〔1002﹣100〕﹣〔982﹣98〕+〔962﹣96〕+…+〔42﹣4〕﹣〔22﹣2〕=〔1002﹣982+962﹣942+...+42﹣22〕﹣〔100+98+96+ (2)=〔1002﹣982〕+〔962﹣942〕﹣…+〔42﹣22〕﹣〔100+2〕×50÷2=198×2+190×2+…+6×2﹣2550=〔198+190+182+…+6〕×2﹣2550=〔198+6〕×33÷2×2﹣2550=6732﹣2550=4182点评:通过转化的数学思想,巧妙灵敏地运用运算定律,使复杂的问题简单化.第 5 页【解析】试题分析:分析:从1到10有2,8;,从11到20,即这样每10个数中有一个个位数是3的数,一个个位数是8的数.如1到10里,有3和8;11到20里有13和18,这两个数的差都是5,如8﹣3=5,18﹣13=5.又1000÷10=100,所以A与B的差是5×100=500.解:8﹣3=51000÷10=100,100×5=500.答:A与B的差是500.点评:完成此类题目要注意分析数据,从中找出规律后解答.17.510.【解析】试题分析:每一行把第一个与第九个相加,第二个与第把个相加,第三个与第七个相加,第四个与第六个相加,再加第五个,第一行是4个18与9;第二行4个20与10;第三行4个22与11;第四行4个24与12;第五行4个26与13相加即可.解:18×4+9+20×4+10+22×4+11+24×4+12+26×4+13=72+9+80+10+88+11+96+12+104+13=510.点评:此题考察了数字和问题,关键是得出第一行是4个18与9;第二行4个20与10;第三行4个22与11;第四行4个24与12;第五行4个26与13.18.210.【解析】试题分析:把算式进展必要的变形,进而利用平方差公式计算得解.解:202﹣192+182﹣172+162﹣152+…+22﹣12=〔20+19〕〔20﹣19〕+〔18+17〕〔18﹣17〕+〔16+15〕〔16﹣15〕+…+〔2+1〕〔2﹣1〕=39+35+31+…+3=〔39+3〕+〔35+7〕+〔31+11〕+〔27+15〕+〔23+19〕=42+42+42+42+42=210.点评:此题考察了平方差公式的应用.关键是把原式化为〔20+19〕〔20﹣19〕+〔18+17〕〔18﹣17〕+〔16+15〕〔16﹣15〕+…+〔2+1〕〔2﹣1〕.19.900003.【解析】试题分析:先算乘法,再算减法,由此顺序计算即可.解:951×949﹣52×48=902499﹣2496=900003.点评:整数混合运算的关键是抓住运算顺序,正确按运算顺序计算即可.20.30;40.【解析】试题分析:规定运算“Θ〞为:aΘb=a+2b﹣2,第一个数加上第二个数的2倍再减去2,按照这个规律即可;有括号先算括号里面的.解:因为aΘb=a+2b﹣2,〔1〕〔8Θ7〕Θ6=〔8+2×7﹣2〕Θ6=20Θ6=20+2×6﹣2=32﹣2=30〔2〕8Θ〔7Θ6〕=8Θ〔7+2×6﹣2〕=8Θ17=8+2×17﹣2=8+34﹣2=40点评:此题考察根据新运算规那么计算:正确找准计算规那么是关键.21.4.【解析】试题分析:根据题意a○b=〔a+1〕×〔b﹣2〕,即为第一个加1与第二个数减去2的差的乘积;设□○5=x,6○〔□○5〕=91就变为6○x=91,据此解出x,然后代入即可求得□.解:设□○5=x因为:a○b=〔a+1〕×〔b﹣2〕所以:6○〔□○5〕=91即为:6○x=91〔6+1〕×〔x﹣2〕=917x﹣14=917x﹣14+14=91+147x=1057x÷7=105÷7x=15所以:□○5=15〔□+1〕×〔5﹣2〕=153□+3=153□+3﹣3=15﹣33□=123□÷3=12÷3□=4答:方格内应该填4.点评:此题考察根据新运算规那么计算:正确找准计算规那么是关键.22.99.【解析】第 7 页试题分析:因为符号“△〞为选择两数中较大的数的运算,“▽〞为选择两数中较小的数的运算,而△2△3▽4△5△6▽7△…▽100,两个向上的,一个向下的,3个是一周期,△取大,▽取小,所以正好是取3的倍数,到最后还剩99,据此解答即可.解:因为3△5=5,3▽5=31△2△3▽4△5△6▽7△…▽100两个向上的,一个向下的,3个是一周期,△取大,▽取小,所以正好是取3的倍数,到最后还剩99,所以:1△2△3▽4△5△6▽7△…▽100=2△3▽4△5△6▽7△…▽100=3▽4△5△6▽7△…▽100=3△5△6▽7△…▽100=6▽7△…▽100=6△8…▽100=99▽100=99点评:此题考察根据新运算规那么计算:正确找准计算规那么是关键.23.这四个数为24,18,12,6;24+18﹣12﹣6;24.【解析】试题分析:通过分析可知,每四个数为一循环,每一循环的第一个数相差24,后边的数相差6,所以最后4个自然数分别24,18,12,6,为24+18﹣12﹣6,据解答即可.解:根据规律可知,这四个数为24,18,12,6,算式为24+18﹣12﹣6结果为:24+18﹣12﹣6=24答:这四个数为24,18,12,6;24+18﹣12﹣6;24.点评:先找到各数量之间的关系,再根据这个关系求解.24.750.【解析】试题分析:在1、2、3、4、5、6、7、8、9、10这10个数中,奇数为1,3,5,7,9;偶数为2,4,6,8,10.奇数与偶数各5个,那么每个奇数都可与其它5个偶数相乘得到5个不同的积,它们的和为:1×2+1×4+1×6+1×8+1×10=〔2+4+6+8+10〕×1,同理3与这五个偶数相乘积的和为〔2+4+6+8+10〕×3,由此可我们根据乘法分配律即求出在1、2、3、4、5、6、7、8、9、10这10个数中,每次取一个奇数和一个偶数相乘,它们所有积和的大小.解:〔1×2+1×4+1×6+1×8+1×10〕+〔3×2+3×4+…+3×10〕+…+〔9×2+9×4+…+9×10〕=〔2+4+6+8+10〕×1+〔2+4+6+8+10〕×3+…+〔2+4+6+8+10〕×9,=〔1+3+5+7+9〕×〔2+4+6+8+10〕,=25×30,=750.点评:在列出算式的根底上通过分析找出算式中数据之间的特点及内在联络,然后连续运用乘法分配律是完成此题的关键.25.2500.【解析】试题分析:我们观察这个算式中的每一项,3=1+2,6=1+2+3,10=1+2+3+4,....4990=1+2+3 (99)那么原式变为:1﹣〔1+2〕+〔1+2+3〕﹣〔1+2+3+4〕+…+〔1+2+3+…+99〕,计算即可.解:1﹣3+6﹣10+15﹣21+28﹣…+4950=1﹣〔1+2〕+〔1+2+3〕﹣〔1+2+3+4〕+...+〔1+2+3+ (99)=1+3+5+…+99=〔1+99〕×50÷2=2500点评:仔细观察算式,根据数据特点,把数据进展拆分,变成从第二项开场相邻两式局部一样的式子,通过加减互相抵消,变成1+3+5+…+99,运用高斯求和公式计算求得结果.26.10100.【解析】试题分析:解答此题先运用平方差公式把相邻两个偶数或两个奇数平方的差转化成因数相乘的形式进展计算即可求解.解:1002+992﹣982﹣972+962+952﹣942﹣932+…+42+32﹣22﹣12=〔1002﹣982〕+〔992﹣972〕+〔962﹣942〕+〔952﹣932〕+…+〔42﹣22〕+〔32﹣12〕=〔100﹣98〕×〔100+98〕+〔99﹣97〕×〔99+97〕+…+〔4﹣2〕×〔4+2〕+〔3﹣1〕×〔3+1〕=2×〔100+98〕+2×〔99+97〕+…+2×〔4+2〕+2×〔3+1〕=2×〔100+98+99+97+4+2+3+1〕=2×=101×100=10100.点评:解答此题主要运用平方差公式、乘法分配律、加法结合律,高斯求和公式进展计算.27.165;10.【解析】试题分析:由题意可知:这种新运算是从第一个数开场,连续自然数相加,加数的个数就是后一个数;〔2〕设□Θ7=x,根据条件求出x,然后根据新运算规那么再求得方框即可.解:因为4Θ3=4+5+6=15,5Θ4=5+6+7+8=26,所以:〔1〕4Θ15=4+5+6+7+ (18)=〔4+17〕×7+18=21×7+18=147+18=165〔2〕因为:〔□Θ7〕Θ11=1056设□Θ7=x,原算式变为:x+〔x+1〕+…〔x+10〕=105611x+〔1+10〕×5=105611x+55=105611x+55﹣55=1056﹣5511x=100111x÷11=1001÷11x=91第 9 页所以□Θ7=91□+〔□+1〕+…〔□+6〕=917□+21=917□+21﹣21=91﹣217□=707□÷7=70÷7□=10答;方框里的数应该是10.点评:此题考察根据新运算规那么计算:正确找准计算规那么是关键.28.﹣7Ω{﹣[〔 3∀4 〕Ω 5]}=3.【解析】试题分析:根据aΩb=a﹣b+1,a∀b=a×b+1,要屡次实验到底用几个Ω,几个∀,或者是单独用其中一个符号,让右边等于3即可.解:因为aΩb=a﹣b+1,a∀b=a×b+13∀4=3×4+1=1313Ω5=13﹣5+1=9﹣7Ω〔﹣9〕=﹣7+9+1=3所以:﹣7Ω{﹣[〔 3∀4 〕Ω 5]}=3.点评:此题考察根据新运算规那么计算:正确找准计算规那么是关键.29.〔1〕4176﹣7416﹣3708﹣7308﹣708﹣700〔2〕即经过7次可以得到0.〔3〕234经过①得117,再经过③得711,再经过④得710.【解析】试题分析:〔1〕〔2〕根据操作规那么进展分析操作即可得出相应结果.〔3〕第一问可选择一个数根据操作规那么进展操作得出结果即可,第二问可按不同的操作顺序分析完成.解:〔1〕4176依次进展③①③②④操作后的结果:4176﹣7416﹣3708﹣7308﹣708﹣700〔2〕从655687开场,655687经过“一分为二〞的操作,得到327844;再经过“丢三落四〞的操作,得到278;再经过“七上八下〞的操作,得到728;再经过经过“一分为二〞的操作,得到364;再经过“丢三落四〞的操作,得到6;最后经过“十全十美〞的操作,得到0.共6步完成操作,得到0.655687经过①得327844﹣经过②得278﹣经过①得139﹣经过②得19﹣经过①得10﹣经过①得5﹣经过④得0.即经过7次可以得到0.〔3〕一个三位数除了“丢三落四〞外,其他三个操作各进展一次之后得到的结果是如:234经过①得117,再经过③得711,再经过④得710.步骤①③④,经过步骤①之后个位含有7,百位含有1的,有10个;分别是214,234,254,274,294,314,334,354,374,394;经过步骤①之后十位含有7,百位为1,有10个;分别是340,342,344,346,348,350,352,354,356,358.重复354;总共有10+10﹣1=19个.步骤①④③,经过步骤①之后十位含有7,百位含有1,有10个;分别是340,342,344,346,348,350,352,354,356,358步骤③①④,③④①,都没有步骤④①③,个位数有10种可能,分别是340,341,342,343,344,345,346,347,348,349步骤④③①,没有.根据上面的分类,除去重复的数据,那么总共有:19+5=24个.故答案为:710.点评:完成此题要注意条件中所给的操作规那么,然后按操作规那么分析即可.30.1155.【解析】试题分析:根9的乘法口诀表,把表中的各个乘积相加即可得出结论.解:〔1+2+3+4+5+6+7+8+9〕+〔4+6+8+10+12+14+16+18〕+〔9+12+15+18+21+24+27〕+〔16+20+24+28+32+36〕+〔25+30+35+40+45〕+〔36+42+48+54〕+〔49+56+63〕+〔64+72〕+81=[〔1+9〕×4+5]+[〔4+18〕×4]+[〔9+27〕×3+18]+[〔16+36〕×3]+[〔25+45〕×2+35]+[〔36+54〕×2]+168+136+81=45+88+126+156+175+180+168+136+81=1155点评:此题也可以按行累计九九乘法表里共有:1个1,1+2个2,1+2+3个3…以此类推,得1个1,3个2,6个3,10个4,15个5,21个6,28个7,36个8,45个9,由此解答即可.第 11 页。
小学的奥数面积计算(综合题型)

第十八周面积计算(一)专题简析:计算平面图形的面积时,有些问题乍一看,在已知条件与所求问题之间找不到任何联系,会使你感到无从下手。
这时,如果我们能认真观察图形,分析、研究已知条件,并加以深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题的小“桥”,就会使你顺利达到目的。
有些平面图形的面积计算必须借助于图形本身的特征,添加一些辅助线,运用平移旋转、剪拼组合等方法,对图形进行恰当合理的变形,再经过分析推导,方能寻求出解题的途径。
图形面积)简单的面积计算是小学数学的一项重要内容.要会计算面积,首先要能识别一些特别的图形:正方形、三角形、平行四边形、梯形等等,然后会计算这些图形的面积.如果我们把这些图形画在方格纸上,不但容易识别,而且容易计算.上面左图是边长为4的正方形,它的面积是4×4=16(格);右图是3×5的长方形,它的面积是3×5=15(格).上面左图是一个锐角三角形,它的底是5,高是4,面积是5×4÷2=10(格);右图是一个钝角三角形,底是4,高也是4,它的面积是4×4÷2=8(格).这里特别说明,这两个三角形的高线一样长,钝角三角形的高线有可能在三角形的外面.上面左图是一个平行四边形,底是5,高是3,它的面积是5×3=15(格);右图是一个梯形,上底是4,下底是7,高是4,它的面积是(4+7)×4÷2=22(格).上面面积计算的单位用“格”,一格就是一个小正方形.如果小正方形边长是1厘米,1格就是1平方厘米;如果小正方形边长是1米,1格就是1平方米.也就是说我们设定一个方格的边长是1个长度单位,1格就是一个面积单位.在这一讲中,我们直接用数表示长度或面积,省略了相应的长度单位和面积单位.一、三角形的面积用直线组成的图形,都可以划分成若干个三角形来计算面积.三角形面积的计算公式是:三角形面积= 底×高÷2.这个公式是许多面积计算的基础.因此我们不仅要掌握这一公式,而且要会灵活运用.例1 右图中BD长是4,DC长是2,那么三角形ABD的面积是三角形ADC面积的多少倍呢?解:三角形ABD与三角形ADC的高相同.三角形ABD面积=4×高÷2.三角形ADC面积=2×高÷2.因此三角形ABD的面积是三角形ADC面积的2倍.注意:三角形的任意一边都可以看作是底,这条边上的高就是三角形的高,所以每个三角形都可看成有三个底,和相应的三条高.例2右图中,BD,DE,EC的长分别是2,4,2.F是线段AE的中点,三角形ABC的高为4.求三角形DFE的面积.解:BC=2+4+2=8.三角形ABC面积= 8×4÷2=16.我们把A和D连成线段,组成三角形ADE,它与三角形ABC的高相同,而DE长是4,也是BC的一半,因此三角形ADE面积是三角形ABC面积的一半.同样道理,EF是AE的一半,三角形DFE面积是三角形ADE面积的一半.三角形DFE面积= 16÷4=4.例3右图中长方形的长是20,宽是12,求它的内部阴影部分面积.解:ABEF也是一个长方形,它内部的三个三角形阴影部分高都与BE一样长.而三个三角形底边的长加起来,就是FE的长.因此这三个三角形的面积之和是FE×BE÷2,它恰好是长方形ABEF面积的一半.同样道理,FECD也是长方形,它内部三个三角形(阴影部分)面积之和是它的面积的一半.因此所有阴影的面积是长方形ABCD面积的一半,也就是20×12÷2=120.通过方格纸,我们还可以从另一个途径来求解.当我们画出中间两个三角形的高线,把每个三角形分成两个直角三角形后,图中每个直角三角形都是某个长方形的一半,而长方形ABCD是由这若干个长方形拼成.因此所有这些直角三角形(阴影部分)的面积之和是长方形ABCD面积的的一半.例4 右图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?解:把A和C连成线段,四边形ABCD就分成了两个,三角形ABC和三角形ADC.对三角形ABC来说,AB是底边,高是10,因此面积=4×10÷2=20.对三角形ADC来说,DC是底边,高是8,因此面积=7×8÷2=28.四边形ABCD面积= 20+28=48.这一例题再一次告诉我们,钝角三角形的高线有可能是在三角形的外面.例5在边长为6的正方形内有一个三角形BEF,线段AE=3,DF=2,求三角形BEF 的面积.解:要直接求出三角形BEF的面积是困难的,但容易求出下面列的三个直角三角形的面积三角形ABE面积=3×6×2=9.三角形BCF面积= 6×(6-2)÷2=12.三角形DEF面积=2×(6-3)÷2=3.我们只要用正方形面积减去这三个直角三角形的面积就能算出:三角形BEF面积=6×6-9-12-3=12.例6 在右图中,ABCD是长方形,三条线段的长度如图所示,M是线段DE的中点,求四边形ABMD(阴影部分)的面积.解:四边形ABMD中,已知的太少,直接求它面积是不可能的,我们设法求出三角形DCE与三角形MBE的面积,然后用长方形ABCD的面积减去它们,由此就可以求得四边形ABMD的面积.把M与C用线段连起来,将三角形DCE分成两个三角形.三角形DCE的面积是7×2÷2=7.因为M是线段DE的中点,三角形DMC与三角形MCE面积相等,所以三角形MCE 面积是7÷2=3.5.因为BE=8是CE=2的4倍,三角形MBE与三角形MCE高一样,因此三角形MBE面积是3.5×4=14.长方形ABCD面积=7×(8+2)=70.四边形ABMD面积=70-7- 14=49.二、有关正方形的问题先从等腰直角三角形讲起.一个直角三角形,它的两条直角边一样长,这样的直角三角形,就叫做等腰直角三角形.它有一个直角(90度),还有两个角都是45度,通常在一副三角尺中.有一个就是等腰直角三角形.两个一样的等腰直角三角形,可以拼成一个正方形,如图(a).四个一样的等腰直角三角形,也可以拼成一个正方形,如图(b).一个等腰直角三角形,当知道它的直角边长,从图(a)知,它的面积是直角边长的平方÷2.当知道它的斜边长,从图(b)知,它的面积是斜边的平方÷4例7 右图由六个等腰直角三角形组成.第一个三角形两条直角边长是8.后一个三角形的直角边长,恰好是前一个斜边长的一半,求这个图形的面积.解:从前面的图形上可以知道,前一个等腰直角三角形的两个拼成的正方形,等于后一个等腰直角三角形四个拼成的正方形.因此后一个三角形面积是前一个三角形面积的一半,第一个等腰直角三角形的面积是8×8÷2=32.这一个图形的面积是32+16+8+ 4 +2+1=63.例8 如右图,两个长方形叠放在一起,小长形的宽是2,A点是大长方形一边的中点,并且三角形ABC是等腰直角三角形,那么图中阴影部分的总面积是多少?解:为了说明的方便,在图上标上英文字母D,E,F,G.三角形ABC的面积=2×2÷2=2.三角形ABC,ADE,EFG都是等腰直角三角形.三角形ABC的斜边,与三角形ADE的直角边一样长,因此三角形ADE面积=ABC面积×2=4.三角形EFG的斜边与三角形ABC的直角边一样长.因此三角形EFG面积=ABC面积÷2=1.阴影部分的总面积是4+1=5.例9如右图,已知一个四边形ABCD的两条边的长度AD=7,BC=3,三个角的度数:角B和D是直角,角A是45°.求这个四边形的面积.解:这个图形可以看作是一个等腰直角三角形ADE,切掉一个等腰直角三角形BCE.因为A是45°,角D是90°,角E是180°-45°-90°=45°,所以ADE是等腰直角三角形,BCE也是等腰直角三角形.四边形ABCD的面积,是这两个等腰直角三角形面积之差,即7×7÷2-3×3÷2=20.这是1994小学数学奥林匹克决赛试题.原来试题图上并没有画出虚线三角形.参赛同学是不大容易想到把图形补全成为等腰直角三角形.因此做对这道题的人数不多.但是有一些同学,用直线AC把图形分成两个直角三角形,并认为这两个直角三角形是一样的,这就大错特错了.这样做,角A是45°,这一条件还用得上吗?图形上线段相等,两个三角形相等,是不能靠眼睛来测定的,必须从几何学上找出根据,小学同学尚未学过几何,千万不要随便对图形下结论.我们应该从题目中已有的条件作为思考的线索.有45°和直角,你应首先考虑等腰直角三角形.现在我们转向正方形的问题.例10 在右图11×15的长方形内,有四对正方形(标号相同的两个正方形为一对),每一对是相同的正方形,那么中间这个小正方形(阴影部分)面积是多少?解:长方形的宽,是“一”与“二”两个正方形的边长之和,长方形的长,是“一”、“三”与“二”三个正方形的边长之和.长-宽=15-11=4是“三”正方形的边长.宽又是两个“三”正方形与中间小正方形的边长之和,因此中间小正方形边长=11-4×2=3.中间小正方形面积=3×3=9.如果把这一图形,画在方格纸上,就一目了然了.例11从一块正方形土地中,划出一块宽为1米的长方形土地(见图),剩下的长方形土地面积是15.75平方米.求划出的长方形土地的面积.解:剩下的长方形土地,我们已知道长-宽=1(米).还知道它的面积是15.75平方米,那么能否从这一面积求出长与宽之和呢?如果能求出,那么与上面“差”的算式就形成和差问题了.我们把长和宽拼在一起,如右图.从这个图形还不能算出长与宽之和,但是再拼上同样的两个正方形,如下图就拼成一个大正方形,这个正方形的边长,恰好是长方形的长与宽之和.可是这个大正方形的中间还有一个空洞.它也是一个正方形,仔细观察一下,就会发现,它的边长,恰好是长方形的长与宽之差,等于1米.现在,我们就可以算出大正方形面积:15.75×4+1×1=64(平方米).64是8×8,大正方形边长是8米,也就是说长方形的长+宽=8(米).因此长=(8+1)÷2=4.5(米).宽=8-4.5=3.5(米).那么划出的长方形面积是4.5×1=4. 5(平方米).例12 如右图.正方形ABCD与正方形EFGC并放在一起.已知小正方形EFGC的边长是6,求三角形AEG(阴影部分)的面积.解:四边形AECD是一个梯形.它的下底是AD,上底是EC,高是CD,因此四边形AECD面积=(小正方形边长+大正方形边长)×大正方形边长÷2三角形ADG是直角三角形,它的一条直角边长DG=(小正方形边长+大正方形边长),因此三角形ADG面积=(小正方形边长+大正方形边长)×大正方形边长÷2.四边形AECD与三角形ADG面积一样大.四边形AHCD是它们两者共有,因此,三角形AEH与三角形HCG面积相等,都加上三角形EHG面积后,就有阴影部分面积=三角形ECG面积=小正方形面积的一半= 6×6÷2=18.十分有趣的是,影阴部分面积,只与小正方形边长有关,而与大正方形边长却没有关系.三、其他的面积这一节将着重介绍求面积的常用思路和技巧.有些例题看起来不难,但可以给你启发的内容不少,请读者仔细体会.例13 画在方格纸上的一个用粗线围成的图形(如右图),求它的面积.解:直接计算粗线围成的面积是困难的,我们通过扣除周围正方形和直角三角形来计算.周围小正方形有3个,面积为1的三角形有5个,面积为1.5的三角形有1个,因此围成面积是4×4-3-5-1.5=6.5.例6与本题在解题思路上是完全类同的.例14 下图中ABCD是6×8的长方形,AF长是4,求阴影部分三角形AEF的面积.解:三角形AEF中,我们知道一边AF,但是不知道它的高多长,直接求它的面积是困难的.如果把它扩大到三角形AEB,底边AB,就是长方形的长,高是长方形的宽,即BC 的长,面积就可以求出.三角形AEB的面积是长方形面积的一半,而扩大的三角形AFB是直角三角形,它的两条直角边的长是知道的,很容易算出它的面积.因此三角形AEF面积=(三角形AEB面积)-(三角形AFB面积)=8×6÷2-4×8÷2=8.这一例题告诉我们,有时我们把难求的图形扩大成易求的图形,当然扩大的部分也要容易求出,从而间接地解决了问题.前面例9的解法,也是这种思路.例15 下左图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积(阴影部分)有多大?解:我们首先要弄清楚,平行四边形面积有多大.平行四边形的面积是底×高.从图上可以看出,底是2,高恰好是长方形的宽度.因此这个平行四边形的面积与10×2的长方形面积相等.可以设想,把这个平行四边形换成10×2的长方形,再把横竖两条都移至边上(如前页右图),草地部分面积(阴影部分)还是与原来一样大小,因此草地面积=(16-2)×(10-2)=112.例16 右图是两个相同的直角三角形叠在一起,求阴影部分的面积.解:实际上,阴影部分是一个梯形,可是它的上底、下底和高都不知道,不能直接来求它的面积.阴影部分与三角形BCE合在一起,就是原直角三角形.你是否看出,ABCD也是梯形,它和三角形BCE合在一起,也是原直角三角形.因此,梯形ABCD的面积与阴影部分面积一样大.梯形ABCD的上底BC,是直角边AD的长减去3,高就是DC的长.因此阴影部分面积等于梯形ABCD面积=(8+8-3)×5÷2=32.5.上面两个例子都启发我们,如何把不容易算的面积,换成容易算的面积,数学上这叫等积变形.要想有这种“换”的本领,首先要提高对图形的观察能力.例17 下图是两个直角三角形叠放在一起形成的图形.已知AF,FE,EC都等于3,CB,BD都等于4.求这个图形的面积.解:两个直角三角形的面积是很容易求出的.三角形ABC面积=(3+3+3)×4÷2=18.三角形CDE面积=(4+4)×3÷2=12.这两个直角三角形有一个重叠部分--四边形BCEG,只要减去这个重叠部分,所求图形的面积立即可以得出.因为AF=FE=EC=3,所以AGF,FGE,EGC是三个面积相等的三角形.因为CB=BD=4,所以CGB,BGD是两个面积相等的三角形.2×三角形DEC面积= 2×2×(三角形GBC面积)+2×(三角形GCE面积).三角形ABC面积= (三角形GBC面积)+3×(三角形GCE面积).四边形BCEG面积=(三角形GBC面积)+(三角形GCE面积)=(2×12+18)÷5=8.4.所求图形面积=12+18- 8.4=21.6.例18 如下页左图,ABCG是4×7长方形,DEFG是2×10长方形.求三角形BCM与三角形DEM面积之差.解:三角形BCM与非阴影部分合起来是梯形ABEF.三角形DEM与非阴影部分合起来是两个长方形的和.(三角形BCM面积)-(三角形DEM面积)=(梯形ABEF面积)-(两个长方形面积之和=(7+10)×(4+2)÷2-(4×7 +2×10)=3.例19 上右图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?解:所求的影阴部分,恰好是三角形ABC 与三角形CDE 的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC 与三角形CDE 盖住的部分,因此(三角形 ABC 面积)+(三角形CDE 面积)+(13+49+35)=(长方形面积)+(阴影部分面积).三角形ABC ,底是长方形的长,高是长方形的宽;三角形CDE ,底是长方形的宽,高是长方形的长.因此,三角形ABC 面积,与三角形CDE 面积,都是长方形面积的一半,就有阴影部分面积=13 + 49+ 35= 97.例题1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数专题第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 182621358 1333416⨯+⨯-÷【分析与解】原式=712372317 461224 1488128 131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5 199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×0.5.具体过程如下:原式=5919(3 5.22)19930.41.6 910() 52719950.51995 19(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.5 9() 519950.419950.5 191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143.计算:1111111987 -+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少?【分析与解】方法一:1118x68114x112x711 1+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25.方法二:有11131118821x4+==+++,所以18222133x4+==++;所以13x42+=,那么x =1.25.5.求944,43,443,...,44...43个这10个数的和.【分析与解】方法一: 944+43+443...44...43++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44...49++++-个=1094(999999...999...9)99⨯++++-个 =1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个 =914111.1009=49382715919⨯-个.方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=; 再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=; 再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=; 再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=; 再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=;再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=; 再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=;再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4. 所以,这10个数的和为4938271591.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少?【分析与解】 因为每个端点均有三条线段通过,所以这6条线段的长度之和为: 1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○2.9=2.9○3.5=3.5.符号“△”表示选择两数中较小数的运算,例如:3.5△2.9=2.9△3.5=2.9.请计算:23155(0.625)(0.4)333841235(0.3)( 2.25)3104⨯+ 【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少?【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1?【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如1.892915929.那么在所有这种数中。
最大的一个是多少?【分析与解】有整数部分尽可能大,十分位尽可能大,则有92918……较大,于是最大的为9.291892915.11.请你举一个例子,说明“两个真分数的和可以是一个真分数,而且这三个分数的分母谁也不是谁的约数”.【分析与解】有11461015+=,11110156+=,111351410+=评注:本题实质可以说是寻找孪生质数,为什么这么说呢?注意到11c aa b c b a b c++=⨯⨯⨯⨯,当a c b+=时,有11c a1a b c b a b c a c++==⨯⨯⨯⨯⨯.当a、b、c两两互质时,显然满足题意.显然当a、b、c为质数时一定满足,那么两个质数的和等于另一个质数,必定有一个质数为2,不妨设a为2,那么有2c b+=,显然b、c为一对孪生质数.即可得出一般公式:1112(c2c(c2)2c+=⨯+⨯+⨯),c与c+2均为质数即可.12.计算:111 (11 (1)22331010 -⨯-⨯⨯-⨯⨯⨯)()【分析与解】原式=(21)(21)(31)(31)(101)(101) (22331010)-⨯+-⨯+-⨯+⨯⨯⨯⨯⨯⨯ =13243546576879810911223344 (1010)⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=12334455...991011223344...991010⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=121011221010⨯⨯⨯⨯⨯⨯=1120.13.已知11661267136814691570a=10011651266136714681569⨯+⨯+⨯+⨯+⨯⨯⨯+⨯+⨯+⨯+⨯.问a 的整数部分是多少?【分析与解】11661267136814691570a=10011651266136714681569⨯+⨯+⨯+⨯+⨯⨯⨯+⨯+⨯+⨯+⨯=11(651)12(661)13(671)14(681)1569110011651266136714681569⨯++⨯++⨯++⨯++⨯+⨯⨯+⨯+⨯+⨯+⨯()=1112131415110011651266136714681569+++++⨯⨯+⨯+⨯+⨯+⨯()=11121314151001001165+1266136714681569+++++⨯⨯⨯+⨯+⨯+⨯.因为1112131001165+1266136714681569++++⨯⨯⨯+⨯+⨯+⨯<111213141510010011121314+156565++++⨯=+++⨯() 所以a <10035100+1016565=.同时11121310011651266136714681569++++⨯⨯+⨯+⨯+⨯+⨯>111213141510010011121314+156969++++⨯=+++⨯() 所以a >100311001016969+=.综上有3110169<a <3510165.所以a 的整数部分为101.14.问135799...2468100⨯⨯⨯⨯⨯与110相比,哪个更大,为什么?【分析与解】方法一:令135799...2468100A ⨯⨯⨯⨯⨯=,2468100 (3579101)B ⨯⨯⨯⨯⨯=, 有13579924681001 (24681003579101101)A B ⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯==. 而B 中分数对应的都比A 中的分数大,则它们的乘积也是B >A ,有A ×A <4×B 1101(=)<1111001010⨯=,所以有A ×A <111010⨯,那么A <110. 即135799...2468100⨯⨯⨯⨯⨯与110相比,110更大. 方法二:设13579799 (246898100)A ⨯⨯⨯⨯⨯⨯=, 则21133559999 (224466100100)A ⨯⨯⨯⨯⨯⨯⨯⨯= =1335577...9797999912244668...969898100100⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯, 显然1322⨯⨯、3544⨯⨯、5766⨯⨯、…、97999898⨯⨯、99100都是小于1的,所以有A 2<1100,于是A<110.15.下面是两个1989位整数相乘:1989119891111...11111...11⨯个个.问:乘积的各位数字之和是多少?【分析与解】在算式中乘以9,再除以9,则结果不变.因为19891111...11个能被9整除,所以将一个19891111...11个乘以9,另一个除以9,使原算式变成:198991988999......99123456790......012345679⨯个共位数=1989019881000......001123456790......012345679-⨯个共位数()=1988198901988123456790......012345679000......00123456790......012345679-共位数个共位数=19881980123456790......012345679123456789876543209......987654320987654321共位数共位数得到的结果中有1980÷9=220个“123456790”和“987654320”及一个“12345678”和一个“987654321”,所以各位数之和为: 1234567922098765432220+++++++⨯++++++++⨯()() +1234567898765432117901++++++++++++++++=()() 评注:111111111÷9=12345679; M ×k 9999...9个的数字和为9×k .(其中M ≤k 9999...9个).可以利用上面性质较快的获得结果.。
