2020高考数学二轮微专题圆锥曲线的方程及几何性质精选试题(5页)

合集下载

2020高考数学圆锥曲线试题(含答案)

2020高考虽然延期，但是每天练习一定要跟上，加油！圆锥曲线一．选择题：1.（福建卷11)又曲线22221x y a b==（a ＞0,b ＞0）的两个焦点为F 1、F 2,若P 为其上一点，且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为BA.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞2.（海南卷11）已知点P 在抛物线y 2 = 4x 上，那么点P 到点Q （2，－1）的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为（ A ）A. （41，－1） B. （41，1）C. （1，2）D. （1，－2）3.(湖北卷10)如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P 轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P 点第三次变轨进入以F 为圆心的圆形轨道Ⅲ绕月飞行，若用12c 和22c 分别表示椭轨道Ⅰ和Ⅱ的焦距，用12a 和22a 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子： ①1122a c a c +=+; ②1122a c a c -=-; ③1212c a a c >; ④11c a ＜22c a . 其中正确式子的序号是BA. ①③B. ②③C. ①④D. ②④4.（湖南卷8）若双曲线22221x y a b -=（a ＞0,b ＞0）上横坐标为32a的点到右焦点的距离大于它到左准线的距离，则双曲线离心率的取值范围是( B ) A.(1,2)B.(2,+∞)C.(1,5)D. (5,+∞)5.（江西卷7）已知1F 、2F 是椭圆的两个焦点，满足120MF MF ⋅=的点M 总在椭圆内部，则椭圆离心率的取值范围是C A ．(0,1) B ．1(0,]2C．(0,2 D．,1)26.（辽宁卷10）已知点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为（ A ） AB ．3 CD ．927.（全国二9）设1a >，则双曲线22221(1)x y a a -=+的离心率e 的取值范围是（ B ）A． B． C ．(25)， D．(28.（山东卷(10)设椭圆C 1的离心率为135，焦点在X 轴上且长轴长为ABCD-26.若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8，则曲线C 2的标准方程为A（A ）1342222=-y x (B)15132222=-y x(C)1432222=-y x (D)112132222=-y x9.（陕西卷8）双曲线22221x y a b-=（0a >，0b >）的左、右焦点分别是12F F ，，过1F 作倾斜角为30的直线交双曲线右支于M 点，若2MF 垂直于x 轴，则双曲线的离心率为（ B ）ABC D10.（四川卷12）已知抛物线2:8C y x =的焦点为F ，准线与x 轴的交点为K ，点A 在C 上且AK AF =，则AFK ∆的面积为( B )（Ａ）4 （Ｂ）8 （Ｃ）16 （Ｄ）3211.（天津卷（7）设椭圆22221x y m n+=（0m >，0n >）的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为B（A ）2211216x y += （B ）2211612x y += （C ）2214864x y += （D ）2216448x y += 12.（浙江卷7）若双曲线12222=-by a x 的两个焦点到一条准线的距离之比为3：2,则双曲线的离心率是D（A ）3 （B ）5 （C ）3 （D ）5 13.（浙江卷10）如图，AB 是平面a 的斜线段，A 为斜足，若点P 在平面a 内运动，使得△ABP 的面积为定值，则动点P 的轨迹是B（A ）圆（B ）椭圆（C ）一条直线（D ）两条平行直线14.（重庆卷(8)已知双曲线22221x y a b-=（a ＞0,b ＞0）的一条渐近线为y =kx (k ＞0),离心率e 5k ,则双曲线方程为C（A ）22x a －224y a =1(B)222215x y a a -= (C)222214x y b b-=(D)222215x y b b-=二．填空题：1.（海南卷14）过双曲线221916x y -=的右顶点为A ，右焦点为F 。

2020年各地高考数学二轮总复习圆锥曲线题整理精品

2020年各地高考圆锥曲线题整理1. （本小题满分13分）已知椭圆E 经过点A （2，3），对称轴为坐标轴，焦点1F ，2F 在x 轴上，离心率12e =．（Ⅰ）求椭圆E 的方程；（Ⅱ）求∠1F A 2F 的角平分线所在直线l 的方程；（Ⅲ）在椭圆E 上是否存在关于直线l 对称的相异两点？若存在．请找出；若不存在，说明理由．（本小题满分13分）本题考查椭圆的定义及标准方程，椭圆的简单几何性质，直线的点斜式方程与一般方程，点到直线的距离公式，点关于直线的对称等基础知识；考查解析几何的基本思想、综合运算能力、探究意识与创新意识.解：（Ⅰ）设椭圆E 的方程为22221x y a b +=2222222211,,2,3,221.43c e a c b a c c a x yc c ====-=∴+=由即得椭圆方程具有形式将A （2，3）代入上式，得22131,2,c c c+==解得 ∴椭圆E 的方程为221.1612x y += （Ⅱ）解法1：由（Ⅰ）知12(2,0),(2,0)F F -，所以直线AF 1的方程为：3(2),3460,4y x x y =+-+=即直线AF 2的方程为： 2.x =由点A 在椭圆E 上的位置知，直线l 的斜率为正数. 设(,)P x y l 为上任一点，则|346||2|.5x y x -+=-若346510,280x y x x y -+=-+-=得（因其斜率为负，舍去）. 于是，由346510,10x y x x y -+=-+--=得2 所以直线l 的方程为：210.x y --=解法2：1212 12121(2,3),(2,0),(2,0),(4,3),(0,3).114(4,3)(0,3)(1,2).535||||2,:32(1),210.A F F AF AFAF AFAF AFk l y x x y-∴=--=-∴+=--+-=-∴=∴-=---=u u u r u u u u rQu u u r u u u u ru u u r u u u u r即得一元二次方程2222134()48,120,2x x m x mx m +-+=-+-=即则12x x 与是该方程的两个根，由韦达定理得12,x x m +=于是121213()2,22m y y x x m +=-++= ∴B ，C 的中点坐标为3(,).24m m又线段BC 的中点在直线321,1, 4.4my x m m =-∴=-=上得即B ，C 的中点坐标为（2，3），与点A 重合，矛盾. ∴不存在满足题设条件的相异两点. 2. （本小题共14分）在平面直角坐标系xOy 中，点B 与点A （-1,1）关于原点O 对称，P 是动点，且直线AP 与BP 的斜率之积等于13-. (Ⅰ)求动点P 的轨迹方程；(Ⅱ)设直线AP 和BP 分别与直线x =3交于点M,N ，问：是否存在点P 使得△PAB 与△PMN 的面积相等？若存在，求出点P 的坐标；若不存在，说明理由。

圆锥曲线知识点+例题+练习含答案(整理)(20201128025357)

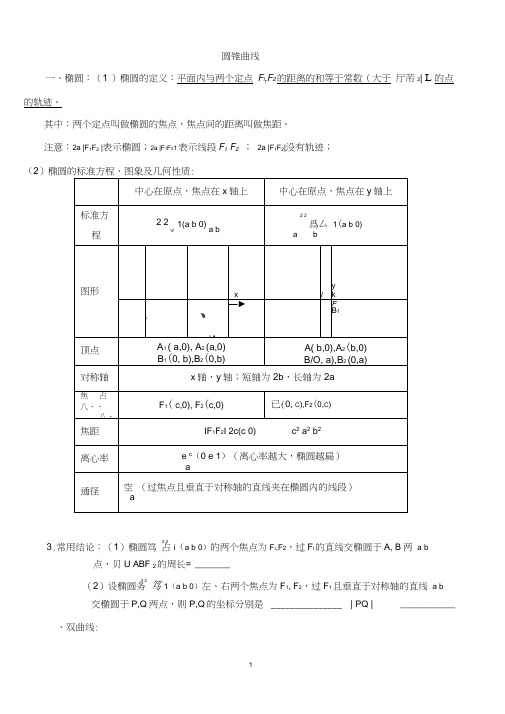
圆锥曲线一、椭圆：（1 ）椭圆的定义：平面内与两个定点F I,F2的距离的和等于常数（大于厅芾2| L 的点的轨迹。

其中：两个定点叫做椭圆的焦点，焦点间的距离叫做焦距。

注意：2a |F1F2 |表示椭圆；2a |F1F21表示线段F1 F2；2a |F1F2|没有轨迹；（2）椭圆的标准方程、图象及几何性质:2 23.常用结论：（1）椭圆笃占i（a b 0）的两个焦点为F I,F2，过F i的直线交椭圆于A, B两 a b点，贝U ABF 2的周长= _______2 2（2）设椭圆务笃1（a b 0）左、右两个焦点为F1, F2，过F1且垂直于对称轴的直线 a b交椭圆于P,Q两点，则P,Q的坐标分别是_______________ | PQ | ___________ 、双曲线:（1）双曲线的定义：平面内与两个定点 F i , F 2的距离的差的绝对值等于常数（小于 | F 1F 2 |）的点的轨迹。

其中：两个定点叫做双曲线的焦点，焦点间的距离叫做焦距。

注意：|PFj IPF 2I 2a 与 | PF 2 | | PF i | 2a （ 2a | F 1F 2 |）表示双曲线的一支。

2a | F 1F 2 |表示两条射线；2a | F 1F 2 |没有轨迹;（2）双曲线的标准方程、图象及几何性质:顶点 A 1( a,0), A 2(a,0)B 1(0, a),B 2(0,a)对称轴x 轴，y 轴；虚轴为 2b，实轴为2a 焦占八、、八、、F 1( C ,0),F 2(C ,0)F 1 (0, C ), F 2(0,C )焦距El2C (C 0) 2 C2.2a b离心率e C (e 1) a（离心率越大，开口越大）渐近线b y —xaa y— xb通径2 b 2a（4）等轴双曲线为x 2 y 2 t 2，其离心率为 2中心在原点，焦点在x 轴上中心在原点，焦点在y 轴上标准方程2x~2 a2y1( a 0,b0)b2y~2a2（3）双曲线的渐近线：①求双曲线匚〔的渐近线，可令其右边的1为0,即得乂 .2 ' 2a 2b 22yb 2，因式分解得到A y 0。

2020高考—圆锥曲线(解答+答案)

2020年高考——圆锥曲线1.(20全国Ⅰ文21)（12分）已知A 、B 分别为椭圆E ：2221x y a+=（a >1）的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线x =6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.2.(20全国Ⅰ理20)（12分）已知A 、B 分别为椭圆E ：2221x y a+=（a >1）的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线x =6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.3.（20全国Ⅱ文19）(12 分)已知椭圆C 1：22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴重直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |．（1）求C 1的离心率；（2）若C 1的四个顶点到C 2的准线距离之和为12，求C 1与C 2的标准方程．4.（20全国Ⅱ理19）（12分）已知椭圆C 1：22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |．（1）求C 1的离心率；（2）设M 是C 1与C 2的公共点，若|MF |=5，求C 1与C 2的标准方程．5.（20全国Ⅲ文21）（12分）已知椭圆222:1(05)25x y C m m +=<<，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，求APQ △的面积．6.（20全国Ⅲ理20）（12分）已知椭圆222:1(05)25x y C m m+=<<，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，求APQ △的面积．7.（20新高考Ⅰ22）（12分）已知椭圆C ：22221(0)x y a b a b +=>>的离心率为2，且过点A （2，1）．（1）求C 的方程：（2）点M ，N 在C 上，且AM ⊥AN ，AD ⊥MN ，D 为垂足．证明：存在定点Q ，使得|DQ |为定值．8.(20天津18)（本小题满分15分）已知椭圆22221(0)x y a b a b+=>>的一个顶点为(0,3)A -，右焦点为F ，且||||OA OF =，其中O 为原点．（Ⅰ）求椭圆的方程；（Ⅱ）已知点C 满足3OC OF =，点B 在椭圆上（B 异于椭圆的顶点），直线AB 与以C 为圆心的圆相切于点P ，且P 为线段AB 的中点．求直线AB 的方程．9.(20浙江21)（本题满分15分）如图，已知椭圆221:12x C y +=，抛物线22:2(0)C y px p =>，点A 是椭圆1C 与抛物线2C 的交点，过点A 的直线l 交椭圆1C 于点B ，交抛物线2C 于点M （B ，M 不同于A ）．（Ⅰ）若116p =，求抛物线2C 的焦点坐标；（Ⅱ）若存在不过原点的直线l 使M 为线段AB 的中点，求p 的最大值．10.（20江苏18）（本小题满分16分）在平面直角坐标系xOy 中，已知椭圆22:143x y E +=的左、右焦点分别为F 1，F 2，点A在椭圆E 上且在第一象限内，AF 2⊥F 1F 2，直线AF 1与椭圆E 相交于另一点B ．（1）求12AF F △的周长；（2）在x 轴上任取一点P ，直线AP 与椭圆E 的右准线相交于点Q ，求OP QP ⋅的最小值；（3）设点M 在椭圆E 上，记OAB △与MAB △的面积分别为S 1，S 2，若213S S =，求点M 的坐标．11.(20北京20)（本小题15分）已知椭圆2222:1x y C a b+=过点(2,1)A --，且2a b =．（Ⅰ）求椭圆C 的方程：（Ⅱ）过点(4,0)B -的直线l 交椭圆C 于点,M N ,直线,MA NA 分别交直线4x =-于点,P Q ．求||||PB BQ 的值．参考答案：1．解：（1）由题设得(,0),(,0),(0,1)A a B a G -．则(,1)AG a =，(,1)GB a =-．由8AG GB ⋅=得218a -=，即3a =．所以E 的方程为2219x y +=．（2）设1122(,),(,),(6,)C x y D x y P t ．若0t ≠，设直线CD 的方程为x my n =+，由题意可知33n -<<．由于直线PA 的方程为(3)9t y x =+，所以11(3)9ty x =+．直线PB 的方程为(3)3t y x =-，所以22(3)3ty x =-．可得12213(3)(3)y x y x -=+．由于222219x y +=，故2222(3)(3)9x x y +-=-，可得121227(3)(3)y y x x =-++，即221212(27)(3)()(3)0m y y m n y y n ++++++=．①将x my n =+代入2219xy +=得222(9)290m y mny n +++-=．所以212122229,99mn n y y y y m m -+=-=-++．代入①式得2222(27)(9)2(3)(3)(9)0m n m n mn n m +--++++=．解得3n =-（舍去），32n =．故直线CD 的方程为32x my =+，即直线CD 过定点3(,0)2．若0t =，则直线CD 的方程为0y =，过点3(,0)2．综上，直线CD 过定点3(,0)2．2．解：（1）由题设得A （–a ，0），B （a ，0），G （0，1）.则(,1)AG a =，GB =（a ，–1）.由AG GB ⋅=8得a 2–1=8，即a =3.所以E 的方程为29x +y 2=1．（2）设C （x 1，y 1），D （x 2，y 2），P （6，t ）.若t ≠0，设直线CD 的方程为x =my +n ，由题意可知–3<n <3. 由于直线PA 的方程为y =9t （x +3），所以y 1=9t （x 1+3）.直线PB 的方程为y =3t （x –3），所以y 2=3t（x 2–3）.可得3y 1（x 2–3）=y 2（x 1+3）.由于222219x y +=，故2222(3)(3)9x x y +-=-，可得121227(3)(3)y y x x =-++，即221212(27)(3)()(3)0.m y y m n y y n ++++++=①将x my n =+代入2219xy +=得222(9)290.m y mny n +++-=所以12229mn y y m +=-+，212299n y y m -=+．代入①式得2222(27)(9)2(3)(3)(9)0.m n m n mn n m +--++++= 解得n =–3（含去），n =32.故直线CD 的方程为3=2x my +，即直线CD 过定点（32，0）．若t =0，则直线CD 的方程为y =0，过点（32，0）.综上，直线CD 过定点（32，0）.3．解：（1）由已知可设2C 的方程为24y cx =，其中c =不妨设,A C 在第一象限，由题设得,A B 的纵坐标分别为2b a ，2b a -；,C D 的纵坐标分别为2c ，2c -，故22||b AB a=，||4CD c =.由4||||3CD AB =得2843b c a=，即2322()c c a a ⨯=-，解得2c a =-（舍去），12c a =.所以1C 的离心率为12.（2）由（1）知2a c =，b =，故22122:143x y C c c+=，所以1C 的四个顶点坐标分别为(2,0)c ，(2,0)c -，)，(0,)，2C 的准线为x c =-. 由已知得312c c c c +++=，即2c =.所以1C 的标准方程为2211612x y +=，2C 的标准方程为28y x =.4．解：（1）由已知可设2C 的方程为24y cx =，其中c =不妨设,A C 在第一象限，由题设得,A B 的纵坐标分别为2b a ，2b a -；,C D 的纵坐标分别为2c ，2c -，故22||b AB a=，||4CD c =.由4||||3CD AB =得2843b c a=，即2322()c c a a ⨯=-，解得2c a =-（舍去），12c a =.所以1C 的离心率为12.（2）由（1）知2a c =，b =，故22122:143x y C c c+=，设00(,)M x y ，则220022143x y c c +=，2004y cx =，故20024143x x c c+=.①由于2C 的准线为x c =-，所以0||MF x c =+，而||5MF =，故05x c =-，代入①得22(5)4(5)143c c c c --+=，即2230c c --=，解得1c =-（舍去），3c =. 所以1C 的标准方程为2213627x y +=，2C 的标准方程为212y x =.5．解：（1）由题设可得54=，得22516m =，所以C 的方程为221252516x y +=. （2）设(,),(6,)P P Q P x y Q y ，根据对称性可设0Q y >，由题意知0P y >，由已知可得(5,0)B ，直线BP 的方程为1(5)Qy x y =--，所以||BP y =，||BQ =，因为||||BP BQ =，所以1P y =，将1P y =代入C 的方程，解得3P x =或3-. 由直线BP 的方程得2Q y =或8.所以点,P Q 的坐标分别为1122(3,1),(6,2);(3,1),(6,8)P Q P Q -.11||PQ 11PQ 的方程为13y x =，点(5,0)A -到直线11PQ，故11APQ △的面积为1522=. 22||PQ =22P Q 的方程为71093y x =+，点A 到直线22P Q的距离为26，故22AP Q △的面积为152262⨯=. 综上，APQ △的面积为52.6．解：（1）由题设可得54=，得22516m =，所以C 的方程为221252516x y +=. （2）设(,),(6,)P P Q P x y Q y ，根据对称性可设0Q y >，由题意知0P y >，由已知可得(5,0)B ，直线BP 的方程为1(5)Qy x y =--，所以||BP y =，||BQ =，因为||||BP BQ =，所以1P y =，将1P y =代入C 的方程，解得3P x =或3-. 由直线BP 的方程得2Q y =或8.所以点,P Q 的坐标分别为1122(3,1),(6,2);(3,1),(6,8)P Q P Q -.11||PQ 11PQ 的方程为13y x =，点(5,0)A -到直线11PQ 的距离为2，故11APQ △的面积为1522=.22||PQ =22P Q 的方程为71093y x =+，点A 到直线22P Q故22AP Q △的面积为1522=. 综上，APQ △的面积为52.7．解：（1）由题设得22411a b +=，22212a b a -=，解得26a =，23b =．所以C 的方程为22163x y +=．（2）设11(,)M x y ，22(,)N x y ．若直线MN 与x 轴不垂直，设直线MN 的方程为y kx m =+，代入22163x y +=得222(12)4260k x kmx m +++-=．于是2121222426,1212km m x x x x k k -+=-=++．①由AM AN ⊥知0AM AN ⋅=，故1212(2)(2)(1)(1)0x x y y --+--=，可得221212(1)(2)()(1)40k x x km k x x m ++--++-+=．将①代入上式可得22222264(1)(2)(1)401212m kmk km k m k k-+---+-+=++．整理得(231)(21)0k m k m +++-=．因为(2,1)A 不在直线MN 上，所以210k m +-≠，故2310k m ++=，1k ≠．于是MN 的方程为21()(1)33y k x k =--≠. 所以直线MN 过点21(,)33P -. 若直线MN 与x 轴垂直，可得11(,)N x y -.由0AM AN ⋅=得1111(2)(2)(1)(1)0x x y y --+---=. 又2211163x y +=，可得2113840x x -+=.解得12x =（舍去），123x =. 此时直线MN 过点21(,)33P -. 令Q 为AP 的中点，即41(,)33Q . 若D 与P 不重合，则由题设知AP 是Rt ADP △的斜边，故1||||2DQ AP ==. 若D 与P 重合，则1||||2DQ AP =. 综上，存在点41(,)33Q ，使得||DQ 为定值.8．（Ⅰ）解：由已知可得3b =．记半焦距为c ，由||||OF OA =可得3c b ==．又由222a b c =+，可得218a =．所以，椭圆的方程为221189x y +=．（Ⅱ）解：因为直线AB 与以C 为圆心的圆相切于点P ，所以AB CP ⊥．依题意，直线AB 和直线CP 的斜率均存在．设直线AB 的方程为3y kx =-．由方程组223,1,189y kx x y =-⎧⎪⎨+=⎪⎩消去y ，可得()2221120k x kx +-=，解得0x =，或21221k x k =+.依题意，可得点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭．因为P 为线段AB 的中点，点A 的坐标为(0,3)-，所以点P 的坐标为2263,2121k k k -⎛⎫ ⎪++⎝⎭．由3OC OF =，得点C 的坐标为(1,0)，故直线CP 的斜率为2230216121k k k --+-+，即23261k k -+．又因为AB CP ⊥，所以231261k k k ⋅=--+，整理得22310k k -+=，解得12k =，或1k =．所以，直线AB 的方程为132y x =-，或3y x =-．9.（Ⅰ）由116p =得2C 的焦点坐标是1(,0)32．（Ⅱ）由题意可设直线:(0,0)l x my t m t =+≠≠，点00(,)A x y ．将直线l 的方程代入椭圆221:12x C y +=得222(2)220m y mty t +++-=，所以点M 的纵坐标22M mt y m =-+．将直线l 的方程代入抛物线22:2C y px =得2220y pmy pt --=，所以02M y y pt =-，解得202(2)p m y m+=，因此22022(2)p m x m+=．由220012x y +=得2421224()2()160m m p m m =+++≥，所以当m，t =时，p．10.解：（1）椭圆22:143x y E +=的长轴长为2a ，短轴长为2b ，焦距为2c ，则2224,3,1a b c ===.所以12AF F △的周长为226a c +=.（2）椭圆E 的右准线为4x =.设(,0),(4,)P x Q y ，则(,0),(4,)OP x QP x y ==--，2(4)(2)44,OP QP x x x ⋅=-=--≥-在2x =时取等号.所以OP QP ⋅的最小值为4-.（3）因为椭圆22:143x y E +=的左、右焦点分别为12,F F ，点A 在椭圆E 上且在第一象限内，212AF F F ⊥，则123(1,0),(1,0),(1,)2F F A -. 所以直线:3430.AB x y -+= 设(,)M x y ，因为213S S =，所以点M 到直线AB 距离等于点O 到直线AB 距离的3倍. 由此得|343||30403|355x y -+⨯-⨯+=⨯，则34120x y -+=或3460x y --=. 由2234120,143x y x y -+=⎧⎪⎨+=⎪⎩得2724320x x ++=，此方程无解；由223460,143x y x y --=⎧⎪⎨+=⎪⎩得271240x x --=，所以2x =或27x =-. 代入直线:3460l x y --=，对应分别得0y =或127y =-. 因此点M 的坐标为(2,0)或212(,)77--.11.。

2020高考数学(文科)二轮专题精讲《圆锥曲线的方程与性质》

3．(2018·全国卷Ⅱ)已知F1，F2是椭圆C的两个焦点，P是C上的一点．若PF1⊥
PF2，且∠PF2F1＝60°，则C的离心率为( )
A．1－
3 2
B．2－ 3
3－1 C. 2
D. 3－1
解析：选 D 不妨设椭圆方程为ax22＋by22＝1(a＞b＞0)．
在Rt△F1PF2中，因为∠PF2F1＝60°，|F1F2|＝2c，所以|PF2|＝c，|PF1|＝ 3c. 由椭圆的定义得|PF1|＋|PF2|＝2a，即 3c＋c＝2a，所以椭圆的离心率e＝ac＝ 32＋1＝ 3－1.故选D.
2．求解圆锥曲线标准方程的方法是“先定型，后计算” (1)定型：就是指定类型，也就是确定圆锥曲线的焦点位置，从而设出标准方程． (2)计算：即利用待定系数法求出方程中的a2，b2或p.另外，当焦点位置无法确定时，抛物线方程常设为y2＝2ax或x2＝2ay(a≠0)，椭圆方程常设为mx2＋ny2＝1(m＞ 0，n＞0，且m≠n)，双曲线方程常设为mx2－ny2＝1(mn＞0)．
(2)当 0＜m＜3 时，椭圆 C 的焦点在 x 轴上，如图(1)，A(－ 3，0)，B( 3，0)．
当点 M 运动到短轴的端点时，∠AMB 取最大值，此时∠AMB≥120°. 则|MO|≤1，即 0＜m≤1；
当 m＞3 时，椭圆 C 的焦点在 y 轴上，如图(2)，A(0， m)，B(0，－ m)．
A. 2
B．2
C.3 2 2
D．2 2
解析：选D ∵e＝ac＝
1＋ba2＝ 2，且a＞0，b＞0，
∴ba＝1，∴C的渐近线方程为y＝±x，
∴点(4,0)到C的渐近线的距离为 |42| ＝2 2.
2．(2019·大连模拟)已知椭圆C：

高二数学圆锥曲线与方程试题答案及解析

高二数学圆锥曲线与方程试题答案及解析1.若动点与定点和直线的距离相等，则动点的轨迹是（）A．椭圆B．双曲线C．抛物线D．直线【答案】D【解析】因为定点F（1，1）在直线上，所以到定点F的距离和到定直线l的距离相等的点的轨迹是直线，就是经过定点A与直线，垂直的直线．故选D．【考点】1．抛物线的定义；2．轨迹方程．2. F1、F2是定点，|F1F2|=6，动点M满足|MF1|+|MF2|=6，则点M的轨迹是（）A．椭圆B．直线C．线段D．圆【答案】C【解析】主要考查椭圆的定义、椭圆的标准方程。

解：因为|MF1|+|MF2|=6=|F1F2|，所以点M的轨迹是线段，故选C。

3.椭圆内有一点P（3，2）过点P的弦恰好以P为中点，那么这弦所在直线的方程为（）A．B．C．D．【答案】B【解析】主要考查椭圆的定义、直线与椭圆的位置关系。

利用“点差法”求弦的斜率，由点斜式写出方程。

故选B。

4.如果抛物线y 2=ax的准线是直线x=-1，那么它的焦点坐标为（）A．（1, 0）B．（2, 0）C．（3, 0）D．（－1, 0）【答案】A【解析】由已知，所以=4，抛物线的焦点坐标为（1, 0），故选A。

【考点】本题主要考查抛物线的定义、标准方程、几何性质。

点评：熟记抛物线的标准方程及几何性质。

5.圆心在抛物线y 2=2x上，且与x轴和该抛物线的准线都相切的一个圆的方程是（）A．x2+ y 2-x-2 y -=0B．x2+ y 2+x-2 y +1="0"C．x2+ y 2-x-2 y +1=0D．x2+ y 2-x-2 y +=0【答案】D【解析】由抛物线定义知，此圆心到焦点距离等于到准线距离，因此圆心横坐标为焦点横坐标，代入抛物线方程的圆心纵坐标,1，且半径为1，故选D。

【考点】本题主要考查抛物线的定义、标准方程、几何性质，同时考查了圆的切线问题。

点评：抛物线问题与圆的切线问题有机结合，利用抛物线定义，简化了解答过程。

精选最新版2020高考数学《圆锥曲线方程》专题训练完整考试题(含参考答案)

2019年高中数学单元测试卷圆锥曲线与方程学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．1 ．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））如图,21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点,B A ,分别是1C ,2C 在第二、四象限的公共点.若四边形21BF AF 为矩形,则2C 的离心率是（）A ．2B ．3C ．23 D ．26 2．(2005全国2文)双曲线22149x y -=的渐近线方程是（）（A ）23y x =±（B ）49y x =±（C ）32y x =±（D ）94y x =± 3．（2000全国11）过抛物线y =ax 2（a ＞0）的焦点F 用一直线交抛物线于P 、Q 两点，若线段PF 与FQ 的长分别是p 、q ，则qp 11+等于（）A ．2aB ．a21 C ．4a D ．a4 4．（2010四川）已知两定点()()2,0,1,0A B -，如果动点P 满足2PA PB =，则点P 的轨迹所包围的图形的面积等于（）（A ）π （B ）4π （C ）8π （D ）9π5．已知抛物线x y 42=的准线与双曲线1222=-y ax )0(>a 相交于B A ,两点，且F 是抛物线的焦点，若FAB ∆是直角三角形，则双曲线的离心率为（） A ．3 B ．6C ．2D ．3二、填空题6．在平面直角坐标系xOy 中，若双曲线 x 2m －y 2m 2＋4＝1的离心率为5，则m 的值为▲ .7．设椭圆22221x y m n+=（0>>n m ）的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为。

8．已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12(,0),(,0)F c F c -，若椭圆上存在一点P 使1221sin sin a c PF F PF F =，则该椭圆的离心率的取值范围为． 9．双曲线C:-=1(a ＞b ＞0)中，F 1、F 2是它的焦点，设抛物线l 的焦点与双曲线C的右焦点F 2重合，l 的准线与C 的左准线重合，P 是C 与l 的一个交点，那么=______________.【答案】【解析】设|PF 1|=m,|PF 2|=n,由抛物线定义有|PF 2|=|PN|(N 为点P 在左准线上的射影),又=e,=e=, ①又|PF 1|-|PF 2|=2a ，即m-n=2a. ②由①②得m=.∴原式=-=e-2c ·=1.10．已知F 1、F 2是两个定点，点P 是以F 1和F 2为公共焦点的椭圆和双曲线的一个交点，并且PF 1⊥PF 2，e 1和e 2分别是上述椭圆和双曲线的离心率，则有A.+=4 B.+=2C.e 12+e 22=4 D.e12+e 22=211．双曲线的渐近线方程是023=±y x ，焦点在y 轴上，则该双曲线的离心率等于 .12．若12F F 、是椭圆22+1169x y =的两个焦点,过1F 作直线与椭圆交于A B 、,则2ABF ∆的周长为 ▲ ．13．已知F 是椭圆2222:1x y C a b+= (0)a b >>的右焦点，点P 在椭圆C 上，线段PF 与圆22214x y b +=相切于点Q ，且→→=QF PQ ，则椭圆C 的离心率为 ▲ ．14．若双曲线22221(0,0)x y a b a b-=>>的一个焦点到一条渐近线的距离等于焦距的14，则该双曲线的渐近线方程是 .15．．已知圆x 2+y 2－6x －7=0与抛物线y 2=-2px (p ＞0)的准线相切，则p = ▲ ．分析: 圆方程化为16)3(22=+-y x ，垂直于x 轴的圆的切线为x =-1,x =7，由于抛物线方程是标准方程，故准线方程为x =7，解得p =14 16．对于顶点在原点的抛物线，给出下列条件： ①焦点在y 轴上；②焦点在x 轴上；③抛物线上横坐标为1的点到焦点的距离等于6； ④抛物线的通径的长为5；⑤由原点向过焦点的某条直线作垂线，垂足坐标为（2，1）．能使这抛物线方程为y 2＝10x 的条件是．（要求填写合适条件的序号）（2002全国文，16）三、解答题17．（本小题满分16分）已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率e ＝32，椭圆C 的上、下顶点分别为A 1，A 2，左、右顶点分别为B 1，B 2,左、右焦点分别为F 1，F 2．原点到直线A 2B 2的距离为255．（1）求椭圆C 的方程；（2）过原点且斜率为12的直线l ，与椭圆交于E ，F 点，试判断∠EF 2F 是锐角、直角还是钝角，并写出理由；（3）P 是椭圆上异于A 1，A 2的任一点,直线PA 1，PA 2，分别交x 轴于点N ，M ,若直线OT 与过点M ，N 的圆G 相切，切点为T .证明：线段OT 的长为定值,并求出该定值.（2）由⎩⎨⎧x 24＋y 2＝1，y ＝12x ，得E (2，22)，F (－2，－22)．……………………………….7分又F 2(3，0)，所以F 2E →＝(2－3，22)，F 2F →＝(－2－3，－22)，所以F 2E →·F 2F →＝(2－3)×(－2－3)＋22×(－22)＝12＞0．所以∠EF 2F 是锐角． ………………… 10分【结束】18．已知A 、B 为椭圆x 24＋y 23＝1的左、右顶点，F 为椭圆的右焦点，P 是椭圆上异于A 、B的任意一点，直线AP 、BP 分别交直线l ：x ＝m (m >2)于M 、N 两点，l 交x 轴于C 点． (1)当PF ∥l 时，求点P 的坐标；(2)是否存在实数m ，使得以MN 为直径的圆过点F ？若存在，求出实数m 的值；若不存在，请说明理由．19．已知以原点O 为中心的双曲线的一条准线方程为5x =，离心率e =求该双曲线的方程；（Ⅱ）点A 的坐标为(0)，B 是圆22(1x y +=上的点，点M 在双曲线右支上，求MA MB +的最小值，并求此时M 点的坐标w.w.k.s.5.u.c.o.m .5.u.c.o.m20．求适合下列条件的曲线的标准方程：（1）3a b =，经过点(3,0)M 的椭圆；（2）52=a ，经过点)5,2(-N ，焦点在y 轴上的双曲线．21．椭圆2222:1(0)x y C a b a b +=>>的离心率为35，两焦点分别为12F F ,，点00(,)M x y 是椭圆C 上一点，且12F F M ∆的周长为16，设线段MO （O 为坐标原点）与圆222O x y r :+=交于点N ，且线段MN 长度的最小值为154. （1）求椭圆C 以及圆O 的方程;（2）当点00(,)M x y 在椭圆C 上运动时,判断直线00:1l x x y y +=与圆O 的位置关系.22．写出适合下列条件的椭圆的标准方程：（1）两个焦点坐标分别是(-4,0)、（4，0），椭圆上一点P 到两焦点的距离之和等于10；（2）两个焦点坐标分别是（0，－2）和（0,2）且过点P （23-,25）。

精选最新2020高考数学《圆锥曲线方程》专题训练考核题(含答案)

2019年高中数学单元测试卷圆锥曲线与方程学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．1 ．（2013年高考四川卷（文））抛物线28y x =的焦点到直线0x -=的距离是（）A ．B ．2CD ．12．（2008天津文7）设椭圆22221x y m n+=（0m >，0n >）的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为 ( ) A .2211216x y += B .2211612x y += C .2214864x y += D .2216448x y += 3．（2010山东文）已知抛物线22(0)y px p =>，过其焦点且斜率为1的直线交抛物线于,A B 两点，若线段AB 的中点的纵坐标为2，则该抛物线的标准方程为( )A ．1x =B ．1x =-C ．2x =D ．2x =-4．（2009浙江文）已知椭圆22221(0)x y a b a b+=>>的左焦点为F ，右顶点为A ，点B在椭圆上，且BF x ⊥轴，直线AB 交y 轴于点P ．若2AP PB =，则椭圆的离心率是（）DA B ．2 C ．13 D ．125．（2005年高考上海）过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点，它们的横坐标之和等于5，则这样的直线（） A ．有且仅有一条B ．有且仅有两条 C ．有无穷多条D ．不存在二、填空题6．已知椭园2222:1x y C a b+= (0)a b >>，(2,0)A 为长轴的一个端点，弦BC 过椭圆的中心O ，且0AC BC ⋅=，2OB OC BC BA -=-，则其短轴长为7．（3分）在平面直角坐标系中，准线方程为y=4的抛物线标准的方程为 x 2=﹣16y ． =48．椭圆5x 2＋ky 2＝5的一个焦点是(0,2)，那么k 的值为9．如图，在平面直角坐标系xoy 中，已知椭圆22221(0)x y a b a b+=>>的左顶点为A ，左焦点为F ，上顶点为B ，若090BAO BFO ∠+∠=，则椭圆的离心率是．10．已知双曲线()222210,0x y C a b a b-=>>：的右焦点为F ,过F C于A B 、两点，若4AF FB =,则C 的离心率为____________．11．正方形ABCD 的边AB 在直线y =x +4上，C 、D 两点在抛物线y 2=x 上，则正方形ABCD 的面积为_________12．如图，已知12,F F 是椭圆2222:1x y C a b+= (0)a b >>的左、右焦点，点P 在椭圆C 上，线段2PF 与圆222x y b += 相切于点Q ，且点Q 为线段2PF 的中点，则椭圆C 的离心率为 .第11题13．抛物线2x y =在1=x 处的切线与两坐标轴围成三角形区域为D (包含三角形内部和边界) ．若点),(y x P 是区域D 内的任意一点，则y x 2+的取值范围是．14．已知椭圆22221(0)y x a b a b +=>>的中心为O ，右焦点为F 、右顶点为A ，右准线与x 轴的交点为H ，则||||FA OH 的最大值为 ▲15．渐近线方程为750x y ±=且过点的双曲线的标准方程是______________16．在平面直角坐标系xOy 中，已知双曲线C ：2221x y a-=（0a >）的一条渐近线与直线l ：210x y -+= 垂直，则实数=a ★ ；17．设P 是椭圆1162522=+y x 上任意一点，A 和F 分别是椭圆的左顶点和右焦点，则AF PA PF PA ⋅+⋅41的最小值为 ▲ ．18．抛物线24y mx =(0)m >的焦点到双曲线221169x y -=的一条渐近线的距离为3，则此抛物线的方程为 ▲ ．19．设双曲线2222by a x -=1（0＜a ＜b ）的半焦距为c ，直线l 过（a ，0），（0，b ）两点.已知原点到直线l 的距离为43c ，则双曲线的离心率为____________三、解答题20．已知以原点O 为中心的双曲线的一条准线方程为5x =，离心率e =求该双曲线的方程；（Ⅱ）点A的坐标为(0)，B是圆22(1x y +=上的点，点M 在双曲线右支上，求MA MB +的最小值，并求此时M 点的坐标w.w.k.s.5.u.c.o.m .5.u.c.o.m21．如图，在平面直角坐标系xOy 中，椭圆22221(0)x y a b a b +=>>的左、右焦点分别为1(0)F c -，，2(0)F c ，．已知(1)e ，和e ⎛ ⎝都在椭圆上，其中e 为椭圆的离心率．（1）求椭圆的离心率；（2）设A ，B 是椭圆上位于x 轴上方的两点，且直线1AF 与直线2BF 平行，2AF 与1BF 交于点P ．（i）若12AF BF -=，求直线1AF 的斜率；（ii ）求证：12PF PF +是定值．【答案及解析】（第19题）【点评】本题主要考查椭圆的定义、几何性质以及直线与椭圆的关系．本题注意解题中，待定系数法在求解椭圆的标准方程应用，曲线和方程的关系.在利用条件2621=-BF AF时，需要注意直线1AF 和直线2BF 平行这个条件.本题属于中档题． 22． (本小题满分16分)已知椭圆E 的中心在坐标原点O ，经过两点).55,2(),552,1(-B A 圆C 以点（2，0）为圆心，椭圆的短半轴长为半径。

精选2020高考数学《圆锥曲线方程》专题训练完整考题(含答案)

2019年高中数学单元测试卷圆锥曲线与方程学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．1 ．（2013年高考四川卷（文））抛物线28y x =的焦点到直线0x -=的距离是（）A ．B ．2CD ．12．(2006广东)已知双曲线9322=-y x ,则双曲线右支上的点P 到右焦点的距离与点P 到右准线的距离之比等于 A. 2 B.332 C. 2 D.4 依题意可知 3293,322=+=+==b a c a ，2332===a c e ，故选C. 3．（2010湖南文5）设抛物线28y x =上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是( )A ． 4B ． 6C ． 8D ． 124．（1993山东理11)一动圆与两圆x 2+y 2=1和x 2+y 2－8x +12=0都外切，则动圆圆心轨迹为( )(A) 圆 (B) 椭圆 (C) 双曲线的一支 (D) 抛物5．（2007四川文）（5）如果双曲线2422y x -＝1上一点P 到双曲线右焦点的距离是2,那么点P 到y 轴的距离是（） (A)364 (B)362 (C)62(D)326．设抛物线的顶点在原点，准线方程为2x =-，则抛物线的方程是（A ）28y x =- （B ）28y x = （C ）24y x =- （D ）24y x =(2011年高考陕西卷理科2)二、填空题7．过抛物线24y x =的焦点的直线交抛物线于A 、B 两点，O 为坐标原点，则⋅= ▲ .8．与双曲线12222=-y x 有相同的焦点,且离心率互为倒数的椭圆的方程为 . 9．已知过椭圆的左焦点F 1且倾斜角为60°的直线交椭圆于A 、B 两点，若F 1A ＝2F 1B ，则椭圆的离心率为________．10．已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线方程是y ＝3x ，它的一个焦点与抛物线y 2＝16x 的焦点相同，则双曲线的方程为________．11．以椭圆的右焦点2F 为圆心作一个圆，使此圆过椭圆中心并交椭圆于点M ，N ，若过椭圆左焦点1F 的直线MF 1是圆2F 的切线，则椭圆的离心率为 12．过椭圆x 2a 2＋y 2b2＝1(a >b >0)的左顶点A 作斜率为1的直线，与椭圆的另一个交点为M ，与y 轴的交点为B ，若AM ＝MB ，则该椭圆的离心率为________．解析：A 点坐标为(－a,0)，l 的方程为y ＝x ＋a ，所以B 点的坐标为(0，a )，故M 点的坐标为⎝⎛⎭⎫－a 2，a 2，代入椭圆方程得a 2＝3b 2，∴c 2＝2b 2，∴e ＝63.13．双曲线221416x y -=的渐近线方程为。

精选2020高考数学《圆锥曲线方程》专题训练完整考题(含标准答案)

2019年高中数学单元测试卷圆锥曲线与方程学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．1 ．（2013年高考课标Ⅱ卷（文））设抛物线C:y 2=4x 的焦点为F,直线L 过F 且与C 交于A, B 两点.若|AF|=3|BF|,则L 的方程为（）A ．y=x-1或y=-x+1B ．y=(X-1)或y=-(x-1)C ．y=(x-1)或y=-(x-1)D ．y=(x-1)或y=-(x-1)2．2 ．（2012江西文）椭圆22221(0)x y a b a b+=>>的左、右顶点分别是A,B,左、右焦点分别是F 1,F 2.若|AF 1|,|F 1F 2|,|F 1B|成等比数列,则此椭圆的离心率为（）A ．14B C ．12D3．(2006辽宁理)直线2y k =与曲线2222918k x y k x += (,)k R ∈≠且k 0的公共点的个数为(A)1 (B)2 (C)3 (D)44．（2010安徽理数）5、双曲线方程为2221x y -=，则它的右焦点坐标为（）A 、,02⎛⎫ ⎪ ⎪⎝⎭B 、2⎛⎫⎪ ⎪⎝⎭C 、2⎛⎫⎪ ⎪⎝⎭D 、)5．（2010山东文数9）已知抛物线22(0)y px p =>，过其焦点且斜率为1的直线交抛物线与A 、B 两点，若线段AB 的中点的纵坐标为2，则该抛物线的准线方程为（）（A ）1x = (B)1x =- (C)2x = (D)2x =-6．（1998山东理）(12) 椭圆31222y x +=1的焦点为F 1和F 2，点P 在椭圆上，如果线段PF 1的中点在y 轴上，那么|P F 1|是|P F 2|的 ( ) (A) 7倍 (B) 5倍 (C) 4倍 (D) 37．（2007重庆文）已知以F 1（2,0），F 2（2,0）为焦点的椭圆与直线043=++y x 有且仅有一个交点，则椭圆的长轴长为（） A .23B .62C .72D .248．已知椭圆2222:1(0)x y C a b a b+=>>双曲线221x y -=的渐近线与椭圆C 有四个交点，以这四个焦点为顶点的四边形的面积为16，则椭圆C 的方程为（A ）22182x y += （B ）221126x y += （C ）221164x y += （D ）221205x y +=二、填空题9．双曲线2214y x -=的渐进线被圆226210x y x y +--+=所截得的弦长为． 10．椭圆x 249＋y 224＝1上一点P 与椭圆的两个焦点F 1，F 2的连线互相垂直，则△PF 1F 2的面积为 2411．已知双曲线22221x y a b -=的一条渐近线方程为20x y -=，则该双曲线的离心率为 ▲ ．12．已知1F ，2F 是椭圆2212516x y +=的两个焦点，P 为椭圆上一点，则△12PF F 的周长为 16 。

精选2020高考数学《圆锥曲线方程》专题训练完整题(含标准答案)

2019年高中数学单元测试卷圆锥曲线与方程学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．(2005全国3理)设椭圆的两个焦点分别为F 1.F 2，过F 2作椭圆长轴的垂线交椭圆于点P ，若三角形F 1PF 2为等腰直角三角形，则椭圆的离心率为（） A.22 B.212- C.22- D.12- 2．（2007宁夏理6）已知抛物线22(0)y px p =>的焦点为F ，点111222()()P x y P x y ，，，，333()P x y ，在抛物线上，且2132x x x =+，则有（）Ａ．123FP FP FP += Ｂ．222123FP FP FP +=Ｃ．2132FP FP FP =+Ｄ．2213FP FP FP =·3．（2000北京安徽春季3）双曲线2222ay b x -＝1的两条渐近线互相垂直，那么该双曲线的离心率是（） A ．2 B ．3C ．2D ．234．（1994全国2）如果方程x 2＋ky 2＝2表示焦点在y 轴上的椭圆，那么实数k 的取值范围是（） A ．（0，＋∞）B ．（0，2）C ．（1，＋∞）D ．（0，1）5．（2005年高考上海）过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点，它们的横坐标之和等于5，则这样的直线（） A ．有且仅有一条B ．有且仅有两条C ．有无穷多条D ．不存在6．设抛物线的顶点在原点，准线方程为2x =-，则抛物线的方程是（A ）28y x =- （B ）28y x = （C ）24y x =- （D ）24y x =(2011年高考陕西卷理科2)二、填空题7．已知正方形ABCD 的坐标分别是A (1,0)-,B (0,1),C (1,0)，D (0,1)-，动点M 满足：MB MD k k ⋅ 则MA MC += ．8．椭圆上一点A 看两焦点的视角为直角，设AF 1的延长线交椭圆于B ，又|AB|＝|AF 2|，则椭圆的离心率e ＝____________9．若动点P 到点(0,2)A 的距离比到直线:4l y =-的距离小2，则动点P 的轨迹方程为____________10．抛物线22y px =的准线经过双曲线2213x y -=的左焦点，则p = ．11．已知点P 在抛物线24y x =上，那么点P 到点(21)Q -，的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为______________.12．已知A ，B ，P 是双曲线22221x y a b -=上不同的三点，且A ，B 连线经过坐标原点，若直线PA ，PB 的斜率乘积23PA PB k k ⋅=，则该双曲线的离心率为 ▲ ．13．已知点P 是抛物线24y x =上的动点，点A 的坐标是()4,1，F 点是抛物线的焦点，则||||PA PF +的最小值是．14．已知点（－2，3）与抛物线y 2=2px （p ＞0）的焦点的距离是5，则p =_____.（1996全国文，16）15．已知双曲线22221(0)x y a b a b-=>>的左右焦点分别为21,F F ,点P 在双曲线的右支上，且214PF PF =,则此双曲线的离心率e 的最大值为 ___ ．16．已知抛物线y 2＝2px 过点M (2，2)，则点M 到抛物线焦点的距离为 ▲ ．17．圆锥曲线G 的一个焦点是F ，与之对应的准线是l ，过F 作直线与圆锥曲线G 交于A 、B 两点，以AB 为直径作圆M ，圆M 与l 的位置关系决定G 是何种曲线之间的关系是：18．设椭圆12622=+y x 和双曲线1322=-y x 的公共焦点为F1、F2，P 是两曲线的一个公共点，则21cos PF F ∠的值等于 ____________ 19．双曲线2233x y －＝的渐近线方程是20．已知直线l 1：4x －3y ＋11＝0和直线l 2：x ＝－1，抛物线y 2＝4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是21．若直线1y kx =-与双曲线224x y -=始终有公共点，则k 取值范围是 ▲ ．22．点(3,1)P -在椭圆22221(0)x y a b a b +=>>的左准线上，过点P 沿斜率52-的直线入射的光线,经直线2y =-反射后通过椭圆的左焦点,则这个椭圆的离心率为 ▲ 23．以下四个关于圆锥曲线的命题中：①设A 、B 为两个定点，k 为非零常数，||||PA PB k -=，则动点P 的轨迹为双曲线； ②过定圆C 上动点A 作水平直径所在直线的垂线AB ，垂足为点B ,若1,2AM AB =则点M 的轨迹为椭圆；③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率；④双曲线13519252222=+=-y x y x 与椭圆有相同的焦点. 其中真命题的序号为．24．已知P 是椭圆16410022=+y x 上一点，21F F 、为该椭圆的焦点，若321π=∠PF F ，则21PF F ∆的面积为三、解答题25．（本题满分14分）如图，已知椭圆E 的中心为O ，长轴的两个端点为A ，B ，右焦点为F ，且，椭圆E的右准线l 的方程为（I ）求椭圆E 的标准方程；（II ）若N 为准线l 上一点（在x 轴上方），AN 与椭圆交于点M ，且26．已知点P （4，4），圆C ：22()5(3)x m y m -+=<与椭圆E ：22221(0)x y a b a b+=>>有一个公共点A （3，1），F 1、F 2分别是椭圆的左、右焦点，直线PF 1与圆C 相切．（Ⅰ）求m 的值与椭圆E 的方程；（Ⅱ）设Q 为椭圆E 上的一个动点，求AP AQ ⋅的取值范围．27．（本题满分15分）椭圆)0(12222>>=+b a by a x 的两个焦点为21,F F ，点P 在椭圆上，且211F F PF ⊥，314,3421==PF PF . （1）求椭圆的标准方程；（2）若直线l 过圆02422=-++y x y x 的圆心M ，交椭圆于A 、B 两点，且A 、B 关于点M 对称，求直线l 的方程.28．如图，已知椭圆22221(0)x y a b a b+=>>的长轴为AB ，点)1,0(恰好是椭圆的一个顶点,且椭圆的离心率e =，过点B 的直线l 与x 轴垂直．（1）求椭圆的标准方程；（2）设P 是椭圆上异于A 、B 的任意一点，PH x ⊥轴，H 为垂足，延长HP 到点Q 使得HP PQ =，连结AQ 延长交直线l 于点M ，N 为MB 的中点． ②点Q 的轨迹；②判断直线QN 与以AB 为直径的圆O 的位置关系．（本题满分15分）29．已知椭圆22221(0)x y a b a b +=>>的右准线1:l x =，右焦点F 到短轴一个端点的距离为2，过动点A （4，m ）引椭圆的两条切线AP 、AQ ，切点分别为P 、Q ． (I ）求椭圆的方程；(Ⅱ）求证：直线PQ 过定点，并求出定点的坐标； (Ⅲ）要使||APQ S PQ ∆最小，求AQ AP ⋅的值．关键字：已知准线；求椭圆方程；解几中恒过定点问题；求数量积；已知最值；基本不等式30．设椭圆的中心为原点O ，一个焦点为F （0，1），长轴和短轴的长度之比为t ． (1）求椭圆的方程；(2）设经过原点且斜率为t 的直线与椭圆在y 轴右边部分的交点为Q 、点P 在该直线上，且1||||2-=t t OQ OP ，当t 变化时，求点P 的轨迹方程，并说明轨迹是什么图形. （1994上海，24）。

精编2020高考数学《圆锥曲线方程》专题训练完整考题(含参考答案)

2019年高中数学单元测试卷圆锥曲线与方程学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．(2006江西理)设O 为坐标原点，F 为抛物线y 2＝4x 的焦点，A 是抛物线上一点，若OA F A ∙＝－4则点A 的坐标是（B ）A ．（2，±） B. (1，±2) C.（1，2）D.(2，)2．(2005江苏)抛物线24x y =上的一点M 到焦点的距离为1，则点M 的纵坐标是（）A ．1617 B ．1615 C ．87 D ．0 3．（2010福建文11）若点O 和点F 分别为椭圆22143x y +=的中心和左焦点，点P 为椭圆上的任意一点，则OP FP 的最大值为（）A ．2 B ．3 C ．6 D ．84．（2007陕西文3）抛物线y x =2的准线方程是( )（A ）014=+x（B ）014=+y （C ）012=+x （D ）012=+y 5．已知F 1、F 2为双曲线C ：x ²-y ²=2的左、右焦点，点P 在C 上，|PF 1|=|2PF 2|，则cos ∠F 1PF 2= (A)14 （B ）35 (C)34 (D)456．已知双曲线C ：22x a -22y b=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C 的方程为A ．220x -25y =1 B.25x -220y =1 C.280x -220y =1 D.220x -280y =17．1 ．（2012辽宁文）已知P,Q 为抛物线x 2=2y 上两点,点P,Q 的横坐标分别为4,-2,过P,Q 分别作抛物线的切线,两切线交于点A,则点A 的纵坐标为（）A ．1B ．3C ．-4D ．-8二、填空题 8．点A 、B 是双曲线15422=-y x 右支上的两点，AB 中点到y 轴的距离为4，则AB 的最大值为 .9．过椭圆22154x y +=的右焦点作一条斜率为2的直线与椭圆交于A 、B 两点，O 为坐标原点，则△OAB 的面积为______________10．若椭圆)0(12222>>=+b a by a x 的左、右焦点分别为21,F F ，线段21F F 被抛物线bx y 22=的焦点F 分成5﹕3的两段，则此椭圆的离心率为．11．已知21F F 、为椭圆192522=+y x 的两个焦点，过1F 的直线交椭圆于A 、B 两点,若1222=+B F A F ，则AB =___________.12．若双曲线22221(00)x y a b a b-=>>，，则其渐近线方程为 ▲ ．13．若动圆M 经过点(3,0)A 且与直线:3l x =-相切，则动圆的圆心M 的轨迹方程是________14．动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等，则P 的轨迹方程为 28y x =。

圆锥曲线求方程真题练习(解析版)

圆锥曲线求方程真题练习（解析版）学校:___________姓名：___________班级：___________考号：___________一、解答题1．设抛物线2:2(0)C y px p =>的焦点为F ，点(),0D p ，过F 的直线交C 于M ，N 两点．当直线MD 垂直于x 轴时，3MF =．(1)求C 的方程；(2)设直线,MD ND 与C 的另一个交点分别为A ，B ，记直线,MN AB 的倾斜角分别为,αβ．当αβ-取得最大值时，求直线AB 的方程．2．已知椭圆E 的中心为坐标原点，对称轴为x 轴、y 轴，且过()30,2,,12A B ⎛--⎫ ⎪⎝⎭两点． (1)求E 的方程；(2)设过点()1,2P -的直线交E 于M ，N 两点，过M 且平行于x 轴的直线与线段AB 交于点T ，点H 满足MT TH =．证明：直线HN 过定点．3．已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为(2,0)F ，渐近线方程为y =． (1)求C 的方程；(2)过F 的直线与C 的两条渐近线分别交于A ，B 两点，点()()1122,,,P x y Q x y 在C 上，且1210,0x x y >>>．过P 且斜率为Q M .从下面①①①中选取两个作为条件，证明另外一个成立：①M 在AB 上；①PQ AB ∥；①||||MA MB =．注：若选择不同的组合分别解答，则按第一个解答计分.4．已知点(2,1)A 在双曲线2222:1(1)1x y C a a a -=>-上，直线l 交C 于P ，Q 两点，直线,AP AQ 的斜率之和为0．(1)求l 的斜率；(2)若tan PAQ ∠=PAQ △的面积．（1）求椭圆C 的方程；（2）设M ，N 是椭圆C 上的两点，直线MN 与曲线222(0)x y b x +=>相切．证明：M ，N ，F 三点共线的充要条件是||MN =6．在平面直角坐标系xOy 中，已知点()1F 、)2122F MF MF -=，，点M 的轨迹为C .（1）求C 的方程；（2）设点T 在直线12x =上，过T 的两条直线分别交C 于A 、B 两点和P ，Q 两点，且TA TB TP TQ ⋅=⋅，求直线AB 的斜率与直线PQ 的斜率之和.（1）求C 的方程：（2）点M ，N 在C 上，且AM AN ⊥，AD MN ⊥，D 为垂足．证明：存在定点Q ，使得DQ 为定值．8．已知椭圆C ：22221(0)x y a b a b+=>>过点M （2，3）,点A 为其左顶点，且AM 的斜率为12 ，（1）求C 的方程；（2）点N 为椭圆上任意一点，求①AMN 的面积的最大值.9．已知抛物线()2:20C x py p =>的焦点为F ，且F 与圆22:(4)1M x y ++=上点的距离的最小值为4．（1）求p ；（2）若点P 在M 上，,PA PB 是C 的两条切线，,A B 是切点，求PAB 面积的最大值．10．抛物线C 的顶点为坐标原点O ．焦点在x 轴上，直线l ：1x =交C 于P ，Q 两点，且OP OQ ⊥．已知点()2,0M ，且M 与l 相切．（1）求C ，M 的方程；（2）设123,,A A A 是C 上的三个点，直线12A A ，13A A 均与M 相切．判断直线23A A 与M 的位置关系，并说明理由．【答案】（1）抛物线2:C y x =，M 方程为22(2)1x y -+=；（2）相切，理由见解析11．已知A 、B 分别为椭圆E ：2221x y a+=（a >1）的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线x =6上的动点，P A 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.12．已知椭圆C 1：22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |. （1）求C 1的离心率；（2）设M 是C 1与C 2的公共点，若|MF |=5，求C 1与C 2的标准方程.13．已知椭圆222:1(05)25x y C m m +=<<A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，求APQ △的面积．14．已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C 的两条切线，切点分别为A ，B .（1）证明：直线AB 过定点：（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.15．已知点A (−2,0)，B (2,0)，动点M (x ,y )满足直线AM 与BM 的斜率之积为−12.记M 的轨迹为曲线C .（1）求C 的方程，并说明C 是什么曲线；（2）过坐标原点的直线交C 于P ，Q 两点，点P 在第一象限，PE ①x 轴，垂足为E ，连结QE 并延长交C 于点G .（i ）证明：PQG 是直角三角形；（ii ）求PQG 面积的最大值.（1C 上. （①）求C 的方程；（①）设直线l 不经过P 2点且与C 相交于A ，B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点.17．设O 为坐标原点，动点M 在椭圆C 22:12x y +=上，过M 作x 轴的垂线，垂足为N ，点P 满足2NP NM =.（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=.证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .【答案】（1）222x y +=；（2）见解析.18．已知点()0,2A -，椭圆E ：22221(0)x y a b a b +=>>F 是椭圆的焦点，直线AFO 为坐标原点． (1)求E 的方程； (2)设过点A 的直线l 与E 相交于,P Q 两点，当OPQ △的面积最大时，求l 的方程．19．平面直角坐标系xOy 中，过椭圆 M ：22221x y a b +=（ 0a b >>）右焦点的直线0x y +交 M 于A ，B 两点，P 为AB 的中点，且 OP 的斜率为12.（①）求椭圆M 的方程；（①）C ， D 为M 上的两点，若四边形ACBD的对角线 CD AB ⊥，求四边形ACBD 面积的最大值.20．已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ，长轴长为4，离心率为12．过点(4,0)Q 的直线l 与椭圆C 交于A ，B 两点．(1)求椭圆C 的标准方程；(2)设直线,AF BF 的斜率分别为()122,0k k k ≠，求证：12k k 为定值．。

2020高考数学二轮微专题圆锥曲线的方程及几何性质考点考向考题(58张)

第6页
考情分析典型例题课后作业
微专题十一圆锥曲线的方程及几何性质
(2) y＝112x2 或 y＝－316x2 解析：抛物线标准方程为 x2＝1ay(a≠0)，当 a＞0 时，开口向上，准线方程为 y＝－41a，则点 M 到准线的距离为 3＋41a＝6，解得 a＝112，则抛物线方程为 y＝112x2；当 a＜0 时，开口向下，准线方程为 y＝－41a，则点 M 到准线的距离为－41a－3＝6，解得 a＝－316，则抛物线方程为 y＝－316x2.
＞0)的焦点到双曲线 C1 的渐近线的距离为 2，则抛物线 C2 的方程是________． x2＝16y 解析：因为双曲线 C1：ax22－by22＝1(a＞0，b＞0)的离心率为 2，所以ac＝2，
即a2＋a2b2＝4，所以ba22＝3.因为双曲线的渐近线方程为 bx±ay＝0，抛物线 C2：x2＝
第3页
考情分析典型例题课后作业
微专题十一圆锥曲线的方程及几何性质
(3) 设椭圆ax22＋by22＝1(a＞b＞0)的左、右焦点分别为 F1，F2，点 D 在椭圆上，DF1 ⊥F1F2，FD1FF12＝2 2，△DF1F2 的面积为 22，求该椭圆的标准方程．
第4页
考情分析典型例题课后作业
填空题 T8双曲线的几何性质 T8双曲线的几何性质 T7双曲线的几何性质
解答题 T17椭圆的标准方程 T18椭圆的标准方程 T17 椭圆标准方程及其几何性质
第2页
考情分析典型例题课后作业
微专题十一圆锥曲线的方程及几何性质
典课型时例作题业
目标 1 圆锥曲线方程的求解例 1 (1) 已知双曲线 C：ax22－by22＝1(a>0，b>0)的一条渐近线方程为 y＝ 25x，且与椭圆1x22 ＋y32＝1 有公共焦点，则 C 的方程为________． (2) 点 M(5,3)到抛物线 y＝ax2(a≠0)的准线的距离为 6，那么抛物线的方程是 ________．