SPSS处理多元方差分析例子
spss多因素方差分析报告例子

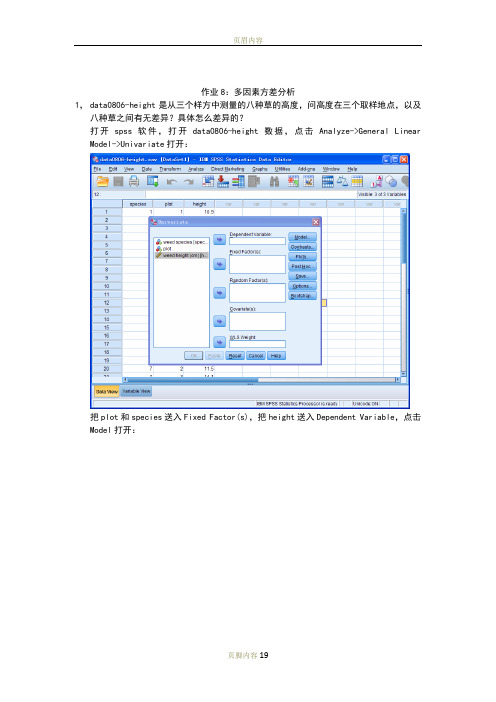
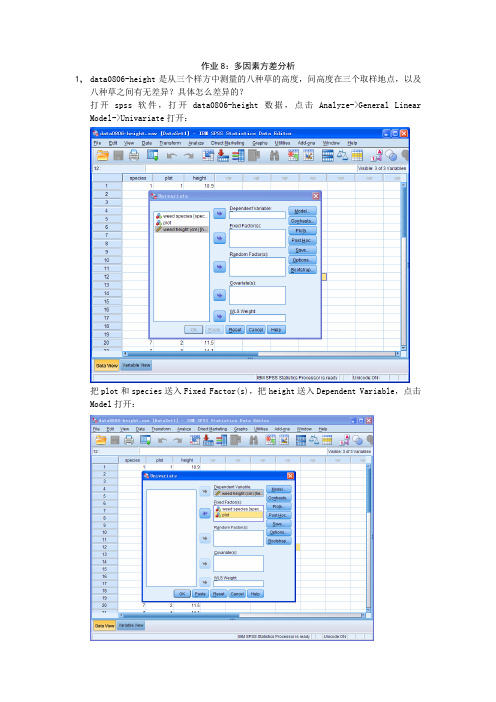
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
使用SPSS软件进行多因素方差分析

使用SPSS软件进行多因素方差分析使用SPSS软件进行多因素方差分析一、引言多因素方差分析是一种重要的统计方法,用于分析多个自变量对因变量的影响。
它可以帮助研究人员确定不同因素对研究对象的差异产生的影响,以及这些因素之间是否存在交互作用。
SPSS软件是一款功能强大且易于使用的统计分析工具,可以帮助用户在进行多因素方差分析时快速、准确地得出结果。
本文将介绍使用SPSS软件进行多因素方差分析的步骤,并通过一个案例来具体说明。
二、SPSS软件介绍SPSS(Statistical Package for the Social Sciences)是一款专业的统计分析软件,被广泛应用于社会科学、医学、商业等领域。
它提供了丰富的统计方法和分析工具,并具备数据清洗、可视化、报告生成等功能。
在多因素方差分析中,SPSS 可以帮助用户进行方差分析表的生成、方差分析的可视化、方差齐性检验和事后比较等操作,大大简化了分析过程。
三、多因素方差分析的步骤1. 数据准备:将需要分析的数据录入SPSS软件,并确定自变量和因变量的测量水平。
一般自变量为定类变量,而因变量可以是定量或定类变量。
2. 方差分析表的生成:选择“分析”菜单中的“一元方差分析”选项,然后将因变量添加到依赖变量框中,将自变量添加到因子框中。
接下来,点击“选项”按钮设置参数,如设定显著性水平和置信区间。
点击“确定”后,SPSS会生成方差分析表。
3. 方差分析的可视化:在方差分析表中,用户可以查看各个因素的主效应和交互作用,以及统计指标如F值、p值等。
此外,SPSS还提供了绘制效应图、交互作用图等功能,帮助用户更直观地理解分析结果。
4. 方差齐性检验:方差齐性检验用于验证因变量的变异是否在各组间具有相同的方差。
SPSS软件可以通过选择“分析”菜单中的“Compare Means”选项,进而进行多个组间方差齐性检验。
5. 事后比较:当发现方差分析存在显著差异时,需要进一步进行事后比较以确定差异所在。
spss多因素方差分析报告例子
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction 的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
spss 方差分析(多因素方差分析)实验报告

大学经济管理学院学生实验报告实验课程名称:统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质:演示性 验证性综合性设计性实验项目名称方差分析(多因素方差分析)指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法,并能够解释软件运行结果。
二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例:为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数据。
销售量日期周一至周三周四至周五周末地区一5000 6000 40006000 8000 30004000 7000 5000地区二700080008000 500050006000500060004000地区三300020004000 600060005000800090006000(1)选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。
在SPSS输入数据。
(2)利用多因素方差分析法,分析不同地区和不同日期对该商品的销售是否产生了显著影响。
1. 选择菜单Analyze,General Linear Model,Univariate;2. 指定观测变量销售额到Dependant Variable框中;3. 指定固定效应的控制变量到Fixed Factors框中,4. OK,得到分析结果。
(3)地区和日期是否对该商品的销售产生了交互影响?若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
三、实验结论(包括SPSS输出结果及分析解释)。
spss方差分析操作示范步骤例子

第五节方差分析的SPSS操作一、完全随机设计的单因素方差分析1.数据采用本章第二节所用的例1中的数据,在数据中定义一个group变量来表示五个不同的组,变量math表示学生的数学成绩。
数据输入格式如图6-3(为了节省空间,只显示部分数据的输入):图6-3 单因素方差分析数据输入将上述数据文件保存为“6-6-1.sav”。
2.理论分析要比较不同组学生成绩平均值之间是否存在显著性差异,从上面数据来看,总共分了5个组,也就是说要解决比较多个组(两组以上)的平均数是否有显著的问题。
从要分析的数据来看,不同组学生成绩之间可看作相互独立,学生的成绩可以假设从总体上服从正态分布,在各组方差满足齐性的条件下,可以用单因素的方差分析来解决这一问题。
单因素方差分析不仅可以检验多组均值之间是否存在差异,同时还可进一步采取多种方法进行多重比较,发现存在差异的究竟是哪些均值。
3.单因素方差分析过程(1)主效应的检验假如我们现在想检验五组被试的数学成绩(math)的均值差异是否显著性,可依下列操作进行。
①单击主菜单Analyze/Compare Means/One-W ay Anova…,进入主对话框,请把math选入到因变量表列(Dependent list)中去,把group选入到因素(factor)中去,如图6-4所示:图6-4:One-Way Anova主对话框②对于方差分析,要求数据服从正态分布和不同组数据方差齐性,对于正态性的假设在后面非参数检验一章再具体介绍;One-Way Anova可以对数据进行方差齐性的检验,单击铵钮Options,进入它的主对话框,在Homogeneity-of-variance项上选中即可。
设置如下图6-5所示:图6-5:One-Way Anova的Options对话框点击Continue,返回主对话框。
③在主对话框中点击OK,得到单因素方差分析结果4.结果及解释(1)输出方差齐性检验结果Test of Homogeneity of VariancesMATHLevene Statistic df1 df2 Sig.1.238 4 35 .313上表结果显示,Levene方差齐性检验统计量的值为1.238,Sig=0.313>0.05,所以五个组的方差满足方差齐性的前提条件,如果不满足方差齐性的前提条件,后面方差分析计算F统计量的方法要稍微复杂,本章我们只考虑方差齐性条件满足的情况。
SPSS多因素方差分析(二类参照)

体育统计与SPSS读书笔记(八)—多因素方差分析(1)具有两个或两个以上因素的方差分析称为多因素方差分析。
多因素是我们在试验中会经常遇到的,比如我们前面说的单因素方差分析的时候,如果做试验的不是一个年级,而是多个年纪,那就成了双因素了:不同教学方法的班级,不同年级。
如果再加上性别上的因素,那就成了三因素了。
如果我们把实验前和试验后的数据用一个时间的变量来表示,那又多了一个时间的因素。
如果每个年级都是不同的老师来上,那又多了一个老师的因素,等等等等,所以我们在设计试验的时候都要进行充分考虑,并确定自己只研究哪些因素。
下面用例子的形式来说说多因素方差分析的运用。
还是用前面说单因素的例子,前面的例子说了只在五年级抽三个班进行不同教学方法的试验,现在我们还要在初二和高二各抽三个班进行不同教学方法的试验。
形成年级和不同教学法班级双因素。
分析:1.根据实验方案我们划出双因素分析的表格,可以看出每个单元格都是有重复数据(也就是不只一个数据),年级不同教学方法的班级定性班定量班定性定量班五年级(班级每个人)(班级每个人)(班级每个人)初中二年级(班级每个人)(班级每个人)(班级每个人)高中二年级(班级每个人)(班级每个人)(班级每个人)2.因为有重复数据,所以存在在数据交互效应的可能。
我们来看看交效应的含义:如果在A因素的不同水平上,B因素对因变量的影响不同,则说明A、B两因素间存在交互作用。
交互作用是多因素实验分析的一个非常重要的内容。
如因素间存在交互作用而又被忽视,则常会掩盖因素的主效应的显著性,另一方面,如果对因变量Y,因素A与B之间存在交互作用,则已说明这两个因素都Y对有影响,而不管其主效应是否具有显著性。
在统计模型中考虑交互作用,是系统论思想在统计方法中的反映。
在大多数场合,交互作用的信息比主效应的信息更为有用。
根据上面的判断。
根据上面的说法,我也无法判断是否有交互作用,不像身高和体重那么直接。
这里假设他们之间有交互作用。
(完整word版)SPSS方差分析案例实例

SPSS第二次作业——方差分析1、案例背景:在一些大型考试中,为了保证结果的准确和一致性,通常针对一些主观题,都采取由多个老师共同评审的办法。
在评分过程中,老师对学生的信息不可见,同时也无法看到其他评分,保证了结果的公正性。
然而也有特殊情况的发生,导致了成绩的不稳定,这就使得对不同教师的评分标准考察变得十分必要。
2、案例所需资料及数据的获取方式和表述,变量的含义以及类型:所需资料:抽样某地某次考试中不同教师对不同的题目的学生成绩的评分;获取方式:让一组学生前后参加四次考试,由三位教师进行批改后收集数据;变量含义、类型:一份试卷的每道主观题由三名教师进行评定,3个教师的评定结果可看成事从同一总体中抽出的3个区组,它们在四次评定的成绩是相关样本。
表1如下:3、分析方法:用方差分析的方法对四个总体的平均数差异进行综合性的F检验。
4、数据的检验和预处理:a) 奇异点的剔除:经检验得无奇异点的剔除;b) 缺失值的补齐:无;c) 变量的转换(虚拟变量、变量变换):无;d) 对于所用方法的假设条件的检验:进行正态性和方差齐性的检验。
✓正态性,用QQ图进行分析得下图:得到近似满足正态性。
✓对方差齐性的检验:用SPSS对方差齐性的分析得下表:Test of Homogeneity of Variances分数Levene Statistic df1 df2 Sig..732 2 9 .508易知P〉0.05,接受方差齐性的假设。
5、分析过程:a) 所用方法:单因素方差分析;方差分析中的多重比较。
b) 方法细节:●单因素方差分析第一步,提出假设:H0:μ1=μ2=μ3;(教师的评定基本合理,即均值相同)H1:μi(i=1,2,3)不全相等;(教师的评定不够合理,均值有差异)第二步,为检验H0是否成立,首先计算以下统计量:1,计算水平均值及总体均值:表2 三位教师评选结果的均值2-计算平方和和自由度:总离差平方和:SST=211)-(∑∑==ki n j iij x x =16.947,自由度为n-1=11组内离差平方和:SSE=211)x -(i ∑∑==ki n j iij x =16.275,自由度为n-k=9组间平方和:SSA=211)-(∑∑==ki n j ii x x =0.672,自由度为k-1=23-计算均方:MSA=1SSA -k =0.336MSE=kn -SSE =1.8084-计算检验的统计量F : F=MSEMSA ~F(k-1,n-k) 计算F=0.186将结果汇集到表中:第三步,统计决断:查F 值表得F 0.01(2,11)=7.21>0.186。
spss多因素方差分析例子

1, data0806-height 是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打 开 spss 软 件 , 打 开 data0806-height 数 据 , 点 击 Analyze->General Linear Model->Univariate 打开:把 plot 和 species 送入 Fixed Factor(s) ,把 height 送入 Dependent Variable ,点击 Model 打开:选择 Full factorial , Type III Sum of squares , Include intercept in model (即 全部默认选项) ,点击 Continue 回到 Univariate 主对话框,对其他选项卡不做任何选 择, 结果输出:因无法计算 ???? ??rror ,即无法分开 ???? intercept的影响,无法进行方差分析,重新 Analyze->General Linear Model->Univariate 打开:选择好 Dependent Variable 和 Fixed Factor(s) 点击Custom,把主效应变量 species 和plot 送入 Model 框,点击 Continue 回到Univariate 主对话框,点击 Plots : 把 date 送入 Horizontal Axis ,把 depth 送入 Separate Lines ,点击 Add ,点击 Continue 回到 Univariate 对话框,点击 Options :把 OVERALL,species, plot 送入 Display Means for 框,选择 Compare main effects , Bonferroni ,点击 Continue 回到 Univariate 对话框,输出结果:可以看到: SS species =, df species =7, MS species= ;SS plot =, df plot =7, MS plot= ;SS error =, df error =14, MS error= ;Fspecies= , p=<;Fplot=,p=<;所以故认为在 5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
SPSS软件的应用——多元统计分析

多元统计分析学院:理学与信息科学学院专业班级:信息与计算科学 2012级01 班姓名:韩祖良(20125991)****:***2015 年6月1日作业1 方差分析三组贫血患者的血红蛋白浓度(%,X1)及红细胞计数(万/mm3,X2)如下表:1、方差分析的前提条件要求各总体服从正态分布,请给出正态分布的检验结果,另要求各总体方差齐性,给出方差齐性检验结果。
2、检验三组贫血患者的指标x1,x2间是否有显著差异,进行多元方差分析。
如果有显著差异,分析三组患者间x1指标是否有显著差异,x2指标是否有显著差异?3、最后进行两两比较,给出更具体的分析结果。
4. 画出三组患者x1,x2两指标的均值图。
答:1.将所需分析数据输入到SPSS中,首先判断各总体是否服从正态分布:对文件进行拆分:数据→拆分文件→按组组织输出→确定。
然后进行正态性检验:文件→描述统计→探索,在绘制对话框中,选择按因子水平分组和带检验的正态图,最后单击确定按钮。
最后得出结果如图(1),(2),(3)所示:表(1)由表(1)可以看出,A组的X1指标的Sig=0.907,X2的Sig=0.914,在检验标准为0.05的条件下,接受H0,拒绝H1,故得A组服从正态分布。
表(2)由表(2)可以看出,B组的X1指标的Sig=0.406,X2的Sig=0.765,在检验标准为0.05的条件下,接受H0,拒绝H1,故得B组服从正态分布。
表(3)由表(3)可以看出,C组的X1指标的Sig=0.337,X2的Sig=0.839,在检验标准为0.05的条件下,接受H0,拒绝H1,故得C组服从正态分布。
再检验各总体是否满足方差齐性:首先取消文件的拆分,对所有个案进行分析。
然后进行方差齐性检验:分析→一般线性模型→多变量,在选项对话框中,选择方差齐性检验,所得结果如下:表(4)上表是对协方差阵相等的检验,由Sig=0.670>0.05,故在显著性水平为0.05的条件下,接受H0,拒绝H1,即观测到的因变量的协方差矩阵在所有组中均相等,可得三组符合方差齐性。
spss多因素方差分析报告例子
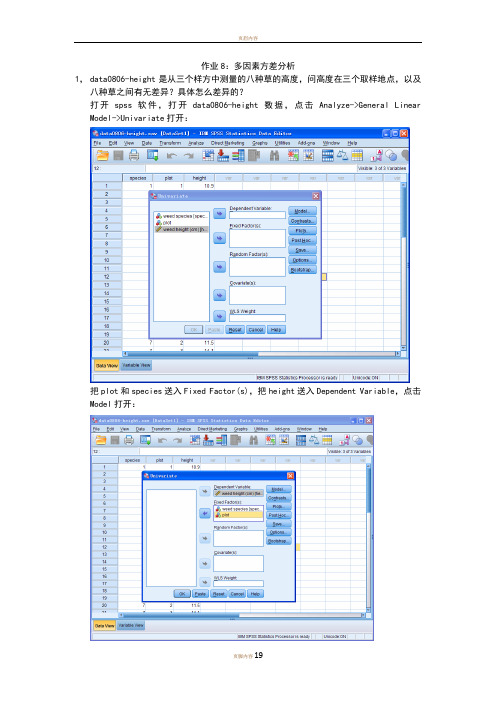
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction 的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
多元方差分析

多元方差分析在SPSS软件的数据窗口依次定义变量并输入数据,由题可知数据来自三个不同的总体,下面对不同组的贫血患者比较其血红蛋白浓度及红细胞计数是否存在差异。
一、对总体进行多元正态分布检验首先将数据进行分组,然后通过SPSS软件分析—描述统计—探索得到检验结果如下:上述两个表给出了对每一个变量进行正态检验的结果,由表可以看出血红蛋白浓度和红细胞计数的显著性水平均大于0.05,即接受原假设,所以这两个变量均遵从正态分布。
下面判断总体是否满足方差齐性:上表是对协方差阵相等的检验,检验统计量是Box’s M,由Sig.值可以看出,0.670显著的大于0.05,所以在0.05的显著性水平下接受协方差阵相等的原假设。
即可以认为三组的协方差阵是相等的,符合方差齐性。
二、多元方程分析上表为多变量检验表,该表给出了几个统计量,显著性水平均为0.001显著的小于0.05,拒绝原假设,故无论从哪个统计量来看,三组不同患者的血红蛋白浓度和红细胞计数这两个指标间均存在显著差异。
下面分别分析三组患者间x1指标是否有显著差异,x2指标是否有显著差异,结果如下:由上表GROUP行可以看到:血红蛋白浓度和红细胞计数这两个指标的显著性水平分别为0.003和0.002均小于0.05,这说明三个组在血红蛋白浓度和红细胞计数这两个指标上均有显著差异。
三、对各组进行两两比较,给出更具体的分析结果通过软件操作得到比较结果如下表:由表中数据可以看出:①在血红蛋白浓度这个指标上A组和B组、B组和C组的显著性水平均小于0.05,拒绝原假设,故A组和B组、B组和C组在血红蛋白浓度这个指标上有显著差异,且B组的血红蛋白浓度显著高于A组和C组。
②在红细胞计数这个指标上A组和C组的显著性水平为0.014小于0.05,故A组和C组在红细胞计数指标上有显著差异,且C组的红细胞计数远远高于B 组。
四、画出三组患者x1,x2两指标的均值图由软件绘图得到均值图如下:由上图可以看出,A组与B组、C组与B组的红蛋白浓度有显著差异,而A组与C组的血红蛋白浓度没有显著差别,大致在一水平线上。
spss相关分析案例多因素方差分析
Dependent Variable
人均副食支出(元/人)
人均日用杂品支出(元/人)
人均衣着支出(元/人)
Level 1 vs。Level 3
Contrast Estimate
38.213
2.437
4。124
Hypothesized Value
0
0
0
Difference(Estimate - Hypothesized)
表五
Multivariate Test Results
Value
F
Hypothesis df
Error df
Sig.
Pillai’s trace
.465
2。725
6。000
54.000
.022
Wilks’ lambda
.555
2.970a
6.000
52。000
。014
Hotelling's trace
Sig.
.668
。343
。638
95% Confidence Interval for Difference
Lower Bound
—28。967
—3。642
—10.797
Upper Bound
18.849
1。309
17。331
a. Reference category = 3
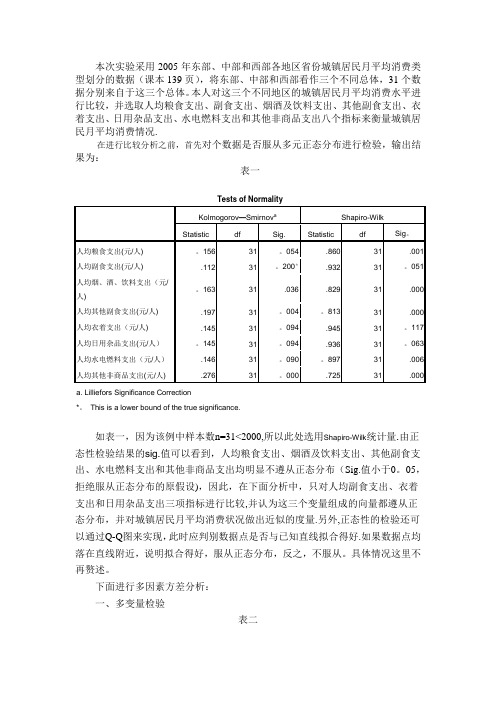
如表四,在0。05显著水平下,东部和西部的人均副食支出(Sig.值为0.001)和日用杂品支出(Sig.值为0.036)指标有明显差别(小于0。05,拒绝原假设),而在人均衣着支出(Sig。值为0.517)指标上没有明显的差别。并且东部的人均副食支出、衣着支出和日用杂品支出三项指标均高于西部地区,说明东部的城镇居民月平均消费水平较西部来说,高出很多,符合实际的情况。另外,中部和西部的人均副食支出、衣着支出和日用杂品支出(Sig。值分别为0.668、0.343、0。638,均大于显著水平)三个指标均无明显差别,但中部的人均副食支出和日用杂品支出指标低于西部地区,人均衣着支出指标高于西部,说明中、西部的城镇居民月平均消费水平差不多,但消费结构有差异,符合实际的情况。
spss多因素方差分析报告报告材料例子
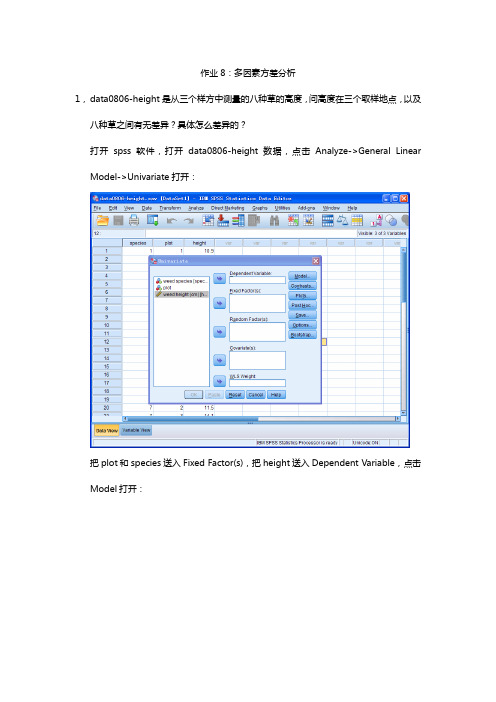
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
spss多因素方差分析报告例子
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction 的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
spss超详细操作两因素多元方差分析(two-way manova)

SPSS超详细操作:两因素多元方差分析(Two-way Manova)每种方差分析的应用场景,以及该如何进行SPSS操作和解读结果,各位伙伴请点击相应的文章链接查看~~今天,我们再来介绍一种统计方法:两因素多元方差分析(Two-way Manova)。
一、问题与数据某研究者想研究三种干预方式(regular—常规干预;rote—死记硬背式干预;reasoning—推理式干预)对学生学习成绩的影响。
研究者记录了学生两门考试的成绩:文科成绩(humanities_score)和理科成绩(science_score)。
另外,基于之前的知识,研究者假设干预方式对男女两种性别学生的效果可能不同。
换言之,研究者想知道不同干预方式对学习成绩的影响在男女学生中是否不同。
也就是说,干预方式和性别两个自变量之间是否存在交互作用(interaction effect)。
注:交互作用是指某一自变量对因变量的效应在另一个自变量的不同水平会不同。
在本例中,就是要比较①男性中干预方式对学习成绩的影响和②女性中干预方式对学习成绩的影响。
这两个效应就成为单独效应(simple main effects),也就是说,单独效应是指在一个自变量的某一水平,另一个自变量对因变量的影响。
因此,交互作用也可以看做是对单独效应间是否存在差异的检验。
在本研究中,共有三个效应:性别的主效应;干预方式的主效应;性别和干预方式的交互作用。
研究者选取30名男学生和30名女学生,并将其随机分配到三个干预组中,每个干预组中共有10名男学生和10名女学生。
部分数据如下:二、对问题的分析使用两因素多元方差分析法进行分析时,需要考虑10个假设。
对研究设计的假设:1. 因变量有2个或以上,为连续变量;2. 有两个自变量,为二分类或多分类变量;3. 各观察对象之间相互独立;对数据的假设:4. 自变量的各个组内,各因变量间存在线性关系;5. 自变量的各个组内,各因变量间没有多重共线性;6. ①没有单因素离群值(univariate outliers)与②多因素离群值(multivariate outliers):单因素离群值是指自变量的各个组中因变量是否是离群值;多因素离群值是指每个研究对象(case)的各因变量组合是否是一个离群值;7. 各因变量服从多元正态分布;8. 样本量足够;9. 自变量的各组观察对象之间因变量的方差协方差矩阵相等;10. 每个因变量在自变量的各个组中方差相等。
《2024年使用SPSS软件进行多因素方差分析》范文

《使用SPSS软件进行多因素方差分析》篇一一、引言在社会科学、医学、生物科学等众多领域中,我们常常需要探讨多个因素对某一结果变量的影响程度。
为了深入分析这些因素间的相互作用和差异,我们通常会采用多因素方差分析(Multivariate Analysis of Variance,MANOVA)方法。
本范文将介绍如何使用SPSS软件进行多因素方差分析,以及该方法的理论背景、适用情境、数据处理流程等。
二、理论背景多因素方差分析是一种统计学方法,旨在同时考察多个因素对某一结果变量的影响。
它通过对每个因素及各因素间交互作用进行假设检验,分析因素间是否存在显著差异,以及这种差异是否与结果变量相关。
SPSS软件提供了进行多因素方差分析的工具,使研究人员能够便捷地开展相关研究。
三、方法与材料本研究以某公司的销售数据为例,探讨销售人员技能、公司市场策略及客户满意度对销售业绩的影响。
研究假设包括:销售人员技能与市场策略、销售人员技能与客户满意度以及市场策略与客户满意度之间存在交互作用,共同影响销售业绩。
数据来源:某公司销售数据集,包括销售人员技能、市场策略、客户满意度和销售业绩等变量。
软件:SPSS软件(版本号:xxx)四、实验设计本实验采用多因素方差分析方法,以销售人员技能、市场策略和客户满意度为自变量,销售业绩为因变量。
首先,对数据进行预处理,包括缺失值处理、异常值处理等;然后,进行多因素方差分析,考察各因素及交互作用对销售业绩的影响;最后,根据分析结果得出结论。
五、数据分析与结果1. 数据预处理在SPSS软件中导入数据后,首先对数据进行描述性统计分析,了解数据的分布特征。
然后,对数据进行缺失值和异常值处理,确保数据质量。
2. 多因素方差分析在SPSS软件中,选择“Analyze”菜单下的“General Linear Model”选项,然后选择“Multivariate”进行多因素方差分析。
在分析过程中,需要设定因变量和自变量,以及交互项。
《2024年使用SPSS软件进行多因素方差分析》范文

《使用SPSS软件进行多因素方差分析》篇一一、引言多因素方差分析是一种统计分析方法,它通过考察多个因素及其交互作用对一个因变量的影响,以评估这些因素之间的关系。
随着科技和大数据的发展,越来越多的学者开始关注和采用这种统计分析方法。
本范文旨在详细阐述如何使用SPSS软件进行多因素方差分析。
二、方法本文将通过以下步骤进行多因素方差分析:1. 数据收集与整理:收集研究所需的数据,并进行整理,确保数据的准确性和完整性。
2. 导入SPSS软件:将数据导入SPSS软件中,以便进行后续的统计分析。
3. 描述性统计分析:对数据进行描述性统计分析,以了解数据的分布情况和基本特征。
4. 多因素方差分析:运用SPSS软件进行多因素方差分析,探讨多个因素对因变量的影响及其交互作用。
三、数据分析本部分以一个具体的研究案例为例,详细介绍如何使用SPSS 软件进行多因素方差分析。
1. 导入数据:将数据导入SPSS软件中,确保数据格式正确无误。
2. 描述性统计分析:对数据进行描述性统计分析,包括均值、标准差、最大值、最小值等统计量。
通过对数据的初步分析,我们可以了解数据的分布情况和基本特征。
3. 多因素方差分析:选择“Analyze”菜单中的“General Linear Model”选项,然后选择“Univariate”子选项进行多因素方差分析。
在设置中,选择因变量和自变量,以及需要进行交互的变量。
4. 结果解读:查看SPSS输出的结果,包括每个因素的均值、标准差、检验结果等。
通过结果解读,我们可以了解各因素对因变量的影响程度以及因素之间的交互作用。
四、结果与讨论根据SPSS软件输出的结果,我们可以得出以下结论:1. 各个因素对因变量的影响程度不同,其中某些因素的影响更为显著。
这表明在研究过程中需要重点关注这些因素。
2. 某些因素之间的交互作用对因变量的影响不可忽视。
这提示我们在研究过程中需要综合考虑各因素之间的相互作用。
3. 通过多因素方差分析,我们可以更全面地了解各因素对因变量的影响及其交互作用,为制定有效的研究策略提供依据。
SPSS教程-多因素方差分析(优质参考)
多因素方差分析多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS调用“Univariate”过程,检验不同水平组合之间因变量均数,由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用,也可以分析因素之间的交互作用,以及分析协方差,以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来,且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量,协变量与因变量不彼此独立。
因素变量是分类变量,可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。
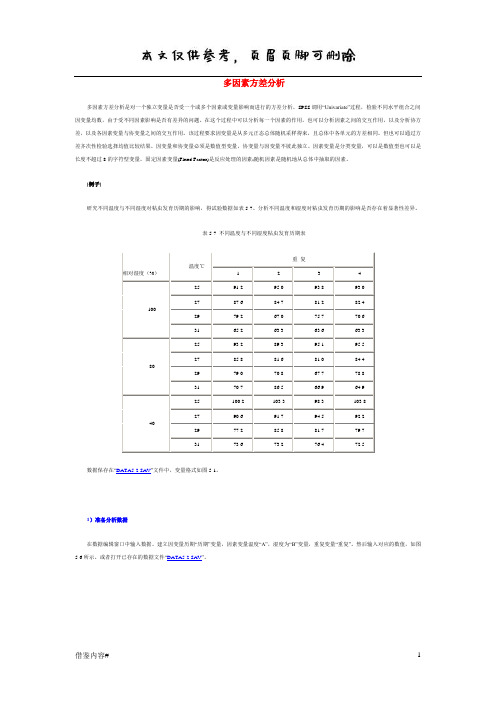
[例子]研究不同温度与不同湿度对粘虫发育历期的影响,得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表相对湿度(%)温度℃重复1 2 3 4100 25 91.2 95.0 93.8 93.0 27 87.6 84.7 81.2 82.4 29 79.2 67.0 75.7 70.6 31 65.2 63.3 63.6 63.380 25 93.2 89.3 95.1 95.5 27 85.8 81.6 81.0 84.4 29 79.0 70.8 67.7 78.8 31 70.7 86.5 66.9 64.940 25 100.2 103.3 98.3 103.8 27 90.6 91.7 94.5 92.2 29 77.2 85.8 81.7 79.7 31 73.6 73.2 76.4 72.5数据保存在“DATA5-2.SAV”文件中,变量格式如图5-1。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量,因素变量温度“A”,湿度为“B”变量,重复变量“重复”。
