2011年南通市中考数学试卷
南通数学中考卷.docx

南通市2011年初中毕业、升学考试试卷数学—— --------------- 注重事项考生在答HttWU*阅读*注重事项:】.本试卷共6萸.椅分为150分,考■试时间为,2。
分的.与试结电后,请捋奉试卷和答瞠卡一, 并交回.2.答题前,请务必将自己的姓名,考试证号用°-5*米黑色字卷的签字笔填写在试卷及答题 卡上指定的位置・ 〔3.答案必须按妾京填涂•书写在答矍卡上,在试卷、草暗我上芬题-律无数.一、选择题(本大题共10小题.每小鹿3分.共30分.在每小睑治出的四个逸项中,检有一项是符合噎目要求的.谓将正嘛小的字2代号坟涂在巷鼠飞学区您里上)1. 如果60 m 表示"向北走60 m".W 么"向南走40 m”可以&小为4. 下列长度的三条线段,不能组成三角形的是• ・ 3.计算国的结果.足A, 120,C. 100,A. ±3^3B. 3V35. 巳知:如图,AB 〃CD.,DCE-80",JH/BEF 的度救为B. 110*A. — 20 mB. — 40 tn C, 20 m2. 下面的图形中.既是轴对称图形又是中心对林图形的矩A. 3,8,4B. 4・9,6C. 15.20.86.下列水平放置的几何体中.俯视(8压蛆彪的是D. 68.如ffi.OO 的弦AB-8.M 是AB 的中点,且OM-3.R3O 的半径等于A. 8B. 4D. 59.甲、乙购人沿相同的路线由A 地到B 地勾速前进.A.J3两地间的路程为20千米.他们耕史 的路程为式单位:千米).甲出发后的时间为可单位:小时),甲、乙前进的路程与时闻的词数 图象如图所示.根据国象信息,F 列说法正确的是A.C. 甲的速度第4千米/小时 乙的速度是10千米/小时乙比甲晚出发1小时 甲比乙晚到B 地3小时10.设 m>n>0.E : + ”:=4,e.SM 竺二^的ff!等于 ranB. V3 Q 76二、填空通(本大题共8小48.每小慝3分,共24分.不需写出解答过程.请把答案直接填写在 旨革专单度但星上)11. 巳知匕『・20•.则/<,的余角等于 ▲ 度.12. 计算:而一搪=▲.*+213.函数岩中,自变量N 的取值范圈是 A.14.七位女生的体直(单位:kg )分别是36.42,38.42.35.45.40,则这七位女生体直的中位二▲ kg.7-巳如3是关于工的方fBx l -5x+c-0的一个机.财这个方fg 的另一个根是A. —2B. 215. 如图,矩形旋片ABCD 中,AB-2 cm,点E 在BC 上.且 AAE-EC.若将蛾片沿AE 折建.点B 恰好与AC 上的威8'重合.则 AC- A erm16. 分解珥式;3m(2x —y)T —3mn : =-▲ 17.如图.测量河竟AB (假设河的两岸平行),在C^MWZACB = 3O\D AMftZADB-60..又CD-60 m.J«河宛AB 为 ▲ m 《结果保留根号).18.巳知;如图,三个半06依次相外切•它们的08心都在X 袖的正半轴上.并与直蟆y-yx 相 切.设牛08 G 、半跚C :,半IM C,的半径分别是r.r.r ,购当r = 1时,,=.▲ •rt /三、解答题(本大题共10小题.共96分.靖在内作答.解答时应写出必要的文字说明、证明过程或演算步骤)19. (本小厩滴分10分)(1)计算 2,+(-1)4 +('/?-2)0-|-3| I(2〉先化简.再求值:。
2011年南通数学中考卷

专业课原理概述部分一、选择题(每题1分,共5分)1. 若a是实数,且(a1)²=0,则a的值为()A. 0B. 1C. 1D. 22. 下列函数中,既是奇函数又是偶函数的是()A. y=x³B. y=x²C. y=|x|D. y=cos(x)3. 已知等差数列{an}的公差为3,且a3=7,则a1的值为()A. 1B. 4C. 7D. 104. 在直角坐标系中,点P(2, 2)关于原点的对称点是()A. (2, 2)B. (2, 2)C. (2, 2)D. (2, 2)5. 下列命题中,正确的是()A. 任何两个实数的和都是一个实数B. 任何两个实数的乘积都是一个实数C. 任何两个实数的商都是一个实数D. 任何两个实数的差都是一个实数二、判断题(每题1分,共5分)1. 若函数f(x)在区间(a,b)上单调递增,则f'(x)>0。
()2. 两个平行线的斜率相等。
()3. 等差数列的通项公式为an=a1+(n1)d。
()4. 向量a与向量b垂直的充分必要条件是a·b=0。
()5. 任何两个复数都可以进行四则运算。
()三、填空题(每题1分,共5分)1. 已知函数f(x)=x²2x+1,则f(x)的零点为______。
2. 若向量a=(3,4),则向量a的模长是______。
3. 已知等差数列{an}的公差为2,a1=1,则a5的值为______。
4. 设复数z=2+3i,则z的共轭复数为______。
5. 若函数f(x)=|x1|,则f(x)在x=1处的导数为______。
四、简答题(每题2分,共10分)1. 简述实数与虚数的关系。
2. 解释等差数列与等比数列的区别。
3. 如何判断一个函数的单调性?4. 什么是向量的数量积(点积)?5. 简述复数乘法的运算规律。
五、应用题(每题2分,共10分)1. 已知函数f(x)=x²4x+3,求f(x)在区间[0, 3]上的最大值和最小值。
2011年南通数学中考卷

2011年南通市初中毕业、升学考试数学试卷一、选择题(每题3分,共30分)1. 下列各数中,比3大且与|3|相等的是()A. 3B. 3C. |3|D. |3|2. 下列图形中,既是轴对称图形又是中心对称图形的是()A. 等边三角形B. 矩形C. 直角三角形D. 平行四边形3. 下列计算正确的是()A. (3)² = 9B. (3)³ = 9C. 3² = 9D. (3)² = 94. 下列各式中,能用平方差公式分解的是()A. x² + 2x + 1B. x² 2x + 1C. x² 5x + 6D. x² 95. 下列关于x的方程中,属于一元一次方程的是()A. 2x + 3 = 5B. 2x² + 3x = 5C. 2x + 3y = 5D. 1/x = 56. 下列图形中,是正方体的展开图的是()(此处插入正方体展开图的选项)7. 在平面直角坐标系中,点(2,3)关于原点对称的点的坐标是()A. (2, 3)B. (2, 3)C. (2, 3)D. (2, 3)8. 下列各式中,是二次根式的是()A. √9B. √9C. √(x² 5)D. √(x² + 5)9. 下列函数中,是正比例函数的是()A. y = 2x + 1B. y = x²C. y = 2/xD. y = 2x10. 下列关于x的不等式中,解集是全体实数的是()A. x > 0B. x < 0C. x ≠ 0D. x ≥ 0二、填空题(每题3分,共30分)11. 计算:(2)×(3)= ______。
12. 已知a = 2,b = 3,则a² + b² = ______。
13. 已知函数y = (x + 1)²,当x = 3时,y的值为 ______。
2011年南通中考数学试卷
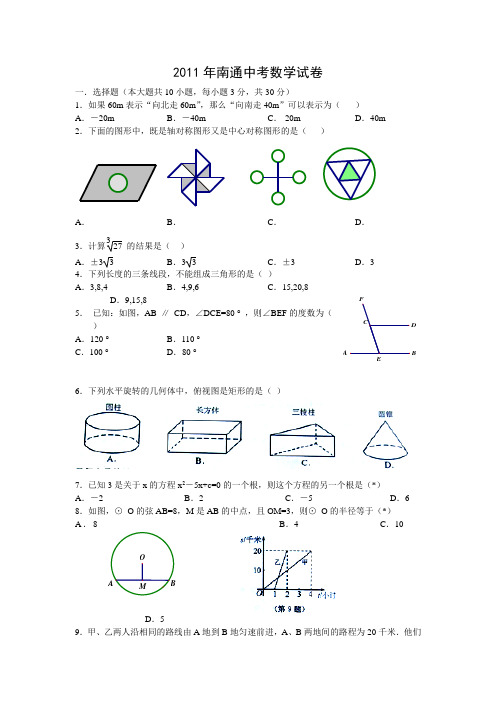
ABCDEF OABM2011年南通中考数学试卷一.选择题(本大题共10小题,每小题3分,共30分) 1.如果60m 表示“向北走60m ”,那么“向南走40m ”可以表示为( )A .-20mB .-40mC . 20mD .40m2.下面的图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .3.计算327 的结果是( )A .±3 3B .3 3C .±3D .34.下列长度的三条线段,不能组成三角形的是( ) A .3,8,4 B .4,9,6 C .15,20,8 D .9,15,85. 已知:如图,AB ∥ CD ,∠DCE=80 ° ,则∠BEF 的度数为( ) A .120 ° B .110 ° C .100 ° D .80 °6.下列水平旋转的几何体中,俯视图是矩形的是( )7.已知3是关于x 的方程x 2-5x+c=0的一个根,则这个方程的另一个根是(*) A .-2 B .2 C .-5 D .6 8.如图,⊙ O 的弦AB=8,M 是AB 的中点,且OM=3,则⊙ O 的半径等于(*) A .8 B .4 C .10D .59.甲、乙两人沿相同的路线由A 地到B 地匀速前进,A 、B 两地间的路程为20千米.他们ABC DEB'前进的路程为s (单位:千米),甲出发后的时间为t (单位:小时),甲、乙前进的路程与时间的函数图像如图所示,根据图像信息,下列说法正确的是(*) A .甲的速度 4千米/小时 B .乙的速度 10千米/小时 C .乙比甲晚出发1小时 D .甲比乙晚到B 地3小时10.设m > n > 0, m 2+n 2=4mn,则m 2-n 2mn的值等于(*)A .2 3B . 3C . 6D .3二.填空题(本大题共8小题,每小题3分,共24分) 11.已知∠α ° ,则∠α的余角等于 度. 12.计算:8 - 2 = .13.函数y=x+2x -1中,自变量x 的取值范围是 .14.七位女生的体重(单位:Kg )分别是36、42、38、42、35、45、40,则这七位女生的体重的中位数为 Kg .15.如图,矩形纸片A BCD ,AB=2cm ,点E 在BC 上,且AE=EC ,若将纸片折叠,点B 恰好与AC 上的点B ′重合,则AC= cm . 16.分解因式:3m(2x -y)2-3mn 2= . 17.如图,测量河宽AB (假设河的两岸平行),在C 点测得∠ ACB=30 ° ,点D 测得∠ ADB=60 ° ,又CD=60m ,则河宽AB 为 m (结果保留根号).18.已知:如图,三个半圆依次相外切,它们的圆心都在x 轴的正半轴上,并与直线y=33x 相切,设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3,则当r 1=1时,r 3=三.解答题(本大题共10小题,共96分) 19.(本小题满分10分) (1)计算:22+(-1)4+( 5 -2)0-︱-3︱(2)先化简,再求值: (4ab 3-8a 2b 2)÷ 4ab+(2a+b)(2a -b),其中a=2,b=1.20.(本小题满分8分) ABD C求不等式组⎩⎨⎧3x -6≥x -42x+1>3(x -1)的解集,并写出它的整数解.21.(本小题满分9分)某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类)并将调查的结果绘制成如下的两幅不完整的统计图.请根据图中提供的信息,解答下面的问题: (1)参加调查的学生共有 人;在扇形图中,表示“其他球类”的扇形的圆心角为 度 (2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有 人. 22.(本小题满分8分)如图,AM 为⊙ O 的切线,A 为切点,BD ⊥ AM 于点D ,BD 交⊙ O 于点C ,OC 平分∠ AOB .求∠ B 的度数.23.(本小题满分8分)列方程解应用题:在社区全民健身活动中,父子俩参加跳绳比赛,相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个? 24.(本小题满分8分)比较正五边形与正六边形,可以发现它们的相同点与不同点. 例如 它们的一个相同点:正五边形的各边相等,正六边形的各边也相等. 它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形. 请你再写出它们的两个相同点和两个不同点. 3060120其他球类足球乒乓球篮球12090600项目人数30CO A M B DAD 其他球类篮球中球乒乓球篮球 乒乓球 足球相同点:(1) (2) 不同点:(1) (2) 25.(本小题满分9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测,某次检测设有A 、B 两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力. (1) 求甲、乙、丙三名学生在同一处检测视力的概率;(2) 求甲、乙、丙三名学生中至少有两人在B 处检测视力的概率. 26.(本小题满分10分)已知:如图1,O 为正方形ABCD 的中心,分别延长OA 到点F ,OD 到点E ,使OF=2OA ,OE=2OD ,连接EF ,将△ FOE 绕点O 逆时针旋转α角得到△ F ′OE ′(如图2). (1) 探究AE ′与BF ′的数量关系,并给予证明;(2) 当α=30 ° 时,求证:△AOE ′为直角三角形.27.(本小题满分12分)已知A (1,0),B (0,-1),C (-1,2),D (2,-1),E (4,2)五个点,抛物线y=a(x -1)2+k(a > 0),经过其中三个点.(1) 求证:C 、E 两点不可能同时在抛物线y=a(x -1)2+k(a > 0)上. (2) 点A 抛物线y=a(x -1)2+k(a > 0)上吗?为什么? (3) 求a 与k 的值. 28.(本小题满分14分) 如图,直线l 经过点A (1,0),且与曲线y=m x (x > 0)交于点B (2,1),过点P (p ,p -1)(p > 1)作x 轴的平行线分别交曲线y=m x (x > 0)和y=-mx (x < 0)于M 、N 两点.(1) 求m 的值及直线l 的解析式;(2) 若点P 在直线y=2上,求证:△PMB ∽ △PNA ;(3) 是否存在实数p ,使得S △AMN =4S △APM ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.a E'F'O C D E F OC D ABB A xylOBA2011年南通中考数学试题参考答案1-10:B.C.D.A.C.B.B.D.C.A.11.7012. 213.x≠114. 4015.416.3m(2x-y+n)(2x-y-n)17.30 318.9.19.(1)3 (2)4a²-2ab, 12.20.1≤x<4, 整数解为:1、2、321.(1)300 36 (2)略(3)80022.60度23.父亲每分钟跳120个,儿子每分钟跳140个24.正五边形的各内角相等,正六边形各内角相等;正五边形是轴对称图形,正六边形也是轴对称图形.正五边形不能密铺,正六边形可以密铺;正五边形的各边不平行,正六边形的对边平行.25.1/4, 1/226.(1)用边角边证明△AOE’和△BOF’全等,即可证得AE’=BF’(2)取OE ’的中点G,得到等边△AOG ,等到∠AGO=60°,又由AG=E ’G 得到∠AE ’O =30°,从而得到∠OAE ’是90°,即为直角三角形。
江苏省2011年中考数学试题(13份含有解析)-7

盐城市二○一一年高中阶段教育招生统一考试数 学 试 题注意事项:1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上) 1.-2的绝对值是 A .-2 B .- 12C .2D .12【答案】C 。
【考点】绝对值。
【分析】根据绝对值的定义,直接得出结果。
2.下列运算正确的是A .x 2+ x 3= x 5B .x 4·x 2= x 6 C .x 6÷x 2 = x 3D .( x 2)3 = x 8【答案】B 。
【考点】同底幂的乘法。
【分析】42426x x x x +⋅==3.下面四个几何体中,俯视图为四边形的是【答案】D 。
【考点】几何体的三视图。
【分析】根据几何体的三视图,直接得出结果。
4.已知a -b =1,则代数式2a -2b -3的值是A .-1B .1C .-5D .5【答案】A 。
【考点】代数式代换。
【分析】()22323231a b a b --=--=-=-5.若⊙O 1、⊙O 2的半径分别为4和6,圆心距O 1O 2=8,则⊙O 1与⊙O 2的位置关系是 A .内切 B .相交 C .外切 D .外离A B CD【答案】B 。
【考点】圆心距。
【分析】126464<O O <-+∴ 两圆相交。
6.对于反比例函数y = 1x,下列说法正确的是A .图象经过点(1,-1)B .图象位于第二、四象限C .图象是中心对称图形D .当x <0时,y 随x 的增大而增大 【答案】C 。
【考点】反比例函数。
【分析】根据反比例函数性质,直接得出结果。
11--13南通中考数学

11--13年南通中考数学试题一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)1.下列各数中,小于﹣3的数是()A.2B.1C.﹣2 D.﹣42.计算(-x)2·x3的结果是()A.x5B.-x5C.x6D.-x63.下面的图形中,既是轴对称图形又是中心对称图形的是【】4.有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为()A.1B.2C.3D.45.已知x2+16x+k是完全平方式,则常数k等于【】A.64 B.48 C.32 D.166.下列水平放置的几何体中,俯视图是矩形的为【】7.如图,在△ABC中,∠C=70º,沿图中虚线截去∠C,则∠1+∠2=【】A.360ºB.250ºC.180ºD.140º8.若3是关于方程x2-5x+c=的一个根,则这个方程的另一个根是【】A.-2 B.2 C.-5 D.59.已知点A(-1,y1)、B(2,y2)都在双曲线y=3+2mx上,且y1>y2,则m的取值范围是【】A.D.圆柱长方体三棱柱圆锥A.m<0 B.m>0 C.m>-3 2D.m<-3210.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于【】A.8 B.4 C.10 D.5二、填空题(本大题共8小题,每小题3分,共24分.)11.单项式3x2y的系数为.12.计算:8-2=.13.某校9名同学的身高(单位:cm)分别是:163、165、167、164、165、166、165、164、166,则这组数据的众数为14.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是.15.如图,在矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=cm.16.如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),则不等式4x+2<kx+b<0的解集为.17.设m、n是一元二次方程x2+3x-7=0的两个根,则m2+4m+n=.18.如图,在▱ABCD中,AB=6cm,AD=9cm,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4cm,则EF+CF的长为cm.A BOMABB1CD三、解答题(本大题共8小题,共96分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤) 19.(11分)(1)计算:;(2)先化简,再求代数式的值:,其中m =1.20.(8分)求不等式组⎩⎨⎧3x -6≥x -42x +1>3(x -1)的解集,并写出它的整数解21.某水果批发市场将一批苹果分为A ,B ,C ,D 四个等级,统计后将结果制成条形图,已知A 等级苹果的重量占这批苹果总重量的30%. 回答下列问题:(1)这批苹果总重量为 kg ; (2)请将条形图补充完整;(3)若用扇形图表示统计结果,则C 等级苹果所对应扇形的圆心角为 度.22、在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?23、光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某次检测设有A 、B 两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.(1)求甲、乙、丙三名学生在同一处检测视力的概率;(2)求甲、乙、丙三名学生中至少有两人在B 处检测视力的概率.24、如图,△ABC 内接于⊙O ,AB 是⊙O 的直径,∠BAC =2∠B ,⊙O 的切线AP 与OC 的延长线相交于点P ,若P A =cm ,求AC 的长.25、如图,某测量船位于海岛P 的北偏西60º方向,距离海岛100海里的A 处,它沿正南方向航行一段时间后,到达位于海岛P 的西南方向上的B 处.求测量船从A 处航行到B 处的路程(结果保留根号).26、如图,已知直线l 经过点A (1,0),与双曲线y =m x(x >0)交于点B (2,1).过点P (p ,p -1)(p >1)作x 轴的平 行线分别交双曲线y =m x (x >0)和y =-mx(x <0)于点M 、N .(1)求m 的值和直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;OABlxy。
2005-2011年江苏省南通市中考数学试卷及答案(7套)

四川省南充市二○○八年高中阶段学校招生统一考试数学试卷(满分100分,考试时间90分钟)一、细心选一选(本大题共8个小题,每小题3分,共24分)每小题都有代号为A ,B ,C ,D 四个答案选项,其中只有一个是正确的,请把正确选项的代号填在相应的括号内.填写正确记3分,不填、填错或填出的代号超过一个记0分. 1.计算2(2)2--的结果是( )A .6-B .2C .2-D .6 2.如图,下列选项中不是正六棱柱三视图的是( )3.某地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:34,35,36,34,36,37,37,36,37,37(单位:℃),则这组数据的中位数和众数分别是( ) A .36,37 B .37,36 C .36.5,37 D .37,36.5 4.若1O 的半径为3cm ,2O 的半径为4cm ,且圆心距121cm OO =,则1O 与2O 的位置关系是( )A .外离B .内切C .相交D .内含5.已知数据13,7-,2.5,π) A .20% B .40% C .60% D .80% 6.“5·12”汶川大地震后,世界各国人民为抗震救灾,积极捐款捐物,截止2008年5月27日12时,共捐款人民币327.22亿元,用科学计数法(保留两位有效数字)表示为( ) A .103.2710⨯B .103.210⨯C .103.310⨯D .113.310⨯7.如图,AB 是O 直径,130AOC ∠=,则D ∠=( ) A .65B .25C .15D .35A .B .C .D .(第2题图)8.二次函数2y ax bx c =++的图像如图所示,则点c Q a b ⎛⎫ ⎪⎝⎭,在( ) A .第一象限B .第二象限C .第三象限D .第四象限二、认真填一填(本大题共4个小题,每小题3分,共12分)请将答案直接写在题中横线上.9.如图,四边形ABCD 中,E F G H ,,,分别是边AB BC CD DA ,,,的中点.请你添加一个条件,使四边形EFGH 为菱形,应添加的条件是 .10.根据下面的运算程序,若输入13x =y = .11.某商场为了解本商场的服务质量,随机调查了本商场的200名顾客,调查的结果如图所示.根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有 人.12.如图,从O 外一点P 引O 的两条切线PA PB ,,切点分别是A B ,,若8c m PA =,C 是AB 上的一个动点(点C 与A B ,两点不重合),过点C 作O 的切线,分别交PA PB ,于点D E ,,则PED △的周长是 .三、(本大题共2个小题,每小题6分,共12分) 13.计算:(第12题图) 输入x输出y2(0)y x x =-<221(01)y x x x =++<≤ 221(1)y x x x =+-≥(第10题图)(第8题图)x D BOAC(第7题图) A D HGC FBE (第9题图) A :满意 B :基本满意 C :说不清 D :不满意 (第11题图)11-14.化简2111xx x x⎛⎫-÷⎪--⎝⎭,并选择你最喜欢的数代入求值.四、(本大题共2个小题,每小题6分,共12分)15.如图,ABCD的对角线相交于点O,过点O任引直线交AD于E,交BC于F,则OE OF(填“>”“=”“<”),说明理由.16.桌面上放有质地均匀、反面相同的3张卡片,正面分别标有数字1,2,3,这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出1张,记下卡片上的数字后仍反面朝上放回洗匀,乙再从中任意抽出1张,记下卡片上的数字,然后将这两数相加.(1)请用列表或画树形图的方法求两数和为4的概率;(2)若甲与乙按上述方式做游戏,当两数之和为4时,甲胜,反之则乙胜;若甲胜一次得6分,那么乙胜一次得多少分,这个游戏才对双方公平?五、(本大题共2个小题,每小题8分,共16分)A E DOCFB(第15题图)17.在“5·12”汶川大地震的“抗震救灾”中,某部队接受了抢修映秀到汶川的“213”国道的任务.需要整修的路段长为4800m ,为了加快抢修进度,获得抢救伤员的时间,该部队实际工作效率比原计划提高了20%,结果提前2小时完成任务,求原计划每小时抢修的路线长度.18.如图,已知(4)A n -,,(24)B -,是一次函数y kx b =+的图像和反比例函数my x=的图像的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线AB 与x 轴的交点C 的坐标及三角形AOB六、(本大题8分)19.如图,已知O 的直径AB 垂直于弦CD 于点E ,过C 点作CG AD ∥交AB 的延长线于点G ,连接CO 并延长交AD 于点F ,且CF AD ⊥. (1)试问:CG 是O 的切线吗?说明理由; (2)请证明:E 是OB 的中点; (3)若8AB =,求CD 的长.xADF E OCB G(第19题图)七、(本大题8分)20.某乒乓球训练馆准备购买10副某种品牌的乒乓球拍,每副球拍配(3)x x ≥个乒乓球,已知A B ,两家超市都有这个品牌的乒乓球拍和乒乓球出售,且每副球拍的标价都为20元,每个乒乓球的标价都为1元,现两家超市正在促销,A 超市所有商品均打九折(按原价的90%付费)销售,而B 超市买1副乒乓球拍送3个乒乓球,若仅考虑购买球拍和乒乓球的费用,请解答下列问题:(1)如果只在某一家超市购买所需球拍和乒乓球,那么去A 超市还是B 超市买更合算? (2)当12x =时,请设计最省钱的购买方案.八、(本大题8分)21.如图,已知平面直角坐标系中,有一矩形纸片OABC ,O 为坐标原点,AB x ∥轴,(B -,现将纸片按如图折叠,AD DE ,为折痕,30OAD ∠=.折叠后,点O 落在点1O ,点C 落在线段AB 上的1C 处,并且1DO 与1DC 在同一直线上. (1)求1C 的坐标;(2)求经过三点1O C C ,,的抛物线的解析式;x(3)若P 的半径为R ,圆心P 在(2)的抛物线上运动, P 与两坐标轴都相切时,求P 半径R 的值.参考答案及评分意见一、细心选一选(本大题共8个小题,每小题3分,共24分) 1.B ; 2.A ; 3.A ; 4.B ; 5.B ; 6.C ; 7.B ; 8.C . 二、认真填一填(本大题共4个小题,每小题3分,共12分)9.AC BD =或EG HF ⊥或EF FG =等(任填一个满足题意的均可); 10.13-11.14;12.16cm .三、(本大题共2个小题,每小题6分,共12分)13.解:原式11)= ······································································ 4分11= ··························································································· 5分22=-···································································································· 6分 14.解:原式111(1)x x x x x --=÷-- ···································································· 2分 1(1)11x x x --=⨯- ··························································································· 4分 x =- ··········································································································· 5分选取除0与1以外的任何值,求代数式的值 ························································· 6分 注:若选取的值为0与1,该步骤不得分. 四、(本大题共2个小题,每小题6分,共12分)15.解:填“=”理由:四边形ABCD 是平行四边形 OA OC ∴=,AD BC ∥ ············································· 3分 12∴∠=∠,34∠=∠ ················································ 4分 在AOE △和COF △中3412OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩AOE COF ∴△≌△. ···················································································· 5分OE OF ∴= ·································································································· 6分16.解:(1)······························ 2分 31(4)93P ==两数之和为 ················································································· 4分 (2)由(1)(4)13P =两数之和为,(4)23P =两数之和不为设乙胜一次得x 分,这个游戏才对双方公平,根据题意得12633x ⨯= 3x =答:乙胜一次得3分,这个游戏才对双方公平. ··················································· 6分 五、(本大题共2个小题,每小题8分,共16分)17.解:设原计划每小时抢修的路线长为m x ,根据题意,得480048002(120)x x =++% ··················································································· 5分 解之得400x = ······································································································· 7分 检验:400x =是原方程的解,且符合题的实际意义.答:原计划每小时抢修的路线长为400m . ··························································· 8分 18.解:(1)(24)B -,在my x=上 8m ∴=-.∴反比例函数的解析式为:8y x=-. ··························· 1分 AEDOCF B(第15题图)1 34 21 2 3 1 1 2 32 1 23 3 甲:乙: x点(4)A n -,在8y x=-上 2n ∴=(42)A ∴-, ···································································································· 2分 y kx b =+经过(42)A -,,(24)B -,,4224k b k b -+=⎧∴⎨+=-⎩ 解之得12k b =-⎧⎨=-⎩∴一次函数的解析式为:2y x =-- ·································································· 4分 (2)C 是直线AB 与x 轴的交点∴当0y =时,2x =-∴点(20)C -,································································································ 5分 2OC ∴= ····································································································· 6分AOB ACO BCO S S S ∴=+△△△11222422=⨯⨯+⨯⨯ 6= ············································································································· 8分六、(本大题8分) 19.(1)解:CG 是O 的切线 ········································································ 1分理由:CG AD ∥180FCG CFD ∴∠+∠= CF AD ⊥90CFD ∴∠= 90FCG ∴∠=即OC CG ⊥.CG ∴是O 的切线. ····················································································· 2分 (2)第一种方法:证明:连接AC ,如图(第19题图1) CF AD ⊥,AE CD ⊥ 且CF AE ,过圆心OADF EOCAC AD ∴=,AC CD =AC AD CD ∴==ACD ∴△是等边三角形. ··········································· 3分60D ∴∠=30FCD ∴∠= ······························································································ 4分在Rt COE △中,12OE OC =12OE OB ∴=∴点E 为OB 的中点 ······················································································· 5分 第二种方法:证明:连接BD ,如图(第19题图2) AB 为O 的直径90ADB ∴∠=又90AFO ∠=ADB AFO ∴∠=∠CF BD ∴∥BDE OCE ∴△∽△ ······················································································· 3分 BE DE OE CE ∴= AE CD ⊥ 且AE 过圆心O CE DE ∴= ·································································································· 4分 BE OE ∴=∴点E 为OB 的中点. ···················································································· 5分 (3)解:8AB =142OC AB ∴==又BE OE = 2OE ∴= ····································································································· 6分cot 3023CE OE ∴=⨯=············································································ 7分AB CD ⊥2CD CE ∴==······················································································ 8分 七、(本大题8分)20.解:(1)去A 超市购买所需费用0.9(201010)A y x =⨯+DF E OCBG (第19题图2)A即9180A y x =+ ···························································································· 1分 去B 超市购买所需费用201010(3)B y x =⨯+-即10170B y x =+ ··························································································· 2分 当A B y y <时,即918010170x x +<+10x >当A B y y =时,即918010170x x +=+10x =当A B y y >时,即918010170x x +>+10x <·········································································································· 4分 综上所述:当10x >时,去A 超市购买更合算;当10x =时,去A 超市或B 超市购买一样;当310x <≤时,去B 超市购买更合算. ···························································· 5分 (2)当12x =时,即购买10副球拍应配120个乒乓球 若只去A 超市购买的费用为:9180912180288x +=⨯+=(元) ·································································· 6分 若在B 超市购买10副球拍,去A 超市购买余下的乒乓球的费用为:2000.9(123)10281+-⨯=(元) ···································································· 7分 281288<∴最佳方案为:只在B 超市购买10副球拍,同时获得送30个乒乓球,然后去A 超市按九折购买90个乒乓球. ······················································································ 8分 八、(本大题8分)21.解:(1)过1C 作1C F x ⊥轴于点F ,如图(第21题图) 在Rt ADO △中,30OAD ∠=,AO BC =tan 301OD OA =⨯== ····························1分由对称性可知:160ADO ADO ∠=∠= 160FDC ∴∠=1cot 60313DF C F ∴=⨯== ································································· 2分 112OF DF DO ∴=+=+=x∴点1C的坐标为(2- ················································································ 3分 (2)设经过1O C C ,,的抛物线的解析式为2y ax bx c =++,则220(2)2(3)30c a b c a b c =⎧⎪--+=⎨⎪--+=⎩··················································································· 4分 解之得220a b c ⎧=-⎪⎪⎪⎪=-⎨⎪=⎪⎪⎪⎩∴抛物线的解析式为:2333y x x = ························································ 5分 (3)P 与两坐标轴相切∴圆心P 应在第一、三象限或第二、四象限的角平分线上.即在直线y x =或y x =-上 ·············································································· 6分 若点P 在直线y x =上,根据题意有233322x x x =-- 解之得10x =,23x =-0R >∴33R x ==+ ······················································································· 7分 若点P 在直线y x =-上,根据题意有222x x x -=-- 解之得10x =,23x =。
2011年江苏南通市中考数学试卷

一、选择题(本大题共10小题,每小题3分,满分30分)1、(2011•南通)如果60m表示“向北走60m”,那么“向南走40m”可以表示为()A、﹣20mB、﹣40mC、20mD、40m考点:正数和负数。
分析:本题需先根据已知条件得出正数表示向北走,从而得出向南走需用负数表示,最后即可得出答案.解答:解:60m表示“向北走60m”,那么“向南走40m”可以表示﹣40米.故选B.点评:本题主要考查了正数和负数,在解题时要能根据正数和负数分别表示什么意义是本题的关键.2、(2011•南通)下面的图形中,既是轴对称图形又是中心对称图形的是()A、B、C、D、考点:中心对称图形;轴对称图形。
分析:结合轴对称图形与中心对称图形的定义进行分析解答:解:A项是中心对称图形,不是轴对称图形,故本项错误,B项为中心对称图形,不是轴对称图形,故本项错误,C项为中心对称图形,也是轴对称图形,故本项正确,D项为轴对称图形,不是中心对称图形,故本项错误故答案选择﹣﹣C.点评:本题主要考察轴对称图象的定义和中心对称图形的定义,解题的关键是找到图形是否符合轴对称图形和中心对称图形的定义3、(2011•南通)的结果是()A、±B、C、±3D、3考点:立方根。
专题:探究型。
分析:根据立方根的定义进行解答即可.解答:解:∵33=27,.故选D.点评:本题考查的是立方根的定义,即如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果x3=a,那么x叫做a.4、(2011•南通)下列长度的三条线段,不能组成三角形的是()A、3,8,4B、4,9,6C、15,20,8D、9,15,8考点:三角形三边关系。
专题:计算题。
分析:根据三角形三边关系定理:三角形两边之和大于第三边,进行判定即可.解答:解:A,∵3+4<8∴不能构成三角形;B,∵4+6>9∴能构成三角形;C,∵8+15>20∴能构成三角形;D,∵8+9>15∴能构成三角形.故选A.点评:此题主要考查学生对运用三角形三边关系判定三条线段能否构成三角形的掌握情况,注意只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.5、(2011•南通)如图,AB∥CD,∠DCE=80°,则∠BEF=()A、120°B、110°C、100°D、80°考点:平行线的性质;对顶角、邻补角。
最新DOC-江苏南通中考数学试题及答案_图文优秀名师资料

(DOC)-2011年江苏南通中考数学试题及答案_图文2011年江苏南通中考数学试题及答案_图文8112. (4ab3-8a2b2)?4ab+(2a+b)(2a-b),其中a=2,b=1.20. (本小题满分8分)x+213. 函数y=中,x-114. 38,42,35,45,位数为________kg15. 如图,矩形纸片BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点重合,则3x,6?x,4求不等式组的解集,并写出它2x,1,3x,1,,的整数解.AC=_____cm.21. (本小题满分9分)某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.根据图中提供跟信息,解答下面的问题: (1)参加调查的学生共有人;在扇形图中,表示“其他球类”的扇形的圆心角为度;16. 分解因式:3m(2x17. 如图,测量河宽AB点测得?ACB=30CD=60m,则河宽18. 心都在x切.设半圆C1、r1,r2,r3,则当19. (本小题满分102(1)计算2+(-1)(2(2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有人.22. (本小题满分8分)如图,AM为?O的切线,A为切点.BD?AM于点D,BD交?O于点C,OC平分?AOB.求?B的度数.23. (本小题满分8分)列方程解应用题:在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个,24. (本小题满分8分)比较正五边形和正六边形,可以发现它们的相同点与不同点.例如它们的一个相同点:正五边形的各边相等,正六边形的各边也相等.它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.请你再写出它们的两个相同点和两个不同点. 相同点:(1); (2). 不同点:(1);(2).83正五边形正六边形25. (本小题满分9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某此检测设有A,B两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.(1)求甲、乙、丙三名学生在同一处检测视力的概率;ADM(2)求甲、乙、丙三名学生中至少有两人在B处检测视力的概率.26. (本小题满分10分)已知:如图1,O为正方形ABCD的中心,分别延长OA到点F,OD到点E,使OF=2OA,OE=2OD,连接EF.将?FOE绕点O逆时针旋转α角得到?F'OE'’(如图2).(1)探究AE'与BF'的数量关系,并给予证明; (2)当α=30?时,求证:?AOE'为直角三角形.F'F图1图227. (本小题满分12分)已知A(1,0),B(0,-1),C(-1,2),D(2,-1),E(4,2)五个点,抛物线28. (本小题满分12分)如图,直线l经过点A(1,0),且与曲线y=m(x,0)交于点B(2,1).xy=a(x-1)+k(a,0)经过其中三个点.(1)求证:C,E两点不可能同时在抛物线2过点P(p,p-1)(p,1)作x轴的平行线分别y=a(x-1)+k(a,0)上;(2)点A在抛物线y=a(x-1)+k(a,0)上吗,为什么, (3)求a与k的值.8422mm()x,0和y=-(x,0)于M、交曲线y=Nxx两点.(1)求m的值及直线l的解析式;(2)若点P在直线y=2上,求证:?PMB??PNA;(3)是否存在实数p,使得,,若存在,请求出所有满足条件的p的值;若不存在,请说明理由.27.(1)略参考答案(声明:此处所提供答案仅为简略版的参考答案,详细答案及重点题目的精彩解析敬请登陆观看免费在线视频,谢谢您的关注~)江苏南通一、选择题(2)不在1k,,2或a,k (3)a,,28.(1)m,2,y,x,1 (2)略(3)i)当P,2时,p3811 8ii)当p,2时不成立 iii)当1,p,2时,p12二、填空题70;1213. x?1; 11(14.40;15.4;16.3m(2x-y+n)(2x-y-n); 17.;18.9.三、解答题19.(1)3;(2)12. 20.1、2、3. 21.(1)300、36;(2)足球:300×30,=90(人); (3)800. 22. ?B=60?.23.父亲:120个;儿子:140个.24.相同点:(1)轴对称图形;(2)正五边形各角都相等.不同点:(1)对称轴条数不同;(2)边角数量不同,内角大小不同. 25.(1)11;(2). 4426.(1)AE′=BF′证明:由?E′OA=?BOF′,OB=OA,OF′=OE′ 可得?OAE′??OBF′ (2)证明略85。
2011年南通市中考数学试题(word)(含答案解析)

2011年江苏省南通市中考数学试题一、选择题(本大题共10小题,每小题3分,满分30分)1.如果60m 表示“向北走60m”,那么“向南走40m”可以表示为【 】A .-20mB .-40mC .20mD .40m【答案】B .【考点】相反数。
【分析】向北与向南是相反方向两个概念,向北为+,向南则为负。
故根据相反数的定义,可直接得出结果2.下面的图形中,既是轴对称图形又是中心对称图形的是【 】【答案】C .【考点】轴对称图形,中心对称图形。
【分析】根据轴对称图形和中心对称图形的定义,可知A 是中心对称图形而不是轴对称图形;B 也是中心对称图形而不是轴对称图形;C 既是轴对称图形又是中心对称图形,它有四条对称轴,分别是连接三个小圆线段所在的水平和竖直直线,这水平和竖直直线之间的两条角平分线;D 既不是轴对称图形也不是中心对称图形。
3.计算327的结果是【 】A .±3 3B .3 3C .±3D .3【答案】D .【考点】立方根。
【分析】根据立方根的定义,因为33=273。
4.下列长度的三条线段,不能组成三角形的是【 】A .3,8,4B .4,9,6C .15,20,8D .9,15,8【答案】A .【考点】三角形的构成条件。
【分析】根据三角形任两边之和大于第三边的构成条件,A 中3+4<8,故A 的三条线段不能组成三角形。
5.如图,AB ∥CD ,∠DCE =80°,则∠BEF =【 】A .120°B .110°C .100°D .80°【答案】C .【考点】平行线的性质。
【分析】根据同旁内角互补的平行线性质,由于AB ∥CD ,∠DCE 和∠BEF 是同旁内角,从而∠BEF =00018080100-=。
6.下列水平放置的几何体中,俯视图是矩形的为【 】A . D A EBC F A . B . C .D .圆柱 长方体 三棱柱 圆锥【考点】几何体的三视图。
2011年江苏省南通市海门中学中考数学模拟试卷(二)

一、选择题(共10小题,1-8小题,每小题3分,9-10小题,每小题4分,满分32分)2011年江苏省南通市海门中学中考数学模拟试卷(二)1、(2006•遂宁)计算:|﹣4|=()A、0B、﹣4C、D、42、(2006•遂宁)一组数据:1,3,2,3,1,0,2的中位数是()A、0B、1C、2D、33、(2006•贵港)下列计算中,正确的是()A、x 2•x3=x6B、2a+3b=5abC、3a﹣2a=1D、(a 2)3=a64、(2010•广州)从图中的四张印有汽车品牌标志图案的卡片中任取一张,取出印有汽车品牌标志的图案是中心对称图形的卡片的概率是()A、B、C、D、15、(2010•广州)不等式的解集是()A 、﹣<x≤2B、﹣3<x≤2C 、x≥2D、x<﹣36、(2006•鄂尔多斯)如图,在一个长方体上放着一个小正方体,若这个组合体的俯视图如图所示,则这个组合体的左视图是()A、B、C、D、7、(2006•贵港)已知正比例函数y=kx的图象与反比例函数的图象的一个交点坐标是(1,3),则另一个交点的坐标是()A、(﹣1,﹣3)B、(﹣3,﹣1)C、(﹣1,﹣2)D、(﹣2,﹣3)8、(2006•遂宁)某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为()A、(n﹣m)元/分钟B、(n+m)元/分钟C、(n﹣m)元/分钟D、(n+m)元/分钟9、(2009•枣庄)如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是()A、1:2B、1:4C、1:5D、1:610、(2009•陕西)根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴()x …﹣1 0 1 2 …y …﹣1﹣﹣2﹣…A、只有一个交点B、有两个交点,且它们分别在y轴两侧C、有两个交点,且它们均在y轴同侧D、无交点二、填空题(共8小题,每小题3分,满分24分)11、(2009•内江)分解因式:﹣x3﹣2x2﹣x=_________.12、(2007•烟台)如图,在数轴上,A,B两点之间表示整数的点有_________个.13、(2006•大兴安岭)直线y=kx﹣4与y轴相交所成的锐角的正切值为,则k的值为_________.14、(2006•遂宁)已知样本:3,4,0,﹣2,6,1,那么这个样本的方差是_________.15、(2008•青海)若关于x的方程x2﹣5x+k=0的一个根是0,则另一个根是_________.16、(2007•赤峰)如图,半径为2的两圆⊙O1和⊙O2均与x轴相切于点O,反比例函数(k>0)的图象与两圆分别交于点A,B,C,D,则图中阴影部分的面积是_________.(结果保留π)17、(2007•成都)如图,将一块斜边长为12cm,∠B=60°的直角三角板ABC,绕点C沿逆时针方向旋转90°至△A′B′C′的位置,再沿CB向右平移,使点B′刚好落在斜边AB上,那么此三角板向右平移的距离是_________cm.18、(2009•陕西)如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是_________.三、解答题(共10小题,满分94分)19、计算:.20、(2010•广州)已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求的值.21、(2009•安顺)已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交于BE的延长线于点F,且AF=DC,连接CF.(1)求证:D是BC的中点;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.22、(2009•陕西)某校为了组织一项球类对抗赛,在本校随机调查了若干名学生,对他们每人最喜欢的一项球类运动进行了统计,并绘制成如图①、②所示的条形和扇形统计图.根据统计图中的信息,解答下列问题:(1)求本次被调查的学生人数,并补全条形统计图;(2)若全校有1 500名学生,请你估计该校最喜欢篮球运动的学生人数;(3)根据调查结果,请你为学校即将组织的一项球类对抗赛提出一条合理化建议.23、(2006•大兴安岭)某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程:加工过程中,当油箱中油量为10升时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185分钟才能将这批工件加工完.下图是油箱中油量y(升)与机器运行时间x(分)之间的函数图象,根据图象回答下列问题:(1)求在第一个加工过程中,油箱中油量y(升)与机器运行时间x(分)之间的函数关系式(不必写出自变量x的取值范围);(2)机器运行多少分钟时,第一个加工过程停止;(3)加工完这批工件,机器耗油多少升?24、(2006•贵港)如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.(1)求证:BC与⊙O的位置关系是_________;(2)若OC是BD的垂直平分线,垂足为E,BD=6,CE=4,求AD的长为_________.25、(2009•陕西)甲、乙两同学用一副扑克牌中牌面数字分别是:3,4,5,6的4张牌做抽数学游戏.游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下、洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数.若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请运用概率知识说明理由.26、(2009•陕西)小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB.(结果精确到0.1m)27、(2010•广州)如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.(1)求弦AB的长;(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;(3)记△ABC的面积为S,若=4,求△ABC的周长.28、(2010•广州)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣x+b交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.答案与评分标准一、选择题(共10小题,1-8小题,每小题3分,9-10小题,每小题4分,满分32分)1、(2006•遂宁)计算:|﹣4|=()A、0B、﹣4C、D、4考点:绝对值。
江苏南通中考数学试题解析版.doc

江苏省南通市2011年中考数学试题一、选择题(本大题共10小题,每小题3分,满分30分)1.如果60m 表示“向北走60m”,那么“向南走40m”可以表示为【 】A .-20mB .-40mC .20mD .40m【答案】B .【考点】相反数。
【分析】向北与向南是相反方向两个概念,向北为+,向南则为负。
故根据相反数的定义,可直接得出结果2.下面的图形中,既是轴对称图形又是中心对称图形的是【 】错误!未指定书签。
【答案】C .【考点】轴对称图形,中心对称图形。
【分析】根据轴对称图形和中心对称图形的定义,可知A 是中心对称图形而不是轴对称图形;B 也是中心对称图形而不是轴对称图形;C 既是轴对称图形又是中心对称图形,它有四条对称轴,分别是连接三个小圆线段所在的水平和竖直直线,这水平和竖直直线之间的两条角平分线;D 既不是轴对称图形也不是中心对称图形。
3.计算327的结果是【 】A .±3 3B .3 3C .±3D .3【答案】D .【考点】立方根。
【分析】根据立方根的定义,因为33=273。
4.下列长度的三条线段,不能组成三角形的是【 】A .3,8,4B .4,9,6C .15,20,8D .9,15,8【答案】A .【考点】三角形的构成条件。
【分析】根据三角形任两边之和大于第三边的构成条件,A 中3+4<8,故A 的三条线段不能组成三角形。
5.如图,AB ∥CD ,∠DCE =80°,则∠BEF =【 】 A .120° B .110° C .100° D .80° 【答案】C .【考点】平行线的性质。
【分析】根据同旁内角互补的平行线性质,由于AB ∥CD ,∠DCE 和∠BEF 是同旁内角,从而∠BEF =00018080100-=。
6.下列水平放置的几何体中,俯视图是矩形的为【 】错误!未指定书签。
【答案】B .【考点】几何体的三视图。
2011年江苏南通中考数学试题(含答案)
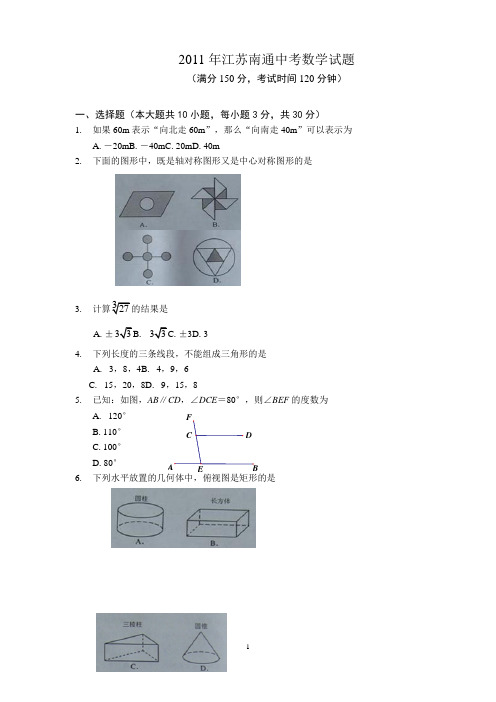
EA BC DF一、选择题(本大题共10小题,每小题3分,共30分)1.如果60m表示“向北走60m”,那么“向南走40m”可以表示为A.-20mB.-40mC.20mD.40m2.下面的图形中,既是轴对称图形又是中心对称图形的是3.计算327的结果是A.±33B. 33C.±3D.34.下列长度的三条线段,不能组成三角形的是A. 3,8,4B. 4,9,6C. 15,20,8D. 9,15,85.已知:如图,AB∥CD,∠DCE=80°,则∠BEF的度数为A. 120°B.110°C.100°D.80°6.下列水平放置的几何体中,俯视图是矩形的是2011年江苏南通中考数学试题(满分150分,考试时间120分钟)MOABt /小时s /千米乙甲2010432A1DA7. 已知3是关于x 的方程250x x c -+=的一个根,则这个方程的另一个根是A .-2B .2C . -5D .68. 如图,⊙O 的弦AB =8,M 是AB 的中点,且OM =3,则⊙O 的半径等于A . 8B . 4C . 10D .59. 甲、乙两人沿相同的路线由A 地到B 地匀速前进,A 、B 两地间的路程为20千米.他们前进的路s (单位:千米),甲出发后的时间为t (单位:小时),甲、乙前进的路程与时间的函数图像如图所示,根据图象信息,下列说法正确的是A .甲的速度是4千米/小时B .乙的速度是10千米/小时C .乙比甲晚出发1小时D .甲比乙晚到B 地3小时10. 设m n 0>>,+=m n mn 224,则-m n mn22的值等于 A .23B .3C .6D .3二、填空题(本题有8个小题,每小题3分,共24分)11. 已知∠α=20°,则∠α的余角等于_______度. 12. 计算-82=_________. 13. 函数+=-x y x 21中,自变量x 的取值范围是_____ 14. 七位女生的体重(单位:kg )分别是36,42,38,42,35,45,40,则这七位女生体重的中位数为________kg .15. 如图,矩形纸片ABCD 中,AB =2cm ,点E 在BC 上,且AE =EC .若将纸片沿AE 折AC 上的点重合,则叠,点B 恰好与xyOC 1C 2C 3AC =_____cm .16. 分解因式:()--m x y mn 22323=__________.17. 如图,测量河宽AB (假设河的两岸平行),在C 点测得∠ACB =30°,D 点测得∠ADB =60°,又CD =60m ,则河宽AB 为____m (结果保留根号).18. 已知:如图,三个半圆依次相外切,它们的圆心都在x 轴的正半轴上,并与直线=y x 3相切.设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1,r 2,r 3,则当r 1=1时,r 3=______.三、解答题(本大题有10个小题,共96分)19. (本小题满分10分)(1)计算()()+-+--04221523;(2)先化简,再求值:()()()--32248422÷++ab a b ab a b a b ,其中=a 2,=b 1.20. (本小题满分8分)求不等式组()3642131x x x x --⎧⎨+-⎩≥>的解集,并写出它的整数解.21. (本小题满分9分)某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.18题图DBCOAM根据图中提供跟信息,解答下面的问题:(1)参加调查的学生共有人;在扇形图中,表示“其他球类”的扇形的圆心角为度;(2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有人.22. (本小题满分8分)如图,AM 为⊙O 的切线,A 为切点.BD ⊥AM 于点D ,BD 交⊙O 于点C ,OC 平分∠AOB .求∠B 的度数.23. (本小题满分8分)列方程解应用题:在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?24. (本小题满分8分)正六边形正五边形F比较正五边形和正六边形,可以发现它们的相同点与不同点.例如 它们的一个相同点:正五边形的各边相等,正六边形的各边也相等. 它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.请你再写出它们的两个相同点和两个不同点. 相同点:(1); (2). 不同点:(1);(2).25. (本小题满分9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某此检测设有A ,B 两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力. (1)求甲、乙、丙三名学生在同一处检测视力的概率;(2)求甲、乙、丙三名学生中至少有两人在B 处检测视力的概率.26. (本小题满分10分)已知:如图1,O 为正方形ABCD 的中心,分别延长OA 到点F ,OD 到点E ,使OF =2OA ,OE =2OD ,连接EF .将△FOE 绕点O 逆时针旋转α角得到△''F OE ’(如图2).(1)探究'AE 与'BF 的数量关系,并给予证明; (2)当α=30°时,求证:△'AOE 为直角三角形.27. (本小题满分12分)已知A (1,0),B (0,-1),C (-1,2),D (2,-1),E (4,2)五个点,抛物线()()=-+y a x k a 210>经过其中三个点.(1)求证:C ,E 两点不可能同时在抛物线()()=-+y a x k a 210>上; (2)点A 在抛物线()()=-+y a x k a 210>上吗?为什么? (3)求a 与k 的值.xylBOA28. (本小题满分12分)如图,直线l 经过点A (1,0),且与曲线()=my x x0>交于点B (2,1).过点P (p ,p -1)(p >1)作x 轴的平行线分别交曲线()=my x x0>和()=-my x x0<于M 、N 两点. (1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ; (3)是否存在实数p ,使得=?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.参考答案江苏南通一、选择题二、填空题11.70;12;13. x ≠1;14.40;15.4;16.3m (2x -y +n )(2x -y -n );17.18.9.三、解答题19.(1)3; (2)12. 20.1、2、3. 21.(1)300、36;(2)足球:300×30%=90(人); (3)800. 22. ∠B =60°.23.父亲:120个;儿子:140个.24.相同点:(1)轴对称图形;(2)正五边形各角都相等.不同点:(1)对称轴条数不同;(2)边角数量不同,内角大小不同. 25.(1)14;(2)14. 26.(1)AE ′=BF ′证明:由∠E ′OA =∠BOF ′,OB =OA ,OF ′=OE ′ 可得△OAE ′≌△OBF ′ (2)证明略 27.(1)略 (2)不在(3)12a k =,=-或31188a k =,=- 28.(1)m =2,1y x =- (2)略(3)i)当P>2时,pii)当p=2时不成立iii)当1<p<2时,12 p=。
2011年江苏省南通市(word)+扫描试题

2011年南通市初中毕业、升学考试试卷数学一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡....上....相应位置1.(11·南通)如果60m表示“向北走60m”,那么“向南走40m”可以表示为A.-20m B.-40m C.20m D.40m【答案】D2.(11·南通)下面的图形中,既是轴对称图形又是中心对称图形的是3.(11·南通)计算327 的结果是A.±3 3 B.3 3 C.±3 D.34.(11·南通)下列长度的三条线段,不能组成三角形的是A.3,8,4 B.4,9,6 C.15,20,8 D.9,15,8 5.(11·南通)已知:如图,AB∥CD,∠DCE=80°,则∠BEF的度数为A.120°B.110°C.100°D.80°6.(11·南通)下列水平放置的几何体中,俯视图是矩形的是7.(11·南通)已知3是关于x的方程x2-5x+c=0的一个根,则这个方程的另一个根是A.-2 B.2 C.-5 D.68.(11·南通)如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于A.8 B.4C.10 D.59.(11·南通)甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的距离为20千米.他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是A.甲的速度是4千米/小时B.乙的速度是10千米/小时C.乙比甲晚出发1小时D.甲比乙晚到B地3小时10.(11·南通)设m>n>0,m2+n2=4mn,则m2-n2mn的值等于A.2 3 B. 3 C. 6 D.3二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答.题卡相应位置......上)11.(11·南通)已知∠α=20°,则∠α的余角等于▲度.12.(11·南通)计算:8-2=▲.13.(11·南通)函数y=x+2x-1中,自变量x的取值范围是▲.14.(11·南通)七位女生的体重(单位:kg)分别是36,42,38,42,35,45,40,则这七位女生体重的中位数为▲kg.15.(11·南通)如图,矩形纸片ABCD 中,AB =2,点E 在BC 上,且AE =BC .若将纸片沿AE折叠,点B 恰好与AC 上的点B ′重合,则AC = ▲ cm .16.(11·南通)分解因式:3m (2x -y)2-3mn 2= ▲ .17.(11·南通)如图,测量河宽AB (假设河的对岸平行),在C 点测得∠ACB =30°,D 点测得∠ADB=60°,又CD =60m ,则河宽AB 为 ▲ m (结果保留根号).18.(11·南通)已知:如图,三个半圆依次相外切,它们的圆心都在x 轴的正半轴上,并与直线y=33x 相切。
2011江苏南通中考数学试卷

18.2011年杭州市各类高中招生文化考试答卷一、选择题(每小题3分, 共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题 (每小题4分, 共24分)11._____________________; 12. __________; 13._____________________; 14. ___________; 15. ; 16. __ ______. 三、解答题(6+6+6+8+8+10+10+12=66分)如图,点A ,B 在数轴上,它们所对应的数分别是4-,2235x x +-,且点A 、B 到原点 的距离相等,求x 的值.17. 计算:02)45cos 1(3)3(︒---+-班级姓名试场号座位号A B4- (第20题)19.20. 已知关于x 的一元二次方程2220x ax b ++=. (1)若a ≥0,b ≥0,方程有实数根,试确定a ,b 之间的大小关系; (2)若a 是从0,1,2,3四个数中任取的一个数,b 是从0,1,2三个数中任取的一个数,请你用树状图或表格表示出所有可能出现的结果,并求出使上述方程有实数根的概率.21.22.23.为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:型号占地面积(单位:m2/个)使用农户数(单位:户/个)造价(单位: 万元/个)A 15 18 2B 20 30 3已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.(1)满足条件的方案共有几种?写出解答过程.(2)通过计算判断,哪种建造方案最省钱24.。
