2016年5.5 等式的性质练习题及答案
五年级等式的性质练习题

五年级等式的性质练习题以下是关于五年级等式的性质练习题的文章:尽管数学在学生们中间可能被视为一门难懂的学科,但它却是我们日常生活中无处不在的。
从简单的计算到复杂的代数方程,数学贯穿在我们的生活中,并帮助我们解决问题。
在数学的世界里,等式是一种非常重要的概念。
等式是表达两个量相等的关系,是解决问题中的基本工具。
在这篇文章中,我们将讨论五年级等式的性质,并介绍一些练习题来加深对等式的理解。
首先,让我们回顾一下等式的定义。
等式将两个量连接起来,并表明它们相等,使用“=”符号来表示。
例如,2 + 3 = 5是一个等式,因为它表明了2和3相加的结果等于5。
在解决等式相关问题时,我们可以使用一些性质和规则来简化计算和推理的过程。
一种常见的等式性质是加法性质。
根据加法性质,如果等式两边加上(或减去)相同的数,等式仍然成立。
这意味着,如果a = b,那么a + c = b + c,其中c是任意数。
以此为基础,我们可以解决一些练习题。
练习题1:如果等式2x = 8成立,求x的值。
解答:首先,我们要将等式化简到最简形式。
根据加法性质,我们可以将8减去2,得到2x - 2 = 8 - 2,即2x - 2 = 6。
接下来,我们将2x - 2的等号右边的数移到左边,得到2x - 2 - 6 = 0。
化简后,我们得到2x - 8 = 0。
再次应用加法性质,让我们将等式两边加上8,得到2x - 8 + 8 = 0 + 8,即2x = 8。
最后,我们将等式两边除以2,得到x = 4。
因此,当2x = 8时,x的值为4。
另一个等式性质是乘法性质。
根据乘法性质,如果等式两边乘以(或除以)相同的数,等式仍然成立。
这意味着,如果a = b,那么ac = bc,其中c是任意数。
我们可以通过解决练习题来展示乘法性质的应用。
练习题2:如果等式3y = 12成立,求y的值。
解答:首先,我们要将等式化简到最简形式。
根据乘法性质,我们可以将12除以3,得到3y ÷ 3 = 12 ÷ 3,即y = 4。
等式的基本性质练习题一

《等式的性质》基础练习11.填空:(1)由,得,这是根据等式的性质_________在等式两边_________.(2)由,得,这是根据等式的性质___________在等式的两边__________________.2.若代数式的值为-2,则=________________.3.长方形的周长为12cm ,长是宽的2倍,则长为____________cm . 4.下列利用等式的性质对方程的变形中,正确的是( )A .由,得B .由,得C .由,得D .由,得5.利用等式的性质解下列方程. (1);(2).6.一家餐馆有能坐4人的方桌,如果多于4人,老板就把桌子拼接起来,成为一张大桌子,2张桌子拼成一行能坐6人.(1)3张桌子拼成一行能坐多少人? (2)完成下表:(3)已知拼成一行的桌子数为14,你能很快算出一共能坐多少人吗?7.中国有很多地方都有大年初一拜年习俗,有一个地区习惯是这样的:每户出1人,只向邻居拜访一次.这个地区有一个村庄只有一横排住户,每户一房,在某年的初一共拜访54次,这村子共有多少户?参考答案1.1,同时加上;2,同时乘以.2.-3【解析】则有.3.4【解析】设宽为cm ,则长为cm .则有故.所以长为4cm .4.D 【解析】A 中,则,有;B 中,得,有;C 中,得,有. 5.(1)(2).6.【解析】(1)8人;(2)拼成一行桌子数1,2,3,4,10,8,9人数4,6,8,10,22,18,20;(3)30人,通过观察可发现:人数=桌子数×2+2.a b =a c b c +=+a b =ac bc =37x +x 521x +=-521x =-03y=3y =114x -=4x =485x -=10x =-2332x -=58x =-c c 372x +=-393x x =-=-.x 2x 26x x +=2x =521x +=-52212x +-=--53x =-03y=303y x ⨯=⨯0y =11114x -+=+24x=8x =94x =-58x =-7.【解析】这是一道实际问题,设共有户,两端的住户,只能拜访一次邻居,因为他们只有一个邻居,其余住户需拜访两次邻居,拜访次.解:设共有户,由题意得2(-2)+2=54.解得=28. 答:该村庄共有28户.x ()22x -x x x。
数学五年级上册等式的性质课时习题(含答案)

522等式的性质一、填空题1.根据等式性质,在横线上填运算符号,在小括号里填数。
(1)890x +=,8-890x +=________(_______)(2)38300x +=,3838300x +-=________(_______)(3)2739x +=,2739x x +-=_______(_______)(4)6423x -=,64x -______(_______)=23_______(_______)2.如果A =B ,根据等式的性质填空A ____(_______)=B +C A ÷4=B ____(_______)3.1只小狗和(_____)只小鸭同样重。
左边放(_____)只小狗,右边放(_____)只小鸭,天平还平衡。
4.已知1个=3个,2个=4个,则1个=(____)个。
5.根据等式的性质在○里填上运算符号,在□里填数。
二、判断题6.如果A =B ,根据等式的性质可知A ×13=B ×13。
(______) 7.等式两边同时除以一个不是0的数,所得结果仍然是等式。
(________)8.在等式3A -6=3B +5的两边都除以3,可得等式A -2=B +5。
(______)9.等式两边加、减、乘同一个数,或除以一个不为0的数,左右两边一定相等。
(____)10.若5x+8=4x,则5x ﹣4x=8。
(___)三、选择题11.500+△600=+□,比较△和□大小,( )正确。
A .△>□B .△=□C .△<□12.运用等式的性质进行的变形,正确的是( )A .如果a b =,那么a b b c +=-B .如果a b c c=,那么 a b = C .如果a b =,那么a b c c = D .如果2a 3a =,那么 a 3=13.李爷爷挑了一挑菜,他觉得左右两边不一样重,于是从左框里拿出8千克放入右筐,这时左右两边一样重了。
初中数学等式的性质习题

初中数学等式的性质习题1. 下列运用等式性质进行的变形,正确的是()A.如果a=b,那么a+c=b−cB.如果a2=3a,那么a=3C.如果a=b,那么ac =bcD.如果ac=bc,那么a=b2. 运用等式性质进行变形,不一定正确的是()A.如果a=b,那么a+c=b+cB.如果a=b,那么ac=bcC.如果a+c=b+c,那么a=bD.如果ac=bc,那么a=b3. 如图,两个天平都平衡,则与2个球体质量相等的正方体的个数为()A.2B.3C.4D.54. 不等式13x<1的解集是( )A.x<13B.x>13C.x>3D.x<35. 某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程ŷ=b为9.4,据此模型预报广告费用为6万元时销售额为( )A.63.6万元B.65.5万元C.67.7万元D.72.0万元6. 线段,点从点开始向点以每秒1个单位长度的速度运动,点从点开始向点以每秒2个单位长度的速度运动,当其中一个点到达终点时另一个点也随之停止运动,当时,的值为________.7. 有一个两位数,个位上的数字为a ,十位上的数字为b ,如果把这个两位数的个位与十位上的数字对调,得到的两位数大于原来的两位数,则a ________b .(选填“>”“<”或“=”)8. 若代数式4x −1与3x −6的值互为相反数,则x 的值为________.9. 由 x −5=3x +1,得 x −3x =1+5,是等式两边同时加上了________.10. 已知3x 2−4x 的值是9,则x 2−43x +6的值为________.11. 将等式3a −2b =2a −2b 变形,过程如下:因为3a −2b =2a −2b ,所以3a =2a (第一步),所以3=2(第二步),上述过程中,第一步的根据是________,第二步得出了明显错误的结论,其原因是________.12. 若x =4是方程kx =1的解,则k =________.13. 解方程(组)(1)解方程:x −2x+13=3x+24−1;(2)解方程组:{x−13=2y,2(x +y )−3(x −2y )=11.14. 某批服装进价为每件200元,商店标价为每件300元.现商店准备将这批服装打折出售,但要保证毛利润不低于8%,商店最低可按标价的几折出售?(通过列不等式进行解答)15. 解方程:1−x 3=x −1−3x−24.16. 阅读材料,解答问题(1);;;…猜想:________.(2)根据以上结论,写出下面式子的结果:________.(3)由以上情形,你能求出下面式子的结果吗?若能求,请直接写出结果,若不能求,请说明理由.________.17. 已知3b−2a+4=3a−2b,利用等式的性质比较a与b的大小.18. 已知7cosα=sinα,求下列各式的值:(1)sinα+cosα;2sinα−cosα(2)sin2α+sinαcosα+3cos2α.19. 用等式性质解下列方程:(1)4x−7=13;(2)3x+2=x+1.参考答案与试题解析初中数学等式的性质习题一、选择题(本题共计 5 小题,每题 3 分,共计15分)1.【答案】D【考点】等式的性质【解析】根据等式的性质即可求出答案.【解答】解:A,当a=b时,a+c=b+c,故A错误;B,当a=0时,此时a≠3,故B错误;C,当c=0时,此时ac 与bc无意义,故C错误;故选D.2.【答案】D【考点】等式的性质【解析】利用等式的性质对每个等式进行变形即可找出答案.【解答】解:A、利用等式性质1,两边都加c,得到a+c=b+c,所以成立;B、利用等式性质2,两边都乘以c,得到a=b,所以B成立;C、利用等式性质1,两边都−c,得到a=b,所以C成立;D、不成立,因为根据等式性质2,c≠0;故选D.3.【答案】D【考点】等式的性质【解析】根据图中物体的质量和天平的平衡情况,设出未知数,列出方程组解答.【解答】解:设球体、圆柱体与正方体的质量分别为x,y,z,根据已知条件,得:{2x=5y,①2z=2y,②①×2−②×5,得:2x=5z,即与2个球体相等质量的正方体的个数为5.故选D.【答案】D【考点】解一元一次不等式【解析】根据不等式的解集的概念即可求出答案.【解答】x<1,解:13解得:x<3.故选D.5.【答案】B【考点】求解线性回归方程【解析】根据表中所给的数据,广告费用x与销售额y(万元)的平均数,得到样本中心点,代入样本中心点求出a的值,写出线性回归方程.将x=6代入回归直线方程,得y,可以预报广告费用为6万元时销售额.【解答】解:由表中数据得:=3.5,x¯=4+2+3+54y¯=49+26+39+54=42,4又回归方程ŷ=b̂x+â中的b̂为9.4,故â=42−9.4×3.5=9.1,∴y=9.4x+9.1.将x=6代入回归直线方程,得y=9.4×6+9.1=65.5(万元).∴此模型预报广告费用为6万元时销售额为65.5万元.故选B.二、填空题(本题共计 7 小题,每题 3 分,共计21分)6.【答案】30或67【考点】解一元一次方程【解析】根据时间与速度可以分别表示出AP、BQ,结合AP=2PQ分别从相遇前和相遇后,利用线段的和差关系计算出:的值.【解答】解:此题可分为两种情况进行讨论:①如图1,B点P、Q相遇前,由题意得4P=t,BQ=2t,PQ=AB−AP−BQ当AP=2PQ时,t=2(15−t−2t)解得t=307②如图2,9PB图2点P、Q相遇后,由题意得AP=t,BQ=2t,PQ=AP+BQQ−AB当AP=2PQ时,t=2t+2t−15)解得t=6或6.综上所述:t的值为307故答案为:30或6.77.【答案】>【考点】不等式的性质【解析】根据题意得到不等式10b+a<10a+b,通过解该不等式即可比较它们的大小.【解答】解:根据题意,得10b+a<10a+b,所以9b<9a,所以b<a,即a>b.故答案为:>.8.【答案】1【考点】相反数解一元一次方程【解析】根据互为相反数的两数之和为0可列出方程,解出即可.【解答】解:由题意可得方程:(4x−1)+(3x−6)=0,解得x=1,故答案为:1.9.【答案】−3x+5【考点】等式的性质【解析】此题暂无解析【解答】解:等式的两边同时加上−3x,得x−3x−5=3x−3x+1,即x−3x−5=1等式的两边再同时加上5,得x−3x−5+5=1+5,即x−3x=1+5;也可以说:等式的两边再同时加上−3x+5,得x−5−3x+5=3x+1−3x+5,即x−3x=1+5,故答案为:−3x+5.10.【答案】9【考点】列代数式求值【解析】将原代数式变形后,利用整体代值的方法即可求解.【解答】解:因为3x2−4x=9,所以x2−43x=3,把x2−43x=3代入x2−43x+6=3+6=9.故答案为:9.11.【答案】等式的基本性质1,没有考虑a=0的情况【考点】等式的性质【解析】利用等式的基本性质判断即可.【解答】将等式3a−2b=2a−2b变形,过程如下:因为3a−2b=2a−2b,所以3a=2a (第一步),所以3=2(第二步),上述过程中,第一步的根据是等式的基本性质1,第二步得出了明显错误的结论,其原因是没有考虑a=0的情况,12.【答案】14【考点】方程的解【解析】将x=4代入方程计算即可得到k的值.【解答】解:把x =4代入方程kx =1得:4k =1,解得:k =14. 故答案为:14.三、 解答题 (本题共计 7 小题 ,每题 3 分 ,共计21分 )13.【答案】解:(1)去分母,得12x −4(2x +1)=3(3x +2)−12,去括号,得12x −8x −4=9x +6−12,移项并合并,得−5x =−2,∴ x =25.(2){x −13=2y,①2(x +y )−3(x −2y )=11,②由①得x =6y +1,③由②2x +2y −3x +6y =11,得x =8y −11,④联立③④可得原方程组的解是{x =37,y =6.【考点】解一元一次方程代入消元法解二元一次方程组【解析】暂无暂无【解答】解:(1)去分母,得12x −4(2x +1)=3(3x +2)−12,去括号,得12x −8x −4=9x +6−12,移项并合并,得−5x =−2,∴ x =25. (2){x −13=2y,①2(x +y )−3(x −2y )=11,②由①得x =6y +1,③由②2x +2y −3x +6y =11,得x =8y −11,④联立③④可得原方程组的解是{x =37,y =6.14.【答案】商店最低可按标价的7.2折出售【考点】一元一次不等式的实际应用【解析】设商店打x折出售,根据利润=售价-成本结合保证毛利润不低于8%,即可得出关于x 的一元一次不等式,解之取其最小值即可得出结论.【解答】设商店打x折出售,−200≥200×8%,依题意,得:300×x10解得:x≥7.2.15.【答案】解:去分母得4(1−x)=12(x−1)−3(3x−2),去括号得4−4x=12x−12−9x+6,整理得7x=10,解得x=10.7【考点】解一元一次方程【解析】暂无【解答】解:去分母得4(1−x)=12(x−1)−3(3x−2),去括号得4−4x=12x−12−9x+6,整理得7x=10,解得x=10.716.【答案】(1)[加加](1)x n+1;(2)x150−1;(3)|x|9+|18+⋯+x++【考点】整式的混合运算【解析】(1)观察已知等式,得到一般性结果,写出即可;(2)原式利用得出的规律计算即可得到结果;(3)原式变形后,约分即可得到结果.【解答】(1)(x−1)(x+1)=x2−1(x−1)(x2+x+1)=x3−(x−1)(x3+x2+x+1)=x4−猜想(x−1)(x n+x n−1+⋯+x2+x+1)=x n+1−(2)根据以上结果,试写出下列式子的结果:(x−1)(x49+x+48+x+1)=x5050(3)由以上情形,求出下面式子的结果:(x20−1)=(x−1)=(x−1)(x19+x18+⋯+x+1)=(x−1)=x19+x19+x+x+1故答案为:(1)xn+1;(2)x50−1;(3)×19+x18…+x+117.【答案】【考点】数列的求和对数的运算性质对数及其运算有理数指数幂的化简求值根式与分数指数幂的互化及其化简运算【解析】此题暂无解析【解答】此题暂无解答18.【答案】解:(1)∵由7cosα=sinα得,tanα=sinαcosα=7,∴sinα+cosα2sinα−cosα=tanα+12tanα−1=814−1=813.(2)∵tanα=7,∴sin2α+sinαcosα+3cos2α=sin2α+sinαcosα+3cos2αsin2α+cos2α=tan2α+tanα+3 tan2α+1=49+7+349+1=5950.【考点】三角函数的恒等变换及化简求值【解析】由条件利用同角三角函数的基本关系,求得要求式子的值.【解答】解:(1)∵由7cosα=sinα得,tanα=sinαcosα=7,∴sinα+cosα2sinα−cosα=tanα+12tanα−1=814−1=813.(2)∵tanα=7,∴sin2α+sinαcosα+3cos2α=sin2α+sinαcosα+3cos2αsin2α+cos2α=tan2α+tanα+3 tan2α+1=49+7+349+1=5950..19.【答案】解:(1)4x−7=13移项得:4x=20,方程两边同时除以4得:x=5;(2)3x+2=x+1移项得:3x−x=−2+1,合并同类项得:2x=−1,.解得:x=−12【考点】等式的性质【解析】(1)利用等式的基本性质分别化简得出即可;(2)利用等式的基本性质分别化简得出即可.【解答】解:(1)4x−7=13移项得:4x=20,方程两边同时除以4得:x=5;(2)3x+2=x+1移项得:3x−x=−2+1,合并同类项得:2x=−1,.解得:x=−12试卷第11页,总11页。
人教版数学五年级上册 第五单元《等式的性质》同步练习(含答案)

《等式的性质》(同步练习)-五年级上册数学人教版一.填空题(共10小题)1.根据“甲数比乙数的3倍多5”写出一个等量关系式。
2.下面式子中等式的有(填序号)。
①5+x=10②19﹣8=11③20﹣3>10④8.5+x⑤7+x<24⑥6(m+2)=423.在6+2=8、27﹣x、52÷2=26、x﹣7>12、a﹣15=32、7x=30、x+y=30中,等式有个,方程有个.4.如果m=n+3,那么根据等式的性质:m÷5=÷5;2m×d=(n+3)×。
5.如果a=b,根据等式的性质填空。
a+3=b+;a﹣=b﹣c;a×d=b×;a÷=b÷10。
6.等式的两边同时加上或减去同一个数,所得的结果仍是.7.等式两边加上或减去,左右两边仍然相等.8.A÷1.8=B÷7.2(AB都不等于0),则A÷B=.9.如果a=b,那么a+3=b+;a÷=b÷10。
10.由2+x=8可得2+x﹣2=8﹣2,这是根据等式两边都,等式仍然成立。
二.选择题(共9小题)11.方程一词,最早出现在我国古代数学书籍《九章算术》中。
下列式子是方程的是()A.3x+2y B.5x÷6>3C.5×3=15D.a﹣2=712.下列各式中,是方程的是()A.5+x=7.5B.5+x>7.5C.5+x D.5+2.5=7.5 13.下面各式中,()是方程.A.3x>12B.21÷3=7C.6.4+x=12D.x+514.等式的两边同时()同一个数,等式两边一定相等。
A.加上或减去B.乘C.除以D.不能确定15.如图所示,在杠杆左侧挂3个钩码,那么在杠杆右侧应挂()个这样的钩码才能保持平衡。
A.5B.6C.7D.816.等式两边乘以同一个数,左右两边()相等。
A.一定B.可能C.不可能D.以上答案都不对17.a+7=b+4,那么a()b。
人教版五年级上册数学 等式的性质 练习题(附答案)

人教版五年级上册数学等式的性质练习题(附答案)一、单选题1.如果x=y,根据等式的基本性质,经过变化后下面的()是错误的。
A. x÷b=y÷6(b≠0)B. x+y=y+yC. x×3×5=15yD. x-y=y-4+32.下列说法中,正确的有()个。
①五(7)班女生人数是男生的56,男生人数就是全班的611。
②等式两边同时除以同一个数,所得结果仍然是等式。
③把35的分子增加6,要使分数的大小不变,它的分母要增加10。
④A、B是不为0的自然数,A=B-1,A和B的最大公因数是1。
A.1B.2C.3D.43.根据等式的性质,由“(3x+5-a)×10=(5y-a)×10”可以推出()。
A. 3x+5=5yB. 3x=yC. x=y4.下列说法正确的是()。
A. 等式两边同时乘或除以一个相同的数,等式仍然成立。
B. 两个不同的质数相加,和可能是奇数也可能是偶数。
C. 一节课的时间是23小时,是把“一节课的时间”看作单位“1”。
二、判断题5.根据x-16=32可以得到x-16+16=32-16()6.等式两边都乘或除以同一个数,等式仍然成立.()7.方程3+x=56,等号两边同减去8,所得结果还是方程。
()8.等式的两边同时乘或除以同一个数,等式依然成立.()三、填空题9.如果b=c,那么b÷10=c÷________,b+________=c+3,bd=c×________。
10.在○填运算符号,□里填数.4x-6=18 4x-6○□=18+6 (从左到右填写) ________11.在式子3+5=8,7y=21,x+y=z,3x+4x=48,59+4m中,方程有________个,等式有________个。
12.方程21x=126时,可以根据等式的性质,在方程左右两边应同时________21。
13.等式的基本性质是________.14.根据等式的性质在横线填上合适的运算符号,在括号里填上合适的数。
人教版小学五年级数学上册《等式的性质》测试题及答案

人教版小学五年级数学上册《等式的性质》测试题及答案一、单选题1.下列说法正确的是()。
A. 等式两边同时乘或除以一个相同的数,等式仍然成立。
B. 两个不同的质数相加,和可能是奇数也可能是偶数。
C. 一节课的时间是小时,是把“一节课的时间”看作单位“1”。
2.x+3=y+5,那么x()y。
A. 大于B. 小于C. 等于D. 无法确定3.如果2m=6n,(m,n均不为0),那么m=()A. nB. 2nC. 3n4.若a+5=b-5,则a+10=()A. b+10B. bC. b-5二、判断题5.方程两边同时乘(或除以)同一个数,等式仍然成立。
()6.等式的两边同时乘或除以同一个数,等式仍然成立。
()7.方程的两边同时加上或减去一个相同的数,等式成立。
()三、填空题8.已知4x+8=10,那么2x+8=________。
9.方程21x=126时,可以根据等式的性质,在方程左右两边应同时________21。
10.根据等式的性质,在下面的横线上填上合适的运算符号或合适的数:如果2(x﹣16)=8,那么2(x﹣16)________________=8÷2.11.如果x=y,则x÷________=y÷8,5x﹣3=________﹣3.12.如果b=c,那么b÷10=c÷________,b+________=c+3,bd=c×________。
13.如果a=b,根据等式的性质填空。
a+5=b+________a-________=b-aa× 1/5 =b×________ a÷________=b÷0.514.若6n=4,则3n=________;若4x=x+5,则3x=________。
15.如果a=b,根据等式的性质填空:a+5=________,________=7b.16.如果m=n,请根据等式的基本性质填空。
等式的性质经典练习题

祖π数学 新人教 七年级上册 之精讲精练 1 【知识点2】等式的性质 (1)等式的性质1:等式的两边同时加(或减) ( ),结果仍相等. 即:如果a=b ,那么a ±c=b .(2)等式的性质2:等式的两边同时乘 ,或除以 数,结果仍相等. 即:如果a=b ,那么ac =bc ;或如果a=b ( ),那么a/c =b/c.【典型例题】1.下列等式变形中,错误的是( )A .由a =b ,得a +5=b +5B .由a =b ,得a -3=b -3C .由x +2=y +2,得x =yD .由-3x =-3y ,得x =-y2.若x =y ,且a≠0,则下面各式中不一定正确的是( )A .ax =ayB .x +a =y +aC .x a =y aD .a x =a y3.下列说法正确的是( )A .在等式ab =ac 两边都除以a ,可得b =c.B .在等式a =b 两边除以c 2+1,可得2211a b c c =++. C .在等式b c a a=两边都除以a ,可得b =c. D .在等式2x =2a-b 两边都除以2,可得x =a-b.4.等式31124x x +-=的下列变形属于等式性质2的变形是( ) A .31214x x +=+ B .31214x x +-= C .3148x x +-= D .311244x x +-= 5. 将103.001.05.02.0=+-x x 的分母化为整数,得( ) A .1301.05.02=+-x x B .1003505=+-x x C .100301.05.020=+-x x D .13505=+-x x 6.根据图所示,对a 、b 、c 三种物体的重量判断正确的是( )A .a <cB .a <bC .a >cD .b <c。
人教版数学五年级上册 第五单元 分层训练 等式的性质 练习题(含答案)
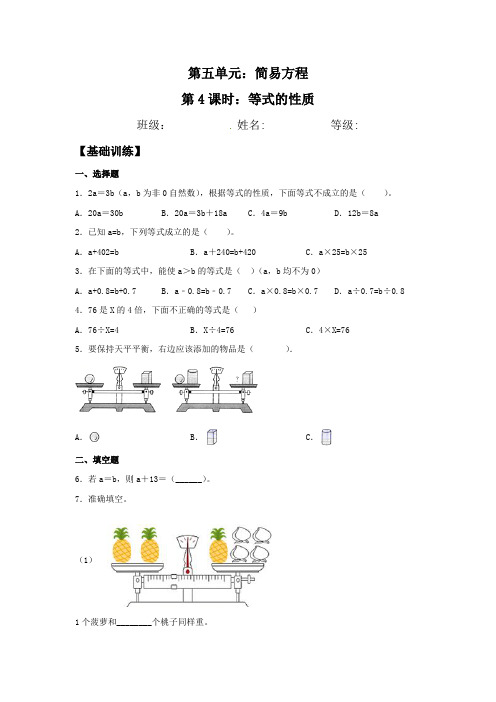
第五单元:简易方程第4课时:等式的性质班级:姓名: 等级:【基础训练】一、选择题1.2a=3b(a,b为非0自然数),根据等式的性质,下面等式不成立的是()。
A.20a=30b B.20a=3b+18a C.4a=9b D.12b=8a2.已知a=b,下列等式成立的是()。
A.a+402=b B.a+240=b+420 C.a×25=b×253.在下面的等式中,能使a>b的等式是()(a,b均不为0)A.a+0.8=b+0.7 B.a﹣0.8=b﹣0.7 C.a×0.8=b×0.7 D.a÷0.7=b÷0.8 4.76是X的4倍,下面不正确的等式是()A.76÷X=4 B.X÷4=76 C.4×X=765.要保持天平平衡,右边应该添加的物品是().A.B.C.二、填空题6.若a=b,则a+13=(______)。
7.准确填空。
(1)1个菠萝和________个桃子同样重。
(2)1只小鸭和________只小鸡同样重。
8.若64n =,则3n =(________);若45x x =+,则3x =(________)。
9.1个文具盒和6支笔共36元,4个文具盒和24支笔要(__________)元钱。
10.运用等式的性质可以(______)。
三、判断题11.方程两边同时乘(或除以)不为零的同一个数,方程仍成立。
(________)12.等式两边同时乘或除以0.2,所得结果仍是等式。
(________)【拓展运用】四、解答题13.一只菠萝的重量等于4根香蕉的重量,两只梨子的重量等于一只菠萝的重量,一只梨子的重量等于几根香蕉的重量?参考答案1.C2.C3.B4.B5.C6.b+137.4 38.2 59.14410.解方程11.√12.√13.1只菠萝的重量=4根香蕉的重量;2只梨子的重量=1只菠萝的重量;则:2只梨子的重量=4根香蕉的重量;2只梨子的重量÷2=4根香蕉的重量÷2;即:1只梨子的重量=2根香蕉的重量。
等式的性质习题及答案

等式的性质课堂评测一、选择:1.下列式子可以用“=”连接的是( )A.5+4_______12-5B.7+(-4)______7-(+4)C.2+4×(-2)______-12D.2×(3-4)_____2×3-42.下列等式变形错误的是( )A.由a=b得a+5=b+5;B.由a=b得- a9=-b9C.由x+2=y+2得x=y;D.由-3x=-3y得x=-y3.运用等式性质进行的变形,正确的是( )A.如果a=b,那么a+c=b-c;B.如果ac=bc,那么a=b;C.如果a=b,那么ac=bc; D.如果a2=3a,那么a=3二、填空:4.用适当的数或式子填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形的:(1)如果x+8=10,那么x=10+_________;(2)如果4x=3x+7,那么4x-_______=7;(3)如果-3x=8,那么x=________;(4)如果13x=-2,那么 =-65.完成下列解方程:(1)3- 13x=4解:两边_________,根据________得3-13x-3=4_______.于是- 13x=_______.两边_________,根据_____ __得x=_________.(2)5x-2=3x+4解:两边_________,根据_______得________=3x+6两边_________,根据_______得2x=________.两边_________,根据________得x=________.三、解答题:6.利用等式的性质解下列方程并检验:(1)x+3=2 (2)- 12x-2=3(3)9x=8x-6 (4)8y=4y+17.解下列方程:(1)7x-6=-5x (2)(3) (4)8.当x 为何值时,式子9.列方程并求解:一个两位数,个位上的数字比十位上的数字大2,个位与十位上的数字之和是10,求这个两位数(提示:设个位上的数字为x)Welcome !!! 欢迎您的下载,资料仅供参考!。
等式的性质习题及答案

、选择:1. 下列式子可以用“=”连接的是()2. 下列等式变形错误的是()3. 运用等式性质进行的变形,正确的是()a b B. 女口果一=-,那么a=b; c ca bC.如果a=b,那么-=-; c c二、填空:4. 用适当的数或式子填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形的:(1) 如果 x+8=10,那么 x=10+ ________(2) 如果 4x=3x+7,那么 4x- ______ =7;(3) 如果-3x=8,那么 x= _______ ;1⑷如果3 x=-2,那么 =-65. 完成下列解方程:1 (1) 3- 3 x=41解:两边 __________ ,根据 ________ 得 3-3 x-3=4 ______ 于是-3 x= ________ ‘两边 __________ ,根据 __________ 得x= _________等式的性质A. _________ 5+4 12-5B. __________ 7+(-4) 7-(+4)C. ____________ 2+4X(-2) -12D. ___________ 2X (3-4) 2 X3-4A.由 a=b 得 a+5=b+5;B. 由 a=b 得-9 =- bC.由 x+2=y+2 得 x=y;D. 由-3x=-3y 得 x=-yA.如果 a=b,那么 a+c=b-c; D. 如果a 2=3a,那么a=3(2) 5x-2=3x+4解:两边 __________,根据 _______ 得 _________ =3x+6两边 _________ ,根据 ________ 得2x= _______ .两边 _________ ,根据 ________ 得 x= _______ .三、解答题:6. 利用等式的性质解下列方程并检验:1 (1) x+3=2 (2)- 2 x-2=34 8. 当 x 为何值时,「 ,: < - I' ■■ - ■.3 9. 列方程并求解:一个两位数,个位上的数字比十位上的数字大 2,个位与十位上的数字之和是 10, 求这个两位数(提示:设个位上的数字为x)10.如果方程2x+a=x-1的解是x=-4,求3a-2的值.(3) 9x=8x-6 (4) 8y=4y+17.解下列方程:(1)7x-6=-5x (2) 3-—K -1=4 (3).. 1 (4厂 \ 7 100 100答案:1.B2.D3.B84. (1)-8,等式性质1;⑵3x,等式性质1;⑶-3,等式性质2;(4) x,等式性质215. (1)都减去3, 等式性质1, -3, 4, 都乘以-3(或除以-3 )等式性质2 3(2) 都加上2, 等式性质1, 5x, -35.都减去3x,等式性质1,6,都除以2,,6. (1)x+3-3=2-3,x=-1, 检验略;(2)-1212x-2+2=3+2,-x=5,x=-10;(3) 9x-8x=8x-6-8x,x=-6; (4)8y-4y=4y+1-4y,4y=1,y=7. (1)x=1-214 ;(2)x=43253; (3)x=- 4;(4)x=15 ? 8.? 列方程x-5+3x+1=9,x=3,9. 设个位上的数字x,列方程得x=10-x+2或x+x-2=10,x=610. 代x=-4 入方程得-8+a=-4-1,a=3,3a-2=711. 因为是一元一次方程,所以(a-2)x2=0,即a-2=0,a=2;x=-12.LE 2.D ERI(If尊式性质:;(2>甌答式性质1; (3)2 爭式•性质2;(・4)马等式性廣23巳(1)都漏去3,等式性质4 7」也都乘以-3〔或睫臥_ ?人等武性质2, -3;〔刀都順上Z弄貳性质1, 5為部緬古盹等式悝质1』£都陰"乙尊式性质Z 3& Q J x^-3^2-3. L1,检蛭瞎;(2)- — 7—2+2=3+2, ——K=S f x=—L0;2 2<3) 3x-6x^Sx-6nSx» x=-6:⑷旳7厂《y+l-切4尸1』y=丄4'1 2、1. (lh=- ;(2)K=-—;'3)K=-1; (l)x=15 *2 3'& •列方程—3彳设卒位上的数宇比列方程得^10-^2或Z+K-2=10,吕1CL代>=-4入方程得・&+玄=~S1*存£ 3a-2=7II■因为足一元一.久方程』所£J\(£r2)1^0,a-Z-Cia-Z^^- 1.。
等式的性质试题精选附答案

6.2.2等式的性质一.选择题(共25小题) 1.(2003•无锡)已知2x=3y (x ≠0),则下列比例式成立的是(,则下列比例式成立的是( ) A . B . C . D .2.(2002•金华)已知:,那么下列式子中一定成立的是(,那么下列式子中一定成立的是( )A .2x=3y B .3x=2y C .x =6y D .x y=63.如图所示,天平右盘里放了一块砖,左盘里放了半块砖和2kg 的砝码,天平两端正好平衡,那么一块砖的重量是(是( )A .1kg B .2kg C .3kg D .4kg4.在下列式子中变形正确的是(.在下列式子中变形正确的是( ) A . 如果a=b ,那么a+c=b ﹣c B . 如果a=b ,那么C . 如果,那么a=2D .如果a ﹣b+c=0,那么a=b+c5.下列说法正确的是(.下列说法正确的是( ) A . 如果ab=ac ,那么b=c B . 如果2x=2a ﹣b ,那么x=a ﹣bC . 如果a=b ,那么D .等式两边同时除以a ,可得b=c6.下列叙述错误的是(.下列叙述错误的是( ) A . 等式两边加(或减)同一个数(或式子),结果仍相等,结果仍相等 B . 等式两边乘以(或除以)同一个数(或式子),结果仍相等,结果仍相等 C . 锐角的补角一定是钝角锐角的补角一定是钝角D . 如果两个角是同一个角的余角,那么它们相等如果两个角是同一个角的余角,那么它们相等7.下列变形中不正确的是(.下列变形中不正确的是( )A . 若x ﹣1=3,则x=4B . 若3x ﹣1=x+3,则2x ﹣1=3C . 若2=x ,则x=2D . 若5x+8=4x ,则5x ﹣4x=88.下列各式中,变形正确的是(.下列各式中,变形正确的是( )A . 若a=b ,则a ﹣c=b ﹣cB . 若2x=a ,则x=a ﹣2C . 若6a=2b ,则a=3bD . 若a=b+2,则3a=3b+29.如果a=b ,则下列等式不一定成立的是(,则下列等式不一定成立的是( )A . a ﹣c=b ﹣cB .a +c=b+c C . D .a c=bc10.下列等式变形错误的是(.下列等式变形错误的是( ) A . 若a+3=b ﹣1,则a+9=3b ﹣3 B . 若2x ﹣6=4y ﹣2,则x ﹣3=2y ﹣1C . 若x 2﹣5=y 2+1,则x 2﹣y 2=6D .若,则2x=3y11.下列方程变形正确的是(.下列方程变形正确的是( )A . 由方程,得3x ﹣2x ﹣2=6B . 由方程,得3(x ﹣1)+2x=1C . 由方程,得2x ﹣1=3﹣6x+3D .由方程,得4x ﹣x+1=412.已知等式a=b 成立,则下列等式不一定成立的是(成立,则下列等式不一定成立的是( )A . a +m=b+mB . ﹣a=﹣bC . ﹣a+1=b ﹣1D .13.下列方程的变形中,正确的是(.下列方程的变形中,正确的是( )①3x+6=0,变形为x+2=0;②x+7=5﹣3x ,变形为4x=﹣2; ③4x=﹣2,变形为x=﹣2;④=3,变形为2x=15.A . ①④;B . ②③;C . ①②④;D . ①②③14.已知5﹣(﹣2x+y )=6,则2x ﹣y=( )A . ﹣1B . 0C . 1D .215.下列说法正确的是(.下列说法正确的是( ) A . 在等式ax=bx 两边都除以x ,可得a=bB . 在等式两边都乘以x ,可得a=bC . 在等式3a=9b 两边都除以3,可得a=3D . 在等式两边都乘以2,可得x=y ﹣116.(2013•东阳市模拟)如图a 和图b 分别表示两架处于平衡状态的简易天平,对a ,b ,c 三种物体的质量判断正确的是(确的是( )A . a <c <bB . a <b <cC . c <b <aD . b <a <c17.已知xy=mn ,则把它改写成比例式后,错误的是(,则把它改写成比例式后,错误的是( ) A . = B . = C . = D . =18.已知mx=my ,下列结论错误的是(,下列结论错误的是( )A . x=yB . a+mx=a+myC . mx ﹣y=my ﹣yD . amx=amy19.若ma=mb ,那么下列等式不一定成立的是(,那么下列等式不一定成立的是( )A . a=bB . ma ﹣6=mb ﹣6C .D . ma+8=mb+820.下列各方程,变形正确的是(.下列各方程,变形正确的是( )A .=1化为x=B . 1﹣[x ﹣(2﹣x )]=x 化为3x=﹣1C .化为3x 一2x+2=1D .化为2(x ﹣3)﹣5(x+4)=1021.下列各式变形错误的是(.下列各式变形错误的是( ) A . 2x+6=0变形为2x=﹣6B .=1﹣x ,变形为x+3=2﹣2xC . ﹣2(x ﹣4)=﹣2,变形为x ﹣4=1D . ,变形为﹣x+1=122.下列变形正确的是(.下列变形正确的是( ) A . 若x 2=y 2,则x=y B . 若axy=a ,则xy=1 C .若﹣x=8,则x=﹣12 D .若=,则x=y23.根据下图所示,对a 、b 、c 三种物体的质量判断正确的是(三种物体的质量判断正确的是( )A . a <cB . a <bC . a >cD . b <c24.如果■●▲表示三种物体,现用天平称了现两次,情况如图所示则下列结论正确的是( )A . ■■=▲B . ■=▲C . ■>●D . ▲▲<■■■25.如图小亮拿了一个天平,测量饼干和糖果的质量(每块饼干质量相同,每颗糖果质量相同),第一次,左盘放两块饼干,右盘放三颗糖果,结果天平平衡;第二次,左盘放10g 砝码,右盘放一块饼干和一颗糖果,结果天平平衡;第三次,左盘放一颗糖果,右盘放一块饼干,下列哪一种方法可使天平再次平衡( )A . 在糖果的秤盘上加2g 砝码砝码B .在饼干的秤盘上加2g 砝码砝码 C . 在糖果的秤盘上加5g 砝码砝码 D .在饼干的秤盘上加5g 砝码砝码二.填空题(共3小题)26.(2001•江西)如果,那么= _________ .27.(2000•台州)已知2y=5x ,则x :y= _________ .28.(1998•宁波)已知3a=2b (b ≠0),那么= _________ .三.解答题(共2小题) 29.由(3a+7)x=4a ﹣b ,得到的是否受一定条件的限制?并说明理由.是否受一定条件的限制?并说明理由.30.将等式5a ﹣3b=4a ﹣3b 变形,过程如下:变形,过程如下: ∵5a ﹣3b=4a ﹣3b ,∴5a=4a (第一步),∴5=4(第二步). 上述过程中,第一步的依据是上述过程中,第一步的依据是 _________ ,第二步得出错误的结论,其原因是,第二步得出错误的结论,其原因是 _________ .6.2.2等式的性质参考答案与试题解析一.选择题(共25小题) 1.(2003•无锡)已知2x=3y (x ≠0),则下列比例式成立的是(,则下列比例式成立的是( )A .B .C .D .考点: 等式的性质. 分析: 根据等式的两边同时乘以或除以同一个不为0的数或字母等式仍成立即可解决.的数或字母等式仍成立即可解决. 解答: 解:根据等式性质2,可判断出只有B 选项正确,选项正确,故选B .点评: 本题考查的是等式的性质:本题考查的是等式的性质:等式性质1:等式的两边加(或减)同一个数(或式子)结果仍相等;:等式的两边加(或减)同一个数(或式子)结果仍相等;等式性质2:等式的两边同乘(或除以)同一个数(除数不为0)结果仍相等.)结果仍相等.2.(2002•金华)已知:,那么下列式子中一定成立的是(,那么下列式子中一定成立的是( )A .2x=3y B .3x=2y C .x =6y D .x y=6考点: 等式的性质.分析: 根据等式的性质,在等式两边同时加、减、乘、除同一个数或式子,结果仍相等可得出答案. 解答: 解:A 、根据等式的性质2,等式两边同时乘以6,即可得2x=3y ;B 、根据等式性质2,等式两边都乘以9,应得3x=y ;C 、根据等式性质2,等式两边都乘以3,应得x=y ;D 、根据等式性质2,等式两边都乘以3y ,应得xy=y 2;故选A . 点评: 本题考查的是等式的性质:题考查的是等式的性质:等式性质1,等式的两边加(或减)同一个数(或式子)结果仍相等;,等式的两边加(或减)同一个数(或式子)结果仍相等;等式性质2,等式的两边同乘(或除以)同一个数(除数不为0)结果仍相等.)结果仍相等.3.如图所示,天平右盘里放了一块砖,左盘里放了半块砖和2kg 的砝码,天平两端正好平衡,那么一块砖的重量是(是( )A .1kg B .2kg C .3kg D .4kg考点: 等式的性质.专题: 应用题.应用题. 分析: 根据题意可知天平两端正好平衡说明左盘里物质的质量等于右盘里物质的质量,可设一块砖的重量是xkg ,利用“天平左盘里物质的质量等于右盘里物质的质量”作为相等关系列方程即可求解.作为相等关系列方程即可求解.解答:解:设一块砖的重量是xkg ,则:2+x=x解得:x=4所以一块砖的重量是4kg . 故选D .点评: 从天平左右两边平衡引出等量关系:天平左盘里物质的质量等于右盘里物质的质量.天平左盘里物质的质量等于右盘里物质的质量.若天平两边同时去掉若天平两边同时去掉半块砖,则可知半块砖头的重量为2kg .同时也体现出了等式的基本性质1:等式的两边同时加上或减去同一个数或字母,等式仍成立.同一个数或字母,等式仍成立.4.在下列式子中变形正确的是(.在下列式子中变形正确的是( ) A . 如果a=b ,那么a+c=b ﹣c B .如果a=b ,那么C .如果,那么a=2D . 如果a ﹣b+c=0,那么a=b+c考点: 等式的性质. 分析: 根据等式的基本性质:①等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时加上或减去同一个数或字母,等式仍成立; ②等式的两边同时乘以或除以同一个不为0的数或字母,等式仍成立.即可解决.的数或字母,等式仍成立.即可解决. 解答: 解:A 、应同加同减,故选项错误;、应同加同减,故选项错误;B 、正确;、正确;C 、a=8,故选项错误;,故选项错误;D 、a=b ﹣c ,故选项错误.,故选项错误. 故选B .点评: 本题主要考查等式的性质.需利用等式的性质对根据已知得到的等式进行变形,从而找到最后的答案.5.下列说法正确的是(.下列说法正确的是( ) A . 如果ab=ac ,那么b=c B . 如果2x=2a ﹣b ,那么x=a ﹣b C .如果a=b ,那么D .等式两边同时除以a ,可得b=c考点: 等式的性质.分析: 根据等式的基本性质对各选项分析判断后利用排除法求解.根据等式的基本性质对各选项分析判断后利用排除法求解. 解答: 解:A 、如果a=0,则不能等式两边都除以a ,故本选项错误;,故本选项错误;B 、等式两边都除以2,应为x=a ﹣,故本选项错误;,故本选项错误;C 、∵c 2+1≥1,∴可以等式两边都除以c 2+1,正确;,正确;D 、是等式两边都乘以a ,而不是都除以a ,故本选项错误.,故本选项错误. 故选C .点评: 本题主要考查等式的基本性质,熟练掌握基本性质是解题的关键,也是为今后更好的学习打下坚实的基础.6.下列叙述错误的是(.下列叙述错误的是( ) A . 等式两边加(或减)同一个数(或式子),结果仍相等,结果仍相等 B . 等式两边乘以(或除以)同一个数(或式子),结果仍相等,结果仍相等 C . 锐角的补角一定是钝角角的补角一定是钝角 D . 如果两个角是同一个角的余角,那么它们相等果两个角是同一个角的余角,那么它们相等考点: 等式的性质;余角和补角. 分析: 根据等式的性质1判断A ;根据等式的性质2判断B ;根据补角的定义判断C ; 根据余角的性质判断D .解答: 解:A 、根据等式的性质1:等式两边加同一个数(或式子),结果仍相等,所以叙述正确,故本选项不符合题意;符合题意;B 、根据等式的性质2:等式两边乘同一个数或除以一个不为零的数,结果仍相等.当除数为0时,除法运算无意义,所以叙述错误,故本选项符合题意;法运算无意义,所以叙述错误,故本选项符合题意;C 、根据和为180°的两个角互为补角,得到锐角的补角一定是钝角,所以叙述正确,故本选项不符合题意;意;D 、根据余角的性:同角的余角相等,所以叙述正确,故本选项不符合题意. 故选B .点评: 本题考查了等式的性质,余角与补角的性质,都是基础知识,需熟练掌握.本题考查了等式的性质,余角与补角的性质,都是基础知识,需熟练掌握.7.下列变形中不正确的是(.下列变形中不正确的是( ) A . 若x ﹣1=3,则x=4 B . 若3x ﹣1=x+3,则2x ﹣1=3 C .若2=x ,则x=2D .若5x+8=4x ,则5x ﹣4x=8考点: 等式的性质. 分析: 根据等式的基本性质进行判断.根据等式的基本性质进行判断. 解答: 解:A 、等式x ﹣1=3的两边同时加上1,等式仍成立,即x=4.故本选项正确;.故本选项正确;B 、等式3x ﹣1=x+3的两边同时减去x ,等式仍成立,即2x ﹣1=3.故本选项正确;.故本选项正确;C 、等式2=x 的两边同时加上(﹣x ﹣2),再除以﹣1,等式仍成立,即x=2.故本选项正确;.故本选项正确;D 、等式5x+8=4x 的两边同时减去(4x+8),等式仍成立,即5x ﹣4x+16=8.故本选项错误;.故本选项错误; 故选D .点评: 本题主要考查了等式的基本性质.本题主要考查了等式的基本性质.等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;、等式的两边同时加上或减去同一个数或字母,等式仍成立;2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.数或字母,等式仍成立.8.下列各式中,变形正确的是(.下列各式中,变形正确的是( )A . 若a=b ,则a ﹣c=b ﹣cB . 若2x=a ,则x=a ﹣2C . 若6a=2b ,则a=3bD . 若a=b+2,则3a=3b+2考点: 等式的性质. 分析: 根据等式的两条性质对四个选项逐一分析,发现只有选项A 正确.正确. 解答: 解:A 、若a=b ,根据等式的性质,等式两边加同一个数(或式子)结果仍得等式,则a ﹣c=b ﹣c ,故选项A 正确;正确;B 、若2x=a ,根据等式的性质,等式两边乘同一个数或除以一个不为零的数,结果仍得等式,则x=a ÷2,故选项B 错误;错误;C 、若6a=2b ,根据等式的性质,等式两边乘同一个数或除以一个不为零的数,结果仍得等式,则a=,故选项C 错误;错误;D 、若a=b+2,根据等式的性质,等式两边乘同一个数或除以一个不为零的数,结果仍得等式,则3a=3b+6,故选项D 错误.错误. 故选A .点评: 本题主要考查等式的两条性质:本题主要考查等式的两条性质:性质1、等式两边加同一个数(或式子)结果仍得等式;、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.9.如果a=b ,则下列等式不一定成立的是(,则下列等式不一定成立的是( )A . a ﹣c=b ﹣cB .a +c=b+c C .D .a c=bc考点: 等式的性质. 专题: 计算题.计算题. 分析: 根据等式两边加上(或减去)同一个数,等式仍然成立可对A 、B 进行判断;根据等式两边同除以一个不为0的数,等式仍然成立对C 进行判断;根据等式两边乘以同一个数,等式仍然成立对D 进行判断.进行判断.解答: 解:A 、若a=b ,则a ﹣c=b ﹣c ,所以A 选项的等式成立;选项的等式成立;B 、若a=b ,则a+c=b+c ,所以B 选项的等式成立;选项的等式成立;C 、当c ≠0,若a=b ,则=,所以C 选项的等式不成立;选项的等式不成立;D 、若a=b ,则ac=bc ,所以D 选项的等式成立.选项的等式成立.故选C .点评: 本题考查了等式的性质:等式两边加上(或减去)同一个数,等式仍然成立;等式两边乘以同一个数,等式仍然成立;等式两边同除以一个不为0的数,等式仍然成立.的数,等式仍然成立.10.下列等式变形错误的是(.下列等式变形错误的是( ) A .若a+3=b ﹣1,则a+9=3b ﹣3 B . 若2x ﹣6=4y ﹣2,则x ﹣3=2y ﹣1C .若x 2﹣5=y 2+1,则x 2﹣y 2=6D .若,则2x=3y考点: 等式的性质. 分析: 根据等式的性质对各选项分析判断后利用排除法求解.根据等式的性质对各选项分析判断后利用排除法求解.解答: 解:A 、a+3=b ﹣1两边都乘以3得,a+9=3b ﹣3,故本选项错误;,故本选项错误;B 、2x ﹣6=4y ﹣2两边都除以2得,x ﹣3=2y ﹣1,故本选项错误;,故本选项错误;C 、x 2﹣5=y 2+1两边都加上5减去y 2得,x 2﹣y 2=6,故本选项错误;,故本选项错误; D 、=两边都乘以6得,2x ﹣2=3y ﹣3,故本选项正确.,故本选项正确.故选D .点评: 本题主要考查了等式的基本性质.本题主要考查了等式的基本性质.等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;、等式的两边同时加上或减去同一个数或字母,等式仍成立; 2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.数或字母,等式仍成立.11.下列方程变形正确的是(.下列方程变形正确的是( ) A .由方程,得3x ﹣2x ﹣2=6 B . 由方程,得3(x ﹣1)+2x=1C .由方程,得2x ﹣1=3﹣6x+3D .由方程,得4x ﹣x+1=4考点: 等式的性质.专题: 计算题.计算题. 分析: 本题需利用等式的性质对等式进行变形,从而解决问题.本题需利用等式的性质对等式进行变形,从而解决问题. 解答: 解:A 、根据等式的性质,等式的两边同时乘以6,得3x ﹣2x+2=6,故本选项错误;,故本选项错误;B 、根据等式的性质,等式的两边同时乘以6,得3(x ﹣1)+2x=6,故本选项错误;,故本选项错误;C 、根据等式的性质,等式的两边同时乘以3,得2x ﹣1=3﹣18x+9,故本选项错误;,故本选项错误;D 、根据等式的性质,等式的两边同时乘以4,得4x ﹣x+1=4,故本选项正确;,故本选项正确; 故选D .点评: 本题考查的是等式的性质:等式性质1:等式的两边加(或减)同一个数(或式子)结果仍相等;:等式的两边加(或减)同一个数(或式子)结果仍相等;等式性质2:等式的两边同乘(或除以)同一个数(除数不为0)结果仍相等;)结果仍相等;12.已知等式a=b 成立,则下列等式不一定成立的是(成立,则下列等式不一定成立的是( ) A .a +m=b+m B . ﹣a=﹣bC . ﹣a+1=b ﹣1D .考点: 等式的性质. 分析: 利用等式的性质对每个等式进行变形即可找出答案.用等式的性质对每个等式进行变形即可找出答案. 解答: 解:A 、根据等式的性质1,a=b 两边同时加m ,得a+m=b+m ;B 、根据等式的性质2,a=b 两边同时乘以﹣1,得﹣a=﹣b ;C 、根据等式1,由﹣a+1=b ﹣1可得a+b=2,所以C 错误;错误;D 、根据等式的性质2,a=b 两边同时除以m ,得=(m ≠0). 故选C .点评: 本题主要考查了等式的性质.题主要考查了等式的性质.等式性质1:等式的两边都加上或者减去同一个数或同一个整式,所得结果仍是等式;:等式的两边都加上或者减去同一个数或同一个整式,所得结果仍是等式; 等式性质2:等式的两边都乘以或者除以同一个数(除数不为零),所得结果仍是等式.,所得结果仍是等式.13.下列方程的变形中,正确的是(.下列方程的变形中,正确的是( ) ①3x+6=0,变形为x+2=0;②x+7=5﹣3x ,变形为4x=﹣2; ③4x=﹣2,变形为x=﹣2;④=3,变形为2x=15. A . ①④;B . ②③;C . ①②④;D . ①②③考点: 等式的性质. 分析: 依据等式的基本性质即可解答.依据等式的基本性质即可解答. 解答: 解:①3x+6=0,两边同时除以3,得到x+2=0,故正确;,故正确;②x+7=5﹣3x ,变形为4x=﹣2,两边同时加上3x ,得到4x+7=5,两边再同时减去7,即可得到4x=﹣2.故正确;正确;③4x=﹣2,两边同时除以4得到:x=﹣,故本选项错误;,故本选项错误; ④=3,两边同时乘以5变形为2x=15.故正确..故正确.综上可得正确的是:①②④. 故选C .点评: 本题属简单题目,只要熟知等式的性质即可.本题属简单题目,只要熟知等式的性质即可.等式性质1:等式的两边都加上或者减去同一个数或同一个整式,所得结果仍是等式;:等式的两边都加上或者减去同一个数或同一个整式,所得结果仍是等式; 等式性质2:等式的两边都乘以或者除以同一个数(除数不为零),所得结果仍是等式.,所得结果仍是等式.14.已知5﹣(﹣2x+y )=6,则2x ﹣y=( ) A . ﹣1 B . 0 C .1 D .2考点: 等式的性质. 分析: 先由去括号法则去掉等式左边的括号,再根据等式的性质两边同时减去5,即可求解.,即可求解.解答: 解:∵5﹣(﹣2x+y )=6,∴5+2x ﹣y=6, ∴2x ﹣y=1. 故选C . 点评: 本题考查了去括号法则,等式的性质,是基础题,比较简单.题考查了去括号法则,等式的性质,是基础题,比较简单.15.下列说法正确的是(.下列说法正确的是( ) A . 在等式ax=bx 两边都除以x ,可得a=b B . 在等式在等式两边都乘以x ,可得a=bC . 在等式3a=9b 两边都除以3,可得a=3D . 在等式两边都乘以2,可得x=y ﹣1考点: 等式的性质. 分析: 根据等式的性质对四个选项进行逐一分析即可.据等式的性质对四个选项进行逐一分析即可. 解答: 解:A 、若x=0时,在等式ax=bx 两边都除以x 则此等式无意义,故本选项错误;则此等式无意义,故本选项错误;B 、由等式的性质2可知,在等式两边都乘以x ,可得a=b ,故本选项正确;,故本选项正确;C 、在等式3a=9b 两边都除以3,可得a=3b ,故本选项错误;,故本选项错误;D 、在等式=﹣1两边都乘以2,可得x=y ﹣2,故本选项错误.,故本选项错误.故选B . 点评: 本题考查的是等式的基本性质,即①等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时加上或减去同一个数或字母,等式仍成立; ②等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.数或字母,等式仍成立.16.(2013•东阳市模拟)如图a 和图b 分别表示两架处于平衡状态的简易天平,对a ,b ,c 三种物体的质量判断正确的是(确的是( )A . a <c <bB . a <b <cC . c <b <aD . b <a <c考点: 等式的性质.专题: 分类讨论.分类讨论. 分析: 根据等式的基本性质:等式的两边同时乘以或除以同一个不为0的数或字母,等式仍成立.分别列出等式,再进行变形,即可解决.式,再进行变形,即可解决.解答:解:由图a 可知,3a=2b ,即a=b ,可知b >a ,由图b 可知,3b=2c ,即b=c ,可知c >b ,∴a <b <c . 故选B .点评: 本题主要考查等式的性质.需利用等式的性质对根据已知得到的等式进行变形,从而找到最后的答案.17.已知xy=mn ,则把它改写成比例式后,错误的是(,则把它改写成比例式后,错误的是( ) A . = B . = C . =D .=分析: 利用等式的性质2:等式的两边同时乘以或除以同一个数(除数不为0),所得的结果仍是等式,可判断各选项正确与否.选项正确与否.解答: 解:A 、两边同时乘以最简公分母ny 得xy=mn ,与原式相等;,与原式相等;B 、两边同时乘以最简公分母mx 得xy=mn ,与原式相等;,与原式相等;C 、两边同时乘以最简公分母mn 得xn=my ,与原式不相等;,与原式不相等;D 、两边同时乘以最简公分母my 得xy=mn ,与原式相等;,与原式相等;故选C .点评: 解答此题应把每一个选项乘以最简公分母后与原式相比较看是否相同.解答此题应把每一个选项乘以最简公分母后与原式相比较看是否相同.18.已知mx=my ,下列结论错误的是(,下列结论错误的是( )A . x =yB . a +mx=a+myC . m x ﹣y=my ﹣yD .a mx=amy考点: 等式的性质.分析: 根据等式的基本性质解答.根据等式的基本性质解答.解答: 解:A 、等式的两边都除以m ,根据等式性质2,m ≠0,而A 选项没有说明,故A 错误;错误;B 、符合等式的性质1,正确.,正确.C 、符合等式的性质1,正确.,正确.D 、符合等式的性质1,正确.,正确.故选A .点评: 本题主要考查了等式的基本性质.本题主要考查了等式的基本性质.等式性质1、等式的两边同时加上或减去同一个数或字母,等式仍成立;、等式的两边同时加上或减去同一个数或字母,等式仍成立;等式性质2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.数或字母,等式仍成立.19.若ma=mb ,那么下列等式不一定成立的是(,那么下列等式不一定成立的是( )A . a=bB . ma ﹣6=mb ﹣6C .D . ma+8=mb+8考点: 等式的性质.分析: 根据等式的基本性质:①等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时加上或减去同一个数或字母,等式仍成立;②等式的两边同时乘以或除以同一个不为0的数或字母,等式仍成立.即可解决.的数或字母,等式仍成立.即可解决.解答: 解:A 、当m=0时,a=b 不一定成立.故选项错误;不一定成立.故选项错误;B 、ma=mb ,根据等式的性质1,两边同时减去6,就得到ma ﹣6=mb ﹣6.故选项正确;.故选项正确;C 、根据等式的性质2,两边同时乘以﹣,即可得到.故选项正确;,即可得到.故选项正确;D 、根据等式的性质1,两边同时加上8就可得到ma+8=mb+8.故正确..故正确.故选A .点评: 本题主要考查等式的性质.需利用等式的性质对根据已知得到的等式进行变形,从而找到最后的答案.20.下列各方程,变形正确的是(.下列各方程,变形正确的是( ) A . =1化为x= B . 1﹣[x ﹣(2﹣x )]=x 化为3x=﹣1C .化为3x 一2x+2=1 D . 化为2(x ﹣3)﹣5(x+4)=10分析: 分别利用性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式求出即可.个不为零的数,结果仍得等式求出即可.解答: 解:A 、﹣=1化为x=﹣3,故此选项错误;,故此选项错误;B 、1﹣[x ﹣(2﹣x )]=x 化为3x=﹣3,故此选项错误;,故此选项错误;C 、﹣=1化为3x ﹣2x+2=6,故此选项错误;,故此选项错误; D 、﹣=1化为2(x ﹣3)﹣5(x+4)=10,此选项正确.,此选项正确.故选:D .点评: 此题主要考查了等式的基本性质,熟练掌握等式的性质是解题关键.题主要考查了等式的基本性质,熟练掌握等式的性质是解题关键.21.下列各式变形错误的是(.下列各式变形错误的是( )A . 2x+6=0变形为2x=﹣6B . =1﹣x ,变形为x+3=2﹣2xC . ﹣2(x ﹣4)=﹣2,变形为x ﹣4=1D . ,变形为﹣x+1=1考点: 等式的性质.分析: 根据等式的性质对各选项分析判断后利用排除法求解.根据等式的性质对各选项分析判断后利用排除法求解.解答: 解:A 、2x+6=0变形为2x=﹣6正确,故本选项错误;正确,故本选项错误;B 、=1﹣x ,变形为x+3=2﹣2x 正确,故本选项错误;正确,故本选项错误;C 、﹣2(x ﹣4)=﹣2,变形为x ﹣4=1正确,故本选项错误;正确,故本选项错误;D 、﹣=变形为﹣x ﹣1=1,故本选项正确.,故本选项正确.故选D .点评: 本题主要考查了等式的基本性质,等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;立;2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.数或字母,等式仍成立.22.下列变形正确的是(.下列变形正确的是( )A . 若x 2=y 2,则x=yB . 若axy=a ,则xy=1C . 若﹣x=8,则x=﹣12D . 若=,则x=y考点: 等式的性质.分析: 利用等式的性质对四个选项逐一判断即可.用等式的性质对四个选项逐一判断即可.解答: 解:A 、当x 与y 互为相反数时,不成立,故本选项错误;互为相反数时,不成立,故本选项错误;B 、当a=0时不成立,故本选项错误;时不成立,故本选项错误;C 、方程两边同乘以﹣得x=﹣,故本选项错误;,故本选项错误;D 、根据分式有意义的条件可以得到a ≠0,所以该选项正确.,所以该选项正确.故选D .点评: 本题考查了等式的性质,在利用等式的性质时,注意所乘因式是否为零.题考查了等式的性质,在利用等式的性质时,注意所乘因式是否为零.23.根据下图所示,对a 、b 、c 三种物体的质量判断正确的是(三种物体的质量判断正确的是( )。
小学等式的性质练习题

小学等式的性质练习题1. 规范等式写法对于小学生来说,学习等式的性质是非常重要的。
一个等式由两边构成,左边和右边使用等号连接。
例如:2 + 3 = 5。
2. 等式的基本性质等式有很多基本性质,我们来看几个典型的例子:a) 可以通过交换等式两边的项来改变等式的顺序。
例如:2 + 3 = 5可以写成3 + 2 = 5。
b) 如果等式两边同时加上或减去相同的数,等式仍然成立。
例如:2 +3 = 5可以写成2 + 3 + 1 = 5 + 1。
c) 如果等式两边同时乘以或除以相同的数,等式仍然成立。
例如:2 +3 = 5可以写成2*2 + 3*2 = 5*2。
3. 练习题一现在让我们来解决一些小学等式的性质练习题:a) 3 + 4 = 7,请用交换性质写出一个等价的等式。
b) 5 - 2 + 1 = 4,请用加减性质写出一个等价的等式。
c) 4 * 3 = 12,请用乘法性质写出一个等价的等式。
4. 练习题一答案a) 4 + 3 = 7b) 5 + 1 - 2 = 4c) 3 * 4 = 125. 练习题二现在我们尝试一些更复杂的等式操作:a) 5 - 3 + 1 = 3,请用加减性质写出一个等价的等式。
b) 6 * 2 - 1 = 11,请用乘法和减法性质写出一个等价的等式。
c) 4 + 3 * 2 = 10,请用加法和乘法性质写出一个等价的等式。
6. 练习题二答案a) 5 + 1 - 3 = 3b) 6 * (2 - 1) = 11c) 4 + (3 * 2) = 107. 总结通过这些练习题,我们可以更好地理解小学等式的性质。
等式的基本操作包括交换、加减和乘法,并且我们可以利用这些性质改变等式的形式,但等式仍然成立。
这些性质为我们解决数学问题提供了便利。
希望本文的练习题能够帮助你更好地掌握小学等式的性质。
通过不断练习,你会发现等式可以是数学问题解决的关键。
加油!。
(完整版)等式性质练习题.docx

一、选择2. 下列等式变形错误的是 ( )A. 由 a=b 得 a+5=b+5;B.由 a=b 得ab;99 C. 由 x+2=y+2 得 x=y;D.由 -3x=-3y 得 x=-y3. 运用等式性质进行的变形 , 正确的是 ( ) A. 如果 a=b, 那么 a+c=b-c;B.如果ab, 那么 a=b;如果 a=b, 那么ab ;ccC. D.如果 a 2=3a, 那么 a=3cc二、填空:4. 用适当的数或式子填空 , 使所得结果仍是等式 , 并说明是根据等式的哪一条性崐质以及怎样变形的:(1) 如果 x+8=10, 那么 x=10+_________; (2) 如果 4x=3x+7, 那么 4x-_______=7;(3) 如果 -3x=8, 那么 x=________; (4) 如果 1x=-2, 那么 _______=-6.35. 完成下列解方程 :(1)3-1x=4 解: 两边 _________, 根据 ________得 3- 1 x-3=4_______. 于是 - 1x=_______.333两边 _________, 根据 _______得 x=_________. (2)5x-2=3x+4解: 两边 _________, 根据 _______得________=3x+6两边 _________, 根据 _______得 2x=________. 两边 _________, 根据 ________得 x=________.三、解答题:6. 利用等式的性质解下列方程并检验 :1 (1)x+3=2(2)-x-2=32(3)9x=8x-6(4)8y=4y+17. 解下列方程 :(1)7x-6=-5x (2)-3x-1=4; (3)2x+3=x-1 (4)3x 2 45 2 5100 1004 8. 当 x 为何值时 , 式子 x-5 与 3x+1 的和等于 9?39. 列方程并求解 :一个两位数 , 个位上的数字比十位上的数字大2, 个位与十位上的数字之和是10 崐 , 求这个两位数 ( 提示 : 设个位上的数字为 x)10. 如果方程 2x+a=x-1 的解是 x=-4, 求 3a-2 的值 .11. 等式 (a-2)x 2+ax+1=0 是关于 x 的一元一次方程( 即 x 未知 ), 求这个方程的解 .1、解方程 1 x 3 x,去分母,得( )62(A ) 1 x 3 3x;(B ) 6 x 3 3x;(C ) 6x 3 3x;( D )1x3 3x.212、下列方程中,是一元一次方程的是()(A ) x 4x 3; (B ) x0; ( C ) x 2y 1;(D ) x 1 .x3.方程 3x 6 0 的解的相反数是 ( )A.2B.-2C.3D.-34 .把方程 3x2x13x 132 去分母正确的是A. 18x 2(2x 1) 18 3( x 1)B.3x (2x 1) 3 ( x1)C. 18x(2x1) 18 ( x 1)D.3x2( 2x 1)3 3(x1)5.方程 -6x-3=0 的解是 ( )(A)x=1(B)x=2 (C)x=-1 (D) x=-22 26. x3 是方程 2( x k ) 5的解 , 则k( ) (A)0.5 (B)0.5 (C)(D)5.57 .解是 x 2 的方程是(A)2( x 1)6 (B)x 10x x 1 x(D) 2x1x 12 (C)23 128.已知关于 x 的方程4x 3m 2 的解是 x=m,则 m 的值是 ()A.2B.-2C.2或 7D.-2或 7二、填空题9.方程 0.25x 1的解是 __________.10.方程 3x-1= 1-2 的解是 ___________?211.若 3x+2 与-5x-8互为相反数 , 则 x-2 的值为 _______?12.已知 x=1 是方程 3x+a=2 的根 , 那么 a=________?13.如果| m3 | (n2)20 , 则方程 3mx 1 x n 的解是 ______.14.已知代数式 5a 1 与 3(a5) 的值相等 , 那么 a___.三、解答题15.解方程 : (1) 3x 5 4 x 1(2) 5x+1=3x-2(3) 4(x0.5) x 7 ( 4) 2x 3 5x 7 9x(5)3 6( x2) 2 (6) 2x-3=3x-(x-2)3316.解方程 .(1)3x 11 5x 7(2)2x 15x 11463 6(3)x 14x 1(4)x 3 2 x1 x2 2326(5)1 yy 3y 2 (6)x2x 11 3x 2341241、下列方程中,是一元一次方程的是 ( )A、x2x 3 x x 2 B 、x4 x0 C、x y 1 D、1x 0 y2、与方程x 1 2x的解相同的方程是 ()A 、x 2 1 2x B、x2x 1C、x 2x 1D、x x 1 23、若关于x的方程mx m 2m 3 0 是一元一次方程,则这个方程的解是()A 、x 0B、x3C、x3D、x 2x x 11去分母后,正确的是()。
