高中物理必修二第六章第15讲 开普勒定律 万有引力定律
必修二第六章-万有引力定律课件ppt

三.万有引力定律:
1.内容:
自然界中任何两个物体都是互相吸引的,引力的 方向在它们的连线上,引力的大小跟这两个物体 的质量m1和m2的乘积成正比,跟它们的距离的 二次方成反比.
2.公式:
m1m2 F G 2 r
3.单位:
质量m----kg,距离r ----m, 力F ----N; 常量G----N· m2/kg2 ,( 数值上等于 两质量各为1Kg的物体相距1米时的万 有引力的大小)。
但是目前为止,我们所做的推导都是源 于开普勒行星运动定律,所以只适用于 太阳与行星间的力。
但苹果落地却引起了牛顿的沉思。 他猜想:行星因为太阳引力没有飞离太阳, 苹果成熟后是否也是因为地球引力才没有飞离地 球呢?这两种力会不会是同一种性质的力呢?月 球是绕地球转动的行星,是否可以利用月球的运 动来进行检验呢?
m1 m2 A、 G 2 r
B、 D、
m m 1 2 C、G 2 (r1 r2 )
r1 r
m1m2 G 2 (r r1 r2 )
r2
m1 m 2 G 2 r1
课堂发散思维:万有引力的重要性!
如果没有万有引力,这个世界可能会发生 何种变化?请举出几种具体的可能发生的 不同于以往的运动情况为例,并简要说明 理论依据。
6、万有引力定律的进一步理解:
(1)普遍性:万有引力是普遍存在于宇宙中的任何有质量 的物体(大到天体小到微观粒子)间的相互吸引力,它 是自然界的物体间的基本相互作用之一. (2)相互性:两个物体相互作用的引力是一对作用力与反 作用力,符合牛顿第三定律. (3)宏观性:通常情况下,万有引力非常小,只有在质量 巨大的天体间或天体与物体间它的存在才有宏观的物理 意义.在微观世界中,粒子的质量都非常小,粒子间的 万有引力很不显著,万有引力可以忽略不计.
人教版高一物理必修二 第六章 万有引力与航天--开普勒定律及万有引力定律(无答案)

开普勒定律及万有引力定律1.开普勒行星运动三定律简介(轨道、面积、比值)丹麦开文学家开普勒信奉日心说,对天文学家有极大的兴趣,并有出众的数学才华,开普勒在其导师弟谷连续20年对行星的位置进行观测所记录的数据研究的基楚上,通过四年多的刻苦计算,最终发现了三个定律。
第一定律:所有行星都在椭圆轨道上运动,太阳则处在这些椭圆轨道的一个焦点上;第二定律:行星沿椭圆轨道运动的过程中,与太阳的连线在单位时间内扫过的面积相等;第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.即k Tr =23开普勒行星运动的定律是在丹麦天文学家弟谷的大量观测数据的基础上概括出的,给出了行星运动的规律。
2.万有引力定律(1) 内容:宇宙间的一切物体都是相互吸引的,两个物体间的引力大小跟它们的质量成积成正比,跟它们的距离平方成反比,引力方向沿两个物体的连线方向。
2r Mm G F =(1687年) 2211/1067.6kg m N G ⋅⨯=-叫做引力常量,它在数值上等于两个质量都是1kg 的物体相距1m 时的相互作用力,1798年由英国物理学家卡文迪许利用扭秤装置测出。
万有引力常量的测定——卡文迪许扭秤实验原理是力矩平衡。
实验中的方法有力学放大(借助于力矩将万有引力的作用效果放大)和光学放大(借助于平面境将微小的运动效果放大)。
万有引力常量的测定使卡文迪许成为“能称出地球质量的人”:对于地面附近的物体m ,有2EE R m m G mg =(式中R E 为地球半径或物体到地球球心间的距离),可得到GgR m E E 2=。
(2)定律的适用条件:严格地说公式只适用于质点间的相互作用,当两个物体间的距离远远大于物体本身的大小时,公式也可近似使用,但此时r 应为两物体重心间的距离.对于均匀的球体,r 是两球心间的距离.当两个物体间的距离无限靠近时,不能再视为质点,万有引力定律不再适用,不能依公式算出F 近为无穷大。
最新人教版高中物理必修2第六章《万有引力定律》教材梳理

庖丁巧解牛知识·巧学一、月—地检验牛顿把牛顿运动定律和开普勒三定律相结合,得出了太阳与行星间的引力关系:引力的大小与太阳、行星的质量成正比,与两者距离的二次方成反比,即F ∝2r Mm 牛顿进一步推断,太阳与行星间的引力和地球对地面上物体的引力是同一种性质的力.为了验证这一结论,牛顿做了“月—地”检验.1.月—地检验的思路假设太阳对行星的引力、行星与卫星之间的引力、地球对月球的引力(维持月球绕地球运动的力)以及地球作用于物体上的重力(使得苹果下落的力)都是同样性质的力的话.根据上述引力公式,对“月—地系统”和地面上的物体分别可得到:月月地月月a m r Mm G =2;2地物r Mm G =m 物a 物=m 物g两式相比,得月球绕地球运动的向心加速度与地球表面物体的重力加速度应有如下关系:a 月=2)(地月地r r g 因为地球和月球之间的距离r 地月约为地球半径r 地的60倍,因此月球绕地球运动的向心加速度应该有如下值:a 月=36001)601(2=g ×9.8 m/s 2=2.7×10-3 m/s 2. 2.观测的结果的对照验证根据天文观测,月球绕地球运动的周期T=27.3 d,地球与月球间距离r 地月=3.85×108 m,因此从运动学公式可直接得到月球运动的向心加速度,应该有:a 月′=224T πr 地月=22)864003.27(4⨯π×3.85×108 m/s 2=2.7×10-3 m/s 2 假设前提下的推理结果与观测下的数据计算结果,两者是一致的,说明地球对月球的引力(维持月球绕地球运动的力)以及地球作用于物体上的重力(使得苹果下落的力)确属同样性质的力.要点剖析 这个结果是牛顿于1666年在家乡避瘟疫时完成的.当时牛顿所知的地球半径数据不精确(我们这里改用了精确的数值),而且牛顿仅得出了圆轨道的引力与半径的平方成反比的关系,对椭圆轨道的情况是否有同样的关系,以及能否把地球质量集中于球心,也尚未严格证明,因此牛顿并未将他的结果发表.二、万有引力定律1.万有引力在宇宙万物中,任何两个物体之间都存在着吸引作用,这种引力称为万有引力.2.万有引力定律(1)内容:任何两个物体都是相互吸引的,引力的大小跟两个物体质量的乘积成正比,跟它们的距离的平方成反比.(2)表达式:设m 1、m 2表示两物体的质量,r 表示它们的距离,则有:F=221r m m G . G 是引力常量,其值为6.67×10-11 N·m 2/kg 2,在数值上等于两个质量都是1 kg 的物体相距1 m 时的相互作用力.使用公式时,注意各量均采用国际单位.(3)万有引力定律适用于可以看作质点的物体间的相互作用.万有引力公式只适用于两质点间的引力的计算,因为对一般物体而言,“两个物体之间的距离”到底是指物体哪两部分的距离,无法确定.实际物体当它们之间的距离远大于它们本身的尺度时,可视为质点.对质量均匀分布的球体,也可以用此公式计算它们之间的引力,其中的距离即两球心之间的距离.但是,对于一般物体间的万有引力,切不可用它们质心间的距离代入上式计算.切不可依据F=221rm m G 得出r→0时F→∞的结论而违背公式的物理含义,因为,此时由于r→0,物体已不能再看作质点,定律已不再适用.深化升华 求一个质点受到多个质点的万有引力时,可先用万有引力公式求出各个质点的引力,再求它们的矢量和.求相距不远而不能看作质点的两物体间的万有引力时,应将每一物体看成一个质点系.物体A 包含的所有质点与物体B 包含的所有质点之间都有引力.如图7-3-1所示,物体B 的各质点m 1′、m 2′、m 3′…m k ′对物体A 的任一质点均有引力,所以质点m 1所受引力的总和为F 1=∑'k k k r m m G211(矢量和).图7-3-1物体B 的各质点m 1′、m 2′、m 3′…m k ′对物体A 的其他质点m 2、m 3、m 4…m i 均有引力,这些力的合力就是物体B 对物体A 的引力,可用下式表示:F=∑'k i ik k i r m m G,2(矢量和).物体A 对物体B 的引力F′与F 大小相等、方向相反.3.理解万有引力定律具有以下特性普遍性:万有引力定律是普遍存在于宇宙中任何有质量的物体间的相互吸引力,它是自然界物体间的基本相互作用力之一.相互性:两个物体间相互作用的万有引力是一对作用力与反作用力,符合牛顿第三定律. 宏观性:通常情况下,万有引力非常小,只有在质量巨大的天体间或天体与物体间,它的存在才有宏观的物理意义.特殊性:两个物体间的万有引力,只与它们本身的质量有关,与它们之间的距离有关,和所在的空间的性质无关,和周围有无其他物体的存在无关.深化升华 万有引力定律,把地面上物体运动的规律与天体运动的规律统一了起来(地面上物体和天体的运动规律相同),揭示了自然界中的一种基本相互作用——万有引力,是17世纪自然科学最伟大的成果之一,对物理学和天文学的发展具有深远的影响.三、引力常量的测定牛顿虽然发现了万有引力定律,却没能给出准确的引力常量,这是因为一般物体间的引力非常小,很难用实验的方法将它显示出来,直到1789年,即在牛顿发现万有引力定律一百多年以后,英国物理学家卡文迪许(1731—1810)才巧妙地利用扭秤装置,第一次在实验室里比较准确地测出了引力常量.通过测量得到G=6.754×10-11 N·m 2/kg 2.卡文迪许通过改变质量和距离,证实了万有引力的存在及万有引力定律的正确性;第一次测出了引力常量,使万有引力定律能进行定量计算,显示出真正的实用价值;它标志着力学实验精密程度的提高,开创了弱力的新时代,同时表明:任何规律的发现总是经过理论上的推理和实验上的反复验证才能完成.深化升华 引力常量的测出不仅用实验证明了万有引力的存在,更使得万有引力定律有了真正的实用(计算)价值.例如,可以用测定地球表面物体重力加速度的方法测定地球的质量,设地球半径为R ,质量为M ,地球表面物体的重力加速度为g ,由牛顿第二定律和万有引力定律可得:2R Mm G =mg ,所以M=GgR 2因为引力常量G 、地球半径R 和地表物体的重力加速度均已知,因此可以计算出地球的质量.也正是由于这一应用,使卡文迪许被人们称为第一个能“称出地球质量的人”. 问题·探究问题1 为什么在日常生活中感觉不到万有引力的存在?探究:引力存在于任何物体之间,只是对于一般质量的物体(例如人与人之间)来说,这个力显得太小,我们无法感觉到罢了.并非人彼此间不存在吸引的力.万有引力是发生在两个有质量的物体之间的力.日常生活中感觉不到万有引力是因为两个物体质量较小,万有引力也较小的缘故.问题2 探究:万有引力常量的测量.探究:卡文迪许实验的巧妙之处是采用“放大法”进行了微小量(万有引力)的间接测量.(1)实验过程中,采用“放大法”把微小的万有引力转变成力矩来反映,并尽可能增大T 形架连接两球的长度L ,使m 、m′之间的万有引力能产生较大力矩,使得金属丝有较大偏转角度,把微小的万有引力的作用效果放大(一次放大)(2)利用光学中“平面镜偏转θ角时,反射光线偏转2θ角”的结论,将金属丝微小形变引起扭转角度θ的效果加以放大,扭转角度通过光标的移动来反映,并尽可能地增大弧形尺与小平面镜间距离,使光标在弧形尺上移动的距离较大(二次放大)(3)让两个球m′同时吸引m (三次放大).卡文迪许扭秤的主要部分是一个轻而坚固的T 形架,倒挂在一根金属丝的下端.T 形架水平部分的两端各装一个质量是m 的小球,T 形架的竖直部分装一面小平面镜M ,它能把射来的光线反射到刻度尺上(图7-3-2),这样就能比较精确地测量金属丝的扭转.图7-3-2实验时,把两个质量都是m′的大球放在图7-3-2所示的位置,它们跟小球的距离相等.由于m 受到m′的吸引,T 形架受到力矩作用而转动,使金属丝发生扭转,产生相反的扭转力矩,阻碍T 形架转动.当这两个力矩平衡时,T 形架停下来不动,这时金属丝扭转的角度可以从小镜M 反射的光点在刻度尺上移动的距离求出,再根据金属丝的扭转力矩跟扭转角度的关系,就可以算出这时的扭转力矩,进而求得m 与m′的引力F.卡文迪许经过多次实验,证明牛顿的万有引力定律是正确的,并测出了引力常量.正是由于卡文迪许测出引力常量G ,才使得万有引力定律在天文学的发展上起了重要的作用.典题·热题例 1 你受太阳的引力是多大?和你受地球的引力比较一下,可得出什么样的结论?太阳的质量是1.99×1030 kg ,地球到太阳的距离为1.5×1011 m ,设你的质量是60 kg.解析:直接应用万有引力公式进行计算加以比较即可得出结论.地球半径为6.4×106 m ,与地球到太阳的距离1.5×1011 m 相比相差近10万倍,因此人距太阳的距离可以认为也是1.5×1011 m.故人受太阳的引力 F=2r m m G '=6.67×10-11×21130)105.1(1099.160⨯⨯⨯ N=0.35 N 人受地球的引力F′=mg=60×9.8 N=588 N168035.0588=='F F 即地球对人的引力要比太阳对人的引力大一千六百多倍.平时计算时可以不考虑人受太阳的万有引力.方法归纳 掌握万有引力定律的意义,体会引力与距离的关系,并能运用万有引力定律计算物体间万有引力的大小.例2 应用万有引力公式证明和计算:(1)在星体上物体做自由落体运动的加速度g 跟运动物体的质量无关,g 的值由星体质量和运动物体所处的位置所决定.(2)如果在离地面高度等于地球半径的高度释放一个物体,让它做自由落体运动,它开始运动的加速度是多大?解析:不考虑物体随星体自转的影响,物体做自由落体运动的加速度是由星体对运动物体的引力产生的.由此求得重力加速度的表达式,代入已知条件进行计算.(1)设物体和星体的质量分别为m 和M ,两者相距r ,则物体所受星体的引力为2R Mm G F = 所以,自由落体加速度为2r M G m F g ==. 可见,g 跟运动物体的质量m 无关,g 的值由星体质量M 和运动物体所处的位置(离星体球心的距离r )所决定.(2)从离地面为R 处做自由落体运动的物体,开始时的加速度 g′=441)2(022g RM G R M G =∙=地地.(g 0为地球表面的重力加速度) 方法归纳 要区分不同星球的重力加速度与同一星球随高度升高而重力加速度减小的问题.例如,要区分在月球轨道上的星球受到地球引力的加速度与月球表面物体的重力加速度.例3 用M 表示地球的质量,R 表示地球的半径,r 月地表示月球到地球的距离.在地球引力作用下:(1)地面上物体的重力加速度g=_____________.(2)月球的加速度a 月=_____________.(3)已知r 月地=60R ,利用(1)(2)求g a 月=___________.(4)已知r 月地=3.8×108 m ,月球绕地球运行的周期T=27.3天,计算月球绕地球运行的向心加速度a 月.(5)已知重力加速度g=9.8 m/s 2,利用(4)中算出的a 月求g a 月的值. (6)比较(3)(5),你能得出什么结论?解析:(1)设物体质量为m ,在地面上时:2R GMm =mg 得g=2R GM (2)月球受地球的万有引力F=2月地月r GMm =m 月a 月得a 月=月地r GM (3)ga 月=222)(月地月地r R R GM r GM==1∶3 600 (4)由a=2)2(Tπ·r 得a 月=2)3600243.272(⨯⨯π×3.8×108 m/s 2=2.69×10-3 m/s 2 (5)364318.91069.23=⨯=-g a 月 (6)比较(3)(5)可知,月球所受引力与地面上物体所受引力遵循相同的规律,因而是同一性质的力.答案:(1)2R GM (2)2月地r GM (3)1∶3 600 (4)2.69×10-3 m/s 2 (5)36431 (6)略方法归纳 ①范例介绍了牛顿著名的“月—地检验”的思路,实际上从“苹果落地”的故事起到牛顿发表万有引力定律,前后经历了20年,大胆的猜测、严谨的求证、不懈的努力使他获得了一个又一个伟大的发现.②距离地面h 高处的重力加速度g′=g h R R h R GM 22)()(+=+,重力加速度随着高度的增加而减小.例4 在一次测量引力常量的实验中,已知一个质量为0.8 kg 的球,以1.3×10-10 N 的力吸引另一个质量为4.0×10-3 kg 的球,这两个球相距4.0×10-2 m ,地球表面的重力加速度为9.8 m/s 2,地球半径为6 400 km.试根据这些数据计算地球的质量.解析:本题考查了引力常量的测定以及地球质量的计算两个知识点,在地面附近的物体,它所受到的重力近似等于物体所受到的万有引力,可用万有引力定律计算地球的质量. 由于地球对物体的引力等于物体所受到的重力,则有:2R Mm G =mg ,所以M 地=GgR 2地 ① 又因为两球之间的万有引力为F=221r m m G 所以有:G=212m m Fr ② ②式代入①式得:M 地=2212Fr m m gR 地代入数据可得地球的质量:M=2210326)100.4(103.1100.48.0)104.6(8.9---⨯⨯⨯⨯⨯⨯⨯⨯ kg=6.2×1024 kg. 方法归纳 本题考查对引力常量G 的理解及应用万有引力定律进行有关计算.万有引力定律中的引力常量G ,无论是在计算天体间的引力还是计算很小微粒间的万有引力时均是相同的.在解答问题的过程中,要视具体情况选择合适的公式使用.例5 有一质量为M 、半径为R 、密度均匀的球体,在距离球心O 为2R 的地方有一质量为m 的质点,现在从M 中挖去一半径为2R 的球体,如图7-3-3所示,求剩下部分对m 的万有引力F 为多大?图7-3-3解析:一个质量均匀分布的球体与球外的一个质点间的万有引力可以用公式221r m m G F =直接进行计算,但当球体被挖去一部分后,由于质量分布不均匀,万有引力定律就不再适用了.此时我们可以用“割补法”进行求解.设想将被挖部分重新补回,则完整球体对质点m 的引力为F 1,可以看作是剩余部分对质点的引力F 与被挖小球对质点的引力F 2的合力,即F 1=F+F 2.设被挖小球的质量为M′,其球心到质点间的距离为r′.由题意,知M′=8M ,r′=23R ;由万有引力定律,得 F 1=224)2(R GMm R Mm G =F 2=22218)23(8R GMm R m M G r m M G =='' 所以剩下部分对m 的万有引力为F=F 1-F 2=2367R GMm . 方法归纳 仔细观察球体挖去部分及完整球体的形状特点,可知,完整部分与质点m 以及挖去部分与质点m 间万有引力均可用公式计算,由此联想到利用等效割补的方式先将剩余部分还原为完整体,计算出万有引力,然后计算出割去部分与质点m 间的万有引力,两者之差即为所求.通过“割补法”的运用,我们可以感受利用直觉思维寻求解题思路的简捷性.。
(word完整版)高一物理必修二第六章《万有引力与航天》知识点总结,推荐文档.docx

万有引力与航天知识点总结一、人类认识天体运动的历史1、 “地心说 ”的内容及代表人物: 托勒密 (欧多克斯、亚里士多德)2、 “日心说 ”的内容及代表人物: 哥白尼(布鲁诺被烧死、伽利略)二、开普勒行星运动定律的内容开普勒第二定律:v 近 v 远开普勒第三定律: K — 与中心天体质量有关,与环绕星体无关的物理量;必须是同一中心天体的星体a 地 3 = a 火 3 a 水 3 =......才可以列比例,太阳系:T 地 2 T 火 2=T 水 2三、万有引力定律1、内容及其推导:应用了开普勒第三定律、牛顿第二定律、牛顿第三定律。
3F m42mmR K①r②F = 4π2K FFF ③r 2T 2T 2r 2FM FMm FG Mmr 2r 2r 22、表达式: F Gm 1m 2r 23、内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1,m2 的乘积成正比,与它们之间的距离r 的二次方成反比。
4.引力常量: G=6.67 ×10-11N/m 2/kg 2,牛顿发现万有引力定律后的 100 多年里, 卡文迪许 在实验室里用扭秤实验测出。
5、适用条件:①适用于两个质点间的万有引力大小的计算。
②对于质量分布均匀的球体,公式中的r 就是它们球心之间的距离 。
③一个均匀球体与球外一个质点的万有引力也适用,其中 r 为球心到质点间的距离。
④两个物体间的距离远远大于物体本身的大小时, 公式也近似的适用, 其中 r 为两物体质心间的距离。
6、推导: GmM4 2R 3GMR 2m2 RT 242T1四、万有引力定律的两个重要推1、在匀球的空腔内任意位置,点受到地壳万有引力的合力零。
2、在匀球体内部距离球心r ,点受到的万有引力就等于半径r 的球体的引力。
五、黄金代若已知星球表面的重力加速度g 和星球半径 R,忽略自的影响,星球物体的万有引力等于物体的重力,有 G Mmmg 所以 MgR2 R2G其中 GM gR2是在有关算中常用到的一个替关系,被称黄金替。
高中物理必修2万有引力定律课文知识点解析

万有引力定律-课文知识点解析天体究竟做怎样的运动一、古代的两种学说1.地心说:宇宙以地球为中心,外边围绕着月亮、水星、金星、太阳、火星、木星、土星,然后是恒星天和最高天这样“九重天”,所有行星和太阳、月亮都有本轮和均轮,而且均轮都是偏心圆,最早于公元前300多年由古希腊哲学家亚里士多德系统提出,至公元前100多年,由天文学家托勒密进一步改进和完善,由于符合天主教的神学,统治人们达1000多年.2.日心说:(heliocentric system)认为太阳是宇宙中心,地球和其他行星都绕太阳转动的学说,又称“日心地动说”或“日心体系”.16世纪,波兰天文学家哥白尼经过近40年的辛勤研究,在分析过去的大量资料和自己长期观测的基础上,于1543年出版的《天体运行论》中,系统地提出了日心体系,认为地球不是宇宙中心,而是一颗普通行星,太阳才是宇宙中心,行星运动的一年周期是地球每年绕太阳公转一周的反映,哥白尼体系另一些内容是:水星、金星、火星、木星、土星五颗行星和地球一样,都在圆形轨道上匀速地绕太阳公转,月球是地球的卫星,它在以地球为中心的圆形轨道上,每月绕地球转一周,同时跟地球一起绕太阳公转,地球每天自转一周,天穹实际上不转动,因地球自转才出现日月星辰每天东升西落的现象,限于当时的科学发展水平,哥白尼学说也有缺点和错误,这就是:把太阳视为宇宙的中心,实际上,太阳只是太阳系的中心天体,不是宇宙中心;沿用了行星在圆轨道上的匀速运动的旧观念,实际上行星轨道是椭圆的,运动也不是匀速的.二、行星运动的描述1.第谷的观测第谷是丹麦的天文学家,是一位出色的观测家,他用了三十年的时间观测、记录了行星、月亮、彗星的位置.第谷本人虽然没有准确描绘出行星运动的规律,但他所记录的数据为后人的研究提供了坚实的基础.2.开普勒三定律德国天文学家开普勒曾经与第谷一起工作过一段时间,第谷去世后,开普勒认真整理了第谷的观测资料,在哥白尼学说的基础上又迈进了一步,抛弃了圆轨道的说法,于1609年在他的著作《新天文学》中提出了著名的三大定律中的前两条,十年后,又提出第三条定律.开普勒第一定律(又叫椭圆轨道定律)所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上.开普勒第二定律(又叫面积定律)太阳和行星的连线在相等的时间内扫过相等的面积.开普勒第三定律(又叫周期定律)所有行星的椭圆轨道的半长轴的三次方跟公转周期的二次方的比值都相等. 全析提示地心说符合人们的日常经验,同时也符合势力强大的宗教神学关于地球是宇宙中心的说法,故地心说统治了人们相当长的时间.日心说能很容易地解释天体的运动,因此日心说逐渐受到人们的重视,到17世纪,就建立了日心说的理论体系.古代的两种说法都不正确,因为不管是地球还是太阳,它们都在不停地运转;不可能静止,鉴于当时人们对自然科学的认识能力,只是日心说比地心说更进一步.开普勒定律是总结行星运动的观察结果而总结归纳出来的规律,它们每一条都是经验定律,都是从观察行星运动所取得的资料中总结出来的,开普勒定律只涉及运动学、几何学方面的内容.不同行星椭圆轨道是不同的.行星近日点的速率大于远日点的速率.思维拓展开普勒定律不仅适用于行星,也适用于卫星,只不过此时23TR=k′,比值数学表达式为23T R =k ,或者为2131T R =2232T R其中R 为椭圆轨道的半长轴,T 为公转周期,k 是与行星无关的常量. 苹果落地的思考:万有引力定律的发现 一、近代物理学家对行星运动本质的认识开普勒三定律清晰地说明了行星是怎样运动的,但行星“为什么会这样运动”?是上帝安排的吗?近代物理学家对此提出了不同的动力学解释:伽利略:认为一切物体都有合并的趋势,这种趋势导致行星做圆周运动.开普勒:行星绕太阳运动,一定是受到了太阳的某种力的作用. 笛卡儿(法国):行星周围有旋转的物质(以太)迫使行星绕太阳运行.胡克、哈雷等人:行星绕太阳运动的原因是因为太阳对行星产生吸引力.牛顿:在前人研究的基础上,凭借其非凡的数学才能,阐明了天体运动的根本原因,提出具有普遍意义的万有引力定律,即行星绕太阳运行的原因是由于太阳与行星之间存在相互吸引的力,称为万有引力.二、万有引力定律的推导思路和方法1.把行星绕太阳的运动近似看成是匀速圆周运动,太阳对行星的万有引力是行星做圆周运动所需的向心力,即F =m rv 2将圆周运动中的线速度与周期的关系式v =T r π2代入上式得F =4π2(23T r )rm据开普勒第三定律知:23Tr =k即 F =4π2k2r m 2.牛顿认为k 是一个与行星无关,但与太阳质量有关的物理量,行星吸引太阳的力和太阳吸引行星的力应大小相等,并且有相同的性质,而太阳对行星的引力F 与行星的质量成正比,自然也应跟太阳的质量成正比,设太阳的质量为M ,则4π2k ∝M ,所以F ∝2r Mm,写成等式为F =G2r Mm,式中G 为常量. 3.牛顿认为太阳与行星的引力跟月球与地球的引力,以及地面上的物体与地球的引力也遵循同样的规律,由此得出万有引力定律F =G221r m m 三、万有引力定律(law of universal gravitation )1.内容:自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比.k ′是由行星的质量所决定的另一恒量,与卫星无关.行星的轨道都跟圆近似,因此计算时可以认为行星是做匀速圆周运动的. 思维拓展对事物的认识总是一步步的,经历了漫长的过程.全析提示万有引力是自然界的一种基本作用力,对它的研究和探讨,促进了物理学的发展,在人类认识自然的历史上起到了巨大的作用.思维拓展对于更一般、且不可看作质点的物体,在计算引力时可采用分隔法:将物体分割成无数个小单元,每个小单元看作质点,求出各质点间的引力,再利用力的合成求出两物体间的引力,对于这样的问题高中阶段一般不涉及,但应了解这种做法.2.公式: F =G2r m m '式中质量的单位用kg ,距离的单位用m ,力的单位用N ,G 为引力常量,标准值为G =6.67259×10-11N ·m 2/kg 2,通常G =6.67×10-11N ·m 2/kg 2. 3.万有引力定律公式使用的条件公式中的r 对于可看作是质点的物体而言指的就是两质点的距离;对于一般物体而言,r 应为两个物体的质量中心的距离,如质量分布均匀的球体,r 可为两球心之间的距离.4.应用万有引力定律时应注意的问题.(1)万有引力的普遍性.万有引力不仅存在于星球间,任何客观存在的有质量的物体之间都存在着这种相互吸引的力.(2)万有引力的相互性.两个物体相互作用的引力是一对作用力和反作用力,它们大小相等,方向相反,分别作用于两个物体上.(3)万有引力的宏观性.在通常情况下,万有引力非常小,只有在质量巨大的星球间或天体与天体附近的物体间,它的存在才有实际的物理意义,故在分析地球表面物体受力时,不考虑地面物体对地球的万有引力.只考虑地球对地面物体的引力.(4)万有引力的特殊性,两个物体间的万有引力只与它们本身的质量有关,与它们间的距离有关,而与所在空间的性质无关,也与周围有无其他物体无关.讨论与交流 1.略2.由于人的质量远小于地球的质量,因此两人之间的吸引力远小于地球对人的吸引力,(即人的重力)两人间的引力不足以克服人与地面间的摩擦力,因而两人不能吸在一起.例如两个质量各为50 kg 的人相距1 m 时他们相互的引力F =G221r m m =211150501067.6⨯⨯⨯-N=1.7×10-7N ,这个引力相当于几百粒尘埃的重量.实践与拓展 1.略2.对F =ma 的理解是当F 一定时a 与m 成反比,而对不同的下落物体重力不同,即合外力不同,不能研究a 与m 的关系.四、引力常量值测定的意义引力常量的测出有着非常重要的意义,不仅用实验证明了万有引力的存在,更使得万有引力定律有了真正的实用价值.例如,可以用测定地球表面物体重力加速度的方法,测定地球的质量,设地球半径为R ,质量为M ,地球表面物体的重力加速度为g ,由牛顿第二定律和万有引力定律可得:G2RMm=mg 所以 M =GgR 2因为引力常量G 、地球半径R 和地表物体的重力加速度均已知,因此要点提炼万有引力虽具有普遍性,但由于一般物体间万有引力较小,可忽略,只有在研究质量很大的天体时,才必须考虑.全析提示采用估算方式进行半定量分析说理.运用万有引力定律可以计算出天体的质量、万有引力常量G 的数值,测得是否准确,对于天体质量计算的准确程度有直接的影响.因此,人类不断改进对基本物理常数G 值的测定技术,使它的数值日益精确.可以计算出地球的质量.也正是由于这一应用,使卡文迪许被人们称为是第一个能称出地球质量的人.高中物理必修2万有引力定律课文知识点解析。
必修二物理第六章万有引力知识点

必修二物理第六章万有引力知识点1. 万有引力定律:两个物体之间的引力与它们的质量成正比,与它们之间的距离的平方成反比。
数学表达式为:F = G × (m1 × m2) / r^2,其中F为两个物体之间的引力,G为万有引力常数,m1和m2分别为两个物体的质量,r为它们之间的距离。
2. 万有引力常数:G为一个固定的常数,其数值为6.674 × 10^-11 N·m^2/kg^2。
它描述了质量和引力之间的比例关系。
3. 地球上的重力:地球对物体的引力称为重力,是物体的质量和地球质量之间的引力作用。
数学表达式为F = mg,其中F为物体所受的重力,m为物体的质量,g为重力加速度(在地球上约为9.8 m/s^2)。
4. 引力的方向:引力的方向始终指向两个物体之间的中心,且大小相等。
5. 引力与质量的关系:引力与物体的质量成正比,质量越大,引力越大。
6. 引力与距离的关系:引力与两个物体之间的距离的平方成反比,距离越远,引力越弱。
7. 引力的作用范围:万有引力是一种长程力,作用范围无限远,即两个物体之间的引力不受距离的限制。
8. 四个基本力中的引力:万有引力是四个基本力之一,其他三个基本力分别为电磁力、强核力和弱核力。
9. 行星运动的引力:行星绕太阳运动是由于太阳对行星的引力作用,根据万有引力定律,太阳对行星的引力提供了向心力,使行星保持在轨道上运动。
10. 引力场:引力形成了一个与质量有关的场,任何在这个场中的物体都会受到引力的作用。
11. 引力势能:两个物体之间的引力势能等于它们之间的引力所做的功,计算公式为Ep = -G × (m1 × m2) / r,其中Ep为引力势能。
12. 开普勒定律:开普勒定律描述了行星运动的规律,其中包括行星轨道的椭圆形状、行星在不同位置上的速度以及行星轨道面与太阳赤道面的关系。
开普勒定律与万有引力定律的结合使得我们能够准确描述行星的运动。
高一物理《开普勒行星运动定律万有引力定律》知识点总结

高一物理《开普勒行星运动定律万有引力定律》知识点总结
一、开普勒定律
1.开普勒第一定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上.
2.开普勒第二定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等.
3.开普勒第三定律:所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相
等.其表达式为a 3
T 2=k ,其中a 代表椭圆轨道的半长轴,T 代表公转周期,比值k 是一个对所有行星都相同的常量.
二、行星运动的近似处理
行星的轨道与圆十分接近,在中学阶段的研究中我们可按圆轨道处理.这样就可以说:
1.行星绕太阳运动的轨道十分接近圆,太阳处在圆心.
2.行星绕太阳做匀速圆周运动.
3.所有行星轨道半径r 的三次方跟它的公转周期T 的二次方的比值都相等,即r 3T 2=k . 三、万有引力定律
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比、与它们之间距离r 的二次方成反比.
2.表达式:F =G m 1m 2r 2,其中G 叫作引力常量. 四、引力常量
牛顿得出了万有引力与物体质量及它们之间距离的关系,但没有测出引力常量G 的值. 英国物理学家卡文迪什通过实验推算出引力常量G 的值.通常取G =6.67×10-11 N·m 2/kg 2.。
新人教版 年 高一物理必修2 第六章 专题:万有引力定律应用-课件

例1.关于万有引力定律和引力常量的发现,下面
说法中哪个是正确的 ( D )
A.万有引力定律是由开普勒发现的,而引 力常量是由伽利略测定的
B.万有引力定律是由开普勒发现的,而引 力常量是由卡文迪许测定的
C.万有引力定律是由牛顿发现的,而引力 常量是由胡克测定的
D.万有引力定律是由牛顿发现的,而引力 常量是由卡文迪许测定的
例2.关于第一宇宙速度,下面说法正确的有( B C ) A. 它是人造卫星绕地球飞行的最小速度 B. 它是发射人造卫星进入近地圆轨道的最小速度 C.它是人造卫星绕地球飞行的最大速度 D. 它是发射人造卫星进入近地圆轨道的最大速度。
(提示:注意发射速度和环绕速度的区别)
练习.已知金星绕太阳公转的周期小于地球绕太阳 公转的周期,它们绕太阳的公转均可看做匀速圆周 运动,则可判定 ( C )
法正确的是 ( B D ) A.卫星的轨道半径越大,它的 运行速度越大 B.卫星的轨道半径越大,它的 运行速度越小 C.卫星的质量一定时,轨道半径越大,它需要的
向心力越大 D.卫星的质量一定时,轨道半径越大,它需要的
向心力越小
例5.一宇宙飞船在离地面h的轨道上做匀速圆周运
动,质量为m的物块用弹簧秤挂起,相对于飞船静
练习.一颗人造地球卫星在离地面高度等于地球半
径的圆形轨道上运行,其运行速度是地球第一宇宙
速度的
2 2
倍.
此处的重力加速度g'= 0.25 g0 .(已知地球表面
处重力加速度为g0)
练习、 从地球上发射的两颗人造地球卫星A和B, 绕地球做匀速圆周运动的半径之比为RA∶RB=4∶1, 求它们的线速度之比和运动周期之比。
n= T1/(T2-T1), ∴ t1 =T1T2/(T2-T1) ,
人教版物理必修二第六章-万有引力与航天知识总结

GgR M R MmG mg 22==第六章 万有引力与航天开普勒行星定律1、开普勒第一定律(轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2、开普勒第二定律(面积定律):对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积。
3、开普勒第三定律(周期定律):所有行星的轨道半径的半长轴的三次方跟它的公转周期的二次方的比值都相等,即32a k T=。
说明:(1)开普勒行星运动定律适用于一切行星(卫星)绕恒星(行星)运动的情况; (2)不同行星绕太阳运动的椭圆轨道是不同的; (3)行星在近日点的速率远大于在远日点的速率;(4)表达式32a k T=中,k 值只与中心天体有关。
引力和重力的关系1、在两极或不考虑地球自转:重力和万有引力相等2R Mm Gmg =2、赤道位置向F mg R MmG+=2 3、重力加速度与高度的关系万有引力定律1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比、与它们之间距离r 的二次方成反比。
2.公式:122m mF G r=(G =6.67×10-11 N·m 2/kg 2)。
G 物理意义:引力常量在数值上等于两个质量都是1 kg 的质点相距1 m 时的相互吸引力。
3.适用范围:(1)质点间引力的计算;(2)质量分布均匀的球体,r 是球体球心间的距离;(3)一均匀球体与球外一个质点间的万有引力的计算,r 是球心到质点的距离; (4)两个物体间的距离远大于物体本身的大小时,r 为两物体质心间的距离。
计算天体的质量和密度1、忽略天体自转,天体表面重力和万有引力相等:2RMmG mg =2)(h R Mm Gg m +='2、测出卫星绕天体做匀速圆周运动的半径r 和周期T 。
(1)由2224πMm rG m r T=得天体的质量2324πr M GT =。
高中物理人教版必修第二册教学课件《万有引力定律》

回顾天体运动规律
开普勒三大定律 开普勒第一定律:(轨道定律) 开普勒第二定律:(面积定律) 开普勒第三定律:(周期定律)
对行星如何绕太阳运动进行了粗略地描述
尝试用所学的知识解释“行星 绕太阳做圆周运动的原因? ”
一、行星与太阳间的引力
概括起来有
则太阳与行星间的引力大小为
G是比例系数,与太阳、行星的质量无关 方向:沿着太阳和行星的连线
a 4 2 r 2.7 103 m / s2
T2
结论
计算表明,地面物体所受地球的引力,月球所
受地球的引力,以及太阳与行星间的引力,都
遵循规律:Байду номын сангаас
F G Mm r2
三、万有引力定律
1.内容:任何两个物体之间都存在相互作用的引力, 引力的大小与这两个物体的质量的乘积成正比,与 这两个物体之间的距离的平方成反比。
太阳对行星的作用力:
行星绕太阳运动遵守这个规律,那么在 其他物体之间是否适用这个规律呢??
牛顿在做了大量研究之后发现:物体间的引力 是普遍存在于宇宙间,并且是由于物体具有质 量而产生的一种力——万有引力。
由苹果落地引发的猜想
牛顿的猜想:地球对苹果的力、地球对 月球的力及太阳对行星的 力是同一种性质的力。
任何有质量的物体间都存在万有引力; 一般情况下,质量较小的物体之间万有引力忽略不计; 只考虑天体间或天体与卫星的万有引力.
G值的精确测定验证了牛顿提出的万有引力 这一规律的正确性,并且可以精确计算出两 物体间的引力,体现这一规律的实用性。
自此,第一次揭示了自然界一种基本相互作 用的规律,把地面物体运动的规律和天体运 动的规律统一起来了。
万有引力与重力的关系
最新人教版高中物理必修2第六章万有引力定律

mm F 2 如果用m´表示太阳的质 r
G是一个常量,对任何行星都是相同的。
2、万有引力定律
(1)定律表述:自然界中任何两个物体都是相互吸 引的,引力的大小跟这两个物体的质量成正比, 跟它们的距离的二次方成反比。
(2)公式表示:
mm F G 2 r
Mm 解:由于 G 2 mg R
所以,地球质量: M
R g G
2
小结:
1、牛顿在前人工作的基础上发现了万有 引力定律。 mm F G 2 r 2、卡文迪许巧妙地利用扭秤实验测定了 引力常量。 3、引力常量 G 6.67 10
11
N m /kg
2
2
中央电教馆资源中心制作
三、引力常量的测量
1686年牛顿发现万有引力定律后,曾经设想过几种 测定引力常量的方法,却没有成功。其间又有科学 家进行引力常量的测量也没有成功。 直到1789年,英国物理学家卡文迪许巧妙地利用了 扭秤装置,第一次在实验室里对两个物体间的引力 大小作了精确的测量和计算,比较准确地测出了引 力常量。
二、万有引力定律
1、定律的推导: 将行星运动的椭圆轨道简化成圆形轨道来讨论, 行星绕太阳的运动是匀速圆周运动,太阳对行星 的引力F是提供行星做圆周运动的向心力,即:
mv2 F r
其中r是太阳和行星间的距离,v是行星运动的线 速度,m是行星的质量。
2r 圆周运动的周期T和速度v的关系 v T 3 r m 2 所以: F 4 T 2 r2
六、万有引力定律的进一步理解
1.普遍性:万有引力是普遍存在于宇宙中的任何有质量 的物体(大到天体小到微观粒子)间的相互吸引力, 它是自然界的物体间的基本相互作用之一。 2.相互性:两个物体相互作用的引力是一对作用力与反 作用力,符合牛顿第三定律。 3.宏观性:通常情况下,万有引力非常小,只有在质量 巨大的天体间或天体与物体间它的存在才有宏观的物 理意义。在微观世界中,粒子的质量都非常小,粒子 间的万有引力很不显著,万有引力可以忽略不计。
高中物理必修二第六章完美总结
(4)地球上成功发射一颗卫星做需的最小发射速度 (即第一宇宙速度)V=7.9Km/s 注意:(1)环绕速度与发射速度是两个不同的概念
(2)近地卫星V发=V环,除此之外,轨道越高的卫星,需要
的发射速度越大,进入轨道后的环绕速度越小
故第一宇宙速度在数值上等于最大的环绕速度
第二宇宙速度v=11.2km/s — 物体刚好能克服地球引力作用,离开地球绕太阳运动所需 的最小发射速度 第三宇宙速度 v=16.7km/s —物体刚好能摆脱太阳引力束缚而飞到太阳系以外所需的最小 发射速度
V近地 V近月
M 地R V 81 1 9 V MR 1 4 2
近地 月 近月 月 地
V近月=16/9Km/s
(2)星球表面的物体受到的重力等于星球对它的万有引力
m
R
M
Mm F引 = G → G 2 mg r
GM gR2
请同学们思考:为什么不能说物体随星球自转需 要的向心力等于星球对它的万有引力?
第六章
开普勒三大定律
基本知识点梳理
行星 太阳
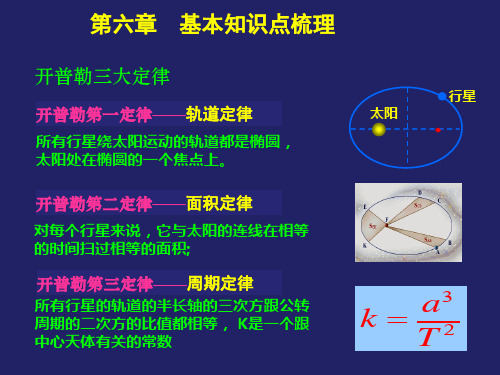
开普勒第一定律——轨道定律
所有行星绕太阳运动的轨道都是椭圆, 太阳处在椭圆的一个焦点上。
开普勒第二定律——面积定律
对每个行星来说,它与太阳的连线在相等 的时间扫过相等的面积;
开普勒第三定律——周期定律
所有行星的轨道的半长轴的三次方跟公转 周期的二次方的比值都相等, K是一个跟 中心天体有关的常数
万有引力定律的应用——两条重要思想的领会:
(1)中心天体—环绕天体模型
处理思想:中心天体施加给环绕天体的引力提供环绕天体做匀速 圆周运动需要的向心力 即 F引 = F向
ma
m F引
必修二物理第六章万有引力知识点

必修二物理第六章万有引力知识点必修二物理第六章万有引力知识点定义:万有引力是由于物体具有质量而在物体之间产生的一种相互作用。
它的大小和物体的质量以及两个物体之间的距离有关。
物体的质量越大,它们之间的万有引力就越大;物体之间的距离越远,它们之间的万有引力就越小。
两个可看作质点的物体之间的万有引力,可以用以下公式计算:F=GmM/r ,即万有引力等于引力常量乘以两物体质量的乘积除以它们距离的平方。
其中G代表引力常量,其值约为6.67×10的负11次方单位N·m2/kg2。
为英国科学家卡文迪许通过扭秤实验测得。
万有引力的推导:若将行星的轨道近似的看成圆形,从开普勒第二定律可得行星运动的角速度是一定的,即:ω=2π/T(周期)如果行星的质量是m,离太阳的距离是r,周期是T,那么由运动方程式可得,行星受到的力的作用大小为mrω =mr(4π )/T另外,由开普勒第三定律可得r /T =常数k’那么沿太阳方向的力为mr(4π )/T =mk’(4π )/r由作用力和反作用力的关系可知,太阳也受到以上相同大小的力。
从太阳的角度看,(太阳的质量M)(k’’)(4π )/r是太阳受到沿行星方向的力。
因为是相同大小的力,由这两个式子比较可知,k’包含了太阳的质量M,k’’包含了行星的质量m。
由此可知,这两个力与两个天体质量的乘积成正比,它称为万有引力。
如果引入一个新的常数(称万有引力常数),再考虑太阳和行星的质量,以及先前得出的4·π2,那么可以表示为万有引力=GmM/r两个通常物体之间的万有引力极其微小,我们察觉不到它,可以不予考虑。
比如,两个质量都是60千克的人,相距0.5米,他们之间的万有引力还不足百万分之一牛顿,而一只蚂蚁拖动细草梗的力竟是这个引力的1000倍!但是,天体系统中,由于天体的质量很大,万有引力就起着决定性的作用。
在天体中质量还算很小的地球,对其他的物体的万有引力已经具有巨大的影响,它把人类、大气和所有地面物体_地球上,它使月球和人造地球卫星绕地球旋转而不离去。
完整版人教版必修二第六章:万有引力与航天简明实用笔记知识要点

一、行星的运动——开普勒三定律 (察看到的,不是实验定律)(环绕,中心天体可视为不动)1、开普勒第必定律——轨道定律(圆周模型)全部的行星环绕太阳运行的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2、开普勒第二定律——面积定律(v 1r 1 v 2 r 2 )对于任意一个行星而言, 太阳和行星的连线在相等的时间内扫过相等的面积。
依据开普勒第二定律可得,行星在远日点的速率较小,在近期点的速率较大。
3、开普勒第三定律——周期定律(a 3 k )T 2全部行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
( a 表示椭圆的半长轴, T 代表公转周期, 同一中心天体 k 是定值 r 3GM T2k42)明显 k 是一个与行星自己没关的量,只与中心体有关 。
开普勒第三定律对全部行星都合用。
对于同一颗行星的卫星,也切合这个运动规律。
二、万有引力定律1、定律的推导。
2、定律的内容:自然界中任何两个物体都互相吸引,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
3、定律的公式: F Gm 1m 2(× 10-112/kg 2. )r 24、万有引力定律公式的合用条件:①质点间 (对于相距很远因此可以看作质点的物体)思虑:在公式中,当 r →0 时, →∞能否有意义?F②对平均的球体 ,可以看作是质量会合于球心上的质点,这是一种等效的简化办理方法。
③不是质点也不可以视为质点的 不可以直接 用公式,但可采纳 微积分 的思想间接求!5、万有引力定律说明①引力的方向 ——两质点的连线上。
②为引力常量 G ——在数值上等于两个质量都是1kg 的物体相距 1m 时的互相作用力, 其数值与单位制有关。
在 SI 制中, G = 6.67 × 10-11N · m 2/kg 2,1687 年牛顿宣布规律,而 1798 年英卡文迪许完成实验之时测定。
卡被称为称出地球质量的人 . 精度不高,可取来运算③一致单位 ——在运用万有引力定律计算时,公式中各量的单位须一致使用国际单位制。
高中物理必修二第6章:万有引力定律-知识点

小初高个性化辅导,助你提升学习力! 1 高中物理必修二第6章:万有引力定律-知识点1、人类对于天体运动的认识:①波兰 天文学家哥白尼 提出日心说 ,②伽利略用望远镜 发现木星的卫星 ,证明地球 并非天体的中心。
③德国 天文学家开普勒 提出开普勒三定律 。
2、开普勒第一定律:各行星都在椭圆轨道上绕太阳运行,太阳处在椭圆的一个焦点上。
开普勒第二定律:行星与太阳的连线在相等时间 内扫过的面积相等 。
3、开普勒第三定律:行星绕太阳运行的椭圆轨道半长轴 a 的三次方 与公转周期T 的二次方 之 比 是一个常数,即 a 3/T 2 =k 。
k 是一个与行星 无关 的常数。
一般我们可近似按圆轨道处理,即 r 3/T 2 =k ,r 是行星圆轨道 的半径。
由该定律可知,人造地球卫星在近地点速度大 ,在远地点速度小 ;同理,地球以及其他行星在近日点速度大 ,在远日点速度小 。
4、牛顿 提出,地球对苹果的引力,地球对月亮的引力与太阳对行星的作用力本质上都相同 。
这种所有物体之间都存在 的相互吸引力就是万有引力 。
5、万有引力定律:自然界中任何两个物体都相互吸引,相互间引力的大小与物体质量的乘积成正比,与它们之间距离的二次方成反比。
公式:F=221r m m G 。
r 是可以看成质点的两物体之间距离,若是质量分布均匀的球体,则是两个球心间的距离。
G 是引力常量,卡文迪许 利用扭秤 装置测得G = 6.67×10-11N ˙m 2/kg 2。
6、“称量”地球的质量:测出地球表面的重力加速度g 地和地球半径r ,利用地球上的物体所受重力 就是万有引力 ,有① mg 地=2r mm 地地G 。
可求得m 地=G 2r g 地地。
②地球的平均密度ρ=V m 地=3r 34m ⋅π地。
7、“称量”太阳的质量:测出地球绕太阳做匀速圆周运动的 轨道半径r 和 周期T ,利用万有引力等于圆周运动的向心力,有2r m m 日地G =22T r 4m π地,可得:m 日=232G T r 4π。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第15讲开普勒定律万有引力定律
考情剖析
1.开普勒定律、万有引力定律一般与天体运动和圆周运动结合综合考查、较少单独出现,但作为基本知识需要了解掌握.
2.预测14年高考中单独考查的可能性很小.
知识整合
知识网络
开普勒定
律万有引力定律三大定律轨道定律周期定律面积定律公式F=
GMm
r2适用条件
两质点
之间
基础自测
一、开普勒定律
1.开普勒第一定律又称轨道定律,它指出:所有行星绕太阳运动的轨道是椭圆,太阳位于椭圆轨道的一个焦点上.远日点是指________,近日点是指________.不同行星的椭圆轨道是不同的,太阳处在这些椭圆的一个公共焦点上.
2.开普勒第二定律又称面积定律.对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积.所以行星在离太阳比较近时,运动速度________.行星在离太阳较远时,运动速度________.
3.开普勒第三定律又称周期定律,内容是:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.该定律的数学表达式是:________.
4.开普勒行星运动定律,不仅适用于行星,也适用于其他卫星的运动.研究行星运动时,开普勒第三定律中的常量k与________有关,研究月球、人造地球卫星运动时,k与________有关.
二、万有引力定律
1.万有引力定律的内容是:自然界中任何两个物体都相互吸引,引力的大小与物体的质量m1和m2的乘积成正比,与它们之间距离r的二次方成反比.其数学表达式是________.万有引力定律的发现,证明了天体运动和地面上运动遵守共同的力学原理,实现了天地间力学的大综合,第一次揭示了自然界中的一种基本相互作用规律.
2.卡文迪许扭秤实验证明了万有引力的存在及正确性,并使得万有引力定律可以定量计算,引力常量G =________.
3.万有引力定律的应用
计算中心天体的质量、密度
若已知一个近地卫星(离地高度忽略,运动半径等于地球半径R )的运行周期是T .有: G Mm R 2=4π2mR T 2,解得地球质量为________;由于地球的体积为V =43
πR 3可以计算地球的密度为: ________.当然同样的道理可以根据某行星绕太阳的运动计算太阳的质量.
随堂 演练
1.地球绕太阳的运行轨道是椭圆,因而地球与太阳之间的距离随季节变化.冬至这天地球离太阳最近,夏至最远.下列关于地球在这两天绕太阳公转速度大小的说法中,正确的是( )
A .地球公转速度是不变的
B .冬至这天地球公转速度大
C .夏至这天地球公转速度大
D .无法确定
第2题图
2.某次,航天飞机在完成对哈勃空间望远镜的维修任务后,在A 点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B 为轨道Ⅱ上的一点,如图,关于航天飞机的运动,下列说法中正确的有( )
A .在轨道Ⅱ上经过A 的速度小于经过
B 的速度
B .在轨道Ⅱ上经过A 的动能小于在轨道Ⅰ上经过A 的动能
C .在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期
D .在轨道Ⅱ上经过A 的加速度小于在轨道Ⅰ上经过A 的加速度
3.2011年8月26日消息,英国曼彻斯特大学的天文学家认为,他们已经在银河系里发现一颗由曾经的庞大恒星转变而成的体积较小的行星,这颗行星完全由钻石构成.若已知万有引力常量,还需知道哪些信息可以计算该行星的质量( )
A .该行星表面的重力加速度及绕行星运行的卫星的轨道半径
B .该行星的自转周期与星体的半径
C .围绕该行星做圆周运动的卫星的公转周期及运行半径
D .围绕该行星做圆周运动的卫星的公转周期及公转线速度
4.一行星绕恒星做圆周运动.由天文观测可得,其运动周期为T ,速度为v ,引力常量为G ,则( )
A .恒星的质量为v 3T 2πG
B .行星的质量为4π2v 3
GT 2
C .行星运动的轨道半径为
v T 2π
D .行星运动的加速度为2πv T
5.1990年4月25日,科学家将哈勃天文望远镜送上距地球表面约600km 的高空,使得人类对宇宙中星体的观测与研究有了极大的进展.假设哈勃天文望远镜沿圆轨道绕地球运
行.已知地球半径约为6.4×106m ,利用地球同步卫星与地球表面的距离为3.6×107m 这一
数据可得到哈勃天文望远镜绕地球运行的周期.以下数据中最接近其运行周期的是( )
A .0.6小时
B .1.6小时
C .4.0小时
D .24小时
6.1798年英国物理学家卡文迪许测出万有引力常量G ,因此卡文迪许被人们称为能称出地球质量的人.若已知万有引力常量G ,地球表面处的重力加速度g ,地球半径R ,地球上一个昼夜的时间T 1(地球自转周期),一年的时间T 2(地球公转周期),地球中心到月球中心的距离L 1,地球中心到太阳中心的距离L 2,你估算出( )
A .地球的质量m 地=gR 2G
B .太阳的质量m 太=4π2L 32GT 22
C .月球的质量m 月=4π2L 31GT 21
D .可求月球、地球及太阳的密度
7.2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,
第7题图
从而建立我国第一个空间实验室.假设T 代表天宫一号,S 代表“神舟八号”,它们绕地球做匀速圆周运动轨道如图所示,则( )
A .T 的周期大于S 的周期
B .T 的速率大于S 的速率
C .T 的向心加速度大于S 的向心加速度
D .S 须加速后才能与T 实现对接
8.已知地球半径为R ,地球表面重力加速度为g ,不考虑地球自转的影响.
(1)推导第一宇宙速度v 1的表达式;
(2)若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h ,求卫星的运行周期T .
第15讲 开普勒定律
万有引力定律
知识整合 基础自测
一、1.离太阳所在焦点较远的长轴端点 离太阳所在焦点较近的长轴端点 2.大 小 3.a 3
T 2=k 4.太阳质量 地球质量 二、1.F =G m 1m 2r 2 2.6.67×10-11N ·m 2/kg 2 3.M =4π2R 3GT 2 ρ=3πGT 2
随堂演练
1.B 【解析】 冬至地球与太阳的连线短,夏至长.根据开普勒第二定律,要在相等的时间内扫过的面积相等,则在相等的时间内冬至时地球运动的路径就要比夏至时长,所以冬至时地球运动的速度比夏至的速度大,答案选B.
2.ABC 【解析】 逐项判断根据开普勒定律,近地点的速度大于远地点的速度,A
正确;由Ⅰ轨道变到Ⅱ轨道要减速,所以B 正确;根据开普勒定律,R 3
T 2=k ,R 2<R 1,所以T 2<T 1,C 正确;根据a =GM R 2,应相等,D 错误. 3.CD 【解析】 由万有引力定律和牛顿第二定律卫星绕中心天体运动的向心力由中
心天体对卫星的万有引力提供,利用牛顿第二定律得G Mm r 2=m v 2r =mrω2=mr 4π2
T 2;若已知卫星的轨道半径r 和卫星的运行周期T 、角速度ω或线速度v ,可求得中心天体的质量为M
=rv 2G =4π2r 3GT 2=ω2r 3G ,所以选项CD 正确. 4.ACD 【解析】由v =2πr T 得到r =vT 2π,C 正确;根据F =G Mm r 2=m 4π2T 2r 及r =vT 2π
得M =v 3T 2πG
,A 正确;根据a =v 2r 及r =vT 2π得知D 正确,故本题答案选ACD. 5.B 【解析】 哈勃天文望远镜绕地球做匀速圆周运动的轨道半径为r 1=R +6×105m =7.0×106m ,地球同步卫星绕地球做匀速圆周运动的轨道半径为r 2=R +3.6×107m =
4.24×107m.已知地球同步卫星绕地球做匀速圆周运动的周期T 2=24h ,由开普勒第三定律T 21/T 22=r 31/r 32可知哈勃天文望远镜绕地球做匀速圆周运动的周期大约为 1.6h.所以正确选项为
B.
6.AB 【解析】 由mg =GMm R 2得m 地=gR 2G ,A 对;地球绕太阳转,由Gm 太·m 地L 22=m 地·4π2T 22·L 2得m 太=4π2L 32GT 22
,B 对;用万有引力公式只能计算中心天体的质量,所以C 错;根据题中的已知量,只能求出地球的密度,D 错.
7.AD 【解析】 本题考查用圆周运动动力学条件研究天体运动及分析能力,根据
万有引力提供圆周运动的向心力有G Mm r 2=m v 2r =mr(2πT )2可知v =GM r ,T =4π2r 3GM
,故A 正确,B 错误;同理,它们的向心加速度a =G M r
2,可知C 错误;S 在低轨加速后做离心运动,达到T 的轨道,才能对接,故D 正确.
8.见解析 【解析】(1)设卫星的质量为m ,地球的质量为M ,在地球表面附近满足G Mm R 2=mg ,得GM =R 2g ①,卫星做圆周运动的向心力等于它受到的万有引力m v 21R =G Mm R 2 ②,①式代入②式,得到v 1=Rg. (2)考虑①式,卫星受到的万有引力为F =G Mm (R +h )2=mgR 2(R +h )2,由牛顿第二定律F =m 4π2T 2(R +h),③④式联立解得T =2π
R (R +h )3g
.。
