安徽省安庆市高三第三次模拟考试
安庆市高三下学期语文第三次模拟考试试卷

安庆市高三下学期语文第三次模拟考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共3题;共8分)1. (4分)(2017·德州模拟) 阅读下面的文字,完成问题。
在我们的日常语言中,真、善、美这三个词常常是相题并论的。
仔细寻思后不难发现,自然的根本性质是真,人生的根本意义为善,艺术的根本价值在于美。
如此看来,真、善、美之间似乎并没有直接的联系,但是在审美的意义上,自然于潜移默化中感发和(涤荡/激荡)着人的情性与思绪,也安顿和抚慰着人的心灵;人则通过审美的思维方式达到______的合谐境界。
可以说,一片自然山水就是一个人诗意栖居的心灵寓所与精神家园。
更为重要的是,每个人的人生都是一道(独特/独到)的风景,具有审美价值,而且整个审美活动的出发点和落脚点就在于(关照/观照)人的生存境况,并努力成就自由完美的人生,使人生得以丰富地展开。
那么,审美人生的具体内容是什么呢?在我看来,审美意义上的人生,一方面是指主体以自然的感性生命为基础,又不滞于感性生命,由切身感悟和内省体验而达到与宇宙精神合一的体道境界;另一方面,主体还以人的社会特质为基础,又不滞于人的社会特质,从心灵中获得精神自由的境界。
这种体道的境界与精神自由的境界在审美思维方式上的贯通合一,即审美的人生境界,这是对现实人生的积极______。
(1)文中划线字的注音和划线词语的字形,都正确的一项是()A . 抚(fǔ)合谐B . 寓(yù)相题并论C . 栖(xī)思绪D . 省(xǐng)贯通合一(2)依次选用文中括号中的词语,最恰当的一项是()A . 涤荡独到观照B . 激荡独特观照C . 涤荡独特关照D . 激荡独到关照(3)在文中两处横线上依次填入词句,衔接最恰当的一项是()A . 物我统一,情景交融提升、拓展与超越B . 物我统一,情景交融拓展、提升与超越C . 情景交融、物我统一拓展、提升与超越D . 情景交融、物我统一提升、拓展与超越。
安徽省安庆市届高三语文第三次模拟试题

高三语文第三次模拟试题第Ⅰ卷做题时,建议先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一部分:听力(共两节,满分 30 分)第一节 (共 5 小题;每小题 1 分,满分 5 分)听下面 5 段对话。
每段对话后有一个小题,从题中所给的 A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有 10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍1.W hat does the man mean?A. The woma n and the man don’t like the same kind of music.B.He didn’t know how the woman found out about thetickets. C. He didn’t realize the woman had wanted toattend the concert.2.W hat is the woman probably doing now?A. Reading a magazine.B. Studying for a test.C. Shopping for shoes.3.W hat does the man mean?A. He has refused the dinner appointment.B.He doesn’t eat out very often.C. He does not like to eat out either.4.W hen will the train for Oxford start?A. At 4:15 p.m.B. At 4:45 p.m.C. At 5:15 p.m.5. What are the speakers probably doing?A. Doing some running.B. Climbing a hill.C. Taking a walk.第二节(共 15 小题,每小题 1. 5 分,满分 22. 5 分)听下面 5 段对话或独白,每段对话或独白后有几个小题,从题中所给的 A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置.听每段对话或独白前,你将有时间阅读各个小题,每小题 5 秒钟;听完后,各小题将给出 5 秒钟的作答时间。
2025届安徽省安庆市下学期高三第三次模拟考试语文试卷含解析

2025届安徽省安庆市下学期高三第三次模拟考试语文试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
1、在下面一段话的空缺处依次填入词语,最恰当的一组是 ( )苏轼,被余秋雨称为的天才,集文学才能与政治才能于一身的天才。
自古以来,文学才能与政治才能似乎是的一对死敌,然而这两者在苏轼身上却得到了最完美的统一,今日西湖的苏堤仍旧着一千多年前这个天才的赫赫政绩。
然而卓越的政治才能并不代表会玩弄肮脏的政治手腕,苏轼的一生命途多舛,与他正直的个性是分不开的。
改革也好,保守也罢,无论当时哪派势力得宠,苏轼都只有一个宗旨:站在良心那边说话!A.千年一遇誓不两立显示B.千载难逢势不两立显示C.千年一遇势不两立昭示D.千载难逢誓不两立昭示2、阅读下面的文字,完成下面小题。
我国城镇化进程的加快以及人民生活水平的提高,生活的垃提总量也在不断加大。
部分城市在市郊露天堆放垃圾,对大气、土壤、水的环境造成污染。
大量餐厨垃圾与其他垃圾混合填理或焚烧,产生有毒物质,威胁着居民健康,这种现象正在向农村地区________。
垃圾分类作为垃圾处理的前端环节,其作用早已得到世界的公认。
分类收集不仅能大幅度减少垃圾给环境带来的污染,节约垃圾无害化处理费用,更能使资源得到________利用。
有人将垃圾称为“放错了地方的资源”。
据保守估计,我国城市每年丢弃的可回收垃圾价值在300亿元左右。
但我国的垃圾分类工作一直难以有效推进,相关调查显示,约四分之一的受访者认为垃圾分类效果不明显或完全没有效果。
有人说:“我辛辛苦苦分了类,环卫车辆却混在一起远走了,分类还有什么意义?”这种现象可以说是________,垃圾分类处理是个复杂的系统工程,各个环节必须配套衔接,才能高效运行。
安徽省安庆市2022届高三第三次模拟考试文科数学试题含解析

安庆2022届高三第三次模拟考试文科数学(答案在最后)本试卷总分150分,考试时间120分钟注意事项:1.答卷前,考试务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本小题12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}=|1A x x ≥,1=|32B y y ⎧⎫≤<⎨⎬⎩⎭那么A B = ()A.1,12⎡⎫⎪⎢⎣⎭ B.(]1,3 C.1,32⎛⎫ ⎪⎝⎭D.[)1,3【答案】D 【解析】【分析】集合A 和集合B 都是数集,由交集运算和区间的表示易得D 选项正确【详解】{}=|1A x x ≥ ,1B=|32y y ⎧⎫≤<⎨⎬⎩⎭{}=|13A B x x ∴⋂≤<,该集合用区间表示为[)1,3.故选:D.2.若复数1i z =+,则下列说法正确的是()A.复数z 的虚部为iB.z 在复平面对应点位于第一象限C.复数i z -为纯虚数D.i z =【答案】B 【解析】【分析】A 选项,根据实数概念得到z 的虚部为1;B 选项,写出复数对应点的坐标,得到其所在象限;C选项,计算得到i z -为实数;D 选项,计算出i 1i z =-+=D 错误.【详解】A 选项,复数z 的虚部为1,A 错误;B 选项,z 在复平面对应点坐标为()1,1,故z 在复平面对应点位于第一象限,B 正确;C 选项,复数i 1i i 1z -=+-=,故i z -为实数,C 错误;D 选项,()2i 11i i i i i z ===-+=+=+,D 错误.故选:B 3.命题:sin 0p θ≠是()2πZ k k θ≠∈的充要条件;命题q :函数sin y x =在,22ππx ⎡⎤∈-⎢⎥⎣⎦不是单调函数,则下列命题是真命题的是()A.p q ∧B.()()p q ⌝∧⌝ C.()p q⌝∨ D.()p q ∨⌝【答案】C 【解析】【分析】先得到p 为假命题,q 为真命题,进而对四个选项一一判断.【详解】sin 0θ≠,解得()11πZ k k θ≠∈,由于()()11πZ 2πZ k k k k θθ≠∈⇒≠∈,但()2πZ k k θ≠∈⇒()11πZ k k θ≠∈,故:sin 0p θ≠不是()2πZ k k θ≠∈的充要条件,p 为假命题,由于()()sin sin f x x x f x -=-==,故sin y x =在,22ππx ⎡⎤∈-⎢⎥⎣⎦上为偶函数,故sin y x =在,22ππx ⎡⎤∈-⎢⎥⎣⎦上不单调,q 为真命题,则p q ∧为假命题,A 错误;()()p q ⌝∧⌝为假命题,B 错误;()p q ⌝∨为真命题,C 正确;()p q ∨⌝为假命题,D 错误.故选:C4.2022年4月23日是第27个世界读书日,以引导全民阅读为出发点,弘扬中华优秀文化,传承中华悠久文明,我校高一年级部举行了“培养阅读习惯,分享智慧人生”为主题的读书竞赛活动.如图所示的茎叶图是甲、乙两个代表队各7名队员参加此次竞赛的成绩,乙队成绩的众数为81m +,则下列关于这两个代表队成绩的叙述中,其中错误的是()A.甲队的众数大于乙队的众数B.甲队的中位数大于乙队的中位数C.甲队的平均数小于乙队的平均数D.甲队的方差小于乙队的方差【答案】D 【解析】【分析】由茎叶图中数据通过计算可得甲队的众数、中位数均大于乙队,甲队的平均数小于乙队的平均数,根据数据波动情况可判断甲队的方差大于乙队的方差.【详解】根据茎叶图可知,甲队的众数为85,乙队的众数为84,所以甲队的众数大于乙队的众数,A 正确;易知甲队的中位数为85,乙队的中位数为84,所以甲队的中位数大于乙队的中位数,B 正确;乙队的众数为84,所以8184m +=,即3m =,甲队的平均数为()17081848585859383.37++++++≈,乙队的平均数为()17984848486879385.37++++++≈,所以甲队的平均数小于乙队的平均数,C 正确;由茎叶图中的数据分步可知,甲队数据偏离平均数的波动性更大,而乙队数据相对比较稳定,因此甲队的方差大于乙队的方差,即D 错误.故选:D5.已知直平行六面体1111ABCD A B C D -中,12,60AA AB BC BAD ===∠=︒,则直线1BC 与DB 所成角的余弦值为()A.4B.12C.14D.0【答案】A 【解析】【分析】作出辅助线,建立空间直角坐标系,写出点的坐标,求出直线1BC 与DB 所成角的余弦值.【详解】取AB 的中点F ,连接DF ,因为2,60AB BC BAD ︒==∠=,所以2AB AD ==,故ABD △为等边三角形,故DF ⊥AB ,所以DF ⊥CD ,又平行六面体1111ABCD A B C D -为直平行六面体,故以D 为坐标原点,1,,DF DC DD 所在直线分别为,,x y z 轴,建立空间直角坐标系,则())()10,0,0,,0,2,2D BC ,设直线1BC 与DB 所成角的大小为θ,则111cos cos ,4BC DB BC DB BC DBθ⋅=====⋅.1BC 与DB 所成角的余弦值为4.故选:A 6.若1cos 64x π⎛⎫-= ⎪⎝⎭,则sin 26x π⎛⎫+= ⎪⎝⎭()A.158B.78C.158-D.78-【答案】D 【解析】【分析】利用诱导公式和二倍角公式化简,即sin 2sin 2cos 26626x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦22cos 16x π⎛⎫=-- ⎪⎝⎭,代值计算即可【详解】解:因为1cos 64x π⎛⎫-= ⎪⎝⎭,所以sin 2sin 2cos 26626x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦22cos 16x π⎛⎫=-- ⎪⎝⎭21214⎛⎫=⨯- ⎪⎝⎭78=-.故选:D .7.某地为方便群众接种新冠疫苗,开设了A ,B ,C ,D 四个接种点,每位接种者可去任一个接种点接种.若甲,乙两人去接种新冠疫苗,则两人不在同一接种点接种疫苗的概率为()A.12B.23C.34 D.14【答案】C 【解析】【分析】根据题意列出甲,乙两人去A ,B ,C ,D 四个接种点接种新冠疫苗的所有选择,然后再求出甲,乙两人不在同一个接种点接种的情况有多少种,从而可求出概率.【详解】甲,乙两人去A ,B ,C ,D 四个接种点接种新冠疫苗的所有选择共有16种,分别为:AA ,AB ,AC ,AD ,BA ,BB ,BC ,BD ,CA ,CB ,CC ,CD ,DA ,DB ,DC ,DD ;其中两人不在同一个接种点接种的情况有12种,从而有123164P ==.故选:C .8.设变量x ,y 满足约束条件211y x y x y ≤⎧⎪+≥⎨⎪-≤⎩,则目标函数313+⎛⎫= ⎪⎝⎭x y z 的最大值为()A.1113⎛⎫ ⎪⎝⎭B.313⎛⎫ ⎪⎝⎭C.3D.4【答案】C 【解析】【分析】作出变量x,y满足约束条件211yx yx y≤⎧⎪+≥⎨⎪-≤⎩可行域,然后将求313+⎛⎫= ⎪⎝⎭x yz的最大值,转化为求u=3x+y的最小值求解.【详解】变量x,y满足约束条件211yx yx y≤⎧⎪+≥⎨⎪-≤⎩可行域如图所示阴影部分:目标函数313+⎛⎫= ⎪⎝⎭x yz,设u=3x+y,欲求313+⎛⎫= ⎪⎝⎭x yz的最大值,等价于求u=3x+y的最小值.u=3x+y可化为y=-3x+u,平移直线y=-3x,当直线y=-3x+u经过点B(-1,2)时,纵截距u取得最小值u min=3×(-1)+2=-1,所以313+⎛⎫= ⎪⎝⎭x yz的最大值1133z-⎛⎫==⎪⎝⎭,故选:C.9.正项等比数列{}n a中,3122a a a=+,若2116m na a a=,则41m n+的最小值等于()A.1B.35 C.136 D.32【答案】D【解析】【分析】设出等比数列的公比,得到方程,求出公比2q=,从而求出6m n+=,再利用基本不等式“1”的妙用求出最小值.【详解】设{}n a的公比为q,则21112a q a a q=+,因为10a>,所以220q q--=,解得2q=或1-(舍去),11222111122216m n m nm na a a a a a--+-=⋅⋅⋅=⋅=,故24m n+-=,即6m n+=,()4114114134156662n mm nm n m n m n⎛⎛⎫⎛⎫+=++=++≥+=⎪ ⎪⎝⎭⎝⎭⎝,当且仅当4n mm n =,即4,2m n ==时,等号成立,故41m n +的最小值等于32故选:D10.已知定义在R 上的函数()(),1f x f x +是偶函数,()2f x +是奇函数,则()2022f 的值为()A.0B.1C.2D.3【答案】A 【解析】【分析】根据已知条件可知()f x 关于点()2,0中心对称,结合偶函数定义可推导得到()f x 的周期,根据周期性和奇偶性可得()()202202=f f =.【详解】()1f x+Q 为偶函数,()()1=1f x f x ∴+-()f x \的图像关于1x =对称,()()2f x f x ∴+=-;()2f x + 是奇函数,()()+22f x f x ∴-=-+,可知()f x 关于点()2,0中心对称,()()22f f ∴=-()20f ∴=,()()()()42,2,f x f x f x f x ∴+=-+∴+=-()()()()()42,f x f x f x f x ∴+=-+=--=()f x \是周期为4的周期函数,()()()20224505+220f f f ∴=⨯==.故选:A.11.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点坐标分别为12,F F ,过1F 作圆222x y a +=的切线交C 的右支于A 点.若122F F F A =,则C 的离心率为()A.B.3C.53D.【答案】C 【解析】【分析】作1OD F A ⊥垂足为D ,由题意12cos bAF F c∠=,在12F F A △中,由余弦定理得222112212112cos 2F A F F F AAF F F A F F +-∠=⋅,化简得223250c ac a +-=,即可得解.【详解】作1OD F A ⊥垂足为D ,由题意OD a =,1OF c =,则1F D b ==,∴12cos b AF F c∠=,122F F F A =,∴22F A c =,122F A a c =+,在12F F A △中,()()222211221211222cos 222222a c F A F F F Aa c AF F F A F F a c c c++-+∠===⋅+⋅,∴2a c bc c+=,结合222b c a =-可得223250c ac a +-=,∴23250e e +-=,由1e >可得53e =.故选:C.【点睛】本题考查了双曲线离心率的求解,考查了运算能力,属于中档题.12.当1a <时,已知()f x ax a =-,()()21xg x x e =-,若存在唯一的整数0x ,使得()()00g x f x <成立,则a 的取值范围是()A.3[,1)2e -B.33[,)24e -C.33[,)2e 4D.3[,1)2e【答案】D 【解析】【分析】根据题设条件,问题转化为存在唯一整数0x 使得点00(,())x g x 在直线y ax a =-的下方,对()g x 求导并探讨其图象及性质,再作出()g x 图象及直线y ax a =-,结合图形即可得解.【详解】由题意知,存在唯一整数0x 使得点00(,())x g x 在直线y ax a =-的下方,()()21x g x e x '=+,12x <-时()0g x '<,12x >-时()0g x '>,即()g x 在1(,]2-∞-上递减,在1[,)2-+∞上递增,min 1()(2g x g =-=,直线y ax a =-恒过定点()1,0且斜率为a ,1a <,如图:又(0)1g =-,(1)g e =,(0)1,(1)0f a f =->-=,于是有(0)(0),(1)(1)g f g f <>,符合题意的唯一整数为0,观察图形得,3(1)(1)2g f a e-≥-⇔-≥-,即32a e ≥,从而得312a e ≤<,所以a 的取值范围是3[,1)2e故选:D第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.13.设A 、B 为曲线C :24x y =上两点,A 与B 的横坐标之和为4,则直线AB 的斜率______.【答案】1【解析】【分析】先设()11,A x y 、()22,B x y ,将A 、B 两点坐标代入抛物线方程,两式作差整理,即可得出直线AB 的斜率.【详解】设()11,A x y 、()22,B x y ,因为A 、B 为曲线C :24x y =上两点,所以21122244x y x y ⎧=⎪⎪⎨⎪=⎪⎩,则()()2212121212444x x x x x x y y -+-=-=,又A 与B 的横坐标之和为4,即124x x +=,因此直线AB 的斜率为12121214AB y yx x k x x -+===-.故答案为:1.14.已知单位向量21,e e 的夹角为1212π,,43a e eb e e λ=+=- ,若a b ⊥ ,则实数λ=___________.【答案】27-【解析】【分析】利用向量数量积公式可得112402a b λλ⋅=-+-=,即可解出实数λ的值.【详解】根据题意可得121== e e ,且1212π1cos 32e e e e ⋅=⋅= ;由a b ⊥ 可得0a b ⋅= ,即()()212121121222144240241e e e e e e e e e e λλλλλ=-⋅+⋅+-=-+=-- ,解得27λ=-.故答案为:27-15.函数()π2πcos 21,33f x x x x ⎛⎫⎡⎤=+-∈-⎪⎢⎥⎣⎦⎝⎭的取值范围是___________.【答案】198⎡-⎢⎣【解析】【分析】先化简()f x ,再根据余弦函数和二次函数的性质求解即可.【详解】()2cos 212cos 11f x x x x x =+-=-+-22cos 2x x =+-,因为π2π,33x ⎡⎤∈-⎢⎥⎣⎦,1cos ,12x ⎡⎤∈-⎢⎥⎣⎦,令cos t x =,1,12t ⎡⎤∈-⎢⎥⎣⎦,所以()222f t t =+-,对称轴为224t =-=-⨯,因为()f t 在1,24t ⎡∈--⎢⎣⎦上单调递减,在14t ⎡⎤∈-⎢⎥⎣⎦上单调递增,所以()2min19224448f t f ⎛⎛⎛=-=⨯-+--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()()max 122f t f ==+=所以函数()π2πcos 21,33f x x x x ⎛⎫⎡⎤=+-∈- ⎪⎢⎥⎣⎦⎝⎭的取值范围是198⎡-⎢⎣.故答案为:198⎡-⎢⎣.16.在三棱锥-P ABC 中,ABC 是边长为2的正三角形,,,PA PB PC E F ==分别是,PA AB 的中点,且CE EF ⊥,则三棱锥-P ABC 外接球的表面积为___________.【答案】6π【解析】【分析】作出辅助线,证明出,,PA PB PC 两两垂直,将三棱锥外接球转化为以,,PA PB PC 为长,宽,高的长方体的外接球,进而求出外接球半径和表面积.【详解】取AC 的中点N ,连接,PN BN ,因为ABC 是边长为2的正三角形,PA PC =,所以,PN AC BN AC ⊥⊥,因为PN BN N Ç=,,PN BN ⊂平面BPN ,所以AC ⊥平面BPN ,因为BP ⊂平面BPN ,所以AC ⊥BP ,因为,E F 分别是,PA AB 的中点,所以EF 是ABP 的中位线,故//EF PB ,因为CE EF ⊥,所以CE PB ⊥,因为,CE AC ⊂平面PAC ,CE AC C = ,所以PB ⊥平面PAC ,因为,PA PC ⊂平面PAC ,所以PB ⊥PA ,PB ⊥PC ,因为2AB BC ==,PA PB PC ==,由勾股定理得PA PB PC ===因为2AC =,所以222PA PC AC +=,由勾股定理逆定理可得PA ⊥PC ,所以,,PA PB PC 两两垂直,故棱锥-P ABC 外接球即为以,,PA PB PC 为长,宽,高的长方体的外接球,设外接球半径为R ,则2R ==,解得2R =,则三棱锥-P ABC 外接球的表面积为24π6πR =.故答案为:6π三、解答题:本大题70分.解答应写出文字说明、证明过程或演算步骤,第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,D 是AC 的中点,已知平面向量m 、n满足()sin sin ,sin sin m A B B C =-- ,(),n a b c =+ ,m n ⊥ .(1)求A ;(2)若BD =,2b c +=ABC 的面积.【答案】(1)3A π=(2)2【解析】【分析】(1)先利用正弦定理角化边得到222b c a bc +-=,再借助余弦定理即可求出A ;(2)先利用余弦定理得到224212c b bc +-=,再化简为()22612b c bc +-=,即可求出6bc =,再利用三角形面积公式求解即可.【小问1详解】∵()sin sin ,sin sin m A B B C =-- ,(),n a b c =+ ,m n ⊥ ,∴()()()sin sin sin sin 0A B a b B C c -++-=.∴()()()0a b a b b c c -++-=,即222b c a bc +-=.∴2221cos 22b c a A bc +-==.∵0A π<<,∴3A π=.【小问2详解】在△ABD 中,由BD =,3A π=和余弦定理,得2222232cos BD AB AD AB AD A AB AD AB AD ==+-⋅=+-⋅.∵D 是AC 的中点,∴2b AD =∴22322b b c c ⎛⎫+-⨯= ⎪⎝⎭,化简得224212c b bc +-=,即()22612b c bc +-=.∵2b c +=∴(2612bc -=,解得6bc =.∴11333sin sin 22342ABC S bc A bc π==== .∴△ABC 的面积为332.18.如图,O 是圆锥底面圆的圆心,AB 是圆O 的直径,PAB 为直角三角形,C 是底面圆周上异于,A B的任一点,D 是线段AC 的中点,E 为母线PA 上的一点,且2PE EA =.(1)证明:平面POD ⊥平面PAC ;(2)若2AC BC ==,求三棱锥P ODE -的体积.【答案】(1)证明见解析;(2【解析】【分析】(1)由圆锥的性质可知,PO ⊥底面圆,再根据线面垂直的性质得出AC PO ⊥,由AB 为直径得出AC BC ⊥,再根据中位线的性质得出OD AC ⊥,最后利用面面垂直的判定定理,即可证明平面POD ⊥平面PAC ;(2)在PD 上取点F ,使得2PF FD =,连接EF ,结合题意可知//EF AC ,从而有EF ⊥平面POD ,得出EF 为三棱锥E POD -的高,最后利用等体积法和三棱锥的体积公式,即可求出三棱锥P ODE -的体积.【小问1详解】证明:由圆锥的性质可知,PO ⊥底面圆,又AC 在底面圆O 上,所以AC PO ⊥,又因为C 在圆O 上,AB 为直径,所以AC BC ⊥,又点O D ,分别为AB AC ,的中点,所以//OD BC ,所以OD AC ⊥,又OD PO O = ,且OD PO ⊂,平面POD ,所以AC ⊥平面POD ,又AC ⊂平面PAC ,所以平面POD ⊥平面PAC .【小问2详解】解:由题可知,2AC BC ==,则12AD AC ==,如图,在PD 上取点F ,使得2PF FD =,连接EF ,由题知2PE EA =,所以//EF AC ,所以22333EF AD ==,又因为AC ⊥平面POD ,所以EF ⊥平面POD ,所以EF 为三棱锥E POD -的高,又232AC BC ==,,所以224AB AC BC =+=,又因为PAB 为等腰直角三角形,所以122PO AB ==,又PO OD ⊥,所以11··21122POD S PO OD ==⨯⨯= ,而11233··13339P ODE E POD POD V V EF S --===⨯⨯= ,所以三棱锥P ODE -2319.安庆某农场主拥有两个面积都是220亩的农场——加盟“生态农场”与“智慧农场”,种植的都是西瓜,西瓜根据品相和质量大小分为优级西瓜、一级西瓜、残次西瓜三个等级.农场主随机抽取了两个农场的西瓜各100千克,得到如下数据:“生态农场”优级西瓜和一级西瓜共95千克,两个农场的残次西瓜一共20千克,优级西瓜数目如下:“生态农场”20千克,“智慧农场”25千克.(1)根据所提供的数据,完成下列22⨯列联表,并判断是否有95%的把握认为残次西瓜率与农场有关?农场非残次西瓜残次西瓜总计生态农场智慧农场总计(2)种植西瓜的成本为0.5元/千克,且西瓜价格如下表:等级优级西瓜一级西瓜残次西瓜价格(元/千克) 2.5 1.50.5-(无害化处理费用)①以样本的频率作为概率,请分别计算两个农场每千克西瓜的平均利润;②由于农场主精力有限,决定售卖其中的一个农场,请你根据以上数据帮他做出决策.(假设两个农场的产量相同)参考公式:()()()()22()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.附表:()20P K k ≥0.1000.0500.0100.0010k 2.7063.841 6.63510.828【答案】(1)答案见解析(2)答案见解析【解析】【分析】(1)根据题目中提供数据即可完成表格,代入计算可得2 5.56 3.841K ≈>,即可得出结论;(2)①分别计算出两农场三种等级的西瓜不同利润盈利的频率,再由期望值公式即可求得结果;②根据两农场每千克西瓜的平均利润的大小可知,售卖利润较低的即可.【小问1详解】根据题意完成22⨯列联表如下:农场非残次西瓜残次西瓜总计生态农场955100智慧农场8515100总计18020200所以可得22200(9515855) 5.56 3.84110010018020K ⨯-⨯=≈⨯⨯⨯>,参考附表可知有95%的把握认为残次西瓜率与农场有关.【小问2详解】①对于“生态农场”,抽到优级西瓜即盈利2元的频率为0.2,抽到一级西瓜即盈利1元的频率为0.75,盈利1-元的频率为0.05;所以“生态农场”农场每千克西瓜的平均利润为20.210.7510.05 1.1⨯+⨯-⨯=(元);对于“智慧农场”,抽到优级西瓜即盈利2元的频率为0.25,抽到一级西瓜即盈利1元的频率为0.6,盈利1-元的频率为0.15;所以“智慧农场”农场每千克西瓜的平均利润为20.2510.610.150.95⨯+⨯-⨯=(元);②由于两个农场的产量相同,所以“生态农场”的利润更大,应该售卖“智慧农场”.20.已知椭圆2222:1(0)x y C a b a b +=>>过点()(),0,0,A a B b --两点,椭圆的离心率为32,O 为坐标原点,且1OAB S = .(1)求椭圆C 的方程;(2)设P 为椭圆C 上第一象限内任意一点,直线PA 与y 轴交于点M ,直线PB 与x 轴交于点N ,求证:四边形ABNM 的面积为定值.【答案】(1)2214x y +=(2)证明见解析【解析】【分析】(1)根据离心率和1OAB S = 可解得224,1a b ==,可写出椭圆C 的方程;(2)设()00,P x y 分别求出直线PA ,PB 的方程并解出,M N 的坐标,可得四边形ABNM 的面积122S AN BM =⋅=.【小问1详解】根据题意可知32c e a ==,又112OAB b S a == ,即可得2ab =,结合222a b c =+,解得2224,1,3a b c ===;即椭圆C 的方程为2214x y +=.【小问2详解】证明:由(1)可知()()2,0,0,1A B --,如下图所示:设()00,P x y ,且000,0x y >>;易知直线PA 的斜率002PA y k x =+,所以PA 的直线方程为()0022y y x x =++;同理直线PB 的斜率001PB y k x +=,所以PB 的直线方程为0011y y x x +=-;由题意解得000020,,,021y x M N x y ⎛⎫⎛⎫ ⎪ ⎪++⎝⎭⎝⎭;所以可得000022,112x y AN BM y x =+=+++,四边形ABNM 的面积()()()()2220000000000000000002224448411212212221222x y x y x y x y x y S AN BM y x x y x y x y ++⎛⎫⎛⎫+++++=⋅=++== ⎪⎪+++++++⎝⎭⎝⎭又220014x y +=,可得220044x y +=,故()()()()220000000000000000000000000042244484444842222222222x y x y x y x y x y x y x y S x y x y x y x y x y x y ++++++++++++====+++++++++,即四边形ABNM 的面积为定值.21.已知函数()x f x e x a =--,对于x ∀∈R ,()0f x ≥恒成立.(1)求实数a 的取值范围;(2)证明:当4 0,x π⎡⎤∈⎢⎥⎣⎦时,cos tan +≤x x x e .【答案】(1)(],1-∞;(2)证明见解析.【解析】【分析】(1)利用参数分离法可知x a e x ≤-,构造函数()xg x e x =-,即()min a g x ≤,利用导数研究函数的最小值即可得解;(2)由(1)得1x e x ≥+恒成立,将不等式的证明转化为证cos tan 1x x x ++≤,构造函数()cos tan 1h x x x x =+--,即证()max 0h x ≤,利用导数研究函数的单调性及最值即可.【详解】(1)由0x e x a --≥恒成立,得x a e x ≤-对x ∀∈R 恒成立.令()x g x e x =-,()1xg x e '=-,令()0g x '=,得0x =当0x >,()0g x '>,()g x 单调递增;当0x <,()0g x '<,()g x 单调减,所以()()min 01g x g ==.故所求实数a 的取值范围为(],1-∞.(2)证明:由(1)得1x e x ≥+恒成立,要证cos tan +≤x x x e ,只需证cos tan 1x x x ++≤即可.令()cos tan 1h x x x x =+--,()()()22222sin sin cos sin sin sin 11sin 1.cos cos cos x x x x x x h x x x x x-+-'=-+-==令()2sin sin 1F x x x =+-,易知()F x 在0,4⎡⎤⎢⎥⎣⎦π单调递增,且()00F <,04⎛⎫> ⎪⎝⎭F π,故存在00,4x π⎛⎫∈ ⎪⎝⎭,使得()00F x =.当[)00,x x ∈时,()0F x <,()0h x '≤,()h x 单调递减;当0,4⎛⎤∈ ⎥⎝⎦x x π时,()0F x >,()0h x '>,()h x 单调递增,又()00h =,0424h ππ⎛⎫=-<⎪⎝⎭,()()max 00h x h ==.故当0,4x π⎡⎤∈⎢⎥⎣⎦时,cos tan +≤x x x e .【点睛】方法点睛:本题考查绝对值不等式的恒成立问题,不等式恒成立问题常见方法:①分离参数()a f x ≥恒成立(()max a f x ≥即可)或()a f x ≤恒成立(()min a f x ≤即可);②数形结合(()y f x =图像在()y g x =上方即可);③讨论最值()min 0f x ≥或()max 0f x ≤恒成立.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.在直角坐标系xOy 中,直线l 的参数方程为315415x t y t ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2221sin ρθ=+,点P的极坐标为4π⎫⎪⎭.(1)求C 的直角坐标方程和P 的直角坐标;(2)设l 与C 交于A ,B 两点,线段AB 的中点为M ,求PM .【答案】(1)2212x y +=,()1,1(2)5541PM =【解析】【分析】(1)利用互化公式把曲线C 化成直角坐标方程,把点P 的极坐标化成直角坐标;(2)把直线l 的参数方程的标准形式代入曲线C 的直角坐标方程,根据韦达定理以及参数t 的几何意义可得.【详解】(1)由ρ2221sin θ=+得ρ2+ρ2sin 2θ=2,将ρ2=x 2+y 2,y =ρsinθ代入上式并整理得曲线C 的直角坐标方程为22x +y 2=1,设点P 的直角坐标为(x ,y ),因为P,4π),所以x =ρcosθ=cos 4π=1,y =ρsinθ=4π=1,所以点P 的直角坐标为(1,1).(2)将315415x t y t ⎧=+⎪⎪⎨⎪=+⎪⎩代入22x +y 2=1,并整理得41t 2+110t +25=0,因为△=1102﹣4×41×25=8000>0,故可设方程的两根为t 1,t 2,则t 1,t 2为A ,B 对应的参数,且t 1+t 211041=-,依题意,点M 对应的参数为122t t +,所以|PM |=|122t t +|5541=.【点睛】本题考查了简单曲线的极坐标方程,属中档题.23.已知函数()2429a b a b f x x x +++=+++-.(1)求证:()5f x ≥;(2)若0,0,1a b a b >>+=,证明:2211252a b a b ⎛⎫⎛⎫+++≥ ⎪ ⎪⎝⎭⎝⎭.【答案】(1)证明见解析(2)证明见解析【解析】【分析】(1)利用绝对值三角不等式与二次函数的性质计算可得;(2)利用基本不等式证明即可.【小问1详解】因为()2429a b a b f x x x +++=+++-()()22429429a b a b a b a b x x ++++++++--=≥-+,当且仅当()()20429a b a b x x ++++-≤+时取等号,又2429a b a b +++-+()22255a b +-+=≥,当且仅当22a b +=,即1a b +=时取等号,所以()5f x ≥.【小问2详解】因为0a >,0b >,且1a b +=,又因为222x y xy +≥,当且仅当x y =时取等号,所以()222222x yx y xy +≥++,即()()2222x y x y +≥+,所以()2222x y x y ++≥,当且仅当x y =时取等号,所以22222111111111222a b a b a b a b a b ab ab ⎛⎫+++ ⎪+⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭+++≥=+=+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,又因为2124a bab+⎛⎫<≤=⎪⎝⎭,当且仅当12a b==时取等号,。
安徽省安庆市第一中学高三第三次模拟考试英语试题参考答案

安徽省安庆市第一中学高三第三次模拟考试英语试题&参考答案第Ⅰ卷做题时,建议先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍1.What does the man mean?A. The woman and the man don’t like the same kind of music.B.He didn’t know how the woman found out about thetickets. C. He didn’t realize the woman had wanted toattend the concert.2.What is the woman probably doing now?A. Reading a magazine.B. Studying for a test.C. Shopping for shoes.3.What does the man mean?A. He has refused the dinner appointment.B.He doesn’t eat out very often.C. He does not like to eat out either.4.When will the train for Oxford start?A. At 4:15 p.m.B. At 4:45 p.m.C. At 5:15 p.m.5. What are the speakers probably doing?A. Doing some running.B. Climbing a hill.C. Taking a walk.第二节(共15小题,每小题 1. 5分,满分22. 5分)听下面5段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置.听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
2023届安徽省安庆市第一中学高三下学期三模理综物理试题

D.由于两线圈 匝数不同,则两线圈产生的电动势的有效值不同,所以磁铁转动一圈电阻的发热量不相同,故D错误。
故选B。
6.如图所示,把倾角为 的粗糙斜面体C置于粗糙水平地面上,质量为 的物块A通过跨过光滑轻定滑轮的轻绳与质量为m的小球B连接,O点为轻绳与定滑轮的接触点,初始时,小球B在水平向右的拉力F作用下,使轻绳 段与水平拉力F的夹角为 ,A、B均保持静止状态。现改变拉力F,并保持夹角 大小不变,将小球B向右上方缓慢拉起至 水平,物块A始终保持静止状态。g为重力加速度,下列关于该过程的说法正确的是( )
A.A、B和弹簧组成的系统满足动量不守恒、机械能守恒
B.若A的速度为 ,B的速度为
C.若A的速度为 ,弹簧与导轨之间的夹角为
D.若弹簧恢复原长时,环B速度为水平向右的 ,则初始状态时弹簧的弹性势能
【答案】BCD
【解析】
【详解】A.平行导轨光滑,对A、B和弹簧组成 系统分析,所受的合外力为0,因此系统动量守恒,系统除系统内弹簧的弹力,没有其他力做功,系统机械能守恒,故A错误;
(2)作出该单色光通过玻璃砖的完整光路图,如图所示
由于玻璃砖两表面平行,两次折射时的法线平行,则 。再结合单色光射出玻璃砖时,由折射定律
则
因此通过玻璃砖的出射光束与入射光束平行。再由图中几何关系可知
12.质量为 的滑板静止在光滑水平地面上,滑板上表面 段水平长度为 段是半径为 的四分之一光滑圆弧,如图所示。质量为 的小物块(小物块可视为质点)以初速度 冲上滑板,已知 ,其中 为重力加速度。小物块与滑板 段的动摩擦因数为 ,在以后的运动过程中:
安徽省安庆市高三第三次模拟考试(文数)
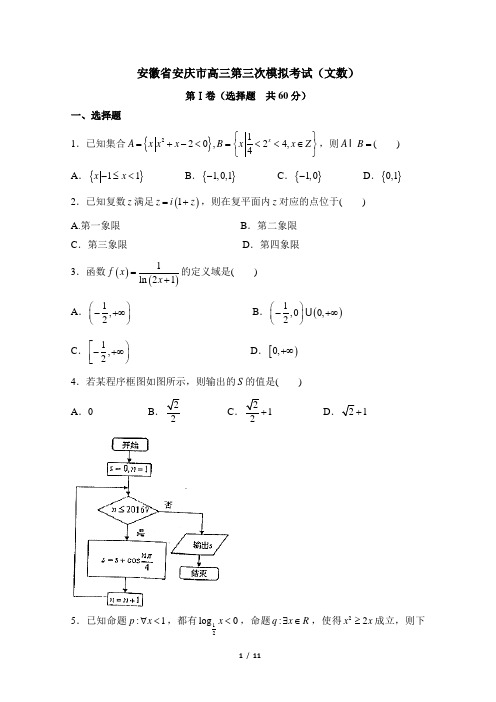
安徽省安庆市高三第三次模拟考试(文数)第Ⅰ卷(选择题 共60分)一、选择题1.已知集合{}2120,24,4x A x x x B x x Z ⎧⎫=+-<=<<∈⎨⎬⎩⎭,则A B =( )A .{}11x x -≤<B .{}1,0,1-C .{}1,0-D .{}0,1 2.已知复数z 满足()1z i z =+,则在复平面内z 对应的点位于( ) A.第一象限 B .第二象限 C .第三象限 D .第四象限 3.函数()()1ln 21f x x =+的定义域是( )A .1,2⎛⎫-+∞ ⎪⎝⎭B .()1,00,2⎛⎫-+∞ ⎪⎝⎭C .1,2⎡⎫-+∞⎪⎢⎣⎭D .[)0,+∞4.若某程序框图如图所示,则输出的S 的值是( )A .0BC 1+D 1+5.已知命题:1p x ∀<,都有12log 0x <,命题:q x R ∃∈,使得22x x ≥成立,则下列命题是真命题的是( )A .()p q ∨⌝B .()()p q ⌝∨⌝C .p q ∨D .p q ∧ 6.某几何体的三视图如图所示,则该几何体的体积为( ) ABCD7.在等比数列{}n a中,若70,n a a >=,则31112a a +的最小值为( ) A. B .4 C .8 D .16 8.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若24,6c b B π===,则A ∠的平分线AD 的长等于( )AB .3 CD9.已知1F 、2F 为双曲线22:1169x y C -=的左、右焦点,点P 在C 上,且123F PF π∠=,则12PF PF ⋅=( )A .6B .9C .12D .1810.已知函数()2log f x x =,在区间[]1,4上随机取一个数x ,使得()f x 的值介于1-到1之间的概率为( )A .13B .34C .12D .2311.已知()()sin ,,,22f x x x x R ππϕϕ⎛⎫=++∈∈- ⎪⎝⎭的图像过,42π⎛⎫⎪⎝⎭点,则()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的值域为( )A .[]5,5-B .[]3,5C .[]3,4D .[]2,512.若函数()22,f x x a x x R =++∈在区间[)3,+∞和[]2,1--上均为增函数,则实数a 的取值范围是( )A .11,33⎡⎤--⎢⎥⎣⎦B .[]6,4--C.3,⎡--⎣ D .[]4,3--第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每题5分,满分20分.13.已知向量()()1,2,,1m =-=a b ,若向量a 在b 方向上的投影长为1,则m =______.14.已知,02πα⎛⎫∈- ⎪⎝⎭,且cos 2sin 2παα⎛⎫=- ⎪⎝⎭,则tan 2α等于______.15.已知x 、y 满足约束条件()2204024x y x y x y ⎧-≥⎪⎪+-≤⎨⎪-+≤⎪⎩,则z x y =+的范围为______.16.如图,已知抛物线24y x =的焦点为F ,过F 的直线AB 交抛物线于A 、B ,交抛物线的准线于点C ,若12BF BC=,则AB =______.三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.(本题满分12分)已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,满足11222233,2,13,2a b a b S T S b ==+==. (Ⅰ)求数列{}n a 、{}n b 通项公式; (Ⅱ)设2nn na cb =,求数列{}n c 的前n 项和为n C . 18.(本题满分12分)某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[]50,60的学生人数为6.(Ⅰ)估计所抽取的数学成绩的众数;(Ⅱ)用分层抽样的方法在成绩为[)80,90和[]90,100这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在[]90,100恰有1人的概率.19.(本题满分12分) 如图,在等腰梯形ABCD 中,,1,60ABCD AD DC CB CF ABC ====∠=︒,四边形ACFE 为矩形,点M 为线段EF 中点,平面ACFE ⊥平面ABCD . (Ⅰ)求证:BC AM ⊥; (Ⅱ)求点A 到平面MBC 的距离.20.(本题满分12分)已知椭圆()2222:10x y C a b a b +=>>与双曲线2213x y -=的离心率互为倒数,且直线20x y --=经过椭圆的右顶点.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)设不过原点O 的直线l 与椭圆C 交于M 、N 两点,且直线OM 、MN 、ON 的斜率依次成等比数列,求直线l 的斜率. 21.(本题满分12分) 已知函数()()ln 1,0,1af x x a x =+-∈+∞-. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若x t =为函数()f x 的极小值点,证明:()1322f t t t<-.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4-4:坐标系与参数方程已知在平面直角坐标系中,曲线C 的参数方程为:3cos 22sin x t y t=⎧⎨=+⎩(t 为参数),P 是C 上任意一点,以x 轴的非负半轴为极轴,原点为极点建立极坐标系,并在两坐标系中取相同的长度单位. (Ⅰ)求曲线C 的直角坐标方程; (Ⅱ)直线l 的极坐标方程为()4R πθρ=∈,求P 到直线l 的最大距离.23.(本小题满分10分)选修4-5:不等式选讲 已知不等式23422x x x --<+的解集为{}x a x b <<. (Ⅰ)求a 、b 的值; (Ⅱ)若(),1,1m n ∈-,且()22,131a a bmn S b m n ==+--,求S 的最小值.安徽省安庆市高三第三次模拟考试(文数)参考答案一、选择题二、填空题13.3414.15.2⎡--⎢⎣16.163三、解答题17.解:(Ⅰ)设等差数列{}n a的公差为d,等比数列{}n b的公比为q,则()()11111112112213233a ba db qa db b qa db q=⎧⎪+=⎪⎨+++=⎪⎪+=⎩,解得112213abdq=⎧⎪=⎪⎨=⎪⎪=⎩,故11,23nn na n b-=+=⋅.………………………………………5分相减得:()()122111111111332717113333313nn n n nC n n----⎛⎫- ⎪⎝⎭=+++⋅⋅⋅+-+⨯=+-+⨯-()21111111525712233223n n n n n ---+⎛⎫=+--+⨯=-⎪⋅⎝⎭. ∴11525443n n n C -+=-⋅……………………………………………………12分 18.解:(Ⅰ)由频率分布直方图可知:样本的众数为75.(Ⅱ)由频率分布直方图可得:第三组[)50,60的频率:0.012100.12⨯=,所以60.1250n =÷=,………………………………………………………4分 ∴第四组[)80,90的频数:0.024105012⨯⨯=: 第五组[]90,100的频数:0.01610508⨯⨯=; 用分层抽样的方法抽取5份得: 第四组[)80,90抽取:125320⨯=;第五组[]90,100抽取:85320⨯=.………………………………7分 记抽到第四组[)80,90的三位同学为123,,A A A ,抽到第五组[]90,100的两位同学为12,B B , 则从5个同学中任取2人的基本事件有:()()()()()()()()()()12131112232122313212,,,,,,,,,,,,,,,,,,,A A A A A B A B A A A B A B A B A B B B ,共10种.其中分数在[]90,100恰有1人有:()()()()()()111221223132,,,,,,,,,,,A B A B A B A B A B A B ,共6种. ∴所求概率:63105P ==.……………………………………………12分19.解:(Ⅰ)证明:在梯形ABCD 中, ∵,1,60ABCD AD DC CB ABC ===∠=︒,∴2AB =,∴2222cos 603AC AB BC AB BC =+-⋅⋅︒=, ∴222AB AC BC =+,∴BC AC ⊥, ∴平面ACFE ⊥平面ABCD ,平面ACFE平面ABCD AC =,BC ⊂平面ABCD ,∴BC ⊥平面ACFE ,∵直线AM ⊂平面ACFE ,∴BC AM ⊥………6分(Ⅱ)由(Ⅰ)可知,,BC AC AC ⊥=,又1BC =,∴11122ABC S AC BC ∆=⨯==,点M 到面ABC 的距离等于1CF =,∴11133AB M ABC C V S CF ∆-=⋅==三棱锥BC ⊥平面ACFE ,∴BC CM ⊥,易得MC =,∴11122MBC S MC BC ∆=⨯==,设点A 平面MBC 的距离为d ,则1133MBC M ABC V S d d ∆-=⋅==三棱锥.=,∴d =………………………………………………12分20.解:,所以椭圆的离心率c e a == 又∵直线20x y --=经过椭圆的右顶点,∴顶点为()2,0,即2a =……………………………………………2分∴1c b ==,∴椭圆方程为2214x y +=…………………………4分(Ⅱ)由题意可设直线l 的方程为:()()()11220,0,,,,y kx m k m M x y N x y =+≠≠联立2214y kx m x y =+⎧⎪⎨+=⎪⎩消去y 并整理得: ()()222148410k xkmx m +++-=……………………5分则()2121222418,1414m km x x x x k k --+==++,于是()22121212y y k x x km x x m =+++…6分 又直线OM 、MN 、ON 的斜率依次成等比数列,∴()2212122121212k x x km x x m y y k x x x x +++⋅== ∴22228014k m m k -+=+,由0m ≠,得214k =,∴12k =±……………12分 21.解:(Ⅰ)若()0,a ∈+∞,函数()f x 定义域为()()0,11,+∞,由()()()22211x a x f x x x -++'=-,∵()2240a ∆=+->,设()0f x '=的两根为1x 、()212x x x <,解得12x x ==,由12122,1x x a x x +=+=,可得1201x x <<<, 当()()120,,x x x ∈+∞时,()0f x '>;当()()12,11,x x x ∈时,()0f x '<.故,函数()f x的单调增区间为⎛ ⎝和⎫+∞⎪⎪⎭,单调递减区间为⎫⎪⎪⎭和⎛ ⎝.……………6分(Ⅱ)由(Ⅰ)知,1t >,函数()f x 的有极小值()ln 11af t t t =+--,而()2210t a t -++=,故()21t a t-=,所以()11ln 1ln t f t t t t t -=+-=-,即证明:113ln 22t t t t-<-, 即证:()11ln 0122t t t t +-<>,设函数()11ln ,122g t t t t t =+->,则()()22102t g t t -'=-<,所以,()g t 函数在()1,+∞上为减函数,从而()()10g t g <=,所以()1322f t t t<- (2)22.解:(Ⅰ)由3cos ,22sin x t y t ==+,消去参数t ,得曲线C 的直角坐标方程为()222194y x -+=.…………………………5分(Ⅱ)直线l 的直角坐标方程为y x =.设与直线l 平行的直线方程为y x m =+,代入()222194y x -+=,整理得()()22131829240x m x m ⎡⎤+-+--=⎣⎦.由()()221824139240m m ⎡⎤∆=--⨯⨯--=⎡⎤⎣⎦⎣⎦,得()2213m -=,所以2m =.当点P位于直线2y x =++与曲线C 的交点(切点)时,点P 到直线l 的距离最=. 或:设点()3cos ,22sin P t t +,则点P 到直线0x y -=的距离为cos ϕϕ==.=. 23.解:11 / 11 (Ⅰ)因为()()()210342214212642x x x x x x x x x +>⎧⎪--<+⇔+-<+⇔⇔<<⎨-<⎪⎩,所以2,6a b ==.……………………5分(Ⅱ)因为2,6a b ==,所以22122,311mn S m n ==+--.22112611S m n ⎛⎫=-+≤-=-≤-=- ⎪--⎝⎭当且仅当m n ==max 6S =-.……………………10分。
安庆市高三模拟考试(三模)语文试题参考答案及评分标准

20XX年安庆市高三模拟考试(三模)语文试题参考答案及评分标准1.(3分)D(A.错在“不属于今”,据“它曾属于昔,已属于今,成了今中之昔”可知,文化传统也属于今;B.错在“秩序的意义”,据原文“并给人类生存带来了秩序和意义”可知,应是“秩序和意义”;C.错在“必能”,据“任何传统都可能成为人们热烈依恋的对象,发挥着预制力功能”可知,应是“可能”。
)2.(3分)D(先后次序混乱,应该是“先”承接上文提出传统始终反不掉的观点,“后”具体分析观点成立的理据。
)3.(3分)①现代社会生活与评判世界的信仰继承了文化传统。
②文化的延续发展与差异理解依赖文化传统。
③每个人都无法摆脱文化传统的命定与掌控。
(每点1分,两点3分。
用原文语句回答,意思对亦可给分。
)4.(3分)A(望:怨恨。
)5.(3分)D(用在动词之后,组成“者”字结构,“……的人”;A.介词,因为/连词,表目的,来;B.放在动词之前构成“所”字结构,指代动作涉及的对象,“……的东西”/用在被动句中,与“为”配合表被动;C.副词,才 /副词,竟然。
)6.(3分)B(此项分析与概括错在“世祖立国之初”,据原文第二段可知,应是更始立国之初。
)7.(10分)(1)(3分)如果放纵贼人不诛杀,那么我就是心怀异志了。
(“纵”、“二心”各1分,语句通顺1分。
)(2)(3分)蒙受您的大恩,我想用性命报答,实在不敢在心里眷顾宗室亲人。
(“效命”、“内顾”各1分,语句通顺1分。
)(3)(4分)世祖就派李忠回到信都,行使太守的职权。
李忠拘押了郡中依附王郎的豪族,诛杀了好几百人。
(“行”、“收”、“大姓附王郎者”定语后置各1分,语句通顺1分。
)8.(3分)C(A.错在“无比的厌恶”,应是“不要厌恶”的意思;B.错在“描写山人饮酒奏乐”,应是描写枭声凄苦;D.错在山人“听枭啼声”,应是交代枭在四季特定时刻啼唱。
)9.(5分)①对比,拿时禽啼唱的媚俗婉转与枭鸟啼叫的凄苦哀怨作对比。
安徽省安庆市高三第三次模拟考试(语文)

安徽省安庆市高三第三次模拟考试(语文)本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
满分150分,考试时间150分钟。
第Ⅰ卷(阅读题共66分)一、(9分)阅读下面文字,同答后面问题。
“丝绸之路”的起与止张骞“凿空”西域,开通丝绸之路,大宛是最知名的地点之一。
大宛,今地在中亚乌兹别克斯坦的费尔干纳盆地。
《史记》将有关西域的内容全部编为《大宛列传》。
大宛是丝绸之路或西域的起止点。
与大宛对应的、中原的丝绸古道起止点,一般认为是西安或洛阳。
西安或洛阳,是汉代行政中心、首都,作为丝绸之路的起点,不容置疑。
商贸起自民间,除了行政中心,还需要有旅客与商品的集散地:人流如织、村落衔接、物产丰饶、宾至如归。
丝绸之路承载着精神文明与物质文明:越贴近基层,它的流动越流畅,脉搏越充满活力,存在越有实效。
由此推断,中原的贴近基层的阶段性起止点、商贸中心,当在伏牛山麓的南阳。
大宛地名,曾引起过争议,争议在于,地名究竟是“大宛”还是大“宛”。
也就是说,大,究竟是当地地名的一部分(如同“大食”“大夏”),还是汉语的修饰成分(如同“大月氏”)岑仲勉先生的结论是:这个西域地名原来是“宛”,大,是汉语的附加成分,他的理由是:《史记》与《汉书》之中,常见“宛宝马”、“使宛”、“许宛之约”、“宛破”等词语,“从知大宛之大,同大月氏之大,意当日汉使艳说宛之广大,故以大冠称,且与小宛对应也”。
“宛”是西域语言,不是汉语。
对此,中外学者从无异说。
然而在中原的地名中,有另外一个“宛”与之对应。
南阳郡别称“宛”,南阳郡的首府名为“宛城”。
“宛”,据《史记》古注,读音为冤(yuān)。
可“宛”的含义是什么呢?费尔干纳盆地是中亚的富庶地区,古代文明的萌生之地,安集延则是盆地中较早出现的重要城镇。
岑仲勉《汉书西域传地理校释》曾引录《西域图志》卷45说:安集延当古道,“与《史记》大宛‘土著有城郭’之说合,则古大宛地,当即今安集延诸城无疑”。
而岑仲勉的结论则是:从读音来说,“余谓‘宛’本安集延之略译,似属无可非议”。
安徽省安庆市高三文综第三次模拟试题

安徽省安庆市2017届高三文综第三次模拟试题第I 卷一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{}{}122,02x M x Z x N xx -=∈-≤≤=<+,则 M N = ( )(A){-2,-1,0} (B) {-1.0,1} (C){0,1} (D){-1,0} (2)已知i 为虚数单位,复数2()1a iZ a R i-=∈-是纯虚数,则1ai -= ( )(3)在等比数列选{}n a 中,已知472568,24a a a a a ==,则2a = ( ) (A)6 (B)4 (C)3 (D)2(4)已知圆221:2440C x y x y +---=。
与圆222:410250C x y x y ++-+=相交于A 、B 两点,则线段AB 的垂直平分线的方程为 (A)(A) 30x y +-= (B) 30x y -+= (C) 310x y +-= (D) 310x y -+= (5)宋代诗词大师欧阳修的《卖油翁》中有一段关于卖油翁的精湛技艺 的细节描写:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之, 自钱孔入,而钱不湿.”如果铜钱是直径为3 cm 的圆,钱中间的正方形孔的边长为1 cm ,则卖油翁向葫芦内注油,油正好进入孔中的概率是 ( ) (A)13 (B) 13π (C) 29 (D) 49π(6)已知1F 、2F 分别是椭圆22221(0)x y a b a b+=>>的左、右焦点,若椭圆上存在点P ,使得120PF PF =,则该椭圆的离心率的取值范围是 ( )(A) ,1)2 (B) (0,2 (C) 1[22 D) [22(7)已知()f x 是定义在R 上的奇函数,且在(0,)+∞上是增函数,若312(log )a f =-,54(log )b f =,c f =,则a ,b ,c 之间的大小关系为 ( )(A) a <b <c (B) a <c <b (C) b <a <c (D) c a b <<。
2023-2024学年安徽省安庆市高考三模数学模拟试题(含解析)

2023-2024学年安徽省安庆市高考三模数学模拟试题一、单选题1.设集合{}2,0,1,2,{2A B xx =-=≤-∣或2}x >,则()R A B ⋂=ð()A .{}2-B .{}1C .2,0,1-D .{}0,1,2【正确答案】D【分析】根据集合的运算求解.【详解】由{2B xx =≤-∣或2}x >得:R {22}B x x =-<≤∣ð,而{}2,0,1,2A =-,所以(){}R 0,1,2A B = ð.故选:D.2.复数20232i z =-+的共轭复数z =()A .2i +B .2i-+C .2i--D .2i-【正确答案】B【分析】根据虚数单位i 的性质求复数z ,再根据共轭复数的概念分析判断.【详解】因为()2023202032i 2i i 2i z =-+=-+⋅=--,所以2i z =-+.故选:B.3.已知两个非零向量a ,b 满足3a b = ,()a b b +⊥ ,则cos ,a b 〈〉= ()A .12B .12-C .13D .13-【正确答案】D【分析】根据向量的数量积运算律和夹角公式求解.【详解】因为()a b b +⊥,所以()0a b b +⋅= ,所以20a b b ⋅+= ,所以2a b b ⋅=- ,221cos ,33b b a b a b a b a b b b--⋅〈〉====-⋅⋅⋅,故选:D.4.在等比数列{}n a 中,2345674,16a a a a a a ==,则8910a a a =()A .4B .8C .32D .64【正确答案】D【分析】根据等比数列的性质求解即可.【详解】由2345674,16a a a a a a ==可得33364,16a a ==,又2639a a a =,故633639a a a =,则239164a =,解得3964a =,即891064a a a =.故选:D5.陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺立体结构图.已知,底面圆的直径12cm AB =,圆柱体部分的高6cm BC =,圆锥体部分的高4cm CD =,则这个陀螺的表面积(单位:2cm )是()A .(144π+B .(144π+C .(108π+D .(108π+【正确答案】C【分析】根据圆柱与圆锥的表面积公式求解.【详解】由题意可得圆锥体的母线长为l =,所以圆锥体的侧面积为112π2⋅⋅=,圆柱体的侧面积为12π672π⨯=,圆柱的底面面积为2π636π⨯=,所以此陀螺的表面积为()()272π36π108cm ++=+,故选:C.6.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知ABC 的面积为4,b =4,8BA AC ⋅=,则a =()A B .C .D 【正确答案】C【分析】由题中的两个等式解得A 与c 的值,再由余弦定理解得a 的值.【详解】∵4b =,||||cos()cos 8BA AC BA AC A bc A π⋅=-=-= ,1=sin 42ABC S bc A =△∴cos 2c A =-①,sin 2c A =②,∴由①②得tan 1A =-,∵(0,)A π∈∴3=4A π∴c =∴22232cos 16824404a b c bc A π=+-=+-⨯⨯=,∴a =故选:C.7.在高三复习经验交流会上,共有3位女同学和6位男同学进行发言.现用抽签的方式决定发言顺序,事件()19,k A k k ≤≤∈N 表示“第k 位发言的是女同学”,则()82P A A =∣()A .14B .712C .16D .13【正确答案】A【分析】根据条件概率公式计算即可.【详解】由题意,()27378299A A 61A 7212P A A ===,()1838299A A 1A 3P A ==所以()()()828221112143P A A P A A P A ===∣,故选:A8.已知函数2()e 2ln ax f x x x ax =--+,若()0f x >恒成立,则实数a 的取值范围为()A .1,e ⎛⎫+∞ ⎪⎝⎭B .(1,)+∞C .2,e ⎛⎫+∞ ⎪⎝⎭D .(e,)+∞【正确答案】C【分析】依题意可得22ln e 2ln e 2ln ax x ax x x x +>+=+,进而可得2ln xa x>在()0,x ∈+∞上恒成立,构造函数2ln ()xh x x=,利用导数研究函数的单调性以及最值,即可求出参数的取值范围.【详解】()0f x >等价于22ln e 2ln e 2ln ax x ax x x x +>+=+.令函数()e x g x x =+,则()e 10x g x '=+>,故()g x 是增函数.2ln e e 2ln ax x ax x +>+等价于2ln (0)ax x x >>,即2ln xa x>.令函数2ln ()xh x x =,则222ln ()x h x x -'=.当(0,e)x ∈时,()0h x '>,()h x 单调递增:当(e,)x ∈+∞时,()0h x '<,()h x 单调递减.max 2()(e)eh x h ==.故实数a 的取值范围为2,e ⎛⎫+∞ ⎪⎝⎭.故选:C.二、多选题9.函数()()sin f x A x ωϕ=+(其中0,0,2A πωϕ>><)的图像如图所示,则下列说法正确的是()A .函数()f x 的最小正周期是2πB .3πϕ=C .为了得到()cos 23g x x π⎛⎫=+ ⎪⎝⎭的图像,只需将()f x 的图像向左平移2π个单位长度D .为了得到()cos 23g x x π⎛⎫=+ ⎪⎝⎭的图像,只需将()f x 的图像向左平移4π个单位长度【正确答案】BD【分析】根据函数图像结合三角函数性质,根据周期,初相判断A,B 选项,根据平移判断C,D 选项即可.【详解】对A ,由图可知,1A =,最小正周期T 满足7πππ41234T =-=,所以πT =,所以函数()f x 的最小正周期是π,故A 错误;对B ,2π2πω==,即()()sin 2f x x ϕ=+,将7π12x =代入可得7π3π22π,122k k ϕ⨯+=+∈Z ,得π2π3k ϕ=+,又π2ϕ<,所以π3ϕ=,故B 正确;对C ,由上述结论可知()πsin 23f x x ⎛⎫=+ ⎪⎝⎭,为了得到()πππ5πcos 2sin 2sin233212g x x x x ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,应将函数()f x 向左平移π4个单位长度.故C 错误,D 正确.故选:BD.10.若甲组样本数据1x ,2x ,…,n x (数据各不相同)的平均数为2,方差为4,乙组样本数据13x a +,23x a +,…,3n x a +的平均数为4,则下列说法正确的是()A .a 的值为-2B .乙组样本数据的方差为36C .两组样本数据的样本中位数一定相同D .两组样本数据的样本极差不同【正确答案】ABD【分析】结合平均数、方差、中位数、极差的概念以及平均数的和差倍分性质,及一组数据同时乘一个数,同时加一个数对方差的影响,逐项分析即可求出结果.【详解】由题意可知:324a ⨯+=,故2a =-,故A 正确;乙组样本数据方差为9436⨯=,故B 正确;设甲组样本数据的中位数为i x ,则乙组样本数据的中位数为32i x -,所以两组样本数据的样本中位数不一定相同,故C 错误;甲组数据的极差为max min x x -,则甲组数据的极差为()()()max min max min 32323x x x x ---=-,所以两组样本数据的样本极差不同,故D 正确;故选:ABD.11.如图,已知四边形,ABCD BCD 是以BD 为斜边的等腰直角三角形,ABD △为等边三角形,2BD =,将ABD △沿对角线BD 翻折到PBD △在翻折的过程中,下列结论中正确的是()A .BD PC⊥B .DP 与BC 可能垂直C .四面体PBCD 33D .直线DP 与平面BCD 所成角的最大值是45 【正确答案】ABC【分析】由折叠平面的变与不变性,对于A ,取BD 中点M ,可得BD ⊥面PMC ,A 选项可判断;对于B ,假设DP 与BC 垂直,则BC ⊥面PCD ,再根据题目所给长度即可判断;对于C ,当面PBD ⊥面BCD 时,此时四面体PBCD 的体积的最大,计算最大体积即可;对于D ,当面PBD ⊥面BCD 时,此时直线DP 与平面BCD 所成角最大,判断即可.【详解】对于A ,如图所示,取BD 的中点M ,连接,PM CM ,BCD △是以BD 为斜边的等腰直角三角形,BD CM ∴⊥,ABD △为等边三角形,BD PM ∴⊥,又,,PM CM M PM CM =⊂ 面PMC ,BD ∴⊥面PMC ,又PC ⊂面PMC ,BD PC ∴⊥,故A 正确.对于B ,假设DP BC ⊥,又,,,BC CD CD DP P CD DP ⊥=⊂ 面PCD ,BC ∴⊥面PCD ,又PC ⊂面PMC ,BC PC ∴⊥,又2,2PB BC ==331PC ⎡⎤∈⎣⎦,当2PC =222BC PC PB +=,故DP 与BC 可能垂直,故B 正确.对于D ,当面PBD ⊥面BCD 时,面PBD 面BCD =BD ,,BD PM PM ⊥⊂平面PBD ,此时PM ⊥面,BCD PDB ∠即为直线DP 与平面BCD 所成角,此时60PDB ∠= ,故D 错误.对于C ,易知当面PBD ⊥面BCD 时,此时四面体PBCD 的体积最大,此时的体积为:1113323BCDV SPM ⎛=⋅=⨯= ⎝,故C 正确.故选:ABC.12.已知数列{}n a 满足328a =,()()1122nn n a n a n --⎡⎤=+≥⎢⎥⎣⎦,*n ∈N ,数列{}n b 的前n 项和为n S ,且()()222212221log log n n n n n b a a a a +-+=⋅-⋅,则下列说法正确的是()A .4221a a =B .1216a a ⋅=C .数列212n n a a -⎧⎫⎨⎬⎩⎭为单调递增的等差数列D .满足不等式50n S ->的正整数n 的最小值为63【正确答案】ABD【分析】由328a =和递推公式()112nn n a n a --⎡⎤=+⎢⎥⎣⎦→28a =→12a =,4168a =→A 选项正确,B 选项正确;()()1122n n n a n a n --⎡⎤=+≥⎢⎥⎣⎦→()112nn n a n a --=+→()212212222n n n a n n a --=+=+为单调递增的等差数列→C 选项不正确;22log 1n n b n +=+→22log 52n n S +=>→62n >→D 选项正确【详解】因为328a =,所以()313222328a a a -=⋅+=,所以28a =,则()21211228a a a -=⋅+=,解得12a =,()4143324168a a a -=⋅+=,所以4221a a =,1216a a ⋅=,所以A 选项正确,B 选项正确;因为()()1122n n n a n a n --⎡⎤=+≥⎢⎥⎣⎦,所以()()1122n n n a n n a --=+≥,所以()212212222n n n a n n a --=+=+,又*n ∈N ,所以22221232222n n n n a a n n a a ----=+-=,*n ∈N 所以221n n a a -⎧⎫⎨⎬⎩⎭为单调递增的等差数列,则数列212n n a a -⎧⎫⎨⎬⎩⎭不是单调递增的等差数列,所以C 选项不正确;()221222122224n n n a n n a +-++=++=+,则()()2221222212221222212log log log log 1n n n n n n n n n a a n b a a a a a a n +-+-++⋅+=-⋅==+,222222341234122log log log log log log 52312312n n n n n n S n n n n +++++⎛⎫=++++=⨯⨯⨯⨯=> ⎪++⎝⎭ ,解得62n >,又*n ∈N ,所以正整数n 的最小值为63,所以D 选项正确.故选:ABD .数列问题,常常需要由递推公式求出通项公式,方法有累加法,累乘法,构造法等,要根据数列特征选择不同的方法.三、填空题13.已知某地最近10天每天的最高气温(单位:C )分别为10,9,13,15,17,16,18,17,20,12,则这10天平均气温的80%分位数为___________C .【正确答案】17.5【分析】根据百分位数的定义求解.【详解】这10天的平均气温的数据按照从小到大的顺序排列为:9,10,12,13,15,16,17,17,18,20,1080%8,⨯= ∴这10天平均气温的80%分位数为171817.5C 2+= .故17.5.14.已知7sin cos 5αα+=,则tan α=________.【正确答案】43或34【分析】利用平方关系式和商数关系式转换求解即可得tan α的值.【详解】解:将7sin cos 5αα+=两边平方得4912sin cos 25αα+=,所以12sin cos 25αα=,所以22sin cos 12sin cos 25αααα=+分式上下同除2cos α得:2tan 12tan 125αα=+整理得:212tan 25tan 120αα-+=,解得:4tan 3α=或3tan 4α=故答案为:43或34.15.已知非负数,x y 满足1x y +=,则1912x y +++的最小值是___________.【正确答案】4【分析】根据题意124x y +++=,再构造等式利用基本不等式求解即可.【详解】由1x y +=,可得()19119124,1212412x y x y x y x y ⎛⎫+++=+=++++ ⎪++++⎝⎭()911219412x y x y ⎛⎫++=+++ ⎪++⎝⎭11044⎛ ≥+= ⎝,当且仅当()231y x +=+,即0,1x y ==时取等号.故416.抛物线22(0)x pyp =>上一点)(1)A m m >到抛物线准线的距离为134,点A 关于y 轴的对称点为B ,O 为坐标原点,OAB ∆的内切圆与OA 切于点E ,点F 为内切圆上任意一点,则•OE OF的取值范围为__________.【正确答案】[3【详解】因为点)A m 在抛物线上,所以3322pm m p=⇒=,点A 到准线的距离为313224p p +=,解得12p =或6p =.当6p =时,114m =<,故6p =舍去,所以抛物线方程为2x y=,∴3)(3)A B ,,所以OAB 是正三角形,边长为22(2)1x y +-=,如图所示,∴32E ⎫⎪⎪⎝⎭,.设点(cos 2sin )F θθ+,(θ为参数),则3π·cos 33226OE OF θθθ⎛⎫=++=++ ⎪⎝⎭,∴·[33OE OF ∈ .本题主要考查抛物线性质的运用,参数方程的运用,三角函数的两角和公式合一变形求最值,属于难题,对于这类题目,首先利用已知条件得到抛物线的方程,进而可得到OAB ∆为等边三角形和内切圆的方程,进而得到点E 的坐标,可利用内切圆的方程设出点F 含参数的坐标,进而得到π·336OE OF θ⎛⎫=++ ⎪⎝⎭ ,从而得到其取值范围,因此正确求出内切圆的方程是解题的关键.四、解答题17.已知函数()21cos 3cos 2f x x x x =+⋅-.(1)求函数()f x 的单调递增区间;(2)求()f x 在区间[0,2π]上的最值.【正确答案】(1),36k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z )(2)最大值为1,最小值为-12.【分析】(1)由三角函数降幂公式与二倍角公式,根据辅助角公式,化简函数为单角三角函数,根据正弦函数的单调性,可得答案;(2)利用整体思想,根据正弦函数的图象性质,可得答案.【详解】(1)()f x =1cos23131cos2sin 2222226x x x x x π+⎛⎫+-=+=+ ⎪⎝⎭.因为y =sin x 的单调递增区间为2,222k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z ),令22,2622x k k πππππ⎡⎤+∈-+⎢⎥⎣⎦(k ∈Z ),得,36x k k ππππ⎡⎤∈-+⎢⎥⎣⎦(k ∈Z ).所以()f x 的单调递增区间为,36k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z ).(2)因为x ∈[0,2π],所以2x +7,666πππ⎡⎤∈⎢⎥⎣⎦.当2x +6π=2π,即x =6π时,()f x 最大值为1,当2x +6π=76π,即x =2π时,()f x 最小值为-12.18.设数列{}n a 的前n 项和n S 满足12n n S a a =-,且1a ,21a -33a -成等比数列.(1)求数列{}n a 的通项公式;(2)设12n n b a ⎧⎫+⎨⎬⎩⎭是首项为1,公差为2的等差数列,求数列{}n b 的通项公式与前n 项和n T .【正确答案】(1)12n n a -=(2)()2212n n b n =--,21222n n T n +=-+【分析】(1)先根据1n n n a S S -=-得到12n n a a -=,利用1a ,21a -33a -成等比数列,可得11a =,可判断数列{}n a 是首项为1,公比为2的等比数列,即可得12n n a -=.(2)由12n n a -=得()2212n n b n =--,利用分组求和法可得.【详解】(1)由已知12n n S a a =-,有()11222n n n n n a S S a a n --=-=-≥,即()122n n a a n -=≥,从而212a a =,32124a a a ==,又因为1a ,21a -33a -成等比数列,即()()221313a a a -=-,所以()()21112143a a a -=-,解得11a =,所以,数列{}n a 是首项为1,公比为2的等比数列,故12n n a -=.(2)因为12n n b a ⎧⎫+⎨⎬⎩⎭是首项为1,公差为2的等差数列,所以()11212n n b a n +=+-,所以数列{}n b 的通项公式为()2212nn b n =--,()()1221321222nn T n ⎡⎤=+++--+++⎣⎦ ()()2121212212nn n -⎡⎤+-⎣⎦=--21222n n +=-+.19.如图,四棱锥P ABCD -中,PA ⊥底面,,ABCD AD BC N ∥为PB 的中点.(1)若点M 在AD 上,32,4AM MD AD BC ==,证明:MN 平面PCD ;(2)若4,5,6PA AB AC AD BC =====,求二面角D AC N --的余弦值.【正确答案】(1)证明见解析(2)【分析】(1)取PC 中点F ,连接,NF DF ,根据已知条件证明四边形NFDM 是平行四边形,即可证明;(2)取BC 中点Q ,根据条件可以证明AQ AD ⊥,所以,,AQ AD AP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,分别求出平面ACN 的法向量和平面ACD 的法向量,再利用公式求解即可.【详解】(1)如图所示:取PC 中点F ,连接,NF DF ,因为2MD AM =,所以23MD AD =,又34AD BC =,所以12MD BC =,因为AD BC ∥,所以MD BC ∥,又因为N 为PB 的中点,所以NF BC ∥且12NF BC =,即有NF MD ∥且NF MD =,所以四边形NFDM 是平行四边形,所以MN DF ∥,又因为MN ⊄平面,PCD DF ⊂平面PCD ,所以MN平面PCD .(2)连接NC ,因为5AB AC ==,所以ABC 为等腰三角形,取BC 中点Q ,连接AQ ,则有AQ BC ⊥,又因为AD BC ∥,所以AQ AD ⊥,又因为PA ⊥底面ABCD ,如图,以,,AQ AD AP 所在直线分别为x 轴,y 轴,z 轴建立空间坐标系,因为4,5,6PA AB AC AD BC =====,则有()()()30,0,0,0,5,0,4,3,0,2,,22A D C N ⎛⎫- ⎪⎝⎭,所以()32,,2,4,3,02AN AC ⎛⎫=-= ⎪⎝⎭,设平面ACN 的法向量为(),,n x y z =r,则有43032202x y x y z +=⎧⎪⎨-+=⎪⎩,则()3,4,6n =-- ,因为PA ⊥底面ABCD ,取平面ACD 的法向量()0,0,1m =,设二面角D AC N --的大小为(θθ为钝角),则有cos cos ,m n m n m n θ⋅===-⋅,即二面角D AC N --的余弦值为61-.20.已知双曲线2222:1x y E a b -=的焦距为4,以原点为圆心,实半轴长为半径的圆和直线0x y -=相切.(1)求双曲线E 的方程;(2)已知点F 为双曲线E 的左焦点,试问在x 轴上是否存在一定点M ,过点M 任意作一条直线l 交双曲线E 于P ,Q 两点,使FP FQ ⋅为定值?若存在,求出此定值和所有的定点M 的坐标;若不存在,请说明理由.【正确答案】(1)22:13x E y -=(2)存在,定值为1,()3M -【分析】(1)利用点到直线的距离公式求得a 的只,再根据焦距,求得b 即可求解;(2)假设存在满足条件的点M ,先在直线垂直于y 轴时,求得定值,再结合根与系数的关系,分析验证直线不垂直于y 轴时,求得此定值的情况,从而得出结论.【详解】(1)原点到直线0x y -=的距离d ==,∴2,c a ==1b ∴=,∴双曲线E 的方程为22:13x E y -=;(2)假设存在点(,0)M m 满足条件,①当直线l 方程为0y =时,则())(),,2,0P Q F -,∴())2,02,01FP FQ ⋅=⋅=;②当直线l 方程不是0y =时,可设直线:l x ty m =+,(t ≠代入22:13x E y -=整理得()(2223230t y mty m t -++-=≠,*由0∆>得223m t +>,设方程*的两个根为1y ,2y ,满足212122223,33mt m y y y y t t -+=-=--,∴()()11222,2,FP FQ ty m y ty m y ⋅=++⋅++()()()()221212122t y y t m y y m =++++++222212153t m m t ---=-,当且仅当2212153m m ++=时,FP FQ ⋅为定值1,解得3m =-,3m =-不满足对任意t 贡0∆>,∴不合题意,舍去.而且3m =-满足0∆>;综上得:过定点()3M -任意作一条直线l 交双曲线E 于P ,Q 两点,使FP FQ ⋅为定值1.21.某校组织“青春心向党,喜迎二十大”主题知识竞赛,每题答对得3分,答错得1分,已知小明答对每道题的概率是12,且每次回答问题是相互独立的.(1)记小明答3题累计得分为X ,求X 的分布列和数学期望;(2)若小明连续答题获得的分数的平均值大于2分,即可获得优秀奖.现有答2n 和22n +道题两种选择,要想获奖概率最大,小明应该如何选择?请说明理由.【正确答案】(1)分布列见解析,数学期望:6(2)小明选择答22n +道题时,获奖的概率更大,理由见解析【分析】(1)由X 的取值为3,5,7,9,再利用独立重复试验求得概率,然后列出分布列进而求得数学期望;(2)分别求出小明选择答2n 道题与22n +道题获得优秀奖的概率,再进行比较即可.【详解】(1)由题意知()303113C 28P X ⎛⎫==⨯= ⎪⎝⎭,()2131135C 228P X ⎛⎫==⨯⨯= ⎪⎝⎭,()2231137C 228P X ⎛⎫==⨯⨯= ⎪⎝⎭,()333119C 28P X ⎛⎫==⨯= ⎪⎝⎭,所以X 的分布列为X3579P18383818()1331357968888E X =⨯+⨯+⨯+⨯=;(2)由题意可知甲同学答一题得3分的概率为12,得1分的概率为12,若选择答2n 道题,此时要能获得优秀奖,则需2n 次游戏的总得分大于4n ,设答2n 道题中,得3分的题数为m ,则()324m n m n +->,则m n >,易知12,2m B n ⎛⎫~ ⎪⎝⎭,故此时获优秀奖的概率:11222122122211111()C C C 22222n n n n nn n n n nn P P m n +-+-++⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=>=⨯⨯+⨯⨯++⨯ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,()21222221CCC2nn n n nnn++⎛⎫=+++⨯ ⎪⎝⎭,()()2201222222222C 11111C C C C 2C 1222222nnn n n n n nn n n n n n ⎛⎫⎛⎫⎛⎫=+++-⨯=-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,同理可以求出当选择答22n +道题,获优秀奖的概率为122222C 1122n n n P +++⎛⎫=- ⎪⎝⎭,因为()()()()()()()()()2222112222222!C 4!!214C 4(1)2122!C C 22212121!1!n n nn n n n n n n n n n n n n n n n n n +++++++====>++++⎡⎤⎡⎤++⎣⎦⎣⎦,所以1222222C C 22n n n n n n +++>,则12P P <,所以小明选择答22n +道题时,获奖的概率更大.22.已知函数()()ln 1f x x =+,()2g x ax x =+.(1)当1x >-时,()()f x g x ≤,求实数a 的取值范围;(2)已知*n ∈N ,证明.111sin sin sin ln2122n n n+++<++ 【正确答案】(1)0a ≥(2)证明见解析【分析】(1)证明出()ln 1x x ≤+,在0a ≥时,可得出()2ln 1x ax x +≤+,在a<0时,010x a=->,分析可知()()00f x g x >,综合可得出实数a 的取值范围;(2)由(1)变形可得()1ln 11x x x ≥->,令111t x =-,可得出()()1ln ln 11t t t t--≥>,可得出()()1ln ln 1n k n k n k≤+-+-+,{}0,1,2,,k n ∈ ,证明出()sin 0x x x <>,可得出()()1sinln ln 1n k n k n k<+-+-+,{}0,1,2,,k n ∈ ,利用不等式的基本性质可证得结论成立.【详解】(1)解:令()()()ln 11h x x x x =+->-,则()1111x h x x x '=-=-++,当10x -<<时,()0h x '>,则函数()h x 在()1,0-上单调递增,当0x >时,()0h x '<,则函数()h x 在()0,∞+上单调递减,所以,()()max 00h x h ==,即()ln 1x x ≤+,所以,当0a ≥时,()2ln 1x x ax x +≤≤+,即()()f x g x ≤,当a<0时,取010x a=->,由于()0ln 1ln10x +>=,而2200110ax x a a a⎛⎫+=⋅--= ⎪⎝⎭,得()2000ln 1x ax x +>+,故()()00f x g x >,不合乎题意.综上所述,0a ≥.(2)证明:当0a =时,由(1)可得()ln 1x x ≤+,则ln 1≤-x x ,可得11ln1x x ≤-,即1ln 1x x -≤-,即()1ln 11x x x≥->,令111t x =-,所以,1t x t =-,所以,1ln1t t t ≥-,即()()1ln ln 11t t t t --≥>,所以,()()1ln ln 1n k n k n k≤+-+-+,{}0,1,2,,k n ∈ ,令()()sin 0g x x x x =->,则()1cos 0g x x '=-≥,且()g x '不恒为零,所以,函数()g x 在()0,∞+上单调递增,故()()00g x g >=,则()sin 0x x x <>,所以,()()11sin ln ln 1n k n k n k n k<≤+-+-++,{}0,1,2,,k n ∈ ,所以,111sinsin sin 122n n n+++++()()()()()ln 1ln ln 2ln 1ln 2ln 21n n n n n n <+-++-+++--⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦()2ln 2ln lnln 2nn n n=-==.方法点睛:利用导数证明不等式问题,方法如下:(1)直接构造函数法:证明不等式()()f x g x >(或()()f x g x <)转化为证明()()0f x g x ->(或()()0f x g x -<),进而构造辅助函数()()()h x f x g x =-;(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.。
安徽省安庆市2021-2022学年高三下学期第三次模拟检测语文试题含解析

安徽省安庆市2021-2022学年高三下学期第三次模拟检测语文试题本试卷总分150分,考试时间150分钟(答案在最后)考生注意事项:1.答题前,务必在试题卷规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中座位号与本人座位号是否一致。
2.答选择题时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
3.答非选择题时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,必须在题号所指示的答题区域作答。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成下列小题。
春秋时期,孔子通过总结和反思夏、商、周三代的文化遗产,继承并发展了古老的“礼”观念,赋予其新的思想内涵,创造性地建立起一套以“礼”为核心价值观念的儒家思想体系。
“礼”既是一种社会政治理想,又是一种伦理道德规范。
它通过对人们思想行为的引导、制约和规范,来维护社会的安定和发展。
在孔子的思想体系中,“仁”与“礼”均处于非常重要的地位。
从《礼记》看来,“礼”是高于“仁”的。
《礼记·曲礼》云:“道德仁义,非礼不成”。
由此可见,连“仁”也是以“礼”为依据的。
中国古代政治是以“礼”为基础的政治。
“礼”与中国古代政治理念、政治行为和政治制度,都有着密不可分的联系。
我国古代社会的宗法制度、爵位制度、土地制度及其他各种政治制度,在古代都属于“礼”的范畴。
“礼”与法制也有密切关系。
“法”源于“礼”,是从“礼”中衍生出来的,《管子·枢言》云:“法出于礼。
”“礼”被赋予了强制力便是“法”。
“礼”是一种社会道德教化工具,“法”是一种事后的惩罚措施。
“礼”和“法”都是人们的行为规范,“礼”依靠道德教化的方式引导人们别贵贱、序尊卑;而“法”则依靠强制力使人们共同遵守礼的有关规范。
在中国古代国家治理模式中,“礼”与“法”紧密地结合在一起,对社会秩序发挥着调节、约束的功能。
许多统治者和政治家还往往以“礼”为依据,进行制度建设或改革。
安徽省安庆市高三理综第三次模拟试题

A、加速度大小为0.5m/s2
B、任意相邻1s内的位移差都为2m
C、第2s内的位移是2m
D、物体第3s内的平均速度大小为2。5m/s
16、近年来我国的探月工程取得了重大成功。在整个卫星的飞行轨道的设计过程中,我们的科研人员通过大量的工作设计了一条特别的地月转移轨道,从“嫦娥一号” 的轨道如图所示,在探月卫星发动机关闭,轨道控制结束,卫星进入地月转移轨道.简化为下图所示,图中MN之间的一段曲线表示转移轨道的一部分,P是轨道上的一点,且在该点地球和月球对卫星的引力大小相等,直线AB过P点且和两边轨道相切.则下面说法中正确的是( )
C.“IR8水稻"拥有抗倒伏的性状,根本原因是体内赤霉素含量较低影响植株的生长
D.SW1基因通过控制酶的合成,间接控制了生物的性状
6. 下表各选项中,符合“M—定能推理得出N结论”的是
选项
M
N
A
花药离体培养
植株体细胞内只有一个染色体组
B
细胞中不存在线粒体
不能发生有氧呼吸
C
孟德尔假说“形成配子时,成对的遗传 因子彼此分离"
B、流过R1的电流有效值等于流过R3的电流有效值。
C、R2两端的电压有效值是R3两端电压有效值的2倍
D、流过R2的电流有效值流过是R4电流有效值的2倍
21、如图所示,金属杆ab、cd置于足够长的平行轨道MN、PQ上,可沿轨道滑动,轨道所在的空间有竖直向上匀强磁场,导轨电阻不计。则下面说法中正确的是( )
C.
D.
10.下列实验操作能达到实验目的的是
A.向苯酚浊液中滴加少量
CO
B.
安徽省安庆市2025届高三语文第三次模拟考试试题

安徽省安庆市2025届高三语文第三次模拟考试试题(考试时间:150分钟满分:150分)留意事项:1.答题前,务必在答题卡规定的地方填写自己的姓名、准考证号和座位号。
2.答题时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.答题时,必需运用0.5毫米的黑色墨水签字笔在答题卡上....书写,要求字体工整、笔迹清晰。
作图题可选用铅笔在答题卡...规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清晰。
必需在题号所指示的答题区域作答,超出答题区域书写........的答案无效.....,在试题卷、草稿纸上答题无效.............。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)保持环境卫生,对于防疫至关重要。
在殷商甲骨文中有大扫除的记载。
《礼记》《治家格言》《周书秘奥造册经》中均强调了保持居室清洁卫生的习惯,同时指出屋宇干净就可以削减疾病的发生。
熏烟蒸洗也是我国古代传统防疫方法。
《周礼·秋官》记载有用莽草、嘉草等烧熏驱蛊防病的方法。
依据出土的竹简我们可以看到,秦时期,凡入城,其车乘和马具都要经过火燎烟熏以消毒防疫。
在敦煌石窟中保存着一幅“殷人洒扫火燎防疫图”,描述了殷商时代以火燎、烟熏方法来杀虫、防疫的情景。
两汉时期是古代瘟疫记录最多的时期,《博物志》中特殊讲到有一次长安大疫,宫中皆疫病,汉武帝焚烧弱水西国所贡香丸一枚“以辟疫气”。
《伤寒杂病论》中具体论述了多种传染性疾病在不同时期的各种治疗方法,熏香便是其中一种防抗和协助疗法。
在中国传统文化中,无论是宫廷生活还是百姓生活,熏香成了各种史料和医药典籍中最为常见的驱瘟防疫有效方法。
空气消毒法出现在晋代。
葛洪认为,通过熏烧药物的方式,可以预防疫病;他在《肘后备急方》中首先提出了空气消毒法。
其后,唐代孙思邈继承和发展了这种防疫方法。
明代李时珍常常运用蒸汽消毒法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省安庆市2012年高三第三次模拟考试理综生物1.科学家以链孢霉胆碱缺陷型突变体为材料,将它们培养在含有3H-胆碱(膜磷脂的前身物)的培养基中,使线粒体中的脂质被同位素标记,然后再将其转移到没有同位素标记物的培养基中,结果发现在以后生长的几代线粒体中都有放射性标记。
该实验证明了A.生物膜具有一定的流动性B.细胞内的生物膜是一个统一的整体C.线粒体内的DNA是半保留复制的D.细胞内的线粒体可进行分裂增殖2.HIV(艾滋病病毒)感染T细胞可使参与细胞周期调控的蛋白质CDK1失活,并使cyclinB 积聚。
CDK1是细胞由DNA复制后进入分裂期的主要酶,cyclinB的降解则是进入分裂期的必要条件,因而HIV的感染造成T淋巴细胞核DNA处于右图所示的A.Ⅰ阶段B. Ⅱ阶段C.Ⅲ阶段 D . Ⅳ阶段3.萝卜的花有白、红、紫三种颜色,该性状由常染色体上的一对等位基因R-r控制。
下表组别亲本子代表现型及数量一紫花×白花紫花428,白花415二紫花×红花紫花413,红花406三紫花×紫花红花198,紫花396,白花202AB.白花植株自交的后代均开白花,红花植株自交的后代均开红花C.白花与红花植株杂交的后代中,既没有红花也没有白花D.可用紫花植株与白花或红花植株杂交验证基因的分离定律4.右图所示的概念关系中,Ⅰ表示整个大方框,包含Ⅱ和Ⅲ,Ⅲ又包含Ⅳ。
下表中对应各项不符合图示关系的是选项ⅠⅡⅢⅣA生物膜系统细胞膜细胞器膜内质网膜B细胞呼吸有氧呼吸无氧呼吸发酵C可遗传变异基因重组突变染色体变异D生态系统非生物的物质和能量生物群落分解者5A.植物生长素是由植物一定部位的细胞分泌的固醇类激素B.生长素在植物体内可以进行极性运输和非极性运输C.顶芽和侧芽因生长素产生量不同而促进或者抑制芽的发育D.生长素的作用具有两重性,不同浓度的生长素其作用效果一定不同A.食物链每个环节的NP仅有很少一部分被下一个营养级利用B.该表显示出能量流动具有单向流动和逐级递减的特点C.表中数据显示这是一个相对封闭的生态系统D.缩短食物链可以提高人类对生态系统的能量利用率29.(19分)回答下列Ⅰ、Ⅱ两小题:Ⅰ.(10分)阅读以下两个与细胞呼吸和光合作用有关的实验,请分析回答:实验一:下图为研究草蜢呼吸速率而设计的实验装置及结果,其中毛细管截面积为Rmm2。
实验二:为了研究某种水草的光补偿点(植物光合作用吸收的二氧化碳量与呼吸作用释放的二氧化碳量相等时的光照强度),科研人员设计了如下图实验。
试管中放入相同的水草和等量的BTB溶液(BTB是一种灵敏的酸碱指示剂,对光不敏感,其一定浓度的水溶液中性时无色,偏碱性时呈蓝色,弱酸性时呈黄色)。
(1)实验一中草蜢的呼吸速率(以吸入氧气的体积为准)应为mm3h-1。
(2)实验二中,一段时间后,距离荧光灯60cm处的试管无颜色变化,这说明。
(3)一段时间后,请预期实验二中2号、5号试管内的颜色分别是、。
(4)实验二中,用荧光灯比白炽灯更好,原因是。
Ⅱ.(9分)右图是从蛙体内剥离出的某反射弧结构模式图,其中①②③④分别表示反射弧的另外四个组成部分,A、B、C、D为神经纤维上的四个实验位点。
该反射弧的效应器为运动神经末梢及其支配的肌肉,当感受器受到刺激时会导致肌肉收缩。
为了探究③是传出神经还是传入神经,请完成以下实验内容。
⑴将微电流计的两个电极分别搭在实验位点B和C的神经纤维膜外,用电刺激仪刺激在实验位点A上给予一定强度的刺激,若微电流计的指针偏转次,则神经③为传出神经;若微电流计的指针偏转次,则神经③为传入神经。
该实验结果表明兴奋在神经细胞间传递的特点为 ,具有这种特点的原因是由于 。
⑵为进一步验证上一实验结果,又进行了以下的实验:在A 、B 之间将神经③剪断,立即用电刺激仪刺激B 点,如果 (能/不能)看到肌肉收缩现象,则神经③为传入神经;假如不剪断神经③,而是在C 、D 之间将神经④剪断,立即用电刺激仪刺激C 点,如果 (能/不能)看到肌肉收缩现象,则神经③为传出神经。
若以上的刺激导致肌肉收缩活动,该活动 (能/不能)称为反射活动,主要原因是 。
30.(15分)某科研所欲开发痢疾疫苗,利用鼷鼠做了一系列实验。
实验的主要过程及结组别 第一次接种(灭活的痢疾杆菌) 第二次接种(灭活的痢疾杆菌)抗体合成程度 甲 正常的鼷鼠 未接种 +乙 正常的鼷鼠 接种 +++++丙 幼年摘除胸腺的鼷鼠 未接种 +丁 幼年摘除胸腺的鼷鼠 接种 +戊 摘除胸腺后注入T 淋巴细胞的鼷鼠 接种 ++++(1) 与甲组相比,乙组内抗体合成程度明显高于甲组的原因是:当第二次接种时,鼷鼠第一次接种产生的一定量的 就会迅速增殖、分化形成新的 ,进而产生更强的特异性免疫反应。
(2) 戊组与丁组对照,说明抗痢疾杆菌抗体的合成过程需要______细胞的帮助。
与乙组相比,丁组抗体合成程度较低的原因是 。
(3) 若将题干中的病原体痢疾杆菌换成病毒,接种病毒后正常鼷鼠往往先通过 免疫来阻止病毒通过血液循环而播散,再通过 免疫彻底消灭它。
(4) 为验证T 细胞是细胞免疫中不可缺少的细胞,请补全实验设计思路和结果.......:①实验组:切除鼷鼠的胸腺后,移植异体器官。
结果:移植器官易保留在小鼠体内。
②对照组:______________ _ 。
结果: 。
③为了进一步验证以上的实验结论,对实验组还需进行以下处理: 。
结果:移植器官被排斥。
31.(20分)回答下列Ⅰ、Ⅱ两小题:Ⅰ.(11分)狗的毛色有白毛、黑毛和棕毛三种,由两对等位基因A-a 和B-b 控制,且基因B 控制黑色素的合成,基因b 控制棕色素的合成,当有基因A 存在时,所有色素均不能合成。
现有纯合白毛狗与纯合黑毛狗杂交,F 1代均为白毛,将F 1代雌雄狗相互交配,得到的F 2代中有118条白毛狗、32条黑毛狗和10条棕毛狗(每种毛色的狗中雌雄比例为1:1)。
(1)亲本的基因型是 。
两对基因A-a 和B-b 的遗传 (能/不能)遵循基因的自由组合定律。
(2) F 2代中白毛性状能稳定遗传的基因型有 、 、 等3种。
(3)若选取F 2代中的白毛狗与纯合棕毛狗杂交,则其子代中狗的表现型及其比例是 。
(4)若要通过一代杂交的方法判断出F 2代中黑毛狗的基因型,请用遗传图解形式表示杂交实验过程(写出基因型、表现型)。
Ⅱ.(9分)据中国古代医学巨著《本草纲目》记载:葡萄酿酒,暖腰身,驻颜色,治补血,耐寒。
请回答下列问题:葡萄酒的酿造离不开酵母菌,首先需要获得纯净的酵母菌菌种,基本程序如下:(1)配制固体培养基的操作步骤有:①计算;②溶化;③灭菌;④倒平板;⑤称量。
下列操作顺序正确的是()A.①②③④⑤B.①⑤③②④C.①⑤②③④D.⑤①②③④(2)微生物接种最常用的方法是和,每次接种之前要对接种环进行,避免接种环上可能存在的微生物污染培养基。
(3)“七分种,三分酿”是葡萄酒生产中品质保障的要决,即决定葡萄酒品质的主要因素是酒的生产原料——葡萄的品质。
为了获得高品质的葡萄,某科研机构采用基因工程技术培育新品种葡萄,在构建基因表达载体时需用、等酶工具,构建的基因表达载体除了目的基因外,还必须有、以及标记基因等,导入葡萄受体细胞时可用基因枪法,培育出的高品质葡萄在短时间内快速繁殖可通过来实现。
1.【答案】D【解析】实验中用3H-胆碱来标记线粒体中的脂质(主要在线粒体膜中),经培养发现在以后生长的几代线粒体中都有放射性标记,这只能说明线粒体可进行分裂增殖,不能说明生物膜的流动性,故A错。
细胞内的生物膜包括细胞膜、细胞器膜和核膜,题干中只涉及线粒体膜,故B错。
没有标记DNA,不能说明DNA是半保留复制的,故C错。
2.【答案】C【解析】根据图解可推知图中Ⅰ、Ⅱ、Ⅲ分别为细胞分裂间期的G1期、S期和G2期,Ⅳ包括分裂期的前期、中期和后期。
由于HIV的感染,造成T淋巴细胞的蛋白质CDK1失活,并使cyclinB积聚,致使T淋巴细胞DNA复制后无法进入分裂期,因此T淋巴细胞的核DNA处于图示的Ⅲ阶段。
3.【答案】A【解析】一对常染色体上的等位基因控制的性状有三种,说明该基因中R对r为不完全显性,即RR、Rr、rr分别对应三种性状。
由组别三可知,紫花植株的基因型为Rr,但三组杂交结果均不能判断出白花和红花植株的基因型是rr、RR,还是RR、rr,所以A选项错误。
白花植株和红花植株均为纯合体,二者自交的后代都不会出现性状分离,二者杂交的后代都为紫花的Rr。
因为该性状为不完全显性,RR、Rr的表现型不同,所以,无论是Rr×rr、还是Rr×RR,后代都会出现1∶1的测交分离比,即都可用来验证基因的分离定律。
4.【答案】A【解析】生物膜系统包括细胞器膜、细胞膜和核膜,故A选项错误。
教材中(必修1第95页)明确指出,微生物的无氧呼吸称为发酵。
在生物进化的相关内容中(必修2第116页),将基因突变与染色体变异统称为突变。
5.【答案】B【解析】植物生长素主要合成部位是幼嫩的芽、叶和发育中的种子,其化学本质是吲哚乙酸,不是固醇类;在胚芽鞘、芽、幼叶和幼根中,生长素进行极性运输,而在成熟组织中生长素可以通过韧皮部进行非极性运输;抑制侧芽生长的生长素来源于顶芽;由于生长素的生理作用具有两重性,因此不同浓度的生长素,其作用效果有可能相同。
6.【答案】C【解析】由图中食物链环节Ⅱ级(田鼠)的NP+R之和远远大于GP,因而可判断该生态系统有迁入,是一个开放的生态系统。
29.Ⅰ.【答案】(10分,每空2分)(1)2R×(L1+L2)(2)距离荧光灯60cm处的光照强度为该水草的光补偿点(3)黄色蓝色(4)荧光灯产生的热量少,可避免温度对实验结果的影响【解析】(1)由实验一中图解可知,因呼吸产生的CO2被固体氢氧化钠被吸收,则30分钟内呼吸消耗氧气体积为(L1+L2)×R,故草蜢的呼吸速率为2R×(L1+L2)mm3h-1。
(2)实验二中距离荧光灯60cm处的试管无颜色变化,说明水草的净光合速率为0,故距离荧光灯60cm处的光照强度为该水草的光补偿点。
(3)根据(2)的结果可推知,2号试管内CO2量增加,溶液呈弱酸性,故呈现黄色;5号试管内CO2量减少,溶液偏碱性,故呈现蓝色。
(4) 实验二荧光灯比白炽灯产热量少,对试管内温度的影响较小。
Ⅱ.【答案】(9分,除标注外每空1分)⑴1 2 单向传递神经递质只能由突触前膜释放,作用于突触后膜受体(2分)⑵能能不能反射弧结构不完整(其他合理答案也给分)【解析】本体考查了神经调节的相关知识。
神经调节的基本方式为反射,其结构基础是反射弧,在反射弧中,兴奋的传导方向是:感受器→传入神经→神经中枢→传出神经→效应器。
