第5章 异方差性
《计量经济学》第五章精选题及答案

第五章 异方差二、简答题1.异方差的存在对下面各项有何影响? (1)OLS 估计量及其方差; (2)置信区间;(3)显著性t 检验和F 检验的使用。
2.产生异方差的经济背景是什么?检验异方差的方法思路是什么? 3.从直观上解释,当存在异方差时,加权最小二乘法(WLS )优于OLS 法。
4.下列异方差检查方法的逻辑关系是什么? (1)图示法 (2)Park 检验 (3)White 检验5.在一元线性回归函数中,假设误差方差有如下结构:()i i i x E 22σε=如何变换模型以达到同方差的目的?我们将如何估计变换后的模型?请列出估计步骤。
三、计算题1.考虑如下两个回归方程(根据1946—1975年美国数据)(括号中给出的是标准差):t t t D GNP C 4398.0624.019.26-+= e s :(2.73)(0.0060) (0.0736)R ²=0.999t t t GNP D GNP GNP C ⎥⎦⎤⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡4315.06246.0192.25 e s : (2.22) (0.0068)(0.0597)R ²=0.875式中,C 为总私人消费支出;GNP 为国民生产总值;D 为国防支出;t 为时间。
研究的目的是确定国防支出对经济中其他支出的影响。
(1)将第一个方程变换为第二个方程的原因是什么?(2)如果变换的目的是为了消除或者减弱异方差,那么我们对误差项要做哪些假设? (3)如果存在异方差,是否已成功地消除异方差?请说明原因。
(4)变换后的回归方程是否一定要通过原点?为什么?(5)能否将两个回归方程中的R²加以比较?为什么?2.1964年,对9966名经济学家的调查数据如下:资料来源:“The Structure of Economists’Employment and Salaries”, Committee on the National Science Foundation Report on the Economics Profession, American Economics Review, vol.55, No.4, December 1965.(1)建立适当的模型解释平均工资与年龄间的关系。
计量经济学课后思考题答案

第五章 异方差性思考题5.1 简述什么是异方差?为什么异方差的出现总是与模型中某个解释变量的变化有关?答 :设模型为),....,,(....n 21i X X Y i i 33i 221i =μ+β++β+β=,如果其他假定均不变,但模型中随机误差项的方差为),...,,()(n 21i Var 2i i =σ=μ,则称i μ具有异方差性。
由于异方差性指的是被解释变量观测值的分散程度是随解释变量的变化而变化的,所以异方差的出现总是与模型中某个解释变量的变化有关。
5.2 试归纳检验异方差方法的基本思想,并指出这些方法的异同。
答:各种异方差检验的共同思想是,基于不同的假定,分析随机误差项的方差与解释变量之间的相关性,以判断随机误差项的方差是否随解释变量变化而变化。
其中,戈德菲尔德-跨特检验、怀特检验、ARCH 检验和Glejser 检验都要求大样本,其中戈德菲尔德-跨特检验、怀特检验和Glejser 检验对时间序列和截面数据模型都可以检验,ARCH 检验只适用于时间序列数据模型中。
戈德菲尔德-跨特检验和ARCH 检验只能判断是否存在异方差,怀特检验在判断基础上还可以判断出是哪一个变量引起的异方差。
Glejser 检验不仅能对异方差的存在进行判断,而且还能对异方差随某个解释变量变化的函数形式进行诊断。
5.3 什么是加权最小二乘法?它的基本思想是什么?答:以一元线性回归模型为例:12i i i Y X u ββ=++经检验i μ存在异方差,公式可以表示为22var()()i i i u f X σσ==。
选取权数 i w ,当2i σ 越小 时,权数i w 越大。
当 2i σ越大时,权数i w 越小。
将权数与 残差平方相乘以后再求和,得到加权的残差平方和:2i 21i 2i i X Y w e w )(**β-β-=∑∑,求使加权残差平方和最小的参数估计值**ˆˆ21ββ和。
这种求解参数估计式的方法为加权最小二乘法。
第五章 异方差性

26
异方差性的检验
问题在于用什么来表示随机误差项的方差 一般的处理方法:
Var(ui ) E(uቤተ መጻሕፍቲ ባይዱ2) ei2
图示检验法
图示检验法
(一)相关图形分析 方差描述的是随机变量取值的(与其均值的)离散程度。因为被解释
变量Y与随机误差项u有相同的方差,所以分析Y与X的相关图,可以初 略地看到Y的离散程度与X之间是否有相关关系。
ui 的某些分布特征,可通过残差 ei 的图形对异方差进行观察。
对于一元回归模型,绘制出ei2 对Xi的散点图,对于多元回归模型,绘制出ei2 对Yi的散点图或ei2 与认为和异方差有关的X的散点图。
31
图示检验法
(二)残差图形分析
e~i 2
e~i 2
X 同方差
e~i 2
X 递增异方差
e~i 2
X 递减异方差
每个企业所处的外部环境对产出量的影响被包含在随机误差项中 每个企业所处的外部环境对产出量的影响程度不同,造成了随机
误差项的异方差性
产生异方差性的原因
产生异方差性的原因
(一)模型设定误差
假设正确的模型是:
Yi 1 2 X2i 3 X3i ui
假如略去了重要的解释变量X3 ,而采用 Yi 1 2 X2i vi
排序,再按戈德菲尔德匡特检验方法回归,否则即使存在异方差,也有可能用戈德菲
尔德匡特方法检验不出来。
用 EViews 给截面数据排序的方法:在 Workfile 窗口点击 Procs 键并选 Sort current page
功能,在打开的 Sort Workfile Series 对话窗填写以哪一个序列为标准(基准序列)排
计量经济学第五章

Variables-Likelihood Ratio • 出现对话框时,写入删除变量名--OK • 对比删除前后的AIC与SC信息值,信息
值小的结论是应采纳的。
9
用Eviews的误设定检验3
• 第一,估计出简单(单纯)方程 • 第二,在命令窗口上写入genr v_hat=resid 或者 Procs/Generate Series中 v_hat=resid 发现 v_hat • 第三,估计出新的回归方程
无约束模型(U)
有约束模型(K) (general to simple)
计算统计量F
F=(RSSK-RSSu)/J RSSu/(n-k-1)
~F(J, n-k)
J 为表示约束条件数, K 为表示自变量数 或者 应估计的参数数, n 为表示样本数(obs)
4
2. LM检验(Lagrange Multiplier
多重共线性多出现在横截面资料上。
16
三、异方差性的检验及对策
Var(ℇi)≠Var(ℇj) (i≠j)时, ℇi中存在异方差性(Herteroskedasticity)。 即随机项中包含着对因变量的影响因素。 异方差性多发生在横截面资料上。
17
异方差性的检验
1.图示检验法 如模型为Yi=0+1X1i+2X2i+…+ℇi 时,
7
用Eviews的误设定检验1
• 首先估计出简单(单纯)方程 • View/Coefficient Tests/Omitted
Variables-Likelihood Ratio • 出现对话框时,写入新变量名 OK • 检验结果出现在上端,如果P值很小时, 拒
计量经济学题库第5章异方差

第5章异 方 差习 题一、单项选择题1. 回归模型中具有异方差性时,仍用OLS 估计模型,则以下说法正确的是( )A. 参数估计值是无偏非有效的B. 参数估计量仍具有最小方差性C. 常用F 检验失效D. 参数估计量是有偏的 2.更容易产生异方差的数据为 ( )A. 时序数据B. 修匀数据C. 横截面数据D. 年度数据 3.在具体运用加权最小二乘法时, 如果变换的结果是则Var(u)是下列形式中的哪一种?( )A. B. C. D.4. 在异方差性情况下,常用的估计方法是( )A .一阶差分法 B. 广义差分法 C .工具变量法 D. 加权最小二乘法 5. 在异方差的情况下,参数估计值的方差不能正确估计的原因是( )A. B.C. D. 6. 设,则对原模型变换的正确形式为( )7. 下列说法不正确的是( )A.异方差是一种随机误差现象B.异方差产生的原因有设定误差C.检验异方差的方法有F 检验法D.修正异方差的方法有加权最小二乘法8. 如果回归模型违背了同方差假定,最小二乘估计是( )A .无偏的,非有效的 B. 有偏的,非有效的011yx ux x x x ββ=++2x σ22xσσ2log x σ22()i E u σ≠()0()i j E u u i j ≠≠()0i i E x u ≠()0i E u ≠)()(,2221i i i i i i x f u Var u x y σσββ==++=01212222212...()()()().()()()()i i i i i i i i i i i i i i i i i A y x u B y x u C f x f x f x f x D y f x f x x f x u f x βββββββ=++=+=++=++C .无偏的,有效的 D. 有偏的,有效的 9. 在检验异方差的方法中,不正确的是( )A. Goldfeld-Quandt 方法B. ARCH 检验法C. White 检验法D. DW 检验法10. 在异方差的情况下,参数估计值仍是无偏的,其原因是( )A.零均值假定成立B.序列无自相关假定成立C.无多重共线性假定成立D.解释变量与随机误差项不相关假定成立11. 在修正异方差的方法中,不正确的是( )A.加权最小二乘法B.对原模型变换的方法C.对模型的对数变换法D.两阶段最小二乘法 12. 下列说法正确的是( )A.异方差是样本现象B.异方差的变化与解释变量的变化有关C.异方差是总体现象D.时间序列更易产生异方差二、多项选择题1. 如果模型中存在异方差现象,则会引起如下后果( )A. 参数估计值有偏B. 参数估计值的方差不能正确确定C. 变量的显著性检验失效D. 预测精度降低E. 参数估计值仍是无偏的2. Goldfeld-Quandt 检验法的应用条件是( )A. 将观测值按解释变量的大小顺序排列B. 样本容量尽可能大C. 随机误差项服从正态分布D. 将排列在中间的约1/4的观测值删除掉 E .除了异方差外,其它假定条件均满足三、计算题1.根据某城市1978——1998年人均储蓄(y)与人均收入(x)的数据资料建立了如下回归模型x y6843.1521.2187ˆ+-=se=(340.0103)(0.0622)下面取时间段1978——1985和1991——1998,分别建立两个模型(括号内为t 值), 模型1:模型2:计算F 统计量,即,对给定的,查F 分布表,得临界值。
庞浩 计量经济学5第五章 异方差性

同方差
递增型异方差
递减型异方差
复杂型异方差
18
2.借助X-e2散点图进行判断 观察散点的纵坐标是否随解释变量Xi的变化而 变化。
~2 e2e i ei e2 ~2
X 同方差 递增异方差
X
e2
~2 e i
~2 e 2 e i
X 递减异方差 复杂型异方差
X
19
二、戈德菲尔德—夸特 (Goldfeld-Quanadt)检验
3
说明1
矩阵表示: Y X u 随机扰动项向量 其方差—协 u1 u 方差矩阵不 2 u 再是: un n1 而是:
2 2 Var Cov ( ui ) 2 nn
ei X i v i
ei
1 vi Xi
ei X i v i 1 ei vi Xi
③利用上述回归的R2、t统计量、F统计量等判断,R2 好、t统计量和F统计量显著,即可判定存在异方差。 28
说明: 1.也可以用 e i 与可能产生异方差的多个解释变 量进行回归模拟; 2.戈里瑟检验的优点在于不仅检验了异方差是否 存在,同时也给出了异方差存在时的具体表现 形式,为克服异方差提供了方便。 3.试验模型选得不好,也可能导致检验不出是否 存在异方差性。
12 2 2 Var Cov ( ui ) 2 n nn
4
说明2
随机扰动项 ui具有异方差性,可理解释为被解释变量 的条件分散程度随解释变量的变化而变化,如下图所 示:var( ui ) i2 2 f ( X i)(i 1,2,, n)
10
第二节 异方差性的后果
计量经济学复习知识点重点难点

计量经济学复习知识点重点难点计量经济学知识点第一章导论1、计量经济学的研究步骤:模型设定、估计参数、模型检验、模型应用。
2、计量经济学是统计学、经济学和数学的结合。
3、计量经济学作为经济学的一门独立学科被正式确立的标志:1930年12月国际计量经济学会的成立。
4、计量经济学是经济学的一个分支学科。
第二章简单线性回归模型1、在总体回归函数中引进随机扰动项的原因:①作为未知影响因素的代表;②作为无法取得数据的已知因素的代表;③作为众多细小影响因素的综合代表;④模型的设定误差;⑤变量的观测误差;⑥经济现象的内在随机性。
2、简单线性回归模型的基本假定:①零均值假定;②同方差假定;③随机扰动项和解释变量不相关假定;④无自相关假定;⑤正态性假定。
3、OLS回归线的性质:①样本回归线通过样本均值;②估计值的均值等于实际值的均值;③剩余项ei的均值为零;④被解释变量的估计值与剩余项不相关;⑤解释变量与剩余项不相关。
4、参数估计量的评价标准:无偏性、有效性、一致性。
5、OLS估计量的统计特征:线性特性、无偏性、有效性。
6、可决系数R2的特点:①可决系数是非负的统计量;②可决系数的取值范围为[0,1];③可决系数是样本观测值的函数,可决系数是随抽样而变动的随机变量。
第三章多元线性回归模型1、多元线性回归模型的古典假定:①零均值假定;②同方差和无自相关假定;③随机扰动项和解释变量不相关假定;④无多重共线性假定;⑤正态性假定。
2、估计多元线性回归模型参数的方法:最小二乘估计、极大似然估计、矩估计、广义矩估计。
3、参数最小二乘估计的性质:线性性质、无偏性、有效性。
4、可决系数必定非负,但是根据公式计算的修正的可决系数可能为负值,这时规定为0。
5、可决系数只是对模型拟合优度的度量,可决系数越大,只是说明列入模型中的解释变量对被解释变量的联合影响程度越大,并非说明模型中各个解释变量对被解释变量的影响程度也大。
6、当R2=0时,F=0;当R2越大时,F值也越大;当R2=1时,F→∞。
第5章 异方差性

5、计算统计量:
RSS2
F
nc ( k 1) nc nc 2 ~ F( k 1, k 1) RSS1 2 2 nc ( k 1) 2
6、在给定的显著性水平下比较判断。
注意: (1) 当模型含有多个解释变量时,应以每一个解释变 量为基准检验异方差。 (2)对于截面样本,计算F统计量之前,必须先把数据 按解释变量的值从小到大排序。 (3)G—Q检验仅适用于检验递增或递减型异方差。 (4)检验结果与数据剔除个数c的选取有关。 (5) G—Q检验无法判定异方差的具体形式。
5.2异方差性的后果
5.2.1对模型参数估计值无偏性的影响
以简单线性回归模型为例,对模型 yt = b0 + b1 xt + ut ˆ 当Var(ut) = t 2,为异方差时,以 b1 为例:
ˆ b1
k
t
yt b1 kt ut
ˆ E (b1 ) E (b1 kt ut ) b1
划分方法是: 把成对(组)的观测值按解释变量的大小顺序排列, 略去c个处于中心位置的观测值 (通常n 30时,取c n/ 4), 余下的n- c个观测值自然分成容量相等,(n- c) / 2的两 个子样本。
{x1, x2, …, xt-1, xt, xt+1, …, x n-1, xn}
n1 = (n-c) / 2
5.2.3对模型参数估计值显著性检验的影响
ee ˆ 并非随机误差项 在异方差情况下, n k 1 方差的无偏估计量。
2
ˆ 导致在此基础上估计的 s ( b j ) 也出现偏误。
ˆ bj 而变量的显著性检验中,构造了t统计量 t ˆ s(b j )
变量的显著性检验失去意义。
第五章-异方差性-答案说课讲解

第五章-异方差性-答案第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T )二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B )A. B. C. D. 7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=A. B. C. D. ∑=i i x y n 1b ˆ 8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模型时,应将模型变换为( C )。
计量经济学第五章 异方差

X 20000
5.3异方差的侦查
利用残差图——绘制残差平方与X散点图
(一般把异方差看成是由于解释变量的变化而引起的)
5.1异方差的概念
三、异方差产生的原因 模型设定误差:省略了重要的解释变量
例:真实模型 Yi 1 2 X 2i 3 X 3i i 采用模型 Yi 1 2 X 2i i
如果X3随着X2的不同而对Y产生不同的影响,则 该影响体现在扰动项中。
测量误差: 一方面,测量误差常常在一定时间内逐渐增加,如X 越大,测量误差就会趋于增大 另一方面,测量误差随时间变化趋于减少,如抽样技 术的改进使得测量误差减少。
)
2 i
5.1异方差的概念
6 Y
4
300 Y
200
2
100
0 0
X
0
X
10
20
30
0
5000
10000
15000
20000
250
Y
二、常见的异方差类型: 200
递增型异方差:
150
100
递减型异方差:
50
条件异方差(略):
0 0
X
10
20
30
时间序列数据和截面数据中都有可能存在异方差。
经济时间序列中的异方差常为递增型异方差。
ˆ 2 ei2 (Yi ˆX i )2 (( ˆ) X i i )2
n 1
n 1
n 1
5.2异方差的后果
E (vaˆr(ˆ ))
E(
ˆ 2
X
2 i
)
E(
(( ˆ)X
(n 1)
异方差

1
1 f ( X 2i )
1Hale Waihona Puke X 1i 21 f ( X 2i )
X 2i
k
X ki
f ( X 2i )
ui
新模型中,存在
V ar( 1 f ( X 2i ) ui ) E ( 1 f ( X 2i ) ui )
2
1 f ( X 2i )
0 . 05
3、White检验 (1)建立回归模型:LS Y C X,回归结果如图5-5
(2)在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图5-6。
4、Park检验 – (1)建立回归模型(结果同图5-5所示)。 – (2)生成新变量序列:GENR LNE2=log(RESID^2) GENR LNX=log(x) – (3)建立新残差序列对解释变量的回归模型: LS LNE2 C LNX,回归结果如图5-7所示。
案例1---我国制造业利润函数模型
一、参数估计 进入EViews软件包,确定时间范围;编辑输 入数据;选择估计方程菜单,估计样本回归函数 如下:
估计结果为:
括号内为t统计量值。
ˆ y i 12 . 0335 0 . 1044 X i ( 0 . 6165 ) R
2
( 12 . 367 ) F 152 . 9322
0 . 8547
二、检验异方差性 1、图形分析检验 ⑴观察销售利润(Y)与销售收入(X)的相关图 (图5-3):SCAT X Y
从图中可以看出,随着销售收入的增加,销售利 润的平均水平不断提高,但离散程度也逐步扩大。这 说明变量之间可能存在递增的异方差性。
异方差

19
几种异方差的检验方法: 几种异方差的检验方法: 非正式的方法(图示法) 一、非正式的方法(图示法)
1、用X-Y的散点图进行判断 、 的散点图进行判断 看是否存在明显的散点扩大 缩小 复杂 散点扩大、缩小 散点扩大 缩小或复杂 型趋势(即不在一个固定的带型域中) 型趋势(即不在一个固定的带型域中)
先将样本一分为二,对子样①和子样② 先将样本一分为二,对子样①和子样②分别 作回归, 作回归,然后利用两个子样的残差平方和之比构 造统计量进行异方差检验。 造统计量进行异方差检验。 由于该统计量服从F分布, 由于该统计量服从 分布,因此假如存在递增 分布 的异方差, 远大于1;反之就会等于1( 的异方差,则F远大于 ;反之就会等于 (同方 远大于 )、或小于 或小于1(递减方差)。 差)、或小于 (递减方差)。
26 26
戈德菲尔德-匡特(Goldfeld Quandt)检验 (Goldfeld3、戈德菲尔德-匡特(Goldfeld-Quandt)检验
G-Q检验以 检验为基础,适用于样本容量较 检验以F检验为基础 检验以 检验为基础, 异方差递增或递减的情况。 大、异方差递增或递减的情况。
G-Q检验的思想: 检验的思想:
所以,当模型出现异方差性时,参数 所以,当模型出现异方差性时,参数OLS 估计值的变异程度增大,从而造成对Y的预测 估计值的变异程度增大,从而造成对 的预测 误差变大,降低预测精度,预测功能失效。 误差变大,降低预测精度,预测功能失效。
18
§5.3 异方差的侦察方法
检验思路: 检验思路:
由于异方差性就是相对于不同的解释 由于异方差性就是相对于不同的解释 异方差性 变量观测值,随机误差项具有不同的方差。 变量观测值,随机误差项具有不同的方差。 那么: 那么 检验异方差性, 检验异方差性,也就是检验随机误差项 的方差与解释变量观测值之间的相关性及 其相关的“形式” 其相关的“形式”。
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
异方差

第一节 异方差的概念
例:以某一行业的企业为样本建立企业生产函数模 型 Yi=Ai1 Ki2 Li3ei 被解释变量:产出量Y 解释变量:资本K、劳动L、技术A, 那么:每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 每个企业所处的外部环境对产出量的影响程度不同 ,造成了随机误差项的异方差性。 这时,随机误差项的方差并不随某一个解释变量观 测值的变化而呈规律性变化,呈现复杂型。
第三节 异方差性的检验
三、戈里瑟(Gleiser)检验 1969年戈里瑟提出的,它不但可以检验异方差是 否存在,而且可以近似探测随机误差项的方差是 怎样随解释变量的变化而变化的。 基本思想:由OLS法得到残差 e i ,取 e i 的绝对 值 ,然后将 对某个 X i回归,根据回归模 ei ei 型的显著性和拟合优度来判断是否存在异方差。
二、异方差性的后果
ˆ
2
e
2 i
n2
ˆ s(1 )
ˆ ki
2
2
ˆ2
(Xi X )
2
但是,在异方差的情况下
ˆ* s( i ) ˆ ki i
2 2
ˆ i ki
2 2
ˆ ki
2
2
i ki ki
2
2
=
ˆ s(i )
i Байду номын сангаасi
第三节 异方差性的检验
计量经济学实验答案--第二版(张晓峒)
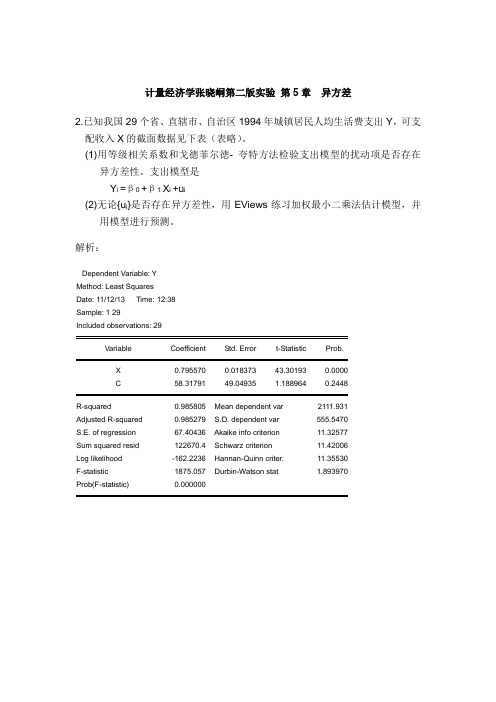
计量经济学张晓峒第二版实验第5章异方差2.已知我国29个省、直辖市、自治区1994年城镇居民人均生活费支出Y,可支配收入X的截面数据见下表(表略)。
(1)用等级相关系数和戈德菲尔徳- 夸特方法检验支出模型的扰动项是否存在异方差性。
支出模型是Y i =β0 +β 1 X i +u i(2)无论{u i}是否存在异方差性,用EViews练习加权最小二乘法估计模型,并用模型进行预测。
解析:Dependent Variable: YMethod: Least SquaresDate: 11/12/13 Time: 12:38Sample: 1 29Included observations: 29Variable Coefficient Std. Error t-Statistic Prob.X 0.795570 0.018373 43.30193 0.0000C 58.31791 49.04935 1.188964 0.2448R-squared 0.985805 Mean dependent var 2111.931Adjusted R-squared 0.985279 S.D. dependent var 555.5470S.E. of regression 67.40436 Akaike info criterion 11.32577Sum squared resid 122670.4 Schwarz criterion 11.42006Log likelihood -162.2236 Hannan-Quinn criter. 11.35530F-statistic 1875.057 Durbin-Watson stat 1.893970Prob(F-statistic) 0.0000001,5002,0002,5003,0003,5004,0001,0002,0003,0004,0005,000可支配收入人均生活费支出(1)略去中心9个样本观测值,将剩下的20个样本观测值分成容量相等的两个子样本,每个子样本的样本观测值个数均为10.由前面的样本回归产生的残差平方和为12363.80,后面样本产生的残差平方和为62996.26.所以F=62996.26/12363.80=5.10,自由度n=10-2=8,查F 分布表得临界值为3.44,因为F=5.10>3.44,所以支出模型的随机误差项存在异方差性。
第五章第三节 异方差性的检验

3、 G-Q检验具体步骤
(1)将样本(观察值)按某个解释变量的大小排序;
(2)将序列中间(段)约 c = 1 / 4 个观察值除去,并使余下的头、尾两段样本容量相同,均为(n-c)/2 个;(3)提出假设:
H0 : ui为同方差; H1:ui为异方差
(4)分别对头、尾两部分样本进行回归,且计算各残差平方和分别为
对(2)式进行回归
R2
a) H0 : 1 2 P H1 : 至少一个i 0
三、Glejser (格里瑟)检验(选学)
四、Breusch—Pagan (布鲁士—佩格)检验(选学) 五、White(怀特)检验 六、ARCH检验
除了图示法以外的检验方法都是构造统计量 实施检验,称为解析法
共同思路
• 异方差性,是相对于不同的样本点,即相对于不 同的X观测值, ui具有不同的方差
ei2
图形分析法是利用残差序列绘制出各种图形,以供分析检验使用。 包括:
1、解释变量为X 轴,残差的平方ei 2 为Y轴的 散点图。
2.解释变量为X 轴,被解释变量为Y轴的X-Y散点图
异方差的类型大致可以分为递增异方差、递减异方差、 复杂异方差三种。 用Y X 作散点图的区域逐渐变宽、变窄、不规则变化, 认为存在异方差; 用ei2 X 作散点图上e2并不近似于某一常数, 则认为存在异方差。
(2)求出残差et , 进而求出et2
(3)估计et2
0
1 X 2t
2 X3t
3
X
2 2t
4
X
2 3t
5 X2t
X 3t
t
(4)针对上述模型作回归,并计算统计量nR2。其中:n为样本
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学课程教案
第五章 异方差性
§5.1 异方差的概念 一、异方差的概念 对于模型
i ki k i ii i X X X Y μββββ+++++= 2210
如果出现
Var i i ()μσ=2
即对于不同的样本点,随机误差项的方差不再是常数,而互不相同,则认为出现了异方差性(Heteroskedasticity)。
将居民按照收入等距离分成n 组,取组平均数为样本观测值。
一般情况下,居民收入服从正态分布:中等收入组人数多,两端收入组人数少。
而人数多的组平均数的误差小,人数少的组平均数的误差大。
所以样本观测值的观测误差随着解释变量观测值的不同而不同,往往引起异方差性。
被解释变量:产出量Y
解释变量:资本K 、劳动L 、技术A ,
那么:每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。
这时,随机误差项的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。
§5.2 异方差性的后果
§5.3 异方差性的检验 检验思路:
由于异方差性就是相对于不同的解释变量观测值,随机误差项具有不同的方差。
那么:检验异方差性,也就是检验随机误差项的方差与解释变量观测值之间的相关性及其相关的“形式”。
问题在于用什么来表示随机误差项的方差。
一般的处理方法:
首先采用OLS 法估计模型,以求得随机误差项的估计量(注意,该估计量是不严格的),我们称之为“近
似估计量”,用
~
e i 表示。
于是有
Var E e i i i ()()~μμ=≈22
~( )e y y i i
i ls =-0
几种异方差的检验方法: 1、图示法
(1)用X-Y 的散点图进行判断
看是否存在明显的散点扩大、缩小或复杂型趋势(即不在一个固定的带型域中)
(2)X-~e i
2
的散点图进行判断
看是否形成一斜率为零的直线
i
ji i X f e ε+=)(~2
i
ji i X f e ε+=)(|~|
i e X X f ji
ji εασ2)(=
i
ji i X e εασ++=ln ln )~ln(22
3、戈德菲尔德-匡特(Goldfeld-Quandt)检验
G-Q 检验以F 检验为基础,适用于样本容量较大、异方差递增或递减的情况。
G-Q 检验的思想:
先将样本一分为二,对子样①和子样②分别作回归,然后利用两个子样的残差平方和之比构造统计量进行异方差检验。
由于该统计量服从F 分布,因此假如存在递增的异方差,则F 远大于1;反之就会等于1(同方差)、或小于1(递减方差)。
G-Q 检验的步骤:
①将n 对样本观察值(X i ,Y i )按观察值X i 的大小排队 ②将序列中间的c=n/4个观察值除去,并将剩下的观察值划分为较小与较大的相同的两个子样本,每个子样样本容量均为(n-c)/2
③对每个子样分别进行OLS 回归,并计算各自的残差平方和
)
12,12(~)12(~)12(~2122------------=∑∑k c
n k c n F k c n e k c n e F i
i
i i i i X X Y μβββ+++=22110
i
i i i i i i i X X X X X X e εαααααα++++++=215224213221102~
注意:
辅助回归仍是检验与解释变量可能的组合的显著性,因此,辅助回归方程中还可引入解释变量的更高次方。
如果存在异方差性,则表明确与解释变量的某种组合有显著的相关性,这时往往显示出有较高的可决系数以及某一参数的t 检验值较大。
当然,在多元回归中,由于辅助回归方程中可能有太多解释变量,从而使自由度减少,有时可去掉交叉项。
§5.4 异方差的修正
模型检验出存在异方差性,可用加权最小二乘法(Weighted Least Squares, WLS )进行估计。
加权最小二乘法的基本思想:
加权最小二乘法是对原模型加权,使之变成一个新的不存在异方差性的模型,然后采用OLS 估计其参数。
2
1102)]
ˆ
ˆˆ([∑∑+++-=k k i i i
i X X Y W e W βββ
2
22)()()(σσμμji i i i X f E Var ===
+++=i ji i ji ji i ji X X f X X f X f Y X f 22110
)
(1)(1)
(1)
(1βββ
i ji ki ji k
X f X X f μβ)
(1)
(1
+
+
2
22)()
(1
))
(1(
))
(1(
σμμμ==
=i ji i ji i ji E X f X f E X f Var
即满足同方差性,可用OLS 法估计。
W μμμμ2)()(0
)(σ='==E Cov E
W =⎡⎣
⎢⎢
⎢⎢⎤⎦
⎥⎥⎥⎥w w w n 1
2
μD X βD Y D 111---+=
***μβX Y +=
1211211111)()()(--------''='=''=''='D D D D D ΩD D μμD D μμD μμ*
*σσE E E
I 2σ=
**1***)(ˆY X X X β''=-
Y
W X X W X Y D D X X D D X 11111111)()(--------''='
'''=
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=221
2~~ˆn e e W σ
这时可直接以
|}
~|/1,
|,
~|/1|,
~|/1{
2
1
1
n
e
e
e
diag
=
-
D
作为权矩阵。
注意:
在实际操作中人们通常采用如下的经验方法:
不对原模型进行异方差性检验,而是直接选择加权最小二乘法,尤其是采用截面数据作样本时。
如果确实存在异方差,则被有效地消除了;
如果不存在异方差性,则加权最小二乘法等价于普通最小二乘法
§5.5 案例--中国农村居民人均消费函数
例4.1.4 中国农村居民人均消费支出主要由人均纯收入来决定。
农村人均纯收入包括(1)从事农业经营的收入,(2)包括从事其他产业的经营性收入(3)工资性收入、(4)财产收入(4)转移支付收入。
考察从事农业经营的收入(X1)和其他收入(X2)对中国农村居民消费支出(Y)增长的影响:
思考题
1、什么是异方差?异方差的实质是什么?
2、检验异方差的基本思想?批出各种方法的异同?
3、加权最小二乘法的基本思想是什么?
4、怎样确权最小二乘法的权数?。
