杨浦区第二学期八年级期中考试数学试卷
杨浦区第二学期八年级期中考试数学试卷

杨浦区2021学年度第二学期初二数学期中考试卷〔考试时间:90分钟总分值100分〕2021、4一、填空题:〔本大题共12题,每题2分,总分值24分〕1.假设函数y(k1)x1是一次函数,那么k的取值范围为.2.一次函数ykxb的图像经过点A(0,2),并与直线y4x平行,那么这个一次函数解析式是_ .3.如果一次函数 y kx 1中y随x的增大而减小,那么这个一次函数一定不经过第___ 象限.4.在图中,将直线OA向上平移3个单位,所得直线的函数解析式为.5.方程2x1x的解是__.第4题图A6.方程组x y2的解为.xy37.十二边形的内角和为_______度.OB C第10题图8.用换元法解方程x233x313.如果设y23,那么原方程可化为y的整x22x式方程是.9.一个多边形的每个外角都为72,那么这个多边形是边形.10.如图,□ABCD的周长是28cm,AC和BD交于O,△OAB的周长比△OBC的周长小2cm,那么AB=,BC=.11.解方程组x2y22时,可先化为和两个方x25xy6y20程组.12.如果直y2x k与两坐所成的三角形面是9,k的.二、〔本大共6,每2分,分12分〕13.函数y x 3,假设当x a,y5;当x b,y3,a和b的大小关系是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕a>b;〔B〕a=b;〔C〕a<b;〔D〕不能确定.14.以下方程中,是二方程的⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕21;〔〕2x0;〔〕8;〔〕.B xCx Dx015.以下方程中, 有数解的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕x610;〔B〕x2;〔C〕x230;〔D〕2xx.x2x216.某灾区恢复生,划在一定内种60蔬菜,播种每天比原划多种3,因此提前一天完成任,种了几天?种了x 天,可列方程⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A63;〔B〕60603;〔C〕60601;〔D〕60601〕600.xx1x1x xx3x3x 17.平行四形的一条14,以下各数中,能分作它的两条角的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕10与16;〔B〕12与16;〔C〕20与22;〔D〕10与18.18.一个面积为2的平行四边形被直线分成面积为x,y的两局部,那么y与x之间的函数关系只可能是〔〕三、简答题〔本大题共5题,每题6分,总分值30分〕19.解关于x的方程:b(x2)4.20.解方程:2x3x.解:解:7,①4y2 21.解方程组:x y22.解方程组:x 22xy291.②x y解:解:23.:如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.求证:∠MAE=∠NCF.四、解答题〔本大题共3题,每题8分,总分值24分〕24.如图,A〔4,a〕,B〔-2,-4〕是一次函数y=kx+b的图象和反比例函数y=m的图象的交点.x1〕求反比例函数和一次函数的解祈式;2〕求△A0B的面积.解:25.某区需修建一条2400米长的封闭式污水处理管道.为了尽量减少施工对市民生活等的影响,实际施工比原方案每天多修10米,结果提前20天完成了任务.试问实际每天修多少米?解:26.如图,:在平行四边形ABCD中,∠C=60°,E、F分别是AB、CD的中点,且AB=2AD.求证:DE∶BD=3∶3.五、〔本大题总分值10分,第〔1〕小题2分,第〔2〕①②小题各4分〕27.如图一次函数y=-x+7与正比例函数y=4x的图象交于点A,且与x轴3交于点B.1〕求点A和点B的坐标;2〕过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O﹣C﹣A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒(t0).①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是QA=QP的等腰三角形?假设存在,求的值;假设不存在,请说明理由.解:。
上海市杨浦区2018-2019学年八年级下学期期中考试数学试卷(解析版)

2018学年第二学期期中初二年级质量调研卷一、填空题(本大题15题,每题2分,满分30分)1.一次函数与x轴的交点是____________2.要使直线不经过第四象限,则该直线至少向上平移__________个单位3.直线与平行,且经过点(2,1),则k=______b=_______4.已知,一次函数的图像经过点A(2,1)(如下图所示),当时,x的取值范围是______5.已知点,是直线上的两点,且当<时,>,则该直线经过______________象限.6.关于x的方程的解是一切实数,那么实数a=_________7.已知方程若设,则原方程可化为关于y的整式方程__8.方程的解是_______________9.将方程组:转化成两个二元二次方程组分别________和____________10.若方程有增根,则a的值为______________11.关于x的方程:是二项方程,k=_____________12.如图,平行四边形ABCD中,对角线AC⊥BD,AC=10,BD=24 ,则AD=____________13.平行四边形ABCD中,∠A:∠B=2:7,则∠C=_________º14.如果从某个多边形的一个顶点出发的对角线共有2 条,那么该多边形的内角和是____度.15.如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”,当协调边为6时,它的周长为______二、选择题(本大题共4题,每题3分,满分12分)16.下列方程组中,属于二元二次方程组的是()A. B. C. D.17.有实数根的方程是()A. B. C. D.18.一个多边形,边数每增加1,内角和是()A. 不变B. 增加1 ºC. 增加180 ºD. 增加360 º19.一次函数,若y 随着x的增大而减小,则该函数的图像经过()A一、二、三 B. 一、二、四 C. 二、三、四 D. 一、三、四三、简答题(本大题共5题,每题6分,满分30分)20.解方程:21.解方程:22.解方程组:23.声音在空气中传播速度y(米/秒)是气温x (摄氏度)的一次函数,下表列出了一组不同气温时的音速。
最新杨浦区学年度第二学期期中考试初二数学学科试卷2014.4

杨浦区2013学年度第二学期期中考试初二数学学科试卷2014.490分钟 100分(基础部分)+50分(拓展部分)基础部分一、填空题(本大题共12题,每题3分,满分36分)1.方程04224=-x x 的解是 。
2.直线12-+=b x y 在y 轴上的截距是2,则b= 。
3.如果一次函数y=kx+b 图像与直线y=2x 平行,且过(-3,5),则这个一次函数的解析式是 。
4.请写出一个二项方程,使其有一解为-2,这个二项方程是: 。
5.直线13+--=m x y 上有两点A (a ,-2)、B (b ,-3),则a b 。
(填“>”、“<”或“=”)6.直角梯形的一腰长6cm ,这条腰与一条底边所成的角为60°,则另一腰长为 。
7.一个多边形的内角和与外角和的度数之比为9:2,则这个多边形的边数是 。
8.矩形的一条对角线长6cm ,它把一个内角分成1:2两部分,则矩形的面积为 平方厘米。
9.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,且AC=8,BD=6,过点O 作OH ⊥AB ,垂足为H ,则点O 到边AB 的距离OH= 。
第9题 第10题10.如图,已知一次函数b x k y +=11的图像与反比例函数xk y 22=的图像交于A (-2,1)和)34,23(-B 两点,当21y y >时,x 的取值范围是 。
11.菱形ABCD 的一条对角线长为6,边AB 的长是方程01272=+-x x 的一个根,则菱形ABCD 的周长为 。
12.如图,在梯形ABCD 中,AD ∥BC ,E 是BC 的中点,AD=5,BC=12,点P 是BC 边上一动点,当PB= 时,以点P 、A 、D 、E 为顶点的四边形为平行四边形。
二、选择题(本大题共4题,每题3分,满分12分)13.右图反映了一辆汽车从甲地开往乙地的过程中,汽车离开甲地的距离s (千米)与所用时间t (分)之间的函数关系。
2018-2019上海市杨浦区八年级(下)期中数学试卷资料

51. 如图,在平面直角坐标系 xOy 中,O 为坐标原点,已知直线 l1 经过点 A (-6,0),它与 y 轴交于点 B,点 B 在 y 轴正半轴上,且 OA=2OB.
52. (1)求直线 l1 的函数解析式; 53. (2)若直线 l2 也经过点 A(-6,0),且与 y 轴交于点 C,如果△ABC
பைடு நூலகம்
5. 一次函数 y=-2x-7 与 x 轴的交点是______.
6. 要使直线 y=3x-2 不经过第四象限,则该直线至少向上平移______个单
位.
7. 直线 y=kx+b 与 y=-5x+1 平行,且过(2,1),则 k=______,
b=______.
8. 已知,一次函数 y=kx+b 的图象经过点 A(2,1)
2018-2019 学年上海 市杨浦区八年级(下)
期中数学试卷
2018-2019 学年上海市杨浦区八年级(下)期中数学试卷
副标题
题号 得分
一
二
三
四
总分
一、选择题(本大题共 4 小题,共 12.0 分)
1. 下列方程组中,属于二元二次方程组的是( )
A.
B.
C.
D.
2. 有实数根的方程是( )
A.
B.
C.
D.
3. 若一个多边形的边数增加 1,它的内角和( )
A. 不变
B. 增加 1°
C. 增加 180° D. 增加 360°
4. 一次函数 y=kx-k,若 y 随着 x 的增大而减小,则该函数的图象经过
()
A. 一、二、三 B. 一、二、四 C. 二、三、四 D. 一、三、四
二、填空题(本大题共 15 小题,共 30.0 分)
杨浦区2013学年第二学期初二数学期终考试试卷最后两题
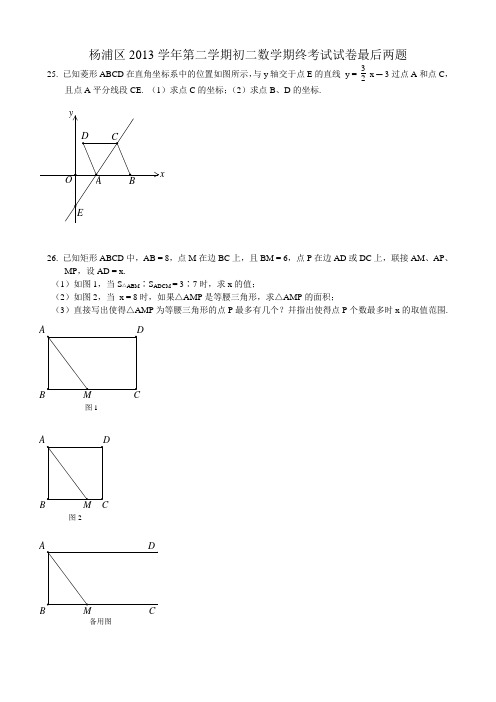
杨浦区2013学年第二学期初二数学期终考试试卷最后两题25. 已知菱形ABCD 在直角坐标系中的位置如图所示,与y 轴交于点E 的直线 y = 32x ─ 3过点A 和点C ,且点A 平分线段CE. (1)求点C 的坐标;(2)求点B 、D 的坐标.26. 已知矩形ABCD 中,AB = 8,点M 在边BC上,且BM = 6,点P 在边AD 或DC 上,联接AM 、AP 、 MP ,设AD = x.(1)如图1,当S △ABM ∶S ADCM = 3∶7时,求x 的值;(2)如图2,当 x = 8时,如果△AMP 是等腰三角形,求△AMP 的面积;(3)直接写出使得△AMP 为等腰三角形的点P 最多有几个?幷指出使得点P 个数最多时x 的取值范围.图1 图2 备用图初二:±⊥─∠°·∥2∣∣×÷.∵∴∶·•≌ a ≠0 <>≤≥△π 2 2 5 3 6 ①②③④⑤⑥⑦⑧⑨⑩αβγθ>22332553343415″′λ6(-8)218612 ─ 112 ─31a 2+1b 2(─8)23─3 18186mna3a 327 x1 , x 2 (1)23213─234314343554152535456516″′ y = k x ( k≠0 ) y =kx( k≠0 )x 41x ab m n→f ( x )△a b m n→f ( x )△一、选择题(本大题共4小题,每题3分,满分12分)二、简答题(本大题共4小题,每题6分,满分24分)三、解答题(本大题共3小题,每题8分,满分24分)四、综合题(本题满分12分)AD。
2020-2021学年上海市杨浦区初二数学第二学期期中数学试卷及解析

2020-2021学年上海市杨浦区初二数学第二学期期中数学试卷一、填空题(每题2分,共30分)1.(2分)一次函数23y x =--的截距是 . 2.(2分)已知一次函数(1)2y m x m =-+-,当m 时,y 随x 的增大而增大.3.(2分)将一次函数23y x =-的图象向上平移 个单位后,图象过原点.4.(2分)当m 取 时,关于x 的方程2mx m x +=无解.5.(2分)已知一次函数32y x k =+-的图象不经过第二象限,则k 的取值范围是 .6.(2分)已知一次函数(0)y kx b k =+≠的图象如图所示,那么关于x 的不等式0kx b +>的解集是 .7.(2分)分式方程2101x x -=-的解是 . 8.(2分)二项方程41802x -=的实数根是 . 9.(2分)如果关于x 的方程220x k -=无实数解,那么k 的取值范围是 .10.(2分)无理方程(4)30x x ++=的解是 .11.(2分)用换元法解分式方程221231x x x x -+=-,若设21x y x-=,则原方程可以化成关于y 的整式方程是 .12.(2分)某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x 套,则根据题意可得方程为 .13.(2分)如果一个正多边形的每个外角都是30︒,那么这个多边形的内角和为 .14.(2分)在平行四边形ABCD 中,AE 平分BAD ∠交直线BC 于点E ,:2:1BE EC =,且6AB =,那么这个四边形的周长是 .15.(2分)在ABCD 中,5AB =,7BC =,对角线AC 和BD 相交于点O ,如果将点A 绕着点O 顺时针旋转90︒后,点A 恰好落在平行四边形ABCD 的边AD 上,那么AC 的长是 .二、选择题(每题3分,共12分)16.(3分)以下函数中,属于一次函数的是( )A .2x y =-B .(y kx b k =+、b 为常数)C .(y c c =为常数)D .2y x = 17.(3分)下列方程中,在实数范围内有解的是( ) A .210x x -+= B .2120x -+= C .1455x x x -=-- D .220x x -+-=18.(3分)已知一次函数y kx k =-,若函数值y 随着自变量x 值的增大而增大,则该函数的图象经过( )A .第一、二、三象限B .第一、二、四象限C .第二、三、四象限D .第一、三、四象限 19.(3分)如图,已知直线:2MN y kx =+交x 轴负半轴于点A ,交y 轴于点B ,30BAO ∠=︒,点C 是x 轴上的一点,且2OC =,则MBC ∠的度数为( )A .75︒B .165︒C .75︒或45︒D .75︒或165︒三、简答题(每题6分,共30分)20.(6分)解方程:2231211x x x x-=--- 21.(63631x x ++.22.(6分)解方程组:2269423x xy y x y ⎧-+=⎨-=⎩①② 23.(6分)某地区为了进一步缓解交通拥堵问题,决定修建一条长8千米的公路.如果平均每天的修建费y (万元)与修建天数x (天)之间在50100x 时具有一次函数关系,如表所示:x (天) 6080 100 y (万元)45 40 35 (1)直接写出y 关于x 的函数解析式是 ;(2)后来在修建的过程中计划发生改变,政府决定多修3千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了21天,求原计划每天的修建费?24.(6分)如图,平行四边形ABCD中,2AD AB=,E为AD的中点,CE的延长线交BA的延长线于点F.(1)求证:FB AD=.(2)若70DAF∠=︒,求EBC∠的度数.四、解答题(每题8分,满分16分)25.(8分)现有一段20千米长,可供长跑爱好者跑步的笔直跑道MN,已知甲、乙两人都从M点出发,甲跑到途中的P点后原地休息了20分钟,之后继续跑到N点,共用时间2小时;乙虽然比甲晚出发半小时,但和甲同时到达N点.假设两人跑步时均为匀速,在甲出发后的2小时内两人离开M点的距离y(千米)与时间x(小时)的函数关系如图所示.请回答下列问题:(1)图中B点的坐标为(2)甲从点P跑到点N的速度为千米/时;(3)求图中线段CD的表达式.并写出定义域.26.(8分)如图,在平面直角坐标系中,直线2y x=与反比例函数kyx=在第一象限内的图象交于点(,2)A m,将直线2y x=向下平移后与反比例函数kyx=在第一象限内的图象交于点P,且POA∆的面积为2.(1)求k的值.(2)求平移后的直线的函数解析式.五、综合题(满分12分)27.(12分)如图,已知一次函数7y x=-+与正比例函数43y x=的图象交于点A,且与x轴交于点B.(1)求点A和点B的坐标;(2)过点A作AC y⊥轴于点C,过点B作直线//l y轴,动点P从点O出发,以每秒1个单位长的速度,沿O C A--的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒(0)t>.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是AP AQ=的等腰三角形?若存在,求t的值;若不存在,请说明理由.参考答案与试题解析一、填空题(每题2分,共30分)1.【解答】解:在一次函数23y x =--中, 3b =-,∴一次函数23y x =--在y 轴上的截距3b =-. 故答案是:3-.2.【解答】解:当10m ->时,y 随x 的增大而增大, 所以1m <.故答案为:1<.3.【解答】解:因为一次函数23y x =-的图象向上平移3个单位后2332y x x =-+=,图象过原点, 故答案为:3.4.【解答】解:移项得:2mx x m -=-,合并同类项得:(2)m x m -=-.关于x 的方程2mx m x +=无解,20m ∴-=.解得:2m =.故答案为:2.5.【解答】解:一次函数32y x k =+-的图象不经过第二象限, 则可能是经过一三象限或一三四象限,经过一三象限时,320k -=,解得23k =, 经过一三四象限时,320k -<.解得23k <故23k . 故答案为23k. 6.【解答】解:当不等式0kx b +>时,一次函数y kx b =+的图象在x 轴上方,故2x >. 故答案为:2x >.7.【解答】解:2101x x -=- 方程两边同乘以1x -得,210x -=则(1)(1)0x x +-=10x ∴+=或10x -=得,1x =-或1x =.检验:1x =-时,10x -≠;1x =时,10x -=,故1x =舍去. 故分式方程的根为:1x =-.故答案为:1x =-.8.【解答】解:41802x -=. ∴221()82x =. 24x ∴=(负值舍去). 2x ∴=±.故答案为:2x =±.9.【解答】解:20x k --=,即2k +无实根, 20k ∴+<,2k ∴<-.故答案为:2k <-.10.【解答】解:(4)0x +40x ∴+=或30x +=,解得4x =-,3x =-,当4x =-时,被开方数无意义;故方程的解为3x =-,故答案为:3x =-.11.【解答】解:21x y x -=, ∴2221x x y =-, 代入原方程得:23y y+=, 方程两边同乘以y 整理得:2320y y -+=. 故答案为:2320y y -+=.12.【解答】解:采用新技术前所用时间为:160x,采用新技术后所用时间为:400160(120%)x-+,∴所列方程为:16040016018(120%)x x-+=+.13.【解答】解:一个多边形的每个外角都是30︒,3603012n∴=︒÷︒=,则内角和为:(122)1801800-︒=︒.故答案为:1800︒.14.【解答】解:四边形ABCD是平行四边形,//AD BC∴,AEB DAE∴∠=∠,AE平分BAD∠,BAE DE∴∠=∠,BAE AEB∴∠=∠,6BE AB∴==,如图1,:2:1BE EC=,3EC∴=,9AD BC∴==,6AB CD==,∴这个四边形的周长是:969630+++=;如图2,:2:1BE EC=,3EC∴=,3AD BC∴==,6AB CD==,∴这个四边形的周长是:363618+++=;∴这个四边形的周长是:30或18.故答案为:30或18.15.【解答】解:如图,过O点作OE AD⊥于E,过C点作CF AD⊥于F,将点A绕着点O顺时针旋转90︒后,点A恰好落在平行四边形ABCD的边AD上,AOA∴∆'是等腰直角三角形,∴△AAC '是等腰直角三角形,设AA x '=,则CF x =,7DF x =-,在Rt CDF ∆中,222(7)5x x +-=,解得14x =,23x =,在Rt CFA ∆中,42AC =或32.故答案为:42或32.二、选择题(每题3分,共12分)16.【解答】解:A 、是一次函数,故A 正确; B 、0k =时,不是一次函数,故B 错误; C 、不含一次项,不是一次函数,故C 错误; D 、未知数x 的次数为1-,不是一次函数,故D 错误. 故选:A .17.【解答】解:A 、1a =,1b =-,1c =,△241430b ac =-=-=-<,方程无实数根,故A 不符合题意;B 、非负数与正数的和是正数,得2122x -,故B 错误;C 、方程两边都乘以(5)x -,得 41x -=,解得5x =,经检验:5x =不是分式方程的根,原分式方程的解,故C 不符合题意; D 220x x --=,得20x -且20x -,解得2x =,故D 符合题意,故选:D .18.【解答】解:一次函数y kx k =-,若函数值y 随着自变量x 值的增大而增大,k∴>,k∴-<,∴此函数的图象经过一、三、四象限.故选:D.19.【解答】解:由已知可得120MBO∠=︒.如图,分两种情况考虑:①当点C在x轴正半轴上时,145C BO∠=︒,11204575MBC∠=︒-︒=︒;②当点C在x轴负半轴上时,212045165MBC∠=︒+︒=︒.故选:D.三、简答题(每题6分,共30分)20.【解答】解:方程两边都乘以(1)(1)x x+-得:232(1)(1)(1)x x x x x-=+-++,23210x x--=,解得:11 3x=-,21x=,经检验:11 3x=-是原方程的解,21x=不是原方程的解,所以原方程的解为13x=-.21.【解答】解:36030xx+⎧⎨+⎩.2x∴-.3631x x++3631x x++.将方程两边平方可得:363123x x x+=++++31x x+=+.再两边平方可得:2321x x x +=++. 整理得:220x x +-=.解得:2x =-或1x =.经检验:当2x =-,左边为1-,右边为1,则左边≠右边, 2x ∴=-不是无理方程的解,当1x =时,左边=右边1=,1x ∴=是无理方程的解.22.【解答】解:由①,得2(3)4x y -=, 32x y ∴-=±,∴原方程组可转化为:3223x y x y -=⎧⎨-=⎩或3223x y x y -=-⎧⎨-=⎩解得1151x y =⎧⎨=⎩或22135x y =⎧⎨=⎩ 所以原方程组的解为:1151x y =⎧⎨=⎩或22135x y =⎧⎨=⎩ 23.【解答】解:(1)设y 关于x 的函数解析式为(0)y kx b k =+≠, 图象过点(60,45),(80,40),∴60458040k b k b +=⎧⎨+=⎩, 解得1460k b ⎧=-⎪⎨⎪=⎩,y ∴关于x 的函数解析式为1604y x =-+. 故答案为:1604y x =-+; (2)设原计划修完这条路需要m 天, 根据题意得81121m m =+, 解得56m =,经检验56m =是原方程的根,50100m ,15660464y ∴=-⨯+=(万元), 答:原计划每天的修建费是46万元.24.【解答】(1)证明E 为AD 的中点,DE AE ∴=,四边形ABCD 是平行四边形,//AB CD ∴,AB DC =,EDC EAF ∴∠=∠,在DEC ∆和AEF ∆中,DEC AEF DE AE EDC EAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,()DEC AEF ASA ∴∆≅∆,DC FA ∴=,2AD AB =,AB DE EA FA ∴===,FB AD ∴=;(2)解:四边形ABCD 是平行四边形,//DA CB ∴,70CBF DAF ∴∠=∠=︒,AEB EBC ∠=∠,又AE AB =,AEB ABE ∴∠=∠,35EBC ABE ∴∠=∠=︒.四、解答题(每题8分,满分16分)25.【解答】解:(1)由题意可得,点B 的横坐标为:2041603+=,纵坐标为:15, ∴点B 的坐标为4(3,15), 故答案为:4(3,15); (2)甲从点P 跑到点N 的速度为:20157.5423-=-千米/时, 故答案为:7.5;(3)由题意可得,点D 的坐标为(0.5,0),点C 的坐标为(2,20), 设线段CD 的函数函数表达式为y kx b =+,0.50220k b k b +=⎧⎨+=⎩,得403203k b ⎧=⎪⎪⎨⎪=-⎪⎩, 即线段CD 的表达式是4020(0.52)33y x x =-. 26.【解答】解:(1)点(,2)A m 在直线2y x =, 22m ∴=,1m ∴=,∴点(1,2)A ,点(1,2)A 在反比例函数k y x=上, 2k ∴=, (2)方法一、如图,设平移后的直线与y 轴相交于B ,过点P 作PM OA ⊥,BN OA ⊥,AC y ⊥轴 由(1)知,(1,2)A ,5OA ∴5sin sin AC BON AOC OA ∠=∠= 115222POA S OA PM PM ∆=⨯==, 45PM ∴= PM OA ⊥,BN OA ⊥,//PM BN ∴,//PB OA ,∴四边形BPMN 是平行四边形,45BN PM ∴==5sin BN BON OB OB ∠==, 4OB ∴=,//PB AO ,(0,4)B ∴-,∴平移后的直线PB 的函数解析式24y x =-, 方法二、如图1,过点P 作PC y ⊥轴交OA 于C ,设点P 的坐标为(n ,2)(1)n n>, 1(C n ∴,2)n, 1PC n n∴=-, POA ∆的面积为2.(1,2)APOA PCO PCA S S S ∆∆∆∴=+112112()()(2)22n n n n n n=-⨯+-- 11()22n n=-⨯ 1n n=- 2=,1n ∴=)或1n =+(1P ∴+2),//PB AO ∴,∴设直线PB 的解析式为2y x b =+,点P 在直线PB 上,22(1b ∴=++,4b ∴=-,∴平移后的直线PB 的函数解析式24y x =-,方法三,过点A 作AM x ⊥轴于M ,过点P 作PN x ⊥轴于N , 点A ,P 是反比例函数2y x=图象上, AOM PON S S ∆∆∴=, 2AOP AMNP S S ∆∴==梯形,(1,2)A ,2AM ∴=,1OM =, 设点2(,)P m m,(1)m > ON m ∴=,2PN m=, 1MN m ∴=-,()()11221222AMNP S PN AM MN m m ⎛⎫∴=+⨯=+⨯-= ⎪⎝⎭梯形, 12m ∴=(舍)或12m =,(12P ∴+222),//PB AO ∴,∴设直线PB 的解析式为2y x b =+,点P 在直线PB 上,2222(12)b ∴=++,4b ∴=-,∴平移后的直线PB 的函数解析式24y x =-,五、综合题(满分12分)27.【解答】解:(1)已知一次函数7y x =-+与正比例函数43y x =的图象交于点A ,且与x 轴交于点B ,(7,0)B ∴,(3,4)A , (2)①当04t <<时,PO t =,4PC t =-,BR T =,7OR t =-, 过A 作AM x ⊥轴于点M ,以A 、P 、R 为顶点的三角形的面积为8,8ACP POR ARB ACOB S S S S ∆∆∆∴---=梯形, ∴1111(37)43(4)(7)482222t t t t +⨯-⨯⨯--⨯⨯--⨯=, 28120t t ∴-+=,解得12t =,26t =(舍),当47t 时,12(7)82S APR AP OC t ∴∆=⨯⨯=-=, 3t ∴=(舍),∴当2t =时,以A 、P 、R 为顶点的三角形的面积为8. ②存在,当04t <时,直线l 与AB 相交于Q ,直线AB 与y 轴交于点N , NO OB =,45OBN ONB ∴∠=∠=︒,直线//l y 轴,RQ RB t ∴==,4AM BM ==,2QB t ∴=,422AQ t =,RB OP QR t ===,//PQ OR ∴,7PQ OR t ==-,AP AQ =,723t ∴-=⨯,1t ∴=,当47t 时,若AP AQ =, 575(7)3t t ∴-=--, 418t ∴=. 1t ∴=或418t =,以A 、P 、Q 为顶点的三角形是AP AQ =的等腰三角形.。
上海杨浦区复旦大学第二附属学校2020-2021学年八年级下学期期中考试数学试题(解析版)

多边形的内角和是: .
故选:B.
【点睛】本题考查了多边形的内角和与外角和公式,熟练掌握公式是解题的关键.
4.下列关于x的方程一定有实数解的是( )
A. B.
C. D.
【4题答案】
【答案】A
【解析】
【分析】根据一元二次方程根的判别式、二次根式有意义的条件、分式方程的增根逐一判断即可得.
2.下列说法正确的是().
A. 是分式方程B. 是无理方程
C. 是二元二次方程组D. 是二项方程
【2题答案】
【答案】C
【解析】
【分析】根据分式方程、无理方程、二元二次方程组、二项方程的定义,即可一一判定.
【详解】解:A选项: 是一元一次方程,故错误;
B选项: 是分式方程,故错误;
C选项: 是二元二次方程组,故正确;
2020~2021学年上海杨浦区复旦大学第二附属学校
一、选择题
1.下列函数中, 是 的一次函数的有().
① ;② ;③ ;④ ;⑤ .
A.1个B.2个C.3个D.4个
【1题答案】
【答案】B
【解析】
【分析】根据一次函数 定义逐一判断即可求解.
【详解】解:① 的次数是1, 是 的一次函数,所以本选项符合题意,故①正确;
【10题答案】
【答案】
【解析】
【分析】根据一元二次方程的解法即可求出答案.
【详解】解:∵
∴ 或 (舍去)
∴
故答案为: .
【点睛】本题考查高次方程的解法,解题的关键是熟练运用一元二次方程的解法,本题属于基础题型.
11.如果 是方程 的一个解,那么 ______.
【11题答案】
【答案】
2020-2021下海杨浦初级中学八年级数学下期中模拟试卷(含答案)
2020-2021下海杨浦初级中学八年级数学下期中模拟试卷(含答案)一、选择题1.下列运算中,正确的是( )A .235+=;B .2(32)32-=-;C .2a a =;D .2()a b a b +=+.2.如右图,点A 的坐标为(0,1),点B 是x 轴正半轴上的一动点,以AB 为边作等腰直角△ABC ,使∠BAC=90°,如果点B 的横坐标为x ,点C 的纵坐标为y ,那么表示y 与x 的函数关系的图像大致是( )A .B .C .D .3.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB BC =时,它是菱形B .当AC BD ⊥时,它是菱形 C .当90ABC ︒∠=时,它是矩形D .当AC BD =时,它是正方形 4.下列结论中,矩形具有而菱形不一定具有的性质是( )A .内角和为360°B .对角线互相平分C .对角线相等D .对角线互相垂直 5.如图,将长方形纸片ABCD 折叠,使边DC 落在对角线AC 上,折痕为,CE 且D 点落在对角线'D 处.若3,4,AB AD ==则ED 的长为( )A .32B .3C .1D .436.函数y =11x x +-中,自变量x 的取值范围是( ) A .x >-1B .x >-1且x ≠1C .x ≥一1D .x ≥-1且x ≠1 7.若一次函数y =(k -3)x -k 的图象经过第二、三、四象限,则k 的取值范围是( )A .k <3B .k <0C .k >3D .0<k <3 8.如图,函数y=2x 和y=ax+4的图象相交于A(m ,3),则不等式2x ax+4<的解集为( )A .3x 2>B .x 3>C .3x 2<D .x 3<9.如图,矩形纸片ABCD ,3AB =,点E 在BC 上,且AE EC =.若将纸片沿AE 折叠,点B 恰好落在AC 上,则矩形ABCD 的面积是( )A .12B .63C .93D .1510.《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x 尺,根据题意,可列方程为 ( )A .82﹢x 2 = (x ﹣3)2B .82﹢(x +3)2= x 2C .82﹢(x ﹣3)2= x 2D .x 2﹢(x ﹣3)2= 8211.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y (米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了32分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米其中正确的结论有( )A .1个B .2个C .3个D .4个12.如图,点E F G H 、、、分别是四边形ABCD 边AB 、BC 、CD 、DA 的中点.则下列说法:①若AC BD =,则四边形EFGH 为矩形;②若AC BD ⊥,则四边形EFGH 为菱形;③若四边形EFGH 是平行四边形,则AC 与BD 互相平分;④若四边形EFGH 是正方形,则AC 与BD 互相垂直且相等.其中正确的个数是( )A .1B .2C .3D .4二、填空题13.若由你选择一个喜欢的数值m ,使一次函数()2y m x m =-+的图象经过第一、二、四象限,则m 的值可以是___________.14.如图所示的网格是正方形网格,则BAC DAE ∠-∠=__________︒(点A ,B ,C ,D ,E 是网格线交点).15.如图,在矩形ABCD 中,AD=9cm ,AB=3cm ,将其折叠,使点D 与点B 重合,则重叠部分(△BEF)的面积为_________cm 2.16.将函数31y x =+的图象平移,使它经过点()1,1,则平移后的函数表达式是____.17.甲、乙两人分别从A ,B 两地相向而行,匀速行进甲先出发且先到达B 地,他们之间的距离s(km)与甲出发的时间t(h)的关系如图所示,则乙由B 地到A 地用了______h .18.化简()213-=_____________;19.如图,ABC V 是以AB 为斜边的直角三角形,4AC =,3BC =,P 为AB 上一动点,且PE AC ⊥于E ,PF BC ⊥于F ,则线段EF 长度的最小值是________.20.如图,已知函数y ax b =+和y kx =的图象交于点P, 则根据图象可得,关于y ax b y kx =+⎧⎨=⎩的二元一次方程组的解是_____________。
杨浦八年级数学试卷

一、选择题(每题4分,共20分)1. 下列各数中,有理数是()A. √9B. √-16C. πD. 0.1010010001…(无限循环小数)2. 已知 a > b > 0,则下列不等式中正确的是()A. a^2 > b^2B. a^3 > b^3C. a^4 > b^4D. a^5 > b^53. 若一个三角形的三边长分别为3,4,5,则该三角形是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 梯形4. 下列函数中,有最小值的是()A. y = x^2 + 2x + 1B. y = x^2 - 2x + 1C. y = -x^2 + 2x - 1D. y = x^2 - 4x + 45. 下列各数中,绝对值最大的是()A. -3B. -2C. 1D. 0二、填空题(每题4分,共20分)6. 已知 a + b = 5,ab = 6,则 a^2 + b^2 的值为______。
7. 一个等腰三角形的底边长为8,腰长为10,则该三角形的面积为______。
8. 若函数 y = kx + b(k≠0)的图像经过点(1,2),则该函数的解析式为______。
9. 在平面直角坐标系中,点A(-2,3)关于原点的对称点为______。
10. 已知等差数列{an}的前三项分别为2,5,8,则该数列的公差为______。
三、解答题(每题10分,共30分)11. 解方程:2x - 3(x - 1) = 5。
12. 已知一个等腰三角形的底边长为10,腰长为8,求该三角形的周长。
13. 已知一次函数 y = kx + b(k≠0)的图像经过点(-1,3),且与y轴的交点为(0,-2),求该函数的解析式。
四、证明题(每题10分,共20分)14. 已知等腰三角形ABC中,AB = AC,AD为底边BC上的高,求证:BD = DC。
15. 已知等差数列{an}中,a1 = 3,d = 2,求证:an + an+1 = 2a1 + (n-1)d。
2020-2021学年上海市杨浦区八年级(下)期中数学试卷(附答案详解)

2020-2021学年上海市杨浦区八年级(下)期中数学试卷1.一次函数y=−2x−3的截距是______ .2.已知一次函数y=(1−m)x+m−2,当m______时,y随x的增大而增大.3.将一次函数y=2x−3的图象向上平移______ 个单位后,图象过原点.4.当m取______ 时,关于x的方程mx+m=2x无解.5.已知一次函数y=x+3k−2的图象不经过第二象限,则k的取值范围是______ .6.已知一次函数y=kx+b(k≠0)的图象如图所示,那么关于x的不等式kx+b>0的解集是______ .7.分式方程x2−1x−1=0的解是______.8.二项方程12x4−8=0的实数根是______ .9.如果关于x的方程2−√x−2+k=0无实数解,那么k的取值范围是______ .10.无理方程(x+4)⋅√x+3=0的解是______ .11.用换元法解分式方程x−1x2+2x2x−1=3,若设y=x−1x2,则原方程可以化成关于y的整式方程是______ .12.某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x套,则根据题意可得方程为______ .13.如果一个正多边形的每个外角都是30°,那么这个多边形的内角和为______.14.在平行四边形ABCD中,AE平分∠BAD交直线BC于点E,BE:EC=2:1,且AB=6,那么这个四边形的周长是______ .15.在▱ABCD中,AB=5,BC=7,对角线AC和BD相交于点O,如果将点A绕着点O顺时针旋转90°后,点A恰好落在平行四边形ABCD的边AD上,那么AC的长是______ .16.以下函数中,属于一次函数的是()A. y=−x2B. y=kx+b(k、b为常数)C. y=c(c为常数)D. y=2x17.下列方程中,在实数范围内有解的是()A. x2−x+1=0B. √2x−1+2=0C. 1x−5=x−4x−5D. √x−2+√2−x=018.已知一次函数y=kx−k若函数值y随着自变量x值的增大而增大,则该函数的图象经过()A. 第一、二、三象限B. 第一、二、四象限C. 第二、三、四象限D. 第一、三、四象限19.如图,已知直线MN:y=kx+2交x轴负半轴于点A,交y轴于点B,∠BAO=30°,点C是x轴上的一点,且OC=2,则∠MBC的度数为()A. 75°B. 165°C. 75°或45°D. 75°或165°20.解方程:3x−x2x2−1=2−11−x21.解方程:√3x+6−√x+3=1.22. 解方程组:{x 2−6xy +9y 2=4 ①x −2y =3 ②23. 某地区为了进一步缓解交通拥堵问题,决定修建一条长8千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在50≤x ≤100时具有一次函数关系,如表所示: x(天) 60 80 100 y(万元)454035(1)直接写出y 关于x 的函数解析式是______ ;(2)后来在修建的过程中计划发生改变,政府决定多修3千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了21天,求原计划每天的修建费?24. 如图,平行四边形ABCD 中,AD =2AB ,E 为AD 的中点,CE 的延长线交BA 的延长线于点F . (1)求证:FB =AD .(2)若∠DAF =70°,求∠EBC 的度数.25.现有一段20千米长,可供长跑爱好者跑步的笔直跑道MN,已知甲、乙两人都从M点出发,甲跑到途中的P点后原地休息了20分钟,之后继续跑到N点,共用时间2小时;乙虽然比甲晚出发半小时,但和甲同时到达N点.假设两人跑步时均为匀速,在甲出发后的2小时内两人离开M点的距离y(千米)与时间x(小时)的函数关系如图所示.请回答下列问题:(1)图中B点的坐标为______(2)甲从点P跑到点N的速度为______ 千米/时;(3)求图中线段CD的表达式.并写出定义域.26.如图,在平面直角坐标系中,直线y=2x与反比例函数y=kx在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=k在第一象限内的图象交于点P,且△POA的面积为2.x(1)求k的值.(2)求平移后的直线的函数解析式.x的图象交于点A,且与x轴交27.如图,已知一次函数y=−x+7与正比例函数y=43于点B.(1)求点A和点B的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l//y轴,动点P从点O出发,以每秒1个单位长的速度,沿O−C−A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒(t>0).①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是AP=AQ的等腰三角形?若存在,求t的值;若不存在,请说明理由.答案和解析1.【答案】−3【解析】解:∵在一次函数y=−2x−3中,b=−3,∴一次函数y=−2x−3在y轴上的截距b=−3.故答案是:−3.一次函数y=kx+b在y轴上的截距是b.本题考查了一次函数图象上点的坐标特征.一次函数图象上的点的坐标,一定满足该函数的关系式.2.【答案】<1【解析】解:当1−m>0时,y随x的增大而增大,所以m<1.故答案为:<1.根据一次函数的性质得1−m>0,然后解不等式即可.本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降;当b>0时,直线与y轴交于正半轴;当b<0时,直线与y轴交于负半轴.3.【答案】3【解析】解:因为一次函数y=2x−3的图象向上平移3个单位后y=2x−3+3=2x,图象过原点,故答案为:3.根据直线y=kx+b向上平移m(m>0)个单位所得直线解析式为y=kx+b+m求解.本题考查了一次函数图象与几何变换:直线y=kx+b向上平移m(m>0)个单位所得直线解析式为y=kx+b+m,直线y=kx+b向下平移m(m>0)个单位所得直线解析式为y=kx+b−m.4.【答案】2【解析】解:移项得:mx−2x=−m,合并同类项得:(m−2)x=−m.∵关于x的方程mx+m=2x无解,∴m−2=0.解得:m=2.故答案为:2.先移项、合并同类项,最后再依据未知数的系数为0求解即可.本题主要考查的是一元一次方程的解,掌握方程无解的条件是解题的关键.5.【答案】k≤23【解析】解:一次函数y=x+3k−2的图象不经过第二象限,则可能是经过一三象限或一三四象限,,经过一三象限时,3k−2=0,解得k=23经过一三四象限时,3k−2<0.解得k<23.故k≤23故答案为k≤2.3根据图象在坐标平面内的位置关系确定k的取值范围,从而求解.本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.6.【答案】x>2【解析】解:当不等式kx+b>0时,一次函数y=kx+b的图象在x轴上方,故x>2.故答案为:x>2.一次函数y=kx+b的图象在x轴上方时,y>0,再根据图象写出解集即可.此题主要考查了一次函数与一元一次不等式的关系,关键是能正确利用数形结合的方法解决问题.7.【答案】x=−1【解析】【分析】根据分式方程,可以先去分母变为整式方程进行解答,解出整式方程的根注意要进行检验.本题考查解答分式方程,解题的关键是解出方程的根要检验.【解答】=0解:x2−1x−1方程两边同乘以x−1得,x2−1=0则(x+1)(x−1)=0∴x+1=0或x−1=0得,x=−1或x=1.检验:x=−1时,x−1≠0;x=1时,x−1=0,故x=1舍去.故分式方程的根为:x=−1.故答案为:x=−1.8.【答案】x=±2x4−8=0.【解析】解:12(x2)2=8.∴12∴x2=4(负值舍去).∴x=±2.故答案为:x=±2.先求x2的解,再求实数根即可.本题考查高次方程的解法,关键在于降次,利用开平方即可降次是关键.9.【答案】k<−2【解析】解:∵2−√x−2+k=0,即2+k=√x−2无实根,∴k+2<0,∴k<−2.故答案为:k<−2.根据题意,可得k+2<0,据此可得答案.此题考查的是一元一次方程的根,掌握二次根式的性质是解决此题关键.10.【答案】x=−3【解析】解:∵(x+4)⋅√x+3=0∴x+4=0或x+3=0,解得x=−4,x=−3,当x=−4时,被开方数无意义;故方程的解为x=−3,故答案为:x=−3.根据ab=0,得a=0或b=0,注意被二次根式开方数大于等于0.本题考查了无理方程,应注意被二次根式开方数大于等于0.11.【答案】y2−3y+2=0【解析】解:∵y=x−1x2,∴2x2x−1=2y,代入原方程得:y+2y=3,方程两边同乘以y整理得:y2−3y+2=0.故答案为:y2−3y+2=0.观察方程的两个分式具备的关系,若设y=x−1x2,则原方程另一个分式为2×1y.可用换元法转化为关于y的分式方程.去分母即可.此题主要考查换元法解分式方程,当分式方程比较复杂时,通常采用换元法使分式方程简化.12.【答案】160x +240(1+20%)⋅x=18【解析】【分析】关键描述语为:“共用了18天完成任务”,那么等量关系为:采用新技术前所用时间+采用新技术后所用时间=18天.找出题目中的关键语,找到相应的等量关系是解决问题的关键.注意工作时间=工作总量÷工作效率.【解答】解:采用新技术前所用时间为:160x ,采用新技术后所用时间为:400−160(1+20%)x , ∴所列方程为:160x +400−160(1+20%)x =18.13.【答案】1800°【解析】解:∵一个多边形的每个外角都是30°,∴n =360°÷30°=12,则内角和为:(12−2)⋅180°=1800°.故答案为:1800°.根据正多边形的性质,边数等于360°除以每一个外角的度数,然后利用多边形的内角和公式计算内角和即可.本题主要考查了利用外角求正多边形的边数的方法以及多边形的内角和公式,解题的关键是掌握任意多边形的外角和都等于360度.14.【答案】30或18【解析】解:∵四边形ABCD 是平行四边形,∴AD//BC ,∴∠AEB =∠DAE ,∵AE 平分∠BAD ,∴∠BAE =∠DE ,∴∠BAE =∠AEB ,∴BE =AB =6,如图1,∵BE :EC =2:1,∴EC =3,∴AD =BC =9,AB =CD =6,∴这个四边形的周长是:9+6+9+6=30;如图2,∵BE :EC =2:1,∴EC =3,∴AD =BC =3,AB =CD =6,∴这个四边形的周长是:3+6+3+6=18;∴这个四边形的周长是:30或18.故答案为:30或18.首先根据题意作图,由AE平分∠BAD交直线BC于点E,可知点E在边BC上或者在其延长线上;分别求解即可求得答案.此题考查了平行四边形的性质、等腰三角形的判定与性质以及角平分线的定义.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.15.【答案】4√2或3√2【解析】解:如图,过O点作OE⊥AD于E,过C点作CF⊥AD于F,∵将点A绕着点O顺时针旋转90°后,点A恰好落在平行四边形ABCD的边AD上,∴△AOA′是等腰直角三角形,∴△AA′C是等腰直角三角形,设AA′=x,则CF=x,DF=7−x,在Rt△CDF中,x2+(7−x)2=52,解得x1=4,x2=3,在Rt△CFA中,AC=4√2或3√2.故答案为:4√2或3√2.如图,过O点作OE⊥AD于E,过C点作CF⊥AD于F,根据旋转的性质可得△AOA′是等腰直角三角形,△AA′C是等腰直角三角形,再根据勾股定理可求AA′,再根据等腰直角三角形的性质即可求解.考查了旋转的性质,平行四边形的性质,以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握旋转前后图形的对应关系,注意掌握数形结合思想的应用.16.【答案】A【解析】【分析】本题主要考查的是一次函数的定义,掌握一次函数的定义是解题的关键.根据一次函数的定义回答即可.【解答】解:A、是一次函数,故A正确;B、k=0时,不是一次函数,故B错误;C、不含一次项,不是一次函数,故C错误;D、自变量x的次数不为1,不是一次函数,故D错误.故选A.17.【答案】D【解析】解:A、a=1,b=−1,c=1,△=b2−4ac=1−4=−3<0,方程无实数根,故A不符合题意;B、非负数与正数的和是正数,得√2x−1+2≥2,故B错误;C、方程两边都乘以(x−5),得x−4=1,解得x=5,经检验:x=5不是分式方程的根,原分式方程的解,故C不符合题意;D、由√x−2+√2−x=0,得x−2≥0且2−x≥0,解得x=2,故D符合题意,故选:D.根据根的判别式,可判断A;根据非负数与正数的和是正数,可判断B;根据解分式方程,可判断C;根据被开方数是非负数,可判断D.本题考查了无理方程,利用了一元二次方程根的判别式,无理方程的被开方数是非负数,注意分式方程要检验.18.【答案】D【解析】【分析】本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,k>0,b<0时,函数的图象在一、三、四象限.先根据一次函数的增减性判断出k的符号,再根据一次函数的性质进行解答即可.【解答】解:∵一次函数y=kx−k,若函数值y随着自变量x值的增大而增大,∴k>0,∴−k<0,∴此函数的图象经过一、三、四象限.故选D.19.【答案】D【解析】【分析】本题考查了一次函数与坐标轴的交点,等腰直角三角形以及分类讨论思想.分两种情况考虑:①C点在x轴正半轴;②C点在x轴负半轴.分别计算出∠MBO、∠OBC 度数,两个角的和差即为所求度数.【解答】解:由已知可得B(0,2),∠MBO=120°.如图,分两种情况考虑:①当点C在x轴正半轴上时,∵OC1=OB=2,∠BOC1=90°,故∠C1BO=45°,∠MBC1=120°−45°=75°;②当点C在x轴负半轴上时,∠MBC2=120°+45°=165°.故选:D.20.【答案】解:方程两边都乘以(x+1)(x−1)得:3x−x2=2(x+1)(x−1)+(x+1),3x2−2x−1=0,,x2=1,解得:x1=−13是原方程的解,x2=1不是原方程的解,经检验:x1=−13所以原方程的解为x =−13.【解析】先把分式方程转化成整式方程,求出方程的解,再进行检验即可. 本题考查了解分式方程,能把分式方程转化成整式方程是解此题的关键.21.【答案】解:∵{3x +6≥0x +3≥0. ∴x ≥−2. 将√3x +6−√x +3=1变形,得:√3x +6=√x +3+1.将方程两边平方可得:3x +6=x +3+1+2√x +3.即:√x +3=x +1. 再两边平方可得:x +3=x 2+2x +1.整理得:x 2+x −2=0.解得:x =−2或x =1.经检验:x =−2或x =1是无理方程的解.【解析】先求出x 的取值范围,再根据等式的性质即可求解.本题考查无理方程的解法,关键在于平分可去根号是关键,同时考虑无理方程有意义.别忘记了最后要检验.22.【答案】解:由①,得(x −3y)2=4,∴x −3y =±2,∴原方程组可转化为:{x −3y =2x −2y =3或{x −3y =−2x −2y =3解得{x 1=5y 1=1或{x 2=13y 2=5所以原方程组的解为:{x 1=5y 1=1或{x 2=13y 2=5【解析】把组中的二次方程因式分解,变形为两个一次方程后和组中的第二个方程组成新的方程组,求解即可.本题考查了高次方程的解法,解决本题的关键是把二次方程转化为两个一次方程,组成新的方程组.23.【答案】y =−14x +60【解析】解:(1)设y 关于x 的函数解析式为y =kx +b(k ≠0),∵图象过点(60,45),(80,40),∴{60k +b =4580k +b =40, 解得{k =−14b =60,∴y 关于x 的函数解析式为y =−14x +60.故答案为:y =−14x +60;(2)设原计划修完这条路需要m 天,根据题意得8m =11m+21,解得m =56,经检验m =56是原方程的根,∵50≤m ≤100,∴y =−14×56+60=46(万元), 答:原计划每天的修建费是46万元.(1)根据题意设出函数解析式,由表格中的数据可以求得函数的解析式;(2)根据题意可以列出相应的方程,求出原计划修路用的天数,从而可以求得原计划每天修建的费用.本题考查一次函数的应用,解题的关键是明确题意,利用待定系数法求出y 关于x 的函数解析式.24.【答案】(1)证明∵E 为AD 的中点,∴DE =AE ,∵四边形ABCD 是平行四边形,∴AB//CD ,AB =DC ,∴∠EDC =∠EAF ,在△DEC 和△AEF 中,{∠DEC =∠AEFDE =AE ∠EDC =∠EAF,∴△DEC≌△AEF(AAS),∴DC =FA ,∵AD =2AB ,∴AB =DE =EA =FA ,∴FB =AD ;(2)解:∵四边形ABCD 是平行四边形,∴DA//CB ,∴∠CBF =∠DAF =70°,∠AEB =∠EBC ,又∵AE =AB ,∴∠AEB =∠ABE ,∴∠EBC =∠ABE =35°.【解析】(1)证△DEC≌△AEF(AAS),得出DC =FA ,进而得出结论;(2)由平行四边形的对边平行证出∠CBF =∠DAF =70°,∠AEB =∠EBC ,由等腰三角形的性质得出∠AEB =∠ABE ,即可得出答案.本题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握平行四边形的性质和等腰三角形的性质,证明三角形全等是解题的关键. 25.【答案】(43,15) 7.5【解析】解:(1)由题意可得,点B 的横坐标为:1+2060=43,纵坐标为:15,∴点B 的坐标为(43,15),故答案为:(43,15);(2)甲从点P 跑到点N 的速度为:20−152−43=7.5千米/时, 故答案为:7.5;(3)由题意可得,点D 的坐标为(0.5,0),点C 的坐标为(2,20),设线段CD 的函数函数表达式为y =kx +b ,{0.5k +b =02k +b =20,得{k =403b =−203, 即线段CD 的表达式是y =403x −203(0.5≤x ≤2).(1)根据题意可以写出点B 的坐标,本题得以解决;(2)根据函数图象中的数据可以求得甲从点P 跑到点N 的速度;(3)根据题意和函数图象中的数据可以写出点D 和点C 的坐标,从而可得到线段CD 的表达式,并写出定义域.本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.26.【答案】解:(1)∵点A(m,2)在直线y =2x ,∴2=2m,∴m=1,∴点A(1,2),∵点A(1,2)在反比例函数y=kx上,∴k=2,(2)方法一、如图,设平移后的直线与y轴相交于B,过点P作PM⊥OA,BN⊥OA,AC⊥y轴由(1)知,A(1,2),∴OA=√5,sin∠BON=sin∠AOC=ACOA =√55,∵S△POA=12OA×PM=12×√5PM=2,∴PM=4√55,∵PM⊥OA,BN⊥OA,∴PM//BN,∵PB//OA,∴四边形BPMN是平行四边形,∴BN=PM=4√55,∵sin∠BON=BNOB =4√55OB=√55,∴OB=4,∵PB//AO,∴B(0,−4),∴平移后的直线PB的函数解析式y=2x−4,方法二、如图1,过点P作PC⊥y轴交OA于C,设点P的坐标为(n,2n)(n>1),∴C(1n ,2n),∴PC=n−1n,∵△POA的面积为2.A(1,2)∴S△POA=S△PCO+S△PCA=12(n−1n)×2n+12(n−1n)(2−2n)=12(n−1n)×2=n−1 n=2,∴n=1−√2(舍)或n=1+√2,∴P(1+√2,2√2−2)∴PB//AO,∴设直线PB的解析式为y=2x+b,∵点P在直线PB上,∴2√2−2=2(1+√2)+b,∴b=−4,∴平移后的直线PB的函数解析式y=2x−4,方法3,过点A作AM⊥x轴于M,过点P作PN⊥x轴于N,∵点A,P是反比例函数y=2x图象上,∴S△AOM=S△PON,∴S△AOP=S梯形AMNP=2,∵A(1,2),∴AM=2,OM=1,设点P(m,2m),(m>1)∴ON=m,PN=2m,∴MN=m−1,∴S梯形AMNP =12(PN+AM)×MN=12(2m+2)×(m−1)=2,∴m=1−√2(舍)或m=1+√2,∴P(1+√2,2√2−2)∴PB//AO,∴设直线PB的解析式为y=2x+b,∵点P在直线PB上,∴2√2−2=2(1+√2)+b,∴b=−4,∴平移后的直线PB的函数解析式y=2x−4,【解析】(1)由点A的纵坐标求得m,即点A的坐标,把点A的坐标代入反比例函数中即可;(2)方法一、先求出PM,再求出BN然后用锐角三角函数求出OB,即可.方法二、先设出点P的坐标,利用△POA的面积为2.建立方程求出点P的坐标,即可得出结论.方法3,先判断出S△AOP=S梯形AMNP,再同方法二,即可得出结论.此题是反比例函数和一次函数的交点问题,主要考查了函数解析式的确定方法,平行四边形的判定和性质,锐角三角函数的意义,解本题的关键是作出辅助线.27.【答案】解:(1)∵已知一次函数y=−x+7与正比例函数y=43x的图象交于点A,且与x轴交于点B,∴B(7,0),A(3,4),(2)①当0<t<4时,PO=t,PC=4−t,BR=T,OR=7−t,过A作AM⊥x轴于点M,∵以A、P、R为顶点的三角形的面积为8,∴S梯形ACOB−S△ACP−S△POR−S△ARB=8,∴12(3+7)×4−12×3×(4−t)−12×t×(7−t)−12×4t=8,∴t2−8t+12=0,解得t1=2,t2=6(舍),当4≤t≤7时,∴S△APR=12×AP×OC=2(7−t)=8,∴t=3(舍),∴当t=2时,以A、P、R为顶点的三角形的面积为8.②存在,当0<t≤4时,直线l与AB相交于Q,直线AB与y轴交于点N,∵NO=OB,∴∠OBN=∠ONB=45°,∵直线l//y轴,∴RQ=RB=t,AM=BM=4,∴QB=√2t,AQ=4√2−√2t,∵RB=OP=QR=t,∴PQ//OR,PQ=OR=7−t,∵AP=AQ,∴7−t=2×3,∴t=1,当4≤t≤7时,若AP=AQ,∴7−t=5−5(7−t),3∴t=41.8∴t=1或t=41,以A、P、Q为顶点的三角形是AP=AQ的等腰三角形.8【解析】(1)利用图象与坐标轴交点求法直接得出;(2)①利用S梯形ACOB−S△ACP−S△POR−S△ARB=8,表示出各个面积,解方程即可;②根据P的位置进行分类讨论,分别解方程.此题考查了一次函数与坐标轴交点求法以及三角形面积的求法和等腰三角形的性质等知识,综合性较强,利用图象表示出各部分长度是解题的关键.。
2021-2022学年上海市杨浦区国和中学八年级(下)期中数学试卷

2021-2022学年上海市杨浦区国和中学八年级(下)期中数学试卷一、选择题(本大题共6题,每题3分,满分18分)1.(3分)以下函数中,属于一次函数的是( )A .y =x 2B .y =2xC .y =c (c 为常数)D .y =kx +b (k 、b 为常数)2.(3分)一个多边形的内角和不可能是( )A .1800°B .540°C .720°D .810° 3.(3分)用换元法解分式方程x−1x −3x x−1+1=0时,如果设x−1x =y ,将原方程化为关于y 的整式方程,那么这个整式方程是( )A .y 2+y ﹣3=0B .y 2﹣3y +1=0C .3y 2﹣y +1=0D .3y 2﹣y ﹣1=04.(3分)下列方程中,有实数根的是( )A .x 2﹣x +2=0B .x 4﹣1=0C .√x −2=−1D .x x−1=1x−15.(3分)下列事件是必然事件的是( )A .疫情期间参加聚会会感染新冠病毒B .抛掷一枚硬币,落地后正面朝上C .打开的电视机正在播放新闻D .13个同学中至少有两个同学同一个月生日6.(3分)下列条件不能判定一个四边形是矩形的是( )A .四个内角都相等B .四条边都相等C .对角线相等且互相平分D .对角线相等的平行四边形二、填空题(本大题共12题,每题2分,满分24分)7.(2分)一次函数y =3x +b 的图象过坐标点(﹣2,4),则该函数的截距为 .8.(2分)从长度为2,3,5,7的四条线段中任意选取三条,这三条线段能构成三角形的概率等于 .9.(2分)已知一次函数y =kx +k ﹣1(其中k 为常数且k ≠0)的图象不经过第二象限,则k 的取值范围是 .10.(2分)二项方程12x 4﹣8=0的实数根是 .11.(2分)方程x 2x−1=1x−1的根是 .12.(2分)方程√1−x (x ﹣2)=0的根是 .13.(2分)已知关于x 的分式方程m x−4=6+x 4−x 有增根,则m = .14.(2分)方程组{x +y =11xy =24的解是 . 15.(2分)把方程x 2﹣2xy ﹣3y 2=0化为两个二元一次方程,它们是 和 .16.(2分)在平行四边形ABCD 中,AE 平分∠BAD 交直线BC 于点E ,BE :EC =2:1,且AB =6,那么这个四边形的周长是 .17.(2分)菱形的边长为10厘米,一条对角线为16厘米,它的面积是 平方厘米.18.(2分)如果把对角线与一边垂直的平行四边形成为“联想平行四边形”,现有一个“联想平行四边形”的一组邻边长为4和2√3,那么它的最小内角为 度.三、简答题(本大题共6题,每题6分,满分0分)19.2x−3−4x =1.20.解方程:√x +1+2x =1.21.解方程组:{x 2−y 2=0x 2+4xy +4y 2=1. 22.已知:如图,四边形ABCD 中,AD ∥BC ,∠ADC =90°,AD =CD ,E 是对角线BD 上一点,且EA =EC .求证:四边形ABCD 是正方形.23.已知在直角坐标系中,菱形ABDC ,顶点A (0,4),B (﹣3,0),点D 在x 轴负半轴,求:(1)求点D 的坐标,(2)求经过点C 的反比例函数解析式.24.为迎接“2010年上海世博会”,甲、乙两个施工队共同完成“阳光”小区绿化改造工程,乙队先单独做2天后,再由两队合作10天就能完成全部工程.已知乙队单独完成此项工程比甲队单独完成此项工程少用5天,求甲、乙两个施工队单独完成此项工程各需多少天?四、解答题(本题10分)25.如图,已知点A(0,6),点C(3,0),将线段AC绕点C顺时针旋转90°,点A落在点B处,点D 是x轴上一动点.(1)求直线BC的解析式;(2)联结B、D.若BD∥AC,求点D的坐标;(3)联结A、D交线段BC于点Q,且∠OAC=∠CAQ.求△BCD的面积.五.综合应用题(本题12分)26.(12分)已知:如图菱形ABCD,点E,F分别为边BC,CD上的动点(不与端点重合),且∠EAF=∠B=60°.(1)求证:AE=AF;(2)如果AB=8,设BE=x,AE=y,求y与x的函数关系式和定义域;(3)在(2)的基础上,当x取何值时,S△AEF与S△CEF面积比值为7.参考答案一、选择题(本大题共6题,每题3分,满分18分)1.A ; 2.D ; 3.A ; 4.B ; 5.D ; 6.B ;二、填空题(本大题共12题,每题2分,满分24分)7.10; 8.14; 9.0<k ≤1; 10.x =±2; 11.x =﹣1; 12.x =1; 13.﹣10; 14.{x =8y =3或{x =3y =8; 15.x ﹣3y =0;x+y =0; 16.30或18; 17.96; 18.30;三、简答题(本大题共6题,每题6分,满分0分)19. ; 20.x =0.; 21.{x 1=1y 1=−1,{x 2=−1y 2=1,{x 3=−13y 3=−13,{x 4=13y 4=13.; 22.证明见解析部分.; 23.(1)D (﹣8,0);(2)y =−20x .; 24. ; 四、解答题(本题10分)25.(1)y =12x −32;(2)(12,0);(3)152.;五.综合应用题(本题12分)26.(1)见解析过程;(2)y =√x 2−8x +64(0<x <8);(3)当x =4±2√2时,S △AEF 与S △CEF 面积比值为7.。
2021-2022学年上海市杨浦区市光中学八年级(下)期中数学试题及答案解析

2021-2022学年上海市杨浦区市光中学八年级(下)期中数学试卷一、选择题(本大题共5小题,共15.0分。
在每小题列出的选项中,选出符合题目的一项)1. 下列函数中,一次函数一共有个.( )(1)y=2x+1;(2)y=kx+b;(3)y=3x;(4)y=(x+1)2−x2;(5)y=x2−2x+1.A. 1B. 2C. 3D. 42. 一次函数y=2x−3的图象不经过( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 用换元法解分式方程x−1x −3xx−1+1=0时,如果设x−1x=y,将原方程化为关于y的整式方程,那么这个整式方程是( )A. y2+y−3=0B. y2−3y+1=0C. 3y2−y+1=0D. 3y2−y−1=04. 下列方程中,有实数根的是( )A. x2−x+2=0B. xx−1=1x−1C. √x−2=−1D. x4−1=0.5. 方程xx−3−3=mx−3有增根,则m的值为( )A. ±√3B. ±3C. −3D. 3二、填空题(本大题共11小题,共33.0分)6. 一次函数y=3x+b的图象过坐标点(−1,−5),则这个一次函数解析式为______.7. 如图,该图象是一个正比例函数的图象,把该图象向右平移两个单位长度,得到的函数图象的解析式为______.8. 已知一次函数的图象过点(3,5)与(−4,−9),则该函数的图象与y轴交点的坐标为______.9. 一次函数的图象过点(0,2),且函数y的值随自变量x的增大而增大,请写出一个符合条件的函数解析式:______ .(答案不唯一)10. 关于x的一元一次方程2x=ax+3的解为______.11. 方程x 2x−1=1x−1的根是______.12. 方程√x −2=2的根是______.13. 方程组{x +y =11xy =24的解是______.14. 把方程x 2−2xy −3y 2=0化为两个二元一次方程,它们是______ 和______ .15. 某企业的年产值从2006年的2亿元增长到2009年的7亿元,如果这三年的年平均增长率相同,均为x ,那么可以列出方程为______.16. 如图,一次函数y =kx +b 的图象经过A ,B 两点,则kx +b >0解集是______ .三、计算题(本大题共2小题,共12.0分)17. 解方程:6x x 2−1+5x−1=x+4x+1.18. 解方程:√x +2=x四、解答题(本大题共4小题,共40.0分。
杨浦区2021学年度第二学期八年级数学期终卷

一、选择题(本大题共6题,每题3分,满分18分)1.一次函数y=2x-1的图像经过()(A)一、二、三象限;(B)二、三、四象限;(C) 一、三、四象限;(D)一、二、四象限.2.下列关于x的方程一定有实数根的是()(A)ax?1?0;(B)ax2?1?0;(C)x?a?0;(D)x2?a?0.3.下列事件中,属于随机事件的是()(A)凸多边形的内角和为500°;(B)凸多边形的外角和为360°;(C)四边形绕它的对角线交点旋转180°能与它本身重合;(D)任何一个三角形的中位线都平行于这个三角形的第三边.4.如果点C、D在线段AB上,AC=BD,那么下列结论中正确的是 ( ) (A)AC与BD是相等向量;(B)AD与BC是相等向量;(C)AD与BD是相反向量;(D)AD与BD是平行向量5.四边形ABCD中,对角线AC、BD交于点O。
给出下列四组条件:①AB//CD,AD//BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB//CD,AD=BC。
其中一定能判定这个四边形是平行四边形的条件共有()(A)1组;(B)2组;(C)3组;(D)4组.6.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路线长为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是()(C )(D ) (第6题图) (A)(B)二、填空题(本大题共12题,每题2分,满分24分)7.若一次函数y?(2?k)x?1中,y随x的增大而减小,则k的取值范围是.8.已知直线y??k?2?x?3与直线y?3x?2平行,那么k= .9.方程x?2?0在实数范围内的解是.3x2?1x2?1x10.用换元法解方程 ?y,那么得到关于y的整式方程为.?2?3时,如果设11.如图,已知一次函数y=kx+b的图像经过点A(5,0)与B(0,-4),那么关于x 的不等式kx+b<0的解集是.12.设关于x的一次函数y?a1x?b1与y?a2x?b2,则称函数y?m(a1x?b1)?n(a2x?b2)(其中m+n?1)为此两个函数的生成函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
杨浦区第二学期八年级期中考试数学试卷
Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT
O A D B 杨浦区2011学年度第二学期初二数学期中考试卷
(考试时间:90分钟 满分100分) 2012、4
一、填空题:(本大题共12题,每题2分, 满分24分)
1.若函数(1)1y k x =-+是一次函数,则k 的取值范围为 .
2.已知一次函数b kx y +=的图像经过点)2,0(-A ,并与直线x y 4-=平行,那么这个
一次函数解析式是 _.
这个
3.如果一次函数1-=kx y 中y 随x 的增大而减小,那么
一次函数一定不经过第___ 象限.
4.在图中,将直线OA 向上平移3个单位,所得直线的函数解析式为 .
5.方程x x =-12的解是 _ _. 6.方程组⎩⎨⎧-==+3
2xy y x 的解为 . 7.十二边形的内角和为_______度. 8.用换元法解方程2
1333322=-+-x x x x .如果设x x y 32-=,则原方程可化为y 的整式方程是 .
9.已知一个多边形的每个外角都为︒72,那么这个多边形是 边形.
10.如图,□ABCD 的周长是28cm ,AC 和BD 交于O ,△OAB 的周长比△OBC 的
周长小2cm ,则AB = ,BC = .
11.解方程组⎪⎩⎪⎨⎧=+-=+0
65202222y xy x y x 时,可先化为 和 两个方程组. 12.如果直线k x y +-=2与两坐标轴所围成的三角形面积是9,则k 的值为 .
二、选择题(本大题共6题,每题2分, 满分12分)
第4题图 第10题图
13.已知函数3-=x y ,若当a x =时,5=y ;当b x =时,3=y ,a 和b 的大小关系
是……………………………………………………………………………… ( )
(A )a>b ; (B )a=b ; (C )a<b ; (D )不能确定.
14.下列方程中,是二项方程的为………………………………………………( )
(A )122=+x x ; (B )02=+x x ; (C )083=-x ; (D )0=x .
15.下列方程中, 有实数解的是…………………………………………………( )
(A )016=+x ; (B )2
22-=-x x x ; (C )032=+-x ; (D )x x =-2. 16. 某灾区恢复生产,计划在一定时间内种60亩蔬菜,实际播种时每天比原
计划多种3亩,因此提前一天完成任务,问实际种了几天现设实际种了x 天,则可列方程…………………………………………………………………………………( )
(A )316060=+-x x ; (B )360160=--x x ; (C )13
6060=+-x x ; (D )160360=--x
x . 17.已知平行四边形的一条边长为14,下列各组数中,能分别作它的两条对角线长的
是…………………………………………………………………………………( )
(A )10与16; (B )12与16; (C )20与22; (D )10与18.
18.一个面积为2的平行四边形被直线分成面积为x ,y 的两部分,则y 与x 之间的函
数关系只可能是………………………………………………………………( )
三、简答题(本大题共5题,每题6分, 满分30分)
19.解关于x 的方程: 4)2(=+x b . 20.解方程:
3x =.
解: 解:
21.解方程组: 517,
311.x y x y x y x y ⎧+=⎪+-⎪⎨⎪-=⎪+-⎩①
②22.解方程组: ⎪⎩⎪⎨⎧=+-=-92 042222y xy x y x
解: 解:
23.已知:如图,O 为平行四边形ABCD 的对角线AC 的中点,过点O 作一条直线分
别与AB 、CD 交于点M 、N ,点E 、F 在直线MN
上,且OE
=OF .
求证:∠MAE =∠NCF .
四、解答题(本大题共3题,每题8分, 满分24分)
24.如图,已知A (4,a ),B (-2,-4)是一次函数y =kx +b 的图象和反比例函数y
=x m 的图象的交点. (1)求反比例函数和一次函数的解祈式;
(2)求△A0B 的面积.
解:
25.某区需修建一条2400米长的封闭式污水处理管道.为了尽量减少施工对市民生
活等的影响,实际施工比原计划每天多修10米,结果提前20天完成了任务.试问实际每天修多少米
解:
26.如图,已知:在平行四边形ABCD 中,∠C =60°,E 、F 分别是AB 、CD 的中
点,且AB =2AD .
求证:DE ∶BD =3∶3.
五、(本大题满分10分,第(1)小题2分,第(2)
①②小题各4分)
27.如图已知一次函数y =-x +7与正比例函数y =
x 3
4的图象交于点A ,且与x 轴交于点B .
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O﹣C﹣A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒)0
t.
(
①当t为何值时,以A、P、R为顶点的三角形的面积为8
②是否存在以A、P、Q为顶点的三角形是QA=QP的等腰三角形若存在,求t的
值;若不存在,请说明理由.
解:。
