弹性力学试题
《弹性力学》试题参考答案

《弹性力学》试题参考答案(答题时间:100分钟)一、填空题(每小题4分)1.最小势能原理等价于弹性力学基本方程中: 平衡微分方程 , 应力边界条件 。
2.一组可能的应力分量应满足: 平衡微分方程 ,相容方程(变形协调条件) 。
3.等截面直杆扭转问题中, M dxdy D=⎰⎰2ϕ的物理意义是 杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M 。
4.平面问题的应力函数解法中,Airy 应力函数ϕ在边界上值的物理意义为 边界上某一点(基准点)到任一点外力的矩 。
5.弹性力学平衡微分方程、几何方程的张量表示为:0,=+i j ij X σ ,)(21,,i j j i ij u u +=ε。
二、简述题(每小题6分)1.试简述力学中的圣维南原理,并说明它在弹性力学分析中的作用。
圣维南原理:如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢与主矩相同),则近处的应力分布将有显著的改变,但远处的应力所受影响可以忽略不计。
作用:(1)将次要边界上复杂的面力(集中力、集中力偶等)作分布的面力代替。
(2)将次要的位移边界条件转化为应力边界条件处理。
2.图示两楔形体,试分别用直角坐标和极坐标写出其应力函数ϕ的分离变量形式。
题二(2)图(a )⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x (b )⎩⎨⎧=+++=)(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3.图示矩形弹性薄板,沿对角线方向作用一对拉力P ,板的几何尺寸如图,材料的弹性模量E 、泊松比 μ 已知。
试求薄板面积的改变量S ∆。
题二(3)图设当各边界受均布压力q 时,两力作用点的相对位移为l ∆。
由q E)1(1με-=得,)1(2222με-+=+=∆Eb a q b a l设板在力P 作用下的面积改变为S ∆,由功的互等定理有:l P S q ∆⋅=∆⋅将l ∆代入得:221b a P ES +-=∆μ显然,S ∆与板的形状无关,仅与E 、μ、l 有关。
弹性力学题库_

弹性力学题库_弹性力学题库第一章绪论1、所谓“完全弹性体”是指(B)。
A、材料应力应变关系满足虎克定律B、材料的应力应变关系与加载时间、历史无关C、本构关系为非线性弹性关系D、应力应变关系满足线性弹性关系2、关于弹性力学的正确认识是(A)。
A、计算力学在工程结构设计中的作用日益重要B、弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C、任何弹性变形材料都是弹性力学的研究对象D、弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析3、下列对象不属于弹性力学研究对象的是(D)。
A、杆件B、板壳C、块体D、质点4、弹性力学研究物体在外力作用下,处于弹性阶段的应力、应变和位移。
5、弹性力学可以解决材料力学无法解决的很多问题;并对杆状结果进行精确分析,以及验算材力结果的适用范围和精度。
与材料力学相比弹性力学的特点有哪些?答:1)研究对象更为普遍;2)研究方法更为严密;3)计算结果更为精确;4)应用范围更为广泛。
6、材料力学研究杆件,不能分析板壳;弹性力学研究板壳,不能分析杆件。
(×)改:弹性力学不仅研究板壳、块体问题,并对杆件进行精确的分析,以及检验材料力学公式的适用范围和精度。
7、弹性力学对杆件分析(C)。
A、无法分析B、得出近似的结果C、得出精确的结果D、需采用一些关于变形的近似假定8、图示弹性构件的应力和位移分析要用什么分析方法?(C)A、材料力学B、结构力学C、弹性力学D、塑性力学解答:该构件为变截面杆,并且具有空洞和键槽。
9、弹性力学与材料力学的主要不同之处在于(B )。
A、任务B、研究对象C、研究方法D、基本假设10、重力、惯性力、电磁力都是体力。
(√)11、下列外力不属于体力的是(D)A、重力B、磁力C、惯性力D、静水压力12、体力作用于物体内部的各个质点上,所以它属于内力。
(×)解答:外力。
它是质量力。
13、在弹性力学和材料力学里关于应力的正负规定是一样的。
弹性力学题库

第一章绪论1、所谓“完全弹性体”是指(B)。
A、材料应力应变关系满足虎克定律B、材料的应力应变关系与加载时间、历史无关C、本构关系为非线性弹性关系D、应力应变关系满足线性弹性关系2、关于弹性力学的正确认识是(A)。
A、计算力学在工程结构设计中的作用日益重要B、弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C、任何弹性变形材料都是弹性力学的研究对象D、弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析3、下列对象不属于弹性力学研究对象的是(D)。
A、杆件B、板壳C、块体D、质点4、弹性力学研究物体在外力作用下,处于弹性阶段的应力、应变和位移。
5、弹性力学可以解决材料力学无法解决的很多问题;并对杆状结果进行精确分析,以及验算材力结果的适用范围和精度。
与材料力学相比弹性力学的特点有哪些?答:1)研究对象更为普遍;2)研究方法更为严密;3)计算结果更为精确;4)应用范围更为广泛。
6、材料力学研究杆件,不能分析板壳;弹性力学研究板壳,不能分析杆件。
(×)改:弹性力学不仅研究板壳、块体问题,并对杆件进行精确的分析,以及检验材料力学公式的适用范围和精度。
7、弹性力学对杆件分析(C)。
A、无法分析B、得出近似的结果C、得出精确的结果D、需采用一些关于变形的近似假定8、图示弹性构件的应力和位移分析要用什么分析方法?(C)A 、材料力学B 、结构力学C 、弹性力学D 、塑性力学解答:该构件为变截面杆,并且具有空洞和键槽。
9、弹性力学与材料力学的主要不同之处在于( B )。
A 、任务B 、研究对象C 、研究方法D 、基本假设10、重力、惯性力、电磁力都是体力。
(√)11、下列外力不属于体力的是(D )A 、重力B 、磁力C 、惯性力D 、静水压力12、体力作用于物体内部的各个质点上,所以它属于内力。
(×)解答:外力。
它是质量力。
13、在弹性力学和材料力学里关于应力的正负规定是一样的。
弹性力学试题及答案

弹性力学试题及答案一、选择题(每题10分,共40分)1. 在弹性力学中,下列哪个物理量表示应变能密度?A. 应力B. 应变C. 位移D. 应力能密度答案:D2. 在平面应力状态下,下列哪个方程是正确的?A. σ_x + σ_y = 0B. σ_x + σ_y = σ_zC. σ_x + σ_y = τ_xyD. σ_x + σ_y = 0答案:D3. 在弹性体中,应力与应变之间的关系可以用下列哪个关系式表示?A. σ = EεB. σ = GγC. τ = μγD. σ = λε答案:A4. 在弹性力学中,下列哪个方程表示平衡方程?A. σ_x + σ_y + σ_z = 0B. ε_x + ε_y +ε_z = 0 C. τ_xy = τ_yx D. σ_x + σ_y + σ_z = F答案:D二、填空题(每题10分,共30分)1. 弹性力学中的基本假设有:连续性假设、线性假设和________假设。
答案:各向同性2. 在三维应力状态下,应力分量可以表示为:σ_x, σ_y, σ_z, τ_xy, τ_xz, τ_yz。
其中,τ_xy表示________面上的切应力。
答案:xOy3. 在弹性力学中,位移与应变之间的关系可以用________方程表示。
答案:几何方程三、计算题(每题30分,共90分)1. 已知一弹性体在平面应力状态下的应力分量为:σ_x = 100 MPa,σ_y = 50 MPa,τ_xy = 25 MPa。
弹性模量E = 200 GPa,泊松比μ = 0.3。
求应变分量ε_x, ε_y, γ_xy。
解:首先,利用胡克定律计算应变分量:ε_x = σ_x / E = 100 MPa / 200 GPa = 0.0005ε_y = σ_y / E = 50 MPa / 200 GPa = 0.00025γ_xy = τ_xy / G = 25 MPa / (E / 2(1 + μ)) = 25 MPa / (200 GPa / 2(1 + 0.3)) = 0.000375答案:ε_x = 0.0005,ε_y = 0.00025,γ_xy = 0.0003752. 一弹性体在三维应力状态下的应力分量为:σ_x = 120 MPa,σ_y = 80 MPa,σ_z = 40 MPa,τ_xy = 30 MPa,τ_xz = 20 MPa,τ_yz = 10 MPa。
(完整版)《弹性力学》试题参考答案

《弹性力学》试题参考答案(答题时间:100分钟)一、填空题(每小题4分)1.最小势能原理等价于弹性力学基本方程中: 平衡微分方程 , 应力边界条件 。
2.一组可能的应力分量应满足: 平衡微分方程 ,相容方程(变形协调条件) 。
3.等截面直杆扭转问题中, 的物理意义是 杆端截面上剪应力对转轴的矩等于M dxdy D=⎰⎰2ϕ杆截面内的扭矩M 。
4.平面问题的应力函数解法中,Airy 应力函数在边界上值的物理意义为 边界上某一点(基准ϕ点)到任一点外力的矩 。
5.弹性力学平衡微分方程、几何方程的张量表示为: ,。
0,=+i j ij X σ)(21,,i j j i ij u u +=ε二、简述题(每小题6分)1.试简述力学中的圣维南原理,并说明它在弹性力学分析中的作用。
圣维南原理:如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢与主矩相同),则近处的应力分布将有显著的改变,但远处的应力所受影响可以忽略不计。
作用:(1)将次要边界上复杂的面力(集中力、集中力偶等)作分布的面力代替。
(2)将次要的位移边界条件转化为应力边界条件处理。
2.图示两楔形体,试分别用直角坐标和极坐标写出其应力函数的分离变量形式。
ϕ题二(2)图(a ) (b )⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x ⎩⎨⎧=+++= )(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3.图示矩形弹性薄板,沿对角线方向作用一对拉力P ,板的几何尺寸如图,材料的弹性模量E 、泊松比 μ 已知。
试求薄板面积的改变量。
S∆题二(3)图设当各边界受均布压力q 时,两力作用点的相对位移为。
由得,l ∆q E)1(1με-=)1(2222με-+=+=∆Eb a q b a l 设板在力P 作用下的面积改变为,由功的互等定理有:S ∆lP S q ∆⋅=∆⋅将代入得:l ∆221b a P ES +-=∆μ显然,与板的形状无关,仅与E 、、l 有关。
弹性力学题库

第一章绪论1、所谓“完全弹性体”是指(B)。
A、材料应力应变关系满足虎克定律B、材料的应力应变关系与加载时间、历史无关C、本构关系为非线性弹性关系D、应力应变关系满足线性弹性关系2、关于弹性力学的正确认识是(A)。
A、计算力学在工程结构设计中的作用日益重要B、弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C、任何弹性变形材料都是弹性力学的研究对象D、弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析3、下列对象不属于弹性力学研究对象的是(D)。
A、杆件B、板壳C、块体D、质点4、弹性力学研究物体在外力作用下,处于弹性阶段的应力、应变和位移。
5、弹性力学可以解决材料力学无法解决的很多问题;并对杆状结果进行精确分析,以及验算材力结果的适用范围和精度。
与材料力学相比弹性力学的特点有哪些?答:1)研究对象更为普遍;2)研究方法更为严密;3)计算结果更为精确;4)应用范围更为广泛。
6、材料力学研究杆件,不能分析板壳;弹性力学研究板壳,不能分析杆件。
(×)改:弹性力学不仅研究板壳、块体问题,并对杆件进行精确的分析,以及检验材料力学公式的适用范围和精度。
7、弹性力学对杆件分析(C)。
A、无法分析B、得出近似的结果C、得出精确的结果D、需采用一些关于变形的近似假定8、图示弹性构件的应力和位移分析要用什么分析方法?(C)A、材料力学B、结构力学C 、弹性力学D 、塑性力学解答:该构件为变截面杆,并且具有空洞和键槽。
9、弹性力学与材料力学的主要不同之处在于( B )。
A 、任务B 、研究对象C 、研究方法D 、基本假设10、重力、惯性力、电磁力都是体力。
(√)11、下列外力不属于体力的是(D )A 、重力B 、磁力C 、惯性力D 、静水压力12、体力作用于物体内部的各个质点上,所以它属于内力。
(×)解答:外力。
它是质量力。
13、在弹性力学和材料力学里关于应力的正负规定是一样的。
《弹性力学》试题

《弹性力学》试题(答题时间:100分钟)一、填空题(每小题4分)1.以应力表示的相容方程其适用性: , 。
2.一组可能的应力分量应满足 , 。
3.等截面直杆扭转问题中,方程0=s ϕ的物理意义是 。
4.应力函数ϕ在边界上值的物理意义是 ,y x ∂∂∂∂ϕϕ,在边界上值的物理意义是 。
5.由平面应力到平面应变问题,其材料弹性常数的转换关系为: ,。
二、简述题(每小题7分)1.图示矩形弹性薄板,沿对角线方向作用一对拉力P ,板的几何尺寸如图,材料的弹性模量E 、泊松比 μ 已知。
试求薄板面积的改变量S ∆。
2.图示两楔形体,试分别用直角坐标和极坐标写出其应力函数ϕ的形式。
题二(1)图 题二(2)图 3.图示曲杆,在b r =边界均布拉应q ,在自由端作用有水平集中力P 。
试写出其边界条件(除固定端外)。
题二(3)图4.下面给出平面应力问题(单连通域)一组应力分量和一组应变分量,试判断它们是否可能。
(1),21y C x C x +=σ,43y C x C y -=σy C x C xy 14-=τ;(2)),(22y x C x +=ε,2Cy y =εCxy xy 2=γ。
5.试用笛卡尔张量写出弹性力学平衡微分方程、几何方程、形变比能1U 的表达式。
三、计算题1.图示顶角为α的楔形体,下端无限长,受水平方向的常体力作用,设单位体积的水平力为p ,试用纯三次多项式为应力函数ϕ求其应力分量。
(15分)2.已知圆环在a r =的内边界上被固定,在b r =的圆周上作用着均匀分布剪应力0τ,如图所示。
试确定圆环内的应力与位移。
(提示:取应力函数θϕA =) (15分)3.一端固定,另一端自由的梁,其跨度为l ,抗弯刚度EI 为常数,分别承受均匀分布载荷q 、集中力P 的作用,如图所示。
若用Ritz 法(或最小势能原理)求解,试:(1)构造两种形式的挠度近似函数)(x w (三角函数形式、多项式);(2)在上述)(x w 中,任选一种求梁的挠度(取一项待定系数)。
弹性力学网考考试题及答案

弹性力学网考考试题及答案一、单项选择题(每题2分,共20分)1. 弹性力学中,应力状态的基本方程是()。
A. 平衡方程B. 几何方程C. 物理方程D. 相容方程答案:A2. 弹性力学中,平面应力问题是指()。
A. 应力分量σx、σy、τxy均不为零B. 应力分量σx、σy、τxy中有一个为零C. 应力分量σx、σy、τxy中有两个为零D. 应力分量σx、σy、τxy中有三个为零答案:C3. 在弹性力学中,圣维南原理适用于()。
A. 静力平衡问题B. 热弹性问题C. 动力学问题D. 流体力学问题答案:A4. 弹性力学中,平面应变问题是指()。
A. 应变分量εx、εy、γxy均不为零B. 应变分量εx、εy、γxy中有一个为零C. 应变分量εx、εy、γxy中有两个为零D. 应变分量εx、εy、γxy中有三个为零答案:B5. 弹性力学中,主应力和主应变之间的关系是()。
A. 线性关系B. 非线性关系C. 没有关系D. 取决于材料的性质答案:A6. 弹性力学中,莫尔圆在σ-τ平面上表示的是()。
A. 应力状态B. 应变状态C. 位移场D. 速度场答案:A7. 弹性力学中,平面应力问题和平面应变问题的区别在于()。
A. 应力分量的数量B. 应变分量的数量C. 位移分量的数量D. 材料的性质答案:B8. 弹性力学中,三向应力状态下的应力分量不包括()。
A. σxB. σyC. σzD. τxy答案:D9. 弹性力学中,应力集中现象通常发生在()。
A. 光滑表面B. 尖锐转角C. 平坦区域D. 均匀区域答案:B10. 弹性力学中,弹性模量E和泊松比μ之间的关系是()。
A. E = 2G(1+μ)B. E = 3G(1-2μ)C. E = 3G(1+2μ)D. E = 2G(1-μ)答案:A二、多项选择题(每题3分,共15分)11. 弹性力学中,下列哪些方程是基本方程?()A. 平衡方程B. 几何方程C. 物理方程D. 相容方程答案:ABCD12. 弹性力学中,下列哪些因素会影响材料的弹性模量E?()A. 材料种类B. 温度C. 应力状态D. 应变状态答案:AB13. 弹性力学中,下列哪些是平面应力问题的特点?()A. 应力分量σz为零B. 应变分量εz不为零C. 位移分量w为零D. 位移分量u和v不为零答案:AC14. 弹性力学中,下列哪些是平面应变问题的特点?()A. 应变分量εz为零B. 应力分量σz不为零C. 位移分量w不为零D. 位移分量u和v不为零答案:AD15. 弹性力学中,下列哪些是应力集中现象的影响因素?()A. 材料性质B. 几何形状C. 载荷类型D. 边界条件答案:BCD三、判断题(每题2分,共20分)16. 弹性力学中,平衡方程是描述物体内部力的平衡状态的方程。
弹性力学复习题---有答案

弹性力学复习题---有答案一、选择题1. 下列材料中,( D )属于各向同性材料。
A. 竹材;B. 纤维增强复合材料;C. 玻璃钢;D. 沥青。
2 关于弹性力学的正确认识是(A )。
A. 计算力学在工程结构设计的中作用日益重要;B. 弹性力学从微分单元体入手分析弹性体,与材料力学不同,不需要对问题作假设;C. 任何弹性变形材料都是弹性力学的研究对象;D. 弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析。
3. 弹性力学与材料力学的主要不同之处在于( B )。
A. 任务;B. 研究对象;C. 研究方法;D. 基本假设。
4. 所谓“完全弹性体”是指( A )。
A. 材料应力应变关系满足胡克定律;B. 材料的应力应变关系与加载时间历史无关;C. 本构关系为非线性弹性关系;D. 应力应变关系满足线性弹性关系。
5. 所谓“应力状态”是指( B )。
A. 斜截面应力矢量与横截面应力矢量不同;B. 一点不同截面的应力随着截面方位变化而改变;C. 3个主应力作用平面相互垂直;D. 不同截面的应力不同,因此应力矢量是不可确定的。
6. 变形协调方程说明( B )。
A. 几何方程是根据运动学关系确定的,因此对于弹性体的变形描述是不正确的;B. 微分单元体的变形必须受到变形协调条件的约束;C. 变形协调方程是保证所有弹性体变形协调条件的必要和充分条件;D. 变形是由应变分量和转动分量共同组成的。
7. 下列关于弹性力学基本方程描述正确的是( A )。
A. 几何方程适用小变形条件;B. 物理方程与材料性质无关;C. 平衡微分方程是确定弹性体平衡的唯一条件;D. 变形协调方程是确定弹性体位移单值连续的唯一条件;8、弹性力学建立的基本方程多是偏微分方程,最后需结合( B )求解这些微分方程,以求得具体问题的应力、应变、位移。
A.几何方程B.边界条件C.数值方法D.附加假定9、弹性力学平面问题的求解中,平面应力问题与平面应变问题的三类基本方程具有下列关系(B )。
弹性力学试题及答案

弹性力学试题及答案一、选择题(每题5分,共20分)1. 弹性力学中,描述材料弹性特性的基本物理量是()。
A. 应力B. 应变C. 弹性模量D. 泊松比答案:C2. 在弹性力学中,下列哪项不是胡克定律的内容?()A. 应力与应变成正比B. 材料是均匀的C. 材料是各向同性的D. 材料是线性的答案:B3. 弹性模量E和泊松比ν之间的关系是()。
A. E = 2(1 + ν)B. E = 3(1 - 2ν)C. E = 3(1 + ν)D. E = 2(1 - ν)答案:D4. 根据弹性力学理论,下列哪种情况下材料会发生塑性变形?()A. 应力小于材料的弹性极限B. 应力达到材料的弹性极限C. 应力超过材料的屈服强度D. 应力小于材料的屈服强度答案:C二、填空题(每题5分,共20分)1. 弹性力学中,应力的定义是单位面积上的______力。
答案:内2. 弹性力学的基本假设之一是______连续性假设。
答案:材料3. 弹性力学中,应变的量纲是______。
答案:无4. 弹性力学中,当外力撤去后,材料能恢复原状的性质称为______。
答案:弹性三、简答题(每题10分,共30分)1. 简述弹性力学中应力和应变的区别。
答案:应力是描述材料内部单位面积上受到的内力,而应变是描述材料在受力后形状和尺寸的变化程度。
2. 解释弹性力学中的杨氏模量和剪切模量。
答案:杨氏模量(E)是描述材料在拉伸或压缩过程中应力与应变比值的物理量,反映了材料的刚度;剪切模量(G)是描述材料在剪切应力作用下剪切应变与剪切应力比值的物理量,反映了材料抵抗剪切变形的能力。
3. 弹性力学中,如何理解材料的各向异性和各向同性?答案:各向异性是指材料的物理性质(如弹性模量、热膨胀系数等)在不同方向上具有不同的值;而各向同性则是指材料的物理性质在各个方向上都是相同的。
四、计算题(每题15分,共30分)1. 已知一圆柱形试件,其直径为50mm,长度为100mm,材料的弹性模量E=210GPa,泊松比ν=0.3。
弹性力学100题

弹性力学100题一、单项选择题1.弹性力学建立的基本方程多是偏微分方程,还必须结合(C )求解这些微分方程,以求得具体问题的应力、应变、位移。
A相容方程 B •近似方法C •边界条件D •附加假定2.根据圣维南原理,作用在物体一小部分边界上的力系可以用(B )的力系代替,则仅在近处应力分布有改变,而在远处所受的影响可以不计。
A.几何上等效B・静力上等效C平衡D •任意3.弹性力学平面问题的求解中,平面应力问题与平面应变问题的三类基本方程不完全相同,其比较关系为(B )。
A •平衡方程、几何方程、物理方程完全相同B •平衡方程、几何方程相同,物理方程不同C •平衡方程、物理方程相同,几何方程不同D •平衡方程相同,物理方程、几何方程不同4.不计体力,在极坐标中按应力求解平面问题时,应力函数必须满足(A )①区域内的相容方程;②边界上的应力边界条件;③满足变分方程;④如果为多连体,考虑多连体中的位移单值条件。
A.①②④B.②③④C.①②③D.①②③④5.如下图1所示三角形薄板,按三结点三角形单元划分后,对于与局部编码ijm对应的整体编码,以下叙述正确的是(D )。
①I单元的整体编码为162②II单元的整体编码为426③II单元的整体编码为246④III单元的整体编码为243⑤IV单元的整体编码为564图1A.①③B.②④C.①④D.③⑤6.平面应变问题的微元体处于(C )A.单向应力状态B.双向应力状态C.三向应力状态,且-是一主应力D.纯剪切应力状态7.圆弧曲梁纯弯时,(CA.应力分量和位移分量都是轴对称的B.应力分量和位移分量都不是轴对称的C.应力分量是轴对称的,位移分量不是轴对称的D.位移分量是轴对称的,应力分量不是轴对称的8.下左图2中所示密度为「的矩形截面柱,应力分量为:匚x =0fy Ay B, xy 0对图(a)和图(b)两种情况由边界条件确定的常数A及B的关系是(C )A.A 相同,B也相同B.A 不相同,B也不相同C.A 相同,B不相同D.A 不相同,B 相同图 2图39、上右图3示单元体剪应变丫应该表示为(B )◎备DA冷B10、设有平面应力状态二X =ax by, ;「y = ex dy, xy dx - ay - x,其中,a,b,c,d 均为常数,为容重。
弹性力学试卷及答案4套
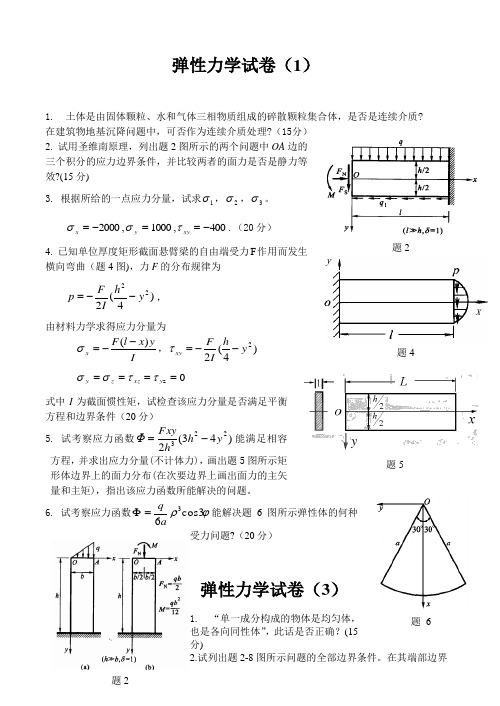
弹性力学试卷(1)1. 土体是由固体颗粒、水和气体三相物质组成的碎散颗粒集合体,是否是连续介质? 在建筑物地基沉降问题中,可否作为连续介质处理?(15分)2. 试用圣维南原理,列出题2图所示的两个问题中OA边的三个积分的应力边界条件,并比较两者的面力是否是静力等效?(15分)3. 根据所给的一点应力分量,试求1σ,2σ,3σ。
400,1000,2000-==-=xyyxτσσ.(20分)4. 已知单位厚度矩形截面悬臂梁的自由端受力F作用而发生横向弯曲(题4图),力F的分布规律为)4(222yhIFp--=,由材料力学求得应力分量为IyxlFx)(--=σ,)4(22yhIFxy--=τz====yxzzyττσσ式中I为截面惯性矩,试检查该应力分量是否满足平衡方程和边界条件(20分)5. 试考察应力函数)43(2223yhhFxyΦ-=能满足相容方程,并求出应力分量(不计体力),画出题5图所示矩形体边界上的面力分布(在次要边界上画出面力的主矢量和主矩),指出该应力函数所能解决的问题。
6.试考察应力函数ϕρcos363aq=Φ能解决题6图所示弹性体的何种受力问题?(20分)弹性力学试卷(3)1. “单一成分构成的物体是均匀体,也是各向同性体”,此话是否正确?(15分)2.试列出题2-8图所示问题的全部边界条件。
在其端部边界题2题2题4y题5题 6上,应用圣维南原理列出三个积分的应力边界条件。
(15分) 3. 根据所给的一点应力分量,试求1σ,2σ,3σ。
1010,50,100===xy y x τσσ.(20分)4. 检验下列应力分量是否是题4图所示问题的解答:q b y x 22=σ,0===yx xy yττσ。
(20分)5. 试证)2(10)134(4332332h y h y qy h y h y qx Φ-+-+-=能满足相容方程,并考察它在题5图所示矩形板和坐标系中能解决什么问题(设矩形板的长度为L ,深度为h ,体力不计)。
《弹性力学》试题参考答案

《弹性力学》试题参考答案(答题时间:100分钟)一、填空题(每小题4分)1.最小势能原理等价于弹性力学基本方程中: 平衡微分方程 , 应力边界条件 。
2.一组可能的应力分量应满足: 平衡微分方程 ,相容方程(变形协调条件) 。
3.等截面直杆扭转问题中,Mdxdy D=⎰⎰ 2ϕ的物理意义是 杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M 。
4.平面问题的应力函数解法中,Airy 应力函数ϕ在边界上值的物理意义为 边界上某一点(基准点)到任一点外力的矩 。
5.弹性力学平衡微分方程、几何方程的张量表示为:0,=+i j ij X σ ,)(21,,i j j i ij u u +=ε。
二、简述题(每小题6分)1.试简述力学中的圣维南原理,并说明它在弹性力学分析中的作用。
圣维南原理:如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢与主矩相同),则近处的应力分布将有显著的改变,但远处的应力所受影响可以忽略不计。
作用:(1)将次要边界上复杂的面力(集中力、集中力偶等)作分布的面力代替。
(2)将次要的位移边界条件转化为应力边界条件处理。
2.图示两楔形体,试分别用直角坐标和极坐标写出其应力函数ϕ的分离变量形式。
题二(2)图(a )⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x (b )⎩⎨⎧=+++=)(),(),(33223θθϕϕf r r dy cxy y bx ax y x3.图示矩形弹性薄板,沿对角线方向作用一对拉力P ,板的几何尺寸如图,材料的弹性模量E 、泊松比 μ 已知。
试求薄板面积的改变量S ∆。
题二(3)图设当各边界受均布压力q 时,两力作用点的相对位移为l ∆。
由q E)1(1με-=得, )1(2222με-+=+=∆Eb a q b a l设板在力P 作用下的面积改变为S ∆,由功的互等定理有:l P S q ∆⋅=∆⋅将l ∆代入得:221b a P ES +-=∆μ显然,S ∆与板的形状无关,仅与E 、μ、l 有关。
弹性力学试题及答案

弹性力学试题及答案一、选择题(每题2分,共20分)1. 弹性力学中的胡克定律描述的是:A. 应力与位移的关系B. 应力与应变的关系C. 应变与位移的关系D. 位移与力的关系2. 以下哪个不是弹性力学的基本假设?A. 连续性假设B. 均匀性假设C. 各向同性假设D. 各向异性假设3. 弹性模量和泊松比的关系是:A. E = 2G(1+ν)B. E = 3K(1-2ν)C. E = 3K(1+ν)D. E = 2G(1-ν)4. 以下哪种材料可以看作是各向同性材料?A. 木材B. 钢筋混凝土C. 单晶硅D. 多晶硅5. 应力集中现象通常发生在:A. 均匀受力区域B. 材料的中间区域C. 材料的边缘或孔洞附近D. 材料的内部二、简答题(每题10分,共30分)6. 简述平面应力和平面应变的区别。
7. 解释什么是圣维南原理,并简述其应用。
8. 描述弹性力学中的主应力和主应变的概念及其意义。
三、计算题(每题25分,共50分)9. 一个长方体材料块,尺寸为L×W×H,受到均匀压力p作用于其顶面,求其内部任意一点处的应力状态。
10. 已知某材料的弹性模量E=200 GPa,泊松比ν=0.3,求其剪切模量G。
答案一、选择题1. 答案:B(应力与应变的关系)2. 答案:D(各向异性假设)3. 答案:A(E = 2G(1+ν))4. 答案:D(多晶硅)5. 答案:C(材料的边缘或孔洞附近)二、简答题6. 答案:平面应力是指材料的一个方向(通常是厚度方向)的应力为零,而平面应变是指材料的一个方向(通常是厚度方向)的应变为零。
平面应力通常用于薄板或薄膜,而平面应变用于长厚比很大的结构。
7. 答案:圣维南原理指出,在远离力作用区域的地方,局部应力分布对整个结构的应力状态影响很小。
这个原理常用于简化复杂结构的应力分析。
8. 答案:主应力是材料内部某一点应力张量的最大值,主应变是材料内部某一点应变张量的最大值。
弹性力学题

弹性力学题Company number:【0089WT-8898YT-W8CCB-BUUT-202108】一、单项选择题1.弹性力学建立的基本方程多是偏微分方程,还必须结合( C )求解这些微分方程,以求得具体问题的应力、应变、位移。
A.相容方程 B.近似方法 C.边界条件 D.附加假定2.根据圣维南原理,作用在物体一小部分边界上的力系可以用( B )的力系代替,则仅在近处应力分布有改变,而在远处所受的影响可以不计。
A.几何上等效 B.静力上等效 C.平衡 D.任意3.弹性力学平面问题的求解中,平面应力问题与平面应变问题的三类基本方程不完全相同,其比较关系为( B )。
A.平衡方程、几何方程、物理方程完全相同B.平衡方程、几何方程相同,物理方程不同C.平衡方程、物理方程相同,几何方程不同D.平衡方程相同,物理方程、几何方程不同4.不计体力,在极坐标中按应力求解平面问题时,应力函数必须满足( A )①区域内的相容方程;②边界上的应力边界条件;③满足变分方程;④如果为多连体,考虑多连体中的位移单值条件。
A.①②④B. ②③④C. ①②③D. ①②③④5.如下图1所示三角形薄板,按三结点三角形单元划分后,对于与局部编码ijm对应的整体编码,以下叙述正确的是( D )。
① I单元的整体编码为162② II单元的整体编码为426③ II单元的整体编码为246④ III单元的整体编码为243⑤ IV单元的整体编码为564图1A. ①③B. ②④C. ①④D. ③⑤6.平面应变问题的微元体处于( C )A.单向应力状态B.双向应力状态是一主应力 D.纯剪切应力状态C.三向应力状态,且z7.圆弧曲梁纯弯时,( C )A.应力分量和位移分量都是轴对称的B.应力分量和位移分量都不是轴对称的C.应力分量是轴对称的,位移分量不是轴对称的D.位移分量是轴对称的,应力分量不是轴对称的8.下左图2中所示密度为ρ的矩形截面柱,应力分量为:0,,0=+==xy y x B Ay τσσ对图(a )和图(b)两种情况由边界条件确定的常数A 及B 的关系是( C )相同,B 也相同 不相同,B 也不相同相同,B 不相同 不相同,B 相同图 2 图 39、上右图3示单元体剪应变γ应该表示为( B )10、设有平面应力状态x ay dx dy cx by ax xy y x γτσσ---=+=+=,,,其中,d c b a ,,,均为常数,γ为容重。
弹性力学试卷及答案

精品文档一、概念题(32分)1、 如图所示三角形截面水坝,其右侧受重度为γ的水压力作用,左侧为自由面。
试列出下述问题的边界条件解:1)右边界(x=0)11 2)左边界(x=ytg β)1 1由: 222、何谓逆解法和半逆解法。
答:1. 所谓逆解法,就是先设定各种形式、满足相容方程的应力函数,利用公式求出应力分量,然后根据应力边界条件考察在各种形状的弹性体上,这些应力分量对应于什么样的面力,从而得知设定的应力函数可以解决什么问题。
4 2. 所谓半逆解法,就是针对所要求解的问题,根据弹性体的边界形状与受力情况,假设部分或全部应力分量为某种形式的函数,从而推出应力函数,然后考察该应力函数是否满足相容方程,以及原来假设的应力分量和由这个应力函数求出的其余应力分量,是否满足应力边界条件和位移单值条件。
如果相容方程和各方面的条件都能满足,就可得到正确解答;如果某一方面不能满足,就需要另作假设,重新考察。
43、已知一点的应力状态,试求主应力的大小及其作用的方向。
200,0,400x y xy MPa MPa σστ===-解:根据公式122x y σσσσ+= 2 和公式11tan xxyσσατ-=,求出主应力和主应力方向: 22000512.31312.322MPa σσ+==- 2000yx x xy x σγτ=-===()()cos ,cos cos ,cos()2sin l n x m n y βπββ====+=-()()()()x y l m x xy s s l m xy y s sf f σττσ+=+=⎫⎪⎬⎪⎭()()()()cos sin 0cos sin 0x xy s s xy y s s σβτβτβσβ-=+=⎫⎪⎬⎪⎭精品文档512200tan 0.7808,3757'11400αα-==-=- 24、最小势能原理等价于 以位移表示的平衡微分 (3) 方程和 应力 (3) 边界条件,选择位移函数仅需满足 位移 (2) 边界条件。
弹性力学题库

C )第一章 绪论1、 所谓“完全弹性体”是指(B )。
A 、 材料应力应变关系满足虎克定律B 、 材料的应力应变关系与加载时间、历史无关C 、 本构关系为非线性弹性关系D 、 应力应变关系满足线性弹性关系2、 关于弹性力学的正确认识是( A )。
A 、 计算力学在工程结构设计中的作用日益重要B 、 弹性力学从微分单元体入手分析弹性体 ,因此与材料力学不同,不需要对问题作假设C 、 任何弹性变形材料都是弹性力学的研究对象D 、 弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析3、 下列对象不属于弹性力学研究对象的是( D )。
A 、杆件B 、板壳C 、块体D 、质点4、 弹性力学研究物体在 外力作用下,处于弹性阶段的应力、应变和位移。
5、 弹性力学可以解决材料力学无法解决的很多问题;并对杆状结果进行精确分析,以及验算材力结果的适用范围和精度。
与材料力学相比弹性力学的特点有哪些?答:1)研究对象更为普遍;2) 研究方法更为严密;3) 计算结果更为精确;4)应用范围更为广泛。
6、材料力学研究杆件,不能分析板壳;弹性力学研究板壳,不能分析杆件。
(X )改:弹性力学不仅研究板壳、块体问题,并对杆件进行精确的分析,以及检验材料力学 公式的适用范围和精度。
8、图示弹性构件的应力和位移分析要用什么分析方法?(7、弹性力学对杆件分析( C )。
A 、无法分析 B 、得出近似的结果 C 、得出精确的结果 D 、需采用一些关于变形的近似假定yz15、按弹性力学规定,下图所示单元体上的剪应力( C )。
D 、静水压力C 、弹性力学D 、塑性力学解答:该构件为变截面杆,并且具有空洞和键槽。
9、弹性力学与材料力学的主要不同之处在于( B )。
10、重力、惯性力、电磁力都是体力。
(V )11、下列外力不属于体力的是( D )A 、重力B 、磁力C 、惯性力 12、体力作用于物体内部的各个质点上,所以它属于内力。
弹性力学100题

一、单项选择题1.弹性力学建立的基本方程多是偏微分方程,还必须结合( C )求解这些微分方程,以求得具体问题的应力、应变、位移。
A .相容方程B .近似方法C .边界条件D .附加假定2.根据圣维南原理,作用在物体一小部分边界上的力系可以用( B )的力系代替,则仅在近处应力分布有改变,而在远处所受的影响可以不计。
A .几何上等效B .静力上等效C .平衡D .任意3.弹性力学平面问题的求解中,平面应力问题与平面应变问题的三类基本方程不完全相同,其比较关系为( B )。
A .平衡方程、几何方程、物理方程完全相同B .平衡方程、几何方程相同,物理方程不同C .平衡方程、物理方程相同,几何方程不同D .平衡方程相同,物理方程、几何方程不同4.不计体力,在极坐标中按应力求解平面问题时,应力函数必须满足( A )①区域内的相容方程;②边界上的应力边界条件;③满足变分方程;④如果为多连体,考虑多连体中的位移单值条件。
A. ①②④B. ②③④C. ①②③D. ①②③④5.如下图1所示三角形薄板,按三结点三角形单元划分后,对于与局部编码ijm 对应的整体编码,以下叙述正确的是( D )。
① I 单元的整体编码为162② II 单元的整体编码为426③ II 单元的整体编码为246④ III 单元的整体编码为243⑤ IV 单元的整体编码为564图1A. ①③B. ②④C. ①④D. ③⑤ 6.平面应变问题的微元体处于( C )A.单向应力状态B.双向应力状态C.三向应力状态,且z 是一主应力D.纯剪切应力状态7.圆弧曲梁纯弯时,( C )A.应力分量和位移分量都是轴对称的 463521I III II IVB.应力分量和位移分量都不是轴对称的C.应力分量是轴对称的,位移分量不是轴对称的D.位移分量是轴对称的,应力分量不是轴对称的8.下左图2中所示密度为ρ的矩形截面柱,应力分量为:0,,0=+==xy y x B Ay τσσ对图(a )和图(b)两种情况由边界条件确定的常数A 及B 的关系是( C )A.A 相同,B 也相同B.A 不相同,B 也不相同C.A 相同,B 不相同D.A 不相同,B 相同图 2 图 39、上右图3示单元体剪应变γ应该表示为( B )10、设有平面应力状态x ay dx dy cx by ax xy y x γτσσ---=+=+=,,,其中,d c b a ,,,均为常数,γ为容重。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章绪论1、所谓“完全弹性体”就是指(B)。
A、材料应力应变关系满足虎克定律B、材料的应力应变关系与加载时间、历史无关C、本构关系为非线性弹性关系D、应力应变关系满足线性弹性关系2、关于弹性力学的正确认识就是(A )。
A、计算力学在工程结构设计中的作用日益重要B、弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C、任何弹性变形材料都就是弹性力学的研究对象D、弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析3、下列对象不属于弹性力学研究对象的就是(D )。
A、杆件B、板壳C、块体D、质点4、弹性力学研究物体在外力作用下,处于(弹性)阶段的(应力)、(应变)与(位移)5、弹性力学可以解决材料力学无法解决的很多问题;并对杆状结果进行精确分析,以及验算材力结果的适用范围与精度。
与材料力学相比弹性力学的特点有哪些?答:1)研究对象更为普遍;2)研究方法更为严密;3)计算结果更为精确;4)应用范围更为广泛。
6、材料力学研究杆件,不能分析板壳;弹性力学研究板壳,不能分析杆件。
(×)改:弹性力学不仅研究板壳、块体问题,并对杆件进行精确的分析,以及检验材料力学公式的适用范围与精度。
7、弹性力学对杆件分析(C)A、无法分析B、得出近似的结果C、得出精确的结果D、需采用一些关于变形的近似假定8、图示弹性构件的应力与位移分析要用什么分析方法?(C)A、材料力学B、结构力学C 、弹性力学D 、塑性力学解答:该构件为变截面杆,并且具有空洞与键槽。
9、弹性力学与材料力学的主要不同之处在于( B )。
A 、任务 B 、研究对象 C 、研究方法 D 、基本假设10、重力、惯性力、电磁力都就是体力。
(√) 11、下列外力不属于体力的就是(D)A 、重力B 、磁力C 、惯性力D 、静水压力 12、体力作用于物体内部的各个质点上,所以它属于内力。
(×) 解答:外力。
它就是质量力。
13、在弹性力学与材料力学里关于应力的正负规定就是一样的。
( × ) 解答:两者正应力的规定相同,剪应力的正负号规定不同。
14、图示单元体右侧面上的剪应力应该表示为(D)A 、xy τB 、yx τC 、zy τD 、yz τ1τ2τ3τ4τOxz15、按弹性力学规定,下图所示单元体上的剪应力( C )。
A 、均为正B 、41,ττ为正,32,ττ为负C 、均为负D 、31,ττ为正,42,ττ为负16、按材料力学规定,上图所示单元体上的剪应力( D ) A 、均为正 B 、41,ττ为正,32,ττ为负 C 、均为负 D 、31,ττ为正,42,ττ为负 17、试分析A 点的应力状态18、上右图示单元体剪应变γ应该表示为( B ) A 、xy γ B 、yz γ C 、zx γ D 、yx γ19、将两块不同材料的金属板焊在一起,便成为一块( D )。
A连续均匀的板B不连续也不均匀的板C不连续但均匀的板D连续但不均匀的板20、下列材料中,( D )属于各向同性材料。
A竹材B纤维增强复合材料C玻璃钢D沥青21、下列那种材料可视为各向同性材料( C )。
A木材B竹材C混凝土D夹层板22、物体的均匀性假定,就是指物体内各点的弹性常数相同。
23、物体就是各向同性的,就是指物体内某点沿各个不同方向的弹性常数相同。
24、格林(1838)应用能量守恒定律,指出各向异性体只有21个独立的弹性常数。
25、如图所示受轴向拉伸的变截面杆,若采用材料力学的方法计算其应力,所得结果就是否总?能满足杆段平衡与微元体平衡27、解答弹性力学问题,必须从( )、( )与( )三方面来考虑。
28、对棱边平行于坐标轴的正平行六面体单元,外法线与坐标轴正方向( )的面称为正面,与坐标轴( )的面称为负面,负面上的应力以沿坐标轴( )方向为正。
29、弹性力学基本方程包括( )方程、( )方程与( )方程,分别反映了物体( )与( ),( )与( ),( )与( )之间的关系。
30、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、应变与位移。
但就是并不直接作强度与刚度分析。
31、弹性力学可分为数学弹性力学与实用弹性力学两个部分。
前者只用精确的数学推演而不引用任何关于应变状态或应力分布的 假定 ;在实用弹性力学里,与材料力学类同,也引用一些关于应变或应力分布的假设,以便简化繁复的数学推演,得出具有相当实用价值 近似解 。
32、弹性力学的研究对象就是完全弹性体。
33、所谓“应力状态”就是指( B )。
A 、 斜截面应力矢量与横截面应力矢量不同B 、 一点不同截面的应力随着截面方位变化而改变C 、 3个主应力作用平面相互垂直D 、 不同截面的应力不同,因此应力矢量就是不可确定的 34、切应力互等定理根据条件( B )成立。
A 、 纯剪切 B 、 任意应力状态 C 、 三向应力状态 D 、 平面应力状态35、在直角坐标系中,已知物体内某点的应力分量为:⎪⎪⎪⎭⎫ ⎝⎛-=01001-001010-001ij σMPa ;试:画出该点的应力单元体。
解:该点的应力单元体如下图(强调指出方向);第二章 平面问题的基本理论1、如图所示的三种情况就是否都属于平面问题?如果就是平面问题,就是平面应力问题还就是平面应变问题?xxyyyyyyOOOOOOZZqqq()z q ()z q ()()b ()c答:平面应力问题、平面应变问题、非平面问题2、当问题可当作平面应力问题来处理时,总有0===yz xz z ττσ。
(√) 解答:平面应力问题,总有0===yz xz z ττσ3、当物体可当作平面应变问题来处理时,总有0===yz xz z γγε。
(√) 解答:平面应变问题,总有0===yz xz z γγε4、图示圆截面柱体R <<l ,问题属于平面应变问题。
(×)lR解答:平面应变问题所受外力应该沿柱体长度方向不变。
5、图示圆截面截头锥体R <<l ,问题属于平面应变问题。
(×)解答:对于平面应变问题,物体应为等截面柱体。
6、严格地说,一般情况下,任何弹性力学问题都就是空间问题,但就是,当弹性体具有某些特殊的形状,且受有某种特殊的外力时,空间问题可简化为平面问题。
7、平面应力问题的几何形状特征就是 等厚度薄板(物体在一个方向的几何尺寸远小于其她两个方向的几何尺寸)。
8、平面应变问题的几何形状特征就是很长的等截面柱体 。
9、下列各图所示结构应力分析问题属于什么问题?薄板属于问题挡土墙属于问题隧道属于问题答:平面应力、平面应变、平面应变10、柱下独立基础的地基属于 问题,条形基础下的地基属于 问题。
答:半空间半平面、平面应变11、高压管属于 平面应变 问题;雨蓬属于 板 问题。
12、平面应变问题的应力、应变与位移与那个(些)坐标无关(纵向为z 轴方向)( C )。
A 、xB 、yC 、zD 、z y x ,, 13、平面应力问题的外力特征就是(A)。
A 只作用在板边且平行于板中面 B 垂直作用在板面C 平行中面作用在板边与板面上D 作用在板面且平行于板中面14、在平面应力问题中(取中面作xy 平面)则 (C)。
A 、0=z σ,0=w B 、0≠z σ,0≠wC 、0=z σ,0≠wD 、0≠z σ,0=w15、在平面应变问题中(取纵向作z 轴)(D)。
A 、0=z σ,0=w ,0=z εB 、0≠z σ,0≠w ,0≠z εC 、0=z σ,0≠w ,0=z εD 、0≠z σ,0=w ,0=z ε16、下列问题可简化为平面应变问题的就是(B)。
A 、墙梁 B 、高压管道 C 、楼板 D 、高速旋转的薄圆盘17、下列关于平面问题所受外力特点的描述错误的就是(D)。
A 、体力分量与z 坐标无关 B 、面力分量与z 坐标无关 C 、z f ,z f 都就是零 D 、z f ,z f 都就是非零常数18、在平面应变问题中,z σ如何计算?(C) A 、0=z σ不需要计算B 、由()[]y x z z Eεεμεσ+-=1直接求 C 、由()y x z σσμσ+=求D 、=z σz f解答:平面应变问题的()[]y x z z Eσσμσε+-=1,所以()y x z σσμσ+= 19、平面应变问题的微元体处于(C)。
A 、单向应力状态 B 、双向应力状态C 、三向应力状态,且z σ就是一主应力D 、纯剪切应力状态解答:因为除了y x σσ,以外,0≠z σ,所以单元体处于三向应力状态;另外z σ作用面上的剪应力0=zx τ,0=zy τ,所以z σ就是一主应力20、对于两类平面问题,从物体内取出的单元体的受力情况 有(平面应变问题的单元体上有z σ ) 差别,所建立的平衡微分方程 无 差别。
21、平面问题的平衡微分方程表述的就是( A )之间的关系。
A 、应力与体力 B 、应力与面力 C 、应力与应变 D 、应力与位移22、设有平面应力状态,by ax x +=σ,dy cx y +=σ,x ay dx xy γτ---=,其中d c b a ,,,均为常数,γ为容重。
该应力状态满足平衡微分方程,其体力就是( D )。
A 、0=x f ,0=y f B 、0≠x f ,0=y f C 、0≠x f ,0≠y f D 、0=x f ,0≠y f解答:代入平衡微分方程直接求解得到23、如图所示,悬臂梁上部受线性分布荷载,梁的厚度为1,不计体力。
试利用材料力学知识写出x σ,xy τ表达式;并利用平面问题的平衡微分方程导出y σ,xy τ表达式。
1分析:该问题属于平面应力问题;在材料力学中用到了纵向纤维互不挤压假定,即无yσ存在,可以瞧出上边界存在直接荷载作用,则会有应力y σ存在,所以材料所得结果就是不精确的;在平衡微分方程二式中都含有xy τ,联系着第一、二式;材料力学与弹性力学中均认为正应力x σ主要由弯矩引起。
解:横截面弯矩:l qx M Z 63-=,横截面正应力y x lhq J y M Z Z x 332-==σ 代入平衡微分方程的第一式得:()x f y x lhq ydy x lh q dy x x xy +==∂∂-=⎰⎰2232336στ(注意未知量就是y x ,的函数),由()02=±=h y xy τ得出()243x lhq x f -=, 可见()2223443h y x lhq xy -=τ 将xy τ代入平衡微分方程的第二式得:()()x g x y h y lhq dy xxy y +--=∂∂-=⎰233342τσ ()02==hy y σ,()x l q x g 2-=,()x h y h y lhq y 3233342+--=σ 24、某一平面问题的应力分量表达式:23x xy Ax σ=-+,32xy By Cx y τ=--,232y Bxy σ=-,体力不计,试求A ,B ,C 的值。
